

10 Problem-Solving Scenarios for High School Students
It is certainly common to come across difficult situations including forgetting an assignment at home or overusing your phone only to miss an important project deadline. We are always surrounded by little difficulties that might become bigger problems if not addressed appropriately.
Whether it is saving your friend from the addiction to social media platforms or communicating your personal boundaries to relatives, problem-solving skills are one of the important skills you need to acquire throughout the journey of life.
Do you think these skills are in-built with other high school students? Certainly not.
It takes innovative learning methodologies just like problem-solving scenarios that help you immerse in the subject matter with precision. With problem-solving scenarios, you come across a range of problems that help you build critical thinking skills, logical reasoning, and analytical techniques.
The article will take you through scenarios that are a combination of various problems that need to be addressed strategically and carefully. As you read ahead, make sure to brainstorm solutions and choose the best one that fits the scenario.
Helpful scenarios to build a problem-solving attitude in high schoolers
Learning through scenarios helps students look at situations from a completely analytical perspective. Problem-solving scenarios offer a combination of various situations that test the thinking skills and growth mindset of high school students. The below-mentioned scenarios are perfect for implementing problem-solving skills simply by allowing open discussions and contributions by students.
1. Uninvited Guests

You have arranged a party at your home after successfully winning the competition at the Science Fair. You invite everyone involved in the project however, one of your friends brings his cousin’s brother along. However, you have limited soft drink cans considering the number of invited people. How would you manage this situation without making anyone feel left out?
2. Communication Issues

A new teacher has joined the high school to teach about environmental conservation. She often involves students in different agriculture activities and workshops. However, one of your friends, John, is not able to understand the subject matter. He is unable to communicate his doubts to the teachers. How would you motivate him to talk to the teacher without the fear of judgment?
3. Friendship or Personal Choice?

The history teacher announced an exciting assignment opportunity that helps you explore ancient civilizations. You and your friend are pretty interested in doing the project as a team. One of your other friends, Jason, wants to join the team with limited knowledge and interest in the topic. Would you respect the friendship or deny him so you can score better on the assignment?
4. Peer Pressure

It is common for high schoolers to follow what their friends do. However, lately, your friends have discovered different ways of showing off their skills. While they do all the fun things, there are certain activities you are not interested in doing. It often puts you in trouble whether to go with friends or take a stand for what is right. Would you take the help of peer mentoring activities in school or try to initiate a direct conversation with them?
5. Team Building

Mr. Jason, the science teacher, assigns different projects and forms teams with random classmates. There are 7 people in each team who need to work towards project completion. As the group starts working, you notice that some members do not contribute at all. How will you ensure that everyone participates and coordinates with the team members?
6. Conflict Resolution
The drama club and the English club are famous clubs in the school. Both clubs organize various events for the students. This time, both clubs have a tiff because of the event venue. Both clubs need the same auditorium for the venue on the same date. How would you mediate to solve the issue and even make sure that club members are on good terms with each other?
7. Stress Management

Your school often conducts different activities or asks students stress survey questions to ensure their happiness and well-being. However, one of your friends always misses them. He gets frustrated and seems stressed throughout the day. What would you do to ensure that your friend gets his issue acknowledged by teachers?
8. Time Management

Your friend is always enthusiastic about new competitions in high school. He is running here and there to enroll and get certificates. In this case, he often misses important lectures and activities in class. Moreover, his parents complain that he misses swimming class too. How would you explain to him the importance of prioritizing and setting goals to solve this issue?
9. Educational Resources
You and your friends are avid readers and often take advice from books. While most must-read books for bibliophiles are read by you, it is important to now look for other books. However, you witness that the school library lacks other important books on philosophy and the non-fiction category. How would you escalate this issue to the higher authorities by addressing the needs of students?
10. Financial Planning

Finance is an important factor and that is why your parents help you plan your pocket money and budgeting. Off lately, they have stopped doing so considering that you can manage on your own. However, after a few months, you have started spending more on games and high-end school supplies. You realize that your spending habits are leading to loss of money and reduced savings. How shall you overcome this situation?
Wrapping Up
Involving students in different learning practices and innovative ways inspires them to think out of the box and make use of imagination skills. With the usage of different problem-solving scenarios, high school students get an opportunity to delve into realistic examples and consequences of different incidents.
Such scenarios offer an excellent way to promote understanding, critical thinking skills and enhance creativity. Ensure to use different activities and games for creating a comprehensive learning environment.

Sananda Bhattacharya, Chief Editor of TheHighSchooler, is dedicated to enhancing operations and growth. With degrees in Literature and Asian Studies from Presidency University, Kolkata, she leverages her educational and innovative background to shape TheHighSchooler into a pivotal resource hub. Providing valuable insights, practical activities, and guidance on school life, graduation, scholarships, and more, Sananda’s leadership enriches the journey of high school students.
Explore a plethora of invaluable resources and insights tailored for high schoolers at TheHighSchooler, under the guidance of Sananda Bhattacharya’s expertise. You can follow her on Linkedin
Leave a Comment Cancel reply
Save my name, email, and website in this browser for the next time I comment.
- Skip to main content
- Skip to primary site menu
Search form
Explore brown university.

Teaching Problem Solving
The other day, a physicist friend was working in the lab with her summer research students. They were talking about the work they’d been doing that summer and how there was no manual or instructions of any sort for any of it; no textbook, no lab procedure. It was as if they were making it up as they went along. Laughing about this, one of the students said, ‘You know what we need? We need an entire course with nothing but problems. Just give us one problem after another, and we figure out how to do them. Because that’s what real research is.’ The rest of the students laughed. And then all of them nodded. -Hanstedt, 2018, p. 41
Employers, college presidents, faculty, and students demonstrate remarkable consensus that problem solving is one of the most important outcomes of a college education (Bok, 2017; Hart Research Associates, 2015; Hora, Benbow, Oleson, 2016; Passow & Passow, 2017). At the time of this newsletter, there were 28 courses offered this year that included the words “problem*” and “solving” in Courses@Brown . Course descriptions ranged from focusing on how to apply techniques or skills, to solving problems, to tackling common problems encountered in the field, and concepts that included “problems” within their title. There are undoubtedly more courses that implicitly and explicitly focus on problem solving across campus. In light of this emphasis, it is important to ask, “What is a problem and what is problem solving?” and “How do I foster problem-solving skills in my course?” and eventually, "How will I be explicit about problem solving in my course and course description?" Although problem solving is often associated with STEM courses, this newsletter offers perspectives and teaching approaches from across the disciplines.
What is a “problem” and problem solving? Problems and problem solving may be context and discipline specific, but the concept and process have overarching components and similarities across contexts. Jonassen (2000, p. 65) defines a problem as an “unknown entity in some situation (the difference between a goal state and a current state)” such that “finding or solving for the unknown must have some social, cultural, or intellectual value.” Within courses, students may encounter a wide variety of current (e.g., a problem statement) and goal (e.g., a solution) states with different motivations for solving them. Students will be exposed to “well-structured” problems at one end of the spectrum, which have a typical solution path and solution, and “ill-structured” problems, which are highly context dependent and have no one solution path (Jonassen, 2000).
We bring in common case scenarios for students and try to develop the frameworks they need to approach a problem rather than just finding the answer. To help students think about the process, we scaffold scenarios over the years through self-study modules that students can complete on their own. The scenarios stay the same, but students can come back to them with new information and frameworks they have learned, a deeper toolbox to pull from in different clinical settings. This allows students to be lifelong learners and more flexible and adaptable in the future. -Dr. Steven Rougas, Director of the Doctoring Program, Alpert Medical School
Problem solving is a “goal-oriented” process that includes creating and manipulating problems as mental models (Jonassen, 2000). Brown faculty from a variety of disciplines were interviewed by Sheridan staff and asked, “What skills do students need to problem solve effectively?” They responded that students need to be able to do the following:
- Reason, observe, and recognize patterns
- Use current information to understand the past
- Know how to break complex problems down into smaller, more manageable components
- Make connections between concepts and disciplines
- Creatively think of multiple solution paths
These skills, among others, target the following problem-solving steps (Pretz, Naples, & Sternbergy, 2003):
- Recognize or identify a problem
- Define and represent the problem mentally
- Develop a solution strategy
- Organize your knowledge about the problem
- Allocate mental and physical resources for solving the problem
- Monitor your progress toward the goal
- Evaluate the solution for accuracy
Problem solving is an iterative process, and as such, these steps do not necessarily progress in a linear fashion. When creating homework assignments, projects, exams, etc., it is helpful to identify the specific skills you want students to practice, the strategies they should use, and how you will evaluate the solutions they produce.
How do I foster problem-solving skills in my course? Instructors can signpost the problem-solving skills students should develop in their courses by adapting existing problem sets to fit recommendations from the Transparency in Learning and Teaching Project (TILT). The process of increasing transparency in assignments includes communicating the assignment’s purpose, task, and criteria to students (Winkelmes et al., 2016):
- The purpose usually links to one learning objective for the course, the skills students will develop as a result of completing the assignment, or a real-world application that students might experience outside of your classroom. In this way, the problem you have presented to the student becomes relevant because it has “some social, cultural, or intellectual value” (Jonassen, 2000, p. 65).
- Next, the task states the strategy or strategies students should take to complete the assignment. This includes guiding students through organizing the information available to develop a strategy.
- Finally, the criteria could be a rubric or annotated examples that are given to students before the assignment is due, so they are aware of the standards for the assignment.
In one study, researchers found that in courses where at least two assignments had features of transparent assignments, students self reported increases in their academic confidence, sense of belonging, and mastery of skills, such as problem solving (Winkelmes et al., 2016). Below are examples of different skills needed for problem solving with suggestions on how you can foster these skills through adapted or new assignments and in-class exercises.
Communication A key skill for problem solving is knowing how to define and represent the problem and its solutions. This is true for all students, regardless of discipline. For example, Berkenkotter (1982, p. 33) states, “A writer is a problem solver of a particular kind. Writers’ ‘solutions’ will be determined by how they frame their problems, the goals they set for themselves, and the means or plans they adopt for achieving those goals.” To help students understand and connect to research in their field, instructors can assign short articles and guide students through rhetorical practices to make expert thinking more explicit. Provide students multiple opportunities to refine their writing allows them to learn “how to frame their problems.”
The distant past can seem uncomfortably strange to modern observers. As we discuss our class readings, one thing I like to do with my students is to explore what seems weird or even offensive to them about our texts and the societies that produced them. Thinking about the disconnect between ancient and modern attitudes, outlooks, beliefs, and values can be an incredibly productive way to think about cultural difference over space and time. - Professor Jonathan Conant, History and Classics
Critical Thinking Critical thinking is the “ability to assess your assumptions, beliefs, and actions” (Merriam & Bierema, 2014, p. 222) with the intent to change your actions in the future and is necessary when solving problems. It is a skill required during all steps of the problem-solving process. Fostering critical thinking in your students is one way to create a more inclusive classroom because you are inherently asking students to challenge their assumptions and biases.
Instructors can use the following conditions to promote critical thinking in your classroom (Merriam & Bierema, 2014):
- Foster critical reflection by examining assumptions (see Promoting Metacognition for specific reflective strategies), e.g., ask students to read a research article and identify possible assumptions that are made in the questions asked, methods used, or the interpretation of the results. For example, to foster critical reflection you could ask students to identify the sources of knowledge they value and use when completing homework and write a reflection on what assumptions they made about those sources. What are the identities of the people creating those sources of knowledge? What systems or people are gatekeepers of that knowledge?
- Build a learning community where the expectation is that students can be wholly present, honest, ask questions, and productively fail (Kapur, 2016).
- Practice dialogical conversation by teaching an awareness of power relations in the classroom such as microaggressions or micro-affirmations and how to use active listening (see Microaggressions and Micro-aggressions for examples and specific practices).
- Provide students the opportunity to make connections between content and their experiences, e.g., by asking students on homework assignments how they apply concepts to a recent experience or asking students why they took your course and how it relates to their career goals.
Collaboration/Teamwork Instructors can develop aspects of problem solving by being intentional about team building, connecting students to alternative perspectives, and being explicit about the expectations of teamwork in the field (e.g., as a researcher, industry partner, consultant, etc.). You can create homework assignments using the TILT framework , which asks students to evaluate both their own and peers’ interactions in teams. There are several models or rubrics for how to assess teamwork, such as the AAC&U Teamwork Value Rubric , which focuses on students’ behaviors or the Comprehensive Assessment of Team Member Effectiveness (CATME) , which is a free packaged tool that gathers information from students and groups them into teams.
We use team-based learning exercises and collaborative problem solving. Students are assigned pre-reading to expand their knowledge so they are able to think through different aspects of a scenario before they come to class. In class, the discussion focuses on a team deciding and agreeing on what the next steps in a case will be. The problem-solving skills that this team discussion focuses on are interpersonal communication, being an active listener, and a collaborative team member. It is not high stakes, but together the team will succeed or fail. - Sarita Warrier, Assistant Dean for Medical Education, Alpert Medical School
A jigsaw is another collaborative approach to teach students how to break up a problem into smaller components. For example, in a class on Romanticism and Romantic philosophies, three groups of students would each be given the following questions about five poems: “How does the writer view nature?” (Group 1), “How does the writer view society?” (Group 2), “How does the writer view the purpose of poetry?” (Group 3). After discussion, three new groups, with representatives from each of these three clusters, might discuss a broader question, such as, “Using the information gathered in the first groups [...] what are Romanticism’s goals? What’s the agenda of the Romantic poets?” (Handstedt, 2018, pp. 121-122).
Reflection Activities or Assignments Expert researchers, practitioners, and educators incorporate reflection and iteration as part of their practice. Key steps of the problem-solving process include being reflective about the process and what is working or not working towards a goal. In a previous newsletter, Promoting Metacognition , the Sheridan Center provided a list of several activities and assignments you could use to help students be reflective in your course. These activities range from short minute papers , to semester-long reflective journals. Think-alouds, or having a student verbally solve a problem with another student, can also help students develop reflective problem-solving skills because it “provides a structure for students to observe both their own and another’s process of learning” (Barkley, 2010, p. 259).
For more strategies on how to engage students in these skills and topics, please see the Sheridan Center’s newsletter, Inclusive Teaching Through Active Learning . It is important to be explicit in how you approach problem solving and convey that information both through your course description, syllabi, and content.
Opportunities at Sheridan for Development of Problem Solving Problem solving is a necessary skill in all disciplines and one that the Sheridan Center is focusing on as part of the Brown Learning Collaborative , which provides students the opportunity to achieve new levels of excellence in six key skills traditionally honed in a liberal arts education – critical reading, writing, research, data analysis, oral communication, and problem solving. To help you think through how to integrate opportunities for students to problem solve effectively in your course, the Sheridan Center offers problem solving professional development opportunities for faculty and students in an effort to engage intergenerational, faculty-student teaching teams.
Problem-Solving Course Design Institute Increasing assignment transparency is at the core of Problem-Solving Course Design Institute (PSCDI). PSCDI is a two-day workshop for faculty, staff, postdocs, and graduate student teams to (re)design assignments that engage students in the problem-solving process. Upon successful completion, faculty participants will receive a $2,000 grant to implement their ideas. For more information on PSCDI and past recipents, please see this Sheridan web resource .
Problem-Solving Fellows Program Undergraduate students who are currently or plan to be peer educators (e.g., UTAs, lab TAs, peer mentors, etc.) are encouraged to take the course, UNIV 1110: The Theory and Teaching of Problem Solving. Within this course, we focus on developing effective problem solvers through students’ teaching practices. We discuss reflective practices necessary for teaching and problem solving; theoretical frames for effective learning; how culture, context, and identity impact problem solving and teaching; and the impact of the problem-solving cycle. For more information, please see this Sheridan web resource and contact Dr. Christina Smith, Sheridan Center (via [email protected] ).
Berkenkotter, C. (1982). Writing and problem solving. In T. Fulwiler & A. Young (Eds.), Language connections: Writing and reading across the curriculum (pp. 33-44). Urbana, Illinois: National Council of Teachers of English.
Barkley, E.F. (2010). Student engagement techniques: A handbook for college faculty . San Francisco, CA: Jossey-Bass.
Bok, D. (2017). The struggle to reform our colleges. Princeton, NJ: Princeton University Press.
Hanstedt, P. (2018). Creating wicked students: Designing courses for a complex world . Sterling, VA: Stylus.
Hart Research Associates. (2015). Falling short? College learning and career success . Survey carried out for AAC&U. Available: https://www.aacu.org/sites/default/files/files/LEAP/2015employerstudents…
Hora, M.T., Benbow, R. J., & Oleson, A. K.. (2016). Beyond the skills gap: Preparing college students for life and work . Cambridge, MA: Harvard University Press.
Jonassen, D. H. (2000). Toward a design theory of problem solving. Educational technology research and development , 48(4), 63-85.
Kapur, M. (2016). Examining productive failure, productive success, unproductive failure, and unproductive success in learning. Educational Psychologist , 51(2), 289-299.
Merriam, S. B., & Bierema, L. L. (2014). Adult learning: Linking theory and practice . John Wiley & Sons.
Passow, H.J., & Passow, C.H. (2017). What competencies should undergraduate engineering programs emphasize? A systematic review. Journal of Engineering Education , 106(3): 475-526.
Pretz, J.E., Naples, A. J., & Sternbergy, R. J. (2003). Recognizing, defining, and representing problems. In J. E. Davidson & R. J. Sternberg (Eds.), The psychology of problem solving (pp. 3-30). New York: Cambridge University Press.
Winkelmes, M.A., Bernacki, M., Butler, J., Zochowski, M., Golanics, J., & Weavil, K. H. (2016). A teaching intervention that increases underserved college students’ success. Peer Review , 18(1/2), 31–36.
Problem-Solving Style Questionnaire
Table of Contents
Here in this post, we are sharing the “Problem-Solving Style Questionnaire”. You can read psychometric and Author information. We have thousands of Scales and questionnaires in our collection ( See Scales and Questionnaires ). You can demand us any scale and questionnaires related to psychology through our community , and we will provide you with a short time. Keep visiting Psychology Roots .
About Problem-Solving Style Questionnaire
Author details.
Thomas Cassidy and Christopher Long Parker
(I still confuse between above two. Some Resources mention 1st one and some on second one. Hope as researcher you can help to verify this)
Translation Availability

Background/Description
The Problem-Solving Style Questionnaire (PSSQ) is a self -report questionnaire that measures four dimensions of problem-solving style: sensing, intuitive, feeling, and thinking. It was developed by Thomas Cassidy and Christopher Long in 1996, based on Carl Jung ’s theory of psychological types.
The PSSQ is a widely used instrument for assessing problem-solving style in a variety of settings, including educational institutions, workplaces, and counseling offices. It has been shown to be a reliable and valid measure of problem-solving style, and it has been used in numerous research studies to investigate the relationship between problem-solving style and other variables, such as academic achievement , job performance, and mental health.
The PSSQ is a relatively short instrument, consisting of 20 items with five items for each dimension. Respondents rate each item on a five-point Likert scale, from 1 (strongly disagree) to 5 (strongly agree). The scores for each dimension are then summed to create a total score for that dimension.
The following is a brief interpretation of the four PSSQ dimensions:
- Sensing: People with a high sensing problem-solving style prefer to learn through concrete experiences and focus on practical details. They may also be good at hands-on tasks and troubleshooting problems.
- Intuitive: People with a high intuitive problem-solving style prefer to learn through abstract concepts and theories and focus on the big picture. They may also be good at thinking creatively and coming up with new ideas.
- Feeling: People with a high feeling problem-solving style prefer to make decisions based on personal values and emotions. They may also be good at empathizing with others and considering their needs .
- Thinking: People with a high thinking problem-solving style prefer to make decisions based on logic and objective reasoning. They may also be good at analyzing information and identifying patterns and trends.
It is important to note that everyone has a unique combination of problem-solving styles. There is no one “best” problem-solving style. The best way to solve a problem is to use the style that is most effective for the specific situation.
The PSSQ can be used in a variety of ways. It can be used to help individuals understand their own problem-solving style and to develop strategies for improving their problem-solving skills. It can also be used to identify individuals who may need additional support in problem-solving.
For example, a student who has a high intuitive problem-solving style may benefit from learning how to break down complex problems into smaller steps. A student who has a high sensing problem-solving style may benefit from learning how to see the big picture and generate ideas.
The PSSQ can also be used in the workplace to help employees understand their own problem-solving style and to develop teams with a variety of problem-solving styles. This can lead to more effective problem-solving and better decision-making.
Administration, Scoring and Interpretation
The Problem-Solving Style Questionnaire (PSSQ) can be administered in a variety of settings, including educational institutions, workplaces, and counseling offices. It is a relatively short instrument, so it can be administered individually or in groups.
To administer the PSSQ, simply provide respondents with a copy of the questionnaire and instruct them to read each item carefully and rate it on a five-point Likert scale, from 1 (strongly disagree) to 5 (strongly agree). Once respondents have completed the questionnaire, collect the questionnaires and score them.
To score the PSSQ, simply sum the responses to the five items for each dimension. The total score for each dimension ranges from 5 to 25. Higher scores indicate a stronger preference for that problem-solving style.
Here are some additional tips for administering the PSSQ:
- Provide respondents with a quiet and comfortable place to complete the questionnaire.
- Allow respondents enough time to complete the questionnaire without feeling rushed.
- Be sure to answer any questions that respondents may have about the questionnaire.
- Once respondents have completed the questionnaire, thank them for their time.
Reliability and Validity
The Problem-Solving Style Questionnaire (PSSQ) has been shown to be a reliable and valid measure of problem-solving style.
Reliability refers to the consistency of a measure. A reliable measure is one that produces similar results when administered to the same people at different times.
Validity refers to the accuracy of a measure. A valid measure is one that measures what it is intended to measure.
The PSSQ has been shown to be reliable in a number of studies. For example, Cassidy and Long (1996) reported that the PSSQ had a Cronbach’s alpha of .77, which is considered to be a good level of reliability .
The PSSQ has also been shown to be valid in a number of studies. For example, Cassidy and Long (1996) found that the PSSQ scores were correlated with other measures of problem-solving style, such as the Myers-Briggs Type Indicator (MBTI).
In addition, the PSSQ has been used in a number of research studies to investigate the relationship between problem-solving style and other variables, such as academic achievement , job performance, and mental health. The results of these studies suggest that the PSSQ is a valid measure of problem-solving style.
Available Versions
Ghodrati, M., Bavandian, L., Moghaddam, M. M., & Attaran, A. (2014). On the relationship between problem-solving trait and the performance on C-test. Theory and practice in language studies , 4 (5), 1093-1100.
Khan, M. J., Younas, T., & Ashraf, S. (2016). Problem Solving Styles as Predictor of Life Satisfaction Among University Students. Pakistan Journal of Psychological Research , 31 (1).
Important Link
- Video Guide
- How to Get Permission
- Sample Email for Permission
- Community Discussions
Scale File:
Frequently asked questions.
What is the Problem-Solving Style Questionnaire (PSSQ)? The PSSQ is a self -report questionnaire that measures four dimensions of problem-solving style: sensing, intuitive, feeling, and thinking.
What are the four dimensions of problem-solving style measured by the PSSQ? The four dimensions of problem-solving style measured by the PSSQ are: Sensing, Intuitive, Feeling, and Thinking.
How is the Problem-Solving Style Questionnaire scored? The PSSQ is scored by summing the responses to the five items for each dimension. The total score for each dimension ranges from 5 to 25. Higher scores indicate a stronger preference for that problem-solving style.
What are the benefits of using the Problem-Solving Style Questionnaire? The PSSQ can be used to help individuals and teams understand their problem-solving styles and develop strategies for improving their problem-solving skills. It can also be used to identify individuals who may need additional support in problem-solving.
Is the PSSQ a reliable and valid measure of problem-solving style? Yes, the PSSQ has been shown to be a reliable and valid measure of problem-solving style. It has been used in a number of research studies to investigate the relationship between problem-solving style and other variables, such as academic achievement , job performance, and mental health.
Please note that Psychology Roots does not have the right to grant permission for the use of any psychological scales or assessments listed on its website. To use any scale or assessment, you must obtain permission directly from the author or translator of the tool. Psychology Roots provides information about various tools and their administration procedures, but it is your responsibility to obtain proper permissions before using any scale or assessment. If you need further information about an author’s contact details, please submit a query to the Psychology Roots team.
Help Us Improve This Article
Have you discovered an inaccuracy? We put out great effort to give accurate and scientifically trustworthy information to our readers. Please notify us if you discover any typographical or grammatical errors. Make a comment. We acknowledge and appreciate your efforts.
Share With Us
If you have any scale or any material related to psychology kindly share it with us at [email protected] . We help others on behalf of you.
Psychology Roots
Problem solving styles scale, psychologist jobs in punjab special education department, related posts, responding desirably on attitudes and opinions..., behavioral activation for depression scale, automatic thoughts questionnaire – positive, autism worries survey – parent version, autism-spectrum quotient (aq) test, autism parenting stress index, leave a comment cancel reply.
You must be logged in to post a comment.
Adblock Detected
- Brain Development
- Childhood & Adolescence
- Diet & Lifestyle
- Emotions, Stress & Anxiety
- Learning & Memory
- Thinking & Awareness
- Alzheimer's & Dementia
- Childhood Disorders
- Immune System Disorders
- Mental Health
- Neurodegenerative Disorders
- Infectious Disease
- Neurological Disorders A-Z
- Body Systems
- Cells & Circuits
- Genes & Molecules
- The Arts & the Brain
- Law, Economics & Ethics
- Neuroscience in the News
- Supporting Research
- Tech & the Brain
- Animals in Research
- BRAIN Initiative
- Meet the Researcher
- Neuro-technologies
- Tools & Techniques
- Core Concepts
- For Educators
- Ask an Expert
- The Brain Facts Book

Test Your Problem-Solving Skills
Personalize your emails.
Personalize your monthly updates from BrainFacts.org by choosing the topics that you care about most!
Find a Neuroscientist
Engage local scientists to educate your community about the brain.
Image of the Week
Check out the Image of the Week Archive.

SUPPORTING PARTNERS
- Privacy Policy
- Accessibility Policy
- Terms and Conditions
- Manage Cookies
Some pages on this website provide links that require Adobe Reader to view.

ChatGPT for Teachers
Trauma-informed practices in schools, teacher well-being, cultivating diversity, equity, & inclusion, integrating technology in the classroom, social-emotional development, covid-19 resources, invest in resilience: summer toolkit, civics & resilience, all toolkits, degree programs, trauma-informed professional development, teacher licensure & certification, how to become - career information, classroom management, instructional design, lifestyle & self-care, online higher ed teaching, current events, 5 problem-solving activities for the classroom.

Problem-solving skills are necessary in all areas of life, and classroom problem solving activities can be a great way to get students prepped and ready to solve real problems in real life scenarios. Whether in school, work or in their social relationships, the ability to critically analyze a problem, map out all its elements and then prepare a workable solution is one of the most valuable skills one can acquire in life.
Educating your students about problem solving skills from an early age in school can be facilitated through classroom problem solving activities. Such endeavors encourage cognitive as well as social development, and can equip students with the tools they’ll need to address and solve problems throughout the rest of their lives. Here are five classroom problem solving activities your students are sure to benefit from as well as enjoy doing:
1. Brainstorm bonanza
Having your students create lists related to whatever you are currently studying can be a great way to help them to enrich their understanding of a topic while learning to problem-solve. For example, if you are studying a historical, current or fictional event that did not turn out favorably, have your students brainstorm ways that the protagonist or participants could have created a different, more positive outcome. They can brainstorm on paper individually or on a chalkboard or white board in front of the class.
2. Problem-solving as a group
Have your students create and decorate a medium-sized box with a slot in the top. Label the box “The Problem-Solving Box.” Invite students to anonymously write down and submit any problem or issue they might be having at school or at home, ones that they can’t seem to figure out on their own. Once or twice a week, have a student draw one of the items from the box and read it aloud. Then have the class as a group figure out the ideal way the student can address the issue and hopefully solve it.
3. Clue me in
This fun detective game encourages problem-solving, critical thinking and cognitive development. Collect a number of items that are associated with a specific profession, social trend, place, public figure, historical event, animal, etc. Assemble actual items (or pictures of items) that are commonly associated with the target answer. Place them all in a bag (five-10 clues should be sufficient.) Then have a student reach into the bag and one by one pull out clues. Choose a minimum number of clues they must draw out before making their first guess (two- three). After this, the student must venture a guess after each clue pulled until they guess correctly. See how quickly the student is able to solve the riddle.
4. Survivor scenarios
Create a pretend scenario for students that requires them to think creatively to make it through. An example might be getting stranded on an island, knowing that help will not arrive for three days. The group has a limited amount of food and water and must create shelter from items around the island. Encourage working together as a group and hearing out every child that has an idea about how to make it through the three days as safely and comfortably as possible.
5. Moral dilemma
Create a number of possible moral dilemmas your students might encounter in life, write them down, and place each item folded up in a bowl or bag. Some of the items might include things like, “I saw a good friend of mine shoplifting. What should I do?” or “The cashier gave me an extra $1.50 in change after I bought candy at the store. What should I do?” Have each student draw an item from the bag one by one, read it aloud, then tell the class their answer on the spot as to how they would handle the situation.
Classroom problem solving activities need not be dull and routine. Ideally, the problem solving activities you give your students will engage their senses and be genuinely fun to do. The activities and lessons learned will leave an impression on each child, increasing the likelihood that they will take the lesson forward into their everyday lives.
You may also like to read
- Classroom Activities for Introverted Students
- Activities for Teaching Tolerance in the Classroom
- 5 Problem-Solving Activities for Elementary Classrooms
- 10 Ways to Motivate Students Outside the Classroom
- Motivating Introverted Students to Excel in the Classroom
- How to Engage Gifted and Talented Students in the Classroom

Categorized as: Tips for Teachers and Classroom Resources
Tagged as: Assessment Tools , Engaging Activities
- Online & Campus Doctorate (EdD) in Higher Edu...
- Degrees and Certificates for Teachers & Educa...
- Programming Teacher: Job Description and Sala...
Your browser is not supported
Sorry but it looks as if your browser is out of date. To get the best experience using our site we recommend that you upgrade or switch browsers.
Find a solution
- Skip to main content
- Skip to navigation

- Back to parent navigation item
- Collections
- Sustainability in chemistry
- Simple rules
- Teacher well-being hub
- Women in chemistry
- Global science
- Escape room activities
- Decolonising chemistry teaching
- Teaching science skills
- Post-lockdown teaching support
- Get the print issue
- RSC Education

- More from navigation items

Source: © Sung Yoon Jo/Shutterstock
Practice makes perfect, but mix it up
By Fraser Scott 2022-03-24T08:30:00+00:00
- No comments
Does question bank design affect student performance?
We know it is important to provide students with repeated opportunities to practise solving questions. In a new study, researchers examined how the presentation and format of practice questions influences students’ problem-solving performance. The study revealed that mixed problem sets are better than questions arranged by topic.
There are two types of question practice teachers can give their students. The first, blocked practice, involves solving multiple problems of the same type, or about the same concept, before moving on to another. Practice worksheets and end-of-chapter questions in textbooks are often blocked practice type questions. They hone students’ algorithmic problem-solving skills, but at the expense of their conceptual understanding of the topic. The second, interleaved practice, shuffles between different types of questions in one session. It is more difficult, because students must identify the type of question being asked, or the concept it relates to, in addition to answering. Shuffled questions are thought to help with long-term learning and are similar to the questioning format in students’ exams.
The researchers investigated the effects of these two kinds of practice. They recruited 79 university students from general chemistry classes. They gave one group assignments with mixed questions and a control group assignments with questions organised into topics or chapters. They compared the groups’ performances through one pre-test and post-test after each of three problem-solving sessions.
Teaching tips
- Source or compile more mixed practice question banks, and avoid solely using topic-specific question sets from textbooks.
- To increase the difficulty and benefits of mixed problem question sets, do not include details identifying the relevant topics or chapters.
- Blocked practice still has a place. Certain topics, particularly those to do with numerical problem-solving, may require extensive blocked practice before students can engage with the benefits of interleaved practice.
Probing the problems
Rather than looking at overall scores, the researchers used a more detailed analysis. They broke each problem into the sub-problems, or steps, required to answer the problem. They then categorised students’ answers to the steps as successful, neutral or unsuccessful. Subcategories provided more insight into the students’ work. For example, the neutral category contained the subcategories ‘not required’, ‘did not know to do’ and ‘did something else’.
The study revealed that students in the interleaved-practice group increased their problem-solving success more than those in the blocked-practice group. Significantly, the achievement gap between the experimental and control groups widened as the study progressed. Following interleaved practice, students’ neutral codes decreased by about 70%, unsuccessful codes decreased by about 40%, and the successful codes increased by about 52%. Even if students were not able to complete the entire problem, they still improved at individual steps.
Importantly, even though A-, B- and C-grade students showed different levels of improvement, they all benefited from interleaved practice. Perhaps unexpectedly, B- and C-grade students improved the most. This might relate to their poorer conceptual understanding of topics or assessment literacy beforehand, which interleaved practice helps to develop.
Fraser Scott
O. Gulacar et al, Chem. Educ. Res. Pract., 2022, DOI: 10.1039/D1RP00334H
O. Gulacar et al, Chem. Educ. Res. Pract., 2022, 23 , 422–435 ( DOI: 10.1039/D1RP00334H )
- Action and context-based research
- Developing teaching practice
- Education research
- Problem solving
Related articles

Your guide to the UK Chemistry Olympiad
2024-06-05T07:00:00Z By Nina Notman
Discover how your school can easily participate in the leading annual chemistry competition for secondary school learners

How to run a successful Chemistry Olympiad club
2024-06-05T07:00:00Z By Lynne Maxwell
Discover effective approaches and essential resources to prepare learners for this competition (and others), recommended by two heads of science

Why you and your students should get involved in the Olympiad
Challenge your learners and ignite a passion for chemistry
No comments yet
Only registered users can comment on this article., more from education research.

Reduce cognitive load with an augmented reality learning environment
2024-05-16T06:00:00Z By Fraser Scott
Discover how to use augmented reality to help students visualise organic mechanisms
How visuospatial thinking boosts chemistry understanding
2024-04-18T06:07:00Z By David Read
Encourage your students to use their hands to help them get to grips with complex chemistry concepts

Understanding how students untangle intermolecular forces
2024-03-14T05:10:00Z By Fraser Scott
Discover how learners use electronegativity to predict the location of dipole−dipole interactions
- Contributors
- Print issue
- Email alerts
Site powered by Webvision Cloud
- Utility Menu
GA4 Tracking Code
fa51e2b1dc8cca8f7467da564e77b5ea
- Make a Gift
- Join Our Email List
- Problem Solving in STEM
Solving problems is a key component of many science, math, and engineering classes. If a goal of a class is for students to emerge with the ability to solve new kinds of problems or to use new problem-solving techniques, then students need numerous opportunities to develop the skills necessary to approach and answer different types of problems. Problem solving during section or class allows students to develop their confidence in these skills under your guidance, better preparing them to succeed on their homework and exams. This page offers advice about strategies for facilitating problem solving during class.
How do I decide which problems to cover in section or class?
In-class problem solving should reinforce the major concepts from the class and provide the opportunity for theoretical concepts to become more concrete. If students have a problem set for homework, then in-class problem solving should prepare students for the types of problems that they will see on their homework. You may wish to include some simpler problems both in the interest of time and to help students gain confidence, but it is ideal if the complexity of at least some of the in-class problems mirrors the level of difficulty of the homework. You may also want to ask your students ahead of time which skills or concepts they find confusing, and include some problems that are directly targeted to their concerns.
You have given your students a problem to solve in class. What are some strategies to work through it?
- Try to give your students a chance to grapple with the problems as much as possible. Offering them the chance to do the problem themselves allows them to learn from their mistakes in the presence of your expertise as their teacher. (If time is limited, they may not be able to get all the way through multi-step problems, in which case it can help to prioritize giving them a chance to tackle the most challenging steps.)
- When you do want to teach by solving the problem yourself at the board, talk through the logic of how you choose to apply certain approaches to solve certain problems. This way you can externalize the type of thinking you hope your students internalize when they solve similar problems themselves.
- Start by setting up the problem on the board (e.g you might write down key variables and equations; draw a figure illustrating the question). Ask students to start solving the problem, either independently or in small groups. As they are working on the problem, walk around to hear what they are saying and see what they are writing down. If several students seem stuck, it might be a good to collect the whole class again to clarify any confusion. After students have made progress, bring the everyone back together and have students guide you as to what to write on the board.
- It can help to first ask students to work on the problem by themselves for a minute, and then get into small groups to work on the problem collaboratively.
- If you have ample board space, have students work in small groups at the board while solving the problem. That way you can monitor their progress by standing back and watching what they put up on the board.
- If you have several problems you would like to have the students practice, but not enough time for everyone to do all of them, you can assign different groups of students to work on different – but related - problems.
When do you want students to work in groups to solve problems?
- Don’t ask students to work in groups for straightforward problems that most students could solve independently in a short amount of time.
- Do have students work in groups for thought-provoking problems, where students will benefit from meaningful collaboration.
- Even in cases where you plan to have students work in groups, it can be useful to give students some time to work on their own before collaborating with others. This ensures that every student engages with the problem and is ready to contribute to a discussion.
What are some benefits of having students work in groups?
- Students bring different strengths, different knowledge, and different ideas for how to solve a problem; collaboration can help students work through problems that are more challenging than they might be able to tackle on their own.
- In working in a group, students might consider multiple ways to approach a problem, thus enriching their repertoire of strategies.
- Students who think they understand the material will gain a deeper understanding by explaining concepts to their peers.
What are some strategies for helping students to form groups?
- Instruct students to work with the person (or people) sitting next to them.
- Count off. (e.g. 1, 2, 3, 4; all the 1’s find each other and form a group, etc)
- Hand out playing cards; students need to find the person with the same number card. (There are many variants to this. For example, you can print pictures of images that go together [rain and umbrella]; each person gets a card and needs to find their partner[s].)
- Based on what you know about the students, assign groups in advance. List the groups on the board.
- Note: Always have students take the time to introduce themselves to each other in a new group.
What should you do while your students are working on problems?
- Walk around and talk to students. Observing their work gives you a sense of what people understand and what they are struggling with. Answer students’ questions, and ask them questions that lead in a productive direction if they are stuck.
- If you discover that many people have the same question—or that someone has a misunderstanding that others might have—you might stop everyone and discuss a key idea with the entire class.
After students work on a problem during class, what are strategies to have them share their answers and their thinking?
- Ask for volunteers to share answers. Depending on the nature of the problem, student might provide answers verbally or by writing on the board. As a variant, for questions where a variety of answers are relevant, ask for at least three volunteers before anyone shares their ideas.
- Use online polling software for students to respond to a multiple-choice question anonymously.
- If students are working in groups, assign reporters ahead of time. For example, the person with the next birthday could be responsible for sharing their group’s work with the class.
- Cold call. To reduce student anxiety about cold calling, it can help to identify students who seem to have the correct answer as you were walking around the class and checking in on their progress solving the assigned problem. You may even want to warn the student ahead of time: "This is a great answer! Do you mind if I call on you when we come back together as a class?"
- Have students write an answer on a notecard that they turn in to you. If your goal is to understand whether students in general solved a problem correctly, the notecards could be submitted anonymously; if you wish to assess individual students’ work, you would want to ask students to put their names on their notecard.
- Use a jigsaw strategy, where you rearrange groups such that each new group is comprised of people who came from different initial groups and had solved different problems. Students now are responsible for teaching the other students in their new group how to solve their problem.
- Have a representative from each group explain their problem to the class.
- Have a representative from each group draw or write the answer on the board.
What happens if a student gives a wrong answer?
- Ask for their reasoning so that you can understand where they went wrong.
- Ask if anyone else has other ideas. You can also ask this sometimes when an answer is right.
- Cultivate an environment where it’s okay to be wrong. Emphasize that you are all learning together, and that you learn through making mistakes.
- Do make sure that you clarify what the correct answer is before moving on.
- Once the correct answer is given, go through some answer-checking techniques that can distinguish between correct and incorrect answers. This can help prepare students to verify their future work.
How can you make your classroom inclusive?
- The goal is that everyone is thinking, talking, and sharing their ideas, and that everyone feels valued and respected. Use a variety of teaching strategies (independent work and group work; allow students to talk to each other before they talk to the class). Create an environment where it is normal to struggle and make mistakes.
- See Kimberly Tanner’s article on strategies to promoste student engagement and cultivate classroom equity.
A few final notes…
- Make sure that you have worked all of the problems and also thought about alternative approaches to solving them.
- Board work matters. You should have a plan beforehand of what you will write on the board, where, when, what needs to be added, and what can be erased when. If students are going to write their answers on the board, you need to also have a plan for making sure that everyone gets to the correct answer. Students will copy what is on the board and use it as their notes for later study, so correct and logical information must be written there.
For more information...
Tipsheet: Problem Solving in STEM Sections
Tanner, K. D. (2013). Structure matters: twenty-one teaching strategies to promote student engagement and cultivate classroom equity . CBE-Life Sciences Education, 12(3), 322-331.
- Designing Your Course
- A Teaching Timeline: From Pre-Term Planning to the Final Exam
- The First Day of Class
- Group Agreements
- Classroom Debate
- Flipped Classrooms
- Leading Discussions
- Polling & Clickers
- Teaching with Cases
- Engaged Scholarship
- Devices in the Classroom
- Beyond the Classroom
- On Professionalism
- Getting Feedback
- Equitable & Inclusive Teaching
- Advising and Mentoring
- Teaching and Your Career
- Teaching Remotely
- Tools and Platforms
- The Science of Learning
- Bok Publications
- Other Resources Around Campus
- WV App Login
- Site Search
- Report Templates
- Speech Helpers
- SLP Resources
- Top 10 Tips
- Getting an Eval
- Certified SLP
- How to Say the R Sound
- 0-18 Months
- 18-36 Months
- 18-30 Months
- 30-36 Months
- 10-11 Years
- Articulation
- Cleft Palate
- Phonological
- Dysphagia Causes
- Dysphagia Treatment
30 Problem Solving Scenarios for Speech Therapy Practice
As promised here are the words for your unlimited use .
If you know others who can use our lists ...
... please share this page using our site share buttons.
Explore Our Goal Reaching, Client Centered Products

SEE ALSO: Houston We Have a Problem! Activities for Problem Solving
Problem solving scenarios.
- Your friends came over to your house for a movie night. One of your friends brought another friend so there are more people than you planned for. You want to pass out the drinks but you only have five cans of soda and you need 6 for everyone to have one. What could you do?
- After basketball practice you go back to the locker room with your team to shower and change. When you are done dressing, you can't find your shoes. What could you do?
- You have been waiting all day for lunch to come because you are starving. Finally class gets over and you get to go to lunch. Except when you go to get to your lunch, it's not there. You probably left it at home. What could you do?
- There is a guy in your class who is always mean to you. He always bumps you when he walks by and he calls you names. He knocks stuff out of your hands and makes you feel stupid. You don't think you can take it anymore. What could you do?
- You really want to invite this new girl/guy to come to your birthday party, but you have never talked to them before. You are worried they will say no. What could you do?
- You rode the bus to school today and on the way in people are pointing and laughing at you. You go in the bathroom and see that you have pink gum all over the back of your pants. What could you do?
- You wake up and see that your alarm never went off. So you are starting your morning 15 minutes later than you planned. It is a really important day at school and you cannot be late. What could you do?
- You are giving a group presentation in front of class and it's your turn to talk. All of the sudden you sneeze. You cover it with your hand, but now your hand is full of stuff you sneezed out. What could you do?
- You are eating dinner at a fancy restaurant with your parents and their friends. You have a really messy dinner and accidentally flip a noodle into the lady's lap. They are busy talking and don't notice it. What could you do?
- You are taking a test and there is no talking allowed. You are writing your answers on the paper and your pencil breaks. What could you do?
- You are taking a test and the guy behind you asks you for help. He wants to know what you put for question number two. What could you do?
- You are at a birthday party and you have waited in line for a long time for your turn to hit the pinata. It is finally going to be your turn and it looks like the next hit will break the pinata. But you suddenly have to go to the bathroom. What could you do?
- You are hanging outside with your friend and she decides to pick your neighbor's flowers. She gives you the pretty handful of flowers and right then your neighbor opens the door. She asks you why you picked her flowers. What could you do?
- You borrowed your sister's skates one day without asking and they broke while you were using them. What could you do?
- You are eating at a friend's house and the mom piles your plate full of food. It looks really good and you want to eat it all but you can't because you just ate a snack. What could you do so you don't hurt her feelings?
SEE ALSO: The Best Free App for Speech Therapy

- Your teacher was working at her desk. You wanted to ask her a question, but she didn't see your hand raised. What should you do?
- You started to do your work, but you weren't sure if you were doing it right. What should you do?
- You were playing tether-ball and were the champion so far. In the next game, you slightly touched the rope. Only one student saw you touch the rope. What will you do?
- The teacher is giving directions, but your friend sitting next to you keeps talking. You can't hear the directions. What should you do?
- You didn't do your homework. Your teacher was upset with you. What should you do?
- You finished eating and felt a burp coming. What are you going to do?
- You were waiting to swing. When it was your turn, another boy jumped in front of you and took the swing. What would you do?
- You waited a long time, but your mom didn't come to pick you up after school. What should you do?
- A bully threatened to beat you up after school. What should you do?
- A boy on the playground keeps pushing you and making you mad. What would you do?
- You were sitting in class doing your work and you hear the fire alarm. What should you do?
- An adult you didn't know came on to the playground and asked if you would help look for his lost dog. What would you do?
- You forgot your lunch at home. What would you do?
- The person sitting behind you keeps tapping your chair with his foot. What should you do?
- You finished your work early. What should you do?
This list of functional words was professionally selected to be the most useful for a child or adult who has difficulty with problem solving scenarios.
We encourage you to use this list when practicing at home.
Home practice will make progress toward meeting individual language goals much faster.
Speech-Language Pathologists (SLPs) are only able to see students/clients 30-60 mins (or less) per week. This is not enough time or practice for someone to handle Problem solving scenarios.
Every day that your loved one goes without practice it becomes more difficult to help them.
SEE ALSO: The Best Books for Speech Therapy Practice

We know life is busy , but if you're reading this you're probably someone who cares about helping their loved one as much as you can.
Practice 5-10 minutes whenever you can, but try to do it on a consistent basis (daily).
Please, please, please use this list to practice.
It will be a great benefit to you and your loved one's progress.
Freebies, Activities, and Specials, Oh My! Sign up for Terrific Therapy Activity Emails
See Past Email Examples
Your information is 100% private & never shared .

Hi! We're Luke and Hollie.
We are both MS CCC-SLPs and fell in love while studying for our degrees. Since then we have done everything together - graduated, worked, and started a family. We spend most of our time with our family and the rest making this site for you.

Top Free Resources
Word vault essential.

# 1 Chronological Age Calculator
Popular Materials
All in one printable flashcards.

Multiple Meaning Word Mega Pack

Complete Articulation Word Search

New! 111 Articulation Stories

Teaching the Sound Books

Multi-Syllabic Words Flashcards

Apps to Save You Time & Help Your Clients
Articulation therapy + pirate adventures = awesomeness.

This App Will Get Your Kids Talking

Image Credits
Copyright © 2010 –
HomeSpeechHome.com | All Rights Reserved

This website contains affiliate links, meaning if you buy something from them we may make some money (at no cost to you). By using our affiliate links, you are helping to support our site which is a U.S.-based, family-run small business :)
Information
- Author Services
Initiatives
You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.
All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .
Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.
Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.
Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.
Original Submission Date Received: .
- Active Journals
- Find a Journal
- Proceedings Series
- For Authors
- For Reviewers
- For Editors
- For Librarians
- For Publishers
- For Societies
- For Conference Organizers
- Open Access Policy
- Institutional Open Access Program
- Special Issues Guidelines
- Editorial Process
- Research and Publication Ethics
- Article Processing Charges
- Testimonials
- Preprints.org
- SciProfiles
- Encyclopedia

Article Menu

- Subscribe SciFeed
- Recommended Articles
- Google Scholar
- on Google Scholar
- Table of Contents
Find support for a specific problem in the support section of our website.
Please let us know what you think of our products and services.
Visit our dedicated information section to learn more about MDPI.
JSmol Viewer
Self-assessment in the development of mathematical problem-solving skills.

1. Introduction
- RQ1: Is there a relation between external (tutors’) assessment and students’ self-assessment?
- RQ2: In which problem-solving phase did students show more difficulties in self-assessing their work?
2. Theoretical Framework
2.1. self-assessment, 2.2. doing and assessing problem solving with technologies, 3. materials and methods, 3.1. self-assessment within the digital math training project.
- A weekly synchronous online tutoring in web-conference, conducted by a tutor and focused on how to use the ACE to solve the problems;
- A discussion forum monitored by tutors in which students can interrelate with the other participants and discuss their solving strategies;
- A questionnaire which guides students to the self-assessment of the submitted problems according to the parameters chosen for grading the problems [ 12 ].
- Comprehension: Analyze the problematic situation, represent, and interpret the data and then turn them into mathematical language;
- Identification of a solving strategy: Employ solving strategies by modeling the problem and by using the most suitable strategy;
- Development of the solving process: Solve the problematic situation consistently, completely, and correctly by applying mathematical rules and by performing the necessary calculations;
- Argumentation: Explain and comment on the chosen strategy, the key steps of the building process and the consistency of the results;
- Use of an ACE: Use the ACE commands appropriately and effectively in order to solve the problem.
- To what level do you think you understood—and showed that you understood—the problematic situation?
- To what level do you think you identified and described the solution strategy?
- To what level do you think you developed the chosen solving process?
- To what level did you discuss your steps clearly and in detail?
- To what level do you think you effectively used Maple?
- Did you find some difficulties in solving this problem?
- To establish and share the evaluation criteria, an assessment rubric has been created and shared through the DLE;
- To show how to apply the established criteria and clarify what a good performance is, the section “Get ready for the training!” has been designed; moreover, proposed solutions to the problems are published after the submission deadline. To increment the range of solving approaches, besides the tutors’ resolution, also some of the most original participants’ submissions are selected;
- To provide feedback to students, the tutors’ assessment is provided though the rubric, which has explicit descriptors; moreover, detailed and personalized comments and tips are released by tutors together with the evaluation;
- To encourage self-assessment, participants receive an explanation about the importance of filling the self-assessment questionnaire. Moreover, they are rewarded with 3 DMC for each questionnaire filled.
3.2. Participants
3.3. research method.
“In solving the problems, how much did the following aspects hinder you? Comprehension of the problematic situation; Identification of a solving strategy; Completion of the solving process; Argumentation; Generalization by using interactive components; Use of Maple.”
4.1. Comprehension of the Problematic Situation
“I found it difficult to select only one strategy because the text could be interpreted differently”; “The text wasn’t so clear”; “I found it more difficult to understand the text than to use Maple. That is why I tried to underline the points in the text from which the different interpretations originated and then I employed my strategy. Furthermore, I found the forum useful because other participants had my doubts and reading the answers to their posts helped me.”
4.2. Identification of a Solving Strategy
4.3. development of the solving process, 4.4. argumentation, 4.5. use of the ace.
“I found it difficult to solve the third task. I had problems in programming the interactive components”; “I found it difficult to develop the interactive components by plotting the moving average”; “I found it difficult to understand some tasks and so I did the best I could, even though I’m not so sure I satisfied the requests”.
5. Discussion
6. conclusions, author contributions, institutional review board statement, informed consent statement, data availability statement, conflicts of interest.
- Problem 1—Gasoline
- How many km can he travel with a liter of gasoline?
- Problem 8—Antibiotic therapy
- If the therapy starts the first day after the medical prescription and is done properly, how many days would it take to remove both bacteria from the organism? Discuss it by using graphical representations.
- Supposing that Marco begins to feel better when only one of the two bacteria has disappeared, and he decides to stop the treatment. What happens to type A bacteria in the 3 following weeks? Does it grow more or less than it would grow if the therapy hadn’t started? Discuss it by using graphical representations.
- Create a system of interactive components which estimates how many days it would take to remove one of the 2 types of bacteria by inserting the initial concentration, the natural increment of the 2 types of bacteria, the competitive decrease (assuming they are the same), the antibiotic sensitivity (in term of the absolute decrease of concentrations). Be careful: It isn’t required to display how many days it would take to remove both bacteria.
- The other problems
| Indicators | Level (Score) | Description |
|---|---|---|
| Comprehension Analyze the problematic situation, represent and interpretate the data and then turn them in mathematical language | L1 (0–3) | You don’t understand the tasks, or you do incorrectly or partially, so that you fail to recognize key points and information, or you recognize some of them, but you interpret them incorrectly. You incorrectly link information, and you use mathematical codes insufficiently and/or with big mistakes. |
| L2 (4–8) | You analyze and you understand the tasks only partially, so that you select just some key points and essential information or, if you identify all of them, you make mistakes by interpreting some of them, by linking topics and/or by using mathematical codes. | |
| L3 (9–13) | You properly analyze the problematic situation by identifying and correctly interpreting the key points, the information and the links between them by recognizing and skipping distractors. You properly use the mathematical codes by employing plots and symbols, but there are some inaccuracies and/or mistakes. | |
| L4 (14–18) | You analyze and interpret the key points, the essential information and the links between them completely and in a relevant way. You are able to skip distractors and use mathematical codes by employing plots and symbols with mastery and accuracy. Even if there are some inaccuracies, these don’t influence the complex comprehension of the problematic situation. | |
| Identification of solving strategy Employ solving strategies by modeling the problem and by using the most suitable strategy | L1 (0–4) | You don’t identify operating strategies, or you identify them improperly. You aren’t able to identify relevant standard model. There isn’t any creative effort to find the solving process. You don’t establish the appropriate formal instruments. |
| L2 (5–10) | You identify operating strategies that are not very effective and sometimes you employ them not very consistently. You use known models with some difficulties. You show little creativity in setting the operating steps. You establish the appropriate formal instruments with difficulties and by doing some mistakes. | |
| L3 (11-16) | You identify operating strategies, even if they aren’t the most appropriate and efficient. You show your knowledge about standard processes and models which you learned in class, but sometimes you don’t employ them correctly. You use some original strategies. You employ the appropriate formal instruments, even though with some uncertainties. | |
| L4 (17–21) | You employ logical links clearly and with mastery. You efficiently identify the correct operating strategies. You employ known models in the best way, and you also propose some new ones. You show creativity and authenticity in employing operating steps. You carefully and accurately identify the appropriate formal instruments. | |
| Development of the solving process Solve the problematic situation consistently, completely and correctly by applying mathematical rules and by performing the necessary calculations | L1 (0–4) | You don’t implement the chosen strategies, or you implement them incorrectly. You don’t develop the solving process, or you employ it incompletely and/or incorrectly. You aren’t able to use procedures and/or theorems or you employ them incorrectly and/or with several mistakes in calculating. The solution isn’t consistent with the problem’s context. |
| L2 (5–10) | You employ the chosen strategies partially and not always properly. You develop the solving process incompletely. You aren’t always able to use procedures and/or theorems or you employ them partially correctly and/or with several mistakes in calculating. The solution is partially consistent with the problem’s context. | |
| L3 (11–16) | You employ the chosen strategy even though with some inaccuracy. You develop the solving process almost completely. You are able to use procedures and/or theorems or rules and you employ them correctly and properly. You make a few mistakes in calculating. The solution is generally consistent with the problem’s context. | |
| L4 (17–21) | You correctly employ the chosen strategy by using models and/or charts and/or symbols. You develop the solving process analytically, completely, clearly and correctly. You employ procedures and/or theorems or rules correctly and properly, with ability and originality. The solution is consistent with the problem’s context. | |
| Argumentation Explain and comment on the chosen strategy, the key steps of the building process and the consistency of the results | L1 (0–3) | You don’t argue or you argue the solving strategy/process and the test phase wrongly by using mathematical language that is improper or very inaccurate. |
| L2 (4–7) | You argue the solving strategy/process or the test phase in a fragmentary way and/or not always consistently. You use broadly suitable, but not always rigorous mathematical language. | |
| L3 (8–11) | You argue the solving process and the test phase correctly but incompletely. You explain the answer, but not the solving strategies employed (or vice versa). You use a pertinent mathematical language, although with some uncertainty. | |
| L4 (12–15) | You argue both the employed strategies and the obtained results consistently, accurately, exhaustively and in depth. You show an excellent command of the scientific language. | |
| Use of an ACE (Maple) Use the ACE commands appropriately and effectively which is the software Maple, in order to solve the problem | L1 (0–5) | You use Maple as a plain white sheet on which you transpose calculus and arguments which are somewhere else employed. You don’t use Maple’s capabilities in order to plot, to perform mathematical operations and to solve the problem. |
| L2 (6–12) | You partially use Maple’s commands in order to perform some non-basic calculus by making decisions about commands and instruments which aren’t always the most pertinent. You only use basic functions and show that you aren’t able to employ advanced features. | |
| L3 (13–19) | You appropriately use basic Maple’s commands and show that you are able to employ advanced features, even with some indecision, several attempts or by making some mistakes, or in a non-effective way in order to represent the data, the solutions and to solve the problem. | |
| L4 (20–25) | You display mastery in the use of Maple, you make correct and efficient decisions about commands and instruments which you employ. You are able to employ them gracefully and with originality by using Maple’s capabilities in order to solve the problem. |
- Klenowski, V. Student Self-evaluation Processes in Student-centred Teaching and Learning Contexts of Australia and England. Assess. Educ. Princ. Policy Pract. 1995 , 2 , 145–163. [ Google Scholar ] [ CrossRef ]
- Black, P.; Wiliam, D. Assessment and Classroom Learning. Assess. Educ. Princ. Policy Pract. 1998 , 5 , 7–74. [ Google Scholar ] [ CrossRef ]
- Ross, J.A. The Reliability, Validity, and Utility of Self-Assessment. Pract. Assess. Res. Eval. 2006 , 11 , 10. [ Google Scholar ] [ CrossRef ]
- Brookhart, S.M.; Andolina, M.; Zuza, M.; Furman, R. Minute Math: An Action Research Study of Student Self-Assessment. Educ. Stud. Math. 2004 , 57 , 213–227. [ Google Scholar ] [ CrossRef ]
- Nicol, D.J.; Macfarlane-Dick, D. Formative Assessment and Self-regulated Learning: A Model and Seven Principles of Good Feedback Practice. Stud. High. Educ. 2006 , 31 , 199–218. [ Google Scholar ] [ CrossRef ]
- Andrade, H.; Valtcheva, A. Promoting Learning and Achievement Through Self-Assessment. Theory Pract. 2009 , 48 , 12–19. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Tachie, S.A. Meta-Cognitive Skills and Strategies Application: How This Helps Learners in Mathematics Problem-Solving. EURASIA J. Math. Sci. Technol. Educ. 2019 , 15 , em1702. [ Google Scholar ] [ CrossRef ]
- Yoong, D.W.K. Helping Your Students to Become Metacognitive in Mathematics: A Decade Later. Math. Newsl. 2002 , 12 , 1–7. [ Google Scholar ]
- Schoenfeld, A. Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In Handbook of Research on Mathematics Teaching and Learning ; Macmillian: New York, NY, USA, 1992; pp. 334–370. [ Google Scholar ]
- Kilpatrick, J. A retrospective account of the past 25 years of research on teaching mathematical problem solving. In Teaching and Learning Mathematical Problem Solving: Multiple Research Perspectives ; Silver, E.A., Ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1985; pp. 1–15. [ Google Scholar ]
- Liljedahl, P.; Santos-Trigo, M.; Malaspina, U.; Bruder, R. Problem Solving in Mathematics Education ; ICME-13 Topical Surveys; Springer: New York, NY, USA, 2016; ISBN 978-3-319-40729-6. [ Google Scholar ]
- Barana, A.; Marchisio, M. From digital mate training experience to alternating school work activities. Mondo Digit. 2016 , 15 , 63–82. [ Google Scholar ]
- Barana, A.; Brancaccio, A.; Conte, A.; Fissore, C.; Floris, F.; Marchisio, M.; Pardini, C. The Role of an Advanced Computing Environment in Teaching and Learning Mathematics through Problem Posing and Solving. In Proceedings of the 15th International Scientific Conference eLearning and Software for Education, Bucharest, Romania, 11–12 April 2019; Volume 2, pp. 11–18. [ Google Scholar ]
- Ninness, H.A.C.; Ninness, S.K.; Sherman, S.; Schotta, C. Augmenting Computer-Interactive Self-Assessment with and Without Feedback. Psychol. Rec. 1998 , 48 , 601–616. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- McDonald, B.; Boud, D. The Impact of Self-Assessment on Achievement: The Effects of Self-Assessment Training on Performance in External Examinations. Assess. Educ. Princ. Policy Pract. 2003 , 10 , 209–220. [ Google Scholar ] [ CrossRef ]
- Black, P.; Wiliam, D. ‘In Praise of Educational Research’: Formative Assessment. Br. Educ. Res. J. 2003 , 29 , 623–637. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Black, P.; Wiliam, D. Developing the Theory of Formative Assessment. Educ. Assess. Eval. Account. 2009 , 21 , 5–31. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Sánchez-Ruiz, L.-M.; Moll-López, S.; Moraño-Fernández, J.-A.; Roselló, M.-D. Dynamical Continuous Discrete Assessment of Competencies Achievement: An Approach to Continuous Assessment. Mathematics 2021 , 9 , 2082. [ Google Scholar ] [ CrossRef ]
- Castoldi, M. Le rubriche valutative. L’Educatore 2006 , 5 , 6–10. [ Google Scholar ]
- Yan, Z. Self-Assessment in the Process of Self-Regulated Learning and Its Relationship with Academic Achievement. Assess. Eval. High. Educ. 2020 , 45 , 224–238. [ Google Scholar ] [ CrossRef ]
- Zimmerman, B.J. Attaining Self-Regulation: A Social Cognitive Perspective. In Handbook of Self-Regulation ; Boekaerts, M., Pintrich, P.R., Zeidner, M., Eds.; Elsevier: San Diego, CA, USA, 2000; pp. 13–39. [ Google Scholar ]
- Ross, J.A.; Hogaboam-Gray, A.; Rolheiser, C. Student Self-Evaluation in Grade 5-6 Mathematics Effects on Problem- Solving Achievement. Educ. Assess. 2002 , 8 , 43–58. [ Google Scholar ] [ CrossRef ]
- English, L.D.; Sriraman, B. Problem Solving for the 21st Century. In Theories of Mathematics Education ; Springer: Berlin/Heidelberg, Germany, 2010; pp. 263–290. [ Google Scholar ]
- Schoenfeld, A. Mathematical Problem Solving ; Academic Press: Cambridge, MA, USA, 1985. [ Google Scholar ]
- Fan, L.; Zhu, Y. From Convergence to Divergence: The Development of Mathematical Problem Solving in Research, Curriculum, and Classroom Practice in Singapore. ZDM 2007 , 39 , 491–501. [ Google Scholar ] [ CrossRef ]
- Chen, P.P. Relationship between Students’ Self-Assessment of Their Capabilities and Their Teachers’ Judgments of Students’ Capabilities in Mathematics Problem-Solving. Psychol. Rep. 2006 , 98 , 765–778. [ Google Scholar ] [ CrossRef ]
- Krathwohl, D.R. A Revision of Bloom’s Taxonomy: An Overview. Theory Pract. 2002 , 41 , 212–218. [ Google Scholar ] [ CrossRef ]
- Semana, S.; Santos, L. Self-Regulation Capacity of Middle School Students in Mathematics. ZDM 2018 , 50 , 743–755. [ Google Scholar ] [ CrossRef ]
- National Council of Teachers of Mathematics. Executive Summary Principles and Standards for School Mathematics ; National Council of Teachers of Mathema: Reston, VA, USA, 2000. [ Google Scholar ]
- Council of the European Union. European Parliament and Council Council Recommendation of 22 May 2018 on Key Competences for Lifelong Learning. Off. J. Eur. Union 2018 , C 189/1 , 1–13.
- Pólya, G. How to Solve It ; Princeton University: Princeton, NJ, USA, 1945. [ Google Scholar ]
- D’Amore, B.; Pinilla, M.I.F. Che problema i problemi! L’insegnamento Della Mat. E Delle Sci. Integr. 2006 , 6 , 645–664. [ Google Scholar ]
- Samo, D.D.; Darhim, D.; Kartasasmita, B. Culture-Based Contextual Learning to Increase Problem-Solving Ability of First Year University Student. J. Math. Educ. 2017 , 9 , 81–94. [ Google Scholar ] [ CrossRef ]
- Bonotto, C.; Baroni, M. Using maths in a daily context: Experiences in Italian compulsory education. In Planting Mathematics, Publication of the Comenius Network Developing Quality in Mathematics Education II—DQME II ; Henn, H.W., Meier, S., Eds.; TU Dortmund: Dortmund, Germany, 2006; pp. 19–47. [ Google Scholar ]
- Acevedo Nistal, A.; Dooren, W.; Clarebout, G.; Elen, J.; Verschaffel, L. Conceptualising, Investigating and Stimulating Representational Flexibility in Mathematical Problem Solving and Learning: A Critical Review. ZDM 2009 , 41 , 627–636. [ Google Scholar ] [ CrossRef ]
- Silver, E.A. Fostering Creativity through Instruction Rich in Mathematical Problem Solving and Problem Posing. ZDM 1997 , 29 , 75–80. [ Google Scholar ] [ CrossRef ]
- Olivares, D.; Lupiáñez, J.L.; Segovia, I. Roles and Characteristics of Problem Solving in the Mathematics Curriculum: A Review. Int. J. Math. Educ. Sci. Technol. 2021 , 52 , 1079–1096. [ Google Scholar ] [ CrossRef ]
- Toh, T.L.; Chan, C.M.E.; Tay, E.G.; Leong, Y.H.; Quek, K.S.; Toh, P.C.; Ho, W.K.; Dindyal, J.; Ho, F.H.; Dong, F. Problem Solving in the Singapore School Mathematics Curriculum. In Mathematics Education in Singapore ; Toh, T.L., Kaur, B., Tay, E.G., Eds.; Mathematics Education—An Asian Perspective; Springer: Singapore, 2019; pp. 141–164. ISBN 9789811335723. [ Google Scholar ]
- Yap, R.A.S.; Leong, Y.H. Using Video Clubs to Learn for Mathematical Problem-Solving Instruction in the Philippines: The Case of Teaching Extensions. In Cases of Mathematics Professional Development in East Asian Countries ; Ng, S.F., Ed.; Springer: Singapore, 2015; pp. 83–106. ISBN 978-981-287-404-7. [ Google Scholar ]
- Leong, Y.H.; Tay, E.G.; Toh, T.L.; Quek, K.S.; Dindyal, J. Reviving Pólya’s “Look Back” in a Singapore School. J. Math. Behav. 2011 , 30 , 181–193. [ Google Scholar ] [ CrossRef ]
- Carreira, S.; Jones, K.; Amado, N.; Jacinto, H.; Nobre, S. Youngsters Solving Mathematical Problems with Technology ; Mathematics Education in the Digital Era; Springer: Cham, Switzerland, 2016; Volume 5, ISBN 978-3-319-24908-7. [ Google Scholar ]
- Lesh, R.; Lehrer, R. Models and Modeling Perspectives on the Development of Students and Teachers. Math. Think. Learn. 2003 , 5 , 109–129. [ Google Scholar ] [ CrossRef ]
- Santos-Trigo, M.; Moreno-Armella, L.; Camacho-Machín, M. Problem Solving and the Use of Digital Technologies within the Mathematical Working Space Framework. ZDM 2016 , 48 , 827–842. [ Google Scholar ] [ CrossRef ]
- Artigue, M. Instrumentation Issues and the Integration of Computer Technologies into Secondary Mathematics Teaching. In Proceedings of the Annual Meeting of the GDM, Potsdam, Germany; 2000; pp. 7–17. Available online: http://webdoc.sub.gwdg.de/ebook/e/gdm/2000/artigue_2000.pdf (accessed on 19 January 2022).
- Kuzniak, A.; Parzysz, B.; Vivier, L. Trajectory of a Problem: A Study in Teacher Training. Math. Enthus. 2013 , 10 , 407–440. [ Google Scholar ] [ CrossRef ]
- Moreno-Armella, L.; Santos-Trigo, M. The use of digital technologies in mathematical practices: Reconciling traditional and emerging approaches. In Handbook of International Research in Mathematics Education ; English, L.D., Kirshner, D., Eds.; Taylor & Francis: New York, NY, USA, 2016; pp. 595–616. [ Google Scholar ]
- Avitzur, R. Graphing Calculator (Version 4.0) ; Pacific Tech.: Berkeley, CA, USA, 2011. [ Google Scholar ]
- Dimiceli, V.A.; Lang, A.S.I.D.; Locke, L.A. Teaching Calculus with Wolfram|Alpha. Int. J. Math. Educ. Sci. Technol. 2010 , 41 , 1061–1071. [ Google Scholar ] [ CrossRef ]
- Hohenwarter, M.; Hohenwarter, J.; Kreis, Y.; Lavicza, Z. Teaching and Learning Calculus with Free Dynamic Mathematics Software GeoGebra. In Proceedings of the 11th International Congress on Mathematics Education, Monterrey, Mexico, 6–13 July 2008; pp. 1–10. [ Google Scholar ]
- Artigue, M. Learning Mathematics in a CAS Environment: The Genesis of a Reflection about Instrumentation and the Dialectics between Technical and Conceptual Work. Int. J. Comput. Math. Learn. 2002 , 7 , 245–274. [ Google Scholar ] [ CrossRef ]
- Barana, A.; Marchisio, M. Analyzing Interactions in Automatic Formative Assessment Activities for Mathematics in Digital Learning Environments. In Proceedings of the 13th International Conference on Computer Supported Education, SCITEPRESS, Online, 23–25 April 2021; Volume 1, pp. 497–504. [ Google Scholar ]
- Barana, A.; Marchisio, M.; Sacchet, M. Interactive Feedback for Learning Mathematics in a Digital Learning Environment. Educ. Sci. 2021 , 11 , 279. [ Google Scholar ] [ CrossRef ]
- Beevers, C.E.; Paterson, J.S. Automatic Assessment of Problem Solving Skills in Mathematics. Act. Learn. High. Educ. 2003 , 4 , 127–144. [ Google Scholar ] [ CrossRef ]
- Goos, M.; Galbraith, P.; Renshaw, P.; Geiger, V. Perspectives on Technology Mediated Learning in Secondary School Mathematics Classrooms. J. Math. Behav. 2003 , 22 , 73–89. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Barana, A.; Fissore, C.; Marchisio, M.; Roman, F. Enhancement of Mathematical Problem Solving by Discussing and Collaborating Asynchronously. In Proceedings of the Edulearn20 Conference, Online, 6–7 July 2020; pp. 2827–2836. [ Google Scholar ]
- Tan, D.Y.; Cheah, C.W. Developing a Gamified AI-Enabled Online Learning Application to Improve Students’ Perception of University Physics. Comput. Educ. Artif. Intell. 2021 , 2 , 100032. [ Google Scholar ] [ CrossRef ]
- Kang, K.; Kushnarev, S.; Wei Pin, W.; Ortiz, O.; Chen Shihang, J. Impact of Virtual Reality on the Visualization of Partial Derivatives in a Multivariable Calculus Class. IEEE Access 2020 , 8 , 58940–58947. [ Google Scholar ] [ CrossRef ]
- Buentello-Montoya, D.A.; Lomelí-Plascencia, M.G.; Medina-Herrera, L.M. The Role of Reality Enhancing Technologies in Teaching and Learning of Mathematics. Comput. Electr. Eng. 2021 , 94 , 107287. [ Google Scholar ] [ CrossRef ]
- Kushnarev, S.; Kang, K.; Goyal, S. Assessing the Efficacy of Personalized Online Homework in a First-Year Engineering Multivariate Calculus Course. In Proceedings of the 2020 IEEE International Conference on Teaching, Assessment, and Learning for Engineering (TALE), Takamatsu, Japan, 8–11 December 2020; pp. 770–773. [ Google Scholar ]
- Cheong, K.H.; Koh, J.M. Integrated Virtual Laboratory in Engineering Mathematics Education: Fourier Theory. IEEE Access 2018 , 6 , 58231–58243. [ Google Scholar ] [ CrossRef ]
- Cheong, K.H.; Koh, J.M.; Yeo, D.J.; Tan, Z.X.; Boo, B.O.E.; Lee, G.Y. Paradoxical Simulations to Enhance Education in Mathematics. IEEE Access 2019 , 7 , 17941–17950. [ Google Scholar ] [ CrossRef ]
- Comoglio, M. Le Nuove Prospettive Della Valutazione Scolasica. L’Educatore 2008 , 11 , 29–34. [ Google Scholar ]
- Leong, Y.H.; Janjaruporn, R. Teaching of Problem Solving in School Mathematics Classrooms. In The Proceedings of the 12th International Congress on Mathematical Education ; Cho, S.J., Ed.; Springer: Cham, Switzerland, 2015; pp. 645–648. ISBN 978-3-319-10685-4. [ Google Scholar ]
- Comoglio, M. La Valutazione Autentica. Orientamenti Pedagog. 2002 , 49 , 93–112. [ Google Scholar ]
- Maple. Available online: https://www.maplesoft.com/products/Maple/ (accessed on 7 August 2019).
- Pajares, F.; Miller, M.D. Mathematics Self-Efficacy and Mathematics Performances: The Need for Specificity of Assessment. J. Couns. Psychol. 1995 , 42 , 190–198. [ Google Scholar ] [ CrossRef ]
- Ewers, C.A.; Wood, N.L. Sex and Ability Differences in Children’s Math Self-Efficacy and Prediction Accuracy. Learn. Individ. Differ. 1993 , 5 , 259–267. [ Google Scholar ] [ CrossRef ]
- Sriraman, B.; Umland, K. Argumentation in Mathematics Education. In Encyclopedia of Mathematics Education ; Lerman, S., Ed.; Springer: Dordrecht, Germany, 2014; pp. 46–48. ISBN 978-94-007-4977-1. [ Google Scholar ]
- Cusi, A.; Olsher, S. Design of Classroom Discussions and the Role of the Expert in Fostering an Effective and Aware Use of Examples as a Means of Argumentation. Int. J. Sci. Math. Educ. 2021 . [ Google Scholar ] [ CrossRef ]
- Boero, P. Argumentation and Mathematical Proof: A Complex, Productive, Unavoidable Relationship in Mathematics and Mathematics Education. Int. Newsl. Teach. Learn. Math. Proof 1999 , 7 , 8. [ Google Scholar ]
| Number of Students | Comprehension | Identification | Development | Argumentation | Use of Maple | |
|---|---|---|---|---|---|---|
| 1st problem | 116 | +0.48 | +0.78 | +0.65 | +0.43 | +0.83 |
| 2nd problem | 120 | +0.83 | +0.64 | +0.45 | +0.45 | +0.57 |
| 3rd problem | 110 | +0.66 | +0.67 | +0.54 | +0.23 | +0.60 |
| 4th problem | 105 | +0.67 | +0.56 | +0.51 | +0.60 | +0.53 |
| 5th problem | 76 | +0.53 | +0.59 | +0.49 | +0.50 | +0.68 |
| 6th problem | 82 | +0.65 | +0.38 | +0.37 | +0.39 | +0.57 |
| 7th problem | 60 | +0.57 | +0.73 | +0.58 | +0.70 | +0.60 |
| 8th problem | 58 | +0.64 | +0.38 | +0.41 | +0.52 | +0.62 |
| Pearson Coefficient | p-Value | |
|---|---|---|
| 1st problem | 0.407 | <0.001 |
| 2nd problem | 0.259 | 0.004 |
| 3rd problem | 0.731 | <0.001 |
| 4th problem | 0.535 | <0.001 |
| 5th problem | 0.556 | <0.001 |
| 6th problem | 0.615 | <0.001 |
| 7th problem | 0.735 | <0.001 |
| 8th problem | 0.515 | <0.001 |
| Pearson Coefficient | p-Value | |
|---|---|---|
| 1st problem | 0.356 | <0.001 |
| 2nd problem | 0.074 | 0.422 |
| 3rd problem | 0.652 | <0.001 |
| 4th problem | 0.379 | <0.001 |
| 5th problem | 0.404 | <0.001 |
| 6th problem | 0.483 | <0.001 |
| 7th problem | 0.662 | <0.001 |
| 8th problem | 0.228 | 0.086 |
| Students’ Answers | Mean | Standard Deviation |
|---|---|---|
| 1 | 0.4143 | 0.15278 |
| 2 | 0.7352 | 0.49100 |
| 3 | 0.8014 | 0.46268 |
| 4 | 0.8586 | 0.61427 |
| 5 | 0.8542 | 0.51875 |
| Pearson Coefficient | p-Value | |
|---|---|---|
| 1st problem | 0.243 | 0.009 |
| 2nd problem | 0.200 | 0.029 |
| 3rd problem | 0.639 | <0.001 |
| 4th problem | 0.411 | <0.001 |
| 5th problem | 0.509 | <0.001 |
| 6th problem | 0.468 | <0.001 |
| 7th problem | 0.653 | <0.001 |
| 8th problem | 0.421 | 0.001 |
| Students’ Answers | Mean | Standard Deviation |
|---|---|---|
| 1 | 0.3452 | 0.13521 |
| 2 | 0.6847 | 0.44823 |
| 3 | 0.8374 | 0.42753 |
| 4 | 0.9793 | 0.31618 |
| 5 | - | - |
| Pearson Coefficient | p-Value | |
|---|---|---|
| 1st problem | 0.300 | 0.001 |
| 2nd problem | 0.277 | 0.002 |
| 3rd problem | 0.632 | <0.001 |
| 4th problem | 0.460 | <0.001 |
| 5th problem | 0.518 | <0.001 |
| 6th problem | 0.553 | <0.001 |
| 7th problem | 0.740 | <0.001 |
| 8th problem | 0.465 | <0.001 |
| Pearson Coefficient | p-Value | |
|---|---|---|
| 1st problem | 0.269 | 0.004 |
| 2nd problem | 0.182 | 0.046 |
| 3rd problem | 0.525 | <0.001 |
| 4th problem | 0.488 | <0.001 |
| 5th problem | 0.307 | 0.007 |
| 6th problem | 0.256 | 0.020 |
| 7th problem | 0.576 | <0.001 |
| 8th problem | 0.346 | 0.008 |
| Students’ Answers | Mean | Standard Deviation |
|---|---|---|
| 1 | 0.4571 | 0.37319 |
| 2 | 0.8515 | 0.49796 |
| 3 | 0.7836 | 0.47839 |
| 4 | 0.9877 | 0.50577 |
| 5 | 0.7143 | 0.62270 |
| Pearson Coefficient | p-Value | |
|---|---|---|
| 1st problem | 0.390 | <0.001 |
| 2nd problem | 0.322 | <0.001 |
| 3rd problem | 0.609 | <0.001 |
| 4th problem | 0.469 | <0.001 |
| 5th problem | 0.477 | <0.001 |
| 6th problem | 0.488 | <0.001 |
| 7th problem | 0.740 | <0.001 |
| 8th problem | 0.465 | <0.001 |
| MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
Share and Cite
Barana, A.; Boetti, G.; Marchisio, M. Self-Assessment in the Development of Mathematical Problem-Solving Skills. Educ. Sci. 2022 , 12 , 81. https://doi.org/10.3390/educsci12020081
Barana A, Boetti G, Marchisio M. Self-Assessment in the Development of Mathematical Problem-Solving Skills. Education Sciences . 2022; 12(2):81. https://doi.org/10.3390/educsci12020081
Barana, Alice, Giulia Boetti, and Marina Marchisio. 2022. "Self-Assessment in the Development of Mathematical Problem-Solving Skills" Education Sciences 12, no. 2: 81. https://doi.org/10.3390/educsci12020081
Article Metrics
Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals
- Prodigy Math
- Prodigy English
- Is a Premium Membership Worth It?
- Promote a Growth Mindset
- Help Your Child Who's Struggling with Math
- Parent's Guide to Prodigy
- Assessments
- Math Curriculum Coverage
- English Curriculum Coverage
- Administrators
- Game Portal
45 Fun and Clever Brain Teasers for Kids with Answers!

Written by Laney Kennedy
Reviewed by Sarah Tino, M.Ed.
Engage and motivate your students with our adaptive, game-based learning platform!
- Game-Based Learning
- What brain teasers are
- The benefits of brain teasers for kids
Math brain teasers for kids
Sometimes keeping your students engaged during a (long) school day feels like a losing battle. How do you gain their full attention while teaching the skills they need to succeed? How do you turn tough and intimidating concepts into fun, entertaining lessons that actually spark life in the classroom?
Brain teasers for kids are a great form of game-based learning that not only entertain children but also inspire some creative thought in the classroom. People of all ages can indulge in these playful — yet challenging — activities.
And some examples of when teachers might want to use brain teasers are on a bulletin board in the classroom, as a partnered activity to start a new concept or lesson, or during a rainy day indoor recess box.
We’ve gathered 45 examples of brain teasers for kids with answers, organized by category:
Table of Contents
Language brain teasers for kids :
Riddles ; Language associations ; Lateral thinking problems.
Math brain teasers for kids :
Math riddles ; Pattern problems ; Prodigy.
Visual brain teasers for kids :
Spot the difference ; Rebus puzzles ; Optical illusions ; Stroop effect test.
Use the list below to find the perfect brain teaser for your class!
What are brain teasers?
Before you explore our examples, you might be wondering what brain teasers actually are.
Cambridge Dictionary defines a brain teaser as “a problem for which it is hard to find the answer, especially one which people enjoy trying to solve as a game.”
Brain teasers are a type of puzzle — and as the list below reveals, they come in many different forms. Often presented as a riddle, question or activity, brain teasers require a little extra brainpower to solve.
It's important to note that if you have any English language learners in your class, brain teasers for kids might pose a challenge for them. If that's the case, they might need you to walk them through the brain teaser more closely, or you can find ones that better suit their language level.
Brain teasers for kids differ from other complex or abstract problems because they’re usually done for fun. Although you can use them to analyze problem-solving and critical thinking skills, they’re often used as an amusing activity to encourage logical and lateral thinking , or thinking “outside the box.”
45 Brain teasers for kids
We’ve compiled a list of language, math and visual brain teasers to get your students thinking. Get inspired by the examples below — including answers!
Language brain teasers for kids
When you hear the term “brain teaser,” a riddle is likely the first thing that comes to mind. Riddles are perplexing — sometimes misleading — questions or statements that require creative thought to solve.
Riddles are usually fun, and plenty of them can add some humour to your classroom.
Enjoy our list of riddles for kids below!
a) Billy’s mother had five children. The first was named Lala, the second was named Lele, the third was named Lili, the fourth was named Lolo. What was the fifth child named?
b) Choose the correct sentence: “The yolk of the egg is white” or “the yolk of the egg is white.��”
c) It’s as light as a feather, but the strongest person can’t hold it for more than five minutes. What is it?
d) The more there is, the less you see. What is it?
e) What gets more wet while it dries?
f) You can find it in Mercury, Earth, Mars, Jupiter and Saturn, but not in Venus or Neptune. What is it?
g) It likes food, but water kills it. What is it?
h) What’s full of holes but can still hold water?
i) Which is heavier, a pound of feathers or a pound of rocks?
j) How far can a dog run into the woods?
k) You’re driving a city bus. At the first stop, three women get on. At the second stop, one woman gets off and a man gets on. At the third stop, two children get on. The bus is blue and it’s raining outside in December. What colour is the bus driver’s hair?
l) There are three houses. One is red, one is blue and one is white. If the red house is to the left of the house in the middle, and the blue house is to the right of the house in the middle, where’s the white house?
m) It’s at the center of gravity and you can find it in Venus, but not Mars. What is it?
n) What goes on four feet in the morning, two in the afternoon and three in the evening? (This is from the classic myth, Oedipus and the Riddle of the Sphinx )
o) What travels faster: heat or cold?
p) A man was walking in the rain in the middle of nowhere without a coat or an umbrella. He got soaked, but not a single hair on his head was wet. How can this be?
q) A cowboy rode into town on Friday. He stayed in town for three days and rode back out on Friday. How is this possible?
b) Neither. Egg yolks are yellow, not white!
f) The letter “R”
h) A sponge
i) Neither. Both weigh a pound!
j) Halfway. Once it reaches halfway, it’s running out of the woods.
k) Whatever colour your hair is. Remember, you’re driving the bus!
l) In Washington, D.C.
m) The letter “V”
n) A human. The times of day represent stages of human life. At the beginning of life, a baby crawls on four “feet.” As a person gets older, they walk on two feet. Later in life, a person will walk on three “feet” (two feet, plus a cane to help them walk).
o) Heat travels faster because you can catch a cold!
p) He was bald.
q) The horse’s name was Friday.
As a bonus, use these riddles to challenge preconceived notions and get students thinking about natural bias .
a) Two boxers are in a match scheduled for 12 rounds. (Pure boxing only - no kicking, UFC takedowns, or anything else). One of the boxers gets knocked out after only six rounds, yet no man throws a punch. How is this possible?
b) A father and son have a car accident and both are very injured. They are taken to separate hospitals for treatment. When the boy is taken in for an operation, the surgeon says, “I can’t do this surgery…. this boy is my son!” How is this possible?
a) The two boxers are women.
b) The surgeon is the boy’s mother.
2. Language associations
These brain teasers for kids explore the complexities of the English language. Use them to boost student knowledge of sounds, words, spelling, categorization and more.a) Word association : find a word that associates with the following sets of words.
- Cake, swiss, cottage
- Glasses, screen, day
- Cream, cube, cap
- Knife, fly, cup
b) Find the mystery word . Replace the third letter of each word with a new letter to create a different word. When read vertically, the new letters will reveal the mystery word.
For example, the word MA K E could become MA R E, MA L E, MA T E and so on. It’s your job to figure out which one works to create the mystery word.
Hint: It’s something you’ll find outside.
c) Find rhyming pairs . Unscramble the words below so that each pair of words rhymes.
- RBAE & HREAS
- WNROED & UTRHNDE
- TUGHAT & HBTUGO
- ODULC & ODOG
Mystery word: FLOWER
- BEAR (or BARE) & SHARE
- WONDER & THUNDER
- TAUGHT & BOUGHT
- COULD & GOOD
You can also use printable brain teasers for kids like this one:

Image source: Spelling Words Well
Answer: The “happy word” is SMILE.
3. Lateral thinking problems
Lateral thinking problems require creative thinking with an indirect approach.
These questions require logic and careful thought to solve. The most notable example of a lateral thinking problem is the classic Monty Hall problem .
Here are two examples of lateral thinking problems kids can try to solve.
a) The river crossing problem

Image source: Popular Mechanics
A farmer is travelling with a fox, a goose, and a bag of beans. During his journey, he comes across a river with a boat to cross it.
The farmer can only fit one thing in the boat with him at a time. If left alone together, the fox will eat the goose or the goose will eat the beans. How does the farmer get everything across the river safely?
b) The light bulb problem

There are three light switches outside of a room-- labeled number one, number two, and number three. The door to the room is closed and you can’t see in. All three switches are off.
You need to figure out which switch belongs to which bulb. You can use the switches however you want to, but can only enter the room once. How do you do it?
a) Here’s the step-by-step solution:
- The farmer brings the goose across the river first (if he leaves the goose alone, it will either eat the beans or be eaten by the fox).
- The farmer brings either the fox or the beans across and leaves the other one alone.
- Now the farmer has two items on the other side of the river, including the goose. If he leaves the goose again, the same problem will occur. So, the farmer must bring the goose back to the other side.
- The farmer brings the other item back (either the fox or the beans) and leaves the goose alone again. The fox and the beans are now on the other side of the river.
- The farmer returns and brings the goose across the river again.
b) Turn on the first switch and leave it on. Turn on the second switch for a few minutes, and then turn it off again. When you enter the room, one light bulb will be on. You’ll know it goes with switch one because you turned it on. Another bulb will be hot. You’ll know that goes with switch two because it was on for a little while. The bulb that’s off and cold goes with switch three because you didn’t touch it.
Like math puzzles , these brain teasers for kids can increase engagement with math content and inspire your students to work on math concepts and problems outside of regular lessons.
1. Math riddles
These riddles are just as amusing as the ones above, but they’re math-focused . Use them to give students some extra math practice and encourage resourceful thinking.
Math riddles
a) Divide 30 by ½ and add 10. What’s the answer?
b) A clerk at the butcher shop is six feet tall and wears size 10 shoes. What does he weigh?
c) A farmer has 19 sheep on his land. One day, a big storm hits and all but seven run away. How many sheep does the farmer have left?
d) Your sock drawer only contains 18 white socks and 18 blue socks. How many times do you need to reach inside the drawer and take out a sock to guarantee a matching pair?
e) You planted sunflower seeds in your back garden. Every day, the number of flowers doubles. If it takes 52 days for the flowers to fill the garden, how many days would it take for them to fill half the garden?
f) Using only addition, how can you use eight eights to get the number 1,000?
g) When Ashley was 15, her mother was 37. Now, her mother is twice her age. How old is Ashley?
a) It's 70. You’re dividing 30 by ½, not by two. Thirty divided by ½ is the same thing as multiplying it by two, which is 60. Plus 10 makes 70!
b) Meat. He works at the butcher shop, so he weighs meat for a living.
c) Seven. The riddle says all but seven run away, meaning there are seven left who didn’t.
d) Three times. On the third time, you’ll get either a white or a blue sock to match with one of the other two you’ve already grabbed.
e) It would take 51 days. If the number of flowers doubles every day, half the garden would be full the day before, on the 51st day.
f) 888 +88 +8 +8 +8
g) Ashley is 22. Her mother is 22 years older, so when Ashley is 22, she’s now half her mother’s age.
2. Pattern problems
These questions require students to identify a pattern before they can answer a particular question. Kids must use creative and logical thinking to find the answers.
4 + 4 = 168
5 + 5 = 2510.
b) What makes this number unique: 8,549,176,320?
c) Solve the pattern puzzle below. Find the missing number to replace the question mark.
Image source: Genius Puzzles
d) Solve the following:
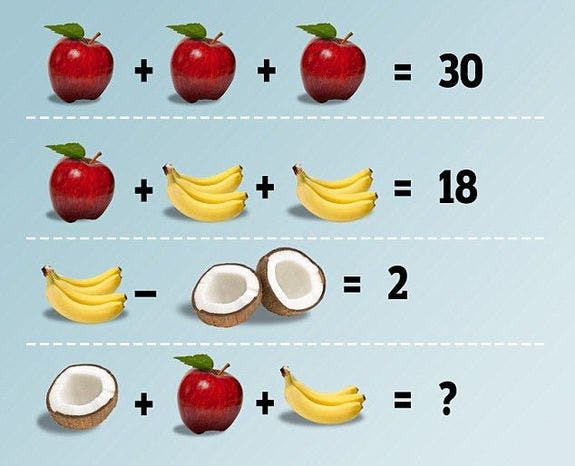
Image source: AOL
a) The missing number is 3612. The answer is the number multiplied by itself and then the number added to itself. Six multiplied by six is 36, and six plus six is 12.
b) It contains each one-digit number, zero through nine, listed in alphabetical order.
c) The missing number is 17. Each number in the circle is the sum of the numbers in the opposite quadrant. In this case, the numbers are eight and nine — added together makes 17.
d) The answer is 14 (or 16), if you’re on the other side of the debate .
3. Prodigy Math Game

This math activity is a bit different from others on the list. It’s not a traditional brain teaser, but it can also be used as a fun, skill-building alternative to traditional math class.
Prodigy is a game-based learning platform that takes your students on an online fantasy adventure while they answer standards-aligned math questions. It’s engaging and effective at teaching necessary skills.
Prodigy's free teacher tools help you differentiate learning, send assessments in-game and even collect student insights!
Visual brain teasers for kids
1. spot the difference.
This ever-popular activity might remind you of your own childhood — and kids still love it! Spot the difference puzzles require lots of deduction and attention to detail.
Here’s an example of a printable spot the difference activity.

Image source: Tim’s Printables

2. Rebus puzzles
A rebus is a visual word puzzle that uses lateral thinking to find its intended meaning. The word or phrase is depicted with a visual illustration, including letters and words. Students must think creatively to figure out the meaning from the clues they’re given.

Image source: Wikipedia

Image source: Stack Exchange
a) Top secret
b) Think outside the box
Visit the link below if you want more fun rebus puzzles for your students:
3. Optical illusions
Get tricky with your students! Optical illusions use visual tricks that alter the perception of what you’re really seeing. Students will love trying to figure out what’s really going on in these examples.
a) How many legs does the elephant have?

Image source: Optics For Kids
b) Are the two squares different colours?

Image source: Brain Den
b) They’re exactly the same colour. If you place your finger over the spot where the squares meet, you can see they’re the same. Try this impossible paper puzzle if you want a more hands-on optical illusion. You can make one to show your class, then have students make their own as a fun brain teaser to show friends and family.
4. Stroop effect test
The Stroop effect was discovered in the 1930s by John Ridley Stroop. During the test, you’re given a list of colour names, with each word being a different colour than what they describe.
The test involves saying the colour of a word, rather than reading the word itself. Your mind must process the two conflicting pieces of information, which slows down reaction speed and requires careful thought to get through.

Image source: The Crafty Classroom
Benefits of brain teasers for kids
You know your students enjoy them, but did you know there are plenty of additional reasons to make brain teasers a regular activity in the classroom?
A study on the attention spans of six-year-olds found children who were given brain teasers were more attentive than those who were not — showing brain teasers were effective at boosting children’s attention spans.
Brain teasers for kids can also:
- Strengthen problem solving and critical thinking skills
- Encourage lateral thinking and build new perspectives
- Improve cognitive abilities like memory and processing speed
- Inspire teamwork and communication
- Engage students and motivate them to learn
- Provide necessary breaks from traditional class work
How to use brain teasers in the classroom
In addition to their many learning advantages, brain teasers are a great way to break up the day and engage your students. Here are just a few ways you can use brain teasers for kids as a teaching strategy and maximize the benefits in your classroom:
- Engagement-boosting activity before or after lessons
- Bonus questions in assignments and tests
- Optional “free time” activity
- Encourage team building — split students into groups to solve them together
- Supplement lessons — choose brain teasers about the subject you’re teaching
Final thoughts on brain teasers for kids
No matter what subject or skill you want to focus on, a brain teaser is a great addition to traditional teaching methods. Plus, it’s something students will actually be excited to do.
Remember that brain teaser are designed to be fun for kids. it’s not about finding the right answer, but the mental exercise they get from trying to find the solution.
Use any of the brain teasers in this list whenever you need a boost of energy in your classroom. Bonus points if you can stump any adults!
Create or log in to your free teacher account on Prodigy – a game-based learning platform for math that’s easy to use for educators and students alike. Aligned with standards across the English-speaking world, it’s used by more than a million teachers and 90 million students.
44 Powerful Problem Solving Activities for Kids
This post and its photos may contain affiliate links, view our disclosure policy.

Inside: Tons of activities that will help boost kids’ problem-solving skills and make them super critical thinkers!
Table of Contents
Who doesn’t love a little challenge now and then? Especially if it’s for our kiddos!
You see, problem-solving isn’t just for the puzzles and math sheets. It’s the magic stuff that shapes our little ones into big thinkers and doers.
Yep, it’s pretty important!
With the right activities, we aren’t just sharpening kids’ brain muscles; we’re also enhancing their creativity, boosting their confidence and critical thinking skills, and (just maybe) buying ourselves five minutes to sip that coffee while it’s still hot.
Stick around, and let’s dive into 44 simple activities to boost your child’s problem-solving skills while having a blast! 🚀💡

Gain access to our library of free printables!
Because we all want our kids to be happy and healthy — not just for right now, but for the rest of their lives.
Why is it Important to Learn Problem-Solving Strategies?
Importance of problem-solving abilities:
Navigating the maze of life requires many skills; it requires the ability to face challenges, find solutions, and adapt.
This is where problem-solving enters the picture, and here’s why it’s so crucial for our kiddos:
Life is Full of Puzzles: From tying shoes to understanding a new math concept, life constantly presents us with puzzles. Equipping our children with problem-solving skills ensures they can tackle each one confidently.
Boosts Independence: As parents or educators, we won’t always be there to hand-hold. When kids can solve problems on their own, they gain a sense of independence, which is essential for their personal growth.
Develops Resilience: Not every attempt to solve a problem will be successful. But with each try, children learn resilience, understanding that it’s okay to fail and important to try again.
Prepares for Real-World Challenges: The real world isn’t a scripted playground. It’s unpredictable. By honing their problem-solving abilities, we’re preparing kids to face the unforeseen challenges of the world outside.
Enhances Cognitive Growth: Otherwise known as cognitive development. Problem-solving isn’t just about finding solutions. It’s about thinking critically, analyzing situations, and making decisions. This cognitive workout helps in the overall brain development of our children.

Fosters Creativity: There’s often more than one way to solve a problem. Encouraging kids to think outside the box helps them see things from different perspectives and nurtures their creative spirit, letting them see possibilities where others might see roadblocks.
Encourages Adaptability: In the face of challenges, it’s important not just to find solutions but to be adaptable. As the world changes, kids with strong problem-solving skills can change with it, learning and growing along the way.
Builds Confidence : Every problem solved is a victory, a testament to their capabilities. This builds a child’s self-esteem, making them believe in their ability to face and overcome obstacles.
So, while it may seem like just another skill on the list, problem-solving is a cornerstone for a well-rounded, resilient, and successful individual.
4 Simple Problem-Solving Steps We Should Know at a Young Age
Problem-solving steps can be thought of as the building blocks for tackling challenges.
They’re like a set of instructions that guide us on our journey to finding different solutions. These steps provide a roadmap for kids, helping them break down big problems into smaller, more manageable pieces.
By following these steps, children can learn how to think critically, make smart decisions, and even discover their own creative problem-solving superpowers.
- First, we need to understand the problem, just like examining the pieces before we start building.
- Next, we brainstorm – this is where we think of different solutions, like trying out various block combinations. Then comes the important part – evaluating the options. We must determine the best solution , just like choosing the right blocks for our structure.
- After that, it’s time to put the plan into action, just like assembling the blocks to create something amazing.
- Finally, we review and see if our solution works, making adjustments if needed.

These problem-solving steps are like our trusty toolkit, helping us build our way to success with creativity and ingenuity.
Whether it’s figuring out a math puzzle, resolving a conflict with a friend, or coming up with a new game, these problem-solving steps will be a guide to helping kids take their next steps.

Featured resource
HeartSmart Social Emotional Curriculum
If you want a program that guides you on how to teach problem-solving along with other essential skills like self-regulation, respect, teamwork, conflict resolution, and more, check this out!
Best Problem-Solving Activities for Kids
In this guide, we have a cool mix of fun problem-solving activities. There are activities for inside, outside, playing in groups, and even on the computer! So take deep breaths, and let’s get to it!
44 Problem-Solving Activities for Kids
Problem-solving games for kids:, card games:.
These are more than just fun; they are brain boosters. In Go Fish , the hunt for matching cards sharpens memory. While in the classic game Uno , it’s all about plotting the right move to take the lead.

The Memory Game:
This game isn’t just about remembering; it’s about strategizing. Matching pairs means we’re not just recalling but also paying close attention. This boosts concentration, focus, and, of course, memory – essential skills for everyday challenges!
Try this animal matching memory game.
Classic Board Games:
Whether it’s Chess , where every move counts, or Monopoly , where every decision can make or break your game, these games teach foresight and strategy.

Maze Games :
Navigating a maze isn’t just about reaching the end; it’s about strategizing the route. These games enhance our ability to plan and foresee, invaluable skills in real-life situations.
Brain-Teasing Sudoku :
Sudoku isn’t merely filling in numbers; it’s about using logic to deduce the correct sequence.
Tangram Puzzles:
These aren’t your average puzzles. With Tangram, you shape a story, crafting images using geometric pieces.
Chess & Strategy-Based Games:
Think of these as mental workouts. Here, every step is a calculated decision, honing your ability to think multiple steps ahead.
For more fun:
- 20 Best Games for 4-Year-Olds
- 15 Board Games Every 9-Year-Old Will Love
Indoor Problem-Solving Activities for Kids
Complete simple tasks:.
Simple tasks are little jobs that you can do to practice problem-solving.
- Matching Socks: Sort through a pile of laundry to pair up matching socks.
- Grocery List Planning: Help create a list for the week’s meals, considering everyone’s preferences.
- Toy Organization: Sort toys into designated bins by type, size, or color.
- Packing Their School Bag: Ensure they have all the necessary items for the next school day.
- Setting the Table: Consider where each plate, fork, and glass should go.
Ask Open-Ended Questions:
Open-ended questions are special questions that don’t have just one answer. They make you think! For instance, instead of asking, “What color is the sky?” you might ask, “Why do you think the sky changes colors?”
Puzzle Games:
Try simple puzzles with fewer pieces for younger kids and more complex puzzles with more pieces for older kids! You figure out how to fit the pieces together, which helps your brain get stronger!
Puzzle games are also great for hand-eye coordination!
Pattern Recognition:
This is all about finding the special patterns in things. Imagine a puzzle with colors or shapes. You have to figure out the pattern to solve it.
Dress-Up and Role-Play:
When you dress up and pretend to be someone else, it’s like stepping into their shoes. You have to think about how they would act and problem-solve what they would say if you were them.

Shape Sorters:
Shape sorters are super fun for young kids. You have to match each shape to the right hole. It’s like a puzzle for shapes! This helps you learn about different shapes and how they fit together.
Building Challenges:
Use Wooden blocks or legos and give kids a theme or structure to replicate. Great for all age groups!

Cooking or Baking:
Cooking and baking are like yummy science experiments! You follow recipes, mix ingredients, and even get to taste your creations. You must figure out how to follow and “solve” the recipe so that your creation tastes delicious!
“What If?” Scenarios:
Present hypothetical situations (e.g., “What if you were invisible for a day?”) and discuss possible solutions or actions.
Homemade Science Experiments:
Homemade science experiments are like being a scientist in your own lab! You get to try out cool experiments and discover how things work.
Quick Experiment example:
Make Dancing Raisins:
- Clear soda (like Sprite or 7-Up)
- A clear glass
- Fill the glass with the soda.
- Drop a few raisins into the glass.
Result: The raisins will initially sink, then start “dancing” up and down due to the carbon dioxide bubbles attaching and detaching from them.
Coding Activities:
Coding is like giving a computer a set of clues to follow. Think of it as telling a story where the computer plays the main character, and your instructions guide its every move. It’s our way of communicating with machines to make them do amazing tasks!
Crossword Puzzles:
Crossword puzzles are fun little word challenges. You must fill in the blanks with the right words and use your smarts to solve tricky clues!
Complex Problems like Brain Teasers:
Brain teasers are like mental gymnastics, making you stretch and flex your thinking muscles. What’s fun about them? There’s often more than one way to reach an answer, so your imagination and logic both get a workout!
Goal Setting Activities:
Goal setting is like making a special plan for what you want to achieve.
Think of goal setting as charting out your very own treasure map, with no wrong answers!
By laying out what you aim to achieve, you’re setting the course toward your treasure: success!
Goals, be they immediate or down the road, act like our personal compasses. They keep you on track and motivated. And every time you hit a goal? That’s you cracking a code and unlocking a new achievement in your adventure!

Setting SMART Goals
This engaging kit focuses on teaching essential skills for setting and achieving smart goals, just like breaking down that LEGO set into manageable sections. We help kids understand the importance of clear objectives, staying motivated, overcoming obstacles, embracing adaptability and more.
Math Challenges:
Think of math challenges as your brain’s personal gym session. These aren’t just any puzzles; they’re crafted to push those thinking caps to the limit.
Debates (Best for older children):
Debates are friendly arguments where you defend your ideas with strong reasons. They’re excellent for problem-solving and for our social skills because they teach us how to think critically and consider different viewpoints. By defending our thoughts in a debate, we learn how to express ourselves clearly, listen to others, and find strong arguments to support our ideas!
Use Worksheets (Teach the Size of the Problem Concepts)
Teach concepts like the size of the problem to help kids determine if their reactions to problems are appropriate and what suitable solutions might be. Use fun visuals and problem-solving worksheets.
You can get this worksheet and more in our HeartSmart curriculum.

STEM Challenges:
STEM challenges are games that use science, technology, engineering, and math to solve problems. They’re awesome for problem-solving because they let us be like inventors and builders. Kids can engage in creative play and design and create things, like bridges or machines, using our smarts and creativity.

Outdoor Problem-Solving Activities for Kids
Nature scavenger hunt or treasure hunt: .
Create a list of natural items for kids to find. For added difficulty, give riddles as clues.
We have some awesome free Scavenger Hunt Bundles you can snag!

Free Scavenger Hunt Bundle
Download this set now, which includes four unique scavenger hunt games
Outdoor Obstacle Course:
Use items like ropes, cones, and hula hoops to design a course that requires navigation.
Garden Planning & Planting :
Design a garden patch, deciding what to plant based on sunlight and spacing needs.
Map & Compass Orienteering:
Teach kids to use a map and compass, then set waypoints for them to find.
Water Relay Challenges:
Carry water from one bucket to another using a sponge or cup, navigating hurdles.

Campsite Setup Simulation Challenge:
Set up a mock campsite considering factors like wind direction, incline, and resource proximity.
Nature Art & Patterns:
Using twigs, leaves, stones, and more, create mosaic patterns or depictions.
Group Problem-Solving Activities for Kids
Tower of spaghetti:.
Using only spaghetti and marshmallows, groups compete to build the tallest stable tower.
Egg Drop Challenge:
Groups are provided with a set of materials (e.g., straws, tape, cotton) to create a protective casing for an egg, which is then dropped from a height.
Silent Line-Up:
Without speaking, kids must line up according to their birthdays or another criterion.
Group Story Time:
One child starts a story with a sentence or two, and each subsequent child adds on, weaving in unexpected twists and turns.

The Human Knot:
Kids stand in a circle, reach across, and grasp two different hands. The challenge is to untangle the knot without releasing hands.
Escape Room:
Everyone is ‘locked’ in a themed room and has to solve a series of clues and puzzles to ‘escape’ within a set time. It’s fantastic for problem-solving because it challenges critical thinking, teamwork, and creativity. Everyone must work together, think outside the box, and use their wits to solve the puzzles and complete the mission before time runs out!
Role-Playing Social Situations:
Role-playing helps you practice how to react and solve problems in different situations. Present the group with a fictional but realistic scenario (e.g., stranded on an island) and brainstorm and act out solutions.
By pretending to be in different roles, you can figure out the best ways to communicate, understand others, and find solutions to problems in a safe and fun way!
Blindfolded Obstacle Course:
In pairs, one blindfolded child is guided through an obstacle course by their partner using only verbal instructions.
Online and App-Based Problem Solving Activities
When tech meets intellect, the digital realm becomes a treasure trove of problem-solving wonder!
Educational Apps:
Best Apps by Age:
- Younger Kids : Dive into the mathematical world with “Moose Math” or kick-start programming concepts playfully with “Bee-Bot.”
- Older Kids: Amp up programming skills with “Cargo-Bot” or embark on a critical thinking journey with “Rush: A Disney Pixar Adventure.”

Online Escape Rooms:
Just like physical escape rooms, but from the comfort of your home! They’re digital adventures, demanding clues to be solved to advance to the next level.
Check out these 10 Family Friendly Online Escape rooms here! I’m especially looking forward to Hogwarts Harry Potter Escape Room .
Virtual Logic Puzzles:
Websites that present logic problems and puzzles, leveling up in complexity as kids solve them.
Top Picks: “Conceptis Puzzles,” “Math Playground Logic Games.”
Benefits: Perfect for sharpening deductive reasoning and pattern recognition.
Interactive E-Books:
These are not your everyday e-books. They demand interaction, choices, and decision-making to progress the story.
Suggestions: “This Book is Perfect” or I love this big list of the best interactive books for kids.
Benefits: Enhance comprehension, decision-making, and experience of how choices shape outcomes.
Online Strategy Games:
These games demand planning, strategic thinking, and foresight.
Check out: “Fish Sticks Strategy Game”
Benefits: Apart from being immensely fun, they teach patience, strategy formulation, and long-term planning.
10 Examples of Problem-Solving Skills Young Children Should Have
Each of these skills not only helps kids tackle problems effectively but also equips them with abilities they’ll use throughout their lives.

- Critical Thinking: Encourage young thinkers to examine situations, ask questions, and view things from different angles before reaching a conclusion.
- Decision-Making Skills: Help children practice making choices by offering them options and discussing the potential outcomes of each decision.
- Creative Thinking: Cultivate creativity by providing opportunities for imaginative play, artistic expression, and activities that encourage thinking outside the box.
- Communication Skills: Show children how to express their thoughts, feelings , and ideas clearly and effectively – a vital skill for problem-solving in social situations.
- Teamwork and Collaboration: Foster the spirit of cooperation by encouraging children to work together on group activities or projects, which helps develop problem-solving skills as a team.
- Resourcefulness: Challenge children to find alternative solutions using the available resources rather than relying solely on adult guidance.
- Flexibility and Adaptability: Teach children how to adapt to changes and unexpected situations, which is crucial for effective problem-solving in real-world scenarios.
- Persistence: Staying determined, even when faced with challenges, and continuing to try until a solution is found.
- Self-reflection: Recognizing one’s own mistakes or misunderstandings in a situation and learning from them for future problem-solving.
- Active Listening: Paying close attention to details when others speak, helping them understand problems more fully and respond effectively.
Must read post:
How to Help Kids with Inflexible Thinking THRIVE
Tips for Parents and Educators: Nurturing Problem-Solving in Kids
When it comes to fostering problem-solving skills in children, both parents and educators play pivotal roles. It’s less about giving the right answers and more about asking the right questions.
Encourage Curiosity. Let kids explore questions like, “What do you think would happen if…?” or “How would you do it differently next time?”.
Embracing mistakes as learning opportunities can be a game-changer.
Set Up Scenarios. Create environments or situations where kids can think and act independently. Whether it’s setting up a puzzle station at home or a role-play corner in the classroom, these controlled scenarios can stimulate their problem-solving faculties. Remember, it’s okay for them to struggle a bit. It’s through overcoming challenges that real learning occurs.
Lastly, Be a Guide, Not a Director. Instead of directing them step-by-step, guide them by providing hints or asking probing questions. This helps them develop the ability to analyze situations and think critically. As they grow, they’ll be more equipped to approach challenges with confidence and creativity.
So, whether you’re a parent or an educator, remember that each day presents countless opportunities to bolster these invaluable skills. Embrace them!
Final Thoughts: Problem Solving Activities for Kids
Being a pro at problem-solving helps us face all types of curveballs life throws at us.
From untangling math puzzles to making big decisions, this skill is our trusty sidekick. And when life changes? No sweat! We can adapt and shine.
In short, mastering problem-solving helps us face challenges, make wise choices, and truly succeed in whatever we tackle!
I hope you enjoyed these problem-solving activities for kids. Tell me, what one is your favorite?

Because we all want our kids to be happy and healthy — not just for right now, but for the rest of their lives.
Tina Williamson is the published author of the growth mindset activity journal for kids - “ Amazing Me ” and the writer and founder here at Mindfulmazing. Passionate about raising mindful, resilient, and compassionate kids we are committed to sharing calming strategies, positive parenting tips, and growth mindset resources. Our resources are now used in over 10,000 homes, schools and counseling offices! Visit the shop here.
Resources You’ll Love
Our shop is filled with printable resources to help you calm the chaos and assist your amazing little humans to believe in the amazing little humans they are!

Calm Down Corner Bundle

Mindful Minute

Feelings Fun Kit

Social Story Bundle

Spring SEL Resources
Now available on tpt.
Splash into spring with these spring-themed social-emotional learning activities
Connect with other parents + teachers
Love this article? Make sure to connect with me on your favorite social platform below, and leave a comment so we can chat!
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Similar Posts

Free Printable Winter Coloring Bookmarks

The BEST Kindness Activities for Elementary Kids (Engaging + Fun)

11 Unique Ways To Encourage Kids to Dream BIG PLUS 20 Dream Big Quotes!

The 10 Best Fidget Toys for School and Home

25 Free Printable Halloween Bingo Cards for Kids

13 Things Happy People Don’t Do
We are passionate about raising mindful, resilient, happy kids.
Our resources are now being used in thousands of homes and classrooms around the world! Welcome to the community.
$$ Bundle & Save $$
Your One-Stop Shop for All Your Kids’ Social-Emotional Needs!

Mega Emotions Super Bundle

Calming Corner Bundle

Growth Mindset Bestsellers Bundle

HeartSmart SEL Program

Amazing Me Journal now available!

Free printables library!
Subscribe for the latest updates plus direct access to our library of free printables! Because we all want our kids to be happy and healthy — not just for right now, but for the rest of their lives.
Shop the store
- Social Emotional Learning
- Coping Skills + Feelings
- Growth Mindset
- Mindfulness
Read the blog
- Selfcare + Mindfulness
- Feelings + Coping Skills
- Kids Games + Activities
- Privacy Policy
Mindfulmazing is a participant in the Amazon Services LLC Associates program, where we earn from qualifying purchases.
- Open access
- Published: 03 January 2020
Students’ problem-solving strategies in qualitative physics questions in a simulation-based formative assessment
- Mihwa Park ORCID: orcid.org/0000-0002-9549-9515 1
Disciplinary and Interdisciplinary Science Education Research volume 2 , Article number: 1 ( 2020 ) Cite this article
9676 Accesses
1 Citations
3 Altmetric
Metrics details
Previous studies on quantitative physics problem solving have been concerned with students’ using equations simply as a numerical computational tool. The current study started from a research question: “How do students solve conceptual physics questions in simulation-based formative assessments?” In the study, three first-year college students’ interview data were analyzed to characterize their problem-solving strategies in qualitative physics questions. Prior to the interview, the participating students completed four formative assessment tasks in physics integrating computer simulations and questions. The formative assessment questions were either constructed-response or two-tiered questions related to the simulations. When interviewing students, they were given two or three questions from each task and asked to think aloud about the questions. The findings showed that students still used equations to answer the qualitative questions, but the ways of using equations differed between students. The study found that when students were able to connect variables to a physical process and to interpret relationships among variables in an equation, equations were used as explanatory or conceptual understanding tools, not just as computational tools.
Introduction
Since the new U.S. science standards, Next Generation Science Standards (NGSS), were released (NGSS Lead States, 2013 ), science assessments have been moving towards revealing students’ reasoning and their ability to apply core scientific ideas in solving problems (National Research Council, 2014 ; Pellegrino, 2013 ). Underwood, Posey, Herrington, Carmel, and Cooper ( 2018 ) suggested types of questions aligned with three-dimensional learning in A Framework for K-12 Science Education (National Research Council, 2012 ). These questions include constructed-response (CR) questions and two-tiered questions. Underwood et al. ( 2018 ) also argued that questions should address core and cross-cutting ideas and ask students to consider how scientific phenomena occur so that they can construct explanations and engage in argumentation. The underlying assumption of this approach could be that qualitative explanation questions (i.e., questions that ask students to explain qualitatively) reveal students’ reasoning and understanding of core scientific concepts better than do traditional multiple-choice and simple-calculation questions. Numerous studies in physics education have examined students’ problem-solving strategies, including studies that have identified differences in the problem-solving strategies employed by experts and novices. Experts tend to start by using general scientific principles to analyze problems conceptually, while novices tend to start by selecting equations and plugging in numbers (Larkin, McDermott, Simon, & Simon, 1980 ; Maloney, 1994 ; Simon & Simon, 1978 ). Thus, giving students opportunities to reason qualitatively about problems could help them to think like experts (van Heuvelen, 1991 ).
Another way to enhance students’ conceptual understanding of scientific ideas could be using computer simulations, because computer simulations help students visualize scientific phenomena that cannot be easily and accurately observed in real life. Many empirical studies support integrating computer simulations into assessments in order to promote students’ engagement in exploring scientific phenomena (de Jong & van Joolingen, 1998 ) and their conceptual understanding (Rutten, van Joolingen, & van der Veen, 2012 ; Trundle & Bell, 2010 ). For example, Quellmalz, Timms, Silberglitt, and Buckley ( 2012 ) developed a simulation-based science assessment, and found that the assessment was effective to reveal students’ knowledge and to find evidence of students’ reasoning. In the current study, computer simulations and conceptual qualitative questions were incorporated as integral parts of formative assessment to reveal students’ problem-solving strategies in answering qualitative physics questions. Therefore, the current study investigated students’ problem-solving strategies in physics, which offered them opportunities to elicit their reasoning by qualitatively explaining what would happen and why it would happen about a given physical situation.
Students’ strategies to solving physics problems
Early research on physics problem solving identified differences between experts and novices in their problem-solving strategies. For example, experts’ knowledge is organized into structures; thus, they demonstrate the effective use of sophisticated strategies to solve problems (Gick, 1986 ). Conversely, novices tend to describe physics problems at best in terms of equations, and spontaneously use superficial analogies (Gick, 1986 ). Experts also effectively use the problem decomposition strategy: breaking down a problem into subproblems, then solving each subproblem and combining them to form the final solution (Dhillon, 1998 ). They also apply relevant principle and laws to solve problems (Chi, Feltovich, & Glaser, 1981 ; Dhillon, 1998 ). By contrast, novices start with selecting equations and cue into surface features (Chi et al., 1981 ). A common finding from studies on differences between experts and novices in problem solving (e.g., Chi et al., 1981 ; Dhillon, 1998 ; Gick, 1986 ; Larkin et al., 1980 ) is that experts demonstrate their expertise in conceptual analysis of the problems using scientific principles and laws, then translate the problem into relevant mathematical equations, while novices jump to mathematical manipulations without the prior process of conceptual analysis (Larkin et al., 1980 ).
Huffman ( 1997 ) incorporated the results of studies on the differences in problem solving between experts and novices to formulate explicit problem-solving procedures for students. The procedures include five steps: (a) performing a qualitative analysis of the problem situation; (b) translating the conceptual analysis into a simplified physics description; (c) translating the physics description into specific mathematical equations to plan the solution; (d) combining the equations according to the plan; and (e) evaluating the solution to ensure it is reasonable and complete (Huffman, 1997 ). In essence, the procedure is designed to ensure students will conceptually reason about the problem first, using relevant scientific principles and laws, before jumping to selecting mathematical equations.
It is possible that students’ problem-solving strategies are influenced by problem representations (verbal, mathematical, graphical, etc.). Kohl and Finkelstein ( 2006 ) investigated how problem representations and student performance were related, and found that student strategies to solve physics problems often varied with different representations. They also found that not only problem representations but a number of other things, including prior knowledge and experience in solving problems from their previous classes, also influenced students’ performance, especially in the case of low-performing students. When asking students not to calculate a science question but to explain it conceptually, a study found that they still used equations or numerical values to solve the problems, indicating that they translated a conceptual qualitative question into a quantitative one (De Cock, 2012 ). Although students may succeed in calculating values in physics problems, it doesn’t always mean that they have good conceptual understanding of the questions (McDermott, 1991 ).
While earlier studies have been concerned with students’ using equations without conceptual understanding when solving problems, mathematical modeling plays a critical role in the epistemology in physics (Redish, 2017 ). Redish emphasized the importance of connecting physical meaning to mathematical representation when solving problems, because in physics, mathematical equations are linked to physical systems, and an equation contains packed conceptual knowledge. Thus, in physics, equations are not only computational tools but also symbolic representations of logical reasoning (Redish, 2005 , 2017 ). As such, students are expected to incorporate mathematical equations into their intuition of the physical world to conceptualize the physical system (Redish & Smith, 2008 ). In a study of students’ quantitative problem solving, Kuo, Hull, Gupta, and Elby ( 2012 ) pointed out the importance of connecting mathematical symbols to conceptual reasoning. Their study was conducted based on an assumption that equations should be blended with conceptual meaning in physics, which turned the attention of researchers on problem solving from how students select equations to how they use the equations. Kuo et al. ( 2012 ) concluded that blending of mathematical operations with conceptual reasoning constitutes good problem solving; thus, this blended process should be a part of problem-solving expertise in physics.
Using computer simulations as an assessment tool
Given that visualization plays a central role in the conceptualization process of physics (Kozhevnikov, Motes, & Hegarty, 2007 ), previous studies have used computer simulations to visualize scientific phenomena, especially those that cannot be accurately observed in real life, and reported their positive effect on students’ learning outcomes (Ardac & Akaygun, 2004 ; Dori & Hameiri, 2003 ). Using computer simulation to facilitate student learning in science was found to be especially effective on student performance, motivation (Rutten et al., 2012 ), and conceptual change (Smetana & Bell, 2012 ).
Computer simulation can be used not only as an instructional tool but also as an assessment tool. For example, Park, Liu, and Waight ( 2017 ) developed computer simulations for U.S. high school chemistry classes to help students conceptualize scientific phenomena, and then integrated the simulations into formative assessments with questions related to the simulations. Quellmalz et al. ( 2012 ) and Srisawasdi and Panjaburee ( 2015 ) also embedded computer simulations into formative assessments for use in science classrooms, and demonstrated positive effects on students’ performance compared to students who experienced only traditional assessments (e.g., paper-and-pencil tests). While many empirical studies have been done to investigate problem-solving strategies of students, there is a lack in studies on students’ strategies to solve physics problems when computer simulations were used as a visual representation and conceptual explanation questions were asked to reveal the students’ reasoning. This study addresses the gap in the body of literature by investigating students’ strategies in solving conceptual explanation questions in a simulation-based formative assessment.
Research procedure and participants
In the study, computer simulations and formative assessment questions were integrated into a web-based formative assessment system for online administration, which allowed students to use it at their convenience (Park, 2019 ). The formative assessment questions were either CR or two-tiered questions related to the simulations. A two-tiered question consists of a simple multiple-choice (MC) question and a justification question for which students write a justification for their answer to the MC question. This format of question was suggested to diagnose possible misconceptions held by students (Treagust, 1985 ) and to provide information about students’ reasoning behind their selected responses (Gurel, Eryılmaz, & McDermott, 2015 ). Computer simulations were selected from the Physics Education Technology (PhET) project ( https://phet.colorado.edu/ ) and embedded into the formative assessment system. The assessments targeted students’ conceptual understanding in physics, thus they were not asked to calculate any values or to demonstrate their mathematical competence (Park, 2019 ). Specifically, the questions presented a scientific situation and asked students to predict what would happen; then the assessment system asked students to run a simulation, posing questions asking for explanation of the phenomena and comparison between their prior ideas and the observed phenomena. Figure 1 presents example questions and simulation for the energy conservation task. After answering the questions, students ran the simulation and responded to questions asking how the skater’s highest speed changed and why they think it happened using evidence found in the simulation.
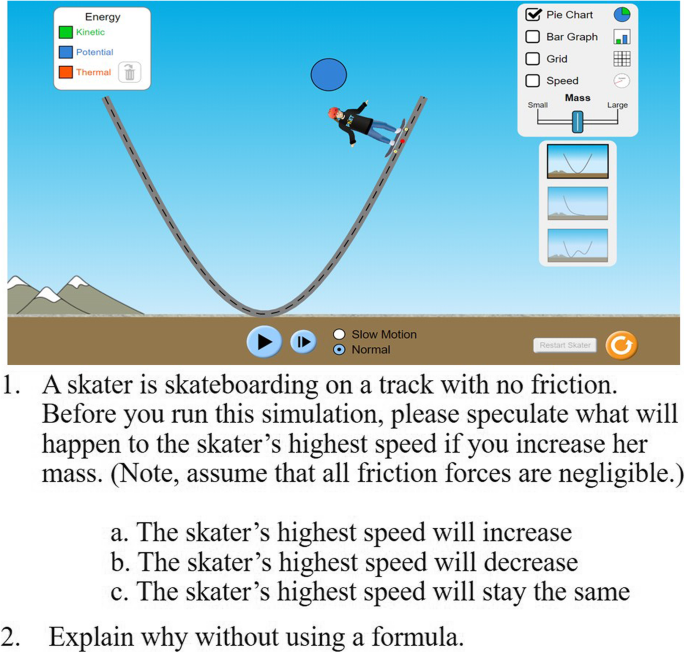
Energy conservation task example questions
Initially, first-year college students were recruited from a calculus-based, introductory level physics course at a large, public university in the United States; no particular demographic was targeted during recruitment. The physics course was offered to students majoring in subjects related to science or engineering and covered mechanics, including kinematics and conservation of energy, so simulations were selected to align with the course content. After selecting simulations from the PhET project, related formative assessment questions were created. As previously mentioned, the questions first asked students to predict what would happen in a given situation. In this case, verbal (expressed in writing) and pictorial representations (including images, diagrams, or graphs) describing the situation were shown on the screen (Fig. 1 ). Next, after the students answered the questions, the simulations were enabled for the students to run, and they were asked to explain the results. In total, four formative assessment tasks were developed and implemented online, and each task contained from 14 to 17 questions. Topics for the four tasks were (1) motion in two dimensions, (2) the laws of motion, (3) motion in one dimension and friction, and (4) conservation of energy. Descriptions of the four tasks are presented below.
Task 1: Students explore what factors will affect an object’s projectile motion when firing a cannon.
Task 2: Students create an applied force such as pulling against or pushing an object and observe how it makes the object move.
Task 3: Students explore the forces at work when a person tries to push a filing cabinet on a frictionless or frictional surface.
Task 4: Students explore a skater’s motion on different shapes of tracks and explore the relationship between the kinetic energy and thermal energy of the skater.
After the participating students completed the online implementations of the four tasks, an interview invitation email was sent to the students who had completed all four tasks, did not skip any questions, and did not answer a question with an off-task response, but included responses that needed further clarification. Initially, we invited six students to clarify and elaborate on their responses so we could better understand what they were thinking. When scoring students’ written responses, some responses needed further clarification. For example, students mentioned that in projectile motion, “mass is not relative to time”; “the greater angle will create a larger x component of velocity in a projectile motion”; or “an object’s speed is broken up evenly resulting in more air time”. In case of the energy conservation task, the responses needing more clarification were “the speed did not change because speed does not depend on mass” or “because a skater’s total energy increases with increase in mass, her speed does not change”. Those responses were not clear to the author. Thus, the author decided to invite them to clarify their responses. During the interviews, the students’ verbal responses inspired the author to explore differences in their problem-solving strategies to answer conceptual physics questions. Three students especially, Alex, Christopher, and Blake (all pseudonyms), demonstrated noticeable differences in their problem-solving strategies; therefore, they are the focus of the analysis in the current study.
Interview context and protocols
Semi-structured interviews were conducted to investigate students’ reasoning when responding to conceptual physics questions. To this end, the students were given two or three questions from each task and asked to think aloud about the questions. After they verbally answered each question, they were given their original written responses to see if their answers had changed, and if so, to explain why. When students used mathematical equations or graphs in their explanations, they were asked to explain why they used those particular strategies and how the strategies helped them to answer the questions. Some example interview questions were; “Please read the question. Will you tell me your answer for the question?”, “How did you answer this question?”, “Could you clarify what this means?”, and “What did you mean by (specific terms that students used)?” Students were interviewed individually by two interviewers. The interviews, which took place in an interview room located at their university, each lasted an hour.
While the interviews were going on, the author wrote memos about the students’ strategies to answer the given questions and their misconceptions about science. Interviews were audio recorded and transcribed verbatim. The transcripts were initially analyzed to prepare and organize data into emergent themes. In this process, the memos were also used. As a result, three initial themes were developed: 1) students’ strategies to answer problems, 2) effects of the assessment on students’ learning, and 3) students’ misconceptions about science. In the study, the first theme—strategies to answer problems—was made a focus in the next level of analysis, as the students demonstrated noticeable differences in using equations to answer conceptual physics problems. After choosing the theme as a main focus, the author analyzed it by open coding the relevant parts of the transcripts of the individual student interviews (interviews about Tasks 1–3) to formulate possible characterizations of students’ problem-solving strategies, especially when they were using equations. The author constantly compared the characterizations to integrate and refine them (Strauss & Corbin, 1998 ). After that, the rest of each individual student interview transcript (interviews about Task 4) was analyzed, using the same categories to confirm the findings. Students’ drawings (i.e., graphs) used to explain their reasoning were also considered as a data source (Creswell, 2016 ). Once characterizations in students’ use of equations in qualitative physics question were identified and compared across cases, the analysis results were given to a physics education researcher to seek an external check (Creswell & Miller, 2000 ).
Previous studies on expert and novice problem-solving strategies were reflected in the design of the formative assessment questions. Specifically, it was hypothesized that conceptual explanation questions would help students think about the questions more conceptually, so that they would start to solve them using scientific concepts and laws. Therefore, short written questions in the tasks asked the students to explain or to justify their answers without using a formula. Nonetheless, when we were interviewing students, we found that they preferred to use equations and mathematical concepts when explaining physical situations. Although the three participating students commonly used equations or mathematical concepts in their explanations, how they used the equations or mathematical concepts differed. Detailed findings are presented below in three subsections representing patterns in problem-solving strategies. Formative assessment Tasks 1, 2, and 3 were designed to address the topic of Motion and Force, while Task 4 covered the topic of Energy Conservation. We analyzed interview data by these two topics. Note that two terms—formula and equation—were not differentiated in the analysis of data; instead, they were considered synonyms.
Alex’s case – using equations as a conceptual understanding tool
Motion and force.
When interviewing Alex, we asked him what would happen if a person pushed a box, then let it go (Task 2). He said, “If it is frictionless, the box will move forever with a constant velocity, and if friction exists, the speed will decrease and eventually the box will stop.” This answer was very similar to his original written response. Next, we asked what would happen to the box’s motion after another box was placed on top of it. Alex said, “I don’t know how to explain this without a formula.” Because the original questions had asked students not to use formulas, he assumed that he was not allowed to use one in this explanation, and obviously he was struggling to explain without it. We told him to use formulas whenever he wanted, and he quickly jumped into using one.
Alex: Resultant force equals mass times acceleration, so if you have a bigger mass. Uh, if the resultant force was 50N, that’s the force you applied, and then you had 10N in friction, for example, then the resultant force is 40. You had, if you had 20kg, the acceleration would be 2. If you had 50kg, the acceleration would be 4 over 5, which is 0.8, which is less than 2. So, the more mass you have the smaller the acceleration is going to be, as a result of the resultant force equals ma equation.
In this statement, Alex explained what would happen in the given situation with algebraic solutions, using F = ma equation, and concluded that mass would affect the object’s acceleration, as he demonstrated. He further described how the eq. ( F = ma ) helped him to explain the given physical situation.
Alex: If you use the formula, then it makes it much easier, because in real life, you never see something moving without friction, so it just clouds your judgment a bit.
In this statement, Alex described the role of equation for him as a conceptual understanding tool, especially in an ideal situation that is not observable in real life. This was something the author had not initially expected from the students during their interviews. When we asked Alex the next question in Task 3, his answer further supported the finding that equations helped him understand physical situations. Specifically, we asked, in a situation when a person was pushing a cabinet on either a frictionless or a frictional surface, what would happen to the cabinet’s motion and why.
Alex: The normal force is, the gravitational force cancels out the y , so the only thing acting on the—in the x -direction, which is the direction being pushed is the applied force, so as small of a force you apply to it, it’s still going to move it because there’s nothing opposing it…if there was friction, I agree that it won’t move. Because the friction, the friction is the coefficient of friction times the normal force, so, since it’s a really big object, it’s going to have a significant amount of friction acting on it.
In his verbal explanation, Alex used a mathematical concept and an equation to explain the given phenomenon, using the vector concept for two components of force and a mathematical equation for frictional force. Obviously, he found equations useful to make sense of physical situations and to explain his understanding to others. Notably, he started his answer by referring to the formula for kinetic friction force and used the formula as a tool to explain why the cabinet wouldn’t move on a frictional surface. His explanation again demonstrated that equations and mathematical concepts were useful to understanding and interpreting scientific phenomena, and not only as a simple computational tool, at least for Alex.
Conservation of energy
Task 4 was designed to investigate students’ conceptions of mechanical energy and its conservation. We asked Alex, when a skater is skateboarding on a track with no friction, what would happen to the skater’s highest speed as the skater’s mass increases? He again asked us if he could use equations. We confirmed that he was allowed to use equations anytime he wanted. Then he immediately started writing equations on the board (see Fig. 2 ). While he was writing, he explained each variable involved in the equations:
Alex: So, her initial, so, um, at the start, her initial energy is mgh + ½ mv 0 2 and then her final [writing on board] mgh + ½ mv f 2 , but the smaller thing to do is that they [mass] all cancel out, so the mass is really, it doesn’t play a role in the height or the velocity. And then, if you wanted to see how the conversion of energy works, if you were initially starting at the maximum height, whatever that is, you could do ½ mv 2 . At the start, her velocity is 0, at the top, so this cancels out, if we’re analyzing it at the bottom, which is her max speed, then this [ h ] is 0, and then you just do gh = v 2 . To find her velocity. Just looking at this, there’s no mass in this, so it doesn’t matter [the skater’s speed]. When you actually work it out, all the masses cancel out, so it doesn’t matter what the mass is, in reality, when you actually calculate it.
This response was different than his original written response to the same question: “If the skater has a larger mass, she will in turn have a larger gravitational potential energy since GPE [gravitational potential energy] has a direct relationship to mass. As a result and according to the principles of conservation of energy, the KE [kinetic energy] will be greater and thus the velocity will be greater.” In this original written response, Alex included a typical misconception that heavier objects fall faster (e.g., Gunstone, Champagne, & Klopfer, 1981 ; Lazonder & Ehrenhard, 2014 ); “If the skater has a larger mass…thus the velocity will be greater” (in his written response). This was the only case of a misconception found in Alex’s written responses. Notably, when he was using equations, he deduced that “it doesn’t matter what the mass is, in reality, when you actually calculate it” from his step-by-step problem-solving procedure using algebraic solutions. Although he solved the problem using equations through algebraic computation, he explained how the object’s velocity and height would change as the object moved: “At the start, her velocity is 0, at the top, so this cancels out, if we’re analyzing it at the bottom, which is her max speed, then this [ h ] is 0, and then you just do gh = v 2 .” Then he connected conceptual meaning to the equation: “Just looking at this, there’s no mass in this, so it doesn’t matter [the skater’s speed].” This confirmed that for Alex, equations were the first tool to make sense of physical situation. In other words, when he applied an equation to a physical situation, he considered variables related to specific situations, then connected conceptual meaning to the variables, which indicated that for him, equations played a role in analyzing and understanding physical situation.
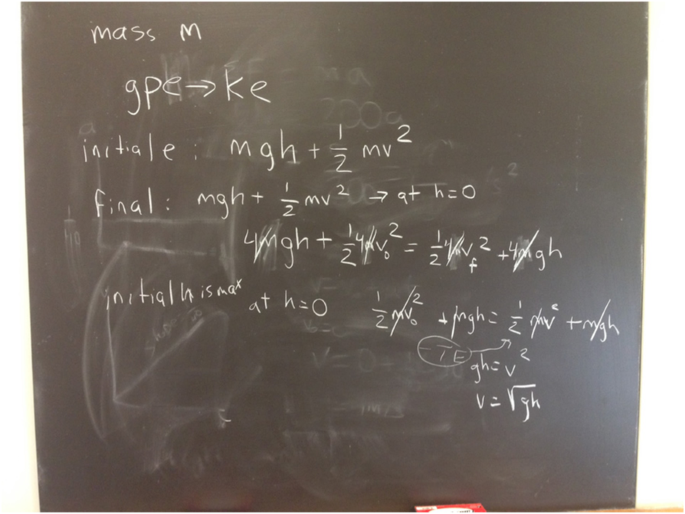
Alex’s explanation
Christopher’s case – using equations as an explanatory tool
We asked Christopher a question—which tank shell would go farther when the initial angles for two tank shells were different (Task 1). In his original written response, he mentioned that “tank A (initial angle: 45 degree)’s speed is broken up more evenly and this results in more air time which leads to more distance covered in the x axis as well.” This answer was similar to Christopher’s thinking-aloud response, so we asked him to elaborate on what he meant by “speed is broken up more evenly.” Below is his response.
Christopher: Because the velocity is a vector quantity, the speed is still the same, but the velocity, the x and y axis are going to be more evenly split [for Tank A, with a 45-degree initial angle], whereas for Tank B [10-degree initial angle] it would have been almost all in the x axis and close to none in the y , so it wouldn’t get that much air time because the force of gravity still stays the same.
As seen in his response, Christopher deduced his answer from a mathematical concept (vector in this case) explaining why the 45-degree shell would have a greater horizontal range than the 10-degree shell one. His problem-solving strategy in the next questions (questions from Tasks 2 and 3) further confirmed that he used mathematical concepts and equations to explain physical situations. For example, when asked to compare two situations from Task 2—a person pushes a box and lets it go, and after placing another box on top of that, a person pushes both boxes and lets them go—Christopher immediately used F = ma and explained the situation.
Christopher: The velocity and the speed will be decreased because, when applying force, force is mass times acceleration. So, if it would be the same exact force with a higher mass, then the acceleration would have to go down significantly in order to keep the same number [force]. So, because of this, it wouldn’t speed up as much, so it would have a lower velocity after the force was applied [compared to the previous situation]. While you are pushing, the acceleration is constant. And if they let it go, there is no acceleration. Then speed will stay the same.
In his statement, he referred to F = ma , and explained why the box’s acceleration would be smaller when its mass increased using algebraic solutions, which is similar to Alex’s case. The difference is that Christopher’s explanation contained an interpretation of the relationship among velocity, acceleration, and applied force: “So, because of this, it wouldn’t speed up as much, so it would have a lower velocity after the force was applied.” This implies that Christopher did not just use the equation as a computational tool, but linked meanings to variables (force, velocity, mass, and acceleration) and interpreted a relationship among them. When we asked him a question from Task 3—when a person is pushing a cabinet, how will the cabinet’s velocity change after passing over the frictionless surface and traveling onto the surface with friction?—his answer reconfirmed that he considered the relationship among variables and gave conceptual meaning not only to the variables but also to the relationship, and used a mathematical concept as an important tool to interpret a physical situation.
Christopher: So, the velocity is 100% dependent on the acceleration, which depends on the force, and then in this scenario, it is the force at first, it has a much higher total net force in the x direction, whereas later on it decreases [on a frictional surface], but there’s still a positive net force in the x direction, so it will continue. The reason why it continues to speed up is because the acceleration is still positive. ‘Cause mass can’t really be negative so that [acceleration] is the only variable [to determine the change of velocity]. So, that’s why velocity continues to increase, it’s just not as much as before.
In his statement, Christopher did not interpret an individual variable separately; rather, he first considered the relationship between force, velocity, and acceleration using the concept of vector and scalar quantity (e.g., mass is not a vector quantity), and explained how each variable was influenced by the other variables’ changes. From the statements above, it is clear that Christopher reasoned through a physical process by interpreting relationships among variables and attaching conceptual meaning to the relationship and the variables.
When we asked Christopher about change in the skater’s highest speed when the skater’s mass increased, his original written and oral responses contained the common answer that the skater’s highest speed would stay the same because gravity acts on all objects equally: “the downward acceleration will be the same.” We further asked him about how total mechanical energy changes. His response is below.
Christopher: Her [the skater’s] mechanical energy would increase because the velocity would stay the same for kinetic, but the mass would go up, so it would make the answer higher. And it’s probably easier to think of it with GPE, can I use the formula to it?
Then he drew a formula on board (Fig. 3 ), and explained why the total mechanical energy would change.
Christopher: This is mg. Since these two [ gh, ½ ] stay the same for both cases, they can be canceled out. So then, these are the only variables in ME (mechanical energy), so if this [ m ] increases, then the whole system[’s energy] will increase, but it won’t change this [ v ] in the specific scenario. If you were to use the equations, once you were to set them equal to each other and solve for the final answer for each, they would still be the same, even though the mass is higher. But because it’s multiplied, you can cancel it [ m ] on both sides for that specific scenario, so it mainly just depends on the constant ½ and then the variable of height and the final velocity which would be the same for this case.
In his response, Christopher first explained the physical situation using the concept of energy and considered the situation as a system: “Her [the skater’s] mechanical energy would increase,” and “so if this [ m ] increases, then the whole system[‘s energy] will increase.” In order to prove why mass doesn’t affect the skater’s speed, he used an equation as an explanatory tool—“And it’s probably easier to think of it with GPE, can I use the formula to it?”—and showed that mass doesn’t affect the skater’s speed: “You can cancel it [ m ] on both sides for that specific scenario.” A noticeable difference from Alex’s approach is that Christopher used equations to prove his claim and to explain it in an easier way, while Alex used equations to make sense of the situation. In other words, equations were in play mainly as explanatory tools for Christopher, whereas they acted as conceptual understanding tools for Alex. Similarly to his previous responses to questions in Motion and Force, Christopher again demonstrated that he considered how all variables were related each other in the system, and attached meaning to the relationship and variables. Interestingly, he often used the phrase “specific scenario,” so we asked what it meant. Below is his response.
Christopher: The equations don’t really help because even though I see it and it’s in my head, but it’s not really useful if I don’t know the scenario. If it’s some problems, I know, are purposefully shaped to muddle it up, and make it purposefully confusing, but usually, when you run the scenario, in a program or in your head, it kind of takes out that confusing stuff.
The above response illustrated that Christopher conceptually interpreted the physical situation first, then translated equations into the physical situation. This strategy shared a commonality with Alex’s in that both students used equations in their explanations and connected how variables in the equations changed as the specific physical situation changed. At the same time, there was a difference between the two students. Christopher’s strategy started with an analysis of the situation, creating a physical scenario and then translating equations into the physical situation, while Alex mentioned relevant equations first, then connected them to the physical situation.
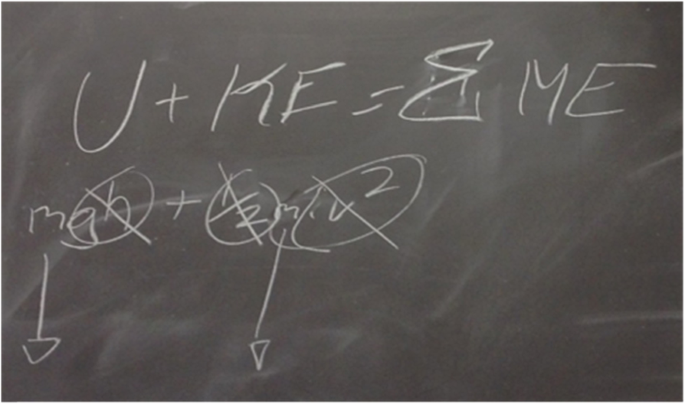
Christopher’s explanation. Note: ME = mechanical energy
Blake’s case – using equations as a computational tool
When we asked Blake which one would go farther when shot from a cannon, a tank shell or a baseball (when air resistance was negligible; Task 1), her original written response and her thinking-aloud response were similar: the mass of an object is not relative to its motion. When we asked her to explain why, she said:
Blake: Because I don’t see kg on the units at all [in the simulation]. kg is the unit for mass, kilograms, so, it’s not written as kg/m/s or something. You could easily compare it with units and mass is not part of the unit.
Her response was interesting in that she used the unit of velocity rather than acceleration. Also, she did not show her conceptual understanding of physical variables and their relationship as Christopher had done. We further asked her what factors should be changed to maximize the horizontal range of the projectile object, in order to elicit her reasoning about a projectile motion. Below is her response.
Blake: You need to throw it faster. Um, because, if you look at gun for example. It’s a really high velocity. So, you just see it going like straight because it’s just high velocity. And, um, if, if I’m throwing this phone, maximum distance it could go is like here [tosses phone, not very far]. Angle? I think…like the maximum distance for x axis and y axis is 45 degrees, but I think it should be a little lower. Around 45 but plus or minus 5 degrees, so like 40 degrees.
Interviewer: Why would you say that?
Blake: It doesn’t get that much time for vertical velocity, but the horizontal velocity will be faster.
In her response, Blake used real-life examples—shooting a gun and throwing a phone—as analogies to reason how to increase the horizontal range of a projectile object. However, when she threw the phone, she tossed it, which started it with a different initial angle from that of a bullet shot from a gun : “You just see it going like straight because it’s just high velocity.” Although she considered two directions of velocity when determining the optimal initial angle, she did not provide a scientifically reasonable explanation for why the initial angle should be lower than 45 degrees. It might be that Blake had learned that 45 degrees is the angle used to maximize range, but that she thought velocity would be more critical than the angle to determine the range, especially that the x -component of velocity would more important than the y -component because an object will fly faster horizontally than vertically when the x- component is greater. Thus, she lowered the initial angle a little bit. In the above statements, Blake did not demonstrate that she could consider the relationship between variables and link conceptual meanings to them (e.g., “Because I don’t see kg on the units at all” and “It doesn’t get that much time for vertical velocity, but the horizontal velocity will be faster”).
For the next question, we asked what would happen to the box’s motion after another box was placed on top of it. She said, “It would still be constant and stay at constant velocity in that motion.” We asked the question again, to clarify if she understood it.
Blake: Yeah. The velocity would be the same. After you let it go. So it will be at constant speed. And the force is proportional to the...wait, well acceleration is proportional to force and mass.
In her response, Blake attempted to apply Newton’s second law ( F = ma ), as the other two students had; however, she didn’t realize that acceleration is inversely proportional to mass, and therefore the velocity would be changed by the different acceleration. As a result, her response involved a misconception that mass doesn’t affect the speed of an object. In other words, she demonstrated her lack of understanding of the relationships between the variables (acceleration, velocity, mass, and force) involved in the situation. Her response to the questions confirmed that she explained scientific phenomena using variables in equations but failed to recognize the relationships among them. Instead she focused on individual variables, e.g., how acceleration will change as force changes, but did not explain how that would change velocity. She also did not explain how two components of velocity affect an object’s motion. Interestingly, she also used the unit of variable to justify her answer without applying conceptual meanings to it. For Blake, equations and units seemed to play important roles in explaining physical situations, but her connection of equations to physical situations was, at best, based on interpretations of individual variables.
When we asked Blake about change in the skater’s highest speed when the skater’s mass increased, her original written response was that her highest speed would increase because the mass of the skater would require more energy. When we interviewed her, her answer was different from her original response.
Blake: I think it should stay the same. I was thinking of the formula.
When we asked her to explain in more detail, she wrote an equation on the board (Fig. 4 ) and explained what it meant.
Blake: The highest point, because there won’t be any kinetic energy. And it’ll be mgh . Also ½ mv 2 and it [ m ] cancels out. It was exactly the same. The speed was the same. But—wasn’t there a bar graph [in the simulation]? Well, the total energy was bigger [in the simulation]. The total energy. But the total energy was same—no bigger.
Similarly to Alex, Blake used an equation to explain that the skater’s speed wouldn’t change because v doesn’t contain m after canceling out. However, she did not describe why kinetic energy is zero at the highest point and why potential energy is zero at the bottom. It might be that she just did not mention this, but it was obvious that she did not understand how the object’s mass affected the system: “But the total energy was same—no bigger.” We further asked her how the total mechanical energy of the skater would change when the skater’s mass increased. This time, she said, “Well, the total energy was bigger. ‘Cause energy depends on mass and either height or speed of a person.” As seen in the response, she thought of variables in equations of gravitational potential energy ( mgh ) and kinetic energy ( \( \frac{1}{2} \) mv 2 ). When asked why she previously had said the total mechanical energy would be the same, she answered, “because energy is always conserved.” This illustrated her misconception that the amount of energy should always be the same regardless of mass; however, when she considered variables in equations of PE and KE, she answered the question accurately. Throughout the interview, we found that Blake’s strategy to solve questions was consistent across different tasks; she used formulas and units as her first approach. However, a difference between Blake and the other two students is that although she used equations and variables, she did not explain how the variables influenced each other; and how they would change as a specific situation changed. In other words, she did not translate equations into physical situations nor link conceptual meanings to the variables and the relationships between them. The findings showed that for Blake, equations were more likely used as a simple computational tool.
Blake’s explanation
Disconnection of students’ problem-solving strategies from physics lecture
The three students all mentioned that they liked simulation-based questions. Alex said that the questions themselves made him think a lot, and running simulations also made him think more deeply: “Beforehand it [the task] just seems really simple, so you don’t put much thought into it. That’s easy. Just write it down, but then, once you run it, it makes you think about it more. So that’s cool too.”
As seen in his responses to the questions in the tasks, Alex used equations as conceptual understanding tools consistently across tasks. When we asked if he had learned this approach from his physics course, he said that his physics class heavily focused on solving problems but mostly by just reading off equations and plugging in numbers.
Alex: Physics is not about reading equations and stuff off a slide. It’s about working things by hand, and my professor, he has all the solutions to the problems in the book. He had them on a clear sheet of paper, and a Sharpie and then, so if he has problem 20, he puts problem 20 on the projector, and then he put that clean sheet there, and then he points to, oh here I did “v = a + blah blah,” so that’s really not effective at all in my opinion.
Christopher mentioned that the formative assessment would be very helpful for a lot of students, because it showed physical scenario. His physics class was more formula-based, with activities such as showing a formula and plugging in numbers to demonstrate how to solve a physics problem, which Christopher felt was disconnected from how he learned science. As he demonstrated, he learned best when he created a physical scenario, then translated it into equations. Alex also mentioned that physics is “about working things by hand,” which implies that he emphasized linking problem-solving procedures to physical situations. In Blake’s case, she mentioned that “It will help students to learn the concept better, but I think students will hate it [the formative assessment] because students will be like, ‘I don’t have time for this. It’s just that I am like too busy for this.’” In sum, the three students had a common opinion that the simulation-based formative assessment had helped them understand the given physical situation better, but the reasons why they liked it differed, as did their problem-solving strategies.
Discussion and conclusion
Previous studies on problem solving were concerned with students’ using equations simply as numerical computational tools by plugging in numbers. While experts tend to start with a conceptual analysis of problems using scientific principles and laws, novices start by selecting and manipulating equations without conceptual analysis (Larkin et al., 1980 ). The difference in solving problems might be more obvious in quantitative questions, in which a mathematically framed physics question may prompt students to use equations without conceptual understanding (Kohl & Finkelstein, 2006 ). The current study started from the research question “How do students solve conceptual physics questions in simulation-based formative assessments?” The findings showed that the students still used equations to answer the questions. However, their utilizations of equations were different. For example, Alex’s and Christopher’s strategies involved using equations to explain or interpret the given physical situation. To do so, they connected variables to physical situations and provided meanings to the variables and the relationships among the variables. Blake, however, used equations and units as tools to find answers for the questions without a clear connection of the variables and equations to the given physical situations. Christopher’s strategy was especially noticeable in that he used equations as effective explanatory tools for a physical situation. He started an analysis of the physical situation, then translated equations into the situation by creating a physical scenario in a system, such as how variables change as the situation changes, and how the variables are related to each other within the physical system. Alex’s explanations illustrated that he utilized equations to understand a physical situation. The difference between him and Christopher is that Alex used equations as major tools to analyze and understand the situation, while Christopher used them to effectively and easily explain the situation. Noticeably, Alex used algebraic computation processes using an equation to understand a given physical process.
Kuo et al. ( 2012 ) argued that linking conceptual reasoning to mathematical formalism indicates a more expert level of understanding and demonstrates robust solutions integrating conceptual and symbolic reasoning. They found that students used equations not just as computational tools but as tools to find conceptual shortcuts to solve physics problems. Although Kuo et al.’s study focused on quantitative problem solving, the current study revealed a similar finding where questions were created qualitatively without asking any calculations. Another difference from Kuo et al.’s study is that they provided an equation to students first, then asked them to explain the equation and apply the equation to a physical situation, whereas the current study provided a physical situation without any equations. As a conclusion, the current study supports that equations can be important in conceptualizing a physical situation by connecting conceptual meanings to equations. Therefore, mathematical equations can be used alternatively in problem solving (Kuo et al., 2012 ). Redish and Smith ( 2008 ) also illuminated the power of equations in solving physics problems and making sense of physical systems when students are able to link physical scenarios to mathematical equations. Thus, the connection of physical meaning to equations should be emphasized in teaching and learning physics in order to help students to conceptualize physical system (Redish & Smith, 2008 ).
Previous studies of quantitative physics problem solving have focused on using equations first when solving a physics question without a conceptual analysis of the problem situation, which indicated equations were in play as a simple computational tool. Although, the current study found a similar case, in which a student used equations as a simple computational tool, we also found that students used equations as a conceptual understanding or an effective explanatory tool. Indeed, using equations helped Alex realize his misconception and explain the situation accurately. While previous studies have emphasized performing a conceptual analysis first using scientific principles when solving a problem, this study argues the positive roles of using equations when it includes a connection between the equations and the physical situation. Therefore, this study contributes to the literature on physics problem solving in that equations can be used for students as tools for a conceptual understanding and as an explanatory tool. In this study, Christopher’s strategy was closer to the strategy used by experts, since he visualized a given situation to analyze by creating a physical scenario, then connected the relevant equations to the situation to explain the physical scenario. On the other hand, Alex used equations first to answer questions by connecting variables to the physical process through an algebraic solution process. Especially for Alex, equations facilitated his physical understanding of the problem and ability to explain the physical process. Although Alex and Blake used equations primarily as tools to answer questions, Blake did not demonstrate her interpretations of variables or the relationships among them in equations; nor did she connect variables to a physical situation. This indicated that her utilization of equations was closer to simple computational tools.
In conclusion, mathematical equations in physics were important when students were conceptually explaining a physical situation. It was revealed that using equations helped them explain a physical situation with more scientifically normative ideas. However, the ways they used equations differed between students. An equation could be an explanatory tool, a conceptual understanding tool, or a computational tool. The essence of the findings was that when students were able to connect variables to a physical process and to interpret relationships among variables in an equation, equations were in play as tools in understanding and explaining a physical situation. On the other hand, without interpretations of variables and connections to a physical situation, equations only served as simple computational tools. The study also found that students’ strategies to answer questions, especially conceptual ones, did not change with different topics in physics.
Implications and study limitations
As some students pointed out, their physics lectures demonstrated how to solve quantitative questions using equations as computational tools. As Christopher’s problem solving strategy was similar to the strategy used by experts, we suggest that his strategy be reflected in teaching physics. To be more specific, physics educators may provide an opportunity for students to visualize the physics phenomena. They could use models or computer simulations to help this procedure. Second, they should emphasize how equations are used to explain the phenomena as a “conceptual shortcut” (Kuo et al., 2012 , p. 39) by connecting equations and variables to the physical situation. In other words, as Alex and Christopher demonstrated, if physics instructions emphasize connections between physical meanings and mathematical expressions, it help students understand physical phenomenon. As we consider physics instructors as experts, perhaps in some cases their expert level of using equations was not reflected in their teaching. A future study topic would be to investigate the reason for the gap between physics experts’ strategies in solving physics problems and their teaching practices when demonstrating how to solve physics problems.
Although the findings of this study suggest an alternative way of using equations as an explanatory or a conceptual analysis tool for a physical situation, the findings might not be generalizable because the study context was limited to an introductory level physics course. Also, it is possible that topics for the tasks (kinematics and mechanical energy conservation) involving several equations might have influenced students’ strategies in answering questions. However, Redish ( 2017 ) emphasizes that a goal of physics is to create mathematical modeling (equations) that can predict and explain physical phenomena. Consequently, mathematical equations are included in physics topics and taught extensively in physics instruction especially in high school and college. We argue that students’ understanding of mathematical modeling in physics should not be considered as a following step after conceptual understanding of scientific principles. Instead, we support the claim that blending of physical meaning with mathematical operations should be emphasized in teaching physics (Kuo et al., 2012 ; Redish, 2005 , 2017 ). We also suggest that future studies should investigate how students’ strategies to answer questions are different in other topics, such as thermodynamics or electricity and magnetism.
Availability of data and materials
Interview data are not available for public.
Abbreviations
Constructed-Response
Gravitational Potential Energy
Kinetic Energy
Next Generation Science Standards
Ardac, D., & Akaygun, S. (2004). Effectiveness of multimedia-based instruction that emphasizes molecular representations on students’ understanding of chemical change. Journal of Research in Science Teaching , 41 (4), 317–337.
Article Google Scholar
Chi, M. T. H., Feltovich, P. J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science , 5 , 121–152.
Creswell, J. W. (2016). 30 essential skills for the qualitative researcher . Thousand Oaks: Sage.
Google Scholar
Creswell, J. W., & Miller, D. L. (2000). Determining validity in qualitative inquiry. Theory Into Practice , 39 , 124–130.
De Cock, M. (2012). Representation use and strategy choice in physics problem solving. Physical Review Special Topics - Physics Education Research , 8 (2), 020117.
de Jong, T., & van Joolingen, W. R. (1998). Scientific discovery learning with computer simulations of conceptual domains. Review of Educational Research , 68 (2), 179–201.
Dhillon, A. S. (1998). Individual differences within problem-solving strategies used in physics. Science Education , 82 (3), 379–405.
Dori, Y. J., & Hameiri, M. (2003). Multidimensional analysis system for quantitative chemistry problems: symbol, macro, micro, and process aspects. Journal of Research in Science Teaching , 40 (3), 278–302.
Gick, M. L. (1986). Problem-solving strategies. Educational Psychologist , 21 (1–2), 99–120. https://doi.org/10.1080/00461520.1986.9653026 .
Gunstone, R. F., Champagne, A. B., & Klopfer, L. E. (1981). Instruction for understanding: a case study: learning research and development center . Pittsburgh: University of Pittsburgh.
Gurel, D. K., Eryılmaz, A., & McDermott, L. C. (2015). A review and comparison of diagnostic instruments to identify students’ misconceptions in science. Eurasia Journal of Mathematics, Science & Technology Education , 11 (5), 989–1008.
Huffman, D. (1997). Effect of explicit problem solving instruction on high school students’ problem-solving performance and conceptual understanding of physics. Journal of Research in Science Teaching , 34 (6), 551–570.
Kohl, P. B., & Finkelstein, N. D. (2006). Effects of representation on students solving physics problems. Physical Review Special Topics - Physics Education Research , 2 (1), 010106.
Kozhevnikov, M., Motes, M. A., & Hegarty, M. (2007). Spatial visualization in physics problem solving. Cognitive Science , 31 (4), 549–579.
Kuo, E., Hull, M. M., Gupta, A., & Elby, A. (2012). How students blend conceptual and formal mathematical reasoning in solving physics problems. Science Education , 97 (1), 32–57.
Larkin, J. H., McDermott, J., Simon, D. P., & Simon, H. A. (1980). Expert and novice performance in solving physics problems. Science , 208 (4450), 1335–1342.
Lazonder, A. W., & Ehrenhard, S. (2014). Relative effectiveness of physical and virtual manipulatives for conceptual change in science: how falling objects fall. Journal of Computer Assisted Learning , 30 (2), 110–120.
Maloney, D. P. (1994). Research on problem solving: physics. In D. L. Gabel (Ed.), Handbook of research in science teaching and learning , (pp. 327–354). New York: Macmillan.
McDermott, L. C. (1991). Millikan lecture 1990: What we teach and what is learned—closing the gap. American Journal of Physics , 59 , 301–315.
National Research Council (2012). A framework for K-12 science education: practices, crosscutting concepts, and core ideas . Washington, DC: National Academies Press.
National Research Council (2014). Developing assessments for the next generation science standards. Committee on developing assessments of science proficiency in K-12. In W. J. W. Pellegrino, M. R. Wilson, J. A. Koenig, & A. S. Beatty (Eds.), Board on testing and assessment and board on science education. Division of behavioral and social sciences and education . Washington, DC: The National Academies Press.
NGSS Lead States. (2013). Next Generation Science Standards: For states, by states. Washington, DC: The National Academies Press.
Park, M. (2019). Effects of simulation-based formative assessments on students’ conceptions in physics. Eurasia Journal of Mathematics, Science and Technology Education , 15 (7), em1722.
Park, M., Liu, X., & Waight, N. (2017). Development of the connected chemistry as formative assessment pedagogy for high school chemistry teaching. Journal of Chemical Education , 94 (3), 273–281.
Pellegrino, J. W. (2013). Proficiency in science: Assessment challenges and opportunities. Science , 340 (6130), 320–323.
Quellmalz, E. S., Timms, M. J., Silberglitt, M. D., & Buckley, B. C. (2012). Science assessments for all: integrating science simulations into balanced state science assessment systems. Journal of Research in Science Teaching , 49 (3), 363–393.
Redish, E. F. (2005). Problem solving and the use of math in physics courses . Delhi: Proceedings of the Conference, World View on Physics Education in 2005: focusing on change.
Redish, E. F. (2017). Analysing the competency of mathematical modelling in physics. In T. Greczyło, & E. Dębowska (Eds.), Key competences in physics teaching and learning , (pp. 25–40). Chum: Springer International Publishing.
Chapter Google Scholar
Redish, E. F., & Smith, K. A. (2008). Looking beyond content: skill development for engineers. Journal of Engineering Education , 97 (3), 295–307.
Rutten, N., van Joolingen, W. R., & van der Veen, J. T. (2012). The learning effects of computer simulations in science education. Computers & Education , 58 (1), 136–153.
Simon, D. P., & Simon, H. A. (1978). Individual differences in solving physics problems. In R. S. Sigler (Ed.), Children’s thinking: what develops? (pp. 325–348). Hillsdale: Erlbaum.
Smetana, L., & Bell, R. L. (2012). Computer simulations to support science instruction and learning: a critical review of the literature. International Journal of Science Education , 34 (9), 1337–1370.
Srisawasdi, N., & Panjaburee, P. (2015). Exploring effectiveness of simulation-based inquiry learning in science with integration of formative assessment. Journal of Computers in Education , 2 (3), 323–352.
Strauss, A. L., & Corbin, J. (1998). Basics of qualitative research: grounded theory procedures and techniques . Newbury Park: Sage.
Treagust, D. F. (1985). Diagnostic tests to evaluate students’ misconceptions in science . French Lick Springs: Paper presented at the annual meeting of the National Association for research in science teaching (NARST).
Trundle, K. C., & Bell, R. L. (2010). The use of a computer simulation to promote conceptual change: a quasi-experimental study. Computers & Education , 54 (4), 1078–1088.
Underwood, S. M., Posey, L. A., Herrington, D. G., Carmel, J. H., & Cooper, M. M. (2018). Adapting assessment tasks to support three-dimensional learning. Journal of Chemical Education , 95 , 207–217.
van Heuvelen, A. (1991). Learning to think like a physicist: a review of research based instructional strategies. American Journal of Physics , 59 , 891–897.
Download references
Acknowledgements
Author information, authors and affiliations.
Department of Curriculum and Instruction, College of Education, Texas Tech University, Box 41071, Lubbock, TX, 79409-1071, USA
You can also search for this author in PubMed Google Scholar
Contributions
First and Corresponding author. Dr. MP (100% contribution). Dr. Park designed the study, collected and analyzed data, and wrote the manuscript entirely. The author read and approved the final manuscript.
Corresponding author
Correspondence to Mihwa Park .
Ethics declarations
Competing interests.
The author declares that he/she has no competing interests
Additional information
Publisher’s note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Reprints and permissions
About this article
Cite this article.
Park, M. Students’ problem-solving strategies in qualitative physics questions in a simulation-based formative assessment. Discip Interdscip Sci Educ Res 2 , 1 (2020). https://doi.org/10.1186/s43031-019-0019-4
Download citation
Received : 14 June 2019
Accepted : 21 November 2019
Published : 03 January 2020
DOI : https://doi.org/10.1186/s43031-019-0019-4
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Formative assessment
- Physics education
- Problem solving
- Bipolar Disorder
- Therapy Center
- When To See a Therapist
- Types of Therapy
- Best Online Therapy
- Best Couples Therapy
- Best Family Therapy
- Managing Stress
- Sleep and Dreaming
- Understanding Emotions
- Self-Improvement
- Healthy Relationships
- Student Resources
- Personality Types
- Guided Meditations
- Verywell Mind Insights
- 2024 Verywell Mind 25
- Mental Health in the Classroom
- Editorial Process
- Meet Our Review Board
- Crisis Support
9 in 10 Teachers Need More Resources to Care for Students' Mental Health
Verywell Mind survey shows teachers are eager to provide support
Sarah Fielding is a freelance writer covering a range of topics with a focus on mental health and women's issues.
:max_bytes(150000):strip_icc():format(webp)/SarahFieldingHeadshot1-afe3609d152d4e409fc179f68c17e652-0ddbe13118414f25ae9e00030fea1fae.jpg)
Another school year is here, and to mark the occasion Verywell Mind surveyed 1,000 middle and high school teachers in the U.S. for our Mental Health in the Classroom Study. Teachers reported on their experiences handling mental health issues, strategies that work, and the kind of resources they need to support their students even more.
The survey found that 81% say teachers feel responsible for their students' mental health, and another 77% believe it’s also their duty to teach students about mental health and relevant self-care strategies.
A vast majority of respondents (89%) agree that they don't have enough resources at their disposal to help students deal with mental health issues.
Teachers have long had a role in society that goes well beyond educating our kids, and a big part of that stems from how much they care about their students.
The past few years have tested teachers’ resolve even further, leaving them trying to guide classrooms of kids through a global pandemic, the deleterious effects of social media, and a world that is increasingly complicated and often cruel.
“There is so much pressure put on teachers today. They are the educator, moral compass, sometimes parents, and always the adults in the room,” says Dr. Tara Lindahl , a licensed clinical psychologist and regional psychotherapy director at Mindpath Health in California. “With so many years of ‘unprecedented times,’ teachers now see how our children’s mental health may be affected. We must remember that this was not part of their training and that they may be feeling out of scope.”
Many Schools Offer Mental Health Training to Teachers
Just over 75% of teachers who took part in the survey reported that their school does offer mental health training for educators, but those working in private schools are more likely to have access at 82%. As a whole, 77% of surveyed educators have previously received training to incorporate mental health awareness and strategies in their teaching. Training rates are higher among teachers who are millennial or younger at 81%, and 86% for private school teachers.
Dr. Kristen Niemczyk-Kistner , a New Jersey-based social worker, is one of the mental health professionals facilitating training for teachers (and parents). Last year, she created and facilitated a pilot training program for staff at the middle school where she works. Niemczyk-Kistner then made weekly psycho-education lesson plans for the teachers to go over with students each Friday during an extended homeroom.
Implementing Calming Spaces
They were also given the vocabulary to create a safe, open space for students to discuss their well-being. Furthermore, the school made “Calming Spaces” for each grade filled with sensory items and comfortable furniture like bean bags. Niemczyk-Kistner reports that administrators, teachers, and students alike positively responded to the pilot program.
Some survey participants have used techniques similar to those laid out by Niemczyk-Kistner: “Mental health awareness strategies are important in making students feel safe in my classroom. I try to take time for at least ten minutes every class period to focus on mental health by discussing their needs and struggles.”
An Ongoing Battle for Resources
Overall, millennial and younger teachers felt both more responsible and more equipped to discuss mental health with their students, suggesting a generational divide in our feelings about mental health. However, many teachers feel that they don’t have enough resources to properly care for students or avenues to point them towards.
As one participant explained, “We need to be adequately trained to not only spot, but to quickly intervene with students who need help, in providing a safe and comfortable space where students can share their thoughts and struggles and know that we can guide them to resources that will help them through their pain, with the promise that there is hope on the other side.”
This is especially critical given that 70% of teachers notice students dealing with poor mental health at least once a month, while 40% notice such issues weekly. 65% of teachers say that students are not getting enough mental health support. Teachers have a strong desire to provide support and are doing what they can, but are too often limited by the tools at their disposal.
Private School Stands Apart
Teachers at private schools—where money tends to be less of an issue—reported more abundant mental health resources, better outcomes, and fewer overall mental health concerns.
Where the Resources Are Going
A majority of teachers (64%) think the support is lacking at the state or federal level for bringing effective mental health training to their schools.
While 71% of teachers say that their school is somewhat or very well-funded, less than half (48%) think the mental health resources available to students are very high or high quality. Amongst private school teachers, 88% say they are somewhat or very well-funded.
Boosting Mental Health Advocacy Can Help Schools Get More Resources
Niemczyk-Kistner stresses the importance of advocacy to create more mental health awareness, training, and resources in schools. “I don't think just because it doesn't exist in your school doesn't mean it can't happen,” she says. “Maybe school districts do not have the staff currently, and they can't afford to have the staff, but they can afford to perhaps hire a consultant to come in to provide this type of coaching.”
She emphasizes the importance of having professionals guiding these undertakings to ensure teachers are aware of when a situation has escalated to the point of further intervention and how to proceed.
“While resources may be limited, teachers can collaborate with school counselors, social workers, and mental health professionals to gain insights and strategies for helping students,” says Angela Ficken , a psychotherapist with a Boston-based private practice. “Leverage community organizations and online mental health resources to enhance your understanding.”
So, How Exactly Are Teachers Approaching Mental Health in Their Classrooms?
Doing something to help students, no matter how small it feels, can be impactful. “A fallacy around mental health is the belief that a big initiative must occur in order to be effective,” says Dr. Sabrina Romanoff, a clinical psychologist and professor at Yeshiva University in New York City. “The benefit of being heard, validated, and acknowledged is immensely valuable. Teachers can demonstrate that they are a safe resource for their students to turn to and can make themselves available during office hours or after class meetings to check in on students.”
Sabrina Romanoff, PsyD
You need to have a strong foundation to draw on in order to help your students. This means taking your own care seriously and scheduling in exercise, sleep, socialization, journaling, and meditation—so you can be an example to model to your students.
The survey found that 81% of teachers integrate mental health awareness and strategies into their teaching. As in other areas, this number increased for teachers who were millennials or younger (86%) and for private school teachers (88%). This appears to be a recent shift, with 71% of teachers reporting that they’ve incorporated this work into their teaching within the last four years.
Yet, when asked which strategies they felt were most effective, individual check-ins, arguably the most time-consuming process, had the highest reported success rate at 37%. Without resources, this kind of one-on-one strategy is much more difficult to pull off.
How Teachers Can Protect Their Own Mental Health
Romanoff stresses how important it is to set realistic expectations for what you can do for your students as someone who only has a part-time role in their life. To this end, it can help to involve parents in watching out for and communicating about their children’s well-being, adds Ficken.
It's important that teachers also look after their own mental health . “You need to have a strong foundation to draw on in order to help your students. This means taking your own care seriously and scheduling in exercise, sleep, socialization, journaling, and meditation—so you can be an example to model to your students,” says Romanoff. Lean on other teachers who understand your experience and can provide guidance.
The Challenges of Mental Health in the Classroom
Teachers cited several issues with integrating mental health awareness strategies into the classroom experience:
- Teachers are too overwhelmed (41%)
- Not enough training (39%)
- Too many other challenges (35%)
- Too many mandates to keep up with (34%)
- Poor quality of trainings (27%)
“Teachers should remember that they are human and cannot be expected to solve every problem,” says Ficken. “Avoid placing excessive guilt on yourself and acknowledge that you are doing your best with available resources.”
Educators also don’t undergo the same level of training as mental health professionals and should keep this in mind as they try to help their students, adds Lindahl. They can offset this by being prepared as to where to direct them.
“While teachers may face challenges balancing their responsibility for students' mental health with limited training and resources, proactive steps can be taken," says Ficken. "Seek professional development, collaborate with school resources, focus on mental health education, set realistic boundaries, and prioritize self-care. Remember that you cannot do it all, but your efforts to create a supportive environment and advocate for students' mental health are valuable.”
Methodology
Verywell Mind surveyed 1,000 middle school and high-school teachers (aged 18+) from July 3rd to 13th, 2023. The survey was fielded online via a self-administered questionnaire to an opt-in panel of respondents from a market research vendor.
Amanda Morelli is the senior director of data journalism at Dotdash Meredith. She has over 10 years of research experience and assists with data visualization and analysis.
:max_bytes(150000):strip_icc():format(webp)/IMG-4419-92ada1eaecb945b2a26705969ac541b1.jpg)
Neetu Gupta is the Director in the Corporate Research & Insights team at Dotdash Meredith. She leads a team of survey programmers, data analysts, panels managers, and researchers
:max_bytes(150000):strip_icc():format(webp)/NeetuGupta-e2e6c6e924e8406da530a2769f200a65.jpg)
Sanskriti Sharma is a Manager in the Consumer Strategy & Insights team at Dotdash Meredith.She helps in executing consumer insight projects for multiple Dotdash Meredith brands by converting data into actionable insights that help simplify brand decisions.
:max_bytes(150000):strip_icc():format(webp)/SanskritiImage-813fafcb02fd493688d18a71c02bfa98.jpg)

Problem-Solving Olympiad Puts Power Skills to the Test
- Share article
The inaugural NXTLVL Problem-Solving Olympiad brought students together online for a day of spirited competition, pushing them to their true potential. Middle school problem-solvers from four continents, including three of the top ten virtual schools ranked by World Schools, navigated complex challenges in teams. These challenges tested timeless Power Skills like creativity, critical thinking, collaboration, communication, emotional intelligence, and resilience.
NXTLVL is a pioneering edtech program that helps students develop Power Skills, preparing them for a rapidly evolving world driven by AI advancements and scientific innovations. Our game-based learning approach combines team challenges with expert coaching, equipping students with the skills needed to take on anything.
Many progressive schools, like those attending the Olympiad, are integrating competency-based education into their curricula, focusing on Power Skills to prepare their students for school, work and life.
Gabriel Hernandez, Director of Technology at our champion school Alverno Heights Academy believes “participation in such interactive activities not only enriches students’ learning experiences but also helps them develop essential skills that are beneficial for their personal and academic growth.”
The new Problem-Solving Olympiad offers an extraordinary learning environment for tomorrow’s problem-solvers to stretch their Power Skills by collaborating under pressure.

Power Skill award winners
To emphasize the importance of Power Skills, we rewarded exceptional examples.
The Emotional Intelligence Award went to Minerva’s Virtual Academy, a globally recognized online school based in the UK, for “anticipating the needs and strategies of allies and opponents to navigate conflicts.”
Williamsburg Academy of Colorado picked up the Resilience Award for “perseverance in pushing through setbacks without losing momentum.”
Laurel Springs School earned the Critical Thinking Award for “demonstrating exceptional analytical thinking, decoding complex problems with logical and strategically sound solutions.”
The Communication and Creativity Awards went to the Prisma Online School for “mastering divergent thinking, consistently generating and synthesizing innovative ideas, while communicating them clearly.”

The Champions
We witnessed the peak of escalating intensity in the Championship Level as four teams battled it out for the main prize. Fourth place went to Prisma Online School, third place to Hill Top Preparatory School, and second place to Minerva’s Virtual Academy.
Our overall champions were a team from Alverno Heights Academy, an independent Catholic school from California. They epitomized teamwork, securing the Power Skill Award for collaboration. With a perfect balance of leadership and emotional intelligence, they leveraged each other’s diverse skills and perspectives. Their dynamism and synchronicity were evident from start to finish. Worthy winners indeed.
Hernandez added, “This Olympiad provides a unique platform for students to engage in communication and critical thinking skills, which are essential in today’s educational landscape. While traditional sports often focus on teamwork and collaboration, this competition allows educators to reach a broader spectrum of students and foster these important skills collectively.”
One of the Alverno Heights Academy students emphasized the importance of “teamwork, communication, and lots of planning before each round,” which was key to their success.

The ultimate contest of wits
The Olympiad was a breathtaking experience. The speed at which all teams adapted to the surmounting challenges reminded us of what students are capable of when given the right platform. In just five hours, students transformed from being curious but uncertain to astute problem-solving teams.
Initially, they dove in without knowing the rules, requiring them to decode the game, develop hypotheses, and fine-tune their tactics. As the game evolved, they had to rework their strategies and adapt on the fly. This journey through failure, setbacks, and upended strategies led them to a finish line where the sweetness of victory was palpable.
The next level
Building on the success of the May event, we’re excited to announce the November Olympiad, which promises to be even more spectacular, expanding over multiple days to welcome more schools.
With early bird access, it’s free for the first four teams until July 1st.
Click here to register and give your students a head start on the future.
We extend a heartfelt thank you to the Elite Academic Academy for their invaluable support in hosting the event and the other schools that made it possible.
Alverno Heights Academy Boston College High School Colégio Bento Benedini Hill Top Preparatory School Laurel Springs School Leadership Academy of Utah Mesa Public Schools Minerva’s Virtual Academy Prisma Online School Repton Abu Dhabi Repton Al Barsha Repton Dubai Williamsburg Academy Williamsburg Academy of Colorado
Sign Up for EdWeek Tech Leader
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 1: Algebra foundations
Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.
The 7 Best AI Tools to Help Solve Math Problems
How do you make seven even? Use these tools to solve the big math problems in life.
Quick Links
The test questions, wolframalpha, microsoft mathsolver.
While OpenAI's ChatGPT is one of the most widely known AI tools, there are numerous other platforms that students can use to improve their math skills.
I tested seven AI tools on two common math problems so you know what to expect from each platform and how to use each of them.
I used two math problems to test each tool and standardize the inputs.
- Solve for b: (2 / (b - 3)) - (6 / (2b + 1)) = 4
- Simplify the expression: (4 / 12) + (9 / 8) x (15 / 3) - (26 / 10)
These two problems give each AI tool a chance to show reasoning, problem-solving, accuracy, and how it can guide a learner through the process.
Thetawise provides more than simple answers; you can also opt to have the AI model tutor you by sharing a detailed step-by-step breakdown of the solution. Using the platform is fairly straightforward, given that all you need to do is navigate to the platform and key in the math problem at hand. Alternatively, you can even upload a photo of the math problem onto the platform, and the AI will analyze the image and provide you with an answer.
The AI platform gave us a step-by-step breakdown of the problem:
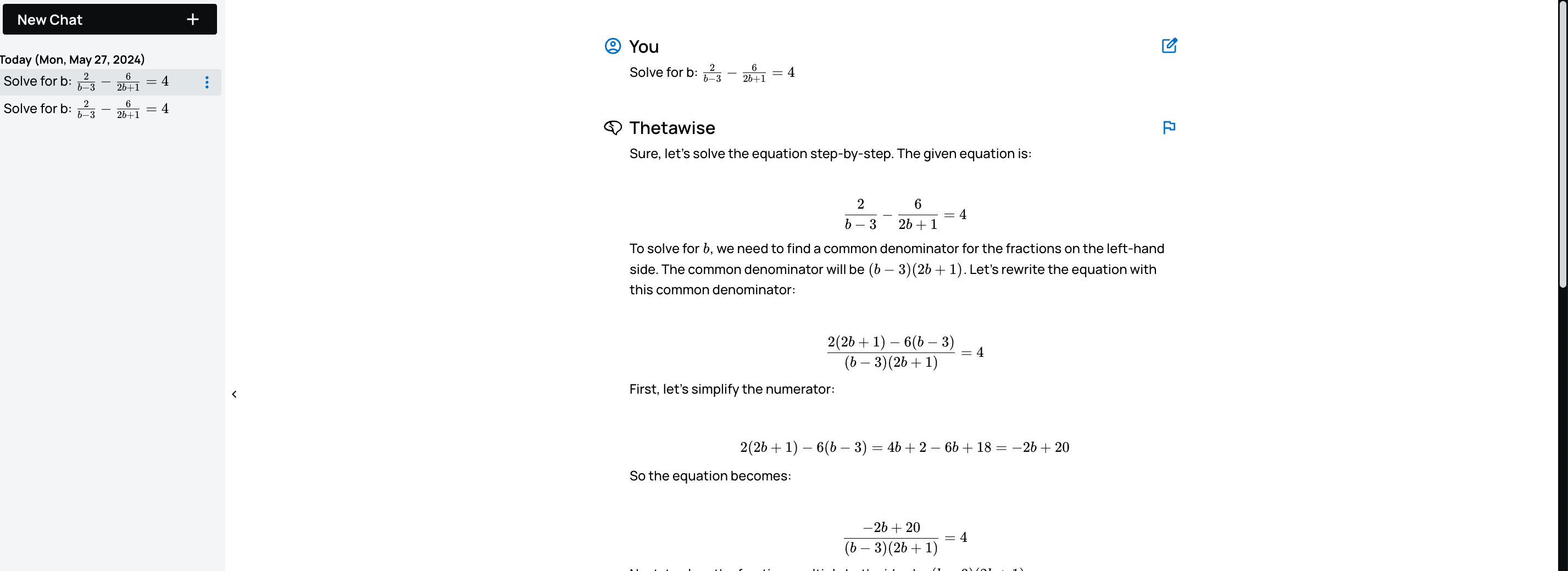
It resulted in the answer:
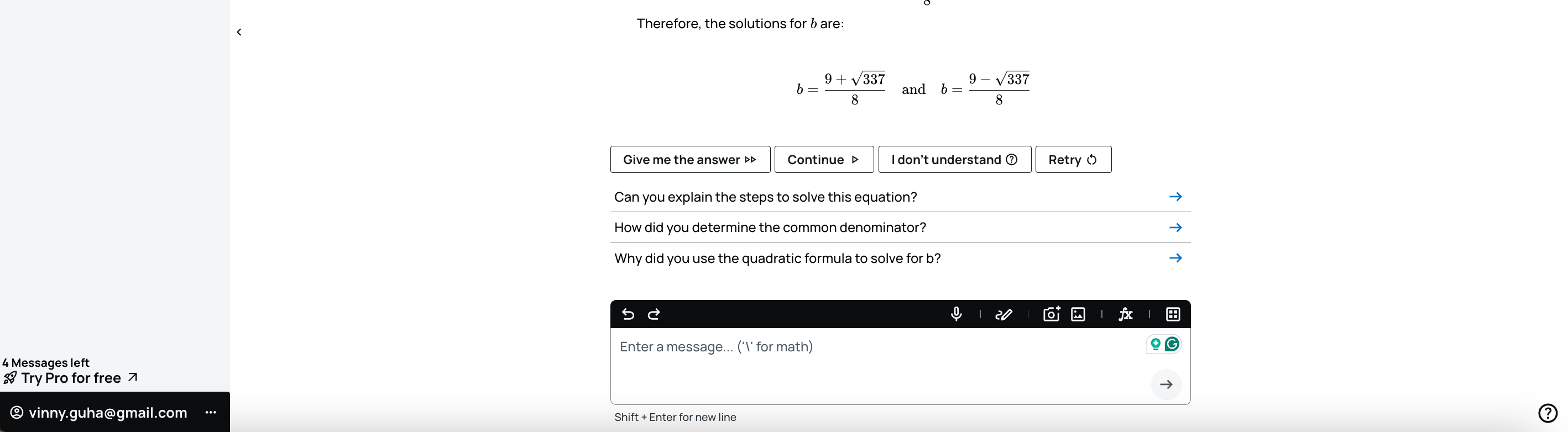
While the answer is correct, the tool also provides further options for students to generate a more detailed breakdown of the steps or ask more specific questions.
WolframAlpha is an AI tool capable of solving advanced arithmetic, calculus, and algebra equations. While WolframAlpha's free version provides you with a direct answer, the paid version of the tool generates step-by-step solutions. If you want to make the best use of WolframAlpha's capabilities, you can sign up for the Pro version, which costs $5 per month for the annual plan if you're a student.
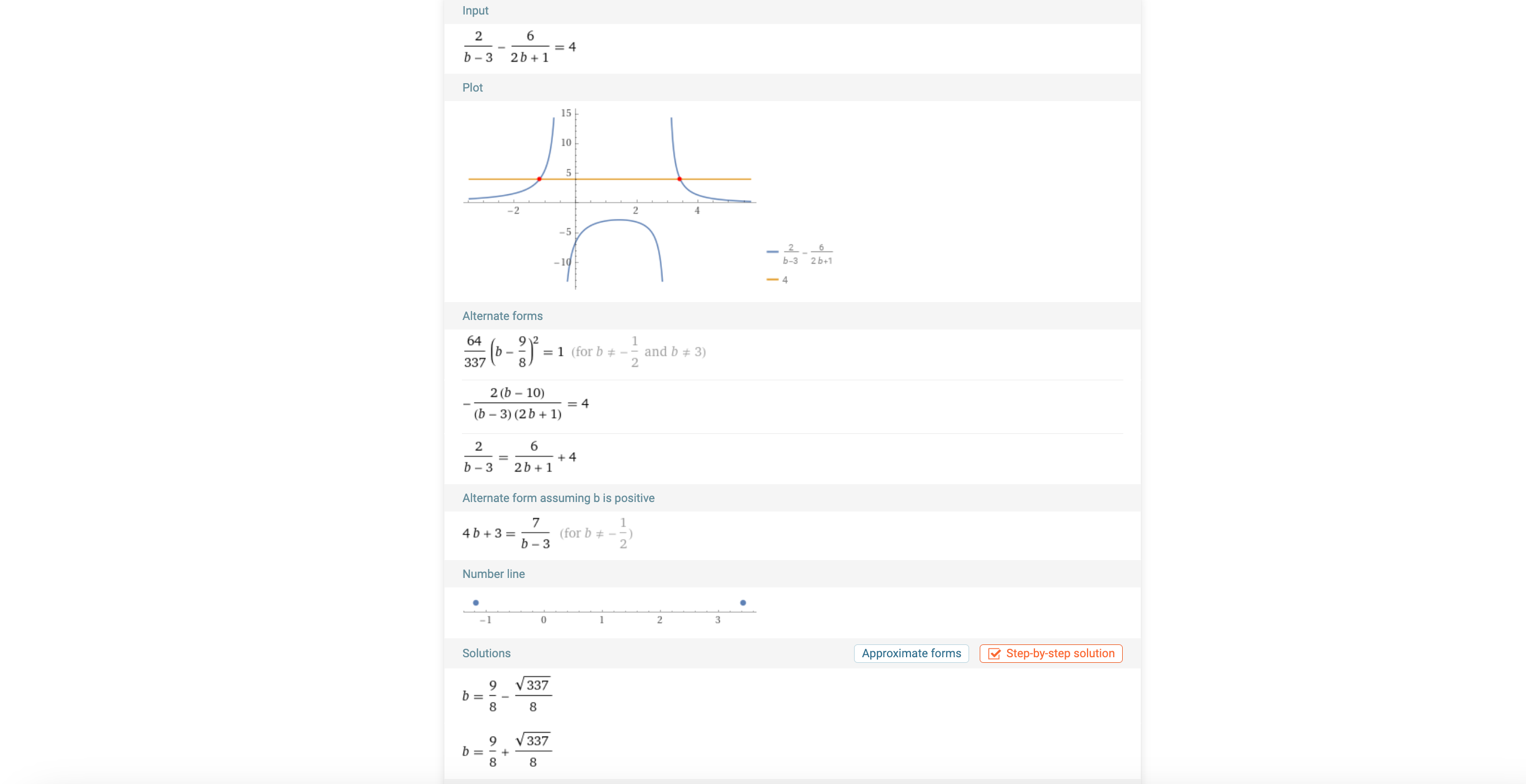
As expected, Wolfram Alpha solved both problems, showcasing its ability to handle different problems and provide precise answers quickly.
Julius works pretty similarly to the other AI tools on this list. That said, the highlight of this platform is that it has a built-in community forum, which users can use to discuss their prompts, results, or even issues they might be facing with the platform. Its active user base helps you quickly exchange ideas and receive feedback or advice. The platform's default version uses a combination of GPT-4 and Calude-3, based on whichever model best suits the prompt you input.
We tested the platform's accuracy by submitting the same problems that we did with the other AI tools. When submitting your prompt, you have the option of typing your question or uploading an image or a Google Sheet.
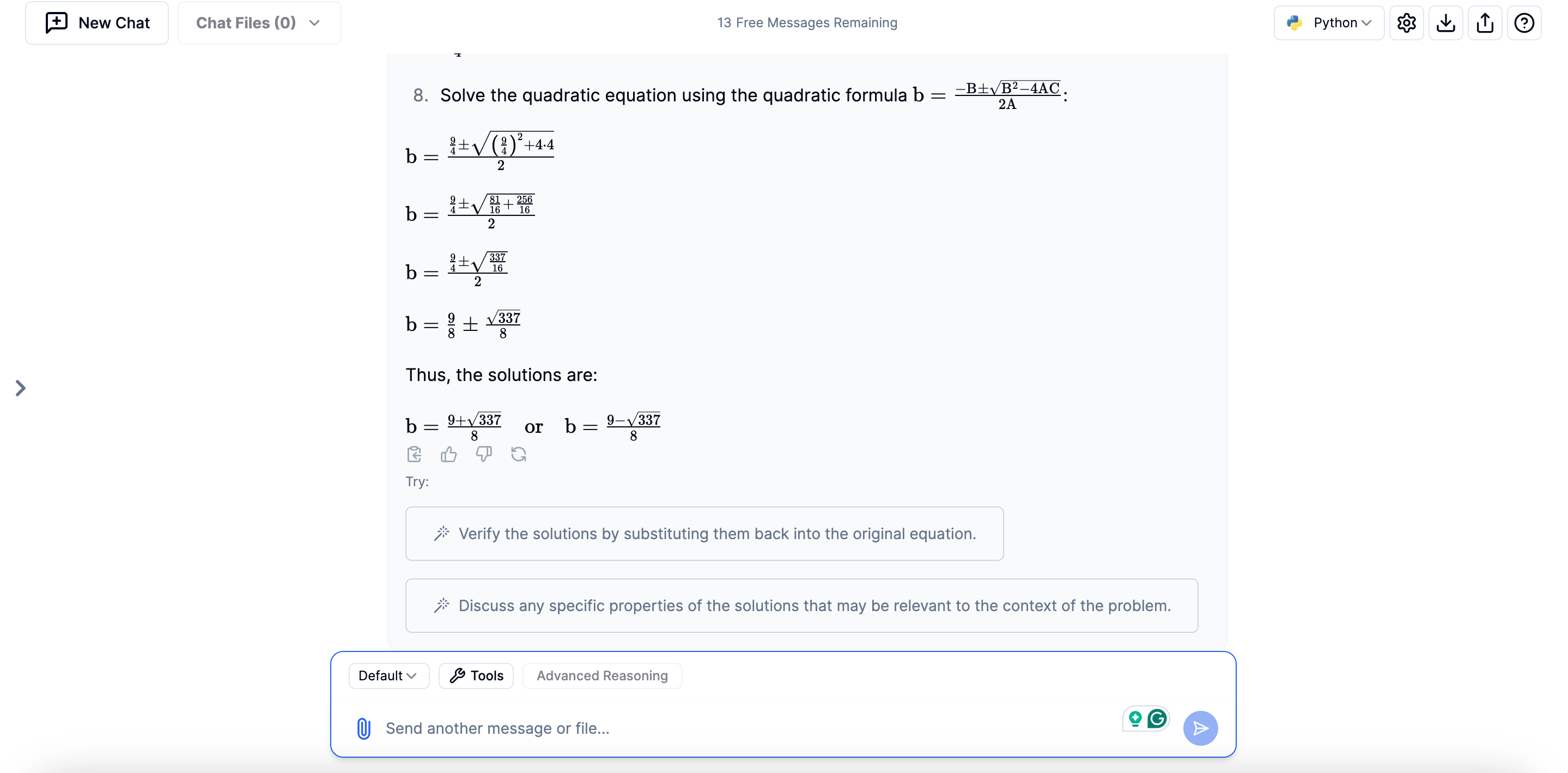
Julius provided correct solutions and offered options to help users verify the solution.
One of the oldest AI platforms, Microsoft's MathSolver is a great option if you want a tool capable of providing free step-by-step solutions to calculus, algebra, and other math problems. Here's how it fared when we submitted our math problems.
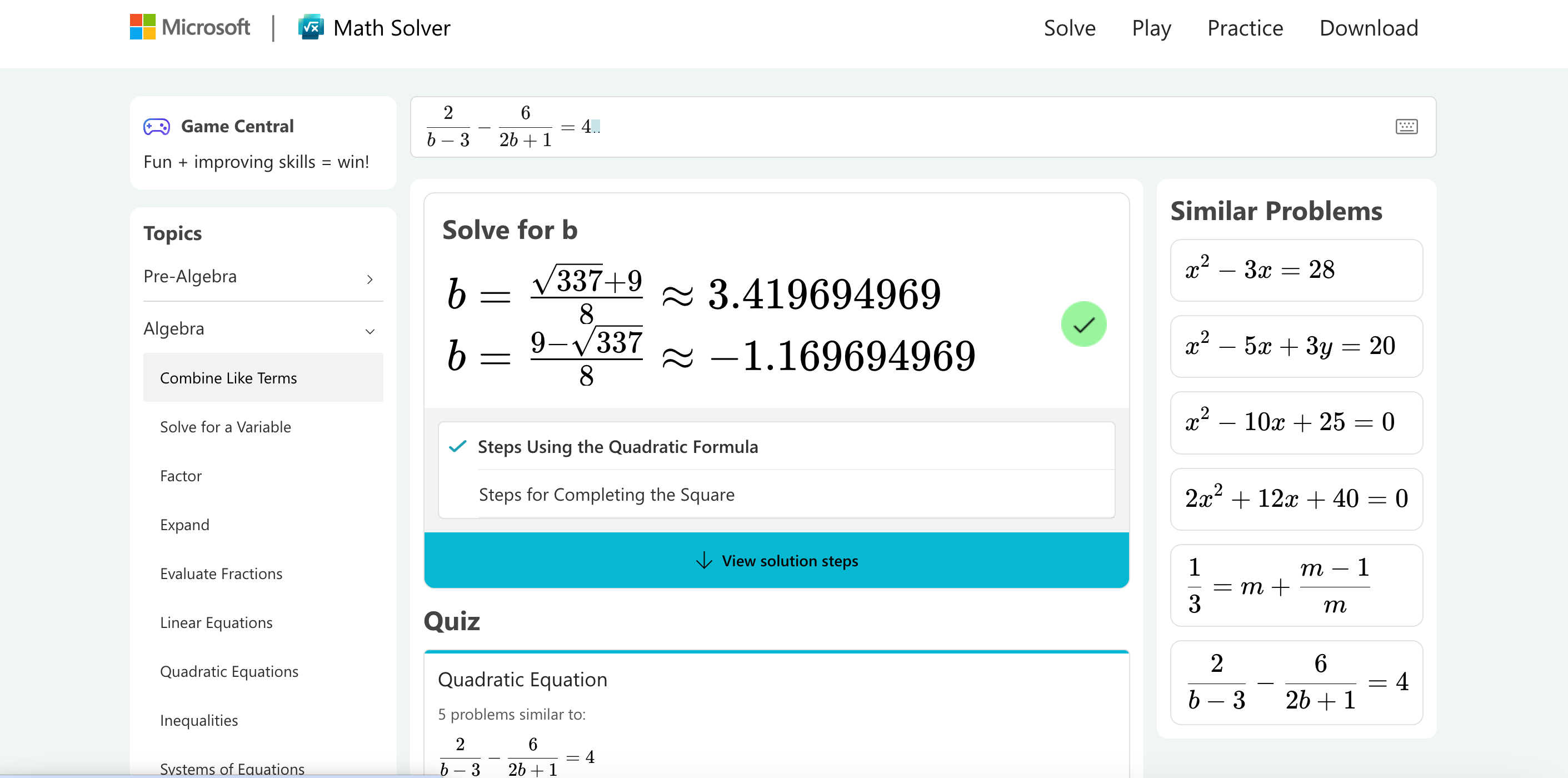
Microsoft's MathSolver provided the correct answers, and you can view the steps to the solution, take a quiz, solve similar problems, and more. This can be a great way to practice and perfect your understanding of different concepts.
Symbolab allows you to practice your math skills via quizzes, track your progress, and provide solutions to mathematical problems of different types, including calculus, fractions, trigonometry, and more. You can also use the Digital Notebook feature to keep track of any math problems you solve and share them with your friends. Another highlight of this platform is that educators can use the tool to create a virtual classroom, generate assessments, and share feedback, among other things.
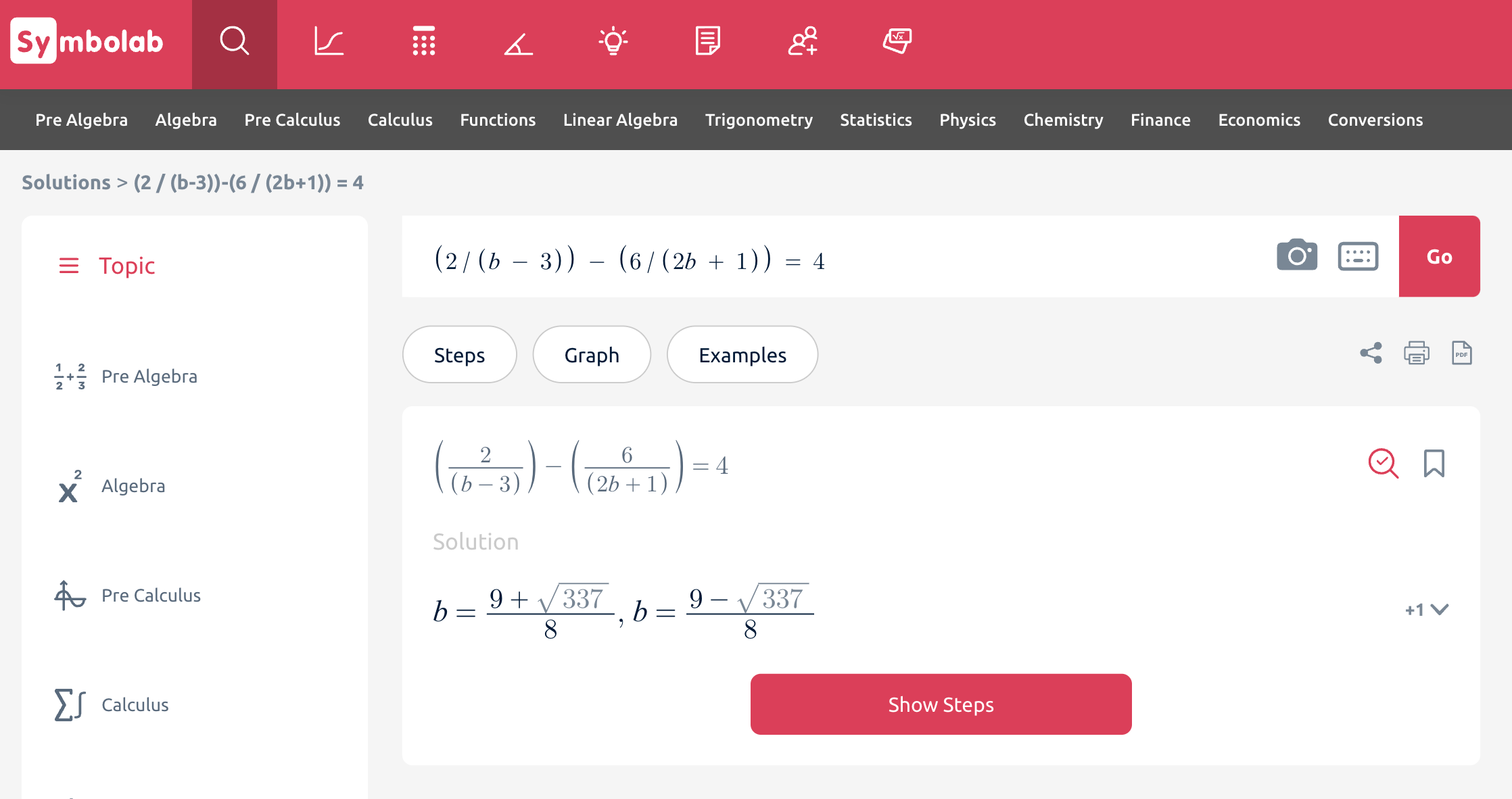
The platform not only displays the answer but also lets you view a breakdown of the steps involved in solving the problem. You can also share the answers and steps via email or social media or print them for reference.
Anthropic launched its Claude 3 AI models in March 2024. Anthropic stated that Claude Opus, the most advanced Claude 3 model, outperforms comparable AI tools on most benchmarks for AI systems, including basic mathematics, undergraduate-level expert knowledge, and graduate-level expert reasoning. To test the platform's accuracy and ease of use, we submitted our two math problems. Here's how the platform performed:

While Claude initially got the answer wrong, probing it and requesting further clarification led to a correct solution.

Remember that we used the free version of Claude to solve this problem; subscribing to Opus (its more advanced model) is recommended if you want to take advantage of Claude's more advanced problem-solving capabilities.
Given that Claude got the previous problem wrong, our second, more basic fraction-based problem will indicate if the AI's performance was an anomaly or part of a consistent pattern.

As you can see, Claude correctly solved this problem and provided a detailed step-by-step breakdown of how it arrived at the answer.
GPT-4 can solve problems with far greater accuracy than its predecessor, GPT-3.5. If you're using the free version of ChatGPT, you'll likely only have access to GPT 3.5 and GPT-4o . However, for $20 per month, you can subscribe to the Plus model, which gives you access to GPT-4 and allows you to input five times the number of messages per day compared to the free version. That said, let's check how it performs with math problems.

In both cases, GPT-4o provided the correct answer with a detailed breakdown of the steps. While the platform is free, unlike other models, it does not have a quiz feature or a community forum.
These AI tools offer unique features and capabilities that make them a good option for math problems. Ultimately, the best way to pick a tool is by testing different models to determine which platform best fits your preferences and learning needs.
Freshman requirements
- Subject requirement (A-G)
- GPA requirement
- Admission by exception
- English language proficiency
- UC graduation requirements
Additional information for
- California residents
- Out-of-state students
- Home-schooled students
Transfer requirements
- Understanding UC transfer
- Preparing to transfer
- UC transfer programs
- Transfer planning tools
International applicants
- Applying for admission
- English language proficiency (TOEFL/IELTS)
- Passports & visas
- Living accommodations
- Health care & insurance
AP & Exam credits
Applying as a freshman
- Filling out the application
- Dates & deadlines
Personal insight questions
- How applications are reviewed
- After you apply
Applying as a transfer
Types of aid
- Grants & scholarships
- Jobs & work-study
- California DREAM Loan Program
- Middle Class Scholarship Program
- Blue and Gold Opportunity Plan
- Native American Opportunity Plan
- Who can get financial aid
- How aid works
- Estimate your aid
Apply for financial aid
- Cal Dream Act application tips
- Tuition & cost of attendance
- Glossary & resources
- Santa Barbara
- Campus program & support services
- Check majors
- Freshman admit data
- Transfer admit data
- Native American Opportunity Plan
- You will have 8 questions to choose from. You must respond to only 4 of the 8 questions.
- Each response is limited to a maximum of 350 words.
- Which questions you choose to answer is entirely up to you. However, you should select questions that are most relevant to your experience and that best reflect your individual circumstances.
Keep in mind
- All questions are equal. All are given equal consideration in the application review process, which means there is no advantage or disadvantage to choosing certain questions over others.
- There is no right or wrong way to answer these questions. It’s about getting to know your personality, background, interests and achievements in your own unique voice.
- Use the additional comments field if there are issues you'd like to address that you didn't have the opportunity to discuss elsewhere on the application. This shouldn't be an essay, but rather a place to note unusual circumstances or anything that might be unclear in other parts of the application. You may use the additional comments field to note extraordinary circumstances related to COVID-19, if necessary.
Questions & guidance
Remember, the personal insight questions are just that—personal. Which means you should use our guidance for each question just as a suggestion in case you need help. The important thing is expressing who you are, what matters to you and what you want to share with UC.
1. Describe an example of your leadership experience in which you have positively influenced others, helped resolve disputes or contributed to group efforts over time. Things to consider: A leadership role can mean more than just a title. It can mean being a mentor to others, acting as the person in charge of a specific task, or taking the lead role in organizing an event or project. Think about what you accomplished and what you learned from the experience. What were your responsibilities?
Did you lead a team? How did your experience change your perspective on leading others? Did you help to resolve an important dispute at your school, church, in your community or an organization? And your leadership role doesn't necessarily have to be limited to school activities. For example, do you help out or take care of your family? 2. Every person has a creative side, and it can be expressed in many ways: problem solving, original and innovative thinking, and artistically, to name a few. Describe how you express your creative side. Things to consider: What does creativity mean to you? Do you have a creative skill that is important to you? What have you been able to do with that skill? If you used creativity to solve a problem, what was your solution? What are the steps you took to solve the problem?
How does your creativity influence your decisions inside or outside the classroom? Does your creativity relate to your major or a future career? 3. What would you say is your greatest talent or skill? How have you developed and demonstrated that talent over time? Things to consider: If there is a talent or skill that you're proud of, this is the time to share it.You don't necessarily have to be recognized or have received awards for your talent (although if you did and you want to talk about it, feel free to do so). Why is this talent or skill meaningful to you?
Does the talent come naturally or have you worked hard to develop this skill or talent? Does your talent or skill allow you opportunities in or outside the classroom? If so, what are they and how do they fit into your schedule? 4. Describe how you have taken advantage of a significant educational opportunity or worked to overcome an educational barrier you have faced. Things to consider: An educational opportunity can be anything that has added value to your educational experience and better prepared you for college. For example, participation in an honors or academic enrichment program, or enrollment in an academy that's geared toward an occupation or a major, or taking advanced courses that interest you; just to name a few.
If you choose to write about educational barriers you've faced, how did you overcome or strive to overcome them? What personal characteristics or skills did you call on to overcome this challenge? How did overcoming this barrier help shape who you are today? 5. Describe the most significant challenge you have faced and the steps you have taken to overcome this challenge. How has this challenge affected your academic achievement? Things to consider: A challenge could be personal, or something you have faced in your community or school. Why was the challenge significant to you? This is a good opportunity to talk about any obstacles you've faced and what you've learned from the experience. Did you have support from someone else or did you handle it alone?
If you're currently working your way through a challenge, what are you doing now, and does that affect different aspects of your life? For example, ask yourself, How has my life changed at home, at my school, with my friends or with my family? 6. Think about an academic subject that inspires you. Describe how you have furthered this interest inside and/or outside of the classroom. Things to consider: Many students have a passion for one specific academic subject area, something that they just can't get enough of. If that applies to you, what have you done to further that interest? Discuss how your interest in the subject developed and describe any experience you have had inside and outside the classroom such as volunteer work, internships, employment, summer programs, participation in student organizations and/or clubs and what you have gained from your involvement.
Has your interest in the subject influenced you in choosing a major and/or future career? Have you been able to pursue coursework at a higher level in this subject (honors, AP, IB, college or university work)? Are you inspired to pursue this subject further at UC, and how might you do that?
7. What have you done to make your school or your community a better place? Things to consider: Think of community as a term that can encompass a group, team or a place like your high school, hometown or home. You can define community as you see fit, just make sure you talk about your role in that community. Was there a problem that you wanted to fix in your community?
Why were you inspired to act? What did you learn from your effort? How did your actions benefit others, the wider community or both? Did you work alone or with others to initiate change in your community? 8. Beyond what has already been shared in your application, what do you believe makes you a strong candidate for admissions to the University of California? Things to consider: If there's anything you want us to know about you but didn't find a question or place in the application to tell us, now's your chance. What have you not shared with us that will highlight a skill, talent, challenge or opportunity that you think will help us know you better?
From your point of view, what do you feel makes you an excellent choice for UC? Don't be afraid to brag a little.
Writing tips
Start early..
Give yourself plenty of time for preparation, careful composition and revisions.
Write persuasively.
Making a list of accomplishments, activities, awards or work will lessen the impact of your words. Expand on a topic by using specific, concrete examples to support the points you want to make.
Use “I” statements.
Talk about yourself so that we can get to know your personality, talents, accomplishments and potential for success on a UC campus. Use “I” and “my” statements in your responses.
Proofread and edit.
Although you will not be evaluated on grammar, spelling or sentence structure, you should proofread your work and make sure your writing is clear. Grammatical and spelling errors can be distracting to the reader and get in the way of what you’re trying to communicate.
Solicit feedback.
Your answers should reflect your own ideas and be written by you alone, but others — family, teachers and friends can offer valuable suggestions. Ask advice of whomever you like, but do not plagiarize from sources in print or online and do not use anyone's words, published or unpublished, but your own.
Copy and paste.
Once you are satisfied with your answers, save them in plain text (ASCII) and paste them into the space provided in the application. Proofread once more to make sure no odd characters or line breaks have appeared.
This is one of many pieces of information we consider in reviewing your application. Your responses can only add value to the application. An admission decision will not be based on this section alone.
Need more help?
Download our worksheets:
- English [PDF]
- Spanish [PDF]

IMAGES
VIDEO
COMMENTS
Problem-Solving Prior to Instruction" (EDU-2019-3907). Questionnaires to assess students' incoming cognitive and motivational characteristics (administered before the problem-solving phase) Effort Regulation (5-point Likert scale from "strongly disagree" to "strongly agree") 1.
The below-mentioned scenarios are perfect for implementing problem-solving skills simply by allowing open discussions and contributions by students. 1. Uninvited Guests. You have arranged a party at your home after successfully winning the competition at the Science Fair. You invite everyone involved in the project however, one of your friends ...
learning is bound to strengthen students' mathematical problem-solving skills. Keywords: assessment strategies, mathematical problem-solving skills, 21st century skills. INTRODUCTION . Following the movement of problem-solving in the United States of America (USA) as it expanded worldwide in the 1980s, problem-solving became the
This allows students to be lifelong learners and more flexible and adaptable in the future. -Dr. Steven Rougas, Director of the Doctoring Program, Alpert Medical School. Problem solving is a "goal-oriented" process that includes creating and manipulating problems as mental models (Jonassen, 2000). Brown faculty from a variety of disciplines ...
The Problem-Solving Style Questionnaire (PSSQ) is a self -report questionnaire that measures four dimensions of problem-solving style: sensing, intuitive, feeling, and thinking. It was developed by Thomas Cassidy and Christopher Long in 1996, based on Carl Jung 's theory of psychological types.
Test Your Problem-Solving Skills. Personalize Your Emails Personalize your monthly updates from BrainFacts.org by choosing the topics that you care about most! Sign Up Find a Neuroscientist Engage local scientists to educate your community about the brain. ...
2. Problem-solving as a group. Have your students create and decorate a medium-sized box with a slot in the top. Label the box "The Problem-Solving Box.". Invite students to anonymously write down and submit any problem or issue they might be having at school or at home, ones that they can't seem to figure out on their own.
in this process, problem posing, is revealed and added by Gonzales (1994) who claims that it is one of the most significant and critical ways to acquire a deeper comprehension of the PS process. In this step, the student amends the problem just solved to obtain a similar one. 1.2. Mathematical Problem-solving
In a new study, researchers examined how the presentation and format of practice questions influences students' problem-solving performance. The study revealed that mixed problem sets are better than questions arranged by topic. There are two types of question practice teachers can give their students. The first, blocked practice, involves ...
Problem Solving in STEM. Solving problems is a key component of many science, math, and engineering classes. If a goal of a class is for students to emerge with the ability to solve new kinds of problems or to use new problem-solving techniques, then students need numerous opportunities to develop the skills necessary to approach and answer ...
A number of research projects in educational assessment reveal that students struggle when it comes to accomplishing problem-solving tasks in Mathematics. Such a struggle is primarily due to the ...
Home practice will make progress toward meeting individual language goals much faster. Speech-Language Pathologists (SLPs) are only able to see students/clients 30-60 mins (or less) per week. This is not enough time or practice for someone to handle Problem solving scenarios. Every day that your loved one goes without practice it becomes more ...
Problem solving skills, student perception of skills, confidence, transfer. Introduction In his Partnership for 21st Century Learning Framework, Ken Kay (2010) invokes certain key skills today's students should develop: critical thinking and problem solving, creativity and innovation, and collaboration and communication. Problem solving skills
to practice self-assessment by: Building students' habits of asking themselves questions they are reading, writing, or solving problems. Providing support for students monitor their learning and assess their progress. Encouraging students to act on their self-assessment and identify what their next steps might be. Practice in Action.
A thinking skills questionnaire QUESTIONS Thinking skills and problem-solving skills are critically essential as we face an uncertain and opportunity-filled future. As lower-skilled and repetitive jobs disappear (e.g. cleaners, factory workers, laundry workers, etc) and working from home becomes more popular, new types of jobs are being created
Self-assessment, in the education framework, is a methodology that motivates students to play an active role in reviewing their performance. It is defined as "the evaluation or judgment of 'the worth' of one's performance and the identification of one's strengths and weaknesses with a view to improving one's learning outcomes". The goal of this research is to study the ...
3. Lateral thinking problems. Lateral thinking problems require creative thinking with an indirect approach. These questions require logic and careful thought to solve. The most notable example of a lateral thinking problem is the classic Monty Hall problem. Here are two examples of lateral thinking problems kids can try to solve.
Dereli-İman, E. (2013). The social problem-solving questionnaire: Evaluation of psychometric properties among Turkish primary school students. Egitim ... adaptation of the social problem-solving scale into Turkish for students in the first stage of primary school, and it analyzes the relationship between social problem solving and aggression.
The game contains problem-solving questions, grouped into three levels of difficulty, and was assessed for its gender-related impact on students' interest and problem-solving skills.
By honing their problem-solving abilities, we're preparing kids to face the unforeseen challenges of the world outside. Enhances Cognitive Growth: Otherwise known as cognitive development. Problem-solving isn't just about finding solutions. It's about thinking critically, analyzing situations, and making decisions.
Previous studies on quantitative physics problem solving have been concerned with students' using equations simply as a numerical computational tool. The current study started from a research question: "How do students solve conceptual physics questions in simulation-based formative assessments?" In the study, three first-year college students' interview data were analyzed to ...
Download scientific diagram | Problem Solving Questionnaire from publication: Promoting social inclusion: A structured intervention for enhancing interpersonal problem-solving skills in children ...
Collaborative problem-solving: Use PBL in a group setting to allow students to share and discuss various strategies for problem-solving. • Step 5: Integrate continuous assessment. Feedback on misconceptions: Provide continuous feedback, especially targeting misconceptions about area and perimeter, and argumentation during problem-solving.
The survey found that 81% say teachers feel responsible for their students' mental health, and another 77% believe it's also their duty to teach students about mental health and relevant self-care strategies. A vast majority of respondents (89%) agree that they don't have enough resources at their disposal to help students deal with mental ...
By Michalis Gkontas, CEO of NXTLVL — June 03, 2024. The inaugural NXTLVL Problem-Solving Olympiad brought students together online for a day of spirited competition, pushing them to their true ...
The Algebra 1 course, often taught in the 9th grade, covers Linear equations, inequalities, functions, and graphs; Systems of equations and inequalities; Extension of the concept of a function; Exponential models; and Quadratic equations, functions, and graphs. Khan Academy's Algebra 1 course is built to deliver a comprehensive, illuminating, engaging, and Common Core aligned experience!
The Test Questions. Thetawise. WolframAlpha. Julius. Microsoft MathSolver. Symbolab. Claude. ChatGPT-4o. While OpenAI's ChatGPT is one of the most widely known AI tools, there are numerous other platforms that students can use to improve their math skills.
See how to get involved: Complete the challenge and get a free Data + Movies t-shirt. join the challenge. Students — double the fun by participating in our Iron Viz: Student Edition competition. learn more. Instructors — download our extra credit opportunity for your classroom. learn more.
Remember, the personal insight questions are just that—personal. Which means you should use our guidance for each question just as a suggestion in case you need help. The important thing is expressing who you are, what matters to you and what you want to share with UC. 1. Describe an example of your leadership experience in which you have ...
Darmawan & Ramlah's research (2021) with the article title analysis of students' mathematical problem-solving abilities in solving TIMSS questions based on Polya stages. Based on the research above, it can be concluded that research related to students' problem-solving abilities is often the object of research.