make a hypothesis drawing

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

How to Write a Great Hypothesis

Hypothesis Definition, Format, Examples, and Tips

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Amy Morin, LCSW, is a psychotherapist and international bestselling author. Her books, including "13 Things Mentally Strong People Don't Do," have been translated into more than 40 languages. Her TEDx talk,  "The Secret of Becoming Mentally Strong," is one of the most viewed talks of all time.

Verywell / Alex Dos Diaz

• The Scientific Method

Hypothesis Format

Falsifiability of a hypothesis.

• Operationalization

Hypothesis Types

Hypotheses examples.

• Collecting Data

A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process.

Consider a study designed to examine the relationship between sleep deprivation and test performance. The hypothesis might be: "This study is designed to assess the hypothesis that sleep-deprived people will perform worse on a test than individuals who are not sleep-deprived."

At a Glance

A hypothesis is crucial to scientific research because it offers a clear direction for what the researchers are looking to find. This allows them to design experiments to test their predictions and add to our scientific knowledge about the world. This article explores how a hypothesis is used in psychology research, how to write a good hypothesis, and the different types of hypotheses you might use.

The Hypothesis in the Scientific Method

In the scientific method , whether it involves research in psychology, biology, or some other area, a hypothesis represents what the researchers think will happen in an experiment. The scientific method involves the following steps:

• Forming a question
• Performing background research
• Creating a hypothesis
• Designing an experiment
• Collecting data
• Analyzing the results
• Drawing conclusions
• Communicating the results

The hypothesis is a prediction, but it involves more than a guess. Most of the time, the hypothesis begins with a question which is then explored through background research. At this point, researchers then begin to develop a testable hypothesis.

Unless you are creating an exploratory study, your hypothesis should always explain what you  expect  to happen.

In a study exploring the effects of a particular drug, the hypothesis might be that researchers expect the drug to have some type of effect on the symptoms of a specific illness. In psychology, the hypothesis might focus on how a certain aspect of the environment might influence a particular behavior.

Remember, a hypothesis does not have to be correct. While the hypothesis predicts what the researchers expect to see, the goal of the research is to determine whether this guess is right or wrong. When conducting an experiment, researchers might explore numerous factors to determine which ones might contribute to the ultimate outcome.

In many cases, researchers may find that the results of an experiment  do not  support the original hypothesis. When writing up these results, the researchers might suggest other options that should be explored in future studies.

In many cases, researchers might draw a hypothesis from a specific theory or build on previous research. For example, prior research has shown that stress can impact the immune system. So a researcher might hypothesize: "People with high-stress levels will be more likely to contract a common cold after being exposed to the virus than people who have low-stress levels."

In other instances, researchers might look at commonly held beliefs or folk wisdom. "Birds of a feather flock together" is one example of folk adage that a psychologist might try to investigate. The researcher might pose a specific hypothesis that "People tend to select romantic partners who are similar to them in interests and educational level."

Elements of a Good Hypothesis

So how do you write a good hypothesis? When trying to come up with a hypothesis for your research or experiments, ask yourself the following questions:

• Is your hypothesis based on your research on a topic?
• Can your hypothesis be tested?
• Does your hypothesis include independent and dependent variables?

Before you come up with a specific hypothesis, spend some time doing background research. Once you have completed a literature review, start thinking about potential questions you still have. Pay attention to the discussion section in the  journal articles you read . Many authors will suggest questions that still need to be explored.

How to Formulate a Good Hypothesis

To form a hypothesis, you should take these steps:

• Collect as many observations about a topic or problem as you can.
• Evaluate these observations and look for possible causes of the problem.
• Create a list of possible explanations that you might want to explore.
• After you have developed some possible hypotheses, think of ways that you could confirm or disprove each hypothesis through experimentation. This is known as falsifiability.

In the scientific method ,  falsifiability is an important part of any valid hypothesis. In order to test a claim scientifically, it must be possible that the claim could be proven false.

Students sometimes confuse the idea of falsifiability with the idea that it means that something is false, which is not the case. What falsifiability means is that  if  something was false, then it is possible to demonstrate that it is false.

One of the hallmarks of pseudoscience is that it makes claims that cannot be refuted or proven false.

The Importance of Operational Definitions

A variable is a factor or element that can be changed and manipulated in ways that are observable and measurable. However, the researcher must also define how the variable will be manipulated and measured in the study.

Operational definitions are specific definitions for all relevant factors in a study. This process helps make vague or ambiguous concepts detailed and measurable.

For example, a researcher might operationally define the variable " test anxiety " as the results of a self-report measure of anxiety experienced during an exam. A "study habits" variable might be defined by the amount of studying that actually occurs as measured by time.

These precise descriptions are important because many things can be measured in various ways. Clearly defining these variables and how they are measured helps ensure that other researchers can replicate your results.

Replicability

One of the basic principles of any type of scientific research is that the results must be replicable.

Replication means repeating an experiment in the same way to produce the same results. By clearly detailing the specifics of how the variables were measured and manipulated, other researchers can better understand the results and repeat the study if needed.

Some variables are more difficult than others to define. For example, how would you operationally define a variable such as aggression ? For obvious ethical reasons, researchers cannot create a situation in which a person behaves aggressively toward others.

To measure this variable, the researcher must devise a measurement that assesses aggressive behavior without harming others. The researcher might utilize a simulated task to measure aggressiveness in this situation.

Hypothesis Checklist

• Does your hypothesis focus on something that you can actually test?
• Does your hypothesis include both an independent and dependent variable?
• Can you manipulate the variables?
• Can your hypothesis be tested without violating ethical standards?

The hypothesis you use will depend on what you are investigating and hoping to find. Some of the main types of hypotheses that you might use include:

• Simple hypothesis : This type of hypothesis suggests there is a relationship between one independent variable and one dependent variable.
• Complex hypothesis : This type suggests a relationship between three or more variables, such as two independent and dependent variables.
• Null hypothesis : This hypothesis suggests no relationship exists between two or more variables.
• Alternative hypothesis : This hypothesis states the opposite of the null hypothesis.
• Statistical hypothesis : This hypothesis uses statistical analysis to evaluate a representative population sample and then generalizes the findings to the larger group.
• Logical hypothesis : This hypothesis assumes a relationship between variables without collecting data or evidence.

A hypothesis often follows a basic format of "If {this happens} then {this will happen}." One way to structure your hypothesis is to describe what will happen to the  dependent variable  if you change the  independent variable .

The basic format might be: "If {these changes are made to a certain independent variable}, then we will observe {a change in a specific dependent variable}."

A few examples of simple hypotheses:

• "Students who eat breakfast will perform better on a math exam than students who do not eat breakfast."
• "Students who experience test anxiety before an English exam will get lower scores than students who do not experience test anxiety."​
• "Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone."
• "Children who receive a new reading intervention will have higher reading scores than students who do not receive the intervention."

Examples of a complex hypothesis include:

• "People with high-sugar diets and sedentary activity levels are more likely to develop depression."
• "Younger people who are regularly exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces."

Examples of a null hypothesis include:

• "There is no difference in anxiety levels between people who take St. John's wort supplements and those who do not."
• "There is no difference in scores on a memory recall task between children and adults."
• "There is no difference in aggression levels between children who play first-person shooter games and those who do not."

Examples of an alternative hypothesis:

• "People who take St. John's wort supplements will have less anxiety than those who do not."
• "Adults will perform better on a memory task than children."
• "Children who play first-person shooter games will show higher levels of aggression than children who do not." 

Collecting Data on Your Hypothesis

Once a researcher has formed a testable hypothesis, the next step is to select a research design and start collecting data. The research method depends largely on exactly what they are studying. There are two basic types of research methods: descriptive research and experimental research.

Descriptive Research Methods

Descriptive research such as  case studies ,  naturalistic observations , and surveys are often used when  conducting an experiment is difficult or impossible. These methods are best used to describe different aspects of a behavior or psychological phenomenon.

Once a researcher has collected data using descriptive methods, a  correlational study  can examine how the variables are related. This research method might be used to investigate a hypothesis that is difficult to test experimentally.

Experimental Research Methods

Experimental methods  are used to demonstrate causal relationships between variables. In an experiment, the researcher systematically manipulates a variable of interest (known as the independent variable) and measures the effect on another variable (known as the dependent variable).

Unlike correlational studies, which can only be used to determine if there is a relationship between two variables, experimental methods can be used to determine the actual nature of the relationship—whether changes in one variable actually  cause  another to change.

The hypothesis is a critical part of any scientific exploration. It represents what researchers expect to find in a study or experiment. In situations where the hypothesis is unsupported by the research, the research still has value. Such research helps us better understand how different aspects of the natural world relate to one another. It also helps us develop new hypotheses that can then be tested in the future.

Thompson WH, Skau S. On the scope of scientific hypotheses .  R Soc Open Sci . 2023;10(8):230607. doi:10.1098/rsos.230607

Taran S, Adhikari NKJ, Fan E. Falsifiability in medicine: what clinicians can learn from Karl Popper [published correction appears in Intensive Care Med. 2021 Jun 17;:].  Intensive Care Med . 2021;47(9):1054-1056. doi:10.1007/s00134-021-06432-z

Eyler AA. Research Methods for Public Health . 1st ed. Springer Publishing Company; 2020. doi:10.1891/9780826182067.0004

Nosek BA, Errington TM. What is replication ?  PLoS Biol . 2020;18(3):e3000691. doi:10.1371/journal.pbio.3000691

Aggarwal R, Ranganathan P. Study designs: Part 2 - Descriptive studies .  Perspect Clin Res . 2019;10(1):34-36. doi:10.4103/picr.PICR_154_18

Nevid J. Psychology: Concepts and Applications. Wadworth, 2013.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

How to Develop a Good Research Hypothesis

The story of a research study begins by asking a question. Researchers all around the globe are asking curious questions and formulating research hypothesis. However, whether the research study provides an effective conclusion depends on how well one develops a good research hypothesis. Research hypothesis examples could help researchers get an idea as to how to write a good research hypothesis.

This blog will help you understand what is a research hypothesis, its characteristics and, how to formulate a research hypothesis

Table of Contents

What is Hypothesis?

Hypothesis is an assumption or an idea proposed for the sake of argument so that it can be tested. It is a precise, testable statement of what the researchers predict will be outcome of the study.  Hypothesis usually involves proposing a relationship between two variables: the independent variable (what the researchers change) and the dependent variable (what the research measures).

What is a Research Hypothesis?

Research hypothesis is a statement that introduces a research question and proposes an expected result. It is an integral part of the scientific method that forms the basis of scientific experiments. Therefore, you need to be careful and thorough when building your research hypothesis. A minor flaw in the construction of your hypothesis could have an adverse effect on your experiment. In research, there is a convention that the hypothesis is written in two forms, the null hypothesis, and the alternative hypothesis (called the experimental hypothesis when the method of investigation is an experiment).

Characteristics of a Good Research Hypothesis

As the hypothesis is specific, there is a testable prediction about what you expect to happen in a study. You may consider drawing hypothesis from previously published research based on the theory.

A good research hypothesis involves more effort than just a guess. In particular, your hypothesis may begin with a question that could be further explored through background research.

To help you formulate a promising research hypothesis, you should ask yourself the following questions:

• Is the language clear and focused?
• What is the relationship between your hypothesis and your research topic?
• Is your hypothesis testable? If yes, then how?
• What are the possible explanations that you might want to explore?
• Does your hypothesis include both an independent and dependent variable?
• Can you manipulate your variables without hampering the ethical standards?
• Does your research predict the relationship and outcome?
• Is your research simple and concise (avoids wordiness)?
• Is it clear with no ambiguity or assumptions about the readers’ knowledge
• Is your research observable and testable results?
• Is it relevant and specific to the research question or problem?

The questions listed above can be used as a checklist to make sure your hypothesis is based on a solid foundation. Furthermore, it can help you identify weaknesses in your hypothesis and revise it if necessary.

Source: Educational Hub

How to formulate a research hypothesis.

A testable hypothesis is not a simple statement. It is rather an intricate statement that needs to offer a clear introduction to a scientific experiment, its intentions, and the possible outcomes. However, there are some important things to consider when building a compelling hypothesis.

1. State the problem that you are trying to solve.

Make sure that the hypothesis clearly defines the topic and the focus of the experiment.

2. Try to write the hypothesis as an if-then statement.

Follow this template: If a specific action is taken, then a certain outcome is expected.

3. Define the variables

Independent variables are the ones that are manipulated, controlled, or changed. Independent variables are isolated from other factors of the study.

Dependent variables , as the name suggests are dependent on other factors of the study. They are influenced by the change in independent variable.

4. Scrutinize the hypothesis

Evaluate assumptions, predictions, and evidence rigorously to refine your understanding.

Types of Research Hypothesis

The types of research hypothesis are stated below:

1. Simple Hypothesis

It predicts the relationship between a single dependent variable and a single independent variable.

2. Complex Hypothesis

It predicts the relationship between two or more independent and dependent variables.

3. Directional Hypothesis

It specifies the expected direction to be followed to determine the relationship between variables and is derived from theory. Furthermore, it implies the researcher’s intellectual commitment to a particular outcome.

4. Non-directional Hypothesis

It does not predict the exact direction or nature of the relationship between the two variables. The non-directional hypothesis is used when there is no theory involved or when findings contradict previous research.

5. Associative and Causal Hypothesis

The associative hypothesis defines interdependency between variables. A change in one variable results in the change of the other variable. On the other hand, the causal hypothesis proposes an effect on the dependent due to manipulation of the independent variable.

6. Null Hypothesis

Null hypothesis states a negative statement to support the researcher’s findings that there is no relationship between two variables. There will be no changes in the dependent variable due the manipulation of the independent variable. Furthermore, it states results are due to chance and are not significant in terms of supporting the idea being investigated.

7. Alternative Hypothesis

It states that there is a relationship between the two variables of the study and that the results are significant to the research topic. An experimental hypothesis predicts what changes will take place in the dependent variable when the independent variable is manipulated. Also, it states that the results are not due to chance and that they are significant in terms of supporting the theory being investigated.

Research Hypothesis Examples of Independent and Dependent Variables

Research Hypothesis Example 1 The greater number of coal plants in a region (independent variable) increases water pollution (dependent variable). If you change the independent variable (building more coal factories), it will change the dependent variable (amount of water pollution).

Research Hypothesis Example 2 What is the effect of diet or regular soda (independent variable) on blood sugar levels (dependent variable)? If you change the independent variable (the type of soda you consume), it will change the dependent variable (blood sugar levels)

You should not ignore the importance of the above steps. The validity of your experiment and its results rely on a robust testable hypothesis. Developing a strong testable hypothesis has few advantages, it compels us to think intensely and specifically about the outcomes of a study. Consequently, it enables us to understand the implication of the question and the different variables involved in the study. Furthermore, it helps us to make precise predictions based on prior research. Hence, forming a hypothesis would be of great value to the research. Here are some good examples of testable hypotheses.

More importantly, you need to build a robust testable research hypothesis for your scientific experiments. A testable hypothesis is a hypothesis that can be proved or disproved as a result of experimentation.

Importance of a Testable Hypothesis

To devise and perform an experiment using scientific method, you need to make sure that your hypothesis is testable. To be considered testable, some essential criteria must be met:

• There must be a possibility to prove that the hypothesis is true.
• There must be a possibility to prove that the hypothesis is false.
• The results of the hypothesis must be reproducible.

Without these criteria, the hypothesis and the results will be vague. As a result, the experiment will not prove or disprove anything significant.

What are your experiences with building hypotheses for scientific experiments? What challenges did you face? How did you overcome these challenges? Please share your thoughts with us in the comments section.

Frequently Asked Questions

The steps to write a research hypothesis are: 1. Stating the problem: Ensure that the hypothesis defines the research problem 2. Writing a hypothesis as an 'if-then' statement: Include the action and the expected outcome of your study by following a ‘if-then’ structure. 3. Defining the variables: Define the variables as Dependent or Independent based on their dependency to other factors. 4. Scrutinizing the hypothesis: Identify the type of your hypothesis

Hypothesis testing is a statistical tool which is used to make inferences about a population data to draw conclusions for a particular hypothesis.

Hypothesis in statistics is a formal statement about the nature of a population within a structured framework of a statistical model. It is used to test an existing hypothesis by studying a population.

Research hypothesis is a statement that introduces a research question and proposes an expected result. It forms the basis of scientific experiments.

The different types of hypothesis in research are: • Null hypothesis: Null hypothesis is a negative statement to support the researcher’s findings that there is no relationship between two variables. • Alternate hypothesis: Alternate hypothesis predicts the relationship between the two variables of the study. • Directional hypothesis: Directional hypothesis specifies the expected direction to be followed to determine the relationship between variables. • Non-directional hypothesis: Non-directional hypothesis does not predict the exact direction or nature of the relationship between the two variables. • Simple hypothesis: Simple hypothesis predicts the relationship between a single dependent variable and a single independent variable. • Complex hypothesis: Complex hypothesis predicts the relationship between two or more independent and dependent variables. • Associative and casual hypothesis: Associative and casual hypothesis predicts the relationship between two or more independent and dependent variables. • Empirical hypothesis: Empirical hypothesis can be tested via experiments and observation. • Statistical hypothesis: A statistical hypothesis utilizes statistical models to draw conclusions about broader populations.

Wow! You really simplified your explanation that even dummies would find it easy to comprehend. Thank you so much.

Thanks a lot for your valuable guidance.

I enjoy reading the post. Hypotheses are actually an intrinsic part in a study. It bridges the research question and the methodology of the study.

Useful piece!

This is awesome.Wow.

It very interesting to read the topic, can you guide me any specific example of hypothesis process establish throw the Demand and supply of the specific product in market

Nicely explained

It is really a useful for me Kindly give some examples of hypothesis

It was a well explained content ,can you please give me an example with the null and alternative hypothesis illustrated

clear and concise. thanks.

So Good so Amazing

Good to learn

Thanks a lot for explaining to my level of understanding

Explained well and in simple terms. Quick read! Thank you

It awesome. It has really positioned me in my research project

Rate this article Cancel Reply

Your email address will not be published.

Enago Academy's Most Popular Articles

• Reporting Research

Choosing the Right Analytical Approach: Thematic analysis vs. content analysis for data interpretation

In research, choosing the right approach to understand data is crucial for deriving meaningful insights.…

Comparing Cross Sectional and Longitudinal Studies: 5 steps for choosing the right approach

The process of choosing the right research design can put ourselves at the crossroads of…

• Industry News

COPE Forum Discussion Highlights Challenges and Urges Clarity in Institutional Authorship Standards

The COPE forum discussion held in December 2023 initiated with a fundamental question — is…

• Career Corner

Unlocking the Power of Networking in Academic Conferences

Embarking on your first academic conference experience? Fear not, we got you covered! Academic conferences…

Research Recommendations – Guiding policy-makers for evidence-based decision making

Research recommendations play a crucial role in guiding scholars and researchers toward fruitful avenues of…

Choosing the Right Analytical Approach: Thematic analysis vs. content analysis for…

Comparing Cross Sectional and Longitudinal Studies: 5 steps for choosing the right…

How to Design Effective Research Questionnaires for Robust Findings

Sign-up to read more

Subscribe for free to get unrestricted access to all our resources on research writing and academic publishing including:

• 2000+ blog articles
• 50+ Webinars
• 10+ Expert podcasts
• 50+ Infographics
• 10+ Checklists
• Research Guides

We hate spam too. We promise to protect your privacy and never spam you.

I am looking for Editing/ Proofreading services for my manuscript Tentative date of next journal submission:

As a researcher, what do you consider most when choosing an image manipulation detector?

Hypothesis Maker Online

Looking for a hypothesis maker? This online tool for students will help you formulate a beautiful hypothesis quickly, efficiently, and for free.

Are you looking for an effective hypothesis maker online? Worry no more; try our online tool for students and formulate your hypothesis within no time.

• 🔎 How to Use the Tool?
• ⚗️ What Is a Hypothesis in Science?

👍 What Does a Good Hypothesis Mean?

• 🧭 Steps to Making a Good Hypothesis

🔗 References

📄 hypothesis maker: how to use it.

Our hypothesis maker is a simple and efficient tool you can access online for free.

If you want to create a research hypothesis quickly, you should fill out the research details in the given fields on the hypothesis generator.

Below are the fields you should complete to generate your hypothesis:

• Who or what is your research based on? For instance, the subject can be research group 1.
• What does the subject (research group 1) do?
• What does the subject affect? - This shows the predicted outcome, which is the object.
• Who or what will be compared with research group 1? (research group 2).

Once you fill the in the fields, you can click the ‘Make a hypothesis’ tab and get your results.

⚗️ What Is a Hypothesis in the Scientific Method?

A hypothesis is a statement describing an expectation or prediction of your research through observation.

It is similar to academic speculation and reasoning that discloses the outcome of your scientific test . An effective hypothesis, therefore, should be crafted carefully and with precision.

A good hypothesis should have dependent and independent variables . These variables are the elements you will test in your research method – it can be a concept, an event, or an object as long as it is observable.

You can observe the dependent variables while the independent variables keep changing during the experiment.

In a nutshell, a hypothesis directs and organizes the research methods you will use, forming a large section of research paper writing.

Hypothesis vs. Theory

A hypothesis is a realistic expectation that researchers make before any investigation. It is formulated and tested to prove whether the statement is true. A theory, on the other hand, is a factual principle supported by evidence. Thus, a theory is more fact-backed compared to a hypothesis.

Another difference is that a hypothesis is presented as a single statement , while a theory can be an assortment of things . Hypotheses are based on future possibilities toward a specific projection, but the results are uncertain. Theories are verified with undisputable results because of proper substantiation.

When it comes to data, a hypothesis relies on limited information , while a theory is established on an extensive data set tested on various conditions.

You should observe the stated assumption to prove its accuracy.

Since hypotheses have observable variables, their outcome is usually based on a specific occurrence. Conversely, theories are grounded on a general principle involving multiple experiments and research tests.

This general principle can apply to many specific cases.

The primary purpose of formulating a hypothesis is to present a tentative prediction for researchers to explore further through tests and observations. Theories, in their turn, aim to explain plausible occurrences in the form of a scientific study.

It would help to rely on several criteria to establish a good hypothesis. Below are the parameters you should use to analyze the quality of your hypothesis.

🧭 6 Steps to Making a Good Hypothesis

Writing a hypothesis becomes way simpler if you follow a tried-and-tested algorithm. Let’s explore how you can formulate a good hypothesis in a few steps:

Step #1: Ask Questions

The first step in hypothesis creation is asking real questions about the surrounding reality.

Why do things happen as they do? What are the causes of some occurrences?

Your curiosity will trigger great questions that you can use to formulate a stellar hypothesis. So, ensure you pick a research topic of interest to scrutinize the world’s phenomena, processes, and events.

Step #2: Do Initial Research

Carry out preliminary research and gather essential background information about your topic of choice.

The extent of the information you collect will depend on what you want to prove.

Your initial research can be complete with a few academic books or a simple Internet search for quick answers with relevant statistics.

Still, keep in mind that in this phase, it is too early to prove or disapprove of your hypothesis.

Step #3: Identify Your Variables

Now that you have a basic understanding of the topic, choose the dependent and independent variables.

Take note that independent variables are the ones you can’t control, so understand the limitations of your test before settling on a final hypothesis.

Step #4: Formulate Your Hypothesis

You can write your hypothesis as an ‘if – then’ expression . Presenting any hypothesis in this format is reliable since it describes the cause-and-effect you want to test.

For instance: If I study every day, then I will get good grades.

Step #5: Gather Relevant Data

Once you have identified your variables and formulated the hypothesis, you can start the experiment. Remember, the conclusion you make will be a proof or rebuttal of your initial assumption.

So, gather relevant information, whether for a simple or statistical hypothesis, because you need to back your statement.

Step #6: Record Your Findings

Finally, write down your conclusions in a research paper .

Outline in detail whether the test has proved or disproved your hypothesis.

Edit and proofread your work, using a plagiarism checker to ensure the authenticity of your text.

We hope that the above tips will be useful for you. Note that if you need to conduct business analysis, you can use the free templates we’ve prepared: SWOT , PESTLE , VRIO , SOAR , and Porter’s 5 Forces .

❓ Hypothesis Formulator FAQ

Updated: Oct 25th, 2023

• How to Write a Hypothesis in 6 Steps - Grammarly
• Forming a Good Hypothesis for Scientific Research
• The Hypothesis in Science Writing
• Scientific Method: Step 3: HYPOTHESIS - Subject Guides
• Hypothesis Template & Examples - Video & Lesson Transcript
• Free Essays
• Writing Tools
• Lit. Guides
• Donate a Paper
• Referencing Guides
• Free Textbooks
• Tongue Twisters
• Job Openings
• Expert Application
• Video Contest
• Writing Scholarship
• Discount Codes
• IvyPanda Shop
• Terms and Conditions
• Privacy Policy
• Cookies Policy
• Copyright Principles
• DMCA Request
• Service Notice

Use our hypothesis maker whenever you need to formulate a hypothesis for your study. We offer a very simple tool where you just need to provide basic info about your variables, subjects, and predicted outcomes. The rest is on us. Get a perfect hypothesis in no time!

How to Write a Hypothesis

Improve your research report and learn how to develop a precise and thorough hypothesis for your research.

A hypothesis is simply a testable statement to find an answer to a specific question; a formalized hypothesis forces the thought about what results to expect in an experiment. 

As a result, a hypothesis can be used for almost anything, such as testing different outcomes in daily tasks, identifying a possible ending in research, forming the basis of a scientific experiment, and so on.

With this article, you will learn the reasoning behind it, the various types of hypotheses as well as how to write a hypothesis more clearly.

What is a Hypothesis?

A hypothesis is a method of forecasting, an attempt to find an answer to something that has not yet been tested, an idea or a proposal based on limited evidence. 

In most cases, this entails proposing relationships between two variables (or more): the independent variable (the change made) and the dependent variable (the measure). For example, suppose you’re used to studying all night before a test, but you’re always too tired to understand the subject clearly, resulting in poor grades.

So, the hypothesis is that if you study during the day, you will understand the subject and, as a result, receive a good grade. In this example, the independent variable is the study time and the dependent variables are the understanding of the subject and the grade. 

As you can see, a hypothesis can be used in almost any situation, but it is most commonly found in research papers or scientific experiments. 

When writing a hypothesis, it is critical to be cautious and thorough before beginning to write it down. Because any hypothesis must be proven through facts, direct testing, and data evidence, even minor flaws or misunderstandings in hypothesis construction can have a negative impact on the quality of your research and its subsequent results. 

Types of Research Hypothesis and Examples

There are various types of hypotheses available depending on the nature or purpose of your hypothesis, whether it is for research or a scientific experiment. 

Before we get into how to write a hypothesis , let’s go over the different types to see which one is best for you. 

Simple Hypothesis

A simple hypothesis will only test and experiment with the relationship between two variables: the independent variable and the dependent one. As we priorly exemplified using study time and grades.

Complex Hypothesis

A more complex hypothesis involves a relationship between more than two variables, let’s say: two independent variables and one dependent variable or vice versa. 

Example: Higher the poverty, higher the illiteracy in society, higher will be the rate of crimes.

Null Hypothesis

A null hypothesis, abbreviated as H0, is one in which there is no relationship between the variables. 

Example: Poverty has nothing to do with a society’s crime rate.

Alternative Hypothesis

In conjunction with a null hypothesis, an alternative hypothesis (H1 or HA) is used. It states the inverse of the null hypothesis, implying that only one must be true. 

Example: Poverty is the cause of society’s crime rate .

Composite Hypothesis

A composite hypothesis is one that does not predict the dependent variable’s exact parameters, distribution, or range. 

We would frequently predict an exact outcome. “23-year-old men are on average 189cm tall,” for example. We are providing an exact parameter here. As a result, the hypothesis is not composite. 

However, we cannot always precisely hypothesize something. In these cases, we might say, “On average, 23-year-old men are not 189cm tall.” We have not established a distribution range or precise parameters for the average height of 23-year-old men. As a result, we’ve introduced a composite hypothesis rather than an exact hypothesis. 

An alternative hypothesis (as discussed above) is generally composite because it is defined as anything other than the null hypothesis. Because this ‘anything except’ does not specify parameters or distribution, it is an example of a composite hypothesis.

Logical Hypothesis

A hypothesis that can be verified logically is known as a logical hypothesis. So, without actual evidence, a logical hypothesis suggests a relationship between variables. 

Example: Alligators have green scales, therefore dinosaurs closely related to them most likely had green scales as well. However, because they are all extinct, we must rely on logic rather than empirical data.

Empirical Hypothesis

An empirical hypothesis is the inverse of a logical hypothesis. It is a hypothesis that is currently being tested through scientific investigation, it relies on concrete data. This is also known as a ‘working hypothesis.’

Example: Cows’ lifespan is reduced by feeding them 1 pound of corn per day.

Statistical Hypothesis

A statistical hypothesis uses representative statistical models to draw conclusions about larger populations. Instead of testing everything, you test a subset and generalize the rest based on previously collected data. 

Example: Natural red hair is found in about 2% of the world’s population.

Directional Hypothesis

A directional hypothesis predicts whether the effect of an intervention will be positive or negative before the test itself. 

Example: Does rainy weather impact the amount of moderate to high intensity exercise people do per week? Positively, rain reduces the amount of moderate to vigorous exercise people do per week.

How to Write a Hypothesis in 6 Steps

1. ask a question.

Writing a hypothesis implies that you have a question to answer. The question should be direct, focused, and specific. To aid in identification, frame this question with the classic six: who, what, where, when, why, or how. But remember that a hypothesis must be a statement and not a question.

2. Gather Primary Research

Collecting background information on the topic may necessitate the reading of several books, academic journals, experiments, and observations, or it may be as simple as an internet search.

Remember to consider your questions from multiple perspectives; conflicting research can be extremely useful when developing a hypothesis; you can use their findings as potential rebuttals and frame your study to address these concerns.

3. Define Your Variables

Once you’ve determined what the question will be, you must identify the independent and dependent variables, as well as the type of hypothesis that applies.

4. Put It in The Form of an If-Then Statement

When constructing a hypothesis, using an if-then format can be helpful. For example: “If I exercise more, I will lose more weight.” This format can be tricky when dealing with multiple variables, but in general, it’s a reliable way of expressing the cause-and-effect relationship you’re testing.

5. Collect More Data to Prove Your Hypothesis

The priority over a hypothesis is answering the question and proving it right or wrong. Once you’ve established your hypothesis and determined your variables, you can begin your experiments. Ideally, you’ll gather data to support your hypothesis.

6. Write it Down

Finally, once you’ve written your hypothesis, analyze all of the data you’ve gathered and draw your conclusions in a research paper format.

Unleash the Power of Infographics with Mind the Graph

Use this opportunity to include a visual tool in your research paper to help clarify your hypothesis. Mind The Graph transforms scientists into designers to increase the visual impact of your research with scientific images and infographic templates.

Subscribe to our newsletter

Exclusive high quality content about effective visual communication in science.

Unlock Your Creativity

Create infographics, presentations and other scientifically-accurate designs without hassle — absolutely free for 7 days!

About Fabricio Pamplona

Fabricio Pamplona is the founder of Mind the Graph - a tool used by over 400K users in 60 countries. He has a Ph.D. and solid scientific background in Psychopharmacology and experience as a Guest Researcher at the Max Planck Institute of Psychiatry (Germany) and Researcher in D'Or Institute for Research and Education (IDOR, Brazil). Fabricio holds over 2500 citations in Google Scholar. He has 10 years of experience in small innovative businesses, with relevant experience in product design and innovation management. Connect with him on LinkedIn - Fabricio Pamplona .

Content tags

Six Steps of the Scientific Method

Learn What Makes Each Stage Important

ThoughtCo. / Hugo Lin 

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

The scientific method is a systematic way of learning about the world around us and answering questions. The key difference between the scientific method and other ways of acquiring knowledge are forming a hypothesis and then testing it with an experiment.

The Six Steps

The number of steps can vary from one description to another (which mainly happens when data and analysis are separated into separate steps), however, this is a fairly standard list of the six scientific method steps that you are expected to know for any science class:

• Purpose/Question Ask a question.
• Research Conduct background research. Write down your sources so you can cite your references. In the modern era, a lot of your research may be conducted online. Scroll to the bottom of articles to check the references. Even if you can't access the full text of a published article, you can usually view the abstract to see the summary of other experiments. Interview experts on a topic. The more you know about a subject, the easier it will be to conduct your investigation.
• Hypothesis Propose a hypothesis . This is a sort of educated guess about what you expect. It is a statement used to predict the outcome of an experiment. Usually, a hypothesis is written in terms of cause and effect. Alternatively, it may describe the relationship between two phenomena. One type of hypothesis is the null hypothesis or the no-difference hypothesis. This is an easy type of hypothesis to test because it assumes changing a variable will have no effect on the outcome. In reality, you probably expect a change but rejecting a hypothesis may be more useful than accepting one.
• Experiment Design and perform an experiment to test your hypothesis. An experiment has an independent and dependent variable. You change or control the independent variable and record the effect it has on the dependent variable . It's important to change only one variable for an experiment rather than try to combine the effects of variables in an experiment. For example, if you want to test the effects of light intensity and fertilizer concentration on the growth rate of a plant, you're really looking at two separate experiments.
• Data/Analysis Record observations and analyze the meaning of the data. Often, you'll prepare a table or graph of the data. Don't throw out data points you think are bad or that don't support your predictions. Some of the most incredible discoveries in science were made because the data looked wrong! Once you have the data, you may need to perform a mathematical analysis to support or refute your hypothesis.
• Conclusion Conclude whether to accept or reject your hypothesis. There is no right or wrong outcome to an experiment, so either result is fine. Accepting a hypothesis does not necessarily mean it's correct! Sometimes repeating an experiment may give a different result. In other cases, a hypothesis may predict an outcome, yet you might draw an incorrect conclusion. Communicate your results. The results may be compiled into a lab report or formally submitted as a paper. Whether you accept or reject the hypothesis, you likely learned something about the subject and may wish to revise the original hypothesis or form a new one for a future experiment.

When Are There Seven Steps?

Sometimes the scientific method is taught with seven steps instead of six. In this model, the first step of the scientific method is to make observations. Really, even if you don't make observations formally, you think about prior experiences with a subject in order to ask a question or solve a problem.

Formal observations are a type of brainstorming that can help you find an idea and form a hypothesis. Observe your subject and record everything about it. Include colors, timing, sounds, temperatures, changes, behavior, and anything that strikes you as interesting or significant.

When you design an experiment, you are controlling and measuring variables. There are three types of variables:

• Controlled Variables:  You can have as many  controlled variables  as you like. These are parts of the experiment that you try to keep constant throughout an experiment so that they won't interfere with your test. Writing down controlled variables is a good idea because it helps make your experiment  reproducible , which is important in science! If you have trouble duplicating results from one experiment to another, there may be a controlled variable that you missed.
• Independent Variable:  This is the variable you control.
• Dependent Variable:  This is the variable you measure. It is called the dependent variable because it  depends  on the independent variable.
• Examples of Independent and Dependent Variables
• Null Hypothesis Examples
• Difference Between Independent and Dependent Variables
• Scientific Method Flow Chart
• What Is an Experiment? Definition and Design
• How To Design a Science Fair Experiment
• What Is a Hypothesis? (Science)
• Scientific Variable
• What Are the Elements of a Good Hypothesis?
• Scientific Method Vocabulary Terms
• Understanding Simple vs Controlled Experiments
• What Is a Variable in Science?
• Null Hypothesis Definition and Examples
• Independent Variable Definition and Examples
• Scientific Method Lesson Plan

How to Write a Hypothesis: A Step-by-Step Guide

Introduction

An overview of the research hypothesis, different types of hypotheses, variables in a hypothesis, how to formulate an effective research hypothesis, designing a study around your hypothesis.

The scientific method can derive and test predictions as hypotheses. Empirical research can then provide support (or lack thereof) for the hypotheses. Even failure to find support for a hypothesis still represents a valuable contribution to scientific knowledge. Let's look more closely at the idea of the hypothesis and the role it plays in research.

As much as the term exists in everyday language, there is a detailed development that informs the word "hypothesis" when applied to research. A good research hypothesis is informed by prior research and guides research design and data analysis , so it is important to understand how a hypothesis is defined and understood by researchers.

What is the simple definition of a hypothesis?

A hypothesis is a testable prediction about an outcome between two or more variables . It functions as a navigational tool in the research process, directing what you aim to predict and how.

What is the hypothesis for in research?

In research, a hypothesis serves as the cornerstone for your empirical study. It not only lays out what you aim to investigate but also provides a structured approach for your data collection and analysis.

Essentially, it bridges the gap between the theoretical and the empirical, guiding your investigation throughout its course.

What is an example of a hypothesis?

If you are studying the relationship between physical exercise and mental health, a suitable hypothesis could be: "Regular physical exercise leads to improved mental well-being among adults."

This statement constitutes a specific and testable hypothesis that directly relates to the variables you are investigating.

What makes a good hypothesis?

A good hypothesis possesses several key characteristics. Firstly, it must be testable, allowing you to analyze data through empirical means, such as observation or experimentation, to assess if there is significant support for the hypothesis. Secondly, a hypothesis should be specific and unambiguous, giving a clear understanding of the expected relationship between variables. Lastly, it should be grounded in existing research or theoretical frameworks , ensuring its relevance and applicability.

Understanding the types of hypotheses can greatly enhance how you construct and work with hypotheses. While all hypotheses serve the essential function of guiding your study, there are varying purposes among the types of hypotheses. In addition, all hypotheses stand in contrast to the null hypothesis, or the assumption that there is no significant relationship between the variables .

Here, we explore various kinds of hypotheses to provide you with the tools needed to craft effective hypotheses for your specific research needs. Bear in mind that many of these hypothesis types may overlap with one another, and the specific type that is typically used will likely depend on the area of research and methodology you are following.

Null hypothesis

The null hypothesis is a statement that there is no effect or relationship between the variables being studied. In statistical terms, it serves as the default assumption that any observed differences are due to random chance.

For example, if you're studying the effect of a drug on blood pressure, the null hypothesis might state that the drug has no effect.

Alternative hypothesis

Contrary to the null hypothesis, the alternative hypothesis suggests that there is a significant relationship or effect between variables.

Using the drug example, the alternative hypothesis would posit that the drug does indeed affect blood pressure. This is what researchers aim to prove.

Simple hypothesis

A simple hypothesis makes a prediction about the relationship between two variables, and only two variables.

For example, "Increased study time results in better exam scores." Here, "study time" and "exam scores" are the only variables involved.

Complex hypothesis

A complex hypothesis, as the name suggests, involves more than two variables. For instance, "Increased study time and access to resources result in better exam scores." Here, "study time," "access to resources," and "exam scores" are all variables.

This hypothesis refers to multiple potential mediating variables. Other hypotheses could also include predictions about variables that moderate the relationship between the independent variable and dependent variable .

Directional hypothesis

A directional hypothesis specifies the direction of the expected relationship between variables. For example, "Eating more fruits and vegetables leads to a decrease in heart disease."

Here, the direction of heart disease is explicitly predicted to decrease, due to effects from eating more fruits and vegetables. All hypotheses typically specify the expected direction of the relationship between the independent and dependent variable, such that researchers can test if this prediction holds in their data analysis .

Statistical hypothesis

A statistical hypothesis is one that is testable through statistical methods, providing a numerical value that can be analyzed. This is commonly seen in quantitative research .

For example, "There is a statistically significant difference in test scores between students who study for one hour and those who study for two."

Empirical hypothesis

An empirical hypothesis is derived from observations and is tested through empirical methods, often through experimentation or survey data . Empirical hypotheses may also be assessed with statistical analyses.

For example, "Regular exercise is correlated with a lower incidence of depression," could be tested through surveys that measure exercise frequency and depression levels.

Causal hypothesis

A causal hypothesis proposes that one variable causes a change in another. This type of hypothesis is often tested through controlled experiments.

For example, "Smoking causes lung cancer," assumes a direct causal relationship.

Associative hypothesis

Unlike causal hypotheses, associative hypotheses suggest a relationship between variables but do not imply causation.

For instance, "People who smoke are more likely to get lung cancer," notes an association but doesn't claim that smoking causes lung cancer directly.

Relational hypothesis

A relational hypothesis explores the relationship between two or more variables but doesn't specify the nature of the relationship.

For example, "There is a relationship between diet and heart health," leaves the nature of the relationship (causal, associative, etc.) open to interpretation.

Logical hypothesis

A logical hypothesis is based on sound reasoning and logical principles. It's often used in theoretical research to explore abstract concepts, rather than being based on empirical data.

For example, "If all men are mortal and Socrates is a man, then Socrates is mortal," employs logical reasoning to make its point.

Let ATLAS.ti take you from research question to key insights

Get started with a free trial and see how ATLAS.ti can make the most of your data.

In any research hypothesis, variables play a critical role. These are the elements or factors that the researcher manipulates, controls, or measures. Understanding variables is essential for crafting a clear, testable hypothesis and for the stages of research that follow, such as data collection and analysis.

In the realm of hypotheses, there are generally two types of variables to consider: independent and dependent. Independent variables are what you, as the researcher, manipulate or change in your study. It's considered the cause in the relationship you're investigating. For instance, in a study examining the impact of sleep duration on academic performance, the independent variable would be the amount of sleep participants get.

Conversely, the dependent variable is the outcome you measure to gauge the effect of your manipulation. It's the effect in the cause-and-effect relationship. The dependent variable thus refers to the main outcome of interest in your study. In the same sleep study example, the academic performance, perhaps measured by exam scores or GPA, would be the dependent variable.

Beyond these two primary types, you might also encounter control variables. These are variables that could potentially influence the outcome and are therefore kept constant to isolate the relationship between the independent and dependent variables . For example, in the sleep and academic performance study, control variables could include age, diet, or even the subject of study.

By clearly identifying and understanding the roles of these variables in your hypothesis, you set the stage for a methodologically sound research project. It helps you develop focused research questions, design appropriate experiments or observations, and carry out meaningful data analysis . It's a step that lays the groundwork for the success of your entire study.

Crafting a strong, testable hypothesis is crucial for the success of any research project. It sets the stage for everything from your study design to data collection and analysis . Below are some key considerations to keep in mind when formulating your hypothesis:

• Be specific : A vague hypothesis can lead to ambiguous results and interpretations . Clearly define your variables and the expected relationship between them.
• Ensure testability : A good hypothesis should be testable through empirical means, whether by observation , experimentation, or other forms of data analysis.
• Ground in literature : Before creating your hypothesis, consult existing research and theories. This not only helps you identify gaps in current knowledge but also gives you valuable context and credibility for crafting your hypothesis.
• Use simple language : While your hypothesis should be conceptually sound, it doesn't have to be complicated. Aim for clarity and simplicity in your wording.
• State direction, if applicable : If your hypothesis involves a directional outcome (e.g., "increase" or "decrease"), make sure to specify this. You also need to think about how you will measure whether or not the outcome moved in the direction you predicted.
• Keep it focused : One of the common pitfalls in hypothesis formulation is trying to answer too many questions at once. Keep your hypothesis focused on a specific issue or relationship.
• Account for control variables : Identify any variables that could potentially impact the outcome and consider how you will control for them in your study.
• Be ethical : Make sure your hypothesis and the methods for testing it comply with ethical standards , particularly if your research involves human or animal subjects.

Designing your study involves multiple key phases that help ensure the rigor and validity of your research. Here we discuss these crucial components in more detail.

Literature review

Starting with a comprehensive literature review is essential. This step allows you to understand the existing body of knowledge related to your hypothesis and helps you identify gaps that your research could fill. Your research should aim to contribute some novel understanding to existing literature, and your hypotheses can reflect this. A literature review also provides valuable insights into how similar research projects were executed, thereby helping you fine-tune your own approach.

Research methods

Choosing the right research methods is critical. Whether it's a survey, an experiment, or observational study, the methodology should be the most appropriate for testing your hypothesis. Your choice of methods will also depend on whether your research is quantitative, qualitative, or mixed-methods. Make sure the chosen methods align well with the variables you are studying and the type of data you need.

Preliminary research

Before diving into a full-scale study, it’s often beneficial to conduct preliminary research or a pilot study . This allows you to test your research methods on a smaller scale, refine your tools, and identify any potential issues. For instance, a pilot survey can help you determine if your questions are clear and if the survey effectively captures the data you need. This step can save you both time and resources in the long run.

Data analysis

Finally, planning your data analysis in advance is crucial for a successful study. Decide which statistical or analytical tools are most suited for your data type and research questions . For quantitative research, you might opt for t-tests, ANOVA, or regression analyses. For qualitative research , thematic analysis or grounded theory may be more appropriate. This phase is integral for interpreting your results and drawing meaningful conclusions in relation to your research question.

Turn data into evidence for insights with ATLAS.ti

Powerful analysis for your research paper or presentation is at your fingertips starting with a free trial.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Science Writing

How to Write a Hypothesis

Last Updated: May 2, 2023 Fact Checked

This article was co-authored by Bess Ruff, MA . Bess Ruff is a Geography PhD student at Florida State University. She received her MA in Environmental Science and Management from the University of California, Santa Barbara in 2016. She has conducted survey work for marine spatial planning projects in the Caribbean and provided research support as a graduate fellow for the Sustainable Fisheries Group. There are 9 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,033,015 times.

A hypothesis is a description of a pattern in nature or an explanation about some real-world phenomenon that can be tested through observation and experimentation. The most common way a hypothesis is used in scientific research is as a tentative, testable, and falsifiable statement that explains some observed phenomenon in nature. [1] X Research source Many academic fields, from the physical sciences to the life sciences to the social sciences, use hypothesis testing as a means of testing ideas to learn about the world and advance scientific knowledge. Whether you are a beginning scholar or a beginning student taking a class in a science subject, understanding what hypotheses are and being able to generate hypotheses and predictions yourself is very important. These instructions will help get you started.

Preparing to Write a Hypothesis

• If you are writing a hypothesis for a school assignment, this step may be taken care of for you.

• Focus on academic and scholarly writing. You need to be certain that your information is unbiased, accurate, and comprehensive. Scholarly search databases such as Google Scholar and Web of Science can help you find relevant articles from reputable sources.
• You can find information in textbooks, at a library, and online. If you are in school, you can also ask for help from teachers, librarians, and your peers.

• For example, if you are interested in the effects of caffeine on the human body, but notice that nobody seems to have explored whether caffeine affects males differently than it does females, this could be something to formulate a hypothesis about. Or, if you are interested in organic farming, you might notice that no one has tested whether organic fertilizer results in different growth rates for plants than non-organic fertilizer.
• You can sometimes find holes in the existing literature by looking for statements like “it is unknown” in scientific papers or places where information is clearly missing. You might also find a claim in the literature that seems far-fetched, unlikely, or too good to be true, like that caffeine improves math skills. If the claim is testable, you could provide a great service to scientific knowledge by doing your own investigation. If you confirm the claim, the claim becomes even more credible. If you do not find support for the claim, you are helping with the necessary self-correcting aspect of science.
• Examining these types of questions provides an excellent way for you to set yourself apart by filling in important gaps in a field of study.

• Following the examples above, you might ask: "How does caffeine affect females as compared to males?" or "How does organic fertilizer affect plant growth compared to non-organic fertilizer?" The rest of your research will be aimed at answering these questions.

• Following the examples above, if you discover in the literature that there is a pattern that some other types of stimulants seem to affect females more than males, this could be a clue that the same pattern might be true for caffeine. Similarly, if you observe the pattern that organic fertilizer seems to be associated with smaller plants overall, you might explain this pattern with the hypothesis that plants exposed to organic fertilizer grow more slowly than plants exposed to non-organic fertilizer.

Formulating Your Hypothesis

• You can think of the independent variable as the one that is causing some kind of difference or effect to occur. In the examples, the independent variable would be biological sex, i.e. whether a person is male or female, and fertilizer type, i.e. whether the fertilizer is organic or non-organically-based.
• The dependent variable is what is affected by (i.e. "depends" on) the independent variable. In the examples above, the dependent variable would be the measured impact of caffeine or fertilizer.
• Your hypothesis should only suggest one relationship. Most importantly, it should only have one independent variable. If you have more than one, you won't be able to determine which one is actually the source of any effects you might observe.

• Don't worry too much at this point about being precise or detailed.
• In the examples above, one hypothesis would make a statement about whether a person's biological sex might impact the way the person is affected by caffeine; for example, at this point, your hypothesis might simply be: "a person's biological sex is related to how caffeine affects his or her heart rate." The other hypothesis would make a general statement about plant growth and fertilizer; for example your simple explanatory hypothesis might be "plants given different types of fertilizer are different sizes because they grow at different rates."

• Using our example, our non-directional hypotheses would be "there is a relationship between a person's biological sex and how much caffeine increases the person's heart rate," and "there is a relationship between fertilizer type and the speed at which plants grow."
• Directional predictions using the same example hypotheses above would be : "Females will experience a greater increase in heart rate after consuming caffeine than will males," and "plants fertilized with non-organic fertilizer will grow faster than those fertilized with organic fertilizer." Indeed, these predictions and the hypotheses that allow for them are very different kinds of statements. More on this distinction below.
• If the literature provides any basis for making a directional prediction, it is better to do so, because it provides more information. Especially in the physical sciences, non-directional predictions are often seen as inadequate.

• Where necessary, specify the population (i.e. the people or things) about which you hope to uncover new knowledge. For example, if you were only interested the effects of caffeine on elderly people, your prediction might read: "Females over the age of 65 will experience a greater increase in heart rate than will males of the same age." If you were interested only in how fertilizer affects tomato plants, your prediction might read: "Tomato plants treated with non-organic fertilizer will grow faster in the first three months than will tomato plants treated with organic fertilizer."

• For example, you would not want to make the hypothesis: "red is the prettiest color." This statement is an opinion and it cannot be tested with an experiment. However, proposing the generalizing hypothesis that red is the most popular color is testable with a simple random survey. If you do indeed confirm that red is the most popular color, your next step may be to ask: Why is red the most popular color? The answer you propose is your explanatory hypothesis .

• An easy way to get to the hypothesis for this method and prediction is to ask yourself why you think heart rates will increase if children are given caffeine. Your explanatory hypothesis in this case may be that caffeine is a stimulant. At this point, some scientists write a research hypothesis , a statement that includes the hypothesis, the experiment, and the prediction all in one statement.
• For example, If caffeine is a stimulant, and some children are given a drink with caffeine while others are given a drink without caffeine, then the heart rates of those children given a caffeinated drink will increase more than the heart rate of children given a non-caffeinated drink.

• Using the above example, if you were to test the effects of caffeine on the heart rates of children, evidence that your hypothesis is not true, sometimes called the null hypothesis , could occur if the heart rates of both the children given the caffeinated drink and the children given the non-caffeinated drink (called the placebo control) did not change, or lowered or raised with the same magnitude, if there was no difference between the two groups of children.
• It is important to note here that the null hypothesis actually becomes much more useful when researchers test the significance of their results with statistics. When statistics are used on the results of an experiment, a researcher is testing the idea of the null statistical hypothesis. For example, that there is no relationship between two variables or that there is no difference between two groups. [8] X Research source

Hypothesis Examples

Community Q&A

• Remember that science is not necessarily a linear process and can be approached in various ways. [10] X Research source Thanks Helpful 0 Not Helpful 0
• When examining the literature, look for research that is similar to what you want to do, and try to build on the findings of other researchers. But also look for claims that you think are suspicious, and test them yourself. Thanks Helpful 0 Not Helpful 0
• Be specific in your hypotheses, but not so specific that your hypothesis can't be applied to anything outside your specific experiment. You definitely want to be clear about the population about which you are interested in drawing conclusions, but nobody (except your roommates) will be interested in reading a paper with the prediction: "my three roommates will each be able to do a different amount of pushups." Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ https://undsci.berkeley.edu/for-educators/prepare-and-plan/correcting-misconceptions/#a4
• ↑ https://owl.purdue.edu/owl/general_writing/common_writing_assignments/research_papers/choosing_a_topic.html
• ↑ https://owl.purdue.edu/owl/subject_specific_writing/writing_in_the_social_sciences/writing_in_psychology_experimental_report_writing/experimental_reports_1.html
• ↑ https://www.grammarly.com/blog/how-to-write-a-hypothesis/
• ↑ https://grammar.yourdictionary.com/for-students-and-parents/how-create-hypothesis.html
• ↑ https://flexbooks.ck12.org/cbook/ck-12-middle-school-physical-science-flexbook-2.0/section/1.19/primary/lesson/hypothesis-ms-ps/
• ↑ https://iastate.pressbooks.pub/preparingtopublish/chapter/goal-1-contextualize-the-studys-methods/
• ↑ http://mathworld.wolfram.com/NullHypothesis.html
• ↑ http://undsci.berkeley.edu/article/scienceflowchart

About This Article

Before writing a hypothesis, think of what questions are still unanswered about a specific subject and make an educated guess about what the answer could be. Then, determine the variables in your question and write a simple statement about how they might be related. Try to focus on specific predictions and variables, such as age or segment of the population, to make your hypothesis easier to test. For tips on how to test your hypothesis, read on! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Onyia Maxwell

Sep 13, 2016

Did this article help you?

Nov 26, 2017

ABEL SHEWADEG

Jun 12, 2018

Connor Gilligan

Jan 2, 2017

Dec 30, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 31289

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

CO-6: Apply basic concepts of probability, random variation, and commonly used statistical probability distributions.

Learning Objectives

LO 6.26: Outline the logic and process of hypothesis testing.

LO 6.27: Explain what the p-value is and how it is used to draw conclusions.

Video: Hypothesis Testing (8:43)

Introduction

We are in the middle of the part of the course that has to do with inference for one variable.

So far, we talked about point estimation and learned how interval estimation enhances it by quantifying the magnitude of the estimation error (with a certain level of confidence) in the form of the margin of error. The result is the confidence interval — an interval that, with a certain confidence, we believe captures the unknown parameter.

We are now moving to the other kind of inference, hypothesis testing . We say that hypothesis testing is “the other kind” because, unlike the inferential methods we presented so far, where the goal was estimating the unknown parameter, the idea, logic and goal of hypothesis testing are quite different.

In the first two parts of this section we will discuss the idea behind hypothesis testing, explain how it works, and introduce new terminology that emerges in this form of inference. The final two parts will be more specific and will discuss hypothesis testing for the population proportion ( p ) and the population mean ( μ, mu).

If this is your first statistics course, you will need to spend considerable time on this topic as there are many new ideas. Many students find this process and its logic difficult to understand in the beginning.

In this section, we will use the hypothesis test for a population proportion to motivate our understanding of the process. We will conduct these tests manually. For all future hypothesis test procedures, including problems involving means, we will use software to obtain the results and focus on interpreting them in the context of our scenario.

General Idea and Logic of Hypothesis Testing

The purpose of this section is to gradually build your understanding about how statistical hypothesis testing works. We start by explaining the general logic behind the process of hypothesis testing. Once we are confident that you understand this logic, we will add some more details and terminology.

To start our discussion about the idea behind statistical hypothesis testing, consider the following example:

A case of suspected cheating on an exam is brought in front of the disciplinary committee at a certain university.

There are two opposing claims in this case:

• The student’s claim: I did not cheat on the exam.
• The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim. The instructor explains that the exam had two versions, and shows the committee members that on three separate exam questions, the student used in his solution numbers that were given in the other version of the exam.

The committee members all agree that it would be extremely unlikely to get evidence like that if the student’s claim of not cheating had been true. In other words, the committee members all agree that the instructor brought forward strong enough evidence to reject the student’s claim, and conclude that the student did cheat on the exam.

What does this example have to do with statistics?

While it is true that this story seems unrelated to statistics, it captures all the elements of hypothesis testing and the logic behind it. Before you read on to understand why, it would be useful to read the example again. Please do so now.

Statistical hypothesis testing is defined as:

• Assessing evidence provided by the data against the null claim (the claim which is to be assumed true unless enough evidence exists to reject it).

Here is how the process of statistical hypothesis testing works:

• We have two claims about what is going on in the population. Let’s call them claim 1 (this will be the null claim or hypothesis) and claim 2 (this will be the alternative) . Much like the story above, where the student’s claim is challenged by the instructor’s claim, the null claim 1 is challenged by the alternative claim 2. (For us, these claims are usually about the value of population parameter(s) or about the existence or nonexistence of a relationship between two variables in the population).
• We choose a sample, collect relevant data and summarize them (this is similar to the instructor collecting evidence from the student’s exam). For statistical tests, this step will also involve checking any conditions or assumptions.
• We figure out how likely it is to observe data like the data we obtained, if claim 1 is true. (Note that the wording “how likely …” implies that this step requires some kind of probability calculation). In the story, the committee members assessed how likely it is to observe evidence such as the instructor provided, had the student’s claim of not cheating been true.
• If, after assuming claim 1 is true, we find that it would be extremely unlikely to observe data as strong as ours or stronger in favor of claim 2, then we have strong evidence against claim 1, and we reject it in favor of claim 2. Later we will see this corresponds to a small p-value.
• If, after assuming claim 1 is true, we find that observing data as strong as ours or stronger in favor of claim 2 is NOT VERY UNLIKELY , then we do not have enough evidence against claim 1, and therefore we cannot reject it in favor of claim 2. Later we will see this corresponds to a p-value which is not small.

In our story, the committee decided that it would be extremely unlikely to find the evidence that the instructor provided had the student’s claim of not cheating been true. In other words, the members felt that it is extremely unlikely that it is just a coincidence (random chance) that the student used the numbers from the other version of the exam on three separate problems. The committee members therefore decided to reject the student’s claim and concluded that the student had, indeed, cheated on the exam. (Wouldn’t you conclude the same?)

Hopefully this example helped you understand the logic behind hypothesis testing.

Interactive Applet: Reasoning of a Statistical Test

To strengthen your understanding of the process of hypothesis testing and the logic behind it, let’s look at three statistical examples.

A recent study estimated that 20% of all college students in the United States smoke. The head of Health Services at Goodheart University (GU) suspects that the proportion of smokers may be lower at GU. In hopes of confirming her claim, the head of Health Services chooses a random sample of 400 Goodheart students, and finds that 70 of them are smokers.

Let’s analyze this example using the 4 steps outlined above:

• claim 1: The proportion of smokers at Goodheart is 0.20.
• claim 2: The proportion of smokers at Goodheart is less than 0.20.

Claim 1 basically says “nothing special goes on at Goodheart University; the proportion of smokers there is no different from the proportion in the entire country.” This claim is challenged by the head of Health Services, who suspects that the proportion of smokers at Goodheart is lower.

• Choosing a sample and collecting data: A sample of n = 400 was chosen, and summarizing the data revealed that the sample proportion of smokers is p -hat = 70/400 = 0.175.While it is true that 0.175 is less than 0.20, it is not clear whether this is strong enough evidence against claim 1. We must account for sampling variation.
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: How surprising is it to get a sample proportion as low as p -hat = 0.175 (or lower), assuming claim 1 is true? In other words, we need to find how likely it is that in a random sample of size n = 400 taken from a population where the proportion of smokers is p = 0.20 we’ll get a sample proportion as low as p -hat = 0.175 (or lower).It turns out that the probability that we’ll get a sample proportion as low as p -hat = 0.175 (or lower) in such a sample is roughly 0.106 (do not worry about how this was calculated at this point – however, if you think about it hopefully you can see that the key is the sampling distribution of p -hat).
• Conclusion: Well, we found that if claim 1 were true there is a probability of 0.106 of observing data like that observed or more extreme. Now you have to decide …Do you think that a probability of 0.106 makes our data rare enough (surprising enough) under claim 1 so that the fact that we did observe it is enough evidence to reject claim 1? Or do you feel that a probability of 0.106 means that data like we observed are not very likely when claim 1 is true, but they are not unlikely enough to conclude that getting such data is sufficient evidence to reject claim 1. Basically, this is your decision. However, it would be nice to have some kind of guideline about what is generally considered surprising enough.

A certain prescription allergy medicine is supposed to contain an average of 245 parts per million (ppm) of a certain chemical. If the concentration is higher than 245 ppm, the drug will likely cause unpleasant side effects, and if the concentration is below 245 ppm, the drug may be ineffective. The manufacturer wants to check whether the mean concentration in a large shipment is the required 245 ppm or not. To this end, a random sample of 64 portions from the large shipment is tested, and it is found that the sample mean concentration is 250 ppm with a sample standard deviation of 12 ppm.

• Claim 1: The mean concentration in the shipment is the required 245 ppm.
• Claim 2: The mean concentration in the shipment is not the required 245 ppm.

Note that again, claim 1 basically says: “There is nothing unusual about this shipment, the mean concentration is the required 245 ppm.” This claim is challenged by the manufacturer, who wants to check whether that is, indeed, the case or not.

• Choosing a sample and collecting data: A sample of n = 64 portions is chosen and after summarizing the data it is found that the sample mean concentration is x-bar = 250 and the sample standard deviation is s = 12.Is the fact that x-bar = 250 is different from 245 strong enough evidence to reject claim 1 and conclude that the mean concentration in the whole shipment is not the required 245? In other words, do the data provide strong enough evidence to reject claim 1?
• Assessing the evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves the following question: If the mean concentration in the whole shipment were really the required 245 ppm (i.e., if claim 1 were true), how surprising would it be to observe a sample of 64 portions where the sample mean concentration is off by 5 ppm or more (as we did)? It turns out that it would be extremely unlikely to get such a result if the mean concentration were really the required 245. There is only a probability of 0.0007 (i.e., 7 in 10,000) of that happening. (Do not worry about how this was calculated at this point, but again, the key will be the sampling distribution.)
• Making conclusions: Here, it is pretty clear that a sample like the one we observed or more extreme is VERY rare (or extremely unlikely) if the mean concentration in the shipment were really the required 245 ppm. The fact that we did observe such a sample therefore provides strong evidence against claim 1, so we reject it and conclude with very little doubt that the mean concentration in the shipment is not the required 245 ppm.

Do you think that you’re getting it? Let’s make sure, and look at another example.

Is there a relationship between gender and combined scores (Math + Verbal) on the SAT exam?

Following a report on the College Board website, which showed that in 2003, males scored generally higher than females on the SAT exam, an educational researcher wanted to check whether this was also the case in her school district. The researcher chose random samples of 150 males and 150 females from her school district, collected data on their SAT performance and found the following:

Again, let’s see how the process of hypothesis testing works for this example:

• Claim 1: Performance on the SAT is not related to gender (males and females score the same).
• Claim 2: Performance on the SAT is related to gender – males score higher.

Note that again, claim 1 basically says: “There is nothing going on between the variables SAT and gender.” Claim 2 represents what the researcher wants to check, or suspects might actually be the case.

• Choosing a sample and collecting data: Data were collected and summarized as given above. Is the fact that the sample mean score of males (1,025) is higher than the sample mean score of females (1,010) by 15 points strong enough information to reject claim 1 and conclude that in this researcher’s school district, males score higher on the SAT than females?
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: If SAT scores are in fact not related to gender (claim 1 is true), how likely is it to get data like the data we observed, in which the difference between the males’ average and females’ average score is as high as 15 points or higher? It turns out that the probability of observing such a sample result if SAT score is not related to gender is approximately 0.29 (Again, do not worry about how this was calculated at this point).
• Conclusion: Here, we have an example where observing a sample like the one we observed or more extreme is definitely not surprising (roughly 30% chance) if claim 1 were true (i.e., if indeed there is no difference in SAT scores between males and females). We therefore conclude that our data does not provide enough evidence for rejecting claim 1.
• “The data provide enough evidence to reject claim 1 and accept claim 2”; or
• “The data do not provide enough evidence to reject claim 1.”

In particular, note that in the second type of conclusion we did not say: “ I accept claim 1 ,” but only “ I don’t have enough evidence to reject claim 1 .” We will come back to this issue later, but this is a good place to make you aware of this subtle difference.

Hopefully by now, you understand the logic behind the statistical hypothesis testing process. Here is a summary:

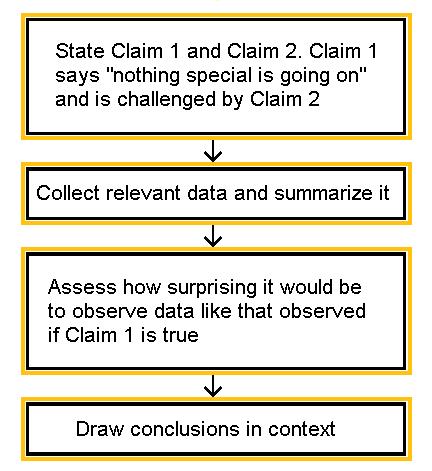
Learn by Doing: Logic of Hypothesis Testing

Did I Get This?: Logic of Hypothesis Testing

Steps in Hypothesis Testing

Video: Steps in Hypothesis Testing (16:02)

Now that we understand the general idea of how statistical hypothesis testing works, let’s go back to each of the steps and delve slightly deeper, getting more details and learning some terminology.

Hypothesis Testing Step 1: State the Hypotheses

In all three examples, our aim is to decide between two opposing points of view, Claim 1 and Claim 2. In hypothesis testing, Claim 1 is called the null hypothesis (denoted “ Ho “), and Claim 2 plays the role of the alternative hypothesis (denoted “ Ha “). As we saw in the three examples, the null hypothesis suggests nothing special is going on; in other words, there is no change from the status quo, no difference from the traditional state of affairs, no relationship. In contrast, the alternative hypothesis disagrees with this, stating that something is going on, or there is a change from the status quo, or there is a difference from the traditional state of affairs. The alternative hypothesis, Ha, usually represents what we want to check or what we suspect is really going on.

Let’s go back to our three examples and apply the new notation:

In example 1:

• Ho: The proportion of smokers at GU is 0.20.
• Ha: The proportion of smokers at GU is less than 0.20.

In example 2:

• Ho: The mean concentration in the shipment is the required 245 ppm.
• Ha: The mean concentration in the shipment is not the required 245 ppm.

In example 3:

• Ho: Performance on the SAT is not related to gender (males and females score the same).
• Ha: Performance on the SAT is related to gender – males score higher.

Learn by Doing: State the Hypotheses

Did I Get This?: State the Hypotheses

Hypothesis Testing Step 2: Collect Data, Check Conditions and Summarize Data

This step is pretty obvious. This is what inference is all about. You look at sampled data in order to draw conclusions about the entire population. In the case of hypothesis testing, based on the data, you draw conclusions about whether or not there is enough evidence to reject Ho.

There is, however, one detail that we would like to add here. In this step we collect data and summarize it. Go back and look at the second step in our three examples. Note that in order to summarize the data we used simple sample statistics such as the sample proportion ( p -hat), sample mean (x-bar) and the sample standard deviation (s).

In practice, you go a step further and use these sample statistics to summarize the data with what’s called a test statistic . We are not going to go into any details right now, but we will discuss test statistics when we go through the specific tests.

This step will also involve checking any conditions or assumptions required to use the test.

Hypothesis Testing Step 3: Assess the Evidence

As we saw, this is the step where we calculate how likely is it to get data like that observed (or more extreme) when Ho is true. In a sense, this is the heart of the process, since we draw our conclusions based on this probability.

• If this probability is very small (see example 2), then that means that it would be very surprising to get data like that observed (or more extreme) if Ho were true. The fact that we did observe such data is therefore evidence against Ho, and we should reject it.
• On the other hand, if this probability is not very small (see example 3) this means that observing data like that observed (or more extreme) is not very surprising if Ho were true. The fact that we observed such data does not provide evidence against Ho. This crucial probability, therefore, has a special name. It is called the p-value of the test.

In our three examples, the p-values were given to you (and you were reassured that you didn’t need to worry about how these were derived yet):

• Example 1: p-value = 0.106
• Example 2: p-value = 0.0007
• Example 3: p-value = 0.29

Obviously, the smaller the p-value, the more surprising it is to get data like ours (or more extreme) when Ho is true, and therefore, the stronger the evidence the data provide against Ho.

Looking at the three p-values of our three examples, we see that the data that we observed in example 2 provide the strongest evidence against the null hypothesis, followed by example 1, while the data in example 3 provides the least evidence against Ho.

• Right now we will not go into specific details about p-value calculations, but just mention that since the p-value is the probability of getting data like those observed (or more extreme) when Ho is true, it would make sense that the calculation of the p-value will be based on the data summary, which, as we mentioned, is the test statistic. Indeed, this is the case. In practice, we will mostly use software to provide the p-value for us.

Hypothesis Testing Step 4: Making Conclusions

Since our statistical conclusion is based on how small the p-value is, or in other words, how surprising our data are when Ho is true, it would be nice to have some kind of guideline or cutoff that will help determine how small the p-value must be, or how “rare” (unlikely) our data must be when Ho is true, for us to conclude that we have enough evidence to reject Ho.

This cutoff exists, and because it is so important, it has a special name. It is called the significance level of the test and is usually denoted by the Greek letter α (alpha). The most commonly used significance level is α (alpha) = 0.05 (or 5%). This means that:

• if the p-value < α (alpha) (usually 0.05), then the data we obtained is considered to be “rare (or surprising) enough” under the assumption that Ho is true, and we say that the data provide statistically significant evidence against Ho, so we reject Ho and thus accept Ha.
• if the p-value > α (alpha)(usually 0.05), then our data are not considered to be “surprising enough” under the assumption that Ho is true, and we say that our data do not provide enough evidence to reject Ho (or, equivalently, that the data do not provide enough evidence to accept Ha).

Now that we have a cutoff to use, here are the appropriate conclusions for each of our examples based upon the p-values we were given.

In Example 1:

• Using our cutoff of 0.05, we fail to reject Ho.
• Conclusion : There IS NOT enough evidence that the proportion of smokers at GU is less than 0.20
• Still we should consider: Does the evidence seen in the data provide any practical evidence towards our alternative hypothesis?

In Example 2:

• Using our cutoff of 0.05, we reject Ho.
• Conclusion : There IS enough evidence that the mean concentration in the shipment is not the required 245 ppm.

In Example 3:

• Conclusion : There IS NOT enough evidence that males score higher on average than females on the SAT.

Notice that all of the above conclusions are written in terms of the alternative hypothesis and are given in the context of the situation. In no situation have we claimed the null hypothesis is true. Be very careful of this and other issues discussed in the following comments.

• Although the significance level provides a good guideline for drawing our conclusions, it should not be treated as an incontrovertible truth. There is a lot of room for personal interpretation. What if your p-value is 0.052? You might want to stick to the rules and say “0.052 > 0.05 and therefore I don’t have enough evidence to reject Ho”, but you might decide that 0.052 is small enough for you to believe that Ho should be rejected. It should be noted that scientific journals do consider 0.05 to be the cutoff point for which any p-value below the cutoff indicates enough evidence against Ho, and any p-value above it, or even equal to it , indicates there is not enough evidence against Ho. Although a p-value between 0.05 and 0.10 is often reported as marginally statistically significant.
• It is important to draw your conclusions in context . It is never enough to say: “p-value = …, and therefore I have enough evidence to reject Ho at the 0.05 significance level.” You should always word your conclusion in terms of the data. Although we will use the terminology of “rejecting Ho” or “failing to reject Ho” – this is mostly due to the fact that we are instructing you in these concepts. In practice, this language is rarely used. We also suggest writing your conclusion in terms of the alternative hypothesis.Is there or is there not enough evidence that the alternative hypothesis is true?
• Let’s go back to the issue of the nature of the two types of conclusions that I can make.
• Either I reject Ho (when the p-value is smaller than the significance level)
• or I cannot reject Ho (when the p-value is larger than the significance level).

As we mentioned earlier, note that the second conclusion does not imply that I accept Ho, but just that I don’t have enough evidence to reject it. Saying (by mistake) “I don’t have enough evidence to reject Ho so I accept it” indicates that the data provide evidence that Ho is true, which is not necessarily the case . Consider the following slightly artificial yet effective example:

An employer claims to subscribe to an “equal opportunity” policy, not hiring men any more often than women for managerial positions. Is this credible? You’re not sure, so you want to test the following two hypotheses:

• Ho: The proportion of male managers hired is 0.5
• Ha: The proportion of male managers hired is more than 0.5

Data: You choose at random three of the new managers who were hired in the last 5 years and find that all 3 are men.

Assessing Evidence: If the proportion of male managers hired is really 0.5 (Ho is true), then the probability that the random selection of three managers will yield three males is therefore 0.5 * 0.5 * 0.5 = 0.125. This is the p-value (using the multiplication rule for independent events).

Conclusion: Using 0.05 as the significance level, you conclude that since the p-value = 0.125 > 0.05, the fact that the three randomly selected managers were all males is not enough evidence to reject the employer’s claim of subscribing to an equal opportunity policy (Ho).

However, the data (all three selected are males) definitely does NOT provide evidence to accept the employer’s claim (Ho).

Learn By Doing: Using p-values

Did I Get This?: Using p-values

Comment about wording: Another common wording in scientific journals is:

• “The results are statistically significant” – when the p-value < α (alpha).
• “The results are not statistically significant” – when the p-value > α (alpha).

Often you will see significance levels reported with additional description to indicate the degree of statistical significance. A general guideline (although not required in our course) is:

• If 0.01 ≤ p-value < 0.05, then the results are (statistically) significant .
• If 0.001 ≤ p-value < 0.01, then the results are highly statistically significant .
• If p-value < 0.001, then the results are very highly statistically significant .
• If p-value > 0.05, then the results are not statistically significant (NS).
• If 0.05 ≤ p-value < 0.10, then the results are marginally statistically significant .

Let’s summarize

We learned quite a lot about hypothesis testing. We learned the logic behind it, what the key elements are, and what types of conclusions we can and cannot draw in hypothesis testing. Here is a quick recap:

Video: Hypothesis Testing Overview (2:20)

Here are a few more activities if you need some additional practice.

Did I Get This?: Hypothesis Testing Overview

• Notice that the p-value is an example of a conditional probability . We calculate the probability of obtaining results like those of our data (or more extreme) GIVEN the null hypothesis is true. We could write P(Obtaining results like ours or more extreme | Ho is True).
• We could write P(Obtaining a test statistic as or more extreme than ours | Ho is True).
• In this case we are asking “Assuming the null hypothesis is true, how rare is it to observe something as or more extreme than what I have found in my data?”
• If after assuming the null hypothesis is true, what we have found in our data is extremely rare (small p-value), this provides evidence to reject our assumption that Ho is true in favor of Ha.
• The p-value can also be thought of as the probability, assuming the null hypothesis is true, that the result we have seen is solely due to random error (or random chance). We have already seen that statistics from samples collected from a population vary. There is random error or random chance involved when we sample from populations.

In this setting, if the p-value is very small, this implies, assuming the null hypothesis is true, that it is extremely unlikely that the results we have obtained would have happened due to random error alone, and thus our assumption (Ho) is rejected in favor of the alternative hypothesis (Ha).

• It is EXTREMELY important that you find a definition of the p-value which makes sense to you. New students often need to contemplate this idea repeatedly through a variety of examples and explanations before becoming comfortable with this idea. It is one of the two most important concepts in statistics (the other being confidence intervals).
• We infer that the alternative hypothesis is true ONLY by rejecting the null hypothesis.
• A statistically significant result is one that has a very low probability of occurring if the null hypothesis is true.
• Results which are statistically significant may or may not have practical significance and vice versa.

Error and Power

LO 6.28: Define a Type I and Type II error in general and in the context of specific scenarios.

LO 6.29: Explain the concept of the power of a statistical test including the relationship between power, sample size, and effect size.

Video: Errors and Power (12:03)

Type I and Type II Errors in Hypothesis Tests

We have not yet discussed the fact that we are not guaranteed to make the correct decision by this process of hypothesis testing. Maybe you are beginning to see that there is always some level of uncertainty in statistics.

Let’s think about what we know already and define the possible errors we can make in hypothesis testing. When we conduct a hypothesis test, we choose one of two possible conclusions based upon our data.

If the p-value is smaller than your pre-specified significance level (α, alpha), you reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is false
• You have made an error ( Type I ) and rejected Ho when in fact Ho is true (your data happened to be a RARE EVENT under Ho)

If the p-value is greater than (or equal to) your chosen significance level (α, alpha), you fail to reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is true
• You have made an error ( Type II ) and failed to reject Ho when in fact Ho is false (the alternative hypothesis, Ha, is true)

The following summarizes the four possible results which can be obtained from a hypothesis test. Notice the rows represent the decision made in the hypothesis test and the columns represent the (usually unknown) truth in reality.

Although the truth is unknown in practice – or we would not be conducting the test – we know it must be the case that either the null hypothesis is true or the null hypothesis is false. It is also the case that either decision we make in a hypothesis test can result in an incorrect conclusion!

A TYPE I Error occurs when we Reject Ho when, in fact, Ho is True. In this case, we mistakenly reject a true null hypothesis.

• P(TYPE I Error) = P(Reject Ho | Ho is True) = α = alpha = Significance Level

A TYPE II Error occurs when we fail to Reject Ho when, in fact, Ho is False. In this case we fail to reject a false null hypothesis.

P(TYPE II Error) = P(Fail to Reject Ho | Ho is False) = β = beta

When our significance level is 5%, we are saying that we will allow ourselves to make a Type I error less than 5% of the time. In the long run, if we repeat the process, 5% of the time we will find a p-value < 0.05 when in fact the null hypothesis was true.

In this case, our data represent a rare occurrence which is unlikely to happen but is still possible. For example, suppose we toss a coin 10 times and obtain 10 heads, this is unlikely for a fair coin but not impossible. We might conclude the coin is unfair when in fact we simply saw a very rare event for this fair coin.

Our testing procedure CONTROLS for the Type I error when we set a pre-determined value for the significance level.

Notice that these probabilities are conditional probabilities. This is one more reason why conditional probability is an important concept in statistics.

Unfortunately, calculating the probability of a Type II error requires us to know the truth about the population. In practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

Comment: As you initially read through the examples below, focus on the broad concepts instead of the small details. It is not important to understand how to calculate these values yourself at this point.

• Try to understand the pictures we present. Which pictures represent an assumed null hypothesis and which represent an alternative?
• It may be useful to come back to this page (and the activities here) after you have reviewed the rest of the section on hypothesis testing and have worked a few problems yourself.

Interactive Applet: Statistical Significance

Here are two examples of using an older version of this applet. It looks slightly different but the same settings and options are available in the version above.

In both cases we will consider IQ scores.

Our null hypothesis is that the true mean is 100. Assume the standard deviation is 16 and we will specify a significance level of 5%.

In this example we will specify that the true mean is indeed 100 so that the null hypothesis is true. Most of the time (95%), when we generate a sample, we should fail to reject the null hypothesis since the null hypothesis is indeed true.

Here is one sample that results in a correct decision:

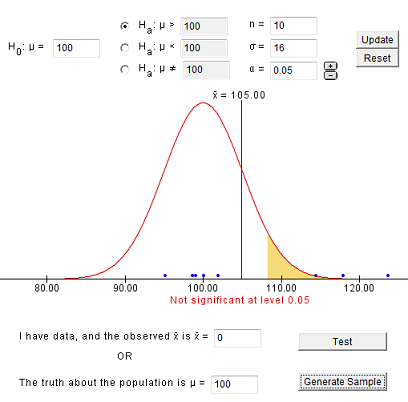
In the sample above, we obtain an x-bar of 105, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true). Notice the sample is shown as blue dots along the x-axis and the shaded region shows for which values of x-bar we would reject the null hypothesis. In other words, we would reject Ho whenever the x-bar falls in the shaded region.

Enter the same values and generate samples until you obtain a Type I error (you falsely reject the null hypothesis). You should see something like this:

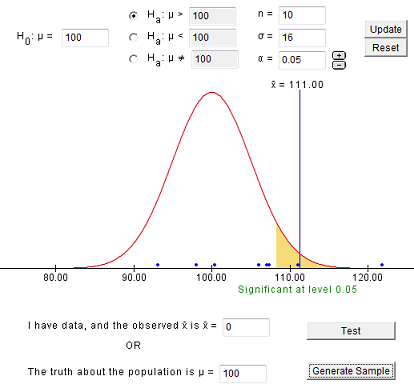
If you were to generate 100 samples, you should have around 5% where you rejected Ho. These would be samples which would result in a Type I error.

The previous example illustrates a correct decision and a Type I error when the null hypothesis is true. The next example illustrates a correct decision and Type II error when the null hypothesis is false. In this case, we must specify the true population mean.

Let’s suppose we are sampling from an honors program and that the true mean IQ for this population is 110. We do not know the probability of a Type II error without more detailed calculations.

Let’s start with a sample which results in a correct decision.

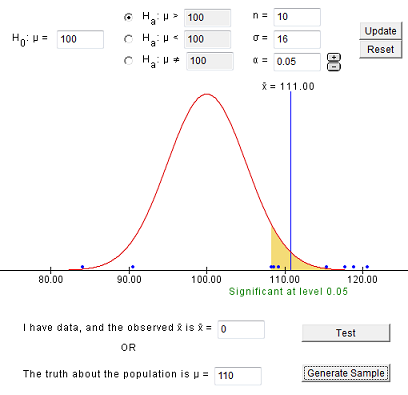
In the sample above, we obtain an x-bar of 111, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true).

Enter the same values and generate samples until you obtain a Type II error (you fail to reject the null hypothesis). You should see something like this:

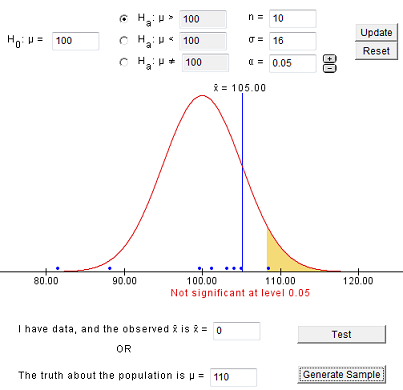
You should notice that in this case (when Ho is false), it is easier to obtain an incorrect decision (a Type II error) than it was in the case where Ho is true. If you generate 100 samples, you can approximate the probability of a Type II error.

We can find the probability of a Type II error by visualizing both the assumed distribution and the true distribution together. The image below is adapted from an applet we will use when we discuss the power of a statistical test.

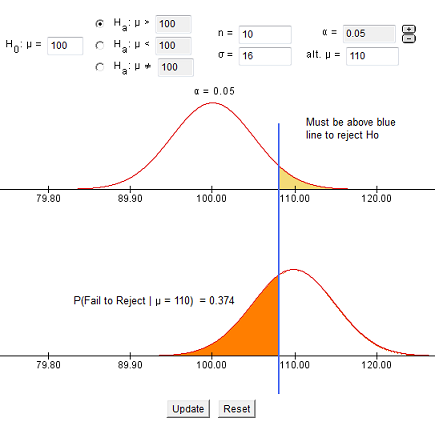
There is a 37.4% chance that, in the long run, we will make a Type II error and fail to reject the null hypothesis when in fact the true mean IQ is 110 in the population from which we sample our 10 individuals.

Can you visualize what will happen if the true population mean is really 115 or 108? When will the Type II error increase? When will it decrease? We will look at this idea again when we discuss the concept of power in hypothesis tests.

• It is important to note that there is a trade-off between the probability of a Type I and a Type II error. If we decrease the probability of one of these errors, the probability of the other will increase! The practical result of this is that if we require stronger evidence to reject the null hypothesis (smaller significance level = probability of a Type I error), we will increase the chance that we will be unable to reject the null hypothesis when in fact Ho is false (increases the probability of a Type II error).
• When α (alpha) = 0.05 we obtained a Type II error probability of 0.374 = β = beta

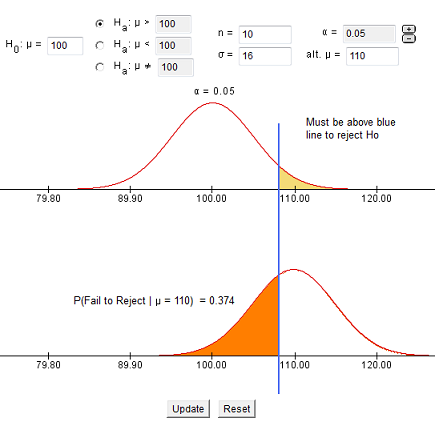
• When α (alpha) = 0.01 (smaller than before) we obtain a Type II error probability of 0.644 = β = beta (larger than before)

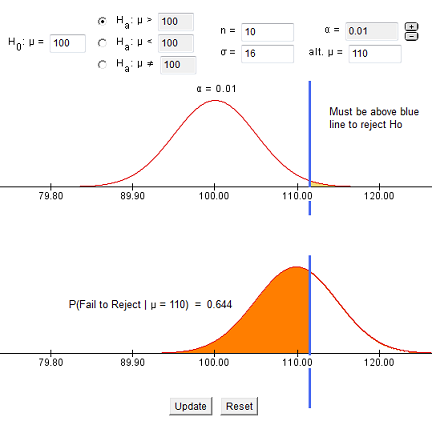
• As the blue line in the picture moves farther right, the significance level (α, alpha) is decreasing and the Type II error probability is increasing.
• As the blue line in the picture moves farther left, the significance level (α, alpha) is increasing and the Type II error probability is decreasing

Let’s return to our very first example and define these two errors in context.

• Ho = The student’s claim: I did not cheat on the exam.
• Ha = The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim.

There are four possible outcomes of this process. There are two possible correct decisions:

• The student did cheat on the exam and the instructor brings enough evidence to reject Ho and conclude the student did cheat on the exam. This is a CORRECT decision!
• The student did not cheat on the exam and the instructor fails to provide enough evidence that the student did cheat on the exam. This is a CORRECT decision!

Both the correct decisions and the possible errors are fairly easy to understand but with the errors, you must be careful to identify and define the two types correctly.

TYPE I Error: Reject Ho when Ho is True

• The student did not cheat on the exam but the instructor brings enough evidence to reject Ho and conclude the student cheated on the exam. This is a Type I Error.

TYPE II Error: Fail to Reject Ho when Ho is False

• The student did cheat on the exam but the instructor fails to provide enough evidence that the student cheated on the exam. This is a Type II Error.

In most situations, including this one, it is more “acceptable” to have a Type II error than a Type I error. Although allowing a student who cheats to go unpunished might be considered a very bad problem, punishing a student for something he or she did not do is usually considered to be a more severe error. This is one reason we control for our Type I error in the process of hypothesis testing.

Did I Get This?: Type I and Type II Errors (in context)

• The probabilities of Type I and Type II errors are closely related to the concepts of sensitivity and specificity that we discussed previously. Consider the following hypotheses:

Ho: The individual does not have diabetes (status quo, nothing special happening)

Ha: The individual does have diabetes (something is going on here)

In this setting:

When someone tests positive for diabetes we would reject the null hypothesis and conclude the person has diabetes (we may or may not be correct!).

When someone tests negative for diabetes we would fail to reject the null hypothesis so that we fail to conclude the person has diabetes (we may or may not be correct!)

Let’s take it one step further:

Sensitivity = P(Test + | Have Disease) which in this setting equals P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1 – beta

Specificity = P(Test – | No Disease) which in this setting equals P(Fail to Reject Ho | Ho is True) = 1 – P(Reject Ho | Ho is True) = 1 – α = 1 – alpha

Notice that sensitivity and specificity relate to the probability of making a correct decision whereas α (alpha) and β (beta) relate to the probability of making an incorrect decision.

Usually α (alpha) = 0.05 so that the specificity listed above is 0.95 or 95%.

Next, we will see that the sensitivity listed above is the power of the hypothesis test!

Reasons for a Type I Error in Practice

Assuming that you have obtained a quality sample:

• The reason for a Type I error is random chance.
• When a Type I error occurs, our observed data represented a rare event which indicated evidence in favor of the alternative hypothesis even though the null hypothesis was actually true.

Reasons for a Type II Error in Practice

Again, assuming that you have obtained a quality sample, now we have a few possibilities depending upon the true difference that exists.

• The sample size is too small to detect an important difference. This is the worst case, you should have obtained a larger sample. In this situation, you may notice that the effect seen in the sample seems PRACTICALLY significant and yet the p-value is not small enough to reject the null hypothesis.
• The sample size is reasonable for the important difference but the true difference (which might be somewhat meaningful or interesting) is smaller than your test was capable of detecting. This is tolerable as you were not interested in being able to detect this difference when you began your study. In this situation, you may notice that the effect seen in the sample seems to have some potential for practical significance.
• The sample size is more than adequate, the difference that was not detected is meaningless in practice. This is not a problem at all and is in effect a “correct decision” since the difference you did not detect would have no practical meaning.
• Note: We will discuss the idea of practical significance later in more detail.

Power of a Hypothesis Test

It is often the case that we truly wish to prove the alternative hypothesis. It is reasonable that we would be interested in the probability of correctly rejecting the null hypothesis. In other words, the probability of rejecting the null hypothesis, when in fact the null hypothesis is false. This can also be thought of as the probability of being able to detect a (pre-specified) difference of interest to the researcher.

Let’s begin with a realistic example of how power can be described in a study.

In a clinical trial to study two medications for weight loss, we have an 80% chance to detect a difference in the weight loss between the two medications of 10 pounds. In other words, the power of the hypothesis test we will conduct is 80%.

In other words, if one medication comes from a population with an average weight loss of 25 pounds and the other comes from a population with an average weight loss of 15 pounds, we will have an 80% chance to detect that difference using the sample we have in our trial.

If we were to repeat this trial many times, 80% of the time we will be able to reject the null hypothesis (that there is no difference between the medications) and 20% of the time we will fail to reject the null hypothesis (and make a Type II error!).

The difference of 10 pounds in the previous example, is often called the effect size . The measure of the effect differs depending on the particular test you are conducting but is always some measure related to the true effect in the population. In this example, it is the difference between two population means.

Recall the definition of a Type II error:

Notice that P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1- beta.

The POWER of a hypothesis test is the probability of rejecting the null hypothesis when the null hypothesis is false . This can also be stated as the probability of correctly rejecting the null hypothesis .

POWER = P(Reject Ho | Ho is False) = 1 – β = 1 – beta

Power is the test’s ability to correctly reject the null hypothesis. A test with high power has a good chance of being able to detect the difference of interest to us, if it exists .

As we mentioned on the bottom of the previous page, this can be thought of as the sensitivity of the hypothesis test if you imagine Ho = No disease and Ha = Disease.

Factors Affecting the Power of a Hypothesis Test

The power of a hypothesis test is affected by numerous quantities (similar to the margin of error in a confidence interval).

Assume that the null hypothesis is false for a given hypothesis test. All else being equal, we have the following:

• Larger samples result in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test.
• If the effect size is larger, it will become easier for us to detect. This results in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test. The effect size varies for each test and is usually closely related to the difference between the hypothesized value and the true value of the parameter under study.
• From the relationship between the probability of a Type I and a Type II error (as α (alpha) decreases, β (beta) increases), we can see that as α (alpha) decreases, Power = 1 – β = 1 – beta also decreases.
• There are other mathematical ways to change the power of a hypothesis test, such as changing the population standard deviation; however, these are not quantities that we can usually control so we will not discuss them here.

In practice, we specify a significance level and a desired power to detect a difference which will have practical meaning to us and this determines the sample size required for the experiment or study.

For most grants involving statistical analysis, power calculations must be completed to illustrate that the study will have a reasonable chance to detect an important effect. Otherwise, the money spent on the study could be wasted. The goal is usually to have a power close to 80%.

For example, if there is only a 5% chance to detect an important difference between two treatments in a clinical trial, this would result in a waste of time, effort, and money on the study since, when the alternative hypothesis is true, the chance a treatment effect can be found is very small.

• In order to calculate the power of a hypothesis test, we must specify the “truth.” As we mentioned previously when discussing Type II errors, in practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

The following activity involves working with an interactive applet to study power more carefully.

Learn by Doing: Power of Hypothesis Tests

The following reading is an excellent discussion about Type I and Type II errors.

(Optional) Outside Reading: A Good Discussion of Power (≈ 2500 words)

We will not be asking you to perform power calculations manually. You may be asked to use online calculators and applets. Most statistical software packages offer some ability to complete power calculations. There are also many online calculators for power and sample size on the internet, for example, Russ Lenth’s power and sample-size page .

Proportions (Introduction & Step 1)

CO-4: Distinguish among different measurement scales, choose the appropriate descriptive and inferential statistical methods based on these distinctions, and interpret the results.

LO 4.33: In a given context, distinguish between situations involving a population proportion and a population mean and specify the correct null and alternative hypothesis for the scenario.

LO 4.34: Carry out a complete hypothesis test for a population proportion by hand.

Video: Proportions (Introduction & Step 1) (7:18)

Now that we understand the process of hypothesis testing and the logic behind it, we are ready to start learning about specific statistical tests (also known as significance tests).

The first test we are going to learn is the test about the population proportion (p).

This test is widely known as the “z-test for the population proportion (p).”

We will understand later where the “z-test” part is coming from.

This will be the only type of problem you will complete entirely “by-hand” in this course. Our goal is to use this example to give you the tools you need to understand how this process works. After working a few problems, you should review the earlier material again. You will likely need to review the terminology and concepts a few times before you fully understand the process.

In reality, you will often be conducting more complex statistical tests and allowing software to provide the p-value. In these settings it will be important to know what test to apply for a given situation and to be able to explain the results in context.

Review: Types of Variables

When we conduct a test about a population proportion, we are working with a categorical variable. Later in the course, after we have learned a variety of hypothesis tests, we will need to be able to identify which test is appropriate for which situation. Identifying the variable as categorical or quantitative is an important component of choosing an appropriate hypothesis test.

Learn by Doing: Review Types of Variables

One Sample Z-Test for a Population Proportion

In this part of our discussion on hypothesis testing, we will go into details that we did not go into before. More specifically, we will use this test to introduce the idea of a test statistic , and details about how p-values are calculated .

Let’s start by introducing the three examples, which will be the leading examples in our discussion. Each example is followed by a figure illustrating the information provided, as well as the question of interest.

A machine is known to produce 20% defective products, and is therefore sent for repair. After the machine is repaired, 400 products produced by the machine are chosen at random and 64 of them are found to be defective. Do the data provide enough evidence that the proportion of defective products produced by the machine (p) has been reduced as a result of the repair?

The following figure displays the information, as well as the question of interest:

The question of interest helps us formulate the null and alternative hypotheses in terms of p, the proportion of defective products produced by the machine following the repair:

• Ho: p = 0.20 (No change; the repair did not help).
• Ha: p < 0.20 (The repair was effective at reducing the proportion of defective parts).

There are rumors that students at a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 100 students from the college, 19 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (This number is reported by the Harvard School of Public Health.)

Again, the following figure displays the information as well as the question of interest:

As before, we can formulate the null and alternative hypotheses in terms of p, the proportion of students in the college who use marijuana:

• Ho: p = 0.157 (same as among all college students in the country).
• Ha: p > 0.157 (higher than the national figure).

Polls on certain topics are conducted routinely in order to monitor changes in the public’s opinions over time. One such topic is the death penalty. In 2003 a poll estimated that 64% of U.S. adults support the death penalty for a person convicted of murder. In a more recent poll, 675 out of 1,000 U.S. adults chosen at random were in favor of the death penalty for convicted murderers. Do the results of this poll provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers (p) changed between 2003 and the later poll?

Here is a figure that displays the information, as well as the question of interest:

Again, we can formulate the null and alternative hypotheses in term of p, the proportion of U.S. adults who support the death penalty for convicted murderers.

• Ho: p = 0.64 (No change from 2003).
• Ha: p ≠ 0.64 (Some change since 2003).

Learn by Doing: Proportions (Overview)

Did I Get This?: Proportions ( Overview )

Recall that there are basically 4 steps in the process of hypothesis testing:

• STEP 1: State the appropriate null and alternative hypotheses, Ho and Ha.
• STEP 2: Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used . If the conditions are met, summarize the data using a test statistic.
• STEP 3: Find the p-value of the test.
• STEP 4: Based on the p-value, decide whether or not the results are statistically significant and draw your conclusions in context.
• Note: In practice, we should always consider the practical significance of the results as well as the statistical significance.

We are now going to go through these steps as they apply to the hypothesis testing for the population proportion p. It should be noted that even though the details will be specific to this particular test, some of the ideas that we will add apply to hypothesis testing in general.

Step 1. Stating the Hypotheses

Here again are the three set of hypotheses that are being tested in each of our three examples:

Has the proportion of defective products been reduced as a result of the repair?

Is the proportion of marijuana users in the college higher than the national figure?

Did the proportion of U.S. adults who support the death penalty change between 2003 and a later poll?

The null hypothesis always takes the form:

• Ho: p = some value

and the alternative hypothesis takes one of the following three forms:

• Ha: p < that value (like in example 1) or
• Ha: p > that value (like in example 2) or
• Ha: p ≠ that value (like in example 3).

Note that it was quite clear from the context which form of the alternative hypothesis would be appropriate. The value that is specified in the null hypothesis is called the null value , and is generally denoted by p 0 . We can say, therefore, that in general the null hypothesis about the population proportion (p) would take the form:

• Ho: p = p 0

We write Ho: p = p 0 to say that we are making the hypothesis that the population proportion has the value of p 0 . In other words, p is the unknown population proportion and p 0 is the number we think p might be for the given situation.

The alternative hypothesis takes one of the following three forms (depending on the context):

Ha: p < p 0 (one-sided)

Ha: p > p 0 (one-sided)

Ha: p ≠ p 0 (two-sided)

The first two possible forms of the alternatives (where the = sign in Ho is challenged by < or >) are called one-sided alternatives , and the third form of alternative (where the = sign in Ho is challenged by ≠) is called a two-sided alternative. To understand the intuition behind these names let’s go back to our examples.

Example 3 (death penalty) is a case where we have a two-sided alternative:

In this case, in order to reject Ho and accept Ha we will need to get a sample proportion of death penalty supporters which is very different from 0.64 in either direction, either much larger or much smaller than 0.64.

In example 2 (marijuana use) we have a one-sided alternative:

Here, in order to reject Ho and accept Ha we will need to get a sample proportion of marijuana users which is much higher than 0.157.

Similarly, in example 1 (defective products), where we are testing:

in order to reject Ho and accept Ha, we will need to get a sample proportion of defective products which is much smaller than 0.20.

Learn by Doing: State Hypotheses (Proportions)

Did I Get This?: State Hypotheses (Proportions)

Proportions (Step 2)

Video: Proportions (Step 2) (12:38)

Step 2. Collect Data, Check Conditions, and Summarize Data

After the hypotheses have been stated, the next step is to obtain a sample (on which the inference will be based), collect relevant data , and summarize them.

It is extremely important that our sample is representative of the population about which we want to draw conclusions. This is ensured when the sample is chosen at random. Beyond the practical issue of ensuring representativeness, choosing a random sample has theoretical importance that we will mention later.

In the case of hypothesis testing for the population proportion (p), we will collect data on the relevant categorical variable from the individuals in the sample and start by calculating the sample proportion p-hat (the natural quantity to calculate when the parameter of interest is p).

Let’s go back to our three examples and add this step to our figures.

As we mentioned earlier without going into details, when we summarize the data in hypothesis testing, we go a step beyond calculating the sample statistic and summarize the data with a test statistic . Every test has a test statistic, which to some degree captures the essence of the test. In fact, the p-value, which so far we have looked upon as “the king” (in the sense that everything is determined by it), is actually determined by (or derived from) the test statistic. We will now introduce the test statistic.

The test statistic is a measure of how far the sample proportion p-hat is from the null value p 0 , the value that the null hypothesis claims is the value of p. In other words, since p-hat is what the data estimates p to be, the test statistic can be viewed as a measure of the “distance” between what the data tells us about p and what the null hypothesis claims p to be.

Let’s use our examples to understand this:

The parameter of interest is p, the proportion of defective products following the repair.

The data estimate p to be p-hat = 0.16

The null hypothesis claims that p = 0.20

The data are therefore 0.04 (or 4 percentage points) below the null hypothesis value.

It is hard to evaluate whether this difference of 4% in defective products is enough evidence to say that the repair was effective at reducing the proportion of defective products, but clearly, the larger the difference, the more evidence it is against the null hypothesis. So if, for example, our sample proportion of defective products had been, say, 0.10 instead of 0.16, then I think you would all agree that cutting the proportion of defective products in half (from 20% to 10%) would be extremely strong evidence that the repair was effective at reducing the proportion of defective products.

The parameter of interest is p, the proportion of students in a college who use marijuana.

The data estimate p to be p-hat = 0.19

The null hypothesis claims that p = 0.157

The data are therefore 0.033 (or 3.3. percentage points) above the null hypothesis value.

The parameter of interest is p, the proportion of U.S. adults who support the death penalty for convicted murderers.

The data estimate p to be p-hat = 0.675

The null hypothesis claims that p = 0.64

There is a difference of 0.035 (or 3.5. percentage points) between the data and the null hypothesis value.

The problem with looking only at the difference between the sample proportion, p-hat, and the null value, p 0 is that we have not taken into account the variability of our estimator p-hat which, as we know from our study of sampling distributions, depends on the sample size.

For this reason, the test statistic cannot simply be the difference between p-hat and p 0 , but must be some form of that formula that accounts for the sample size. In other words, we need to somehow standardize the difference so that comparison between different situations will be possible. We are very close to revealing the test statistic, but before we construct it, let’s be reminded of the following two facts from probability:

Fact 1: When we take a random sample of size n from a population with population proportion p, then

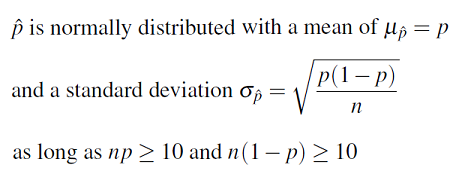
Fact 2: The z-score of any normal value (a value that comes from a normal distribution) is calculated by finding the difference between the value and the mean and then dividing that difference by the standard deviation (of the normal distribution associated with the value). The z-score represents how many standard deviations below or above the mean the value is.

Thus, our test statistic should be a measure of how far the sample proportion p-hat is from the null value p 0 relative to the variation of p-hat (as measured by the standard error of p-hat).

Recall that the standard error is the standard deviation of the sampling distribution for a given statistic. For p-hat, we know the following:

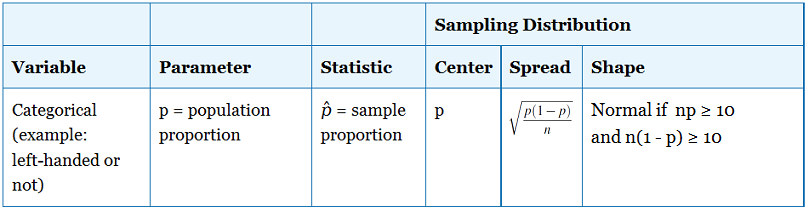
To find the p-value, we will need to determine how surprising our value is assuming the null hypothesis is true. We already have the tools needed for this process from our study of sampling distributions as represented in the table above.

If we assume the null hypothesis is true, we can specify that the center of the distribution of all possible values of p-hat from samples of size 400 would be 0.20 (our null value).

We can calculate the standard error, assuming p = 0.20 as

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}=\sqrt{\dfrac{0.2(1-0.2)}{400}}=0.02\)

The following picture represents the sampling distribution of all possible values of p-hat of samples of size 400, assuming the true proportion p is 0.20 and our other requirements for the sampling distribution to be normal are met (we will review these during the next step).

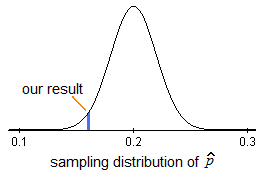
In order to calculate probabilities for the picture above, we would need to find the z-score associated with our result.

This z-score is the test statistic ! In this example, the numerator of our z-score is the difference between p-hat (0.16) and null value (0.20) which we found earlier to be -0.04. The denominator of our z-score is the standard error calculated above (0.02) and thus quickly we find the z-score, our test statistic, to be -2.

The sample proportion based upon this data is 2 standard errors below the null value.

Hopefully you now understand more about the reasons we need probability in statistics!!

Now we will formalize the definition and look at our remaining examples before moving on to the next step, which will be to determine if a normal distribution applies and calculate the p-value.

Test Statistic for Hypothesis Tests for One Proportion is:

\(z=\dfrac{\hat{p}-p_{0}}{\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}}\)

It represents the difference between the sample proportion and the null value, measured in standard deviations (standard error of p-hat).

The picture above is a representation of the sampling distribution of p-hat assuming p = p 0 . In other words, this is a model of how p-hat behaves if we are drawing random samples from a population for which Ho is true.

Notice the center of the sampling distribution is at p 0 , which is the hypothesized proportion given in the null hypothesis (Ho: p = p 0 .) We could also mark the axis in standard error units,

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}\)

For example, if our null hypothesis claims that the proportion of U.S. adults supporting the death penalty is 0.64, then the sampling distribution is drawn as if the null is true. We draw a normal distribution centered at 0.64 (p 0 ) with a standard error dependent on sample size,

\(\sqrt{\dfrac{0.64(1-0.64)}{n}}\).

Important Comment:

• Note that under the assumption that Ho is true (and if the conditions for the sampling distribution to be normal are satisfied) the test statistic follows a N(0,1) (standard normal) distribution. Another way to say the same thing which is quite common is: “The null distribution of the test statistic is N(0,1).”

By “null distribution,” we mean the distribution under the assumption that Ho is true. As we’ll see and stress again later, the null distribution of the test statistic is what the calculation of the p-value is based on.

Let’s go back to our remaining two examples and find the test statistic in each case:

Since the null hypothesis is Ho: p = 0.157, the standardized (z) score of p-hat = 0.19 is

\(z=\dfrac{0.19-0.157}{\sqrt{\dfrac{0.157(1-0.157)}{100}}} \approx 0.91\)

This is the value of the test statistic for this example.

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.19 is 0.91 standard errors above the null value (0.157).

Since the null hypothesis is Ho: p = 0.64, the standardized (z) score of p-hat = 0.675 is

\(z=\dfrac{0.675-0.64}{\sqrt{\dfrac{0.64(1-0.64)}{1000}}} \approx 2.31\)

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.675 is 2.31 standard errors above the null value (0.64).

Learn by Doing: Proportions (Step 2)

Comments about the Test Statistic:

• We mentioned earlier that to some degree, the test statistic captures the essence of the test. In this case, the test statistic measures the difference between p-hat and p 0 in standard errors. This is exactly what this test is about. Get data, and look at the discrepancy between what the data estimates p to be (represented by p-hat) and what Ho claims about p (represented by p 0 ).
• You can think about this test statistic as a measure of evidence in the data against Ho. The larger the test statistic, the “further the data are from Ho” and therefore the more evidence the data provide against Ho.

Learn by Doing: Proportions (Step 2) Understanding the Test Statistic

Did I Get This?: Proportions (Step 2)

• It should now be clear why this test is commonly known as the z-test for the population proportion . The name comes from the fact that it is based on a test statistic that is a z-score.
• Recall fact 1 that we used for constructing the z-test statistic. Here is part of it again:

When we take a random sample of size n from a population with population proportion p 0 , the possible values of the sample proportion p-hat ( when certain conditions are met ) have approximately a normal distribution with a mean of p 0 … and a standard deviation of

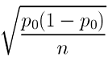
This result provides the theoretical justification for constructing the test statistic the way we did, and therefore the assumptions under which this result holds (in bold, above) are the conditions that our data need to satisfy so that we can use this test. These two conditions are:

i. The sample has to be random.

ii. The conditions under which the sampling distribution of p-hat is normal are met. In other words:

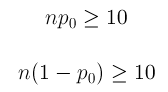
• Here we will pause to say more about condition (i.) above, the need for a random sample. In the Probability Unit we discussed sampling plans based on probability (such as a simple random sample, cluster, or stratified sampling) that produce a non-biased sample, which can be safely used in order to make inferences about a population. We noted in the Probability Unit that, in practice, other (non-random) sampling techniques are sometimes used when random sampling is not feasible. It is important though, when these techniques are used, to be aware of the type of bias that they introduce, and thus the limitations of the conclusions that can be drawn from them. For our purpose here, we will focus on one such practice, the situation in which a sample is not really chosen randomly, but in the context of the categorical variable that is being studied, the sample is regarded as random. For example, say that you are interested in the proportion of students at a certain college who suffer from seasonal allergies. For that purpose, the students in a large engineering class could be considered as a random sample, since there is nothing about being in an engineering class that makes you more or less likely to suffer from seasonal allergies. Technically, the engineering class is a convenience sample, but it is treated as a random sample in the context of this categorical variable. On the other hand, if you are interested in the proportion of students in the college who have math anxiety, then the class of engineering students clearly could not possibly be viewed as a random sample, since engineering students probably have a much lower incidence of math anxiety than the college population overall.

Learn by Doing: Proportions (Step 2) Valid or Invalid Sampling?

Let’s check the conditions in our three examples.

i. The 400 products were chosen at random.

ii. n = 400, p 0 = 0.2 and therefore:

\(n p_{0}=400(0.2)=80 \geq 10\)

\(n\left(1-p_{0}\right)=400(1-0.2)=320 \geq 10\)

i. The 100 students were chosen at random.

ii. n = 100, p 0 = 0.157 and therefore:

\begin{gathered} n p_{0}=100(0.157)=15.7 \geq 10 \\ n\left(1-p_{0}\right)=100(1-0.157)=84.3 \geq 10 \end{gathered}

i. The 1000 adults were chosen at random.

ii. n = 1000, p 0 = 0.64 and therefore:

\begin{gathered} n p_{0}=1000(0.64)=640 \geq 10 \\ n\left(1-p_{0}\right)=1000(1-0.64)=360 \geq 10 \end{gathered}

Learn by Doing: Proportions (Step 2) Verify Conditions

Checking that our data satisfy the conditions under which the test can be reliably used is a very important part of the hypothesis testing process. Be sure to consider this for every hypothesis test you conduct in this course and certainly in practice.

The Four Steps in Hypothesis Testing

With respect to the z-test, the population proportion that we are currently discussing we have:

Step 1: Completed

Step 2: Completed

Step 3: This is what we will work on next.

Proportions (Step 3)

Video: Proportions (Step 3) (14:46)

Calculators and Tables

Step 3. Finding the P-value of the Test

So far we’ve talked about the p-value at the intuitive level: understanding what it is (or what it measures) and how we use it to draw conclusions about the statistical significance of our results. We will now go more deeply into how the p-value is calculated.

It should be mentioned that eventually we will rely on technology to calculate the p-value for us (as well as the test statistic), but in order to make intelligent use of the output, it is important to first understand the details, and only then let the computer do the calculations for us. Again, our goal is to use this simple example to give you the tools you need to understand the process entirely. Let’s start.

Recall that so far we have said that the p-value is the probability of obtaining data like those observed assuming that Ho is true. Like the test statistic, the p-value is, therefore, a measure of the evidence against Ho. In the case of the test statistic, the larger it is in magnitude (positive or negative), the further p-hat is from p 0 , the more evidence we have against Ho. In the case of the p-value , it is the opposite; the smaller it is, the more unlikely it is to get data like those observed when Ho is true, the more evidence it is against Ho . One can actually draw conclusions in hypothesis testing just using the test statistic, and as we’ll see the p-value is, in a sense, just another way of looking at the test statistic. The reason that we actually take the extra step in this course and derive the p-value from the test statistic is that even though in this case (the test about the population proportion) and some other tests, the value of the test statistic has a very clear and intuitive interpretation, there are some tests where its value is not as easy to interpret. On the other hand, the p-value keeps its intuitive appeal across all statistical tests.

How is the p-value calculated?

Intuitively, the p-value is the probability of observing data like those observed assuming that Ho is true. Let’s be a bit more formal:

• Since this is a probability question about the data , it makes sense that the calculation will involve the data summary, the test statistic.
• What do we mean by “like” those observed? By “like” we mean “as extreme or even more extreme.”

Putting it all together, we get that in general:

The p-value is the probability of observing a test statistic as extreme as that observed (or even more extreme) assuming that the null hypothesis is true.

By “extreme” we mean extreme in the direction(s) of the alternative hypothesis.

Specifically , for the z-test for the population proportion:

• If the alternative hypothesis is Ha: p < p 0 (less than) , then “extreme” means small or less than , and the p-value is: The probability of observing a test statistic as small as that observed or smaller if the null hypothesis is true.
• If the alternative hypothesis is Ha: p > p 0 (greater than) , then “extreme” means large or greater than , and the p-value is: The probability of observing a test statistic as large as that observed or larger if the null hypothesis is true.
• If the alternative is Ha: p ≠ p 0 (different from) , then “extreme” means extreme in either direction either small or large (i.e., large in magnitude) or just different from , and the p-value therefore is: The probability of observing a test statistic as large in magnitude as that observed or larger if the null hypothesis is true.(Examples: If z = -2.5: p-value = probability of observing a test statistic as small as -2.5 or smaller or as large as 2.5 or larger. If z = 1.5: p-value = probability of observing a test statistic as large as 1.5 or larger, or as small as -1.5 or smaller.)

OK, hopefully that makes (some) sense. But how do we actually calculate it?

Recall the important comment from our discussion about our test statistic,

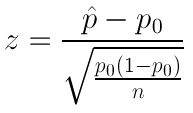
which said that when the null hypothesis is true (i.e., when p = p 0 ), the possible values of our test statistic follow a standard normal (N(0,1), denoted by Z) distribution. Therefore, the p-value calculations (which assume that Ho is true) are simply standard normal distribution calculations for the 3 possible alternative hypotheses.

Alternative Hypothesis is “Less Than”

The probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

Looking at the shaded region, you can see why this is often referred to as a left-tailed test. We shaded to the left of the test statistic, since less than is to the left.

Alternative Hypothesis is “Greater Than”

The probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

Looking at the shaded region, you can see why this is often referred to as a right-tailed test. We shaded to the right of the test statistic, since greater than is to the right.

Alternative Hypothesis is “Not Equal To”

The probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

This is often referred to as a two-tailed test, since we shaded in both directions.

Next, we will apply this to our three examples. But first, work through the following activities, which should help your understanding.

Learn by Doing: Proportions (Step 3)

Did I Get This?: Proportions (Step 3)

The p-value in this case is:

• The probability of observing a test statistic as small as -2 or smaller, assuming that Ho is true.

OR (recalling what the test statistic actually means in this case),

• The probability of observing a sample proportion that is 2 standard deviations or more below the null value (p 0 = 0.20), assuming that p 0 is the true population proportion.

OR, more specifically,

• The probability of observing a sample proportion of 0.16 or lower in a random sample of size 400, when the true population proportion is p 0 =0.20

In either case, the p-value is found as shown in the following figure:

To find P(Z ≤ -2) we can either use the calculator or table we learned to use in the probability unit for normal random variables. Eventually, after we understand the details, we will use software to run the test for us and the output will give us all the information we need. The p-value that the statistical software provides for this specific example is 0.023. The p-value tells us that it is pretty unlikely (probability of 0.023) to get data like those observed (test statistic of -2 or less) assuming that Ho is true.

• The probability of observing a test statistic as large as 0.91 or larger, assuming that Ho is true.
• The probability of observing a sample proportion that is 0.91 standard deviations or more above the null value (p 0 = 0.157), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion of 0.19 or higher in a random sample of size 100, when the true population proportion is p 0 =0.157

Again, at this point we can either use the calculator or table to find that the p-value is 0.182, this is P(Z ≥ 0.91).

The p-value tells us that it is not very surprising (probability of 0.182) to get data like those observed (which yield a test statistic of 0.91 or higher) assuming that the null hypothesis is true.

• The probability of observing a test statistic as large as 2.31 (or larger) or as small as -2.31 (or smaller), assuming that Ho is true.
• The probability of observing a sample proportion that is 2.31 standard deviations or more away from the null value (p 0 = 0.64), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion as different as 0.675 is from 0.64, or even more different (i.e. as high as 0.675 or higher or as low as 0.605 or lower) in a random sample of size 1,000, when the true population proportion is p 0 = 0.64

Again, at this point we can either use the calculator or table to find that the p-value is 0.021, this is P(Z ≤ -2.31) + P(Z ≥ 2.31) = 2*P(Z ≥ |2.31|)

The p-value tells us that it is pretty unlikely (probability of 0.021) to get data like those observed (test statistic as high as 2.31 or higher or as low as -2.31 or lower) assuming that Ho is true.

• We’ve just seen that finding p-values involves probability calculations about the value of the test statistic assuming that Ho is true. In this case, when Ho is true, the values of the test statistic follow a standard normal distribution (i.e., the sampling distribution of the test statistic when the null hypothesis is true is N(0,1)). Therefore, p-values correspond to areas (probabilities) under the standard normal curve.

Similarly, in any test , p-values are found using the sampling distribution of the test statistic when the null hypothesis is true (also known as the “null distribution” of the test statistic). In this case, it was relatively easy to argue that the null distribution of our test statistic is N(0,1). As we’ll see, in other tests, other distributions come up (like the t-distribution and the F-distribution), which we will just mention briefly, and rely heavily on the output of our statistical package for obtaining the p-values.

We’ve just completed our discussion about the p-value, and how it is calculated both in general and more specifically for the z-test for the population proportion. Let’s go back to the four-step process of hypothesis testing and see what we’ve covered and what still needs to be discussed.

With respect to the z-test the population proportion:

Step 3: Completed

Step 4. This is what we will work on next.

Learn by Doing: Proportions (Step 3) Understanding P-values

Proportions (Step 4 & Summary)

Video: Proportions (Step 4 & Summary) (4:30)

Step 4. Drawing Conclusions Based on the P-Value

This last part of the four-step process of hypothesis testing is the same across all statistical tests, and actually, we’ve already said basically everything there is to say about it, but it can’t hurt to say it again.

The p-value is a measure of how much evidence the data present against Ho. The smaller the p-value, the more evidence the data present against Ho.

We already mentioned that what determines what constitutes enough evidence against Ho is the significance level (α, alpha), a cutoff point below which the p-value is considered small enough to reject Ho in favor of Ha. The most commonly used significance level is 0.05.

• Conclusion: There IS enough evidence that Ha is True
• Conclusion: There IS NOT enough evidence that Ha is True

Where instead of Ha is True , we write what this means in the words of the problem, in other words, in the context of the current scenario.

It is important to mention again that this step has essentially two sub-steps:

(i) Based on the p-value, determine whether or not the results are statistically significant (i.e., the data present enough evidence to reject Ho).

(ii) State your conclusions in the context of the problem.

Note: We always still must consider whether the results have any practical significance, particularly if they are statistically significant as a statistically significant result which has not practical use is essentially meaningless!

Let’s go back to our three examples and draw conclusions.

We found that the p-value for this test was 0.023.

Since 0.023 is small (in particular, 0.023 < 0.05), the data provide enough evidence to reject Ho.

Conclusion:

• There IS enough evidence that the proportion of defective products is less than 20% after the repair .

The following figure is the complete story of this example, and includes all the steps we went through, starting from stating the hypotheses and ending with our conclusions:

We found that the p-value for this test was 0.182.

Since .182 is not small (in particular, 0.182 > 0.05), the data do not provide enough evidence to reject Ho.

• There IS NOT enough evidence that the proportion of students at the college who use marijuana is higher than the national figure.

Here is the complete story of this example:

Learn by Doing: Learn by Doing – Proportions (Step 4)

We found that the p-value for this test was 0.021.

Since 0.021 is small (in particular, 0.021 < 0.05), the data provide enough evidence to reject Ho

• There IS enough evidence that the proportion of adults who support the death penalty for convicted murderers has changed since 2003.

Did I Get This?: Proportions (Step 4)

Many Students Wonder: Hypothesis Testing for the Population Proportion

Many students wonder why 5% is often selected as the significance level in hypothesis testing, and why 1% is the next most typical level. This is largely due to just convenience and tradition.

When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly these are arbitrary levels.

The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics; but it’s important to remember that there is really a continuous range of increasing confidence towards the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between a p-value of .049 or .051, and it would be foolish to declare one case definitely a “real” effect and to declare the other case definitely a “random” effect. In either case, the study results were roughly 5% likely by chance if there’s no actual effect.

Whether such a p-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision, and the extent to which the hypothesized effect might contradict our prior experience or previous studies.

Let’s Summarize!!

We have now completed going through the four steps of hypothesis testing, and in particular we learned how they are applied to the z-test for the population proportion. Here is a brief summary:

Step 1: State the hypotheses

State the null hypothesis:

State the alternative hypothesis:

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem. If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! Use only the information given in the problem.

Step 2: Obtain data, check conditions, and summarize data

Obtain data from a sample and:

(i) Check whether the data satisfy the conditions which allow you to use this test.

random sample (or at least a sample that can be considered random in context)

the conditions under which the sampling distribution of p-hat is normal are met

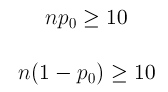
(ii) Calculate the sample proportion p-hat, and summarize the data using the test statistic:

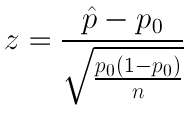
( Recall: This standardized test statistic represents how many standard deviations above or below p 0 our sample proportion p-hat is.)

Step 3: Find the p-value of the test by using the test statistic as follows

IMPORTANT FACT: In all future tests, we will rely on software to obtain the p-value.

When the alternative hypothesis is “less than” the probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

When the alternative hypothesis is “greater than” the probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

When the alternative hypothesis is “not equal to” the probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

Step 4: Conclusion

Reach a conclusion first regarding the statistical significance of the results, and then determine what it means in the context of the problem.

If p-value ≤ 0.05 then WE REJECT Ho Conclusion: There IS enough evidence that Ha is True

If p-value > 0.05 then WE FAIL TO REJECT Ho Conclusion: There IS NOT enough evidence that Ha is True

Recall that: If the p-value is small (in particular, smaller than the significance level, which is usually 0.05), the results are statistically significant (in the sense that there is a statistically significant difference between what was observed in the sample and what was claimed in Ho), and so we reject Ho.

If the p-value is not small, we do not have enough statistical evidence to reject Ho, and so we continue to believe that Ho may be true. ( Remember: In hypothesis testing we never “accept” Ho ).

Finally, in practice, we should always consider the practical significance of the results as well as the statistical significance.

Learn by Doing: Z-Test for a Population Proportion

What’s next?

Before we move on to the next test, we are going to use the z-test for proportions to bring up and illustrate a few more very important issues regarding hypothesis testing. This might also be a good time to review the concepts of Type I error, Type II error, and Power before continuing on.

More about Hypothesis Testing

CO-1: Describe the roles biostatistics serves in the discipline of public health.

LO 1.11: Recognize the distinction between statistical significance and practical significance.

LO 6.30: Use a confidence interval to determine the correct conclusion to the associated two-sided hypothesis test.

Video: More about Hypothesis Testing (18:25)

The issues regarding hypothesis testing that we will discuss are:

• The effect of sample size on hypothesis testing.
• Statistical significance vs. practical importance.
• Hypothesis testing and confidence intervals—how are they related?

Let’s begin.

1. The Effect of Sample Size on Hypothesis Testing

We have already seen the effect that the sample size has on inference, when we discussed point and interval estimation for the population mean (μ, mu) and population proportion (p). Intuitively …

Larger sample sizes give us more information to pin down the true nature of the population. We can therefore expect the sample mean and sample proportion obtained from a larger sample to be closer to the population mean and proportion, respectively. As a result, for the same level of confidence, we can report a smaller margin of error, and get a narrower confidence interval. What we’ve seen, then, is that larger sample size gives a boost to how much we trust our sample results.

In hypothesis testing, larger sample sizes have a similar effect. We have also discussed that the power of our test increases when the sample size increases, all else remaining the same. This means, we have a better chance to detect the difference between the true value and the null value for larger samples.

The following two examples will illustrate that a larger sample size provides more convincing evidence (the test has greater power), and how the evidence manifests itself in hypothesis testing. Let’s go back to our example 2 (marijuana use at a certain liberal arts college).

We do not have enough evidence to conclude that the proportion of students at the college who use marijuana is higher than the national figure.

Now, let’s increase the sample size.

There are rumors that students in a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use . Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (Reported by the Harvard School of Public Health).

Our results here are statistically significant . In other words, in example 2* the data provide enough evidence to reject Ho.

• Conclusion: There is enough evidence that the proportion of marijuana users at the college is higher than among all U.S. students.

What do we learn from this?

We see that sample results that are based on a larger sample carry more weight (have greater power).

In example 2, we saw that a sample proportion of 0.19 based on a sample of size of 100 was not enough evidence that the proportion of marijuana users in the college is higher than 0.157. Recall, from our general overview of hypothesis testing, that this conclusion (not having enough evidence to reject the null hypothesis) doesn’t mean the null hypothesis is necessarily true (so, we never “accept” the null); it only means that the particular study didn’t yield sufficient evidence to reject the null. It might be that the sample size was simply too small to detect a statistically significant difference.

However, in example 2*, we saw that when the sample proportion of 0.19 is obtained from a sample of size 400, it carries much more weight, and in particular, provides enough evidence that the proportion of marijuana users in the college is higher than 0.157 (the national figure). In this case, the sample size of 400 was large enough to detect a statistically significant difference.

The following activity will allow you to practice the ideas and terminology used in hypothesis testing when a result is not statistically significant.

Learn by Doing: Interpreting Non-significant Results

2. Statistical significance vs. practical importance.

Now, we will address the issue of statistical significance versus practical importance (which also involves issues of sample size).

The following activity will let you explore the effect of the sample size on the statistical significance of the results yourself, and more importantly will discuss issue 2: Statistical significance vs. practical importance.

Important Fact: In general, with a sufficiently large sample size you can make any result that has very little practical importance statistically significant! A large sample size alone does NOT make a “good” study!!

This suggests that when interpreting the results of a test, you should always think not only about the statistical significance of the results but also about their practical importance.

Learn by Doing: Statistical vs. Practical Significance

3. Hypothesis Testing and Confidence Intervals

The last topic we want to discuss is the relationship between hypothesis testing and confidence intervals. Even though the flavor of these two forms of inference is different (confidence intervals estimate a parameter, and hypothesis testing assesses the evidence in the data against one claim and in favor of another), there is a strong link between them.

We will explain this link (using the z-test and confidence interval for the population proportion), and then explain how confidence intervals can be used after a test has been carried out.

Recall that a confidence interval gives us a set of plausible values for the unknown population parameter. We may therefore examine a confidence interval to informally decide if a proposed value of population proportion seems plausible.

For example, if a 95% confidence interval for p, the proportion of all U.S. adults already familiar with Viagra in May 1998, was (0.61, 0.67), then it seems clear that we should be able to reject a claim that only 50% of all U.S. adults were familiar with the drug, since based on the confidence interval, 0.50 is not one of the plausible values for p.

In fact, the information provided by a confidence interval can be formally related to the information provided by a hypothesis test. ( Comment: The relationship is more straightforward for two-sided alternatives, and so we will not present results for the one-sided cases.)

Suppose we want to carry out the two-sided test:

• Ha: p ≠ p 0

using a significance level of 0.05.

An alternative way to perform this test is to find a 95% confidence interval for p and check:

• If p 0 falls outside the confidence interval, reject Ho.
• If p 0 falls inside the confidence interval, do not reject Ho.

In other words,

• If p 0 is not one of the plausible values for p, we reject Ho.
• If p 0 is a plausible value for p, we cannot reject Ho.

( Comment: Similarly, the results of a test using a significance level of 0.01 can be related to the 99% confidence interval.)

Let’s look at an example:

Recall example 3, where we wanted to know whether the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64.

We are testing:

and as the figure reminds us, we took a sample of 1,000 U.S. adults, and the data told us that 675 supported the death penalty for convicted murderers (p-hat = 0.675).

A 95% confidence interval for p, the proportion of all U.S. adults who support the death penalty, is:

\(0.675 \pm 1.96 \sqrt{\dfrac{0.675(1-0.675)}{1000}} \approx 0.675 \pm 0.029=(0.646,0.704)\)

Since the 95% confidence interval for p does not include 0.64 as a plausible value for p, we can reject Ho and conclude (as we did before) that there is enough evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003.

You and your roommate are arguing about whose turn it is to clean the apartment. Your roommate suggests that you settle this by tossing a coin and takes one out of a locked box he has on the shelf. Suspecting that the coin might not be fair, you decide to test it first. You toss the coin 80 times, thinking to yourself that if, indeed, the coin is fair, you should get around 40 heads. Instead you get 48 heads. You are puzzled. You are not sure whether getting 48 heads out of 80 is enough evidence to conclude that the coin is unbalanced, or whether this a result that could have happened just by chance when the coin is fair.

Statistics can help you answer this question.

Let p be the true proportion (probability) of heads. We want to test whether the coin is fair or not.

• Ho: p = 0.5 (the coin is fair).
• Ha: p ≠ 0.5 (the coin is not fair).

The data we have are that out of n = 80 tosses, we got 48 heads, or that the sample proportion of heads is p-hat = 48/80 = 0.6.

A 95% confidence interval for p, the true proportion of heads for this coin, is:

\(0.6 \pm 1.96 \sqrt{\dfrac{0.6(1-0.6)}{80}} \approx 0.6 \pm 0.11=(0.49,0.71)\)

Since in this case 0.5 is one of the plausible values for p, we cannot reject Ho. In other words, the data do not provide enough evidence to conclude that the coin is not fair.

The context of the last example is a good opportunity to bring up an important point that was discussed earlier.

Even though we use 0.05 as a cutoff to guide our decision about whether the results are statistically significant, we should not treat it as inviolable and we should always add our own judgment. Let’s look at the last example again.

It turns out that the p-value of this test is 0.0734. In other words, it is maybe not extremely unlikely, but it is quite unlikely (probability of 0.0734) that when you toss a fair coin 80 times you’ll get a sample proportion of heads of 48/80 = 0.6 (or even more extreme). It is true that using the 0.05 significance level (cutoff), 0.0734 is not considered small enough to conclude that the coin is not fair. However, if you really don’t want to clean the apartment, the p-value might be small enough for you to ask your roommate to use a different coin, or to provide one yourself!

Did I Get This?: Connection between Confidence Intervals and Hypothesis Tests

Did I Get This?: Hypothesis Tests for Proportions (Extra Practice)

Here is our final point on this subject:

When the data provide enough evidence to reject Ho, we can conclude (depending on the alternative hypothesis) that the population proportion is either less than, greater than, or not equal to the null value p 0 . However, we do not get a more informative statement about its actual value. It might be of interest, then, to follow the test with a 95% confidence interval that will give us more insight into the actual value of p.

In our example 3,

we concluded that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64. It is probably of interest not only to know that the proportion has changed, but also to estimate what it has changed to. We’ve calculated the 95% confidence interval for p on the previous page and found that it is (0.646, 0.704).

We can combine our conclusions from the test and the confidence interval and say:

Data provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, and we are 95% confident that it is now between 0.646 and 0.704. (i.e. between 64.6% and 70.4%).

Let’s look at our example 1 to see how a confidence interval following a test might be insightful in a different way.

Here is a summary of example 1:

We conclude that as a result of the repair, the proportion of defective products has been reduced to below 0.20 (which was the proportion prior to the repair). It is probably of great interest to the company not only to know that the proportion of defective has been reduced, but also estimate what it has been reduced to, to get a better sense of how effective the repair was. A 95% confidence interval for p in this case is:

\(0.16 \pm 1.96 \sqrt{\dfrac{0.16(1-0.16)}{400}} \approx 0.16 \pm 0.036=(0.124,0.196)\)

We can therefore say that the data provide evidence that the proportion of defective products has been reduced, and we are 95% confident that it has been reduced to somewhere between 12.4% and 19.6%. This is very useful information, since it tells us that even though the results were significant (i.e., the repair reduced the number of defective products), the repair might not have been effective enough, if it managed to reduce the number of defective products only to the range provided by the confidence interval. This, of course, ties back in to the idea of statistical significance vs. practical importance that we discussed earlier. Even though the results are statistically significant (Ho was rejected), practically speaking, the repair might still be considered ineffective.

Learn by Doing: Hypothesis Tests and Confidence Intervals

Even though this portion of the current section is about the z-test for population proportion, it is loaded with very important ideas that apply to hypothesis testing in general. We’ve already summarized the details that are specific to the z-test for proportions, so the purpose of this summary is to highlight the general ideas.

The process of hypothesis testing has four steps :

I. Stating the null and alternative hypotheses (Ho and Ha).

II. Obtaining a random sample (or at least one that can be considered random) and collecting data. Using the data:

Check that the conditions under which the test can be reliably used are met.

Summarize the data using a test statistic.

• The test statistic is a measure of the evidence in the data against Ho. The larger the test statistic is in magnitude, the more evidence the data present against Ho.

III. Finding the p-value of the test. The p-value is the probability of getting data like those observed (or even more extreme) assuming that the null hypothesis is true, and is calculated using the null distribution of the test statistic. The p-value is a measure of the evidence against Ho. The smaller the p-value, the more evidence the data present against Ho.

IV. Making conclusions.

Conclusions about the statistical significance of the results:

If the p-value is small, the data present enough evidence to reject Ho (and accept Ha).

If the p-value is not small, the data do not provide enough evidence to reject Ho.

To help guide our decision, we use the significance level as a cutoff for what is considered a small p-value. The significance cutoff is usually set at 0.05.

Conclusions should then be provided in the context of the problem.

Additional Important Ideas about Hypothesis Testing

• Results that are based on a larger sample carry more weight, and therefore as the sample size increases, results become more statistically significant.
• Even a very small and practically unimportant effect becomes statistically significant with a large enough sample size. The distinction between statistical significance and practical importance should therefore always be considered.
• Confidence intervals can be used in order to carry out two-sided tests (95% confidence for the 0.05 significance level). If the null value is not included in the confidence interval (i.e., is not one of the plausible values for the parameter), we have enough evidence to reject Ho. Otherwise, we cannot reject Ho.
• If the results are statistically significant, it might be of interest to follow up the tests with a confidence interval in order to get insight into the actual value of the parameter of interest.
• It is important to be aware that there are two types of errors in hypothesis testing ( Type I and Type II ) and that the power of a statistical test is an important measure of how likely we are to be able to detect a difference of interest to us in a particular problem.

Means (All Steps)

NOTE: Beginning on this page, the Learn By Doing and Did I Get This activities are presented as interactive PDF files. The interactivity may not work on mobile devices or with certain PDF viewers. Use an official ADOBE product such as ADOBE READER .

If you have any issues with the Learn By Doing or Did I Get This interactive PDF files, you can view all of the questions and answers presented on this page in this document:

• QUESTION/Answer (SPOILER ALERT!)

Tests About μ (mu) When σ (sigma) is Unknown – The t-test for a Population Mean

The t-distribution.

Video: Means (All Steps) (13:11)

So far we have talked about the logic behind hypothesis testing and then illustrated how this process proceeds in practice, using the z-test for the population proportion (p).

We are now moving on to discuss testing for the population mean (μ, mu), which is the parameter of interest when the variable of interest is quantitative.

A few comments about the structure of this section:

• The basic groundwork for carrying out hypothesis tests has already been laid in our general discussion and in our presentation of tests about proportions.

Therefore we can easily modify the four steps to carry out tests about means instead, without going into all of the details again.

We will use this approach for all future tests so be sure to go back to the discussion in general and for proportions to review the concepts in more detail.

• In our discussion about confidence intervals for the population mean, we made the distinction between whether the population standard deviation, σ (sigma) was known or if we needed to estimate this value using the sample standard deviation, s .

In this section, we will only discuss the second case as in most realistic settings we do not know the population standard deviation .

In this case we need to use the t- distribution instead of the standard normal distribution for the probability aspects of confidence intervals (choosing table values) and hypothesis tests (finding p-values).

• Although we will discuss some theoretical or conceptual details for some of the analyses we will learn, from this point on we will rely on software to conduct tests and calculate confidence intervals for us , while we focus on understanding which methods are used for which situations and what the results say in context.

If you are interested in more information about the z-test, where we assume the population standard deviation σ (sigma) is known, you can review the Carnegie Mellon Open Learning Statistics Course (you will need to click “ENTER COURSE”).

Like any other tests, the t- test for the population mean follows the four-step process:

• STEP 1: Stating the hypotheses H o and H a .
• STEP 2: Collecting relevant data, checking that the data satisfy the conditions which allow us to use this test, and summarizing the data using a test statistic.
• STEP 3: Finding the p-value of the test, the probability of obtaining data as extreme as those collected (or even more extreme, in the direction of the alternative hypothesis), assuming that the null hypothesis is true. In other words, how likely is it that the only reason for getting data like those observed is sampling variability (and not because H o is not true)?
• STEP 4: Drawing conclusions, assessing the statistical significance of the results based on the p-value, and stating our conclusions in context. (Do we or don’t we have evidence to reject H o and accept H a ?)
• Note: In practice, we should also always consider the practical significance of the results as well as the statistical significance.

We will now go through the four steps specifically for the t- test for the population mean and apply them to our two examples.

Only in a few cases is it reasonable to assume that the population standard deviation, σ (sigma), is known and so we will not cover hypothesis tests in this case. We discussed both cases for confidence intervals so that we could still calculate some confidence intervals by hand.

For this and all future tests we will rely on software to obtain our summary statistics, test statistics, and p-values for us.

The case where σ (sigma) is unknown is much more common in practice. What can we use to replace σ (sigma)? If you don’t know the population standard deviation, the best you can do is find the sample standard deviation, s, and use it instead of σ (sigma). (Note that this is exactly what we did when we discussed confidence intervals).

Is that it? Can we just use s instead of σ (sigma), and the rest is the same as the previous case? Unfortunately, it’s not that simple, but not very complicated either.

Here, when we use the sample standard deviation, s, as our estimate of σ (sigma) we can no longer use a normal distribution to find the cutoff for confidence intervals or the p-values for hypothesis tests.

Instead we must use the t- distribution (with n-1 degrees of freedom) to obtain the p-value for this test.

We discussed this issue for confidence intervals. We will talk more about the t- distribution after we discuss the details of this test for those who are interested in learning more.

It isn’t really necessary for us to understand this distribution but it is important that we use the correct distributions in practice via our software.

We will wait until UNIT 4B to look at how to accomplish this test in the software. For now focus on understanding the process and drawing the correct conclusions from the p-values given.

Now let’s go through the four steps in conducting the t- test for the population mean.

The null and alternative hypotheses for the t- test for the population mean (μ, mu) have exactly the same structure as the hypotheses for z-test for the population proportion (p):

The null hypothesis has the form:

• Ho: μ = μ 0 (mu = mu_zero)

(where μ 0 (mu_zero) is often called the null value)

• Ha: μ < μ 0 (mu < mu_zero) (one-sided)
• Ha: μ > μ 0 (mu > mu_zero) (one-sided)
• Ha: μ ≠ μ 0 (mu ≠ mu_zero) (two-sided)

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem.

If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! You also cannot use the information from the sample to help you determine the hypothesis. We would not know our data when we originally asked the question.

Now try it yourself. Here are a few exercises on stating the hypotheses for tests for a population mean.

Learn by Doing: State the Hypotheses for a test for a population mean

Here are a few more activities for practice.

Did I Get This?: State the Hypotheses for a test for a population mean

When setting up hypotheses, be sure to use only the information in the research question. We cannot use our sample data to help us set up our hypotheses.

For this test, it is still important to correctly choose the alternative hypothesis as “less than”, “greater than”, or “different” although generally in practice two-sample tests are used.

Obtain data from a sample:

• In this step we would obtain data from a sample. This is not something we do much of in courses but it is done very often in practice!

Check the conditions:

• Then we check the conditions under which this test (the t- test for one population mean) can be safely carried out – which are:
• The sample is random (or at least can be considered random in context).
• We are in one of the three situations marked with a green check mark in the following table (which ensure that x-bar is at least approximately normal and the test statistic using the sample standard deviation, s, is therefore a t- distribution with n-1 degrees of freedom – proving this is beyond the scope of this course):
• For large samples, we don’t need to check for normality in the population . We can rely on the sample size as the basis for the validity of using this test.
• For small samples , we need to have data from a normal population in order for the p-values and confidence intervals to be valid.

In practice, for small samples, it can be very difficult to determine if the population is normal. Here is a simulation to give you a better understanding of the difficulties.

Video: Simulations – Are Samples from a Normal Population? (4:58)

Now try it yourself with a few activities.

Learn by Doing: Checking Conditions for Hypothesis Testing for the Population Mean

• It is always a good idea to look at the data and get a sense of their pattern regardless of whether you actually need to do it in order to assess whether the conditions are met.
• This idea of looking at the data is relevant to all tests in general. In the next module—inference for relationships—conducting exploratory data analysis before inference will be an integral part of the process.

Here are a few more problems for extra practice.

Did I Get This?: Checking Conditions for Hypothesis Testing for the Population Mean

When setting up hypotheses, be sure to use only the information in the res

Calculate Test Statistic

Assuming that the conditions are met, we calculate the sample mean x-bar and the sample standard deviation, s (which estimates σ (sigma)), and summarize the data with a test statistic.

The test statistic for the t -test for the population mean is:

\(t=\dfrac{\bar{x} - \mu_0}{s/ \sqrt{n}}\)

Recall that such a standardized test statistic represents how many standard deviations above or below μ 0 (mu_zero) our sample mean x-bar is.

Therefore our test statistic is a measure of how different our data are from what is claimed in the null hypothesis. This is an idea that we mentioned in the previous test as well.

Again we will rely on the p-value to determine how unusual our data would be if the null hypothesis is true.

As we mentioned, the test statistic in the t -test for a population mean does not follow a standard normal distribution. Rather, it follows another bell-shaped distribution called the t- distribution.

We will present the details of this distribution at the end for those interested but for now we will work on the process of the test.

Here are a few important facts.

• In statistical language we say that the null distribution of our test statistic is the t- distribution with (n-1) degrees of freedom. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t- distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t (n – 1) or Z to calculate the p-values does not make a big difference. However, software will use the t -distribution regardless of the sample size and so will we.

Although we will not calculate p-values by hand for this test, we can still easily calculate the test statistic.

Try it yourself:

Learn by Doing: Calculate the Test Statistic for a Test for a Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistics and we will use the p-values provided to draw our conclusions.

We will use software to obtain the p-value for this (and all future) tests but here are the images illustrating how the p-value is calculated in each of the three cases corresponding to the three choices for our alternative hypothesis.

Note that due to the symmetry of the t distribution, for a given value of the test statistic t, the p-value for the two-sided test is twice as large as the p-value of either of the one-sided tests. The same thing happens when p-values are calculated under the t distribution as when they are calculated under the Z distribution.

We will show some examples of p-values obtained from software in our examples. For now let’s continue our summary of the steps.

As usual, based on the p-value (and some significance level of choice) we assess the statistical significance of results, and draw our conclusions in context.

To review what we have said before:

If p-value ≤ 0.05 then WE REJECT Ho

If p-value > 0.05 then WE FAIL TO REJECT Ho

This step has essentially two sub-steps:

We are now ready to look at two examples.

A certain prescription medicine is supposed to contain an average of 250 parts per million (ppm) of a certain chemical. If the concentration is higher than this, the drug may cause harmful side effects; if it is lower, the drug may be ineffective.

The manufacturer runs a check to see if the mean concentration in a large shipment conforms to the target level of 250 ppm or not.

A simple random sample of 100 portions is tested, and the sample mean concentration is found to be 247 ppm with a sample standard deviation of 12 ppm.

Here is a figure that represents this example:

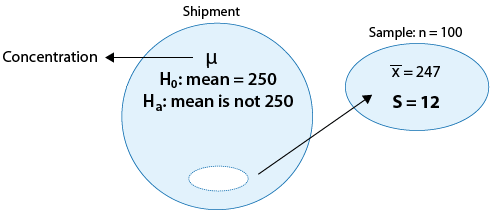
1. The hypotheses being tested are:

• Ha: μ ≠ μ 0 (mu ≠ mu_zero)
• Where μ = population mean part per million of the chemical in the entire shipment

2. The conditions that allow us to use the t-test are met since:

• The sample is random
• The sample size is large enough for the Central Limit Theorem to apply and ensure the normality of x-bar. We do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.
• The test statistic is:

\(t=\dfrac{\bar{x}-\mu_{0}}{s / \sqrt{n}}=\dfrac{247-250}{12 / \sqrt{100}}=-2.5\)

• The data (represented by the sample mean) are 2.5 standard errors below the null value.

3. Finding the p-value.

• To find the p-value we use statistical software, and we calculate a p-value of 0.014.

4. Conclusions:

• The p-value is small (.014) indicating that at the 5% significance level, the results are significant.
• We reject the null hypothesis.
• There is enough evidence to conclude that the mean concentration in entire shipment is not the required 250 ppm.
• It is difficult to comment on the practical significance of this result without more understanding of the practical considerations of this problem.

Here is a summary:

• The 95% confidence interval for μ (mu) can be used here in the same way as for proportions to conduct the two-sided test (checking whether the null value falls inside or outside the confidence interval) or following a t- test where Ho was rejected to get insight into the value of μ (mu).
• We find the 95% confidence interval to be (244.619, 249.381) . Since 250 is not in the interval we know we would reject our null hypothesis that μ (mu) = 250. The confidence interval gives additional information. By accounting for estimation error, it estimates that the population mean is likely to be between 244.62 and 249.38. This is lower than the target concentration and that information might help determine the seriousness and appropriate course of action in this situation.

In most situations in practice we use TWO-SIDED HYPOTHESIS TESTS, followed by confidence intervals to gain more insight.

For completeness in covering one sample t-tests for a population mean, we still cover all three possible alternative hypotheses here HOWEVER, this will be the last test for which we will do so.

A research study measured the pulse rates of 57 college men and found a mean pulse rate of 70 beats per minute with a standard deviation of 9.85 beats per minute.

Researchers want to know if the mean pulse rate for all college men is different from the current standard of 72 beats per minute.

• The hypotheses being tested are:
• Ho: μ = 72
• Ha: μ ≠ 72
• Where μ = population mean heart rate among college men
• The conditions that allow us to use the t- test are met since:
• The sample is random.
• The sample size is large (n = 57) so we do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.

\(t=\dfrac{\bar{x}-\mu}{s / \sqrt{n}}=\dfrac{70-72}{9.85 / \sqrt{57}}=-1.53\)

• The data (represented by the sample mean) are 1.53 estimated standard errors below the null value.
• Recall that in general the p-value is calculated under the null distribution of the test statistic, which, in the t- test case, is t (n-1). In our case, in which n = 57, the p-value is calculated under the t (56) distribution. Using statistical software, we find that the p-value is 0.132 .
• Here is how we calculated the p-value. http://homepage.stat.uiowa.edu/~mbognar/applets/t.html .

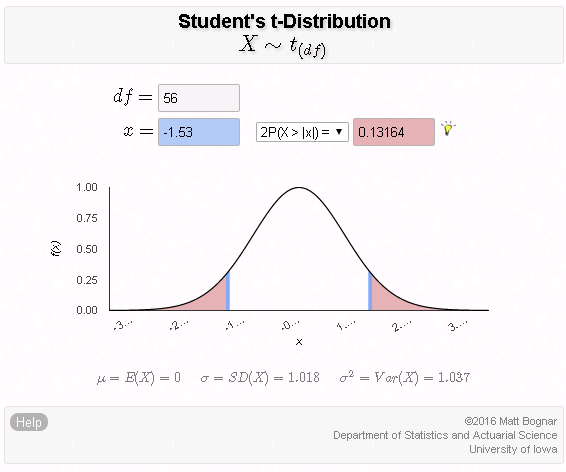
4. Making conclusions.

• The p-value (0.132) is not small, indicating that the results are not significant.
• We fail to reject the null hypothesis.
• There is not enough evidence to conclude that the mean pulse rate for all college men is different from the current standard of 72 beats per minute.
• The results from this sample do not appear to have any practical significance either with a mean pulse rate of 70, this is very similar to the hypothesized value, relative to the variation expected in pulse rates.

Now try a few yourself.

Learn by Doing: Hypothesis Testing for the Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistic and p-value and we will use the p-values provided to draw our conclusions.

That concludes our discussion of hypothesis tests in Unit 4A.

In the next unit we will continue to use both confidence intervals and hypothesis test to investigate the relationship between two variables in the cases we covered in Unit 1 on exploratory data analysis – we will look at Case CQ, Case CC, and Case QQ.

Before moving on, we will discuss the details about the t- distribution as a general object.

We have seen that variables can be visually modeled by many different sorts of shapes, and we call these shapes distributions. Several distributions arise so frequently that they have been given special names, and they have been studied mathematically.

So far in the course, the only one we’ve named, for continuous quantitative variables, is the normal distribution, but there are others. One of them is called the t- distribution.

The t- distribution is another bell-shaped (unimodal and symmetric) distribution, like the normal distribution; and the center of the t- distribution is standardized at zero, like the center of the standard normal distribution.

Like all distributions that are used as probability models, the normal and the t- distribution are both scaled, so the total area under each of them is 1.

So how is the t-distribution fundamentally different from the normal distribution?

• The spread .

The following picture illustrates the fundamental difference between the normal distribution and the t-distribution:

Here we have an image which illustrates the fundamental difference between the normal distribution and the t- distribution:

You can see in the picture that the t- distribution has slightly less area near the expected central value than the normal distribution does, and you can see that the t distribution has correspondingly more area in the “tails” than the normal distribution does. (It’s often said that the t- distribution has “fatter tails” or “heavier tails” than the normal distribution.)

This reflects the fact that the t- distribution has a larger spread than the normal distribution. The same total area of 1 is spread out over a slightly wider range on the t- distribution, making it a bit lower near the center compared to the normal distribution, and giving the t- distribution slightly more probability in the ‘tails’ compared to the normal distribution.

Therefore, the t- distribution ends up being the appropriate model in certain cases where there is more variability than would be predicted by the normal distribution. One of these cases is stock values, which have more variability (or “volatility,” to use the economic term) than would be predicted by the normal distribution.

There’s actually an entire family of t- distributions. They all have similar formulas (but the math is beyond the scope of this introductory course in statistics), and they all have slightly “fatter tails” than the normal distribution. But some are closer to normal than others.

The t- distributions that have higher “degrees of freedom” are closer to normal (degrees of freedom is a mathematical concept that we won’t study in this course, beyond merely mentioning it here). So, there’s a t- distribution “with one degree of freedom,” another t- distribution “with 2 degrees of freedom” which is slightly closer to normal, another t- distribution “with 3 degrees of freedom” which is a bit closer to normal than the previous ones, and so on.

The following picture illustrates this idea with just a couple of t- distributions (note that “degrees of freedom” is abbreviated “d.f.” on the picture):

The test statistic for our t-test for one population mean is a t -score which follows a t- distribution with (n – 1) degrees of freedom. Recall that each t- distribution is indexed according to “degrees of freedom.” Notice that, in the context of a test for a mean, the degrees of freedom depend on the sample size in the study.

Remember that we said that higher degrees of freedom indicate that the t- distribution is closer to normal. So in the context of a test for the mean, the larger the sample size , the higher the degrees of freedom, and the closer the t- distribution is to a normal z distribution .

As a result, in the context of a test for a mean, the effect of the t- distribution is most important for a study with a relatively small sample size .

We are now done introducing the t-distribution. What are implications of all of this?

• The null distribution of our t-test statistic is the t-distribution with (n-1) d.f. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t-distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t(n – 1) or Z to calculate the p-values does not make a big difference.

Chemix is an online editor for drawing lab diagrams and school experiment apparatus. Easy sketching for both students and teachers.

 loading….

Statistical Thinking: A Simulation Approach to Modeling Uncertainty (UM STAT 216 edition)

2.14 drawing conclusions and “statistical significance”.

We have seen that statistical hypothesis testing is a process of comparing the real-world observed result to a null hypothesis where there is no effect . At the end of the process, we compare the observed result to the distribution of simulated results if the null hypothesis were true, and from this we determine whether the observed result is compatible with the null hypothesis.

The conclusions that we can draw form a hypothesis test are based on the comparison between the observed result and the null hypothesis. For example, in the Monday breakups study , we concluded:

The observed result is not compatible with the null hypothesis. This suggests that breakups may be more likely to be reported on Monday.

There are two important point to notice in how this conclusion is written:

• The conclusion is stated in terms of compatibility with the null hypothesis .
• The conclusion uses soft language like “suggests.” This is becuase we did not prove that breakups are more likely to be reported on Monday. Instead, we simply have strong evidence against the null hypothesis (that breakups are equally likely each day). This, in turn, suggests that breakups are more likely to be reported on Mondays.

Similarly, if the observed result had been within the range of likely results if the null hypothesis were true, we would still write the conclusion in terms of compatibility with the null hypothesis:

The observed result is compatible with the null hypothesis. We do not have sufficient evidence to suggest that breakups are more likely to be reported on Monday.

In both cases, notice that the conclusion is limited to whether there is an effect or not. There are many additional aspects that we might be interested in, but the hypothesis test does not tell us about. For example,

• We don’t know what caused the effect.
• We don’t know the size of the effect. Perhaps the true percentage of Monday breakups is 26%. Perhaps it is slightly more or slightly less. We only have evidence that the results are incompatible with the null hypothesis.
• We don’t know the scope of the effect. Perhaps the phenomenon is limited to this particular year, or to breakups that are reported on facebook, etc.

(We will learn about size, scope, and causation later in the course. The key point to understand now is that a hypothesis test, by itself, can not tell us about these things and so the conclusion should not address them.)

2.14.1 Statistical significance

In news reports and scientific literature, we often hear the term, “statistical significance.” What does it mean for a result to be “statistically significant?” In short, it means that the observed result is not compatible with the null hypothesis.

Different scientific communities have different standards for determining whether a result is statistically significant. In the social sciences, there are two common approaches for determining statistical significance.

• Use the range of likely results: The first approach is to determine whether the observed result is within the range of likely results if the null hypothesis were true. If the observed result is outside the range of likely values if the null hypothesis were true, then social scientists consider A second common practice is to use \(p\) -values. Commonly, social scientists consider that to be sufficient evidence that the observed result is not compatible with the null hypothesis, and thus that the observed result is statistically significant.
• Use p < 0.05: A second common approach is to use a \(p\) -value of 0.05 as a threshold. If \(p<0.05\) , social scientists consider that to be sufficient evidence that the observed result is not compatible with the null hypothesis, and thus that the observed result is statistically significant.

Other scientific communities may have different standards. Moreover, there is currently a lot of discussion about whether the current thresholds should be reconsidered, and even whether we should even have a threshold. Some scholars advocate that researchers should just report the \(p\) -value and make an argument as to whether it provides sufficient evidence against the null model.

For our class, you can use either the “range of likely values” approach, the “ \(p<0.05\) ” approach, or the “report the p-value and make an argument” approach to determining whether an observed result is statistically significant. As you become a member of a scientific community, you will learn which approaches that community uses.

2.14.2 Statistical significance vs. practical significance

Don’t confuse statistical significance with practical significance. Often, statistical significance is taken to be a indication of whether the result is meaningful in the real world (i.e., “practically significant”). But statistical significance has nothing to do with real-world importance. Remember, statistical significance just tells us whether the observed result is compatible with the null hypothesis. The question of whether the result is of real-world (or practical) significance cannot be determined statistically. Instead, this is something that people have to make an argument about.

2.14.3 Other things that statistical significance can’t tell us.

Again, statistical significance only tells us that an observed result is not compatible with the null hypothesis. It does not tell us about other important aspects, including:

• Statistical significance does not mean that we have proven something. It only tells us that the there is evidence against a null model, which in turn would suggest that the effect is real.
• Statistical significance says nothing about what caused the effect
• Statistical significance does not tell us the scope of the effect (that is, how broadly the result apply).

2.14.4 Examples

Here is how to write a conclusion to a hypothesis test.

If the result is statistically significant:

The observed result is not compatible with the null hypothesis. This suggests that there may be an effect.

If the result is not statistically significant:

The observed result is compatible with the null hypothesis. We do not have sufficient evidence to suggest that there is an effect.

2.14.5 Summary

The box below summarizes the key points about drawing conclusions and statistical significance. statistical hypothesis testing.

Key points about drawing conclusions and statistical significance

Conclusions from a hypothesis test are stated in terms of compatibility with the null hypothesis

We do not prove anything, so conclusions should use softer language like suggests

Statistical significance simply means that the observed result is not compatible with the null hypothesis

• Statistical significance does not tell us the size of the effect, or whether it is large enough to have real-world importance.

Choose Your Test

Sat / act prep online guides and tips, what is a hypothesis and how do i write one.

General Education

Think about something strange and unexplainable in your life. Maybe you get a headache right before it rains, or maybe you think your favorite sports team wins when you wear a certain color. If you wanted to see whether these are just coincidences or scientific fact, you would form a hypothesis, then create an experiment to see whether that hypothesis is true or not.

But what is a hypothesis, anyway? If you’re not sure about what a hypothesis is--or how to test for one!--you’re in the right place. This article will teach you everything you need to know about hypotheses, including: 

• Defining the term “hypothesis” 
• Providing hypothesis examples 
• Giving you tips for how to write your own hypothesis

So let’s get started!

What Is a Hypothesis?

Merriam Webster defines a hypothesis as “an assumption or concession made for the sake of argument.” In other words, a hypothesis is an educated guess . Scientists make a reasonable assumption--or a hypothesis--then design an experiment to test whether it’s true or not. Keep in mind that in science, a hypothesis should be testable. You have to be able to design an experiment that tests your hypothesis in order for it to be valid. 

As you could assume from that statement, it’s easy to make a bad hypothesis. But when you’re holding an experiment, it’s even more important that your guesses be good...after all, you’re spending time (and maybe money!) to figure out more about your observation. That’s why we refer to a hypothesis as an educated guess--good hypotheses are based on existing data and research to make them as sound as possible.

Hypotheses are one part of what’s called the scientific method .  Every (good) experiment or study is based in the scientific method. The scientific method gives order and structure to experiments and ensures that interference from scientists or outside influences does not skew the results. It’s important that you understand the concepts of the scientific method before holding your own experiment. Though it may vary among scientists, the scientific method is generally made up of six steps (in order):

• Observation
• Asking questions
• Forming a hypothesis
• Analyze the data
• Communicate your results

You’ll notice that the hypothesis comes pretty early on when conducting an experiment. That’s because experiments work best when they’re trying to answer one specific question. And you can’t conduct an experiment until you know what you’re trying to prove!

Independent and Dependent Variables 

After doing your research, you’re ready for another important step in forming your hypothesis: identifying variables. Variables are basically any factor that could influence the outcome of your experiment . Variables have to be measurable and related to the topic being studied.

There are two types of variables:  independent variables and dependent variables. I ndependent variables remain constant . For example, age is an independent variable; it will stay the same, and researchers can look at different ages to see if it has an effect on the dependent variable. 

Speaking of dependent variables... dependent variables are subject to the influence of the independent variable , meaning that they are not constant. Let’s say you want to test whether a person’s age affects how much sleep they need. In that case, the independent variable is age (like we mentioned above), and the dependent variable is how much sleep a person gets. 

Variables will be crucial in writing your hypothesis. You need to be able to identify which variable is which, as both the independent and dependent variables will be written into your hypothesis. For instance, in a study about exercise, the independent variable might be the speed at which the respondents walk for thirty minutes, and the dependent variable would be their heart rate. In your study and in your hypothesis, you’re trying to understand the relationship between the two variables.

Elements of a Good Hypothesis

The best hypotheses start by asking the right questions . For instance, if you’ve observed that the grass is greener when it rains twice a week, you could ask what kind of grass it is, what elevation it’s at, and if the grass across the street responds to rain in the same way. Any of these questions could become the backbone of experiments to test why the grass gets greener when it rains fairly frequently.

As you’re asking more questions about your first observation, make sure you’re also making more observations . If it doesn’t rain for two weeks and the grass still looks green, that’s an important observation that could influence your hypothesis. You'll continue observing all throughout your experiment, but until the hypothesis is finalized, every observation should be noted.

Finally, you should consult secondary research before writing your hypothesis . Secondary research is comprised of results found and published by other people. You can usually find this information online or at your library. Additionally, m ake sure the research you find is credible and related to your topic. If you’re studying the correlation between rain and grass growth, it would help you to research rain patterns over the past twenty years for your county, published by a local agricultural association. You should also research the types of grass common in your area, the type of grass in your lawn, and whether anyone else has conducted experiments about your hypothesis. Also be sure you’re checking the quality of your research . Research done by a middle school student about what minerals can be found in rainwater would be less useful than an article published by a local university.

Writing Your Hypothesis

Once you’ve considered all of the factors above, you’re ready to start writing your hypothesis. Hypotheses usually take a certain form when they’re written out in a research report.

When you boil down your hypothesis statement, you are writing down your best guess and not the question at hand . This means that your statement should be written as if it is fact already, even though you are simply testing it.

The reason for this is that, after you have completed your study, you'll either accept or reject your if-then or your null hypothesis. All hypothesis testing examples should be measurable and able to be confirmed or denied. You cannot confirm a question, only a statement! 

In fact, you come up with hypothesis examples all the time! For instance, when you guess on the outcome of a basketball game, you don’t say, “Will the Miami Heat beat the Boston Celtics?” but instead, “I think the Miami Heat will beat the Boston Celtics.” You state it as if it is already true, even if it turns out you’re wrong. You do the same thing when writing your hypothesis.

Additionally, keep in mind that hypotheses can range from very specific to very broad.  These hypotheses can be specific, but if your hypothesis testing examples involve a broad range of causes and effects, your hypothesis can also be broad.  

The Two Types of Hypotheses

Now that you understand what goes into a hypothesis, it’s time to look more closely at the two most common types of hypothesis: the if-then hypothesis and the null hypothesis.

#1: If-Then Hypotheses

First of all, if-then hypotheses typically follow this formula:

If ____ happens, then ____ will happen.

The goal of this type of hypothesis is to test the causal relationship between the independent and dependent variable. It’s fairly simple, and each hypothesis can vary in how detailed it can be. We create if-then hypotheses all the time with our daily predictions. Here are some examples of hypotheses that use an if-then structure from daily life: 

• If I get enough sleep, I’ll be able to get more work done tomorrow.
• If the bus is on time, I can make it to my friend’s birthday party. 
• If I study every night this week, I’ll get a better grade on my exam. 

In each of these situations, you’re making a guess on how an independent variable (sleep, time, or studying) will affect a dependent variable (the amount of work you can do, making it to a party on time, or getting better grades). 

You may still be asking, “What is an example of a hypothesis used in scientific research?” Take one of the hypothesis examples from a real-world study on whether using technology before bed affects children’s sleep patterns. The hypothesis read s:

“We hypothesized that increased hours of tablet- and phone-based screen time at bedtime would be inversely correlated with sleep quality and child attention.”

It might not look like it, but this is an if-then statement. The researchers basically said, “If children have more screen usage at bedtime, then their quality of sleep and attention will be worse.” The sleep quality and attention are the dependent variables and the screen usage is the independent variable. (Usually, the independent variable comes after the “if” and the dependent variable comes after the “then,” as it is the independent variable that affects the dependent variable.) This is an excellent example of how flexible hypothesis statements can be, as long as the general idea of “if-then” and the independent and dependent variables are present.

#2: Null Hypotheses

Your if-then hypothesis is not the only one needed to complete a successful experiment, however. You also need a null hypothesis to test it against. In its most basic form, the null hypothesis is the opposite of your if-then hypothesis . When you write your null hypothesis, you are writing a hypothesis that suggests that your guess is not true, and that the independent and dependent variables have no relationship .

One null hypothesis for the cell phone and sleep study from the last section might say: 

“If children have more screen usage at bedtime, their quality of sleep and attention will not be worse.” 

In this case, this is a null hypothesis because it’s asking the opposite of the original thesis! 

Conversely, if your if-then hypothesis suggests that your two variables have no relationship, then your null hypothesis would suggest that there is one. So, pretend that there is a study that is asking the question, “Does the amount of followers on Instagram influence how long people spend on the app?” The independent variable is the amount of followers, and the dependent variable is the time spent. But if you, as the researcher, don’t think there is a relationship between the number of followers and time spent, you might write an if-then hypothesis that reads:

“If people have many followers on Instagram, they will not spend more time on the app than people who have less.”

In this case, the if-then suggests there isn’t a relationship between the variables. In that case, one of the null hypothesis examples might say:

“If people have many followers on Instagram, they will spend more time on the app than people who have less.”

You then test both the if-then and the null hypothesis to gauge if there is a relationship between the variables, and if so, how much of a relationship. 

4 Tips to Write the Best Hypothesis

If you’re going to take the time to hold an experiment, whether in school or by yourself, you’re also going to want to take the time to make sure your hypothesis is a good one. The best hypotheses have four major elements in common: plausibility, defined concepts, observability, and general explanation.

#1: Plausibility

At first glance, this quality of a hypothesis might seem obvious. When your hypothesis is plausible, that means it’s possible given what we know about science and general common sense. However, improbable hypotheses are more common than you might think. 

Imagine you’re studying weight gain and television watching habits. If you hypothesize that people who watch more than  twenty hours of television a week will gain two hundred pounds or more over the course of a year, this might be improbable (though it’s potentially possible). Consequently, c ommon sense can tell us the results of the study before the study even begins.

Improbable hypotheses generally go against  science, as well. Take this hypothesis example: 

“If a person smokes one cigarette a day, then they will have lungs just as healthy as the average person’s.” 

This hypothesis is obviously untrue, as studies have shown again and again that cigarettes negatively affect lung health. You must be careful that your hypotheses do not reflect your own personal opinion more than they do scientifically-supported findings. This plausibility points to the necessity of research before the hypothesis is written to make sure that your hypothesis has not already been disproven.

#2: Defined Concepts

The more advanced you are in your studies, the more likely that the terms you’re using in your hypothesis are specific to a limited set of knowledge. One of the hypothesis testing examples might include the readability of printed text in newspapers, where you might use words like “kerning” and “x-height.” Unless your readers have a background in graphic design, it’s likely that they won’t know what you mean by these terms. Thus, it’s important to either write what they mean in the hypothesis itself or in the report before the hypothesis.

Here’s what we mean. Which of the following sentences makes more sense to the common person?

If the kerning is greater than average, more words will be read per minute.

If the space between letters is greater than average, more words will be read per minute.

For people reading your report that are not experts in typography, simply adding a few more words will be helpful in clarifying exactly what the experiment is all about. It’s always a good idea to make your research and findings as accessible as possible. 

Good hypotheses ensure that you can observe the results. 

#3: Observability

In order to measure the truth or falsity of your hypothesis, you must be able to see your variables and the way they interact. For instance, if your hypothesis is that the flight patterns of satellites affect the strength of certain television signals, yet you don’t have a telescope to view the satellites or a television to monitor the signal strength, you cannot properly observe your hypothesis and thus cannot continue your study.

Some variables may seem easy to observe, but if you do not have a system of measurement in place, you cannot observe your hypothesis properly. Here’s an example: if you’re experimenting on the effect of healthy food on overall happiness, but you don’t have a way to monitor and measure what “overall happiness” means, your results will not reflect the truth. Monitoring how often someone smiles for a whole day is not reasonably observable, but having the participants state how happy they feel on a scale of one to ten is more observable. 

In writing your hypothesis, always keep in mind how you'll execute the experiment.

#4: Generalizability 

Perhaps you’d like to study what color your best friend wears the most often by observing and documenting the colors she wears each day of the week. This might be fun information for her and you to know, but beyond you two, there aren’t many people who could benefit from this experiment. When you start an experiment, you should note how generalizable your findings may be if they are confirmed. Generalizability is basically how common a particular phenomenon is to other people’s everyday life.

Let’s say you’re asking a question about the health benefits of eating an apple for one day only, you need to realize that the experiment may be too specific to be helpful. It does not help to explain a phenomenon that many people experience. If you find yourself with too specific of a hypothesis, go back to asking the big question: what is it that you want to know, and what do you think will happen between your two variables?

Hypothesis Testing Examples

We know it can be hard to write a good hypothesis unless you’ve seen some good hypothesis examples. We’ve included four hypothesis examples based on some made-up experiments. Use these as templates or launch pads for coming up with your own hypotheses.

Experiment #1: Students Studying Outside (Writing a Hypothesis)

You are a student at PrepScholar University. When you walk around campus, you notice that, when the temperature is above 60 degrees, more students study in the quad. You want to know when your fellow students are more likely to study outside. With this information, how do you make the best hypothesis possible?

You must remember to make additional observations and do secondary research before writing your hypothesis. In doing so, you notice that no one studies outside when it’s 75 degrees and raining, so this should be included in your experiment. Also, studies done on the topic beforehand suggested that students are more likely to study in temperatures less than 85 degrees. With this in mind, you feel confident that you can identify your variables and write your hypotheses:

If-then: “If the temperature in Fahrenheit is less than 60 degrees, significantly fewer students will study outside.”

Null: “If the temperature in Fahrenheit is less than 60 degrees, the same number of students will study outside as when it is more than 60 degrees.”

These hypotheses are plausible, as the temperatures are reasonably within the bounds of what is possible. The number of people in the quad is also easily observable. It is also not a phenomenon specific to only one person or at one time, but instead can explain a phenomenon for a broader group of people.

To complete this experiment, you pick the month of October to observe the quad. Every day (except on the days where it’s raining)from 3 to 4 PM, when most classes have released for the day, you observe how many people are on the quad. You measure how many people come  and how many leave. You also write down the temperature on the hour. 

After writing down all of your observations and putting them on a graph, you find that the most students study on the quad when it is 70 degrees outside, and that the number of students drops a lot once the temperature reaches 60 degrees or below. In this case, your research report would state that you accept or “failed to reject” your first hypothesis with your findings.

Experiment #2: The Cupcake Store (Forming a Simple Experiment)

Let’s say that you work at a bakery. You specialize in cupcakes, and you make only two colors of frosting: yellow and purple. You want to know what kind of customers are more likely to buy what kind of cupcake, so you set up an experiment. Your independent variable is the customer’s gender, and the dependent variable is the color of the frosting. What is an example of a hypothesis that might answer the question of this study?

Here’s what your hypotheses might look like: 

If-then: “If customers’ gender is female, then they will buy more yellow cupcakes than purple cupcakes.”

Null: “If customers’ gender is female, then they will be just as likely to buy purple cupcakes as yellow cupcakes.”

This is a pretty simple experiment! It passes the test of plausibility (there could easily be a difference), defined concepts (there’s nothing complicated about cupcakes!), observability (both color and gender can be easily observed), and general explanation ( this would potentially help you make better business decisions ).

Experiment #3: Backyard Bird Feeders (Integrating Multiple Variables and Rejecting the If-Then Hypothesis)

While watching your backyard bird feeder, you realized that different birds come on the days when you change the types of seeds. You decide that you want to see more cardinals in your backyard, so you decide to see what type of food they like the best and set up an experiment. 

However, one morning, you notice that, while some cardinals are present, blue jays are eating out of your backyard feeder filled with millet. You decide that, of all of the other birds, you would like to see the blue jays the least. This means you'll have more than one variable in your hypothesis. Your new hypotheses might look like this: 

If-then: “If sunflower seeds are placed in the bird feeders, then more cardinals will come than blue jays. If millet is placed in the bird feeders, then more blue jays will come than cardinals.”

Null: “If either sunflower seeds or millet are placed in the bird, equal numbers of cardinals and blue jays will come.”

Through simple observation, you actually find that cardinals come as often as blue jays when sunflower seeds or millet is in the bird feeder. In this case, you would reject your “if-then” hypothesis and “fail to reject” your null hypothesis . You cannot accept your first hypothesis, because it’s clearly not true. Instead you found that there was actually no relation between your different variables. Consequently, you would need to run more experiments with different variables to see if the new variables impact the results.

Experiment #4: In-Class Survey (Including an Alternative Hypothesis)

You’re about to give a speech in one of your classes about the importance of paying attention. You want to take this opportunity to test a hypothesis you’ve had for a while: 

If-then: If students sit in the first two rows of the classroom, then they will listen better than students who do not.

Null: If students sit in the first two rows of the classroom, then they will not listen better or worse than students who do not.

You give your speech and then ask your teacher if you can hand out a short survey to the class. On the survey, you’ve included questions about some of the topics you talked about. When you get back the results, you’re surprised to see that not only do the students in the first two rows not pay better attention, but they also scored worse than students in other parts of the classroom! Here, both your if-then and your null hypotheses are not representative of your findings. What do you do?

This is when you reject both your if-then and null hypotheses and instead create an alternative hypothesis . This type of hypothesis is used in the rare circumstance that neither of your hypotheses is able to capture your findings . Now you can use what you’ve learned to draft new hypotheses and test again! 

Key Takeaways: Hypothesis Writing

The more comfortable you become with writing hypotheses, the better they will become. The structure of hypotheses is flexible and may need to be changed depending on what topic you are studying. The most important thing to remember is the purpose of your hypothesis and the difference between the if-then and the null . From there, in forming your hypothesis, you should constantly be asking questions, making observations, doing secondary research, and considering your variables. After you have written your hypothesis, be sure to edit it so that it is plausible, clearly defined, observable, and helpful in explaining a general phenomenon.

Writing a hypothesis is something that everyone, from elementary school children competing in a science fair to professional scientists in a lab, needs to know how to do. Hypotheses are vital in experiments and in properly executing the scientific method . When done correctly, hypotheses will set up your studies for success and help you to understand the world a little better, one experiment at a time.

What’s Next?

If you’re studying for the science portion of the ACT, there’s definitely a lot you need to know. We’ve got the tools to help, though! Start by checking out our ultimate study guide for the ACT Science subject test. Once you read through that, be sure to download our recommended ACT Science practice tests , since they’re one of the most foolproof ways to improve your score. (And don’t forget to check out our expert guide book , too.)

If you love science and want to major in a scientific field, you should start preparing in high school . Here are the science classes you should take to set yourself up for success.

If you’re trying to think of science experiments you can do for class (or for a science fair!), here’s a list of 37 awesome science experiments you can do at home

Ashley Sufflé Robinson has a Ph.D. in 19th Century English Literature. As a content writer for PrepScholar, Ashley is passionate about giving college-bound students the in-depth information they need to get into the school of their dreams.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

2.7 Drawing Conclusions and Reporting the Results

Learning objectives.

• Identify the conclusions researchers can make based on the outcome of their studies.
• Describe why scientists avoid the term “scientific proof.”
• Explain the different ways that scientists share their findings.

Drawing Conclusions

Since statistics are probabilistic in nature and findings can reflect type I or type II errors, we cannot use the results of a single study to conclude with certainty that a theory is true. Rather theories are supported, refuted, or modified based on the results of research.

If the results are statistically significant and consistent with the hypothesis and the theory that was used to generate the hypothesis, then researchers can conclude that the theory is supported. Not only did the theory make an accurate prediction, but there is now a new phenomenon that the theory accounts for. If a hypothesis is disconfirmed in a systematic empirical study, then the theory has been weakened. It made an inaccurate prediction, and there is now a new phenomenon that it does not account for.

Although this seems straightforward, there are some complications. First, confirming a hypothesis can strengthen a theory but it can never prove a theory. In fact, scientists tend to avoid the word “prove” when talking and writing about theories. One reason for this avoidance is that the result may reflect a type I error.  Another reason for this  avoidance  is that there may be other plausible theories that imply the same hypothesis, which means that confirming the hypothesis strengthens all those theories equally. A third reason is that it is always possible that another test of the hypothesis or a test of a new hypothesis derived from the theory will be disconfirmed. This  difficulty  is a version of the famous philosophical “problem of induction.” One cannot definitively prove a general principle (e.g., “All swans are white.”) just by observing confirming cases (e.g., white swans)—no matter how many. It is always possible that a disconfirming case (e.g., a black swan) will eventually come along. For these reasons, scientists tend to think of theories—even highly successful ones—as subject to revision based on new and unexpected observations.

A second complication has to do with what it means when a hypothesis is disconfirmed. According to the strictest version of the hypothetico-deductive method, disconfirming a hypothesis disproves the theory it was derived from. In formal logic, the premises “if  A  then  B ” and “not  B ” necessarily lead to the conclusion “not  A .” If  A  is the theory and  B  is the hypothesis (“if  A  then  B ”), then disconfirming the hypothesis (“not  B ”) must mean that the theory is incorrect (“not  A ”). In practice, however, scientists do not give up on their theories so easily. One reason is that one disconfirmed hypothesis could be a missed opportunity (the result of a type II error) or it could be the result of a faulty research design. Perhaps the researcher did not successfully manipulate the independent variable or measure the dependent variable.

A disconfirmed hypothesis could also mean that some unstated but relatively minor assumption of the theory was not met. For example, if Zajonc had failed to find social facilitation in cockroaches, he could have concluded that drive theory is still correct but it applies only to animals with sufficiently complex nervous systems. That is, the evidence from a study can be used to modify a theory.  This practice does not mean that researchers are free to ignore disconfirmations of their theories. If they cannot improve their research designs or modify their theories to account for repeated disconfirmations, then they eventually must abandon their theories and replace them with ones that are more successful.

The bottom line here is that because statistics are probabilistic in nature and because all research studies have flaws there is no such thing as scientific proof, there is only scientific evidence.

Reporting the Results

The final step in the research process involves reporting the results. As described in the section on Reviewing the Research Literature in this chapter, results are typically reported in peer-reviewed journal articles and at conferences.

The most prestigious way to report one’s findings is by writing a manuscript and having it published in a peer-reviewed scientific journal. Manuscripts published in psychology journals typically must adhere to the writing style of the American Psychological Association (APA style). You will likely be learning the major elements of this writing style in this course.

Another way to report findings is by writing a book chapter that is published in an edited book. Preferably the editor of the book puts the chapter through peer review but this is not always the case and some scientists are invited by editors to write book chapters.

A fun way to disseminate findings is to give a presentation at a conference. This can either be done as an oral presentation or a poster presentation. Oral presentations involve getting up in front of an audience of fellow scientists and giving a talk that might last anywhere from 10 minutes to 1 hour (depending on the conference) and then fielding questions from the audience. Alternatively, poster presentations involve summarizing the study on a large poster that provides a brief overview of the purpose, methods, results, and discussion. The presenter stands by his or her poster for an hour or two and discusses it with people who pass by. Presenting one’s work at a conference is a great way to get feedback from one’s peers before attempting to undergo the more rigorous peer-review process involved in publishing a journal article.

Share This Book

• Increase Font Size

Drawing a Hypothesis

DRAWING A HYPOTHESIS - A publication project by Nikolaus Gansterer

Drawing a Hypothesis is an exciting reader on the ontology of forms of visualisation and on the development of the diagrammatic perspective and its use in contemporary art, science and theory. In an intense process of exchange with artists and scientists, Nikolaus Gansterer reveals drawing figures as a media of research which enables the emergence of new narratives and ideas by tracing the speculative potential of diagrams. Based on a discursive analysis of found figures with the artist’s own diagrammatic maps and models, the invited authors create unique correlations between thinking and drawing. The book is a rich compendium of figures of thought, which moves from scientific representation through artistic interpretation and vice versa. Central hypotheses of the publication were later re-transformed into installations and/or performance lectures and presented in various occasions and formats.

Author's note:

"The idea for this book originated during a two-year research project at the Jan van Eyck Academie in the Netherlands. My longheld fascination for diagrams, maps, networks and the graphical forms of visualising complex associations prompted me to approach the field from an artistic point of view. How (else) could these visual artefacts be comprehended? This book has arisen from a five-year exchange with theoreticians, scientists and artists on the question of the hypothetical potential of diagrams. Here I sent my drawings to various interpreters with a request for a written interpretation (micrology), so that in turn I could react to their texts with diagrammatic drawings and models."

"The process worked until the potential for action was exhausted. Through this intensive exchange of thoughts, the most varying ideas, hypotheses, theses and interrelations developed, eventually achieving the form of captions, (sci-fi)stories, and longer essays on the themes of figure, drawing, hypothesis and diagram. The resulting contributions are of very different kinds, reflecting their authors’ particular fields of knowledge in the fractious borderland between art, science and fiction. The design of the book was developed by Simona Koch reflecting the language of classical scientific formats of publications and enquiring how a specific appearance influences the perception of the content itself."

Table of Contents: Index of Figures. - Drawing a Hypothesis (Preface), Nikolaus Gansterer. - A Line with Variable Direction, which Traces No Contour, and Delimits No Form, Susanne Leeb. - I Must Be Seeing Things, Clemens Krümmel. - Subjective Objectivities, Jörg Piringer. - Grapheus Was Here, Anthony Auerbach. - Asynchronous Connections, Kirsten Matheus. - Distancing the If and Then, Emma Cocker. - Drawing Interest / Recording Vitality, Karin Harrasser.  - Nonself Compatibility in Plants, Monika Bakke. - Hypotheses non Fingo or When Symbols Fail, Andreas Schinner, - Wiry Fantasy, Ferdinand Schmatz. - Reading Figures, Helmut Leder. - Collection of Figures of Thoughts, Gerhard Dirmoser. - Radical Cartographies, Philippe Rekacewicz. - 3 Elements, Axel Stockburger. - Dances of Space, Marc Boeckler. - Collection of Emotions and Orientation, Christian Reder.  - On the Importance of Scientific Research in Relation to Humanities, Walter Seidl. - Interpersonal Governance Structures, Katja Mayer. - The Afterthought of Drawing: 6 Hypotheses, Jane Tormey. - The Hand, The Creatures, The Singing Garden & The Night Sky, Moira Roth. - The Unthought Known, Felix de Mendelssohn. - Processing the Routes of Thoughts, Kerstin Bartels. - An Attempted Survey, Section.a. - The Line of Thought, Hanneke Grootenboer. - Strong Evidence for Telon-priming Cell Layers in the Mammalian Olfactory Bulb, M. L. Nardo, A. Adam, P. Brandlmayr, B. F. Fisher. - Expected Anomalies Caused by Increased Radiation, Christina Stadlbauer. - On Pluto 86 Winter Lasts 92 Years, Ralo Mayer.  – Appendix: Personalia. Subindex. Index of Names. Colophon. Notices.

Book presentations with a performance-lecture and/or installation: – 22 Sept 2011: MHKA, Antwerp, Belgium. – 27 Oct 2011: KNAW, Amsterdam, The Netherlands. – 18 Nov 2011: Kunsthall, Bergen, Norway. – 23 Nov 2011: Kunsthalle Project Space, Vienna, Austria.

– March - April 2011: Galerie Lisi Haemmerle, Bregenz – 02 Feb 2012: "Die Materialität der Diagramme", NGBK, Berlin, Germany.

– 03 Feb - 14 March 2012: Archive Books in Berlin , Germany.

– 16 March 2012: "Leipzig book fair", Leipzig, Germany.

– 13 April - 12 May 2012: "A study on Knowledge", Forum Stadtpark, Graz, Austria.

– 20 Sept 2012: Lehrerzimmer, Bern, Switzerland.

– 9 Nov 2012 - 27 Jan 2013 : "Schaubilder", Kunstverein Bielefeld, Bielefeld, Germany.

– 23 Nov 2012: Salon fuer Kunstbuch at the Museum "21er Haus" , Vienna, Austria.

– 17 Nov 2012- 24 Feb, 2013: "World Book Design" exhibition, Printing Museum, Tokyo, Japan.

– 20 March 2013: Subnet Talk, at the KunstQuartier, Salzburg, Austria.

– Sept - Dec 2013: 4th Athens Biennale, Athens, Greece.


– May - Sept 2013: "When Thought becomes Matter...", Kunstraum Niederösterreich, Vienna, Austria.

– 2014: "Inventing Temperature", KCC, London, UK.

– 2014: "My Brain is in my Inkstand", Cranbrook Museum, Detroit, US.

The second corrected edition was released in Spring 2017

5 May 2017, 19:00 – 21:00

“PUBLISHING IN THE CONTEXT OF ARTISTIC RESEARCH - A BOOKISH TABLE TALK”

Launch of the brand new second edition of Drawing  a Hypothesis – Figures of Thought and its sequel publication Choreo-graphic Figures: Deviations from the Line .

Public presentation of a series of new publications discussing the critical role of documenting and publishing in the context of artistic research with invited guests and authors ao. Alex Arteaga, Emma Cocker, Alexander Damianisch, Nikolaus Gansterer, Mariella Greil, Lilia Mestre at AILab – Angewandte Innovation Lab , Franz-Josefs-Kai 3, 1010 Vienna, Austria. 

The publication could be ORDERED HERE!   Please download sample pages HERE!

"Drawing a Hypothesis – Figures of Thought", Springer Verlag Wien/NewYork, Edition Angewandte, 1st Edition, 2011.

ISBN 978-3-7091-0802-4 Library of Congress Control Number: 2011927923

"Drawing a Hypothesis – Figures of Thought", De Gruyter Berlin/Boston, Edition Angewandte,

2nd corrected edition, 2017.

ISBN 978-3-11-054661-3

352 p. 202 illus., 42 in colour. 1 folding map, Softcover

Book concept: Nikolaus Gansterer Book design: Simona Koch All drawings by Nikolaus Gansterer, 2005 - 2011.

Translation: Veronica Buckley, Aileen Derieg Proofreading: Dorrie Tattersall, Petra van der Jeught, Michael Karassowitsch Image proofreading and technical assistance: Jo Frenken

Photography: Nikolaus Gansterer, TimTom

Support: The publication was made possible by the generous funding of the Jan van Eyck Academie, Maaastricht, The Netherlands, the University of Applied Arts, Vienna, Austria and the BKA.

Keywords: Artistic research; Drawing; Diagrams; Figures of thought; Speculative Thinking.

The publication "Drawing a Hypothesis" was honoured to be one of the ten most beautiful books of Austria 2011 and won the bronze medal at the annual book design competition “ Best Books from all over the World - 2012”. The ceremony took place on the 16th of March 2012 at the Leipzig book fair in Germany.

Reviews (click to download files):

– Book Review in Interface by Mark Robert Doyle (in English), 2011

– Book Review by Gert Hasenhuetl (in English), 2012

– Book Review by Gert Hasenhuetl (in German), 2012

– Book Review by Marc Goethals (in Dutch), 2011

– Interview in Radio Orange with Natascha Gruber (in German), 2012

– Interview in Radio Oe1 with Hans Groisz (in German), 2012

– Performance Review: "Gedanken zeichnen / Drawing Thoughts", Roland Fischer, in: Der Bund Online, 21.09.2012

– "The Hand & The Creature" (Nikolaus Gansterer & Moira Roth), by guest editor Maria Fusco, in: "Discipline art journal / Issue 2, Autumn, 2012, Nick Croggon and Helen Hughes (Eds.), Melbourne.

– Nova Benway, Curatorial Assistant at the Drawing Center / New York in conversation with Nikolaus Gansterer, The Bottom Line Blog, 2 May 2013

– "Strukturbilder", Marie Beschorner, Vira Haglund, Cynthia Krell, Oliver M. Reuter, Lars Zumbansen, in: Kunst+Unterricht Nr. 376, Friedrich Verlag, Velber, 2013.

– Schaubilder, Eva Scharrer, in: Frieze, 2013

– Nina Samuel in conversation with Kaegan Sparks, The Drawing Center, New York, in: The Bottom Line, 01/2014

– Interview with Lucy Liu and Matthew Bohne, "Diagrams without context", PROPS Magazine#6, 2016

In advance of the third program in The Drawing Center’s Drafts series, Curatorial Assistant Nova Benway speaks with Vienna-based artist Nikolaus Gansterer about the generative potential of diagrams at the The Bottom Line Blog . Nova Benway: You just had an exhibition in Germany at the Kunstverein Bielefeld titled Schaubilder. Since your work deals with visibility and invisibility, let’s start with the question of what you showed.

Nikolaus Gansterer: I was showing work resulting from my project Drawing a Hypothesis – Figures of Thought (excerpt). For years I have had a strong fascination with diagrams (in German “Schaubilder”) and I was questioning how these relational visual artifacts—graphic forms visualizing complex associations—could be comprehended from an artistic point of view. In an intensive exchange with artists and scientists, I developed new forms of narratives and hypotheses by tracing the speculative potential of diagrams. Based on a discursive process, I sent my drawings to various interpreters with a request for a written interpretation (which I call “micrology”), so that in return I could react to their texts with diagrammatic drawings and models. In 2011 a publication resulted from this five-year exchange of figures of thought and figures of speech, describing, from various angles, the reflexive and dynamic character of diagrams.

My work shown at the exhibition at the Kunstverein Biefeld bears the title Table of Contents—literally displaying an arrangement of key figures of thought distilled/resulting from these inspiring conversations and transferred into fragile materiality. Here, drawing plays a crucial role in producing and communicating our knowledge(s), due to its ability to mediate between perception and reflection. For me drawing is a way to watch the mind working in the making of ideas, revealing thinking as an inter-subjective and translational process. It’s a balancing between visibility and invisibility.

NB: What constitutes a “figure of thought” for you? Does this form have definable parameters, or is it something more vague and intuitive?

NG: For me a “figure of thought” describes something dynamic and flexible, shifting rather than solid and static. My conception of the figure and figuration is deeply rooted in the Greek understanding of the term, which has a choreographic and performative notion, like “a body’s gesture caught in motion.” (See also Roland Barthes: A Lover’s Discourse, 1979.) It is both an elusive and highly lively form and, for me as artist, also a method to frame, name, and question a phenomenon by entering the field of my inquiry with a specific attitude, attention, and awareness. Due to the ambivalent character of the figure of thought, it’s interesting to use it as a vehicle and specific set of frames—maybe comparable to a system of lenses—to operate with.

NB: Can you give examples of interpretations your collaborators made for Drawing a Hypothesis that were particularly interesting to you?

NG: The multitude of explanations was most striking to me. In this project the potential of drawings and diagrams to activate the mind comes clearly to the forefront. I would argue that a diagram is a reflexive sign, empowering the reader in the process of reading and sense-making as it functions in a non-linear way. Thus it is probably closer to the nature of how our mind is organized and operates. Here again the performative character of diagrams plays an essential role. For example, the artist and theoretician Jane Tormey allowed herself to delve with all senses into the drawings and started living within and between the drawn lines. Letting herself be guided by the lines of thought, she directly inscribed her reflections onto the drawings and thus avoided simplistic description.[i]  On the contrary, the radical cartographers Philippe Rekacewicz and Marc Boeckler individually delineated a set of witty captions, reflecting on our basic need for spatio-temporal representations by deconstructing mapping as a practice of topological narrations. The writers Moira Roth and Ferdinand Schmatz wrote beautiful poetic micrologies on modes in-between seeing and sensing. Systems analyst Gerhard Dirmoser developed an extensive alphabet of figures of thought—which I re-translated into a fold-out map. All these written hypotheses served for me as another starting point to develop new drawings, models, installations, or a series of gestures.

NB: What kind of new knowledge do you think was produced?

NG: In my work, the intuitive part of knowing is as vital as the so-called cognitive part. Drawing—which is for me always a performative act in time and space—offered a way to combine these modes of thinking and sensing (in) correlations. Based on my method of “reverse engineering a theory” (by initiating the process of knowing through a speculative approach to reading diagrams, inferring the information they represent), the resulting hypotheses are naturally of very different kinds, reflecting their authors’ particular fields of knowledge in this fractious zone between art, science, and fiction. Each collated reflection—be it a theoretical essay, a poem, or a drawing—produces a very specific form of knowledge, revealing an enticing glance into our sub/consciousness and the possible mental spaces between recognizing and naming. For me “not-(yet)-knowing” is more exciting and inspiring than mere knowing.

NB: You have also done this kind of interpretation live, correct? How does that change the process?

NG: In the last few years I have collaborated with theoreticians and artists in a series of performances which I call TransLectures. Often a text, a drawing, or a material marks the starting point for different layers of interpretations and re-translations. Here drawing—for me a medium of high immediacy—could turn the subject into a score, an ad-hoc diagram, a makeshift model, or an instruction for taking action. Within these performances the process of “drawing beyond drawing” is central and extended along the categories of time, space, and movement: a line of thought becomes a line on the paper, a line in space, a line verbalized, or even a line drawn with the whole body. Together with the writer Emma Cocker I developed a series called Drawing on Drawing a Hypothesis. Using processes of cross-reading and live drawing, we dissected my publication Drawing a Hypothesis in the search for key words and phrases and evocative fragments in order to re-edit its content live. I am now preparing for the next step of TransLectures, which will take place in July at a performance festival in Berlin called Foreign Affairs. Invited philosophers, sociologists, and economists will discuss the omnipresent phenomenon of betting and the desire for speculation, but also the enormous impact of the idea of “futures” on social interrelations. Parallel to the lectures I will be live transforming the speakers’ ideas into ad hoc diagrams and daring card house models (“bodies of theory”) by translating their ideas into fragile forms of materiality.

NB: Your work sounds perfectly suited to Drafts, the program series at The Drawing Center you’ve recently taken part in. Can you describe your participation, and what was interesting for you about the process?

NG: It was indeed a very exciting process. I felt familiar with the rather associative approach of the “cadavre exquis” applied to Drafts through my research into diagrams. It was fascinating to find new visual material relating to explanations and visualizations in the archives of the Reanimation Library. In my first investigation I felt drawn to figures that are rather abstract and open. In my intense exchange with Kaegan Sparks, we worked on a set of figures which, in the end, contained both movements: an “informed openness” combined with a specific speculative and poetic potential. [i] “If I enter the drawing and start living in this world, I can describe this other reality as if I were looking at the ‘scene’ as it unfold before me,” Jane Tormey, “The Afterthought of Drawing: 6 Hypotheses” in Drawing a Hypothesis, pp. 241-258.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Idea behind hypothesis testing
• Examples of null and alternative hypotheses
• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations

Using P-values to make conclusions

• (Choice A)   Fail to reject H 0 ‍   A Fail to reject H 0 ‍  
• (Choice B)   Reject H 0 ‍   and accept H a ‍   B Reject H 0 ‍   and accept H a ‍  
• (Choice C)   Accept H 0 ‍   C Accept H 0 ‍  
• (Choice A)   The evidence suggests that these subjects can do better than guessing when identifying the bottled water. A The evidence suggests that these subjects can do better than guessing when identifying the bottled water.
• (Choice B)   We don't have enough evidence to say that these subjects can do better than guessing when identifying the bottled water. B We don't have enough evidence to say that these subjects can do better than guessing when identifying the bottled water.
• (Choice C)   The evidence suggests that these subjects were simply guessing when identifying the bottled water. C The evidence suggests that these subjects were simply guessing when identifying the bottled water.
• (Choice A)   She would have rejected H a ‍   . A She would have rejected H a ‍   .
• (Choice B)   She would have accepted H 0 ‍   . B She would have accepted H 0 ‍   .
• (Choice C)   She would have rejected H 0 ‍   and accepted H a ‍   . C She would have rejected H 0 ‍   and accepted H a ‍   .
• (Choice D)   She would have reached the same conclusion using either α = 0.05 ‍   or α = 0.10 ‍   . D She would have reached the same conclusion using either α = 0.05 ‍   or α = 0.10 ‍   .
• (Choice A)   The evidence suggests that these bags are being filled with a mean amount that is different than 7.4  kg ‍   . A The evidence suggests that these bags are being filled with a mean amount that is different than 7.4  kg ‍   .
• (Choice B)   We don't have enough evidence to say that these bags are being filled with a mean amount that is different than 7.4  kg ‍   . B We don't have enough evidence to say that these bags are being filled with a mean amount that is different than 7.4  kg ‍   .
• (Choice C)   The evidence suggests that these bags are being filled with a mean amount of 7.4  kg ‍   . C The evidence suggests that these bags are being filled with a mean amount of 7.4  kg ‍   .
• (Choice A)   They would have rejected H a ‍   . A They would have rejected H a ‍   .
• (Choice B)   They would have accepted H 0 ‍   . B They would have accepted H 0 ‍   .
• (Choice C)   They would have failed to reject H 0 ‍   . C They would have failed to reject H 0 ‍   .
• (Choice D)   They would have reached the same conclusion using either α = 0.05 ‍   or α = 0.01 ‍   . D They would have reached the same conclusion using either α = 0.05 ‍   or α = 0.01 ‍   .

Ethics and the significance level α ‍  

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• Architecture and Design
• Asian and Pacific Studies
• Business and Economics
• Classical and Ancient Near Eastern Studies
• Computer Sciences
• Cultural Studies
• Engineering
• General Interest
• Geosciences
• Industrial Chemistry
• Islamic and Middle Eastern Studies
• Jewish Studies
• Library and Information Science, Book Studies
• Life Sciences
• Linguistics and Semiotics
• Literary Studies
• Materials Sciences
• Mathematics
• Social Sciences
• Sports and Recreation
• Theology and Religion
• Publish your article
• The role of authors
• Promoting your article
• Abstracting & indexing
• Publishing Ethics
• Why publish with De Gruyter
• How to publish with De Gruyter
• Our book series
• Our subject areas
• Your digital product at De Gruyter
• Contribute to our reference works
• Product information
• Tools & resources
• Product Information
• Promotional Materials
• Orders and Inquiries
• FAQ for Library Suppliers and Book Sellers
• Repository Policy
• Free access policy
• Open Access agreements
• Database portals
• For Authors
• Customer service
• People + Culture
• Journal Management
• How to join us
• Working at De Gruyter
• Mission & Vision
• De Gruyter Foundation
• De Gruyter Ebound
• Our Responsibility
• Partner publishers

Your purchase has been completed. Your documents are now available to view.

Drawing A Hypothesis

Figures of thought.

• Nikolaus Gansterer
• X / Twitter

Please login or register with De Gruyter to order this product.

• Language: English
• Publisher: De Gruyter
• Copyright year: 2017
• Edition: 2nd corr. ed.
• Audience: An künstl. Forschung, Ästhetik, Zeichnung, Diagrammatik, Philosophie Interessierte
• Main content: 351
• Other: Zahlr. Abb.
• Keywords: Zeichnung ; Diagramm ; Künstlerische Forschung
• Published: April 24, 2017
• ISBN: 9783110546613

Artists priced out of Los Angeles head to this creative hub in the high desert

• Show more sharing options
• Copy Link URL Copied!

At high noon on a Saturday, the last aluminum pour of the day is about to commence at the Yucca Valley Material Lab .

Heidi Schwegler, founder of the Lab, has crawled up to the roof to get the best vantage point for a video. Schwegler has a hard stance on safety while still allowing for wild experimentation — it’s this attitude that makes the compound, with its art and recording studios, gallery, retrofitted campers and workshops like foundry and glass casting — a place of inspiration and community that pulls in people from all over the nation, but especially Angelenos looking for a reprieve from city life.

“This is the closest Derek and I could get to L.A. and afford it,” said Schwegler, referring to her partner, Derek Monypeny, who works with musicians. “And I think if you ask a lot of artists out here, they’ll say the same thing. It’s as close as you can get and be a really decent place to live and have a huge studio and still be within driving distance of an art center.”

It’s this passion and energy that pull artists east. Every workshop sells out, attracting hot-shot artists and retired high school teachers alike. “It’s really amazing to see my art and pedagogical practice come together outside of myself — in the form of a curved metal building plopped in the Mojave Desert,” Schwegler said. “Never would I have imagined this when we bought this property in 2018.”

Travel & Experiences

What’s happening in Joshua Tree is a ‘dream’ — and possibly a curse

More and more people are arriving in the towns along Highway 62 near Joshua Tree National Park. In their eagerness to feel those desert vibes, they’ve set off a full-blown boom.

March 10, 2022

The Lab has become a landing place for out-of-town artists and people looking for a way to plug into the desert scene. Many artists in Yucca Valley moved there on a whim after visiting for a weekend, much like Schwegler.

“I built this program because I was really afraid I would become a total recluse out here, because I didn’t think anybody was out here,” Schwegler said. “Come to find out, it’s just like that saying: ‘If you build it, they will come.’”

An artist and self-proclaimed materials junkie, Schwegler has pulled together funding from various sources, including AHA Projects, a nonprofit organization that supports creators, to cover residency and workshop costs, including airfare for teachers and housing for artists. Schwegler also often works with artists from the desert and Los Angeles for trade.

The Lab’s growing community has been cited as a reason why L.A. artists stay in the high desert — being able to see familiar faces at one or two cultural events a weekend is a balm after the smorgasbord and sprawl of the Southland.

Haydeé Jiménez, an artist in residence at Yucca Valley Material Lab, wears a protective Kevlar apron during a bronze and aluminum workshop.

Students in the foundry casting in bronze and aluminum workshop pour molten aluminum into molds that were made earlier in the week.

In 2016, artists Ry Rocklen and Carolyn Pennypacker Riggs realized that a mortgage in the desert would be cheaper than a storage unit in Los Angeles. “I had a bunch of my ‘Trophy Modern’ furniture in storage and realized we could decorate our house with it and have a place to visit on the weekends,” said Rocklen, of a series of sculptures he made for an exhibit.

After having a child in 2020 and spending more time in nearby Joshua Tree, they moved full-time and converted their garage into studio space. “It was such a strange time, with so many different things going on, adjusting was not really on my mind. It was kind of a blur between our new baby, the pandemic and the move,” said Rocklen, who runs the gallery space Quality Coins in Yucca Valley. “The landscape, however, was our saving grace, as we were able to go on walks through the beautiful rocky hills.”

Back at the metal workshop, the roaring sound of the kiln — which is used in the process of turning molten bronze and aluminum into objects — fills the quiet desert mesa with an ambient soundtrack.

Haydeé Jiménez, a recent artist in residence who splits her time between Los Angeles and Tijuana, crouched outside the metals workshop observation window wearing headphones and sunglasses, with her microphone wind-screened by a cardboard box. Amid the Joshua trees and creosote bushes, she recorded the sounds of the makeshift foundry.

Jiménez, who describes her art practice as revolving around “sound, music and vibrational sound healing,” said she was excited to work with new materials.

“When I first got the invitation to join [the Lab] for a residency, I hoped to work with glass and create little resonant objects for the development of a sort of acoustic ASMR experience,” said Jiménez, referring to Autonomous Sensory Meridian Response, which is when one is soothed by sounds like whispers and taps. Later in the weekend, she’d layer the foundry recording over sounds made using bronze objects from the workshop in a performance with gong-master Tatsuya Nakatani at the Firehouse, a Joshua Tree venue.

Looking for L.A.’s art cool kids? They’re hosting exhibits in laundry rooms and garages

The most exciting exhibit spaces in L.A. have gone in-house, popping up in unlikely homes, empty pools, laundry rooms and beyond.

Feb. 29, 2024

Any given weekend at the compound can be action-packed; that Saturday, Lazy Eye Gallery opened Michelle Ross’ “Before Pictures,” a show of sculptural paintings inside the nave of a water tower converted into a small funnel of a gallery space with a ladder to the roof that affords a view of the mesa.

But as the artists’ community grows, so has interest in real estate in Yucca Valley, Joshua Tree and Twentynine Palms, once considered more affordable areas. Housing prices in Yucca Valley have grown 80% since 2019, according to Zillow , although the steep pandemic rush has since cooled .

Haydeé Jiménez, an artist in residence at Yucca Valley Material Lab, records sounds of students in the foundry pouring molten aluminum into molds. A view of the Lazy Eye gallery at the Yucca Valley Material Lab.

“The presence of Airbnbs is corrosive,” said Riggs, observing that interested buyers have grown beyond “Silver Lake hipsters with a getaway cabin.” Last year, Yucca Valley capped short-term rentals at 10% of its housing stock. According to Redfin , most people searching to buy Yucca Valley homes today are in San Francisco.

Between the expansive landscape, cheaper-than-L.A. studio space and the small-town feel, the desert offers the experience of slow time — which can help some artists tap into a flow state without the day-to-day distraction of city living. But all that free time and space can be intimidating.

Ceramic artist and designer Mansi Shah left Los Angeles in 2020 after another artist friend told her about a house for rent in Yucca Valley; she packed up and headed to the desert within a few weeks. “There was 500 feet of open desert between me and my nearest neighbor. I remember those first few months, I was terrified of everything. The wind, the quiet, the desert critters,” said Shah.

“My introduction to life in America was the desert,” said Shah. She grew up in Palm Springs with her hotel manager father after her family emigrated from India. But later, she’d lived in Los Angeles, then New York and then returned to Los Angeles. “Now moving back here to the high desert, setting up my home and studio, it feels I’ve come back full circle.”

When she moved to L.A. in 2017, she realized that it had radically changed — most noticeably, the rent prices.

“But every exploding colorful sunset, every jackrabbit, every coyote sighting changed my brain chemistry,” said Shah. “I began to soften and ease into the different pace of life here. There’s a reverence for nature here that I hadn’t experienced before.”

In the summer months, the average temperature is 95 degrees Fahrenheit . “My studio schedule revolves around outside temperatures,” said Shah. “I tend to work early mornings and nights in the summer and run the kiln overnight.”

11 places in L.A. to get your creativity flowing. Pottery! Neon bending! Bookbinding!

Whether you want to try candle making, Jaipur block printing, glass blowing, neon bending or woodworking, L.A. has a space for that.

April 27, 2023

Workshops at the Lab are about to wind down for the summer, making the last bronze pour of the day bittersweet.

After pouring hot aluminum into one of her stick-shaped molds and letting it cool in a pile of dirt, a participant took a ball-peen hammer and cracked open the rough silicate mold, like a geode.

The next day, participants buffed their objects and applied chemical solvents to create patinas and finishes before heading back to the city. After the last pour finished, the crucible was set aside to cool.

“That’s a wrap,” said Schwegler, while everyone clapped.

More to Read

Opinion: Studio productions keep moving out of Los Angeles. We need to stop the bleeding

May 21, 2024

Weed changed this California town. Now artsy residents are all in on psychedelics

May 8, 2024

Meow Wolf supercharged the way we experience art. Is L.A. ready for the wild ride?

May 3, 2024

Sign up for our L.A. Times Plants newsletter

At the start of each month, get a roundup of upcoming plant-related activities and events in Southern California, along with links to tips and articles you may have missed.

You may occasionally receive promotional content from the Los Angeles Times.

Los Angeles Times staff photographer Allen J. Schaben is an award-winning journalist capturing a wide range of images over the past 34 years. Before joining The Times, he honed his craft at the Detroit Free Press, Dallas Morning News, Wichita Eagle and Connecticut Post. Schaben earned his bachelor’s degree in journalism at the University of Nebraska-Lincoln in 1993.

More From the Los Angeles Times

Entertainment & Arts

How Maria Friedman and Jonathan Groff cracked the riddle of Sondheim’s ‘Merrily’

May 29, 2024

The 8 best fabric stores in L.A. to score deals for your next project

This must be West Hollywood

World & Nation

U.S. vows to return more looted antiquities as Italy welcomes home 600 artifacts

May 28, 2024

First things first: Before thinking about Texas A&M, UT faces Louisiana in NCAA Tournament

After the Texas baseball team was placed in an NCAA regional hosted by Texas A&M, the discussion at a media availability Monday centered around the Aggies and Longhorns.

"A&M has always been a rivalry. I've never liked them personally, just growing up being a UT fan," Texas first baseman Jared Thomas told reporters.

Here's the thing, though. For as much fun as a Texas-Texas A&M tournament tussle would be — and the volleyball, softball and men's tennis programs at both schools can attest to just how fun those postseason clashes have been during the 2023-24 academic year — there is no guarantee that such a matchup will take place at Blue Bell Park this weekend.

When Texas opens its 63rd appearance in the NCAA Tournament on Friday, the Longhorns will be playing Louisiana . Texas A&M has to worry about Grambling before even thinking about Texas.

"It's just important to take every game one at a time," UT outfielder Max Belyeu said. "If you look too far ahead, it can bite you."

The winners of the Sun Belt Conference's regular season championship, Louisiana boasts a 40-18 record and is actually the No. 2 seed in the College Station regional. Texas is the No. 3 seed. Nationally, Louisiana boasts a top-20 ERA and the 15th-best WHIP in college baseball.

Texas and Louisiana have played 42 times before. Last year, UT opened its NCAA Tournament run with a 4-2 win over Louisiana in a regional hosted by Miami. Texas fans will probably remember that game for former UT standout Dylan Campbell's diving catch in right field .

"The Aggies aren't even in the picture unless we play well against a very good team," Texas coach David Pierce said. "It's interesting that we faced them last year and I think they have a lot of those kids back. Their pitching's definitely improved, (they have) team speed. We'll take a look at their entire roster and then view how we want to approach it with our staff."

OK, OK. Texas and Louisiana will meet at Blue Bell Park at 5 p.m. on Friday in a game that will be televised by ESPNU. If the Longhorns take care of business against the Ragin' Cajuns and Texas A&M (44-13) beats Grambling (26-26), then what?

Then it will be time for the 381st baseball battle between these in-state rivals. Texas has earned a 245-131-5 lead in the all-time series, but Texas A&M owns the most-recent win since it recorded a 9-2 victory in Austin on March 5. The Longhorns have gotten the better of Texas A&M in the regional round in 2014 and 2018, but the Aggies sent UT home from the 2022 College World Series.

"Of course it's a rivalry. It's a beautiful thing," Texas shortstop Jalin Flores said. "It would be the same (amount of animosity from the crowd) if they came and played us here. You've got to embrace it, that's what you've got to do as a Texas Longhorn. We love it. I think going out there and playing A&M, of course handling Louisiana first, it's going to be a good battle."

When asked after the NCAA selection show if he was surprised that Texas was placed in the College Station Regional, Pierce said he wasn't after UT lost both of its games at last week's Big 12 Tournament. The eighth-year coach even joked that after Texas and Texas A&M's softball teams engaged in an entertaining super regional this past weekend, the NCAA decided that "we'll just send Texas (to College Station) and make it just as exciting."

Pierce, though, was surprised that Texas earned a No. 3 seed. Texas was last a No. 3 seed in the NCAA Tournament in 2015. Texas does have some notable losses on its résumé, but the Longhorns finished in third place in the Big 12 standings and most publications listed UT as a No. 2 seed in their tournament projections .

"I think we've been the underdogs all year," Thomas said. "Nobody's expected us to get to the point we're at anyways so we've got nothing to lose. We're going to go out and give it everything we've got, no regrets."

Under Pierce, Texas has compiled a 24-12 record over five appearances in the NCAA Tournament. The Longhorns reached the Men's College World Series in 2018, 2021 and 2022. Last year, UT won a road regional for the first time since 2014.

French Open draw: Nadal’s nightmare draw with Zverev? And who will stop Swiatek?

Follow live coverage of the third day of the French Open 2024 today, with Djokovic and Sabalenka in action

Once upon a time, there was a tennis tournament called the French Open. Plenty of great men’s players triumphed on the red clay, but so did a lot of nice players who never ended up on anyone’s all-time list. Andres Gomez. Carlos Moya. Thomas Muster. Yevgeny Kafelnikov. Gaston Gaudio.

Advertisement

This was the “Open” that really was pretty open, at least for players who had a talent for slogging on soft red clay for four hours. 

And then, the higher minds of tennis made the red clay harder and faster, and along came a young Spaniard who wore funny shorts named Rafael Nadal , and the French Open, at least on the men’s side, was basically never open again.

But as the French Open held its 2024 draw Thursday afternoon, the event had a renewed everything-and-nothing quality, given that the top of men’s tennis has basically become an episode of Grey’s Anatomy during the past month.

Nadal is the episode’s main storyline, patient zero of the chaos, and a 112-3 record at the tournament. Now he has to play the world No 4, Alexander Zverev, in the first round.

Nadal was unseeded, so he could have ended up anywhere from the second slot, right under Novak Djokovic for the 60th time in their careers, undoubtedly with the strangest of circumstances, or next to “TBD” from the qualifying tournament, or somewhere in between.  When it was over, the greatest clay-court player of all time learned that he would have to play a rematch of the 2022 French Open semi-final, where Zverev tore ligaments in his ankle after pushing Nadal to his limits.

It couldn’t really be worse for the 14-time champion, and a gasp rippled through the audience when the pairing was made. He is the greatest floater in the modern history of tennis. Each shot might be his last, but after all he’s done at this tournament, there is the notion of the smallest chance that he will walk onto the grounds and feel all his old magic once more, as though he has just chugged an elixir. Having to face a player as competent on clay as Zverev took the air out of proceedings.

Zverev will be playing over the coming days and weeks while a domestic abuse hearing begins in the German city of Berlin , over charges that he abused a former girlfriend during an argument in 2020.

Ghosts of clay courts past: Rafael Nadal's comeback is really about his legacy

“It all depends on the draw” is one of the age-old cliches of tennis. There is plenty of truth to it at the start of a tournament, before players have had a chance to play themselves into form. It’s still largely a waste of time to look at a first-round draw and start prognostications about semi-final matchups that often don’t end up happening.

That is more true this year than it has been in a while, because of the health calamities at the top of the game. Normally, having to face a top-five favorite in the opening round is pretty much a death sentence. This year, it might not be such a bad thing. 

The first favorite, Carlos Alcaraz , has a balky right forearm that has made a mess of his clay-court campaign. No Monte Carlo, Barcelona or Rome, and defeat to Andrey Rublev in the quarter-finals in Madrid. He will face US lucky loser, JJ Wolf.

Next is Djokovic, the defending champion who really hasn’t played top-tier tennis in six months, and who took a whack on the head from a falling water bottle while signing autographs in Rome. He lost his next match and is competing in a lower-level tournament in Geneva this week, to try to find some form and confidence at the last minute.

In the first round, Djokovic will face Pierre Hugues-Herbert, who can walk onto the court with the confidence of knowing he is facing someone who has lost to both Luca Nardi of Italy and Alejandro Tabilo of Chile since March, and now to Tomas Machac in Geneva .

Then there’s Jannik Sinner , who suffered a hip injury during a weight training session in Madrid. He pulled out of his quarter-final there and then skipped the Italian Open. He will play in Roland Garros, according to his agent, but his health has been touch-and-go for days. For his first-round opponent, Chris Eubanks, there’s never been a better time to face a player likely to take over the No 1 slot in the rankings in the coming weeks.

Perhaps you fancy Stefanos Tsitispas or Casper Ruud. They’re French Open finalists the past three years, and two of the best clay-court players in the world. Tsitsipas found his form on the Monte Carlo clay in early April, but wobbled in Madrid and Rome. He faces Marton Fucsovics, while Ruud, who complained of a “lock” in his back in Rome, has been released from facing promising Czech, Jakub Mensik, who withdrew with injury. Ruud will now play Felipe Meligeni Alves.

More outside bets might be the in-form Chileans: Nicolas Jarry and Alejandro Tabilo, who made the final and semi-finals in Rome respectively. Jarry faces Corentin Moutet, while Tabilo takes on Zizou Bergs.

French Open 2024: Men’s first-round picks

• 🇨🇭 Stan Wawrinka vs 🇬🇧 Andy Murray
• 🇩🇪 Alexander Zverev (4) vs 🇪🇸 Rafael Nadal
• 🇫🇷 Gael Monfils vs 🇧🇷 Thiago Seyboth Wild
• 🇦🇺 Alexei Popyrin vs 🇦🇺 Thanasi Kokkinakis
• 🇵🇹 Nuno Borges vs 🇨🇿 Tomas Machac
• 🇫🇷 Hugo Gaston vs 🇺🇸 (15) Ben Shelton
• 🇩🇰 Holger Rune (13) vs 🇬🇧Dan Evans
• 🇫🇷 Arthur Fils (29) vs 🇮🇹 Matteo Arnaldi

This is how a French Open becomes truly open. 

Iga Swiatek is how it becomes closed. Swiatek will turn 23 next week. She has won three of the past four French Open titles, and has become nearly unbeatable on clay. She lost a semi-final in Stuttgart last month to Elena Rybakina, then won in Madrid and Rome, beating world No 2 Aryna Sabalenka twice.

Given all that, the biggest question wasn’t her opponent in the first round (it’s qualifier Leolia Jeanjean, and she could face Naomi Osaka in the second round) but whether the two players who have proven to be the greatest challenges for her, Rybakina and Jelena Ostapenko, would end up on her side of the draw. Of course, there are other players who can have a career day and beat Swiatek. Linda Noskova, 29th in the world, did it in Australia, but that was on a hard court. 

Like Noskova, Rybakina and Ostapenko are two of the biggest hitters in the game. And Swiatek generally has most of her problems against big hitters, since they take time away from her or have the power to hit the ball through the court.

Ostapenko has beaten Swiatek all four times they have played, and won this tournament in 2017. Rybakina has won four out of six meetings.

They will have to get to her first though. Ostapenko and Swiatek could meet in the semi-finals, while Rybakina would have to wait until the final.

As for the other players with an outside chance of slaying Swiatek, Sabalenka will face Erika Andreeva in the first round, Coco Gauff will play Julia Avdeeva, and Danielle Collins will face compatriot Caroline Dolehide. Collins and Gauff could meet Swiatek in the quarter-finals and semi-finals respectively.

Sabalenka, the winner of the last Grand Slam in Australia and two of the last five, is the second seed, which means she can’t face Swiatek on her favorite court until the finals. If Swiatek is still standing then, chances are she is playing pretty well — she is 4-0 in Grand Slam finals and 19-4 in finals overall.

The women’s draw also has some floaters that no one will really want to face, even if they aren’t as big of a threat as they might have been in the recent past. Osaka hasn’t had the best time on clay, but she’s said she’s leaning into it these days — and is a four-time Grand Slam champion no matter how you slice it. She faces Lucia Bronzetti.

Elsewhere, Mirra Andreeva is dangerous, Madison Keys is on something of a clay-court hot streak, and the Fruhvirtova siblings could cause some chaos if they get through qualification .

French Open 2024: Women’s first-round picks

• 🇨🇦 Bianca Andreescu vs 🇪🇸 Sara Sorribes Tormo
• 🇯🇵 Naomi Osaka vs 🇮🇹 Lucia Bronzetti
• 🇰🇿 Yulia Putintseva vs 🇺🇸 Sloane Stephens
• 🇹🇳 Ons Jabeur (8) vs 🇺🇸 Sachia Vickery
• 🇨🇳 Qinwen Zheng (7) vs 🇫🇷 Alize Cornet
• 🇷🇴 Sorana Cirstea (28) vs 🇷🇺 Anna Blinkova
• 🇬🇧 Katie Boulter (26) vs 🇪🇸 Paola Badosa
• 🇺🇦 Elina Svitolina (15) vs 🇨🇿 Karolina Pliskova

The main draws begin this Sunday, May 26. What are your stand-out first-round ties? And who do you see going all the way? Tell us in the comments…

(Top photos: Clive Mason; Clive Brunskill/Getty Images)

Get all-access to exclusive stories.

Subscribe to The Athletic for in-depth coverage of your favorite players, teams, leagues and clubs. Try a week on us.

Matthew Futterman is an award-winning veteran sports journalist and the author of two books, “Running to the Edge: A Band of Misfits and the Guru Who Unlocked the Secrets of Speed” and “Players: How Sports Became a Business.”Before coming to The Athletic in 2023, he worked for The New York Times, The Wall Street Journal, The Star-Ledger of New Jersey and The Philadelphia Inquirer. He is currently writing a book about tennis, "The Cruelest Game: Agony, Ecstasy and Near Death Experiences on the Pro Tennis Tour," to be published by Doubleday in 2026. Follow Matthew on Twitter @ mattfutterman

Powerball winning numbers for Monday, May 27, 2024 lottery drawing with jackpot at $131M

After there was no grand prize winner from  Saturday's drawing , the jackpot for Monday rose to  $131 million  with cash value of  $61.2 million .

Ready to try your luck with Powerball? Here's everything you need to know.

Powerball winning numbers 5/27/24

The  winning numbers from the Monday, May 27 drawing  were  9-30-39-49-59  and the Powerball was  21 . The Power Play was  5X .

Did anyone win Powerball drawing, Monday, May 27, 2024?

There was no grand prize winner, but there was a Match 5 winner worth $1 million in New York.

The jackpot rose to $143 million with cash value of   $66.8 million .

Powerball winning numbers 5/25/24

The  winning numbers from the Saturday, May 25 drawing  were  6-33-35-36-64  and the Powerball was  24 . The Power Play was  3X .

Did anyone win Powerball drawing, Saturday, May 25, 2024?

There was no grand prize winner, but there was a Match 5 winner worth $1 million in Texas.

Powerball: Winning numbers for Saturday, May 25, 2024 lottery drawing worth $120 million

Mega Millions: Winning numbers for Friday, May 24, 2024 lottery drawing worth $453M

When is the next Powerball drawing?

The next drawing will be Wednesday, May 29, at 10:59 p.m. ET.

What times does Powerball close?

In Delaware, tickets may be purchased until 9:45 p.m. ET on the day of the drawing.

In New Jersey and Pennsylvania, you can purchase tickets until 9:59 p.m.

What days are the Powerball drawings? What time does Powerball go off?

Powerball drawings are held three times a week, every Monday, Wednesday and Saturday at 10:59 p.m. ET.

How much are Powerball tickets?

The Powerball costs $2 per play.

In Pennsylvania, you can buy tickets online:  www.pailottery.com/games/draw-games/ .

Tickets can be bought online as well in New Jersey:  njlotto.com .

To play, select five numbers from 1 to 69 for the white balls, then select one number from 1 to 26 for the red Powerball.

You can choose your lucky numbers on a play slip or let the lottery terminal randomly pick your numbers. 

To win, match one of the nine ways to win:

• 5 white balls + 1 red Powerball = Grand prize.
• 5 white balls = $1 million.
• 4 white balls + 1 red Powerball = $50,000.
• 4 white balls = $100.
• 3 white balls + 1 red Powerball = $100.
• 3 white balls = $7.
• 2 white balls + 1 red Powerball = $7.
• 1 white ball + 1 red Powerball = $4.
• 1 red Powerball = $4.

There's a chance to have your winnings increased two, three, four, five and 10 times through the Power Play for an additional $1 per play. Players can multiply non-jackpot wins up to 10 times when the jackpot is $150 million or less.

All prizes are set cash amounts, except for the grand prize. In California, prize payout amounts are pari-mutuel, meaning it's determined by the sales and the number of winners.

What are the odds of winning the Powerball?

The odds of winning the Powerball grand prize are 1 in 292,201,338. The odds for the lowest prize, $4 for one red Powerball, are 1 in 38.32.

According to Powerball, the overall odds of winning a prize are 1 in 24.87, based on a $2 play and rounded to two decimal places.

What is the  largest Powerball jackpot ?

• $2.04 billion – Nov. 7, 2022 – CA
• $1.765 billion – Oct. 11, 2023 – CA
• $1.586 billion – Jan. 13, 2016 – CA, FL, TN
• $1.3 billion – April 6, 2024 – OR
• $1.08 billion – July 19, 2023 – CA
• $842 million – Jan. 1, 2024 – MI
• $768.4 million – March 27, 2019 – WI
• $758.7 million – Aug. 23, 2017 – MA
• $754.6 million – Feb. 6, 2023 - WA
• $731.1 million – Jan. 20, 2021 – MD

• SI SWIMSUIT
• SI SPORTSBOOK

Mavericks draw first blood with Game 1 win over Timberwolves at Target Center

Nolan o'hara | may 23, 2024.

• Minnesota Timberwolves
• Dallas Mavericks

In a reverse of typical proceedings, Kyrie Irving got the Dallas Mavericks started and Luka Doncic played the part of a closer. The Timberwolves at times struggled to contain both in a 108-105 loss in Game 1 of the Western Conference finals Wednesday night at Target Center in Minneapolis.

Doncic hit a crucial jumper to put the Mavericks up four with 49 seconds remaining in the fourth quarter. While Naz Reid later made a tip-in shot to cut it back to two, Irving made a pair of free throws following the intentional foul that pushed it back to a four-point margin with seven seconds remaining.

The Timberwolves, meanwhile, struggled to find an offensive rhythm late.

"Terrible offense, bad shots, turnovers, no composure," Timberwolves coach Chris Finch said.

Doncic, who tallied 33 points, eight assists and six rebounds, took over during the fourth quarter and made three straight buckets during a 13-0 Mavs run that eventually resulted in an eight-point lead.

Doncic got it all started with a pair of stepback jumpers and a 3 during his own 7-0 run that gave the Mavericks a 91-89 advantage, their first lead of the fourth quarter after trailing by five.

The Timberwolves, however, eventually answered with their own 10-1 run in which they retook the lead with just under five minutes to play. Karl-Anthony Towns was a driving force, hitting a jumper, finding Rudy Gobert for a lob dunk and drilling a 3 that gave the Wolves a 99-98 lead.

Anthony Edwards pushed that to a four-point advantage when he made a 3 for the first bucket following a Mavericks timeout. But Doncic answered with a 3 on the other end, and P.J. Washington later hit another that gave Dallas a lead it would not relinquish.

That all came despite the Timberwolves leading throughout the entire first half and most of the first quarter. Jaden McDaniels came out hot from long range, knocking down a trio of 3s during the first quarter on his way to 19 first-half points. It's the third straight game McDaniels has scored 20 or more points, finishing his night with a team-high 24 points.

"I don't think we played our best basketball (Wednesday)," Edwards said. "One through 15. I think (McDaniels) was the only one that came ready to play (Wednesday). I think everybody else let him down."

Kyle Anderson, who scored 11 points, also got the Wolves going off the bench, particularly early on when he scored seven points in four minutes of action during the first quarter. He even hit a 3-pointer during that stretch. And the Timberwolves led 33-27 after one quarter of action.

But despite maintaining a lead throughout the first half, the Timberwolves did have trouble containing Kyrie Irving, who beat the Wolves up and down the court, finished at the rim and hit an assortment of shots from the midrange. Irving scored 24 of his 30 points in the first half.

Perhaps the five biggest came in the final stretch of the second quarter when he scored five straight points to cut an eight-point margin to three. Irving first got to the rim for a layup and then found his way right back to the paint following a turnover from Edwards. He made a difficult shot in the paint and drew a foul on McDaniels before completing a three-point play to make it 62-59.

NOLAN O'HARA

Another lead slips away as D.C. United sputters to a draw vs. Chicago

United veered off course in the second half and settled for a 1-1 draw against a team with no wins in its past eight.

D.C. United’s first season under Coach Troy Lesesne has brought both thrills and frustration — an anticipated range of emotions as long-term plans take hold. Amid the growing process, though, matches such as Saturday’s against the stumbling Chicago Fire carry higher expectations.

Anything shy of three points would be considered a failure in the moment and a setback to United’s ambitions of returning to the MLS playoffs after four consecutive misses.

United was headed in the right direction before veering off course in the second half and settling for a 1-1 draw before 19,081 at Audi Field.

D.C. (4-5-6) is winless in three straight and fell to 3-3-2 at home. After a run of seven goals in three matches, it has managed two in its past three outings — both by central defenders.

Chicago (2-8-5) is winless in eight (0-5-3) and has scored three goals in that time.

“Chicago was better than us in the second half,” Lesesne said. “We’re fortunate to get a point out of that, and that’s not good enough.”

Christopher McVey scored midway through the first half, but Chicago’s Kellyn Acosta responded early in the second.

United’s frustration was heard throughout the locker room.

“We know how we want to play,” captain Steven Birnbaum said. “We’ve shown spells of it. It’s frustrating to not put a full performance together over the last couple of games, and so that needs to be addressed. We know it needs to be addressed.”

Goalkeeper Alex Bono said: “We come out for the second half, and we look like a different team. It’s self-inflicted. ... We can’t keep playing like this and expect to do what we want to do this year.”

United has failed to protect leads six times, resulting in two defeats and four draws.

“Story of the season,” right back Aaron Herrera said. “Take the lead and then come out the second half super lackadaisical and give them a bad goal. It’s shocking we haven’t figured it out yet. Can’t just keep doing the same thing over and over. It’s getting ridiculous at this point.”

United went ahead in the 20th minute on McVey’s first goal of the season and second in 65 MLS appearances. Mateusz Klich launched a free kick from the center circle. Birnbaum won the header in the penalty area, flicking it into McVey’s path at the top of the six-yard box for a right-footed poke past goalkeeper Chris Brady.

After finishing the half without a shot on goal or corner kick, the Fire set the terms after intermission.

“We were too passive,” Birnbaum said.

“You can see in the first half we disrupted them,” Lesesne said. “We were [performing] in our way. I think you could see our identity. You could not see that in the second half.”

In the 53rd minute, Andrew Gutman’s cross set up one-touch passing between Acosta and Hugo Cuypers before Acosta drove an 18-yarder into the low left corner. United has not recorded a shutout since March 30.

United’s energy remained high, but its execution was poor and its defensive effort conceded ample space. United could not find a rhythm, and top scorer Christian Benteke didn’t receive quality service in the box.

“Second half, we were one-dimensional at best,” Lesesne said.

Late in the game, Birnbaum’s header flew wide of the back post and Chicago’s Maren Haile-Selassie threatened twice.

“We’re past the point of taking small positives and trying to work them into our process,” Bono said. “It’s time the results need to come.”

The match began the start of another stretch of three games in eight days for United, which will visit Montreal (3-7-4) on Wednesday and host Toronto (7-7-1) next Saturday.

Here’s what else to know about United’s draw:

Roster shortage

Winger Martín Rodríguez (concussion) and defender-midfielder Pedro Santos (hip) were ruled out, leaving United with just 15 non-goalkeepers. The 17-man active squad was three fewer than the maximum.

Midfielder Russell Canouse ( colon surgery ) and defender Conner Antley ( ACL ) are out for the year. Left back Mohanad Jeahze’s contract was bought out by the team, people close to the matter said, and David Schnegg (Austria’s Sturm Graz) is expected to debut after the transfer window opens July 18.

National team call-ups

While United is off during the FIFA window June 3 to 11, Herrera will join Guatemala for World Cup qualifiers vs. Dominica and the British Virgin Islands. He will skip the June 14 friendly vs. Argentina in Landover because it falls outside the window and United plays the next day in Charlotte.

Defender Matti Peltola is scheduled to join Finland for friendlies at Portugal and Scotland.

New field planned

Badly scarred by football games, Audi Field’s grass is set to be replaced early this summer, though a date has not been disclosed. The D.C. Defenders’ final home game is June 2. The U.S. women’s national team is scheduled to visit July 16 for its final Olympic tuneup.