what does hypothesis testing means

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses. 

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value  tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results. 

Interpret the results of the hypothesis test in the context of the question being asked. 

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called  alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or  Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related:   What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Search Search Please fill out this field.

What Is Hypothesis Testing?

• How It Works

4 Step Process

The bottom line.

• Fundamental Analysis

Hypothesis Testing: 4 Steps and Example

Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population or a data-generating process. The word "population" will be used for both of these cases in the following descriptions.

Key Takeaways

• Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
• The test provides evidence concerning the plausibility of the hypothesis, given the data.
• Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
• The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

How Hypothesis Testing Works

In hypothesis testing, an  analyst  tests a statistical sample, intending to provide evidence on the plausibility of the null hypothesis. Statistical analysts measure and examine a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.

The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis. Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.

The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.

• State the hypotheses.
• Formulate an analysis plan, which outlines how the data will be evaluated.
• Carry out the plan and analyze the sample data.
• Analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.

Example of Hypothesis Testing

If an individual wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct. Mathematically, the null hypothesis is represented as Ho: P = 0.5. The alternative hypothesis is shown as "Ha" and is identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.

A random sample of 100 coin flips is taken, and the null hypothesis is tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.

If there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."

When Did Hypothesis Testing Begin?

Some statisticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”

What are the Benefits of Hypothesis Testing?

Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.

What are the Limitations of Hypothesis Testing?

Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.

Hypothesis testing refers to a statistical process that helps researchers determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. All hypothesis testing methods have the same four-step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

Sage. " Introduction to Hypothesis Testing ," Page 4.

Elder Research. " Who Invented the Null Hypothesis? "

Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples ."

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3 hypothesis testing.

In reviewing hypothesis tests, we start first with the general idea. Then, we keep returning to the basic procedures of hypothesis testing, each time adding a little more detail.

The general idea of hypothesis testing involves:

• Making an initial assumption.
• Collecting evidence (data).
• Based on the available evidence (data), deciding whether to reject or not reject the initial assumption.

Every hypothesis test — regardless of the population parameter involved — requires the above three steps.

Example S.3.1

Is normal body temperature really 98.6 degrees f section  .

Consider the population of many, many adults. A researcher hypothesized that the average adult body temperature is lower than the often-advertised 98.6 degrees F. That is, the researcher wants an answer to the question: "Is the average adult body temperature 98.6 degrees? Or is it lower?" To answer his research question, the researcher starts by assuming that the average adult body temperature was 98.6 degrees F.

Then, the researcher went out and tried to find evidence that refutes his initial assumption. In doing so, he selects a random sample of 130 adults. The average body temperature of the 130 sampled adults is 98.25 degrees.

Then, the researcher uses the data he collected to make a decision about his initial assumption. It is either likely or unlikely that the researcher would collect the evidence he did given his initial assumption that the average adult body temperature is 98.6 degrees:

• If it is likely , then the researcher does not reject his initial assumption that the average adult body temperature is 98.6 degrees. There is not enough evidence to do otherwise.
• either the researcher's initial assumption is correct and he experienced a very unusual event;
• or the researcher's initial assumption is incorrect.

In statistics, we generally don't make claims that require us to believe that a very unusual event happened. That is, in the practice of statistics, if the evidence (data) we collected is unlikely in light of the initial assumption, then we reject our initial assumption.

Example S.3.2

Criminal trial analogy section  .

One place where you can consistently see the general idea of hypothesis testing in action is in criminal trials held in the United States. Our criminal justice system assumes "the defendant is innocent until proven guilty." That is, our initial assumption is that the defendant is innocent.

In the practice of statistics, we make our initial assumption when we state our two competing hypotheses -- the null hypothesis ( H 0 ) and the alternative hypothesis ( H A ). Here, our hypotheses are:

• H 0 : Defendant is not guilty (innocent)
• H A : Defendant is guilty

In statistics, we always assume the null hypothesis is true . That is, the null hypothesis is always our initial assumption.

The prosecution team then collects evidence — such as finger prints, blood spots, hair samples, carpet fibers, shoe prints, ransom notes, and handwriting samples — with the hopes of finding "sufficient evidence" to make the assumption of innocence refutable.

In statistics, the data are the evidence.

The jury then makes a decision based on the available evidence:

• If the jury finds sufficient evidence — beyond a reasonable doubt — to make the assumption of innocence refutable, the jury rejects the null hypothesis and deems the defendant guilty. We behave as if the defendant is guilty.
• If there is insufficient evidence, then the jury does not reject the null hypothesis . We behave as if the defendant is innocent.

In statistics, we always make one of two decisions. We either "reject the null hypothesis" or we "fail to reject the null hypothesis."

Errors in Hypothesis Testing Section  

Did you notice the use of the phrase "behave as if" in the previous discussion? We "behave as if" the defendant is guilty; we do not "prove" that the defendant is guilty. And, we "behave as if" the defendant is innocent; we do not "prove" that the defendant is innocent.

This is a very important distinction! We make our decision based on evidence not on 100% guaranteed proof. Again:

• If we reject the null hypothesis, we do not prove that the alternative hypothesis is true.
• If we do not reject the null hypothesis, we do not prove that the null hypothesis is true.

We merely state that there is enough evidence to behave one way or the other. This is always true in statistics! Because of this, whatever the decision, there is always a chance that we made an error .

Let's review the two types of errors that can be made in criminal trials:

Table S.3.2 shows how this corresponds to the two types of errors in hypothesis testing.

Note that, in statistics, we call the two types of errors by two different  names -- one is called a "Type I error," and the other is called  a "Type II error." Here are the formal definitions of the two types of errors:

There is always a chance of making one of these errors. But, a good scientific study will minimize the chance of doing so!

Making the Decision Section  

Recall that it is either likely or unlikely that we would observe the evidence we did given our initial assumption. If it is likely , we do not reject the null hypothesis. If it is unlikely , then we reject the null hypothesis in favor of the alternative hypothesis. Effectively, then, making the decision reduces to determining "likely" or "unlikely."

In statistics, there are two ways to determine whether the evidence is likely or unlikely given the initial assumption:

• We could take the " critical value approach " (favored in many of the older textbooks).
• Or, we could take the " P -value approach " (what is used most often in research, journal articles, and statistical software).

In the next two sections, we review the procedures behind each of these two approaches. To make our review concrete, let's imagine that μ is the average grade point average of all American students who major in mathematics. We first review the critical value approach for conducting each of the following three hypothesis tests about the population mean $\mu$:

In Practice

• We would want to conduct the first hypothesis test if we were interested in concluding that the average grade point average of the group is more than 3.
• We would want to conduct the second hypothesis test if we were interested in concluding that the average grade point average of the group is less than 3.
• And, we would want to conduct the third hypothesis test if we were only interested in concluding that the average grade point average of the group differs from 3 (without caring whether it is more or less than 3).

Upon completing the review of the critical value approach, we review the P -value approach for conducting each of the above three hypothesis tests about the population mean \(\mu\). The procedures that we review here for both approaches easily extend to hypothesis tests about any other population parameter.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 31289

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

CO-6: Apply basic concepts of probability, random variation, and commonly used statistical probability distributions.

Learning Objectives

LO 6.26: Outline the logic and process of hypothesis testing.

LO 6.27: Explain what the p-value is and how it is used to draw conclusions.

Video: Hypothesis Testing (8:43)

Introduction

We are in the middle of the part of the course that has to do with inference for one variable.

So far, we talked about point estimation and learned how interval estimation enhances it by quantifying the magnitude of the estimation error (with a certain level of confidence) in the form of the margin of error. The result is the confidence interval — an interval that, with a certain confidence, we believe captures the unknown parameter.

We are now moving to the other kind of inference, hypothesis testing . We say that hypothesis testing is “the other kind” because, unlike the inferential methods we presented so far, where the goal was estimating the unknown parameter, the idea, logic and goal of hypothesis testing are quite different.

In the first two parts of this section we will discuss the idea behind hypothesis testing, explain how it works, and introduce new terminology that emerges in this form of inference. The final two parts will be more specific and will discuss hypothesis testing for the population proportion ( p ) and the population mean ( μ, mu).

If this is your first statistics course, you will need to spend considerable time on this topic as there are many new ideas. Many students find this process and its logic difficult to understand in the beginning.

In this section, we will use the hypothesis test for a population proportion to motivate our understanding of the process. We will conduct these tests manually. For all future hypothesis test procedures, including problems involving means, we will use software to obtain the results and focus on interpreting them in the context of our scenario.

General Idea and Logic of Hypothesis Testing

The purpose of this section is to gradually build your understanding about how statistical hypothesis testing works. We start by explaining the general logic behind the process of hypothesis testing. Once we are confident that you understand this logic, we will add some more details and terminology.

To start our discussion about the idea behind statistical hypothesis testing, consider the following example:

A case of suspected cheating on an exam is brought in front of the disciplinary committee at a certain university.

There are two opposing claims in this case:

• The student’s claim: I did not cheat on the exam.
• The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim. The instructor explains that the exam had two versions, and shows the committee members that on three separate exam questions, the student used in his solution numbers that were given in the other version of the exam.

The committee members all agree that it would be extremely unlikely to get evidence like that if the student’s claim of not cheating had been true. In other words, the committee members all agree that the instructor brought forward strong enough evidence to reject the student’s claim, and conclude that the student did cheat on the exam.

What does this example have to do with statistics?

While it is true that this story seems unrelated to statistics, it captures all the elements of hypothesis testing and the logic behind it. Before you read on to understand why, it would be useful to read the example again. Please do so now.

Statistical hypothesis testing is defined as:

• Assessing evidence provided by the data against the null claim (the claim which is to be assumed true unless enough evidence exists to reject it).

Here is how the process of statistical hypothesis testing works:

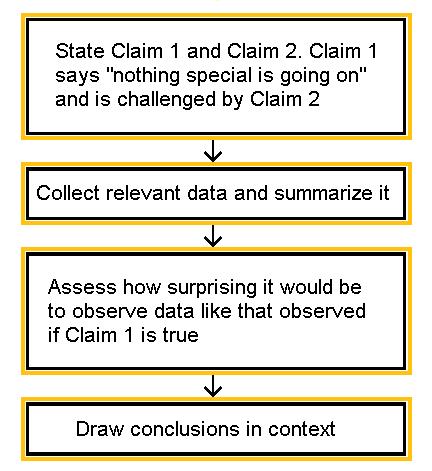
• We have two claims about what is going on in the population. Let’s call them claim 1 (this will be the null claim or hypothesis) and claim 2 (this will be the alternative) . Much like the story above, where the student’s claim is challenged by the instructor’s claim, the null claim 1 is challenged by the alternative claim 2. (For us, these claims are usually about the value of population parameter(s) or about the existence or nonexistence of a relationship between two variables in the population).
• We choose a sample, collect relevant data and summarize them (this is similar to the instructor collecting evidence from the student’s exam). For statistical tests, this step will also involve checking any conditions or assumptions.
• We figure out how likely it is to observe data like the data we obtained, if claim 1 is true. (Note that the wording “how likely …” implies that this step requires some kind of probability calculation). In the story, the committee members assessed how likely it is to observe evidence such as the instructor provided, had the student’s claim of not cheating been true.
• If, after assuming claim 1 is true, we find that it would be extremely unlikely to observe data as strong as ours or stronger in favor of claim 2, then we have strong evidence against claim 1, and we reject it in favor of claim 2. Later we will see this corresponds to a small p-value.
• If, after assuming claim 1 is true, we find that observing data as strong as ours or stronger in favor of claim 2 is NOT VERY UNLIKELY , then we do not have enough evidence against claim 1, and therefore we cannot reject it in favor of claim 2. Later we will see this corresponds to a p-value which is not small.

In our story, the committee decided that it would be extremely unlikely to find the evidence that the instructor provided had the student’s claim of not cheating been true. In other words, the members felt that it is extremely unlikely that it is just a coincidence (random chance) that the student used the numbers from the other version of the exam on three separate problems. The committee members therefore decided to reject the student’s claim and concluded that the student had, indeed, cheated on the exam. (Wouldn’t you conclude the same?)

Hopefully this example helped you understand the logic behind hypothesis testing.

Interactive Applet: Reasoning of a Statistical Test

To strengthen your understanding of the process of hypothesis testing and the logic behind it, let’s look at three statistical examples.

A recent study estimated that 20% of all college students in the United States smoke. The head of Health Services at Goodheart University (GU) suspects that the proportion of smokers may be lower at GU. In hopes of confirming her claim, the head of Health Services chooses a random sample of 400 Goodheart students, and finds that 70 of them are smokers.

Let’s analyze this example using the 4 steps outlined above:

• claim 1: The proportion of smokers at Goodheart is 0.20.
• claim 2: The proportion of smokers at Goodheart is less than 0.20.

Claim 1 basically says “nothing special goes on at Goodheart University; the proportion of smokers there is no different from the proportion in the entire country.” This claim is challenged by the head of Health Services, who suspects that the proportion of smokers at Goodheart is lower.

• Choosing a sample and collecting data: A sample of n = 400 was chosen, and summarizing the data revealed that the sample proportion of smokers is p -hat = 70/400 = 0.175.While it is true that 0.175 is less than 0.20, it is not clear whether this is strong enough evidence against claim 1. We must account for sampling variation.
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: How surprising is it to get a sample proportion as low as p -hat = 0.175 (or lower), assuming claim 1 is true? In other words, we need to find how likely it is that in a random sample of size n = 400 taken from a population where the proportion of smokers is p = 0.20 we’ll get a sample proportion as low as p -hat = 0.175 (or lower).It turns out that the probability that we’ll get a sample proportion as low as p -hat = 0.175 (or lower) in such a sample is roughly 0.106 (do not worry about how this was calculated at this point – however, if you think about it hopefully you can see that the key is the sampling distribution of p -hat).
• Conclusion: Well, we found that if claim 1 were true there is a probability of 0.106 of observing data like that observed or more extreme. Now you have to decide …Do you think that a probability of 0.106 makes our data rare enough (surprising enough) under claim 1 so that the fact that we did observe it is enough evidence to reject claim 1? Or do you feel that a probability of 0.106 means that data like we observed are not very likely when claim 1 is true, but they are not unlikely enough to conclude that getting such data is sufficient evidence to reject claim 1. Basically, this is your decision. However, it would be nice to have some kind of guideline about what is generally considered surprising enough.

A certain prescription allergy medicine is supposed to contain an average of 245 parts per million (ppm) of a certain chemical. If the concentration is higher than 245 ppm, the drug will likely cause unpleasant side effects, and if the concentration is below 245 ppm, the drug may be ineffective. The manufacturer wants to check whether the mean concentration in a large shipment is the required 245 ppm or not. To this end, a random sample of 64 portions from the large shipment is tested, and it is found that the sample mean concentration is 250 ppm with a sample standard deviation of 12 ppm.

• Claim 1: The mean concentration in the shipment is the required 245 ppm.
• Claim 2: The mean concentration in the shipment is not the required 245 ppm.

Note that again, claim 1 basically says: “There is nothing unusual about this shipment, the mean concentration is the required 245 ppm.” This claim is challenged by the manufacturer, who wants to check whether that is, indeed, the case or not.

• Choosing a sample and collecting data: A sample of n = 64 portions is chosen and after summarizing the data it is found that the sample mean concentration is x-bar = 250 and the sample standard deviation is s = 12.Is the fact that x-bar = 250 is different from 245 strong enough evidence to reject claim 1 and conclude that the mean concentration in the whole shipment is not the required 245? In other words, do the data provide strong enough evidence to reject claim 1?
• Assessing the evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves the following question: If the mean concentration in the whole shipment were really the required 245 ppm (i.e., if claim 1 were true), how surprising would it be to observe a sample of 64 portions where the sample mean concentration is off by 5 ppm or more (as we did)? It turns out that it would be extremely unlikely to get such a result if the mean concentration were really the required 245. There is only a probability of 0.0007 (i.e., 7 in 10,000) of that happening. (Do not worry about how this was calculated at this point, but again, the key will be the sampling distribution.)
• Making conclusions: Here, it is pretty clear that a sample like the one we observed or more extreme is VERY rare (or extremely unlikely) if the mean concentration in the shipment were really the required 245 ppm. The fact that we did observe such a sample therefore provides strong evidence against claim 1, so we reject it and conclude with very little doubt that the mean concentration in the shipment is not the required 245 ppm.

Do you think that you’re getting it? Let’s make sure, and look at another example.

Is there a relationship between gender and combined scores (Math + Verbal) on the SAT exam?

Following a report on the College Board website, which showed that in 2003, males scored generally higher than females on the SAT exam, an educational researcher wanted to check whether this was also the case in her school district. The researcher chose random samples of 150 males and 150 females from her school district, collected data on their SAT performance and found the following:

Again, let’s see how the process of hypothesis testing works for this example:

• Claim 1: Performance on the SAT is not related to gender (males and females score the same).
• Claim 2: Performance on the SAT is related to gender – males score higher.

Note that again, claim 1 basically says: “There is nothing going on between the variables SAT and gender.” Claim 2 represents what the researcher wants to check, or suspects might actually be the case.

• Choosing a sample and collecting data: Data were collected and summarized as given above. Is the fact that the sample mean score of males (1,025) is higher than the sample mean score of females (1,010) by 15 points strong enough information to reject claim 1 and conclude that in this researcher’s school district, males score higher on the SAT than females?
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: If SAT scores are in fact not related to gender (claim 1 is true), how likely is it to get data like the data we observed, in which the difference between the males’ average and females’ average score is as high as 15 points or higher? It turns out that the probability of observing such a sample result if SAT score is not related to gender is approximately 0.29 (Again, do not worry about how this was calculated at this point).
• Conclusion: Here, we have an example where observing a sample like the one we observed or more extreme is definitely not surprising (roughly 30% chance) if claim 1 were true (i.e., if indeed there is no difference in SAT scores between males and females). We therefore conclude that our data does not provide enough evidence for rejecting claim 1.
• “The data provide enough evidence to reject claim 1 and accept claim 2”; or
• “The data do not provide enough evidence to reject claim 1.”

In particular, note that in the second type of conclusion we did not say: “ I accept claim 1 ,” but only “ I don’t have enough evidence to reject claim 1 .” We will come back to this issue later, but this is a good place to make you aware of this subtle difference.

Hopefully by now, you understand the logic behind the statistical hypothesis testing process. Here is a summary:

Learn by Doing: Logic of Hypothesis Testing

Did I Get This?: Logic of Hypothesis Testing

Steps in Hypothesis Testing

Video: Steps in Hypothesis Testing (16:02)

Now that we understand the general idea of how statistical hypothesis testing works, let’s go back to each of the steps and delve slightly deeper, getting more details and learning some terminology.

Hypothesis Testing Step 1: State the Hypotheses

In all three examples, our aim is to decide between two opposing points of view, Claim 1 and Claim 2. In hypothesis testing, Claim 1 is called the null hypothesis (denoted “ Ho “), and Claim 2 plays the role of the alternative hypothesis (denoted “ Ha “). As we saw in the three examples, the null hypothesis suggests nothing special is going on; in other words, there is no change from the status quo, no difference from the traditional state of affairs, no relationship. In contrast, the alternative hypothesis disagrees with this, stating that something is going on, or there is a change from the status quo, or there is a difference from the traditional state of affairs. The alternative hypothesis, Ha, usually represents what we want to check or what we suspect is really going on.

Let’s go back to our three examples and apply the new notation:

In example 1:

• Ho: The proportion of smokers at GU is 0.20.
• Ha: The proportion of smokers at GU is less than 0.20.

In example 2:

• Ho: The mean concentration in the shipment is the required 245 ppm.
• Ha: The mean concentration in the shipment is not the required 245 ppm.

In example 3:

• Ho: Performance on the SAT is not related to gender (males and females score the same).
• Ha: Performance on the SAT is related to gender – males score higher.

Learn by Doing: State the Hypotheses

Did I Get This?: State the Hypotheses

Hypothesis Testing Step 2: Collect Data, Check Conditions and Summarize Data

This step is pretty obvious. This is what inference is all about. You look at sampled data in order to draw conclusions about the entire population. In the case of hypothesis testing, based on the data, you draw conclusions about whether or not there is enough evidence to reject Ho.

There is, however, one detail that we would like to add here. In this step we collect data and summarize it. Go back and look at the second step in our three examples. Note that in order to summarize the data we used simple sample statistics such as the sample proportion ( p -hat), sample mean (x-bar) and the sample standard deviation (s).

In practice, you go a step further and use these sample statistics to summarize the data with what’s called a test statistic . We are not going to go into any details right now, but we will discuss test statistics when we go through the specific tests.

This step will also involve checking any conditions or assumptions required to use the test.

Hypothesis Testing Step 3: Assess the Evidence

As we saw, this is the step where we calculate how likely is it to get data like that observed (or more extreme) when Ho is true. In a sense, this is the heart of the process, since we draw our conclusions based on this probability.

• If this probability is very small (see example 2), then that means that it would be very surprising to get data like that observed (or more extreme) if Ho were true. The fact that we did observe such data is therefore evidence against Ho, and we should reject it.
• On the other hand, if this probability is not very small (see example 3) this means that observing data like that observed (or more extreme) is not very surprising if Ho were true. The fact that we observed such data does not provide evidence against Ho. This crucial probability, therefore, has a special name. It is called the p-value of the test.

In our three examples, the p-values were given to you (and you were reassured that you didn’t need to worry about how these were derived yet):

• Example 1: p-value = 0.106
• Example 2: p-value = 0.0007
• Example 3: p-value = 0.29

Obviously, the smaller the p-value, the more surprising it is to get data like ours (or more extreme) when Ho is true, and therefore, the stronger the evidence the data provide against Ho.

Looking at the three p-values of our three examples, we see that the data that we observed in example 2 provide the strongest evidence against the null hypothesis, followed by example 1, while the data in example 3 provides the least evidence against Ho.

• Right now we will not go into specific details about p-value calculations, but just mention that since the p-value is the probability of getting data like those observed (or more extreme) when Ho is true, it would make sense that the calculation of the p-value will be based on the data summary, which, as we mentioned, is the test statistic. Indeed, this is the case. In practice, we will mostly use software to provide the p-value for us.

Hypothesis Testing Step 4: Making Conclusions

Since our statistical conclusion is based on how small the p-value is, or in other words, how surprising our data are when Ho is true, it would be nice to have some kind of guideline or cutoff that will help determine how small the p-value must be, or how “rare” (unlikely) our data must be when Ho is true, for us to conclude that we have enough evidence to reject Ho.

This cutoff exists, and because it is so important, it has a special name. It is called the significance level of the test and is usually denoted by the Greek letter α (alpha). The most commonly used significance level is α (alpha) = 0.05 (or 5%). This means that:

• if the p-value < α (alpha) (usually 0.05), then the data we obtained is considered to be “rare (or surprising) enough” under the assumption that Ho is true, and we say that the data provide statistically significant evidence against Ho, so we reject Ho and thus accept Ha.
• if the p-value > α (alpha)(usually 0.05), then our data are not considered to be “surprising enough” under the assumption that Ho is true, and we say that our data do not provide enough evidence to reject Ho (or, equivalently, that the data do not provide enough evidence to accept Ha).

Now that we have a cutoff to use, here are the appropriate conclusions for each of our examples based upon the p-values we were given.

In Example 1:

• Using our cutoff of 0.05, we fail to reject Ho.
• Conclusion : There IS NOT enough evidence that the proportion of smokers at GU is less than 0.20
• Still we should consider: Does the evidence seen in the data provide any practical evidence towards our alternative hypothesis?

In Example 2:

• Using our cutoff of 0.05, we reject Ho.
• Conclusion : There IS enough evidence that the mean concentration in the shipment is not the required 245 ppm.

In Example 3:

• Conclusion : There IS NOT enough evidence that males score higher on average than females on the SAT.

Notice that all of the above conclusions are written in terms of the alternative hypothesis and are given in the context of the situation. In no situation have we claimed the null hypothesis is true. Be very careful of this and other issues discussed in the following comments.

• Although the significance level provides a good guideline for drawing our conclusions, it should not be treated as an incontrovertible truth. There is a lot of room for personal interpretation. What if your p-value is 0.052? You might want to stick to the rules and say “0.052 > 0.05 and therefore I don’t have enough evidence to reject Ho”, but you might decide that 0.052 is small enough for you to believe that Ho should be rejected. It should be noted that scientific journals do consider 0.05 to be the cutoff point for which any p-value below the cutoff indicates enough evidence against Ho, and any p-value above it, or even equal to it , indicates there is not enough evidence against Ho. Although a p-value between 0.05 and 0.10 is often reported as marginally statistically significant.
• It is important to draw your conclusions in context . It is never enough to say: “p-value = …, and therefore I have enough evidence to reject Ho at the 0.05 significance level.” You should always word your conclusion in terms of the data. Although we will use the terminology of “rejecting Ho” or “failing to reject Ho” – this is mostly due to the fact that we are instructing you in these concepts. In practice, this language is rarely used. We also suggest writing your conclusion in terms of the alternative hypothesis.Is there or is there not enough evidence that the alternative hypothesis is true?
• Let’s go back to the issue of the nature of the two types of conclusions that I can make.
• Either I reject Ho (when the p-value is smaller than the significance level)
• or I cannot reject Ho (when the p-value is larger than the significance level).

As we mentioned earlier, note that the second conclusion does not imply that I accept Ho, but just that I don’t have enough evidence to reject it. Saying (by mistake) “I don’t have enough evidence to reject Ho so I accept it” indicates that the data provide evidence that Ho is true, which is not necessarily the case . Consider the following slightly artificial yet effective example:

An employer claims to subscribe to an “equal opportunity” policy, not hiring men any more often than women for managerial positions. Is this credible? You’re not sure, so you want to test the following two hypotheses:

• Ho: The proportion of male managers hired is 0.5
• Ha: The proportion of male managers hired is more than 0.5

Data: You choose at random three of the new managers who were hired in the last 5 years and find that all 3 are men.

Assessing Evidence: If the proportion of male managers hired is really 0.5 (Ho is true), then the probability that the random selection of three managers will yield three males is therefore 0.5 * 0.5 * 0.5 = 0.125. This is the p-value (using the multiplication rule for independent events).

Conclusion: Using 0.05 as the significance level, you conclude that since the p-value = 0.125 > 0.05, the fact that the three randomly selected managers were all males is not enough evidence to reject the employer’s claim of subscribing to an equal opportunity policy (Ho).

However, the data (all three selected are males) definitely does NOT provide evidence to accept the employer’s claim (Ho).

Learn By Doing: Using p-values

Did I Get This?: Using p-values

Comment about wording: Another common wording in scientific journals is:

• “The results are statistically significant” – when the p-value < α (alpha).
• “The results are not statistically significant” – when the p-value > α (alpha).

Often you will see significance levels reported with additional description to indicate the degree of statistical significance. A general guideline (although not required in our course) is:

• If 0.01 ≤ p-value < 0.05, then the results are (statistically) significant .
• If 0.001 ≤ p-value < 0.01, then the results are highly statistically significant .
• If p-value < 0.001, then the results are very highly statistically significant .
• If p-value > 0.05, then the results are not statistically significant (NS).
• If 0.05 ≤ p-value < 0.10, then the results are marginally statistically significant .

Let’s summarize

We learned quite a lot about hypothesis testing. We learned the logic behind it, what the key elements are, and what types of conclusions we can and cannot draw in hypothesis testing. Here is a quick recap:

Video: Hypothesis Testing Overview (2:20)

Here are a few more activities if you need some additional practice.

Did I Get This?: Hypothesis Testing Overview

• Notice that the p-value is an example of a conditional probability . We calculate the probability of obtaining results like those of our data (or more extreme) GIVEN the null hypothesis is true. We could write P(Obtaining results like ours or more extreme | Ho is True).
• We could write P(Obtaining a test statistic as or more extreme than ours | Ho is True).
• In this case we are asking “Assuming the null hypothesis is true, how rare is it to observe something as or more extreme than what I have found in my data?”
• If after assuming the null hypothesis is true, what we have found in our data is extremely rare (small p-value), this provides evidence to reject our assumption that Ho is true in favor of Ha.
• The p-value can also be thought of as the probability, assuming the null hypothesis is true, that the result we have seen is solely due to random error (or random chance). We have already seen that statistics from samples collected from a population vary. There is random error or random chance involved when we sample from populations.

In this setting, if the p-value is very small, this implies, assuming the null hypothesis is true, that it is extremely unlikely that the results we have obtained would have happened due to random error alone, and thus our assumption (Ho) is rejected in favor of the alternative hypothesis (Ha).

• It is EXTREMELY important that you find a definition of the p-value which makes sense to you. New students often need to contemplate this idea repeatedly through a variety of examples and explanations before becoming comfortable with this idea. It is one of the two most important concepts in statistics (the other being confidence intervals).
• We infer that the alternative hypothesis is true ONLY by rejecting the null hypothesis.
• A statistically significant result is one that has a very low probability of occurring if the null hypothesis is true.
• Results which are statistically significant may or may not have practical significance and vice versa.

Error and Power

LO 6.28: Define a Type I and Type II error in general and in the context of specific scenarios.

LO 6.29: Explain the concept of the power of a statistical test including the relationship between power, sample size, and effect size.

Video: Errors and Power (12:03)

Type I and Type II Errors in Hypothesis Tests

We have not yet discussed the fact that we are not guaranteed to make the correct decision by this process of hypothesis testing. Maybe you are beginning to see that there is always some level of uncertainty in statistics.

Let’s think about what we know already and define the possible errors we can make in hypothesis testing. When we conduct a hypothesis test, we choose one of two possible conclusions based upon our data.

If the p-value is smaller than your pre-specified significance level (α, alpha), you reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is false
• You have made an error ( Type I ) and rejected Ho when in fact Ho is true (your data happened to be a RARE EVENT under Ho)

If the p-value is greater than (or equal to) your chosen significance level (α, alpha), you fail to reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is true
• You have made an error ( Type II ) and failed to reject Ho when in fact Ho is false (the alternative hypothesis, Ha, is true)

The following summarizes the four possible results which can be obtained from a hypothesis test. Notice the rows represent the decision made in the hypothesis test and the columns represent the (usually unknown) truth in reality.

Although the truth is unknown in practice – or we would not be conducting the test – we know it must be the case that either the null hypothesis is true or the null hypothesis is false. It is also the case that either decision we make in a hypothesis test can result in an incorrect conclusion!

A TYPE I Error occurs when we Reject Ho when, in fact, Ho is True. In this case, we mistakenly reject a true null hypothesis.

• P(TYPE I Error) = P(Reject Ho | Ho is True) = α = alpha = Significance Level

A TYPE II Error occurs when we fail to Reject Ho when, in fact, Ho is False. In this case we fail to reject a false null hypothesis.

P(TYPE II Error) = P(Fail to Reject Ho | Ho is False) = β = beta

When our significance level is 5%, we are saying that we will allow ourselves to make a Type I error less than 5% of the time. In the long run, if we repeat the process, 5% of the time we will find a p-value < 0.05 when in fact the null hypothesis was true.

In this case, our data represent a rare occurrence which is unlikely to happen but is still possible. For example, suppose we toss a coin 10 times and obtain 10 heads, this is unlikely for a fair coin but not impossible. We might conclude the coin is unfair when in fact we simply saw a very rare event for this fair coin.

Our testing procedure CONTROLS for the Type I error when we set a pre-determined value for the significance level.

Notice that these probabilities are conditional probabilities. This is one more reason why conditional probability is an important concept in statistics.

Unfortunately, calculating the probability of a Type II error requires us to know the truth about the population. In practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

Comment: As you initially read through the examples below, focus on the broad concepts instead of the small details. It is not important to understand how to calculate these values yourself at this point.

• Try to understand the pictures we present. Which pictures represent an assumed null hypothesis and which represent an alternative?
• It may be useful to come back to this page (and the activities here) after you have reviewed the rest of the section on hypothesis testing and have worked a few problems yourself.

Interactive Applet: Statistical Significance

Here are two examples of using an older version of this applet. It looks slightly different but the same settings and options are available in the version above.

In both cases we will consider IQ scores.

Our null hypothesis is that the true mean is 100. Assume the standard deviation is 16 and we will specify a significance level of 5%.

In this example we will specify that the true mean is indeed 100 so that the null hypothesis is true. Most of the time (95%), when we generate a sample, we should fail to reject the null hypothesis since the null hypothesis is indeed true.

Here is one sample that results in a correct decision:

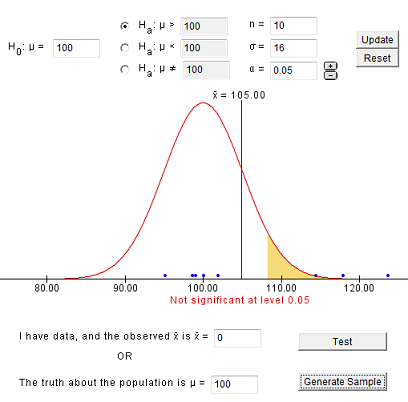
In the sample above, we obtain an x-bar of 105, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true). Notice the sample is shown as blue dots along the x-axis and the shaded region shows for which values of x-bar we would reject the null hypothesis. In other words, we would reject Ho whenever the x-bar falls in the shaded region.

Enter the same values and generate samples until you obtain a Type I error (you falsely reject the null hypothesis). You should see something like this:

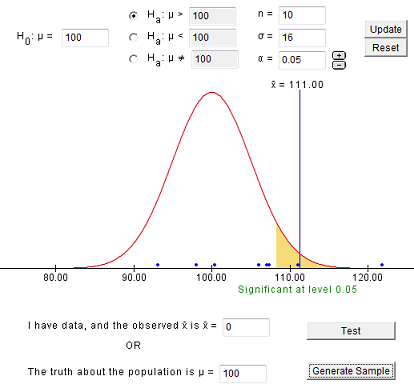
If you were to generate 100 samples, you should have around 5% where you rejected Ho. These would be samples which would result in a Type I error.

The previous example illustrates a correct decision and a Type I error when the null hypothesis is true. The next example illustrates a correct decision and Type II error when the null hypothesis is false. In this case, we must specify the true population mean.

Let’s suppose we are sampling from an honors program and that the true mean IQ for this population is 110. We do not know the probability of a Type II error without more detailed calculations.

Let’s start with a sample which results in a correct decision.

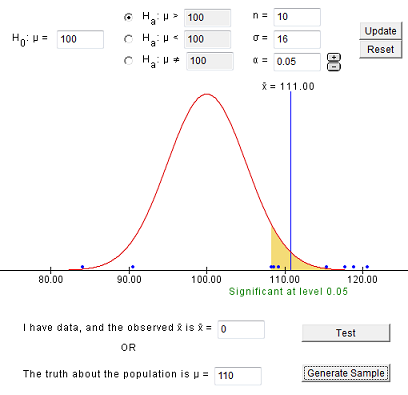
In the sample above, we obtain an x-bar of 111, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true).

Enter the same values and generate samples until you obtain a Type II error (you fail to reject the null hypothesis). You should see something like this:

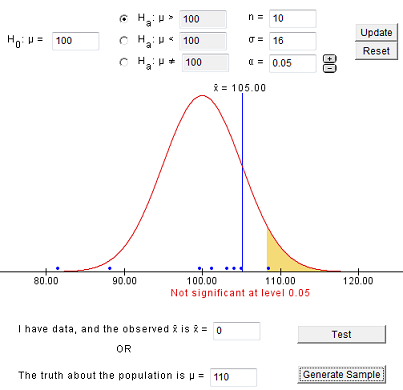
You should notice that in this case (when Ho is false), it is easier to obtain an incorrect decision (a Type II error) than it was in the case where Ho is true. If you generate 100 samples, you can approximate the probability of a Type II error.

We can find the probability of a Type II error by visualizing both the assumed distribution and the true distribution together. The image below is adapted from an applet we will use when we discuss the power of a statistical test.

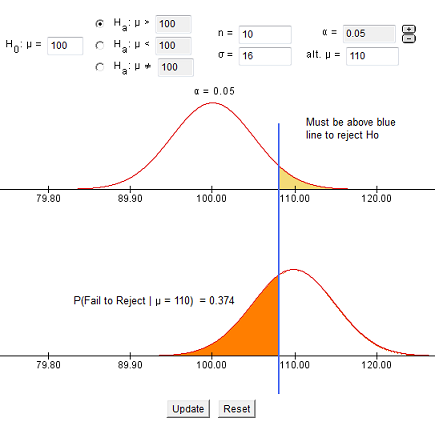
There is a 37.4% chance that, in the long run, we will make a Type II error and fail to reject the null hypothesis when in fact the true mean IQ is 110 in the population from which we sample our 10 individuals.

Can you visualize what will happen if the true population mean is really 115 or 108? When will the Type II error increase? When will it decrease? We will look at this idea again when we discuss the concept of power in hypothesis tests.

• It is important to note that there is a trade-off between the probability of a Type I and a Type II error. If we decrease the probability of one of these errors, the probability of the other will increase! The practical result of this is that if we require stronger evidence to reject the null hypothesis (smaller significance level = probability of a Type I error), we will increase the chance that we will be unable to reject the null hypothesis when in fact Ho is false (increases the probability of a Type II error).
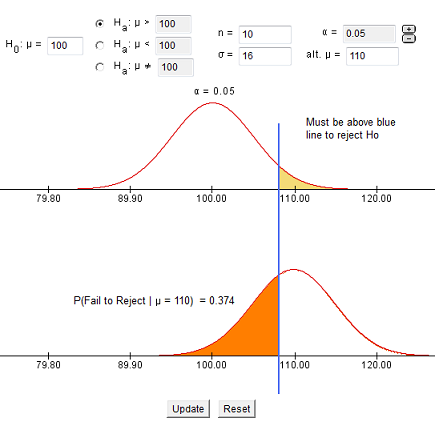
• When α (alpha) = 0.05 we obtained a Type II error probability of 0.374 = β = beta

• When α (alpha) = 0.01 (smaller than before) we obtain a Type II error probability of 0.644 = β = beta (larger than before)

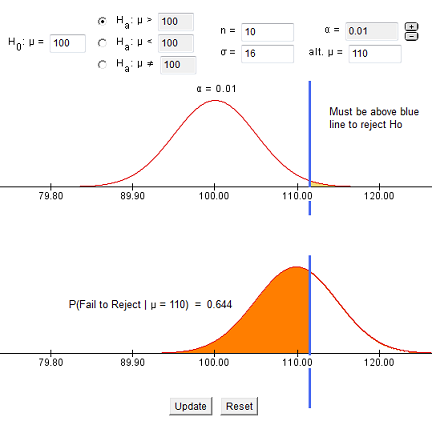
• As the blue line in the picture moves farther right, the significance level (α, alpha) is decreasing and the Type II error probability is increasing.
• As the blue line in the picture moves farther left, the significance level (α, alpha) is increasing and the Type II error probability is decreasing

Let’s return to our very first example and define these two errors in context.

• Ho = The student’s claim: I did not cheat on the exam.
• Ha = The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim.

There are four possible outcomes of this process. There are two possible correct decisions:

• The student did cheat on the exam and the instructor brings enough evidence to reject Ho and conclude the student did cheat on the exam. This is a CORRECT decision!
• The student did not cheat on the exam and the instructor fails to provide enough evidence that the student did cheat on the exam. This is a CORRECT decision!

Both the correct decisions and the possible errors are fairly easy to understand but with the errors, you must be careful to identify and define the two types correctly.

TYPE I Error: Reject Ho when Ho is True

• The student did not cheat on the exam but the instructor brings enough evidence to reject Ho and conclude the student cheated on the exam. This is a Type I Error.

TYPE II Error: Fail to Reject Ho when Ho is False

• The student did cheat on the exam but the instructor fails to provide enough evidence that the student cheated on the exam. This is a Type II Error.

In most situations, including this one, it is more “acceptable” to have a Type II error than a Type I error. Although allowing a student who cheats to go unpunished might be considered a very bad problem, punishing a student for something he or she did not do is usually considered to be a more severe error. This is one reason we control for our Type I error in the process of hypothesis testing.

Did I Get This?: Type I and Type II Errors (in context)

• The probabilities of Type I and Type II errors are closely related to the concepts of sensitivity and specificity that we discussed previously. Consider the following hypotheses:

Ho: The individual does not have diabetes (status quo, nothing special happening)

Ha: The individual does have diabetes (something is going on here)

In this setting:

When someone tests positive for diabetes we would reject the null hypothesis and conclude the person has diabetes (we may or may not be correct!).

When someone tests negative for diabetes we would fail to reject the null hypothesis so that we fail to conclude the person has diabetes (we may or may not be correct!)

Let’s take it one step further:

Sensitivity = P(Test + | Have Disease) which in this setting equals P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1 – beta

Specificity = P(Test – | No Disease) which in this setting equals P(Fail to Reject Ho | Ho is True) = 1 – P(Reject Ho | Ho is True) = 1 – α = 1 – alpha

Notice that sensitivity and specificity relate to the probability of making a correct decision whereas α (alpha) and β (beta) relate to the probability of making an incorrect decision.

Usually α (alpha) = 0.05 so that the specificity listed above is 0.95 or 95%.

Next, we will see that the sensitivity listed above is the power of the hypothesis test!

Reasons for a Type I Error in Practice

Assuming that you have obtained a quality sample:

• The reason for a Type I error is random chance.
• When a Type I error occurs, our observed data represented a rare event which indicated evidence in favor of the alternative hypothesis even though the null hypothesis was actually true.

Reasons for a Type II Error in Practice

Again, assuming that you have obtained a quality sample, now we have a few possibilities depending upon the true difference that exists.

• The sample size is too small to detect an important difference. This is the worst case, you should have obtained a larger sample. In this situation, you may notice that the effect seen in the sample seems PRACTICALLY significant and yet the p-value is not small enough to reject the null hypothesis.
• The sample size is reasonable for the important difference but the true difference (which might be somewhat meaningful or interesting) is smaller than your test was capable of detecting. This is tolerable as you were not interested in being able to detect this difference when you began your study. In this situation, you may notice that the effect seen in the sample seems to have some potential for practical significance.
• The sample size is more than adequate, the difference that was not detected is meaningless in practice. This is not a problem at all and is in effect a “correct decision” since the difference you did not detect would have no practical meaning.
• Note: We will discuss the idea of practical significance later in more detail.

Power of a Hypothesis Test

It is often the case that we truly wish to prove the alternative hypothesis. It is reasonable that we would be interested in the probability of correctly rejecting the null hypothesis. In other words, the probability of rejecting the null hypothesis, when in fact the null hypothesis is false. This can also be thought of as the probability of being able to detect a (pre-specified) difference of interest to the researcher.

Let’s begin with a realistic example of how power can be described in a study.

In a clinical trial to study two medications for weight loss, we have an 80% chance to detect a difference in the weight loss between the two medications of 10 pounds. In other words, the power of the hypothesis test we will conduct is 80%.

In other words, if one medication comes from a population with an average weight loss of 25 pounds and the other comes from a population with an average weight loss of 15 pounds, we will have an 80% chance to detect that difference using the sample we have in our trial.

If we were to repeat this trial many times, 80% of the time we will be able to reject the null hypothesis (that there is no difference between the medications) and 20% of the time we will fail to reject the null hypothesis (and make a Type II error!).

The difference of 10 pounds in the previous example, is often called the effect size . The measure of the effect differs depending on the particular test you are conducting but is always some measure related to the true effect in the population. In this example, it is the difference between two population means.

Recall the definition of a Type II error:

Notice that P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1- beta.

The POWER of a hypothesis test is the probability of rejecting the null hypothesis when the null hypothesis is false . This can also be stated as the probability of correctly rejecting the null hypothesis .

POWER = P(Reject Ho | Ho is False) = 1 – β = 1 – beta

Power is the test’s ability to correctly reject the null hypothesis. A test with high power has a good chance of being able to detect the difference of interest to us, if it exists .

As we mentioned on the bottom of the previous page, this can be thought of as the sensitivity of the hypothesis test if you imagine Ho = No disease and Ha = Disease.

Factors Affecting the Power of a Hypothesis Test

The power of a hypothesis test is affected by numerous quantities (similar to the margin of error in a confidence interval).

Assume that the null hypothesis is false for a given hypothesis test. All else being equal, we have the following:

• Larger samples result in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test.
• If the effect size is larger, it will become easier for us to detect. This results in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test. The effect size varies for each test and is usually closely related to the difference between the hypothesized value and the true value of the parameter under study.
• From the relationship between the probability of a Type I and a Type II error (as α (alpha) decreases, β (beta) increases), we can see that as α (alpha) decreases, Power = 1 – β = 1 – beta also decreases.
• There are other mathematical ways to change the power of a hypothesis test, such as changing the population standard deviation; however, these are not quantities that we can usually control so we will not discuss them here.

In practice, we specify a significance level and a desired power to detect a difference which will have practical meaning to us and this determines the sample size required for the experiment or study.

For most grants involving statistical analysis, power calculations must be completed to illustrate that the study will have a reasonable chance to detect an important effect. Otherwise, the money spent on the study could be wasted. The goal is usually to have a power close to 80%.

For example, if there is only a 5% chance to detect an important difference between two treatments in a clinical trial, this would result in a waste of time, effort, and money on the study since, when the alternative hypothesis is true, the chance a treatment effect can be found is very small.

• In order to calculate the power of a hypothesis test, we must specify the “truth.” As we mentioned previously when discussing Type II errors, in practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

The following activity involves working with an interactive applet to study power more carefully.

Learn by Doing: Power of Hypothesis Tests

The following reading is an excellent discussion about Type I and Type II errors.

(Optional) Outside Reading: A Good Discussion of Power (≈ 2500 words)

We will not be asking you to perform power calculations manually. You may be asked to use online calculators and applets. Most statistical software packages offer some ability to complete power calculations. There are also many online calculators for power and sample size on the internet, for example, Russ Lenth’s power and sample-size page .

Proportions (Introduction & Step 1)

CO-4: Distinguish among different measurement scales, choose the appropriate descriptive and inferential statistical methods based on these distinctions, and interpret the results.

LO 4.33: In a given context, distinguish between situations involving a population proportion and a population mean and specify the correct null and alternative hypothesis for the scenario.

LO 4.34: Carry out a complete hypothesis test for a population proportion by hand.

Video: Proportions (Introduction & Step 1) (7:18)

Now that we understand the process of hypothesis testing and the logic behind it, we are ready to start learning about specific statistical tests (also known as significance tests).

The first test we are going to learn is the test about the population proportion (p).

This test is widely known as the “z-test for the population proportion (p).”

We will understand later where the “z-test” part is coming from.

This will be the only type of problem you will complete entirely “by-hand” in this course. Our goal is to use this example to give you the tools you need to understand how this process works. After working a few problems, you should review the earlier material again. You will likely need to review the terminology and concepts a few times before you fully understand the process.

In reality, you will often be conducting more complex statistical tests and allowing software to provide the p-value. In these settings it will be important to know what test to apply for a given situation and to be able to explain the results in context.

Review: Types of Variables

When we conduct a test about a population proportion, we are working with a categorical variable. Later in the course, after we have learned a variety of hypothesis tests, we will need to be able to identify which test is appropriate for which situation. Identifying the variable as categorical or quantitative is an important component of choosing an appropriate hypothesis test.

Learn by Doing: Review Types of Variables

One Sample Z-Test for a Population Proportion

In this part of our discussion on hypothesis testing, we will go into details that we did not go into before. More specifically, we will use this test to introduce the idea of a test statistic , and details about how p-values are calculated .

Let’s start by introducing the three examples, which will be the leading examples in our discussion. Each example is followed by a figure illustrating the information provided, as well as the question of interest.

A machine is known to produce 20% defective products, and is therefore sent for repair. After the machine is repaired, 400 products produced by the machine are chosen at random and 64 of them are found to be defective. Do the data provide enough evidence that the proportion of defective products produced by the machine (p) has been reduced as a result of the repair?

The following figure displays the information, as well as the question of interest:

The question of interest helps us formulate the null and alternative hypotheses in terms of p, the proportion of defective products produced by the machine following the repair:

• Ho: p = 0.20 (No change; the repair did not help).
• Ha: p < 0.20 (The repair was effective at reducing the proportion of defective parts).

There are rumors that students at a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 100 students from the college, 19 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (This number is reported by the Harvard School of Public Health.)

Again, the following figure displays the information as well as the question of interest:

As before, we can formulate the null and alternative hypotheses in terms of p, the proportion of students in the college who use marijuana:

• Ho: p = 0.157 (same as among all college students in the country).
• Ha: p > 0.157 (higher than the national figure).

Polls on certain topics are conducted routinely in order to monitor changes in the public’s opinions over time. One such topic is the death penalty. In 2003 a poll estimated that 64% of U.S. adults support the death penalty for a person convicted of murder. In a more recent poll, 675 out of 1,000 U.S. adults chosen at random were in favor of the death penalty for convicted murderers. Do the results of this poll provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers (p) changed between 2003 and the later poll?

Here is a figure that displays the information, as well as the question of interest:

Again, we can formulate the null and alternative hypotheses in term of p, the proportion of U.S. adults who support the death penalty for convicted murderers.

• Ho: p = 0.64 (No change from 2003).
• Ha: p ≠ 0.64 (Some change since 2003).

Learn by Doing: Proportions (Overview)

Did I Get This?: Proportions ( Overview )

Recall that there are basically 4 steps in the process of hypothesis testing:

• STEP 1: State the appropriate null and alternative hypotheses, Ho and Ha.
• STEP 2: Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used . If the conditions are met, summarize the data using a test statistic.
• STEP 3: Find the p-value of the test.
• STEP 4: Based on the p-value, decide whether or not the results are statistically significant and draw your conclusions in context.
• Note: In practice, we should always consider the practical significance of the results as well as the statistical significance.

We are now going to go through these steps as they apply to the hypothesis testing for the population proportion p. It should be noted that even though the details will be specific to this particular test, some of the ideas that we will add apply to hypothesis testing in general.

Step 1. Stating the Hypotheses

Here again are the three set of hypotheses that are being tested in each of our three examples:

Has the proportion of defective products been reduced as a result of the repair?

Is the proportion of marijuana users in the college higher than the national figure?

Did the proportion of U.S. adults who support the death penalty change between 2003 and a later poll?

The null hypothesis always takes the form:

• Ho: p = some value

and the alternative hypothesis takes one of the following three forms:

• Ha: p < that value (like in example 1) or
• Ha: p > that value (like in example 2) or
• Ha: p ≠ that value (like in example 3).

Note that it was quite clear from the context which form of the alternative hypothesis would be appropriate. The value that is specified in the null hypothesis is called the null value , and is generally denoted by p 0 . We can say, therefore, that in general the null hypothesis about the population proportion (p) would take the form:

• Ho: p = p 0

We write Ho: p = p 0 to say that we are making the hypothesis that the population proportion has the value of p 0 . In other words, p is the unknown population proportion and p 0 is the number we think p might be for the given situation.

The alternative hypothesis takes one of the following three forms (depending on the context):

Ha: p < p 0 (one-sided)

Ha: p > p 0 (one-sided)

Ha: p ≠ p 0 (two-sided)

The first two possible forms of the alternatives (where the = sign in Ho is challenged by < or >) are called one-sided alternatives , and the third form of alternative (where the = sign in Ho is challenged by ≠) is called a two-sided alternative. To understand the intuition behind these names let’s go back to our examples.

Example 3 (death penalty) is a case where we have a two-sided alternative:

In this case, in order to reject Ho and accept Ha we will need to get a sample proportion of death penalty supporters which is very different from 0.64 in either direction, either much larger or much smaller than 0.64.

In example 2 (marijuana use) we have a one-sided alternative:

Here, in order to reject Ho and accept Ha we will need to get a sample proportion of marijuana users which is much higher than 0.157.

Similarly, in example 1 (defective products), where we are testing:

in order to reject Ho and accept Ha, we will need to get a sample proportion of defective products which is much smaller than 0.20.

Learn by Doing: State Hypotheses (Proportions)

Did I Get This?: State Hypotheses (Proportions)

Proportions (Step 2)

Video: Proportions (Step 2) (12:38)

Step 2. Collect Data, Check Conditions, and Summarize Data

After the hypotheses have been stated, the next step is to obtain a sample (on which the inference will be based), collect relevant data , and summarize them.

It is extremely important that our sample is representative of the population about which we want to draw conclusions. This is ensured when the sample is chosen at random. Beyond the practical issue of ensuring representativeness, choosing a random sample has theoretical importance that we will mention later.

In the case of hypothesis testing for the population proportion (p), we will collect data on the relevant categorical variable from the individuals in the sample and start by calculating the sample proportion p-hat (the natural quantity to calculate when the parameter of interest is p).

Let’s go back to our three examples and add this step to our figures.

As we mentioned earlier without going into details, when we summarize the data in hypothesis testing, we go a step beyond calculating the sample statistic and summarize the data with a test statistic . Every test has a test statistic, which to some degree captures the essence of the test. In fact, the p-value, which so far we have looked upon as “the king” (in the sense that everything is determined by it), is actually determined by (or derived from) the test statistic. We will now introduce the test statistic.

The test statistic is a measure of how far the sample proportion p-hat is from the null value p 0 , the value that the null hypothesis claims is the value of p. In other words, since p-hat is what the data estimates p to be, the test statistic can be viewed as a measure of the “distance” between what the data tells us about p and what the null hypothesis claims p to be.

Let’s use our examples to understand this:

The parameter of interest is p, the proportion of defective products following the repair.

The data estimate p to be p-hat = 0.16

The null hypothesis claims that p = 0.20

The data are therefore 0.04 (or 4 percentage points) below the null hypothesis value.

It is hard to evaluate whether this difference of 4% in defective products is enough evidence to say that the repair was effective at reducing the proportion of defective products, but clearly, the larger the difference, the more evidence it is against the null hypothesis. So if, for example, our sample proportion of defective products had been, say, 0.10 instead of 0.16, then I think you would all agree that cutting the proportion of defective products in half (from 20% to 10%) would be extremely strong evidence that the repair was effective at reducing the proportion of defective products.

The parameter of interest is p, the proportion of students in a college who use marijuana.

The data estimate p to be p-hat = 0.19

The null hypothesis claims that p = 0.157

The data are therefore 0.033 (or 3.3. percentage points) above the null hypothesis value.

The parameter of interest is p, the proportion of U.S. adults who support the death penalty for convicted murderers.

The data estimate p to be p-hat = 0.675

The null hypothesis claims that p = 0.64

There is a difference of 0.035 (or 3.5. percentage points) between the data and the null hypothesis value.

The problem with looking only at the difference between the sample proportion, p-hat, and the null value, p 0 is that we have not taken into account the variability of our estimator p-hat which, as we know from our study of sampling distributions, depends on the sample size.

For this reason, the test statistic cannot simply be the difference between p-hat and p 0 , but must be some form of that formula that accounts for the sample size. In other words, we need to somehow standardize the difference so that comparison between different situations will be possible. We are very close to revealing the test statistic, but before we construct it, let’s be reminded of the following two facts from probability:

Fact 1: When we take a random sample of size n from a population with population proportion p, then

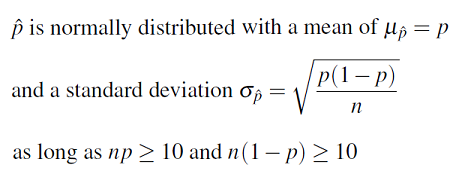
Fact 2: The z-score of any normal value (a value that comes from a normal distribution) is calculated by finding the difference between the value and the mean and then dividing that difference by the standard deviation (of the normal distribution associated with the value). The z-score represents how many standard deviations below or above the mean the value is.

Thus, our test statistic should be a measure of how far the sample proportion p-hat is from the null value p 0 relative to the variation of p-hat (as measured by the standard error of p-hat).

Recall that the standard error is the standard deviation of the sampling distribution for a given statistic. For p-hat, we know the following:

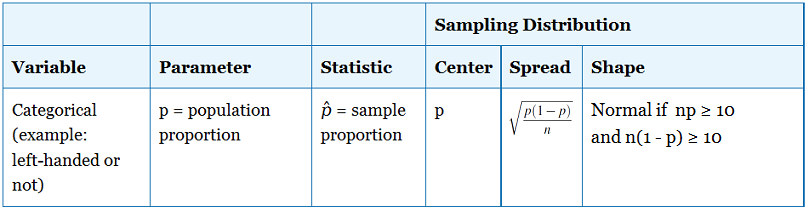
To find the p-value, we will need to determine how surprising our value is assuming the null hypothesis is true. We already have the tools needed for this process from our study of sampling distributions as represented in the table above.

If we assume the null hypothesis is true, we can specify that the center of the distribution of all possible values of p-hat from samples of size 400 would be 0.20 (our null value).

We can calculate the standard error, assuming p = 0.20 as

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}=\sqrt{\dfrac{0.2(1-0.2)}{400}}=0.02\)

The following picture represents the sampling distribution of all possible values of p-hat of samples of size 400, assuming the true proportion p is 0.20 and our other requirements for the sampling distribution to be normal are met (we will review these during the next step).

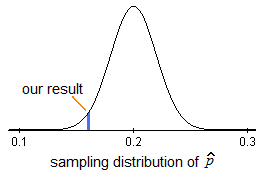
In order to calculate probabilities for the picture above, we would need to find the z-score associated with our result.

This z-score is the test statistic ! In this example, the numerator of our z-score is the difference between p-hat (0.16) and null value (0.20) which we found earlier to be -0.04. The denominator of our z-score is the standard error calculated above (0.02) and thus quickly we find the z-score, our test statistic, to be -2.

The sample proportion based upon this data is 2 standard errors below the null value.

Hopefully you now understand more about the reasons we need probability in statistics!!

Now we will formalize the definition and look at our remaining examples before moving on to the next step, which will be to determine if a normal distribution applies and calculate the p-value.

Test Statistic for Hypothesis Tests for One Proportion is:

\(z=\dfrac{\hat{p}-p_{0}}{\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}}\)

It represents the difference between the sample proportion and the null value, measured in standard deviations (standard error of p-hat).

The picture above is a representation of the sampling distribution of p-hat assuming p = p 0 . In other words, this is a model of how p-hat behaves if we are drawing random samples from a population for which Ho is true.

Notice the center of the sampling distribution is at p 0 , which is the hypothesized proportion given in the null hypothesis (Ho: p = p 0 .) We could also mark the axis in standard error units,

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}\)

For example, if our null hypothesis claims that the proportion of U.S. adults supporting the death penalty is 0.64, then the sampling distribution is drawn as if the null is true. We draw a normal distribution centered at 0.64 (p 0 ) with a standard error dependent on sample size,

\(\sqrt{\dfrac{0.64(1-0.64)}{n}}\).

Important Comment:

• Note that under the assumption that Ho is true (and if the conditions for the sampling distribution to be normal are satisfied) the test statistic follows a N(0,1) (standard normal) distribution. Another way to say the same thing which is quite common is: “The null distribution of the test statistic is N(0,1).”

By “null distribution,” we mean the distribution under the assumption that Ho is true. As we’ll see and stress again later, the null distribution of the test statistic is what the calculation of the p-value is based on.

Let’s go back to our remaining two examples and find the test statistic in each case:

Since the null hypothesis is Ho: p = 0.157, the standardized (z) score of p-hat = 0.19 is

\(z=\dfrac{0.19-0.157}{\sqrt{\dfrac{0.157(1-0.157)}{100}}} \approx 0.91\)

This is the value of the test statistic for this example.

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.19 is 0.91 standard errors above the null value (0.157).

Since the null hypothesis is Ho: p = 0.64, the standardized (z) score of p-hat = 0.675 is

\(z=\dfrac{0.675-0.64}{\sqrt{\dfrac{0.64(1-0.64)}{1000}}} \approx 2.31\)

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.675 is 2.31 standard errors above the null value (0.64).

Learn by Doing: Proportions (Step 2)

Comments about the Test Statistic:

• We mentioned earlier that to some degree, the test statistic captures the essence of the test. In this case, the test statistic measures the difference between p-hat and p 0 in standard errors. This is exactly what this test is about. Get data, and look at the discrepancy between what the data estimates p to be (represented by p-hat) and what Ho claims about p (represented by p 0 ).
• You can think about this test statistic as a measure of evidence in the data against Ho. The larger the test statistic, the “further the data are from Ho” and therefore the more evidence the data provide against Ho.

Learn by Doing: Proportions (Step 2) Understanding the Test Statistic

Did I Get This?: Proportions (Step 2)

• It should now be clear why this test is commonly known as the z-test for the population proportion . The name comes from the fact that it is based on a test statistic that is a z-score.
• Recall fact 1 that we used for constructing the z-test statistic. Here is part of it again:

When we take a random sample of size n from a population with population proportion p 0 , the possible values of the sample proportion p-hat ( when certain conditions are met ) have approximately a normal distribution with a mean of p 0 … and a standard deviation of

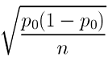
This result provides the theoretical justification for constructing the test statistic the way we did, and therefore the assumptions under which this result holds (in bold, above) are the conditions that our data need to satisfy so that we can use this test. These two conditions are:

i. The sample has to be random.

ii. The conditions under which the sampling distribution of p-hat is normal are met. In other words:

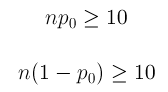
• Here we will pause to say more about condition (i.) above, the need for a random sample. In the Probability Unit we discussed sampling plans based on probability (such as a simple random sample, cluster, or stratified sampling) that produce a non-biased sample, which can be safely used in order to make inferences about a population. We noted in the Probability Unit that, in practice, other (non-random) sampling techniques are sometimes used when random sampling is not feasible. It is important though, when these techniques are used, to be aware of the type of bias that they introduce, and thus the limitations of the conclusions that can be drawn from them. For our purpose here, we will focus on one such practice, the situation in which a sample is not really chosen randomly, but in the context of the categorical variable that is being studied, the sample is regarded as random. For example, say that you are interested in the proportion of students at a certain college who suffer from seasonal allergies. For that purpose, the students in a large engineering class could be considered as a random sample, since there is nothing about being in an engineering class that makes you more or less likely to suffer from seasonal allergies. Technically, the engineering class is a convenience sample, but it is treated as a random sample in the context of this categorical variable. On the other hand, if you are interested in the proportion of students in the college who have math anxiety, then the class of engineering students clearly could not possibly be viewed as a random sample, since engineering students probably have a much lower incidence of math anxiety than the college population overall.

Learn by Doing: Proportions (Step 2) Valid or Invalid Sampling?

Let’s check the conditions in our three examples.

i. The 400 products were chosen at random.

ii. n = 400, p 0 = 0.2 and therefore:

\(n p_{0}=400(0.2)=80 \geq 10\)

\(n\left(1-p_{0}\right)=400(1-0.2)=320 \geq 10\)

i. The 100 students were chosen at random.

ii. n = 100, p 0 = 0.157 and therefore:

\begin{gathered} n p_{0}=100(0.157)=15.7 \geq 10 \\ n\left(1-p_{0}\right)=100(1-0.157)=84.3 \geq 10 \end{gathered}

i. The 1000 adults were chosen at random.

ii. n = 1000, p 0 = 0.64 and therefore:

\begin{gathered} n p_{0}=1000(0.64)=640 \geq 10 \\ n\left(1-p_{0}\right)=1000(1-0.64)=360 \geq 10 \end{gathered}

Learn by Doing: Proportions (Step 2) Verify Conditions

Checking that our data satisfy the conditions under which the test can be reliably used is a very important part of the hypothesis testing process. Be sure to consider this for every hypothesis test you conduct in this course and certainly in practice.

The Four Steps in Hypothesis Testing

With respect to the z-test, the population proportion that we are currently discussing we have:

Step 1: Completed

Step 2: Completed

Step 3: This is what we will work on next.

Proportions (Step 3)

Video: Proportions (Step 3) (14:46)

Calculators and Tables

Step 3. Finding the P-value of the Test

So far we’ve talked about the p-value at the intuitive level: understanding what it is (or what it measures) and how we use it to draw conclusions about the statistical significance of our results. We will now go more deeply into how the p-value is calculated.

It should be mentioned that eventually we will rely on technology to calculate the p-value for us (as well as the test statistic), but in order to make intelligent use of the output, it is important to first understand the details, and only then let the computer do the calculations for us. Again, our goal is to use this simple example to give you the tools you need to understand the process entirely. Let’s start.

Recall that so far we have said that the p-value is the probability of obtaining data like those observed assuming that Ho is true. Like the test statistic, the p-value is, therefore, a measure of the evidence against Ho. In the case of the test statistic, the larger it is in magnitude (positive or negative), the further p-hat is from p 0 , the more evidence we have against Ho. In the case of the p-value , it is the opposite; the smaller it is, the more unlikely it is to get data like those observed when Ho is true, the more evidence it is against Ho . One can actually draw conclusions in hypothesis testing just using the test statistic, and as we’ll see the p-value is, in a sense, just another way of looking at the test statistic. The reason that we actually take the extra step in this course and derive the p-value from the test statistic is that even though in this case (the test about the population proportion) and some other tests, the value of the test statistic has a very clear and intuitive interpretation, there are some tests where its value is not as easy to interpret. On the other hand, the p-value keeps its intuitive appeal across all statistical tests.

How is the p-value calculated?

Intuitively, the p-value is the probability of observing data like those observed assuming that Ho is true. Let’s be a bit more formal:

• Since this is a probability question about the data , it makes sense that the calculation will involve the data summary, the test statistic.
• What do we mean by “like” those observed? By “like” we mean “as extreme or even more extreme.”

Putting it all together, we get that in general:

The p-value is the probability of observing a test statistic as extreme as that observed (or even more extreme) assuming that the null hypothesis is true.

By “extreme” we mean extreme in the direction(s) of the alternative hypothesis.

Specifically , for the z-test for the population proportion:

• If the alternative hypothesis is Ha: p < p 0 (less than) , then “extreme” means small or less than , and the p-value is: The probability of observing a test statistic as small as that observed or smaller if the null hypothesis is true.
• If the alternative hypothesis is Ha: p > p 0 (greater than) , then “extreme” means large or greater than , and the p-value is: The probability of observing a test statistic as large as that observed or larger if the null hypothesis is true.
• If the alternative is Ha: p ≠ p 0 (different from) , then “extreme” means extreme in either direction either small or large (i.e., large in magnitude) or just different from , and the p-value therefore is: The probability of observing a test statistic as large in magnitude as that observed or larger if the null hypothesis is true.(Examples: If z = -2.5: p-value = probability of observing a test statistic as small as -2.5 or smaller or as large as 2.5 or larger. If z = 1.5: p-value = probability of observing a test statistic as large as 1.5 or larger, or as small as -1.5 or smaller.)

OK, hopefully that makes (some) sense. But how do we actually calculate it?

Recall the important comment from our discussion about our test statistic,

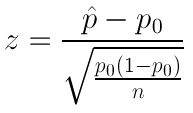
which said that when the null hypothesis is true (i.e., when p = p 0 ), the possible values of our test statistic follow a standard normal (N(0,1), denoted by Z) distribution. Therefore, the p-value calculations (which assume that Ho is true) are simply standard normal distribution calculations for the 3 possible alternative hypotheses.

Alternative Hypothesis is “Less Than”

The probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

Looking at the shaded region, you can see why this is often referred to as a left-tailed test. We shaded to the left of the test statistic, since less than is to the left.

Alternative Hypothesis is “Greater Than”

The probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

Looking at the shaded region, you can see why this is often referred to as a right-tailed test. We shaded to the right of the test statistic, since greater than is to the right.

Alternative Hypothesis is “Not Equal To”

The probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

This is often referred to as a two-tailed test, since we shaded in both directions.

Next, we will apply this to our three examples. But first, work through the following activities, which should help your understanding.

Learn by Doing: Proportions (Step 3)

Did I Get This?: Proportions (Step 3)

The p-value in this case is:

• The probability of observing a test statistic as small as -2 or smaller, assuming that Ho is true.

OR (recalling what the test statistic actually means in this case),

• The probability of observing a sample proportion that is 2 standard deviations or more below the null value (p 0 = 0.20), assuming that p 0 is the true population proportion.

OR, more specifically,

• The probability of observing a sample proportion of 0.16 or lower in a random sample of size 400, when the true population proportion is p 0 =0.20

In either case, the p-value is found as shown in the following figure:

To find P(Z ≤ -2) we can either use the calculator or table we learned to use in the probability unit for normal random variables. Eventually, after we understand the details, we will use software to run the test for us and the output will give us all the information we need. The p-value that the statistical software provides for this specific example is 0.023. The p-value tells us that it is pretty unlikely (probability of 0.023) to get data like those observed (test statistic of -2 or less) assuming that Ho is true.

• The probability of observing a test statistic as large as 0.91 or larger, assuming that Ho is true.
• The probability of observing a sample proportion that is 0.91 standard deviations or more above the null value (p 0 = 0.157), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion of 0.19 or higher in a random sample of size 100, when the true population proportion is p 0 =0.157

Again, at this point we can either use the calculator or table to find that the p-value is 0.182, this is P(Z ≥ 0.91).

The p-value tells us that it is not very surprising (probability of 0.182) to get data like those observed (which yield a test statistic of 0.91 or higher) assuming that the null hypothesis is true.

• The probability of observing a test statistic as large as 2.31 (or larger) or as small as -2.31 (or smaller), assuming that Ho is true.
• The probability of observing a sample proportion that is 2.31 standard deviations or more away from the null value (p 0 = 0.64), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion as different as 0.675 is from 0.64, or even more different (i.e. as high as 0.675 or higher or as low as 0.605 or lower) in a random sample of size 1,000, when the true population proportion is p 0 = 0.64

Again, at this point we can either use the calculator or table to find that the p-value is 0.021, this is P(Z ≤ -2.31) + P(Z ≥ 2.31) = 2*P(Z ≥ |2.31|)

The p-value tells us that it is pretty unlikely (probability of 0.021) to get data like those observed (test statistic as high as 2.31 or higher or as low as -2.31 or lower) assuming that Ho is true.

• We’ve just seen that finding p-values involves probability calculations about the value of the test statistic assuming that Ho is true. In this case, when Ho is true, the values of the test statistic follow a standard normal distribution (i.e., the sampling distribution of the test statistic when the null hypothesis is true is N(0,1)). Therefore, p-values correspond to areas (probabilities) under the standard normal curve.

Similarly, in any test , p-values are found using the sampling distribution of the test statistic when the null hypothesis is true (also known as the “null distribution” of the test statistic). In this case, it was relatively easy to argue that the null distribution of our test statistic is N(0,1). As we’ll see, in other tests, other distributions come up (like the t-distribution and the F-distribution), which we will just mention briefly, and rely heavily on the output of our statistical package for obtaining the p-values.

We’ve just completed our discussion about the p-value, and how it is calculated both in general and more specifically for the z-test for the population proportion. Let’s go back to the four-step process of hypothesis testing and see what we’ve covered and what still needs to be discussed.

With respect to the z-test the population proportion:

Step 3: Completed

Step 4. This is what we will work on next.

Learn by Doing: Proportions (Step 3) Understanding P-values

Proportions (Step 4 & Summary)

Video: Proportions (Step 4 & Summary) (4:30)

Step 4. Drawing Conclusions Based on the P-Value

This last part of the four-step process of hypothesis testing is the same across all statistical tests, and actually, we’ve already said basically everything there is to say about it, but it can’t hurt to say it again.

The p-value is a measure of how much evidence the data present against Ho. The smaller the p-value, the more evidence the data present against Ho.

We already mentioned that what determines what constitutes enough evidence against Ho is the significance level (α, alpha), a cutoff point below which the p-value is considered small enough to reject Ho in favor of Ha. The most commonly used significance level is 0.05.

• Conclusion: There IS enough evidence that Ha is True
• Conclusion: There IS NOT enough evidence that Ha is True

Where instead of Ha is True , we write what this means in the words of the problem, in other words, in the context of the current scenario.

It is important to mention again that this step has essentially two sub-steps:

(i) Based on the p-value, determine whether or not the results are statistically significant (i.e., the data present enough evidence to reject Ho).

(ii) State your conclusions in the context of the problem.

Note: We always still must consider whether the results have any practical significance, particularly if they are statistically significant as a statistically significant result which has not practical use is essentially meaningless!

Let’s go back to our three examples and draw conclusions.

We found that the p-value for this test was 0.023.

Since 0.023 is small (in particular, 0.023 < 0.05), the data provide enough evidence to reject Ho.

Conclusion:

• There IS enough evidence that the proportion of defective products is less than 20% after the repair .

The following figure is the complete story of this example, and includes all the steps we went through, starting from stating the hypotheses and ending with our conclusions:

We found that the p-value for this test was 0.182.

Since .182 is not small (in particular, 0.182 > 0.05), the data do not provide enough evidence to reject Ho.

• There IS NOT enough evidence that the proportion of students at the college who use marijuana is higher than the national figure.

Here is the complete story of this example:

Learn by Doing: Learn by Doing – Proportions (Step 4)

We found that the p-value for this test was 0.021.

Since 0.021 is small (in particular, 0.021 < 0.05), the data provide enough evidence to reject Ho

• There IS enough evidence that the proportion of adults who support the death penalty for convicted murderers has changed since 2003.

Did I Get This?: Proportions (Step 4)

Many Students Wonder: Hypothesis Testing for the Population Proportion

Many students wonder why 5% is often selected as the significance level in hypothesis testing, and why 1% is the next most typical level. This is largely due to just convenience and tradition.

When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly these are arbitrary levels.

The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics; but it’s important to remember that there is really a continuous range of increasing confidence towards the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between a p-value of .049 or .051, and it would be foolish to declare one case definitely a “real” effect and to declare the other case definitely a “random” effect. In either case, the study results were roughly 5% likely by chance if there’s no actual effect.

Whether such a p-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision, and the extent to which the hypothesized effect might contradict our prior experience or previous studies.

Let’s Summarize!!

We have now completed going through the four steps of hypothesis testing, and in particular we learned how they are applied to the z-test for the population proportion. Here is a brief summary:

Step 1: State the hypotheses

State the null hypothesis:

State the alternative hypothesis:

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem. If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! Use only the information given in the problem.

Step 2: Obtain data, check conditions, and summarize data

Obtain data from a sample and:

(i) Check whether the data satisfy the conditions which allow you to use this test.

random sample (or at least a sample that can be considered random in context)

the conditions under which the sampling distribution of p-hat is normal are met

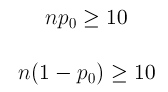
(ii) Calculate the sample proportion p-hat, and summarize the data using the test statistic:

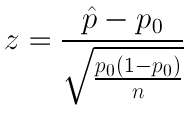
( Recall: This standardized test statistic represents how many standard deviations above or below p 0 our sample proportion p-hat is.)

Step 3: Find the p-value of the test by using the test statistic as follows

IMPORTANT FACT: In all future tests, we will rely on software to obtain the p-value.

When the alternative hypothesis is “less than” the probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

When the alternative hypothesis is “greater than” the probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

When the alternative hypothesis is “not equal to” the probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

Step 4: Conclusion

Reach a conclusion first regarding the statistical significance of the results, and then determine what it means in the context of the problem.

If p-value ≤ 0.05 then WE REJECT Ho Conclusion: There IS enough evidence that Ha is True

If p-value > 0.05 then WE FAIL TO REJECT Ho Conclusion: There IS NOT enough evidence that Ha is True

Recall that: If the p-value is small (in particular, smaller than the significance level, which is usually 0.05), the results are statistically significant (in the sense that there is a statistically significant difference between what was observed in the sample and what was claimed in Ho), and so we reject Ho.

If the p-value is not small, we do not have enough statistical evidence to reject Ho, and so we continue to believe that Ho may be true. ( Remember: In hypothesis testing we never “accept” Ho ).

Finally, in practice, we should always consider the practical significance of the results as well as the statistical significance.

Learn by Doing: Z-Test for a Population Proportion

What’s next?

Before we move on to the next test, we are going to use the z-test for proportions to bring up and illustrate a few more very important issues regarding hypothesis testing. This might also be a good time to review the concepts of Type I error, Type II error, and Power before continuing on.

More about Hypothesis Testing

CO-1: Describe the roles biostatistics serves in the discipline of public health.

LO 1.11: Recognize the distinction between statistical significance and practical significance.

LO 6.30: Use a confidence interval to determine the correct conclusion to the associated two-sided hypothesis test.

Video: More about Hypothesis Testing (18:25)

The issues regarding hypothesis testing that we will discuss are:

• The effect of sample size on hypothesis testing.
• Statistical significance vs. practical importance.
• Hypothesis testing and confidence intervals—how are they related?

Let’s begin.

1. The Effect of Sample Size on Hypothesis Testing

We have already seen the effect that the sample size has on inference, when we discussed point and interval estimation for the population mean (μ, mu) and population proportion (p). Intuitively …

Larger sample sizes give us more information to pin down the true nature of the population. We can therefore expect the sample mean and sample proportion obtained from a larger sample to be closer to the population mean and proportion, respectively. As a result, for the same level of confidence, we can report a smaller margin of error, and get a narrower confidence interval. What we’ve seen, then, is that larger sample size gives a boost to how much we trust our sample results.

In hypothesis testing, larger sample sizes have a similar effect. We have also discussed that the power of our test increases when the sample size increases, all else remaining the same. This means, we have a better chance to detect the difference between the true value and the null value for larger samples.

The following two examples will illustrate that a larger sample size provides more convincing evidence (the test has greater power), and how the evidence manifests itself in hypothesis testing. Let’s go back to our example 2 (marijuana use at a certain liberal arts college).

We do not have enough evidence to conclude that the proportion of students at the college who use marijuana is higher than the national figure.

Now, let’s increase the sample size.

There are rumors that students in a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use . Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (Reported by the Harvard School of Public Health).

Our results here are statistically significant . In other words, in example 2* the data provide enough evidence to reject Ho.

• Conclusion: There is enough evidence that the proportion of marijuana users at the college is higher than among all U.S. students.

What do we learn from this?

We see that sample results that are based on a larger sample carry more weight (have greater power).

In example 2, we saw that a sample proportion of 0.19 based on a sample of size of 100 was not enough evidence that the proportion of marijuana users in the college is higher than 0.157. Recall, from our general overview of hypothesis testing, that this conclusion (not having enough evidence to reject the null hypothesis) doesn’t mean the null hypothesis is necessarily true (so, we never “accept” the null); it only means that the particular study didn’t yield sufficient evidence to reject the null. It might be that the sample size was simply too small to detect a statistically significant difference.

However, in example 2*, we saw that when the sample proportion of 0.19 is obtained from a sample of size 400, it carries much more weight, and in particular, provides enough evidence that the proportion of marijuana users in the college is higher than 0.157 (the national figure). In this case, the sample size of 400 was large enough to detect a statistically significant difference.

The following activity will allow you to practice the ideas and terminology used in hypothesis testing when a result is not statistically significant.

Learn by Doing: Interpreting Non-significant Results

2. Statistical significance vs. practical importance.

Now, we will address the issue of statistical significance versus practical importance (which also involves issues of sample size).

The following activity will let you explore the effect of the sample size on the statistical significance of the results yourself, and more importantly will discuss issue 2: Statistical significance vs. practical importance.

Important Fact: In general, with a sufficiently large sample size you can make any result that has very little practical importance statistically significant! A large sample size alone does NOT make a “good” study!!

This suggests that when interpreting the results of a test, you should always think not only about the statistical significance of the results but also about their practical importance.

Learn by Doing: Statistical vs. Practical Significance

3. Hypothesis Testing and Confidence Intervals

The last topic we want to discuss is the relationship between hypothesis testing and confidence intervals. Even though the flavor of these two forms of inference is different (confidence intervals estimate a parameter, and hypothesis testing assesses the evidence in the data against one claim and in favor of another), there is a strong link between them.

We will explain this link (using the z-test and confidence interval for the population proportion), and then explain how confidence intervals can be used after a test has been carried out.

Recall that a confidence interval gives us a set of plausible values for the unknown population parameter. We may therefore examine a confidence interval to informally decide if a proposed value of population proportion seems plausible.

For example, if a 95% confidence interval for p, the proportion of all U.S. adults already familiar with Viagra in May 1998, was (0.61, 0.67), then it seems clear that we should be able to reject a claim that only 50% of all U.S. adults were familiar with the drug, since based on the confidence interval, 0.50 is not one of the plausible values for p.

In fact, the information provided by a confidence interval can be formally related to the information provided by a hypothesis test. ( Comment: The relationship is more straightforward for two-sided alternatives, and so we will not present results for the one-sided cases.)

Suppose we want to carry out the two-sided test:

• Ha: p ≠ p 0

using a significance level of 0.05.

An alternative way to perform this test is to find a 95% confidence interval for p and check:

• If p 0 falls outside the confidence interval, reject Ho.
• If p 0 falls inside the confidence interval, do not reject Ho.

In other words,

• If p 0 is not one of the plausible values for p, we reject Ho.
• If p 0 is a plausible value for p, we cannot reject Ho.

( Comment: Similarly, the results of a test using a significance level of 0.01 can be related to the 99% confidence interval.)

Let’s look at an example:

Recall example 3, where we wanted to know whether the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64.

We are testing:

and as the figure reminds us, we took a sample of 1,000 U.S. adults, and the data told us that 675 supported the death penalty for convicted murderers (p-hat = 0.675).

A 95% confidence interval for p, the proportion of all U.S. adults who support the death penalty, is:

\(0.675 \pm 1.96 \sqrt{\dfrac{0.675(1-0.675)}{1000}} \approx 0.675 \pm 0.029=(0.646,0.704)\)

Since the 95% confidence interval for p does not include 0.64 as a plausible value for p, we can reject Ho and conclude (as we did before) that there is enough evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003.

You and your roommate are arguing about whose turn it is to clean the apartment. Your roommate suggests that you settle this by tossing a coin and takes one out of a locked box he has on the shelf. Suspecting that the coin might not be fair, you decide to test it first. You toss the coin 80 times, thinking to yourself that if, indeed, the coin is fair, you should get around 40 heads. Instead you get 48 heads. You are puzzled. You are not sure whether getting 48 heads out of 80 is enough evidence to conclude that the coin is unbalanced, or whether this a result that could have happened just by chance when the coin is fair.

Statistics can help you answer this question.

Let p be the true proportion (probability) of heads. We want to test whether the coin is fair or not.

• Ho: p = 0.5 (the coin is fair).
• Ha: p ≠ 0.5 (the coin is not fair).

The data we have are that out of n = 80 tosses, we got 48 heads, or that the sample proportion of heads is p-hat = 48/80 = 0.6.

A 95% confidence interval for p, the true proportion of heads for this coin, is:

\(0.6 \pm 1.96 \sqrt{\dfrac{0.6(1-0.6)}{80}} \approx 0.6 \pm 0.11=(0.49,0.71)\)

Since in this case 0.5 is one of the plausible values for p, we cannot reject Ho. In other words, the data do not provide enough evidence to conclude that the coin is not fair.

The context of the last example is a good opportunity to bring up an important point that was discussed earlier.

Even though we use 0.05 as a cutoff to guide our decision about whether the results are statistically significant, we should not treat it as inviolable and we should always add our own judgment. Let’s look at the last example again.

It turns out that the p-value of this test is 0.0734. In other words, it is maybe not extremely unlikely, but it is quite unlikely (probability of 0.0734) that when you toss a fair coin 80 times you’ll get a sample proportion of heads of 48/80 = 0.6 (or even more extreme). It is true that using the 0.05 significance level (cutoff), 0.0734 is not considered small enough to conclude that the coin is not fair. However, if you really don’t want to clean the apartment, the p-value might be small enough for you to ask your roommate to use a different coin, or to provide one yourself!

Did I Get This?: Connection between Confidence Intervals and Hypothesis Tests

Did I Get This?: Hypothesis Tests for Proportions (Extra Practice)

Here is our final point on this subject:

When the data provide enough evidence to reject Ho, we can conclude (depending on the alternative hypothesis) that the population proportion is either less than, greater than, or not equal to the null value p 0 . However, we do not get a more informative statement about its actual value. It might be of interest, then, to follow the test with a 95% confidence interval that will give us more insight into the actual value of p.

In our example 3,

we concluded that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64. It is probably of interest not only to know that the proportion has changed, but also to estimate what it has changed to. We’ve calculated the 95% confidence interval for p on the previous page and found that it is (0.646, 0.704).

We can combine our conclusions from the test and the confidence interval and say:

Data provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, and we are 95% confident that it is now between 0.646 and 0.704. (i.e. between 64.6% and 70.4%).

Let’s look at our example 1 to see how a confidence interval following a test might be insightful in a different way.

Here is a summary of example 1:

We conclude that as a result of the repair, the proportion of defective products has been reduced to below 0.20 (which was the proportion prior to the repair). It is probably of great interest to the company not only to know that the proportion of defective has been reduced, but also estimate what it has been reduced to, to get a better sense of how effective the repair was. A 95% confidence interval for p in this case is:

\(0.16 \pm 1.96 \sqrt{\dfrac{0.16(1-0.16)}{400}} \approx 0.16 \pm 0.036=(0.124,0.196)\)

We can therefore say that the data provide evidence that the proportion of defective products has been reduced, and we are 95% confident that it has been reduced to somewhere between 12.4% and 19.6%. This is very useful information, since it tells us that even though the results were significant (i.e., the repair reduced the number of defective products), the repair might not have been effective enough, if it managed to reduce the number of defective products only to the range provided by the confidence interval. This, of course, ties back in to the idea of statistical significance vs. practical importance that we discussed earlier. Even though the results are statistically significant (Ho was rejected), practically speaking, the repair might still be considered ineffective.

Learn by Doing: Hypothesis Tests and Confidence Intervals

Even though this portion of the current section is about the z-test for population proportion, it is loaded with very important ideas that apply to hypothesis testing in general. We’ve already summarized the details that are specific to the z-test for proportions, so the purpose of this summary is to highlight the general ideas.

The process of hypothesis testing has four steps :

I. Stating the null and alternative hypotheses (Ho and Ha).

II. Obtaining a random sample (or at least one that can be considered random) and collecting data. Using the data:

Check that the conditions under which the test can be reliably used are met.

Summarize the data using a test statistic.

• The test statistic is a measure of the evidence in the data against Ho. The larger the test statistic is in magnitude, the more evidence the data present against Ho.

III. Finding the p-value of the test. The p-value is the probability of getting data like those observed (or even more extreme) assuming that the null hypothesis is true, and is calculated using the null distribution of the test statistic. The p-value is a measure of the evidence against Ho. The smaller the p-value, the more evidence the data present against Ho.

IV. Making conclusions.

Conclusions about the statistical significance of the results:

If the p-value is small, the data present enough evidence to reject Ho (and accept Ha).

If the p-value is not small, the data do not provide enough evidence to reject Ho.

To help guide our decision, we use the significance level as a cutoff for what is considered a small p-value. The significance cutoff is usually set at 0.05.

Conclusions should then be provided in the context of the problem.

Additional Important Ideas about Hypothesis Testing

• Results that are based on a larger sample carry more weight, and therefore as the sample size increases, results become more statistically significant.
• Even a very small and practically unimportant effect becomes statistically significant with a large enough sample size. The distinction between statistical significance and practical importance should therefore always be considered.
• Confidence intervals can be used in order to carry out two-sided tests (95% confidence for the 0.05 significance level). If the null value is not included in the confidence interval (i.e., is not one of the plausible values for the parameter), we have enough evidence to reject Ho. Otherwise, we cannot reject Ho.
• If the results are statistically significant, it might be of interest to follow up the tests with a confidence interval in order to get insight into the actual value of the parameter of interest.
• It is important to be aware that there are two types of errors in hypothesis testing ( Type I and Type II ) and that the power of a statistical test is an important measure of how likely we are to be able to detect a difference of interest to us in a particular problem.

Means (All Steps)

NOTE: Beginning on this page, the Learn By Doing and Did I Get This activities are presented as interactive PDF files. The interactivity may not work on mobile devices or with certain PDF viewers. Use an official ADOBE product such as ADOBE READER .

If you have any issues with the Learn By Doing or Did I Get This interactive PDF files, you can view all of the questions and answers presented on this page in this document:

• QUESTION/Answer (SPOILER ALERT!)

Tests About μ (mu) When σ (sigma) is Unknown – The t-test for a Population Mean

The t-distribution.

Video: Means (All Steps) (13:11)

So far we have talked about the logic behind hypothesis testing and then illustrated how this process proceeds in practice, using the z-test for the population proportion (p).

We are now moving on to discuss testing for the population mean (μ, mu), which is the parameter of interest when the variable of interest is quantitative.

A few comments about the structure of this section:

• The basic groundwork for carrying out hypothesis tests has already been laid in our general discussion and in our presentation of tests about proportions.

Therefore we can easily modify the four steps to carry out tests about means instead, without going into all of the details again.

We will use this approach for all future tests so be sure to go back to the discussion in general and for proportions to review the concepts in more detail.

• In our discussion about confidence intervals for the population mean, we made the distinction between whether the population standard deviation, σ (sigma) was known or if we needed to estimate this value using the sample standard deviation, s .

In this section, we will only discuss the second case as in most realistic settings we do not know the population standard deviation .

In this case we need to use the t- distribution instead of the standard normal distribution for the probability aspects of confidence intervals (choosing table values) and hypothesis tests (finding p-values).

• Although we will discuss some theoretical or conceptual details for some of the analyses we will learn, from this point on we will rely on software to conduct tests and calculate confidence intervals for us , while we focus on understanding which methods are used for which situations and what the results say in context.

If you are interested in more information about the z-test, where we assume the population standard deviation σ (sigma) is known, you can review the Carnegie Mellon Open Learning Statistics Course (you will need to click “ENTER COURSE”).

Like any other tests, the t- test for the population mean follows the four-step process:

• STEP 1: Stating the hypotheses H o and H a .
• STEP 2: Collecting relevant data, checking that the data satisfy the conditions which allow us to use this test, and summarizing the data using a test statistic.
• STEP 3: Finding the p-value of the test, the probability of obtaining data as extreme as those collected (or even more extreme, in the direction of the alternative hypothesis), assuming that the null hypothesis is true. In other words, how likely is it that the only reason for getting data like those observed is sampling variability (and not because H o is not true)?
• STEP 4: Drawing conclusions, assessing the statistical significance of the results based on the p-value, and stating our conclusions in context. (Do we or don’t we have evidence to reject H o and accept H a ?)
• Note: In practice, we should also always consider the practical significance of the results as well as the statistical significance.

We will now go through the four steps specifically for the t- test for the population mean and apply them to our two examples.

Only in a few cases is it reasonable to assume that the population standard deviation, σ (sigma), is known and so we will not cover hypothesis tests in this case. We discussed both cases for confidence intervals so that we could still calculate some confidence intervals by hand.

For this and all future tests we will rely on software to obtain our summary statistics, test statistics, and p-values for us.

The case where σ (sigma) is unknown is much more common in practice. What can we use to replace σ (sigma)? If you don’t know the population standard deviation, the best you can do is find the sample standard deviation, s, and use it instead of σ (sigma). (Note that this is exactly what we did when we discussed confidence intervals).

Is that it? Can we just use s instead of σ (sigma), and the rest is the same as the previous case? Unfortunately, it’s not that simple, but not very complicated either.

Here, when we use the sample standard deviation, s, as our estimate of σ (sigma) we can no longer use a normal distribution to find the cutoff for confidence intervals or the p-values for hypothesis tests.

Instead we must use the t- distribution (with n-1 degrees of freedom) to obtain the p-value for this test.

We discussed this issue for confidence intervals. We will talk more about the t- distribution after we discuss the details of this test for those who are interested in learning more.

It isn’t really necessary for us to understand this distribution but it is important that we use the correct distributions in practice via our software.

We will wait until UNIT 4B to look at how to accomplish this test in the software. For now focus on understanding the process and drawing the correct conclusions from the p-values given.

Now let’s go through the four steps in conducting the t- test for the population mean.

The null and alternative hypotheses for the t- test for the population mean (μ, mu) have exactly the same structure as the hypotheses for z-test for the population proportion (p):

The null hypothesis has the form:

• Ho: μ = μ 0 (mu = mu_zero)

(where μ 0 (mu_zero) is often called the null value)

• Ha: μ < μ 0 (mu < mu_zero) (one-sided)
• Ha: μ > μ 0 (mu > mu_zero) (one-sided)
• Ha: μ ≠ μ 0 (mu ≠ mu_zero) (two-sided)

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem.

If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! You also cannot use the information from the sample to help you determine the hypothesis. We would not know our data when we originally asked the question.

Now try it yourself. Here are a few exercises on stating the hypotheses for tests for a population mean.

Learn by Doing: State the Hypotheses for a test for a population mean

Here are a few more activities for practice.

Did I Get This?: State the Hypotheses for a test for a population mean

When setting up hypotheses, be sure to use only the information in the research question. We cannot use our sample data to help us set up our hypotheses.

For this test, it is still important to correctly choose the alternative hypothesis as “less than”, “greater than”, or “different” although generally in practice two-sample tests are used.

Obtain data from a sample:

• In this step we would obtain data from a sample. This is not something we do much of in courses but it is done very often in practice!

Check the conditions:

• Then we check the conditions under which this test (the t- test for one population mean) can be safely carried out – which are:
• The sample is random (or at least can be considered random in context).
• We are in one of the three situations marked with a green check mark in the following table (which ensure that x-bar is at least approximately normal and the test statistic using the sample standard deviation, s, is therefore a t- distribution with n-1 degrees of freedom – proving this is beyond the scope of this course):
• For large samples, we don’t need to check for normality in the population . We can rely on the sample size as the basis for the validity of using this test.
• For small samples , we need to have data from a normal population in order for the p-values and confidence intervals to be valid.

In practice, for small samples, it can be very difficult to determine if the population is normal. Here is a simulation to give you a better understanding of the difficulties.

Video: Simulations – Are Samples from a Normal Population? (4:58)

Now try it yourself with a few activities.

Learn by Doing: Checking Conditions for Hypothesis Testing for the Population Mean

• It is always a good idea to look at the data and get a sense of their pattern regardless of whether you actually need to do it in order to assess whether the conditions are met.
• This idea of looking at the data is relevant to all tests in general. In the next module—inference for relationships—conducting exploratory data analysis before inference will be an integral part of the process.

Here are a few more problems for extra practice.

Did I Get This?: Checking Conditions for Hypothesis Testing for the Population Mean

When setting up hypotheses, be sure to use only the information in the res

Calculate Test Statistic

Assuming that the conditions are met, we calculate the sample mean x-bar and the sample standard deviation, s (which estimates σ (sigma)), and summarize the data with a test statistic.

The test statistic for the t -test for the population mean is:

\(t=\dfrac{\bar{x} - \mu_0}{s/ \sqrt{n}}\)

Recall that such a standardized test statistic represents how many standard deviations above or below μ 0 (mu_zero) our sample mean x-bar is.

Therefore our test statistic is a measure of how different our data are from what is claimed in the null hypothesis. This is an idea that we mentioned in the previous test as well.

Again we will rely on the p-value to determine how unusual our data would be if the null hypothesis is true.

As we mentioned, the test statistic in the t -test for a population mean does not follow a standard normal distribution. Rather, it follows another bell-shaped distribution called the t- distribution.

We will present the details of this distribution at the end for those interested but for now we will work on the process of the test.

Here are a few important facts.

• In statistical language we say that the null distribution of our test statistic is the t- distribution with (n-1) degrees of freedom. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t- distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t (n – 1) or Z to calculate the p-values does not make a big difference. However, software will use the t -distribution regardless of the sample size and so will we.

Although we will not calculate p-values by hand for this test, we can still easily calculate the test statistic.

Try it yourself:

Learn by Doing: Calculate the Test Statistic for a Test for a Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistics and we will use the p-values provided to draw our conclusions.

We will use software to obtain the p-value for this (and all future) tests but here are the images illustrating how the p-value is calculated in each of the three cases corresponding to the three choices for our alternative hypothesis.

Note that due to the symmetry of the t distribution, for a given value of the test statistic t, the p-value for the two-sided test is twice as large as the p-value of either of the one-sided tests. The same thing happens when p-values are calculated under the t distribution as when they are calculated under the Z distribution.

We will show some examples of p-values obtained from software in our examples. For now let’s continue our summary of the steps.

As usual, based on the p-value (and some significance level of choice) we assess the statistical significance of results, and draw our conclusions in context.

To review what we have said before:

If p-value ≤ 0.05 then WE REJECT Ho

If p-value > 0.05 then WE FAIL TO REJECT Ho

This step has essentially two sub-steps:

We are now ready to look at two examples.

A certain prescription medicine is supposed to contain an average of 250 parts per million (ppm) of a certain chemical. If the concentration is higher than this, the drug may cause harmful side effects; if it is lower, the drug may be ineffective.

The manufacturer runs a check to see if the mean concentration in a large shipment conforms to the target level of 250 ppm or not.

A simple random sample of 100 portions is tested, and the sample mean concentration is found to be 247 ppm with a sample standard deviation of 12 ppm.

Here is a figure that represents this example:

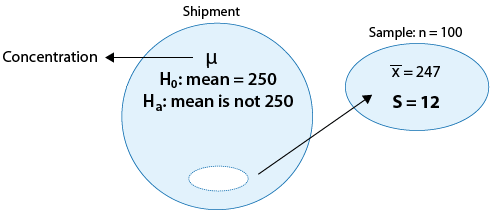
1. The hypotheses being tested are:

• Ha: μ ≠ μ 0 (mu ≠ mu_zero)
• Where μ = population mean part per million of the chemical in the entire shipment

2. The conditions that allow us to use the t-test are met since:

• The sample is random
• The sample size is large enough for the Central Limit Theorem to apply and ensure the normality of x-bar. We do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.
• The test statistic is:

\(t=\dfrac{\bar{x}-\mu_{0}}{s / \sqrt{n}}=\dfrac{247-250}{12 / \sqrt{100}}=-2.5\)

• The data (represented by the sample mean) are 2.5 standard errors below the null value.

3. Finding the p-value.

• To find the p-value we use statistical software, and we calculate a p-value of 0.014.

4. Conclusions:

• The p-value is small (.014) indicating that at the 5% significance level, the results are significant.
• We reject the null hypothesis.
• There is enough evidence to conclude that the mean concentration in entire shipment is not the required 250 ppm.
• It is difficult to comment on the practical significance of this result without more understanding of the practical considerations of this problem.

Here is a summary:

• The 95% confidence interval for μ (mu) can be used here in the same way as for proportions to conduct the two-sided test (checking whether the null value falls inside or outside the confidence interval) or following a t- test where Ho was rejected to get insight into the value of μ (mu).
• We find the 95% confidence interval to be (244.619, 249.381) . Since 250 is not in the interval we know we would reject our null hypothesis that μ (mu) = 250. The confidence interval gives additional information. By accounting for estimation error, it estimates that the population mean is likely to be between 244.62 and 249.38. This is lower than the target concentration and that information might help determine the seriousness and appropriate course of action in this situation.

In most situations in practice we use TWO-SIDED HYPOTHESIS TESTS, followed by confidence intervals to gain more insight.

For completeness in covering one sample t-tests for a population mean, we still cover all three possible alternative hypotheses here HOWEVER, this will be the last test for which we will do so.

A research study measured the pulse rates of 57 college men and found a mean pulse rate of 70 beats per minute with a standard deviation of 9.85 beats per minute.

Researchers want to know if the mean pulse rate for all college men is different from the current standard of 72 beats per minute.

• The hypotheses being tested are:
• Ho: μ = 72
• Ha: μ ≠ 72
• Where μ = population mean heart rate among college men
• The conditions that allow us to use the t- test are met since:
• The sample is random.
• The sample size is large (n = 57) so we do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.

\(t=\dfrac{\bar{x}-\mu}{s / \sqrt{n}}=\dfrac{70-72}{9.85 / \sqrt{57}}=-1.53\)

• The data (represented by the sample mean) are 1.53 estimated standard errors below the null value.
• Recall that in general the p-value is calculated under the null distribution of the test statistic, which, in the t- test case, is t (n-1). In our case, in which n = 57, the p-value is calculated under the t (56) distribution. Using statistical software, we find that the p-value is 0.132 .
• Here is how we calculated the p-value. http://homepage.stat.uiowa.edu/~mbognar/applets/t.html .

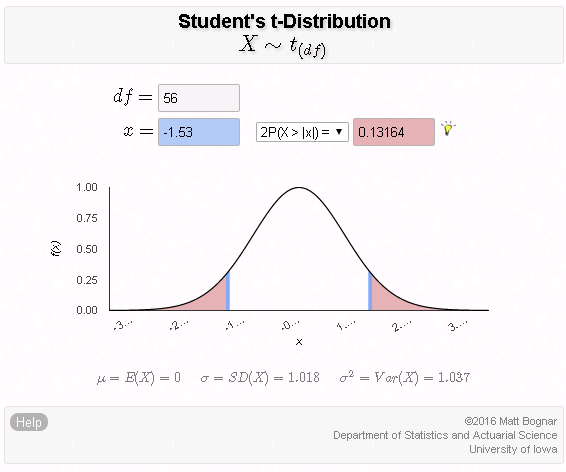
4. Making conclusions.

• The p-value (0.132) is not small, indicating that the results are not significant.
• We fail to reject the null hypothesis.
• There is not enough evidence to conclude that the mean pulse rate for all college men is different from the current standard of 72 beats per minute.
• The results from this sample do not appear to have any practical significance either with a mean pulse rate of 70, this is very similar to the hypothesized value, relative to the variation expected in pulse rates.

Now try a few yourself.

Learn by Doing: Hypothesis Testing for the Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistic and p-value and we will use the p-values provided to draw our conclusions.

That concludes our discussion of hypothesis tests in Unit 4A.

In the next unit we will continue to use both confidence intervals and hypothesis test to investigate the relationship between two variables in the cases we covered in Unit 1 on exploratory data analysis – we will look at Case CQ, Case CC, and Case QQ.

Before moving on, we will discuss the details about the t- distribution as a general object.

We have seen that variables can be visually modeled by many different sorts of shapes, and we call these shapes distributions. Several distributions arise so frequently that they have been given special names, and they have been studied mathematically.

So far in the course, the only one we’ve named, for continuous quantitative variables, is the normal distribution, but there are others. One of them is called the t- distribution.

The t- distribution is another bell-shaped (unimodal and symmetric) distribution, like the normal distribution; and the center of the t- distribution is standardized at zero, like the center of the standard normal distribution.

Like all distributions that are used as probability models, the normal and the t- distribution are both scaled, so the total area under each of them is 1.

So how is the t-distribution fundamentally different from the normal distribution?

• The spread .

The following picture illustrates the fundamental difference between the normal distribution and the t-distribution:

Here we have an image which illustrates the fundamental difference between the normal distribution and the t- distribution:

You can see in the picture that the t- distribution has slightly less area near the expected central value than the normal distribution does, and you can see that the t distribution has correspondingly more area in the “tails” than the normal distribution does. (It’s often said that the t- distribution has “fatter tails” or “heavier tails” than the normal distribution.)

This reflects the fact that the t- distribution has a larger spread than the normal distribution. The same total area of 1 is spread out over a slightly wider range on the t- distribution, making it a bit lower near the center compared to the normal distribution, and giving the t- distribution slightly more probability in the ‘tails’ compared to the normal distribution.

Therefore, the t- distribution ends up being the appropriate model in certain cases where there is more variability than would be predicted by the normal distribution. One of these cases is stock values, which have more variability (or “volatility,” to use the economic term) than would be predicted by the normal distribution.

There’s actually an entire family of t- distributions. They all have similar formulas (but the math is beyond the scope of this introductory course in statistics), and they all have slightly “fatter tails” than the normal distribution. But some are closer to normal than others.

The t- distributions that have higher “degrees of freedom” are closer to normal (degrees of freedom is a mathematical concept that we won’t study in this course, beyond merely mentioning it here). So, there’s a t- distribution “with one degree of freedom,” another t- distribution “with 2 degrees of freedom” which is slightly closer to normal, another t- distribution “with 3 degrees of freedom” which is a bit closer to normal than the previous ones, and so on.

The following picture illustrates this idea with just a couple of t- distributions (note that “degrees of freedom” is abbreviated “d.f.” on the picture):

The test statistic for our t-test for one population mean is a t -score which follows a t- distribution with (n – 1) degrees of freedom. Recall that each t- distribution is indexed according to “degrees of freedom.” Notice that, in the context of a test for a mean, the degrees of freedom depend on the sample size in the study.

Remember that we said that higher degrees of freedom indicate that the t- distribution is closer to normal. So in the context of a test for the mean, the larger the sample size , the higher the degrees of freedom, and the closer the t- distribution is to a normal z distribution .

As a result, in the context of a test for a mean, the effect of the t- distribution is most important for a study with a relatively small sample size .

We are now done introducing the t-distribution. What are implications of all of this?

• The null distribution of our t-test statistic is the t-distribution with (n-1) d.f. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t-distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t(n – 1) or Z to calculate the p-values does not make a big difference.

• Comprehensive Learning Paths
• 150+ Hours of Videos
• Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

• September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

• What is Hypothesis Testing?
• Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
• Example : Testing a new drug.
• Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

• Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
• Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
• p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
• Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

• Symbolized by the Greek letter alpha (α).
• Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
• The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
• Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

• Symbolized by the Greek letter beta (β).
• Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
• The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

• If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
• If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

• Set up Hypotheses : Before starting, you make a prediction:
• Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
• Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

• The average healing time in the Drug Group is 2 hours.
• The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

• P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
• P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
• If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
• If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

More Articles

Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, what is hypothesis testing in statistics types and examples, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

The Ultimate Ticket to Top Data Science Job Roles

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Hypothesis testing is a statistical method to determine if there is enough evidence in a sample of data to infer that a certain condition is true for the entire population. Here’s a breakdown of the typical steps involved in hypothesis testing:

Formulate Hypotheses

• Null Hypothesis (H0): This hypothesis states that there is no effect or difference, and it is the hypothesis you attempt to reject with your test.
• Alternative Hypothesis (H1 or Ha): This hypothesis is what you might believe to be true or hope to prove true. It is usually considered the opposite of the null hypothesis.

Choose the Significance Level (α)

The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. Common choices for α are 0.05 (5%), 0.01 (1%), and 0.10 (10%).

Select the Appropriate Test

Choose a statistical test based on the type of data and the hypothesis. Common tests include t-tests, chi-square tests, ANOVA, and regression analysis . The selection depends on data type, distribution, sample size, and whether the hypothesis is one-tailed or two-tailed.

Collect Data

Gather the data that will be analyzed in the test. This data should be representative of the population to infer conclusions accurately.

Calculate the Test Statistic

Based on the collected data and the chosen test, calculate a test statistic that reflects how much the observed data deviates from the null hypothesis.

Determine the p-value

The p-value is the probability of observing test results at least as extreme as the results observed, assuming the null hypothesis is correct. It helps determine the strength of the evidence against the null hypothesis.

Make a Decision

Compare the p-value to the chosen significance level:

• If the p-value ≤ α: Reject the null hypothesis, suggesting sufficient evidence in the data supports the alternative hypothesis.
• If the p-value > α: Do not reject the null hypothesis, suggesting insufficient evidence to support the alternative hypothesis.

Report the Results

Present the findings from the hypothesis test, including the test statistic, p-value, and the conclusion about the hypotheses.

Perform Post-hoc Analysis (if necessary)

Depending on the results and the study design, further analysis may be needed to explore the data more deeply or to address multiple comparisons if several hypotheses were tested simultaneously.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Become a Data Scientist through hands-on learning with hackathons, masterclasses, webinars, and Ask-Me-Anything! Start learning now!

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales.  If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Our Data Scientist Master's Program covers core topics such as R, Python, Machine Learning, Tableau, Hadoop, and Spark. Get started on your journey today!

Why Is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

• Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
• Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
• Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
• Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

When Did Hypothesis Testing Begin?

Hypothesis testing as a formalized process began in the early 20th century, primarily through the work of statisticians such as Ronald A. Fisher, Jerzy Neyman, and Egon Pearson. The development of hypothesis testing is closely tied to the evolution of statistical methods during this period.

• Ronald A. Fisher (1920s): Fisher was one of the key figures in developing the foundation for modern statistical science. In the 1920s, he introduced the concept of the null hypothesis in his book "Statistical Methods for Research Workers" (1925). Fisher also developed significance testing to examine the likelihood of observing the collected data if the null hypothesis were true. He introduced p-values to determine the significance of the observed results.
• Neyman-Pearson Framework (1930s): Jerzy Neyman and Egon Pearson built on Fisher’s work and formalized the process of hypothesis testing even further. In the 1930s, they introduced the concepts of Type I and Type II errors and developed a decision-making framework widely used in hypothesis testing today. Their approach emphasized the balance between these errors and introduced the concepts of the power of a test and the alternative hypothesis.

The dialogue between Fisher's and Neyman-Pearson's approaches shaped the methods and philosophy of statistical hypothesis testing used today. Fisher emphasized the evidential interpretation of the p-value. At the same time, Neyman and Pearson advocated for a decision-theoretical approach in which hypotheses are either accepted or rejected based on pre-determined significance levels and power considerations.

The application and methodology of hypothesis testing have since become a cornerstone of statistical analysis across various scientific disciplines, marking a significant statistical development.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

Learn All The Tricks Of The BI Trade

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore the Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is H0 and H1 in statistics?

In statistics, H0​ and H1​ represent the null and alternative hypotheses. The null hypothesis, H0​, is the default assumption that no effect or difference exists between groups or conditions. The alternative hypothesis, H1​, is the competing claim suggesting an effect or a difference. Statistical tests determine whether to reject the null hypothesis in favor of the alternative hypothesis based on the data.

3. What is a simple hypothesis with an example?

A simple hypothesis is a specific statement predicting a single relationship between two variables. It posits a direct and uncomplicated outcome. For example, a simple hypothesis might state, "Increased sunlight exposure increases the growth rate of sunflowers." Here, the hypothesis suggests a direct relationship between the amount of sunlight (independent variable) and the growth rate of sunflowers (dependent variable), with no additional variables considered.

4. What are the 2 types of hypothesis testing?

• One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
• Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our PL-300 Microsoft Power BI Certification Training Online Classroom training classes in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

• Simple hypothesis testing (Opens a modal)
• Idea behind hypothesis testing (Opens a modal)
• Examples of null and alternative hypotheses (Opens a modal)
• P-values and significance tests (Opens a modal)
• Comparing P-values to different significance levels (Opens a modal)
• Estimating a P-value from a simulation (Opens a modal)
• Using P-values to make conclusions (Opens a modal)
• Simple hypothesis testing Get 3 of 4 questions to level up!
• Writing null and alternative hypotheses Get 3 of 4 questions to level up!
• Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

• Introduction to Type I and Type II errors (Opens a modal)
• Type 1 errors (Opens a modal)
• Examples identifying Type I and Type II errors (Opens a modal)
• Introduction to power in significance tests (Opens a modal)
• Examples thinking about power in significance tests (Opens a modal)
• Consequences of errors and significance (Opens a modal)
• Type I vs Type II error Get 3 of 4 questions to level up!
• Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

• Constructing hypotheses for a significance test about a proportion (Opens a modal)
• Conditions for a z test about a proportion (Opens a modal)
• Reference: Conditions for inference on a proportion (Opens a modal)
• Calculating a z statistic in a test about a proportion (Opens a modal)
• Calculating a P-value given a z statistic (Opens a modal)
• Making conclusions in a test about a proportion (Opens a modal)
• Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
• Conditions for a z test about a proportion Get 3 of 4 questions to level up!
• Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
• Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
• Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

• Writing hypotheses for a significance test about a mean (Opens a modal)
• Conditions for a t test about a mean (Opens a modal)
• Reference: Conditions for inference on a mean (Opens a modal)
• When to use z or t statistics in significance tests (Opens a modal)
• Example calculating t statistic for a test about a mean (Opens a modal)
• Using TI calculator for P-value from t statistic (Opens a modal)
• Using a table to estimate P-value from t statistic (Opens a modal)
• Comparing P-value from t statistic to significance level (Opens a modal)
• Free response example: Significance test for a mean (Opens a modal)
• Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
• Conditions for a t test about a mean Get 3 of 4 questions to level up!
• Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
• Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
• Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

More significance testing videos

• Hypothesis testing and p-values (Opens a modal)
• One-tailed and two-tailed tests (Opens a modal)
• Z-statistics vs. T-statistics (Opens a modal)
• Small sample hypothesis test (Opens a modal)
• Large sample proportion hypothesis testing (Opens a modal)

• Hypothesis Testing: Definition, Uses, Limitations + Examples

Hypothesis testing is as old as the scientific method and is at the heart of the research process. 

Research exists to validate or disprove assumptions about various phenomena. The process of validation involves testing and it is in this context that we will explore hypothesis testing. 

What is a Hypothesis? 

A hypothesis is a calculated prediction or assumption about a population parameter based on limited evidence. The whole idea behind hypothesis formulation is testing—this means the researcher subjects his or her calculated assumption to a series of evaluations to know whether they are true or false. 

Typically, every research starts with a hypothesis—the investigator makes a claim and experiments to prove that this claim is true or false . For instance, if you predict that students who drink milk before class perform better than those who don’t, then this becomes a hypothesis that can be confirmed or refuted using an experiment.  

Read: What is Empirical Research Study? [Examples & Method]

What are the Types of Hypotheses? 

1. simple hypothesis.

Also known as a basic hypothesis, a simple hypothesis suggests that an independent variable is responsible for a corresponding dependent variable. In other words, an occurrence of the independent variable inevitably leads to an occurrence of the dependent variable. 

Typically, simple hypotheses are considered as generally true, and they establish a causal relationship between two variables. 

Examples of Simple Hypothesis  

• Drinking soda and other sugary drinks can cause obesity. 
• Smoking cigarettes daily leads to lung cancer.

2. Complex Hypothesis

A complex hypothesis is also known as a modal. It accounts for the causal relationship between two independent variables and the resulting dependent variables. This means that the combination of the independent variables leads to the occurrence of the dependent variables . 

Examples of Complex Hypotheses  

• Adults who do not smoke and drink are less likely to develop liver-related conditions.
• Global warming causes icebergs to melt which in turn causes major changes in weather patterns.

3. Null Hypothesis

As the name suggests, a null hypothesis is formed when a researcher suspects that there’s no relationship between the variables in an observation. In this case, the purpose of the research is to approve or disapprove this assumption. 

Examples of Null Hypothesis

• This is no significant change in a student’s performance if they drink coffee or tea before classes. 
• There’s no significant change in the growth of a plant if one uses distilled water only or vitamin-rich water. 

Read: Research Report: Definition, Types + [Writing Guide]

4. Alternative Hypothesis 

To disapprove a null hypothesis, the researcher has to come up with an opposite assumption—this assumption is known as the alternative hypothesis. This means if the null hypothesis says that A is false, the alternative hypothesis assumes that A is true. 

An alternative hypothesis can be directional or non-directional depending on the direction of the difference. A directional alternative hypothesis specifies the direction of the tested relationship, stating that one variable is predicted to be larger or smaller than the null value while a non-directional hypothesis only validates the existence of a difference without stating its direction. 

Examples of Alternative Hypotheses  

• Starting your day with a cup of tea instead of a cup of coffee can make you more alert in the morning. 
• The growth of a plant improves significantly when it receives distilled water instead of vitamin-rich water. 

5. Logical Hypothesis

Logical hypotheses are some of the most common types of calculated assumptions in systematic investigations. It is an attempt to use your reasoning to connect different pieces in research and build a theory using little evidence. In this case, the researcher uses any data available to him, to form a plausible assumption that can be tested. 

Examples of Logical Hypothesis

• Waking up early helps you to have a more productive day. 
• Beings from Mars would not be able to breathe the air in the atmosphere of the Earth. 

6. Empirical Hypothesis  

After forming a logical hypothesis, the next step is to create an empirical or working hypothesis. At this stage, your logical hypothesis undergoes systematic testing to prove or disprove the assumption. An empirical hypothesis is subject to several variables that can trigger changes and lead to specific outcomes. 

Examples of Empirical Testing 

• People who eat more fish run faster than people who eat meat.
• Women taking vitamin E grow hair faster than those taking vitamin K.

7. Statistical Hypothesis

When forming a statistical hypothesis, the researcher examines the portion of a population of interest and makes a calculated assumption based on the data from this sample. A statistical hypothesis is most common with systematic investigations involving a large target audience. Here, it’s impossible to collect responses from every member of the population so you have to depend on data from your sample and extrapolate the results to the wider population. 

Examples of Statistical Hypothesis  

• 45% of students in Louisiana have middle-income parents. 
• 80% of the UK’s population gets a divorce because of irreconcilable differences.

What is Hypothesis Testing? 

Hypothesis testing is an assessment method that allows researchers to determine the plausibility of a hypothesis. It involves testing an assumption about a specific population parameter to know whether it’s true or false. These population parameters include variance, standard deviation, and median. 

Typically, hypothesis testing starts with developing a null hypothesis and then performing several tests that support or reject the null hypothesis. The researcher uses test statistics to compare the association or relationship between two or more variables. 

Explore: Research Bias: Definition, Types + Examples

Researchers also use hypothesis testing to calculate the coefficient of variation and determine if the regression relationship and the correlation coefficient are statistically significant.

How Hypothesis Testing Works

The basis of hypothesis testing is to examine and analyze the null hypothesis and alternative hypothesis to know which one is the most plausible assumption. Since both assumptions are mutually exclusive, only one can be true. In other words, the occurrence of a null hypothesis destroys the chances of the alternative coming to life, and vice-versa. 

Interesting: 21 Chrome Extensions for Academic Researchers in 2021

What Are The Stages of Hypothesis Testing?  

To successfully confirm or refute an assumption, the researcher goes through five (5) stages of hypothesis testing; 

• Determine the null hypothesis
• Specify the alternative hypothesis
• Set the significance level
• Calculate the test statistics and corresponding P-value
• Draw your conclusion
• Determine the Null Hypothesis

Like we mentioned earlier, hypothesis testing starts with creating a null hypothesis which stands as an assumption that a certain statement is false or implausible. For example, the null hypothesis (H0) could suggest that different subgroups in the research population react to a variable in the same way. 

• Specify the Alternative Hypothesis

Once you know the variables for the null hypothesis, the next step is to determine the alternative hypothesis. The alternative hypothesis counters the null assumption by suggesting the statement or assertion is true. Depending on the purpose of your research, the alternative hypothesis can be one-sided or two-sided. 

Using the example we established earlier, the alternative hypothesis may argue that the different sub-groups react differently to the same variable based on several internal and external factors. 

• Set the Significance Level

Many researchers create a 5% allowance for accepting the value of an alternative hypothesis, even if the value is untrue. This means that there is a 0.05 chance that one would go with the value of the alternative hypothesis, despite the truth of the null hypothesis. 

Something to note here is that the smaller the significance level, the greater the burden of proof needed to reject the null hypothesis and support the alternative hypothesis.

Explore: What is Data Interpretation? + [Types, Method & Tools]

• Calculate the Test Statistics and Corresponding P-Value 

Test statistics in hypothesis testing allow you to compare different groups between variables while the p-value accounts for the probability of obtaining sample statistics if your null hypothesis is true. In this case, your test statistics can be the mean, median and similar parameters. 

If your p-value is 0.65, for example, then it means that the variable in your hypothesis will happen 65 in100 times by pure chance. Use this formula to determine the p-value for your data: 

• Draw Your Conclusions

After conducting a series of tests, you should be able to agree or refute the hypothesis based on feedback and insights from your sample data.  

Applications of Hypothesis Testing in Research

Hypothesis testing isn’t only confined to numbers and calculations; it also has several real-life applications in business, manufacturing, advertising, and medicine. 

In a factory or other manufacturing plants, hypothesis testing is an important part of quality and production control before the final products are approved and sent out to the consumer. 

During ideation and strategy development, C-level executives use hypothesis testing to evaluate their theories and assumptions before any form of implementation. For example, they could leverage hypothesis testing to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales. 

In addition, hypothesis testing is used during clinical trials to prove the efficacy of a drug or new medical method before its approval for widespread human usage. 

What is an Example of Hypothesis Testing?

An employer claims that her workers are of above-average intelligence. She takes a random sample of 20 of them and gets the following results: 

Mean IQ Scores: 110

Standard Deviation: 15 

Mean Population IQ: 100

Step 1: Using the value of the mean population IQ, we establish the null hypothesis as 100.

Step 2: State that the alternative hypothesis is greater than 100.

Step 3: State the alpha level as 0.05 or 5% 

Step 4: Find the rejection region area (given by your alpha level above) from the z-table. An area of .05 is equal to a z-score of 1.645.

Step 5: Calculate the test statistics using this formula

Z = (110–100) ÷ (15÷√20) 

10 ÷ 3.35 = 2.99 

If the value of the test statistics is higher than the value of the rejection region, then you should reject the null hypothesis. If it is less, then you cannot reject the null. 

In this case, 2.99 > 1.645 so we reject the null. 

Importance/Benefits of Hypothesis Testing 

The most significant benefit of hypothesis testing is it allows you to evaluate the strength of your claim or assumption before implementing it in your data set. Also, hypothesis testing is the only valid method to prove that something “is or is not”. Other benefits include: 

• Hypothesis testing provides a reliable framework for making any data decisions for your population of interest. 
• It helps the researcher to successfully extrapolate data from the sample to the larger population. 
• Hypothesis testing allows the researcher to determine whether the data from the sample is statistically significant. 
• Hypothesis testing is one of the most important processes for measuring the validity and reliability of outcomes in any systematic investigation. 
• It helps to provide links to the underlying theory and specific research questions.

Criticism and Limitations of Hypothesis Testing

Several limitations of hypothesis testing can affect the quality of data you get from this process. Some of these limitations include: 

• The interpretation of a p-value for observation depends on the stopping rule and definition of multiple comparisons. This makes it difficult to calculate since the stopping rule is subject to numerous interpretations, plus “multiple comparisons” are unavoidably ambiguous. 
• Conceptual issues often arise in hypothesis testing, especially if the researcher merges Fisher and Neyman-Pearson’s methods which are conceptually distinct. 
• In an attempt to focus on the statistical significance of the data, the researcher might ignore the estimation and confirmation by repeated experiments.
• Hypothesis testing can trigger publication bias, especially when it requires statistical significance as a criterion for publication.
• When used to detect whether a difference exists between groups, hypothesis testing can trigger absurd assumptions that affect the reliability of your observation.

Connect to Formplus, Get Started Now - It's Free!

• alternative hypothesis
• alternative vs null hypothesis
• complex hypothesis
• empirical hypothesis
• hypothesis testing
• logical hypothesis
• simple hypothesis
• statistical hypothesis
• busayo.longe

You may also like:

Type I vs Type II Errors: Causes, Examples & Prevention

This article will discuss the two different types of errors in hypothesis testing and how you can prevent them from occurring in your research

What is Pure or Basic Research? + [Examples & Method]

Simple guide on pure or basic research, its methods, characteristics, advantages, and examples in science, medicine, education and psychology

Internal Validity in Research: Definition, Threats, Examples

In this article, we will discuss the concept of internal validity, some clear examples, its importance, and how to test it.

Alternative vs Null Hypothesis: Pros, Cons, Uses & Examples

We are going to discuss alternative hypotheses and null hypotheses in this post and how they work in research.

Formplus - For Seamless Data Collection

Collect data the right way with a versatile data collection tool. try formplus and transform your work productivity today..

Hypothesis Testing (cont...)

Hypothesis testing, the null and alternative hypothesis.

In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.

The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:

Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:

Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.

Significance levels

The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?

So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.

Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions

When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:

The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.

Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.

Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:

In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.

Rejecting or failing to reject the null hypothesis

Let's return finally to the question of whether we reject or fail to reject the null hypothesis.

If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.

Hypothesis Testing for Means & Proportions

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This is the first of three modules that will addresses the second area of statistical inference, which is hypothesis testing, in which a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The process of hypothesis testing involves setting up two competing hypotheses, the null hypothesis and the alternate hypothesis. One selects a random sample (or multiple samples when there are more comparison groups), computes summary statistics and then assesses the likelihood that the sample data support the research or alternative hypothesis. Similar to estimation, the process of hypothesis testing is based on probability theory and the Central Limit Theorem.  

This module will focus on hypothesis testing for means and proportions. The next two modules in this series will address analysis of variance and chi-squared tests. 

Learning Objectives

After completing this module, the student will be able to:

• Define null and research hypothesis, test statistic, level of significance and decision rule
• Distinguish between Type I and Type II errors and discuss the implications of each
• Explain the difference between one and two sided tests of hypothesis
• Estimate and interpret p-values
• Explain the relationship between confidence interval estimates and p-values in drawing inferences
• Differentiate hypothesis testing procedures based on type of outcome variable and number of sample

Introduction to Hypothesis Testing

Techniques for hypothesis testing  .

The techniques for hypothesis testing depend on

• the type of outcome variable being analyzed (continuous, dichotomous, discrete)
• the number of comparison groups in the investigation
• whether the comparison groups are independent (i.e., physically separate such as men versus women) or dependent (i.e., matched or paired such as pre- and post-assessments on the same participants).

In estimation we focused explicitly on techniques for one and two samples and discussed estimation for a specific parameter (e.g., the mean or proportion of a population), for differences (e.g., difference in means, the risk difference) and ratios (e.g., the relative risk and odds ratio). Here we will focus on procedures for one and two samples when the outcome is either continuous (and we focus on means) or dichotomous (and we focus on proportions).

General Approach: A Simple Example

The Centers for Disease Control (CDC) reported on trends in weight, height and body mass index from the 1960's through 2002. 1 The general trend was that Americans were much heavier and slightly taller in 2002 as compared to 1960; both men and women gained approximately 24 pounds, on average, between 1960 and 2002.   In 2002, the mean weight for men was reported at 191 pounds. Suppose that an investigator hypothesizes that weights are even higher in 2006 (i.e., that the trend continued over the subsequent 4 years). The research hypothesis is that the mean weight in men in 2006 is more than 191 pounds. The null hypothesis is that there is no change in weight, and therefore the mean weight is still 191 pounds in 2006.  

In order to test the hypotheses, we select a random sample of American males in 2006 and measure their weights. Suppose we have resources available to recruit n=100 men into our sample. We weigh each participant and compute summary statistics on the sample data. Suppose in the sample we determine the following:

Do the sample data support the null or research hypothesis? The sample mean of 197.1 is numerically higher than 191. However, is this difference more than would be expected by chance? In hypothesis testing, we assume that the null hypothesis holds until proven otherwise. We therefore need to determine the likelihood of observing a sample mean of 197.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true or under the null hypothesis). We can compute this probability using the Central Limit Theorem. Specifically,

(Notice that we use the sample standard deviation in computing the Z score. This is generally an appropriate substitution as long as the sample size is large, n > 30. Thus, there is less than a 1% probability of observing a sample mean as large as 197.1 when the true population mean is 191. Do you think that the null hypothesis is likely true? Based on how unlikely it is to observe a sample mean of 197.1 under the null hypothesis (i.e., <1% probability), we might infer, from our data, that the null hypothesis is probably not true.

Suppose that the sample data had turned out differently. Suppose that we instead observed the following in 2006:

How likely it is to observe a sample mean of 192.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true)? We can again compute this probability using the Central Limit Theorem. Specifically,

There is a 33.4% probability of observing a sample mean as large as 192.1 when the true population mean is 191. Do you think that the null hypothesis is likely true?  

Neither of the sample means that we obtained allows us to know with certainty whether the null hypothesis is true or not. However, our computations suggest that, if the null hypothesis were true, the probability of observing a sample mean >197.1 is less than 1%. In contrast, if the null hypothesis were true, the probability of observing a sample mean >192.1 is about 33%. We can't know whether the null hypothesis is true, but the sample that provided a mean value of 197.1 provides much stronger evidence in favor of rejecting the null hypothesis, than the sample that provided a mean value of 192.1. Note that this does not mean that a sample mean of 192.1 indicates that the null hypothesis is true; it just doesn't provide compelling evidence to reject it.

In essence, hypothesis testing is a procedure to compute a probability that reflects the strength of the evidence (based on a given sample) for rejecting the null hypothesis. In hypothesis testing, we determine a threshold or cut-off point (called the critical value) to decide when to believe the null hypothesis and when to believe the research hypothesis. It is important to note that it is possible to observe any sample mean when the true population mean is true (in this example equal to 191), but some sample means are very unlikely. Based on the two samples above it would seem reasonable to believe the research hypothesis when x̄ = 197.1, but to believe the null hypothesis when x̄ =192.1. What we need is a threshold value such that if x̄ is above that threshold then we believe that H 1 is true and if x̄ is below that threshold then we believe that H 0 is true. The difficulty in determining a threshold for x̄ is that it depends on the scale of measurement. In this example, the threshold, sometimes called the critical value, might be 195 (i.e., if the sample mean is 195 or more then we believe that H 1 is true and if the sample mean is less than 195 then we believe that H 0 is true). Suppose we are interested in assessing an increase in blood pressure over time, the critical value will be different because blood pressures are measured in millimeters of mercury (mmHg) as opposed to in pounds. In the following we will explain how the critical value is determined and how we handle the issue of scale.

First, to address the issue of scale in determining the critical value, we convert our sample data (in particular the sample mean) into a Z score. We know from the module on probability that the center of the Z distribution is zero and extreme values are those that exceed 2 or fall below -2. Z scores above 2 and below -2 represent approximately 5% of all Z values. If the observed sample mean is close to the mean specified in H 0 (here m =191), then Z will be close to zero. If the observed sample mean is much larger than the mean specified in H 0 , then Z will be large.  

In hypothesis testing, we select a critical value from the Z distribution. This is done by first determining what is called the level of significance, denoted α ("alpha"). What we are doing here is drawing a line at extreme values. The level of significance is the probability that we reject the null hypothesis (in favor of the alternative) when it is actually true and is also called the Type I error rate.

α = Level of significance = P(Type I error) = P(Reject H 0 | H 0 is true).

Because α is a probability, it ranges between 0 and 1. The most commonly used value in the medical literature for α is 0.05, or 5%. Thus, if an investigator selects α=0.05, then they are allowing a 5% probability of incorrectly rejecting the null hypothesis in favor of the alternative when the null is in fact true. Depending on the circumstances, one might choose to use a level of significance of 1% or 10%. For example, if an investigator wanted to reject the null only if there were even stronger evidence than that ensured with α=0.05, they could choose a =0.01as their level of significance. The typical values for α are 0.01, 0.05 and 0.10, with α=0.05 the most commonly used value.  

Suppose in our weight study we select α=0.05. We need to determine the value of Z that holds 5% of the values above it (see below).

The critical value of Z for α =0.05 is Z = 1.645 (i.e., 5% of the distribution is above Z=1.645). With this value we can set up what is called our decision rule for the test. The rule is to reject H 0 if the Z score is 1.645 or more.  

With the first sample we have

Because 2.38 > 1.645, we reject the null hypothesis. (The same conclusion can be drawn by comparing the 0.0087 probability of observing a sample mean as extreme as 197.1 to the level of significance of 0.05. If the observed probability is smaller than the level of significance we reject H 0 ). Because the Z score exceeds the critical value, we conclude that the mean weight for men in 2006 is more than 191 pounds, the value reported in 2002. If we observed the second sample (i.e., sample mean =192.1), we would not be able to reject the null hypothesis because the Z score is 0.43 which is not in the rejection region (i.e., the region in the tail end of the curve above 1.645). With the second sample we do not have sufficient evidence (because we set our level of significance at 5%) to conclude that weights have increased. Again, the same conclusion can be reached by comparing probabilities. The probability of observing a sample mean as extreme as 192.1 is 33.4% which is not below our 5% level of significance.

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.  

• Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);  

H 1 : Research hypothesis (investigator's belief); α =0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is a single number that summarizes the sample information.   An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

• Step 3.  Set up decision rule.  

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

• The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value.  In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
• The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.  
• The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value.   For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.  

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

• Step 4. Compute the test statistic.  

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

• Step 5. Conclusion.  

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).  

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .  

• Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191                 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

• Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

• Step 3. Set up decision rule.  

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05.   Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.  

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.                  

Type I and Type II Errors

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

 The most common reason for a Type II error is a small sample size.

Tests with One Sample, Continuous Outcome

Hypothesis testing applications with a continuous outcome variable in a single population are performed according to the five-step procedure outlined above. A key component is setting up the null and research hypotheses. The objective is to compare the mean in a single population to known mean (μ 0 ). The known value is generally derived from another study or report, for example a study in a similar, but not identical, population or a study performed some years ago. The latter is called a historical control. It is important in setting up the hypotheses in a one sample test that the mean specified in the null hypothesis is a fair and reasonable comparator. This will be discussed in the examples that follow.

Test Statistics for Testing H 0 : μ= μ 0

• if n > 30
• if n < 30

Note that statistical computing packages will use the t statistic exclusively and make the necessary adjustments for comparing the test statistic to appropriate values from probability tables to produce a p-value. 

The National Center for Health Statistics (NCHS) published a report in 2005 entitled Health, United States, containing extensive information on major trends in the health of Americans. Data are provided for the US population as a whole and for specific ages, sexes and races.  The NCHS report indicated that in 2002 Americans paid an average of $3,302 per year on health care and prescription drugs. An investigator hypothesizes that in 2005 expenditures have decreased primarily due to the availability of generic drugs. To test the hypothesis, a sample of 100 Americans are selected and their expenditures on health care and prescription drugs in 2005 are measured.   The sample data are summarized as follows: n=100, x̄

=$3,190 and s=$890. Is there statistical evidence of a reduction in expenditures on health care and prescription drugs in 2005? Is the sample mean of $3,190 evidence of a true reduction in the mean or is it within chance fluctuation? We will run the test using the five-step approach. 

• Step 1.  Set up hypotheses and determine level of significance

H 0 : μ = 3,302 H 1 : μ < 3,302           α =0.05

The research hypothesis is that expenditures have decreased, and therefore a lower-tailed test is used.

This is a lower tailed test, using a Z statistic and a 5% level of significance.   Reject H 0 if Z < -1.645.

•   Step 4. Compute the test statistic.  

We do not reject H 0 because -1.26 > -1.645. We do not have statistically significant evidence at α=0.05 to show that the mean expenditures on health care and prescription drugs are lower in 2005 than the mean of $3,302 reported in 2002.  

Recall that when we fail to reject H 0 in a test of hypothesis that either the null hypothesis is true (here the mean expenditures in 2005 are the same as those in 2002 and equal to $3,302) or we committed a Type II error (i.e., we failed to reject H 0 when in fact it is false). In summarizing this test, we conclude that we do not have sufficient evidence to reject H 0 . We do not conclude that H 0 is true, because there may be a moderate to high probability that we committed a Type II error. It is possible that the sample size is not large enough to detect a difference in mean expenditures.      

The NCHS reported that the mean total cholesterol level in 2002 for all adults was 203. Total cholesterol levels in participants who attended the seventh examination of the Offspring in the Framingham Heart Study are summarized as follows: n=3,310, x̄ =200.3, and s=36.8. Is there statistical evidence of a difference in mean cholesterol levels in the Framingham Offspring?

Here we want to assess whether the sample mean of 200.3 in the Framingham sample is statistically significantly different from 203 (i.e., beyond what we would expect by chance). We will run the test using the five-step approach.

H 0 : μ= 203 H 1 : μ≠ 203                       α=0.05

The research hypothesis is that cholesterol levels are different in the Framingham Offspring, and therefore a two-tailed test is used.

•   Step 3. Set up decision rule.  

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or is Z > 1.960.

We reject H 0 because -4.22 ≤ -1. .960. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level in the Framingham Offspring is different from the national average of 203 reported in 2002.   Because we reject H 0 , we also approximate a p-value. Using the two-sided significance levels, p < 0.0001.  

Statistical Significance versus Clinical (Practical) Significance

This example raises an important concept of statistical versus clinical or practical significance. From a statistical standpoint, the total cholesterol levels in the Framingham sample are highly statistically significantly different from the national average with p < 0.0001 (i.e., there is less than a 0.01% chance that we are incorrectly rejecting the null hypothesis). However, the sample mean in the Framingham Offspring study is 200.3, less than 3 units different from the national mean of 203. The reason that the data are so highly statistically significant is due to the very large sample size. It is always important to assess both statistical and clinical significance of data. This is particularly relevant when the sample size is large. Is a 3 unit difference in total cholesterol a meaningful difference?  

Consider again the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. Suppose a new drug is proposed to lower total cholesterol. A study is designed to evaluate the efficacy of the drug in lowering cholesterol.   Fifteen patients are enrolled in the study and asked to take the new drug for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows:   n=15, x̄ =195.9 and s=28.7. Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new drug for 6 weeks? We will run the test using the five-step approach. 

H 0 : μ= 203 H 1 : μ< 203                   α=0.05

•  Step 2. Select the appropriate test statistic.  

Because the sample size is small (n<30) the appropriate test statistic is

This is a lower tailed test, using a t statistic and a 5% level of significance. In order to determine the critical value of t, we need degrees of freedom, df, defined as df=n-1. In this example df=15-1=14. The critical value for a lower tailed test with df=14 and a =0.05 is -2.145 and the decision rule is as follows:   Reject H 0 if t < -2.145.

We do not reject H 0 because -0.96 > -2.145. We do not have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower than the national mean in patients taking the new drug for 6 weeks. Again, because we failed to reject the null hypothesis we make a weaker concluding statement allowing for the possibility that we may have committed a Type II error (i.e., failed to reject H 0 when in fact the drug is efficacious).

This example raises an important issue in terms of study design. In this example we assume in the null hypothesis that the mean cholesterol level is 203. This is taken to be the mean cholesterol level in patients without treatment. Is this an appropriate comparator? Alternative and potentially more efficient study designs to evaluate the effect of the new drug could involve two treatment groups, where one group receives the new drug and the other does not, or we could measure each patient's baseline or pre-treatment cholesterol level and then assess changes from baseline to 6 weeks post-treatment. These designs are also discussed here.

Video - Comparing a Sample Mean to Known Population Mean (8:20)

Link to transcript of the video

Tests with One Sample, Dichotomous Outcome

Hypothesis testing applications with a dichotomous outcome variable in a single population are also performed according to the five-step procedure. Similar to tests for means, a key component is setting up the null and research hypotheses. The objective is to compare the proportion of successes in a single population to a known proportion (p 0 ). That known proportion is generally derived from another study or report and is sometimes called a historical control. It is important in setting up the hypotheses in a one sample test that the proportion specified in the null hypothesis is a fair and reasonable comparator.    

In one sample tests for a dichotomous outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the sample proportion which is computed by taking the ratio of the number of successes to the sample size,

We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formula for the test statistic is given below.

Test Statistic for Testing H 0 : p = p 0

if min(np 0 , n(1-p 0 )) > 5

The formula above is appropriate for large samples, defined when the smaller of np 0 and n(1-p 0 ) is at least 5. This is similar, but not identical, to the condition required for appropriate use of the confidence interval formula for a population proportion, i.e.,

Here we use the proportion specified in the null hypothesis as the true proportion of successes rather than the sample proportion. If we fail to satisfy the condition, then alternative procedures, called exact methods must be used to test the hypothesis about the population proportion.

Example:  

The NCHS report indicated that in 2002 the prevalence of cigarette smoking among American adults was 21.1%.  Data on prevalent smoking in n=3,536 participants who attended the seventh examination of the Offspring in the Framingham Heart Study indicated that 482/3,536 = 13.6% of the respondents were currently smoking at the time of the exam. Suppose we want to assess whether the prevalence of smoking is lower in the Framingham Offspring sample given the focus on cardiovascular health in that community. Is there evidence of a statistically lower prevalence of smoking in the Framingham Offspring study as compared to the prevalence among all Americans?

H 0 : p = 0.211 H 1 : p < 0.211                     α=0.05

We must first check that the sample size is adequate.   Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 3,536(0.211), 3,536(1-0.211))=min(746, 2790)=746. The sample size is more than adequate so the following formula can be used:

This is a lower tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.645.

We reject H 0 because -10.93 < -1.645. We have statistically significant evidence at α=0.05 to show that the prevalence of smoking in the Framingham Offspring is lower than the prevalence nationally (21.1%). Here, p < 0.0001.  

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

Calculate this on your own before checking the answer.

Video - Hypothesis Test for One Sample and a Dichotomous Outcome (3:55)

Tests with Two Independent Samples, Continuous Outcome

There are many applications where it is of interest to compare two independent groups with respect to their mean scores on a continuous outcome. Here we compare means between groups, but rather than generating an estimate of the difference, we will test whether the observed difference (increase, decrease or difference) is statistically significant or not. Remember, that hypothesis testing gives an assessment of statistical significance, whereas estimation gives an estimate of effect and both are important.

Here we discuss the comparison of means when the two comparison groups are independent or physically separate. The two groups might be determined by a particular attribute (e.g., sex, diagnosis of cardiovascular disease) or might be set up by the investigator (e.g., participants assigned to receive an experimental treatment or placebo). The first step in the analysis involves computing descriptive statistics on each of the two samples. Specifically, we compute the sample size, mean and standard deviation in each sample and we denote these summary statistics as follows:

for sample 1:

for sample 2:

The designation of sample 1 and sample 2 is arbitrary. In a clinical trial setting the convention is to call the treatment group 1 and the control group 2. However, when comparing men and women, for example, either group can be 1 or 2.  

In the two independent samples application with a continuous outcome, the parameter of interest in the test of hypothesis is the difference in population means, μ 1 -μ 2 . The null hypothesis is always that there is no difference between groups with respect to means, i.e.,

The null hypothesis can also be written as follows: H 0 : μ 1 = μ 2 . In the research hypothesis, an investigator can hypothesize that the first mean is larger than the second (H 1 : μ 1 > μ 2 ), that the first mean is smaller than the second (H 1 : μ 1 < μ 2 ), or that the means are different (H 1 : μ 1 ≠ μ 2 ). The three different alternatives represent upper-, lower-, and two-tailed tests, respectively. The following test statistics are used to test these hypotheses.

Test Statistics for Testing H 0 : μ 1 = μ 2

• if n 1 > 30 and n 2 > 30
• if n 1 < 30 or n 2 < 30

NOTE: The formulas above assume equal variability in the two populations (i.e., the population variances are equal, or s 1 2 = s 2 2 ). This means that the outcome is equally variable in each of the comparison populations. For analysis, we have samples from each of the comparison populations. If the sample variances are similar, then the assumption about variability in the populations is probably reasonable. As a guideline, if the ratio of the sample variances, s 1 2 /s 2 2 is between 0.5 and 2 (i.e., if one variance is no more than double the other), then the formulas above are appropriate. If the ratio of the sample variances is greater than 2 or less than 0.5 then alternative formulas must be used to account for the heterogeneity in variances.    

The test statistics include Sp, which is the pooled estimate of the common standard deviation (again assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples as follows:

Because we are assuming equal variances between groups, we pool the information on variability (sample variances) to generate an estimate of the variability in the population. Note: Because Sp is a weighted average of the standard deviations in the sample, Sp will always be in between s 1 and s 2 .)

Data measured on n=3,539 participants who attended the seventh examination of the Offspring in the Framingham Heart Study are shown below.  

Suppose we now wish to assess whether there is a statistically significant difference in mean systolic blood pressures between men and women using a 5% level of significance.  

H 0 : μ 1 = μ 2

H 1 : μ 1 ≠ μ 2                       α=0.05

Because both samples are large ( > 30), we can use the Z test statistic as opposed to t. Note that statistical computing packages use t throughout. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The guideline suggests investigating the ratio of the sample variances, s 1 2 /s 2 2 . Suppose we call the men group 1 and the women group 2. Again, this is arbitrary; it only needs to be noted when interpreting the results. The ratio of the sample variances is 17.5 2 /20.1 2 = 0.76, which falls between 0.5 and 2 suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is

We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.

Notice that the pooled estimate of the common standard deviation, Sp, falls in between the standard deviations in the comparison groups (i.e., 17.5 and 20.1). Sp is slightly closer in value to the standard deviation in the women (20.1) as there were slightly more women in the sample.   Recall, Sp is a weight average of the standard deviations in the comparison groups, weighted by the respective sample sizes.  

Now the test statistic:

We reject H 0 because 2.66 > 1.960. We have statistically significant evidence at α=0.05 to show that there is a difference in mean systolic blood pressures between men and women. The p-value is p < 0.010.  

Here again we find that there is a statistically significant difference in mean systolic blood pressures between men and women at p < 0.010. Notice that there is a very small difference in the sample means (128.2-126.5 = 1.7 units), but this difference is beyond what would be expected by chance. Is this a clinically meaningful difference? The large sample size in this example is driving the statistical significance. A 95% confidence interval for the difference in mean systolic blood pressures is: 1.7 + 1.26 or (0.44, 2.96). The confidence interval provides an assessment of the magnitude of the difference between means whereas the test of hypothesis and p-value provide an assessment of the statistical significance of the difference.  

Above we performed a study to evaluate a new drug designed to lower total cholesterol. The study involved one sample of patients, each patient took the new drug for 6 weeks and had their cholesterol measured. As a means of evaluating the efficacy of the new drug, the mean total cholesterol following 6 weeks of treatment was compared to the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. At the end of the example, we discussed the appropriateness of the fixed comparator as well as an alternative study design to evaluate the effect of the new drug involving two treatment groups, where one group receives the new drug and the other does not. Here, we revisit the example with a concurrent or parallel control group, which is very typical in randomized controlled trials or clinical trials (refer to the EP713 module on Clinical Trials).  

A new drug is proposed to lower total cholesterol. A randomized controlled trial is designed to evaluate the efficacy of the medication in lowering cholesterol. Thirty participants are enrolled in the trial and are randomly assigned to receive either the new drug or a placebo. The participants do not know which treatment they are assigned. Each participant is asked to take the assigned treatment for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows.

Is there statistical evidence of a reduction in mean total cholesterol in patients taking the new drug for 6 weeks as compared to participants taking placebo? We will run the test using the five-step approach.

H 0 : μ 1 = μ 2 H 1 : μ 1 < μ 2                         α=0.05

Because both samples are small (< 30), we use the t test statistic. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The ratio of the sample variances, s 1 2 /s 2 2 =28.7 2 /30.3 2 = 0.90, which falls between 0.5 and 2, suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is:

This is a lower-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table (in More Resources to the right). In order to determine the critical value of t we need degrees of freedom, df, defined as df=n 1 +n 2 -2 = 15+15-2=28. The critical value for a lower tailed test with df=28 and α=0.05 is -1.701 and the decision rule is: Reject H 0 if t < -1.701.

Now the test statistic,

We reject H 0 because -2.92 < -1.701. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower in patients taking the new drug for 6 weeks as compared to patients taking placebo, p < 0.005.

The clinical trial in this example finds a statistically significant reduction in total cholesterol, whereas in the previous example where we had a historical control (as opposed to a parallel control group) we did not demonstrate efficacy of the new drug. Notice that the mean total cholesterol level in patients taking placebo is 217.4 which is very different from the mean cholesterol reported among all Americans in 2002 of 203 and used as the comparator in the prior example. The historical control value may not have been the most appropriate comparator as cholesterol levels have been increasing over time. In the next section, we present another design that can be used to assess the efficacy of the new drug.

Video - Comparison of Two Independent Samples With a Continuous Outcome (8:02)

Tests with Matched Samples, Continuous Outcome

In the previous section we compared two groups with respect to their mean scores on a continuous outcome. An alternative study design is to compare matched or paired samples. The two comparison groups are said to be dependent, and the data can arise from a single sample of participants where each participant is measured twice (possibly before and after an intervention) or from two samples that are matched on specific characteristics (e.g., siblings). When the samples are dependent, we focus on difference scores in each participant or between members of a pair and the test of hypothesis is based on the mean difference, μ d . The null hypothesis again reflects "no difference" and is stated as H 0 : μ d =0 . Note that there are some instances where it is of interest to test whether there is a difference of a particular magnitude (e.g., μ d =5) but in most instances the null hypothesis reflects no difference (i.e., μ d =0).  

The appropriate formula for the test of hypothesis depends on the sample size. The formulas are shown below and are identical to those we presented for estimating the mean of a single sample presented (e.g., when comparing against an external or historical control), except here we focus on difference scores.

Test Statistics for Testing H 0 : μ d =0

A new drug is proposed to lower total cholesterol and a study is designed to evaluate the efficacy of the drug in lowering cholesterol. Fifteen patients agree to participate in the study and each is asked to take the new drug for 6 weeks. However, before starting the treatment, each patient's total cholesterol level is measured. The initial measurement is a pre-treatment or baseline value. After taking the drug for 6 weeks, each patient's total cholesterol level is measured again and the data are shown below. The rightmost column contains difference scores for each patient, computed by subtracting the 6 week cholesterol level from the baseline level. The differences represent the reduction in total cholesterol over 4 weeks. (The differences could have been computed by subtracting the baseline total cholesterol level from the level measured at 6 weeks. The way in which the differences are computed does not affect the outcome of the analysis only the interpretation.)

Because the differences are computed by subtracting the cholesterols measured at 6 weeks from the baseline values, positive differences indicate reductions and negative differences indicate increases (e.g., participant 12 increases by 2 units over 6 weeks). The goal here is to test whether there is a statistically significant reduction in cholesterol. Because of the way in which we computed the differences, we want to look for an increase in the mean difference (i.e., a positive reduction). In order to conduct the test, we need to summarize the differences. In this sample, we have

The calculations are shown below.  

Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new medication for 6 weeks? We will run the test using the five-step approach.

H 0 : μ d = 0 H 1 : μ d > 0                 α=0.05

NOTE: If we had computed differences by subtracting the baseline level from the level measured at 6 weeks then negative differences would have reflected reductions and the research hypothesis would have been H 1 : μ d < 0. 

• Step 2 . Select the appropriate test statistic.

This is an upper-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table at the right, with df=15-1=14. The critical value for an upper-tailed test with df=14 and α=0.05 is 2.145 and the decision rule is Reject H 0 if t > 2.145.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

We reject H 0 because 4.61 > 2.145. We have statistically significant evidence at α=0.05 to show that there is a reduction in cholesterol levels over 6 weeks.  

Here we illustrate the use of a matched design to test the efficacy of a new drug to lower total cholesterol. We also considered a parallel design (randomized clinical trial) and a study using a historical comparator. It is extremely important to design studies that are best suited to detect a meaningful difference when one exists. There are often several alternatives and investigators work with biostatisticians to determine the best design for each application. It is worth noting that the matched design used here can be problematic in that observed differences may only reflect a "placebo" effect. All participants took the assigned medication, but is the observed reduction attributable to the medication or a result of these participation in a study.

Video - Hypothesis Testing With a Matched Sample and a Continuous Outcome (3:11)

Tests with Two Independent Samples, Dichotomous Outcome

There are several approaches that can be used to test hypotheses concerning two independent proportions. Here we present one approach - the chi-square test of independence is an alternative, equivalent, and perhaps more popular approach to the same analysis. Hypothesis testing with the chi-square test is addressed in the third module in this series: BS704_HypothesisTesting-ChiSquare.

In tests of hypothesis comparing proportions between two independent groups, one test is performed and results can be interpreted to apply to a risk difference, relative risk or odds ratio. As a reminder, the risk difference is computed by taking the difference in proportions between comparison groups, the risk ratio is computed by taking the ratio of proportions, and the odds ratio is computed by taking the ratio of the odds of success in the comparison groups. Because the null values for the risk difference, the risk ratio and the odds ratio are different, the hypotheses in tests of hypothesis look slightly different depending on which measure is used. When performing tests of hypothesis for the risk difference, relative risk or odds ratio, the convention is to label the exposed or treated group 1 and the unexposed or control group 2.      

For example, suppose a study is designed to assess whether there is a significant difference in proportions in two independent comparison groups. The test of interest is as follows:

H 0 : p 1 = p 2 versus H 1 : p 1 ≠ p 2 .  

The following are the hypothesis for testing for a difference in proportions using the risk difference, the risk ratio and the odds ratio. First, the hypotheses above are equivalent to the following:

• For the risk difference, H 0 : p 1 - p 2 = 0 versus H 1 : p 1 - p 2 ≠ 0 which are, by definition, equal to H 0 : RD = 0 versus H 1 : RD ≠ 0.
• If an investigator wants to focus on the risk ratio, the equivalent hypotheses are H 0 : RR = 1 versus H 1 : RR ≠ 1.
• If the investigator wants to focus on the odds ratio, the equivalent hypotheses are H 0 : OR = 1 versus H 1 : OR ≠ 1.  

Suppose a test is performed to test H 0 : RD = 0 versus H 1 : RD ≠ 0 and the test rejects H 0 at α=0.05. Based on this test we can conclude that there is significant evidence, α=0.05, of a difference in proportions, significant evidence that the risk difference is not zero, significant evidence that the risk ratio and odds ratio are not one. The risk difference is analogous to the difference in means when the outcome is continuous. Here the parameter of interest is the difference in proportions in the population, RD = p 1 -p 2 and the null value for the risk difference is zero. In a test of hypothesis for the risk difference, the null hypothesis is always H 0 : RD = 0. This is equivalent to H 0 : RR = 1 and H 0 : OR = 1. In the research hypothesis, an investigator can hypothesize that the first proportion is larger than the second (H 1 : p 1 > p 2 , which is equivalent to H 1 : RD > 0, H 1 : RR > 1 and H 1 : OR > 1), that the first proportion is smaller than the second (H 1 : p 1 < p 2 , which is equivalent to H 1 : RD < 0, H 1 : RR < 1 and H 1 : OR < 1), or that the proportions are different (H 1 : p 1 ≠ p 2 , which is equivalent to H 1 : RD ≠ 0, H 1 : RR ≠ 1 and H 1 : OR ≠

1). The three different alternatives represent upper-, lower- and two-tailed tests, respectively.  

The formula for the test of hypothesis for the difference in proportions is given below.

Test Statistics for Testing H 0 : p 1 = p

The formula above is appropriate for large samples, defined as at least 5 successes (np > 5) and at least 5 failures (n(1-p > 5)) in each of the two samples. If there are fewer than 5 successes or failures in either comparison group, then alternative procedures, called exact methods must be used to estimate the difference in population proportions.

The following table summarizes data from n=3,799 participants who attended the fifth examination of the Offspring in the Framingham Heart Study. The outcome of interest is prevalent CVD and we want to test whether the prevalence of CVD is significantly higher in smokers as compared to non-smokers.

The prevalence of CVD (or proportion of participants with prevalent CVD) among non-smokers is 298/3,055 = 0.0975 and the prevalence of CVD among current smokers is 81/744 = 0.1089. Here smoking status defines the comparison groups and we will call the current smokers group 1 (exposed) and the non-smokers (unexposed) group 2. The test of hypothesis is conducted below using the five step approach.

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2                 α=0.05

• Step 2.  Select the appropriate test statistic.  

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group. In this example, we have more than enough successes (cases of prevalent CVD) and failures (persons free of CVD) in each comparison group. The sample size is more than adequate so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5. Conclusion.

We do not reject H 0 because -1.960 < 0.927 < 1.960. We do not have statistically significant evidence at α=0.05 to show that there is a difference in prevalent CVD between smokers and non-smokers.  

A 95% confidence interval for the difference in prevalent CVD (or risk difference) between smokers and non-smokers as 0.0114 + 0.0247, or between -0.0133 and 0.0361. Because the 95% confidence interval for the risk difference includes zero we again conclude that there is no statistically significant difference in prevalent CVD between smokers and non-smokers.    

Smoking has been shown over and over to be a risk factor for cardiovascular disease. What might explain the fact that we did not observe a statistically significant difference using data from the Framingham Heart Study? HINT: Here we consider prevalent CVD, would the results have been different if we considered incident CVD?

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We now test whether there is a statistically significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using the five step approach.  

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2              α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group, i.e.,

In this example, we have min(50(0.46), 50(1-0.46), 50(0.22), 50(1-0.22)) = min(23, 27, 11, 39) = 11. The sample size is adequate so the following formula can be used

We reject H 0 because 2.526 > 1960. We have statistically significant evidence at a =0.05 to show that there is a difference in the proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever.

A 95% confidence interval for the difference in proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever is 0.24 + 0.18 or between 0.06 and 0.42. Because the 95% confidence interval does not include zero we concluded that there was a statistically significant difference in proportions which is consistent with the test of hypothesis result. 

Again, the procedures discussed here apply to applications where there are two independent comparison groups and a dichotomous outcome. There are other applications in which it is of interest to compare a dichotomous outcome in matched or paired samples. For example, in a clinical trial we might wish to test the effectiveness of a new antibiotic eye drop for the treatment of bacterial conjunctivitis. Participants use the new antibiotic eye drop in one eye and a comparator (placebo or active control treatment) in the other. The success of the treatment (yes/no) is recorded for each participant for each eye. Because the two assessments (success or failure) are paired, we cannot use the procedures discussed here. The appropriate test is called McNemar's test (sometimes called McNemar's test for dependent proportions).  

Vide0 - Hypothesis Testing With Two Independent Samples and a Dichotomous Outcome (2:55)

Here we presented hypothesis testing techniques for means and proportions in one and two sample situations. Tests of hypothesis involve several steps, including specifying the null and alternative or research hypothesis, selecting and computing an appropriate test statistic, setting up a decision rule and drawing a conclusion. There are many details to consider in hypothesis testing. The first is to determine the appropriate test. We discussed Z and t tests here for different applications. The appropriate test depends on the distribution of the outcome variable (continuous or dichotomous), the number of comparison groups (one, two) and whether the comparison groups are independent or dependent. The following table summarizes the different tests of hypothesis discussed here.

• Continuous Outcome, One Sample: H0: μ = μ0
• Continuous Outcome, Two Independent Samples: H0: μ1 = μ2
• Continuous Outcome, Two Matched Samples: H0: μd = 0
• Dichotomous Outcome, One Sample: H0: p = p 0
• Dichotomous Outcome, Two Independent Samples: H0: p1 = p2, RD=0, RR=1, OR=1

Once the type of test is determined, the details of the test must be specified. Specifically, the null and alternative hypotheses must be clearly stated. The null hypothesis always reflects the "no change" or "no difference" situation. The alternative or research hypothesis reflects the investigator's belief. The investigator might hypothesize that a parameter (e.g., a mean, proportion, difference in means or proportions) will increase, will decrease or will be different under specific conditions (sometimes the conditions are different experimental conditions and other times the conditions are simply different groups of participants). Once the hypotheses are specified, data are collected and summarized. The appropriate test is then conducted according to the five step approach. If the test leads to rejection of the null hypothesis, an approximate p-value is computed to summarize the significance of the findings. When tests of hypothesis are conducted using statistical computing packages, exact p-values are computed. Because the statistical tables in this textbook are limited, we can only approximate p-values. If the test fails to reject the null hypothesis, then a weaker concluding statement is made for the following reason.

In hypothesis testing, there are two types of errors that can be committed. A Type I error occurs when a test incorrectly rejects the null hypothesis. This is referred to as a false positive result, and the probability that this occurs is equal to the level of significance, α. The investigator chooses the level of significance in Step 1, and purposely chooses a small value such as α=0.05 to control the probability of committing a Type I error. A Type II error occurs when a test fails to reject the null hypothesis when in fact it is false. The probability that this occurs is equal to β. Unfortunately, the investigator cannot specify β at the outset because it depends on several factors including the sample size (smaller samples have higher b), the level of significance (β decreases as a increases), and the difference in the parameter under the null and alternative hypothesis.    

We noted in several examples in this chapter, the relationship between confidence intervals and tests of hypothesis. The approaches are different, yet related. It is possible to draw a conclusion about statistical significance by examining a confidence interval. For example, if a 95% confidence interval does not contain the null value (e.g., zero when analyzing a mean difference or risk difference, one when analyzing relative risks or odds ratios), then one can conclude that a two-sided test of hypothesis would reject the null at α=0.05. It is important to note that the correspondence between a confidence interval and test of hypothesis relates to a two-sided test and that the confidence level corresponds to a specific level of significance (e.g., 95% to α=0.05, 90% to α=0.10 and so on). The exact significance of the test, the p-value, can only be determined using the hypothesis testing approach and the p-value provides an assessment of the strength of the evidence and not an estimate of the effect.

Answers to Selected Problems

Dental services problem - bottom of page 5.

• Step 1: Set up hypotheses and determine the level of significance.

α=0.05

• Step 2: Select the appropriate test statistic.

First, determine whether the sample size is adequate.

Therefore the sample size is adequate, and we can use the following formula:

• Step 3: Set up the decision rule.

Reject H0 if Z is less than or equal to -1.96 or if Z is greater than or equal to 1.96.

• Step 4: Compute the test statistic
• Step 5: Conclusion.

We reject the null hypothesis because -6.15<-1.96. Therefore there is a statistically significant difference in the proportion of children in Boston using dental services compated to the national proportion.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Data Analysis with Python

Introduction to Data Analysis

• What is Data Analysis?
• Data Analytics and its type
• How to Install Numpy on Windows?
• How to Install Pandas in Python?
• How to Install Matplotlib on python?
• How to Install Python Tensorflow in Windows?

Data Analysis Libraries

• Pandas Tutorial
• NumPy Tutorial - Python Library
• Data Analysis with SciPy
• Introduction to TensorFlow

Data Visulization Libraries

• Matplotlib Tutorial
• Python Seaborn Tutorial
• Plotly tutorial
• Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis
• Measures of Central Tendency in Statistics
• Measures of spread - Range, Variance, and Standard Deviation
• Interquartile Range and Quartile Deviation using NumPy and SciPy
• Anova Formula
• Skewness of Statistical Data
• How to Calculate Skewness and Kurtosis in Python?
• Difference Between Skewness and Kurtosis
• Histogram | Meaning, Example, Types and Steps to Draw
• Interpretations of Histogram
• Quantile Quantile plots
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
• Using pandas crosstab to create a bar plot
• Exploring Correlation in Python
• Mathematics | Covariance and Correlation
• Factor Analysis | Data Analysis
• Data Mining - Cluster Analysis
• MANOVA Test in R Programming
• Python - Central Limit Theorem
• Probability Distribution Function
• Probability Density Estimation & Maximum Likelihood Estimation
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Poisson Distribution | Definition, Formula, Table and Examples
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret
• Z-Score in Statistics
• How to Calculate Point Estimates in R?
• Confidence Interval
• Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

• ML | Data Preprocessing in Python
• ML | Overview of Data Cleaning
• ML | Handling Missing Values
• Detect and Remove the Outliers using Python

Data Transformation

• Data Normalization Machine Learning
• Sampling distribution Using Python

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data
• Basic DateTime Operations in Python
• Time Series Analysis & Visualization in Python
• How to deal with missing values in a Timeseries in Python?
• How to calculate MOVING AVERAGE in a Pandas DataFrame?
• What is a trend in time series?
• How to Perform an Augmented Dickey-Fuller Test in R
• AutoCorrelation

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects
• Step by Step Predictive Analysis - Machine Learning
• 6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing. 

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

• Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
• The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
• Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Similar reads.

• data-science
• Data Science
• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Quality Improvement
• Talk To Minitab

Understanding Hypothesis Tests: Significance Levels (Alpha) and P values in Statistics

Topics: Hypothesis Testing , Statistics

What do significance levels and P values mean in hypothesis tests? What is statistical significance anyway? In this post, I’ll continue to focus on concepts and graphs to help you gain a more intuitive understanding of how hypothesis tests work in statistics.

To bring it to life, I’ll add the significance level and P value to the graph in my previous post in order to perform a graphical version of the 1 sample t-test. It’s easier to understand when you can see what statistical significance truly means!

Here’s where we left off in my last post . We want to determine whether our sample mean (330.6) indicates that this year's average energy cost is significantly different from last year’s average energy cost of $260.

The probability distribution plot above shows the distribution of sample means we’d obtain under the assumption that the null hypothesis is true (population mean = 260) and we repeatedly drew a large number of random samples.

I left you with a question: where do we draw the line for statistical significance on the graph? Now we'll add in the significance level and the P value, which are the decision-making tools we'll need.

We'll use these tools to test the following hypotheses:

• Null hypothesis: The population mean equals the hypothesized mean (260).
• Alternative hypothesis: The population mean differs from the hypothesized mean (260).

What Is the Significance Level (Alpha)?

The significance level, also denoted as alpha or α, is the probability of rejecting the null hypothesis when it is true. For example, a significance level of 0.05 indicates a 5% risk of concluding that a difference exists when there is no actual difference.

These types of definitions can be hard to understand because of their technical nature. A picture makes the concepts much easier to comprehend!

The significance level determines how far out from the null hypothesis value we'll draw that line on the graph. To graph a significance level of 0.05, we need to shade the 5% of the distribution that is furthest away from the null hypothesis.

In the graph above, the two shaded areas are equidistant from the null hypothesis value and each area has a probability of 0.025, for a total of 0.05. In statistics, we call these shaded areas the critical region for a two-tailed test. If the population mean is 260, we’d expect to obtain a sample mean that falls in the critical region 5% of the time. The critical region defines how far away our sample statistic must be from the null hypothesis value before we can say it is unusual enough to reject the null hypothesis.

Our sample mean (330.6) falls within the critical region, which indicates it is statistically significant at the 0.05 level.

We can also see if it is statistically significant using the other common significance level of 0.01.

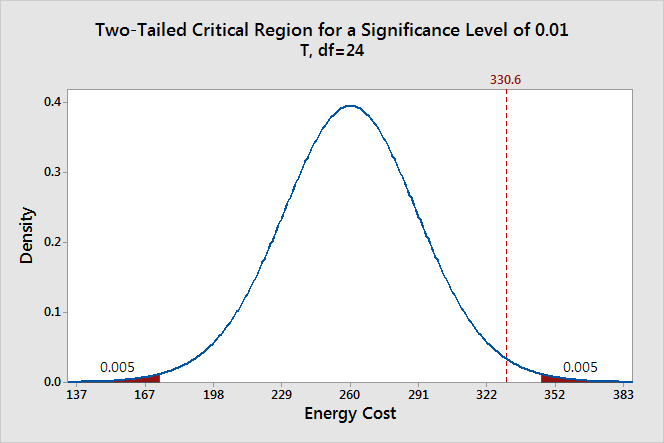
The two shaded areas each have a probability of 0.005, which adds up to a total probability of 0.01. This time our sample mean does not fall within the critical region and we fail to reject the null hypothesis. This comparison shows why you need to choose your significance level before you begin your study. It protects you from choosing a significance level because it conveniently gives you significant results!

Thanks to the graph, we were able to determine that our results are statistically significant at the 0.05 level without using a P value. However, when you use the numeric output produced by statistical software , you’ll need to compare the P value to your significance level to make this determination.

Ready for a demo of Minitab Statistical Software? Just ask! 

What Are P values?

P-values are the probability of obtaining an effect at least as extreme as the one in your sample data, assuming the truth of the null hypothesis.

This definition of P values, while technically correct, is a bit convoluted. It’s easier to understand with a graph!

To graph the P value for our example data set, we need to determine the distance between the sample mean and the null hypothesis value (330.6 - 260 = 70.6). Next, we can graph the probability of obtaining a sample mean that is at least as extreme in both tails of the distribution (260 +/- 70.6).

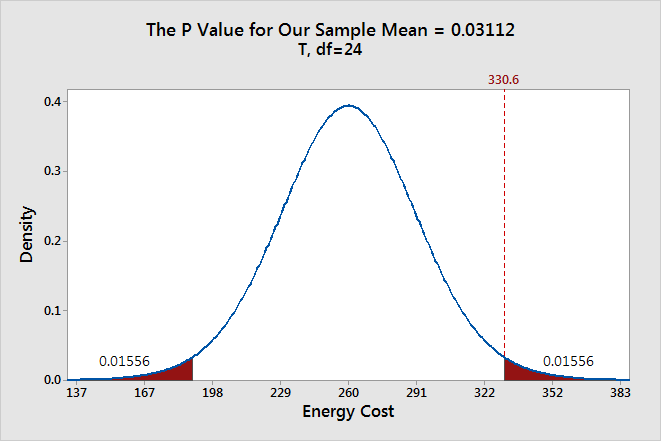
In the graph above, the two shaded areas each have a probability of 0.01556, for a total probability 0.03112. This probability represents the likelihood of obtaining a sample mean that is at least as extreme as our sample mean in both tails of the distribution if the population mean is 260. That’s our P value!

When a P value is less than or equal to the significance level, you reject the null hypothesis. If we take the P value for our example and compare it to the common significance levels, it matches the previous graphical results. The P value of 0.03112 is statistically significant at an alpha level of 0.05, but not at the 0.01 level.

If we stick to a significance level of 0.05, we can conclude that the average energy cost for the population is greater than 260.

A common mistake is to interpret the P-value as the probability that the null hypothesis is true. To understand why this interpretation is incorrect, please read my blog post  How to Correctly Interpret P Values .

Discussion about Statistically Significant Results

A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. A test result is statistically significant when the sample statistic is unusual enough relative to the null hypothesis that we can reject the null hypothesis for the entire population. “Unusual enough” in a hypothesis test is defined by:

• The assumption that the null hypothesis is true—the graphs are centered on the null hypothesis value.
• The significance level—how far out do we draw the line for the critical region?
• Our sample statistic—does it fall in the critical region?

Keep in mind that there is no magic significance level that distinguishes between the studies that have a true effect and those that don’t with 100% accuracy. The common alpha values of 0.05 and 0.01 are simply based on tradition. For a significance level of 0.05, expect to obtain sample means in the critical region 5% of the time when the null hypothesis is true . In these cases, you won’t know that the null hypothesis is true but you’ll reject it because the sample mean falls in the critical region. That’s why the significance level is also referred to as an error rate!

This type of error doesn’t imply that the experimenter did anything wrong or require any other unusual explanation. The graphs show that when the null hypothesis is true, it is possible to obtain these unusual sample means for no reason other than random sampling error. It’s just luck of the draw.

Significance levels and P values are important tools that help you quantify and control this type of error in a hypothesis test. Using these tools to decide when to reject the null hypothesis increases your chance of making the correct decision.

If you like this post, you might want to read the other posts in this series that use the same graphical framework:

• Previous: Why We Need to Use Hypothesis Tests
• Next: Confidence Intervals and Confidence Levels

If you'd like to see how I made these graphs, please read: How to Create a Graphical Version of the 1-sample t-Test .

You Might Also Like

• Trust Center

© 2023 Minitab, LLC. All Rights Reserved.

• Terms of Use
• Privacy Policy
• Cookies Settings

Teach yourself statistics

Hypothesis Test: Difference Between Means

This lesson explains how to conduct a hypothesis test for the difference between two means. The test procedure, called the two-sample t-test , is appropriate when the following conditions are met:

• The sampling method for each sample is simple random sampling .
• The samples are independent .
• Each population is at least 20 times larger than its respective sample .
• The population distribution is normal.
• The population data are symmetric , unimodal , without outliers , and the sample size is 15 or less.
• The population data are slightly skewed , unimodal, without outliers, and the sample size is 16 to 40.
• The sample size is greater than 40, without outliers.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of null and alternative hypotheses. Each makes a statement about the difference d between the mean of one population μ 1 and the mean of another population μ 2 . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

When the null hypothesis states that there is no difference between the two population means (i.e., d = 0), the null and alternative hypothesis are often stated in the following form.

H o : μ 1 = μ 2

H a : μ 1 ≠ μ 2

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the two-sample t-test to determine whether the difference between means found in the sample is significantly different from the hypothesized difference between means.

Analyze Sample Data

Using sample data, find the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.

SE = sqrt[ (s 1 2 /n 1 ) + (s 2 2 /n 2 ) ]

DF = (s 1 2 /n 1 + s 2 2 /n 2 ) 2 / { [ (s 1 2 / n 1 ) 2 / (n 1 - 1) ] + [ (s 2 2 / n 2 ) 2 / (n 2 - 1) ] }

t = [ ( x 1 - x 2 ) - d ] / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, having the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two sample problems illustrate how to conduct a hypothesis test of a difference between mean scores. The first problem involves a two-tailed test; the second problem, a one-tailed test.

Problem 1: Two-Tailed Test

Within a school district, students were randomly assigned to one of two Math teachers - Mrs. Smith and Mrs. Jones. After the assignment, Mrs. Smith had 30 students, and Mrs. Jones had 25 students.

At the end of the year, each class took the same standardized test. Mrs. Smith's students had an average test score of 78, with a standard deviation of 10; and Mrs. Jones' students had an average test score of 85, with a standard deviation of 15.

Test the hypothesis that Mrs. Smith and Mrs. Jones are equally effective teachers. Use a 0.10 level of significance. (Assume that student performance is approximately normal.)

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.

Null hypothesis: μ 1 - μ 2 = 0

Alternative hypothesis: μ 1 - μ 2 ≠ 0

• Formulate an analysis plan . For this analysis, the significance level is 0.10. Using sample data, we will conduct a two-sample t-test of the null hypothesis.

SE = sqrt[(s 1 2 /n 1 ) + (s 2 2 /n 2 )]

SE = sqrt[(10 2 /30) + (15 2 /25] = sqrt(3.33 + 9)

SE = sqrt(12.33) = 3.51

DF = (10 2 /30 + 15 2 /25) 2 / { [ (10 2 / 30) 2 / (29) ] + [ (15 2 / 25) 2 / (24) ] }

DF = (3.33 + 9) 2 / { [ (3.33) 2 / (29) ] + [ (9) 2 / (24) ] } = 152.03 / (0.382 + 3.375) = 152.03/3.757 = 40.47

t = [ ( x 1 - x 2 ) - d ] / SE = [ (78 - 85) - 0 ] / 3.51 = -7/3.51 = -1.99

where s 1 is the standard deviation of sample 1, s 2 is the standard deviation of sample 2, n 1 is the size of sample 1, n 2 is the size of sample 2, x 1 is the mean of sample 1, x 2 is the mean of sample 2, d is the hypothesized difference between the population means, and SE is the standard error.

Since we have a two-tailed test , the P-value is the probability that a t statistic having 40 degrees of freedom is more extreme than -1.99; that is, less than -1.99 or greater than 1.99.

We use the t Distribution Calculator to find P(t < -1.99) is about 0.027.

• If you enter 1.99 as the sample mean in the t Distribution Calculator, you will find the that the P(t ≤ 1.99) is about 0.973. Therefore, P(t > 1.99) is 1 minus 0.973 or 0.027. Thus, the P-value = 0.027 + 0.027 = 0.054.
• Interpret results . Since the P-value (0.054) is less than the significance level (0.10), we cannot accept the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the samples were independent, the sample size was much smaller than the population size, and the samples were drawn from a normal population.

Problem 2: One-Tailed Test

The Acme Company has developed a new battery. The engineer in charge claims that the new battery will operate continuously for at least 7 minutes longer than the old battery.

To test the claim, the company selects a simple random sample of 100 new batteries and 100 old batteries. The old batteries run continuously for 190 minutes with a standard deviation of 20 minutes; the new batteries, 200 minutes with a standard deviation of 40 minutes.

Test the engineer's claim that the new batteries run at least 7 minutes longer than the old. Use a 0.05 level of significance. (Assume that there are no outliers in either sample.)

Null hypothesis: μ 1 - μ 2 <= 7

Alternative hypothesis: μ 1 - μ 2 > 7

where μ 1 is battery life for the new battery, and μ 2 is battery life for the old battery.

• Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a two-sample t-test of the null hypothesis.

SE = sqrt[(40 2 /100) + (20 2 /100]

SE = sqrt(16 + 4) = 4.472

DF = (40 2 /100 + 20 2 /100) 2 / { [ (40 2 / 100) 2 / (99) ] + [ (20 2 / 100) 2 / (99) ] }

DF = (20) 2 / { [ (16) 2 / (99) ] + [ (2) 2 / (99) ] } = 400 / (2.586 + 0.162) = 145.56

t = [ ( x 1 - x 2 ) - d ] / SE = [(200 - 190) - 7] / 4.472 = 3/4.472 = 0.67

where s 1 is the standard deviation of sample 1, s 2 is the standard deviation of sample 2, n 1 is the size of sample 1, n 2 is the size of sample 2, x 1 is the mean of sample 1, x 2 is the mean of sample 2, d is the hypothesized difference between population means, and SE is the standard error.

Here is the logic of the analysis: Given the alternative hypothesis (μ 1 - μ 2 > 7), we want to know whether the observed difference in sample means is big enough (i.e., sufficiently greater than 7) to cause us to reject the null hypothesis.

Interpret results . Suppose we replicated this study many times with different samples. If the true difference in population means were actually 7, we would expect the observed difference in sample means to be 10 or less in 75% of our samples. And we would expect to find an observed difference to be more than 10 in 25% of our samples Therefore, the P-value in this analysis is 0.25.

• Skip to primary navigation
• Skip to main content
• Skip to primary sidebar
• Skip to footer

Understanding Science

How science REALLY works...

• Understanding Science 101
• Misconceptions
• Testing ideas with evidence from the natural world is at the core of science.
• Scientific testing involves figuring out what we would  expect  to observe if an idea were correct and comparing that expectation to what we  actually  observe.
• Scientific arguments are built from an idea and the evidence relevant to that idea.
• Scientific arguments can be built in any order. Sometimes a scientific idea precedes any evidence relevant to it, and other times the evidence helps inspire the idea.

Misconception:  Science proves ideas.

Misconception:  Science can only disprove ideas.

Correction:  Science neither proves nor disproves. It accepts or rejects ideas based on supporting and refuting evidence, but may revise those conclusions if warranted by new evidence or perspectives.  Read more about it.

The core of science: Relating evidence and ideas

In this case, the term  argument  refers not to a disagreement between two people, but to an evidence-based line of reasoning — so scientific arguments are more like the closing argument in a court case (a logical description of what we think and why we think it) than they are like the fights you may have had with siblings. Scientific arguments involve three components: the idea (a  hypothesis  or theory), the  expectations  generated by that idea (frequently called predictions), and the actual observations relevant to those expectations (the evidence). These components are always related in the same logical way:

• What would we expect to see if this idea were true (i.e., what is our expected observation)?
• What do we actually observe?
• Do our expectations match our observations?

PREDICTIONS OR EXPECTATIONS?

When scientists describe their arguments, they frequently talk about their expectations in terms of what a hypothesis or theory predicts: “If it were the case that smoking causes lung cancer, then we’d  predict  that countries with higher rates of smoking would have higher rates of lung cancer.” At first, it might seem confusing to talk about a prediction that doesn’t deal with the future, but that refers to something going on right now or that may have already happened. In fact, this is just another way of discussing the expectations that the hypothesis or theory generates. So when a scientist talks about the  predicted  rates of lung cancer, he or she really means something like “the rates that we’d expect to see if our hypothesis were correct.”

If the idea generates expectations that hold true (are actually observed), then the idea is more likely to be accurate. If the idea generates expectations that don’t hold true (are not observed), then we are less likely to  accept  the idea. For example, consider the idea that cells are the building blocks of life. If that idea were true, we’d expect to see cells in all kinds of living tissues observed under a microscope — that’s our expected observation. In fact, we do observe this (our actual observation), so evidence supports the idea that living things are built from cells.

Though the structure of this argument is consistent (hypothesis, then expectation, then actual observation), its pieces may be assembled in different orders. For example, the first observations of cells were made in the 1600s, but cell theory was not postulated until 200 years later — so in this case, the evidence actually helped inspire the idea. Whether the idea comes first or the evidence comes first, the logic relating them remains the same.

Here, we’ll explore scientific arguments and how to build them. You can investigate:

Putting the pieces together: The hard work of building arguments

• Predicting the past
• Arguments with legs to stand on

Or just click the  Next  button to dive right in!

• Take a sidetrip
• Teaching resources

Scientific arguments rely on testable ideas. To learn what makes an idea testable, review our  Science Checklist .

• Forming hypotheses — scientific explanations — can be difficult for students. It is often easier for students to generate an expectation (what they think will happen or what they expect to observe) based on prior experience than to formulate a potential explanation for that phenomena. You can help students go beyond expectations to generate real, explanatory hypotheses by providing sentence stems for them to fill in: “I expect to observe A because B.” Once students have filled in this sentence you can explain that B is a hypothesis and A is the expectation generated by that hypothesis.
• You can help students learn to distinguish between hypotheses and the expectations generated by them by regularly asking students to analyze lecture material, text, or video. Students should try to figure out which aspects of the content were hypotheses and which were expectations.

Summing up the process

Subscribe to our newsletter

• The science flowchart
• Science stories
• Grade-level teaching guides
• Teaching resource database
• Journaling tool

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.4: Distribution Needed for Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 155549

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Earlier in the course, we discussed sampling distributions. Particular distributions are associated with hypothesis testing. Perform tests of a population mean using a normal distribution or a Student's \(t\)-distribution. (Remember, use a Student's \(t\)-distribution when the population standard deviation is unknown and the distribution of the sample mean is approximately normal.) We perform tests of a population proportion using a normal distribution (usually \(n\) is large or the sample size is large).

If you are testing a single population mean, the distribution for the test is for means :

\[\bar{X} \sim N\left(\mu_{x}, \frac{\sigma_{x}}{\sqrt{n}}\right)\]

The population parameter is \(\mu\). The estimated value (point estimate) for \(\mu\) is \(\bar{x}\), the sample mean.

If you are testing a single population proportion, the distribution for the test is for proportions or percentages:

\[P' \sim N\left(p, \sqrt{\frac{p-q}{n}}\right)\]

The population parameter is \(p\). The estimated value (point estimate) for \(p\) is \(p′\). \(p' = \frac{x}{n}\) where \(x\) is the number of successes and n is the sample size.

Assumptions

When you perform a hypothesis test of a single population mean \(\mu\) using a Student's \(t\)-distribution (often called a \(t\)-test), there are fundamental assumptions that need to be met in order for the test to work properly. Your data should be a simple random sample that comes from a population that is approximately normally distributed. You use the sample standard deviation to approximate the population standard deviation. (Note that if the sample size is sufficiently large, a \(t\)-test will work even if the population is not approximately normally distributed).

When you perform a hypothesis test of a single population mean \(\mu\) using a normal distribution (often called a \(z\)-test), you take a simple random sample from the population. The population you are testing is normally distributed or your sample size is sufficiently large. You know the value of the population standard deviation which, in reality, is rarely known.

When you perform a hypothesis test of a single population proportion \(p\), you take a simple random sample from the population. You must meet the conditions for a binomial distribution which are: there are a certain number \(n\) of independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of a success \(p\). The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities \(np\) and \(nq\) must both be greater than five \((np > 5\) and \(nq > 5)\). Then the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with \(\mu = p\) and \(\sigma = \sqrt{\frac{pq}{n}}\). Remember that \(q = 1 – p\).

In order for a hypothesis test’s results to be generalized to a population, certain requirements must be satisfied.

When testing for a single population mean:

• A Student's \(t\)-test should be used if the data come from a simple, random sample and the population is approximately normally distributed, or the sample size is large, with an unknown standard deviation.
• The normal test will work if the data come from a simple, random sample and the population is approximately normally distributed, or the sample size is large, with a known standard deviation.

When testing a single population proportion use a normal test for a single population proportion if the data comes from a simple, random sample, fill the requirements for a binomial distribution, and the mean number of successes and the mean number of failures satisfy the conditions: \(np > 5\) and \(nq > 5\) where \(n\) is the sample size, \(p\) is the probability of a success, and \(q\) is the probability of a failure.

Formula Review

If there is no given preconceived \(\alpha\), then use \(\alpha = 0.05\).

Types of Hypothesis Tests

• Single population mean, known population variance (or standard deviation): Normal test .
• Single population mean, unknown population variance (or standard deviation): Student's \(t\)-test .
• Single population proportion: Normal test .
• For a single population mean , we may use a normal distribution with the following mean and standard deviation. Means: \(\mu = \mu_{\bar{x}}\) and \(\\sigma_{\bar{x}} = \frac{\sigma_{x}}{\sqrt{n}}\)
• A single population proportion , we may use a normal distribution with the following mean and standard deviation. Proportions: \(\mu = p\) and \(\sigma = \sqrt{\frac{pq}{n}}\).
• It is continuous and assumes any real values.
• The pdf is symmetrical about its mean of zero. However, it is more spread out and flatter at the apex than the normal distribution.
• It approaches the standard normal distribution as \(n\) gets larger.
• There is a "family" of \(t\)-distributions: every representative of the family is completely defined by the number of degrees of freedom which is one less than the number of data items.

Lara Trump Failed the Hogan Test

I n this era of political correctness and cancel culture, it’s amazing what you just can’t say anymore. Like, for example, that the rule of law is good and worthy of respect.

That’s what the Republican U.S. Senate candidate Larry Hogan is finding out. Last week, minutes before a jury announced that it had found former President Donald Trump guilty of 34 felonies , Hogan, who is running in Maryland, posted on X : “Regardless of the result, I urge all Americans to respect the verdict and the legal process. At this dangerously divided moment in our history, all leaders—regardless of party—must not pour fuel on the fire with more toxic partisanship. We must reaffirm what has made this nation great: the rule of law.”

This is extremely mild stuff. Once upon a time, respecting the rule of law was not controversial. Not anymore. Chris LaCivita, a Trump aide who is also a top Republican National Committee official, replied , “You just ended your campaign.” And on CNN’s State of the Union on Sunday, the RNC co-chair (and Trump daughter-in-law) Lara Trump refused to say whether the RNC would support Hogan’s campaign but attacked the anodyne statement furiously.

[ Adam Serwer: Trump wishes his trial were rigged ]

“I will tell you one thing. I don't support what he just said there. I think it's ridiculous,” she said . “He doesn't deserve the respect of anyone in the Republican Party at this point and, quite frankly, anybody in America, if that's the way you feel. That's very upsetting to hear that.”

This is deeply corrosive. Lara Trump is well within her rights to be upset about anyone criticizing her father-in-law. The RNC can even cut Hogan off if it wants; political parties can back or not back whomever they choose. And anyone is entitled to questionable arguments about the verdict. But although Trump wasn’t ready to announce anything as drastic as a decision about political spending, she had no hesitations about blasting Hogan for respecting the rule of law, a hallmark of the American experiment.

(One person who’s probably not upset about all of this is Hogan, a former governor who’s trying to win a Senate seat in a very blue state and who has been running ads on TV saying that the GOP can’t rely on his vote. What better way to demonstrate that than a public feud with the RNC?)

Less than 15 years ago, when Barack Obama criticized the Supreme Court for its ruling in Citizens United in his 2010 State of the Union speech, he faced a chorus of critics from both the right and the left , saying that such a public attack on the justices was inappropriate. Today, as Lara Trump attacks the rule of law itself, “responsible” Trump-skeptical conservatives are criticizing her, but rather than recoiling from the substance, they seem mostly worried that she is endangering the GOP’s chances at winning a Senate seat: “Internecine warfare may make for some lively prime-time cable news segments, but it’s no way to run a national party,” writes Noah Rothman. What about a nation, though?

In a separate interview over the weekend, Donald Trump suggested—or, depending on your view, made a veiled threat—that if he were sentenced to jail, mass violence might result . These flashy statements rightly drew a great deal of attention. But as my colleagues Ali Breland and Juliette Kayyem wrote, the immediate danger of serious violence seems low.

[ Read: The MAGA internet calls for war ]

Lara Trump’s statements are less flashy, but they, too, pose a great danger in the long run. Scholars who study threats to democracy have found that the words and actions of political leaders are an essential factor in driving the spread and effect of anti-democratic attitudes. The presidential scholar and occasional Atlantic contributor Tim Naftali predicted on Friday that trashing the judicial system would become a new litmus test for any Republican who wants to remain in Donald Trump’s good graces. He’s already being proved right.

The FDA Wants To Reschedule Cannabis. Does That Mean All Employees Can Soon Legally Use It?

On May 21, 2024, the Drug Enforcement Agency (DEA) issued a notice of proposed rulemaking indicating that the U.S Food and Drug Administration (FDA) intends to transfer marijuana from Schedule I to Schedule III of the Controlled Substances Act (CSA). This notice is consistent with opinions from the Department of Health and Human Services (HHS) acknowledging that marijuana has currently accepted medical uses as well as HHS’s views about marijuana’s abuse potential and level of physical or psychological dependence. But assuming that the proposed rescheduling goes through, does that mean that cannabis is now federally legal, leaving employees free to consume cannabis like any other legal substances such as alcohol?

The short answer is “no.”

While rescheduling cannabis as a Schedule III drug may go a long way to opening doors for additional cannabis research and generally changing perceptions on cannabis use, such rescheduling does not make possession or use of cannabis “legal” at the federal level. The federal ban, though, is still against the weight of the direction many states are heading across the country. Recreational cannabis is now legal in 24 states and the District of Columbia. Considering that just 12 years ago there were only two states with legal recreational cannabis, it is not hard to see where the trend is heading. In fact, when accounting for medical cannabis programs, there are now only six states that do not offer any sort of legalized cannabis.

Perhaps unsurprisingly, recent drug testing data suggests that the increasing legality at the state level is resulting in increased cannabis use across the country. Positive drug tests for cannabis are on the rise. In Michigan, for example, positive cannabis drug tests have more than tripled since 2008. Notably, while cannabis positive tests are on the rise, use of other drugs such as opiates and cocaine have been steadily decreasing. Another study related to drug testing showed that employees are increasingly trying to thwart these drug tests. In 2023, drug tests with signs of tampering increased an astonishing 633% — the highest rate in more than 30 years.

With all these factors in mind, what might the “best practice” be for employers as it relates to the treatment of cannabis among their workforce? Of course, the answer is not a “one-size-fits-all” issue. The decision will depend on a number of factors, including certain jurisdictions’ prohibition on testing for cannabis , anti-discrimination laws protecting the use of cannabis, laws requiring drug testing for certain jobs, and position-specific questions surrounding job duties (e.g., desk job versus operating heavy machinery or other safety-sensitive positions). Still, what many employers may have considered as a best practice for years is one that should be reconsidered in light of these rapid developments.

Foley’s Labor & Employment Group, with the support of Foley’s Cannabis Law Team, is ready to help employers navigate this ever-evolving landscape.

Patrick J. McMahon

Senior Counsel

Related Insights

Nineteen states sue to enjoin new eeoc harassment guidance, proceed with caution when taking the human out of human resources: the colorado artificial intelligence act will have immediate impact on employers, proposed warehouse worker protection act could have major implications for businesses employing warehouse workers.

Salesforce is closed for new business in your area.