two sample hypothesis test worksheet

• Number Theory
• Data Structures
• Cornerstones

Exercises - Hypothesis Testing (Two Samples)

Accessibility options:

• Jump to content
• Accessibility

For the help you need to support your course

• Communities

Find resources by…

• Case study  
• Topic e.g. The Steps Glossary
• Resource type e.g. Video, Paper based
• Let me choose See all
• Resource types
• 03. Teach Yourself Worksheets - Two-Sample t-tests

Two-Sample t-tests resources

Show me all resources applicable to both students & staff students only staff only

03. Teach Yourself Worksheets (4)

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Minitab quick guide.

Minitab ®

Access Minitab Web , using Google Chrome  .

Click on the section to view the Minitab procedures.

After saving the Minitab File to your computer or cloud location, you must first open Minitab .

• To open a Minitab project (.mpx file): File > Open > Project
• To open a data file (.mtw, .csv or .xlsx): File > Open > Worksheet

Descriptive, graphical

• Bar Chart : Graph > Bar Chart > Counts of unique values > One Variable
• Pie Chart : Graph > Pie Chart > Counts of unique values > Select Options > Under Label Slices With choose Percent

Descriptive, numerical

• Frequency Tables : Stat > Tables > Tally Individual Variables

Inference (one proportion)

Hypothesis Test

• With raw data : Stat > Basic Statistics > 1 Proportion > Select variable > Check Perform hypothesis test and enter null value > Select Options tab > Choose correct alternative > Under method , choose Normal approximation
• With summarized data : Stat > Basic Statistics > 1 Proportion > Choose Summarized data from the dropdown menu > Enter data > Check Perform hypothesis test and enter null value > Select Options tab > Choose correct alternative > Under method, choose Normal approximation

Confidence Interval

• With raw data : Stat > Basic Statistics > 1 Proportion > Select variable > Select Options tab > Enter correct confidence level, make sure the alternative is set as not-equal, and choose Normal approximation method
• Histogram : Graph > Histogram > Simple
• Dotplot : Graph > Dotplot > One Y, Simple
• Boxplot : Graph > Boxplot > One Y, Simple
• Mean, Std. Dev., 5-number Summary, etc .: Stat > Basic Statistics > Display Descriptive Statistics > Select Statistics tab to choose exactly what you want to display

Inference (one mean)

• With raw data : Stat > Basic Statistics > 1-Sample t > Select variable > Check Perform hypothesis test and enter null value > Select Options tab > Choose the correct alternative
• With summarized data : Stat > Basic Statistics > 1-Sample t > Select Summarized data from the dropdown menu > Enter data (n, x-bar, s) > Check Perform hypothesis test and enter null value > Select Options tab > Choose correct alternative
• With raw data : Stat > Basic Statistics > 1-Sample t > Select variable > Select Options tab > Enter correct confidence level and make sure the alternative is set as not-equal
• With summarized data : Stat > Basic Statistics > 1-Sample t > Select Summarized data from the dropdown menu > Enter data (n, x-bar, s) > Select Options tab > Enter correct confidence level and make sure the alternative is set as not-equal
• Side-by-side Histograms : Graph > Histogram > Under One Y Variable , select Groups Displayed Separately > Enter the categorical variable under Group Variables > Choose In separate panels of one graph under Display Groups
• Side-by-side Dotplots : Graph > Dotplot > One Y Variable , Groups Displayed on the Scale
• Side-by-side Boxplots : Graph > Boxplot > One Y, With Categorical Variables
• Mean, Std. Dev., 5-number Summary, etc .: Stat > Basic Statistics > Display Descriptive Statistics > Select variables (enter the categorical variable under By variables ) > Select Statistics tab to choose exactly what you want to display

Inference (independent samples)

• With raw data : Stat > Basic Statistics > 2-Sample t > Select variables (response/quantitative as Samples and explanatory/categorical as Sample IDs ) > Select Options tab > Choose correct alternative
• With summarized data : Stat > Basic Statistics > 2-Sample t > Select Summarized data from the dropdown menu > Enter data > Select Options tab > Choose correct alternative
• Same as above, choose confidence level and make sure the alternative is set as not-equal

Inference (paired difference)

• Stat > Basic Statistics > Paired t > Enter correct columns in Sample 1 and Sample 2 boxes > Select Options tab > Choose correct alternative
• Scatterplot : Graph > Scatterplot > Simple > Enter the response variable under Y variables and the explanatory variable under X variables
• Fitted Line Plot : Stat > Regression > Fitted Line Plot > Enter the response variable under Response (y) and the explanatory variable under Predictor (x)
• Correlation : Stat > Basic Statistics > Correlation > Select Graphs tab > Click Statistics to display on plot and select Correlations
• Correlation : Stat > Basic Statistics > Correlation > Select Graphs tab > Click Statistics to display on plot and select Correlations and p-values
• Regression Line : Stat > Regression > Regression > Fit Regression Model > Enter the response variable under Responses and the explanatory variable under Continuous predictors > Select Results tab > Click Display of results and select Basic tables ( Note : if you want the confidence interval for the population slope, change “display of results” to “expanded table.” With the expanded table, you will get a lot of information on the output that you will not understand.)
• Side-by-side Bar Charts with raw data : Graph > Bar Chart > Counts of unique values > Multiple Variables
• Side-by-side Bar Charts with a two-way table : Graph > Bar Chart > Summarized Data in a Table > Under Two-Way Table choose Clustered or Stacked > Enter the columns that contain the data under Y-variables and enter the column that contains your row labels under Row labels
• Two-way Table : Stat > Tables > Cross Tabulation and Chi-square

Inference (difference in proportions)

• Using a dataset : Stat > Basic Statistics > 2 Proportions > Select variables (enter response variable as Samples and explanatory variable as Sample IDs ) > Select Options tab > Choose correct alternative
• Using a summary table : Stat > Basic Statistics > 2 Proportions > Select Summarized data from the dropdown menu > Enter data > Select Options tab > Choose correct alternative
• Same as above, choose confidence level and make sure the alternative is set as not equal

Inference (Chi-squared test of association)

• Stat > Tables > Chi-Square Test for Association > Choose correct data option (raw or summarized) > Select variables > Select Statistics tab to choose the statistics you want to display
• Fit multiple regression model : Stat > Regression > Regression > Fit Regression Model > Enter the response variable under Responses , the quantitative explanatory variables under Continuous predictors , and any categorical explanatory variables under Categorical predictors > Select Results tab > Click Display of results and select Basic tables ( Note : if you want the confidence intervals for the coefficients, change display of results to expanded table . You will get a lot of information on the output that you will not understand.)
• Make a prediction or prediction interval using a fitted model : Stat > Regression > Regression > Predict > Enter values for each explanatory variable

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.5: Hypothesis Testing for Two Means and Two Proportions (Worksheet)

• Last updated
• Save as PDF
• Page ID 113364

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

Student Learning Outcomes

• The student will select the appropriate distributions to use in each case.
• The student will conduct hypothesis tests and interpret the results.
• the business section from two consecutive days’ newspapers
• three small packages of M&Ms®
• five small packages of Reese's Pieces®

Increasing Stocks Survey

• \(H_{0}\): _________
• \(H_{a}\) : _________
• In words, define the random variable.
• The distribution to use for the test is _____________.
• Calculate the test statistic using your data.

• Calculate the \(p\text{-value}\).
• Do you reject or not reject the null hypothesis? Why?
• Write a clear conclusion using a complete sentence.

Decreasing Stocks Survey

• \(H_{0}\): ________
• \(H_{a}\) : ________

• Calculate the \(p\text{-value}\):

Candy Survey

Buy three small packages of M&Ms and five small packages of Reese's Pieces (same net weight as the M&Ms). Test whether or not the mean number of candy pieces per package is the same for the two brands.

• \(H_{a}\): ________
• What distribution should be used for this test?

Shoe Survey

Test whether women have, on average, more pairs of shoes than men. Include all forms of sneakers, shoes, sandals, and boots. Use your class as the sample.

• The distribution to use for the test is ________________.

5 Ways to Find P-Value in Microsoft Excel

If you’re wondering how to find p-values in Excel, you’ve reached the right resource. Keep reading!

Microsoft Excel offers a little over 100 statistical analysis functions. However, you won’t find a function that says p-value. If you’re an expert in statistics and Excel you’ll know that the output of certain statistical formulas are p-values and there’s no need to create a dedicated formula named p-value.

If you’re new to statistics and Excel this article is just for you.

Determining the p-value for different types of hypothesis testing in Excel is a complicated skill. You must choose the Excel functions or tools carefully and verify if the underlying formulas align with the statistical analysis you’re doing.

In this effortless Excel tutorial, I’ll explain all popular Excel functions and tools you can use to calculate p-values in easy steps. I’ll also mention which method is suitable for which experiments of hypothesis. Furthermore, you’ll find here real-world datasets so you can easily relate to the problem at hand.

Moreover, you’ll discover advanced Excel automation techniques that enable you to find p-values more intuitively than all conventional methods.

Let’s dive in!

What Is P-Value?

Think of the p-value (the probability value) like a detective’s clue in a mystery. It tells you if the evidence (data) you have is strong enough to believe a certain idea.

For example, let’s say you have a hypothesis that eating breakfast makes you smarter. You do a study and find a p-value of 0.03 . This means there’s only a 3% chance the results are due to luck or random chance.

So, a low p-value suggests your idea might be true, like finding a strong clue in a mystery. But a high p-value , like 0.5 , means the evidence isn’t very convincing, like finding a weak clue that might not lead anywhere.

In short, the p-value helps you decide if your findings are worth believing, just like a detective uses clues to solve a case.

Find P-Value Using the T.TEST Function

The T.TEST function in Excel is a statistical function you can use to determine whether two samples are correlated. Whether it’s likely or not likely to have come from the same two underlying populations with the same mean.

It’s also known as the Student’s t-test and the function returns the probability associated ( p-value ) with the null hypothesis of your study.

The null hypothesis in which the T.TEST function be used could be as outlined below:

“ You’re assuming that there’s no significant difference between the means of the two populations from which you’ve drawn the samples. “

Scenarios where you can use this method could be:

• Medical trials to determine if a new drug treatment yields significantly different outcomes compared to a control group.
• To analyze if there’s a significant difference in customer response rates to different advertising strategies in different marketing campaigns.
• To compare the effectiveness of two training methods by analyzing the performance metrics of employees who underwent each.

Whenever you need to test if the null hypothesis mentioned above is true or not for two given lists of values as in Sample 1 and Sample 2 , you can use the T.TEST function.

Organize your input dataset as shown in the above screenshot.

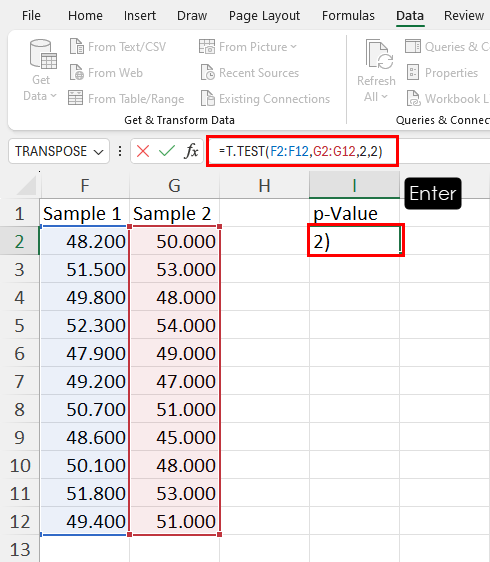
Go to I2 or wherever you want to get the p-value and enter the following formula in it:

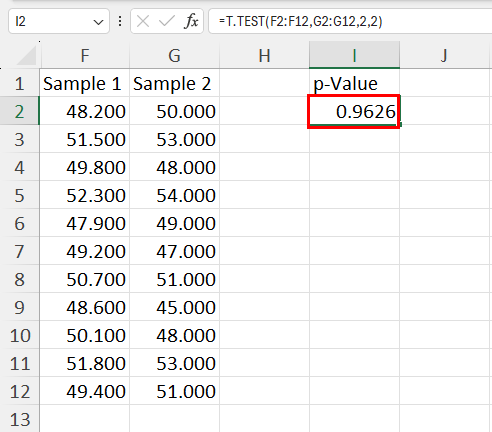
Hit Enter to calculate the p-value .

In the above formula, F2:F12 and G2:G12 are references for Sample 1 and Sample 2 . The first numeric value 2 tells Excel that you’re looking for a two-tailed distribution and the second numeric value 2 indicates that you’ve opted for a two-sample equal variance t-Test . So, customize your inputs according to the specific statistical problem you’re solving.

A higher p-value , often more than 0.05 indicates that there’s a solid ground that the null hypothesis is true. The datasets in Sample 1 and Sample 2 are related because I pulled them from two similar populations having a matching average or mean value.

However, it depends on the alpha or the level of significance you’ve chosen when starting the experiment.

Find P-Value Using the Z.TEST Function

You can use Z.TEST to calculate the p-value which is the one-tailed probability value of the following null hypothesis:

“ There’s no significant difference between the sample mean and the population mean. “

In this case, you know the mean and standard deviation of the population.

Find below some common statistical experiments where you can use the Z.TEST function:

• Analyzing the performance of students on a standardized test and determining if their average score differs significantly from the national average.
• Testing the effectiveness of a new drug treatment by comparing the average recovery time of patients to a known population average.
• Assessing whether the average wait times in two different customer service queues are statistically different from each other.

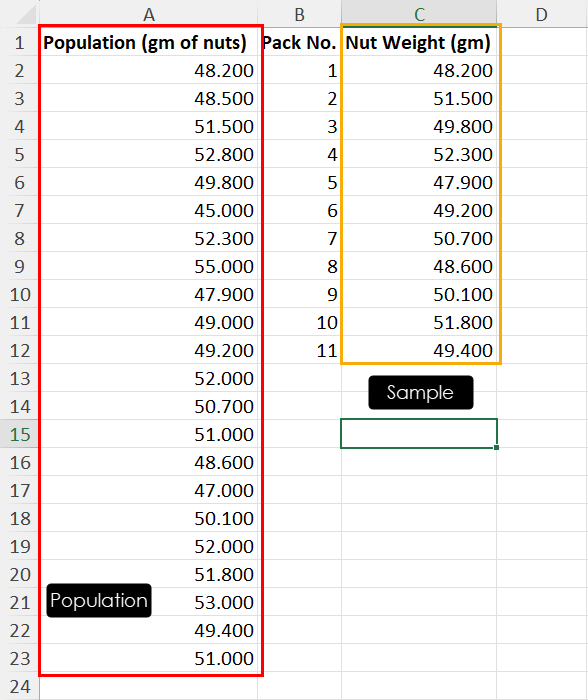
In the above dataset, I’ve drawn 11 samples from a population of 22 chocolate nutty bars. I aim to prove that the mean weight of the nuts in the population isn’t significantly different from the mean weight of nuts in the drawn sample.

I’ve also calculated the required basic statistics for the population data as shown above.

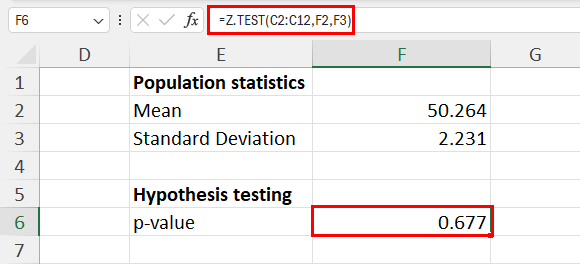
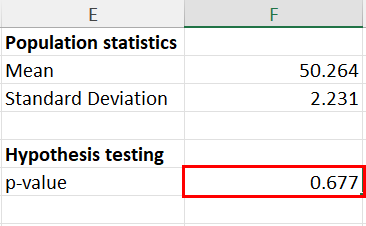
Now, I can easily find the p-value for this experiment in F6 by entering this formula:

In the above formula, you simply need to enter the cell range for the sample dataset ( C2:C12 ), the mean of the population ( F2 ), and the standard deviation of the population ( F3 ).

The p-value of this Z-test experiment is 0.677 which suggests that the null hypothesis is true.

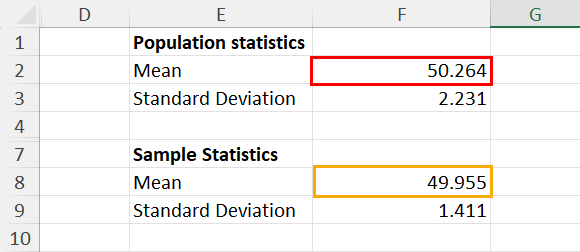
The mean of the population and sample datasets aren’t significantly different.

Find P-Value Using the F.TEST Function

The F.TEST function helps prove whether the following null hypothesis value is true or not by generating a p-value as the output:

“ That the variances of the two populations are equal. “

If the p-value is below the significance level value or the alpha of the experiment, suppose, 0.05 , then the null hypothesis isn’t true, and vice versa.

So, when you’re comparing the variance of two samples drawn potentially from different populations you use F.TEST to calculate the p-value and not any other methods explained so far.

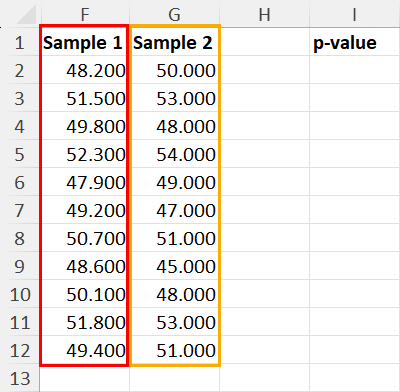
Using this method is too easy. Just arrange the input datasets of two different samples as shown above.

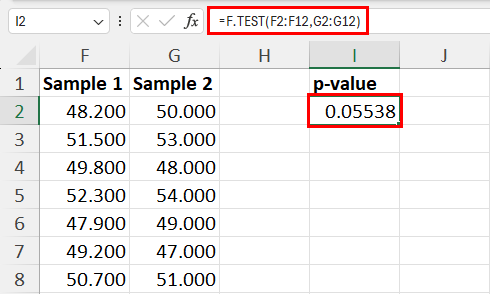
Now, use the following formula in the cell where you’d like to generate the p-value of the F-test:

You only need to enter the references of the two sample datasets in any order.

The p-value of the example dataset is 0.553 which is more than the alpha ( 0.05 ) set for the experiment. Hence, the null hypothesis is valid.

Find P-Value Using Data Analysis ToolPak

The Data Analysis ToolPak add-in allows you to find the p-value using a graphical user interface. Also, there are additional inputs you can use to refine the results. However, you must possess some previous experience in statistical data analysis to use the add-in effectively.

Using Regression

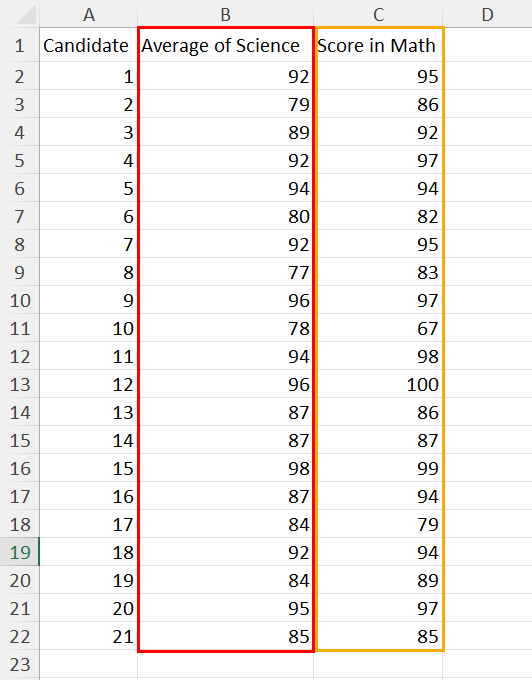
Suppose, you’ve got a dataset as shown above. Here, you’re studying if there’s any correlation between the average grades of the science subjects and that of the individual math grades.

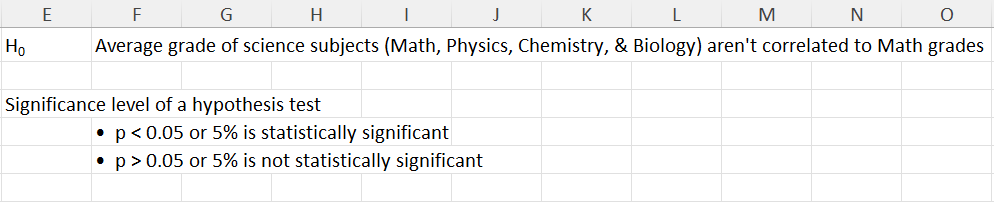
In this problem, your null hypothesis should be as outlined below:

“ Average grades of science subjects (Math, Physics, Chemistry, & Biology) aren’t correlated to Math grades. “

You’ve aimed for an alpha or significance level 0.05 as the cut-off to determine if the null hypothesis stands or not.

Now, follow this simple Excel tutorial to activate the Data Analysis ToolPak add-in in your Excel desktop app:

📒 Read More : How to Install Data Analysis Toolpak in Microsoft Excel

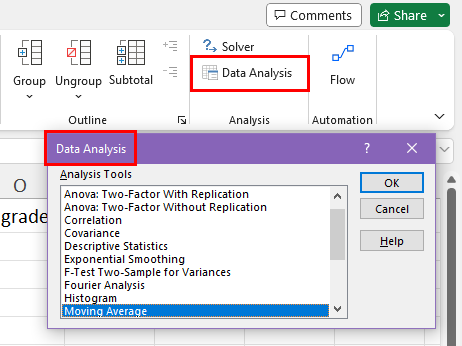
If you’ve already done it, go to the Data tab and click on the Data Analysis command inside the Analysis block.

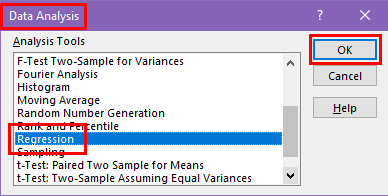
You shall see the Data Analysis dialog box.

Scroll down the scroll bar to find the Regression tool, select it, and click the OK button.

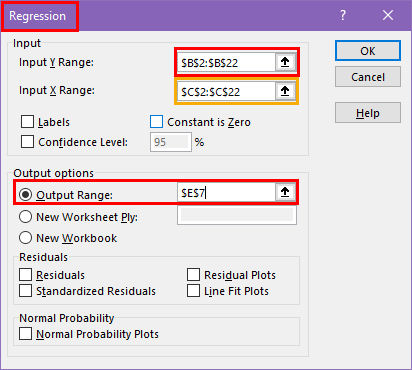
You should now see the Regression analysis configuration dialog.

Choose the dependent variable or the outcome variable that you are trying to predict or explain in the Input Y Range field. In the current exercise, it’s the Average of Science column.

Select the independent variables or predictors that are believed to influence the dependent variable in the Input X Range field. In the present example, it’s the Score in Math .

Click on the Output Range option and select a blank cell on the active worksheet. From this cell, Excel shall start printing the result of the Regression analysis.

Click OK to start the analysis.

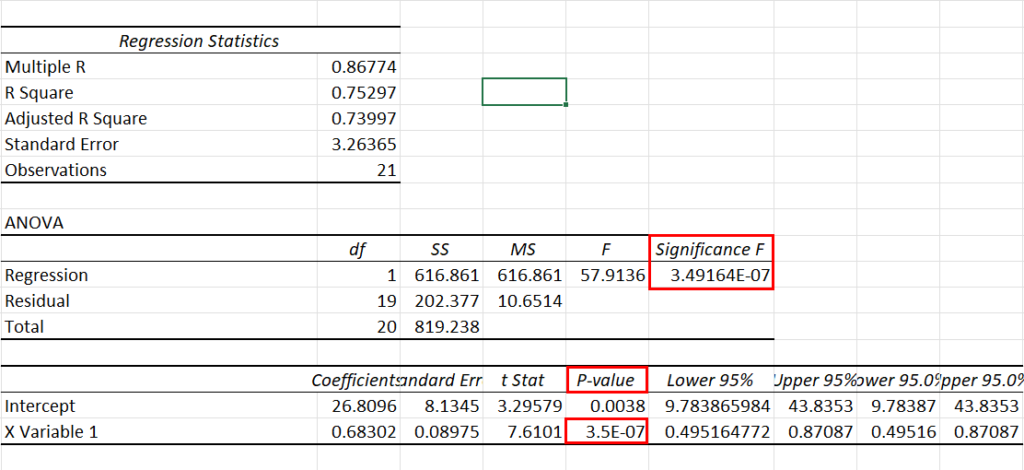
You’ll see a Regression analysis chart as shown above. In the screenshot, I’ve highlighted the cells where you’ll find the p-value.

The p-value calculated in this example is 0.0000003 . This is far lower than the alpha value of 0.05 . It indicates that the null hypothesis doesn’t stand. There’s a correlation between the grades obtained in all the subjects of science and individual grades in math.

Using t-Test

If you wish to perform advanced t-Test on Excel you can use various t-Test tools available in the Data Analysis ToolPak add-in.

Follow the steps mentioned earlier to bring up the Data Analysis dialog.

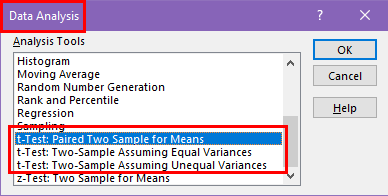
Scroll down to find three different types of t-Tests you can choose from.

Let’s go ahead with the t-Test: Paired Two Sample for Means . Click OK to bring up the dialog box.

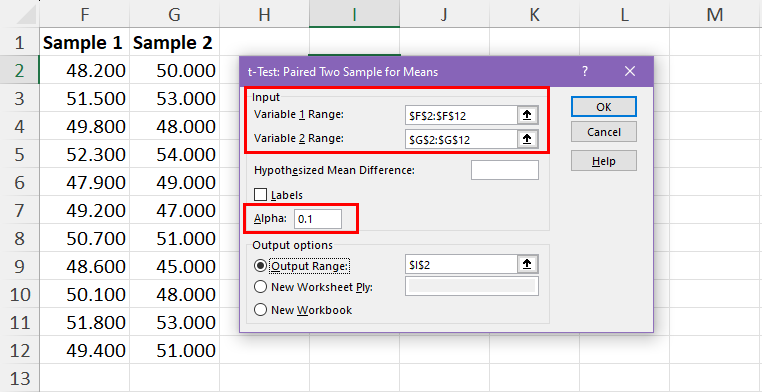
Enter the sample dataset ranges in the Variable 1 Range and Variable 2 Range fields.

Enter the significance level you’re aiming for in the Alpha field.

Select the Output Range and choose a cell as the destination for the results.

Click OK to perform the t-Test .

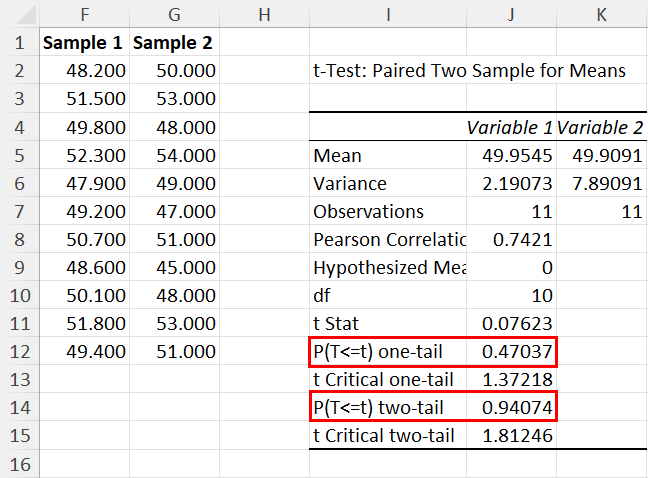
I’ve highlighted the cells in the above screenshot where you should find the p-values .

Find P-Value Using Excel VBA

Suppose, you find it challenging to remember various formula syntaxes and arguments of Excel functions. Or, you’d like to automate the task of finding the p-value using a programmatic method. In both scenarios, you can use Excel VBA.

You can create a VBA macro using the following script:

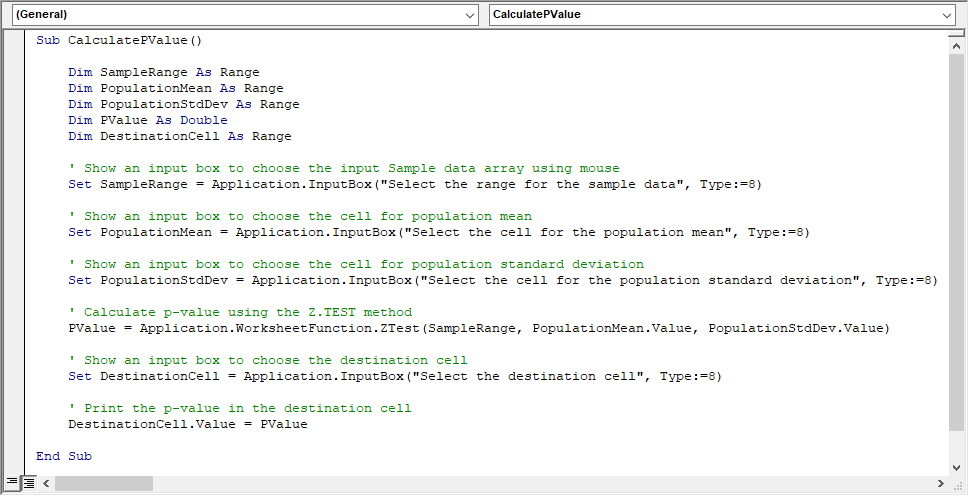
To learn the steps to create a VBA macro using a VBA script, read this Excel article now:

📒 Read More : How To Use The VBA Code You Find Online

The above script visually guides you to calculate p-values using the Z.TEST function.

You shall see the following prompts if you ruin the macro:

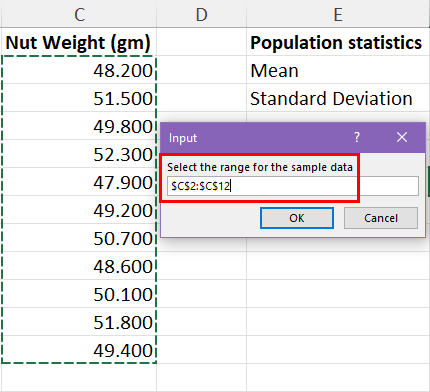
• Input box for the sample dataset

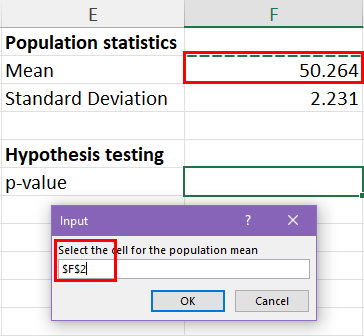
• Prompt for the population mean

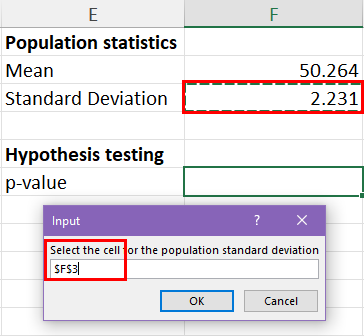
• Input box for the population standard deviation

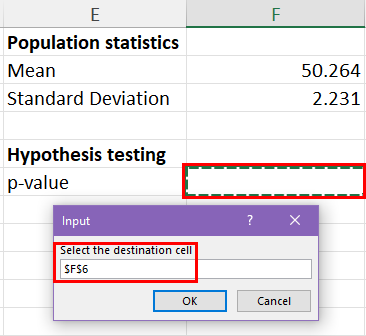
• Prompt for destination cell range

When you go through the above steps, Excel calculates the p-value in the selected cell.

If you wish to calculate the p-value with the t-Test, use the following script:

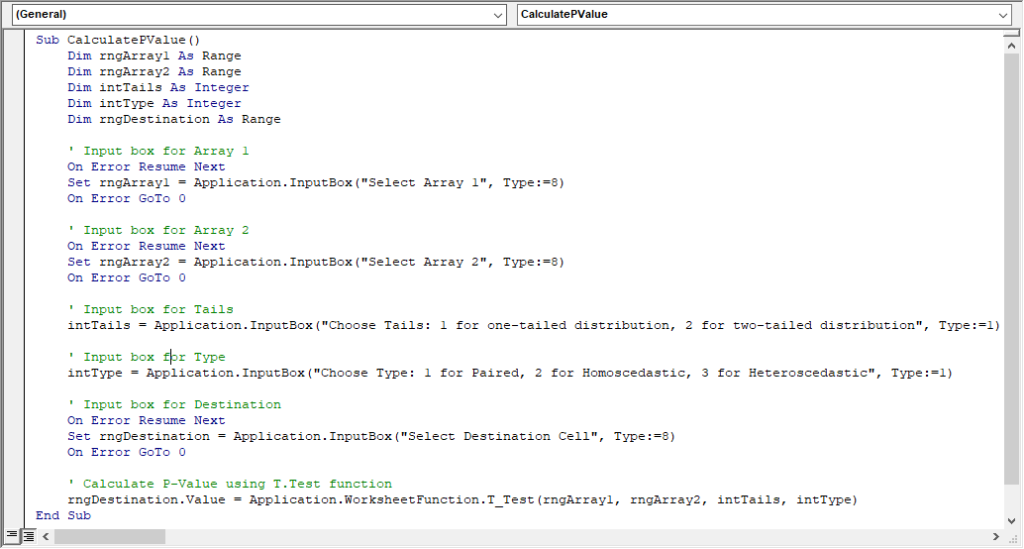
You just need to create a VBA macro using the above script.

Then, the VBA script input boxes shall visually guide you through the process.

⚠️ Warning : Excel VBA doesn’t allow the use of Excel undo features to revert back to the original workbook structure. So, create a backup copy of the workbook before running any VBA macros.

Conclusions

Before going through this Excel tutorial, if you thought calculating p-value in statistical analysis was a complex tax, your perception should have changed by now. So far, you must have learned that it’s pretty easy to find the p-value of a statistical experiment to disprove or establish a null hypothesis. All you need to do is follow the manual and automatic methods mentioned above.

Did the article help you to clear your doubts about p-value or probability value calculation in Excel? Comment below!

About the Author

Bipasha Nath

Subscribe for awesome Microsoft Excel videos 😃

John MacDougall

I’m John , and my goal is to help you Excel!

You’ll find a ton of awesome tips , tricks , tutorials , and templates here to help you save time and effort in your work.

• Pivot Table Tips and Tricks You Need to Know
• Everything You Need to Know About Excel Tables
• The Complete Guide to Power Query
• Introduction To Power Query M Code
• The Complete List of Keyboard Shortcuts in Microsoft Excel
• The Complete List of VBA Keyboard Shortcuts in Microsoft Excel

Related Posts

How To Find Z-Score in Excel

May 14, 2024

Learn how to find Z-score in Excel in this quick and easy-to-remember...

4 Ways to Calculate Weighted Average in Excel

Aug 14, 2023

You must be precise if you're analyzing data for actionable insights. Enter...

3 Ways to Calculate a Pearson’s Correlation Coefficient in Excel

Aug 23, 2020

Learn 3 easy ways to calculate the Pearson’s Correlation Coefficient statistic in Excel.

Submit a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Submit Comment

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Get the Latest Microsoft Excel Tips

Follow us to stay up to date with the latest in Microsoft Excel!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.6: Hypothesis Testing for Two Means and Two Proportions (Worksheet)

• Last updated
• Save as PDF
• Page ID 782

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

Student Learning Outcomes

• The student will select the appropriate distributions to use in each case.
• The student will conduct hypothesis tests and interpret the results.
• the business section from two consecutive days’ newspapers
• three small packages of M&Ms®
• five small packages of Reese's Pieces®

Increasing Stocks Survey

• \(H_{0}\): _________
• \(H_{a}\) : _________
• In words, define the random variable.
• The distribution to use for the test is _____________.
• Calculate the test statistic using your data.

• Calculate the \(p\text{-value}\).
• Do you reject or not reject the null hypothesis? Why?
• Write a clear conclusion using a complete sentence.

Decreasing Stocks Survey

• \(H_{0}\): ________
• \(H_{a}\) : ________

• Calculate the \(p\text{-value}\):

Candy Survey

Buy three small packages of M&Ms and five small packages of Reese's Pieces (same net weight as the M&Ms). Test whether or not the mean number of candy pieces per package is the same for the two brands.

• \(H_{a}\): ________
• What distribution should be used for this test?

Shoe Survey

Test whether women have, on average, more pairs of shoes than men. Include all forms of sneakers, shoes, sandals, and boots. Use your class as the sample.

• The distribution to use for the test is ________________.