representation of number definition

• Math Article

We use numbers in our day to day life. They are often called numerals. Without numbers, we cannot do counting of things, date, time, money, etc. Sometimes these numbers are used for measurement and sometimes they are used for labelling. The properties of numbers make them capable of performing  arithmetic operations on them.  These numbers are expressed in numeric forms and also in words. For example, 2 is written as two in words, 25 is written as twenty-five in words, etc. Students can practice writing the numbers from 1 to 100 in words to learn more.

There are different types of numbers in Maths, which we learn. They are natural and whole numbers, odd and even numbers, rational and irrational numbers , etc. We will discuss all the types here in this article. Apart from these, the numbers are used in various applications such as forming number series, maths tables, etc.

Table of contents:

Numbers in Words

Special numbers, numbers definition.

A number is an arithmetic value used for representing the quantity and used in making calculations. A written symbol like “3” which represents a number is known as numerals. A number system is a writing system for denoting numbers using digits or symbols in a logical manner. The numeral system:

• Represents a useful set of numbers
• Reflects the arithmetic and algebraic structure of a number
• Provides standard representation

We use the digits from 0 to 9 to form all other numbers. 

With the help of these digits, we can create infinite numbers.

For example, 12, 3456, 1298, etc

Counting Numbers:

We use numbers to count different things or objects such as 1, 2, 3, 4, etc. Humans have been using numbers to count things from the past thousands of years. For example, there are 7 cows in the field. The counting numbers start from 1 and it goes till infinity.

The Number Zero:

The concept of the number “Zero (0)” place an important role in Mathematics and it is used as a placeholder in the place value number system. The number 0, acts as an additive identity for the real numbers, and other algebraic structures. We use the number “0” to show nothing. For example, there were 3 apples, but now there are none. To represent nothing, we can use zero.

Watch The Below Video To Know About Numbers

Types of Numbers

The numbers can be classified  into sets known as the number system. The different types of numbers in maths are:

• Natural Numbers: Natural numbers are known as counting numbers that contain the positive integers from 1 to infinity. The set of natural numbers is denoted as “N” and it includes N = {1, 2, 3, 4, 5, ……….}
• Whole Numbers: Whole numbers are known as non-negative integers and it does not include any fractional or decimal part. It is denoted as “W” and the set of whole numbers includes W = {0,1, 2, 3, 4, 5, ……….}
• Integers: Integers are the set of all whole numbers but it includes a negative set of natural numbers also. “Z” represents integers and the set of integers are Z = { -3, -2, -1, 0, 1, 2, 3}
• Real Numbers: All the positive and negative integers, fractional and decimal numbers without imaginary numbers are called real numbers. It is represented by the symbol “R”.
• Rational Numbers: Any number that can be written as a ratio of one number over another number is written as rational numbers. This means that any number that can be written in the form of p/q. The symbol “Q” represents the rational number.
• Irrational Numbers: The number that cannot be expressed as the ratio of one over another is known as irrational numbers and it is represented by the symbol ”P”.
• Complex Numbers: The number that can be written in the form of a+bi where “a and b” are the real number and “i” is an imaginary number is known as complex numbers “C”.
• Imaginary Numbers: The imaginary numbers are the complex numbers that can be written in the form of the product of a real number and the imaginary unit “i”

Also, read:

Apart from the above, there exist other numbers namely even and odd numbers ,  prime numbers and composite numbers.  These can be defined as given below:

Even Numbers: The numbers which are exactly divisible by 2, are called even numbers. These can be positive or negative integers such as -42, -36, -12, 2, 4, 8 and so on.

Get more information about even numbers here.

Odd Numbers: The numbers which are not exactly divisible by 2, are called odd numbers. These can be both positive and negative integers such as -3, -15, 7, 9, 17, 25 and so on.

Prime Numbers: Prime numbers are the numbers that have two factors only. (i.e.,) 1 and the number itself. In other words, the number which is divided by 1 and the number itself is called prime numbers. For example, 2, 3, 5, 7, 11, etc.

Composite Numbers : A composite number is a number that has more than two factors. For example, 4 is a composite number, as the number 4 is divisible by 1, 2, and 4. Other examples of composite numbers are 6, 8, 9, 10, and so on.

Note: The number “1” is neither prime nor composite.

Numbers Chart

Below is the chart for the classification of numbers:

The list of numbers in words from 1 to 100 is given below:

Number Series

In mathematics, the number series consists of a series of numbers in which the next term is obtained by adding or subtracting the constant term to the previous term. For example, consider the series 1, 3, 5, 7, 9, … In this series, the next term is obtained by adding the constant term “2” to the previous term. There are different types of number series namely,

• Perfect Square series
• Two-stage type series
• The odd man out series
• Perfect cube series
• Geometric series
• Mixed series

Cardinal Numbers : Cardinal number defines how many of something are there in a list, such as one, five, ten, etc.

Ordinal Numbers : Ordinal numbers explain the position of something in a list, such as first, second, third, fourth, and so on.

Nominal Numbers : Nominal number is used only as a name. It does not denote an actual value or the position of something.

Pi (π): Pi is a special number, which is approximately equal to 3.14159. Pi (π) is defined as the ratio of the circumference of the circle divided by the diameter of the circle.

(i.e.,) Circumference/ Diameter = π = 3.14159.

Euler’s Number (e): Euler’s number is one of the important numbers in Maths, and it is approximately equal to 2.7182818. It is an irrational number and it is the base of the natural logarithm.

Golden Ratio (φ): A golden ratio is a special number and it is approximately equal to 1.618. It is an irrational number and the digits do not follow any pattern.

Properties of Numbers

The  properties of numbers are basically stated for real numbers. Th e common properties are:

Commutative Property:  If  a and b are two real numbers, then according to commutative property;

Example: 2+3 = 3+2

and 2 × 3 = 3 × 2

Associative Property: If a, b and c are three real numbers, then according to associative property;

(a+b)+c = a+(b+c)

(a.b).c = a.(b.c)

Example: (1+2)+3 = 1+(2+3)

(1.2).3 = 1.(2.3)

Distributive Property:  If a, b and c are three real numbers, then according to distributive property;

a × (b + c) = a×b + a×c

Example: 2 × (3 + 4) = 2×3 + 2×4

2 × 7 = 6 + 8

Closure Property:  If a number is added to another number, then the result will be a number only, such as;

a+b = c ; where a, b and c are three real numbers.

Example: 1+2 = 3

Identity Property:  If we add zero to a number or multiply by 1, the number will remain unchanged.

Example: 5+0 = 5 and 5 x 1 = 5

Additive Inverse:  If a number is added to its own negative number, then the result is zero.

Example: 3+(-3) = 3-3 = 0

Multiplicative Inverse:  If a number apart from 0, is multiplied to its own reciprocal then the result is 1.

a x (1/a) = 1

Example: 23 x (1/23) = 1

Zero Product Property:  If a.b = 0, then;

either a = 0 or b = 0.

Example: 7 x 0 = 0 or 0 x 6 = 6

Reflexive Property:  This property reflects the number itself.

Example: 9 = 9

The properties which are explained above can vary based on the different types of numbers. To learn the properties of different types of numbers, please check the link given below:

Read: Types of Numbers Watch The Below Video To Know The History Of Numbers

Solved Problems

Example 1: 

Prove the associative property of addition and multiplication.

We know that the associative property of addition and multiplication are:

Now, assume that a = 2, b= 4 and c = 5

Proving associative property of addition:

Now, substitute the values in the property

(2+4)+5 = 2+(4+5)

L.H.S = R.H.S

Hence, (a+b)+c = a+(b+c) is proved.

Proving associative property of multiplication:

(2.4).5 = 2.(4.5)

(8).5 = 2.(20)

Hence, (a.b).c = a.(b.c) is proved.

Example 2:  

Solve the given algebraic expression 4.(3+2) using the distributive property

Given expression: We know that the distributive property is a × (b + c) = (a×b) + (a×c)

Now, take a= 4, b= 3 and c= 2

Now, substituting values, we get

4.(3+2) =  (a×b) + (a×c)

= (4×3) + (4×2)

Hence, 4.(3+2) is 20.

Alternate method:

The expression can be solved using BODMAS Rule also

Apply, BODMAS rule in the given expression:4.(3+2) 

According to this rule, we have the simplify the value inside the brackets first, so we get

4.(3+2) = 4. 5

Now, multiply the values

4.(3+2) = 20.

Frequently Asked Questions on Numbers – FAQs

What are the different properties of numbers.

The different properties of numbers are: Associative property Commutative property Distributive property Closure property Identity Property Inverse property Reflexive property Zero product property

Write down the properties for real numbers

The properties of the real number are: The real numbers obey associative and commutative property It obeys distributive property under addition and multiplication The additive identity of real numbers is 0 and the multiplicative identity is 1.

What is the difference between rational and irrational numbers?

The rational number is defined as the ratio of two numbers, and it is expressed in the form p/q, where q is not equal to 0. But the irrational number cannot be expressed as the ratio of two numbers.

Write down the associative property of numbers.

The associative property of addition is (a+b)+c = a+(b+c) The associative property of multiplication is (a.b).c = a.(b.c)

What are the additive and multiplicative inverse of numbers?

If “x” is a number, the additive inverse of x is -x. The additive inverse property is given as x+ (-x) = 0 If “y” is a number, the multiplicative inverse of y is 1/y. The multiplicative inverse property is given by y. (1/y) = 1.

To know more about numbers and number systems in mathematics, register with BYJU’S – The Learning App to learn with ease.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Decimal Representation of Rational Numbers: Definition, Types, Facts

What is the decimal representation of rational numbers, writing rational numbers in the decimal form, decimal form of a rational number chart, solved examples on decimal representation of rational numbers, practice problems on decimal representation of rational numbers, frequently asked questions on decimal representation of rational numbers.

Decimal representation of rational numbers is a method of finding decimal expansion of the given rational number or converting a rational number into an equivalent decimal number using long division.  

Decimal form of a rational number example: $\frac{5}{4} = 5\div4= 1.25$

Rational numbers are the numbers of the form $\frac{p}{q}$, where p and q are integers and $q\neq0$. Decimals are the numbers that have a whole number part and a fractional part separated by a decimal point. Every rational number is either a terminating or repeating decimal.

To convert the rational number $\frac{p}{q}$ into a decimal, we divide the number p by the number q using the long division process. Writing rational numbers in decimal form involves two cases. The decimal form of a rational number we get can be of 2 types:

• When Remainder $= 0$ , the decimal expansion is terminating.  

Terminating decimal is the decimal number in which there is an end-digit. There are a finite number of digits after the decimal point. 

For example, if we divide 5 by 1, we get 0.2. The number terminates and doesn’t continue after 2. So, it’s a terminating number.

• When Remainder $\neq0$ , the decimal expansion is non-terminating and repeating.

In a non-terminating and repeating decimal, a single digit or a block of digits repeat themselves infinitely after the decimal point. 

For example, we get $0.\overline{09}=0.09090909$ … on dividing 1 by 11. Here, the group of digits, 09, keep on repeating. 

So, how are rational numbers written as decimals? Let’s discuss both the cases.

Related Worksheets

Terminating Decimal Representation of Rational Numbers

When the decimal expansion of $\frac{p}{q}$, $q\neq 0$ comes to an end after a finite number of digits, the decimal expansion is called terminating. In this case, when we divide p by q using the long division method, we get remainder 0.

Example 1: Find the decimal representation of the rational number $\frac{4}{5}$ .

Thus, $\frac{4}{5} = 0.8$ … terminating decimal expansion

Example 2: Find the decimal representation of the rational number $\frac{3}{4}$.

Here, $\frac{3}{4} = 0.75$ … terminating decimal expansion

Non-terminating and Repeating Decimal Representation of Rational Numbers

In some cases, when we divide p by q to find the decimal expansion of $\frac{p}{q}$, $q\neq 0$, the remainder never becomes 0. Also, the remainder repeats after some steps, which results in a non-terminating and recurring decimal expansion.

Example 1: $\frac{10}{3} = 3.333$…

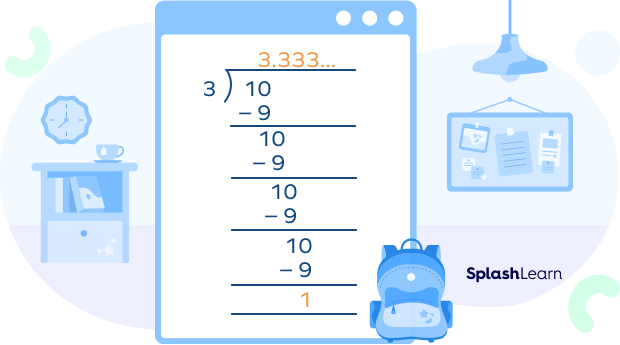
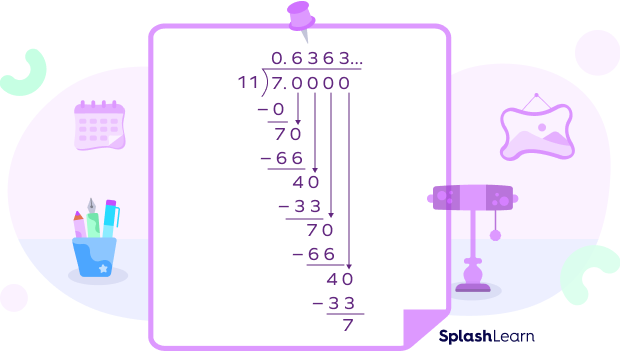
Example 2: $\frac{7}{11} = 0.636363$ …

Facts about Decimal Representation of Rational Numbers

• A rational number has either a terminating decimal expansion or a non-terminating and recurring (repeating) decimal expansion.
• The converse of the above statement is also true. If the decimal expansion of a number is terminating or non-terminating and recurring (repeating), then the number is a rational number.
• The decimal expansion of an irrational number is non-terminating and non-repeating.

In this article, we learned about the two types of decimal expansions of rational numbers. Let’s solve a few examples and practice problems for revision.

• Express $\frac{3}{8}$ in the form of a decimal.

Solution: 

Divide 3 by 8 using the long division method.

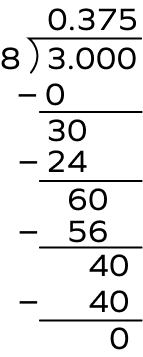
The rational number $\frac{3}{8}$ has a terminating decimal expansion.  

$\frac{3}{8} = 0.375$

• What is the decimal expansion of the rational number $\frac{20}{11}$ ?

Divide 20 by 11.

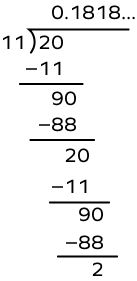
The rational number $\frac{20}{11}$ has a non-terminating and recurring decimal expansion. 

$\frac{20}{11} = 0.181818$…

• Write the rational numbers in the decimal form?

i) $\frac{2}{10}$ ii) $\frac{174}{100}$ ii) $\frac{56}{1000}

i) $\frac{2}{10} = 0.2$

ii) $\frac{174}{100} = 1.74$

iii) $\frac{56}{1000} = 0.056$

Attend this quiz & Test your knowledge.

What will be the decimal equivalent of the number $\frac{22}{4}$?

The decimal expansion of a rational number is either terminating or, is 1.5 a rational number.

How do you know if a decimal is rational?

If the decimal expansion of a number is “terminating” or “non-terminating and recurring (repeating),” then the number is a rational number.

What cannot be the decimal representation of a rational number?

A rational number cannot have a non-terminating and non-repeating decimal expansion.

What is the difference between rational numbers and fractions?

Rational numbers are the numbers of the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q\neq0$. Fractions represent part of a whole. A fraction is written in the form of $\frac{a}{b}$, where $b\neq0$ and a & b are natural numbers. Here, “a” is the numerator that represents the number of parts taken and “b” is the denominator that represents the total number of parts of the whole.

RELATED POSTS

• Algebraic Identities: Definition, Factorization, Proof, Examples, FAQs
• Coplanar – Definition With Examples
• Isosceles Trapezoid: Definition, Formula, Properties, Examples
• Slope of Parallel Line: Formula, Derivation, Example
• Inches to Centimeter Conversion: Definition, Chart, Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.25: The Base b Representation of n

• Last updated
• Save as PDF
• Page ID 82307

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Definition \(\PageIndex{1}\)

Let \(b\ge 2\) and \(n>0\) . We write \[\label{eq:1} n=\left[a_k,a_{k-1},\dotsc,a_1,a_0\right]_b \] if and only if for some \(k\ge 0\) \[n=a_kb^k+a_{k-1}b^{k-1}+\dotsb+a_1b+a_0\nonumber \] where \(a_i\in\{0,1,\dotsc,b-1\}\) for \(i=0,1,\dotsc,k\) . \(\left[a_k,a_{k-1},\dotsc,a_1,a_0\right]\) is called a base \(b\) representation of \(n\) .

Remark \(\PageIndex{1}\)

Base \(b\) is called \[\begin{aligned} binary \quad & \text{if }b=2, \\ ternary \quad & \text{if }b=3, \\ octal \quad & \text{if }b=8, \\ decimal \quad & \text{if }b=10, \\ hexadecimal \quad & \text{if }b=16.\end{aligned}\] If \(b\) is understood, especially if \(b=10\) , we write \(a_ka_{k-1}\dotsm a_1a_0\) in place of \(\left[a_k,a_{k-1},\dotsc,a_1,a_0\right]_{10}\) . In the case of \(b=16\) , which is used frequently in computer science, the “digits” \(10\) , \(11\) , \(12\) , \(13\) , \(14\) and \(15\) are replaced by \(A\) , \(B\) , \(C\) , \(D\) , \(E\) and \(F\) , respectively.

For a fixed base \(b\ge 2\) , the numbers \(a_i\in\{0,1,2,\dotsc,b-1\}\) in equation (1) are called the digits of the base \(b\) representation of \(n\) . In the binary case \(a_i\in\{0,1\}\) and the \(a_i\) ’s are called bits ( bi nary digi ts ).

Here are a few examples:

• \(267=[5,3,1]_7\) since \(267 = 5 \cdot 7^2+3\cdot 7 +1\) .
• \(147=[1,0,0,1,0,0,1,1]_2\) since \(147=1\cdot 2^7+0\cdot 2^6+0\cdot 2^5+1\cdot 2^4+0\cdot 2^3+0\cdot 2^2+1\cdot 2+1\) .
• \(4879=[4,8,7,9]_{10}\) since \(4879 = 4\cdot 10^3+8\cdot 10^2 + 7\cdot 10 + 9\) .
• \(10705679=[A,3,5,B,0,F]_{16}\) since \(10705679=10\cdot 16^5+3\cdot 16^4+5\cdot 16^3+11\cdot 16^2+0\cdot 16+15\) .
• \(107056791=[107, 56, 791]_{1000}\) since \(107056791=107\cdot 1000^2+56\cdot 1000 +791\) .

Theorem \(\PageIndex{1}\)

If \(b\ge 2\) , then every \(n>0\) has a unique base \(b\) representation of the form \(n=\left[a_k,\dotsc,a_1,a_0\right]_b\) with \(a_k>0\) .

Apply repeatedly the Division Algorithm as follows: \[\begin{aligned} n &=bq_0+r_0,\quad 0\le r_0<b \\ q_0 &=bq_1+r_1,\quad 0\le r_1<b \\ q_1 &=bq_2+r_2,\quad 0\le r_2<b \\ &\qquad\vdots \\ q_{k-1} &=bq_k+r_k,\quad 0\le r_k<b \\ q_k &=bq_{k+1}+r_{k+1},\quad 0\le r_{k+1}<b.\end{aligned}\] It is easy to see that if \(q_k>0\) : \[n>q_0>q_1>\dotsm>q_k.\nonumber \] Since this cannot go on forever we eventually obtain \(q_\ell=0\) for some \(\ell\) . Then we have \[q_{\ell-1}=b\cdot 0+r_\ell.\nonumber \] I claim that \(n=\left[r_\ell,r_{\ell-1},\dotsc,r_0\right]\) if \(\ell\) is the smallest integer such that \(q_\ell=0\) . To see this, note that \[n=bq_0+r_0\nonumber \] and \[q_0=bq_1+r_1.\nonumber \] Hence \[\begin{aligned} n &=b\left(bq_1+r_1\right)+r_0 \\ n &=b^2q_1+br_1+r_0.\end{aligned}\] Continuing in this way we find that \[n=b^{\ell+1}q_{\ell}+b^\ell r_\ell+\dotsb+br_1+r_0.\nonumber \] And, since \(q_\ell=0\) we have \[\label{eq:2} n=b^\ell r_\ell+\dotsb+br_1+r_0, \] which shows that \[n=\left[r_\ell,\dotsc,r_1,r_0\right]_b.\nonumber \] To see that this representation is unique, note that from \(\eqref{eq:2}\) we have \[n=b\left(b^{\ell-1}r_\ell+\dotsb+r_1\right)+r_0,\quad 0\le r_0<b.\nonumber \] By the Division Algorithm it follows that \(r_0\) is uniquely determined by \(n\) , as is the quotient \(q=b^{\ell-1}r_\ell+\dotsb+r_1\) . A similar argument shows that \(r_1\) is uniquely determined. Continuing in this way we see that all the digits \(r_\ell,r_{\ell-1},\dotsc,r_0\) are uniquely determined.

Example \(\PageIndex{1}\)

• We find the base \(7\) representation of \(1\) , \(749\) . \[\begin{aligned} 1749 &=249\cdot 7+6 \\ 249 &=35\cdot 7+4 \\ 35 &=5\cdot 7+0 \\ 5 &=0\cdot 7+5\end{aligned}\] Hence \(1749=[5,0,4,6]_7\) .
• We find the base \(12\) representation of \(19\) , \(151\) . \[\begin{aligned} 19,151 &=1595\cdot 12+11 \\ 1,595 &=132\cdot 12+11 \\ 132 &=11\cdot 12+0 \\ 11 &=0\cdot 12+11\end{aligned}\] \(\therefore 19,151=[11,0,11,11]_{12}\) .
• Find the base \(10\) representation of \(1\) , \(203\) . \[\begin{aligned} 1203 &=120\cdot 10+3 \\ 120 &= 12\cdot 10+0 \\ 12 &=1\cdot 10+2 \\ 1 &=0\cdot 10+1\end{aligned}\] \(\therefore 1203=[1,2,0,3]_{10}\) .
• Find the base \(2\) ( binary ) representation of \(137\) . \[\begin{aligned} 137 &=2\cdot 68+1 \\ 68 &=2\cdot 34+0 \\ 34 &=2\cdot 17+0 \\ 17 &=2\cdot 8+1 \\ 8 &=2\cdot 4+0 \\ 4 &=2\cdot 2+0 \\ 2 &=2\cdot 1+0 \\ 1 &=2\cdot 0+1\end{aligned}\] \(\therefore 137=[1,0,0,0,1,0,0,1]_2\) .

Exercise \(\PageIndex{1}\)

Generalize the following observations \[\begin{aligned} 3 &=[1,1]_2 \\ 7 &=[1,1,1]_2 \\ 15 &=[1,1,1,1]_2 \\ 31 &=[1,1,1,1,1]_2 \\ 63 &=[1,1,1,1,1,1]_2\end{aligned}\] Prove your generalization.

See Exercise 2.5

Exercise \(\PageIndex{2}\)

Generalize the following observation: \[\begin{aligned} 8 &=[2,2]_3 \\ 26 &=[2,2,2]_3 \\ 80 &=[2,2,2,2]_3 \\ 242 &=[2,2,2,2,2]_3\end{aligned}\] Prove your generalization.

Exercise \(\PageIndex{3}\)

Generalize Exercises \(\PageIndex{1}\) and \(\PageIndex{2}\) to an arbitrary base \(b\ge 2\) .

Remark \(\PageIndex{2}\)

To find the binary representation of a small number, the following method is often easier than the above method:

Given \(n>0\) let \(2^{n_1}\) be the largest power of \(2\) satisfying \(2^{n_1}\le n\) . Let \(2^{n_2}\) be the largest power of \(2\) satisfying \[2^{n_2}\le n-2^{n_1}.\nonumber \] Let \(2^{n_3}\) be the largest power of \(2\) satisfying \[2^{n_3}\le n-2^{n_1}-2^{n_2}.\nonumber \] Note that at this point we have \[0\le n-\left(2^{n_1}+2^{n_2}+2^{n_3}\right)<n-\left(2^{n_1}+2^{n_2}\right)<n-2^{n_1}<n.\nonumber \] Continuing in this way, eventually we get \[0=n-\left(2^{n_1}+2^{n_2}+\dotsb+2^{n_k}\right).\nonumber \] Then \(n=2^{n_1}+2^{n_2}+\dotsb+2^{n_k}\) , and this gives the binary representation of \(n\) .

Example \(\PageIndex{2}\)

Take \(n=137\) . Note that \(2^1=2\) , \(2^2=4\) , \(2^3=8\) , \(2^4=16\) , \(2^5=32\) , \(2^6=64\) , \(2^7=128\) , and \(2^8=256\) . Using the above method we compute: \[\begin{aligned} 137-2^7 &=137-128=9, \\ 9-2^3 &=1, \\ 1-2^0 &=0.\end{aligned}\] So we have \[\begin{gathered} 137=2^7+9=2^7+2^3+1, \\ \therefore 137=2^7+02^6+02^5+02^4+2^3+02^2+0\cdot 2+1.\end{gathered}\] So \(137=[1,0,0,0,1,0,0,1]_2\) .

Exercise \(\PageIndex{4}\)

Show how to use both methods to find the binary representation of \(455\) .

Exercise \(\PageIndex{5}\)

Make a vertical list of the binary representation of the integers 1 to 16.

Sets in mathematics, are simply a collection of distinct objects forming a group. A set can have any group of items, be it a collection of numbers, days of a week, types of vehicles, and so on. Every item in the set is called an element of the set. Curly brackets are used while writing a set. A very simple example of a set would be like this. Set A = {1, 2, 3, 4, 5}. In set theory, there are various notations to represent elements of a set. Sets are usually represented using a roster form or a set builder form. Let us discuss each of these terms in detail.

Sets Definition

In mathematics, a set is defined as a well-defined collection of objects. Sets are named and represented using capital letters. In the set theory, the elements that a set comprises can be any kind of thing: people, letters of the alphabet, numbers, shapes, variables, etc.

Sets in Maths Examples

Some standard sets in maths are:

• Set of natural numbers , ℕ = {1, 2, 3, ...}
• Set of whole numbers , W = {0, 1, 2, 3, ...}
• Set of integers , ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}
• Set of rational numbers , ℚ = {p/q | q is an integer and q ≠ 0}
• Set of irrational numbers , ℚ' = {x | x is not rational}
• Set of real numbers , ℝ = ℚ ∪ ℚ'

All these are infinite sets. But there can be finite sets as well. For example, the collection of even natural numbers less than 10 can be represented in the form of a set, A = {2, 4, 6, 8}, which is a finite set.

Let us use this example to understand the basic terminology associated with sets in math.

Elements of a Set

The items present in a set are called either elements or members of a set. The elements of a set are enclosed in curly brackets separated by commas. To denote that an element is contained in a set, the symbol '∈' is used. In the above example, 2 ∈ A. If an element is not a member of a set, then it is denoted using the symbol '∉'. For example, 3 ∉ A.

Cardinal Number of a Set

The cardinal number, cardinality , or order of a set denotes the total number of elements in the set. For natural even numbers less than 10, n(A) = 4. Sets are defined as a collection of unique elements. One important condition to define a set is that all the elements of a set should be related to each other and share a common property. For example, if we define a set with the elements as the names of months in a year, then we can say that all the elements of the set are the months of the year.

Representation of Sets in Set Theory

There are different set notations used for the representation of sets in set theory. They differ in the way in which the elements are listed. The three set notations used for representing sets are:

• Semantic form
• Roster form
• Set builder form

Let us understand each of these forms with an example.

Semantic Form

Semantic notation describes a statement to show what are the elements of a set. For example, a set of the first five odd numbers .

Roster Form

The most common form used to represent sets is the roster notation in which the elements of the sets are enclosed in curly brackets separated by commas. For example, Set B = {2,4,6,8,10}, which is the collection of the first five even numbers. In a roster form, the order of the elements of the set does not matter, for example, the set of the first five even numbers can also be defined as {2,6,8,10,4}. Also, if there is an endless list of elements in a set, then they are defined using a series of dots at the end of the last element. For example, infinite sets are represented as, X = {1, 2, 3, 4, 5 ...}, where X is the set of natural numbers. To sum up the notation of the roster form, please take a look at the examples below.

Finite Roster Notation of Sets : Set A = {1, 2, 3, 4, 5} (The first five natural numbers)

Infinite Roster Notation of Sets : Set B = {5, 10, 15, 20 ....} (The multiples of 5 )

Set Builder Form

The set builder notation has a certain rule or a statement that specifically describes the common feature of all the elements of a set. The set builder form uses a vertical bar in its representation, with a text describing the character of the elements of the set. For example, A = { k | k is an even number, k ≤ 20}. The statement says, all the elements of set A are even numbers that are less than or equal to 20. Sometimes a ":" is used in the place of the "|".

Visual Representation of Sets Using Venn Diagram

Venn Diagram is a pictorial representation of sets, with each set represented as a circle. The elements of a set are present inside the circles . Sometimes a rectangle encloses the circles, which represents the universal set . The Venn diagram represents how the given sets are related to each other.

Sets Symbols

Set symbols are used to define the elements of a given set. The following table shows the set theory symbols and their meaning.

Types of Sets

There are different types of sets in set theory. Some of these are singleton, finite, infinite, empty, etc.

Singleton Sets

A set that has only one element is called a singleton set or also called a unit set. Example, Set A = { k | k is an integer between 3 and 5} which is A = {4}.

Finite Sets

As the name implies, a set with a finite or countable number of elements is called a finite set . Example, Set B = {k | k is a prime number less than 20}, which is B = {2,3,5,7,11,13,17,19}

Infinite Sets

A set with an infinite number of elements is called an infinite set. Example: Set C = { Multiples of 3 }.

Empty or Null Sets

A set that does not contain any element is called an empty set or a null set. An empty set is denoted using the symbol '∅'. It is read as ' phi '. Example: Set X = { }.

If two sets have the same elements in them, then they are called equal sets . Example: A = {1,2,3} and B = {1,2,3}. Here, set A and set B are equal sets. This can be represented as A = B.

Unequal Sets

If two sets have at least one different element, then they are unequal sets. Example: A = {1,2,3} and B = {2,3,4}. Here, set A and set B are unequal sets. This can be represented as A ≠ B.

Equivalent Sets

Two sets are said to be equivalent sets when they have the same number of elements, though the elements are different. Example: A = {1,2,3,4} and B = {a,b,c,d}. Here, set A and set B are equivalent sets since n(A) = n(B)

Overlapping Sets

Two sets are said to be overlapping if at least one element from set A is present in set B. Example: A = {2,4,6} B = {4,8,10}. Here, element 4 is present in set A as well as in set B. Therefore, A and B are overlapping sets.

Disjoint Sets

Two sets are disjoint if there are no common elements in both sets. Example: A = {1,2,3,4} B = {5,6,7,8}. Here, set A and set B are disjoint sets.

Subset and Superset

For two sets A and B, if every element in set A is present in set B, then set A is a subset of set B(A ⊆ B) and in this case, B is the superset of set A(B ⊇ A). Example: Consider the sets A = {1,2,3} and B = {1,2,3,4,5,6}. Here:

• A ⊆ B, since all the elements in set A are present in set B.
• B ⊇ A denotes that set B is the superset of set A.

Universal Set

A universal set is the collection of all the elements regarding a particular subject. The universal set is denoted by the letter 'U'. Example: Let U = {The list of all road transport vehicles}. Here, a set of cars is a subset for this universal set, the set of cycles, trains are all subsets of this universal set.

Power set is the set of all subsets that a set could contain. Example: Set A = {1,2,3}. Power set of A is = {∅, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.

Operations on Sets

Some important operations on sets in set theory include union, intersection, difference, the complement of a set, and the cartesian product of a set. A brief explanation of set operations is as follows.

Union of Sets

Union of sets, which is denoted as A U B, lists the elements in set A and set B or the elements in both set A and set B. For example, {1, 3} ∪ {1, 4} = {1, 3, 4}

Intersection of Sets

The intersection of sets which is denoted by A ∩ B lists the elements that are common to both set A and set B. For example, {1, 2} ∩ {2, 4} = {2}

Set Difference

Set difference which is denoted by A - B, lists the elements in set A that are not present in set B. For example, A = {2, 3, 4} and B = {4, 5, 6}. A - B = {2, 3}.

Set Complement

Set complement which is denoted by A', is the set of all elements in the universal set that are not present in set A. In other words, A' is denoted as U - A, which is the difference in the elements of the universal set and set A.

Cartesian Product of Sets

The cartesian product of two sets which is denoted by A × B, is the product of two non-empty sets, wherein ordered pairs of elements are obtained. For example, {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}.

In the above figure, the shaded portions in "blue" show the set that they are labelled with.

Sets Formulas in Set Theory

Sets find their application in the field of algebra , statistics , and probability . There are some important set theory formulas in set theory as listed below.

For any two overlapping sets A and B,

• n(A U B) = n(A) + n(B) - n(A ∩ B)
• n (A ∩ B) = n(A) + n(B) - n(A U B)
• n(A) = n(A U B) + n(A ∩ B) - n(B)
• n(B) = n(A U B) + n(A ∩ B) - n(A)
• n(A - B) = n(A U B) - n(B)
• n(A - B) = n(A) - n(A ∩ B)

For any two sets A and B that are disjoint,

• n(A U B) = n(A) + n(B)
• n(A - B) = n(A)

Properties of Sets

Similar to numbers, sets also have properties like associative property, commutative property, and so on. There are six important properties of sets . Given, three sets A, B, and C, the properties for these sets are as follows.

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Sets Examples

Example 1: Find the elements of the sets represented as follows and write the cardinal number of each set. a) Set A is the first 8 multiples of 7 b) Set B = {a,e,i,o,u} c) Set C = {x | x are even numbers between 20 and 40}

a) Set A = {7,14,21,28,35,42,49,56}. These are the first 8 multiples of 7 .

Since there are 8 elements in the set, cardinal number n (A) = 8

b) Set B = {a,e,i,o,u}. There are five elements in the set,

Therefore, the cardinal number of set B, n(B) = 5. c) Set C = {22,24,26,28,30,32,34,36,38}. These are the even numbers between 20 and 40, which make up the elements of the set C.

Therefore, the cardinal number of set C, n(C) = 9.

Answer: (a) 8 (b) 5 (c) 9

Example 2: If Set A = {a,b,c}, Set B = {a,b,c,p,q,r}, U = {a,b,c,d,p,q,r,s}, find the following using sets formulas, a) A U B b) A ∩ B c) A' d) Is A ⊆ B? (Here 'U' is the universal set).

a) A U B = writing the elements of A and B together in one set by removing duplicates = {a,b,c,p,q,r}

b) A ∩ B = writing common elements of A and B in a set = {a,b,c}

c) A' = writing elements of U that are NOT present in A = {d,p,q,r,s}

d) A ⊆ B, (Set A is a subset of set B) since all the elements in set A are present in set B.

Answer: (a) {a,b,c,p,q,r} (b) {a,b,c} (c) {d,p,q,r,s} (d) Yes

Example 3: Express the given set in set-builder form: A = {2, 4, 6, 8, 10, 12, 14}

Solution: Given: A = {2, 4, 6, 8, 10, 12, 14}

Using sets notations, we can represent the given set A in set-builder form as,

A = {x | x is an even natural number less than 15}

Answer: A = {x | x is an even natural number less than 15}

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Sets

Faqs on sets, what is set in math.

Sets are a collection of distinct elements, which are enclosed in curly brackets, separated by commas. The list of items in a set is called the elements of a set. Examples are a collection of fruits, a collection of pictures. Sets are represented by the symbol { }. i.e., the elements of the set are written inside these brackets. Example: Set A = {a,b,c,d}. Here, a,b,c, and d are the elements of set A.

What are Different Sets Notations to Represent Sets?

Sets can be represented in three ways. Representing sets means a way of listing the elements of the set. They are as follows.

• Semantic Notation: The elements of a set are represented by a single statement. For example, Set A is the number of days in a week.
• Roster Notation: This form of representation of sets uses curly brackets to list the elements of the set. For example, Set A = {10,12,14,16,18}}
• Set Builder Notation: A set builder form represents the elements of a set by a common rule or a property. For example, {x | x is a prime number less than 20}

What are the Types of Sets?

Sets differ from each depending upon elements present in them. Based on this, we have the following types of sets . They are singleton sets, finite and infinite sets, empty or null sets, equal sets, unequal sets, equivalent sets, overlapping sets, disjoint sets, subsets, supersets, power sets, and universal sets.

What are the Properties of Sets in Set-Theory?

Different properties associated with sets in math are,

• Commutative Property: A U B = B U A and A ∩ B = B ∩ A
• Associative Property: (A ∩ B) ∩ C = A ∩ (B ∩ C) and (A U B) U C = A U (B U C)
• Distributive Property: A U (B ∩ C) = (A U B) ∩ (A U C) and A ∩ (B U C) = (A ∩ B) U (A ∩ C)
• Identity Property: A U ∅ = A and A ∩ U = A
• Complement Property: A U A' = U
• Idempotent Property: A ∩ A = A and A U A = A

What is the Union of Sets?

The union of two sets A and B are the elements from both set A and B, or both combined together. It is denoted using the symbol 'U'. For example, if set A = {1,2,3} and set B = {4,5,6}, then A U B = {1,2,3,4,5,6}. A U B is read as 'A union B'.

What is the Intersection of Sets?

The intersection of two sets A and B are the elements that are common to both set A and B. It is denoted using the symbol '∩'. For example, if set A = {1,2,3} and set B = {3,4,5}, then A ∩ B = {3}. A ∩ B is read as 'A intersection B'.

What are Subsets and Supersets?

If every element in a set A is present in set B, then set B is the superset of set A and set A is a subset of set B. Example: A = {1,4,5} B = {1,2,3,4,5,6}, here since all elements of set A are present in set B ⇒ A ⊆ B and B ⊇ A.

What are Universal Sets?

A universal set, denoted by the letter 'U', is the collection of all the elements in regard to a particular subject. Example: Let U = {All types of cycles}. Here, a set of cycles of a specific company is a subset of this universal set.

What Does Sets Class 11 Contain?

The sets in class 11 is an important chapter that deals with various components of set theory. It starts with definition of sets, and extends to types of sets, properties of sets, set operations, etc. It also has some real-life applications related to sets. To solve more applications related to sets class 11, click here . ☛Also Check:

• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.1
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.2
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.3
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.4
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.5
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.6
• NCERT Solutions Class 11 Maths Chapter 1 Miscellaneous Exercise

What is Complement in Sets?

The complement of a set which is denoted by A', is the set of all elements in the universal set that are not present in set A. In other words, A' is denoted as U - A, which is the difference in the elements of the universal set and set A.

What is Cartesian Product in Sets?

Cartesian product of two sets, denoted by A×B, is the product of two non-empty sets, wherein ordered pairs of elements are obtained. For example, if A = {1,2} and B = {3,4}, then A×B = {(1,3), (1,4), (2,3), (2,4)}.

What is the Use of Venn Diagram in Set Theory?

Venn Diagram is a pictorial representation of the relationship between two or more sets. Circles are used to represent sets. Each circle represents a set. A rectangle that encloses the circles represents the universal set.