hypothesis test proportion small sample

Teach yourself statistics

Hypothesis Test of a Proportion (Small Sample)

This lesson explains how to test a hypothesis about a proportion when a simple random sample has fewer than 10 successes or 10 failures - a situation that often occurs with small samples. (In a previous lesson , we showed how to conduct a hypothesis test for a proportion when a simple random sample includes at least 10 successes and 10 failures.)

The approach described in this lesson is appropriate, as long as the sample includes at least one success and one failure. The key steps are:

• Formulate the hypotheses to be tested. This means stating the null hypothesis and the alternative hypothesis .
• Determine the sampling distribution of the proportion. If the sample proportion is the outcome of a binomial experiment , the sampling distribution will be binomial. If it is the outcome of a hypergeometric experiment , the sampling distribution will be hypergeometric.
• Specify the significance level . (Researchers often set the significance level equal to 0.05 or 0.01, although other values may be used.)
• Based on the hypotheses, the sampling distribution, and the significance level, define the region of acceptance .
• Test the null hypothesis. If the sample proportion falls within the region of acceptance, do not reject the null hypothesis; otherwise, reject the null hypothesis.

The following examples illustrate how to test hypotheses with small samples. The first example involves a binomial experiment; and the second example, a hypergeometric experiment.

Example 1: Sampling With Replacement

Suppose an urn contains 30 marbles. Some marbles are red, and the rest are green. A researcher hypothesizes that the urn contains 15 or more red marbles. The researcher randomly samples five marbles, with replacement , from the urn. Two of the selected marbles are red, and three are green. Based on the sample results, should the researcher reject the null hypothesis? Use a significance level of 0.20.

Solution: There are five steps in conducting a hypothesis test, as described in the previous section. We work through each of the five steps below:

Null hypothesis: P >= 0.50

Alternative hypothesis: P < 0.50

Given those inputs (a binomial distribution where the true population proportion is equal to 0.50), the sampling distribution of the proportion can be determined. It appears in the table below, which shows individual probabilities for single events and cumulative probabilities for multiple events. (Elsewhere on this website, we showed how to compute binomial probabilities that form the body of the table.)

• Specify significance level . The significance level was set at 0.20. (This means that the probability of making a Type I error is 0.20, assuming that the null hypothesis is true.)

However, we can define a region of acceptance for which the significance level would be no more than 0.20. From the table, we see that if the true population proportion is equal to 0.50, we would be very unlikely to pick 0 or 1 red marble in our sample of 5 marbles. The probability of selecting 1 or 0 red marbles would be 0.1875. Therefore, if we let the significance level equal 0.1875, we can define the region of rejection as any sampled outcome that includes only 0 or 1 red marble (i.e., a sampled proportion equal to 0 or 0.20). We can define the region of acceptance as any sampled outcome that includes at least 2 red marbles. This is equivalent to a sampled proportion that is greater than or equal to 0.40.

• Test the null hypothesis . Since the sample proportion (0.40) is within the region of acceptance, we cannot reject the null hypothesis.

Example 2: Sampling Without Replacement

The Acme Advertising company has 25 clients. Account executives at Acme claim that 80 percent of these clients are very satisfied with the service they receive. To test that claim, Acme's CEO commissions a survey of 10 clients. Survey participants are randomly sampled, without replacement , from the client population. Six of the ten sampled customers (i.e., 60 percent) say that they are very satisfied. Based on the sample results, should the CEO accept or reject the hypothesis that 80 percent of Acme's clients are very satisfied. Use a significance level of 0.10.

Null hypothesis: P >= 0.80

Alternative hypothesis: P < 0.80

Given those inputs (a hypergeometric distribution where 20 of 25 clients are very satisfied), the sampling distribution of the proportion can be determined. It appears in the table below, which shows individual probabilities for single events and cumulative probabilities for multiple events. (Elsewhere on this website, we showed how to compute hypergeometric probabilities that form the body of the table.)

• Specify significance level . The significance level was set at 0.10. (This means that the probability of making a Type I error is 0.10, assuming that the null hypothesis is true.)

However, we can define a region of acceptance for which the significance level would be no more than 0.10. From the table, we see that if the true proportion of very satisfied clients is equal to 0.80, we would be very unlikely to have fewer than 7 very satisfied clients in our sample. The probability of having 6 or fewer very satisfied clients in the sample would be 0.064. Therefore, if we let the significance level equal 0.064, we can define the region of rejection as any sampled outcome that includes 6 or fewer very satisfied customers. We can define the region of acceptance as any sampled outcome that includes 7 or more very satisfied customers. This is equivalent to a sample proportion that is greater than or equal to 0.70.

• Test the null hypothesis . Since the sample proportion (0.60) is outside the region of acceptance, we cannot accept the null hypothesis at the 0.064 level of significance.

Hypothesis Testing for Means & Proportions

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This is the first of three modules that will addresses the second area of statistical inference, which is hypothesis testing, in which a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The process of hypothesis testing involves setting up two competing hypotheses, the null hypothesis and the alternate hypothesis. One selects a random sample (or multiple samples when there are more comparison groups), computes summary statistics and then assesses the likelihood that the sample data support the research or alternative hypothesis. Similar to estimation, the process of hypothesis testing is based on probability theory and the Central Limit Theorem.  

This module will focus on hypothesis testing for means and proportions. The next two modules in this series will address analysis of variance and chi-squared tests. 

Learning Objectives

After completing this module, the student will be able to:

• Define null and research hypothesis, test statistic, level of significance and decision rule
• Distinguish between Type I and Type II errors and discuss the implications of each
• Explain the difference between one and two sided tests of hypothesis
• Estimate and interpret p-values
• Explain the relationship between confidence interval estimates and p-values in drawing inferences
• Differentiate hypothesis testing procedures based on type of outcome variable and number of sample

Introduction to Hypothesis Testing

Techniques for hypothesis testing  .

The techniques for hypothesis testing depend on

• the type of outcome variable being analyzed (continuous, dichotomous, discrete)
• the number of comparison groups in the investigation
• whether the comparison groups are independent (i.e., physically separate such as men versus women) or dependent (i.e., matched or paired such as pre- and post-assessments on the same participants).

In estimation we focused explicitly on techniques for one and two samples and discussed estimation for a specific parameter (e.g., the mean or proportion of a population), for differences (e.g., difference in means, the risk difference) and ratios (e.g., the relative risk and odds ratio). Here we will focus on procedures for one and two samples when the outcome is either continuous (and we focus on means) or dichotomous (and we focus on proportions).

General Approach: A Simple Example

The Centers for Disease Control (CDC) reported on trends in weight, height and body mass index from the 1960's through 2002. 1 The general trend was that Americans were much heavier and slightly taller in 2002 as compared to 1960; both men and women gained approximately 24 pounds, on average, between 1960 and 2002.   In 2002, the mean weight for men was reported at 191 pounds. Suppose that an investigator hypothesizes that weights are even higher in 2006 (i.e., that the trend continued over the subsequent 4 years). The research hypothesis is that the mean weight in men in 2006 is more than 191 pounds. The null hypothesis is that there is no change in weight, and therefore the mean weight is still 191 pounds in 2006.  

In order to test the hypotheses, we select a random sample of American males in 2006 and measure their weights. Suppose we have resources available to recruit n=100 men into our sample. We weigh each participant and compute summary statistics on the sample data. Suppose in the sample we determine the following:

Do the sample data support the null or research hypothesis? The sample mean of 197.1 is numerically higher than 191. However, is this difference more than would be expected by chance? In hypothesis testing, we assume that the null hypothesis holds until proven otherwise. We therefore need to determine the likelihood of observing a sample mean of 197.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true or under the null hypothesis). We can compute this probability using the Central Limit Theorem. Specifically,

(Notice that we use the sample standard deviation in computing the Z score. This is generally an appropriate substitution as long as the sample size is large, n > 30. Thus, there is less than a 1% probability of observing a sample mean as large as 197.1 when the true population mean is 191. Do you think that the null hypothesis is likely true? Based on how unlikely it is to observe a sample mean of 197.1 under the null hypothesis (i.e., <1% probability), we might infer, from our data, that the null hypothesis is probably not true.

Suppose that the sample data had turned out differently. Suppose that we instead observed the following in 2006:

How likely it is to observe a sample mean of 192.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true)? We can again compute this probability using the Central Limit Theorem. Specifically,

There is a 33.4% probability of observing a sample mean as large as 192.1 when the true population mean is 191. Do you think that the null hypothesis is likely true?  

Neither of the sample means that we obtained allows us to know with certainty whether the null hypothesis is true or not. However, our computations suggest that, if the null hypothesis were true, the probability of observing a sample mean >197.1 is less than 1%. In contrast, if the null hypothesis were true, the probability of observing a sample mean >192.1 is about 33%. We can't know whether the null hypothesis is true, but the sample that provided a mean value of 197.1 provides much stronger evidence in favor of rejecting the null hypothesis, than the sample that provided a mean value of 192.1. Note that this does not mean that a sample mean of 192.1 indicates that the null hypothesis is true; it just doesn't provide compelling evidence to reject it.

In essence, hypothesis testing is a procedure to compute a probability that reflects the strength of the evidence (based on a given sample) for rejecting the null hypothesis. In hypothesis testing, we determine a threshold or cut-off point (called the critical value) to decide when to believe the null hypothesis and when to believe the research hypothesis. It is important to note that it is possible to observe any sample mean when the true population mean is true (in this example equal to 191), but some sample means are very unlikely. Based on the two samples above it would seem reasonable to believe the research hypothesis when x̄ = 197.1, but to believe the null hypothesis when x̄ =192.1. What we need is a threshold value such that if x̄ is above that threshold then we believe that H 1 is true and if x̄ is below that threshold then we believe that H 0 is true. The difficulty in determining a threshold for x̄ is that it depends on the scale of measurement. In this example, the threshold, sometimes called the critical value, might be 195 (i.e., if the sample mean is 195 or more then we believe that H 1 is true and if the sample mean is less than 195 then we believe that H 0 is true). Suppose we are interested in assessing an increase in blood pressure over time, the critical value will be different because blood pressures are measured in millimeters of mercury (mmHg) as opposed to in pounds. In the following we will explain how the critical value is determined and how we handle the issue of scale.

First, to address the issue of scale in determining the critical value, we convert our sample data (in particular the sample mean) into a Z score. We know from the module on probability that the center of the Z distribution is zero and extreme values are those that exceed 2 or fall below -2. Z scores above 2 and below -2 represent approximately 5% of all Z values. If the observed sample mean is close to the mean specified in H 0 (here m =191), then Z will be close to zero. If the observed sample mean is much larger than the mean specified in H 0 , then Z will be large.  

In hypothesis testing, we select a critical value from the Z distribution. This is done by first determining what is called the level of significance, denoted α ("alpha"). What we are doing here is drawing a line at extreme values. The level of significance is the probability that we reject the null hypothesis (in favor of the alternative) when it is actually true and is also called the Type I error rate.

α = Level of significance = P(Type I error) = P(Reject H 0 | H 0 is true).

Because α is a probability, it ranges between 0 and 1. The most commonly used value in the medical literature for α is 0.05, or 5%. Thus, if an investigator selects α=0.05, then they are allowing a 5% probability of incorrectly rejecting the null hypothesis in favor of the alternative when the null is in fact true. Depending on the circumstances, one might choose to use a level of significance of 1% or 10%. For example, if an investigator wanted to reject the null only if there were even stronger evidence than that ensured with α=0.05, they could choose a =0.01as their level of significance. The typical values for α are 0.01, 0.05 and 0.10, with α=0.05 the most commonly used value.  

Suppose in our weight study we select α=0.05. We need to determine the value of Z that holds 5% of the values above it (see below).

The critical value of Z for α =0.05 is Z = 1.645 (i.e., 5% of the distribution is above Z=1.645). With this value we can set up what is called our decision rule for the test. The rule is to reject H 0 if the Z score is 1.645 or more.  

With the first sample we have

Because 2.38 > 1.645, we reject the null hypothesis. (The same conclusion can be drawn by comparing the 0.0087 probability of observing a sample mean as extreme as 197.1 to the level of significance of 0.05. If the observed probability is smaller than the level of significance we reject H 0 ). Because the Z score exceeds the critical value, we conclude that the mean weight for men in 2006 is more than 191 pounds, the value reported in 2002. If we observed the second sample (i.e., sample mean =192.1), we would not be able to reject the null hypothesis because the Z score is 0.43 which is not in the rejection region (i.e., the region in the tail end of the curve above 1.645). With the second sample we do not have sufficient evidence (because we set our level of significance at 5%) to conclude that weights have increased. Again, the same conclusion can be reached by comparing probabilities. The probability of observing a sample mean as extreme as 192.1 is 33.4% which is not below our 5% level of significance.

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.  

• Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);  

H 1 : Research hypothesis (investigator's belief); α =0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is a single number that summarizes the sample information.   An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

• Step 3.  Set up decision rule.  

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

• The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value.  In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
• The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.  
• The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value.   For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.  

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

• Step 4. Compute the test statistic.  

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

• Step 5. Conclusion.  

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).  

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .  

• Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191                 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

• Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

• Step 3. Set up decision rule.  

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05.   Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.  

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.                  

Type I and Type II Errors

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

 The most common reason for a Type II error is a small sample size.

Tests with One Sample, Continuous Outcome

Hypothesis testing applications with a continuous outcome variable in a single population are performed according to the five-step procedure outlined above. A key component is setting up the null and research hypotheses. The objective is to compare the mean in a single population to known mean (μ 0 ). The known value is generally derived from another study or report, for example a study in a similar, but not identical, population or a study performed some years ago. The latter is called a historical control. It is important in setting up the hypotheses in a one sample test that the mean specified in the null hypothesis is a fair and reasonable comparator. This will be discussed in the examples that follow.

Test Statistics for Testing H 0 : μ= μ 0

• if n > 30
• if n < 30

Note that statistical computing packages will use the t statistic exclusively and make the necessary adjustments for comparing the test statistic to appropriate values from probability tables to produce a p-value. 

The National Center for Health Statistics (NCHS) published a report in 2005 entitled Health, United States, containing extensive information on major trends in the health of Americans. Data are provided for the US population as a whole and for specific ages, sexes and races.  The NCHS report indicated that in 2002 Americans paid an average of $3,302 per year on health care and prescription drugs. An investigator hypothesizes that in 2005 expenditures have decreased primarily due to the availability of generic drugs. To test the hypothesis, a sample of 100 Americans are selected and their expenditures on health care and prescription drugs in 2005 are measured.   The sample data are summarized as follows: n=100, x̄

=$3,190 and s=$890. Is there statistical evidence of a reduction in expenditures on health care and prescription drugs in 2005? Is the sample mean of $3,190 evidence of a true reduction in the mean or is it within chance fluctuation? We will run the test using the five-step approach. 

• Step 1.  Set up hypotheses and determine level of significance

H 0 : μ = 3,302 H 1 : μ < 3,302           α =0.05

The research hypothesis is that expenditures have decreased, and therefore a lower-tailed test is used.

This is a lower tailed test, using a Z statistic and a 5% level of significance.   Reject H 0 if Z < -1.645.

•   Step 4. Compute the test statistic.  

We do not reject H 0 because -1.26 > -1.645. We do not have statistically significant evidence at α=0.05 to show that the mean expenditures on health care and prescription drugs are lower in 2005 than the mean of $3,302 reported in 2002.  

Recall that when we fail to reject H 0 in a test of hypothesis that either the null hypothesis is true (here the mean expenditures in 2005 are the same as those in 2002 and equal to $3,302) or we committed a Type II error (i.e., we failed to reject H 0 when in fact it is false). In summarizing this test, we conclude that we do not have sufficient evidence to reject H 0 . We do not conclude that H 0 is true, because there may be a moderate to high probability that we committed a Type II error. It is possible that the sample size is not large enough to detect a difference in mean expenditures.      

The NCHS reported that the mean total cholesterol level in 2002 for all adults was 203. Total cholesterol levels in participants who attended the seventh examination of the Offspring in the Framingham Heart Study are summarized as follows: n=3,310, x̄ =200.3, and s=36.8. Is there statistical evidence of a difference in mean cholesterol levels in the Framingham Offspring?

Here we want to assess whether the sample mean of 200.3 in the Framingham sample is statistically significantly different from 203 (i.e., beyond what we would expect by chance). We will run the test using the five-step approach.

H 0 : μ= 203 H 1 : μ≠ 203                       α=0.05

The research hypothesis is that cholesterol levels are different in the Framingham Offspring, and therefore a two-tailed test is used.

•   Step 3. Set up decision rule.  

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or is Z > 1.960.

We reject H 0 because -4.22 ≤ -1. .960. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level in the Framingham Offspring is different from the national average of 203 reported in 2002.   Because we reject H 0 , we also approximate a p-value. Using the two-sided significance levels, p < 0.0001.  

Statistical Significance versus Clinical (Practical) Significance

This example raises an important concept of statistical versus clinical or practical significance. From a statistical standpoint, the total cholesterol levels in the Framingham sample are highly statistically significantly different from the national average with p < 0.0001 (i.e., there is less than a 0.01% chance that we are incorrectly rejecting the null hypothesis). However, the sample mean in the Framingham Offspring study is 200.3, less than 3 units different from the national mean of 203. The reason that the data are so highly statistically significant is due to the very large sample size. It is always important to assess both statistical and clinical significance of data. This is particularly relevant when the sample size is large. Is a 3 unit difference in total cholesterol a meaningful difference?  

Consider again the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. Suppose a new drug is proposed to lower total cholesterol. A study is designed to evaluate the efficacy of the drug in lowering cholesterol.   Fifteen patients are enrolled in the study and asked to take the new drug for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows:   n=15, x̄ =195.9 and s=28.7. Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new drug for 6 weeks? We will run the test using the five-step approach. 

H 0 : μ= 203 H 1 : μ< 203                   α=0.05

•  Step 2. Select the appropriate test statistic.  

Because the sample size is small (n<30) the appropriate test statistic is

This is a lower tailed test, using a t statistic and a 5% level of significance. In order to determine the critical value of t, we need degrees of freedom, df, defined as df=n-1. In this example df=15-1=14. The critical value for a lower tailed test with df=14 and a =0.05 is -2.145 and the decision rule is as follows:   Reject H 0 if t < -2.145.

We do not reject H 0 because -0.96 > -2.145. We do not have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower than the national mean in patients taking the new drug for 6 weeks. Again, because we failed to reject the null hypothesis we make a weaker concluding statement allowing for the possibility that we may have committed a Type II error (i.e., failed to reject H 0 when in fact the drug is efficacious).

This example raises an important issue in terms of study design. In this example we assume in the null hypothesis that the mean cholesterol level is 203. This is taken to be the mean cholesterol level in patients without treatment. Is this an appropriate comparator? Alternative and potentially more efficient study designs to evaluate the effect of the new drug could involve two treatment groups, where one group receives the new drug and the other does not, or we could measure each patient's baseline or pre-treatment cholesterol level and then assess changes from baseline to 6 weeks post-treatment. These designs are also discussed here.

Video - Comparing a Sample Mean to Known Population Mean (8:20)

Link to transcript of the video

Tests with One Sample, Dichotomous Outcome

Hypothesis testing applications with a dichotomous outcome variable in a single population are also performed according to the five-step procedure. Similar to tests for means, a key component is setting up the null and research hypotheses. The objective is to compare the proportion of successes in a single population to a known proportion (p 0 ). That known proportion is generally derived from another study or report and is sometimes called a historical control. It is important in setting up the hypotheses in a one sample test that the proportion specified in the null hypothesis is a fair and reasonable comparator.    

In one sample tests for a dichotomous outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the sample proportion which is computed by taking the ratio of the number of successes to the sample size,

We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formula for the test statistic is given below.

Test Statistic for Testing H 0 : p = p 0

if min(np 0 , n(1-p 0 )) > 5

The formula above is appropriate for large samples, defined when the smaller of np 0 and n(1-p 0 ) is at least 5. This is similar, but not identical, to the condition required for appropriate use of the confidence interval formula for a population proportion, i.e.,

Here we use the proportion specified in the null hypothesis as the true proportion of successes rather than the sample proportion. If we fail to satisfy the condition, then alternative procedures, called exact methods must be used to test the hypothesis about the population proportion.

Example:  

The NCHS report indicated that in 2002 the prevalence of cigarette smoking among American adults was 21.1%.  Data on prevalent smoking in n=3,536 participants who attended the seventh examination of the Offspring in the Framingham Heart Study indicated that 482/3,536 = 13.6% of the respondents were currently smoking at the time of the exam. Suppose we want to assess whether the prevalence of smoking is lower in the Framingham Offspring sample given the focus on cardiovascular health in that community. Is there evidence of a statistically lower prevalence of smoking in the Framingham Offspring study as compared to the prevalence among all Americans?

H 0 : p = 0.211 H 1 : p < 0.211                     α=0.05

We must first check that the sample size is adequate.   Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 3,536(0.211), 3,536(1-0.211))=min(746, 2790)=746. The sample size is more than adequate so the following formula can be used:

This is a lower tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.645.

We reject H 0 because -10.93 < -1.645. We have statistically significant evidence at α=0.05 to show that the prevalence of smoking in the Framingham Offspring is lower than the prevalence nationally (21.1%). Here, p < 0.0001.  

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

Calculate this on your own before checking the answer.

Video - Hypothesis Test for One Sample and a Dichotomous Outcome (3:55)

Tests with Two Independent Samples, Continuous Outcome

There are many applications where it is of interest to compare two independent groups with respect to their mean scores on a continuous outcome. Here we compare means between groups, but rather than generating an estimate of the difference, we will test whether the observed difference (increase, decrease or difference) is statistically significant or not. Remember, that hypothesis testing gives an assessment of statistical significance, whereas estimation gives an estimate of effect and both are important.

Here we discuss the comparison of means when the two comparison groups are independent or physically separate. The two groups might be determined by a particular attribute (e.g., sex, diagnosis of cardiovascular disease) or might be set up by the investigator (e.g., participants assigned to receive an experimental treatment or placebo). The first step in the analysis involves computing descriptive statistics on each of the two samples. Specifically, we compute the sample size, mean and standard deviation in each sample and we denote these summary statistics as follows:

for sample 1:

for sample 2:

The designation of sample 1 and sample 2 is arbitrary. In a clinical trial setting the convention is to call the treatment group 1 and the control group 2. However, when comparing men and women, for example, either group can be 1 or 2.  

In the two independent samples application with a continuous outcome, the parameter of interest in the test of hypothesis is the difference in population means, μ 1 -μ 2 . The null hypothesis is always that there is no difference between groups with respect to means, i.e.,

The null hypothesis can also be written as follows: H 0 : μ 1 = μ 2 . In the research hypothesis, an investigator can hypothesize that the first mean is larger than the second (H 1 : μ 1 > μ 2 ), that the first mean is smaller than the second (H 1 : μ 1 < μ 2 ), or that the means are different (H 1 : μ 1 ≠ μ 2 ). The three different alternatives represent upper-, lower-, and two-tailed tests, respectively. The following test statistics are used to test these hypotheses.

Test Statistics for Testing H 0 : μ 1 = μ 2

• if n 1 > 30 and n 2 > 30
• if n 1 < 30 or n 2 < 30

NOTE: The formulas above assume equal variability in the two populations (i.e., the population variances are equal, or s 1 2 = s 2 2 ). This means that the outcome is equally variable in each of the comparison populations. For analysis, we have samples from each of the comparison populations. If the sample variances are similar, then the assumption about variability in the populations is probably reasonable. As a guideline, if the ratio of the sample variances, s 1 2 /s 2 2 is between 0.5 and 2 (i.e., if one variance is no more than double the other), then the formulas above are appropriate. If the ratio of the sample variances is greater than 2 or less than 0.5 then alternative formulas must be used to account for the heterogeneity in variances.    

The test statistics include Sp, which is the pooled estimate of the common standard deviation (again assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples as follows:

Because we are assuming equal variances between groups, we pool the information on variability (sample variances) to generate an estimate of the variability in the population. Note: Because Sp is a weighted average of the standard deviations in the sample, Sp will always be in between s 1 and s 2 .)

Data measured on n=3,539 participants who attended the seventh examination of the Offspring in the Framingham Heart Study are shown below.  

Suppose we now wish to assess whether there is a statistically significant difference in mean systolic blood pressures between men and women using a 5% level of significance.  

H 0 : μ 1 = μ 2

H 1 : μ 1 ≠ μ 2                       α=0.05

Because both samples are large ( > 30), we can use the Z test statistic as opposed to t. Note that statistical computing packages use t throughout. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The guideline suggests investigating the ratio of the sample variances, s 1 2 /s 2 2 . Suppose we call the men group 1 and the women group 2. Again, this is arbitrary; it only needs to be noted when interpreting the results. The ratio of the sample variances is 17.5 2 /20.1 2 = 0.76, which falls between 0.5 and 2 suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is

We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.

Notice that the pooled estimate of the common standard deviation, Sp, falls in between the standard deviations in the comparison groups (i.e., 17.5 and 20.1). Sp is slightly closer in value to the standard deviation in the women (20.1) as there were slightly more women in the sample.   Recall, Sp is a weight average of the standard deviations in the comparison groups, weighted by the respective sample sizes.  

Now the test statistic:

We reject H 0 because 2.66 > 1.960. We have statistically significant evidence at α=0.05 to show that there is a difference in mean systolic blood pressures between men and women. The p-value is p < 0.010.  

Here again we find that there is a statistically significant difference in mean systolic blood pressures between men and women at p < 0.010. Notice that there is a very small difference in the sample means (128.2-126.5 = 1.7 units), but this difference is beyond what would be expected by chance. Is this a clinically meaningful difference? The large sample size in this example is driving the statistical significance. A 95% confidence interval for the difference in mean systolic blood pressures is: 1.7 + 1.26 or (0.44, 2.96). The confidence interval provides an assessment of the magnitude of the difference between means whereas the test of hypothesis and p-value provide an assessment of the statistical significance of the difference.  

Above we performed a study to evaluate a new drug designed to lower total cholesterol. The study involved one sample of patients, each patient took the new drug for 6 weeks and had their cholesterol measured. As a means of evaluating the efficacy of the new drug, the mean total cholesterol following 6 weeks of treatment was compared to the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. At the end of the example, we discussed the appropriateness of the fixed comparator as well as an alternative study design to evaluate the effect of the new drug involving two treatment groups, where one group receives the new drug and the other does not. Here, we revisit the example with a concurrent or parallel control group, which is very typical in randomized controlled trials or clinical trials (refer to the EP713 module on Clinical Trials).  

A new drug is proposed to lower total cholesterol. A randomized controlled trial is designed to evaluate the efficacy of the medication in lowering cholesterol. Thirty participants are enrolled in the trial and are randomly assigned to receive either the new drug or a placebo. The participants do not know which treatment they are assigned. Each participant is asked to take the assigned treatment for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows.

Is there statistical evidence of a reduction in mean total cholesterol in patients taking the new drug for 6 weeks as compared to participants taking placebo? We will run the test using the five-step approach.

H 0 : μ 1 = μ 2 H 1 : μ 1 < μ 2                         α=0.05

Because both samples are small (< 30), we use the t test statistic. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The ratio of the sample variances, s 1 2 /s 2 2 =28.7 2 /30.3 2 = 0.90, which falls between 0.5 and 2, suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is:

This is a lower-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table (in More Resources to the right). In order to determine the critical value of t we need degrees of freedom, df, defined as df=n 1 +n 2 -2 = 15+15-2=28. The critical value for a lower tailed test with df=28 and α=0.05 is -1.701 and the decision rule is: Reject H 0 if t < -1.701.

Now the test statistic,

We reject H 0 because -2.92 < -1.701. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower in patients taking the new drug for 6 weeks as compared to patients taking placebo, p < 0.005.

The clinical trial in this example finds a statistically significant reduction in total cholesterol, whereas in the previous example where we had a historical control (as opposed to a parallel control group) we did not demonstrate efficacy of the new drug. Notice that the mean total cholesterol level in patients taking placebo is 217.4 which is very different from the mean cholesterol reported among all Americans in 2002 of 203 and used as the comparator in the prior example. The historical control value may not have been the most appropriate comparator as cholesterol levels have been increasing over time. In the next section, we present another design that can be used to assess the efficacy of the new drug.

Video - Comparison of Two Independent Samples With a Continuous Outcome (8:02)

Tests with Matched Samples, Continuous Outcome

In the previous section we compared two groups with respect to their mean scores on a continuous outcome. An alternative study design is to compare matched or paired samples. The two comparison groups are said to be dependent, and the data can arise from a single sample of participants where each participant is measured twice (possibly before and after an intervention) or from two samples that are matched on specific characteristics (e.g., siblings). When the samples are dependent, we focus on difference scores in each participant or between members of a pair and the test of hypothesis is based on the mean difference, μ d . The null hypothesis again reflects "no difference" and is stated as H 0 : μ d =0 . Note that there are some instances where it is of interest to test whether there is a difference of a particular magnitude (e.g., μ d =5) but in most instances the null hypothesis reflects no difference (i.e., μ d =0).  

The appropriate formula for the test of hypothesis depends on the sample size. The formulas are shown below and are identical to those we presented for estimating the mean of a single sample presented (e.g., when comparing against an external or historical control), except here we focus on difference scores.

Test Statistics for Testing H 0 : μ d =0

A new drug is proposed to lower total cholesterol and a study is designed to evaluate the efficacy of the drug in lowering cholesterol. Fifteen patients agree to participate in the study and each is asked to take the new drug for 6 weeks. However, before starting the treatment, each patient's total cholesterol level is measured. The initial measurement is a pre-treatment or baseline value. After taking the drug for 6 weeks, each patient's total cholesterol level is measured again and the data are shown below. The rightmost column contains difference scores for each patient, computed by subtracting the 6 week cholesterol level from the baseline level. The differences represent the reduction in total cholesterol over 4 weeks. (The differences could have been computed by subtracting the baseline total cholesterol level from the level measured at 6 weeks. The way in which the differences are computed does not affect the outcome of the analysis only the interpretation.)

Because the differences are computed by subtracting the cholesterols measured at 6 weeks from the baseline values, positive differences indicate reductions and negative differences indicate increases (e.g., participant 12 increases by 2 units over 6 weeks). The goal here is to test whether there is a statistically significant reduction in cholesterol. Because of the way in which we computed the differences, we want to look for an increase in the mean difference (i.e., a positive reduction). In order to conduct the test, we need to summarize the differences. In this sample, we have

The calculations are shown below.  

Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new medication for 6 weeks? We will run the test using the five-step approach.

H 0 : μ d = 0 H 1 : μ d > 0                 α=0.05

NOTE: If we had computed differences by subtracting the baseline level from the level measured at 6 weeks then negative differences would have reflected reductions and the research hypothesis would have been H 1 : μ d < 0. 

• Step 2 . Select the appropriate test statistic.

This is an upper-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table at the right, with df=15-1=14. The critical value for an upper-tailed test with df=14 and α=0.05 is 2.145 and the decision rule is Reject H 0 if t > 2.145.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

We reject H 0 because 4.61 > 2.145. We have statistically significant evidence at α=0.05 to show that there is a reduction in cholesterol levels over 6 weeks.  

Here we illustrate the use of a matched design to test the efficacy of a new drug to lower total cholesterol. We also considered a parallel design (randomized clinical trial) and a study using a historical comparator. It is extremely important to design studies that are best suited to detect a meaningful difference when one exists. There are often several alternatives and investigators work with biostatisticians to determine the best design for each application. It is worth noting that the matched design used here can be problematic in that observed differences may only reflect a "placebo" effect. All participants took the assigned medication, but is the observed reduction attributable to the medication or a result of these participation in a study.

Video - Hypothesis Testing With a Matched Sample and a Continuous Outcome (3:11)

Tests with Two Independent Samples, Dichotomous Outcome

There are several approaches that can be used to test hypotheses concerning two independent proportions. Here we present one approach - the chi-square test of independence is an alternative, equivalent, and perhaps more popular approach to the same analysis. Hypothesis testing with the chi-square test is addressed in the third module in this series: BS704_HypothesisTesting-ChiSquare.

In tests of hypothesis comparing proportions between two independent groups, one test is performed and results can be interpreted to apply to a risk difference, relative risk or odds ratio. As a reminder, the risk difference is computed by taking the difference in proportions between comparison groups, the risk ratio is computed by taking the ratio of proportions, and the odds ratio is computed by taking the ratio of the odds of success in the comparison groups. Because the null values for the risk difference, the risk ratio and the odds ratio are different, the hypotheses in tests of hypothesis look slightly different depending on which measure is used. When performing tests of hypothesis for the risk difference, relative risk or odds ratio, the convention is to label the exposed or treated group 1 and the unexposed or control group 2.      

For example, suppose a study is designed to assess whether there is a significant difference in proportions in two independent comparison groups. The test of interest is as follows:

H 0 : p 1 = p 2 versus H 1 : p 1 ≠ p 2 .  

The following are the hypothesis for testing for a difference in proportions using the risk difference, the risk ratio and the odds ratio. First, the hypotheses above are equivalent to the following:

• For the risk difference, H 0 : p 1 - p 2 = 0 versus H 1 : p 1 - p 2 ≠ 0 which are, by definition, equal to H 0 : RD = 0 versus H 1 : RD ≠ 0.
• If an investigator wants to focus on the risk ratio, the equivalent hypotheses are H 0 : RR = 1 versus H 1 : RR ≠ 1.
• If the investigator wants to focus on the odds ratio, the equivalent hypotheses are H 0 : OR = 1 versus H 1 : OR ≠ 1.  

Suppose a test is performed to test H 0 : RD = 0 versus H 1 : RD ≠ 0 and the test rejects H 0 at α=0.05. Based on this test we can conclude that there is significant evidence, α=0.05, of a difference in proportions, significant evidence that the risk difference is not zero, significant evidence that the risk ratio and odds ratio are not one. The risk difference is analogous to the difference in means when the outcome is continuous. Here the parameter of interest is the difference in proportions in the population, RD = p 1 -p 2 and the null value for the risk difference is zero. In a test of hypothesis for the risk difference, the null hypothesis is always H 0 : RD = 0. This is equivalent to H 0 : RR = 1 and H 0 : OR = 1. In the research hypothesis, an investigator can hypothesize that the first proportion is larger than the second (H 1 : p 1 > p 2 , which is equivalent to H 1 : RD > 0, H 1 : RR > 1 and H 1 : OR > 1), that the first proportion is smaller than the second (H 1 : p 1 < p 2 , which is equivalent to H 1 : RD < 0, H 1 : RR < 1 and H 1 : OR < 1), or that the proportions are different (H 1 : p 1 ≠ p 2 , which is equivalent to H 1 : RD ≠ 0, H 1 : RR ≠ 1 and H 1 : OR ≠

1). The three different alternatives represent upper-, lower- and two-tailed tests, respectively.  

The formula for the test of hypothesis for the difference in proportions is given below.

Test Statistics for Testing H 0 : p 1 = p

The formula above is appropriate for large samples, defined as at least 5 successes (np > 5) and at least 5 failures (n(1-p > 5)) in each of the two samples. If there are fewer than 5 successes or failures in either comparison group, then alternative procedures, called exact methods must be used to estimate the difference in population proportions.

The following table summarizes data from n=3,799 participants who attended the fifth examination of the Offspring in the Framingham Heart Study. The outcome of interest is prevalent CVD and we want to test whether the prevalence of CVD is significantly higher in smokers as compared to non-smokers.

The prevalence of CVD (or proportion of participants with prevalent CVD) among non-smokers is 298/3,055 = 0.0975 and the prevalence of CVD among current smokers is 81/744 = 0.1089. Here smoking status defines the comparison groups and we will call the current smokers group 1 (exposed) and the non-smokers (unexposed) group 2. The test of hypothesis is conducted below using the five step approach.

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2                 α=0.05

• Step 2.  Select the appropriate test statistic.  

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group. In this example, we have more than enough successes (cases of prevalent CVD) and failures (persons free of CVD) in each comparison group. The sample size is more than adequate so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5. Conclusion.

We do not reject H 0 because -1.960 < 0.927 < 1.960. We do not have statistically significant evidence at α=0.05 to show that there is a difference in prevalent CVD between smokers and non-smokers.  

A 95% confidence interval for the difference in prevalent CVD (or risk difference) between smokers and non-smokers as 0.0114 + 0.0247, or between -0.0133 and 0.0361. Because the 95% confidence interval for the risk difference includes zero we again conclude that there is no statistically significant difference in prevalent CVD between smokers and non-smokers.    

Smoking has been shown over and over to be a risk factor for cardiovascular disease. What might explain the fact that we did not observe a statistically significant difference using data from the Framingham Heart Study? HINT: Here we consider prevalent CVD, would the results have been different if we considered incident CVD?

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We now test whether there is a statistically significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using the five step approach.  

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2              α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group, i.e.,

In this example, we have min(50(0.46), 50(1-0.46), 50(0.22), 50(1-0.22)) = min(23, 27, 11, 39) = 11. The sample size is adequate so the following formula can be used

We reject H 0 because 2.526 > 1960. We have statistically significant evidence at a =0.05 to show that there is a difference in the proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever.

A 95% confidence interval for the difference in proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever is 0.24 + 0.18 or between 0.06 and 0.42. Because the 95% confidence interval does not include zero we concluded that there was a statistically significant difference in proportions which is consistent with the test of hypothesis result. 

Again, the procedures discussed here apply to applications where there are two independent comparison groups and a dichotomous outcome. There are other applications in which it is of interest to compare a dichotomous outcome in matched or paired samples. For example, in a clinical trial we might wish to test the effectiveness of a new antibiotic eye drop for the treatment of bacterial conjunctivitis. Participants use the new antibiotic eye drop in one eye and a comparator (placebo or active control treatment) in the other. The success of the treatment (yes/no) is recorded for each participant for each eye. Because the two assessments (success or failure) are paired, we cannot use the procedures discussed here. The appropriate test is called McNemar's test (sometimes called McNemar's test for dependent proportions).  

Vide0 - Hypothesis Testing With Two Independent Samples and a Dichotomous Outcome (2:55)

Here we presented hypothesis testing techniques for means and proportions in one and two sample situations. Tests of hypothesis involve several steps, including specifying the null and alternative or research hypothesis, selecting and computing an appropriate test statistic, setting up a decision rule and drawing a conclusion. There are many details to consider in hypothesis testing. The first is to determine the appropriate test. We discussed Z and t tests here for different applications. The appropriate test depends on the distribution of the outcome variable (continuous or dichotomous), the number of comparison groups (one, two) and whether the comparison groups are independent or dependent. The following table summarizes the different tests of hypothesis discussed here.

• Continuous Outcome, One Sample: H0: μ = μ0
• Continuous Outcome, Two Independent Samples: H0: μ1 = μ2
• Continuous Outcome, Two Matched Samples: H0: μd = 0
• Dichotomous Outcome, One Sample: H0: p = p 0
• Dichotomous Outcome, Two Independent Samples: H0: p1 = p2, RD=0, RR=1, OR=1

Once the type of test is determined, the details of the test must be specified. Specifically, the null and alternative hypotheses must be clearly stated. The null hypothesis always reflects the "no change" or "no difference" situation. The alternative or research hypothesis reflects the investigator's belief. The investigator might hypothesize that a parameter (e.g., a mean, proportion, difference in means or proportions) will increase, will decrease or will be different under specific conditions (sometimes the conditions are different experimental conditions and other times the conditions are simply different groups of participants). Once the hypotheses are specified, data are collected and summarized. The appropriate test is then conducted according to the five step approach. If the test leads to rejection of the null hypothesis, an approximate p-value is computed to summarize the significance of the findings. When tests of hypothesis are conducted using statistical computing packages, exact p-values are computed. Because the statistical tables in this textbook are limited, we can only approximate p-values. If the test fails to reject the null hypothesis, then a weaker concluding statement is made for the following reason.

In hypothesis testing, there are two types of errors that can be committed. A Type I error occurs when a test incorrectly rejects the null hypothesis. This is referred to as a false positive result, and the probability that this occurs is equal to the level of significance, α. The investigator chooses the level of significance in Step 1, and purposely chooses a small value such as α=0.05 to control the probability of committing a Type I error. A Type II error occurs when a test fails to reject the null hypothesis when in fact it is false. The probability that this occurs is equal to β. Unfortunately, the investigator cannot specify β at the outset because it depends on several factors including the sample size (smaller samples have higher b), the level of significance (β decreases as a increases), and the difference in the parameter under the null and alternative hypothesis.    

We noted in several examples in this chapter, the relationship between confidence intervals and tests of hypothesis. The approaches are different, yet related. It is possible to draw a conclusion about statistical significance by examining a confidence interval. For example, if a 95% confidence interval does not contain the null value (e.g., zero when analyzing a mean difference or risk difference, one when analyzing relative risks or odds ratios), then one can conclude that a two-sided test of hypothesis would reject the null at α=0.05. It is important to note that the correspondence between a confidence interval and test of hypothesis relates to a two-sided test and that the confidence level corresponds to a specific level of significance (e.g., 95% to α=0.05, 90% to α=0.10 and so on). The exact significance of the test, the p-value, can only be determined using the hypothesis testing approach and the p-value provides an assessment of the strength of the evidence and not an estimate of the effect.

Answers to Selected Problems

Dental services problem - bottom of page 5.

• Step 1: Set up hypotheses and determine the level of significance.

α=0.05

• Step 2: Select the appropriate test statistic.

First, determine whether the sample size is adequate.

Therefore the sample size is adequate, and we can use the following formula:

• Step 3: Set up the decision rule.

Reject H0 if Z is less than or equal to -1.96 or if Z is greater than or equal to 1.96.

• Step 4: Compute the test statistic
• Step 5: Conclusion.

We reject the null hypothesis because -6.15<-1.96. Therefore there is a statistically significant difference in the proportion of children in Boston using dental services compated to the national proportion.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.8 Hypothesis Tests for a Population Proportion

Learning objectives.

• Conduct and interpret hypothesis tests for a population proportion.

Some notes about conducting a hypothesis test:

• The null hypothesis [latex]H_0[/latex] is always an “equal to.”  The null hypothesis is the original claim about the population parameter.
• The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.”  The form of the alternative hypothesis depends on the context of the question.
• If the alternative hypothesis is a “less than”, then the test is left-tail.  The p -value is the area in the left-tail of the distribution.
• If the alternative hypothesis is a “greater than”, then the test is right-tail.  The p -value is the area in the right-tail of the distribution.
• If the alternative hypothesis is a “not equal to”, then the test is two-tail.  The p -value is the sum of the area in the two-tails of the distribution.  Each tail represents exactly half of the p -value.
• Think about the meaning of the p -value.  A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller p -value (for example, 0.001 as opposed to 0.04) even if using a significance level of 0.05. Similarly, for a large p -value such as 0.4, as opposed to a p -value of 0.056 (a significance level of 0.05 is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
• The significance level must be identified before collecting the sample data and conducting the test.  Generally, the significance level will be included in the question.  If no significance level is given, a common standard is to use a significance level of 5%.

Suppose the hypotheses for a hypothesis test are:

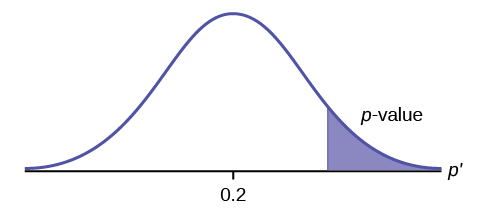
[latex]\begin{eqnarray*} H_0: & & p=20 \% \\ H_a: & & p \gt 20\% \end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\gt[/latex], this is a right-tail test.  The p -value is the area in the right-tail of the distribution.

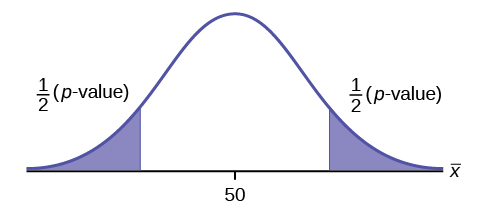
[latex]\begin{eqnarray*} H_0: & & p=50 \% \\ H_a: & & p \neq  50\% \end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\neq[/latex], this is a two-tail test.  The p -value is the sum of the areas in the two tails of the distribution.  Each tail contains exactly half of the p -value.

[latex]\begin{eqnarray*} H_0: & & p=10\% \\ H_a: & & p \lt  10\% \end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tail test.  The p -value is the area in the left-tail of the distribution.

Steps to Conduct a Hypothesis Test for a Population Proportion

• Write down the null and alternative hypotheses in terms of the population proportion [latex]p[/latex].  Include appropriate units with the values of the proportion.
• Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
• Collect the sample information for the test and identify the significance level.
• If [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution with [latex]\displaystyle{z=\frac{\hat{p}-p}{\sqrt{\frac{p \times (1-p)}{n}}}}[/latex].
• If one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use a binomial distribution.
• The results of the sample data are significant.  There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
• The results of the sample data are not significant.  There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
• Write down a concluding sentence specific to the context of the question.

USING EXCEL TO CALCULE THE P -VALUE FOR A HYPOTHESIS TEST ON A POPULATION PROPORTION

The p -value for a hypothesis test on a population proportion is the area in the tail(s) of distribution of the sample proportion.  If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution to find the p -value.  If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use the binomial distribution to find the p -value.

If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex]:

• For x , enter the value for [latex]\hat{p}[/latex].
• For [latex]\mu[/latex] , enter the mean of the sample proportions [latex]p[/latex].  Note:  Because the test is run assuming the null hypothesis is true, the value for [latex]p[/latex] is the claim from the null hypothesis.
• For [latex]\sigma[/latex] , enter the standard error of the proportions [latex]\displaystyle{\sqrt{\frac{p \times (1-p)}{n}}}[/latex].
• For the logic operator , enter true .  Note:  Because we are calculating the area under the curve, we always enter true for the logic operator.
• Use the appropriate technique with the norm.dist function to find the area in the left-tail or the area in the right-tail.

If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex]:

• The p -value is found using the binomial distribution.
• For x , enter the number of successes.
• For n , enter the sample size.
• For p , enter the the value of the population proportion [latex]p[/latex] from the null hypothesis.
• For the logic operator , enter true .  Note:  Because we are calculating an at most probability, the logic operator is always true.
• For p , enter the the value of the population proportion [latex]p[/latex] in the null hypothesis.
• For the logic operator , enter true .  Note:  Because we are calculating an at least probability, the logic operator is always true.

Marketers believe that 92% of adults own a cell phone.  A cell phone manufacturer believes that number is actually lower.  In a sample of 200 adults, 87% own a cell phone.  At the 1% significance level, determine if the proportion of adults that own a cell phone is lower than the marketers’ claim.

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & p=92\% \mbox{ of adults own a cell phone} \\ H_a: & & p \lt 92\% \mbox{ of adults own a cell phone} \end{eqnarray*}[/latex]

From the question, we have [latex]n=200[/latex], [latex]\hat{p}=0.87[/latex], and [latex]\alpha=0.01[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.92[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 200 \times 0.92=184 \geq 5 \\ n \times (1-p) & = & 200 \times (1-0.92)=16 \geq 5\end{eqnarray*}[/latex]

Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p)  \geq 5[/latex] we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the area in the left tail of the distribution.

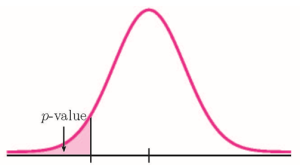
So the p -value[latex]=0.0046[/latex].

Conclusion:

Because p -value[latex]=0.0046 \lt 0.01=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 1% significance level there is enough evidence to suggest that the proportion of adults who own a cell phone is lower than 92%.

• The null hypothesis [latex]p=92\%[/latex] is the claim that 92% of adults own a cell phone.
• The alternative hypothesis [latex]p \lt 92\%[/latex] is the claim that less than 92% of adults own a cell phone.
• The function is norm.dist because we are finding the area in the left tail of a normal distribution.
• Field 1 is the value of [latex]\hat{p}[/latex].
• Field 2 is the value of [latex]p[/latex] from the null hypothesis.  Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.92[/latex].
• Field 3 is the standard deviation for the sample proportions [latex]\displaystyle{\sqrt{\frac{p \times (1-p)}{n}}}[/latex].
• The p -value of 0.0046 tells us that under the assumption that 92% of adults own a cell phone (the null hypothesis), there is only a 0.46% chance that the proportion of adults who own a cell phone in a sample of 200 is 87% or less.  This is a small probability, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.  In other words, the proportion of adults who own a cell phone is most likely less than 92%.

A consumer group claims that the proportion of households that have at least three cell phones is 30%.  A cell phone company has reason to believe that the proportion of households with at least three cell phones is much higher.  Before they start a big advertising campaign based on the proportion of households that have at least three cell phones, they want to test their claim.  Their marketing people survey 150 households with the result that 54 of the households have at least three cell phones.  At the 1% significance level, determine if the proportion of households that have at least three cell phones is less than 30%.

[latex]\begin{eqnarray*} H_0: & & p=30\% \mbox{ of household have at least 3 cell phones} \\ H_a: & & p \gt 30\% \mbox{ of household have at least 3 cell phones} \end{eqnarray*}[/latex]

From the question, we have [latex]n=150[/latex], [latex]\displaystyle{\hat{p}=\frac{54}{150}=0.36}[/latex], and [latex]\alpha=0.01[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.3[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 150 \times 0.3=45 \geq 5 \\ n \times (1-p) & = & 150 \times (1-0.3)=105 \geq 5\end{eqnarray*}[/latex]

Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p)  \geq  5[/latex] we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right tail of the distribution.

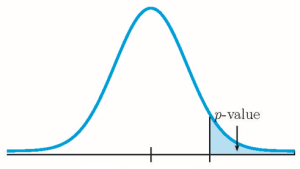
So the p -value[latex]=0.0544[/latex].

Because p -value[latex]=0.0544 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis.  At the 1% significance level there is not enough evidence to suggest that the proportion of households with at least three cell phones is more than 30%.

• The null hypothesis [latex]p=30\%[/latex] is the claim that 30% of households have at least three cell phones.
• The alternative hypothesis [latex]p \gt 30\%[/latex] is the claim that more than 30% of households have at least three cell phones.
• The function is 1-norm.dist because we are finding the area in the right tail of a normal distribution.
• Field 2 is the value of [latex]p[/latex] from the null hypothesis.  Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.3[/latex].
• The p -value of 0.0544 tells us that under the assumption that 30% of households have at least three cell phones (the null hypothesis), there is a 5.44% chance that the proportion of households with at least three cell phones in a sample of 150 is 36% or more.  Compared to the 1% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the claim that 30% of households have at least three cell phones is most likely correct.

A teacher believes that 70% of students in the class will want to go on a field trip to the local zoo.  The students in the class believe the proportion is much higher and ask the teacher to verify her claim.  The teacher samples 50 students and 39 reply that they would want to go to the zoo.  At the 5% significance level, determine if the proportion of students who want to go on the field trip is higher than 70%.

[latex]\begin{eqnarray*} H_0: & & p = 70\% \mbox{ of students want to go on the field trip}  \\ H_a: & & p \gt 70\% \mbox{ of students want to go on the field trip}   \end{eqnarray*}[/latex]

From the question, we have [latex]n=50[/latex], [latex]\displaystyle{\hat{p}=\frac{39}{50}=0.78}[/latex], and [latex]\alpha=0.05[/latex].

[latex]\begin{eqnarray*} n \times p & = & 50 \times 0.7=35 \geq 5 \\ n \times (1-p) & = & 50 \times (1-0.7)=15 \geq 5\end{eqnarray*}[/latex]

Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p)  \geq 5[/latex] we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right tail of the distribution.

So the p -value[latex]=0.1085[/latex].

Because p -value[latex]=0.1085 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is not enough evidence to suggest that the proportion of students who want to go on the field trip is higher than 70%.

• The null hypothesis [latex]p=70\%[/latex] is the claim that 70% of the students want to go on the field trip.
• The alternative hypothesis [latex]p \gt 70\%[/latex] is the claim that more than 70% of students want to go on the field trip.
• The p -value of 0.1085 tells us that under the assumption that 70% of students want to go on the field trip (the null hypothesis), there is a 10.85% chance that the proportion of students who want to go on the field trip in a sample of 50 students is 78% or more.  Compared to the 5% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the teacher’s claim that 70% of students want to go on the field trip is most likely correct.

Joan believes that 50% of first-time brides in the United States are younger than their grooms.  She performs a hypothesis test to determine if the percentage is the same or different from 50%.  Joan samples 100 first-time brides and 56 reply that they are younger than their grooms.  Use a 5% significance level.

[latex]\begin{eqnarray*} H_0: & & p=50\% \mbox{ of first-time brides are younger than the groom} \\ H_a: & & p \neq 50\% \mbox{ of first-time brides are younger than the groom} \end{eqnarray*}[/latex]

From the question, we have [latex]n=100[/latex], [latex]\displaystyle{\hat{p}=\frac{56}{100}=0.56}[/latex], and [latex]\alpha=0.05[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.5[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 100 \times 0.5=50 \geq 5 \\ n \times (1-p) & = & 100 \times (1-0.5)=50 \geq 5\end{eqnarray*}[/latex]

Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p)  \geq 5[/latex] we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of area in the tails of the distribution.

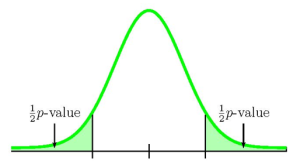
Because there is only one sample, we only have information relating to one of the two tails, either the left or the right.  We need to know if the sample relates to the left or right tail because that will determine how we calculate out the area of that tail using the normal distribution.  In this case, the sample proportion [latex]\hat{p}=0.56[/latex] is greater than the value of the population proportion in the null hypothesis [latex]p=0.5[/latex] ([latex]\hat{p}=0.56>0.5=p[/latex]), so the sample information relates to the right-tail of the normal distribution.  This means that we will calculate out the area in the right tail using 1-norm.dist .  However, this is a two-tailed test where the p -value is the sum of the area in the two tails and the area in the right-tail is only one half of the p -value.  The area in the left tail equals the area in the right tail and the p -value is the sum of these two areas.

So the area in the right tail is 0.1151 and  [latex]\frac{1}{2}[/latex]( p -value)[latex]=0.1151[/latex].  This is also the area in the left tail, so

p -value[latex]=0.1151+0.1151=0.2302[/latex]

Because p -value[latex]=0.2302 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is not enough evidence to suggest that the proportion of first-time brides that are younger than the groom is different from 50%.

• The null hypothesis [latex]p=50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is 50%.
• The alternative hypothesis [latex]p \neq 50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is different from 50%.
• We use norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\mbox{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the left tail.  The area in the right tail equals the area in the left tail, so we can find the p -value by adding the output from this function to itself.
• We use 1-norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\mbox{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the right tail.  The area in the left tail equals the area in the right tail, so we can find the p -value by adding the output from this function to itself.
• The p -value of 0.2302  is a large probability compared to the 5% significance level, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the claim that the proportion of first-time brides who are younger than the groom is most likely correct.

Watch this video: Hypothesis Testing for Proportions: z -test by ExcelIsFun [7:27] 

An online retailer believes that 93% of the visitors to its website will make a purchase.   A researcher in the marketing department thinks the actual percent is lower than claimed.  The researcher examines a sample of 50 visits to the website and finds that 45 of the visits resulted in a purchase.  At the 1% significance level, determine if the proportion of visits to the website that result in a purchase is lower than claimed.

[latex]\begin{eqnarray*} H_0: & & p=93\% \mbox{ of visitors make a purchase} \\ H_a: & & p \lt 93\% \mbox{ of visitors make a purchase} \end{eqnarray*}[/latex]

From the question, we have [latex]n=50[/latex], [latex]x=45[/latex], and [latex]\alpha=0.01[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.93[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 50 \times 0.93=46.5 \geq 5 \\ n \times (1-p) & = & 50 \times (1-0.93)=3.5 \lt 5\end{eqnarray*}[/latex]

Because [latex]n \times (1-p)  \lt 5[/latex] we use a binomial distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the probability of getting at most 45 successes in 50 trials.

So the p -value[latex]=0.2710[/latex].

Because p -value[latex]=0.2710 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis.  At the 1% significance level there is not enough evidence to suggest that the proportion of visitors who make a purchase is lower than 93%.

• The null hypothesis [latex]p=93\%[/latex] is the claim that 93% of visitors to the website make a purchase.
• The alternative hypothesis [latex]p \lt 93\%[/latex] is the claim that less than 93% of visitors to the website make a purchase.
• The function is binom.dist because we are finding the probability of at most 45 successes.
• Field 1 is the number of successes [latex]x[/latex].
• Field 2 is the sample size [latex]n[/latex].
• Field 3 is the probability of success [latex]p[/latex].  This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.93[/latex].
• The p -value of 0.2710 tells us that under the assumption that 93% of visitors make a purchase (the null hypothesis), there is a 27.10% chance that the number of visitors in a sample of 50 who make a purchase is 45 or less.  This is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the proportion of visitors to the website who make a purchase adults is most likely 93%.

A drug company claims that only 4% of people who take their new drug experience any side effects from the drug.  A researcher believes that the percent is higher than drug company’s claim.  The researcher takes a sample of 80 people who take the drug and finds that 10% of the people in the sample experience side effects from the drug.  At the 5% significance level, determine if the proportion of people who experience side effects from taking the drug is higher than claimed.

[latex]\begin{eqnarray*} H_0: & & p=4\% \mbox{ of people experience side effects} \\ H_a: & & p \gt 4\% \mbox{ of people experience side effects} \end{eqnarray*}[/latex]

From the question, we have [latex]n=80[/latex], [latex]\hat{p}=0.1[/latex], and [latex]\alpha=0.05[/latex].

To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex].  For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.04[/latex]).

[latex]\begin{eqnarray*} n \times p & = & 80 \times 0.04=3.2 \lt 5\end{eqnarray*}[/latex]

Because [latex]n \times p  \lt 5[/latex] we use a binomial distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the probability of getting at least 8 successes in 80 trials.  (Note:  In the sample of size 80, 10% have the characteristic of interest, so this means that [latex]80 \times 0.1=8[/latex] people in the sample have the characteristic of interest.)

So the p -value[latex]=0.0147[/latex].

Because p -value[latex]=0.0147 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 5% significance level there is enough evidence to suggest that the proportion of people who experience side effects from taking the drug is higher than 4%.

• The null hypothesis [latex]p=4\%[/latex] is the claim that 4% of the people experience side effects from taking the drug.
• The alternative hypothesis [latex]p \gt 4\%[/latex] is the claim that more than 4% of the people experience side effects from taking the drug.
• The function is 1-binom.dist because we are finding the probability of at least 8 successes.
• Field 1 is [latex]x-1[/latex] where [latex]x[/latex] is the number of successes.  In this case, we are using the compliment rule to change the probability of at least 8 successes into 1 minus the probability of at most 7 successes.
• Field 3 is the probability of success [latex]p[/latex].  This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.04[/latex].
• The p -value of 0.0147 tells us that under the assumption that 4% of people experience side effects (the null hypothesis), there is a 1.47% chance that the number of people in a sample of 80 who experience side effects is 8 or more.  This is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.  In other words, the proportion of people who experience side effects is most likely greater than 4%.

Concept Review

The hypothesis test for a population proportion is a well-established process:

• Find the p -value (the area in the corresponding tail) for the test using the appropriate distribution (normal or binomial).
• Compare the p -value to the significance level and state the outcome of the test.

Attribution

“ 9.6   Hypothesis Testing of a Single Mean and Single Proportion “ in Introductory Statistics by OpenStax  is licensed under a  Creative Commons Attribution 4.0 International License.

Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.4: Small Sample Tests for a Population Mean

• Last updated
• Save as PDF
• Page ID 522

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• To learn how to apply the five-step test procedure for test of hypotheses concerning a population mean when the sample size is small.

In the previous section hypotheses testing for population means was described in the case of large samples. The statistical validity of the tests was insured by the Central Limit Theorem, with essentially no assumptions on the distribution of the population. When sample sizes are small, as is often the case in practice, the Central Limit Theorem does not apply. One must then impose stricter assumptions on the population to give statistical validity to the test procedure. One common assumption is that the population from which the sample is taken has a normal probability distribution to begin with. Under such circumstances, if the population standard deviation is known, then the test statistic

\[\frac{(\bar{x}-\mu _0)}{\sigma /\sqrt{n}} \nonumber \]

still has the standard normal distribution, as in the previous two sections. If \(\sigma\) is unknown and is approximated by the sample standard deviation \(s\), then the resulting test statistic

\[\dfrac{(\bar{x}-\mu _0)}{s/\sqrt{n}} \nonumber \]

follows Student’s \(t\)-distribution with \(n-1\) degrees of freedom.

Standardized Test Statistics for Small Sample Hypothesis Tests Concerning a Single Population Mean

 If \(\sigma\) is known: \[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}} \nonumber \]

If \(\sigma\) is unknown: \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}} \nonumber \]

• The first test statistic (\(\sigma\) known) has the standard normal distribution.
• The second test statistic (\(\sigma\) unknown) has Student’s \(t\)-distribution with \(n-1\) degrees of freedom.
• The population must be normally distributed.

The distribution of the second standardized test statistic (the one containing \(s\)) and the corresponding rejection region for each form of the alternative hypothesis (left-tailed, right-tailed, or two-tailed), is shown in Figure \(\PageIndex{1}\). This is just like Figure 8.2.1 except that now the critical values are from the \(t\)-distribution. Figure 8.2.1 still applies to the first standardized test statistic (the one containing (\(\sigma\)) since it follows the standard normal distribution.

The \(p\)-value of a test of hypotheses for which the test statistic has Student’s \(t\)-distribution can be computed using statistical software, but it is impractical to do so using tables, since that would require \(30\) tables analogous to Figure 7.1.5, one for each degree of freedom from \(1\) to \(30\). Figure 7.1.6 can be used to approximate the \(p\)-value of such a test, and this is typically adequate for making a decision using the \(p\)-value approach to hypothesis testing, although not always. For this reason the tests in the two examples in this section will be made following the critical value approach to hypothesis testing summarized at the end of Section 8.1, but after each one we will show how the \(p\)-value approach could have been used.

Example \(\PageIndex{1}\)

The price of a popular tennis racket at a national chain store is \(\$179\). Portia bought five of the same racket at an online auction site for the following prices:

\[155\; 179\; 175\; 175\; 161 \nonumber \]

Assuming that the auction prices of rackets are normally distributed, determine whether there is sufficient evidence in the sample, at the \(5\%\) level of significance, to conclude that the average price of the racket is less than \(\$179\) if purchased at an online auction.

• Step 1 . The assertion for which evidence must be provided is that the average online price \(\mu\) is less than the average price in retail stores, so the hypothesis test is \[H_0: \mu =179\\ \text{vs}\\ H_a: \mu <179\; @\; \alpha =0.05 \nonumber \]
• Step 2 . The sample is small and the population standard deviation is unknown. Thus the test statistic is \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}} \nonumber \] and has the Student \(t\)-distribution with \(n-1=5-1=4\) degrees of freedom.
• Step 3 . From the data we compute \(\bar{x}=169\) and \(s=10.39\). Inserting these values into the formula for the test statistic gives \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{169-179}{10.39/\sqrt{5}}=-2.152 \nonumber \]
• Step 4 . Since the symbol in \(H_a\) is “\(<\)” this is a left-tailed test, so there is a single critical value, \(-t_\alpha =-t_{0.05}[df=4]\). Reading from the row labeled \(df=4\) in Figure 7.1.6 its value is \(-2.132\). The rejection region is \((-\infty ,-2.132]\).
• Step 5 . As shown in Figure \(\PageIndex{2}\) the test statistic falls in the rejection region. The decision is to reject \(H_0\). In the context of the problem our conclusion is:

The data provide sufficient evidence, at the \(5\%\) level of significance, to conclude that the average price of such rackets purchased at online auctions is less than \(\$179\).

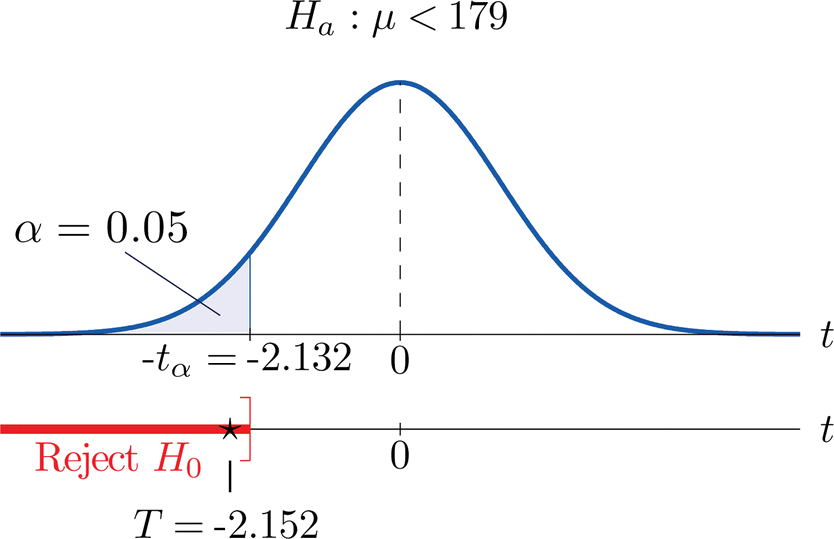
To perform the test in Example \(\PageIndex{1}\) using the \(p\)-value approach, look in the row in Figure 7.1.6 with the heading \(df=4\) and search for the two \(t\)-values that bracket the unsigned value \(2.152\) of the test statistic. They are \(2.132\) and \(2.776\), in the columns with headings \(t_{0.050}\) and \(t_{0.025}\). They cut off right tails of area \(0.050\) and \(0.025\), so because \(2.152\) is between them it must cut off a tail of area between \(0.050\) and \(0.025\). By symmetry \(-2.152\) cuts off a left tail of area between \(0.050\) and \(0.025\), hence the \(p\)-value corresponding to \(t=-2.152\) is between \(0.025\) and \(0.05\). Although its precise value is unknown, it must be less than \(\alpha =0.05\), so the decision is to reject \(H_0\).

Example \(\PageIndex{2}\)

A small component in an electronic device has two small holes where another tiny part is fitted. In the manufacturing process the average distance between the two holes must be tightly controlled at \(0.02\) mm, else many units would be defective and wasted. Many times throughout the day quality control engineers take a small sample of the components from the production line, measure the distance between the two holes, and make adjustments if needed. Suppose at one time four units are taken and the distances are measured as

Determine, at the \(1\%\) level of significance, if there is sufficient evidence in the sample to conclude that an adjustment is needed. Assume the distances of interest are normally distributed.

• Step 1 . The assumption is that the process is under control unless there is strong evidence to the contrary. Since a deviation of the average distance to either side is undesirable, the relevant test is \[H_0: \mu =0.02\\ \text{vs}\\ H_a: \mu \neq 0.02\; @\; \alpha =0.01 \nonumber \] where \(\mu\) denotes the mean distance between the holes.
• Step 2 . The sample is small and the population standard deviation is unknown. Thus the test statistic is \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}} \nonumber \] and has the Student \(t\)-distribution with \(n-1=4-1=3\) degrees of freedom.
• Step 3 . From the data we compute \(\bar{x}=0.02075\) and \(s=0.00171\). Inserting these values into the formula for the test statistic gives \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{0.02075-0.02}{0.00171\sqrt{4}}=0.877 \nonumber \]
• Step 4 . Since the symbol in \(H_a\) is “\(\neq\)” this is a two-tailed test, so there are two critical values, \(\pm t_{\alpha/2} =-t_{0.005}[df=3]\). Reading from the row in Figure 7.1.6 labeled \(df=3\) their values are \(\pm 5.841\). The rejection region is \((-\infty ,-5.841]\cup [5.841,\infty )\).
• Step 5 . As shown in Figure \(\PageIndex{3}\) the test statistic does not fall in the rejection region. The decision is not to reject \(H_0\). In the context of the problem our conclusion is:

The data do not provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the mean distance between the holes in the component differs from \(0.02\) mm.

To perform the test in "Example \(\PageIndex{2}\)" using the \(p\)-value approach, look in the row in Figure 7.1.6 with the heading \(df=3\) and search for the two \(t\)-values that bracket the value \(0.877\) of the test statistic. Actually \(0.877\) is smaller than the smallest number in the row, which is \(0.978\), in the column with heading \(t_{0.200}\). The value \(0.978\) cuts off a right tail of area \(0.200\), so because \(0.877\) is to its left it must cut off a tail of area greater than \(0.200\). Thus the \(p\)-value, which is the double of the area cut off (since the test is two-tailed), is greater than \(0.400\). Although its precise value is unknown, it must be greater than \(\alpha =0.01\), so the decision is not to reject \(H_0\).

Key Takeaway

• There are two formulas for the test statistic in testing hypotheses about a population mean with small samples. One test statistic follows the standard normal distribution, the other Student’s \(t\)-distribution.
• The population standard deviation is used if it is known, otherwise the sample standard deviation is used.
• Either five-step procedure, critical value or \(p\)-value approach, is used with either test statistic.

Statistics Tutorial

Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a proportion.

A population proportion is the share of a population that belongs to a particular category .

Hypothesis tests are used to check a claim about the size of that population proportion.

Hypothesis Testing a Proportion

The following steps are used for a hypothesis test:

• Check the conditions
• Define the claims
• Decide the significance level
• Calculate the test statistic

For example:

• Population : Nobel Prize winners
• Category : Born in the United States of America

And we want to check the claim:

" More than 20% of Nobel Prize winners were born in the US"

By taking a sample of 40 randomly selected Nobel Prize winners we could find that:

10 out of 40 Nobel Prize winners in the sample were born in the US

The sample proportion is then: \(\displaystyle \frac{10}{40} = 0.25\), or 25%.

From this sample data we check the claim with the steps below.

1. Checking the Conditions

The conditions for calculating a confidence interval for a proportion are:

• The sample is randomly selected
• Being in the category
• Not being in the category
• 5 members in the category
• 5 members not in the category

In our example, we randomly selected 10 people that were born in the US.

The rest were not born in the US, so there are 30 in the other category.

The conditions are fulfilled in this case.

Note: It is possible to do a hypothesis test without having 5 of each category. But special adjustments need to be made.

2. Defining the Claims

We need to define a null hypothesis (\(H_{0}\)) and an alternative hypothesis (\(H_{1}\)) based on the claim we are checking.

The claim was:

In this case, the parameter is the proportion of Nobel Prize winners born in the US (\(p\)).

The null and alternative hypothesis are then:

Null hypothesis : 20% of Nobel Prize winners were born in the US.

Alternative hypothesis : More than 20% of Nobel Prize winners were born in the US.

Which can be expressed with symbols as:

\(H_{0}\): \(p = 0.20 \)

\(H_{1}\): \(p > 0.20 \)

This is a ' right tailed' test, because the alternative hypothesis claims that the proportion is more than in the null hypothesis.

If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.

Advertisement

3. Deciding the Significance Level

The significance level (\(\alpha\)) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.

The significance level is a percentage probability of accidentally making the wrong conclusion.

Typical significance levels are:

• \(\alpha = 0.1\) (10%)
• \(\alpha = 0.05\) (5%)
• \(\alpha = 0.01\) (1%)

A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.

There is no "correct" significance level - it only states the uncertainty of the conclusion.

Note: A 5% significance level means that when we reject a null hypothesis:

We expect to reject a true null hypothesis 5 out of 100 times.

4. Calculating the Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

The formula for the test statistic (TS) of a population proportion is:

\(\displaystyle \frac{\hat{p} - p}{\sqrt{p(1-p)}} \cdot \sqrt{n} \)

\(\hat{p}-p\) is the difference between the sample proportion (\(\hat{p}\)) and the claimed population proportion (\(p\)).

\(n\) is the sample size.

In our example:

The claimed (\(H_{0}\)) population proportion (\(p\)) was \( 0.20 \)

The sample size (\(n\)) was \(40\)

So the test statistic (TS) is then:

\(\displaystyle \frac{0.25-0.20}{\sqrt{0.2(1-0.2)}} \cdot \sqrt{40} = \frac{0.05}{\sqrt{0.2(0.8)}} \cdot \sqrt{40} = \frac{0.05}{\sqrt{0.16}} \cdot \sqrt{40} \approx \frac{0.05}{0.4} \cdot 6.325 = \underline{0.791}\)

You can also calculate the test statistic using programming language functions:

With Python use the scipy and math libraries to calculate the test statistic for a proportion.

With R use the built-in prop.test() function to calculate the test statistic for a proportion.

5. Concluding

There are two main approaches for making the conclusion of a hypothesis test:

• The critical value approach compares the test statistic with the critical value of the significance level.
• The P-value approach compares the P-value of the test statistic and with the significance level.

Note: The two approaches are only different in how they present the conclusion.

The Critical Value Approach

For the critical value approach we need to find the critical value (CV) of the significance level (\(\alpha\)).

For a population proportion test, the critical value (CV) is a Z-value from a standard normal distribution .

This critical Z-value (CV) defines the rejection region for the test.

The rejection region is an area of probability in the tails of the standard normal distribution.

Because the claim is that the population proportion is more than 20%, the rejection region is in the right tail:

Choosing a significance level (\(\alpha\)) of 0.05, or 5%, we can find the critical Z-value from a Z-table , or with a programming language function:

Note: The functions find the Z-value for an area from the left side.

To find the Z-value for a right tail we need to use the function on the area to the left of the tail (1-0.05 = 0.95).

With Python use the Scipy Stats library norm.ppf() function find the Z-value for an \(\alpha\) = 0.05 in the right tail.

With R use the built-in qnorm() function to find the Z-value for an \(\alpha\) = 0.05 in the right tail.

Using either method we can find that the critical Z-value is \(\approx \underline{1.6449}\)

For a right tailed test we need to check if the test statistic (TS) is bigger than the critical value (CV).

If the test statistic is bigger than the critical value, the test statistic is in the rejection region .

When the test statistic is in the rejection region, we reject the null hypothesis (\(H_{0}\)).

Here, the test statistic (TS) was \(\approx \underline{0.791}\) and the critical value was \(\approx \underline{1.6449}\)

Here is an illustration of this test in a graph:

Since the test statistic was smaller than the critical value we do not reject the null hypothesis.

This means that the sample data does not support the alternative hypothesis.

And we can summarize the conclusion stating:

The sample data does not support the claim that "more than 20% of Nobel Prize winners were born in the US" at a 5% significance level .

The P-Value Approach

For the P-value approach we need to find the P-value of the test statistic (TS).

If the P-value is smaller than the significance level (\(\alpha\)), we reject the null hypothesis (\(H_{0}\)).

The test statistic was found to be \( \approx \underline{0.791} \)

For a population proportion test, the test statistic is a Z-Value from a standard normal distribution .

Because this is a right tailed test, we need to find the P-value of a Z-value bigger than 0.791.

We can find the P-value using a Z-table , or with a programming language function:

Note: The functions find the P-value (area) to the left side of Z-value.

To find the P-value for a right tail we need to subtract the left area from the total area: 1 - the output of the function.

With Python use the Scipy Stats library norm.cdf() function find the P-value of a Z-value bigger than 0.791:

With R use the built-in pnorm() function find the P-value of a Z-value bigger than 0.791:

Using either method we can find that the P-value is \(\approx \underline{0.2145}\)

This tells us that the significance level (\(\alpha\)) would need to be bigger than 0.2145, or 21.45%, to reject the null hypothesis.

This P-value is bigger than any of the common significance levels (10%, 5%, 1%).

So the null hypothesis is kept at all of these significance levels.

The sample data does not support the claim that "more than 20% of Nobel Prize winners were born in the US" at a 10%, 5%, or 1% significance level .

Note: It may still be true that the real population proportion is more than 20%.

But there was not strong enough evidence to support it with this sample.

Calculating a P-Value for a Hypothesis Test with Programming

Many programming languages can calculate the P-value to decide outcome of a hypothesis test.

Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.

The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.

With Python use the scipy and math libraries to calculate the P-value for a right tailed hypothesis test for a proportion.

Here, the sample size is 40, the occurrences are 10, and the test is for a proportion bigger than 0.20.

With R use the built-in prop.test() function find the P-value for a right tailed hypothesis test for a proportion.

Note: The conf.level in the R code is the reverse of the significance level.

Here, the significance level is 0.05, or 5%, so the conf.level is 1-0.05 = 0.95, or 95%.

Left-Tailed and Two-Tailed Tests

This was an example of a right tailed test, where the alternative hypothesis claimed that parameter is bigger than the null hypothesis claim.

You can check out an equivalent step-by-step guide for other types here:

• Left-Tailed Test
• Two-Tailed Test

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.5 - hypothesis testing for two-sample proportions.

We are now going to develop the hypothesis test for the difference of two proportions for independent samples. The hypothesis test follows the same steps as one group.

These notes are going to go into a little bit of math and formulas to help demonstrate the logic behind hypothesis testing for two groups. If this starts to get a little confusion, just skim over it for a general understanding! Remember we can rely on the software to do the calculations for us, but it is good to have a basic understanding of the logic!

We will use the sampling distribution of \(\hat{p}_1-\hat{p}_2\) as we did for the confidence interval.

For a test for two proportions, we are interested in the difference between two groups. If the difference is zero, then they are not different (i.e., they are equal). Therefore, the null hypothesis will always be:

\(H_0\colon p_1-p_2=0\)

Another way to look at it is \(H_0\colon p_1=p_2\). This is worth stopping to think about. Remember, in hypothesis testing, we assume the null hypothesis is true. In this case, it means that \(p_1\) and \(p_2\) are equal. Under this assumption, then \(\hat{p}_1\) and \(\hat{p}_2\) are both estimating the same proportion. Think of this proportion as \(p^*\).

Therefore, the sampling distribution of both proportions, \(\hat{p}_1\) and \(\hat{p}_2\), will, under certain conditions, be approximately normal centered around \(p^*\), with standard error \(\sqrt{\dfrac{p^*(1-p^*)}{n_i}}\), for \(i=1, 2\).

We take this into account by finding an estimate for this \(p^*\) using the two-sample proportions. We can calculate an estimate of \(p^*\) using the following formula:

\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\)

This value is the total number in the desired categories \((x_1+x_2)\) from both samples over the total number of sampling units in the combined sample \((n_1+n_2)\).

Putting everything together, if we assume \(p_1=p_2\), then the sampling distribution of \(\hat{p}_1-\hat{p}_2\) will be approximately normal with mean 0 and standard error of \(\sqrt{p^*(1-p^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\), under certain conditions.

\(z^*=\dfrac{(\hat{p}_1-\hat{p}_2)-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...will follow a standard normal distribution.

Finally, we can develop our hypothesis test for \(p_1-p_2\).

Hypothesis Testing for Two-Sample Proportions

Conditions :

\(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than five

Test Statistic:

\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)

...where \(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\).

The critical values, p-values, and decisions will all follow the same steps as those from a hypothesis test for a one-sample proportion.