fractions and percentages problem solving

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Percentage Word Problems

Welcome to our Basic Percentage Word Problems. In this area, we have a selection of basic percentage problem worksheets designed for 6th grade students who are just starting to learn about percentages to help them to solve a range of simple percentage problems.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Percentage Learning

Percentages are another area that children can find quite difficult. There are several key areas within percentages which need to be mastered in order.

Our selection of percentage worksheets will help you to find percentages of numbers and amounts, as well as working out percentage increases and decreases and converting percentages to fractions or decimals.

Key percentage facts:

• 50% = 0.5 = ½
• 25% = 0.25 = ¼
• 75% = 0.75 = ¾
• 10% = 0.1 = 1 ⁄ 10
• 1% = 0.01 = 1 ⁄ 100

How to work out Percentages of a number

This page will help you learn to find the percentage of a given number.

There is also a percentage calculator on the page to support you work through practice questions.

• Percentage Of Calculator

This is the calculator to use if you want to find a percentage of a number.

Simple choose your number and the percentage and the calculator will do the rest.

Basic Percentage Word Problems

Here you will find a selection of worksheets on percentages designed to help your child practise how to apply their knowledge to solve a range of percentage problems..

The sheets are graded so that the easier ones are at the top.

The sheets have been split up into sections as follows:

• spot the percentage problems where the aim is to use the given facts to find the missing percentage;
• solving percentage of number problems, where the aim is to work out the percentage of a number.

Each of the sheets on this page has also been split into 3 different worksheets:

• Sheet A which is set at an easier level;
• Sheet B which is set at a medium level;
• Sheet C which is set at a more advanced level for high attainers.

Spot the Percentages Problems

• Spot the Percentage 1A
• PDF version
• Spot the Percentage 1B
• Spot the Percentage 1C
• Spot the Percentage 2A
• Spot the Percentage 2B
• Spot the Percentage 2C

Percentage of Number Word Problems

• Percentage of Number Problems 1A
• Percentage of Number Problems 1B
• Percentage of Number Problems 1C
• Percentage of Number Problems 2A
• Percentage of Number Problems 2B
• Percentage of Number Problems 2C
• Percentage of Number Problems 3A
• Percentage of Number Problems 3B
• Percentage of Number Problems 3C

More Recommended Math Worksheets

Take a look at some more of our worksheets similar to these.

6th Grade Percentage Word Problems

The sheets in this area are at a harder level than those on this page.

The problems involve finding the percentage of numbers and amounts, as well as finding the amounts when the percentage is given.

• 6th Grade Percent Word Problems
• Percentage Increase and Decrease Worksheets

We have created a range of worksheets based around percentage increases and decreases.

Our worksheets include:

• finding percentage change between two numbers;
• finding a given percentage increase from an amount;
• finding a given percentage decrease from an amount.

Percentage of Money Amounts

Often when we are studying percentages, we look at them in the context of money.

The sheets on this page are all about finding percentages of different amounts of money.

• Money Percentage Worksheets

Percentage of Number Worksheets

If you would like some practice finding the percentage of a range of numbers, then try our Percentage Worksheets page.

You will find a range of worksheets starting with finding simple percentages such as 1%, 10% and 50% to finding much trickier ones.

• Percentage of Numbers Worksheets

Converting Percentages to Fractions

To convert a fraction to a percentage follows on simply from converting a fraction to a decimal.

Simply divide the numerator by the denominator to give you the decimal form. Then multiply the result by 100 to change the decimal into a percentage.

The printable learning fraction page below contains more support, examples and practice converting fractions to decimals.

• Converting Fractions to Percentages

• Convert Percent to Fraction

Online Percentage Practice Zone

Our online percentage practice zone gives you a chance to practice finding percentages of a range of numbers.

You can choose your level of difficulty and test yourself with immediate feedback!

• Online Percentage Practice
• Ratio Part to Part Worksheets

These sheets are a great way to introduce ratio of one object to another using visual aids.

The sheets in this section are at a more basic level than those on this page.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to 5th Grade Math Worksheets

Return from Percentage Word Problems page to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

Decimals, Fractions and Percentages

Decimals, Fractions and Percentages are just different ways of showing the same value:

Here, have a play with it yourself:

Example Values

Here is a table of commonly used values shown in Percent, Decimal and Fraction form:

Conversions!

From percent to decimal.

To convert from percent to decimal divide by 100 and remove the % sign.

An easy way to divide by 100 is to move the decimal point 2 places to the left :

Don't forget to remove the % sign!

From Decimal to Percent

To convert from decimal to percent multiply by 100%

An easy way to multiply by 100 is to move the decimal point 2 places to the right :

 Don't forget to add the % sign!

From Fraction to Decimal

To convert a fraction to a decimal divide the top number by the bottom number:

Example: Convert 2 5 to a decimal

Divide 2 by 5: 2 ÷ 5 = 0.4

Answer: 2 5 = 0.4

From Decimal to Fraction

To convert a decimal to a fraction needs a little more work.

Example: To convert 0.75 to a fraction

From fraction to percentage.

To convert a fraction to a percentage divide the top number by the bottom number, then multiply the result by 100%

Example: Convert 3 8 to a percentage

First divide 3 by 8: 3 ÷ 8 = 0.375

Then multiply by 100%: 0.375 × 100% = 37.5%

Answer: 3 8 = 37.5%

From Percentage to Fraction

To convert a percentage to a fraction , first convert to a decimal (divide by 100), then use the steps for converting decimal to fractions (like above).

Example: To convert 80% to a fraction

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.2.1: Solving Percent Problems

• Last updated
• Save as PDF
• Page ID 62169

• The NROC Project

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Identify the amount, the base, and the percent in a percent problem.
• Find the unknown in a percent problem.

Introduction

Percents are a ratio of a number and 100, so they are easier to compare than fractions, as they always have the same denominator, 100. A store may have a 10% off sale. The amount saved is always the same portion or fraction of the price, but a higher price means more money is taken off. Interest rates on a saving account work in the same way. The more money you put in your account, the more money you get in interest. It’s helpful to understand how these percents are calculated.

Parts of a Percent Problem

Jeff has a coupon at the Guitar Store for 15% off any purchase of $100 or more. He wants to buy a used guitar that has a price tag of $220 on it. Jeff wonders how much money the coupon will take off the original $220 price.

Problems involving percents have any three quantities to work with: the percent , the amount , and the base .

• The percent has the percent symbol (%) or the word “percent.” In the problem above, 15% is the percent off the purchase price.
• The base is the whole amount. In the problem above, the whole price of the guitar is $220, which is the base.
• The amount is the number that relates to the percent. It is always part of the whole. In the problem above, the amount is unknown. Since the percent is the percent off , the amount will be the amount off of the price.

You will return to this problem a bit later. The following examples show how to identify the three parts: the percent, the base, and the amount.

Identify the percent, amount, and base in this problem.

30 is 20% of what number?

Percent: The percent is the number with the % symbol: 20%.

Base : The base is the whole amount, which in this case is unknown.

Amount: The amount based on the percent is 30.

Percent=20%

Base=unknown

The previous problem states that 30 is a portion of another number. That means 30 is the amount. Note that this problem could be rewritten: 20% of what number is 30?

Identify the percent, base, and amount in this problem:

What percent of 30 is 3?

The percent is unknown, because the problem states " What percent?" The base is the whole in the situation, so the base is 30. The amount is the portion of the whole, which is 3 in this case.

Solving with Equations

Percent problems can be solved by writing equations. An equation uses an equal sign (=) to show that two mathematical expressions have the same value.

Percents are fractions, and just like fractions, when finding a percent (or fraction, or portion) of another amount, you multiply.

The percent of the base is the amount.

Percent of the Base is the Amount.

\[\ \text { Percent } {\color{red}\cdot}\text { Base }{\color{blue}=}\text { Amount } \nonumber \]

In the examples below, the unknown is represented by the letter \(\ n\). The unknown can be represented by any letter or a box \(\ \square\) or even a question mark.

Write an equation that represents the following problem.

\(\ 20 \% \cdot n=30\)

Once you have an equation, you can solve it and find the unknown value. To do this, think about the relationship between multiplication and division. Look at the pairs of multiplication and division facts below, and look for a pattern in each row.

Multiplication and division are inverse operations. What one does to a number, the other “undoes.”

When you have an equation such as \(\ 20 \% \cdot n=30\), you can divide 30 by 20% to find the unknown: \(\ n=30 \div 20 \%\).

You can solve this by writing the percent as a decimal or fraction and then dividing.

\(\ n=30 \div 20 \%=30 \div 0.20=150\)

What percent of 72 is 9?

\(\ 12.5 \% \text { of } 72 \text { is } 9\).

You can estimate to see if the answer is reasonable. Use 10% and 20%, numbers close to 12.5%, to see if they get you close to the answer.

\(\ 10 \% \text { of } 72=0.1 \cdot 72=7.2\)

\(\ 20 \% \text { of } 72=0.2 \cdot 72=14.4\)

Notice that 9 is between 7.2 and 14.4, so 12.5% is reasonable since it is between 10% and 20%.

What is 110% of 24?

\(\ 26.4 \text { is } 110 \% \text { of } 24\).

This problem is a little easier to estimate. 100% of 24 is 24. And 110% is a little bit more than 24. So, 26.4 is a reasonable answer.

18 is what percent of 48?

• \(\ 0.375 \%\)
• \(\ 8.64 \%\)
• \(\ 37.5 \%\)
• \(\ 864 \%\)

Incorrect. You may have calculated properly, but you forgot to move the decimal point when you rewrote your answer as a percent. The equation for this problem is \(\ n \cdot 48=18\). The corresponding division is \(\ 18 \div 48\), so \(\ n=0.375\). Rewriting this decimal as a percent gives the correct answer, \(\ 37.5 \%\).

Incorrect. You may have used \(\ 18\) or \(\ 48\) as the percent, rather than the amount or base. The equation for this problem is \(\ n \cdot 48=18\). The corresponding division is \(\ 18 \div 48\), so \(\ n=0.375\). Rewriting this decimal as a percent gives the correct answer, \(\ 37.5 \%\).

Correct. The equation for this problem is \(\ n \cdot 48=18\). The corresponding division is \(\ 18 \div 48\), so \(\ n=0.375\). Rewriting this decimal as a percent gives \(\ 37.5 \%\).

Incorrect. You probably used 18 or 48 as the percent, rather than the amount or base, and also forgot to rewrite the percent as a decimal before multiplying. The equation for this problem is \(\ n \cdot 48=18\). The corresponding division is \(\ 18 \div 48\), so \(\ n=0.375\). Rewriting this decimal as a percent gives the correct answer, \(\ 37.5 \%\).

Using Proportions to Solve Percent Problems

Percent problems can also be solved by writing a proportion. A proportion is an equation that sets two ratios or fractions equal to each other. With percent problems, one of the ratios is the percent, written as \(\ \frac{n}{100}\). The other ratio is the amount to the base.

\(\ \text { Percent }=\frac{\text { amount }}{\text { base }}\)

Write a proportion to find the answer to the following question.

30 is 20% of 150.

18 is 125% of what number?

• \(\ 0.144\)
• \(\ 694 \frac{4}{9}\) (or about \(\ 694.4\))

Incorrect. You probably didn’t write a proportion and just divided 18 by 125. Or, you incorrectly set up one fraction as \(\ \frac{18}{125}\) and set this equal to the base, \(\ n\). The percent in this case is 125%, so one fraction in the proportion should be \(\ \frac{125}{100}\). The base is unknown and the amount is 18, so the other fraction is \(\ \frac{18}{n}\). Solving the proportion \(\ \frac{125}{100}=\frac{18}{n}\) gives \(\ n=14.4\).

Correct. The percent in this case is 125%, so one fraction in the proportion should be \(\ \frac{125}{100}\). The base is unknown and the amount is 18, so the other fraction is \(\ \frac{18}{n}\). Solving the proportion \(\ \frac{125}{100}=\frac{18}{n}\) gives \(\ n=14.4\).

Incorrect. You probably put the amount (18) over 100 in the proportion, rather than the percent (125). Perhaps you thought 18 was the percent and 125 was the base. The correct percent fraction for the proportion is \(\ \frac{125}{100}\). The base is unknown and the amount is 18, so the other fraction is \(\ \frac{18}{n}\). Solving the proportion \(\ \frac{125}{100}=\frac{18}{n}\) gives \(\ n=14.4\).

Incorrect. You probably confused the amount (18) with the percent (125) when you set up the proportion. The correct percent fraction for the proportion is \(\ \frac{125}{100}\). The base is unknown and the amount is 18, so the other fraction is \(\ \frac{18}{n}\). Solving the proportion \(\ \frac{125}{100}=\frac{18}{n}\) gives \(\ n=14.4\).

Let’s go back to the problem that was posed at the beginning. You can now solve this problem as shown in the following example.

Jeff has a coupon at the Guitar Store for 15% off any purchase of $100 or more. He wants to buy a used guitar that has a price tag of $220 on it. Jeff wonders how much money the coupon will take off of the $220 original price .

The coupon will take $33 off the original price.

You can estimate to see if the answer is reasonable. Since 15% is half way between 10% and 20%, find these numbers.

\(\ \begin{array}{l} 10 \% \text { of } 220=0.1 \cdot 220=22 \\ 20 \% \text { of } 220=0.2 \cdot 220=44 \end{array}\)

The answer, 33, is between 22 and 44. So $33 seems reasonable.

There are many other situations that involve percents. Below are just a few.

Evelyn bought some books at the local bookstore. Her total bill was $31.50, which included 5% tax. How much did the books cost before tax?

The books cost $30 before tax.

Susana worked 20 hours at her job last week. This week, she worked 35 hours. In terms of a percent, how much more did she work this week than last week?

Since 35 is 175% of 20, Susana worked 75% more this week than she did last week. (You can think of this as, “Susana worked 100% of the hours she worked last week, as well as 75% more.”)

Percent problems have three parts: the percent, the base (or whole), and the amount. Any of those parts may be the unknown value to be found. To solve percent problems, you can use the equation, \(\ \text { Percent } \cdot \text { Base }=\text { Amount }\), and solve for the unknown numbers. Or, you can set up the proportion, \(\ \text { Percent }=\frac{\text { amount }}{\text { base }}\), where the percent is a ratio of a number to 100. You can then use cross multiplication to solve the proportion.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2013 Revised 2019

Exploring Fractions

• The first group  gives you some starting points to explore with your class, which are applicable to a wide range of ages.  The tasks in this first group will build on children's current understanding of fractions and will help them get to grips with the concept of the part-whole relationship. 
• The second group of tasks  focuses on the progression of ideas associated with fractions, through a problem-solving lens.  So, the tasks in this second group are curriculum-linked but crucially also offer opportunities for learners to develop their problem-solving and reasoning skills.   

• are applicable to a range of ages;
• provide contexts in which to explore the part-whole relationship in depth;
• offer opportunities to develop conceptual understanding through talk.

PROBLEM SOLVING WITH FRACTIONS DECIMALS AND PERCENTAGES WORKSHEET

Problems with fractions.

(1)  A fruit merchant bought mangoes in bulk. He sold 5/8  of the mangoes. 1/16 of the mangoes were spoiled. 300 mangoes remained with him. How many mangoes did he buy? 

(2)  A family requires 2 1/2 liters of milk per day. How much milk would family require in a month of 31 days?  

(3)  A ream of paper weighs 12 1/2 kg.  What is the weight per quire ?

(4)   It was Richard's birthday. He distributed 6 kg of candies to his friends. If he had given 1/8  kg of candies to each friend, how many friends were there ?

(5)  Rachel bought a pizza and ate 2/5 of it. If he had given 2/3 of the remaining to his friend, what fraction of the original pizza will be remaining now ?

Answer Key :

(1)  960 mangoes

(2)   77 1/2 liter

(3)  5/8 kg

(4)   48 friends

(5)  1/5

Fraction Word Problems Mixed Operations

(1)  Linda walked 2 1/3 miles on the first day and 3 2/5   miles on the next day. How many miles did she walk in all ?                Solution

(2)   David ate 2 1/7 pizzas and he gave 1 3/14    pizzas to his mother. How many pizzas did David have initially ?

(3)   Mr. A has 3 2/3 acres of land. He gave 1 1/4 acres of land to his friend. How many acres of land does Mr. A have now ?          Solution

(4)   Lily added 3 1/3 cups of walnuts to a batch of trail mix. Later she added 1 1/3 cups of almonds. How many cups of nuts did Lily put in the trail mix in all? 

(5)   In the first hockey games of the year, Rodayo played 1 1/2 periods and 1 3/4 periods. How many periods in all did he play ?         Solution

(6)   A bag can hold 1 1/2 pounds of flour. If Mimi has 7 1/2 pounds of flour, then how many bags of flour can Mimi make ?        Solution

(7)   Jack and John went fishing Jack caught 3 3/4 kg of fish and while John  caught 2 1/5 kg of fish. What is the total weight of the fish they caught?

(8)   Amy has 3 1/2 bottles in her refrigerator. She used 3/5 bottle in the morning 1 1/4 bottle in the afternoon. How many bottles of milk does Amy have left over ?  

(9)   A tank has 82 3/4 liters of water. 24 4/5 liters of water were used and the tank was filled with another 18 3/4 liters. What is the final volume of the water in the tank ?

(10)   A trader prepared 21 1/2 liters of lemonade. At the end of the day he had 2 5/8 liters left over. How many liters of lemonade was sold by the Trader? 

Answer key :

Problems on Decimals

(1)  A chemist mixed 6.35 grams of one compound with 2.45 grams of another compound. How many grams were there in the mixture.      Solution

(2)   If the cost of a pen is $10.50, a book is $25.75 and a bag is $45.50, the  find the total cost of 2 books, 3 pens and 1 bag.         Solution

(3)    John wants to buy a bicycle that cost $ 450.75. He has saved $ 125.35. How much more money must John save in order to have enough money to buy the bicycle ?

(4)   Jennifer bought 6.5 kg of sugar. she used 3750 grams. How many kilograms of sugar were left ?

(5)   The inner radius of a pipe is 12.625 mm and the outer radius is 18.025 mm. Find the thickness of the pipe.          Solution

(6)   A copy of English book weighs 0.45 kg. What is the weight of 20 copies ?          Solution

(7)   Find the weight of 25.5 meters of copper wire in kilograms, if one meter weighs 10 grams.          Solution

(8)   Robert paid $140 for 2.8 kg of cooking oil. How much did 1 kg of the cooking oil cost ?         Solution

(9)   If $20.70 is earned in 6 hours, how much money will be earned in 5 hours ?            Solution

(10)   A pipe is 76.8 meters long. What will the greatest number of pieces of pipe each 8 meters long that can be cut from this pipe ?          Solution

Answers Key :

Problems on Percentage

(1)  In a particular store the number of TV's sold the week of Black Friday was 685. The number of TVs sold the following week was 500. TV sales the week following Black Friday were what percent less than TV sales the week of Black Friday ?

(A)  17%   (B)  27%   (C)  37%   (D)  47%

(2)  In March, a city zoo attracted 32000 visitors to its polar bear exhibit. In April, the number of visitors to the exhibit increased by 15%. How many visitors did the zoo attract to its polar bear exhibit in April ?

(A)  32150   (B)  32480   (C)  35200  (D)  36800

(3)  A charity organization collected 2140 donations last month. With the help of 50 additional volunteers, the organization collected 2690 donations this month. To the nearest tenth of a percent, what was the percent increase in the number of donations the charity organization collected ?

(A) 20.4%   (B)  20.7%    (C)  25.4%   (D)  25.7%

(4)  The discount price of a book is 20% less than the retail price. James manages to purchase the book at 30% off the discount price at the special book sale. What percent of the retail price did James pay ?

(A)  42%   (B)  48%    (C)  50%   (D)  56%

(5)  Each day, Robert eats 40% of the pistachios left in his jar at the time. At the end of the second day, 27 pistachios remain. How many pistachios were in the jar at the start of the first day ?

(A)  75   (B)  80   (C)  85  (D)  95

(6) Joanne bought a doll at a 10 percent discount off the original price of $105.82. However, she had to pay a sales tax of x% on the discounted price. If the total amount she paid for the doll was $100, what is the value of x ?

(A)  2   (B)  3   (C)  4  (D)  5

(7)  In 2010, the number of houses built in Town A was 25 percent greater than the number of houses built in Town B. If 70 houses were built in Town A during 2010, how many were built in Town B ?

(A)  56   (B)  50    (C)  48   (D)  20

(8)  Over two week span, John ate 20 pounds of chicken wings and 15 pounds of hot dogs. Kyle ate 20 percent more chicken wings and 40 percent more hot dogs. Considering only chicken wings and hot dogs, Kyle ate approximately x percent more food, by weight, than John, what is x (rounded to the nearest percent) ?

(A)  25   (B)  27    (C)  29   (D)  30

(9) Due to deforestation, researchers, expect the deer population to decline by 6 percent every year. If the current deer population is 12000, what is the approximate expected population size in 10 years from now ?

(A)  25000   (B)  48000    (C)  56000   (D)  30000

(10)  In 2000 the price of a house was $72600. By 2010 the price of the house has increased to 125598.

(A)  70%    (B)  62%    (C)  73%    (D)  90%

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

The Mean Value Theorem Worksheet

May 14, 24 08:53 AM

Mean Value Theorem

May 14, 24 02:48 AM

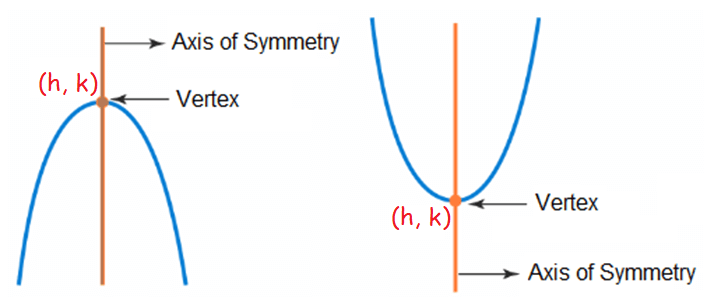
How to Find the Vertex of a Parabola

May 12, 24 10:03 PM

Ratio: Expressing as a Fraction/Percentage Textbook Exercise

Click here for questions, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• International
• Schools directory
• Resources Jobs Schools directory News Search

Convert Percent to a Fraction Number Conversion Worksheets Math Problems

Subject: Mathematics

Age range: 7-11

Resource type: Worksheet/Activity

Last updated

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Convert Percent to a Fraction Number Conversion Worksheets Math Problems Make learning percentages and decimals engaging with our comprehensive set of worksheets designed to reinforce understanding and mastery of these essential mathematical concepts. Whether you’re a teacher looking for classroom resources or a parent seeking supplementary materials for at-home learning, our worksheets cater to various skill levels and learning styles. Variety of Problems: Each worksheet offers a diverse range of problems, including converting between percentages and decimals, calculating percentages of numbers, and solving word problems involving percentages and decimals. Progressive Difficulty: Worksheets are organized by difficulty level, allowing learners to gradually build their skills from basic to advanced concepts. Answer Keys: Each worksheet comes with an answer key for easy grading and self-assessment, facilitating independent learning. Enhanced Understanding: Through repeated practice, students develop a deeper comprehension of percentages and decimals, paving the way for proficiency in more advanced mathematical concepts. Improved Problem-Solving Skills: By tackling a variety of problems, learners sharpen their analytical and critical-thinking abilities, essential for solving mathematical problems and real-world challenges. Confidence Boost: Success in solving problems boosts students’ confidence and enthusiasm for learning mathematics, fostering a positive attitude towards the subject. Whether you’re introducing percentages and decimals for the first time or reinforcing existing knowledge, our worksheets provide valuable resources to support effective teaching and learning. Empower your students to excel in mathematics with our engaging and comprehensive materials. Worksheets are made in 8.5” x 11” Standard Letter Size. This resource is helpful in students’ assessment, Independent Studies, group activities, practice and homework. This product is available in PDF format and ready to print as well.

Tes paid licence How can I reuse this?

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 7th grade   >   Unit 2

• Solving percent problems
• Equivalent expressions with percent problems
• Percent word problem: magic club

Percent problems

• Percent word problems: tax and discount
• Tax and tip word problems
• Percent word problem: guavas
• Discount, markup, and commission word problems
• Multi-step ratio and percent problems
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍