vector and scalar presentation

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Physics library

Course: physics library > unit 1, intro to vectors and scalars.

Introduction to reference frames
What is displacement?
Calculating average velocity or speed
Solving for time
Displacement from time and velocity example
Instantaneous speed and velocity
What is velocity?
Position vs. time graphs
What are position vs. time graphs?
Average velocity and average speed from graphs
Instantaneous velocity and instantaneous speed from graphs

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

2.1 Scalars and Vectors

Learning objectives.

By the end of this section, you will be able to:

Describe the difference between vector and scalar quantities.
Identify the magnitude and direction of a vector.
Explain the effect of multiplying a vector quantity by a scalar.
Describe how one-dimensional vector quantities are added or subtracted.
Explain the geometric construction for the addition or subtraction of vectors in a plane.
Distinguish between a vector equation and a scalar equation.

Many familiar physical quantities can be specified completely by giving a single number and the appropriate unit. For example, “a class period lasts 50 min” or “the gas tank in my car holds 65 L” or “the distance between two posts is 100 m.” A physical quantity that can be specified completely in this manner is called a scalar quantity . Scalar is a synonym of “number.” Time, mass, distance, length, volume, temperature, and energy are examples of scalar quantities.

Scalar quantities that have the same physical units can be added or subtracted according to the usual rules of algebra for numbers. For example, a class ending 10 min earlier than 50 min lasts 50 min − 10 min = 40 min 50 min − 10 min = 40 min . Similarly, a 60-cal serving of corn followed by a 200-cal serving of donuts gives 60 cal + 200 cal = 260 cal 60 cal + 200 cal = 260 cal of energy. When we multiply a scalar quantity by a number, we obtain the same scalar quantity but with a larger (or smaller) value. For example, if yesterday’s breakfast had 200 cal of energy and today’s breakfast has four times as much energy as it had yesterday, then today’s breakfast has 4 ( 200 cal ) = 800 cal 4 ( 200 cal ) = 800 cal of energy. Two scalar quantities can also be multiplied or divided by each other to form a derived scalar quantity. For example, if a train covers a distance of 100 km in 1.0 h, its speed is 100.0 km/1.0 h = 27.8 m/s, where the speed is a derived scalar quantity obtained by dividing distance by time.

Many physical quantities, however, cannot be described completely by just a single number of physical units. For example, when the U.S. Coast Guard dispatches a ship or a helicopter for a rescue mission, the rescue team must know not only the distance to the distress signal, but also the direction from which the signal is coming so they can get to its origin as quickly as possible. Physical quantities specified completely by giving a number of units (magnitude) and a direction are called vector quantities . Examples of vector quantities include displacement, velocity, position, force, and torque. In the language of mathematics, physical vector quantities are represented by mathematical objects called vectors ( Figure 2.2 ). We can add or subtract two vectors, and we can multiply a vector by a scalar or by another vector, but we cannot divide by a vector. The operation of division by a vector is not defined.

Let’s examine vector algebra using a graphical method to be aware of basic terms and to develop a qualitative understanding. In practice, however, when it comes to solving physics problems, we use analytical methods, which we’ll see in the next section. Analytical methods are more simple computationally and more accurate than graphical methods. From now on, to distinguish between a vector and a scalar quantity, we adopt the common convention that a letter in bold type with an arrow above it denotes a vector, and a letter without an arrow denotes a scalar. For example, a distance of 2.0 km, which is a scalar quantity, is denoted by d = 2.0 km, whereas a displacement of 2.0 km in some direction, which is a vector quantity, is denoted by d → d → .

Suppose you tell a friend on a camping trip that you have discovered a terrific fishing hole 6 km from your tent. It is unlikely your friend would be able to find the hole easily unless you also communicate the direction in which it can be found with respect to your campsite. You may say, for example, “Walk about 6 km northeast from my tent.” The key concept here is that you have to give not one but two pieces of information—namely, the distance or magnitude (6 km) and the direction (northeast).

Displacement is a general term used to describe a change in position , such as during a trip from the tent to the fishing hole. Displacement is an example of a vector quantity. If you walk from the tent (location A ) to the hole (location B ), as shown in Figure 2.3 , the vector D → D → , representing your displacement , is drawn as the arrow that originates at point A and ends at point B . The arrowhead marks the end of the vector. The direction of the displacement vector D → D → is the direction of the arrow. The length of the arrow represents the magnitude D of vector D → D → . Here, D = 6 km. Since the magnitude of a vector is its length, which is a positive number, the magnitude is also indicated by placing the absolute value notation around the symbol that denotes the vector; so, we can write equivalently that D ≡ | D → | D ≡ | D → | . To solve a vector problem graphically, we need to draw the vector D → D → to scale. For example, if we assume 1 unit of distance (1 km) is represented in the drawing by a line segment of length u = 2 cm, then the total displacement in this example is represented by a vector of length d = 6 u = 6 ( 2 cm ) = 12 cm d = 6 u = 6 ( 2 cm ) = 12 cm , as shown in Figure 2.4 . Notice that here, to avoid confusion, we used D = 6 km D = 6 km to denote the magnitude of the actual displacement and d = 12 cm to denote the length of its representation in the drawing.

Suppose your friend walks from the campsite at A to the fishing pond at B and then walks back: from the fishing pond at B to the campsite at A . The magnitude of the displacement vector D → A B D → A B from A to B is the same as the magnitude of the displacement vector D → B A D → B A from B to A (it equals 6 km in both cases), so we can write D A B = D B A D A B = D B A . However, vector D → A B D → A B is not equal to vector D → B A D → B A because these two vectors have different directions: D → A B ≠ D → B A D → A B ≠ D → B A . In Figure 2.3 , vector D → B A D → B A would be represented by a vector with an origin at point B and an end at point A , indicating vector D → B A D → B A points to the southwest, which is exactly 180 ° 180 ° opposite to the direction of vector D → A B D → A B . We say that vector D → B A D → B A is antiparallel to vector D → A B D → A B and write D → A B = − D → B A D → A B = − D → B A , where the minus sign indicates the antiparallel direction.

Two vectors that have identical directions are said to be parallel vectors —meaning, they are parallel to each other. Two parallel vectors A → A → and B → B → are equal, denoted by A → = B → A → = B → , if and only if they have equal magnitudes | A → | = | B → | | A → | = | B → | . Two vectors with directions perpendicular to each other are said to be orthogonal vectors . These relations between vectors are illustrated in Figure 2.5 .

Check Your Understanding 2.1

Two motorboats named Alice and Bob are moving on a lake. Given the information about their velocity vectors in each of the following situations, indicate whether their velocity vectors are equal or otherwise. (a) Alice moves north at 6 knots and Bob moves west at 6 knots. (b) Alice moves west at 6 knots and Bob moves west at 3 knots. (c) Alice moves northeast at 6 knots and Bob moves south at 3 knots. (d) Alice moves northeast at 6 knots and Bob moves southwest at 6 knots. (e) Alice moves northeast at 2 knots and Bob moves closer to the shore northeast at 2 knots.

Algebra of Vectors in One Dimension

Vectors can be multiplied by scalars, added to other vectors, or subtracted from other vectors. We can illustrate these vector concepts using an example of the fishing trip seen in Figure 2.6 .

Suppose your friend departs from point A (the campsite) and walks in the direction to point B (the fishing pond), but, along the way, stops to rest at some point C located three-quarters of the distance between A and B , beginning from point A ( Figure 2.6 (a)). What is his displacement vector D → A C D → A C when he reaches point C ? We know that if he walks all the way to B , his displacement vector relative to A is D → A B D → A B , which has magnitude D A B = 6 km D A B = 6 km and a direction of northeast. If he walks only a 0.75 fraction of the total distance, maintaining the northeasterly direction, at point C he must be 0.75 D A B = 4.5 km 0.75 D A B = 4.5 km away from the campsite at A . So, his displacement vector at the rest point C has magnitude D A C = 4.5 km = 0.75 D A B D A C = 4.5 km = 0.75 D A B and is parallel to the displacement vector D → A B D → A B . All of this can be stated succinctly in the form of the following vector equation :

In a vector equation, both sides of the equation are vectors. The previous equation is an example of a vector multiplied by a positive scalar (number) α = 0.75 α = 0.75 . The result, D → A C D → A C , of such a multiplication is a new vector with a direction parallel to the direction of the original vector D → A B D → A B .

In general, when a vector A → A → is multiplied by a positive scalar α α , the result is a new vector B → B → that is parallel to A → A → :

The magnitude | B → | | B → | of this new vector is obtained by multiplying the magnitude | A → | | A → | of the original vector, as expressed by the scalar equation :

In a scalar equation, both sides of the equation are numbers. Equation 2.2 is a scalar equation because the magnitudes of vectors are scalar quantities (and positive numbers). If the scalar α α is negative in the vector equation Equation 2.1 , then the magnitude | B → | | B → | of the new vector is still given by Equation 2.2 , but the direction of the new vector B → B → is antiparallel to the direction of A → A → . These principles are illustrated in Figure 2.7 (a) by two examples where the length of vector A → A → is 1.5 units. When α = 2 α = 2 , the new vector B → = 2 A → B → = 2 A → has length B = 2 A = 3.0 units B = 2 A = 3.0 units (twice as long as the original vector) and is parallel to the original vector. When α = −2 α = −2 , the new vector C → = −2 A → C → = −2 A → has length C = | − 2 | A = 3.0 units C = | − 2 | A = 3.0 units (twice as long as the original vector) and is antiparallel to the original vector.

Now suppose your fishing buddy departs from point A (the campsite), walking in the direction to point B (the fishing hole), but he realizes he lost his tackle box when he stopped to rest at point C (located three-quarters of the distance between A and B , beginning from point A ). So, he turns back and retraces his steps in the direction toward the campsite and finds the box lying on the path at some point D only 1.2 km away from point C (see Figure 2.6 (b)). What is his displacement vector D → A D D → A D when he finds the box at point D ? What is his displacement vector D → D B D → D B from point D to the hole? We have already established that at rest point C his displacement vector is D → A C = 0.75 D → A B D → A C = 0.75 D → A B . Starting at point C , he walks southwest (toward the campsite), which means his new displacement vector D → C D D → C D from point C to point D is antiparallel to D → A B D → A B . Its magnitude | D → C D | | D → C D | is D C D = 1.2 km = 0.2 D A B D C D = 1.2 km = 0.2 D A B , so his second displacement vector is D → C D = −0.2 D → A B D → C D = −0.2 D → A B . His total displacement D → A D D → A D relative to the campsite is the vector sum of the two displacement vectors: vector D → A C D → A C (from the campsite to the rest point) and vector D → C D D → C D (from the rest point to the point where he finds his box):

The vector sum of two (or more) vectors is called the resultant vector or, for short, the resultant . When the vectors on the right-hand-side of Equation 2.3 are known, we can find the resultant D → A D D → A D as follows:

When your friend finally reaches the pond at B , his displacement vector D → A B D → A B from point A is the vector sum of his displacement vector D → A D D → A D from point A to point D and his displacement vector D → D B D → D B from point D to the fishing hole: D → A B = D → A D + D → D B D → A B = D → A D + D → D B (see Figure 2.6 (c)). This means his displacement vector D → D B D → D B is the difference of two vectors :

Notice that a difference of two vectors is nothing more than a vector sum of two vectors because the second term in Equation 2.5 is vector − D → A D − D → A D (which is antiparallel to D → A D ) D → A D ) . When we substitute Equation 2.4 into Equation 2.5 , we obtain the second displacement vector:

This result means your friend walked D D B = 0.45 D A B = 0.45 ( 6.0 km ) = 2.7 km D D B = 0.45 D A B = 0.45 ( 6.0 km ) = 2.7 km from the point where he finds his tackle box to the fishing hole.

When vectors A → A → and B → B → lie along a line (that is, in one dimension), such as in the camping example, their resultant R → = A → + B → R → = A → + B → and their difference D → = A → − B → D → = A → − B → both lie along the same direction. We can illustrate the addition or subtraction of vectors by drawing the corresponding vectors to scale in one dimension, as shown in Figure 2.7 .

To illustrate the resultant when A → A → and B → B → are two parallel vectors, we draw them along one line by placing the origin of one vector at the end of the other vector in head-to-tail fashion (see Figure 2.7 (b)). The magnitude of this resultant is the sum of their magnitudes: R = A + B . The direction of the resultant is parallel to both vectors. When vector A → A → is antiparallel to vector B → B → , we draw them along one line in either head-to-head fashion ( Figure 2.7 (c)) or tail-to-tail fashion. The magnitude of the vector difference, then, is the absolute value D = | A − B | D = | A − B | of the difference of their magnitudes. The direction of the difference vector D → D → is parallel to the direction of the longer vector.

In general, in one dimension—as well as in higher dimensions, such as in a plane or in space—we can add any number of vectors and we can do so in any order because the addition of vectors is commutative ,

and associative ,

Moreover, multiplication by a scalar is distributive :

We used the distributive property in Equation 2.4 and Equation 2.6 .

When adding many vectors in one dimension, it is convenient to use the concept of a unit vector . A unit vector, which is denoted by a letter symbol with a hat, such as u ^ u ^ , has a magnitude of one and does not have any physical unit so that | u ^ | ≡ u = 1 | u ^ | ≡ u = 1 . The only role of a unit vector is to specify direction. For example, instead of saying vector D → A B D → A B has a magnitude of 6.0 km and a direction of northeast, we can introduce a unit vector u ^ u ^ that points to the northeast and say succinctly that D → A B = ( 6.0 km ) u ^ D → A B = ( 6.0 km ) u ^ . Then the southwesterly direction is simply given by the unit vector − u ^ − u ^ . In this way, the displacement of 6.0 km in the southwesterly direction is expressed by the vector

Example 2.1

A ladybug walker.

The total displacement D → D → is the resultant of all its displacement vectors.

In this calculation, we use the distributive law given by Equation 2.9 . The result reads that the total displacement vector points away from the 100-cm mark (initial landing site) toward the end of the meter stick that touches the wall. The end that touches the wall is marked 0 cm, so the final position of the ladybug is at the (100 – 32)cm = 68-cm mark.

Check Your Understanding 2.2

A cave diver enters a long underwater tunnel. When her displacement with respect to the entry point is 20 m, she accidentally drops her camera, but she doesn’t notice it missing until she is some 6 m farther into the tunnel. She swims back 10 m but cannot find the camera, so she decides to end the dive. How far from the entry point is she? Taking the positive direction out of the tunnel, what is her displacement vector relative to the entry point?

Algebra of Vectors in Two Dimensions

When vectors lie in a plane—that is, when they are in two dimensions—they can be multiplied by scalars, added to other vectors, or subtracted from other vectors in accordance with the general laws expressed by Equation 2.1 , Equation 2.2 , Equation 2.7 , and Equation 2.8 . However, the addition rule for two vectors in a plane becomes more complicated than the rule for vector addition in one dimension. We have to use the laws of geometry to construct resultant vectors, followed by trigonometry to find vector magnitudes and directions. This geometric approach is commonly used in navigation ( Figure 2.9 ). In this section, we need to have at hand two rulers, a triangle, a protractor, a pencil, and an eraser for drawing vectors to scale by geometric constructions.

For a geometric construction of the sum of two vectors in a plane, we follow the parallelogram rule . Suppose two vectors A → A → and B → B → are at the arbitrary positions shown in Figure 2.10 . Translate either one of them in parallel to the beginning of the other vector, so that after the translation, both vectors have their origins at the same point. Now, at the end of vector A → A → we draw a line parallel to vector B → B → and at the end of vector B → B → we draw a line parallel to vector A → A → (the dashed lines in Figure 2.10 ). In this way, we obtain a parallelogram. From the origin of the two vectors we draw a diagonal that is the resultant R → R → of the two vectors: R → = A → + B → R → = A → + B → ( Figure 2.10 (a)). The other diagonal of this parallelogram is the vector difference of the two vectors D → = A → − B → D → = A → − B → , as shown in Figure 2.10 (b). Notice that the end of the difference vector is placed at the end of vector A → A → .

It follows from the parallelogram rule that neither the magnitude of the resultant vector nor the magnitude of the difference vector can be expressed as a simple sum or difference of magnitudes A and B , because the length of a diagonal cannot be expressed as a simple sum of side lengths. When using a geometric construction to find magnitudes | R → | | R → | and | D → | | D → | , we have to use trigonometry laws for triangles, which may lead to complicated algebra. There are two ways to circumvent this algebraic complexity. One way is to use the method of components, which we examine in the next section. The other way is to draw the vectors to scale, as is done in navigation, and read approximate vector lengths and angles (directions) from the graphs. In this section we examine the second approach.

If we need to add three or more vectors, we repeat the parallelogram rule for the pairs of vectors until we find the resultant of all of the resultants. For three vectors, for example, we first find the resultant of vector 1 and vector 2, and then we find the resultant of this resultant and vector 3. The order in which we select the pairs of vectors does not matter because the operation of vector addition is commutative and associative (see Equation 2.7 and Equation 2.8 ). Before we state a general rule that follows from repetitive applications of the parallelogram rule, let’s look at the following example.

Suppose you plan a vacation trip in Florida. Departing from Tallahassee, the state capital, you plan to visit your uncle Joe in Jacksonville, see your cousin Vinny in Daytona Beach, stop for a little fun in Orlando, see a circus performance in Tampa, and visit the University of Florida in Gainesville. Your route may be represented by five displacement vectors A → , A → , B → B → , C → C → , D → D → , and E → E → , which are indicated by the red vectors in Figure 2.11 . What is your total displacement when you reach Gainesville? The total displacement is the vector sum of all five displacement vectors, which may be found by using the parallelogram rule four times. Alternatively, recall that the displacement vector has its beginning at the initial position (Tallahassee) and its end at the final position (Gainesville), so the total displacement vector can be drawn directly as an arrow connecting Tallahassee with Gainesville (see the green vector in Figure 2.11 ). When we use the parallelogram rule four times, the resultant R → R → we obtain is exactly this green vector connecting Tallahassee with Gainesville: R → = A → + B → + C → + D → + E → R → = A → + B → + C → + D → + E → .

Drawing the resultant vector of many vectors can be generalized by using the following tail-to-head geometric construction . Suppose we want to draw the resultant vector R → R → of four vectors A → A → , B → B → , C → C → , and D → D → ( Figure 2.12 (a)). We select any one of the vectors as the first vector and make a parallel translation of a second vector to a position where the origin (“tail”) of the second vector coincides with the end (“head”) of the first vector. Then, we select a third vector and make a parallel translation of the third vector to a position where the origin of the third vector coincides with the end of the second vector. We repeat this procedure until all the vectors are in a head-to-tail arrangement like the one shown in Figure 2.12 . We draw the resultant vector R → R → by connecting the origin (“tail”) of the first vector with the end (“head”) of the last vector. The end of the resultant vector is at the end of the last vector. Because the addition of vectors is associative and commutative, we obtain the same resultant vector regardless of which vector we choose to be first, second, third, or fourth in this construction.

Example 2.2

Geometric construction of the resultant.

For (c), we can start with vector −3 B → −3 B → and draw the remaining vectors tail-to-head as shown in Figure 2.15 . In vector addition, the order in which we draw the vectors is unimportant, but drawing the vectors to scale is very important. Next, we draw vector S → S → from the origin of the first vector to the end of the last vector and place the arrowhead at the end of S → S → . We use a ruler to measure the length of S → S → , and find that its magnitude is S = 36.9 cm. We use a protractor and find that its direction angle is θ S = 52.9 ° θ S = 52.9 ° . This solution is shown in Figure 2.15 .

Check Your Understanding 2.3

Using the three displacement vectors A → A → , B → B → , and F → F → in Figure 2.13 , choose a convenient scale, and use a ruler and a protractor to find vector G → G → given by the vector equation G → = A → + 2 B → − F → G → = A → + 2 B → − F → .

Interactive

Observe the addition of vectors in a plane by visiting this vector calculator , and by engaging the Phet simulation below.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

Authors: William Moebs, Samuel J. Ling, Jeff Sanny
Publisher/website: OpenStax
Book title: University Physics Volume 1
Publication date: Sep 19, 2016
Location: Houston, Texas
Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
Section URL: https://openstax.org/books/university-physics-volume-1/pages/2-1-scalars-and-vectors

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Skip to navigation (Press Enter)
Skip to main content (Press Enter)

Math Insight

An introduction to vectors, definition of a vector.

A vector is an object that has both a magnitude and a direction. Geometrically, we can picture a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.

Two vectors are the same if they have the same magnitude and direction. This means that if we take a vector and translate it to a new position (without rotating it), then the vector we obtain at the end of this process is the same vector we had in the beginning.

Two examples of vectors are those that represent force and velocity. Both force and velocity are in a particular direction. The magnitude of the vector would indicate the strength of the force or the speed associated with the velocity.

We denote vectors using boldface as in $\vc{a}$ or $\vc{b}$. Especially when writing by hand where one cannot easily write in boldface, people will sometimes denote vectors using arrows as in $\vec{a}$ or $\vec{b}$, or they use other markings. We won't need to use arrows here. We denote the magnitude of the vector $\vc{a}$ by $\|\vc{a}\|$. When we want to refer to a number and stress that it is not a vector, we can call the number a scalar . We will denote scalars with italics, as in $a$ or $b$.

You can explore the concept of the magnitude and direction of a vector using the below applet. Note that moving the vector around doesn't change the vector, as the position of the vector doesn't affect the magnitude or the direction. But if you stretch or turn the vector by moving just its head or its tail, the magnitude or direction will change. (This applet also shows the coordinates of the vector, which you can read about in another page .)

The magnitude and direction of a vector. The blue arrow represents a vector $\vc{a}$. The two defining properties of a vector, magnitude and direction, are illustrated by a red bar and a green arrow, respectively. The length of the red bar is the magnitude $\|\vc{a}\|$ of the vector $\vc{a}$. The green arrow always has length one, but its direction is the direction of the vector $\vc{a}$. The one exception is when $\vc{a}$ is the zero vector (the only vector with zero magnitude), for which the direction is not defined. You can change either end of $\vc{a}$ by dragging it with your mouse. You can also move $\vc{a}$ by dragging the middle of the vector; however, changing the position of the $\vc{a}$ in this way does not change the vector, as its magnitude and direction remain unchanged.

More information about applet.

There is one important exception to vectors having a direction. The zero vector , denoted by a boldface $\vc{0}$, is the vector of zero length. Since it has no length, it is not pointing in any particular direction. There is only one vector of zero length, so we can speak of the zero vector.

Operations on vectors

We can define a number of operations on vectors geometrically without reference to any coordinate system. Here we define addition , subtraction , and multiplication by a scalar . On separate pages, we discuss two different ways to multiply two vectors together: the dot product and the cross product .

Addition of vectors

Given two vectors $\vc{a}$ and $\vc{b}$, we form their sum $\vc{a}+\vc{b}$, as follows. We translate the vector $\vc{b}$ until its tail coincides with the head of $\vc{a}$. (Recall such translation does not change a vector.) Then, the directed line segment from the tail of $\vc{a}$ to the head of $\vc{b}$ is the vector $\vc{a}+\vc{b}$.

The vector addition is the way forces and velocities combine. For example, if a car is travelling due north at 20 miles per hour and a child in the back seat behind the driver throws an object at 20 miles per hour toward his sibling who is sitting due east of him, then the velocity of the object (relative to the ground!) will be in a north-easterly direction. The velocity vectors form a right triangle, where the total velocity is the hypotenuse. Therefore, the total speed of the object (i.e., the magnitude of the velocity vector) is $\sqrt{20^2+20^2}=20\sqrt{2}$ miles per hour relative to the ground.

Addition of vectors satisfies two important properties.

The commutative law, which states the order of addition doesn't matter: $$\vc{a}+\vc{b}=\vc{b}+\vc{a}.$$ This law is also called the parallelogram law, as illustrated in the below image. Two of the edges of the parallelogram define $\vc{a}+\vc{b}$, and the other pair of edges define $\vc{b}+\vc{a}$. But, both sums are equal to the same diagonal of the parallelogram.

The parallelogram law, or commutative law, of vector addition

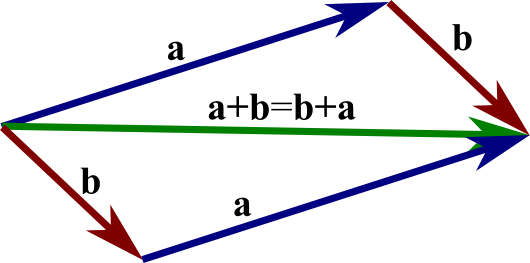
The associative law, which states that the sum of three vectors does not depend on which pair of vectors is added first: $$(\vc{a}+\vc{b})+\vc{c} = \vc{a} + (\vc{b}+\vc{c}).$$

You can explore the properties of vector addition with the following applet. (This applet also shows the coordinates of the vectors, which you can read about in another page .)

The sum of two vectors. The sum $\vc{a}+\vc{b}$ of the vector $\vc{a}$ (blue arrow) and the vector $\vc{b}$ (red arrow) is shown by the green arrow. As vectors are independent of their starting position, both blue arrows represent the same vector $\vc{a}$ and both red arrows represent the same vector $\vc{b}$. The sum $\vc{a}+\vc{b}$ can be formed by placing the tail of the vector $\vc{b}$ at the head of the vector $\vc{a}$. Equivalently, it can be formed by placing the tail of the vector $\vc{a}$ at the head of the vector $\vc{b}$. Both constructions together form a parallelogram, with the sum $\vc{a}+\vc{b}$ being a diagonal. (For this reason, the commutative law $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ is sometimes called the parallelogram law.) You can change $\vc{a}$ and $\vc{b}$ by dragging the yellow points.

Vector subtraction

Before we define subtraction, we define the vector $-\vc{a}$, which is the opposite of $\vc{a}$. The vector $-\vc{a}$ is the vector with the same magnitude as $\vc{a}$ but that is pointed in the opposite direction.

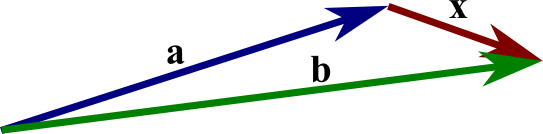
We define subtraction as addition with the opposite of a vector: $$\vc{b}-\vc{a} = \vc{b} + (-\vc{a}).$$ This is equivalent to turning vector $\vc{a}$ around in the applying the above rules for addition. Can you see how the vector $\vc{x}$ in the below figure is equal to $\vc{b}-\vc{a}$? Notice how this is the same as stating that $\vc{a}+\vc{x}=\vc{b}$, just like with subtraction of scalar numbers.

Scalar multiplication

Given a vector $\vc{a}$ and a real number ( scalar ) $\lambda$, we can form the vector $\lambda\vc{a}$ as follows. If $\lambda$ is positive, then $\lambda\vc{a}$ is the vector whose direction is the same as the direction of $\vc{a}$ and whose length is $\lambda$ times the length of $\vc{a}$. In this case, multiplication by $\lambda$ simply stretches (if $\lambda>1$) or compresses (if $0 < \lambda <1$) the vector $\vc{a}$.

If, on the other hand, $\lambda$ is negative, then we have to take the opposite of $\vc{a}$ before stretching or compressing it. In other words, the vector $\lambda\vc{a}$ points in the opposite direction of $\vc{a}$, and the length of $\lambda\vc{a}$ is $|\lambda|$ times the length of $\vc{a}$. No matter the sign of $\lambda$, we observe that the magnitude of $\lambda\vc{a}$ is $|\lambda|$ times the magnitude of $\vc{a}$: $\| \lambda \vc{a}\| = |\lambda| \|\vc{a}\|$.

Scalar multiplications satisfies many of the same properties as the usual multiplication.

$s(\vc{a}+\vc{b}) = s\vc{a} + s\vc{b}$ (distributive law, form 1)
$(s+t)\vc{a} = s\vc{a}+t\vc{a}$ (distributive law, form 2)
$1\vc{a} = \vc{a}$
$(-1)\vc{a} = -\vc{a}$
$0\vc{a} = \vc{0}$

In the last formula, the zero on the left is the number 0, while the zero on the right is the vector $\vc{0}$, which is the unique vector whose length is zero.

If $\vc{a} = \lambda\vc{b}$ for some scalar $\lambda$, then we say that the vectors $\vc{a}$ and $\vc{b}$ are parallel. If $\lambda$ is negative, some people say that $\vc{a}$ and $\vc{b}$ are anti-parallel, but we will not use that language.

We were able to describe vectors, vector addition, vector subtraction, and scalar multiplication without reference to any coordinate system. The advantage of such purely geometric reasoning is that our results hold generally, independent of any coordinate system in which the vectors live. However, sometimes it is useful to express vectors in terms of coordinates, as discussed in a page about vectors in the standard Cartesian coordinate systems in the plane and in three-dimensional space.

Thread navigation

Vector algebra.

Next: Vectors in two- and three-dimensional Cartesian coordinates

Math 2241, Spring 2023

Previous: For-loops in R

Vectors in two- and three-dimensional Cartesian coordinates
The cross product
Cross product examples
The formula for the cross product
The scalar triple product
Scalar triple product example
Multiplying matrices and vectors
Matrix and vector multiplication examples
Vectors in arbitrary dimensions
The transpose of a matrix
More similar pages
The zero vector
The dot product
Examples of n-dimensional vectors

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

2.3: Scalars and Vectors

Last updated
Save as PDF
Page ID 68709

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Vectors are essential to physics and engineering. Many fundamental physical quantities are vectors, including displacement, velocity, force, and electric and magnetic vector fields. Scalar products of vectors define other fundamental scalar physical quantities, such as energy. Vector products of vectors define still other fundamental vector physical quantities, such as torque and angular momentum. In other words, vectors are a component part of physics in much the same way as sentences are a component part of literature.

A photograph of a signpost with distances to numerous locations in different directions.

In introductory physics, vectors are Euclidean quantities that have geometric representations as arrows in one dimension (in a line), in two dimensions (in a plane), or in three dimensions (in space). They can be added, subtracted, or multiplied.

Learning Objectives

Describe the difference between vector and scalar quantities.
Identify the magnitude and direction of a vector.
Explain the effect of multiplying a vector quantity by a scalar.
Describe how one-dimensional vector quantities are added or subtracted.
Explain the geometric construction for the addition or subtraction of vectors in a plane.
Distinguish between a vector equation and a scalar equation.

Scalar quantities that have the same physical units can be added or subtracted according to the usual rules of algebra for numbers. For example, a class ending 10 min earlier than 50 min lasts 50 min − 10 min = 40 min. Similarly, a 60-cal serving of corn followed by a 200-cal serving of donuts gives 60 cal + 200 cal = 260 cal of energy. When we multiply a scalar quantity by a number, we obtain the same scalar quantity but with a larger (or smaller) value. For example, if yesterday’s breakfast had 200 cal of energy and today’s breakfast has four times as much energy as it had yesterday, then today’s breakfast has 4(200 cal) = 800 cal of energy. Two scalar quantities can also be multiplied or divided by each other to form a derived scalar quantity. For example, if a train covers a distance of 100 km in 1.0 h, its speed is 100.0 km/1.0 h = 27.8 m/s, where the speed is a derived scalar quantity obtained by dividing distance by time.

Many physical quantities, however, cannot be described completely by just a single number of physical units. For example, when the U.S. Coast Guard dispatches a ship or a helicopter for a rescue mission, the rescue team must know not only the distance to the distress signal, but also the direction from which the signal is coming so they can get to its origin as quickly as possible. Physical quantities specified completely by giving a number of units (magnitude) and a direction are called vector quantities . Examples of vector quantities include displacement, velocity, position, force, and torque. In the language of mathematics, physical vector quantities are represented by mathematical objects called vectors (Figure $\PageIndex{1}$). We can add or subtract two vectors, and we can multiply a vector by a scalar or by another vector, but we cannot divide by a vector. The operation of division by a vector is not defined.

A photo of a dog. Below the photo is a horizontal arrow which starts below the dog’s tail and ends below the dog’s nose. The arrow is labeled Vector D, and its length is labeled as magnitude D. The start (tail) of the arrow is labeled “From rail of a vector origin” and its end (head) is labeled “To head of a vector end.”

Let’s examine vector algebra using a graphical method to be aware of basic terms and to develop a qualitative understanding. In practice, however, when it comes to solving physics problems, we use analytical methods. Analytical methods are more simple computationally and more accurate than graphical methods. From now on, to distinguish between a vector and a scalar quantity, we adopt the common convention that a letter with an arrow above it denotes a vector, and a letter without an arrow denotes a scalar. For example, a distance of 2.0 km, which is a scalar quantity, is denoted by d = 2.0 km, whereas a displacement of 2.0 km in some direction, which is a vector quantity, is denoted by $\vec{d}$.

Displacement is a general term used to describe a change in position, such as during a trip from the tent to the fishing hole. Displacement is an example of a vector quantity. If you walk from the tent (location A) to the hole (location B), as shown in Figure $\PageIndex{2}$, the vector $\vec{D}$, representing your displacement , is drawn as the arrow that originates at point A and ends at point B. The arrowhead marks the end of the vector. The direction of the displacement vector $\vec{D}$ is the direction of the arrow. The length of the arrow represents the magnitude (or size) D of vector $\vec{D}$. Here, D = 6 km. Since the magnitude of a vector is its length, which is a positive number, the magnitude is also indicated by placing the absolute value notation around the symbol that denotes the vector; so, we can write equivalently that D ≡ |$\vec{D}$|. To solve a vector problem graphically, we need to draw the vector $\vec{D}$ to scale. For example, if we assume 1 unit of distance (1 km) is represented in the drawing by a line segment of length u = 2 cm, then the total displacement in this example is represented by a vector of length d = 6u = 6(2 cm) = 12 cm , as shown in Figure $\PageIndex{3}$. Notice that here, to avoid confusion, we used D = 6 km to denote the magnitude of the actual displacement and d = 12 cm to denote the length of its representation in the drawing.

An illustration of a lake, some distance northeast from a tent. North is up on the page, east to the right. The tent is labeled as location A, and the lake as location B. A straight arrow starts at A and ends at B. Three meandering paths, shown as dashed lines, also start at A and end at B.

Suppose your friend walks from the campsite at A to the fishing pond at B and then walks back: from the fishing pond at B to the campsite at A. The magnitude of the displacement vector $\vec{D}_{AB}$ from A to B is the same as the magnitude of the displacement vector $\vec{D}_{BA}$ from B to A (it equals 6 km in both cases), so we can write $\vec{D}_{AB}$ = $\vec{D}_{BA}$. However, vector $\vec{D}_{AB}$ is not equal to vector $\vec{D}_{BA}$ because these two vectors have different directions: $\vec{D}_{AB}$ ≠ $\vec{D}_{BA}$. In Figure 2.3, vector $\vec{D}_{BA}$ would be represented by a vector with an origin at point B and an end at point A, indicating vector $\vec{D}_{BA}$ points to the southwest, which is exactly 180° opposite to the direction of vector $\vec{D}_{AB}$. We say that vector $\vec{D}_{BA}$ is antiparallel to vector $\vec{D}_{AB}$ and write $\vec{D}_{AB}$ = $-\vec{D}_{BA}$, where the minus sign indicates the antiparallel direction.

Two vectors that have identical directions are said to be parallel vectors —meaning, they are parallel to each other. Two parallel vectors $\vec{A}$ and $\vec{B}$ are equal, denoted by $\vec{A}$ = $\vec{B}$, if and only if they have equal magnitudes |$\vec{A}$| = |$\vec{B}$|. Two vectors with directions perpendicular to each other are said to be orthogonal vectors . These relations between vectors are illustrated in Figure $\PageIndex{4}$.

Figure a: Two examples of vector A parallel to vector B. In one, A and B are on the same line, one after the other, but A is longer than B. In the other, A and B are parallel to each other with their tails aligned, but A is shorter than B. Figure b: An example of vector A antiparallel to vector B. Vector A points to the left and is longer than vector B, which points to the right. The angle between them is 180 degrees. Figure c: An example of vector A antiparallel to minus vector A: A points to the right and –A points to the left. Both are the same length. Figure d: Two examples of vector A equal to vector B: In one, A and B are on the same line, one after the other, and both are the same length. In the other, A and B are parallel to each other with their tails aligned, and both are the same length. Figure e: Two examples of vector A orthogonal to vector B: In one, A points down and B points to the right, meeting at a right angle, and both are the same length. In the other, points down and to the right and B points down and to the left, meeting A at a right angle. Both are the same length.

Algebra of Vectors in One Dimension

Vectors can be multiplied by scalars, added to other vectors, or subtracted from other vectors. We can illustrate these vector concepts using an example of the fishing trip seen in Figure $\PageIndex{5}$.

Three illustrations of the same tent and lake northeast of the tent. North is up on the page. The tent location is point A, and the lake location is point B. A location between A and B, about 2/3 of the way from A to B, is labeled as point C. In figure a, the vector from A to B is shown as a blue arrow, starting at A and ending at B, and labeled vector D sub A B. The vector from A to C is shown as a red arrow, starting at A and ending at C and labeled vector D sub A C. Three meandering paths are shown as dashed lines that start at A and end at B. Figure b adds the following to the illustration of figure a: Point D is added about half way between point A and B. The vector from A to D is shown as a purple arrow, starting at A and ending at D and labeled vector D sub A D. The vector from D to B is shown as an orange arrow, starting at D and ending at B and labeled vector D sub D B. Figure c adds a green arrow from point C to point D and is labeled vector D sub C D. Vector D sub C D points in the direction opposite to that of the other vectors, toward the tent rather than toward the lake.

Suppose your friend departs from point A (the campsite) and walks in the direction to point B (the fishing pond), but, along the way, stops to rest at some point C located three-quarters of the distance between A and B, beginning from point A (Figure $\PageIndex{5a}$). What is his displacement vector $\vec{D}_{AC}$ when he reaches point C? We know that if he walks all the way to B, his displacement vector relative to A is $\vec{D}_{AB}$, which has magnitude D AB = 6 km and a direction of northeast. If he walks only a 0.75 fraction of the total distance, maintaining the northeasterly direction, at point C he must be 0.75 D AB = 4.5 km away from the campsite at A. So, his displacement vector at the rest point C has magnitude D AC = 4.5 km = 0.75 D AB and is parallel to the displacement vector $\vec{D}_{AB}$. All of this can be stated succinctly in the form of the following vector equation :

\[\vec{D}_{AC} = 0.75\; \vec{D}_{AB} \ldotp \nonumber\]

In a vector equation, both sides of the equation are vectors. The previous equation is an example of a vector multiplied by a positive scalar (number) $\alpha$ = 0.75. The result, $\vec{D}_{AC}$, of such a multiplication is a new vector with a direction parallel to the direction of the original vector $\vec{D}_{AB}$. In general, when a vector $\vec{D}_{A}$ is multiplied by a positive scalar $\alpha$, the result is a new vector $\vec{D}_{B}$ that is parallel to $\vec{D}_{A}$:

\[\vec{B} = \alpha \vec{A} \label{2.1}\]

The magnitude |$\vec{B}$| of this new vector is obtained by multiplying the magnitude |$\vec{A}$| of the original vector, as expressed by the scalar equation :

\[ B = | \alpha | A \ldotp \label{2.2}\]

In a scalar equation, both sides of the equation are numbers. Equation \ref{2.2} is a scalar equation because the magnitudes of vectors are scalar quantities (and positive numbers). If the scalar $\alpha$ is negative in the vector equation Equation \ref{2.1}, then the magnitude |$\vec{B}$| of the new vector is still given by Equation \ref{2.2}, but the direction of the new vector $\vec{B}$ is antiparallel to the direction of $\vec{A}$. These principles are illustrated in Figure $\PageIndex{6a}$ by two examples where the length of vector $\vec{A}$ is 1.5 units. When $\alpha$ = 2, the new vector $\vec{B}$ = 2$\vec{A}$ has length B = 2A = 3.0 units (twice as long as the original vector) and is parallel to the original vector. When $\alpha$ = −2, the new vector $\vec{C}$ = −2$\vec{A}$ has length C = |−2| A = 3.0 units (twice as long as the original vector) and is antiparallel to the original vector.

Figure a shows vector A pointing to the right. It has magnitude A=1.5. Vector B=2 time vector A points to the right and has magnitude B = 2 A = 3.0. Vector C = -2 times vector A and has magnitude B = 2.0. Figure b shows vector A points to the right and has magnitude A=1.5. Vector B is shown below vector A, with their tails aligned. Vector B points to the right and has magnitude 2.0. In another view, Vector A is shown with vector B starting at the head of A and extending further to the right. Below them is a vector, labeled as vector R = vector A plus vector B, pointing to the right whose tail is aligned with the tail of vector A and whose head is aligned with the head of vector B. The magnitude of vector R is equal to magnitude A plus magnitude B = 3.5. Figure c shows vector A points to the right and has magnitude A=1.5. Vector B is shown below vector A, with their tails aligned. Vector minus B points to the right and has magnitude 3.2. In another view, Vector A is shown with vector minus B pointing to the left and with its head meeting the head of vector A. Below them is a vector, labeled as vector D = vector A minus vector B, shorter than B and pointing to the left whose head is aligned with the head of vector B. The magnitude of vector D is equal to magnitude of quantity A minus B = 1.7.

Now suppose your fishing buddy departs from point A (the campsite), walking in the direction to point B (the fishing hole), but he realizes he lost his tackle box when he stopped to rest at point C (located three-quarters of the distance between A and B, beginning from point A). So, he turns back and retraces his steps in the direction toward the campsite and finds the box lying on the path at some point D only 1.2 km away from point C (see Figure $\PageIndex{5b}$). What is his displacement vector $\vec{D}_{AD}$ when he finds the box at point D? What is his displacement vector $\vec{D}_{DB}$ from point D to the hole? We have already established that at rest point C his displacement vector is $\vec{D}_{AC}$ = 0.75 $\vec{D}_{AB}$. Starting at point C, he walks southwest (toward the campsite), which means his new displacement vector $\vec{D}_{CD}$ from point C to point D is antiparallel to $\vec{D}_{AB}$. Its magnitude |$\vec{D}_{CD}$| is D CD = 1.2 km = 0.2 D AB , so his second displacement vector is $\vec{D}_{CD}$ = −0.2 $\vec{D}_{AB}$. His total displacement $\vec{D}_{AD}$ relative to the campsite is the vector sum of the two displacement vectors: vector $\vec{D}_{AC}$ (from the campsite to the rest point) and vector $\vec{D}_{CD}$ (from the rest point to the point where he finds his box):

\[\vec{D}_{AD} = \vec{D}_{AC} + \vec{D}_{CD} \ldotp \label{2.3}\]

The vector sum of two (or more vectors is called the resultant vector or, for short, the resultant . When the vectors on the right-hand-side of Equation \ref{2.3} are known, we can find the resultant $\vec{D}_{AD}$ as follows:

\[\vec{D}_{AD} = \vec{D}_{AC} + \vec{D}_{CD} = 0.75\; \vec{D}_{AB} - 0.2\; \vec{D}_{AB} = (0.75 - 0.2) \vec{D}_{AB} = 0.55 \vec{D}_{AB} \ldotp \label{2.4}\]

When your friend finally reaches the pond at B, his displacement vector $\vec{D}_{AB}$ from point A is the vector sum of his displacement vector $\vec{D}_{AD}$ from point A to point D and his displacement vector $\vec{D}_{DB}$ from point D to the fishing hole: $\vec{D}_{AB}$ = $\vec{D}_{AD}$ + $\vec{D}_{DB}$ (see Figure $\PageIndex{5c}$). This means his displacement vector $\vec{D}_{DB}$ is the difference of two vectors:

\[\vec{D}_{DB} = \vec{D}_{AB} − \vec{D}_{AD} = \vec{D}_{AB} + (− \vec{D}_{AD}) \ldotp \label{2.5}\]

Notice that a difference of two vectors is nothing more than a vector sum of two vectors because the second term in Equation \ref{2.5} is vector $- \vec{D}_{AD}$ (which is antiparallel to $\vec{D}_{AD}$). When we substitute Equation \ref{2.4} into Equation \ref{2.5}, we obtain the second displacement vector:

\[\vec{D}_{DB} = \vec{D}_{AB} − \vec{D}_{AD} = \vec{D}_{AB} − 0.55\; \vec{D}_{AB} = (1.0 − 0.55)\; \vec{D}_{AB} = 0.45\; \vec{D}_{AB} \ldotp \label{2.6}\]

This result means your friend walked D DB = 0.45 D AB = 0.45(6.0 km) = 2.7 km from the point where he finds his tackle box to the fishing hole.

When vectors $\vec{A}$ and $\vec{B}$ lie along a line (that is, in one dimension), such as in the camping example, their resultant $\vec{R}$ = $\vec{A}$ + $\vec{B}$ and their difference $\vec{D}$ = $\vec{A}$ − $\vec{B}$ both lie along the same direction. We can illustrate the addition or subtraction of vectors by drawing the corresponding vectors to scale in one dimension, as shown in Figure $\PageIndex{6}$.

To illustrate the resultant when $\vec{A}$ and $\vec{B}$ are two parallel vectors, we draw them along one line by placing the origin of one vector at the end of the other vector in head-to-tail fashion (see Figure (\PageIndex{6b}\)). The magnitude of this resultant is the sum of their magnitudes: R = A + B. The direction of the resultant is parallel to both vectors. When vector $\vec{A}$ is antiparallel to vector $\vec{B}$, we draw them along one line in either head-to-head fashion (Figure (\PageIndex{6c}\)) or tail-to-tail fashion. The magnitude of the vector difference, then, is the absolute value D = |A − B| of the difference of their magnitudes. The direction of the difference vector $\vec{D}$ is parallel to the direction of the longer vector.

\[\vec{A} + \vec{B} = \vec{B} + \vec{A} \ldotp \label{2.7}\]

and associative,

\[ (\vec{A} + \vec{B}) + \vec{C} = \vec{A} + (\vec{B} + \vec{C}) \ldotp \label{2.8}\]

Moreover, multiplication by a scalar is distributive :

\[ \alpha_{1} \vec{A} + \alpha_{2} \vec{A} = (\alpha_{1} + \alpha_{2}) \vec{A} \ldotp \label{2.9}\]

We used the distributive property in Equation \ref{2.4} and Equation \ref{2.6}.

When adding many vectors in one dimension, it is convenient to use the concept of a unit vector . A unit vector, which is denoted by a letter symbol with a hat, such as $\hat{u}$, has a magnitude of one and does not have any physical unit so that |$\hat{u}$| ≡ u = 1. The only role of a unit vector is to specify direction. For example, instead of saying vector $\vec{D}_{AB}$ has a magnitude of 6.0 km and a direction of northeast, we can introduce a unit vector $\hat{u}$ that points to the northeast and say succinctly that $\vec{D}_{AB}$ = (6.0 km) $\hat{u}$. Then the southwesterly direction is simply given by the unit vector$- \hat{u}$. In this way, the displacement of 6.0 km in the southwesterly direction is expressed by the vector

\[\vec{D}_{BA} = (−6.0\; km)\; \hat{u} \ldotp \nonumber\]

Example $\PageIndex{1}$: A Ladybug Walker

A long measuring stick rests against a wall in a physics laboratory with its 200-cm end at the floor. A ladybug lands on the 100-cm mark and crawls randomly along the stick. It first walks 15 cm toward the floor, then it walks 56 cm toward the wall, then it walks 3 cm toward the floor again. Then, after a brief stop, it continues for 25 cm toward the floor and then, again, it crawls up 19 cm toward the wall before coming to a complete rest (Figure $\PageIndex{1}$). Find the vector of its total displacement and its final resting position on the stick.

\[ \begin{align*} \vec{D}_{1} &= (15\; cm)( + \hat{u}), \\[4pt] \vec{D}_{2} &= (56\; cm)( - \hat{u}), \\[4pt] \vec{D}_{3} &= (3\; cm)( + \hat{u}), \\[4pt] \vec{D}_{4} &= (25\; cm)( + \hat{u}), \; and \\[4pt] \vec{D}_{5} &= (19\; cm)( - \hat{u}) \ldotp \end{align*}\]

The total displacement $\vec{D}$ is the resultant of all its displacement vectors.

Five illustrations of a ladybug on a ruler leaning against a wall. The +u hat direction is toward the floor parallel to the ruler, and the – u hat direction is up along the ruler. In the first illustration, the ladybug is located near the middle of the ruler and vector D sub 1 points down the ruler. In the second illustration, the ladybug is located lower, where the head of vector D sub 1 is in the first illustration, and vector D sub 2 points up the ruler. In the third illustration, the ladybug is located higher, where the head of vector D sub 2 is in the second illustration, and vector D sub 3 points down the ruler. In the fourth illustration, the ladybug is located lower, where the head of vector D sub 3 is in the third illustration, and vector D sub 4 points down the ruler. In the fifth illustration, the ladybug is located lower, where the head of vector D sub 4 is in the fourth illustration, and vector D sub 5 points up the ruler.

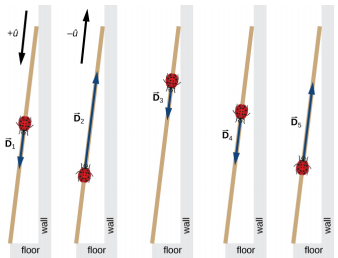
The resultant of all the displacement vectors is

\[ \begin{align*} \vec{D} &= \vec{D}_{1} + \vec{D}_{2} + \vec{D}_{3} + \vec{D}_{4} + \vec{D}_{5} \\[4pt] &= (15\; cm)( + \hat{u} ) + (56\; cm)( −\hat{u} ) + (3\; cm)( + \hat{u} ) + (25\; cm)( + \hat{u}) + (19\; cm)( − \hat{u}) \\[4pt] &= (15 − 56 + 3 + 25 − 19) cm\; \hat{u} \\[4pt] &= −32\; cm\; \hat{u} \ldotp \end{align*}\]

In this calculation, we use the distributive law given by Equation 2.2.9 . The result reads that the total displacement vector points away from the 100-cm mark (initial landing site) toward the end of the meter stick that touches the wall. The end that touches the wall is marked 0 cm, so the final position of the ladybug is at the (100 – 32) cm = 68-cm mark.

Algebra of Vectors in Two Dimensions

When vectors lie in a plane—that is, when they are in two dimensions—they can be multiplied by scalars, added to other vectors, or subtracted from other vectors in accordance with the general laws expressed by Equation 2.2.1 , Equation 2..2.2 , Equation 2.2.7 , and Equation 2.2.8 . However, the addition rule for two vectors in a plane becomes more complicated than the rule for vector addition in one dimension. We have to use the laws of geometry to construct resultant vectors, followed by trigonometry to find vector magnitudes and directions. This geometric approach is commonly used in navigation (Figure $\PageIndex{2}$). In this section, we need to have at hand two rulers, a triangle, a protractor, a pencil, and an eraser for drawing vectors to scale by geometric constructions.

A photograph of someone measuring distance on a map using calipers and a ruler.

For a geometric construction of the sum of two vectors in a plane, we follow the parallelogram rule . Suppose two vectors $\vec{A}$ and $\vec{B}$ are at the arbitrary positions shown in Figure $\PageIndex{3}$. Translate either one of them in parallel to the beginning of the other vector, so that after the translation, both vectors have their origins at the same point. Now, at the end of vector $\vec{A}$ we draw a line parallel to vector $\vec{B}$ and at the end of vector $\vec{B}$ we draw a line parallel to vector $\vec{A}$ (the dashed lines in Figure $\PageIndex{3}$). In this way, we obtain a parallelogram. From the origin of the two vectors we draw a diagonal that is the resultant $\vec{R}$ of the two vectors: $\vec{R}$ = $\vec{A}$ + $\vec{B}$ (Figure $\PageIndex{3a}$). The other diagonal of this parallelogram is the vector difference of the two vectors $\vec{D}$ = $\vec{A}$ − $\vec{B}$, as shown in Figure $\PageIndex{3b}$. Notice that the end of the difference vector is placed at the end of vector $\vec{A}$.

The parallelogram method for adding vectors is illustrated. In figure a, vectors A and B are shown. Vector A points to the right and down and vector B points right and up. Vectors A and B are then shown as solid arrows with their tails together, and their directions as before. A dashed line parallel to vector A but shifted so it starts at the head of B is shown. A second dashed line, parallel to B and starting at the head of A is also shown. The vectors A and B and the two dashed lines form a parallelogram. A third vector, labeled vector R = vector A plus vector B, is shown. The tail of vector R is at the tails of vectors A and B, and the head of vector R is where the dashed lines meet each other, diagonally across the parallelogram. We note that the magnitude of R is not equal to the magnitude of A plus the magnitude of B. In figure b, vectors A and minus B are shown. Vector minus B is vector B from part a, rotated 180 degrees. Vector A points to the right and down and vector minus B points left and down. Vectors A and B are then shown as solid arrows with their tails together, and their directions as before. A dashed line parallel to vector A but shifted so it starts at the head of B is shown. A second dashed line, parallel to B and starting at the head of A is also shown. The vectors A and B and the two dashed lines form a parallelogram. A third vector, labeled vector D is shown. The tail of vector D is at the head of vector B, and the head of vector D is at the head of vector A, diagonally across the parallelogram. We note that vector D is equal to vector A minus vector B, but the magnitude of D is not equal to the magnitude of A minus the B.

It follows from the parallelogram rule that neither the magnitude of the resultant vector nor the magnitude of the difference vector can be expressed as a simple sum or difference of magnitudes A and B, because the length of a diagonal cannot be expressed as a simple sum of side lengths. When using a geometric construction to find magnitudes |$\vec{R}$| and |$\vec{D}$|, we have to use trigonometry laws for triangles, which may lead to complicated algebra. There are two ways to circumvent this algebraic complexity. One way is to use the method of components, which we examine in the next section. The other way is to draw the vectors to scale, as is done in navigation, and read approximate vector lengths and angles (directions) from the graphs. In this section we examine the second approach.

If we need to add three or more vectors, we repeat the parallelogram rule for the pairs of vectors until we find the resultant of all of the resultants. For three vectors, for example, we first find the resultant of vector 1 and vector 2, and then we find the resultant of this resultant and vector 3. The order in which we select the pairs of vectors does not matter because the operation of vector addition is commutative and associative (see Equation 2.2.7 and Equation 2.2.8 ). Before we state a general rule that follows from repetitive applications of the parallelogram rule, let’s look at the following example.

Suppose you plan a vacation trip in Florida. Departing from Tallahassee, the state capital, you plan to visit your uncle Joe in Jacksonville, see your cousin Vinny in Daytona Beach, stop for a little fun in Orlando, see a circus performance in Tampa, and visit the University of Florida in Gainesville. Your route may be represented by five displacement vectors $\vec{A}$, $\vec{B}$, $\vec{C}$, $\vec{D}$, and $\vec{E}$, which are indicated by the red vectors in Figure $\PageIndex{4}$. What is your total displacement when you reach Gainesville? The total displacement is the vector sum of all five displacement vectors, which may be found by using the parallelogram rule four times. Alternatively, recall that the displacement vector has its beginning at the initial position (Tallahassee) and its end at the final position (Gainesville), so the total displacement vector can be drawn directly as an arrow connecting Tallahassee with Gainesville (see the green vector in Figure $\PageIndex{4}$). When we use the parallelogram rule four times, the resultant $\vec{R}$ we obtain is exactly this green vector connecting Tallahassee with Gainesville: $\vec{R}$ = $\vec{A}$ + $\vec{B}$ + $\vec{C}$ + $\vec{D}$ + $\vec{E}$.

A map of Florida with the following vectors shown in red: Vector A from Tallahassee to Jacksonville, almost due west. Vector B from Jacksonville to Daytona Beach, southeast. Vector C from Daytona Beach to Orlando, southwest. Vector D from Orlando to Tampa, southwest (but less vertical than vector C). Vector E from Tampa to Gainesville, slightly east of north. Vector R from Tallahassee to Gainsville is shown as a green arrow.

Drawing the resultant vector of many vectors can be generalized by using the following tail-to-head geometric construction. Suppose we want to draw the resultant vector $\vec{R}$ of four vectors $\vec{A}$, $\vec{B}$, $\vec{C}$, and $\vec{D}$ (Figure $\PageIndex{5a}$). We select any one of the vectors as the first vector and make a parallel translation of a second vector to a position where the origin (“tail”) of the second vector coincides with the end (“head”) of the first vector. Then, we select a third vector and make a parallel translation of the third vector to a position where the origin of the third vector coincides with the end of the second vector. We repeat this procedure until all the vectors are in a head-to-tail arrangement like the one shown in Figure $\PageIndex{5}$. We draw the resultant vector $\vec{R}$ by connecting the origin (“tail”) of the first vector with the end (“head”) of the last vector. The end of the resultant vector is at the end of the last vector. Because the addition of vectors is associative and commutative, we obtain the same resultant vector regardless of which vector we choose to be first, second, third, or fourth in this construction.

In figure a, four vectors, labeled A, B, C, and D are shown individually. In figure b, the vectors are shown arranged head to tail: Vector A’s tail is at the head of D. Vector C’s tail is at the head of A. And vector B’s tail is at the head of C. Each vector is pointing in the same direction as it is in figure a. A fifth vector, R, starts at the tail of vector D and ends at the head of vector B.

Example $\PageIndex{2}$: Geometric Construction of the Resultant

The three displacement vectors $\vec{A}$, $\vec{B}$, and $\vec{C}$ in Figure $\PageIndex{6}$ are specified by their magnitudes A = 10.0, B = 7.0, and C = 8.0, respectively, and by their respective direction angles with the horizontal direction $\alpha$ = 35°, $\beta$ = −110°, and $\gamma$ = 30°. The physical units of the magnitudes are centimeters. Choose a convenient scale and use a ruler and a protractor to find the following vector sums: (a) $\vec{R}$ = $\vec{A}$ + $\vec{B}$, (b) $\vec{D}$ = $\vec{A}$ − $\vec{B}$, and (c) $\vec{S}$ = $\vec{A}$ − $3 \vec{B}$ + $\vec{C}$.

Vector A has magnitude 10.0 and is at an angle alpha = 35 degrees counterclockwise from the horizontal. It points up and right. Vector B has magnitude 7.0 and is at an angle beta = -110 degrees clockwise from the horizontal. It points down and left. Vector C has magnitude 8.0 and is at an angle gamma = 30 degrees counterclockwise from the horizontal. It points up and right. Vector F has magnitude 20.0 and is at an angle phi = 110 degrees counterclockwise from the horizontal. It points up and left.

In geometric construction, to find a vector means to find its magnitude and its direction angle with the horizontal direction. The strategy is to draw to scale the vectors that appear on the right-hand side of the equation and construct the resultant vector. Then, use a ruler and a protractor to read the magnitude of the resultant and the direction angle. For parts (a) and (b) we use the parallelogram rule. For (c) we use the tail-to-head method.

For parts (a) and (b), we attach the origin of vector $\vec{B}$ to the origin of vector $\vec{A}$, as shown in Figure $\PageIndex{7}$, and construct a parallelogram. The shorter diagonal of this parallelogram is the sum $\vec{A}$ + $\vec{B}$. The longer of the diagonals is the difference $\vec{A}$ − $\vec{B}$. We use a ruler to measure the lengths of the diagonals, and a protractor to measure the angles with the horizontal. For the resultant $\vec{R}$, we obtain R = 5.8 cm and $\theta_{R}$ ≈ 0°. For the difference $\vec{D}$, we obtain D = 16.2 cm and $\theta_{D}$ = 49.3°, which are shown in Figure $\PageIndex{7}$.

Three diagrams of vectors A and B. Vectors A and B are shown placed tail to tail. Vector A points up and right and has magnitude 10.0. Vector B points down and left and has magnitude 7.0. The angle between vectors A and B is 145 degrees. In the second diagram, Vectors A and B are shown again along with the dashed lines completing the parallelogram. Vector R equaling the sum of vectors A and B is shown as the vector from the tails of A and B to the opposite vertex of the parallelogram. The magnitude of R is 5.8. In the third diagram, Vectors A and B are shown again along with the dashed lines completing the parallelogram. Vector D equaling the difference of vectors A and B is shown as the vector from the head of B to the head of A. The magnitude of D is 16.2, and the angle between D and the horizontal is 49.3 degrees. Vector R in the second diagram is much shorter than vector D in the third diagram.

For (c), we can start with vector −3 $\vec{B}$ and draw the remaining vectors tail-to-head as shown in Figure $\PageIndex{8}$. In vector addition, the order in which we draw the vectors is unimportant, but drawing the vectors to scale is very important. Next, we draw vector $\vec{S}$ from the origin of the first vector to the end of the last vector and place the arrowhead at the end of $\vec{S}$. We use a ruler to measure the length of $\vec{S}$, and find that its magnitude is S = 36.9 cm. We use a protractor and find that its direction angle is $\theta_{S}$ = 52.9°. This solution is shown in Figure $\PageIndex{8}$.

Three vectors are shown in blue and placed head to tail: Vector minus 3 B points up and right and has magnitude 3 B = 21.0. Vector A starts at the head of B, points up and right, and has a magnitude of A=10.0. The angle between vector A and vector minus 3 B is 145 degrees. Vector C starts at the head of A and has magnitude C=8.0. Vector S is green and goes from the tail of minus 3 B to the head of C. Vector S equals vector A minus 3 vector B plus vector C, has a magnitude of S=36.9 and makes an angle of 52.9 degrees counterclockwise with the horizontal.

Science Notes Posts
Contact Science Notes
Todd Helmenstine Biography
Anne Helmenstine Biography
Free Printable Periodic Tables (PDF and PNG)
Periodic Table Wallpapers
Interactive Periodic Table
Periodic Table Posters
How to Grow Crystals
Chemistry Projects
Fire and Flames Projects
Holiday Science
Chemistry Problems With Answers
Physics Problems
Unit Conversion Example Problems
Chemistry Worksheets
Biology Worksheets
Periodic Table Worksheets
Physical Science Worksheets
Science Lab Worksheets
My Amazon Books

Scalar vs Vector – Definitions and Examples

In mathematics and physics, a scalar is a quantity that only has magnitude (size), while a vector has both magnitude and direction. Examples of scalar quantities include pure numbers, mass, speed, temperature, energy, volume, and time. Examples of vector quantities include velocity, acceleration, momentum, displacement, and forces, such as weight and friction.

Examples of Scalars

Here are some examples of scalar quantities:

Temperature

Examples of Vectors

Here are some examples of vector quantities:

Acceleration

Scalar vs Vector – Test Your Understanding

(1) The car is going 75 mph.

This is a scalar value because you don’t know which direction the car is going.

(2) You walked 4 mph toward the store.

This is a vector because you have both a magnitude and a direction.

(3) The box in the west corner of the room has a mass of 12 kilograms.

The mass of the box is a scalar quantity. Even though you know the location of the box, this fact has nothing to do with its mass.

(5) The time is 12:30 pm.

This is a scalar. There is no direction.

(6) The pressure inside a balloon is 2 atmospheres.

Pressure has a magnitude, but it does not have a direction. Another way of looking at it is that pressure acts in all directions at once.

(7) The cat weighs 8 pounds.

Mass and weight can be confusing, when it comes to distinguishing between scalar and vector quantities. The pound is a unit of weight, so this value is a vector. The implied direction is down, toward the Earth’s center of gravity. If the “weight” of the cat was given in kilograms, it would be a scalar value (for mass, not weight). A cat’s weight is different on the Moon or Mars, but its mass remains the same.

Related Terms

A unit vector is a vector that has a magnitude of 1. Usually, it’s indicated by placing a carat ( ^ ) over it. The unit vector x , with a carat over it, is read as “x-hat” because the vector looks somewhat like it’s wearing a hat.
The null vector or zero vector is a vector with a magnitude of zero. While it has no magnitude, it has a direction. For example, you could use a null vector to describe which direction a compass is pointing.
Ashcroft, Neil; Mermin, N. David (1976). Solid State Physics . Toronto: Thomson Learning. ISBN 978-0-03-083993-1.
Banach, Stefan (1922). “Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)”. Fundamenta Mathematicae (in French). 3: 133–181. doi: 10.4064/fm-3-1-133-181
Lay, David C. (2006). Linear Algebra and Its Applications (3rd ed.). Addison–Wesley. ISBN 0-321-28713-4.
Strang, Gilbert (2006). Linear Algebra and Its Applications (4th ed.). Brooks Cole. ISBN 0-03-010567-6.

Scalars and Vectors

Mar 12, 2019

330 likes | 528 Views

Section 1 Introduction to Vectors. Chapter 3. Scalars and Vectors. A scalar is a physical quantity that has magnitude but no direction. Examples: speed, volume, the number of pages in your textbook A vector is a physical quantity that has both magnitude and direction.

Share Presentation

axis points
stunt dummy
displacement vectors
section 1 introduction
section 2 vector operations

Presentation Transcript

Section 1 Introduction to Vectors Chapter 3 Scalars and Vectors • A scalaris a physical quantity that has magnitude but no direction. • Examples: speed, volume, the number of pages in your textbook • Avectoris a physical quantity that has both magnitude and direction. • Examples: displacement, velocity, acceleration • In this book, scalar quantities are initalics. Vectors are represented byboldfacesymbols.

Section 1 Introduction to Vectors Chapter 3 Triangle Method of Addition • Vectors can be movedparallelto themselves in a diagram. • Thus, you can draw one vector with its tail starting at the tip of the other as long as the size and direction of each vector do not change. • Theresultant vectorcan then be drawn from the tail of the first vector to the tip of the last vector.

Section 1 Introduction to Vectors Chapter 3 Properties of Vectors • Vectors can be added in any order. • To subtract a vector, add its opposite. • Multiplying or dividingvectors by scalars results in vectors.

Section 2 Vector Operations Chapter 3 Coordinate Systems in Two Dimensions • One method for diagraming the motion of an object employsvectorsand the use of thex- and y-axes. • Axes are often designated usingfixed directions. • In the figure shown here, thepositive y-axispoints northand thepositive x-axispointseast.

Section 2 Vector Operations Chapter 3 Determining Resultant Magnitude and Direction • In Section 1, the magnitude and direction of a resultant were found graphically. • With this approach, the accuracy of the answer depends on how carefully the diagram is drawn and measured. • A simpler method uses thePythagorean theoremand thetangent function.

Section 2 Vector Operations Chapter 3 Determining Resultant Magnitude and Direction The Pythagorean Theorem • Use thePythagorean theoremto find the magnitude of the resultant vector. • The Pythagorean theorem states that for anyright triangle,thesquare of the hypotenuse—the side opposite the right angle—equals the sum of the squares of the other two sides, or legs.

Section 2 Vector Operations Chapter 3 Determining Resultant Magnitude and Direction, continued The Trigonometry Functions • SOHCAHTOA – sin q = opp/hyp, cos q = opp/adj, tan q = opp/adj

Section 2 Vector Operations Chapter 3 Sample Problem Finding Resultant Magnitude and Direction An archaeologist climbs the Great Pyramid in Giza, Egypt. The pyramid’s height is 136 m and its width is 2.30  102 m. What is the magnitude and the direction of the displacement of the archaeologist after she has climbed from the bottom of the pyramid to the top?

Section 2 Vector Operations Chapter 3 Sample Problem, continued 1. Define Given: Dy = 136 m Dx = 1/2(width) = 115 m Unknown: d= ? q = ? Diagram: Choose the archaeologist’s starting position as the origin of the coordinate system, as shown above.

Section 2 Vector Operations Chapter 3 Sample Problem, continued 2. Plan Choose an equation or situation: The Pythagorean theorem can be used to find the magnitude of the archaeologist’s displacement. The direction of the displacement can be found by using the inverse tangent function. Rearrange the equations to isolate the unknowns:

Section 2 Vector Operations Chapter 3 Sample Problem, continued 3. Calculate • Evaluate Because d is the hypotenuse, the archaeologist’s displacement should be less than the sum of the height and half of the width. The angle is expected to be more than 45 because the height is greater than half of the width.

Section 2 Vector Operations Chapter 3 Adding Vectors That Are Not Perpendicular • Suppose that a plane travels first5 kmat an angle of35°,then climbs at10°for22 km,as shown below. How can you find thetotal displacement? • Because the original displacement vectors do not form a right triangle, you can not directly apply the tangent function or the Pythagorean theorem. d2 d1

Section 2 Vector Operations Chapter 3 Adding Vectors That Are Not Perpendicular, continued • You can find the magnitude and the direction of the resultant by resolving each of the plane’s displacement vectors into its x and y components. • Then the components along each axis can be added together. As shown in the figure, these sums will be the two perpendicular components of the resultant, d. The resultant’s magnitude can then be found by using the Pythagorean theorem, and its direction can be found by using the inverse tangent function.

Section 2 Vector Operations Chapter 3 Sample Problem Adding Vectors Algebraically A hiker walks 27.0 km from her base camp at 35° south of east. The next day, she walks 41.0 km in a direction 65° north of east and discovers a forest ranger’s tower. Find the magnitude and direction of her resultant displacement

Section 2 Vector Operations Chapter 3 Sample Problem, continued 1 . Select a coordinate system. Then sketch and label each vector. Given: d1 = 27.0 km q1 = –35° d2 = 41.0 km q2 = 65° Tip:q1 is negative, because clockwise movement from the positive x-axis is negative by convention. Unknown: d = ? q = ?

Section 2 Vector Operations Chapter 3 Sample Problem, continued 2 . Find the x and y components of all vectors. Make a separate sketch of the displacements for each day. Use the cosine and sine functions to find the components.

Section 2 Vector Operations Chapter 3 Sample Problem, continued 3 . Find the x and y components of the total displacement. 4 . Use the Pythagorean theorem to find the magnitude of the resultant vector.

Section 2 Vector Operations Chapter 3 Sample Problem, continued 5 . Use a suitable trigonometric function to find the angle.

Section 3 Projectile Motion Chapter 3 Projectiles • Objects that are thrown or launched into the air and are subject to gravity are calledprojectiles. • Projectile motionis the curved path that an object follows when thrown, launched,or otherwise projected near the surface of Earth. • If air resistance is disregarded, projectiles followparabolic trajectories.

Section 3 Projectile Motion Chapter 3 Sample Problem Projectiles Launched At An Angle A zookeeper finds an escaped monkey hanging from a light pole. Aiming her tranquilizer gun at the monkey, she kneels 10.0 m from the light pole,which is 5.00 m high. The tip of her gun is 1.00 m above the ground. At the same moment that the monkey drops a banana, the zookeeper shoots. If the dart travels at 50.0 m/s,will the dart hit the monkey, the banana, or neither one?

Section 3 Projectile Motion Chapter 3 Sample Problem, continued 1 . Select a coordinate system. The positive y-axis points up, and the positive x-axis points along the ground toward the pole. Because the dart leaves the gun at a height of 1.00 m, the vertical distance is 4.00 m.

Section 3 Projectile Motion Chapter 3 Sample Problem, continued 2 . Use the inverse tangent function to find the angle that the initial velocity makes with the x-axis.

Section 3 Projectile Motion Chapter 3 Sample Problem, continued 3 . Choose a kinematic equation to solve for time. Rearrange the equation for motion along the x-axis to isolate the unknown Dt, which is the time the dart takes to travel the horizontal distance.

Section 3 Projectile Motion Chapter 3 Sample Problem, continued 4 . Find out how far each object will fall during this time. Use the free-fall kinematic equation in both cases. For the banana, vi = 0. Thus: Dyb = ½ay(Dt)2 = ½(–9.81 m/s2)(0.215 s)2 = –0.227 m The dart has an initial vertical component of velocity equal to vi sin q, so: • Dyd = (vi sin q)(Dt) + ½ay(Dt)2 • Dyd = (50.0 m/s)(sin 21.8)(0.215 s) +½(–9.81 m/s2)(0.215 s)2 • Dyd = 3.99 m – 0.227 m = 3.76 m

Section 3 Projectile Motion Chapter 3 Sample Problem, continued 5 . Analyze the results. Find the final height of both the banana and the dart. ybanana, f = yb,i+ Dyb = 5.00 m + (–0.227 m) ybanana, f = 4.77 m above the ground ydart, f = yd,i+ Dyd = 1.00 m + 3.76 m ydart, f = 4.76 m above the ground The dart hits the banana. The slight difference is due to rounding.

Section 4 Relative Motion Chapter 3 Frames of Reference, continued Consider a stunt dummy dropped from a plane. (a)When viewed from the plane, the stunt dummy falls straight down. (b)When viewed from a stationary position on the ground, the stunt dummy follows a parabolic projectile path.

More by User

Scalars and Vectors. Scalars are quantities which are fully described by a size alone. Eg. Temperature, Distance, Time, Speed, Mass, Length. Vectors are quantities which are fully described by both a size and a direction. Eg. Velocity, Acceleration, Force, Thrust, Drag.

482 views • 9 slides

Vectors And Scalars

Vectors and Scalars. All quantities we deal with in Physics can be classified as vectors or scalars (note the spelling!)Scalars can be described simply with a number indicating the magnitude (size)Mass of 2 kgTemperature of 22

640 views • 12 slides

Vectors and Scalars

Vectors and Scalars. Physics. Bell Ringer (5 mins) in your notebook. Bell ringer. Bell ringer. Bell ringer. Bell ringer. Objective. We will draw vectors & find the resultant to describe motion in 2-Dimensions

723 views • 40 slides

Vectors and Scalars. Learning outcomes. Understand scalar and vector quantities Determine resultant vector by graphical method Parallelogram Head to tail method. PHYSICAL QUANTITIES. BASE QUANTITIES. DERIVED QUANTITIES. PHYSICAL QUANTITIES. SCALARS. VECTORS.

600 views • 17 slides

VECTORS AND SCALARS

VECTORS AND SCALARS. SCALARS. Vectors. Symbol for vectors:. Typed: v, a, F, x Written: . Multiplying vectors by scalars. Vector x scalar = vector. Multiplying vectors by scalars. Comparing vectors. Which vectors have the same magnitude?. Which vectors have the same direction?.

1.1k views • 47 slides

Vectors and Scalars. A SCALAR is ANY quantity in physics that has MAGNITUDE , but NOT a direction associated with it. Magnitude – A numerical value with units. A VECTOR is ANY quantity in physics that has BOTH MAGNITUDE and DIRECTION. x. displacement x = 6 cm, 25 0.

6.44k views • 33 slides

Vectors and Scalars. Honors Physics. Scalar. A SCALAR is ANY quantity in physics that has MAGNITUDE , but NOT a direction associated with it. Magnitude – A numerical value with units. Vector. A VECTOR is ANY quantity in physics that has BOTH MAGNITUDE and DIRECTION.

371 views • 13 slides

Scalars and vectors

Scalars and vectors. Which of the following is the odd one out? Mass Speed Force Temperature Distance Elephant. Which of the following is the odd one out? Mass Speed Force Temperature Distance Elephant. Scalars. Scalar quantities have a magnitude (size) only . For example:

903 views • 20 slides

Vectors and Scalars.

997 views • 41 slides

Scalars and Vectors. define scalar and vector quantities and give examples. ( b) draw and use a vector triangle to determine the resultant of two vectors such as displacement, velocity and force. (c) Use trigonometry to determine the resultant of two vectors. Scalars and Vectors.

1.01k views • 17 slides

Vectors and Scalars. Adding and Subtracting. Pythagorean Theorem. a 2 + b 2 = c 2 10 8 6 4 3

242 views • 11 slides

Vectors and Scalars. Scalars have magnitude only e.g. mass, speed, distance Vectors have magnitude and direction e.g. force of 10 N to the left.. Velocity, displacement, weight ,acceleration……. Adding Vectors. Vectors are represented by arrows : 10 N to left or - 10 N

535 views • 35 slides

Vectors and Scalars. Chapter 2. Definitions. A vector is a quantity that has both direction and magnitude. Examples of vectors include: position, velocity, acceleration, force, and torque. A scalar is a quantity that has only magnitude.

278 views • 14 slides

VECTORS AND SCALARS A scalar quantity has only magnitude and is completely specified by a number and a unit. Examples are: mass (2 kg), volume (1.5 L), and frequency (60 Hz). Scalar quantities of the same kind are added by using ordinary arithmetic.

1.21k views • 89 slides

Vectors and Scalars. Vectors & Scalars. Vectors are the physical quantities having ; 1- Magnitude 2- Direction 3- Should obey the parallelogram law of addition

648 views • 31 slides

Scalars and Vectors. A scalar quantity is one that can be described by a single number: temperature, speed, mass. A vector quantity deals inherently with both magnitude and direction : velocity, force, displacement, acceleration. Scalars and Vectors.

292 views • 11 slides

VECTORS AND SCALARS A scalar quantity has only magnitude and is completely specified by a number and a unit. Examples are mass (a stone has a mass of 2 kg), volume (1.5 L), and frequency (60 Hz). Scalar quantities of the same kind are added by using ordinary arithmetic.

1.25k views • 54 slides

Vectors and Scalars. I know where I’m going. A scalar is a quantity described by just a number, usually with units. It can be positive, negative, or zero. Examples : Distance Time Temperature Speed

667 views • 32 slides

Vectors and Scalars. AP Physics. Scalar. A SCALAR is ANY quantity in physics that has MAGNITUDE , but NOT a direction associated with it. Magnitude – A numerical value with units. Vector. A VECTOR is ANY quantity in physics that has BOTH MAGNITUDE and DIRECTION.

483 views • 30 slides

Vectors and Scalars. AP Physics B. Scalar. A SCALAR is ANY quantity in physics that has MAGNITUDE , but NOT a direction associated with it. Magnitude – A numerical value with units. Vector. A VECTOR is ANY quantity in physics that has BOTH MAGNITUDE and DIRECTION.

208 views • 13 slides

Scalars and Vectors. MR. KEMUEL DE CASTRO. “You can’t control the direction of the WIND but you can always adjust your SAIL”. Definition of Terms. It is the space between two points. It is change of place or position.

489 views • 34 slides

Scalars and Vectors

Motion of objects in physics are expressed by distance, displacement, speed, velocity, and acceleration which are associated with mathematical quantities called scalar and vector. Read less

1. By Prof. Liwayway Memije-Cruz Scalars and Vectors
2. Introduction  Physics is a mathematical science.  Its concepts and principles have a mathematical basis.  Mo tio n o f o bje cts in physics are e xpre sse d by distance , displace m e nt, spe e d, ve lo city, and acce le ratio n which are asso ciate d with mathematical quantities.  Mathematical quantities used to describe the motion of objects are vector and a scalar.
4. Mathematical Quantities  Scalars are quantities that are fully described by a magnitude (or numerical value) alone.  Vectors are quantities that are fully described by both a magnitude and a direction.
5. Consider the following quantities listed below. Be able to categorize each quantity as being either a vector or a scalar. Quantity Category 20 s 80 km 4000 cal 70 m South 30 m/sec, East 25 degrees Celsius 5 hrs
6. Resultant and Equilibrant  Resultant is the vector sum of two or more vectors.  Equilibrant is a force capable of balancing another force and producing equilibrium.
7. Methods of Finding the Resultant  Head to Tail Method 1. Place the two vectors next to each other such that the head of the one vector is touching the tail of the other vector. 2. Draw the resultant vector by starting where
8. Answer  To find the resultant vector's magnitude, use the Pythagorean theorem.
9. Exercise 1 1. You left your house to visit your sister. You got in your car drove 40 miles east, then got on a highway and went 50 miles north. 2. Draw a vector from the beginning of your journey, your home, and the end, your friend’s house.
10. Answer  How long is the vector that you drew?
11. Exercise 2  What is the sum of the two vectors? Use the head to tail method to calculate the resultant vector in the picture on the right
13. Parallelogram Method  Basic sine, cosine and tangent (SOHCAHTOA)
14. To which triangle(s) below does SOHCAHTOA apply?
16. Law of Cosine
17. Law of Sines  The law of sines provides a formula that relates the sides with the angles of a triangle. This formula allows you to relatively easily find the side length or the angle of any triangle.
18. Properties of Parallelogram
19. Exercise 3  To best understand how the parallelogram method works, examine the two vectors below. The vectors have magnitudes of 17 and 28 and the angle between them is 66°. Use the parallelogram method to determine the magnitude of the resultant.
20.  Step 1) Draw a parallelogram based on the two vectors that you already have. These vectors will be two sides of the parallelogram (not the opposite sides since they have the angle between them)  Step 2) We now have a parallelogram and know two angles (opposite angles of parallelograms are congruent). We can also figure out the other pair of angles since the other pair are congruent and all four angles must add up to 360.
21. Step 3 Draw the parallelograms diagonal. This diagonal is the resultant vector. Step 4 Use the law of cosines to determine the length of the resultant
22.  Use the law of cosines to calculate the resultant.
23. References:  http://www.mathwarehouse.com/vectors/result ant-vector.php#headToTailMethod  http://www.s-cool.co.uk/a- level/physics/vectors-and-scalars-and-linear- motion/revise-it/resolving  http://www.physicsclassroom.com/class/vector s/Lesson-1/Vector-Addition  http://www.physicsclassroom.com/class/vector s/Lesson-1/Resultants

Scalars And Vectors

Scalar and Vector

In Physics, we often use the terms force, speed, velocity and work, and these quantities are classified as a scalar or vector quantities. A scalar quantity is a physical quantity with only magnitudes, such as mass and electric charge. On the other hand, a vector quantity is a physical quantity that has both magnitudes and directions like force and weight. In this article, let us familiarize ourselves with vectors and scalars.

What Is a Scalar Quantity?

A scalar quantity is defined as the physical quantity with only magnitude and no direction. Such physical quantities can be described just by their numerical value without directions. The addition of these physical quantities follows the simple rules of algebra, and here, only their magnitudes are added.

Examples of Scalar Quantities

Some examples of scalar include:

Temperature

What Is a Vector Quantity?

A vector quantity is defined as the physical quantity that has both directions as well as magnitude. A vector with a value of magnitude equal to one is called a unit vector and is represented by a lowercase alphabet with a “hat” circumflex, i.e. “ û “.

Visualise Unit Vector with the Help of the Video Given Below

Examples of Vector Quantities

Examples of vector quantity include:

Linear momentum
Acceleration
Displacement
Angular velocity
Electric field
Polarization

Difference Between Scalars and Vectors

The difference between Scalars and Vectors is crucial to understand in physics learning.

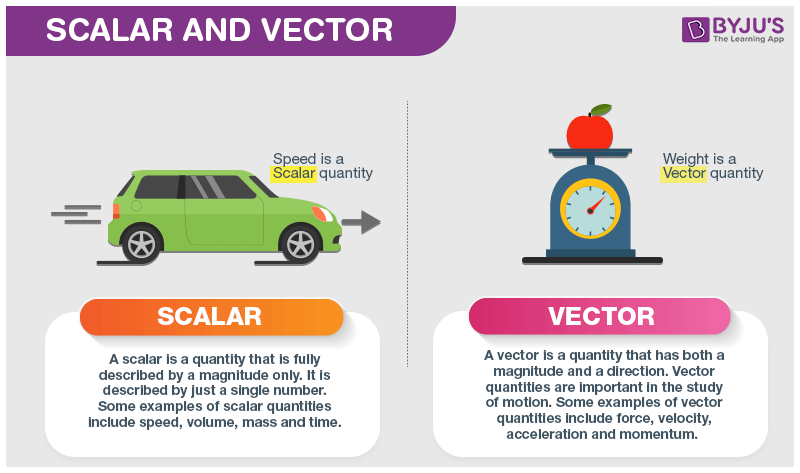
We have listed the various differences between a scalar and vector in the table below:

Vector Addition and Subtraction

After understanding what is a vector, let’s learn vector addition and subtraction. The addition and subtraction of vector quantities do not follow the simple arithmetic rules. A special set of rules are followed for the addition and subtraction of vectors. Following are some points to be noted while adding vectors:

Addition of vectors means finding the resultant of a number of vectors acting on a body.
The component vectors whose resultant is to be calculated are independent of each other. Each vector acts as if the other vectors were absent.
Vectors can be added geometrically but not algebraically.
Vector addition is commutative in nature, i.e., $\begin{array}{l}\underset{A}{\rightarrow}+\underset{B}{\rightarrow}=\underset{B}{\rightarrow}+\underset{A}{\rightarrow}\end{array} $

Now, about vector subtraction, it is the same as adding the negative of the vector to be subtracted. To better understand, let us look at the example given below.

Let us consider two vectors, A and B, as shown in the figure below. We need to subtract vector B from vector A. It is just the same as adding vector B and vector A. The resultant vector is shown in the figure below.

Vector Notation

For vector quantity usually, an arrow is used on the top as shown below, which represents the vector value of the velocity and also explains that the quantity has both magnitudes as well as direction.

Scalar and Vector Solved Problems

Q1: Given below is a list of quantities. Categorize each quantity as being either a vector or a scalar.

Q2: Ashwin walks 10 m north, 12 m east, 3 m west and 5 m south and then stops to drink water. What is the magnitude of his displacement from his original point?

Answer: We know that displacement is a vector quantity; hence the direction Ashwin walks will be positive or negative along an axis.

To find the total distance travelled along the y-axis, let us consider the movement towards the north to be positive and the south to be negative.

$\begin{array}{l}\sum y=10\,m-5\,m=5\,m\end{array} $

He moved a net of 5 meters to the north along the y-axis.

Similarly, let us consider his movement towards the east to be positive and the west to be negative.

$\begin{array}{l}\sum y=-3\,m+12\,m=9\,m\end{array} $

He moved a net of 9 m to the east.

Using Pythagoras theorem, the resultant displacement can be found as follows:

Substituting the values, we get

Q3. What is the magnitude of a unit vector?

Answer: The magnitude of a unit vector is unity. A unit vector has no units or dimensions.

Frequently Asked Questions – FAQS

What is vector and scalar quantity in physics, how are vector and scalar different, how are vectors and scalars quantities alike, what are the examples of scalar, what are the examples of vectors.

Stay tuned to BYJU’S and Fall in Loev with Learning !

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with BYJU'S & Download Free PDFs

STEM Ambassadors
School trusts
ITE and governors
Invest in schools
STEM careers inspiration
Benefits and impact
Our supporters
Become a STEM Ambassador
Request a STEM Ambassador
Employer information
Training and support
STEM Ambassadors Partners
Working with community groups
Search icon
Join the STEM Community

Vectors and Scalars

the distinction between vector and scalar quantities
resolution of vectors into two components at right angles
addition rule for two vectors
calculations for two perpendicular vectors

Those students who studied separate sciences at GCSE are likely to have encountered the concept of vectors before, while those who studied dual award will need a little more support.

It is important the students are aware of the differences between vector and scalar properties; that being that vectors have a direction. Once they can identify which quantities are which they need to be able to resolve vectors into their two components at right angles, add them and then move on to more complicated calculations involving perpendicular vectors.

Some students, naturally, will struggle with the maths of this, and some may also find visualising this concept difficult. There is some work that can be done to help visualise, including making arrows to represent vectors and arranging these appropriately.

Whilst this list provides a source of information and ideas for experimental work, it is important to note that recommendations can date very quickly. Do NOT follow suggestions which conflict with current advice from CLEAPSS or recent safety guides. eLibrary users are responsible for ensuring that any activity, including practical work, which they carry out is consistent with current regulations related to Health and Safety and that they carry an appropriate risk assessment. Further information is provided in our Health and Safety guidance.

Episode 201: Scalars and Vectors

Quality Assured Category: Science Publisher: Institute of Physics

A suggested teaching order which is part of the 'Teaching Advanced Physics' scheme from Institute of Physics.

It gives a clear overview of the topic, including teacher notes, student notes, worked examples and practice questions, and will prove invaluable to those new to teaching A level physics.

Teachers new to teaching A level physics will appreciate the practical advice on the last page

Vectors suitable for home teaching

Quality Assured Category: Mathematics Publisher: Mathcentre

These resources are provided by Mathcentre . Some of the topics covered include an introduction to vectors and the cartesian components of vectors.

Comprehensive notes, with clear descriptions, for each resource are provided, together with relevant diagrams and examples. Each pdf contains worked examples as well as practice questions. The 'Key points' section in the notes provide a useful summary of the ideas presented.

Written from a maths point of view, the first (Introduction to vectors) and last (Cartesian components of vectors) sections of this resource will be useful to a physics teacher to see how vectors are taught and notated in maths lessons and could be used to help plan lessons, as well as to consolidate subject knowledge where necessary.

Vectors Introduction

Quality Assured Category: Mathematics Publisher: University of Leicester

This interactive resource, produced by the University of Leicester, is designed to enable students to explore vectors, beginning with the definition of a vector followed by the algebra of vectors and the scalar product.

Khan Academy presents a video on Vectors. A vector has both magnitude and direction. We use vectors to describe the velocity of moving objects. In this video, you will learn how to write and draw vectors.

Physics Classroom - Resolution of Vectors

These are notes on how to resolve vectors into two components at right angles.

This is best used as either something to help teachers plan a series of lessons around the subject, or set as homework for the students to read, take notes and support learning that they have done in class.

International
Schools directory
Resources Jobs Schools directory News Search

KS4 Lesson: Scalars and Vectors

Subject: Physics

Age range: 14-16

Resource type: Other

Last updated

22 February 2018

Share through email
Share through twitter
Share through linkedin
Share through facebook
Share through pinterest

Tes paid licence How can I reuse this?

Get this resource as part of a bundle and save up to 20%

A bundle is a package of resources grouped together to teach a particular topic, or a series of lessons, in one place.

Physics Fundamentals Lesson Bundle

A set of three lessons designed to introduce key concepts in physics to students who are new to studying the subject. Originally designed for the Edexcel 9-1 specification, these lessons would support any curriculum that introduces these concepts. Each lesson includes a starter activity, a plenary quiz, and accompanying lesson notes sheets for students. This bundle also includes differentiated worksheets on unit conversions, and standard form and significant figures. Lessons are designed to be presented in the following order: Lesson 1: SI Units and Unit Conversions Lesson 2: Standard Form and Significant Figures Lesson 3: Scalars and Vectors The price of this bundle represents a 20% savings on the cost of purchasing each resource individually.

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

COMMENTS

Scalars & vectors
57. Multiplying a vector by a vector • There are two ways to multiply a vector by a vector: • The first way produces a scalar quantity and called as scalar product (dot product). • The second way produces a vector quantity and called as vector product (cross product). 58. Scalar product A B θ A ∙ B = AB cos θ. 59.
1. Scalars and Vectors
1 Tuesday, September 09, 2014 G481 Scalars & Vectors Learning Objectives By the end of this lesson, you should be able to: 4. Define scalar and vector quantities and give examples. 5. Draw and use vector triangles. 6. Calculate the resultant of two perpendicular vectors. Displacement and velocity A runner completes one lap of an athletics track.
PPT
Presentation Transcript. Vectors and Scalars. A SCALAR is ANY quantity in physics that has MAGNITUDE, but NOT a direction associated with it. Magnitude - A numerical value with units. A VECTOR is ANY quantity in physics that has BOTH MAGNITUDE and DIRECTION. x displacement x = 6 cm, 250 A picture is worth a thousand word, at least they say so.
Intro to vectors and scalars (video)
Transcript. Scalars and vectors are two kinds of quantities that are used in physics and math. Scalars are quantities that only have magnitude (or size), while vectors have both magnitude and direction. Explore some examples of scalars and vectors, including distance, displacement, speed, and velocity. Created by Sal Khan.
3.2: Scalars and Vectors (Part 1)
Figure 3.2.1 3.2. 1: We draw a vector from the initial point or origin (called the "tail" of a vector) to the end or terminal point (called the "head" of a vector), marked by an arrowhead. Magnitude is the length of a vector and is always a positive scalar quantity. (credit: modification of work by Cate Sevilla)
2.1 Scalars and Vectors
Figure 2.2 We draw a vector from the initial point or origin (called the "tail" of a vector) to the end or terminal point (called the "head" of a vector), marked by an arrowhead. Magnitude is the length of a vector and is always a positive scalar quantity. (credit "photo": modification of work by Cate Sevilla)
An introduction to vectors
A vector is an object that has both a magnitude and a direction. Geometrically, we can picture a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head. Two vectors are the same if they have the same magnitude and direction.
2.3: Scalars and Vectors
Equation 2.3.2 is a scalar equation because the magnitudes of vectors are scalar quantities (and positive numbers). If the scalar α is negative in the vector equation Equation 2.3.1, then the magnitude | →B | of the new vector is still given by Equation 2.3.2, but the direction of the new vector →B is antiparallel to the direction of →A.
Scalars and Vectors
Scalars and Vectors. A scalar quantity is a mathematical quantity that describes only the magnitude (the number). Examples. Speed. Time. Distance. A vector quantity is a mathematical quantity that describes both the magnitude AND the direction. Examples. Displacement.
PDF LECTURE 1: INTRODUCING VECTORS
1.1 Scalars I A scalar is a quantity with magnitude but no direction, any mathematical entity that can be represented by a number. I Examples: Mass, temperature, energy, charge ... I Scalar addition, subtraction, division, multiplication are deﬁned by the algebra of the real numbers representing the scalars. I M total= M 1 + M 2, V = I R etc. But scalars are not enough if a physical
PDF SCALAR AND VECTORS
Position. The word 'position' in this class implies a vector quantity, like the position of an object relative to a reference point or the position change when moving from point. to point B. B. The scalar part is the straight-line distance between two points, and the direction is from starting point to ending point. VECTOR QUANTITY EXAMPLES.
Episode 201: Scalars and vectors
Episode 201: Scalars and vectors. Lesson for 16-19. Activity time 90 minutes. Level Advanced. Although many students will be familiar with the definition of vector and scalar quantities others may have glossed over these ideas. Such students may feel nervous about vector quantities and will find simple mathematical analysis quite daunting at ...
Scalar vs Vector
In mathematics and physics, a scalar is a quantity that only has magnitude (size), while a vector has both magnitude and direction. Examples of scalar quantities include pure numbers, mass, speed, temperature, energy, volume, and time. Examples of vector quantities include velocity, acceleration, momentum, displacement, and forces, such as ...
PPT
330 likes | 514 Views. Section 1 Introduction to Vectors. Chapter 3. Scalars and Vectors. A scalar is a physical quantity that has magnitude but no direction. Examples: speed, volume, the number of pages in your textbook A vector is a physical quantity that has both magnitude and direction. Download Presentation. vectors.
Physics 1.3 scalars and vectors
Draw one vector. Draw the next. Carry on doing. Join the. Measure the resultant's. What is. This is done. Example. Physics 1.3 scalars and vectors - Download as a PDF or view online for free.
Scalars and Vectors
7. Methods of Finding the Resultant Head to Tail Method 1. Place the two vectors next to each other such that the head of the one vector is touching the tail of the other vector. 2. Draw the resultant vector by starting where. 8. Answer To find the resultant vector's magnitude, use the Pythagorean theorem.
Vector and Scalar
We have listed the various differences between a scalar and vector in the table below: Vector. Scalar. Definition. A physical quantity with both the magnitude and direction. A physical quantity with only magnitude. Representation. A number (magnitude), direction using unit cap or arrow at the top and unit. A number (magnitude) and unit.
Scalars and Vectors
Subject: Physics. Age range: 14-16. Resource type: Other. File previews. pptx, 546.69 KB. Scalars and Vectors introduction for low to mid ability students. Includes powerpoint with worksheet embedded. Powerpoint has differentiated lesson objectives linked to questions in the worksheet. Based on the new physics AQA GCSE specification for 2018.
Vector and Scalar Quantities Physics Powerpoint Presentation
Subject: Physics. Age range: 11 - 18. Resource type: Other. File previews. pptx, 1.71 MB. Vector and Scalar Quantities Physics Powerpoint Presentation. This Powerpoint will help your students to learn about the difference between vector and scalar quantities. You might also like: Vectors and Scalars Worksheet.
SCALAR & VECTOR
Good day learners! This is EarthPen. This time we are going to talk about "Scalar and Vector Quantities".The mathematical quantities that are used to describ...
Scalar and vector quantities presentation
Scalar and vector quantities presentation. A simple power point outlining the main differences between scalars and vectors. Aimed at AS level mechanics students, as an introduction to the topic. I hope you find it useful. to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.
Vectors and Scalars
Vectors and Scalars. Those students who studied separate sciences at GCSE are likely to have encountered the concept of vectors before, while those who studied dual award will need a little more support. It is important the students are aware of the differences between vector and scalar properties; that being that vectors have a direction. Once ...
KS4 Lesson: Scalars and Vectors
Presentation and accompanying lesson notes on scalars and vectors. Originally designed to support the Edexcel 9-1 GCSE specification (outcomes 2.1-2.4), this lesson would be suitable for introducing the concept of scalar and vector quantities under any curriculum. This lesson includes a starter activity on writing directions, specification ...

Physics library

Want to join the conversation?

Video transcript

2.1 Scalars and Vectors

Check Your Understanding 2.1

Algebra of Vectors in One Dimension

Example 2.1

Check Your Understanding 2.2

Algebra of Vectors in Two Dimensions

Example 2.2

Check Your Understanding 2.3

Interactive

Math Insight

Operations on vectors

Addition of vectors

Vector subtraction

Scalar multiplication

Thread navigation

Math 2241, Spring 2023

Similar pages

Margin Size

2.3: Scalars and Vectors

Learning Objectives

Algebra of Vectors in One Dimension

Example \(\PageIndex{1}\): A Ladybug Walker

Algebra of Vectors in Two Dimensions

Example \(\PageIndex{2}\): Geometric Construction of the Resultant

Scalar vs Vector – Definitions and Examples

Examples of Scalars

Examples of Vectors

Scalar vs Vector – Test Your Understanding

Related Terms

Related Posts

Scalars and Vectors

Share Presentation

Presentation Transcript

Vectors And Scalars

Vectors and Scalars

VECTORS AND SCALARS

Scalars and vectors

Scalars and Vectors

Recommended

Scalar and Vector

What Is a Scalar Quantity?

Examples of Scalar Quantities

What Is a Vector Quantity?

Visualise Unit Vector with the Help of the Video Given Below

Examples of Vector Quantities

Difference Between Scalars and Vectors

Vector Addition and Subtraction

Vector Notation

Scalar and Vector Solved Problems

Frequently Asked Questions – FAQS

Leave a Comment Cancel reply

Register with BYJU'S & Download Free PDFs

Vectors and Scalars

Episode 201: Scalars and Vectors

Vectors *suitable for home teaching*

Vectors Introduction

Physics Classroom - Resolution of Vectors

KS4 Lesson: Scalars and Vectors

Get this resource as part of a bundle and save up to 20%

Physics Fundamentals Lesson Bundle

Not quite what you were looking for? Search by keyword to find the right resource:

COMMENTS

Vectors suitable for home teaching