how to write multiple null hypothesis

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\(H_0\)) and an alternative hypothesis (\(H_a\)).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

• At this point we can write hypotheses for a single mean (\(\mu\)), paired means(\(\mu_d\)), a single proportion (\(p\)), the difference between two independent means (\(\mu_1-\mu_2\)), the difference between two proportions (\(p_1-p_2\)), a simple linear regression slope (\(\beta\)), and a correlation (\(\rho\)). 
• The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
• The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., \(\mu_0\) and \(p_0\)). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., \(p\) and \(\mu\)).  The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• College University and Postgraduate
• Academic Writing

Writing Null Hypotheses in Research and Statistics

Last Updated: January 17, 2024 Fact Checked

This article was co-authored by Joseph Quinones and by wikiHow staff writer, Jennifer Mueller, JD . Joseph Quinones is a High School Physics Teacher working at South Bronx Community Charter High School. Joseph specializes in astronomy and astrophysics and is interested in science education and science outreach, currently practicing ways to make physics accessible to more students with the goal of bringing more students of color into the STEM fields. He has experience working on Astrophysics research projects at the Museum of Natural History (AMNH). Joseph recieved his Bachelor's degree in Physics from Lehman College and his Masters in Physics Education from City College of New York (CCNY). He is also a member of a network called New York City Men Teach. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 25,408 times.

Are you working on a research project and struggling with how to write a null hypothesis? Well, you've come to the right place! Start by recognizing that the basic definition of "null" is "none" or "zero"—that's your biggest clue as to what a null hypothesis should say. Keep reading to learn everything you need to know about the null hypothesis, including how it relates to your research question and your alternative hypothesis as well as how to use it in different types of studies.

Things You Should Know

• Write a research null hypothesis as a statement that the studied variables have no relationship to each other, or that there's no difference between 2 groups.

• Adjust the format of your null hypothesis to match the statistical method you used to test it, such as using "mean" if you're comparing the mean between 2 groups.

What is a null hypothesis?

• Research hypothesis: States in plain language that there's no relationship between the 2 variables or there's no difference between the 2 groups being studied.
• Statistical hypothesis: States the predicted outcome of statistical analysis through a mathematical equation related to the statistical method you're using.

Examples of Null Hypotheses

Null Hypothesis vs. Alternative Hypothesis

• For example, your alternative hypothesis could state a positive correlation between 2 variables while your null hypothesis states there's no relationship. If there's a negative correlation, then both hypotheses are false.

• You need additional data or evidence to show that your alternative hypothesis is correct—proving the null hypothesis false is just the first step.
• In smaller studies, sometimes it's enough to show that there's some relationship and your hypothesis could be correct—you can leave the additional proof as an open question for other researchers to tackle.

How do I test a null hypothesis?

• Group means: Compare the mean of the variable in your sample with the mean of the variable in the general population. [6] X Research source
• Group proportions: Compare the proportion of the variable in your sample with the proportion of the variable in the general population. [7] X Research source
• Correlation: Correlation analysis looks at the relationship between 2 variables—specifically, whether they tend to happen together. [8] X Research source
• Regression: Regression analysis reveals the correlation between 2 variables while also controlling for the effect of other, interrelated variables. [9] X Research source

Templates for Null Hypotheses

• Research null hypothesis: There is no difference in the mean [dependent variable] between [group 1] and [group 2].

• Research null hypothesis: The proportion of [dependent variable] in [group 1] and [group 2] is the same.

• Research null hypothesis: There is no correlation between [independent variable] and [dependent variable] in the population.

• Research null hypothesis: There is no relationship between [independent variable] and [dependent variable] in the population.

Expert Q&A

You Might Also Like

Expert Interview

Thanks for reading our article! If you’d like to learn more about physics, check out our in-depth interview with Joseph Quinones .

• ↑ https://online.stat.psu.edu/stat100/lesson/10/10.1
• ↑ https://online.stat.psu.edu/stat501/lesson/2/2.12
• ↑ https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistics/basic-statistics/supporting-topics/basics/null-and-alternative-hypotheses/
• ↑ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5635437/
• ↑ https://online.stat.psu.edu/statprogram/reviews/statistical-concepts/hypothesis-testing
• ↑ https://education.arcus.chop.edu/null-hypothesis-testing/
• ↑ https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_hypothesistest-means-proportions/bs704_hypothesistest-means-proportions_print.html

About This Article

• Send fan mail to authors

Reader Success Stories

Dec 3, 2022

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Level up your tech skills and stay ahead of the curve

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 23459

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 66\)
• \(H_{a}: \mu \_ 66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 5\)
• \(H_{a}: \mu < 5\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 45\)
• \(H_{a}: \mu \_ 45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p \_ 0.40\)
• \(H_{a}: p \_ 0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 14 May 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Null Hypothesis Examples

ThoughtCo / Hilary Allison

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating ​a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.

The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.

What Is the Null Hypothesis?

The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not​ need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.

To distinguish it from other hypotheses , the null hypothesis is written as ​ H 0  (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.

Examples of the Null Hypothesis

To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.

Other Types of Hypotheses

In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."

Key Takeaways

• In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
• Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
• By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
• What 'Fail to Reject' Means in a Hypothesis Test
• What Is a Hypothesis? (Science)
• Null Hypothesis Definition and Examples
• What Are the Elements of a Good Hypothesis?
• Scientific Method Vocabulary Terms
• Definition of a Hypothesis
• Six Steps of the Scientific Method
• What Is the Difference Between Alpha and P-Values?
• Hypothesis Test for the Difference of Two Population Proportions
• Understanding Simple vs Controlled Experiments
• Null Hypothesis and Alternative Hypothesis
• What Are Examples of a Hypothesis?
• What It Means When a Variable Is Spurious
• Hypothesis Test Example
• How to Conduct a Hypothesis Test
• What Is a P-Value?

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7 Addressing the Null & Alternate Hypotheses

Forming Hypotheses

After coming up with an experimental question, scientists develop hypotheses and predictions.

The null hypothesis H 0 states that there will be no effect of the treatment on the dependent variable, while the alternate hypothesis H A states the opposite, that there will be an effect.

Every hypothesis should include the following information:

• Name of organism (common and Latin name)
• Name of variable being manipulated (independent variable) with units
• Which response will be measured (dependent variable) with units

Example of Null and Alternate Hypotheses

Null hypothesis (H 0 ) : Temperature ( o C) will have no effect on the pulse rate, measured in beats per minute, of mice ( Mus musculus ).

Alternate hypothesis (H A ) : Temperature ( o C) will have an effect on the pulse rate, measured in beats per minute, of mice ( Mus musculus ).

Reject or Fail to Reject the Null Hypothesis

To determine if two groups are different from one another, we look to see whether or not their respective 95% confidence intervals overlap and then relate this conclusion back to our two hypotheses.

If the 95% confidence intervals of two sample means do overlap (e.g., a treatment and the control), we are less than 95% sure (i.e. not sure enough) that these two groups reflect a true difference in the populations. This results in a failure to reject the null hypothesis , as there is insufficient evidence to support our alternative hypothesis that there was an effect.

If the 95% confidence intervals do not overlap, we are 95% sure that these two groups reflect a true difference in the populations. This result allows us to reject our null hypothesis and provide support for our alternative hypothesis. It should be noted that calculating confidence intervals only allows us to compare two groups at one time.

Interpreting Confidence Intervals

For example, the 95% confidence intervals of the 30 o C and 35 o C degrees treatment groups do not overlap with the confidence intervals of the 25 o C (control) (Figure 1). In this case, we reject the null hypothesis and provide support for the alternate hypothesis. We conclude that temperature ( o C) will have an effect on the pulse rate, measured in beats per minute, of mice ( Mus musculus ).

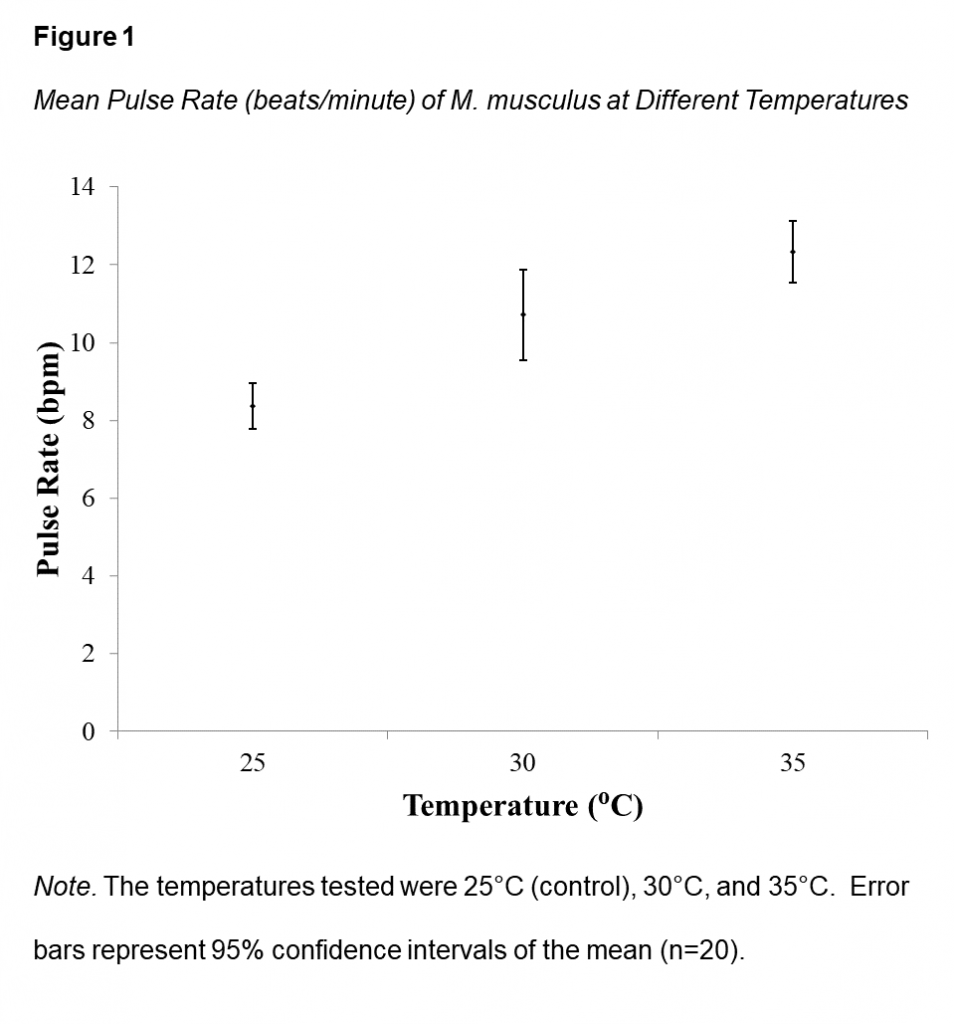
How to Address the Null and Alternate Hypotheses in the Discussion

In the Discussion section of your report you will need to discuss whether or not the 95% confidence intervals of the treatment groups overlap with the control.

When addressing the null and alternate hypothesis in the Discussion:

• State whether the confidence intervals overlap with the control (be specific about which treatment(s) overlap).
• If you reject or fail to reject the null hypothesis (use this language).
• A full restatement of the supported hypothesis.

Click on the hotspots below to learn about how to address the null and alternate hypotheses in the Discussion.

How to Address the Null & Alternate Hypotheses in the Discussion

Results and Discussion Writing Workshop Part 1 Copyright © by Melissa Bodner. All Rights Reserved.

Share This Book

Statistics Made Easy

Understanding the Null Hypothesis for Linear Regression

Linear regression is a technique we can use to understand the relationship between one or more predictor variables and a response variable .

If we only have one predictor variable and one response variable, we can use simple linear regression , which uses the following formula to estimate the relationship between the variables:

ŷ = β 0 + β 1 x

• ŷ: The estimated response value.
• β 0 : The average value of y when x is zero.
• β 1 : The average change in y associated with a one unit increase in x.
• x: The value of the predictor variable.

Simple linear regression uses the following null and alternative hypotheses:

• H 0 : β 1 = 0
• H A : β 1 ≠ 0

The null hypothesis states that the coefficient β 1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.

The alternative hypothesis states that β 1 is not equal to zero. In other words, there is a statistically significant relationship between x and y.

If we have multiple predictor variables and one response variable, we can use multiple linear regression , which uses the following formula to estimate the relationship between the variables:

ŷ = β 0 + β 1 x 1 + β 2 x 2 + … + β k x k

• β 0 : The average value of y when all predictor variables are equal to zero.
• β i : The average change in y associated with a one unit increase in x i .
• x i : The value of the predictor variable x i .

Multiple linear regression uses the following null and alternative hypotheses:

• H 0 : β 1 = β 2 = … = β k = 0
• H A : β 1 = β 2 = … = β k ≠ 0

The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically significant relationship with the response variable, y.

The alternative hypothesis states that not every coefficient is simultaneously equal to zero.

The following examples show how to decide to reject or fail to reject the null hypothesis in both simple linear regression and multiple linear regression models.

Example 1: Simple Linear Regression

Suppose a professor would like to use the number of hours studied to predict the exam score that students will receive in his class. He collects data for 20 students and fits a simple linear regression model.

The following screenshot shows the output of the regression model:

The fitted simple linear regression model is:

Exam Score = 67.1617 + 5.2503*(hours studied)

To determine if there is a statistically significant relationship between hours studied and exam score, we need to analyze the overall F value of the model and the corresponding p-value:

• Overall F-Value:  47.9952
• P-value:  0.000

Since this p-value is less than .05, we can reject the null hypothesis. In other words, there is a statistically significant relationship between hours studied and exam score received.

Example 2: Multiple Linear Regression

Suppose a professor would like to use the number of hours studied and the number of prep exams taken to predict the exam score that students will receive in his class. He collects data for 20 students and fits a multiple linear regression model.

The fitted multiple linear regression model is:

Exam Score = 67.67 + 5.56*(hours studied) – 0.60*(prep exams taken)

To determine if there is a jointly statistically significant relationship between the two predictor variables and the response variable, we need to analyze the overall F value of the model and the corresponding p-value:

• Overall F-Value:  23.46
• P-value:  0.00

Since this p-value is less than .05, we can reject the null hypothesis. In other words, hours studied and prep exams taken have a jointly statistically significant relationship with exam score.

Note: Although the p-value for prep exams taken (p = 0.52) is not significant, prep exams combined with hours studied has a significant relationship with exam score.

Additional Resources

Understanding the F-Test of Overall Significance in Regression How to Read and Interpret a Regression Table How to Report Regression Results How to Perform Simple Linear Regression in Excel How to Perform Multiple Linear Regression in Excel

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “Understanding the Null Hypothesis for Linear Regression”

Thank you Zach, this helped me on homework!

Great articles, Zach.

I would like to cite your work in a research paper.

Could you provide me with your last name and initials.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Miles D. Williams

Visiting Assistant Professor | Denison University

• Download My CV
• Send Me an Email
• View My LinkedIn
• Follow Me on Twitter

When the Research Hypothesis Is the Null

Posted on May 13, 2024 by Miles Williams in Methods   Statistics  

Back to Blog

What should you do if your research hypothesis is the null hypothesis? In other words, how should you approach hypothesis testing if your theory predicts no effect between two variables? I and a coauthor are working on a paper where a couple of our proposed hypotheses look like this, and we got some push-back from a reviewer about it. This prompted me to go down a rabbit hole of journal articles and message boards to see how others handle this situation. I quickly found that I waded into a contentious issue that’s connected to a bigger philosophical debate about the merits of hypothesis testing in general and whether the null hypothesis in particular as a bench-mark for hypothesis testing is even logically sound.

There’s too much to unpack with this debate for me to cover in a single blog post (and I’m sure I’d get some of the key points wrong anyway if I tried). The main issue I want to explore in this post is the practical problem of how to approach testing a null research hypothesis. From an applied perspective, this is a tricky problem that raises issues with how we calculate and interpret p-values. Thankfully, there is a sound solution for the null research hypothesis which I explore in greater detail below. It’s called a two one-sided test, and it’s easy to implement once you know what it is.

The usual approach

Most of the time when doing research, a scientist usually has a research hypothesis that goes something like X has a positive effect on Y . For example, a political scientist might propose that a get-out-the-vote (GOTV) campaign ( X ) will increase voter turnout ( Y ).

The typical approach for testing this claim might be to estimate a regression model with voter turnout as the outcome and the GOTV campaign as the explanatory variable of interest:

Y = α + β X + ε

If the parameter β > 0, this would support the hypothesis that GOTV campaigns improve voter turnout. To test this hypothesis, in practice the researcher would actually test a different hypothesis that we call the null hypothesis. This is the hypothesis that says there is no true effect of GOTV campaigns on voter turnout.

By proposing and testing the null, we now have a point of reference for calculating a measure of uncertainty—that is, the probability of observing an empirical effect of a certain magnitude or greater if the null hypothesis is true. This probability is called a p-value, and by convention if it is less than 0.05 we say that we can reject the null hypothesis.

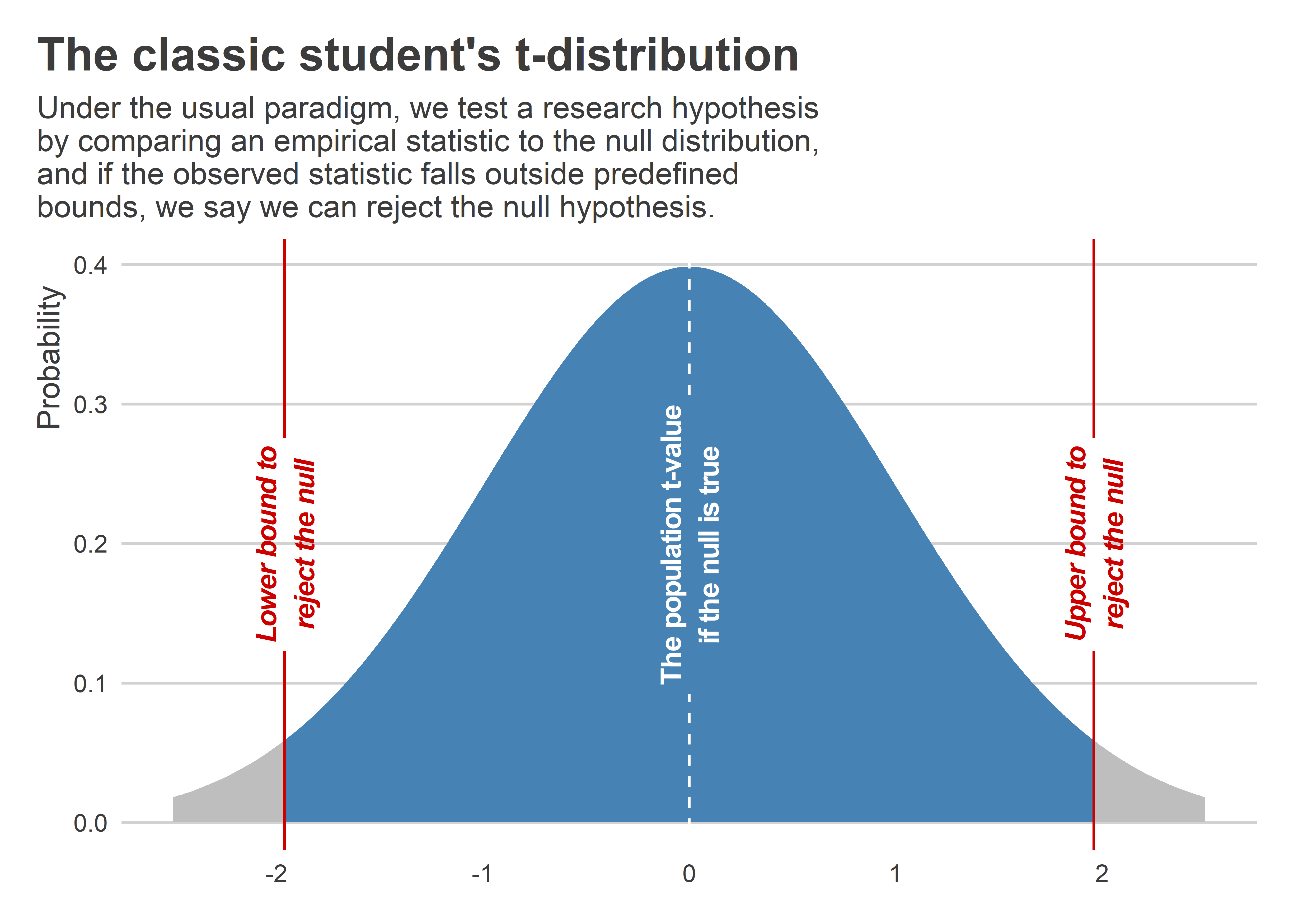
For the hypothetical regression model proposed above, to get this p-value we’d estimate β, then calculate its standard error, and then we’d take the ratio of the former to the latter giving us what’s called a t-statistic or t-value. Under the null hypothesis, the t-value has a known distribution which makes it really easy to map any t-value to a p-value. The below figure illustrates using a hypothetical data sample of size N = 200. You can see that the t-statistic’s distribution has a distinct bell shape centered around 0. You can also see the range of t-values in blue where if we observed them in our empirical data we’d fail to reject the null hypothesis at the p < 0.05 level. Values in gray are t-values that would lead us to reject the null hypothesis at this same level.

When the null is the research hypothesis we want to test

There’s nothing new or special here. If you have even a basic stats background (particularly with Frequentist statistics), the conventional approach to hypothesis testing is pretty ubiquitous. Things get more tricky when our research hypothesis is that there is no effect. Say for a certain set of theoretical reasons we think that GOTV campaigns are basically useless at increasing voter turnout. If this argument is true, then if we estimate the following regression model, we’d expect β = 0.

The problem here is that our substantive research hypothesis is also the one that we want to try to find evidence against. We could just proceed like usual and just say that if we fail to reject the null this is evidence in support of our theory, but the problem with doing this is that failure to reject the null is not the same thing as finding support for the null hypothesis.

There are a few ideas in the literature for how we should approach this instead. Many of these approaches are Bayesian, but most of my research relies on Frequentist statistics, so these approaches were a no-go for me. However, there is one really simple approach that is consistent with the Frequentist paradigm: equivalence testing . The idea is simple. Propose some absolute effect size that is of minimal interest and then test whether an observed effect is different from it. This minimum effect is called the “smallest effect size of interest” (SESOI). I read about the approach in an article by Harms and Lakens (2018) in the Journal of Clinical and Translational Research .

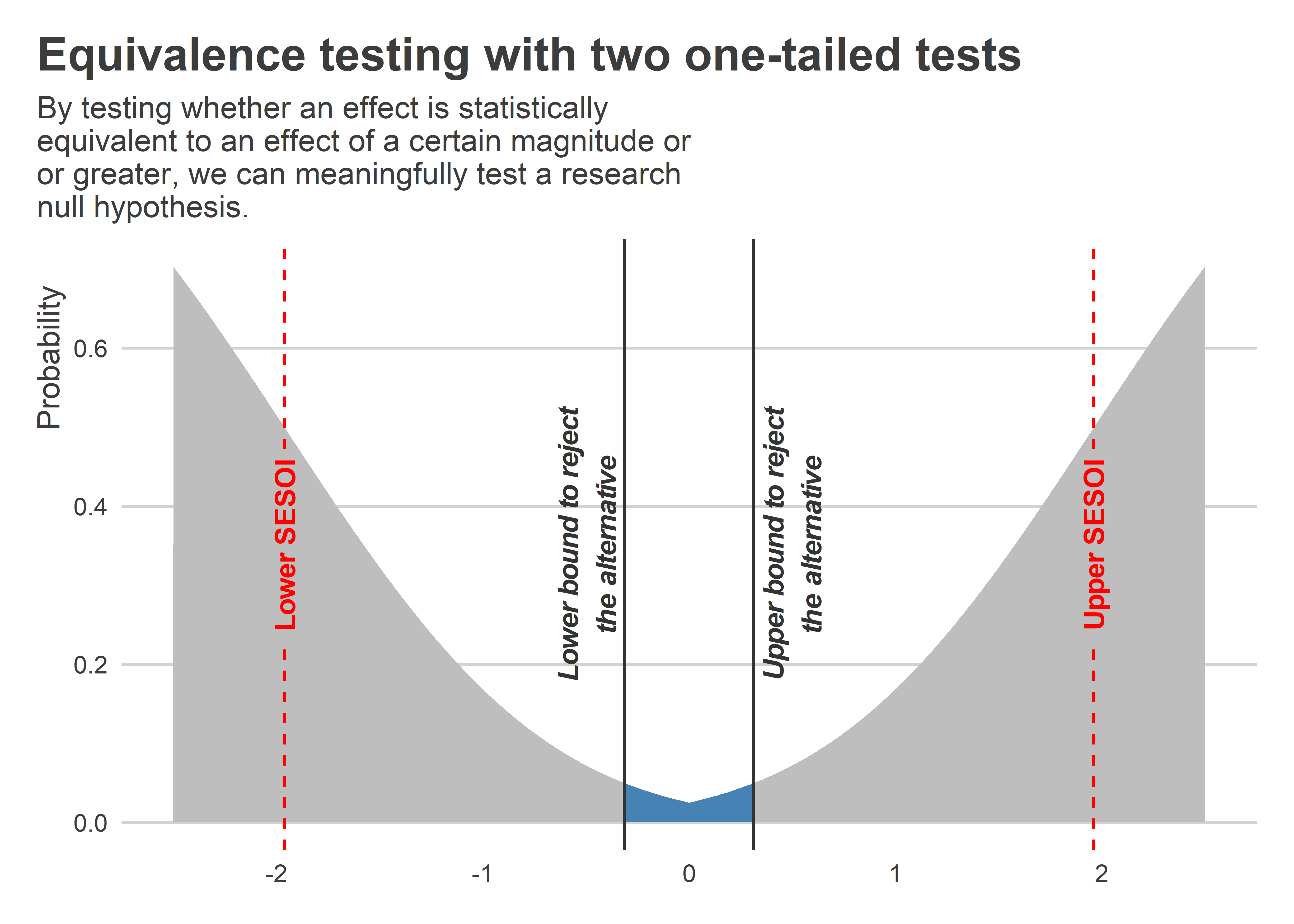
Say, for example, that we deemed a t-value of +/-1.96 (the usual threshold for rejecting the null hypothesis) as extreme enough to constitute good evidence of a non-zero effect. We could make the appropriate adjustments to our t-distribution to identify a new range of t-values that would allow us to reject the hypothesis that an effect is non-zero. This is illustrated in the below figure. We can now see a range of t-values in the middle where we’d have t-values such that we could reject the non-zero hypothesis at the p < 0.05 level. This distribution looks like it’s been inverted relative to the usual null distribution. The reason is that with this approach what we’re doing is conducting a pair of alternative one-tailed tests. We’re testing both the hypothesis that β / se(β) - 1.96 > 0 and β / se(β) + 1.96 < 0. In the Harms and Lakens paper cited above, they call this approach two one-sided tests or TOST (I’m guessing this is pronounced “toast”).

Something to pay attention to with this approach is that the observed t-statistic needs to be very small in absolute magnitude for us to reject the hypothesis of a non-zero effect. This means that the bar for testing a null research hypothesis is actually quite high. This is demonstrated using the following simulation in R. Using the {seerrr} package, I had R generate 1,000 random draws (each of size 200) for a pair of variables x and y where the former is a binary “treatment” and the latter is a random normal “outcome.” By design, there is no true causal relationship between these variables. Once I simulated the data, I then generated a set of estimates of the effect of x on y for each simulated dataset and collected the results in an object called sim_ests . I then visualized two metrics that that I calculated with the simulated results: (1) the rejection rate for the null hypothesis test and (2) the rejection rate for the two one-sided equivalence tests. As you can see, if we were to try to test a research null hypothesis the usual way, we’d expect to be able to fail to reject the null about 95% of the time. Conversely, if we were to use the two one-sided equivalence tests, we’d expect to reject the non-zero alternative hypothesis only about 25% of the time. I tested out a few additional simulations to see if a larger sample size would lead to improvements in power (not shown), but no dice.

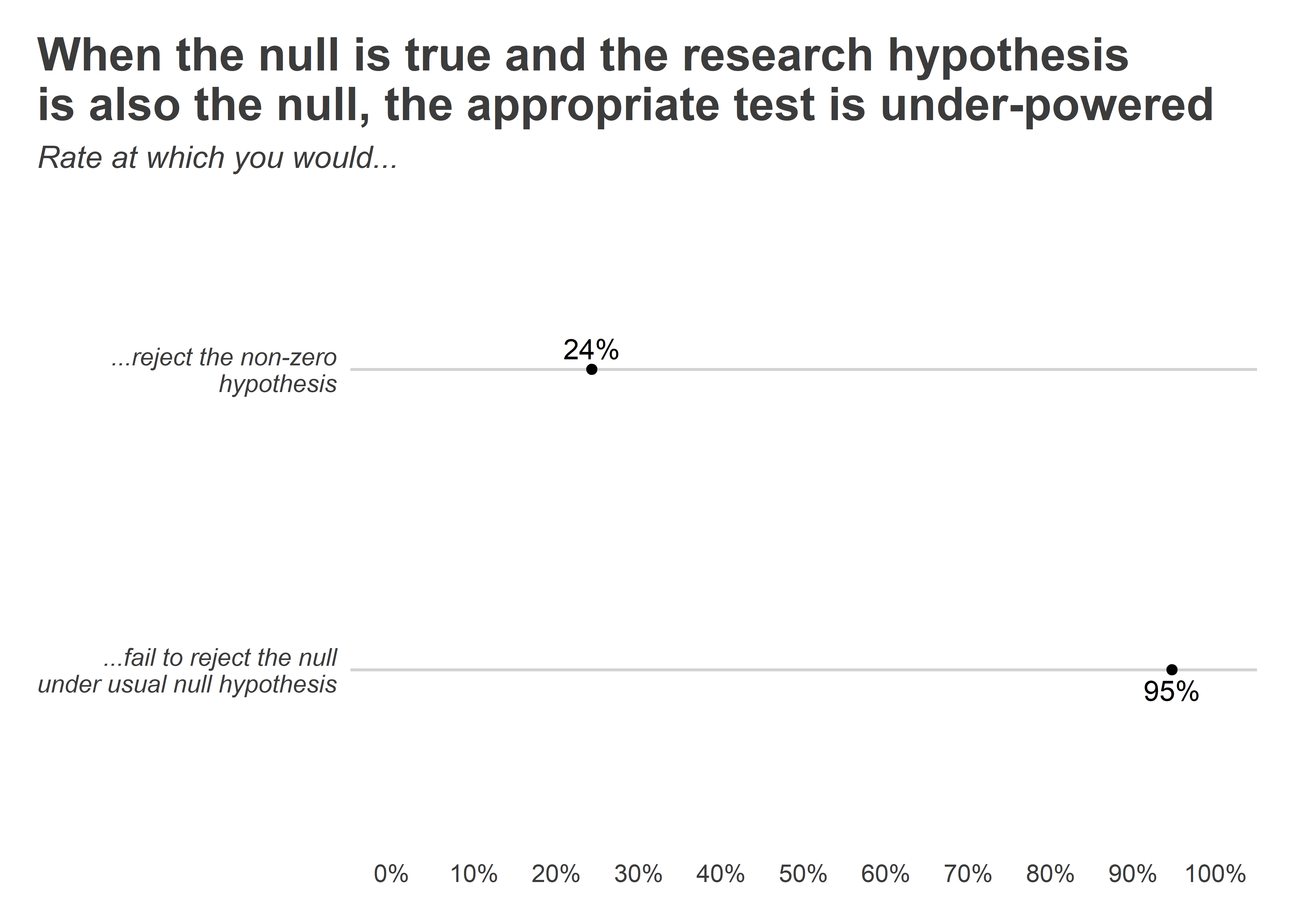
The two one-sided tests approach strikes me as a nice method when dealing with a null research hypothesis. It’s actually pretty easy to implement, too. The one downside is that this test is under-powered. If the null is true, it will only reject the alternative 25% of the time (though you could select a different non-zero alternative which would possibly give you more power). However, this isn’t all bad. The flip side of the coin is that this is a really conservative test, so if you can reject the alternative that puts you on solid rhetorical footing to show the data really do seem consistent with the null.

OPINION article

All animals are conscious in their own way: comparing the markers hypothesis with the universal consciousness hypothesis.

• Cognition in Action Lab, University of Milan, Milan, Italy

1 Introduction

Consciousness in non-human animals can be explored philosophically through two central questions: the distribution question, which enquires which animals are conscious, and the phenomenological question, which seeks to understand what the experiences of animals are like ( Allen and Trestman, 2024 ).

The distribution question is considered empirically tractable by those scientists who believe that markers, such as traits or behaviors, can be used to assess the presence of consciousness in animals. Bayne et al. (2024) have recently offered a version of this markers approach. They also aim to make the phenomenological question empirically tractable by targeting phenomenological experience through potential C-tests with the aim of identifying conscious entities across a spectrum of beings, including humans, animals, and artificial systems. Indirectly, Andrews (2024) also advocates for the empirical tractability of the phenomenological question and indirectly criticizes the marker-based approach, highlighting its inadequacies in addressing the “distribution question” of consciousness—namely, which animals are conscious. She argues for a paradigm shift that favors an inclusive presumption that all animals possess consciousness, challenging the premise of needing C-tests to distinguish conscious from non-conscious entities.

Acknowledging the complexity of applying C-tests to non-human entities, Bayne et al. reference Dung and Newen (2023) , who propose a species-sensitive, two-tier account of animal consciousness, aiming to assess not just whether animals are conscious (the distribution question) but also how their conscious experiences differ (the phenomenological question). Both approaches highlight the diversity of conscious experiences in the animal kingdom and encourage ethical considerations regarding the treatment of other animal species.

Andrews does not engage with Dung and Newen directly. Her focus is on proposing a foundational shift in how we approach the study of animal consciousness, arguing for the assumption that all animals are conscious as a starting point for research. This approach contrasts with seeking specific markers or dimensions of consciousness, as Bayne et al. and Dung and Newen suggested frameworks do, or Birch et al. (2020) before them, by instead questioning the very methodologies we use to infer consciousness in non-human animals.

Bayne et al. champion the utilization of precise markers, or C-tests, to demarcate conscious entities. Their methodology, underscored by a commitment to scientific rigor, seeks to establish a clear boundary between conscious and non-conscious beings. This approach, whilst promising methodological clarity, may inadvertently overlook the intricate and varied nature of consciousness, potentially imposing anthropocentric limitations on the understanding of animal consciousness. However, Andrews's broad ethical presumption of consciousness across all animals may risk diluting the specificity required to discern the diverse manifestations of consciousness across species.

Each perspective presents its merits—Bayne et al.'s methodological clarity, and Andrews' ethical inclusivity. It is Dung and Newen's account that appears to provide a preferable methodological synthesis where the identification of markers is informed by an ethical commitment to presume consciousness broadly, all whilst acknowledging diversity across species.

2 The markers hypothesis

Bayne et al. (2024) introduce the concept of C-tests, emphasizing the urgent need for validated methods to determine consciousness across different systems, including humans at various developmental stages, non-human animals, AI, and more recent innovations such as neural organoids and xenobots. Bayne et al. highlight the general consensus on consciousness in healthy, awake adult humans but acknowledge the debate on the presence of consciousness in other entities or states, such as during human development, in sleep, under anesthesia, and in various brain-damaged conditions. They also point out the controversies over consciousness in non-human animals.

The authors propose a four-dimensional space for classifying potential C-tests. These dimensions include the target population (identify which entities the C-test is applicable to, such as humans, specific animals, or artificial systems), specificity (measure the false-positive rate of the C-test since a test with high specificity accurately indicates consciousness when it is present), sensitivity (the test's ability to correctly identify true positives—genuinely conscious entities), and rational confidence (the degree of trust in the test's specificity and sensitivity assessments). To validate C-tests, Bayne et al. suggest three strategies:

The redeployment strategy: using variants of widely accepted tests for consciousness.

The theory-based strategy: grounding tests in consciousness theories.

The iterative natural kind strategy: an iterative process of refining and validating tests, treating consciousness as a natural kind.

This latter, indicated as the preferred strategy, posits that C-tests should be applied hierarchically, beginning with “consensus cases” (e.g., neurotypical, adult humans) and extending to “neighboring” and then more “alien” populations.

The authors recognize the moral implications of consciousness assessment, especially since consciousness is often linked to moral status ( Shepherd, 2018 , 2023 ). They acknowledge the importance of aligning C-tests with ethical considerations, as consciousness may dictate how various entities should be treated.

Bayne et al. also address the challenge of applying these tests to non-human subjects, particularly when certain abilities required by the test may be specific to humans, such as language or certain patterns of neural activity.

The significance of Bayne et al.'s studies lies not only in the advancement of C-tests but also in the broader philosophical and ethical discourse on consciousness. By considering different population targets and validating the sensitivity and specificity of these tests, Bayne et al.'s studies directly contribute to the ongoing dialogue on animal consciousness and how to appropriately measure it.

Bayne et al.'s (2024) proposal exemplify methodological rigor through its systematic and interdisciplinary approach. It sets forth a comprehensive framework to classify tests as C-tests, considering diverse entities from human development to artificial systems. This framework is underpinned by a precise categorization based on the target population, specificity, sensitivity, and rational confidence, each dimension addressing distinct validation challenges. The authors expand the robustness of their approach by critically assessing three validation strategies: redeployment, theory-based, and iterative NK, thus avoiding reliance on a single, potentially narrow methodological pathway. The authors advocate for an iterative NK strategy that emphasizes flexibility and adaptability, allowing for the refinement of hypotheses and methods in light of new evidence. By transparently discussing the inherent limitations and crucial decision points of developing C-tests, the authors exhibit a conscientious understanding of the complexity of their research question. This self-reflective stance not only clarifies the methodological boundaries but also ensures that the research advances with clarity and precision.

Although not directly addressing it, their paper can be understood as a response to Andrews' (2024) view that “all animals are conscious” and challenges it by proposing a structured, methodological framework for assessing consciousness across a broad spectrum of entities. This may sound in contrast with Andrews' position, which promotes an assumption of consciousness across all animals as a foundational starting point for research. Instead, Bayne et al.'s methodology could offer a systematic way to test Andrews' assertion and investigate the dimensions of consciousness she suggests should be the focus of research.

3 Universal consciousness

Andrews (2024) advocates for a paradigmatic shift in consciousness studies: the scientific community should adopt the stance that all animals are conscious by default and then work to explore dimensions of consciousness rather than laboring to mark consciousness in different species.

This approach, she argues, is limited by its reliance on initial markers—pretheoretical indicators such as language, social responsiveness, and emotional expression—and its development of derived markers—indicators that emerge from scientific investigation.

Andrews points out that as research progresses, the number of derived markers for consciousness increases, leading to a higher probability of ascribing consciousness to various species, potentially even those such as Caenorhabditis elegans and Hydra, which traditionally might not be considered conscious.

Andrews suggests that this approach creates an illusion of progress on the distribution question of consciousness because it can only increase the confidence in an animal's consciousness, not decrease it.

Initial markers are simply characteristics observed that set a baseline for the study of consciousness but are insufficient as proof. For instance, the fact that an entity displays pain behavior or engages in goal-directed activities does not conclusively demonstrate consciousness. This is particularly true in organisms whose physical forms or neural architectures differ significantly from humans or in the case of artificial intelligence. Conversely, derived markers arise through more theoretical means and often reveal aspects of consciousness not immediately evident through initial markers. These can encompass a range of behaviors that pass certain tests, or they can be mechanistic, rooted in the neurophysiology or biochemistry of the entity in question. These markers are less human-centric, recognizing behaviors and structures distinct from those typically found in humans, as long as they fulfill similar functional roles. The derived marker approach accommodates the multiple realizability of psychological properties, indicating a move toward a more inclusive and varied recognition of consciousness markers.

Andrews recommends that scientists default to the assumption that all animals are conscious and then investigate the various expressions and intensities of consciousness. This change in the scientific stance could catalyze more comprehensive and productive research, facilitating the development of a rich and inclusive theory of consciousness built on data spanning a vast array of life forms.

In essence, Andrews' argument is both pragmatic and methodological. She suggests that accepting the premise that all animals are conscious would eliminate biases that could hinder research and would leverage simpler organisms to gain insights into consciousness that might be obfuscated in more complex beings. Embracing this foundational shift would not only enhance the study of animal minds but could also have ethical implications for their treatment, emphasizing the importance of understanding the subjective experiences of non-human beings.

4 Between markers and dimensions

Dung and Newen (2023) propose a framework between markers and dimensions by addressing simultaneously the distribution question (which animals are conscious) and the phenomenological question (how consciousness experiences differ between animals).

The framework establishes 10 dimensions of consciousness with species-sensitive operationalizations, which allows for a comprehensive comparison of consciousness profiles across different animal species. This approach differentiates between strong and weak indicators of consciousness, enabling researchers to assign a multi-faceted profile to animal species, reflecting their conscious experiences. Strong indicators are direct evidence of consciousness, whilst weak indicators require multiple instances or higher degrees of the behavior to suggest conscious experience. Dung and Newen build upon previous studies by Birch et al. (2020) , whilst making four key advancements in their methodology: (1) a distinction between the distribution and the phenomenological question; (2) a structured taxonomy with strong and weak indicators; (3) the inclusion of dimensions for cognitive processing strategies beyond content features of conscious experience; and (4) a more extensive set of ten dimensions as opposed to the five suggested by Birch et al. (2020) . The five dimensions included: perceptual richness (how fine-grained is perception), evaluative richness (how fine-grained is valence), integration at a time (how temporally integrated is an experience), integration across time (how continuous or fragmented is an experience), and self-consciousness (how conscious of being a specific entity separate from the environment). Whereas, Dung and Newen add three dimensions of cognitive processing strategies: complex forms of reasoning (such as transitive inferences and causal reasoning), some forms of learning, and abstract categorization of specific sensory stimuli or events. They also include two further dimensions: the experience of body and mental agency and that of body ownership. The experience of agency pertains to whether an animal perceives its actions, including mental actions, as self-generated and under its voluntary command, rather than as occurrences that exceed their control (such as, mind wandering). The experience of ownership determines whether an animal recognizes its body parts as intrinsic to its being or merely as objects existing within the external environment.

They argue that these 10 dimensions are core for any general investigation of animal consciousness, but they are adaptable for more specific comparisons, such as between two species or different stages of ontogenetic development.

The operationalizations for these dimensions draw from a variety of behaviors and cognitive abilities. For example, perceptual categorization can be measured through tests such as discrimination learning and motivational trade-offs, whereas agency might be gauged through tasks testing delay of gratification or response inhibition.

Their studies contribute to the understanding of animal consciousness by offering a structured framework that can inform both empirical research and ethical considerations about the treatment of animals. Their approach specifically seeks to recognize indicators of consciousness that are potentially unique to non-human animals, which could differ significantly from human consciousness markers. In addition, the introduction of strong and weak indicators adds a layer of complexity to the evaluation of consciousness. This distinction acknowledges that not all indicators provide the same level of evidence for consciousness, and a set of weaker indicators can collectively signal the presence of consciousness in an animal. Process-oriented indicators for cognitive processes such as reasoning, learning, and abstraction reflect a deeper inquiry into how consciousness operates rather than just its outward manifestations. This shows an interest in the mechanisms of consciousness, providing a richer picture than what might be obtained through more static, trait-based markers. A defining feature of their framework is its adaptability and openness to revision based on empirical findings. This flexibility is an acknowledgment of the evolving nature of consciousness science. Their framework is not just theoretical but comes with concrete operationalizations for each dimension, providing tangible, testable manifestations of consciousness. This aspect is particularly valuable as it moves the field beyond theoretical speculation to empirical investigation. Furthermore, the authors recognize the limitations of current methodologies and introduce what they term pragmatic idealizations. This approach is intended to guide and refine research without making unwarranted assertions, which marks a departure from the sometimes binary perspective of traditional markers.

Dung and Newen's perspective can be seen as an intermediary between the marker-based approach of Bayne et al. and the universal consciousness claim argued by Andrews. Whilst they utilize a form of marker through their structured taxonomy, their approach is species-sensitive and acknowledges the diversity and richness of consciousness across species.

5 Conclusion

A balanced perspective on animal consciousness requires both empirical and ethical sensitivities. The C-tests proposed by Bayne et al. (2024) bring a necessary scientific precision to the field, whilst Andrews (2024) ethical presumption of universal consciousness ensures the moral consideration of all animals. Dung and Newen (2023) multi-dimensional framework integrates these aspects, offering a methodological approach that is both scientifically informed and ethically aware, incorporating the strengths of each perspective.

Author contributions

AK: Conceptualization, Methodology, Resources, Writing – original draft, Writing – review & editing.

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Allen, C., and Trestman, M. (2024). “Animal consciousness,” The Stanford Encyclopedia of Philosophy (Spring 2024 Edition) , eds. E. N. Zalta and U. Nodelman. Available online at: https://plato.stanford.edu/archives/spr2024/entries/consciousness-animal/

Google Scholar

Andrews, K. (2024). “All animals are conscious”: shifting the null hypothesis in consciousness science. Mind Lang . 1–19. doi: 10.1111/mila.12498

Crossref Full Text | Google Scholar

Bayne, T., Seth, A. K., Massimini, M., Shepherd, J., Cleeremans, A., Fleming, S. M., et al. (2024). Tests for consciousness in humans and beyond. Trends Cogn. Sci . doi: 10.1016/j.tics.2024.01.010

PubMed Abstract | Crossref Full Text | Google Scholar

Birch, J., Schnell, A. K., and Clayton, N. S. (2020). Dimensions of animal consciousness. Trends Cogn. Sci. 24, 789–801. doi: 10.1016/j.tics.2020.07.007

Dung, L., and Newen, A. (2023). Profiles of animal consciousness: a species-sensitive, two-tier account to quality and distribution. Cognition 235:105409. doi: 10.1016/j.cognition.2023.105409

Shepherd, J. (2018). Consciousness and Moral Status . Oxford: Taylor and Francis, 122. doi: 10.4324/9781315396347

Shepherd, J. (2023). Non-human moral status: problems with phenomenal consciousness. AJOB Neurosci. 14, 148–157. doi: 10.1080/21507740.2022.2148770

Keywords: animal consciousness, markers hypothesis, dimensions, distribution, animal cognition

Citation: Kaufmann A (2024) All animals are conscious in their own way: comparing the markers hypothesis with the universal consciousness hypothesis. Front. Psychol. 15:1405394. doi: 10.3389/fpsyg.2024.1405394

Received: 22 March 2024; Accepted: 19 April 2024; Published: 13 May 2024.

Reviewed by:

Copyright © 2024 Kaufmann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Angelica Kaufmann, angelica.kaufmann@gmail.com

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.