how data analysis can aid problem solving and decision making

How Should Data Analysis Impact Your Decision-Making Process?

Contrary to popular belief, no statistician can turn uncertainty into certainty for you. If you’re looking for facts or truth, you won’t find them by adding more equations to the mix; the only way is to collect so much data that you don’t need a statistician. How much is that? Bluntly put, all of it.

So, what’s a statistician for, in that case?

As a trained statistician myself, I’ve seen many people struggle to grasp what it means to do hypothesis testing in the face of uncertainty, so in this article, I’ll take a stab at clarifying those slippery stumbling blocks by taking an unusual approach: a touch of mythology!

More From Cassie Kozyrkov What Does It Mean to ‘Work With AI’?

How Does Hypothesis Testing Work?

Let’s put ourselves in the shoes of supernatural all-knowing beings … were they to have shoes at all. If you’re a lover of the classics, perhaps you might imagine yourself among the Greek gods and goddesses, looking down upon us mortals from Mount Olympus. In a slight departure from Homer’s deities — ever fallible and bickering — let’s imagine that we know everything about past, present, and future.

There we are on Olympus, watching little mortals going about their daily business and notice — aha! — that one of them has a default action. Because we have a perfect grasp of reality, we naturally know all about statistical decision-making, including how to set up a hypothesis test. It’s fun to be all-knowing. So let’s summarize what we know so we can get back to our usual business of laughing at the ridiculousness of the human condition:

Statistical Decision-Making 101

The default action is the option that you find palatable under ignorance. It’s what you’ll do if you’re forced to make a snap decision.
The alternative action is what you’ll do if the data analysis talks you out of your default action.
The null hypothesis is a (mathematical) description of all the realities in which our default action would be a happy choice. If that sounds confusing, here’s a straightforward example .
The alternative hypothesis is a description of all the realities not covered by the null hypothesis.

A default action is the physical action/decision that you commit to making if you don’t gather any (more) evidence. When I’m performing the role of decision advisor, one of my early questions tends to be, “What would you commit to doing if you knew you had to make the decision right this moment?” If you’re curious to learn more about default actions, I have a whole article for you here .

Picking your default action is one of the most important judgments in a statistical decision process, but I’ve never seen it taught explicitly in a traditional statistics textbook. It is the pivotal concept, though, so I prefer to drag it out into the open and name it explicitly since it will shape the entire hypothesis test.

But hush, the mortal may be about to do something stupid! Let’s watch.

What Can We Learn From Data?

This little mortal’s default action is to not launch a new version of their product. Because we deities are omniscient, we know that it’s the best action to take — we happen to know that the product is expensive to launch but customers won’t like it as much as the current version. Everyone would be better off if the new version were abandoned. Unfortunately, the mortal can’t know this — the poor thing has to live with uncertainty and limited information. But we deities know all things.

We start laughing ourselves silly, “Look at this ridiculous mortal!” If the mortal is too lazy to be bothered with data analysis , they’ll execute the default action (which we happen to know is correct) and everything will be dandy with their little life. But this mortal is not lazy. This mortal is honorable and diligent … and is going to analyze data! They want to be data-driven in all things!!

The mortal goes off to collect market data, then toils and toils over the numbers. What are they going to learn from their foray into statistics?

Well, in the best possible case, they’ll learn nothing. That, in a nutshell, is the right thing to learn when you perform a hypothesis test and find no evidence to reject your null hypothesis in favor of the alternative, which would have triggered a switch away from the default action. If that explanation zoomed past you too quickly, I’ve got a gentle primer on the logic of hypothesis testing for you here .

Learning nothing would be a wonderful outcome for this little mortal, though it’s hard on the emotions — it’s awfully disappointing to spend all that effort on data analysis and come away without anything that feels like a eureka moment serenaded by celestial trumpets. But the important thing is that the poor dear will end up taking the right action . They won’t know it’s the right action (that would be, as Shakespeare might put it, more than mortal knowledge), but they’ll end up in the same happy place as the couch potato who spent their time binging Netflix. Ah, these mortals and their Sisyphean data analysis. They were going to do the right thing anyway!

What Is the Point of Statistical Analysis?

The key insight for you, dear reader, is that the poor mortal can’t possibly know this. That’s why we are doing this rather odd exercise of putting ourselves on Mount Olympus. It’s not a normal perspective for readers to take during your statistics-article-reading loo break.

What we have been snickering at so far was the absolute best case for this mortal’s data analysis: learning nothing at all and performing their default action. Now, what’s the worst possible thing this little mortal could learn from the data? Something!

Because upon learning something, they will do … something stupid. In classical statistical inference, learning something about the population means rejecting the null hypothesis, feeling ridiculous about the default action, and switching their course of action to the (incorrect) alternative. This mortal will pat themselves on the back for statistical significance and launch a bad product.

That’s so tragicomic that we’re falling out of our supernatural chairs with laughter.

Thanks to the silly mortal’s data-driven diligence and their mathematical savvy, they’ve managed to talk themselves out of doing what they should have done. If they’d been lazy, they would have been better off! Puny mortals, so brave and so good — so hilarious.

Why would a mortal end up learning something incorrectly like that? Unfortunately, randomness is random. There’s a luck of the draw element to data. Your sample might be a freak accident that leads you to the wrong conclusion. Alas, when luck’s involved, bad things can happen to good people.

Omniscient beings may have the privilege of reasoning in advance about what the right decision is, but mortals aren’t so lucky. Mortals must contend with uncertainty and incomplete information, which means they can make mistakes. Unlike supernatural, omniscient beings, people haven’t got enough information to say which actions are correct or not.

They’ll only find that out later, in hindsight , once the universe catches up with them. In the meantime, all people can do is make the best decision they can with the incomplete information they have. Sometimes that leads them off a cliff. Uncertainty is a jerk like that, which is why I do sympathize with the desire to shower data gurus with boatloads of cash in the hopes that they’ll make the uncertainty go away. But there’s a name for someone who promises you that certainty is for sale when your data is incomplete: a charlatan. Unfortunately, data charlatans are everywhere these days . Buyer beware!

More on Data-Driven Thinking Is 'Statistical Significance' in Research Just a Strawman?

Am I Making Decisions Intelligently?

So, let’s put ourselves back in the shoes we belong in: those of puny mortals. All we have is our data set, which — when we’re doing statistics — is an incomplete snapshot of our world. We don’t have the facts that allow us to be sure we’re making the right decision. We can’t know if we’ve made a mistake or not until it’s too late. We only know what our data set looks like.

It’s always possible that, thanks to uncertainty, all our mathematical huffing and puffing talks us out of a perfectly reasonable default action. We can never be sure that we’re not making the deeply embarrassing error of toiling ourselves into a worse decision than what we would have had by spending the time with a trashy novel instead of with our data. We must remember that we are not gods and thus we haven’t got the privilege of reasoning as though we’re all-knowing.

That’s why we mortals must ask ourselves, “Am I making the decision intelligently?” instead of “Am I making the right decision?”

The mortal’s mistake — actively mathing themselves into a stupid course of action — adds insult to injury. There’s an asymmetry here that makes the mistake extra painful. It comes from the fact that they have a preferred default action in the first place. Our default action is what we fundamentally lean towards doing, even under ignorance.

The analysis would be different if there were no default action. In that case, staying lazily on the couch would not be an option — indifference between options forces you to glance at the data, but it lets you get away with a less involved approach, as I explain here .

Alas, true indifference seems rather rare in the human animal. We often enter the decision-making process with a preference for one course of action over another, which means we do have a default action that represents a happy, comfortable choice we’d need the data to talk us out of.

Instead, we’re hardly indifferent. If we were indifferent, we’d be doing this a different way — we’d simply be making a best guess based on the data. It wouldn’t matter how much data you used — just grab hold of as much data as you can afford and go with the best-looking action, statistical significance be damned.

By preferring one of the actions by default, you’re making a value judgment about what you consider to be the worst mistake you can make: stupidly leaving this cozy default action. You’re only okay with abandoning it if you get on a strong-enough cease-and-desist signal from your data. Otherwise, you’re happy to stay there. You’d appreciate avoiding the mistake of staying with a bad default action, but that situation doesn’t represent as grievous a wound to you as the other mistake you could make — leaving your comfort zone incorrectly.

Statistics Is the Science of Changing Your Mind

Statistics is the science of changing your mind , and the mechanics of its most popular methods are powered by the imbalance in your preferences about the actions that are on the table for you. The worst possible thing that you could do is talk yourself into stupidly changing your mind. And yet, because randomness is random, you could get some bad luck — it’s entirely possible that this will be exactly what happens to you. You’re a mere mortal, after all. Is there anything you can do about it? Sort of. You can’t guarantee you’ll make the right decision, but you can turn the dial on the size of the gamble you’re willing to take. It’s your best attempt at indemnifying yourself against the vagaries of chance.

In fact, that’s the main payoff to formal statistical hypothesis testing: it gives you control over the maximum up-front probability of stupidly changing your mind. It allows you to search your soul, discover your own appetite for risk, and make your decision in a way that delivers the action that best blends your data, your assumptions , and your risk preferences.

When you’re dealing with uncertainty, truly knowing is not for us mortals. You can’t make certainty out of uncertainty and you certainly can’t get it by paying a statistician to mumble some equation-filled mumbo jumbo for you. All you can know is how your data pans out in light of your assumptions. That’s what your friendly statistician helps you with. Hypothesis testing is a decision tool. What it gives you is powerful but not perfect: the ability to control your decision’s risk settings mathematically.

Thinking With Data How Ontology and Data Go Hand-in-Hand

Statistics Offers Control, Not Certainty

To summarize our discussion: you’d have to have omniscience to know if your decision is correct . Until it’s too late, of course. With uncertainty and partial information (a sample of your population), mistakes are possible even though you’ll have done the best you can with what little you know. There’s always the possibility that you — dear little mortal — will make the terrible mistake of analyzing yourself out of a perfectly good default action. What statistics allows you to do is to control the probability of that sad event.

I may be biased in my love for statistics — I’ve been a statistician since my teens, after all — but when there are really important data-driven decisions to make, I’m deeply grateful that I’m able to have control over the risk and quality of my decision process. This is why I’m frequently baffled that decision-makers engage in the pantomime of statistics without ever availing themselves of that control panel. It defeats the entire point of all that mathematical jiujitsu!

Built In’s expert contributor network publishes thoughtful, solutions-oriented stories written by innovative tech professionals. It is the tech industry’s definitive destination for sharing compelling, first-person accounts of problem-solving on the road to innovation.

Great Companies Need Great People. That's Where We Come In.

The Role of Data Analysis in Decision-Making: A Comprehensive Guide

In today’s data-driven world, organizations of all sizes are recognizing the immense value of data in making informed decisions. Data analysis has emerged as a critical process in extracting meaningful insights from raw data, enabling businesses to identify patterns, trends, and correlations that can guide strategic decision-making.

Understanding Data-Driven Decision Making

Data-driven decision-making refers to the process of making informed choices and taking actions based on objective analysis of relevant data. It involves collecting, analyzing, and interpreting data to extract meaningful insights that guide decision-making processes. By relying on data rather than intuition or assumptions, organizations can reduce biases, improve accuracy, and increase the chances of making optimal decisions.

Data-driven decision-making enables businesses to identify trends, patterns, and correlations, uncover hidden opportunities, mitigate risks, and drive strategic initiatives. It empowers decision-makers to rely on evidence-based insights, ultimately leading to better outcomes and a competitive edge in today’s data-driven world.

Understanding the Importance of Data Analysis

Types of data analysis techniques.

There are several techniques employed in data analysis, each serving a specific purpose. Some common types of data analysis techniques include:

Descriptive Analysis

Diagnostic analysis.

Diagnostic analysis aims to uncover the root causes of specific events or trends. By examining data and applying various statistical methods, it helps identify factors that contribute to observed outcomes, allowing organizations to address underlying issues.

Predictive Analysis

Predictive analysis makes use of statistical modeling techniques and historical data to predict future outcomes. By identifying patterns and relationships in data, organizations can make predictions about future trends, customer behavior, market dynamics, and more.

Prescriptive Analysis

Prescriptive analysis goes beyond predicting future outcomes. It suggests optimal courses of action based on the available data, taking into account constraints and objectives. It helps decision-makers explore different scenarios and make informed choices.

The Data Analysis Process

Data collection.

Gathering relevant data from various sources, ensuring data quality and accuracy.

Data Cleaning and Preparation

Cleaning and transforming the data to remove errors, inconsistencies, and missing values. This step also involves organizing and formatting the data for analysis.

Exploratory Data Analysis (EDA)

Statistical analysis.

Applying statistical methods to analyze data, test hypotheses, and draw meaningful conclusions. Techniques such as regression analysis, hypothesis testing, and correlation analysis are commonly used.

Data Visualization

Presenting the findings of the analysis through visual representations like charts, graphs, and dashboards to enhance understanding and facilitate decision-making.

Interpretation and Decision-Making

Interpreting the results of the analysis, extracting actionable insights, and using them to inform decision-making processes.

Tools and Technologies for Data Analysis

Data analysis relies on a variety of tools and technologies to handle and process vast amounts of data efficiently. Some popular tools include:

Spreadsheet Software

Tools like Microsoft Excel and Google Sheets offer basic data analysis capabilities, including sorting, filtering, and basic statistical functions.

Statistical Software

Business intelligence (bi) tools.

BI tools like Tableau, Power BI, and QlikView enable businesses to create interactive visualizations, reports, and dashboards for data analysis and decision-making.

Machine Learning (ML) Platforms

ML platforms like TensorFlow and scikit-learn allow organizations to build predictive models and perform advanced data analysis tasks.

Challenges and Best Practices in Data Analysis

Data analysis comes with its own set of challenges, including data quality issues, data privacy concerns, and the need for skilled analysts. To ensure successful data analysis, organizations should adopt best practices such as:

Defining Clear Objectives

Data governance, continuous learning.

Encourage a culture of continuous learning and upskilling among data analysts to keep up with evolving techniques and technologies.

Companies Who Put Analytics Into Practice

Companies across various industries harness the power of analytics to gain insights, improve operational efficiency, enhance customer experiences, and drive business growth.

Netflix is renowned for its data-driven approach to content recommendations and production. By analyzing user viewing patterns, ratings, and feedback, Netflix can tailor personalized recommendations to its subscribers. Additionally, they leverage data analysis to make strategic decisions in content creation and acquisition. Netflix analyzes viewer data to identify popular genres, cast members, and storylines, which helps them develop original content that aligns with audience preferences, increasing the likelihood of successful shows and attracting and retaining subscribers.

Privacy Overview

5 Reasons Why Data Analytics is Important in Problem Solving

Data analytics is important in problem solving and it is a key sub-branch of data science. Even though there are endless data analytics applications in a business, one of the most crucial roles it plays is problem-solving.

Using data analytics not only boosts your problem-solving skills, but it also makes them a whole lot faster and efficient, automating a majority of the long and repetitive processes.

Whether you’re fresh out of university graduate or a professional who works for an organization, having top-notch problem-solving skills is a necessity and always comes in handy.

Everybody keeps facing new kinds of complex problems every day, and a lot of time is invested in overcoming these obstacles. Moreover, much valuable time is lost while trying to find solutions to unexpected problems, and your plans also get disrupted often.

This is where data analytics comes in. It lets you find and analyze the relevant data without too much of human-support. It’s a real time-saver and has become a necessity in problem-solving nowadays. So if you don’t already use data analytics in solving these problems, you’re probably missing out on a lot!

As the saying goes from the chief analytics officer of TIBCO,

“Think analytically, rigorously, and systematically about a business problem and come up with a solution that leverages the available data .”

– Michael O’Connell.

In this article, I will explain the importance of data analytics in problem-solving and go through the top 5 reasons why it cannot be ignored. So, let’s dive into it right away.

Highly Recommended Articles:

13 Reasons Why Data Analytics is Important in Decision Making

This is Why Business Analytics is Vital in Every Business

Is Data Analysis Qualitative or Quantitative? (We find Out!)

Will Algorithms Erode our Decision-Making Skills?

What is Data Analytics?

Data analytics is the art of automating processes using algorithms to collect raw data from multiple sources and transform it. This results in achieving the data that’s ready to be studied and used for analytical purposes, such as finding the trends, patterns, and so forth.

Why is Data Analytics Important in Problem Solving?

Problem-solving and data analytics often proceed hand in hand. When a particular problem is faced, everybody’s first instinct is to look for supporting data. Data analytics plays a pivotal role in finding this data and analyzing it to be used for tackling that specific problem.

Although the analytical part sometimes adds further complexities, since it’s a whole different process that might get challenging sometimes, it eventually helps you get a better hold of the situation.

Also, you come up with a more informed solution, not leaving anything out of the equation.

Having strong analytical skills help you dig deeper into the problem and get all the insights you need. Once you have extracted enough relevant knowledge, you can proceed with solving the problem.

However, you need to make sure you’re using the right, and complete data, or using data analytics may even backfire for you. Misleading data can make you believe things that don’t exist, and that’s bound to take you off the track, making the problem appear more complex or simpler than it is.

Let’s see a very straightforward daily life example to examine the importance of data analytics in problem-solving; what would you do if a question appears on your exam, but it doesn’t have enough data provided for you to solve the question?

Obviously, you won’t be able to solve that problem. You need a certain level of facts and figures about the situation first, or you’ll be wandering in the dark.

However, once you get the information you need, you can analyze the situation and quickly develop a solution. Moreover, getting more and more knowledge of the situation will further ease your ability to solve the given problem. This is precisely how data analytics assists you. It eases the process of collecting information and processing it to solve real-life problems.

5 Reasons Why Data Analytics Is Important in Problem Solving

Now that we’ve established a general idea of how strongly connected analytical skills and problem-solving are, let’s dig deeper into the top 5 reasons why data analytics is important in problem-solving .

1. Uncover Hidden Details

Data analytics is great at putting the minor details out in the spotlight. Sometimes, even the most qualified data scientists might not be able to spot tiny details existing in the data used to solve a certain problem. However, computers don’t miss. This enhances your ability to solve problems, and you might be able to come up with solutions a lot quicker.

Data analytics tools have a wide variety of features that let you study the given data very thoroughly and catch any hidden or recurring trends using built-in features without needing any effort. These tools are entirely automated and require very little programming support to work. They’re great at excavating the depths of data, going back way into the past.

2. Automated Models

Automation is the future. Businesses don’t have enough time nor the budget to let manual workforces go through tons of data to solve business problems.

Instead, what they do is hire a data analyst who automates problem-solving processes, and once that’s done, problem-solving becomes completely independent of any human intervention.

The tools can collect, combine, clean, and transform the relevant data all by themselves and finally using it to predict the solutions. Pretty impressive, right?

However, there might be some complex problems appearing now and then, which cannot be handled by algorithms since they’re completely new and nothing similar has come up before. But a lot of the work is still done using the algorithms, and it’s only once in a blue moon that they face something that rare.

However, there’s one thing to note here; the process of automation by designing complex analytical and ML algorithms might initially be a bit challenging. Many factors need to be kept in mind, and a lot of different scenarios may occur. But once it goes up and running, you’ll be saving a significant amount of manpower as well as resources.

3. Explore Similar Problems

If you’re using a data analytics approach for solving your problems, you will have a lot of data available at your disposal. Most of the data would indirectly help you in the form of similar problems, and you only have to figure out how these problems are related.

Once you’re there, the process gets a lot smoother because you get references to how such problems were tackled in the past.

Such data is available all over the internet and is automatically extracted by the data analytics tools according to the current problems. People run into difficulties all over the world, and there’s no harm if you follow the guidelines of someone who has gone through a similar situation before.

Even though exploring similar problems is also possible without the help of data analytics, we’re generating a lot of data nowadays , and searching through tons of this data isn’t as easy as you might think. So, using analytical tools is the smart choice since they’re quite fast and will save a lot of your time.

4. Predict Future Problems

While we have already gone through the fact that data analytics tools let you analyze the data available from the past and use it to predict the solutions to the problems you’re facing in the present, it also goes the other way around.

Whenever you use data analytics to solve any present problem, the tools you’re using store the data related to the problem and saves it in the form of variables forever. This way, similar problems faced in the future don’t need to be analyzed again. Instead, you can reuse the previous solutions you have, or the algorithms can predict the solutions for you even if the problems have evolved a bit.

This way, you’re not wasting any time on the problems that are recurring in nature. You jump directly onto the solution whenever you face a situation, and this makes the job quite simple.

5. Faster Data Extraction

However, with the latest tools, the data extraction is greatly reduced, and everything is done automatically with no human intervention whatsoever.

Moreover, once the appropriate data is mined and cleaned, there are not many hurdles that remain, and the rest of the processes are done without a lot of delays.

When businesses come across a problem, around 70%-80% is their time is consumed while gathering the relevant data and transforming it into usable forms. So, you can estimate how quick the process could get if the data analytics tools automate all this process.

Even though many of the tools are open-source, if you’re a bigger organization that can spend a bit on paid tools, problem-solving could get even better. The paid tools are literal workhorses, and in addition to generating the data, they could also develop the models to your solutions, unless it’s a very complex one, without needing any support of data analysts.

What problems can data analytics solve? 3 Real-World Examples

Employee performance problems .

Imagine a Call Center with over 100 agents

By Analyzing data sets of employee attendance, productivity, and issues that tend to delay in resolution. Through that, preparing refresher training plans, and mentorship plans according to key weak areas identified.

Sales Efficiency Problems

Imagine a Business that is spread out across multiple cities or regions

By analyzing the number of sales per area, the size of the sales reps’ team, the overall income and disposable income of potential customers, you can come up with interesting insights as to why some areas sell more or less than the others. Through that, prepping a recruitment and training plan or area expansion in order to boost sales could be a good move.

Business Investment Decisions Problems

Imagine an Investor with a portfolio of apps/software)

By analyzing the number of subscribers, sales, the trends in usage, the demographics, you can decide which peace of software has a better Return on Investment over the long term.

Throughout the article, we’ve seen various reasons why data analytics is very important for problem-solving.

Many different problems that may seem very complex in the start are made seamless using data analytics, and there are hundreds of analytical tools that can help us solve problems in our everyday lives.

Emidio Amadebai

As an IT Engineer, who is passionate about learning and sharing. I have worked and learned quite a bit from Data Engineers, Data Analysts, Business Analysts, and Key Decision Makers almost for the past 5 years. Interested in learning more about Data Science and How to leverage it for better decision-making in my business and hopefully help you do the same in yours.

.css-s5s6ko{margin-right:42px;color:#F5F4F3;}@media (max-width: 1120px){.css-s5s6ko{margin-right:12px;}} AI that works. Coming June 5, Asana redefines work management—again. .css-1ixh9fn{display:inline-block;}@media (max-width: 480px){.css-1ixh9fn{display:block;margin-top:12px;}} .css-1uaoevr-heading-6{font-size:14px;line-height:24px;font-weight:500;-webkit-text-decoration:underline;text-decoration:underline;color:#F5F4F3;}.css-1uaoevr-heading-6:hover{color:#F5F4F3;} .css-ora5nu-heading-6{display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;-webkit-align-items:center;-webkit-box-align:center;-ms-flex-align:center;align-items:center;-webkit-box-pack:start;-ms-flex-pack:start;-webkit-justify-content:flex-start;justify-content:flex-start;color:#0D0E10;-webkit-transition:all 0.3s;transition:all 0.3s;position:relative;font-size:16px;line-height:28px;padding:0;font-size:14px;line-height:24px;font-weight:500;-webkit-text-decoration:underline;text-decoration:underline;color:#F5F4F3;}.css-ora5nu-heading-6:hover{border-bottom:0;color:#CD4848;}.css-ora5nu-heading-6:hover path{fill:#CD4848;}.css-ora5nu-heading-6:hover div{border-color:#CD4848;}.css-ora5nu-heading-6:hover div:before{border-left-color:#CD4848;}.css-ora5nu-heading-6:active{border-bottom:0;background-color:#EBE8E8;color:#0D0E10;}.css-ora5nu-heading-6:active path{fill:#0D0E10;}.css-ora5nu-heading-6:active div{border-color:#0D0E10;}.css-ora5nu-heading-6:active div:before{border-left-color:#0D0E10;}.css-ora5nu-heading-6:hover{color:#F5F4F3;} Get early access .css-1k6cidy{width:11px;height:11px;margin-left:8px;}.css-1k6cidy path{fill:currentColor;}

Product overview
All features
App integrations

CAPABILITIES

project icon Project management
Project views
Custom fields
Status updates
goal icon Goals and reporting
Reporting dashboards
workflow icon Workflows and automation
portfolio icon Resource management
Time tracking
my-task icon Admin and security
Admin console
asana-intelligence icon Asana Intelligence
list icon Personal
premium icon Starter
briefcase icon Advanced
Goal management
Organizational planning
Campaign management
Creative production
Marketing strategic planning
Request tracking
Resource planning
Project intake
View all uses arrow-right icon
Project plans
Team goals & objectives
Team continuity
Meeting agenda
View all templates arrow-right icon
Work management resources Discover best practices, watch webinars, get insights
What's new Learn about the latest and greatest from Asana
Customer stories See how the world's best organizations drive work innovation with Asana
Help Center Get lots of tips, tricks, and advice to get the most from Asana
Asana Academy Sign up for interactive courses and webinars to learn Asana
Developers Learn more about building apps on the Asana platform
Community programs Connect with and learn from Asana customers around the world
Events Find out about upcoming events near you
Partners Learn more about our partner programs
Support Need help? Contact the Asana support team
Asana for nonprofits Get more information on our nonprofit discount program, and apply.

Data-driven decision making: A step-by-step guide

Data-driven decision making article banner image

Data-driven decision making is the process of collecting data based on your company’s key performance indicators (KPIs) and transforming that data into actionable insights. This process is a crucial element of modern business strategy. In this article, we’ll discuss the benefits of data-driven decision making and provide tips so you can make informed decisions at work.

If there’s a looming decision ahead of you at work, it’s often hard to know which direction to go. If you go with your gut feeling, you may feel more confident in your choices, but will those choices be right for your team members? When you use facts to make decisions, you can feel more at ease knowing your choices are based on data and meant to maximize business impact.

Whether outshining competitors or increasing profitability, data-driven decision making is a crucial part of business strategy in the modern world. Below, we dive into the benefits of data-driven decision making and provide tips for making these decisions at work.

Decision-making tools for agile businesses

In this ebook, learn how to equip employees to make better decisions—so your business can pivot, adapt, and tackle challenges more effectively than your competition.

Make good choices, fast: How decision-making processes can help businesses stay agile ebook banner image

What is data-driven decision making (DDDM)?

You can use business intelligence (BI) reporting tools during this process, which make big data collection fast and fruitful. These tools simplify data visualization, making data analytics accessible to those without advanced technical know-how.

What does being data-driven mean?

In short, the concept of being data-driven refers to using facts, or data, to find patterns, inferences, and insights to inform your decision making process.

Essentially, being data-driven means that you try to make decisions without bias or emotion. As a result, you can ensure that your company’s goals and roadmap are based on evidence and the patterns you’ve extracted from it, rather than what you like or dislike.

Why is data-driven decision making important?

Data-driven decision making is important because it helps you make decisions based on facts instead of biases. If you’re in a leadership position, making objective decisions is the best way to remain fair and balanced.

The most informed decisions stem from data that measure your business goals and populates in real time. You can aggregate the data you need to see patterns and make predictions with reporting software .

Some decisions you can make with support from data include:

How to drive profits and sales

How to establish good management behavior

How to optimize operations

How to improve team performance

While not every decision will have data to back it up, many of the most important decisions will.

5 steps for making data-driven decisions

Making data-driven decisions takes practice. If you want to improve your leadership skills , then you’ll need to know how to turn raw data into actionable steps that work toward your company initiatives. The following steps can help you make better decisions when analyzing data.

1. Know your vision

Before you can make informed decisions, you need to understand your company’s vision for the future . This helps you use both data and strategy to form your decisions. Graphs and figures have little meaning without context to support them.

Tip: Use your company’s yearly objectives and key results ( OKRs ) or quarterly team KPIs to make data-backed decisions.

2. Find data sources

Once you’ve identified the goal you’re working towards, you can start collecting data.

The tools and data sources you use will depend on the type of data you’re collecting. If your goal is to analyze data sets pertaining to internal company processes, use a universal reporting tool. Reporting tools offer a single point of reference for keeping track of how work across your organization is progressing. Some reporting tools like Microsoft’s Power BI let you gather data from various external sources. If you want to analyze marketing trends or competitor metrics, you can use one of those tools.

Some general success metrics you may want to measure include:

Gross profit margin: Gross profit margin is measured by subtracting the cost of goods sold from the company's net sales.

Return on investment (ROI): The ratio between the income and investment, ROI is commonly used to decide whether or not an initiative is worth investing time or money in. When used as a business metric, it often tracks how well an investment is performing.

Productivity: This is the measurement of how efficiently your company is producing goods or services. You can calculate this by dividing the total output by the total input.

Total number of customers: This is a simple but effective metric to track. The more paid customers, the more money earned for the business.

Recurring revenue : Commonly used by SaaS companies, this is the amount of revenue generated by all of your current active subscribers during a specific period. It's commonly measured either monthly or annually.

You can measure a variety of other data sets based on your job role and the vision you’re working toward. Machine learning makes aggregating real time data simpler than ever before.

Tip: Try to create a connected story through these metrics. If revenue is down, look at productivity and see if you can draw a connection. Keep digging through these metrics until you find a “why” for whatever problem you’re trying to solve.

3. Organize your data

Organizing your data to improve data visualization is crucial for making effective business decisions. If you can’t see all your relevant data in one place and understand how it connects, then it’s difficult to ensure you’re making the most informed decisions.

Tip: One way to organize your data is with an executive dashboard . An executive dashboard is a customizable interface that usually comes as a feature of your universal reporting tool. This dashboard will display the data that’s most critical to achieving your goals, whether those goals are strategic, tactical, analytical, or operational.

[Product UI] Universal reporting interactive dashboards in Asana (Search & Reporting)

4. Perform data analysis

Once you’ve organized your data, you can begin your data-driven analysis. This is when you’ll extract actionable insights from your data that will help you in the decision-making process .

Depending on your goals, you may want to analyze the data from your executive dashboard in tandem with user research such as case studies, surveys, or testimonials so your conclusions include the customer experience.

Does your team want to improve their SEO tools to make it more competitive with other options on the market? The data sets you can use to determine necessary improvements may include:

Competitors’ performance data

Current SEO software performance data

Current customer satisfaction data

User research on a variety of SEO/marketing tools

While some of this information will come from your organization, you may need to obtain some of it from external sources. Analyzing these data sets as a whole can be helpful because you’ll draw a different conclusion than you would if you were to analyze each data set individually.

Tip: Share your analytics tools with your whole team or organization. Just like any collaborative effort, data analysis is most effective when viewed from many perspectives. While you may notice one pattern in the data, it’s entirely possible a teammate may see something completely different.

5. Draw conclusions

As you perform your data analysis, you’ll likely begin to draw conclusions about what you see. However, your conclusions deserve their own section because it’s important to flesh out what you see in the data so you can share your findings with others.

The main questions to ask yourself when drawing conclusions include:

What am I seeing that I already knew about this data?

What new information did I learn from this data?

How can I use the information I’ve gained to meet my business goals?

Once you can answer these questions, you’ve successfully performed data analysis and should be ready to make data-driven decisions for your business.

Tip: A natural next step after data analysis is writing down some SMART goals . Now that you’ve dug into the facts, you can establish achievable goals based on what you’ve learned.

Data-driven decision making examples

While the data analysis itself happens behind the scenes, the way data-driven decisions affect the consumer is very apparent. Some examples of data-driven decision making in different industries include:

E-commerce

Have you ever been shopping online and wondered why you’re getting certain recommendations? Well, it’s probably because you bought something similar in the past or clicked on a certain product.

Online marketplaces like Amazon track customer journeys and use metrics like click-through rate and bounce rate to identify what items you’re engaging with most. Using this data, retailers are able to show you what you might want without you having to search for it.

Financial institutions use data in a multitude of different ways, ranging from assessing risk to customer segmentation. Risk is especially prevalent in the financial sector, so it’s important that companies are able to determine the risk factor before making any significant decisions. Historical data is the best way to understand potential risks, threats, and the likelihood they occur.

Financial institutions also use customer data to determine their target market. By grouping consumers based on socioeconomic status, spending habits, and more, financial companies can infer what consumers have the greatest lifetime value and target them.

Transportation

Data science additionally plays a huge role in determining safe transportation. The U.S. Department of Transportation’s Safety Data Initiative underscores the role that data plays in improving transportation safety.

The report pulls data from all types of motor crashes and evaluates factors like weather and road conditions to discover the source of problems. Using the hard facts, the department can work toward implementing more safety measures.

Benefits of data-driven decision making

Analytics-based decision making is more than just a helpful skill—it’s a crucial one if you want to lead by example and foster a data-driven culture.

When you use data to make decisions, you can ensure your business remains fair, goal-oriented, and focused on improvement.

[inline illustration] Benefits of data driven decision-making (infographic)

Make confident decisions

The businesses that outlast their competitors do so because they’re confident in their ability to succeed. If the decision-makers within a business waiver in their choices, it can lead to mistakes, high team member turnover, and poor risk management .

When you use data to make the most important business decisions, you’ll feel confident in those decisions, which will push you and your team forward. Confidence can lead to higher team morale and better performance.

Guard against biases

Using data to make decisions will guard against any biases among business leaders. While you may not be aware of your biases, having internal favoritism or values can affect the way you make decisions.

Making decisions directly based on the facts and numbers keeps your decisions objective and fair. It also means you have something to back up your decisions when team members or stakeholders ask why you chose to do what you did.

Find unresolved questions

Without using data, there are many questions that go unanswered. There may also be questions you didn’t know you had until your data sets revealed them. Any amount of data can benefit your team by providing better visualization into areas you can’t see without statistics, graphs, and charts.

When you bring those questions to the surface, you can feel confident knowing your decisions were made by considering every bit of relevant information.

Set measurable goals

Using data is one of the simplest ways to set measurable goals for your team and successfully meet those goals. By looking at internal data on past performance, you can determine what you need to improve and get as granular as possible with your targets. For example, your team may use data to identify the following goals:

Increase number of customers by 20% year over year

Reduce overall budget spend by $20,000 each quarter

Reduce project budget spend by $500

Increase hiring by 10 team members each quarter

Reduce cost per hire by $500

Without data, it would be difficult for your company to see where they’re spending their money and where they’d like to cut costs. Setting measurable goals ultimately leads to data-driven decisions because once these goals are set, you’ll determine how to reduce the overall budget or increase the number of customers.

Improve company processes

There are ways to improve company processes without using data, but when you observe trends in team member performance using numbers or analyzing company spending patterns with graphs, the process improvements you make will be based on more than observation alone.

Processes you can improve with data may include:

Risk management based on financial data

Cost estimation based on market pricing data

Team member onboarding based on new hire performance data

Customer service based on customer feedback data

Changing a company process can be difficult if you aren’t sure about the result, but you can be confident in your decisions when the facts are in front of you.

Tips for becoming more data-driven

Data-driven organizations are able to parse through the numbers and charts and find the meaning behind them. Creating a more data-driven culture starts with simply using data more often. However, this is easier said than done. If you’re ready to get started, try these tips to become more data-driven.

Find the story

The key to analyzing data, numbers, and charts is to look for the story. Without the “why,” the data itself isn’t much help, and the decision process is far more difficult. If you’re trying to become more data-driven in your decision making, look for the story the data is telling. This will be integral in making the right decisions.

Consult the data

Before making any organizational decision, ask yourself: Does the data support this? Data is everywhere and can be applied to any major decision. So why not consult it when making tough choices? Data is so helpful because it’s naturally void of bias, so make sure you’re consulting the facts before any decision.

Learn data visualization

Finding the story behind the data becomes easier when you’re able to visualize it clearly. While learning how to visualize data is often the toughest aspect of establishing a data-driven culture, it’s the best way to recognize patterns and discrepancies in the data.

Familiarize yourself with different tools and techniques for data visualization. Try to get creative with the different ways to present data. If you’re well-versed in data visualization, your data storytelling skills will skyrocket.

Make data-driven decisions easy with reporting software

You’ll need the right data in front of you to make meaningful decisions for your team. Universal reporting software aggregates data from your company and presents it on your executive dashboard so you can view it in an organized and graphical way.

Related resources

7 steps to complete a social media audit (with template)

3 visual project management layouts (and how to use them)

Grant management: A nonprofit’s guide

Everything you need to know about waterfall project management

How to analyze a problem

May 7, 2023 Companies that harness the power of data have the upper hand when it comes to problem solving. Rather than defaulting to solving problems by developing lengthy—sometimes multiyear—road maps, they’re empowered to ask how innovative data techniques could resolve challenges in hours, days or weeks, write senior partner Kayvaun Rowshankish and coauthors. But when organizations have more data than ever at their disposal, which data should they leverage to analyze a problem? Before jumping in, it’s crucial to plan the analysis, decide which analytical tools to use, and ensure rigor. Check out these insights to uncover ways data can take your problem-solving techniques to the next level, and stay tuned for an upcoming post on the potential power of generative AI in problem-solving.

The data-driven enterprise of 2025

How data can help tech companies thrive amid economic uncertainty

How to unlock the full value of data? Manage it like a product

Data ethics: What it means and what it takes

Author Talks: Think digital

Five insights about harnessing data and AI from leaders at the frontier

Real-world data quality: What are the opportunities and challenges?

How a tech company went from moving data to using data: An interview with Ericsson’s Sonia Boije

Harnessing the power of external data

What is Data Analysis?

Data are everywhere nowadays. And with each passing year, the amount of data we are producing will only continue to increase.

There is a large amount of data available, but what do we do with all that data? How is it all used? And what does all that data mean?

It’s not much use if we just collect and store data in a spreadsheet or database and don't look at it, explor it, or research it.

Data analysts use tools and processes to derive meaning from data. They are responsible for collecting, manipulating, investigating, analyzing, gathering insights, and gaining knowledge from it.

This is one of the reasons data analysts are very high in demand: they play an integral role in business and science.

In this article, I will first go over what data analysis means as a term and explain why it is so important.

I will also break down the data analysis process and list some of the necessary skills required for conducting data analysis.

Here is an overview of what we will cover:

What is data?
What is data analysis?
Effective customer targeting
Measure success and performance
Problem solving
Step 1: recognising and identifying the questions that need answering
Step 2: collecting raw data
Step 3: cleaning the data
Step 4: analyzing the data
Step 5: sharing the results
A good grasp of maths and statistics

Knowledge of SQL and Relational Databases

Knowledge of a programming language

Knowledge of data visualization tools

Knowledge of excel, what is data meaning and definition of data.

Data refers to collections of facts and individual pieces of information.

Data is vital for decision-making, planning, and even telling a story.

There are two broad and general types of data:

Qualitative data
Quantitative data

Qualitative data is data expressed in non-numerical characters.

It is expressed as images, videos, text documents, or audio.

This type of data can’t be measured or counted.

It is used to determine how people feel about something – it’s about people's feelings, motivations, opinions, perceptions and involves bias.

It is descriptive and aims to answer questions such as ‘Why’, ‘How’, and ‘What’.

Qualitative data is gathered from observations, surveys, or user interviews.

Quantitative data is expressed in numerical characters.

This type of data is countable, measurable, and comparable.

It is about amounts of numbers and involves things such as quantity and the average of numbers.

It aims to answer questions such as ‘How much, ‘How many’, ‘How often’, ‘and 'How long’.

The act of collecting, analyzing, and interpreting quantitative data is known as performing statistical analysis.

Statistical analysis helps uncover underlying patterns and trends in data.

What Is Data Analysis? A Definition For Beginners

Data analysis is the act of turning raw, messy data into useful insights by cleaning the data up, transforming it, manipulating it, and inspecting it.

The insights gathered from the data are then presented visually in the form of charts, graphs, or dashboards.

The insights discovered can help aid the company’s or organization’s growth. Decision-makers will be able to come to an actionable conclusion and make the right business decisions.

Extracting knowledge from raw data will help the company/organization take steps towards achieving greater customer reach, improving performance, and increasing profit.

At its core, data analysis is about identifying and predicting trends and figuring out patterns, correlations, and relationships in the available data, and finding solutions to complex problems.

Why Is Data Analysis Important?

Data equals knowledge.

This means that data analysis is integral for every business.

It can be useful and greatly beneficial for every department, whether it's administration, accounting, logistics, marketing, design, or engineering, to name a few.

Below I will explain why exploring data and giving data context and meaning is really important.

Data Analysis Improves Customer Targeting

By analyzing data, you understand your competitors, and you will be able to match your product/service to the current market needs.

It also helps you determine the appropriate audience and demographic best suited to your product or service.

This way, you will be able to come up with an effective pricing strategy to make sure that your product/service will be profitable.

You will also be able to create more targeted campaigns and know what methods and forms of advertising and content to use to reach your audience directly and effectively.

Knowing the right audience for your product or service will transform your whole strategy. It will become more customer-oriented and customized to fit customers' needs.

Essentially, with the appropriate information and tools, you will be able to figure out how your product or service can be of value and high quality.

You'll also be able to make sure that your product or service helps solve a problem for your customers.

This is especially important in the product development phases since it cuts down on expenses and saves time.

Data Analysis Measures Success and Performance

By analyzing data, you can measure how well your product/service performs in the market compared to others.

You are able to identify the stronger areas that have seen the most success and desired results. And you will be able to identify weaker areas that are facing problems.

Additionally, you can predict what areas could possibly face problems before the problem actually occurs. This way, you can take action and prevent the problem from happening.

Analyzing data will give you a better idea of what you should focus more on and what you should focus less on going forward.

By creating performance maps, you can then go on to set goals and identify potential opportunities.

Data Analysis Can Aid Problem Solving

By performing data analysis on relevant, correct, and accurate data, you will have a better understanding of the right choices you need to make and how to make more informed and wiser decisions.

Data analysis means having better insights, which helps improve decision-making and leads to solving problems.

All the above will help a business grow.

Not analyzing data, or having insufficient data, could be one of the reasons why your business is not growing.

If that is the case, performing data analysis will help you come up with a more effective strategy for the future.

And if your business is growing, analyzing data will help it grow even further.

It will help reach its full potential and meet different goals – such as boosting customer retention, finding new customers, or providing a smoother and more pleasant customer experience.

An Overview Of The Data Analysis Process

Step 1: recognising and identifying the questions that need answering.

The first step in the data analysis process is setting a clear objective.

Before setting out to gather a large amount of data, it is important to think of why you are actually performing the data analysis in the first place.

What problem are you trying to solve?

What is the purpose of this data analysis?

What are you trying to do?

What do you want to achieve?

What is the end goal?

What do you want to gain from the analysis?

Why do you even need data analysis?

At this stage, it is paramount to have an insight and understanding of your business goals.

Start by defining the right questions you want to answer and the immediate and long-term business goals.

Identify what is needed for the analysis, what kind of data you would need, what data you want to track and measure, and think of a specific problem you want to solve.

Step 2: Collecting Raw Data

The next step is to identify what type of data you want to collect – whether it will be qualitative (non-numerical, descriptive ) or quantitative (numerical).

The way you go about collecting the data and the sources you gather from will depend on whether it is qualitative or quantitative.

Some of the ways you could collect relevant and suitable data are:

By viewing the results of user groups, surveys, forms, questionnaires, internal documents, and interviews that have already been conducted in the business.
By viewing customer reviews and feedback on customer satisfaction.
By viewing transactions and purchase history records, as well as sales and financial figure reports created by the finance or marketing department of the business.
By using a customer relationship management system (CRM) in the company.
By monitoring website and social media activity and monthly visitors.
By monitoring social media engagement.
By tracking commonly searched keywords and search queries.
By checking which ads are regularly clicked on.
By checking customer conversion rates.
By checking email open rates.
By comparing the company’s data to competitors using third-party services.
By querying a database.
By gathering data through open data sets using web scraping. Web scraping is the act of extracting and collecting data and content from websites.

Step 3: Cleaning The Data

Once you have gathered the data from multiple sources, it is important to understand the structure of that data.

It is also important to check if you have gathered all the data you needed and if any crucial data is missing.

If you used multiple sources for the data collection, your data will likely be unstructured.

Raw, unstructured data is not usable. Not all data is necessarily good data.

Cleaning data is the most important part of the data analysis process and one on which data analysts spend most of their time.

Data needs to be cleaned, which means correcting errors, polishing, and sorting through the data.

This could include:

Looking for outliers (values that are unusually big or small).
Fixing typos.
Removing errors.
Removing duplicate data.
Managing inconsistencies in the format.
Checking for missing values or correcting incorrect data.
Checking for inconsistencies
Getting rid of irrelevant data and data that is not useful or needed for the analysis.

This step will ensure that you are focusing on and analyzing the correct and appropriate data and that your data is high-quality.

If you analyze irrelevant or incorrect data, it will affect the results of your analysis and have a negative impact overall.

So, the accuracy of your end analysis will depend on this step.

Step 4: Analyzing The Data

The next step is to analyze the data based on the questions and objectives from step 1.

There are four different data analysis techniques used, and they depend on the goals and aims of the business:

Descriptive Analysis : This step is the initial and fundamental step in the analysis process. It provides a summary of the collected data and aims to answer the question: “ What happened?”. It goes over the key points in the data and emphasizes what has already taken place.
Diagnostic Analysis : This step is about using the collected data and trying to understand the cause behind the issue at hand and identify patterns. It aims to answer the question: “ Why has this happened?”.
Predictive Analysis : This step is about detecting and predicting future trends and is important for the future growth of the business. It aims to answer the question: “ What is likely to happen in the future?
Prescriptive Analysis: This step is about gathering all the insights from the three previous steps, making recommendations for the future, and creating an actionable plan. It aims to answer the question: “ What needs to be done? ”

Step 5: Sharing The Results

The last step is to interpret your findings.

This is usually done by creating reports, charts, graphs, or interactive dashboards using data visualization tools.

All the above will help support the presentation of your findings and the results of your analysis to stakeholders, business executives, and decision-makers.

Data analysts are storytellers, which means having strong communication skills is important.

They need to showcase the findings and present the results in a clear, concise, and straightforward way by taking the data and creating a narrative.

This step will influence decision-making and the future steps of the business.

What Skills Are Required For Data Analysis?

A good grasp of maths and statistics.

The amount of maths you will use as a data analyst will vary depending on the job. Some jobs may require working with maths more than others.

You don’t necessarily need to be a math wizard, but with that said, having at least a fundamental understanding of math basics can be of great help.

Here are some math courses to get you started:

College Algebra – Learn College Math Prerequisites with this Free 7-Hour Course
Precalculus – Learn College Math Prerequisites with this Free 5-Hour Course
Math for Programmers Course

Data analysts need to have good knowledge of statistics and probability for gathering and analyzing data, figuring out patterns, and drawing conclusions from the data.

To get started, take an intro to statistics course, and then you can move on to more advanced topics:

Learn College-level Statistics in this free 8-hour course
If you want to learn Data Science, take a few of these statistics classes

Data analysts need to know how to interact with relational databases to extract data.

A database is an electronic storage localization for data. Data can be easily retrieved and searched through.

A relational database is structured in format and all data items stored have pre-defined relationships with each other.

SQL stands for S tructured Q uery L anguage and is the language used for querying and interacting with relational databases.

By writing SQL queries you can perform CRUD (Create, Read, Update, and Delete) operations on data.

To learn SQL, check out the following resources:

SQL Commands Cheat Sheet – How to Learn SQL in 10 Minutes
Learn SQL – Free Relational Database Courses for Beginners
Relational Database Certification

Knowledge Of A Programming Language

To further organize and manipulate databases, data analysts benefit from knowing a programming language.

Two of the most popular ones used in the data analysis field are Python and R.

Python is a general-purpose programming language, and it is very beginner-friendly thanks to its syntax that resembles the English language. It is also one of the most used technical tools for data analysis.

Python offers a wealth of packages and libraries for data manipulation, such as Pandas and NumPy, as well as for data visualization, such as Matplotlib.

To get started, first see how to go about learning Python as a complete beginner .

Once you understand the fundamentals, you can move on to learning about Pandas, NumPy, and Matplotlib.

Here are some resources to get you started:

How to Get Started with Pandas in Python – a Beginner's Guide
The Ultimate Guide to the Pandas Library for Data Science in Python
The Ultimate Guide to the NumPy Package for Scientific Computing in Python
Learn NumPy and start doing scientific computing in Python
How to Analyze Data with Python, Pandas & Numpy - 10 Hour Course
Matplotlib Course – Learn Python Data Visualization
Python Data Science – A Free 12-Hour Course for Beginners. Learn Pandas, NumPy, Matplotlib, and More.

R is a language used for statistical analysis and data analysis. That said, it is not as beginner-friendly as Python.

To get started learning it, check out the following courses:

R Programming Language Explained
Learn R programming language basics in just 2 hours with this free course on statistical programming

Data visualization is the graphical interpretation and presentation of data.

This includes creating graphs, charts, interactive dashboards, or maps that can be easily shared with other team members and important stakeholders.

Data visualization tools are essentially used to tell a story with data and drive decision-making.

One of the most popular data visualization tools used is Tableau.

To learn Tableau, check out the following course:

Tableau for Data Science and Data Visualization - Crash Course

Excel is one of the most essential tools used in Data analysis.

It is used for storing, structuring, and formatting data, performing calculations, summarizing data and identifying trends, sorting data into categories, and creating reports.

You can also use Excel to create charts and graphs.

To learn how to use Excel, check out the following courses:

Learn Microsoft Excel - Full Video Course
Excel Classes Online – 11 Free Excel Training Courses
Data Analysis with Python for Excel Users Course

This marks the end of the article – thank you so much for making it to the end!

Hopefully this guide was helpful, and it gave you some insight into what data analysis is, why it is important, and what skills you need to enter the field.

Thank you for reading!

7 Data Analysis for Effective Decision Making

Hoi K. Suen, Department of Educational Psychology, School Psychology, and Special Education, The Pennsylvania State University, University Park, PA

Pui-Wa Lei, Department of Educational Psychology, School Psychology, and Special Education, The Pennsylvania State University, University Park, PA

Hongli Li, Department of Educational Psychology, School Psychology, and Special Education, The Pennsylvania State University, University Park, PA

Published: 21 November 2012
Cite Icon Cite
Permissions Icon Permissions

Data analyses are statistical manipulations of numbers to help discern patterns in the data. As such, they need guidance from substantive theories in order to decide what patterns to look for, and to make sense of these patterns. The core outcomes of these manipulations are summary descriptors used to reduce the amount of information a researcher needs to digest. When such descriptors summarize data from a sample, and a researcher wishes to make inferences from the sample descriptors to the population, various inferential techniques are used. These techniques approach the inferential task from three different angles: significance testing, parameter estimation, and statistical modeling. For decisions regarding a single individual, reliability and validity of information need to be assessed. For the evaluation of the efficacy of intervention on an individual, however, the typical design used is that of an interrupted time-series analysis.

Data analyses are no more than statistical manipulations of numerical data to reveal patterns, trends and relationships otherwise not obvious from the original, often unwieldy raw data. Yet, interpretations of these trends and patterns, as well as the original raw data, are only as meaningful as the research process through which these data are collected. A random collection of facts rarely lead to any meaningful pattern that can be used for decisions. Therefore, prior to any data analysis, it is important to examine how the data are collected to begin with.

The Reciprocal Relationship Among Theory, Practice, and Data Collection

Research data collection activities, particularly in clinical and applied fields such as school psychology, do not exist in a vacuum. The purpose of research data collection in school psychology is most often to obtain information to guide real-life decisions regarding a child, a group, or a program. As such, clinical and educational concerns provide the guidance needed to pose the proper research or evaluation question. In order to provide answers to such a research or evaluation question, appropriate data or information needs to be gathered. Yet, a research or evaluation question alone provides no indication as to what data are most appropriate, nor directions for how to go about gathering the data. A model, theory, or even “hunch” is needed to provide some tentative conceptual structure for possible answers to the research questions. Through such theoretical structure, we are able to discern the type and manner of data to be collected. Therefore, a theory, no matter how informal or casual, “seat of the pants,” is critical to data collection and data analyses. Results of data analyses provide empirical support for the tentative theoretical structure, which in turn provides evidence to support a particular clinical or educational decision. In this manner, practice, theory, and data analyses form an inseparable tripartite relationship, each providing guidance and support to another, and each a critical component of the overall process to guide decisions.

The need for guidance from theory and practice exists even for research or evaluation studies that are euphemistically called “exploratory” or “data driven.” Performing data analyses and interpreting results without the guidance of a theoretical framework is not different from trying to read tea leaves to tell a fortune—with the results about as meaningful and useful. A case in point is the so-called “exploratory factor analysis” method. The name gives the impression that this is a data-driven analytic technique, and that the results will “uncover” the hidden structure among a number of unobserved constructs. In reality, both exploratory and confirmatory factor analyses start with a theoretical structure. The difference is that for the former, that structure is not entered as input into the analysis, while it is an integral part of the data input for the latter. For confirmatory factor analysis, the analytic steps involve evaluating mathematically whether the structure of the data is consistent with the theoretical structure that the researcher has input into the analysis. For exploratory factor analyses, the analytic steps produce the best and most reasonable and internally consistent structure, based on the data and a set of chosen numerical rules alone. The researcher makes the judgment as to whether the data-based structure thus produced is consistent with the theoretical structure. The actual data analysis itself is fundamentally a series of numerical transformations and manipulations, changing from one set of numbers to another set of numbers based on some mathematical or statistical rules—not totally unlike playing Sudoku, except much more complicated. Theories and structures of unobserved constructs do not magically appear from nothing through such numerical transformations. In other words, in both cases, an a priori theory is central to both data analysis and the interpretation of results.

Influenced by the U.S. federal government’s preference for research and evaluation activities that use certain types of methodology in funding decisions in the past decade, the particular approach to research data collection design referred to as “evidence based” has been in vogue. It is important to clarify what constitutes evidence-based research; and not to confuse it with data-driven research. The central criterion of excellence for evidence-based research is strong internal validity. As such, randomized trial experimentation is viewed as the sine qua non of data collection designs. To further maximize internal validity, data reliability and statistical power are emphasized. These designs lend themselves to the use of numerical data and statistical analysis techniques. However, the use of empirical, quantitative data, and sophisticated statistical data analysis techniques, does not by itself constitute evidence-based research; nor should evidence-based research be confused with atheoretical, “empirical research,” for which the common mantra has been “let the data speak for themselves.” In reality, data do not speak at all; instead, theories speak through the language of data. Evidence-based research data collection without the proper guidance of theory and practice is essentially a manifestation of the now refuted radical epistemology of logical positivism, as was advocated by the Vienna Circle (Hahn, Neurath, & Carnap, 1929 ). As the great Hungarian philosopher Imre Lakatos cautioned us against:

…patched up, unimaginative series of pedestrian “empirical” adjustments which are so frequent, for instance, in modern social psychology. Such adjustments may, with the help of so-called “statistical techniques,” grant some “novel” predictions and may even conjure up some irrelevant grains of truth in them. But this theorizing has no unifying idea, no heuristic power, no continuity. They do not add up to a genuine research program and are, on the whole, worthless.( Lakatos , 1970 , p. 176)

The officially sanctioned evidence-based approach to data collection is not without critics. Many feel that the approach is particularly not appropriate for field research, or for clinical program evaluation activities. The major objections have to do with the need for external validity, and the impracticality of randomized trials in many situations (see for example the debate among Brooks-Gunn, 2004 ; Cook, 2004 ; Cottingham, 2004 ; and McCall & Green 2004 ). However, few, regardless of their position about evidence-based research, challenged the need to guide research and evaluation data collection activities and analyses through theory and practice; in turn, results of data analyses help to clarify and revise theories.

Basic Data Reduction

Guided by theories and practice, school psychologists conduct research and evaluation activities by collecting and analyzing data. Data may be collected from a single individual, without any generalization to a larger population, or from a sample of people, with an intention to generalize results to a larger population. The data collected may be used as overt signs of some unobserved, covert psychological constructs. Alternatively, they may be no more than a sample of directly observable behaviors without further inferences to any latent traits or covert constructs. The nature of the data collected may be simple or complex, crossed or nested, single- or multileveled, univariate or multivariate. The theory or model that drives the data collection activities may involve a simple direct relationship, a complex set of direct and indirect relationships, or relationships among observed variables and unobserved theoretical constructs. In other words, school psychologists work with a very large variety of data types and structures, with a large array of different objectives. These require a large variety of data analytic tools. Additionally, some of these analyses are performed to help confirm larger, generalizable principles, while others are performed in order to provide information regarding the efficacy of a particular individual intervention.

Regardless of the nature, structure, and complexity of the data, and regardless of the goals, objectives, and underlying theories, the first and foremost purpose of statistical data analysis is to summarize an otherwise unwieldy set of raw sample data. That is, before we can make inferences about populations, about trends, about latent structures, about theories, or generalizations to other situations, we need first to obtain a clear picture of the actual, tangible, sample data in hand. However, sample data can be unwieldy, messy, idiosyncratic, and unorganized. The picture presented by sample data is, at first glance, murky and confusing. To understand this data, we need to reorganize the information so that we can characterize the data through manageably fewer pieces of information. To accomplish this, we use descriptive statistics. There are a number of fundamental descriptive statistics that will apply to most, if not all, sample data to help us gain a better understanding of the data at hand. Some combination of these descriptive statistics should be applied whenever feasible to the sample data, whether we end up reporting them or not, just so that we have a more complete perspective about the sample. First, it is often informative to summarize the data graphically through either a histogram, a polygon, a stem-and-leaf diagram, a boxplot, a scatterplot, or some other graphic format as appropriate. Basic univariate descriptive statistics such as mean, variance, median, and/or mode are usually informative. For data with more than one variable, there is a large array of descriptors of relationships, ranging from Pearson’s r to Kendall’s tau, Somer’s d, Cohen’s kappa, to various proportionate reduction in error (PRE) statistics.

One particularly important category of descriptive statistics is effect size statistics. The very first effect size statistic was Karl Pearson’s r developed a century ago; but the concept of effect size was formally introduced through Jacob Cohen’s d statistic in the 1960s. Since then, the concept of effect size has been much more broadly conceived as the magnitude of the effect that is attributable to the independent variable. This concept applies to describing the effect in a variety of experimental and quasi-experimental, as well as correlational studies, and is a central focus in meta-analytic studies. In addition to Pearson’s r and Cohen’s d, some common alternative effect size measures include the eta-square statistic in analyses of variance and r-square in regression. Effect size statistics are a particularly important category of sample descriptors, because the reporting of effect size has been required for over a decade for studies published in journals sponsored by the American Psychological Association, and many of those sponsored by the American Educational Research Association and other organizations.

Inferences About Population Parameters

The group of individuals from whom we collect the data is either the target population or a sample drawn from the target population. If these individuals constitute the entire target population, no legitimate inference beyond these individuals would be made. In this case, no inferential statistical analysis is necessary. At the same time, however, results of descriptive analyses cannot be extrapolated or generalized beyond the individuals actually studied. Except for some case studies and clinical, single-subject interventions, the majority of research studies in school psychology treat the individuals in the study from whom the data are collected as a sample of a larger population, to whom the results of the study are generalized. The reason for the use of a sample when the object of interest is a larger population is a practical one: it is much more economical to collect data from a small sample than it is from a large population. For this economical practice to be reasonable, the data collected from the sample need to be representative of those that we would have otherwise collected from the population; i.e., the sample data need to provide a microcosm of the larger population. Yet, samples almost never accurately represent populations. It is very rare that data from a sample form an exact microcosm of data from the population. The only exceptions are data collected via certain sampling procedures such as proportional stratified sampling; but even with these methods, the sample is a microcosm of the larger population only with respect to the stratifying variable(s) and nothing else. For example, if we were to draw a sample such that the sex ratio of the sample is the same as that of the population, the sample would be assured to be representative of the population only in terms of sex ratio, but nothing else.

If a sample is unlikely to be a microcosm of the larger population, how do we justify drawing conclusions about the population based on information from the sample? In statistical analyses, sample representation is treated as a probabilistic concept. When a scientific sample such as a simple random sample is drawn, there is some probability that the sample forms a microcosm of the population. It is somewhat less probable that the sample deviates slightly from the population; and even less probable that the sample deviates substantially from the population. However, even though there is a probability that the sample is a microcosm of the population, that probability can potentially be quite small. Since data from a sample may or may not be a microcosm of the population, what can we say about the population when all we have are data from a sample? The inference to the population is accomplished through some combination, or all, of three parallel approaches. These approaches are based on applications of probability theories.

The most fundamental approach is to develop descriptive statistics for the sample, such that these statistics are unbiased estimators of the corresponding quantities for the population. The objective here is not an accurate microcosm, but a fair and unbiased representation. These sample statistics may overestimate or underestimate the corresponding values in the population; but they are as probable to have overestimated as they are to have underestimated the corresponding population statistics (called parameters ). Therefore, in the long run, under repeated estimations, the over- and underestimations would probably cancel each other out, resulting in the correct value of the population. Examples of these unbiased sample statistics include the arithmetic mean, and the adjusted variance calculated by dividing the sum of squared deviations by the degree of freedom of N-1.

Unbiased estimates from sample data are only fair in the long run. A single estimate calculated from a particular sample is most probably not an accurate or precise representation of the corresponding population parameter. To supplement the use of unbiased sample statistics, one or both of two approaches have been used.

Significance Testing

The first supplement is a negation approach developed by Ronald Fisher, commonly known as significance testing . With this approach, we postulate a worst-case scenario hypothesis that there is no relationship or difference in the population, and the sample statistic value is an artifact of random sampling fluctuation. If the sampling fluctuation hypothesis is incorrect, it removes the worst-case scenario of no relationship/difference from consideration. The sample statistic may still not represent the population parameter, but at least we know that the situation with the population is unlikely to be that of the worst-case scenario.

In practice, the methodology of significance testing will not determine whether the no relationship/difference scenario is true or not in the population. Instead, it determines whether it is plausible to obtain the sample statistics if there is no relationship/difference in the population. When it is implausible, we can safely rule out the idea that the observed sample statistics are a random sampling fluctuation artifact from a population of no relationship/difference. This situation is described as “statistically significant.” Conversely, when it is plausible to obtain such sample statistics from a no-relationship/difference population, we are unable to negate the competing hypothesis of random sampling fluctuation. The results of the research are thus inconclusive, and the situation is described as “statistically not significant.” There is no situation under which one can “prove” that there is no relationship/difference in the population, nor a situation in which one can conclude that the observed sample statistics accurately reflect the value in the population. As Ronald Fisher explained:

… tests of significance, when used accurately, are capable of rejecting or invalidating (null) hypotheses, in so far as they are contradicted by the data; but they are never capable of establishing them as certainly true…( cited in Salsburg , 2001 , p. 108)

The plausibility of the sampling fluctuation hypothesis is determined by evaluating a particular conditional probability value: the probability that, through random sampling fluctuations alone, one can obtain a sample statistic as large or larger than the one obtained by the researcher—given that the true difference/relationship in the population is zero (or equals some other meaningful value predetermined by the researcher). Note that this is a conditional probability of obtaining the sample statistics value or larger through random sampling fluctuation, given the condition of zero relationship/difference. It is not the probability that the population has a zero relationship/difference. That is a given condition for this conditional probability, and is therefore assumed to be true to begin with, prior to calculating probability values.

The threshold between a high and a low probability value is called the alpha value , and this threshold value is determined by conventional professional consensus. The most typical alpha value used is 5%, or .05. The alpha value is also referred to as the “Type I error rate” for certain decisions.

Dependent on the mathematical nature of the measurement metric used in the collection of sample data, the conditional probability value can be calculated directly or indirectly from the sample data. For certain data metrics such as frequencies, rates, and proportions, the conditional probability of obtaining the sample value by random sampling fluctuation can often be calculated directly. Some examples of methods used to calculate these conditional probabilities include the binomial test, the Poisson test, and the Weibull test. For situations other than the use of frequencies, rates, and proportions, however, the measurement metric is undetermined a priori and can be different from study to study. For example, the scoring metric used to measure reading ability may be different from instrument to instrument, and from study to study; or, the metric to scale “persistence” or “depression” may be a function of the instrument used, as well as the scaling technique employed. For these situations with a variable metric, a different approach is needed to calculate the conditional probability.

To calculate the conditional probability when the measurement metric is undetermined, we use an indirect approach. Instead of assessing the conditional probability of obtaining the sample descriptive statistic, such as the sample mean or the sample variance, we assess the conditional probability of obtaining the value of a ratio between the actual obtained sample statistic, and the typical random sampling fluctuation expected. One particular example of this approach is the chi-square test. The ratio used is called the chi-square value, and it is the ratio between observed frequencies beyond expectation and the frequencies expected under the random sampling fluctuation scenario. Another example is the two-sample independent t -test. The ratio, called t , is the ratio of the observed difference in mean scores between two samples, and the expected fluctuation of mean difference values under the random sampling fluctuation scenario. Other examples of such an approach include the F-ratio and the z-test.

It should be noted that in the attempt to negate various scenarios in the population, there are two alternatives to Fisher’s significance testing scheme. One is the Neyman-Pearson approach, which pits one hypothesis against another and rejects the one that is less probable. Yet another is the Bayesian approach, which attempts to identify the most probable scenario inductively, through the sequential accumulation of data from many studies. These two approaches to significance testing, however, are rarely used in school psychology.

Parameter Estimation

The significance testing approach has clear limitations. Through the significance testing process, we can only ascertain that the worst-case null scenario is implausible and can be safely rejected. Yet, we gain no information as to what are the exact population parameters, and whether the sample statistics are accurate reflections of these population parameters. In contrast to Ronald Fisher’s significance testing approach, Karl Pearson developed the “goodness of fit” approach in the early twentieth century, in the form of a chi-square goodness of fit test. The underlying idea for this approach is one of trying to estimate the population parameters directly, based on sample data. With Pearson’s goodness-of-fit method, one postulates a set of possible population parameters, and then evaluates the probability that the sample data could have been drawn from such a population. If the probability is high, we would describe the data as fitting those parameters.

The general conceptual approach is thus one of first postulating some theoretical model regarding either the population parameters, or the relationship between sample statistics and population parameters. Based on these postulated models and relationships, we would estimate the population parameter values directly. Today, this general approach has been expanded to include a very large array of different inferential statistical techniques. These techniques can be categorized into those methods that use confidence intervals, and those that use statistical modeling.

Confidence Interval Approach

Confidence intervals are built around a sample statistic to provide a range of values within which the true population parameter is likely to be. Confidence intervals are calculated by the following generic form:

Population parameters of common interest include mean, proportion, and difference in mean or proportion. Standard errors are computed differently for sample estimates of different population parameters (see Appendix A for some common standard error formulas, and Glass & Hopkins, 1995 , or Kirk, 1998 , for an introductory text on statistics). Standard error gauges the magnitude of random sampling fluctuation of sample estimates, if different random samples are drawn from the population. Critical value is determined by the desired confidence level, and the sampling distribution of the sample estimates. The larger the desired confidence level (e.g., 95% vs. 68%), the larger the critical value is, and the wider the interval becomes. The most common sampling distribution used to form confidence intervals is probably the standard normal (z) distribution. Using the standard normal distribution is often adequate when sample size is large (i.e., large sample approximation).

Suppose that a research question is: Does depression affect reading comprehension? One way to tackle this question is to form two groups (e.g., depressed vs. not-depressed) based on scores on a depression inventory. A reading comprehension test can be administered to the two groups. Table 7.1 provides the simple descriptive statistics of reading comprehension for the two hypothetical groups.

One can form a confidence interval around each of two means (using standard error calculated with equation 1 in Appendix A), and see if the two resulting ranges of possible population parameter values are far from each other. If the confidence intervals do not overlap, then there is evidence to suggest that the depressed sample and the not-depressed sample are drawn from different populations. One can then conclude that the mean comprehension scores are different between these two populations. In this example, neither the 68% nor the 95% confidence intervals for the two groups overlap. That is, the upper limits for the depressed group (93.7 and 96.31 respectively for 68% and 95%) are lower than the lower limits for the not-depressed group (108.9 and 107.69 respectively for the 68% and 95%). These hypothetical data suggest that the population mean of reading comprehension for the depressed group is generally lower than the population mean for the not-depressed group. Alternatively, one can take the difference between the two group means (18.98 in this example), which estimates the difference in population mean values. A confidence interval can be formed for that difference (using standard error calculated with equation 2 in Appendix A) to determine the range of likely differences in reading comprehension between depressed and not-depressed individuals. For the numerical example, the difference ranged from 15.74 to 22.21 68% of the time, and from 12.58 to 25.38 95% of the time 1 .

Suppose an intervention program has been implemented to reduce incidents of depression. The investigator can establish a baseline level of depression for participants before program intervention. The baseline scores can be used to match respondents, to form pairs of treatment and control subjects. After intervention, all subjects are measured again on their level of depression. Due to the matching by baseline depression scores, post-intervention depression scores for the matched pair become dependent, because their scores are expected to be more similar to each other than to scores from respondents in different pairs. This dependence calls for a different estimate of standard error (equation 3 in Appendix A), which is usually smaller than the standard error estimate for independent group difference. Table 7.2 shows descriptive statistics for a hypothetical matched pair sample. In this example, subjects in the treatment condition had lower posttest depression scores than subjects in the control condition, and the estimated population difference ranged from 2.21 to 7.79 points 95% of the time.

The intervention program can also be evaluated via a proportion estimation approach. That is, depression scores for treatment and control subjects in each pair are compared, and the proportion of the matched pairs in which the treatment subject had lower depression score than the control subject can be tabulated. If the estimated proportion is higher than .50, then there is an indication that subjects receiving the treatment have lower depression scores compared to subjects receiving no treatment. The estimated proportion for this example ranged from .538 to .729 95% of the time, suggesting that the proportion is generally higher than .50 and that the intervention program appeared to be somewhat effective in reducing depression. This proportion estimation approach arrived at the same conclusion as the paired mean difference approach in this example. However, the proportion approach only compares the paired values, and disregards the magnitude of difference. The loss of metric information renders the proportion estimates relatively less precise.

Statistical Modeling

As opposed to finding a probable range of values for individual population parameters, statistical modeling is a general approach to estimating multiple population parameters simultaneously. Modeling starts with the postulation of a statistical model to describe relationships among variables in the population. Multiple parameters, representing various relationships of the postulated model, are estimated from sample data at the same time. Goodness-of-fit of the postulated model to sample data is evaluated by certain mathematical criteria. Different estimation methods employ different criteria. For example, the least square estimation method minimizes the sum of squared differences between observed and fitted values. In contrast, the maximum likelihood method maximizes the likelihood of observed data given the model parameters, and the resulting parameter estimates will be the most probable among all possible parameter values for the observed data. The choice of estimation methods is often based on the properties of the resulting parameter estimates, such as unbiasedness, consistency, and efficiency. Under regular conditions, the least square estimation method is the best linear unbiased estimator for general linear models (GLM), and the maximum likelihood estimator is asymptotically unbiased (i.e., becomes increasingly unbiased as the sample size increases), consistent, and efficient, and is commonly used for more complicated models (e.g., generalized linear models with categorical outcomes and structural equation modeling).

Modeling Linear Relationships

When there is only one outcome variable with one or more independent variables, the model is considered univariate. One family of well known univariate models is the general linear model (GLM) in which the outcome variable is continuous. General linear models include analysis of variance (ANOVA) models and linear regression models. The question about whether depression affects reading comprehension in the population, in one of the previous examples, can be answered by fitting a GLM to the data. In this GLM model, reading comprehension score is a continuous outcome variable, and depression score on a depression measurement scale (not the depressed vs. not-depressed categories) is a predictor variable and is assumed to be linearly related to reading comprehension scores. Based on our data that generated the statistics in Table 7.1 , the estimated regression model for this hypothetical example can be expressed as: predicted reading score = 148.94 – .87×(depression score). That is, reading comprehension score was expected to be .87 lower (or from .70 to 1.05 lower 95% of the time) for each score point increased in depression. Had all variables been standardized before fitting the regression model, the resulting regression coefficients would be on a standardized metric, and are customarily referred to as the standardized coefficients . For this example, the standardized regression coefficient was -.57, suggesting that reading score was expected to drop by .57 standard deviations for each standard deviation unit increased in depression score.

If the depression variable was dichotomously coded as 1 for “depressed” and 0 for “not- depressed,” and was used instead as the predictor variable in the linear regression model, the estimated regression equation became: predicted reading score = 110.13 – 18.98 × (depressed/not-depressed indicator). That means the depressed group on average scored 18.98 points lower on reading comprehension than the not-depressed group. The estimated coefficients in both models suggested a negative effect of depression on reading comprehension in this hypothetical example.

Model assumptions for general linear models include independent residuals (i.e., prediction error), normal distribution of residuals, and same variance of residuals (i.e., homogeneity of variance for ANOVA models, or homoscedasticity for linear regression models) conditional on independent variables, as well as linear relationship between outcome and independent variables. When these model assumptions hold, estimates of model parameters from sample data will have such desirable properties as being unbiased, consistent, and efficient. In practice, the choice of model and estimator depends greatly on the satisfaction of model assumptions. When one or more of these assumptions are violated, Type I error (i.e., incorrectly rejecting a null hypothesis when null is in fact true) rate will be higher or lower than the alpha level used to make inference decisions, and confidence levels will be likewise incorrect.

Modeling Nonlinear Relationships

When the relationship between the outcome measure and predictor variables is nonlinear, but normality and homoscedasticity approximately hold, polynomial regression models can be used to model the nonlinear relationship. Power functions of predictor variables are used in polynomial regression models, but the models are still linear in model parameters (i.e., regression coefficients). Suppose that the relationship between reading comprehension score and depression score is nonlinear, in that the relationship is quite weak for low depression scores but becomes strong negative as depression score increases from a certain point. A hypothetical scatter plot of reading comprehension score on depression score is provided, with fitted linear and quadratic trends superimposed, in Figure 7.1 .

A Hypothetical Scatter Plot of Reading Comprehension Score on Depression Score

The estimated linear equation is: predicted reading score = 163.75 – 1.28×(depression score), R 2 =.72. R 2 indicates the proportion of accounted-for variance in the outcome variable, and may be used as a measure of predictive power of the model. The estimated quadratic equation is: predicted reading score = 55.22 + 3.23 × (depression score) - .045 × (depression score) 2 , R 2 =.86. The incremental R 2 due to the quadratic term is .14, p < .0001, indicating that the estimated quadratic trend fitted the sample data better than the estimated linear trend. For this example, examination of residual plots for the quadratic model did not reveal substantial departure from normality or homoscedasticity. The quadratic model appeared to be adequate for the sample data.

When the normality assumption is violated (e.g., when the continuous outcome variable is skewed) or the residual variances are heteroscedastic, the outcome variable can be transformed to normalize the residual distribution, stabilize the residual variances, or both, as long as the relationship between the transformed outcome variable and the predictor variables remains linear. If the transformation results in an approximately normal distribution and stabilizes the variances, ordinary general linear models can be applied to the transformed outcome variable. Because transformation is more or less a trial-and-error exercise, we do not address this issue here. For more extensive discussion of nonlinear transformations, see Cohen, Cohen, West, and Aiken ( 2003 , p.221–249).

When the outcome variable is categorical or discrete (e.g., binary outcome or count), however, using GLM on transformed outcome variable is usually not satisfactory. Non-normality and heteroscedasticity often remain problematic in these cases despite transformation, and the fitted values may go out of bound. Nonlinear models are generally more appropriate for categorical outcome variables, such as logistic regression for binary outcome and Poisson regression for count outcome. Nonlinear models are, by definition, not linear in model parameters in the original metric of the outcome variable. However, models belonging to the family of generalized linear models can be expressed as a linear function in model parameters by a suitable transformation (referred to as the link function that relates the predicted outcome to the original outcome variable), and different forms of probability distributions in the exponential family can be assumed for residuals, to allow for variances to vary as a function of the fitted value. In logistic regression models, for instance, binomial distribution is assumed for the dichotomous outcome variable (e.g., event vs. nonevent) and the logit (or log odds transformation of the predicted probability of event) is modeled as a linear function of predictor variables (referred to as the systematic component of the model). As in ordinary regression, predictor variables for the systematic component of generalized linear models can be categorical or continuous, or nonlinear functions of the predictor variables, such as product terms for interactions or power functions for polynomial regression.

Suppose one is interested in the effect of depression on the proportion of students passing a difficult reading comprehension test, or making adequate yearly progress in reading. The outcome variable is dichotomized based on a cut point on the reading comprehension test (e.g., 1=passed, 0=failed). Because this outcome variable is binary, logistic regression can be used to model the relationship between the dichotomous passing score and the continuous depression score. Simple descriptive statistics for a synthetic data set are given in Table 7.3 .

The estimated logistic regression equation for this example was: logit(passed) = 6.6 - .12 × (depression score). The estimated odds ratio for depression score was .889 (95% confidence interval was between .855 and .924). That is, the odds of passing for those who scored 1 point higher on depression was .889 times the odds for those who scored 1 point lower. Alternatively, the odds of passing for those who scored 1 point lower on depression was 1.125 (1/.889) times the odds for those who scored 1 point higher; the odds of passing was .125 higher for those who scored 1 point lower on depression. Fitted probabilities, along with the estimated 95% confidence interval, are plotted as a function of depression scores in Figure 7.2 . The probability of passing appeared to drop quickly as depression score went above 40. The model seemed to fit the data quite well as indicated by the Hosmer and Lemeshow goodness-of-fit test (Hosmer & Lemeshow, 2000 ), chi-squared (df=8, N=202) = 9.41, p=.309.

Predicted Probabilities and 95% Confidence Interval

When the outcome or response variable is direct frequency count of the occurrence of some event, Poisson regression, also known as loglinear modeling , is appropriate. Poisson distribution is assumed for the count outcome variable (e.g., number of rare incidences in a period of time) and the natural logarithm transformation of count is modeled as a linear function of predictor variables.

Suppose the number of occurrences of a particular depression symptom within a week was measured as the outcome variable in the evaluation of program effect on depression, and that subjects were randomly assigned to a new intervention (treatment) and a traditional intervention (control) condition (coded 1 and 0 respectively). Because the number of symptom occurrences is discrete, and the occurrence of events is rare, the most frequent scores will concentrate at the low end, and the resulting frequency distribution will be highly positively skewed. The frequency distribution of number of symptom occurrences for a hypothetical sample is provided in Figure 7.3 , and the associated descriptive statistics are given in Table 7.4 . The observed variance was similar to the observed mean for each of the intervention conditions, suggesting that a Poisson regression model might fit the data well.

The estimated Poisson regression equation based on the hypothetical sample was: log(expected number of occurrences) = .425 – 1.070 × (treatment). The coefficient of –1.07 indicates that the expected mean number of occurrences for treatment group subjects was .343 times that for control group subjects.

Loglinear models can also be used to model associations among two or more categorical variables. The response variable is frequency count for every combination of the categorical variables in the model, and it is assumed to have a Poisson distribution. Natural logarithm transformation of the expected frequencies is modeled as a linear function of the categorical variables. To determine the best fitting model, successive hierarchically less complicated models are usually fitted. The estimated models are compared by model fit indices. Simpler models with fewer model parameters are preferred for the sake of better interpretability and parsimony, if the loss in model–data fit is small.

To illustrate, in studying the relationship between depression, reading comprehension, and treatment effect, suppose that a pass or fail decision was made based on a subject’s reading comprehension score, and a depressed or not-depressed classification was made based on a subject’s depression test score. The relationship among treatment (1 = treatment condition, 0 = control condition), depression (1 = not-depressed, 0 = depressed), and passing reading comprehension (1 = passed, 0 = failed) can be examined by loglinear models. An example of the 2×2×2 frequency table for this hypothetical scenario is given in Table 7.5 . Fit indices for the estimated hierarchical models are provided in Table 7.6 .

Frequency Distribution of Number of Symptom Occurrences

According to the fit statistics (i.e., Δ deviance) in Table 7.6 , the all 2-way associations model did not fit the data significantly worse than the 3-way association model, and the Passed x Treatment with Passed x Not-depressed model did not fit the data significantly worse than the all 2-way associations model. Because the other two models with two 2-way association terms fit the data significantly worse than the all 2-way associations model, the Passed x Treatment with Passed x Not-depressed model would be preferred. In addition, dropping one of the 2-way association terms from the Passed x Treatment with Passed x Not-depressed model significantly worsened the model fit to the data. As a result, the Passed x Treatment with Passed x Not-depressed model would be retained. The estimated equation for this model was: Log(expected frequency) = 2.8085 – 1.9855 × passed – 1.1192 × treatment + .6702 × not-depressed + 1.6106 × (passed × treatment) + 2.4133 × (passed × not-depressed). Taking the exponentiation of the coefficients gives the multiplicative factors for expected frequencies. For instance, the value of exp(–1.9855) = .137 indicated that the expected number of passing was .137 times that of failing for depressed subjects in the control condition (i.e., when treatment=0 and not-depressed=0). The expected number of passing was exp(-1.9855+2.4133) = 1.53 times that of failing (or 53% higher than that of failing) for not-depressed subjects in the control condition. Estimated frequencies based on this model are quite similar to the corresponding observed frequencies (see Table 7.5 ). This was expected, as both the Pearson chi-squared (value=1.3163, df=2, p=.6581) and deviance (value=1.2824, df=2, p=.6412) tests for goodness of fit indicated good fit of the model to the data. The results for this hypothetical example suggested that treatment was associated with passing the reading comprehension test, but their association did not depend on depression status. Similarly, depression status was associated with passing the reading comprehension test, but their association did not depend on treatment condition.

Multilevel Models

Another important assumption made by general linear models is independence of observations. This assumption is violated when random sampling occurs at the cluster level (e.g., classrooms, schools, districts), or subjects are measured repeatedly over time or by a set of related variables. In essence, the data will exhibit a nesting or multilevel structure. For example, subjects can be nested in classrooms in the cluster sampling case, and measures can be nested in subjects in the repeated measures case, regardless of whether the same instrument is administered at different points in time (e.g., growth models) or multiple measures are used to indicate the same general construct (e.g., item response models that account for measurement error). Dependence occurs among observations in the lower level of the multilevel structure. For instance, subjects sharing the same classroom and teacher are expected to be more similar to each other than to subjects in a different classroom with a different teacher. Likewise, scores measuring the same construct received by the same subjects are expected to be more similar to each other than to scores measuring the same construct received by other subjects. In these cases, estimators assuming simple random sampling or independence will provide underestimated standard errors and hence inflate Type I error in statistical inference. Multilevel models (also known as mixed, or hierarchical linear models (HLM)), are generally used to account for such dependence among observations sharing the same higher-level unit.

Suppose that a researcher wanted to evaluate the effectiveness of a reading program on improving reading comprehension, controlling for the effect of depression. Classrooms, instead of subjects, were randomly assigned to treatment (integrating the reading program into regular instruction) and control (regular instruction) conditions. Subjects are considered level-1 units and are nested within classrooms, which are considered level-2 units. Variables that are associated with level-1 units are distinguished from those that are associated with level-2 units. In this example, reading comprehension and depression were level-1 variables, while reading program treatment was a level-2 variable. Participating subjects were administered a depression scale prior to the experiment, and a reading comprehension test after the experiment. Using the multilevel notation, the level-1 equation is:

a Highest order term fitted along with all the lower order terms.

b Comparison model is the 3-way association model.

c Comparison model is the all 2-way associations model.

d Comparison model is the Passed x Treatment and Passed x Not-depressed model because it does not fit the data significantly worse than all 2-way associations model.

where the subscript i indexes subject, and j indexes cluster.

The level-2 equations are:

The two-level equations can be combined into a single equation as:

In the equations above, e ij is a random error associated with student i in classroom j and r 0j is a random component associated with classroom j. These random components are usually assumed to be normally distributed and their variances are often assumed to be homoscedastic.

Compared to an ordinary regression model, the single equation for this two-level model (i.e., equation 5) has an extra random component that is due to classroom differences. The larger are the classroom differences on the outcome measure relative to the differences between individuals within classrooms, the larger will be the magnitude of dependence within classrooms. The level of dependence within classrooms is measured by an intra-class correlation, which is equal to the variance due to classrooms, divided by the sum of variance due to classrooms and variance due to individuals within classrooms.

Descriptive statistics by treatment condition and level for a synthetic data set are provided in Table 7.7 . Parameter estimates and their associated standard error estimates by the ordinary regression and multilevel models are presented in Table 7.8 . The OLS regression coefficient estimates were nearly identical to the corresponding estimates from the multilevel model, which supported the claim that parameter estimates were generally not biased when dependence due to clustering was ignored. As expected, standard errors estimated

Note. Table entries are means (standard deviations).

from the OLS model were smaller than standard errors estimated from the multilevel model, except for the depression score covariate. Intra-class correlation estimated based on the unconditional model was .08 [=32.38/(32.38+364.44)]. It could be interpreted as the estimated correlation between any two students in the same class. The estimated between-class variance was also statistically significant at the .05 level by a large sample z-test (see Table 7.8 ) indicating that the level of within-class dependence was not trivial. Hence, the effect of ignoring this level of dependence on standard error estimates was not small.

Dependence among observations due to repeated measurement of the same subjects, such as when the growth of individual child is modeled, can be handled in the same way as clustering in multilevel modeling.

In fact, the class of multilevel models subsumes general linear models, and is very broad and versatile. It is beyond the scope of this chapter to discuss the large variety of multilevel models in depth. Interested readers should consult Kreft and de Leeuw ( 1998 ), Snijders and Bosker ( 1999 ), or Raudenbush and Bryk ( 2002 ).

Structural Equation Modeling (SEM) 2

When there are many dependent variables, including variables that are both independent and dependent, the Structural Equation Modeling (SEM) approach might be more convenient than the modeling approaches discussed hitherto. Like the class of multilevel models, SEM represents an extension of general linear models. One of the primary advantages of SEM (versus other applications of GLM) is that it can be used to study the relationships among latent constructs that are indicated by multiple measures. It is also applicable to both experimental and nonexperimental data, as well as cross-sectional and longitudinal data. SEM takes a confirmatory (hypothesis-testing) approach to the multivariate analysis of a structural theory, one that stipulates causal relations among multiple variables. The causal pattern of intervariable relations within the theory is specified a priori. The goal is to determine whether a hypothesized theoretical model is consistent with data collected to reflect this theory. The consistency is evaluated through model-data fit, which indicates the extent to which the postulated network of relations among variables is plausible. SEM is a large-sample technique (usually N >200; e.g., Kline, 2005 , pp.111, 178), and the sample size required is somewhat dependent on model complexity, the estimation method used, and the distributional characteristics of observed variables (Kline, pp.14-15). SEM has a number of synonyms and special cases in the literature, including path analysis, causal modeling, and covariance structure analysis. We briefly introduce the most common and basic SEM models in the following, and discuss some of the issues widely encountered in practice. Readers are referred to Kline ( 2005 ) for an accessible introductory text.

Note. Table entries are estimates (standard errors). All parameter estimates are significantly different from zero at the .05 level by large sample z-tests.

Path Models

Path analysis is an extension of multiple regression, in that it involves various multiple regression models or equations that are estimated simultaneously. This provides a more effective and direct way of modeling mediation, indirect effects, and other complex relationships among variables. Path analysis can be considered a special case of SEM, in which structural relations among overt, observable variables are modeled. Structural relations are hypotheses about directional influences or causal relations of multiple variables (e.g., how intervention will affect depression scores, which will in turn affect reading comprehension scores).

In SEM in general, a variable can serve both as a source variable (called an exogenous variable, which is analogous to an independent variable) and a result variable (called an endogenous variable, which is analogous to a dependent variable) in a chain of causal hypotheses. When a variable is both a source and a result, it is often called a mediator . As an example, suppose that depression has a direct effect on brain activity which, in turn, is hypothesized to affect reading comprehension. In this case, brain activity is a mediator between depression and reading comprehension; it is the source variable for reading comprehension, and the result variable for depression. Furthermore, feedback loops among variables (e.g., reading comprehension can, in turn, affect depression in the example) are permissible in SEM, as are reciprocal effects (e.g., depression and reading comprehension affect each other).

In path analyses, specific, observed variables are treated as if they are measured without error, which is an assumption that does not likely hold in most social and behavioral sciences. When observed variables contain error, estimates of path coefficients may be biased in unpredictable ways, especially for complex models (e.g., Bollen, 1989 , pp. 151–178). Estimates of reliability for the measured variables, if available, can be incorporated into the model to fix their error variances (e.g., squared standard error of measurement via classical test theory, see later sections on reliability and on parameter estimation in individual assessment ).

Measurement or Factor Analysis Model

Alternatively, if multiple observed variables that are supposed to measure the same latent constructs are available, then a measurement (or factor analysis) model can be used to separate the common variances of the observed variables from their error variances, thus correcting the coefficients in the model for unreliability. The measurement of latent variables originated from psychometric theories. Unobserved latent variables cannot be measured directly, but are indicated or inferred by responses to a number of observable variables (indicators). Latent constructs such as depression or reading ability are often gauged by responses to a battery of items that are designed to tap those constructs. Responses of a study participant to those items are supposed to reflect where the participant stands on the latent variable. Statistical techniques such as factor analysis, exploratory or confirmatory, have been widely used to examine the number of latent constructs underlying the observed responses, and to evaluate the adequacy of individual items or variables as indicators for the latent constructs they are supposed to measure.

The measurement model in SEM is evaluated through confirmatory factor analysis (CFA). The number of factors in CFA is assumed known. In SEM, these factors correspond to the latent constructs represented in the model. Once the measurement model has been specified by the researcher, structural relations of the latent factors are then modeled essentially the same way as they are in path models. The combination of confirmatory factor analysis models with path models on the latent constructs represents the general SEM framework in analyzing covariance structures.

In general, every SEM analysis goes through the steps of model specification, model estimation, model evaluation, and, possibly, model modification, provided that the modification makes theoretical sense. A sound model is theory-based. Theory is based on findings in the literature, knowledge in the field, or one’s logical deduction, or even educated guesses, from which causes and effects among variables within the theory are specified. Recall the above research interest in the relationship between depression and reading comprehension. Because depression and reading comprehension ability are not directly observed, but inferred from individuals’ responses to a battery of items, they are considered latent variables. One can model the effect of the latent depression variable on children’s latent reading comprehension ability by incorporating a measurement model for each latent construct in the general framework of SEM, to take into account measurement error and unique variances of individual indicator variables. The structural relationship between the latent depression variable and latent reading comprehension ability would be of main interest.

SEM is a large-sample technique. That is, model estimation and statistical inference or hypothesis testing regarding the specified model and individual parameters are appropriate only if sample size is not too small for the estimation method chosen. The sample size required to provide unbiased parameter estimates and accurate model fit information for SEM models depends on model characteristics such as model size, as well as score characteristics of measured variables such as score scale and distribution. Larger models require larger samples to provide stable parameter estimates, and larger samples are required for categorical or non-normally distributed variables than for continuous or normally distributed variables. A general rule of thumb is that the minimum sample size should be no less than 200 (preferably no less than 400, especially when observed variables are not multivariate normally distributed) or 5 to 20 times the number of parameters to be estimated, whichever is larger (e.g., Kline, 2005 , pp.111, 178). Larger models often contain a larger number of model parameters, and hence demand larger sample sizes.

A measurement instrument may be theorized to have hierarchically structured factors. Many published measurement instruments provide scores for several subscales, presumably based on factor analysis results of item level responses. Observed subscale scores are often sum, mean, or some other simple linear functions of item responses to the group of items that share a large amount of common variance. For instance, the Children’s Depression Inventory (CDI; Kovacs, 1992 ) contains 27 items, from which 5 subscales (first order latent variables) are derived. The 5 subscales are negative mood , interpersonal problems , ineffectiveness , anhedonia (i.e., impaired ability to experience pleasure, including losing energy, sleep, and appetite), and negative self-esteem (Kovacs, 1992 ). The 5 subscales can serve as indicators for the general latent depression variable. Whether one should use the 5 subscales, or a single general scale of depression, depends on one’s interest and the strength of correlation among the subscales. If the interest is in the effect of individual subscales, then it makes little sense to combine them into a single scale, especially if intercorrelations between subscales are not very high. On the other hand, if the subscales are highly correlated, and using 5 individual scales may make the model substantially more complicated, then it is more convenient to combine them into a single scale.

The CDI appears to have hierarchical factor structure. The question is whether one should include a hierarchical factor model in a full SEM model. A number of factors need to be considered before a decision can be made. If a hierarchical factor model is included, the lowest level observed indicator variables are item level responses. Most item level responses are categorical (e.g., dichotomous—correct or incorrect for achievement tests, 5- or 7-point Likert type scale). Categorical responses are, by definition, not normally distributed and require alternative treatment, as the normality assumption for common estimation methods is violated. Alternative estimation methods, such as weighted least squares or robust statistics, usually require larger sample sizes to provide unbiased parameter and standard error estimates (e.g., Boomsma & Hoogland, 2000 ). Compared to a simple CFA model using subscales as observed indicator variables for the latent depression construct, the hierarchical CFA model contains substantially larger number of parameters. Accordingly, sample size required will be larger for the hierarchical CFA model than for the simple CFA model, if one follows the 5–20 per parameter recommendation. That is, the answer depends at least partly on sample size.

Compared to simpler models with fewer parameters and continuous outcome variables, complex models and categorical outcome variables are more likely to encounter estimation problems such as nonconvergence or improper solutions (i.e., some parameter estimates are out of range; e.g., correlation greater than 1, negative variance). These problems may result if a model is ill-specified (e.g., the model is not “identified,” indicating that there does not exist a unique solution), the data are problematic (e.g., sample size is too small, variables are highly correlated, etc.), or both. Standard error for individual parameters may not be properly estimated if multicollinearity (i.e., some variables are linearly dependent or strongly correlated) occurs. In any event, nonconverged solutions or improper solutions are not interpretable. In that case, it may be a necessity to deal with data problems prior to estimating the model of interest, or simplify the model if the problem does not appear to be related to data characteristics.

In the case of the CDI example, one can probably use observed subscale scores as indicators for the latent depression variable instead of using a hierarchical factor analysis model (see Figure 7.4 for the conceptual model of modeling the effect of depression on reading comprehension). This will not only simplify the model, but also alleviate the categorical indicator variable concern, because subscale scores are composites of item scores and have more unique score points. The publisher of CDI provides T-scores for each of the 5 subscales. Table 7.9 presents simple descriptive statistics for a hypothetical data set with 5 subscale scores of CDI, and reading comprehension scores on the T-scale (i.e., population mean = 50 and population standard deviation = 10).

The conceptual model of Figure 7.4 was fitted to the hypothetical data using maximum likelihood estimation. The overall model goodness-of-fit is reflected by the magnitude of discrepancy between the sample covariance matrix and the covariance matrix implied by the model with the parameter estimates. When sample size is large, a chi-square test of model goodness-of-fit is often used. Unfortunately, this test statistic has been found to be extremely sensitive to sample size. That is, the model may fit the data reasonably well, but the chi-square test may reject the model because of large sample size.

Conceptual Model for Modeling The Effect of Depression on Reading Comprehension (Note. For illustration purpose, a simple model with one latent variable instead of two is used.)

Note. NM=Negative mood; IP=interpersonal problems; IE=ineffectiveness; AH= anhedonia; NS=negative self-esteem; RC=reading comprehension.

A variety of alternative goodness-of-fit indices has been developed to supplement the chi-square statistic. Incremental fit indices measure the increase in fit relative to a baseline model (often one in which all observed variables are uncorrelated). Examples of incremental fit indices include Tucker-Lewis Index (TLI; Tucker & Lewis, 1973 ) and Comparative Fit Index (CFI; Bentler, 1989 , 1990 ). Higher values of incremental fit indices indicate larger improvement over the baseline model in fit. Values in the .90s (or, more recently, ≥ .95) are generally accepted as indications of good fit. Absolute fit indices measure the extent to which the specified model of interest reproduces the sample covariance matrix. Examples of absolute fit indices include standardized root mean square residual (SRMR; Bentler, 1995 ) and the root mean square error of approximation (RMSEA; Steiger & Lind, 1980 ). Lower values of SRMR and RMSEA indicate better model–data fit.

It is generally recommended that multiple indices be considered simultaneously when overall model fit is evaluated. For instance, Hu and Bentler ( 1999 ) proposed a 2-index strategy; that is, reporting SRMR along with one of the fit indices (e.g., CFI or RMSEA). They also suggested the following criteria for an indication of good model-data fit using those indices: CFI ≥ .95, SRMR ≤ .08, and RMSEA ≤ .06. For the hypothetical example, the model appeared to fit the data well. Chi-squared (df = 9, N = 500) = 3.334, p = .95, indicated that the discrepancy between observed and model-implied covariance matrices was not statistically significant. Using the 2-index strategy recommended by Hu and Bentler ( 1999 ), SRMR and RMEAS for the model were .01 (<.08) and .00 (<.06) respectively, which also support the good fit of the model to the data.

Individual parameter and standard error estimates of the model are provided in Table 7.10 . All parameter and standard error estimates appeared to be reasonable in magnitude and direction. All standardized factor loading estimates for depression are higher than .60. The unstandardized estimate for the effect of the latent depression variable on the observed reading comprehension variable was -.306. That is, reading comprehension T-scores were expected to decrease by .306 for one unit increase in depression on the T-score scale. Note that the observed variables do not need to be on the same scale; the same T-score scale was used in this example for convenience. The corresponding standardized estimate was -.241, suggesting that reading comprehension scores were expected to decrease by .241 standard deviation units per each standard deviation increase in depression. Although the estimated effect was significantly different from zero at the .05 significance level (|-.306/.061| = 5.02 > 1.96), the standardized residual variance for reading comprehension indicated that 94.2% of the variance in reading comprehension scores was unaccounted for by depression.

Note. Table values are Maximum Likelihood estimates. NM=Negative mood; IP=interpersonal problems; IE=ineffectiveness; AH= anhedonia; NS=negative self-esteem; RC=reading comprehension.

a Fixed parameter to set the scale of the latent variable.

Had the model failed to fit the data, post hoc modifications can be made based on the evaluation of modification indices and expected change in parameter estimates, provided that such modifications are supported by theory. However, it is often more defensible to consider multiple alternative models a priori. That is, multiple models (e.g., based on competing theories or different sides of an argument) should be specified prior to model fitting, and the best fitting model selected among the alternatives.

Other Models

Current developments in SEM include the modeling of mean structures in addition to covariance structures, the modeling of changes over time (growth models) and latent classes or profiles, the modeling of data having nesting structures (i.e., multilevel models), as well as the modeling of nonlinear effects (e.g., interaction). Models can also be different for different groups by analyzing multiple sample-specific models simultaneously (multiple sample analysis). Moreover, sampling weights or design effects can be incorporated for complex survey sampling designs. See Marcoulides and Schumacker ( 2001 ) and Marcoulides and Moustaki ( 2002 ) for more detailed discussions of the more recent developments in SEM.

Pros and Cons of Various Approaches

All statistical models introduced here, including generalized linear models, HLM, and SEM, can estimate linear or nonlinear relationships between variables, as well as moderating and mediating effects. Because SEM can simultaneously estimate multiple equations, it can model mediating effects more directly, along with reciprocal and feedback effects. Moreover, latent variables can be specified explicitly in SEM models.

In general, more recently advanced modeling frameworks like SEM and HLM allow greater flexibility in model specification. Hence, a variety of models can be conceived to test different theoretical hypotheses. In fact, it can be shown that more conventional analysis approaches, such as GLM or generalized linear models, are merely special cases in these more advanced frameworks. In addition, new applications of these models are continually emerging. As an example, it has been demonstrated over the last few years that certain item response theory models, which were developed in the field of psychometrics and must be estimated using specialized software programs, can be modeled in both the SEM and HLM framework. Also, random coefficients of HLM models can be treated as latent variables in SEM. That is, conceptually equivalent models can be specified under different modeling frameworks.

However, parameter estimates obtained from different modeling frameworks as implemented in different software programs might be slightly different, because different estimation techniques might be used. For GLM models, estimation is usually more efficient and straightforward, as there are often closed form solutions (i.e., there are finite solutions that can be calculated through a formula). For other generalized linear models (e.g., logistic regression models, loglinear models), HLM, and SEM, iterative estimation procedures are required, as there are frequently no closed form solutions (i.e., solutions cannot be calculated directly, but are successively approximated in iterative steps). Consequently, the evaluation of modeling results is more complicated, and larger sample sizes are typically required, for iterative estimation procedures. The burden of making sure that the model parameters are properly estimated rests on the shoulders of modelers. Practitioners or researchers who are interested in statistical modeling should familiarize themselves with not only modeling procedures, but also their associated estimation issues and limitations.

As briefly illustrated in this section, the same research question can be examined in different ways. Many data collection decisions (e.g., the choice of measurement instruments, the selection of variables, the number of data collection times, etc.), once implemented, are irreversible in practice. Therefore, it is essential to consider data analysis options and their limitations before starting to collect data.

Decisions about Individuals

School psychologists are researcher-practitioners. On the one hand, they conduct research to help confirm principles and to develop theoretical models to understand child behaviors and other school-related issues, and to guide practice. On the other hand, they design and implement interventions and programs to help students and families to succeed in school. Data are collected to evaluate the efficacy of these interventions. School psychologists also conduct educational and psychological assessments of individual children for placement and diagnostic purposes. While their research activities to test principles generally require the use of groups of participants as samples, their intervention evaluation and assessment activities most probably have only a single client or a few clients as the focus. For these activities, the “population” of interest is the single client or family, and no generalization is intended beyond that client or that family.

Even though no generalization to a larger population of people would be made for these individual assessments and/or interventions, this does not imply that no inference is to be made beyond the actual data obtained. In practice, these single-subject assessments and evaluations do involve sampling, and inferences are made beyond sample data. Specifically, for these situations, instead of drawing a sample of people from a larger population, we draw a sample of the child’s performance or the parents’ behaviors from all possible similar performances or incidents. That is, data are collected from within-subject sampling probes. Based on the data in this sample of performances or behaviors, we infer to other times, situations, conditions, and occasions. As such, inferential statistics do play a role in the analyses of these data. The general approach used in these single-subject situations depends on whether the decision to be made is one of assessing some trait of an individual, or one of evaluating the efficacy of an individual intervention program for a single person.

Individual Measurements

School psychologists routinely conduct individual assessments to evaluate a child’s achievement, intelligence, preferences, compliance, and a host of other behaviors, traits, and psychological constructs. The results of these assessments are used either as baseline information for intervention, or to help diagnosis, placement, or classification, among other types of decisions. Individual assessments, whether in the form of a mental test, a series of naturalistic observations, interviews or other formats, are inherently a sampling process. Through these assessment activities, we draw a sample of either natural behaviors or responses to a sample of assessment probes. Inferences are made from sample statistics to population parameters, except that the sample statistic in this context is called the “observed score” of the individual, and the corresponding population parameter of interest is called the “true score” of that same individual.

For inferential analyses of group statistics, discussed earlier, we use a combination of several strategies: unbiased sample estimators, significance testing, confidence intervals, and modeling. Similar strategies are used in individual assessments to infer from observed scores to true scores, with one exception: the significance testing approach is not used in individual assessments. In its place, an evaluative index called the reliability coefficient is used to describe the extent to which the observed scores represent the true scores. Unbiased observed scores are not obtained via statistical adjustments; instead, they are obtained via procedural safeguards. Specifically, assessment procedures are standardized such that the process through which observed scores are obtained is as identical as possible from person to person, and from situation to situation. Steps include strict adherence to standard assessment environment, administrative procedures, rater training, scoring protocol, and so on; such that there is as little as possible systematic and random variation between the assessments of different clients.

Reliability

In addition to attempting to obtain unbiased observed scores, a reliability coefficient is estimated for the observed scores. A reliability coefficient is the square of the correlation between observed scores and the corresponding theoretical true scores. The value of the reliability coefficient indicates the proportion of the variation in observed scores that is attributable to the variation in true scores. For example, a reliability coefficient of 0.8 indicates that 80% of the variance in observed scores among individuals assessed is due to variance in true scores. Reliability coefficients cannot be estimated directly. Instead, they are estimated indirectly through various strategies, under different mathematical or statistical assumptions, that would theoretically lead us to the values of the reliability coefficients. Most reliability coefficients today are estimated through strategies that are based on a set of assumptions called classical parallel tests assumptions. Under these assumptions, if we are able to identify two tests that meet a set of very restrictive statistical conditions (e.g., identical true scores, independence between true and error scores, identical variances), the correlation between the observed scores from these two tests is numerically equal to the reliability coefficient (i.e., square of correlation between observed and true scores) for either of the two tests. Strategies to obtain these parallel tests have included the test-retest method, equivalent forms method, and internal consistency methods. With the test-retest method, the same test is given to the same pilot sample of individuals at two points in time, generally several weeks apart. The correlation between the two sets of observed scores is an estimate of the reliability coefficient value. With the equivalent forms method, two interchangeable versions of the same test are administered to a pilot sample simultaneously, and the correlation between the two sets of observed scores is another estimate of the reliability coefficient value. Finally, with the internal consistency strategy, parallel tests are “created” internally within a single test. The most basic internal consistency strategy is the split-half method which takes half of the items within a single test as those of one parallel test, and the other items as those of another parallel test. The correlation between the observed scores of the two halves would be taken as an estimate of the reliability coefficients. This strategy provides an underestimation of the reliability coefficient. Generally, the Spearman-Brown prophecy formula (see Lord & Novick, 1968 , pp. 112-114) is applied to correct for the underestimation. Another alternative internal consistency strategy is to treat a K-item test as if there were K parallel 1-item tests. The average inter-item correlation, after correcting for length via the Spearman-Brown prophecy formula, would then be taken as an estimate of the reliability coefficient value. The result of this internal consistency strategy is called standardized item alpha . The result is numerically equal to the average of all possible split-half estimates from a single test, estimated from splitting the same test repeatedly into two halves in every possible manner.

A very popular method that employs the internal consistency method is the Cronbach alpha method. It is conceptually similar to the standardized item alpha method, but is based on a set of slightly more relaxed statistical assumptions, called the essentially tau-equivalent assumption s. As such, it is a slightly more realistic method than the other internal consistency methods. In practice, if all item scores are converted to standard z-scores before calculation, the Cronbach alpha value equals that of the standardized item alpha. If item scores are not converted to z-scores, Cronbach alpha is expected to be less than or equal to the value of standardized item alpha. An earlier method to estimate reliability developed in the 1930s, called the Kuder-Richardson Formula-20 (KR-20), is in fact a special case of Cronbach alpha when items are scored dichotomously. It is, essentially, a computationally more convenient method to calculate Cronbach alpha when items are dichotomous. With computers today, KR-20 is essentially obsolete. Another index, called Kuder-Richardson Formula-21 (KR-21), is a computationally quick conservative estimate of KR-20. Again, with high-speed computers today, KR-21 is not needed.

The above methods are within a general theoretical approach called the Classical Theory of Measurement . Within this approach, true score is defined as the mean of all possible observed scores that would be obtained by the same individual in an undefined, infinitely large universe under a variety of unspecified conditions. In other words, true score is an ill-defined, rather nebulous concept. An alternative approach that is particularly suited for multifaceted assessments, such as naturalistic observations, authentic assessments, and performance assessments, is that of the Generalizability Theory (G-theory). With the G-theory, true scores are very circumscribed. Specifically, to assess reliability one needs to specify the dimensions to which the scores are to be generalized. For example, the observations of a child’s behavior will be confined to only classroom behaviors during school hours, as observed by teachers or teachers’ assistants and as recorded by the items on a particular behavior checklist. True score in this case is the average of all possible observations within this well-defined set of conditions. It is theoretically possible that the same child might have a different true score for other situations. For example, the true score might be different from observations made at home by parents in the evening.

Given a particular assessment method, a person can potentially have numerous different true scores—called universe scores in G-theory. Therefore, for a given assessment method, there are potentially many reliability coefficients, called G-coefficients; one for each generalization and application scenario. G-coefficients are “constructed” indirectly, rather than estimated directly, from data. Data are collected within the confines of the circumscribed dimensions of generalization. These data are analyzed via the general analysis of variance (ANOVA) approach. Instead of evaluating F-ratios to test for significance in its usual application, ANOVA is used to estimate the variances of the dimensions and their interactions within the circumscribed universe/population. These variances form the building blocks to “construct” G-coefficients. To estimate a G-coefficient, one needs to project a usage scenario in terms of a number of practical considerations. These include such considerations as whether the interpretation will be norm-referenced or criterion-referenced, whether each dimension will be crossed or nested, random or fixed, how many items, raters, occasions, and any other relevant factors, will be used in the actual assessment. Based on these considerations, the variances estimated from the ANOVA are separated into those that may be considered components of the true variance, those that are components of the error variance, and those that are irrelevant to the situation. They are further adjusted by the projected sample size of each dimension in the application (e.g., number of observers used, number of items used during application under the usage scenario). G-coefficient is then calculated by:

Increasingly, many standardized achievement and clinical assessment tools used by school psychologists are being scaled via the Item Response theoretic approach, particularly via the Rasch model. Item Response Theory methods, including the Rasch model, do not lead to a reliability coefficient per se. Instead, they produce an information function, which is a conceptual, though not statistical, analog to the reliability coefficient.

Parameter Estimation In Individual Assessment

Reliability and G coefficients are indices used to evaluate the precision of assessment scores. Assessment analogs to parameter estimations in individual assessment include the building of confidence intervals, and the direct estimation of true scores. Confidence intervals are built by identifying a margin of error around the observed score of the individual. This is accomplished via the standard error of measurement statistic, which is calculated by:

where σ x is the standard deviation of the observed scores. We can build 68% confidence intervals by adding and subtracting 1 standard error of measurement from an observed score; or we can build a 95% confidence interval by adding and subtracting 1.96 standard errors of measurement from an observed score. The interpretation of these confidence intervals is that the true score of the individual is likely, with either a 68% confidence or a 95% confidence, respectively, to be within the range of scores encompassed by the confidence interval.

A more direct method is to estimate the true score of the individual via:

where ρ xx is the reliability or G coefficient, x is the observed score of the individual and μ x is the mean observed score of the norm group. Note, however, that this estimated true score will effectively be a linear transformation of the original raw score.

One particular consideration for school psychologists is that the reliability coefficient and its corresponding standard error of measurement commonly reported by test publishers, including those discussed above, can be viewed as the average reliability and standard error across all score levels. Reliability and standard errors can vary substantially for different scores. Since school psychologists most often work with children closer to the extreme ends of score range, where reliability and standard errors are particularly different from the average, they should consider estimating their own reliability coefficients and standard errors for the particular scores that they use. Methods to estimate these can be found in such references as Haertel ( 2006 , pp. 82-84) and Feldt and Brennan ( 1989 , pp. 123–124).

Rater/Observer Interchangeability

Many individual assessments used by school psychologists involve the use of raters or observers. One particular area of common data concern is rater/observer interchangeability. The issue of interest is whether the data obtained are independent of the particular rater/observer used in the assessment, which is taken to be a sign of data objectivity. To ascertain this, we calculate and evaluate inter-rater or inter-observer reliability, or agreement indices. These include correlations, proportion agreement indices, and/or kappa coefficients between the scores obtained by two independent raters or observers. It should be noted that inter-observer or inter-rater reliability is somewhat of a misnomer. Technically, reliability is a characteristic of scores, not raters/observers. The reliability coefficient value indicates the proportion of observed score variance that is due to true variance across subjects. Consistency between raters/observers does not assure score reliability. Therefore, inter-observer or inter-rater reliability is better described as rater/observer interchangeability. This interchangeability will enhance, but not guarantee, score reliability.

To evaluate score reliability by taking rater consistency, or the lack thereof, into account, one would need to conduct a multifaceted generalizability analysis in which raters are one of the facets of measurement. Brennan ( 2001 ) provides specific designs and procedures to accomplish this.

Validity And Classification Decisions

Validity in individual assessment refers to the adequacy of evidence to support the interpretation of assessment scores, and the decisions made on the basis of the scores. Validity evidence may be gathered from a variety of sources via different methodologies, which can range from qualitative to quantitative methods involving the analyses of objective, judgmental, or textual data. A variety of general statistical techniques can be applied for some particular pieces of validity evidence. Particularly common is the use of exploratory or confirmatory factor analyses to produce evidence that the internal structure of the response data from the assessment is consistent with the theoretical internal structure of the construct or trait being measured. Another cogent data analytic framework is the multitrait-multimethod matrix design (Campbell & Fiske, 1959 ) which can be implemented by a variety of statistical techniques, ranging from a correlation matrix, to analysis of variance, to confirmatory factor analytic procedures. The result is two particular compelling pieces of validity evidence, called convergent and discriminant validity, and is well within the conceptual frame of a cogent approach to validity known as the nomological net (Cronbach & Meehl, 1955 ). The Generalizability Theory approach can also be used to gathered validity evidence (see, for example, Kane 1982 . Also see Kane ( 2006 ) and Messick ( 1989 ) for a comprehensive discussion of validity issues.)

One area of validity concerns that is particularly relevant to school psychologists is evidence to support the validity of classifications of children or other individuals. Examples include classifying a child as gifted, as mentally retarded, as having a learning disability, or as suffering from attention deficit hyperactive disorder. At least parts of these decisions are based on test scores being above or below certain cutoff thresholds (e.g., having an IQ score of higher than a cutoff score of 130 may be part of the criteria to classify a child as being gifted), or having a score profile similar to that of a particular known category of children. Evidence to support the validity of these classification decisions includes questions of classification accuracy and clinical utility.

Classification accuracy includes such statistics as hit rate, kappa coefficient, sensitivity and specificity. Clinical utility includes such statistics as positive predictive power, negative predictive power, false positive rate, and false negative rate. These statistics are estimated either through data gathered from a sample of subjects with known classifications, or those who can be classified through some alternative “gold standard” criterion. The test of interest is administered to the sample, and the individuals in the sample are classified into the categories based solely on their scores on the test, and whether the scores are above or below the predetermined cutoff score. The consistency between classifications based on test scores, and the known classifications based on the gold standard, would be evaluated from various angles to produce a set of classification accuracy and clinical utility statistics, which include hit rate, sensitivity, specificity, positive predictive power, negative predictive power, false positive rate, and false negative rate. Appendix B provides a summary of how each of these indices is calculated from sample data. The context for the table in Appendix B is one in which a child is classified as either learning disabled or not, based on a test, and the gold standard is determined by whether the child needs special help or not, after following the child for three years without actually classifying the child.

Efficacy of Single-Subject Interventions

In addition to individual assessments, school psychologists often implement individualized interventions. Since these interventions involve only one or few subjects, many of the group data analysis techniques discussed early in this chapter cannot be applied directly to evaluate the efficacy of the interventions. Instead, internally valid conclusions are drawn regarding intervention efficacy, based on a coordinated orchestration between the manipulation of interrupted time-series data collection designs and corresponding parametric or nonparametric statistical analyses.

The most basic of interrupted time-series designs is the A-B Design, which consists of a no-intervention baseline “A” phase, and an intervention “B” phase, over a period of time in which observations of some behavior of the single subject are made. Figure 7.5 shows the frequency of disruptive behavior exhibited by a child in a hypothetical A-B design single-case study. The child shows disruptive behaviors in the classroom, and after observing and recording the behavior without intervention for five days, a school psychologist attempts an intervention

A-B Design with a Stable Baseline

(e.g., giving warnings) and continues to observe and record for a number of days afterwards. The efficacy of the intervention is evaluated by comparing the frequency of disruptive behaviors in the A phase against that in the B phase. If the intervention is effective, one would expect a decline in frequency in the intervention phase, as is shown in the hypothetical example in Figure 7.5 .

The A-B design is the most basic single-subject design. However, as a quasi-experimental design, it cannot eliminate some known potential threats to internal validity. Some of these threats may include maturation and autocorrelation. To control for additional threats to internal validity, features have been added to the basic A-B design, resulting in improved designs that may be applied in specific situations. One such improvement is the A-B-A design. In this design, a third phase is added, when feasible, to the end of the A-B design, by returning to a non-intervention phase from the intervention phase at some point. If there is a change in data (i.e., frequency or score returns to a level similar to that of the original baseline phase), the conclusion of intervention effectiveness is very cogent.

A particularly powerful alternative design is the multiple baseline design, which can be used if there are at least several subjects for whom the intervention can be appropriately implemented, individually and independently. For each subject, an A-B design is used and the same intervention is implemented. The A phase starts at the same time for all subjects. Observations are made at the same intervals and for the same duration for all subjects. The only difference across subjects is that the time point at which the intervention is initiated is staggered across subjects, each intervention starting at a different point. Ideally, the starting point of intervention for each subject is determined randomly, but after at least a certain number of baseline observations. Wolf and Risley ( 1971 ) recommended the use of 3 or 4 subjects with this design.

A design that is slightly more complicated than the A-B or the A-B-A design is the A-B-C-A-C-B design. This design is particularly appropriate when a second intervention, C, is attempted after the first intervention, B, shows little effect. A potential threat to the validity of conclusions regarding the effectiveness of C is multiple treatment interference; namely, that intervention C might be effective only with the prior help of intervention B. With the A-B-C-A-C-B design, at some point after the implementation of intervention C, we return to a no-intervention baseline phase. This non-intervention phase is then followed by the two interventions in a reversed order. By counterbalancing the order of the two interventions, the data would reveal whether multiple treatment interference has occurred.

In lieu of statistical analyses of these single-subject time-series data, visual inspections of graphic presentations have been widely used, and often advocated. Efficacy of intervention is determined by whether the data in the intervention phase are different from the data in the baseline phase. Although it has the merits of simplicity and convenience for use, there has been concern over whether judgment based on visual inspection is reliable and accurate. According to Brossart, Parker, Olson, and Mahadevan ( 2006 ), several studies found inter-rater consistencies of visual inspections to range from .40 to .60 (DeProspero & Cohen, 1979 ; Harbst, Ottenbacher, & Harris, 1991 ; Ottenbacher, 1990 ; Park, Marascuilo, & Gaylord-Ross, 1990 ). Park et al. ( 1990 ) found that even among expert raters, inter-rater agreements were 27% for graphs with statistically significant results, and 67% for graphs without significant results. Training did not seem to improve inter-rater agreements.

Statistical tests of significance seem to be a good alternative to mere visual inspections. Recently, there appears to be an increased interest in the use of statistical analysis in single-case studies. Kazdin ( 1982 ) suggests that statistical procedures may be used when (a) there is no stable baseline; (b) expected treatment effects cannot be well predicted, as with a new treatment; and (c) statistical control is needed for extraneous factors in naturalistic environments. Huitema ( 1986 ) further recommends that statistical analyses should be added whenever unambiguous results must be shared with other professionals.

However, the use of statistical tests for single-case study is still limited due to the problem of autocorrelation among errors, though it has been argued that this equally jeopardizes the validity of visual inspections. Autocorrelation refers to the dependence between observations at successive time points. Busk and Marascuilo ( 1988 ) computed lag-1 autocorrelations for 248 independent data sets from 44 studies in the Journal of Applied Behavior Analysis, published from 1975 to 1985. They found that 80% of the autocorrelations ranged from .10 to .49 for phases of size 5 to 18 observations; 40% of the baseline autocorrelations were greater than .25, and 59% of intervention phase autocorrelations were above .25. The existence of autocorrelation makes it inappropriate to use the traditional general linear model techniques, which assumes that residual errors are random, uncorrelated, normally distributed, and have constant variances (see earlier discussion on GLM). It has been found that when residuals in single-case data are positively autocorrelated, the standard errors for most traditional tests will be undesirably reduced, and the size of the resulting test statistics will be increased, as will the rate of Type I errors (Suen & Ary, 1987 ). Variations of general linear models have been proposed to compensate for autocorrelation; however, they did not necessarily remove or reduce the autocorrelation (Kazdin, 1976 ). One consequence of autocorrelation is that common significance testing techniques, such as t-test or F-ratios, cannot be used to analyze single-case study data.

Time-series analysis techniques, such as Box-Jenkins’ Autoregressive Integrated Moving Average (ARIMA), provide a valid set of procedures to be used in single-case designs. Time-series analysis attempts to apply the General Linear Model to determine if there is a slope change between the baseline and intervention phases. This determination is made only after trends and autocorrelations have been removed from the original time-series data. A major limitation of time-series technique when applied to single-subject data is that time-series methods such as ARIMA require a large number of observations, usually difficult to obtain in typical single-subject intervention situations. The general recommendation is to have at least 35 to 40 observations (Box & Jenkins, 1970 ; Gottman & Glass, 1978 ) for each phase in order to justify the model. Consequently, time-series statistical techniques are not widely used in the evaluation of the efficacy of single-subject interventions. See Glass, Willson, and Gottman ( 1975 ) for detailed discussions of the application of time-series analyses in single-subject behavioral observation research. See Box and Jenkins ( 1970 ) for in-depth treatment of the subject.

Randomization tests are another important set of methods that have been recommended for analyzing time-series data from single-subject studies. Originally developed by Fisher (see Fisher, 1951 ) in the 1930s, randomization tests do not make prior assumptions about the form of distribution from which the data comes (Todman & Dugard, 2001 ), and they also ameliorate the dependency problem by randomly assigning treatments (e.g. A and B treatments) to different occasions. The basic approach is one of significance testing, rather than attempting to model the parameters. With the obtained data, we generate the probability distribution of the test statistic, which is then used to determine the probability that the observed sample value can be the artifact of randomization, instead of being the effect of intervention (Marascuilo & Busk, 1988 ). For instance, in a single-subject A-B design, there are N A observations in the A Phase, and N B observations in the B Phase. The mean difference D ¯ s . = Y ¯ A − Y ¯ B would be the statistic of interest. To generate the probability distribution of D ¯ values, we calculate all possible values of D ¯ when the B phase is initiated, at each of the possible points in the time series. By dividing the number of D ¯ values thus calculated that is equal to or exceeds the observed D ¯ , by the total number of D ¯ values, we obtain the probability value for significance testing. If the probability is less than .05, the null hypothesis of the observed D ¯ being an artifact of random sampling fluctuation is rejected. Edgington ( 1967 , 1969 , 1975 ) provided a number of illustrative examples of how to implement this method.

The calculation of all the possible treatment assignments and their corresponding mean differences can be very labor-intensive. Marascuilo and Busk ( 1988 ) proposed to use rank tests, which is easier to perform and is available in some statistical software. Todman and Dugard ( 2001 ) have also provided detailed procedures for how to use SPSS, Minitab, and Excel respectively, to analyze randomization test data.

The above randomized A-B design is the simplest design, in which all A (baseline) treatment blocks precede all B treatment blocks. Wampold and Worsham ( 1986 ) developed a randomized multiple-baseline design, in which the experimenter employed a random selection of intervention times. The test statistic used in this design is based on the sum across S subjects of the difference in phase means. W = D ¯ 1 + D ¯ 2 + D ¯ 3 + D ¯ 4 + ... where D ¯ s . = Y ¯ A s − Y ¯ B s is the difference in phase means for subject S. For S subjects, there are a total of S! possible permutations for the random assignment of intervention time. We need to determine the proportion of these S! assignments in which the calculated W value is as large or larger than the W value obtained in the current data.

In the randomized multiple baseline design proposed by Marascuilo and Busk ( 1988 ), however, the random assignment of intervention to different subjects is different. If there are S subjects with T possible intervention points, the researcher would randomly select one of the T intervention points independently, for each of the S subjects. This allows for S T possible configurations of intervention initiation points. For example, for 5 subjects each having 5 potential points of initiation, there are a total of 5 5 = 3125 unique combinations of intervention arrangements. Compared to the Wampold-Worsham design, this design leads to more possible assignments, smaller p values and potentially more power (Ferron & Sentovich, 2002 ). In general, the principles and procedures for obtaining the probability value for significance testing for different designs are very similar. For more details about using randomization tests for multiple-baseline A-B and replicated A-B-A-B designs, see Marascuilo and Busk ( 1988 ).

In practice, randomization tests require that treatment be randomly assigned to occasions upon which the response measurements are obtained. The power of randomization tests varies depending on designs. Some empirical studies (Ferron, Foster-Johnson, & Kromrey, 2003 ; Ferron & Ware, 1995 ) show that it has an acceptable control over Type I error. Marascuilo and Busk ( 1988 ) also reported that risks of Type I error rates less than .05 could usually be generated with two or more subjects. In general, the power of the test can be increased by having a larger number of observations and experimental units (either individuals or groups) to which the intervention is applied.

Observations and Limitations

We are the beneficiaries of decades, and in some cases centuries, of creative and ingenious mathematical and statistical minds that have developed some very elegant, efficient, and powerful data analytic procedures to help us discern patterns, trends, and associations from otherwise unwieldy sample data. Without these analytical techniques, many statistical patterns and relations would have been otherwise buried deep in our data, obscured by the apparent chaos of the data. These analytic techniques have become increasingly sophisticated. They are now capable of extracting very complex patterns from our data that would not have been revealed by existing methods just a few decades ago. Yet, in spite of the sophistication of these methods, we cannot lose sight of the fact that they only point at patterns and associations in the existing data that we have collected. They are inherently incapable of providing explanations, interpretations, causal inferences, policy, or clinical implications. These necessarily need to come from the researcher and evaluator, based on theory and clinical considerations and guided by reason and experience.

The role of an a priori substantive theory, which is based on literature, experience, reasoning and practice, cannot be overemphasized. Increasingly, newer sophisticated modeling techniques are favored over the simpler conventional significance testing or confidence interval approaches for inferences from sample to the population. The logic of these modeling techniques in general is confirmatory in nature. One postulates one or several possible theory-based models in the population, and then examines whether sample data fit the model or which of several models fits the sample data best. This is the case whether the method used is one of general linear modeling, generalized linear modeling, hierarchical linear modeling, or structural equation modeling; whether there is an explicit statistic called a fit index or not; or whether the analysis is based on a least-squared criterion, or a maximum-likelihood criterion. The logic of this approach, however, can only work in one direction, not in the reversed direction. That is, the process is one in which, starting from theory or practice, we postulate a model. From the model, we decide what data to collect and then examine the data to see if the model is supported. However, we cannot start from data collection without a model, and then examine patterns and associations in the data in order to “find” a model. This is because, for any given set of sample data, there are many possible, some drastically different, models that will fit the data about equally well—including many models that the researcher has yet to imagine.

Results of data analysis may, in some limited situations, help to trigger insights toward the formulation of alternative theories, models, and explanations. This function becomes possible when data are from very large samples, and/or when the analyses have been replicated a number of times and all results have led to the same consistent pattern. These new insights would need to be confirmed via either a replication or, when appropriate, new data collection.

In general, for inferences to the population, large sample sizes are preferred when feasible, and in some cases are required. With larger sample sizes, parameter estimates will be more precise and statistical tests will be more powerful. More complex models require larger minimum sample sizes to provide adequate parameter estimates. Although simpler models such as GLM are more tolerant of smaller sample sizes, test statistics are generally more robust to violation of model assumptions with large samples.

There are practical limitations to data analysis techniques today, and not all theoretical relations or models can be analyzed. Scope of data collection for complex models is more extensive, and may require more resources than simpler models. Complex models are likely to have more variables and require more measures and larger sample sizes. Human and other resources are needed to administer measures, score responses, check and enter data. Lengthy questionnaires, tests, performances, or other measures that require extensive time to complete, may also diminish subjects’ motivation to participate or provide complete, careful responses. Consequently, missing data or unusable data may result.

The use of the significance testing approach has been under persistent criticism over the last several decades, primarily due to the widespread misuses and misinterpretation of results from this approach. Books and numerous academic journal articles have been written, and are continually being written, on this controversy. Many have advocated for an end to the use of significance testing, while others have defended its role in data analysis. There is nothing inherently wrong with significance testing per se, and significance testing remains one of the useful tools in data analysis. The problem arises from widespread attempts, some misguided by textbook authors, to over-interpret the results of significance tests, which have led to many erroneous conclusions. The logic of significance testing is convoluted, and the proper interpretation of results is very narrow and restrictive. Very restrictively, “significance” means that it is reasonable to refute the competing explanation that the pattern (statistics) observed in the sample data is an artifact of random sampling fluctuation. Conversely, nonsignificance means that random sampling fluctuation remains a viable competing explanation for the sample pattern. Most attempts to interpret significance beyond the confines of this narrow meaning have led to misinterpretations.

The advantages of large sample sizes, as well as issues of inferences to a larger population, are moot in single-subject research. Results of single-subject research inherently cannot be generalized to other subjects; albeit, when the study has been designed properly, results may be generalized to the same subject in other occasions and situations. There does not exist any data analysis technique that would enable one to generalize the results of a single-subject study to a larger population or to any other subjects. Generalization to a larger population needs to be built over time through replications of the study with other subjects. Generalization to other occasions and situations may, however, be made in single-subject research via the significance testing approach, such as when one of the variations of the randomization test method is employed. However, the use of randomization tests requires the ability to randomize the time point for the initiation of intervention, which may be unrealistic in many clinical situations.

Given that data analysis methods are techniques to find patterns and associations in a set of existing numerical data, the results of data analyses can only be as trustworthy and as meaningful as that of the original data. Therefore, reliability and validity of the sample data are of foremost importance prior to data analyses. Of the two, validity is by far more critical. Poor reliability will reduce statistical power. However, it is possible to compensate for the reduced statistical power to some extent via other contributors of power, such as large sample sizes, large effect sizes, or homogenous population. When there is a lack of evidence to support valid interpretation or use of the scores or other forms of data in the study, however, data analyses may prove to be little more than numerical exercises.

These two approaches to comparing independent group means are not mathematically equivalent, and may occasionally result in different conclusions about population mean differences.

Part of the introduction is based on Lei ( 2006 ) and Lei and Wu ( 2007 ).

Appendix A Formulas of standard errors for some common parameters

Standard error of the mean: σ ^ x ¯ = s n , where s = ∑ i= 1 n X i − X ¯ ) 2 n − 1 , n is the sample size.

Standard error for independent group mean difference: σ ^ X ¯ 1 − X ¯ 2 = ( n 1 − 1 ) s 1 2 + ( n 2 − 1 ) s 2 2 n 1 + n 2 − 2 ( 1 n 1 + 1 n 2 ) , where S 1 and S 2 are S for the two independent groups 1 and 2, respectively; n 1 and n 2 are sample sizes for groups 1 and 2, respectively.

Standard error for dependent group mean difference ( D ¯ = X ¯ 1 − X ¯ 2 ): σ ^ D ¯ = s D n , where s D = ∑ i = 1 n ( X 1 i − X 2 i ) 2 n − 1 , and n is the number of pairs.

Standard error for proportion with large sample size: σ ^ p = p ( 1 − p ) n − 1 , where p is the sample proportion.

where p 0 is the hit rate and p c is chance agreement, which can be calculated by:

Bentler, P. M. ( 1989 ). EQS structural equations program manual . Los Angeles, CA: BMDP Statistical Software.

Google Scholar

Google Preview

Bentler, P. M. ( 1990 ). Comparative fit indexes in structural models. Psychological Bulletin , 107 , 238–246.

Bentler, P. M. ( 1995 ). EQS structural equations program manual . Encino, CA: Multivariate Software, Inc.

Bollen, K. A. ( 1989 ). Structural equations with latent variables . New York: Wiley.

Boomsma, A. & Hoogland, J. J. ( 2000 ). The robustness of LISREL modeling revisited. In R. Cudeck, S. H. C. du Toit, & D. Sörbom (Eds.). Structural equation modeling: Present and future (pp. 139–168). Lincolnwood, IL: Scientific Software International, Inc.

Box, G. E. P. & Jenkins, G. M. ( 1970 ). Time-series analysis: Forecasting and control . San Francisco: Holden Day.

Brennan, R. L. ( 2001 ) Generalizability Theory . New York: Springer-Verlag.

Brooks-Gunn, J. ( 2004 ). Don’t throw out the baby with the bathwater: Incorporating behavioral research into evaluation. Social Policy Report , 18 (2), 14–15.

Brossart, D. F., Parker, R. I., Olson, E. A., & Mahadevan, L. ( 2006 ). The relationship between visual analysis and five statistical analyses in a simple AB single-case research design. Behavior Modification , 30 (5), 531–563.

Busk, P. L., & Marascuilo, L. A. ( 1988 ). Autocorrelation in single-subject research: A counter argument to the myth of no autocorrelation. Behavioral Assessment , 10 , 229–242.

Campbell, D. T., & Fiske, D. W. ( 1959 ). Convergent and discriminant validity in the multitrait–multimethod matrix. Psychological Bulletin , 56 , 81–105.

Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. ( 2003 ). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah, NJ: Lawrence Erlbaum Associates.

Cook, T. D. ( 2004 ). Beyond advocacy: Putting history and research on research into debates about the merits of social experiments. Social Policy Report , 18 (2), 5–6.

Cottingham, P. ( 2004 ). Why we need more, not fewer, gold standard evaluations. Social Policy Report , 18 (2), 13.

Cronbach, L. J. & Meehl, P. E. ( 1955 ). Construct validity in psychological tests. Psychological Bulletin , 52 , 281–301.

DeProspero, A. & Cohen, S. ( 1979 ). Inconsistent visual analyses of intrasubject data. Journal of Applied Behavior Analysis , 12 , 573–579.

Edgington, E.S. ( 1967 ). Statistical inference from N = 1 experiments. Journal of Psychology , 65 , 195–199.

Edgington, E. S. ( 1969 ). Approximate randomization tests. Journal of Psychology , 72 , 143–179.

Edgington, E.S. ( 1975 ). Randomization tests for one-subject operant experiments. Journal of Psychology , 90 , 57–68.

Feldt, L. S. & Brennan, R. L. ( 1989 ). Reliability. In R. L. Linn (Ed.). Educational measurement (3 rd ed., pp. 105–146). New York: Macmillan.

Ferron, J., Foster-Johnson, L., & Kromrey, J. D. ( 2003 ). The functioning of single-case randomization tests with and without random assignment. The Journal of Experimental Education , 71 , 267–288.

Ferron, J. & Sentovich, C. ( 2002 ). Statistical power of randomization tests used with multiple-baseline designs. The Journal of Experimental Education , 70 (2), 165–178.

Ferron, J. & Ware, W. ( 1995 ). Analyzing single-case data: The power of randomization tests. The Journal of Experimental Education , 63 , 167–178.

Fisher, R. A. ( 1951 ). The design of experiments (6th ed.). New York: Hafner.

Glass, G. V. & Hopkins, K. D. ( 1995 ). Statistical methods in education and psychology (3rd ed.). Boston, MA: Allyn and Bacon.

Glass, G. V., Willson, V. L., & Gottman, J. M. ( 1975 ). Design and analysis of time-series experiments . Boulder: Colorado Associated University Press.

Gottman, J. M. & Glass, G. V. ( 1978 ). Analysis of interrupted time-series experiments. In T. R. Kratochwill (Ed.). Single subject research: Strategies for evaluating change (pp. 197–235). New York: Academic Press.

Haertel, E. H. ( 2006 ). Reliability. In R. L. Brennan (Ed.), Educational measurement (4 th ed., pp. 65–110). Westport, CT: Praeger.

Hahn, H., Neurath, O., & Carnap, R. ( 1929 ). Wissenschaftliche weltauffassung: Der wiener kreis (A scientific world-view: The Vienna circle). Vienna: Ernst Mach Society.

Harbst, K. B., Ottenbacher, K. J., & Harris, S. R. ( 1991 ). Interrater reliability of therapists’ judgments of graphed data. Physical Therapy , 71 , 107–115.

Hosmer, D.W. Jr., & Lemeshow, S. ( 2000 ). Applied logistic regression (2nd ed.). New York: John Wiley & Sons, Inc.

Hu, L.-T. & Bentler, P. ( 1999 ). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling , 6 , 1–55.

Huitema, B. E. ( 1986 ). Autocorrelation in behavioral research: Wherefore art thou? In A. Poling & R. W. Fuqua (Eds.). Research methods in applied behavior analysis: Issues and advances . (pp. 187–208). New York: Plenum Press.

Kane, M. T. ( 1982 ). A sampling model for validity. Applied Psychological Measurement , 6 (2), 125–160.

Kane, M. T. ( 2006 ). Validation. In R. L. Brennan (Ed.). Educational measurement (4 th ed., pp. 17–64). Westport, CT: Praeger.

Kazdin, A. E. ( 1976 ). Statistical analyses for single-case experimental designs. In M. Hersen & D. H. Barlow (Eds.). Single case experimental designs: Strategies for behavioral change (pp. 265–316). New York: Pergamon Press.

Kazdin, A. E. ( 1982 ). Single-case research designs: Methods for clinical and applied settings . New York: Oxford University Press.

Kirk, R. E. ( 1998 ). Statistics: An introduction (4th ed.). New York, NY: Harcourt Brace College Publishers.

Kline, R. B. ( 2005 ). Principles and practice of structural equation modeling (2nd ed.). New York: Guilford Press.

Kovacs, M. ( 1992 ). Children’s depression inventory . North Tonawanda, NY: Multi-Health System.

Kreft, I. & de Leeuw, J. ( 1998 ). Introducing multilevel modeling . London: Sage.

Lakatos, I. ( 1970 ). Falsification and the methodology of scientific research programmes. In I. Lakatos and A. Musgraove (Eds.). Criticism and the growth of knowledge . London: Cambridge University Press.

Lei, P.-W. ( 2006 ). Structural equation modeling (SEM). In N. J. Salkind & K. L. Rasmussen (Eds.). Encyclopedia of measurement and statistics (pp. 973–976). Thousand Oaks, CA: Sage.

Lei, P.-W. & Wu, Q. ( 2007 ). Introduction to structural equation modeling: Issues and practical considerations. Educational Measurement: Issues and Practices , 26 (3), 33–43.

Lord, F. M. & Novick, M. R. ( 1968 ). Statistical theories of mental test scores . Reading, MA: Addison-Wesley.

Marascuilo, L.A. & Busk, P. L. ( 1988 ). Combining statistics for multiple-baseline AB and replicated ABAB designs across subjects. Behavioral Assessment , 10 , 1–28.

Marcoulides, G. A. & Moustaki, I. ( 2002 ). Latent variable and latent structure models . Mahwah, NJ: Lawrence Erlbaum Associates.

Marcoulides, G. A. & Schumacker, R. E. (Eds.). ( 2001 ). New developments and techniques in structural equation modeling . Mahwah, NJ: Lawrence Erlbaum Associates.

McCall, R. B. & Green, B. L. ( 2004 ). Beyond the methodological gold standards of behavioral research: Considerations for practice and policy. Policy Report , 18 (2), 1, 3–4, 6–19.

Messick, S. ( 1989 ). Validity. In R. L. Linn (Ed.). Educational measurement (3rd ed., pp. 13–104). New York: Macmillan.

Ottenbacher, K. J. ( 1990 ). When is a picture worth a thousand p values? A comparison of visual and quantitative methods to analyze single subject data. Journal of Special Education , 23 , 436–449.

Park, H., Marascuilo, L., & Gaylord-Ross, R. ( 1990 ). Visual inspection and statistical analysis of single-case designs. Journal of Experimental Education , 58 , 311–320.

Raudenbush, S. W. & Bryk, A. S. ( 2002 ). Hierarchical linear models: Applications and data analysis methods (2nd ed.). Thousand Oaks, CA: Sage.

Salsburg, D. ( 2001 ). The lady tasting tea: How statistics revolutionized science in the twentieth century . New York: Freeman

Snijders, T. & Bosker, R. ( 1999 ). Multilevel analysis: An introduction to basic and advanced multilevel modeling . London: Sage.

Steiger, J. H. & Lind, J. C. ( 1980 , May). Statistically based tests for the number of common factors . Paper presented at the annual meeting of the Psychometric Society, Iowa City, IA.

Suen, H. K. & Ary, D. ( 1987 ). Autocorrelation in applied behavior analysis: Myth or reality? Behavioral Assessment , 9 , 125–130.

Todman, J. B. & Dugard, P. ( 2001 ). Single-case and small-n experimental design: A practical guide to randomization tests . Mahwah, NJ: Lawrence Erlbaum Associates.

Tucker, L. R., & Lewis, C. ( 1973 ). A reliability coefficient for maximum likelihood factor analysis. Psychometrika , 38 , 1–10.

Wampold, B. E., & Worsham, N. L. ( 1986 ). Randomization tests for multiple-baseline designs. Behavioral Assessment , 8 , 135–143.

Wolf, M. M. & Risley, T. R. ( 1971 ). Reinforcement: Applied research. In R. Glaser (Ed.). The nature of reinforcement . pp. (310–325). New York: Academic Press.

About Oxford Academic
Publish journals with us
University press partners
What we publish
New features
Open access
Institutional account management
Rights and permissions
Get help with access
Accessibility
Advertising
Media enquiries
Oxford University Press
Oxford Languages
University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

Copyright © 2024 Oxford University Press
Cookie settings
Cookie policy
Privacy policy
Legal notice

This Feature Is Available To Subscribers Only

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

Home » Data Analysis – Process, Methods and Types

Data Analysis – Process, Methods and Types

Table of Contents

Data Analysis

Definition:

Data analysis refers to the process of inspecting, cleaning, transforming, and modeling data with the goal of discovering useful information, drawing conclusions, and supporting decision-making. It involves applying various statistical and computational techniques to interpret and derive insights from large datasets. The ultimate aim of data analysis is to convert raw data into actionable insights that can inform business decisions, scientific research, and other endeavors.

Data Analysis Process

The following are step-by-step guides to the data analysis process:

Define the Problem

The first step in data analysis is to clearly define the problem or question that needs to be answered. This involves identifying the purpose of the analysis, the data required, and the intended outcome.

Collect the Data

The next step is to collect the relevant data from various sources. This may involve collecting data from surveys, databases, or other sources. It is important to ensure that the data collected is accurate, complete, and relevant to the problem being analyzed.

Clean and Organize the Data

Once the data has been collected, it needs to be cleaned and organized. This involves removing any errors or inconsistencies in the data, filling in missing values, and ensuring that the data is in a format that can be easily analyzed.

Analyze the Data

The next step is to analyze the data using various statistical and analytical techniques. This may involve identifying patterns in the data, conducting statistical tests, or using machine learning algorithms to identify trends and insights.

Interpret the Results

After analyzing the data, the next step is to interpret the results. This involves drawing conclusions based on the analysis and identifying any significant findings or trends.

Communicate the Findings

Once the results have been interpreted, they need to be communicated to stakeholders. This may involve creating reports, visualizations, or presentations to effectively communicate the findings and recommendations.

Take Action

The final step in the data analysis process is to take action based on the findings. This may involve implementing new policies or procedures, making strategic decisions, or taking other actions based on the insights gained from the analysis.

Types of Data Analysis

Types of Data Analysis are as follows:

Descriptive Analysis

This type of analysis involves summarizing and describing the main characteristics of a dataset, such as the mean, median, mode, standard deviation, and range.

Inferential Analysis

This type of analysis involves making inferences about a population based on a sample. Inferential analysis can help determine whether a certain relationship or pattern observed in a sample is likely to be present in the entire population.

Diagnostic Analysis

This type of analysis involves identifying and diagnosing problems or issues within a dataset. Diagnostic analysis can help identify outliers, errors, missing data, or other anomalies in the dataset.

Predictive Analysis

This type of analysis involves using statistical models and algorithms to predict future outcomes or trends based on historical data. Predictive analysis can help businesses and organizations make informed decisions about the future.

Prescriptive Analysis

This type of analysis involves recommending a course of action based on the results of previous analyses. Prescriptive analysis can help organizations make data-driven decisions about how to optimize their operations, products, or services.

Exploratory Analysis

This type of analysis involves exploring the relationships and patterns within a dataset to identify new insights and trends. Exploratory analysis is often used in the early stages of research or data analysis to generate hypotheses and identify areas for further investigation.

Data Analysis Methods

Data Analysis Methods are as follows:

Statistical Analysis

This method involves the use of mathematical models and statistical tools to analyze and interpret data. It includes measures of central tendency, correlation analysis, regression analysis, hypothesis testing, and more.

Machine Learning

This method involves the use of algorithms to identify patterns and relationships in data. It includes supervised and unsupervised learning, classification, clustering, and predictive modeling.

Data Mining

This method involves using statistical and machine learning techniques to extract information and insights from large and complex datasets.

Text Analysis

This method involves using natural language processing (NLP) techniques to analyze and interpret text data. It includes sentiment analysis, topic modeling, and entity recognition.

Network Analysis

This method involves analyzing the relationships and connections between entities in a network, such as social networks or computer networks. It includes social network analysis and graph theory.

Time Series Analysis

This method involves analyzing data collected over time to identify patterns and trends. It includes forecasting, decomposition, and smoothing techniques.

Spatial Analysis

This method involves analyzing geographic data to identify spatial patterns and relationships. It includes spatial statistics, spatial regression, and geospatial data visualization.

Data Visualization

This method involves using graphs, charts, and other visual representations to help communicate the findings of the analysis. It includes scatter plots, bar charts, heat maps, and interactive dashboards.

Qualitative Analysis

This method involves analyzing non-numeric data such as interviews, observations, and open-ended survey responses. It includes thematic analysis, content analysis, and grounded theory.

Multi-criteria Decision Analysis

This method involves analyzing multiple criteria and objectives to support decision-making. It includes techniques such as the analytical hierarchy process, TOPSIS, and ELECTRE.

Data Analysis Tools

There are various data analysis tools available that can help with different aspects of data analysis. Below is a list of some commonly used data analysis tools:

Microsoft Excel: A widely used spreadsheet program that allows for data organization, analysis, and visualization.
SQL : A programming language used to manage and manipulate relational databases.
R : An open-source programming language and software environment for statistical computing and graphics.
Python : A general-purpose programming language that is widely used in data analysis and machine learning.
Tableau : A data visualization software that allows for interactive and dynamic visualizations of data.
SAS : A statistical analysis software used for data management, analysis, and reporting.
SPSS : A statistical analysis software used for data analysis, reporting, and modeling.
Matlab : A numerical computing software that is widely used in scientific research and engineering.
RapidMiner : A data science platform that offers a wide range of data analysis and machine learning tools.

Applications of Data Analysis

Data analysis has numerous applications across various fields. Below are some examples of how data analysis is used in different fields:

Business : Data analysis is used to gain insights into customer behavior, market trends, and financial performance. This includes customer segmentation, sales forecasting, and market research.
Healthcare : Data analysis is used to identify patterns and trends in patient data, improve patient outcomes, and optimize healthcare operations. This includes clinical decision support, disease surveillance, and healthcare cost analysis.
Education : Data analysis is used to measure student performance, evaluate teaching effectiveness, and improve educational programs. This includes assessment analytics, learning analytics, and program evaluation.
Finance : Data analysis is used to monitor and evaluate financial performance, identify risks, and make investment decisions. This includes risk management, portfolio optimization, and fraud detection.
Government : Data analysis is used to inform policy-making, improve public services, and enhance public safety. This includes crime analysis, disaster response planning, and social welfare program evaluation.
Sports : Data analysis is used to gain insights into athlete performance, improve team strategy, and enhance fan engagement. This includes player evaluation, scouting analysis, and game strategy optimization.
Marketing : Data analysis is used to measure the effectiveness of marketing campaigns, understand customer behavior, and develop targeted marketing strategies. This includes customer segmentation, marketing attribution analysis, and social media analytics.
Environmental science : Data analysis is used to monitor and evaluate environmental conditions, assess the impact of human activities on the environment, and develop environmental policies. This includes climate modeling, ecological forecasting, and pollution monitoring.

When to Use Data Analysis

Data analysis is useful when you need to extract meaningful insights and information from large and complex datasets. It is a crucial step in the decision-making process, as it helps you understand the underlying patterns and relationships within the data, and identify potential areas for improvement or opportunities for growth.

Here are some specific scenarios where data analysis can be particularly helpful:

Problem-solving : When you encounter a problem or challenge, data analysis can help you identify the root cause and develop effective solutions.
Optimization : Data analysis can help you optimize processes, products, or services to increase efficiency, reduce costs, and improve overall performance.
Prediction: Data analysis can help you make predictions about future trends or outcomes, which can inform strategic planning and decision-making.
Performance evaluation : Data analysis can help you evaluate the performance of a process, product, or service to identify areas for improvement and potential opportunities for growth.
Risk assessment : Data analysis can help you assess and mitigate risks, whether it is financial, operational, or related to safety.
Market research : Data analysis can help you understand customer behavior and preferences, identify market trends, and develop effective marketing strategies.
Quality control: Data analysis can help you ensure product quality and customer satisfaction by identifying and addressing quality issues.

Purpose of Data Analysis

The primary purposes of data analysis can be summarized as follows:

To gain insights: Data analysis allows you to identify patterns and trends in data, which can provide valuable insights into the underlying factors that influence a particular phenomenon or process.
To inform decision-making: Data analysis can help you make informed decisions based on the information that is available. By analyzing data, you can identify potential risks, opportunities, and solutions to problems.
To improve performance: Data analysis can help you optimize processes, products, or services by identifying areas for improvement and potential opportunities for growth.
To measure progress: Data analysis can help you measure progress towards a specific goal or objective, allowing you to track performance over time and adjust your strategies accordingly.
To identify new opportunities: Data analysis can help you identify new opportunities for growth and innovation by identifying patterns and trends that may not have been visible before.

Examples of Data Analysis

Some Examples of Data Analysis are as follows:

Social Media Monitoring: Companies use data analysis to monitor social media activity in real-time to understand their brand reputation, identify potential customer issues, and track competitors. By analyzing social media data, businesses can make informed decisions on product development, marketing strategies, and customer service.
Financial Trading: Financial traders use data analysis to make real-time decisions about buying and selling stocks, bonds, and other financial instruments. By analyzing real-time market data, traders can identify trends and patterns that help them make informed investment decisions.
Traffic Monitoring : Cities use data analysis to monitor traffic patterns and make real-time decisions about traffic management. By analyzing data from traffic cameras, sensors, and other sources, cities can identify congestion hotspots and make changes to improve traffic flow.
Healthcare Monitoring: Healthcare providers use data analysis to monitor patient health in real-time. By analyzing data from wearable devices, electronic health records, and other sources, healthcare providers can identify potential health issues and provide timely interventions.
Online Advertising: Online advertisers use data analysis to make real-time decisions about advertising campaigns. By analyzing data on user behavior and ad performance, advertisers can make adjustments to their campaigns to improve their effectiveness.
Sports Analysis : Sports teams use data analysis to make real-time decisions about strategy and player performance. By analyzing data on player movement, ball position, and other variables, coaches can make informed decisions about substitutions, game strategy, and training regimens.
Energy Management : Energy companies use data analysis to monitor energy consumption in real-time. By analyzing data on energy usage patterns, companies can identify opportunities to reduce energy consumption and improve efficiency.

Characteristics of Data Analysis

Characteristics of Data Analysis are as follows:

Objective : Data analysis should be objective and based on empirical evidence, rather than subjective assumptions or opinions.
Systematic : Data analysis should follow a systematic approach, using established methods and procedures for collecting, cleaning, and analyzing data.
Accurate : Data analysis should produce accurate results, free from errors and bias. Data should be validated and verified to ensure its quality.
Relevant : Data analysis should be relevant to the research question or problem being addressed. It should focus on the data that is most useful for answering the research question or solving the problem.
Comprehensive : Data analysis should be comprehensive and consider all relevant factors that may affect the research question or problem.
Timely : Data analysis should be conducted in a timely manner, so that the results are available when they are needed.
Reproducible : Data analysis should be reproducible, meaning that other researchers should be able to replicate the analysis using the same data and methods.
Communicable : Data analysis should be communicated clearly and effectively to stakeholders and other interested parties. The results should be presented in a way that is understandable and useful for decision-making.

Advantages of Data Analysis

Advantages of Data Analysis are as follows:

Better decision-making: Data analysis helps in making informed decisions based on facts and evidence, rather than intuition or guesswork.
Improved efficiency: Data analysis can identify inefficiencies and bottlenecks in business processes, allowing organizations to optimize their operations and reduce costs.
Increased accuracy: Data analysis helps to reduce errors and bias, providing more accurate and reliable information.
Better customer service: Data analysis can help organizations understand their customers better, allowing them to provide better customer service and improve customer satisfaction.
Competitive advantage: Data analysis can provide organizations with insights into their competitors, allowing them to identify areas where they can gain a competitive advantage.
Identification of trends and patterns : Data analysis can identify trends and patterns in data that may not be immediately apparent, helping organizations to make predictions and plan for the future.
Improved risk management : Data analysis can help organizations identify potential risks and take proactive steps to mitigate them.
Innovation: Data analysis can inspire innovation and new ideas by revealing new opportunities or previously unknown correlations in data.

Limitations of Data Analysis

Data quality: The quality of data can impact the accuracy and reliability of analysis results. If data is incomplete, inconsistent, or outdated, the analysis may not provide meaningful insights.
Limited scope: Data analysis is limited by the scope of the data available. If data is incomplete or does not capture all relevant factors, the analysis may not provide a complete picture.
Human error : Data analysis is often conducted by humans, and errors can occur in data collection, cleaning, and analysis.
Cost : Data analysis can be expensive, requiring specialized tools, software, and expertise.
Time-consuming : Data analysis can be time-consuming, especially when working with large datasets or conducting complex analyses.
Overreliance on data: Data analysis should be complemented with human intuition and expertise. Overreliance on data can lead to a lack of creativity and innovation.
Privacy concerns: Data analysis can raise privacy concerns if personal or sensitive information is used without proper consent or security measures.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

Cluster Analysis – Types, Methods and Examples

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Discriminant Analysis – Methods, Types and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

reflective data

How Data Analysis Improve Decision Making

Big data is a game changer in the business world, so companies are starting to ramp up their digital transformation. The result has been a huge surge in demand for data analytics. We are seeing more trends being given birth due to the rise of data. Data analysis decision making has become the go-to strategy for success in 2019.

Data analysis is giving small businesses the opportunity to be even more competitive through the use of analytics.
Artificial intelligence and machine learning are disruptive technologies that are revolutionizing the landscape.

Big data has become adopted by more companies in recent years. We’ve seen the demand increase from 17% to 59% in just three years! As a result, businesses that use data analytics experienced an increase in profit that reached as high as 10%. Furthermore, those same businesses experienced a reduction in costs that also reached as high as 10%.

Data Analysis is helping companies make smarter decisions that lead to higher productivity and more efficient operations. It provides a significant competitive advantage.

Data Analysis is Making Smarter Decisions

Small businesses are experiencing the greatest impact of analysis, and this is not expected to slow down. The truth is that if your business does not follow through with these trends, then you’re going to find yourself at a significant disadvantage. It has become the cornerstone for all strategic business decisions.

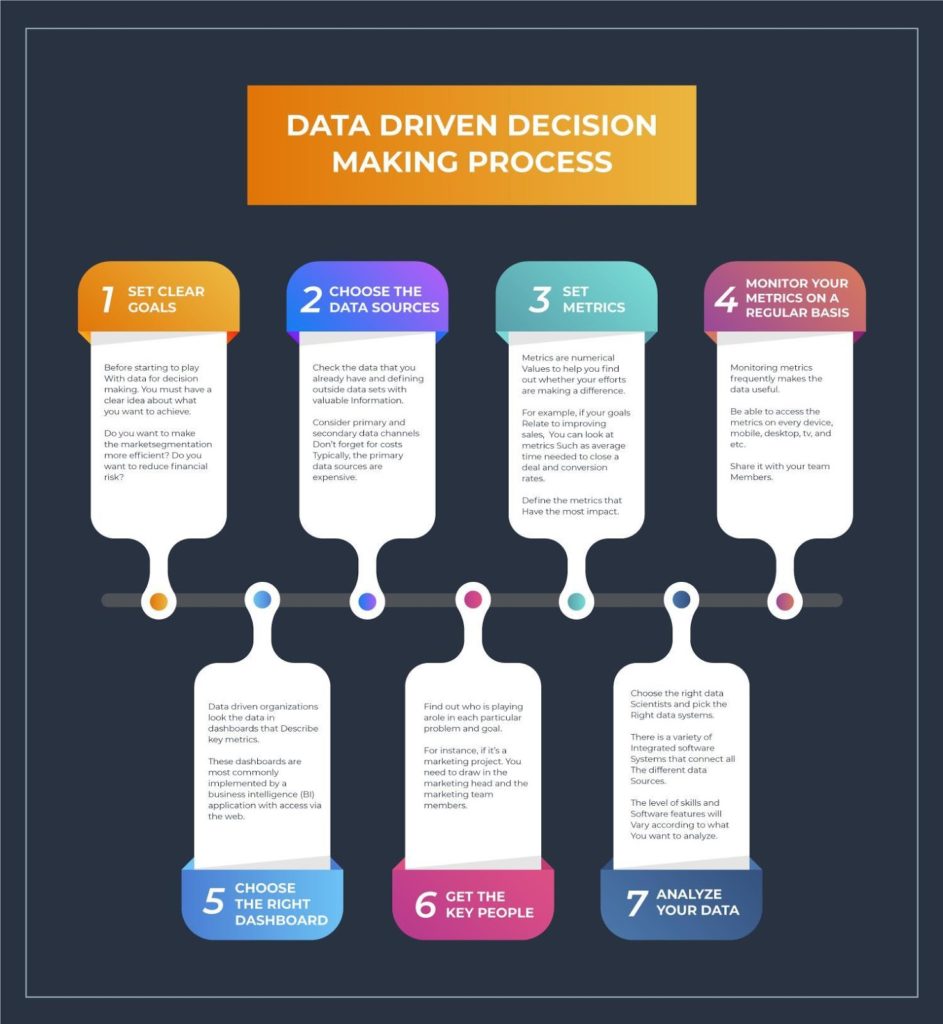
Finding the right audience is an important step to making better decisions moving forward. Business analytics gathers data from popular hubs like Facebook and Instagram, and this data is used to create a demographic of a brand’s ideal customers. In turn, this profile determines what types of features your customers want or need from specific products. So it is a powerful tool while deciding about how to improve current products and services; this is a powerful tool.

Using Data Analysis to Make the Most out of Consumer Patterns

Today’s businesses must know what their customers want to make the proper decisions moving forward. If the brick and mortar stores are not stocking the right products on their shelves, then they are going to experience a decrease in sales. If online providers are not offering the right services, then they will lose customers. The first step in business is to make sure you’re selling the right products to the right people.

That’s where business analytics comes into play. It provides the information necessary to make sure that your business is providing the right products and services. This process is known as predictive analysis and uses four methods:

Segmentation: Uses information about target customers to split them into separate categories based on demographics, behavior, and attitudes. Then specific products or services are targeted to these segments.
Forecasting: Uses analytics to predict specific patterns that allow businesses to understand the demand for a product or service beforehand.
Pricing: This is the process of analyzing data from various sources – usually competition – to determine how much a target market is willing to pay for a specific product or service.
Customer Satisfaction: Improving the customer journey is important, and customers today are not afraid to share what you’re doing wrong. Use this data to improve their experience.

In this era, consumers hold all of the power in business. A company must conform to the needs of its customers, or else they will be ignored. Customers expect preferential treatment. More importantly, consumers provide so much information that they expect businesses to know their patterns. Analytics allows for better planning and insight based on the patterns of their customers.

Companies that fully utilize their customer behaviors to make decisions outperform their competition by a whopping 85% ! Those same businesses also experienced an increase of 25% in their profits. It shows us that analytics is powerful because it identifies buying patterns. This information is then used to make important marketing decisions.

Data can Drive Performance

Small businesses can expect to spend a considerable amount of time analyzing data to identify buying patterns, but it is just as important to focus on performance. Data analysis plays a vital role internally within a company by providing insight into decision-based on improvements in efficiency. The idea is to streamline these business operations so that they are more time-efficient. Some examples include operational costs, product development, and workforce planning. Using insight provides a unique insight into complex internal business scenarios.

Businesses can use analytics to improve their profit margins by developing more efficient processes.

Risk Mitigation is Improved through Analytics

One of the biggest reasons why businesses need to use analytics to make better decisions is due to the risk being posed by the sheer amount of data being gathered. There is so much unstructured data being delivered that it’s easy to make the wrong decisions unless it’s properly analyzed. With that said, having the right data analytics strategy in place will predict risk and help make better decisions moving forward.

Business analytics also makes expansions much less risky since businesses have access to valuable information before they make their final decision. It’s also possible to interact with the information so that it can be used to create an actionable plan.

Companies that have a baseline standard for measuring risk are going to be able to incorporate exact numbers into their decision modelling process. In short, they can predict certain scenarios and plan for them in advance.

Final Thoughts

Data insights are a disruptive technology, so businesses must be prepared to keep their systems up to date. Small businesses must be able to identify new opportunities as quickly as possible because it provides a significant competitive advantage.

Businesses must stay focused on analytics because data is a valuable aspect of making core business decision in today’s market. It allows businesses to stay in front of this digital disruption, ensuring continued success. Companies like the Research Optimus helps businesses to better decision making through data analytics process.

6 thoughts on “ How Data Analysis Improve Decision Making ”

Pingback: Using data science for business decisions | Agile Recruit
Pingback: Pourquoi la prise de décision s'applique-t-elle à l'analyse commerciale ? - Taj.ma
Pingback: Client Reporting Tools That Are Going to Save Your Business Time IT Voice | Online IT Media | IT Magazine
Pingback: Using data science for business decisions | new.agilerecruit.com
Pingback: How Real Estate Agents are Using Property Data to their Advantage – The Pinnacle List

Sign up for Reflective Data

Please enter your email

After submitting your email, we will send you the registration form.

Integrated Approach
Testimonials
Business Process Reengineering
Career Development
Competency Development

Data Analytics

Innovation Strategy
Innovation Readiness Survey (IRS)
Innovative Leader Survey (ILS)
Exploring Innovation
Lean Six Sigma Methodology
Lean Six Sigma and Data Analytics
Strategic Workforce Planning
iiP – Investing in People
Innovation and Change
Innovation and Productivity
Lean Six Sigma
Lean Innovation Training (LIT)
Articles and Case Studies
Data Analytics for OD
Lean Six Sigma Nuggets
Leadership Competency Cards
Lean Innovation Tool Kit
Bridging Cards
Data Science für Einsteiger
Praxisbuch Lean Six Sigma
Data Analytics with R
Sign up for Newsletter

Introducing Data Analytics and Data Science into Your Organisation with Carefully Crafted Solutions.

“I only believe in statistics that I doctored myself.” Winston Churchill

Data analytics, or data analysis , is the process of screening, cleaning, transforming, and modeling data with the objective of discovering useful information, suggesting conclusions, and supporting problem solving as well as decision making. There are multiple approaches, including a variety of techniques and tools used for data analytics. Data analytics finds applications in many different environments. As such, it usually covers two steps, graphical analysis and statistical analysis. The selection of tools for a given data analytics task depends on the overall objective, the source and types of data given.

Above all, Data Analytics, as part of Data Science, marks the foundation of all disciplines that are part of Artificial Intelligence (AI).

Objectives of Data Analytics

The objective of the data analytics task can be to screen or inspect the data in order to find out whether the data fulfils certain requirements. These requirements can be a certain distribution, a certain homogeneity of the dataset (no outliers) or just the behaviour of the data under certain stratification conditions (using demographics).

More often than not, another objective would be the analysis of data, in particular survey data , to determine the reliability of the survey instrument used to the collect data. Cronbach’s Alpha is often applied to perform this task. Cronbach’s Alpha determines whether survey items (questions/statements) that belong to the same factor are really behaving in a similar way, i.e. showing the same characteristic as other items in that factor. Testing reliability of a survey instrument is a prerequisite for further analysis using the dataset in question.

Data Preparation Before Data Analysis

Often enough, data is not ready for analysis. This can be due to a data collection format that is not in sync with subsequent analysis tools. This can also be due to a distribution that makes it harder to analyse the data. Hence, reorganising , standardising or transforming (to normal distribution) the dataset might be necessary.

Data Analytics with Descriptive Statistics

Descriptive Statistics includes a set of tools that is used to quantitatively describe a set of data. It usually indicates central tendency, variability, minimum, maximum as well as distribution and deviation from this distribution ( kurtosis , skewness ). Descriptive statistics might also highlight potential outliers for further inspection and action.

Data Analytics with Predictive Statistics

In contrast to descriptive statistics characterising a certain given set of data, inferential statistics uses a subset of the population, a sample, to draw conclusions regarding the population. The inherent risk depends on the required confidence level, confidence interval and the sample size at hand as well as the variation in the data set. Hence, the test result indicates this risk.

Data Analytics with Factor Analysis

Factor Analysis helps determine clusters in datasets, i.e. it finds empirical variables that show a similar variability. These variables may therefore construct the same factor. A factor is a dependent, unobserved variable that includes multiple observed variables in the same cluster. Under certain circumstances, this can lead to a reduction of observed variables and hence the increase of sample size in the remaining unobserved variables (factors). So, both outcomes improve the power of subsequent statistical analysis of the data.

Factor analysis can use different approaches to pursue a multitude of objectives. Exploratory factor analysis (EFA) is used to identify complex interrelationships among items and determine clusters/factors whilst there is no predetermination of factors. Confirmatory factor analysis (CFA) is used to test the hypothesis that the items are associated with specific factors. In this case, factors are predetermined before the analysis.

Data Analytics For Problem Solving

Data analytics can be helpful in problem solving by establishing the significance of the relationship between problems (Y) and potential root causes (X). As a result, a large variety of tools is available. The selection of tools for a given data analytics task depends on the overall objective, the source and types of data. Discrete data, such as counts or attributes require different tools than continuous data, such as measurements. Whilst continuous data are transformable into discrete data for decision making, this process is irreversible.

Depending on the data in X and Y, regression analysis or hypothesis testing will be used to answer the question whether there is a relationship between problem and alleged root cause. These tools do not take away the decision, they rather tell the risk for a certain conclusion. The decision is still to be made by the process owner ( example ).

Analytics was never intended to replace intuition, but to supplement it instead. Stuart Farrand, Data Scientist at Pivotal Insight

Applications for data analytics are evident in all private and public organisations without limits. For example, already some decades ago, companies like Motorola and General Electric discovered the power of data analytics and made this the core of their Six Sigma movement. As a result, these organisations made sure, that problem solving is based on data and applied data analytics wherever appropriate. Nowadays, data analytics or data science is vital part of problem solving and most Lean Six Sigma projects. So, Six Sigma Black Belts are usually well-versed in this kind of data analysis and make good candidates for a Data Scientist career track.

To sum it up, we offer multiple training solutions as public and in-house courses. Please, check out our upcoming events .

Internet of Things for Starters

Managers need data analytics, automating a mess yields an automated mess, data analysis – plot the data, plot the data, plot the data, can we predict when our staff is leaving, leading digital-ready workforce, analytical storytelling, great, we have improved … or not, do you understand your survey results, making sense of the wilcoxon test, making sense of chi-squared test – finding differences in proportions, making sense of test for equal variances, make use of your survey data – kano them, making sense of the two-proportions test, making sense of linear regression.

Architect of High-Performing Organisations

+65 61000 263

[email protected]

Our Locations

home button
Executive development

Data Analytics for Decision-Making and Problem-Solving for Executives and Managers

Available dates coming soon.

Location/Format: In-person or Virtual (Zoom) | --> Cost: $2,840

There is very high demand for Data Scientists, in fact it is one of the leading professions in the market at the moment. Harvard Business Review called it " The Sexiest Job of the 21st Century ".

According to Glassdoor, the average base pay for Data Scientists is $120,931 .

There is a reason Data Scientists are in such high demand. Employers all over the world are looking to make their firms more data-driven, more disciplined, and with a far better decision-making capability.

Course Description

Now more than ever from baseball to politics and from supply chain to marketing, data analytics is helping decision makers understand information can be used to design and deploy superior strategies that produce superior results. Managers and leaders from all levels of the organization need to understand how to define the challenges they face and how to employ analytics to address those challenges. This course will help you apply analytical business strategy by putting data analytics to valuable use inside of your company creating a solid base of knowledge which will allow you to go out and solve real world business problems.

This course presents an overview as well as practical guidelines for applying analytics and data to complex business decisions as they arise. The textbook used in the course will be Profit from Science, written by the instructor.

Course Cost

Norman Johnson Professor and Chair of Decision and Information Sciences C. T. Bauer College of Business

Problem Analysis Techniques: Tools for Effective Decision Making

Discover key problem analysis techniques for smart decision making. Unlock tools and methods to enhance your strategic thinking.

The multifaceted nature of issues within the professional domain necessitates a comprehensive understanding of problem analysis, a skill set increasingly recognized as pivotal in crafting effective solutions. This foundational approach offers a structured pathway to dissect complex situations, enabling a thorough assessment that aids decision-makers across industries.

As we delve into the realm of problem analysis, we shall explore its significance within different contexts, exemplifying its value in enhancing strategic outcomes. Whether employed within a problem solving course or utilized in a business setting, problem analysis stands out as a cornerstone of successful operational management.

Understanding Problem Analysis

Definition and basics of problem analysis.

Problem analysis is a diagnostic process that allows individuals to identify the core of a complication with precision, thereby paving the way toward a feasible solution. The core of this concept lies in a systematic examination that seeks to separate a problem into manageable parts. This enables decision-makers to ascertain not only the symptoms but also the underlying causes.

Organizations across the globe incorporate problem analysis into their fundamental practices, ensuring robust decision-making and facilitating a problem-solving ethos that can be further bolstered by various online certificate programs .

Importance of problem analysis

At the strategic level, problem analysis is indispensable. It underpins strategic planning by providing clarity, allowing leaders to envision a roadmap that circumvents potential obstacles while maximizing resources efficiently.

Moreover, its influence on productivity cannot be overstated. By simplifying the convoluted, problem analysis enhances an organization's ability to streamline its operations. Effective utility in risk management is yet another beneficial facet; problem analysis allows for the anticipation and mitigation of risks, safeguarding an organization’s assets and reputation.

Various Techniques of Problem Analysis

The 5 why's.

One foundational technique in problem analysis is the 5 Why's . This method, in essence, employs a series of questions, with each answer forming the basis of the next question. The simplicity of repeatedly asking 'Why?' aids in peeling back the layers of an issue, much like an onion, to uncover the fundamental cause.

Though straightforward, this iterative interrogative approach yields profound insights, often leading to solutions that are both effective and surprisingly simple.

Cause and Effect Diagram

Another critical tool within a problem analyst's repertoire is the Cause and Effect Diagram , often termed the Ishikawa or fishbone diagram. The strength of this technique lies in its visual representation of the relationship between a problem and its possible causes. It guides users to systematically dissect the factors contributing to an issue, distinguishing between the significant and the inconsequential—thus forming a hierarchy of concerns that can be addressed according to their impact on the overall problem.

Pareto Analysis

Pareto Analysis, or the 80/20 rule, posits that roughly 80% of effects come from 20% of causes. This technique is particularly useful for prioritizing tasks, making it a staple in both managerial decision-making and problem solving course curricula. By focusing on the critical few causes, this analysis aids in resource allocation, ensuring that efforts are channeled toward the most impactful issues.

Root Cause Analysis

Lastly, Root Cause Analysis is a thorough method used to dissect complex problems, avoid recurrence, and establish a clear course of action for future reference. This methodology is all about digging deeper – much akin to a detective searching for the underlying truth. Emphasizing a systematic approach, it seeks not just to treat the symptoms, but to eradicate the source of issues, thereby preventing a mere superficial fix.

Choosing the Right Problem Analysis Technique

Key factors to be considered.

Selection of the appropriate problem analysis technique is contingent upon several critical factors. The nature and scale of the problem, available resources, and timeline, are all essential elements requiring careful consideration.

The unique aspects of each scenario will invariably influence the choice of technique, with some methods lending themselves to particular types of problems more so than others. The capacity to rationalize the selection process is an indicator of both critical thinking and professionalism.

Guideline on selection among different techniques

Determining which technique to apply hinges on a comprehensive situational analysis, examining both the strengths and weaknesses inherent to each method. A detailed overview of the current challenge underpins an informed decision, guiding the analyst to the most suited approach.

Additionally, understanding the complexity and scope of a problem is crucial as it informs the depth and breadth of analysis needed. In scenarios where the complexity is high, techniques such as Root Cause Analysis may be preferable due to their detailed nature.

In conclusion, problem analysis serves as an indispensable tool in the cascade of decision-making processes. By breaking down issues into their constituent parts, professionals are well-positioned to devise strategic solutions that are both insightful and effective. The techniques described herein, from the 5 Why's to Root Cause Analysis, offer a compendium of approaches best suited to the diverse array of challenges that may arise.

As such, the importance of these problem analysis techniques cannot be overstated, and there's a growing impetus for their application across a wide range of professional fields. Whether by enrolling in a online certificate programs or by undertaking a problem solving course , the mastery of these methods is vital for any thriving enterprise or individual seeking to navigate the complexities of the modern world with skill and agility.

What are the key components of effective problem analysis techniques in decision-making processes?

Understanding the problem.

Effective problem analysis starts with clarity. One must understand the issue at hand fully. Ask critical questions. These narrow the problem's scope. Identify goals, needs, and limitations. This structured approach eases subsequent steps.

Gathering Relevant Information

One cannot analyze problems in isolation. Information forms the analysis's backbone. Seek data from diverse sources. Collect historical, empirical, and anecdotal evidence. Cross-reference facts. This builds a comprehensive knowledge base.

Identifying Key Factors

Every problem has underlying factors. Recognize these to focus the analysis. Differentiate between cause and effect. Assign priorities to each factor. Understand their interrelations. This step shapes potential solutions.

Employing Analytical Tools

Use established tools for structured analysis. Models like SWOT or PESTLE offer frameworks. Apply Decision Matrix Analysis or Root Cause Analysis to dig deeper. These tools bring objectivity. They help avoid cognitive biases.

Generating Alternatives

Do not fixate on a single solution. Develop many potential answers. Creativity plays a crucial role here. Brainstorming sessions can fuel innovation. Ensure diversity in thought among participants. This enhances the breadth of options.

Evaluating Alternatives

Consider the feasibility of each alternative. Assess their alignment with goals. Perform cost-benefit analysis. Check for unintended consequences. Make comparisons easier with ranking or scoring systems. This aids in discerning the optimal choice.

Making the Decision

After thorough evaluation, decide on the best alternative. Ensure it aligns with the goals identified earlier. It should address key factors effectively. Prepare to act decisively. Confidence in the choice grounds the decision in logic.

Reviewing the Decision

Post-implementation review is vital. Monitor for expected outcomes. Adapt based on feedback and results. This step ensures continuous improvement. It is critical for long-term decision-making success.

Practical Tips:

- Break problems down into smaller parts.

- Engage stakeholders for varied perspectives.

- Keep the analysis flexible; adapt as you learn.

- Document assumptions for transparency.

- Communicate analysis clearly to relevant parties.

In summary, effective problem analysis integrates these components seamlessly. It demands both discipline and flexibility. By following these guidelines, decision-makers can approach complex problems systematically and make informed decisions that stand the test of uncertainty and scrutiny.

How does the application of these techniques enhance the validity and reliability of managerial decisions?

The importance of techniques in decision-making.

Managerial decision-making requires accuracy. It hinges on reliable data. Various techniques aid this process. These methods sharpen the insight of managers. Improved decisions lead to better outcomes.

Data Analysis Enhances Understanding

Data analysis is vital. It clarifies complex situations. Managers analyze trends through this. They detect patterns in consumer behavior. Predictive analytics can foresee market changes. This leads to proactive decision-making.

Modeling Reduces Uncertainty

Modeling offers hypothetical scenarios. Managers test various outcomes here. Risk assessment becomes more precise. Uncertainty in decisions reduces significantly. This technique validates the predicted results. Managers make informed choices.

Benchmarking Sets Performance Standards

Benchmarking compares business processes. It looks at industry best practices. Managers identify performance gaps through it. Quality improvements follow next. This method ensures continual improvement. Benchmarking validates strategic priorities.

Cost-Benefit Analysis Justifies Financial Decisions

Cost-benefit analysis weighs options financially. Every potential action is examined. Costs compare against possible benefits. This justifies investment decisions. It promotes financial prudence. Reliability in financial decisions increases.

Sensitivity Analysis Uncovers Risk

Sensitivity analysis tests assumptions. It explores the 'what-ifs'. Managers understand the impact of change. They prepare better for volatility. This strengthens the robustness of plans.

Decision Trees Provide Visual Clarity

Decision trees map choices visually. They outline consequences stepwise. Managers grasp complex choices easily. It simplifies understanding. Each decision path becomes clear. Better decision-making ensues.

SWOT Analysis Reveals Opportunities and Risks

SWOT analysis focuses on strengths, weaknesses, opportunities, threats. Managers use it for strategic planning. Internal and external factors are weighed. It spots critical issues. This analysis guides strategic shifts.

Feedback Mechanisms Promote Continuous Learning

Feedback mechanisms improve ongoing processes. They involve staff and customers. Feedback solicits different perspectives. It uncovers potential flaws early. Continuous learning becomes part of the culture. It iteratively enhances decision quality.

The Balanced Scorecard Aligns Decisions with Strategy

The balanced scorecard links everyday actions to strategy. It measures from four perspectives: financial, customer, internal processes, learning and growth. Managers see how actions affect objectives. Decisions align with long-term goals.

Applying these techniques creates a multidimensional analysis framework. It incorporates quantitative and qualitative insights. Managers make decisions based on a 360-degree viewpoint. Validity and reliability in managerial decisions build a resilient organization. Each technique complements others. They mitigate bias. They encourage objectivity. Collectively, they lead to more scientifically grounded decisions. Businesses thrive on sound decisions. Managers who leverage these techniques drive success.

Can problem analysis techniques be customized or modified to suit specific organizational contexts and if so, how?

Customizing problem analysis techniques.

Organizations face unique challenges. These stem from their specific contexts. Hence, problem analysis techniques seldom fit all uniformly. Such techniques require adaptation. They must reflect organizational culture, structure, and goals.

Understanding Organizational Context

Each organization operates distinctly. They have their own cultures, processes, and strategies. Recognizing these nuances is critical. It fuels effective customization of problem analysis methods.

Problem analysis is not one-size-fits-all. Managers should first understand their organizational dynamics. Then, they can tailor analysis methods appropriately.

Steps for Customization

- Assess the organization

- Identify challenges

- Consider available resources

- Acknowledge constraints

Assessment reveals specific needs. Identification prioritizes problems. Consideration recognizes tools at disposal. Acknowledgement of limitations sets realistic boundaries.

Modifying Existing Frameworks

Existing problem analysis frameworks are starting points. They are not final solutions. Modification requires creativity and insight.

- Simplify complex steps

- Add relevant stages

- Remove redundant elements

- Integrate organizational knowledge

Simplification aids comprehension. Addition fills in gaps. Removal concentrates efforts. Integration leverages internal wisdom.

Case-by-Case Approach

Each problem is distinct. Solutions must reflect that uniqueness. Customize techniques for each challenge. This demands flexibility and responsiveness.

- Analyze individually

- Customize meticulously

- Apply selectively

Individual analysis ensures attention to detail. Meticulous customization ensures precision. Selective application promises relevance.

Involving Stakeholders

Stakeholders provide valuable insights. Their involvement is crucial. They inform customization processes. Their perspectives often highlight otherwise hidden nuances.

- Collaborate with teams

- Seek diverse opinions

- Incorporate feedback

Collaboration fosters understanding. Seeking diverse opinions enhances creativity. Incorporating feedback refines the approach.

Reflecting on Effectiveness

Effectiveness measurement is indispensable. It confirms whether the customization is successful. Feedback loops prompt continuous improvement.

- Set measurable goals

- Monitor progress

- Adjust as necessary

Setting goals provides direction. Monitoring progress tracks success. Adjusting ensures ongoing relevance.

Customizing problem analysis techniques is vital. It acknowledges that organizations are not monolithic. Tailoring these techniques to fit specific contexts is a dynamic process. It requires insight, creativity, and adaptability. Through such customization, organizations enhance problem-solving capabilities. They become more resilient and equipped to tackle unique challenges effectively.

A middle-aged man is seen wearing a pair of black-rimmed glasses. His hair is slightly tousled, and he looks off to the side, suggesting he is deep in thought. He is wearing a navy blue sweater, and his hands are folded in front of him. His facial expression is one of concentration and contemplation. He appears to be in an office, with a white wall in the background and a few bookshelves visible behind him. He looks calm and composed.

He is a content producer who specializes in blog content. He has a master's degree in business administration and he lives in the Netherlands.

Plato shines a light of knowledge reminding us to keep our hearts open to the power of emotion and desire BeMonthofPlato

Plato: A Beacon of Influence Through Desire, Emotion, & Knowledge

Master decision-making with our strategic Decision Tree guide. Improve choices, outcomes, and efficiency swiftly and effectively.

Decision Tree: A Strategic Approach for Effective Decision Making

Unlock strategic decision-making with advanced DSS tools. Elevate your strategy for optimal business outcomes.

Decision Support Systems: Advancing Effective Strategic Choices

Unlock decision-making mastery with Problem Framing strategies for effective solutions. Elevate your strategic approach today!

Problem Framing: A Strategic Approach to Decision Making

Business Essentials
Leadership & Management
Credential of Leadership, Impact, and Management in Business (CLIMB)
Entrepreneurship & Innovation
Digital Transformation
Finance & Accounting
Business in Society
For Organizations
Support Portal
Media Coverage
Founding Donors
Leadership Team

Harvard Business School →
HBS Online →
Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

Career Development
Communication
Decision-Making
Earning Your MBA
Negotiation
News & Events
Productivity
Staff Spotlight
Student Profiles
Work-Life Balance
AI Essentials for Business
Alternative Investments
Business Analytics
Business Strategy
Business and Climate Change
Design Thinking and Innovation
Digital Marketing Strategy
Disruptive Strategy
Economics for Managers
Entrepreneurship Essentials
Financial Accounting
Global Business
Launching Tech Ventures
Leadership Principles
Leadership, Ethics, and Corporate Accountability
Leading with Finance
Management Essentials
Negotiation Mastery
Organizational Leadership
Power and Influence for Positive Impact
Strategy Execution
Sustainable Business Strategy
Sustainable Investing
Winning with Digital Platforms

5 Key Decision-Making Techniques for Managers

Business manager engaging in decision-making with his team

31 Mar 2020

Decision-making is an essential business skill that drives organizational performance. A survey of more than 750 companies by management consulting firm Bain found a 95 percent correlation between decision-making effectiveness and financial results. The data also showed companies that excel at making and executing strategic decisions generate returns nearly six percent higher than those of their competitors.

At many organizations, it’s up to managers to make the key decisions that influence business strategy. Research by consulting firm McKinsey , however, shows that 61 percent of them believe at least half the time they spend doing so is ineffective.

If you want to avoid falling into this demographic, here are five decision-making techniques you can employ to improve your management skills and help your organization succeed.

Access your free e-book today.

Decision-Making Techniques for Managers

1. take a process-oriented approach.

One of your primary responsibilities as a manager is to get things done with and through others, which involves leveraging organizational processes to accomplish goals and produce results. According to Harvard Business School Professor Len Schlesinger, who’s featured in the online course Management Essentials , decision-making is one of the processes you can use to your advantage.

“The majority of people think about making decisions as an event,” Schlesinger says. “It’s very rare to find a single point in time where a ‘decision of significance’ is made and things go forward from there. What we’re really talking about is a process. The role of the manager in overseeing that process is straightforward, yet, at the same time, extraordinarily complex.”

When establishing your decision-making process , first frame the issue at hand to ensure you ask the right questions and everyone agrees on what needs to be decided. From there, build your team and manage group dynamics to analyze the problem and craft a viable solution. By following a structured, multi-step process, you can make informed decisions and achieve the desired outcome.

2. Involve Your Team in the Process

Decision-making doesn’t have to be done in a vacuum. To avoid relying on managerial decisions alone, involve your team in the process to bring multiple viewpoints into the conversation and stimulate creative problem-solving .

Research in the journal Royal Society Open Science shows team decision-making is highly effective because it pools individuals’ collective knowledge and experience, leading to more innovative solutions and helping to surface and overcome hidden biases among groups.

Considering others’ perspectives on how to approach and surmount a specific challenge is an ideal alternative because it helps you become more aware of your implicit biases and manage your team with greater emotional intelligence .

Related: Emotional Intelligence Skills: What They Are & How to Develop Them

3. Foster a Collaborative Mindset

Fostering the right mindset early in the decision-making process is critical to ensuring your team works collaboratively—not contentiously.

When facing a decision, there are two key mindsets to consider:

Decision-Making Mindsets: Advocacy vs. Inquiry

Advocacy: A mindset that regards decision-making as a contest. In a group with an advocacy mindset, individuals try to persuade others, defend their positions, and downplay their weaknesses.
Inquiry: A mindset that navigates decision-making with collaborative problem-solving. An inquiry mindset centers on individuals testing and evaluating assumptions by presenting balanced arguments, considering alternatives, and being open to constructive criticism.

“On the surface, advocacy and inquiry approaches look deceptively similar,” HBS Professor David Garvin says in Management Essentials . “Both involve individuals engaged in debates, drawing on data, developing alternatives, and deciding on future directions. But, despite these similarities, inquiry and advocacy produce very different results.”

A study by software company Cloverpop found that decisions made and executed by diverse teams deliver 60 percent better results. Strive to instill your team members with an inquiry mindset so they’re empowered to think critically and feel their perspectives are welcomed and valued rather than discouraged and dismissed.

4. Create and Uphold Psychological Safety

For your team members to feel comfortable sharing their diverse perspectives and working collaboratively, it’s crucial to create and maintain a psychologically safe environment. According to research by technology company Google , psychological safety is the most important dynamic found among high-performing teams.

“Psychological safety is essential—first and foremost—for getting the information and perspectives out,” HBS Professor Amy Edmondson says in Management Essentials . “It’s helpful to be able to talk about what we know and think in an effective and thoughtful way before coming to a final conclusion.”

To help your team feel psychologically safe, be respectful and give fair consideration when listening to everyone’s opinions. When voicing your own point of view, be open and transparent, and adapt your communication style to meet the group’s needs. By actively listening and being attuned to your colleagues’ emotions and attitudes, you can forge a stronger bond of trust, make them feel more engaged and foster an environment that allows for more effective decisions.

Related: 5 Tips for Managing Change in the Workplace

5. Reiterate the Goals and Purpose of the Decision

Throughout the decision-making process, it’s vital to avoid common management pitfalls and lose sight of the goals and purpose of the decision on the table.

The goals you’re working toward need to be clearly articulated at the outset of the decision-making process—and constantly reiterated throughout—to ensure they’re ultimately achieved.

“It’s easy, as you get into these conversations, to get so immersed in one substantive part of the equation that you lose track of what the actual purpose is,” Schlesinger says.

Revisiting purpose is especially important when making decisions related to complex initiatives—such as organizational change —to ensure your team feels motivated and aligned and understands how their contributions tie into larger objectives.

Why Are Decision-Making Skills Important?

Effective decision-making can immensely impact organizational performance. By developing your decision-making skills, you can exercise sound judgment and guide your team through the appropriate frameworks and processes—resulting in more data-driven decisions .

You can also anticipate and navigate organizational challenges while analyzing the outcomes of previous efforts, which can have lasting effects on your firm’s success.

Management Essentials | Get the job done | Learn More

Improve Your Decision-Making Skills

Enhancing your decision-making capabilities can be an integral part of your journey to becoming a better manager , reaching your business goals, and advancing your career. In addition to real-world experience, furthering your education by taking a management training course can equip you with a wide range of skills and knowledge that enable both your team and organization to thrive.

Do you want to design, direct, and shape organizational processes to your advantage? Explore Management Essentials , one of our online leadership and management courses , and discover how you can influence the context and environment in which decisions get made.

This post was updated on December 21, 2022. It was originally published on March 31, 2020.

About the Author

Understanding data analysis: A beginner's guide

Before data can be used to tell a story, it must go through a process that makes it usable. Explore the role of data analysis in decision-making.

What is data analysis?

Data analysis is the process of gathering, cleaning, and modeling data to reveal meaningful insights. This data is then crafted into reports that support the strategic decision-making process.

Types of data analysis

There are many different types of data analysis. Each type can be used to answer a different question.

Descriptive analytics

Descriptive analytics refers to the process of analyzing historical data to understand trends and patterns. For example, success or failure to achieve key performance indicators like return on investment.

An example of descriptive analytics is generating reports to provide an overview of an organization's sales and financial data, offering valuable insights into past activities and outcomes.

Predictive analytics

Predictive analytics uses historical data to help predict what might happen in the future, such as identifying past trends in data to determine if they’re likely to recur.

Methods include a range of statistical and machine learning techniques, including neural networks, decision trees, and regression analysis.

Diagnostic analytics

Diagnostic analytics helps answer questions about what caused certain events by looking at performance indicators. Diagnostic analytics techniques supplement basic descriptive analysis.

Generally, diagnostic analytics involves spotting anomalies in data (like an unexpected shift in a metric), gathering data related to these anomalies, and using statistical techniques to identify potential explanations.

Cognitive analytics

Cognitive analytics is a sophisticated form of data analysis that goes beyond traditional methods. This method uses machine learning and natural language processing to understand, reason, and learn from data in a way that resembles human thought processes.

The goal of cognitive analytics is to simulate human-like thinking to provide deeper insights, recognize patterns, and make predictions.

Prescriptive analytics

Prescriptive analytics helps answer questions about what needs to happen next to achieve a certain goal or target. By using insights from prescriptive analytics, organizations can make data-driven decisions in the face of uncertainty.

Data analysts performing prescriptive analysis often rely on machine learning to find patterns in large semantic models and estimate the likelihood of various outcomes.

analyticsText analytics

Text analytics is a way to teach computers to understand human language. It involves using algorithms and other techniques to extract information from large amounts of text data, such as social media posts or customer previews.

Text analytics helps data analysts make sense of what people are saying, find patterns, and gain insights that can be used to make better decisions in fields like business, marketing, and research.

The data analysis process

Compiling and interpreting data so it can be used in decision making is a detailed process and requires a systematic approach. Here are the steps that data analysts follow:

1. Define your objectives.

Clearly define the purpose of your analysis. What specific question are you trying to answer? What problem do you want to solve? Identify your core objectives. This will guide the entire process.

2. Collect and consolidate your data.

Gather your data from all relevant sources using data analysis software . Ensure that the data is representative and actually covers the variables you want to analyze.

3. Select your analytical methods.

Investigate the various data analysis methods and select the technique that best aligns with your objectives. Many free data analysis software solutions offer built-in algorithms and methods to facilitate this selection process.

4. Clean your data.

Scrutinize your data for errors, missing values, or inconsistencies using the cleansing features already built into your data analysis software. Cleaning the data ensures accuracy and reliability in your analysis and is an important part of data analytics.

5. Uncover valuable insights.

Delve into your data to uncover patterns, trends, and relationships. Use statistical methods, machine learning algorithms, or other analytical techniques that are aligned with your goals. This step transforms raw data into valuable insights.

6. Interpret and visualize the results.

Examine the results of your analyses to understand their implications. Connect these findings with your initial objectives. Then, leverage the visualization tools within free data analysis software to present your insights in a more digestible format.

7. Make an informed decision.

Use the insights gained from your analysis to inform your next steps. Think about how these findings can be utilized to enhance processes, optimize strategies, or improve overall performance.

By following these steps, analysts can systematically approach large sets of data, breaking down the complexities and ensuring the results are actionable for decision makers.

The importance of data analysis

Data analysis is critical because it helps business decision makers make sense of the information they collect in our increasingly data-driven world. Imagine you have a massive pile of puzzle pieces (data), and you want to see the bigger picture (insights). Data analysis is like putting those puzzle pieces together—turning that data into knowledge—to reveal what’s important.

Whether you’re a business decision maker trying to make sense of customer preferences or a scientist studying trends, data analysis is an important tool that helps us understand the world and make informed choices.

Primary data analysis methods

A person working on his desktop an open office environment

Quantitative analysis

Quantitative analysis deals with numbers and measurements (for example, looking at survey results captured through ratings). When performing quantitative analysis, you’ll use mathematical and statistical methods exclusively and answer questions like ‘how much’ or ‘how many.’

Two people looking at tablet screen showing a word document

Qualitative analysis

Qualitative analysis is about understanding the subjective meaning behind non-numerical data. For example, analyzing interview responses or looking at pictures to understand emotions. Qualitative analysis looks for patterns, themes, or insights, and is mainly concerned with depth and detail.

Data analysis solutions and resources

Turn your data into actionable insights and visualize the results with ease.

Microsoft 365

Process data and turn ideas into reality with innovative apps, including Excel.

Importance of backing up data

Learn how to back up your data and devices for peace of mind—and added security.

Copilot in Excel

Go deeper with your data using Microsoft Copilot—your AI assistant.

Excel expense template

Organize and track your business expenses using Excel.

Excel templates

Boost your productivity with free, customizable Excel templates for all types of documents.

Chart designs

Enhance presentations, research, and other materials with customizable chart templates.

Follow Microsoft

COMMENTS

The Importance of Data Analysis in Problem Solving
Data crunching, business analysis and finding unique insights is a very essential part of management analysis and decision making. There are several tools and techniques that are used. But what I have realized is that more than the tools, what is important is how you think and approach problem solving using data. The tool can be as simple as MS ...
The Advantages of Data-Driven Decision-Making
Today's largest and most successful organizations use data to their advantage when making high-impact business decisions. To better understand how your organization can incorporate data analytics into its decision-making process, consider the success stories of these well-known businesses. 1. Leadership Development at Google.
8 Types of Data Analytics to Improve Decision-Making
By automating decision-making to a certain extent, prescriptive analytics empowers organizations to make faster and more informed choices. Specific Types of Data Analytics For Decision-Making. Within the types of analytics, there are many ways that you can make data-driven decisions. Here are some of the most common methods: 5. Text Analytics
4 Types of Data Analytics to Improve Decision-Making
4 Key Types of Data Analytics. 1. Descriptive Analytics. Descriptive analytics is the simplest type of analytics and the foundation the other types are built on. It allows you to pull trends from raw data and succinctly describe what happened or is currently happening.
How Data Analytics Can Improve Decision-Making
Cost efficiency analysis. Pricing optimization. By providing insights on the above, data analytics can improve decision-making in terms of mitigating risk. Through establishing clear metrics against which to measure risk, companies can use analytics to make informed, productive, and safer choices across the board.
What is Data Analysis? An Expert Guide With Examples
Similarly, in the finance sector, data analysis can help in risk assessment, fraud detection, and investment decision-making. The Data Analysis Process: A Step-by-Step Guide. The process of data analysis is a systematic approach that involves several stages, each crucial to ensuring the accuracy and usefulness of the results.
How Should Data Analysis Impact Your Decision-Making Process?
Statistical Decision-Making 101. The default action is the option that you find palatable under ignorance. It's what you'll do if you're forced to make a snap decision. The alternative action is what you'll do if the data analysis talks you out of your default action. The null hypothesis is a (mathematical) description of all the ...
The Role of Data Analysis in Decision-Making: A Comprehensive Guide
Data analysis plays a pivotal role in decision-making by providing objective evidence and insights. It allows organizations to move beyond gut feelings and intuitions, empowering them to make informed choices based on data-driven evidence. By leveraging data analysis, businesses can gain a competitive edge, optimize processes, identify new ...
5 Reasons Why Data Analytics Is Important In Problem Solving
Now that we've established a general idea of how strongly connected analytical skills and problem-solving are, let's dig deeper into the top 5 reasons why data analytics is important in problem-solving. 1. Uncover Hidden Details. Data analytics is great at putting the minor details out in the spotlight.
Data-driven decision making: A step-by-step guide
Decision-making tools for agile businesses. In this ebook, learn how to equip employees to make better decisions—so your business can pivot, adapt, and tackle challenges more effectively than your competition. Get the insights. Data-driven decision-making (DDDM) involves collecting data and using it to make decisions.
How to analyze a problem
Before jumping in, it's crucial to plan the analysis, decide which analytical tools to use, and ensure rigor. Check out these insights to uncover ways data can take your problem-solving techniques to the next level, and stay tuned for an upcoming post on the potential power of generative AI in problem-solving. The data-driven enterprise of 2025.
What is Data Analysis?
Data Analysis Can Aid Problem Solving . By performing data analysis on relevant, correct, and accurate data, you will have a better understanding of the right choices you need to make and how to make more informed and wiser decisions. Data analysis means having better insights, which helps improve decision-making and leads to solving problems.
Data Analysis for Effective Decision Making
33 Problem Solving Consultation: Applications in Evidence-Based Prevention and Intervention Notes. Notes. Notes. Expand Part 7 ... ' Data Analysis for Effective Decision Making', in Melissa A. Bray, and Thomas J. Kehle (eds), The Oxford Handbook of School Psychology, ...
How to Use Data for Better Problem Solving
1 Data sources. One of the first steps in problem solving is to gather relevant and reliable data from various sources. Depending on the nature and scope of the problem, you may need to use ...
Data Analysis
Here are some specific scenarios where data analysis can be particularly helpful: Problem-solving: When you encounter a problem or challenge, ... To inform decision-making: Data analysis can help you make informed decisions based on the information that is available. By analyzing data, you can identify potential risks, opportunities, and ...
How Data Analysis Improve Decision Making
As a result, businesses that use data analytics experienced an increase in profit that reached as high as 10%. Furthermore, those same businesses experienced a reduction in costs that also reached as high as 10%. Data Analysis is helping companies make smarter decisions that lead to higher productivity and more efficient operations.
Data Analytics for Problem Solving and Decision Making
Data analytics, or data analysis, is the process of screening, cleaning, transforming, and modeling data with the objective of discovering useful information, suggesting conclusions, and supporting problem solving as well as decision making.There are multiple approaches, including a variety of techniques and tools used for data analytics. Data analytics finds applications in many different ...
Workforce Development: Problem Solving and Data Analysis
Analyzing Data Using the DASA Model. Learn how to use the Data as a Strategic Asset (DASA) Model to identify and answer relevant business questions based on data-driven insights. Effective Problem Solving and Decision-Making Tools. Learn about different types of decisions, and discover three decision-making tools. Presenting Visually Compelling ...
Data Analytics for Decision-Making and Problem-Solving for Executives
Employers all over the world are looking to make their firms more data-driven, more disciplined, and with a far better decision-making capability. Course Description Now more than ever from baseball to politics and from supply chain to marketing, data analytics is helping decision makers understand information can be used to design and deploy ...
Information Processing and Data Analytics for Decision Making: A
to aid in problem solving and decision making. A model-dr iven DSS ma y be based on a single plan or a mixture of two or more types depending on the requirement of the users.
Problem Analysis Techniques: Tools for Effective Decision Making
Pareto Analysis. Pareto Analysis, or the 80/20 rule, posits that roughly 80% of effects come from 20% of causes. This technique is particularly useful for prioritizing tasks, making it a staple in both managerial decision-making and problem solving course curricula. By focusing on the critical few causes, this analysis aids in resource ...
Effective Problem-Solving and Decision-Making
There are 4 modules in this course. Problem-solving and effective decision-making are essential skills in today's fast-paced and ever-changing workplace. Both require a systematic yet creative approach to address today's business concerns. This course will teach an overarching process of how to identify problems to generate potential ...
5 Key Decision-Making Techniques for Managers
3. Foster a Collaborative Mindset. Fostering the right mindset early in the decision-making process is critical to ensuring your team works collaboratively—not contentiously. When facing a decision, there are two key mindsets to consider: Advocacy: A mindset that regards decision-making as a contest.
Understanding Data Analysis: A Beginner's Guide
Data analysis is the process of gathering, cleaning, and modeling data to reveal meaningful insights. This data is then crafted into reports that support the strategic decision-making process. Descriptive analytics refers to the process of analyzing historical data to understand trends and patterns ...
Enhance Non-Profit Problem Solving with Data
As a non-profit manager, you're constantly faced with challenges that require effective problem solving. Fortunately, data and analytics can be powerful tools in your decision-making arsenal.

How Should Data Analysis Impact Your Decision-Making Process?

How Does Hypothesis Testing Work?

Statistical Decision-Making 101

What Can We Learn From Data?

What Is the Point of Statistical Analysis?

Am I Making Decisions Intelligently?

Statistics Is the Science of Changing Your Mind

Statistics Offers Control, Not Certainty

Great Companies Need Great People. That's Where We Come In.

The Role of Data Analysis in Decision-Making: A Comprehensive Guide

Understanding Data-Driven Decision Making

Understanding the Importance of Data Analysis

Descriptive Analysis

Predictive Analysis

Prescriptive Analysis

The Data Analysis Process

Data Cleaning and Preparation

Exploratory Data Analysis (EDA)

Data Visualization

Interpretation and Decision-Making

Tools and Technologies for Data Analysis

Spreadsheet Software

Statistical Software

Machine Learning (ML) Platforms

Challenges and Best Practices in Data Analysis

Defining Clear Objectives

Companies Who Put Analytics Into Practice

Privacy Overview

5 Reasons Why Data Analytics is Important in Problem Solving

What is Data Analytics?

Why is Data Analytics Important in Problem Solving?

5 Reasons Why Data Analytics Is Important in Problem Solving

1. Uncover Hidden Details

2. Automated Models

3. Explore Similar Problems

4. Predict Future Problems

5. Faster Data Extraction

What problems can data analytics solve? 3 Real-World Examples

Sales Efficiency Problems

Business Investment Decisions Problems

Recent Posts

CAPABILITIES

Featured Reads

Data-driven decision making: A step-by-step guide

Decision-making tools for agile businesses

What is data-driven decision making (DDDM)?

What does being data-driven mean?

Why is data-driven decision making important?

5 steps for making data-driven decisions

1. Know your vision

2. Find data sources

3. Organize your data

4. Perform data analysis

5. Draw conclusions

Data-driven decision making examples

E-commerce

Transportation

Benefits of data-driven decision making

Make confident decisions

Guard against biases

Find unresolved questions

Set measurable goals

Improve company processes

Tips for becoming more data-driven

Find the story

Consult the data

Learn data visualization

Make data-driven decisions easy with reporting software

Related resources

7 steps to complete a social media audit (with template)

3 visual project management layouts (and how to use them)

Grant management: A nonprofit’s guide

Everything you need to know about waterfall project management

How to analyze a problem

What is Data Analysis?

Knowledge of SQL and Relational Databases

Knowledge of data visualization tools

What Is Data Analysis? A Definition For Beginners

Why Is Data Analysis Important?

Data Analysis Improves Customer Targeting