Problem Solving on Subtraction
Problem solving on subtraction will help us to get the idea on how to solve the basic subtraction statement problems.
1. Eight birds sat on a wire. Three birds flew away. How many were left?
Total number of birds sat on a wire = 8
Number of birds flew away = 3
Therefore, number of birds left = 8 - 3 = 5
2. Sam had 7 dollars. He spent 4 dollars. How many dollars is he left with?
Total amount of money Sam had = $7
He spent = $4
Therefore, amount of money left with him = $7 - $4 = $3
3. Five boats were tied up. Four of the boats sailed away. How many were left?
Total number of boats tied up = 5
Number of boats sailed away = 4
Therefore, number of boats were left = 5 - 4 = 1
4. Ron had 10 stamps. His father took 2 stamps. How many stamps does Ron have now?
Total number of stamps Ron had = 10
Number of stamps his father took = 2
Therefore, number of stamps he have now = 10 - 2 = 8
5. Diana had 18 toffees. She gave 5 toffees to her friend. How many toffees left with her?
Total number of toffees Diana had = 18
Number of toffees she gave to her friend = 5
Therefore, number of toffees left = 18 - 5 = 13
More examples on statement problem solving on subtraction:
6. Mr. Daniel had 39 goats in a pasture. When he opened the pasture gate, 13 goats went out. How many goats remained in?
Total number of goats in a pasture Mr. Daniel had = 39
Number of goats went out = 13
Therefore, number of goats remained in = 39 - 13 = 26
7. Derek’s father is 47 years old. His mother is 35 years old. What is the difference of their ages?
Age of Derek’s father = 47 years
Age of his mother = 35 years
Therefore, difference of their ages = 47 - 35 = 12 years
2nd Grade Math Practice From Problem Solving on Subtraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy

Recent Articles
Numbers | Notation | Numeration | Numeral | Estimation | Examples
May 12, 24 06:28 PM
Face Value and Place Value|Difference Between Place Value & Face Value
May 12, 24 06:23 PM
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
May 12, 24 06:09 PM
Worksheet on Bar Graphs | Bar Graphs or Column Graphs | Graphing Bar
May 12, 24 04:59 PM
Worksheet on Pictographs | Picture Graph Worksheets | Pictograph Works
May 12, 24 04:31 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
Subtraction Word Problems (1-step word problems)
These lessons look at some examples of subtraction word problems that can be solved in one step, illustrating the use of bar models or block diagrams in the solution process.
Related Pages 2-step Subtraction Word Problems Using Bar Models Solving Word Problems Using Bar Models Singapore Math More Word Problems
We will illustrate how block diagrams can be used to help you to visualize the subtraction word problems in terms of the information given and the data that needs to be found. The block diagrams or block modeling method is used in Singapore Math.
Example: Jessica has 1135 beads. 604 beads are red and the rest are blue. How many blue beads does she have?
1135 – 604 = 531
She has 531 blue beads.
Example: James and Ken donated $2300 to a charitable organization. Ken donated $658. How much did James donate?
2300 – 658 = 1642 James donated $1642.
Example: The price of a car is $2795 and the price of a motorbike is $1063. What is the difference between the prices of the 2 vehicles?
Solution: 2795 – 1063 = 1732
The difference between the prices of the 2 vehicles is $1732.
Example: There are 967 chairs in a hall. During an event, 761 chairs were occupied. How many chairs were not occupied?
967 – 761 = 206 206 chairs were not occupied.
Examples of subtraction word problems
134 girls and 119 boys took part in an art competition. How many more girls than boys were there?
Mei Lin saved $184. She saved $63 more than Betty. How much did Betty saved?
John read 32 pages in the morning. He read 14 pages less in the afternoon. a) How many pages did he read in the afternoon? b) How many pages did they read altogether?
A visual way to solve world problems using bar modeling This type of word problem uses the part-whole model.
Example: Mr. Oliver bought 88 pencils. he sold 26 of them. How many pencils did he have left?
A visual way to solve world problems using bar modeling This type of word problem uses the part-whole model. Because the part is missing, this is a subtraction problem.
Example: There are 98 hats, 20 of them are pink and the rest are yellow. How many yellow hats are there?
Example: Cayla did 88 sit-ups in the morning. Nekira did 32 sit-ups at night. How many more sit-ups did Cayla do than Nekira?
How to use bar modeling in Singapore math to solve word problems that deal with comparing?
Example: Adam has 11 fewer lollipops than Hope. If Adam has 16 lollipops, how many lollipop does Hope have?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Subtraction
Subtraction is the process of taking away a number from another. It is a primary arithmetic operation that is denoted by a subtraction symbol (-) and is the method of calculating the difference between two numbers.
What Is Subtraction?
Subtraction is an operation used to find the difference between numbers . When you have a group of objects and you take away a few objects from it, the group becomes smaller. For example, you bought 9 cupcakes for your birthday party and your friends ate 7 cupcakes. Now you are left with 2 cupcakes. This can be written in the form of a subtraction expression: 9 - 7 = 2 and is read as "nine minus seven equals two". When we subtract 7 from 9, (9 - 7) we get 2. Here, we performed the subtraction operation on two numbers 9 and 7 to get the difference of 2.
Subtraction Symbol
In mathematics, we have different symbols. The subtraction symbol is one of the important math symbols that we use while performing subtraction. In the above section, we read about subtracting two numbers 9 and 7. If we observe this subtraction: (9 - 7 = 2), the symbol (-) connects the two numbers and completes the given expression. This symbol is also known as the minus sign.
Subtraction Formula
When we subtract two numbers, we use some terms which are used in the subtraction expression:
- Minuend: The number from which the other number is subtracted.
- Subtrahend: The number which is to be subtracted from the minuend.
- Difference: The final result after subtracting the subtrahend from the minuend.
The subtraction formula is written as: Minuend - Subtrahend = Difference
Let us understand the subtraction formula or the mathematical equation of subtraction with an example.

Here, 9 is the minuend, 7 is the subtrahend, and 2 is the difference.
How To Solve Subtraction Problems?
While solving subtraction problems, one-digit numbers can be subtracted in a simple way, but for larger numbers, we split the numbers into columns using their respective place values , like Ones, Tens, Hundreds, Thousands, and so on. While solving such problems we may encounter some cases with borrowing and some without borrowing. Subtraction with borrowing is also known as subtraction with regrouping. When the minuend is smaller than the subtrahend, we use the regrouping method. While regrouping, we borrow 1 number from the preceding column to make the minuend bigger than the subtrahend. Let us understand this with the help of a few examples.
Subtraction Without Regrouping
Example: Subtract 25632 from 48756.
Note: In subtraction, we always subtract the smaller number from the larger number to get the correct answer.
Solution: Follow the given steps and try to relate them with the following figure.
Step 1: Start with the digit at ones place. (6 - 2 = 4) Step 2: Move to the tens place. (5 - 3 = 2) Step 3: Now subtract the digits at hundreds place. (7 - 6 = 1) Step 4: Now subtract the digits at thousands place. (8 - 5 = 3) Step 5: Finally, subtract the digits at ten thousands place. (4 - 2 = 2) Step 6: Therefore, the difference between the two given numbers is: 48756 - 25632 = 23124.

Subtraction With Regrouping
Example: Subtract 3678 from 8162.
Solution: Follow the given steps and try to relate them with the following figure. We need to solve: 8162 - 3678 Step 1: Start subtracting the digits at ones place. We can see that 8 is greater than 2. So, we will borrow 1 from the tens column which will make it 12. Now, 12 - 8 = 4 ones. Step 2: After giving 1 to the ones column in the previous step, 6 becomes 5. Now, let us subtract the digits at the tens place (5 - 7). Here, 7 is greater than 5, so we will borrow 1 from the hundreds column. This will make it 15. So,15 - 7 = 8 tens. Step 3: In step 2 we had given 1 to the tens column, so we are left with 0 at the hundreds place. To subtract the digits on the hundreds place, i.e., (0 - 6) we will borrow 1 from the thousands column. This will make it 10. So, 10 - 6 = 4 hundreds. Step 4: Now, let us subtract the digits at the thousands place. After giving 1 to the hundreds column, we have 7. So, 7 - 3 = 4 Step 5: Therefore, the difference between the two given numbers is: 8162 - 3678 = 4484

Subtraction Using Number Line
A number line is a visual aid that helps us understand subtraction because it allows us to jump backward and forward on each number. To understand how this works, let us explore subtraction using a number line. Let us subtract 4 from 9 using a number line. We will start by marking the number 9 on the number line. When we subtract using a number line, we count by moving one number at a time towards the left-hand side. Since we are subtracting 4 from 9, we will move 4 times to the left. The number on which you land after 4 backward jumps, is the answer. Thus, 9 - 4 = 5.

Real Life Subtraction Word Problems
The concept of subtraction is often used in our day-to-day activities. Let us understand how to solve real-life subtraction word problems with the help of an interesting example.
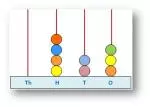
Example: A soccer match had a total of 4535 spectators. After the first innings, 2332 spectators left the stadium. Find the number of remaining spectators.
Solution: Given: The total number of spectators present in the first innings = 4535; The number of spectators who left the stadium after the first innings = 2332 Here, 4535 is the minuend and 2332 is the subtrahend.
Th H T O 4 5 3 5 -2 3 3 2 2 2 0 3
Therefore, the number of remaining spectators = 2203.
Important Notes on Subtraction:
Here are a few important notes that you can follow while performing subtraction in your everyday life.
- Any subtraction problem can be transformed into an addition problem and vice-versa.
- Subtracting 0 from any number gives the number itself as the difference.
- When 1 is subtracted from any number, the difference equals the predecessor of the number.
- Words like "Minus", "Less", "Difference", "Decrease", "Take Away" and "Deduct" indicate that you need to subtract one number from another.
Topics Related to Subtraction
Check out these interesting articles to know about subtraction and its related topics.
- Binary Subtraction
- Subtraction Calculator
- Addition and Subtraction of Fractions
- Subtraction of Complex Numbers
- Subtraction of Fractions
Subtraction Examples
Example 1: In an International cricket match, Sri Lanka scored 236 runs and India scored 126 runs. How many more runs should India score to be equal to the number of runs scored by Sri Lanka?
Runs scored by Sri Lanka = 236; Runs scored by India = 126 To find the number of runs that India should score more to be equal to the number of runs scored by Sri Lanka, we will subtract 126 from 236.
H T O 2 3 6 - 1 2 6 1 1 0
Therefore, India must score 110 more runs to be equal to Sri Lanka's runs.
Example 2: Jerry collected 189 seashells and Eva collected 54 shells. Who collected more seashells and by how much?
Number of shells collected by Jerry = 189; Number of shells collected by Eva = 54
This shows that Jerry collected more seashells. Let us subtract 189 - 54 to get the difference.
H T O 1 8 9 - 0 5 4 1 3 5
Therefore, Jerry collected 135 seashells more than Eva.
Example 3: During an annual Easter egg hunt, the participants found 2469 eggs in the clubhouse, out of which 54 Easter eggs were broken. Can you find out the number of unbroken eggs?
The number of easter eggs found in the Clubhouse = 2469; Number of easter eggs that were broken = 54; The total number of unbroken eggs=?
Now, we will subtract the number of broken eggs from the total number of eggs.
Th H T O 2 4 6 9 - 5 4 2 4 1 5
Therefore, the number of unbroken eggs are 2415.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Subtraction
go to slide go to slide
FAQs on Subtraction
Where do we use subtraction.
Subtraction is used in our day-to-day life. For example, if we want to know how much money we spent on the items that we bought, or, how much money is left with us, or, if we want to calculate the time left in finishing a task, we use subtraction.
What Are the Types of Subtraction?
The types of subtraction mean the various methods used in subtraction. For example, subtraction with and without regrouping, subtraction using number charts, subtraction using number line, the subtraction of small numbers using you fingers, and so on.
What Are Subtraction Strategies?
Subtraction strategies are different ways in which subtraction can be learned. For example, using a number line, with the help of a Place Value Chart, separating the Tens and Ones and then subtracting them separately, and many others.
Give Some Subtraction Examples.
There can be various real-life examples of subtraction. For example, if you have 5 apples and your friend ate 3 apples. Using subtraction, we can find out the number of remaining apples: 5 - 3 = 2. So, 2 apples are left with you. Similarly, if there are 16 students in a class, out of which 9 are girls, then we can find out the number of boys in the class by subtracting 9 from 16. (16 - 9 = 7). So, we know that there are 7 boys in the class.
What Are the Three Parts of Subtraction?
The 3 parts of subtraction are named as follows:
- Minuend: The number from which we subtract the other number is known as the minuend.
- Subtrahend: The number which is subtracted from the minuend is known as the subtrahend.
- Difference: The final result obtained after performing subtraction is known as the difference.
How Do You Write a Subtraction?
While writing subtraction, the two important symbols are '-' (minus) and '=' (equal to). The minus sign means when one number is being subtracted from the other number. And the equal to sign delivers the final result.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 2: Addition and subtraction
About this unit.
In this topic, we will add and subtract whole numbers. The topic starts with 1+1=2 and goes through adding and subtracting within 1000. We will cover regrouping, borrowing, and word problems.
Basic addition and subtraction
- Basic addition (Opens a modal)
- Basic subtraction (Opens a modal)
- Add and subtract: pieces of fruit (Opens a modal)
- Relating addition and subtraction (Opens a modal)
- Add within 5 7 questions Practice
- Subtract within 5 7 questions Practice
- Add within 10 7 questions Practice
- Subtract within 10 7 questions Practice
- Relate addition and subtraction 7 questions Practice
- Getting to 10 by filling boxes (Opens a modal)
- Adding to 10 (Opens a modal)
- Make 10 (grids and number bonds) 7 questions Practice
- Make 10 7 questions Practice
Addition and subtraction word problems within 10
- Addition word problems within 10 (Opens a modal)
- Subtraction word problems within 10 (Opens a modal)
- Addition word problems within 10 7 questions Practice
- Subtraction word problems within 10 7 questions Practice
Addition and subtraction within 20
- Adding within 20 using place value blocks (Opens a modal)
- Adding within 20 using ten frames (Opens a modal)
- Adding 7 + 6 (Opens a modal)
- Adding 8 + 7 (Opens a modal)
- Adding with arrays (Opens a modal)
- Subtracting different ways (Opens a modal)
- Subtract within 20 using a number line (Opens a modal)
- Subtract within 20 using place value blocks (Opens a modal)
- Subtract within 20 using ten frames (Opens a modal)
- Subtracting 14 - 6 (Opens a modal)
- Add within 20 visually 7 questions Practice
- Add within 20 7 questions Practice
- Adding with arrays 4 questions Practice
- Subtract within 20 visually 7 questions Practice
- Subtract within 20 7 questions Practice
- Find missing number (add and subtract within 20) 7 questions Practice
- Add & subtract within 20 7 questions Practice
Word problems within 20
- Addition and subtraction word problems: superheroes (Opens a modal)
- Addition and subtraction word problems: gorillas (Opens a modal)
- Addition and subtraction word problems 1 7 questions Practice
- Addition and subtraction word problems 2 7 questions Practice
- Add and subtract within 20 word problems 7 questions Practice
Word problems with "more" and "fewer"
- Comparison word problems: marbles (Opens a modal)
- Comparison word problems: roly-polies (Opens a modal)
- Word problems with "more" and "fewer" 2 7 questions Practice
Intro to addition with 2-digit numbers
- Adding 2-digit numbers without regrouping (Opens a modal)
- Adding 2-digit numbers without regrouping 1 (Opens a modal)
- Example: Adding 2-digit numbers (no carrying) (Opens a modal)
- Breaking apart 2-digit addition problems (Opens a modal)
- Regrouping to add 1-digit number (Opens a modal)
- Adding up to four 2-digit numbers 4 questions Practice
- Break apart 2-digit addition problems 4 questions Practice
- Regroup when adding 1-digit numbers 7 questions Practice
Intro to subtraction with 2-digit numbers
- Subtracting two-digit numbers without regrouping (Opens a modal)
- Subtracting 2-digit numbers without regrouping 1 (Opens a modal)
- Subtracting a 1-digit number with regrouping (Opens a modal)
- Subtract within 100 using place value blocks 4 questions Practice
- Subtract within 100 using a number line 4 questions Practice
- Subtract 1-digit numbers with regrouping 7 questions Practice
Strategies for adding and subtracting within 100
- Adding 53+17 by making a group of 10 (Opens a modal)
- Adding by making a group of 10 (Opens a modal)
- Strategies for adding 2-digit numbers (Opens a modal)
- Addition and subtraction with number lines (Opens a modal)
- Add 2-digit numbers by making tens 4 questions Practice
- Add 2-digit numbers by making tens 2 4 questions Practice
- Select strategies for adding within 100 4 questions Practice
- Add within 100 using a number line 4 questions Practice
Addition within 100
- Understanding place value when adding ones (Opens a modal)
- Understanding place value when adding tens (Opens a modal)
- Adding with regrouping (Opens a modal)
- Add within 100 using place value blocks 4 questions Practice
Subtraction within 100
- Subtracting with regrouping (borrowing) (Opens a modal)
Word problems within 100
- Adding and subtracting on number line word problems (Opens a modal)
- Adding two digit numbers on a number line (Opens a modal)
- Subtraction word problem: tennis balls (Opens a modal)
- Addition word problem: horses (Opens a modal)
- Subtraction word problem: snow (Opens a modal)
- Subtraction word problem: crayons (Opens a modal)
- Multi step addition word problem (Opens a modal)
- Multi-step subtraction word problem (Opens a modal)
- Add and subtract on the number line word problems 4 questions Practice
- Addition word problems within 100 4 questions Practice
- Subtraction word problems within 100 4 questions Practice
- 2-step addition word problems within 100 4 questions Practice
- 2-step subtraction word problems within 100 4 questions Practice
Adding 1s, 10s, and 100s
- Adding 10 or 100 (Opens a modal)
- Adding 1s, 10s, and 100s (Opens a modal)
- Adding 3-digit numbers (no regrouping) (Opens a modal)
- Add 10s and 100s (no regrouping) 4 questions Practice
- Add within 1,000 using place value blocks 4 questions Practice
Subtracting 1s, 10s, and 100s
- Subtracting 1, 10, or 100 (Opens a modal)
- Subtracting 1s, 10s, and 100s (Opens a modal)
- Subtracting 3-digit numbers (no regrouping) (Opens a modal)
- Subtract 10s and 100s (no regrouping) 7 questions Practice
- Subtract within 1,000 using place value blocks 4 questions Practice
Strategies for adding 2- and 3-digit numbers
- Breaking apart 3-digit addition problems (Opens a modal)
- Solving 3-digit addition in your head (Opens a modal)
- Addition using groups of 10 and 100 (Opens a modal)
- Adding and subtracting on number line (Opens a modal)
- Break apart 3-digit addition problems 4 questions Practice
- Add using groups of 10 and 100 4 questions Practice
- Add on a number line 4 questions Practice
- Select strategies for adding within 1000 4 questions Practice
Addition with regrouping within 1000
- Using place value to add 3-digit numbers: part 2 (Opens a modal)
- Adding 3-digit numbers (Opens a modal)
- Add within 1000 4 questions Practice
Subtraction with regrouping within 1000
- Worked example: Subtracting 3-digit numbers (regrouping) (Opens a modal)
- Worked example: Subtracting 3-digit numbers (regrouping twice) (Opens a modal)
- Worked example: Subtracting 3-digit numbers (regrouping from 0) (Opens a modal)
- Subtracting in your head (no regrouping) (Opens a modal)
- Subtract on a number line 4 questions Practice
- Subtract within 1000 4 questions Practice
Addition and subtraction missing value problems
- Missing numbers in addition and subtraction (Opens a modal)
- Missing number for 3-digit addition within 1000 (Opens a modal)
- Find the missing number (add and subtract within 100) 4 questions Practice
- Find the missing number (add and subtract within 1000) 4 questions Practice
Addition and subtraction greater than 1000
- Relate place value to standard algorithm for multi-digit addition (Opens a modal)
- Multi-digit addition with regrouping (Opens a modal)
- Multi-digit subtraction with regrouping: 6798-3359 (Opens a modal)
- Multi-digit subtraction with regrouping: 7329-6278 (Opens a modal)
- Multi-digit subtraction with regrouping twice (Opens a modal)
- Alternate mental subtraction method (Opens a modal)
- Adding multi-digit numbers: 48,029+233,930 (Opens a modal)
- Relate place value to standard algorithm for multi-digit subtraction (Opens a modal)
- Multi-digit subtraction: 389,002-76,151 (Opens a modal)
- Multi-digit addition 4 questions Practice
- Multi-digit subtraction 4 questions Practice
- Pre-algebra lessons
- Pre-algebra word problems
- Algebra lessons
Algebra word problems
- Algebra proofs
- Advanced algebra
- Geometry lessons
- Geometry word problems
- Geometry proofs
- Trigonometry lessons
- Consumer math
- Baseball math
- Math for nurses
- Statistics made easy
- High school physics
- Basic mathematics store
- SAT Math Prep
- Math skills by grade level
- Ask an expert
- Other websites
- K-12 worksheets
- Worksheets generator
- Algebra worksheets
- Geometry worksheets
- Free math problem solver
- Pre-algebra calculators
- Algebra Calculators
- Geometry Calculators
- Math puzzles
- Math tricks
- Member login
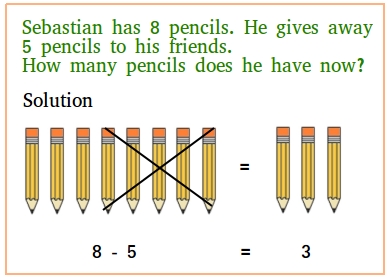
Subtraction word problems
In the problem below, Sebastian has 8 pencils and he gives away 5 pencils to his friends. Sebastian is experiencing a loss of 5 pencils, so the subtraction problem to solve to get the answer is 8 - 5 and 8 - 5 = 3.
Sebastian is left with 3 pencils.
Here are a few more interesting subtraction word problems along with their solutions.
A stock bottle of medication contains 500 mg of a drug. You used 125 mg for one prescription and 62.5 mg for a second prescription, while the third prescription was for a child and only 25.25 mg were necessary.
A. What quantity (mg) of the medication has been used? Round to the nearest hundredths.
B. What quantity (mg) of the original medication is left in the stock bottle? Round to the nearest tenths.
A. We can find the quantity that has been used by adding 125 mg, 62.5 mg, and 25.25 mg together.
125 mg + 62.5 + 25.25 = 212.75 mg
212.75 rounded to the nearest hundredths is 212.75
B. We can find the quantity that is left in the stock bottle by subtracting 212.75 mg from 500 mg.
500 - 212.75 = 287.25
287.25 rounded to the nearest tenths is 287.3
Have A Great Basic Math Word Problem?
Share it here with a very detailed solution!
Enter Your Title
Add a Picture/Graphic Caption (optional)
Click here to upload more images (optional)
Author Information (optional)
To receive credit as the author, enter your information below.
Submit Your Contribution
- Check box to agree to these submission guidelines .
- I am at least 16 years of age.
- I understand and accept the privacy policy .
- I understand that you will display my submission on your website.
(You can preview and edit on the next page)
What Other Visitors Have Said
Click below to see contributions from other visitors to this page...
Click here to write your own.
Addition word problems
Recent Articles
How to divide any number by 5 in 2 seconds.
Feb 28, 24 11:07 AM
Math Trick to Square Numbers from 50 to 59
Feb 23, 24 04:46 AM
Sum of Consecutive Odd Numbers
Feb 22, 24 10:07 AM

100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

Recommended
About me :: Privacy policy :: Disclaimer :: Donate Careers in mathematics
Copyright © 2008-2021. Basic-mathematics.com. All right reserved

Child Login
- Kindergarten
- Number charts
- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even
- Prime and Composite
- Roman Numerals
- Ordinal Numbers
- In and Out Boxes
- Number System Conversions
- More Number Sense Worksheets
- Size Comparison
- Measuring Length
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- More Measurement Worksheets
- Writing Checks
- Profit and Loss
- Simple Interest
- Compound Interest
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem-and-leaf Plot
- Box-and-whisker Plot
- Permutation and Combination
- Probability
- Venn Diagram
- More Statistics Worksheets
- Shapes - 2D
- Shapes - 3D
- Lines, Rays and Line Segments
- Points, Lines and Planes
- Transformation
- Quadrilateral
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel, Perpendicular and Intersecting Lines
- Scale Factor
- Surface Area
- Pythagorean Theorem
- More Geometry Worksheets
- Converting between Fractions and Decimals
- Significant Figures
- Convert between Fractions, Decimals, and Percents
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Squaring Numbers
- Square Roots
- Scientific Notations
- Speed, Distance, and Time
- Absolute Value
- More Pre-Algebra Worksheets
- Translating Algebraic Phrases
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Algebraic Identities
- Quadratic Equations
- Systems of Equations
- Polynomials
- Inequalities
- Sequence and Series
- Complex Numbers
- More Algebra Worksheets
- Trigonometry
- Math Workbooks
- English Language Arts
- Summer Review Packets
- Social Studies
- Holidays and Events
- Worksheets >
- Number Sense >
- Subtraction >
Subtraction Word Problem Worksheets
The extensive set of subtraction word problems featured here will require the learner to find the difference between minuends and subtrahends, which includes problems with regrouping and without regrouping. This large collection of printable word problem worksheets, ideal for children in kindergarten through grade 4 features scenarios that involve single-digit subtraction, two-digit subtraction, three-digit subtraction, and subtraction of large numbers up to six digits. Give yourself a head-start with our free subtraction worksheets!

Word Problems for Beginners: 0 to 10
Find the difference between the numbers that ranges from 0 to 10 in the set of kindergarten worksheets featured here. Use the answer key to verify your responses.
- Download the set

Subtraction within 20
Ascend from a beginner to a proficient in performing subtraction up to 20 as you explore this bunch of well-researched word problems and work out the difference within 20.

Two-digit Subtraction: No Regrouping (No Borrowing)
The series of worksheets for grade 1 and grade 2 presented here involve two-digit subtraction word problems that do not require regrouping. Find the differences between the two-digit subtrahends and minuends featured here.

Two-digit Subtraction: Regrouping (Borrowing)
The two-digit subtraction word problems presented in the 2nd grade worksheets here require regrouping (borrowing). Determine the difference between the two-digit numbers by following the place value columns correctly.

Theme based Subtraction Problems
The colorful theme-based worksheet pdfs for kids in 1st grade through 3rd grade are based on three engaging real-life themes - Beach, Italian Ice and Birthday Party.

Three-digit and Two-digit Subtraction
The set of subtraction word problem pdfs featured here will require grade 3 student to find the difference between three-digit minuends and two-digit subtrahends. Use the answer keys to verify your responses.

Three-digit Subtraction Word Problems
Each printable worksheet contains five word problems finding difference between three-digit numbers. Some problems may require regrouping.

Four-digit Subtraction Word Problems
This section contains subtraction word problems on finding the difference between four-digit numbers. Both borrowing and no borrowing problems are included. Some problems may involve subtraction across zero.

Advanced: Large Number Subtraction
The word problems featured in the 4th grade pdf worksheets here include large numbers with minuends and subtrahends up to six digits. Determine the difference between the large numbers by following the place value columns correctly.
Related Worksheets
» Addition Word Problems
» Subtraction within 10
» 2-Digit Subtraction
» Word Problems
Become a Member
Membership Information
Privacy Policy
What's New?
Printing Help
Testimonial
Copyright © 2024 - Math Worksheets 4 Kids
This is a members-only feature!

Subtraction Worksheets
Welcome to the Subtraction Worksheets page at Math-Drills.com where you will get less of an experience than our other pages! This page includes Subtraction worksheets on topics such as five minute frenzies, one-, two-, three- and multi-digit subtraction and subtracting across zeros.
Subtraction has been around for several years now... well maybe more than a few, so it's probably a good thing for students to learn. People experience subtraction every minute of their lives from banks and the government taking away your money to the cookies in the jar mysteriously disappearing. With a good knowledge of subtraction, you can understand why your bank account reaches zero and do something to prevent it from happening.
Some students do have difficulty with subtraction, so take it easy on them. Help them to learn their addition facts first. Once they know those, they will need a few more strategies to successfully subtract. Teaching with manipulatives like base ten blocks or cereal or insects in the park can help students gain a deeper understanding of subtraction. The subtracting worksheets on this page are meant to support good teaching practices, so only use them for independent learning if students are practising skills they already know.
We use the words, minuend, subtrahend and difference on this page. Please refer to the following, so you know which word means which part of a subtraction question.
Minuend - Subtrahend = Difference
Most Popular Subtraction Worksheets this Week

Subtraction Facts Tables
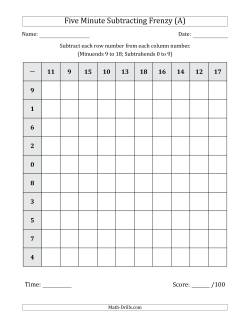
Five minute subtraction frenzies are timed practice charts that help students develop subtraction fact recall speed. These charts are similar to the addition and multiplication frenzy charts, but due to the nature of how subtraction works, we could not focus solely on the single digit fact families. For example, you might get questions like 18 - 4 = 14. You also have to be aware that you must subtract the row number from the column number to get a positive number (or zero). Other than that, they should be a nice way to practice some mental subtraction. As with most of these pages, please only use them as a timed activity with students who will experience success. If a student does not have the necessary skills to complete a frenzy in under five minutes, you may need to take a different approach to how you deliver this page. For all others, students should be able to complete this page in under five minutes with a 98% or greater accuracy and improve their time as they get more practice.
- Five Minute Subtraction Frenzies Five Minute Subtraction Frenzy (Minuends 9 to 18; Subtrahends 0 to 9) Five Minute Subtraction Frenzy (Minuends 29 to 38; Subtrahends 10 to 19) Five Minute Subtraction Frenzy (Minuends 41 to 50; Subtrahends 16 to 25)
Most of the subtraction tables in this section are meant to be used as a reference for students learning their subtraction facts. After a while, most students will remember the facts and recall them easily when completing math problems.
- Subtraction Facts Tables 0 to 11 Subtraction Facts 0 to 11 in Grey Subtraction Facts 0 to 11 in Color Subtraction Facts 0 to 11 with Facts Highlighted Subtraction Facts 0 to 11 in Montessori Colors Subtraction Facts 0 to 11 in Montessori Colors with Facts Highlighted
- Subtraction Facts Tables 1 to 12 Subtraction Facts Tables in Gray 1 to 12 Subtraction Facts Tables in Color 1 to 12 Subtraction Facts Tables in Montessori Colors 1 to 12 Subtraction Facts 1 to 12 with Facts Highlighted Subtraction Facts 1 to 12 in Montessori Colors with Facts Highlighted
- Compact Subtraction Facts Tables Compact Subtraction Table (Filled) Compact Subtraction Table (Blank)
Single-Digit Subtraction Facts

Subtracting single-digit facts is a skill that students generally learn after or while they are learning single-digit addition facts. The subtraction worksheets in this section are meant to be used for practice, testing or with teacher guidance. They will not teach students how to subtract or what the connection is between addition and subtraction; for that, students require a teacher or parent.
Some students might find it easier to start with subtraction facts with minuends (the first number) limited to 9 or lower. This way, they don't need to count across 10 eliminating that extra pesky digit... for now.
- Subtracting Single-Digit from Single-Digit Numbers 100 Subtraction Questions with Minuends up to 9 64 Subtraction Questions with Minuends up to 9 25 Subtraction Questions with Minuends up to 9
In relation to addition facts, the following worksheets cover the facts from 0 to 9, and the worksheets after that cover the addition facts from 1 to 9. The minuends are the amounts to be subtracted from, so a minuend of 18 means that both the subtrahend (the amount being subtracted) and the difference will be 9. The worksheets marked with an asterisk (*) include all possible questions in a random order on each version of the worksheet.
- Subtraction Facts from (0 − 0) to (18 − 9) Subtraction Facts from (0 − 0) to (18 − 9) (100* Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (81 Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (64 Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (50 Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (25 Large Print Questions) ✎ Subtraction Facts from (0 − 0) to (18 − 9) (12 Very Large Print Questions) ✎
- Subtraction Facts from (2 − 1) to (18 − 9) (No Zeros) Subtraction Facts from (2 − 1) to (18 − 9) (100 Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (81* Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (64 Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (50 Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (25 Large Print Questions) ✎ Subtraction Facts from (2 − 1) to (18 − 9) (12 Very Large Print Questions) ✎
- Subtraction Facts with Minuends from 10 to 18 100 Subtraction Questions with Minuends from 10 to 18 and All Regrouping (100 Questions) 64 Subtraction Questions with Minuends from 10 to 18 and All Regrouping (64 Questions) 25 Subtraction Questions with Minuends from 10 to 18 and All Regrouping (25 Large Print Questions)
Sometimes students just need to reinforce a single number at a time which is where these worksheets come in. There are three sets of worksheets in this section, each with a different number of questions. The last set is the most interesting as there are no questions repeated. Eleven and Twelve have been included as they are essentially subtracting by 10 and 1 or 2 more.
- Subtracting Individual Focus or Target Facts (50 Questions per Page) Subtracting 0 (50 Questions) ✎ Subtracting 1 (50 Questions) ✎ Subtracting 2 (50 Questions) ✎ Subtracting 3 (50 Questions) ✎ Subtracting 4 (50 Questions) ✎ Subtracting 5 (50 Questions) ✎ Subtracting 6 (50 Questions) ✎ Subtracting 7 (50 Questions) ✎ Subtracting 8 (50 Questions) ✎ Subtracting 9 (50 Questions) ✎ Subtracting 10 (50 Questions) ✎ Subtracting 11 (50 Questions) ✎ Subtracting 12 (50 Questions) ✎
- Subtracting Individual Focus or Target Facts (25 Questions per Page) Subtracting Zero (0) (25 Large Print Questions) ✎ Subtracting One (1) (25 Large Print Questions) ✎ Subtracting Two (2) (25 Large Print Questions) ✎ Subtracting Three (3) (25 Large Print Questions) ✎ Subtracting Four (4) (25 Large Print Questions) ✎ Subtracting Five (5) (25 Large Print Questions) ✎ Subtracting Six (6) (25 Large Print Questions) ✎ Subtracting Seven (7) (25 Large Print Questions) ✎ Subtracting Eight (8) (25 Large Print Questions) ✎ Subtracting Nine (9) (25 Large Print Questions) ✎
- Subtracting Individual Focus or Target Facts with Differences of 0 to 99 (100 Unique Questions per Page) Subtracting One (1) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Two (2) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Three (3) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Four (4) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Five (5) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Six (6) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Seven (7) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Eight (8) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Nine (9) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Ten (10) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Eleven (11) with Differences 0 to 99 (100 Unique Questions) ✎ Subtracting Twelve (12) with Differences 0 to 99 (100 Unique Questions) ✎
- Horizontally Arranged Subtraction Facts with Minuends to 18 Horizontal Subtraction Facts with Minuends to 18 (100 Questions) ✎ Horizontal Subtraction Facts with Minuends to 18 (50 Questions) ✎ Horizontal Subtraction Facts with Minuends to 18 (25 Questions; Large Print) ✎
- Horizontally Arranged Subtracting 1 to 5 from 1 to 10 Horizontal Subtracting 1 to 5 from 1 to 10 (100 Questions) ✎ Horizontal Subtracting 1 to 5 from 1 to 10 (50 Questions) ✎ Horizontal Subtracting 1 to 5 from 1 to 10 (25 Questions; Large Print) ✎
- Horizontally Arranged Subtracting 1s and 2s from Single-Digit Minuends Horizontal Subtracting Ones from Single-Digit Minuends (25 per page) ✎ Horizontal Subtracting Twos from Single-Digit Minuends (25 per page) ✎
- Horizontally Arranged Subtracting Individual Focus Facts Horizontal Subtracting 0s (100 per page) ✎ Horizontal Subtracting 1s (100 per page) ✎ Horizontal Subtracting 2s (100 per page) ✎ Horizontal Subtracting 3s (100 per page) ✎ Horizontal Subtracting 4s (100 per page) ✎ Horizontal Subtracting 5s (100 per page) ✎ Horizontal Subtracting 6s (100 per page) ✎ Horizontal Subtracting 7s (100 per page) ✎ Horizontal Subtracting 8s (100 per page) ✎ Horizontal Subtracting 9s (100 per page) ✎
- Horizontally Arranged Subtracting Pairs of Individual Focus Facts Horizontal Subtracting 0s and 1s (100 per page) ✎ Horizontal Subtracting 2s and 3s (100 per page) ✎ Horizontal Subtracting 4s and 5s (100 per page) ✎ Horizontal Subtracting 6s and 7s (100 per page) ✎ Horizontal Subtracting 8s and 9s (100 per page) ✎
- Subtracting a Number from Itself Subtracting a Number from Itself (Range 1 to 20)
The make ten subtraction strategy involves "spliting" the subtrahend (amount being subtracted) into two parts. The first part should be the exact amount that will reduce the minuend (the first number) to ten (or multiple of ten as the case may be) and the second part is the leftover amount. The strategy helps students internalize a mental strategy for subtracting across tens. For example, with the question 15 - 9, students first recognize that they need to subtract 5 to get 10, so they split the 9 into 5 and 4. Subtracting 5 from 15 results in 10 and subtracting 4 more results in 6, so 15 - 9 = 6. This strategy can be used any time students need to subtract "over" a multiple of ten and there are many worksheets in this section to practice it. For example, subtracting 84 - 8, students recognize that they must subtract 4 from 84 to get 80 which leaves 4 more to subtract from 80 to get 76.
- Make Ten Strategy Worksheets with 10 and Multiples of 10 Make 10 Subtraction Strategy Make 20 Subtraction Strategy Make 30 Subtraction Strategy Make 40 Subtraction Strategy Make 50 Subtraction Strategy Make 60 Subtraction Strategy Make 70 Subtraction Strategy Make 80 Subtraction Strategy Make 90 Subtraction Strategy Make Multiples of 10 Subtraction Strategy
Long Subtraction Worksheets

Try teaching a mental math strategy for subtraction called counting up. Here is how it is done:
Start with the second number (the subtrahend) and count up by tens until you find the closest value to the first number (the minuend). Keep track of how many tens you counted. Add or subtract a single digit number to get the minuend exactly then adjust the tens by that amount. For the question, 84 - 35, start at 35, and count, 45, 55, 65, 75, 85 (five tens) and one down to get 84. Five tens minus one is 49. For the question 65 - 22, start at 22 and count, 32, 42, 52, 62 (four tens) and three up to get 65. Four tens and three is 43. The previous examples used two-digit numbers, but the strategy can swiftly be modified for larger numbers. How far can your students go with it? Here is an example with three-digit numbers:
Let's use the question 927 - 648. First, count up by hundreds to 948 (that's 300). Then count down by tens to 928 (that's -20). Finally count down by ones to 927 (that's one). 300 - 20 - 1 = 279. That's almost easier than adding!
The multi-digit or long subtraction worksheets in the first part of this section are classic long subtraction worksheets with randomly generated numbers. Regrouping should be necessary about half of the time. Versions with ALL regrouping and NO regrouping follow. If you would like to see numbers with thousands separators, look a little further down and choose the appropriate version for your location.
- Subtracting up to 3-Digit Numbers with Some Regrouping Subtracting 2-Digit from 2-Digit Numbers with Some Regrouping ✎ Subtracting 2-Digit from 3-Digit Numbers with Some Regrouping ✎ Subtracting 3-Digit from 3-Digit Numbers with Some Regrouping ✎ 3-Digit Expanded Form Subtraction Subtracting 3-Digit from 4-Digit Numbers with Some Regrouping ✎
- Subtracting up to 3-Digit Numbers with Some Regrouping (Large Print) Subtracting 1-Digit from 2-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 2-Digit from 2-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 1-Digit from 3-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 2-Digit from 3-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 3-Digit from 3-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 1- to 3-Digit from 1- to 3-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 3-Digit from 4-Digit Numbers with Some Regrouping ( Large Print ) ✎
- Subtracting 4- to 9-Digit Numbers with Some Regrouping Subtracting 4-Digit from 4-Digit Numbers with Some Regrouping ✎ Subtracting 4-Digit from 5-Digit Numbers with Some Regrouping ✎ Subtracting 5-Digit from 5-Digit Numbers with Some Regrouping ✎ Subtracting 5-Digit from 6-Digit Numbers with Some Regrouping ✎ Subtracting 6-Digit from 6-Digit Numbers with Some Regrouping ✎ Subtracting 6-Digit from 7-Digit Numbers with Some Regrouping ✎ Subtracting 7-Digit from 7-Digit Numbers with Some Regrouping ✎ Subtracting 7-Digit from 8-Digit Numbers with Some Regrouping ✎ Subtracting 8-Digit from 8-Digit Numbers with Some Regrouping ✎ Subtracting 8-Digit from 9-Digit Numbers with Some Regrouping ✎ Subtracting 9-Digit from 9-Digit Numbers with Some Regrouping ✎
- Subtracting 4- to 6-Digit Numbers with Some Regrouping (Large Print) Subtracting 4-Digit from 4-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 4-Digit from 5-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 5-Digit from 5-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 5-Digit from 6-Digit Numbers with Some Regrouping ( Large Print ) ✎ Subtracting 6-Digit from 6-Digit Numbers with Some Regrouping ( Large Print ) ✎
For students who need a little extra help with lining things up, these long subtraction worksheets have the digits spaced farther apart on a grid. The answer keys also show the carrying values to help diagnose where things went wrong (but hopefully they won't).
- Long Subtraction Worksheets with Grid Support 2-Digit Minus 2-Digit Subtraction With Grid Support 3-Digit Minus 2-Digit Subtraction With Grid Support 3-Digit Minus 3-Digit Subtraction With Grid Support 4-Digit Minus 3-Digit Subtraction With Grid Support 4-Digit Minus 4-Digit Subtraction With Grid Support 5-Digit Minus 4-Digit Subtraction With Grid Support 5-Digit Minus 5-Digit Subtraction With Grid Support 6-Digit Minus 5-Digit Subtraction With Grid Support 6-Digit Minus 6-Digit Subtraction With Grid Support 2- to 4-Digit Minus 2- to 4-Digit Subtraction With Grid Support 3- to 6-Digit Minus 3- to 6-Digit Subtraction With Grid Support
The next long subtraction worksheets include questions that require regrouping at every step. They can be frustrating and difficult for students who are not familiar with the concept of subtraction. Try showing them with base ten blocks how regrouping works.
- Subtracting up to 3-Digit Numbers with All Regrouping Subtracting 1-Digit Numbers with ALL Regrouping ✎ Subtracting 2-Digit Numbers with ALL Regrouping ✎ Subtracting 3-Digit Numbers with ALL Regrouping ✎
- Subtracting up to 3-Digit Numbers with All Regrouping (Large Print) Subtracting 1-Digit Numbers with ALL Regrouping ( Large Print ) ✎ Subtracting 2-Digit Numbers with ALL Regrouping ( Large Print ) ✎ Subtracting 3-Digit Numbers with ALL Regrouping ( Large Print ) ✎
- Subtracting 4- to 8-Digit Numbers with All Regrouping Subtracting 4-Digit Numbers with ALL Regrouping ✎ Subtracting 5-Digit Numbers with ALL Regrouping ✎ Subtracting 6-Digit Numbers with ALL Regrouping ✎ Subtracting 7-Digit Numbers with ALL Regrouping ✎ Subtracting 8-Digit Numbers with ALL Regrouping ✎
- Subtracting 4- to 6-Digit Numbers with All Regrouping (Large Print) Subtracting 4-Digit Numbers with ALL Regrouping ( Large Print ) ✎ Subtracting 5-Digit Numbers with ALL Regrouping ( Large Print ) ✎ Subtracting 6-Digit Numbers with ALL Regrouping ( Large Print ) ✎
Some students require a little extra help when learning to subtract large numbers. These subtraction worksheets include questions where the regrouping step has been eliminated. This might help students learn a subtraction algorithm before learning about regrouping.
- Subtracting up to 3-Digit Numbers with No Regrouping Subtracting 2-Digit from 2-Digit Numbers with NO Regrouping ✎ Subtracting 2-Digit from 3-Digit Numbers with NO Regrouping ✎ Subtracting 3-Digit from 3-Digit Numbers with NO Regrouping ✎ Subtracting 2-Digit from 4-Digit Numbers with NO Regrouping ✎ Subtracting 3-Digit from 4-Digit Numbers with NO Regrouping ✎
- Subtracting up to 3-Digit Numbers with No Regrouping (Large Print) Subtracting 2-Digit from 2-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 2-Digit from 3-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 3-Digit from 3-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 2-Digit from 4-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 3-Digit from 4-Digit Numbers with NO Regrouping ( Large Print ) ✎
- Subtracting 4- to 9-Digit Numbers with No Regrouping Subtracting 4-Digit from 4-Digit Numbers with NO Regrouping ✎ Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping ✎ Subtracting 7-Digit from 7-Digit Numbers with NO Regrouping ✎ Subtracting 8-Digit from 8-Digit Numbers with NO Regrouping ✎ Subtracting 9-Digit from 9-Digit Numbers with NO Regrouping ✎
- Subtracting 4- to 6-Digit Numbers with No Regrouping (Large Print) Subtracting 4-Digit from 4-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping ( Large Print ) ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping ( Large Print ) ✎
Why horizontal subtraction worksheets? Students can show their understanding of place value and number sense if they do not already have the numbers lined up. Vertical subtraction is often learned based on a student's understanding of single-digit subtraction, but looking at the whole number is lost in the algorithm.
- Horizontally Arranged 2-Digit Minus 1-Digit Questions 2-digit Minus 1-Digit Horizontal Subtraction (100 Questions) ✎ 2-digit Minus 1-Digit Horizontal Subtraction (50 Questions) ✎ 2-digit Minus 1-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
- Horizontally Arranged 2-Digit Minus 2-Digit Questions 2-digit Minus 2-Digit Horizontal Subtraction (100 Questions) ✎ 2-digit Minus 2-Digit Horizontal Subtraction (50 Questions) ✎ 2-digit Minus 2-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
- Horizontally Arranged 3-Digit Minus 1-Digit Questions 3-digit Minus 1-Digit Horizontal Subtraction (100 Questions) ✎ 3-digit Minus 1-Digit Horizontal Subtraction (50 Questions) ✎ 3-digit Minus 1-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
- Horizontally Arranged 3-Digit Minus 2-Digit Questions 3-digit Minus 2-Digit Horizontal Subtraction (50 Questions) ✎ 3-digit Minus 2-Digit Horizontal Subtraction (25 Questions; Large Print) ✎ 3-Digit Minus 2-Digit Horizontal Subtraction ( All Regrouping ; 100 Questions)
- Horizontally Arranged 3-Digit Minus 3-Digit Questions 3-Digit Minus 3-Digit Horizontal Subtraction (50 Questions) ✎ 3-Digit Minus 3-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
- Horizontally Arranged Various-Digit Minus Various-Digit Questions Various-Digit Minus Various-Digit Horizontal Subtraction (50 Questions) ✎ Various-Digit Minus Various-Digit Horizontal Subtraction (25 Questions; Large Print) ✎
Many students in English-speaking countries are used to seeing numbers with comma-separated thousands.
- Long Subtraction Worksheets with Comma Separated Thousands Subtracting 2-Digit from 4-Digit Numbers (Comma Separated) ✎ Subtracting 3-Digit from 4-Digit Numbers (Comma Separated) ✎ Subtracting 4-Digit from 4-Digit Numbers (Comma Separated) ✎ Subtracting 2-Digit from 5-Digit Numbers (Comma Separated) ✎ Subtracting 3-Digit from 5-Digit Numbers (Comma Separated) ✎ Subtracting 4-Digit from 5-Digit Numbers (Comma Separated) ✎ Subtracting 5-Digit from 5-Digit Numbers (Comma Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 4 digits (Comma Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 5 digits (Comma Separated) ✎
- Long Subtraction Worksheets with Comma Separated Thousands and All Regrouping Subtracting 4-Digit Numbers with ALL Regrouping (Comma Separated) ✎ Subtracting 5-Digit Numbers with ALL Regrouping (Comma Separated) ✎ Subtracting 6-Digit Numbers with ALL Regrouping (Comma Separated) ✎ Subtracting 7-Digit Numbers with ALL Regrouping (Comma Separated) ✎ Subtracting 8-Digit Numbers with ALL Regrouping (Comma Separated) ✎
- Long Subtraction Worksheets with Comma Separated Thousands and No Regrouping Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping (Comma Separated) ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping (Comma Separated) ✎ Subtracting 7-Digit from 7-Digit Numbers with NO Regrouping (Comma Separated) ✎ Subtracting 8-Digit from 8-Digit Numbers with NO Regrouping (Comma Separated) ✎ Subtracting 9-Digit from 9-Digit Numbers with NO Regrouping (Comma Separated) ✎
Space-separated thousands are becoming more widely used, including in the United States. Canadian students have used both comma separated and space separated thousands for many years.
- Long Subtraction Worksheets with Space Separated Thousands Subtracting 2-Digit from 4-Digit Numbers (Space Separated) ✎ Subtracting 3-Digit from 4-Digit Numbers (Space Separated) ✎ Subtracting 4-Digit from 4-Digit Numbers (Space Separated) ✎ Subtracting 2-Digit from 5-Digit Numbers (Space Separated) ✎ Subtracting 3-Digit from 5-Digit Numbers (Space Separated) ✎ Subtracting 4-Digit from 5-Digit Numbers (Space Separated) ✎ Subtracting 5-Digit from 5-Digit Numbers (Space Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 4 digits (Space Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 5 digits (Space Separated) ✎
- Long Subtraction Worksheets with Space Separated Thousands and All Regrouping Subtracting 4-Digit Numbers with ALL Regrouping (Space Separated) ✎ Subtracting 5-Digit Numbers with ALL Regrouping (Space Separated) ✎ Subtracting 6-Digit Numbers with ALL Regrouping (Space Separated) ✎ Subtracting 7-Digit Numbers with ALL Regrouping (Space Separated) ✎ Subtracting 8-Digit Numbers with ALL Regrouping (Space Separated) ✎
- Long Subtraction Worksheets with Space Separated Thousands and No Regrouping Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping (Space Separated) ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping (Space Separated) ✎ Subtracting 7-Digit from 7-Digit Numbers with NO Regrouping (Space Separated) ✎ Subtracting 8-Digit from 8-Digit Numbers with NO Regrouping (Space Separated) ✎ Subtracting 9-Digit from 9-Digit Numbers with NO Regrouping (Space Separated) ✎
Even though period separated thousands are not common in the English-speaking world, we provide these for our friends in other countries who may find them useful.
- Long Subtraction Worksheets with Period Separated Thousands Subtracting 2-Digit from 4-Digit Numbers (Period Separated) ✎ Subtracting 3-Digit from 4-Digit Numbers (Period Separated) ✎ Subtracting 4-Digit from 4-Digit Numbers (Period Separated) ✎ Subtracting 2-Digit from 5-Digit Numbers (Period Separated) ✎ Subtracting 3-Digit from 5-Digit Numbers (Period Separated) ✎ Subtracting 4-Digit from 5-Digit Numbers (Period Separated) ✎ Subtracting 5-Digit from 5-Digit Numbers (Period Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 4 digits (Period Separated) ✎ Mixture of Multi-Digit Subtraction from 2 to 5 digits (Period Separated) ✎
- Long Subtraction Worksheets with Period Separated Thousands and All Regrouping Subtracting 4-Digit Numbers with ALL Regrouping (Period Separated) ✎ Subtracting 5-Digit Numbers with ALL Regrouping (Period Separated) ✎ Subtracting 6-Digit Numbers with ALL Regrouping (Period Separated) ✎ Subtracting 7-Digit Numbers with ALL Regrouping (Period Separated) ✎ Subtracting 8-Digit Numbers with ALL Regrouping (Period Separated) ✎
- Long Subtraction Worksheets with Period Separated Thousands and No Regrouping Subtracting 5-Digit from 5-Digit Numbers with NO Regrouping (Period Separated) ✎ Subtracting 6-Digit from 6-Digit Numbers with NO Regrouping (Period Separated) ✎ Subtracting 7-Digit from 7-Digit Numbers with NO Regrouping (Period Separated) ✎ Subtracting 8-Digit from 8-Digit Numbers with NO Regrouping (Period Separated) ✎ Subtracting 9-Digit from 9-Digit Numbers with NO Regrouping (Period Separated) ✎
Various Other Long Subtraction Worksheets

Generally, a student would not regroup to determine the complements of 10, 100, 1000, etc. One strategy that could be used is as follows: working from left to right, a student would take each digit in the subtrahend and figure out its nines complement. If the digit was 3, for example, the nines complement of 3 is 6. For the last digit (ones), the student would use the tens complement. For example, a typical question is 1000 - 456. The nines complement of 4 is 5, the nines complement of 5 is 4 and the tens complement of 6 is 4. Putting it all together, the student would get 5 4 4 or 544 = 1000 - 456.
- Calculating Complements of Powers of Ten (Subtracting Across Zeros) Complements of 10 Complements of 100 Complements of 1000 Complements of 10000 Complements of 100 and 1000 Complements of 1000 and 10000 Complements of 100, 1000 and 10000
A similar strategy is employed with the next worksheets except students must adapt to calculating the largest place value number.
- Calculating Complements of Multiples of Powers of Ten (Subtracting Across Zeros) Subtracting from multiples of 10 Subtracting from multiples of 100 Subtracting from multiples of 1000 Subtracting from multiples of 10000 Subtracting from a mixture of multiples of 100 and 1000 Subtracting from a mixture of multiples of 1000 and 10000 Subtracting from a mixture of multiples of 100, 1000 and 10000
These worksheets are meant to give students practice dealing with 0's in the middles of subtraction questions. Whether using pencil and paper or mental arithmetic, it is always a good idea to make sure students know what to do when they encounter zeros.
- Subtracting Across Zeros in the Middle (Ones Always Need Regrouping) 3-Digit Subtraction across zeros in the middle ( Ones always need regrouping ) 4-Digit Subtraction across zeros in the middle ( Ones always need regrouping ) 5-Digit Subtraction across zeros in the middle ( Ones always need regrouping )
- Subtracting Across Zeros in the Middle (Ones Sometimes Need Regrouping) 3-Digit Subtraction across zeros in the middle ( Ones sometimes need regrouping ) 4-Digit Subtraction across zeros in the middle ( Ones sometimes need regrouping ) 5-Digit Subtraction across zeros in the middle ( Ones sometimes need regrouping )
Subtracting numbers in number systems other than decimal numbers including binary, quaternary, octal, duodecimal and hexadecimal numbers.
- Subtracting in Other Base Number Systems Subtracting Binary Numbers (Base 2) Subtracting Ternary Numbers (Base 3) Subtracting Quaternary Numbers (Base 4) Subtracting Quinary Numbers (Base 5) Subtracting Senary Numbers (Base 6) Subtracting Octal Numbers (Base 8) Subtracting Duodecimal Numbers (Base 12) Subtracting Hexadecimal Numbers (Base 16) Subtracting Vigesimal Numbers (Base 20) Subtracting Hexatrigesimal Numbers (Base 36) Subtracting Various Numbers (Various Bases)
Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.

Subtraction – Definition, Symbol, Examples, Practice Problems
What is subtraction in math, symbol of subtraction, regrouping in math, solved examples on subtraction, practice problems on subtraction, frequently asked questions on subtraction, subtraction: introduction.
Suppose we purchase ice cream for a certain amount of money, say $\$140$, and we give $\$200$ to the cashier. Now, the cashier returns the excess amount by performing subtraction such as $200 − 140 = 60$. Then, the cashier will return $\$60$.
What is exactly happening here?
The answer to this question is subtraction.

Subtraction is one of the four basic arithmetic operations in mathematics. The other three being addition , multiplication , and division .
We can observe the applications of subtraction in our day-to-day life in different situations.
For example, if we have 3 candies and our friend asks us for 1 candy, how many candies are we left with? Simply,
$3 − 1 = 2$
Let’s understand the concept with the help of the following example of apples.

In the example above, if Harry has 6 apples and he gives 3 apples to Jim, How many apples are left with him?
We can calculate this by subtracting 3 from 6:
$6 − 3 = 3$
Harry is left with 3 apples.
Related Worksheets

Definition of Subtraction
The operation or process of finding the difference between two numbers or quantities is known as subtraction. To subtract a number from another number is also referred to as ‘taking away one number from another’. Some instances where we use subtraction are while making payments, transferring money to our friends and many more.
In mathematics, we have generally used different symbols for different operators. We have symbols like $+, −, /, *$ and many more. The subtraction symbol $“−”$ is one of the most important math symbols that we use. In the above section, we read about subtracting two numbers 6 and 3. If we observe this expression: $(6 − 3 = 3)$, the symbol $(−)$ between the two numbers is what denotes subtraction. This symbol is also known as the minus $(−)$ sign.
Formula of Subtraction Operation
When we subtract two numbers, we commonly use some terms that are used in a subtraction expression:
Minuend : A minuend is the number from which the other number is subtracted.
Subtrahend : A subtrahend is the number which is to be subtracted from the minuend.
Difference : A difference is the final result after subtracting the subtrahend from the minuend.
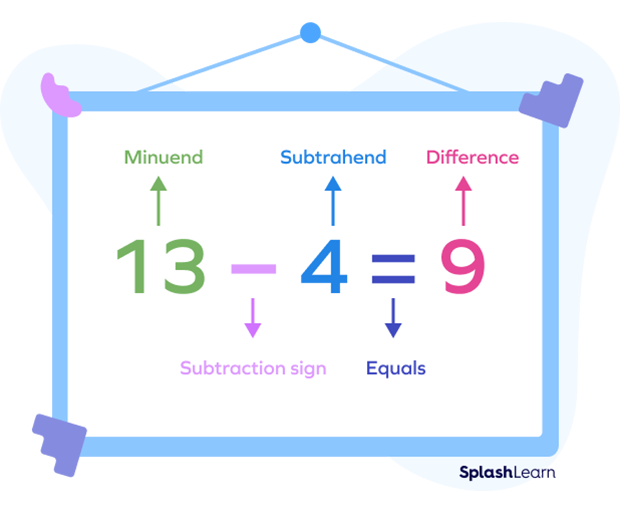
The subtraction formula is written as
Minuend $−$ Subtrahend $=$ Difference
For example,
$7 − 3 = 4$
Here,
$7 =$ Minuend
$3 =$ Subtrahend
$4 =$ Difference
What Is Minus in Math?
Minus is a sign or a symbol that is represented by a horizontal line .

We use minus in mathematics for multiple representations.
Uses of Minus Sign
Subtraction operation.
Minus represents the arithmetic operation of subtraction between two numbers. We use minus sign to denote subtract, decreased by, take away, etc.
For example,
Minus sign also means how much is one value more than the other value.
For example, Darby has 8 gingerbread with her and Olive has 3 gingerbreads.
Darby has more gingerbreads by $(8 − 3) = 5$
To Represent Negative Integers
Integers are the numbers that are not in decimal or fractional form and include positive and negative numbers along with 0. We use the minus sign to represent the negative integers, i.e., the whole numbers which are less than zero (no fractions).
For representing a negative integer, we add a negative or minus sign in front of a whole number. For example, negative integer 5 is represented as: $(− 5)$
Use in Measurement
We also use the minus sign in measurement specially in temperature.
For example, a temperature of $− 4^{\circ} \text{C}$ means 4 degrees below zero.
Another example: The temperature is $5^{\circ} \text{C}$ and then drops $− 10^{\circ} \text{C}$. What is the temperature now?
The temperature now $= 5 − 10 = − 5^{\circ} \text{C}$

To Represent Opposite Directions
We also use the minus sign to represent a negative direction on a graph paper to show the coordinates.
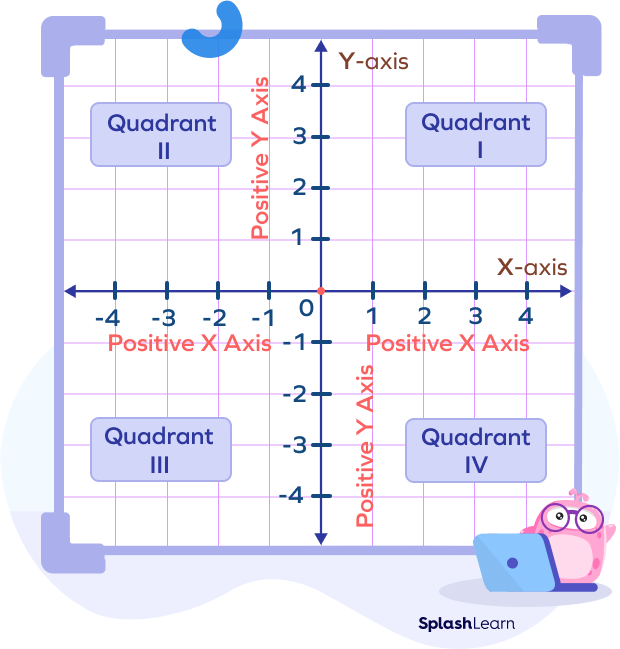
The graph also runs in the negative direction.
- In the first quadrant, the coordinates are of the form $(x,y)$.
- In the second quadrant, the coordinates are of the form $(−x,y)$.
- In the third quadrant, the coordinates are of the form $(−x,−y)$.
- In the fourth quadrant, the coordinates are of the form $(x,−y)$.
Mathematical Operations on Integers Using “Minus” Sign
- Multiplication of two negative numbers gives a positive number.
Negative $\times$ Negative $=$ Positive
For example, $(− 5) \times (− 15) = + 75$
- Multiplication of a negative number and a positive number gives a negative number.
Negative $\times$ Positive $=$ Negative
For example, $(− 5) \times (15) = − 75$
- Addition of a negative number with a negative number will always give a negative number.
Negative $+$ Negative $=$ Negative
For example, $(− 3) + (− 4) = (− 7)$
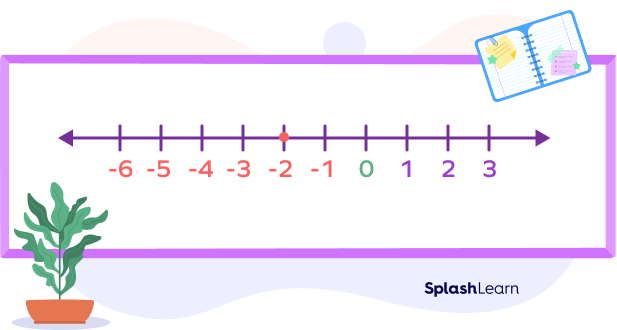
- Subtracting a positive number from a negative number will always give a negative number.
If we subtract a positive number from a negative number, we start at the negative number and count backwards.
Negative $−$ Positive $=$ Negative
Using the number line, let’s start at $− 3$.
For example: Say, we have the problem $(− 2) − 3$.
Now count backwards 3 units. So, keep counting back three spaces from $− 2$ on the number line, we get
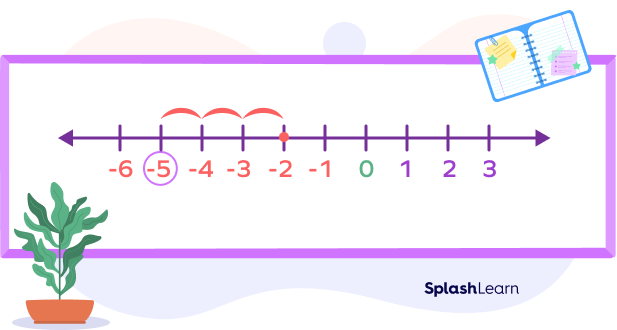
The answer is $(− 2) − 3 = − 5$.
- Subtracting a negative number from a negative number
A negative sign followed by a negative sign, turns the two signs into a positive sign. So, instead of subtracting a negative, you are adding a positive. The answer could be either positive or negative, depending on the magnitude of the numbers.
Negative $−$ Negative $=$ Negative $+$ Positive
Basically, $− (− 5)$ becomes $+ 5$, and then you add the numbers.
For example, we have $(− 2) − (− 5)$. We can read it as “negative two minus negative 5”. We’re changing the two negative signs into a positive, so the equation now becomes $(− 2) + 5$.
On the number line, it starts at $− 2$.
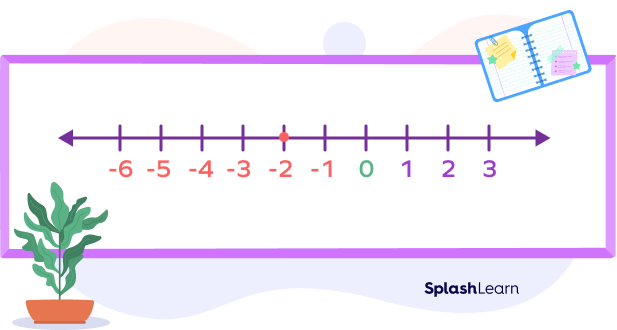
Then we move forward 5 units: $+ 5$.
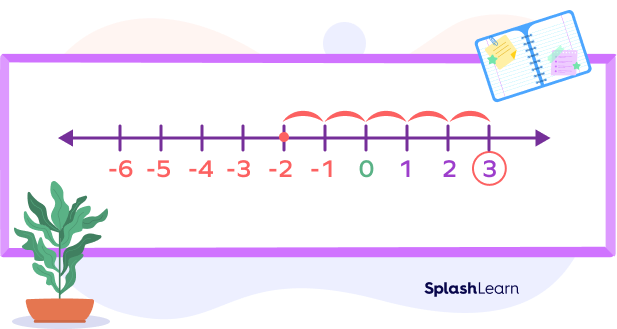
The answer is $− 2 − (− 5) = 3$.
- Subtracting a negative number from a positive number will always give a positive number.
When we subtract a negative number from a positive number, we turn the subtraction sign followed by a negative sign into a plus sign. So, instead of subtracting a negative, you’re adding a positive. So the equation turns into a simple addition problem.
Positive – Negative = Positive + Positive
For example, let’s say we have the problem $2 − (− 4)$. This reads “two minus negative four.” The $− (− 4)$ turns into $+ 4$.
On the number line we start at 2.
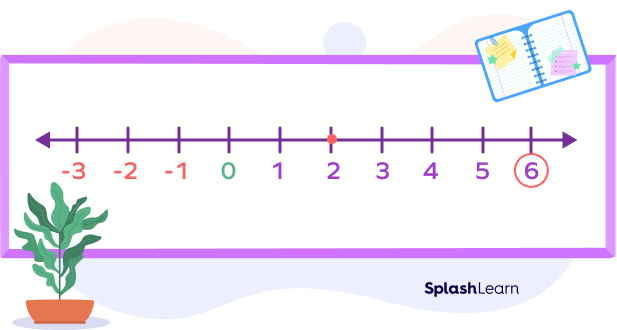
Then we move forward three units: $2 + 4$.
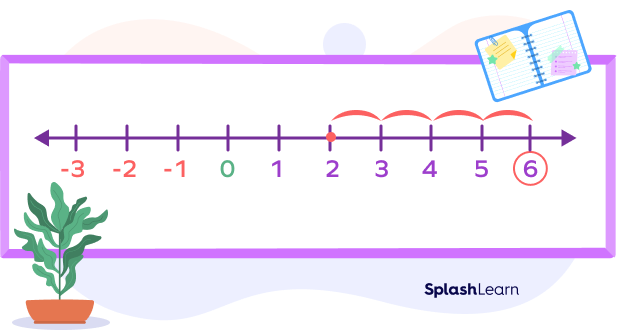
The answer is $2 − (− 4) = 6$.
Methods of Subtraction
There are various methods for subtraction. In this article, we shall be discussing three of them.
Visual representation
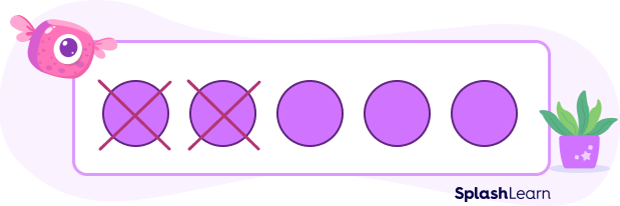
One of the methods is to use a diagram showing what you start with, what you are taking away, and what you are left with.
For example, we have 5 balls, now a friend asks for 2 balls, we can easily calculate that we are left with 2 balls using the concept of subtraction by depicting it through a diagram as given below:
Another method to perform subtraction is by using a number line.
Subtraction on Number Lines
If we want to calculate 5 minus 2, we start from 5. Since we need to subtract 2, we take 2 steps back. Finally we observe that we are standing at 3.
So, this is how $5 − 2$ is calculated on the number line.
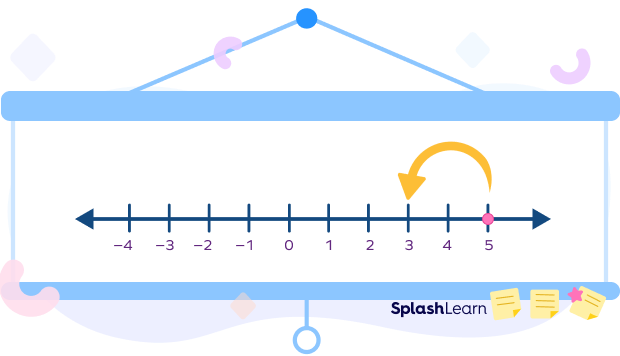
This is a number line representation of the expression.
Column method
The generally used method is the column method of subtraction, where we separate the numbers into ones, tens, hundreds and so on and write the minuend above the subtrahend, where all the ones are in one column, all the tens are in another column and so on. In this method, we always start the subtraction with the ones and proceed from right to left.

Regrouping in math can be defined as the process of making/breaking groups when carrying out operations like addition and subtraction. To regroup means to rearrange groups in place value to carry out an operation. We use regrouping in subtraction, when digits in the minuend are smaller than the digits in the same place of the subtrahend.
This process is called regrouping as we are regrouping numbers or rearranging them into their place value to carry out this process. When we use regrouping in subtraction, it is also sometimes called borrowing.

Subtraction with Regrouping
In subtraction, we sometimes use the concept of regrouping between numbers. When the numbers are subtracted using the column method and the bottom digit is greater than the upper digit, we regroup the numbers to be able to subtract.
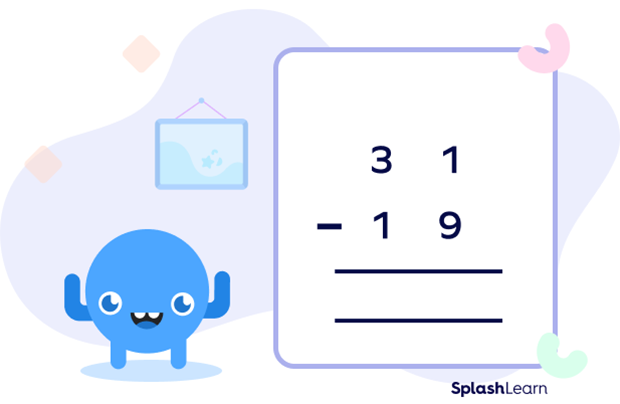
Let us understand subtraction using this regrouping example, which includes finding the answer to the expression $31 − 19$.
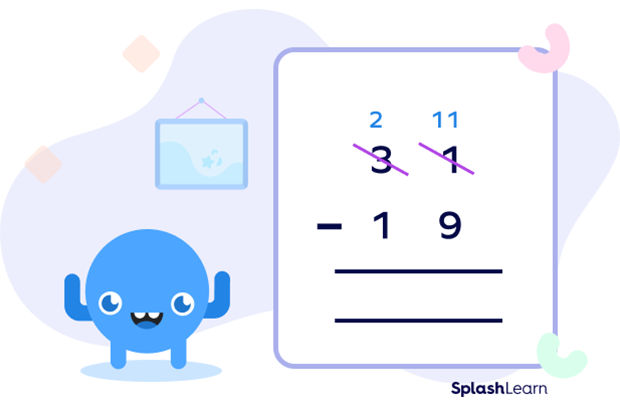
Here, we first subtract the unit place digit of the number in the lower slot with the upper slot. If the number in the lower slot is larger than the number in the upper slot, regrouping takes place, also called borrowing. In this case, we subtract one from the tens place digit from the upper slot number and write the remaining number above it, that is, we take 1 from 3 making it 2 which we wrote above 3, while this 1 that we subtracted is “borrowed” to the unit place, making it a 10 and adding it to the unit place existing number, giving us a two digit number. In simpler words 10 is borrowed from the tens place digit and added to the unit place digit. In the above example, 10 is added to the unit place digit i.e. 1 and we write 11 above the unit place digit.
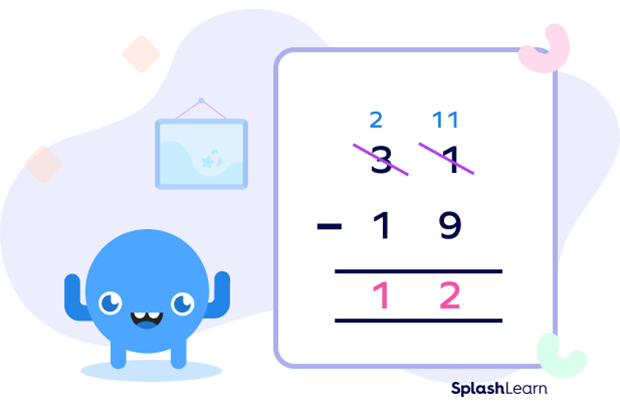
Now, we move on to the real subtraction of the two numbers. The number of the unit place of the upper slot can now be subtracted from the unit place number of the lower slot, i.e. $11 − 9$ giving us 2. While we normally take the remaining number from the upper slot i.e. 2 and subtract the lower slot number from it, i.e., $2 − 1$, giving us 1, which leaves us with 12 as the final answer.
Here’s how we regroup hundred and tens to subtract 182 from 427:
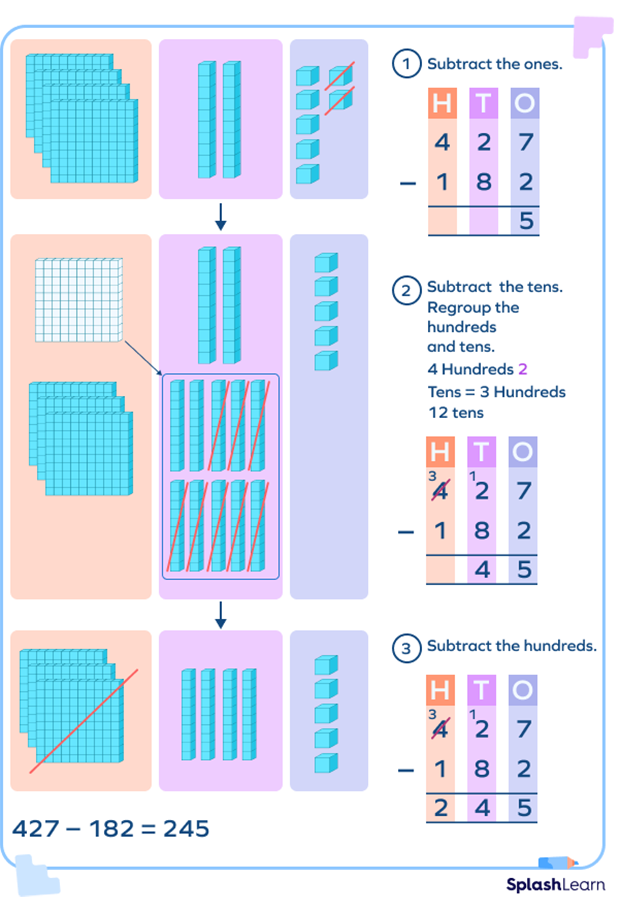
Properties of Subtraction
Here are a few important properties of subtraction in our everyday life.
- Commutative property of subtraction:
Commutative property states that swapping of numbers does not alter the result. But in subtraction, we cannot get the same output when we put minuend in place of subtrahend and vice versa. Hence, commutative property is not possible in case of subtraction.
For example, $8 − 5$ is not equal to $5 − 8$.
- Identity property of subtraction:
Identity property states that when we subtract “0” from a number, the resultant is the number itself.
For example, $5 − 0 = 5$.
- Inverse Property of Subtraction (Subtracting a number by itself):
When we subtract a number from itself, the resultant is always “0.”
$\text{A} − \text{A} = 0$
For example, $9 − 9 = 0$.
- Subtraction Property of Equality
According to the property, if we subtract any number on both sides of an equation, the equality of the equation still holds.
For the given algebra equation;
$\Rightarrow \times − 3 = 5$
If we subtract the same number on both sides, the equation will still hold true. Here we will subtract 8 from both sides.
$\Rightarrow \times − 3 − 8 = 5 − 8$
$\Rightarrow \times − 11 = − 3$
- Distributive Property of Subtraction
According to the property, the multiplication of subtraction of numbers is equal to subtraction of the multiplication of individual numbers.
$\text{A} \times (\text{B} − \text{C}) = \text{A} \times \text{B} − \text{A} \times \text{C}$
For example: $3 \times (5 − 2) = 3 \times 3 = 9$ and $3 \times 5 − 3 \times 2 = 15 − 6 = 9$
In this article, we have learned about subtraction, its definition with example, the symbols used for it, the common methods used for subtraction. We also learned about the minus sign. The minus sign is used for different purposes. Let’s practice our understanding with a few solved examples and practice problems and solved examples.
1. In a soccer match, Team A scored 5 goals and Team B scored 9 goals. Which team scored more goals and by how much?
Goals scored by Team $\text{A} = 5$;
Goals scored by Team $\text{B} = 9$
We can clearly see that Team B scored more goals. To calculate the numbers of goals by which Team B exceeded, we will subtract 5 from 9.
$9 − 5 = 4$
Therefore, Team B scored 4 more goals than Team A.
2. Jeff has 120 pens. Her friend Tim has 50 pens less than Jeff. How many pens does Tim have?
As we know, the term “less than” refers to the operation subtraction.
Jeff $= 120$
Tim $= 120 − 50 = 70$
Therefore, Tim has 70 pens.
3. During an annual Easter egg hunt, the participants found 52 eggs in the clubhouse, out of which 14 Easter eggs were broken. Can you find out the exact number of unbroken eggs?
The number of easter eggs found in the Clubhouse $= 52$;
Number of easter eggs that were broken $= 14$;
The total number of unbroken eggs $=$ ?
Now, we will subtract the number of broken eggs from the total number of eggs.
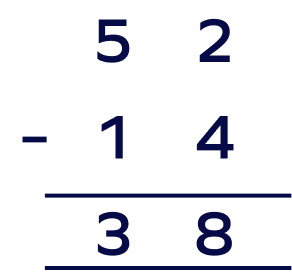
Therefore, the number of unbroken eggs is 38.
4. Jerry collected 194 fishes and Evan collected 132 fishes. Who collected more fish and by how much?
Number of fishes collected by Jerry $= 194$;
Number of fishes collected by Evan $= 132$
This shows that Jerry collected more fish. Let us subtract $194 − 132$ to get the difference.
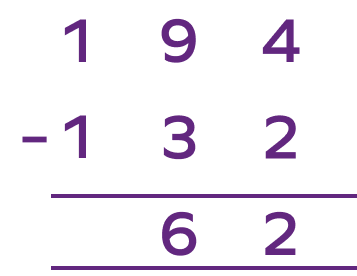
Therefore, Jerry collected 62 fish more than Evan.
5. By how much is 5251 less than 6556?
From the given, it is clear that 6556 is greater than 5251 .
Now subtract 5251 from 6556.
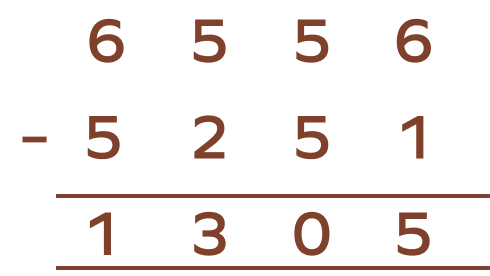
$6556 − 5251 = 1305$
Therefore, 5251 is less than 6556 by 1305.
6. What is the value of 794 minus 658?
Solution: $794 − 658 = 136$
7. When Steve woke up, his temperature was $101^{\circ} \text{F}$ . Two hours later, it was 3º lower. What was his temperature after two hours?
Solution: Temperature at the time of Steve waking up $= 101^{\circ} \text{F}$
Temperature after 2 hours $= 101^{\circ} \text{F} − 3^{\circ} \text{F} = 98^{\circ} \text{F}$
8. What will be the coordinates of A if $x = −5$ and $y = − 7$ . In which quadrant will A lie?
Solution: Since it is given that $x = − 5$ and $y = − 7$, the coordinates of A will be $(− 5, − 7)$. Also, as both the coordinates are negative, i.e., $( − x, − y)$, A will lie in the third quadrant.
9. An elevator is on the eighteenth floor. It goes down 13 floors. What floor is the elevator on now?
Solution: The floor on which the elevator is now $= 18 − 13 = 5$th floor
10. Is $(4 − 6) = (6 − 4)$ ?
Solution: Let us find the solution to both of them.
On the left side, $4 − 6 = − 2$
Whereas, on the right side, $6 − 4 = 2$
We can clearly see that $2 \neq − 2$.
So, $(4 − 6)$ is not equal to $(6 − 4)$.
Subtract - Definition with Examples
Attend this quiz & Test your knowledge.
On subtracting 69 from 108, we get
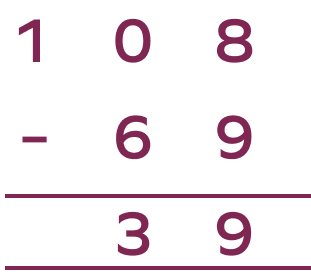
What is the difference between 155 and 56?
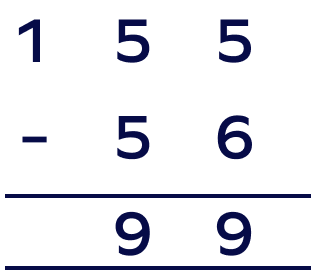
Derek has 25 apples and he gave 18 apples to his brother. How many apples is Derek left with?
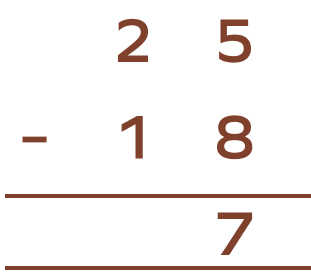
Look at the given number line. What equation would correctly match the solution on the number line?
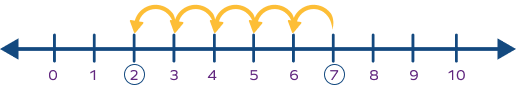
On subtracting 1267 from 1513, we get
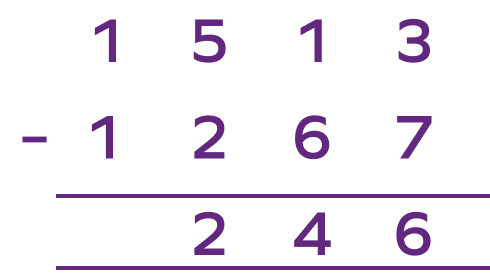
Why is the answer to a subtraction problem called the difference?
Because if you subtract a smaller number from a bigger number the result is the difference between the two numbers.
Example: Subtract 2 from 6
$6 − 2 = 4$
But, the number 6 is also 4 bigger than 2. It is the difference between the two numbers.
Which other operation has the output smaller than the input?
Another operation where the output is smaller than the input is division.
Is subtraction associative?
No, subtraction is not associative. Let us look at it using an example. $10 − (5 − 1) \neq (10 − 5) − 1$
Can we subtract a larger number from a smaller number?
Yes, we can subtract a larger number from a smaller number. The resultant will be a negative number.
Mathematically speaking, why does subtraction by “counting up” work?
When we subtract 2 numbers, we can do it in two ways. Let’s take an example of subtracting 5 from 8. You can either take 8 and subtract 5 from it, or you can begin with 5 and count up to 8. When you begin with 5 and count up to 8, you do it 3 times: 6, 7 and 8. So, 3 will be the difference between 5 and 8.
What is the difference between minus sign and plus sign?
Minus sign is denoted by a horizontal symbol, i.e., $−$, and it means to subtract or take away. Whereas, the plus sign is denoted by intersection of horizontal and vertical lines, i.e., $+$ which means to add or find the sum.
Does commutative property hold true for subtraction?
The commutative property does not hold for subtraction. It means for any two whole numbers, $\text{A} − \text{B} \neq \text{B} − \text{A}$.For example: $3 − 5 = − 2$ and $5 − 3 = 2$ and $− 2 \neq 2$.
Does Associative property hold true for subtraction?
The associative property does not hold for subtraction. It means for any three whole numbers A, B, and C.
$\text{A} – (\text{B} – \text{C}) \neq (\text{A} – \text{B}) – \text{C}$ For example: $(2 – 3) – 5 = – 1 – 5 = – 6$ and $2 – (3 – 5) = 2 + 2$ and $– 6 \neq 4$.
What is a minuend and a subtrahend?
In a subtraction equation, minuend is the highest number from which a component would be subtracted. A subtrahend is the term that denotes the number being subtracted from another.
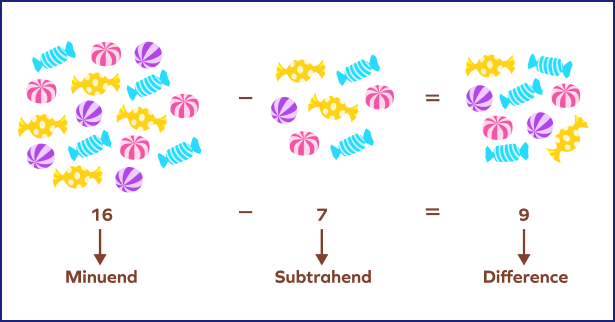
Who discovered the minus sign?
Robert Recorde introduced the modern use of minus to the UK in 1557. The first appearance of the minus sign was given by Johannes Widmann in 1489 and was found in his book called “Mercantile Arithmetic.”
RELATED POSTS
- Difference in Math – Definition With Examples
- Liters to Gallons Conversion
- Multiplying Fractions with Mixed Numbers – Steps, Examples, FAQs
- Round to the Nearest Hundredth – Definition, Method, Examples
- Minuend – Definition With Examples

Math & ELA | PreK To Grade 5
Kids see fun., you see real learning outcomes..
Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.
Parents, Try for Free Teachers, Use for Free
Subtraction by "Regrouping"
(Also called "borrowing" or "trading")
To subtract numbers with more than one digit:
- write down the larger number first and the smaller number directly below it making sure to line up the columns!
- then do subtractions one column at a time like this (press play button):
Smaller Number - Bigger Number
But what if a column has a smaller number on the top?
How do we do 2 − 5 ?
The Solution : Make the "2" larger by "regrouping" (press arrow button):
- the "3" means 3 tens ,
- the "2" means 2 ones ,
- reduce the 3 by 1
- increase the 2 by 10
And we get:
And here is how to do it with a pencil and paper:
We use this method whenever a column has a smaller number on top , as in this example:
But we can't regroup from zero ...
But we can make a "0" into a "10" by regrouping it first, them carry on normally, like this:
Now, you can practice with these Subtraction Worksheets
Subtraction Word Problems — Examples & Practice - Expii
Subtraction word problems — examples & practice, explanations (3).

Words to Math: Subtraction
In this section, we will learn to translate phrases into a mathematical expression by identifying key words that indicate subtraction .
When talking about subtraction, you will most likely see the terms " subtract ", " less than ", " minus ", " difference ", and " decreased by ". There are different such terms for addition , multiplication , and division .
Let’s take a look at an example.
Sam has 6 pencils. His friend, Jack, has 3 pencils less than Sam. How many pencils does Jack have?
We know that the term " less than " often refers to subtraction, so the operator ‘−’ is required.
Since Sam has 6 pencils and Jack had 3 less than Sam, we can rewrite this as a mathematical expression.
Jack = Sam (6 Pencils) − 3 Pencils = 3 Pencils
, via [pixabay.com](https://cdn.pixabay.com/photo/2012/04/01/17/29/pencil-23648_960_720.png)](https://d20khd7ddkh5ls.cloudfront.net/subtraction_property_of_equality_4.jpg)
When talking about equality, you will most likely see the terms " equal to ", " is ", " the same as ", and " amounts to ".
Here are some phrases about subtraction translated into a mathematical expression.
- 2 less than 6 is 4→6−2=4
- 13 minus 1 equals to 12→13−1=12
- The difference between 10 and 7 is 3→10−7=3
This technique is useful for solving equations too. In that case, we're subtracting the same number from both sides of an equation.
We are now going to take a look at some of the types of problems you might encounter about subtraction word problems.
Example 1 Translate the following into a mathematical expression: 15 minus 8 is 7.
Related Lessons
Word problems with subtraction.
The key to solving word problems is to translate them into mathematical expressions. This is made easier if you can pick out key phrases that tell you what type of operation the problem is asking for. We'll call these signal words .

Image source: By OpenClipartVectors CC0 , via pixabay.com
Which subtraction signal word is included in this word problem?
(Video) Writing an Algebraic Expression from a Word Problem
by mrmaisonet
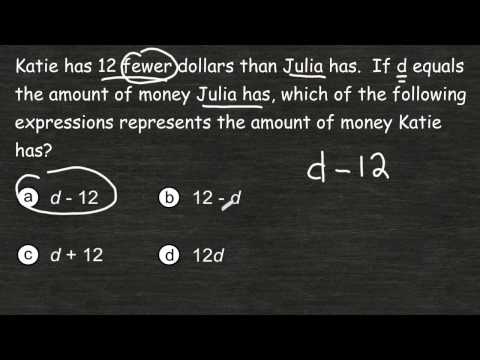
This video by mrmaisonet works through a few word problem examples with an identification of key words.
The problem he looks at is:
Katie has 12 fewer dollars than Julia has. If d equals the amount of money Julia has, write an expression for the amount of money Katie has.
Here d is a variable . Our expression will have the variable in it somewhere. The key phrase is 12 fewer. This means Katie has the same as Julia minus 12. Therefore, we can say Katie has: d−12
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Addition and subtraction
Here you will learn strategies on how to add and subtract, including using visual models, the number line, and algorithms.
Students will first learn about addition and subtraction in kindergarten, continue to add and subtract larger numbers in 2 nd and 3 rd grade, and learn the standard algorithm in 4 th grade. In 7 th grade, students learn to add and subtract with integers and then rational numbers.
What are addition and subtraction?
Addition is the operation of combining two or more numbers together. Subtraction is the operation of taking away from a number.
Students as early as pre-k have a basic, informal understanding of addition and subtraction. By the end of Kindergarten, students can operate within 10, heavily relying on models like counters or 10 frames to solve.
By the end of first grade, students should be able to add and subtract fluently within 20. As students work on repeatedly adding and subtracting with single digit numbers, they deepen their number sense around the operations by solving in different ways.
This includes beginning to build number bonds.
For example,
- Seeing 5+4 and knowing the sum is 9 without having to solve.
- Seeing 9-4 and knowing the difference is 5 without having to solve.
This aids students as they go into 2 nd and 3 rd grade and learn to add and subtract multi-digit numbers (within 1,000 ). At this level, students are still relying on number relationships, properties of operations, place value ideas, models, etc. to solve.
When adding 3- digit numbers, students may combine each place value of the addends separately.
Hundreds \hspace{1.1cm} Tens \hspace{1.2cm} Ones
200 + 100 \hspace{1cm} 30 + 40 \hspace{1cm} 5 + 9 \hspace{1cm}
= 300 \hspace{1.5cm} = 70 \hspace{1.3cm} = 14
And then add in the partial sums:
300+70+14=384
When subtracting numbers that are larger, students may use what they know about place value to solve.
The distance from 781-395 is the same as 786-400, it is just shifted up 5 on the number line.
Now solve 786-400 by taking away 4 hundreds.
786-400=386, so 781-395=386.
Once students have developed a flexible understanding of multi-digit addition and multi-digit subtraction in 2 nd grade and 3 rd grade, they learn the standard algorithm in 4 th grade.
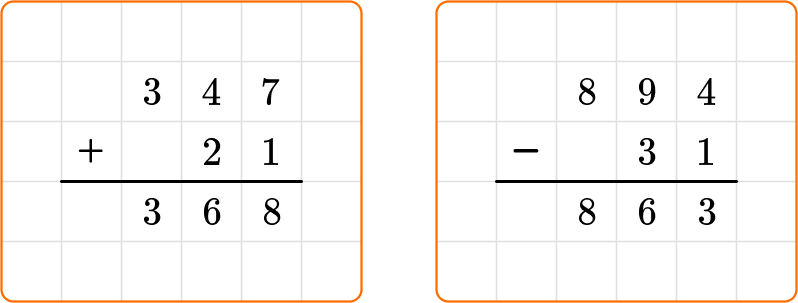
It is important to consider the place value of each digit and line up the corresponding digits in each number.
In 5 th grade and 6 th grade, students continue to add and subtract with whole numbers and apply these strategies to decimal operations.
See also: Adding and subtracting decimals
In 7 th grade, students learn to add and subtract integers and rational numbers.
You can add and subtract integers using visual models or a number line.
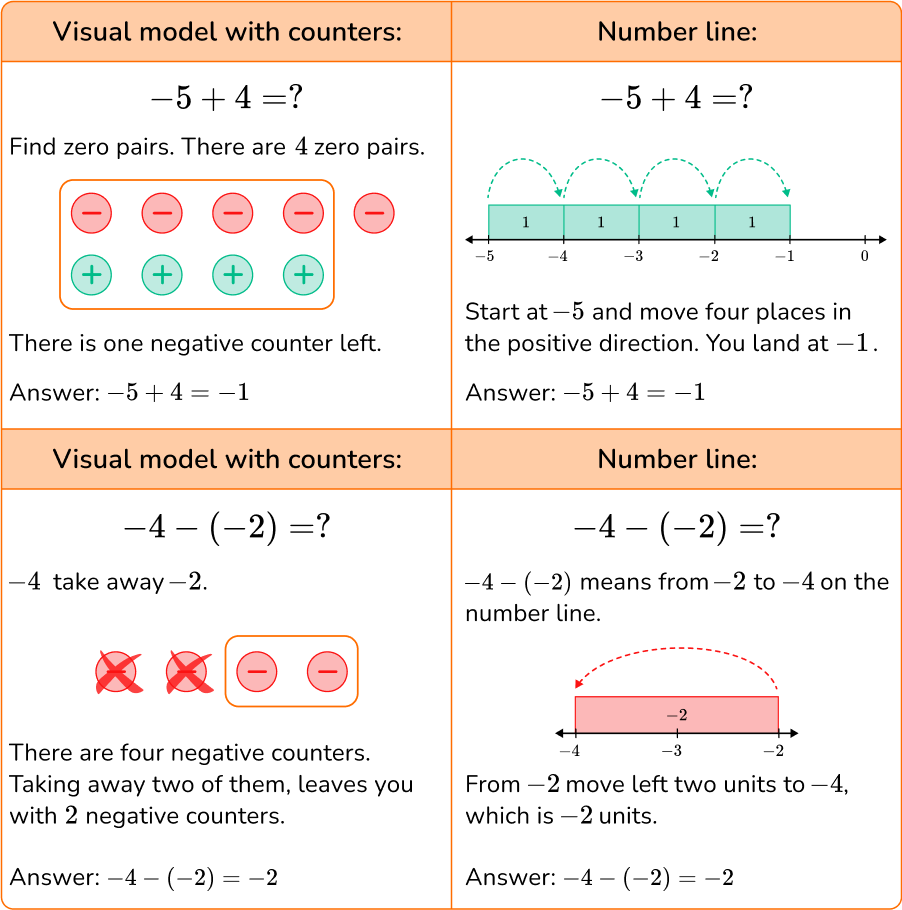
Step-by-step guide: Adding and subtracting integers
You can also add and subtract rational numbers using visual models or a number line.
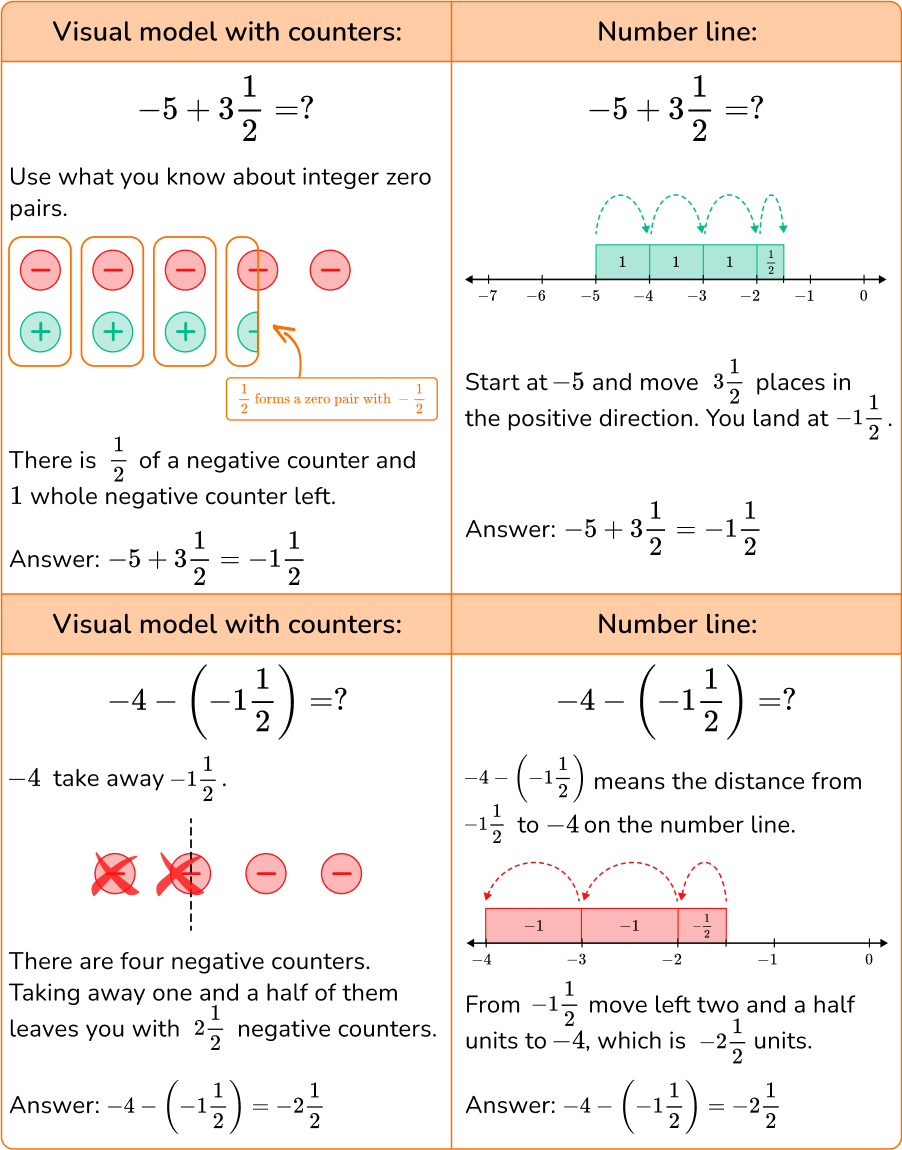
[FREE] Addition and Subtraction Worksheet (Grade 2 to 7)
Use this quiz to check your grade 2, 3, 4 and 7 students’ understanding of addition and subtraction. 15+ questions with answers covering a range of 2nd, 3rd, 4th and 7th grade addition and subtraction topics to identify areas of strength and support!
Common Core State Standards
How does this apply to 2 nd grade math, 3 rd grade math, 4 th grade, and 7 th grade math?
- Kindergarten – Operations and Algebraic Thinking (K.OA.A.2) Solve addition and subtraction word problems, and add and subtract within 10, e.g., by using objects or drawings to represent the problem.
- Grade 1 – Operations and Algebraic Thinking (1.OA.C.6) Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8+6=8+2+4=10+4=14 ); decomposing a number leading to a ten (e.g., 13-4=13-3-1=10-1=9 ); using the relationship between addition and subtraction (e.g., knowing that 8+4=12, one knows 12-8=4 ); and creating equivalent but easier or known sums (e.g., adding 6+7 by creating the known equivalent 6+6+1=12+1=13 ).
- Grade 2 – Operations and Algebraic Thinking (2.OA.A.1) Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
- Grade 2 – Numbers and Operations in Base Ten (2.NBT.B.5) Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
- Grade 3 – Numbers and Operations in Base Ten (3.NBT.A.2) Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
- Grade 4 – Numbers and Operations in Base Ten (4.NBT.A.4) Fluently add and subtract multi-digit whole numbers using the standard algorithm.
- Grade 7- The Number System (7.NS.A.1) Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram.
- Grade 7- The Number System (7.NS.A.3) Solve real-world and mathematical problems involving the four operations with rational numbers.
How to add and subtract
There are a lot of ways to add and subtract. For more specific step-by-step guides, check out the individual pages linked in the “What are addition and subtraction?” section above or read through the examples below.
Addition and subtraction examples
Example 1: two digit addition.
Solve 34 + 58.
Choose a strategy.
You can use a model of the tens and ones.

Combine the tens and ones.

You can create one new group of ten from 10 ones.
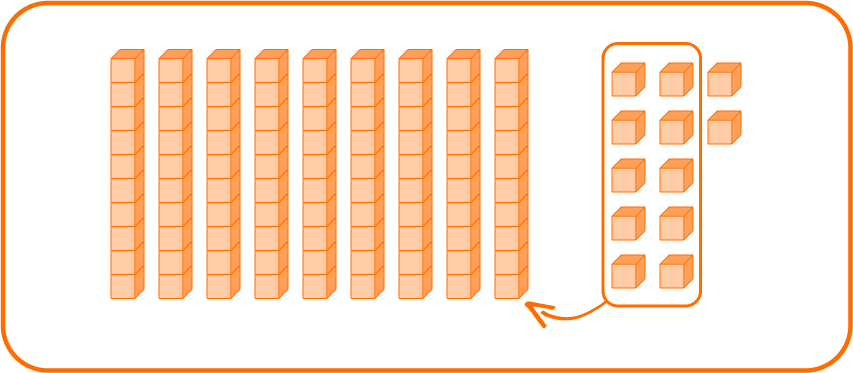
This leaves 9 tens and 2 ones, which is 92.

So, 34+58=92.
Example 2: three digit subtraction
Solve 340-291.
You can use a number line to count up to 340 from 291.

The difference between 291 and 340 is 49.
So, 340-291=49.
Example 3: addition with the algorithm
Add 4,297 + 381 with the algorithm.
Stack the numbers and line up the place values.

Add each column from right to left and regroup the numbers when necessary.

Write your final answer and check to make sure your answer is reasonable.
You can estimate to decide if your answer is reasonable.
4,297 rounds to 4,300.
381 rounds to 400.
4,300+400=4,700, so the answer should be close to 4,700. Since 4,678 is close, the answer is reasonable.
4,297+381=4,678
Example 4: subtraction word problem with the algorithm
After the harvest, a farmer has 2,148 pears. 213 of the pears are rotten and cannot be sold. If the farmer sells the rest, how many pears will she sell?
Write an equation that represents the word problem.
2,148 - 213 = ⬜

Subtract each column from right to left and exchange for a \bf{10} when necessary.
2,148 rounds to 2,000.
213 rounds to 200.
2,000-200=1,800, so the answer should be close to 1,800. Since 1,935 is close, the answer is reasonable.
2,148-213=1,935
Example 5: subtracting integers with models
Subtract: -4 -(-6)=?
Represent the problem with counters, identifying zero pairs with addition or adding zero pairs when necessary for subtraction.
-4 - (-6) starts with -4 and removes -6. Add 2 zero pairs in order to remove -6.

The answer is the leftover counters.
There are two positive counters left.
Example 6: adding rational numbers with the algorithm
Solve -34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right) .
Make sense of the calculation – relating to positive numbers when necessary.
-34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right) combines two negative amounts, which do not create zero pairs.
This means the answer will be even more negative. You can use the algorithm for addition to see what the total amount is.
Use an algorithm.
\begin{aligned}& 34 \frac{2}{3}+567 \frac{3}{4} \\\\ & =34 \frac{2 \times 4}{3 \times 4}+567 \frac{3 \times 3}{4 \times 3} \\\\ & =34 \frac{8}{12}+567 \frac{9}{12} \\\\ & =601 \frac{17}{12} \text { or } 602 \frac{5}{12}\end{aligned}
Decide if the final answer is positive or negative.
Adding two negative numbers results in a negative number. For example, if you started on the number line and went back 34 \cfrac{2}{3} and then you went back 567 \cfrac{3}{4} more, you are further down the negative side of the number line.
-34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right)=-602 \cfrac{5}{12}
Teaching tips for addition and subtraction
- Sufficient time using place value blocks, 100 s charts, grids and other interactive manipulatives should be provided to students when they are first learning to operate with any new set of numbers. The Common Core Standards intentionally allow time for students to develop an understanding of the operation, before learning how to use the algorithm.
- When students are first learning, encourage them to make connections between addition problems and subtraction problems. As students learn how to operate with any new set of numbers (whole, integer, or rational), it is crucial that they see the connection, as this opens the door to solving strategies, helps them make sense of the algorithms, and can be used to decide if an answer is reasonable. Understanding this relationship is also important for later topics like solving equations.
- When choosing printable math worksheets, look for resources that have missing numbers in all parts of the equation (start unknown, change unknown, result unknown). This helps students develop flexible ideas about the operations and can help prevent mindlessly grabbing numbers from word problems.
- Instead of giving students subtraction worksheets that have dozens of questions to solve, prioritize worksheets that allow students to solve in more than one way and that encourage them to consider the reasonableness of their answer. While there may be times that students are expected to solve in a larger quantity (for example, when learning the algorithm or completing a math review packet), the majority of student work should focus on depth not breadth.
Easy mistakes to make
- Not considering the place value of numbers when solving When using strategies to solve, students may choose a strategy they do not fully understand, causing them to misuse place value. For example, 56 + 78 Thinking that they can just add 5+6+7+8.
- Thinking subtraction always leads to a smaller number (and vice versa with addition) Students often create this false idea because subtracting a larger number from a smaller number or adding negative numbers are not addressed in elementary school. As students begin to operate with integers, it is important to consistently ask them to make sense of an equation before operating. This may be explaining the operation in their own words or using a model to show what is happening.

- Not making sense of operations with rational numbers By the time students operate with rational numbers, they will have learned many algorithms. Though algorithms can be useful, if used in a rush it is easy to make mistakes. Encourage students to think about a reasonable answer before solving. This can help them catch mistakes.
Practice addition and subtraction questions
1. Solve 39 + 46.

This leaves 8 tens and 5 ones, which is 85.
2. Solve 763-594.
You can use a number line to count up to 594 from 763.
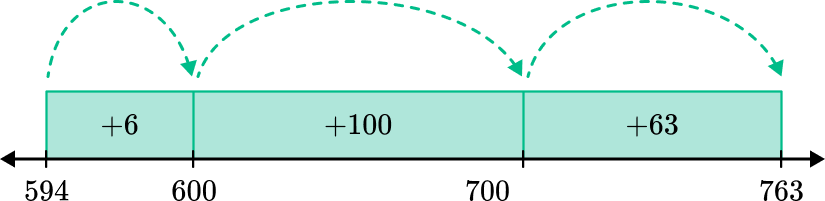
The difference between 594 and 763 is 169.
So, 763-594=169.
3. Solve 5,621 + 3,570.
To use the standard algorithm, stack the numbers and line up the place values.

5,621 rounds to 6,000.
3,570 rounds to 4,000.
6,000+4,000=10,000, so the answer should be close to 10,000.
Since 9,191 is close, the answer is reasonable.
5,621+3,570=9,191
4. Jerome has 18,341 points in a game. Yasmine has 8,239 points in the same game. How many more points does Jerome have?
18,341-8,239 = ⬜
To solve with the standard algorithm, stack the numbers and line up the place values.
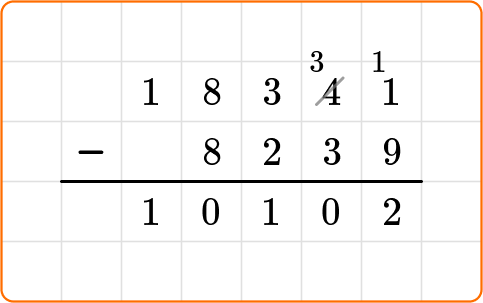
18,341 rounds to 18,000.
8,239 rounds to 8,000.
18,000-8,000=10,000, so the answer should be close to 10,000.
Since 10,102 is close, the answer is reasonable.
18,341-8,239=10,102
5. Subtract: -12-3= \, ?
-12-3 starts with -12 and removes 3 positives. Add 3 zero pairs in order to remove 3.

There are 15 negative counters left.
You can also think of this as the distance from 3 to -12.
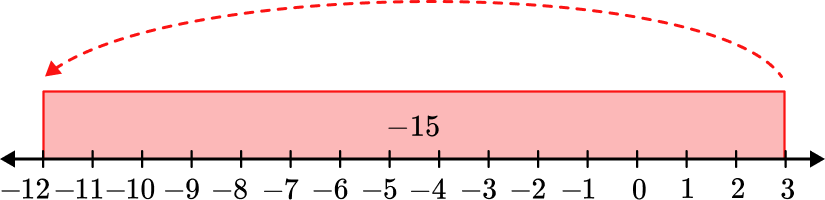
6. Solve -84.4+391.02= \, ?.
-84.4 + 391.02 combines negative and positive values, which creates zero pairs. This means that -84.4+391.02=391.02-84.4, so you can use the standard algorithm to solve.
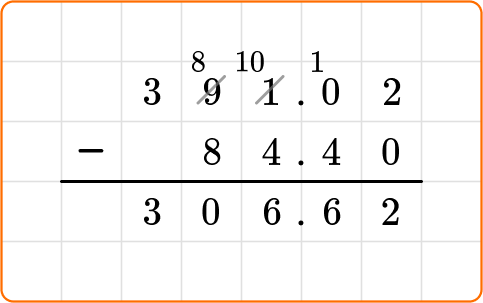
Adding a smaller negative number to a larger positive results in a positive answer.
-84.4+321.02=306.62
Addition and subtraction FAQs
Regrouping is when you are adding and have more than 10 ones, tens, hundreds, etc. and you need to regroup to create a new group of ten, hundred, etc. For example, if you add 27 + 18, you will have 3 tens and 15 ones. You regroup 10 of the ones to be a new group of ten, so you are left with 4 tens and 5 ones, or 45.
Exchanging is when you are subtracting and you do not have enough ones, tens, hundreds, etc. to take away and you need to exchange for a new group of ten, hundred, etc. For example, if you subtract 27 - 18, you start with 7 ones and need to take away 8. There are not enough, so you exchange one of the tens in 27 for ones. Then you have 1 ten and 17 ones. Now you can subtract 8 ones from 17 ones, leaving 9 ones.
In 4 th grade students learn to add and subtract fractions with common denominators. In fifth grade they learn to add and subtraction fractions with uncommon denominators. Then in 7 th grade they are expected to add and subtract negative fractions. See also: Adding and subtracting fractions
The next lessons are
- Multiplication and division
- Types of numbers
- Rounding numbers
- Adding and subtracting rational numbers
- Adding and subtracting negative numbers
- Add and subtract within 100
- Standard algorithm addition
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview

Reading & Math for K-5
- Kindergarten
- Learning numbers
- Comparing numbers
- Place Value
- Roman numerals
- Subtraction
- Multiplication
- Order of operations
- Drills & practice
- Measurement
- Factoring & prime factors
- Proportions
- Shape & geometry
- Data & graphing
- Word problems
- Children's stories
- Leveled Stories
- Context clues
- Cause & effect
- Compare & contrast
- Fact vs. fiction
- Fact vs. opinion
- Main idea & details
- Story elements
- Conclusions & inferences
- Sounds & phonics
- Words & vocabulary
- Reading comprehension
- Early writing
- Numbers & counting
- Simple math
- Social skills
- Other activities
- Dolch sight words
- Fry sight words
- Multiple meaning words
- Prefixes & suffixes
- Vocabulary cards
- Other parts of speech
- Punctuation
- Capitalization
- Narrative writing
- Opinion writing
- Informative writing
- Cursive alphabet
- Cursive letters
- Cursive letter joins
- Cursive words
- Cursive sentences
- Cursive passages
- Grammar & Writing
Breadcrumbs
- Word Problems
- Subtract 1-3 digits

Download & Print Only $7.90
Subtraction word problems (1-3 digits)
Word problem worksheets: subtracting numbers below 1,000.
These word problems involve the subtraction of 1-3 digit numbers. The calculations are relatively simple, however we include irrelevant data to encourage students to read carefully.

These worksheets are available to members only.
Join K5 to save time, skip ads and access more content. Learn More
More word problem worksheets
Explore all of our math word problem worksheets , from kindergarten through grade 5.
What is K5?
K5 Learning offers free worksheets , flashcards and inexpensive workbooks for kids in kindergarten to grade 5. Become a member to access additional content and skip ads.
Our members helped us give away millions of worksheets last year.
We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.
Members skip ads and access exclusive features.
Learn about member benefits
This content is available to members only.
- Forgot Password?
- Math Article
Subtraction
Subtraction is one of the four basic arithmetic operations in mathematics. We can observe the applications of subtraction in our everyday life in different situations. For example, when we purchase fruits and vegetables for a certain amount of money say Rs. 150 and we have given a Rs. 200 note to the vendor. Now, the vendor returns the excess amount by performing subtraction such as 200 – 150 = 50. Then, the vendor will return Rs. 50.
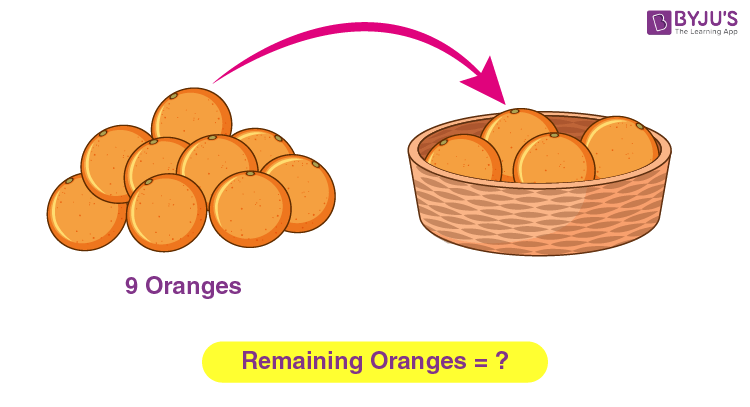
In this article, you will learn the meaning and definition of subtraction in maths, the symbol for subtraction, rules, how to subtract numbers in different ways such as subtraction of numbers on the number line along with examples and properties of subtraction.
Subtraction Meaning
Subtraction represents the operation of removing objects from a collection. The minus sign signifies subtraction −. For example, there are nine oranges arranged as a stack (as shown in the above figure), out of which four oranges are transferred to a basket, then there will be 9 – 4 oranges left in the stack, i.e. five oranges. Therefore, the difference between 9 and 4 is 5, i.e., 9 − 4 = 5. Subtraction is not only applied to natural numbers but also can be incorporated for different types of numbers. That means we can also describe decreasing or removing physical and abstract quantities with various sets of objects such as negative numbers, fractions, rational & irrational numbers, decimals, functions, matrices and vectors.
Subtraction Symbol and Parts
The symbol “-” signifies subtraction. A subtraction process consists of three parts of numbers, namely minuend, subtrahend and difference. The number in a subtraction sentence from which we subtract another number is called a minuend, which means the minuend is the first number in a subtraction process.
Example: 8 – 6 = 2
8 = Minuend
6 = Subtrahend
2 = Difference
And, “-” is the minus, i.e. the symbol for subtraction and “=” is the equal sign .
However, the parts of the subtraction can be shown as:

Subtraction Table
Let’s have a look at the subtraction table of simple subtractions of numbers.
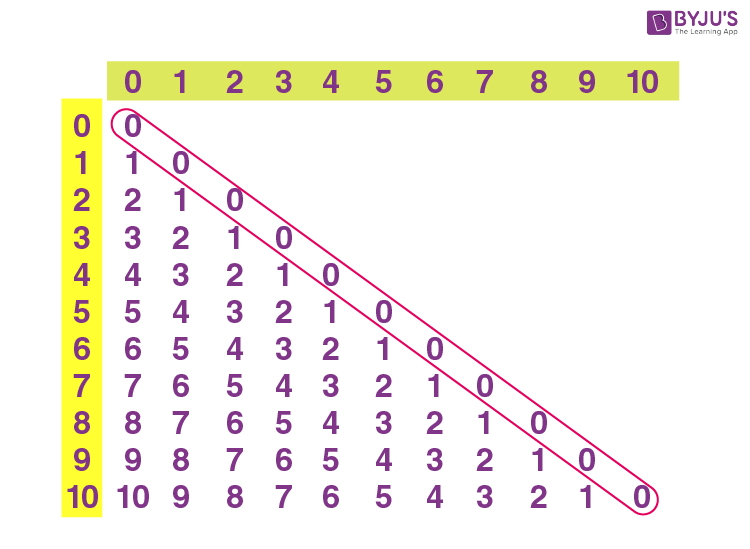
Here, we can observe that the subtraction of equal numbers always results in 0, i.e. 2 – 2 = 0, 3 – 3 = 0 and so on.
Subtraction sums
Subtraction can be performed on single-digit, double-digit, triple-digit numbers and so on. Single-digit subtraction is quite simple as shown in the below examples.
Single digit subtraction:
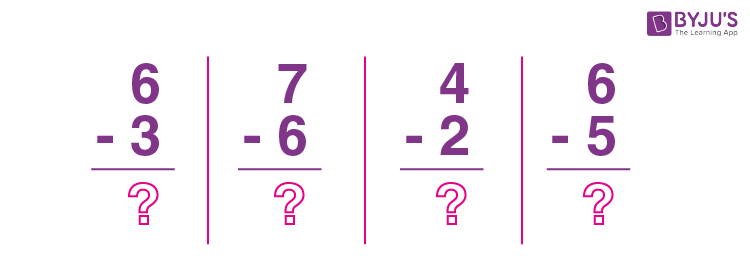
Here, 6 – 3 = 3, 7 – 6 = 1, 4 – 2 = 2 and 6 – 5 = 1.
Subtraction of a single digit from a two-digit number:

In this case, subtraction of digits may involve borrowing from the adjacent digit.
Consider the second sum from the above figure.
70 – 5; here first we have to perform subtraction for unit digits, i.e. for 0 and 5.
0 is less than 5 hence we have to borrow 1 from the adjacent digit, i.e. we have to take 1 from 7 so that 7 will become 6 and 0 will become 10.
Now, 10 -5 = 5 and the leftover digit is 6. Therefore, 70 – 5 = 65.
Subtraction of two digit numbers:

Here, 78 – 18 = 60
85 – 75 = 10
68 – 47 = 21
70 – 41 = 29
Similarly, we can subtract two-digit or three-digit numbers from three-digit numbers. Large numbers can also be subtracted from each other.
Subtraction of Fractions
Subtraction of fractions can be done depending on the types of fractions given. This can be done as follows.
- If the given fractions are like fractions, then subtract the numerators and keep the denominator as it is. Then simplify the fraction if possible to get the result.
- If the given fractions are unlike fractions, then convert them into like fractions and follow the procedure as mentioned above.
- (7/9) – (4/9) = (7 – 4)/9 = 3/9 = ⅓
- (5/6) – (2/3) Here, 2/3 ⇒ (2/3) × (2/2) = 4/6 Now, (5/6) – (2/3) = (5/6) – (4/6) = 1/6
Subtraction of Integers
The subtraction of integers involves three possibilities such as:
- Subtraction between two positive numbers
- Subtraction between two negative numbers
- Subtraction between a positive number and a negative number
For easy computation, we have to convert the subtraction problems into additional problems. This contains two steps as given below:
Step 1: Convert the subtraction sign into an addition sign.
Step 2: After converting the sign, take the inverse of the number which comes after the sign.
The properties of subtraction of integers are tabulated below.
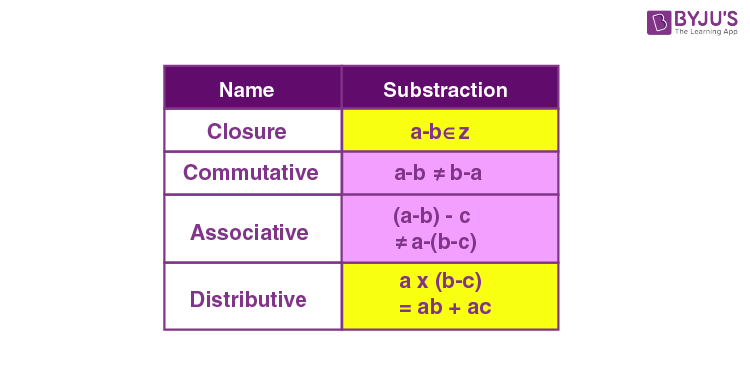
Subtraction on Number line
Let us consider the below example to understand the subtraction of numbers on the number line .
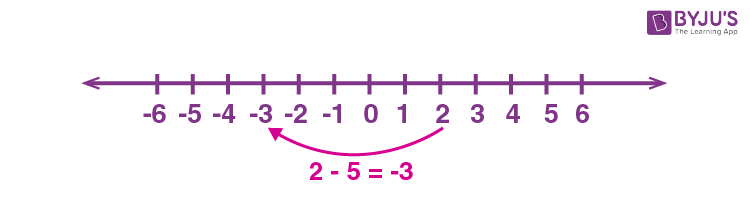
Here, subtraction of 5 from 2 gives -3.
Consider another example 6 – 5:
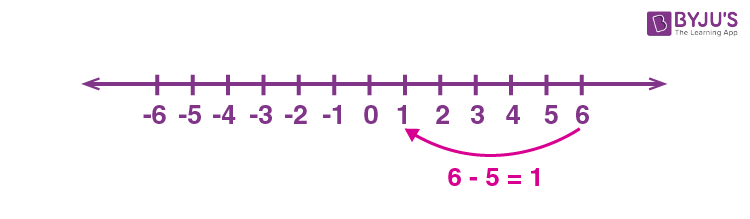
Subtraction word problems
An important key for solving word problems on subtraction is given below.
Few words such as “minus, difference, less, deduct, take away, decrease” often represent subtraction.
Suma has 12 pens. Her friend Jessi has 5 pens less than Suma. How many pens does Jessi have?
As we know, the term “less than” refers to the incorporation of subtraction.
Jessi = 12 – 5 = 7
Therefore, Jessi has 7 pens.
By how much is 3576 less than 5344?
From the given, it is clear that 5344 is greater than 3576.
Now subtract 3576 from 5344.
5344 – 3576 = 1768
Therefore, 3576 is less than 5344 by 1768.
Subtraction Properties
Subtraction of numbers possess some properties as given below:
- We can transform any subtraction problem into a problem with addition and vice-versa.
- Subtracting 0 from any number gives the number itself, i.e. the difference is nothing.
- When we subtract 1 from any number, the difference always equals the predecessor of the number.
- The subtraction of numbers is anti-commutative.
- Subtraction of numbers is non-associative.
Practice Questions
- Subtract 64 from 103.
- Subtract 6 from -4 using the number line.
- What is the difference between 247 and 358?
- Varsha has 19 apples and she gave 8 apples to her brother. How many apples did Varsha left with?
Frequently Asked Questions on Subtraction
What is subtraction give an example., what is the subtraction rule, where do we use subtraction, what is the symbol of subtraction, what are the parts of a subtraction sentence, leave a comment cancel reply.
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
- Share Share
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.


Subtraction Practice Questions
Click here for questions, click here for answers.
GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
Helping with Math
Solving Word Problems involving Addition and Subtraction of numbers within 120 1st Grade Math Worksheets
Download solving word problems involving addition and subtraction of numbers within 120 worksheets.
Click the button below to get instant access to these premium worksheets for use in the classroom or at a home.

Download this Worksheet
This download is exclusively for Helping With Math Premium members!
To download this worksheet collection, click the button below to signup (it only takes a minute) and you'll be brought right back to this page to start the download!
Edit this Worksheet
Editing worksheet collections is available exclusively for Helping With Math Premium members.
To edit this worksheet collection, click the button below to signup (it only takes a minute) and you'll be brought right back to this page to start editing!
This worksheet can be edited by Premium members using the free Google Slides online software. Click the Edit button above to get started.
Download free sample
Not ready to purchase a subscription yet? Click here to download a FREE sample of this worksheet pack.
Solving word problems both rely the development of reading and language skills. Addition means “putting together” groups of objects and finding how many they are in total while subtraction tells “how many are left” or “how many more or less”.
Steps in Problem Solving:
- Identify the Problem. Understand what is asked.
- Encircle important numbers.
- Underline the keywords. Analyze if it is for addition or subtraction .
- Solve the problem.
- Present the answer.
Addition: in all, sum, total, more than, plus, altogether, increased by add
Subtraction: fewer, left, less than, take away, minus, difference, remain, decreased
There are 6 surfboards and the surfer bought another 8 pieces. How many surfboards are there in all?
There were 8 beach balls but 5 of them were damaged. How many beach balls were left?
8 – 5 = 3
Solving Word Problems Involving Addition and Subtraction of Numbers within 120 Worksheets
This is a fantastic bundle which includes everything you need to know about Solving Word Problems Involving Addition and Subtraction of Numbers within 120 across 15+ in-depth pages. These are ready-to-use Common core aligned Grade 1 Math worksheets . Each ready to use worksheet collection includes 10 activities and an answer guide. Not teaching common core standards ? Don’t worry! All our worksheets are completely editable so can be tailored for your curriculum and target audience.
Resource Examples
Click any of the example images below to view a larger version.
Even More Math Worksheets
- Addition and Subtraction of Numbers within 20 1st Grade Math Worksheets
- Word Problems on Addition and Subtraction of Numbers 1st Grade Math Worksheets
- Determining the Unknown Whole Number in an Addition or Subtraction Equation 1st Grade Math Worksheets
- Addition and Subtraction of Time 3rd Grade Math Worksheets
- Understanding Commutative and Associative Property of Addition 1st Grade Math Worksheets
- Understanding the Basic Number Properties of Addition 1st Grade Math Worksheets
- Partitioning Shapes 1st Grade Math Worksheets
- Problem Solving - Addition and Subtraction (World Teachers' Day Themed) Math Worksheets
- Adding Numbers within 20 1st Grade Math Worksheets
Lifetime Membership Offer
Exclusive, limited time offer! One payment, lifetime access.
While we continue to grow our extensive math worksheet library, you can get all editable worksheets available now and in the future. We add 100+ K-8, common core aligned worksheets every month.
To find out more and sign up for a very low one-time payment , click now!
Similar Worksheets
The worksheets listed below are suitable for the same age and grades as Solving Word Problems involving Addition and Subtraction of numbers within 120 1st Grade Math.
Classifying Shapes by Lines and Angles 4th Grade Math Worksheets

Understanding Number and Shape Patterns 4th Grade Math Worksheets

Prime and Composite Numbers 4th Grade Math Worksheets

Comparing Multi-digit Numbers 4th Grade Math Worksheets

Solving Word Problems Involving Perimeter and Area of Rectangle 4th Grade Math Worksheets

Understanding Decimal Notations 4th Grade Math Worksheets

Multiplicative Comparisons and Equations 4th Grade Math Worksheets

Writing Multi-Digit Numbers Using Base 10 Numerals 4th Grade Math Worksheets

Understanding Angles and Its Measures 4th Grade Math Worksheets

Kindergarten Geometry Free Bundle


IMAGES
VIDEO
COMMENTS
These lessons look at simple examples of subtraction word problems. Words like 'difference', 'less', 'take away', 'loss' usually means that subtraction is involved. For subtraction, take note which number has to be subtracted from which number. Subtracting in the wrong order will give you the wrong answer. Andy has 53 marbles.
Problem Solving on Subtraction. Problem solving on subtraction will help us to get the idea on how to solve the basic subtraction statement problems. 1. Eight birds sat on a wire. Three birds flew away. How many were left? Total number of birds sat on a wire = 8. Number of birds flew away = 3. Therefore, number of birds left = 8 - 3 = 5.
Singapore Math More Word Problems. We will illustrate how block diagrams can be used to help you to visualize the subtraction word problems in terms of the information given and the data that needs to be found. The block diagrams or block modeling method is used in Singapore Math. Example: Jessica has 1135 beads. 604 beads are red and the rest ...
Example: Subtract 25632 from 48756. Note: In subtraction, we always subtract the smaller number from the larger number to get the correct answer. Solution: Follow the given steps and try to relate them with the following figure. Step 6: Therefore, the difference between the two given numbers is: 48756 - 25632 = 23124.
In the next video I'll just do as many basic subtraction problems I can do in 10 minutes. And then you'll be ready to do the exercises. See you soon. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free ...
Identify your areas for growth in this lesson: Addition and subtraction greater than 1000. Unit test. Test your understanding of with these NaN questions. In this topic, we will add and subtract whole numbers. The topic starts with 1+1=2 and goes through adding and subtracting within 1000. We will cover regrouping, borrowing, and word problems.
Think of subtraction as removing parts from a whole. Consider the following word problem. In the problem below, Sebastian has 8 pencils and he gives away 5 pencils to his friends. Sebastian is experiencing a loss of 5 pencils, so the subtraction problem to solve to get the answer is 8 - 5 and 8 - 5 = 3. Sebastian is left with 3 pencils.
The word problems featured in the 4th grade pdf worksheets here include large numbers with minuends and subtrahends up to six digits. Determine the difference between the large numbers by following the place value columns correctly. Download the set. Explore these subtraction word problem worksheets that deal with real-life situations.
Subtraction Worksheets. No Negative Answers (subtrahend no larger than minuend) Some Negative Answers (subtrahend can be larger than minuend) Math explained in easy language, plus puzzles, games, quizzes, videos and worksheets. For K-12 kids, teachers and parents.
Hence, it is essential for kids to practice subtraction questions thoroughly. Learn more about subtraction. Subtraction Questions with Solutions. Below are the questions based on subtraction operation for practice, along with solutions. Question 1: Evaluate the following: (i) 23 - 9 (ii) 89 - 67 (ii) 7 - 5 (iv) 65 - 34. Solution:
After a while, most students will remember the facts and recall them easily when completing math problems. Subtraction Facts Tables 0 to 11. ... The strategy helps students internalize a mental strategy for subtracting across tens. For example, with the question 15 - 9, students first recognize that they need to subtract 5 to get 10, so they ...
Names. Other names used in subtraction are Minus, Less, Difference, Decrease, Take Away, Deduct.. The names of the numbers in a subtraction fact are: Minuend − Subtrahend = Difference. Minuend: The number that is to be subtracted from.. Subtrahend: The number that is to be subtracted.. Difference: The result of subtracting one number from another. ...
Subtracting a positive number from a negative number will always give a negative number. If we subtract a positive number from a negative number, we start at the negative number and count backwards. Negative $−$ Positive $=$ Negative. Using the number line, let's start at $− 3$. For example: Say, we have the problem $(− 2) − 3$.
Subtraction by "Regrouping". (Also called "borrowing" or "trading") To subtract numbers with more than one digit: write down the larger number first and the smaller number directly below it. making sure to line up the columns! then do subtractions one column at a time like this (press play button):
This technique is useful for solving equations too. In that case, we're subtracting the same number from both sides of an equation. We are now going to take a look at some of the types of problems you might encounter about subtraction word problems. Example 1 Translate the following into a mathematical expression: 15 minus 8 is 7. 15−7=8. 15 ...
These grade 3 word problems use simple (horizontal) subtraction. The student should read the problem, write a subtraction equation from it and then answer the problem. Students should understand the meaning of subtraction and have studied their subtraction math facts prior to attempting these worksheets. Worksheet #1 Worksheet #2 Worksheet #3 ...
How does this apply to 2 nd grade math, 3 rd grade math, 4 th grade, and 7 th grade math? Kindergarten - Operations and Algebraic Thinking (K.OA.A.2) Solve addition and subtraction word problems, and add and subtract within 10, e.g., by using objects or drawings to represent the problem. Grade 1 - Operations and Algebraic Thinking (1.OA.C.6)
The calculations are relatively simple, however we include irrelevant data to encourage students to read carefully. Worksheet #1 Worksheet #2 Worksheet #3 Worksheet #4. Worksheet #5 Worksheet #6. Similar: Word problems with addition of numbers below 1,000 Mixed addition and subtraction word problems (two digits)
Consider another example 6 - 5: Subtraction word problems. An important key for solving word problems on subtraction is given below. Few words such as "minus, difference, less, deduct, take away, decrease" often represent subtraction. Example 1: Suma has 12 pens. Her friend Jessi has 5 pens less than Suma.
Previous: Surface Area of Cubes and Cuboids Practice Questions Next: Non-linear Simultaneous Equations Practice Questions GCSE Revision Cards
This is a fantastic bundle which includes everything you need to know about Solving Word Problems Involving Addition and Subtraction of Numbers within 120 across 15+ in-depth pages. These are ready-to-use Common core aligned Grade 1 Math worksheets. Each ready to use worksheet collection includes 10 activities and an answer guide.
Subtracting Integers Practice Problems with Answers The following ten (10) practice problems are all about subtracting integers. Keep practicing and you will get better in no time! Have fun! Note: To subtract integers, change the operation from subtraction to addition but take the opposite sign of the second integer. Then proceed with regular integer addition...
We follow the following steps to subtract polynomials: Step 1: Remove all parentheses. To facilitate visualization, it is advisable to write the problem and each process vertically. When we remove the parentheses, we have to distribute the negative sign, which will cause each of the terms to change the sign. Step 2: Combine like terms.