essay math questions

260 Interesting Math Topics for Essays & Research Papers

Mathematics is the science of numbers and shapes. Writing about it can give you a fresh perspective and help to clarify difficult concepts. You can even use mathematical writing as a tool in problem-solving.

In this article, you will find plenty of interesting math topics. Besides, you will learn about branches of mathematics that you can choose from. And if the thought of letters and numbers makes your head swim, try our custom writing service . Our professionals will craft a paper for you in no time!

And now, let’s proceed to math essay topics and tips.

🔝 Top 10 Interesting Math Topics

✅ branches of mathematics, ✨ fun math topics.

• 🏫 Math Topics for High School
• 🎓 College Math Topics
• 🤔 Advanced Math
• 📚 Math Research
• ✏️ Math Education
• 💵 Business Math

🔍 References

• Number theory in everyday life.
• Logicist definitions of mathematics.
• Multivariable vs. vector calculus.
• 4 conditions of functional analysis.
• Random variable in probability theory.
• How is math used in cryptography?
• The purpose of homological algebra.
• Concave vs. convex in geometry.
• The philosophical problem of foundations.
• Is numerical analysis useful for machine learning?

What exactly is mathematics ? First and foremost, it is very old. Ancient Greeks and Persians were already utilizing mathematical tools. Nowadays, we consider it an interdisciplinary language.

Biologists, linguists, and sociologists alike use math in their work. And not only that, we all deal with it in our daily lives. For instance, it manifests in the measurement of time. We often need it to calculate how much our groceries cost and how much paint we need to buy to cover a wall.

Simply put, mathematics is a universal instrument for problem-solving. We can divide pure math into three branches: geometry, arithmetic, and algebra. Let’s take a closer look:

• Geometry By studying geometry, we try to comprehend our physical surroundings. Geometric shapes can be simple, like a triangle. Or, they can form complicated figures, like a rhombicosidodecahedron.
• Arithmetic Arithmetic deals with numbers and simple operations: subtraction, addition, division, and multiplication.
• Algebra Algebra is used when the exact numbers are unclear. Instead, they are replaced with letters. Businesses often need algebra to predict their sales.

It’s true that most high school students don’t like math. However, that doesn’t mean it can’t be a fun and compelling subject. In the following section, you will find plenty of enthralling mathematical topics for your paper.

If you’re struggling to start working on your essay, we have some fun and cool math topics to offer. They will definitely engage you and make the writing process enjoyable. Besides, fun math topics can show everyone that even math can be entertaining or even a bit silly.

• The link between mathematics and art – analyzing the Golden Ratio in Renaissance-era paintings.
• An evaluation of Georg Cantor’s set theory.
• The best approaches to learning math facts and developing number sense.
• Different approaches to probability as explored through analyzing card tricks.
• Chess and checkers – the use of mathematics in recreational activities.
• The five types of math used in computer science.
• Real-life applications of the Pythagorean Theorem .
• A study of the different theories of mathematical logic.
• The use of game theory in social science.
• Mathematical definitions of infinity and how to measure it.
• What is the logic behind unsolvable math problems?
• An explanation of mean, mode, and median using classroom math grades.
• The properties and geometry of a Möbius strip.
• Using truth tables to present the logical validity of a propositional expression.
• The relationship between Pascal’s Triangle and The Binomial Theorem.
• The use of different number types: the history.
• The application of differential geometry in modern architecture.
• A mathematical approach to the solution of a Rubik’s Cube.
• Comparison of predictive and prescriptive statistical analyses.
• Explaining the iterations of the Koch snowflake.
• The importance of limits in calculus.
• Hexagons as the most balanced shape in the universe.
• The emergence of patterns in chaos theory.
• What were Euclid’s contributions to the field of mathematics?
• The difference between universal algebra and abstract algebra.

🏫 Math Essay Topics for High School

When writing a math paper, you want to demonstrate that you understand a concept. It can be helpful if you need to prepare for an exam. Choose a topic from this section and decide what you want to discuss.

• Explain what we need Pythagoras’ theorem for.
• What is a hyperbola?
• Describe the difference between algebra and arithmetic.
• When is it unnecessary to use a calculator ?
• Find a connection between math and the arts.
• How do you solve a linear equation?
• Discuss how to determine the probability of rolling two dice.
• Is there a link between philosophy and math?
• What types of math do you use in your everyday life?
• What is the numerical data?
• Explain how to use the binomial theorem.
• What is the distributive property of multiplication?
• Discuss the major concepts in ancient Egyptian mathematics .
• Why do so many students dislike math?
• Should math be required in school?
• How do you do an equivalent transformation?
• Why do we need imaginary numbers?
• How can you calculate the slope of a curve?
• What is the difference between sine, cosine, and tangent?
• How do you define the cross product of two vectors?
• What do we use differential equations for?
• Investigate how to calculate the mean value.
• Define linear growth.
• Give examples of different number types.
• How can you solve a matrix?

🎓 College Math Topics for a Paper

Sometimes you need more than just formulas to explain a complex idea. That’s why knowing how to express yourself is crucial. It is especially true for college-level mathematics. Consider the following ideas for your next research project:

• What do we need n-dimensional spaces for?
• Explain how card counting works.
• Discuss the difference between a discrete and a continuous probability distribution .
• How does encryption work?
• Describe extremal problems in discrete geometry.
• What can make a math problem unsolvable?
• Examine the topology of a Möbius strip.

• What is K-theory?
• Discuss the core problems of computational geometry.
• Explain the use of set theory .
• What do we need Boolean functions for?
• Describe the main topological concepts in modern mathematics.
• Investigate the properties of a rotation matrix.
• Analyze the practical applications of game theory.
• How can you solve a Rubik’s cube mathematically?
• Explain the math behind the Koch snowflake.
• Describe the paradox of Gabriel’s Horn.
• How do fractals form?
• Find a way to solve Sudoku using math.
• Why is the Riemann hypothesis still unsolved?
• Discuss the Millennium Prize Problems.
• How can you divide complex numbers?
• Analyze the degrees in polynomial functions.
• What are the most important concepts in number theory?
• Compare the different types of statistical methods.

🤔 Advanced Topics in Math to Write a Paper on

Once you have passed the trials of basic math, you can move on to the advanced section. This area includes topology, combinatorics, logic, and computational mathematics. Check out the list below for enticing topics to write about:

• What is an abelian group?
• Explain the orbit-stabilizer theorem.
• Discuss what makes the Burnside problem influential.
• What fundamental properties do holomorphic functions have?
• How does Cauchy’s integral theorem lead to Cauchy’s integral formula?
• How do the two Picard theorems relate to each other?
• When is a trigonometric series called a Fourier series?
• Give an example of an algorithm used for machine learning.
• Compare the different types of knapsack problems.
• What is the minimum overlap problem?
• Describe the Bernoulli scheme.
• Give a formal definition of the Chinese restaurant process.
• Discuss the logistic map in relation to chaos.
• What do we need the Feigenbaum constants for?
• Define a difference equation.
• Explain the uses of the Fibonacci sequence.
• What is an oblivious transfer?
• Compare the Riemann and the Ruelle zeta functions.
• How can you use elementary embeddings in model theory?
• Analyze the problem with the wholeness axiom and Kunen’s inconsistency theorem.
• How is Lie algebra used in physics ?
• Define various cases of algebraic cycles.
• Why do we need étale cohomology groups to calculate algebraic curves?
• What does non-Euclidean geometry consist of?
• How can two lines be ultraparallel?

📚 Math Research Topics for a Paper

Choosing the right topic is crucial for a successful research paper in math. It should be hard enough to be compelling, but not exceeding your level of competence. If possible, stick to your area of knowledge. This way your task will become more manageable. Here are some ideas:

• Write about the history of calculus.
• Why are unsolved math problems significant?
• Find reasons for the gender gap in math students.
• What are the toughest mathematical questions asked today?
• Examine the notion of operator spaces.
• How can we design a train schedule for a whole country?
• What makes a number big?

• How can infinities have various sizes?
• What is the best mathematical strategy to win a game of Go?
• Analyze natural occurrences of random walks in biology.
• Explain what kind of mathematics was used in ancient Persia.
• Discuss how the Iwasawa theory relates to modular forms.
• What role do prime numbers play in encryption?
• How did the study of mathematics evolve?
• Investigate the different Tower of Hanoi solutions.
• Research Napier’s bones. How can you use them?
• What is the best mathematical way to find someone who is lost in a maze?
• Examine the Traveling Salesman Problem. Can you find a new strategy?
• Describe how barcodes function.
• Study some real-life examples of chaos theory. How do you define them mathematically?
• Compare the impact of various ground-breaking mathematical equations .
• Research the Seven Bridges of Königsberg. Relate the problem to the city of your choice.
• Discuss Fisher’s fundamental theorem of natural selection.
• How does quantum computing work?
• Pick an unsolved math problem and say what makes it so difficult.

✏️ Math Education Research Topics

For many teachers, the hardest part is to keep the students interested. When it comes to math, it can be especially challenging. It’s crucial to make complicated concepts easy to understand. That’s why we need research on math education.

• Compare traditional methods of teaching math with unconventional ones.
• How can you improve mathematical education in the U.S.?
• Describe ways of encouraging girls to pursue careers in STEM fields.
• Should computer programming be taught in high school?
• Define the goals of mathematics education .
• Research how to make math more accessible to students with learning disabilities .
• At what age should children begin to practice simple equations?
• Investigate the effectiveness of gamification in algebra classes.
• What do students gain from taking part in mathematics competitions?
• What are the benefits of moving away from standardized testing ?
• Describe the causes of “ math anxiety .” How can you overcome it?
• Explain the social and political relevance of mathematics education.
• Define the most significant issues in public school math teaching.
• What is the best way to get children interested in geometry?
• How can students hone their mathematical thinking outside the classroom?
• Discuss the benefits of using technology in math class.
• In what way does culture influence your mathematical education?
• Explore the history of teaching algebra.
• Compare math education in various countries.

• How does dyscalculia affect a student’s daily life?
• Into which school subjects can math be integrated?
• Has a mathematics degree increased in value over the last few years?
• What are the disadvantages of the Common Core Standards?
• What are the advantages of following an integrated curriculum in math?
• Discuss the benefits of Mathcamp.

🧮 Algebra Topics for a Paper

The elegance of algebra stems from its simplicity. It gives us the ability to express complex problems in short equations. The world was changed forever when Einstein wrote down the simple formula E=mc². Now, if your algebra seminar requires you to write a paper, look no further! Here are some brilliant prompts:

• Give an example of an induction proof.
• What are F-algebras used for?
• What are number problems?
• Show the importance of abstract algebraic thinking .
• Investigate the peculiarities of Fermat’s last theorem.
• What are the essentials of Boolean algebra?
• Explore the relationship between algebra and geometry.
• Compare the differences between commutative and noncommutative algebra.
• Why is Brun’s constant relevant?
• How do you factor quadratics?
• Explain Descartes’ Rule of Signs.
• What is the quadratic formula?
• Compare the four types of sequences and define them.
• Explain how partial fractions work.
• What are logarithms used for?
• Describe the Gaussian elimination.
• What does Cramer’s rule state?
• Explore the difference between eigenvectors and eigenvalues.
• Analyze the Gram-Schmidt process in two dimensions.
• Explain what is meant by “range” and “domain” in algebra.
• What can you do with determinants?
• Learn about the origin of the distance formula.
• Find the best way to solve math word problems.
• Compare the relationships between different systems of equations.
• Explore how the Rubik’s cube relates to group theory.

📏 Geometry Topics for a Research Paper

Shapes and space are the two staples of geometry. Since its appearance in ancient times, it has evolved into a major field of study. Geometry’s most recent addition, topology, explores what happens to an object if you stretch, shrink, and fold it. Things can get pretty crazy from here! The following list contains 25 interesting geometry topics:

• What are the Archimedean solids?
• Find real-life uses for a rhombicosidodecahedron.
• What is studied in projective geometry?
• Compare the most common types of transformations.
• Explain how acute square triangulation works.
• Discuss the Borromean ring configuration.
• Investigate the solutions to Buffon’s needle problem.
• What is unique about right triangles?

• Describe the notion of Dirac manifolds.
• Compare the various relationships between lines.
• What is the Klein bottle?
• How does geometry translate into other disciplines, such as chemistry and physics?
• Explore Riemannian manifolds in Euclidean space.
• How can you prove the angle bisector theorem?
• Do a research on M.C. Escher’s use of geometry.
• Find applications for the golden ratio .
• Describe the importance of circles.
• Investigate what the ancient Greeks knew about geometry.
• What does congruency mean?
• Study the uses of Euler’s formula.
• How do CT scans relate to geometry?
• Why do we need n-dimensional vectors?
• How can you solve Heesch’s problem?
• What are hypercubes?
• Analyze the use of geometry in Picasso’s paintings.

➗ Calculus Topics to Write a Paper on

You can describe calculus as a more complicated algebra. It’s a study of change over time that provides useful insights into everyday problems. Applied calculus is required in a variety of fields such as sociology, engineering, or business. Consult this list of compelling topics on a calculus paper:

• What are the differences between trigonometry, algebra, and calculus?
• Explain the concept of limits.
• Describe the standard formulas needed for derivatives.
• How can you find critical points in a graph?
• Evaluate the application of L’Hôpital’s rule.
• How do you define the area between curves?
• What is the foundation of calculus?

• How does multivariate calculus work?
• Discuss the use of Stokes’ theorem.
• What does Leibniz’s integral rule state?
• What is the Itô stochastic integral?
• Explore the influence of nonstandard analysis on probability theory.
• Research the origins of calculus.
• Who was Maria Gaetana Agnesi?
• Define a continuous function.
• What is the fundamental theorem of calculus?
• How do you calculate the Taylor series of a function?
• Discuss the ways to resolve Runge’s phenomenon.
• Explain the extreme value theorem.
• What do we need predicate calculus for?
• What are linear approximations?
• When does an integral become improper?
• Describe the Ratio and Root Tests.
• How does the method of rings work?
• Where do we apply calculus in real-life situations?

💵 Business Math Topics to Write About

You don’t have to own a company to appreciate business math. Its topics range from credits and loans to insurance, taxes, and investment. Even if you’re not a mathematician, you can use it to handle your finances. Sounds interesting? Then have a look at the following list:

• What are the essential skills needed for business math?
• How do you calculate interest rates?
• Compare business and consumer math.
• What is a discount factor?
• How do you know that an investment is reasonable?
• When does it make sense to pay a loan with another loan?
• Find useful financing techniques that everyone can use.
• How does critical path analysis work?
• Explain how loans work.
• Which areas of work utilize operations research?
• How do businesses use statistics?
• What is the economic lot scheduling problem?
• Compare the uses of different chart types.
• What causes a stock market crash?
• How can you calculate the net present value?
• Explore the history of revenue management.
• When do you use multi-period models?
• Explain the consequences of depreciation.
• Are annuities a good investment?
• Would the U.S. financially benefit from discontinuing the penny?
• What caused the United States housing crash in 2008?
• How do you calculate sales tax?
• Describe the notions of markups and markdowns.
• Investigate the math behind debt amortization.
• What is the difference between a loan and a mortgage?

With all these ideas, you are perfectly equipped for your next math paper. Good luck!

• What Is Calculus?: Southern State Community College
• What Is Mathematics?: Tennessee Tech University
• What Is Geometry?: University of Waterloo
• What Is Algebra?: BBC
• Ten Simple Rules for Mathematical Writing: Ohio State University
• Practical Algebra Lessons: Purplemath
• Topics in Geometry: Massachusetts Institute of Technology
• The Geometry Junkyard: All Topics: Donald Bren School of Information and Computer Sciences
• Calculus I: Lamar University
• Business Math for Financial Management: The Balance Small Business
• What Is Mathematics: Life Science
• What Is Mathematics Education?: University of California, Berkeley
• Share to Facebook
• Share to Twitter
• Share to LinkedIn
• Share to email

Cause and effect essays examine how an event happened and what consequences it had. Gaining weight after eating lots of fast food is an example of a cause-and-effect relationship. Possible topics cover a variety of subjects ranging from mental health to history and politics. This article gives you an outline...

An analysis essay aims to break down the subject in order to understand it. You can choose to analyze a text, a process, or an idea. This article will help you write a great essay! Selecting an interesting topic makes writing a lot easier. We’ve prepared a list of excellent...

Everybody knows that being healthy requires effort. We should exercise regularly and maintain a balanced diet. However, the reward is worth it. A healthy lifestyle prevents chronic illnesses and leads to better body performance. Besides, if you improve your physical well-being, your mental health will strengthen as well! In this...

Environment affects us all, whether we want it or not. Political leaders and students alike discuss ways to tackle environmental topics & issues. Some might argue about the role humans play in all this. The fact remains that our environment is a delicate matter. That’s why we must educate ourselves...

Our code of ethics is derived from what we think is right or wrong. On top of that, we have to agree to the moral standards established by the society we live in. Conventional norms generally label theft, murder, or harassment as bad. However, there are many influences that impact...

A definition explains the meaning of a term or a concept. In a dictionary, you’ll find a definition in a single sentence. A definition paper, however, encompasses several paragraphs. Such an essay, amongst other things, can include personal experience and examples. To write a successful definition paper, you need to...

As simple as it is, the purpose of the descriptive essay is to explain or portray its subject. It can focus on any topic or issue you want to write about. Be sure that any middle school, high school, or college student can manage this type of creative writing assignment!...

Rhetorical analysis essay focuses on assessing the method used for delivering a message. This assignment isn’t about giving an opinion on the topic. The purpose is to analyze how the author presents the argument and whether or not they succeeded. Keep reading to find out more strategies and prompts for...

A narrative essay tells a story about a series of events. At the core of this kind of essay can be a personal experience or a fictional plot. Any story can be a basis for a narrative essay! Narratives can look similar to descriptions. Still, they are different. A descriptive...

Similar to the instructions in a recipe book, process essays convey information in a step-by-step format. In this type of paper, you follow a structured chronological process. You can also call it a how-to essay. A closely related type is a process analysis essay. Here you have to carefully consider...

In a classification essay, you divide the subject into categories. To create these categories, you single out certain attributes of things. You can classify them according to their characteristics, themes, or traits. Sounds complicated? Be sure that any high school or college student can manage this type of essay!

Throughout your high school years, you are likely to write many evaluative papers. In an evaluation essay you aim is to justify your point of view through evidence.

I need a writer on algebra. I am a PhD student.Can i be helped by anybody/expert?

Please I want to do my MPhil research on algebra if you can help me

shall your university help me on research in mathematics ?

how I get the full pdf of those tittles

Print as pdf.

Math Essay Ideas for Students: Exploring Mathematical Concepts

Are you a student who's been tasked with writing a math essay? Don't fret! While math may seem like an abstract and daunting subject, it's actually full of fascinating concepts waiting to be explored. In this article, we'll delve into some exciting math essay ideas that will not only pique your interest but also impress your teachers. So grab your pens and calculators, and let's dive into the world of mathematics!

• The Beauty of Fibonacci Sequence

Have you ever wondered why sunflowers, pinecones, and even galaxies exhibit a mesmerizing spiral pattern? It's all thanks to the Fibonacci sequence! Explore the origin, properties, and real-world applications of this remarkable mathematical sequence. Discuss how it manifests in nature, art, and even financial markets. Unveil the hidden beauty behind these numbers and show how they shape the world around us.

• The Mathematics of Music

Did you know that music and mathematics go hand in hand? Dive into the relationship between these two seemingly unrelated fields and develop your writing skills . Explore the connection between harmonics, frequencies, and mathematical ratios. Analyze how musical scales are constructed and why certain combinations of notes create pleasant melodies while others may sound dissonant. Explore the fascinating world where numbers and melodies intertwine.

• The Geometry of Architecture

Architects have been using mathematical principles for centuries to create awe-inspiring structures. Explore the geometric concepts that underpin iconic architectural designs. From the symmetry of the Parthenon to the intricate tessellations in Islamic art, mathematics plays a crucial role in creating visually stunning buildings. Discuss the mathematical principles architects employ and how they enhance the functionality and aesthetics of their designs.

• Fractals: Nature's Infinite Complexity

Step into the mesmerizing world of fractals, where infinite complexity arises from simple patterns. Did you know that the famous Mandelbrot set , a classic example of a fractal, has been studied extensively and generated using computers? In fact, it is estimated that the Mandelbrot set requires billions of calculations to generate just a single image! This showcases the computational power and mathematical precision involved in exploring the beauty of fractal geometry.

Explore the beauty and intricacy of fractal geometry, from the famous Mandelbrot set to the Sierpinski triangle. Discuss the self-similarity and infinite iteration that define fractals and how they can be found in natural phenomena such as coastlines, clouds, and even in the structure of our lungs. Examine how fractal mathematics is applied in computer graphics, art, and the study of chaotic systems. Let the captivating world of fractals unfold before your eyes.

• The Game Theory Revolution

Game theory isn't just about playing games; it's a powerful tool used in various fields, from economics to biology. Dive into the world of strategic decision-making and explore how game theory helps us understand human behavior and predict outcomes. Discuss in your essay classic games like The Prisoner's Dilemma and examine how mathematical models can shed light on complex social interactions. Explore the cutting-edge applications of game theory in diverse fields, such as cybersecurity and evolutionary biology. If you still have difficulties choosing an idea for a math essay, find a reliable expert online. Ask them to write me an essay or provide any other academic assistance with your math assignments.

• Chaos Theory and the Butterfly Effect

While writing an essay, explore the fascinating world of chaos theory and how small changes can lead to big consequences. Discuss the famous Butterfly Effect and how it exemplifies the sensitive dependence on initial conditions. Delve into the mathematical principles behind chaotic systems and their applications in weather forecasting, population dynamics, and cryptography. Unravel the hidden order within apparent randomness and showcase the far-reaching implications of chaos theory.

• The Mathematics Behind Cryptography

In an increasingly digital world, cryptography plays a vital role in ensuring secure communication and data protection. Did you know that the global cybersecurity market is projected to reach a staggering $248.26 billion by 2023? This statistic emphasizes the growing importance of cryptography in safeguarding sensitive information.

Explore the mathematical foundations of cryptography and how it allows for the creation of unbreakable codes and encryption algorithms. Discuss the concepts of prime numbers, modular arithmetic, and public-key cryptography. Delve into the fascinating history of cryptography, from ancient times to modern-day encryption methods. In your essay, highlight the importance of mathematics in safeguarding sensitive information and the ongoing challenges faced by cryptographers.

Writing a math essay doesn't have to be a daunting task. By choosing a captivating topic and exploring the various mathematical concepts, you can turn your essay into a fascinating journey of discovery. Whether you're uncovering the beauty of the Fibonacci sequence, exploring the mathematical underpinnings of music, or delving into the game theory revolution, there's a world of possibilities waiting to be explored. So embrace the power of mathematics and let your creativity shine through your words!

Remember, these are just a few math essay ideas to get you started. Feel free to explore other mathematical concepts that ignite your curiosity. The world of mathematics is vast, and each concept has its own unique story to tell. So go ahead, unleash your inner mathematician, and embark on an exciting journey through the captivating realm of mathematical ideas!

Tobi Columb, a math expert, is a dedicated educator and explorer. He is deeply fascinated by the infinite possibilities of mathematics. Tobi's mission is to equip his students with the tools needed to excel in the realm of numbers. He also advocates for the benefits of a gluten-free lifestyle for students and people of all ages. Join Tobi on his transformative journey of mathematical mastery and holistic well-being.

Related Calculators

In case you have any suggestion, or if you would like to report a broken solver/calculator, please do not hesitate to contact us .

log in to your account

Reset password.

Extended Essay: Group 5: Mathematics

• General Timeline
• Group 1: English Language and Literature
• Group 2: Language Acquisition
• Group 3: Individuals and Societies
• Group 4: Sciences
• Group 5: Mathematics
• Group 6: The Arts
• Interdisciplinary essays
• Six sub-categories for WSEE
• IB Interdisciplinary EE Assessment Guide
• Brainstorming
• Pre-Writing
• Research Techniques
• The Research Question
• Paraphrasing, Summarising and Quotations
• Writing an EE Introduction
• Writing the main body of your EE
• Writing your EE Conclusion
• Sources: Finding, Organising and Evaluating Them
• Conducting Interviews and Surveys
• Citing and Referencing
• Check-in Sessions
• First Formal Reflection
• Second Formal Reflection
• Final Reflection (Viva Voce)
• Researcher's Reflection Space (RRS) Examples
• Information for Supervisors
• How is the EE Graded?
• EE Online Resources
• Stavanger Public Library
• Exemplar Essays
• Extended Essay Presentations
• ISS High School Academic Honesty Policy

Mathematics

An extended essay (EE) in mathematics is intended for students who are writing on any topic that has a mathematical focus and it need not be confined to the theory of mathematics itself.

Essays in this group are divided into six categories:

• the applicability of mathematics to solve both real and abstract problems
• the beauty of mathematics—eg geometry or fractal theory
• the elegance of mathematics in the proving of theorems—eg number theory
• the history of mathematics: the origin and subsequent development of a branch of mathematics over a period of time, measured in tens, hundreds or thousands of years
• the effect of technology on mathematics:
• in forging links between different branches of mathematics,
• or in bringing about a new branch of mathematics, or causing a particular branch to flourish.

These are just some of the many different ways that mathematics can be enjoyable or useful, or, as in many cases, both.

For an Introduction in a Mathematics EE look HERE . 

Choice of topic

The EE may be written on any topic that has a mathematical focus and it need not be confined to the theory of mathematics itself.

Students may choose mathematical topics from fields such as engineering, the sciences or the social sciences, as well as from mathematics itself.

Statistical analyses of experimental results taken from other subject areas are also acceptable, provided that they focus on the modeling process and discuss the limitations of the results; such essays should not include extensive non-mathematical detail.

A topic selected from the history of mathematics may also be appropriate, provided that a clear line of mathematical development is demonstrated. Concentration on the lives of, or personal rivalries between, mathematicians would be irrelevant and would not score highly on the assessment criteria.

It should be noted that the assessment criteria give credit for the nature of the investigation and for the extent that reasoned arguments are applied to an appropriate research question.

Students should avoid choosing a topic that gives rise to a trivial research question or one that is not sufficiently focused to allow appropriate treatment within the requirements of the EE.

Students will normally be expected either to extend their knowledge beyond that encountered in the Diploma Programme mathematics course they are studying or to apply techniques used in their mathematics course to modeling in an appropriately chosen topic.

However, it is very important to remember that it is an essay that is being written, not a research paper for a journal of advanced mathematics, and no result, however impressive, should be quoted without evidence of the student’s real understanding of it.

Example and Treatment of Topic

Examples of topics

These examples are just for guidance. Students must ensure their choice of topic is focused (left-hand column) rather than broad (right-hand column

Treatment of the topic

Whatever the title of the EE, students must apply good mathematical practice that is relevant to the

chosen topic, including:

• data analysed using appropriate techniques

• arguments correctly reasoned

• situations modeled using correct methodology

• problems clearly stated and techniques at the correct level of sophistication applied to their solution.

Research methods

Students must be advised that mathematical research is a long-term and open-ended exploration of a set of related mathematical problems that are based on personal observations. 

The answers to these problems connect to and build upon each other over time.

Students’ research should be guided by analysis of primary and secondary sources.

A primary source for research in mathematics involves:

• data-gathering

• visualization

• abstraction

• conjecturing

• proof.

A secondary source of research refers to a comprehensive review of scholarly work, including books, journal articles or essays in an edited collection.

A literature review for mathematics might not be as extensive as in other subjects, but students are expected to demonstrate their knowledge and understanding of the mathematics they are using in the context of the broader discipline, for example how the mathematics they are using has been applied before, or in a different area to the one they are investigating.

Writing the essay

Throughout the EE students should communicate mathematically:

• describing their way of thinking

• writing definitions and conjectures

• using symbols, theorems, graphs and diagrams

• justifying their conclusions.

There must be sufficient explanation and commentary throughout the essay to ensure that the reader does not lose sight of its purpose in a mass of mathematical symbols, formulae and analysis.

The unique disciplines of mathematics must be respected throughout. Relevant graphs and diagrams are often important and should be incorporated in the body of the essay, not relegated to an appendix.

However, lengthy printouts, tables of results and computer programs should not be allowed to interrupt the development of the essay, and should appear separately as footnotes or in an appendix. Proofs of key results may be included, but proofs of standard results should be either omitted or, if they illustrate an important point, included in an appendix.

Examples of topics, research questions and suggested approaches

Once students have identified their topic and written their research question, they can decide how to

research their answer. They may find it helpful to write a statement outlining their broad approach. These

examples are for guidance only.

An important note on “double-dipping”

Students must ensure that their EE does not duplicate other work they are submitting for the Diploma Programme. For example, students are not permitted to repeat any of the mathematics in their IA in their EE, or vice versa.

The mathematics EE and internal assessment

An EE in mathematics is not an extension of the internal assessment (IA) task. Students must ensure that they understand the differences between the two.

• The EE is a more substantial piece of work that requires formal research
• The IA is an exploration of an idea in mathematics.

It is not appropriate for a student to choose the same topic for an EE as the IA. There would be too much danger of duplication and it must therefore be discouraged.

• << Previous: Group 4: Sciences
• Next: Group 6: The Arts >>
• Last Updated: May 30, 2024 9:48 AM
• URL: https://isstavanger.libguides.com/c.php?g=695888

IB Maths EE examples

Filter exemplars, to what extent prime counting function and the riemann zeta function are similar, and what is the importance of their similarities, how are elliptic curves used in cryptography to make information secure in today’s world, want to get full marks for your ee allow us to review it for you 🎯, how does elliptic curve cryptography ensure secure communication of information on the internet, to what extent is the naive bayes classifier effective in classifying iris plants data set, to what extent is the insight into the concepts of consonance and dissonance in music theory provided by the mathematical descriptions of the string motions within stringed instruments described by the fourier series, fast track your coursework with mark schemes moderated by ib examiners. upgrade now 🚀, how can laplace transformation be used to solve differential equations in undamped vibration and kirchhoff's laws of current and voltage, to what length does the lotka-volterra model help us understand the predator-prey relation in an ecosystem, how does the implementation of pell's equation in rsa cryptography affect its efficiency, and what is the security of the prime fake modulus variant against fermat's factorization and wiener's attack, how do laplace transformations and complex exponential substitution enable the solution of a first order differential equation to obtain the sinusoidal current in a basic rl circuit, the analysis of approaches and extension of a combinatorial geometry problem, to what extent, statistically, are the causal effects of parenting programs on rural chinese toddlers’ cognition different between genders, to what extent is the mathematical proof of ‘ac ohm’s law’ applicable to ac circuits, dans quelle mesure, l’utilisation de pi (π) est-il devenu un facteur important dans la vie quotidienne et l’évolution du monde, how can matrix analysis of game theory be used to guide foreign policy in the ongoing us-iran nuclear tensions, how does the idea of transpositions from group theory apply itself to the solution of the futurama problem, how can the surface area of a violin's top plate be calculated, what is the height and number of towers in a suspension bridge between tuas and jurong island such that it will bear the heaviest possible load and have the lowest cost, how trigonomotry applied in astronomy, to what extent do trigonometry, elliptical geometry and calculus aid forensic analysts in blood spatter analysis and the estimation of the time of death of a corpse, how does the fourier series is used as a musical signal for chord structure, what is modular arithmetic, and how can it be applied to solve problems in the field of number theory, to what extent do the motion of strings within stringed instruments described by fourier series give insight into consonance and dissonance in music theory, how can we use fourier series to analyse and produce an electrocardiogram signal, (35/36) hyperbolic flyby trajectories in orbital mechanicss, analyzing the distribution of cards in the "egg game”, to what extent the areas of mathematics such as differ- ential geometry and calculus of variations can be used to generalize the brachis- tochrone problem at planes to curved surfaces embedded in three dimensions, generating arbitrary uniform probability distributions, what are some ways the riemann zeta function is connected to the prime numbers, that helps us investigate and better understand them, probability factors that influence the game of roulette, we will investigate whether the supply and demand affect the performance of a stock in the us equity market, to what extent does the distance between the path that goes through the gold nucleus and one of the asymptotes of the α particle’s hyperbolic trajectory affect the trajectory of the α particle in rutherford's gold foil experiment, what is the most optimal point on football field to score a goal, how does abstract mathematics apply to physical phenomena in the process of the development of schrodinger’s equations, the rsa algorithm and its vulnerabilities, how can mathematics be used to work out the optimal distance from the try line to position the ball for a conversion kick in rugby union.

Essays About Math: Top 10 Examples and Writing Prompts 

Love it or hate it, an understanding of math is said to be crucial to success. So, if you are writing essays about math, read our top essay examples.  

Mathematics is the study of numbers, shapes, and space using reason and usually a special system of symbols and rules for organizing them . It can be used for a variety of purposes, from calculating a business’s profit to estimating the mass of a black hole. However, it can be considered “controversial” to an extent.

Most students adore math or regard it as their least favorite. No other core subject has the same infamy as math for generating passionate reactions both for and against it. It has applications in every field, whether basic operations or complex calculus problems. Knowing the basics of math is necessary to do any work properly. 

If you are writing essays about Math, we have compiled some essay examples for you to get started. 

1. Mathematics: Problem Solving and Ideal Math Classroom by Darlene Gregory 

2. math essay by prasanna, 3. short essay on the importance of mathematics by jay prakash.

• 4.  Math Anxiety by Elias Wong

5. Why Math Isn’t as Useless as We Think by Murtaza Ali

1. mathematics – do you love or hate it, 2. why do many people despise math, 3. how does math prepare you for the future, 4. is mathematics an essential skill, 5. mathematics in the modern world.

“The trait of the teacher that is being strict is we know that will really help the students to change. But it will give a stress and pressure to students and that is one of the causes why students begin to dislike math. As a student I want a teacher that is not so much strict and giving considerations to his students. A teacher that is not giving loads of things to do and must know how to understand the reasons of his students.”

Gregory discusses the reasons for most students’ hatred of math and how teachers handle the subject in class. She says that math teachers do not explain the topics well, give too much work, and demand nothing less than perfection. To her, the ideal math class would involve teachers being more considerate and giving less work. 

You might also be interested in our ordinal number explainer.

“Math is complicated to learn, and one needs to focus and concentrate more. Math is logical sometimes, and the logic needs to be derived out. Maths make our life easier and more straightforward. Math is considered to be challenging because it consists of many formulas that have to be learned, and many symbols and each symbol generally has its significance.”

In her essay, Prasanna gives readers a basic idea of what math is and its importance. She additionally lists down some of the many uses of mathematics in different career paths, namely managing finances, cooking, home modeling and construction, and traveling. Math may seem “useless” and “annoying” to many, but the essay gives readers a clear message: we need math to succeed. 

“In this modern age of Science and Technology, emphasis is given on Science such as Physics, Chemistry, Biology, Medicine and Engineering. Mathematics, which is a Science by any criterion, also is an efficient and necessary tool being employed by all these Sciences. As a matter of fact, all these Sciences progress only with the aid of Mathematics. So it is aptly remarked, ‘Mathematics is a Science of all Sciences and art of all arts.’”

As its title suggests, Prakash’s essay briefly explains why math is vital to human nature. As the world continues to advance and modernize, society emphasizes sciences such as medicine, chemistry, and physics. All sciences employ math; it cannot be studied without math. It also helps us better our reasoning skills and maximizes the human mind. It is not only necessary but beneficial to our everyday lives. 

4.   Math Anxiety by Elias Wong

“Math anxiety affects different not only students but also people in different ways. It’s important to be familiar with the thoughts you have about yourself and the situation when you encounter math. If you are aware of unrealistic or irrational thoughts you can work to replace those thoughts with more positive and realistic ones.”

Wong writes about the phenomenon known as “math anxiety.” This term is used to describe many people’s hatred or fear of math- they feel that they are incapable of doing it. This anxiety is caused mainly by students’ negative experiences in math class, which makes them believe they cannot do well. Wong explains that some people have brains geared towards math and others do not, but this should not stop people from trying to overcome their math anxiety. Through review and practice of basic mathematical skills, students can overcome them and even excel at math. 

“We see that math is not an obscure subject reserved for some pretentious intellectual nobility. Though we may not be aware of it, mathematics is embedded into many different aspects of our lives and our world — and by understanding it deeply, we may just gain a greater understanding of ourselves.”

Similar to some of the previous essays, Ali’s essay explains the importance of math. Interestingly, he tells a story of the life of a person name Kyle. He goes through the typical stages of life and enjoys typical human hobbies, including Rubik’s cube solving. Throughout this “Kyle’s” entire life, he performed the role of a mathematician in various ways. Ali explains that math is much more prevalent in our lives than we think, and by understanding it, we can better understand ourselves. 

Writing Prompts on Essays about Math

Math is a controversial subject that many people either passionately adore or despise. In this essay, reflect on your feelings towards math, and state your position on the topic. Then, give insights and reasons as to why you feel this way. Perhaps this subject comes easily to you, or perhaps it’s a subject that you find pretty challenging. For an insightful and compelling essay, you can include personal anecdotes to relate to your argument. 

It is well-known that many people despise math. In this essay, discuss why so many people do not enjoy maths and struggle with this subject in school. For a compelling essay, gather interview data and statistics to support your arguments. You could include different sections correlating to why people do not enjoy this subject.

In this essay, begin by reading articles and essays about the importance of studying math. Then, write about the different ways that having proficient math skills can help you later in life. Next, use real-life examples of where maths is necessary, such as banking, shopping, planning holidays, and more! For an engaging essay, use some anecdotes from your experiences of using math in your daily life.

Many people have said that math is essential for the future and that you shouldn’t take a math class for granted. However, many also say that only a basic understanding of math is essential; the rest depends on one’s career. Is it essential to learn calculus and trigonometry? Choose your position and back up your claim with evidence. 

Prasanna’s essay lists down just a few applications math has in our daily lives. For this essay, you can choose any activity, whether running, painting, or playing video games, and explain how math is used there. Then, write about mathematical concepts related to your chosen activity and explain how they are used. Finally, be sure to link it back to the importance of math, as this is essentially the topic around which your essay is based. 

If you are interested in learning more, check out our essay writing tips !

For help with your essays, check out our round-up of the best essay checkers

Martin is an avid writer specializing in editing and proofreading. He also enjoys literary analysis and writing about food and travel.

View all posts

IB Math EE - Math Extended Essay Guide

The IB Math Extended Essay is a challenging yet rewarding academic endeavor that allows students to explore and delve deeper into various mathematical concepts and techniques. This article aims to provide valuable insights and guidance on how to successfully navigate through the process of writing an IB Math Extended Essay.

With a focus on conducting effective research, applying mathematical concepts, developing a coherent argument, and managing time and organization, this article offers practical tips to help students overcome challenges and roadblocks they may encounter along the way.

Furthermore, this article emphasizes the importance of showcasing personal engagement in the essay by demonstrating genuine curiosity and passion for the chosen topic. By doing so, students can celebrate their accomplishment in producing a well-written piece that reflects their dedication and understanding of mathematics.

Whether you are just beginning your journey or already immersed in your IB Math Extended Essay, this informative guide will equip you with essential tools to excel in your academic pursuit while ensuring safety within an objective academic writing style.

Key Takeaways

• IB Math Extended Essay is a challenging academic endeavor that allows students to explore mathematical concepts and techniques.
• The essay requires effective research, application of mathematical concepts, coherent argument, and time management.
• Personal engagement and passion are important for a successful extended essay.
• Effective research strategies include consulting scholarly articles, books, and reputable online resources, and following clear plans and systematic methodologies.

Understanding the IB Math Extended Essay

The IB Math Extended Essay is a research project that requires students to investigate a mathematical topic of their choice in depth, demonstrating their understanding and application of mathematical principles. It serves as an opportunity for students to engage in independent research and explore the subject matter beyond the scope of the standard math curriculum. The essay allows students to delve into complex mathematical concepts, develop logical arguments, and present their findings in a structured manner.

To ensure safety within this academic pursuit, it is crucial for students to adhere to ethical guidelines when conducting their research. This includes citing all sources accurately and giving credit where it is due. Additionally, students should prioritize data integrity by using reliable sources and verifying information before incorporating it into their essays.

In order to conduct effective research for the IB Math Extended Essay, students must employ various strategies such as consulting scholarly articles, books, and reputable online resources. They should also consider seeking guidance from experts or professionals who can provide valuable insights on their chosen topic. By utilizing these resources effectively, students can enhance the quality of their research and ultimately produce a comprehensive essay that contributes meaningfully to the field of mathematics.

Transitioning into the next section on conducting effective research without explicitly stating "step," it is essential for students to approach their investigation with a clear plan and systematic methodology.

Conducting Effective Research

To effectively conduct research for an IB Math extended essay, it is essential to approach the task with an objective and impersonal mindset. This ensures that the research is conducted in a systematic and unbiased manner, allowing for reliable and valid results. Here are four helpful tips to consider when conducting research for your IB Math extended essay:

• Define your research question clearly: Start by identifying a specific problem or topic within the field of mathematics that you want to explore. Clearly define your research question to provide focus and direction throughout the process.
• Gather relevant sources: Conduct a thorough literature review to identify existing theories, models, and studies related to your research question. This will help you build a solid foundation of knowledge and understand previous findings in order to contribute something new to the field.
• Collect and analyze data: Depending on your chosen topic, collect data using appropriate methods such as surveys, experiments, or simulations. Ensure that your data collection process is rigorous and follows ethical guidelines.
• Draw meaningful conclusions: Analyze your data using appropriate mathematical techniques and interpret the results objectively. Draw meaningful conclusions that address your research question's objectives while considering any limitations or uncertainties present in the study.

By following these steps, you can conduct effective research for your IB Math extended essay that contributes valuable insights into the field of mathematics. Moving forward into applying mathematical concepts and techniques…

Read More About:

IB Design Technology IA Guide

IB Economics IA Guide

IB Economics Syllabus New Pattern & Changes

IB ESS (Environmental Systems and Societies) IA - Step By Step Guide

IB Exams Guide - Essential Study Tips

Applying Mathematical Concepts and Techniques

Applying mathematical concepts and techniques involves seamlessly integrating complex equations, formulas, and algorithms into practical real-world scenarios, unlocking the potential for innovative solutions and transformative insights. By harnessing the power of mathematics, researchers can analyze data, model systems, and make predictions with precision and accuracy. Mathematical tools provide a structured framework to explore relationships between variables, identify patterns, and test hypotheses.

To illustrate the significance of applying mathematical concepts in research, let us consider a 2-column table:

Mathematical ConceptPractical ApplicationProbability theoryAssessing risks in safety engineeringOptimizationOptimizing resource allocation in disaster managementStatistical analysisAnalyzing crime patterns for effective law enforcement

This table demonstrates how mathematical concepts can be applied to enhance safety measures. Probability theory enables engineers to assess risks associated with different design choices. Optimization techniques help allocate limited resources efficiently during emergencies. Statistical analysis allows law enforcement agencies to identify crime hotspots for targeted interventions.

By incorporating mathematical concepts and techniques into research methodologies, researchers can derive meaningful insights that contribute to safe and reliable solutions. In the subsequent section about 'writing a strong introduction,' we will explore how an effective opening sets the stage for further investigation without being overly prescriptive or formulaic.

Writing a Strong Introduction

Engaging the reader and providing context is crucial in writing a strong introduction for an essay. By presenting relevant background information or posing thought-provoking questions, the writer can capture the reader's attention and create a sense of relevance to the topic. Additionally, formulating a clear thesis statement in the introductory paragraph helps establish the main argument of the essay and provides a roadmap for what will be discussed. Lastly, outlining the structure and scope of the essay allows readers to understand how different sections will be organized and what specific aspects will be explored, ensuring clarity and coherence throughout the paper.

Engaging the reader and providing context

In order to fully immerse the reader into the world of mathematics, it is crucial to provide a rich contextual backdrop that allows for a clearer understanding and appreciation of the subject matter. Mathematics can often seem abstract and disconnected from everyday life, leading some individuals to view it as intimidating or irrelevant. By engaging the reader through relatable examples and real-world applications, we can create a safe and approachable environment for learning. Exploring how mathematical concepts are applied in various fields such as engineering, finance, or computer science not only helps students see the practicality of mathematics but also fosters an interest in further exploration. Moreover, providing historical context can highlight the development and significance of different branches within mathematics. This sets the stage for formulating a clear thesis statement that builds upon this foundation of knowledge.

Formulating a clear thesis statement

To effectively convey the main focus of a mathematical exploration, it is crucial to craft a concise and clear thesis statement that serves as a guiding framework for the subsequent analysis. A well-formulated thesis statement not only states the main argument or hypothesis but also provides a roadmap for the reader to follow throughout the essay. In an academic style of writing, it is important to maintain objectivity and impersonality, eliminating personal pronouns to create a sense of professionalism and neutrality. By presenting the thesis statement in an objective manner, the writer can engage with an audience that desires safety and assurance in their understanding of complex mathematical concepts. With a solid thesis statement in place, the subsequent section will outline the structure and scope of the essay seamlessly, ensuring clarity and coherence in presenting mathematical ideas.

Outlining the structure and scope of the essay

In the previous subtopic, we discussed the importance of formulating a clear thesis statement for an IB Math Extended Essay. Now, let's move on to outlining the structure and scope of the essay. This step is crucial as it helps provide a roadmap for the reader to navigate through your work. By clearly outlining the structure and scope, you ensure that all relevant aspects are covered while maintaining coherence and logical flow.

To achieve this, consider incorporating an unordered 3 item bullet list in markdown format:

• Begin with an introduction that introduces the topic and provides context.
• Divide your essay into sections or chapters based on different aspects or arguments.
• Conclude with a summary of key findings and a reflection on their significance.

By following these guidelines, you can create a well-structured essay that effectively communicates your ideas. Transitioning into the next section about developing a coherent argument, it is essential to build upon this foundation by presenting compelling evidence and reasoning to support your thesis statement.

Developing a Coherent Argument

Developing a coherent argument requires the use of logical reasoning and well-structured evidence. When constructing an argument, it is essential to present facts and information in a clear and organized manner. This involves avoiding personal biases and emotions, as well as eliminating personal pronouns to maintain objectivity.

To ensure a strong argument, it is crucial to rely on credible sources and data that support the claims being made. Using evidence from reputable academic journals or textbooks helps establish credibility and adds weight to the argument being presented. Additionally, incorporating logical reasoning allows for connections to be made between different pieces of evidence, further strengthening the overall coherence of the argument.

When writing for an audience that desires safety, it is important to use language that is appropriate and sensitive. Avoiding inflammatory or offensive language ensures that readers feel respected and engaged with the content. By presenting arguments in a respectful manner, readers are more likely to consider different perspectives without feeling attacked or threatened.

Developing a coherent argument requires logical reasoning backed by well-structured evidence. By employing these strategies, writers can effectively communicate their ideas while maintaining objectivity. In the subsequent section about using clear and concise language, we will explore how this aspect contributes to the overall coherence of an essay's argumentation process.

Using Clear and Concise Language

Using precise and concise language enhances the clarity and impact of an argument, captivating readers and facilitating their understanding. When writing academically, it is important to eliminate personal pronouns and adopt an objective and impersonal tone. This approach allows the focus to remain on the content rather than the writer's subjective perspective. By using clear and concise language, writers can effectively convey complex ideas without overwhelming or confusing their audience.

In an academic setting, it is crucial to cater to an audience that values safety in their reading material. Using language appropriate for this type of audience ensures that readers feel secure in engaging with the content. It also helps build trust between the writer and the reader, as clear communication fosters a sense of reliability.

Transitioning into the subsequent section about formatting and citations, it is essential to maintain precision throughout all aspects of academic writing. Formatting guidelines ensure consistency in presenting information while citations acknowledge sources used in support of arguments. These elements contribute to establishing credibility within academia by demonstrating a thorough understanding of scholarly norms.

By adhering to these rules of using clear and concise language, as well as following proper formatting guidelines and including accurate citations, writers can effectively communicate their ideas while maintaining professionalism within academic discourse.

Formatting and Citations

This paragraph will discuss the importance of following the IB guidelines for formatting and citation style, using proper citations and references, and creating a bibliography or works cited page. Following the IB guidelines is crucial to ensure consistency and professionalism in academic writing. Proper citations and references are essential to give credit to the original authors and avoid plagiarism. Creating a bibliography or works cited page helps readers locate and verify the sources used in research.

Following the IB guidelines for formatting and citation style

To adhere to the IB guidelines for formatting and citation style, it is essential to employ an academic writing style that maintains objectivity and avoids personal pronouns, thus conveying a sense of professionalism and scholarly rigor to the intended readership. One effective way to enhance the readability of academic writing is through the use of tables. Tables provide a clear and organized format for presenting data or information in a concise manner. They allow readers to quickly grasp key points and make comparisons between different elements. In this context, a 2 column by 4 row table can be utilized, providing a visually appealing layout that facilitates understanding. By incorporating tables into academic writing, authors can effectively communicate complex ideas while maintaining clarity and coherence.

Moving forward, it is important to also consider the importance of using proper citations and references in order to acknowledge the sources of information used in academic writing without plagiarizing.

Using proper citations and references

A crucial aspect of scholarly writing involves the integration of accurate citations and references, which serve to acknowledge the sources of information employed in academic discourse while maintaining integrity and avoiding plagiarism. By providing proper citations, researchers ensure that their work is transparent and reliable, allowing readers to verify claims and build upon established knowledge. Additionally, citations demonstrate respect for intellectual property rights and ethical research practices. In an academic setting where safety is a priority, precise referencing becomes even more important as it enables readers to access relevant sources and evaluate the reliability of information provided. Moving forward into the next section about creating a bibliography or works cited page, attention to citation details will continue to play a pivotal role in upholding academic standards and fostering a culture of accountability in research endeavors.

Creating a bibliography or works cited page

The creation of a bibliography or works cited page is an essential step in scholarly writing, as it provides a comprehensive list of all the sources referenced in an academic work, enabling readers to access and evaluate the reliability of the information presented. By including a bibliography, authors demonstrate transparency and accountability by acknowledging the contributions of other scholars and researchers. This not only strengthens their own arguments but also allows readers to verify the credibility of the sources used. A well-constructed bibliography typically includes information such as author names, publication dates, titles, and any relevant page numbers. It is important to adhere to specific citation styles, such as APA or MLA, to ensure consistency and accuracy throughout the document. With a complete bibliography in place, authors can confidently move on to seeking feedback and revisions for their work.

Seeking Feedback and Revisions

Revising and seeking feedback on the IB Math EE is an essential step in ensuring a well-rounded and academically rigorous research project. The process of seeking feedback allows for constructive criticism, which can help identify areas for improvement and strengthen the overall quality of the Extended Essay. Here are three key reasons why seeking feedback and revisions are crucial:

• Enhancing clarity: Feedback from teachers, peers, or subject experts can provide valuable insights into areas that may be unclear or confusing. This allows the researcher to refine their arguments and ensure that their ideas are effectively communicated.
• Identifying errors: Through feedback, researchers can identify any mistakes or inaccuracies in their work. This could include mathematical errors, incorrect data analysis techniques, or flawed reasoning. Addressing these issues helps maintain the integrity and accuracy of the research.
• Strengthening analysis: Seeking feedback enables researchers to evaluate whether their analysis is comprehensive and thorough enough to support their claims. It encourages critical thinking by challenging assumptions and highlighting potential gaps in reasoning.

By actively seeking feedback and making necessary revisions based on this input, researchers can produce a more polished and robust IB Math EE. Transitioning into the subsequent section on time management and organization, careful planning is also crucial for successfully completing this project within given timelines.

Time Management and Organization

Efficient time management and effective organization are crucial in successfully completing the IB Math EE within designated timelines. The process of researching, analyzing data, and writing a comprehensive extended essay requires careful planning and allocation of time. By creating a detailed schedule that outlines specific tasks and deadlines, students can ensure that they stay on track throughout the research and writing process.

To effectively manage their time, students should prioritize their tasks based on urgency and importance. Breaking down the project into smaller, manageable chunks allows for a more systematic approach to research and writing. Setting realistic goals for each stage of the EE helps to prevent procrastination and ensures progress is made consistently.

Furthermore, maintaining an organized workspace is paramount to staying focused and minimizing distractions. Keeping research materials, notes, and drafts neatly organized not only saves time but also aids in efficiently retrieving information when needed.

By adhering to these principles of time management and organization, students can confidently navigate through the various stages of their IB Math EE while meeting deadlines. In the upcoming section about dealing with challenges and roadblocks, we will explore strategies for overcoming obstacles that may arise during this demanding process.

Dealing with Challenges and Roadblocks

This paragraph introduces a discussion on dealing with challenges and roadblocks in the context of writing an IB Math EE. It highlights three key points: overcoming writer's block and lack of motivation, managing stress and pressure, and seeking help and support when needed. These issues are important to address in order to maintain productivity and achieve success in the research process.

Overcoming writer's block and lack of motivation

Overcoming writer's block and lack of motivation can be a significant challenge when working on an IB Math Extended Essay. To help navigate these obstacles, it is important to implement strategies that promote productivity and maintain focus. Here are five effective approaches:

• Break the task into smaller, manageable parts.
• Establish a routine that includes dedicated work sessions.
• Seek support from teachers, peers, or online communities.
• Engage in activities that promote relaxation and reduce stress.
• Set realistic goals and celebrate achievements along the way.

Implementing these strategies can create a sense of structure and purpose, which can help overcome writer's block and lack of motivation. By incorporating these practices into your writing process, you can increase productivity while maintaining a healthy balance. Transitioning into managing stress and pressure requires acknowledging the importance of self-care and adopting coping mechanisms to ensure overall well-being.

Managing stress and pressure

Having discussed strategies to overcome writer's block and lack of motivation, it is crucial to address the issue of managing stress and pressure in order to maintain a healthy state of mind during the IB Math Extended Essay (EE) process. The demanding nature of this task can often lead students to feel overwhelmed and stressed, affecting their ability to perform well. It is important for students to develop effective stress management techniques such as time management, relaxation exercises, and seeking support from friends and family. Additionally, engaging in physical activities or hobbies can provide a much-needed break from academic pressures. By learning how to manage stress effectively, students can maintain focus and productivity throughout their EE journey. However, there may be instances when additional help and support are required. Thus, it becomes imperative to understand the significance of seeking assistance when needed while navigating through this challenging task without compromising mental well-being.

Seeking help and support when needed

To ensure a successful completion of the IB Math Extended Essay, it is important for students to recognize the value of seeking assistance and support when facing challenges or difficulties. When students seek help, they are not admitting weakness but rather acknowledging that everyone encounters obstacles at some point. Seeking assistance from teachers, peers, or online resources can provide valuable insights and guidance to overcome any hurdles encountered during the research process. Additionally, reaching out for support can alleviate stress and pressure, promoting a healthier mindset and overall well-being. By actively seeking help when needed, students demonstrate maturity and a commitment to their academic growth. This willingness to seek assistance sets them up for success in showcasing their personal engagement with their chosen topic in the subsequent section.

Showcasing Your Personal Engagement

Demonstrating personal engagement is crucial in an IB Math Extended Essay as it showcases the depth of the student's involvement and passion for the chosen topic. By showcasing personal engagement, students highlight their commitment to exploring complex mathematical concepts and applying them to real-world scenarios. This level of involvement not only allows students to develop a deeper understanding of their chosen topic but also demonstrates their ability to think critically and independently.

To showcase personal engagement effectively, students should clearly articulate their motivation for selecting the particular research question or topic. They should provide a comprehensive overview of their thought process, including any challenges they encountered along the way and how they overcame them. Moreover, students should demonstrate a genuine interest in investigating alternative viewpoints or methodologies related to their research question.

In addition, students can exhibit personal engagement by actively seeking out feedback from teachers, peers, and other experts in the field. This shows a willingness to learn from others' perspectives and incorporate constructive criticism into their work.

By demonstrating personal engagement throughout the essay, students not only establish themselves as credible researchers but also contribute valuable insights to the field of mathematics. Celebrating this accomplishment requires reflecting on one's growth throughout the research process while acknowledging that there is always room for further exploration and improvement.

Celebrating Your Accomplishment

Recognizing the hard work and dedication involved in completing an IB Math EE is essential. The process of researching, analyzing data, and writing the essay requires a significant amount of time and effort. Embracing the learning experience gained from undertaking such a substantial project can lead to personal growth and development as a student.

Sharing your knowledge and insights with others in the IB community is not only an act of celebration but also a way to contribute to the collective learning experience. By disseminating your findings, you can inspire others to explore similar topics or provide valuable guidance for those who may be embarking on their own EE journey. Ultimately, celebrating your accomplishment goes beyond personal satisfaction; it becomes an opportunity to engage with others in meaningful discussions and foster intellectual curiosity within the IB community.

Recognizing the hard work and dedication involved

The arduous journey of an IB Math Extended Essay involves hours spent poring over complex mathematical concepts and tirelessly analyzing data sets. To recognize the hard work and dedication involved in completing this task, it is important to acknowledge the following:

• Intellectual rigor: The IB Math Extended Essay requires students to engage in critical thinking, problem-solving, and independent research. It demands a high level of intellectual rigor and analytical skills.
• Time commitment: Students invest a significant amount of time in conducting experiments, collecting data, and writing their essay. This commitment demonstrates their perseverance and determination to excel academically.
• Attention to detail: Success in the IB Math Extended Essay requires meticulous attention to detail. Students must ensure accuracy in calculations, interpretation of results, and adherence to formatting guidelines.

By recognizing the challenging nature of the IB Math Extended Essay process, we can better appreciate the accomplishments achieved by students. Embracing this learning experience allows for further growth and development in mathematical understanding.

Embracing the learning experience

Embracing the learning experience of completing an IB Math Extended Essay involves immersing oneself in intricate mathematical concepts and adopting a mindset of curiosity and continual growth. It requires a willingness to explore complex problems, analyze data, and formulate logical arguments. Throughout the process, students are encouraged to develop a deep understanding of mathematical principles and apply them in real-world contexts. This kind of engagement fosters intellectual rigor and critical thinking skills, preparing students for future academic pursuits. Additionally, embracing the learning experience allows individuals to appreciate the beauty and elegance of mathematics as they uncover connections between different areas of study. By actively seeking out new knowledge and challenging themselves, students can gain confidence in their abilities while nurturing a passion for mathematics. Ultimately, this mindset sets the stage for sharing one's knowledge and insights with others in the IB community, fostering collaboration and mutual growth within this supportive network.

Sharing your knowledge and insights with others in the IB community

Sharing knowledge and insights with others in the IB community can foster a collaborative learning environment that encourages mutual growth and intellectual development. By sharing our expertise, we contribute to the collective understanding of complex concepts and enhance the quality of education within the IB program. One way to facilitate this exchange is through online forums and discussion platforms, where students can seek guidance from their peers or mentors. Engaging in respectful and inclusive conversations allows for diverse perspectives to be heard, fostering an atmosphere of safety and inclusivity. Additionally, active participation in group study sessions or study groups promotes effective communication skills, critical thinking, and problem-solving abilities. Through this process of sharing knowledge, individuals not only reinforce their own understanding but also contribute to the academic success of others within the IB community.

Frequently Asked Questions

Can you provide a step-by-step guide on how to choose a research question for my ib math extended essay.

Choosing a research question for the IB Math Extended Essay involves considering personal interests, access to data, and relevance to mathematics. It is important to formulate a clear and focused question that can be answered using mathematical methods and analysis techniques.

What are some common mistakes to avoid when conducting research for an IB Math Extended Essay?

Common mistakes to avoid when conducting research for an IB Math extended essay include: insufficient planning, lack of clarity in the research question, inadequate data collection methods, ignoring relevant sources, and neglecting to analyze and interpret the results accurately.

Is it necessary to use advanced mathematical concepts and techniques in my IB Math Extended Essay, or can I stick to basic concepts?

Advanced mathematical concepts and techniques are not necessary for an IB Math extended essay. While basic concepts can be sufficient, it is important to demonstrate a thorough understanding and application of those concepts in a rigorous and logical manner.

How can I effectively incorporate real-life examples and applications of mathematics in my IB Math Extended Essay?

To effectively incorporate real-life examples and applications of mathematics in the IB Math Extended Essay, one should choose relevant and relatable topics, gather accurate data, analyze it using appropriate mathematical techniques, and draw conclusions that reflect a practical understanding of the subject matter.

Are there any specific formatting guidelines or citation styles that I should follow when writing my IB Math Extended Essay?

Yes, there are specific formatting guidelines and citation styles that should be followed when writing an IB Math Extended Essay. These guidelines ensure clarity, consistency, and academic integrity in the essay.

The IB Math Extended Essay is a challenging but rewarding task that requires effective research, application of mathematical concepts and techniques, strong introduction, coherent argument development, time management and organization skills. It is important to be prepared for challenges and roadblocks along the way while showcasing personal engagement in the essay. By following these guidelines, students can successfully complete their IB Math EE and celebrate their accomplishment.

Hire a Tutor & Get Free Trial

Choose Your Test

Sat / act prep online guides and tips, the complete ib extended essay guide: examples, topics, and ideas.

International Baccalaureate (IB)

IB students around the globe fear writing the Extended Essay, but it doesn't have to be a source of stress! In this article, I'll get you excited about writing your Extended Essay and provide you with the resources you need to get an A on it.

If you're reading this article, I'm going to assume you're an IB student getting ready to write your Extended Essay. If you're looking at this as a potential future IB student, I recommend reading our introductory IB articles first, including our guide to what the IB program is and our full coverage of the IB curriculum .

IB Extended Essay: Why Should You Trust My Advice?

I myself am a recipient of an IB Diploma, and I happened to receive an A on my IB Extended Essay. Don't believe me? The proof is in the IBO pudding:

If you're confused by what this report means, EE is short for Extended Essay , and English A1 is the subject that my Extended Essay topic coordinated with. In layman's terms, my IB Diploma was graded in May 2010, I wrote my Extended Essay in the English A1 category, and I received an A grade on it.

What Is the Extended Essay in the IB Diploma Programme?

The IB Extended Essay, or EE , is a mini-thesis you write under the supervision of an IB advisor (an IB teacher at your school), which counts toward your IB Diploma (learn more about the major IB Diploma requirements in our guide) . I will explain exactly how the EE affects your Diploma later in this article.

For the Extended Essay, you will choose a research question as a topic, conduct the research independently, then write an essay on your findings . The essay itself is a long one—although there's a cap of 4,000 words, most successful essays get very close to this limit.

Keep in mind that the IB requires this essay to be a "formal piece of academic writing," meaning you'll have to do outside research and cite additional sources.

The IB Extended Essay must include the following:

• A title page
• Contents page
• Introduction
• Body of the essay
• References and bibliography

Additionally, your research topic must fall into one of the six approved DP categories , or IB subject groups, which are as follows:

• Group 1: Studies in Language and Literature
• Group 2: Language Acquisition
• Group 3: Individuals and Societies
• Group 4: Sciences
• Group 5: Mathematics
• Group 6: The Arts

Once you figure out your category and have identified a potential research topic, it's time to pick your advisor, who is normally an IB teacher at your school (though you can also find one online ). This person will help direct your research, and they'll conduct the reflection sessions you'll have to do as part of your Extended Essay.

As of 2018, the IB requires a "reflection process" as part of your EE supervision process. To fulfill this requirement, you have to meet at least three times with your supervisor in what the IB calls "reflection sessions." These meetings are not only mandatory but are also part of the formal assessment of the EE and your research methods.

According to the IB, the purpose of these meetings is to "provide an opportunity for students to reflect on their engagement with the research process." Basically, these meetings give your supervisor the opportunity to offer feedback, push you to think differently, and encourage you to evaluate your research process.

The final reflection session is called the viva voce, and it's a short 10- to 15-minute interview between you and your advisor. This happens at the very end of the EE process, and it's designed to help your advisor write their report, which factors into your EE grade.

Here are the topics covered in your viva voce :

• A check on plagiarism and malpractice
• Your reflection on your project's successes and difficulties
• Your reflection on what you've learned during the EE process

Your completed Extended Essay, along with your supervisor's report, will then be sent to the IB to be graded. We'll cover the assessment criteria in just a moment.

We'll help you learn how to have those "lightbulb" moments...even on test day!  

What Should You Write About in Your IB Extended Essay?

You can technically write about anything, so long as it falls within one of the approved categories listed above.

It's best to choose a topic that matches one of the IB courses , (such as Theatre, Film, Spanish, French, Math, Biology, etc.), which shouldn't be difficult because there are so many class subjects.

Here is a range of sample topics with the attached extended essay:

• Biology: The Effect of Age and Gender on the Photoreceptor Cells in the Human Retina
• Chemistry: How Does Reflux Time Affect the Yield and Purity of Ethyl Aminobenzoate (Benzocaine), and How Effective is Recrystallisation as a Purification Technique for This Compound?
• English: An Exploration of Jane Austen's Use of the Outdoors in Emma
• Geography: The Effect of Location on the Educational Attainment of Indigenous Secondary Students in Queensland, Australia
• Math: Alhazen's Billiard Problem
• Visual Arts: Can Luc Tuymans Be Classified as a Political Painter?

You can see from how varied the topics are that you have a lot of freedom when it comes to picking a topic . So how do you pick when the options are limitless?

How to Write a Stellar IB Extended Essay: 6 Essential Tips

Below are six key tips to keep in mind as you work on your Extended Essay for the IB DP. Follow these and you're sure to get an A!

#1: Write About Something You Enjoy

You can't expect to write a compelling essay if you're not a fan of the topic on which you're writing. For example, I just love British theatre and ended up writing my Extended Essay on a revolution in post-WWII British theatre. (Yes, I'm definitely a #TheatreNerd.)

I really encourage anyone who pursues an IB Diploma to take the Extended Essay seriously. I was fortunate enough to receive a full-tuition merit scholarship to USC's School of Dramatic Arts program. In my interview for the scholarship, I spoke passionately about my Extended Essay; thus, I genuinely think my Extended Essay helped me get my scholarship.

But how do you find a topic you're passionate about? Start by thinking about which classes you enjoy the most and why . Do you like math classes because you like to solve problems? Or do you enjoy English because you like to analyze literary texts?

Keep in mind that there's no right or wrong answer when it comes to choosing your Extended Essay topic. You're not more likely to get high marks because you're writing about science, just like you're not doomed to failure because you've chosen to tackle the social sciences. The quality of what you produce—not the field you choose to research within—will determine your grade.

Once you've figured out your category, you should brainstorm more specific topics by putting pen to paper . What was your favorite chapter you learned in that class? Was it astrophysics or mechanics? What did you like about that specific chapter? Is there something you want to learn more about? I recommend spending a few hours on this type of brainstorming.

One last note: if you're truly stumped on what to research, pick a topic that will help you in your future major or career . That way you can use your Extended Essay as a talking point in your college essays (and it will prepare you for your studies to come too!).

#2: Select a Topic That Is Neither Too Broad nor Too Narrow

There's a fine line between broad and narrow. You need to write about something specific, but not so specific that you can't write 4,000 words on it.

You can't write about WWII because that would be a book's worth of material. You also don't want to write about what type of soup prisoners of war received behind enemy lines, because you probably won’t be able to come up with 4,000 words of material about it. However, you could possibly write about how the conditions in German POW camps—and the rations provided—were directly affected by the Nazis' successes and failures on the front, including the use of captured factories and prison labor in Eastern Europe to increase production. WWII military history might be a little overdone, but you get my point.

If you're really stuck trying to pinpoint a not-too-broad-or-too-narrow topic, I suggest trying to brainstorm a topic that uses a comparison. Once you begin looking through the list of sample essays below, you'll notice that many use comparisons to formulate their main arguments.

I also used a comparison in my EE, contrasting Harold Pinter's Party Time with John Osborne's Look Back in Anger in order to show a transition in British theatre. Topics with comparisons of two to three plays, books, and so on tend to be the sweet spot. You can analyze each item and then compare them with one another after doing some in-depth analysis of each individually. The ways these items compare and contrast will end up forming the thesis of your essay!

When choosing a comparative topic, the key is that the comparison should be significant. I compared two plays to illustrate the transition in British theatre, but you could compare the ways different regional dialects affect people's job prospects or how different temperatures may or may not affect the mating patterns of lightning bugs. The point here is that comparisons not only help you limit your topic, but they also help you build your argument.

Comparisons are not the only way to get a grade-A EE, though. If after brainstorming, you pick a non-comparison-based topic and are still unsure whether your topic is too broad or narrow, spend about 30 minutes doing some basic research and see how much material is out there.

If there are more than 1,000 books, articles, or documentaries out there on that exact topic, it may be too broad. But if there are only two books that have any connection to your topic, it may be too narrow. If you're still unsure, ask your advisor—it's what they're there for! Speaking of advisors...

Don't get stuck with a narrow topic!

#3: Choose an Advisor Who Is Familiar With Your Topic

If you're not certain of who you would like to be your advisor, create a list of your top three choices. Next, write down the pros and cons of each possibility (I know this sounds tedious, but it really helps!).

For example, Mr. Green is my favorite teacher and we get along really well, but he teaches English. For my EE, I want to conduct an experiment that compares the efficiency of American electric cars with foreign electric cars.

I had Ms. White a year ago. She teaches physics and enjoyed having me in her class. Unlike Mr. Green, Ms. White could help me design my experiment.

Based on my topic and what I need from my advisor, Ms. White would be a better fit for me than would Mr. Green (even though I like him a lot).

The moral of my story is this: do not just ask your favorite teacher to be your advisor . They might be a hindrance to you if they teach another subject. For example, I would not recommend asking your biology teacher to guide you in writing an English literature-based EE.

There can, of course, be exceptions to this rule. If you have a teacher who's passionate and knowledgeable about your topic (as my English teacher was about my theatre topic), you could ask that instructor. Consider all your options before you do this. There was no theatre teacher at my high school, so I couldn't find a theatre-specific advisor, but I chose the next best thing.

Before you approach a teacher to serve as your advisor, check with your high school to see what requirements they have for this process. Some IB high schools require your IB Extended Essay advisor to sign an Agreement Form , for instance.

Make sure that you ask your IB coordinator whether there is any required paperwork to fill out. If your school needs a specific form signed, bring it with you when you ask your teacher to be your EE advisor.

#4: Pick an Advisor Who Will Push You to Be Your Best

Some teachers might just take on students because they have to and aren't very passionate about reading drafts, only giving you minimal feedback. Choose a teacher who will take the time to read several drafts of your essay and give you extensive notes. I would not have gotten my A without being pushed to make my Extended Essay draft better.

Ask a teacher that you have experience with through class or an extracurricular activity. Do not ask a teacher that you have absolutely no connection to. If a teacher already knows you, that means they already know your strengths and weaknesses, so they know what to look for, where you need to improve, and how to encourage your best work.

Also, don't forget that your supervisor's assessment is part of your overall EE score . If you're meeting with someone who pushes you to do better—and you actually take their advice—they'll have more impressive things to say about you than a supervisor who doesn't know you well and isn't heavily involved in your research process.

Be aware that the IB only allows advisors to make suggestions and give constructive criticism. Your teacher cannot actually help you write your EE. The IB recommends that the supervisor spends approximately two to three hours in total with the candidate discussing the EE.

#5: Make Sure Your Essay Has a Clear Structure and Flow

The IB likes structure. Your EE needs a clear introduction (which should be one to two double-spaced pages), research question/focus (i.e., what you're investigating), a body, and a conclusion (about one double-spaced page). An essay with unclear organization will be graded poorly.

The body of your EE should make up the bulk of the essay. It should be about eight to 18 pages long (again, depending on your topic). Your body can be split into multiple parts. For example, if you were doing a comparison, you might have one third of your body as Novel A Analysis, another third as Novel B Analysis, and the final third as your comparison of Novels A and B.

If you're conducting an experiment or analyzing data, such as in this EE , your EE body should have a clear structure that aligns with the scientific method ; you should state the research question, discuss your method, present the data, analyze the data, explain any uncertainties, and draw a conclusion and/or evaluate the success of the experiment.

#6: Start Writing Sooner Rather Than Later!

You will not be able to crank out a 4,000-word essay in just a week and get an A on it. You'll be reading many, many articles (and, depending on your topic, possibly books and plays as well!). As such, it's imperative that you start your research as soon as possible.

Each school has a slightly different deadline for the Extended Essay. Some schools want them as soon as November of your senior year; others will take them as late as February. Your school will tell you what your deadline is. If they haven't mentioned it by February of your junior year, ask your IB coordinator about it.

Some high schools will provide you with a timeline of when you need to come up with a topic, when you need to meet with your advisor, and when certain drafts are due. Not all schools do this. Ask your IB coordinator if you are unsure whether you are on a specific timeline.

Below is my recommended EE timeline. While it's earlier than most schools, it'll save you a ton of heartache (trust me, I remember how hard this process was!):

• January/February of Junior Year: Come up with your final research topic (or at least your top three options).
• February of Junior Year: Approach a teacher about being your EE advisor. If they decline, keep asking others until you find one. See my notes above on how to pick an EE advisor.
• April/May of Junior Year: Submit an outline of your EE and a bibliography of potential research sources (I recommend at least seven to 10) to your EE advisor. Meet with your EE advisor to discuss your outline.
• Summer Between Junior and Senior Year: Complete your first full draft over the summer between your junior and senior year. I know, I know—no one wants to work during the summer, but trust me—this will save you so much stress come fall when you are busy with college applications and other internal assessments for your IB classes. You will want to have this first full draft done because you will want to complete a couple of draft cycles as you likely won't be able to get everything you want to say into 4,000 articulate words on the first attempt. Try to get this first draft into the best possible shape so you don't have to work on too many revisions during the school year on top of your homework, college applications, and extracurriculars.
• August/September of Senior Year: Turn in your first draft of your EE to your advisor and receive feedback. Work on incorporating their feedback into your essay. If they have a lot of suggestions for improvement, ask if they will read one more draft before the final draft.
• September/October of Senior Year: Submit the second draft of your EE to your advisor (if necessary) and look at their feedback. Work on creating the best possible final draft.
• November-February of Senior Year: Schedule your viva voce. Submit two copies of your final draft to your school to be sent off to the IB. You likely will not get your grade until after you graduate.

Remember that in the middle of these milestones, you'll need to schedule two other reflection sessions with your advisor . (Your teachers will actually take notes on these sessions on a form like this one , which then gets submitted to the IB.)

I recommend doing them when you get feedback on your drafts, but these meetings will ultimately be up to your supervisor. Just don't forget to do them!

The early bird DOES get the worm!

How Is the IB Extended Essay Graded?

Extended Essays are graded by examiners appointed by the IB on a scale of 0 to 34 . You'll be graded on five criteria, each with its own set of points. You can learn more about how EE scoring works by reading the IB guide to extended essays .

• Criterion A: Focus and Method (6 points maximum)
• Criterion B: Knowledge and Understanding (6 points maximum)
• Criterion C: Critical Thinking (12 points maximum)
• Criterion D: Presentation (4 points maximum)
• Criterion E: Engagement (6 points maximum)

How well you do on each of these criteria will determine the final letter grade you get for your EE. You must earn at least a D to be eligible to receive your IB Diploma.

Although each criterion has a point value, the IB explicitly states that graders are not converting point totals into grades; instead, they're using qualitative grade descriptors to determine the final grade of your Extended Essay . Grade descriptors are on pages 102-103 of this document .

Here's a rough estimate of how these different point values translate to letter grades based on previous scoring methods for the EE. This is just an estimate —you should read and understand the grade descriptors so you know exactly what the scorers are looking for.

Here is the breakdown of EE scores (from the May 2021 bulletin):

How Does the Extended Essay Grade Affect Your IB Diploma?

The Extended Essay grade is combined with your TOK (Theory of Knowledge) grade to determine how many points you get toward your IB Diploma.

To learn about Theory of Knowledge or how many points you need to receive an IB Diploma, read our complete guide to the IB program and our guide to the IB Diploma requirements .

This diagram shows how the two scores are combined to determine how many points you receive for your IB diploma (3 being the most, 0 being the least). In order to get your IB Diploma, you have to earn 24 points across both categories (the TOK and EE). The highest score anyone can earn is 45 points.

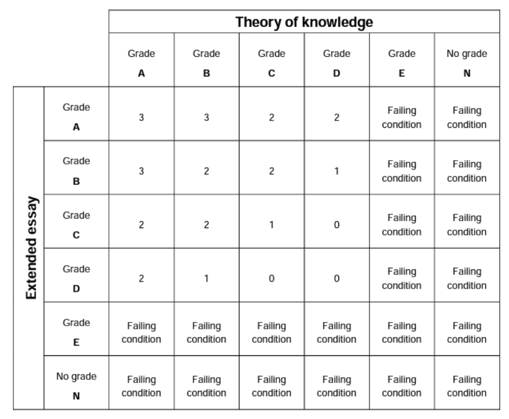
Let's say you get an A on your EE and a B on TOK. You will get 3 points toward your Diploma. As of 2014, a student who scores an E on either the extended essay or TOK essay will not be eligible to receive an IB Diploma .

Prior to the class of 2010, a Diploma candidate could receive a failing grade in either the Extended Essay or Theory of Knowledge and still be awarded a Diploma, but this is no longer true.

Figuring out how you're assessed can be a little tricky. Luckily, the IB breaks everything down here in this document . (The assessment information begins on page 219.)

40+ Sample Extended Essays for the IB Diploma Programme

In case you want a little more guidance on how to get an A on your EE, here are over 40 excellent (grade A) sample extended essays for your reading pleasure. Essays are grouped by IB subject.

• Business Management 1
• Chemistry 1
• Chemistry 2
• Chemistry 3
• Chemistry 4
• Chemistry 5
• Chemistry 6
• Chemistry 7
• Computer Science 1
• Economics 1
• Design Technology 1
• Design Technology 2
• Environmental Systems and Societies 1
• Geography 1
• Geography 2
• Geography 3
• Geography 4
• Geography 5
• Geography 6
• Literature and Performance 1
• Mathematics 1
• Mathematics 2
• Mathematics 3
• Mathematics 4
• Mathematics 5
• Philosophy 1
• Philosophy 2
• Philosophy 3
• Philosophy 4
• Philosophy 5
• Psychology 1
• Psychology 2
• Psychology 3
• Psychology 4
• Psychology 5
• Social and Cultural Anthropology 1
• Social and Cultural Anthropology 2
• Social and Cultural Anthropology 3
• Sports, Exercise and Health Science 1
• Sports, Exercise and Health Science 2
• Visual Arts 1
• Visual Arts 2
• Visual Arts 3
• Visual Arts 4
• Visual Arts 5
• World Religion 1
• World Religion 2
• World Religion 3

What's Next?

Trying to figure out what extracurriculars you should do? Learn more about participating in the Science Olympiad , starting a club , doing volunteer work , and joining Student Government .

Studying for the SAT? Check out our expert study guide to the SAT . Taking the SAT in a month or so? Learn how to cram effectively for this important test .

Not sure where you want to go to college? Read our guide to finding your target school . Also, determine your target SAT score or target ACT score .

As an SAT/ACT tutor, Dora has guided many students to test prep success. She loves watching students succeed and is committed to helping you get there. Dora received a full-tuition merit based scholarship to University of Southern California. She graduated magna cum laude and scored in the 99th percentile on the ACT. She is also passionate about acting, writing, and photography.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

SAT Essay Questions

We have a collection of the new SAT Essay Questions from March 2005 till the most recent test released by College Board.

October 2007

If you took the October 2007 SAT Reasoning Test, you would have been given one of the essay prompts below:

Think carefully about the issue presented in the following excerpt and the assignment below.

A person does not simply "receive" his or her identity. Identity is much more than the name or features one is born with. True identity is something people must create for themselves by making choices that are significant and that require a courageous commitment in the face of challenges. Identity means having ideas and values that one lives by.

Adapted from Thomas Merton, Contemplation in a World of Action

Assignment: Is identity something people are born with or given, or is it something people create for themselves? Plan and write an essay in which you develop your point of view on this issue. Support your position with reasoning and examples taken from your reading, studies, experience, or observations.

We value uniqueness and originality, but it seems that everywhere we turn, we are surrounded by ideas and things that are copies or even copies of copies. Writers, artists, and musicians seek new ideas for paintings, books, songs, and movies, but many sadly realize, "It's been done." The same is true for scientists, scholars, and businesspeople. Everyone wants to create something new, but at best we can hope only to repeat or imitate what has already been done.

Assignment: Can people ever be truly original? Plan and write an essay in which you develop your point of view on this issue. Support your position with reasoning and examples taken from your reading, studies, experience, or observations.

All people who have achieved greatness in something knew what they excelled at. These people identified the skills that made them special—good judgment, or courage, or a special artistic or literary talent—and focused on developing these skills. Yet most people achieve superiority in nothing because they fail to identify and develop their greatest attribute.

Adapted from Baltasar Gracián y Morales, The Art of Worldly Wisdom

Adapted from Stephen J. Carter, Integrity

Assignment: Do people achieve greatness only by finding out what they are especially good at and developing that attribute above all else? Plan and write an essay in which you develop your point of view on this issue. Support your position with reasoning and examples taken from your reading, studies, experience, or observations.

Having many admirers is one way to become a celebrity, but it is not the way to become a hero. Heroes are self-made. Yet in our daily lives we see no difference between "celebrities" and "heroes." For this reason, we deprive ourselves of real role models. We should admire heroes—people who are famous because they are great—but not celebrities—people who simply seem great because they are famous.

Adapted from Daniel Boorstin, The Image: A Guide to Pseudo-Events in America

Assignment: Should we admire heroes but not celebrities? Plan and write an essay in which you develop your point of view on this issue. Support your position with reasoning and examples taken from your reading, studies, experience, or observations.

More SAT essay prompts at SAT preparation.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Math Essay Examples and Topics

Leonardo da vinci and his contribution to the development of mathematics.

• Words: 1413

The Importance of Geometry in Our Daily Life

• Words: 1414

Oblique Triangles in Everyday Life

Mathematics: discovered or created, statistics: chi-square test and regression analysis.

• Words: 1989

History of Algebra Brief Overview

Parabolas and their application in the real life, mathematical analysis of the pyramid of the louvre.

• Words: 1523

Debate on Mathematics: An Art or a Science

• Words: 2719

Sofia Kovalevskaya’s Contributions to Math

Spatial modeling: types, pros and cons, the life and works of archimedes.

• Words: 2513

Pythagorean Theorem: History, Formula, and Proof

• Words: 1524

Reflection on Statistics Learning Goals

Measurements’ standarts, the use of polynomials in the real world, problem solving process in mathematics, t-test discussion, optimizing the cross section of a gutter, implicit differentiation in the business sector, pythagoras theories.

• Words: 1918

Linear Equations Comprehensive Study

Fourier transform: the behavior of the image in the frequency domain.

• Words: 2889

History of Calculus: Brief Review One of the Branches of Mathematics

• Words: 1169

Math Functions in Economics

• Words: 2443

Calculus-Integration

• Words: 1074

Correlation

• Words: 1036

Mathematics – Concept of Multiplication

• Words: 1161

Arthur Cayley: Life, Career, and Achievements

Pizza box optimization: packaging problem.

• Words: 1867

Algebra in the Real World and Everyday Life

Teaching math: number sense instruction.

• Words: 1191

Prime Numbers Role in People’s Life

Mathematics: the language of nature, fundamental theorem of calculus in modern world, correlation as a statistical analysis tool, binomial logistic regression, misconceptions and errors in math, statistical analysis of the relationship between the two variables, math: factoring using the p-1 method, positive and negative association between variables, why casino always wins: a mathematician’s view, mathematical and statistical investigation.

• Words: 1798

The Concept of the Derivative of a Function

• Words: 2257

Algebra: Y-Intercept and X-Intercept

Mathematics and business relationship.

• Words: 2480

Statistical Process in Data Analysis

Qualitative research method analysis.

• Words: 1766

Probability Concepts and Applications

Qualitative research design and methods, a comparison of observations to measurement instruments, quantitative data analysis, the central limit theorem and its applications, graph theory’s origins and development, a-level math aqa : specification.

• Words: 4304

Pierre de Fermat: One of the Most Prominent Mathematicians

The discipline of criminal justice: the use of mathematics, leonardo pisano fibonacci’s life and contributions, statistics abuse: how, why, and when.

• Words: 2836

Number Theory and Major Contributors to the Field

• Words: 1136

Statistically Significant but Not Meaningful

Hamilton-jacobi-bellman equation and linear pearson coefficient, rational functions and their real-world applications, carl friedrich gauss: mathematician and innovator, charting a career in mathematics: from teaching to actuarial practice.

• Words: 1057

Navigating the Math Maze: A Strategic Policy Framework

• Words: 1226

Deduction in Ancient Greece and Egypt

Aspects of the mathematics problem solving.

• Words: 1154

The Life Accomplishments of John von Neumann

Report: tow tank statistical analysis.

• Words: 1409

Determining the Area of the Isosceles Triangles

Mathematical operations with positive and negative numbers.

• Words: 1460

Construction of Regular Polygons: Octagon

A random variable and binomial experiment, evaluating the effectiveness of an instructional design.

• Words: 1210

Determining the Strongest Predictors of Kappa Number in Kraft Pulp

The genesis of mathematics storytelling: god’s own, mathematical explorations: quantitative reasoning, multiple linear regression critique, importance of math during trip from us to japan, mathematics: problem-solving tasks, the spicp-ms approach: paraphrasing, articulation principle in solving algebra problems, using mathematics in trading metrics, math: a differential calculus lesson analysis, the formal mathematical language and its importance, using the weibull distribution to study failure intensity, the perfect square trinomial and the sum of cubes, finding a hypotenuse of an ipad pro tablet, functional mathematics implementation, the value of mathematics in antonsen’s ted talk, the pythagorean theorem and its origin, the use of mathematics in advertisements, math: aspects of hiv modeling.

• Words: 1107

Order of Operations: Connecting to Real Life

Aspects of probability theory, researching of advanced forecasting methods, chapter 5 of weapons of math destruction by o’neil, the concept of coterminal angles, the exponential function in analytic algebra, sophie germain’s story of a woman mathematician, compound interest as mathematical fact.

• Words: 3827

A Real-World Linear Regression Model

• Words: 1400

Math: Compound Interest as a Future Problem

Mathematician john wilder tukey’s biography, dangers of false representation in mathematics.

• Words: 1438

Slope Desciption and Necessity

Thinking in terms of vectors in daily life, physiologically-structured population models and their ordinary differential equations reduction, mathematical biology: explaining population extinction, statistical and stochastic modeling applied to social processes.

• Words: 1666

Bouncing Ball as an Example of a Conic Section

Probability theory: descriptive statistics, math assignment: graph visualization, mathematical models addressing the covid-19 pandemic, “is-lm model” by dudley cooke, mathematical laws in the real world.

• Words: 1146

Mathematics: An Art or a Science

• Words: 1864

Geometry Web Quest for Soccer, Baseball, Basketball, Bowling, Golf, Volleyball and Pool

Mathematical and physical concepts.

• Customer Reviews
• Extended Essays
• IB Internal Assessment
• Theory of Knowledge
• Literature Review
• Dissertations
• Essay Writing
• Research Writing
• Assignment Help
• Capstone Projects
• College Application
• Online Class

IB Math Extended Essay Topics: 20+ Ideas for Inspiration

by  Antony W

September 3, 2022

Do you feel stuck on searching for and choosing the best IB Math Extended Essay topics? Or maybe you already have a topic for consideration but it isn’t viable enough to fit the scope of the assignment?

You’ve come to the right place.

In this guide, we’ll give you 15+ IB Math ideas that you can use as inspiration to come up with your own topic or modify and investigate further in your extended essay.

What’s the Purpose of IB Math Extended Essay?

An extended essay in mathematics gives you the chance to demonstrate an understanding of any part of the subject.

You can give an expression on the beauty of mathematics in geometry or fractal theory, the elegance of mathematics in the proving of theorems, and the origin and subsequent development of a branch of mathematics over a period.

The extended essay also allows you to demonstrate the link between the different branches of mathematics and the powerful structures that enable many different problems to be solved by a single theory and the way in which mathematics is applied to real-world situations.

Your essay requires a well-defined and focused research question. An abstract is no longer necessary in an extended essay , but you’re welcome to include it if you believe it will summarizes your strategy to solving the research question and your findings

Math Extended Essay Writing Assistance

While Math opens up an opportunity to explore complex issues beyond the IB Diploma course , the subject can be extremely challenging for some IB students.

If you’re one of the students who chose Math for the Extended Essay project but you find the subject challenging, you can get help online from experts in the subject.

Help for Assessment offers the most  comprehensive Extended Essay help   in Mathematics, even on a topic that you would consider too complex to handle. With our help, you’ll find complex concepts easy to understand, not to mention you’ll get your Math assignment completed on time.

We understand that Math tasks can be costly and involving. However, we’ve made our writing service as affordable as possible, so you can get professional writing help.

We can write you first draft before the first reflection session with your supervisor and equally help you fine-tune the last draft for the final submission.

IB Math Extended Essay Topics

The following are examples of IB Math Extended Essay topics that you might find worth investigating further: 

• What is the return percentage of a certain three-reel slot machine?
• What are the alternatives to Euclidean geometry and what are their practical applications?
• Comparison of population growth models for Country X for the past n years, with projections for the future.
• The exploration of geometric series in musical instruments, such as the fret position on a guitar
• How many convex polygons can you construct from seven tangram pieces?
• An examination of the alteration of a message's truthful substance during transmission between persons
• Is there a connection between the golden ratio and human’s perception on natural beauty, with a focus on the human face and form?
• Is there a relationship between SAT scores and school test results/GPA?
• Leibniz and Newton independently developed calculus at around the same time. Compare their techniques and analyze which notation is currently more prevalent.
• What is the Binomial Theorem, and how has it contributed to human history?
• Complex number problem-solving techniques: What types of real-world issues do complex numbers assist solve?
• Applying Newton's Forward Difference Formula to predict the number of triangles created by subdividing the sides of an equilateral triangle n times.
• RSA Public Key Cryptography's use of modular arithmetic and huge prime integers to achieve anonymity
• Investigating the link between Pascal's Triangle and the Fibonacci sequence
• How can mathematical modeling that employs differential equations determine population growth patterns for a predator and its prey?
• How can the population of cells be determined throughout time? Which mathematical model approximates an actual experiment more precisely?
• A study of Riemann Sums (conventional integration to get areas) and Numerical Integration
• Vedic Mathematics: an investigation of its effectiveness and exploration of its applications
• How are Laplace transforms utilized in the solution of second-order differential equations?
• A statistical examination of the impact of background music on pupils' short-term memory ability
• Analytical and geometric formulations of parabolic and cubic Bezier curves as used in computer graphics software
• A quantitative analysis of the efficacy of two herbs for treating impetigo skin condition
• A study of the nature of beats and the relative consonance of pure-tone dyads
• The link between logical-mathematical intelligence and academic achievement at the undergraduate level
• A study of the link between a bond's coupon rate, yield to maturity, and its clean price
• Using the addition of sine curves to analyze the harmony of Chinese and Western musical scales
• The correlation between students' attitudes toward mathematics and their mathematical performance
• How near is the approximation of the Taylor Series to the original function
• What criteria determine whether the movement of employees on a building site achieves "equilibrium"?
• The efficacy of an English Tuition Program in enhancing the English skills of participants
• A statistical examination of the causes of fatal traffic accidents throughout the holiday season
• Does studying a third language have any influence on the short-term memory retention of lower secondary students?

Keep in mind that this list is not exhaustive by any means. So if none of these topic ideas appeals to you, doing additional research can make a difference.

Related Reading

• The Complete Guide for IB Math Extended Essay
• Get a List of Psychology Extended Essay Topics Here
• Learn More About Physics Extended Essay Assignment

Some Tips to Help You Choose a Relevant Math EE Topic

You can write an extended essay in math on any subject with a mathematical focus. Because IB doesn’t limit the assignment to mathematical theories, you may select mathematical themes from engineering, sciences, and the social sciences.

Statistical analyses of experimental results from other disciplines are also appropriate, as long as they focus on the modeling method and address the limits of the results.

A topic chosen from the history of mathematics may also be acceptable, provided you bring out a clear progression of mathematical growth.

Focusing on the lives of mathematicians or their personal rivalry would be irrelevant and would not score highly on the grading criteria.

Notably, the evaluation criteria provide points for the nature of the inquiry and the extent to which reasoned arguments are suitable for a research issue.

You need to avoid selecting a topic that generates a trivial research question or is insufficiently concentrated to permit suitable presentation in an essay of the right length.

Typically, you will have to challenge yourself to either extend their knowledge beyond the Diploma Program course or apply techniques learned in their mathematics course to the modeling of an adequately chosen topic.

Final Thoughts

One of the most important thing to keep in mind once you find a suitable Math EE topic is that you will be working on an essay, not a research article for a journal of advanced mathematics.

Also, no finding, no matter how remarkable, should appear in your work without proof of your actual understanding of it. 

About the author 

Antony W is a professional writer and coach at Help for Assessment. He spends countless hours every day researching and writing great content filled with expert advice on how to write engaging essays, research papers, and assignments.

Mathematics Extended Essay Topics for IB

Table of contents

• Writing Metier

Ever felt the exhilaration that comes with cracking a complex math problem? That’s the sheer beauty of mathematics – it’s a world where numbers dance, patterns emerge, and solutions await the keen observer. Felt that? Hah?

Now, imagine channeling that same enthusiasm and zest into your Math Extended essay. It might sound like a challenge, but isn’t that what we thrive on? With the right Math EE topic, you can showcase your mathematical prowess and leave an indelible mark on your IB evaluators following the general criteria. 

To help you with that, I’ve curated a list of Math extended essay ideas that span the spectrum from the accessible to the intricate. 

So, let’s begin.

IB Math extended essay ideas

These aren’t just topics; they’re gateways to exploration, understanding, and innovation. 

Ready to get started?

Easy-to-approach topics

For those looking for a gentler introduction to the Math Extended essay, below is a list of 10 engaging and manageable IB Math EE topic ideas, each with a research question and a brief description on how to approach it:

Patterns in Pascal’s Triangle

Research Question: 

How do patterns emerge in Pascal’s Triangle?

Description: 

Begin with the construction of Pascal’s Triangle, then delve into the exploration of its patterns, such as triangular numbers and the Fibonacci sequence.

Mathematics of Voting Systems

How do different voting systems weigh individual votes mathematically?

Introduce various voting systems, then analyze the mathematical principles behind each, discussing fairness and potential biases.

Geometry in Art

Research Question:  

How is geometry used to create visual appeal in art?

Explore various art pieces, highlighting the geometric principles employed, and discuss their impact on aesthetics.

The Math Behind Baking

How do ratios in baking recipes affect the final product?

Investigate the importance of maintaining specific ratios in baking recipes and experiment with variations to observe changes in outcomes.

Probability in Card Games

How does understanding probability enhance success in card games like Poker?

Delve into the rules of Poker and then analyze various hands and scenarios using probability principles.

Symmetry in Nature

How is symmetry exhibited in natural formations?

Explore the concept of symmetry mathematically and then identify and analyze its presence in various natural formations like leaves, flowers, and animals.

Mathematics of Music

How do mathematical patterns influence musical scales and rhythms?

Investigate the structure of musical scales, rhythms, and time signatures, highlighting the underlying mathematical patterns.

Simple Interest vs. Compound Interest

How do simple and compound interest methods impact savings over time?

Define both interest methods and then use mathematical modeling to compare their effects on savings over various periods.

The Golden Ratio in Architecture

How is the Golden Ratio applied in iconic architectural designs?

Introduce the concept of the Golden Ratio and then analyze its application in various famous architectural structures.

Mathematics of Juggling

How do mathematical patterns and sequences dictate juggling techniques?

Explore basic juggling techniques and patterns, analyzing the mathematical sequences that jugglers use to maintain rhythm and control.

Each of these topic ideas and RQs is approachable yet offers ample scope for exploration and analysis within the realm of mathematics.

Intermediate topics

For those seeking a bit more challenge without diving into the deep end, the topics below offer a balanced blend of complexity and accessibility.

Here’s a list of 10 average-difficulty IB Math Extended essay topics, each with a research question and a brief description of how to approach it:

Game Theory in Economics

How does game theory provide insights into competitive market behaviors?

Introduce game theory principles and use business world case studies to show strategic decision-making influenced by game theory.

Fractals and Nature

How do fractal patterns manifest in natural phenomena?

Description:  

Delve into the mathematical concept of fractals and explore their appearance in various natural settings, such as coastlines, mountains, and plants.

Mathematics of Population Growth Models

How do mathematical models accurately predict population growth in urban areas?

Introduce population growth models and use real urban area data to validate these models, discussing influencing factors.

Cryptography and Internet Security

How do modern cryptographic techniques ensure data security on the internet?

Explore the evolution of cryptography, focusing on modern techniques, and discuss their role in ensuring data security in online transactions.

Mathematical Modeling of Epidemics

How can mathematical models predict the spread of infectious diseases?

Introduce basic epidemiological models and analyze their effectiveness in predicting disease spread using real-world data.

Topology and Coffee Cups

How does topology explain the mathematical similarity between a coffee cup and a donut?

Dive into the basics of topology and use it to explain the often-cited comparison between coffee cups and donuts, emphasizing the concept of homeomorphism.

Chaos Theory and Weather Forecasting

How does chaos theory impact the accuracy of long-term weather forecasts?

Introduce chaos theory, then delve into its application in meteorology, discussing the challenges and limitations in predicting weather.

Mathematics Behind Neural Networks

How do mathematical algorithms drive the functioning of neural networks in artificial intelligence?

Explore the structure of neural networks and delve into the mathematical algorithms that enable their learning and functioning.

Optimization Problems in Logistics

How can mathematical optimization improve efficiency in supply chain logistics?

Investigate real-world logistics challenges and demonstrate how mathematical optimization techniques can offer solutions.

Number Theory in Modern Cryptography

How does advanced number theory underpin modern cryptographic techniques?

Delve into number theory concepts and their application in modern cryptographic methods, emphasizing their role in ensuring data security.

These topics and research questions offer a balanced blend of complexity and accessibility, making them suitable for students seeking a moderate challenge in their Math Extended essay.

Advanced topics (with potential for higher rewards)

For the brave hearts ready to dive deep, these topics are challenging but can yield impressive results when tackled effectively.

The list of 10 challenging IB Math Extended essay ideas, each with a research question and a brief description:

Navier–Stokes Existence and Smoothness

What are the mathematical implications of the unsolved Navier–Stokes existence and smoothness problem in fluid dynamics?

Delve deep into the Navier–Stokes equations, exploring their significance in fluid dynamics and the challenges surrounding their unsolved problems.

Riemann Hypothesis and Prime Numbers

How does the Riemann Hypothesis relate to the distribution of prime numbers?

Investigate the Riemann Hypothesis, its historical context, and its profound implications for the distribution of prime numbers.

Quantum Cryptography and Key Distribution

How does quantum cryptography enhance security in key distribution?

Explore the principles of quantum mechanics applied to cryptography, focusing on the advantages and challenges of quantum key distribution.

Elliptic Curves and Cryptography

How do elliptic curves underpin modern cryptographic techniques?

Dive into the mathematics of elliptic curves and their pivotal role in modern cryptographic algorithms.

Four Color Theorem and Graph Theory

How does the Four Color Theorem demonstrate the complexities of graph coloring?

Investigate the history and proof of the Four Color Theorem, discussing its implications and challenges in graph theory.

Complex Analysis in Quantum Mechanics

How does complex analysis influence the mathematical foundations of quantum mechanics?

Delve into the principles of complex analysis and explore their applications and significance in quantum mechanics.

Twin Prime Conjecture

What are the implications and challenges of the Twin Prime Conjecture in number theory?

Investigate the Twin Prime Conjecture, its history, and its significance in the realm of number theory.

Knot Theory and DNA Replication

How does knot theory provide insights into the process of DNA replication?

Explore the mathematical intricacies of knot theory and its applications in understanding the complexities of DNA replication.

Ergodic Theory and Thermodynamics

How does ergodic theory connect with the principles of statistical thermodynamics?

Dive deep into ergodic theory, exploring its foundational concepts and its connections to statistical thermodynamics.

Langlands Program and Number Theory

What is the Langlands Program, and how does it seek to unify different areas of mathematics?

Investigate the Langlands Program, its objectives, and its profound implications in unifying disparate areas of mathematics, particularly number theory.

These topics are undoubtedly challenging but can yield impressive results when tackled effectively. They offer a deep dive into complex mathematical concepts and theories, making them ideal for students aiming for the highest grades in their Math Extended essay.

Get extended essay help

Before continuing to the next block, I suggest our Math EE writing or editing services . Our company has been working with numerous IB students and helped them write custom IB extended essays.

Join a team of happy IB students who have followed the IB extended essay rubric and criteria and gained better results with Writing Metier and our Math assignments help !

Overused Math EE topics (proceed with caution)

While these topics are popular, they’ve been explored extensively. If you choose one, ensure you bring a fresh perspective:

• The Fibonacci Sequence in Nature.
• Pi and its Mysteries.
• The Monty Hall Problem.
• The Birthday Paradox.
• Exploring Pascal’s Triangle.
• The Mathematics of the Pyramids.
• The Tower of Hanoi Problem.
• Benford’s Law.
• The Four Color Theorem.
• The Mathematics of the Rubik’s Cube.

Keep in mind that selecting such a topic will require hard work to find a new custom angle of research and sometimes might not lead to higher grades .

In Conclusion

Alright, IB champs, that wraps up our curated selection of Math EE topics, each with its unique flavor and challenge. The topic is just the starting point. The real magic happens when you infuse it with your insights, analysis, and unique perspective. 

Mathematics isn’t just about numbers; it’s about stories and trips within the confines of equations and graphs. As you gear up to tackle your Extended essay, keep that passion alive, keep questioning, and most importantly, enjoy the process. 

Don’t forget to reserve extra space because it may take time to write an extended essay . And if you’re ever in doubt, remember that Writing Metier is here to guide you through every step of the process.

Free topic suggestions

Vasy kafidoff.

Vasyl Kafidoff is a co-founder and CEO at WritingMetier. He is interested in education and how modern technology makes it more accessible. He wants to bring awareness about new learning possibilities as an educational specialist. When Vasy is not working, he’s found behind a drum kit.

Similar posts

Economics extended essay topic ideas for ib students.

This article serves as a launchpad for students crafting their Economics Extended Essays, offering a diverse array of topics that span from the intricacies of microeconomic market structures to the broad strokes of macroeconomic policy. It provides a rich tapestry of ideas, inviting exploration into the complex interplay between economic theory and real-world application across various branches such as labor, environmental, and health economics.

Extended Essay Grading in the IB Program

Check the latest nuances of the IB Extended Essay with Writing Metier. From grading insights to firsthand experiences, we've got your EE queries covered. Let our seasoned team guide you to unlock success in your Extended Essay.

37 IB SL Math IA Topic Ideas that Actually Work!

If you are here because you are stuck with an idea for your IB Mathematics Standard Level (SL) essay topic, you have come to the right place. We understand that the IB Math is the toughest subject (no kidding, we feel you) and therefore, we are here to aid you as much as we can.

IB Math AA vs. IB Math AI: What Are The Differences?

Curious about the distinctions between IB Math AA and IB Math AI? Discover the key differences between these International Baccalaureate (IB) math courses in this comprehensive article. From curriculum structure to content focus, we delve into the unique features of each program, helping you make an informed decision about which course aligns best with your academic goals. Uncover the dissimilarities between IB Math AA and IB Math AI, empowering yourself with the knowledge to choose the right path for your mathematical journey.

Math IA Grading Boundaries from Writing Metier Perspective

Math IA grading criteria in the IB program. Dive into the nuances from 'Outstanding' to 'Insufficient'. Grasp a deeper understanding of what each grade truly signifies, learn the benchmarks for each level, and gather insights on how to aim for and achieve excellence in your assessments

IB Math AA Topic Ideas | Explained

Discover valuable tips for composing an exceptional Math AA topic in this comprehensive guide. If you need help with topic suggestions or writing your Math AA from scratch, our experienced IB writers are here to assist. Don't miss out on expert advice for crafting a standout Math AA topic!

We rely on cookies to give you the best experince on our website. By browsing, you agree to it. Read more

• Essay on the 21st century technology
• Essay on Technology and Society
• Social issues essay example
• 20 topics on Chemistry
• Writing a strong essay about education problems
• Tips for a political science essay introduction
• Essay on technology forecasting
• Technology in education essay
• Ideas for physical education essay
• 6 Sources to check
• Places where students can buy essay cheap

12 Strong Topic Ideas For A Math Extended Essay

Writing a math extended essay can be quite a challenge unless you are using an IB extended essay writing service . You have many factors to consider such as following the right format, choosing the best approach for your study, and defending your thesis (if required). So choosing an engaging topic that pertains to today’s issues is a crucial first step when you are in the planning stages.

Obviously, mathematics are your primary interest or else you wouldn’t have this assignment, to begin with due to not being enrolled in a course that goes above and beyond Algebra 102 or Geometry 104. (Even if you’re forced to endure a statistics course, you would have some interest in mathematical data or at least possess an awareness of working with numbers in your chosen field.) So one bit of advice on selecting a topic for your extended essay topics is to combine your intrigue with math with a problem, scenario or specific career domain (e.g.: medical, technology, sociology, business, etc.) that will not only hold your attention but also relate to current trends or events.

So here some suggestions for fascinating math essay topics to get you started:

In the area of education, some possible themes are:

• Possible correlation between district-level standardized test scores or GPA’s and performance on the SAT
• Prevalence of stress and coping skills of secondary university-bound students (Think ratios and statistics)
• Effectiveness of literacy programs (school or community-wide) towards improving reading skills (You can probably narrow down to an age range or grade level(s))

For the medical field, the possibilities are endless. Consider these three suggestions:

• Possible direct correlation between usage of “antibacterial” products, like hand sanitizer for instance and the rise of the “Super Bug.”
• The odds of another pandemic, similar to the 1918 worldwide influenza outbreak, occurring
• The impact of advertising on childhood obesity (Again, think ratios, statistics, and probability)

In the realm of computer technology, you can look into any one of these subjects:

• Best formula and combinations for SEO
• The use of prime numbers and modular arithmetic to maintain privacy with RSA Public Key Cryptography
• Correlation between the use of electronic pay services (Skrill for example) and users’ professions.

Of course, there are a variety of areas to explore within the content of math itself and its applications. Some possibilities include the following:

• Study of alternatives to Euclidean geometry and their applications
• Close study of Sophie Germain’s Theorem
• Real life dilemmas that can be solved with strategies of complex number problem-solving

As you can see, there are many different subjects to explore when writing about mathematical concepts and how they relate to the real world. You can dive more into the content area of science and hypothesize the route(s) of a comet that could impact the earth. Concerning sociological and psychological studies, you can look into various statistical investigations of human behavior. Another rather amusing numerical investigation could involve a study of probability in gambling venues or about other types of gaming, like Fantasy Football. (Be careful with your finances, though.)

However, some tips to remember as you examine these topics is to choose the “sub-area” that interests you the most (unless it’s all about the math), as you will devote a lot of time to this project; make sure you have a clear and measurable hypothesis; and clarify any questions on format with your instructor. With these recommendations and a lot of calculating, you will compose the perfect paper.

Helpful Sources

Writing Tips

• Essay intro on math algorithms
• Paper about the chemistry of water

ESSAY SAUCE

FOR STUDENTS : ALL THE INGREDIENTS OF A GOOD ESSAY

• Mathematics essays

Our free mathematics essay examples include popular topics such as algorithms, applied mathematics, calculus, knot theory, linear algebra, and more.

Euler’s identity

Euler’s identity is an equality found in mathematics that has been compared to a Shakespearean sonnet and described as “the most beautiful equation.” It is a special case of a foundational equation in complex arithmetic called Euler’s Formula, which the late great physicist Richard Feynman called in his lectures “our jewel” and “the most remarkable formula in … Read more

The Banach-Tarski paradox

Mathematics is seen by many as a mysterious and often unsettling subject. Answers often hide behind layers and layers of complicated equations, formulas and ciphers, the application of advanced concepts to real life is limited and I often find myself more confused after class than when I first entered. However, the real beauty of Mathematics … Read more

Pascal’s triangle, binomial theorem

What is Pascal’s Triangle? Pascal’s Triangle was named after Blaise Pascal. Pascal’s triangle starts with the number 1 and goes down the scale. When you start with one, add more numbers in a triangular shape, like a pyramid of some sort. All the numbers on the surrounding right and left sides of the triangle are … Read more

My journey of teaching and learning mathematics since embarking on a PGCE Mathematics course

Before I came to study a Post Graduate Certificate (PGCE) Mathematics course at University College London Institute of Education (UCL IOE), I had been working as an Academic Tutor at a behavioural centre, linked to a mainstream secondary school for the past 7 months. Students placed here had either learning difficulties or behaviour issues experienced … Read more

Aircraft – mathematics

Math SL Internal Assessment Lift and Drag Introduction When you look at aircrafts, they look like they shouldn’t be able to leave the ground because of how big they are. I always watched aircrafts, take off and land, over and over. According to Newton’s Third Law, every action has an equal and opposite reaction, lift … Read more

The World of Mathematics

Mathematics is often considered a useless discipline because people think they do not use advanced math in their life. It is a misunderstanding. Not using advanced math does not mean it is not vital. If you trade stocks, you will read many stock analysis reports. These reports use mathematical knowledge. Many students in the United … Read more

The history of algebra

We all use algebra. Even if it’s for the simple stuff, we use some form of algebra in our everyday lives. While reading chapters 1-10, I came across the word algebra and became quite curious about the subject for I have never really understood nor cared for it honestly, I just figured it’s the usual … Read more

Mathematics introduction

Mathematics belongs to the science discourse community. The word science means knowledge and comes from the Latin “Scientia”. In university, science is made up of a lot of discourse communities, such as Mathematics, Physics, and Chemistry. By searching the definition of science in Webster’s New Collegiate Dictionary, science is “knowledge covering general truths of the … Read more

Niels Henrik Abel

For over two centuries, mathematicians had trouble in finding a solution to the quintic equation, that is until Niels Henrik Abel formulated a theory. Abel was a Norwegian mathematician born on August 5, 1802, and his talent and potential in the field of mathematics was already present at a young age, leading him to become … Read more

The narrative of zero

Numbers surround us. They stamp our days, light our evenings, foresee our climate, and keep us on course. They drive business and support human progress. The beginning of the numerals makes disarray between the historical backdrop of mathematics and the historical backdrop of our modern numerals. The narrative of zero alludes to something can be … Read more

Emmy Noether

She was more than a mathematician to the people she met and to the people she inspired. She even has managed to inspire people long after she has passed. Emmy Noether was born on March 23, 1882 in Bavaria Germany. Growing up she wanted to go to college but back then women weren’t allowed to … Read more

Bitopological Approximation Space with Application to Data Reduction in Multivalued Information Systems

Abstract: In this work we generalize Pawlak approximation space to bitopological approximation space. One binary relation can define two subbases of two topological spaces. Membership, equillity and inclusion relations using rough approximations are defined and studied in bitopological aapproximation space. Some new measures that measure the accuracy and the quality of approximations are defined and … Read more

Statistics overview

Statistics is a form of mathematical analysis that uses quantified models, representations and synopses for a given set of experimental data or real life studies. Statistical analysis involves the process of gathering and evaluating data and then summarizing the data into a mathematical form. Statistics is a term used to summarize a process that a … Read more

Numerical Weather Prediction

You turn on the television, and often the first channel that pops up is the weather. It’s going 24/7 with predictions that go from weekly all the way down to hourly, with conditions that go from humidity to temperature. But what goes on behind the scenes is heavily entrenched in mathematics– meteorology’s backbone is a … Read more

The Mathematics of Our Universe

Abstract In this report, we start by defining key aspects of classical Lagrangian mechanics including the principle of least action and how one can use this to derive the Euler-Lagrange equations. Momentum and Conservation laws shall also be introduced, deriving relations between position, momenta and the Lagrangian of a given system. Following this, we develop … Read more

Ideas for your next mathematics essay

Stuck for a title for your next essay? Here are some ideas to inspire you:

• The Mathematics of Music: Exploring the Relationship between Mathematics and Music – This essay would examine the connections between music and mathematics, including the use of mathematical concepts in musical composition and the study of the mathematics of sound.
• The Golden Ratio: A Mathematical and Aesthetic Marvel – This essay would discuss the concept of the golden ratio and its applications in art, architecture, and design. It would explore the beauty and symmetry of this mathematical principle.
• Mathematics in Sports: Analyzing the Numbers Behind Athletic Performance – This essay would explore the use of mathematics in sports, including the use of statistics and analytics to analyze athletic performance and predict outcomes.
• Chaos Theory: The Science of Nonlinear Systems – This essay would discuss the concept of chaos theory and its applications in various fields, such as meteorology, physics, and economics. It would explore the idea that small changes in initial conditions can have a significant impact on the final outcome of a system.
• The Mathematics of Cryptography: Securing Information in the Digital Age – This essay would examine the use of mathematics in cryptography, including the principles of encryption and decryption, and how these concepts are applied to secure information in the digital age.
• Fractals: The Beauty of Infinite Complexity – This essay would explore the concept of fractals and their applications in art, nature, and science. It would discuss the beauty and complexity of these repeating patterns found in nature and how they are used in various fields of study.
• Mathematical Models in Biology: Understanding the Complexities of Life – This essay would discuss the use of mathematical models in biology, including the modeling of population growth, the spread of disease, and the behavior of organisms. It would explore how these models help scientists understand the complex systems that make up living organisms.
• The Mathematics of Finance: Analyzing Investments and Markets – This essay would examine the use of mathematics in finance, including the principles of financial analysis, investments, and risk management. It would explore how mathematics is used to understand and predict market trends.
• Geometry in Art: The Intersection of Math and Creativity – This essay would discuss the use of geometry in art, including the use of shapes, patterns, and symmetry. It would explore how artists use mathematical concepts to create beautiful and compelling works of art.
• The History of Mathematics: From Ancient Times to Modern-Day Advances – This essay would trace the history of mathematics, from its origins in ancient civilizations to modern-day advancements in the field. It would explore the contributions of key mathematicians throughout history and the evolution of mathematical concepts and principles over time.

Essay Categories:

• Accounting essays
• Architecture essays
• Business essays
• Computer science essays
• Criminology essays
• Economics essays
• Education essays
• Engineering essays
• English language essays
• Environmental studies essays
• Essay examples
• Finance essays
• Geography essays
• Health essays
• History essays
• Hospitality and tourism essays
• Human rights essays
• Information technology essays
• International relations
• Leadership essays
• Linguistics essays
• Literature essays
• Management essays
• Marketing essays
• Media essays
• Medicine essays
• Military essays
• Miscellaneous essays
• Music Essays
• Nursing essays
• Philosophy essays
• Photography and arts essays
• Politics essays
• Project management essays
• Psychology essays
• Religious studies and theology essays
• Sample essays
• Science essays
• Social work essays
• Sociology essays
• Sports essays
• Types of essay
• Zoology essays

• SAT BootCamp
• SAT MasterClass
• SAT Private Tutoring
• SAT Proctored Practice Test
• ACT Private Tutoring
• Academic Subjects
• College Essay Workshop
• Academic Writing Workshop
• AP English FRQ BootCamp
• 1:1 College Essay Help
• Online Instruction
• Free Resources

Hardest SAT Math Problems (updated for Digital SAT)

Bonus Material: The Hardest SAT Math Problems Quiz

Aiming for a really great score on the SAT? Wondering if your math skills are up to the challenge of the hardest problems?

If you want to be able to get a perfect score, you have to be able to solve the hardest SAT math problems.

We used our extensive test-prep experience to find the questions that many students miss. The examples below are real problems from past official SATs. 

Give each of these 16 hard math problems a try, then read our step-by-step explanations to see if you’re solving them correctly.

If you’re thinking about getting SAT tutoring to help you tackle problems like these on the real SAT, be sure to check out our list of the 15 best SAT Tutoring Services

Then, download this quiz with 20 more of the hardest real SAT problems ever to see if you’re on track for a perfect score! 

Bonus Material: 20 of the All-Time Hardest SAT Math Problems

Math on the SAT

Math accounts for half of your Total SAT Score, regardless of whether you’re taking the old paper SAT or the new Digital SAT.

On the traditional, paper SAT (which will be phased out in early 2024), the Math section comprises section 3, which contains 20 questions, is 25 minutes long and does not allow you to use a calculator; and section 4, which contains 38 questions, is 55 minutes long and does allow a calculator.

On the upcoming digital SAT (which will come into place in spring of 2024), the format is considerably different. You’ll be given two 35-minute “modules” with 22 questions in each, with the difficulty level of the second one depending on your performance on the first one. In other words, if you do really poorly on the first set of 22 questions, the second set will be easier–but your overall math score will be negatively affected. You can use your calculator on both.

Every SAT covers the following math material:

Heart of Algebra: 33% of test . Linear equations and inequalities and their graphs and systems.

Problem Solving and Data Analysis: 29% of test . Ratios, proportions, percentages, and units; analyzing graphical data, probabilities, and statistics.

Passport to Advanced Math: 28% of test . Identifying and creating equivalent expressions; quadratic and nonlinear equations/functions and their graphs.

Additional Topics in Math: 10% of test . A wide variety of topics, including geometry, trigonometry, radians and the unit circle, and complex numbers.

On the old SAT , open-ended questions came at the end of each Math section. Many students find them harder because you can’t guess or work backwards from multiple-choice options.

However, what many students don’t know is that the first 1–3 of these grid-in questions will actually be easier than the last few multiple-choice questions. 

That’s because the math questions on the SAT get increasingly difficult over the course of each section, but the difficulty level starts over again with the grid-in questions.

The savvy student will know this and skip the harder multiple-choice questions to go answer the easier grid-in questions first. Of course, if you’re aiming for a perfect score, (on most tests) you’ll have to answer every question correctly . 

But on the new Digital SAT, these open-ended questions will pop up at different points throughout both modules. You may see them in the beginning, the middle, or the end: there’s no set place for these to appear. Nor is there a set difficulty: generally, we’ve seen these questions be slightly on the easier side, but this varies significantly from test to test.

Because there’s obviously no bubble sheet on the digital SAT, you’ll simply type your answer into the text box. Be sure to look for instructions in the question about how they want the answer formatted!

To work with us for one-on-one tutoring or for our group SAT classes, schedule a free consultation with our team .

Why these problems are essential if you’re aiming at a top school

A perfect score on the SAT Math is 800. The only way to get this score is to answer every question correctly . 

In order to score a 750, you can only miss 2 or 3 questions across both math sections .

A 750 Math SAT may sound like a very high score—and it is! It’s a very high score.

But at the very best schools in the US, three quarters of the students scored a 750 Math or better.

In fact, at the Ivy League and other top schools, at least a quarter of the students had a perfect score!

The average math scores are even higher at the top engineering schools. Three quarters of the students at CalTech had a 790 or 800, and three quarters of the students at MIT had at least a 780.

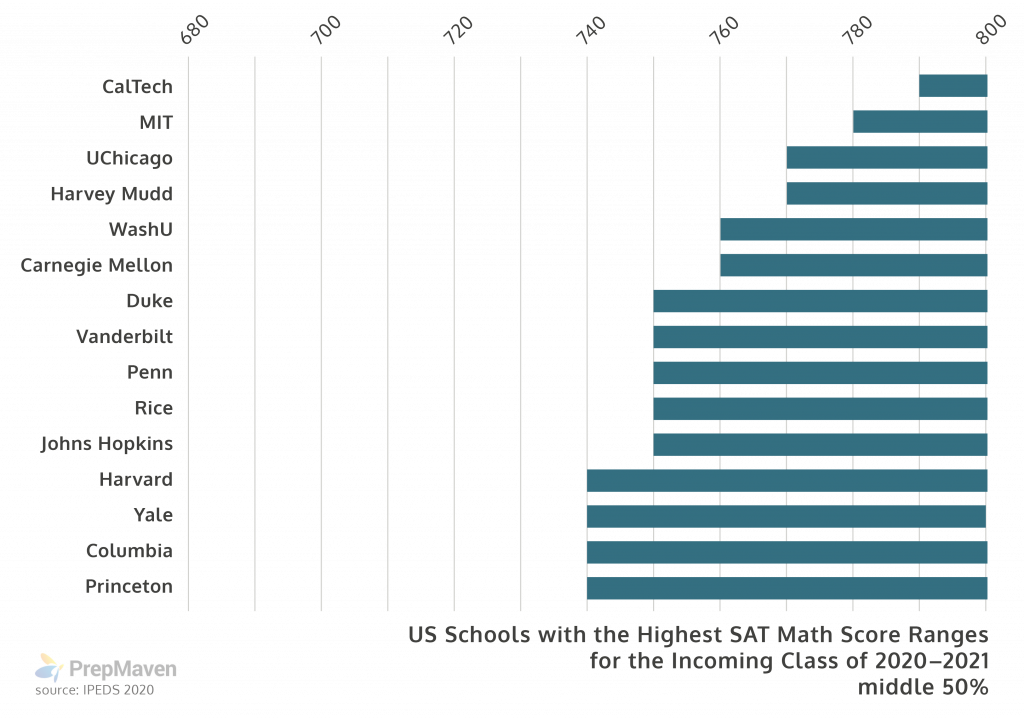
In order to be a competitive applicant to these schools, your SAT Math score should be within the “middle 50%” of the students at that school—in other words, more or less an average score for that school.

So if you’re aiming at an Ivy or one of the other top schools, you can only miss 2 or 3 questions out of the 58 math questions on the whole SAT.

If that’s your goal, make sure that you understand the problems explained below, and then try our quiz of 20 more real SAT questions that rank among the hardest questions ever.

SAT Problem #1

At first glance, this looks like a geometry question, since it talks about planes and lines and points . But this is actually an algebra question, dressed up with some geometric trappings. 

The key is to realize: 

1) We don’t need to solve for p and r individually. We just need to solve for (r/p) . 

2) The points themselves (p,r) and (2p, 5r) represent X and Y values on the line itself. (For example if p = 2 and r = 3 then that’s the same thing as an x-coordinate of 2 and a y-coordinate of 3.)

So let’s take a look at it. 

First, let’s plug in the p and r points for the x and y values to see what equations we end up with. 

y = x + b becomes r = p + b

y = 2x + b becomes 5r = 2(2p) + b or 5r = 4p + b

At this point we might get a little anxious because we have three variables. 

But we have to remember we don’t need to get the value of the individual letters, just the value of the relationship between r and p. 

That’s where b actually becomes helpful. Because we can now set both equations equal to b , plug in, and then see if we can manipulate the r and p to get them to express the same relationship we want. 

So, first set both equations equal to b to get: 

b = r – p

b = 5r – 4p

And since, obviously b = b … 

r – p = 5r – 4p

Let’s now use some basic algebra to put the like variables together, so:

Now we’re nearly home. All we have to do is manipulate the problem so r/p .

So, divide both sides by  3p :

4r / 3p = 1

Then multiply both sides by 3: 

And finally divide by 4, which gives us: 

CHOICE B  

Download the Hard SAT Math Problems quiz

SAT Problem #2

This is a question that can cause all sorts of problems if you forget your exponent rules—but it’s otherwise very straightforward. 

So let’s go over a few of those rules, just to get comfortable . . . and notice a pattern. I’ve included three below:

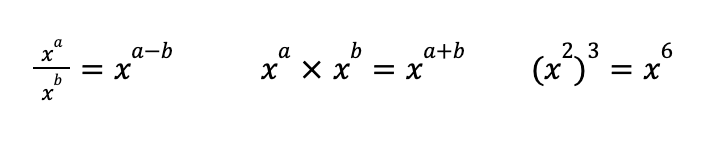
Two things to pay attention to:

First, when we divide variables with exponents, we keep the base and subtract the exponent. When we multiply variables with exponents, we keep the base and add the exponents. When we take a variable with an exponent to an additional power, we multiply the exponents. 

Second, in order to use the first two of these rules, the two numbers must have the same base . 

There is a base x on both the top and bottom of that fraction or the left and right side of that multiplication sign. 

So how does that help us here? 

Let’s forget the first half of the problem and look at the second:

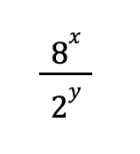
We might look back at these exponent rules and throw our hands up—the top and bottom parts of this fraction don’t have the same base, so what am I supposed to do here? 

Except… 

8 and 2 actually DO have the same base. Base 2. 

Isn’t 2^3 equal to 8? 

So if we re-write the problem, plugging in 2^3 for 8, and thinking about that third exponent rule I gave you above, the equation will look like this: 

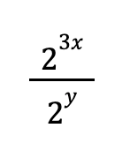
Now let’s go back to our exponent rules once more, and look at the first one. 

Because that tells us that… 

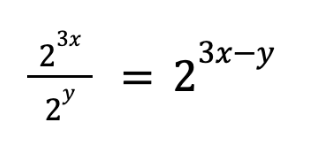
Well, hold on a second! 

We know the value of 3x – y . 

The problem tells us it’s 12.  

So we just plug in and get our answer… 

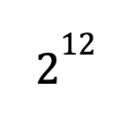
Which is CHOICE A. 

Keep up the practice! If you’d like help honing your skills, reach out to us for a free test prep consultation. All of our tutors are top 1% scorers who attended top-tier schools like Harvard and Princeton. That makes them uniquely qualified to help high-scoring students improve.

SAT Problem #3

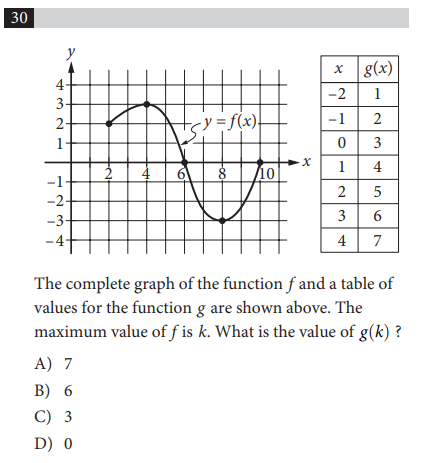
A question like this confuses a lot of students because they either forget how minimums and maximums work or find it hard to keep track of which numbers they are plugging in and where. 

In order to solve it, it’s helpful to think of a function as a machine . We enter an input into the machine (an x value)—it acts on it—and then it gives us an output (a y value). 

Let’s also remember that when we’re talking about minimum and maximums we’re talking about the y value when the function is at its highest and lowest point . 

With these two facts in mind, the problem is going to be much simpler, so let’s take it on in parts…

Since the question is asking us for g(k) and k represents the maximum value of f , it’s going to be helpful to first… 

Find k .  

So what is the maximum value of f , the graphed function? Well, the maximum value (as we realized earlier) is the y value when the function is at its highest. 

Looking at the graph, it looks the function is at highest when x = 4 , and more importantly, when 

Therefore, k = 3 .

Now let’s consider our functions as machines. 

When the problem asks us for g(k) , it’s telling us that k is going to act as the input (the x value for the function). So g(k) , the value after the machine acts upon the function, is going to be the output , or the y value . 

So, g(k) is the same as g(x) , except we’re plugging in our value of k , which is 3, for our x value. 

The rest is very simple. 

We go to the table and find where x = 3 , then move our finger across to see the output for that value, which is 6.

CHOICE B. 

Test your SAT math knowledge with our quiz

SAT Problem #4

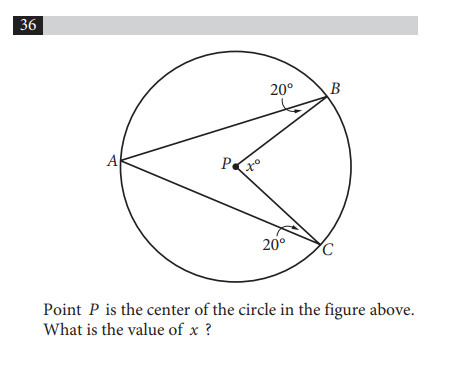
A version of this question has appeared on the SAT multiple times in recent years, and it often stumps students!

Here we have something that resembles a rotated version of the logo from Star Trek, and we’re asked to find the value of a degree inside the circle, between two points of the pointed figure.

We’re given a point that represents the center of the circle, along with two degree measurements inside the triangle-like figure. 

Generally, when we’re given a figure that looks unfamiliar to us—like the figure inside the circle— it can be extremely helpful to find a way to fix it (or cut it up) so that it’s made up of parts of shapes that are more familiar . 

So looking inside this circle, how might we “fix” this figure so that it becomes a little friendlier. 

Well, if we draw a line to the center of the circle ( P ) from the edge of the circle ( A ), then this unfamiliar figure suddenly becomes two triangles. 

And with triangles, unlike the figure we were originally given, we can apply some rules . 

Rules, for example, that dictate opposite sides of the triangle that have the same length will have the same opposite angles. 

And if we look at our drawing we see that two sides of our triangle are the same length because they’re both the radius …

And so we also know that the opposite angles of those sides will be the same… 

And we’ve been given one of those angles! 

Therefore, angles ⦣ABP and ⦣PAB will be the same—both 20 degrees. Let’s fill that in. 

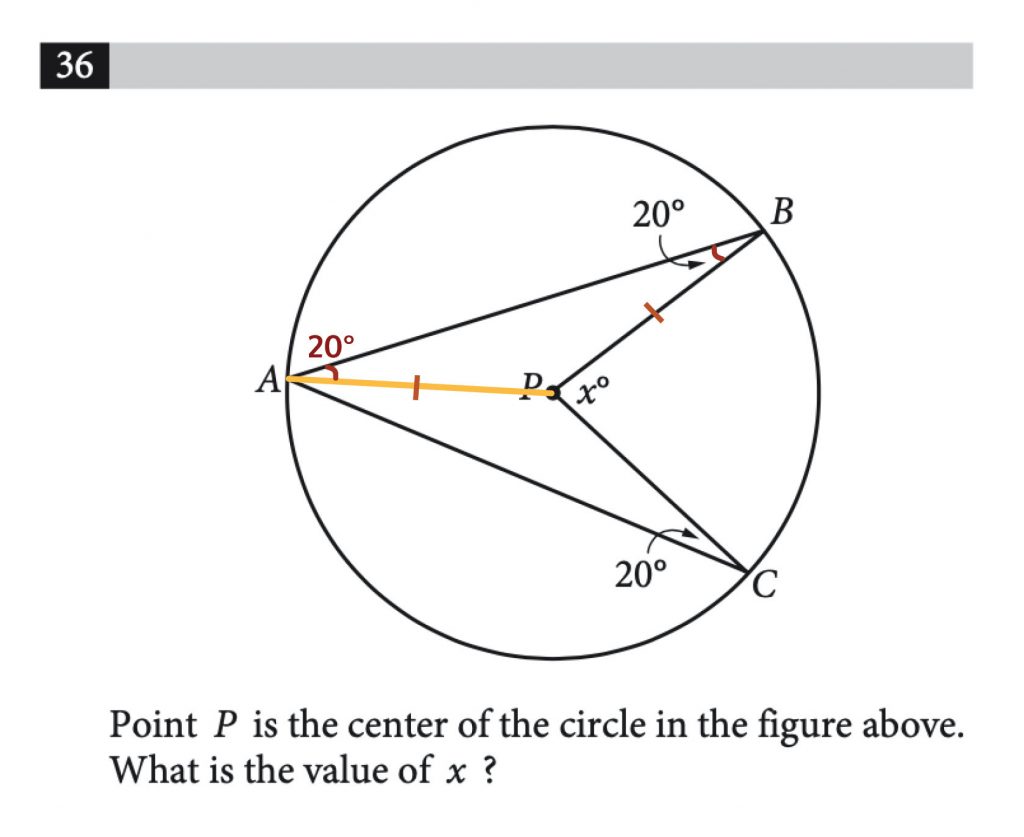
Now again—because we have a triangle—we can apply another rule as well. 

We know that degrees of a triangle will add up to 180 degrees. 

So if we know one of the inner degrees of the triangle is 20, and the other is 20—the remaining angle has to be 140 degrees. (Because 180 – 40 = 140. )

We have two of these triangles, so we know the larger inner angles of both add up to 280. 

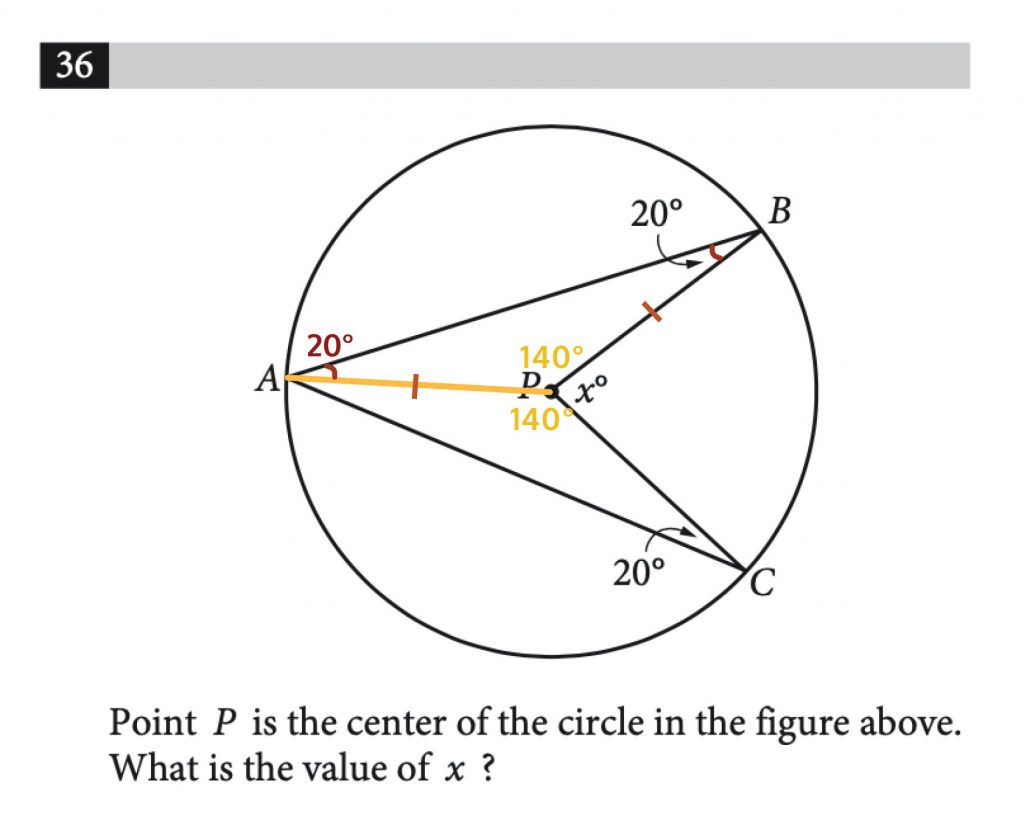
Because a circle is 360 degrees, the number of degrees “left over” when 280 is subtracted from 360 is 80. 

So X equals 80. 

There is actually a second clever way to solve this problem, involving arc measures. Can you spot it? (If not, don’t worry! Ask us how we did it here .)

SAT Problem #5

Here we have a problem that looks quite complicated—and one I find students often waste a lot of time on. They either try to plug in answers and work backwards… 

…or they waste time trying to combine the two terms on the right side of the equation and simplifying. 

It turns out the easiest way to solve this problem is by polynomial division , because we’ve already been given the answer! It’s the right-hand side of the equation: (-8x – 3) – (53 / (ax – 2)) .

That means that this is our answer to when (24x^2 + 25x – 47) is divided by ax – 2 .

So how does that help us get a value for a ? 

Well, let’s set this up as a polynomial division problem.

We’d write it as follows: 

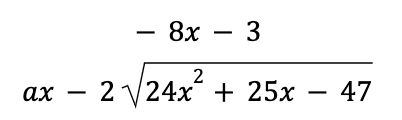
(I’m not putting the second half of the right side of the equation on top because that’s going to be our remainder.) 

So now we have a simple question. What number divided into 24 , gives me -8 ? 

Well, that’s easy. It’s -3 , right? 

Because -3 * -8 gives me 24 . 

So a equals -3 ,   CHOICE B .

Now, you could spend time plugging in -3 for a and dividing through the rest of the problem to make sure your answer matches the one on the exam—but generally on a timed test you really shouldn’t do more work than necessary. 

In fact, by setting this up as a polynomial division problem, we’ve saved time precisely because we don’t have to complete all the work . . . just enough to get us our answer. 

Try the quiz

SAT Problem #6

Because the SAT is a timed test, “difficult” includes not only questions that are hard to solve, but also those that—if a few wrong decisions are made—take a long time to solve. 

Sure, you may get the right answer, but those extra seconds or minutes wasted will inevitably cost you on other questions later on the exam.

Generally speaking, you should be able to answer each question in about a minute. If you spend more than 60 seconds on a single question, you should put down your best guess and move on (and hope that you have extra time at the end to return to this question).

To that end, let’s look at this question. You’re asked to find the value of 3x – 2 , and you’re given this equation:

(⅔)(9x – 6) – 4 = (9x – 6)

Many students will immediately think: “This is totally straightforward: Solve for x and plug it back into the equation.” 

They’ll distribute the ⅔ and end up with something like this: 

6x – 4 – 4 = 9x – 6

and then go through all the algebra from there, to get… 3x = -2 . 

These students will then find that x = (-⅔) . 

A few unlucky students will then forget that they have to plug in, and they’ll choose the trap answer C. 

The lucky ones will plug the (-⅔) back into 3x – 2 and get the correct answer, -4 , A . 

However, it turns out there is actually a much quicker way to solve this problem! 

We can solve it without ever having to plug into a second equation. 

If we simply subtract (⅔)(9x-6) from both sides, we end up with… 

-4 = (⅓)(9x-6) . 

We can realize that (⅓) of 9x-6 is the same as 3x-2 . 

And, what do you know… 

-4 = 3x – 2 . 

Ready to try some of these problems on your own? Try our quiz with 20 more of the hardest real SAT problems ever to see if you could get a perfect score on the SAT Math!

SAT Problem #7

This is a question you could muscle through, but it’s going to be a lot easier if we find a few shortcuts and work from there. Remember, a hard question isn’t necessarily difficult because of the conceptual and mathematical effort it asks from you but also because of the time it might require.

So how do we save ourselves some time? 

First, let’s notice that in the answer choices none of these numbers repeat . There are eight distinct numbers in the answer choices. Therefore, if we were pressed for time we only really have to find one of the values of c , choose the corresponding answer choice, and then move on. 

Second, let’s look at the other piece of information this problem gives us besides the quadratic. 

It tell us that a + b = 8.

This should be especially helpful because we know from FOIL (and what the rest of the problem gives us) that a * b = 15 , because abx^2 is going to be equal to 15x^2. 

Because a + b = 8 and ab = 15 , we know that the values of a and b are going to be 3 and 5. 

(We don’t know which one is which, and that’s precisely why this problem has two possible values for c .)

At this point we’ve done most of the “hard” work to save time in this problem, and it hasn’t even been particularly hard!

Now all we have to do is assign one of 3 or 5 to a , assign the other to b , FOIL out the problem, and pick whichever choice corresponds to one of the values of c . 

Let’s say a = 3 and b = 5 .

It will work like this: 

(3x + 2)(5x + 7) = 15x^2 + 21x + 10x + 14 .

Which simplifies to… 

15x^2 + 31x + 14 .

Which means c = 31 .

31 only appears once in our answer choices, so the answer must be CHOICE D.  

SAT Problem #8

When you’re faced with one of these more difficult system-of-equations problems—specifically the ones that ask you for no solutions or infinite solutions —it’s going to be much, much easier to think about the problems geometrically. 

In other words, as two line equations. 

So what does it mean for two lines to have no solutions ?

Well, for two lines to have no solutions, they’d have to never intersect , correct? 

(Just like if one of these problems asks you about two lines with infinite solutions , they’re saying that the lines are the same . They’re laid on top of each other. )

In other words, they’d have to be… parallel lines . 

And parallel lines have the same… slope! 

So this question is asking you to find the correct value for the variable that gives these lines the equivalent slope . 

Obviously, the first step is to put both of these equations in slope-intercept form. We’d end up with:

y = (-a/2)x + 2

Now the rest is very simple. All we need is a value of a that makes the slopes equal, so that it solves the equation (-a/2) = 3 .

With some basic algebra, we end up with -a = 6 . This is the same as a = -6 .

So the answer is CHOICE A, -6. 

Are these problems feeling super hard for you? Want to work on more similar problems? Check out our one-on-one tutoring with Ivy-League instructors. A great experienced tutor can help you focus on the concepts that are the hardest for you until you understand them thoroughly.

SAT Problem 9

This is another type of problem that students often have conceptual difficulty with, causing them to waste much more time than they should. 

(Remember, basically every problem in the SAT math section is designed to be solved in a minute and half or less. If you’re taking three or four minutes on a math problem, you’ve probably made a mistake!)

Some students will see that (u-t) is defined but not u or t individually, so they’ll try either solving for u in terms of t (or vice versa), or they’ll try squaring (u-t) to get a solution. (Which is closer to the correct way to solve the problem, but still incorrect). 

Instead, to solve this problem we need to remember the difference of squares . 

Remember, that the difference of squares states the following… 

(x+y)(x-y) = x^2 – xy + xy – y^2 .

Which means… 

(x+y)(x-y) = x^2 – y^2 .

And doesn’t that look awfully familiar to… u^2 – t^2 ?

In fact, we can now replace  u^2 – t^2 with (u + t)(u – t) .

So the whole problem would now read: (u + t)(u – t)(u – t) . Since we know the value of (u + t) and (u – t) , this would simply be the same as (2)(5)(2) .

Which equals our answer… 

Ready to see how you’re doing? Download the quiz

SAT Problem #10

What makes this question confusing is that students often get thrown off by the repetition of the (⅓). 

They forget that when the ⅓ gets factored out of the parenthesis like that, it means it’s going to apply to the whole equation: both the  x^2 AND the -2 . 

Once we remember that, we can solve this problem by difference of squares . This will save us the time of having to brute force the answer choices and FOIL each one through for the different values of k. 

We’ll simply square k and subtract it from the  x^2 for each choice. 

That will give us the following four choices: 

(⅓)(x^2  – 4)

(⅓)(x^2 – 36)

(⅓)(x^2 – 2)

(⅓) (x^2 – 6)

A student might rush to choose the third answer choice, since it appears to look like the expression at the beginning of the problem, but remember what I told you at the beginning: 

We’re going to apply that ⅓ to both the x^2 AND the k ! 

If we multiply that ⅓ through, the choices suddenly look like this…  

(⅓)(x^2) – (4/3)

(⅓)(x^2) –  (12)

(⅓)(x^2) – (⅔)

(⅓)(x^2) – (2)

. . . and so the correct answer is actually the fourth choice, CHOICE D . 

Ready to try more hard problems on your own? Download our free quiz to try 20 more of the hardest ever (real) SAT problems.

SAT Problem #11

There are not many problems on the SAT that involve knowing the equation for a circle—in fact, circle equation problems don’t show up on every test—but that’s precisely why students often find a problem like this more difficult. 

First, let’s do a quick refresher on what the numbers in the equation of a circle mean. 

Any equation for a circle is going to be in this form: 

(x – h)^2 + (y – k)^2 = r^2

Where h and k represent the coordinates of the center and r is the radius. 

Let’s apply that to our problem here… 

(x + 3)^2 + (y – 1)^2 = 25.

Remember: because in the form of the circle equation the numbers inside the parenthesis are subtracted from x and y , when they appear inside the parenthesis as positives , that indicates the coordinate point will be negative. 

Therefore the center of this circle is at point (-3, 1) .

Because the radius is expressed as r^2 , then the 25 indicates the radius will be 5 . 

So we have a circle centered on the point (-3,1) and with a radius of 5 . 

So… now what? 

How do we figure out which of these points is not inside the circle? 

First, let’s draw the circle itself and look at it. On the SAT itself, you won’t have graph paper, so just draw a rough sketch!

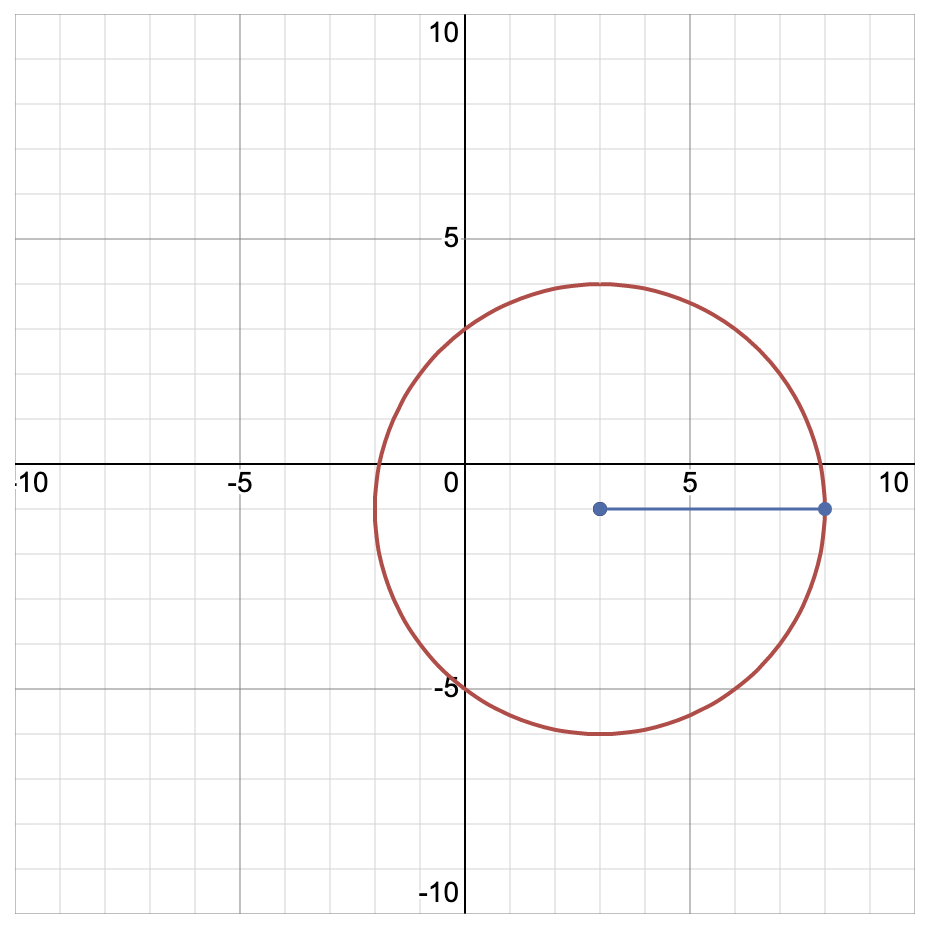
Of course if we’re truly flummoxed we could graph the points, eliminate what we can . . . and guess. 

But that’s not ideal, obviously! 

Instead, let’s think about what the radius means. 

The radius demarcates the boundaries of the circle from the center. 

In other words, any points with a distance less-than-the-radius away from the center will lie within the circle. 

And any points more-than-the-radius distance from the center will lie outside of it. 

(Any points exactly-the-radius distance from the center will lie on the circle itself.) 

So all we have to do is find the point that is more than 5 units away from our center, and that will be our answer. 

To do this requires the distance formula. 

Remember, the distance formula is

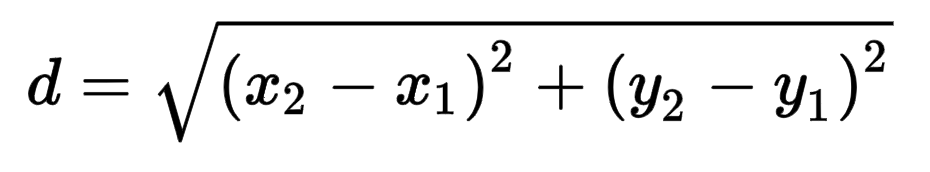
A quick note: if you ever forget the distance formula, simply plot the two points on a graph, make a triangle with the distance between the two points and the hypotenuse, and use the Pythagorean Theorem to find the length of the hypotenuse, like this: 

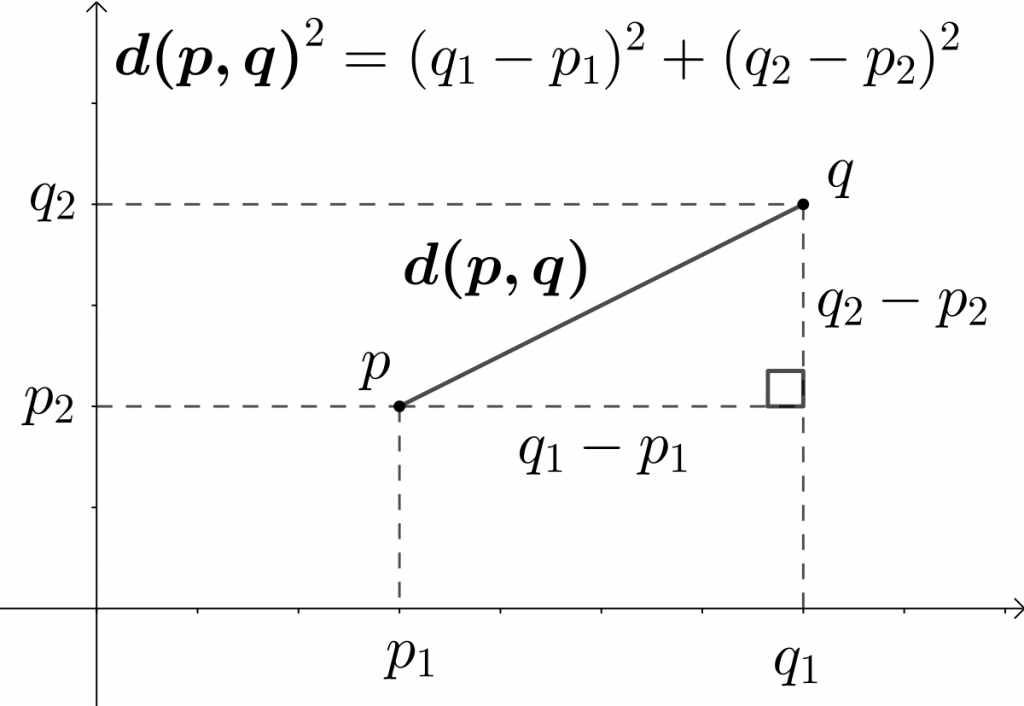
Going back to our problem, let’s plug each of the points in along with our radius to the equation. (I’ll include the second point here, although since that’s our center we need not actually bother with it when we’re going through the problem.) We end up with: 

√(-3 – (-7))^2 +(1-(3))^2) = √20

√(-3 – (-3))^2 +(1-(1))^2) = √0

√(-3 – (0))^2 +(1-(0))^2) = √10

√(-3 – (3))^2 +(1-(2))^2) = √37

Only the square root of 37—choice D—is an answer that is larger than five. 

So that’s our correct choice, D . 

Want more hand-picked problems? Get the quiz

SAT Problem #12

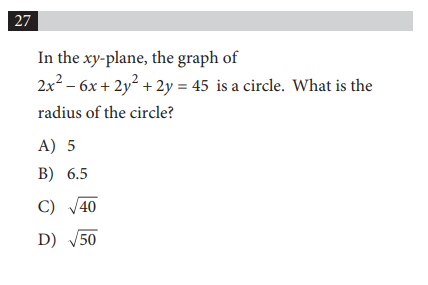
More circles! Let’s recall how the equation for a circle looked. It’s… 

(x – h)^2 + (y – k)^2 = r^2 

What the problem gives us, unfortunately, does not resemble that equation… 

…so our goal is to get the equation in the problem to look like a normal equation for a circle. 

Once we do this, we’ll just have to take the square root of whatever is on the right side of the equation, and that will give us our answer.

But how? 

We need to do something called completing the square . 

For the SAT, this concept is slightly obscure—it’s one you may see only once (or not at all) on a given exam. It makes the question a bit more difficult. 

Completing the square is normally a process reserved for solving a quadratic equation, but if you look closely at the way this problem is set up – 

2x^2 – 6x + 2y^2 + 2y = 45

we see that what we really have here are two quadratic equations, so we just have to complete the square twice. 

First we have to get rid of the coefficient in front of the x and y squared, so we have to divide through by 2 . 

This gives us  x^2 – 3x + y^2 + y = 22.5 .

Now we’re reading to complete the square!

Let’s deal with the x terms first. We have to think of what number, if we had it here in the equation, would allow us to factor x^2 – 3x into something of the form (x – z)^2 , where z is a constant. If we think about it, we realize that z has to be half of b . In this case, that means half of -3 , so -1.5 .

When we pop that into our setup, we get (x – 1.5)^2 . If we FOIL this out, however, we see that we get x^2 – 3x + 2.25 .

So it turns out that in order to be able to rewrite our expression in the form we want, we need to add 2.25 to our equation. As always in algebra, we do the same thing to both sides, so now we have:

x^2 – 3x + 2.25 + y^2 + y = 22.5 + 2.25.

Now we do the same thing for the y terms! Again, we need to add something to the equation so that we could rewrite the y part of the expression in the form (y – z)^2 . To get this number, we take half of the b term and square it: 1 divided by 2 , then squared, so 0.5^2 or 0.25.

Again, we have to add this number to both sides of the equation. Now we’ve got:

x^2 – 3x + 2.25 + y^2 + y + 0.25 = 22.5 + 2.25 + 0.25.

We can factor and rewrite this like:

( x – 1.5)^2 + (y + 0.5)^2 = 25.

Alright, now this is finally in the right format for the equation for a circle!

The final step is to use this equation to find the radius.

We know that the equation for a circle is (x – h)^2 + (y – k)^2 = r^2  . Fortunately this works out really nicely, since 25 is just 5^2. The radius must be 5, CHOICE A .

We’ve tutored thousands of students and used that experience to assemble a list of 20 more problems that students frequently miss. Can you answer them correctly? Download the quiz now to find out!

SAT Problem #13

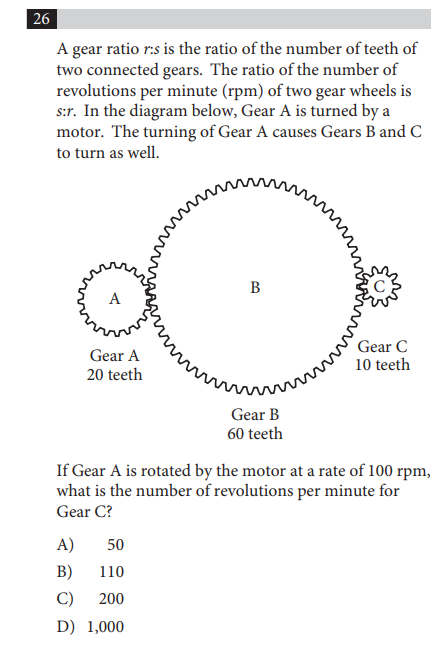
This question involves a number of moving parts and thus can be a little overwhelming for students to follow. 

It asks us to find, based on the rotation of the first gear, the rotation of the third. 

I find many students trip up on this problem by making two errors that are simple to fix, but relatively common. They fail to take the problem step by step… and they fail to write down their work as they track through the material. 

With that in mind, let’s work through the problem. 

Because gears A and C do not connect directly, but instead through gear B, we should first try to figure out the rotational relationship between A and B (at 100 rpm) before applying that to B and C. 

Because B is larger than A (and has more gears), A is going to rotate fully multiple times before B rotates once. 

How many times? Here it’s helpful to consider a ratio. 

A has 20 gears. 

B has 60 gears. 

So A is going to have to rotate three times before B rotates once . (20 goes into 60 three times.) 

Therefore, the ratio of rotation between A and B is 3 : 1 . 

Let’s write that down and then apply the same method to figure out the ratio between B and C. 

C has 10 gears. 

Here B only has to rotate a sixth of its distance for C to rotate once, so the ratio of rotation between B and C is 1 : 6 .

Now we take the number of RPMs the problem gives us, start with the gear on the left and multiply through with our ratios. 

So if Gear A rotates 100 times RPMS per minute, Gear B will rotate a third of that distance… 

So we divide 100 by 3. 

Because we know Gear C rotates six times as fast as Gear B, we then take our answer and multiply it by 6. 

So we get (100)(⅓)(6) . 

Which gives us 200 rpm. 

CHOICE C. 

SAT Problem #14

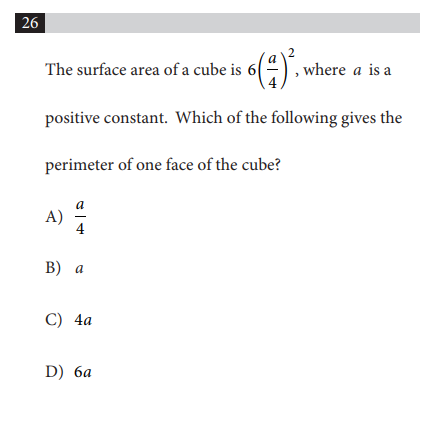
This question appears complicated—and students often get tripped up trying to either plug in numbers (which can be time consuming) or by searching for an equation that explains the relationship between the surface area and perimeter of the cube itself. 

This is especially tempting because while the question gives us the equation for the entire surface area of the cube, it only asks for the perimeter of one of the cube’s faces. 

However… 

If we think about the properties of a cube, this question actually becomes quite simple. 

First, let’s draw a cube.  

Again, the equation the problem gives us is for the entire surface area of the cube: 6(a/4)^2 .

But when we look at the cube, we may notice that it has, in fact, six faces. 

Therefore, each face would have one sixth of the surface area of the entire cube. 

So by dividing the equation by six, we get the surface area for one face of the cube, which is: 

But the question asks for the perimeter of one face of the cube. 

Let’s examine the drawing of the cube one more time. 

What shape is each cube face? It’s a square. 

And because each side of a square (let’s call each side x ) is equal to the other, the area of the square is going to be x^2, or the length of the side times itself. 

Well, wait a moment… 

If we go back to our equation for the surface area of ONE face of the cube, (a/4)^2 , we might notice that it’s in the same form as the equation for area of the square, except instead of x being squared, it’s (a/4) . 

And if we replace the x with (a/4) , we find that each side of the square is equivalent to (a/4) . 

Which makes finding the perimeter of this square quite simple, because it has four sides. 

So we merely add the four sides together: 

(a/4) + (a/4) + (a/4) + (a/4) . . .

which equals a . 

Which in this case is CHOICE B . 

Want more practice? We collected 20 more of the hardest SAT math problems. Download the quiz and take it with a 25-minute timer to mimic the real test!

SAT Problem #15

We have a lot of variables in this question, so it’s easiest to try to incorporate the extra piece of information we’re given, b = c – (½) , as best we can and then try to simplify the problem and solve from there. 

So how can we do that? 

The problem tells us b = c – (½) , which can also be expressed as b – c = -(½) .

(Once we put the b and c together on one side, it becomes easier to replace them together with a number). 

So what’s the best way to manipulate these two equations so that we’ll have b – c , which we can then replace with the (-½) and be left with x and y ? 

Because let’s remember that the problem does not ask us to solve for x and y individually. 

Just their relationship. 

So once we’re left with x and y as our only two variables, we should be able to make good progress. 

Anyhow, looking back over these two equations it seems the easiest way to be left with b – c is to… 

…subtract the bottom equation from the top one. 

When we do so, we’re left with the following: 

(3x – 3y) + (b – c) = (5x – 5y) + (-7 – (-7))

We replace b – c with -½  

And then combine like terms to get… 

(-½) = (5x – 3x) – (5y + 3y)

(-½) = 2x – 2y

Divide through by 2 … 

-¼ = x – y

Or x = y – (¼)

So our an answer is x = y – ¼ , CHOICE A .

Download 20 more of the hardest problems ever

SAT Problem #16

There are a few ways to solve this problem. The easiest one is simply to know the “remainder theorem.”

I don’t want to get too sidetracked with details, but remainder theorem states that when polynomial g(x) is divided by (x – a) , the remainder is g(a) .

In other words, when p(x) is divided by  (x-3) here, the remainder would be p(3) , which, according to the information we’re given, is -2 . 

That leads to CHOICE D . 

But what if, like many students, you don’t know the remainder theorem? (It’s pretty obscure and there’s a good chance you won’t see a problem about it on the entire exam.) 

Let’s look at an alternative way to solve the problem. 

If p(3) equals -2 , let’s imagine a function where that might be the case. 

We could do as simple one, like y = 3x – 11 , or a more complex one, like y = x^2 + 3x – 20 .

Either way, if I plug 3 into either of these functions for x , I get -2 as a y value. 

I should also notice immediately that (x – 5) , (x – 2) , and (x + 2) are not factors of either of them.

Clearly choices A, B, and C are not things that must be true. 

This also, by process of elimination, leads to CHOICE D. 

But just to check, let’s divide x – 3 into one of these functions – say 3x – 11 – and see what happens: 

The x goes into 3x three times – and three times (x-3) equals 3x – 9 .

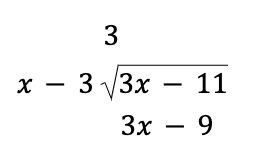
When I subtract 3x – 9 from 3x – 11 , I get -2 , which is my remainder. 

Which points us, again, to CHOICE D .

Test your knowledge with 20 more problems

If these problems feel really hard, don’t panic—you can still do well on the SAT without answering every question correctly. 

The average SAT Math score for US students in 2022 was 52 8, and you have to answer about 32 out of 58 math questions correctly to get this score. That’s only a little over half of the questions!

However, if you want a high score—or a perfect score—you’ll have to be able to answer tough questions like these. You’ll need a very high score to be a competitive applicant for Harvard, Stanford, MIT, or other highly competitive schools.

The good news is that it’s very possible to raise your math score! 

In fact, it’s typically easier to improve your SAT Math score than your Reading & Writing score. Good preparation (on your own or with a tutor ) will fill in the knowledge gaps for any concepts that might be shaky and then practice the most common problem types until they feel easy.

We’ve worked with students who were able to see a 200-point increase on the Math section alone, through lots of hard work and practice.

To see how your math skills stack up against the toughest parts of the SAT, download our quiz with 20 more of the hardest SAT math questions, taken from real tests administered in recent years.

Once you know where you stand, keep up the practice!

If you’re interested in customized one-on-one tutoring support from an expert SAT tutor who can help you understand these tough problems, schedule a free consultation with Jessica or one of our founders . Our Ivy-League tutors are top scorers themselves who can help you with these more advanced concepts and strategies.

Bonus Material: Quiz: 20 of the All-Time Hardest SAT Math Problems

Emily graduated  summa cum laude  from Princeton University and holds an MA from the University of Notre Dame. She was a National Merit Scholar and has won numerous academic prizes and fellowships. A veteran of the publishing industry, she has helped professors at Harvard, Yale, and Princeton revise their books and articles. Over the last decade, Emily has successfully mentored hundreds of students in all aspects of the college admissions process, including the SAT, ACT, and college application essay. 

CHECK OUT THESE RELATED POSTS

Your Guide to the SSAT’s Format

June 3, 2024

Wondering about SSAT format, length, or content? In this post, we cover everything you need to know about the structure of this high stakes test so that you can prepare for …

6 SSAT Reading Strategies From the Experts

May 29, 2024

With these 6 SSAT Reading strategies, you'll be prepared to maximize your raw score on this difficult section.

15 College Essays That Worked

May 13, 2024

In this regularly updated post, we share the college essays that helped students get into their dream schools -- including Ivy Leagues.

SSAT Score Release Dates – When You’ll Get That Score Report

May 2, 2024

You've studied hard. You've taken the SSAT. Now when will you get that score report? Find SSAT score release dates and more in this regularly updated post.

SSAT Prep Resources: Your Guide

Preparing to take the SSAT? What SSAT prep resources should you be utilizing? We weigh in on the best SSAT test prep tools in this post.

Scoring on the SSAT: Your 2024 Guide

Understanding your SSAT score report can be challenging. With this detailed breakdown of SSAT scores, you'll have a firm grasp on what to expect in no time!

What is a Good SSAT Score for 2024?

What is a good SSAT score? What percentile ranking do you need to get into the school of your dreams? Find out more in this comprehensive post.

Princeton Review vs Kaplan: Which SAT Prep Service is Better?

April 29, 2024

Princeton Review and Kaplan are two of the biggest test prep services, but which one is better? Detailed review of pricing, course materials, instructor qualifications, and customer service. Choose the best SAT prep to help you raise your score…

Kaplan SAT Prep Review: Rating All of Kaplan’s SAT Prep Options

Comprehensive review of Kaplan's SAT prep services: pricing, instructor qualifications, online platform, customer service, and educational quality.

Princeton Review vs Kaplan: Which ACT Prep Service is Better?

Princeton Review and Kaplan are two of the biggest test prep services, but which one is better? Detailed review of pricing, course materials, instructor qualifications, and customer service. Choose the best ACT prep to help you raise your score…

Privacy Preference Center

Privacy preferences.

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Essays and thoughts on mathematics

Many distinguished mathematicians, at some point of their career, collected their thoughts on mathematics (its aesthetic, purposes, methods, etc .) and on the work of a mathematician in written form.

For instance:

• W. Thurston wrote the lovely essay On proof and progress in mathematics in response to an article by Jaffe and Quinn ; some points made there are also presented in an answer given on MathOverflow ( What's a mathematician to do? ).
• More recently, T. Tao shared some personal thoughts and opinions on what makes "good quality mathematics" in What is good mathematics? .
• G. Hardy wrote the famous little book A Mathematician's Apology , which influenced, at least to some extent, several generations of mathematicians.

Personally, I've been greatly inspired by the two writings listed under (1.) -- they are one of the main reasons why I started studying mathematics -- and, considering that one of them appeared on MathOverflow , I'd like to propose here -- if it is appropriate -- to create a " big-list " of the kind of works described in the above blockquote.

I'd suggest (again, if it is appropriate) to give one title (or link) per answer with a short summary.

• A related question, which I've found very interesting, is Good papers/books/essays about the thought process behind mathematical research .
• Only slightly related (but surely interesting): Which mathematicians have influenced you the most?
• A single paper everyone should read? is not quite related, but still somewhat relevant (especially the most up-voted answer).
• reference-request
• soft-question
• 1 $\begingroup$ Hardy's apology is available here: math.ualberta.ca/~mss/misc/A%20Mathematician%27s%20Apology.pdf $\endgroup$ –  Goldstern Oct 5, 2015 at 15:33
• $\begingroup$ This seems a little broad--can you be a bit more specific? I gave one answer, but do you want things like Dyson's "Birds and Frogs" or Gower's "Two cultures"? $\endgroup$ –  Kimball Oct 5, 2015 at 22:29
• $\begingroup$ @Kimball, first of all, thanks for your answer, the book you suggested seems very interesting. Then, yes, I've read both those articles and, although they didn't come to my mind when I asked the question, they are surely two very insightful additions to this list. Thanks again. :) $\endgroup$ –  user81051 Oct 6, 2015 at 18:12

22 Answers 22

There are many snippets that can be found. I like the following bit of the foreword by Thurston to J. H. Hubbard's Teichmüller Theory . I share the remarks because I think you simply can't have enough of Bill Thurston's insights:

"Mathematics is a paradoxical, elusive subject, with the habit of appearing clear and straightforward, then zooming away and leaving us stranded in a blank haze. Why? It is easy to forget that mathematics is primarily a tool for human thought. Mathematical thought is far better defined and far more logical than everyday thought, and people can be fooled into thinking of mathematics as logical, formal, symbolic reasoning. But this is far from reality. Logic, formalization, and symbols can be very powerful tools for humans to use, but we are actually very poor at purely formal reasoning; computers are far better at formal computation and formal reasoning, but humans are far better mathematicians. The most important thing about mathematics is how it resides in the human brain. Mathematics is not something we sense directly: it lives in our imagination and we sense it only indirectly. The choices of how it flows in our brains are not standard and automatic, and can be very sensitive to cues and context. Our minds depend on many interconnected special-purpose but powerful modules. We allocate everyday tasks to these various modules instinctively and subconsciously. The term `geometry', for instance, refers to a pattern of processing within our brains related to our spatial and visual senses, more than it refers to a separate content area of mathematics. One illustration of this is the concept of correlation between two measurements on a set, which is formally nearly identical with the concept of cosine of the angle between two vectors. The content is almost the same (for correlation, you first project to a hyperplane before measuring the cosine of the angle), but the human psychology is very different. Each mode of thinking has its own power, and ideally, people harness both modes of thought to work together. However, in formalized expositions, this psychological > difference vanishes. In the same way, any idea in mathematics can be thought about in many different ways, with competing advantages. When mathematics is explained, formalized and written down, there is a strong tendency to favor symbolic modes of thought at the expense of everything else, because symbols are easier to write and more standardized than other modes of reasoning. But when mathematics loses its connection to our minds, it dissolves into a haze. I've loved to read all my life. I went to New College of Sarasota, Florida, a small college that was just starting up with a strong emphasis on independent study, so I ended up learning a good deal of mathematics by reading mathematics books. At that time, I prided myself in reading quickly. I was really amazed by my first encounters with serious mathematics textbooks. I was very interested and impressed by the quality of the reasoning, but it was quite hard to stay alert and focused. After a few experiences of reading a few pages only to discover that I really had no idea what I'd just read, I learned to drink lots of coffee, slow way down, and accept that I needed to read these books at 1/10th or 1/50th standard reading speed, pay attention to every single word and backtrack to look up all the obscure numbers of equations and theorems in order to follow the arguments. Even so, when something was ``left to the reader'', I generally left it as well. At the time, I could appreciate that the mathematics was an impressive intellectual edifice, and I could follow the steps of proofs. I assumed that such an elaborate buildup must be leading to a fantastic denouement, which I eagerly awaited -- and waited, and waited. It was only much later, after much of the mathematics I had studied had come alive for me that I came to appreciate how ineffective and denatured the standard ((definition theorem proof)^n remark)^m style is for communicating mathematics. When I reread some of these early texts, I was stunned by how well their formalism and indirection hid the motivation, the intuition and the multiple ways to think about their subjects: they were unwelcoming to the full human mind. John Hubbard approaches mathematics with his whole mind. If you page through the current book, you will see many intriguing figures. That is a first sign: figures are one of the most important ways to keep our thought processes going in our whole brains, rather than settling down into the linguistic, symbol-handling areas. Of course, the figures in your imagination are even more important. Geometric ideas can be conveyed with words and with symbols, sometimes more effectively than with pictures, but a lack of figures is a good indication of a lack of geometry. Another important part of human thinking is the emotional aspect. In mathematics, what is intriguing, puzzling, interesting, surprising, boring, tedious, exciting is crucial; they are not incidental, they shape how we think. Personally, my thinking was shaped by boredom: I develop intense urges to come up with `easy' methods in order to avoid tedious computations that are opaque to me. Hubbard, a principal participant in the mathematics he is discussing, has done an excellent job in conveying the drama."

There are also many very good interviews that can be found, such as this one with Connes , as well as the advice to young mathematicians in the Princeton Companion to Mathematics .

A Mathematician's lament by Paul Lockhart: Reflections on how badly mathematics are taught these days. Imagining how it would be if music was taught the same way.

Indiscrete Thoughts by Gian-Carlo Rota and Discrete Thoughts by Kac, Rota, and Schwartz.

Proofs and Refutations: The Logic of Mathematical Discovery by Imre Lakatos: The sequence of steps through which mathematical ideas can be made to grow in an informal setting is explained through Socratic dialogues between a teacher and students. A beautiful read.

Since you mentioned A Mathematician's Apology : Michael Harris' Mathematics Without Apology .

Here's an excerpt explaining the title:

These attempts at justifications are the 'apologies' of the title. They usually take one of three forms. Pure research in mathematics as in other fields is good because it often leads to useful consequences (Steven Shapin calls this the Golden Goose argument); it is true because it offers a privileged access to certain truths; it is beautiful , an art form. To claim that these virtues are present in mathematics is not wrong, but it sheds little light on what is distinctively mathematical and even less about pure mathematicians' intentions . Intentions lie at the core of this book. I want to give the reader a sense of the mathematical life -- what it feels like to be a mathematician in a society of mathematicians where the first and second lives overlap.

Love and Math: The Heart of Hidden Reality by Edward Frenkel is, in my opinion, a lot better than Lockhart's lament.

The Mathematical Experience by Philip J. Davis and Reuben Hersh is a wonderful collection of essays on mathematics and on the experiences and culture of mathematicians. Written back in the 1980's, it has extremely insightful discussions of many of the same topics that nowadays are discussed on MO. For example, the essay "The Ideal Mathematician," which describes a hypothetical "ideal" mathematician working on the made-up area of "non-Riemannian hypersquares" is absolutely hilarious. Highly recommended!

• 1 $\begingroup$ The "Ideal Mathematician" is, to my mind, a poor mathematician. (It was a caricature, yes, but one which was a little too extreme for me.) $\endgroup$ –  Todd Trimble ♦ Oct 5, 2015 at 16:29
• 1 $\begingroup$ @ToddTrimble, I disliked it too. For myself, the more bearing what I'm working on has on undergraduate or even high-school mathematics, the more excited I am about it. $\endgroup$ –  goblin GONE Aug 23, 2016 at 14:55

Mathematics as Metaphor by Yuri Manin (both the title of the linked book which is a collection of essays, as well as the title of one particular essay in there). At least some of the essays you can find online.

I Want to be a Mathematician , by Paul Halmos.

• $\begingroup$ Indeed I love that book. Thanks for adding it. $\endgroup$ –  user81051 Oct 6, 2015 at 18:13

Eugene Wigner: The Unreasonable Effectiveness of Mathematics in the Natural Sciences

The statement that the laws of nature are written in the language of mathematics was probably made three hundred years ago [It is attributed to Galileo]. It is now more true than ever before … Surely complex numbers are far from natural or simple and they cannot be suggested by physical observations. Furthermore, the use of complex numbers is close to being a necessity in the formulation of the laws of quantum mechanics. It is difficult to avoid the impression that a miracle confronts us here , quite comparable in its striking nature to the miracle that the human mind can string a thousand arguments together without getting itself into contradictions, or to the two miracles of the existence of laws of nature and of the human mind’s capacity to divine them. The closest explanation [for this mathematical universe] is Einstein’s statement that “the only physical theories which we are willing to accept are the beautiful ones” … the concepts of mathematics have this quality of beauty.

• 2 $\begingroup$ I have to disagree. Wigner's assertion that "mathematics is the science of skillful operations with concepts and rules invented just for this purpose" is the whole basis of his piece, and it doesn't have much to do with mathematics. The article is quasi-religious speculation based on this false premise. (The example that Wigner opens the article with is a case in point - he marvels at the appearance of $\sqrt{\pi}$ in the pdf for the normal distribution, as if this were magic. But probability theory was developed with very practical applications in mind.) $\endgroup$ –  Paul Levy May 23, 2017 at 9:31

A Drifter of Dadaist Persuasion by Matilde Marcolli, published in Art in the Life of Mathematicians (Edited by Anna Kepes Szemerédi) American Mathematical Society, 2015, pp.210-231

The Psychology of Invention in the Mathematical Field (Jacques Hadamard's 1945 essay)

• $\begingroup$ This book was very influential to me, and made a huge difference in helping me understand m own process of doing mathematics. $\endgroup$ –  Zach H Jul 17, 2017 at 17:13
• $\begingroup$ I love "the Poincare-Hadamard metaphor" described there! It says that our thoughts conscious and unconscious ones and their interactions could be explained via a mechanical model of states of a system of particles(the details inside). Very inspiring and still I haven't found an enough obstruction to the presented point of view there to the modern neuroscience, but I do not know much about it. An expertise needed! :) $\endgroup$ –  P. Grabowski Apr 14, 2020 at 18:42

The Mathematician by John Von Neumannn.

Enigmas of Chance , by Mark Kac.

I would add "Letters to a Young Mathematician" by Ian Stewart

I recommend:

Vladimir Arnold: Yesterday and Long Ago . This is a very enjoyable and highly interesting collection of anecdotes and historical remarks. The latest Russian edition of this book contains some more chapters. Richard Hamming: You and Your Research , transcribed and edited by J F Kaiser, reprinted in Tveito et al: Simula Research Laboratory . This is the text of a lecture of Hamming.

Birth of a Theorem , by French candidate for Parliament Cédric Villani

• 4 $\begingroup$ Now French member of Parliament Cédric Villani. $\endgroup$ –  Michael Lugo Jul 17, 2017 at 15:16

Here are additional mathematicians' thoughts.

S. Ulam, Adventures of a mathematician .A recollection of his life, from Lwow to Los Alamos. I am linking to excerpts. The book is still available for purchase.

Advices to a Young mathematician , a collection of advice and anecdotes by M. Atiyah, B. Bollobas, A. Connes, D. McDuff and P. Sarnak.

A. Borel, Art and science (Math. Intelligencer vol.5 1983, translation from German). A text for a general audience about the relationship between art and mathematics.

R. P. Langlands Is there beauty in mathematical theories? , this text is actually about number theory, old and new.

T. Gowers The two cultures of mathematics , another take on the dichotomy between problem solving and theory building.

A. Connes A view of mathematics , a thorough exposition of A. Connes'philosophical stance about space and physics. Targeted at a scientific audience.

D. Mumford, the dawning of the age of stochasticity , from algebraic geometry to statistics.

Y. Manin, Interrelations between Mathematics and Physics , on the divergence between mathematics and physics in the XXe century.

M. Gromov, ergobrain , one of the most surprising inquiry about life and mathematics.

I end that list with a text from a french mathematician about the future of mathematics: Poincare, l'avenir des mathematiques .

Perhaps a little broader in range/scope than the original question intended — but then again, perhaps not — the essays collected in

Mathématiques, mathematiciens et société. Publications Mathématiques d'Orsay no. 86 74-16 (1974)

I was led to this when someone somewhere posted a link to Vergne's Témoignage d'une mathématicienne , which is one of the essays in this volume, and — I must confess — is the only one I've read, although the other ones do look interesting

In the Princeton Companion to Mathematics , there is a section entitled Advice to a Young Mathematician (pdf), containing essays by Atiyah, Bollobás, Connes, McDuff and Sarnak.

A Mathematician's Miscellany (reprinted, with additional material, as Littlewood's Miscellany by CUP in 1986) is worthwhile reading.

Clifford Truesdell published a series of essays as An Idiot's Fugitive Essays on Science Methods, Criticism, Training, Circumstances (Springer, 1984), which sets out in a forthright manner the author's views on mathematics and science.

A really nice article by Andrei Toom about mathematical education, especially in the US, got recently mentioned in a comment to this question.

• Featured on Meta
• Testing a new version of Stack Overflow Jobs
• What deliverables would you like to see out of a working group?

• Forums New posts Search Forums
• Members Registered members Current visitors Recent Activity
• Free Assessment

Updates WAEC Mathematics Essay & Obj Answers 2024

• Thread starter clutech
• Start date Tuesday at 10:38 AM

Note: Pay #1,500 and get Questions and Answers now Click to expand...

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson