case study questions based on applications of trigonometry

• Bihar Board
• RBSE 12th Result 2024

SRM University

• RBSE 10th Result 2024
• Maharashtra HSC Result
• MBSE Result 2024
• TBSE Result 2024
• CBSE Board Result 2024
• Shiv Khera Special
• Education News
• Web Stories
• Current Affairs
• नए भारत का नया उत्तर प्रदेश
• School & Boards
• College Admission
• Govt Jobs Alert & Prep
• GK & Aptitude
• CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 9 - Some Applications of Trigonometry (Published By CBSE)

Check case study questions for cbse class 10 maths chapter 9 - some applications of trigonometry. these questions are published by the cbse itself for class 10 students..

Case study based questions are new for class 10 students. Therefore, it is quite essential that students practice with more of such questions so that they do not have problem in solving them in their Maths board exam. We have provided here the case study questions for CBSE Class 10 Maths Chapter 9 - Some Applications of Trigonometry. All these questions have been published by the Central Board of Secondary Education (CBSE) for the class 10 students. Therefore, students must solve all the questions seriously so that they may score the desired marks in their Maths exam.

Check Case Study Questions for Class 10 Maths Chapter 9:

CASE STUDY 1:

A group of students of class X visited India Gate on an education trip. The teacher and students had interest in history as well. The teacher narrated that India Gate, official name Delhi Memorial, originally called All-India War Memorial, monumental sandstone arch in New Delhi, dedicated to the troops of British India who died in wars fought between 1914 and 1919. The teacher also said that India Gate, which is located at the eastern end of the Rajpath (formerly called the Kingsway), is about 138 feet (42 metres) in height.

1. What is the angle of elevation if they are standing at a distance of 42m away from the monument?

Answer: b) 45 o

2. They want to see the tower at an angle of 60 o . So, they want to know the distance where they should stand and hence find the distance.

Answer: a) 25.24 m

3. If the altitude of the Sun is at 60 o , then the height of the vertical tower that will cast a shadow of length 20 m is

a) 20√3 m

b) 20/ √3 m

c) 15/ √3 m

d) 15√3 m

Answer: a) 20√3 m

4. The ratio of the length of a rod and its shadow is 1:1. The angle of elevation of the Sun is

5. The angle formed by the line of sight with the horizontal when the object viewed is below the horizontal level is

a) corresponding angle

b) angle of elevation

c) angle of depression

d) complete angle

Answer: a) corresponding angle

CASE STUDY 2:

A Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka, them being Nanda Devi(height 7,816m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite, to the top of Nanda Devi and Mullayanagiri are 30° and 60° respectively. If the distance between the peaks of the two mountains is 1937 km, and the satellite is vertically above the midpoint of the distance between the two mountains.

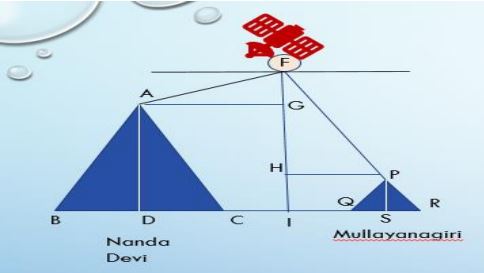
1. The distance of the satellite from the top of Nanda Devi is

a) 1139.4 km

b) 577.52 km

d) 1025.36 km

Answer: a) 1139.4 km

2. The distance of the satellite from the top of Mullayanagiri is

Answer: c) 1937 km

3. The distance of the satellite from the ground is

Answer: b) 577.52 km

4. What is the angle of elevation if a man is standing at a distance of 7816m from Nanda Devi?

5.If a mile stone very far away from, makes 45 o to the top of Mullanyangiri mountain. So, find the distance of this mile stone from the mountain.

a) 1118.327 km

b) 566.976 km

Also Check:

Case Study Questions for All Chapters of CBSE Class 10 Maths

Tips to Solve Case Study Based Questions Accurately

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check  Board Result 2024  for Class 10 and Class 12 like  CBSE Board Result ,  UP Board Result ,  Bihar Board Result ,  MP Board Result ,  Rajasthan Board Result  and Other States Boards.

• Rajasthan Board 12th Result 2024
• rajeduboard.rajasthan.gov.in Result 2024
• Rajasthan Board Class 12th Result 2024
• 12th Result 2024 Rajasthan Board
• rajresults.nic.in Result 2024
• RBSE 12th Toppers List 2024
• Jagran Josh 12th Result 2024 RBSE
• rajresults.nic.in 12th Result 2024
• 12th Result 2024 RBSE Roll Number और Name wise
• CBSE Study Material
• CBSE Class 10

Latest Education News

Class 9 Chemistry Project Ideas 2024-25 For Summer Vacation

[यहाँ देखें] RBSE 12th Result 2024: Check आरबीएसई Rajasthan Class 12 Arts, Science, Commerce Results at rajeduboard.rajasthan.gov.in with Roll Number and Name-wise

UPSC CDS 2 Eligibility Criteria 2024: Check Age Limit, Qualification and Nationality

Driving License Rules Changed: Here are all the details you need to know

JK Bank Recruitment 2024 Notification Out for 276 Apprentice Posts; Check Eligibility, Salary & More

IPL Qualifier, Eliminator Schedule 2024: Match Dates, Time, Venue and How to Watch Live Stream

RBSE 12th Result 2024 OUT: रिजल्ट जारी, कला वर्ग में तरुणा बनी प्रदेश टॉपर, 10th का रिजल्ट कब होगा जारी, जानें

[कला रिजल्ट] Rajasthan Board 12th Result 2024: 12वीं आर्ट्स में 96.88% छात्र पास, Umang App और Digilocker पर तुरंत देखें रिजल्ट

[चेक करें] rajresults.nic.in 2024 Result: राजस्थान 12वीं रिजल्ट का लिंक, Roll Number से परिणाम देखे और डाउनलोड करें Inter की Marksheet

Upcoming Government Jobs 2024 LIVE: Employment News May (18-24) 2024, Notifications, Admit Card, Exam Date, Result and much more

JAC 8th Result 2024 Link: झारखंड बोर्ड 8वीं का रिजल्ट jacresults.com पर, यहां Roll Number से डाउनलोड कर सकेंगे मार्कशीट

Indian Army Dental Corps Recruitment 2024: Apply Online For Various Posts, Check Eligibility

Heat Waves Causes Early Summer Vacation for Punjab Schools, Schools to Remain Closed from Tomorrow

[डायरेक्ट लिंक] jac.jharkhand.gov.in 8th Result 2024: झारखंड बोर्ड कक्षा 8वीं का रिजल्ट jacresults.com पर जल्द, रोल नंबर से यहां देखें जेएसी 9वीं, 11वीं के नतीजे

UGC NET 2024 Application Correction: Direct Link, Steps to Edit June 2024 Forms

केंद्र में सरकार बनाने के लिए कितने बहुमत की जरूरत होती है, जानें

UPSC CSE Prelims Important Questions 2024 for General Studies (GS) with Answers

[LIVE] RBSE 12th Result 2024 OUT: राजस्थान बोर्ड 12वीं रिजल्ट Direct Link rajeduboard.rajasthan.gov.in, rajresults.nic.in पर एक्टिव, यहां Roll Number और नाम से करें चेक

ट्रेन का टिकट खोने या फटने पर क्या करें, यहां पढ़ें

DBRAU Result 2024 Out: डॉ. भीमराव अंबेडकर यूनिवर्सिटी रिजल्ट dbrau.ac.in पर जारी, देखें आगरा यूनिवर्सिटी यूजी और पीजी सेमेस्टर मार्कशीट डाउनलोड लिंक

CBSE Expert

Class 10 Maths: Case Study Questions of Chapter 9 Some Applications of Trigonometry PDF

Case study Questions on the Class 10 Mathematics Chapter 9  are very important to solve for your exam. Class 10 Maths Chapter 9 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 10 Maths Chapter 9 Some Applications of Trigonometry

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on  Assertion and Reason . There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Some Applications of Trigonometry Case Study Questions With answers

Here, we have provided case-based/passage-based questions for Class 10 Maths  Chapter 9 Some Applications of Trigonometry

Case Study/Passage Based Questions

There are two temples on each bank of a river. One temple is 50 m high. A man, who is standing on the top of a 50 m high temple, observed from the top that the angle of depression of the top and foot of other temples are 30° and 60° respectively.

The measure of ∠ADF is equal to (a) 45° (b) 60° (c) 30° (d) 90°

Answer: (c) 30°

A measure of ∠ACB is equal to (a) 45° (b) 60° (c) 30° (d) 90°

Answer: (b) 60°

Width of the river is (a) 28.90 m (b) 26.75 m (c) 25 m (d) 27 m

Answer: (a) 28.90 m

The height of the other temple is (a) 32.5 m (b) 35 m (c) 33.33 m (d) 40 m

Answer: (c) 33.33 m

The angle of depression is always (a) reflex angle (b) straight (c) an obtuse angle (d) an acute angle

Answer: (d) an acute angle

Rohit is standing at the top of the building observes a car at an angle of 30°, which is approaching the foot of the building at a uniform speed. 6 seconds later, the angle of depression of the car formed to be 60°, whose distance at that instant from the building is 25 m.

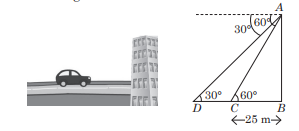
The height of the building is (a) 25√2 m (b) 50 m (c) 25√3 m (d) 25 m

Answer: (c) 25√3 m

Distance between two positions of the car is (a) 40 m (b) 50 m (c) 60 m (d) 75 m

Answer: (b) 50 m

Total time is taken by the car to reach the foot of the building from the starting point is (a) 4 secs (b) 3 secs (c) 6 secs (d) 9 secs

Answer: (d) 9 secs

The distance of the observer from the car when it makes an angle of 60° is (a) 25 m (b) 45 m (c) 50 m (d) 75 m

Answer: (c) 50 m

The angle of elevation increases (a) when point of observation moves towards the object (b) when point of observation moves away from the object (c) when object moves away from the observer (d) None of these

Answer: (a) when point of observation moves towards the object

Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 9 Some Applications of Trigonometry with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 10 Maths Some Applications of Trigonometry Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 10 Maths Chapter 9 Applications of Trigonometry

• Last modified on: 10 months ago
• Reading Time: 9 Minutes

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies as well. In that, a paragraph will be given, and then the MCQ questions or subjective questions based on it will be asked.

Here, we have provided case based/passage-based questions for Class 10 Maths Chapter 9 Applications of Trigonometry

Case Study Questions:

Question 1:

A Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka, them being Nanda Devi (height 7,816m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite to the top of Nanda Devi and Mullayanagiri are 30° and 60° respectively. If the distance between the peaks of two mountains is 1937 km, and the satellite is vertically above the midpoint of the distance between the two mountains.

(i) The distance of the satellite from the top of Mullayanagiri is

(a) 1139.4 km

(b) 577.52 km

(c) 1937 km

(d) 1025.36 km

(ii) If a mile stone very far away from, makes 45 to the top of Mullanyangiri mountain. So, find the distance of this milestone form the mountain.

(a) 1118.327 km

(b) 566.976 km

(iii) The distance of the satellite from the ground is

(iv) The distance of the satellite from the top of Nanda Devi is

(v) What is the angle of elevation if a man is standing at a distance of 7816m from Nanda Devi?

Question 2:

A group of students of class X visited India Gate on an educational trip. The teacher and students had interest in history as well. The teacher narrated that India Gate, official name Delhi Memorial, originally called All-India War Memorial, monumental sandstone arch in New Delhi, dedicated to the troops of British India who died in wars fought between 1914 and 1919.The teacher also said that India Gate, which is located at the eastern end of the Rajpath (formerly called the Kingsway), is about 138 feet (42 m) in height.

(i) What is the angle of elevation if they are standing at a distance of 42 m away from the monument? (a) 30° (b) 45° (c) 60° (d) 0°

(ii) They want to see the tower at an angle of 60°. So, they want to know the distance where they should stand and hence find the distance. (a) 25.24 m (b) 20.12 m (c) 42 m (d) 24.24 m

(iii) If the altitude of the Sun is at 60°, then the height of the vertical tower that will cast a shadow of length 20 m is (a) 20 √ 3 m (b) 20/ √ 3 m (c) 15/ √ 3 m (d) 15 √ 3 m

(iv) The ratio of the length of a rod and its shadow is 1 : 1. The angle of elevation of the Sun is (a) 30° (b) 45° (c) 60° (d) 90°

(v) The angle formed by the line of sight with the horizontal when the object viewed is below the horizontal level is (a) corresponding angle (b) angle of elevation (c) angle of depression (d) complete angle

✨ Free Quizzes, Test Series and Learning Videos for CBSE Class 10 Maths

You may also like:

Chapter 1 Real Numbers Chapter 2 Polynomials Chapter 3 Pair of Linear Equations in Two Variables C hapter 4 Quadratic Equations Chapter 5 Arithmetic Progressions Chapter 6 Triangles Chapter 7 Coordinate Geometry Chapter 8 Introduction to Trigonometry Chapter 9 Some Applications of Trigonometry Chapter 10 Circles Chapter 11 Constructions Chapter 12 Areas Related to Circles Chapter 13 Surface Areas and Volumes Chapter 14 Statistics Chapter 15 Probability

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

Class 10 Maths Case Study Questions Chapter 8 Introduction to Trigonometry

• Post author: studyrate
• Post published:
• Post category: class 10th
• Post comments: 0 Comments

Case study Questions in the Class 10 Mathematics Chapter 8  are very important to solve for your exam. Class 10 Maths Chapter 8 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving Class 10 Maths Case Study Questions Chapter 8  Introduction to Trigonometry

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Introduction to Trigonometry Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 10 Maths  Chapter 8 Introduction to Trigonometry

Case Study/Passage-Based Questions

Question 1:

Answer: (d) 6m

(ii) Measure of ∠A =

Answer: (c) 45°

(iii) Measure of ∠C =

(iv) Find the value of sinA + cosC.

Answer: (d) 2√2

(v) Find the value of tan 2 C + tan 2  A.

Answer: (c) 2

Question 2:

Answer: (a) 30°

(ii) The measure of  ∠C is

Answer: (c) 60°

(iii) The length of AC is 

Answer: (d)6√3m

(iv) cos2A =

Answer: (b)1/2

Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 10 Maths Introduction to Trigonometry Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

You Might Also Like

Cbse class 10 english term 2 mcq questions with answers pdf download, assertion reason questions class 10 science chapter 9 heredity and evolution.

Class 10 Science Topper’s Answer Sheet Latest PDF Download FREE

Leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11: Applications of Trigonometry

• Last updated
• Save as PDF
• Page ID 80825

• Carl Stitz & Jeff Zeager
• Lakeland Community College & Lorain County Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

• 11.1: Applications of Sinusoids In the same way exponential functions can be used to model a wide variety of phenomena in nature, the cosine and sine functions can be used to model their fair share of natural behaviors
• 11.2: The Law of Sines Trigonometry literally means 'measuring triangles', we are more than prepared to do just that. The main goal of this section and the next is to develop theorems which allow us to 'solve' triangles -- that is, find the length of each side of a triangle and the measure of each of its angles.
• 11.3: The Law of Cosines The Law of Sines to enable us to solve triangles in the 'Angle-Angle-Side' (AAS), the 'Angle-Side-Angle' (ASA) and the ambiguous 'Angle-Side-Side' (ASS) cases. In this section, we develop the Law of Cosines which handles solving triangles in the 'Side-Angle-Side' (SAS) and 'Side-Side-Side' (SSS) cases.
• 11.4: Polar Coordinates Cartesian coordinates of a point are often called 'rectangular' coordinates. In this section, we introduce a new system for assigning coordinates to points in the plane -- polar coordinates. We start with an origin point, called the pole, and a ray called the polar axis. We then locate a point PP using two coordinates, (r,θ), where r represents a directed distance from the pole.
• 11.5: Graphs of Polar Equations In this section, we discuss how to graph equations in polar coordinates on the rectangular coordinate plane.
• 11.6: Hooked on Conics Again In this section, we revisit our friends the Conic Sections which we began studying in Chapter 7. Our first task is to formalize the notion of rotating axes.  Armed with polar coordinates, we can generalize the process of rotating axes as shown below.
• 11.7: Polar Form of Complex Numbers In this section, we return to our study of complex numbers. We associate each complex number z=a+biz=a+bi with the point (a,b)(a,b) on the coordinate plane. In this case, the xx -axis is relabeled as the real axis, which corresponds to the real number line as usual, and the yy -axis is relabeled as the imaginary axis, which is demarcated in increments of the imaginary unit ii . The plane determined by these two axes is called the complex plane.
• 11.8: Vectors To answer questions that involve both a quantitative answer, or magnitude, along with a direction, we use the mathematical objects called vectors. The word 'vector' comes from the Latin vehere meaning 'to convey' or 'to carry.' A vector is represented geometrically as a directed line segment where the magnitude of the vector is taken to be the length of the line segment and the direction is made clear with the use of an arrow at one endpoint of the segment.
• 11.9: The Dot Product and Projection Previously, we learned how add and subtract vectors and how to multiply vectors by scalars. In this section, we define a product of vectors.
• 11.10: Parametric Equations There are scores of interesting curves which, when plotted in the xy-plane, neither represent y as a function of x nor x as a function of y. In this section, we present a new concept which allows us to use functions to study these kinds of curves.

CBSE Case Study Questions for Class 10 Maths Trigonometry Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 10 Maths Trigonometry  in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 10 Maths Trigonometry PDF

Checkout our case study questions for other chapters.

• Chapter 6 Triangles Case Study Questions
• Chapter 7 Coordinate Geometry Case Study Questions
• Chapter 9 Some Applications of Trigonometry Case Study Questions
• Chapter 10 Circles Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Contact Form

Privacy Policy

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

CBSE Class 10 Sample Paper for 2022 Boards - Maths Standard [Term 2]

• CBSE Class 10 Sample Paper for 2024 Boards - Maths Standard
• CBSE Class 10 Sample Paper for 2023 Boards - Maths Standard
• Practice Questions CBSE - Maths Class 10 (2023 Boards)
• CBSE Class 10 Sample Paper for 2023 Boards - Maths Basic
• CBSE Class 10 Sample Paper for 2022 Boards - Maths Basic [Term 2]
• CBSE Class 10 Sample Paper for 2022 Boards - Maths Standard [MCQ]
• CBSE Class 10 Sample Paper for 2022 Boards - Maths Basic [MCQ]
• CBSE Class 10 Sample Paper for 2021 Boards - Maths Standard
• CBSE Class 10 Sample Paper for 2021 Boards - Maths Basic
• CBSE Class 10 Sample Paper for 2020 Boards - Maths Standard
• CBSE Class 10 Sample Paper for 2020 Boards - Maths Basic
• CBSE Class 10 Sample Paper for 2019 Boards
• CBSE Class 10 Sample Paper for 2018 Boards

Question 13 - Case Study - CBSE Class 10 Sample Paper for 2022 Boards - Maths Standard [Term 2] - Solutions of Sample Papers for Class 10 Boards

Last updated at April 16, 2024 by Teachoo

Trigonometry in the form of triangulation forms the basis of navigation, whether it is by land, sea or air. GPS a radio navigation system helps to locate our position on earth with the help of satellites. A guard, stationed at the top of a 240m tower, observed an unidentified boat coming towards it. A clinometer or inclinometer is an instrument used fo measuring angles or slopes(tilt). The guard used the clinometer to measure the angle of depression of the boat coming towards the lighthouse and found it to be 30°.(Lighthouse of Mumbai Harbour. Picture credits - Times of India Travel) i) Make a labelled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation tower.

Ii) after 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(√3 - 1) m. he immediately raised the alarm. what was the new angle of depression of the boat from the top of the observation tower.

This question is similar to Ex 9.1, 13 Chapter 9 Class 10 - Some Applications of Trigonometry

Trigonometry in the form of triangulation forms the basis of navigation, whether it is by land, sea or air. GPS a radio navigation system helps to locate our position on earth with the help of satellites. A guard, stationed at the top of a 240m tower, observed an unidentified boat coming towards it. A clinometer or inclinometer is an instrument used fo measuring angles or slopes(tilt). The guard used the clinometer to measure the angle of depression of the boat coming towards the lighthouse and found it to be 30°. (Lighthouse of Mumbai Harbour. Picture credits - Times of India Travel) i) Make a labelled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation tower. ii) After 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(√3 - 1) m. He immediately raised the alarm. What was the new angle of depression of the boat from the top of the observation tower? Making a labelled figure Given that height of the lighthouse is 240 m Hence, AC = 240 m And angle of depression of boat is 30° So, ∠ PAB = 30 ° Since Angle of depression = Angle of elevation ∴ ∠ ABC = 30° Question 13 (i) Make a labelled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation tower. We need to find distance between boat and tower, i.e. BC In right angled triangle ΔABC, tan B = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐵)/(𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐵) tan 30° = 𝐴𝐶/𝐵𝐶 (" " 1)/√3 = (" " 240)/𝐵𝐶 BC = 240√𝟑 m Question 13 (ii) After 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(√3−1) m. He immediately raised the alarm. What was the new angle of depression of the boat from the top of the observation tower? Let Boat be now at point D Since Distance of tower is reduced by 240(√3−1) m Hence, BD = 𝟐𝟒𝟎(√𝟑−𝟏) m Let angle of depression of boat now be θ So, ∠ PAD = θ ° Since Angle of depression = Angle of elevation ∴ ∠ ADC = θ Also, CD = BC − BD = 240√3 −240(√3−1) = 240√3 −240√3+240 = 𝟐𝟒𝟎 m Now, In right angled triangle ΔABC, tan D = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐵)/(𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝐵) tan θ = 𝐴𝐶/𝐶𝐷 tan θ = 𝟐𝟒𝟎/𝟐𝟒𝟎 tan θ = 1 ∴ θ = 45° Thus, required angle of depression is 45°

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

• New QB365-SLMS
• NEET Materials
• JEE Materials
• Banking first yr Materials
• TNPSC Materials
• DIPLOMA COURSE Materials
• 5th Standard Materials
• 12th Standard Materials
• 11th Standard Materials
• 10th Standard Materials
• 9th Standard Materials
• 8th Standard Materials
• 7th Standard Materials
• 6th Standard Materials
• 12th Standard CBSE Materials
• 11th Standard CBSE Materials
• 10th Standard CBSE Materials
• 9th Standard CBSE Materials
• 8th Standard CBSE Materials
• 7th Standard CBSE Materials
• 6th Standard CBSE Materials
• Tamilnadu Stateboard
• Scholarship Exams
• Scholarships

CBSE 10th Standard Maths Subject Introduction to Trigonometry Case Study Questions 2021

By QB365 on 22 May, 2021

QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get  more marks in Exams

QB365 - Question Bank Software

10th Standard CBSE

Final Semester - June 2015

Case Study Questions

(ii) The measure of   \(\angle\) C is

(iii) The length of AC is 

(iv) cos2A =

(v) sin  \(\left(\frac{C}{2}\right)\) =

(ii) Find cot B

(iii) Find tanA.

(iv) Find secA.

(v) Find cosecB.

(ii) The value of sec  \(\theta\)   =

(iii) The value of  \(\frac{\tan \theta}{1+\tan ^{2} \theta}=\)

(iv) The value of  \(\cot ^{2} \theta-\operatorname{cosec}^{2} \theta=\)  

(v) The value of  \(\sin ^{2} \theta+\cos ^{2} \theta=\)

(ii) The value of \(\angle\) K =

(iii) Find the value of tanM.

(iv) sec 2 M - 1 =

(v) The value of  \(\frac{\tan ^{2} 45^{\circ}-1}{\tan ^{2} 45^{\circ}+1}\)   is

(ii) Measure of \(\angle\) A =

(iii) Measure of \(\angle\) C =

(iv) Find the value of sinA + cosC.

(v) Find the value of tan 2 C + tan 2 A.

*****************************************

Cbse 10th standard maths subject introduction to trigonometry case study questions 2021 answer keys.

(i) (a): We have, AB = 9 m, BC = 3 \(\sqrt{3}\) m In   \(\Delta\) ABC, we have \(\tan A=\frac{B C}{A B}=\frac{3 \sqrt{3}}{9}=\frac{1}{\sqrt{3}} \) \(\Rightarrow \tan A=\tan 30^{\circ} \Rightarrow \angle A=30^{\circ}\) (ii) (c): Similarly,  \(\tan C=\frac{A B}{B C}=\frac{9}{3 \sqrt{3}}=\sqrt{3}\) \(\Rightarrow \tan C=\tan 60^{\circ} \Rightarrow \angle C=60^{\circ}\) (iii) (d): Since  \(\sin A=\frac{B C}{A C} \Rightarrow \sin 30^{\circ}=\frac{B C}{A C}\) \(\Rightarrow \frac{1}{2}=\frac{3 \sqrt{3}}{A C} \Rightarrow A C=6 \sqrt{3} \mathrm{~m}\) (iv) (b) :   \(\because \angle A=30^{\circ}\)   [From (1)] \(\therefore \quad \cos 2 A=\cos \left(2 \times 30^{\circ}\right)=\cos 60^{\circ}=\frac{1}{2}\)   (v) (b):   \(\because \angle C=60^{\circ}\)   [Using (2)] \(\therefore \quad \sin \left(\frac{C}{2}\right)=\sin \left(\frac{60^{\circ}}{2}\right)=\sin 30^{\circ}=\frac{1}{2}\)

(i) (d) :   \(\text { In } \Delta A P Q, \tan \theta=\frac{A Q}{P Q}=\frac{1.2}{1.6}=\frac{3}{4}\) (ii) (d) :   \(\text { In } \Delta P B Q, \cot B=\frac{Q B}{P Q}=\frac{3}{1.6}=\frac{15}{8}\)  ... (i) (iii) (c):   \(\text { In } \Delta A P Q, \tan A=\frac{P Q}{A Q}=\frac{1.6}{1.2}=\frac{4}{3}\)   ...(ii) (iv) (d) : We have, tan 2 A + 1 = sec 2 A \(\Rightarrow \sec A =\sqrt{\left(\frac{4}{3}\right)^{2}+1} \) \(=\sqrt{\frac{16}{9}+1}=\sqrt{\frac{25}{9}}=\frac{5}{3}\) (v) (a): Since  \(\operatorname{cosec} B=\sqrt{\cot ^{2} B+1}\) \(\begin{array}{l} =\sqrt{\left(\frac{15}{8}\right)^{2}+1} \\ =\frac{17}{8} \end{array}\)

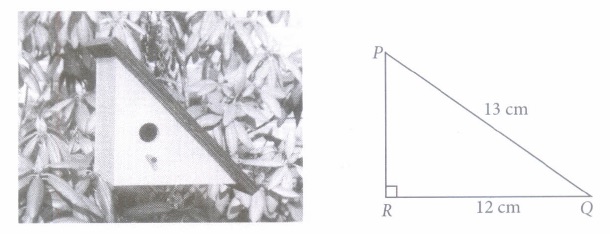
\(\because \Delta\) PQR is a right angled triangle. \(\therefore\)   PR 2 + RQ 2 = PQ 2 \(\Rightarrow P R^{2}=(13)^{2}-(12)^{2}=25 \Rightarrow P R=5 \mathrm{~cm}\) (i) (c) :  \(\cos \theta=\frac{Q R}{P Q}=\frac{12}{13} \) (ii) (c) :   \(\sec \theta=\frac{1}{\cos \theta}=\frac{13}{12} \) (iii) (c) :   \(\tan \theta=\frac{P R}{R Q}=\frac{5}{12}\) \(\therefore \frac{\tan \theta}{1+\tan ^{2} \theta}=\frac{\frac{5}{12}}{1+\frac{25}{144}}=\frac{\frac{5}{12}}{\frac{169}{144}}=\frac{60}{169}\) (iv) (a):  \(\cot \theta=\frac{1}{\tan \theta}=\frac{12}{5}\)      [Using (1)] \(\operatorname{cosec} \theta=\frac{P Q}{P R}=\frac{13}{5} \) \(\therefore \quad \cot ^{2} \theta-\operatorname{cosec}^{2} \theta=\frac{144}{25}-\frac{169}{25}=-1\) (v) (b):   \(\sin ^{2} \theta+\cos ^{2} \theta=1\)   (Using identity)

We have, KL = 4 cm, ML = 4 \(\sqrt{3}\) m, KM = 8 cm (i) (a):   \(\tan M=\frac{K L}{L M}=\frac{4}{4 \sqrt{3}}=\frac{1}{\sqrt{3}}\) \(\Rightarrow \tan M=\tan 30^{\circ} \Rightarrow \angle M=30^{\circ}\) (ii) (c) :   \(\tan K=\frac{M L}{K L}=\frac{4 \sqrt{3}}{4}=\sqrt{3}=\tan 60^{\circ}\) \(\Rightarrow \angle K=60^{\circ}\) (iii) (b) (iv) (c) (v) (a) :  \(\frac{\tan ^{2} 45^{\circ}-1}{\tan ^{2} 45^{\circ}+1}=\frac{(1)^{2}-1}{1^{2}+1}=\frac{0}{2}=0\)

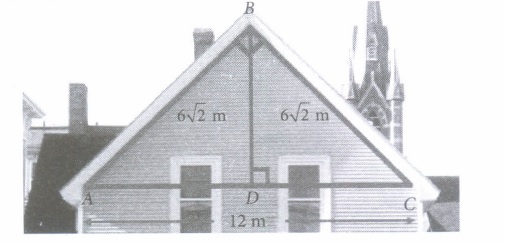
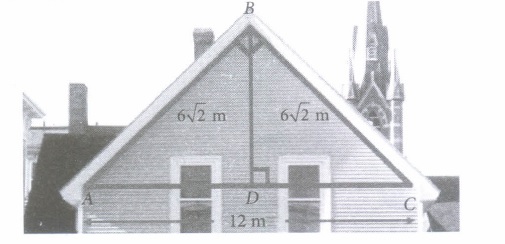
We have, AB = BC = 6 \(\sqrt{2}\) m and AC=12m . (i) (d) : \(\because\)   Dis mid point of AC. \(\therefore\)   AD=DC=6m Now, AB 2 = BD 2 + AD 2 ( \(\therefore\) \(\Delta\) ABD is a right triangle) \(\Rightarrow B D^{2}=(6 \sqrt{2})^{2}-6^{2}=72-36=36 \) \(\Rightarrow B D=6 \mathrm{~m}\) (ii) (c) :  \(\operatorname{In} \Delta A B D, \sin A=\frac{B D}{A B}=\frac{6}{6 \sqrt{2}}=\frac{1}{\sqrt{2}}\) \(\Rightarrow \sin A=\sin 45^{\circ} \Rightarrow \angle A=45^{\circ}\) (iii) (c) :  \(\operatorname{In} \Delta B D C, \tan C=\frac{B D}{D C}=\frac{6}{6}\) \(\Rightarrow \tan C=1=\tan 45^{\circ} \Rightarrow \angle C=45^{\circ}\) (iv) (d) :  \(\sin A=\frac{1}{\sqrt{2}}, \cos C=\cos 45^{\circ}=\frac{1}{\sqrt{2}}\) \(\therefore \quad \sin A+\cos C=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\) (v) (c):  \((v) \quad(c): \tan C=1, \tan A=\tan 45^{\circ}=1\) \(\Rightarrow \tan ^{2} C+\tan ^{2} A=1+1=2\)  

Related 10th Standard CBSE Maths Materials

10th standard cbse syllabus & materials, cbse 10th social science the making of a global world chapter case study question with answers, cbse 10th social science nationalism in india chapter case study question with answers, cbse 10th social science the rise of nationalism in europe chapter case study question with answers, cbse 10th science metals and non metals chapter case study question with answers, cbse 10th science acids, bases and salts chapter case study question with answers, cbse 10th science chemical reactions and equations chapter case study question with answers, class 10th science - our environment case study questions and answers 2022 - 2023, class 10th science - magnetic effects of electric current case study questions and answers 2022 - 2023, class 10th science - electricity case study questions and answers 2022 - 2023, class 10th science - human eye and the colourful world case study questions and answers 2022 - 2023, class 10th science - light reflection and refraction case study questions and answers 2022 - 2023, class 10th science - heredity and evolution case study questions and answers 2022 - 2023, class 10th science - how do organisms reproduce case study questions and answers 2022 - 2023, class 10th science - life processes case study questions and answers 2022 - 2023, class 10th science - periodic classification of elements case study questions and answers 2022 - 2023.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

10th Standard CBSE Study Materials

10th Standard CBSE Subjects

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• ML Aggarwal Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• HOTS Question
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Crash Course
• JEE Previous Year Paper
• Important Info
• JEE Mock Test
• JEE Sample Papers
• SRM-JEEE Mock Test
• VITEEE Mock Test
• BITSAT Mock Test
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• COMEDK Previous Year Paper
• GUJCET Previous Year Paper
• KCET Previous Year Paper
• KEAM Previous Year Paper
• Manipal Previous Year Paper
• MHT CET Previous Year Paper
• WBJEE Previous Year Paper
• AMU Previous Year Paper
• TS EAMCET Previous Year Paper
• SRM-JEEE Previous Year Paper
• VITEEE Previous Year Paper
• BITSAT Previous Year Paper
• UPSEE Previous Year Paper
• CGPET Previous Year Paper
• CUSAT Previous Year Paper
• AEEE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

Case Study on Introduction to Trigonometry Class 10 Maths PDF

The passage-based questions are commonly known as case study questions. Students looking for Case Study on Introduction to Trigonometry Class 10 Maths can use this page to download the PDF file. 

The case study questions on Introduction to Trigonometry are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Introduction to Trigonometry case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.

Case Study on Introduction to Trigonometry Class 10 Maths with Solutions in PDF

Our experts have also kept in mind the challenges students may face while solving the case study on Introduction to Trigonometry, therefore, they prepared a set of solutions along with the case study questions on Introduction to Trigonometry.

The case study on Introduction to Trigonometry Class 10 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Introduction to Trigonometry case study questions are very easy to grasp from the PDF - download links are given on this page.

Why Solve Introduction to Trigonometry Case Study Questions on Class 10 Maths?

There are three major reasons why one should solve Introduction to Trigonometry case study questions on Class 10 Maths - all those major reasons are discussed below:

• To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 10 Maths students, therefore, it is important to solve Introduction to Trigonometry Case study questions as it will help better prepare for the Class 10 board exam preparation.
• Develop Problem-Solving Skills: Class 10 Maths Introduction to Trigonometry case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any profession rather than Class 10 board exam preparation.
• Understand Real-Life Applications: Several Introduction to Trigonometry Class 10 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Introduction to Trigonometry as well as real-life implications of those learnings too.

How to Answer Case Study Questions on Introduction to Trigonometry?

Students can choose their own way to answer Case Study on Introduction to Trigonometry Class 10 Maths, however, we believe following these three steps would help a lot in answering Class 10 Maths Introduction to Trigonometry Case Study questions.

• Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
• Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Introduction to Trigonometry questions quickly.
• Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Introduction to Trigonometry Class 10 Maths case study questions make sure you are approaching each question in a step-wise manner.

What to Know to Solve Case Study Questions on Class 10 Introduction to Trigonometry?

 A few essential things to know to solve Case Study Questions on Class 10 Introduction to Trigonometry are -

• Basic Formulas of Introduction to Trigonometry: One of the most important things to know to solve Case Study Questions on Class 10 Introduction to Trigonometry is to learn about the basic formulas or revise them before solving the case-based questions on Introduction to Trigonometry.
• To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 10 Maths Introduction to Trigonometry case study questions.
• Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.

Where to Find Case Study on Introduction to Trigonometry Class 10 Maths?

Use Selfstudys.com to find Case Study on Introduction to Trigonometry Class 10 Maths. For ease, here is a step-wise procedure to download the Introduction to Trigonometry Case Study for Class 10 Maths in PDF for free of cost.

Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Introduction to Trigonometry. To help others reach this page let them know these steps:

• Open Selfstudys.com on your computer/laptop or Smartphone 
• Once the website gets loaded, click on the navigation button

• Find CBSE from the given menu

• Click on Case Study

• Choose Class 10 
• Search Maths and then navigate to the Introduction to Trigonometry Class 10 Maths Case Study

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences

One Last Step...

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

• Class 10 Maths

Important Questions Class 10 Maths Chapter 9 Applications of Trigonometry

Important questions for Class 10 Maths Chapter 9 Some Applications of Trigonometry are provided here for the board exams preparation. The questions are based on the new pattern of CBSE and are as per the revised syllabus. Students who are preparing CBSE 2022-2023 Maths exam are advised to practice these important questions of Some Applications of Trigonometry For Class 10 . Solving these questions will help students to score high marks in the questions asked from this chapter.

Trigonometry has more applications in our daily existence, and hence, the chapter is crucial for the board exam and valuable in many other fields. Most of the questions from this chapter are also asked in the competitive exams such as JEE etc.

• Applications of Trigonometry
• Trigonometry Formula For Class 10
• Trigonometry Table

Below, we have provided the questions of Chapter 9 Applications of Trigonometry with the solutions. Students can als o find additional qu estions without solutions for their practice.

Important Questions & Answers For Class 10 Maths Chapter 9 – Some Applications of Trigonometry

Q.1: The shadow of a tower standing on level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.

Let AB be the tower and BC be the length of its shadow when the sun’s altitude (angle of elevation from the top of the tower to the tip of the shadow) is 60° and DB be the length of the shadow when the angle of elevation is 30°.

Let us assume, AB = h m, BC = x m

DB = (40 +x) m

In the right triangle ABC,

tan 60° = AB/BC

h = √3 x……….(i)

In the right triangle ABD,

tan 30° = AB/BD

1/√3 =h/(x + 40) ……..(ii)

From (i) and (ii),

x(√3 )(√3 ) = x + 40

3x = x + 40

Substituting x = 20 in (i),

Hence, the height of the tower is 20√3 m.

Q. 2: A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

Using given instructions, draw a figure. Let AC be the broken part of the tree. Angel C = 30 degrees.

To Find: Height of the tree, which is AB

From figure: Total height of the tree is the sum of AB and AC i.e. AB+AC

In right ΔABC,

Using Cosine and tangent angles,

cos 30° = BC/AC

We know that, cos 30° = √3/2

√3/2 = 8/AC

AC = 16/√3 …(1)

tan 30° = AB/BC

1/√3 = AB/8

AB = 8/√3 ….(2)

From (1) and (2),

Total height of the tree = AB + AC = 16/√3 + 8/√3 = 24/√3 = 8√3 m.

Q. 3: Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

Let AB and CD be the poles of equal height.

O is the point between them from where the height of elevation is taken. BD is the distance between the poles.

As per the above figure, AB = CD,

OB + OD = 80 m

In right ΔCDO,

tan 30° = CD/OD

1/√3 = CD/OD

CD = OD/√3 … (1)

In right ΔABO,

tan 60° = AB/OB

√3 = AB/(80-OD)

AB = √3(80-OD)

AB = CD (Given)

√3(80-OD) = OD/√3 (Using equation (1))

3(80-OD) = OD

240 – 3 OD = OD

Substituting the value of OD in equation (1)

CD = 20√3 m

⇒ OB = (80-60) m = 20 m

Therefore, the height of the poles are 20√3 m and the distance from the point of elevation are 20 m and 60 m respectively.

Q. 4:  An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.

Let AB be the height of the observer and PR be the height of the tower.

Also, PB is the distance between the foot of the tower and the observer.

Consider θ as the angle of elevation of the top of the tower from the eye of the observer.

From the above figure,

AB = PQ = 1.5 m

PB = QA = 20 m

QR = PR – PQ = 22 – 1.5 = 20.5 m

In the right triangle AQR,

tan θ = QR/AQ

tan θ = 20.5/20.5 = 1

⇒ tan θ = tan 45°

Hence, the angle of elevation is 45°.

Q. 5: The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is √st.

Let BC = s; PC = t

Let the height of the tower be AB = h.

∠ABC = θ and ∠APC = 90° – θ

(∵ the angle of elevation of the top of the tower from two points P and B are complementary)

In triangle ABC,

tan θ = AC/BC = h/s ………..(i)

In triangle APC,

tan (90° – θ) = AC/PC = h/t

cot θ = h/t ………..(ii)

Multiplying (i) and (ii),

tan θ × cot θ = (h/s) × (h/t)

1 = h 2 /st

Hence, the height of the tower is √st.

Q.6: The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.

Let AB be the height of the tower.

The angle of elevation of the top of a tower from point P is 30°, i.e. ∠APB = 30°.

Given that, when the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°.

Thus, PQ = 20 m

Also, ∠AQB = 30° + 15° = 45°.

In right triangle ABQ,

tan 45° = AB/QB

h = x….(i)

In right triangle ABP,

tan 30° = AB/PB

1/√3 = h/(x + 20)

x + 20 = √3h  {from (i)}

h + 20 = √3h

√3h – h = 20

h = 20/(√3 – 1)

h = [20/(√3 – 1)] × [(√3 + 1)/(√3 + 1)]

= 20(√3 + 1)/(3 – 1)

= 20(√3 + 1)/2

= 10(√3 + 1)

Therefore, the height of the tower is 10(√3 + 1) m.

Q.7: A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

Let AB be the vertical pole and AC be the length of the rope.

Also, the angle of elevation = ∠ACB = 30°

In right triangle ABC,

sin 30 = AB/AC

1/2 = AB/20

AB = 20/2 = 10

Therefore, the height of the vertical pole is 10 m.

Q.8: From the top of a 7 m high building, the angle of elevation of the top of a cable tower is

60° and the angle of depression of its foot is 45°. Determine the height of the tower.

Let AB be the height of the building and CE be the height of the tower.

Also, A be the point from where the elevation of the tower is 60° and the angle of depression of its foot is 45°.

EC = DE + CD

From the figure,

CD = AB = 7 m

tan 45° = AB/BC

BC = 7 {since BC = AD}

Thus, AD = 7 m

In right triangle ADE,

tan 60° = DE/AD

⇒ DE = 7√3 m

EC = DE + CD = (7√3 + 7) = 7(√3 + 1)

Therefore, the height of the tower is 7(√3 + 1) m.

Video Lesson on Applications of Trigonometry

Practice Questions For Class 10 Maths Chapter 9 Some Applications of Trigonometry

• The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 50 m high, what is the height of the hill? [Answer: 150 m]
• A bridge across the river makes an angle of 45° with the river bank. If the length of the bridge across the river is 150 m, what is the width of the river? [Answer: 75√2 m]
• There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are the points directly opposite to each other on the two banks, and in a line with the tree. If the angles of elevation of the top of the tree from P and Q are 30° and 45° respectively, find the height of the tree. [Answer: 36.6.m]
• From a point 20m away from the foot of a tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower. [Answer: 11.56 m]
• A flagstaff stands at the top of a 5m high tower. From a point on the ground, the angle of elevation of the top of the flagstaff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flagstaff. [Answer: 3.65 m]
• A tower subtends an angle α at a point A in the place of its base and the angle of depression of the foot of the tower at a point b ft. just above A is β. Prove that the height of the tower is b tan α cot β.
• A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane, the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the flagstaff is 45°. Find the height of the tower. [Answer: 9.55m]
• The angle of elevation of a cloud from a point h metres above the surface of a lake is θ and the angle of depression of its reflection in the lake is φ. Prove that the height of the cloud above the lake is h[(tan φ + tan θ)/ (tan φ – tan θ)].
• The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building and the distance between the two buildings. [Answer: 4(3 + √3) m]
• A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower at a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point. [Answer: 3 sec]

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.