hypothesis testing in statistics lecture notes

1014SCG Statistics - Lecture Notes

Chapter 4 week 5/6 - t-tests.

Outline: Hypothesis Testing – General Process The Concept The Basic Steps for Hypothesis Testing – 10 steps The Scientific Problem and Question The Research Hypothesis Resources, Required Detectable Differences, Significance Level Required The Statistical Hypotheses One and Two Tailed Hypotheses Theoretical Models used in Testing Hypotheses The Test Statistic, its Null Distribution, Significance Level and Critical Region Sample Collection and Calculation of Sample Test Statistic Comparison of Sample Test Statistic with Null Distribution The \(p\) -Value of a Test Conclusions and Interpretation Possible Errors Power of a Statistical Test Specific Tests of Hypotheses I Hypothesis Testing: The Proportion versus a Stated Value Hypothesis Testing: The Mean versus a Stated Value (One-sample t-test) Hypothesis Testing: Difference Between Two Means I – Independent Samples (Two-Sample t-test) Hypothesis Testing: Difference Between Two Means II –Paired Samples Using R Functions for probability \(Pr(X \leq x)\) : pnorm() , pt() . Calculating and Testing a Mean: The One-Sample t-test. Testing the Difference Between Two Means - The Two-Sample t-test. The Paired t-test. Workshop for Week 5 Keep working with your project data; Normal Distribution, Test of Independence, Binomial and normal approximation; Assignment help– applicable to Assignment 1. Project Requirements for Weeks 5 & 6 Proceed with your project - it is due at the end of week 6! Things YOU must do in Week 5 & 6 Revise and summarise the lecture notes for week 3 & 4; Read your week 5 & 6 lecture notes before the lecture; Read the workshop on learning@griffith before your workshop; Submit your assignment in week 6.

4.1 Hypothesis Testing – The General Process

4.1.1 the concept.

The first area of statistical inference that we discuss involves using sample data to test some sort of belief. The second branch of statistical inference, estimation, will be discussed later.

Do the sample data support the claim made by the researcher? In such situations there are two main types of question:

• Question asked is:

Is the value (parameter) as proposed?

Is the proportion of males equal to 0.5?

Is the standard deviation of leaf area greater than 10% of its mean?

Is the maximum energy output greater than 10kw?

Is the mean dissolved oxygen (DO) in the Brisbane river below the critical level for fish survival?

Are the parameters the same for different groups/situations/etc?

Is the mean level of NOX (nitrogen oxide) in the atmosphere increasing – time 1 versus time 2?

Is a particular grass species more tolerant to pressure from foot traffic than another grass species?

Is the average house loan through a particular bank the same this year as at the same time last?

4.1.2 The Basic Steps for Hypothesis Testing – the HT 10 steps

Identify clearly the scientific problem and question.

From the identified question, clearly define the research hypothesis at issue.

Decide on the resources, required detectable difference and significance level.

Formulate the statistical hypotheses: null and alternative.

Determine the theoretical model - based on null hypothesis and assumptions.

Identify the test statistic, its null distribution, and the relevant critical region.

Obtain the sample data and calculate the sample test statistic.

Compare the sample test statistic with the null distribution using the critical region OR evaluate the p-value for the test.

Make statistical conclusion and interpret result in terms of original question.

Consider the possible errors - type I, type II.

4.1.3 The Scientific Problem and Question

It is the duty of the researcher to identify and explain the problem being studied. If this is not carried out with care improper, incorrect, and/or misleading conclusions may occur.

4.1.4 The Research Hypothesis

• A specific belief about some feature of the population variable – eg a mean, proportion, range.
• The feature will describe the variable in some way.
• The feature must be measurable or observable (not necessarily quantitative).
• Also known as a scientific hypothesis or an English hypothesis.
• Refers to a situation, problem, question.

Dictionary Definitions of the English word hypothesis

Supposition made as basis for reasoning, without assumption of its truth, or as starting-point for investigation (The Concise Oxford Dictionary, 1975)

A proposition assumed as a premise in an argument; a proposition (or set of propositions) proposed as an explanation for the occurrence of some specified group of phenomena, either asserted or merely as a provisional conjecture to guide investigation (Macquarie Concise Dictionary, 1996)

One of the most common problem areas in research design is inadequate clarification of the research hypothesis – it must be specific and unambiguous; it must be clear what is to be measured. What may seem obvious to the researcher at the time may be less than obvious to someone else, for example a research assistant actually collecting the data, and may be no longer obvious to anyone at a later date!

Decide whether each of the following is a good research hypothesis.

36% of Australian females between 15 and 24 years of age smoke cigarettes.

The probability that a cyclone first located in the Coral Sea will cross the Queensland coast is 0.20.

Budgerigars in inland Australia have a smaller range of body weights than do budgerigars on the coast.

The minimum temperature in Brisbane never goes below 0 \(^{\circ}\) C.

The average Mastercard debt is $600.

Toyota Corollas are better cars than Ford Lasers.

Most people eat meat.

OPs in Private Schools cover a smaller range than OPs in State Schools.

Five percent of women who take the contraceptive pill still fall pregnant.

The average level of hydrocarbon concentration in body tissues increases up the food chain indicating an accumulation process.

The noise levels from the freeway are above the maximum decibel level set by the Australian standards.

Difficulties in defining the research hypothesis

The following are common difficulties encountered by researchers when they are attempting to define the research hypothesis. - Identifying the problem of interest - Defining the population - Identifying the specific question which is being asked - Stating the specific belief

Remember, the feature describes the population variable

Example: Identify the variables, populations and research hypotheses for some of the examples given in the example above.

4.1.5 Resources, Required Detectable Differences, Significance Level Required

Resources: The resources that are available for the study need to be assessed at the beginning of the project and compared with the resources required to achieve the desired aim. If the two are not compatible, proceeding with the research may be a complete waste of time and money. Statistical input can help with this process, and ‘clever’ designs may enable research that would otherwise not be possible.

Detectable Differences: It is important to recognise the difference between ‘statistical difference’ and ‘observed difference’. For example, two sample means may have different values, but because of the variation associated with the measurement, it is not possible to say that they come from different populations – they are not statistically different. The researcher needs to think about the minimum difference he wishes to be able to detect – this will influence the size of the sample needed in the experimental design. It may also mean that the resources will not be sufficient; this will mean further thinking and maybe the decision not to go ahead with the study.

The Significance Level: The chance the researcher is willing to take of incorrectly supporting the research hypothesis – usually designated by \(\alpha\) (alpha). - Traditionally the level is set at 0.05 or 0.01, why? - The level depends on the situation. - 0.05 and 0.01 are like hair lengths, different people and/or problems require different reliabilities - be yourself! - The possible error if the conclusion is to reject the null hypothesis.

4.1.6 The Statistical Hypotheses

The Alternative Hypothesis – \(H_1\) or \(H_a\)

• The ‘research’ hypothesis – possibly reformulated in statistical jargon.
• The ‘belief’ we want to prove true.
• The opposite of the null hypothesis.
• By disproving the null, we say we have ‘proved’ the alternative.
• Usually represented as H1

The Null Hypothesis - \(H_0\)

• Restatement of the research hypothesis in a form that is testable – usually involves negation.
• Expresses the belief about the feature describing the variable in a way that is testable.
• There must be a known theoretical model relating to the distribution of the feature OR a way of obtaining an empirical null distribution (resampling or bootstrapping).
• Is true if and only if the alternative is false. We can never prove it true.

Hypotheses are statements about the population not about the sample.

4.1.7 One and Two Tailed Hypotheses

Where do the tails fit in?

Tails play a significant (pun intended!) role in statistical inference – depends on question being asked.

Two Tailed: Null contains: equals

Alternative contains: not equals

One Tailed: Null contains: equals and greater than OR equals and less than

Alternative contains: less than OR greater than

A comparative study is to be carried out on the populations of fiddler crabs in the Tweed River and the Brisbane River. One aspect to be studied is the weight of an adult crab, a component of interest to a potential marketing venture. Write the hypotheses for the following:

• Belief: crabs in the Tweed River have a different weight from those in the Brisbane River.
• Belief: crabs in the Tweed River weigh more than those in the Brisbane River.
• Belief: crabs in the Tweed River weigh less than those in the Brisbane River.

4.1.8 Theoretical Models used in Testing Hypotheses

Theoretical models are used to specify the null distribution , that is, the distribution of the test statistic if the null hypothesis is true .

The model will depend on the measurement and on the feature of interest in the research hypothesis. For example:

• A study involves a series of Bernoulli trials; feature of interest is a count or proportion - the theoretical model will be the Binomial;
• If a continuous measurement such as weight is to be investigated and the mean is of interest - the Normal or t- distribution may be an appropriate model;
• If the aim is to test the goodness of fit of some data to a specified distribution - the chi-squared model could be used.

The feature of interest is usually converted to a test statistic which has a known distribution, assuming the null hypothesis is true (the Null Distribution).

All theoretical models involve assumptions. Violations of these assumptions may or may not have a dramatic effect on the outcome of any inference undertaken. If you are ever in any doubts regarding assumptions and your data, consult a statistician for advice.

4.1.9 The Test Statistic, its Null Distribution, Significance Level and Critical Region

The Test Statistic:

Usually a function of the ‘feature of interest’ and is known to have a particular distribution – this contributes to the ‘testability’ of the process.

Should be something that has meaning in the context of the feature of interest – if you want to determine if two things are different, you might decide to look at their absolute difference, and include some sort of weighting – a difference of two has more impact if the values are near10 than if the values are near 1000

For example, when testing hypotheses about the population mean the equivalent Z score (or t- value if the standard deviation is estimated) becomes a test statistic.

The null distribution

• Is the probability distribution of the test statistic, assuming the null hypothesis is true.
• If \(H_0\) is true, this is the distribution we would expect the feature (or some expression based on it) to have.
• The distribution for the population of ‘feature values’ if H0 is true – eg, the distribution of the sample mean .

Significance Level – alpha, \(\alpha\)

The risk you are willing to take that you will reject the null hypothesis when it is really true. The probability of a Type I error. It defines the ‘cut off’ point for the test statistic.

Critical Region

• Determined by the specified significance level, \(\alpha\)
• The region of the null distribution where it is considered unlikely for a value of the test statistic to occur.
• If sample value lies here, it is regarded as evidence to reject \(H_0\) in favour of \(H_1\) .

The relationships of the test statistic to the sample and population are critical.

4.1.10 Sample Collection and Calculation of Sample Test Statistic

Ways of selecting the sample are discussed at length in various introductory texts. In general, samples should be random and representative of the population they are taken from. The test statistic is calculated as per the definition of whatever ‘meaningful’ feature has been selected, given the question asked and the available data – eg a count or a mean or a sum of deviations or …

4.1.11 Comparison of Sample Test Statistic with Null Distribution

• The sample test statistic is calculated from the observed data and compared with the null distribution which reflects the population if \(H_0\) is true.
• If the sample test statistic lies in the ‘critical region’ the null hypothesis is rejected at the specified level of significance.
• If it does not lie in the critical region the null hypothesis is not rejected – the data do not provide evidence to reject the null hypothesis in favour of the research (alternative) hypothesis.

4.1.12 The p-Value of a Test

• Probability of observing a value of the test statistic as extreme as, or more extreme than , that seen in the sample.
• Calculated from the null distribution.
• Called the p-value for the sample test statistic
• Is the probability of selecting a sample at least as favourable to the research hypothesis (alternative) as the observed sample.
• It represents the attained level of significance for the test.

4.1.13 Conclusion and Interpretation

• Depends on whether we reject or fail to reject the null hypothesis.
• Remember, failing to reject the null hypothesis does not mean the null hypothesis is true

4.1.14 Consider Possible Errors:

Two basic types of error can occur whenever hypothesis testing is carried out. These are summarised in the following table:

The LEVEL OF SIGNIFICANCE is the probability of making a Type I error and is under the control of the person carrying out the statistical test. The symbol used is \(\alpha\) (alpha).

The PROBABILITY OF A TYPE II ERROR depends on the true alternative hypothesis (and several other things) and is thus usually unknown. The symbol used is \(\beta\) (beta).

4.1.15 Power of a Statistical Test

• The power of a statistical test is the probability of correctly rejecting the null hypothesis.
• The probability of correctly detecting a valid alternative hypothesis.
• Power is calculated as one minus the probability of a Type II error. Power = 1 - \(\beta\)
• A test with low power results in a higher chance of not rejecting the null hypothesis when it should in fact be rejected.

For example, if we conclude that the null hypothesis: equal numbers of males and females cannot be rejected, then it may be that the test of proportion being used has a low power and we are simply not detecting the actual difference.

This may be a case of no statistical difference when there is a meaningful real difference .

Note: It is also possible to find a statistically significant difference that is not a scientifically significant or meaningful effect. Being a slave to p-values can lead you into trouble - there is no substitute for common sense and scientific knowledge. You should always ask yourself" “Does this result make sense?”

4.2 Specific Tests of Hypotheses I

4.2.1 hypothesis testing: the proportion versus a stated value.

See the week 3/4 lecture notes for theory, details and examples.

Use binomial if sample size no more than 20.

Use normal approximation for sample size > 20.

4.2.2 Hypothesis Testing: The Mean versus a Stated Value (The one-sample t-test)

Two-tailed hypotheses: \[\begin{align*} H_0: & \mu = \mu_0\\ H_1: & \mu \neq \mu_0 \end{align*}\]

One-tailed Upper hypotheses: \[\begin{align*} H_0: & \mu \leq \mu_0\\ H_1: & \mu > \mu_0 \end{align*}\]

One-tailed Lower hypotheses: \[\begin{align*} H_0: & \mu \geq\mu_0\\ H_1: & \mu < \mu_0 \end{align*}\]

Using theory: If \(X \sim N(\mu, \sigma^2)\) then \(\overline{X}_n \sim N(\mu, \frac{\sigma^2}{n})\) . Applying the standard normal ( \(Z\) ) transform we get the test statistic:

\[ T = \frac{\overline{X}_n - \mu_0}{\sigma/\sqrt{n}} \sim N(0, 1). \]

Generally, however, we do not know the population standard deviation \(\sigma\) . Instead, we estimate it using the sample standard deviation \(s\) . Introducing this extra level of uncertainty into the test statistic changes the distribution of the test statistic to a Student’s \(t\) :

\[ T = \frac{\overline{X}_n - \mu_0}{s/\sqrt{n}} \sim t_{n-1}. \]

The hypothesised value for \(\mu\) ( \(\mu_0\) ) is substituted into the formula along with the values calculated from the sample – mean and standard deviation – to obtain the sample test statistic. The calculated sample test statistic is compared with the relevant critical value from the Student’s \(t\) distribution with \(n-1\) degrees of freedom.

THE QUESTION: Fiddler crabs in the Tweed River appear to be heavier than those reported in the literature, where the mean weight is given as 230gm. Is this true? IDENTIFY A FEATURE WHICH WILL HAVE MEANING FOR THE QUESTION: The mean weight. THE RESEARCH HYPOTHESIS: The mean weight of fiddler crabs in the Tweed river is greater than 230gm. DETERMINE THE RESOURCES , DETECTABLE DIFFERENCE , LEVEL OF SIGNIFICANCE Estimation of sample size for a given detectable difference is discussed in a later section. Assume for this example that a sample of 16 crabs will be taken. STATISTICAL HYPOTHESES: \[\begin{align*} H_0: & \mu \leq 230\\ H_1: & \mu > 230 \end{align*}\] where \(\mu\) is the population mean weight of fiddler crabs in the Tweed river. DEDUCE A THEORETICAL MODEL FOR THE FEATURE: Continuous data, possibly normal – a genetic & environmental derivation. Interested in testing the mean – central limit theorem gives the distribution of the sample mean as normal with mean \(\mu\) and variance \(\sigma^2/16\) . Standard deviation, \(\sigma\) , is not known and will have to be estimated from the sample using \(s\) . This means our null distribution is the Student’s \(t\) distribution. TEST STATISTIC , NULL DISTRIBUTION & CRITICAL REGION: The mean of a random sample of size \(n\) from a variable with a normal distribution \(N(\mu, \sigma^2)\) has a normal distribution \(N(\mu, \sigma^2/n)\) . Converting this to a \(Z\) format, and acknowledging that the population standard deviation of the weights of crabs in the Tweed River is not known gives a test statistic: \[ T = \frac{\overline{X}_n - \mu_0}{s/\sqrt{n}} \sim t_{n-1}. \] where \(s\) is the estimated standard deviation calculated from the sample. This test statistic has a \(t\) distribution with \((n – 1)\) degrees of freedom if \(H_0\) is true. Since a sample size of 16 has been proposed, the degrees of freedom will be 15 and the critical region relevant for a level of significance of \(\alpha = 0.05\) and a one-tailed test ( \(H_1\) has a ‘greater than’ not a ‘not equals to’) is found from the \(t\) -table (see table at end of notes) to be: \(t > 1.75\) . COLLECT THE DATA: The data have been collected. CALCULATE THE TEST STATISTIC: Calculations on observations: sample mean \(\overline{X} = 240\) , and sample standard deviation \(s= 24\) . Compute sample test statistic, \[ T = \frac{240 - 230}{24/\sqrt{16}} = \frac{10}{6} = 1.667. \] COMPARE THE TEST STATISTIC WITH THE NULL DISTRIBUTION: Does T lie in critical region? No. Calculated \(T\) of \(1.667 < 1.7531\) . OR: What is the \(p\) - value for \(T\) ? R using: 1 - pt(1.6667, 15) [1] 0.05815621 The \(p\) -value for the calculated \(T\) of 1.667 on 15 df is 0.058. (This is larger than 0.05.) MAKE CONCLUSION AND INFERENCES: There is insufficient evidence to reject the null hypothesis ( \(p \geq 0.05\) ). The sample data do not support the research hypothesis that the mean weight of crabs in the Tweed is greater than that reported in the literature (230gm), at the 0.05 level of significance. SPECIFY THE ERROR YOU MAY BE MAKING IN YOUR INFERENTIAL CONCLUSIONS: The researcher may be incorrect in not rejecting the null hypothesis in favour of the research hypothesis – a type II error. The probability associated with this error is unknown unless the true alternative value of the mean weight for Tweed river crabs is known. The failure to reject the null may simply reflect a low powered test. Question: What if the standard deviation for the sample had been 20?

R: A one-sample t-test can be carried out using t.test() in R. See R section for details.

4.2.3 Hypothesis Testing: Difference Between Two Means I –Independent Samples (The two-sample t-test)

Two-tailed hypotheses: \[\begin{align*} H_0: & \mu_1 = \mu_2\\ H_1: & \mu_1 \neq \mu_2 \end{align*}\]

where \(\mu_1\) and \(\mu_2\) are the respective means of the two populations to be compared.

One-tailed Hypothesis: \[\begin{align*} H_0: & \mu_1 \leq \mu_2\\ H_1: & \mu_1 > \mu_2 \end{align*}\]

One-tailed Hypothesis: \[\begin{align*} H_0: & \mu_1 \geq\mu_2\\ H_1: & \mu_1 < \mu_2 \end{align*}\]

Note that in the two-sample t-test the tail of a one-tailed hypothesis test (upper or lower) depends on how you calculate the test statistic. This will be discussed in lectures.

Using theory: If \(X_1 \sim N(\mu_1, \sigma_1^2)\) and \(X_2 \sim N(\mu_2, \sigma_2^2)\) then \((\overline{X}_1 - \overline{X}_2) \sim N(\mu_1 - \mu_2, \sigma_{\overline{X}_1 - \overline{X}_2}^2)\) .

The situation where \(\sigma_1\) and \(\sigma_2\) are known is most unlikely and will not be discussed.

The estimation of \(\sigma_{\overline{X}_1 - \overline{X}_2}^2\) depends on whether or not \(\sigma_1\) and \(\sigma_2\) can be assumed equal.

Let \(n_1\) and \(n_2\) denote the sample sizes taken from populations 1 and 2, respectively. Let \(s_1\) and \(s_2\) denote the standard deviations of each sample taken from populations 1 and 2, respectively.

Standard deviations unknown but assumed equal (Pooled Procedure)

\[ \widehat{\sigma_{\overline{X}_1 - \overline{X}_2}^2} = s_p^2 = \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}. \]

\[ s_p = \sqrt{\frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}}. \]

The Test Statistic is:

\[ T = \frac{(\overline{X}_1 - \overline{X}_2) - (\mu_1 - \mu2)}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t_{n_1 + n_2 -2} \text{ if } H_0 \text{ is true.} \]

\(s_p\) is known as the pooled sample standard deviation .

Standard deviations unknown but cannot be assumed equal

\[ T = \frac{(\overline{X}_1 - \overline{X}_2) - (\mu_1 - \mu2)}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \sim t_{n_1 + n_2 -2} \text{ if } H_0 \text{ is true.} \]

• For large sample sizes, \(T \sim Z\) .
• for small sample sizes, \(T \sim t\) with weighted DF.

In this course, the situation of unequal standard deviations and small samples will not be considered further.

Question: Why would a test to compare means be of interest if populations have unequal standard deviations?

The hypothesised value for \((\mu_1 - \mu_2)\) under \(H_0\) is substituted into the formula along with the values calculated from the sample (means and standard deviations) to obtain sample test statistic. The calculated sample test statistic is compared with the relevant critical value of \(t\) .

NOTE: When comparing the means from two populations using the test statistic shown above, the choice of which sample mean is subtracted from the other is arbitrary. For two-tailed hypotheses this is not an issue. However, it can create an issue for one-tailed tests when deciding whether the test is upper or lower tailed. This will be discussed further in lectures.

THE QUESTION: Fiddler crabs in the Tweed River appear to be heavier than fiddler crabs in the Brisbane River. Is this true? IDENTIFY A FEATURE WHICH WILL HAVE MEANING FOR THE QUESTION: The difference between the mean weights of crabs in the two locations. THE RESEARCH HYPOTHESIS: Mean weight for Tweed River crabs is greater than the mean weight for Brisbane River crabs. DETERMINE THE RESOURCES , DETECTABLE DIFFERENCE , LEVEL OF SIGNIFICANCE Sample size? Assume sample sizes of 16 and 25 have been taken from Tweed and Brisbane rivers respectively. Following tradition, take the level of significance to be \(\alpha = 0.05\) . STATISTICAL HYPOTHESES: \[\begin{align*} H_0: & \mu_{\text{T}} \leq \mu_{\text{B}}\\ H_1: & \mu_{\text{T}} > \mu_{\text{B}} \end{align*}\] where \(\mu_{\text{T}}\) and \(\mu_{\text{B}}\) are the population mean weights of fiddler crabs in the Tweed and Brisbane rivers, respectively. DEDUCE A THEORETICAL MODEL FOR THE FEATURE: Assume weight has a normal distribution. Assume the standard deviations are unknown but the same. TEST STATISTIC , NULL DISTRIBUTION & CRITICAL REGION: The Test Statistic is: \[ T = \frac{(\overline{X}_1 - \overline{X}_2) - (\mu_1 - \mu2)}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t_{n_1 + n_2 -2} \text{ if } H_0 \text{ is true.} \] where \[ s_p^2 = \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}. \] Degrees of freedom = \(16 + 25 - 2 = 39\) . From \(t\) -tables, \(t_{39}(0.95) = 1.69\) (or \(-1.69\) - see discussion below). COLLECT THE DATA: Take a sample of 16 crabs from the Tweed river; take a sample of 25 crabs from the Brisbane river. CALCULATE THE TEST STATISTIC: Using the sample crab weight data from each river, calculate means and std deviations: Tweed: mean = 240, standard deviation = 24, n = 16 Brisbane: mean = 215, standard deviation = 18, n = 25 \(s_p^2 =\) \(T =\)

COMPARE THE TEST STATISTIC WITH THE NULL DISTRIBUTION: MAKE CONCLUSION AND INFERENCES: SPECIFY THE ERROR YOU MAY BE MAKING IN YOUR INFERENTIAL CONCLUSIONS:

R: Two-sample t-tests can be carried out using t.test() - see Using R section.

4.2.4 Hypothesis Testing: Difference Between Two Means I –Paired Samples (the Paired t-test)

The same experimental unit is measured twice. E.g. Standing and lying down blood pressures. In these cases the data are not independent.

Here, we first calculate the difference between the two measures on each individual. Then we apply the one-sample t-test to the ** difference variable.

Twelve randomly selected individuals had their blood pressure measured in both standing and lying down positions. The data is given in the table below.

Two-tailed Paired t-test

\(H_0:\) There is no difference between the mean blood pressures in the two populations

\(H_1:\) There is a difference between the mean blood pressures in the two populations

Since the two populations are paired (ie the same indivicuals are measured twice), we are actually testing the whether the population mean difference ( \(\mu_D\) )is zero or not:

\[\begin{align*} H_0: & \mu_{D} = 0 \\ H_1: & \mu_{D} \neq 0 \end{align*}\]

This is just a one-sample t-test on the difference data: ie, use the difference data as the sample and caclulate its sample mean ( \(\overline{X}_D\) ) and sample standard deviation ( \(s_D\) ). We can then use these in the one-sample t-test test statistic:

\[\begin{align*} T &= \frac{\overline{X}_n - \mu_0}{s/\sqrt{n}} \\ &= \frac{\overline{X}_D - \mu_D}{s_D/\sqrt{n}} \\ &= \frac{2.5 - 0}{5.5/\sqrt{12}} \\ &= 1.574. \end{align*}\]

From tables, \(t_{11}(0.975) = \pm 2.2010\) . Since \(T = 1.574\) is not greater than 2.010 (or less than -2.010) we cannot reject the null at the 0.05 level of significance. We conclude there is insufficient evidence to suggest that the mean standing blood pressure differs from the mean lying blood pressure.

One-tailed versions will be discussed during lectures .

4.3 Using R

4.3.1 more probability functions:.

Use the functions: pnorm(z, mean, sd) and pt(t, df) to find the cumulative probability for particular values of \(Z\) and the calculated t-test statistic, \(T\) based on Specified degrees of freedom ( df ).

Eg: An art auction produces normally distributed sale prices with a mean of 1600 dollars and a standard deviation of 220 dollars. What is the probability that a particular painting will cost at least 2000 dollars?

Let \(X\) denote sales prices. We want to find \(Pr(X > 2000) = 1 - Pr(X \leq 2000)\) .

(Exercise: Modify the above code to find the probability that a painting will cost 5000 dollars or less.)

Suppose now that the standard deviation given above had been estimated from a random sample of 10 of the paintings. Student’s \(t\) should be used (with df = 9) rather than the normal. Note you should convert the figure to a Z-value first before using the pt function:

4.3.2 Testing a Mean – The One-Sample t- test

Use the t.test() function in R:

t.test(x, alternative, mu)

EG: Student’s sleep data (1908) contain data on the extra amount of sleep gained (hours) from two types of soporific drug. Twenty patients were randomly assigned to either drug 1 or drug 2 (10 patients in each group) and their extra amount of sleep obtained was recorded. [NB: Actually the data are paired - 10 patients measured twice, but we are going to pretend they are independent groups of patients for the next two exercises].

Let’s test whether the mean amount of extra sleep is greater than 0 hours, across both groups. In other words, do both the drugs increase mean hours of sleep?

The data are in R already, so we just need to use the t.test() function:

(Exercise: How would you modify the above code if you wanted to test whether the mean extra hours of sleep is significantly less than 1 hour?)

4.3.3 Testing the Difference Between Two Means – The Two-Sample t-test

Again, we use the t.test() function in R to do two-sample t-tests.

Suppose in the sleep example we want to test whether the mean extra hours of sleep differs between the two drugs. We simply do the two-sample t-test comparing the two groups (drugs) using the t.test() function:

(Exercise: Investigate what R means when it says “Welch Two Sample t-test” in the output. Start by looking at the help for t.test() using ?t.test in the R console).

4.3.4 Testing the Mean Difference Between Paired Data – The Paired t- test

Recall the blood pressure example. Enter the data and then do the test.

(Exercise: Can you work out how to do a paired t-test on Student’s sleep data? Remember, the data are actually paired.)

Browse Course Material

Course info.

• Emery N Brown

Departments

• Brain and Cognitive Sciences

As Taught In

• Probability and Statistics
• Cognitive Science

Learning Resource Types

Statistics for brain and cognitive science, hypothesis testing i & ii.

This file contains information regarding hypothesis testing I & II.

You are leaving MIT OpenCourseWare

Hypothesis Testing in Statistics – Short Notes + PPT

“Truth can be stated in a thousand different ways, yet each one can be true…” Swami Vivekananda

What is ‘Test of Hypothesis’?

Ø   Test of Hypothesis (Hypothesis Testing) is a process of testing of the significance regarding the parameters of the population on the basis of sample drawn from it. Ø   Test of hypothesis is also called as ‘Test of Significance’. Ø   J. Neyman and E.S. Pearson initiated the practice of testing of hypothesis in statistics.

What is the purpose of Hypothesis Testing?

Ø   The main purpose of hypothesis testing is to help the researcher in reaching a conclusion regarding the population by examining a sample taken from that population. Ø   The hypothesis testing does not provide proof for the hypothesis. Ø   The test only indicates whether the hypothesis is supported or not supported by the available data.

What is Hypothesis?

Ø   Hypothesis is a statement about one or more populations.

Ø   It is a statement about the parameters of the population about which the statement is made.

Ø   Example:

$   A doctor hypothesized: “The drug ‘X’ is ineffective in 99% of cases of which it is used”.

$   “The average pass percentage of central university degree programme is 98”.

Ø   Through the hypothesis testing the researcher or investigator can determine whether or not such statements are compatible with the available data.

Types of Hypothesis

Ø   There are TWO types of hypothesis.

                        (A).   Research Hypothesis

                        (B).   Statistical Hypothesis

(A). Research Hypothesis

Ø   Research Hypothesis is “a tentative solution for the problem being investigated”.

Ø   It is the supposition (guess) that motivates the research.

Ø   In research, the researcher determines whether or not their supposition can be supported through scientific investigation.

Ø   The research hypothesis directly leads to statistical hypothesis.

(B). Statistical Hypothesis

Details of the Statistical hypothesis are discussed in the “Steps or Components in Testing of Statistical Hypothesis”.

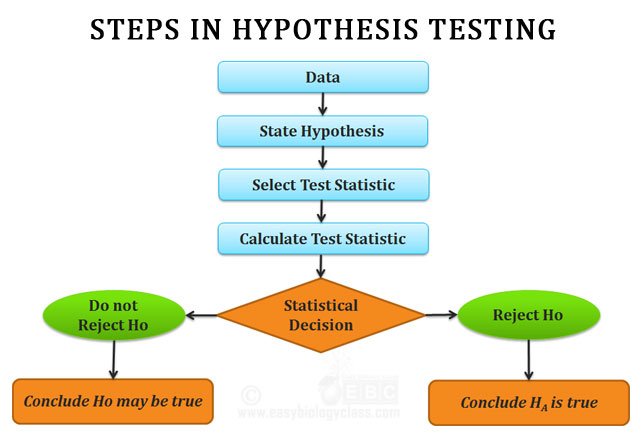
Steps / Components in Testing of Statistical Hypothesis:

Ø   The statistical hypothesis testing consists of following Steps / Components

(1).      Data (variable)

(2).      Statistical Hypothesis

(3).      Test Statistic

(4).      Decision Rule

(5).      Significance Level

(6).      Statistical Decision

(7).      p – Value

(1). Data (variable)

Ø   Data is the information collected from the population.

Ø   It may be the observation of a natural phenomenon, Result of an experiment, Data from a survey or a secondary data.

Ø   The nature of data determines the type of statistical test to be selected.

Ø   All the features of the data such as continuous, discontinuous, quantitative or qualitative etc. matters in the process of hypothesis testing.

(2). Statistical Hypothesis

Ø   Statistical hypothesis is a statement about the population which we want to verify on the basis of information available from the sample.

Ø   A statistical hypothesis is stated in such a way that they may be evaluated by appropriate statistical techniques.

Ø   There are TWO types of statistical hypothesizes:

(a).  Null hypothesis

(b).  Alternative hypothesis

(a). Null Hypothesis

Ø   The Null hypothesis is the hypothesis to be tested by test statistic.

Ø  Null hypothesis is denoted as H 0 .

Ø   Usually the null hypothesis stated as the ‘Hypothesis of No Difference’.

Ø   The statement is created complementary to the conclusion that the researcher is seeking to reach through his research.

Ø   Usually stated in the negative terms of the original research hypothesis.

Ø   Example: The drug ‘X’ DO NOT induces apoptosis in cancerous cells.

Ø   In the statistical testing process, the null hypothesis is either:

$   Rejected

$   Not rejected (Fail to be rejected / accepted)

Ø   If the null hypothesis is not rejected, we say that the data on which the test is based do not provide sufficient evidence to cause the rejection of null hypothesis.

Ø   If the null hypothesis is rejected in the testing process, we say that the data at hand are not compatible with the null hypothesis but are supportive for some other hypothesis (commonly called as alternative hypothesis).

(b). Alternative Hypothesis

Ø   Alternate hypothesis is created in a negative meaning of the null hypothesis.

Ø   It is denoted as H 1 or H A .

Ø   Usually the alternative hypothesis and research hypothesis are the same.

Ø   Example: The drug ‘X’ induces apoptosis in cancerous cells.

How to state the statistical hypothesis?

Ø   The null hypothesis should contain an equality sign (=, ≤ or ≥).

Ø   Example: The population mean (μ) is not 100.

$   H0:       μ = 100

$   H1:       μ ≠ 100

Ø   Example: The population means is greater than 100.

$   H0:       μ ≤ 100

$   H1:       μ > 100

Ø   Example: The population mean is less than 100.

$   H0:       μ ≥ 100

$   H1:       μ < 100

Things to remember when constructing the Null Hypothesis:

$   What you expected to conclude with the study should be placed in the alternative hypothesis.

$   The null hypothesis should contain a statement of equality (=, ≤, ≥).

$   The null hypothesis is the hypothesis to be tested.

$   The null hypothesis and alternative hypothesis should be complementary.

(3). Test Statistic

Ø   Test statistic is the statistic computed from the data sample.

Ø   There are many possible values that the test statistic can adopt.

Ø   Test value of the statistic depends on the nature of the sample.

Ø   The test statistic is the decision maker in hypothesis testing.

Ø   Decision is to reject or not reject the null hypothesis.

Ø   General formula for test statistic: (applicable to most of the test statistic but not to all)

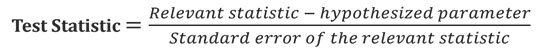
x̄            : mean

μ0         : hypothesized value of population mean

σ/√n     : Standard error

(4). Decision Rule

Ø   All the possible values that the test statistic can assume are points on the horizontal axis of a graph of the distribution of the test statistic.

Ø   The values are divided into two groups:

1.      Values of the rejection region

2.      Values of the non-rejection region

Ø   The decision rule tell us to reject the null hypothesis if the values of the test statistic that we compute from our sample is one of the values in the rejection region and not to reject the null hypothesis if the computed values of the test statistic is on the values in the non-rejection region.

(5) Significance Level

Ø   Level of significance is the probability of rejecting a true null hypothesis in the statistical testing procedure.

Ø   The level of significance is a probability value and it is denoted as ‘α’.

Ø   The significance level decide the decision value to go the rejection region or to the non-rejection region.

Ø  Due to the ‘Level of significance’ the test statistic is often called as ‘Significance Test’.

Ø   If we reject a true null hypothesis we are committed an error.

Ø   Thus, you have to ensure that the probability of rejecting a true null hypothesis is very small.

Ø   Thus, we select a small value of α to ensure the probability of rejecting a true null hypothesis is very less.

Ø   The frequently used α values are 0.01 (99%), 0.05 (95%).

Ø   Explanation : if we select 0.01 (99%) as the significance level, it means that we are 99% confident in our decision but still there is 1% change for our decision being false.

(6). Statistical Decision

Ø   It is the decision of rejecting or not rejecting the null hypothesis.

Ø   We reject the null hypothesis if the computed value of the test statistic is fall in the rejection region.

Ø   We will NOT reject the null hypothesis if the computed value falls in the non-rejection region.

Ø   Conclusion:

Ø   If we reject H 0 , we conclude that H A is true.

Ø   If we fail to reject H 0 , we conclude that the H 0 may be true.

Ø   When a null hypothesis is not rejected one should not say that the null hypothesis accepted but we say that null hypothesis is not rejected.

Ø   We usually avoid the usage ‘accept’, because we may have committed a type II error.

Learn more: Statistical Errors (Type I and Type II Errors)

(7). p-Value

Ø   p-value is the smallest value of α for which we can reject a null hypothesis.

Ø   A p-value is the probability that the computed value for a test statistic is at least as extreme as specified value of the test statistic when the null hypothesis is true.

Daniel, W.W., 1999. Biostatistics: A foundation for analysis in the health sciences 9th edition. John Wiley & Sons inc.: USA.

Khan, I.A. and Khanum, A., 2012, Fundamentals of Biostatistics, 3rd edition (revised), Ukaaz Publications, Hyderabad, India.

Kothari, C.R., 2004. Research methodology: Methods and techniques. New Age International, India.

<<< Back to Statistics Note Papte

Do you have any Queries? Please leave me a COMMENT in the Comments Section below. I will be Happy to Read your Comments and Reply.

Download the PPT of this Topic

You might also like…

@. Introduction to Biostatistics

@. Data Collection Methods in Statistics

@. Difference between Type I and Type II Errors

@. Biostatistics PPTs.

More Lecture Notes from Easy Biology Class…

Botany Zoology Biochemistry Genetics Molecular Biology Biotechnology Endocrinology Physiology Microbiology Immunology Embryology Ecology Evolution Biophysics Research Methodology Biostatistics Chemistry for Biologists Physics for Biologists

Browse more in Easy Biology Class…

Lecture Notes Biology PPTs Video Tutorials Biology MCQ Question Bank Difference between Practical Aids Mock Tests (Online) Biology Exams

Related posts:

• Principles of Experimental Designs in Statistics – Replication, Randomization & Local Control
• Types of Experimental Designs in Statistics (RBD, CRD, LSD, Factorial Designs)
• Difference between Primary and Secondary Data
• MCQ on Hypothesis Testing in Statistics
• What is Data in Statistics?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Privacy Overview

Statistics: Lecture Notes

• Definitions
• Generating Random Numbers on the TI-82
• Sampling Lab designed to expose the student to each of the five types of sampling
• Creating Grouped Frequency Distributions
• Introduction to Statistics and Lists on the TI-82
• Creating Histograms, Box Plots , and Grouped Frequency Distributions on the TI-82
• Creating an Ogive on the TI-82
• Creating Pie Charts on the TI-82 using the PIE program
• Measures of Central Tendency
• Measures of Variation
• Measures of Position
• Counting Principles
• Introduction to Probability
• Addition and Multiplication Rules
• Conditional Probability
• Probability Distributions
• Binomial Probabilities
• Other Distributions : Multinomial, Poisson, HyperGeometric
• Introduction to Normal Probabilities
• Table - Standard Normal Probabilities
• Central Limit Theorem
• Approximating the Binomial with the Normal
• Introduction to Estimation
• Estimating the Population Mean
• Table - Student's T Probabilities
• Estimating the Population Proportion
• Sample Size Determination
• Introduction to Hypothesis Testing
• Determining the type of test
• Using confidence intervals to do hypothesis testing
• Steps to Hypothesis Testing
• Testing of Means
• Hypothesis test example: Does pi = 3.2?
• Testing of Proportions
• Dependent Samples - The Mean of the Difference
• Independent Samples - The Difference of the Means
• Two Proportions
• Scatter Plots and Regression Lines on the TI-82
• Correlation
• Correlation and Regression on the TI-82
• Coefficient of Determination
• Introduction to the chi-square distribution
• Testing a single population variance
• Chi-square goodness-of-fit test
• Chi-square goodness-of-fit tests on the TI-82
• Chi-square test for independence
• Contingency tables on the TI-82
• F distribution and F-test
• One-Way Analysis of Variance
• One-Way Analysis of Variance on the TI-82
• Scheffe' and Tukey Tests
• Two-Way Analysis of Variance