factorisation class 8 assignment

CBSE NCERT Solutions

NCERT and CBSE Solutions for free

Class 8 Mathematics Factorisation Assignments

We have provided below free printable Class 8 Mathematics Factorisation Assignments for Download in PDF. The Assignments have been designed based on the latest NCERT Book for Class 8 Mathematics Factorisation . These Assignments for Grade 8 Mathematics Factorisation cover all important topics which can come in your standard 8 tests and examinations. Free printable Assignments for CBSE Class 8 Mathematics Factorisation , school and class assignments, and practice test papers have been designed by our highly experienced class 8 faculty. You can free download CBSE NCERT printable Assignments for Mathematics Factorisation Class 8 with solutions and answers. All Assignments and test sheets have been prepared by expert teachers as per the latest Syllabus in Mathematics Factorisation Class 8. Students can click on the links below and download all Pdf Assignments for Mathematics Factorisation class 8 for free. All latest Kendriya Vidyalaya Class 8 Mathematics Factorisation Assignments with Answers and test papers are given below.

Mathematics Factorisation Class 8 Assignments Pdf Download

We have provided below the biggest collection of free CBSE NCERT KVS Assignments for Class 8 Mathematics Factorisation . Students and teachers can download and save all free Mathematics Factorisation assignments in Pdf for grade 8th. Our expert faculty have covered Class 8 important questions and answers for Mathematics Factorisation as per the latest syllabus for the current academic year. All test papers and question banks for Class 8 Mathematics Factorisation and CBSE Assignments for Mathematics Factorisation Class 8 will be really helpful for standard 8th students to prepare for the class tests and school examinations. Class 8th students can easily free download in Pdf all printable practice worksheets given below.

Topicwise Assignments for Class 8 Mathematics Factorisation Download in Pdf

Advantages of Class 8 Mathematics Factorisation Assignments

• As we have the best and largest collection of Mathematics Factorisation assignments for Grade 8, you will be able to easily get full list of solved important questions which can come in your examinations.
• Students will be able to go through all important and critical topics given in your CBSE Mathematics Factorisation textbooks for Class 8 .
• All Mathematics Factorisation assignments for Class 8 have been designed with answers. Students should solve them yourself and then compare with the solutions provided by us.
• Class 8 Students studying in per CBSE, NCERT and KVS schools will be able to free download all Mathematics Factorisation chapter wise worksheets and assignments for free in Pdf
• Class 8 Mathematics Factorisation question bank will help to improve subject understanding which will help to get better rank in exams

Frequently Asked Questions by Class 8 Mathematics Factorisation students

At https://www.cbsencertsolutions.com, we have provided the biggest database of free assignments for Mathematics Factorisation Class 8 which you can download in Pdf

We provide here Standard 8 Mathematics Factorisation chapter-wise assignments which can be easily downloaded in Pdf format for free.

You can click on the links above and get assignments for Mathematics Factorisation in Grade 8, all topic-wise question banks with solutions have been provided here. You can click on the links to download in Pdf.

We have provided here topic-wise Mathematics Factorisation Grade 8 question banks, revision notes and questions for all difficult topics, and other study material.

We have provided the best collection of question bank and practice tests for Class 8 for all subjects. You can download them all and use them offline without the internet.

Related Posts

Class 8 Marathi Assignments

Class 8 Kannada Assignments

Class 8 Social Science Assignments

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

You are learning...

Chapter 12 Class 8 Factorisation

Click on any of the links below to start learning from Teachoo ...

Get solutions of all NCERT Exercise Questions and Examples of Chapter 12 Class 8 Factorisation free at Teachoo (टीचू). In this chapter, first the concepts are explained, and then answers to each and every question, including examples is given.

This chapter comes under Algebra. So, we will use the concepts which we studied in Chapter 8 Class 8 Algebra Expressions.

In this chapter, we will learn

• What are factors of numbers
• What are factors of Algebra Expressions
• What is Factorisation
• Factorization using Method of Common Factors
• Factorisation by regrouping terms
• Factorisation using Algebra Identities - (a + b) 2 , (a - b) 2 , a 2 - b 2
• Factorisation of the form (x + a) (x + b) - Splitting the middle term factorisation
• Division of a monomial by another monomial
• Division of a polynomial by a monomial
• Division of Polynomial by a Polynomial
• Finding error while solving an algebra expression (This is in Ex 14.4)

Click on exercise or topic link below to start doing the chapter

Note : When you click on a link, the first of the exercise will open. To open other questions, there is a list at the bottom of the page (it has arrows). That has all the questions of that exercise.  We have also marked important questions in that list, you can check them out.

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

NCERT Solutions Class 8 Maths Chapter 14 Factorization

NCERT Solutions for Class 8 Maths Chapter 14 Factorization covers all the topics as well as subtopics related to factorization and its applications. Factorization of algebraic expressions is an important skill vital for advanced math studies. Learning factorization of expressions is a complex process and requires a deep step-by-step understanding of factors and the methods to list them. With the thorough practice of NCERT Solutions Class 8 Maths Chapter 14, students can quickly acquire this knowledge to prepare well for exams. These solutions also enable students to gain confidence for various competitive studies.

These NCERT Solutions are a well-structured resource highly competent to lay a strong math foundation. With the thorough practice of all the questions available in these solutions, students can easily explore interesting ways to learn this topic. The range of problems provided in these Class 8 Maths NCERT Solutions Chapter 14 will promote students’ problem-solving skills. You can find some of these exercises provided in the links below.

• NCERT Solutions Class 8 Maths Chapter 14 Ex 14.1
• NCERT Solutions Class 8 Maths Chapter 14 Ex 14.2
• NCERT Solutions Class 8 Maths Chapter 14 Ex 14.3
• NCERT Solutions Class 8 Maths Chapter 14 Ex 14.4

NCERT Solutions for Class 8 Maths Chapter 14 PDF

NCERT Solutions for Class 8 Maths Chapter 14 are well-formed by highly qualified teachers and math experts to enhance the learnability in students. The self-explanatory format of these solutions is highly appropriate to impart deep subject knowledge. To prepare with these solutions, click on the links of the pdf files given below.

☛ Download Class 8 Maths NCERT Solutions Chapter 14 Factorization

NCERT Class 8 Maths Chapter 14   Download PDF

NCERT Solutions for Class 8 Maths Chapter 14 Factorization

NCERT solutions Class 8 Maths Chapter 14 Factorization is written as per the NCERT textbook to provide comprehensive learning of the whole syllabus. The simplistic format of these solutions will allow students to learn and explore this topic with ease. The appropriately placed exercises and sample problems offer strategic learning of each and every concept. To practice the exercise-wise NCERT Solutions Class 8 Maths Factorization , try the links given below.

• Class 8 Maths Chapter 14 Ex 14.1 - 3 Questions
• Class 8 Maths Chapter 14 Ex 14.2 - 5 Questions
• Class 8 Maths Chapter 14 Ex 14.3 - 5 Questions
• Class 8 Maths Chapter 14 Ex 14.4 - 20 Questions

☛ Download Class 8 Maths Chapter 14 NCERT Book

Topics Covered: NCERT solutions Class 8 Maths Chapter 14 covers all major topics of factorization, including factors of natural numbers , factors of algebraic expressions , methods of factorization, and division of algebraic expressions.

Total Questions: Class 8 Maths Chapter 14 Factorization has 33 questions that are mostly short answer-type questions with subparts. These problems are primarily based on factoring algebraic expressions and dividing polynomials by polynomials .

List of Formulas in NCERT Solutions Class 8 Maths Chapter 14

Learning the important methods used for the factorization of numbers and algebraic expressions is an important skill. Mastering this topic will also enable students to score well in exams. NCERT Solutions Class 8 Maths Chapter 14 covers all the necessary methods used for factorization with appropriate examples. Some of the methods used for factorization of algebraic expressions explained in these solutions are listed below:

• Method of Common Factors: By using this method, an expression can be expressed as a product of terms. For example, ax + ay = a x (x+y).
• Regrouping of Factors: By regrouping terms of an expression, it can be represented as the product of its factors. For example, a 2 + bc + ab + ac = (a + b) (a + c).
• Factorization using Identities: Factorization using identities is an easy method to factorize algebraic expressions. For example, a 2 + 2ab + b 2 = (a + b) 2
• Factors of the Form (a+x)(b+x): These expressions are not perfect squares and can be factorized using this form. x 2 + (a + b) x + ab = (x + a) (x + b)

Important Questions for Class 8 Maths NCERT Solutions Chapter 14

Ncert solutions for class 8 maths video chapter 14, faqs on ncert solutions class 8 maths chapter 14, what is the importance of ncert solutions for class 8 maths chapter 14 factorization.

NCERT Solutions for Class 8 Maths Chapter 14 Factorization are highly reliable resources formulated as per the latest CBSE syllabus to help students learn maths. Students can attain conceptual fluency and the right problem-solving approach required for math studies with the regular practice of the questions and sample problems included in these solutions. The practical examples readily available in these solutions make it quite simple for students to grasp difficult steps and solutions.

What are the Important Topics Covered in NCERT Solutions Class 8 Maths Chapter 14?

The important topics explained in the NCERT Solutions Class 8 Maths Chapter 14 are factors of numbers as well as algebraic expressions, factorization methods of algebraic expressions, and division of algebraic expressions. It is necessary for students to give ample time to all topics are prepare them well.

Do I Need to Practice all Questions Provided in Class 8 Maths NCERT Solutions Factorization?

NCERT Solutions Class 8 Maths Factorization is an elaborated guide that explains all the important terms, formulas, and methods with examples to provide an in-depth understanding of factorization. Practicing each and every question present in these solutions will enable the students to attain comprehensive knowledge to excel in exams.

How Many Questions are there in Class 8 Maths NCERT Solutions Chapter 14 Factorization?

NCERT Solutions for Class 8 Maths Chapter 14 Factorization has 33 questions in 4 exercises. These four exercises effectively cover the whole topic, including methods, terms, and formulas related to Factorization. These problems are gradually placed in an efficient manner to offer step-by-step error-free learning and preparation.

What are the Important Formulas in NCERT Solutions Class 8 Maths Chapter 14?

NCERT Solutions Class 8 Maths Chapter 14 includes some of the most important formulas and methods used to factorize algebraic expressions. These solutions comprise questions based on finding common factors, regrouping expressions, and using identities for factorization. These well-formed resources have sample problems and examples that competently impart a clear knowledge of many complex concepts.

Why Should I Practice NCERT Solutions Class 8 Maths Factorization Chapter 14?

NCERT Solutions for Class 8 Maths Factorization are well-structured resources that offer complete guidance and practice to prepare for exams. The topics covered in the CBSE Class 8 maths Chapter 14 are based on NCERT textbooks to ensure positive results. The format of these solutions is quite reliable and promotes the problem-solving abilities of students for math success.

Talk to our experts

1800-120-456-456

NCERT Solutions for Class 8 Maths Chapter 14 - Factorisation

• NCERT Solutions
• Chapter 14 Factorisation

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation - Free PDF Download

Vedantu’s NCERT Solutions for Class 8 maths chapter 14 is a good platform for the students to explore more knowledge and can gain command over the chapter. All the concepts are explained in your step-by-step process with plenty of examples. The test of papers provided in our solutions is good enough to make the students get to practice. Science Students who are looking for NCERT Solutions for Class 8 Science will also find the Solutions curated by our Master Teachers really Helpful. You can also Download NCERT Solution for Class 8 Maths to help you to revise the complete Syllabus and score more marks in your examinations. Also, these materials are available to download from the official website of Vedantu.

Important Topics of NCERT Class 8 Math Chapter 14 Factorisation

Factorization, NCERT Class 8 Math Chapter 14 is an important topic covered in the syllabus. It is a scoring chapter from the exam point of view, so you must focus on Class 8 Math Chapter 14 to score well in your exam. 

Remember that factorization of expressions can seem complex in the beginning but will feel easy with practice. The Class 8 Math NCERT Solutions Chapter 14 will help you cover this chapter with ease. 

Here’s a table of all topics that you will study in NCERT Solutions Math Class 8 Chapter 14 Factorisation. 

Access NCERT Solutions for Class 8 Maths Chapter 14 – Factorization

Exercise (14.1)

1. Find the common factors of the terms

i. $12x,36$

Ans:  Write the factors of each term separately:

$12x=2\times 2\times 3\times x$

$36=2\times 2\times 3\times 3$

The factors that appear in both the lists are the common factors. 

Hence, the common factors are $2,2,3$. 

Multiply the common factors, $2\times 2\times 3=12$

ii.   $2y,22xy$

Ans: Write the factors of each term separately:

$2y=2\times y$

$22xy=2\times 11\times x\times y$

Hence, the common factors are $2,y$. 

Multiply the common factors, $2\times y=2y$. 

iii. $14pq,28{{p}^{2}}{{q}^{2}}$

$14pq=2\times 7\times p\times q$

$28{{p}^{2}}{{q}^{2}}=2\times 2\times 7\times p\times p\times q\times q$

Hence, the common factors are$2,7,p,q$. 

Multiply the common factors, $2\times 7\times p\times q=14pq$. 

iv. \[2x,3{{x}^{2}},4\]

$2x=2\times x$

$3{{x}^{2}}=3\times x\times x$

$4=2\times 2$

Hence, the common factor is $1$. 

v. $6abc,24a{{b}^{2}},12{{a}^{2}}b$

$6abc=2\times 3\times a\times b\times c$

$24a{{b}^{2}}=2\times 2\times 2\times 3\times a\times b\times b$

$12{{a}^{2}}b=2\times 2\times 3\times a\times a\times b$

Hence, the common factors are$2,3,a,b$. 

Multiply the common factors, $2\times 3\times a\times b=6ab$. 

vi. $16{{x}^{3}},-4{{x}^{2}},32x$

$16{{x}^{3}}=2\times 2\times 2\times 2\times x\times x\times x$

$-4{{x}^{2}}=-1\times 2\times 2\times x\times x$

$32x=2\times 2\times 2\times 2\times 2\times x$

Hence, the common factors are$2,2,x$ 

Multiply the common factors, $2\times 2\times x=4x$

vii. $10pq,20qr,30rp$

$10pq=2\times 5\times p\times q$

$20qr=2\times 2\times 5\times q\times r$

$30rp=2\times 3\times 5\times r\times p$

Hence, the common factors are $2,5$.

Multiply the common factors, $2\times 5=10$. 

viii. $3{{x}^{2}}{{y}^{3}},10{{x}^{3}}{{y}^{2}},6{{x}^{2}}{{y}^{2}}z$

$3{{x}^{2}}{{y}^{3}}=3\times x\times x\times y\times y\times y$

$10{{x}^{3}}{{y}^{2}}=2\times 5\times x\times x\times x\times y\times y$

$6{{x}^{2}}{{y}^{2}}z=2\times 3\times x\times x\times y\times y\times z$

Hence, the common factors are $2\times 7\times p\times q=14pq$. 

2. Factorise the following expressions

Ans: Take out the common factors from all the terms to factorize. 

$\text{ }7x=7\times x$

$42=2\times 3\times 7$

The common factor is 7

$\therefore 7x-42=(7\times x)-(2\times 3\times 7)=7(x-6)$

ii. $6p-12q$

$6p=2\times 3\times p$

$12q=2\times 2\times 3\times q$

The common factors are $2$ and $3$.

$6p-12q=(2\times 3\times p)-(2\times 2\times 3\times q)$

$=2\times 3[p-(2\times q)]$

iii. $7{{a}^{2}}+14a$

$7{{a}^{2}}=7\times a\times a$

$14a=2\times 7\times a$

The common factors are $7$ and \[a\]

$\therefore 7{{a}^{2}}+14a=(7\times a\times a)+(2\times 7\times a)$

$=7\times a[a+2]$

iv. $-16z+20{{z}^{3}}$

$\text{ }16z=2\times 2\times 2\times 2\times z$

$20{{z}^{3}}=2\times 2\times 5\times z\times z\times z$

The common factors are $2,2$, and $z$ .

$-16z+20{{z}^{3}}=-(2\times 2\times 2\times 2\times z)+(2\times 2\times 5\times z\times z\times z)$

$=(2\times 2\times z)[-(2\times 2)+(5\times z\times z)]$

$=4z\left( -4+5{{z}^{2}} \right)$

v. $20{{l}^{2}}m+30\text{alm}$

$20{{l}^{2}}m=2\times 2\times 5\times 1\times 1\times m\text{ }$

$\text{30alm }=2\times 3\times 5\times a\times 1\times m$

The common factors are \[2,5,1,\] and $m$.

$\therefore 20{{l}^{2}}m+30alm=(2\times 2\times 5\times 1\times 1\times m)+(2\times 3\times 5\times a\times 1\times m)$

$=(2\times 5\times 1\times m)[(2\times l)+(3\times a)]$

$=10lm(2l+3a)$

vi. $5{{x}^{2}}y-15x{{y}^{2}}$

$5{{x}^{2}}y=5\times x\times x\times y$

$15x{{y}^{2}}=3\times 5\times x\times y\times y$

The common factors are$5,x$, and$y$.

$5{{x}^{2}}y-15x{{y}^{2}}=(5\times x\times x\times y)-(3\times 5\times x\times y\times y)$

$=5\times x\times y[x-(3\times y)]$

$=5xy(x-3y)$

vii. $10{{a}^{2}}-15{{b}^{2}}+20{{c}^{2}}$

$10{{a}^{2}}=2\times 5\times a\times a$

$15{{b}^{2}}=3\times 5\times b\times b$

$20{{c}^{2}}=2\times 2\times 5\times c\times c$

The common factor is $5$

$10{{a}^{2}}-15{{b}^{2}}+20{{c}^{2}}=(2\times 5\times a\times a)-(3\times 5\times b\times b)+(2\times 2\times 5\times c\times c)$

$=5[(2\times a\times a)-(3\times b\times b)+(2\times 2\times c\times c)]$

$=5\left( 2{{a}^{2}}-3{{b}^{2}}+4{{c}^{2}} \right)$

viii. $-4{{a}^{2}}+4ab-4ca$

$4{{a}^{2}}=2\times 2\times a\times a$

$4ab=2\times 2\times a\times b$

$4ca=2\times 2\times c\times a$

The common factors are $2,2$, and $a$

$-4{{a}^{2}}+4ab-4ca=-(2\times 2\times a\times a)+(2\times 2\times a\times b)-(2\times 2\times c\times a)$

$=2\times 2\times a[-(a)+b-c]$

$=4a(-a+b-c)\text{ }$

ix. ${{x}^{2}}yz+x{{y}^{2}}z+xy{{z}^{2}}$

${{x}^{2}}yz=x\times x\times y\times z$

$x{{y}^{2}}z=x\times y\times y\times z$

$xy{{z}^{2}}=x\times y\times z\times z$

The common factors are$x,y$, and \[z\]

${{x}^{2}}yz+x{{y}^{2}}z+xy{{z}^{2}}=(x\times x\times y\times z)+(x\times y\times y\times z)+(x\times y\times z\times z)$

$=x\times y\times z[x+y+z]$

$=xyz(x+y+z)$

x. $a{{x}^{2}}y+bx{{y}^{2}}+cxyz$

$a{{x}^{2}}y=a\times x\times x\times y$

$bx{{y}^{2}}=b\times x\times y\times y$

$\operatorname{cxyz}=c\times x\times y\times z$

The common factors are$x$and $y$.

$a{{x}^{2}}y+bx{{y}^{2}}+cxyz=(a\times x\times x\times y)+(b\times x\times y\times y)+(c\times x\times y\times z)$

$=(x\times y)[(a\times x)+(b\times y)+(c\times z)]$

$=xy(ax+by+cz)$

3.   Factorise

i. ${{x}^{2}}+xy+8x+8y$

Write each term in terms of its factors and take out the common factors. 

${{x}^{2}}+xy+8x+8y=x\times x+x\times y+8\times x+8\times y$

$=x(x+y)+8(x+y)$

$=(x+y)(x+8)$

ii. $15xy-6x+5y-2$

$15xy-6x+5y-2=3\times 5\times x\times y-3\times 2\times x+5\times y-2$

$=3x(5y-2)+1(5y-2)$

$=(5y-2)(3x+1)$

iii. $ax+bx-ay-by$

$ax+bx-ay-by=a\times x+b\times x-a\times y-b\times y$

$=x(a+b)-y(a+b)$

$=(a+b)(x-y)$

iv. $15pq+15+9q+25p$

$15pq+15+9q+25p=15pq+9q+25p+15$

$=3\times 5\times p\times q+3\times 3\times q+5\times 5\times p+3\times 5$

$ =3\text{ }q\left( 5\text{ }p+3 \right)+5\left( 5\text{ }p+3 \right) $

$  =\left( 5\text{ }p+3 \right)\left( 3\text{ }q+5 \right) $

v.   $z-7+7xy-xyz$

$z-7+7xy-xyz=z-x\times y\times z-7+7\times x\times y$

\[=z\left( 1-x\text{ }y \right)-7\left( 1-x\text{ }y \right)\]

$=(1-xy)(z-7)$

Exercise (14.2)

1. Factorise the following expressions.

i. ${{a}^{2}}+8a+16$

Ans: Use the formula \[\left[ {{(x+y)}^{2}}={{x}^{2}}+2xy+{{y}^{2}} \right]\] to factorize.

 \[{{a}^{2}}+8a+16={{(a)}^{2}}+2\times a\times 4+{{(4)}^{2}}\]

\[={{(a+4)}^{2}}\]

ii. ${{p}^{2}}-10p+25$

${{p}^{2}}-10p+25={{(p)}^{2}}-2\times p\times 5+{{(5)}^{2}}$

$={{(p-5)}^{2}}$

iii. $25{{m}^{2}}+30m+9$

$25{{m}^{2}}+30m+9={{(5m)}^{2}}+2\times 5m\times 3+{{(3)}^{2}}$

$={{(5m+3)}^{2}}$

iv. $49{{y}^{2}}+84yz+36{{z}^{2}}$

$49{{y}^{2}}+84yz+36{{z}^{2}}={{(7y)}^{2}}+2\times (7y)\times (6z)+{{(6z)}^{2}}$

$={{(11b-4c)}^{2}}$

v. $4{{x}^{2}}-8x+4$

$4{{x}^{2}}-8x+4={{(2x)}^{2}}-2(2x)(2)+{{(2)}^{2}}$

$={{(2x-2)}^{2}}$

$={{[(2)(x-1)]}^{2}}$

$=4{{(x-1)}^{2}}$

vi. $121{{b}^{2}}-88bc+16{{c}^{2}}$

$121{{b}^{2}}-88bc+16{{c}^{2}}={{(11b)}^{2}}-2(11b)(4c)+{{(4c)}^{2}}$

vii. ${{(l+m)}^{2}}-4lm$ (Hint: Expand ${{(l+m)}^{2}}$first)

Ans: Use identity $\left[ {{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}} \right]$to factorize.

${{(l+m)}^{2}}-4lm={{l}^{2}}+2lm+{{m}^{2}}-4lm$

$={{l}^{2}}-2lm+{{m}^{2}}$

$={{(l-m)}^{2}}$

viii. ${{a}^{4}}+2{{a}^{2}}{{b}^{2}}+{{b}^{4}}$

Ans: Use identity $\left[ {{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}} \right]$to factorize. 

${{a}^{4}}+2{{a}^{2}}{{b}^{2}}+{{b}^{4}}={{\left( {{a}^{2}} \right)}^{2}}+2\left( {{a}^{2}} \right)\left( {{b}^{2}} \right)+{{\left( {{b}^{2}} \right)}^{2}}$

$={{\left( {{a}^{2}}+{{b}^{2}} \right)}^{2}}$

2. Factorise

i. $4{{p}^{2}}-9{{q}^{2}}$

Ans: Use the identity $\left[ {{a}^{2}}-{{b}^{2}}=(a-b)(a+b) \right]$ for factorizing. 

$4{{p}^{2}}-9{{q}^{2}}={{(2p)}^{2}}-{{(3q)}^{2}}$ 

$=(2p+3q)(2p-3q)$

ii. $63{{a}^{2}}-112{{b}^{2}}$

$63{{a}^{2}}-112{{b}^{2}}=7\left( 9{{a}^{2}}-16{{b}^{2}} \right)$

$=7\left[ {{(3a)}^{2}}-{{(4b)}^{2}} \right]$

$=7(3a+4b)(3a-4b)$

iii. $49{{x}^{2}}-36$

$49{{x}^{2}}-36={{(7x)}^{2}}-{{(6)}^{2}}$

$=(7x-6)(7x+6)$

iv. $16{{x}^{5}}-144{{x}^{3}}$

$16{{x}^{5}}-144{{x}^{3}}=16{{x}^{3}}\left( {{x}^{2}}-9 \right)$

$=16{{x}^{3}}\left[ {{(x)}^{2}}-{{(3)}^{2}} \right]$

$=16{{x}^{3}}(x-3)(x+3)$

v. ${{(l+m)}^{2}}-{{(l-m)}^{2}}$

${{(l+m)}^{2}}-{{(l-m)}^{2}}=[(l+m)-(l-m)][(l+m)+(l-m)]$ \[=\left( l+m-1+m \right)\left( I+m+l-m \right)\]

$=2m\times 2l$

$=4\text{ml}$

vi. \[9{{x}^{2}}{{y}^{2}}-16\]

$9{{x}^{2}}{{y}^{2}}-16={{(3xy)}^{2}}-{{(4)}^{2}}$

$=(3xy-4)(3xy+4)$

vii. $\left( {{x}^{2}}-2xy+{{y}^{2}} \right)-{{z}^{2}}$

$\left( {{x}^{2}}-2xy+{{y}^{2}} \right)-{{z}^{2}}={{(x-y)}^{2}}-{{(z)}^{2}}$

$=(x-y-z)(x-y+z)$

viii. $25{{a}^{2}}-4{{b}^{2}}+28bc-49{{c}^{2}}$

$25{{a}^{2}}-4{{b}^{2}}+28bc-49{{c}^{2}}=25{{a}^{2}}-\left( 4{{b}^{2}}-28bc+49{{c}^{2}} \right)$   $={{(5a)}^{2}}-\left[ {{(2b)}^{2}}-2\times 2b\times 7c+{{(7c)}^{2}} \right]$

$={{(5a)}^{2}}-\left[ {{(2b-7c)}^{2}} \right]$

\[=\left[ 5\text{ }a+\left( 2\text{ }b-7\text{ }c \right) \right]\left[ 5\text{ }a-\left( 2\text{ }b-7\text{ }c \right) \right]\]

\[=\left( 5\text{ }a+2\text{ }b-7\text{ }c \right)\left( 5\text{ }a-2\text{ }b+7\text{ }c \right)\]

3. Factorise the expressions

i. $a{{x}^{2}}+bx$

Ans: Take the common factors out to factorize. 

$a{{x}^{2}}+bx=a\times x\times x+b\times x$

ii. $7{{p}^{2}}+21{{q}^{2}}$

$7{{p}^{2}}+21{{q}^{2}}=7\times p\times p+3\times 7\times q\times q$

$=7\left( {{p}^{2}}+3{{q}^{2}} \right)$

iii. $2{{x}^{3}}+2x{{y}^{2}}+2x{{z}^{2}}$

$2{{x}^{3}}+2x{{y}^{2}}+2x{{z}^{2}}=2x\left( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \right)$

iv. $a{{m}^{2}}+b{{m}^{2}}+b{{n}^{2}}+a{{n}^{2}}$

$a{{m}^{2}}+b{{m}^{2}}+b{{n}^{2}}+a{{n}^{2}}=a{{m}^{2}}+b{{m}^{2}}+a{{n}^{2}}+b{{n}^{2}}$

$={{m}^{2}}(a+b)+{{n}^{2}}(a+b)$

$=(a+b)\left( {{m}^{2}}+{{n}^{2}} \right)$

v. $(lm+l)+m+l$

$(lm+l)+m+1=1m+m+1+1$

$=m(l+1)+1(l+1)$

$=(l+1)(m+1)$

vi. $y(y+z)+9(y+z)$

$y(y+z)+9(y+z)=(y+z)(y+9)$

vii. $5{{y}^{2}}-20y-8z+2yz$

$5{{y}^{2}}-20y-8z+2yz=5{{y}^{2}}-20y+2yz-8z$

\[=5y(y-4)+2z(y-4)\]

\[=(y-4)(5y+2z)\]

viii. $10ab+4a+5b+2$

$10ab+4a+5b+2=10ab+5b+4a+2$

\[=5\text{ }b\left( 2\text{ }a+1 \right)+2\left( 2\text{ }a+1 \right)\]

\[=\left( 2\text{ }a+1 \right)\left( 5\text{ }b+2 \right)\]

ix. $6xy-4y+6-9x$

 \[6xy-4\text{ }y+6-9x=6xy-9x-4y+6\]

 \[=3x\left( 2y-3 \right)-2\left( 2y-3 \right)\]

\[=\left( 2y-3 \right)\left( 3x-2 \right)\]

4. Factorise

i. ${{a}^{4}}-{{b}^{4}}$

${{a}^{4}}-{{b}^{4}}={{\left( {{a}^{2}} \right)}^{2}}-{{\left( {{b}^{2}} \right)}^{2}}$

$=\left( {{a}^{2}}-{{b}^{2}} \right)\left( {{a}^{2}}+{{b}^{2}} \right)$

$=(a-b)(a+b)\left( {{a}^{2}}+{{b}^{2}} \right)$

ii. ${{p}^{4}}-81$

${{p}^{4}}-81={{\left( {{p}^{2}} \right)}^{2}}-{{(9)}^{2}}$

$=\left( {{p}^{2}}-9 \right)\left( {{p}^{2}}+9 \right)$

$=\left[ {{(p)}^{2}}-{{(3)}^{2}} \right]\left( {{p}^{2}}+9 \right)$

$=(p-3)(p+3)\left( {{p}^{2}}+9 \right)$

iii. ${{x}^{4}}-{{(y+z)}^{4}}$

${{x}^{4}}-{{(y+z)}^{4}}={{\left( {{x}^{2}} \right)}^{2}}-{{\left[ {{(y+z)}^{2}} \right]}^{2}}$

$=\left[ {{x}^{2}}-{{(y+z)}^{2}} \right]\left[ {{x}^{2}}+{{(y+z)}^{2}} \right]$

$=[x-(y+z)][x+(y+z)]\left[ {{x}^{2}}+{{(y+z)}^{2}} \right]$

$=(x-y-z)(x+y+z)\left[ {{x}^{2}}+{{(y+z)}^{2}} \right]$

iv. ${{x}^{4}}-{{(x-z)}^{4}}$

${{x}^{4}}-{{(x-z)}^{4}}={{\left( {{x}^{2}} \right)}^{2}}-{{\left[ {{(x-z)}^{2}} \right]}^{2}}$

$=\left[ {{x}^{2}}-{{(x-z)}^{2}} \right]\left[ {{x}^{2}}+{{(x-z)}^{2}} \right]$

$=[x-(x-z)][x+(x-z)]\left[ {{x}^{2}}+{{(x-z)}^{2}} \right]$

$=z(2x-z)\left[ {{x}^{2}}+{{x}^{2}}-2xz+{{z}^{2}} \right]$

$=z(2x-z)\left( 2{{x}^{2}}-2xz+{{z}^{2}} \right)$

v. ${{a}^{4}}-2{{a}^{2}}{{b}^{2}}+{{b}^{4}}$

Ans: Use the identity $\left[ {{a}^{2}}-{{b}^{2}}=(a-b)(a+b) \right]$ for factorizing.${{a}^{4}}-2{{a}^{2}}{{b}^{2}}+{{b}^{4}}={{\left( {{a}^{2}} \right)}^{2}}-2\left( {{a}^{2}} \right)\left( {{b}^{2}} \right)+{{\left( {{b}^{2}} \right)}^{2}}$

$={{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}$

$={{[(a-b)(a+b)]}^{2}}$

$={{(a-b)}^{2}}{{(a+b)}^{2}}$

5. Factorise the following expressions

i. ${{p}^{2}}+6p+8$

Ans: We can see that, $8=4\times 2$and $4+2=6$

$\therefore {{p}^{2}}+6p+8={{p}^{2}}+2p+4p+8$

\[=p\left( p+2 \right)+4\left( p+2 \right)\]

\[=\left( p+2 \right)\left( p+4 \right)\]

ii. ${{q}^{2}}-10q+21$

Ans: We can see that, $21=(-7)\times (-3)$and $(-7)+(-3)=-10$

$\therefore {{q}^{2}}-10q+21={{q}^{2}}-7q-3q+21$

\[=q\left( q-7 \right)-3\left( q-7 \right)\]

\[=\left( q-7 \right)\left( q-3 \right)\]

iii. ${{p}^{2}}+6p-16$

Ans: We can see that, $16=(-2)\times 8$ and $8+(-2)=6$

${{p}^{2}}+6p-16={{p}^{2}}+8p-2p-16$

\[=p\left( p+8 \right)-2\left( p+8 \right)\]

\[=\left( p+8 \right)\left( p-2 \right)\]

Exercise (14.3)

1. Carry out the following divisions.

i. $28{{x}^{4}}\div 56x$

Ans: Write the numerator and denominator in its factors and divide. 

$28{{x}^{4}}=2\times 2\times 7\times x\times x\times x\times x$

$56x=2\times 2\times 2\times 7\times x$

$28{{x}^{4}}\div 56x=\dfrac{2\times 2\times 7\times x\times x\times x\times x}{2\times 2\times 2\times 7\times x}$

$=\dfrac{{{x}^{3}}}{2}$

$=\dfrac{1}{2}{{x}^{3}}$

ii. $-36{{y}^{3}}\div 9{{y}^{2}}$

$ 36{{y}^{3}}=2\times 2\times 3\times 3\times y\times y\times y$

$9{{y}^{2}}=3\times 3\times y\times y$

$-36{{y}^{3}}\div 9{{y}^{2}}=\dfrac{-2\times 2\times 3\times 3\times y\times y\times y}{3\times 3\times y\times y}$

iii. $66p{{q}^{2}}{{r}^{3}}\div 11q{{r}^{2}}$

$66p{{q}^{2}}{{r}^{3}}=2\times 3\times 11\times p\times q\times q\times r\times r\times r$

$11q{{r}^{2}}=11\times q\times r\times r$

$66p{{q}^{2}}{{r}^{3}}\div 11q{{r}^{2}}=\dfrac{2\times 3\times 11\times p\times q\times q\times r\times r\times r}{11\times q\times r\times r}=6pqr$ 

iv. $34{{x}^{3}}{{y}^{3}}{{z}^{3}}\div 51x{{y}^{2}}{{z}^{3}}$

$34{{x}^{3}}{{y}^{3}}{{z}^{3}}=2\times 17\times x\times x\times x\times y\times y\times y\times z\times z\times z$

$51x{{y}^{2}}{{z}^{3}}=3\times 17\times x\times y\times y\times z\times z\times z$

$34{{x}^{3}}{{y}^{3}}{{z}^{3}}\div 51x{{y}^{2}}{{z}^{3}}=\dfrac{2\times 17\times x\times x\times x\times y\times y\times y\times z\times z\times z}{3\times 17\times x\times y\times y\times z\times z\times z}$

$=\dfrac{2}{3}{{x}^{2}}y$

v. $12{{a}^{3}}{{b}^{8}}\div \left( -6{{a}^{6}}{{b}^{4}} \right)$

$12{{a}^{8}}{{b}^{8}}=2\times 2\times 3\times {{a}^{8}}\times {{b}^{8}}$

$6{{a}^{6}}{{b}^{4}}=2\times 3\times {{a}^{6}}\times {{b}^{4}}$

$12{{a}^{8}}{{b}^{8}}\div \left( -6{{a}^{6}}{{b}^{4}} \right)=\dfrac{2\times 2\times 3\times {{a}^{8}}\times {{b}^{8}}}{-2\times 3\times {{a}^{6}}\times {{b}^{4}}}$

$=-2{{a}^{2}}{{b}^{4}}$

2. Divide the given polynomial by the given monomial.

i. $\left( 5{{x}^{2}}-6x \right)\div 3x$

Ans: Write the numerator its factors and divide. 

$5{{x}^{2}}-6x=x(5x-6)$ 

$\left. 5{{x}^{2}}-6x \right)\div 3x=\dfrac{x(5x-6)}{3x}$

$=\dfrac{1}{3}(5x-6)$

ii. $\left( 3{{y}^{8}}-4{{y}^{6}}+5{{y}^{4}} \right)\div {{y}^{4}}$

Ans: Write the numerator its factors and divide.

$3{{y}^{8}}-4{{y}^{6}}+5{{y}^{4}}={{y}^{4}}\left( 3{{y}^{4}}-4{{y}^{2}}+5 \right)$

$\left( 3{{y}^{8}}-4{{y}^{6}}+5{{y}^{4}} \right)\div {{y}^{4}}=\dfrac{{{y}^{4}}\left( 3{{y}^{4}}-4{{y}^{2}}+5 \right)}{{{y}^{4}}}$

$=3{{y}^{4}}-4{{y}^{2}}+5$

iii.   $8\left( {{x}^{3}}{{y}^{2}}{{z}^{2}}+{{x}^{2}}{{y}^{3}}{{z}^{2}}+{{x}^{2}}{{y}^{2}}{{z}^{3}} \right)\div 4{{x}^{2}}{{y}^{2}}{{z}^{2}}$

Ans: Write the numerator its factors and divide.  

$8\left( {{x}^{3}}{{y}^{2}}{{z}^{2}}+{{x}^{2}}{{y}^{3}}{{z}^{2}}+{{x}^{2}}{{y}^{2}}{{z}^{3}} \right)=8{{x}^{2}}{{y}^{2}}{{z}^{2}}(x+y+z)$

$8\left( {{x}^{3}}{{y}^{2}}{{z}^{2}}+{{x}^{2}}{{y}^{3}}{{z}^{2}}+{{x}^{2}}{{y}^{2}}{{z}^{3}} \right)\div 4{{x}^{2}}{{y}^{2}}{{z}^{2}}=\dfrac{8{{x}^{2}}{{y}^{2}}{{z}^{2}}(x+y+z)}{4{{x}^{2}}{{y}^{2}}{{z}^{2}}}$

$=2(x+y+z)$

iv. $\left( {{x}^{3}}+2{{x}^{2}}+3x \right)\div 2x$

${{x}^{3}}+2{{x}^{2}}+3x=x\left( {{x}^{2}}+2x+3 \right)$

$\left( {{x}^{3}}+2{{x}^{2}}+3x \right)\div 2x=\dfrac{x\left( {{x}^{2}}+2x+3 \right)}{2x}$

$=\dfrac{1}{2}\left( {{x}^{2}}+2x+3 \right)$

v. $\left( {{p}^{3}}{{q}^{6}}-{{p}^{6}}{{q}^{3}} \right)\div {{p}^{3}}{{q}^{3}}$

) ${{p}^{3}}{{q}^{6}}-{{p}^{6}}{{q}^{3}}={{p}^{3}}{{q}^{3}}\left( {{q}^{3}}-{{p}^{3}} \right)$

$\left( {{p}^{3}}{{q}^{6}}-{{p}^{6}}{{q}^{3}} \right)\div {{p}^{3}}{{q}^{3}}=\dfrac{{{p}^{3}}{{q}^{3}}\left( {{q}^{3}}-{{p}^{3}} \right)}{{{p}^{3}}{{q}^{3}}}$

$={{q}^{3}}-{{p}^{3}}$

3. Work out the following divisions.

i. $(10x-25)\div 5$

$(10x-25)\div 5=\dfrac{2\times 5\times x-5\times 5}{5}$

$=\dfrac{5(2x-5)}{5}$

ii. $(10x-25)\div (2x-5)$

$(10x-25)\div (2x-5)=\dfrac{2\times 5\times x-5\times 5}{(2x-5)}$

$=\dfrac{5(2x-5)}{2x-5}$

iii. $10y(6y+21)\div 5(2y+7)$

$10y(6y+21)\div 5(2y+7)=\dfrac{2\times 5\times y[2\times 3\times y+3\times 7]}{5(2y+7)}$

 $=\dfrac{2\times 5\times y\times 3(2y+7)}{5(2y+7)}$

iv. $9{{x}^{2}}{{y}^{2}}(3z-24)\div 27xy(z-8)$

$9{{x}^{2}}{{y}^{2}}(3z-24)\div 27xy(z-8)=\dfrac{9{{x}^{2}}{{y}^{2}}[3\times z-2\times 2\times 2\times 3]}{27xy(z-8)}$

  $=\dfrac{xy\times 3(z-8)}{3(z-8)}$

v. $96abc(3a-12)(5b-30)\div 144(a-4)(b-6)$

$96abc(3a-12)(5b-30)\div 144(a-4)(b-6)$

$=\dfrac{96abc(3\times a-3\times 4)(5\times b-2\times 3\times 5)}{144(a-4)(b-6)}$

$=\dfrac{2abc\times 3(a-4)\times 5(b-6)}{3(a-4)(b-6)}$

4. Divide as directed.

i. $5(2x+1)(3x+5)\div (2x+1)$

$5(2x+1)(3x+5)\div (2x+1)=\dfrac{5(2x+1)(3x+1)}{(2x+1)}$

ii. $26xy(x+5)(y-4)\div 13x(y-4)$

$26xy(x+5)(y-4)\div 13x(y-4)=\dfrac{2\times 13\times xy(x+5)(y-4)}{13x(y-4)}$

iii. $52pqr(p+q)(q+r)(r+p)\div 104pq(q+r)(r+p)$

$52pqr(p+q)(q+r)(r+p)\div 104pq(q+r)(r+p)$

$=\dfrac{2\times 2\times 13\times p\times q\times r\times (p+q)\times (q+r)\times (r+p)}{2\times 2\times 2\times 13\times p\times q\times (q+r)\times (r+p)}$

$=\dfrac{1}{2}r(p+q)$

iv. $20(y+4)\left( {{y}^{2}}+5y+3 \right)\div 5(y+4)$

$20(y+4)\left( {{y}^{2}}+5y+3 \right)=2\times 2\times 5\times (y+4)\left( {{y}^{2}}+5y+3 \right)$

$20(y+4)\left( {{y}^{2}}+5y+3 \right)\div 5(y+4)=\dfrac{2\times 2\times 5\times (y+4)\times \left( {{y}^{2}}+5y+3 \right)}{5\times (y+4)}$                    $=4\left( {{y}^{2}}+5y+3 \right)$ 

v. $x(x+1)(x+2)(x+3)\div x(x+1)$

$x(x+1)(x+2)(x+3)\div x(x+1)=\dfrac{x(x+1)(x+2)(x+3)}{x(x+1)}$

\[=\left( x+2 \right)\left( x+3 \right)\]

5. Factorise the expressions and divide them as directed.

i. $\left( {{y}^{2}}+7y+10 \right)\div (y+5)$

Ans: Factorise the given terms separately.

$\left( {{y}^{2}}+7y+10 \right)={{y}^{2}}+2y+5y+10$

$=y(y+2)+5(y+2)$

$=(y+2)(y+5)$

Divide the two terms. 

$\left( {{y}^{2}}+7y+10 \right)\div (y+5)=\dfrac{(y+5)(y+2)}{(y+5)}$

ii. $\left( {{m}^{2}}-14m-32 \right)\div (m+2)$

${{m}^{2}}-14m-32={{m}^{2}}+2m-16m-32$

$=m(m+2)-16(m+2)$

$=(m+2)(m-16)$

$\left( {{m}^{2}}-14m-32 \right)\div (m+2)=\dfrac{(m+2)(m-16)}{(m+2)}$

iii. $\left( 5{{p}^{2}}-25p+20 \right)\div (p-1)$

$5{{p}^{2}}-25p+20=5\left( {{p}^{2}}-5p+4 \right)$

=5[p(p-1)-4(p-1)]

$=5(p-1)(p-4)$

$\left( 5{{p}^{2}}-25p+20 \right)\div (p-1)=\dfrac{5(p-1)(p-4)}{(p-1)}$

iv. $4yz\left( {{z}^{2}}+6z-16 \right)\div 2y(z+8)$

$4yz\left( {{z}^{2}}+6z-16 \right)=4yz\left[ {{z}^{2}}-2z+8z-16 \right]$

\[=4\text{ }y\text{ }z\left[ z\left( z-2 \right)+8\left( z-2 \right) \right]\]

\[=4\text{ }y\text{ }z\left( z-2 \right)\left( z+8 \right)\]

$4yz\left( {{z}^{2}}+6z-16 \right)\div 2y(z+8)=\dfrac{4yz(z-2)(z+8)}{2y(z+8)}$

v. $5pq\left( {{p}^{2}}-{{q}^{2}} \right)\div 2p(p+q)$

$5pq\left( {{p}^{2}}-{{q}^{2}} \right)=5pq(p-q)(p+q)$

$5pq\left( {{p}^{2}}-{{q}^{2}} \right)\div 2p(p+q)=\dfrac{5pq(p-q)(p+q)}{2p(p+q)}$

$=\dfrac{5}{2}q(p-q)$

vi. $12xy\left( 9{{x}^{2}}-16{{y}^{2}} \right)\div 4xy(3x+4y)$

$12xy\left( 9{{x}^{2}}-16{{y}^{2}} \right)=12xy\left[ {{(3x)}^{2}}-{{(4y)}^{2}} \right]$

$=12xy(3x-4y)(3x+4y)$

$12xy\left( 9{{x}^{2}}-16{{y}^{2}} \right)\div 4xy(3x+4y)$

$=\dfrac{2\times 2\times 3\times x\times y\times (3x-4y)\times (3x+4y)}{2\times 2\times x\times y\times (3x+4y)}$

\[=3\left( 3\text{ }x-4\text{ }y \right)\]

vii. $39{{y}^{3}}\left( 50{{y}^{2}}-98 \right)\div 26{{y}^{2}}(5y+7)$

$39{{y}^{3}}\left( 50{{y}^{2}}-98 \right)=3\times 13\times y\times y\times y\times 2\left[ \left( 25{{y}^{2}}-49 \right) \right]$

$=3\times 13\times 2\times y\times y\times y\times \left[ {{(5y)}^{2}}-{{(7)}^{2}} \right]$

$=3\times 13\times 2\times y\times y\times y(5y-7)(5y+7)$

$26{{y}^{2}}(5y+7)=2\times 13\times y\times y\times (5y+7)$

\[39{{y}^{3}}\left( 50{{y}^{2}}-98 \right)\div 26{{y}^{2}}(5y+7)=\dfrac{3\times 13\times 2\times y\times y\times y(5y-7)(5y+7)}{2\times 13\times y\times y\times (5y+7)}\]

\[=3y(5y-7)\]

\[=15{{y}^{2}}-21y\]

Exercise (14.4)

1.   Find and correct the errors in the statement: $4(x-5)=4x-5$

Ans: Compare the L.HS. with the R.H.S.

L.H.S $4(x-5)=4x-20 \ne $R.H.S.

The correct statement is  $4(x-5)=4x-20$

2.   Find and correct the errors in the statement: $x(3x+2)=3x^2 +2$

L.H.S $x(3x+2)=3x^2 +2x \ne $R.H.S.

3.   Find and correct the errors in the statement: $2x+3y=5xy$

L.H.S $=2x+3y=2x+3y\ne $R.H.S.

The correct statement is $2x+3y=2x+3y$

4. Find and correct the errors in the statement: $x+2x+3x=5x$

L.H.S \[=x+2x+3x=1x+2x+3x=x(1+2+3)=6x\ne RHS\]

The correct statement is $x+2x+3x=6x$

5. Find and correct the errors in the statement: $5y+2y+y-7y=0$

L.H.S. $=5y+2y+y-7y=8y-7y=y\ne \$R.H.S$

The correct statement is $5y+2y+y-7y=y$

6. Find and correct the errors in the statement: $3x+2x=5{{x}^{2}}$

L.H.S. $=3x+2x=5x\ne \$R.H.S$

The correct statement is $3x+2x=5x$.

7.   Find and correct the errors in the statement: ${{(2x)}^{2}}+4(2x)+7=2{{x}^{2}}+8x+7$

Ans: Compare the L.H.S with the R.H.S. 

L.H.S$={{(2x)}^{2}}+4(2x)+7=4{{x}^{2}}+8x+7\ne $R.H.S 

The correct statement is ${{(2x)}^{2}}+4(2x)+7=4{{x}^{2}}+8x+7$

8. Find and correct the errors in the statement: ${{(2x)}^{2}}+5x=4x+5x=9x$

LH.S $={{(2x)}^{2}}+5x=4{{x}^{2}}+5x\ne \$R.H.S.$

The correct statement is ${{(2x)}^{2}}+5x=4{{x}^{2}}+5x$

9. Find and correct the errors in the statement: ${{(3x+2)}^{2}}=3{{x}^{2}}+6x+4$

Use the property $\left[ {{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}} \right]$.

$\text{ L}\text{.H}\text{.S}\text{. }={{(3x+2)}^{2}}={{(3x)}^{2}}+2(3x)(2)+{{(2)}^{2}}\text{ =}9{{x}^{2}}+12x+4\ne \text{ R}\text{.H}\text{.S }$

The correct statement is ${{(3x+2)}^{2}}=9{{x}^{2}}+12x+4$.

10. Find and correct the errors in the following mathematical statement. Substituting $x=-3$ in

a. ${{x}^{2}}+5x+4$  gives ${{(-3)}^{2}}+5(-3)+4=9+2+4=15$

Ans: Put the value $x=-3$ and solve. 

${{x}^{2}}+5x+4={{(-3)}^{2}}+5(-3)+4$

Hence the given statement is wrong. 

The correct statement is: ${{x}^{2}}+5x+4$ gives $-2$

b. ${{x}^{2}}-5x+4$ gives ${{(-3)}^{2}}-5(-3)+4=9-15+4=-2$

Ans: Put the value $x=-3$ and solve.

${{x}^{2}}-5x+4={{(-3)}^{2}}-5(-3)+4$ 

The correct statement is: ${{x}^{2}}-5x+4$ gives $28$

c. ${{x}^{2}}+5x$  gives  ${{(-3)}^{2}}+5(-3)=-9-15=-24$

${{x}^{2}}+5x={{(-3)}^{2}}+5(-3)$

The correct statement is: ${{x}^{2}}+5x$ gives $-6$. 

11. Find and correct the errors in the statement: ${{(y-3)}^{2}}={{y}^{2}}-9$

Use the property $\left[ {{(a-b)}^{2}}={{a}^{2}}-2ab+{{b}^{2}} \right]$

L.H.S $={{(y-3)}^{2}}={{(y)}^{2}}-2(y)(3)+{{(3)}^{2}}={{y}^{2}}-6y+9\ne R.H.S$

The correct statement is ${{(y-3)}^{2}}={{y}^{2}}-6y+9$

12. Find and correct the errors in the statement: ${{(z+5)}^{2}}={{z}^{2}}+25$

Use the property $\left[ {{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}} \right]$. 

$\text{ L}\text{.H}\text{.S }={{(z+5)}^{2}}={{(z)}^{2}}+2(z)(5)+{{(5)}^{2}}={{z}^{2}}+10z+25\ne \text{ R}\text{.H}\text{.S }$

The correct statement is ${{(z+5)}^{2}}={{z}^{2}}+10z+25$

13. Find and correct the errors in the statement: $(2a+3b)(a-b)=2{{a}^{2}}-3{{b}^{2}}$

Ans: Compare the L.HS. with the R.H.S. 

$=(2a+3b)(a-b)$

$=2a\times a+3b\times a-2a\times b-3b\times b$

$=2{{a}^{2}}+3ab-2ab-3{{b}^{2}}$ 

$=2{{a}^{2}}+ab-3{{b}^{2}}\ne \text{ R}\text{.H}\text{.S}\text{. }$

The correct statement is $(2a+3b)(a-b)=2{{a}^{2}}+ab-3{{b}^{2}}$

14. Find and correct the errors in the statement: $(a+4)(a+2)={{a}^{2}}+8$

$\text{ L}\text{.H}\text{.S}\text{. }=(a+4)(a+2)={{(a)}^{2}}+(4+2)(a)+4\times 2={{a}^{2}}+6a+8\ne \text{ R}\text{.H}\text{.S }$

The correct statement is $(a+4)(a+2)={{a}^{2}}+6a+8$

15. Find and correct the errors in the statement: $(a-4)(a-2)={{a}^{2}}-8$

$L.H.S.=(a-4)(a-2)={{(a)}^{2}}+[(-4)+(-2)](a)+(-4)(-2)={{a}^{2}}-6a+8\ne \text{ R}\text{.H}\text{.S}\text{. }$

The correct statement is $(a-4)(a-2)={{a}^{2}}-6a+8$

16. Find and correct the errors in the statement: $\dfrac{3{{x}^{2}}}{3{{x}^{2}}}=0$

$\text{ L}\text{.H}\text{.S }=\dfrac{3{{x}^{2}}}{3{{x}^{2}}}=\dfrac{3\times x\times x}{3\times x\times x}=1\ne \text{ R}\text{.H}\text{.S}\text{. }$

The correct statement is $\dfrac{3{{x}^{2}}}{3{{x}^{2}}}=1$

17. Find and correct the errors in the statement : $\dfrac{3{{x}^{2}}+1}{3{{x}^{2}}}=1+1=2$

$\dfrac{3{{x}^{2}}+1}{3{{x}^{2}}}=\dfrac{3{{x}^{2}}}{3{{x}^{2}}}+\dfrac{1}{3{{x}^{2}}}=1+\dfrac{1}{3{{x}^{2}}}\ne \text{ R}\text{.H}\text{.S}\text{. }$

The correct statement is $\dfrac{3{{x}^{2}}+1}{3{{x}^{2}}}=1+\dfrac{1}{3{{x}^{2}}}$

18. Find and correct the errors in the statement: $\dfrac{3x}{3x+2}=\dfrac{1}{2}$

$\text{ L}.\text{H}.\text{S=}\dfrac{\text{3x}}{\text{3x+2}}\ne \text{ R}\text{.H}\text{.S}\text{. }$

The correct statement is $\dfrac{3x}{3x+2}=\dfrac{3x}{3x+2}$

19. Find and correct the errors in the statement: $\dfrac{3}{4x+3}=\dfrac{1}{4x}$

$\text{L}\text{.H}\text{.S}=\dfrac{3}{4x+3}\ne \text{R}\text{.H}.\text{S}$

The correct statement is $\dfrac{3}{4x+3}=\dfrac{3}{4x+3}$

20. Find and correct the errors in the statement: $\dfrac{4x+5}{4x}=5$

L.H.S. $=\dfrac{4x+5}{4x}=\dfrac{4x}{4x}+\dfrac{5}{4x}=1+\dfrac{5}{4x}\ne R.H.S$

The correct statement is $\dfrac{4x+5}{4x}=1+\dfrac{5}{4x}$

21. Find and correct the errors in the statement: $\dfrac{7x+5}{5}=7x$

L.H.S. $=\dfrac{7x+5}{5}=\dfrac{7x}{5}+\dfrac{5}{5}=\dfrac{7x}{5}+1\ne R.H.S.$

The correct statement is $\dfrac{7x+5}{5}=\dfrac{7x}{5}+1$.

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Free PDF

Students can have the benefit of downloading NCERT Solutions for Class 8 Factorisation in a pdf format for free of cost. Take a physical copy for the uninterrupted study hours of the student as these hard copies can be taken anywhere to practice any time, along with friends also. Also, these can be stored and utilised during the time of examinations and can revise while attending olympiads and competitive exams.

NCERT Solutions for Class 8 Factorisation

14.1 introduction.

The first section of every chapter might be the same in most cases. It is the Introduction part. Here the introduction may remind the knowledge of factors for the students which they have studied in the earlier classes. Students have already learned to find factors for natural numbers and the meaning of factors for algebraic expressions. Then in this chapter, they are going to learn the factorisation of big expressions using different methods in detail.

14.2 What is Factorisation?

The 8th class maths chapter 12 factorisation Pdf explains the meaning of factorisation. The factorisation is a process of representing the given expression in the form of the product of two factors. These factors may be either of the numbers or variables or algebraic expressions themselves. The PDF also explains that it has several systematic approaches to find factors for the given expressions. Let's see the available methods to find the factors.

14.2.1 Method of Common Factors

It is the first method of finding factors for the given expression. According to NCERT Solutions Class 8 Factorisation, the given expression can be expressed in the product of terms. This can be understood clearly by observing two or more examples given in the PDF.

14.2.2 Factorization by Regrouping Terms

The next section of this chapter deals with another method of factorization. Chapter 14 Class 8 explains that while finding the factors of the given expression, we will take an individual term as common and consider it as a common factor. This can be done by forming two groups. For an instance,

= 6𝑝 − (6 × 2)𝑞

= 6(𝑝 − 2𝑞)(taking 6 as common)

Exercise 14.1 with three short answer type questions.

14.2.3 Factorization Using Identities

NCERT Class 8 Maths Chapter 14 came to the third method of factorization in this section. Here students need to find out the identical terms and then separate those terms which give the factors directly.

14.2.4 Factors of the form (x+a)(x+b)

This is the 4th method of solving factorization. The Class 8 Maths Solutions Chapter 14 explains that this method was usually used if the expression doesn't have perfect squares. Even though it is suitable for perfect squares, without having perfect squares, also we can use this method to get factors of the given expression. Even though we have different methods to find factors, the solution is one and the same, but the procedures may differ.

Exercise 14.2 has five short answer type questions in which each question has some set of expressions to solve.

14.3 Division of Algebraic Expressions

The Maths Class 8 NCERT Solutions Chapter 14 explains an advanced concept in factorization. As the students have learned addition, subtraction, multiplication of algebraic expressions, now class 8 maths factorization explains how to divide two or more expressions. But it has two sub-concepts. Because the division can be made based on the degree of expression. From the notes of NCERT Solutions Chapter 14 Class 8, we have:

Division of monomial by another monomial.

Division of polynomial by monomial.

14.4 Division of Algebraic Expressions Continued

Class 8 Maths Factorisation Solutions has explained that this section is the extension of the above section. Here the division of expressions can be made by two or more polynomials. It explains how to divide the Algebraic Expressions of higher degrees.

Exercise 14.3 contains five long answer type questions each question has a set of sums.

14.5  Can You Find the Error

The chapter of Factorisation questions for Class 8 NCERT has ended with this last section of correcting errors on the expressions. It is also known as verification and making the right-hand side terms and left-hand side terms equal. In this equalisation process, students can correct the errors.

Exercise 14.4 with 20 short answer type questions.

Key Takeaways of NCERT Solutions Class 8 Maths Chapter 14 Free PDF

Students can enjoy various benefits by using Factorisation class 8 NCERT. Some of them are:

The previous papers can help the students to practice and understand the question pattern, allotment of marks.

Well-experienced mathematicians prepare the PDFs based on the current syllabus.

These are available for free in both English and Hindi.

Why Should You Study Class 8 Math NCERT Solutions on Vedantu?

1. Vedantu's Math NCERT Solutions are comprehensive, ensuring a clear and easy-to-understand presentation.

2. Detailed solutions to every question in the Class 8 Math NCERT book are available here, enhancing understanding.

3. Crafted by subject experts, our NCERT Solutions offer precise and correct step-by-step solutions for effective learning.

4. Accessible for free download in PDF format, providing convenience for students.

5. Vedantu prioritizes concept clarity, offering insights into Math NCERT chapters to enhance exam preparation.

NCERT Class 8 Maths Chapter wise Solutions in Hindi

Chapter 1 - Rational Numbers in Hindi

Chapter 2 - Linear Equations in One Variable in Hindi

Chapter 3 - Understanding Quadrilaterals in Hindi

Chapter 4 - Practical Geometry in Hindi

Chapter 5 - Data Handling in Hindi

Chapter 6 - Squares and Square Roots in Hindi

Chapter 7 - Cubes and Cube Roots in Hindi

Chapter 8 - Comparing Quantities in Hindi

Chapter 9 - Algebraic Expressions and Identities in Hindi

Chapter 10 - Visualising Solid Shapes in Hindi

Chapter 11 - Mensuration in Hindi

Chapter 12 - Exponents and Powers in Hindi

Chapter 13 - Direct and Inverse Proportions in Hindi

Chapter 14 - Factorisation in Hindi

Chapter 15 - Introduction to Graphs in Hindi

Chapter 16 - Playing with Number in Hindi

NCERT Solutions for Class 8 Maths - Chapterwise Solutions

Chapter 1 - Rational Numbers

Chapter 2 - Linear Equations in One Variable

Chapter 3 - Understanding Quadrilaterals

Chapter 4 - Practical Geometry

Chapter 5 - Data Handling

Chapter 6 - Squares and Square Roots

Chapter 7 - Cubes and Cube Roots

Chapter 8 - Comparing Quantities

Chapter 9 - Algebraic Expressions and Identities

Chapter 10 - Visualising Solid Shapes

Chapter 11 - Mensuration

Chapter 12 - Exponents and Powers

Chapter 13 - Direct and Inverse Proportions

Chapter 15 - Introduction to Graphs

Chapter 16 - Playing with Numbers

NCERT Solutions plays a crucial role in Class 8 exam prep. Start by thoroughly reading the textbook chapter. After that, solve the NCERT questions for Class 8 Maths Chapter 14 - Factorisation. You can find detailed solutions on Vedantu, aligning with CBSE guidelines. Download the free NCERT Solutions for Class 8 Maths Chapter 14 - Factorisation to guide your exam preparation with expert-reviewed answers.

FAQs on NCERT Solutions for Class 8 Maths Chapter 14 - Factorisation

1. Solve 49𝑦 2 + 84𝑦𝑧 + 36𝑧 2

49𝑦 2 + 84𝑦𝑧 + 36𝑧 2

49𝑦 2  + 84𝑦𝑧 + 36𝑧 2

= (7𝑦) 2 + 84𝑦𝑧 + (6𝑧) 2

= (7𝑦) 2   + 2 × 7𝑦 × 6𝑧 + (6𝑧) 2

= (7𝑦) 2 + (6𝑧) 2 + 2 × 7𝑦 × 6𝑧

Using (𝑎 + 𝑏) 2 = 𝑎 2   + 𝑏 2   + 2𝑎𝑏

Here, 𝑎 = 7𝑦 and 𝑏 = 6𝑧

= (7𝑦 + 6𝑧) 2

It is the solution.

2. Solve a 4 + 2a 2 b 2 + b 4

Given expression is, 𝑎 4 + 2𝑎 2 𝑏 2 + 𝑏 4

It is a fourth-degree expression.

= 𝑎 4 + 2𝑎 2 𝑏 2 + 𝑏 4

Using the formula, (𝑎 m ) n = 𝑎 m*n

∴ (𝑎 2 ) 2 = 𝑎 2*2 = 𝑎 4

= (𝑎 2 ) 2 + 2𝑎 2 𝑏 2 + (b 2 ) 2

= (𝑎 2 ) 2 + 2(𝑎 2 × 𝑏 2 ) + (𝑏 2 ) 2

= (𝑎 2 ) 2 + (𝑏 2 ) 2 + 2(𝑎 2 × 𝑏 2 )

Using (𝑥 + 𝑦) 2   = x 2 + y 2   + 2xy, we can substitute as,

Here, 𝑥 = 𝑎 2 and 𝑦 = 𝑏 2

= (a 2   + b 2 ) 2

Hence it is solved.

3. How to study Chapter 14 “Factorisation” of Class 8 Maths using Vedantu’s NCERT Solutions?

To use Vedantu's NCERT Solutions for Chapter 14 “Factorisation” of Class 8 Maths effectively for your studies:

Read the NCERT textbook well and practice all of its exercise questions.

Refer to Vedantu's NCERT Solutions of this chapter for perfectly crafted step-by-step answers.

Use Vedantu's explanations provided below the solutions for an added understanding of the chapter.

These explanations are also useful for revision purposes.

You may also attend Vedantu's live classes to study the chapter with our master teachers.

4. What are the main topics covered in the NCERT Solutions for Chapter 14 of Class 8 Maths?

Chapter 14 "Factorisation" of Class 8 Maths contains the following foundational topics significant in various mathematical operations:

Factors of natural numbers

Factors of algebraic expressions

Method of on factors

Factorization by regrouping terms

Factorization using identities

Factors of the form ( x + a) ( x + b)

Division of Algebraic Expressions

Can you find the error?

5. How many exercises are there in NCERT Solutions for Chapter 14 of Class 8 Maths?

Chapter 14 “Factorisation” of Class 8 Maths contains a total of four exercises.

All four exercises are important from the examination point of view.

Factorization is a significant chapter and students must have the basics of this chapter clear in their minds. You can look up Vedantu's explanations of this chapter for further clarity.

You need to practice the exercises from this chapter diligently to master the conceptual understanding of this chapter. Refer to the NCERT Solutions for Chapter 14 of Class 8 Maths available free of cost on the Vedantu website and the Vedantu app.

6. What do you mean by factorization according to Chapter 14 of Class 8 Maths?

Factorization is the process of breaking down a number into smaller numbers which when multiplied together produces the original number.

In simple terms Factorisation of an algebraic expression is the process of writing the expression as a product of its factors. These factors may be numbers, algebraic variables, or algebraic expressions.

"Factorisation" is an important chapter as it lays down the basic foundations of several mathematical operations. 

7. Explain the common factor method in factorization according to Chapter 14 of Class 8 Maths.

The Common Factor method is an organized way of factorizing an expression.

Here is how you can systematically factorize an expression using the common factor method: 

Write each term of the expression as a product of irreducible factors. 

Look for the common factors and separate them.

Combine the remaining factors in each term in accordance with the distributive law.

Exercise 14.1 of Chapter 14 of Class 8 Maths is based on the common factor method. You can download the solutions for this exercise in pdf format here.

NCERT Solutions for Class 8 Maths

Ncert solutions for class 8.

Mathematics | Factorisation

This is an introductory lesson on factorisation of algebraic expressions and explores some techniques involved

• Questions & Answers

Introduction to CBSE Class 8 Mathematics Chapter "Factorisation"

“Factorisation” is a key chapter in the CBSE Class 8 Mathematics syllabus that delves into breaking down algebraic expressions into their simplest form. This chapter introduces students to the concept of factors of natural numbers, which are then extended to polynomial expressions. It begins with the factorisation of common terms and advances to techniques such as regrouping terms, splitting the middle term, and using identities to simplify and solve quadratic and cubic polynomial expressions.

The chapter aims to strengthen students’ understanding of how factorisation is applied to simplify algebraic expressions and solve equations efficiently. By mastering factorisation, students can solve a variety of problems, including those involving finding values of algebraic expressions for specific values of variables. Factorisation also plays a significant role in finding the LCM and GCD of polynomials, thereby linking arithmetic to algebra.

Assignments for CBSE Class 8 Mathematics Chapter “Factorisation”

• Factor Hunt : Factorise different algebraic expressions and identify their factors.
• Real-life Application : Describe a real-life situation where factorisation might be used and demonstrate how to apply it.
• Exploring Identities : Use algebraic identities to factorise given expressions and verify the results by expansion.
• Creative Factors : Craft a story problem that involves factorisation and present the solution.
• Puzzle Time : Create and solve a puzzle where the clues lead to factorisation of polynomials.

Conclusion The chapter “Factorisation” in CBSE Class 8 Mathematics serves as an essential building block for understanding algebraic expressions and equations. It equips students with a fundamental skill set that not only aids in simplifying and solving algebraic challenges but also lays the groundwork for future studies in mathematics and sciences.

"Preparing for the Class 6 exam? Notebook is your go-to resource for learning anytime, anywhere. With courses, docs, videos, and tests covering the complete syllabus, Notebook has the perfect solution for all your study needs. Join Notebook today to get everything you need in one place.

Questions and Answers for CBSE Class 8 Mathematics Chapter "Factorisation"

• Q1: What is factorisation? ANS : Factorisation is the process of breaking down a complex expression into simpler factors that, when multiplied together, give the original expression.
• Q2: Why is factorisation important in mathematics? ANS : Factorisation is important because it simplifies expressions, making it easier to solve equations and understand algebraic structures.
• Q3: What is a common factor in algebraic expressions? ANS : A common factor is a term that is present in all terms of an expression, which can be factored out to simplify the expression.
• Q4: How do you factorise a polynomial using the middle term splitting method? ANS : To factorise a polynomial using the middle term splitting method, you split the middle term into two terms such that their product is equal to the product of the squared term coefficient and the constant term.
• Q5: Can all algebraic expressions be factorised? ANS : Most algebraic expressions can be factorised, but some cannot be broken down into simpler factors over the set of integers.
• Q6: What role do algebraic identities play in factorisation? ANS : Algebraic identities help in factorisation by providing standard forms that can be used to quickly factorise certain types of expressions.
• Q7: How does factorisation help in finding the LCM and GCD of polynomials? ANS : Factorisation allows us to break down polynomials into their prime factors, making it easier to identify the least common multiples (LCM) and greatest common divisors (GCD).
• Q8: What is a factor tree, and how is it used in factorisation? ANS : A factor tree is a diagram used to break down a number into its prime factors. It’s not commonly used for algebraic expressions but can help understand factorisation of numbers.
• Q9: How do you check if your factorisation is correct? ANS : You can check factorisation by multiplying the factors and verifying if the product is the original expression.
• Q10: How can factorisation be used to solve quadratic equations? ANS : Factorisation can be used to solve quadratic equations by setting the factored form of the equation to zero and solving for the variable, which gives the roots of the equation.

Want access to all premium tests, videos & docs?

Learn next topic:, science | conservation of plants and animals, previous post science | crop production and management, next post mathematics | direct and inverse proportions.

Comments are closed.

Augmented Storytelling

Welcome to the world of beautiful hand drawn picures

Get maximum value for each minute spent

Content Pedagogy

Generating curiosity- maximising takeaway

Download the Mobile App to watch more videos.

In Partnership with Notebook.

In Partnership with

Quick Links

• About Notebook
• Enquiry about Notebook
• Notebook Media
• Notebook Courses

+91 080 41650688

[email protected].

©2024 All Rights Reserved by CBSE Guide.

• Factorisation

NCERT curriculum (for CBSE/ICSE) Class 8 - Factorisation

Unlimited worksheets.

Every time you click the New Worksheet button, you will get a brand new printable PDF worksheet on Factorisation . You can choose to include answers and step-by-step solutions.

Unlimited Online Practice

Unlimited adaptive online practice on Factorisation . Practice that feels like play! Get shields, trophies, certificates and scores. Master Factorisation as you play.

Unlimited Online Tests

Take unlimited online tests on Factorisation . Get instant scores and step-by-step solutions on submission. Make sure you always get your answers right in Factorisation .

Contents: Factorisation

Factorisation - Factorisation of Polynomials.

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• ML Aggarwal Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• HOTS Question
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Crash Course
• JEE Previous Year Paper
• Important Info
• JEE Mock Test
• JEE Sample Papers
• SRM-JEEE Mock Test
• VITEEE Mock Test
• BITSAT Mock Test
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• COMEDK Previous Year Paper
• GUJCET Previous Year Paper
• KCET Previous Year Paper
• KEAM Previous Year Paper
• Manipal Previous Year Paper
• MHT CET Previous Year Paper
• WBJEE Previous Year Paper
• AMU Previous Year Paper
• TS EAMCET Previous Year Paper
• SRM-JEEE Previous Year Paper
• VITEEE Previous Year Paper
• BITSAT Previous Year Paper
• UPSEE Previous Year Paper
• CGPET Previous Year Paper
• CUSAT Previous Year Paper
• AEEE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

Factorisation Worksheet Class 8 PDF with Answers

These Factorisation worksheet PDF can be helpful for both teachers and students. Teachers can track their student’s performance in the chapter Factorisation. Students can easily identify their strong points and weak points by solving questions from the worksheet. Accordingly, students can work on both weak points and strong points. 

All students studying in CBSE class 8th, need to practise a lot of questions for the chapter Factorisation. Students can easily practise questions from the Factorisation problems worksheet PDF. By practising a lot of questions, students can improve their confidence level. With the help of confidence level, students can easily cover all the concepts included in the chapter Factorisation. 

Factorisation Worksheets with Solutions

Solutions is the written reply for all questions included in the worksheet. With the help of Factorisation worksheets with solutions, students can solve all doubts regarding questions. Students can have deep learning in the chapter Factorisation by solving all their doubts. By solving doubts, students can also score well in the chapter Factorisation. 

Factorisation Worksheet PDF

Worksheet is a sheet which includes many questions to solve for class 8th students. The Factorisation worksheet PDF provides an opportunity for students to enhance their learning skills. Through these skills, students can easily score well in the chapter Factorisation. Students can solve the portable document format (PDF) of the worksheet from their own comfort zone. 

How to Download the Factorisation Worksheet PDF? 

To solve questions from the Factorisation worksheet PDF, students can easily go through the given steps. Those steps are- 

• Open Selfstudys website.

• Bring the arrow towards CBSE which can be seen in the navigation bar. 

• Drop down menu will appear, select KVS NCERT CBSE Worksheet. 

• A new page will appear, select class 8th from the given list of classes. 
• Select Mathematics from the given list of subjects. Now click the chapter’s name that is Factorisation. 

Features of the Factorisation Worksheet PDF

Before starting to solve questions from the Factorisation problems worksheet PDF, students need to know everything about the worksheet. Those features are- 

• Variety of questions are included:  The Factorisation Maths Worksheet for Class 8 includes varieties of questions. Those varieties of questions are- one mark questions, two mark questions, three mark questions, etc. 
• Solutions are provided:  Doubts regarding each question can be easily solved through the solutions given. Through solving questions, a student's comprehensive skill can be increased. 
• All concepts are covered:  By solving questions from the Factorisation problems worksheet, students can easily cover all the concepts included in the chapter.  
• Created by Expert:  These worksheets are personally created by the subject experts. These Factorisation worksheet pdf are created with proper research. 
• Provides plenty of questions:  The Factorisation worksheet provides plenty of questions to practise. Through good practice, students can get engaged in the learning process. 

Benefits of the Factorisation Worksheet PDF

With the help of Factorisation problems worksheet PDF, students can easily track their performance. This is the most crucial benefit, other than this there are more benefits. Those benefits are- 

• Builds a strong foundation:  Regular solving questions from the worksheet can help students to build a strong foundation. Through the strong foundation, students can score well in the chapter Factorisation. 
• Improves speed and accuracy:  While solving questions from the chapter Factorisation, students need to maintain the speed and accuracy. Speed and accuracy can be easily maintained and improved by solving questions from the Factorisation worksheet PDF. 
• Acts as a guide:  Factorisation worksheets with solutions acts as guide for both the teachers and students. Through the worksheet, teachers can guide their students according to the answers given by them. Students can also analyse themselves with the help of answers and can improve accordingly. 
• Enhances the learning process:  Regular solving of questions from the worksheet can help students enhance their learning process. According to the learning skills, students can easily understand all topics and concepts included in the chapter Factorisation.  
• Improvisation of grades:  Regular solving of questions from the worksheet can help students to improve their marks and grades. With the help of good marks and good grades, students can select their desired field further. 

Tips to Score Good Marks in Factorisation Worksheet

Students are requested to follow some tips to score good marks in the Factorisation worksheet. Those tips are-

• Complete all the concepts:  First and the most crucial step is to understand all the concepts included in the chapter Factorisation.  
• Practise questions:  Next step is to practise questions from the Factorisation problems worksheet. Through this students can identify all types of questions: easy, moderate, difficult, etc.  
• Note down the mistakes:  After practising questions, students need to note down the wrong sums that have been done earlier. 
• Rectify the mistakes:  After noting down the mistakes, students need to rectify all the mistakes made. 
• Maintain a positive attitude:  Students are requested to maintain a positive attitude while solving worksheets. By maintaining a positive attitude, students can improve speed and accuracy while solving the worksheets. 
• Remain focused:  Students need to remain focused while solving questions from the Factorisation problems worksheet pdf. As it helps students to solve the questions as fast as possible. 

When should a student start solving the Factorisation Worksheet PDF?

Students studying in class 8 should start solving worksheets after covering each and every concept included in the chapter. Regular solving questions from the Factorisation worksheet PDF, can help students to have a better understanding of the chapter. Better understanding of the chapter Factorisation can help students to score well in the class 8th board exam. 

Regular solving questions from the Factorisation Worksheet PDF can help students to build a strong foundation for the chapter Factorisation. Strong foundation of the chapter Factorisation can help students to understand further chapters. 

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences

One Last Step...

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

• Factorisations
• Active page
• Factorization

Factorisations of Class 8

Factoringis the process by which we go about determining what we multiplied to get the given quantity.  An important part of this process is being able to express a complicated polynomial into a product of simpler polynomials. This involves factorisation.

We do this all the time with numbers.  For instance, here are a variety of ways to  factor 12.

12 = (2) (6) 12 = (3) (4) 12 = (2) (2) (3)

There are many more possible ways to factor 12, but these are representative of many of them. 

A common method of factoring numbers is to completely factor the number into positive prime factors.  A prime number is a number whose only positive factors are 1 and itself.  For example 2, 3, 5, and 7 are all examples of prime numbers. Examples of numbers that aren’t prime are 4, 6, and 12 to pick a few.

If we completely factor a number into positive prime factors there will only be one way of doing it.  That is the reason for factoring things in this way.  For our example above with 12 the complete factorization is,

12 = (2) (2) (3) 12 = (2) (2) (3)

Here are a couple of examples.

x2 – 16 = (x + 4) (x – 4)

This is completely factored since neither of the two factors on the right can be further factored.

  Likewise,

x4 – 16 = (x2 + 4) (x2 – 4)

is not completely factored because the second factor can be further factored.  Note that the first factor is completely factored however.  Here is the complete factorization of this polynomial.

x4 – 16 = (x2 + 4) (x + 2) (x – 2)

The purpose of this section is to familiarize ourselves with many of the techniques for factoring polynomials.

FACTORING BINOMIALS:

The simplest method of factoring binomials is to remove factors that are common to different terms. This method does not work in all situations. The formulas listed below can be used to factor binomials that fit the specific situation.

Difference of Squares:

x2 – y2 = (x – y) (x + y)

Sum of Cubes

x3 + y3 = (x + y) (x2 – xy + y2)

Difference of Cubes

x3 – y3 = (x – y) (x2 + xy + y2)

e.g. Factor the following:

•  2x3 + 10x2 – 4x = 2x(x2 + 5x – 2)
• x3y3 + 2x2y + 2xy2 + xy = xy (x2y2 + 2x + 2y + 1)

NCERT solutions for class 8 Maths   prepared by Physics Wallah will help you to solve your NCERT text book exercise. 

• Factorisation class 8
• Division of a polynomial by a polynomial
• Identity property
• Solved questions
• Exercise 3 (Fill in the blanks)
• Exercise 4 (True and False)

Talk to Our counsellor

• CBSE Notes For Class 8
• CBSE Notes Class 8 Maths
• Chapter 14: Factorisation

Factorisation Class 8 Notes Chapter 14

According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 12.

What are Factors?

An expression can be factorised into the product of its factors. These factors can be algebraic expressions, variables and numbers also.

To know more about Factors, visit here .

Division of a monomial by another monomial

Division of a monomial by another monomial:

i) Division of 9x 2 by 3:

9x 2 ÷ 3 = 3(3x 2 ) / 3 = 3x 2

ii) Division of 6x 2 y by 2y:

6x 2 y÷2y = (6x 2 )y / 2y = 2y(3x 2 ) / 2y = 3x 2

Division of a polynomial by a monomial

A polynomial 2x 3 + 4x 2 + 6xis divided by monomial 2x as shown below:

(2x 3 +4x 2 +6x)2x = 2x 3 / 2x + 4x 2 2x + 6x / 2x = x 2 + 2x + 3

Division of a polynomial by a polynomial

Long division method is used to divide a polynomial by a polynomial. Example:Division of 3x 2 + 3x – 5 by (x – 1) is shown below:

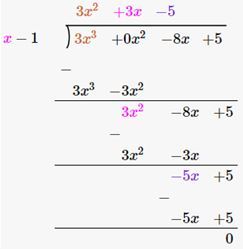
To know more about Polynomial Division, visit here .

Factors of natural numbers

Every number can be expressed in the form of product of prime factors. This is called prime factor form.

Example: Prime factor form of 42 is2 x 3 x 7, where 2, 3 and 7 are factors of 42.

Algebraic expressions

An algebraic expression is defined as a mathematical expression which consists of variables, numbers, and operations. The values of this expression are not constant, for example: x + 1, p – q, 3x, 2x+3y, 5a/6b etc.

Factors of algebraic expressions and factorisation

An  irreducible  factor is a factor which cannot be expressed further as a product of factors. Algebraic expressions  can be expressed in irreducible form.

To know more about Factorisation of algebraic expression, visit here .

Method of Common Factors

For more information on common factors, watch the below video..

Factorisation by common factors

To factorise an algebraic expression, the  highest common factors  are determined.

Example: Algebraic expression -2y 2 + 8y can be written as 2y(-y+4), where 2y is the highest common factor in the expression.

Factorisation by regrouping terms

In some algebraic expressions, it is not possible that every term has a common factor. Therefore, to factorise those algebraic expressions, terms having common factors are  grouped  together.

= 12a + n – na – 12

= 12a-12+n-na

= 12(a-1)-n(a-1)

= (12-n)(a-1)

(12-n) and (a-1)are factors of the expression 12a+n-na-12

Method of Identities

Algebraic identities.

The algebraic equations which are true for all values of variables in them are called algebraic identities.

Some of the identities are,

(a+b) 2 = a 2 + 2ab + b 2

(a-b) 2 = a 2 – 2ab + b 2

(a+b)(a-b)= a 2 – b 2

Factorisation using algebraic identities

Algebraic identities can be used for factorisation

Example: (i)9x 2 + 12xy + 4y 2

= ( 3x) 2 + 2 x 3x x 2y+(2y) 2

= (3x+4y) 2

(ii)4a 2 – b 2 = (2a-b)(2a+b)

For more information on Algebraic Identities, watch the below videos.

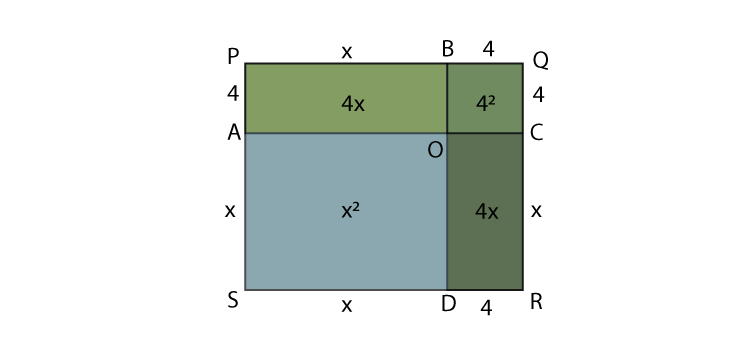
Visualisation of factorisation

Frequently Asked Questions on CBSE Class 8 Maths Notes Chapter 14 Factorisation

A number or algebraic expression that divides another number or expression evenly—i.e., with no remainder is said to be a factor of the primary number.

What is a common multiple?

A multiple of each of two or more numbers is said to be ‘common mutiple’ of both the numbers.

What is Factorisation?

Factorisation is when a number is broken down into smaller numbers that, multiplied together, give the original number.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 11: Factorisation

Factors of a monomial.

• Worked example: finding the missing monomial factor (Opens a modal)
• Factor monomials Get 3 of 4 questions to level up!

Factorisation using common factors

• Greatest common factor of monomials (Opens a modal)
• Taking common factor from binomial (Opens a modal)
• Greatest common factor of monomials Get 3 of 4 questions to level up!
• Factor polynomials: common factor Get 3 of 4 questions to level up!

Factorisation using identities

• Difference of squares intro (Opens a modal)
• Perfect square factorization intro (Opens a modal)
• Difference of squares Get 3 of 4 questions to level up!
• Perfect squares Get 3 of 4 questions to level up!
• Factor polynomials using structure Get 3 of 4 questions to level up!

Factors of the form (x+a)(x+b)

• Factoring quadratics as (x+a)(x+b) (Opens a modal)
• More examples of factoring quadratics as (x+a)(x+b) (Opens a modal)
• Factoring quadratics intro Get 3 of 4 questions to level up!
• Factor quadratics by grouping Get 3 of 4 questions to level up!

Dividing polynomials by monomials

• Divide polynomials by x (with remainders) (Opens a modal)
• Divide polynomials by monomials (with remainders) (Opens a modal)
• Divide polynomials by monomials (with remainders) Get 3 of 4 questions to level up!

Dividing polynomials by polynomials

• Dividing polynomials with remainders (Opens a modal)
• Divide polynomials by linear expressions Get 3 of 4 questions to level up!
• Divide polynomials with remainders Get 3 of 4 questions to level up!

AssignmentsBag.com

Assignments For Class 8 Mathematics Factorisation

Assignments for Class 8 Mathematics Factorisation have been developed for Standard 8 students based on the latest syllabus and textbooks applicable in CBSE, NCERT and KVS schools. Parents and students can download the full collection of class assignments for class 8 Mathematics Factorisation from our website as we have provided all topic wise assignments free in PDF format which can be downloaded easily. Students are recommended to do these assignments daily by taking printouts and going through the questions and answers for Grade 8 Mathematics Factorisation. You should try to do these test assignments on a daily basis so that you are able to understand the concepts and details of each chapter in your Mathematics Factorisation book and get good marks in class 8 exams.

Assignments for Class 8 Mathematics Factorisation as per CBSE NCERT pattern

All students studying in Grade 8 Mathematics Factorisation should download the assignments provided here and use them for their daily routine practice. This will help them to get better grades in Mathematics Factorisation exam for standard 8. We have made sure that all topics given in your textbook for Mathematics Factorisation which is suggested in Class 8 have been covered ad we have made assignments and test papers for all topics which your teacher has been teaching in your class. All chapter wise assignments have been made by our teachers after full research of each important topic in the textbooks so that you have enough questions and their solutions to help them practice so that they are able to get full practice and understanding of all important topics. Our teachers at https://www.assignmentsbag.com have made sure that all test papers have been designed as per CBSE, NCERT and KVS syllabus and examination pattern. These question banks have been recommended in various schools and have supported many students to practice and further enhance their scores in school and have also assisted them to appear in other school level tests and examinations. Its easy to take print of thee assignments as all are available in PDF format.

Some advantages of Free Assignments for Class 8 Mathematics Factorisation

• Solving Assignments for Mathematics Factorisation Class 8 helps to further enhance understanding of the topics given in your text book which will help you to get better marks
• By solving one assignments given in your class by Mathematics Factorisation teacher for class 8 will help you to keep in touch with the topic thus reducing dependence on last minute studies
• You will be able to understand the type of questions which are expected in your Mathematics Factorisation class test
• You will be able to revise all topics given in the ebook for Class 8 Mathematics Factorisation as all questions have been provided in the question banks
• NCERT Class 8 Mathematics Factorisation Workbooks will surely help you to make your concepts stronger and better than anyone else in your class.
• Parents will be able to take print out of the assignments and give to their child easily.

All free Printable practice assignments are in PDF single lick download format and have been prepared by Class 8 Mathematics Factorisation teachers after full study of all topics which have been given in each chapter so that the students are able to take complete benefit from the worksheets. The Chapter wise question bank and revision assignments can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 8 Mathematics Factorisation Assignments PDF.

You can download free assignments for class 8 Mathematics Factorisation from https://www.assignmentsbag.com

You can get free PDF downloadable assignments for Grade 8 Mathematics Factorisation from our website which has been developed by teachers after doing extensive research in each topic.

On our website we have provided assignments for all subjects in Grade 8, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.

You can easily get question banks, topic wise notes and questions and other useful study material from https://www.assignmentsbag.com without any charge

Yes all test papers for Mathematics Factorisation Class 8 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all assignments.

https://www.assignmentsbag.com is the best portal to download all assignments for all classes without any charges.

Related Posts

Assignments For Class 9 Biology

Assignments For Class 6 French

Assignments For Class 7 Mathematics Perimeter and Area