adding and subtracting fractions reasoning and problem solving

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.5: Add and Subtract Fractions with Common Denominators

• Last updated
• Save as PDF
• Page ID 114897

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Model fraction addition
• Add fractions with a common denominator
• Model fraction subtraction
• Subtract fractions with a common denominator

Be Prepared 4.9

Before you get started, take this readiness quiz.

Simplify: 2 x + 9 + 3 x − 4 . 2 x + 9 + 3 x − 4 . If you missed this problem, review Example 2.22.

Be Prepared 4.10

Draw a model of the fraction 3 4 . 3 4 . If you missed this problem, review Example 4.2.

Be Prepared 4.11

Simplify: 3 + 2 6 . 3 + 2 6 . If you missed this problem, review Example 4.48.

Model Fraction Addition

How many quarters are pictured? One quarter plus 2 2 quarters equals 3 3 quarters.

Remember, quarters are really fractions of a dollar. Quarters are another way to say fourths. So the picture of the coins shows that

1 4 2 4 3 4 one quarter + two quarters = three quarters 1 4 2 4 3 4 one quarter + two quarters = three quarters

Let’s use fraction circles to model the same example, 1 4 + 2 4 . 1 4 + 2 4 .

So again, we see that

1 4 + 2 4 = 3 4 1 4 + 2 4 = 3 4

Manipulative Mathematics

Example 4.52.

Use a model to find the sum 3 8 + 2 8 . 3 8 + 2 8 .

There are five 1 8 1 8 pieces, or five-eighths. The model shows that 3 8 + 2 8 = 5 8 . 3 8 + 2 8 = 5 8 .

Try It 4.103

Use a model to find each sum. Show a diagram to illustrate your model.

1 8 + 4 8 1 8 + 4 8

Try It 4.104

1 6 + 4 6 1 6 + 4 6

Add Fractions with a Common Denominator

Example 4.52 shows that to add the same-size pieces—meaning that the fractions have the same denominator —we just add the number of pieces.

Fraction Addition

If a , b , a , b , and c c are numbers where c ≠ 0 , c ≠ 0 , then

a c + b c = a + b c a c + b c = a + b c

To add fractions with a common denominator, add the numerators and place the sum over the common denominator.

Example 4.53

Find the sum: 3 5 + 1 5 . 3 5 + 1 5 .

Try It 4.105

Find each sum: 3 6 + 2 6 . 3 6 + 2 6 .

Try It 4.106

Find each sum: 3 10 + 7 10 . 3 10 + 7 10 .

Example 4.54

Find the sum: x 3 + 2 3 . x 3 + 2 3 .

Note that we cannot simplify this fraction any more. Since x x and 2 2 are not like terms, we cannot combine them.

Try It 4.107

Find the sum: x 4 + 3 4 . x 4 + 3 4 .

Try It 4.108

Find the sum: y 8 + 5 8 . y 8 + 5 8 .

Example 4.55

Find the sum: − 9 d + 3 d . − 9 d + 3 d .

We will begin by rewriting the first fraction with the negative sign in the numerator.

− a b = − a b − a b = − a b

Try It 4.109

Find the sum: − 7 d + 8 d . − 7 d + 8 d .

Try It 4.110

Find the sum: − 6 m + 9 m . − 6 m + 9 m .

Example 4.56

Find the sum: 2 n 11 + 5 n 11 . 2 n 11 + 5 n 11 .

Try It 4.111

Find the sum: 3 p 8 + 6 p 8 . 3 p 8 + 6 p 8 .

Try It 4.112

Find the sum: 2 q 5 + 7 q 5 . 2 q 5 + 7 q 5 .

Example 4.57

Find the sum: − 3 12 + ( − 5 12 ) . − 3 12 + ( − 5 12 ) .

Try It 4.113

Find each sum: − 4 15 + ( − 6 15 ) . − 4 15 + ( − 6 15 ) .

Try It 4.114

Find each sum: − 5 21 + ( − 9 21 ) . − 5 21 + ( − 9 21 ) .

Model Fraction Subtraction

Subtracting two fractions with common denominators is much like adding fractions. Think of a pizza that was cut into 12 12 slices. Suppose five pieces are eaten for dinner. This means that, after dinner, there are seven pieces (or 7 12 7 12 of the pizza) left in the box. If Leonardo eats 2 2 of these remaining pieces (or 2 12 2 12 of the pizza), how much is left? There would be 5 5 pieces left (or 5 12 5 12 of the pizza).

7 12 − 2 12 = 5 12 7 12 − 2 12 = 5 12

Let’s use fraction circles to model the same example, 7 12 − 2 12 . 7 12 − 2 12 .

Start with seven 1 12 1 12 pieces. Take away two 1 12 1 12 pieces. How many twelfths are left?

Again, we have five twelfths, 5 12 . 5 12 .

Example 4.58

Use fraction circles to find the difference: 4 5 − 1 5 . 4 5 − 1 5 .

Start with four 1 5 1 5 pieces. Take away one 1 5 1 5 piece. Count how many fifths are left. There are three 1 5 1 5 pieces left.

Try It 4.115

Use a model to find each difference. Show a diagram to illustrate your model.

7 8 − 4 8 7 8 − 4 8

Try It 4.116

5 6 − 4 6 5 6 − 4 6

Subtract Fractions with a Common Denominator

We subtract fractions with a common denominator in much the same way as we add fractions with a common denominator.

Fraction Subtraction

a c − b c = a − b c a c − b c = a − b c

To subtract fractions with a common denominator, we subtract the numerators and place the difference over the common denominator.

Example 4.59

Find the difference: 23 24 − 14 24 . 23 24 − 14 24 .

Try It 4.117

Find the difference: 19 28 − 7 28 . 19 28 − 7 28 .

Try It 4.118

Find the difference: 27 32 − 11 32 . 27 32 − 11 32 .

Example 4.60

Find the difference: y 6 − 1 6 . y 6 − 1 6 .

The fraction is simplified because we cannot combine the terms in the numerator.

Try It 4.119

Find the difference: x 7 − 2 7 . x 7 − 2 7 .

Try It 4.120

Find the difference: y 14 − 13 14 . y 14 − 13 14 .

Example 4.61

Find the difference: − 10 x − 4 x . − 10 x − 4 x .

Remember, the fraction − 10 x − 10 x can be written as −10 x . −10 x .

Try It 4.121

Find the difference: − 9 x − 7 x . − 9 x − 7 x .

Try It 4.122

Find the difference: − 17 a − 5 a . − 17 a − 5 a .

Now lets do an example that involves both addition and subtraction.

Example 4.62

Simplify: 3 8 + ( − 5 8 ) − 1 8 . 3 8 + ( − 5 8 ) − 1 8 .

Try It 4.123

Simplify: 2 5 + ( − 4 5 ) − 3 5 . 2 5 + ( − 4 5 ) − 3 5 .

Try It 4.124

Simplify: 5 9 + ( − 4 9 ) − 7 9 . 5 9 + ( − 4 9 ) − 7 9 .

ACCESS ADDITIONAL ONLINE RESOURCES

• Adding Fractions With Pattern Blocks
• Adding Fractions With Like Denominators
• Subtracting Fractions With Like Denominators

Section 4.4 Exercises

Practice makes perfect.

In the following exercises, use a model to add the fractions. Show a diagram to illustrate your model.

2 5 + 1 5 2 5 + 1 5

3 10 + 4 10 3 10 + 4 10

1 6 + 3 6 1 6 + 3 6

3 8 + 3 8 3 8 + 3 8

In the following exercises, find each sum.

4 9 + 1 9 4 9 + 1 9

2 9 + 5 9 2 9 + 5 9

6 13 + 7 13 6 13 + 7 13

9 15 + 7 15 9 15 + 7 15

x 4 + 3 4 x 4 + 3 4

y 3 + 2 3 y 3 + 2 3

7 p + 9 p 7 p + 9 p

8 q + 6 q 8 q + 6 q

8 b 9 + 3 b 9 8 b 9 + 3 b 9

5 a 7 + 4 a 7 5 a 7 + 4 a 7

−12 y 8 + 3 y 8 −12 y 8 + 3 y 8

−11 x 5 + 7 x 5 −11 x 5 + 7 x 5

− 1 8 + ( − 3 8 ) − 1 8 + ( − 3 8 )

− 1 8 + ( − 5 8 ) − 1 8 + ( − 5 8 )

− 3 16 + ( − 7 16 ) − 3 16 + ( − 7 16 )

− 5 16 + ( − 9 16 ) − 5 16 + ( − 9 16 )

− 8 17 + 15 17 − 8 17 + 15 17

− 9 19 + 17 19 − 9 19 + 17 19

6 13 + ( − 10 13 ) + ( − 12 13 ) 6 13 + ( − 10 13 ) + ( − 12 13 )

5 12 + ( − 7 12 ) + ( − 11 12 ) 5 12 + ( − 7 12 ) + ( − 11 12 )

In the following exercises, use a model to subtract the fractions. Show a diagram to illustrate your model.

5 8 − 2 8 5 8 − 2 8

5 6 − 2 6 5 6 − 2 6

In the following exercises, find the difference.

4 5 − 1 5 4 5 − 1 5

4 5 − 3 5 4 5 − 3 5

11 15 − 7 15 11 15 − 7 15

9 13 − 4 13 9 13 − 4 13

11 12 − 5 12 11 12 − 5 12

7 12 − 5 12 7 12 − 5 12

4 21 − 19 21 4 21 − 19 21

− 8 9 − 16 9 − 8 9 − 16 9

y 17 − 9 17 y 17 − 9 17

x 19 − 8 19 x 19 − 8 19

5 y 8 − 7 8 5 y 8 − 7 8

11 z 13 − 8 13 11 z 13 − 8 13

− 8 d − 3 d − 8 d − 3 d

− 7 c − 7 c − 7 c − 7 c

− 23 u − 15 u − 23 u − 15 u

− 29 v − 26 v − 29 v − 26 v

6 c 7 − 5 c 7 6 c 7 − 5 c 7

12 d 11 − 9 d 11 12 d 11 − 9 d 11

−4 r 13 − 5 r 13 −4 r 13 − 5 r 13

−7 s 3 − 7 s 3 −7 s 3 − 7 s 3

− 3 5 − ( − 4 5 ) − 3 5 − ( − 4 5 )

− 3 7 − ( − 5 7 ) − 3 7 − ( − 5 7 )

− 7 9 − ( − 5 9 ) − 7 9 − ( − 5 9 )

− 8 11 − ( − 5 11 ) − 8 11 − ( − 5 11 )

Mixed Practice

In the following exercises, perform the indicated operation and write your answers in simplified form.

− 5 18 · 9 10 − 5 18 · 9 10

− 3 14 · 7 12 − 3 14 · 7 12

n 5 − 4 5 n 5 − 4 5

6 11 − s 11 6 11 − s 11

− 7 24 + 2 24 − 7 24 + 2 24

− 5 18 + 1 18 − 5 18 + 1 18

8 15 ÷ 12 5 8 15 ÷ 12 5

7 12 ÷ 9 28 7 12 ÷ 9 28

Everyday Math

Trail Mix Jacob is mixing together nuts and raisins to make trail mix. He has 6 10 6 10 of a pound of nuts and 3 10 3 10 of a pound of raisins. How much trail mix can he make?

Baking Janet needs 5 8 5 8 of a cup of flour for a recipe she is making. She only has 3 8 3 8 of a cup of flour and will ask to borrow the rest from her next-door neighbor. How much flour does she have to borrow?

Writing Exercises

Greg dropped his case of drill bits and three of the bits fell out. The case has slots for the drill bits, and the slots are arranged in order from smallest to largest. Greg needs to put the bits that fell out back in the case in the empty slots. Where do the three bits go? Explain how you know. Bits in case: 1 16 1 16 , 1 8 1 8 , ___, ___, 5 16 5 16 , 3 8 3 8 , ___, 1 2 1 2 , 9 16 9 16 , 5 8 5 8 . Bits that fell out: 7 16 7 16 , 3 16 3 16 , 1 4 1 4 .

After a party, Lupe has 5 12 5 12 of a cheese pizza, 4 12 4 12 of a pepperoni pizza, and 4 12 4 12 of a veggie pizza left. Will all the slices fit into 1 1 pizza box? Explain your reasoning.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Module 1A: Problem Solving and Proportional Reasoning

Adding and subtracting fractions, learning outcomes.

• Find the common denominator of two or more fractions
• Use the common denominator to add or subtract fractions
• Simplify a fraction to its lowest terms

Introduction

Before we get started, here is some important terminology that will help you understand the concepts about working with fractions in this section.

• product:  the result of  multiplication
• factor: something being multiplied – for  [latex]3 \cdot 2 = 6[/latex] , both 3 and 2 are factors of 6
• numerator: the top part of a fraction – the numerator in the fraction [latex]\frac{2}{3}[/latex] is 2
• denominator: the bottom part of a fraction – the denominator in the fraction [latex]\frac{2}{3}[/latex] is 3

Note About Instructions

Many different words are used by math textbooks and teachers to provide students with instructions on what they are to do with a given problem. For example, you may see instructions such as “Find” or “Simplify” in the example in this module. It is important to understand what these words mean so you can successfully work through the problems in this course. Here is a short list of the words you may see that can help you know how to work through the problems in this module.

Adding Fractions

When you need to add or subtract fractions, you will need to first make sure that the fractions have the same denominator. The denominator tells you how many pieces the whole has been broken into, and the numerator tells you how many of those pieces you are using.

The “parts of a whole” concept can be modeled with pizzas and pizza slices. For example, imagine a pizza is cut into 4 pieces, and someone takes 1 piece. Now, [latex]\frac{1}{4}[/latex] of the pizza is gone and [latex]\frac{3}{4}[/latex] remains. Note that both of these fractions have a denominator of 4, which refers to the number of slices the whole pizza has been cut into. What if you have another pizza that had been cut into 8 equal parts and 3 of those parts were gone, leaving [latex]\frac{5}{8}[/latex]?

How can you describe the total amount of pizza that is left with one number rather than two different fractions? You need a common denominator, technically called the least common multiple. Remember that if a number is a multiple of another, you can divide them and have no remainder.

One way to find the least common multiple of two or more numbers is to first multiply each by 1, 2, 3, 4, etc.  For example, find the least common multiple of 2 and 5.

The smallest multiple they have in common will be the common denominator for the two!

Describe the amount of pizza left using common terms.

Find the least common multiple of the denominators. This is the least common denominator.

Multiples of 4: 4, 8 , 12, 16

Multiples of 8: 8 , 16, 24

The least common denominator is 8—the smallest multiple they have in common.

Rewrite [latex] \frac{3}{4}[/latex] with a denominator of 8. You have to multiply both the top and bottom by 2 so you don’t change the relationship between them.

[latex] \frac{3}{4}\cdot \frac{2}{2}=\frac{6}{8}[/latex]

We don’t need to rewrite [latex] \frac{5}{8}[/latex] since it already has the common denominator.

Both [latex]\frac{6}{8}[/latex] and [latex] \frac{5}{8}[/latex] have the same denominator, and you can describe how much pizza is left with common terms.

To add fractions with unlike denominators, first rewrite them with like denominators. Then, you know what to do! The steps are shown below.

Adding Fractions with Unlike Denominators

• Find a common denominator.
• Rewrite each fraction using the common denominator.
• Now that the fractions have a common denominator, you can add the numerators.
• Simplify by canceling out all common factors in the numerator and denominator.

Simplifying a Fraction

Often, if the answer to a problem is a fraction, you will be asked to write it in lowest terms. This is a common convention used in mathematics, similar to starting a sentence with a capital letter and ending it with a period. In this course, we will not go into great detail about methods for reducing fractions because there are many. The process of simplifying a fraction is often called reducing the fraction . We can simplify by canceling (dividing) the common factors in a fraction’s numerator and denominator.  We can do this because a fraction represents division.

For example, to simplify [latex]\frac{6}{9}[/latex] you can rewrite 6 and 9 using the smallest factors possible as follows:

[latex]\frac{6}{9}=\frac{2\cdot3}{3\cdot3}[/latex]

Since there is a 3 in both the numerator and denominator, and fractions can be considered division, we can divide the 3 in the top by the 3 in the bottom to reduce to 1.

[latex]\frac{6}{9}=\frac{2\cdot\cancel{3}}{3\cdot\cancel{3}}=\frac{2\cdot1}{3}=\frac{2}{3}[/latex]

Rewriting fractions with the smallest factors possible is often called prime factorization.

In the next example you are shown how to add two fractions with different denominators, then simplify the answer.

Add [latex] \frac{2}{3}+\frac{1}{5}[/latex]. Simplify the answer.

[latex]3\cdot5=15[/latex]

Rewrite each fraction with a denominator of 15.

[latex]\begin{array}{c}\frac{2}{3}\cdot \frac{5}{5}=\frac{10}{15}\\\\\frac{1}{5}\cdot \frac{3}{3}=\frac{3}{15}\end{array}[/latex]

Add the fractions by adding the numerators and keeping the denominator the same. Make sure the fraction cannot be simplified.

[latex] \frac{10}{15}+\frac{3}{15}=\frac{13}{15}[/latex]

[latex] \frac{2}{3}+\frac{1}{5}=\frac{13}{15}[/latex]

You can find a common denominator by finding the common multiples of the denominators. The least common multiple is the easiest to use.

Add [latex] \frac{3}{7}+\frac{2}{21}[/latex]. Simplify the answer.

Multiples of 7: 7, 14, 21

Multiples of 21: 21

Rewrite each fraction with a denominator of 21.

[latex]\begin{array}{c}\frac{3}{7}\cdot \frac{3}{3}=\frac{9}{21}\\\\\frac{2}{21}\end{array}[/latex]

[latex] \frac{9}{21}+\frac{2}{21}=\frac{11}{21}[/latex]

[latex] \frac{3}{7}+\frac{2}{21}=\frac{11}{21}[/latex]

In the following video you will see an example of how to add two fractions with different denominators.

You can also add more than two fractions as long as you first find a common denominator for all of them. An example of a sum of three fractions is shown below. In this example, you will use the prime factorization method to find the LCM.

Think About It

Add [latex] \frac{3}{4}+\frac{1}{6}+\frac{5}{8}[/latex].  Simplify the answer and write as a mixed number.

What makes this example different than the previous ones? Use the box below to write down a few thoughts about how you would add three fractions with different denominators together.

[latex]4=2\cdot2\\6=3\cdot2\\8=2\cdot2\cdot2\\\text{LCM}:\,\,2\cdot2\cdot2\cdot3=24[/latex]

Rewrite each fraction with a denominator of 24.

[latex]\begin{array}{c}\frac{3}{4}\cdot \frac{6}{6}=\frac{18}{24}\\\\\frac{1}{6}\cdot \frac{4}{4}=\frac{4}{24}\\\\\frac{5}{8}\cdot \frac{3}{3}=\frac{15}{24}\end{array}[/latex]

Add the fractions by adding the numerators and keeping the denominator the same.

[latex]\frac{18}{24}+\frac{4}{24}+\frac{15}{24}=\frac{37}{24}[/latex]

Write the improper fraction as a mixed number and simplify the fraction.

[latex] \frac{37}{24}=1\,\,\frac{13}{24}[/latex]

[latex]\frac{3}{4}+\frac{1}{6}+\frac{5}{8}=1\frac{13}{24}[/latex]

Subtracting Fractions

When you subtract fractions, you must think about whether they have a common denominator, just like with adding fractions. Below are some examples of subtracting fractions whose denominators are not alike.

Subtract [latex]\frac{1}{5}-\frac{1}{6}[/latex]. Simplify the answer.

[latex]5\cdot6=30[/latex]

Rewrite each fraction as an equivalent fraction with a denominator of 30.

[latex]\begin{array}{c}\frac{1}{5}\cdot \frac{6}{6}=\frac{6}{30}\\\\\frac{1}{6}\cdot \frac{5}{5}=\frac{5}{30}\end{array}[/latex]

Subtract the numerators. Simplify the answer if needed.

[latex] \frac{6}{30}-\frac{5}{30}=\frac{1}{30}[/latex]

[latex] \frac{1}{5}-\frac{1}{6}=\frac{1}{30}[/latex]

The example below shows how to use multiples to find the least common multiple, which will be the least common denominator.

Subtract [latex]\frac{5}{6}-\frac{1}{4}[/latex]. Simplify the answer.

Multiples of 6: 6, 12 , 18, 24

Multiples of 4: 4, 8 12 , 16, 20

12 is the least common multiple of 6 and 4.

Rewrite each fraction with a denominator of 12.

[latex]\begin{array}{c}\frac{5}{6}\cdot \frac{2}{2}=\frac{10}{12}\\\\\frac{1}{4}\cdot \frac{3}{3}=\frac{3}{12}\end{array}[/latex]

Subtract the fractions. Simplify the answer if needed.

[latex]\frac{10}{12}-\frac{3}{12}=\frac{7}{12}[/latex]

[latex] \frac{5}{6}-\frac{1}{4}=\frac{7}{12}[/latex]

In the following video you will see an example of how to subtract fractions with unlike denominators.

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Ex: Add Fractions with Unlike Denominators (Basic with Model). Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/zV4q7j1-89I . License : CC BY-SA: Attribution-ShareAlike
• Ex: Subtract Fractions with Unlike Denominators (Basic with Model). Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/RpHtOMjeI7g . License : CC BY-SA: Attribution-ShareAlike
• Unit 2: Fractions and Mixed Numbers, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. License : CC BY: Attribution

Privacy Policy

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Fractions  - Adding and Subtracting Fractions

Fractions  -, adding and subtracting fractions, fractions adding and subtracting fractions.

Fractions: Adding and Subtracting Fractions

Lesson 3: adding and subtracting fractions.

/en/fractions/comparing-and-reducing-fractions/content/

Adding and subtracting fractions

In the previous lessons, you learned that a fraction is part of a whole. Fractions show how much you have of something, like 1/2 of a tank of gas or 1/3 of a cup of water.

In real life, you might need to add or subtract fractions. For example, have you ever walked 1/2 of a mile to work and then walked another 1/2 mile back? Or drained 1/4 of a quart of gas from a gas tank that had 3/4 of a quart in it? You probably didn't think about it at the time, but these are examples of adding and subtracting fractions.

Click through the slideshow to learn how to set up addition and subtraction problems with fractions.

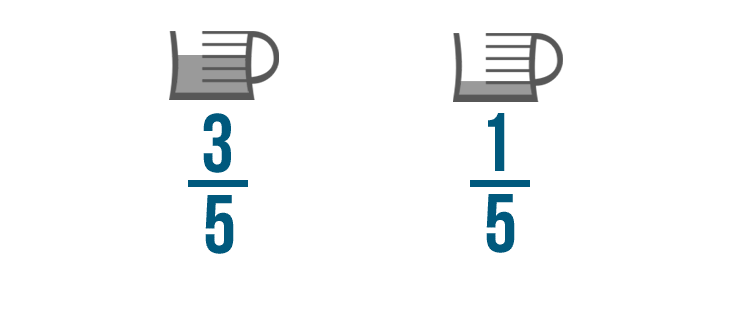
Let's imagine that a cake recipe tells you to add 3/5 of a cup of oil to the batter.

You also need 1/5 of a cup of oil to grease the pan. To see how much oil you'll need total, you can add these fractions together.

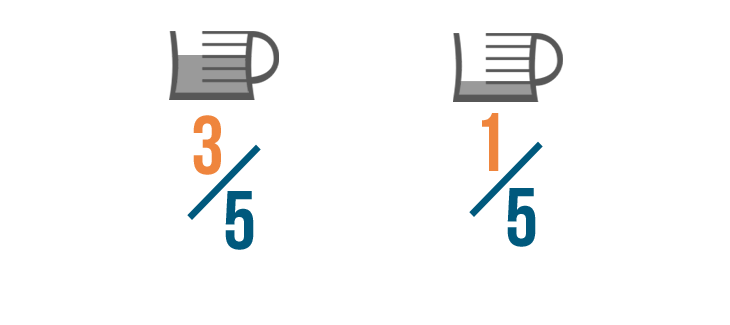
When you add fractions, you just add the top numbers, or numerators .

That's because the bottom numbers, or denominators , show how many parts would make a whole.

We don't want to change how many parts make a whole cup ( 5 ). We just want to find out how many parts we need total.

So we only need to add the numerators of our fractions.

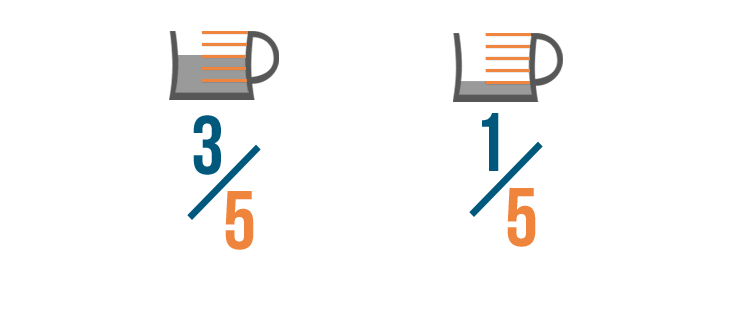
We can stack the fractions so the numerators are lined up. This will make it easier to add them.

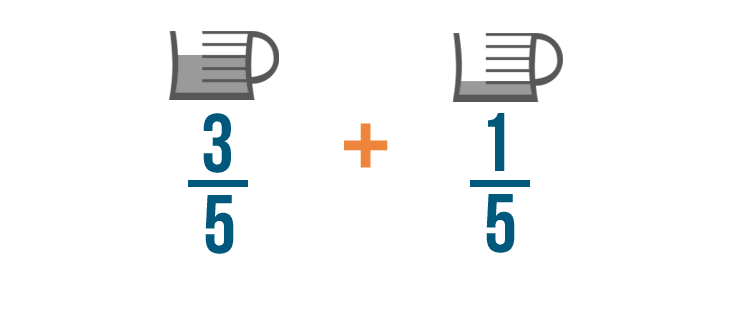
And that's all we have to do to set up an addition example with fractions. Our fractions are now ready to be added.

We'll do the same thing to set up a subtraction example. Let's say you had 3/4 of a tank of gas when you got to work.

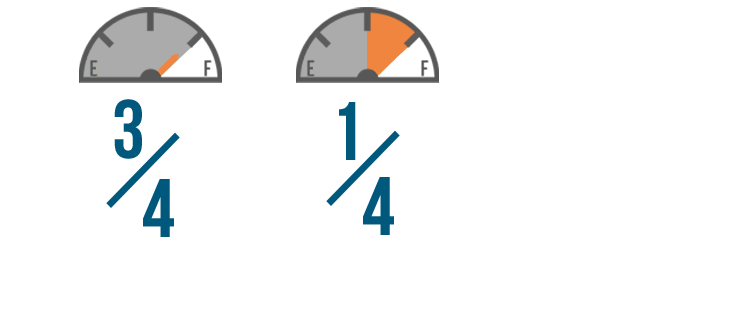
If you use 1/4 of a tank to drive home, how much will you have left? We can subtract these fractions to find out.

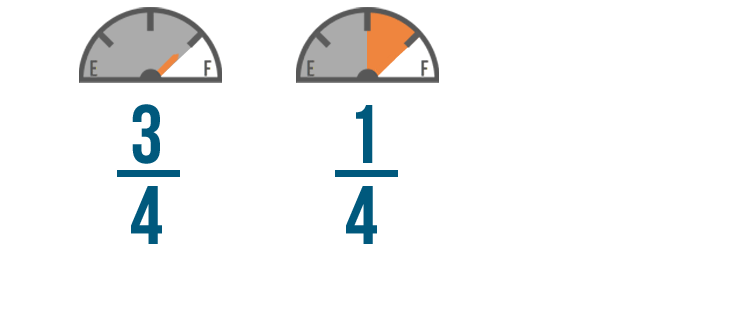
Just like when we added, we'll stack our fractions to keep the numerators lined up.

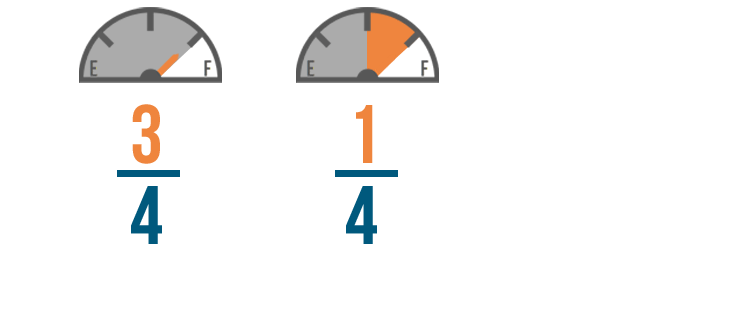
This is because we want to subtract 1 part from 3 parts.

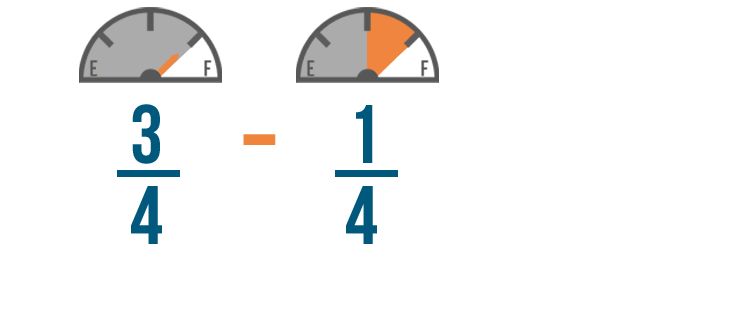
Now that our example is set up, we're ready to subtract!

Try setting up these addition and subtraction problems with fractions. Don't try solving them yet!

You run 4/10 of a mile in the morning. Later, you run for 3/10 of a mile.

You had 7/8 of a stick of butter and used 2/8 of the stick while cooking dinner.

Your gas tank is 2/5 full, and you put in another 2/5 of a tank.

Solving addition problems with fractions

Now that we know how to write addition problems with fractions, let's practice solving a few. If you can add whole numbers , you're ready to add fractions.

Click through the slideshow to learn how to add fractions.

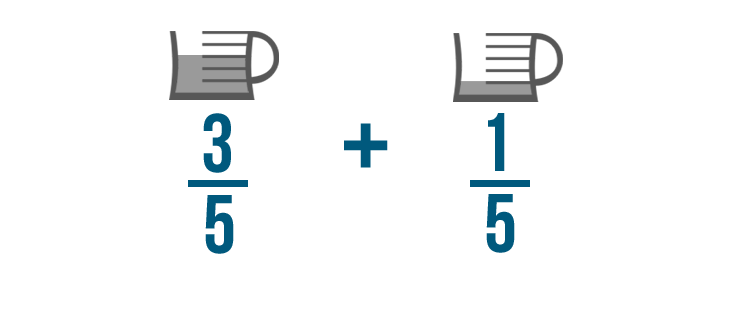
Let's continue with our previous example and add these fractions: 3/5 of cup of oil and 1/5 of a cup of oil.

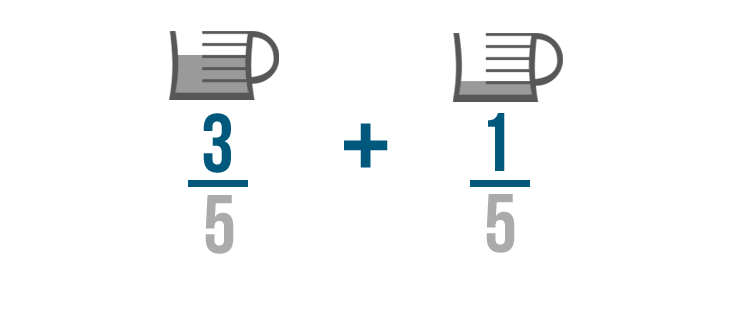
Remember, when we add fractions, we don't add the denominators.

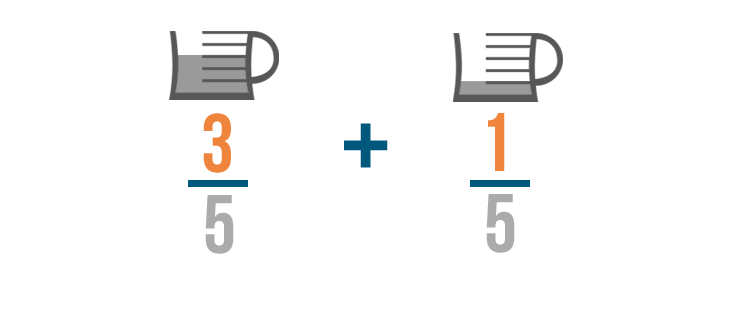
This is because we're finding how many parts we need total. The numerators show the parts we need, so we'll add 3 and 1 .

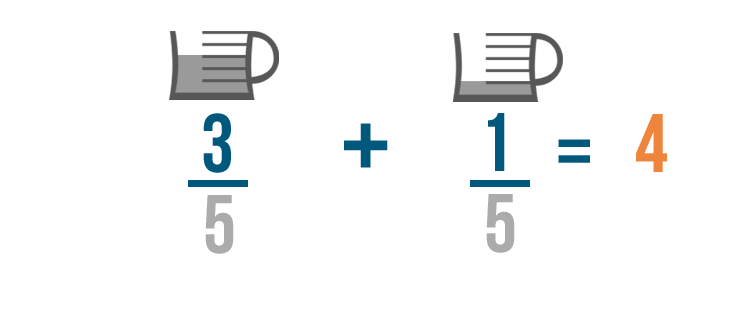
3 plus 1 equals 4 . Make sure to line up the 4 with the numbers you just added.

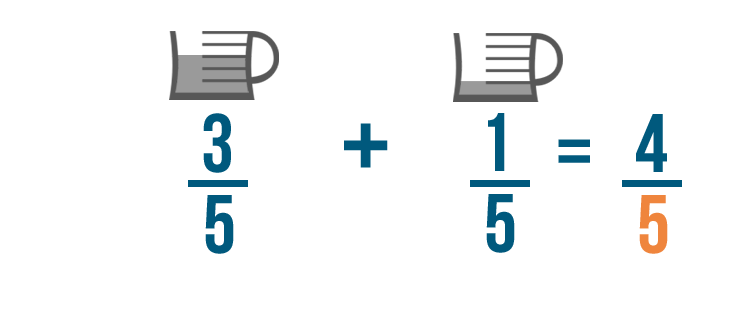
The denominators will stay the same, so we'll write 5 on the bottom of our new fraction.

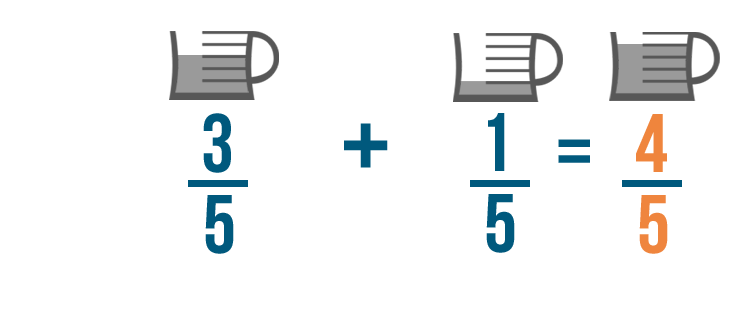
3/5 plus 1/5 equals 4/5 . So you'll need 4/5 of a cup of oil total to make your cake.

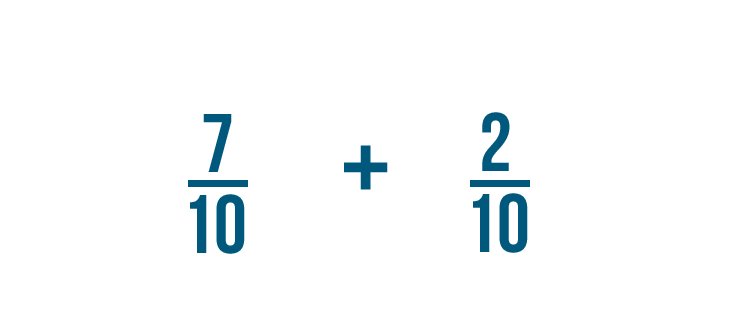
Let's try another example: 7/10 plus 2/10 .

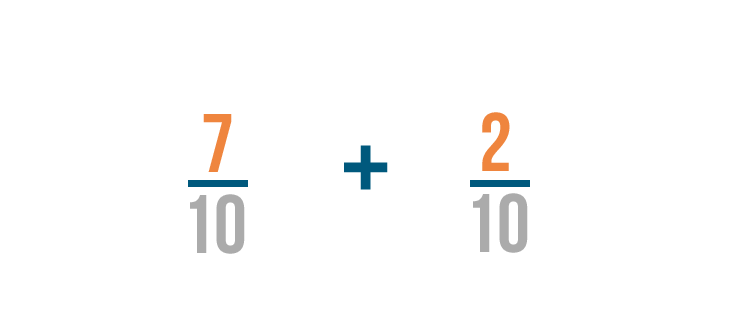
Just like before, we're only going to add the numerators. In this example, the numerators are 7 and 2 .

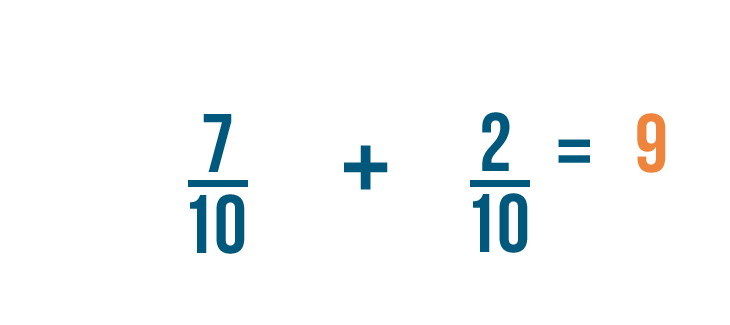
7 plus 2 equals 9 , so we'll write that to the right of the numerators.

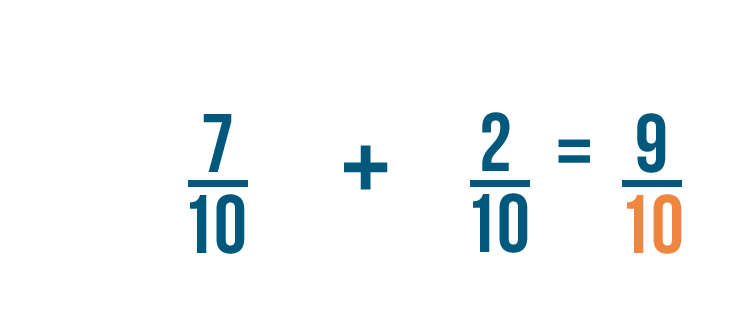
Just like in our earlier example, the denominator stays the same.

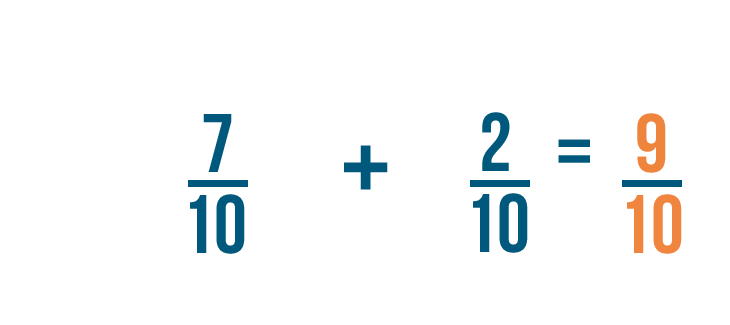
So 7/10 plus 2/10 equals 9/10 .

Try solving some of the addition problems below.

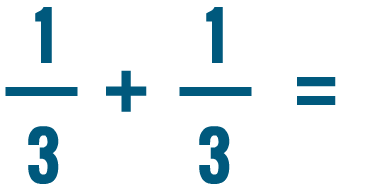
Solving subtraction problems with fractions

Subtracting fractions is a lot like regular subtraction. If you can subtract whole numbers , you can subtract fractions too!

Click through the slideshow to learn how to subtract fractions.

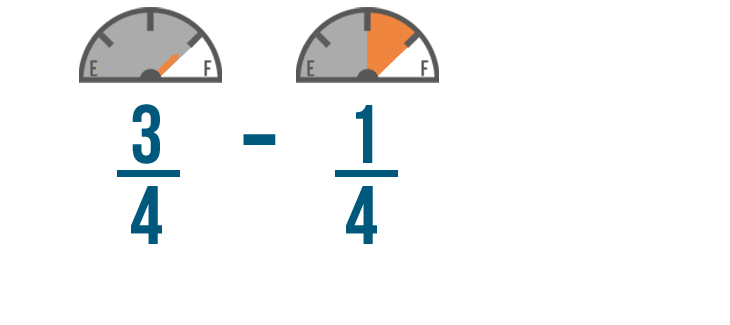
Let's use our earlier example and subtract 1/4 of a tank of gas from 3/4 of a tank.

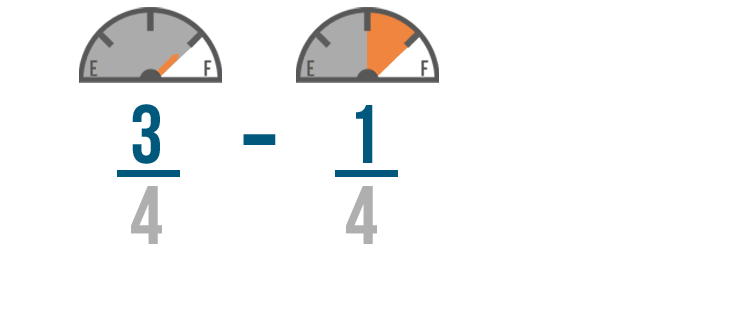
Just like in addition, we're not going to change the denominators.

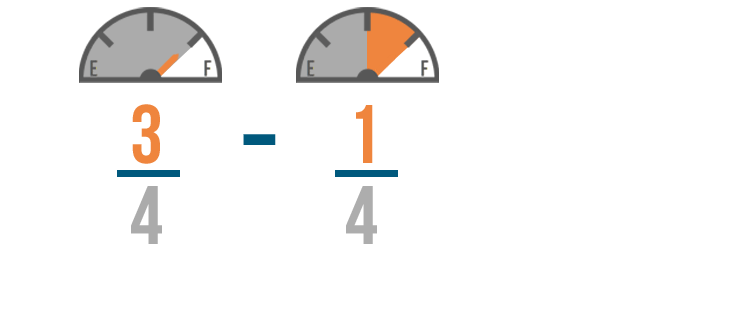
We don't want to change how many parts make a whole tank of gas. We just want to know how many parts we'll have left.

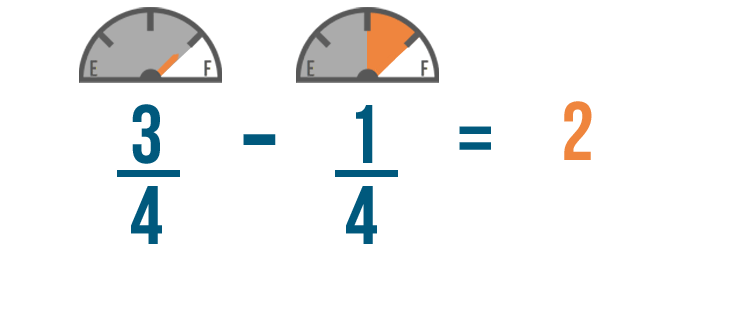
We'll start by subtracting the numerators. 3 minus 1 equals 2 , so we'll write 2 to the right of the numerators.

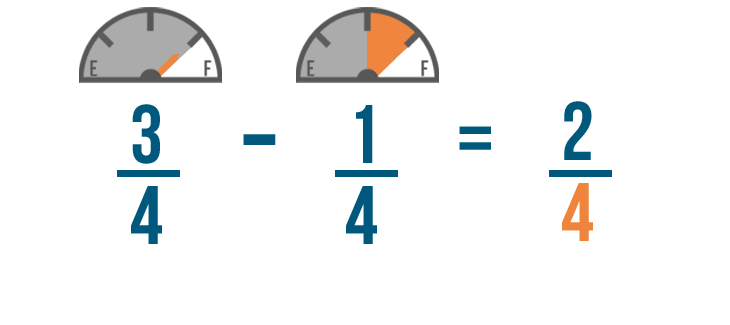
Just like when we added, the denominator of our answer will be the same as the other denominators.

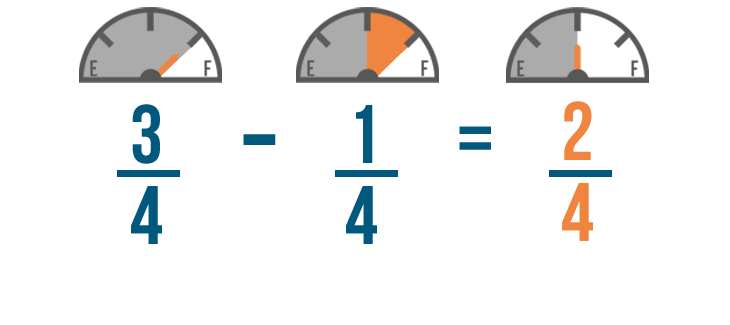
So 3/4 minus 1/4 equals 2/4 . You'll have 2/4 of a tank of gas left when you get home.

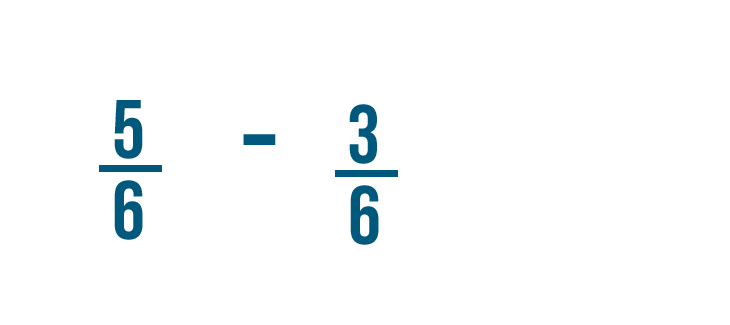
Let's try solving another problem: 5/6 minus 3/6 .

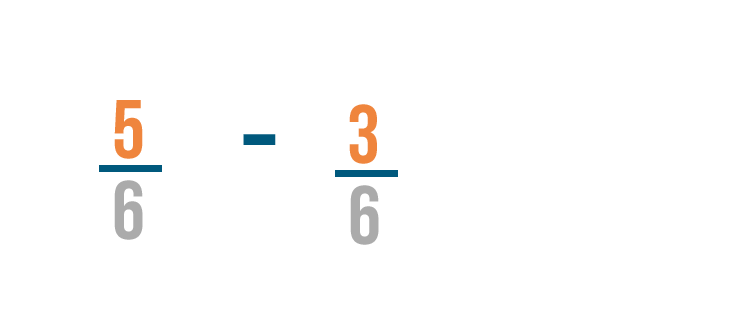
We'll start by subtracting the numerators.

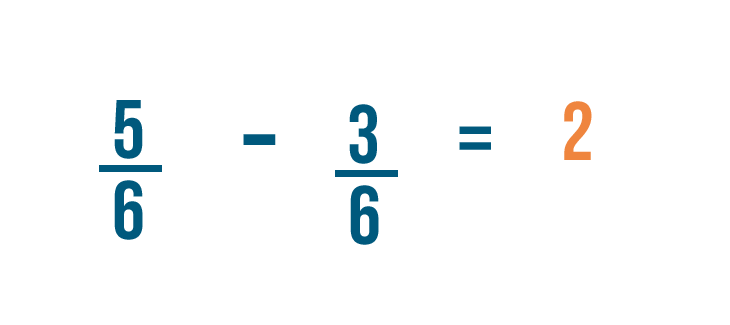
5 minus 3 equals 2 . So we'll put a 2 to the right of the numerators.

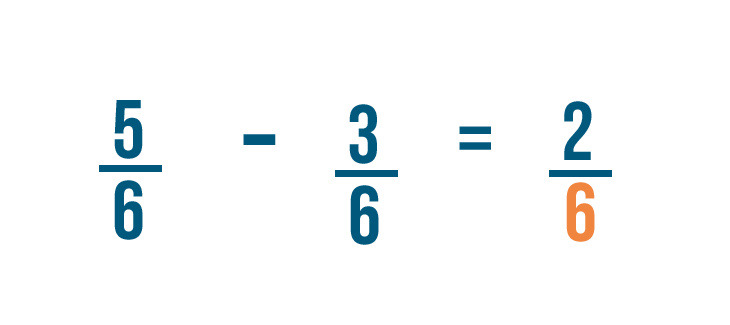
As usual, the denominator stays the same.

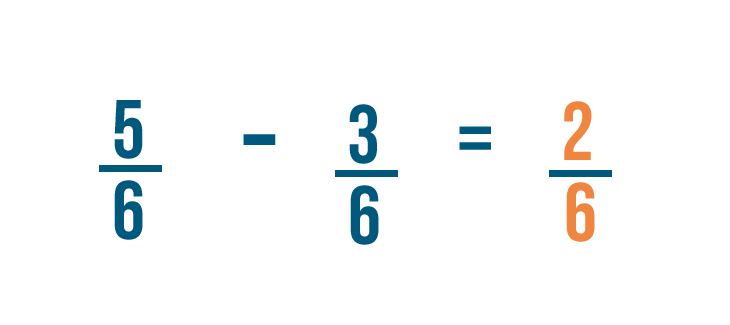
So 5/6 minus 3/6 equals 2/6 .

Try solving some of the subtraction problems below.

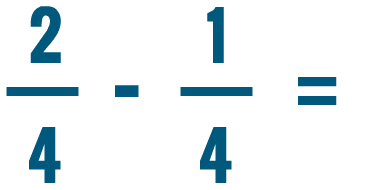
After you add or subtract fractions, you may sometimes have a fraction that can be reduced to a simpler fraction. As you learned in Comparing and Reducing Fractions , it's always best to reduce a fraction to its simplest form when you can. For example, 1/4 plus 1/4 equals 2/4 . Because 2 and 4 can both be divided 2 , we can reduce 2/4 to 1/2 .

Adding fractions with different denominators

On the last page, we learned how to add fractions that have the same denominator, like 1/4 and 3/4 . But what if you needed to add fractions with different denominators? For example, our cake recipe might say to blend 1/4 cup of milk in slowly and then dump in another 1/3 of a cup.

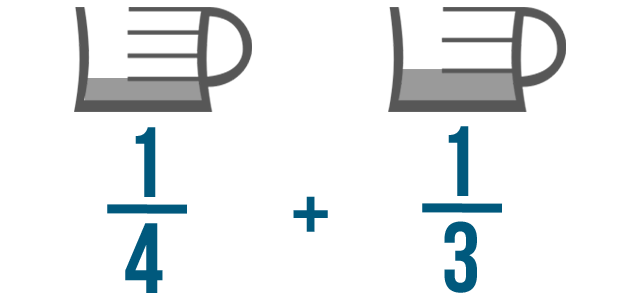
In Comparing and Reducing Fractions , we compared fractions with a different bottom number, or denominator. We had to change the fractions so their denominators were the same. To do that, we found the lowest common denominator , or LCD .

We can only add or subtract fractions if they have the same denominators. So we'll need to find the lowest common denominator before we add or subtract these fractions. Once the fractions have the same denominator, we can add or subtract as usual.

Click through the slideshow to learn how to add fractions with different denominators.

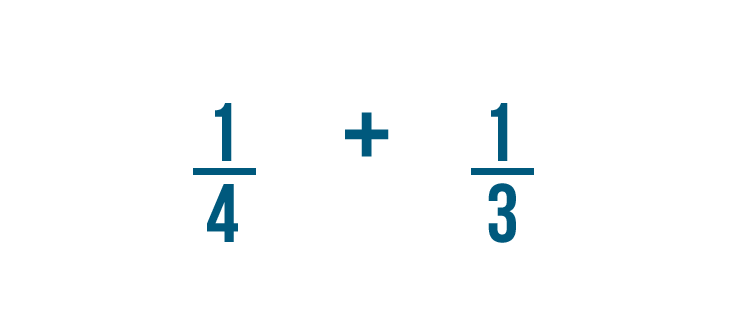
Let's add 1/4 and 1/3 .

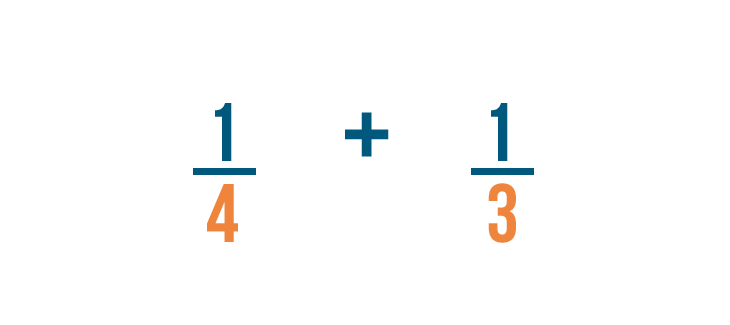
Before we can add these fractions, we'll need to change them so they have the same denominator .

To do that, we'll have to find the LCD , or lowest common denominator, of 4 and 3 .

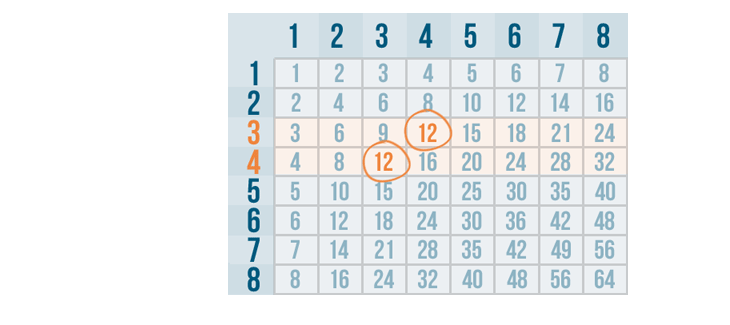
It looks like 12 is the smallest number that can be divided by both 3 and 4, so 12 is our LCD .

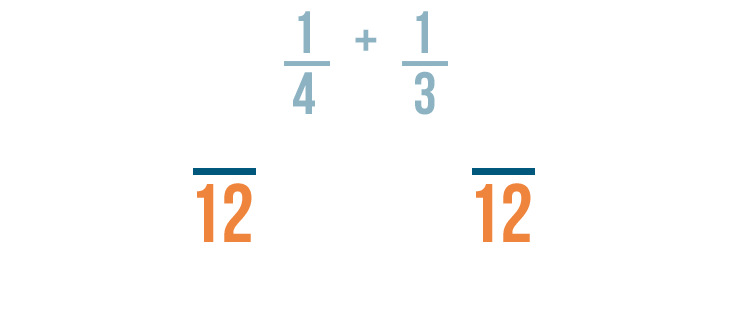
Since 12 is the LCD, it will be the new denominator for our fractions.

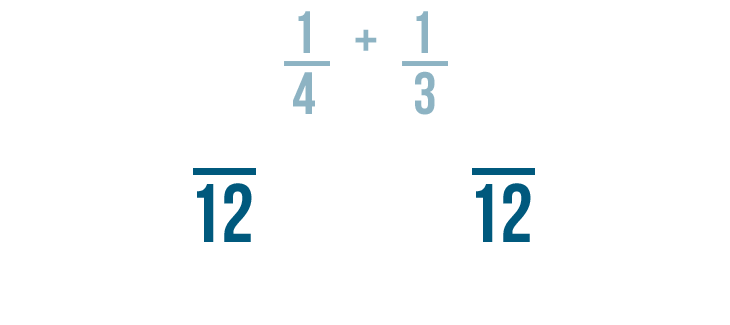
Now we'll change the numerators of the fractions, just like we changed the denominators.

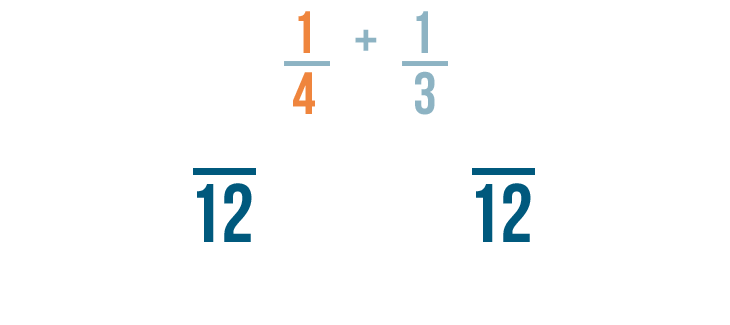
First, let's look at the fraction on the left: 1/4 .

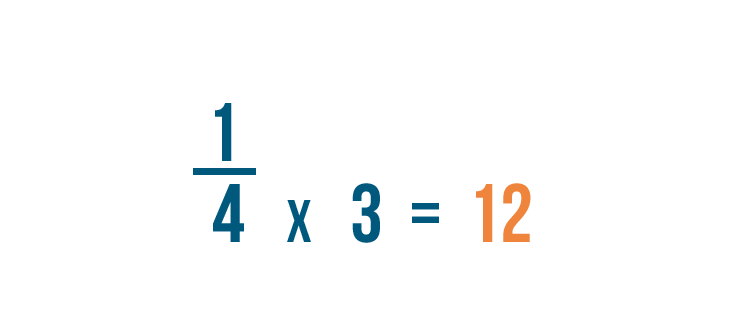
To change 4 into 12 , we multiplied it by 3 .

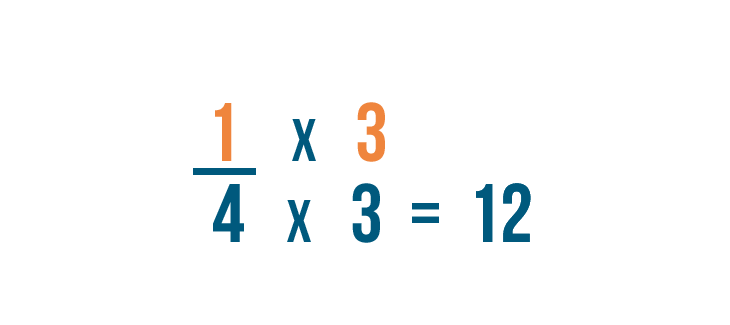
Since the denominator was multiplied by 3 , we'll also multiply the numerator by 3 .

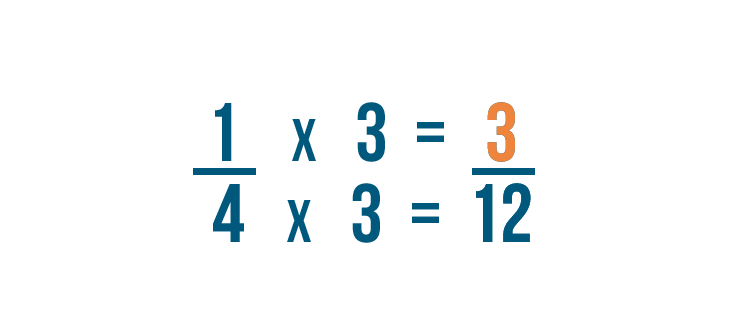
1 times 3 equals 3 .

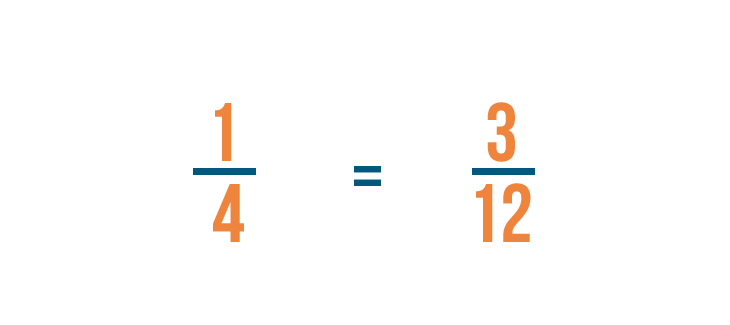
1/4 is equal to 3/12 .

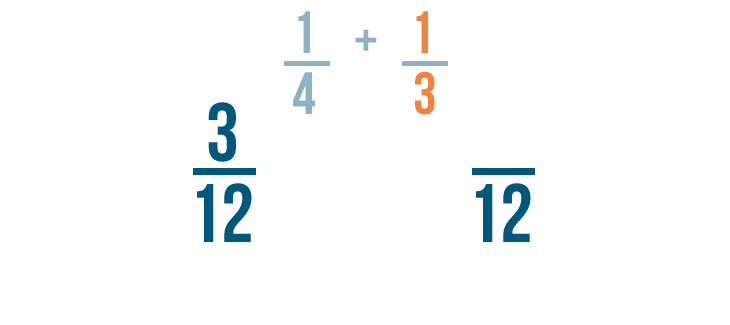
Now let's look at the fraction on the right: 1/3 . We changed its denominator to 12 as well.

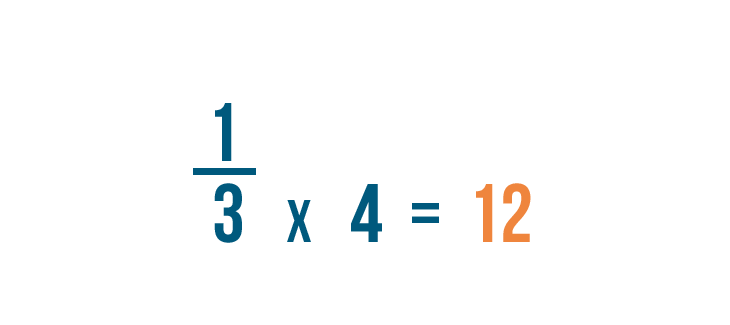
Our old denominator was 3 . We multiplied it by 4 to get 12.

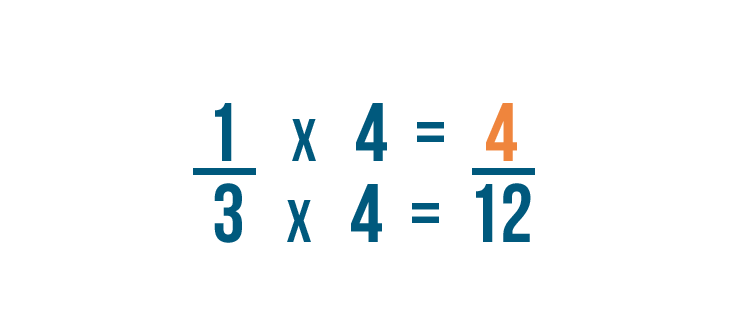
We'll also multiply the numerator by 4 . 1 times 4 equals 4 .

So 1/3 is equal to 4/12 .

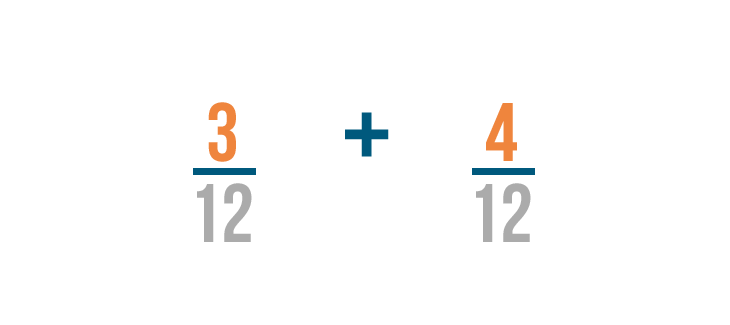
Now that our fractions have the same denominator, we can add them like we normally do.

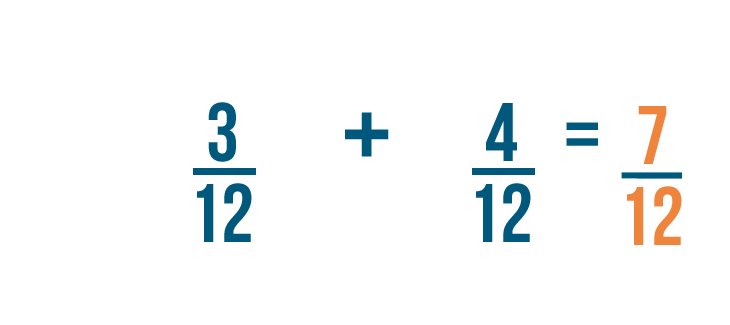
3 plus 4 equals 7 . As usual, the denominator stays the same. So 3/12 plus 4/12 equals 7/12 .

Try solving the addition problems below.

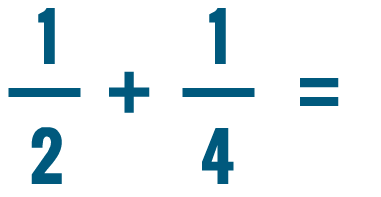
Subtracting fractions with different denominators

We just saw that fractions can only be added when they have the same denominator. The same thing is true when we're subtracting fractions. Before we can subtract, we'll have to change our fractions so they have the same denominator.

Click through the slideshow to learn how to subtract fractions with different denominators.

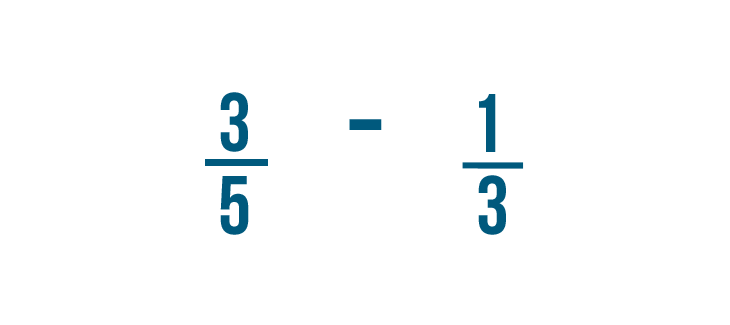
Let's try subtracting 1/3 from 3/5 .

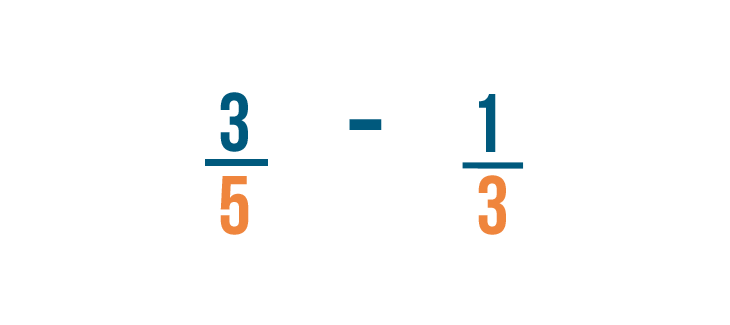
First, we'll change the denominators of both fractions to be the same by finding the lowest common denominator .

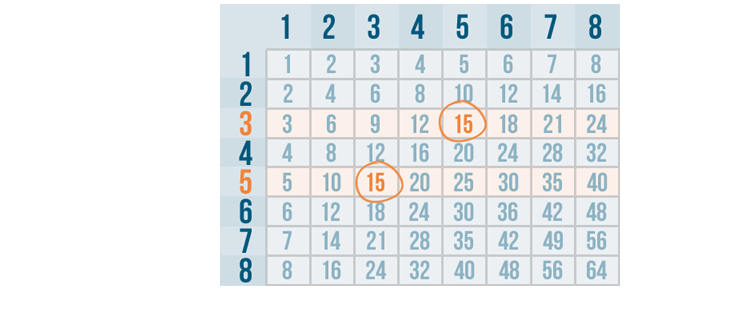
It looks like 15 is the smallest number that can be divided evenly by 3 and 5 , so 15 is our LCD.

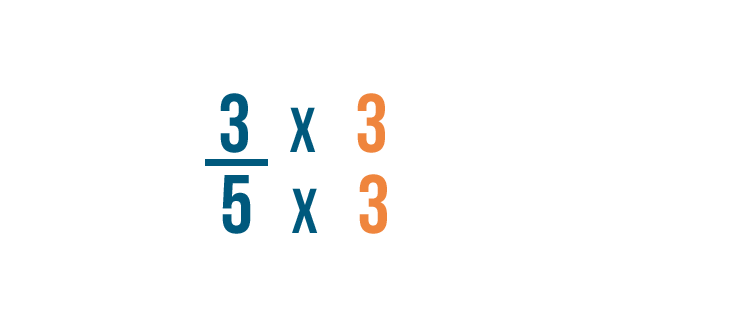
Now we'll change our first fraction. To change the denominator to 15 , we'll multiply the denominator and the numerator by 3 .

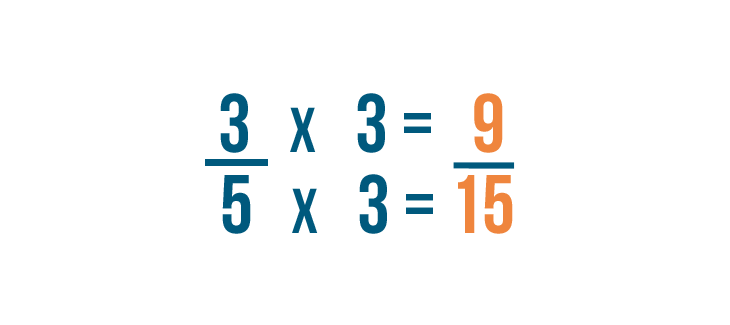
5 times 3 equals 15 . So our fraction is now 9/15 .

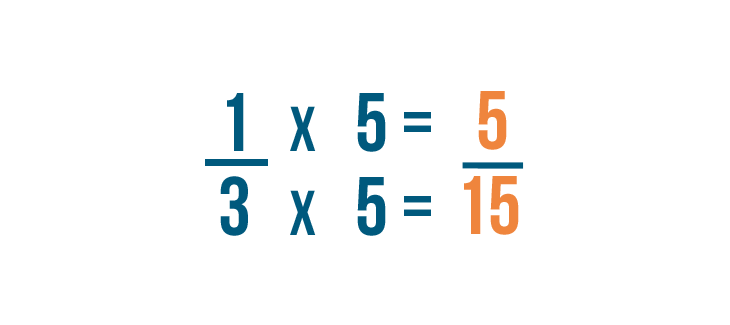
Now let's change the second fraction. To change the denominator to 15 , we'll multiply both numbers by 5 to get 5/15 .

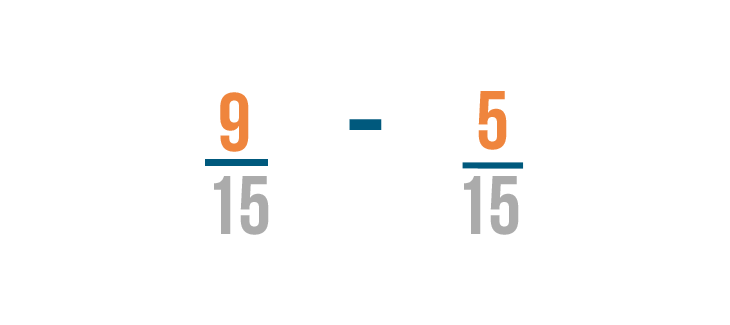
Now that our fractions have the same denominator, we can subtract like we normally do.

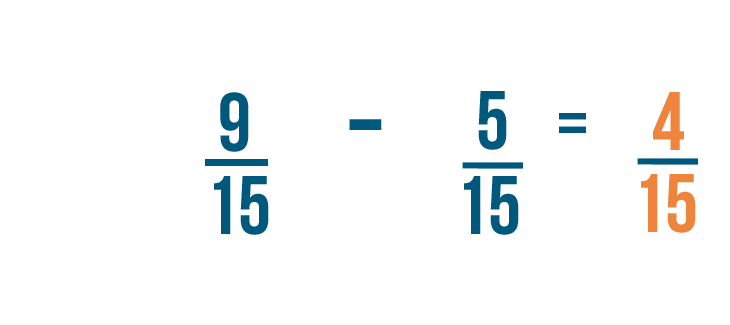
9 minus 5 equals 4 . As always, the denominator stays the same. So 9/15 minus 5/15 equals 4/15 .

Try solving the subtraction problems below.

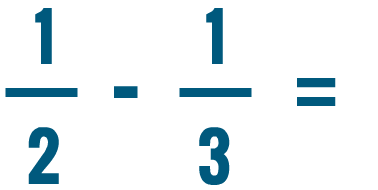
Adding and subtracting mixed numbers

Over the last few pages, you've practiced adding and subtracting different kinds of fractions. But some problems will need one extra step. For example, can you add the fractions below?

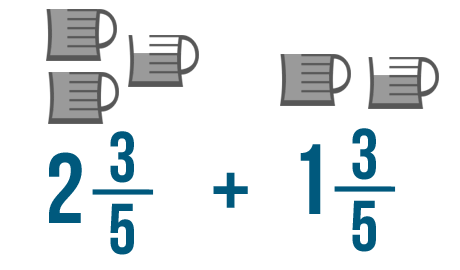
In Introduction to Fractions , you learned about mixed numbers . A mixed number has both a fraction and a whole number . An example is 2 1/2 , or two-and-a-half . Another way to write this would be 5/2 , or five-halves . These two numbers look different, but they're actually the same.

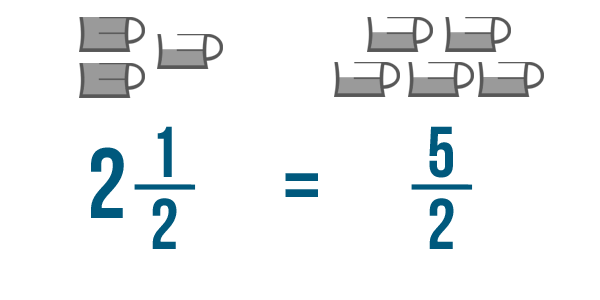
5/2 is an improper fraction . This just means the top number is larger than the bottom number. Even though improper fractions look strange, you can add and subtract them just like normal fractions. Mixed numbers aren't easy to add, so you'll have to convert them into improper fractions first.

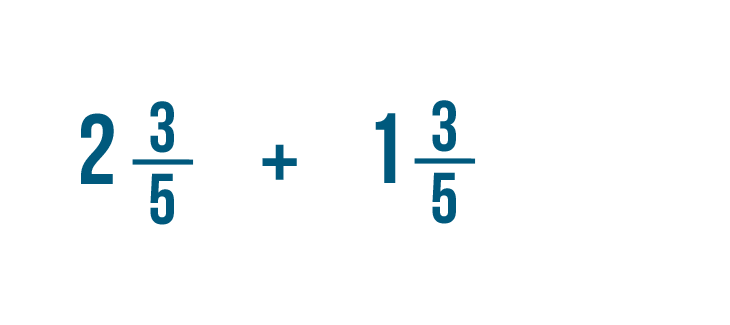
Let's add these two mixed numbers: 2 3/5 and 1 3/5 .

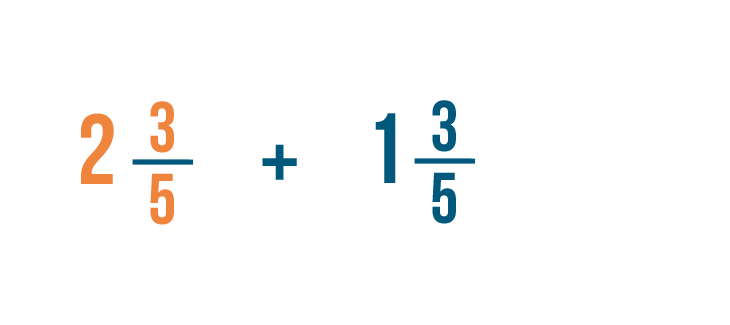
We'll need to convert these mixed numbers to improper fractions. Let's start with 2 3/5 .

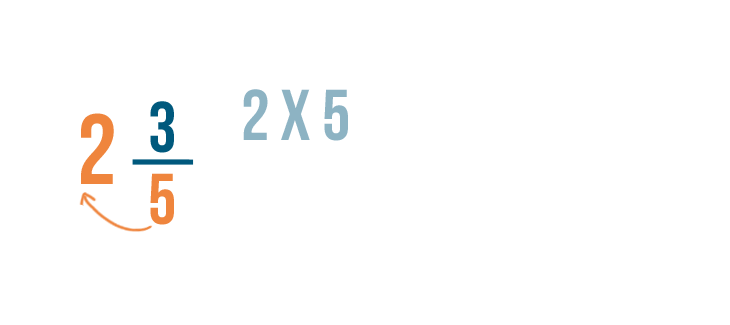
As you learned in Lesson 2 , we'll multiply the whole number, 2 , by the bottom number, 5 .

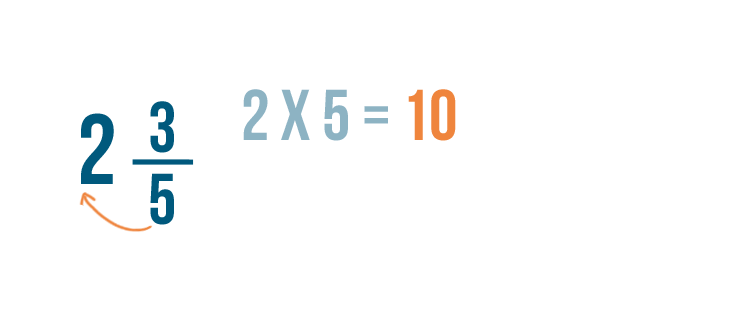
2 times 5 equals 10 .

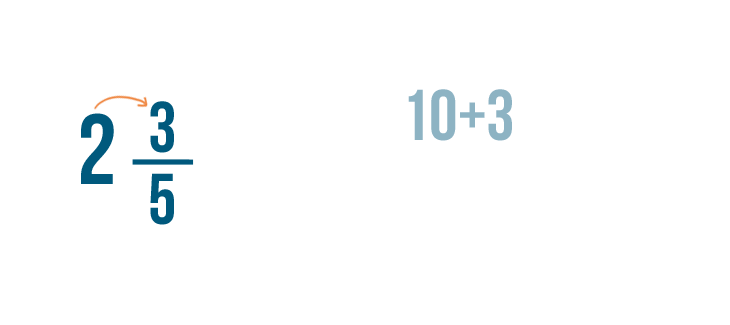
Now, let's add 10 to the numerator, 3 .

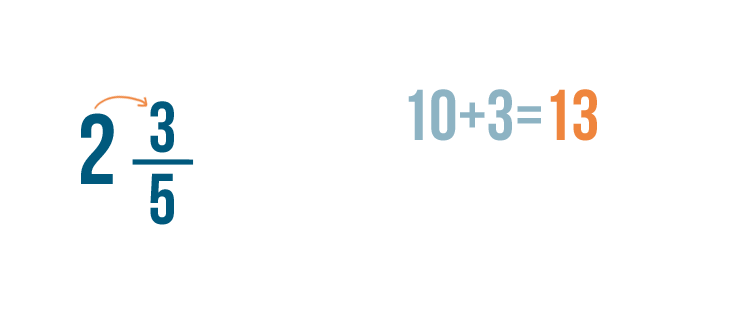
10 + 3 equals 13 .

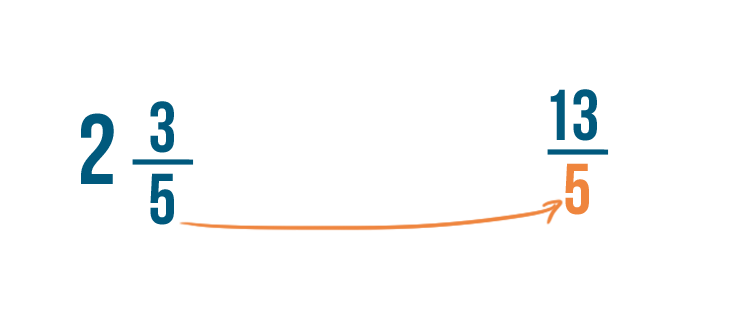
Just like when you add fractions, the denominator stays the same. Our improper fraction is 13/5 .

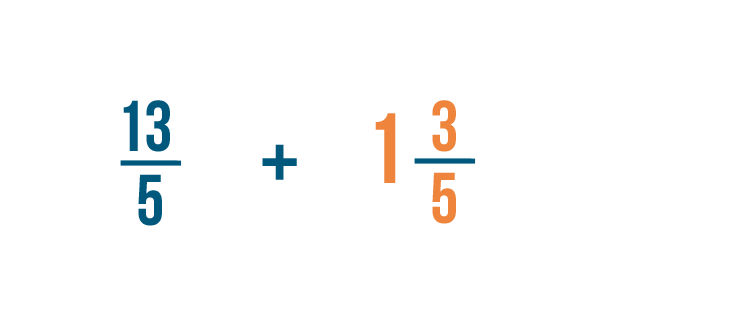
Now we'll need to convert our second mixed number: 1 3/5 .

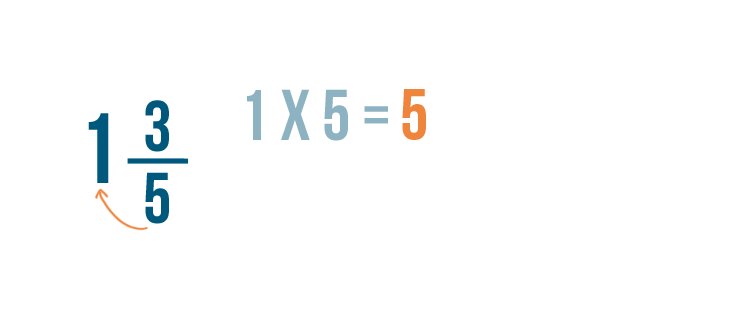
First, we'll multiply the whole number by the denominator. 1 x 5 = 5 .

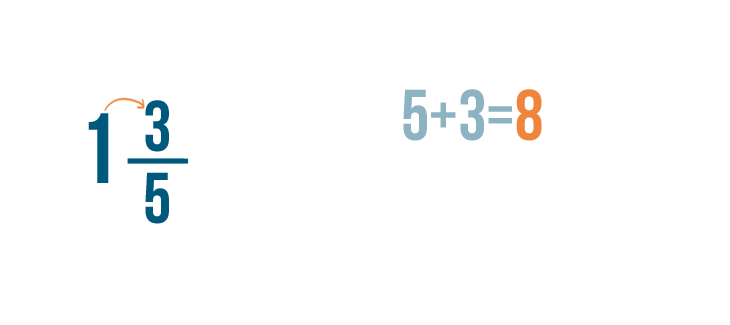
Next, we'll add 5 to the numerators. 5 + 3 = 8 .

Just like last time, the denominator remains the same. So we've changed 1 3/5 to 8/5 .

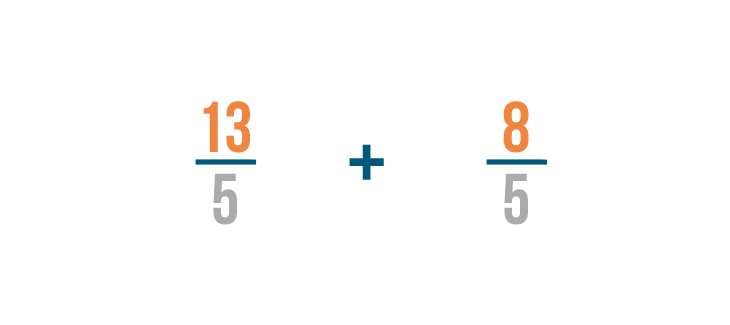
Now that we've changed our mixed numbers to improper fractions, we can add like we normally do.

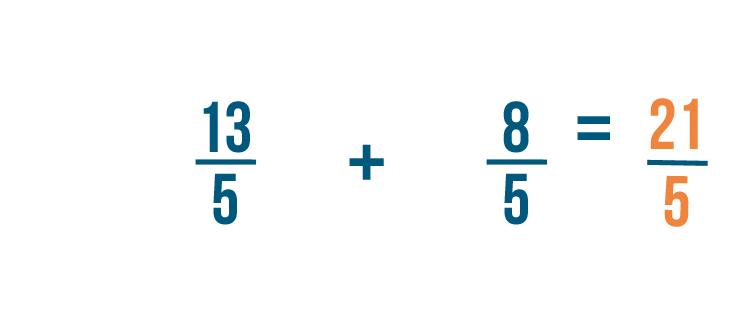
13 plus 8 equals 21 . As usual, the denominator will stay the same. So 13/5 + 8/5 = 21/5 .

Because we started with a mixed number, let's convert this improper fraction back into a mixed number.

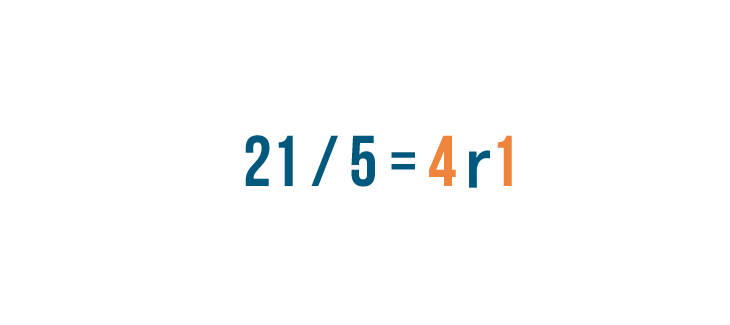
As you learned in the previous lesson , divide the top number by the bottom number. 21 divided by 5 equals 4, with a remainder of 1 .

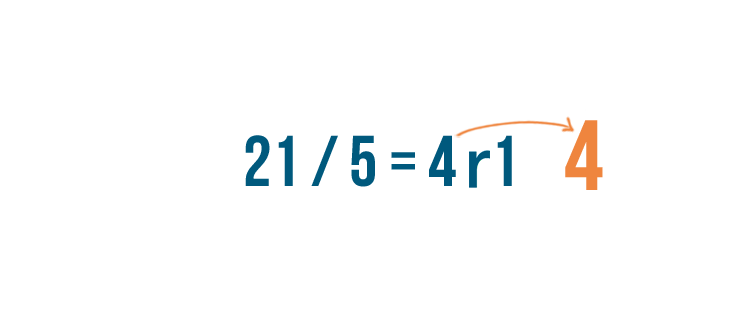
The answer, 4, will become our whole number.

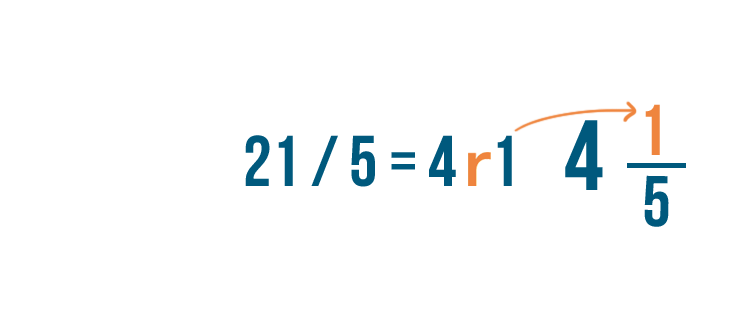
And the remainder , 1, will become the numerator of the fraction.

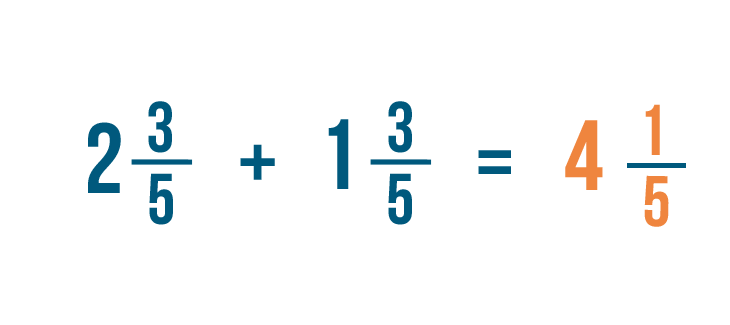
So 2 3/5 + 1 3/5 = 4 1/5 .

/en/fractions/multiplying-and-dividing-fractions/content/

We're sorry, but we don't support Internet Explorer anymore. Please use a different browser .

Add and Subtract Fractions Online practice for grades 3-7

On this page, you can practice addition and subtraction of fractions. Each practice set will automatically include both addition and subtraction problems.

The options are:

• You can limit the fractions in the problems to like fractions (fractions with the same denominator), for example: 1/6 + 4/6.
• You can limit the script to use only proper fractions—fractions that are less than 1. With this option, the script will make problems such as 1/4 + 2/5, but will not make problems such as 8/5 − 4/5.
• When you choose problems that use simplified fractions, the script will only include fractions in the problems that are in lowest terms. For example, you could get a problem such as 5/6 + 3/5, but you would not see 2/4 + 6/8.
• The last option, when chose, allows or accepts answers to not be in lowest terms. In other words, the script will accept an answer such as 8/10.

Note: ALL answers have to be given as mixed numbers, when possible. In other words, your answer cannot be left as an improper fraction.

You may use the space below to write the intermediate step. Your work in this area will not be checked.

Generate Quick Link

Addition and Subtraction of Fraction: Methods, Examples, Facts, FAQs

What is addition and subtraction of fractions, methods of addition and subtraction of fractions, addition and subtraction of mixed numbers, solved examples on addition and subtraction of fractions, practice problems on addition and subtraction of fractions, frequently asked questions on addition and subtraction of fractions.

Addition and subtraction of fractions are the fundamental operations on fractions that can be studied easily using two cases:

• Addition and subtraction of like fractions (fractions with same denominators)
• Addition and subtraction of unlike fractions (fractions with different denominators)

A fraction represents parts of a whole. For example, the fraction 37 represents 3 parts out of 7 equal parts of a whole. Here, 3 is the numerator and it represents the number of parts taken. 7 is the denominator and it represents the total number of parts of the whole.

Adding and subtracting fractions is simple and straightforward when it comes to like fractions. In the case of unlike fractions, we first need to make the denominators the same. Let’s take a closer look at both these cases.

Before adding and subtracting fractions, we first need to make sure that the fractions have the same denominators. 

When the denominators are the same, we simply add the numerators and keep the denominator as it is. To add or subtract unlike fractions, we first need to learn how to make the denominators alike. Let’s learn how to add fractions and how to subtract fractions in both cases.

Related Worksheets

Addition and Subtraction of Like Fractions

The rules for adding fractions with the same denominator are really simple and straightforward. 

Let’s learn with the help of examples and visual bar models.

Addition of Like Fractions

Here are the steps to add fractions with the same denominator:

Step 1: Add the numerators of the given fractions. 

Step 2: Keep the denominator the same. 

Step 3: Simplify.          

$\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}$  …$c \neq 0$

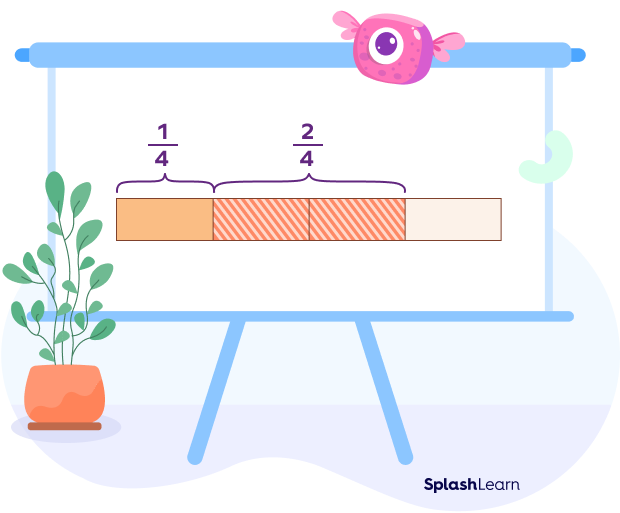
Example 1: Find $\frac{1}{4} + \frac{2}{4}$ .

$\frac{1}{4} + \frac{2}{4} = \frac{1 + 2}{4} = \frac{3}{4}$

We can visualize this addition using a bar model:

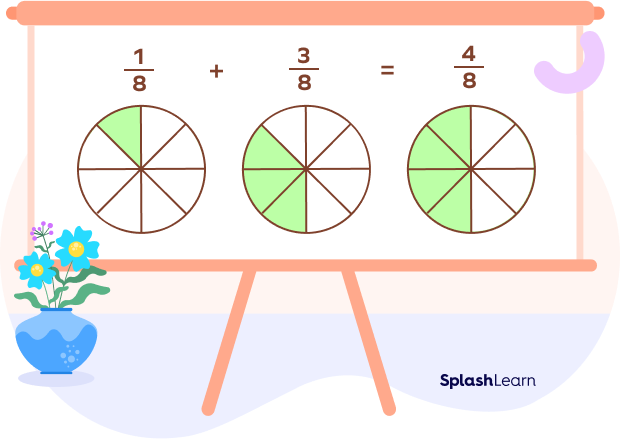
Example 2: $\frac{1}{8} + \frac{3}{8} = \frac{1 + 3}{8} = \frac{4}{8} = \frac{1}{2}$

Subtraction of Like Fractions

Here are the steps to subtract fractions with the same denominator:

Step 1: Subtract the numerators of the given fractions. 

Step 3: Simplify. 

$\frac{a}{c}\;-\;\frac{b}{c} = \frac{a \;-\; b}{c}$ …$c \neq 0$

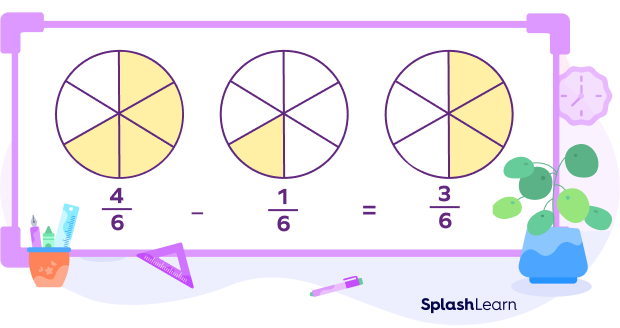
Example 1: Find $\frac{4}{6} \;-\; \frac{1}{6}$.

$\frac{4}{6}\;-\;\frac{1}{6} = \frac{4-1}{6} = \frac{3}{6} = \frac{1}{2}$

Addition and Subtraction of Unlike Fractions

Addition and subtraction of fractions with unlike denominators can be a little bit tricky since the denominators are not the same. So, we need to first convert the unlike fractions into like fractions. Let’s look at a few ways to do this!

Addition of Unlike Fractions

We can make the denominators the same by finding the LCM of the two denominators. Once we calculate the LCM, we multiply both the numerator and the denominator with an appropriate number so that we get the LCM value in the denominator. 

Example: $\frac{3}{5} + \frac{3}{2}$

Step 1: Find the LCM (Least Common Multiple) of the two denominators.

The LCM of 5 and 2 is 10.

Step 2: Convert both the fractions into like fractions by making the denominators same.  

$\frac{3 \times 2}{5 \times 2} = \frac{6}{10}$  

$\frac{3 \times 5}{2 \times 5} = \frac{15}{10}$

Step 3: Add the numerators. The denominator stays the same.

$\frac{6}{10} + \frac{15}{10} = \frac{21}{10}$

Step 4: Convert the resultant fraction to its simplest form if the GCF of the numerator and denominator is not 1. 

In this case, GCF (21,10) $= 1$

The fraction $\frac{21}{10}$ is already in its simplest form. 

Thus, $\frac{3}{5} + \frac{3}{2} = \frac{21}{10}$

Subtraction of Unlike Fractions

Let’s learn how to subtract fractions when denominators are not the same. To subtract unlike fractions, we use the LCM method. The process is similar to what we discussed in the previous example.

Example: $\frac{5}{6} \;-\; \frac{2}{9}$

Step 1: Find the LCM of the two denominators.

LCM of 6 and $9 = 18$

Step 2: Convert both the fractions into like fractions by making the denominators same.

$\frac{5 \times 3}{6 \times 3} = \frac{15}{18}$   

$\frac{2 \times 2}{9 \times 2} = \frac{4}{18}$

Step 3: Subtract the numerators. The denominator stays the same.

$\frac{15}{18} \;-\; \frac{4}{18} = \frac{11}{18}$

In this case, the GCF (11,18) $= 1$

So, it is already in its simplest form. 

Thus, $\frac{5}{6}\;-\; 29 = \frac{11}{18}$

A mixed number is a type of fraction that has two parts: a whole number and a proper fraction. It is also known as a mixed fraction. Any mixed number can be written in the form of an improper fraction and vice-versa. 

Adding and subtracting mixed fractions is done by converting mixed numbers into improper fractions .

Addition and Subtraction of Mixed Fractions with Same Denominators

The steps of adding and subtracting mixed numbers with the same denominators are the same. The only difference is the operation.

Step 1: Convert the given mixed fractions to improper fractions.

Step 2: Add/Subtract the like fractions obtained in step 1.

Step 3: Reduce the fraction to its simplest form.

Step 4: Convert the resulting fraction into a mixed number.

Example 1: $2\frac{1}{5} + 1\frac{3}{5}$

$2\frac{1}{5} = \frac{(5 \times 2) + 1}{5} = \frac{11}{5}$

$1\frac{3}{5} = \frac{(5 \times 1) + 3}{5} = \frac{8}{5}$

Thus, $2\frac{1}{5} + 1\frac{3}{5} = \frac{11}{5} + \frac{8}{5} = \frac{19}{5}$

Converting $\frac{19}{5}$ into a mixed number, we get

$\frac{19}{5} = 3\frac{4}{5}$

Example 2: $2\frac{1}{5} + 1\frac{3}{5} = \frac{11}{5} \;-\; \frac{8}{5} = \frac{3}{5}$

Addition and Subtraction of Mixed Fractions with Unlike Denominators

Step 2: Convert both the fractions into like fractions by finding the least common denominator.

Step 3: Add the fractions. (or subtract the fractions.)

Step 4: Reduce the fraction if possible or convert back to a mixed number 

Let us understand the addition of mixed numbers with unlike denominators with the help of an example.

Example 1: Find the value of $1\frac{3}{5} + 2\frac{1}{2}$.

Convert the given mixed fractions to improper fractions.

$1\frac{3}{5} = \frac{8}{5}$ and $2\frac{1}{2} = \frac{5}{2}$

Step 2: Convert both the fractions into like fractions by making the denominators the same.

Here, LCM of 5 and 2 is 10.

Thus, $\frac{8 \times 2}{5 \times 2} = \frac{16}{10}$ and $\frac{5\times 5}{2 \times 5} = \frac{25}{10}$

Step 3: Add the fractions by adding the numerators.

$\frac{16}{10} + \frac{25}{10} = \frac{41}{10}$

Step 4: Convert back into a mixed number. 

Thus, $\frac{41}{10}$ will become  $4\frac{1}{10}$

Therefore, $1\frac{3}{5} + 2\frac{1}{2} =  4\frac{1}{10}$

Here’s an example for subtraction. It follows the same steps.

Example 2 : $6\frac{1}{2} \;-\; 1\frac{3}{4}$

Step 1: Convert the mixed numbers into improper fractions.

     $6\frac{1}{2} \;-\; 1\frac{3}{4} = \frac{13}{2} \;-\; \frac{7}{4}$

Step 2: Make the denominators equal.

LCM of 2 and 4 is 4. 

   $\frac{13 \times 2}{2 \times 2} = \frac{26}{4}$ 

Step 3: Subtract the fractions.

        $\frac{26}{4} \;-\;  \frac{7}{4} = \frac{19}{4}$

Step 4: Convert the fraction as a mixed number.

            $\frac{19}{4}  = 4\frac{3}{4}$  

Thus, $6\frac{1}{2} \;-\; 1\frac{3}{4}  =   4\frac{3}{4}$  

Facts about Addition and Subtraction of Fractions

• We cannot add or subtract fractions without converting them into like fractions.
• Like fractions are fractions that have the same denominator, and unlike fractions are fractions that have different denominators.
• Equivalent fractions are two different fractions that represent the same value.
• The LCD (least common denominator) of two fractions is the LCM of the denominators.

In this article, we have learned about addition and subtraction of fractions (like fractions, unlike fractions, mixed fractions), methods of addition and subtraction of these fractions along with the steps. Let’s solve some examples on adding and subtracting fractions to understand the concept better.

• Solve: $\frac{2}{4} + \frac{1}{4}$ .

Solution: 

Here, the denominators are the same.

Thus, we add the numerators by keeping the denominators as it is.

$\frac{2}{4} + \frac{1}{4} = \frac{2 + 1}{4}$ 

$\frac{2}{4} + \frac{1}{4} = \frac{3}{4}$

2. Find the sum of the fractions $\frac{3}{5}$ and $\frac{5}{2}$ by using the LCM method.

$\frac{3}{5}$ and $\frac{5}{2}$ are unlike fractions.

The LCM of 2 and 5 is 10.

Thus, we can write

$\frac{3}{5} + \frac{5}{2} = \frac{3 \times 2}{5 \times 2} + \frac{5 \times 5}{2 \times 5}$

$= \frac{6}{10} + \frac{25}{10}$

            $= \frac{6}{10} + \frac{25}{10}$

            $= \frac{31}{10}$

Thus, $\frac{3}{5} + \frac{5}{2} =  \frac{31}{10}$

3. Find $\frac{4}{16} + \frac{5}{8}$.

Solution:  

To add two fractions with different denominators, we first need to find the LCM of the denominators.

The LCM of 16 and 8 is 16.

$\frac{4}{16} + \frac{5}{8} = \frac{4 \times 1}{16\times 1} + \frac{5 \times 2}{8 \times 2}$ 

            $= \frac{10}{16} + \frac{4}{16}$ 

            $= \frac{14}{16}$

$= \frac{7}{8}$

4. From a rope $12\frac{1}{2}$ ft. long, a $7 \frac{6}{8}\;-$ ft-long piece is cut off. Find the length of the remaining rope.

Total length of the rope $= 12\frac{1}{2}$ ft.

Length of the rope that was cut off $= 7 \frac{6}{8}$ ft. 

The length of the remaining rope $= 12\frac{1}{2} \;-\; 7 \frac{6}{8}$

$12\frac{1}{2} \;-\; 7 \frac{6}{8} = \frac{25}{2} \;-\; \frac{62}{8}$

         $= \frac{25 \times 4}{2 \times 4} \;-\; \frac{62 \times 1}{8\times 1}$

         $= \frac{100}{8} \;-\; \frac{62}{8}$

         $= \frac{38}{8}$

         $= \frac{19}{4}$

Converting it into a mixed fraction, $\frac{19}{4}$ becomes $4 \frac{3}{4}$.

Thus, the length of the remaining rope is $4\frac{3}{4}$ ft.

Attend this quiz & Test your knowledge.

Find $\frac{2}{4} + \frac{2}{4}$.

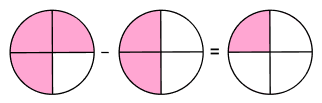
$\frac{7}{24} + \frac{5}{16} =$, what is the least common denominator of $\frac{1}{2}$ and $\frac{1}{3}$, $\frac{3}{6} \;-\; \frac{1}{6} =$, what equation does the following figure represent.

How do we add and subtract negative fractions?

Negative fractions are simply fractions with a negative sign. The steps to add and subtract the negative fractions remain the same. We need to follow the rules for addition/subtraction with negative signs.

How can we convert an improper fraction into a mixed number?

To convert an improper fraction into a mixed number, we divide the numerator by the denominator. The denominator stays the same. The quotient represents the whole number part. The remainder represents the numerator of the mixed number.

Example: $\frac{14}{3} = 4\; \text{R}\; 2$

Quotient $= 4$

Remainder $= 2$

$\frac{14}{3} = 4\frac{2}{3}$

How do we divide two fractions?

To divide one fraction by another, we multiply the first fraction by the reciprocal of the second fraction.

$\frac{A}{B} \div \frac{C}{D} = \frac{A}{B} \times \frac{D}{C}$

For example, $\frac{1}{2} \div \frac{3}{5} = \frac{1}{2} \times \frac{5}{3} = \frac{5}{6}$

What are the rules of adding and subtracting fractions?

• Before adding or subtracting, we check if the fractions have the same denominator.
• If the denominators are equal, then we add/subtract the numerators keeping the common denominator.
• If the denominators are different, then we make the denominators equal by using the LCM method. Once the fractions have the same denominator, we can add/subtract the numerators keeping the common denominator as it is.

How do we add and subtract fractions with whole numbers?

• Convert the whole number to a fraction. To do this, give the whole number a denominator of 1.
• Convert to fractions of like denominators. 
• Add/subtract the numerators. Now that the fractions have the same denominators, you can treat the numerators as a normal addition/subtraction problem.

RELATED POSTS

• Cube Numbers – Definition, Examples, Facts, Practice Problems
• Volume of Hemisphere: Definition, Formula, Examples
• CPCTC: Definition, Postulates, Theorem, Proof, Examples
• Dividend – Definition with Examples
• Reflexive Property – Definition, Equality, Examples, FAQs

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

• Word Problems
• Add/subtract fractions

Download & Print From only $2.60

Add & subtract fractions word problems

Like & unlike denominators.

Below are our grade 5 math word problem worksheet on adding and subtracting fractions.  The problems include both like and unlike denominators , and may include more than two terms.

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

More word problem worksheets

Explore all of our math word problem worksheets , from kindergarten through grade 5.

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

• Forgot Password?

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 4: Understand fractions

About this unit.

From cooking measurements to geometry, fractions are all around us. By understanding how the numerator and denominator work together, you'll be able to break down numbers into smaller parts, compare different fractions, and get a grasp on concepts like equivalent fractions.

Fractions intro

• Intro to fractions (Opens a modal)
• Cutting shapes into equal parts (Opens a modal)
• Cut shapes into equal parts Get 5 of 7 questions to level up!

What fractions mean

• Identifying numerators and denominators (Opens a modal)
• Recognize fractions (Opens a modal)
• Recognizing fractions greater than 1 (Opens a modal)
• Understand numerators and denominators Get 5 of 7 questions to level up!
• Recognize fractions Get 5 of 7 questions to level up!
• Recognize fractions greater than 1 Get 3 of 4 questions to level up!

Fractions on the number line

• Fractions on a number line (Opens a modal)
• Fractions on number line widget (Opens a modal)
• Finding 1 on the number line (Opens a modal)
• Fractions greater than 1 on the number line (Opens a modal)
• Fractions on the number line Get 5 of 7 questions to level up!
• Find 1 on the number line Get 5 of 7 questions to level up!
• Fractions greater than 1 on the number line Get 3 of 4 questions to level up!

Fractions and whole numbers

• Representing 1 as a fraction (Opens a modal)
• Whole numbers as fractions (Opens a modal)
• Writing whole numbers as fractions (Opens a modal)
• Write whole numbers as fractions Get 5 of 7 questions to level up!

Equivalent fractions

• Equivalent fractions with visuals (Opens a modal)
• Equivalent fraction models (Opens a modal)
• Equivalent fraction visually (Opens a modal)
• Creating equivalent fractions (Opens a modal)
• Equivalent fraction models Get 5 of 7 questions to level up!
• Equivalent fractions on the number line Get 3 of 4 questions to level up!
• Equivalent fractions Get 3 of 4 questions to level up!

Adding Fractions Practice Questions

Click here for questions, click here for answers.

Addition, Adding

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• International
• Education Jobs
• Schools directory
• Resources Education Jobs Schools directory News Search

Adding and Subtracting Fractions - Reasoning Challenges and Skill Drill

Subject: Mathematics

Age range: 7-11

Resource type: Worksheet/Activity

Last updated

25 May 2017

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Creative Commons "Sharealike"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

AuntSally22

Empty reply does not make any sense for the end user

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource: