types of hypothesis testing

• > Machine Learning
• > Statistics

What is Hypothesis Testing? Types and Methods

• Soumyaa Rawat
• Jul 23, 2021

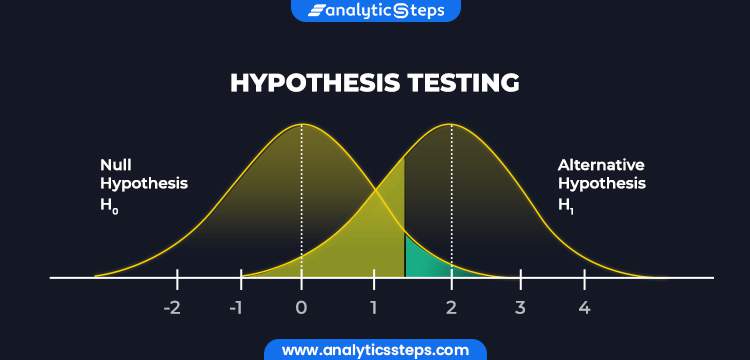
Hypothesis Testing  

Hypothesis testing is the act of testing a hypothesis or a supposition in relation to a statistical parameter. Analysts implement hypothesis testing in order to test if a hypothesis is plausible or not. 

In data science and statistics , hypothesis testing is an important step as it involves the verification of an assumption that could help develop a statistical parameter. For instance, a researcher establishes a hypothesis assuming that the average of all odd numbers is an even number. 

In order to find the plausibility of this hypothesis, the researcher will have to test the hypothesis using hypothesis testing methods. Unlike a hypothesis that is ‘supposed’ to stand true on the basis of little or no evidence, hypothesis testing is required to have plausible evidence in order to establish that a statistical hypothesis is true. 

Perhaps this is where statistics play an important role. A number of components are involved in this process. But before understanding the process involved in hypothesis testing in research methodology, we shall first understand the types of hypotheses that are involved in the process. Let us get started! 

Types of Hypotheses

In data sampling, different types of hypothesis are involved in finding whether the tested samples test positive for a hypothesis or not. In this segment, we shall discover the different types of hypotheses and understand the role they play in hypothesis testing.

Alternative Hypothesis

Alternative Hypothesis (H1) or the research hypothesis states that there is a relationship between two variables (where one variable affects the other). The alternative hypothesis is the main driving force for hypothesis testing. 

It implies that the two variables are related to each other and the relationship that exists between them is not due to chance or coincidence. 

When the process of hypothesis testing is carried out, the alternative hypothesis is the main subject of the testing process. The analyst intends to test the alternative hypothesis and verifies its plausibility.

Null Hypothesis

The Null Hypothesis (H0) aims to nullify the alternative hypothesis by implying that there exists no relation between two variables in statistics. It states that the effect of one variable on the other is solely due to chance and no empirical cause lies behind it. 

The null hypothesis is established alongside the alternative hypothesis and is recognized as important as the latter. In hypothesis testing, the null hypothesis has a major role to play as it influences the testing against the alternative hypothesis. 

(Must read: What is ANOVA test? )

Non-Directional Hypothesis

The Non-directional hypothesis states that the relation between two variables has no direction. 

Simply put, it asserts that there exists a relation between two variables, but does not recognize the direction of effect, whether variable A affects variable B or vice versa. 

Directional Hypothesis

The Directional hypothesis, on the other hand, asserts the direction of effect of the relationship that exists between two variables. 

Herein, the hypothesis clearly states that variable A affects variable B, or vice versa. 

Statistical Hypothesis

A statistical hypothesis is a hypothesis that can be verified to be plausible on the basis of statistics. 

By using data sampling and statistical knowledge, one can determine the plausibility of a statistical hypothesis and find out if it stands true or not. 

(Related blog: z-test vs t-test )

Performing Hypothesis Testing  

Now that we have understood the types of hypotheses and the role they play in hypothesis testing, let us now move on to understand the process in a better manner. 

In hypothesis testing, a researcher is first required to establish two hypotheses - alternative hypothesis and null hypothesis in order to begin with the procedure. 

To establish these two hypotheses, one is required to study data samples, find a plausible pattern among the samples, and pen down a statistical hypothesis that they wish to test. 

A random population of samples can be drawn, to begin with hypothesis testing. Among the two hypotheses, alternative and null, only one can be verified to be true. Perhaps the presence of both hypotheses is required to make the process successful. 

At the end of the hypothesis testing procedure, either of the hypotheses will be rejected and the other one will be supported. Even though one of the two hypotheses turns out to be true, no hypothesis can ever be verified 100%. 

(Read also: Types of data sampling techniques )

Therefore, a hypothesis can only be supported based on the statistical samples and verified data. Here is a step-by-step guide for hypothesis testing.

Establish the hypotheses

First things first, one is required to establish two hypotheses - alternative and null, that will set the foundation for hypothesis testing. 

These hypotheses initiate the testing process that involves the researcher working on data samples in order to either support the alternative hypothesis or the null hypothesis. 

Generate a testing plan

Once the hypotheses have been formulated, it is now time to generate a testing plan. A testing plan or an analysis plan involves the accumulation of data samples, determining which statistic is to be considered and laying out the sample size. 

All these factors are very important while one is working on hypothesis testing.

Analyze data samples

As soon as a testing plan is ready, it is time to move on to the analysis part. Analysis of data samples involves configuring statistical values of samples, drawing them together, and deriving a pattern out of these samples. 

While analyzing the data samples, a researcher needs to determine a set of things -

Significance Level - The level of significance in hypothesis testing indicates if a statistical result could have significance if the null hypothesis stands to be true.

Testing Method - The testing method involves a type of sampling-distribution and a test statistic that leads to hypothesis testing. There are a number of testing methods that can assist in the analysis of data samples. 

Test statistic - Test statistic is a numerical summary of a data set that can be used to perform hypothesis testing.

P-value - The P-value interpretation is the probability of finding a sample statistic to be as extreme as the test statistic, indicating the plausibility of the null hypothesis. 

Infer the results

The analysis of data samples leads to the inference of results that establishes whether the alternative hypothesis stands true or not. When the P-value is less than the significance level, the null hypothesis is rejected and the alternative hypothesis turns out to be plausible. 

Methods of Hypothesis Testing

As we have already looked into different aspects of hypothesis testing, we shall now look into the different methods of hypothesis testing. All in all, there are 2 most common types of hypothesis testing methods. They are as follows -

Frequentist Hypothesis Testing

The frequentist hypothesis or the traditional approach to hypothesis testing is a hypothesis testing method that aims on making assumptions by considering current data. 

The supposed truths and assumptions are based on the current data and a set of 2 hypotheses are formulated. A very popular subtype of the frequentist approach is the Null Hypothesis Significance Testing (NHST). 

The NHST approach (involving the null and alternative hypothesis) has been one of the most sought-after methods of hypothesis testing in the field of statistics ever since its inception in the mid-1950s. 

Bayesian Hypothesis Testing

A much unconventional and modern method of hypothesis testing, the Bayesian Hypothesis Testing claims to test a particular hypothesis in accordance with the past data samples, known as prior probability, and current data that lead to the plausibility of a hypothesis. 

The result obtained indicates the posterior probability of the hypothesis. In this method, the researcher relies on ‘prior probability and posterior probability’ to conduct hypothesis testing on hand. 

On the basis of this prior probability, the Bayesian approach tests a hypothesis to be true or false. The Bayes factor, a major component of this method, indicates the likelihood ratio among the null hypothesis and the alternative hypothesis. 

The Bayes factor is the indicator of the plausibility of either of the two hypotheses that are established for hypothesis testing.  

(Also read - Introduction to Bayesian Statistics ) 

To conclude, hypothesis testing, a way to verify the plausibility of a supposed assumption can be done through different methods - the Bayesian approach or the Frequentist approach. 

Although the Bayesian approach relies on the prior probability of data samples, the frequentist approach assumes without a probability. A number of elements involved in hypothesis testing are - significance level, p-level, test statistic, and method of hypothesis testing. 

(Also read: Introduction to probability distributions )

A significant way to determine whether a hypothesis stands true or not is to verify the data samples and identify the plausible hypothesis among the null hypothesis and alternative hypothesis. 

Share Blog :

Be a part of our Instagram community

Trending blogs

5 Factors Influencing Consumer Behavior

Elasticity of Demand and its Types

What is PESTLE Analysis? Everything you need to know about it

An Overview of Descriptive Analysis

What is Managerial Economics? Definition, Types, Nature, Principles, and Scope

5 Factors Affecting the Price Elasticity of Demand (PED)

6 Major Branches of Artificial Intelligence (AI)

Dijkstra’s Algorithm: The Shortest Path Algorithm

Scope of Managerial Economics

Different Types of Research Methods

Latest Comments

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses. 

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value  tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results. 

Interpret the results of the hypothesis test in the context of the question being asked. 

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called  alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or  Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related:   What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Hypothesis testing.

Key Topics:

• Basic approach
• Null and alternative hypothesis
• Decision making and the p -value
• Z-test & Nonparametric alternative

Basic approach to hypothesis testing

• State a model describing the relationship between the explanatory variables and the outcome variable(s) in the population and the nature of the variability. State all of your assumptions .
• Specify the null and alternative hypotheses in terms of the parameters of the model.
• Invent a test statistic that will tend to be different under the null and alternative hypotheses.
• Using the assumptions of step 1, find the theoretical sampling distribution of the statistic under the null hypothesis of step 2. Ideally the form of the sampling distribution should be one of the “standard distributions”(e.g. normal, t , binomial..)
• Calculate a p -value , as the area under the sampling distribution more extreme than your statistic. Depends on the form of the alternative hypothesis.
• Choose your acceptable type 1 error rate (alpha) and apply the decision rule : reject the null hypothesis if the p-value is less than alpha, otherwise do not reject.
• \(\frac{\bar{X}-\mu_0}{\sigma / \sqrt{n}}\)
• general form is: (estimate - value we are testing)/(st.dev of the estimate)
• z-statistic follows N(0,1) distribution
• 2 × the area above |z|, area above z,or area below z, or
• compare the statistic to a critical value, |z| ≥ z α/2 , z ≥ z α , or z ≤ - z α
• Choose the acceptable level of Alpha = 0.05, we conclude …. ?

Making the Decision

It is either likely or unlikely that we would collect the evidence we did given the initial assumption. (Note: “likely” or “unlikely” is measured by calculating a probability!)

If it is likely , then we “ do not reject ” our initial assumption. There is not enough evidence to do otherwise.

If it is unlikely , then:

• either our initial assumption is correct and we experienced an unusual event or,
• our initial assumption is incorrect

In statistics, if it is unlikely, we decide to “ reject ” our initial assumption.

Example: Criminal Trial Analogy

First, state 2 hypotheses, the null hypothesis (“H 0 ”) and the alternative hypothesis (“H A ”)

• H 0 : Defendant is not guilty.
• H A : Defendant is guilty.

Usually the H 0 is a statement of “no effect”, or “no change”, or “chance only” about a population parameter.

While the H A , depending on the situation, is that there is a difference, trend, effect, or a relationship with respect to a population parameter.

• It can one-sided and two-sided.
• In two-sided we only care there is a difference, but not the direction of it. In one-sided we care about a particular direction of the relationship. We want to know if the value is strictly larger or smaller.

Then, collect evidence, such as finger prints, blood spots, hair samples, carpet fibers, shoe prints, ransom notes, handwriting samples, etc. (In statistics, the data are the evidence.)

Next, you make your initial assumption.

• Defendant is innocent until proven guilty.

In statistics, we always assume the null hypothesis is true .

Then, make a decision based on the available evidence.

• If there is sufficient evidence (“beyond a reasonable doubt”), reject the null hypothesis . (Behave as if defendant is guilty.)
• If there is not enough evidence, do not reject the null hypothesis . (Behave as if defendant is not guilty.)

If the observed outcome, e.g., a sample statistic, is surprising under the assumption that the null hypothesis is true, but more probable if the alternative is true, then this outcome is evidence against H 0 and in favor of H A .

An observed effect so large that it would rarely occur by chance is called statistically significant (i.e., not likely to happen by chance).

Using the p -value to make the decision

The p -value represents how likely we would be to observe such an extreme sample if the null hypothesis were true. The p -value is a probability computed assuming the null hypothesis is true, that the test statistic would take a value as extreme or more extreme than that actually observed. Since it's a probability, it is a number between 0 and 1. The closer the number is to 0 means the event is “unlikely.” So if p -value is “small,” (typically, less than 0.05), we can then reject the null hypothesis.

Significance level and p -value

Significance level, α, is a decisive value for p -value. In this context, significant does not mean “important”, but it means “not likely to happened just by chance”.

α is the maximum probability of rejecting the null hypothesis when the null hypothesis is true. If α = 1 we always reject the null, if α = 0 we never reject the null hypothesis. In articles, journals, etc… you may read: “The results were significant ( p <0.05).” So if p =0.03, it's significant at the level of α = 0.05 but not at the level of α = 0.01. If we reject the H 0 at the level of α = 0.05 (which corresponds to 95% CI), we are saying that if H 0 is true, the observed phenomenon would happen no more than 5% of the time (that is 1 in 20). If we choose to compare the p -value to α = 0.01, we are insisting on a stronger evidence!

So, what kind of error could we make? No matter what decision we make, there is always a chance we made an error.

Errors in Criminal Trial:

Errors in Hypothesis Testing

Type I error (False positive): The null hypothesis is rejected when it is true.

• α is the maximum probability of making a Type I error.

Type II error (False negative): The null hypothesis is not rejected when it is false.

• β is the probability of making a Type II error

There is always a chance of making one of these errors. But, a good scientific study will minimize the chance of doing so!

The power of a statistical test is its probability of rejecting the null hypothesis if the null hypothesis is false. That is, power is the ability to correctly reject H 0 and detect a significant effect. In other words, power is one minus the type II error risk.

\(\text{Power }=1-\beta = P\left(\text{reject} H_0 | H_0 \text{is false } \right)\)

Which error is worse?

Type I = you are innocent, yet accused of cheating on the test. Type II = you cheated on the test, but you are found innocent.

This depends on the context of the problem too. But in most cases scientists are trying to be “conservative”; it's worse to make a spurious discovery than to fail to make a good one. Our goal it to increase the power of the test that is to minimize the length of the CI.

We need to keep in mind:

• the effect of the sample size,
• the correctness of the underlying assumptions about the population,
• statistical vs. practical significance, etc…

(see the handout). To study the tradeoffs between the sample size, α, and Type II error we can use power and operating characteristic curves.

What type of error might we have made?

Type I error is claiming that average student height is not 65 inches, when it really is. Type II error is failing to claim that the average student height is not 65in when it is.

We rejected the null hypothesis, i.e., claimed that the height is not 65, thus making potentially a Type I error. But sometimes the p -value is too low because of the large sample size, and we may have statistical significance but not really practical significance! That's why most statisticians are much more comfortable with using CI than tests.

There is a need for a further generalization. What if we can't assume that σ is known? In this case we would use s (the sample standard deviation) to estimate σ.

If the sample is very large, we can treat σ as known by assuming that σ = s . According to the law of large numbers, this is not too bad a thing to do. But if the sample is small, the fact that we have to estimate both the standard deviation and the mean adds extra uncertainty to our inference. In practice this means that we need a larger multiplier for the standard error.

We need one-sample t -test.

One sample t -test

• Assume data are independently sampled from a normal distribution with unknown mean μ and variance σ 2 . Make an initial assumption, μ 0 .
• t-statistic: \(\frac{\bar{X}-\mu_0}{s / \sqrt{n}}\) where s is a sample st.dev.
• t-statistic follows t -distribution with df = n - 1
• Alpha = 0.05, we conclude ….

Testing for the population proportion

Let's go back to our CNN poll. Assume we have a SRS of 1,017 adults.

We are interested in testing the following hypothesis: H 0 : p = 0.50 vs. p > 0.50

What is the test statistic?

If alpha = 0.05, what do we conclude?

We will see more details in the next lesson on proportions, then distributions, and possible tests.

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, a complete guide on hypothesis testing in statistics, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

 We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Step 1: specify your null and alternate hypotheses.

It is critical to rephrase your original research hypothesis (the prediction that you wish to study) as a null (Ho) and alternative (Ha) hypothesis so that you can test it quantitatively. Your first hypothesis, which predicts a link between variables, is generally your alternate hypothesis. The null hypothesis predicts no link between the variables of interest.

Step 2: Gather Data

For a statistical test to be legitimate, sampling and data collection must be done in a way that is meant to test your hypothesis. You cannot draw statistical conclusions about the population you are interested in if your data is not representative.

Step 3: Conduct a Statistical Test

Other statistical tests are available, but they all compare within-group variance (how to spread out the data inside a category) against between-group variance (how different the categories are from one another). If the between-group variation is big enough that there is little or no overlap between groups, your statistical test will display a low p-value to represent this. This suggests that the disparities between these groups are unlikely to have occurred by accident. Alternatively, if there is a large within-group variance and a low between-group variance, your statistical test will show a high p-value. Any difference you find across groups is most likely attributable to chance. The variety of variables and the level of measurement of your obtained data will influence your statistical test selection.

Step 4: Determine Rejection Of Your Null Hypothesis

Your statistical test results must determine whether your null hypothesis should be rejected or not. In most circumstances, you will base your judgment on the p-value provided by the statistical test. In most circumstances, your preset level of significance for rejecting the null hypothesis will be 0.05 - that is, when there is less than a 5% likelihood that these data would be seen if the null hypothesis were true. In other circumstances, researchers use a lower level of significance, such as 0.01 (1%). This reduces the possibility of wrongly rejecting the null hypothesis.

Step 5: Present Your Results 

The findings of hypothesis testing will be discussed in the results and discussion portions of your research paper, dissertation, or thesis. You should include a concise overview of the data and a summary of the findings of your statistical test in the results section. You can talk about whether your results confirmed your initial hypothesis or not in the conversation. Rejecting or failing to reject the null hypothesis is a formal term used in hypothesis testing. This is likely a must for your statistics assignments.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

Future-Proof Your AI/ML Career: Top Dos and Don'ts

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales.  If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Why is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

• Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
• Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
• Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
• Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore Simplilearn’s Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is hypothesis testing and its types?

Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating two hypotheses: the null hypothesis (H0), which represents the default assumption, and the alternative hypothesis (Ha), which contradicts H0. The goal is to assess the evidence and determine whether there is enough statistical significance to reject the null hypothesis in favor of the alternative hypothesis.

Types of hypothesis testing:

• One-sample test: Used to compare a sample to a known value or a hypothesized value.
• Two-sample test: Compares two independent samples to assess if there is a significant difference between their means or distributions.
• Paired-sample test: Compares two related samples, such as pre-test and post-test data, to evaluate changes within the same subjects over time or under different conditions.
• Chi-square test: Used to analyze categorical data and determine if there is a significant association between variables.
• ANOVA (Analysis of Variance): Compares means across multiple groups to check if there is a significant difference between them.

3. What are the steps of hypothesis testing?

The steps of hypothesis testing are as follows:

• Formulate the hypotheses: State the null hypothesis (H0) and the alternative hypothesis (Ha) based on the research question.
• Set the significance level: Determine the acceptable level of error (alpha) for making a decision.
• Collect and analyze data: Gather and process the sample data.
• Compute test statistic: Calculate the appropriate statistical test to assess the evidence.
• Make a decision: Compare the test statistic with critical values or p-values and determine whether to reject H0 in favor of Ha or not.
• Draw conclusions: Interpret the results and communicate the findings in the context of the research question.

4. What are the 2 types of hypothesis testing?

• One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
• Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: The Fundamentals of Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 2883

• Diane Kiernan
• SUNY College of Environmental Science and Forestry via OpenSUNY

The previous two chapters introduced methods for organizing and summarizing sample data, and using sample statistics to estimate population parameters. This chapter introduces the next major topic of inferential statistics: hypothesis testing.

A hypothesis is a statement or claim about a property of a population.

The Fundamentals of Hypothesis Testing

When conducting scientific research, typically there is some known information, perhaps from some past work or from a long accepted idea. We want to test whether this claim is believable. This is the basic idea behind a hypothesis test:

• State what we think is true.
• Quantify how confident we are about our claim.
• Use sample statistics to make inferences about population parameters.

For example, past research tells us that the average life span for a hummingbird is about four years. You have been studying the hummingbirds in the southeastern United States and find a sample mean lifespan of 4.8 years. Should you reject the known or accepted information in favor of your results? How confident are you in your estimate? At what point would you say that there is enough evidence to reject the known information and support your alternative claim? How far from the known mean of four years can the sample mean be before we reject the idea that the average lifespan of a hummingbird is four years?

Definition: hypothesis testing

Hypothesis testing is a procedure, based on sample evidence and probability, used to test claims regarding a characteristic of a population.

A hypothesis is a claim or statement about a characteristic of a population of interest to us. A hypothesis test is a way for us to use our sample statistics to test a specific claim.

Example \(\PageIndex{1}\):

The population mean weight is known to be 157 lb. We want to test the claim that the mean weight has increased.

Example \(\PageIndex{2}\):

Two years ago, the proportion of infected plants was 37%. We believe that a treatment has helped, and we want to test the claim that there has been a reduction in the proportion of infected plants.

Components of a Formal Hypothesis Test

The null hypothesis is a statement about the value of a population parameter, such as the population mean (µ) or the population proportion ( p ). It contains the condition of equality and is denoted as H 0 (H-naught).

H 0 : µ = 157 or H0 : p = 0.37

The alternative hypothesis is the claim to be tested, the opposite of the null hypothesis. It contains the value of the parameter that we consider plausible and is denoted as H 1 .

H 1 : µ > 157 or H1 : p ≠ 0.37

The test statistic is a value computed from the sample data that is used in making a decision about the rejection of the null hypothesis. The test statistic converts the sample mean ( x̄ ) or sample proportion ( p̂ ) to a Z- or t-score under the assumption that the null hypothesis is true. It is used to decide whether the difference between the sample statistic and the hypothesized claim is significant.

The p-value is the area under the curve to the left or right of the test statistic. It is compared to the level of significance (α).

The critical value is the value that defines the rejection zone (the test statistic values that would lead to rejection of the null hypothesis). It is defined by the level of significance.

The level of significance (α) is the probability that the test statistic will fall into the critical region when the null hypothesis is true. This level is set by the researcher.

The conclusion is the final decision of the hypothesis test. The conclusion must always be clearly stated, communicating the decision based on the components of the test. It is important to realize that we never prove or accept the null hypothesis. We are merely saying that the sample evidence is not strong enough to warrant the rejection of the null hypothesis. The conclusion is made up of two parts:

1) Reject or fail to reject the null hypothesis, and 2) there is or is not enough evidence to support the alternative claim.

Option 1) Reject the null hypothesis (H0). This means that you have enough statistical evidence to support the alternative claim (H 1 ).

Option 2) Fail to reject the null hypothesis (H0). This means that you do NOT have enough evidence to support the alternative claim (H 1 ).

Another way to think about hypothesis testing is to compare it to the US justice system. A defendant is innocent until proven guilty (Null hypothesis—innocent). The prosecuting attorney tries to prove that the defendant is guilty (Alternative hypothesis—guilty). There are two possible conclusions that the jury can reach. First, the defendant is guilty (Reject the null hypothesis). Second, the defendant is not guilty (Fail to reject the null hypothesis). This is NOT the same thing as saying the defendant is innocent! In the first case, the prosecutor had enough evidence to reject the null hypothesis (innocent) and support the alternative claim (guilty). In the second case, the prosecutor did NOT have enough evidence to reject the null hypothesis (innocent) and support the alternative claim of guilty.

The Null and Alternative Hypotheses

There are three different pairs of null and alternative hypotheses:

Table \(PageIndex{1}\): The rejection zone for a two-sided hypothesis test.

where c is some known value.

A Two-sided Test

This tests whether the population parameter is equal to, versus not equal to, some specific value.

Ho: μ = 12 vs. H 1 : μ ≠ 12

The critical region is divided equally into the two tails and the critical values are ± values that define the rejection zones.

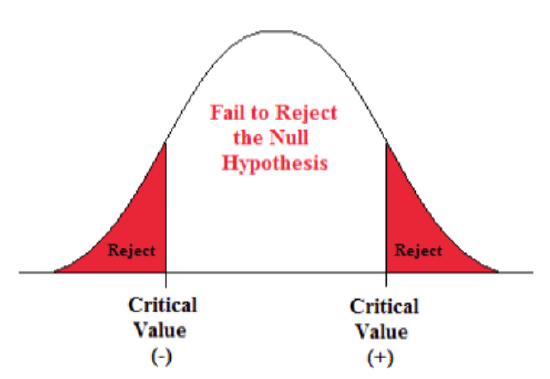
Example \(\PageIndex{3}\):

A forester studying diameter growth of red pine believes that the mean diameter growth will be different if a fertilization treatment is applied to the stand.

• Ho: μ = 1.2 in./ year
• H 1 : μ ≠ 1.2 in./ year

This is a two-sided question, as the forester doesn’t state whether population mean diameter growth will increase or decrease.

A Right-sided Test

This tests whether the population parameter is equal to, versus greater than, some specific value.

Ho: μ = 12 vs. H 1 : μ > 12

The critical region is in the right tail and the critical value is a positive value that defines the rejection zone.

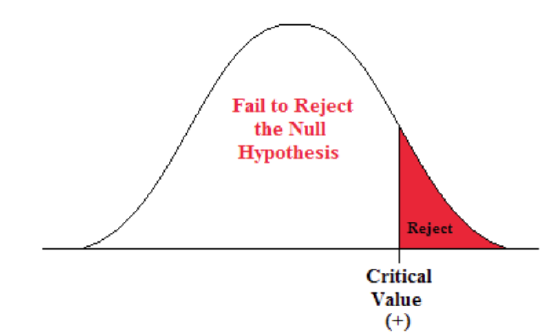
Example \(\PageIndex{4}\):

A biologist believes that there has been an increase in the mean number of lakes infected with milfoil, an invasive species, since the last study five years ago.

• Ho: μ = 15 lakes
• H1: μ >15 lakes

This is a right-sided question, as the biologist believes that there has been an increase in population mean number of infected lakes.

A Left-sided Test

This tests whether the population parameter is equal to, versus less than, some specific value.

Ho: μ = 12 vs. H 1 : μ < 12

The critical region is in the left tail and the critical value is a negative value that defines the rejection zone.

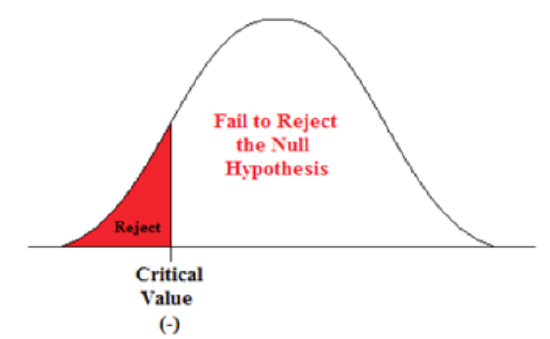
Example \(\PageIndex{5}\):

A scientist’s research indicates that there has been a change in the proportion of people who support certain environmental policies. He wants to test the claim that there has been a reduction in the proportion of people who support these policies.

• Ho: p = 0.57
• H 1 : p < 0.57

This is a left-sided question, as the scientist believes that there has been a reduction in the true population proportion.

Statistically Significant

When the observed results (the sample statistics) are unlikely (a low probability) under the assumption that the null hypothesis is true, we say that the result is statistically significant, and we reject the null hypothesis. This result depends on the level of significance, the sample statistic, sample size, and whether it is a one- or two-sided alternative hypothesis.

Types of Errors

When testing, we arrive at a conclusion of rejecting the null hypothesis or failing to reject the null hypothesis. Such conclusions are sometimes correct and sometimes incorrect (even when we have followed all the correct procedures). We use incomplete sample data to reach a conclusion and there is always the possibility of reaching the wrong conclusion. There are four possible conclusions to reach from hypothesis testing. Of the four possible outcomes, two are correct and two are NOT correct.

Table \(\PageIndex{2}\). Possible outcomes from a hypothesis test.

A Type I error is when we reject the null hypothesis when it is true. The symbol α (alpha) is used to represent Type I errors. This is the same alpha we use as the level of significance. By setting alpha as low as reasonably possible, we try to control the Type I error through the level of significance.

A Type II error is when we fail to reject the null hypothesis when it is false. The symbol β(beta) is used to represent Type II errors.

In general, Type I errors are considered more serious. One step in the hypothesis test procedure involves selecting the significance level ( α ), which is the probability of rejecting the null hypothesis when it is correct. So the researcher can select the level of significance that minimizes Type I errors. However, there is a mathematical relationship between α, β, and n (sample size).

• As α increases, β decreases
• As α decreases, β increases
• As sample size increases (n), both α and β decrease

The natural inclination is to select the smallest possible value for α, thinking to minimize the possibility of causing a Type I error. Unfortunately, this forces an increase in Type II errors. By making the rejection zone too small, you may fail to reject the null hypothesis, when, in fact, it is false. Typically, we select the best sample size and level of significance, automatically setting β.

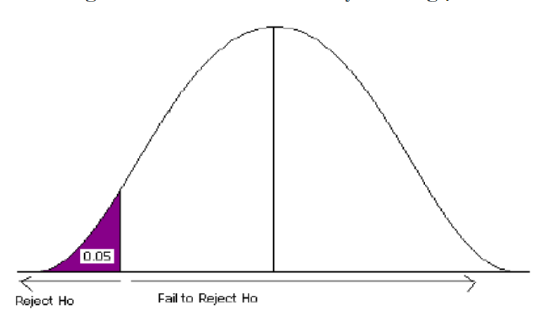
Power of the Test

A Type II error (β) is the probability of failing to reject a false null hypothesis. It follows that 1-β is the probability of rejecting a false null hypothesis. This probability is identified as the power of the test, and is often used to gauge the test’s effectiveness in recognizing that a null hypothesis is false.

Definition: power of the test

The probability that at a fixed level α significance test will reject H0, when a particular alternative value of the parameter is true is called the power of the test.

Power is also directly linked to sample size. For example, suppose the null hypothesis is that the mean fish weight is 8.7 lb. Given sample data, a level of significance of 5%, and an alternative weight of 9.2 lb., we can compute the power of the test to reject μ = 8.7 lb. If we have a small sample size, the power will be low. However, increasing the sample size will increase the power of the test. Increasing the level of significance will also increase power. A 5% test of significance will have a greater chance of rejecting the null hypothesis than a 1% test because the strength of evidence required for the rejection is less. Decreasing the standard deviation has the same effect as increasing the sample size: there is more information about μ.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

• Simple hypothesis testing (Opens a modal)
• Idea behind hypothesis testing (Opens a modal)
• Examples of null and alternative hypotheses (Opens a modal)
• P-values and significance tests (Opens a modal)
• Comparing P-values to different significance levels (Opens a modal)
• Estimating a P-value from a simulation (Opens a modal)
• Using P-values to make conclusions (Opens a modal)
• Simple hypothesis testing Get 3 of 4 questions to level up!
• Writing null and alternative hypotheses Get 3 of 4 questions to level up!
• Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

• Introduction to Type I and Type II errors (Opens a modal)
• Type 1 errors (Opens a modal)
• Examples identifying Type I and Type II errors (Opens a modal)
• Introduction to power in significance tests (Opens a modal)
• Examples thinking about power in significance tests (Opens a modal)
• Consequences of errors and significance (Opens a modal)
• Type I vs Type II error Get 3 of 4 questions to level up!
• Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

• Constructing hypotheses for a significance test about a proportion (Opens a modal)
• Conditions for a z test about a proportion (Opens a modal)
• Reference: Conditions for inference on a proportion (Opens a modal)
• Calculating a z statistic in a test about a proportion (Opens a modal)
• Calculating a P-value given a z statistic (Opens a modal)
• Making conclusions in a test about a proportion (Opens a modal)
• Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
• Conditions for a z test about a proportion Get 3 of 4 questions to level up!
• Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
• Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
• Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

• Writing hypotheses for a significance test about a mean (Opens a modal)
• Conditions for a t test about a mean (Opens a modal)
• Reference: Conditions for inference on a mean (Opens a modal)
• When to use z or t statistics in significance tests (Opens a modal)
• Example calculating t statistic for a test about a mean (Opens a modal)
• Using TI calculator for P-value from t statistic (Opens a modal)
• Using a table to estimate P-value from t statistic (Opens a modal)
• Comparing P-value from t statistic to significance level (Opens a modal)
• Free response example: Significance test for a mean (Opens a modal)
• Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
• Conditions for a t test about a mean Get 3 of 4 questions to level up!
• Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
• Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
• Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

More significance testing videos

• Hypothesis testing and p-values (Opens a modal)
• One-tailed and two-tailed tests (Opens a modal)
• Z-statistics vs. T-statistics (Opens a modal)
• Small sample hypothesis test (Opens a modal)
• Large sample proportion hypothesis testing (Opens a modal)

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

9.5: Types of Hypothesis Testing

Chapter 1: understanding statistics, chapter 2: summarizing and visualizing data, chapter 3: measure of central tendency, chapter 4: measures of variation, chapter 5: measures of relative standing, chapter 6: probability distributions, chapter 7: estimates, chapter 8: distributions, chapter 9: hypothesis testing, chapter 10: analysis of variance, chapter 11: correlation and regression, chapter 12: statistics in practice.

The JoVE video player is compatible with HTML5 and Adobe Flash. Older browsers that do not support HTML5 and the H.264 video codec will still use a Flash-based video player. We recommend downloading the newest version of Flash here, but we support all versions 10 and above.

Consider the example of testing a claim about the proportion of healthy and scabbed apples from a cultivar.

In this case, the null hypothesis is stated as the cultivar produces an equal number of healthy and scabbed apples.

Here, the alternative hypothesis can be expressed in three different ways, and based on that, the type of hypothesis test is decided.

One way to state the alternative hypothesis is that the cultivar produces more healthy apples than scabbed apples. In this case, the right-tailed hypothesis test is applicable as the critical region would be at the right tail of the distribution.

When we state that the cultivar produces less number of healthy apples, the critical region would be at the left tail of the distribution. Here, the left-tailed hypothesis test is applicable.

In case of uncertainty of the direction of the hypothesis, we may state that the cultivar produces an unequal number of healthy and scabbed apples. As the critical region would be at both the tails equally, the two-tailed hypothesis test would be applicable.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed.

When the null and alternative hypotheses are stated, it is observed that the null hypothesis is a neutral statement against which the alternative hypothesis is tested. The alternative hypothesis is a claim that instead has a certain direction. If the null hypothesis claims that p = 0.5, the alternative hypothesis would be an opposing statement to this and can be put either p > 0.5, p < 0.5, or p ≠ 0.5. In all these alternative hypotheses statements, the inequality symbols indicate the direction of the hypothesis. Based on the direction mentioned in the hypothesis, the type of hypothesis test can be decided for the given population parameter.

When the alternative hypothesis claims p > 0.5 (notice the 'greater than symbol), the critical region would fall at the right side of the probability distribution curve. In this case, the right-tailed hypothesis test is used.

When the alternative hypothesis claims p < 0.5 (notice the 'less than' symbol), the critical region would fall at the left side of the probability distribution curve. In this case, the left-tailed hypothesis test is used.

In the case of the alternative hypothesis p ≠ 0.5, a definite direction cannot be decided, and therefore the critical region falls at both the tails of the probability distribution curve. In this case, the  two-tailed test should be used.

Get cutting-edge science videos from J o VE sent straight to your inbox every month.

mktb-description

We use cookies to enhance your experience on our website.

By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.

Hypothesis Testing: Understanding the Basics, Types, and Importance

Hypothesis testing is a statistical method used to determine whether a hypothesis about a population parameter is true or not. This technique helps researchers and decision-makers make informed decisions based on evidence rather than guesses. Hypothesis testing is an essential tool in scientific research, social sciences, and business analysis. In this article, we will delve deeper into the basics of hypothesis testing, types of hypotheses, significance level, p-values, and the importance of hypothesis testing.

• Introduction

What is a hypothesis?

What is hypothesis testing, types of hypotheses, null hypothesis, alternative hypothesis, one-tailed and two-tailed tests, significance level and p-values, avoiding type i and type ii errors, making informed decisions, testing business strategies, a/b testing, formulating the null and alternative hypotheses, selecting the appropriate test, setting the level of significance, calculating the p-value, making a decision, common misconceptions about hypothesis testing, understanding hypothesis testing.

A hypothesis is an assumption or a proposition made about a population parameter. It is a statement that can be tested and either supported or refuted. For example, a hypothesis could be that a new medication reduces the severity of symptoms in patients with a particular disease.

Hypothesis testing is a statistical method that helps to determine whether a hypothesis is true or not. It is a procedure that involves collecting and analyzing data to evaluate the probability of the null hypothesis being true. The null hypothesis is the hypothesis that there is no significant difference between a sample and the population.

In hypothesis testing, there are two types of hypotheses: null and alternative.

The null hypothesis, denoted by H0, is a statement of no effect, no relationship, or no difference between the sample and the population. It is assumed to be true until there is sufficient evidence to reject it. For example, the null hypothesis could be that there is no significant difference in the blood pressure of patients who received the medication and those who received a placebo.

The alternative hypothesis, denoted by H1, is a statement of an effect, relationship, or difference between the sample and the population. It is the opposite of the null hypothesis. For example, the alternative hypothesis could be that the medication reduces the blood pressure of patients compared to those who received a placebo.

There are two types of alternative hypotheses: one-tailed and two-tailed. A one-tailed test is used when there is a directional hypothesis. For example, the hypothesis could be that the medication reduces blood pressure. A two-tailed test is used when there is a non-directional hypothesis. For example, the hypothesis could be that there is a significant difference in blood pressure between patients who received the medication and those who received a placebo.

The significance level, denoted by α, is the probability of rejecting the null hypothesis when it is true. It is set at the beginning of the test, usually at 5% or 1%. The p-value is the probability of obtaining a test statistic as extreme as

or more extreme than the observed one, assuming that the null hypothesis is true. If the p-value is less than the significance level, we reject the null hypothesis.

Importance of Hypothesis Testing

Hypothesis testing helps to avoid Type I and Type II errors. Type I error occurs when we reject the null hypothesis when it is actually true. Type II error occurs when we fail to reject the null hypothesis when it is actually false. By setting a significance level and calculating the p-value, we can control the probability of making these errors.

Hypothesis testing helps researchers and decision-makers make informed decisions based on evidence. For example, a medical researcher can use hypothesis testing to determine the effectiveness of a new drug. A business analyst can use hypothesis testing to evaluate the performance of a marketing campaign. By testing hypotheses, decision-makers can avoid making decisions based on guesses or assumptions.

Hypothesis testing is widely used in business analysis to test strategies and make data-driven decisions. For example, a business owner can use hypothesis testing to determine whether a new product will be profitable. By conducting A/B testing, businesses can compare the performance of two versions of a product and make data-driven decisions.

Examples of Hypothesis Testing

• A/B testing is a popular technique used in online marketing and web design. It involves comparing two versions of a webpage or an advertisement to determine which one performs better. By conducting A/B testing, businesses can optimize their websites and advertisements to increase conversions and sales.

A t-test is used to compare the means of two samples. It is commonly used in medical research, social sciences, and business analysis. For example, a researcher can use a t-test to determine whether there is a significant difference in the cholesterol levels of patients who received a new drug and those who received a placebo.

Analysis of Variance (ANOVA) is a statistical technique used to compare the means of more than two samples. It is commonly used in medical research, social sciences, and business analysis. For example, a business owner can use ANOVA to determine whether there is a significant difference in the sales performance of three different stores.

Steps in Hypothesis Testing

The first step in hypothesis testing is to formulate the null and alternative hypotheses. The null hypothesis is the hypothesis that there is no significant difference between the sample and the population, while the alternative hypothesis is the opposite.

The second step is to select the appropriate test based on the type of data and the research question. There are different types of tests for different types of data, such as t-test for continuous data and chi-square test for categorical data.

The third step is to set the level of significance, which is usually 5% or 1%. The significance level represents the probability of rejecting the null hypothesis when it is actually true.

The fourth step is to calculate the p-value, which represents the probability of obtaining a test statistic as extreme as or more extreme than the observed one, assuming that the null hypothesis is true.

The final step is to make a decision based on the p-value and the significance level. If the p-value is less than the significance level, we reject the null hypothesis. Otherwise, we fail to reject the null hypothesis.

There are several common misconceptions about hypothesis testing. One of the most common misconceptions is that rejecting the null hypothesis means that the alternative hypothesis is true. However

this is not necessarily the case. Rejecting the null hypothesis only means that there is evidence against it, but it does not prove that the alternative hypothesis is true. Another common misconception is that hypothesis testing can prove causality. However, hypothesis testing can only provide evidence for or against a hypothesis, and causality can only be inferred from a well-designed experiment.

Hypothesis testing is an important statistical technique used to test hypotheses and make informed decisions based on evidence. It helps to avoid Type I and Type II errors, and it is widely used in medical research, social sciences, and business analysis. By following the steps in hypothesis testing and avoiding common misconceptions, researchers and decision-makers can make data-driven decisions and avoid making decisions based on guesses or assumptions.

• What is the difference between Type I and Type II errors in hypothesis testing?
• Type I error occurs when we reject the null hypothesis when it is actually true, while Type II error occurs when we fail to reject the null hypothesis when it is actually false.
• How do you select the appropriate test in hypothesis testing?
• The appropriate test is selected based on the type of data and the research question. There are different types of tests for different types of data, such as t-test for continuous data and chi-square test for categorical data.
• Can hypothesis testing prove causality?
• No, hypothesis testing can only provide evidence for or against a hypothesis, and causality can only be inferred from a well-designed experiment.
• Why is hypothesis testing important in business analysis?
• Hypothesis testing is important in business analysis because it helps businesses make data-driven decisions and avoid making decisions based on guesses or assumptions. By testing hypotheses, businesses can evaluate the effectiveness of their strategies and optimize their performance.
• What is A/B testing?

If you want to learn more about statistical analysis, including central tendency measures, check out our  comprehensive statistical course . Our course provides a hands-on learning experience that covers all the essential statistical concepts and tools, empowering you to analyze complex data with confidence. With practical examples and interactive exercises, you’ll gain the skills you need to succeed in your statistical analysis endeavors. Enroll now and take your statistical knowledge to the next level!

If you’re looking to jumpstart your career as a data analyst, consider enrolling in our comprehensive  Data Analyst Bootcamp with Internship program . Our program provides you with the skills and experience necessary to succeed in today’s data-driven world. You’ll learn the fundamentals of statistical analysis, as well as how to use tools such as SQL, Python, Excel, and PowerBI to analyze and visualize data. But that’s not all – our program also includes a 3-month internship with us where you can showcase your Capstone Project.

2 Responses

This is a great and comprehensive article on hypothesis testing, covering everything from the basics to practical examples. I particularly appreciate the section on common misconceptions, as it’s important to understand what hypothesis testing can and cannot do. Overall, a valuable resource for anyone looking to understand this statistical technique.

Thanks, Ana Carol for your Kind words, Yes these topics are very important to know in Artificial intelligence.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Search Search Please fill out this field.

What Is Hypothesis Testing?

How hypothesis testing works, 4 step process, the bottom line.

• Fundamental Analysis

Hypothesis Testing: 4 Steps and Example

Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population or a data-generating process. The word "population" will be used for both of these cases in the following descriptions.

Key Takeaways

• Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
• The test provides evidence concerning the plausibility of the hypothesis, given the data.
• Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
• The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

In hypothesis testing, an  analyst  tests a statistical sample, intending to provide evidence on the plausibility of the null hypothesis. Statistical analysts measure and examine a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.

The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis. Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.

The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.

• State the hypotheses.
• Formulate an analysis plan, which outlines how the data will be evaluated.
• Carry out the plan and analyze the sample data.
• Analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.

Example of Hypothesis Testing

If an individual wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct. Mathematically, the null hypothesis is represented as Ho: P = 0.5. The alternative hypothesis is shown as "Ha" and is identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.

A random sample of 100 coin flips is taken, and the null hypothesis is tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.

If there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."

When Did Hypothesis Testing Begin?

Some statisticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”

What are the Benefits of Hypothesis Testing?

Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.

What are the Limitations of Hypothesis Testing?

Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.

Hypothesis testing refers to a statistical process that helps researchers determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. All hypothesis testing methods have the same four-step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

Sage. " Introduction to Hypothesis Testing. " Page 4.

Elder Research. " Who Invented the Null Hypothesis? "

Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples. "

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Talk to our experts

1800-120-456-456

• Hypothesis Testing

What is Hypothesis Testing?

Hypothesis testing in statistics refers to analyzing an assumption about a population parameter. It is used to make an educated guess about an assumption using statistics. With the use of sample data, hypothesis testing makes an assumption about how true the assumption is for the entire population from where the sample is being taken.  

Any hypothetical statement we make may or may not be valid, and it is then our responsibility to provide evidence for its possibility. To approach any hypothesis, we follow these four simple steps that test its validity.

First, we formulate two hypothetical statements such that only one of them is true. By doing so, we can check the validity of our own hypothesis.

The next step is to formulate the statistical analysis to be followed based upon the data points.

Then we analyze the given data using our methodology.

The final step is to analyze the result and judge whether the null hypothesis will be rejected or is true.

Let’s look at several hypothesis testing examples:

It is observed that the average recovery time for a knee-surgery patient is 8 weeks. A physician believes that after successful knee surgery if the patient goes for physical therapy twice a week rather than thrice a week, the recovery period will be longer. Conduct hypothesis for this statement. 

David is a ten-year-old who finishes a 25-yard freestyle in the meantime of 16.43 seconds. David’s father bought goggles for his son, believing that it would help him to reduce his time. He then recorded a total of fifteen 25-yard freestyle for David, and the average time came out to be 16 seconds. Conduct a hypothesis.

A tire company claims their A-segment of tires have a running life of 50,000 miles before they need to be replaced, and previous studies show a standard deviation of 8,000 miles. After surveying a total of 28 tires, the mean run time came to be 46,500 miles with a standard deviation of 9800 miles. Is the claim made by the tire company consistent with the given data? Conduct hypothesis testing. 

All of the hypothesis testing examples are from real-life situations, which leads us to believe that hypothesis testing is a very practical topic indeed. It is an integral part of a researcher's study and is used in every research methodology in one way or another. 

Inferential statistics majorly deals with hypothesis testing. The research hypothesis states there is a relationship between the independent variable and dependent variable. Whereas the null hypothesis rejects this claim of any relationship between the two, our job as researchers or students is to check whether there is any relation between the two.  

Hypothesis Testing in Research Methodology

Now that we are clear about what hypothesis testing is? Let's look at the use of hypothesis testing in research methodology. Hypothesis testing is at the centre of research projects. 

What is Hypothesis Testing and Why is it Important in Research Methodology?

Often after formulating research statements, the validity of those statements need to be verified. Hypothesis testing offers a statistical approach to the researcher about the theoretical assumptions he/she made. It can be understood as quantitative results for a qualitative problem. 

(Image will be uploaded soon)

Hypothesis testing provides various techniques to test the hypothesis statement depending upon the variable and the data points. It finds its use in almost every field of research while answering statements such as whether this new medicine will work, a new testing method is appropriate, or if the outcomes of a random experiment are probable or not.

Procedure of Hypothesis Testing

To find the validity of any statement, we have to strictly follow the stepwise procedure of hypothesis testing. After stating the initial hypothesis, we have to re-write them in the form of a null and alternate hypothesis. The alternate hypothesis predicts a relationship between the variables, whereas the null hypothesis predicts no relationship between the variables.

After writing them as H 0 (null hypothesis) and H a (Alternate hypothesis), only one of the statements can be true. For example, taking the hypothesis that, on average, men are taller than women, we write the statements as:

H 0 : On average, men are not taller than women.

H a : On average, men are taller than women. 

Our next aim is to collect sample data, what we call sampling, in a way so that we can test our hypothesis. Your data should come from the concerned population for which you want to make a hypothesis. 

What is the p value in hypothesis testing? P-value gives us information about the probability of occurrence of results as extreme as observed results.

You will obtain your p-value after choosing the hypothesis testing method, which will be the guiding factor in rejecting the hypothesis. Usually, the p-value cutoff for rejecting the null hypothesis is 0.05. So anything below that, you will reject the null hypothesis. 

A low p-value means that the between-group variance is large enough that there is almost no overlapping, and it is unlikely that these came about by chance. A high p-value suggests there is a high within-group variance and low between-group variance, and any difference in the measure is due to chance only.

What is statistical hypothesis testing?

When forming conclusions through research, two sorts of errors are common: A hypothesis must be set and defined in statistics during a statistical survey or research. A statistical hypothesis is what it is called. It is, in fact, a population parameter assumption. However, it is unmistakable that this idea is always proven correct. Hypothesis testing refers to the predetermined formal procedures used by statisticians to determine whether hypotheses should be accepted or rejected. The process of selecting hypotheses for a given probability distribution based on observable data is known as hypothesis testing. Hypothesis testing is a fundamental and crucial issue in statistics. 

Why do I Need to Test it? Why not just prove an alternate one?

The quick answer is that you must as a scientist; it is part of the scientific process. Science employs a variety of methods to test or reject theories, ensuring that any new hypothesis is free of errors. One protection to ensure your research is not incorrect is to include both a null and an alternate hypothesis. The scientific community considers not incorporating the null hypothesis in your research to be poor practice. You are almost certainly setting yourself up for failure if you set out to prove another theory without first examining it. At the very least, your experiment will not be considered seriously.

Types of Hypothesis Testing

There are several types of hypothesis testing, and they are used based on the data provided. Depending on the sample size and the data given, we choose among different hypothesis testing methodologies. Here starts the use of hypothesis testing tools in research methodology.

Normality- This type of testing is used for normal distribution in a population sample. If the data points are grouped around the mean, the probability of them being above or below the mean is equally likely. Its shape resembles a bell curve that is equally distributed on either side of the mean.

T-test- This test is used when the sample size in a normally distributed population is comparatively small, and the standard deviation is unknown. Usually, if the sample size drops below 30, we use a T-test to find the confidence intervals of the population. 

Chi-Square Test- The Chi-Square test is used to test the population variance against the known or assumed value of the population variance. It is also a better choice to test the goodness of fit of a distribution of data. The two most common Chi-Square tests are the Chi-Square test of independence and the chi-square test of variance.

ANOVA- Analysis of Variance or ANOVA compares the data sets of two different populations or samples. It is similar in its use to the t-test or the Z-test, but it allows us to compare more than two sample means. ANOVA allows us to test the significance between an independent variable and a dependent variable, namely X and Y, respectively.

Z-test- It is a statistical measure to test that the means of two population samples are different when their variance is known. For a Z-test, the population is assumed to be normally distributed. A z-test is better suited in the case of large sample sizes greater than 30. This is due to the central limit theorem that as the sample size increases, the samples are considered to be distributed normally. 

FAQs on Hypothesis Testing

1. Mention the types of hypothesis Tests.

There are two types of a hypothesis tests:

Null Hypothesis: It is denoted as H₀.

Alternative Hypothesis: IT is denoted as H₁ or Hₐ.

2. What are the two errors that can be found while performing the null Hypothesis test?

While performing the null hypothesis test there is a possibility of occurring two types of errors,

Type-1: The type-1 error is denoted by (α), it is also known as the significance level. It is the rejection of the true null hypothesis. It is the error of commission.

Type-2: The type-2 error is denoted by (β). (1 - β) is known as the power test. The false null hypothesis is not rejected. It is the error of the omission. 

3. What is the p-value in hypothesis testing?

During hypothetical testing in statistics, the p-value indicates the probability of obtaining the result as extreme as observed results. A smaller p-value provides evidence to accept the alternate hypothesis. The p-value is used as a rejection point that provides the smallest level of significance at which the null hypothesis is rejected. Often p-value is calculated using the p-value tables by calculating the deviation between the observed value and the chosen reference value. 

It may also be calculated mathematically by performing integrals on all the values that fall under the curve and areas far from the reference value as the observed value relative to the total area of the curve. The p-value determines the evidence to reject the null hypothesis in hypothesis testing.

4. What is a null hypothesis?

The null hypothesis in statistics says that there is no certain difference between the population. It serves as a conjecture proposing no difference, whereas the alternate hypothesis says there is a difference. When we perform hypothesis testing, we have to state the null hypothesis and alternative hypotheses such that only one of them is ever true. 

By determining the p-value, we calculate whether the null hypothesis is to be rejected or not. If the difference between groups is low, it is merely by chance, and the null hypothesis, which states that there is no difference among groups, is true. Therefore, we have no evidence to reject the null hypothesis.

• Machine Learning Tutorial
• Data Analysis Tutorial
• Python - Data visualization tutorial
• Machine Learning Projects
• Machine Learning Interview Questions
• Machine Learning Mathematics
• Deep Learning Tutorial
• Deep Learning Project
• Deep Learning Interview Questions
• Computer Vision Tutorial
• Computer Vision Projects
• NLP Project
• NLP Interview Questions
• Statistics with Python
• 100 Days of Machine Learning
• Data Analysis with Python

Introduction to Data Analysis

• What is Data Analysis?
• Data Analytics and its type
• How to Install Numpy on Windows?
• How to Install Pandas in Python?
• How to Install Matplotlib on python?
• How to Install Python Tensorflow in Windows?

Data Analysis Libraries

• Pandas Tutorial
• NumPy Tutorial - Python Library
• Data Analysis with SciPy
• Introduction to TensorFlow

Data Visulization Libraries

• Matplotlib Tutorial
• Python Seaborn Tutorial
• Plotly tutorial
• Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis
• Measures of Central Tendency in Statistics
• Measures of spread - Range, Variance, and Standard Deviation
• Interquartile Range and Quartile Deviation using NumPy and SciPy
• Anova Formula
• Skewness of Statistical Data
• How to Calculate Skewness and Kurtosis in Python?
• Difference Between Skewness and Kurtosis
• Histogram | Meaning, Example, Types and Steps to Draw
• Interpretations of Histogram
• Quantile Quantile plots
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
• Using pandas crosstab to create a bar plot
• Exploring Correlation in Python
• Mathematics | Covariance and Correlation
• Factor Analysis | Data Analysis
• Data Mining - Cluster Analysis
• MANOVA Test in R Programming
• Python - Central Limit Theorem
• Probability Distribution Function
• Probability Density Estimation & Maximum Likelihood Estimation
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Poisson Distribution - Definition, Formula, Table and Examples
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret
• Z-Score in Statistics
• How to Calculate Point Estimates in R?
• Confidence Interval
• Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

• ML | Data Preprocessing in Python
• ML | Overview of Data Cleaning
• ML | Handling Missing Values
• Detect and Remove the Outliers using Python

Data Transformation

• Data Normalization Machine Learning
• Sampling distribution Using Python

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data
• Basic DateTime Operations in Python
• Time Series Analysis & Visualization in Python
• How to deal with missing values in a Timeseries in Python?
• How to calculate MOVING AVERAGE in a Pandas DataFrame?
• What is a trend in time series?
• How to Perform an Augmented Dickey-Fuller Test in R
• AutoCorrelation

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects
• Step by Step Predictive Analysis - Machine Learning
• 6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing. 

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

• Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
• The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
• Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Similar reads.

• data-science
• Data Science
• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Get science-backed answers as you write with Paperpal's Research feature

How to Write a Hypothesis? Types and Examples 

All research studies involve the use of the scientific method, which is a mathematical and experimental technique used to conduct experiments by developing and testing a hypothesis or a prediction about an outcome. Simply put, a hypothesis is a suggested solution to a problem. It includes elements that are expressed in terms of relationships with each other to explain a condition or an assumption that hasn’t been verified using facts. 1 The typical steps in a scientific method include developing such a hypothesis, testing it through various methods, and then modifying it based on the outcomes of the experiments.  

A research hypothesis can be defined as a specific, testable prediction about the anticipated results of a study. 2 Hypotheses help guide the research process and supplement the aim of the study. After several rounds of testing, hypotheses can help develop scientific theories. 3 Hypotheses are often written as if-then statements. 

Here are two hypothesis examples: 

Dandelions growing in nitrogen-rich soils for two weeks develop larger leaves than those in nitrogen-poor soils because nitrogen stimulates vegetative growth. 4  

If a company offers flexible work hours, then their employees will be happier at work. 5  

Table of Contents

• What is a hypothesis? 
• Types of hypotheses 
• Characteristics of a hypothesis 
• Functions of a hypothesis 
• How to write a hypothesis 
• Hypothesis examples 
• Frequently asked questions 

What is a hypothesis?

A hypothesis expresses an expected relationship between variables in a study and is developed before conducting any research. Hypotheses are not opinions but rather are expected relationships based on facts and observations. They help support scientific research and expand existing knowledge. An incorrectly formulated hypothesis can affect the entire experiment leading to errors in the results so it’s important to know how to formulate a hypothesis and develop it carefully.

A few sources of a hypothesis include observations from prior studies, current research and experiences, competitors, scientific theories, and general conditions that can influence people. Figure 1 depicts the different steps in a research design and shows where exactly in the process a hypothesis is developed. 4  

There are seven different types of hypotheses—simple, complex, directional, nondirectional, associative and causal, null, and alternative. 

Types of hypotheses

The seven types of hypotheses are listed below: 5 , 6,7  

• Simple : Predicts the relationship between a single dependent variable and a single independent variable. 

Example: Exercising in the morning every day will increase your productivity.  

• Complex : Predicts the relationship between two or more variables. 

Example: Spending three hours or more on social media daily will negatively affect children’s mental health and productivity, more than that of adults.  

• Directional : Specifies the expected direction to be followed and uses terms like increase, decrease, positive, negative, more, or less. 

Example: The inclusion of intervention X decreases infant mortality compared to the original treatment.  

• Non-directional : Does not predict the exact direction, nature, or magnitude of the relationship between two variables but rather states the existence of a relationship. This hypothesis may be used when there is no underlying theory or if findings contradict prior research. 

Example: Cats and dogs differ in the amount of affection they express.  

• Associative and causal : An associative hypothesis suggests an interdependency between variables, that is, how a change in one variable changes the other.  

Example: There is a positive association between physical activity levels and overall health.  

A causal hypothesis, on the other hand, expresses a cause-and-effect association between variables. 

Example: Long-term alcohol use causes liver damage.  

• Null : Claims that the original hypothesis is false by showing that there is no relationship between the variables. 

Example: Sleep duration does not have any effect on productivity.  

• Alternative : States the opposite of the null hypothesis, that is, a relationship exists between two variables. 

Example: Sleep duration affects productivity.  

Characteristics of a hypothesis

So, what makes a good hypothesis? Here are some important characteristics of a hypothesis. 8,9  

• Testable : You must be able to test the hypothesis using scientific methods to either accept or reject the prediction. 
• Falsifiable : It should be possible to collect data that reject rather than support the hypothesis. 
• Logical : Hypotheses shouldn’t be a random guess but rather should be based on previous theories, observations, prior research, and logical reasoning. 
• Positive : The hypothesis statement about the existence of an association should be positive, that is, it should not suggest that an association does not exist. Therefore, the language used and knowing how to phrase a hypothesis is very important. 
• Clear and accurate : The language used should be easily comprehensible and use correct terminology. 
• Relevant : The hypothesis should be relevant and specific to the research question. 
• Structure : Should include all the elements that make a good hypothesis: variables, relationship, and outcome. 

Functions of a hypothesis

The following list mentions some important functions of a hypothesis: 1  

• Maintains the direction and progress of the research. 
• Expresses the important assumptions underlying the proposition in a single statement. 
• Establishes a suitable context for researchers to begin their investigation and for readers who are referring to the final report. 
• Provides an explanation for the occurrence of a specific phenomenon. 
• Ensures selection of appropriate and accurate facts necessary and relevant to the research subject. 

To summarize, a hypothesis provides the conceptual elements that complete the known data, conceptual relationships that systematize unordered elements, and conceptual meanings and interpretations that explain the unknown phenomena. 1  

How to write a hypothesis

Listed below are the main steps explaining how to write a hypothesis. 2,4,5  

• Make an observation and identify variables : Observe the subject in question and try to recognize a pattern or a relationship between the variables involved. This step provides essential background information to begin your research.  

For example, if you notice that an office’s vending machine frequently runs out of a specific snack, you may predict that more people in the office choose that snack over another. 

• Identify the main research question : After identifying a subject and recognizing a pattern, the next step is to ask a question that your hypothesis will answer.  

For example, after observing employees’ break times at work, you could ask “why do more employees take breaks in the morning rather than in the afternoon?” 

• Conduct some preliminary research to ensure originality and novelty : Your initial answer, which is your hypothesis, to the question is based on some pre-existing information about the subject. However, to ensure that your hypothesis has not been asked before or that it has been asked but rejected by other researchers you would need to gather additional information.  

For example, based on your observations you might state a hypothesis that employees work more efficiently when the air conditioning in the office is set at a lower temperature. However, during your preliminary research you find that this hypothesis was proven incorrect by a prior study. 

• Develop a general statement : After your preliminary research has confirmed the originality of your proposed answer, draft a general statement that includes all variables, subjects, and predicted outcome. The statement could be if/then or declarative.  
• Finalize the hypothesis statement : Use the PICOT model, which clarifies how to word a hypothesis effectively, when finalizing the statement. This model lists the important components required to write a hypothesis. 

P opulation: The specific group or individual who is the main subject of the research 

I nterest: The main concern of the study/research question 

C omparison: The main alternative group 

O utcome: The expected results  

T ime: Duration of the experiment 

Once you’ve finalized your hypothesis statement you would need to conduct experiments to test whether the hypothesis is true or false. 

Hypothesis examples

The following table provides examples of different types of hypotheses. 10 ,11  

Key takeaways  

Here’s a summary of all the key points discussed in this article about how to write a hypothesis. 

• A hypothesis is an assumption about an association between variables made based on limited evidence, which should be tested. 
• A hypothesis has four parts—the research question, independent variable, dependent variable, and the proposed relationship between the variables.   
• The statement should be clear, concise, testable, logical, and falsifiable. 
• There are seven types of hypotheses—simple, complex, directional, non-directional, associative and causal, null, and alternative. 
• A hypothesis provides a focus and direction for the research to progress. 
• A hypothesis plays an important role in the scientific method by helping to create an appropriate experimental design. 

Frequently asked questions

Hypotheses and research questions have different objectives and structure. The following table lists some major differences between the two. 9  

Here are a few examples to differentiate between a research question and hypothesis. 

Yes, here’s a simple checklist to help you gauge the effectiveness of your hypothesis. 9   1. When writing a hypothesis statement, check if it:  2. Predicts the relationship between the stated variables and the expected outcome.  3. Uses simple and concise language and is not wordy.  4. Does not assume readers’ knowledge about the subject.  5. Has observable, falsifiable, and testable results. 

As mentioned earlier in this article, a hypothesis is an assumption or prediction about an association between variables based on observations and simple evidence. These statements are usually generic. Research objectives, on the other hand, are more specific and dictated by hypotheses. The same hypothesis can be tested using different methods and the research objectives could be different in each case.     For example, Louis Pasteur observed that food lasts longer at higher altitudes, reasoned that it could be because the air at higher altitudes is cleaner (with fewer or no germs), and tested the hypothesis by exposing food to air cleaned in the laboratory. 12 Thus, a hypothesis is predictive—if the reasoning is correct, X will lead to Y—and research objectives are developed to test these predictions. 

Null hypothesis testing is a method to decide between two assumptions or predictions between variables (null and alternative hypotheses) in a statistical relationship in a sample. The null hypothesis, denoted as H 0 , claims that no relationship exists between variables in a population and any relationship in the sample reflects a sampling error or occurrence by chance. The alternative hypothesis, denoted as H 1 , claims that there is a relationship in the population. In every study, researchers need to decide whether the relationship in a sample occurred by chance or reflects a relationship in the population. This is done by hypothesis testing using the following steps: 13   1. Assume that the null hypothesis is true.  2. Determine how likely the sample relationship would be if the null hypothesis were true. This probability is called the p value.  3. If the sample relationship would be extremely unlikely, reject the null hypothesis and accept the alternative hypothesis. If the relationship would not be unlikely, accept the null hypothesis. 

To summarize, researchers should know how to write a good hypothesis to ensure that their research progresses in the required direction. A hypothesis is a testable prediction about any behavior or relationship between variables, usually based on facts and observation, and states an expected outcome.  

We hope this article has provided you with essential insight into the different types of hypotheses and their functions so that you can use them appropriately in your next research project. 

References  

• Dalen, DVV. The function of hypotheses in research. Proquest website. Accessed April 8, 2024. https://www.proquest.com/docview/1437933010?pq-origsite=gscholar&fromopenview=true&sourcetype=Scholarly%20Journals&imgSeq=1  
• McLeod S. Research hypothesis in psychology: Types & examples. SimplyPsychology website. Updated December 13, 2023. Accessed April 9, 2024. https://www.simplypsychology.org/what-is-a-hypotheses.html  
• Scientific method. Britannica website. Updated March 14, 2024. Accessed April 9, 2024. https://www.britannica.com/science/scientific-method  
• The hypothesis in science writing. Accessed April 10, 2024. https://berks.psu.edu/sites/berks/files/campus/HypothesisHandout_Final.pdf  
• How to develop a hypothesis (with elements, types, and examples). Indeed.com website. Updated February 3, 2023. Accessed April 10, 2024. https://www.indeed.com/career-advice/career-development/how-to-write-a-hypothesis  
• Types of research hypotheses. Excelsior online writing lab. Accessed April 11, 2024. https://owl.excelsior.edu/research/research-hypotheses/types-of-research-hypotheses/  
• What is a research hypothesis: how to write it, types, and examples. Researcher.life website. Published February 8, 2023. Accessed April 11, 2024. https://researcher.life/blog/article/how-to-write-a-research-hypothesis-definition-types-examples/  
• Developing a hypothesis. Pressbooks website. Accessed April 12, 2024. https://opentext.wsu.edu/carriecuttler/chapter/developing-a-hypothesis/  
• What is and how to write a good hypothesis in research. Elsevier author services website. Accessed April 12, 2024. https://scientific-publishing.webshop.elsevier.com/manuscript-preparation/what-how-write-good-hypothesis-research/  
• How to write a great hypothesis. Verywellmind website. Updated March 12, 2023. Accessed April 13, 2024. https://www.verywellmind.com/what-is-a-hypothesis-2795239  
• 15 Hypothesis examples. Helpfulprofessor.com Published September 8, 2023. Accessed March 14, 2024. https://helpfulprofessor.com/hypothesis-examples/ 
• Editage insights. What is the interconnectivity between research objectives and hypothesis? Published February 24, 2021. Accessed April 13, 2024. https://www.editage.com/insights/what-is-the-interconnectivity-between-research-objectives-and-hypothesis  
• Understanding null hypothesis testing. BCCampus open publishing. Accessed April 16, 2024. https://opentextbc.ca/researchmethods/chapter/understanding-null-hypothesis-testing/#:~:text=In%20null%20hypothesis%20testing%2C%20this,said%20to%20be%20statistically%20significant  

Paperpal is a comprehensive AI writing toolkit that helps students and researchers achieve 2x the writing in half the time. It leverages 21+ years of STM experience and insights from millions of research articles to provide in-depth academic writing, language editing, and submission readiness support to help you write better, faster.  

Get accurate academic translations, rewriting support, grammar checks, vocabulary suggestions, and generative AI assistance that delivers human precision at machine speed. Try for free or upgrade to Paperpal Prime starting at US$19 a month to access premium features, including consistency, plagiarism, and 30+ submission readiness checks to help you succeed.  

Experience the future of academic writing – Sign up to Paperpal and start writing for free!  

Related Reads:

• Empirical Research: A Comprehensive Guide for Academics 
• How to Write a Scientific Paper in 10 Steps 
• What is a Literature Review? How to Write It (with Examples)
• What are Journal Guidelines on Using Generative AI Tools

Measuring Academic Success: Definition & Strategies for Excellence

What are scholarly sources and where can you find them , you may also like, 4 ways paperpal encourages responsible writing with ai, what are scholarly sources and where can you..., what is academic writing: tips for students, why traditional editorial process needs an upgrade, paperpal’s new ai research finder empowers authors to..., what is hedging in academic writing  , how to use ai to enhance your college..., ai + human expertise – a paradigm shift..., how to use paperpal to generate emails &....