how to write hypothesis for t test

Independent t-test for two samples

Introduction.

The independent t-test, also called the two sample t-test, independent-samples t-test or student's t-test, is an inferential statistical test that determines whether there is a statistically significant difference between the means in two unrelated groups.

Null and alternative hypotheses for the independent t-test

The null hypothesis for the independent t-test is that the population means from the two unrelated groups are equal:

H 0 : u 1 = u 2

In most cases, we are looking to see if we can show that we can reject the null hypothesis and accept the alternative hypothesis, which is that the population means are not equal:

H A : u 1 ≠ u 2

To do this, we need to set a significance level (also called alpha) that allows us to either reject or accept the alternative hypothesis. Most commonly, this value is set at 0.05.

What do you need to run an independent t-test?

In order to run an independent t-test, you need the following:

• One independent, categorical variable that has two levels/groups.
• One continuous dependent variable.

Unrelated groups

Unrelated groups, also called unpaired groups or independent groups, are groups in which the cases (e.g., participants) in each group are different. Often we are investigating differences in individuals, which means that when comparing two groups, an individual in one group cannot also be a member of the other group and vice versa. An example would be gender - an individual would have to be classified as either male or female – not both.

Assumption of normality of the dependent variable

The independent t-test requires that the dependent variable is approximately normally distributed within each group.

Note: Technically, it is the residuals that need to be normally distributed, but for an independent t-test, both will give you the same result.

You can test for this using a number of different tests, but the Shapiro-Wilks test of normality or a graphical method, such as a Q-Q Plot, are very common. You can run these tests using SPSS Statistics, the procedure for which can be found in our Testing for Normality guide. However, the t-test is described as a robust test with respect to the assumption of normality. This means that some deviation away from normality does not have a large influence on Type I error rates. The exception to this is if the ratio of the smallest to largest group size is greater than 1.5 (largest compared to smallest).

What to do when you violate the normality assumption

If you find that either one or both of your group's data is not approximately normally distributed and groups sizes differ greatly, you have two options: (1) transform your data so that the data becomes normally distributed (to do this in SPSS Statistics see our guide on Transforming Data ), or (2) run the Mann-Whitney U test which is a non-parametric test that does not require the assumption of normality (to run this test in SPSS Statistics see our guide on the Mann-Whitney U Test ).

Assumption of homogeneity of variance

The independent t-test assumes the variances of the two groups you are measuring are equal in the population. If your variances are unequal, this can affect the Type I error rate. The assumption of homogeneity of variance can be tested using Levene's Test of Equality of Variances, which is produced in SPSS Statistics when running the independent t-test procedure. If you have run Levene's Test of Equality of Variances in SPSS Statistics, you will get a result similar to that below:

This test for homogeneity of variance provides an F -statistic and a significance value ( p -value). We are primarily concerned with the significance value – if it is greater than 0.05 (i.e., p > .05), our group variances can be treated as equal. However, if p < 0.05, we have unequal variances and we have violated the assumption of homogeneity of variances.

Overcoming a violation of the assumption of homogeneity of variance

If the Levene's Test for Equality of Variances is statistically significant, which indicates that the group variances are unequal in the population, you can correct for this violation by not using the pooled estimate for the error term for the t -statistic, but instead using an adjustment to the degrees of freedom using the Welch-Satterthwaite method. In all reality, you will probably never have heard of these adjustments because SPSS Statistics hides this information and simply labels the two options as "Equal variances assumed" and "Equal variances not assumed" without explicitly stating the underlying tests used. However, you can see the evidence of these tests as below:

From the result of Levene's Test for Equality of Variances, we can reject the null hypothesis that there is no difference in the variances between the groups and accept the alternative hypothesis that there is a statistically significant difference in the variances between groups. The effect of not being able to assume equal variances is evident in the final column of the above figure where we see a reduction in the value of the t -statistic and a large reduction in the degrees of freedom (df). This has the effect of increasing the p -value above the critical significance level of 0.05. In this case, we therefore do not accept the alternative hypothesis and accept that there are no statistically significant differences between means. This would not have been our conclusion had we not tested for homogeneity of variances.

Reporting the result of an independent t-test

When reporting the result of an independent t-test, you need to include the t -statistic value, the degrees of freedom (df) and the significance value of the test ( p -value). The format of the test result is: t (df) = t -statistic, p = significance value. Therefore, for the example above, you could report the result as t (7.001) = 2.233, p = 0.061.

Fully reporting your results

In order to provide enough information for readers to fully understand the results when you have run an independent t-test, you should include the result of normality tests, Levene's Equality of Variances test, the two group means and standard deviations, the actual t-test result and the direction of the difference (if any). In addition, you might also wish to include the difference between the groups along with a 95% confidence interval. For example:

Inspection of Q-Q Plots revealed that cholesterol concentration was normally distributed for both groups and that there was homogeneity of variance as assessed by Levene's Test for Equality of Variances. Therefore, an independent t-test was run on the data with a 95% confidence interval (CI) for the mean difference. It was found that after the two interventions, cholesterol concentrations in the dietary group (6.15 ± 0.52 mmol/L) were significantly higher than the exercise group (5.80 ± 0.38 mmol/L) ( t (38) = 2.470, p = 0.018) with a difference of 0.35 (95% CI, 0.06 to 0.64) mmol/L.

To know how to run an independent t-test in SPSS Statistics, see our SPSS Statistics Independent-Samples T-Test guide. Alternatively, you can carry out an independent-samples t-test using Excel, R and RStudio .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

13.3: The Independent Samples t-test (Student Test)

• Last updated
• Save as PDF
• Page ID 4023

• Danielle Navarro
• University of New South Wales

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Although the one sample t-test has its uses, it’s not the most typical example of a t-test 189 . A much more common situation arises when you’ve got two different groups of observations. In psychology, this tends to correspond to two different groups of participants, where each group corresponds to a different condition in your study. For each person in the study, you measure some outcome variable of interest, and the research question that you’re asking is whether or not the two groups have the same population mean. This is the situation that the independent samples t-test is designed for.

Suppose we have 33 students taking Dr Harpo’s statistics lectures, and Dr Harpo doesn’t grade to a curve. Actually, Dr Harpo’s grading is a bit of a mystery, so we don’t really know anything about what the average grade is for the class as a whole. There are two tutors for the class, Anastasia and Bernadette. There are N 1 =15 students in Anastasia’s tutorials, and N 2 =18 in Bernadette’s tutorials. The research question I’m interested in is whether Anastasia or Bernadette is a better tutor, or if it doesn’t make much of a difference. Dr Harpo emails me the course grades, in the harpo.Rdata file. As usual, I’ll load the file and have a look at what variables it contains:

As we can see, there’s a single data frame with two variables, grade and tutor . The grade variable is a numeric vector, containing the grades for all N=33 students taking Dr Harpo’s class; the tutor variable is a factor that indicates who each student’s tutor was. The first six observations in this data set are shown below:

We can calculate means and standard deviations, using the mean() and sd() functions. Rather than show the R output, here’s a nice little summary table:

To give you a more detailed sense of what’s going on here, I’ve plotted histograms showing the distribution of grades for both tutors (Figure 13.6 and 13.7). Inspection of these histograms suggests that the students in Anastasia’s class may be getting slightly better grades on average, though they also seem a little more variable.

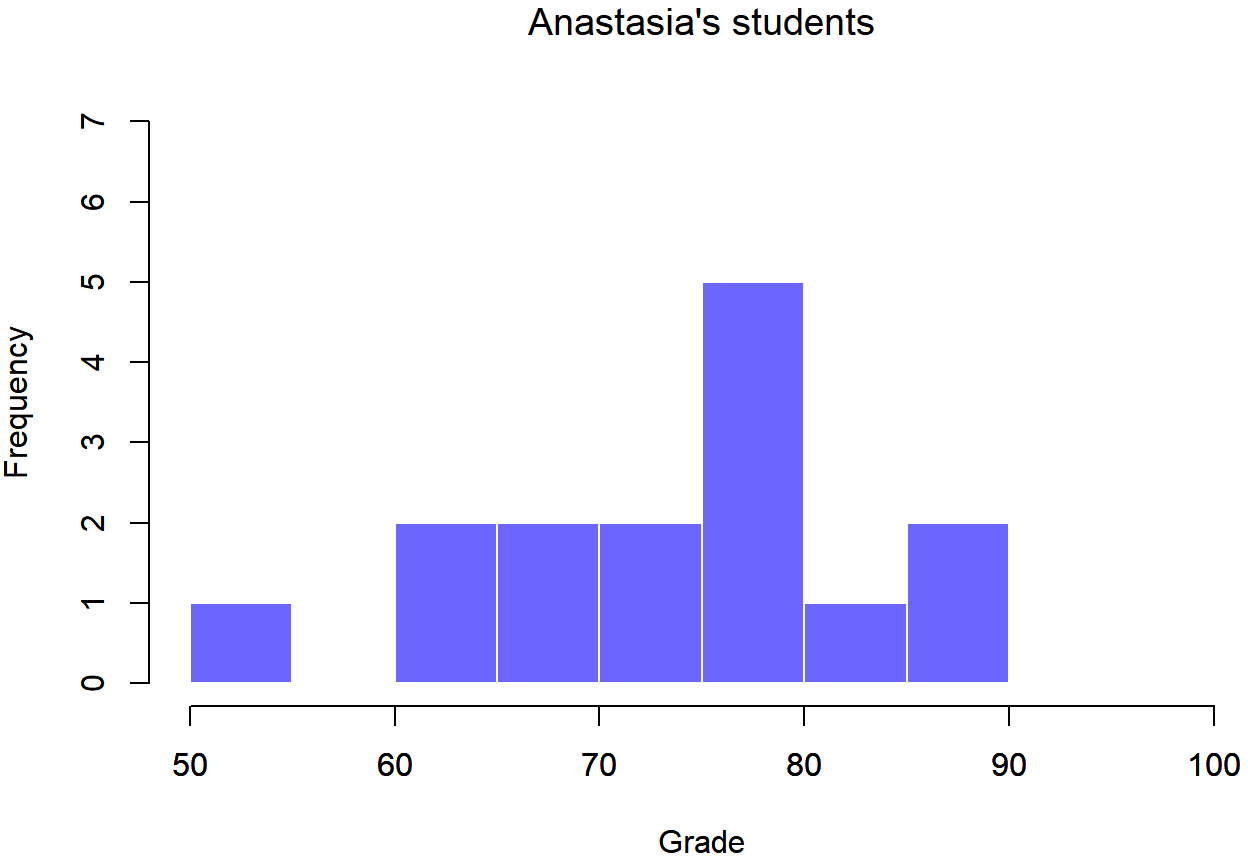
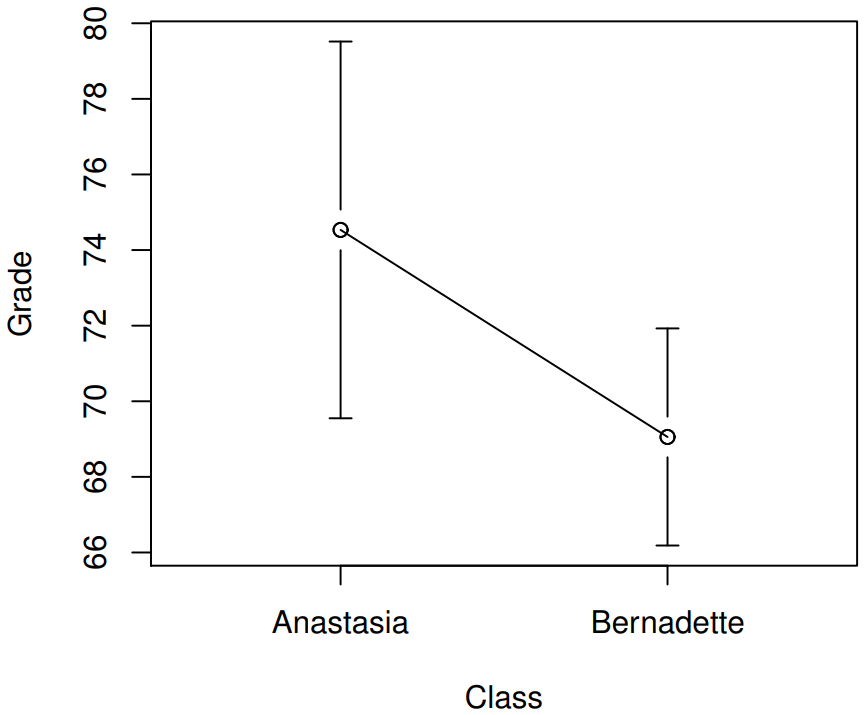
Here is a simpler plot showing the means and corresponding confidence intervals for both groups of students (Figure 13.8).

Introducing the test

The independent samples t-test comes in two different forms, Student’s and Welch’s. The original Student t-test – which is the one I’ll describe in this section – is the simpler of the two, but relies on much more restrictive assumptions than the Welch t-test. Assuming for the moment that you want to run a two-sided test, the goal is to determine whether two “independent samples” of data are drawn from populations with the same mean (the null hypothesis) or different means (the alternative hypothesis). When we say “independent” samples, what we really mean here is that there’s no special relationship between observations in the two samples. This probably doesn’t make a lot of sense right now, but it will be clearer when we come to talk about the paired samples t-test later on. For now, let’s just point out that if we have an experimental design where participants are randomly allocated to one of two groups, and we want to compare the two groups’ mean performance on some outcome measure, then an independent samples t-test (rather than a paired samples t-test) is what we’re after.

Okay, so let’s let μ 1 denote the true population mean for group 1 (e.g., Anastasia’s students), and μ 2 will be the true population mean for group 2 (e.g., Bernadette’s students), 190 and as usual we’ll let \(\bar{X}_{1}\) and \(\bar{X}_{2}\) denote the observed sample means for both of these groups. Our null hypothesis states that the two population means are identical (μ 1 =μ 2 ) and the alternative to this is that they are not (μ 1 ≠μ 2 ). Written in mathematical-ese, this is…

H 0 :μ 1 =μ 2

H 1 :μ 1 ≠μ 2

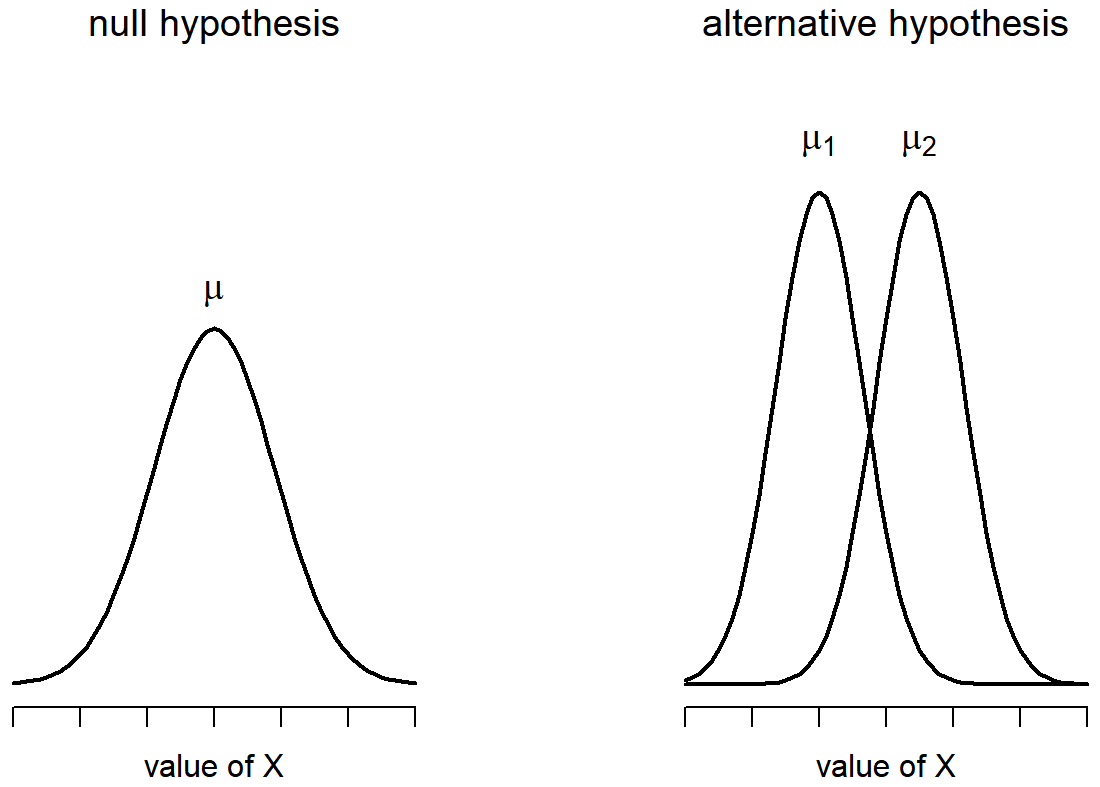
To construct a hypothesis test that handles this scenario, we start by noting that if the null hypothesis is true, then the difference between the population means is exactly zero, μ 1 −μ 2 =0 As a consequence, a diagnostic test statistic will be based on the difference between the two sample means. Because if the null hypothesis is true, then we’d expect

\(\bar{X}_{1}\) - \(\bar{X}_{2}\)

to be pretty close to zero. However, just like we saw with our one-sample tests (i.e., the one-sample z-test and the one-sample t-test) we have to be precise about exactly how close to zero this difference

\(\ t ={\bar{X}_1 - \bar{X}_2 \over SE}\)

We just need to figure out what this standard error estimate actually is. This is a bit trickier than was the case for either of the two tests we’ve looked at so far, so we need to go through it a lot more carefully to understand how it works.

“pooled estimate” of the standard deviation

In the original “Student t-test”, we make the assumption that the two groups have the same population standard deviation: that is, regardless of whether the population means are the same, we assume that the population standard deviations are identical, σ 1 =σ 2 . Since we’re assuming that the two standard deviations are the same, we drop the subscripts and refer to both of them as σ. How should we estimate this? How should we construct a single estimate of a standard deviation when we have two samples? The answer is, basically, we average them. Well, sort of. Actually, what we do is take a weighed average of the variance estimates, which we use as our pooled estimate of the variance . The weight assigned to each sample is equal to the number of observations in that sample, minus 1. Mathematically, we can write this as

\(\ \omega_{1}\)=N 1 −1

\(\ \omega_{2}\)=N 2 −1

Now that we’ve assigned weights to each sample, we calculate the pooled estimate of the variance by taking the weighted average of the two variance estimates, \(\ \hat{\sigma_1}^2\) and \(\ \hat{\sigma_2}^2\)

\(\ \hat{\sigma_p}^2 ={ \omega_{1}\hat{\sigma_1}^2+\omega_{2}\hat{\sigma_2}^2 \over \omega_{1}+\omega_{2}}\)

Finally, we convert the pooled variance estimate to a pooled standard deviation estimate, by taking the square root. This gives us the following formula for \(\ \hat{\sigma_p}\),

\(\ \hat{\sigma_p} =\sqrt{\omega_1\hat{\sigma_1}^2+\omega_2\hat{\sigma_2}^2\over \omega_1+\omega_2} \)

And if you mentally substitute \(\ \omega_1\)=N1−1 and \(\ \omega_2\)=N2−1 into this equation you get a very ugly looking formula; a very ugly formula that actually seems to be the “standard” way of describing the pooled standard deviation estimate. It’s not my favourite way of thinking about pooled standard deviations, however. 191

same pooled estimate, described differently

I prefer to think about it like this. Our data set actually corresponds to a set of N observations, which are sorted into two groups. So let’s use the notation X ik to refer to the grade received by the i-th student in the k-th tutorial group: that is, X 11 is the grade received by the first student in Anastasia’s class, X 21 is her second student, and so on. And we have two separate group means \(\ \bar{X_1}\) and \(\ \bar{X_2}\), which we could “generically” refer to using the notation \(\ \bar{X_k}\), i.e., the mean grade for the k-th tutorial group. So far, so good. Now, since every single student falls into one of the two tutorials, and so we can describe their deviation from the group mean as the difference

\(\ X_{ik} - \bar{X_k}\)

So why not just use these deviations (i.e., the extent to which each student’s grade differs from the mean grade in their tutorial?) Remember, a variance is just the average of a bunch of squared deviations, so let’s do that. Mathematically, we could write it like this:

\(\ ∑_{ik} (X_{ik}-\bar{X}_k)^2 \over N \)

where the notation “∑ ik ” is a lazy way of saying “calculate a sum by looking at all students in all tutorials”, since each “ik” corresponds to one student. 192 But, as we saw in Chapter 10, calculating the variance by dividing by N produces a biased estimate of the population variance. And previously, we needed to divide by N−1 to fix this. However, as I mentioned at the time, the reason why this bias exists is because the variance estimate relies on the sample mean; and to the extent that the sample mean isn’t equal to the population mean, it can systematically bias our estimate of the variance. But this time we’re relying on two sample means! Does this mean that we’ve got more bias? Yes, yes it does. And does this mean we now need to divide by N−2 instead of N−1, in order to calculate our pooled variance estimate? Why, yes…

\(\hat{\sigma}_{p}\ ^{2}=\dfrac{\sum_{i k}\left(X_{i k}-X_{k}\right)^{2}}{N-2}\)

Oh, and if you take the square root of this then you get \(\ \hat{\sigma_{P}}\), the pooled standard deviation estimate. In other words, the pooled standard deviation calculation is nothing special: it’s not terribly different to the regular standard deviation calculation.

Completing the test

Regardless of which way you want to think about it, we now have our pooled estimate of the standard deviation. From now on, I’ll drop the silly p subscript, and just refer to this estimate as \(\ \hat{\sigma}\). Great. Let’s now go back to thinking about the bloody hypothesis test, shall we? Our whole reason for calculating this pooled estimate was that we knew it would be helpful when calculating our standard error estimate. But, standard error of what ? In the one-sample t-test, it was the standard error of the sample mean, SE (\(\ \bar{X}\)), and since SE (\(\ \bar{X}=\sigma/ \sqrt{N}\) that’s what the denominator of our t-statistic looked like. This time around, however, we have two sample means. And what we’re interested in, specifically, is the the difference between the two \(\ \bar{X_1}\) - \(\ \bar{X_2}\). As a consequence, the standard error that we need to divide by is in fact the standard error of the difference between means. As long as the two variables really do have the same standard deviation, then our estimate for the standard error is

\(\operatorname{SE}\left(\bar{X}_{1}-\bar{X}_{2}\right)=\hat{\sigma} \sqrt{\dfrac{1}{N_{1}}+\dfrac{1}{N_{2}}}\)

and our t-statistic is therefore

\(t=\dfrac{\bar{X}_{1}-\bar{X}_{2}}{\operatorname{SE}\left(\bar{X}_{1}-\bar{X}_{2}\right)}\)

(shocking, isn’t it?) as long as the null hypothesis is true, and all of the assumptions of the test are met. The degrees of freedom, however, is slightly different. As usual, we can think of the degrees of freedom to be equal to the number of data points minus the number of constraints. In this case, we have N observations (N1 in sample 1, and N2 in sample 2), and 2 constraints (the sample means). So the total degrees of freedom for this test are N−2.

Doing the test in R

Not surprisingly, you can run an independent samples t-test using the t.test() function (Section 13.7), but once again I’m going to start with a somewhat simpler function in the lsr package. That function is unimaginatively called independentSamplesTTest() . First, recall that our data look like this:

The outcome variable for our test is the student grade , and the groups are defined in terms of the tutor for each class. So you probably won’t be too surprised to see that we’re going to describe the test that we want in terms of an R formula that reads like this grade ~ tutor . The specific command that we need is:

The first two arguments should be familiar to you. The first one is the formula that tells R what variables to use and the second one tells R the name of the data frame that stores those variables. The third argument is not so obvious. By saying var.equal = TRUE , what we’re really doing is telling R to use the Student independent samples t-test. More on this later. For now, lets ignore that bit and look at the output:

The output has a very familiar form. First, it tells you what test was run, and it tells you the names of the variables that you used. The second part of the output reports the sample means and standard deviations for both groups (i.e., both tutorial groups). The third section of the output states the null hypothesis and the alternative hypothesis in a fairly explicit form. It then reports the test results: just like last time, the test results consist of a t-statistic, the degrees of freedom, and the p-value. The final section reports two things: it gives you a confidence interval, and an effect size. I’ll talk about effect sizes later. The confidence interval, however, I should talk about now.

It’s pretty important to be clear on what this confidence interval actually refers to: it is a confidence interval for the difference between the group means. In our example, Anastasia’s students had an average grade of 74.5, and Bernadette’s students had an average grade of 69.1, so the difference between the two sample means is 5.4. But of course the difference between population means might be bigger or smaller than this. The confidence interval reported by the independentSamplesTTest() function tells you that there’s a 95% chance that the true difference between means lies between 0.2 and 10.8.

In any case, the difference between the two groups is significant (just barely), so we might write up the result using text like this:

The mean grade in Anastasia’s class was 74.5% (std dev = 9.0), whereas the mean in Bernadette’s class was 69.1% (std dev = 5.8). A Student’s independent samples t-test showed that this 5.4% difference was significant (t(31)=2.1, p<.05, CI 95 =[0.2,10.8], d=.74), suggesting that a genuine difference in learning outcomes has occurred.

Notice that I’ve included the confidence interval and the effect size in the stat block. People don’t always do this. At a bare minimum, you’d expect to see the t-statistic, the degrees of freedom and the p value. So you should include something like this at a minimum: t(31)=2.1, p<.05. If statisticians had their way, everyone would also report the confidence interval and probably the effect size measure too, because they are useful things to know. But real life doesn’t always work the way statisticians want it to: you should make a judgment based on whether you think it will help your readers, and (if you’re writing a scientific paper) the editorial standard for the journal in question. Some journals expect you to report effect sizes, others don’t. Within some scientific communities it is standard practice to report confidence intervals, in other it is not. You’ll need to figure out what your audience expects. But, just for the sake of clarity, if you’re taking my class: my default position is that it’s usually worth includng the effect size, but don’t worry about the confidence interval unless the assignment asks you to or implies that you should.

Positive and negative t values

Before moving on to talk about the assumptions of the t-test, there’s one additional point I want to make about the use of t-tests in practice. The first one relates to the sign of the t-statistic (that is, whether it is a positive number or a negative one). One very common worry that students have when they start running their first t-test is that they often end up with negative values for the t-statistic, and don’t know how to interpret it. In fact, it’s not at all uncommon for two people working independently to end up with R outputs that are almost identical, except that one person has a negative t values and the other one has a positive t value. Assuming that you’re running a two-sided test, then the p-values will be identical. On closer inspection, the students will notice that the confidence intervals also have the opposite signs. This is perfectly okay: whenever this happens, what you’ll find is that the two versions of the R output arise from slightly different ways of running the t-test. What’s happening here is very simple. The t-statistic that R is calculating here is always of the form

\(t=\dfrac{(\text { mean } 1)-(\text { mean } 2)}{(\mathrm{SE})}\)

If “mean 1” is larger than “mean 2” the t statistic will be positive, whereas if “mean 2” is larger then the t statistic will be negative. Similarly, the confidence interval that R reports is the confidence interval for the difference “(mean 1) minus (mean 2)”, which will be the reverse of what you’d get if you were calculating the confidence interval for the difference “(mean 2) minus (mean 1)”.

Okay, that’s pretty straightforward when you think about it, but now consider our t-test comparing Anastasia’s class to Bernadette’s class. Which one should we call “mean 1” and which one should we call “mean 2”. It’s arbitrary. However, you really do need to designate one of them as “mean 1” and the other one as “mean 2”. Not surprisingly, the way that R handles this is also pretty arbitrary. In earlier versions of the book I used to try to explain it, but after a while I gave up, because it’s not really all that important, and to be honest I can never remember myself. Whenever I get a significant t-test result, and I want to figure out which mean is the larger one, I don’t try to figure it out by looking at the t-statistic. Why would I bother doing that? It’s foolish. It’s easier just look at the actual group means, since the R output actually shows them!

Here’s the important thing. Because it really doesn’t matter what R printed out, I usually try to report the t-statistic in such a way that the numbers match up with the text. Here’s what I mean… suppose that what I want to write in my report is “Anastasia’s class had higher grades than Bernadette’s class”. The phrasing here implies that Anastasia’s group comes first, so it makes sense to report the t-statistic as if Anastasia’s class corresponded to group 1. If so, I would write

Anastasia’s class had higher grades than Bernadette’s class (t(31)=2.1,p=.04).

(I wouldn’t actually emphasise the word “higher” in real life, I’m just doing it to emphasise the point that “higher” corresponds to positive t values). On the other hand, suppose the phrasing I wanted to use has Bernadette’s class listed first. If so, it makes more sense to treat her class as group 1, and if so, the write up looks like this:

Bernadette’s class had lower grades than Anastasia’s class (t(31)=−2.1,p=.04).

Because I’m talking about one group having “lower” scores this time around, it is more sensible to use the negative form of the t-statistic. It just makes it read more cleanly.

One last thing: please note that you can’t do this for other types of test statistics. It works for t-tests, but it wouldn’t be meaningful for chi-square testsm F-tests or indeed for most of the tests I talk about in this book. So don’t overgeneralise this advice! I’m really just talking about t-tests here and nothing else!

Assumptions of the test

As always, our hypothesis test relies on some assumptions. So what are they? For the Student t-test there are three assumptions, some of which we saw previously in the context of the one sample t-test (see Section 13.2.3):

• Normality . Like the one-sample t-test, it is assumed that the data are normally distributed. Specifically, we assume that both groups are normally distributed. In Section 13.9 we’ll discuss how to test for normality, and in Section 13.10 we’ll discuss possible solutions.
• Independence . Once again, it is assumed that the observations are independently sampled. In the context of the Student test this has two aspects to it. Firstly, we assume that the observations within each sample are independent of one another (exactly the same as for the one-sample test). However, we also assume that there are no cross-sample dependencies. If, for instance, it turns out that you included some participants in both experimental conditions of your study (e.g., by accidentally allowing the same person to sign up to different conditions), then there are some cross sample dependencies that you’d need to take into account.
• Homogeneity of variance (also called “homoscedasticity”). The third assumption is that the population standard deviation is the same in both groups. You can test this assumption using the Levene test, which I’ll talk about later on in the book (Section 14.7). However, there’s a very simple remedy for this assumption, which I’ll talk about in the next section.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 11.

• Hypotheses for a two-sample t test

Example of hypotheses for paired and two-sample t tests

• Writing hypotheses to test the difference of means
• Two-sample t test for difference of means
• Test statistic in a two-sample t test
• P-value in a two-sample t test
• Conclusion for a two-sample t test using a P-value
• Conclusion for a two-sample t test using a confidence interval
• Making conclusions about the difference of means

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Statistics Made Easy

Two Sample t-test: Definition, Formula, and Example

A two sample t-test is used to determine whether or not two population means are equal.

This tutorial explains the following:

• The motivation for performing a two sample t-test.
• The formula to perform a two sample t-test.
• The assumptions that should be met to perform a two sample t-test.
• An example of how to perform a two sample t-test.

Two Sample t-test: Motivation

Suppose we want to know whether or not the mean weight between two different species of turtles is equal. Since there are thousands of turtles in each population, it would be too time-consuming and costly to go around and weigh each individual turtle.

Instead, we might take a simple random sample of 15 turtles from each population and use the mean weight in each sample to determine if the mean weight is equal between the two populations:

However, it’s virtually guaranteed that the mean weight between the two samples will be at least a little different. The question is whether or not this difference is statistically significant . Fortunately, a two sample t-test allows us to answer this question.

Two Sample t-test: Formula

A two-sample t-test always uses the following null hypothesis:

• H 0 : μ 1  = μ 2 (the two population means are equal)

The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:

• H 1 (two-tailed): μ 1  ≠ μ 2 (the two population means are not equal)
• H 1 (left-tailed): μ 1  < μ 2  (population 1 mean is less than population 2 mean)
• H 1 (right-tailed):  μ 1 > μ 2  (population 1 mean is greater than population 2 mean)

We use the following formula to calculate the test statistic t:

Test statistic:  ( x 1  –  x 2 )  /  s p (√ 1/n 1  + 1/n 2 )

where  x 1  and  x 2 are the sample means, n 1 and n 2  are the sample sizes, and where s p is calculated as:

s p = √  (n 1 -1)s 1 2  +  (n 2 -1)s 2 2  /  (n 1 +n 2 -2)

where s 1 2  and s 2 2  are the sample variances.

If the p-value that corresponds to the test statistic t with (n 1 +n 2 -1) degrees of freedom is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis.

Two Sample t-test: Assumptions

For the results of a two sample t-test to be valid, the following assumptions should be met:

• The observations in one sample should be independent of the observations in the other sample.
• The data should be approximately normally distributed.
• The two samples should have approximately the same variance. If this assumption is not met, you should instead perform Welch’s t-test .
• The data in both samples was obtained using a random sampling method .

Two Sample t-test : Example

Suppose we want to know whether or not the mean weight between two different species of turtles is equal. To test this, will perform a two sample t-test at significance level α = 0.05 using the following steps:

Step 1: Gather the sample data.

Suppose we collect a random sample of turtles from each population with the following information:

• Sample size n 1 = 40
• Sample mean weight  x 1  = 300
• Sample standard deviation s 1 = 18.5
• Sample size n 2 = 38
• Sample mean weight  x 2  = 305
• Sample standard deviation s 2 = 16.7

Step 2: Define the hypotheses.

We will perform the two sample t-test with the following hypotheses:

• H 0 :  μ 1  = μ 2 (the two population means are equal)
• H 1 :  μ 1  ≠ μ 2 (the two population means are not equal)

Step 3: Calculate the test statistic  t .

First, we will calculate the pooled standard deviation s p :

s p = √  (n 1 -1)s 1 2  +  (n 2 -1)s 2 2  /  (n 1 +n 2 -2)  = √  (40-1)18.5 2  +  (38-1)16.7 2  /  (40+38-2)  = 17.647

Next, we will calculate the test statistic  t :

t = ( x 1  –  x 2 )  /  s p (√ 1/n 1  + 1/n 2 ) =  (300-305) / 17.647(√ 1/40 + 1/38 ) =  -1.2508

Step 4: Calculate the p-value of the test statistic  t .

According to the T Score to P Value Calculator , the p-value associated with t = -1.2508 and degrees of freedom = n 1 +n 2 -2 = 40+38-2 = 76 is  0.21484 .

Step 5: Draw a conclusion.

Since this p-value is not less than our significance level α = 0.05, we fail to reject the null hypothesis. We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.

Note:  You can also perform this entire two sample t-test by simply using the Two Sample t-test Calculator .

Additional Resources

The following tutorials explain how to perform a two-sample t-test using different statistical programs:

How to Perform a Two Sample t-test in Excel How to Perform a Two Sample t-test in SPSS How to Perform a Two Sample t-test in Stata How to Perform a Two Sample t-test in R How to Perform a Two Sample t-test in Python How to Perform a Two Sample t-test on a TI-84 Calculator

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “Two Sample t-test: Definition, Formula, and Example”

I like the detailed information and simplified in the way I can understand and relate easily. Thank you

It seems a couple of parenthesis is missed at the pooled standard deviation formula. Under square root you have (n1-1)s12 + (n2-1)s22 / (n1+n2-2) but it should be [(n1-1)s12 + (n2-1)s22] / (n1+n2-2) I used square bracket

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Python for Machine Learning
• Machine Learning with R
• Machine Learning Algorithms
• Math for Machine Learning
• Machine Learning Interview Questions
• ML Projects
• Deep Learning
• Computer vision
• Data Science
• Artificial Intelligence
• Machine Learning Mathematics

Linear Algebra and Matrix

• Scalar and Vector
• Python Program to Add Two Matrices
• Python program to multiply two matrices
• Vector Operations
• Product of Vectors
• Scalar Product of Vectors
• Dot and Cross Products on Vectors
• Transpose a matrix in Single line in Python
• Transpose of a Matrix
• Adjoint and Inverse of a Matrix
• How to inverse a matrix using NumPy
• Determinant of a Matrix
• Program to find Normal and Trace of a matrix
• Data Science | Solving Linear Equations
• Data Science - Solving Linear Equations with Python
• System of Linear Equations
• System of Linear Equations in three variables using Cramer's Rule
• Eigenvalues
• Applications of Eigenvalues and Eigenvectors
• How to compute the eigenvalues and right eigenvectors of a given square array using NumPY?

Statistics for Machine Learning

• Descriptive Statistic
• Measures of Central Tendency
• Measures of Dispersion | Types, Formula and Examples
• Mean, Variance and Standard Deviation
• Calculate the average, variance and standard deviation in Python using NumPy
• Random Variables
• Difference between Parametric and Non-Parametric Methods
• Probability Distribution - Function, Formula, Table
• Confidence Interval
• Mathematics | Covariance and Correlation
• Program to find correlation coefficient
• Robust Correlation
• Normal Probability Plot
• Quantile Quantile plots
• True Error vs Sample Error
• Bias-Variance Trade Off - Machine Learning
• Understanding Hypothesis Testing
• Paired T-Test - A Detailed Overview
• P-value in Machine Learning
• F-Test in Statistics
• Residual Leverage Plot (Regression Diagnostic)
• Difference between Null and Alternate Hypothesis
• Mann and Whitney U test
• Wilcoxon Signed Rank Test
• Kruskal Wallis Test
• Friedman Test
• Mathematics | Probability

Probability and Probability Distributions

• Mathematics - Law of Total Probability
• Bayes's Theorem for Conditional Probability
• Mathematics | Probability Distributions Set 1 (Uniform Distribution)
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Mathematics | Probability Distributions Set 5 (Poisson Distribution)
• Uniform Distribution Formula
• Mathematics | Probability Distributions Set 2 (Exponential Distribution)
• Mathematics | Probability Distributions Set 3 (Normal Distribution)
• Mathematics | Beta Distribution Model
• Gamma Distribution Model in Mathematics
• Chi-Square Test for Feature Selection - Mathematical Explanation
• Student's t-distribution in Statistics
• Python - Central Limit Theorem
• Mathematics | Limits, Continuity and Differentiability
• Implicit Differentiation

Calculus for Machine Learning

• Engineering Mathematics - Partial Derivatives
• Advanced Differentiation
• How to find Gradient of a Function using Python?
• Optimization techniques for Gradient Descent
• Higher Order Derivatives
• Taylor Series
• Application of Derivative - Maxima and Minima | Mathematics
• Absolute Minima and Maxima
• Optimization for Data Science
• Unconstrained Multivariate Optimization
• Lagrange Multipliers
• Lagrange's Interpolation
• Linear Regression in Machine learning
• Ordinary Least Squares (OLS) using statsmodels

Regression in Machine Learning

In statistics, various tests are used to compare different samples or groups and draw conclusions about populations. These tests, known as statistical tests, focus on analyzing the likelihood or probability of obtaining the observed data under specific assumptions or hypotheses. They provide a framework for assessing evidence in support of or against a particular hypothesis.

A statistical test begins by formulating a null hypothesis (H 0 ) and an alternative hypothesis (H a ). The null hypothesis represents the default assumption, typically stating no effect or no difference, while the alternative hypothesis suggests a specific relationship or effect.

There are different statistical tests like Z-test , T-test, Chi-squared tests , ANOVA , Z-test , and F-test , etc. which are used to compute the p-value. In this article, we will learn about the T-test.

Table of Content

What is T-Test?

Assumptions in t-test, prerequisites for t-test, types of t-tests, one sample t-test, independent sample t-test, paired two-sample t-test, frequently asked questions on t-test.

The t-test is named after William Sealy Gosset’s Student’s t-distribution, created while he was writing under the pen name “Student.”

A t-test is a type of inferential statistic test used to determine if there is a significant difference between the means of two groups. It is often used when data is normally distributed and population variance is unknown.

The t-test is used in hypothesis testing to assess whether the observed difference between the means of the two groups is statistically significant or just due to random variation.

• Independence : The observations within each group must be independent of each other. This means that the value of one observation should not influence the value of another observation. Violations of independence can occur with repeated measures, paired data, or clustered data.
• Normality : The data within each group should be approximately normally distributed i.e the distribution of the data within each group being compared should resemble a normal (bell-shaped) distribution. This assumption is crucial for small sample sizes (n < 30).
• Homogeneity of Variances (for independent samples t-test) : The variances of the two groups being compared should be equal. This assumption ensures that the groups have a similar spread of values. Unequal variances can affect the standard error of the difference between means and, consequently, the t-statistic.
• Absence of Outliers: There should be no extreme outliers in the data as outliers can disproportionately influence the results, especially when sample sizes are small.

Let’s quickly review some related terms before digging deeper into the specifics of the t-test.

A t-test is a statistical method used to compare the means of two groups to determine if there is a significant difference between them. The t-test is a parametric test, meaning it makes certain assumptions about the data. Here are the key prerequisites for conducting a t-test.

Hypothesis Testing :

Hypothesis testing is a statistical method used to make inferences about a population based on a sample of data.

The p-value is the probability of observing a test statistic (or something more extreme) given that the null hypothesis is true.

• A small p-value (typically less than the chosen significance level) suggests that the observed data is unlikely to have occurred by random chance alone, leading to the rejection of the null hypothesis.
• A large p-value suggests that the observed data is likely to have occurred by random chance, and there is not enough evidence to reject the null hypothesis.

Degree of freedom (df):

Significance Level :

The significance level is the predetermined threshold that is used to decide whether to reject the null hypothesis. Commonly used significance levels are 0.05, 0.01, or 0.10. A significance level of 0.05 indicates that the researcher is willing to accept a 5% chance of making a Type I error (incorrectly rejecting a true null hypothesis).

T-statistic :

The t-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

• If the t-value is large => the two groups belong to different groups. 
• If the t-value is small => the two groups belong to the same group.

T-Distribution

The t-distribution , commonly known as the Student’s t-distribution, is a probability distribution with tails that are thicker than those of the normal distribution.

Statistical Significance

Statistical significance is determined by comparing the p-value to the chosen significance level.

• If the p-value is less than or equal to the significance level, the result is considered statistically significant, and the null hypothesis is rejected.
• If the p-value is greater than the significance level, the result is not statistically significant, and there is insufficient evidence to reject the null hypothesis.

In the context of a t-test, these concepts are applied to compare means between two groups. The t-test assesses whether the means are significantly different from each other, taking into account the variability within the groups. The p-value from the t-test is then compared to the significance level to make a decision about the null hypothesis.

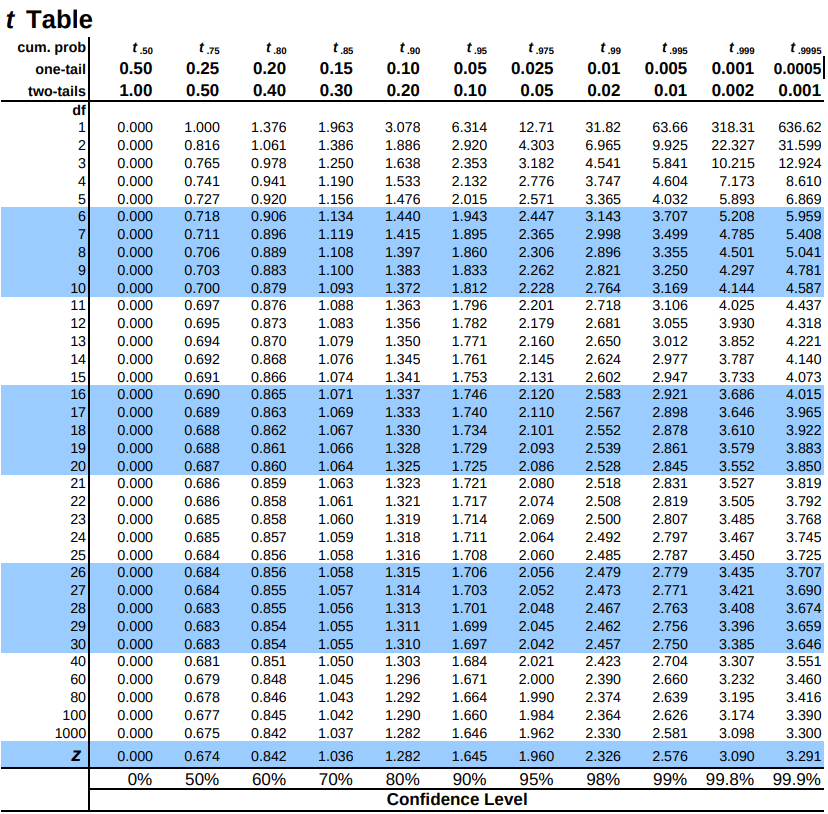
A t-table, or a t-distribution table, is a reference table that provides critical values for the t-test. The table is organized by degrees of freedom and significance levels (usually 0.05 or 0.01). The t-table is used to find the critical t-value corresponding to their specific degrees of freedom and chosen significance level. If the calculated t-value is greater than the critical value from the table, it suggests that the observed difference is statistically significant.

There are three types of t-tests, and they are categorized as dependent and independent t-tests.

• One sample t-test test: The mean of a single group against a known mean.
• Independent samples t-test: compares the means for two groups.
• Paired sample t-test: compares means from the same group at different times (say, one year apart).

One sample t-test is one of the widely used t-tests for comparison of the sample mean of the data to a particularly given value. Used for comparing the sample mean to the true/population mean.

We can use this when the sample size is small. (under 30) data is collected randomly and it is approximately normally distributed. It can be calculated as:

• t = t-value
• x_bar = sample mean
• μ = true/population mean
• σ = standard deviation
• n = sample size

Example Problem

Consider the following example. The weights of 25 obese people were taken before enrolling them into the nutrition camp. The population mean weight is found to be 45 kg before starting the camp. After finishing the camp, for the same 25 people, the sample mean was found to be 75 with a standard deviation of 25. Did the fitness camp work?

One-Sample T-test in Python

The T-value of 6.0 is significantly greater than the critical t-value, leading to rejection of the null hypothesis therefore, we can conclude there is a significant difference in weight before and after the fitness camp. The fitness camp had an effect on the weights of the participants.

The results strongly suggest that the fitness camp was effective in producing a statistically significant change in weight for the participants.

• The T-value and p-value both provide consistent evidence for rejecting the null hypothesis.
• The practical significance should also be considered to understand the real-world impact of this weight change.

An Independent sample t-test, commonly known as an unpaired sample t-test is used to find out if the differences found between two groups is actually significant or just a random occurrence. 

We can use this when:

• the population mean or standard deviation is unknown. (information about the population is unknown)
• the two samples are separate/independent. For eg. boys and girls (the two are independent of each other)

It can be calculated using:

Researchers are investigating whether there is a significant difference in the exam scores of two different teaching methods, A and B. Two independent samples, each representing a different teaching method, have been collected. The objective is to determine if there is enough evidence to suggest that one teaching method leads to higher exam scores compared to the other. Suppose, two independent sample data A and B are given, with the following values. We have to perform the Independent samples t-test for this data.

Two-Sample t-test in Python (Independent)

With T-Value, of 0.989 is less than the critical t-value of 2.1009. Therefore, No significant difference is found between the exam scores of Teaching Method A and Teaching Method B based on the T-value.

With P-Value, of 0.336 is greater than the significance level of 0.05. There is no evidence to reject the null hypothesis, indicating no significant difference between the two teaching methods based on the P-value.

In conclusion, The results suggest that, statistically, there is no significant difference in exam scores between Teaching Method A and Teaching Method B. Therefore, based on this analysis, there is no clear evidence to suggest that one teaching method leads to higher exam scores compared to the other.

Paired sample t-test, commonly known as dependent sample t-test is used to find out if the difference in the mean of two samples is 0. The test is done on dependent samples, usually focusing on a particular group of people or things. In this, each entity is measured twice, resulting in a pair of observations. 

We can use this when :

• Two similar (twin like) samples are given. [Eg, Scores obtained in English and Math (both subjects)]
• The dependent variable (data) is continuous.
• The observations are independent of one another.
• The dependent variable is approximately normally distributed.

It can be calculated using,

• (s_d) is the standard deviation of the differences.
• (n) is the number of paired observations.

Consider the following example. Scores (out of 25) of the subjects Math1 and Math2 are taken for a sample of 10 students. We have to perform the paired sample t-test for this data. 

Paired Two-Sample T-test in Python

The paired sample t-test suggests that there is a statistically significant difference in scores between Math1 and Math2 as T-value of -4.95 is less than the critical t-value of -2.2622 and P-value of 0.00079 is less than the significance level of 0.05. Therefore, based on this analysis, it can be concluded that there is evidence to support the claim that the two sets of scores are different, and the difference is not due to random chance.

The above-discussed types of t-tests are widely used in the fields of research in hospitals by experts to gain important information about the medical data given to them about the effects of various medicines and drugs on the population and help them draw out important inferences regarding the same. However, it is the responsibility of the person to see to it that which t-test would bring out the best results and that all the assumptions of that t-test are adhered to. For any doubt/query, comment below. 

In conclusion, t-test, play a crucial role in hypothesis testing, comparing means, and drawing conclusions about populations. The test can be one-sample, independent two-sample, or paired two-sample, each with specific use cases and assumptions. Interpretation of results involves considering T-values, P-values, and critical values.

These tests aid researchers in making informed decisions based on statistical evidence.

Q. What is the t-test for mean in Python?

The t-test for mean in Python is a statistical method used to determine if there is a significant difference between the means of two groups.

Q. What is the t-test function?

The t-test function is a statistical tool used to compare means and assess the significance of differences between groups, considering factors like sample size and variability.

Q. What is the p-value in t-test Python?

The p-value in a t-test Python indicates the probability of observing the data or more extreme results assuming the null hypothesis is true. A small p-value suggests evidence against the null hypothesis.

Q. Why is it called t-test?

The t-test is named after William Sealy Gosset, who published under the pseudonym “Student.” The name “t” refers to the t-distribution used in the test, particularly applicable for small sample sizes.

Please Login to comment...

Similar reads.

• Machine Learning
• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?