area of cuboid presentation

• Math Article
• Surface Area Of Cuboid

Surface Area of Cuboid

A cuboid is a three-dimensional figure bounded by six rectangular planes, having a different magnitude of length, width and height. If you look around and you can see a box, brick or anything in the shape of a rectangle, it could be cuboid. A cuboid (3-dimensional) can be seen made up of rectangles (2-dimensional) of different dimensions when seen from any of the ends. In this article, we are going to discuss the definition of cuboid, total and lateral surface area of a cuboid in a detailed way. Table of Contents:

Cuboid Definition

• Total Surface Area
• Lateral Surface Area

Total Surface Area of a Cuboid Derivation

A cuboid is a three-dimensional figure or solid which has six rectangular sides called faces. Each face of a cuboid is a rectangle and all of its corners are 90-degrees. It has 8 vertices and 12 edges. The opposite faces of a cuboid are always equal. It means that the opposite surfaces of the cuboid are in the same dimension. The measures of the cuboid are the Total Surface Area (TSA), Lateral or curved Surface Area (CSA) and volume. The surface areas are measured in terms of square units, whereas the volume of the cube is measured in terms of cubic units.

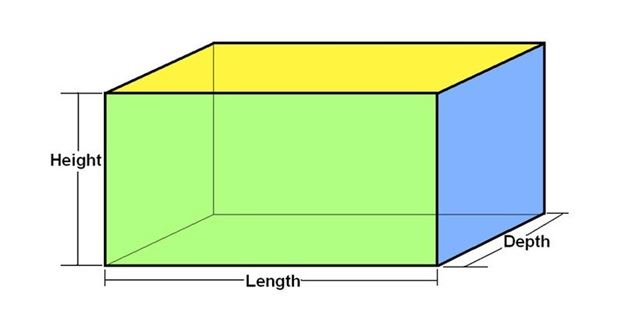
Area of Cuboid

The area of a cuboid refers to the surface area as the cuboid is a three dimensional solid. Thus, the area of cuboid can be calculated using the formula of area of rectangle , since the faces of a cuboid are in a rectangular shape.

Cuboid Surface Area

The surface area of the cuboid can be of two types-

(i) Total Surface Area

(ii) Lateral Surface Area or Curved Surface Area

Surface Area of Cuboid Formula

Before going into the concept of area, let us denote the dimensions of a cuboid, which are,

Length, Width, and Height are represented by l, w, h, respectively.

Total Surface Area of a Cuboid

The Total surface area of a cuboid (TSA) is equal to the sum of the areas of it’s 6 rectangular faces, which is given by:

Total Surface Area of a Cuboid (TSA) = 2 (lw + wh + lh) square units

The above formula gives the total surface area of a cuboid having all six faces.

Lateral Surface Area of a Cuboid

The lateral surface area of a cuboid is the sum of 4 planes of a rectangle, leaving the top (upper) and the base (lower) surface. Mathematically, the Lateral Surface Area of a cuboid (LSA) is given as:

Lateral Surface Area of a cuboid (LSA) = 2 (lh + wh) = 2 h (l + w) square units

Also, learn:

• Cuboid and Cube
• Volume of a Cuboid
• Surface area and Volumes
• Difference Between Cube and Cuboid

As the cuboid has six rectangular faces, the total surface area of the cuboid is calculated as follows:

Assume that, l, w, h be the length, width, and height of the cuboid respectively.

The front face area of cuboid = l x h

The back face area of the cuboid = l x h

The top face area of the cuboid = l x w

The bottom face area of the cuboid = l x w

The left face area of the cuboid = h x w

The right face area of cuboid = h x w

Hence, the total surface area is the sum of all the faces of a cuboid, then the TSA of a cuboid is:

Total Surface Area of Cuboid = lh + lh + lw+ lw+ hw+ hw

Total Surface Area of Cuboid  = 2 lh + 2 lw + 2 hw

Total Surface Area of Cuboid  = 2 (lh + lw+ hw) 

Therefore, the total surface area of the cuboid is 2 (lh + lw+ hw) square units.

Surface Area of Cuboid Example

Given below is a cuboid having its dimension given as length = 8 cm, width = 6 cm and height = 5 cm, find the TSA of a cuboid.

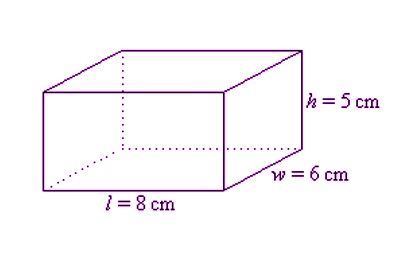
Using the formula: TSA = 2 (lw + wh + hl)

2( (8×6) + (6×5) + (5×8))

= 2(48 + 30 + 40)

So, the total surface area of this cuboid is 236 cm².

The dimensions of a cuboid are given as follows:

Length = 4.8 cm

Width = 3.4 cm

Height = 7.2 cm.

Find the Total Surface area and the Lateral Surface area.

The total surface area is given as

TSA = 2 (lw + wh + hl)

=2((4.8 ×3.4) + (3.4×7.2) + (7.2×4.8))

= 2(16.32 +24.48 +34.56)

= 2(75.36) cm²

Therefore, TSA of a cuboid= 150.72 cm

Also, the lateral surface area = 2 h (l + w)

= 2×7.2 (4.8 + 3.4)

= 14.4 (8.2) = 118.08

Therefore, LSA of a cuboid = 118.08 cm²

Frequently Asked Questions on Surface Area of Cuboid

What is the surface area of the cube and cuboid, what is the latest surface area of a cuboid, how do you find the surface area and volume of a cuboid, what is the total surface area and lateral surface area, what is the difference between total surface area and the curved surface area.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Awesome explanation.

Satisfied with answer.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Surface Area of Cuboid

The surface area of a cuboid is the total space occupied by it. A cuboid is a six-faced three-dimensional shape in which each face is in the shape of a rectangle. If l, w, and h are the length, width, and the height of a cuboid, then the surface area of a cuboid formula is 2 lw + 2 wh + 2hl.

This formula can be derived by observing that a cuboid has three pairs of faces, each pair having the same area (because opposite faces are congruent), and adding up the areas of all six faces. Let us learn more about the formula of the surface area of the cuboid and solve problems based on it.

What is the Surface Area of Cuboid?

The surface area of a cuboid is the total area of all its 6 faces. Since a cuboid is a three-dimensional solid shape , the value of its surface area depends on the dimensions of its length, width, and height. The change in any of the dimensions of a cuboid changes the value of its surface area. The surface area of a cuboid is expressed in square units.

The surface area of a cuboid is an important metric as it is useful in a wide range of applications such as construction, manufacturing, and packaging. For example, when determining how much paint is needed to cover a cuboidal box, or when calculating the amount of material required to manufacture a cuboidal object, the surface area of the cuboid is an essential measurement.

Surface Area of Cuboid Formula

The formula for the surface area of a cuboid depends on the type of surface area that has been asked for. A cuboid has two kinds of surface areas:

• TSA of Cuboid : Total Surface Area (also known just as "surface area")
• LSA (or) CSA of Cuboid: Lateral Surface Area (or) Curved Surface Area

The total surface area of the cuboid is obtained by adding the area of all the 6 faces while the lateral surface area of the cuboid is calculated by finding the area of each face excluding the base and the top. The total surface area and the lateral surface area of a cuboid can be expressed in terms of length (l), width (w), and height of cuboid (h) as:

Total Surface Area of Cuboid = 2 (lw + wh + lh) Lateral Surface Area of Cuboid = 2h (l + w)

If the surface area is given or asked without any specifications, it means that it refers to the total surface area. Let us see how to derive the formulas for the surface area of the cuboid by opening up a cuboidal box.

Total Surface Area of Cuboid (TSA)

The TSA of cuboid is sometimes just referred to as surface area of cuboid itself. A cuboid has 6 rectangular faces. Now, in order to find the total surface area of a cuboid, we need to add the area of all the 6 rectangular faces. Since each face of a cuboid is a rectangle , hence the area of the rectangle for each face is calculated and added to get the total surface area of the cuboid. Let us understand this with the help of the figure given below.

The faces of cuboid are numbered as 1, 2, 3, 4, 5, and 6 as shown in the figure given above. In other words, if we see the cuboid in the form of a two-dimensional figure as a net , we get this figure.

• Area of Rectangles 1 and 2: the area of the rectangles of the top and bottom faces = lw + lw = 2lw
• Area of Rectangles 3 and 4: the area of the rectangles of the left and right sides = wh + wh = 2wh
• Area of Rectangles 5 and 6: area of the rectangles on the front and back faces = lh + lh = 2lh

Hence, the total surface area (TSA) of the six faces = 2lw + 2wh + 2lh.

Thus, the TSA of a cuboid of dimensions l, w, and h is 2 (lw + wh + lh).

Lateral Surface Area of Cuboid (LSA)

The lateral surface area (LSA) of a cuboid is also known as the curved surface area of cuboid (CSA). This is the combined surface area of the four lateral (side) faces. In the figure given above, if we remove the top and bottom faces, we will get the area of the lateral surface area of the cuboid. The LSA (or) CSA of cuboid is,

Lateral Surface Area = Area of the four side faces

= 2lh + 2wh

= 2h(l + w)

It is important to note that CSA of cuboid only includes the vertical faces and does not include the top and bottom faces, so it is always less than the total surface area of the cuboid.

To understand this with the help of a real-life example let us imagine a room in the shape of a cuboid. The total surface area will be the combined area of the six faces of the room (the four vertical walls + the floor + the ceiling) while the lateral surface area will be the combined surface area of the four vertical walls (the areas of the floor and the ceiling are not added).

Difference Between TSA and CSA of Cuboid

The main difference between TSA and CSA of the cuboid is that TSA includes all six faces of the cuboid, whereas CSA only includes the vertical faces of the cuboid. TSA is a measure of the total area that needs to be covered or painted on the cuboid, while CSA is a measure of the area of the curved surface that wraps around the cuboid. The following table summarizes the differences between the total surface area and curved surface area of cuboid in detail.

How to Find the Surface Area of Cuboid?

The surface area of a cuboid is the total area of each surface of a cuboid. Let us use the following steps to calculate the total surface area of a cuboid.

• Step 1: Check if the given dimensions of cuboids are in the same units or not. If not, convert the dimensions into the same units.
• Step 2: Use the formula for total surface area = 2(lw + wh + lh) if we need TSA and lateral surface area = 2h(l + w) if we need LSA.
• Step 3: Substitute the given values to get the area and express it in square units.

Example: Find the total surface area and the lateral surface area of a cuboid whose length = 6 inches, width = 4 inches, and height = 3 inches.

Solution: Here, length (l) = 6 inches, width (w) = 4 inches and height (h) = 3 inches

• Total surface area of cuboid = 2 (lw + wh + lh) = 2 [(6 × 4) + (4 × 3) + (6 × 3)] = 108 in 2
• Lateral surface area of cuboid = 2h(l + w) = (2 × 3)(6 + 4) = 60 in 2

Applications of Surface Area of Cuboid

The surface area of a cuboid has various real-world applications in various fields such as engineering, construction, manufacturing, architecture, etc. Here are a few applications.

Packaging : Knowing the surface area of a cuboid can help companies determine the amount of material required and ensure that the product fits properly inside the packaging.

Painting : The information about the amount of paint needed to cover a rectangular box or cuboid is crucial for painters to estimate the cost of paint required for a project.

Manufacturing : In manufacturing, the surface area of cuboids is used to calculate the amount of material needed to manufacture a product.

Heat Transfer : The surface area of a cuboid is also used to calculate the rate of heat transfer in a solid object and hence surface area of a material is a critical factor in its thermal conductivity.

☛ Related Articles

• Surface Area of Cube
• Volume of Cube
• Volume of Cuboid
• Difference Between Area and Surface Area

Examples on Surface Area of Cuboid

Example 1: Find the lateral surface area of a cuboid whose length = 20 inches, width = 10 inches, and height = 15 inches.

Solution: As we know, the lateral surface area of a cuboid is L = 2h(l + w) and it is given that,

length (l) = 20 in

width (w) = 10 in

height (h) = 15 in

Let us substitute the values in the formula,

LSA of cuboid = 2h(l + w)

= 2 × 15 (20 + 10)

= 30 (20 + 10)

= 900 square inches

Answer: The lateral surface area of the cuboid is 900 square inches.

Example 2: Find the total surface area of a cuboid which is 8 m long, 5 m broad, and 4 m high.

Solution: Given, length of the cuboid (l) = 8 m, width (w) = 5 m, height (h) = 4 m.

The total surface area of the cuboid = 2 (lw + wh + lh)

So, let us substitute the values in the formula.

TSA of the cuboid = 2 (lw + wh + lh)

= 2 [(8 × 5) + (5 × 4) + (8 × 4)]

= 2 [40 + 20 + 32]

Answer: The total surface area of the cuboid is 184 m 2

Example 3: State true or false.

a.) A cuboid has 7 rectangular faces.

b.) In order to find the total surface area of a cuboid, we need to add the area of all 6 rectangular faces.

a.) False, a cuboid has only 6 rectangular faces.

b.) True, in order to find the TSA of a cuboid, we need to add the area of all 6 rectangular faces.

Answer: (a) False (b) True

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Surface Area of Cuboid

go to slide go to slide

FAQs on Surface Area of Cuboid

What does the total surface area of cuboid mean.

The total surface area of a cuboid is the sum of all its surfaces. In order to find the total surface area of a cuboid, we need to add the area of all the 6 rectangular faces. The formula for the total surface area of a cuboid is 2 (lw + wh + lh) where l = length, w = width, and h = height of the cuboid.

What is the Lateral Surface Area of a Cuboid?

The lateral surface area of a cuboid is the value of the surface area of a cuboid excluding its top and bottom surfaces. The formula for the lateral surface area of a cuboid is expressed as, 2h(l + w) where l = length, w = width, and h = height of the cuboid.

Where to Find the Surface Area of Cuboid Calculator?

The area of cuboid can be calculated using the calculator . It shows the surface area just by entering the values of length, width, and height of the cuboid.

What is the Difference Between the TSA and the LSA of a Cuboid?

The difference between total surface area and the lateral surface area of a cuboid is given below:

• The total surface area of a cuboid is the sum of the areas of all 6 faces and is calculated by the formula 2(lw + wh + lh).
• The lateral surface area of a cuboid is the sum of the areas of faces excluding the top and the base and is calculated by the formula 2h(l + w)

What is the Total Surface Area of a Cuboidal Box Without Lid?

The total surface area of a cuboidal box without a lid can be given in two ways:

• Method 1: Total surface area of a cuboidal box without lid = Total surface area of the cuboid - 1 rectangular face;
• Method 2: Total surface area of a cuboidal box without lid = Lateral surface area of cuboid + 1 rectangular face;

It should be noted that both the methods result in the same answer.

What is the Unit for Surface Area of Cuboid?

The surface area of a cuboid is expressed in square units like cm 2 , m 2 , inch 2 , and so on. This is because surface area is also area .

What is the TSA and CSA of a Cuboid?

The TSA and CSA of a cuboid are the abbreviations of the Total Surface Area (TSA) and Curved Surface Area (CSA) of a cuboid. The total surface area is the sum of the surface area of all 6 faces while curved surface area is the measure of surface area excluding the top and bottom faces.

What is the Total Surface Area of a Cuboid Formula?

The formula that is used to find the total surface area of a cuboid is 2 (lw + wh + lh); where l = length, w = width, and h = height of the cuboid.

What is the Lateral Surface Area of a Cuboid Formula?

The formula that is used to find the lateral surface area of a cuboid is 2h(l + w) where l, w, and h are the length, width, and height of the cuboid respectively.

• Basic Math Formulas
• Trigonometry Formulas
• Integration Formulas
• Differentiation Formula
• Algebra Formulas
• Mensuration Formula
• Statistics Formulas
• Basic Geometry Formulas
• Sequences and Series Formulas
• Coordinate Geometry Formulas
• Trigonometric Table
• CBSE Class 8 Maths Formulas
• CBSE Class 9 Maths Formulas
• CBSE Class 10 Maths Formulas
• CBSE Class 11 Maths Formulas
• Mensuration in Maths | Formulas for 2D and 3D Shapes, Examples

Introduction to Mensuration

• Geometric Shapes in Maths
• Visualizing Solid Shapes
• Volume of Combination of Solids
• Mensuration Formulas
• Perimeter of Triangle
• How to find the perimeter of an equilateral triangle?
• Perimeter of an Isosceles Triangle
• Perimeter of Rectangle
• Perimeter of Square | Formula, Derivation, Examples
• Perimeter of a Parallelogram
• Perimeter of A Rhombus
• How to find the perimeter of a trapezium?
• Circumference of Circle - Definition, Perimeter Formula, and Examples
• Area of Triangle | Formula and Examples
• Area of Equilateral Triangle
• Right Angled Triangle | Properties and Formula
• Heron's Formula
• Area of Square
• Area of Rectangle
• Area of Parallelogram (Definition, Formulas & Examples)
• Area of Rhombus: Formula, Derivation and Examples
• Area of Trapezium - Mensuration | Class 8 Maths
• Area of a Circle: Formula, Derivation, Examples
• How to Calculate Area of Sector of Circle?
• Segment of a Circle
• Find the area of the shaded region formed by the intersection of four semicircles in a square
• Volume of a Cube
• Diagonal of a Cube Formula
• Volume of Cuboid | Formula and Examples
• Volume of a Sphere
• Volume of Hemisphere
• Volume of Cone: Formula, Derivation and Examples
• Volume of a Cylinder: Formula, Definition and Examples
• Mensuration 3D - Hollow sphere
• Volume of a Hollow Cylinder
• Convert Cubic Meter To Liter (m³ to l)

Total Surface Area

• Surface Area of Cube

Surface Area of Cuboid

• Surface Area of Sphere: Formula, Derivation and Solved Examples
• Surface Area of a Hemisphere
• Surface Area of Cone
• Surface Area of Cylinder

Lateral or Curved Surface Area

• Area of Hollow Cylinder

The surface area of a cuboid is the total space occupied by all its surfaces/sides. In geometry, a three-dimensional shape having six rectangular faces is called a cuboid. A cuboid is also known as a regular hexahedron and has six rectangular faces, eight vertices, and twelve edges with congruent, opposite faces. It is a three-dimensional form of a rectangle with four lateral faces and two faces at the top and bottom. Some examples of cuboids that we regularly see are bricks, geometric boxes, shoe boxes, packaging boxes, etc. Let’s learn in detail about the surface area of a cuboid, along with examples.

What is the Surface Area of a Cuboid?

The surface area of a cuboid is the total area covered by all of its surfaces, and since the cuboid is the 3-D form of a rectangle, therefore, along with length and breadth, the height of the cuboid is also involved in finding the surface area. Surface area and volume are calculated in 3-D figures. The surface area of a cuboid is measured in square units (For example, cm 2 , m 2 , etc).

Surface Area of a Cuboid Formula

A cuboid has 2 kinds of surface area. The surface area of a cuboid is calculated based on what type of surface area is required. The formulas for both types of surface areas are different. They are:

• Total surface area of a cuboid
• Lateral surface area of a cuboid

The total surface area of a cuboid is the area of all 6 sides of the cuboid. However, the lateral surface area of a cuboid is the area of only 4 sides (base and top excluded). Imagine there is a room in the shape of a cuboid; if only the walls of the room (excluding the ceiling) require painting, then the lateral surface area of the room will be taken into account for the paint used, and the total surface area of the room is the sum of the 4 walls + ceiling + floor. Both the total surface area and lateral surface area of a cuboid are calculated in terms of length (l), breadth(b), and height(h). The formulas are:

Lateral surface area of a cuboid = 2h(l + b) square units Total surface area of a cuboid = 2 (lb + bh + lh) square units

Note: If the surface area is asked without giving any information or specification, then the total surface area of the cuboid is calculated.

Derivation of Surface Area of a Cuboid

The lateral and total surface areas of a cuboid are the two types of surface areas of a cuboid. The lateral surface area of a cuboid is the area occupied by its lateral faces, whereas the total surface area of a cuboid is the area occupied by all its six rectangular faces.

Total Surface Area of Cuboid

The total surface area of a cuboid can be calculated by first calculating the area of all the sides and then adding all six sides. Let us consider that “l” is the length of the cuboid, “b” is the breadth of the cuboid, and “h” is the height of the cuboid.

We know that in a cuboid, opposite faces are equal, i.e., ABCD = PQRS, APSD = BQRC, and ABQP = DCRS. Now, the total surface area of the cuboid is equal to the sum of the areas of its six rectangular faces. The total surface area of the cuboid = Area of [ABCD + APSD + ABQP + PQRS + BQRS + DCRS].

Area of [ABCD +APSD + ABQP + ABCD +APSD + ABQP] = 2 Area of [ABCD +APSD + ABQP]

• The area of the rectangle ABCD = l × h
• The area of the rectangle APSD = b × h
• The area of the rectangle ABQP = l × b

Therefore, 

Total surface area of the cuboid (TSA) = 2 (lb + bh + lh) square units

Lateral Surface Area of a Cuboid

The lateral surface area of a cuboid is the area occupied by its lateral faces. Hence, the lateral surface area of the cuboid = The total surface area of the cuboid – The area of the top and bottom faces of the cuboid

= 2 (lb + bh + lh) – Area of [ABPQ + CDRS}

= 2 (lb + bh + lh) – 2 Area of (ABPQ)

= 2 (lb + bh + lh) – 2lb

= 2 (bh + lh) = 2h(l + b)

Lateral surface area of a cuboid (LSA) = 2h(l + b) square units

How to Find the Surface Area of Cuboid?

The surface area of a cuboid is the total area of all the sides/surfaces of the cuboid. In order to understand how to find the surface area of a cuboid, let’s take a look at the given steps:

Step 1: Observe and note down the dimensions of each size. In case the dimensions have different units, convert them into one unit.

Step 2: Use the formula for the total surface area of the cuboid: that is, TSA = 2 (lb + bh + lh) square units

Step 3: Note down the area contained in proper units.

Let’s consider an example to determine the surface area of the cuboid using its formula.

Example: Calculate the total surface area of a cuboid if its length, breadth, and height are 8 cm, 3 cm, and 5 cm, respectively.

Step 1: Note down the dimensions of the given sphere. Here, the length, breadth, and height are 8 cm, 3 cm, and 5 cm. Step 2: We know that the total surface area of a cuboid = 2 (lb + bh + lh). So, substitute the value of the given dimensions in the equation = 2 [(8 × 3) + (3 × 5) + (8 × 5)] = 158 sq. cm. Step 3: Hence, the total surface area of a cuboid is 158 sq. cm.

Related Articles

Surface Area of a Cube Surface area of a Sphere Surface area of a Hemisphere

Solved Examples on Surface Area of a Cuboid

Example 1: Determine the lateral surface area of a cuboid if its length, breadth, and height are 15 in, 8 in, and 12 in, respectively.

Given data, The length of a cuboid (l) = 15 in The breadth of a cuboid (b) = 8 in The height of a cuboid (h) = 12 in We have, Lateral surface area of a cuboid = 2h(l + b) = 2 × 12 (15 + 8) = 24 × 23 = 552 square inches. Hence, the lateral surface area of the given cuboid is 552 square inches.

Example 2: What is the total surface area of a cuboid shown in the figure below:

Given data, The length of a cuboid (l) = 18 cm The breadth of a cuboid (b) = 13 cm The height of a cuboid (h) = 15 cm We have, Total surface area of a cuboid = 2 (lb + bh + lh) = 2 [(18 × 13) + (13 × 15) + (18 × 15)] = 2 [234 + 195 + 270] = 2 [699] = 1398 cm 2 Hence, the total surface area of the given cuboid is 1398 cm 2 .

Example 3: Calculate the height of the cuboid whose lateral surface area is 360 square units and whose length and breadth are 12 units and 8 units, respectively.

Given data, The length of a cuboid (l) = 12 units The breadth of a cuboid (b) = 8 units The lateral surface area = 360 square units We have, Lateral surface area of a cuboid = 2h(l + b) ⇒ 2h (12 + 8) = 360 ⇒ h × (20) = 360/2 = 180 ⇒ 20h = 180⇒ h = 180/20 ⇒ h = 9 units Hence, the height of the given cuboid is 9 units.

Example 4: Determine the length and the total surface area of a cuboid whose lateral surface area is 960 sq. in and whose breadth and height are 12 in and 16 in, respectively.

Given data, The breadth of a cuboid (b) = 12 in The height of a cuboid (h) = 16 in The lateral surface area = 960 square inches We know that, Lateral surface area of a cuboid = 2h(l + b) ⇒ 2 × 16 (l + 12) = 960 ⇒ 32 (l + 12) = 960 ⇒ (l + 12) = 960/32 = 30 ⇒ l = 30 – 12 = 18 in We have, Total surface area of a cuboid = 2 (lb + bh + lh) = 2 [(18 × 12) + (12 × 16) + (18 × 16)] = 2 [ 216 + 192 + 288] = 2 × [696] = 1398 square inches Hence, the length and the total surface area of the cuboid are 18 in and 1398 sq. in, respectively.

Example 5: Calculate the total surface area of a cuboid if its length, breadth, and height are 10 in, 5 in, and 8 in, respectively.

Given data, The length of a cuboid (l) = 10 in The breadth of a cuboid (b) = 5 in The height of a cuboid (h) = 8 in We have, Total surface area of a cuboid = 2 (lb + bh + lh) = 2 [(10 × 5) + (5 × 8) + (10 × 8)] = 2 × [50 + 40 + 80] = 2 × (170) = 340 sq. in Hence, the total surface area of the given cuboid is 340 sq. in.

Example 6: Determine the lateral and total surface areas of a cuboid whose length, breadth, and height are 21 cm, 16 cm, and 18 cm, respectively.

Given data, The length of a cuboid (l) = 21 cm The breadth of a cuboid (b) = 16 cm The height of a cuboid (h) = 18 cm We have, Lateral surface area of a cuboid = 2h(l + b) = 2 × 18 (21 + 16) = 36 × 37 = 1332 sq. cm Total surface area of a cuboid = 2 (lb + bh + lh) = 2 [(21 × 16) + (16 × 18) + (21 × 18)] = 2 [336 + 288+ 378] = 2 × 1002 = 2004 sq. cm Therefore, the lateral surface area and the total surface area of a cuboid are 1332 sq. cm and 2004 sq. cm, respectively.

FAQs on Surface Area of a Cuboid

Question 1: What is the difference between the total surface area of a cuboid and the lateral surface area of a cuboid?

Difference between the total surface area of cuboid and lateral surface area of cuboid: The total surface area of a cuboid is the sum of all six sides, while the lateral surface area of a cuboid is the sum of only 4 sides of the cuboid; the base and the top side are not involved while solving for the lateral surface area of the cuboid. The formulas for total surface area and lateral surface area are different; they are, Lateral surface area of a cuboid = 2h(l + b) square units and Total surface area of a cuboid = 2 (lb + bh + lh) square units.

Question 2: What do you mean by TSA and LSA of a cuboid?

TSA is short for the total surface area of a cuboid. The total surface area is the sum of all 6 sides. LSA stands for the lateral surface area of the cuboid, and the lateral surface area is the sum of the four sides of the cuboid (base and top are excluded).

Question 3: What is the unit used for the surface area of a cuboid?

The surface area of a cuboid is measured in square units. For example: cm 2 , m 2 , inch 2 , etc.

Question 4: What is the total surface area of a cuboid?

The total surface area of a cuboid is defined as the sum of the area of all sides of a cuboid. A cuboid has 6 sides (4 lateral sides, 1 base, 1 top) and therefore, the sum of the area of all six sides gives the total surface area of a cuboid. The formula for the total surface area of a cuboid is given: TSA = 2 (lb + bh + lh) square units.

Question 5: How to find the lateral surface area of a cuboid?

The lateral surface area of a cuboid is the area of all the lateral sides/surfaces of the cuboid. In order to understand how to find the lateral surface area of a cuboid, let’s take a look at the given steps: Step 1: Observe and note down the dimensions of each size. In case the dimensions have different units, convert them into one unit. Step 2: Use the formula for the total surface area of the cuboid: that is, LSA = 2h(l + b) square units. Step 3: Note down the area contained in proper units.

Question 6: Find the volume and surface area of a cuboid.

The volume of a cuboid is the space occupied by the 3-dimensional cuboid. The formula for the volume of a cuboid is l × b × h cubic units, l is the length, b is the breadth, and h is the height of the cuboid. The surface area of a cuboid is the region covered cuboid in 2-dimensional space. The formula for the surface area of a cuboid is 2 (lb + bh + lh) square units.

Please Login to comment...

Similar reads.

• Math-Concepts
• Maths-Formulas
• Mensuration 3D
• Mathematics
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Surface Area Of A Cuboid

Here we will learn about the surface area of a cuboid and how to calculate it.

There are also volume and surface area of a cuboid worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the surface area of a cuboid?

The surface area of a cuboid is the total area of all of the faces of a cuboid (or rectangular prism).

The 3 dimensions of a cuboid are width, length and height.

Cuboids have three pairs of identical faces – top and bottom, front and back, and left and right.

To work out the total surface area of a cuboid, we need to work out the area of each rectangular face and add them all together.

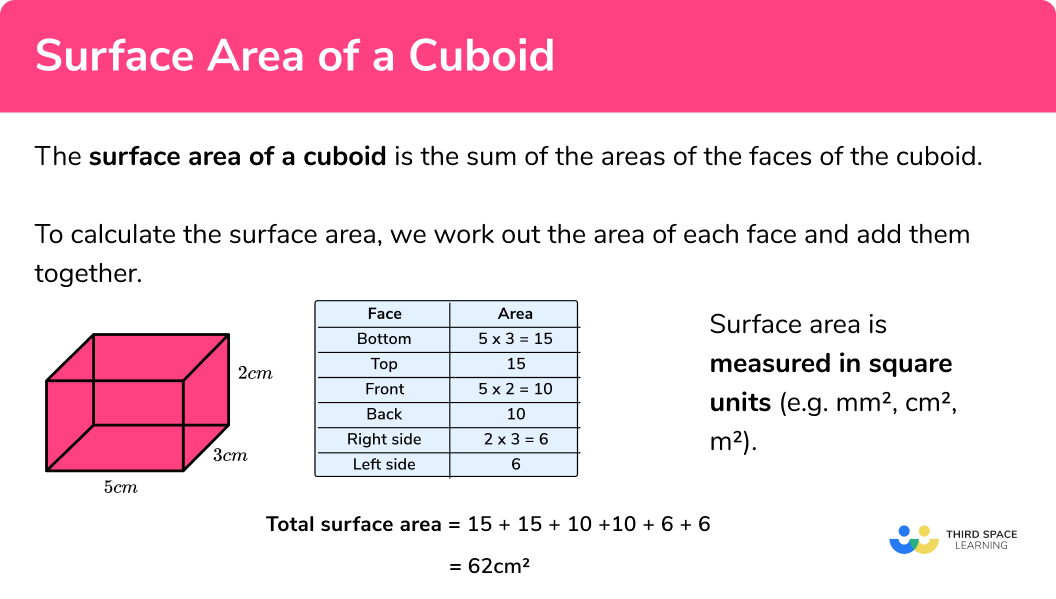
E.g. Find the surface area of a cuboid.

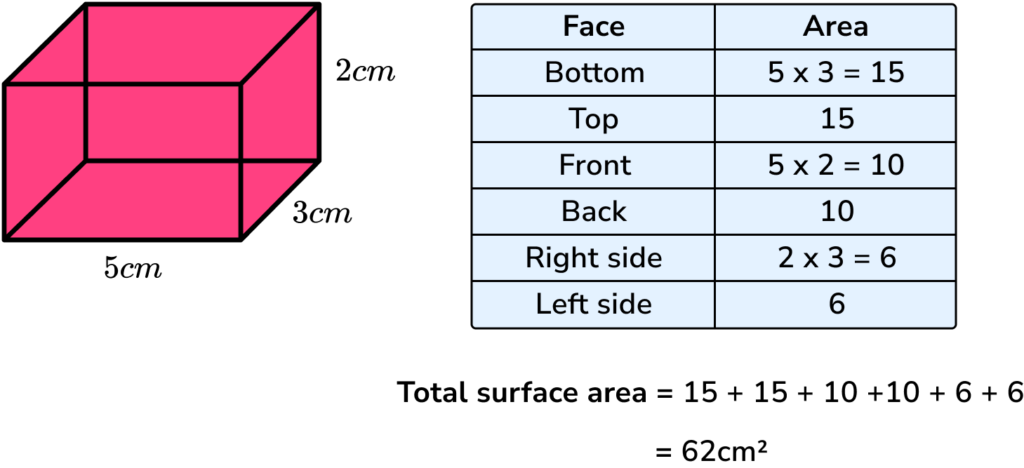
Since it is an area, surface area is measured in square units (e.g. mm^2, cm^2, m^2 etc).

How to calculate the surface area of a cuboid

In order to work out the surface area of a cuboid:

Work out the area of each face.

Add the six areas together.

Include the units.

Surface area of a cuboid worksheet

Get your free surface area of a cuboid worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Surface area of a cuboid examples

Example 1: surface area of a cuboid.

Work out the surface area of the cuboid

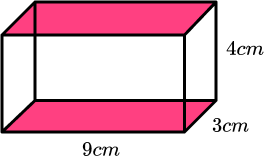
The area of the bottom is 9\times3=27cm^2 .

The top face is the same as the bottom face so the area of the top is also 27cm^2 .

The area of the front is 9\times4=36cm^2 .

The back face is the same as the front face so the area of the back is also 36cm^2 .

The area of the right hand side is 3\times4=12cm^2 .

The left side face is the same as the right side face so the area of the left side is also 12cm^2 .

It will make our working clearer if we use a table:

2 Add the six areas together.

The sum of the areas is: 27+27+36+36+12+12=150

3 Include the units.

The measurements on the cuboid are in cm therefore the total surface area of the cuboid = 150cm^2 .

Example 2: surface area of a cuboid

The measurements on the cuboid are in mm therefore the total surface area of the cuboid = 198mm^2 .

Example 3: surface area of a cube

Work out the surface area of this cube

Each face of a cube is the same. For this cube, the area of each face is 8\times8=64cm^2

The measurements on the cube are in cm therefore the total surface area of the cube = 384cm^2 .

Example 4: surface area with different units

Work out the surface area of this cuboid

Notice that one of the measurements is in metres and the rest are in centimetres. Before we can calculate any areas, we need to ensure all units are the same. In this case, 0.1m=10cm so we can use 10cm .

The measurements we have used are in cm therefore the total surface area = 250cm^2 .

Example 5: surface area using algebra

Work out the surface area of this cuboid.

The measurements we have used are in cm therefore the total surface area = (40x+168) cm^2 .

If we are told the value of the surface area, we can use the expression we have found to work out the value of x .

Let’s say the surface area of this cuboid is 328cm^2 . Then we can say:

40x+168=328 .

Now we can solve this equation:

The width of this cuboid is 4cm .

Example 6: surface area using algebra

The measurements we have used are in m therefore the total surface area = (16y^2+120y) m^2 .

Common misconceptions

• Calculating volume instead of surface area

Volume and surface area are different things – volume is the space within the shape whereas surface area is the total area of the faces. To find surface area, we need to work out the area of each face and add them together.

• Equal faces

A common mistake is to think that four of the faces are equal.

E.g. The first pair of faces are equal to each other. The second pair of faces are equal to each other. The third pair of faces are equal to each other.

Related lessons

Surface area of a cuboid is part of our series of lessons to support revision on cuboid. You may find it helpful to start with the main cuboid lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Volume of a cuboid
• Volume of a cube
• Surface area of a cube

Practice surface area of a cuboid questions

1. Work out the surface area of the cuboid

Work out the area of each of the six faces:

\text{Total surface area: }105+105+45+45+21+21=342\mathrm{cm}^{2}

2. Work out the surface area of this cube

Since it is a cube, all of the faces are the same. The area of each face is 4\times 4=16\mathrm{cm}^{2} . There are six identical faces therefore the total surface area of the cube is 6 \times 16=96 \mathrm{cm}^{2}

3. Work out the surface area of this cuboid

Some of the measurements are in m and one is in cm. We need all of the measurements to be in the same units so convert the metres to centimetres. 0.7m=70cm and 0.4m=40cm . Now we can calculate the areas:

4. Work out the surface area of this cuboid

5. Work out the surface area of the cuboid

6. Given that the surface area of this cuboid is 142\mathrm{cm}^{2} find the value of x .

Since we know the surface area is  142\mathrm{cm}^{2} we can say: 20x+42=142\\ 20x=100\\ x=5\mathrm{cm}

Surface area of a cuboid GCSE questions

1. Calculate the surface area of the cuboid.

Two of: 12\times 3.5=42\\ 12\times 4=48\\ 4\times 3.5=14

2. A breakfast cereal producer wants to produce a cereal box with a volume of 4800cm^3 . The company wants to use as little cardboard as possible for each box. Should they use box A or box B ? You must show your working.

Box A surface area: 160+160+600+600+240+240

Box B surface area: 192+192+480+480+250+250

They should use box B

3. John wants to paint 4 identical doors, as shown below.

1 litre of paint will cover 10\mathrm{m}^{2} John has 1 litre of paint. Does he have enough paint to cover all 4 doors? You must show your working.

Surface area of 1 door: 0.03+0.03+1.2+1.2+0.1+0.1

No he does not have enough paint

Learning checklist

You have now learned how to:

• Calculate the surface area of a cuboid
• Use the properties of faces, surfaces, edges and vertices of cubes and cuboids to solve problems in 3D

The next lessons are

• Volume of a prism
• Volume of a triangular prism
• Pythagoras’ theorem
• Trigonometry

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Cuboid – Definition, Shape, Formulas, Properties, Examples, FAQs

What is a cuboid, properties of a cuboid, cuboid shaped objects around us, solved examples on cuboid, practice problems on cuboid, frequently asked questions about cuboid.

A cuboid is a three-dimensional shape having length, width and height. A cuboid is also called a rectangular prism .

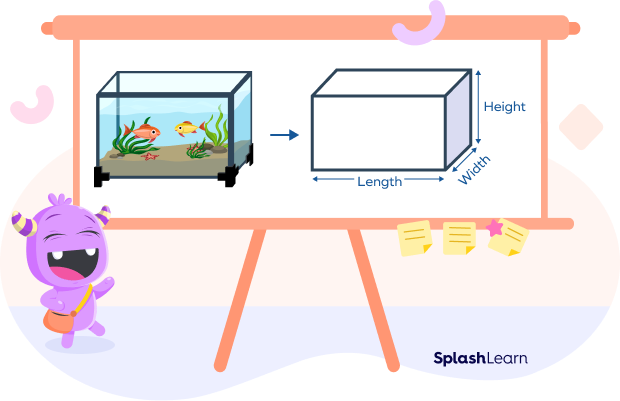
Observe the shape of the fish tank shown here. What is its shape? Can you identify? This is a three-dimensional shape bounded by six rectangular faces. It is called cuboid.

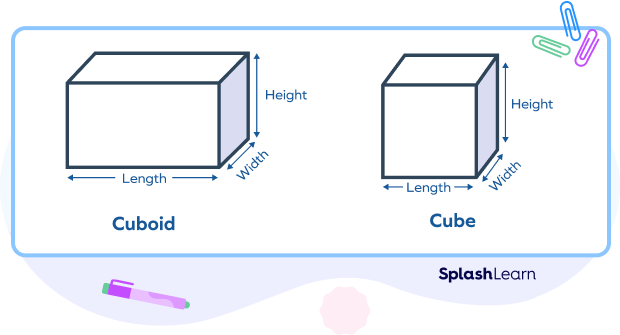
A cube is a special type of cuboid where the length, width and height are all equal.

Cuboid Shape

A cuboid shape is a 3D geometric solid whose each face is a rectangle . The cuboid shape is shown below. 

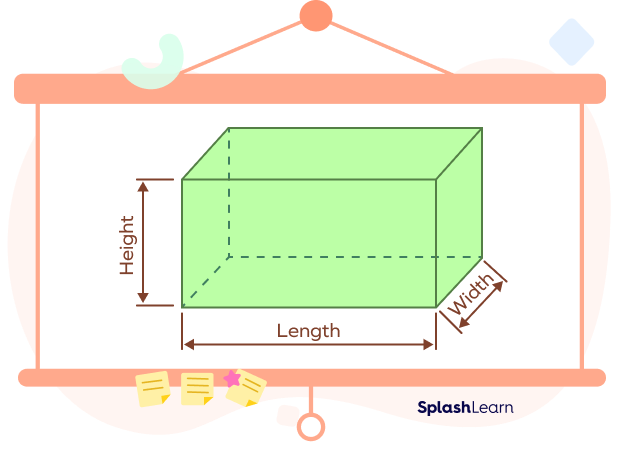
Dimensions of a Cuboid

The cuboid shape is determined by its 3 dimensions . Dimensions of a cuboid include its length, height, and width as shown in the figure.

Faces, Edges, and Vertices of a Cuboid

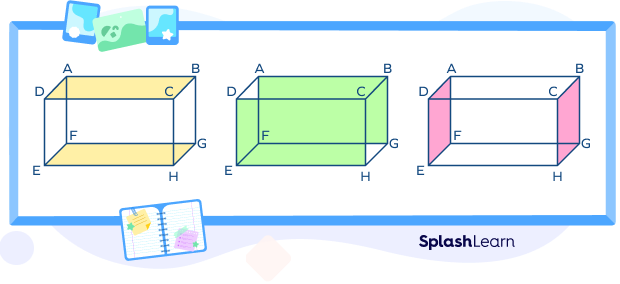
Every geometric solid has a finite number of faces, edges, and vertices. Vertices refer to the corner points. The vertices are joined by the edges. The flat surface bounded by the edges is called the face of a solid. Cuboid has 6 faces, 12 edges, and 8 vertices.

• Faces of a cuboid

Cuboid has 6 faces: 4 lateral, 2 identical faces at the top and bottom. All faces are rectangular in shape. Opposite faces are parallel. 

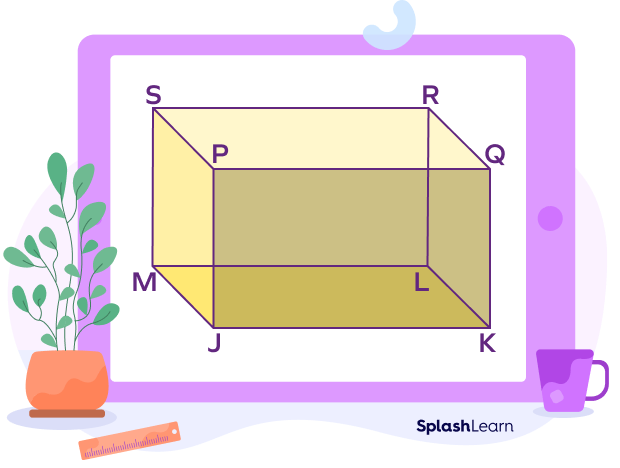
Here, the faces are: ABCD, EFGH, ADEF, BCHG, ABFG and DCHE

The identical faces are ABCD and EFGH; ABFG and DCHE ; ADEF and BCHG.

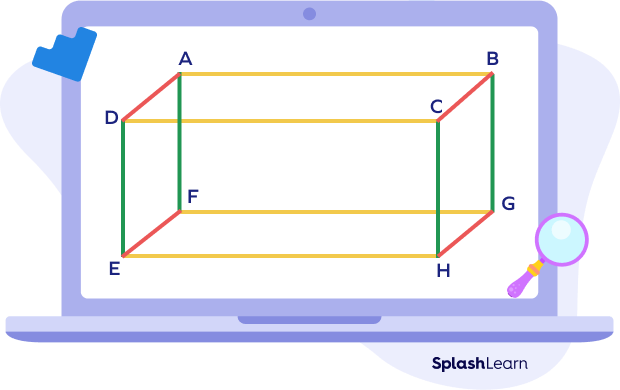
• Edges of a cube

A cuboid has 12 edges. The line segments AB, BC, CD, DA, DE, EF, FG, GH, EH, AF, BG and CH are edges of the given cuboid. 

In cuboid, opposite edges are equal and parallel to each other.

Here, 

AB = CD = EH = FG

AD = EF = GH = CD

And DE = AF = BG = CH

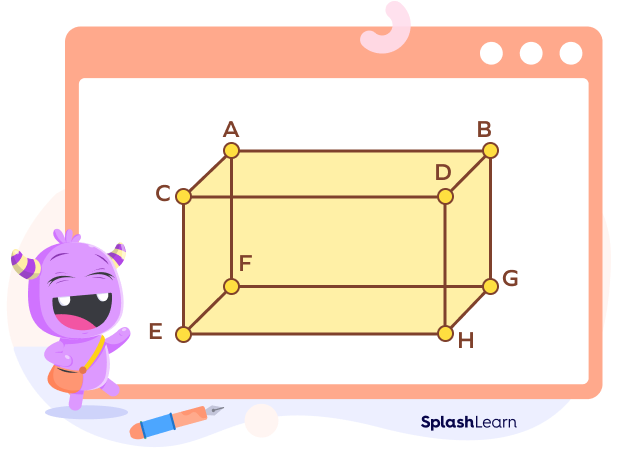
• Vertices of a cuboid

A cuboid has 8 vertices.

Here, the corner points A, B, C, D, E, F, G and H are the vertices of the given cuboid.

• Vertices, Faces, Edges : A cuboid has 6 faces, 8 vertices, and 12 edges.
• A cuboid is a three-dimensional shape; it has length, width, and height.
• All the faces of a cuboid are rectangular in shape.
• All the angles that are formed at the vertices are right angles.
• All the opposite edges of a cuboid are parallel and equal to each other.

Net of a Cuboid

Net of a three-dimensional shape is the 2 dimensional shape we get when we unfold the solid and lay flat. Nets can be folded up to again make the 3D shapes. 

Here,  the view of the cuboid shape helps in identifying the sides that are rectangular in shape. Once the flattened shape is folded back together, the shape of a cuboid is formed. 

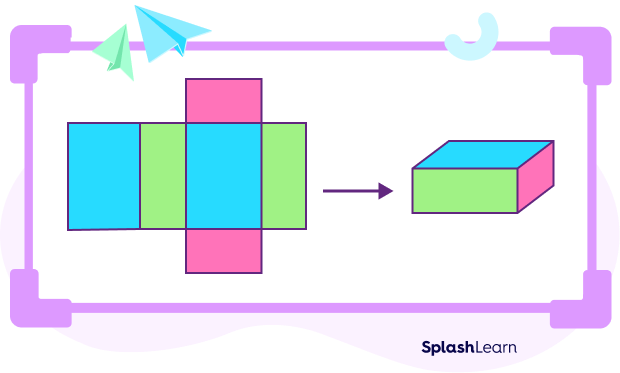
Surface Area of Cuboid

The surface area of a cuboid can be divided into two types.

• Lateral surface area(LSA) of cuboid 

Let l, w, and h be the length, breadth and height of a cuboid respectively.

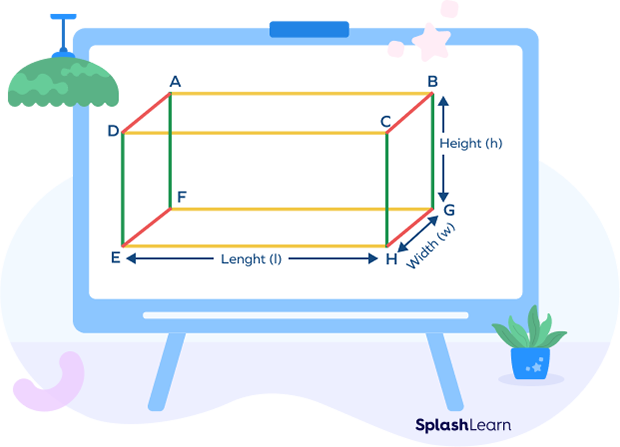
Lateral surface area (LSA) of a cuboid is the sum of areas of its four lateral faces except the top and bottom faces. 

The unit of cuboid Lateral surface area (LSA) is measured in square units. 

The lateral surface area of the cuboid =  Area of face DEHC + Area of face CHGB + Area of face ABGF + Area of face DAFE

LSA of cuboid =  (l × h) + (w × h) + (l × h) + (w × h) square units

LSA of cuboid = 2(l × h) + 2(w × h) square units

LSA of cuboid = 2h(l + w) square units.

• Total surface area of a cuboid:

Total surface area (TSA) of a cuboid = Sum of the areas of all its 6 rectangular faces.

TSA of cuboid = Area of face (ABCD + CDEH + CHGB + ABGF + DAFE)

TSA of cuboid = (l × w) + (l × w) + (w × h) + (w × h) + (l × h) + (l × h) square units        

TSA of cuboid = (2lw + 2wh + 2lh) square units

TSA of cuboid = 2(lw + wh + lh) square units

Volume of a Cuboid

The volume of a cuboid is the space occupied by a cuboid. The volume of the cuboid is equal to the product of the base area (area of the rectangular face) and height. The volume is measured in cubic units . 

Therefore, the formula to calculate the volume of a cuboid is:

Volume = (Length × width) × Height

              = (l × w) × h 

              = lwh 

Diagonals of a Cuboid

There are two types of diagonals in a cuboid:

• Face Diagonals
• Space Diagonals

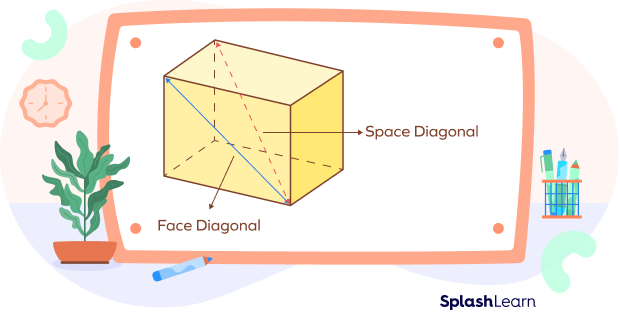
Generally In cuboid, we deal with space diagonal only. For each face there are two face diagonals. The total face diagonals in a cuboid are 6 faces $\times 2 = 12$.

• Formula for space diagonal of cuboid

Diagonal of cuboid whose length is l, width is w and height is h:

Length of space diagonal $= sqrt{l^{2} + w^{2} + h^{2}}$ units

Perimeter of a Cuboid

The perimeter of a cuboid is the sum of the lengths of all the edges. 

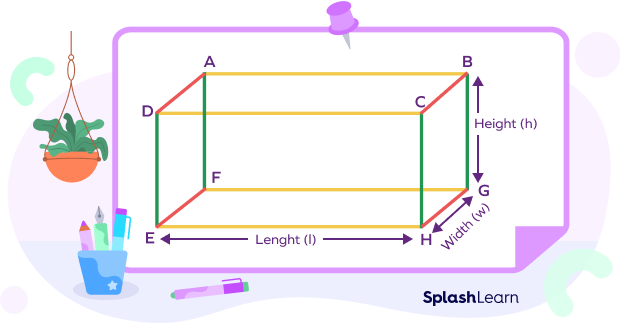
From the given figure, we have

• AB = CD = EH = FG = l (length)
• BC = AD = EF = HG = w (width)
• BG = CH = DE = AF = h (height)

Perimeter of a cuboid = AB + CD + EH + FG + BC + AD + EF + HG + BG + CH + DE + AF

                                      = (l + l + l + l) + (w + w + w + w) + (h + h + h + h) units

                                     = (4l + 4w + 4h) units

                                     = 4(l + w + h) units

Cuboid Formulas Chart

The table below shows the formulas of a cuboid of length (l), width (w) and height (h).

There are many examples of cuboid you can identify in daily life. Take a look at various objects around us that have a cuboid shape!

Facts about Cuboid

• In geometry, a cuboid is a polyhedron. It is a hexahedron, a six-faced solid. 
• A cuboid contains only right angles at their corner points. If there is any other type of angle, then it is not a cuboid.   
• A cuboid is also a prism since it has a rectangular cross-section all the way through. It’s known as a rectangular prism.
• Every cube is also a cuboid, but every cuboid is not a cube.
• By the Euler’s formula the numbers of faces F , of vertices V , and of edges E of any convex polyhedron are related by the formula F + V = E + 2. In the case of a cuboid, this gives 6 + 8  = 12 + 2.
• Euler brick is a rectangular cuboid whose edges and face diagonals have integer lengths. A perfect cuboid is an Euler brick whose space diagonal also has an integer length.

In this article we learnt that a cuboid is a solid three-dimensional shape having length, width and height. It has 6 faces, 12 edges and 8 vertices. Each of its faces is a rectangle. It is also called a rectangular prism. 

Example 1:  Calculate the lateral surface area of a cuboid of dimensions 11 cm × 5 cm × 4 cm.

Solution: Given dimensions of a cuboid are: 11 cm × 5 cm × 4 cm.

Let length(l) = 11 cm, width (w) = 5 cm, height (h) = 4 cm

Lateral surface area (LSA) = 2h(l + w) square units

                                              = 2 × 4 (11 + 4) cm 2                        

                                              = (8 × 15) cm 2 

                                               = 120 cm 2 

Example 2:  Find the total surface area (TSA) of this cuboid.

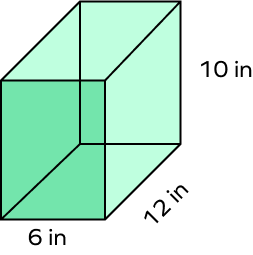
Length (l) = 12 in, width (w) = 6 in, and height (h) = 10 in.

Total surface area of a cuboid = 2(lw + wh + lh) square units.

TSA = 2 {(12 × 6) + (6 × 10) + (12 × 10)} in²                                                                                          

TSA = 2 (72 + 60 + 120) in²

TSA = 2 (252) 

TSA = 504 in²

Therefore, the required total surface area is 504 cm².

Example 3: Find out the volume of a rectangular prism with base length 9 inches, base width 6 inches, and height 18 inches, respectively.

As we know the rectangular prism is a cuboid, we use the formula for the volume of the cuboid.

Length (l) = 9 inches

Width (w) = 6 inches

Height (h) = 18 inches

So, the volume of the given rectangular prism = l × w × h = 9 × 6 × 18 = 972 cubic inches.

  Example 4: Find the length of the diagonal of a cuboid whose dimensions are 4 × 4 × 3 units.

The length of the diagonal of a cuboid formula $= \sqrt{l^{2} + w^{2} + h^{2}}$ units.

Given length (l) = 4 units, width (w) = 4 units and height (h) = 3 units.

Therefore, the length of diagonal $= \sqrt{4^{2} + 4^{2} + 3^{2}}$ units

                                                            $= \sqrt{16 + 16 + 9}$ units

                                                            $= \sqrt{41}$ units

Therefore, the length of the diagonal is $\sqrt{41}$ units.

Example 5: Find the perimeter of a cuboid whose dimensions are 7 m × 4 m × 5 m. 

Solution : 

Length (l) = 7 m, width (w) = 4 m, and height (h) = 5 m

Perimeter of cuboid = 4 (l + w + h)

Perimeter of cuboid = 4 (7 + 4 + 5) m   

P = (4  × 16) m

Cuboid - Definition, Shape, Formulas, Properties, Examples, FAQs

Attend this quiz & Test your knowledge.

What is the lateral surface area of a cuboid whose Length $= 3 \;cm$, Width $= 2 \;cm$ and Height $= 1 \;cm$?

What is the total surface area of a cuboid whose length $= 2\; cm$, width $= 2\; cm$ and height $= 2\; cm$, sarah has a cuboidal box of dimensions $12 \times 7 \times 5$ inches. what is the volume of the box, what is the perimeter of a cuboid whose length $= 4\; cm$, width $= 11\; cm$ and height $= 2\; cm$, find the length of the diagonal of a cuboid whose dimensions are $10 \times 2 \times 4$ units..

How can we define a cuboid?

A cuboid is defined as a three-dimensional shape that has six rectangular faces, eight vertices and twelve edges.

What is the main difference between a cuboid and a cube?

The main difference between a cube and cuboid is that a cube has all square faces and a cuboid has rectangular faces.

What is the difference between a rectangle and a cuboid?

The key difference is that a rectangle is a two-dimensional shape whereas a cuboid is a three-dimensional shape. Hence, a cuboid has an extra dimension, which is its height.

RELATED POSTS

• Union of Sets – Definition, Formula, Examples, Facts, FAQs
• Right Circular Cone – Definition, Properties, Formulas, Examples
• Slide in Maths
• Pythagorean Triples
• Sector of a Circle: Definition, Formula, Area, Perimeter, Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Surface Area of a cuboid – Explanation & Examples

Surface Area of a Cuboid – Explanation & Examples

In geometry, a cuboid is a 3-dimensional figure with a length, width, and height. A cuboid has 6 rectangular faces. Ultimately, a cuboid has the shape of a rectangular prism or a box.

In a cuboid, the horizontal longer side is the length (l), and the shorter horizontal side is the width (w) or breadth (b). The height (h) of a cuboid is the vertical side.

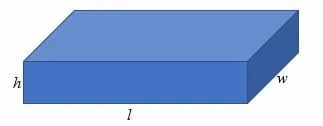
The surface area of a cuboid is the sum of the area of the 6 rectangular faces that cover it.

In this article, we will learn how to find the surface area using a cuboid formula’s surface area.

How to Find the Surface Area of a Cuboid?

To find the surface area of a cuboid, you need to calculate the area of each rectangular face and then sum up all the areas to get the total surface area i.e.

• Area of the top and bottom face = lw+ lw = 2lw
• Area of the front and back face = lh+ lh = 2lh
• Area of the two side faces = wh+ wh = 2wh

The total surface area of a cuboid is equal to the sum of the face areas;

Surface area of cuboid = 2lw + 2lh + 2wh 

Note: The cuboid’s total surface area is not the same as the lateral surface area of a cuboid. The lateral surface of a cuboid is the sum of the area of the rectangular faces excluding the top and bottom face;

Lateral surface area of a cuboid ( LSA ) = 2h (l +b)

Surface area of a cuboid formula

From the above illustration, the formula for the total surface area of a cuboid can be represented as:

Total surface area of a cuboid (TSA) = 2 (lw + wh + lh)

The units for the surface area of a cuboid are square units.

Let’s practice some example problems below.

The dimensions of a cuboid are given as follows:

Length = 5 cm

Width = 3 cm

Height = 4 cm.

Find the total surface area of the cuboid.

By the formula,

Total surface area of a cuboid = 2 (lw + wh + lh)

Substitute.

TSA = 2(5 x 3 + 3 x 4 + 5 x 4)

= 2(15 + 12 + 20)

= 2 x 47 = 94 cm 2

Therefore, the total surface area of the cuboid is 94 cm 2

The surface area of a cuboid is 126 ft 2 . If the cuboid’s length and height are 6 feet and 3 feet, find the width of the cuboid.

Total surface area = 126 ft 2

Length = 6 ft

Height = 3 ft

⇒126 = 2 (lw + wh + lh)

⇒126 = 2 (6w + 3w + 6 x 3)

⇒126 = 2(9w + 18)

⇒126 = 18 w + 36

Subtract by 36 on both sides and then divide by 18

Therefore, the width of the cuboid is 5 feet.

Given the dimensions of a cuboid as:

Length = 10 m

width = 5 width

Height = 9 m

By how much is the total surface area of the cuboid more than the lateral surface area?

Total surface area = 2 (lw + wh + lh)

= 2 (10 x 5 + 5 x 9 + 10 x 9)

= 2(50 + 45 + 90)

TSA = 2 x 185

The lateral surface area of a cuboid = 2h (l + b)

= 2 x 9(10 + 5)

Total surface area – lateral surface area = 370 – 270

Therefore, the total surface area of the cuboid is 100 m 2 more than the lateral surface area.

The length and width of a cardboard are 20 m by 10 m, respectively. How many cuboids can be made from the cardboard if each cuboid must be 4 m long, 3 m wide, and 1 m high.

Area of the cardboard = l x w

Total surface area of the cuboid = 2 (lw + wh + lh)

= 2 (4 x 3 + 3 x 1 + 4 x 1)

= 2 (12 + 3 + 4)

The number of cuboids = area of the cardboard/total surface area of a cuboid

= 200 m/38 m 2

= 5 cuboids

Compare the total surface area of a cube of length 8 cm and a cuboid of length 8 cm, width, 3 cm, and height, 4 cm.

Total surface area of a cube = 6a 2

= 2(8 x 3 + 3 x 4 + 8 x 4)

= 2(24 +12 + 32)

Therefore, the surface area of the cube is more than the surface area of the cuboid.

Practice Questions

Previous lesson  |  main page | next lesson.

Cuboid Calculator

Table of contents

Are you struggling with cuboid calculations? Our cuboid calculator is just the tool you need to help solve those math problems. Keep reading to learn:

• What is a cuboid;
• How to use our cuboid calculator;
• The surface area and volume of a cuboid formula; and
• How to manually calculate the surface area and volume of a cuboid.

What is a cuboid?

A cuboid is a three-dimensional shape that has six rectangular faces. A cuboid's length, width, and height are of different measurements. The corners of these faces form right angles. Cuboids have eight vertices and twelve edges.

How to use our cuboid calculator

Our cuboid calculator calculates the surface area of a cuboid as well as the volume. To calculate either of these two unknowns, you simply need to enter the length ( l ), width ( w ), and height ( h ) of the shape, and the result will be generated in real-time.

As a bonus, you will also be able to see the diagonal of the shape.

How to calculate the volume of a cuboid

To calculate the volume of a cuboid , we use the following formula:

So if we have the following problem: Find the volume of a cuboid whose length is 12 cm, width is 9 cm, and height is 10 cm.

Using the above formula, we can then say:

How to calculate the surface area of a cuboid

We calculate the surface area of a cuboid by finding the sum of the area of its six faces. To calculate the surface area of a cuboid ( SAC ), we use the following formula:

So if we need to find the total surface area of a cuboid whose length is 8 cm , width is 7 cm , and height is 6 cm , using the above, we begin by substituting the values:

Similar calculators?

Are you interested in other similar calculators? Be sure to check out the ones below:

• Rectangular prism calculator ;
• Cuboid surface area calculator ;
• Cuboid volume calculator .

What is the difference between a cube and a cuboid?

The main difference between a cube and a cuboid is that the length, width, and height of a cube are of equal measurements. On the other hand, a cuboid has length, width, and height that are of different sizes.

How do I calculate the volume of a cuboid?

To calculate the volume of a cuboid you need to:

• Get the length, width, and height.
• Put the dimensions into the formula: volume = (l × w × h) cubic unit.
• Do the calculation to find the answer.

© Omni Calculator

Surface area

Diagonal (d)

To use this resource a subscription to Go Teach Maths is required. A subscription gives you access to every resource on the website!

Individual Subscription

School subscription.

• Comprehensive topic coverage
• Over 7000 classroom resources
• GCSE & IGCSE coverage

A subscription to Go Teach Maths gives you access to every resource on the website!

Log in to your individual or school account

Or subscribe from only £25 per year!

Reset your password

Please enter the registered email address for your individual or school subscription.

Surface Area of a Cuboid

Presentations.

Answer Maze

Digit Puzzle

Teacher-Led Activities

Noughts & Crosses

Exam Questions

AQA Foundation

9-1 Foundation

2-Minute Feedback Form

[email protected]

• About Go Teach Maths
• What Do Teachers Say About GTM?
• Terms & Conditions

© Go Teach Maths

Privacy Overview

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Biology

Course: ap®︎/college biology   >   unit 2.

• Scale of cells
• Introduction to cilia, flagella and pseudopodia
• Surface area to volume ratio of cells

Surface area of a box (cuboid)

• Volume of a sphere

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Cubes and Cuboids

A complete lesson with a starter on areas of rectangles. "What's the same and what's different?" to encourage discussion and derive formula for volume of a cuboid. Investigation with an Easter theme included, then surface area of cuboids. Answers included.

CUBE and CUBOID

Sep 26, 2014

760 likes | 2.81k Views

CUBE and CUBOID. To calculate the volume and surface area of cube and cuboid. Created by Cep Andi Alim Subarkah for mathlabsky.wordpress.com. Created by Cep Andi Alim Subarkah for mathlabsky.wordpress.com. CUBE. H. G. F. E. r cm. D. C. r cm. A. B. r cm.

Share Presentation

Presentation Transcript

CUBE and CUBOID To calculate the volume and surface area of cube and cuboid Created by CepAndiAlimSubarkah for mathlabsky.wordpress.com Created by CepAndiAlimSubarkah for mathlabsky.wordpress.com

CUBE H G F E r cm D C r cm A B r cm Example 1 Example 2 Example 3 3

Given the measure edges of a cube is 5cm. Calculate a. The length of diagonal c. The surface area b. The volume Answer: a. L.O.D = r = 5 = = = 8 cm b. Vol = = = = 125 cm3 c. S. A = = = = cm2

Given a cube has length of face diagonal is cm. Calculate a. The volume b. The surface area Answer: L.O.F.D = cm = = : = = 6cm a. Vol= = = = 216 cm3 b. S. A= = = = 216 cm2

Given a cube has surface area is 150cm2 . Calculate a. The length of face diagonal b. The Volume Answer: S. A = 150 cm2 = 150 = 150 : 6 = 25 = = cm a. L.OF.D= = = = cm b. Vol = = = = cm3

CUBOID G H F E h cm D C ) w cm A B l cm Example 1 Example 2 Example 3

Given a cuboid has measurement 6cm x 4cm x 7cm. Calculate: a. Length of diagonal c. The volume b. The surface area Answer: b. S.A = 2(l.w + l.h + w.h) = 2(6x4 + 6x7 + 4x7) = 2(24 + 42 + 28) = 2(94) = 118 cm2 a. L.O.D = = = = c. Vol = l x w x h = 6 x 4 x 7 = 168 cm3

Given a cuboid has measure edges of based is 5cm x 4cm, and the sum of edges is 68 cm. Calculate: a. The volume b. The surface area Answer: a. Vol= l x w x h = 5 x 4 x 8 = 160 cm3 S.O.E = 68 cm 4 (l + w + h) = 68 4 (5 + 4 + h) = 68 4 (9 + h) = 68 9 + h = 68 : 4 = 17 h = 17 – 9 = 8 cm b. S.A= 2(l.w + l.h + w.h) = 2(5x4 + 5x8 + 4x 8) = 2(20 + 40 + 32) = 2 (92) = 184 cm2

Given a cuboid has measure edges of based is 5cm x 8cm, and the surface area is 184cm2. Calculate: a. The volume b. The length of diagonal a. Vol = l x w x h = 5 x 8 x 4 = 160 cm3 Answer: The Surface Area = 184 2(l.w + l.h + w.h) = 184 2(5x8 + 5xh + 8xh) = 184 40 + 5h + 8h = 184 : 2 = 92 13h = 92 – 40 = 52 h = 52 : 13 = 4 cm b. L,O,D = = = = cm

• More by User

Square, root and cube

Square, root and cube This slide show intends to support the teacher in the concept of square numbers, square roots and cubes. It is intended to be used in class with a data projector. Liz Philip. 2 x 2 = 4. 2. 2. 3 x 3 = 9. 3. 3. 4 x 4 = 16. 4. 4. 5 x 5 = 25. 5. 5. 2.

461 views • 13 slides

Cubes and Cube roots

Η. Κ. Σ. Ι. Ε. Ζ. Ω. Φ. Cubes and Cube roots. Γ. Θ. Β. Α. θ. Δ. Contents. Introduction Perfect Cubes Cube root Cube root by prime factorisation Cube root by estimation. introduction.

7.48k views • 14 slides

Cube Printing with a Cube

Cube Printing with a Cube. Using 3D Printers. Produced By- Dave White. Head of D&T Clevedon School. Before you start. Before printing you should ensure that you have… Installed the Cube software Set up the Cube Created an account at Cubify.com Activated at Cubify.com

400 views • 15 slides

Cosmic Cube

Cosmic Cube. Team Lead/Programmer: Kenneth Spradley Lead ECE: Matthew Gibson ECE Assistant: Don Lundi Lead ME: Cole Gray Financial Advisor: Crystal Hill . Presentation Outline . Crystal Hill Project Executive Summary Risk Assessment Schedule Budget Deliverables Don Lundi

622 views • 51 slides

Square and Cube Roots

Square and Cube Roots. Perimeter. The Distance Around Add all the sides For a SQUARE – Multiply the length of the side by 4 (SIDE LENGTH) ∙ 4 Examples. If Perimeter of a SQUARE is Given to You. Divide the Perimeter by 4 Example:

302 views • 10 slides

Cube Roots . Math notebook, calculator & pencil . Last Week. Last week we focused on factoring the square roots of numbers and solving equations with square roots Today, we will be focusing on cube roots. Can any one tell me what a “cube root” is?. Square Roots.

325 views • 8 slides

cube. The cube. Geometry.

264 views • 5 slides

Cubes in a Skeleton Cuboid

Cubes in a Skeleton Cuboid. An Investigation. Here is a picture of a skeleton cuboid that has been made by sticking together a lot of cubes, each of edge 1cm. You can easily check that the base of the skeleton cuboid shown above measures 12cm by 6cm and that the height of the cuboid is 10cm.

217 views • 6 slides

Cubes and Cube Roots

Cubes and Cube Roots. Arithmetic. 5cm. 3cm. Cubes and cube roots ( all measurements will be assumed to be in centimetres ) The volume of the cube shown is 5  5  5 which is 125 cm 3 . What is the volume of this cube ?. 8cm. 4cm. Cubes and cube roots

542 views • 9 slides

Cube. Assignment #2 Programming Language, Spring 2003. Cube. Cube 3 by 3 by 3 cube built of 27 smaller cubes Cube is fallen apart into 7 pieces 7 pieces can be assembled in many ways to again form the cube. Assembled Cube. Representation Linearized form string

496 views • 8 slides

CUBE. Secure VoIP. Outline. Who? CUBE Members Why? Motivation What? Project Description How? Design and Implementation. Outline. Who? CUBE Members Why? Motivation What? Project Description How?

418 views • 21 slides

CUBE and CUBOID. To calculate the sum of edges, length of face/plane diagonal, and diagonal, also area of diagonal plane. Created by Cep Andi Alim Subarkah for mathlabsky.wordpress.com. Created by Cep Andi Alim Subarkah for mathlabsky.wordpress.com. CUBE. H. G. F.

916 views • 13 slides

1. CUBE. Borrow a Mathematics Chart from Mr. Rosas and use the centimeter ruler to measure the perimeter of the figure below to the nearest centimeter. 2. TRIANGLE BASED PYRAMID. The models below represents the length and width of two rectangles. Model K. Model M. = 1 square meter.

230 views • 5 slides

Cube. By Andrea Larry. This is how many faces a cube have in 3-D shape is 4 faces. The number of edges dose a cube have is 12 edges. the number of vertices is 8 total. The number of bases in a cube has 2 bases.

217 views • 5 slides

Cube. By: Shaqwiten Morine. The number of face’s a cube has is {12}. The number of edges a cube has is {12}. The number of vertices a cube has is {8}. The number of bases a cube has is {2}.

219 views • 5 slides

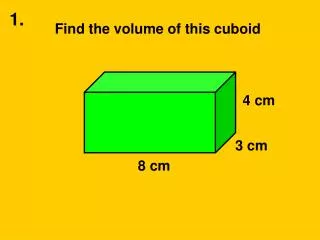
Find the volume of this cuboid

1. Find the volume of this cuboid. 4 cm. 3 cm. 8 cm. 2. Find the area. 5 cm. 3. Work out 437 x 24. 4. Find the HCF of 90 and 135. 5. Find the LCM of 90 and 135. 6. Find the missing side. 5 cm. 3 cm. 7. Find the volume. 7 cm. 6 cm. 3 cm. 10 cm. 8. Write 80% as a fraction

712 views • 10 slides

Cube Materialization: Full Cube, Iceberg Cube, Closed Cube, and Shell Cube

Cube Materialization: Full Cube, Iceberg Cube, Closed Cube, and Shell Cube. Introducing iceberg cubes will lessen the burden of computing trivial aggregate cells in a data cube. However, we could still end up with a large number of uninteresting cells to compute.

1.01k views • 62 slides

Simple Squamous & cuboid Epithelia

Simple Squamous & cuboid Epithelia. Simple columnar/ciliated Epithelia. Pseudo stratified columnar ciliated epithelia. Stratified squamous keratinised. Stratified squamous non keratinised. Transitional epithelia. Points of identification. Simple Squamous Epithelia

113 views • 9 slides

Volume Cube & Cuboid

Volume. Volume Cube & Cuboid. Volume of a Prism. Volume of a Cylinder. www.mathsrevision.com. Capacity. Starter Questions. 10cm. Q1. Find the area of the triangle. 3cm. 4cm. Q2. Expand out and simplify 2w 2 – 3(2w – 5). www.mathsrevision.com. Q3. True or false.

806 views • 34 slides

Presentation on Volume of Cuboid and Cube

177 views • 6 slides

• International
• Schools directory
• Resources Jobs Schools directory News Search

Volume and Surface Area of a Cuboid

Subject: Mathematics

Age range: 14-16

Resource type: Lesson (complete)

Last updated

7 September 2020

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Creative Commons "Attribution"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

ElizabethMaryElliott

Gorgeous! Clear and complete, thank you !

Empty reply does not make any sense for the end user

jellybaby 1

If the PP already had worksheet ready to go with space for working out. Perhaps link this to density and volume?

Great resource - thank you<br />

one of the few lessons on TES I have not felt the need to edit before delivering! amazing!

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource: