unit analysis method of problem solving

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

1.7: Problem Solving Process

Last updated
Save as PDF
Page ID 91453

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Learning how to use a structured problem solving process will help you to be more organized and support your future courses. Also, it will train your brain how to approach problems. Just like basketball players practice jump shots over and over to train their body how to act in high pressure scenarios, if you are comfortable and familiar with a structured problem solving process, when you’re in a high pressure situation like a test, you can just jump into the problem like muscle memory.

6 Step Problem Solving Method:

Write out the answer with all necessary information that is given to you. It feels like it takes forever, but it’s important to have the problem and solution next to each other.
Draw the problem, this is usually a free-body diagram (don’t forget a coordinate frame). Eventually, as you get further into the course, you might need a few drawings. One would be a quick sketch of the problem in the real world, then modelling it into a simplified engineering drawing, and finally the free-body diagram.
Write out a list of the known/given values with the variable and unit, i.e m = 14 kg (variable = number unit)
Write out a list of the unknown values that you will have to solve for in order to solve the problem
You can also add any assumptions you made here that change the problem.
Also state any constants, i.e. g = 32.2 ft/m 2 or g = 9.81 m/s 2
This step helps you to have all of the information in one place when you solve the problem. It’s also important because each number should include units, so you can see if the units match or if you need to convert some numbers so they are all in English or SI. This also gives you the variables side by side to ensure they are unique (so you don’t accidentally have 2 ‘d’ variables and can rename one with a subscript).
Write a simple sentence or phrase explaining what method/approach you will be using to solve the problem.
For example: ‘use method of joints’, or equilibrium equations for a rigid body, MMOI for a certain shape, etc.
This is going to be more important when you get to the later chapters and especially next semester in Dynamics where you can solve the same problem many ways. Might as well practice now!
This is the actual solving step. This is where you show all the work you have done to solve the problem.
When you get an answer, restate the variable you are solving for, include the unit, and put a box around the answer.
Write a simple sentence explaining why (or why not) your answer makes sense. Use logic and common sense for this step.
When possible, use a second quick numerical analysis to verify your answer. This is the “gut check” to do a quick calculation to ensure your answer is reasonable.
This is the most confusing step as students often don’t know what to put here and up just writing ‘The number looks reasonable’. This step is vitally important to help you learn how to think about your answer. What does that number mean? What is it close to? For example, if you find that x = 4000 m, that’s a very large distance! In the review, I would say, ‘the object is 4 km long which is reasonable for a long bridge’. See how this is compared to something similar? Or you could do a second calculation to verify the number is correct, such as adding up multiple parts of the problem to confirm the total length is accurate i.e. ‘x + y + z = total, yes it works!’

Additional notes for this course:

It’s important to include the number and label the steps so it’s clear what you’re doing, as shown in the example below.
It’s okay if you make mistakes, just put a line through it and keep going.
Remember your header should include your name, the page number, total number of pages, the course number, and the assignment number. If a problem spans a number of pages, you should include it in the header too.

Key Takeaways

Basically: Use a 6-step structured problem solving process: 1. Problem, 2. Draw, 3. Known & Unknown, 4. Approach, 5. Analysis (Solve), 6. Review

Application: In your future job there is likely a structure for analysis reports that will be used. Each company has a different approach, but most have a standard that should be followed. This is good practice.

Looking ahead: This will be part of every homework assignment.

Written by Gayla & Libby

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

2: Units, Dimensional Analysis, Problem Solving, and Estimation

Last updated
Save as PDF
Page ID 24430

Peter Dourmashkin
Massachusetts Institute of Technology via MIT OpenCourseWare

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

But we must not forget that all things in the world are connected with one another and depend on one another, and that we ourselves and all our thoughts are also a part of nature. It is utterly beyond our power to measure the changes of things by time. Quite the contrary, time is an abstraction, at which we arrive by means of the change of things; made because we are not restricted to any one definite measure, all being interconnected. A motion is termed uniform in which equal increments of space described correspond to equal increments of space described by some motion with which we form a comparison, as the rotation of the earth. A motion may, with respect to another motion, be uniform. But the question whether a motion is in itself uniform, is senseless. With just as little justice, also, may we speak of an “absolute time” --- of a time independent of change. This absolute time can be measured by comparison with no motion; it has therefore neither a practical nor a scientific value; and no one is justified in saying that he knows aught about it. It is an idle metaphysical conception [1] - Ernst Mach

2.1: The Speed of light
2.2: International System of Units The system of units most commonly used throughout science and technology today is the Système International (SI).
2.3: Dimensions of Commonly Encountered Quantities Many physical quantities are derived from the base quantities by a set of algebraic relations defining the physical relation between these quantities. The dimension of the derived quantity is written as a power of the dimensions of the base quantities.
2.4: Order of Magnitude Estimates - Fermi Problems Counting is the first mathematical skill we learn. We came to use this skill by distinguishing elements into groups of similar objects, but counting becomes problematic when our desired objects are not easily identified, or there are too many to count. Rather than spending a huge amount of effort to attempt an exact count, we can try to estimate the number of objects.

[1] E. Mach, The Science of Mechanics, translated by Thomas J. McCormack, Open Court Publishing Company, La Salle, Illinois, 1960, p. 273.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

2.3: Scientific Dimensional Analysis

Last updated
Save as PDF
Page ID 74086

Allison Soult
University of Kentucky

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Learning Outcomes

Convert values among units.
Use dimensional analysis to solve problems.

Dimensional analysis (also called factor label method or unit analysis) is used to convert from one set of units to another. This method is used for both simple (feet to inches) and complex ($\text{g/cm}^3$ to $\text{kg}$/gallon) conversions and uses relationships or conversion factors between different sets of units. While the terms are frequently used interchangeably, conversion factors and relationships are different. Conversion factors are quantities that are equal to one another, such as $100 \: \text{cm} = 1 \: \text{m}$, in which both values describe a length. Relationships are between two values that are not necessarily a measure of the same quantity. For example, the density of water is $1.00 \: \text{g/mL}$. Grams are a measure of mass while milliliters measure volume so this is considered a relationship rather than a conversion factor. Either way, we depend on units to help set up and solve the calculation. We will see additional examples of relationships as we explore other details about chemical substance.

Importance of using Correct Conversions

In healthcare professions, a calculation error can quite literally have a life or death consequence. Read the short article, Med-Math Errors and the Nursing Student at http://www.alysion.org/dimensional/matherrors.htm , to better understand the importance of units and correct calculations.

Conversion Factors

Many quantities can be expressed in several different ways. The English system measurement of 4 cups is also equal to 2 pints, 1 quart, and $\ce{1/4}$ of a gallon. $4 \: \text{cups} = 2 \: \text{pints} = 1 \: \text{quart} = 0.25 \: \text{gallon}$. Notice that the numerical component of each quantity is different, while the actual amount of material that it represents is the same. That is because the units are different. We can establish the same set of equalities for the metric system: $1 \: \text{meter} = 10 \: \text{decimeters} = 100 \: \text{centimeters} = 1000 \: \text{millimeters}$. The metric system's use of powers of 10 for all conversions makes this quite simple. We can write conversion factors between any pair of equivalent quantities. In each conversion factor, the numerator and denominator represent equal quantities so they are all valid conversion factors. Additionally, these conversion factors can be inverted or used in combination with other conversion factors in a dimensional analysis problem.

\[ \dfrac{\text{4 cups}}{\text{2 pints}} =\dfrac{\text{1 quart}}{\text{4 cups}} = \dfrac{\text{0.25 gallen}}{\text{1 quarter}}=1 \nonumber\]

\[ \dfrac{\text{1 meter}}{\text{10 decimeters}} =\dfrac{\text{100 centimeters}}{\text{1000 milimeters}} = \dfrac{\text{1000 milimeters}}{\text{1 meter}}=1 \nonumber\]

Example $\PageIndex{1}$

How many centimeters are in $3.4 \: \text{m}$?

This problem requires the conversion from one unit to another so we can use dimensional analysis to solve the problem. We need to identify the units that are given $\left( \text{m} \right)$, the units for the answer $\left( \text{cm} \right)$, and any relationships that relate the units of the known and unknown values. In this case, we will use the relationship of $1 \: \text{m} = 100 \: \text{cm}$. Start with the known value and its unit.

\[3.4 \: \text{m} \times \dfrac{?}{?} \nonumber\]

Then, we look at the units of our relationship to see which value goes in the numerator and which value goes in the denominator. Remember, we are trying to find the value in centimeters. Since our known value is in units of meters, we need meters to be in the denominator so that it will cancel. As a result, centimeters will be in the numerator.

\[3.4 \: \text{m} \times \dfrac{100 \: \text{cm}}{1 \: \text{m}} \nonumber\]

Note that the numbers stay with the appropriate unit (100 with centimeters and 1 with meters). Now, the meters will cancel out and we are left with units of centimeters. Always check that your problem is set up completely and that your units cancel correctly before you do the actual calculation.

\[\begin{align*}3.4 \: \cancel{\text{m}} \times \dfrac{100 \: \text{cm}}{1 \: \cancel{\text{m}}} &= 340 \: \text{cm} \\[5pt] &= 3.4 \times 10^2 \: \text{cm} \end{align*}\]

We find the answer to be $340 \: \text{cm}$ or $3.4 \times 10^2 \: \text{cm}$.

Derived Units

Using dimensional analysis with derived units requires special care. When units are squared or cubed as with area or volume, the conversion factors themselves must also be squared or cubed. Two convenient volume units are the liter, which is equal to a cubic decimeter, and the milliliters, which is equal to a cubic centimeter. There are thus $1000 \: \text{cm}^3$ in $1 \: \text{dm}^3$, which is the same thing as saying there are $1000 \: \text{mL}$ in $1 \: \text{L}$. The conversion factor of $1 \: \text{cm}^3 = 1 \: \text{mL}$ is a very useful conversion.

There are $1000 \: \text{cm}^3$ in $1 \: \text{dm}^3$. Since a $\text{cm}^3$ is equal to a $\text{mL}$, and a $\text{dm}^3$ is equal to a $\text{L}$, we can say that there are $1000 \: \text{mL}$ in $1 \: \text{L}$.

Example $\PageIndex{2}$

Convert $3.6 \: \text{mm}^3$ to $\text{mL}$.

Determine the units of the known value $\left( \text{mm}^3 \right)$ and the units of the unknown value $\left( \text{mL} \right)$. The starting and ending units will help guide the setup of the problem. Next, list any known conversion factors that might be helpful.

$1 \: \text{m} = 1000 \: \text{mm}$
$1 \: \text{mL} = 1 \: \text{cm}^3$
$1 \: \text{m} = 100 \: \text{cm}$

Now, we can set up the problem to find the value in units of $\text{mL}$. Once we know the starting units, we can then use the conversion factors to find the answer.

\[3.6 \: \text{mm}^3 \times \left( \dfrac{?}{?} \right) \nonumber\]

Continue to use the conversion factors between the units to set up the rest of the problem. Note that all of the units cancel except $\text{mL}$, which are the requested units for the answer. Since the values in these conversion factors are exact numbers, they will not affect the number of significant figures in the answer. Only the original value (3.6) will be considered in determining significant figures.

\[3.6 \: \text{mm}^3 \times \left( \dfrac{1 \: \text{m}}{1000 \: \text{mm}} \right)^3 \times \left( \dfrac{?}{?} \right) \nonumber\]

Once you have solved the problem, always ask if the answer seems reasonable. Remember, a millimeter is very small and a cubic millimeter is also very small. Therefore, we would expect a small volume which means $0.0036 \: \text{mL}$ is reasonable.

If you find that you forgot to cube numbers as well as units, you can setup the problem in an expanded form which is the equivalent to the previous method to cube the numerical values.

Contributors and Attributions

Allison Soult , Ph.D. (Department of Chemistry, University of Kentucky)

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Join the 150,000+ facilitators  using SessionLab.

How do you identify problems?

How do you identify the right solution.

Tips for more effective problem-solving

Complete problem-solving methods

Problem-solving techniques to identify and analyze problems
Problem-solving techniques for developing solutions

Problem-solving warm-up activities

Closing activities for a problem-solving process.

Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve.

Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward.

Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.

Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.

Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.

With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.

Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.

After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!

Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.

Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.

In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.

The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!

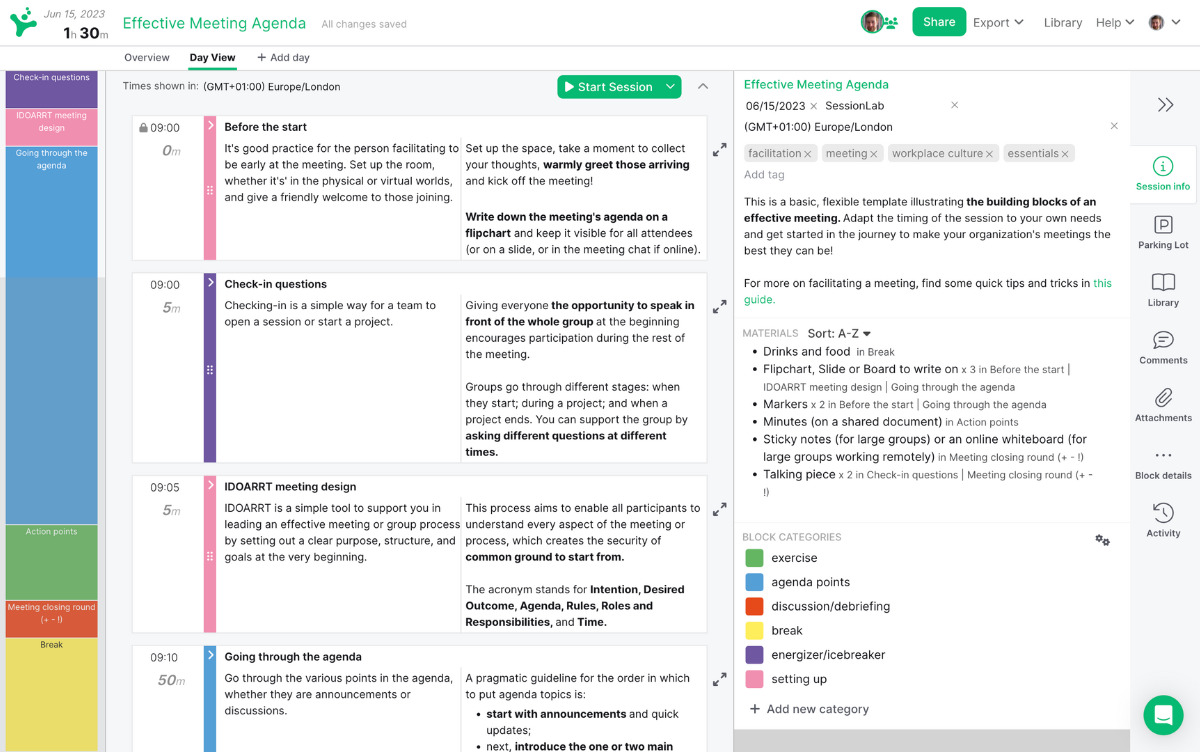
Tips for more effective problem solving

Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.

Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!

Clearly define the problem

Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.

This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.

Don’t jump to conclusions

It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.

The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.

Try different approaches

Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.

Don’t take it personally

Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.

You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.

Get the right people in the room

Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!

If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.

Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.

Document everything

The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!

Bring a facilitator

Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!

Develop your problem-solving skills

It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.

You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!

Design a great agenda

Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.

Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!

In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.

If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.

Six Thinking Hats
Lightning Decision Jam
Problem Definition Process
Discovery & Action Dialogue

Design Sprint 2.0

Open Space Technology

1. Six Thinking Hats

Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.

Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.

Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.

2. Lightning Decision Jam

Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.

Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.

In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.

From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on.

By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages.

Lightning Decision Jam (LDJ) #action #decision making #problem solving #issue analysis #innovation #design #remote-friendly The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow

3. Problem Definition Process

While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design.

By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.

Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.

This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!

Problem Definition #problem solving #idea generation #creativity #online #remote-friendly A problem solving technique to define a problem, challenge or opportunity and to generate ideas.

4. The 5 Whys

Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges.

The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results.

By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.

The 5 Whys #hyperisland #innovation This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.

5. World Cafe

World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.

World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!

Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold.

World Cafe #hyperisland #innovation #issue analysis World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.

6. Discovery & Action Dialogue (DAD)

One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.

With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!

This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.

Discovery & Action Dialogue (DAD) #idea generation #liberating structures #action #issue analysis #remote-friendly DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.

7. Design Sprint 2.0

Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.

Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.

Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.

8. Open space technology

Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.

Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.

Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!

Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.

Open Space Technology #action plan #idea generation #problem solving #issue analysis #large group #online #remote-friendly Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation

Techniques to identify and analyze problems

Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.

While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.

We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.

Let’s take a look!

The Creativity Dice
Fishbone Analysis
Problem Tree
SWOT Analysis
Agreement-Certainty Matrix
The Journalistic Six
LEGO Challenge
What, So What, Now What?
Journalists

Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?

Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed.

Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.

No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.

Flip It! #gamestorming #problem solving #action Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.

10. The Creativity Dice

One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed.

In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.

Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable.

The Creativity Dice #creativity #problem solving #thiagi #issue analysis Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.

11. Fishbone Analysis

Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.

Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around.

Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish.

Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.

Fishbone Analysis #problem solving ##root cause analysis #decision making #online facilitation A process to help identify and understand the origins of problems, issues or observations.

12. Problem Tree

Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them.

In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.

Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.

Problem tree #define intentions #create #design #issue analysis A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.

13. SWOT Analysis

Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.

Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.

Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward.

SWOT analysis #gamestorming #problem solving #action #meeting facilitation The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.

14. Agreement-Certainty Matrix

Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.

The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results.

If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause.

Agreement-Certainty Matrix #issue analysis #liberating structures #problem solving You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic . A problem is simple when it can be solved reliably with practices that are easy to duplicate. It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably. A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail. Chaotic is when the context is too turbulent to identify a path forward. A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.” The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.

Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process.

Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.

It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.

SQUID #gamestorming #project planning #issue analysis #problem solving When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.

16. Speed Boat

To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.

Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.

In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!

Speed Boat #gamestorming #problem solving #action Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.

17. The Journalistic Six

Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.

Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.

The Journalistic Six – Who What When Where Why How #idea generation #issue analysis #problem solving #online #creative thinking #remote-friendly A questioning method for generating, explaining, investigating ideas.

18. LEGO Challenge

Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills.

The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.

What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO!

LEGO Challenge #hyperisland #team A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.

19. What, So What, Now What?

If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.

The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems.

Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.

Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken.

This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.

W³ – What, So What, Now What? #issue analysis #innovation #liberating structures You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!

20. Journalists

Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.

Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.

In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.

Journalists #vision #big picture #issue analysis #remote-friendly This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.

Problem-solving techniques for developing solutions

The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.

Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.

Improved Solutions
Four-Step Sketch
15% Solutions
How-Now-Wow matrix
Impact Effort Matrix

21. Mindspin

Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly.

With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation.

This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex.

MindSpin #teampedia #idea generation #problem solving #action A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.

22. Improved Solutions

After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result.

One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution.

Improved Solutions #creativity #thiagi #problem solving #action #team You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.

23. Four Step Sketch

Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged.

By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.

Four-Step Sketch #design sprint #innovation #idea generation #remote-friendly The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper, Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint

24. 15% Solutions

Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change.

Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.

Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.

It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change.

15% Solutions #action #liberating structures #remote-friendly You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference. 15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change. With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.

25. How-Now-Wow Matrix

The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process.

When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.

Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud.

How-Now-Wow Matrix #gamestorming #idea generation #remote-friendly When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.

26. Impact and Effort Matrix

All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice.

The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.

Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them.

Impact and Effort Matrix #gamestorming #decision making #action #remote-friendly In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.

27. Dotmocracy

If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action?

Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus.

One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively.

Dotmocracy #action #decision making #group prioritization #hyperisland #remote-friendly Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.

All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.

Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.

Check-in/Check-out
Doodling Together
Show and Tell
Constellations
Draw a Tree

28. Check-in / Check-out

Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.

Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute.

If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!

Check-in / Check-out #team #opening #closing #hyperisland #remote-friendly Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.

29. Doodling Together

Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start.

Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems.

Doodling Together #collaboration #creativity #teamwork #fun #team #visual methods #energiser #icebreaker #remote-friendly Create wild, weird and often funny postcards together & establish a group’s creative confidence.

30. Show and Tell

You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.

Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.

By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team!

Show and Tell #gamestorming #action #opening #meeting facilitation Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.

31. Constellations

Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.

Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible.

Constellations #trust #connection #opening #coaching #patterns #system Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.

32. Draw a Tree

Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.

Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic.

Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.

All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.

Draw a Tree #thiagi #opening #perspectives #remote-friendly With this game you can raise awarness about being more mindful, and aware of the environment we live in.

Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.

Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.

One Breath Feedback
Who What When Matrix
Response Cards

How do I conclude a problem-solving process?

All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.

At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space.

The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.

Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.

33. One Breath Feedback

Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round.

One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them.

One breath feedback #closing #feedback #action This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.

34. Who What When Matrix

Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.

The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward.

Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved.

Who/What/When Matrix #gamestorming #action #project planning With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.

35. Response cards

Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out!

Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.

Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised.

Response Cards #debriefing #closing #structured sharing #questions and answers #thiagi #action It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.

Save time and effort discovering the right solutions

A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?

With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks to build your agenda. When you make changes or update your agenda, your session timing adjusts automatically , saving you time on manual adjustments.

Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.

Explore how to use SessionLab to design effective problem solving workshops or watch this five minute video to see the planner in action!

Over to you

The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.

Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you!

thank you very much for these excellent techniques

Certainly wonderful article, very detailed. Shared!

Your list of techniques for problem solving can be helpfully extended by adding TRIZ to the list of techniques. TRIZ has 40 problem solving techniques derived from methods inventros and patent holders used to get new patents. About 10-12 are general approaches. many organization sponsor classes in TRIZ that are used to solve business problems or general organiztational problems. You can take a look at TRIZ and dwonload a free internet booklet to see if you feel it shound be included per your selection process.

Design your next workshop with SessionLab

Join the 150,000 facilitators using SessionLab

Become a math whiz with AI Tutoring, Practice Questions & more.

Unit Analysis

Unit analysis means using the rules of multiplying and reducing fractions to solve problems involving different units.

A desk is 4 1 2 feet long. Find the length of the desk in inches.

There are 12 inches in 1 foot. Write this relationship as a fraction, and multiply it by the given length.

4 1 2 ft × 12 in 1 ft = 9 ft 2 × 12 in 1 ft

= 9 ft × 12 in 2 × 1 ft

= 108 in 2

= 54 in

Note that you can cancel the unit "ft" just as though it were a number being multiplied.

A car can drive 80 miles on $ 6 worth of gasoline. If 1 gallon of gasoline costs $ 2.50 , find how far the car can travel in kilometers on 1 liter of gasoline.

To solve this problem you need to know some conversions.

1 kilometer ( km ) ≈ 0.62 miles ( mi )

1 gallon ( gal ) ≈ 3.79 liters ( L )

Write all the conversions as fractions, so that the unwanted units will cancel.

80 mi $ 6 × $ 2.50 1 gal × 1 gal 3.79 L × 1 km 0.62 mi

= 80 mi × $ 2 .50 × 1 gal × 1 km $ 6 × 1 gal × 3.79 L × 0.62 mi

= 200 km 14.0988 L

≈ 14.2 km / L

9th Grade Writing Tutors
Arizona Bar Exam Test Prep
AWS Certification - Amazon Web Services Certification Training
Fortran Tutors
Actuarial Exam P Test Prep
CCI - Cardiovascular Credentialing International Tutors
Insurance License Test Prep
OAT Test Prep
SAT Subject Test in Biology E/M Test Prep
Google Cloud Certified - Professional Cloud Architect Courses & Classes
HSPT Tutors
CBEST - The California Basic Educational Skills Test Test Prep
SAT Subject Test in Modern Hebrew Tutors
California Proficiency Program (CPP) Test Prep
CMT - Chartered Market Technician Test Prep
Delaware Bar Exam Courses & Classes
Washington Bar Exam Courses & Classes
Image Editing Tutors
Alabama Bar Exam Courses & Classes
CGEIT - Certified in the Governance of Enterprise IT Courses & Classes
Las Vegas Tutoring
Miami Tutoring
Ann Arbor Tutoring
Virginia Beach Tutoring
Detroit Tutoring
Tulsa Tutoring
Indianapolis Tutoring
Sacramento Tutoring
San Diego Tutoring
Jacksonville Tutoring
Algebra Tutors in Philadelphia
Reading Tutors in Houston
Spanish Tutors in Washington DC
Computer Science Tutors in Chicago
SSAT Tutors in New York City
MCAT Tutors in San Diego
Algebra Tutors in Los Angeles
GMAT Tutors in Los Angeles
GMAT Tutors in Boston
Biology Tutors in Miami

Unit Analysis Problem Solving:

Corwin's text: chapter 2 section 2.9, sample problems.

Problem 1 If the sun is 93,000,000 miles from the Earth, how many kilometers is the distance? (Given: One mile equals 1.61 kilometers.)

Problem 2 If the sun is 93,000,000 miles from the Earth, how many minutes does it take for sunlight to reach the Earth? (Given: The velocity of light is 186,000 miles per second.)

Problem 3 Find the mass in grains of a 325 milligram aspirin tablet. (Given: 1.00 g = 15.4 grains)

Problem 4 Insurance statistics state that a person loses 8 minutes of average life for each cigarette smoked. If there are 20 cigarettes in a pack and the average cost of cigarette is $5.00 per pack over the next 25 years, how many years of average life would a person lose for smoking 1.5 packs a day for 25 years?

Problem 5 What is the density of water in lb/ft 3 , if the density of water at 25 o C is 1.00 g/ml? [Hint: There are 2.54 cm = 1 in (or 16.48 cm 3 = 1 in 3 ); 454 g = 1 lb ]

Problem 6 Calculate the velocity of a car traveling car traveling 65 miles/hr in ft/sec.

Problem 7 How many milligrams does a 0.750 carat diamond weigh? (Hint: 1 carat = 0.200 g)

Problem 8 Diamond has a density of 3.513 g/cm 3 . The mass of a diamond is often measured in carats, 1 carat equaling 0.200 g. What is the volume of a 1.50 carat diamond?

Problem 9 Liquor used to be sold in fifths. A fifth is one fifth of a gallon. A gallon is 128 fluid ounces. Today liquor is sold in bottle sizes of 750 ml to equate to the old fifth. If there are 946 ml in a quart, calculate the number of milliliters in a fifth. How many milliliters difference is there in the bottling?

The True Story On July 23, 1983, Air Canada Flight 143 was flying at an altitude of 26,000 ft from Montreal to Edmonton. Warning buzzers sounded in the cockpit of the Boeing 767. One of the world's larger planes was now a glider-the plane had ran out of fuel! Like all Boeing 767s, the plane had a sophisticated fuel gauge, but it was not working properly. However, the plane was still allowed to fly, because there is an alternate method for determining fuel. The Mechanics have a dip stick, calibrated in centimeters, and translated into volume in liters. The Mechanics calculated the three tanks had a total of 7682L of fuel. Pilots always calculate fuel quantities in mass, because they need to know the total mass of the plane before takeoff. Air Canada pilots had always calculated the mass in pounds, but the new 767s fuel consumption was given in kilograms. This involved using the fuel's density to convert 7682 L to a mass in kilograms, so that the pilot could calculate the mass of fuel that had to be added. The First Officer of the plane asked the Mechanic for the conversion factor to calculate volume-to-mass conversion, and the Mechanic replied "1.77". Using that number, the officer and the Mechanic calculated that 4917 L of fuel should be added. The required amount for the trip was 22,300 kg. The mechanic never gave the First Officer the conversion units which was for pounds per liter, not kg/liter as the First Officer assumed. The rest of the story is that the Pilot could not make it to the nearest airport, Winnipeg, but to a little town Gimli which had a former Royal Canadian Air Force runway converted to a race track. For 30 minutes the plane glided to Gimil and managed to land.

Now The Problem 10 The Gimli Glider was a Boeing 767 that ran out of fuel. Read the story above, then verify that the ground crew should have added 20,163 L of fuel instead 4916. The crucial piece of information is the density of the fuel. The crew used 1.77, but did not recognize the units were pounds per liter. To solve the problem you need first to find the density in units of kilograms per liter (Hint: 1 lb = 453.6 grams).

Problem Reworded

1. On July 23, 1983 Air Canada Flight 143, flying at 26,000 feet from Montreal to Edmonton, ran out of fuel because the first officer ask the mechanic for the conversion factor of mass to volume at Montreal. The mechanic gave the first officer the answer 1.77 with no units. The plane had 7682 L of fuel at Montreal. The pilot knew he needed 22,300 kg of fuel to make the trip. The mechanic's answer of 1.77 was pounds per liter not kilograms per liter caused the error such that only 4917 L of fuel was added. If there are 2.205 pounds in a kilogram, how many liters of fuel were needed for the trip? How many liters minimum of fuel should have been added at Montreal before takeoff?

Before 1982 the US Mint cast penny coins from an alloy of copper and zinc. A 1980 Penny weighs 3.051 g and contains 2.898 g of pure copper. In 1982 the US Mint stopped making copper pennies, because the price of copper was worth more than the penny. The post 1982 penny contains only a layer of copper over zinc. A 1990 penny weighs 2.554 g and contains 2.490 g of zinc. If the mint melted down one pound of 1980 pennies, how many 1990 pennies can be made from the total copper from the 1980 pennies?

Problems 12

An Olympic size swimming pool is 50.0 m long and 25.0 m wide. How many gallons of water ( d = 1.0g/mL )are needed to fill the pool to an average depth of 5.5 feet.

A furniture factory needs 29.5 ft 2 of fabric to upholster one chair. A Europen supplier sends the fabric in bolts of exactly 200 m 2 . What is the maximum number of chirs that can be upholstered by three bolts of fabric. Hint: 1 m - 3.281 ft)?

My throw away car gets 23.4 mi/gal and hold 70.1 L of gasoline. How far can I drive on a tankful of gas?

If gas cost $2.20/gal; how much does a tankful of gas cost?

If the average speed on a trip is 92.2 km/hr, How many hours may I drive the car on the trip before I run out of gas?

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

3 Chemical Problem Solving Strategies

Video Transcript

Unit Analysis and Problem Solving

Original quantity x conversion factor = equivalent quantity for example converting between length units given that 1 meter = 39.37 inches conversion factors or the same relationship, just invert as necessary to give you the units you need, calculations: using unit analysis.

The more you use the “long method” of converting units, the fewer errors you will make!

Problem Solving Examples

How many moles of oxygen atoms are there in a 10 ml volume of water, convert volume of water to moles of oxygen.

$H_{2}O \rightarrow$

= There are 0.55 moles of oxygen atoms. Always Check Units!

Problems set, below are two documents. one is practice problems, the second is the same problems with solutions. they can be downloaded and changed to suit your needs..

Be Prepared! Everything you should know for 1st year Chemistry Copyright © by Andrew Vreugdenhil and Kelly Wright is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

How to master the seven-step problem-solving process

In this episode of the McKinsey Podcast , Simon London speaks with Charles Conn, CEO of venture-capital firm Oxford Sciences Innovation, and McKinsey senior partner Hugo Sarrazin about the complexities of different problem-solving strategies.

Podcast transcript

Simon London: Hello, and welcome to this episode of the McKinsey Podcast , with me, Simon London. What’s the number-one skill you need to succeed professionally? Salesmanship, perhaps? Or a facility with statistics? Or maybe the ability to communicate crisply and clearly? Many would argue that at the very top of the list comes problem solving: that is, the ability to think through and come up with an optimal course of action to address any complex challenge—in business, in public policy, or indeed in life.

Looked at this way, it’s no surprise that McKinsey takes problem solving very seriously, testing for it during the recruiting process and then honing it, in McKinsey consultants, through immersion in a structured seven-step method. To discuss the art of problem solving, I sat down in California with McKinsey senior partner Hugo Sarrazin and also with Charles Conn. Charles is a former McKinsey partner, entrepreneur, executive, and coauthor of the book Bulletproof Problem Solving: The One Skill That Changes Everything [John Wiley & Sons, 2018].

Charles and Hugo, welcome to the podcast. Thank you for being here.

Hugo Sarrazin: Our pleasure.

Charles Conn: It’s terrific to be here.

Simon London: Problem solving is a really interesting piece of terminology. It could mean so many different things. I have a son who’s a teenage climber. They talk about solving problems. Climbing is problem solving. Charles, when you talk about problem solving, what are you talking about?

Charles Conn: For me, problem solving is the answer to the question “What should I do?” It’s interesting when there’s uncertainty and complexity, and when it’s meaningful because there are consequences. Your son’s climbing is a perfect example. There are consequences, and it’s complicated, and there’s uncertainty—can he make that grab? I think we can apply that same frame almost at any level. You can think about questions like “What town would I like to live in?” or “Should I put solar panels on my roof?”

You might think that’s a funny thing to apply problem solving to, but in my mind it’s not fundamentally different from business problem solving, which answers the question “What should my strategy be?” Or problem solving at the policy level: “How do we combat climate change?” “Should I support the local school bond?” I think these are all part and parcel of the same type of question, “What should I do?”

I’m a big fan of structured problem solving. By following steps, we can more clearly understand what problem it is we’re solving, what are the components of the problem that we’re solving, which components are the most important ones for us to pay attention to, which analytic techniques we should apply to those, and how we can synthesize what we’ve learned back into a compelling story. That’s all it is, at its heart.

I think sometimes when people think about seven steps, they assume that there’s a rigidity to this. That’s not it at all. It’s actually to give you the scope for creativity, which often doesn’t exist when your problem solving is muddled.

Simon London: You were just talking about the seven-step process. That’s what’s written down in the book, but it’s a very McKinsey process as well. Without getting too deep into the weeds, let’s go through the steps, one by one. You were just talking about problem definition as being a particularly important thing to get right first. That’s the first step. Hugo, tell us about that.

Hugo Sarrazin: It is surprising how often people jump past this step and make a bunch of assumptions. The most powerful thing is to step back and ask the basic questions—“What are we trying to solve? What are the constraints that exist? What are the dependencies?” Let’s make those explicit and really push the thinking and defining. At McKinsey, we spend an enormous amount of time in writing that little statement, and the statement, if you’re a logic purist, is great. You debate. “Is it an ‘or’? Is it an ‘and’? What’s the action verb?” Because all these specific words help you get to the heart of what matters.

Want to subscribe to The McKinsey Podcast ?

Simon London: So this is a concise problem statement.

Hugo Sarrazin: Yeah. It’s not like “Can we grow in Japan?” That’s interesting, but it is “What, specifically, are we trying to uncover in the growth of a product in Japan? Or a segment in Japan? Or a channel in Japan?” When you spend an enormous amount of time, in the first meeting of the different stakeholders, debating this and having different people put forward what they think the problem definition is, you realize that people have completely different views of why they’re here. That, to me, is the most important step.

Charles Conn: I would agree with that. For me, the problem context is critical. When we understand “What are the forces acting upon your decision maker? How quickly is the answer needed? With what precision is the answer needed? Are there areas that are off limits or areas where we would particularly like to find our solution? Is the decision maker open to exploring other areas?” then you not only become more efficient, and move toward what we call the critical path in problem solving, but you also make it so much more likely that you’re not going to waste your time or your decision maker’s time.

How often do especially bright young people run off with half of the idea about what the problem is and start collecting data and start building models—only to discover that they’ve really gone off half-cocked.

Hugo Sarrazin: Yeah.

Charles Conn: And in the wrong direction.

Simon London: OK. So step one—and there is a real art and a structure to it—is define the problem. Step two, Charles?

Charles Conn: My favorite step is step two, which is to use logic trees to disaggregate the problem. Every problem we’re solving has some complexity and some uncertainty in it. The only way that we can really get our team working on the problem is to take the problem apart into logical pieces.

What we find, of course, is that the way to disaggregate the problem often gives you an insight into the answer to the problem quite quickly. I love to do two or three different cuts at it, each one giving a bit of a different insight into what might be going wrong. By doing sensible disaggregations, using logic trees, we can figure out which parts of the problem we should be looking at, and we can assign those different parts to team members.

Simon London: What’s a good example of a logic tree on a sort of ratable problem?

Charles Conn: Maybe the easiest one is the classic profit tree. Almost in every business that I would take a look at, I would start with a profit or return-on-assets tree. In its simplest form, you have the components of revenue, which are price and quantity, and the components of cost, which are cost and quantity. Each of those can be broken out. Cost can be broken into variable cost and fixed cost. The components of price can be broken into what your pricing scheme is. That simple tree often provides insight into what’s going on in a business or what the difference is between that business and the competitors.

If we add the leg, which is “What’s the asset base or investment element?”—so profit divided by assets—then we can ask the question “Is the business using its investments sensibly?” whether that’s in stores or in manufacturing or in transportation assets. I hope we can see just how simple this is, even though we’re describing it in words.

When I went to work with Gordon Moore at the Moore Foundation, the problem that he asked us to look at was “How can we save Pacific salmon?” Now, that sounds like an impossible question, but it was amenable to precisely the same type of disaggregation and allowed us to organize what became a 15-year effort to improve the likelihood of good outcomes for Pacific salmon.

Simon London: Now, is there a danger that your logic tree can be impossibly large? This, I think, brings us onto the third step in the process, which is that you have to prioritize.

Charles Conn: Absolutely. The third step, which we also emphasize, along with good problem definition, is rigorous prioritization—we ask the questions “How important is this lever or this branch of the tree in the overall outcome that we seek to achieve? How much can I move that lever?” Obviously, we try and focus our efforts on ones that have a big impact on the problem and the ones that we have the ability to change. With salmon, ocean conditions turned out to be a big lever, but not one that we could adjust. We focused our attention on fish habitats and fish-harvesting practices, which were big levers that we could affect.

People spend a lot of time arguing about branches that are either not important or that none of us can change. We see it in the public square. When we deal with questions at the policy level—“Should you support the death penalty?” “How do we affect climate change?” “How can we uncover the causes and address homelessness?”—it’s even more important that we’re focusing on levers that are big and movable.

Would you like to learn more about our Strategy & Corporate Finance Practice ?

Simon London: Let’s move swiftly on to step four. You’ve defined your problem, you disaggregate it, you prioritize where you want to analyze—what you want to really look at hard. Then you got to the work plan. Now, what does that mean in practice?

Hugo Sarrazin: Depending on what you’ve prioritized, there are many things you could do. It could be breaking the work among the team members so that people have a clear piece of the work to do. It could be defining the specific analyses that need to get done and executed, and being clear on time lines. There’s always a level-one answer, there’s a level-two answer, there’s a level-three answer. Without being too flippant, I can solve any problem during a good dinner with wine. It won’t have a whole lot of backing.

Simon London: Not going to have a lot of depth to it.

Hugo Sarrazin: No, but it may be useful as a starting point. If the stakes are not that high, that could be OK. If it’s really high stakes, you may need level three and have the whole model validated in three different ways. You need to find a work plan that reflects the level of precision, the time frame you have, and the stakeholders you need to bring along in the exercise.

Charles Conn: I love the way you’ve described that, because, again, some people think of problem solving as a linear thing, but of course what’s critical is that it’s iterative. As you say, you can solve the problem in one day or even one hour.

Charles Conn: We encourage our teams everywhere to do that. We call it the one-day answer or the one-hour answer. In work planning, we’re always iterating. Every time you see a 50-page work plan that stretches out to three months, you know it’s wrong. It will be outmoded very quickly by that learning process that you described. Iterative problem solving is a critical part of this. Sometimes, people think work planning sounds dull, but it isn’t. It’s how we know what’s expected of us and when we need to deliver it and how we’re progressing toward the answer. It’s also the place where we can deal with biases. Bias is a feature of every human decision-making process. If we design our team interactions intelligently, we can avoid the worst sort of biases.

Simon London: Here we’re talking about cognitive biases primarily, right? It’s not that I’m biased against you because of your accent or something. These are the cognitive biases that behavioral sciences have shown we all carry around, things like anchoring, overoptimism—these kinds of things.

Both: Yeah.

Charles Conn: Availability bias is the one that I’m always alert to. You think you’ve seen the problem before, and therefore what’s available is your previous conception of it—and we have to be most careful about that. In any human setting, we also have to be careful about biases that are based on hierarchies, sometimes called sunflower bias. I’m sure, Hugo, with your teams, you make sure that the youngest team members speak first. Not the oldest team members, because it’s easy for people to look at who’s senior and alter their own creative approaches.

Hugo Sarrazin: It’s helpful, at that moment—if someone is asserting a point of view—to ask the question “This was true in what context?” You’re trying to apply something that worked in one context to a different one. That can be deadly if the context has changed, and that’s why organizations struggle to change. You promote all these people because they did something that worked well in the past, and then there’s a disruption in the industry, and they keep doing what got them promoted even though the context has changed.

Simon London: Right. Right.

Hugo Sarrazin: So it’s the same thing in problem solving.

Charles Conn: And it’s why diversity in our teams is so important. It’s one of the best things about the world that we’re in now. We’re likely to have people from different socioeconomic, ethnic, and national backgrounds, each of whom sees problems from a slightly different perspective. It is therefore much more likely that the team will uncover a truly creative and clever approach to problem solving.

Simon London: Let’s move on to step five. You’ve done your work plan. Now you’ve actually got to do the analysis. The thing that strikes me here is that the range of tools that we have at our disposal now, of course, is just huge, particularly with advances in computation, advanced analytics. There’s so many things that you can apply here. Just talk about the analysis stage. How do you pick the right tools?

Charles Conn: For me, the most important thing is that we start with simple heuristics and explanatory statistics before we go off and use the big-gun tools. We need to understand the shape and scope of our problem before we start applying these massive and complex analytical approaches.

Simon London: Would you agree with that?

Hugo Sarrazin: I agree. I think there are so many wonderful heuristics. You need to start there before you go deep into the modeling exercise. There’s an interesting dynamic that’s happening, though. In some cases, for some types of problems, it is even better to set yourself up to maximize your learning. Your problem-solving methodology is test and learn, test and learn, test and learn, and iterate. That is a heuristic in itself, the A/B testing that is used in many parts of the world. So that’s a problem-solving methodology. It’s nothing different. It just uses technology and feedback loops in a fast way. The other one is exploratory data analysis. When you’re dealing with a large-scale problem, and there’s so much data, I can get to the heuristics that Charles was talking about through very clever visualization of data.

You test with your data. You need to set up an environment to do so, but don’t get caught up in neural-network modeling immediately. You’re testing, you’re checking—“Is the data right? Is it sound? Does it make sense?”—before you launch too far.

Simon London: You do hear these ideas—that if you have a big enough data set and enough algorithms, they’re going to find things that you just wouldn’t have spotted, find solutions that maybe you wouldn’t have thought of. Does machine learning sort of revolutionize the problem-solving process? Or are these actually just other tools in the toolbox for structured problem solving?

Charles Conn: It can be revolutionary. There are some areas in which the pattern recognition of large data sets and good algorithms can help us see things that we otherwise couldn’t see. But I do think it’s terribly important we don’t think that this particular technique is a substitute for superb problem solving, starting with good problem definition. Many people use machine learning without understanding algorithms that themselves can have biases built into them. Just as 20 years ago, when we were doing statistical analysis, we knew that we needed good model definition, we still need a good understanding of our algorithms and really good problem definition before we launch off into big data sets and unknown algorithms.

Simon London: Step six. You’ve done your analysis.

Charles Conn: I take six and seven together, and this is the place where young problem solvers often make a mistake. They’ve got their analysis, and they assume that’s the answer, and of course it isn’t the answer. The ability to synthesize the pieces that came out of the analysis and begin to weave those into a story that helps people answer the question “What should I do?” This is back to where we started. If we can’t synthesize, and we can’t tell a story, then our decision maker can’t find the answer to “What should I do?”

Simon London: But, again, these final steps are about motivating people to action, right?

Charles Conn: Yeah.

Simon London: I am slightly torn about the nomenclature of problem solving because it’s on paper, right? Until you motivate people to action, you actually haven’t solved anything.

Charles Conn: I love this question because I think decision-making theory, without a bias to action, is a waste of time. Everything in how I approach this is to help people take action that makes the world better.

Simon London: Hence, these are absolutely critical steps. If you don’t do this well, you’ve just got a bunch of analysis.

Charles Conn: We end up in exactly the same place where we started, which is people speaking across each other, past each other in the public square, rather than actually working together, shoulder to shoulder, to crack these important problems.

Simon London: In the real world, we have a lot of uncertainty—arguably, increasing uncertainty. How do good problem solvers deal with that?

Hugo Sarrazin: At every step of the process. In the problem definition, when you’re defining the context, you need to understand those sources of uncertainty and whether they’re important or not important. It becomes important in the definition of the tree.

You need to think carefully about the branches of the tree that are more certain and less certain as you define them. They don’t have equal weight just because they’ve got equal space on the page. Then, when you’re prioritizing, your prioritization approach may put more emphasis on things that have low probability but huge impact—or, vice versa, may put a lot of priority on things that are very likely and, hopefully, have a reasonable impact. You can introduce that along the way. When you come back to the synthesis, you just need to be nuanced about what you’re understanding, the likelihood.

Often, people lack humility in the way they make their recommendations: “This is the answer.” They’re very precise, and I think we would all be well-served to say, “This is a likely answer under the following sets of conditions” and then make the level of uncertainty clearer, if that is appropriate. It doesn’t mean you’re always in the gray zone; it doesn’t mean you don’t have a point of view. It just means that you can be explicit about the certainty of your answer when you make that recommendation.

Simon London: So it sounds like there is an underlying principle: “Acknowledge and embrace the uncertainty. Don’t pretend that it isn’t there. Be very clear about what the uncertainties are up front, and then build that into every step of the process.”

Hugo Sarrazin: Every step of the process.

Simon London: Yeah. We have just walked through a particular structured methodology for problem solving. But, of course, this is not the only structured methodology for problem solving. One that is also very well-known is design thinking, which comes at things very differently. So, Hugo, I know you have worked with a lot of designers. Just give us a very quick summary. Design thinking—what is it, and how does it relate?

Hugo Sarrazin: It starts with an incredible amount of empathy for the user and uses that to define the problem. It does pause and go out in the wild and spend an enormous amount of time seeing how people interact with objects, seeing the experience they’re getting, seeing the pain points or joy—and uses that to infer and define the problem.

Simon London: Problem definition, but out in the world.

Hugo Sarrazin: With an enormous amount of empathy. There’s a huge emphasis on empathy. Traditional, more classic problem solving is you define the problem based on an understanding of the situation. This one almost presupposes that we don’t know the problem until we go see it. The second thing is you need to come up with multiple scenarios or answers or ideas or concepts, and there’s a lot of divergent thinking initially. That’s slightly different, versus the prioritization, but not for long. Eventually, you need to kind of say, “OK, I’m going to converge again.” Then you go and you bring things back to the customer and get feedback and iterate. Then you rinse and repeat, rinse and repeat. There’s a lot of tactile building, along the way, of prototypes and things like that. It’s very iterative.

Simon London: So, Charles, are these complements or are these alternatives?

Charles Conn: I think they’re entirely complementary, and I think Hugo’s description is perfect. When we do problem definition well in classic problem solving, we are demonstrating the kind of empathy, at the very beginning of our problem, that design thinking asks us to approach. When we ideate—and that’s very similar to the disaggregation, prioritization, and work-planning steps—we do precisely the same thing, and often we use contrasting teams, so that we do have divergent thinking. The best teams allow divergent thinking to bump them off whatever their initial biases in problem solving are. For me, design thinking gives us a constant reminder of creativity, empathy, and the tactile nature of problem solving, but it’s absolutely complementary, not alternative.

Simon London: I think, in a world of cross-functional teams, an interesting question is do people with design-thinking backgrounds really work well together with classical problem solvers? How do you make that chemistry happen?

Hugo Sarrazin: Yeah, it is not easy when people have spent an enormous amount of time seeped in design thinking or user-centric design, whichever word you want to use. If the person who’s applying classic problem-solving methodology is very rigid and mechanical in the way they’re doing it, there could be an enormous amount of tension. If there’s not clarity in the role and not clarity in the process, I think having the two together can be, sometimes, problematic.

The second thing that happens often is that the artifacts the two methodologies try to gravitate toward can be different. Classic problem solving often gravitates toward a model; design thinking migrates toward a prototype. Rather than writing a big deck with all my supporting evidence, they’ll bring an example, a thing, and that feels different. Then you spend your time differently to achieve those two end products, so that’s another source of friction.

Now, I still think it can be an incredibly powerful thing to have the two—if there are the right people with the right mind-set, if there is a team that is explicit about the roles, if we’re clear about the kind of outcomes we are attempting to bring forward. There’s an enormous amount of collaborativeness and respect.

Simon London: But they have to respect each other’s methodology and be prepared to flex, maybe, a little bit, in how this process is going to work.

Hugo Sarrazin: Absolutely.

Simon London: The other area where, it strikes me, there could be a little bit of a different sort of friction is this whole concept of the day-one answer, which is what we were just talking about in classical problem solving. Now, you know that this is probably not going to be your final answer, but that’s how you begin to structure the problem. Whereas I would imagine your design thinkers—no, they’re going off to do their ethnographic research and get out into the field, potentially for a long time, before they come back with at least an initial hypothesis.

Want better strategies? Become a bulletproof problem solver

Hugo Sarrazin: That is a great callout, and that’s another difference. Designers typically will like to soak into the situation and avoid converging too quickly. There’s optionality and exploring different options. There’s a strong belief that keeps the solution space wide enough that you can come up with more radical ideas. If there’s a large design team or many designers on the team, and you come on Friday and say, “What’s our week-one answer?” they’re going to struggle. They’re not going to be comfortable, naturally, to give that answer. It doesn’t mean they don’t have an answer; it’s just not where they are in their thinking process.

Simon London: I think we are, sadly, out of time for today. But Charles and Hugo, thank you so much.

Charles Conn: It was a pleasure to be here, Simon.

Hugo Sarrazin: It was a pleasure. Thank you.

Simon London: And thanks, as always, to you, our listeners, for tuning into this episode of the McKinsey Podcast . If you want to learn more about problem solving, you can find the book, Bulletproof Problem Solving: The One Skill That Changes Everything , online or order it through your local bookstore. To learn more about McKinsey, you can of course find us at McKinsey.com.

Charles Conn is CEO of Oxford Sciences Innovation and an alumnus of McKinsey’s Sydney office. Hugo Sarrazin is a senior partner in the Silicon Valley office, where Simon London, a member of McKinsey Publishing, is also based.

Explore a career with us

Strategy to beat the odds

Five routes to more innovative problem solving

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

1.7: Dimensional Analysis- a Problem Solving Method Used in Chemistry

Last updated
Save as PDF
Page ID 358362

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Learning Objectives

Explain the dimensional analysis (factor label) approach to mathematical calculations involving quantities.
Describe how to use dimensional analysis to carry out unit conversions for a given property and computations involving two or more properties.
Convert between the three main temperature units: Fahrenheit, Celsius, and Kelvin.

It is often the case that a quantity of interest may not be easy (or even possible) to measure directly but instead must be calculated from other directly measured properties and appropriate mathematical relationships. For example, consider measuring the average speed of an athlete running sprints. This is typically accomplished by measuring the time required for the athlete to run from the starting line to the finish line, and the distance between these two lines, and then computing speed from the equation that relates these three properties:

\[\mathrm{speed=\dfrac{distance}{time}}\]

An Olympic-quality sprinter can run 100 m in approximately 10 s, corresponding to an average speed of

\[\mathrm{\dfrac{100\: m}{10\: s}=10\: m/s}\]

Note that this simple arithmetic involves dividing the numbers of each measured quantity to yield the number of the computed quantity (100/10 = 10) and likewise dividing the units of each measured quantity to yield the unit of the computed quantity (m/s = m/s). Now, consider using this same relation to predict the time required for a person running at this speed to travel a distance of 25 m. The same relation between the three properties is used, but in this case, the two quantities provided are a speed (10 m/s) and a distance (25 m). To yield the sought property, time, the equation must be rearranged appropriately:

\[\mathrm{time=\dfrac{distance}{speed}}\]

The time can then be computed as:

\[\mathrm{\dfrac{25\: m}{10\: m/s}=2.5\: s}\]

Again, arithmetic on the numbers (25/10 = 2.5) was accompanied by the same arithmetic on the units (m/m/s = s) to yield the number and unit of the result, 2.5 s. Note that, just as for numbers, when a unit is divided by an identical unit (in this case, m/m), the result is “1”—or, as commonly phrased, the units “cancel.”

These calculations are examples of a versatile mathematical approach known as dimensional analysis (or the factor-label method ). Dimensional analysis is based on this premise: the units of quantities must be subjected to the same mathematical operations as their associated numbers . This method can be applied to computations ranging from simple unit conversions to more complex, multi-step calculations involving several different quantities.

Conversion Factors and Dimensional Analysis

A ratio of two equivalent quantities expressed with different measurement units can be used as a unit conversion factor . For example, the lengths of 2.54 cm and 1 in. are equivalent (by definition), and so a unit conversion factor may be derived from the ratio,

\[\mathrm{\dfrac{2.54\: cm}{1\: in.}\:(2.54\: cm=1\: in.)\: or\: 2.54\:\dfrac{cm}{in.}}\]

Several other commonly used conversion factors are given in Table $\PageIndex{1}$.

When we multiply a quantity (such as distance given in inches) by an appropriate unit conversion factor, we convert the quantity to an equivalent value with different units (such as distance in centimeters). For example, a basketball player’s vertical jump of 34 inches can be converted to centimeters by:

\[\mathrm{34\: \cancel{in.} \times \dfrac{2.54\: cm}{1\:\cancel{in.}}=86\: cm}\]

Since this simple arithmetic involves quantities , the premise of dimensional analysis requires that we multiply both numbers and units . The numbers of these two quantities are multiplied to yield the number of the product quantity, 86, whereas the units are multiplied to yield

\[\mathrm{\dfrac{in.\times cm}{in.}}.\]

Just as for numbers, a ratio of identical units is also numerically equal to one,

\[\mathrm{\dfrac{in.}{in.}=1}\]

and the unit product thus simplifies to cm . (When identical units divide to yield a factor of 1, they are said to “cancel.”) Using dimensional analysis, we can determine that a unit conversion factor has been set up correctly by checking to confirm that the original unit will cancel, and the result will contain the sought (converted) unit.

Example $\PageIndex{1}$: Using a Unit Conversion Factor

The mass of a competition Frisbee is 125 g. Convert its mass to ounces using the unit conversion factor derived from the relationship 1 oz = 28.349 g (Table $\PageIndex{1}$).

If we have the conversion factor, we can determine the mass in kilograms using an equation similar the one used for converting length from inches to centimeters.

\[x\:\mathrm{oz=125\: g\times unit\: conversion\: factor}\nonumber\]

We write the unit conversion factor in its two forms:

\[\mathrm{\dfrac{1\: oz}{28.349\: g}\:and\:\dfrac{28.349\: g}{1\: oz}}\nonumber\]

The correct unit conversion factor is the ratio that cancels the units of grams and leaves ounces.

\[\begin{align*} x\:\ce{oz}&=\mathrm{125\:\cancel{g}\times \dfrac{1\: oz}{28.349\:\cancel{g}}}\\ &=\mathrm{\left(\dfrac{125}{28.349}\right)\:oz}\\ &=\mathrm{4.41\: oz\: (three\: significant\: figures)} \end{align*}\]

Exercise $\PageIndex{1}$

Convert a volume of 9.345 qt to liters.

Beyond simple unit conversions, the factor-label method can be used to solve more complex problems involving computations. Regardless of the details, the basic approach is the same—all the factors involved in the calculation must be appropriately oriented to insure that their labels (units) will appropriately cancel and/or combine to yield the desired unit in the result. This is why it is referred to as the factor-label method. As your study of chemistry continues, you will encounter many opportunities to apply this approach.

Example $\PageIndex{2}$: Computing Quantities from Measurement Results

What is the density of common antifreeze in units of g/mL? A 4.00-qt sample of the antifreeze weighs 9.26 lb.

Since $\mathrm{density=\dfrac{mass}{volume}}$, we need to divide the mass in grams by the volume in milliliters. In general: the number of units of B = the number of units of A $\times$ unit conversion factor. The necessary conversion factors are given in Table 1.7.1: 1 lb = 453.59 g; 1 L = 1.0567 qt; 1 L = 1,000 mL. We can convert mass from pounds to grams in one step:

\[\mathrm{9.26\:\cancel{lb}\times \dfrac{453.59\: g}{1\:\cancel{lb}}=4.20\times 10^3\:g}\nonumber \]

We need to use two steps to convert volume from quarts to milliliters.

Convert quarts to liters.

\[\mathrm{4.00\:\cancel{qt}\times\dfrac{1\: L}{1.0567\:\cancel{qt}}=3.78\: L}\nonumber\]

Convert liters to milliliters.

\[\mathrm{3.78\:\cancel{L}\times\dfrac{1000\: mL}{1\:\cancel{L}}=3.78\times10^3\:mL}\nonumber\]

\[\mathrm{density=\dfrac{4.20\times10^3\:g}{3.78\times10^3\:mL}=1.11\: g/mL}\nonumber\]

Alternatively, the calculation could be set up in a way that uses three unit conversion factors sequentially as follows:

\[\mathrm{\dfrac{9.26\:\cancel{lb}}{4.00\:\cancel{qt}}\times\dfrac{453.59\: g}{1\:\cancel{lb}}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\:\cancel{L}}{1000\: mL}=1.11\: g/mL}\nonumber\]

Exercise $\PageIndex{2}$

What is the volume in liters of 1.000 oz, given that 1 L = 1.0567 qt and 1 qt = 32 oz (exactly)?

$\mathrm{2.956\times10^{-2}\:L}$

Example $\PageIndex{3}$: Computing Quantities from Measurement Results

While being driven from Philadelphia to Atlanta, a distance of about 1250 km, a 2014 Lamborghini Aventador Roadster uses 213 L gasoline.

What (average) fuel economy, in miles per gallon, did the Roadster get during this trip?
If gasoline costs $3.80 per gallon, what was the fuel cost for this trip?

(a) We first convert distance from kilometers to miles:

\[\mathrm{1250\: km\times\dfrac{0.62137\: mi}{1\: km}=777\: mi}\nonumber\]

and then convert volume from liters to gallons:

\[\mathrm{213\:\cancel{L}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\: gal}{4\:\cancel{qt}}=56.3\: gal}\nonumber\]

\[\mathrm{(average)\: mileage=\dfrac{777\: mi}{56.3\: gal}=13.8\: miles/gallon=13.8\: mpg}\nonumber\]

Alternatively, the calculation could be set up in a way that uses all the conversion factors sequentially, as follows:

\[\mathrm{\dfrac{1250\:\cancel{km}}{213\:\cancel{L}}\times\dfrac{0.62137\: mi}{1\:\cancel{km}}\times\dfrac{1\:\cancel{L}}{1.0567\:\cancel{qt}}\times\dfrac{4\:\cancel{qt}}{1\: gal}=13.8\: mpg}\nonumber \]

(b) Using the previously calculated volume in gallons, we find:

\[\mathrm{56.3\: gal\times\dfrac{$3.80}{1\: gal}=$214}\nonumber \]

Exercise $\PageIndex{3}$

A Toyota Prius Hybrid uses 59.7 L gasoline to drive from San Francisco to Seattle, a distance of 1300 km (two significant digits).

What (average) fuel economy, in miles per gallon, did the Prius get during this trip?
If gasoline costs $3.90 per gallon, what was the fuel cost for this trip?

Conversion of Temperature Units

We use the word temperature to refer to the hotness or coldness of a substance. One way we measure a change in temperature is to use the fact that most substances expand when their temperature increases and contract when their temperature decreases. The mercury or alcohol in a common glass thermometer changes its volume as the temperature changes. Because the volume of the liquid changes more than the volume of the glass, we can see the liquid expand when it gets warmer and contract when it gets cooler.

To mark a scale on a thermometer, we need a set of reference values: Two of the most commonly used are the freezing and boiling temperatures of water at a specified atmospheric pressure. On the Celsius scale, 0 °C is defined as the freezing temperature of water and 100 °C as the boiling temperature of water. The space between the two temperatures is divided into 100 equal intervals, which we call degrees. On the Fahrenheit scale, the freezing point of water is defined as 32 °F and the boiling temperature as 212 °F. The space between these two points on a Fahrenheit thermometer is divided into 180 equal parts (degrees).

Defining the Celsius and Fahrenheit temperature scales as described in the previous paragraph results in a slightly more complex relationship between temperature values on these two scales than for different units of measure for other properties. Most measurement units for a given property are directly proportional to one another (y = mx). Using familiar length units as one example:

\[\mathrm{length\: in\: feet=\left(\dfrac{1\: ft}{12\: in.}\right)\times length\: in\: inches}\]

y = length in feet,
x = length in inches, and
the proportionality constant, m, is the conversion factor.

The Celsius and Fahrenheit temperature scales, however, do not share a common zero point, and so the relationship between these two scales is a linear one rather than a proportional one ($y = mx + b$). Consequently, converting a temperature from one of these scales into the other requires more than simple multiplication by a conversion factor, m, it also must take into account differences in the scales’ zero points ($b$).

The linear equation relating Celsius and Fahrenheit temperatures is easily derived from the two temperatures used to define each scale. Representing the Celsius temperature as $x$ and the Fahrenheit temperature as $y$, the slope, $m$, is computed to be:

\[\begin{align*} m &=\dfrac{\Delta y}{\Delta x} \\[4pt] &= \mathrm{\dfrac{212\: ^\circ F - 32\: ^\circ F}{100\: ^\circ C-0\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{180\: ^\circ F}{100\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{9\: ^\circ F}{5\: ^\circ C} }\end{align*} \]

The y-intercept of the equation, b , is then calculated using either of the equivalent temperature pairs, (100 °C, 212 °F) or (0 °C, 32 °F), as:

\[\begin{align*} b&=y-mx \\[4pt] &= \mathrm{32\:^\circ F-\dfrac{9\:^\circ F}{5\:^\circ C}\times0\:^\circ C} \\[4pt] &= \mathrm{32\:^\circ F} \end{align*} \]

The equation relating the temperature scales is then:

\[\mathrm{\mathit{T}_{^\circ F}=\left(\dfrac{9\:^\circ F}{5\:^\circ C}\times \mathit{T}_{^\circ C}\right)+32\:^\circ C}\]

An abbreviated form of this equation that omits the measurement units is:

\[\mathrm{\mathit{T}_{^\circ F}=\dfrac{9}{5}\times \mathit{T}_{^\circ C}+32}\]

Rearrangement of this equation yields the form useful for converting from Fahrenheit to Celsius:

\[\mathrm{\mathit{T}_{^\circ C}=\dfrac{5}{9}(\mathit{T}_{^\circ F}+32)}\]

As mentioned earlier in this chapter, the SI unit of temperature is the kelvin (K). Unlike the Celsius and Fahrenheit scales, the kelvin scale is an absolute temperature scale in which 0 (zero) K corresponds to the lowest temperature that can theoretically be achieved. The early 19th-century discovery of the relationship between a gas's volume and temperature suggested that the volume of a gas would be zero at −273.15 °C. In 1848, British physicist William Thompson, who later adopted the title of Lord Kelvin, proposed an absolute temperature scale based on this concept (further treatment of this topic is provided in this text’s chapter on gases).

The freezing temperature of water on this scale is 273.15 K and its boiling temperature 373.15 K. Notice the numerical difference in these two reference temperatures is 100, the same as for the Celsius scale, and so the linear relation between these two temperature scales will exhibit a slope of $\mathrm{1\:\dfrac{K}{^\circ\:C}}$. Following the same approach, the equations for converting between the kelvin and Celsius temperature scales are derived to be:

\[T_{\ce K}=T_{\mathrm{^\circ C}}+273.15\]

\[T_\mathrm{^\circ C}=T_{\ce K}-273.15\]

The 273.15 in these equations has been determined experimentally, so it is not exact. Figure $\PageIndex{1}$ shows the relationship among the three temperature scales. Recall that we do not use the degree sign with temperatures on the kelvin scale.

Although the kelvin (absolute) temperature scale is the official SI temperature scale, Celsius is commonly used in many scientific contexts and is the scale of choice for nonscience contexts in almost all areas of the world. Very few countries (the U.S. and its territories, the Bahamas, Belize, Cayman Islands, and Palau) still use Fahrenheit for weather, medicine, and cooking.

Example $\PageIndex{4}$: Conversion from Celsius

Normal body temperature has been commonly accepted as 37.0 °C (although it varies depending on time of day and method of measurement, as well as among individuals). What is this temperature on the kelvin scale and on the Fahrenheit scale?

\[\mathrm{K= {^\circ C}+273.15=37.0+273.2=310.2\: K}\nonumber \]

\[\mathrm{^\circ F=\dfrac{9}{5}\:{^\circ C}+32.0=\left(\dfrac{9}{5}\times 37.0\right)+32.0=66.6+32.0=98.6\: ^\circ F}\nonumber \]

Exercise $\PageIndex{4}$

Convert 80.92 °C to K and °F.

354.07 K, 177.7 °F

Example $\PageIndex{5}$: Conversion from Fahrenheit

Baking a ready-made pizza calls for an oven temperature of 450 °F. If you are in Europe, and your oven thermometer uses the Celsius scale, what is the setting? What is the kelvin temperature?

\[\mathrm{^\circ C=\dfrac{5}{9}(^\circ F-32)=\dfrac{5}{9}(450-32)=\dfrac{5}{9}\times 418=232 ^\circ C\rightarrow set\: oven\: to\: 230 ^\circ C}\hspace{20px}\textrm{(two significant figures)}\nonumber\]

\[\mathrm{K={^\circ C}+273.15=230+273=503\: K\rightarrow 5.0\times 10^2\,K\hspace{20px}(two\: significant\: figures)}\nonumber\]

Exercise $\PageIndex{5}$

Convert 50 °F to °C and K.

10 °C, 280 K

Measurements are made using a variety of units. It is often useful or necessary to convert a measured quantity from one unit into another. These conversions are accomplished using unit conversion factors, which are derived by simple applications of a mathematical approach called the factor-label method or dimensional analysis. This strategy is also employed to calculate sought quantities using measured quantities and appropriate mathematical relations.

Key Equations

$T_\mathrm{^\circ C}=\dfrac{5}{9}\times T_\mathrm{^\circ F}-32$
$T_\mathrm{^\circ F}=\dfrac{9}{5}\times T_\mathrm{^\circ C}+32$
$T_\ce{K}={^\circ \ce C}+273.15$
$T_\mathrm{^\circ C}=\ce K-273.15$

Contributors and Attributions

Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] ).

Big Chemical Encyclopedia

Chemical substances, components, reactions, process design ....

IMAGES

5 step problem solving method
What Is Problem-Solving? Steps, Processes, Exercises to do it Right
An Overview Of 9 Step Problem Solving Model
Problem Solving Methods Steps Process Examples
what is the 4 step problem solving method
The problem-solving process chart

VIDEO

How Maths Unitary Methods problem solving by class 5 students step by step explained Aikik Niyam
Dimensional Analysis Part 1
Chapter 1
Part 3: One Way ANOVA
How to Use Unit Analysis
Exercise 1.1, Question 02

COMMENTS

PDF Unit Analysis and Problem Solving Script
efficient way to minimize errors in a multi-step calculation. Solving problems with this method provides the units for the final answer, and an easy to follow solution. All chemical calculation problems should be solved using unit analysis. To layout a problem with unit analysis, string together a series of multiplication or division calculations.
Chemistry Problem Solving
A powerful technique for solving problems is called unit analysis method, sometimes referred to as dimensional analysis method, or factor label method of problem solving. Unit analysis cannot solve every chemistry word problem, but it is very effective for the problems we encounter in begining and college chemistry.
Unit Equations, Unit Factors and Unit Analysis Method
The basics of writing unit equations, their corresponding unit factors and using them to perform the unit analysis method of problem solving.
1.7: Problem Solving Process
Analysis This is the actual solving step. This is where you show all the work you have done to solve the problem. When you get an answer, restate the variable you are solving for, include the unit, and put a box around the answer. Review Write a simple sentence explaining why (or why not) your answer makes sense.
PDF Unit Analysis Instructor Guide
4:54 Chapter 2: example from physics Presents and solves a problem from physics to compute the work done by a machine on an object. Uses unit analysis to check work along the way. 5:05 Animation of problem scenario Maple animation of the position function of the object in the problem. 5:31 Work Illustration of the concept of work.
PDF 3.1 DIMENSIONAL ANALYSIS
dimensional analysis, also known as factor-label method and unit analysis. Dimensional analysis is a general problem solving method that uses the dimensions (units) associated with numbers as a guide in setting up and checking calculations. Dimensional analysis is a consistent and predictable technique, yet many teachers are not experienced
2.9: PSS.9- Unit Analysis Problem Solving
Unit conversion is a powerful mathematical technique in chemistry that must be mastered. Exact numbers do not affect the determination of significant figures. 2.9: PSS.9- Unit Analysis Problem Solving is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by LibreTexts.
1.7: Problem Solving Using the Unit Analysis Method (the unit
Unit Analysis or Factor Analysis or Dimensional Analysis MethodHow to convert between different units using this method
2: Units, Dimensional Analysis, Problem Solving, and Estimation
This page titled 2: Units, Dimensional Analysis, Problem Solving, and Estimation is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Peter Dourmashkin (MIT OpenCourseWare) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.
2.3: Scientific Dimensional Analysis
Dimensional analysis (also called factor label method or unit analysis) is used to convert from one set of units to another. This method is used for both simple (feet to inches) and complex ($\text{g/cm}^3$ to $\text{kg}$/gallon) conversions and uses relationships or conversion factors between different sets of units.
35 problem-solving techniques and methods for solving complex problems
Problem-solving methods are primarily designed to help a group or team through a process of first identifying problems and challenges, ... unit, or community to ... Chances are you've heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested ...
2.6: Problem Solving and Unit Conversions
Here is what we would have gotten: 3.55 m × 1 m 100 cm = 0.0355m2 cm 3.55 m × 1 m 100 c m = 0.0355 m 2 c m. For the answer to be meaningful, we have to construct the conversion factor in a form that causes the original unit to cancel out. Figure 2.6.1 2.6. 1 shows a concept map for constructing a proper conversion.
PDF Chapter 2 Units, Dimensional Analysis, Problem Solving, and
Solution: The standard kilogram is an alloy of 90% platinum and 10% iridium. The density of platinum is 21.45g ⋅cm−3 and the density of iridium is 22.55g ⋅cm−3. Thus the density of the standard kilogram, ρ = 21.56 g ⋅ cm−3, and its volume is. V = m / ρ ≅ 1000 g / 22 g ⋅ cm−3 ≅ 46.38cm3.
2: Units and Dimensional Analysis
2.1: Scientific Dimensional Analysis. Dimensional analysis (also called factor label method or unit analysis) is used to convert from one set of units to another. This method uses relationships or conversion factors between different sets of units. While the terms are frequently used interchangeably, conversion factors and relationships are ...
PDF THIRTEEN PROBLEM-SOLVING MODELS
The Six-Step method provides a focused procedure for the problem solving (PS) group. It ensures consistency, as everyone understands the approach to be used. By using data, it helps eliminate bias and preconceptions, leading to greater objectivity. It helps to remove divisions and encourages collaborative working.
Unit Analysis
Unit Analysis Unit analysis means using the rules of multiplying and reducing fractions to solve problems ... To solve this problem you need to know some conversions. ... experts, educators, and other professionals on the platform are independent contractors, who use their own styles, methods, and materials and create their own lesson plans ...
What is Problem Solving? Steps, Process & Techniques
Finding a suitable solution for issues can be accomplished by following the basic four-step problem-solving process and methodology outlined below. Step. Characteristics. 1. Define the problem. Differentiate fact from opinion. Specify underlying causes. Consult each faction involved for information. State the problem specifically.
Math Skills
Dimensional Analysis (also called Factor-Label Method or the Unit Factor Method) is a problem-solving method that uses the fact that any number or expression can be multiplied by one without changing its value. It is a useful technique. The only danger is that you may end up thinking that chemistry is simply a math problem - which it definitely ...
Dimensional Analysis Calculator
Solving problems by unit analysis is a simple three step process: Step 1. Read the problem and determine the unit required in the answer. Step 2. Analyze the problem and determine the given value related to the answer. Step 3. Apply unit factors to convert the unit of the given to the unit in the answer. Back to CHEM 1001 Home Page.
3 Chemical Problem Solving Strategies
Unit analysis helps avoid errors in a multi-step calculation and provides the units for the final answer. 1) Write the units with every number you include in a series of calculations. 2) String your calculations together as a series of multiplications or divisions before doing any math. 3) Cancel your units to see the calculation evolve.
How to master the seven-step problem-solving process
Looked at this way, it's no surprise that McKinsey takes problem solving very seriously, testing for it during the recruiting process and then honing it, in McKinsey consultants, through immersion in a structured seven-step method. To discuss the art of problem solving, I sat down in California with McKinsey senior partner Hugo Sarrazin and ...
1.7: Dimensional Analysis- a Problem Solving Method Used in Chemistry
1.7: Dimensional Analysis- a Problem Solving Method Used in Chemistry is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts. Measurements are made using a variety of units. It is often useful or necessary to convert a measured quantity from one unit into another.
Unit analysis method
Unit analysis method The unit analysis method of problem solving is extremely versatile. You can use it to convert between units or to solve some formula problems. If you forget a formula during a test, you may still be able to solve the problem using unit analysis. The unit analysis method involves analyzing the units and setting up conversion ...

Margin Size

1.7: Problem Solving Process

6 Step Problem Solving Method:

Margin Size

2: Units, Dimensional Analysis, Problem Solving, and Estimation

Margin Size

2.3: Scientific Dimensional Analysis

Conversion Factors

Derived Units

Contributors and Attributions

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Recommended Articles

How do you identify problems?

Complete problem-solving methods

Problem-solving warm-up activities

Tips for more effective problem solving

Clearly define the problem

Don’t jump to conclusions

Try different approaches

Don’t take it personally

Get the right people in the room

Document everything

Bring a facilitator

Develop your problem-solving skills

Design a great agenda

1. Six Thinking Hats

2. Lightning Decision Jam

3. Problem Definition Process

4. The 5 Whys

5. World Cafe

6. Discovery & Action Dialogue (DAD)

7. Design Sprint 2.0

8. Open space technology

Techniques to identify and analyze problems

10. The Creativity Dice

11. Fishbone Analysis

12. Problem Tree

13. SWOT Analysis

14. Agreement-Certainty Matrix

16. Speed Boat

17. The Journalistic Six

18. LEGO Challenge

19. What, So What, Now What?

20. Journalists

Problem-solving techniques for developing solutions

21. Mindspin

22. Improved Solutions

23. Four Step Sketch

24. 15% Solutions

25. How-Now-Wow Matrix

26. Impact and Effort Matrix

27. Dotmocracy

28. Check-in / Check-out

29. Doodling Together

30. Show and Tell

31. Constellations

32. Draw a Tree

How do I conclude a problem-solving process?

33. One Breath Feedback

34. Who What When Matrix

35. Response cards

Save time and effort discovering the right solutions

Over to you

Leave a Comment Cancel reply

Design your next workshop with SessionLab

Unit Analysis

Unit Analysis Problem Solving:

Problem Reworded

Problems 12

3 Chemical Problem Solving Strategies

Unit Analysis and Problem Solving

Problem Solving Examples

= There are 0.55 moles of oxygen atoms. Always Check Units!

Share This Book

How to master the seven-step problem-solving process

Want to subscribe to The McKinsey Podcast ?

Would you like to learn more about our Strategy & Corporate Finance Practice ?

Want better strategies? Become a bulletproof problem solver

Explore a career with us