problem solving about quadratic equation with solution

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.6: Solve Applications of Quadratic Equations

• Last updated
• Save as PDF
• Page ID 5177

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Solve applications modeled by quadratic equations

Before you get started, take this readiness quiz.

• The sum of two consecutive odd numbers is \(−100\). Find the numbers. If you missed this problem, review Example 2.18.
• Solve: \(\frac{2}{x+1}+\frac{1}{x-1}=\frac{1}{x^{2}-1}\). If you missed this problem, review Example 7.35.
• Find the length of the hypotenuse of a right triangle with legs \(5\) inches and \(12\) inches. If you missed this problem, review Example 2.34.

Solve Applications Modeled by Quadratic Equations

We solved some applications that are modeled by quadratic equations earlier, when the only method we had to solve them was factoring. Now that we have more methods to solve quadratic equations, we will take another look at applications.

Let’s first summarize the methods we now have to solve quadratic equations.

Methods to Solve Quadratic Equations

• Square Root Property
• Completing the Square
• Quadratic Formula

As you solve each equation, choose the method that is most convenient for you to work the problem. As a reminder, we will copy our usual Problem-Solving Strategy here so we can follow the steps.

Use a Problem-Solving Strategy

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Solve the equation using algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

We have solved number applications that involved consecutive even and odd integers, by modeling the situation with linear equations. Remember, we noticed each even integer is \(2\) more than the number preceding it. If we call the first one \(n\), then the next one is \(n+2\). The next one would be \(n+2+2\) or \(n+4\). This is also true when we use odd integers. One set of even integers and one set of odd integers are shown below.

\(\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}\)

\(\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}\)

Some applications of odd or even consecutive integers are modeled by quadratic equations. The notation above will be helpful as you name the variables.

Example \(\PageIndex{1}\)

The product of two consecutive odd integers is \(195\). Find the integers.

Step 1 : Read the problem

Step 2 : Identify what we are looking for.

We are looking for two consecutive odd integers.

Step 3 : Name what we are looking for.

Let \(n=\) the first odd integer.

\(n+2=\) the next odd integer.

Step 4 : Translate into an equation. State the problem in one sentence.

“The product of two consecutive odd integers is \(195\).” The product of the first odd integer and the second odd integer is \(195\).

Translate into an equation.

\(n(n+2)=195\)

Step 5 : Solve the equation. Distribute.

\(n^{2}+2 n=195\)

Write the equation in standard form.

\(n^{2}+2 n-195=0\)

\((n+15)(n-13)=0\)

Use the Zero Product Property.

\(n+15=0 \quad n-13=0\)

Solve each equation.

\(n=-15, \quad n=13\)

There are two values of \(n\) that are solutions. This will give us two pairs of consecutive odd integers for our solution.

\(\begin{array}{cc}{\text { First odd integer } n=13} & {\text { First odd integer } n=-15} \\ {\text { next odd integer } n+2} & {\text { next odd integer } n+2} \\ {13+2} & {-15+2} \\ {15} & {-13}\end{array}\)

Step 6 : Check the answer.

Do these pairs work? Are they consecutive odd integers?

\(\begin{aligned} 13,15 & \text { yes } \\-13,-15 & \text { yes } \end{aligned}\)

Is their product \(195\)?

\(\begin{aligned} 13 \cdot 15 &=195 &\text{yes} \\-13(-15) &=195 & \text { yes } \end{aligned}\)

Step 7 : Answer the question.

Two consecutive odd integers whose product is \(195\) are \(13,15\) and \(-13,-15\).

Exercise \(\PageIndex{1}\)

The product of two consecutive odd integers is \(99\). Find the integers.

The two consecutive odd integers whose product is \(99\) are \(9, 11\), and \(−9, −11\).

Exercise \(\PageIndex{2}\)

The product of two consecutive even integers is \(168\). Find the integers.

The two consecutive even integers whose product is \(128\) are \(12, 14\) and \(−12, −14\).

We will use the formula for the area of a triangle to solve the next example.

Definition \(\PageIndex{1}\)

Area of a Triangle

For a triangle with base, \(b\), and height, \(h\), the area, \(A\), is given by the formula \(A=\frac{1}{2} b h\).

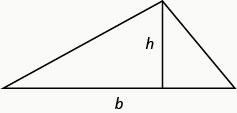
Recall that when we solve geometric applications, it is helpful to draw the figure.

Example \(\PageIndex{2}\)

An architect is designing the entryway of a restaurant. She wants to put a triangular window above the doorway. Due to energy restrictions, the window can only have an area of \(120\) square feet and the architect wants the base to be \(4\) feet more than twice the height. Find the base and height of the window.

Exercise \(\PageIndex{3}\)

Find the base and height of a triangle whose base is four inches more than six times its height and has an area of \(456\) square inches.

The height of the triangle is \(12\) inches and the base is \(76\) inches.

Exercise \(\PageIndex{4}\)

If a triangle that has an area of \(110\) square feet has a base that is two feet less than twice the height, what is the length of its base and height?

The height of the triangle is \(11\) feet and the base is \(20\) feet.

In the two preceding examples, the number in the radical in the Quadratic Formula was a perfect square and so the solutions were rational numbers. If we get an irrational number as a solution to an application problem, we will use a calculator to get an approximate value.

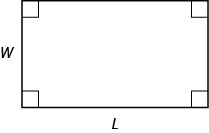
We will use the formula for the area of a rectangle to solve the next example.

Definition \(\PageIndex{2}\)

Area of a Rectangle

For a rectangle with length, \(L\), and width, \(W\), the area, \(A\), is given by the formula \(A=LW\).

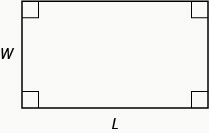
Example \(\PageIndex{3}\)

Mike wants to put \(150\) square feet of artificial turf in his front yard. This is the maximum area of artificial turf allowed by his homeowners association. He wants to have a rectangular area of turf with length one foot less than \(3\) times the width. Find the length and width. Round to the nearest tenth of a foot.

Exercise \(\PageIndex{5}\)

The length of a \(200\) square foot rectangular vegetable garden is four feet less than twice the width. Find the length and width of the garden, to the nearest tenth of a foot.

The length of the garden is approximately \(18\) feet and the width \(11\) feet.

Exercise \(\PageIndex{6}\)

A rectangular tablecloth has an area of \(80\) square feet. The width is \(5\) feet shorter than the length.What are the length and width of the tablecloth to the nearest tenth of a foot?

The length of the tablecloth is approximately \(11.8\) feet and the width \(6.8\) feet.

The Pythagorean Theorem gives the relation between the legs and hypotenuse of a right triangle. We will use the Pythagorean Theorem to solve the next example.

Definition \(\PageIndex{3}\)

Pythagorean Theorem

• In any right triangle, where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse, \(a^{2}+b^{2}=c^{2}\).

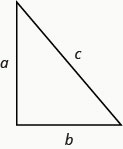
Example \(\PageIndex{4}\)

Rene is setting up a holiday light display. He wants to make a ‘tree’ in the shape of two right triangles, as shown below, and has two \(10\)-foot strings of lights to use for the sides. He will attach the lights to the top of a pole and to two stakes on the ground. He wants the height of the pole to be the same as the distance from the base of the pole to each stake. How tall should the pole be?

Exercise \(\PageIndex{7}\)

The sun casts a shadow from a flag pole. The height of the flag pole is three times the length of its shadow. The distance between the end of the shadow and the top of the flag pole is \(20\) feet. Find the length of the shadow and the length of the flag pole. Round to the nearest tenth.

The length of the flag pole’s shadow is approximately \(6.3\) feet and the height of the flag pole is \(18.9\) feet.

Exercise \(\PageIndex{8}\)

The distance between opposite corners of a rectangular field is four more than the width of the field. The length of the field is twice its width. Find the distance between the opposite corners. Round to the nearest tenth.

The distance between the opposite corners is approximately \(7.2\) feet.

The height of a projectile shot upward from the ground is modeled by a quadratic equation. The initial velocity, \(v_{0}\), propels the object up until gravity causes the object to fall back down.

Definition \(\PageIndex{4}\)

The height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds is given by the formula

\(h=-16 t^{2}+v_{0} t\)

We can use this formula to find how many seconds it will take for a firework to reach a specific height.

Example \(\PageIndex{5}\)

A firework is shot upwards with initial velocity \(130\) feet per second. How many seconds will it take to reach a height of \(260\) feet? Round to the nearest tenth of a second.

Exercise \(\PageIndex{9}\)

An arrow is shot from the ground into the air at an initial speed of \(108\) ft/s. Use the formula \(h=-16 t^{2}+v_{0} t\) to determine when the arrow will be \(180\) feet from the ground. Round the nearest tenth.

The arrow will reach \(180\) feet on its way up after \(3\) seconds and again on its way down after approximately \(3.8\) seconds.

Exercise \(\PageIndex{10}\)

A man throws a ball into the air with a velocity of \(96\) ft/s. Use the formula \(h=-16 t^{2}+v_{0} t\) to determine when the height of the ball will be \(48\) feet. Round to the nearest tenth.

The ball will reach \(48\) feet on its way up after approximately \(.6\) second and again on its way down after approximately \(5.4\) seconds.

We have solved uniform motion problems using the formula \(D=rt\) in previous chapters. We used a table like the one below to organize the information and lead us to the equation.

The formula \(D=rt\) assumes we know \(r\) and \(t\) and use them to find \(D\). If we know \(D\) and \(r\) and need to find \(t\), we would solve the equation for \(t\) and get the formula \(t=\frac{D}{r}\).

Some uniform motion problems are also modeled by quadratic equations.

Example \(\PageIndex{6}\)

Professor Smith just returned from a conference that was \(2,000\) miles east of his home. His total time in the airplane for the round trip was \(9\) hours. If the plane was flying at a rate of \(450\) miles per hour, what was the speed of the jet stream?

This is a uniform motion situation. A diagram will help us visualize the situation.

We fill in the chart to organize the information.

We are looking for the speed of the jet stream. Let \(r=\) the speed of the jet stream.

When the plane flies with the wind, the wind increases its speed and so the rate is \(450 + r\).

When the plane flies against the wind, the wind decreases its speed and the rate is \(450 − r\).

The speed of the jet stream was \(50\) mph.

Exercise \(\PageIndex{11}\)

MaryAnne just returned from a visit with her grandchildren back east. The trip was \(2400\) miles from her home and her total time in the airplane for the round trip was \(10\) hours. If the plane was flying at a rate of \(500\) miles per hour, what was the speed of the jet stream?

The speed of the jet stream was \(100\) mph.

Exercise \(\PageIndex{12}\)

Gerry just returned from a cross country trip. The trip was \(3000\) miles from his home and his total time in the airplane for the round trip was \(11\) hours. If the plane was flying at a rate of \(550\) miles per hour, what was the speed of the jet stream?

Work applications can also be modeled by quadratic equations. We will set them up using the same methods we used when we solved them with rational equations.We’ll use a similar scenario now.

Example \(\PageIndex{7}\)

The weekly gossip magazine has a big story about the presidential election and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes \(12\) hours more than Press #2 to do the job and when both presses are running they can print the job in \(8\) hours. How long does it take for each press to print the job alone?

This is a work problem. A chart will help us organize the information.

We are looking for how many hours it would take each press separately to complete the job.

Exercise \(\PageIndex{13}\)

The weekly news magazine has a big story naming the Person of the Year and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes \(6\) hours more than Press #2 to do the job and when both presses are running they can print the job in \(4\) hours. How long does it take for each press to print the job alone?

Press #1 would take \(12\) hours, and Press #2 would take \(6\) hours to do the job alone.

Exercise \(\PageIndex{14}\)

Erlinda is having a party and wants to fill her hot tub. If she only uses the red hose it takes \(3\) hours more than if she only uses the green hose. If she uses both hoses together, the hot tub fills in \(2\) hours. How long does it take for each hose to fill the hot tub?

The red hose take \(6\) hours and the green hose take \(3\) hours alone.

Access these online resources for additional instruction and practice with solving applications modeled by quadratic equations.

• Word Problems Involving Quadratic Equations
• Quadratic Equation Word Problems
• Applying the Quadratic Formula

Key Concepts

• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
• Solve the equation using good algebra techniques.
• For a triangle with base, \(b\), and height, \(h\), the area, \(A\), is given by the formula \(A=\frac{1}{2}bh\).

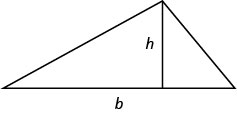
• For a rectangle with length,\(L\), and width, \(W\), the area, \(A\), is given by the formula \(A=LW\).

• The height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds is given by the formula \(h=-16 t^{2}+v_{0} t\).

Quadratic Equation Solver

We can help you solve an equation of the form " ax 2 + bx + c = 0 " Just enter the values of a, b and c below :

Is it Quadratic?

Only if it can be put in the form ax 2 + bx + c = 0 , and a is not zero .

The name comes from "quad" meaning square, as the variable is squared (in other words x 2 ).

These are all quadratic equations in disguise:

How Does this Work?

The solution(s) to a quadratic equation can be calculated using the Quadratic Formula :

The "±" means we need to do a plus AND a minus, so there are normally TWO solutions !

The blue part ( b 2 - 4ac ) is called the "discriminant", because it can "discriminate" between the possible types of answer:

• when it is positive, we get two real solutions,
• when it is zero we get just ONE solution,
• when it is negative we get complex solutions.

Learn more at Quadratic Equations

Quadratic Equation Solver

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Step-By-Step Example

Example (click to try), choose your method, solve by factoring.

Example: 3x^2-2x-1=0

Complete The Square

Example: 3x^2-2x-1=0 (After you click the example, change the Method to 'Solve By Completing the Square'.)

Take the Square Root

Example: 2x^2=18

Quadratic Formula

Example: 4x^2-2x-1=0

About quadratic equations

Need more problem types? Try MathPapa Algebra Calculator

Clear Quadratic Equation Solver »

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve a Quadratic Equation: A Step-by-Step Guide

Last Updated: May 3, 2024 Fact Checked

Factoring the Equation

Using the quadratic formula, completing the square, practice problems and answers, expert q&a.

This article was co-authored by David Jia . David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math. There are 9 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,415,043 times.

A quadratic equation is a polynomial equation in a single variable where the highest exponent of the variable is 2. [1] X Research source There are three main ways to solve quadratic equations: 1) to factor the quadratic equation if you can do so, 2) to use the quadratic formula, or 3) to complete the square. If you want to know how to master these three methods, just follow these steps.

Quadradic Formula for Solving Equations

• Then, use the process of elimination to plug in the factors of 4 to find a combination that produces -11x when multiplied. You can either use a combination of 4 and 1, or 2 and 2, since both of those numbers multiply to get 4. Just remember that one of the terms should be negative, since the term is -4. [3] X Research source

• 3x = -1 ..... by subtracting
• 3x/3 = -1/3 ..... by dividing
• x = -1/3 ..... simplified
• x = 4 ..... by subtracting
• x = (-1/3, 4) ..... by making a set of possible, separate solutions, meaning x = -1/3, or x = 4 seem good.

• So, both solutions do "check" separately, and both are verified as working and correct for two different solutions.

• 4x 2 - 5x - 13 = x 2 -5
• 4x 2 - x 2 - 5x - 13 +5 = 0
• 3x 2 - 5x - 8 = 0

• {-b +/-√ (b 2 - 4ac)}/2
• {-(-5) +/-√ ((-5) 2 - 4(3)(-8))}/2(3) =
• {-(-5) +/-√ ((-5) 2 - (-96))}/2(3)

• {-(-5) +/-√ ((-5) 2 - (-96))}/2(3) =
• {5 +/-√(25 + 96)}/6
• {5 +/-√(121)}/6

• (5 + 11)/6 = 16/6
• (5-11)/6 = -6/6

• x = (-1, 8/3)

• 2x 2 - 9 = 12x =
• In this equation, the a term is 2, the b term is -12, and the c term is -9.

• 2x 2 - 12x - 9 = 0
• 2x 2 - 12x = 9

• 2x 2 /2 - 12x/2 = 9/2 =
• x 2 - 6x = 9/2

• -6/2 = -3 =
• (-3) 2 = 9 =
• x 2 - 6x + 9 = 9/2 + 9

• x = 3 + 3(√6)/2
• x = 3 - 3(√6)/2)

• If the number under the square root is not a perfect square, then the last few steps run a little differently. Here is an example: [14] X Research source Thanks Helpful 0 Not Helpful 0
• If the "b" is an even number, the formula is : {-(b/2) +/- √(b/2)-ac}/a. Thanks Helpful 3 Not Helpful 0
• As you can see, the radical sign did not disappear completely. Therefore, the terms in the numerator cannot be combined (because they are not like terms). There is no purpose, then, to splitting up the plus-or-minus. Instead, we divide out any common factors --- but ONLY if the factor is common to both of the constants AND the radical's coefficient. Thanks Helpful 1 Not Helpful 0

You Might Also Like

• ↑ https://www.mathsisfun.com/definitions/quadratic-equation.html
• ↑ http://www.mathsisfun.com/algebra/factoring-quadratics.html
• ↑ https://www.mathportal.org/algebra/solving-system-of-linear-equations/elimination-method.php
• ↑ https://www.cuemath.com/algebra/quadratic-equations/
• ↑ https://www.purplemath.com/modules/solvquad4.htm
• ↑ http://www.purplemath.com/modules/quadform.htm
• ↑ https://uniskills.library.curtin.edu.au/numeracy/algebra/quadratic-equations/
• ↑ http://www.mathsisfun.com/algebra/completing-square.html
• ↑ http://www.umsl.edu/~defreeseca/intalg/ch7extra/quadmeth.htm

About This Article

To solve quadratic equations, start by combining all of the like terms and moving them to one side of the equation. Then, factor the expression, and set each set of parentheses equal to 0 as separate equations. Finally, solve each equation separately to find the 2 possible values for x. To learn how to solve quadratic equations using the quadratic formula, scroll down! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Sep 24, 2022

Did this article help you?

Kalo Morris

Mar 12, 2017

Matthew Mathers

Mar 25, 2017

Kapela Davis

Oct 10, 2017

Jan 29, 2018

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Level up your tech skills and stay ahead of the curve

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Solving Equations
• Quadratic Equation Solver

Quadratic equation solver

This step-by-step calculator solves quadratic equations using three different methods: the quadratic formula method , completing the square , and the factoring method . Calculator shows all the work and provides detailed explanation on how to solve an equation.

• Factoring Polynomials
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Rationalize Denominator
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance calculator
• Midpoint Calculator
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

How to use this calculator

The most commonly used methods for solving quadratic equations are:

1 . Factoring method

2 . Solving quadratic equations by completing the square

3 . Using quadratic formula

In the following sections, we'll go over these methods.

Method 1A : Factoring method

If a quadratic trinomial can be factored, this is the best solving method.

We often use this method when the leading coefficient is equal to 1 or -1. If this is not the case, then it is better to use some other method.

Example 01: Solve $ x^2 \color{red}{-8}x \color{blue}{+ 15} = 0 $ by factoring.

Here we see that the leading coefficient is 1, so the factoring method is our first choice.

To factor this equation, we must find two numbers ( $ a $ and $ b $ ) with a sum is $ a + b = \color{red}{8} $ and a product of $ a \cdot b = \color{blue}{15} $.

After some trials and errors, we see that $ a = 3 $ and $ b = 5 $.

Now we use formula $ x^2 - 8x + 15 = (x - a)(x - b) $ to get factored form:

Divide the factored form into two linear equations to get solutions.

Method 1B : Factoring - special cases

Example 02: Solve $ x^2 -8x = 0 $ by factoring.

In this case, (when the coefficient c = 0 ) we can factor out $ \color{blue}{x} $ out of $ x^2 - 8x $.

Example 03: Solve $ x^2 - 16 = 0 $ by factoring.

In this case, ( when the middle term is equal 0) we can use the difference of squares formula.

Method 3 : Solve using quadratic formula

This method solves all types of quadratic equations. It works best when solutions contain some radicals or complex numbers.

Example 05: Solve equation $ 2x^2 + 3x - 2 = 0$ by using quadratic formula.

Step 1 : Read the values of $a$, $b$, and $c$ from the quadratic equation. ( $a$ is the number in front of $x^2$ , $b$ is the number in front of $x$ and $c$ is the number at the end)

Step 2 :Plug the values for a, b, and c into the quadratic formula and simplify.

Step 3 : Solve for $x_1$ and $x_2$

Method 2 : Completing the square

This method can be used to solve all types of quadratic equations, although it can be complicated for some types of equations. The method involves seven steps.

Example 04: Solve equation $ 2x^2 + 8x - 10= 0$ by completing the square.

Step 1 : Divide the equation by the number in front of the square term.

Step 2 : move $-5$ to the right:

Step 3 : Take half of the x-term coefficient $ \color{blue}{\dfrac{4}{2}} $, square it $ \color{blue}{\left(\dfrac{4}{2} \right)^2} $ and add this value to both sides.

Step 4 : Simplify left and right side.

Step 5 : Write the perfect square on the left.

Step 6 : Take the square root of both sides.

Step 7 : Solve for $x_1$ and $x_2$ .

1. Quadratic Equation — step-by-step examples, video tutorials with worked examples.

2. Completing the Square — video on Khan Academy

3. Completing the Square — video on Khan Academy

4. Polynomial equation solver

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

• NCERT Solutions
• NCERT Solutions for Class 10
• NCERT Solutions for Class 10 Maths
• Chapter 4: Quadratic Equations

NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations

Ncert solutions class 10 maths chapter 4 – cbse free pdf download.

NCERT Solutions Class 10 Maths Chapter 4 Quadratic Equations  contain all the solutions to the problems provided in the Class 10 Maths NCERT textbook for CBSE exam preparations. The questions from every section are framed and solved accurately by the subject experts. NCERT Solutions for Class 10 are detailed and step-by-step guides to all the queries of the students. The exercises present in the chapter should be dealt with utmost sincerity if one wants to score well in the examinations. Maths is a subject that requires a good understanding and a lot of practice. The tips and tricks to solve the problems easily are also provided here. A quadratic equation in the variable x is an equation of the form ax 2 + bx + c = 0, where a, b, c are real numbers, a ≠ 0. That is, ax 2 + bx + c = 0, a ≠ 0 is called the standard form of a quadratic equation.

Download Exclusively Curated Chapter Notes for Class 10 Maths Chapter – 4 Quadratic Equations

Download most important questions for class 10 maths chapter – 4 quadratic equations.

Quadratic equations arise in several situations around us. Hence, students should give special attention to learning the concepts related to this chapter of the latest CBSE Syllabus for 2023-24 thoroughly to excel in Class 10 Maths examinations. NCERT Solutions help the students in learning these concepts as well as in evaluating themselves. Practising these solutions repeatedly is bound to help the students in overcoming their shortcomings. Maths has either a correct answer or a wrong one. Therefore, it is imperative to concentrate while solving the questions to score full marks.

• Chapter 1 Real Numbers
• Chapter 2 Polynomials
• Chapter 3 Pair of Linear Equations in Two Variables
• Chapter 4 Quadratic Equations
• Chapter 5 Arithmetic Progressions
• Chapter 6 Triangles
• Chapter 7 Coordinate Geometry
• Chapter 8 Introduction to Trigonometry
• Chapter 9 Some Applications of Trigonometry
• Chapter 10 Circles
• Chapter 11 Constructions
• Chapter 12 Areas Related to Circles
• Chapter 13 Surface Areas and Volumes
• Chapter 14 Statistics
• Chapter 15 Probability
• Exercise 4.1
• Exercise 4.2
• Exercise 4.3
• Exercise 4.4

NCERT Solutions Class 10 Maths Chapter 4 – Quadratic Equations

carouselExampleControls112

Previous Next

Access answers to NCERT Class 10 Maths Chapter 4 – Quadratic Equations

Exercise 4.1 page: 73.

1. Check whether the following are quadratic equations:

(i) (x + 1) 2 = 2(x – 3)

(ii) x 2 – 2x = (–2) (3 – x)

(iii) (x – 2)(x + 1) = (x – 1)(x + 3)

(iv) (x – 3)(2x +1) = x(x + 5)

(v) (2x – 1)(x – 3) = (x + 5)(x – 1)

(vi) x 2 + 3x + 1 = (x – 2) 2

(vii) (x + 2) 3 = 2x (x 2 – 1)

(viii) x 3 – 4x 2 – x + 1 = (x – 2) 3

(x + 1) 2 = 2(x – 3)

By using the formula for (a+b) 2 = a 2 +2ab+b 2

⇒ x 2  + 2x + 1 = 2x – 6

⇒ x 2  + 7 = 0

The above equation is in the form of ax 2 + bx + c = 0

Therefore, the given equation is a quadratic equation.

(ii) Given, x 2 – 2x = (–2) (3 – x)

⇒ x 2  –   2x = -6 + 2x

⇒ x 2  – 4x + 6 = 0

(iii) Given, (x – 2)(x + 1) = (x – 1)(x + 3)

By multiplication,

⇒ x 2  – x – 2 = x 2  + 2x – 3

⇒ 3x – 1 = 0

The above equation is not in the form of ax 2 + bx + c = 0

Therefore, the given equation is not a quadratic equation.

(iv) Given, (x – 3)(2x +1) = x(x + 5)

⇒ 2x 2  – 5x – 3 = x 2  + 5x

⇒  x 2  – 10x – 3 = 0

(v) Given, (2x – 1)(x – 3) = (x + 5)(x – 1)

⇒ 2x 2  – 7x + 3 = x 2  + 4x – 5

⇒ x 2  – 11x + 8 = 0

The above equation is in the form of ax 2  + bx + c = 0.

(vi) Given, x 2  + 3x + 1 = (x – 2) 2

By using the formula for (a-b) 2 =a 2 -2ab+b 2

⇒ x 2  + 3x + 1 = x 2  + 4 – 4x

⇒ 7x – 3 = 0

(vii) Given, (x + 2) 3  = 2x(x 2  – 1)

By using the formula for (a+b) 3  = a 3 +b 3 +3ab(a+b)

⇒ x 3  + 8 + x 2  + 12x = 2x 3  – 2x

⇒ x 3  + 14x – 6x 2  – 8 = 0

(viii) Given, x 3  – 4x 2  – x + 1 = (x – 2) 3

By using the formula for (a-b) 3  = a 3 -b 3 -3ab(a-b)

⇒  x 3  – 4x 2  – x + 1 = x 3  – 8 – 6x 2   + 12x

⇒ 2x 2  – 13x + 9 = 0

2. Represent the following situations in the form of quadratic equations:

(i) The area of a rectangular plot is 528 m 2 . The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.

(ii) The product of two consecutive positive integers is 306. We need to find the integers.

(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.

(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken

(i) Let us consider,

The breadth of the rectangular plot = x m

Thus, the length of the plot = (2x + 1) m

As we know,

Area of rectangle = length × breadth = 528 m 2

Putting the value of the length and breadth of the plot in the formula, we get,

(2x + 1) × x = 528

⇒ 2x 2  + x =528

⇒ 2x 2  + x – 528 = 0

Therefore, the length and breadth of the plot satisfy the quadratic equation, 2x 2  + x – 528 = 0, which is the required representation of the problem mathematically.

(ii) Let us consider,

The first integer number = x

Thus, the next consecutive positive integer will be = x + 1

Product of two consecutive integers = x × (x +1) = 306

⇒ x 2  + x = 306

⇒ x 2  + x – 306 = 0

Therefore, the two integers x and x+1 satisfy the quadratic equation, x 2  + x – 306 = 0, which is the required representation of the problem mathematically.

(iii) Let us consider,

Age of Rohan’s = x  years

Therefore, as per the given question,

Rohan’s mother’s age = x + 26

After 3 years,

Age of Rohan’s = x + 3

Age of Rohan’s mother will be = x + 26 + 3 = x + 29

The product of their ages after 3 years will be equal to 360, such that

(x + 3)(x + 29) = 360

⇒ x 2  + 29x + 3x + 87 = 360

⇒ x 2  + 32x + 87 – 360 = 0

⇒ x 2  + 32x – 273 = 0

Therefore, the age of Rohan and his mother satisfies the quadratic equation, x 2  + 32x – 273 = 0, which is the required representation of the problem mathematically.

(iv) Let us consider,

The speed of the train = x   km/h

Time taken to travel 480 km = 480/x km/hr

As per second condition, the speed of train = ( x  – 8) km/h

Also given, the train will take 3 hours to cover the same distance.

Therefore, time taken to travel 480 km = (480/x)+3 km/h

Speed × Time = Distance

( x  – 8)(480/ x  )+ 3 = 480

⇒ 480 + 3 x  – 3840/ x  – 24 = 480

⇒ 3 x  – 3840/ x  = 24

⇒ x 2  – 8 x  – 1280 = 0

Therefore, the speed of the train satisfies the quadratic equation, x 2  – 8 x  – 1280 = 0, which is the required representation of the problem mathematically.

Exercise 4.2 Page: 76

1. Find the roots of the following quadratic equations by factorisation:

(i) x 2  – 3x – 10 = 0 (ii) 2x 2  + x – 6 = 0 (iii) √2 x 2  + 7x + 5√2 = 0 (iv) 2x 2  – x +1/8 = 0 (v) 100x 2  – 20x + 1 = 0

(i) Given,  x 2  – 3 x  – 10 =0

Taking L.H.S.,

=> x 2  – 5 x  + 2 x  – 10

=> x ( x  – 5) + 2( x  – 5)

=>( x  – 5)( x  + 2)

The roots of this equation, x 2  – 3 x  – 10 = 0 are the values of x for which ( x  – 5)( x  + 2) = 0

Therefore,  x  – 5 = 0 or  x  + 2 = 0

=>  x  = 5 or  x  = -2

(ii) Given, 2 x 2  +  x  – 6 = 0

=> 2 x 2  + 4 x  – 3 x  – 6

=> 2 x ( x  + 2) – 3( x  + 2)

=> ( x  + 2)(2 x  – 3)

The roots of this equation, 2 x 2  +  x  – 6=0 are the values of x for which ( x x  + 2)(2 x  – 3) = 0

Therefore,  x  + 2 = 0 or 2 x  – 3 = 0

=>  x  = -2 or  x  = 3/2

(iii) √2  x 2  + 7 x  + 5√2=0

=> √2  x 2  + 5 x  + 2 x  + 5√2

=>  x  (√2 x  + 5) + √2(√2 x  + 5)= (√2 x  + 5)( x  + √2)

The roots of this equation, √2  x 2  + 7 x  + 5√2=0 are the values of x for which (√2 x  + 5)( x  + √2) = 0

Therefore, √2 x  + 5 = 0 or  x  + √2 = 0

=>  x  = -5/√2 or  x  = -√2

(iv) 2 x 2  –  x  +1/8 = 0

=1/8 (16 x 2   – 8 x  + 1)

= 1/8 (16 x 2   – 4 x  -4 x  + 1)

= 1/8 (4 x (4 x    – 1) -1(4 x  – 1))

= 1/8 (4 x  – 1) 2

The roots of this equation, 2 x 2  –  x  + 1/8 = 0, are the values of x for which (4 x  – 1) 2 = 0

Therefore, (4 x  – 1) = 0 or (4 x  – 1) = 0

⇒  x  = 1/4 or  x  = 1/4

(v) Given, 100x 2  – 20x + 1=0

= 100x 2  – 10x – 10x + 1

= 10x(10x – 1) -1(10x – 1)

= (10x – 1) 2

The roots of this equation, 100x 2  – 20x + 1=0, are the values of x for which (10x – 1) 2 = 0

∴ (10x – 1) = 0 or (10x – 1) = 0

⇒x = 1/10 or x = 1/10

2. Solve the problems given in Example 1.

Represent the following situations mathematically:

(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.

(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was Rs. 750. We would like to find out the number of toys produced on that day.

(i) Let us say the number of marbles John has = x

Therefore, the number of marble Jivanti has = 45 – x

After losing 5 marbles each,

Number of marbles John has = x  – 5

Number of marble Jivanti has = 45 – x  – 5 = 40 –  x

Given that the product of their marbles is 124.

∴ ( x  – 5)(40 –  x ) = 124

⇒  x 2  – 45 x  + 324 = 0

⇒  x 2  – 36 x  – 9 x  + 324 = 0

⇒  x ( x  – 36) -9( x  – 36) = 0

⇒ ( x  – 36)( x  – 9) = 0

Thus, we can say,

x  – 36 = 0 or  x  – 9 = 0

⇒  x  = 36 or  x  = 9

If John’s marbles = 36

Then, Jivanti’s marbles = 45 – 36 = 9

And if John’s marbles = 9

Then, Jivanti’s marbles = 45 – 9 = 36

(ii) Let us say the number of toys produced in a day is x .

Therefore, cost of production of each toy = Rs(55 –  x )

Given the total cost of production of the toys = Rs 750

∴  x (55 –  x ) = 750

⇒  x 2  – 55 x  + 750 = 0

⇒  x 2  – 25 x  – 30 x  + 750 = 0

⇒  x ( x  – 25) -30( x  – 25) = 0

⇒ ( x  – 25)( x  – 30) = 0

Thus, either x  -25 = 0 or  x  – 30 = 0

⇒  x  = 25 or  x  = 30

Hence, the number of toys produced in a day will be either 25 or 30.

3. Find two numbers whose sum is 27 and product is 182.

Let us say the first number is x, and the second number is 27 – x.

Therefore, the product of two numbers

x(27 – x) = 182

⇒ x 2  – 27x – 182 = 0

⇒ x 2  – 13x – 14x + 182 = 0

⇒ x(x – 13) -14(x – 13) = 0

⇒ (x – 13)(x -14) = 0

Thus, either, x = -13 = 0 or x – 14 = 0

⇒ x = 13 or x = 14

Therefore, if first number = 13, then second number = 27 – 13 = 14

And if first number = 14, then second number = 27 – 14 = 13

Hence, the numbers are 13 and 14.

4. Find two consecutive positive integers, the sum of whose squares is 365.

Let us say the two consecutive positive integers are x  and  x  + 1.

Therefore, as per the given questions,

x 2  + ( x  + 1) 2  = 365

⇒  x 2  +  x 2  + 1 + 2 x  = 365

⇒ 2 x 2  + 2x – 364 = 0

⇒  x 2  +  x  – 182 = 0

⇒  x 2  + 14 x  – 13 x  – 182 = 0

⇒  x ( x  + 14) -13( x  + 14) = 0

⇒ ( x  + 14)( x  – 13) = 0

Thus, either, x  + 14 = 0 or  x  – 13 = 0,

⇒  x  = – 14 or  x  = 13

Since the integers are positive, x can be 13 only.

∴  x  + 1 = 13 + 1 = 14

Therefore, two consecutive positive integers will be 13 and 14.

5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.

Let us say the base of the right triangle is x cm.

Given, the altitude of right triangle = (x – 7) cm

From Pythagoras’ theorem, we know,

Base 2  + Altitude 2  = Hypotenuse 2

∴ x 2  + (x – 7) 2  = 13 2

⇒ x 2  + x 2  + 49 – 14x = 169

⇒ 2x 2  – 14x – 120 = 0

⇒ x 2  – 7x – 60 = 0

⇒ x 2  – 12x + 5x – 60 = 0

⇒ x(x – 12) + 5(x – 12) = 0

⇒ (x – 12)(x + 5) = 0

Thus, either x – 12 = 0 or x + 5 = 0,

⇒ x = 12 or x = – 5

Since sides cannot be negative, x can only be 12.

Therefore, the base of the given triangle is 12 cm, and the altitude of this triangle will be (12 – 7) cm = 5 cm.

6. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs.90, find the number of articles produced and the cost of each article.

Let us say the number of articles produced is x .

Therefore, cost of production of each article = Rs (2 x  + 3)

Given the total cost of production is Rs.90

∴  x (2 x  + 3) = 90

⇒ 2 x 2  + 3 x  – 90 = 0

⇒ 2 x 2  + 15 x  -12 x  – 90 = 0

⇒  x (2 x  + 15) -6(2 x  + 15) = 0

⇒ (2 x  + 15)( x  – 6) = 0

Thus, either 2 x  + 15 = 0 or  x  – 6 = 0

⇒  x  = -15/2 or  x  = 6

As the number of articles produced can only be a positive integer, x can only be 6.

Hence, the number of articles produced = 6

Cost of each article = 2 × 6 + 3 = Rs 15

Exercise 4.3 Page: 87

1. Find the roots of the following quadratic equations, if they exist, by the method of completing the square:

(i) 2 x 2  – 7 x  +3 = 0

(ii) 2 x 2  +  x  – 4 = 0 (iii) 4 x 2  + 4√3 x  + 3 = 0

(iv) 2 x 2  +  x  + 4 = 0

(i) 2 x 2  – 7 x  + 3 = 0

⇒ 2 x 2  – 7 x  = – 3

Dividing by 2 on both sides, we get

⇒ x 2 -7x/2 = -3/2

⇒ x 2 -2 × x ×7/4 = -3/2

On adding (7/4) 2 to both sides of the equation, we get

⇒ (x) 2 -2×x×7/4 +(7/4) 2 = (7/4) 2 -3/2

⇒ (x-7/4) 2 = (49/16) – (3/2)

⇒(x-7/4) 2 = 25/16

⇒(x-7/4) 2 = ±5/4

⇒  x  = 7/4 ± 5/4

⇒  x  = 7/4 + 5/4 or x = 7/4 – 5/4

⇒ x = 12/4 or x = 2/4

⇒ x = 3 or x = 1/2

(ii) 2x 2  + x – 4 = 0

⇒ 2x 2  + x = 4

Dividing both sides of the equation by 2, we get

⇒ x 2  +x/2 = 2

Now on adding (1/4) 2  to both sides of the equation, we get,

⇒ (x) 2  + 2 × x × 1/4 + (1/4) 2  = 2 + (1/4) 2

⇒ (x + 1/4) 2  = 33/16

⇒ x + 1/4 = ± √33/4

⇒ x = ± √33/4 – 1/4

⇒ x = (± √33-1)/4

Therefore, either x = (√33-1)/4 or x = (-√33-1)/4

(iii) 4x 2  + 4√3x + 3 = 0

Converting the equation into a 2 +2ab+b 2 form, we get,

⇒ (2x) 2  + 2 × 2x × √3 + (√3) 2  = 0

⇒ (2x + √3) 2  = 0

⇒ (2x + √3) = 0 and (2x + √3) = 0

Therefore, either x = -√3/2 or x = -√3/2

(iv) 2x 2  + x + 4 = 0

⇒ 2x 2  + x = -4

⇒ x 2  + 1/2x = 2

⇒ x 2  + 2 × x × 1/4 = -2

By adding (1/4) 2  to both sides of the equation, we get

⇒ (x) 2  + 2 × x × 1/4 + (1/4) 2  = (1/4) 2  – 2

⇒ (x + 1/4) 2  = 1/16 – 2

⇒ (x + 1/4) 2  = -31/16

As we know, the square of numbers cannot be negative.

Therefore, there is no real root for the given equation, 2x 2 + x + 4 = 0

2. Find the roots of the quadratic equations given in Q.1 above by applying the quadratic formula.

(i) 2x 2  – 7x + 3 = 0

On comparing the given equation with ax 2  + bx + c = 0, we get,

a = 2, b = -7 and c = 3

By using the quadratic formula, we get,

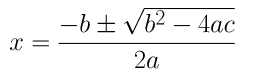
⇒ x = (7±√(49 – 24))/4

⇒ x = (7±√25)/4

⇒ x = (7±5)/4

⇒ x = (7+5)/4 or x = (7-5)/4

⇒ x = 12/4 or 2/4

∴  x = 3 or 1/2

a = 2, b = 1 and c = -4

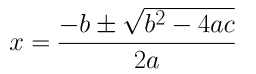
⇒x = (-1±√1+32)/4

⇒x = (-1±√33)/4

∴ x = (-1+√33)/4 or x = (-1-√33)/4

(iii) 4x 2  + 4√3x + 3 = 0

On comparing the given equation with ax 2  + bx + c = 0, we get

a = 4, b = 4√3 and c = 3

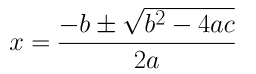
⇒ x = (-4√3±√48-48)/8

⇒ x = (-4√3±0)/8

∴ x = -√3/2 or x = -√3/2

(iv) 2x 2  + x + 4 = 0

a = 2, b = 1 and c = 4

By using the quadratic formula, we get

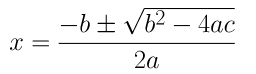
⇒ x = (-1±√1-32)/4

⇒ x = (-1±√-31)/4

As we know, the square of a number can never be negative. Therefore, there is no real solution for the given equation.

3. Find the roots of the following equations:

(i) x-1/x = 3, x ≠ 0 (ii) 1/x+4 – 1/x-7 = 11/30, x = -4, 7

(i) x-1/x = 3

⇒ x 2  – 3x -1 = 0

a = 1, b = -3 and c = -1

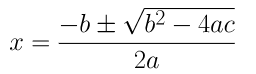
⇒ x = (3±√9+4)/2

⇒ x = (3±√13)/2

∴ x = (3+√13)/2 or x = (3-√13)/2

(ii) 1/x+4 – 1/x-7 = 11/30 ⇒ x-7-x-4/(x+4)(x-7) = 11/30

⇒ -11/(x+4)(x-7) = 11/30

⇒ (x+4)(x-7) = -30

⇒ x 2  – 3x – 28 = 30

⇒ x 2  – 3x + 2 = 0

We can solve this equation by factorisation method now.

⇒ x 2  – 2x – x + 2 = 0

⇒ x(x – 2) – 1(x – 2) = 0

⇒ (x – 2)(x – 1) = 0

⇒ x = 1 or 2

4. The sum of the reciprocals of Rehman’s age (in years) 3 years ago and 5 years from now is 1/3. Find his present age.

Let us say the present age of Rahman is x  years.

Three years ago, Rehman’s age was ( x  – 3) years.

Five years after, his age will be ( x  + 5) years.

Given the sum of the reciprocals of Rehman’s ages 3 years ago and after 5 years is equal to 1/3.

∴ 1/ x -3 + 1/ x -5 = 1/3

(x +5+ x -3)/( x -3)( x +5) = 1/3

(2 x +2)/( x -3)( x +5) = 1/3

⇒ 3(2 x  + 2) = ( x -3)( x +5)

⇒ 6 x  + 6 =  x 2  + 2 x  – 15

⇒  x 2  – 4 x  – 21 = 0

⇒  x 2  – 7 x  + 3 x  – 21 = 0

⇒  x ( x  – 7) + 3( x  – 7) = 0

⇒ ( x  – 7)( x  + 3) = 0

⇒  x  = 7, -3

As we know, age cannot be negative.

Therefore, Rahman’s present age is 7 years.

5. In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.

Let us say the marks of Shefali in Maths be x.

Then, the marks in English will be 30 – x.

As per the given question,

(x + 2)(30 – x – 3) = 210

(x + 2)(27 – x) = 210

⇒ -x 2  + 25x + 54 = 210

⇒ x 2  – 25x + 156 = 0

⇒ x 2  – 12x – 13x + 156 = 0

⇒ x(x – 12) -13(x – 12) = 0

⇒ (x – 12)(x – 13) = 0

⇒ x = 12, 13

Therefore, if the marks in Maths are 12, then marks in English will be 30 – 12 = 18, and if the marks in Maths are 13, then marks in English will be 30 – 13 = 17 .

6. The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.

Let us say the shorter side of the rectangle is x  m.

Then, larger side of the rectangle = ( x  + 30) m

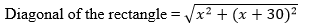
As given, the length of the diagonal is = x + 30 m

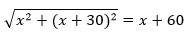
⇒  x 2  + ( x  + 30) 2  = ( x  + 60) 2

⇒  x 2  +  x 2  + 900 + 60 x  =  x 2  + 3600 + 120 x

⇒  x 2  – 60 x  – 2700 = 0

⇒  x 2  – 90 x  + 30 x  – 2700 = 0

⇒  x ( x  – 90) + 30( x  -90) = 0

⇒ ( x  – 90)( x  + 30) = 0

⇒  x  = 90, -30

However, the side of the field cannot be negative. Therefore, the length of the shorter side will be 90 m.

And the length of the larger side will be (90 + 30) m = 120 m.

7. The difference of the squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.

Let us say the larger and smaller number be x  and  y,  respectively.

As per the question given,

x 2  –  y 2  = 180 and  y 2  = 8 x

⇒  x 2  – 8 x  = 180

⇒  x 2  – 8 x  – 180 = 0

⇒  x 2  – 18 x  + 10 x  – 180 = 0

⇒  x ( x  – 18) +10( x  – 18) = 0

⇒ ( x  – 18)( x  + 10) = 0

⇒  x  = 18, -10

However, the larger number cannot be considered a negative number, as 8 times the larger number will be negative, and hence, the square of the smaller number will be negative, which is not possible.

Therefore, the larger number will be 18 only.

∴  y 2  = 8x = 8 × 18 = 144

⇒  y  = ±√144 = ±12

∴ Smaller number = ±12

Therefore, the numbers are 18 and 12 or 18 and -12.

8. A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

It is given that

Distance = 360 km

Consider x as the speed, then the time taken

If the speed is increased by 5 km/h, the speed will be (x + 5) km/h.

Distance will be the same.

t = 360/(x + 5)

We know that

Time with original speed – Time with increased speed = 1

360/x – 360/(x + 5) = 1

LCM = x (x + 5)

360 x + 1800 – 360x = x (x + 5)

x 2  + 5x = 1800

x 2  + 5x – 1800 = 0

x 2  + 45x – 40x – 1800 = 0

x (x + 45) – 40 (x + 45) = 0

(x – 40) (x + 45) = 0

x = 40 km/hr

As we know, the value of speed cannot be negative.

Therefore, the speed of the train is 40 km/h.

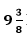
Let the time taken by the smaller pipe to fill the tank = x hr.

Time taken by the larger pipe = ( x  – 10) hr

Part of the tank filled by smaller pipe in 1 hour = 1/ x

Part of the tank filled by larger pipe in 1 hour = 1/( x  – 10)

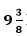
1/ x  + 1/ x -10 = 8/75

x -10+ x / x ( x -10) = 8/75

⇒ 2 x -10/ x ( x -10) = 8/75

⇒ 75(2 x  – 10) = 8 x 2  – 80 x

⇒ 150 x  – 750 = 8 x 2  – 80 x

⇒ 8 x 2  – 230 x  +750 = 0

⇒ 8 x 2  – 200 x  – 30 x  + 750 = 0

⇒ 8 x ( x  – 25) -30( x  – 25) = 0

⇒ ( x  – 25)(8 x  -30) = 0

⇒  x  = 25, 30/8

Time taken by the smaller pipe cannot be 30/8 = 3.75 hours, as the time taken by the larger pipe will become negative, which is logically not possible.

Therefore, the time taken individually by the smaller pipe and the larger pipe will be 25 and 25 – 10 =15 hours, respectively.

10. An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.

Let us say the average speed of the passenger train =   x  km/h.

Average speed of express train = ( x  + 11) km/h

Given the time taken by the express train to cover 132 km is 1 hour less than the passenger train to cover the same distance. Therefore,

(132/x) – (132/(x+11)) = 1

132(x+11-x)/(x(x+11)) = 1

132 × 11 /(x(x+11)) = 1

⇒ 132 × 11 =  x ( x  + 11)

⇒  x 2  + 11 x  – 1452 = 0

⇒  x 2  +  44 x  -33 x  -1452 = 0

⇒  x ( x  + 44) -33( x  + 44) = 0

⇒ ( x  + 44)( x  – 33) = 0

⇒  x  = – 44, 33

As we know, speed cannot be negative.

Therefore, the speed of the passenger train will be 33 km/h and thus, the speed of the express train will be 33 + 11 = 44 km/h.

11. Sum of the areas of two squares is 468 m 2 . If the difference between their perimeters is 24 m, find the sides of the two squares.

Let the sides of the two squares be  x  m and  y  m.

Therefore, their perimeter will be 4 x  and 4 y,  respectively

And the area of the squares will be x 2  and  y 2,  respectively.

4 x  – 4 y  = 24

x  –  y  = 6

x  =  y  + 6

Also,  x 2  +   y 2  = 468

⇒ (6 +  y 2 ) +  y 2  = 468

⇒ 36 +  y 2  + 12 y  +  y 2  = 468

⇒ 2 y 2  + 12 y  + 432 = 0

⇒  y 2  + 6y – 216 = 0

⇒  y 2  + 18 y  – 12 y  – 216 = 0

⇒  y ( y  +18) -12( y  + 18) = 0

⇒ ( y  + 18)( y  – 12) = 0

⇒  y  = -18, 12

As we know, the side of a square cannot be negative.

Hence, the sides of the squares are 12 m and (12 + 6) m = 18 m.

Exercise 4.4 Page: 91

1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them. (i) 2 x 2  – 3 x  + 5 = 0 (ii) 3 x 2  – 4√3 x  + 4 = 0 (iii) 2 x 2  – 6 x  + 3 = 0

2x 2  – 3 x  + 5 = 0

Comparing the equation with  ax 2  +  bx  +  c  = 0, we get

a  = 2,  b  = -3 and  c  = 5

We know, Discriminant =  b 2  – 4 ac

=  ( – 3) 2  – 4 (2) (5) = 9 – 40

As you can see, b 2  – 4ac < 0

Therefore, no real root is possible for the given equation, 2x 2  – 3 x + 5 = 0

(ii) 3 x 2  – 4√3 x  + 4 = 0

a  = 3,  b  = -4√3 and  c  = 4

= (-4√3) 2  – 4(3)(4)

= 48 – 48 = 0

As  b 2  – 4 ac  = 0,

Real roots exist for the given equation, and they are equal to each other.

Hence, the roots will be – b /2 a  and – b /2 a .

– b /2 a  = -(-4√3)/2×3 = 4√3/6 = 2√3/3 = 2/√3

Therefore, the roots are 2/√3 and 2/√3.

(iii) 2 x 2  – 6 x  + 3 = 0

a  = 2,  b  = -6,  c  = 3

As we know, Discriminant =  b 2  – 4 ac

= (-6) 2  – 4 (2) (3)

= 36 – 24 = 12

As  b 2  – 4 ac  > 0,

Therefore, there are distinct real roots that exist for this equation, 2 x 2  – 6 x + 3 = 0

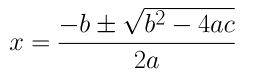
= (-(-6) ± √(-6 2 -4(2)(3)) )/ 2(2)

= (6±2√3 )/4

Therefore, the roots for the given equation are (3+√3)/2 and (3-√3)/2

2. Find the values of  k for each of the following quadratic equations so that they have two equal roots. (i) 2 x 2  +  kx  + 3 = 0 (ii)  kx  ( x  – 2) + 6 = 0

(i) 2 x 2  +  kx  + 3 = 0

Comparing the given equation with  ax 2  +  bx  +  c  = 0, we get,

a  = 2,  b  = k and  c  = 3

= ( k ) 2  – 4(2) (3)

=  k 2  – 24

For equal roots, we know,

Discriminant = 0

k 2  – 24 = 0

k = ±√24 = ±2√6

(ii)  kx ( x  – 2) + 6 = 0

or  kx 2  – 2 kx  + 6 = 0

Comparing the given equation with  ax 2  +  bx  +  c  = 0, we get

a  =  k ,  b  = – 2 k  and  c  = 6

= ( – 2 k ) 2 – 4 ( k ) (6)

= 4 k 2 – 24 k

b 2 – 4 ac  = 0

4 k 2 – 24 k  = 0

4 k  ( k  – 6) = 0

Either 4 k  = 0 or  k  = 6 = 0

k  = 0 or  k  = 6

However, if  k  = 0, then the equation will not have the terms ‘ x 2 ‘ and ‘ x ‘.

Therefore, if this equation has two equal roots,  k  should be 6 only.

3. Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m 2 ? If so, find its length and breadth.

Let the breadth of the mango grove be l .

The length of the mango grove will be 2 l .

Area of the mango grove = (2 l ) ( l )= 2 l 2

2 l 2  = 800

l 2  = 800/2 = 400

l 2  – 400 =0

a  = 1,  b  = 0,  c  = 400

=> (0) 2  – 4 × (1) × ( – 400) = 1600

Here,  b 2  – 4 ac  > 0

Thus, the equation will have real roots. And hence, the desired rectangular mango grove can be designed.

As we know, the value of length cannot be negative.

Therefore, the breadth of the mango grove = 20 m

Length of mango grove = 2 × 20 = 40 m

4. Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their age in years was 48.

Let’s say the age of one friend is x years.

Then, the age of the other friend will be (20 – x) years.

Four years ago,

Age of First friend = ( x  – 4) years

Age of Second friend = (20 –  x  – 4) = (16 –  x ) years

As per the given question, we can write,

( x  – 4) (16 –  x ) = 48

16 x – x 2  – 64 + 4 x  = 48

 – x 2  + 20 x –  112 = 0

x 2  – 20 x +  112 = 0

a  =  1 ,  b  = -2 0  and  c  = 112

Discriminant =  b 2  – 4 ac

= (- 20 ) 2  – 4 × 112

= 400 – 448 = -48

b 2  – 4 ac  < 0

Therefore, there will be no real solution possible for the equations. Hence, the condition doesn’t exist.

5. Is it possible to design a rectangular park of perimeter 80 and an area of 400 m2? If so, find its length and breadth.

Let the length and breadth of the park be l and b.

Perimeter of the rectangular park = 2 ( l + b ) = 80

So, l + b  = 40

Or,  b  = 40 –  l

Area of the rectangular park =  l×b = l(40 – l) =  40 l  –  l 2 = 400

l 2   –    40 l  + 400   = 0, which is a quadratic equation.

a  = 1,  b  = -40,  c  = 400

Since, Discriminant =  b 2  – 4 ac

=(- 40 ) 2  – 4 × 400

= 1600 – 1600 = 0

Thus, b 2  – 4 ac  = 0

Therefore, this equation has equal real roots. Hence, the situation is possible.

The root of the equation,

l  = – b /2 a

l  = -(-40)/2(1) = 40/2 = 20

Therefore, the length of the rectangular park, l  = 20 m

And the breadth of the park, b  = 40 –  l  = 40 – 20 = 20 m.

NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations

A 1-mark question was asked from Chapter 4 Quadratic Equations in the year 2018. However, in the year 2017, a total of 13 marks were asked from the topic Quadratic Equations. Therefore, students need to have a thorough understanding of the topic. The topics and sub-topics provided in this chapter include:

4.1 Introduction

If we equate the polynomial  ax 2 + bx + c, a ≠ 0 to zero, we get a quadratic equation. Quadratic equations come up when we deal with many real-life situations. In this chapter, students will study quadratic equations and various ways of finding their roots. They will also see some applications of quadratic equations in daily life situations.

4.2 Quadratic Equations

A quadratic equation in the variable x is an equation of the form ax 2 + bx + c = 0, where a, b, c are real numbers, a ≠ 0. In fact, any equation of the form p(x) = 0, where p(x) is a polynomial of degree 2, is a quadratic equation. But when we write the terms of p(x) in descending order of their degrees, then we get the standard form of the equation. That is, ax 2 + bx + c = 0, a ≠ 0 is called the standard form of a quadratic equation.

4.3 Solution of Quadratic Equations by Factorisation

A real number α is called a root of the quadratic equation ax 2  + bx + c = 0, a ≠ 0 if a α 2 + bα + c = 0. We also say that x = α is a solution of the quadratic equation or that α satisfies the quadratic equation. Note that the zeroes of the quadratic polynomial ax 2 + bx + c and the roots of the quadratic equation ax 2  + bx + c = 0 are the same.

4.4 Solution of a Quadratic Equation by Completing the Square

Finding the value that makes a quadratic equation a square trinomial is called  completing the square. The square trinomial can then be solved easily by factorising.

4.5 Nature of Roots

If b 2  – 4ac < 0, then there is no real number whose square is b 2  – 4ac. Therefore, there are no real roots for the given quadratic equation in this case. Since b 2  – 4ac determines whether the quadratic equation ax 2  + bx + c = 0 has real roots or not, b 2  – 4ac is called the discriminant of this quadratic equation. So, a quadratic equation ax 2  + bx + c = 0 has (i) two distinct real roots, if b 2  – 4ac > 0, (ii) two equal real roots, if b 2 – 4ac = 0, (iii) no real roots, if b 2 – 4ac < 0. 4.6

List of exercises we covered in NCERT Solutions for Class 10 Maths Chapter 4

Exercise 4.1 Solutions – 2 Questions Exercise 4.2 Solutions – 6 Questions Exercise 4.3 Solutions – 11 Questions Exercise 4.4 Solutions – 5 Questions

In a quadratic equation, x represents an unknown form, and a, b, and c are the known values. An equation to be quadratic “a” should not be equal to 0. The equation is of the form ax 2 + bx + c = 0. The values of a, b, and c are always real numbers. A quadratic equation can be calculated by completing the square. A quadratic equation has

• Two different real roots
• No real roots
• Two equal roots

Key Features of NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations

• The highly experienced faculty at BYJU’S designs NCERT Solutions with utmost care.
• The solutions are 100% accurate and can be used by the students while preparing for their CBSE board exams.
• All the minute concepts are also covered to help students face other competitive exams more confidently.
• The exercise questions present in the NCERT Textbook have been answered in a step-wise manner so that students attain good scores not only on the final answer but also on each step.

For more questions to practise, students can refer to the other study materials which are given at BYJU’S.

• RD Sharma Solutions for Class 10 Maths Chapter 8 Quadratic Equations

Disclaimer – 

Dropped Topics –  4.4 Solution of a quadratic equation by completing the squares

Frequently Asked Questions on NCERT Solutions for Class 10 Maths Chapter 4

How many exercises are there in ncert solutions for class 10 maths chapter 4, is byju’s website providing answers for ncert solutions for class 10 maths chapter 4 quadratic equations, mention the important concepts you learn in ncert solutions for class 10 maths chapter 4 quadratic equations., leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

It is good learning app

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Trial Class

Quadratic Formula Calculator

Enter the equation you want to solve using the quadratic formula.

The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. For equations with real solutions, you can use the graphing tool to visualize the solutions.

Quadratic Formula : x = − b ± b 2 − 4 a c 2 a

Click the blue arrow to submit. Choose "Solve Using the Quadratic Formula" from the topic selector and click to see the result in our Algebra Calculator !

Solve Using the Quadratic Formula Apply the Quadratic Formula

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^4-5x^2+4=0
• \sqrt{x-1}-x=-7
• \left|3x+1\right|=4
• \log _2(x+1)=\log _3(27)
• 3^x=9^{x+5}
• What is the completing square method?
• Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
• What is the golden rule for solving equations?
• The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
• How do you simplify equations?
• To simplify equations, combine like terms, remove parethesis, use the order of operations.
• How do you solve linear equations?
• To solve a linear equation, get the variable on one side of the equation by using inverse operations.

equation-calculator

• Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series. Over the next few weeks, we'll be showing how Symbolab...

Please add a message.

Message received. Thanks for the feedback.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 14

• Solve by completing the square: Integer solutions
• Solve by completing the square: Non-integer solutions
• Solve equations by completing the square
• Worked example: completing the square (leading coefficient ≠ 1)
• Completing the square
• Solving quadratics by completing the square: no solution
• Proof of the quadratic formula

Solving quadratics by completing the square

• Completing the square review
• Quadratic formula proof review

What you should be familiar with before taking this lesson

• Solving quadratic equations by taking the square root
• Solving quadratic equations by factoring

What you will learn in this lesson

Solving quadratic equations by completing the square, what happened here, how to complete the square.

• The coefficient of x ‍   , which we know to be 6 ‍   , should be equal to 2 a ‍   . This means that a = 3 ‍   .
• The constant number we need to add is equal to a 2 ‍   , which is 3 2 = 9 ‍   .
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍