lesson 6 homework practice scientific notation answer key

Worksheet and Answer Key

• Scientific Notation
• Operations with Scientific Notation

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 7: Exponents and scientific notation

Lesson 4: dividing powers of 10.

• The 0 & 1st power (Opens a modal)

Lesson 6: What about other bases?

• Exponent properties with products (Opens a modal)
• Exponent properties with quotients (Opens a modal)
• Negative exponent intuition (Opens a modal)
• Multiplying & dividing powers (integer exponents) (Opens a modal)
• Multiply powers Get 3 of 4 questions to level up!
• Powers of powers Get 3 of 4 questions to level up!
• Divide powers Get 3 of 4 questions to level up!
• Negative exponents Get 3 of 4 questions to level up!
• Multiply & divide powers (integer exponents) Get 5 of 7 questions to level up!

Lesson 8: Combining bases

• Exponent properties with parentheses (Opens a modal)
• Exponent properties review (Opens a modal)

Extra practice: Exponents

• No videos or articles available in this lesson
• Powers of products & quotients Get 3 of 4 questions to level up!

Lesson 12: Applications of arithmetic with powers of 10

• Multiplying multiples of powers of 10 (Opens a modal)
• Approximating with powers of 10 (Opens a modal)
• Multiplication and division with powers of ten Get 5 of 7 questions to level up!
• Approximating with powers of 10 Get 3 of 4 questions to level up!

Lesson 13: Definition of scientific notation

• Scientific notation example: 0.0000000003457 (Opens a modal)
• Scientific notation examples (Opens a modal)
• Scientific notation review (Opens a modal)
• Scientific notation Get 5 of 7 questions to level up!

Lesson 14: Multiplying, dividing, and estimating with scientific notation

• Multiplying in scientific notation example (Opens a modal)
• Multiplying & dividing in scientific notation (Opens a modal)
• Scientific notation word problem: U.S. national debt (Opens a modal)
• Multiplying & dividing in scientific notation Get 3 of 4 questions to level up!

Lesson 15: Adding and subtracting with scientific notation

• Adding & subtracting in scientific notation Get 3 of 4 questions to level up!
• Scientific notation word problems Get 3 of 4 questions to level up!

• Notifications 0

• Add Friend ($5)

As a registered member you can:

• View all solutions for free
• Request more in-depth explanations for free
• Ask our tutors any math-related question for free
• Email your homework to your parent or tutor for free
• Grade 8 McGraw Hill Glencoe - Answer Keys

Explanation:

\(1.1\times10^{-4} =\)

\(2.52\times10^{-5} =\)

Write each number in scientific notation.

\(43,000 =\)

• Type below:

\(0.0072 =\)

\(0.0000901 =\)

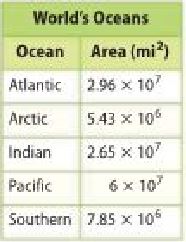
The areas of the world's oceans are listed in the table. Order the oceans according to their area from least to greatest.

The space shuttle can travel about \(8\times10^{5}\) centimeters per second. Is it more appropiate to report this rate as \(8\times10^{5}\) centimeters per second or 8 kilometers per second? Explain.

The inside diameter of a certain size of ring is \(1.732\times10^{-2}\) meter. Is it more appropriate to report the ring diameter as \(1.732\times10^{-2}\) meter or 17.32 millimeters? Explain.

Fill in with <,>, or = to make a true statement.

Yes, email page to my online tutor. ( if you didn't add a tutor yet, you can add one here )

Thank you for doing your homework!

Submit Your Question

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2: Exponents and Scientific Notation

• Last updated
• Save as PDF
• Page ID 61961

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Various rules of Exponents

Scientific Notation

Mathematicians, scientists, and economists commonly encounter very large and very small numbers. But it may not be obvious how common such figures are in everyday life. For instance, a pixel is the smallest unit of light that can be perceived and recorded by a digital camera. A particular camera might record an image that is \(2,048\) pixels by \(1,536\) pixels, which is a very high resolution picture. It can also perceive a color depth (gradations in colors) of up to \(48\) bits per frame, and can shoot the equivalent of \(24\) frames per second. The maximum possible number of bits of information used to film a one-hour (\(3,600\)-second) digital film is then an extremely large number.

Using a calculator, we enter \(2,048×1\), \(536×48×24×3\), \(600\) and press ENTER. The calculator displays \(1.304596316E13\). What does this mean? The “\(E13\)” portion of the result represents the exponent \(13\) of ten, so there are a maximum of approximately \(1.3\times10^{13}\) bits of data in that one-hour film. In this section, we review rules of exponents first and then apply them to calculations involving very large or small numbers.

Using the Product Rule of Exponents

Consider the product \(x^3\times x^4\). Both terms have the same base, \(x\), but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.

\[ \begin{align*} x^3 \times x^4 &= \overbrace{x \times x \times x}^{\text{3 factors}} \times \overbrace{ x \times x \times x\times x}^{\text{4 factors}} \\[4pt] &= \overbrace{x\times x\times x\times x\times x\times x\times x}^{\text{7 factors}} \\[4pt] &=x^7 \end{align*}\]

The result is that \(x^3\times x^4=x^{3+4}=x^7\).

Notice that the exponent of the product is the sum of the exponents of the terms. In other words, when multiplying exponential expressions with the same base, we write the result with the common base and add the exponents. This is the product rule of exponents.

\[a^m\times a^n=a^{m+n}\]

Now consider an example with real numbers.

\(2^3\times2^4=2^{3+4}=2^7\)

We can always check that this is true by simplifying each exponential expression. We find that \(2^3\) is \(8\), \(2^4\) is \(16\), and \(2^7\) is \(128\). The product \(8\times16\) equals \(128\), so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents.

THE PRODUCT RULE OF EXPONENTS

For any real number a and natural numbers \(m\) and \(n\), the product rule of exponents states that

\[a^m\times a^n=a^{m+n} \label{prod}\]

Example \(\PageIndex{1}\): Using the Product Rule

Write each of the following products with a single base. Do not simplify further.

• \(t^5\times t^3\)
• \((−3)^5\times(−3)\)
• \(x^2\times x^5\times x^3\)

Use the product rule (Equation \ref{prod}) to simplify each expression.

• \(t^5\times t^3=t^{5+3}=t^8\)
• \((−3)^5\times(−3)=(−3)^5\times(−3)^1=(−3)^{5+1}=(−3)^6\)

At first, it may appear that we cannot simplify a product of three factors. However, using the associative property of multiplication, begin by simplifying the first two.

\[x^2\times x^5\times x^3=(x^2\times x^5) \times x^3=(x^{2+5})\times x^3=x^7\times x^3=x^{7+3}=x^{10} \nonumber\]

Notice we get the same result by adding the three exponents in one step.

\[x^2\times x^5\times x^3=x^{2+5+3}=x^{10} \nonumber\]

Exercise \(\PageIndex{1}\)

• \(k^6\times k^9\)
• \(\left(\dfrac{2}{y}\right)^4\times\left(\dfrac{2}{y}\right)\)
• \(t^3\times t^6\times t^5\)

\(\left(\dfrac{2}{y}\right)^5\)

Using the Quotient Rule of Exponents

The quotient rule of exponents allows us to simplify an expression that divides two numbers with the same base but different exponents. In a similar way to the product rule, we can simplify an expression such as \(\dfrac{y^m}{y^n}\), where \(m>n\). Consider the example \(\dfrac{y^9}{y^5}\). Perform the division by canceling common factors.

\[\begin{align*} \dfrac{y^9}{y^5} &= \dfrac{y\cdot y\cdot y\cdot y\cdot y\cdot y\cdot y\cdot y\cdot y}{y\cdot y\cdot y\cdot y\cdot y}\\ &= \dfrac{y\cdot y\cdot y\cdot y}{1}\\ &= y^4 \end{align*}\]

Notice that the exponent of the quotient is the difference between the exponents of the divisor and dividend.

\[\dfrac{a^m}{a^n}=a^{m−n}\]

In other words, when dividing exponential expressions with the same base, we write the result with the common base and subtract the exponents.

\(\dfrac{y^9}{y^5}=y^{9−5}=y^4\)

For the time being, we must be aware of the condition \(m>n\). Otherwise, the difference \(m-n\) could be zero or negative. Those possibilities will be explored shortly. Also, instead of qualifying variables as nonzero each time, we will simplify matters and assume from here on that all variables represent nonzero real numbers.

THE QUOTIENT RULE OF EXPONENTS

For any real number \(a\) and natural numbers \(m\) and \(n\), such that \(m>n\), the quotient rule of exponents states that

\[\dfrac{a^m}{a^n}=a^{m−n} \label{quot}\]

Example \(\PageIndex{2}\): Using the Quotient Rule

• \(\dfrac{(−2)^{14}}{(−2)^{9}}\)
• \(\dfrac{t^{23}}{t^{15}}\)
• \(\dfrac{(z\sqrt{2})^5}{z\sqrt{2}}\)

Use the quotient rule (Equation \ref{quot}) to simplify each expression.

• \(\dfrac{(−2)^{14}}{(−2)^{9}}=(−2)^{14−9}=(−2)^5\)
• \(\dfrac{t^{23}}{t^{15}}\)=t^{23−15}=t^8\)
• \(\dfrac{(z\sqrt{2})^5}{z\sqrt{2}}=(z\sqrt{2})^{5−1}=(z\sqrt{2})^4\)

Exercise \(\PageIndex{2}\)

• \(\dfrac{s^{75}}{s^{68}}\)
• \(\dfrac{(−3)^6}{−3}\)
• \(\dfrac{(ef^2)^5}{(ef^2)^3}\)

\((−3)^5\)

\((ef^2)^2\)

Using the Power Rule of Exponents

Suppose an exponential expression is raised to some power. Can we simplify the result? Yes. To do this, we use the power rule of exponents. Consider the expression \((x^2)^3\). The expression inside the parentheses is multiplied twice because it has an exponent of \(2\). Then the result is multiplied three times because the entire expression has an exponent of \(3\).

\[\begin{align*} (x^2)^3 &= (x^2)\times(x^2)\times(x^2)\\ &= x\times x\times x\times x\times x\times x\\ &= x^6 \end{align*}\]

The exponent of the answer is the product of the exponents: \((x^2)^3=x^{2⋅3}=x^6\). In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.

\[(a^m)^n=a^{m⋅n}\]

Be careful to distinguish between uses of the product rule and the power rule. When using the product rule, different terms with the same bases are raised to exponents. In this case, you add the exponents. When using the power rule, a term in exponential notation is raised to a power. In this case, you multiply the exponents.

THE POWER RULE OF EXPONENTS

For any real number a and positive integers m and n, the power rule of exponents states that

\[(a^m)^n=a^{m⋅n} \label{power}\]

Example \(\PageIndex{3}\): Using the Power Rule

• \((x^2)^7\)
• \(((2t)^5)^3\)
• \(((−3)^5)^{11}\)

Use the power rule (Equation \ref{power}) to simplify each expression.

• \((x^2)^7=x^{2⋅7}=x^{14}\)
• \(((2t)^5)^3=(2t)^{5⋅3}=(2t)^{15}\)
• \(((−3)^5)^{11}=(−3)^{5⋅11}=(−3)^{55}\)

Exercise \(\PageIndex{3}\)

• \(((3y)^8)^3\)
• \((t^5)^7\)
• \(((−g)^4)^4\)

\((3y)^{24}\)

\((−g)^{16}\)

Using the Zero Exponent Rule of Exponents

Return to the quotient rule. We made the condition that \(m>n\) so that the difference \(m−n\) would never be zero or negative. What would happen if \(m=n\) ? In this case, we would use the zero exponent rule of exponents to simplify the expression to \(1\). To see how this is done, let us begin with an example.

\[\dfrac{t^8}{t^8}=1 \nonumber\]

If we were to simplify the original expression using the quotient rule, we would have

\[\dfrac{t^8}{t^8}=t^{8−8}=t^0 \nonumber\]

If we equate the two answers, the result is \(t^0=1\). This is true for any nonzero real number, or any variable representing a real number.

\[a^0=1 \nonumber\]

The sole exception is the expression \(0^0\). This appears later in more advanced courses, but for now, we will consider the value to be undefined.

THE ZERO EXPONENT RULE OF EXPONENTS

For any nonzero real number a, the zero exponent rule of exponents states that

Example \(\PageIndex{4}\): Using the Zero Exponent Rule

Simplify each expression using the zero exponent rule of exponents.

• \(\dfrac{c^3}{c^3}\)
• \(\dfrac{-3x^5}{x^5}\)
• \(\dfrac{(j^2k)^4}{(j^2k)\times(j^2k)^3}\)
• \(\dfrac{5(rs^2)^2}{(rs^2)^2}\)

Use the zero exponent and other rules to simplify each expression.

a. \[\begin{align*} \dfrac{c^3}{c^3} &= c^{3-3}\\ &= c^0\\ &= 1 \end{align*}\]

b. \[\begin{align*} \dfrac{-3x^5}{x^5} &= -3\times\dfrac{x^5}{x^5}\\ &= -3\times x^{5-5}\\ &= -3\times x^0\\ &= -3\times 1\\ &= -3 \end{align*}\]

c. \[\begin{align*} \dfrac{(j^2k)^4}{(j^2k)\times(j^2k)^3} &= \dfrac{(j^2k)^4}{(j^2k)^{1+3}} && \text{ Use the product rule in the denominator}\\ &= \dfrac{(j^2k)^4}{(j^2k)^4} && \text{ Simplify}\\ &= (j^2k)^{4-4} && \text{ Use the quotient rule}\\ &= (j^2k)^0 && \text{ Simplify}\\ &= 1 \end{align*}\]

d. \[\begin{align*} \dfrac{5(rs^2)^2}{(rs^2)^2} &= 5(rs^2)^{2-2} && \text{ Use the quotient rule}\\ &= 5(rs^2)^0 && \text{ Simplify}\\ &= 5\times1 && \text{ Use the zero exponent rule}\\ &= 5 && \text{ Simplify} \end{align*}\]

Exercise \(\PageIndex{4}\)

• \(\dfrac{t^7}{t^7}\)
• \(\dfrac{(de^2)^{11}}{2(de^2)^{11}}\)
• \(\dfrac{w^4\times w^2}{w^6}\)
• \(\dfrac{t^3\times t^4}{t^2\times t^5}\)

\(\dfrac{1}{2}\)

Using the Negative Rule of Exponents

Another useful result occurs if we relax the condition that \(m>n\) in the quotient rule even further. For example, can we simplify \(\dfrac{t^3}{t^5}\)? When \(m<n\) —that is, where the difference \(m−n\) is negative—we can use the negative rule of exponents to simplify the expression to its reciprocal.

Divide one exponential expression by another with a larger exponent. Use our example, \(\dfrac{t^3}{t^5}\).

\[\begin{align*} \dfrac{t^3}{t^5} &= \dfrac{t\times t\times t}{t\times t\times t\times t\times t} \\ &= \dfrac{1}{t\times t}\\ &= \dfrac{1}{h^2} \end{align*}\]

\[\begin{align*} \dfrac{t^3}{t^5} &= h^{3-5} \\ &= h^{-2} \end{align*}\]

Putting the answers together, we have \(h^{−2}=\dfrac{1}{h^2}\). This is true for any nonzero real number, or any variable representing a nonzero real number.

A factor with a negative exponent becomes the same factor with a positive exponent if it is moved across the fraction bar—from numerator to denominator or vice versa.

We have shown that the exponential expression an is defined when \(n\) is a natural number, \(0\), or the negative of a natural number. That means that an is defined for any integer \(n\). Also, the product and quotient rules and all of the rules we will look at soon hold for any integer \(n\).

THE NEGATIVE RULE OF EXPONENTS

For any nonzero real number a and natural number n, the negative rule of exponents states that

\[a^{−n}=\dfrac{1}{a^n}\]

Example \(\PageIndex{5}\): Using the Negative Exponent Rule

Write each of the following quotients with a single base. Do not simplify further. Write answers with positive exponents.

• \(\dfrac{\theta^3}{\theta^{10}}\)
• \(\dfrac{z^2\times z}{z^4}\)
• \(\dfrac{(-5t^3)^4}{(-5t^3)^8}\)
• \(\dfrac{\theta^3}{\theta^{10}}=\theta^{3-10}=\theta^{-7}=\dfrac{1}{\theta^7}\)
• \(\dfrac{z^2\times z}{z^4}=\dfrac{z^{2+1}}{z^4}=\dfrac{z^3}{z^4}=z^{3-4}=z^{-1}=\dfrac{1}{z}\)
• \(\dfrac{(-5t^3)^4}{(-5t^3)^8}=(-5t^3)^{4-8}=(-5t^3)^{-4}=\dfrac{1}{(-5t^3)^4}\)

Exercise \(\PageIndex{5}\)

• \(\dfrac{(-3t)^2}{(-3t)^8}\)
• \(\dfrac{f^{47}}{f^{49}\times f}\)
• \(\dfrac{2k^4}{5k^7}\)

\(\dfrac{1}{(-3t)^6}\)

\(\dfrac{1}{f^3}\)

\(\dfrac{2}{5k^3}\)​

Example \(\PageIndex{6}\): Using the Product and Quotient Rules

Write each of the following products with a single base. Do not simplify further. Write answers with positive exponents.

• \(b^2\times b^{-8}\)
• \((-x)^5\times(-x)^{-5}\)
• \(\dfrac{-7z}{(-7z)^5}\)
• \(b^2\times b^{-8}=b^{2-8}=b^{-6}=\dfrac{1}{b^6}\)
• \((-x)^5\times(-x)^{-5}=(-x)^{5-5}=(-x)^0=1\)
• \(\dfrac{-7z}{(-7z)^5}= \dfrac{(-7z)^1}{(-7z)^5}=(-7z)^{1-5}=(-7z)^{-4}=\dfrac{1}{(-7z)^4}\)

Exercise \(\PageIndex{6}\)

• \(t^{-11}\times t^6\)
• \(\dfrac{25^{12}}{25^{13}}\)

\(t^{-5}=\dfrac{1}{t^5}\)

\(\dfrac{1}{25}\)

Finding the Power of a Product

To simplify the power of a product of two exponential expressions, we can use the power of a product rule of exponents, which breaks up the power of a product of factors into the product of the powers of the factors. For instance, consider \((pq)^3\). We begin by using the associative and commutative properties of multiplication to regroup the factors.

\[\begin{align*} (pq)^3 &= (pq)\times(pq)\times(pq)\\ &= p\times q\times p\times q\times p\times q\\ &= p^3\times q^3 \end{align*}\]

In other words, \((pq)^3=p^3\times q^3\).

THE POWER OF A PRODUCT RULE OF EXPONENTS

For any real numbers a and b and any integer n, the power of a product rule of exponents states that

\[(ab)^n=a^nb^n\]​

Example \(\PageIndex{7}\): Using the Power of a Product Rule

Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.

• \((ab^2)^3\)
• \((2t)^{15}\)
• \((-2w^3)^3\)
• \(\dfrac{1}{(-7z)^4}\)
• \((e^{-2}f^2)^7\)

Use the product and quotient rules and the new definitions to simplify each expression.

a. \((ab^2)^3=(a)^3\times(b^2)^3=a^{1\times3}\times b^{2\times3}=a^3b^6\)

b. \((2t)^{15}=(2)^{15}\times(t)^{15}=2^{15}t^{15}=32,768t^{15}\)

c. \((−2w^3)^3=(−2)^3\times(w^3)^3=−8\times w^{3\times3}=−8w^9\)

d. \(\dfrac{1}{(-7z)^4}=\dfrac{1}{(-7)^4\times(z)^4}=\dfrac{1}{2401z^4}\)

e. \((e^{-2}f^2)^7=(e^{−2})^7\times(f^2)^7=e^{−2\times7}\times f^{2\times7}=e^{−14}f^{14}=\dfrac{f^{14}}{e^{14}}\)

Exercise \(\PageIndex{7}\)

• \((g^2h^3)^5\)
• \((-3y^5)^3\)
• \(\dfrac{1}{(a^6b^7)^3}\)
• \((r^3s^{-2})^4\)

\(g^{10}h^{15}\)

\(-27y^{15}\)

\(\dfrac{1}{a^{18}b^{21}}\)

\(\dfrac{r^{12}}{s^8}\)

Finding the Power of a Quotient

To simplify the power of a quotient of two expressions, we can use the power of a quotient rule, which states that the power of a quotient of factors is the quotient of the powers of the factors. For example, let’s look at the following example.

\[(e^{−2}f^2)^7=\dfrac{f^{14}}{e^{14}}\]

Let’s rewrite the original problem differently and look at the result.

\[\begin{align*} (e^{-2}f^2)^7 &= \left(\dfrac{f^2}{e^2}\right)^7\\ &= \dfrac{f^{14}}{e^{14}} \end{align*}\]

It appears from the last two steps that we can use the power of a product rule as a power of a quotient rule.

\[\begin{align*} (e^{-2}f^2)^7 &= \left(\dfrac{f^2}{e^2}\right)^7\\ &= \dfrac{(f^2)^7}{(e^2)^7}\\ &= \dfrac{f^{2\times7}}{e^{2\times7}}\\ &= \dfrac{f^{14}}{e^{14}} \end{align*}\]

THE POWER OF A QUOTIENT RULE OF EXPONENTS

For any real numbers a and b and any integer n, the power of a quotient rule of exponents states that

\[\left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}\]

Example \(\PageIndex{8}\): Using the Power of a Quotient Rule

Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.

• \(\left(\dfrac{4}{z^{11}}\right)^3\)
• \(\left(\dfrac{p}{q^3}\right)^6\)
• \(\left(\dfrac{-1}{t^2}\right)^{27}\)
• \((j^3k^{-2})^4\)
• \((m^{-2}n^{-2})^3\)

a. \(\left(\dfrac{4}{z^{11}}\right)^3=\dfrac{(4)^3}{(z^{11})^3}=\dfrac{64}{z^{11\times3}}=\dfrac{64}{z^{33}}\)

b. \(\left(\dfrac{p}{q^3}\right)^6=\dfrac{(p)^6}{(q^3)^6}=\dfrac{p^{1\times6}}{q^{3\times6}}=\dfrac{p^6}{q^{18}}\)

c. \(\left(\dfrac{-1}{t^2}\right)^{27}=\dfrac{(-1)^{27}}{(t^2)^{27}}=\dfrac{-1}{t^{2\times27}}=\dfrac{-1}{t^{54}}=-\dfrac{1}{t^{54}}\)

d. \((j^3k^{-2})^4=\left(\dfrac{j^3}{k^2}\right)^4=\dfrac{(j^3)^4}{(k^2)^4}=\dfrac{j^{3\times4}}{k^{2\times4}}=\dfrac{j^{12}}{k^8}\)

e. \((m^{-2}n^{-2})^3=\left(\dfrac{1}{m^2n^2}\right)^3=\dfrac{(1)^3}{(m^2n^2)^3}=\dfrac{1}{(m^2)^3(n^2)^3}=\dfrac{1}{m^{2\times3}n^{2\times3}}=\dfrac{1}{m^6n^6}\)

Exercise \(\PageIndex{8}\)

• \(\left(\dfrac{b^5}{c}\right)^3\)
• \(\left(\dfrac{5}{u^8}\right)^4\)
• \(\left(\dfrac{-1}{w^3}\right)^{35}\)
• \((p^{-4}q^3)^8\)
• \((c^{-5}d^{-3})^4\)

\(\dfrac{b^{15}}{c^3}\)

\(\dfrac{625}{u^{32}}\)

\(\dfrac{-1}{w^{105}}\)

\(\dfrac{q^{24}}{p^{32}}\)

\(\dfrac{1}{c^{20}d^{12}}\) 

Simplifying Exponential Expressions

Recall that to simplify an expression means to rewrite it by combing terms or exponents; in other words, to write the expression more simply with fewer terms. The rules for exponents may be combined to simplify expressions.

Example \(\PageIndex{9}\): Simplifying Exponential Expressions

Simplify each expression and write the answer with positive exponents only.

• \((6m^2n^{-1})^3\)
• \(17^5\times17^{-4}\times17^{-3}\)
• \(\left(\dfrac{u^{-1}v}{v^{-1}}\right)^2\)
• \((-2a^3b^{-1})(5a^{-2}b^2)\)
• \((x^2\sqrt{2})^4(x^2\sqrt{2})^{-4}\)
• \(\dfrac{(3w^2)^5}{(6w^{-2})^2}\)

a. \[\begin{align*} (6m^2n^{-1})^3 &= (6)^3(m^2)^3(n^{-1})^3 && \text{ The power of a product rule}\\ &= 6^3m^{2\times3}n^{-1\times3} && \text{ The power rule}\\ &= 216m^6n^{-3} && \text{ The power rule}\\ &= \dfrac{216m^6}{n^3} && \text{ The negative exponent rule} \end{align*}\]

b. \[\begin{align*} 17^5\times17^{-4}\times17^{-3} &= 17^{5-4-3} && \text{ The product rule}\\ &= 17^{-2} && \text{ Simplify}\\ &= \dfrac{1}{17^2} \text{ or } \dfrac{1}{289} && \text{ The negative exponent rule} \end{align*}\]

c. \[\begin{align*} \left ( \dfrac{u^{-1}v}{v^{-1}} \right )^2 &= \dfrac{(u^{-1}v)^2}{(v^{-1})^2} && \text{ The power of a quotient rule}\\ &= \dfrac{u^{-2}v^2}{v^{-2}} && \text{ The power of a product rule}\\ &= u^{-2}v^{2-(-2)} && \text{ The quotient rule}\\ &= u^{-2}v^4 && \text{ Simplify}\\ &= \dfrac{v^4}{u^2} && \text{ The negative exponent rule} \end{align*}\]

d. \[\begin{align*} \left (-2a^3b^{-1} \right ) \left(5a^{-2}b^2 \right ) &= \left (x^2\sqrt{2} \right )^{4-4} && \text{ Commutative and associative laws of multiplication}\\ &= -10\times a^{3-2}\times b^{-1+2} && \text{ The product rule}\\ &= -10ab && \text{ Simplify} \end{align*}\]

e. \[\begin{align*} \left (x^2\sqrt{2})^4(x^2\sqrt{2} \right )^{-4} &= \left (x^2\sqrt{2} \right )^{4-4} && \text{ The product rule}\\ &= \left (x^2\sqrt{2} \right )^0 && \text{ Simplify}\\ &= 1 && \text{ The zero exponent rule} \end{align*}\]

f. \[\begin{align*} \dfrac{(3w^2)^5}{(6w^{-2})^2} &= \dfrac{(3)^5\times(w^2)^5}{(6)^2\times(w^{-2})^2} && \text{ The power of a product rule}\\ &= \dfrac{3^5w^{2\times5}}{6^2w^{-2\times2}} && \text{ The power rule}\\ &= \dfrac{243w^{10}}{36w^{-4}} && \text{ Simplify}\\ &= \dfrac{27w^{10-(-4)}}{4} && \text{ The quotient rule and reduce fraction}\\ &= \dfrac{27w^{14}}{4} && \text{ Simplify} \end{align*}\]

Using Scientific Notation

Recall at the beginning of the section that we found the number \(1.3\times10^{13}\) when describing bits of information in digital images. Other extreme numbers include the width of a human hair, which is about \(0.00005\; m\), and the radius of an electron, which is about \(0.00000000000047\; m\). How can we effectively work read, compare, and calculate with numbers such as these?

A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of \(10\). To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between \(1\) and \(10\). Count the number of places \(n\) that you moved the decimal point. Multiply the decimal number by \(10\) raised to a power of \(n\). If you moved the decimal left as in a very large number, \(n\) is positive. If you moved the decimal right as in a small large number, \(n\) is negative.

For example, consider the number \(2,780,418\). Move the decimal left until it is to the right of the first nonzero digit, which is \(2\).

We obtain \(2.780418\) by moving the decimal point \(6\) places to the left. Therefore, the exponent of \(10\) is \(6\), and it is positive because we moved the decimal point to the left. This is what we should expect for a large number.

Working with small numbers is similar. Take, for example, the radius of an electron, \(0.00000000000047\; m\). Perform the same series of steps as above, except move the decimal point to the right.

Be careful not to include the leading \(0\) in your count. We move the decimal point \(13\) places to the right, so the exponent of \(10\) is \(13\). The exponent is negative because we moved the decimal point to the right. This is what we should expect for a small number.

SCIENTIFIC NOTATION

A number is written in scientific notation if it is written in the form \(a\times{10}^n\), where \(1≤|a|<10\) and \(n\) is an integer.

Example \(\PageIndex{10}\): Converting Standard Notation to Scientific Notation

Write each number in scientific notation.

• Distance to Andromeda Galaxy from Earth: \(24,000,000,000,000,000,000,000\; m\)
• Diameter of Andromeda Galaxy: \(1,300,000,000,000,000,000,000\; m\)
• Number of stars in Andromeda Galaxy: \(1,000,000,000,000\)
• Diameter of electron: \(0.00000000000094\; m\)
• Probability of being struck by lightning in any single year: \(0.00000143\)

a. \(24,000,000,000,000,000,000,000\; m\) \(22\) places

\(2.4\times{10}^{22}\; m\)

b. \(1,300,000,000,000,000,000,000\; m\) \(21\) places

\(1.3\times{10}^{21}\; m\)

c. \(1,000,000,000,000\) \(12\) places

\(1\times{10}^{12}\)

d. \(0.00000000000094\; m\) \(13\) places

\(9.4\times{10}^{-13}\; m\)

e. \(0.00000143\) \(6\) places

\(1.43\times{10}^6\)

Observe that, if the given number is greater than \(1\), as in examples a–c, the exponent of \(10\) is positive; and if the number is less than \(1\), as in examples d–e, the exponent is negative.

Exercise \(\PageIndex{10}\)

• U.S. national debt per taxpayer (April 2014): \(\$152,000\)
• World population (April 2014): \(7,158,000,000\)
• World gross national income (April 2014): \(\$85,500,000,000,000\)
• Time for light to travel \(1\; m: 0.00000000334\; s\)
• Probability of winning lottery (match \(6\) of \(49\) possible numbers): \(0.0000000715\)

\(\$1.52\times{10}^5\)

\(7.158\times{10}^9\)

\(\$8.55\times{10}^{13}\)

\(3.34\times{10}^{-9}\)

\(7.15\times{10}^{-8}\)

Converting from Scientific to Standard Notation

To convert a number in scientific notation to standard notation, simply reverse the process. Move the decimal n places to the right if \(n\) is positive or \(n\) places to the left if \(n\) is negative and add zeros as needed. Remember, if \(n\) is positive, the value of the number is greater than \(1\), and if \(n\) is negative, the value of the number is less than one.

Example \(\PageIndex{11}\): Converting Scientific Notation to Standard Notation

Convert each number in scientific notation to standard notation.

• \(3.547\times{10}^{14}\)
• \(−2\times{10}^6\)
• \(7.91\times{10}^{−7}\)
• \(−8.05\times{10}^{−12}\)

a. \(3.547\times{10}^{14}\)

\(3.54700000000000\)

\(\rightarrow14\) places

\(354,700,000,000,000\)

b. \(−2\times{10}^6\)

\(−2.000000\)

\(\rightarrow6\) places

\(−2,000,000\)

c. \(7.91\times{10}^{−7}\)

\(0000007.91\)

\(\rightarrow7\) places

\(0.000000791\)

d. \(−8.05\times{10}^{−12}\)

\(−000000000008.05\)

\(\rightarrow12\) places

\(−0.00000000000805\)

Exercise \(\PageIndex{11}\)

• \(7.03\times{10}^5\)
• \(−8.16\times{10}^{11}\)
• \(−3.9\times{10}^{−13}\)
• \(8\times{10}^{−6}\)

\(703,000\)

\(−816,000,000,000\)

\(−0.00000000000039\)

\(0.000008\)

Using Scientific Notation in Applications

Scientific notation, used with the rules of exponents, makes calculating with large or small numbers much easier than doing so using standard notation. For example, suppose we are asked to calculate the number of atoms in \(1\; L\) of water. Each water molecule contains \(3\) atoms (\(2\) hydrogen and \(1\) oxygen). The average drop of water contains around \(1.32\times{10}{21}\) molecules of water and \(1\; L\) of water holds about \(1.22\times{10}^{4}\) average drops. Therefore, there are approximately \(3⋅(1.32\times{10}^{21})⋅(1.22\times{10}^4)≈4.83\times{10}^{25}\) atoms in \(1\; L\) of water. We simply multiply the decimal terms and add the exponents. Imagine having to perform the calculation without using scientific notation!

When performing calculations with scientific notation, be sure to write the answer in proper scientific notation. For example, consider the product \((7\times{10}^4)⋅(5\times{10}^6)=35\times{10}^{10}\). The answer is not in proper scientific notation because \(35\) is greater than \(10\). Consider \(35\) as \(3.5\times10\). That adds a ten to the exponent of the answer.

\((35)\times{10}^{10}=(3.5\times10)\times{10}^{10}=3.5\times(10\times{10}^{10})=3.5\times{10}^{11}\)

Example \(\PageIndex{12}\): Using Scientific Notation

Perform the operations and write the answer in scientific notation.

• \((8.14\times{10}^{−7})(6.5\times{10}^{10})\)
• \((4\times{10}^5)÷(−1.52\times{10}^{9})\)
• \((2.7\times{10}^5)(6.04\times{10}^{13})\)
• \((1.2\times{10}^8)÷(9.6\times{10}^5)\)
• \((3.33\times{10}^4)(−1.05\times{10}^7)(5.62\times{10}^5)\)

a. \[\begin{align*} (8.14\times{10}^{-7})(6.5\times{10}^{10}) &= (8.14\times6.5)({10}^{-7}\times{10}^{10}) \text{ Commutative and associative properties of multiplication}\\ &= (52.91)({10}^3) \text{ Product rule of exponents}\\ &= 5.291\times{10}^4 \text{ Scientific notation} \end{align*}\]

b. \[\begin{align*} (4\times{10}^5)\div (-1.52\times{10}^{9}) &= \left(\dfrac{4}{-1.52}\right)\left(\dfrac{{10}^5}{{10}^9}\right) \text{ Commutative and associative properties of multiplication}\\ &\approx (-2.63)({10}^{-4}) \text{ Quotient rule of exponents}\\ &= -2.63\times{10}^{-4} \text{ Scientific notation} \end{align*}\]

c. \[\begin{align*} (2.7\times{10}^5)(6.04\times{10}^{13}) &= (2.7\times6.04)({10}^5\times{10}^{13}) \text{ Commutative and associative properties of multiplication}\\ &= (16.308)({10}^{18}) \text{ Product rule of exponents}\\ &= 1.6308\times{10}^{19} \text{ Scientific notation} \end{align*}\]

d. \[\begin{align*} (1.2\times{10}^8)÷(9.6\times{10}^5) &= \left(\dfrac{1.2}{9.6}\right)\left(\dfrac{{10}^8}{{10}^5}\right) \text{ Commutative and associative properties of multiplication}\\ &= (0.125)({10}^3) \text{ Quotient rule of exponents}\\ &= 1.25\times{10}^2 \text{ Scientific notation} \end{align*}\]

e. \[\begin{align*} (3.33\times{10}^4)(-1.05\times{10}^7)(5.62\times{10}^5) &= [3.33\times(-1.05)\times5.62]({10}^4\times{10}^7\times{10}^5)\\ &\approx (-19.65)({10}^{16})\\ &= -1.965\times{10}^{17} \end{align*}\]

Exercise \(\PageIndex{12}\)

• \((−7.5\times{10}^8)(1.13\times{10}^{−2})\)
• \((1.24\times{10}^{11})÷(1.55\times{10}^{18})\)
• \((3.72\times{10}^9)(8\times{10}^3)\)
• \((9.933\times{10}^{23})÷(−2.31\times{10}^{17})\)
• \((−6.04\times{10}^9)(7.3\times{10}^2)(−2.81\times{10}^2)\)

\(−8.475\times{10}^6\)

\(8\times{10}^{−8}\)

\(2.976\times{10}^{13}\)

\(−4.3\times{10}^6\)

\(≈1.24\times{10}^{15}\)

Example \(\PageIndex{13}\): Applying Scientific Notation to Solve Problems

In April 2014, the population of the United States was about \(308,000,000\) people. The national debt was about \(\$17,547,000,000,000\). Write each number in scientific notation, rounding figures to two decimal places, and find the amount of the debt per U.S. citizen. Write the answer in both scientific and standard notations.

The population was \(308,000,000=3.08\times{10}^8\).

The national debt was \($17,547,000,000,000≈$1.75\times{10}^{13}\).

To find the amount of debt per citizen, divide the national debt by the number of citizens.

\[\begin{align*} (1.75\times{10}^{13})\div (3.08\times{10}^8)&=\left(\dfrac{1.75}{3.08}\right)({10}^5)\\ &\approx 0.57\times{10}^5\\ &=5.7\times{10}^4 \end{align*}\]

The debt per citizen at the time was about \($5.7\times{10}^4\), or \($57,000\).

Exercise \(\PageIndex{13}\)

An average human body contains around \(30,000,000,000,000\) red blood cells. Each cell measures approximately \(0.000008\; m\) long. Write each number in scientific notation and find the total length if the cells were laid end-to-end. Write the answer in both scientific and standard notations.

Number of cells: \(3\times{10}^{13}\); length of a cell: \(8\times{10}^{−6}\; m\); total length: \(2.4\times{10}^8\; m\) or \(240,000,000\; m\).

Access these online resources for additional instruction and practice with exponents and scientific notation.

Exponential Notation

Properties of Exponents

Zero Exponent

Simplify Exponent Expressions

Quotient Rule for Exponents

Converting to Decimal Notation

Key Equations

Key concepts.

• Products of exponential expressions with the same base can be simplified by adding exponents. See Example .
• Quotients of exponential expressions with the same base can be simplified by subtracting exponents. See Example .
• Powers of exponential expressions with the same base can be simplified by multiplying exponents. See Example .
• An expression with exponent zero is defined as 1. See Example .
• An expression with a negative exponent is defined as a reciprocal. See Example and Example .
• The power of a product of factors is the same as the product of the powers of the same factors. See Example .
• The power of a quotient of factors is the same as the quotient of the powers of the same factors. See Example .
• The rules for exponential expressions can be combined to simplify more complicated expressions. See Example .
• Scientific notation uses powers of 10 to simplify very large or very small numbers. See Example and Example .
• Scientific notation may be used to simplify calculations with very large or very small numbers. See Example and Example .

Finished Papers

Customer Reviews

How will you prove that the drafts are original and unique?

Customer Reviews

Business Enquiries

How much does an essay cost.

Starting your search for an agency, you need to carefully study the services of each option. There are a lot of specialists in this area, so prices vary in a wide range. But you need to remember that the quality of work directly depends on the cost. Decide immediately what is more important to you - financial savings or the result.

Companies always indicate how much 1000 characters of text costs, so that the client understands what price to expect and whether it is worth continuing to cooperate.

At Essayswriting, it all depends on the timeline you put in it. Professional authors can write an essay in 3 hours, if there is a certain volume, but it must be borne in mind that with such a service the price will be the highest. The cheapest estimate is the work that needs to be done in 14 days. Then 275 words will cost you $ 10, while 3 hours will cost you $ 50. Please, take into consideration that VAT tax is totally included in the mentioned prices. The tax will be charged only from EU customers.

When choosing an agency, try to pay more attention to the level of professionalism, and then evaluate the high cost of work.

Order Number

Finished Papers

Writing my essay with the top-notch writers!

The writers you are supposed to hire for your cheap essay writer service are accomplished writers. First of all, all of them are highly skilled professionals and have higher academic degrees like Masters and PhDs. Secondly, all the writers have work experience of more than 5 years in this domain of academic writing. They are responsible for

• Omitting any sign of plagiarism
• Formatting the draft
• Delivering order before the allocated deadline

Perfect Essay

Customer Reviews

Writing my essay with the top-notch writers!

The writers you are supposed to hire for your cheap essay writer service are accomplished writers. First of all, all of them are highly skilled professionals and have higher academic degrees like Masters and PhDs. Secondly, all the writers have work experience of more than 5 years in this domain of academic writing. They are responsible for

• Omitting any sign of plagiarism
• Formatting the draft
• Delivering order before the allocated deadline

1555 Lakeside Drive, Oakland

Extra spacious rarely available courtyard facing unit at the Lakeside…

Andre Cardoso

Why is the best essay writing service?

On the Internet, you can find a lot of services that offer customers to write huge articles in the shortest possible time at a low price. It's up to you to agree or not, but we recommend that you do not rush to make a choice. Many of these sites will take your money and disappear without getting the job done. Some low-skilled writers will still send you an essay file, but the text will not meet the required parameters.

is the best essay writing service because we provide guarantees at all stages of cooperation. Our polite managers will answer all your questions and help you determine the details. We will sign a contract with you so that you can be sure of our good faith.

The team employs only professionals with higher education. They will write you a high-quality essay that will pass all anti-plagiarism checks, since we do not steal other people's thoughts and ideas, but create new ones.

You can always contact us and make corrections, and we will be happy to help you.

Finished Papers

Niamh Chamberlain

Customer Reviews

• Terms & conditions
• Privacy policy
• Referral program

Finished Papers

Gustavo Almeida Correia