go math grade 5 answer key homework book chapter 6

• Apalachee Elementary
• Astoria Park Elementary
• Bond Elementary
• Buck Lake Elementary
• Canopy Oaks Elementary
• Chaires Elementary
• Conley Elementary
• DeSoto Trail Elementary
• Gilchrist Elementary
• Hartsfield Elementary
• Hawks Rise Elementary
• Kate Sullivan Elementary
• Killearn Lakes Elementary
• Oak Ridge Elementary
• Pineview Elementary
• Riley Elementary
• Roberts Elementary
• Ruediger Elementary
• Sabal Palm Elementary
• Sealey Elementary
• Springwood Elementary
• W.T. Moore Elementary
• Cobb Middle School
• Deerlake Middle
• Fairview Middle
• Griffin Middle
• Montford Middle
• Nims Middle
• Swift Creek Middle
• Chiles High
• Lincoln High
• Rickards High
• Ft. Braden PreK-8
• Second Chance at Ghazvini Learning Center
• Success Academy at Ghazvini Learning Center
• Woodville PreK-8
• Early Childhood Programs
• Dining Services
• Student Admissions
• Transportation & Buses
• LCS - 20223 Night of Celebration
• LCS - 2024 Graduation

Astoria Park Elementary School

Home of the Panthers! #Building Great Minds!

• 5th Grade Go Math
• Go Math Chapter 6

Z_Jones, Ryan B._Transfer

Page navigation.

• Sunshine State Readers
• FCAT Practice Materials
• Go Math Videos
• 5th Grade Chapter 1 Textbook Pages
• 5th Grade Chapter 1 Workbook Pages
• 5th Grade Chapter 1 Enrich Pages
• 5th Grade Chapter 2 Textbook Pages
• 5th Grade Chapter 2 Workbook Pages
• 5th Grade Chapter 2 Reteach Pages
• 5th Grade Chapter 2 Enrich Pages
• 5th Grade Chapter 3 Textbook Pages
• 5th Grade Chapter 3 Workbook Pages
• 5th Grade Chapter 3 Reteach Pages
• 5th Grade Chapter 3 Enrich Pages
• 5th Grade Chapter 4 Textbook Pages
• 5th Grade Chapter 4 Workbook Pages
• 5th Grade Chapter 4 Reteach Pages
• 5th Grade Chapter 4 Enrich Pages
• 5th Grade Chapter 5 Textbook Pages
• 5th Grade Chapter 5 Workbook Pages
• 5th Grade Chapter 5 Reteach Pages
• 5th Grade Chapter 5 Enrich Pages
• 5th Grade Chapter 6 Textbook Pages
• 5th Grade Chapter 6 Workbook Pages
• 5th Grade Chapter 6 Reteach Pages
• 5th Grade Chapter 6 Enrich Pages
• 5th Grade Chapter 7 Textbook Pages
• 5th Grade Chapter 7 Workbook Pages
• 5th Grade Chapter 7 Reteach Pages
• 5th Grade Chapter 7 Enrich Pages
• 5th Grade Chapter 8 Textbook Pages
• 5th Grade Chapter 8 Workbook Pages
• 5th Grade Chapter 8 Reteach Pages
• 5th Grade Chapter 8 Enrich Pages
• 5th Grade Chapter 9 Textbook Pages
• 5th Grade Chapter 9 Workbook Pages
• 5th Grade Chapter 9 Reteach Pages
• 5th Grade Chapter 9 Enrich Pages
• 5th Grade Chapter 10 Textbook Pages
• 5th Grade Chapter 10 Workbook Pages
• 5th Grade Chapter 10 Reteach Pages
• 5th Grade Chapter 10 Enrich Pages
• 5th Grade Chapter 11 Textbook Pages
• 5th Grade Chapter 11 Workbook Pages
• 5th Grade Chapter 11 Reteach Pages
• 5th Grade Chapter 11 Enrich Pages

Add and Subtract Fractions with Unlike Denominators

Lesson(s): 6.1–6.3, 6.9

Use equivalent fractions as a strategy to add and subtract fractions. MAFS.5.NF.1.2 Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers.

Lesson(s): 6.4–6.8, 6.10

Use equivalent fractions as a strategy to add and subtract fractions. MAFS.5.NF.1.1 Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators.

Student Workbook Chapter 6

Enrich chapter 6, reteach chapter 6, student textbook chapter 6.

• Questions or Feedback? |
• Web Community Manager Privacy Policy (Updated) |

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Go Math Grade 5 Answer Key Chapter 6 Add and Subtract Fractions with Unlike Denominators

Go Math Grade 5 Answer Key Chapter 6 Add and Subtract Fractions with Unlike Denominators can be downloaded free of cost from here. HMH Go Math Grade 5 Answer Key includes topics such as Addition and Subtraction with unlike denominators, Estimate fraction sums and differences, Least Common Denominators, etc. Begin your preparation from Go Math Grade 5 Chapter 6 Solution Key Add and Subtract Fractions with Unlike Denominators and score better grades in your exams.

The Go Math Grade 5 Answer Key Add and Subtract Fractions with Unlike Denominators covers all the Questions in Chapter Tests, Practice Tests, etc., and has detailed solutions for all of them. Try to solve as many problems as possible from the  Go Math Answer Key for Grade 5 Chapter 6 Add and Subtract Fractions with Unlike Denominators and know the concepts behind them easily. Access the Topics in 5th Grade Go Math Ch 6 Add and Subtract Fractions with Unlike Denominators via quick links available in the forthcoming modules.

Lesson 1: Investigate • Addition with Unlike Denominators

Share and Show – Page No. 244

• Investigate • Addition with Unlike Denominators Page No. 245

Problem Solving – Page No. 246

Lesson 2: Investigate • Subtraction with Unlike Denominators

Share and Show – Page No. 248

• Investigate • Subtraction with Unlike Denominators Page No. 249

UNLOCK the Problem – Page No. 250

Lesson 3: Estimate Fraction Sums and Differences

Share and Show – Page No. 253

Problem solving – page no. 254.

Lesson 4: Common Denominators and Equivalent Fractions

Share and Show – Page No. 256

• Common Denominators and Equivalent Fractions Page No. 257

UNLOCK the Problem – Page No. 258

Lesson 5: Add and Subtract Fractions

Share and Show – Page No. 260

On your own – page no. 261, problem solving – page no. 262.

Mid-Chapter Checkpoint

Mid-Chapter Checkpoint – Vocabulary – Page No. 263

Mid-chapter checkpoint – page no. 264.

Lesson 6: Add and Subtract Mixed Numbers

Share and Show – Page No. 266

Page no. 267, problem solving – page no. 268.

Lesson 7: Subtraction with Renaming

Share and Show – Page No. 270

• Subtraction with Renaming Page No. 271
• Subtraction with Renaming Page No. 272

Lesson 8: Algebra • Patterns with Fractions

Share and Show – Page No. 275

Problem solving – page no. 276.

Lesson 9: Problem Solving • Practice Addition and Subtraction

Share and Show – Page No. 279

On your own – page no. 280.

Lesson 10: Algebra • Use Properties of Addition

Share and Show – Page No. 283

Problem solving – page no. 284.

Chapter 6 Review/Test

Chapter Review/Test – Vocabulary – Page No. 285

Chapter review/test – page no. 286, chapter review/test – page no. 287, chapter review/test – page no. 288.

Use fraction strips to find the sum. Write your answer in simplest form.

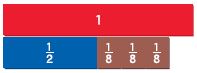
Answer: \(\frac{7}{8}\) Explanation: Step 1: Place three \(\frac{1}{8}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{2}\) fraction strip beside the three \(\frac{1}{8}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{2}\) and \(\frac{3}{8}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{4}{4}\) = \(\frac{4}{8}\) \(\frac{3}{8}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{4}{8}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\)

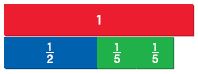
Answer: \(\frac{9}{10}\) Explanation: Step 1: Place two \(\frac{1}{5}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{2}\) fraction strip beside the two \(\frac{1}{5}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{2}\) and \(\frac{2}{5}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{2}\) = \(\frac{1}{2}\) × \(\frac{5}{5}\) = \(\frac{5}{10}\) \(\frac{2}{5}\) = \(\frac{2}{5}\) × \(\frac{2}{2}\) = \(\frac{4}{10}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{5}{10}\) + \(\frac{4}{10}\) = \(\frac{9}{10}\) Thus, \(\frac{1}{2}\) + \(\frac{2}{5}\) = \(\frac{9}{10}\)

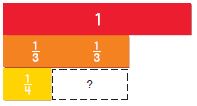
Page No. 245

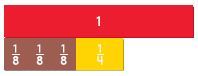
Answer: \(\frac{5}{8}\) Explanation: Step 1: Place three \(\frac{1}{8}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{4}\) fraction strip beside the three \(\frac{1}{8}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{4}\) and \(\frac{3}{8}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{4}\) × \(\frac{2}{2}\) = \(\frac{2}{8}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{2}{8}\) + \(\frac{3}{8}\) = \(\frac{5}{8}\)

Answer: 1 \(\frac{1}{12}\) Explanation: Step 1: Place three \(\frac{3}{4}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{3}\) fraction strip beside the three \(\frac{1}{4}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{3}\) and \(\frac{3}{4}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{3}\) × \(\frac{4}{4}\) = \(\frac{4}{12}\) \(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{4}{12}\) + \(\frac{9}{12}\) = \(\frac{13}{12}\) = 1 \(\frac{1}{12}\)

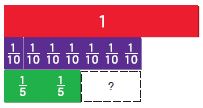
Question 5. \(\frac{2}{5}+\frac{3}{10}=\) \(\frac{□}{□}\)

Answer: \(\frac{7}{10}\) Explanation: Step 1: Place three \(\frac{1}{10}\) fractions strips under the 1 whole strip on your Mathboard. Then place a two \(\frac{2}{5}\) fraction strip beside the three \(\frac{1}{10}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{2}{5}\) and \(\frac{3}{10}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{2}{5}\) • \(\frac{2}{2}\) = \(\frac{4}{10}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{4}{10}\) + \(\frac{3}{10}\) = \(\frac{7}{10}\)

Question 6. \(\frac{1}{4}+\frac{1}{12}=\) \(\frac{□}{□}\)

Answer: \(\frac{4}{12}\) Explanation: Step 1: Place \(\frac{1}{12}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{4}\) fraction strip beside the \(\frac{1}{12}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{12}\) and \(\frac{1}{4}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{4}\) • \(\frac{3}{3}\) = \(\frac{3}{12}\) \(\frac{1}{12}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{3}{12}\) + \(\frac{1}{12}\) = \(\frac{4}{12}\)

Question 7. \(\frac{1}{2}+\frac{3}{10}=\) \(\frac{□}{□}\)

Answer: \(\frac{8}{10}\) Explanation: Step 1: Place three \(\frac{1}{10}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{2}\) fraction strip beside the three \(\frac{1}{10}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{2}\) and \(\frac{3}{10}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{2}\) • \(\frac{5}{5}\) = \(\frac{5}{10}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{5}{10}\) + \(\frac{3}{10}\) = \(\frac{8}{10}\)

Question 8. \(\frac{2}{3}+\frac{1}{6}=\) \(\frac{□}{□}\)

Answer: \(\frac{5}{6}\) Explanation: Step 1: Place two \(\frac{1}{3}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{6}\) fraction strip beside the two \(\frac{1}{3}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{6}\) and \(\frac{2}{3}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{2}{3}\) = \(\frac{2}{3}\) • \(\frac{2}{2}\) = \(\frac{4}{6}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{4}{6}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\)

Question 9. \(\frac{5}{8}+\frac{1}{4}=\) \(\frac{□}{□}\)

Answer: \(\frac{7}{8}\) Explanation: Step 1: Place five \(\frac{1}{8}\) fractions strips under the 1 whole strip on your Mathboard. Then place a \(\frac{1}{4}\) fraction strip beside the five \(\frac{1}{8}\) strips. Step 2: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{4}\) and \(\frac{5}{8}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{4}\) • \(\frac{2}{2}\) = \(\frac{2}{8}\) Step 3: Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{2}{8}\) + \(\frac{5}{8}\) = \(\frac{7}{8}\)

Question 10. \(\frac{1}{2}+\frac{1}{5}=\) \(\frac{□}{□}\)

Answer: \(\frac{7}{10}\) Explanation: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{5}\) and \(\frac{1}{2}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{5}\) • \(\frac{2}{2}\) = \(\frac{2}{10}\) \(\frac{1}{2}\) • \(\frac{5}{5}\) = \(\frac{5}{10}\) Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\)

Question 11. \(\frac{3}{4}+\frac{1}{6}=\) \(\frac{□}{□}\)

Answer: \(\frac{11}{12}\) Explanation: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{3}{4}\) and \(\frac{1}{6}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{3}{4}\) • \(\frac{3}{3}\) = \(\frac{9}{12}\) \(\frac{1}{6}\) • \(\frac{2}{2}\)  = \(\frac{2}{12}\) Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{9}{12}\) + \(\frac{2}{12}\) = \(\frac{11}{12}\)

Question 12. \(\frac{1}{2}+\frac{2}{3}=\) ______ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{6}\) Explanation: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{2}{3}\) and \(\frac{1}{2}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{2}{3}\) • \(\frac{2}{2}\) = \(\frac{4}{6}\) \(\frac{1}{2}\) • \(\frac{3}{3}\) = \(\frac{3}{6}\) Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{4}{6}\) + \(\frac{3}{6}\) = \(\frac{7}{6}\) \(\frac{7}{6}\) is greater than 1. Convert the fraction into the mixed fraction \(\frac{7}{6}\) = 1 \(\frac{1}{6}\)

Question 13. \(\frac{7}{8}+\frac{1}{4}=\) ______ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{8}\) Explanation: Find fraction strips, all with the same denominator, that are equivalent to \(\frac{7}{8}\) and \(\frac{1}{4}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions. \(\frac{1}{4}\) • \(\frac{2}{2}\) = \(\frac{2}{8}\) Add the fractions with like denominators. Use the 1 whole strip to rename the sum in the simplest form. \(\frac{7}{8}\) + \(\frac{2}{8}\) = \(\frac{9}{8}\) Convert \(\frac{9}{8}\) into the mixed fraction. \(\frac{9}{8}\) = 1 \(\frac{1}{8}\)

Question 14. Explain how using fraction strips with like denominators makes it possible to add fractions with unlike denominators. Type below: _________

Answer: The strips for both fractions need to be the same size. Finding like denominators is done by trying smaller strips so they can all be the same size.

Question 15. Maya makes trail mix by combining \(\frac{1}{3}\) cup of mixed nuts and \(\frac{1}{4}\) cup of dried fruit. What is the total amount of ingredients in her trail mix? \(\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\) Maya uses \(\frac{1}{12}\) cup of ingredients. Write a new problem using different amounts for each ingredient. Each amount should be a fraction with a denominator of 2, 3, or 4. Then use fraction strips to solve your problem. Pose a problem                          Solve your problem. Draw a picture of the fraction strips you use to solve the problem. Explain why you chose the amounts you did for your problem. Type below: _________

Answer: \(\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\) Maya uses \(\frac{1}{12}\) cup of ingredients. Maya makes trail mix by combining \(\frac{1}{2}\) cup of mixed nuts and \(\frac{1}{3}\) cup of dried fruit and \(\frac{1}{4}\) cup of chocolate morsels. What is the total amount of ingredients in her trail mix? \(\frac{1}{2}\) + \(\frac{1}{3}\) + \(\frac{1}{4}\) = x 2 • \(\frac{1}{2}\) +  2 • \(\frac{1}{3}\) +  2 • \(\frac{1}{4}\) =  2 • x 1 + \(\frac{2}{3}\) + \(\frac{1}{2}\) = 2x Now multiply with 3 on both sides 3 • 1 + 3 • \(\frac{2}{3}\) + 3 • \(\frac{1}{2}\) = 3 • 2x 3 + 2 + \(\frac{3}{2}\) = 6x 6 + 4 + 1 = 12 x 11 = 12x x = \(\frac{11}{12}\) \(\frac{1}{2}\) + \(\frac{1}{3}\) + \(\frac{1}{4}\) = \(\frac{11}{12}\)

Use fraction strips to find the difference. Write your answer in simplest form.

Answer: \(\frac{7}{10}\) – \(\frac{2}{5}\) \(\frac{7}{10}\) – \(\frac{2}{5}\) • \(\frac{2}{2}\) \(\frac{7}{10}\) – \(\frac{4}{10}\) = \(\frac{3}{10}\)

Answer: \(\frac{2}{3}\) – \(\frac{1}{4}\) Now we have to make the fractions like denominators \(\frac{2}{3}\) • \(\frac{4}{4}\) – \(\frac{1}{4}\) • \(\frac{3}{3}\) \(\frac{8}{12}\) – \(\frac{3}{12}\) = \(\frac{5}{12}\)

Page No. 249

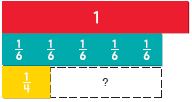
Answer: Step 1: Find fraction strips, all with the same denominator, that fit exactly under the difference \(\frac{5}{6}-\frac{1}{4}\) Step 2: Find another set of fraction strips, all with the same the denominator, that fit exactly under the difference \(\frac{5}{6}-\frac{1}{4}\) Step 3: Find other fraction strips, all with the same denominator, that fit exactly under the difference \(\frac{5}{6}-\frac{1}{4}\) \(\frac{5}{6}\) • \(\frac{4}{4}\) – \(\frac{1}{4}\) • \(\frac{6}{6}\) \(\frac{20}{24}\) – \(\frac{6}{24}\) = \(\frac{14}{24}\) = \(\frac{7}{12}\) Thus, \(\frac{5}{6}-\frac{1}{4}\) = \(\frac{7}{12}\)

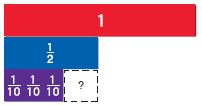
Answer: \(\frac{1}{2}-\frac{3}{10}\) \(\frac{1}{2}\) • \(\frac{5}{5}\) – \(\frac{3}{10}\) \(\frac{5}{10}\) – \(\frac{3}{10}\) = \(\frac{2}{10}\)

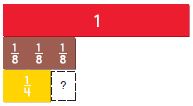
Answer: \(\frac{3}{8}-\frac{1}{4}\) \(\frac{3}{8}\) – \(\frac{1}{4}\) • \(\frac{2}{2}\) = \(\frac{3}{8}\) – \(\frac{2}{8}\) = \(\frac{1}{8}\)

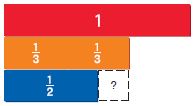
Answer: \(\frac{2}{3}-\frac{1}{2}\) \(\frac{2}{3}\) • \(\frac{2}{2}\) – \(\frac{1}{2}\) • \(\frac{3}{3}\) \(\frac{4}{6}-\frac{3}{6}\) = \(\frac{1}{6}\)

Question 7. \(\frac{3}{5}-\frac{3}{10}=\) \(\frac{□}{□}\)

Answer: \(\frac{3}{5}-\frac{3}{10}\) \(\frac{3}{5}\) • \(\frac{2}{2}\) – \(\frac{3}{10}\) = \(\frac{6}{10}\) – \(\frac{3}{10}\) = \(\frac{3}{10}\)

Question 8. \(\frac{5}{12}-\frac{1}{3}=\) \(\frac{□}{□}\)

Answer: \(\frac{5}{12}-\frac{1}{3}\) Make the denominators equal and then subtract the subtract the fraction with lide denominators. \(\frac{5}{12}\) – \(\frac{1}{3}\) • \(\frac{4}{4}\) \(\frac{5}{12}\) – \(\frac{4}{12}\) = \(\frac{1}{12}\)

Question 9. \(\frac{1}{2}-\frac{1}{10}=\) \(\frac{□}{□}\)

Answer: \(\frac{1}{2}-\frac{1}{10}\) Make the denominators equal and then subtract the subtract the fraction with lide denominators. \(\frac{1}{2}\) • \(\frac{5}{5}\) – \(\frac{1}{10}\) \(\frac{5}{10}\) – \(\frac{1}{10}\) = \(\frac{4}{10}\)

Question 10. \(\frac{3}{5}-\frac{1}{2}=\) \(\frac{□}{□}\)

Answer: \(\frac{3}{5}-\frac{1}{2}\) Make the denominators equal and then subtract the subtract the fraction with lide denominators. \(\frac{3}{5}\) • \(\frac{2}{2}\) – \(\frac{1}{2}\) • \(\frac{5}{5}\) \(\frac{6}{10}-\frac{5}{10}\) = \(\frac{1}{10}\)

Question 11. \(\frac{7}{8}-\frac{1}{4}=\) \(\frac{□}{□}\)

Answer: \(\frac{7}{8}-\frac{1}{4}\) Make the denominators equal and then subtract the subtract the fraction with lide denominators. \(\frac{7}{8}\) – \(\frac{1}{4}\) • \(\frac{2}{2}\) \(\frac{7}{8}\) – \(\frac{2}{8}\) = \(\frac{5}{8}\)

Question 12. \(\frac{5}{6}-\frac{2}{3}=\) \(\frac{□}{□}\)

Answer: \(\frac{5}{6}-\frac{2}{3}\) Make the denominators equal and then subtract the subtract the fraction with lide denominators. \(\frac{5}{6}\) – \(\frac{2}{3}\) • \(\frac{2}{2}\) \(\frac{5}{6}\) – \(\frac{4}{6}\) \(\frac{1}{6}\)

Question 13. \(\frac{3}{4}-\frac{1}{3}=\) \(\frac{□}{□}\)

Answer: \(\frac{3}{4}-\frac{1}{3}\) \(\frac{3}{4}\) • \(\frac{3}{3}\) – \(\frac{1}{3}\) • \(\frac{4}{4}\) \(\frac{9}{12}\) – \(\frac{4}{12}\) = \(\frac{5}{12}\)

Question 14. \(\frac{5}{6}-\frac{1}{2}=\) \(\frac{□}{□}\)

Answer: \(\frac{5}{6}-\frac{1}{2}\) \(\frac{5}{6}\) – \(\frac{1}{2}\) • \(\frac{3}{3}\) \(\frac{5}{6}\) – \(\frac{3}{6}\) = \(\frac{2}{6}\) \(\frac{5}{6}-\frac{1}{2}=\) \(\frac{2}{6}\)

Question 15. \(\frac{3}{4}-\frac{7}{12}=\) \(\frac{□}{□}\)

Answer: \(\frac{3}{4}-\frac{7}{12}\) \(\frac{3}{4}\) • \(\frac{3}{3}\) – \(\frac{7}{12}\) \(\frac{9}{12}\) – \(\frac{7}{12}\) = \(\frac{2}{12}\) \(\frac{3}{4}-\frac{7}{12}=\) \(\frac{2}{12}\)

Question 16. Explain how your model for \(\frac{3}{5}-\frac{1}{2}\) is different from your model for \(\frac{3}{5}-\frac{3}{10}\). Type below: _________

Answer: \(\frac{3}{5}-\frac{3}{10}\) \(\frac{3}{5}\) • \(\frac{2}{2}\) – \(\frac{3}{10}\) \(\frac{6}{10}\) – \(\frac{3}{10}\) = \(\frac{3}{10}\)

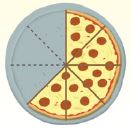
Answer: I am asked to solve which subtraction sentence represents the amount of pizza that is remaining after dinner.

Question 17. b. How will you use the diagram to solve the problem? Type below: _________

Answer: I will use number of slices left in the pizza to solve the problem.

Question 17. c. Jason eats \(\frac{1}{4}\) of the whole pizza. How many slices does he eat? ______ slices

Answer: 2 slices

Explanation: Given that, Jason eats \(\frac{1}{4}\) of the whole pizza. The pizza is cut into 8 slices. So, 8 × \(\frac{1}{4}\) = 2 slices. Thus Jason ate 2 slices.

Question 17. d. Redraw the diagram of the pizza. Shade the sections of pizza that are remaining after Jason eats his dinner. Type below: _________

Question 17. e. Write a fraction to represent the amount of pizza that is remaining. \(\frac{□}{□}\) of a pizza

Answer: \(\frac{3}{8}\) of a pizza

Explanation: The fraction of pizzz Jason ate = \(\frac{1}{4}\) Number of slices left = \(\frac{5}{8}\) Now subtract \(\frac{5}{8}\) – \(\frac{1}{4}\) = \(\frac{3}{8}\) Thus the fraction to represent the amount of pizza that is remaining is \(\frac{3}{8}\)

Question 17. f. Fill in the bubble for the correct answer choice above. Options: a. 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\) b. \(\frac{5}{8}\) – \(\frac{1}{4}\) = \(\frac{3}{8}\) c. \(\frac{3}{8}\) – \(\frac{1}{4}\) = \(\frac{2}{8}\) d. 1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)

Answer: B The fraction of pizzz Jason ate = \(\frac{1}{4}\) Number of slices left = \(\frac{5}{8}\) Now subtract \(\frac{5}{8}\) – \(\frac{1}{4}\) = \(\frac{3}{8}\) Thus the correct answer is option B.

Answer: \(\frac{1}{3}\) yard

Explanation: The original yard of fabric is 6 Tina uses \(\frac{2}{3}\) yard of fabric for a project. \(\frac{1}{1}\) – \(\frac{2}{3}\) \(\frac{3}{3}\) – \(\frac{2}{3}\) = \(\frac{1}{3}\) yard

Estimate the sum or difference.

Question 1. \(\frac{5}{6}+\frac{3}{8}\) a. Round \(\frac{5}{6}\) to its closest benchmark. ____ b. Round \(\frac{3}{8}\) to its closest benchmark. ____ c. Add to find the estimate. ____ + ____ = ____ _____ \(\frac{□}{□}\)

Answer: a. Round \(\frac{5}{6}\) to its closest benchmark. \(\frac{6}{6}\) or 1. b. Round \(\frac{3}{8}\) to its closest benchmark. \(\frac{4}{8}\) or \(\frac{1}{2}\) c. Add to find the estimate. ____ + ____ = ____ 1 + \(\frac{1}{2}\) = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\)

Question 2. \(\frac{5}{9}-\frac{3}{8}\) _____

Explanation: Step 1: Place a point at \(\frac{5}{9}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\). The fraction rounded to \(\frac{5}{9}\) is \(\frac{1}{2}\) Step 2: Place a point at \(\frac{3}{8}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\). The fraction rounded to \(\frac{3}{8}\) is \(\frac{1}{2}\). \(\frac{1}{2}\) – \(\frac{1}{2}\) = 0

Question 3. \(\frac{6}{7}+2 \frac{4}{5}\) _____

Explanation: Step 1: Place a point at \(\frac{6}{7}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{4}{5}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. 1 + 3 = 4

Question 4. \(\frac{5}{6}+\frac{2}{5}\) _____ \(\frac{□}{□}\)

Answer: 1 \(\frac{1}{2}\)

Explanation: Step 1: Place a point at \(\frac{5}{6}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{2}{5}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\). 1 + \(\frac{1}{2}\) = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\)

Question 5. \(3 \frac{9}{10}-1 \frac{2}{9}\) _____

Explanation:

Step 1: Place a point at \(\frac{9}{10}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{2}{9}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\). 3 × 1 – 1 × 0 = 3 – 0 = 3 \(3 \frac{9}{10}-1 \frac{2}{9}\) = 3

Question 6. \(\frac{4}{6}+\frac{1}{9}\) \(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Step 1: Place a point at \(\frac{4}{6}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{1}{9}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\). So, \(\frac{1}{2}\) + 0 = \(\frac{1}{2}\) \(\frac{4}{6}+\frac{1}{9}\) = \(\frac{1}{2}\)

Question 7. \(\frac{9}{10}-\frac{1}{9}\) _____

Explanation: Step 1: Place a point at \(\frac{9}{10}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{1}{9}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\). 1 – 0 = 1 \(\frac{9}{10}-\frac{1}{9}\) = 1

On Your Own

Question 8. \(\frac{5}{8}-\frac{1}{5}\) \(\frac{□}{□}\)

Explanation: Step 1: Place a point at \(\frac{5}{8}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{1}{5}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\). 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)

Question 9. \(\frac{1}{6}+\frac{3}{8}\) \(\frac{□}{□}\)

Explanation: Step 1: Place a point at \(\frac{1}{6}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) Step 2: Place a point at \(\frac{3}{8}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) 0 + \(\frac{1}{2}\) = \(\frac{1}{2}\)

Question 10. \(\frac{6}{7}-\frac{1}{5}\) _____

Explanation: Step 1: Place a point at \(\frac{6}{7}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{1}{5}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) 1 – 0 = 1 \(\frac{6}{7}-\frac{1}{5}\) = 1

Question 11. \(\frac{11}{12}+\frac{6}{10}\) _____ \(\frac{□}{□}\)

Explanation: Step 1: Place a point at \(\frac{11}{12}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1 Step 2: Place a point at \(\frac{6}{10}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1 1 + \(\frac{1}{2}\) = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\) \(\frac{11}{12}+\frac{6}{10}\) = 1 \(\frac{1}{2}\)

Question 12. \(\frac{9}{10}-\frac{1}{2}\) \(\frac{□}{□}\)

Explanation: Step 1: Place a point at \(\frac{9}{10}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{1}{2}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\) \(\frac{9}{10}-\frac{1}{2}\) = \(\frac{1}{2}\)

Question 13. \(\frac{3}{6}+\frac{4}{5}\) _____ \(\frac{□}{□}\)

Explanation: Step 1: Place a point at \(\frac{3}{6}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) Step 2: Place a point at \(\frac{4}{5}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1 \(\frac{1}{2}\) + 1 = \(\frac{3}{2}\) = 1 \(\frac{1}{2}\) \(\frac{3}{6}+\frac{4}{5}\) = 1 \(\frac{1}{2}\)

Question 14. \(\frac{5}{6}-\frac{3}{8}\) \(\frac{□}{□}\)

Explanation: Step 1: Place a point at \(\frac{5}{6}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place a point at \(\frac{3}{8}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\) \(\frac{5}{6}-\frac{3}{8}\) = \(\frac{1}{2}\)

Question 15. \(\frac{1}{7}+\frac{8}{9}\) _____

Explanation: Step 1: Place a point at \(\frac{1}{7}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) Step 2: Place a point at \(\frac{8}{9}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. 0 + 1 = 1 \(\frac{1}{7}+\frac{8}{9}\) = 1

Question 16. \(3 \frac{5}{12}-3 \frac{1}{10}\) \(\frac{□}{□}\)

Explanation: Step 1: Place a point at \(\frac{5}{12}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) Step 2: Place a point at \(\frac{1}{10}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\) \(\frac{1}{2}\) – 0 = \(\frac{1}{2}\) \(3 \frac{5}{12}-3 \frac{1}{10}\) = \(\frac{1}{2}\)

Question 17. Lisa and Valerie are picnicking in Trough Creek State Park in Pennsylvania. Lisa has brought a salad that she made with \(\frac{3}{4}\) cup of strawberries, \(\frac{7}{8}\) cup of peaches, and \(\frac{1}{6}\) cup of blueberries. About how many total cups of fruit are in the salad? _____ cups

Answer: 2 cups

Explanation: Lisa and Valerie are picnicking in Trough Creek State Park in Pennsylvania. Lisa has brought a salad that she made with \(\frac{3}{4}\) cup of strawberries, \(\frac{7}{8}\) cup of peaches, and \(\frac{1}{6}\) cup of blueberries. Step 1: Place \(\frac{3}{4}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 2: Place \(\frac{7}{8}\) on the number line. The fraction is between \(\frac{1}{2}\) and 1. Step 3: Place \(\frac{1}{6}\) on the number line. The fraction is between 0 and \(\frac{1}{2}\). 1 + 1 + 0 = 2 Thus 2 cups of fruit are in the salad.

Question 18. At Trace State Park in Mississippi, there is a 25-mile mountain bike trail. If Tommy rode \(\frac{1}{2}\) of the trail on Saturday and \(\frac{1}{5}\) of the trail on Sunday, about what fraction of the trail did he ride? \(\frac{□}{□}\)

Explanation: At Trace State Park in Mississippi, there is a 25-mile mountain bike trail. If Tommy rode \(\frac{1}{2}\) of the trail on Saturday and \(\frac{1}{5}\) of the trail on Sunday Step 1: Place \(\frac{1}{2}\) on the number line. \(\frac{1}{2}\) lies between 0 and \(\frac{1}{2}\) Step 2: Place \(\frac{1}{5}\) on the number line. \(\frac{1}{5}\) 0 and \(\frac{1}{2}\) The number closer to \(\frac{1}{5}\) is 0 \(\frac{1}{2}\) – 0 = \(\frac{1}{2}\) The estimated fraction of the trail he ride is \(\frac{1}{2}\)

Question 19. Explain how you know that \(\frac{5}{8}+\frac{6}{10}\) is greater than 1. Type below: __________

Answer: Step 1: Place \(\frac{5}{8}\) on the number line. \(\frac{5}{8}\) is closer to \(\frac{1}{2}\) Step 2: Place \(\frac{6}{10}\) on the number line. \(\frac{6}{10}\) lies between \(\frac{1}{2}\) and 1. \(\frac{6}{10}\) is closer to \(\frac{1}{2}\) \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1

Question 20. Nick estimated that \(\frac{5}{8}+\frac{4}{7}\) is about 2. Explain how you know his estimate is not reasonable. Type below: __________

Answer: Step 1: Place \(\frac{5}{8}\) on the number line. \(\frac{5}{8}\) is closer to \(\frac{1}{2}\) Step 2: Place \(\frac{4}{7}\) on the number line. \(\frac{4}{7}\) lies between \(\frac{1}{2}\) and 1. \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1 By this, we can say that Nick’s estimation was wrong.

Question 21. Test Prep Jake added \(\frac{1}{8}\) cup of sunflower seeds and \(\frac{4}{5}\) cup of banana chips to his sundae. Which is the best estimate of the total amount of toppings Jake added to his sundae? Options: a. about \(\frac{1}{2}\) cup b. about 1 cup c. about 1 \(\frac{1}{2}\) cups d. about 2 cups

Answer: about 1 cup

Explanation: Given, Test Prep Jake added \(\frac{1}{8}\) cup of sunflower seeds and \(\frac{4}{5}\) cup of banana chips to his sundae Step 1: Place \(\frac{1}{8}\) on the number line. \(\frac{1}{8}\) lies between 0 and \(\frac{1}{2}\) Step 2: Place \(\frac{4}{5}\) on the number line. \(\frac{4}{5}\) lies between \(\frac{1}{2}\) and 1. 0 + 1 = 1 The best estimate of the total amount of toppings Jake added to his sundae is about 1 cup.

Question 1. Find a common denominator of \(\frac{1}{6}\) and \(\frac{1}{9}\) . Rewrite the pair of fractions using the common denominator. • Multiply the denominators. A common denominator of \(\frac{1}{6}\) and \(\frac{1}{9}\) is ____. • Rewrite the pair of fractions using the common denominator. Type below: _________

Answer: Common denominator is 18. \(\frac{1}{6}\) × \(\frac{3}{3}\) = \(\frac{3}{18}\) \(\frac{1}{9}\) × \(\frac{2}{2}\) = \(\frac{2}{18}\) The pair of fractions using the common denominator is \(\frac{3}{18}\), \(\frac{2}{18}\)

Use a common denominator to write an equivalent fraction for each fraction.

Question 2. \(\frac{1}{3}, \frac{1}{5}\) common denominator: _________ Type below: _________

Explanation: Multiply the denominators of the fraction. \(\frac{1}{3}\) × \(\frac{1}{5}\) = \(\frac{1}{15}\) Thus the common denominator is 15.

Question 3. \(\frac{2}{3}, \frac{5}{9}\) common denominator: _________ Type below: _________

Explanation: Multiply the denominators \(\frac{2}{3}\) × \(\frac{5}{9}\) = 3 × 9 = 27 Thus the common denominator of \(\frac{2}{3}, \frac{5}{9}\) is 27.

Question 4. \(\frac{2}{9}, \frac{1}{15}\) common denominator: _________ Type below: _________

Explanation: Multiply the denominators \(\frac{2}{9}\) × \(\frac{1}{15}\) The least common denominator of 15 and 9 is 45. So, the common denominator of \(\frac{2}{9}, \frac{1}{15}\) is 45.

Page No. 257

Use the least common denominator to write an equivalent fraction for each fraction.

Question 5. \(\frac{1}{4}, \frac{3}{8}\) least common denominator: ______ Type below: _________

First multiply the denominators of the fractions \(\frac{1}{4}, \frac{3}{8}\) 4 × 8 = 32 The least common denominator is 8 The equivalent fractions with LCD \(\frac{1}{4}\) = \(\frac{2}{8}\) \(\frac{3}{8}\) = \(\frac{3}{8}\)

Question 6. \(\frac{11}{12}, \frac{5}{8}\) least common denominator: ______ Type below: _________

Explanation: First, multiply the denominators of the fractions. 12 × 8 = 96 The least common denominator of 12 and 8 is 24. The equivalent fractions with LCD \(\frac{11}{12}\) × \(\frac{2}{2}\)= \(\frac{22}{24}\) \(\frac{5}{8}\) × \(\frac{3}{3}\) = \(\frac{15}{24}\)

Question 7. \(\frac{4}{5}, \frac{1}{6}\) least common denominator: ______ Type below: _________

Explanation: First, multiply the denominators of the fractions. 5 × 6 = 30 The least common denominator (LCD) = 30 \(\frac{4}{5}\) × \(\frac{6}{6}\)= \(\frac{24}{30}\) \(\frac{1}{6}\) × \(\frac{5}{5}\) = \(\frac{5}{30}\)

Question 8. \(\frac{3}{5}, \frac{1}{4}\) common denominator: ______ Type below: _________

Explanation: Multiply the denominators of the fractions to find the common denominator. 5 × 4 = 20 So, the common denominator of \(\frac{3}{5}, \frac{1}{4}\) is 20.

Question 9. \(\frac{5}{8}, \frac{1}{5}\) common denominator: ______ Type below: _________

Explanation: Multiply the denominators of the fractions to find the common denominator. 8 × 5 = 40 So, the common denominator of \(\frac{5}{8}, \frac{1}{5}\) is 40.

Question 10. \(\frac{1}{12}, \frac{1}{2}\) common denominator: ______ Type below: _________

Explanation: Multiply the denominators of the fractions to find the common denominator. 12 × 2 = 24 The common denominator of \(\frac{1}{12}, \frac{1}{2}\) is 24.

Practice: Copy and Solve Use the least common denominator to write an equivalent fraction for each fraction.

Question 11. \(\frac{1}{6}, \frac{4}{9}\) Type below: _________

Answer: \(\frac{3}{18}, \frac{8}{18}\)

Explanation: Multiply the denominators of the fractions. The Least Common Denominator = 18 Now rewrite the fractions \(\frac{1}{6}\) × \(\frac{3}{3}\) = \(\frac{3}{18}\) \(\frac{4}{9}\) × \(\frac{2}{2}\) = \(\frac{8}{18}\)

Question 12. \(\frac{7}{9}, \frac{8}{27}\) Type below: _________

Answer: \(\frac{21}{27}, \frac{8}{27}\)

Explanation: Multiply the denominators of the fractions. The Least Common Denominator = 27 Now rewrite the fractions \(\frac{7}{9}\) × \(\frac{3}{3}\) = \(\frac{21}{27}\) \(\frac{8}{27}\) × \(\frac{1}{1}\) = \(\frac{8}{27}\)

Question 13. \(\frac{7}{10}, \frac{3}{8}\) Type below: _________

Answer: \(\frac{28}{40}, \frac{15}{40}\)

Explanation: Multiply the denominators of the fractions. The Least Common Denominator = 40 Now rewrite the fractions \(\frac{7}{10}\) × \(\frac{4}{4}\) = \(\frac{28}{40}\) \(\frac{3}{8}\) × \(\frac{5}{5}\) = \(\frac{15}{40}\)

Question 14. \(\frac{1}{3}, \frac{5}{11}\) Type below: _________

Answer: \(\frac{11}{33}, \frac{15}{33}\)

Explanation: Multiply the denominators of the fractions. The Least Common Denominator = 33 Now rewrite the fractions \(\frac{1}{3}\) × \(\frac{11}{11}\) = \(\frac{11}{33}\) \(\frac{5}{11}\) × \(\frac{3}{3}\) = \(\frac{15}{33}\)

Question 15. \(\frac{5}{9}, \frac{4}{15}\) Type below: _________

Answer: \(\frac{25}{45}, \frac{12}{45}\)

Explanation: Multiply the denominators of the fractions. The Least Common Denominator of \(\frac{5}{9}, \frac{4}{15}\)= 45 Now rewrite the input fractions \(\frac{5}{9}\) × \(\frac{5}{5}\) = \(\frac{25}{45}\) \(\frac{4}{15}\) × \(\frac{3}{3}\) = \(\frac{12}{45}\)

Question 16. \(\frac{1}{6}, \frac{4}{21}\) Type below: _________

Answer: \(\frac{7}{42}, \frac{8}{42}\)

Explanation: Multiply the denominators of the fractions. The Least Common Denominator = 42 Now rewrite the fractions \(\frac{1}{6}\) × \(\frac{7}{7}\) = \(\frac{7}{42}\) \(\frac{4}{21}\) × \(\frac{2}{2}\) = \(\frac{8}{42}\)

Question 17. \(\frac{5}{14}, \frac{8}{42}\) Type below: _________

Answer: \(\frac{15}{42}, \frac{8}{42}\)

Explanation: Multiply the denominators of the fractions. The Least Common Denominator = 42 Now rewrite the fractions \(\frac{5}{14}\) × \(\frac{3}{3}\) = \(\frac{15}{42}\) \(\frac{8}{42}\) × \(\frac{1}{1}\) = \(\frac{8}{42}\)

Question 18. \(\frac{7}{12}, \frac{5}{18}\) Type below: _________

Answer: \(\frac{21}{36}, \frac{10}{36}\)

Explanation: Multiply the denominators of the fractions. The Least Common Denominator = 36 Now rewrite the fractions \(\frac{7}{12}\) × \(\frac{3}{3}\) = \(\frac{21}{36}\) \(\frac{5}{18}\) × \(\frac{2}{2}\) = \(\frac{10}{36}\)

Algebra Write the unknown number for each ■.

Question 19. \(\frac{1}{5}, \frac{1}{8}\) least common denominator: ■ ■ = ______

Explanation: Multiply the denominators of the fractions. 5 × 8 = 40 Therefore, ■ = 40

Question 20. \(\frac{2}{5}, \frac{1}{■}\) least common denominator: 15 ■ = ______

Explanation: Multiply the denominators of the fractions. 5 × ■ = 15 ■ = 15/5 = 3 Thus ■ = 3

Question 21. \(\frac{3}{■}, \frac{5}{6}\) least common denominator: 42 ■ = ______

Explanation: \(\frac{3}{■}, \frac{5}{6}\) ■ × 6 = 42 ■ = 42/6 ■ = 7

Question 22. Katie made two pies for the bake sale. One was cut into three equal slices and the other into 5 equal slices. She will continue to cut the pies so each one has the same number of equal-sized slices. What is the least number of equal-sized slices each pie could have? a. What information are you given? Type below: _________

Answer: I have the information about the two pies for the bake sale. One was cut into three equal slices and the other into 5 equal slices. She will continue to cut the pies so each one has the same number of equal-sized slices.

Question 22. b. What problem are you being asked to solve? Type below: _________

Answer: I am asked to solve the least number of equal-sized slices each pie could have.

Question 22. c. When Katie cuts the pies more, can she cut each pie the same number of times and have all the slices the same size? Explain. Type below: _________

Answer: Yes she can cut into more equal pieces. Katie can cut the pie into 6 equal pieces and 10 equal pieces. But the least number of equal-sized slices each pie could have is 3 and 5.

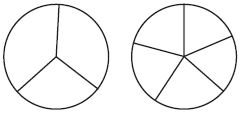
Answer: There are 2 pies. One pie is cut into 3 equal pieces and the second pie is cut into 5 equal pieces. So, there are 15 pieces of pies.

Question 22. e. Complete the sentences. The least common denominator of \(\frac{1}{3}\) and \(\frac{1}{5}\) is ____. Katie can cut each piece of the first pie into ____ and each piece of the second pie into ____ . That means that Katie can cut each pie into pieces that are ____ of the whole pie. Type below: _________

Answer: The least common denominator of \(\frac{1}{3}\) and \(\frac{1}{5}\) is 15 5 × 3 = 15 Katie can cut each piece of the first pie into three and each piece of the second pie into five. That means that Katie can cut each pie into pieces that are 15 of the whole pie.

Question 23. A cookie recipe calls for \(\frac{1}{3}\) cup of brown sugar and \(\frac{1}{8}\) cup of walnuts. Find the least common denominator of the fractions used in the recipe. ____

A cookie recipe calls for \(\frac{1}{3}\) cup of brown sugar and \(\frac{1}{8}\) cup of walnuts. We can calculate the LCD by multiplying the denominators of the fraction. 3 × 8 = 24.

Question 24. Test Prep Which fractions use the least common denominator and are equivalent to \(\frac{5}{8}\) and \(\frac{7}{10}\) ? Options: a. \(\frac{10}{40} \text { and } \frac{14}{40}\) b. \(\frac{25}{40} \text { and } \frac{28}{40}\) c. \(\frac{25}{80} \text { and } \frac{21}{80}\) d. \(\frac{50}{80} \text { and } \frac{56}{80}\)

Answer: \(\frac{50}{80} \text { and } \frac{56}{80}\)

Explanation: The least common denominator of \(\frac{5}{8}\) and \(\frac{7}{10}\) is 80. \(\frac{5}{8}\) × \(\frac{10}{10}\) and \(\frac{7}{10}\) × \(\frac{8}{8}\) = \(\frac{50}{80} \text { and } \frac{56}{80}\) Thus the correct answer is option D.

Find the sum or difference. Write your answer in simplest form.

Question 1. \(\frac{5}{12}+\frac{1}{3}\) \(\frac{□}{□}\)

Answer: Find a common denominator by multiplying the denominators. \(\frac{5}{12}+\frac{1}{3}\) \(\frac{5}{12}\) + \(\frac{1}{3}\) × \(\frac{4}{4}\) \(\frac{5}{12}\) + \(\frac{4}{12}\) \(\frac{9}{12}\)

Question 2. \(\frac{2}{5}+\frac{3}{7}\) \(\frac{□}{□}\)

Answer: Find a common denominator by multiplying the denominators. Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form. \(\frac{2}{5}+\frac{3}{7}\) \(\frac{2}{5}\) × \(\frac{7}{7}\) + \(\frac{3}{7}\) × \(\frac{5}{5}\) \(\frac{14}{35}+\frac{15}{35}\) = \(\frac{29}{35}\) \(\frac{2}{5}+\frac{3}{7}\) = \(\frac{29}{35}\)

Question 3. \(\frac{1}{6}+\frac{3}{4}\) \(\frac{□}{□}\)

Answer: Find a common denominator by multiplying the denominators. Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form. \(\frac{1}{6}\) × \(\frac{2}{2}\) + \(\frac{3}{4}\) × \(\frac{3}{3}\) \(\frac{2}{12}+\frac{9}{12}\) = \(\frac{11}{12}\) So, \(\frac{1}{6}+\frac{3}{4}\) = \(\frac{11}{12}\)

Question 4. \(\frac{3}{4}-\frac{1}{8}\) \(\frac{□}{□}\)

Answer: First, find a common denominator by multiplying the denominators. Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form. \(\frac{3}{4}-\frac{1}{8}\) \(\frac{3}{4}\) × \(\frac{2}{2}\) – \(\frac{1}{8}\) \(\frac{6}{8}\) – \(\frac{1}{8}\) = \(\frac{5}{8}\) Thus \(\frac{3}{4}-\frac{1}{8}\) = \(\frac{5}{8}\)

Question 5. \(\frac{1}{4}-\frac{1}{7}\) \(\frac{□}{□}\)

Answer: First, find a common denominator by multiplying the denominators. Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form. \(\frac{1}{4}-\frac{1}{7}\) \(\frac{1}{4}\) × \(\frac{7}{7}\) – \(\frac{1}{7}\) × \(\frac{4}{4}\) \(\frac{7}{28}\) – \(\frac{4}{28}\) = \(\frac{3}{28}\) \(\frac{1}{4}-\frac{1}{7}\) = \(\frac{3}{28}\)

Question 6. \(\frac{9}{10}-\frac{1}{4}\) \(\frac{□}{□}\)

Answer: First, find a common denominator by multiplying the denominators. Use the common denominator to write equivalent fractions with like denominators. Then add, and write your answer in simplest form. \(\frac{9}{10}-\frac{1}{4}\) \(\frac{9}{10}\) × \(\frac{4}{4}\) – \(\frac{1}{4}\) × \(\frac{10}{10}\) \(\frac{36}{40}\) – \(\frac{10}{40}\) = \(\frac{26}{40}\) \(\frac{9}{10}-\frac{1}{4}\) = \(\frac{26}{40}\)

Question 7. \(\frac{3}{8}+\frac{1}{4}\) \(\frac{□}{□}\)

Answer: \(\frac{5}{8}\)

Explanation: \(\frac{3}{8}+\frac{1}{4}\) = \(\frac{3}{8}\) + \(\frac{1}{4}\) LCD = 8 \(\frac{3}{8}\) + \(\frac{1}{4}\) × \(\frac{2}{2}\) \(\frac{3}{8}\) + \(\frac{2}{8}\) = \(\frac{5}{8}\) Thus \(\frac{3}{8}+\frac{1}{4}\) = \(\frac{5}{8}\)

Question 8. \(\frac{7}{8}+\frac{1}{10}\) \(\frac{□}{□}\)

Answer: \(\frac{7}{8}+\frac{1}{10}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 40 \(\frac{7}{8}\) × \(\frac{5}{5}\) + \(\frac{1}{10}\) × \(\frac{4}{4}\) \(\frac{35}{40}\) + \(\frac{4}{40}\) = \(\frac{39}{40}\) \(\frac{7}{8}+\frac{1}{10}\) = \(\frac{39}{40}\)

Question 9. \(\frac{2}{7}+\frac{3}{10}\) \(\frac{□}{□}\)

Answer: \(\frac{2}{7}+\frac{3}{10}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 70 \(\frac{2}{7}\) × \(\frac{10}{10}\) + \(\frac{3}{10}\) × \(\frac{7}{7}\) \(\frac{20}{70}\) + \(\frac{21}{70}\) = \(\frac{41}{70}\) \(\frac{2}{7}+\frac{3}{10}\) = \(\frac{41}{70}\)

Question 10. \(\frac{5}{6}+\frac{1}{8}\) \(\frac{□}{□}\)

Answer: \(\frac{5}{6}+\frac{1}{8}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. \(\frac{5}{6}\) + \(\frac{1}{8}\) LCD = 24 \(\frac{5}{6}\) × \(\frac{4}{4}\) + \(\frac{1}{8}\) × \(\frac{3}{3}\) \(\frac{20}{24}\) + \(\frac{3}{24}\) = \(\frac{23}{24}\) \(\frac{5}{6}+\frac{1}{8}\) = \(\frac{23}{24}\)

Question 11. \(\frac{5}{12}+\frac{5}{18}\) \(\frac{□}{□}\)

Answer: \(\frac{5}{12}+\frac{5}{18}\) = \(\frac{5}{12}\) + \(\frac{5}{18}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 36 \(\frac{5}{12}\) × \(\frac{3}{3}\) + \(\frac{5}{18}\) × \(\frac{2}{2}\) \(\frac{15}{36}\) + \(\frac{10}{36}\) = \(\frac{25}{36}\) \(\frac{5}{12}+\frac{5}{18}\) = \(\frac{25}{36}\)

Question 12. \(\frac{7}{16}+\frac{1}{4}\) \(\frac{□}{□}\)

Answer: \(\frac{7}{16}+\frac{1}{4}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 16 \(\frac{7}{16}\) + \(\frac{1}{4}\) = \(\frac{7}{16}\) + \(\frac{1}{4}\) × \(\frac{4}{4}\) \(\frac{7}{16}\) + \(\frac{4}{16}\) = \(\frac{11}{16}\)

Question 13. \(\frac{5}{6}+\frac{3}{8}\) \(\frac{□}{□}\)

Answer: \(\frac{5}{6}+\frac{3}{8}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. \(\frac{5}{6}\) + \(\frac{3}{8}\) LCD = 24 \(\frac{5}{6}\) × \(\frac{4}{4}\) + \(\frac{3}{8}\) × \(\frac{3}{3}\) = \(\frac{20}{24}\) + \(\frac{9}{24}\) = \(\frac{29}{24}\) \(\frac{5}{6}+\frac{3}{8}\) = \(\frac{29}{24}\)

Question 14. \(\frac{3}{4}+\frac{1}{2}\) \(\frac{□}{□}\)

Answer: \(\frac{3}{4}+\frac{1}{2}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. \(\frac{3}{4}\) + \(\frac{1}{2}\) LCD = 4 \(\frac{3}{4}\) + \(\frac{1}{2}\) × \(\frac{2}{2}\) = \(\frac{3}{4}\) + \(\frac{2}{4}\) = \(\frac{5}{4}\) The miced fractiion of \(\frac{5}{4}\) is 1 \(\frac{1}{4}\)

Question 15. \(\frac{5}{12}+\frac{1}{4}\) \(\frac{□}{□}\)

Answer: \(\frac{5}{12}+\frac{1}{4}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. \(\frac{5}{12}\) + \(\frac{1}{4}\) LCD = 12 \(\frac{5}{12}\) + \(\frac{1}{4}\) × \(\frac{3}{3}\) \(\frac{5}{12}\) + \(\frac{3}{12}\) = \(\frac{8}{12}\) = \(\frac{2}{3}\)

Practice: Copy and Solve Find the sum or difference. Write your answer in simplest form.

Question 16. \(\frac{1}{3}+\frac{4}{18}\) \(\frac{□}{□}\)

Answer: \(\frac{1}{3}+\frac{4}{18}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 18 \(\frac{1}{3}\) + \(\frac{4}{18}\) \(\frac{1}{3}\) × \(\frac{6}{6}\) + \(\frac{4}{18}\) \(\frac{6}{18}\) + \(\frac{4}{18}\) = \(\frac{10}{18}\) = \(\frac{5}{9}\) \(\frac{1}{3}+\frac{4}{18}\) = \(\frac{5}{9}\)

Question 17. \(\frac{3}{5}+\frac{1}{3}\) \(\frac{□}{□}\)

Answer: \(\frac{3}{5}+\frac{1}{3}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 15 \(\frac{3}{5}\) + \(\frac{1}{3}\) \(\frac{3}{5}\) × \(\frac{3}{3}\) + \(\frac{1}{3}\) × \(\frac{5}{5}\) \(\frac{9}{15}\) + \(\frac{5}{15}\) = \(\frac{14}{15}\) \(\frac{3}{5}+\frac{1}{3}\) = \(\frac{14}{15}\)

Question 18. \(\frac{3}{10}+\frac{1}{6}\) \(\frac{□}{□}\)

Answer: \(\frac{3}{10}+\frac{1}{6}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 30 \(\frac{3}{10}\) + \(\frac{1}{6}\) \(\frac{3}{10}\) × \(\frac{3}{3}\) + \(\frac{1}{6}\) × \(\frac{5}{5}\) \(\frac{9}{30}\) + \(\frac{5}{30}\) = \(\frac{14}{30}\) \(\frac{3}{10}+\frac{1}{6}\) = \(\frac{14}{30}\)

Question 19. \(\frac{1}{2}+\frac{4}{9}\) \(\frac{□}{□}\)

Answer: \(\frac{1}{2}+\frac{4}{9}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 18 \(\frac{1}{2}\) + \(\frac{4}{9}\) \(\frac{1}{2}\) × \(\frac{9}{9}\) + \(\frac{4}{9}\) × \(\frac{2}{2}\) = \(\frac{9}{18}\) + \(\frac{8}{18}\) = \(\frac{17}{18}\) \(\frac{1}{2}+\frac{4}{9}\) = \(\frac{17}{18}\)

Question 20. \(\frac{1}{2}-\frac{3}{8}\) \(\frac{□}{□}\)

Answer: \(\frac{1}{2}-\frac{3}{8}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 8 \(\frac{1}{2}\) – \(\frac{3}{8}\) \(\frac{1}{2}\) × \(\frac{4}{4}\) – \(\frac{3}{8}\) \(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\) \(\frac{1}{2}-\frac{3}{8}\) = \(\frac{1}{8}\)

Question 21. \(\frac{5}{7}-\frac{2}{3}\) \(\frac{□}{□}\)

Answer: \(\frac{5}{7}-\frac{2}{3}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 21 \(\frac{5}{7}\) – \(\frac{2}{3}\) \(\frac{5}{7}\) × \(\frac{3}{3}\) – \(\frac{2}{3}\) × \(\frac{7}{7}\) \(\frac{15}{21}\) – \(\frac{14}{21}\) = \(\frac{1}{21}\) \(\frac{5}{7}-\frac{2}{3}\) = \(\frac{1}{21}\)

Question 22. \(\frac{4}{9}-\frac{1}{6}\) \(\frac{□}{□}\)

Answer: \(\frac{4}{9}-\frac{1}{6}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 18 \(\frac{4}{9}\) – \(\frac{1}{6}\) \(\frac{4}{9}\) × \(\frac{2}{2}\) – \(\frac{1}{6}\) × \(\frac{3}{3}\) \(\frac{8}{18}\) – \(\frac{3}{18}\) = \(\frac{5}{18}\) \(\frac{4}{9}-\frac{1}{6}\) = \(\frac{5}{18}\)

Question 23. \(\frac{11}{12}-\frac{7}{15}\) \(\frac{□}{□}\)

Answer: \(\frac{11}{12}-\frac{7}{15}\) First, find the Least Common Denominator and rewrite the fractions with the common denominator. LCD = 60 \(\frac{11}{12}\) – \(\frac{7}{15}\) \(\frac{11}{12}\) × \(\frac{5}{5}\) – \(\frac{7}{15}\) × \(\frac{4}{4}\) \(\frac{55}{60}\) – \(\frac{28}{60}\) = \(\frac{27}{60}\) \(\frac{11}{12}-\frac{7}{15}\) = \(\frac{27}{60}\) = \(\frac{9}{20}\)

Algebra Find the unknown number.

Question 24. \(\frac{9}{10}\) − ■ = \(\frac{1}{5}\) ■ = \(\frac{□}{□}\)

Answer: \(\frac{9}{10}\) – \(\frac{1}{5}\) = ■ ■ = \(\frac{9}{10}\) – \(\frac{1}{5}\) ■ = \(\frac{9}{10}\) – \(\frac{2}{10}\) = \(\frac{7}{10}\) ■ = \(\frac{7}{10}\)

Question 25. \(\frac{5}{12}\) + ■ = \(\frac{1}{2}\) ■ = \(\frac{□}{□}\)

Answer: \(\frac{5}{12}\) + ■ = \(\frac{1}{2}\) \(\frac{5}{12}\) − \(\frac{1}{2}\) = – ■ – ■ = \(\frac{5}{12}\) − \(\frac{1}{2}\) – ■ = \(\frac{5}{12}\) − \(\frac{1}{2}\) × \(\frac{6}{6}\) – ■ = \(\frac{5}{12}\) − \(\frac{6}{12}\) = – \(\frac{1}{12}\) ■ = \(\frac{1}{12}\)

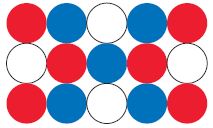
Question 26. Sara is making a key chain using the bead design shown. What fraction of the beads in her design are either blue or red? \(\frac{□}{□}\)

Answer: \(\frac{11}{15}\)

Explanation: Total number of red beads = 6 Total number of blue beads = 5 Total number of beads = 6 + 5 = 11 The fraction of beads = \(\frac{11}{15}\)

Question 27. In making the key chain, Sara uses the pattern of beads 3 times. After the key chain is complete, what fraction of the beads in the key chain are either white or blue? ______ \(\frac{□}{□}\)

Answer: 1 \(\frac{4}{5}\)

Explanation: In making the key chain, Sara uses the pattern of beads 3 times. Given that Sara uses the pattern of beads 3 times. Total number of blue beads = 5 5 × 3 = 15 Number of white beads = 4 4 × 3 = 12 15 + 12 = 27 Actual number of beads = 15 So, the fraction is \(\frac{27}{15}\) = \(\frac{9}{5}\) The mixed fraction of \(\frac{9}{5}\) is 1 \(\frac{4}{5}\)

Question 28. Jamie had \(\frac{4}{5}\) of a spool of twine. He then used \(\frac{1}{2}\) of a spool of twine to make friendship knots. He claims to have \(\frac{3}{10}\) of the original spool of twine left over. Explain how you know whether Jamie’s claim is reasonable. Type below: _________

Answer: Jamie’s claim is reasonable

Explanation: Jamie had \(\frac{4}{5}\) of a spool of twine. He then used \(\frac{1}{2}\) of a spool of twine to make friendship knots. He claims to have \(\frac{3}{10}\) of the original spool of twine left over. To know whether his estimation is reasonable or not we have to subtract the total spool of twine from used spool of twine. \(\frac{4}{5}\) – \(\frac{1}{2}\) LCD = 10 \(\frac{4}{5}\) × \(\frac{2}{2}\)  – \(\frac{1}{2}\) × \(\frac{5}{5}\) \(\frac{8}{10}\) – \(\frac{5}{10}\) = \(\frac{3}{10}\) By this is can that Jamie’s claim is reasonable.

Answer: [atex]\frac{1}{2}+\frac{1}{4}=\frac{3}{4}[/latex]

Explanation: Number of green beads = 4 = [atex]\frac{1}{2}[/latex] Number of blue beads = 3 = [atex]\frac{3}{4}[/latex] Number of yellow beads = 1 [atex]\frac{1}{4}[/latex] The fraction of beads that are green or yellow is [atex]\frac{1}{2}+\frac{1}{4}=\frac{3}{4}[/latex] The correct answer is option B.

Question 1. A ________ is a number that is a multiple of two or more numbers. ________

Answer: Common Multiple A Common Multiple is a number that is a multiple of two or more numbers.

Question 2. A ________ is a common multiple of two or more denominators. ________

Answer: Common denominator A Common denominator is a common multiple of two or more denominators.

Concepts and Skills

Question 3. \(\frac{8}{9}+\frac{4}{7}\) about ______ \(\frac{□}{□}\)

Place \(\frac{8}{9}\) on the number line. \(\frac{8}{9}\) lies between \(\frac{1}{2}\) and 1. \(\frac{8}{9}\) is closer to 1. Place \(\frac{4}{7}\) on the number line. \(\frac{4}{7}\) lies between \(\frac{1}{2}\) and 1. \(\frac{4}{7}\) is closer to \(\frac{1}{2}\). 1 + \(\frac{1}{2}\) = 1 \(\frac{1}{2}\)

Question 4. \(3 \frac{2}{5}-\frac{5}{8}\) about ______

Explanation: Place \(\frac{2}{5}\) on the number line. \(\frac{2}{5}\) lies between 0 and \(\frac{1}{2}\) \(\frac{2}{5}\) is closer to \(\frac{1}{2}\) Place \(\frac{5}{8}\) on the number line. \(\frac{5}{8}\) lies between \(\frac{1}{2}\) and 1. \(\frac{5}{8}\) is closer to \(\frac{1}{2}\) 3 + \(\frac{1}{2}\) – \(\frac{1}{2}\) = 3 \(3 \frac{2}{5}-\frac{5}{8}\) = 3

Question 5. \(1 \frac{5}{6}+2 \frac{2}{11}\) about ______

Explanation: Place \(\frac{5}{6}\) on the number line. \(\frac{5}{6}\) lies between \(\frac{1}{2}\) and 1. \(\frac{5}{6}\) is closer to 1. Place \(\frac{2}{11}\) on the number line. \(\frac{2}{11}\) lies between \(\frac{1}{2}\) and 0. \(\frac{2}{11}\) is closer to 0 1 + 1 + 2 + 0 = 4 \(1 \frac{5}{6}+2 \frac{2}{11}\) = 4

Question 6. \(\frac{1}{6}, \frac{1}{9}\) common denominator: Type below: __________

Answer: 54 Multiply the denominators 6 × 9 = 54 Thus the common denominator of \(\frac{1}{6}, \frac{1}{9}\) is 54

Question 7. \(\frac{3}{8}, \frac{3}{10}\) common denominator: Type below: __________

Answer: 80 Multiply the denominators 8 × 10 = 80 The common denominator of \(\frac{3}{8}, \frac{3}{10}\) is 80

Question 8. \(\frac{1}{9}, \frac{5}{12}\) common denominator: Type below: __________

Answer: 36 Multiply the denominators 9 × 12 = 108 The common denominator of \(\frac{1}{9}, \frac{5}{12}\) is 108

Question 9. \(\frac{2}{5}, \frac{1}{10}\) least common denominator: ______ Explain: __________

Explanation: Multiply the denominators 5 × 10 = 50 The least common denominators of \(\frac{2}{5}, \frac{1}{10}\) is 10.

Question 10. \(\frac{5}{6}, \frac{3}{8}\) least common denominator: ______ Explain: __________

Explanation: Multiply the denominators The least common denominator of 6 and 8 is 24 Thus the LCD of \(\frac{5}{6}, \frac{3}{8}\) is 24

Question 11. \(\frac{1}{3}, \frac{2}{7}\) least common denominator: ______ Explain: __________

Explanation: Multiply the denominators The least common denominator of 3 and 7 is 21. Thus the LCD of \(\frac{1}{3}, \frac{2}{7}\) is 21.

Question 12. \(\frac{11}{18}-\frac{1}{6}\) \(\frac{□}{□}\)

Answer: \(\frac{8}{18}\)

Explanation: Make the fractions like denominators. \(\frac{11}{18}\) – \(\frac{1}{6}\) \(\frac{1}{6}\) × \(\frac{3}{3}\) = \(\frac{3}{18}\) \(\frac{11}{18}\) – \(\frac{3}{18}\) = \(\frac{8}{18}\)

Question 13. \(\frac{2}{7}+\frac{2}{5}\) \(\frac{□}{□}\)

Answer: \(\frac{24}{35}\)

Explanation: Make the fractions like denominators. \(\frac{2}{7}\) × \(\frac{5}{5}\) = \(\frac{10}{35}\) \(\frac{2}{5}\) × \(\frac{7}{7}\) = \(\frac{14}{35}\) \(\frac{10}{35}\) + \(\frac{14}{35}\) = \(\frac{24}{35}\) Thus \(\frac{2}{7}+\frac{2}{5}\) = \(\frac{24}{35}\)

Question 14. \(\frac{3}{4}-\frac{3}{10}\) \(\frac{□}{□}\)

Answer: \(\frac{18}{40}\)

Explanation: Make the fractions like denominators. \(\frac{3}{4}\) × \(\frac{10}{10}\) = \(\frac{30}{40}\) \(\frac{3}{10}\) × \(\frac{4}{4}\) = \(\frac{12}{40}\) \(\frac{30}{40}\) – \(\frac{12}{40}\) = \(\frac{18}{40}\)

Answer: \(\frac{1}{4}\)

Explanation: Mrs. Vargas bakes a pie for her book club meeting. The shaded part of the diagram below shows the amount of pie left after the meeting. So, the fraction of the pie is \(\frac{1}{2}\) That evening, Mr. Vargas eats \(\frac{1}{4}\) of the whole pie. \(\frac{1}{2}\) – \(\frac{1}{4}\) = \(\frac{1}{4}\) Thus the fraction represents the amount of pie remaining is \(\frac{1}{4}\)

Question 16. Keisha makes a large sandwich for a family picnic. She takes \(\frac{1}{2}\) of the sandwich to the picnic. At the picnic, her family eats \(\frac{3}{8}\) of the whole sandwich. What fraction of the whole sandwich does Keisha bring back from the picnic? \(\frac{□}{□}\)

Answer: \(\frac{1}{8}\)

Explanation: Keisha makes a large sandwich for a family picnic. She takes \(\frac{1}{2}\) of the sandwich to the picnic. At the picnic, her family eats \(\frac{3}{8}\) of the whole sandwich. \(\frac{1}{2}\) – \(\frac{3}{8}\) \(\frac{1}{2}\) × \(\frac{4}{4}\) – \(\frac{3}{8}\) \(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\) Thus Keisha brought \(\frac{1}{8}\) of the sandwich from the picnic.

Question 17. Mike is mixing paint for his walls. He mixes \(\frac{1}{6}\) gallon blue paint and \(\frac{5}{8}\) gallon green paint in a large container. What fraction represents the total amount of paint Mike mixes? \(\frac{□}{□}\)

Answer: \(\frac{19}{24}\)

Explanation: Mike is mixing paint for his walls. He mixes \(\frac{1}{6}\) gallon blue paint and \(\frac{5}{8}\) gallon green paint in a large container. \(\frac{1}{6}\) + \(\frac{5}{8}\) \(\frac{1}{6}\) × \(\frac{8}{8}\)  + \(\frac{5}{8}\) × \(\frac{6}{6}\) \(\frac{8}{48}\)  + \(\frac{30}{48}\) \(\frac{38}{48}\) = \(\frac{19}{24}\) Therefore the total amount of paint Mike mixes is \(\frac{19}{24}\)

Question 1. Use a common denominator to write equivalent fractions with like denominators and then find the sum. Write your answer in simplest form. 7 \(\frac{2}{5}\) = ■ + 4 \(\frac{3}{4}\) = + ■ ————————— ■ _____ \(\frac{□}{□}\)

Answer: 12 \(\frac{3}{20}\)

Explanation: First convert the mixed fraction to proper fraction. 7 \(\frac{2}{5}\) = \(\frac{37}{5}\) 4 \(\frac{3}{4}\) = \(\frac{19}{4}\) \(\frac{37}{5}\) + \(\frac{19}{4}\) = \(\frac{37}{5}\) × \(\frac{4}{4}\) = \(\frac{148}{20}\) \(\frac{19}{4}\) × \(\frac{5}{5}\) = \(\frac{95}{20}\) \(\frac{148}{20}\) + \(\frac{95}{20}\) = \(\frac{243}{20}\) Now convert it into mixed fraction = 12 \(\frac{3}{20}\)

Find the sum. Write your answer in simplest form.

Question 2. \(2 \frac{3}{4}+3 \frac{3}{10}\) _____ \(\frac{□}{□}\)

Answer: 6 \(\frac{1}{20}\)

Explanation: First convert the mixed fraction to proper fraction. \(2 \frac{3}{4}\) = \(\frac{11}{4}\) 3 \(\frac{3}{10}\) = \(\frac{33}{10}\) Now make the common denominators of the above fractions. \(\frac{11}{4}\) × \(\frac{10}{10}\) = \(\frac{110}{40}\) \(\frac{33}{10}\) × \(\frac{4}{4}\) = \(\frac{132}{40}\) = \(\frac{121}{20}\) Now convert the fraction into mixed fraction. \(\frac{121}{20}\) = 6 \(\frac{1}{20}\)

Question 3. \(5 \frac{3}{4}+1 \frac{1}{3}\) _____ \(\frac{□}{□}\)

Answer: 7 \(\frac{1}{12}\)

Explanation: First convert the mixed fraction to proper fraction. 5 \(\frac{3}{4}\) = \(\frac{23}{4}\) 1 \(\frac{1}{3}\) = \(\frac{4}{3}\) \(\frac{23}{4}\) + \(\frac{4}{3}\) \(\frac{23}{4}\) × \(\frac{3}{3}\) = \(\frac{69}{12}\) \(\frac{4}{3}\) × \(\frac{4}{4}\) = \(\frac{16}{12}\) \(\frac{69}{12}\) + \(\frac{16}{12}\) = \(\frac{85}{12}\) The mixed fraction of \(\frac{85}{12}\) = 7 \(\frac{1}{12}\)

Question 4. \(3 \frac{4}{5}+2 \frac{3}{10}\) _____ \(\frac{□}{□}\)

Answer: 6 \(\frac{1}{10}\)

Explanation: First convert the mixed fraction to proper fraction. 3 \(\frac{4}{5}\) = \(\frac{19}{5}\) 2 \(\frac{3}{10}\) = \(\frac{23}{10}\) \(\frac{19}{5}\) + \(\frac{23}{10}\) Now make the common denominators of the above fractions. \(\frac{19}{5}\) × \(\frac{2}{2}\) = \(\frac{38}{10}\) \(\frac{38}{10}\) + \(\frac{23}{10}\) = \(\frac{61}{10}\) The mixed fraction of \(\frac{61}{10}\) = 6 \(\frac{1}{10}\)

Find the difference. Write your answer in simplest form.

Question 5. \(9 \frac{5}{6}-2 \frac{1}{3}\) _____ \(\frac{□}{□}\)

Answer: 7 \(\frac{1}{2}\)

Explanation: \(9 \frac{5}{6}-2 \frac{1}{3}\) = \(\frac{59}{6}\) – \(\frac{14}{6}\) = \(\frac{45}{6}\) = \(\frac{15}{2}\) = 7 \(\frac{1}{2}\)

Question 6. \(10 \frac{5}{9}-9 \frac{1}{6}\) _____ \(\frac{□}{□}\)

Answer: 1 \(\frac{7}{18}\)

Explanation: \(10 \frac{5}{9}-9 \frac{1}{6}\) = \(\frac{95}{9}\) – \(\frac{55}{6}\) = \(\frac{190}{18}\) – \(\frac{165}{18}\) = \(\frac{25}{18}\) = 1 \(\frac{7}{18}\) \(10 \frac{5}{9}-9 \frac{1}{6}\) = 1 \(\frac{7}{18}\)

Question 7. \(7 \frac{2}{3}-3 \frac{1}{6}\) _____ \(\frac{□}{□}\)

Answer: 4 \(\frac{1}{2}\)

Explanation: \(7 \frac{2}{3}-3 \frac{1}{6}\) \(\frac{23}{3}\) – \(\frac{19}{6}\) = \(\frac{46}{6}\) – \(\frac{19}{6}\) = \(\frac{27}{6}\) = 4 \(\frac{1}{2}\) \(7 \frac{2}{3}-3 \frac{1}{6}\) = 4 \(\frac{1}{2}\)

Question 8. \(1 \frac{3}{10}+2 \frac{2}{5}\) _____ \(\frac{□}{□}\)

Answer: 3 \(\frac{7}{10}\)

Explanation: \(1 \frac{3}{10}+2 \frac{2}{5}\) \(\frac{13}{10}\) + \(\frac{12}{5}\) = \(\frac{13}{10}\) + \(\frac{24}{10}\) = \(\frac{37}{10}\) = 3 \(\frac{7}{10}\) Thus \(1 \frac{3}{10}+2 \frac{2}{5}\) = 3 \(\frac{7}{10}\)

Question 9. \(3 \frac{4}{9}+3 \frac{1}{2}\) _____ \(\frac{□}{□}\)

Answer: 6 \(\frac{17}{18}\)

Explanation: \(3 \frac{4}{9}+3 \frac{1}{2}\) \(\frac{31}{9}\) + \(\frac{7}{2}\) = \(\frac{62}{18}\) + \(\frac{63}{18}\) \(\frac{125}{18}\) = 6 \(\frac{17}{18}\) \(3 \frac{4}{9}+3 \frac{1}{2}\) = 6 \(\frac{17}{18}\)

Question 10. \(2 \frac{1}{2}+2 \frac{1}{3}\) _____ \(\frac{□}{□}\)

Answer: 4 \(\frac{5}{6}\)

Explanation: \(2 \frac{1}{2}+2 \frac{1}{3}\) = \(\frac{5}{2}\) + \(\frac{7}{3}\) \(\frac{15}{6}\) + \(\frac{14}{6}\)= \(\frac{29}{6}\) The mixed fraction of \(\frac{29}{6}\) is 4 \(\frac{5}{6}\)

Question 11. \(5 \frac{1}{4}+9 \frac{1}{3}\) _____ \(\frac{□}{□}\)

Answer: 14 \(\frac{7}{12}\)

Explanation: \(5 \frac{1}{4}+9 \frac{1}{3}\) = \(\frac{21}{4}\) + \(\frac{28}{3}\) \(\frac{63}{12}\) + \(\frac{112}{12}\) = \(\frac{175}{12}\) The mixed fraction of \(\frac{175}{12}\) is 14 \(\frac{7}{12}\)

Question 12. \(8 \frac{1}{6}+7 \frac{3}{8}\) _____ \(\frac{□}{□}\)

Answer: 15 \(\frac{13}{24}\)

Explanation: \(8 \frac{1}{6}+7 \frac{3}{8}\) = \(\frac{49}{6}\) + \(\frac{59}{8}\) \(\frac{196}{24}\) + \(\frac{177}{24}\) = \(\frac{373}{24}\) The mixed fraction of \(\frac{373}{24}\) is 15 \(\frac{13}{24}\)

Question 13. \(14 \frac{7}{12}-5 \frac{1}{4}\) _____ \(\frac{□}{□}\)

Answer: 9 \(\frac{1}{3}\)

Explanation: \(14 \frac{7}{12}-5 \frac{1}{4}\) = \(\frac{175}{12}\) – \(\frac{21}{4}\) \(\frac{175}{12}\) – \(\frac{63}{12}\) = \(\frac{112}{12}\) The mixed fraction of \(\frac{112}{12}\) is 9 \(\frac{1}{3}\)

Question 14. \(12 \frac{3}{4}-6 \frac{1}{6}\) _____ \(\frac{□}{□}\)

Answer: 6 \(\frac{7}{12}\)

Explanation: \(12 \frac{3}{4}-6 \frac{1}{6}\) = \(\frac{51}{4}\) – \(\frac{37}{6}\) \(\frac{153}{12}\) – \(\frac{74}{12}\) = \(\frac{79}{12}\) The mixed fraction of \(\frac{79}{12}\) is 6 \(\frac{7}{12}\)

Question 15. \(2 \frac{5}{8}-1 \frac{1}{4}\) _____ \(\frac{□}{□}\)

Answer: 1 \(\frac{3}{8}\)

Explanation: \(2 \frac{5}{8}-1 \frac{1}{4}\) \(\frac{21}{8}\) – \(\frac{5}{4}\) = \(\frac{21}{8}\) – \(\frac{10}{8}\) = \(\frac{11}{8}\) The mixed fraction of \(\frac{11}{8}\) is 1 \(\frac{3}{8}\)

Question 16. \(10 \frac{1}{2}-2 \frac{1}{5}\) _____ \(\frac{□}{□}\)

Answer: 8 \(\frac{3}{10}\)

Explanation: \(10 \frac{1}{2}-2 \frac{1}{5}\) = \(\frac{21}{2}\) – \(\frac{11}{5}\) \(\frac{105}{10}\) – \(\frac{22}{10}\) = \(\frac{83}{10}\) The mixed fraction of \(\frac{83}{10}\) is 8 \(\frac{3}{10}\)

Question 17. \(1 \frac{5}{12}+4 \frac{1}{6}\) _____ \(\frac{□}{□}\)

Answer: 5 \(\frac{7}{12}\)

Explanation: \(1 \frac{5}{12}+4 \frac{1}{6}\) = \(\frac{17}{12}\) + \(\frac{25}{6}\) \(\frac{17}{12}\) + \(\frac{50}{12}\) = \(\frac{67}{12}\) The mixed fraction of \(\frac{67}{12}\) is 5 \(\frac{7}{12}\)

Question 18. \(8 \frac{1}{2}+6 \frac{3}{5}\) _____ \(\frac{□}{□}\)

Answer: 15 \(\frac{1}{10}\)

Explanation: \(8 \frac{1}{2}+6 \frac{3}{5}\) = \(\frac{17}{2}\) + \(\frac{33}{5}\) \(\frac{85}{10}\) + \(\frac{66}{10}\) = \(\frac{151}{10}\) The mixed fraction of \(\frac{151}{10}\) is 15 \(\frac{1}{10}\) \(8 \frac{1}{2}+6 \frac{3}{5}\) = 15 \(\frac{1}{10}\)

Question 19. \(2 \frac{1}{6}+4 \frac{5}{9}\) _____ \(\frac{□}{□}\)

Answer: 6 \(\frac{13}{18}\)

Explanation: \(2 \frac{1}{6}+4 \frac{5}{9}\) = \(\frac{13}{6}\) + \(\frac{41}{9}\) \(\frac{39}{18}\) + \(\frac{82}{18}\) = \(\frac{121}{18}\) The mixed fraction of \(\frac{121}{18}\) is 6 \(\frac{13}{18}\) \(2 \frac{1}{6}+4 \frac{5}{9}\) = 6 \(\frac{13}{18}\)

Question 20. \(20 \frac{5}{8}+\frac{5}{12}\) _____ \(\frac{□}{□}\)

Answer: 21 \(\frac{1}{24}\)

Explanation: \(20 \frac{5}{8}+\frac{5}{12}\) = \(\frac{165}{8}\) + \(\frac{5}{12}\) \(\frac{495}{24}\) + \(\frac{10}{24}\) = \(\frac{505}{24}\) The mixed fraction of \(\frac{505}{24}\) is 21 \(\frac{1}{24}\) \(20 \frac{5}{8}+\frac{5}{12}\) = 21 \(\frac{1}{24}\)

Question 21. \(3 \frac{2}{3}-1 \frac{1}{6}\) _____ \(\frac{□}{□}\)

Answer: 2 \(\frac{1}{2}\)

Explanation: \(3 \frac{2}{3}-1 \frac{1}{6}\) = \(\frac{11}{3}\) – \(\frac{7}{6}\) \(\frac{22}{6}\) – \(\frac{7}{6}\) = \(\frac{15}{6}\) = \(\frac{5}{2}\) The mixed fraction of \(\frac{5}{2}\) is 2 \(\frac{1}{2}\) \(3 \frac{2}{3}-1 \frac{1}{6}\) = 2 \(\frac{1}{2}\)

Question 22. \(5 \frac{6}{7}-1 \frac{2}{3}\) _____ \(\frac{□}{□}\)

Answer: 4 \(\frac{4}{21}\)

Explanation: \(5 \frac{6}{7}-1 \frac{2}{3}\) = \(\frac{41}{7}\) – \(\frac{5}{3}\) \(\frac{123}{21}\) – \(\frac{35}{21}\) = \(\frac{88}{21}\) The mixed fraction of \(\frac{88}{21}\) is 4 \(\frac{4}{21}\)

Question 23. \(2 \frac{7}{8}-\frac{1}{2}\) _____ \(\frac{□}{□}\)

Answer: 2 \(\frac{3}{8}\)

Explanation: \(2 \frac{7}{8}-\frac{1}{2}\) = \(\frac{23}{8}\) – \(\frac{1}{2}\) = \(\frac{23}{8}\) – \(\frac{4}{8}\) = \(\frac{19}{8}\) The mixed fraction of \(\frac{19}{8}\) is 2 \(\frac{3}{8}\) So, \(2 \frac{7}{8}-\frac{1}{2}\) = 2 \(\frac{3}{8}\)

Question 24. \(4 \frac{7}{12}-1 \frac{2}{9}\) _____ \(\frac{□}{□}\)

Answer: 3 \(\frac{13}{36}\)

Explanation: \(4 \frac{7}{12}-1 \frac{2}{9}\) = \(\frac{55}{12}\) – \(\frac{11}{9}\) \(\frac{165}{36}\) – \(\frac{44}{36}\) = \(\frac{121}{36}\) The mixed fraction of \(\frac{121}{36}\) is 3 \(\frac{13}{36}\)

Question 25. Gavin is mixing a batch of Sunrise Orange paint for an art project. How much paint does Gavin mix? _____ \(\frac{□}{□}\) ounces

Answer: 5 \(\frac{7}{8}\) ounces

Explanation: Gavin is mixing a batch of Sunrise Orange paint for an art project. 2 \(\frac{5}{8}\) + 3 \(\frac{1}{4}\) Solving the whole numbers 2 + 3 = 5 Add the fraction parts \(\frac{5}{8}\) + \(\frac{1}{4}\) LCD = 8 \(\frac{5}{8}\) + \(\frac{2}{8}\) = \(\frac{7}{8}\) 5 + \(\frac{7}{8}\) = 5 \(\frac{7}{8}\) ounces

Question 26. Gavin plans to mix a batch of Tangerine paint. He expects to have a total of 5 \(\frac{3}{10}\) ounces of paint after he mixes the amounts of red and yellow. Explain how you can tell if Gavin’s expectation is reasonable. Type below: _________

Answer: Gavin plans to mix a batch of Tangerine paint. He expects to have a total of 5 \(\frac{3}{10}\) ounces of paint after he mixes the amounts of red and yellow. To mix a batch of Tangerine paint he need 3 \(\frac{9}{10}\) red and 2 \(\frac{3}{8}\) yellow paint. Add the fractions 3 + \(\frac{9}{10}\) + 2 + \(\frac{3}{8}\) Solving the whole numbers 3 + 2 = 5 \(\frac{9}{10}\) + \(\frac{3}{8}\) LCD = 40 \(\frac{9}{10}\) + \(\frac{3}{8}\) = \(\frac{36}{40}\) + \(\frac{15}{40}\) = \(\frac{51}{40}\) = 1 \(\frac{11}{40}\) 5 + 1 \(\frac{11}{40}\) = 6 \(\frac{11}{40}\)

Question 27. For a special project, Gavin mixes the amount of red from one shade of paint with the amount of yellow from a different shade. He mixes the batch so he will have the greatest possible amount of paint. What amounts of red and yellow from which shades are used in the mixture for the special project? Explain your answer. Type below: _________

Answer: Gavin used red paint from mango and yellow paint from Sunrise Orange. 5 \(\frac{5}{6}\) + 3 \(\frac{1}{4}\) Solving the whole numbers parts 5 + 3 = 8 Solving the fraction part \(\frac{5}{6}\) + \(\frac{1}{4}\) LCD = 12 \(\frac{10}{12}\) + \(\frac{3}{12}\) = \(\frac{13}{12}\) \(\frac{13}{12}\) = 1 \(\frac{1}{12}\)

Question 28. Gavin needs to make 2 batches of Mango paint. Explain how you could find the total amount of paint Gavin mixed. Type below: _________

Answer: Gavin used Red paint and Yellow Paint to make Mango shade. For one batch he need to add 5 \(\frac{5}{6}\) + 5 \(\frac{5}{6}\) Foe 2 batches 5 \(\frac{5}{6}\)+ 5 \(\frac{5}{6}\) + 5 \(\frac{5}{6}\) + 5 \(\frac{5}{6}\) Solving the whole numbers 5 + 5 + 5 + 5 = 20 Solving the fractions part \(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\) = \(\frac{20}{6}\) = \(\frac{10}{3}\) Gavin mixed \(\frac{10}{3}\) of paint to make 2 batches of Mango Paint.

Question 29. Test Prep Yolanda walked 3 \(\frac{6}{10}\) miles. Then she walked 4 \(\frac{1}{2}\) more miles. How many miles did Yolanda walk? Options: a. 7 \(\frac{1}{10}\) miles b. 7 \(\frac{7}{10}\) miles c. 8 \(\frac{1}{10}\) miles d. 8 \(\frac{7}{10}\) miles

Answer: 8 \(\frac{1}{10}\) miles

Explanation: Test Prep Yolanda walked 3 \(\frac{6}{10}\) miles. Then she walked 4 \(\frac{1}{2}\) more miles. 3 \(\frac{6}{10}\) + 4 \(\frac{1}{2}\) = 3 + \(\frac{6}{10}\) + 4 + \(\frac{1}{2}\) Add whole numbers 3 + 4 = 7 Add the fractions \(\frac{6}{10}\) + \(\frac{1}{2}\) LCD = 10 \(\frac{6}{10}\) + \(\frac{5}{10}\) = \(\frac{11}{10}\) \(\frac{11}{10}\) = 8 \(\frac{1}{10}\) miles Thus the correct answer is option C.

Estimate. Then find the difference and write it in simplest form.

Question 1. Estimate: ______ 1 \(\frac{3}{4}-\frac{7}{8}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 1 Difference: \(\frac{7}{8}\)

Explanation: Estimation: 1 + \(\frac{3}{4}\) – \(\frac{7}{8}\) \(\frac{7}{8}\) is close to 1. \(\frac{3}{4}\) is close to 1. 1 + 1 – 1 = 1 Difference: 1 \(\frac{3}{4}-\frac{7}{8}\) 1 + \(\frac{3}{4}\) – \(\frac{7}{8}\) \(\frac{3}{4}\) – \(\frac{7}{8}\) \(\frac{3}{4}\) × \(\frac{8}{8}\) – \(\frac{7}{8}\) × \(\frac{4}{4}\) \(\frac{24}{32}\) – \(\frac{28}{32}\) = – \(\frac{1}{8}\) 1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)

Question 2. Estimate: ______ \(12 \frac{1}{9}-7 \frac{1}{3}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 5 Difference: 4 \(\frac{7}{9}\)

Explanation: Estimate: 12 + 0 – 7 – 0 = 5 Difference: 12 + \(\frac{1}{9}\) – 7 – \(\frac{1}{3}\) 12 – 7 = 5 \(\frac{1}{9}\) – \(\frac{1}{3}\) = \(\frac{1}{9}\) – \(\frac{3}{9}\) = – \(\frac{2}{9}\) 5 – \(\frac{2}{9}\) = 4 \(\frac{7}{9}\)

Page No. 271

Question 3. Estimate: ________ \(4 \frac{1}{2}-3 \frac{4}{5}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: \(\frac{1}{2}\) Difference: \(\frac{7}{10}\)

Explanation: \(4 \frac{1}{2}-3 \frac{4}{5}\) 4 – \(\frac{1}{2}\) – 3 – 1 = \(\frac{1}{2}\) Difference: \(4 \frac{1}{2}-3 \frac{4}{5}\) 4 \(\frac{1}{2}\) – 3 \(\frac{4}{5}\) Solving the whole number parts 4 – 3 = 1 Solving the fraction parts \(\frac{1}{2}\) – \(\frac{4}{5}\) LCD = 10 \(\frac{5}{10}\) – \(\frac{8}{10}\) = – \(\frac{3}{10}\) 1 – \(\frac{3}{10}\) = \(\frac{7}{10}\)

Question 4. Estimate: ________ \(9 \frac{1}{6}-2 \frac{3}{4}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 6 Difference: 6 \(\frac{5}{12}\)

Explanation: \(9 \frac{1}{6}-2 \frac{3}{4}\) 9 + 0 – 2 – 1 = 6 Difference: \(9 \frac{1}{6}-2 \frac{3}{4}\) 9 + \(\frac{1}{6}\) – 2 – \(\frac{3}{4}\) 9 – 2 = 7 \(\frac{1}{6}\) – \(\frac{3}{4}\) LCD = 12 \(\frac{2}{12}\) – \(\frac{9}{12}\) = – \(\frac{7}{12}\) 7 – \(\frac{7}{12}\) = 6 \(\frac{5}{12}\) \(9 \frac{1}{6}-2 \frac{3}{4}\) = 6 \(\frac{5}{12}\)

Question 5. Estimate: ________ \(3 \frac{2}{3}-1 \frac{11}{12}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 2 Difference: 1 \(\frac{3}{4}\)

Explanation: Estimate: \(3 \frac{2}{3}-1 \frac{11}{12}\) \(\frac{2}{3}\) is close to 1. \(\frac{11}{12}\) is close to 1. 3 + 1 – 1 – 1 = 2 Difference: \(3 \frac{2}{3}-1 \frac{11}{12}\) 3 + \(\frac{2}{3}\) – 1 – \(\frac{11}{12}\) 3 – 1 = 2 Solving the fractions part \(\frac{2}{3}\) – \(\frac{11}{12}\) LCD = 12 \(\frac{8}{12}\) – \(\frac{11}{12}\) = – \(\frac{3}{12}\) = – \(\frac{1}{4}\) 3 – \(\frac{1}{4}\) = 1 \(\frac{3}{4}\) \(3 \frac{2}{3}-1 \frac{11}{12}\) = 1 \(\frac{3}{4}\)

Question 6. Estimate: ________ \(4 \frac{1}{4}-2 \frac{1}{3}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 2 Difference: 1 \(\frac{11}{12}\)

Explanation: \(4 \frac{1}{4}-2 \frac{1}{3}\) \(\frac{1}{4}\) is close to 0. \(\frac{1}{3}\) is close to 0. 4 – 2 = 2 Solving the fractions part \(\frac{1}{4}\) – \(\frac{1}{3}\) LCD = 12 \(\frac{1}{4}\) × \(\frac{3}{3}\) – \(\frac{1}{3}\) × \(\frac{4}{4}\) \(\frac{3}{12}\) – \(\frac{4}{12}\) = – \(\frac{1}{12}\) 2 – \(\frac{1}{12}\) = 1 \(\frac{11}{12}\)

Question 7. Estimate: ________ \(5 \frac{2}{5}-1 \frac{1}{2}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 4 Difference: 3 \(\frac{9}{10}\)

Explanation: Estimate: \(5 \frac{2}{5}-1 \frac{1}{2}\) 5 + \(\frac{1}{2}\) – 1 – \(\frac{1}{2}\) 5 – 1 = 4 Solving the fractions part \(5 \frac{2}{5}-1 \frac{1}{2}\) LCD = 10 \(\frac{4}{10}\) – \(\frac{5}{10}\) = – \(\frac{1}{10}\) 4 – \(\frac{1}{10}\) = 3 \(\frac{9}{10}\)

Question 8. \(7 \frac{5}{9}-2 \frac{5}{6}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 4 \(\frac{1}{2}\) Difference: 4 \(\frac{13}{18}\)

Explanation: Estimate: \(7 \frac{5}{9}-2 \frac{5}{6}\) \(\frac{5}{9}\) is close to \(\frac{1}{2}\) \(\frac{5}{6}\) is close to 1. 7 + \(\frac{1}{2}\) – 2 – 1 4 \(\frac{1}{2}\) Difference: \(7 \frac{5}{9}-2 \frac{5}{6}\) 7 + \(\frac{5}{9}\) – 2 – \(\frac{5}{6}\) Solving the whole numbers 7 – 2 = 5 Solving the fraction part \(\frac{5}{9}\) – \(\frac{5}{6}\) LCD = 18 \(\frac{10}{18}\) – \(\frac{15}{18}\) = – \(\frac{5}{18}\) 5 – \(\frac{5}{18}\) = 4 \(\frac{13}{18}\)

Question 9. Estimate: ________ \(7-5 \frac{2}{3}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 1 Difference: 1 \(\frac{1}{3}\)

Explanation: Estimate: \(7-5 \frac{2}{3}\) 7 – 5 – \(\frac{2}{3}\) 7 – 5 – 1 = 1 Difference: \(7-5 \frac{2}{3}\) 7 – 5 = 2 2 – \(\frac{2}{3}\) = 1 \(\frac{1}{3}\) Thus \(7-5 \frac{2}{3}\) = 1 \(\frac{1}{3}\)

Question 10. Estimate: ________ \(2 \frac{1}{5}-1 \frac{9}{10}\) Estimate: _____ \(\frac{□}{□}\) Difference: _____ \(\frac{□}{□}\)

Answer: Estimate: 0 Difference: \(\frac{3}{10}\)

Explanation: Estimate: \(2 \frac{1}{5}-1 \frac{9}{10}\) 2 + 0 – 1 – 1 = 0 Difference: \(2 \frac{1}{5}-1 \frac{9}{10}\) 2 \(\frac{1}{5}\) – 1 \(\frac{9}{10}\) 2 + \(\frac{1}{5}\) – 1 – \(\frac{9}{10}\) Solving the whole number parts 2 – 1 = 1 \(\frac{1}{5}\) – \(\frac{9}{10}\) LCD = 10 \(\frac{2}{10}\) – \(\frac{9}{10}\) = – \(\frac{7}{10}\) 1 – \(\frac{7}{10}\) = \(\frac{3}{10}\)

Practice: Copy and Solve Find the difference and write it in simplest form.

Question 11. \(11 \frac{1}{9}-3 \frac{2}{3}\) _____ \(\frac{□}{□}\)

Answer: 7 \(\frac{4}{9}\)

Explanation: Rewriting our equation with parts separated 11 + \(\frac{1}{9}\) – 3 – \(\frac{2}{3}\) Solving the whole number parts 11 – 3 = 8 Solving the fraction parts LCD = 9 \(\frac{1}{9}\) – \(\frac{2}{3}\) \(\frac{1}{9}\) – \(\frac{6}{9}\) = – \(\frac{5}{9}\) 8 – \(\frac{5}{9}\) = 7 \(\frac{4}{9}\)

Question 12. \(6-3 \frac{1}{2}\) _____ \(\frac{□}{□}\)

Explanation: Rewriting our equation with parts separated 6 – 3 – \(\frac{1}{2}\) 3 – \(\frac{1}{2}\) = 2 \(\frac{1}{2}\)

Question 13. \(4 \frac{3}{8}-3 \frac{1}{2}\) \(\frac{□}{□}\)

Answer: \(\frac{7}{8}\)

Explanation: Rewriting our equation with parts separated 4 + \(\frac{3}{8}\) – 3 – \(\frac{1}{2}\) Solving the whole number parts 4 – 3 = 1 Solving the fraction parts \(\frac{3}{8}\) – \(\frac{1}{2}\) = \(\frac{3}{8}\) – \(\frac{4}{8}\) = – \(\frac{1}{8}\) 1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)

Question 14. \(9 \frac{1}{6}-3 \frac{5}{8}\) _____ \(\frac{□}{□}\)

Answer: 5 \(\frac{13}{24}\)

Explanation: Rewriting our equation with parts separated 9 + \(\frac{1}{6}\) – 3 – \(\frac{5}{8}\) Solving the whole number parts 9 – 3 = 6 Solving the fraction parts \(\frac{1}{6}\) – \(\frac{5}{8}\) \(\frac{4}{24}\) – \(\frac{15}{24}\) = – \(\frac{11}{24}\) 6 – \(\frac{11}{24}\) = 5 \(\frac{13}{24}\)

Question 15. \(1 \frac{1}{5}-\frac{1}{2}\) \(\frac{□}{□}\)

Answer: \(\frac{7}{10}\)

Explanation: Rewriting our equation with parts separated 1 + \(\frac{1}{5}\) – \(\frac{1}{2}\) Solving the whole number parts 1 + 0 = 1 Solving the fraction parts \(\frac{1}{5}\) – \(\frac{1}{2}\) LCD = 10 \(\frac{2}{10}\) – \(\frac{5}{10}\) = – \(\frac{3}{10}\) 1 – \(\frac{3}{10}\) = \(\frac{7}{10}\)

Question 16. \(13 \frac{1}{6}-3 \frac{4}{5}\) _____ \(\frac{□}{□}\)

Answer: 9 \(\frac{11}{30}\)

Explanation: Rewriting our equation with parts separated 13 + \(\frac{1}{6}\) – 3 – \(\frac{4}{5}\) Solving the whole number parts 13 – 3 = 10 Solving the fraction parts \(\frac{1}{6}\) – \(\frac{4}{5}\) LCD = 30 \(\frac{5}{30}\) – \(\frac{24}{30}\) = – \(\frac{19}{30}\) 10 – \(\frac{19}{30}\) = 9 \(\frac{11}{30}\)

Question 17. \(12 \frac{2}{5}-5 \frac{3}{4}\) _____ \(\frac{□}{□}\)

Answer: 6 \(\frac{13}{20}\)

Explanation: Rewriting our equation with parts separated 12 + \(\frac{2}{5}\) – 5 – \(\frac{3}{4}\) Solving the whole number parts 12 – 5 = 7 Solving the fraction parts \(\frac{2}{5}\) – \(\frac{3}{4}\) LCD = 20 \(\frac{8}{20}\) – \(\frac{15}{20}\) = – \(\frac{7}{20}\) 7 – \(\frac{7}{20}\) = 6 \(\frac{13}{20}\)

Question 18. \(7 \frac{3}{8}-2 \frac{7}{9}\) _____ \(\frac{□}{□}\)

Answer: 4 \(\frac{43}{72}\)

Explanation: 7 + \(\frac{3}{8}\) – 2 – \(\frac{7}{9}\) 7 – 2 = 5 \(\frac{3}{8}\) – \(\frac{7}{9}\) = \(\frac{27}{72}\) – \(\frac{56}{72}\) – \(\frac{29}{72}\) 5 – \(\frac{29}{72}\) = 4 \(\frac{43}{72}\)

Page No. 272

Summarize An amusement park in Sandusky, Ohio, offers 17 amazing roller coasters for visitors to ride. One of the roller coasters runs at 60 miles per hour and has 3,900 feet of twisting track. This coaster also has 3 trains with 8 rows per train. Riders stand in rows of 4, for a total of 32 riders per train.

The operators of the coaster recorded the number of riders on each train during a run. On the first train, the operators reported that 7 \(\frac{1}{4}\) rows were filled. On the second train, all 8 rows were filled, and on the third train, 5 \(\frac{1}{2}\) rows were filled. How many more rows were filled on the first train than on the third train?

When you summarize, you restate the most important information in a shortened form to more easily understand what you have read. Summarize the information given. ______________________ Use the summary to solve.

Question 19. Solve the problem above. Type below: _________

Answer: On the first train, the operators reported that 7 \(\frac{1}{4}\) rows were filled. On the third train, 5 \(\frac{1}{2}\) rows were filled. 7 \(\frac{1}{4}\) – 5 \(\frac{1}{2}\) Solving the whole numbers 7 – 5 = 2 Solving the fractions \(\frac{1}{4}\) – \(\frac{1}{2}\) = – \(\frac{1}{4}\) 2 – \(\frac{1}{4}\) = 1 \(\frac{3}{4}\) 1 \(\frac{3}{4}\) more rows were filled on the first train than on the third train.

Question 20. How many rows were empty on the third train? How many additional riders would it take to fill the empty rows? Explain your answer. Type below: _________

Answer: The coaster also has 3 trains with 8 rows per train. The third train has 8 rows. On the third train, 5 \(\frac{1}{2}\) rows were filled. 8 – 5 \(\frac{1}{2}\) 8 – 5 – \(\frac{1}{2}\) = 2 \(\frac{1}{2}\) 2 \(\frac{1}{2}\) rows are empty. So, it takes 10 additional riders to fill the empty rows on the third train.

Write a rule for the sequence.

Question 1. \(\frac{1}{4}, \frac{1}{2}, \frac{3}{4}, \cdots\) Think: Is the sequence increasing or decreasing? Rule: _________ Type below: _________

Answer: The sequence is increasing order with difference \(\frac{1}{4}\)

Question 2. \(\frac{1}{9}, \frac{1}{3}, \frac{5}{9}, \ldots\) Type below: _________

Answer: The sequence is increasing order with difference 2 in numerataor.

Write a rule for the sequence. Then, find the unknown term.

Question 3. \(\frac{3}{10}, \frac{2}{5}\), \(\frac{□}{□}\) , \(\frac{3}{5}, \frac{7}{10}\)

Answer: The sequence is increasing order with difference \(\frac{1}{2}\) LCD = 10 Add \(\frac{1}{2}\) to each term Let the unknown fraction be x \(\frac{3}{10}\), \(\frac{4}{10}\), x, \(\frac{6}{10}\), \(\frac{7}{10}\) x = \(\frac{5}{10}\) = \(\frac{1}{2}\)

Question 4. \(10 \frac{2}{3}, 9 \frac{11}{18}, 8 \frac{5}{9}\), ______ \(\frac{□}{□}\) , \(6 \frac{4}{9}\)

Explanation: \(\frac{32}{3}\), \(\frac{173}{18}\), \(\frac{77}{9}\), x, \(\frac{58}{9}\) LCD = 54 \(\frac{576}{54}\), \(\frac{519}{54}\), \(\frac{462}{54}\), x, \(\frac{348}{54}\) According to the series x = \(\frac{405}{54}\) = \(\frac{15}{2}\) The mixed fraction of \(\frac{15}{2}\) is 7 \(\frac{1}{2}\)

Question 5. \(1 \frac{1}{6}\), ______ \(\frac{□}{□}\) , \(1, \frac{11}{12}, \frac{5}{6}\)

Answer: 1 \(\frac{1}{12}\)

Explanation: \(1 \frac{1}{6}\), ______ \(\frac{□}{□}\) , \(1, \frac{11}{12}, \frac{5}{6}\) The LCD of the above fractons is 12 Convert them into improper fractions \(\frac{14}{12}\), x, \(\frac{12}{12}\), \(\frac{11}{12}\), \(\frac{10}{12}\) According to the series x = \(\frac{13}{12}\) The mixed fraction of \(\frac{13}{12}\) is 1 \(\frac{1}{12}\)

Question 6. \(2 \frac{3}{4}, 4,5 \frac{1}{4}, 6 \frac{1}{2}\), ______ \(\frac{□}{□}\)

Answer: 7 \(\frac{3}{4}\)

Explanation: \(2 \frac{3}{4}, 4,5 \frac{1}{4}, 6 \frac{1}{2}\), ______ \(\frac{□}{□}\) Convert the mixed fractions into improper fractions \(\frac{11}{4}\), \(\frac{4}{1}\), \(\frac{21}{4}\), \(\frac{13}{2}\), x \(\frac{11}{4}\), \(\frac{16}{4}\), \(\frac{21}{4}\), \(\frac{26}{4}\), x According to the series x = \(\frac{31}{4}\) The mixed fraction of \(\frac{31}{4}\) is 7 \(\frac{3}{4}\)

Question 7. \(\frac{1}{8}, \frac{1}{2}\), \(\frac{□}{□}\) , \(1 \frac{1}{4}, 1 \frac{5}{8}\)

Explanation: \(\frac{1}{8}, \frac{1}{2}\), \(1 \frac{1}{4}, 1 \frac{5}{8}\), x LCD = 8 \(\frac{1}{8}, \frac{4}{8}\), \(\frac{10}{8}, \frac{26}{8}\), x \(\frac{1}{8}\), \(\frac{4}{8}\), x, \(\frac{10}{8}\), \(\frac{26}{8}\) The difference between the series is 3 in numerator. x = \(\frac{7}{8}\)

Question 8. \(1 \frac{2}{3}, 1 \frac{3}{4}, 1 \frac{5}{6}, 1 \frac{11}{12}\), ______

Explanation: 1 \(\frac{2}{3}\), 1 \(\frac{3}{4}\), 1 \(\frac{5}{6}\), 1 \(\frac{11}{12}\) Convert the mixed fractions into improper fractions \(\frac{5}{3}\), \(\frac{7}{4}\), \(\frac{11}{6}\), \(\frac{23}{12}\), x The LCD is 12 \(\frac{20}{12}\), \(\frac{21}{12}\), \(\frac{22}{12}\), \(\frac{23}{12}\), x x = \(\frac{24}{12}\) = 2

Question 9. \(12 \frac{7}{8}, 10 \frac{3}{4}\), ______ \(\frac{□}{□}\) , \(6 \frac{1}{2}, 4 \frac{3}{8}\)

Answer: 8 \(\frac{5}{8}\)

Explanation: \(12 \frac{7}{8}, 10 \frac{3}{4}\), x , \(6 \frac{1}{2}, 4 \frac{3}{8}\) Convert the mixed fractions into improper fractions \(\frac{103}{8}\), \(\frac{43}{4}\), x, \(\frac{13}{2}\), \(\frac{35}{8}\) The LCD is 8 \(\frac{103}{8}\), \(\frac{86}{8}\), x, \(\frac{52}{8}\), \(\frac{35}{8}\) x = \(\frac{69}{8}\) The mixed fraction of \(\frac{69}{8}\) is 8 \(\frac{5}{8}\)

Question 10. \(9 \frac{1}{3}\), ______ \(\frac{□}{□}\) , \(6 \frac{8}{9}, 5 \frac{2}{3}, 4 \frac{4}{9}\)

Answer: 8 \(\frac{1}{9}\)

Explanation: \(9 \frac{1}{3}\), x , \(6 \frac{8}{9}, 5 \frac{2}{3}, 4 \frac{4}{9}\) Convert the mixed fractions into improper fractions \(\frac{28}{3}\), x, \(\frac{62}{9}\), \(\frac{17}{3}\), \(\frac{40}{9}\) LCD = 9 \(\frac{84}{9}\), x, \(\frac{62}{9}\), \(\frac{51}{9}\), \(\frac{40}{9}\) According to the series x =  \(\frac{73}{9}\) = 8 \(\frac{1}{9}\)

Write the first four terms of the sequence.

Question 11. Rule: start at 5 \(\frac{3}{4}\), subtract \(\frac{5}{8}\) First term: ______ \(\frac{□}{□}\) Second term: ______ \(\frac{□}{□}\) Third term: ______ \(\frac{□}{□}\) Fourth term: ______ \(\frac{□}{□}\)

Answer: Let the first term be 5 \(\frac{3}{4}\) Second term = 5 \(\frac{3}{4}\) – \(\frac{5}{8}\) = \(\frac{41}{8}\) = 5 \(\frac{1}{8}\) Third term = 5 \(\frac{1}{8}\) – \(\frac{5}{8}\) = \(\frac{36}{8}\) = 4 \(\frac{1}{2}\) Fourth term = \(\frac{36}{8}\) – \(\frac{5}{8}\) = \(\frac{31}{8}\) = 3 \(\frac{7}{8}\)

Question 12. Rule: start at \(\frac{3}{8}\), add \(\frac{3}{16}\) Type below: _________

Answer: Let the first term be \(\frac{3}{8}\) Second term = \(\frac{3}{8}\) + \(\frac{3}{16}\) = \(\frac{9}{16}\) Third term = \(\frac{9}{16}\) + \(\frac{3}{16}\) = \(\frac{12}{16}\) Fourth term = \(\frac{12}{16}\) + \(\frac{3}{16}\) = \(\frac{15}{16}\)

Question 13. Rule: start at 2 \(\frac{1}{3}\), add 2 \(\frac{1}{4}\) First term: ______ \(\frac{□}{□}\) Second term: ______ \(\frac{□}{□}\) Third term: ______ \(\frac{□}{□}\) Fourth term: ______ \(\frac{□}{□}\)

Answer: Let the first term be 2 \(\frac{1}{3}\) Second term = 2 \(\frac{1}{3}\) + 2 \(\frac{1}{4}\) = \(\frac{7}{3}\) + \(\frac{9}{4}\) = \(\frac{55}{12}\) = 4 \(\frac{7}{12}\) Third term = 4 \(\frac{7}{12}\) + 2 \(\frac{1}{4}\) = 6 \(\frac{5}{6}\) Fourth term = 6 \(\frac{5}{6}\) + 2 \(\frac{1}{4}\) = 9 \(\frac{1}{12}\)

Question 14. Rule: start at \(\frac{8}{9}\), subtract \(\frac{1}{18}\) Type below: _________

Answer: Let the first term be \(\frac{8}{9}\) Second term = \(\frac{8}{9}\) – \(\frac{1}{18}\) = \(\frac{15}{18}\) = \(\frac{5}{6}\) Third term = \(\frac{15}{18}\) – \(\frac{1}{18}\) = \(\frac{14}{18}\) = \(\frac{7}{9}\) Fourth term = \(\frac{14}{18}\) – \(\frac{1}{18}\) = \(\frac{13}{18}\)

Question 15. When Bill bought a marigold plant, it was \(\frac{1}{4}\) inch tall. After the first week, it measured 1 \(\frac{1}{12}\) inches tall. After the second week, it was 1 \(\frac{11}{12}\) inches. After week 3, it was 2 \(\frac{3}{4}\) inches tall. Assuming the growth of the plant was constant, what was the height of the plant at the end of week 4? ______ \(\frac{□}{□}\) inches

Answer: 3 \(\frac{7}{12}\) inches

The sequence is the increasing where the first term is \(\frac{1}{4}\) LCD = 12 First week is \(\frac{3}{12}\) Second week = \(\frac{13}{12}\) = 1 \(\frac{1}{12}\) Third week = 1 \(\frac{11}{12}\) = \(\frac{23}{12}\) Fourth week = \(\frac{33}{12}\) = 2 \(\frac{3}{4}\) At the end of fourth week = \(\frac{43}{12}\) = 3 \(\frac{7}{12}\) inches The height of the plant at the end of the week is 3 \(\frac{7}{12}\) inches.

Question 16. What if Bill’s plant grew at the same rate but was 1 \(\frac{1}{2}\) inches when he bought it? How tall would the plant be after 3 weeks? ______ inches

Answer: 4 inches

Explanation: The sequence is increasing. First week 1 \(\frac{1}{2}\) Let the first term is \(\frac{6}{12}\) Second term is 1 \(\frac{16}{12}\) Third term is 1 \(\frac{26}{12}\) Fourth week is 1 \(\frac{36}{12}\) 1 \(\frac{36}{12}\) = 1 \(\frac{3}{1}\) = 1 + 3 = 4 After 4 weeks the plant grew 4 inches.

Question 17. Vicki wanted to start jogging. The first time she ran, she ran \(\frac{3}{16}\) mile. The second time, she ran \(\frac{3}{8}\) mile, and the third time, she ran \(\frac{9}{16}\) mile. If she continued this pattern, when was the first time she ran more than 1 mile? Explain. Type below: _________

Answer: Sixth time

Explanation: Vicki wanted to start jogging. The first time she ran, she ran \(\frac{3}{16}\) mile. The second time, she ran \(\frac{3}{8}\) mile, and the third time, she ran \(\frac{9}{16}\) mile. The difference is \(\frac{3}{16}\) First time = \(\frac{3}{16}\) mile Second time = \(\frac{3}{16}\) + \(\frac{3}{16}\) = \(\frac{3}{8}\) mile Third time = \(\frac{3}{8}\) + \(\frac{3}{16}\) = \(\frac{9}{16}\) mile Fourth time = \(\frac{9}{16}\) + \(\frac{3}{16}\) = \(\frac{12}{16}\) mile Fifth time = \(\frac{12}{16}\) + \(\frac{3}{16}\) = \(\frac{15}{16}\) mile Sixth time = \(\frac{15}{16}\) + \(\frac{3}{16}\) = \(\frac{18}{16}\) mile \(\frac{18}{16}\) = 1 \(\frac{2}{16}\) = 1 \(\frac{1}{8}\)

Question 18. Mr. Conners drove 78 \(\frac{1}{3}\) miles on Monday, 77 \(\frac{1}{12}\) miles on Tuesday, and 75 \(\frac{5}{6}\) miles on Wednesday. If he continues this pattern on Thursday and Friday, how many miles will he drive on Friday? ______ \(\frac{□}{□}\) miles

Answer: Given that, Mr. Conners drove 78 \(\frac{1}{3}\) miles on Monday, 77 \(\frac{1}{12}\) miles on Tuesday, and 75 \(\frac{5}{6}\) miles on Wednesday. The sequence is the decreasing where the first term is 78 \(\frac{4}{12}\) 78 \(\frac{4}{12}\) – 77 \(\frac{1}{12}\) = 1 \(\frac{3}{12}\) The difference between the term is 1 \(\frac{3}{12}\) On thursday, 75 \(\frac{5}{6}\) – 1 \(\frac{3}{12}\) = 74 \(\frac{7}{12}\) On friday, 74 \(\frac{7}{12}\) – 1 \(\frac{3}{12}\) = 73 \(\frac{4}{12}\) = 73 \(\frac{1}{3}\)

Question 19. Test Prep Zack watered his garden with 1 \(\frac{3}{8}\) gallons of water the first week he planted it. He watered it with 1 \(\frac{3}{4}\) gallons the second week, and 2 \(\frac{1}{8}\) gallons the third week. If he continued watering in this pattern, how much water did he use on the fifth week? Options: a. 2 \(\frac{1}{2}\) gallons b. 2 \(\frac{7}{8}\) gallons c. 3 \(\frac{1}{4}\) gallons d. 6 \(\frac{7}{8}\) gallons

Answer: 2 \(\frac{7}{8}\) gallons

Explanation: First term = 1 \(\frac{3}{8}\) The difference is \(\frac{3}{4}\) – \(\frac{3}{8}\) = \(\frac{3}{8}\) Second term is 1 \(\frac{3}{8}\) + \(\frac{3}{8}\) = 1 \(\frac{3}{4}\) Third term = 1 \(\frac{3}{4}\) + \(\frac{3}{8}\) = 1 + 1 \(\frac{1}{8}\) = 2 \(\frac{1}{8}\) Fourth term = 2 \(\frac{1}{8}\) + \(\frac{3}{8}\) = 2 \(\frac{1}{2}\) Fifth term = 2 \(\frac{1}{2}\) + \(\frac{3}{8}\) = 2 \(\frac{7}{8}\) gallons Thus the correct answer is option B.

Question 1. Caitlin has 4 \(\frac{3}{4}\) pounds of clay. She uses 1 \(\frac{1}{10}\) pounds to make a cup, and another 2 pounds to make a jar. How many pounds are left? First, write an equation to model the problem. Type below: _________

Answer: 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2

Explanation: Subtract the total pound of clay from used clay. So, the equation of the clay leftover is 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2

Question 1. Next, work backwards and rewrite the equation to find x. Type below: _________

Answer: 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2 = x

Explanation: Let the leftover clay be x 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2 = x x = 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2

Question 1. Solve. _____________________ So, ________ pounds of clay remain. Type below: _________

Answer: 1 \(\frac{13}{20}\) pounds

Explanation: 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2 4 + \(\frac{3}{4}\) – 1 – \(\frac{1}{10}\) – 2 4 – 3 = 1 \(\frac{3}{4}\) – \(\frac{1}{10}\) = \(\frac{13}{20}\) 1 + \(\frac{13}{20}\) = 1 \(\frac{13}{20}\) pounds

Question 2. What if Caitlin had used more than 2 pounds of clay to make a jar? Would the amount remaining have been more or less than your answer to Exercise 1? Type below: _________

Answer: Let us assume that Catlin used 2 \(\frac{1}{4}\) pounds of clay to make a jar and 1 \(\frac{1}{10}\) pounds to make a cup. 4 \(\frac{3}{4}\) – 1 \(\frac{1}{10}\) – 2 \(\frac{1}{4}\) = 2 \(\frac{1}{20}\)

Question 3. A pet store donated 50 pounds of food for adult dogs, puppies, and cats to an animal shelter. 19 \(\frac{3}{4}\) pounds was adult dog food and 18 \(\frac{7}{8}\) pounds was puppy food. How many pounds of cat food did the pet store donate? ______ \(\frac{□}{□}\) pounds of cat food

Answer: 11 \(\frac{3}{8}\) pounds of cat food

Explanation: A pet store donated 50 pounds of food for adult dogs, puppies, and cats to an animal shelter. 19 \(\frac{3}{4}\) pounds was adult dog food and 18 \(\frac{7}{8}\) pounds was puppy food. 19 \(\frac{3}{4}\) + 18 \(\frac{7}{8}\) = 38 \(\frac{5}{8}\) 50 – 38 \(\frac{5}{8}\) = 11 \(\frac{3}{8}\) pounds of cat food Thus the pet store donate 11 \(\frac{3}{8}\) pounds of cat food

Question 4. Thelma spent \(\frac{1}{6}\) of her weekly allowance on dog toys, \(\frac{1}{4}\) on a dog collar, and \(\frac{1}{3}\) on dog food. What fraction of her weekly allowance is left? \(\frac{□}{□}\) of her weekly allowance

Explanation: Given that, Thelma spent \(\frac{1}{6}\) of her weekly allowance on dog toys, \(\frac{1}{4}\) on a dog collar, and \(\frac{1}{3}\) on dog food. \(\frac{1}{6}\) + \(\frac{1}{4}\) + \(\frac{1}{3}\)  = \(\frac{3}{4}\) 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\) \(\frac{1}{4}\) of her weekly allowance.

Question 5. Martin is making a model of a Native American canoe. He has 5 \(\frac{1}{2}\) feet of wood. He uses 2 \(\frac{3}{4}\) feet for the hull and 1 \(\frac{1}{4}\) feet for the paddles and struts. How much wood does he have left? ______ \(\frac{□}{□}\) feet

Answer: 1 \(\frac{1}{2}\) feet

Explanation: Martin is making a model of a Native American canoe. He has 5 \(\frac{1}{2}\) feet of wood. He uses 2 \(\frac{3}{4}\) feet for the hull and 1 \(\frac{1}{4}\) feet for the paddles and struts. 2 \(\frac{3}{4}\) + 1 \(\frac{1}{4}\) 2 + \(\frac{3}{4}\) + 1 + \(\frac{1}{4}\) 2 + 1 = 3 \(\frac{3}{4}\) + \(\frac{1}{4}\) = 1 3 + 1 = 4 5 \(\frac{1}{2}\) – 4 = 1 \(\frac{1}{2}\)

Question 6. What if Martin makes a hull and two sets of paddles and struts? How much wood does he have left?

Answer: 1 \(\frac{1}{4}\)

Explanation: He has 5 \(\frac{1}{2}\) feet of wood. If Martin makes a hull and two sets of paddles and struts 1 \(\frac{1}{4}\) + 1 \(\frac{1}{4}\) = 2 \(\frac{1}{2}\) 2 \(\frac{1}{2}\) + 2 \(\frac{3}{4}\) = 4 \(\frac{1}{4}\) 5 \(\frac{1}{2}\) – 4 \(\frac{1}{4}\) 5 + \(\frac{1}{2}\) – 4 – \(\frac{1}{4}\) 1 + \(\frac{1}{4}\) = 1 \(\frac{1}{4}\)

Question 7. Beth’s summer vacation lasted 87 days. At the beginning of her vacation, she spent 3 weeks at soccer camp, 5 days at her grandmother’s house, and 13 days visiting Glacier National Park with her parents. How many vacation days remained? ______ days

Answer: 48 days

Explanation: Given, Beth’s summer vacation lasted 87 days. At the beginning of her vacation, she spent 3 weeks at soccer camp, 5 days at her grandmother’s house, and 13 days visiting Glacier National Park with her parents. 87 – 21 – 5 – 13 = 48 days The remaining vacation days are 48.

Question 8. You can buy 2 DVDs for the same price you would pay for 3 CDs selling for $13.20 apiece. Explain how you could find the price of 1 DVD. $ ______

Answer: $19.8

Explanation: To find what is the price of 1 DVD we will find what is the price of 3 DVDs and then because 2 DVDs price is the same than 3 CDs we can easily find the price of 1 DVD. $13.20 × 3 = $39.6 We will divide $39.6 by 2. $39.6 ÷ 2 = $19.8 The price of 1 DVD is $19.8

Question 9. Test Prep During the 9 hours between 8 A.M. and 5 P.M., Bret spent 5 \(\frac{3}{4}\) hours in class and 1 \(\frac{1}{2}\) hours at band practice. How much time did he spend on other activities? Options: a. \(\frac{3}{4}\) hour b. 1 \(\frac{1}{4}\) hour c. 1 \(\frac{1}{2}\) hour d. 1 \(\frac{3}{4}\) hour

Answer: 1 \(\frac{3}{4}\) hour

Explanation: Test Prep During the 9 hours between 8 A.M. and 5 P.M., Bret spent 5 \(\frac{3}{4}\) hours in class and 1 \(\frac{1}{2}\) hours at band practice. 5 \(\frac{3}{4}\) + 1 \(\frac{1}{2}\) = 7 \(\frac{1}{4}\) hour 9 – 7 \(\frac{1}{4}\) hour 8 + 1 – 7 – \(\frac{1}{4}\) 1 \(\frac{3}{4}\) hour The correct answer is option D.

Use the properties and mental math to solve. Write your answer in simplest form.

Question 1. \(\left(2 \frac{5}{8}+\frac{5}{6}\right)+1 \frac{1}{8}\) ______ \(\frac{□}{□}\)

Answer: \(\left(2 \frac{5}{8}+\frac{5}{6}\right)+1 \frac{1}{8}\) 2 \(\frac{5}{8}\) + \(\frac{5}{6}\) 2 + \(\frac{5}{8}\) + \(\frac{5}{6}\) LCD = 24 \(\frac{15}{24}\) + \(\frac{20}{24}\) = \(\frac{35}{24}\) \(\frac{35}{24}\) = 1 \(\frac{11}{24}\) 2 + 1 \(\frac{11}{24}\) = 3 \(\frac{11}{24}\) 3 \(\frac{11}{24}\) + 1 \(\frac{1}{8}\) = 4 \(\frac{7}{12}\)

Question 2. \(\frac{5}{12}+\left(\frac{5}{12}+\frac{3}{4}\right)\) ______ \(\frac{□}{□}\)

Answer: \(\frac{5}{12}+\left(\frac{5}{12}+\frac{3}{4}\right)\) \(\frac{5}{12}\) + \(\frac{3}{4}\) LCD = 12 \(\frac{5}{12}\) + \(\frac{3}{4}\) × \(\frac{3}{3}\) \(\frac{5}{12}\) + \(\frac{9}{12}\) = \(\frac{14}{12}\) \(\frac{5}{12}\) + \(\frac{14}{12}\) = \(\frac{19}{12}\) \(\frac{19}{12}\) = 1 \(\frac{7}{12}\)

Question 3. \(\left(3 \frac{1}{4}+2 \frac{5}{6}\right)+1 \frac{3}{4}\) ______ \(\frac{□}{□}\)

\(\left(3 \frac{1}{4}+2 \frac{5}{6}\right)\) 2 + \(\frac{5}{6}\) + 3 + \(\frac{1}{4}\) 2 + 3 = 5 \(\frac{5}{6}\) + \(\frac{1}{4}\) LCD = 12 \(\frac{5}{6}\) × \(\frac{2}{2}\) + \(\frac{1}{4}\) × \(\frac{3}{3}\) \(\frac{10}{12}\) + \(\frac{3}{12}\) = \(\frac{13}{12}\) = 1 \(\frac{1}{12}\) 5 + 1 \(\frac{1}{12}\) = 6 \(\frac{1}{12}\) 6 \(\frac{1}{12}\) + 1 \(\frac{3}{4}\) 6 + \(\frac{1}{12}\) + 1 + \(\frac{3}{4}\) 6 + 1 = 7 \(\frac{1}{12}\) + \(\frac{3}{4}\) \(\frac{1}{12}\) + \(\frac{9}{12}\) = \(\frac{10}{12}\) = \(\frac{5}{6}\) 7 + \(\frac{5}{6}\) = 7 \(\frac{5}{6}\)

Question 4. \(\left(\frac{2}{7}+\frac{1}{3}\right)+\frac{2}{3}\) ______ \(\frac{□}{□}\)

Answer: \(\left(\frac{2}{7}+\frac{1}{3}\right)+\frac{2}{3}\) \(\left(\frac{2}{7}+\frac{1}{3}\right)\) LCD = 21 \(\left(\frac{6}{21}+\frac{7}{21}\right)\) = \(\frac{13}{21}\) \(\frac{13}{21}\) + \(\frac{2}{3}\) LCD = 21 \(\frac{13}{21}\) + \(\frac{14}{21}\) \(\frac{27}{21}\) = \(\frac{9}{7}\) = 1 \(\frac{2}{7}\)

Question 5. \(\left(\frac{1}{5}+\frac{1}{2}\right)+\frac{2}{5}\) ______ \(\frac{□}{□}\)

Answer: \(\left(\frac{1}{5}+\frac{1}{2}\right)\) \(\frac{1}{5}\) + \(\frac{1}{2}\) LCD = 10 \(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\) \(\frac{7}{10}\) + \(\frac{2}{5}\) \(\frac{7}{10}\) + \(\frac{4}{10}\) = \(\frac{11}{10}\) \(\frac{11}{10}\) = 1 \(\frac{1}{10}\)

Question 6. \(\left(\frac{1}{6}+\frac{3}{7}\right)+\frac{2}{7}\) \(\frac{□}{□}\)

Answer: \(\left(\frac{1}{6}+\frac{3}{7}\right)\) LCD = 42 \(\left(\frac{7}{42}+\frac{18}{42}\right)\) = \(\frac{25}{42}\) \(\frac{25}{42}\) + \(\frac{2}{7}\) LCD = 42 \(\frac{25}{42}\) + \(\frac{12}{42}\) = \(\frac{37}{42}\) \(\left(\frac{1}{6}+\frac{3}{7}\right)+\frac{2}{7}\) = \(\frac{37}{42}\)

Question 7. \(\left(2 \frac{5}{12}+4 \frac{1}{4}\right)+\frac{1}{4}\) ______ \(\frac{□}{□}\)

Answer: \(\left(2 \frac{5}{12}+4 \frac{1}{4}\right)\) 2 \(\frac{5}{12}\) + 4 \(\frac{1}{4}\) 2 + \(\frac{5}{12}\) + 4 + \(\frac{1}{4}\) 2 + 4 = 6 \(\frac{5}{12}\) + \(\frac{1}{4}\) = \(\frac{8}{12}\) 6 \(\frac{8}{12}\) = 6 \(\frac{2}{3}\) 6 \(\frac{2}{3}\) + \(\frac{1}{4}\) = 6 \(\frac{11}{12}\)

Question 8. \(1 \frac{1}{8}+\left(5 \frac{1}{2}+2 \frac{3}{8}\right)\) ______

Answer: 5 \(\frac{1}{2}\) + 2 \(\frac{3}{8}\) 5 + 2 = 7 \(\frac{1}{2}\) + \(\frac{3}{8}\) LCD = 8 \(\frac{4}{8}\) + \(\frac{3}{8}\) = \(\frac{7}{8}\) = 7 \(\frac{7}{8}\) 1 \(\frac{1}{8}\) + 7 \(\frac{7}{8}\) = 9

Question 9. \(\frac{5}{9}+\left(\frac{1}{9}+\frac{4}{5}\right)\) ______ \(\frac{□}{□}\)

Answer: \(\frac{1}{9}\) + \(\frac{4}{5}\) LCD = 45 \(\frac{5}{45}\) + \(\frac{36}{45}\) = \(\frac{41}{45}\) \(\frac{41}{45}\) + \(\frac{5}{9}\) LCD = 45 \(\frac{41}{45}\) + \(\frac{25}{45}\) = \(\frac{66}{45}\) \(\frac{66}{45}\) = 1 \(\frac{7}{15}\)

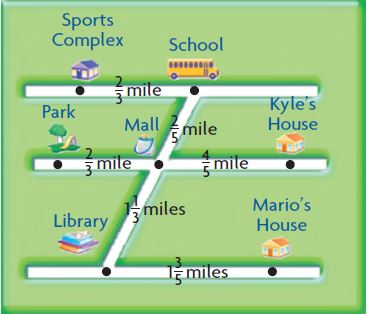
Question 10. In the morning, Julie rides her bike from the sports complex to the school. In the afternoon, she rides from the school to the mall, and then to Kyle’s house. How far does Julie ride her bike? ______ \(\frac{□}{□}\) miles

Answer: 1 \(\frac{13}{15}\) miles

Explanation: Julie rides her bike from the sports complex to the school = \(\frac{2}{3}\) mile In the afternoon, she rides from the school to the mall, and then to Kyle’s house. = \(\frac{2}{5}\) + \(\frac{4}{5}\) = \(\frac{6}{5}\) = 1 \(\frac{1}{5}\) 1 \(\frac{1}{5}\) + \(\frac{2}{3}\) mile = 1 \(\frac{13}{15}\) miles

Question 11. On one afternoon, Mario walks from his house to the library. That evening, Mario walks from the library to the mall, and then to Kyle’s house. Describe how you can use the properties to find how far Mario walks. ______ \(\frac{□}{□}\) miles

Answer: Mario walks from his house to the library = 1 \(\frac{3}{5}\) miles Mario walks from the library to the mall, and then to Kyle’s house = 1 \(\frac{1}{3}\) and \(\frac{4}{5}\) 1 \(\frac{3}{5}\) + (1 \(\frac{1}{3}\) + \(\frac{4}{5}\)) 1 \(\frac{3}{5}\) + 2 \(\frac{2}{15}\) = 3 \(\frac{11}{15}\) miles

Question 12. Pose a Problem Write and solve a new problem that uses the distances between four locations. Type below: _________

Answer: In the evening Kyle rides his bike from the sports complex to school. Then he rides from School to the mall and then to his house. How far does Kyle ride his bike? The distance from Sports complex to School is \(\frac{2}{3}\) mile The distance from School to the mall is \(\frac{2}{5}\) The distance from the mall to Kyle house is \(\frac{4}{5}\) \(\frac{2}{3}\) + (\(\frac{2}{5}\) + \(\frac{4}{5}\)) \(\frac{2}{3}\) + \(\frac{6}{5}\) = 1 \(\frac{13}{15}\) miles

Question 13. Test Prep Which property or properties does the problem below use? \(\frac{1}{9}+\left(\frac{4}{9}+\frac{1}{6}\right)=\left(\frac{1}{9}+\frac{4}{9}\right)+\frac{1}{6}\) Options: a. Commutative Property b. Associative Property c. Commutative Property and Associative Property d. Distributive Property

Answer: Associative Property The associative property states that you can add or multiply regardless of how the numbers are grouped. By ‘grouped’ we mean ‘how you use parenthesis’. In other words, if you are adding or multiplying it does not matter where you put the parenthesis.

Question 1. A _________ is a number that is a common multiple of two or more denominators. _________

Answer: Common Denominator

Question 2. \(\frac{2}{5}, \frac{1}{8}\) common denominator: ______ Explain: _________

Answer: 40 Multiply the denominators of the fractions 5 × 8 = 40

Question 3. \(\frac{3}{4}, \frac{1}{2}\) common denominator: ______ Explain: _________

Answer: 8 Multiply the denominators of the fractions 4 × 2 = 8

Question 4. \(\frac{2}{3}, \frac{1}{6}\) common denominator: ______ Explain: _________

Answer: 18 Multiply the denominators of the fractions 3 × 6 = 18

Find the sum or difference. Write your answer in simplest form

Question 5. \(\frac{5}{6}+\frac{7}{8}\) ______ \(\frac{□}{□}\)

Answer: 1 \(\frac{17}{24}\)

Explanation: \(\frac{5}{6}+\frac{7}{8}\) = \(\frac{20}{24}\) + \(\frac{21}{24}\) = \(\frac{41}{24}\) = 1 \(\frac{17}{24}\)

Question 6. \(2 \frac{2}{3}-1 \frac{2}{5}\) ______ \(\frac{□}{□}\)

Answer: 1 \(\frac{4}{15}\)

Question 7. \(7 \frac{3}{4}+3 \frac{7}{20}\) ______ \(\frac{□}{□}\)

Answer: 11 \(\frac{1}{10 }\)

Question 8. \(1 \frac{2}{5}-\frac{2}{3}\) Type below: ________

Answer: Estimate: \(\frac{1}{2}\) Difference: Rewriting our equation with parts separated 1 + \(\frac{2}{5}\) – \(\frac{2}{3}\) \(\frac{7}{5}\) – \(\frac{2}{3}\) \(\frac{7}{5}\) × \(\frac{3}{3}\) – \(\frac{2}{3}\) × \(\frac{5}{5}\) = \(\frac{21}{15}\) – \(\frac{10}{15}\) = \(\frac{11}{15}\)

Question 9. \(7-\frac{3}{7}\) Type below: ________

Answer: 6 \(\frac{4}{7}\)

Explanation: \(7-\frac{3}{7}\) = \(\frac{49}{7}\) – \(\frac{3}{7}\) \(\frac{46}{7}\) = 6 \(\frac{4}{7}\) \(7-\frac{3}{7}\) = 6 \(\frac{4}{7}\)

Question 10. \(5 \frac{1}{9}-3 \frac{5}{6}\) Type below: ________

Answer: 1 \(\frac{5}{18}\)

Explanation: \(5 \frac{1}{9}-3 \frac{5}{6}\) = 5 + \(\frac{1}{9}\) – 3 – \(\frac{5}{6}\) 5 – 3 = 2 \(\frac{1}{9}\) – \(\frac{5}{6}\) = \(\frac{2}{18}\) – \(\frac{15}{18}\) = – \(\frac{13}{18}\) 2 – \(\frac{13}{18}\) = 1 \(\frac{5}{18}\)

Question 11. \(\left(\frac{3}{8}+\frac{2}{3}\right)+\frac{1}{3}\) ______ \(\frac{□}{□}\)

Explanation: \(\frac{3}{8}\) + \(\frac{2}{3}\) = \(\frac{9}{24}\) + \(\frac{16}{24}\) = \(\frac{25}{24}\) \(\frac{25}{24}\) + \(\frac{1}{3}\) = \(\frac{25}{24}\) + \(\frac{8}{24}\) = \(\frac{33}{24}\) = \(\frac{11}{8}\) The mixed fraction of \(\frac{11}{8}\) is 1 \(\frac{3}{8}\).

Question 12. \(1 \frac{4}{5}+\left(2 \frac{3}{20}+\frac{3}{5}\right)\) ______ \(\frac{□}{□}\)

Answer: 4 \(\frac{11}{20}\)

Explanation: Rewriting our equation with parts separated 2 \(\frac{3}{20}\) + \(\frac{3}{5}\) = \(\frac{43}{20}\) + \(\frac{3}{5}\) \(\frac{43}{20}\) + \(\frac{3}{5}\) = \(\frac{215}{100}\) + \(\frac{60}{100}\) = \(\frac{275}{100}\) = 2 \(\frac{3}{4}\) 2 \(\frac{3}{4}\) + 1 \(\frac{4}{5}\) = 2 + \(\frac{3}{4}\) + 1 + \(\frac{4}{5}\) 2 + 1 = 3 \(\frac{3}{4}\) + \(\frac{4}{5}\) = \(\frac{15}{20}\) + \(\frac{16}{20}\) = \(\frac{31}{20}\) \(\frac{31}{20}\) = 4 \(\frac{11}{20}\)

Question 13. \(3 \frac{5}{9}+\left(1 \frac{7}{9}+2 \frac{5}{12}\right)\) ______ \(\frac{□}{□}\)

Explanation: 1 \(\frac{7}{9}\) + 2 \(\frac{5}{12}\) 1 + 2 = 3 \(\frac{7}{9}\) + \(\frac{5}{12}\) LCD is 36 \(\frac{28}{36}\) + \(\frac{15}{36}\) = \(\frac{43}{36}\) \(\frac{43}{36}\) = 1 \(\frac{7}{36}\) 3 + 1 + \(\frac{7}{36}\) = 4 \(\frac{7}{36}\) 4 \(\frac{7}{36}\) + 3 \(\frac{5}{9}\) 4 + \(\frac{7}{36}\) + 3 + \(\frac{5}{9}\) 4 + 3 = 7 \(\frac{7}{36}\) + \(\frac{5}{9}\) = \(\frac{7}{36}\) + \(\frac{20}{36}\) = \(\frac{27}{36}\) = \(\frac{3}{4}\) 7 + \(\frac{3}{4}\) = 7 \(\frac{3}{4}\)

Question 14. Ursula mixed 3 \(\frac{1}{8}\) cups of dry ingredients with 1 \(\frac{2}{5}\) cups of liquid ingredients. Which answer represents the best estimate of the total amount of ingredients Ursula mixed? Options: a. about 4 cups b. about 4 \(\frac{1}{2}\) cups c. about 5 cups d. about 5 \(\frac{1}{2}\) cups

Answer: about 4 \(\frac{1}{2}\) cups

Explanation: Ursula mixed 3 \(\frac{1}{8}\) cups of dry ingredients with 1 \(\frac{2}{5}\) cups of liquid ingredients. 3 + 1 = 4 \(\frac{1}{8}\) is closer to 0. \(\frac{2}{5}\) is closer to \(\frac{1}{2}\) 4 + \(\frac{1}{2}\) = 4 \(\frac{1}{2}\) Thus the correct answer is option B.

Question 15. Samuel walks in the Labor Day parade. He walks 3 \(\frac{1}{4}\) miles along the parade route and 2 \(\frac{5}{6}\) miles home. How many miles does Samuel walk? Options: a. \(\frac{5}{10}\) mile b. 5 \(\frac{1}{12}\) miles c. 5 \(\frac{11}{12}\) miles d. 6 \(\frac{1}{12}\) miles

Answer: 6 \(\frac{1}{12}\) miles

Explanation: Samuel walks in the Labor Day parade. He walks 3 \(\frac{1}{4}\) miles along the parade route and 2 \(\frac{5}{6}\) miles home. 3 + \(\frac{1}{4}\) + 2 + \(\frac{5}{6}\) 3 + 2 =5 \(\frac{5}{6}\) + \(\frac{1}{4}\) = \(\frac{10}{12}\) + \(\frac{3}{12}\) = \(\frac{13}{12}\) \(\frac{13}{12}\) = 6 \(\frac{1}{12}\) miles Thus the correct answer is option D.

Question 16. A gardener has a container with 6 \(\frac{1}{5}\) ounces of liquid plant fertilizer. On Sunday, the gardener uses 2 \(\frac{1}{2}\) ounces on a flower garden. How many ounces of liquid plant fertilizer are left? Options: a. 3 \(\frac{7}{10}\) ounces b. 5 \(\frac{7}{10}\) ounces c. 6 \(\frac{7}{10}\) ounces d. 9 \(\frac{7}{10}\) ounces

Answer: 9 \(\frac{7}{10}\) ounces

Explanation: A gardener has a container with 6 \(\frac{1}{5}\) ounces of liquid plant fertilizer. On Sunday, the gardener uses 2 \(\frac{1}{2}\) ounces on a flower garden. 6 + \(\frac{1}{5}\) + 2 + \(\frac{1}{2}\) 6 + 2 = 8 \(\frac{1}{5}\) + \(\frac{1}{2}\) LCD = 10 \(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\) 8 \(\frac{7}{10}\)

Question 17. Aaron is practicing for a triathlon. On Sunday, he bikes 12 \(\frac{5}{8}\) miles and swims 5 \(\frac{2}{3}\) miles. On Monday, he runs 6 \(\frac{3}{8}\) miles. How many total miles does Aaron cover on the two days? Options: a. 23 \(\frac{1}{6}\) miles b. 24 \(\frac{7}{12}\) miles c. 24 \(\frac{2}{3}\) miles d. 25 \(\frac{7}{12}\) miles

Answer: 24 \(\frac{2}{3}\) miles

Explanation: Aaron is practicing for a triathlon. On Sunday, he bikes 12 \(\frac{5}{8}\) miles and swims 5 \(\frac{2}{3}\) miles. On Monday, he runs 6 \(\frac{3}{8}\) miles. 5 \(\frac{2}{3}\) + 6 \(\frac{3}{8}\) = 12 \(\frac{1}{24}\) 12 \(\frac{1}{24}\) + 12 \(\frac{5}{8}\) miles 12 + \(\frac{1}{24}\) + 12 + \(\frac{5}{8}\) 12 + 12 = 24 \(\frac{1}{24}\) + \(\frac{5}{8}\) = \(\frac{1}{24}\) + \(\frac{15}{24}\) = \(\frac{16}{24}\) = \(\frac{2}{3}\) 24 + \(\frac{2}{3}\) = 24 \(\frac{2}{3}\) mile The correct answer is option D.

Fill in the bubble completely to show your answer.

Answer: 1 \(\frac{5}{8}\)

Explanation: The fraction for the above figure is 1 \(\frac{7}{8}\) The fraction for the second figure is \(\frac{1}{4}\) 1 + \(\frac{7}{8}\) – \(\frac{1}{4}\) \(\frac{7}{8}\) – \(\frac{1}{4}\) = \(\frac{7}{8}\) – \(\frac{2}{8}\) \(\frac{7}{8}\) – \(\frac{2}{8}\) = \(\frac{5}{8}\) 1 + \(\frac{5}{8}\) = 1 \(\frac{5}{8}\) The correct answer is option C.

Question 19. Cody is designing a pattern for a wood floor. The length of the pieces of wood are 1 \(\frac{1}{2}\) inches, 1 \(\frac{13}{16}\) inches, and 2 \(\frac{1}{8}\) inches. What is the length of the 5th piece of wood if the pattern continues? Options: a. 2 \(\frac{7}{6}\) inches b. 2 \(\frac{3}{4}\) inches c. 3 \(\frac{1}{2}\) inches d. 4 inches

Answer: 2 \(\frac{3}{4}\) inches

Explanation: The length of the pieces of wood are 1 \(\frac{1}{2}\) inches, 1 \(\frac{13}{16}\) inches, and 2 \(\frac{1}{8}\) inches 1 \(\frac{1}{2}\) = \(\frac{3}{2}\) 1 \(\frac{13}{16}\) inches = \(\frac{29}{16}\) \(\frac{29}{16}\) – \(\frac{3}{2}\) = latex]\frac{5}{16}[/latex] 5th piece = \(\frac{3}{2}\) + latex]\frac{5}{16}[/latex] (5 – 1) = \(\frac{3}{2}\) + latex]\frac{5}{16}[/latex] 4 = \(\frac{3}{2}\) + latex]\frac{20}{16}[/latex] = \(\frac{3}{2}\) × latex]\frac{8}{8}[/latex] + latex]\frac{20}{16}[/latex] = latex]\frac{44}{16}[/latex] = 2 latex]\frac{3}{4}[/latex] Thus the correct answer is option B.

Question 20. Julie spends \(\frac{3}{4}\) hour studying on Monday and \(\frac{1}{6}\) hour studying on Tuesday. How many hours does Julie study on those two days? Options: a. \(\frac{1}{3}\) hour b. \(\frac{2}{5}\) hour c. \(\frac{5}{6}\) hour d. \(\frac{11}{12}\) hour

Answer: \(\frac{11}{12}\) hour

Explanation: Julie spends \(\frac{3}{4}\) hour studying on Monday and \(\frac{1}{6}\) hour studying on Tuesday. \(\frac{3}{4}\) + \(\frac{1}{6}\) LCD = 12 \(\frac{9}{12}\) + \(\frac{2}{12}\) = \(\frac{11}{12}\) hour So, the correct answer is option D.

Constructed Response

Question 21. A class uses 8 \(\frac{5}{6}\) sheets of white paper and 3 \(\frac{1}{12}\) sheets of red paper for a project. How much more white paper is used than red paper? Show your work using words, pictures, or numbers. Explain how you know your answer is reasonable. ______ \(\frac{□}{□}\) sheet of white paper

Answer: 5 \(\frac{3}{4}\) sheet of white paper

Explanation: A class uses 8 \(\frac{5}{6}\) sheets of white paper and 3 \(\frac{1}{12}\) sheets of red paper for a project. 8 \(\frac{5}{6}\) – 3 \(\frac{1}{12}\) 8 + \(\frac{5}{6}\) – 3 – \(\frac{1}{12}\) 8 – 3 = 5 \(\frac{5}{6}\) – \(\frac{1}{12}\) \(\frac{10}{12}\) – \(\frac{1}{12}\) = \(\frac{9}{12}\) \(\frac{9}{12}\) = \(\frac{3}{4}\) 5 + \(\frac{3}{4}\) = 5 \(\frac{3}{4}\)

Performance Task

Answer: He may use \(\frac{1}{4}\) gallon lime juice for one batch of the lemon-lime punch.

Question 22. B). If Marcos needs to make two batches of the recipe, how much of each ingredient will he need? How many gallons of punch will he have? Show your math solution and explain your thinking when you solve both questions. Type below: ________

Answer: \(\frac{2}{3}\) gallon lime juice

Question 22. C). Marcos had 1 \(\frac{1}{3}\) gallons of punch left over. He poured all of it into several containers for family members to take home. Use fractional parts of a gallon to suggest a way he could have shared the punch in three different-sized containers. Type below: ________

Answering the concepts in Go Math Grade 5 Chapter 6 Solution Key helps students to attempt the exam with confidence and prepare accordingly. Once you get to know the concept better you can solve any kind of question framed on Addition and Subtraction of Fractions with Unlike Denominators. Check your knowledge by taking an Assessment Test on Chapter 6 available.

Leave a Comment Cancel Reply

You must be logged in to post a comment.

• Texas Go Math
• Big Ideas Math
• enVision Math
• EngageNY Math
• McGraw Hill My Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Go Math Grade 6 Answer Key Chapter 7 Exponents

In order to excel in exams, we suggest the students check out the solutions in the Go Math Grade 6 Answer Key Chapter 7 Exponents. The solutions of Go Math Answer Key for Chapter 7 Exponents are available in simple PDF which can be downloaded by the students. The Answer of Go Math Grade 6 Chapter 7 can be used as a model of reference by the students to enhance the math skills.

In grade 6, students studied whole-number exponents. In this unit, they extend the definition of exponents to include all integers, and in the process codify the properties of exponents. This chapter includes concepts such as Exponents, Algebraic expressions, combine like terms, identify equivalent expressions, etc.

Click on the links in topic wise to get the question and answers for the exercise problems. Students can get solutions for homework problems, mid-chapter problems also. Hence make use of the links given below and learn the simple techniques to solve the problems in exponents.

Lesson 1: Exponents

Share and Show – Page No. 359

Bacterial growth – page no. 360, exponents – page no. 361, lesson check – page no. 362.

Lesson 2: Evaluate Expressions Involving Exponents

Share and Show – Page No. 365

Problem solving + applications – page no. 366, evaluate expressions involving exponents – page no. 367, lesson check – page no. 368.

Lesson 3: Write Algebraic Expressions

Share and Show – Page No. 371

Unlock the problem – page no. 372, write algebraic expressions – page no. 373, lesson check – page no. 374.

Lesson 4: Identify Parts of Expressions

Share and Show – Page No. 377

Problem solving + applications – page no. 378, identify parts of expressions – page no. 379, lesson check – page no. 380.

Lesson 5: Evaluate Algebraic Expressions and Formulas

Share and Show – Page No. 383

Problem solving + applications – page no. 384, evaluate algebraic expressions and formulas – page no. 385, lesson check – page no. 386.

Mid-Chapter Checkpoint

• Mid-Chapter Checkpoint Vocabulary – Page No. 387
• Mid-Chapter Checkpoint Page No. 388

Lesson 6: Use Algebraic Expressions

Share and Show – Page No. 391

Problem solving + applications – page no. 392, use algebraic expressions – page no. 393, lesson check – page no. 394.

Lesson 7: Problem Solving • Combine Like Terms

Share and Show – Page No. 397

On your own – page no. 398, problem solving combine like terms – page no. 399, lesson check – page no. 400, share and show – page no. 403, problem solving + applications – page no. 404.

Lesson 8: Generate Equivalent Expressions

Generate Equivalent Expressions – Page No. 405

Lesson check – page no. 406, share and show – page no. 409, problem solving + applications – page no. 410.

Lesson 9: Identify Equivalent Expressions

Identify Equivalent Expressions – Page No. 411

Lesson check – page no. 412.

Chapter 7 Review/Test

Chapter 7 Review/Test – Page No. 413

Chapter 7 review/test – page no. 414, chapter 7 review/test – page no. 415, chapter 7 review/test – page no. 416, chapter 7 review/test – page no. 417, chapter 7 review/test – page no. 418.

Question 1. Write 2 4 by using repeated multiplication. Then find the value of 2 4 . ___________

Explanation: The repeated factor is 2 The number 2 is repeated 4 times. The repeated multiplication of 2 4 is 2 × 2 × 2 × 2 = 16 Thus the value of 2 4 is 16.

Use one or more exponents to write the expression.

Question 2. 7 × 7 × 7 × 7 Type below: _____________

Answer: 7 4

Explanation: The repeated factor is 7. 7 is repeated four times. The exponent of the repeated multiplication 7 × 7 × 7 × 7 is 7 4

Question 3. 5 × 5 × 5 × 5 × 5 Type below: _____________

Answer: 5 5

Explanation: The repeated factor is 5. The number 5 is repeated five times. The exponent of the repeated multiplication 5 × 5 × 5 × 5 × 5 is 5 5

Question 4. 3 × 3 × 4 × 4 Type below: _____________

Answer: 3 2 × 4 2

Explanation: The exponent of the repeated multiplication 3 × 3 is 3 2 The exponent of the repeated multiplication 4 × 4 is 4 2 Thus the exponent for 3 × 3 × 4 × 4 is 3 2 × 4 2

On Your Own

Find the value.

Question 5. 20 2 ______

Answer: 20 × 20 = 400

Explanation: The repeated factor is 20 Write the factor 2 times. 20 × 20 = 400 The value of 20 2 = 400

Question 6. 82 1 ______

Explanation: The repeated factor is 82 Write the factor 1 time. The value of 82 1 is 82

Question 7. 3 5

Answer: 3 × 3 × 3 × 3 × 3 = 243

Explanation: The repeated factor is 3 Write the factor 5 times. The value of 3 5 is 343

Lesson 7 Problem Set 7.1 Answer Key Question 8. Write 32 as a number with an exponent by using 2 as the base. Type below: _____________

Answer: 2 5

Explanation: The exponent of 32 by using the base 2 is 2 × 2 × 2 × 2 × 2  = 2 5

Complete the statement with the correct exponent.

Question 9. 5 ? = 125 ______

Answer: 5 3

Explanation: The exponential form of 125 is 5 × 5 × 5 = 5 3 5 ? = 125 5 ? = 5 3 When bases are equal powers should be equated. Thus the exponent is 3

Question 10. 16 ? = 16 ______

Explanation: The exponential form of 16 is 16 1 16 ? = 16 1 When bases are equal powers should be equated. Thus the exponent is 1.

Question 11. 30 ? = 900 ______

Explanation: The exponential form of 900 is 30 × 30 = 30 2 30 ? = 30 2 When bases are equal powers should be equated. Thus the exponent is 2.

Identifying Parts in An Algebraic Expression Worksheet 7.1 Answer Key Question 12. Use Repeated Reasoning Find the values of 4 1 , 4 2 , 4 3 , 4 4 , and 4 5 . Look for a pattern in your results and use it to predict the ones digit in the value of 4 6 . Type below: _____________

Answer: The value of 4 1 is 4. The value of 4 2 is 4 × 4 = 16 The value of 4 3 is 4 × 4 × 4 = 64 The value of 4 4 is 4 × 4 × 4 × 4 = 256 The value of 4 5 is 4 × 4 × 4 × 4 × 4 = 1024 The value of 4 6 is 4 × 4 × 4 × 4 × 4 × 4 = 4096

Question 13. Select the expressions that are equivalent to 32. Mark all that apply. Options: a. 2 5 b. 8 4 c. 2 3 × 4 d. 2 × 4 × 4

Explanation: The exponent of 32 by using the base 2 is 2 × 2 × 2 × 2 × 2  = 2 5 32 = 2 5 Thus the correct answer is option A.

Bacteria are tiny, one-celled organisms that live almost everywhere on Earth. Although some bacteria cause disease, other bacteria are helpful to humans, other animals, and plants. For example, bacteria are needed to make yogurt and many types of cheese.

Under ideal conditions, a certain type of bacterium cell grows larger and then splits into 2 “daughter” cells. After 20 minutes, the daughter cells split, resulting in 4 cells. This splitting can happen again and again as long as conditions remain ideal.

Question 14. What power of 2 shows the number of cells after 3 hours? How many cells are there after 3 hours? Type below: _____________

Answer: 2 9

Explanation: So, each cell doubles every 20 mins. After 20 minutes, you have 1(2) = 2 cells. After 40 minutes, you have 2(2) = 4 cells, etc. 1 hour = 60 minutes 3 hours = 3 × 60 minutes = 180 minutes 180/20 = 9 divisions Thus 2 9 cells are there after 3 hours.

Question 15. How many minutes would it take to have a total of 4,096 cells? _______ minutes

Answer: 240 minutes

Explanation: First, convert the cells into the exponential form. The exponential form of 4096 is 2 × 2 × 2 × 2 × 2 × 2× 2 × 2× 2 × 2× 2 × 2 = 2 12 Multiply the power with 20 12 × 20 = 240 Thus it would take 240 minutes to have a total of 4,096 cells

Question 1. 6 × 6 Type below: _____________

Answer: The number 6 is used as a repeated factor. 6 is used as a factor 2 times. Now write the base and exponent for 6 × 6 = 6 2

Question 2. 11 × 11 × 11 × 11 Type below: _____________

Answer: The number 11 is used as a repeated factor. 11 is used as a factor 4 times. Now write the base and exponent for 11 × 11 × 11 × 11 = 11 4

Question 3. 9 × 9 × 9 × 9 × 7 × 7 Type below: _____________

Answer: The number 9 and 7 is used as a repeated factor. 9 is used as a factor 4 times and 7 is used 2 times. Now write the base and exponent for 9 × 9 × 9 × 9 × 7 × 7 = 9 4 × 7 2

Question 4. 6 4 _______

Answer: The repeated factor is 6. Write the factor 4 times. The value of 6 4 is 6 × 6 × 6 × 6 = 1296

Question 5. 1 6 _______

Answer: The repeated factor is 1. Write the factor 6 times. The value of 1 6 is 1 × 1 × 1 × 1 × 1 × 1 = 1

Question 6. 10 5 _______

Answer: The repeated factor is 10. Write the factor 5 times. The value of 10 5 is 10 × 10 × 10 × 10 × 10 = 1,00,000

Question 7. Write 144 with an exponent by using 12 as the base. Type below: _____________

Answer: 12 × 12 = 12 2 The exponential form of 144 is 12 × 12 = 12 2

Question 8. Write 343 with an exponent by using 7 as the base. Type below: _____________

Answer: The exponential form of 343 is 7 × 7 × 7 = 7 3

Question 9. Each day Sheila doubles the number of push-ups she did the day before. On the fifth day, she does 2 × 2 × 2 × 2 × 2 push-ups. Use an exponent to write the number of push-ups Shelia does on the fifth day. Type below: _____________

Answer: The number 2 is the repeated factor. 2 is repeated 5 times. The exponential form of 2 × 2 × 2 × 2 × 2 is 2 5

Lesson 7.1 Homework Answer Key Question 10. The city of Beijing has a population of more than 10 7 people. Write 10 7 without using an exponent. _______

Answer: The repeated factor is 10. Write the factor 7 times. The value of 10 7 is 10 × 10 × 10 × 10 × 10 × 10 × 10 = 10,000,000

Question 11. Explain what the expression 4 5 means and how to find its value. Type below: _____________

Answer: The repeated factor is 4. Write the factor 5 times. The value of 4 5 is 4 × 4 × 4 × 4 × 4 = 1024

Question 1. The number of games in the first round of a chess tournament is equal to 2 × 2 × 2 × 2 × 2 × 2. Write the number of games using an exponent. Type below: _____________

Answer: 2 6

Explanation:

The number 2 is the repeated factor. 2 is repeated 6 times. 2 × 2 × 2 × 2 × 2 × 2 = 2 6

Question 2. The number of gallons of water in a tank at an aquarium is equal to 8 3 . How many gallons of water are in the tank? _______ gallons

Answer: 512 gallons

Explanation: The repeated factor is 8. Write the factor 3 times. The value of 8 3 is 8 × 8 × 8 = 512 gallons Therefore there are 512 gallons of water in the tank.

Spiral Review

Answer: 5 : 15

Explanation: By using the above table we can find the ratio of strawberry juice to lemonade. 2 : 6 = 1 : 3 The ratio of strawberry juice to lemonade next to 4 : 12 is 5 : 15

Question 4. Which percent is equivalent to the fraction \(\frac{37}{50}\)? _______ %

Answer: 74%

Explanation: \(\frac{37}{50}\) × 100 0.74 × 100 = 74 Thus 74% is equivalent to the fraction \(\frac{37}{50}\)

Lesson 7.1 Answer Key 6th Grade Question 5. How many milliliters are equivalent to 2.7 liters? _______ milliliters

Answer: 2700 milliliters

Explanation: Convert from liters to milliliters. 1 liter = 1000 milliliters 2.7 liters = 2.7 × 1000 milliliters = 2700 milliliters 2.7 liters is equivalent to 2700 milliliters.

Question 6. Use the formula d = rt to find the distance traveled by a car driving at an average speed of 50 miles per hour for 4.5 hours. _______ miles

Answer: 225 miles

Explanation: Given, r = 50 miles/hour t = 4.5 hours Use the formula d = rt d = 50 × 4.5 = 225 miles Thus the distance traveled by a car driving at an average speed of 50 miles per hour for 4.5 hours is 225 miles.

Question 1. Evaluate the expression 9 + (5 2 − 10) _______

Explanation: First, write the square for 5 2 5 2 is 25 Now simplify the expression 9 + (25 – 10) 9 + 15 = 24 So, 9 + (5 2 − 10) = 24

Evaluate the expression.

Question 2. 6 + 3 3 ÷ 9 _______

Explanation: 6 + 3 3 ÷ 9 6 + (3 3 ÷ 9) Write the factor for 3 3 3 3 = 3 × 3 × 3 = 27 6 + (27 ÷ 9) 27 ÷ 9 = 3 6 + 3 = 9 Thus 6 + 3 3 ÷ 9 = 9

Question 3. (15 − 3) 2 ÷ 9 _______

Explanation: First subtract 15 – 3 = 12 (12) 2 ÷ 9 (12) 2 = 12 × 12 = 144 144 ÷ 9 9 divides 144 16 times. 144 ÷ 9 = 16 Thus (15 − 3) 2 ÷ 9 = 16

Question 4. (8 + 9 2 ) − 4 × 10 _______

Explanation: First multiply 9 × 9 = 81 (8 + 81) – (4 × 10) Multiply 4 and 10. 4 × 10 = 40 (8 + 81) – (40) 89 – 40 = 49 (8 + 9 2 ) − 4 × 10 = 49

Evaluate the expression

Question 5. 10 + 6 2 × 2 ÷ 9 _______

Explanation: 10 + (6 2 × 2) ÷ 9 Multiply 6 × 6 = 36 10 + (36 × 2) ÷ 9 Multiply 36 and 2 and then divide by 9. 10 + (72 ÷ 9) 10 + 8 = 18 So, 10 + 6 2 × 2 ÷ 9 = 18

Question 6. 6 2 − (2 3 + 5) _______

The value of 6 2 is 6 × 6 = 36 The value of 2 3 is 2 × 2 × 2 = 8 36 – (8 + 5) 36 – 13 = 23 Thus the answer for the expression for 6 2 − (2 3 + 5) is 23.

Question 7. 16 + 18 ÷ 9 + 3 4 _______

Explanation: 16 + (18 ÷ 9) + 3 4 First divide 18 by 9 16 + 2 + 3 4 18 + 3 4 The value of 3 4 is 3 × 3 × 3 × 3 = 81 18 + 81 = 99 Thus the answer for the expression 16 + (18 ÷ 9) + 3 4 is 99.

Place parentheses in the expression so that it equals the given value.

Question 8. 10 2 − 50 ÷ 5 value: 10 Type below: _____________

Explanation: 10 2 − 50 ÷ 5 The factor of 10 2 is 10 × 10 = 100 (10 2 − 50) ÷ 5 50 ÷ 5 = 10 10 2 − 50 ÷ 5 = 10 The value of 10 2 − 50 ÷ 5 = 10

Question 9. 20 + 2 × 5 + 4 1 value: 38 Type below: _____________

Explanation: 20 + 2 × 5 + 4 1 The value of 4 1 is 4. 20 + 2 × (5 + 4) 20 + 2 × 9 Now multiply 2 and 9. 20 + 18 = 38 The value of 20 + 2 × 5 + 4 1 = 38

Question 10. 28 ÷ 2 2 + 3 value: 4 Type below: _____________

Explanation: 28 ÷ 2 2 + 3 28 ÷ (2 2 + 3) The value of 2 2 is 4 28 ÷ (4 + 3) 28 ÷ 7 = 4 The value of 28 ÷ 2 2 + 3 is 4.

Question 11. Write an Expression To find the cost of a window, multiply its area in square feet by the price per square foot. Write and evaluate an expression to find the cost of a knot window $ _______

Answer: 108

Explanation: To find the cost of the knot window multiply the area with the price per square foot. Area per square feet is 2 2 Price per square foot is $27 Cost = 2 2 × 27 = 4 × 27 = 108 Thus the cost of a knot window is $108

Question 12. A builder installs 2 rose windows and 2 tulip windows. Write and evaluate an expression to find the combined area of the windows. _______ square feet

Explanation: The area of rose window is 3 2 The area of tulip windows is 2 2 Combines area of rose and tulip window is 3 2 + 2 2 = 5 2 5 2 × 2 = 25 × 2 = 50 Thus the area of the combined windows is 50 square feet.

Evaluate Expressions Involving Exponents Lesson 7.2 Question 13. DeShawn bought a tulip window. Emma bought a rose window. Write and evaluate an expression to determine how much more DeShawn paid for his window than Emma paid for hers. $ _______

Answer: 258

Explanation: Given that, DeShawn bought a tulip window. DeShawn bought it for 4 2 × $33 = 16 × $33 = 528 Emma bought a rose window Emma bought it for 3 2 × 30 = 9 × 30 = 270 $528 – $270 = $258 DeShawn paid $258 for his window and Emma paid for hers.

Question 14. What’s the Error? Darius wrote 17 − 2 2 = 225. Explain his error. Type below: _____________

Answer: 17 – 4 is actually 13 but not 225.

Question 15. Ms. Hall wrote the expression 2 × (3 + 5) 2 ÷ 4 on the board. Shyann said the first step is to evaluate 52. Explain Shyann’s mistake. Then evaluate the expression _______

Explanation: 2 × (3 + 5) 2 ÷ 4 First, add 3 and 5. 2 × (8) 2 ÷ 4 The square of 8 × 8 is 64. 2 × (64 ÷ 4) = 2 × 16 = 32

Question 1. 5 + 17 − 10 2 ÷ 5 _______

Explanation: 5 + 17 – (100 ÷ 5) Divide 100 by 5 (5 + 17) – 20 22 – 20 = 2 So, the value for the expression 5 + 17 − 10 2 ÷ 5 = 2

Question 2. 7 2 − 3 2 × 4 _______

Explanation: 7 2 − 3 2 × 4 7 2 − (3 2 × 4) 7 2 − (9 × 4) 49 – 36 = 13 Thus, 7 2 − 3 2 × 4 = 13

Question 3. 2 4 ÷ (7 − 5) _______

Explanation: 2 4 ÷ (7 − 5) 2 4 ÷ 2 2 4 = 2 × 2 × 2 × 2 = 16 16 ÷ 2 = 8 2 4 ÷ (7 − 5) = 8

Lesson 7 Problem Set 7.2 Answer Key Question 4. (8 2 + 36) ÷ (4 × 5 2 ) _______

Explanation: (8 2 + 36) ÷ (4 × 5 2 ) 8 2 = 8 × 8 = 64 5 2 = 5 × 5 = 25 (64 + 36) ÷ (4 × 25) 100 ÷ 100 = 1 So, (8 2 + 36) ÷ (4 × 5 2 ) = 1

Question 5. 12 + 21 ÷ 3 + (2 2 × 0) _______

Explanation: 12 + 21 ÷ 3 + 0 12 + (21 ÷ 3) 12 + 7 = 19 12 + 21 ÷ 3 + (2 2 × 0) = 19

Question 6. (12 − 8) 3 − 24 × 2 _______

Explanation: (12 − 8) 3 − 24 × 2 = (4) 3 − 24 × 2 64 – (24 × 2) = 64 – 48 = 16 (12 − 8) 3 − 24 × 2 = 16

Question 7. 12 × 2 + 2 3 value: 120 Type below: _____________

Answer: 12 × (2 + 2 3 ) 12 × (2 + 8) 12 × 10 = 120 12 × 2 + 2 3 = 120

Question 8. 7 2 + 1 − 5 × 3 value: 135 Type below: _____________

Answer: (7 2 + 1 − 5) × 3 (49 + 1 – 5) × 3 (50 – 5) × 3 45 × 3 = 135 7 2 + 1 − 5 × 3 = 135

Problem Solving

Question 9. Hugo is saving for a new baseball glove. He saves $10 the first week, and $6 each week for the next 6 weeks. The expression 10 + 6 2 represents the total amount in dollars he has saved. What is the total amount Hugo has saved? $ _______

Answer: $46

Explanation: Hugo is saving for a new baseball glove. He saves $10 the first week, and $6 each week for the next 6 weeks. The expression 10 + 6 2 represents the total amount in dollars he has saved. 10 + 6 2 = 10 + 36 = 46 The total amount Hugo has saved is $46

Practice and Homework Lesson 7.2 Answer Key Question 10. A scientist placed 5 fish eggs in a tank. Each day, twice the number of eggs from the previous day hatch. The expression 5 × 2 6 represents the number of eggs that hatch on the seventh day. How many eggs hatch on the seventh day? _______ eggs

Answer: 320 eggs

Explanation: A scientist placed 5 fish eggs in a tank. Each day, twice the number of eggs from the previous day hatch. The expression 5 × 2 6 represents the number of eggs that hatch on the seventh day. 5 × 2 6 = 5 × 64 = 320 eggs Therefore 320 eggs hatch on the seventh day.

Question 11. Explain how you could determine whether a calculator correctly performs the order of operations. Type below: _____________

Answer: Create a problem that must use the order of operations and isn’t solved by just left to right. Solve it going left to right. Then solve it using the order of operations. Solve it on the calculator. Your answer on the calculator will match the one using the order of operations.

Question 1. Ritchie wants to paint his bedroom ceiling and four walls. The ceiling and each of the walls are 8 feet by 8 feet. A gallon of paint covers 40 square feet. Write an expression that can be used to find the number of gallons of paint Ritchie needs to buy. Type below: _____________

Answer: Ritchie wants to paint his bedroom ceiling and four walls. The ceiling and each of the walls are 8 feet by 8 feet. A gallon of paint covers 40 square feet. 8 × 8 × (4 + 1) ÷ 40 8 2 (4 + 1) ÷ 40 Thus the expression that can be used to find the number of gallons of paint Ritchie needs to buy is 8 2 (4 + 1) ÷ 40

Question 2. A Chinese restaurant uses about 225 pairs of chopsticks each day. The manager wants to order a 30-day supply of chopsticks. The chopsticks come in boxes of 750 pairs. How many boxes should the manager order? _______ boxes

Answer: 9 boxes

Explanation: A Chinese restaurant uses about 225 pairs of chopsticks each day. The manager wants to order a 30-day supply of chopsticks. Multiply the number of pairs with the number of days 225 × 30 = 6750 The chopsticks come in boxes of 750 pairs. Now divide the number of chopsticks by the number of pairs. 6750 ÷ 750 = 9 boxes.

Question 3. Annabelle spent $5 to buy 4 raffle tickets. How many tickets can she buy for $20? _______ tickets

Answer: 16 tickets

Explanation: Annabelle spent $5 to buy 4 raffle tickets. To find the number of tickets she can buy for $20. ($20 ÷ $5) × 4 4 × 4 = 16 tickets That means she can buy 16 tickets for $20.

Question 4. Gavin has 460 baseball players in his collection of baseball cards, and 15% of the players are pitchers. How many pitchers are in Gavin’s collection? _______ pitchers

Answer: 69 pitchers

Explanation: Gavin has 460 baseball players in his collection of baseball cards, and 15% of the players are pitchers. The decimal form of 15% is 0.15 Now multiply 460 with 0.15 460 × 0.15 = 69.00 Thus there are 69 pitchers in Gavin’s collection.

Question 5. How many pounds are equivalent to 40 ounces? _______ pounds

Answer: 2.5 pounds

Explanation: Convert from ounces to pounds. 1 pound = 16 ounces 1 ounce = 1/16 pound 40 ounces = 40 × 1/16 pound 40 ounces = 2.5 pounds Thus, 2.5 pounds are equivalent to 40 ounces

Question 6. List the expressions in order from least to greatest. 1 5 3 3 4 2 8 1 Type below: _____________

Answer: 1 5 3 3 4 2 8 1 1 5 = 1 × 1 × 1 × 1 × 1 = 1 3 3 = 3 × 3 × 3 = 27 4 2 = 4 × 4 = 16 8 1 = 8 Thus the order from least to greatest. 1 5 8 1 4 2 3 3

Question 1. Write an algebraic expression for the product of 6 and p. What operation does the word “product” indicate? Type below: _____________

Answer: 6 × p Explanation: The word product indicates multiplication. Multiply 6 with p. The algebraic expression for the product of 6 and p is 6 × p.

Write an algebraic expression for the word expression.

Question 2. 11 more than e Type below: _____________

Answer: 11 + e

Explanation: The word more than indicates addition operation. So, the algebraic expression is 11 + e

Question 3. 9 less than the quotient of n and 5 Type below: _____________

Answer: 9 – (n ÷ 5)

Explanation: The word “less than” indicates subtraction and the “quotient” indicates division. So, the expression is 9 – (n ÷ 5)

Question 4. 20 divided by c Type below: _____________

Answer: 20 ÷ c

Explanation: Here we have to divide 20 by c. The expression is 20 ÷ c

Question 5. 8 times the product of 5 and t Type below: _____________

Answer: 8 × (5t)

Explanation: The word times indicate multiplication and the product indicates multiplication. Here we have to multiply 8 with 5 and t. Thus the expression is 8 × 5 × t = 8 × 5t

Question 6. There are 12 eggs in a dozen. Write an algebraic expression for the number of eggs in d dozen. Type below: _____________

Answer: 12d

Explanation: Given, There are 12 eggs in a dozen. d represents the number of eggs in a dozen So, we have to multiply 12 with d. Thus the algebraic expression is 12d.

Write Algebraic Expressions Lesson 7.3 Answer Key Question 7. A state park charges a $6.00 entry fee plus $7.50 per night of camping. Write an algebraic expression for the cost in dollars of entering the park and camping for n nights. Type below: _____________

Answer: $6.00 + $7.50 n

Explanation: Given that, A state park charges a $6.00 entry fee plus $7.50 per night of camping. Find the camping for n nights. The product of $7.50 camping for n nights. $7.50 × n Now add park charges to the camping nights. $6.00 + $7.50 n Thus the algebraic expression for the cost in dollars of entering the park and camping for n nights is $6.00 + $7.50 n

Question 8. Look for Structure At a bookstore, the expression 2c + 8g gives the cost in dollars of c comic books and g graphic novels. Next month, the store’s owner plans to increase the price of each graphic novel by $3. Write an expression that will give the cost of c comic books and g graphic novels next month. Type below: _____________

Answer: 2c + 11g

Explanation: Look for Structure At a bookstore, the expression 2c + 8g gives the cost in dollars of c comic books and g graphic novels. Next month, the store’s owner plans to increase the price of each graphic novel by $3. Here we have to add $3 to 8 g = 3g + 8g = 11g The sum of cost of c comic books and g graphic novels Thus the expression is 2c + 11g

Answer: Pay a low monthly fee of $50. Receive $10 off your first month’s fee.

Question 9. b. Write an expression for the monthly fee in dollars for m months. Type below: _____________

Answer: M is the number of months. 50 × m Given that $10 off on the first-month fee. 50m + (50-10) 50m + $40

Question 9. c. What operation can you use to show the discount of $10 for the first month? Type below: _____________

Answer: We have to use subtraction operations to show a discount of $10 for the first month.

Question 9. d. Write an expression for the total cost of the plan in dollars for m months Type below: _____________

Answer: 50m + 40

Question 10. A group of n friends evenly share the cost of dinner. The dinner costs $74. After dinner, each friend pays $11 for a movie. Write an expression to represent what each friend paid for dinner and the movie. Type below: _____________

Answer: 74 ÷ n + 11n

Explanation: Given, A group of n friends evenly share the cost of dinner. The dinner costs $74. After dinner, each friend pays $11 for a movie. The word share represents the division operation. That means we have to divide 74 by n. 74 ÷ n After that n friends paid $11 for movie Multiply 11 with n. Thus the expression to represent what each friend paid for dinner and the movie is 74 ÷ n + 11n

Question 11. A cell phone company charges $40 per month plus $0.05 for each text message sent. Select the expressions that represent the cost in dollars for one month of cell phone usage and sending m text messages. Mark all that apply. Options: a. 40m + 0.05 b. 40 + 0.05m c. 40 more than the product of 0.05 and m d. the product of 40 and m plus 0.05

Answer: 40 + 0.05m

Explanation: A cell phone company charges $40 per month plus $0.05 for each text message sent. Let m represent the messages sent. 40m + 0.05m Thus the answer is option B.

Question 1. 13 less than p Type below: _____________

Answer: 13 – p

Explanation: Less than is nothing but subtraction. So the expression for 13 less than p is 13 – p

Question 2. the sum of x and 9 Type below: _____________

Answer: x + 9

Explanation: The sum is nothing but an addition. Thus the expression for the sum of x and 9 is x + 9.

Question 3. 6 more than the difference of b and 5 Type below: _____________

Answer: 6 + (b – 5)

Explanation: More than is nothing but addition and difference means subtraction. The expression for 6 more than the difference of b and 5 is 6 + (b – 5)

Question 4. the sum of 15 and the product of 5 and v Type below: _____________

Answer: 15 + 5v

Explanation: Product is nothing but multiplication and sum is nothing but an addition. So, the expression for the sum of 15 and the product of 5 and v is 15 + 5 × v

Question 5. the difference of 2 and the product of 3 and k Type below: _____________

Answer: 2 – 3k

Explanation: The difference means subtraction and Product is nothing but the multiplication So, the difference of 2 and the product of 3 and k is 2 – 3 × k 2 – 3k

Question 6. 12 divided by the sum of h and 2 Type below: _____________

Answer: 12 ÷ h + 2

Explanation: 12 divided by the sum of h and 2 Divide 12 by sum of h and 2. 12 ÷ (h + 2)

Question 7. the quotient of m and 7 Type below: _____________

Answer: m ÷ 7

Explanation: Given the quotient of m and 7 That means we have to divide m by 7. Thus the answer is m ÷ 7

Question 8. 9 more than 2 multiplied by f Type below: _____________

Answer: 9 + 2f

Explanation: 9 more than 2 multiplied by f We have to add 9 to 2 × f So, the expression is 9 + 2f

Question 9. 6 minus the difference of x and 3 Type below: _____________

Answer: 6 – (x – 3)

Explanation: First, subtract 3 from x The expression for 6 minus the difference of x and 3 is 6 – (x – 3)

Question 10. 10 less than the quotient of g and 3 Type below: _____________

Answer: 10 – (g ÷ 3)

Explanation: The quotient of g and 3 is nothing but divide g by 3 g ÷ 3 Now subtract g ÷ 3 from 10. So, the expression for 10 less than the quotient of g and 3 is 10 – (g ÷ 3)

Question 11. the sum of 4 multiplied by a and 5 multiplied by b Type below: _____________

Answer: 4a + 5b

Explanation: First, multiply 4 with a and then multiply 5 with b After that add both the expressions. 4a + 5b So, the sum of 4 multiplied by a and 5 multiplied by b is 4a + 5b

Question 12. 14 more than the difference of r and s Type below: _____________

Answer: 14 + (r – s)

Explanation: Subtract r and s And then add 14 to that r -s 14 + (r – s)

Question 13. Let h represent Mark’s height in inches. Suzanne is 7 inches shorter than Mark. Write an algebraic expression that represents Suzanne’s height in inches. Type below: _____________

Answer: h – 7

Explanation: Let h represent Mark’s height in inches. Suzanne is 7 inches shorter than Mark. That means we have to subtract 7 from h. i.e., h – 7 Thus Suzanne’s height is h – 7 inches.

Question 14. A company rents bicycles for a fee of $10 plus $4 per hour of use. Write an algebraic expression for the total cost in dollars for renting a bicycle for h hours. Type below: _____________

Answer: 10 + 4h

Explanation: A company rents bicycles for a fee of $10 plus $4 per hour of use. Multiply 4 with hours And then 10 to 4h 10 + 4h Thus the total cost in dollars for renting a bicycle for h hours is 10 + 4h

Question 15. Give an example of a real-world situation involving two unknown quantities. Then write an algebraic expression to represent the situation. Type below: _____________

Answer: Cooper bikes so many miles per day and does it for 7 months. The expression for the question is 6m × 7

Question 1. The female lion at a zoo weighs 190 pounds more than the female cheetah. Let c represent the weight in pounds of the cheetah. Write an expression that gives the weight in pounds of the lion. Type below: _____________

Answer: c + 190

Explanation: Given that, The female lion at a zoo weighs 190 pounds more than the female cheetah. Let c represent the weight in pounds of the cheetah. We have to add 190 to the weight in pounds of the cheetah. That means c + 190 Thus the expression that gives the weight in pounds of the lion is c + 190.

Question 2. Tickets to a play cost $8 each. Write an expression that gives the ticket cost in dollars for a group of g girls and b-boys. Type below: _____________

Answer: 8 × (g + b)

Explanation: First add girls group and boys group. g + b And then multiply 8 with the group of girls and boys. 8 × (g + b) So, the expression that gives the ticket cost in dollars for a group of g girls and b-boys is 8 × (g + b).

Question 3. A bottle of cranberry juice contains 32 fluid ounces and costs $2.56. What is the unit rate? $ _______ per fluid ounce

Answer: 0.08

Explanation: A bottle of cranberry juice contains 32 fluid ounces and costs $2.56. Divide the number of fluid ounces by the cost. 32 ÷ $2.56 32/2.56 = 0.08 The unit rate is 0.08 per fluid ounce.

Question 4. There are 32 peanuts in a bag. Elliott takes 25% of the peanuts from the bag. Then Zaire takes 50% of the remaining peanuts. How many peanuts are left in the bag? _______ peanuts

Explanation: First, we have to find 25% of 32. 25% of 32 its 0.25 × 32=8 Now we have to subtract 32 and 8 32 – 8=24 Now we have to find 50% of 24 50% of 24 = 12 24-12=12. Thus 12 peanuts are left in the bag.

Question 5. Hank earns $12 per hour for babysitting. How much does he earn for 15 hours of babysitting? $ _______

Answer: 180

Explanation: Hank earns $12 per hour for babysitting. Multiply $12 with 15 12 × 15 = $180 He earned $180 for 15 hours of babysitting.

Answer: 7 2 – 2 2

Explanation: The area of the square is 7 cm × 7 cm = 7 2 The area of the square is 2 cm × 2 cm = 2 2 Now subtract a small square from the large square. The expression that represents the area of the figure is 7 2 – 2 2

Identify the parts of the expression. Then, write a word expression for the numerical or algebraic expression.

Question 1. 7 × (9 ÷ 3) Type below: _____________

Answer: The quotient of 9 and 3 and then multiply with 7. Word expression: Product of 7 with the quotient of 9 and 3.

Question 2. 5m + 2n Type below: _____________

Answer: Product of 5 and m and product of 2 and n Now add both the product of 5 and m and 2 and n. Word Expression: Product of 5 and m plus the product of 2 and n.

Practice: Copy and Solve Identify the parts of the expression. Then write a word expression for the numerical or algebraic expression.

Question 3. 8 + (10 − 7) Type below: _____________

Answer: Subtraction is the difference between 10 and 7. Addition to the subtraction of 10 and 7. Word expression: Add 8 to the difference between 10 and 7.

Question 4. 1.5 × 6 + 8.3 Type below: _____________

Answer: The addition is the sum of 6 and 8.3 and then multiply the sum to 1.5. Word expression: 1.5 times the sum of 6 and 8.3

Question 5. b + 12x Type below: _____________

Answer: Product of 12 and x. Add b to the product of 12 and x. Word expression: Sum of b to the product of 12 and x.

Question 6. 4a ÷ 6 Type below: _____________

Answer: The division is the quotient of 4a and 6. Multiply 4 and a. The expression is the product of 4 and a divided by 6. Word expression: The quotient of the product 4 and a and 6.

Identify the terms of the expression. Then, give the coefficient of each term.

Question 7. k − \(\frac{1}{3}\)d Type below: _____________

Answer: The terms of the expression are k and \(\frac{1}{3}\)d Coefficients – 1 and \(\frac{1}{3}\)

Question 8. 0.5x + 2.5y Type below: _____________

Answer: The terms of the expression are 0.5x and 2.5y Coefficients – 0.5 and 2.5

Question 9. Connect Symbols and Words Ava said she wrote an expression with three terms. She said the first term has the coefficient 7, the second term has the coefficient 1, and the third term has the coefficient 0.1. Each term involves a different variable. Write an expression that could be the expression Ava wrote Type below: _____________

Answer: Connect Symbols and Words Ava said she wrote an expression with three terms. She said the first term has the coefficient 7, the second term has the coefficient 1, and the third term has the coefficient 0.1. The expression for the first term is 7x The expression for the second term is 1y The expression for the third term is 0.1z 7x + y + 0.1z

Question 10. A football team scored 2 touchdowns and 2 extra points. Their opponent scored 1 touchdown and 2 field goals. Write a numerical expression for the points scored in the game. Type below: _____________

Answer: A football team scored 2 touchdowns and 2 extra points. 2 touchdowns = 2 × 6 2 extra points = 2 × 1 Their opponent scored 1 touchdown and 2 field goals. 1 touchdown = 1 × 6 2 field goals = 2 × 3 Thue the numerical expression is 12 + 2 + 6 + 6 14 + 12 The numerical expression for the points scored in the game is 14 + 12.

Question 11. Write an algebraic expression for the number of points scored by a football team that makes t touchdowns, f field goals, and e extra points Type below: _____________

Answer: 6t + 3f + e

Explanation: The number of points scored by a football team that makes t touchdowns, f field goals, and e extra points. The table shows that touchdown has 6 points, field goal has 3 points and extra point has 1 point. So we need to add all the points to make the expressions That means 6t + 3f + e

Question 12. Identify the parts of the expression you wrote in Exercise 11. Type below: _____________

Question 13. Give an example of an expression involving multiplication in which one of the factors is a sum. Explain why you do or do not need parentheses in your expression Type below: _____________

Answer: 6 × 2 + 3 In this expression, there is no need for parentheses because there are no exponents or multiple operations.

Question 14. Kennedy bought a pounds of almonds at $5 per pound and p pounds of peanuts at $2 per pound. Write an algebraic expression for the cost of Kennedy’s purchase. Type below: _____________

Answer: 5 + 2p = x

Explanation: Kennedy bought a pounds of almonds at $5 per pound and p pounds of peanuts at $2 per pound. We have to multiply p with $2 per pound. The algebraic expression for the cost of Kennedy’s purchase is the sum of 5 and the product of p and 2 Thus the expression is 5 + 2p = x

Identify the parts of the expression. Then write a word expression for the numerical or algebraic expression.

Question 1. (16 − 7) ÷ 3 Type below: _____________

Answer: Subtraction is the difference between 16 and 7. The division is the quotient of the difference and 3 Word expression: the quotient of the difference 16 and 7 and 3.

Question 2. 8 + 6q + q Type below: _____________

Answer: Sum of 8 and the product of 6 and q added to q. Addition – Sum of 8 plus the product of 6 and q plus q. Addition – 6 times q and the sum of q. Multiply – the product of 6 and q.

Identify the terms of the expression. Then give the coefficient of each term.

Question 3. 11r + 7s Type below: _____________

Answer: The terms of the expression are 11r and 7s The coefficient of each term is 11 and 7.

Question 4. 6g − h Type below: _____________

Answer: The terms of the expression are 6g and h The coefficient of each term is 6 and 1.

Question 5. Adam bought granola bars at the store. The expression 6p + 5n gives the number of bars in p boxes of plain granola bars and n boxes of granola bars with nuts. What are the terms of the expression? Type below: _____________

Answer: Adam bought granola bars at the store. The expression 6p + 5n gives the number of bars in p boxes of plain granola bars and n boxes of granola bars with nuts. The terms of the expression are 6p and 5n.

Question 6. In the sixth grade, each student will get 4 new books. There is one class of 15 students and one class of 20 students. The expression 4 × (15 + 20) gives the total number of new books. Write a word expression for the numerical expression. Type below: _____________

Answer: In the sixth grade, each student will get 4 new books. There is one class of 15 students and one class of 20 students. The expression 4 × (15 + 20) gives the total number of new books. The product of 4 the sum of 15 and 20.

Question 7. Explain how knowing the order of operations helps you write a word expression for a numerical or algebraic expression. Type below: _____________

Answer: Because if you don’t know and use the order of operations you can get an entirely different answer.

Question 1. A fabric store sells pieces of material for $5 each. Ali bought 2 white pieces and 8 blue pieces. She also bought a pack of buttons for $3. The expression 5 × (2 + 8) + 3 gives the cost in dollars of Ali’s purchase. How can you describe the term (2 + 8) in words? Type below: _____________

Answer: the sum of 2 and 8

Explanation: A fabric store sells pieces of material for $5 each. Ali bought 2 white pieces and 8 blue pieces. She also bought a pack of buttons for $3. The expression 5 × (2 + 8) + 3 gives the cost in dollars of Ali’s purchase. The word expression for the term 2 + 8 is the sum of 2 and 8.

Question 2. A hotel offers two different types of rooms. The expression k + 2f gives the number of beds in the hotel where k is the number of rooms with a king-size bed and f is the number of rooms with 2 full-size beds. What are the terms of the expression? Type below: _____________

Answer: k and 2f

Explanation: The terms for the expression k + 2f is k and 2f.

Question 3. Meg paid $9 for 2 tuna sandwiches. At the same rate, how much does Meg pay for 8 tuna sandwiches? $ _______

Explanation: Meg paid $9 for 2 tuna sandwiches. To find how much does Meg pay for 8 tuna sandwiches 2 – $9 8 -? $9 × 8/2 = 72/2 = 36 Thus Meg pays $36 for 8 tuna sandwiches.

Question 4. Jan is saving for a skateboard. She has saved $30 already, which is 20% of the total price. How much does the skateboard cost? $ _______

Answer: 150

Explanation: Jan is saving for a skateboard. She has saved $30 already, which is 20% of the total price. Divide $30 by 20% 30 ÷ 20% 30 ÷ 20 × 1/100 30 ÷ 1/5 30 × 5 = 150 Thus the cost of the skateboard is $150.

Question 5. It took Eduardo 8 hours to drive from Buffalo, NY, to New York City, a distance of about 400 miles. Find his average speed. _______ miles per hour

Explanation: Given, It took Eduardo 8 hours to drive from Buffalo, NY, to New York City, a distance of about 400 miles. We can use the formula d = rt r = d/t r = 400 miles/8 hours r = 50 miles per hour

Question 6. Write an expression that represents the value, in cents, of n nickels. Type below: _____________

Answer: 0.05n

Explanation: An expression does not have an equal sign. Since the value of a nickel is 5 cents and you want to find out the value of n nickels (which means if you had any number of nickels) the expression would be .05n

Question 1. Evaluate 5k + 6 for k = 4. _______

Explanation: The expression is 5k + 6 Substitute the value k = 4 5(4) + 6 = 20 + 6 = 26 5k + 6 = 26

Evaluate the expression for the given value of the variable.

Question 2. m − 9 for m = 13 _______

Explanation: m – 9 Substitute the value of m in the expression 13 – 9 = 4 Thus m – 9 = 4

Question 3. 16 − 3b for b = 4 _______

Explanation: Given the expression 16 – 3b Now substitute the value of b in the expression. 16 – 3b = 16 – 3(4) = 16 – 12 = 4 16 – 3b = 4

Question 4. p 2 + 4 for p = 6 _______

Explanation: Given the expression p 2 + 4 Substitute the value of p in the expression 6 2 + 4 = 36 + 4 = 40 Thus the value of p 2 + 4 is 40.

Question 5. The formula A = lw gives the area A of a rectangle with length l and width w. What is the area in square feet of a United States flag with a length of 12 feet and a width of 8 feet? _______ square feet

Answer: 96 square feet

Explanation: Use the formula A = lw Length = 12 feet Width = 8 feet A = lw A = 12 feet × 8 feet = 96 square feet Thus the area of the United States flag is 96 square feet.

Practice: Copy and Solve Evaluate the expression for the given value of the variable.

Question 6. 7s + 5 for s = 3 _______

Explanation: Given the expression 7s + 5 Substitute  the value of S in the above expression 7(3) + 5 = 21 + 5 = 26

Question 7. 21 − 4d for d = 5 _______

Explanation: Given the expression 21 – 4d Substitute  the value d = 5 in the above expression 21 – 4(5) = 21 – 20 = 1

Question 8. (t − 6) 2 for t = 11 _______

Explanation: Given the expression (t − 6) 2 Substitute the value t = 11 Thus (t − 6) 2 = (11 − 6) 2 = 5 × 5 = 25

9.6 × (2v − 3) for v = 5 _______

Explanation: Given the expression 6 × (2v – 3) Substitute the value of v in the above expression. 6 × (2v – 3) = 6 × (2 × 5 – 3) 6 × (10 – 3) 6 × 7 = 42 Thus the value of 6 × (2v – 3) = 42

Question 10. 2 × (k 2 − 2) for k = 6 _______

Explanation: Given the expression 2 × (k 2 − 2) Substitute the value of k in the above expression 2 × (k 2 − 2) = 2 × (6 2 − 2) 2 × (36 – 2) = 2 × 34 = 68 Thus the value of 2 × (k 2 − 2) is 68

Question 11. 5 × (f − 32) ÷ 9 for f = 95 _______

Explanation: The expression is 5 × (f – 32) ÷ 9 Substitute  the value f = 95 5 × (f – 32) ÷ 9 = 5 × (95 – 32) ÷ 9 5 × (63 ÷ 9) = 5 × 7 = 35 The value of 5 × (63 ÷ 9) = 35

Question 12. The formula P = 4s gives the perimeter P of a square with side length s. How much greater is the perimeter of a square with a side length of 5 \(\frac{1}{2}\) inches than a square with a side length of 5 inches? _______ inches

Answer: 2 inches

Explanation: We have to use the formula P = 4s to find the perimeter of the square. 4 × 5 \(\frac{1}{2}\) Convert the mixed fraction to the improper fraction. 4 × 11/2 = 2 × 11 = 22 inches 4 × 5 inches = 20 inches To find which has the greater  perimeter  we have to subtract 20 inches from 22 inches 22 inches – 20 inches = 2 inches Thus the perimeter of a square with 5 \(\frac{1}{2}\) inches is 2 inches greater than a square with a side length of 5 inches.

Question 13. Complete the table. Type below: _____________

Question 14. A skateboard club has $200 to spend on new wheels this year. What is the greatest number of packs of wheels the club can order? _______ packs

Answer: 3 packs

Explanation: A skateboard club has $200 to spend on new wheels this year. From the above table, we can say that the club can order 3 packs of wheels.

Evaluate Algebraic Expressions and Formulas Lesson 7.5 Answer Key Question 15. Make Sense of Problems A sporting goods store placed an order for 12 packs of wheels on the first day of each month last year. How much did the sporting goods store spend on these orders last year? $ _______

Answer: 7284

Explanation: Make Sense of Problems A sporting goods store placed an order for 12 packs of wheels on the first day of each month last year. Substitute n = 7 in the expression 50 × n + 7 We get, 50 × 12 + 7 600 + 7 = 607 Now multiply 607 with 12 607 × 12 = 7284 Therefore the sporting goods store spent $7284 on these orders last year.

Question 16. What’s the Error? Bob used these steps to evaluate 3m − 3 ÷ 3 for m = 8. Explain his error. 3 × 8 − 3 ÷ 3 = 24 − 3 ÷ 3 = 21 ÷ 3 = 7 Type below: _____________

Answer: First, he has to subtract 8 and 3. But he first multiplied and then subtracted 24 and 3. 3 × 8 − 3 ÷ 3 = 3 × (8 − 3) ÷ 3 3 × 5 ÷ 3 15 ÷ 3 = 5

Question 17. The surface area of a cube can be found by using the formula 6s 2 , where s represents the length of the side of the cube. The surface area of a cube that has a side length of 3 meters is _____ meters squared. The surface area of a cube that has a side length                       meters of 3 meters is _____________ squared

Explanation: The surface area of a cube can be found by using the formula 6s 2 he surface area of a cube that has a side length of 3 meters s 2  = 3 2  = 9 6 × 9 = 54 square meters

Evaluate the expression for the given values of the variables.

Question 1. w + 6 for w = 11 _______

Explanation: Given the expression w + 6 Substitute the value w = 6 in the expression w + 6 = 11 + 6 = 17

Question 2. 17 − 2c for c = 7 _______

Explanation: Substitute  the value c = 7 in the given expression 17 – 2(7) = 17 – 14 = 3 Thus the value for 17 – 2c is 3.

Question 3. b 2 − 4 for b = 5 _______

Explanation: Substitute the value b = 5 in the expression b 2 − 4 = 5 2 − 4 = 25 – 4 = 21 Thus the value for the expression b 2 − 4 is 21.

Question 4. (h − 3) 2 for h = 5 _______

Explanation: We have to substitute the value h = 5 (h − 3) 2 = (5 − 3) 2 = (2) 2 = 4 Therefore the value of (h − 3) 2 is 4.

Question 5. m + 2m + 3 for m = 12 _______

Explanation: Given the expression m + 2m + 3 Now substitute the value m = 12 in the above expression. 12 + 2(12) + 3 = 12 + 24 + 3 = 39. The value for m + 2m + 3 = 39.

Question 6. 4 × (21 − 3h) for h = 5 _______

Explanation: Substitute h = 5 in the given expression. 4 × (21 – 3h) = 4 × (21 – 3(5)) 4 × (21 – 15) = 4 × 6 = 24 Therefore the value for 4 × (21 – 3h) is 24.

Question 7. 7m − 9n for m = 7 and n = 5 _______

Explanation: Substitute the values m = 7 and n = 5 in the above expression. 7m – 9n = 7 × 7 – 9 × 5 = 49 – 45 = 4 Thus 7m – 9n = 4.

Question 8. d 2 − 9k + 3 for d = 10 and k = 9 _______

Explanation: Given the expression d 2 − 9k + 3 Now substitute d = 10 and k = 9 in the expression. d 2 − 9k + 3 = 10 2 − 9(9) + 3 100 – 81 + 3 = 22 Thus the value for the expression d 2 − 9k + 3 is 22.

Question 9. 3x + 4y ÷ 2 for x = 7 and y = 10 _______

Explanation: Substitute the values x = 7 and y = 10 in the expression. 3x + 4y ÷ 2 = 3(7) + 4(10) ÷ 2 21 + 40 ÷ 2 = 21 + 20 = 41 Thus the value for 3x + 4y ÷ 2 is 41.

Question 10. The formula P = 2l + 2w gives the perimeter P of a rectangular room with length l and width w. A rectangular living room is 26 feet long and 21 feet wide. What is the perimeter of the room? _______ feet

Answer: 94 feet

Explanation: Use the formula  of the perimeter  of a rectangle P = 2l + 2w L = 26 feet W = 21 feet P = 2(26) + 2(21) P = 52 feet + 42 feet P = 94 feet Therefore the perimeter of a room is 94 feet.

Question 11. The formula C = 5(F − 32) ÷ 9 gives the Celsius temperature in C degrees for a Fahrenheit temperature of F degrees. What is the Celsius temperature for a Fahrenheit temperature of 122 degrees? _______ degrees Celsius

Explanation: C = 5(F – 32) ÷ 9 We know that F = 122 degrees Substitute the value of F in the formula C = 5(122 – 32) ÷ 9 C = 5(90) ÷ 9 C = 450 ÷ 9 = 50 Thus the answer is 50 degrees Celsius.

Question 12. Explain how the terms variable, algebraic expression, and evaluate are related. Type below: _____________

Answer: To evaluate an algebraic expression, you have to substitute a number for each variable and perform the arthematic operations. If we know the variables, we can replace the variables with their values and then evaluate the expression.

Question 1. When Debbie baby-sits, she charges $5 to go to the house plus $8 for every hour she is there. The expression 5 + 8h gives the amount in dollars she charges. How much will she charge to baby-sit for 5 hours? $ _______

Explanation: When Debbie baby-sits, she charges $5 to go to the house plus $8 for every hour she is there. The expression 5 + 8h gives the amount in dollars she charges. If h = 5 hours Substitute the value h in the above expression. 5 + 8h = 5 + 8(5) = 5 + 40 = 45 Thus she charges $45 to baby-sit for 5 hours.

Question 2. The formula to find the cost C in dollars of a square sheet of glass is C = 25s 2 where s represents the length of a side in feet. How much will Ricardo pay for a square sheet of glass that is 3 feet on each side? $ _______

Answer: $225

Explanation: Use the formula C = 25s 2 s represents the length of a side in feet. s = 3 feet Substitute the value s in the above formula. C = 25s 2 C = 25(3 2 ) C = 25(9) = 225 Ricardo pays $225 for a square sheet of glass that is 3 feet on each side.

Question 3. Evaluate using the order of operations. \(\frac{3}{4}+\frac{5}{6} \div \frac{2}{3}\) _______

Explanation: \(\frac{3}{4}\) + [/latex]\frac{5}{6}[/latex] ÷ [/latex]\frac{2}{3}[/latex] [/latex]\frac{5}{6}[/latex] ÷ [/latex]\frac{2}{3}[/latex] = [/latex]\frac{5}{6}[/latex] × [/latex]\frac{3}{2}[/latex] = [/latex]\frac{15}{12}[/latex] = [/latex]\frac{5}{4}[/latex] Now convert the improper fraction to the mixed fraction. [/latex]\frac{5}{4}[/latex] = 1 [/latex]\frac{1}{4}[/latex] 1 [/latex]\frac{1}{4}[/latex] + \(\frac{3}{4}\) 1 + [/latex]\frac{1}{4}[/latex] + \(\frac{3}{4}\) = 1 + 1 = 2 \(\frac{3}{4}+\frac{5}{6} \div \frac{2}{3}\) = 2

Practice and Homework Lesson 7.5 Answer Key Question 4. Patricia scored 80% on a math test. She missed 4 problems. How many problems were on the test? _______ problems

Explanation: Patricia scored 80% on a math test. She missed 4 problems. 4 ÷ 80% 4 × [/latex]\frac{100}{80}[/latex] = 4 × 5 = 20 Therefore there are 20 questions in the test.

Question 5. What is the value of 7 3 ? _______

Answer: 343

Explanation: 7 3 = 7 × 7 × 7 = 49 × 7 = 343 Thus the value of 7 3  is 343.

Question 6. James and his friends ordered b hamburgers that cost $4 each and f fruit cups that cost $3 each. Write an algebraic expression for the total cost in dollars of their purchases. Type below: _____________

Answer: 4b + 3f

Explanation: Given that, James and his friends ordered b hamburgers that cost $4 each and f fruit cups that cost $3 each. Multiply b with $4 and multiply $3 with f Add 4b and 3f Thus the expression is 4b + 3f.

Vocabulary – Page No. 387

Question 1. A(n) _____ tells how many times a base is used as a factor. Type below: _____________

Answer: Exponent An Exponent tells how many times a base is used as a factor.

Question 2. The mathematical phrase 5+2×18 is an example of a(n) _____. Type below: _____________

Answer: Numerical expression The mathematical phrase 5+2×18 is an example of Numerical expression.

Concepts and Skills

Question 3. 5 4 ________

Answer: 5 × 5 × 5 × 5 = 625

Explanation: The number 5 is the repeated factor. 5 is used 4 times. Multiply 5 four times. 5 × 5 × 5 × 5 = 625

Question 4. 21 2 ________

Answer: 21 × 21 = 441

Explanation: The number 21 is the repeated factor. 21 is used 2 times. Multiply 21 two times. 21 × 21 = 441

Question 5. 8 3 ________

Answer: 8 × 8 × 8 = 512

Explanation: The number 8 is the repeated factor. 8 is used 3 times. 8 × 8 × 8 = 512

Question 6. 9 2 × 2 − 4 2 ________

Answer: 146

Explanation: 9 2 × 2 − 4 2 9 2 = 9 × 9 = 81 4 2 = 4 × 4 = 16 81 × 2 – 16 = 162 – 16 = 146 Thus 9 2 × 2 − 4 2 = 146

Question 7. 2 × (10 − 2) ÷ 2 2 ________

Explanation: 2 × (10 − 2) ÷ 2 2 2 × (10 − 2) ÷ 4 2 × 8 ÷ 4 = 16 ÷ 4 = 4 Thus 2 × (10 − 2) ÷ 2 2 = 4

Question 8. 30 − (3 3 − 8) ________

Explanation: 3 3 = 3 × 3 × 3 = 27 30 − (3 3 − 8) = 30 – (27 – 8) = 30 – 19 = 11 30 − (3 3 − 8) = 11 So, 30 − (3 3 − 8) is 11.

Question 9. the quotient of c and 8 Type below: _____________

Answer: c ÷ 8 The quotient is nothing but the division of c by 8. So, the expression is c ÷ 8.

Question 10. 16 more than the product of 5 and p Type below: _____________

Answer: 16 + 5p

Explanation: The operation for more than is addition. Here we have to add 16 to the product of 5 and p. The product is the operation for multiplication. Multiply 5 and p and then add 16 to it. The expression of the word is 16 + 5p.

Question 11. 9 less than the sum of x and 5 Type below: _____________

Answer: 9 – x + 5

Explanation: First, we have to evaluate the expression x and 5. Sum of is nothing but adding x and 5. Difference between 9 and x and 5 The expression is 9 – x + 5.

Question 12. 5 × (h + 3) for h = 7 ________

Explanation: Given expression is 5 × (h + 3) Substitute h = 7 in the above expression. 5 × (h + 3) = 5 × (7 + 3) 5 × 10 = 50 5 × (h + 3) = 50

Question 13. 2 × (c 2 − 5) for c = 4 ________

Explanation: Given 2 × (c 2 − 5) Substitute c = 4 in the expression 2 × (c 2 − 5) = 2 × (4 2 − 5) = 2 × (16 – 5) = 2 × 11 = 22 2 × (c 2 − 5) = 22

Question 14. 7a − 4a for a = 8 ________

Explanation: Given, 7a − 4a Subtract the like terms 7a − 4a = 3a Now substitute the value a = 8 in the above expression 3a = 3 × 8 = 24 7a − 4a = 24

Page No. 388

Question 15. The greatest value of any U.S. paper money ever printed is 10 5 dollars. What is this amount written in standard form? ________

Answer: 100000

Explanation: 10 5 dollars = 10 × 10 × 10 × 10 × 10 10 is a repeated factor. 10 repeated 5 times. 10 × 10 × 10 × 10 × 10 = 100000 dollars

Question 16. A clothing store is raising the price of all its sweaters by $3.00. Write an expression that could be used to find the new price of a sweater that originally cost d dollars. Type below: _____________

Answer: d + 3

Explanation: A clothing store is raising the price of all its sweaters by $3.00. The cost of the sweater is d dollars. The store is going to add $3. So, the new price of a sweater is the sum of d dollars and $3. The expression is d + 3.

Question 17. Kendra bought a magazine for $3 and 4 paperback books for $5 each. The expression 3 + 4 × 5 represents the total cost in dollars of her purchases. What are the terms in this expression? Type below: _____________

Answer: 3 and 4 × 5

Explanation: Kendra bought a magazine for $3 and 4 paperback books for $5 each. The expression 3 + 4 × 5 represents the total cost in dollars of her purchases. The terms in the expression are 3, 4, and 5.

Question 18. The expression 5c + 7m gives the number of people who can ride in c cars and m minivans. What are the coefficients in this expression? Type below: _____________

Answer: The coefficients in the expression 5c + 7m are 5 and 7.

Question 19. The formula P = a + b + c gives the perimeter P of a triangle with side lengths a, b, and c. How much greater is the perimeter of a triangular field with sides that measure 33 yards, 56 yards, and 65 yards than the perimeter of a triangular field with sides that measure 26 yards, 49 yards, and 38 yards? ________ yards

Answer: 41 yards

Explanation: First, we have to calculate the perimeter of the 1st triangle. Given: a = 33 yards b = 56 yards c = 65 yards P1 = a + b + c P1 = 33 + 56 + 65 = 154 yards Now we have to calculate the perimeter of 2nd triangle. Given: a = 26 yards b = 49 yards c = 38 yards P2 = a + b + c P2 = 26 + 49 + 38 = 113 yards Now we have to calculate which triangle has greater perimeter and how much greater. P1 – P2 = 154 yards – 113 yards = 41 yards Therefore, 41 yards greater is the perimeter of the 1st triangular field than the perimeter of the 2nd triangular field.

Louisa read that the highest elevation of Mount Everest is 8,848 meters. She wants to know how much higher Mount Everest is than Mount Rainier. Use this information for 1–2.

Question 1. Write an expression to represent the difference in the heights of the two mountains. Tell what the variable in your expression represents. Type below: _____________

Answer: 8848 – h, where h represents the height of the Mount Rainier

Explanation: Given that, the height of the Mount Everest is 8848 meters Let the height of the Mount Rainier is h The difference in height of Mount Everest and height of the Mount Rainier is 8848 – h.

Question 2. Louisa researches the highest elevation of Mount Rainier and finds that it is 4,392 meters. Use your expression to find the difference in the mountains’ heights. ________ meters

Answer: 4456 meters

Explanation: The height of the Mount Rainier = 4392 meters Replace the value of height of the Mount Rainier in the above expression. 8848 – h = 8848 meters – 4392 meters = 4456 meters Thus the difference between the height of the two mountains is 4456 meters.

A muffin recipe calls for 3 times as much flour as sugar. Use this information for 3–5.

Question 3. Write an expression that can be used to find the amount of flour needed for a given amount of sugar. Tell what the variable in your expression represents. Type below: _____________

Answer: Let the amount of sugar used represents the variable is s. The expression to find the amount of flour needed for a given amount of sugar is 3 × m i.e., 3m

Question 4. Use your expression to find the amount of flour needed when \(\frac{3}{4}\) cup of sugar is used. ______ \(\frac{□}{□}\)

Answer: 2 \(\frac{1}{4}\)

Explanation: Given that, A muffin recipe calls for 3 times as much flour as sugar. The amount of flour needed when \(\frac{3}{4}\) cup of sugar used is 3 × \(\frac{3}{4}\) = \(\frac{9}{4}\) Convert the improper fraction into the mixed fraction. \(\frac{9}{4}\) = 2 \(\frac{1}{4}\) Therefore 2 \(\frac{1}{4}\) amount of flour needed when \(\frac{3}{4}\) cup of sugar is used.

Question 5. Reason Quantitatively Is the value of the variable in your expression restricted to a particular set of numbers? Explain. Type below: _____________

Answer: The values that make the denominator equal to zero for a rational expression are known as restricted values. The solutions are the restricted values since they result in a denominator of zero when replaced for the variable(s).

Practice: Copy and Solve Write an algebraic expression for each word expression. Then evaluate the expression for these values of the variable: \(\frac{1}{2}\), 4, and 6.5.

Question 6. the quotient of p and 4 Type below: _____________

Answer: p ÷ 4

Explanation: The expression is p ÷ 4 p = \(\frac{1}{2}\) \(\frac{1}{2}\) ÷ 4 \(\frac{1}{2}\)/4 = \(\frac{1}{8}\) p ÷ 4 when p = \(\frac{1}{2}\) is \(\frac{1}{8}\) p = 4 4 ÷ 4 = 1 p = 6.5 6.5 ÷ 4 = 1.625

Question 7. 4 less than the sum of x and 5 Type below: _____________

Answer: 4 – (x + 5)

Explanation: The expression is 4 – (x + 5) x = 1/2 4 – (x + 5) = 4 – 1/2 + 5 3 1/2 + 5 = 8 1/2 x = 4 4 – x + 5 4 – 4 + 5 = 5 x = 6.5 4 – 6.5 + 5 = 2.5

Question 8. Write expressions for the distance in feet that each animal could run at top speed in a given amount of time. Tell what the variable in your expressions represents. Type below: _____________

Answer: The expression for distance in feet for Elephant = 22t The expression for distance in feet for Cheetah = 103t The expression for distance in feet for Giraffe = 51t The expression for distance in feet for hippopotamus = 21t Where t represents the time.

Question 9. How much farther could a cheetah run in 20 seconds at top speed than a hippopotamus could? ______ feet

Answer: 1640 feet

Explanation: The expression for distance in feet for Cheetah = 103t where t = 20 sec 103t = 103 × 20 sec = 2060 feet The expression for distance in feet for hippopotamus = 21t where t = 20 sec 21t = 21 × 20 = 420 feet Now we have to find How much farther could a cheetah run in 20 seconds at top speed than a hippopotamus could 2060 feet – 420 feet = 1640 feet

Question 10. A giraffe runs at top speed toward a tree that is 400 feet away. Write an expression that represents the giraffe’s distance in feet from the tree after s seconds. Type below: _____________

Answer: The expression representing the giraffe’s distance from tree after s seconds, if the rate is 51 ft per second. 7 43/60 seconds in all

Jeff sold the pumpkins he grew for $7 each at the farmer’s market.

Question 1. Write an expression to represent the amount of money in dollars Jeff made selling the pumpkins. Tell what the variable in your expression represents Type below: _____________

Answer: 7p, where p is the number of pumpkins

Question 2. If Jeff sold 30 pumpkins, how much money did he make? $ ________

Answer: 210

Explanation: The expression is 7p p = 30 pumpkins 7 × 30 = 210 Thus Jeff sold 30 pumpkins for $210.

An architect is designing a building. Each floor will be 12 feet tall.

Question 3. Write an expression for the number of floors the building can have for a given building height. Tell what the variable in your expression represents. Type below: _____________

Answer: The expression for the number of floors is h/12, where h is the height of the building.

Question 4. If the architect is designing a building that is 132 feet tall, how many floors can be built? ________ floors

Answer: 11 floors

Explanation: Given the height of the building is 132 feet Substitute h in the above expression h/12 = 132/12 = 11 floors Thus 11 floors can be built.

Write an algebraic expression for each word expression. Then evaluate the expression for these values of the variable: 1, 6, 13.5.

Question 5. the quotient of 300 and the sum of b and 24 Type below: _____________

Answer: 300 ÷ (b + 24)

Explanation: For b = 1 300 ÷ (b + 24) = 300 ÷ (1 + 24) 300 ÷ 25 = 12 Thus 300 ÷ (b + 24) when b = 1 is 12. For b = 6 300 ÷ (b + 24) = 300 ÷ (6 + 24) 300 ÷ 30 = 10 Thus 300 ÷ (b + 24) when b = 6 is 10. For b = 13.5 300 ÷ (b + 24) = 300 ÷ (13.5 + 24) 300 ÷ 37.5 = 8 300 ÷ (b + 24) when b = 13.5 is 8.

Question 6. 13 more than the product of m and 5 Type below: _____________

Answer: 13 + 5m

Explanation: For m = 1 13 + 5m = 13 + 5(1) = 13 + 6 = 19 For m = 6 13 + 5m = 13 + 5(6) = 13 + 30 = 43 For m = 13.5 13 + 5m = 13 + 5(13.5) = 13 + 67.5 = 80.5

Question 7. In the town of Pleasant Hill, there is an average of 16 sunny days each month. Write an expression to represent the approximate number of sunny days for any number of months. Tell what the variable represents. Type below: _____________

Answer: 16m, m for months

Explanation: In the town of Pleasant Hill, there is an average of 16 sunny days each month. Write an expression to represent the approximate number of sunny days for any number of months. we have to multiply the number of months with 16 The expression will be 16 times of m = 16m

Question 8. How many sunny days can a resident of Pleasant Hill expect to have in 9 months? ________ days

Answer: 144 days

Explanation: The expression to represent the approximate number of sunny days for any number of months is 16m m = 9 Substitute the value of m in the expression. 16m = 16 × 9 = 144 days

Question 9. Describe a situation in which a variable could be used to represent any whole number greater than 0. Type below: _____________

Answer: To represent the number of people any answer can be accepted.

Question 1. Oliver drives 45 miles per hour. Write an expression that represents the distance in miles he will travel for h hours driven. Type below: _____________

Answer: 45h

Explanation: It is given that Oliver drives 45 miles per hour. Let the number of hours he drove be h. The distance is the product of speed and time. The distance travel by Oliver is defined by the expression is 45h.

Question 2. Socks cost $5 per pair. The expression 5p represents the cost in dollars of p pairs of socks. Why must p be a whole number? Type below: _____________

Answer: p must be a whole number because in almost 100% of all stores it is not allowed to buy a single sock, you must always buy a pair of socks.

Question 3. Sterling silver consists of 92.5% silver and 7.5% copper. What decimal represents the portion of the silver in sterling silver? ________

Answer: 0.925

Explanation: If Sterling silver is 92.5% silver, that means it has 92.5/100 * 100% silver The fraction 92.5/100 can be simplified by just moving the decimal 2 places to the left: 92.5/100 = .925

Question 4. How many pints are equivalent to 3 gallons? ________ pints

Explanation: Convert from gallons to pints. 1 gallon = 8 pints 3 gallons = 3 × 8 pints = 24 pints 24 pints are equivalent to 3 gallons.

Question 5. Which operation should be done first to evaluate 10 + (66 – 6 2 )? Type below: _____________

Answer: Square 6

Question 6. Evaluate the algebraic expression h(m + n) ÷ 2 for h = 4, m = 5, and n = 6. ________

Explanation: Given the expression h(m + n) ÷ 2 h = 4 m = 5 n = 6 h(m + n) ÷ 2 = 4 (5 + 6) ÷ 2 4 (11) ÷ 2 = 44 ÷ 2 = 22 h(m + n) ÷ 2 = 22

Question 1. Museum admission costs $7, and tickets to the mammoth exhibit cost $5. The expression 7p + 5p represents the cost in dollars for p people to visit the museum and attend the exhibit. Simplify the expression by combining like terms. Type below: _____________

Answer: 12p

7p+5p When you combine like terms, you just add all the terms that have the same variable so you get 7p + 5p = 12p

Question 2. What if the cost of tickets to the exhibit was reduced to $3? Write an expression for the new cost in dollars for p people to visit the museum and attend the exhibit. Then, simplify the expression by combining like terms. Type below: _____________

Answer: 10p

Explanation: Museum admission costs $7, and tickets to the mammoth exhibit cost $5. The expression 7p + 5p represents the cost in dollars for p people to visit the museum and attend the exhibit. The cost of tickets to the mammoth exhibit is $5. If it is reduced to $3 then the cost will be $5 – $2 = $3 12p – 2p = 10p

Question 3. A store receives tomatoes in boxes of 40 tomatoes each. About 4 tomatoes per box cannot be sold due to damage. The expression 40b − 4b gives the number of tomatoes that the store can sell from a shipment of b boxes. Simplify the expression by combining like terms. Type below: _____________

Answer: 36b

Explanation: Given, A store receives tomatoes in boxes of 40 tomatoes each. About 4 tomatoes per box cannot be sold due to damage. The expression 40b − 4b gives the number of tomatoes that the store can sell from a shipment of b boxes. Subtract 40b and 4b 40b – 4b = 36b

Question 4. Each cheerleading uniform includes a shirt and a skirt. The shirts cost $12 each, and skirts cost $18 each. The expression 12u + 18u represents the cost in dollars of buying u uniforms. Simplify the expression by combining like terms. Type below: _____________

Answer: 30u

Explanation: The expression 12u + 18u represents the cost in dollars of buying u uniforms. 12u and 18u are the like terms. So add the two terms 12u + 18u = 30u

Question 5. A shop sells vases holding 9 red roses and 6 white roses. The expression 9v + 6v represents the total number of roses needed for v vases. Simplify the expression by combining like terms. Type below: _____________

Answer: 15v

Explanation: A shop sells vases holding 9 red roses and 6 white roses. The expression 9v + 6v represents the total number of roses needed for v vases. The like terms are 9v and 6v 9v + 6v = 15v

Question 6. Marco received a gift card. He used it to buy 2 bike lights for $10.50 each. Then he bought a handlebar bag for $18.25. After these purchases, he had $0.75 left on the card. How much money was on the gift card when Marco received it? $ _______

Answer: Marco received a gift card. He used it to buy 2 bike lights for $10.50 each. Then he bought a handlebar bag for $18.25. After these purchases, he had $0.75 left on the card. Add total amount = 2 × $10.50 + $18.25 + $0.75 $21 + $19 = $40 $40 was on the gift card when Marco received it.

Question 7. Lydia collects shells. She has 24 sea snail shells, 16 conch shells, and 32 scallop shells. She wants to display the shells in equal rows, with only one type of shell in each row. What is the greatest number of shells Lydia can put in each row? _______ shells

Answer: 8 shells

Explanation: Lydia collects shells. She has 24 sea snail shells, 16 conch shells, and 32 scallop shells. She wants to display the shells in equal rows, with only one type of shell in each row. The possible shells in equal rows are 8 because 16, 24, and 32 are the multiples of 8. Thus the greatest number of shells Lydia can put in each row is 8.

Question 8. The three sides of a triangle measure 3x + 6 inches, 5x inches, and 6x inches. Write an expression for the perimeter of the triangle in inches. Then simplify the expression by combining like terms. Type below: _____________

Answer: Perimeter of the triangle = a + b + c Let a = 3x + 6 inches b = 5x inches c = 6x inches P = a + b + c P = 3x + 6 + 5x + 6x Combine the like terms 3x, 5x, 6x P = 14x + 6 Thus the perimeter of the triangle is 14x + 6.

Question 9. Verify the Reasoning of Others Karina states that you can simplify the expression 20x + 4 by combining like terms to get 24x. Does Karina’s statement make sense? Explain. Type below: _____________

Answer: Karina’s statement doesn’t make sense. Because the 20x + 4 are not the like terms. We can add only the like terms. 20x + 4 ≠ 24x

Question 10. Vincent is ordering accessories for his surfboard. A set of fins costs $24 each and a leash costs $15. The shipping cost is $4 per order. The expression 24b + 15b + 4 can be used to find the cost in dollars of buying b fins and b leashes plus the cost of shipping. For numbers 10a–10c, select True or False for each statement. 10a. The terms are 24b, 15b and 4. 10b. The like terms are 24b and 15b. 10c. The simplified expression is 43b. 10a. _____________ 10b. _____________ 10c. _____________

Answer: 10a. True 10b. True 10c. False

Explanation: a. The terms of the expression 24b + 15b + 4 area 24b, 15b, 4. b. The terms are said to be like if they have the common variable. So, the common terms are 24b, 15b. c. Combine the like terms 24b and 15b 24b + 15b = 39b Thus the statement is false.

Read each problem and solve.

Question 1. A box of pens costs $3 and a box of markers costs $5. The expression 3p + 5p represents the cost in dollars to make p packages that include 1 box of pens and 1 box of markers. Simplify the expression by combining like terms. Type below: _____________

Answer: 3p + 5p = 8p

Explanation: A box of pens costs $3 and a box of markers costs $5. The expression 3p + 5p represents the cost in dollars to make p packages that include 1 box of pens and 1 box of markers. Adding the like terms 3p + 5p is 8p.

Question 2. Riley’s parents got a cell phone plan that has a $40 monthly fee for the first phone. For each extra phone, there is a $15 phone service charge and a $10 text service charge. The expression 40 + 15e + 10e represents the total phone bill in dollars, where e is the number of extra phones. Simplify the expression by combining like terms. Type below: _____________

Answer: 25e + 40

Explanation: Given that, Riley’s parents got a cell phone plan that has a $40 monthly fee for the first phone. For each extra phone, there is a $15 phone service charge and a $10 text service charge. The expression 40 + 15e + 10e represents the total phone bill in dollars, We have to combine the like terms here The like terms in the expression are 15e and 10e. That means 40 + 15e + 10e = 25e + 40

Question 3. A radio show lasts for h hours. For every 60 minutes of air time during the show, there are 8 minutes of commercials. The expression 60h – 8h represents the air time in minutes available for talk and music. Simplify the expression by combining like terms. Type below: _____________

Answer: 52h

Explanation: A radio show lasts for h hours. For every 60 minutes of air time during the show, there are 8 minutes of commercials. The expression 60h – 8h represents the air time in minutes available for talk and music. Now we have to Subtract the like terms 60h – 8h = 52h

Question 4. A sub shop sells a meal that includes an Italian sub for $6 and chips for $2. If a customer purchases more than 3 meals, he or she receives a $5 discount. The expression 6m + 2m – 5 shows the cost in dollars of the customer’s order for m meals, where m is greater than 3. Simplify the expression by combining like terms. Type below: _____________

Answer: 8m – 5

Explanation: The expression is 6m + 2m – 5 Now combine the like terms 6m + 2m – 5 = 8m – 5

Question 5. Explain how combining like terms is similar to adding and subtracting whole numbers. How are they different? Type below: _____________

Answer: It’s the same because you are adding or subtracting numbers but it’s different because they can only be added or subtracted if the variable attached is the same. There are no variables when adding/subtracting regular whole numbers.

Question 1. For each gym class, a school has 10 soccer balls and 6 volleyballs. All of the classes share 15 basketballs. The expression 10c + 6c + 15 represents the total number of balls the school has for c classes. What is a simpler form of the expression? Type below: _____________

Answer: 16c + 15

Explanation: For each gym class, a school has 10 soccer balls and 6 volleyballs. All of the classes share 15 basketballs. c represents classes. The expression is 10c + 6c + 15 Combine the like terms 10c and 6c Now add common terms 10c + 6c + 15 = 16c + 15

Question 2. A public library wants to place 4 magazines and 9 books on each display shelf. The expression 4s + 9s represents the total number of items that will be displayed on s shelves. Simplify this expression. Type below: _____________

Answer: 13s

Explanation: A public library wants to place 4 magazines and 9 books on each display shelf. The expression is 4s + 9s Combine the like terms 4s + 9s = 13s

Question 3. A bag has 8 bagels. Three of the bagels are cranberry. What percent of the bagels are cranberry? ________ %

Answer: 37.5%

Explanation: [/latex]\frac{3}{8}[/latex] = 0.375 0.375 × 100 = 37.5 % 37.5% of the bagels are cranberry.

Question 4. How many kilograms are equivalent to 3,200 grams? ________ kilograms

Answer: 3.2 kg

Explanation: Convert from grams into kilograms 1000 grams = 1kg 3200 grams = 3200 × 1/1000 kg = 3.2 kg 3.2 kilograms are equivalent to 3,200 grams.

Question 5. Toni earns $200 per week plus $5 for every magazine subscription that she sells. Write an expression that represents how much she will earn in dollars in a week in which she sells s subscriptions. Type below: _____________

Answer: 200 + 5s

Explanation: Toni earns $200 per week plus $5 for every magazine subscription that she sells. s represents subscriptions. 200 + 5 × s Thus the expression that represents how much she will earn in dollars in a week is 200 + 5s

Question 6. At a snack stand, drinks cost $1.50. Write an expression that could be used to find the total cost in dollars of d drinks. Type below: _____________

Answer: 1.5d

Explanation: At a snack stand, drinks cost $1.50. To find the total cost in dollars of d drinks we have to multiply 1.50 with d. 1.50 × d Thus the expression that could be used to find the total cost in dollars of d drinks is 1.5d

Use properties of operations to write an equivalent expression by combining like terms.

Question 1. \(3 \frac{7}{10} r-1 \frac{1}{5} r\) Type below: _____________

Answer: 2 \(frac{5}{10}\)r

Explanation: 3 \(frac{7}{10}\)r – 1 \(frac{1}{5}\)r 3 + \(frac{7}{10}\)r – 1 – \(frac{1}{5}\)r 3 – 1 = 2 \(frac{7}{10}\)r – \(frac{1}{5}\)r \(frac{7}{10}\)r – \(frac{2}{10}\)r = \(frac{5}{10}\)r \(3 \frac{7}{10} r-1 \frac{1}{5} r\) = 2 \(frac{5}{10}\)r

Question 2. 20a + 18 + 16a Type below: _____________

Answer: 36a + 18

Explanation: Combine  the like terms first 16a and 20a are like terms in the given expression. Add 16a and 20a 16a + 20a +18 = 36a + 18

Question 3. 7s + 8t + 10s + 12t Type below: _____________

Answer: 17s + 20t

Explanation: There are 4 terms in the expression they are 7s, 10s, 8t, 12t. Now combine the like terms 7s + 10s + 8t + 12t = 17s + 20t

Use the Distributive Property to write an equivalent expression.

Question 4. 8(h + 1.5) Type below: _____________

Answer: 8h + 12

Explanation: Here we have to use the distributive property for the above expression. 8(h + 1.5) = 8 × h + 1.5 × 8 = 8h + 12 Thus 8(h + 1.5) is 8h + 12.

Question 5. 4m + 4p Type below: _____________

Answer: 4(m + p)

Explanation: Here we have to take 4 as a common factor from the expression. 4m + 4p = 4 × m + 4 × p That implies 4 × (m + p)

Question 6. 3a + 9b Type below: _____________

Answer: 3(a + 3b)

Explanation: Let us take 4 as a common factor from the expression. 3a + 9b = 3 × a + 9 × b 3(a + 3b) 3a + 9b = 3(a + 3b)

Practice: Copy and Solve Use the Distributive Property to write an equivalent expression.

Question 7. 3.5(w + 7) Type below: _____________

Answer: 3.5w + 24.5

Explanation: Use the distributive property. Multiply within the parentheses. 3.5(w + 7) = 3.5 × w + 3.5 × 7 3.5w + 24.5 Thus 3.5(w + 7) = 3.5w + 24.5

Question 8. \(\frac{1}{2}\)(f + 10) Type below: _____________

Answer: \(\frac{1}{2}\)f + 5

Explanation: \(\frac{1}{2}\)(f + 10) Use the distributive property. Multiply within the parentheses. \(\frac{1}{2}\) × f + \(\frac{1}{2}\) × 10 = \(\frac{1}{2}\)f + 5 Thus \(\frac{1}{2}\)(f + 10) = \(\frac{1}{2}\)f + 5

Question 9. 4(3z + 2) Type below: _____________

Answer: 12z + 8

Explanation: Use the distributive property. Multiply within the parentheses. 4(3z + 2) = 4 × 3z + 4 × 2 = 12z + 8 So, 4(3z + 2) = 12z + 8

Question 10. 20b + 16c Type below: _____________

Answer: 4(5b + 4c)

Explanation: 20b + 16c Use the distributive property. Multiply within the parentheses. Take 4 as a common factor. 20b + 16c = 4 × 5b + 4 × 4c = 4 (5b + 4c) Thus the expression 20b + 16c = 4 (5b + 4c)

Question 11. 30d + 18 Type below: _____________

Answer: 6(5d + 3)

Explanation: 30 and 18 are the factors of 6. So, take 6 as a common factor. 30d + 18 = 6 × 5d + 6 × 3 6 (5d + 3) 30d + 18 = 6 (5d + 3)

Question 12. 24g − 8h Type below: _____________

Answer: 8(3g – h)

Explanation: Given the expression 24g − 8h 24 and 8 are the factors of 8. So, let us take 8 as a common factor. 24g − 8h = 8 × 3g – 8 × 1h = 8(3g – h)

Question 13. Write an Expression The lengths of the sides of a triangle are 3t, 2t + 1, and t + 4. Write an expression for the perimeter (sum of the lengths). Then, write an equivalent expression with 2 terms. Type below: _____________

Answer: 6t + 5

Explanation: Given that, The lengths of the sides of a triangle are 3t, 2t + 1, and t + 4. We know that the perimeter of the triangle is P = a + b + c P = 3t + 2t + 1 + t + 4 Combine the like terms. P = 6t + 5

Question 14. Use properties of operations to write an expression equivalent to the sum of the expressions 3(g + 5) and 2(3g − 6). Type below: _____________

Answer: 3(3g + 1)

Explanation: Given two expressions 3(g + 5) and 2(3g − 6). Use the distributive property to simplify the expressions. 3(g + 5) = 3 × g + 3 × 5 = 3g + 15 2(3g − 6) = 2 × 3g – 2 × 6 = 6g – 12 Add both the expressions and combine the like terms 3g + 15 + 6g – 12 = 9g + 3 = 3(3g + 1)

Question 15. Sense or Nonsense Peter and Jade are using what they know about properties to write an expression equivalent to 2 × (n + 6) + 3. Whose answer makes sense? Whose answer is nonsense? Explain your reasoning. Peter’s Work: Expression: 2 × (n + 6) + 3 Associative Property of Addition: 2 × n + (6 + 3) Add within parentheses: 2 × n + 9 Multiply: 2n + 9

Jade’s Work: Expression: 2 × (n + 6) + 3 Distributive Property: (2 × n) + (2 × 6) + 3 Multiply within parentheses: 2n + 12 + 3 Associative Property of Addition: 2n + (12 + 3) Add within parentheses: 2n + 15 For the answer that is nonsense, correct the statement. Type below: _____________

Answer: Jade’s Work makes sense. Peter’s Work makes non-sense because He must have multiplied n + 6 with 2 but he added 6 with 3. 2 × (n + 6) + 3 2 × n + 2 × 6 + 3 = 2n + 12 + 3 = 2n + 15

Answer: 6(z + 5) = 6 × z + 6 × 5 = 6z + 30 6z + 5z = z(6 + 5) = 11z 2 + 6z + 3 = 6z + 5

Question 1. 7h − 3h Type below: _____________

Explanation: Combine the like terms 7h and 3h are the common terms Now subtract 3h from 7h 7h – 3h = 4h

Question 2. 5x + 7 + 2x Type below: _____________

Answer: 7x + 7

Explanation: The given expression is 5x + 7 + 2x The common terms are 5x and 2x Combine the like terms 5x + 7 + 2x = 7x + 7

Question 3. 16 + 13p − 9p Type below: _____________

Answer: 16 + 4p

Combine the like terms for the above expressions. The like terms are 13p and 9p 16 + 13p − 9p = 16 + 4p

Question 4. y 2 + 13y − 8y Type below: _____________

Answer: y 2 + 5y

Explanation: The given expression is y 2 + 13y − 8y The like terms are 13y and 8y y 2 + 13y − 8y = y 2 + 5y

Question 5. 5(2h + 3) + 3h Type below: _____________

Answer: 13h + 15

Explanation: 5(2h + 3) + 3h = 10h + 15 + 3h The like terms are 10h and 3h 10h + 15 + 3h = 13h + 15

Question 6. 12 + 18n + 7 − 14n Type below: _____________

Answer: 19 + 4n

Explanation: The expression is 12 + 18n + 7 − 14n The like terms are 18n and 14n 12 + 18n + 7 − 14n = 19 + 4n

Question 7. 2(9 + 5k) Type below: _____________

Answer: 18 + 10k

Explanation: Use the Distributive property Multiply within the parentheses. 2(9 + 5k) = (2 × 9) + (2 × 5k) (2 × 9) + (2 × 5k) = 18 + 10k

Question 8. 4d + 8 Type below: _____________

Answer: 4(d + 2)

Explanation: Use the Distributive property Multiply within the parentheses. 4d + 8 = 4 × d + 4 × 2 The common term is 4. Take 4 as a common factor. 4d + 8 = 4 (d + 2)

Question 9. 21p + 35q Type below: _____________

Answer: 7(3p + 5q)

Explanation: Use the Distributive property Multiply within the parentheses. 7 × 3p + 7 × 5q The common term is 7. 7(3p + 5q) 21p + 35q = 7(3p + 5q)

Question 10. The expression 15n + 12n + 100 represents the total cost in dollars for skis, boots, and a lesson for n skiers. Simplify the expression 15n + 12n + 100. Then find the total cost for 8 skiers. Type below: _____________

Answer: 27n + 100, $316

Explanation: The terms that have n can be operated: 15n +12n + 100 = 27n +100. Then, we have that total cost = 27n +100 for n skiers. So, for 8 skiers we have total cost = 27(8) +100 = 216 + 100 = 316. Then, the total cost of 8 skiers is $316.

Question 11. Casey has n nickels. Megan has 4 times as many nickels as Casey has. Write an expression for the total number of nickels Casey and Megan have. Then simplify the expression. Type below: _____________

Answer: n + 4n; 5n

Explanation: Casey has n nickels. Megan has 4 times as many nickels as Casey has. Sum of n and 4n Add the common terms n and 4n. n + 4n = 5n

Question 12. Explain how you would use properties to write an expression equivalent to 7y + 4b – 3y. Type below: _____________

Answer: 1st you combine like terms so subtract 7y and 3y and you get 4y. So this is the final answer: 4y+4b.

Question 1. A ticket to a museum costs $8. A ticket to the dinosaur exhibit costs $5. The expression 8n + 5n represents the cost in dollars for n people to visit the museum and the exhibit. What is a simpler form of the expression 8n + 5n? Type below: _____________

Answer: 13n

Explanation: A ticket to a museum costs $8. A ticket to the dinosaur exhibit costs $5. The expression is the sum of 8n and 5n. Thus the simpler form of the expression is 8n + 5n = 13n

Question 2. What is an expression that is equivalent to 3(2p – 3)? Type below: _____________

Answer: 6p – 9

Explanation: Use the distributive property to find the equivalent expression. 3(2p – 3) = 3 × 2p – 3 × 3 = 6p – 9 Thus the expression that is equivalent to 3(2p – 3) is 6p – 9.

Question 3. A Mexican restaurant received 60 take-out orders. The manager found that 60% of the orders were for tacos and 25% of the orders were for burritos. How many orders were for other items? ______ orders

Answer: 9 orders

Explanation: Given, A Mexican restaurant received 60 take-out orders. The manager found that 60% of the orders were for tacos and 25% of the orders were for burritos. The answer is 9 because 25% of 60 is 15 plus 60% of 60 is 36 so 36+15=51 and 60-51=9 Thus 9 orders were for other items.

Question 4. The area of a rectangular field is 1,710 square feet. The length of the field is 45 feet. What is the width of the field? ______ feet

Answer: 38 feet

Explanation: The area of a rectangular field is 1,710 square feet. The length of the field is 45 feet. The width of the field is x feet A = l × w 1710 square feet = 45 feet × x x = 1710/45 = 38 feet Thus the width of the rectangular field is 38 feet.

Question 5. How many terms are in 2 + 4x + 7y? ______ terms

Explanation: Given expression 2 + 4x + 7y There are 3 terms in the expression 2, 4x, 7y.

Question 6. Boxes of cereal usually cost $4, but they are on sale for $1 off. A gallon of milk costs $3. The expression 4b – 1b + 3 can be used to find the cost in dollars of buying b boxes of cereal and a gallon of milk. Write the expression in a simpler form. Type below: _____________

Answer: 3b + 3

Explanation: Boxes of cereal usually cost $4, but they are on sale for $1 off. A gallon of milk costs $3. The expression is 4b – 1b + 3 Combine the like terms for the above expression. 4b – 1b + 3 = 3b + 3 = 3(b + 1)

Use properties of operations to determine whether the expressions are equivalent.

Question 1. 7k + 4 + 2k and 4 + 9k The expressions are _____________

Answer: equivalent

Explanation: 7k + 4 + 2k Combine the like terms 7k and 2k Add the like terms 7k + 2k + 4 = 9k + 4 9k + 4 and 4 + 9k are equivalent.

Question 2. 9a × 3 and 12a The expressions are _____________

Answer: not equivalent

Explanation: Multiply 9a with 3. 9a × 3 = 27a 27a and 12a are not equivalent. Thus the expressions are not equivalent.

Question 3. 8p + 0 and 8p × 0 The expressions are ______

Explanation: 8p + 0 = 8p 8p × 0 = 0 8p and 0 are not equivalent. The expressions 8p + 0 and 8p × 0 are not equivalent.

Question 4. 5(a + b) and (5a + 2b) + 3b The expressions are _____________

Explanation: 5(a + b) = 5a + 5b (5a + 2b) + 3b The like terms are 5a and 2b, 3b Add the combine terms 5a + 2b + 3b = 5a + 5b Thus the expressions 5(a + b) and (5a + 2b) + 3b are equivalent.

Question 5. 3(v + 2) + 7v and 16v The expressions are _____________

Explanation: 3(v + 2) + 7v Combine the like terms 3v and 7v 3(v + 2) + 7v = 3v + 6 + 7v = 10v + 6 The expressions 10v + 6 and 16v are not equivalent.

Question 6. 14h + (17 + 11h) and 25h + 17 The expressions are _____________

Explanation: 14h + (17 + 11h) Combine the like terms 14h and 11h. 14h + 17 + 11h = 25h + 17 The expressions 14h + (17 + 11h) and 25h + 17 are equivalent.

Question 7. 4b × 7 and 28b The expressions are _____________

Explanation: Multiply 4b with 7. 4b × 7 = 28b The expressions 4b × 7 and 28b are equivalent.

Question 8. Each case of dog food contains c cans. Each case of cat food contains 12 cans. Four students wrote the expressions below for the number of cans in 6 cases of dog food and 1 case of cat food. Which of the expressions are correct? 6c + 12     6c × 12      6(c + 2)      (2c + 4) × 3 Type below: _____________

Answer: The correct expressions are 6c + 12, 6(c + 2), (2c + 4) × 3 6(c + 2) is the distributive form of the expression.

Question 9. Marcus bought 4 packets of baseball cards and 4 packets of animal cards. Write an algebraic expression for the total number of cards Marcus bought. Type below: _____________

Answer: 4a + 4b

Explanation: Marcus bought 4 packets of baseball cards and 4 packets of animal cards. b represents the number per packet Multiply 4 with b 4 × b = 4b a represents the number per packet of animal cards. Multiply 4 with a. 4 × a = 4a Therefore the algebraic expression for the total number of cards Marcus bought is the sum of 4a and 4b. The expression is 4a + 4b

Question 10. Make Arguments Is the expression for the number of cards Marcus bought equivalent to 4(a + b)? Justify your answer. Type below: _____________

Answer: Yes Use the distributive property to simplify the expression 4a + 4b. Take 4 as the common factor for the expression 4a + 4b. 4a + 4b = 4(a + b)

Question 11. Angelica buys 3 packets of movie cards and 6 packets of cartoon cards and adds these to the 3 packets of movie cards she already has. Write three equivalent algebraic expressions for the number of cards Angelica has now Type below: _____________

Answer: 3m + 6c + 3m

Explanation: Angelica buys 3 packets of movie cards and 6 packets of cartoon cards and adds these to the 3 packets of movie cards she already has. The expression for 3 packets of movie cards is 3m The expression for 6 packets of cartoon cards is 6c. Now we have to add 3m to the expression. 3m + 6c + 3m Thus the three equivalent algebraic expressions for the number of cards Angelica has now is 3m + 6c + 3m

Question 12. Select the expressions that are equivalent to 3(x + 2). Mark all that apply. Options: a. 3x + 6 b. 3x + 2 c. 5x d. x + 5

Answer: 3x + 6

Explanation: Use distributive property to solve the expression 3(x + 2). 3(x + 2) = 3 × x + 3 × 2 = 3x + 6 Thus the correct answer is option A.

Question 1. 2s + 13 + 15s and 17s + 13 The expressions are _____________

Explanation: 2s + 13 + 15s Combine the like terms 2s + 13 + 15s = 17s + 13 17s + 13 = 17s + 13 Thus the expressions 2s + 13 + 15s and 17s + 13 are equivalent.

Question 2. 5 × 7h and 35h The expressions are _____________

Explanation: 5 × 7h = 35h 35h = 35h The expressions 5 × 7h and 35h are equivalent.

Question 3. 10 + 8v − 3v and 18 − 3v The expressions are _____________

Explanation: Combine the like terms 8v and 3v 10 + 8v − 3v = 10 + 5v 10 + 5v ≠ 18 − 3v Thus the expressions 10 + 8v − 3v and 18 − 3v are not equivalent.

Question 4. (9w × 0)−12 and 9w – 12 The expressions are _____________

Explanation: (9w × 0)−12 = 0 – 12 = – 12 – 12 ≠ 9w – 12 So, the expressions (9w × 0)−12 and 9w – 12 are not equivalent.

Question 5. 11(p + q) and 11p + (7q + 4q) The expressions are _____________

Explanation: 11(p + q) = 11p + 11q Combine the terms 7q and 4q 11p + (7q + 4q) = 11p + 11q = 11(p + q) So, the expressions 11(p + q) and 11p + (7q + 4q) are equivalent.

Question 6. 6(4b + 3d) and 24b + 3d The expressions are _____________

Explanation: 6(4b + 3d) = 24b + 18d 24b + 18d ≠ 24b + 3d So, the expressions 6(4b + 3d) and 24b + 3d are not equivalent.

Question 7. 14m + 9 − 6m and 8m + 9 The expressions are _____________

Explanation: Combine the like terms 14m and 6m 14m + 9 − 6m = 8m + 9 8m + 9 = 8m + 9 Thus the expressions are equivalent.

Question 8. (y × 1) + 2 and y + 2 The expressions are _____________

Explanation: (y × 1) + 2 = y + 2 y + 2 = y + 2 Thus the expressions (y × 1) + 2 and y + 2 are equivalent.

Question 9. 4 + 5(6t + 1) and 9 + 30t The expressions are _____________

Explanation: 4 + 5(6t + 1) = 4 + 30t + 5 = 9 + 30t 9 + 30t = 9 + 30t Thus the expressions 4 + 5(6t + 1) and 9 + 30t are equivalent.

Question 10. 9x + 0 + 10x and 19x + 1 The expressions are _____________

Explanation: 9x + 0 + 10x Combine the like terms 9x and 10x. 9x + 10x = 19x 19x ≠ 19x + 1 Thus the expressions 9x + 0 + 10x and 19x + 1 are not equivalent.

Question 11. 12c − 3c and 3(4c − 1) The expressions are _____________

Explanation: 12c − 3c Take 3 as a common factor. 3c(4 – 1) or 3 (4c – 1c) 3 (4c – 1c) ≠ 3(4c − 1) Thus the expressions 12c − 3c and 3(4c − 1) are not equivalent.

Question 12. 6a × 4 and 24a The expressions are _____________

Explanation: 6a × 4 = 24a 24a = 24a The expressions 6a × 4 and 24a are equivalent.

Question 13. Rachel needs to write 3 book reports with b pages and 3 science reports with s pages during the school year. Write an algebraic expression for the total number of pages Rachel will need to write. Type below: _____________

Answer: 3b + 3s

Explanation: Rachel needs to write 3 book reports with b pages and 3 science reports with s pages during the school year. Multiply 3 book reports with b pages = 3b. Multiply 3 science books with s pages = 3s. The algebraic expression for the total number of pages Rachel will need to write is 3b + 3s.

Question 14. Rachel’s friend Yassi has to write 3(b + s) pages for reports. Use properties of operations to determine whether this expression is equivalent to the expression for the number of pages Rachel has to write. This expression is _____________

Explanation: Rachel’s friend Yassi has to write 3(b + s) pages for reports. The equivalent expression of 3(b + s) = 3b + 3s

Question 15. Use properties of operations to show whether 7y + 7b + 3y and 7(y + b) + 3b are equivalent expressions. Explain your reasoning. Type below: _____________

Answer: Use Distributive property to simplify the expressions. The equivalent expression of 7y + 7b + 3y = 7(y + b) + 3y Thus 7y + 7b + 3y and 7(y + b) + 3b are equivalent.

Question 1. Ian had 4 cases of comic books and 6 adventure books. Each case holds c comic books. He gave 1 case of comic books to his friend. Write an expression that gives the total number of books Ian has left. Type below: _____________

Answer: 3c + 6

Explanation: Ian had 4 cases of comic books and 6 adventure books. Each case holds c comic books. He gave 1 case of comic books to his friend. 4c + 6 – 1c Combine the like terms 3c + 6

Question 2. In May, Xia made 5 flower planters with f flowers in each planter. In June, she made 8 flower planters with f flowers in each planter. Write an expression in the simplest form that gives the number of flowers Xia has in the planters. Type below: _____________

Answer: 13f

Explanation: In May, Xia made 5 flower planters with f flowers in each planter. The expression is 5f In June, she made 8 flower planters with f flowers in each planter. The expression is 8f. Sum of 5f and 8f is 8f + 5f = 13f

Question 3. Keisha wants to read for 90 minutes. So far, she has read 30% of her goal. How much longer does she need to read to reach her goal? ________ minutes

Answer: 63 min

Explanation: Keisha wants to read for 90 minutes. So far, she has read 30% of her goal. 30% = 30/100 = 0.3 Multiply 90 with 0.3 90 × 0.3 = 27 Subtract 27 from 90 90 – 27 = 63 She needs to read 63 minutes to reach her goal.

Question 4. Marvyn travels 105 miles on his scooter. He travels for 3 hours. What is his average speed? ________ miles per hour

Answer: 35 miles per hour

Explanation: Divide the number of miles by hours traveled. Average speed = 105 miles/3 hours = 35 miles per hour Thus the average speed is 35 miles per hour.

Question 5. The expression 5(F − 32) ÷ 9 gives the Celsius temperature for a Fahrenheit temperature of F degrees. The noon Fahrenheit temperature in Centerville was 86 degrees. What was the temperature in degrees Celsius? ________ degrees Celsius

Answer: 30 degrees Celsius

Explanation: The expression is 5(F − 32) ÷ 9 F = 86 degrees Substitute F in the above expression. 5(86 − 32) ÷ 9 = 5(54) ÷ 9 270 ÷ 9 = 30 The temperature is 30 degrees Celsius

Question 6. At the library book sale, hardcover books sell for $4 and paperbacks sell for $2. The expression 4b + 2b represents the total cost for b hardcover books and b paperbacks. Write a simpler expression that is equivalent to 4b + 2b. Type below: _____________

Explanation: Given expression is 4b + 2b The terms are 4b and 2b Now combine the like terms That means 4b + 2b = 6b

Question 1. Use exponents to rewrite the expression. 3 × 3 × 3 × 3 × 5 × 5 Type below: _____________

Answer: 3 4 × 5 2

Explanation: 3 is a repeated factor. The number 3 is repeated four times. 5 is a repeated factor. The number 5 is repeated two times. The exponential form of 3 × 3 × 3 × 3 × 5 × 5 is 3 4 × 5 2

Question 2. A plumber charges $10 for transportation and $55 per hour for repairs. Write an expression that can be used to find the cost in dollars for a repair that takes h hours. Type below: _____________

Answer: 10 + 55h

Explanation: A plumber charges $10 for transportation and $55 per hour for repairs. Multiply 55 with an hour Sum of 10 and product of 55 and h. The expression is 10 + 55h.

Question 3. Ellen is 2 years older than her brother Luke. Let k represent Luke’s age. Identify the expression that can be used to find Ellen’s age. Options: a. k−2 b. k+2 c. 2k d. \(\frac{k}{2}\)

Answer: k+2

Explanation: Given, Ellen is 2 years older than her brother Luke. Let k represent Luke’s age. Older is nothing but more so we have to add 2 years to k. That means k + 2. Thus the correct answer is option B.

Question 4. Write 4 3 using repeated multiplication. Then find the value of 4 3 . ________

Answer: 4 3 = 4 × 4 × 4 = 64 The value of 4 3 is 64.

Question 5. Jasmine is buying beans. She bought r pounds of red beans that cost $3 per pound and b pounds of black beans that cost $2 per pound. The total amount of her purchase is given by the expression 3r + 2b. Select the terms of the expression. Mark all that apply Options: a. 2 b. 2b c. 3 d. 3r

Answer: B, D

Explanation: The expression is 3r + 2b The terms of the expressions are 3r and 2b. Thus the correct answers are B and D.

Question 6. Choose the number that makes the sentence true. The formula V= s 3 gives the volume V of a cube with side length s. The volume of a cube that has a side length of 8 inches inches is _____________ cubed

Answer: 512

Explanation: Use the formula V= s 3 s = 8 V = 8 3 = 8 × 8 × 8 = 512

Question 7. Liang is ordering new chairs and cushions for his dining room table. A new chair costs $88 and a new cushion costs $12. Shipping costs $34. The expression 88c + 12c + 34 gives the total cost for buying c sets of chairs and cushions. Simplify the expression by combining like terms. Type below: _____________

Answer: 100c + 34

Explanation: Liang is ordering new chairs and cushions for his dining room table. A new chair costs $88 and a new cushion costs $12. Shipping costs $34. The expression is 88c + 12c + 34. Combine the like terms 88c + 12c + 34 = 100c + 34

Question 8. Mr. Ruiz writes the expression 5 × (2 + 1) 2 ÷ 3 on the board. Chelsea says the first step is to evaluate 1 2 . Explain Chelsea’s mistake. Then, evaluate the expression _____________

Answer: She should have done what was in the parentheses (2 + 1) and then the exponent 3 2 = 9 5 × (2 + 1) 2 ÷ 3 = 5 × 9 ÷ 3 5 × 3 = 15

Answer: The expression is 7m Replace m = 4 with m 7m = 7 × 4 = 28

Question 11. Logan works at a florist. He earns $600 per week plus $5 for each floral arrangement he delivers. Write an expression that gives the amount in dollars that Logan earns for delivering f floral arrangements. Use the expression to find the amount Logan will earn if he delivers 45 floral arrangements in one week. Show your work. $ ________

Answer: $825

Explanation: Logan works at a florist. He earns $600 per week plus $5 for each floral arrangement he delivers. Write an expression that gives the amount in dollars that Logan earns for delivering f floral arrangements. The expression is 600 + 5f f = 45 600 + 5f = 600 + 5(45) 600 + 225 = 825 Thus Logan earned $825 for delivering f floral arrangements.

Question 12. Choose the word that makes the sentence true. Dara wrote the expression 7 × (d + 4) in her notebook. She used the _____ Property to write the equivalent expression 7d + 28. Answer: Dara wrote the expression 7 × (d + 4) in her notebook. She used the Distributive Property to write the equivalent expression 7d + 28. Use the distributive property to simplify the expression. 7 × (d + 4) = 7d + 28

Question 13. Use properties of operations to determine whether 5(n + 1) + 2n and 7n + 1 are equivalent expressions. The expressions are _____________

Answer: 5n + 5 + 2n is Distributive property 5n + 2n + 5 is Commutative property of addition 7n + 5 combine like term 5n + 5 + 2n is equivalent to 7n + 5 Since it is not equivalent to 7n + 1, 7n + 5 is not equivalent to 7n.

Question 14. Alisha buys 5 boxes of peanut butter granola bars and 5 boxes of cinnamon granola bars. Let p represent the number of bars in a box of peanut butter granola bars and c represents the number of bars in a box of cinnamon granola bars. Jaira and Emma each write an expression that represents the total number of granola bars Alisha bought. Are the equivalent of the expression? Justify your answer Jaira 5p + 5c Emma 5(p + c) Type below: _____________

Answer: They are equivalent statements. 5p + 5c = 5(p + c) by the distributive property.

Question 15. Abe is 3 inches taller than Chen. Select the expressions that represent Abe’s height if Chen’s height is h inches. Mark all that apply Options: a. h−3 b. h+3 c. the sum of h and 3 d. the difference between h and 3

Answer: Abe is 3 inches taller than Chen. Let Chen’s height is h. The expression is the sum of Chen’s height and 3. So, the suitable answers are h + 3 and the sum of h and 3. Thus the correct answers are option B and C.

Answer: 3(k + 2) = 3k + 6 3k + 2k = 5k 2 + 6k + 3 = 6k + 5

Question 19. An online sporting goods store charges $12 for a pair of athletic socks. Shipping is $2 per order Part A Write an expression that Hana can use to find the total cost in dollars for ordering n pairs of socks. Type below: _____________

Answer: 12n + 2

Explanation: Let n represents a pair of socks. Multiply the price of pair of athletic socks with pair of socks = 12 × n Shipping is $2 per order The expression for the total cost in dollars for ordering n pairs of socks is 12n + 2

Question 19. Part B Hana orders 3 pairs of athletic socks and her friend, Charlie, order 2 pairs of athletic socks. What is the total cost, including shipping, for both orders? Show your work. $ ________

Answer: The cost of Hannah’s order is 12 × 3 + 2 = 36 + 2 = 38 The cost of Charlie’s order is 12 × 2 + 2 = 24 + 2 = 26 The total cost for both is 38 + 26 = 64

Question 20. Fernando simplifies the expression (6 + 2) 2 – 4 × 3. Part A Fernando shows his work on the board. Use numbers and words to explain his mistake. (6 + 2) 2 – 4 × 3 (6 + 4) – 4 × 3 10 − 4 × 3 6 × 3 18 Type below: _____________

Answer: Fernando did not use the correct order of operations. He should have added 6 and 2, then evaluate the exponent. He also subtracted before multiplying. He should have multiplied first.

Question 20. Part B Simplify the expression (6 + 2) 2 − 4 × 3 using the order of operations. _______

Explanation: (6 + 2) 2 − 4 × 3 First, add 6 and 2 and then subtract with 12. 8 2 – 4 × 3 = 64 – 12 = 52 (6 + 2) 2 − 4 × 3 = 52

Conclusion:

You can also get the solutions for the review test at the end of the chapter. So, test your knowledge by solving the problems in Mid Chapter Checkpoint and Review test. So, Download Go Math Grade 6 Answer Key Chapter 7 Exponents to score good marks in the exams. To get solutions for all Grade 6 chapter wise we suggest you follow our Go Math Answer Key page.

Share this:

Leave a comment cancel reply.

You must be logged in to post a comment.

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice

Measurement

• Factoring & prime factors

Proportions

• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

Download & Print From only $2.60

Sixth Grade Math Worksheets

Free grade 6 worksheets from k5 learning.

Our printable grade 6 math worksheets delve deeper into earlier grade math topics (4 operations, fractions, decimals, measurement, geometry) as well as introduce exponents, proportions, percents and integers .

Choose your grade 6 topic:

4 operations.

Place Value & Scientific Notation

Add & Subtract

Multiply & Divide

Decimals & Percents

Fractions to / from Decimals

Decimals - Add and Subtract

Decimals  - Multiply

Decimals - Divide

Add & Subtract Fractions

Multiply & Divide Fractions

Converting Fractions

Sample Grade 6 Math Worksheet

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

Join K5 to save time, skip ads and access more content. Learn More

• Forgot Password?

• 888-309-8227
• 732-384-0146

New User Registration

Forgot Password

Go Math! 6 Common Core Edition, Grade: 6 Publisher: Houghton Mifflin Harcourt

Go math 6 common core edition, title : go math 6 common core edition, publisher : houghton mifflin harcourt, isbn : 547587783, isbn-13 : 9780547587783, use the table below to find videos, mobile apps, worksheets and lessons that supplement go math 6 common core edition., textbook resources.

• Call us toll-free
• FAQs – Frequently Asked Questions
• Contact Lumos Learning – Proven Study Programs by Expert Teachers

Follow us: Lumos Learning -->

• 2024 © Lumos Learning
• Privacy Policy - Terms of Service - Disclaimers

PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc... Read More

PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc., the Partnership for the Assessment of Readiness for College and Careers, nor any state of the Union. Neither PARCC, Inc., nor The Partnership for the Assessment of Readiness for College and Careers, nor any member state has endorsed this product. No portion of any fees or charges paid for any products or services Lumos Learning offers will be paid or inure to the benefit of PARCC, Inc., or any state of the Union

SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not aff... Read More

SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not affiliated to Lumos Learning. The Regents of the University of California – Smarter Balanced Assessment Consortium, was not involved in the production of, and does not endorse these products or this site.

ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC, was not... Read More

ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC,was not involved in the production of, and does not endorse these products or this site.

Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the... Read More

Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the production of, and does not endorse these products or this site.

Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the... Read More

Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the production of, and does not endorse these products or this site.

Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved... Read More

Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved in the production of, and does not endorse these products or this site.

Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the prod... Read More

Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the production of, and does not endorse these products or this site.

Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved... Read More

Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved in the production of, and does not endorse these products or this site.

Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved... Read More

Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved in the production of, and does not endorse these products or this site.

Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved... Read More

Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved in the production of, and does not endorse these products or this site.

Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved... Read More

Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved in the production of, and does not endorse these products or this site.