explain presentation of statistical data classification

• Accountancy
• Business Studies
• Organisational Behaviour
• Human Resource Management
• Entrepreneurship
• CBSE Class 11 Statistics for Economics Notes

Chapter 1: Concept of Economics and Significance of Statistics in Economics

• Statistics for Economics | Functions, Importance, and Limitations

Chapter 2: Collection of Data

• Data Collection & Its Methods
• Sources of Data Collection | Primary and Secondary Sources
• Direct Personal Investigation: Meaning, Suitability, Merits, Demerits and Precautions
• Indirect Oral Investigation : Suitability, Merits, Demerits and Precautions
• Difference between Direct Personal Investigation and Indirect Oral Investigation
• Information from Local Source or Correspondents: Meaning, Suitability, Merits, and Demerits
• Questionnaires and Schedules Method of Data Collection
• Difference between Questionnaire and Schedule
• Qualities of a Good Questionnaire and types of Questions
• What are the Published Sources of Collecting Secondary Data?
• What Precautions should be taken before using Secondary Data?
• Two Important Sources of Secondary Data: Census of India and Reports & Publications of NSSO
• What is National Sample Survey Organisation (NSSO)?
• What is Census Method of Collecting Data?
• Sample Method of Collection of Data
• Methods of Sampling
• Father of Indian Census
• What makes a Sampling Data Reliable?
• Difference between Census Method and Sampling Method of Collecting Data
• What are Statistical Errors?

Chapter 3: Organisation of Data

• Organization of Data
• Objectives and Characteristics of Classification of Data

Classification of Data in Statistics | Meaning and Basis of Classification of Data

• Concept of Variable and Raw Data
• Types of Statistical Series
• Difference between Frequency Array and Frequency Distribution
• Types of Frequency Distribution

Chapter 4: Presentation of Data: Textual and Tabular

• Textual Presentation of Data: Meaning, Suitability, and Drawbacks
• Tabular Presentation of Data: Meaning, Objectives, Features and Merits
• Different Types of Tables
• Classification and Tabulation of Data

Chapter 5: Diagrammatic Presentation of Data

• Diagrammatic Presentation of Data: Meaning , Features, Guidelines, Advantages and Disadvantages
• Types of Diagrams
• Bar Graph | Meaning, Types, and Examples
• Pie Diagrams | Meaning, Example and Steps to Construct
• Histogram | Meaning, Example, Types and Steps to Draw
• Frequency Polygon | Meaning, Steps to Draw and Examples
• Ogive (Cumulative Frequency Curve) and its Types
• What is Arithmetic Line-Graph or Time-Series Graph?
• Diagrammatic and Graphic Presentation of Data

Chapter 6: Measures of Central Tendency: Arithmetic Mean

• Measures of Central Tendency in Statistics
• Arithmetic Mean: Meaning, Example, Types, Merits, and Demerits
• What is Simple Arithmetic Mean?
• Calculation of Mean in Individual Series | Formula of Mean
• Calculation of Mean in Discrete Series | Formula of Mean
• Calculation of Mean in Continuous Series | Formula of Mean
• Calculation of Arithmetic Mean in Special Cases
• Weighted Arithmetic Mean

Chapter 7: Measures of Central Tendency: Median and Mode

• Median(Measures of Central Tendency): Meaning, Formula, Merits, Demerits, and Examples
• Calculation of Median for Different Types of Statistical Series
• Calculation of Median in Individual Series | Formula of Median
• Calculation of Median in Discrete Series | Formula of Median
• Calculation of Median in Continuous Series | Formula of Median
• Graphical determination of Median
• Mode: Meaning, Formula, Merits, Demerits, and Examples
• Calculation of Mode in Individual Series | Formula of Mode
• Calculation of Mode in Discrete Series | Formula of Mode
• Grouping Method of Calculating Mode in Discrete Series | Formula of Mode
• Calculation of Mode in Continuous Series | Formula of Mode
• Calculation of Mode in Special Cases
• Calculation of Mode by Graphical Method
• Mean, Median and Mode| Comparison, Relationship and Calculation

Chapter 8: Measures of Dispersion

• Measures of Dispersion | Meaning, Absolute and Relative Measures of Dispersion
• Range | Meaning, Coefficient of Range, Merits and Demerits, Calculation of Range
• Calculation of Range and Coefficient of Range
• Interquartile Range and Quartile Deviation
• Partition Value | Quartiles, Deciles and Percentiles
• Quartile Deviation and Coefficient of Quartile Deviation: Meaning, Formula, Calculation, and Examples
• Quartile Deviation in Discrete Series | Formula, Calculation and Examples
• Quartile Deviation in Continuous Series | Formula, Calculation and Examples
• Mean Deviation: Coefficient of Mean Deviation, Merits, and Demerits
• Calculation of Mean Deviation for different types of Statistical Series
• Mean Deviation from Mean | Individual, Discrete, and Continuous Series
• Mean Deviation from Median | Individual, Discrete, and Continuous Series
• Standard Deviation: Meaning, Coefficient of Standard Deviation, Merits, and Demerits
• Standard Deviation in Individual Series
• Methods of Calculating Standard Deviation in Discrete Series
• Methods of calculation of Standard Deviation in frequency distribution series
• Combined Standard Deviation: Meaning, Formula, and Example
• How to calculate Variance?
• Coefficient of Variation: Meaning, Formula and Examples
• Lorenz Curveb : Meaning, Construction, and Application

Chapter 9: Correlation

• Correlation: Meaning, Significance, Types and Degree of Correlation
• Methods of measurements of Correlation
• Calculation of Correlation with Scattered Diagram
• Spearman's Rank Correlation Coefficient
• Karl Pearson's Coefficient of Correlation
• Karl Pearson's Coefficient of Correlation | Methods and Examples

Chapter 10: Index Number

• Index Number | Meaning, Characteristics, Uses and Limitations
• Methods of Construction of Index Number
• Unweighted or Simple Index Numbers: Meaning and Methods
• Methods of calculating Weighted Index Numbers
• Fisher's Index Number as an Ideal Method
• Fisher's Method of calculating Weighted Index Number
• Paasche's Method of calculating Weighted Index Number
• Laspeyre's Method of calculating Weighted Index Number
• Laspeyre's, Paasche's, and Fisher's Methods of Calculating Index Number
• Consumer Price Index (CPI) or Cost of Living Index Number: Construction of Consumer Price Index|Difficulties and Uses of Consumer Price Index
• Methods of Constructing Consumer Price Index (CPI)
• Wholesale Price Index (WPI) | Meaning, Uses, Merits, and Demerits
• Index Number of Industrial Production : Characteristics, Construction & Example
• Inflation and Index Number

Important Formulas in Statistics for Economics

• Important Formulas in Statistics for Economics | Class 11

What is Classification of Data?

For performing statistical analysis, various kinds of data are gathered by the investigator or analyst. The information gathered is usually in raw form which is difficult to analyze. To make the analysis meaningful and easy, the raw data is converted or classified into different categories based on their characteristics. This grouping of data into different categories or classes with similar or homogeneous characteristics is known as the Classification of Data . Each division or class of the gathered data is known as a Class. The different basis of classification of statistical information are Geographical, Chronological, Qualitative (Simple and Manifold), and Quantitative or Numerical.

For example, if an investigator wants to determine the poverty level of a state, he/she can do so by gathering the information of people of that state and then classifying them on the basis of their income, education, etc.

According to Conner , “Classification is the process of arranging things (either actually or notionally) in groups or classes according to their resemblances and affinities, and gives expression to the unity of attributes that may exist amongst a diversity of individuals.”

The main objectives of Classification of Data are as follows:

• Explain similarities and differences of data
• Simplify and condense data’s mass
• Facilitate comparisons
• Study the relationship
• Prepare data for tabular presentation
• Present a mental picture of the data

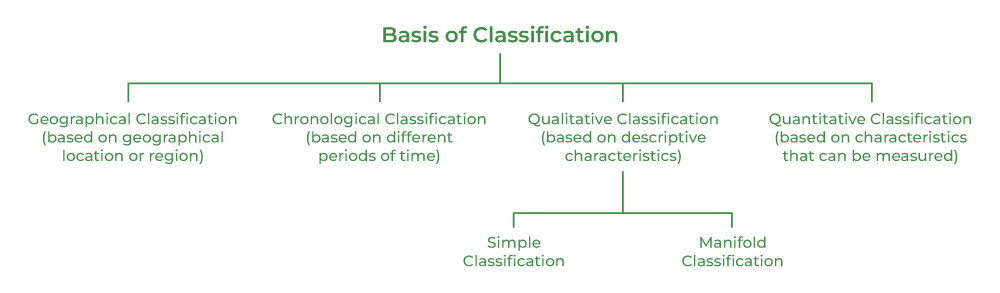
Basis of Classification of Data

The classification of statistical data is done after considering the scope, nature, and purpose of an investigation and is generally done on four bases; viz., geographical location, chronology, qualitative characteristics, and quantitative characteristics. 

1. Geographical Classification

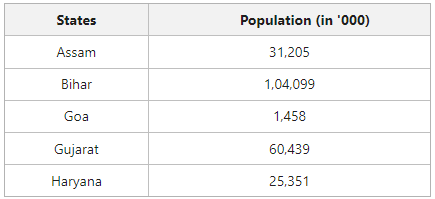
The classification of data on the basis of geographical location or region is known as Geographical or Spatial Classification. For example, presenting the population of different states of a country is done on the basis of geographical location or region. 

2. Chronological Classification

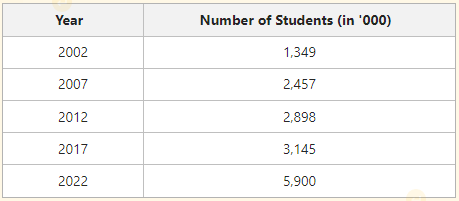
The classification of data with respect to different time periods is known as Chronological or Temporal Classification. For example, the number of students in a school in different years can be presented on the basis of a time period. 

3. Qualitative Classification

The classification of data on the basis of descriptive or qualitative characteristics like region, caste, sex, gender, education, etc., is known as Qualitative Classification. A qualitative classification can not be quantified and can be of two types; viz., Simple Classification and Manifold Classification. 

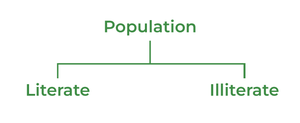
Simple Classification

When based on only one attribute, the given data is classified into two classes, which is known as Simple Classification . For example, when the population is divided into literate and illiterate, it is a simple classification. 

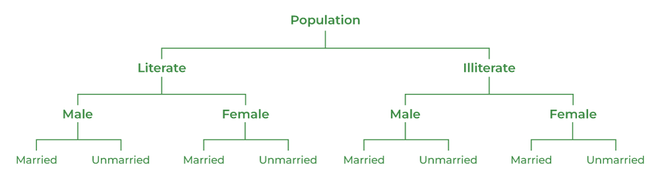
Manifold Classification

When based on more than one attribute, the given data is classified into different classes, and then sub-divided into more sub-classes, which is known as Manifold Classification. For example, when the population is divided into literate and illiterate, then sub-divided into male and female, and further sub-divided into married and unmarried, it is a manifold classification.

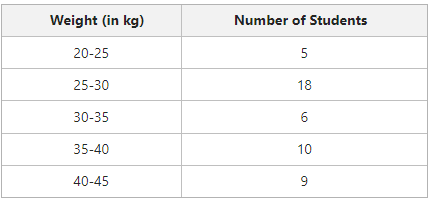
4. Quantitative Classification

The classification of data on the basis of the characteristics, such as age, height, weight, income, etc., that can be measured in quantity is known as Quantitative Classification. For example, the weight of students in a class can be classified as quantitative classification.

Please Login to comment...

Similar reads.

• Statistics for Economics

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.3: Presentation of Data

• Last updated
• Save as PDF
• Page ID 577

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• To learn two ways that data will be presented in the text.

In this book we will use two formats for presenting data sets. The first is a data list, which is an explicit listing of all the individual measurements, either as a display with space between the individual measurements, or in set notation with individual measurements separated by commas.

Example \(\PageIndex{1}\)

The data obtained by measuring the age of \(21\) randomly selected students enrolled in freshman courses at a university could be presented as the data list:

\[\begin{array}{cccccccccc}18 & 18 & 19 & 19 & 19 & 18 & 22 & 20 & 18 & 18 & 17 \\ 19 & 18 & 24 & 18 & 20 & 18 & 21 & 20 & 17 & 19 &\end{array} \nonumber \]

or in set notation as:

\[ \{18,18,19,19,19,18,22,20,18,18,17,19,18,24,18,20,18,21,20,17,19\} \nonumber \]

A data set can also be presented by means of a data frequency table, a table in which each distinct value \(x\) is listed in the first row and its frequency \(f\), which is the number of times the value \(x\) appears in the data set, is listed below it in the second row.

Example \(\PageIndex{2}\)

The data set of the previous example is represented by the data frequency table

\[\begin{array}{c|cccccc}x & 17 & 18 & 19 & 20 & 21 & 22 & 24 \\ \hline f & 2 & 8 & 5 & 3 & 1 & 1 & 1\end{array} \nonumber \]

The data frequency table is especially convenient when data sets are large and the number of distinct values is not too large.

Key Takeaway

• Data sets can be presented either by listing all the elements or by giving a table of values and frequencies.

1.1 Definitions of Statistics, Probability, and Key Terms

The science of statistics deals with the collection, analysis, interpretation, and presentation of data . We see and use data in our everyday lives.

Collaborative Exercise

In your classroom, try this exercise. Have class members write down the average time—in hours, to the nearest half-hour—they sleep per night. Your instructor will record the data. Then create a simple graph, called a dot plot, of the data. A dot plot consists of a number line and dots, or points, positioned above the number line. For example, consider the following data:

5, 5.5, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7, 7, 8, 8, 9.

The dot plot for this data would be as follows:

Does your dot plot look the same as or different from the example? Why? If you did the same example in an English class with the same number of students, do you think the results would be the same? Why or why not?

Where do your data appear to cluster? How might you interpret the clustering?

The questions above ask you to analyze and interpret your data. With this example, you have begun your study of statistics.

In this course, you will learn how to organize and summarize data. Organizing and summarizing data is called descriptive statistics . Two ways to summarize data are by graphing and by using numbers, for example, finding an average. After you have studied probability and probability distributions, you will use formal methods for drawing conclusions from good data. The formal methods are called inferential statistics . Statistical inference uses probability to determine how confident we can be that our conclusions are correct.

Effective interpretation of data, or inference, is based on good procedures for producing data and thoughtful examination of the data. You will encounter what will seem to be too many mathematical formulas for interpreting data. The goal of statistics is not to perform numerous calculations using the formulas, but to gain an understanding of your data. The calculations can be done using a calculator or a computer. The understanding must come from you. If you can thoroughly grasp the basics of statistics, you can be more confident in the decisions you make in life.

Statistical Models

Statistics, like all other branches of mathematics, uses mathematical models to describe phenomena that occur in the real world. Some mathematical models are deterministic. These models can be used when one value is precisely determined from another value. Examples of deterministic models are the quadratic equations that describe the acceleration of a car from rest or the differential equations that describe the transfer of heat from a stove to a pot. These models are quite accurate and can be used to answer questions and make predictions with a high degree of precision. Space agencies, for example, use deterministic models to predict the exact amount of thrust that a rocket needs to break away from Earth’s gravity and achieve orbit.

However, life is not always precise. While scientists can predict to the minute the time that the sun will rise, they cannot say precisely where a hurricane will make landfall. Statistical models can be used to predict life’s more uncertain situations. These special forms of mathematical models or functions are based on the idea that one value affects another value. Some statistical models are mathematical functions that are more precise—one set of values can predict or determine another set of values. Or some statistical models are mathematical functions in which a set of values do not precisely determine other values. Statistical models are very useful because they can describe the probability or likelihood of an event occurring and provide alternative outcomes if the event does not occur. For example, weather forecasts are examples of statistical models. Meteorologists cannot predict tomorrow’s weather with certainty. However, they often use statistical models to tell you how likely it is to rain at any given time, and you can prepare yourself based on this probability.

Probability

Probability is a mathematical tool used to study randomness. It deals with the chance of an event occurring. For example, if you toss a fair coin four times, the outcomes may not be two heads and two tails. However, if you toss the same coin 4,000 times, the outcomes will be close to half heads and half tails. The expected theoretical probability of heads in any one toss is 1 2 1 2 or .5. Even though the outcomes of a few repetitions are uncertain, there is a regular pattern of outcomes when there are many repetitions. After reading about the English statistician Karl Pearson who tossed a coin 24,000 times with a result of 12,012 heads, one of the authors tossed a coin 2,000 times. The results were 996 heads. The fraction 996 2,000 996 2,000 is equal to .498 which is very close to .5, the expected probability.

The theory of probability began with the study of games of chance such as poker. Predictions take the form of probabilities. To predict the likelihood of an earthquake, of rain, or whether you will get an A in this course, we use probabilities. Doctors use probability to determine the chance of a vaccination causing the disease the vaccination is supposed to prevent. A stockbroker uses probability to determine the rate of return on a client's investments.

In statistics, we generally want to study a population . You can think of a population as a collection of persons, things, or objects under study. To study the population, we select a sample . The idea of sampling is to select a portion, or subset, of the larger population and study that portion—the sample—to gain information about the population. Data are the result of sampling from a population.

Because it takes a lot of time and money to examine an entire population, sampling is a very practical technique. If you wished to compute the overall grade point average at your school, it would make sense to select a sample of students who attend the school. The data collected from the sample would be the students' grade point averages. In presidential elections, opinion poll samples of 1,000–2,000 people are taken. The opinion poll is supposed to represent the views of the people in the entire country. Manufacturers of canned carbonated drinks take samples to determine if a 16-ounce can contains 16 ounces of carbonated drink.

From the sample data, we can calculate a statistic. A statistic is a number that represents a property of the sample. For example, if we consider one math class as a sample of the population of all math classes, then the average number of points earned by students in that one math class at the end of the term is an example of a statistic. Since we do not have the data for all math classes, that statistic is our best estimate of the average for the entire population of math classes. If we happen to have data for all math classes, we can find the population parameter. A parameter is a numerical characteristic of the whole population that can be estimated by a statistic. Since we considered all math classes to be the population, then the average number of points earned per student over all the math classes is an example of a parameter.

One of the main concerns in the field of statistics is how accurately a statistic estimates a parameter. In order to have an accurate sample, it must contain the characteristics of the population in order to be a representative sample . We are interested in both the sample statistic and the population parameter in inferential statistics. In a later chapter, we will use the sample statistic to test the validity of the established population parameter.

A variable , usually notated by capital letters such as X and Y , is a characteristic or measurement that can be determined for each member of a population. Variables may describe values like weight in pounds or favorite subject in school. Numerical variables take on values with equal units such as weight in pounds and time in hours. Categorical variables place the person or thing into a category. If we let X equal the number of points earned by one math student at the end of a term, then X is a numerical variable. If we let Y be a person's party affiliation, then some examples of Y include Republican, Democrat, and Independent. Y is a categorical variable. We could do some math with values of X —calculate the average number of points earned, for example—but it makes no sense to do math with values of Y —calculating an average party affiliation makes no sense.

Data are the actual values of the variable. They may be numbers or they may be words. Datum is a single value.

Two words that come up often in statistics are mean and proportion . If you were to take three exams in your math classes and obtain scores of 86, 75, and 92, you would calculate your mean score by adding the three exam scores and dividing by three. Your mean score would be 84.3 to one decimal place. If, in your math class, there are 40 students and 22 are males and 18 females, then the proportion of men students is 22 40 22 40 and the proportion of women students is 18 40 18 40 . Mean and proportion are discussed in more detail in later chapters.

The words mean and average are often used interchangeably. In this book, we use the term arithmetic mean for mean.

Example 1.1

Determine what the population, sample, parameter, statistic, variable, and data referred to in the following study.

We want to know the mean amount of extracurricular activities in which high school students participate. We randomly surveyed 100 high school students. Three of those students were in 2, 5, and 7 extracurricular activities, respectively.

The population is all high school students.

The sample is the 100 high school students interviewed.

The parameter is the mean amount of extracurricular activities in which all high school students participate.

The statistic is the mean amount of extracurricular activities in which the sample of high school students participate.

The variable could be the amount of extracurricular activities by one high school student. Let X = the amount of extracurricular activities by one high school student.

The data are the number of extracurricular activities in which the high school students participate. Examples of the data are 2, 5, 7.

Find an article online or in a newspaper or magazine that refers to a statistical study or poll. Identify what each of the key terms—population, sample, parameter, statistic, variable, and data—refers to in the study mentioned in the article. Does the article use the key terms correctly?

Example 1.2

Determine what the key terms refer to in the following study.

A study was conducted at a local high school to analyze the average cumulative GPAs of students who graduated last year. Fill in the letter of the phrase that best describes each of the items below.

1. Population ____ 2. Statistic ____ 3. Parameter ____ 4. Sample ____ 5. Variable ____ 6. Data ____

• a) all students who attended the high school last year
• b) the cumulative GPA of one student who graduated from the high school last year
• c) 3.65, 2.80, 1.50, 3.90
• d) a group of students who graduated from the high school last year, randomly selected
• e) the average cumulative GPA of students who graduated from the high school last year
• f) all students who graduated from the high school last year
• g) the average cumulative GPA of students in the study who graduated from the high school last year

1. f ; 2. g ; 3. e ; 4. d ; 5. b ; 6. c

Example 1.3

As part of a study designed to test the safety of automobiles, the National Transportation Safety Board collected and reviewed data about the effects of an automobile crash on test dummies (The Data and Story Library, n.d.). Here is the criterion they used.

Cars with dummies in the front seats were crashed into a wall at a speed of 35 miles per hour. We want to know the proportion of dummies in the driver’s seat that would have had head injuries, if they had been actual drivers. We start with a simple random sample of 75 cars.

The population is all cars containing dummies in the front seat.

The sample is the 75 cars, selected by a simple random sample.

The parameter is the proportion of driver dummies—if they had been real people—who would have suffered head injuries in the population.

The statistic is proportion of driver dummies—if they had been real people—who would have suffered head injuries in the sample.

The variable X = whether driver dummies—if they had been real people—would have suffered head injuries.

The data are either: yes, had head injury, or no, did not.

Example 1.4

An insurance company would like to determine the proportion of all medical doctors who have been involved in one or more malpractice lawsuits. The company selects 500 doctors at random from a professional directory and determines the number in the sample who have been involved in a malpractice lawsuit.

The population is all medical doctors listed in the professional directory.

The parameter is the proportion of medical doctors who have been involved in one or more malpractice suits in the population.

The sample is the 500 doctors selected at random from the professional directory.

The statistic is the proportion of medical doctors who have been involved in one or more malpractice suits in the sample.

The variable X records whether a doctor has or has not been involved in a malpractice suit.

The data are either: yes, was involved in one or more malpractice lawsuits; or no, was not.

Do the following exercise collaboratively with up to four people per group. Find a population, a sample, the parameter, the statistic, a variable, and data for the following study: You want to determine the average—mean—number of glasses of milk college students drink per day. Suppose yesterday, in your English class, you asked five students how many glasses of milk they drank the day before. The answers were 1, 0, 1, 3, and 4 glasses of milk.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/1-1-definitions-of-statistics-probability-and-key-terms

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

A Primer of Statistical Methods for Classification

• First Online: 29 June 2019

Cite this chapter

• Rajarshi Dey 3 &
• Madhuri S. Mulekar 3  

Part of the book series: STEAM-H: Science, Technology, Engineering, Agriculture, Mathematics & Health ((STEAM))

1094 Accesses

Classification techniques are commonly used by scientists and businesses alike for decision-making. They involve assignment of objects (or information) to pre-defined groups (or classes) using certain known characteristics such as classifying emails as real or spam using information in subject field of email. Here we describe two soft and four hard classifiers popularly used by statisticians in practice. To demonstrate their applications, two simulated and three real-life datasets are used to develop classification criteria. The results of different classifiers are compared using misclassification rate and an uncertainty measure.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Agresti, A.: Categorical Data Analysis. Wiley, Hoboken (2013)

MATH   Google Scholar  

Aizerman, M.A., Braverman, E.M., Rozonoer, L.I.: Theoretical foundations of the potential function method in pattern recognition learning. Autom. Remote. Control. 25 , 821–837 (1964)

Anderson, E.: The irises of the Gaspe Peninsula. Bull. Am. Iris Soc. 59 , 2–5 (1935)

Google Scholar  

Asparoukhov, O.K., Krzanowski, W.J.: A comparison of discriminant procedures for binary variables. Comput. Stat. Data Anal. 38 , 139–160 (2001)

Article   MathSciNet   MATH   Google Scholar  

Bayes, T.: An essay towards solving a problem in the doctrine of chances. Philos. Trans. 53 , 370–418 (1763)

Berkson, J.: Applications of the logistic function to bioassay. J. Am. Stat. Assoc. 9 , 357–365 (1944)

Bhatt, R.B., Sharma, G., Dhall, A., Chaudhury, S.: Efficient Skin Region Segmentation Using Low Complexity Fuzzy Decision Tree Model. IEEE-Indicon, Ahmedabad (2009)

Book   Google Scholar  

Bhattacharya, S., Sanjeev, J., Tharakunnel, K., Westland, J.C.: Data mining for credit card fraud: a comparative study. Decis. Support. Syst. 50 , 602–613 (2011)

Article   Google Scholar  

Boser, B.E., Guyon, I.M., Vapnik, V.N.: A training algorithm for optimal margin classifiers. In: Proceedings of the Fifth Annual Workshop on Computational Learning Theory – COLT ’92. p. 144 (1992)

Bottou, L., Cortes, C., Denker, J.S., Drucker, L., Guyon, I., Jackel, L., LeCun, Y., Muller, U.A., Sackinger, E., Simard, P., Vapnik, V.N.: Comparison of classifier methods: a case study in handwriting digit recognition. Int. Conf. Pattern Recognit. 2 , 77–87 (1994)

Breiman, L.: Bagging predictors. Mach. Learn. 24 (2), 123–140 (1996)

Breiman, L.: Random forests. Mach. Learn. 45 , 5–32 (2001)

Article   MATH   Google Scholar  

Breiman, L., Friedman, J.H., Olshen, R.A., Stone, C.J.: Classification and Regression Trees. Wadsworth, Belmont (1984)

Burrus, C.S., Barreto, J.A., Selesnick, I.W.: Iterative reweighted least squares design of FIR filters. IEEE Trans. Signal Process. 42 (11), 2922–2936 (1994)

Chipman, H.A., George, E.I., McCulloch, R.E.: Bayesian CART model search. J. Am. Stat. Assoc. 93 , 935–948 (1998)

Chomboon, K., Pasapichi, C., Pongsakorn, T., Kerdprasop, K., Kerdprasop, N.: An empirical study of distance mreics for K-nearest neighbor algorithm. 3 rd International Conference on Industrial Application Engineering, 280–285 (2015)

Cortes, C., Vapnik, V.: Support-vector networks. Mach. Learn. 20 (3), 273–297 (1995)

Cover, T., Hart, P.: Nearest neighbor pattern classification. IEEE Trans. Inf. Theory. 13 (1), 21–27 (1967)

Cox, D.R.: Analysis of Binary Data. Chapman and Hall, London (1969)

Cramer, J.S.: The origins and development of the logit model. In: Cramer, J.S. (ed.) Logit Models from Economics and Other Fields, pp. 149–158. Cambridge University Press, Cambridge (2003)

Chapter   MATH   Google Scholar  

Denison, D.G.T., Mallick, B.K., Smith, A.F.M.: A Bayesian CART algorithm. Biometrika. 85 , 363–377 (1998)

Farcomeni, A., Greco, L.: Robust Methods for Data Reduction. CRC Press, Boca Raton (2015)

Finch, W.H., Schneider, M.K.: Misclassification rates for four methods of group classification. Educ. Psychol. Meas. 66 (2), 240–257 (2006)

Article   MathSciNet   Google Scholar  

Fisher, R.A.: The use of multiple measurements in taxonomic problems. Ann. Eugenics. 7 (2), 179–188 (1936)

Freund, Y., Schapire, R.E.: A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 5 (1), 119–139 (1997)

Grabusts, P.: The choice of metrics for clustering algorithms. Proceedinhs of the 8th International Scientific and Practical Conference, 11 , 70–76 (2011)

Gurland, J., Lee, I., Dahm, P.A.: Polychotomous quantal response in biological assay. Biometrics. 16 , 382–398 (1960)

Hamming, R.W.: Error detecting and error correcting codes. Bell Syst. Tech. J. 29 (2), 147–160 (1950)

Hand, D.J.: Classifier technology and the illusion of progress. Stat. Sci. 21 , 1–14 (2006)

Hand, D.J.: Assessing the performance of classification methods. Int. Stat. Rev. 80 , 400–414 (2012)

Hand, D.J., Yu, K.: Idiot’s Bayes - not so stupid after all? Int. Stat. Rev. 69 (3), 385–399 (2001)

Har-Peled, S., Indyk, P., Motwani, R.: Approximate nearest neighbor: towards removing the curse of dimensionality. Theory Comput. 8 , 321–350 (2012)

Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning: Data Mining, Inference and Prediction. Springer, New York (2001)

Book   MATH   Google Scholar  

Hosmer, T., Hosmer, D.W., Fisher, L.L.: A comparison of the maximum likelihood and discriminant function estimators of the coefficients of the logistic regression model for mixed continuous and discrete variables. Commun. Stat. 12 , 577–593 (1983)

Hsu, C.W., Lin, C.J.: A comparison of methods for multi-class support vector machines. IEEE Trans. Neural Netw. 13 (2), 415–425 (2002)

Izenman, A.J.: Modern Multivariate Statistical Techniques: Regression, Classification and Manifold Learning. Springer, New York (2008)

James, G., Witten, D., Hastie, T., Tibshirani, R.: An Introduction to Statistical Learning: With Applications in R. Springer, New York (2013)

Kiang, M.: A comparative assessment of classification methods. Decis. Support. Syst. 35 , 441–454 (2003)

Kleinbaum, D.G., Klein, M.: Logistic Regression: A Self-learning Text, 3rd edn. Springer, New York (2010)

Kressel, U.H.G.: Pairwise classification and support vector machines. In: Advances in Kernel Methods: Support Vector Learning, pp. 255–268. MIT Press, Cambridge (1998)

Lange, K.: MM Optimization Algorithms. SIAM, Philadelphia (2016)

Lichman, M.: UCI Machine Learning Repository [ http://archive.ics.uci.edu/ml ]. University of California, Irvine 2013

Liu, W.Z., White, A.P.: A comparison of nearest neighbor and tree-based methods of non-parametric discriminant analysis. J. Stat. Comput. Simul. 53 , 41–50 (1995)

Liu, Y., Zhang, H.H., Wu, Y.: Hard or soft classification? Large-margin unified machines. J. Am. Stat. Assoc. 106 (493), 166–177 (2011)

Loh, W.Y.: Improving the precision of classification trees. Ann. Appl. Stat. 3 , 1710–1737 (2009)

Mahalanobis, P.C.: On the generalized distance in statistics. Proceedings of the National Institute of Science in India, 2 (1), 49–55, (1936)

Mai, Q., Zou, H.: Semiparametric sparse discriminant analysis in ultra-high dimensions. J. Multivar. Anal. 135 , 175–188 (2015)

Mantel, N.: Models for complex contingency tables and polychotomous response curves. Biometrics. 22 , 83–110 (1966)

McLachlan, G.J.: Discriminant Analysis and Statistical Pattern Recognition. Wiley-Interscience, New York (2004)

McLachlan, G.J., Byth, K.: Expected error rates for logistic regression versus normal discriminant analysis. Biom. J. 21 , 47–56 (1979)

Menard, S.: Applied Logistic Regression Analysis, 2nd edn. Sage Publications, Thousand Oaks (2002)

Meshbane, A., Morris, J.D.: A method for selecting between linear and quadratic classification models in discriminant analysis. J. Exp. Educ. 63 (3), 263–273 (1996)

Messenger, R., Mandell, L.: A modal search technique for predictive nominal scale multivariate analysis. J. Am. Stat. Assoc. 67 , 768–772 (1972)

Mills, P.: Efficient statistical classification of satellite measurements. Int. J. Remote Sens. 32 , 6109–6132 (2011)

Mulekar, M.S., Brown, C.S.: Distance and similarity measures. In: Alhaji, R., Rekne, J. (eds.) Encyclopedia of Social Network and Mining (ESNAM), pp. 385–400. Springer, New York (2014)

Murphy, K.P.: Machine Learning: A Probabilistic Perspective. MIT Press, Cambridge (2012)

Nigam, K., McCallum, A., Thrun, S., Mitchell, T.: Text classification from labeled and unlabeled documents using EM. Mach. Learn. 39 (2-3), 103–134 (2000)

Nilsson, N.: Learning Machines: Foundations of Trainable Pattern-Classifying Systems. McGraw-Hill, New York (1965)

Quenouille, M.H.: Problems in plane sampling. Ann. Math. Stat. 20 (3), 355–375 (1949)

Quenouille, M.H.: Notes on bias in estimation. Biometrika. 43 (3-4), 353–360 (1956)

Rao, R.C.: The utilization of multiple measurements in problems of biological classification. J. R. Stat. Soc. Ser. B. 10 (2), 159–203 (1948)

MathSciNet   MATH   Google Scholar  

Rish, I.: An empirical study of the naive Bayes classifier. In: IJCAI Workshop on Empirical Methods in AI, Sicily, Italy (2001)

Samworth, R.J.: Optimal weighted nearest neighbour classifiers. Ann. Stat. 40 (5), 2733–2763 (2012)

Schölkopf, B., Sung, K., Burges, C., Girosi, F., Niyogi, P., Poggio, T., Vapnik, V.: Comparing support vector machines with Gaussian kernels to radial basis function classifiers. IEEE Trans. Signal Process. 45 , 2758–2765 (1997)

Sebestyen, G.S.: Decision-making Process in Pattern Recognition. McMillan, New York (1962)

Snell, E.J.: A scaling procedure for ordered categorical data. Biometrics. 20 , 592–607 (1964)

Soria, D., Garibaldi, J.M., Ambrogi, F., Biganzoli, E.M., Ellis, I.O.: A non-parametric version of the naive Bayes classifier. Knowl.-Based Syst. 24 (6), 775–784 (2011)

Srivastava, S., Gupta, M.R., Frigyik, B.A.: Bayesian quadratic discriminant analysis. J. Mach. Learn. Res. 8 , 1287–1314 (2007)

Steel, S.J., Louw, N., Leroux, N.J.: A comparison of the post selection error rate behavior of the normal and quadratic linear discriminant rules. J. Stat. Comput. Simul. 65 , 157–172 (2000)

Steinwart, I., Christmann, A.: Support Vector Machines. Springer, New York (2008)

Theil, H.: A multinomial extension of the linear logit model. Int. Econ. Rev. 10 (3), 251–259 (1969)

Tjalling, J.Y.: Historical development of the Newton-Raphson method. SIAM Rev. 37 (4), 531–551 (1995)

Tukey, J.W.: Bias and confidence in not quite large samples. Ann. Math. Stat. 29 (2), 614–623 (1958)

Vapnik, V., Lerner, A.: Pattern recognition using generalized portrait method. Autom. Remote. Control. 24 , 774–780 (1963)

Wahba, G.: Soft and hard classification by reproducing Kernel Hilbert space methods. Proc. Natl. Acad. Sci. 99 , 16524–16530 (2002)

Witten, I., Frank, E., Hall, M.: Data Mining. Morgan Kaufmann, Burlington (2011)

Download references

Author information

Authors and affiliations.

Department of Mathematics and Statistics, University of South Alabama, Mobile, AL, USA

Rajarshi Dey & Madhuri S. Mulekar

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Madhuri S. Mulekar .

Editor information

Editors and affiliations.

Department of Mathematics and Statistics, Old Dominion University, Norfolk, VA, USA

Norou Diawara

Rights and permissions

Reprints and permissions

Copyright information

© 2019 Springer Nature Switzerland AG

About this chapter

Dey, R., Mulekar, M.S. (2019). A Primer of Statistical Methods for Classification. In: Diawara, N. (eds) Modern Statistical Methods for Spatial and Multivariate Data. STEAM-H: Science, Technology, Engineering, Agriculture, Mathematics & Health. Springer, Cham. https://doi.org/10.1007/978-3-030-11431-2_6

Download citation

DOI : https://doi.org/10.1007/978-3-030-11431-2_6

Published : 29 June 2019

Publisher Name : Springer, Cham

Print ISBN : 978-3-030-11430-5

Online ISBN : 978-3-030-11431-2

eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

AI, Analytics & Data Science: Towards Analytics Specialist

Statistics for Beginners: From Data Collection to Classification and Tabulation in Statistics with Python

Article Outline

I. Introduction - Brief overview of the importance of data in statistical analysis and the role of effective data management practices. - Introduction to the concepts of collection, classification, and tabulation of data.

II. Data Collection in Statistics - Explanation of data collection, including primary and secondary methods. - Discussing the importance of clear objectives and methodologies in data collection. - Overview of tools and techniques for data collection, with a focus on Python for web scraping and APIs for secondary data collection.

III. Data Classification in Statistics - Definition and importance of data classification in statistical analysis. - Types of data classification: Qualitative vs. Quantitative, and further subdivisions. - Practical examples of data classification using Python, including the use of Pandas for categorizing datasets.

IV. Data Tabulation in Statistics - Explaining data tabulation and its significance in statistical analysis. - Types of tables: Frequency distribution tables, cross-tabulations, and more. - Demonstrating data tabulation techniques with Python, utilizing Pandas and NumPy to create and manipulate tables.

V. Integrating Collection, Classification, and Tabulation - A step-by-step guide on integrating these processes for statistical analysis using Python. - Case study: Applying these methods to a publicly available dataset (e.g., Iris dataset, Census data). - Highlighting best practices in data management and analysis throughout the process.

VI. Advanced Techniques and Considerations - Discussing advanced data classification and tabulation techniques, such as hierarchical clustering and multidimensional tables. - Addressing challenges in data collection, classification, and tabulation, including data quality issues and large datasets management.

VII. Tools and Libraries in Python for Effective Data Management - Overview of Python libraries relevant to data collection, classification, and tabulation (e.g., Scrapy for collection, Pandas for classification and tabulation). - Tips for selecting the right tool based on the specific needs of a statistical analysis project.

VIII. Conclusion - Recap of the key points discussed in the article. - Emphasizing the importance of effective data management in statistical analysis and the power of Python in facilitating these processes. - Encouragement for readers to leverage Python for their data collection, classification, and tabulation needs in statistics.

This outline provides a comprehensive framework on the entire process of data management in statistics, from collection to classification and tabulation, with a strong emphasis on practical implementation using Python. It covers theoretical aspects, practical application with Python code examples, and addresses advanced techniques and challenges, offering readers a thorough understanding of how to effectively manage data for statistical analysis.

Keep reading with a 7-day free trial

Subscribe to AI, Analytics & Data Science: Towards Analytics Specialist to keep reading this post and get 7 days of free access to the full post archives.

• Comprehensive Learning Paths
• 150+ Hours of Videos
• Complete Access to Jupyter notebooks, Datasets, References.

Types of Data in Statistics – A Comprehensive Guide

• September 15, 2023

Statistics is a domain that revolves around the collection, analysis, interpretation, presentation, and organization of data. To appropriately utilize statistical methods and produce meaningful results, understanding the types of data is crucial.

In this Blog post we will learn

• Qualitative Data (Categorical Data) 1.1. Nominal Data: 1.2. Ordinal Data:
• Quantitative Data (Numerical Data) 2.1. Discrete Data: 2.2. Continuous Data:
• Time-Series Data:

Let’s explore the different types of data in statistics, supplemented with examples and visualization methods using Python.

1. Qualitative Data (Categorical Data)

We often term qualitative data as categorical data, and you can divide it into categories, but you cannot measure or quantify it.

1.1. Nominal Data:

Nominal data represents categories or labels without any inherent order, ranking, or numerical significance as a type of categorical data. In other words, nominal data classifies items into distinct groups or classes based on some qualitative characteristic, but the categories have no natural or meaningful order associated with them.

Key Characteristics

No Quantitative Meaning: Unlike ordinal, interval, or ratio data, nominal data does not imply any quantitative or numerical meaning. The categories are purely qualitative and serve as labels for grouping.

Arbitrary Assignment: The assignment of items to categories in nominal data is often arbitrary and based on some subjective or contextual criteria. For example, assigning items to categories like “red,” “blue,” or “green” for colors is arbitrary.

No Mathematical Operations: Arithmetic operations like addition, subtraction, or multiplication are not meaningful with nominal data because there is no numerical significance to the categories.

Examples of nominal data include:

• Gender categories (e.g., “male,” “female,” “other”).
• Marital status (e.g., “single,” “married,” “divorced,” “widowed”).
• Types of animals (e.g., “cat,” “dog,” “horse,” “bird”).
• Ethnicity or race (e.g., “Caucasian,” “African American,” “Asian,” “Hispanic”).

1.2. Ordinal Data:

Ordinal data is a type of categorical data that represents values with a meaningful order or ranking but does not have a consistent or evenly spaced numerical difference between the values. In other words, ordinal data has categories that can be ordered or ranked, but the intervals between the categories are not uniform or measurable.

Non-Numeric Labels: The categories in ordinal data are typically represented by non-numeric labels or symbols, such as “low,” “medium,” and “high” for levels of satisfaction or “small,” “medium,” and “large” for T-shirt sizes.

No Fixed Intervals: Unlike interval or ratio data, where the intervals between values have a consistent meaning and can be measured, ordinal data does not have fixed or uniform intervals. In other words, you cannot say that the difference between “low” and “medium” is the same as the difference between “medium” and “high.”

Limited Arithmetic Operations: Arithmetic operations like addition and subtraction are not meaningful with ordinal data because the intervals between categories are not quantifiable. However, some basic operations like counting frequencies, calculating medians, or finding modes can still be performed.

Examples of ordinal data include:

• Educational attainment levels (e.g., “high school,” “bachelor’s degree,” “master’s degree”).
• Customer satisfaction ratings (e.g., “very dissatisfied,” “somewhat dissatisfied,” “neutral,” “satisfied,” “very satisfied”).
• Likert scale responses (e.g., “strongly disagree,” “disagree,” “neutral,” “agree,” “strongly agree”).

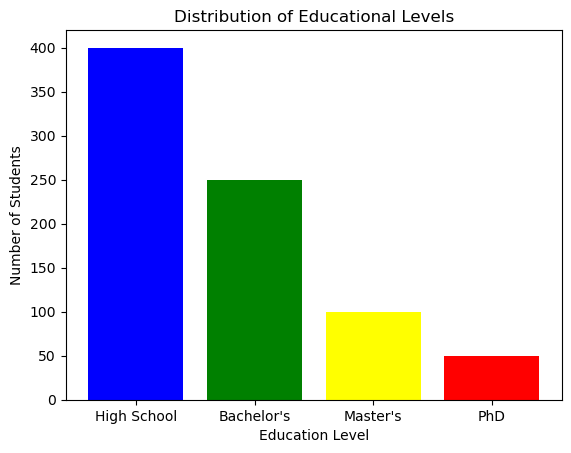
2. Quantitative Data (Numerical Data)

Quantitative data represents quantities and can be measured.

2.1. Discrete Data:

Discrete data refers to a type of data that consists of distinct, separate values or categories. These values are typically counted and are often whole numbers, although they don’t have to be limited to integers. Discrete data can only take on specific, finite values within a defined range.

Key characteristics of discrete data include:

a. Countable Values : Discrete data represents individual, separate items or categories that can be counted or enumerated. For example, the number of students in a classroom, the number of cars in a parking lot, or the number of pets in a household are all discrete data.

b. Distinct Categories : Each value in discrete data represents a distinct category or class. These categories are often non-overlapping, meaning that an item can belong to one category only, with no intermediate values.

c. Gaps between Values : There are gaps or spaces between the values in discrete data. For example, if you are counting the number of people in a household, you can have values like 1, 2, 3, and so on, but you can’t have values like 1.5 or 2.75.

d. Often Represented Graphically with Bar Charts : Discrete data is commonly visualized using bar charts or histograms, where each category is represented by a separate bar, and the height of the bar corresponds to the frequency or count of that category.

* Examples of discrete data include:

The number of children in a family. The number of defects in a batch of products. The number of goals scored by a soccer team in a season. The number of days in a week (Monday, Tuesday, etc.). The types of cars in a parking lot (sedan, SUV, truck).

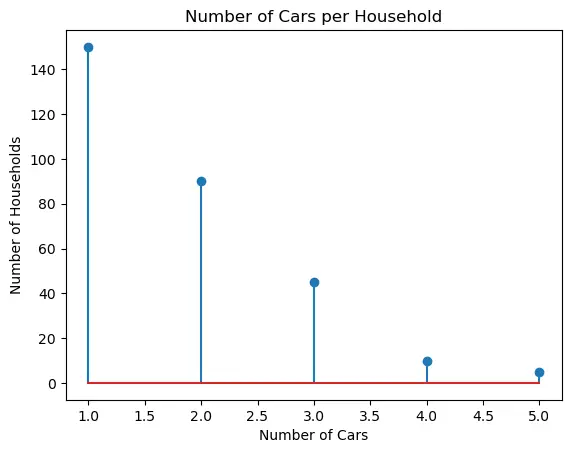
2.2. Continuous Data:

Continuous data, also known as continuous variables or quantitative data, is a type of data that can take on an infinite number of values within a given range. It represents measurements that can be expressed with a high level of precision and are typically numeric in nature. Unlike discrete data, which consists of distinct, separate values, continuous data can have values at any point along a continuous scale.

Precision: Continuous data is often associated with high precision, meaning that measurements can be made with great detail. For example, temperature, height, and weight can be measured to multiple decimal places.

No Gaps or Discontinuities: There are no gaps, spaces, or jumps between values in continuous data. You can have values that are very close to each other without any distinct categories or separations.

Graphical Representation: Continuous data is commonly visualized using line charts or scatter plots, where data points are connected with lines to show the continuous nature of the data.

Examples of continuous data include:

• Temperature readings, such as 20.5°C or 72.3°F.
• Height measurements, like 175.2 cm or 5.8 feet.
• Weight measurements, such as 68.7 kg or 151.3 pounds.
• Time intervals, like 3.45 seconds or 1.25 hours.
• Age of individuals, which can include decimals (e.g., 27.5 years).

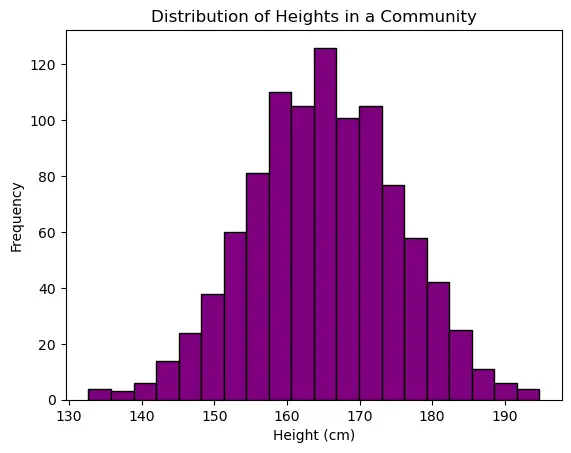
3. Time-Series Data:

Time-series data is a type of data that is collected or recorded over a sequence of equally spaced time intervals. It represents how a particular variable or set of variables changes over time. Each data point in a time series is associated with a specific timestamp, which can be regular (e.g., hourly, daily, monthly) or irregular (e.g., timestamps recorded at random intervals).

Equally Spaced or Irregular Intervals: Time series can have equally spaced intervals, such as daily stock prices, or irregular intervals, like timestamped customer orders. The choice of interval depends on the nature of the data and the context of the analysis.

Seasonality and Trends: Time-series data often exhibits seasonality, which refers to repeating patterns or cycles, and trends, which represent long-term changes or movements in the data. Understanding these patterns is crucial for forecasting and decision-making.

Noise and Variability: Time series may contain noise or random fluctuations that make it challenging to discern underlying patterns. Statistical techniques are often used to filter out noise and identify meaningful patterns.

Applications: Time-series data is widely used in various fields, including finance (stock prices, economic indicators), meteorology (weather data), epidemiology (disease outbreaks), and manufacturing (production processes), among others. It is valuable for making predictions, monitoring trends, and understanding the dynamics of processes over time.

Visualization : Line charts are most suitable for time-series data.

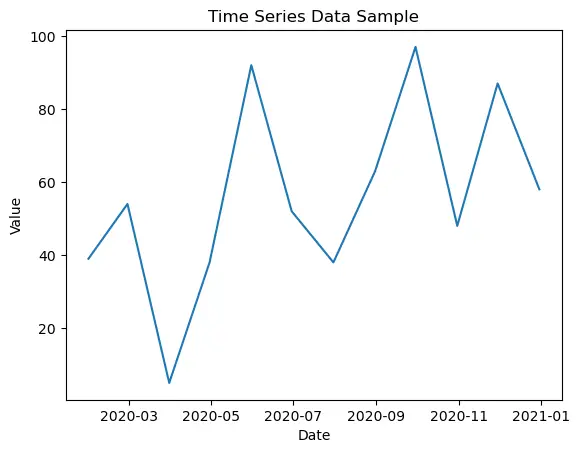
4. Conclusion

Understanding the types of data is crucial as each type requires different methods of analysis. For instance, you wouldn’t use the same statistical test for nominal data as you would for continuous data. By categorizing your data correctly, you can apply the most suitable statistical tools and draw accurate conclusions.

More Articles

Correlation – connecting the dots, the role of correlation in data analysis, hypothesis testing – a deep dive into hypothesis testing, the backbone of statistical inference, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Korean J Anesthesiol
• v.70(3); 2017 Jun

Statistical data presentation

1 Department of Anesthesiology and Pain Medicine, Dongguk University Ilsan Hospital, Goyang, Korea.

Sangseok Lee

2 Department of Anesthesiology and Pain Medicine, Sanggye Paik Hospital, Inje University College of Medicine, Seoul, Korea.

Data are usually collected in a raw format and thus the inherent information is difficult to understand. Therefore, raw data need to be summarized, processed, and analyzed. However, no matter how well manipulated, the information derived from the raw data should be presented in an effective format, otherwise, it would be a great loss for both authors and readers. In this article, the techniques of data and information presentation in textual, tabular, and graphical forms are introduced. Text is the principal method for explaining findings, outlining trends, and providing contextual information. A table is best suited for representing individual information and represents both quantitative and qualitative information. A graph is a very effective visual tool as it displays data at a glance, facilitates comparison, and can reveal trends and relationships within the data such as changes over time, frequency distribution, and correlation or relative share of a whole. Text, tables, and graphs for data and information presentation are very powerful communication tools. They can make an article easy to understand, attract and sustain the interest of readers, and efficiently present large amounts of complex information. Moreover, as journal editors and reviewers glance at these presentations before reading the whole article, their importance cannot be ignored.

Introduction

Data are a set of facts, and provide a partial picture of reality. Whether data are being collected with a certain purpose or collected data are being utilized, questions regarding what information the data are conveying, how the data can be used, and what must be done to include more useful information must constantly be kept in mind.

Since most data are available to researchers in a raw format, they must be summarized, organized, and analyzed to usefully derive information from them. Furthermore, each data set needs to be presented in a certain way depending on what it is used for. Planning how the data will be presented is essential before appropriately processing raw data.

First, a question for which an answer is desired must be clearly defined. The more detailed the question is, the more detailed and clearer the results are. A broad question results in vague answers and results that are hard to interpret. In other words, a well-defined question is crucial for the data to be well-understood later. Once a detailed question is ready, the raw data must be prepared before processing. These days, data are often summarized, organized, and analyzed with statistical packages or graphics software. Data must be prepared in such a way they are properly recognized by the program being used. The present study does not discuss this data preparation process, which involves creating a data frame, creating/changing rows and columns, changing the level of a factor, categorical variable, coding, dummy variables, variable transformation, data transformation, missing value, outlier treatment, and noise removal.

We describe the roles and appropriate use of text, tables, and graphs (graphs, plots, or charts), all of which are commonly used in reports, articles, posters, and presentations. Furthermore, we discuss the issues that must be addressed when presenting various kinds of information, and effective methods of presenting data, which are the end products of research, and of emphasizing specific information.

Data Presentation

Data can be presented in one of the three ways:

–as text;

–in tabular form; or

–in graphical form.

Methods of presentation must be determined according to the data format, the method of analysis to be used, and the information to be emphasized. Inappropriately presented data fail to clearly convey information to readers and reviewers. Even when the same information is being conveyed, different methods of presentation must be employed depending on what specific information is going to be emphasized. A method of presentation must be chosen after carefully weighing the advantages and disadvantages of different methods of presentation. For easy comparison of different methods of presentation, let us look at a table ( Table 1 ) and a line graph ( Fig. 1 ) that present the same information [ 1 ]. If one wishes to compare or introduce two values at a certain time point, it is appropriate to use text or the written language. However, a table is the most appropriate when all information requires equal attention, and it allows readers to selectively look at information of their own interest. Graphs allow readers to understand the overall trend in data, and intuitively understand the comparison results between two groups. One thing to always bear in mind regardless of what method is used, however, is the simplicity of presentation.

Values are expressed as mean ± SD. Group C: normal saline, Group D: dexmedetomidine. SBP: systolic blood pressure, DBP: diastolic blood pressure, MBP: mean blood pressure, HR: heart rate. * P < 0.05 indicates a significant increase in each group, compared with the baseline values. † P < 0.05 indicates a significant decrease noted in Group D, compared with the baseline values. ‡ P < 0.05 indicates a significant difference between the groups.

Text presentation

Text is the main method of conveying information as it is used to explain results and trends, and provide contextual information. Data are fundamentally presented in paragraphs or sentences. Text can be used to provide interpretation or emphasize certain data. If quantitative information to be conveyed consists of one or two numbers, it is more appropriate to use written language than tables or graphs. For instance, information about the incidence rates of delirium following anesthesia in 2016–2017 can be presented with the use of a few numbers: “The incidence rate of delirium following anesthesia was 11% in 2016 and 15% in 2017; no significant difference of incidence rates was found between the two years.” If this information were to be presented in a graph or a table, it would occupy an unnecessarily large space on the page, without enhancing the readers' understanding of the data. If more data are to be presented, or other information such as that regarding data trends are to be conveyed, a table or a graph would be more appropriate. By nature, data take longer to read when presented as texts and when the main text includes a long list of information, readers and reviewers may have difficulties in understanding the information.

Table presentation

Tables, which convey information that has been converted into words or numbers in rows and columns, have been used for nearly 2,000 years. Anyone with a sufficient level of literacy can easily understand the information presented in a table. Tables are the most appropriate for presenting individual information, and can present both quantitative and qualitative information. Examples of qualitative information are the level of sedation [ 2 ], statistical methods/functions [ 3 , 4 ], and intubation conditions [ 5 ].

The strength of tables is that they can accurately present information that cannot be presented with a graph. A number such as “132.145852” can be accurately expressed in a table. Another strength is that information with different units can be presented together. For instance, blood pressure, heart rate, number of drugs administered, and anesthesia time can be presented together in one table. Finally, tables are useful for summarizing and comparing quantitative information of different variables. However, the interpretation of information takes longer in tables than in graphs, and tables are not appropriate for studying data trends. Furthermore, since all data are of equal importance in a table, it is not easy to identify and selectively choose the information required.

For a general guideline for creating tables, refer to the journal submission requirements 1) .

Heat maps for better visualization of information than tables

Heat maps help to further visualize the information presented in a table by applying colors to the background of cells. By adjusting the colors or color saturation, information is conveyed in a more visible manner, and readers can quickly identify the information of interest ( Table 2 ). Software such as Excel (in Microsoft Office, Microsoft, WA, USA) have features that enable easy creation of heat maps through the options available on the “conditional formatting” menu.

All numbers were created by the author. SBP: systolic blood pressure, DBP: diastolic blood pressure, MBP: mean blood pressure, HR: heart rate.

Graph presentation

Whereas tables can be used for presenting all the information, graphs simplify complex information by using images and emphasizing data patterns or trends, and are useful for summarizing, explaining, or exploring quantitative data. While graphs are effective for presenting large amounts of data, they can be used in place of tables to present small sets of data. A graph format that best presents information must be chosen so that readers and reviewers can easily understand the information. In the following, we describe frequently used graph formats and the types of data that are appropriately presented with each format with examples.

Scatter plot

Scatter plots present data on the x - and y -axes and are used to investigate an association between two variables. A point represents each individual or object, and an association between two variables can be studied by analyzing patterns across multiple points. A regression line is added to a graph to determine whether the association between two variables can be explained or not. Fig. 2 illustrates correlations between pain scoring systems that are currently used (PSQ, Pain Sensitivity Questionnaire; PASS, Pain Anxiety Symptoms Scale; PCS, Pain Catastrophizing Scale) and Geop-Pain Questionnaire (GPQ) with the correlation coefficient, R, and regression line indicated on the scatter plot [ 6 ]. If multiple points exist at an identical location as in this example ( Fig. 2 ), the correlation level may not be clear. In this case, a correlation coefficient or regression line can be added to further elucidate the correlation.

Bar graph and histogram

A bar graph is used to indicate and compare values in a discrete category or group, and the frequency or other measurement parameters (i.e. mean). Depending on the number of categories, and the size or complexity of each category, bars may be created vertically or horizontally. The height (or length) of a bar represents the amount of information in a category. Bar graphs are flexible, and can be used in a grouped or subdivided bar format in cases of two or more data sets in each category. Fig. 3 is a representative example of a vertical bar graph, with the x -axis representing the length of recovery room stay and drug-treated group, and the y -axis representing the visual analog scale (VAS) score. The mean and standard deviation of the VAS scores are expressed as whiskers on the bars ( Fig. 3 ) [ 7 ].

By comparing the endpoints of bars, one can identify the largest and the smallest categories, and understand gradual differences between each category. It is advised to start the x - and y -axes from 0. Illustration of comparison results in the x - and y -axes that do not start from 0 can deceive readers' eyes and lead to overrepresentation of the results.

One form of vertical bar graph is the stacked vertical bar graph. A stack vertical bar graph is used to compare the sum of each category, and analyze parts of a category. While stacked vertical bar graphs are excellent from the aspect of visualization, they do not have a reference line, making comparison of parts of various categories challenging ( Fig. 4 ) [ 8 ].

A pie chart, which is used to represent nominal data (in other words, data classified in different categories), visually represents a distribution of categories. It is generally the most appropriate format for representing information grouped into a small number of categories. It is also used for data that have no other way of being represented aside from a table (i.e. frequency table). Fig. 5 illustrates the distribution of regular waste from operation rooms by their weight [ 8 ]. A pie chart is also commonly used to illustrate the number of votes each candidate won in an election.

Line plot with whiskers

A line plot is useful for representing time-series data such as monthly precipitation and yearly unemployment rates; in other words, it is used to study variables that are observed over time. Line graphs are especially useful for studying patterns and trends across data that include climatic influence, large changes or turning points, and are also appropriate for representing not only time-series data, but also data measured over the progression of a continuous variable such as distance. As can be seen in Fig. 1 , mean and standard deviation of systolic blood pressure are indicated for each time point, which enables readers to easily understand changes of systolic pressure over time [ 1 ]. If data are collected at a regular interval, values in between the measurements can be estimated. In a line graph, the x-axis represents the continuous variable, while the y-axis represents the scale and measurement values. It is also useful to represent multiple data sets on a single line graph to compare and analyze patterns across different data sets.

Box and whisker chart

A box and whisker chart does not make any assumptions about the underlying statistical distribution, and represents variations in samples of a population; therefore, it is appropriate for representing nonparametric data. AA box and whisker chart consists of boxes that represent interquartile range (one to three), the median and the mean of the data, and whiskers presented as lines outside of the boxes. Whiskers can be used to present the largest and smallest values in a set of data or only a part of the data (i.e. 95% of all the data). Data that are excluded from the data set are presented as individual points and are called outliers. The spacing at both ends of the box indicates dispersion in the data. The relative location of the median demonstrated within the box indicates skewness ( Fig. 6 ). The box and whisker chart provided as an example represents calculated volumes of an anesthetic, desflurane, consumed over the course of the observation period ( Fig. 7 ) [ 9 ].

Three-dimensional effects

Most of the recently introduced statistical packages and graphics software have the three-dimensional (3D) effect feature. The 3D effects can add depth and perspective to a graph. However, since they may make reading and interpreting data more difficult, they must only be used after careful consideration. The application of 3D effects on a pie chart makes distinguishing the size of each slice difficult. Even if slices are of similar sizes, slices farther from the front of the pie chart may appear smaller than the slices closer to the front ( Fig. 8 ).

Drawing a graph: example

Finally, we explain how to create a graph by using a line graph as an example ( Fig. 9 ). In Fig. 9 , the mean values of arterial pressure were randomly produced and assumed to have been measured on an hourly basis. In many graphs, the x- and y-axes meet at the zero point ( Fig. 9A ). In this case, information regarding the mean and standard deviation of mean arterial pressure measurements corresponding to t = 0 cannot be conveyed as the values overlap with the y-axis. The data can be clearly exposed by separating the zero point ( Fig. 9B ). In Fig. 9B , the mean and standard deviation of different groups overlap and cannot be clearly distinguished from each other. Separating the data sets and presenting standard deviations in a single direction prevents overlapping and, therefore, reduces the visual inconvenience. Doing so also reduces the excessive number of ticks on the y-axis, increasing the legibility of the graph ( Fig. 9C ). In the last graph, different shapes were used for the lines connecting different time points to further allow the data to be distinguished, and the y-axis was shortened to get rid of the unnecessary empty space present in the previous graphs ( Fig. 9D ). A graph can be made easier to interpret by assigning each group to a different color, changing the shape of a point, or including graphs of different formats [ 10 ]. The use of random settings for the scale in a graph may lead to inappropriate presentation or presentation of data that can deceive readers' eyes ( Fig. 10 ).

Owing to the lack of space, we could not discuss all types of graphs, but have focused on describing graphs that are frequently used in scholarly articles. We have summarized the commonly used types of graphs according to the method of data analysis in Table 3 . For general guidelines on graph designs, please refer to the journal submission requirements 2) .

Conclusions

Text, tables, and graphs are effective communication media that present and convey data and information. They aid readers in understanding the content of research, sustain their interest, and effectively present large quantities of complex information. As journal editors and reviewers will scan through these presentations before reading the entire text, their importance cannot be disregarded. For this reason, authors must pay as close attention to selecting appropriate methods of data presentation as when they were collecting data of good quality and analyzing them. In addition, having a well-established understanding of different methods of data presentation and their appropriate use will enable one to develop the ability to recognize and interpret inappropriately presented data or data presented in such a way that it deceives readers' eyes [ 11 ].

<Appendix>

Output for presentation.

Discovery and communication are the two objectives of data visualization. In the discovery phase, various types of graphs must be tried to understand the rough and overall information the data are conveying. The communication phase is focused on presenting the discovered information in a summarized form. During this phase, it is necessary to polish images including graphs, pictures, and videos, and consider the fact that the images may look different when printed than how appear on a computer screen. In this appendix, we discuss important concepts that one must be familiar with to print graphs appropriately.

The KJA asks that pictures and images meet the following requirement before submission 3)

“Figures and photographs should be submitted as ‘TIFF’ files. Submit files of figures and photographs separately from the text of the paper. Width of figure should be 84 mm (one column). Contrast of photos or graphs should be at least 600 dpi. Contrast of line drawings should be at least 1,200 dpi. The Powerpoint file (ppt, pptx) is also acceptable.”

Unfortunately, without sufficient knowledge of computer graphics, it is not easy to understand the submission requirement above. Therefore, it is necessary to develop an understanding of image resolution, image format (bitmap and vector images), and the corresponding file specifications.

Resolution is often mentioned to describe the quality of images containing graphs or CT/MRI scans, and video files. The higher the resolution, the clearer and closer to reality the image is, while the opposite is true for low resolutions. The most representative unit used to describe a resolution is “dpi” (dots per inch): this literally translates to the number of dots required to constitute 1 inch. The greater the number of dots, the higher the resolution. The KJA submission requirements recommend 600 dpi for images, and 1,200 dpi 4) for graphs. In other words, resolutions in which 600 or 1,200 dots constitute one inch are required for submission.

There are requirements for the horizontal length of an image in addition to the resolution requirements. While there are no requirements for the vertical length of an image, it must not exceed the vertical length of a page. The width of a column on one side of a printed page is 84 mm, or 3.3 inches (84/25.4 mm ≒ 3.3 inches). Therefore, a graph must have a resolution in which 1,200 dots constitute 1 inch, and have a width of 3.3 inches.

Bitmap and Vector

Methods of image construction are important. Bitmap images can be considered as images drawn on section paper. Enlarging the image will enlarge the picture along with the grid, resulting in a lower resolution; in other words, aliasing occurs. On the other hand, reducing the size of the image will reduce the size of the picture, while increasing the resolution. In other words, resolution and the size of an image are inversely proportionate to one another in bitmap images, and it is a drawback of bitmap images that resolution must be considered when adjusting the size of an image. To enlarge an image while maintaining the same resolution, the size and resolution of the image must be determined before saving the image. An image that has already been created cannot avoid changes to its resolution according to changes in size. Enlarging an image while maintaining the same resolution will increase the number of horizontal and vertical dots, ultimately increasing the number of pixels 5) of the image, and the file size. In other words, the file size of a bitmap image is affected by the size and resolution of the image (file extensions include JPG [JPEG] 6) , PNG 7) , GIF 8) , and TIF [TIFF] 9) . To avoid this complexity, the width of an image can be set to 4 inches and its resolution to 900 dpi to satisfy the submission requirements of most journals [ 12 ].

Vector images overcome the shortcomings of bitmap images. Vector images are created based on mathematical operations of line segments and areas between different points, and are not affected by aliasing or pixelation. Furthermore, they result in a smaller file size that is not affected by the size of the image. They are commonly used for drawings and illustrations (file extensions include EPS 10) , CGM 11) , and SVG 12) ).

Finally, the PDF 13) is a file format developed by Adobe Systems (Adobe Systems, CA, USA) for electronic documents, and can contain general documents, text, drawings, images, and fonts. They can also contain bitmap and vector images. While vector images are used by researchers when working in Powerpoint, they are saved as 960 × 720 dots when saved in TIFF format in Powerpoint. This results in a resolution that is inappropriate for printing on a paper medium. To save high-resolution bitmap images, the image must be saved as a PDF file instead of a TIFF, and the saved PDF file must be imported into an imaging processing program such as Photoshop™(Adobe Systems, CA, USA) to be saved in TIFF format [ 12 ].

1) Instructions to authors in KJA; section 5-(9) Table; https://ekja.org/index.php?body=instruction

2) Instructions to Authors in KJA; section 6-1)-(10) Figures and illustrations in Manuscript preparation; https://ekja.org/index.php?body=instruction

3) Instructions to Authors in KJA; section 6-1)-(10) Figures and illustrations in Manuscript preparation; https://ekja.org/index.php?body=instruction

4) Resolution; in KJA, it is represented by “contrast.”

5) Pixel is a minimum unit of an image and contains information of a dot and color. It is derived by multiplying the number of vertical and horizontal dots regardless of image size. For example, Full High Definition (FHD) monitor has 1920 × 1080 dots ≒ 2.07 million pixel.

6) Joint Photographic Experts Group.

7) Portable Network Graphics.

8) Graphics Interchange Format

9) Tagged Image File Format; TIFF

10) Encapsulated PostScript.

11) Computer Graphics Metafile.

12) Scalable Vector Graphics.

13) Portable Document Format.

• List of Commerce Articles
• Meaning And Objectives Of Classification Of Data

Meaning and Objectives of Classification of Data

Meaning of classification of data.

•     It is the process of arranging data into homogeneous (similar) groups according to their common characteristics.
•     Raw data cannot be easily understood, and it is not fit for further analysis and interpretation. Arrangement of data helps users in comparison and analysis.
• For example, the population of a town can be grouped according to sex, age, marital status, etc.

Classification of data

The method of arranging data into homogeneous classes according to the common features present in the data is known as classification.

A planned data analysis system makes the fundamental data easy to find and recover. This can be of particular interest for legal discovery, risk management, and compliance. Written methods and sets of guidelines for data classification should determine what levels and measures the company will use to organise data and define the roles of employees within the business regarding input stewardship.

Once a data -classification scheme has been designed, the security standards that stipulate proper approaching practices for each division and the storage criteria that determines the data’s lifecycle demands should be discussed.

Objectives of Data Classification

The primary objectives of data classification are:

•     To consolidate the volume of data in such a way that similarities and differences can be quickly understood. Figures can consequently be ordered in sections with common traits.
•     To aid comparison.
•     To point out the important characteristics of the data at a flash.
•     To give importance to the prominent data collected while separating the optional elements.
• To allow a statistical method of the materials gathered.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

This is a Very nice app to learn and make notes of any chapter

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Key Differences

Know the Differences & Comparisons

Difference Between Classification and Tabulation

After the collection of data is completed, it is prepared for analysis. As the data is raw, it needs to be transformed in such a way, that it is appropriate for analysis. The form of data, highly influences the result of analysis and so, to get positive results, the data preparation should be proper. There are various steps of data preparation, which include editing, coding, classification, tabulation, graphical representation and so on.

For a layperson, classification and tabulation are same, but the fact is they are different, as the former is a means to sort data, for further analysis while the latter is used to present data.

Content: Classification Vs Tabulation

Comparison chart, definition of classification.

Classification refers to a process, wherein data is arranged based on the characteristic under consideration, into classes, or groups, as per resemblance of observations. Classification puts the data in a condensed form, as it removes unnecessary details that helps to easily comprehend data.

The data collected for the first time is raw data and so it is arranged in haphazard manner, which does not provide a clear picture. The classification of data reduces the large volume of raw data into homogeneous groups, i.e. data having common characteristics or nature are placed in one group and thus, the whole data is bifurcated into a number of groups. there are four types of classification:

• Qualitative Classification or Ordinal Classification
• Quantitative Classification
• Chronological or Temporal Classification
• Geographical or Spatial Classification

Definition of Tabulation

Tabulation refers to a logical data presentation, wherein raw data is summarized and displayed in a compact form, i.e. in statistical tables. In other words, it is a systematic arrangement of data in columns and rows, that represents data in concise and attractive way. One should follow the given guidelines for tabulation.

• A serial number should be allotted to the table, in addition to the self explanatory title.
• The statistical table is required to be divided into four parts, i.e. Box head, Stub, Caption and Body. The complete upper part of the table that contains columns and sub-columns, along with caption, is the Box Head. The left part of the table, giving description of rows is called stub. The part of table that contains numerical figures and other content is its body.
• Length and Width of the table should be perfectly balanced.
• Presentation of data should be such that it takes less time and labor to make comparison between various figures.
• Footnotes, explaining the source of data or any other thing, are to be presented at the bottom of the table.

Key Differences Between Classification and Tabulation

The paramount differences between classification and tabulation are discussed in the points given below:

• The process of arranging data into different categories, on the basis of nature, behavior, or common characteristics is called classification. A process of condensing data and presenting it in a compact form, by putting data into statistical table, is called tabulation.
• Classification of data is done after data collection process is completed. On the other hand, tabulation follows classification.
• Data classification is based on similar attributes and variables of the observations. Conversely, in tabulation the data is arranged in rows and columns, in a systematic way.
• Classification of data is performed with the objective of analysing data in order to draw inferences. Unlike tabulation, which aims at presenting data, to ensure easy comparison of various figures.
• In classification, data is bifurcated into categories and sub-categories while in tabulation data is divided into headings and sub-headings.

When the collection and verification of data is completed on the basis of homogeneity and consistency, it needs to be summarized and presented in a clear and compact manner which highlights the relevant features of data. Both classification and tabulation, enhances the readability and attractiveness of data, by presenting it in a mannner that looks more appealing to the eyes.

You Might Also Like:

September 3, 2020 at 1:01 am

Thanks for the explanation that too in a lucid manner. Concept of classification and tabulation was very easy to understand

May 25, 2021 at 10:14 pm

Priyanshi says

January 27, 2022 at 10:00 pm

This is very useful for us….This is so easy and simple for learning and understanding…..

Thank you so much……

Manisha says

February 8, 2022 at 10:54 am

Very well explained Thanks

Gangongmei says

April 25, 2022 at 1:59 pm

The best explanation for the topic classification and tabulation.

[email protected] says

December 11, 2023 at 2:28 pm

Thanks a lot

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

The world is getting “smarter” every day, and to keep up with consumer expectations, companies are increasingly using machine learning algorithms to make things easier. You can see them in use in end-user devices (through face recognition for unlocking smartphones) or for detecting credit card fraud (like triggering alerts for unusual purchases).

Within  artificial intelligence  (AI) and  machine learning , there are two basic approaches: supervised learning and unsupervised learning. The main difference is that one uses labeled data to help predict outcomes, while the other does not. However, there are some nuances between the two approaches, and key areas in which one outperforms the other. This post clarifies the differences so you can choose the best approach for your situation.

Supervised learning  is a machine learning approach that’s defined by its use of labeled data sets. These data sets are designed to train or “supervise” algorithms into classifying data or predicting outcomes accurately. Using labeled inputs and outputs, the model can measure its accuracy and learn over time.

Supervised learning can be separated into two types of problems when  data mining : classification and regression:

• Classification  problems use an algorithm to accurately assign test data into specific categories, such as separating apples from oranges. Or, in the real world, supervised learning algorithms can be used to classify spam in a separate folder from your inbox. Linear classifiers, support vector machines, decision trees and  random forest  are all common types of classification algorithms.
• Regression  is another type of supervised learning method that uses an algorithm to understand the relationship between dependent and independent variables. Regression models are helpful for predicting numerical values based on different data points, such as sales revenue projections for a given business. Some popular regression algorithms are linear regression, logistic regression, and polynomial regression.

Unsupervised learning  uses machine learning algorithms to analyze and cluster unlabeled data sets. These algorithms discover hidden patterns in data without the need for human intervention (hence, they are “unsupervised”).

Unsupervised learning models are used for three main tasks: clustering, association and dimensionality reduction:

• Clustering  is a data mining technique for grouping unlabeled data based on their similarities or differences. For example, K-means clustering algorithms assign similar data points into groups, where the K value represents the size of the grouping and granularity. This technique is helpful for market segmentation, image compression, and so on.
• Association  is another type of unsupervised learning method that uses different rules to find relationships between variables in a given data set. These methods are frequently used for market basket analysis and recommendation engines, along the lines of “Customers Who Bought This Item Also Bought” recommendations.
• Dimensionality reduction  is a learning technique that is used when the number of features (or dimensions) in a given data set is too high. It reduces the number of data inputs to a manageable size while also preserving the data integrity. Often, this technique is used in the preprocessing data stage, such as when autoencoders remove noise from visual data to improve picture quality.

The main distinction between the two approaches is the use of labeled data sets. To put it simply, supervised learning uses labeled input and output data, while an unsupervised learning algorithm does not.

In supervised learning, the algorithm “learns” from the training data set by iteratively making predictions on the data and adjusting for the correct answer. While supervised learning models tend to be more accurate than unsupervised learning models, they require upfront human intervention to label the data appropriately. For example, a supervised learning model can predict how long your commute will be based on the time of day, weather conditions and so on. But first, you must train it to know that rainy weather extends the driving time.

Unsupervised learning models, in contrast, work on their own to discover the inherent structure of unlabeled data. Note that they still require some human intervention for validating output variables. For example, an unsupervised learning model can identify that online shoppers often purchase groups of products at the same time. However, a data analyst would need to validate that it makes sense for a recommendation engine to group baby clothes with an order of diapers, applesauce, and sippy cups.

• Goals:  In supervised learning, the goal is to predict outcomes for new data. You know up front the type of results to expect. With an unsupervised learning algorithm, the goal is to get insights from large volumes of new data. The machine learning itself determines what is different or interesting from the data set.
• Applications: Supervised learning models are ideal for spam detection, sentiment analysis, weather forecasting and pricing predictions, among other things. In contrast, unsupervised learning is a great fit for anomaly detection, recommendation engines, customer personas and medical imaging.
• Complexity:  Supervised learning is a simple method for machine learning, typically calculated by using programs like R or Python. In unsupervised learning, you need powerful tools for working with large amounts of unclassified data. Unsupervised learning models are computationally complex because they need a large training set to produce intended outcomes.
• Drawbacks: Supervised learning models can be time-consuming to train, and the labels for input and output variables require expertise. Meanwhile, unsupervised learning methods can have wildly inaccurate results unless you have human intervention to validate the output variables.

Choosing the right approach for your situation depends on how your data scientists assess the structure and volume of your data, as well as the use case. To make your decision, be sure to do the following:

• Evaluate your input data:  Is it labeled or unlabeled data? Do you have experts that can support extra labeling?
• Define your goals:  Do you have a recurring, well-defined problem to solve? Or will the algorithm need to predict new problems?
• Review your options for algorithms:  Are there algorithms with the same dimensionality that you need (number of features, attributes, or characteristics)? Can they support your data volume and structure?

Classifying big data can be a real challenge in supervised learning, but the results are highly accurate and trustworthy. In contrast, unsupervised learning can handle large volumes of data in real time. But, there’s a lack of transparency into how data is clustered and a higher risk of inaccurate results. This is where semi-supervised learning comes in.

Can’t decide on whether to use supervised or unsupervised learning?  Semi-supervised learning  is a happy medium, where you use a training data set with both labeled and unlabeled data. It’s particularly useful when it’s difficult to extract relevant features from data—and when you have a high volume of data.

Semi-supervised learning is ideal for medical images, where a small amount of training data can lead to a significant improvement in accuracy. For example, a radiologist can label a small subset of CT scans for tumors or diseases so the machine can more accurately predict which patients might require more medical attention.

Machine learning models are a powerful way to gain the data insights that improve our world. To learn more about the specific algorithms that are used with supervised and unsupervised learning, we encourage you to delve into the Learn Hub articles on these techniques. We also recommend checking out the blog post that goes a step further, with a detailed look at deep learning and neural networks.

• What is Supervised Learning?
• What is Unsupervised Learning?
• AI vs. Machine Learning vs. Deep Learning vs. Neural Networks: What’s the difference?

To learn more about how to build machine learning models, explore the free tutorials on the  IBM® Developer Hub .

Get the latest tech insights and expert thought leadership in your inbox.

The Data Differentiator: Learn how to weave a single technology concept into a holistic data strategy that drives business value.

Get our newsletters and topic updates that deliver the latest thought leadership and insights on emerging trends.

• Aboriginal and Torres Strait Islander Health Performance Framework
• Australian Mesothelioma Registry
• GEN Aged Care Data
• Housing data
• Indigenous Mental Health and Suicide Prevention Clearinghouse
• Metadata Online Registry (METEOR)
• Regional Insights for Indigenous Communities
• Help & tools
• Increase text size
• Decrease text size

Palliative care services in Australia

Australian Institute of Health and Welfare (2024) Palliative care services in Australia , AIHW, Australian Government, accessed 23 May 2024.

Australian Institute of Health and Welfare. (2024). Palliative care services in Australia. Retrieved from https://www.aihw.gov.au/reports/palliative-care/palliative-care-services-in-australia

Palliative care services in Australia. Australian Institute of Health and Welfare, 23 May 2024, https://www.aihw.gov.au/reports/palliative-care/palliative-care-services-in-australia

Australian Institute of Health and Welfare. Palliative care services in Australia [Internet]. Canberra: Australian Institute of Health and Welfare, 2024 [cited 2024 May. 23]. Available from: https://www.aihw.gov.au/reports/palliative-care/palliative-care-services-in-australia

Australian Institute of Health and Welfare (AIHW) 2024, Palliative care services in Australia , viewed 23 May 2024, https://www.aihw.gov.au/reports/palliative-care/palliative-care-services-in-australia

Get citations as an Endnote file : Endnote

Classifications

Australian statistical geographical standard for remoteness areas.

The Australian Statistical Geographical Standard (ASGS) for Remoteness Areas was developed by the Australian Bureau of Statistics (ABS) to collect and disseminate geographically classified statistics (ABS 2011; ABS 2016; ABS 2021).

The ASGS’s remoteness structure categorises geographical areas in Australia into five remoteness areas:

• Major cities
• Inner regional
• Outer regional
• Very remote.

The ABS website includes detailed information on ASGS, including the key changes made between each edition.

Data on remoteness of geographical location in the National Hospital Morbidity Database (NHMD) are collected based on patients’ usual residential address and in the National Public Hospital Establishments Database (NPHED), this is determined by hospital street address. This release provides hospital data on remoteness using 2021–22 NHMD (ASGS 2016 edition). Further information on the quality of the usual residence of the patient data in the NHMD can be found in National Hospital Morbidity Database (NHMD) Technical appendices/notes 2021–22 .

Index of Relative Socio-economic Disadvantage 

The Index of Relative Socio-economic Disadvantage (IRSD) is one of four Socio-Economic Indexes for Areas (SEIFA) developed by the ABS (ABS 2018). The IRSD represents the socioeconomic position of Australian communities by measuring aspects of disadvantage, such as low income, low educational attainment, high unemployment, and jobs in relatively unskilled occupations. Areas are then ranked according to their level of disadvantage.

When the IRSD is used in this report, people living in the 20% of areas with the greatest overall level of disadvantage are described as living in the ‘lowest socioeconomic areas’. The 20% of people at the other end of the scale – those living in areas with the least overall level of disadvantage – are described as living in the ‘highest socioeconomic areas’.

It is important to note that the IRSD reflects the overall or average socioeconomic position of the population of an area; it does not show how individuals living in the same area might differ from each other in their socioeconomic position.

International Statistical Classification of Diseases and Related Health Problems 

The International Statistical Classification of Diseases and Related Health Problems (ICD), which was developed by the World Health Organization (WHO), is the international standard for coding morbidity and mortality statistics. It was designed to promote international comparability in collecting, processing, classifying and presenting these statistics. The ICD is periodically reviewed to reflect changes in clinical and research settings (WHO 2022).

The version currently used in Australia to code causes of death, ICD-10 (WHO 1992), was endorsed in May 1990 and officially came into use in WHO member states from 1994. The 11th revision of the ICD was released in June 2018. Member States will begin reporting health data using ICD-11 in 2022. Further information on the ICD is available from the WHO website .

Diagnosis, procedure and external cause hospital data for 2021–22 were reported to the NHMD by all states and territories using the 11th edition of the Australian Modification of ICD-10, referred to as the ICD-10-AM. ICD-10-AM, is based on ICD-10 (NCCC 2013). ICD-10 was modified for the Australian setting by the National Centre for Classification in Health to make it more relevant to Australian clinical practice. Compatibility with ICD-10 at the higher levels (that is, up to 4-character codes) of the classification has been maintained. ICD-10-AM has been used to classify diagnoses in admitted patient hospital records in all Australian states and territories since 1999–2000 (AIHW 2000).

The ICD-10-AM disease classification is hierarchical; a small number of summary disease chapters are divided into a large number of more specific disease groupings (represented by 3-character codes). Most of the 3-character disease groupings can be divided into an even larger number of very specific disease categories represented by 4- character and 5-character codes (see Table 1 in Technical information: Disease-related information ).

ABS (Australian Bureau of Statistics) (2011) Australian Statistical Geography Standard (ASGS), Volume 1 – Main Structure and Greater City Statistical Areas , ABS Website, accessed 26 March 2024.

ABS (2016) Australian Statistical Geography Standard (ASGS), Volume 1 – Main Structure and Greater Capital City Statistical Areas , ABS Website, accessed 26 March 2024.

ABS (2018) Census of Population and Housing: Socio-Economic Indexes for Areas (SEIFA), Australia, 2016 , ABS Website, accessed 26 March 2024.

ABS (2021) Australian Statistical Geography Standard (ASGS) Edition 3 , ABS Website, accessed 28 March 2024.

AIHW (Australian Institute of Health and Welfare) (2000) Australian hospital statistics 1998–99 , AIHW, Australian Government, accessed 29 August 2023.

NCCC (National Casemix and Classification Centre) (2013) The International Statistical Classification of Diseases and Related Health Problems, Tenth Revision, Australian Modification (ICD-10-AM) - Eighth Edition . Sydney: NCCC, Australian Health Services Research Institute, University of Wollongong.

WHO (World Health Organisation) (1992) International Statistical Classification of Diseases and Related Health Problems, tenth revision. Vol. 1 . Geneva: WHO.

WHO (2022) International Classification of Diseases (ICD) , WHO website, accessed 11 February 2023.

This website needs JavaScript enabled in order to work correctly; currently it looks like it is disabled. Please enable JavaScript to use this website as intended.

We'd love to know any feedback that you have about the AIHW website, its contents or reports.

Required fields

The browser you are using to browse this website is outdated and some features may not display properly or be accessible to you. Please use a more recent browser for the best user experience.

An official website of the United States government.

Here’s how you know

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Occupational Safety and Health Administration

• 中文（简体） (Chinese-Simplified)
• 繁體中文 (Chinese-Traditional)
• Kreyòl ayisyen (Haitian Creole)
• 한국어 (Korean)
• Español (Spanish)
• Filipino/Tagalog
• Tiếng Việt (Vietnamese)
• Federal Registers
• Hazard Communication Standard; Final Rule
• Publication Date: 05/20/2024
• Publication Type: Final Rule
• Fed Register #: 89:44144-44461
• Standard Number: 1910.1200
• Title: Hazard Communication Standard; Final Rule

The Federal Register

The daily journal of the united states government, request access.

Due to aggressive automated scraping of FederalRegister.gov and eCFR.gov, programmatic access to these sites is limited to access to our extensive developer APIs.

If you are human user receiving this message, we can add your IP address to a set of IPs that can access FederalRegister.gov & eCFR.gov; complete the CAPTCHA (bot test) below and click "Request Access". This process will be necessary for each IP address you wish to access the site from, requests are valid for approximately one quarter (three months) after which the process may need to be repeated.

An official website of the United States government.

If you want to request a wider IP range, first request access for your current IP, and then use the "Site Feedback" button found in the lower left-hand side to make the request.