example of research using chi square

Statistics Made Easy

4 Examples of Using Chi-Square Tests in Real Life

In statistics, there are two different types of Chi-Square tests:

1. The Chi-Square Goodness of Fit Test – Used to determine whether or not a categorical variable follows a hypothesized distribution.

2. The Chi-Square Test of Independence – Used to determine whether or not there is a significant association between two categorical variables.

In this article, we share several examples of how each of these types of Chi-Square tests are used in real-life situations.

Example 1: Chi-Square Goodness of Fit Test

Suppose a shop owner claims that an equal number of customers come into his shop each weekday.

To test this hypothesis, he records the number of customers that come into the shop on a given week and finds the following:

• Monday:  50 customers
• Tuesday:  60 customers
• Wednesday:  40 customers
• Thursday:  47 customers
• Friday:  53 customers

He can use a Chi-Square Goodness of Fit Test to determine if the distribution of the customers that come in each day is consistent with his hypothesized distribution.

Using the Chi-Square Goodness of Fit Test Calculator , he can find that the p-value of the test is 0.359 .

Since this p-value is not less than .05, there is not sufficient evidence to say that the true distribution of customers is different from the distribution that the shop owner claimed.

Example 2: Chi-Square Goodness of Fit Test

Suppose a biologist claims that an equal number of four different species of deer enter a certain wooded area in a forest each week.

To test this hypothesis, she records the number of each species of deer that enter the wooded area over the course of one week:

• Species #1: 22 
• Species #2: 20
• Species #3: 23
• Species #4: 35

She can use a Chi-Square Goodness of Fit Test to determine if the distribution of the deer species that enter the wooded area in the forest each week is consistent with his hypothesized distribution.

Using the Chi-Square Goodness of Fit Test Calculator , she can find that the p-value of the test is 0.137 .

Since this p-value is not less than .05, there is not sufficient evidence to say that the true distribution of deer is different from the distribution that the biologist claimed.

Example 3: Chi-Square Test of Independence

Suppose a policy maker in a certain town wants to know whether or not gender is associated with political party preference.

He decides to take a simple random sample of 500 voters and survey them on their political party preference. The following table shows the results of the survey:

He can use a Chi-Square Test of Independence to determine if there is a statistically significant association between the two variables.

Using the Chi-Square Test of Independence Calculator , he can find that the p-value of the test is 0.649 .

Since the p-value is not less than .05, there is not sufficient evidence to say that there is an association between gender and political party preference.

Example 4: Chi-Square Test of Independence

Suppose a researcher wants to know whether or not marital status is associated with education level.

He decides to take a simple random sample of 300 individuals and obtains the following results:

Using the Chi-Square Test of Independence Calculator , he can find that the p-value of the test is 0.000011 .

Since the p-value is less than .05, there is sufficient evidence to say that there is an association between marital status and education level.

Additional Resources

The following tutorials provide an introduction to the different types of Chi-Square Tests:

• Chi-Square Test of Independence
• Chi-Square Goodness of Fit Test

The following tutorials explain the difference between Chi-Square tests and other statistical tests:

• Chi-Square Test vs. T-Test
• Chi-Square Test vs. ANOVA

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.4 chi-square tests, chi-square test of independence section  .

Do you remember how to test the independence of two categorical variables? This test is performed by using a Chi-square test of independence.

Recall that we can summarize two categorical variables within a two-way table, also called an r × c contingency table, where r = number of rows, c = number of columns. Our question of interest is “Are the two variables independent?” This question is set up using the following hypothesis statements:

 \[E=\frac{\text{row total}\times\text{column total}}{\text{sample size}}\]

We will compare the value of the test statistic to the critical value of \(\chi_{\alpha}^2\) with the degree of freedom = ( r - 1) ( c - 1), and reject the null hypothesis if \(\chi^2 \gt \chi_{\alpha}^2\).

Example S.4.1 Section  

Is gender independent of education level? A random sample of 395 people was surveyed and each person was asked to report the highest education level they obtained. The data that resulted from the survey are summarized in the following table:

Question : Are gender and education level dependent at a 5% level of significance? In other words, given the data collected above, is there a relationship between the gender of an individual and the level of education that they have obtained?

Here's the table of expected counts:

So, working this out, \(\chi^2= \dfrac{(60−50.886)^2}{50.886} + \cdots + \dfrac{(57 − 48.132)^2}{48.132} = 8.006\)

The critical value of \(\chi^2\) with 3 degrees of freedom is 7.815. Since 8.006 > 7.815, we reject the null hypothesis and conclude that the education level depends on gender at a 5% level of significance.

• Search Search Please fill out this field.

What Is a Chi-Square Statistic?

• What Does It Tell You?

When to Use a Chi-Square Test

• How to Perform It
• Limitations

The Bottom Line

• Business Leaders
• Math and Statistics

Chi-Square (χ2) Statistic: What It Is, Examples, How and When to Use the Test

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

Paige McLaughlin / Investopedia

A chi-square ( χ 2 ) statistic is a test that measures how a model compares to actual observed data. The data used in calculating a chi-square statistic must be random, raw, mutually exclusive , drawn from independent variables, and drawn from a large-enough sample . For example, the results of tossing a fair coin meet these criteria.

Chi-square tests are often used to test hypotheses . The chi-square statistic compares the size of any discrepancies between the expected results and the actual results, given the size of the sample and the number of variables in the relationship.

For these tests, degrees of freedom are used to determine if a certain  null hypothesis  can be rejected based on the total number of variables and samples within the experiment. As with any statistic, the larger the sample size, the more reliable the results.

Chi-Square Is a Test of...

...how a model compares to actual observed data.

Key Takeaways

• A chi-square ( χ 2 ) statistic is a measure of the difference between the observed and expected frequencies of the outcomes of a set of events or variables.
• Chi-square is useful for analyzing such differences in categorical variables, especially those nominal in nature.
• χ 2 depends on the size of the difference between actual and observed values, the degrees of freedom, and the sample size.
• χ 2 can be used to test whether two variables are related or independent of each other.
• It can also be used to test the goodness of fit between an observed distribution and a theoretical distribution of frequencies.

Formula for Chi-Square

 χ c 2 = ∑ ( O i − E i ) 2 E i where: c = Degrees of freedom O = Observed value(s) \begin{aligned}&\chi^2_c = \sum \frac{(O_i - E_i)^2}{E_i} \\&\textbf{where:}\\&c=\text{Degrees of freedom}\\&O=\text{Observed value(s)}\\&E=\text{Expected value(s)}\end{aligned} ​ χ c 2 ​ = ∑ E i ​ ( O i ​ − E i ​ ) 2 ​ where: c = Degrees of freedom O = Observed value(s) ​ 

What Does a Chi-Square Statistic Tell You?

There are two main kinds of chi-square tests:

• The test of independence, which asks a question of relationship, such as, “Is there a relationship between student gender and course choice?”
• The  goodness-of-fit test , which asks something like, “How well does the coin in my hand match a theoretically fair coin?”

Chi-square analysis is applied to categorical variables and is especially useful when those variables are nominal (where order doesn’t matter, like marital status or gender).

Independence

When considering student gender and course choice, a χ 2 test for independence could be used. To do this test, the researcher would collect data on the two chosen variables (gender and courses picked) and then compare the frequencies at which male and female students select among the offered classes using the formula given above and a χ 2 statistical table.

If there is no relationship between gender and course selection (that is if they are independent), then the actual frequencies at which male and female students select each offered course should be expected to be approximately equal, or conversely, the proportion of male and female students in any selected course should be approximately equal to the proportion of male and female students in the sample.

A χ 2 test for independence can tell us how likely it is that random chance can explain any observed difference between the actual frequencies in the data and these theoretical expectations.

Goodness of Fit

χ 2 provides a way to test how well a sample of data matches the (known or assumed) characteristics of the larger population that the sample is intended to represent. This is known as goodness of fit.

If the sample data do not fit the expected properties of the population in which we are interested, then we would not want to use this sample to draw conclusions about the larger population.

An Example of Chi-Square

For example, consider an imaginary coin with exactly a 50/50 chance of landing heads or tails and a real coin that you toss 100 times. If this coin is fair, then it will also have an equal probability of landing on either side, and the expected result of tossing the coin 100 times is that heads will come up 50 times and tails will come up 50 times.

In this case, χ 2 can tell us how well the actual results of 100 coin flips compare to the theoretical model that a fair coin will give 50/50 results. The actual toss could come up 50/50, or 60/40, or even 90/10. The farther away the actual results of the 100 tosses are from 50/50, the less good the fit of this set of tosses is to the theoretical expectation of 50/50, and the more likely we might conclude that this coin is not actually a fair coin.

A chi-square test is used to help determine if observed results are in line with expected results and to rule out that observations are due to chance.

A chi-square test is appropriate for this when the data being analyzed are from a random sample , and when the variable in question is a categorical variable. A categorical variable consists of selections such as type of car, race, educational attainment, male or female, or how much somebody likes a political candidate (from very much to very little).

These types of data are often collected via survey responses or questionnaires. Therefore, chi-square analysis is often most useful in analyzing this type of data.

How to Perform a Chi-Square Test

These are the basic steps whether you are performing a goodness-of-fit test or a test of independence:

• Create a table of the observed and expected frequencies.
• Use the formula to calculate the chi-square value.
• Find the critical chi-square value using a chi-square value table or statistical software.
• Determine whether the chi-square value or the critical value is the larger of the two.
• Reject or accept the null hypothesis.

Limitations of the Chi-Square Test

The chi-square test is sensitive to sample size. Relationships may appear to be significant when they aren’t simply because a very large sample is used.

In addition, the chi-square test cannot establish whether one variable has a causal relationship with another. It can only establish whether two variables are related.

What Is a Chi-Square Test Used for?

Chi-square is a statistical test used to examine the differences between categorical variables from a random sample in order to judge the goodness of fit between expected and observed results.

Who Uses Chi-Square Analysis?

Since chi-square applies to categorical variables, it is most used by researchers who are studying survey response data. This type of research can range from demography to consumer and marketing research to political science and economics.

Is Chi-Square Analysis Used When the Independent Variable Is Nominal or Ordinal?

A nominal variable is a categorical variable that differs by quality, but whose numerical order could be irrelevant. For instance, asking somebody their favorite color would produce a nominal variable. Asking somebody’s age, on the other hand, would produce an ordinal set of data. Chi-square can be best applied to nominal data.

There are two types of chi-square tests: the test of independence and the test of goodness of fit. Both are used to determine the validity of a hypothesis or an assumption. The result is a piece of evidence that can be used to make a decision.

For example:

In a test of independence, a company may want to evaluate whether its new product, an herbal supplement that promises to give people an energy boost, is reaching the people who are most likely to be interested. It is being advertised on websites related to sports and fitness, on the assumption that active and health-conscious people are most likely to buy it. It does an extensive poll that is intended to evaluate interest in the product by demographic group. The poll suggests no correlation between interest in this product and the most health-conscious people.

In a test of goodness of fit, a marketing professional is considering launching a new product that the company believes will be irresistible to women over age 45. The company has conducted product testing panels of 500 potential buyers of the product. The marketing professional has information about the age and gender of the test panels. This allows the construction of a chi-square test showing the distribution by age and gender of the people who said they would buy the product. The result will show whether or not the likeliest buyer is a woman over 45. If the test shows that men over age 45 or women ages 18 to 44 are just as likely to buy the product, then the marketing professional will revise the advertising, promotion, and placement of the product to appeal to this wider group of customers.

The Open University, via Internet Archive Wayback Machine. “ Chi Square Analysis ,” Page 2.

Kent State University, University Libraries. “ SPSS Tutorials: Chi-Square Test of Independence .”

The Open University, via Internet Archive Wayback Machine. “ Chi Square Analysis ,” Page 3.

The Open University, via Internet Archive Wayback Machine. “ Chi Square Analysis ,” Pages 3–5.

Scribbr. “ Chi-Square ( χ 2) Tests | Types, Formula & Examples .”

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

LEARN STATISTICS EASILY

Learn Data Analysis Now!

How to Report Chi-Square Test Results in APA Style: A Step-By-Step Guide

In this article, we guide you through how to report Chi-Square Test results, including essential components like the Chi-Square statistic (χ²), degrees of freedom (df), p-value, and Effect Size , aligning with established guidelines for clarity and reproducibility.

Introduction

The Chi-Square Test of Independence is a cornerstone in the field of statistical analysis when researchers aim to examine associations between categorical variables. For instance, in healthcare research, it could be employed to determine whether smoking status is independent of lung cancer incidence within a particular demographic. This statistical technique can decipher the intricacies of frequencies or proportions across different categories, thereby providing robust conclusions on the presence or absence of significant associations.

Conforming to the American Psychological Association (APA) guidelines for statistical reporting not only bolsters the credibility of your findings but also facilitates comprehension among a diversified audience, which may include scholars, healthcare professionals, and policy-makers. Adherence to the APA style is imperative for ensuring that the statistical rigor and the nuances of the Chi-Square Test are communicated effectively and unequivocally.

• The Chi-Square Test evaluates relationships between categorical variables.
• Reporting the Chi-Square, degrees of freedom, p-value, and effect size enhances scientific rigor.
• A p-value under the significance level (generally 0.01 or 0.05) signifies statistical significance.
• For tables larger than 2×2, use adjusted residuals; 5% thresholds are -1.96 and +1.96.
• Cramer’s V and Phi measure effect size and direction.

Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.

Guide to Reporting Chi-Square Test Results

1. state the chi-square test purpose.

Before you delve into the specifics of the Chi-Square Test, clearly outline the research question you aim to answer. The research question will guide your analysis, and it generally revolves around investigating how certain categorical variables might be related to one another.

Once you have a well-framed research question, you must state your hypothesis clearly . The hypothesis will predict what you expect to find in your study. The researcher needs to have a clear understanding of both the null and alternative hypotheses. These hypotheses function as the backbone of the statistical analysis, providing the framework for evaluating the data.

2. Report Sample Size and Characteristics

The sample size is pivotal for the reliability of your results. Indicate how many subjects or items were part of your study and describe the method used for sample size determination.

Offer any relevant demographic information, such as age, gender, socioeconomic status, or other categorical variables that could impact the results. Providing these details will enhance the clarity and comprehensibility of your report.

3. Present Observed Frequencies

For each category or class under investigation, present the observed frequencies . These are the actual counts of subjects or items in each category collected through your research.

The expected frequencies are what you would anticipate if the null hypothesis is true, suggesting no association between the variables. If you prefer, you can also present these expected frequencies in your report to provide additional context for interpretation.

4. Report the Chi-Square Statistic and Degrees of Freedom

Clearly state the Chi-Square value that you calculated during the test. This is often denoted as χ² . It is the test statistic that you’ll compare to a critical value to decide whether to reject the null hypothesis.

In statistical parlance, degrees of freedom refer to the number of values in a study that are free to vary. When reporting your Chi-Square Test results, it is vital to mention the degrees of freedom, typically denoted as “ df .”

5. Indicate the p-value

The p-value is a critical component in statistical hypothesis testing, representing the probability that the observed data would occur if the null hypothesis were true. It quantifies the evidence against the null hypothesis.

Values below 0.05 are commonly considered indicators of statistical significance. This suggests that there is less than a 5% probability of observing a test statistic at least as extreme as the one observed, assuming that the null hypothesis is true. It implies that the association between the variables under study is unlikely to have occurred by random chance alone.

6. Report Effect Size

While a statistically significant p-value can inform you of an association between variables, it does not indicate the strength or magnitude of the relationship. This is where effect size comes into play. Effect size measures such as Cramer’s V or Phi coefficient offer a quantifiable method to determine how strong the association is.

Cramer’s V and Phi coefficient are the most commonly used effect size measures in Chi-Square Tests. Cramer’s V is beneficial for tables larger than 2×2, whereas Phi is generally used for 2×2 tables. Both are derived from the Chi-Square statistic and help compare results across different studies or datasets.

Effect sizes are generally categorized as small (0.1), medium (0.3), or large (0.5). These categories help the audience in making practical interpretations of the study findings.

7. Interpret the Results

Based on the Chi-Square statistic, degrees of freedom, p-value, and effect size, you need to synthesize all this data into coherent and clear conclusions. Here, you must state whether your results support the null hypothesis or suggest that it should be rejected.

Interpreting the results also involves detailing the real-world relevance or practical implications of the findings. For instance, if a Chi-Square Test in a medical study finds a significant association between a particular treatment and patient recovery rates, the practical implication could be that the treatment is effective and should be considered in clinical guidelines.

8. Additional Information

When working with contingency tables larger than 2×2, analyzing the adjusted residuals for each combination of categories between the two nominal qualitative variables becomes necessary. Suppose the significance level is set at 5%. In that case, adjusted residuals with values less than -1.96 or greater than +1.96 indicate an association in the analyzed combination. Similarly, at a 1% significance level, adjusted residuals with values less than -2.576 or greater than +2.576 indicate an association.

Charts , graphs , or tables can be included as supplementary material to represent the statistical data visually. This helps the reader grasp the details and implications of the study more effectively.

Vaccine Efficacy in Two Age Groups

Suppose a study aims to assess whether a new vaccine is equally effective across different age groups: those aged 18-40 and those aged 41-60. A sample of 200 people is randomly chosen, half from each age group. After administering the vaccine, it is observed whether or not the individuals contracted the disease within a specified timeframe.

Observed Frequencies

• Contracted Disease: 12
• Did Not Contract Disease: 88
• Contracted Disease: 28
• Did Not Contract Disease: 72

Expected Frequencies

If there were no association between age group and vaccine efficacy, we would expect an equal proportion of individuals in each group to contract the disease. The expected frequencies would then be:

• Contracted Disease: (12+28)/2 = 20
• Did Not Contract Disease: (88+72)/2 = 80
• Contracted Disease: 20
• Did Not Contract Disease: 80

Chi-Square Test Results

• Chi-Square Statistic (χ²) : 10.8
• Degrees of Freedom (df) : 1
• p-value : 0.001
• Effect Size (Cramer’s V) : 0.23

Interpretation

• Statistical Significance : The p-value being less than 0.05 indicates a statistically significant association between age group and vaccine efficacy.
• Effect Size : The effect size of 0.23, although statistically significant, is on the smaller side, suggesting that while age does have an impact on vaccine efficacy, the practical significance is moderate.
• Practical Implications : Given the significant but moderate association, healthcare providers may consider additional protective measures for the older age group but do not necessarily need to rethink the vaccine’s distribution strategy entirely.

Results Presentation

To evaluate the effectiveness of the vaccine across two different age groups, a Chi-Square Test of Independence was executed. The observed frequencies revealed that among those aged 18-40, 12 contracted the disease, while 88 did not. Conversely, in the 41-60 age group, 28 contracted the disease, and 72 did not. Under the assumption that there was no association between age group and vaccine efficacy, the expected frequencies were calculated to be 20 contracting the disease and 80 not contracting the disease for both age groups. The analysis resulted in a Chi-Square statistic (χ²) of 10.8, with 1 degree of freedom. The associated p-value was 0.001, below the alpha level of 0.05, suggesting a statistically significant association between age group and vaccine efficacy. Additionally, an effect size was calculated using Cramer’s V, which was found to be 0.23. While this effect size is statistically significant, it is moderate in magnitude.

Alternative Results Presentation

To assess the vaccine’s effectiveness across different age demographics, we performed a Chi-Square Test of Independence. In the age bracket of 18-40, observed frequencies indicated that 12 individuals contracted the disease, in contrast to 88 who did not (Expected frequencies: Contracted = 20, Not Contracted = 80). Similarly, for the 41-60 age group, 28 individuals contracted the disease, while 72 did not (Expected frequencies: Contracted = 20, Not Contracted = 80). The Chi-Square Test yielded significant results (χ²(1) = 10.8, p = .001, V = .23). These results imply a statistically significant, albeit moderately sized, association between age group and vaccine efficacy.

Reporting Chi-Square Test results in APA style involves multiple layers of detail. From stating the test’s purpose, presenting sample size, and explaining the observed and expected frequencies to elucidating the Chi-Square statistic, p-value, and effect size, each component serves a unique role in building a compelling narrative around your research findings.

By diligently following this comprehensive guide, you empower your audience to gain a nuanced understanding of your research. This not only enhances the validity and impact of your study but also contributes to the collective scientific endeavor of advancing knowledge.

Recommended Articles

Interested in learning more about statistical analysis and its vital role in scientific research? Explore our blog for more insights and discussions on relevant topics.

• Mastering the Chi-Square Test: A Comprehensive Guide

What is the Difference Between the T-Test vs. Chi-Square Test?

• Understanding the Null Hypothesis in Chi-Square

Effect Size for Chi-Square Tests: Unveiling its Significance

Understanding the assumptions for chi-square test of independence.

• Assumptions for Chi-Square Test (Story)
• Chi-Square Calculator: Enhance Your Data Analysis Skills
• Chi Square Test – an overview (Exte rnal Link)

Frequently Asked Questions (FAQs)

The Chi-Square Test of Independence is a statistical method used to evaluate the relationship between two or more categorical variables. It is commonly employed in various research fields to determine if there are significant associations between variables.

Use a Chi-Square Test to examine the relationship between two or more categorical variables. This test is often applied in healthcare, social sciences, and marketing research, among other disciplines.

The p-value represents the probability that the observed data occurred by chance if the null hypothesis is true. A p-value less than 0.05 generally indicates a statistically significant relationship between the variables being studied.

To report the results in APA style, state the purpose, sample size, observed frequencies, Chi-Square statistic, degrees of freedom, p-value, effect size, and interpretation of the findings. Additional information, such as adjusted residuals and graphical representations, may also be included.

Effect size measures like Cramer’s V or Phi coefficient quantify the strength and direction of the relationship between variables. Effect sizes are categorized as small (0.1), medium (0.3), or large (0.5).

Interpret the effect size in terms of its practical implications. For example, a small effect size, although statistically significant, might not be practically important. Conversely, a large effect size would likely have significant real-world implications.

In contingency tables larger than 2×2, adjusted residuals are calculated to identify which specific combinations of categories are driving the observed associations. Thresholds commonly used are -1.96 and +1.96 at a 5% significance level.

Chi-square tests are more reliable with larger sample sizes. For small sample sizes, it is advisable to use an alternative test like Fisher’s Exact Test.

While a t-test is used to compare the means of two groups, a Chi-Square Test is used to examine the relationship between two or more categorical variables. Both tests provide different types of information and are used under other conditions.

Yes, options like the Fisher’s Exact Test for small samples and the Kruskal-Wallis test for ordinal data are available. These are used when the assumptions for a Chi-Square Test cannot be met.

Similar Posts

How to Report Results of Multiple Linear Regression in APA Style

Master how to report results of multiple linear regression in APA style, covering coefficients, model fit, and diagnostics.

APA Style T-Test Reporting Guide

How to report t-test in APA style? Learn now! Tips, examples, and effect size calculation included. Learn how to report t-test results.

Discover the significance of effect size for chi square in data science, understand standard measures like Cramer’s V and Phi coefficient, and learn how to calculate them.

Explore the fundamental differences between the t-test vs. chi-square test, crucial tools in statistics and data analysis.

How to Report One-Way ANOVA Results in APA Style: A Step-by-Step Guide

Learn how to report the results of ANOVA in APA style with our step-by-step guide, covering key elements, effect sizes, and interpretation.

Explore the assumptions and applications of the Chi-Square Test of Independence, a crucial tool for analyzing categorical data in various fields.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Chi-Square (Χ²) Test & How To Calculate Formula Equation

Benjamin Frimodig

Science Expert

B.A., History and Science, Harvard University

Ben Frimodig is a 2021 graduate of Harvard College, where he studied the History of Science.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

On This Page:

Chi-square (χ2) is used to test hypotheses about the distribution of observations into categories with no inherent ranking.

What Is a Chi-Square Statistic?

The Chi-square test (pronounced Kai) looks at the pattern of observations and will tell us if certain combinations of the categories occur more frequently than we would expect by chance, given the total number of times each category occurred.

It looks for an association between the variables. We cannot use a correlation coefficient to look for the patterns in this data because the categories often do not form a continuum.

There are three main types of Chi-square tests, tests of goodness of fit, the test of independence, and the test for homogeneity. All three tests rely on the same formula to compute a test statistic.

These tests function by deciphering relationships between observed sets of data and theoretical or “expected” sets of data that align with the null hypothesis.

What is a Contingency Table?

Contingency tables (also known as two-way tables) are grids in which Chi-square data is organized and displayed. They provide a basic picture of the interrelation between two variables and can help find interactions between them.

In contingency tables, one variable and each of its categories are listed vertically, and the other variable and each of its categories are listed horizontally.

Additionally, including column and row totals, also known as “marginal frequencies,” will help facilitate the Chi-square testing process.

In order for the Chi-square test to be considered trustworthy, each cell of your expected contingency table must have a value of at least five.

Each Chi-square test will have one contingency table representing observed counts (see Fig. 1) and one contingency table representing expected counts (see Fig. 2).

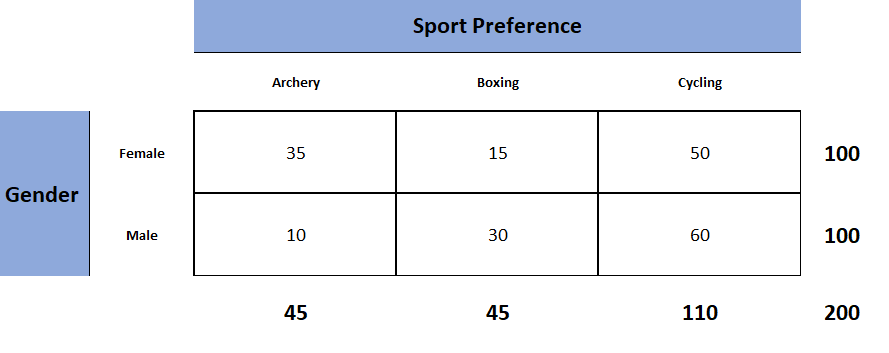
Figure 1. Observed table (which contains the observed counts).

To obtain the expected frequencies for any cell in any cross-tabulation in which the two variables are assumed independent, multiply the row and column totals for that cell and divide the product by the total number of cases in the table.

Figure 2. Expected table (what we expect the two-way table to look like if the two categorical variables are independent).

To decide if our calculated value for χ2 is significant, we also need to work out the degrees of freedom for our contingency table using the following formula: df= (rows – 1) x (columns – 1).

Formula Calculation

Calculate the chi-square statistic (χ2) by completing the following steps:

• Calculate the expected frequencies and the observed frequencies.
• For each observed number in the table, subtract the corresponding expected number (O — E).
• Square the difference (O —E)².
• Divide the squares obtained for each cell in the table by the expected number for that cell (O – E)² / E.
• Sum all the values for (O – E)² / E. This is the chi-square statistic.
• Calculate the degrees of freedom for the contingency table using the following formula; df= (rows – 1) x (columns – 1).

Once we have calculated the degrees of freedom (df) and the chi-squared value (χ2), we can use the χ2 table (often at the back of a statistics book) to check if our value for χ2 is higher than the critical value given in the table. If it is, then our result is significant at the level given.

Interpretation

The chi-square statistic tells you how much difference exists between the observed count in each table cell to the counts you would expect if there were no relationship at all in the population.

Small Chi-Square Statistic: If the chi-square statistic is small and the p-value is large (usually greater than 0.05), this often indicates that the observed frequencies in the sample are close to what would be expected under the null hypothesis.

The null hypothesis usually states no association between the variables being studied or that the observed distribution fits the expected distribution.

In theory, if the observed and expected values were equal (no difference), then the chi-square statistic would be zero — but this is unlikely to happen in real life.

Large Chi-Square Statistic : If the chi-square statistic is large and the p-value is small (usually less than 0.05), then the conclusion is often that the data does not fit the model well, i.e., the observed and expected values are significantly different. This often leads to the rejection of the null hypothesis.

How to Report

To report a chi-square output in an APA-style results section, always rely on the following template:

χ2 ( degrees of freedom , N = sample size ) = chi-square statistic value , p = p value .

In the case of the above example, the results would be written as follows:

A chi-square test of independence showed that there was a significant association between gender and post-graduation education plans, χ2 (4, N = 101) = 54.50, p < .001.

APA Style Rules

• Do not use a zero before a decimal when the statistic cannot be greater than 1 (proportion, correlation, level of statistical significance).
• Report exact p values to two or three decimals (e.g., p = .006, p = .03).
• However, report p values less than .001 as “ p < .001.”
• Put a space before and after a mathematical operator (e.g., minus, plus, greater than, less than, equals sign).
• Do not repeat statistics in both the text and a table or figure.

p -value Interpretation

You test whether a given χ2 is statistically significant by testing it against a table of chi-square distributions , according to the number of degrees of freedom for your sample, which is the number of categories minus 1. The chi-square assumes that you have at least 5 observations per category.

If you are using SPSS then you will have an expected p -value.

For a chi-square test, a p-value that is less than or equal to the .05 significance level indicates that the observed values are different to the expected values.

Thus, low p-values (p< .05) indicate a likely difference between the theoretical population and the collected sample. You can conclude that a relationship exists between the categorical variables.

Remember that p -values do not indicate the odds that the null hypothesis is true but rather provide the probability that one would obtain the sample distribution observed (or a more extreme distribution) if the null hypothesis was true.

A level of confidence necessary to accept the null hypothesis can never be reached. Therefore, conclusions must choose to either fail to reject the null or accept the alternative hypothesis, depending on the calculated p-value.

The four steps below show you how to analyze your data using a chi-square goodness-of-fit test in SPSS (when you have hypothesized that you have equal expected proportions).

Step 1 : Analyze > Nonparametric Tests > Legacy Dialogs > Chi-square… on the top menu as shown below:

Step 2 : Move the variable indicating categories into the “Test Variable List:” box.

Step 3 : If you want to test the hypothesis that all categories are equally likely, click “OK.”

Step 4 : Specify the expected count for each category by first clicking the “Values” button under “Expected Values.”

Step 5 : Then, in the box to the right of “Values,” enter the expected count for category one and click the “Add” button. Now enter the expected count for category two and click “Add.” Continue in this way until all expected counts have been entered.

Step 6 : Then click “OK.”

The four steps below show you how to analyze your data using a chi-square test of independence in SPSS Statistics.

Step 1 : Open the Crosstabs dialog (Analyze > Descriptive Statistics > Crosstabs).

Step 2 : Select the variables you want to compare using the chi-square test. Click one variable in the left window and then click the arrow at the top to move the variable. Select the row variable and the column variable.

Step 3 : Click Statistics (a new pop-up window will appear). Check Chi-square, then click Continue.

Step 4 : (Optional) Check the box for Display clustered bar charts.

Step 5 : Click OK.

Goodness-of-Fit Test

The Chi-square goodness of fit test is used to compare a randomly collected sample containing a single, categorical variable to a larger population.

This test is most commonly used to compare a random sample to the population from which it was potentially collected.

The test begins with the creation of a null and alternative hypothesis. In this case, the hypotheses are as follows:

Null Hypothesis (Ho) : The null hypothesis (Ho) is that the observed frequencies are the same (except for chance variation) as the expected frequencies. The collected data is consistent with the population distribution.

Alternative Hypothesis (Ha) : The collected data is not consistent with the population distribution.

The next step is to create a contingency table that represents how the data would be distributed if the null hypothesis were exactly correct.

The sample’s overall deviation from this theoretical/expected data will allow us to draw a conclusion, with a more severe deviation resulting in smaller p-values.

Test for Independence

The Chi-square test for independence looks for an association between two categorical variables within the same population.

Unlike the goodness of fit test, the test for independence does not compare a single observed variable to a theoretical population but rather two variables within a sample set to one another.

The hypotheses for a Chi-square test of independence are as follows:

Null Hypothesis (Ho) : There is no association between the two categorical variables in the population of interest.

Alternative Hypothesis (Ha) : There is no association between the two categorical variables in the population of interest.

The next step is to create a contingency table of expected values that reflects how a data set that perfectly aligns the null hypothesis would appear.

The simplest way to do this is to calculate the marginal frequencies of each row and column; the expected frequency of each cell is equal to the marginal frequency of the row and column that corresponds to a given cell in the observed contingency table divided by the total sample size.

Test for Homogeneity

The Chi-square test for homogeneity is organized and executed exactly the same as the test for independence.

The main difference to remember between the two is that the test for independence looks for an association between two categorical variables within the same population, while the test for homogeneity determines if the distribution of a variable is the same in each of several populations (thus allocating population itself as the second categorical variable).

Null Hypothesis (Ho) : There is no difference in the distribution of a categorical variable for several populations or treatments.

Alternative Hypothesis (Ha) : There is a difference in the distribution of a categorical variable for several populations or treatments.

The difference between these two tests can be a bit tricky to determine, especially in the practical applications of a Chi-square test. A reliable rule of thumb is to determine how the data was collected.

If the data consists of only one random sample with the observations classified according to two categorical variables, it is a test for independence. If the data consists of more than one independent random sample, it is a test for homogeneity.

What is the chi-square test?

The Chi-square test is a non-parametric statistical test used to determine if there’s a significant association between two or more categorical variables in a sample.

It works by comparing the observed frequencies in each category of a cross-tabulation with the frequencies expected under the null hypothesis, which assumes there is no relationship between the variables.

This test is often used in fields like biology, marketing, sociology, and psychology for hypothesis testing.

What does chi-square tell you?

The Chi-square test informs whether there is a significant association between two categorical variables. Suppose the calculated Chi-square value is above the critical value from the Chi-square distribution.

In that case, it suggests a significant relationship between the variables, rejecting the null hypothesis of no association.

How to calculate chi-square?

To calculate the Chi-square statistic, follow these steps:

1. Create a contingency table of observed frequencies for each category.

2. Calculate expected frequencies for each category under the null hypothesis.

3. Compute the Chi-square statistic using the formula: Χ² = Σ [ (O_i – E_i)² / E_i ], where O_i is the observed frequency and E_i is the expected frequency.

4. Compare the calculated statistic with the critical value from the Chi-square distribution to draw a conclusion.

Related Articles

Exploratory Data Analysis

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

Convergent Validity: Definition and Examples

Content Validity in Research: Definition & Examples

Construct Validity In Psychology Research

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Inference for categorical data: Chi-square

About this unit.

Learn to test how well sample counts of a categorical variable fit some hypothesized distribution, or, if the distribution of a categorical variable is similar or not across multiple groups.

Chi-square test for goodness of fit

• Chi-square statistic for hypothesis testing (Opens a modal)
• Chi-square goodness-of-fit example (Opens a modal)
• Expected counts in a goodness-of-fit test Get 3 of 4 questions to level up!
• Conditions for a goodness-of-fit test Get 3 of 4 questions to level up!
• Test statistic and P-value in a goodness-of-fit test Get 3 of 4 questions to level up!
• Conclusions in a goodness-of-fit test Get 3 of 4 questions to level up!

Chi square tests for relationships (homogeneity or independence)

• Introduction to the chi-square test for homogeneity (Opens a modal)
• Chi-square test for association (independence) (Opens a modal)
• Expected counts in chi-squared tests with two-way tables Get 3 of 4 questions to level up!
• Test statistic and P-value in chi-square tests with two-way tables Get 3 of 4 questions to level up!
• Making conclusions in chi-square tests for two-way tables Get 3 of 4 questions to level up!

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability, a comprehensive look at percentile in statistics, the best guide to understand bayes theorem, everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test.

A Complete Guide on Hypothesis Testing in Statistics

Understanding the Fundamentals of Arithmetic and Geometric Progression

The definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution, all you need to know about bias in statistics, a complete guide to get a grasp of time series analysis.

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is a chi-square test formula, examples & application.

Lesson 9 of 24 By Avijeet Biswal

Table of Contents

The world is constantly curious about the Chi-Square test's application in machine learning and how it makes a difference. Feature selection is a critical topic in machine learning , as you will have multiple features in line and must choose the best ones to build the model. By examining the relationship between the elements, the chi-square test aids in the solution of feature selection problems. In this tutorial, you will learn about the chi-square test and its application.

What Is a Chi-Square Test?

The Chi-Square test is a statistical procedure for determining the difference between observed and expected data. This test can also be used to determine whether it correlates to the categorical variables in our data. It helps to find out whether a difference between two categorical variables is due to chance or a relationship between them.

Chi-Square Test Definition

A chi-square test is a statistical test that is used to compare observed and expected results. The goal of this test is to identify whether a disparity between actual and predicted data is due to chance or to a link between the variables under consideration. As a result, the chi-square test is an ideal choice for aiding in our understanding and interpretation of the connection between our two categorical variables.

A chi-square test or comparable nonparametric test is required to test a hypothesis regarding the distribution of a categorical variable. Categorical variables, which indicate categories such as animals or countries, can be nominal or ordinal. They cannot have a normal distribution since they can only have a few particular values.

For example, a meal delivery firm in India wants to investigate the link between gender, geography, and people's food preferences.

It is used to calculate the difference between two categorical variables, which are:

• As a result of chance or
• Because of the relationship

Your Data Analytics Career is Around The Corner!

Formula For Chi-Square Test

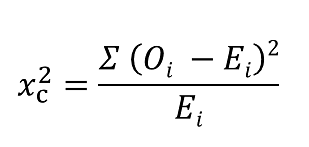
c = Degrees of freedom

O = Observed Value

E = Expected Value

The degrees of freedom in a statistical calculation represent the number of variables that can vary in a calculation. The degrees of freedom can be calculated to ensure that chi-square tests are statistically valid. These tests are frequently used to compare observed data with data that would be expected to be obtained if a particular hypothesis were true.

The Observed values are those you gather yourselves.

The expected values are the frequencies expected, based on the null hypothesis. 

Fundamentals of Hypothesis Testing

Hypothesis testing is a technique for interpreting and drawing inferences about a population based on sample data. It aids in determining which sample data best support mutually exclusive population claims.

Null Hypothesis (H0) - The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

Alternate Hypothesis(H1 or Ha) - The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Become a Data Science Expert & Get Your Dream Job

What Are Categorical Variables?

Categorical variables belong to a subset of variables that can be divided into discrete categories. Names or labels are the most common categories. These variables are also known as qualitative variables because they depict the variable's quality or characteristics.

Categorical variables can be divided into two categories:

• Nominal Variable: A nominal variable's categories have no natural ordering. Example: Gender, Blood groups
• Ordinal Variable: A variable that allows the categories to be sorted is ordinal variables. Customer satisfaction (Excellent, Very Good, Good, Average, Bad, and so on) is an example.

Why Do You Use the Chi-Square Test?

Chi-square is a statistical test that examines the differences between categorical variables from a random sample in order to determine whether the expected and observed results are well-fitting.

Here are some of the uses of the Chi-Squared test:

• The Chi-squared test can be used to see if your data follows a well-known theoretical probability distribution like the Normal or Poisson distribution.
• The Chi-squared test allows you to assess your trained regression model's goodness of fit on the training, validation, and test data sets.

Become an Expert in Data Analytics!

What Does A Chi-Square Statistic Test Tell You?

A Chi-Square test ( symbolically represented as  2 ) is fundamentally a data analysis based on the observations of a random set of variables. It computes how a model equates to actual observed data. A Chi-Square statistic test is calculated based on the data, which must be raw, random, drawn from independent variables, drawn from a wide-ranging sample and mutually exclusive. In simple terms, two sets of statistical data are compared -for instance, the results of tossing a fair coin. Karl Pearson introduced this test in 1900 for categorical data analysis and distribution. This test is also known as ‘Pearson’s Chi-Squared Test’. 

Chi-Squared Tests are most commonly used in hypothesis testing. A hypothesis is an assumption that any given condition might be true, which can be tested afterwards. The Chi-Square test estimates the size of inconsistency between the expected results and the actual results when the size of the sample and the number of variables in the relationship is mentioned. 

These tests use degrees of freedom to determine if a particular null hypothesis can be rejected based on the total number of observations made in the experiments. Larger the sample size, more reliable is the result.

There are two main types of Chi-Square tests namely -

Independence 

• Goodness-of-Fit 

The Chi-Square Test of Independence is a derivable ( also known as inferential ) statistical test which examines whether the two sets of variables are likely to be related with each other or not. This test is used when we have counts of values for two nominal or categorical variables and is considered as non-parametric test. A relatively large sample size and independence of obseravations are the required criteria for conducting this test.

For Example- 

In a movie theatre, suppose we made a list of movie genres. Let us consider this as the first variable. The second variable is whether or not the people who came to watch those genres of movies have bought snacks at the theatre. Here the null hypothesis is that th genre of the film and whether people bought snacks or not are unrelatable. If this is true, the movie genres don’t impact snack sales. 

Future-Proof Your AI/ML Career: Top Dos and Don'ts

Goodness-Of-Fit

In statistical hypothesis testing, the Chi-Square Goodness-of-Fit test determines whether a variable is likely to come from a given distribution or not. We must have a set of data values and the idea of the distribution of this data. We can use this test when we have value counts for categorical variables. This test demonstrates a way of deciding if the data values have a “ good enough” fit for our idea or if it is a representative sample data of the entire population. 

Suppose we have bags of balls with five different colours in each bag. The given condition is that the bag should contain an equal number of balls of each colour. The idea we would like to test here is that the proportions of the five colours of balls in each bag must be exact. 

Who Uses Chi-Square Analysis?

Chi-square is most commonly used by researchers who are studying survey response data because it applies to categorical variables. Demography, consumer and marketing research, political science, and economics are all examples of this type of research.

Let's say you want to know if gender has anything to do with political party preference. You poll 440 voters in a simple random sample to find out which political party they prefer. The results of the survey are shown in the table below:

To see if gender is linked to political party preference, perform a Chi-Square test of independence using the steps below.

Step 1: Define the Hypothesis

H0: There is no link between gender and political party preference.

H1: There is a link between gender and political party preference.

Step 2: Calculate the Expected Values

Now you will calculate the expected frequency.

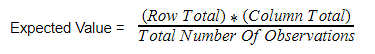
For example, the expected value for Male Republicans is: 

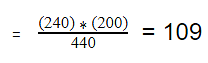
Similarly, you can calculate the expected value for each of the cells.

Step 3: Calculate (O-E)2 / E for Each Cell in the Table

Now you will calculate the (O - E)2 / E for each cell in the table.

Step 4: Calculate the Test Statistic X2

X2  is the sum of all the values in the last table

 =  0.743 + 2.05 + 2.33 + 3.33 + 0.384 + 1

Before you can conclude, you must first determine the critical statistic, which requires determining our degrees of freedom. The degrees of freedom in this case are equal to the table's number of columns minus one multiplied by the table's number of rows minus one, or (r-1) (c-1). We have (3-1)(2-1) = 2.

Finally, you compare our obtained statistic to the critical statistic found in the chi-square table. As you can see, for an alpha level of 0.05 and two degrees of freedom, the critical statistic is 5.991, which is less than our obtained statistic of 9.83. You can reject our null hypothesis because the critical statistic is higher than your obtained statistic.

This means you have sufficient evidence to say that there is an association between gender and political party preference.

When to Use a Chi-Square Test?

A Chi-Square Test is used to examine whether the observed results are in order with the expected values. When the data to be analysed is from a random sample, and when the variable is the question is a categorical variable, then Chi-Square proves the most appropriate test for the same. A categorical variable consists of selections such as breeds of dogs, types of cars, genres of movies, educational attainment, male v/s female etc. Survey responses and questionnaires are the primary sources of these types of data. The Chi-square test is most commonly used for analysing this kind of data. This type of analysis is helpful for researchers who are studying survey response data. The research can range from customer and marketing research to political sciences and economics. 

The Ultimate Ticket to Top Data Science Job Roles

Chi-Square Distribution 

Chi-square distributions (X2) are a type of continuous probability distribution. They're commonly utilized in hypothesis testing, such as the chi-square goodness of fit and independence tests. The parameter k, which represents the degrees of freedom, determines the shape of a chi-square distribution.

A chi-square distribution is followed by very few real-world observations. The objective of chi-square distributions is to test hypotheses, not to describe real-world distributions. In contrast, most other commonly used distributions, such as normal and Poisson distributions, may explain important things like baby birth weights or illness cases per year.

Because of its close resemblance to the conventional normal distribution, chi-square distributions are excellent for hypothesis testing. Many essential statistical tests rely on the conventional normal distribution.

In statistical analysis , the Chi-Square distribution is used in many hypothesis tests and is determined by the parameter k degree of freedoms. It belongs to the family of continuous probability distributions . The Sum of the squares of the k independent standard random variables is called the Chi-Squared distribution. Pearson’s Chi-Square Test formula is - 

Where X^2 is the Chi-Square test symbol

Σ is the summation of observations

O is the observed results

E is the expected results 

The shape of the distribution graph changes with the increase in the value of k, i.e. degree of freedoms. 

When k is 1 or 2, the Chi-square distribution curve is shaped like a backwards ‘J’. It means there is a high chance that X^2 becomes close to zero. 

Courtesy: Scribbr

When k is greater than 2, the shape of the distribution curve looks like a hump and has a low probability that X^2 is very near to 0 or very far from 0. The distribution occurs much longer on the right-hand side and shorter on the left-hand side. The probable value of X^2 is (X^2 - 2).

When k is greater than ninety, a normal distribution is seen, approximating the Chi-square distribution.

Become a Data Scientist With Real-World Experience

Chi-Square P-Values

Here P denotes the probability; hence for the calculation of p-values, the Chi-Square test comes into the picture. The different p-values indicate different types of hypothesis interpretations. 

• P <= 0.05 (Hypothesis interpretations are rejected)
• P>= 0.05 (Hypothesis interpretations are accepted) 

The concepts of probability and statistics are entangled with Chi-Square Test. Probability is the estimation of something that is most likely to happen. Simply put, it is the possibility of an event or outcome of the sample. Probability can understandably represent bulky or complicated data. And statistics involves collecting and organising, analysing, interpreting and presenting the data. 

Finding P-Value

When you run all of the Chi-square tests, you'll get a test statistic called X2. You have two options for determining whether this test statistic is statistically significant at some alpha level:

• Compare the test statistic X2 to a critical value from the Chi-square distribution table.
• Compare the p-value of the test statistic X2 to a chosen alpha level.

Test statistics are calculated by taking into account the sampling distribution of the test statistic under the null hypothesis, the sample data, and the approach which is chosen for performing the test. 

The p-value will be as mentioned in the following cases.

• A lower-tailed test is specified by: P(TS ts | H0 is true) p-value = cdf (ts)
• Lower-tailed tests have the following definition: P(TS ts | H0 is true) p-value = cdf (ts)
• A two-sided test is defined as follows, if we assume that the test static distribution  of H0 is symmetric about 0. 2 * P(TS |ts| | H0 is true) = 2 * (1 - cdf(|ts|))

P: probability Event

TS: Test statistic is computed observed value of the test statistic from your sample cdf(): Cumulative distribution function of the test statistic's distribution (TS)

Types of Chi-square Tests

Pearson's chi-square tests are classified into two types:

• Chi-square goodness-of-fit analysis
• Chi-square independence test

These are, mathematically, the same exam. However, because they are utilized for distinct goals, we generally conceive of them as separate tests.

The chi-square test has the following significant properties:

• If you multiply the number of degrees of freedom by two, you will receive an answer that is equal to the variance.
• The chi-square distribution curve approaches the data is normally distributed as the degree of freedom increases.
• The mean distribution is equal to the number of degrees of freedom.

Properties of Chi-Square Test 

• Variance is double the times the number of degrees of freedom.
• Mean distribution is equal to the number of degrees of freedom.
• When the degree of freedom increases, the Chi-Square distribution curve becomes normal.

Limitations of Chi-Square Test

There are two limitations to using the chi-square test that you should be aware of. 

• The chi-square test, for starters, is extremely sensitive to sample size. Even insignificant relationships can appear statistically significant when a large enough sample is used. Keep in mind that "statistically significant" does not always imply "meaningful" when using the chi-square test.
• Be mindful that the chi-square can only determine whether two variables are related. It does not necessarily follow that one variable has a causal relationship with the other. It would require a more detailed analysis to establish causality.

Get In-Demand Skills to Launch Your Data Career

Chi-Square Goodness of Fit Test

When there is only one categorical variable, the chi-square goodness of fit test can be used. The frequency distribution of the categorical variable is evaluated for determining whether it differs significantly from what you expected. The idea is that the categories will have equal proportions, however, this is not always the case.

When you want to see if there is a link between two categorical variables, you perform the chi-square test. To acquire the test statistic and its related p-value in SPSS, use the chisq option on the statistics subcommand of the crosstabs command. Remember that the chi-square test implies that each cell's anticipated value is five or greater.

In this tutorial titled ‘The Complete Guide to Chi-square test’, you explored the concept of Chi-square distribution and how to find the related values. You also take a look at how the critical value and chi-square value is related to each other.

If you want to gain more insight and get a work-ready understanding in statistical concepts and learn how to use them to get into a career in Data Analytics , our Post Graduate Program in Data Analytics in partnership with Purdue University should be your next stop. A comprehensive program with training from top practitioners and in collaboration with IBM, this will be all that you need to kickstart your career in the field. 

Was this tutorial on the Chi-square test useful to you? Do you have any doubts or questions for us? Mention them in this article's comments section, and we'll have our experts answer them for you at the earliest!

1) What is the chi-square test used for? 

The chi-square test is a statistical method used to determine if there is a significant association between two categorical variables. It helps researchers understand whether the observed distribution of data differs from the expected distribution, allowing them to assess whether any relationship exists between the variables being studied.

2) What is the chi-square test and its types? 

The chi-square test is a statistical test used to analyze categorical data and assess the independence or association between variables. There are two main types of chi-square tests: a) Chi-square test of independence: This test determines whether there is a significant association between two categorical variables. b) Chi-square goodness-of-fit test: This test compares the observed data to the expected data to assess how well the observed data fit the expected distribution.

3) What is the chi-square test easily explained? 

The chi-square test is a statistical tool used to check if two categorical variables are related or independent. It helps us understand if the observed data differs significantly from the expected data. By comparing the two datasets, we can draw conclusions about whether the variables have a meaningful association.

4) What is the difference between t-test and chi-square? 

The t-test and the chi-square test are two different statistical tests used for different types of data. The t-test is used to compare the means of two groups and is suitable for continuous numerical data. On the other hand, the chi-square test is used to examine the association between two categorical variables. It is applicable to discrete, categorical data. So, the choice between the t-test and chi-square test depends on the nature of the data being analyzed.

5) What are the characteristics of chi-square? 

The chi-square test has several key characteristics:

1) It is non-parametric, meaning it does not assume a specific probability distribution for the data.

2) It is sensitive to sample size; larger samples can result in more significant outcomes.

3) It works with categorical data and is used for hypothesis testing and analyzing associations.

4) The test output provides a p-value, which indicates the level of significance for the observed relationship between variables.

5)It can be used with different levels of significance (e.g., 0.05 or 0.01) to determine statistical significance.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Getting Started with Google Display Network: The Ultimate Beginner’s Guide

Sanity Testing Vs Smoke Testing: Know the Differences, Applications, and Benefits Of Each

Fundamentals of Software Testing

The Building Blocks of API Development

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Biochem Med (Zagreb)
• v.23(2); 2013 Jun

The Chi-square test of independence

The Chi-square statistic is a non-parametric (distribution free) tool designed to analyze group differences when the dependent variable is measured at a nominal level. Like all non-parametric statistics, the Chi-square is robust with respect to the distribution of the data. Specifically, it does not require equality of variances among the study groups or homoscedasticity in the data. It permits evaluation of both dichotomous independent variables, and of multiple group studies. Unlike many other non-parametric and some parametric statistics, the calculations needed to compute the Chi-square provide considerable information about how each of the groups performed in the study. This richness of detail allows the researcher to understand the results and thus to derive more detailed information from this statistic than from many others.

The Chi-square is a significance statistic, and should be followed with a strength statistic. The Cramer’s V is the most common strength test used to test the data when a significant Chi-square result has been obtained. Advantages of the Chi-square include its robustness with respect to distribution of the data, its ease of computation, the detailed information that can be derived from the test, its use in studies for which parametric assumptions cannot be met, and its flexibility in handling data from both two group and multiple group studies. Limitations include its sample size requirements, difficulty of interpretation when there are large numbers of categories (20 or more) in the independent or dependent variables, and tendency of the Cramer’s V to produce relative low correlation measures, even for highly significant results.

Introduction

The Chi-square test of independence (also known as the Pearson Chi-square test, or simply the Chi-square) is one of the most useful statistics for testing hypotheses when the variables are nominal, as often happens in clinical research. Unlike most statistics, the Chi-square (χ 2 ) can provide information not only on the significance of any observed differences, but also provides detailed information on exactly which categories account for any differences found. Thus, the amount and detail of information this statistic can provide renders it one of the most useful tools in the researcher’s array of available analysis tools. As with any statistic, there are requirements for its appropriate use, which are called “assumptions” of the statistic. Additionally, the χ 2 is a significance test, and should always be coupled with an appropriate test of strength.

The Chi-square test is a non-parametric statistic, also called a distribution free test. Non-parametric tests should be used when any one of the following conditions pertains to the data:

• The level of measurement of all the variables is nominal or ordinal.
• The sample sizes of the study groups are unequal; for the χ 2 the groups may be of equal size or unequal size whereas some parametric tests require groups of equal or approximately equal size.
• The distribution of the data was seriously skewed or kurtotic (parametric tests assume approximately normal distribution of the dependent variable), and thus the researcher must use a distribution free statistic rather than a parametric statistic.
• The data violate the assumptions of equal variance or homoscedasticity.
• For any of a number of reasons ( 1 ), the continuous data were collapsed into a small number of categories, and thus the data are no longer interval or ratio.

Assumptions of the Chi-square

As with parametric tests, the non-parametric tests, including the χ 2 assume the data were obtained through random selection. However, it is not uncommon to find inferential statistics used when data are from convenience samples rather than random samples. (To have confidence in the results when the random sampling assumption is violated, several replication studies should be performed with essentially the same result obtained). Each non-parametric test has its own specific assumptions as well. The assumptions of the Chi-square include:

• The data in the cells should be frequencies, or counts of cases rather than percentages or some other transformation of the data.
• The levels (or categories) of the variables are mutually exclusive. That is, a particular subject fits into one and only one level of each of the variables.
• Each subject may contribute data to one and only one cell in the χ 2 . If, for example, the same subjects are tested over time such that the comparisons are of the same subjects at Time 1, Time 2, Time 3, etc., then χ 2 may not be used.
• The study groups must be independent. This means that a different test must be used if the two groups are related. For example, a different test must be used if the researcher’s data consists of paired samples, such as in studies in which a parent is paired with his or her child.
• There are 2 variables, and both are measured as categories, usually at the nominal level. However, data may be ordinal data. Interval or ratio data that have been collapsed into ordinal categories may also be used. While Chi-square has no rule about limiting the number of cells (by limiting the number of categories for each variable), a very large number of cells (over 20) can make it difficult to meet assumption #6 below, and to interpret the meaning of the results.
• The value of the cell expecteds should be 5 or more in at least 80% of the cells, and no cell should have an expected of less than one ( 3 ). This assumption is most likely to be met if the sample size equals at least the number of cells multiplied by 5. Essentially, this assumption specifies the number of cases (sample size) needed to use the χ 2 for any number of cells in that χ 2 . This requirement will be fully explained in the example of the calculation of the statistic in the case study example.

To illustrate the calculation and interpretation of the χ 2 statistic, the following case example will be used:

The owner of a laboratory wants to keep sick leave as low as possible by keeping employees healthy through disease prevention programs. Many employees have contracted pneumonia leading to productivity problems due to sick leave from the disease. There is a vaccine for pneumococcal pneumonia, and the owner believes that it is important to get as many employees vaccinated as possible. Due to a production problem at the company that produces the vaccine, there is only enough vaccine for half the employees. In effect, there are two groups; employees who received the vaccine and employees who did not receive the vaccine. The company sent a nurse to every employee who contracted pneumonia to provide home health care and to take a sputum sample for culture to determine the causative agent. They kept track of the number of employees who contracted pneumonia and which type of pneumonia each had. The data were organized as follows:

• Group 1: Not provided with the vaccine (unvaccinated control group, N = 92)
• Group 2: Provided with the vaccine (vaccinated experimental group, N = 92)

In this case, the independent variable is vaccination status (vaccinated versus unvaccinated). The dependent variable is health outcome with three levels:

• contracted pneumoccal pneumonia;
• contracted another type of pneumonia; and
• did not contract pneumonia.

The company wanted to know if providing the vaccine made a difference. To answer this question, they must choose a statistic that can test for differences when all the variables are nominal. The χ 2 statistic was used to test the question, “Was there a difference in incidence of pneumonia between the two groups?” At the end of the winter, Table 1 was constructed to illustrate the occurrence of pneumonia among the employees.

Results of the vaccination program.

Calculating Chi-square

With the data in table form, the researcher can proceed with calculating the χ 2 statistic to find out if the vaccination program made any difference in the health outcomes of the employees. The formula for calculating a Chi-Square is:

The first step in calculating a χ 2 is to calculate the sum of each row, and the sum of each column. These sums are called the “marginals” and there are row marginal values and column marginal values. The marginal values for the case study data are presented in Table 2 .

Calculation of marginals.

The second step is to calculate the expected values for each cell. In the Chi-square statistic, the “expected” values represent an estimate of how the cases would be distributed if there were NO vaccine effect. Expected values must reflect both the incidence of cases in each category and the unbiased distribution of cases if there is no vaccine effect. This means the statistic cannot just count the total N and divide by 6 for the expected number in each cell. That would not take account of the fact that more subjects stayed healthy regardless of whether they were vaccinated or not. Chi-Square expecteds are calculated as follows:

Specifically, for each cell, its row marginal is multiplied by its column marginal, and that product is divided by the sample size. For Cell 1, the math is as follows: (28 × 92)/184 = 13.92. Table 3 provides the results of this calculation for each cell. Once the expected values have been calculated, the cell χ 2 values are calculated with the following formula:

The cell χ 2 for the first cell in the case study data is calculated as follows: (23−13.93) 2 /13.93 = 5.92. The cell χ 2 value for each cellis the value in parentheses in each of the cells in Table 3 .

Cell expected values and (cell Chi-square values).

Once the cell χ 2 values have been calculated, they are summed to obtain the χ 2 statistic for the table. In this case, the χ 2 is 12.35 (rounded). The Chi-square table requires the table’s degrees of freedom (df) in order to determine the significance level of the statistic. The degrees of freedom for a χ 2 table are calculated with the formula:

For example, a 2 × 2 table has 1 df. (2−1) × (2−1) = 1. A 3 × 3 table has (3−1) × (3−1) = 4 df. A 4 × 5 table has (4−1) × (5−1) = 3 × 4 = 12 df. Assuming a χ 2 value of 12.35 with each of these different df levels (1, 4, and 12), the significance levels from a table of χ 2 values, the significance levels are: df = 1, P < 0.001, df = 4, P < 0.025, and df = 12, P > 0.10. Note, as degrees of freedom increase, the P-level becomes less significant, until the χ 2 value of 12.35 is no longer statistically significant at the 0.05 level, because P was greater than 0.10.

For the sample table with 3 rows and 2 columns, df = (3−1) × (2−1) = 2 × 1 = 2. A Chi-square table of significances is available in many elementary statistics texts and on many Internet sites. Using a χ 2 table, the significance of a Chi-square value of 12.35 with 2 df equals P < 0.005. This value may be rounded to P < 0.01 for convenience. The exact significance when the Chi-square is calculated through a statistical program is found to be P = 0.0011.

As the P-value of the table is less than P < 0.05, the researcher rejects the null hypothesis and accepts the alternate hypothesis: “There is a difference in occurrence of pneumococcal pneumonia between the vaccinated and unvaccinated groups.” However, this result does not specify what that difference might be. To fully interpret the result, it is useful to look at the cell χ 2 values.

Interpreting cell χ 2 values

It can be seen in Table 3 that the largest cell χ 2 value of 5.92 occurs in Cell 1. This is a result of the observed value being 23 while only 13.92 were expected. Therefore, this cell has a much larger number of observed cases than would be expected by chance. Cell 1 reflects the number of unvaccinated employees who contracted pneumococcal pneumonia. This means that the number of unvaccinated people who contracted pneumococcal pneumonia was significantly greater than expected. The second largest cell χ 2 value of 4.56 is located in Cell 2. However, in this cell we discover that the number of observed cases was much lower than expected (Observed = 5, Expected = 12.57). This means that a significantly lower number of vaccinated subjects contracted pneumococcal pneumonia than would be expected if the vaccine had no effect. No other cell has a cell χ 2 value greater than 0.99.

A cell χ 2 value less than 1.0 should be interpreted as the number of observed cases being approximately equal to the number of expected cases, meaning there is no vaccination effect on any of the other cells. In the case study example, all other cells produced cell χ 2 values below 1.0. Therefore the company can conclude that there was no difference between the two groups for incidence of non-pneumococcal pneumonia. It can be seen that for both groups, the majority of employees stayed healthy. The meaningful result was that there were significantly fewer cases of pneumococcal pneumonia among the vaccinated employees and significantly more cases among the unvaccinated employees. As a result, the company should conclude that the vaccination program did reduce the incidence of pneumoccal pneumonia.

Very few statistical programs provide tables of cell expecteds and cell χ 2 values as part of the default output. Some programs will produce those tables as an option, and that option should be used to examine the cell χ 2 values. If the program provides an option to print out only the cell χ 2 value (but not cell expecteds), the direction of the χ 2 value provides information. A positive cell χ 2 value means that the observed value is higher than the expected value, and a negative cell χ 2 value (e.g. −12.45) means the observed cases are less than the expected number of cases. When the program does not provide either option, all the researcher can conclude is this: The overall table provides evidence that the two groups are independent (significantly different because P < 0.05), or are not independent (P > 0.05). Most researchers inspect the table to estimate which cells are overrepresented with a large number of cases versus those which have a small number of cases. However, without access to cell expecteds or cell χ 2 values, the interpretation of the direction of the group differences is less precise. Given the ease of calculating the cell expecteds and χ 2 values, researchers may want to hand calculate those values to enhance interpretation.

Chi-square and closely related tests

One might ask if, in this case, the Chi-square was the best or only test the researcher could have used. Nominal variables require the use of non-parametric tests, and there are three commonly used significance tests that can be used for this type of nominal data. The first and most commonly used is the Chi-square. The second is the Fisher’s exact test, which is a bit more precise than the Chi-square, but it is used only for 2 × 2 Tables ( 4 ). For example, if the only options in the case study were pneumonia versus no pneumonia, the table would have 2 rows and 2 columns and the correct test would be the Fisher’s exact. The case study example requires a 2 × 3 table and thus the data are not suitable for the Fisher’s exact test.

The third test is the maximum likelihood ratio Chi-square test which is most often used when the data set is too small to meet the sample size assumption of the Chi-square test. As exhibited by the table of expected values for the case study, the cell expected requirements of the Chi-square were met by the data in the example. Specifically, there are 6 cells in the table. To meet the requirement that 80% of the cells have expected values of 5 or more, this table must have 6 × 0.8 = 4.8 rounded to 5. This table meets the requirement that at least 5 of the 6 cells must have cell expected of 5 or more, and so there is no need to use the maximum likelihood ratio chi-square. Suppose the sample size were much smaller. Suppose the sample size was smaller and the table had the data in Table 4 .

Example of a table that violates cell expected values.

Sample raw data presented first, sample expected values in parentheses, and cell follow the slash.

Although the total sample size of 39 exceeds the value of 5 cases × 6 cells = 30, the very low distribution of cases in 4 of the cells is of concern. When the cell expecteds are calculated, it can be seen that 4 of the 6 cells have expecteds below 5, and thus this table violates the χ 2 test assumption. This table should be tested with a maximum likelihood ratio Chi-square test.

When researchers use the Chi-square test in violation of one or more assumptions, the result may or may not be reliable. In this author’s experience of having output from both the appropriate and inappropriate tests on the same data, one of three outcomes are possible:

First, the appropriate and the inappropriate test may give the same results.

Second, the appropriate test may produce a significant result while the inappropriate test provides a result that is not statistically significant, which is a Type II error.

Third, the appropriate test may provide a non-significant result while the inappropriate test may provide a significant result, which is a Type I error.

Strength test for the Chi-square

The researcher’s work is not quite done yet. Finding a significant difference merely means that the differences between the vaccinated and unvaccinated groups have less than 1.1 in a thousand chances of being in error (P = 0.0011). That is, there are 1.1 in one thousand chances that there really is no difference between the two groups for contracting pneumococcal pneumonia, and that the researcher made a Type I error. That is a sufficiently remote probability of error that in this case, the company can be confident that the vaccination made a difference. While useful, this is not complete information. It is necessary to know the strength of the association as well as the significance.

Statistical significance does not necessarily imply clinical importance. Clinical significance is usually a function of how much improvement is produced by the treatment. For example, if there was a significant difference, but the vaccine only reduced pneumonias by two cases, it might not be worth the company’s money to vaccinate 184 people (at a cost of $20 per person) to eliminate only two cases. In this case study, the vaccinated group experienced only 5 cases out of 92 employees (a rate of 5%) while the unvaccinated group experienced 23 cases out of 92 employees (a rate of 25%). While it is always a matter of judgment as to whether the results are worth the investment, many employers would view 25% of their workforce becoming ill with a preventable infectious illness as an undesirable outcome. There is, however, a more standardized strength test for the Chi-Square.

Statistical strength tests are correlation measures. For the Chi-square, the most commonly used strength test is the Cramer’s V test. It is easily calculated with the following formula:

Where n is the number of rows or number of columns, whichever is less. For the example, the V is 0.259 or rounded, 0.26 as calculated below.

The Cramer’s V is a form of a correlation and is interpreted exactly the same. For any correlation, a value of 0.26 is a weak correlation. It should be noted that a relatively weak correlation is all that can be expected when a phenomena is only partially dependent on the independent variable.

In the case study, five vaccinated people did contract pneumococcal pneumonia, but vaccinated or not, the majority of employees remained healthy. Clearly, most employees will not get pneumonia. This fact alone makes it difficult to obtain a moderate or high correlation coefficient. The amount of change the treatment (vaccine) can produce is limited by the relatively low rate of disease in the population of employees. While the correlation value is low, it is statistically significant, and the clinical importance of reducing a rate of 25% incidence to 5% incidence of the disease would appear to be clinically worthwhile. These are the factors the researcher should take into account when interpreting this statistical result.

Summary and conclusions

The Chi-square is a valuable analysis tool that provides considerable information about the nature of research data. It is a powerful statistic that enables researchers to test hypotheses about variables measured at the nominal level. As with all inferential statistics, the results are most reliable when the data are collected from randomly selected subjects, and when sample sizes are sufficiently large that they produce appropriate statistical power. The Chi-square is also an excellent tool to use when violations of assumptions of equal variances and homoscedascity are violated and parametric statistics such as the t-test and ANOVA cannot provide reliable results. As the Chi-Square and its strength test, the Cramer’s V are both simple to compute, it is an especially convenient tool for researchers in the field where statistical programs may not be easily accessed. However, most statistical programs provide not only the Chi-square and Cramer’s V, but also a variety of other non-parametric tools for both significance and strength testing.

Potential conflict of interest

None declared.

Is there a statistically significant relationship between a student’s Year 11 truancy and his or her enrolment in full time education after secondary school?

A chi-square test is a statistical test used to compare observed results with expected results. The purpose of this test is to determine if a difference between observed data and expected data is due to chance, or if it is due to a relationship between the variables you are studying. Therefore, a chi-square test is an excellent choice to help us better understand and interpret the relationship between our two categorical variables.

To perform a chi-square exploring the statistical significance of the relationship between s2q10 and s1truan , select Analyze , Descriptive Statistics , and then Crosstabs .

Find s2q10 in the variable list on the left, and move it to the Row(s) box. Find s1truan in the variable list on the left, and move it to the Column(s) box. Click Statistics , and select Chi-square .

Click Continue and then OK to run the analysis. Your output should look like the table on the right.

Take a look at the column on the far right of this output table. It is the Asymptotic Significance, or p-value, of the chi-square we’ve just run in SPSS. This value determines the statistical significance of the relationship we’ve just tested. In all tests of significance, if p < 0.05, we can say that there is a statistically significant relationship between the two variables. The p-value in our chi-square output is p = 0.000. This means that the relationship between Year 11 truancy and enrolment in full time education after secondary school is significant. It’s worth mentioning now that this test, like all tests of significance, only illuminates that there is a relationship and that that relationship has statistical significance (meaning, it is not due to chance). Running a chi-square test cannot tell you anything about a causal relationship between truancy and later educational enrolment. Let’s run one more chi square test together. Thinking about other individual characteristics that may influence a young person’s enrolment in full time education after secondary school, we may be interested in the impact parental educational attainment has on a student’s future plans. Therefore, let’s use s1q62a , which concerns whether or not a young person’s father obtained a degree, in another chi square test with s2q10 .

Before we use s1q62a , we should check its frequencies to make sure the data is ready for bivariate analysis. Go to Analyze , Descriptive Statistics , and then Frequencies . Move s1q62a into the Variable(s) box on the right side of the dialogue box. Click OK to run a frequency test. Notice in the frequency output table that along with the answers “Yes,” “No,” and “Not sure,” which we are interested in, there is the category “Not answered.” Because these survey respondents haven’t responded to this question, their answers are missing. We should code this information as missing data before we run our chi square test, so that we are only performing the test on data relevant to our research question. Luckily, doing this is very easy. First, find s1q62a in the Variable View window of the SPSS Data Editor . (You can do this easily by clicking to highlight any cell in the Name column on the far left of the Variable View screen, and hitting Ctrl + F . This will open up a Find and Replace dialogue box. Just enter s1q62a into the text bar and click Find Next . This will find the s1q62a row in the dataset.)

When you’ve found s1q62a , move across its row until you find the Values column. Click this cell to open it. Now you should see a dialogue box that lists all the numerical values of the categories of this variable. In this dialogue box, you can see that “Not answered,” the missing data category, is listed as -9.00. In addition, there are categories “Item not applicable” (with a value of 4.00) and “Not answered (9)” (with a value of 5.00) listed. We‘ll include these in our recoding, as they also represent missing data. To recode these categories as missing data, all you need to do is move over one column to the Missing column. The Missing column in the s1q62a row should say “None,” as no data is classed as missing just yet. Click to open that cell. In the dialogue box that opens, select Discrete missing values and enter -9.00 , 4.00 , and 5.00 into the three text boxes provided. These are the numerical codes for the three categories that include missing data. Click OK . You should now see that our three missing codes are saved in the Missing cell of the s1q62a row. To make sure that the missing data is no longer included in tests we run using this variable, run a frequency check on s1q62a . In this new frequency table, the “Not answered” category is listed as Missing, so our recoding has been successful. And, because we have cleaned up s1q62a , we are ready to run our chi square test. Select Analyze , Descriptive Statistics , and then Crosstabs . Find s2q10 in the variable list on the left, and move it to the Row(s) box. Find s1q62a in the variable list on the left, and move it to the Column(s) box.

Click Statistics , and select Chi-square . Click Continue and then OK to run the analysis. Your output should look like the table on the left.

Take a look at the Asymptotic Significance of this chi square test. Using this information, what can we say about the relationship between paternal degree and full time enrolment in education after secondary school?

Run another chi square to test the significance of the relationship between s1q10 and s1q62b , a variable that concerns whether or not a survey respondent’s mother has obtained a degree. Before you run the chi square, make sure to check the frequencies in s1q62b and make any corrections you think are necessary. Is there a statistically significant relationship between maternal degree and full time education after secondary school?

Using a chi square test, you’ve just determined that there is, in fact, a statistically significant relationship between our two categorical variables, s2q10 and s1truan. In addition, you’ve run another chi square, determining that there is a statistically significant relationship between s2q10 and s1q62a, a measure of whether or not a respondent’s father had obtained a degree. Remember that you are simply able to say now that paternal degree and Year 11 truancy both have relationships with respondent enrolment in full time education after secondary school. You cannot say, for example, that a paternal degree causes enrolment in full time education.

Note: as we are making changes to a dataset we’ll continue using for the rest of this section, please make sure to save your changes before you close down SPSS. This will save you having to repeat sections you’ve already completed.

Useful Downloads

• Chi Square PDF

• Math Article
• Chi Square Test

Chi-Square Test

A chi-squared test  (symbolically represented as  χ 2 ) is basically a data analysis on the basis of observations of a random set of variables. Usually, it is a comparison of two statistical data sets. This test was introduced by Karl Pearson in 1900 for categorical data analysis and distribution . So it was mentioned as Pearson’s chi-squared test .

The chi-square test is used to estimate how likely the observations that are made would be, by considering the assumption of the null hypothesis as true.

A hypothesis is a consideration that a given condition or statement might be true, which we can test afterwards. Chi-squared tests are usually created from a sum of squared falsities or errors over  the sample variance.

Chi-Square Distribution

When we consider, the null speculation is true, the sampling distribution of the test statistic is called as chi-squared distribution . The chi-squared test helps to determine whether there is a notable difference between the normal frequencies and the observed frequencies in one or more classes or categories. It gives the probability of independent variables.

Note: Chi-squared test is applicable only for categorical data, such as men and women falling under the categories of Gender, Age, Height, etc.

Finding P-Value

P stands for probability here. To calculate the p-value, the chi-square test is used in statistics. The different values of p indicates the different hypothesis interpretation, are given below:

• P≤ 0.05; Hypothesis rejected
• P>.05; Hypothesis Accepted

Probability is all about chance or risk or uncertainty. It is the possibility of the outcome of the sample or the occurrence of an event. But when we talk about statistics, it is more about how we handle various data using different techniques. It helps to represent complicated data or bulk data in a very easy and understandable way. It describes the collection, analysis, interpretation, presentation, and organization of data. The concept of both probability and statistics is related to the chi-squared test.

Also, read:

The following are the important properties of the chi-square test:

• Two times the number of degrees of freedom is equal to the variance.
• The number of degree of freedom is equal to the mean distribution
• The chi-square distribution curve approaches the normal distribution when the degree of freedom increases.

The chi-squared test is done to check if there is any difference between the observed value and expected value. The formula for chi-square can be written as;

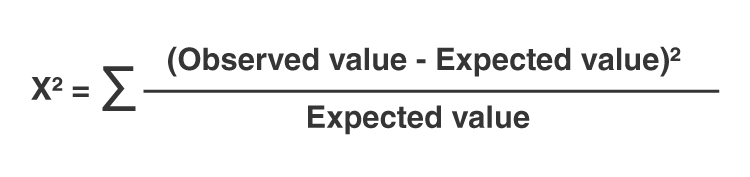
χ 2  = ∑(O i – E i ) 2 /E i

where O i is the observed value and E i is the expected value.

Chi-Square Test of Independence

The chi-square test of independence also known as the chi-square test of association which is used to determine the association between the categorical variables. It is considered as a non-parametric test . It is mostly used to test statistical independence.

The chi-square test of independence is not appropriate when the categorical variables represent the pre-test and post-test observations. For this test, the data must meet the following requirements:

• Two categorical variables
• Relatively large sample size
• Categories of variables (two or more)
• Independence of observations

Example of Categorical Data

Let us take an example of a categorical data where there is a society of 1000 residents with four neighbourhoods, P, Q, R and S. A random sample of 650 residents of the society is taken whose occupations are doctors, engineers and teachers. The null hypothesis is that each person’s neighbourhood of residency is independent of the person’s professional division. The data are categorised as:

Assume the sample living in neighbourhood P, 150, to estimate what proportion of the whole 1,000 people live in neighbourhood P. In the same way, we take 349/650 to calculate what ratio of the 1,000 are doctors. By the supposition of independence under the hypothesis, we should “expect” the number of doctors in neighbourhood P is;

150 x 349/650  ≈ 80.54

So by  the chi-square test formula for that particular cell in the table, we get;

(Observed – Expected) 2 /Expected Value = (90-80.54) 2 /80.54  ≈ 1.11

Some of the exciting facts about the Chi-square test are given below:

The Chi-square statistic can only be used on numbers. We cannot use them for data in terms of percentages, proportions, means or similar statistical contents. Suppose, if we have 20% of 400 people, we need to convert it to a number, i.e. 80, before running a test statistic.

A chi-square test will give us a p-value. The p-value will tell us whether our test results are significant or not. 

However, to perform a chi-square test and get the p-value, we require two pieces of information:

(1) Degrees of freedom. That’s just the number of categories minus 1.

(2) The alpha level(α). You or the researcher chooses this. The usual alpha level is 0.05 (5%), but you could also have other levels like 0.01 or 0.10.

In elementary statistics, we usually get questions along with the degrees of freedom(DF) and the alpha level. Thus, we don’t usually have to figure out what they are. To get the degrees of freedom, count the categories and subtract 1.

The chi-square distribution table with three probability levels is provided here. The statistic here is used to examine whether distributions of certain variables vary from one another. The categorical variable will produce data in the categories and numerical variables will produce data in numerical form.

The distribution of χ 2 with (r-1)(c-1) degrees of freedom(DF) , is represented in the table given below. Here, r represents the number of rows in the two-way table and c represents the number of columns.

Solved Problem

 A survey on cars had conducted in 2011 and determined that 60% of car owners have  only one car, 28% have two cars, and 12% have three or more. Supposing that you have decided to conduct your own survey and have collected the data below, determine whether your data supports the results of the study.

Use a significance level of 0.05. Also, given that, out of 129 car owners, 73 had one car and 38 had two cars.

Let us state the null and alternative hypotheses.

H 0 : The proportion of car owners with one, two or three cars is 0.60, 0.28 and 0.12 respectively.

H 1 : The proportion of car owners with one, two or three cars does not match the proposed model.

A Chi-Square goodness of fit test is appropriate because we are examining the distribution of a single categorical variable. 

Let’s tabulate the given information and calculate the required values.

Therefore, χ 2  = ∑(O i  – E i ) 2 /E i  = 0.7533

Let’s compare it to the chi-square value for the significance level 0.05. 

The degrees for freedom = 3 – 1 = 2

Using the table, the critical value for a 0.05 significance level with df = 2 is 5.99. 

That means that 95 times out of 100, a survey that agrees with a sample will have a χ 2  value of 5.99 or less. 

The Chi-square statistic is only 0.7533, so we will accept the null hypothesis.

Frequently Asked Questions – FAQs

What is the chi-square test write its formula, how do you calculate chi squared, what is a chi-square test used for, how do you interpret a chi-square test, what is a good chi-square value, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Open access
• Published: 20 May 2024

Development and internal validation of a clinical prediction model for osteopenia in Chinese middle-aged and elderly men: a prospective cohort study

• Ting Li 1   na1 ,
• Jing Zeng 1   na1 ,
• Zimo Pan 1 ,
• Xiaoyan Cai 2 ,
• Xinjiang Wang 3 ,
• Guanzhong Liu 3 ,
• Xinghe Hu 3 ,
• Xinli Deng 4 ,
• Meiliang Gong 4 ,
• Xue Yang 5 ,
• Yanping Gong 1 ,
• Nan Li   ORCID: orcid.org/0000-0003-3820-0692 1 &
• Chunlin Li   ORCID: orcid.org/0000-0003-3723-5703 1  

BMC Musculoskeletal Disorders volume  25 , Article number:  394 ( 2024 ) Cite this article

52 Accesses

Metrics details

Early identification of patients at risk of osteopenia is an essential step in reducing the population at risk for fractures. We aimed to develop and validate a prediction model for osteopenia in Chinese middle-aged and elderly men that provides individualized risk estimates.

In this prospective cohort study, 1109 patients who attend regular physical examinations in the Second Medical Centre of Chinese PLA General Hospital were enrolled from 2015.03 to 2015.09. The baseline risk factors included dietary habits, exercise habits, medical histories and medication records. Osteopenia during follow-up were collected from Electronic Health Records (EHRs) and telephone interviews. Internal validation was conducted using bootstrapping to correct the optimism. The independent sample T-test analysis, Mann_Whitney U test, Chi-Square Test and multivariable Cox regression analysis were utilized to identify predictive factors for osteopenia in Chinese middle-aged and elderly men. A nomogram based on the seven variables was built for clinical use. Concordance index (C-index), receiver operating characteristic curve (ROC), decision curve analysis (DCA) and calibration curve were used to evaluate the efficiency of the nomogram.

The risk factors included in the prediction model were bone mineral density at left femoral neck (LNBMD), hemoglobin (Hb), serum albumin (ALB), postprandial blood glucose (PBG), fatty liver disease (FLD), smoking and tea consumption. The C-index for the risk nomogram was 0.773 in the prediction model, which presented good refinement. The AUC of the risk nomogram at different time points ranged from 0.785 to 0.817, exhibiting good predictive ability and performance. In addition, the DCA showed that the nomogram had a good clinical application value. The nomogram calibration curve indicated that the prediction model was consistent.

Conclusions

Our study provides a novel nomogram and a web calculator that can effectively predict the 7-year incidence risk of osteopenia in Chinese middle-aged and elderly men. It is convenient for clinicians to prevent fragility fractures in the male population.

Peer Review reports

According to a working group of the World Health Organization (WHO), osteopenia(low bone mass, LBM) is defined as a T score that is higher than − 2.5 but less than − 1.0 [ 1 ]. With the rapid growth of aging population worldwide, osteopenia has become a major public health problem because of high prevalence and serious health hazard in the elderly. The National Osteoporosis Foundation (NOF) estimates that 10.2 million Americans have osteoporosis (OP) and that an additional 43.4 million have LBM [ 2 ]. Meanwhile, in China, the overall prevalence rate of OP in people over 50 years old is 19.2%, and the prevalence rate in men is 6.0%; the overall prevalence rate in people with osteopenia who need prevention and treatment is 46.4%, and in men, it is as high as 46.9% [ 3 ]. Although the risk of fracture is greater among patients with OP than among those with osteopenia, the much larger number of persons with osteopenia means that this group represents a substantial portion of the population at risk for fracture [ 4 ]. OP and fragility fractures associated with LBM pose a huge economic burden and health risk to the whole society. A report regarding the economic burden of OP in the European Union estimated the costs of incident and prior fragility fractures at €37 billion, with an expected increase by 25% in 2025 [ 5 ]. Moreover, active prevention of osteoporotic fracture can be beneficial to prolong life expectancy and improve quality of life for the elderly [ 6 ].

There are many well-known OP or fracture risk assessment tools (International Osteoporosis Foundation (IOF), fracture risk assessment tool (FRAX®) and Qfracture score) were available by far [ 7 ]. However, prediction models for osteopenia are almost absent. Therefore, it is necessary to establish a prediction model of LBM based on the need for the advanced diagnosis and treatment of chronic diseases. The current techniques used for diagnosis of OP and fracture risk models developed for prediction of fracture risk based on risk factors are primarily for postmenopausal women, and similar effective measurement tools for men are not available [ 8 , 9 , 10 ]. However, the incidence of LBM or OP in elderly men is not low. In addition, osteoporotic fractures in men may have more serious consequences, higher morbidity and mortality than those in women [ 11 , 12 ].

Therefore, we believe that it is important to develop predictive models of LBM in men. The goal of this study was to develop and validate a clinical prediction model to estimate the risk of osteopenia in Chinese middle-aged and elderly men.

Study participants

Patients of this prospective study were enrolled during the period between March 2015 and September 2015, from the Second Medical Centre of Chinese PLA General Hospital. All enrolled patients had comprehensive physical examination results and had a definite outcome of either osteopenia or not. This study was approved by the Ethics Committee of Chinese PLA General Hospital (ID: S2021-094-01). The inclusion criteria were as follows: (i)patients with normal bone mineral density (BMD) that were measured by dual-energy X-ray absorptiometry (DXA); (ii)age ≥ 45 years old; (iii)Chinese male patients. Meanwhile, the exclusion criteria were as follows: (i)patients with history of osteopenia, OP and fragility fracture and anti-osteoporosis drugs use; (ii)patients combined with secondary OP. Finally, 1185 non-OP patients at the baseline were included for a 7-year non-interventional follow-up. The follow-up period was from March 2015 to September 2022. The follow-up time for each patient was calculated from baseline to diagnosis of LBM or the end of follow-up period in months. Ultimately, 1109 patients completed the second survey and were included in the study. The follow-up response rate was 93.6%, and the detailed research flow chart is shown in Fig.  1 .

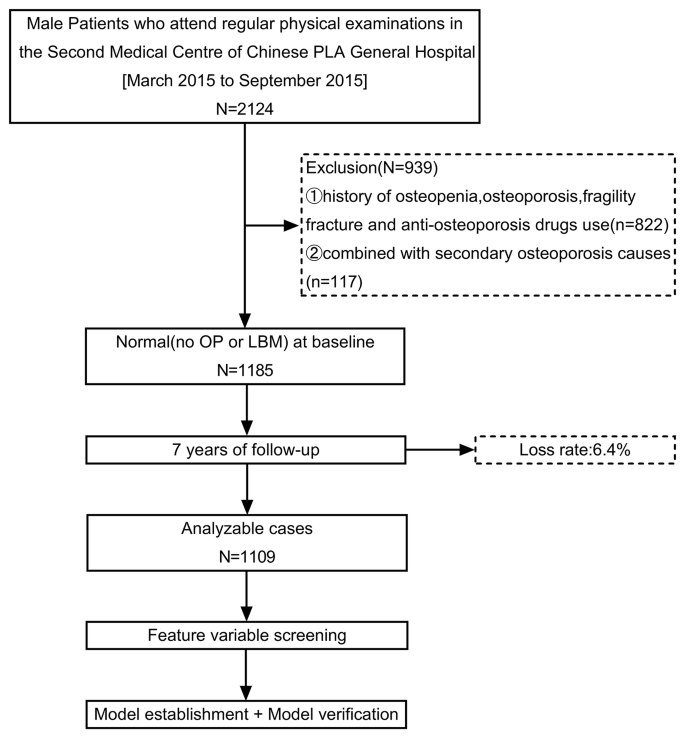
Flow diagram of study design

LBM, low bone mass; OP, osteoporosis

Data collection

On one side, the standardized self-administered questionnaires pertaining to personal history (histories of smoking, drinking, coffee, carbonated beverage and tea consumption), dietary habits (such as staple food, egg, red meat, white meat, dairy products, soy products) and exercise habits (exercise frequency, exercise duration, exercise intensity) were conducted by trained residents. We inquired about smoking, drinking, coffee, carbonated beverage and tea consumption as ‘never’ and ‘past or current’. On the other side, any medical or fracture histories (such as hypertension, dyslipidemia, diabetes, coronary heart disease (CHD), cerebrovascular disease (CVD), chronic kidney disease (CKD), fatty liver disease (FLD), benign prostatic hyperplasia (BPH), cataract) and medication records (such as antihypertensive drugs, oral hypoglycemic drugs, insulin, statins, acid inhibitors, sleeping pills) were collected in detail from electronic medical records of these patients. In order to minimize sampling bias, data were obtained by communicating effectively with medical workers and double checking with them.

The height, weight, waist circumference (WC), respiratory rate (RR), heart rate (HR), and blood pressure (BP) were measured by uniformly trained investigators. The subjects wore thin shirts and stood upright on the bottom plate of a stadiometer to measure their height and weight. WC was measured at the thinnest part of the waist (the horizontal circumference of the waist through the umbilical point). body mass index (BMI) was then calculated by weight (kg)/height (m 2 ). The BP, HR and RR were measured after the subjects rested for 10 min. An electronic sphygmomanometer (Omron) was used to measure BP three times, and the average value was taken as the data analysis.

Biochemical measurements were performed using standardized methods in the central laboratory of our institution. Blood samples with fasting for more than 8 h were extracted to detect for white blood cell count, red blood cell count, platelet count, hemoglobin (Hb), serum calcium, serum phosphorus, serum magnesium, fasting blood glucose (FBG), hemoglobin A1c (HbA1c), serum albumin (ALB), alanine aminotransferase (ALT), aspartate aminotransferase (AST), gamma-glutamyltransferase (GGT), serum creatinine (Cr), blood urea nitrogen (BUN), triglyceride (TG), total cholesterol (TC), high density lipoprotein cholesterol (HDL), low density lipoprotein cholesterol (LDL), prothrombin time (PT), activate part plasma prothrombin time (APTT), prothrombin time (TT), fibrinogen (FIB), thyroid stimulating hormone (TSH), total triiodothyronine (TT3), total thyroxine (TT4), free triiodothyronine (FT3), free thyroxine (FT4), luteinizing hormone (LH), follicle-stimulating hormone (FSH), testosterone (T), estradiol (E2), progesterone (P), osteocalcin (OST), type I procollagen amino-terminal peptide (P1NP), β isomer of C-terminal telopeptide of type I collagen (β-CTX), parathyroid hormone (PTH), 25-hydroxy-vitamin D [25(OH)D] and alkaline phosphatase (ALP). The same day, blood samples with breakfast after 2 h were extracted to detect for postprandial blood glucose (PBG).

BMD scores were obtained from completed DXA scans by chart abstraction for each patient. At our hospital, we use a GE Lunar DXA (GE Healthcare, Madison, WI, USA). According to the diagnostic criteria from the WHO, the definition of normal is T-score ≥–1, the definition of osteopenia is − 2.5 < T-score <–1, and the definition for OP is T-score ≤ − 2.5.

Statistical analysis

Continuous variables were expressed as mean ± standard deviation or median (interquartile range, IQR), while categorical variables were presented as frequencies (percentages, %). To compare the difference between groups, we use chi-squared test for categorical variables, T-test analysis and Mann_Whitney U test for continuous variables. Variables found to be associated with LBM at a p  value <0.05 were then entered into multivariable Cox proportional hazard model identify significantly the predictive factors associated with osteopenia. Both proportional hazards assumption and schoenfeld residuals were used to prove that it conforms to the Cox model requires that the ratio of the hazards of the occurrence of the outcome for any 2 individuals remains constant during the entire follow-up. Subsequently, factors with prognostic significance in the multivariable Cox regression analysis were utilized to build a prediction model for osteopenia in Chinese middle-old men and a nomogram was used to visualize the model. Internal validation was conducted using bootstrapping to correct the optimism. Areas under the receiver operating characteristic curve (ROC) curve (AUC), and decision curve analysis (DCA) were used to assess discrimination of the model, while the calibration plot was used to graphically evaluate the calibration of the nomogram in our prospective cohorts. All analyses were conducted using R software (version 4.3.0), and p  values less than 0.05 were considered statistically significant in each statistical analysis.

Characteristics of the study cohort

This was a 7-year retrospective cohort study. We collected data from 1109 patients from the Second Medical Centre of Chinese PLA General Hospital between March 2015 and September 2015. After a follow-up time of 7 years, 451 participants had an osteopenia, with an overall incidence rate of 40.67%. Those with LBM were more likely to be older male, with lower BMI, lower PINP, lower BMD at left femoral neck (LNBMD), lower Hb, lower ALB, lower PROG, history of smoke, history of tea consumption, FLD, cataract, assisted walking, higher PBG and higher TT3(Table  1 ).

Model development and web-based calculator

To screen risk factors for osteopenia, we performed univariate analysis of patients with and without osteopenia, as shown in Table  1 . Then we included all variables with p  < 0.05 in the univariate analysis into the multivariable COX regression analysis. Results of the multivariate Cox regression analysis are shown in Table  2 ; and verify that all variables are consistent with the Proportional Hazards assumption (Table  3 ; Fig.  2 ). The above multivariable COX regression analysis (Table  2 ) suggests that the prediction model finally identifies seven predictors, including LNBMD, Hb, PBG, ALB, smoking, tea consumption and FLD. Low LNBMD (HR, 0.00345; 95% CI, 0.00097–0.01224; p  < 0.001), low Hb level (HR, 0.99113; 95% CI, 0.98289–0.99945; p  = 0.037), higher PBG level (HR, 1.09922; 95% CI, 1.06192–1.13783; p  < 0.001), low ALB concentration (HR, 0.82394; 95% CI, 0.79446–0.85452; p  < 0.001), smoking (HR, 1.64669; 95% CI, 1.36069–1.99281; p  < 0.001), tea consumption (HR, 1.58007; 95% CI, 1.24279–2.00888; p  < 0.001), FLD (HR, 1.37232; 95% CI, 1.12944–1.66744; p  = 0.001) were significantly associated with increased risk of osteopenia in the model. The fitted regression risk model was then rendered as a nomogram that can effectively predict the 7-year incidence risk of osteopenia in Chinese middle-aged and elderly men (Fig.  3 ). An example interpretation of this nomogram is as follows: a male patient with LNBMD = 1.00 g/cm 2 , Hb = 120 g/L, PBG = 12mmol/L, ALB = 46 g/L, smoking, never drinking tea, and a history of FLD. The seven features attract the scores of 71.5,16,19,39,12.5,0 and 8, respectively (total 166). The nomogram indicates that the risk of an osteopenia is almost 76%.

Schoenfeld residuals

ALB, albumin; β, partial regression coefficient; Hb, hemoglobin; HR hazard ratio, CI confidential interval, FLD, fatty liver disease; LNBMD, bone mineral density of left femoral neck; PBG, postprandial blood glucose

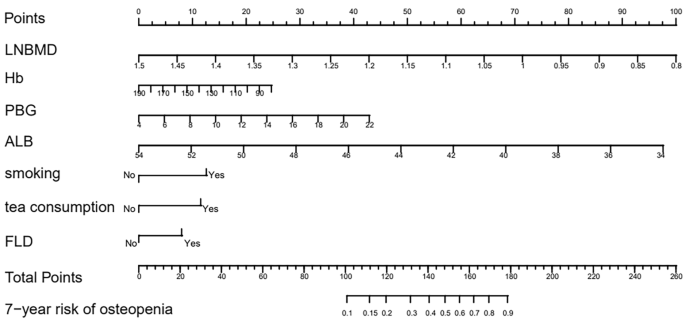
Nomogram prediction for the risk of osteopenia

Predictors contained in the prediction nomogram included LNBMD, Hb, 2hPG, ALB, smoke, tea, FLD. ALB, albumin; β, partial regression coefficient; Hb, hemoglobin; HR hazard ratio, CI confidential interval, FLD, fatty liver disease; LNBMD, bone mineral density of left femoral neck; PBG, postprandial blood glucose

An online web-based calculator based on our predictive model was developed to allow clinicians to enter the values of the 7 variables required for the risk score with automatic calculation of the likelihood (with 95% CIs) that a male patient will develop osteopenia ( https://fafa717.shinyapps.io/DynNomapp/ ) (Fig.  4 ).

The online web-based calculatora for predicting osteopenia among Chinese middle-old male patients

a: https://fafa717.shinyapps.io/DynNomapp/

Model validation

On the one hand, the Concordance index (C-index) for the prediction model in the cohort was 0.773 (95% CI, 0.772–0.786; Likelihood ratio test: p  < 0.001) and was 0.762 by bootstrapping validation (95% CI, 0.759–0.766), indicating that the model had good refinement. The AUC of the risk nomogram were 0.785 at the 80th month, 0.789 at the 82th month and 0.801 at the 84th month(Fig.  5 a), which suggested that the model had adequate predictive capabilities and great discrimination. On the other hand, the calibration curve for the risk nomogram at different points in time exhibited good calibration in our prospective cohort (Fig. 5b1-3). Furthermore, the threshold probability was defined as the probability of having osteopenia during the study follow-up time (at 84-month) and Fig.  5 c shows the clinical DCA for the risk nomogram at the 84th month. In DCA, the curve for our model showed a positive net benefit for the threshold probabilities between 23% and 90% compared to the strategies of assuming that all or none of the patients had osteopenia. The DCA shows that using this risk nomogram to predict the 7-year risk for osteopenia was beneficial in clinical work.

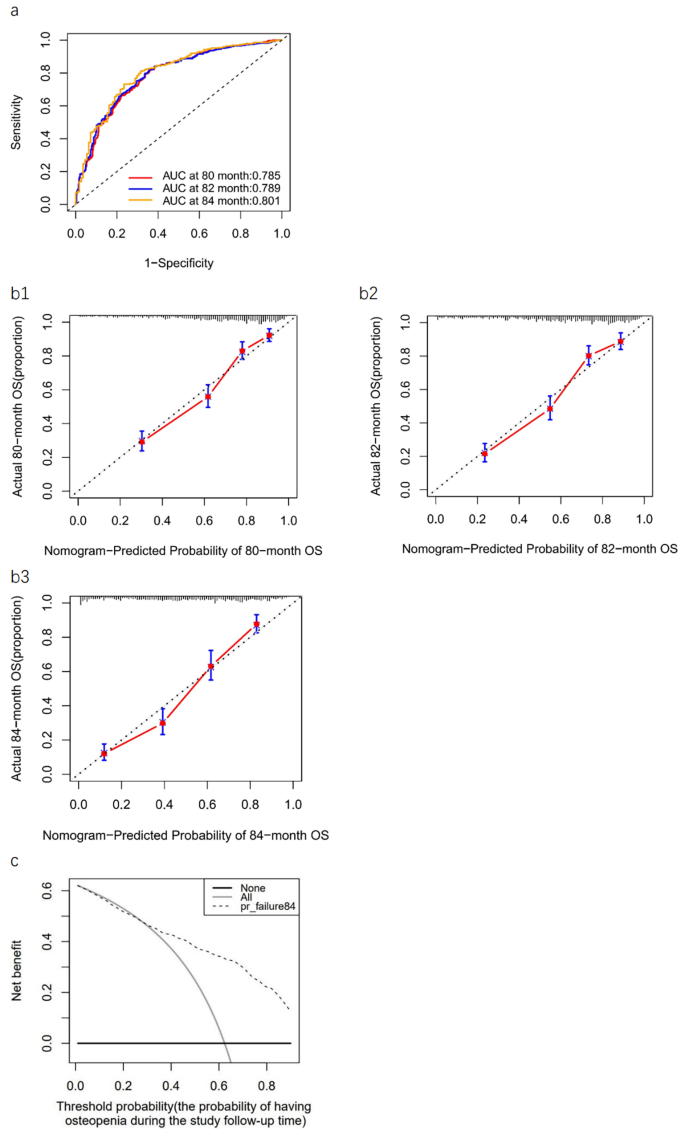
Receiver operating characteristic curve, clinical decision curve analysis, and calibration curves

( a ) ROC curve of the predictive osteopenia risk nomogram. The y-axis represents the sensitivity of the risk prediction, the x-axis represents the 1-specificity of the risk prediction. The red line represents the performance of the nomogram at 80 month. The blue line represents the performance of the nomogram at 82 month. The orange line represents the performance of the nomogram at 84 month. (b1-b3) Calibration curve of the predictive osteopenia risk nomogram. The y-axis represents actual diagnosed cases of osteopenia, the x-axis represents the predicted risk of osteopenia. The diagonal dotted line represents a perfect prediction by an ideal model, the solid line represents the predictive power of the actual model, with the results indicating that a closer fit to the diagonal dotted line represents a better prediction. ( c ) DCA curve of the predictive osteopenia risk nomogram at 84 month. The y-axis represents the net benefit. The thick solid line represents the assumption that no patients have osteopenia, the thin solid line represents the assumption that all patients have osteopenia, the dotted line represents the osteopenia risk nomogram.ROC, receiver operating characteristic; DCA, decision curve analysis

Based on the characteristics of OP and osteoporotic fracture, early prevention is particularly more important than treatment [ 13 ]. Therefore, a simple and accurate tool to identify the risk of osteopenia is very important in developing countries such as the People’s Republic of China. Current tools for OP or fracture prediction suffer from a number of major weaknesses. A study reported poor results when attempting to validate the use of Osteoporosis Self-assessment Tool for Asians (OSTA) for identifying postmenopausal OP in a Chinese cohort as diagnosed with lumbar spine DXA BMD measurements [ 14 ]. Meanwhile, due to regional differences, lack of appropriate cohort data, and design flaws, some studies have found that FRAX® has limitations in clinical use [ 15 ]. The study of Harvey et al. [ 16 ]showed that the accuracy of using FRAX® to predict fracture risk in men may be lower than in women. A possible explanation of the relative underestimation of fractures by FRAX® could be its design, which adjusts fracture risk based on expected mortality rates, resulting in a decline of absolute risk for those aged over 80 years [ 17 ]. Therefore, we believe that it is very meaningful clinical work to study the prediction of LBM in elderly men. In this study, we developed a predictive model applicable for middle-aged and elderly men to help guide the strategy of LBM. Seven predictors were finally selected as the most appropriate features to build this model: LNBMD, Hb, ALB, PBG, FLD, smoking and tea consumption.

Baseline BMD

The BMD measurements play an important role in assessing bone mass and predicting the risk of fractures. Moreover, we found that BMD at any site was still associated with the risk of fracture in women who did not fracture over the first decade after the BMD measurement [ 18 ]. Melton et al. showed in 225 postmenopausal women followed up for a median of 16 years that femoral neck BMD predicted the risk of osteoporotic fracture as well in the first 10 years of follow-up as in the subsequent 10 years [ 19 ]. Bone loss rates are variable [ 20 ], but because bone loss proceeds at a rate of only a few percent per year, evidence shows that baseline BMD would still predict a sufficiently large proportion of the variation in BMD after several years to be clinically useful for deriving intervention thresholds [ 21 ]. However, many osteoporosis prediction models do not include this index, which may be because most baseline BMD data is not readily available in clinical work. Whereas, we have detailed BMD data in our database so that we can use BMD at baseline to predict osteopenia. At the same time, considering that degenerative changes in the elderly, aortic calcification or other spinal morphological abnormalities may affect the DXA detection of lumbar BMD, the LNBMD detected by DXA was selected as the study variable. Finally, our study found that LNBMD at baseline was an important protective factor for osteopenia in middle-aged and elderly men. Our results are also generally consistent with studies performed outside of China regarding associations between baseline BMD and osteoporotic fracture risk. Moreover, we innovatively incorporated the baseline BMD in the clinical predition model.

Nutritional status (Hb/ALB)

Nutritional status are strongly associated with BMD. Hb and ALB levels are important indicators of patients’ nutritional status. Recently, different studies indicated that a low Hb level was associated with a high risk of OP in the adult population [ 22 , 23 , 24 , 25 ]. On the one hand, relative hypoxia caused by decreased Hb may increase the differentiation and activity of osteoclasts by increasing the expression of hypoxia-inducible factors and osteoclast-specific factors and the formation of extracellular acidic environment, resulting in increased bone resorption [ 24 , 26 ]. On the other hand, the effects of hypoxia on osteoblasts, including inhibition of proliferation and differentiation and alteration of bone mineralization, suppress bone formation [ 27 ]. Meanwhile, other studies came to the conclusion that low ALB concentration was significantly and independently associated with low BMD [ 28 , 29 ]. In fact, hypoalbuminemia activates osteoclasts and inhibits osteoblasts through nuclear factor kappaB (NFκB) factors and other infammatory cytokines [ 30 ]. Moreover,

hypoalbumine mia causes a decrease in insulin-like growth factor-1 synthesis, thereby leading to a decreased number of osteoblasts, decreased cellular activity, increased osteo clast lifespan, increased bone resorption, and decreased bone remodeling [ 31 ]. Overall, in our model, we similarly found that the low Hb level and low ALB concentration were risk factors for osteopenia.

Glycolipid metabolism and FLD

Abnormal glycolipid metabolism is another risk factor that may be associated with low BMD. In a previous study, similar to diabetics, high prediabetics have lower trabecular bone score (TBS) than normoglycemic individuals [ 32 ]. And another study revealed the significant causal effect of HbA1c on BMD [ 33 ]. In insulin resistant states, insulin signaling leads to expansion of bone marrow adipose tissue and decreased trabecular BMD [ 34 ]. Recent reports indicated that the chronic inflammatory microenvironment induced by hyperglycaemia activates the NLR Family Pyrin Domain Containing 3 (Nlrp3) inflammasome and promotes the production of inflammatory factors, leading to the inhibition of proliferation and differentiation of osteoblasts [ 35 ]. Meanwhile, exposure to high glucose inhibits nuclear factor erythroid 2­related factor 2 (Nrf2)/ Kelch­Like ECH­Associated Protein 1 (Keap1) signalling, leading to oxidative stress induction, assembly of Nlrp3, activation of Caspase1, and subsequent initiation of pyroptosis.This cascade culminates in disrupted bone remodelling and exacerbated osteoporosis [ 36 ]. In this study, we discovered that after adjusting for age, BMI, and other confounding factors, Chinese middle-aged and elderly men with high PBG levels have a higher risk for osteopenia. Therefore, actively controlling blood sugar has a positive effect on preventing osteopenia.

Moreover, nonalcoholic fatty liver disease (NAFLD) is now widely recognized as a highly prevalent metabolic disease. Multiple studies suggested that NAFLD was associated with decreased BMD and an increased risk of OP or osteoporotic fractures [ 37 , 38 , 39 ]. In the circumstance of liver inflammation and fibrosis, hepatic stellate cells are activated and release oncofetal fibronectin, which acts on osteoblasts to decrease bone formation [ 40 ]. Furthermore, liver also secretes peripheral colony-stimulating factor-1 (CSF1) and inflammatory cytokine-like tumor necrosis factor (TNF) which respectively bind the colony-stimulating factor-1 receptor (c-Fms) and TNF receptor on osteoclast precursors, thereby increasing bone resorption [ 41 ]. Our prospective cohort study in China showed that middle-aged and elderly men with FLD were at a higher risk of osteopenia than non-FLD men.

It is widely known that smoking is a risk factor for bone loss and plays a key role in osteopenia. Studies showed that being a smoker was associated with the prevalence of OP or osteopenia compared with being a nonsmoker and that there was a strong nonlinear positive dose-response relationship between serum cotinine levels and OP and osteopenia [ 42 , 43 ]. Our result are consistent with the above findings. At present, the mechanism through which smoke causes bone loss is becoming clearer. A study found that cigarette smoke exposure enhanced bone remodeling stimulated by mechanical force and increased osteoclast numbers [ 44 ]. Also, cigarette smoke extract increased the number of osteoclasts by inhibiting osteoclast apoptosis via the mitochondrial reactive oxygen species/cytochrome C/caspase 3 pathway [ 44 ]. Other findings suggest that smoke exposure induces RANKL activation-mediated by NFκB, which could be a “smoke sensor” for bone remodeling [ 45 ].

Tea consumption

There is still no consistent conclusion about the effect of tea consumption on osteopenia. Some studies suggesting a potential link between tea consumption and reduced BMD or increased fracture risk. Caffeine, a regular part of tea, has also been suggested to affect bone through derangement of calcium metabolism, alteration of vitamin D responses, and other mechanisms [ 46 ]. Whereas, other studies found that tea consumption was linked to a lower risk of OP, particularly among women and middle-aged people [ 47 , 48 ]. Catechin, the main polyphenols found in green tea with potent anti-oxidant and anti-inflammatory properties, can enhance osteoblastogenesis by enhancing osteogenic differentiation of mesenchymal stem cells (MSCs) and increasing osteoblastic survival, proliferation, differentiation, and mineralization [ 49 ]. In addition, a two-sample Mendelian randomization study discovered that there was no statistical power to confirm a causal relationship between tea consumption and the risk of OP [ 50 ]. However, in this study, we found that tea consumption was a risk factor for osteopenia. And we believe that differences in methodology, selected populations, and duration/timing of the studies may account for study outcome discrepancies. Since, a large-scale, placebo-controlled, long-term randomized trial with a tea regimen intervention of optimal duration is required to determine its efficacy on osteopenia.

In summary, our study has several strengths. First, to our knowledge, this is the first prospective study that addressed LBM prediction in a study cohort that included Chinese middle-aged and elderly men. Second, the included population in this study attend regular physical examinations in the Second Medical Centre of Chinese PLA General Hospital, so the follow-up population was highly stable. Third, as the seven predictors in our model were both accessible at a common enough physical examination, the early prevention of osteopenia-related factors may reduce the risk of OP and osteoporotic fracture. Fourth, in middle-aged and elderly men, this model could screen patients with a high risk of osteopenia and help clinicians to make correct health guiding decisions for each patient.

Limitations

However, there are several shortcomings in our study. First, our model was developed based on Chinese middle-aged and elderly men at a single-center, and the lack of an external validation cohort limits the universality of the model for application in other regions. Second, our study was an observational prospective cohort study; we controlled for numerous relevant confounders, but the possibility of residual confounding remains. Third, during follow-up, information about the dosage and duration of anti-osteoporosis drugs and other drugs that influence bone metabolism was not obtained, which might affect the evaluation of osteopenia risk.

A nomogram and online web-based calculator for osteopenia in Chinese middle-old men was built and demonstrated good discrimination and calibration. By assessing individual risks, we can formulate effective interventions for patients and provide health education according to their lifestyles. This will be of great significance for the early prevention and management of middle-old men with high osteopenia risk.

Data availability

Data availability Some or all data sets generated during and/or analyzed during the present study are not publicly available due to privacy restrictions but are available from the corresponding author on reasonable request.

Abbreviations

Electronic Health Records

Concordance index

receiver operating characteristic curve

decision curve analysis

bone mineral density at left femoral neck

serum albumin

postprandial blood glucose

fatty liver disease

World Health Organization

low bone mass

National Osteoporosis Foundation

osteoporosis

International Osteoporosis Foundation

fracture risk assessment tool

bone mineral density

dual-energy X-ray absorptiometry

waist circumference

respiratory rate

blood pressure

body mass index

fasting blood glucose

hemoglobin A1c

alanine aminotransferase

aspartate aminotransferase

gamma-glutamyltransferase

serum creatinine

blood urea nitrogen

triglyceride

total cholesterol

high density lipoprotein cholesterol

low density lipoprotein cholesterol

prothrombin time

activate part plasma prothrombin time

thyroid stimulating hormone

total triiodothyronine

total thyroxine

free triiodothyronine

free thyroxine

luteinizing hormone

follicle-stimulating hormone

testosterone

progesterone

osteocalcin

type I procollagen amino-terminal peptide

βisomer of C-terminal telopeptide of type I collagen

parathyroid hormone

25-hydroxy-vitamin D

alkaline phosphatase

coronary heart disease

cerebrovascular disease

chronic kidney disease

benign prostatic hyperplasia

interquartile range

areas under the ROC curve

Osteoporosis Self-assessment Tool for Asians

nuclear factor kappaB

trabecular bone score

NLR Family Pyrin Domain Containing 3

nuclear factor erythroid 2­related factor 2

Kelch­Like ECH­Associated Protein 1

nonalcoholic fatty liver disease

colony-stimulating factor-1

tumor necrosis factor

colony-stimulating factor-1 receptor

mesenchymal stem cells

Assessment of fracture risk. And its application to screening for postmenopausal osteoporosis. Report of a WHO Study Group. World Health Organ Tech Rep Ser. 1994;843:1–129.

Google Scholar  

Camacho PM, Petak SM, Binkley N, Diab DL, Eldeiry LS, Farooki A, AMERICAN ASSOCIATION OF CLINICAL ENDOCRINOLOGISTS/AMERICAN COLLEGE OF ENDOCRINOLOGY CLINICAL PRACTICE GUIDELINES FOR THE DIAGNOSIS AND TREATMENT OF POSTMENOPAUSAL OSTEOPOROSIS-2020 UPDATE, et al. Endocr Pract. 2020;26(Suppl 1):1–46.

Article   PubMed   Google Scholar  

Chinese Society of Osteoporosis and Bone Mineral Research. Epidemiological survey of osteoporosis in China and the results of the ‘healthy bones’ special action released. Chin J Osteoporos Bone Mineral Res. 2019;12:1017–33.

Khosla S, Melton LJ. 3rd. Clinical practice. Osteopenia. N Engl J Med. 2007;356(22):2293–300.

Article   CAS   PubMed   Google Scholar  

Bliuc D, Nguyen ND, Nguyen TV, Eisman JA, Center JR. Compound risk of high mortality following osteoporotic fracture and refracture in elderly women and men. J Bone Min Res. 2013;28(11):2317–24.

Article   Google Scholar  

Viswanathan M, Reddy S, Berkman N, Cullen K, Middleton JC, Nicholson WK, et al. Screening to prevent osteoporotic fractures: updated evidence report and systematic review for the US Preventive Services Task Force. JAMA. 2018;319(24):2532–51.

El-Hajj Fuleihan G, Chakhtoura M, Cauley JA, Chamoun N. Worldwide Fracture Prediction. J Clin Densitom. 2017;20(3):397–424.

Shoback D, Rosen CJ, Black DM, Cheung AM, Murad MH, Eastell R. Pharmacological management of osteoporosis in Postmenopausal women: an Endocrine Society Guideline Update. J Clin Endocrinol Metab. 2020;105(3):dgaa048.

Areeckal AS, Kocher M. Current and emerging diagnostic imaging-based techniques for Assessment of osteoporosis and fracture risk. IEEE Rev Biomed Eng. 2019;12:254–68.

Rubin KH, Friis-Holmberg T, Hermann AP, Abrahamsen B, Brixen K. Risk assessment tools to identify women with increased risk of osteoporotic fracture: complexity or simplicity? A systematic review. J Bone Min Res. 2013;28(8):1701–17.

Center JR, Nguyen TV, Schneider D, Sambrook PN, Eisman JA. Mortality after all major types of osteoporotic fracture in men and women: an observational study. Lancet. 1999;353(9156):878–82.

Johnell O, Kanis JA. An estimate of the worldwide prevalence and disability associated with osteoporotic fractures. Osteoporos Int. 2006;17(12):1726–33.

Eastell R, Rosen CJ, Black DM, Cheung AM, Murad MH, Shoback D. Pharmacological management of osteoporosis in postmenopausal women: an endocrine society clinical practice guideline. J Clin Endocrinol Metab. 2019;104(5):1595–622.

Zha XY, Hu Y, Pang XN, Chang GL, Li L. Diagnostic value of osteoporosis self-assessment tool for asians (OSTA) and quantitative bone ultrasound (QUS) in detecting high-risk populations for osteoporosis among elderly Chinese men. J Bone Min Metab. 2015;33(2):230–8.

Abrahamsen B, Screening. FRAX in clinical practice. Nat Rev Rheumatol. 2011;7(12):686–8.

Harvey NC, McCloskey E, Kanis JA. Use of FRAX(®) in men. Joint Bone Spine. 2016;83(5):477–8.

Article   PubMed   PubMed Central   Google Scholar  

Kanis JA, Oden A, Johansson H, McCloskey E. Pitfalls in the external validation of FRAX. Osteoporos Int. 2012;23(2):423–31.

El Maghraoui A, Rezqi A, El Mrahi S, Sadni S, Ghozlani I, Mounach A. Osteoporosis, vertebral fractures and metabolic syndrome in postmenopausal women. BMC Endocr Disord. 2014;14:93.

Melton LJ 3rd, Beck TJ, Amin S, Khosla S, Achenbach SJ, Oberg AL, et al. Contributions of bone density and structure to fracture risk assessment in men and women. Osteoporos Int. 2005;16(5):460–7.

Abrahamsen B, Stilgren LS, Hermann AP, Tofteng CL, Bärenholdt O, Vestergaard P, et al. Discordance between changes in bone mineral density measured at different skeletal sites in perimenopausal women–implications for assessment of bone loss and response to therapy: the Danish osteoporosis Prevention Study. J Bone Min Res. 2001;16(7):1212–9.

Article   CAS   Google Scholar  

Abrahamsen B, Rejnmark L, Nielsen SP, Rud B, Nissen N, Mosekilde L, et al. Ten-year prediction of osteoporosis from baseline bone mineral density: development of prognostic thresholds in healthy postmenopausal women. The Danish osteoporosis Prevention Study. Osteoporos Int. 2006;17(2):245–51.

Valderrábano RJ, Buzkova P, Chang PY, Zakai NA, Fink HA, Robbins JA, et al. Associations of hemoglobin and change in hemoglobin with risk of incident hip fracture in older men and women: the cardiovascular health study. Osteoporos Int. 2021;32(8):1669–77.

Kim SY, Yoo DM, Min C, Choi HG. Association between osteoporosis and low hemoglobin levels: a nested case-control study using a National Health Screening Cohort. Int J Environ Res Public Health. 2021;18(16):8598.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Chuang MH, Chuang TL, Koo M, Wang YF. Low hemoglobin is Associated with Low Bone Mineral density and high risk of bone fracture in male adults: a Retrospective Medical Record Review study. Am J Mens Health. 2019;13(3):1557988319850378.

Kim HS, Park HM, Lee HS, Lee YJ. Hemoglobin levels and low bone mineral density in non-anemic older adults: secondary analysis of the Korean National Health and Nutrition Examination Survey. Exp Gerontol. 2019;126:110706.

Sun KT, Chen MY, Tu MG, Wang IK, Chang SS, Li CY. MicroRNA-20a regulates autophagy related protein-ATG16L1 in hypoxia-induced osteoclast differentiation. Bone. 2015;73:145–53.

Tan JK, Mohamad Hazir NS, Alias E. Impacts of Hypoxia on Osteoclast formation and activity: systematic review. Int J Mol Sci. 2021;22(18):10146.

Nagayama Y, Ebina K, Tsuboi H, Hirao M, Hashimoto J, Yoshikawa H, et al. Low serum albumin concentration is associated with increased risk of osteoporosis in postmenopausal patients with rheumatoid arthritis. J Orthop Sci. 2022;27(6):1283–90.

Ji Y, Geng N, Niu Y, Zhao H, Fei W, Chen S, et al. Relationship between geriatric nutritional risk index and osteoporosis in type 2 diabetes in Northern China. BMC Endocr Disord. 2022;22(1):308.

Zheng CM, Wu CC, Lu CL, Hou YC, Wu MS, Hsu YH, et al. Hypoalbuminemia differently affects the serum bone turnover markers in hemodialysis patients. Int J Med Sci. 2019;16(12):1583–92.

Afshinnia F, Wong KK, Sundaram B, Ackermann RJ, Pennathur S. Hypoalbuminemia and osteoporosis: reappraisal of a controversy. J Clin Endocrinol Metab. 2016;101(1):167–75.

Shieh A, Greendale GA, Cauley JA, Karvonen-Gutierriez C, Harlow SD, Finkelstein JS, et al. Prediabetes and insulin resistance are associated with lower trabecular bone score (TBS): cross-sectional results from the study of women’s Health across the Nation TBS study. Osteoporos Int. 2022;33(6):1365–72.

Ji X, Hong J, Qu Z, Yang W, Wang Y, Lin J, et al. HemoglobinA1c is a risk factor for changes of bone Mineral density: a mendelian randomization study. Front Endocrinol (Lausanne). 2022;13:942878.

Tencerova M, Figeac F, Ditzel N, Taipaleenmäki H, Nielsen TK, Kassem M. High-Fat Diet-Induced obesity promotes expansion of bone marrow adipose tissue and impairs skeletal stem cell functions in mice. J Bone Min Res. 2018;33(6):1154–65.

Sharma BR, Kanneganti TD. NLRP3 inflammasome in cancer and metabolic diseases. Nat Immunol. 2021;22(5):550–9.

Zhu C, Shen S, Zhang S, Huang M, Zhang L, Chen X. Autophagy in bone remodeling: a Regulator of oxidative stress. Front Endocrinol (Lausanne). 2022;13:898634.

Su YH, Chien KL, Yang SH, Chia WT, Chen JH, Chen YC. Nonalcoholic fatty liver disease is Associated with decreased bone Mineral density in adults: a systematic review and Meta-analysis. J Bone Min Res. 2023;38(8):1092–103.

Xie R, Liu M. Relationship between non-alcoholic fatty liver disease and degree of hepatic steatosis and bone Mineral Density. Front Endocrinol (Lausanne). 2022;13:857110.

Pan B, Cai J, Zhao P, Liu J, Fu S, Jing G, et al. Relationship between prevalence and risk of osteoporosis or osteoporotic fracture with non-alcoholic fatty liver disease: a systematic review and meta-analysis. Osteoporos Int. 2022;33(11):2275–86.

Nakchbandi IA, van der Merwe SW. Current understanding of osteoporosis associated with liver disease. Nat Rev Gastroenterol Hepatol. 2009;6(11):660–70.

Nara Y, Kitaura H, Ogawa S, Shen WR, Qi J, Ohori F, et al. Anti-c-fms antibody prevents osteoclast formation and bone resorption in co-culture of Osteoblasts and osteoclast precursors in Vitro and in Ovariectomized mice. Int J Mol Sci. 2020;21(17):6120.

Hou W, Chen S, Zhu C, Gu Y, Zhu L, Zhou Z. Associations between smoke exposure and osteoporosis or osteopenia in a US NHANES population of elderly individuals. Front Endocrinol (Lausanne). 2023;14:1074574.

Chen YY, Kao TW, Wang CC, Wu CJ, Zhou YC, Chen WL. Association between polycyclic aromatic hydrocarbons exposure and bone turnover in adults. Eur J Endocrinol. 2020;182(3):333–41.

Qin Y, Liu Y, Jiang Y, Mei S, Liu Y, Feng J, et al. Cigarette smoke exposure inhibits Osteoclast apoptosis via the mtROS pathway. J Dent Res. 2021;100(12):1378–86.

Lu Y, Di YP, Chang M, Huang X, Chen Q, Hong N, et al. Cigarette smoke-associated inflammation impairs bone remodeling through NFκB activation. J Transl Med. 2021;19(1):163.

Berman NK, Honig S, Cronstein BN, Pillinger MH. The effects of caffeine on bone mineral density and fracture risk. Osteoporos Int. 2022;33(6):1235–41.

Huang YP, Chen LS, Feng SH, Liang YS, Pan SL. Tea consumption and the risks of osteoporosis and hip fracture: a population-based longitudinal follow-up study. Osteoporos Int. 2023;34(1):101–9.

Lee DB, Song HJ, Paek YJ, Park KH, Seo YG, Noh HM. Relationship between regular green tea intake and osteoporosis in Korean Postmenopausal women: a Nationwide Study. Nutrients. 2021;14(1):87.

Huang HT, Cheng TL, Lin SY, Ho CJ, Chyu JY, Yang RS, et al. Osteoprotective Roles Green Tea Catechins Antioxid (Basel). 2020;9(11):1136.

CAS   Google Scholar  

Chen S, Chen T, Chen Y, Huang D, Pan Y, Chen S. Causal Association between Tea Consumption and Bone Health: a mendelian randomization study. Front Nutr. 2022;9:872451.

Download references

Acknowledgements

The authors thank all the study participants.

National Key Research and Development Program of China (No. 2020YFC2004900).

Multi-center RCT Clinical Project of the National Clinical Research Centre for Geriatric Diseases, Chinese PLA General Hospital (No. NCRCG-PLAGH-2023001).

The Open Project of the National Clinical Research Centre for Geriatric Diseases, Chinese PLA General Hospital (No. NCRCG-PLAGH-2022016).

Author information

Ting Li and Jing Zeng contributed equally to this work.

Authors and Affiliations

Department of Endocrinology, the Second Medical Centre & National Clinical Research Centre for Geriatric Disease, Chinese PLA General Hospital, Beijing, China

Ting Li, Jing Zeng, Zimo Pan, Fan Hu, Yanping Gong, Nan Li & Chunlin Li

Department of Nephrology, the Second Medical Centre & National Clinical Research Centre for Geriatric Disease, Chinese PLA General Hospital, Beijing, China

Xiaoyan Cai

Department of Radiology, the Second Medical Centre & National Clinical Research Centre for Geriatric Disease, Chinese PLA General Hospital, Beijing, China

Xinjiang Wang, Guanzhong Liu & Xinghe Hu

Department of Clinical Laboratory, the Second Medical Centre & National Clinical Research Centre for Geriatric Disease, Chinese PLA General Hospital, Beijing, China

Xinli Deng & Meiliang Gong

Department of Outpatient, the Second Medical Centre & National Clinical Research Centre for Geriatric Disease, Chinese PLA General Hospital, Beijing, China

You can also search for this author in PubMed   Google Scholar

Contributions

Study concept and design: TL, NL, CL. Data acquisition: XC, XW, GL, XH, XD, MG and XY. Data analysis and interpretation: TL, JZ. Statistical analysis: TL, JZ, ZP, FH and YG. Drafting of the manuscript: TL, JZ. Critical revision of the manuscript: TL, JZ, NL and YG. Manuscript review: NL, CL.

Corresponding authors

Correspondence to Nan Li or Chunlin Li .

Ethics declarations

Ethics approval and consent to participate.

This study has been approved by the Ethics Committee of Chinese PLA General Hospital (ID: S2021-094-01) and has been performed in accordance with the ethical standards as laid down in the 1964 Declaration of Helsinki and its later amendments or comparable ethical standards.

All participants in the study have signed informed consent forms.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Li, T., Zeng, J., Pan, Z. et al. Development and internal validation of a clinical prediction model for osteopenia in Chinese middle-aged and elderly men: a prospective cohort study. BMC Musculoskelet Disord 25 , 394 (2024). https://doi.org/10.1186/s12891-024-07526-7

Download citation

Received : 31 August 2023

Accepted : 15 May 2024

Published : 20 May 2024

DOI : https://doi.org/10.1186/s12891-024-07526-7

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Risk factors
• Cohort study

BMC Musculoskeletal Disorders

ISSN: 1471-2474

• Submission enquiries: [email protected]
• General enquiries: [email protected]