
- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons

Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

4.2E: Exercises
- Last updated
- Save as PDF
- Page ID 120152
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
In Exercises 1 - 16, use the six-step procedure to graph the rational function. Be sure to draw any asymptotes as dashed lines.
- \(f(x) = \dfrac{4}{x + 2}\)
- \(f(x) = \dfrac{5x}{6 - 2x}\)
- \(f(x) = \dfrac{1}{x^{2}}\)
- \(f(x) = \dfrac{1}{x^{2} + x - 12}\)
- \(f(x) = \dfrac{2x - 1}{-2x^{2} - 5x + 3}\)
- \(f(x) = \dfrac{x}{x^{2} + x - 12}\)
- \(f(x) = \dfrac{4x}{x^2+4}\)
- \(f(x) = \dfrac{4x}{x^2-4}\)
- \(f(x) = \dfrac{x^2-x-12}{x^2+x-6}\)
- \(f(x) = \dfrac{3x^2-5x-2}{x^2-9}\)
- \(f(x) = \dfrac{x^2-x-6}{x+1}\)
- \(f(x) = \dfrac{x^2-x}{3-x}\)
- \(f(x) = \dfrac{x^3+2x^2+x}{x^2-x-2}\)
- \(f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9}\)
- \(f(x) = \dfrac{x^3-2x^2+3x}{2x^2+2}\)
- \(f(x) = \dfrac{x^{2} - 2x + 1}{x^{3} + x^{2} - 2x}\)
In Exercises 17 - 20, graph the rational function by applying transformations to the graph of \(y = \dfrac{1}{x}\).
- \(f(x) = \dfrac{1}{x - 2}\)
- \(g(x) = 1 - \dfrac{3}{x}\)
- \(h(x) = \dfrac{-2x + 1}{x}\) (Hint: Divide)
- \(j(x) = \dfrac{3x - 7}{x - 2}\) (Hint: Divide)
- Discuss with your classmates how you would graph \(f(x) = \dfrac{ax + b}{cx + d}\). What restrictions must be placed on \(a, b, c\) and \(d\) so that the graph is indeed a transformation of \(y = \dfrac{1}{x}\)?
- In Example 3.1.1 in Section 3.1 we showed that \(p(x) = \frac{4x+x^3}{x}\) is not a polynomial even though its formula reduced to \(4 + x^{2}\) for \(x \neq 0\). However, it is a rational function similar to those studied in the section. With the help of your classmates, graph \(p(x)\).
- Let \(g(x) = \displaystyle \frac{x^{4} - 8x^{3} + 24x^{2} - 72x + 135}{x^{3} - 9x^{2} + 15x - 7}.\;\) With the help of your classmates, find the \(x\)- and \(y\)- intercepts of the graph of \(g\). Find the intervals on which the function is increasing, the intervals on which it is decreasing and the local extrema. Find all of the asymptotes of the graph of \(g\) and any holes in the graph, if they exist. Be sure to show all of your work including any polynomial or synthetic division. Sketch the graph of \(g\), using more than one picture if necessary to show all of the important features of the graph.
Example 4.2.4 showed us that the six-step procedure cannot tell us everything of importance about the graph of a rational function. Without Calculus, we need to use our graphing calculators to reveal the hidden mysteries of rational function behavior. Working with your classmates, use a graphing calculator to examine the graphs of the rational functions given in Exercises 24 - 27. Compare and contrast their features. Which features can the six-step process reveal and which features cannot be detected by it?
- \(f(x) = \dfrac{1}{x^{2} + 1}\)
- \(f(x) = \dfrac{x}{x^{2} + 1}\)
- \(f(x) = \dfrac{x^{2}}{x^{2} + 1}\)
- \(f(x) = \dfrac{x^{3}}{x^{2} + 1}\)
\(f(x) = \dfrac{4}{x + 2}\) Domain: \((-\infty, -2) \cup (-2, \infty)\) No \(x\)-intercepts \(y\)-intercept: \((0, 2)\) Vertical asymptote: \(x = -2\) As \(x \rightarrow -2^{-}, \; f(x) \rightarrow -\infty\) As \(x \rightarrow -2^{+}, \; f(x) \rightarrow \infty\) Horizontal asymptote: \(y = 0\) As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\) As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)
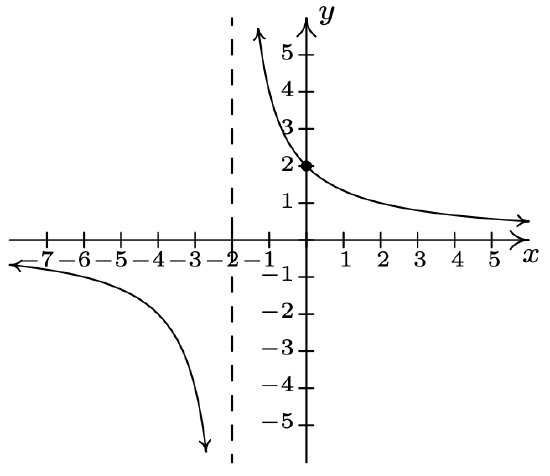
\(f(x) = \dfrac{5x}{6 - 2x}\) Domain: \((-\infty, 3) \cup (3, \infty)\) \(x\)-intercept: \((0, 0)\) \(y\)-intercept: \((0, 0)\) Vertical asymptote: \(x = 3\) As \(x \rightarrow 3^{-}, \; f(x) \rightarrow \infty\) As \(x \rightarrow 3^{+}, \; f(x) \rightarrow -\infty\) Horizontal asymptote: \(y = -\frac{5}{2}\) As \(x \rightarrow -\infty, \; f(x) \rightarrow -\frac{5}{2}^{+}\) As \(x \rightarrow \infty, \; f(x) \rightarrow -\frac{5}{2}^{-}\)
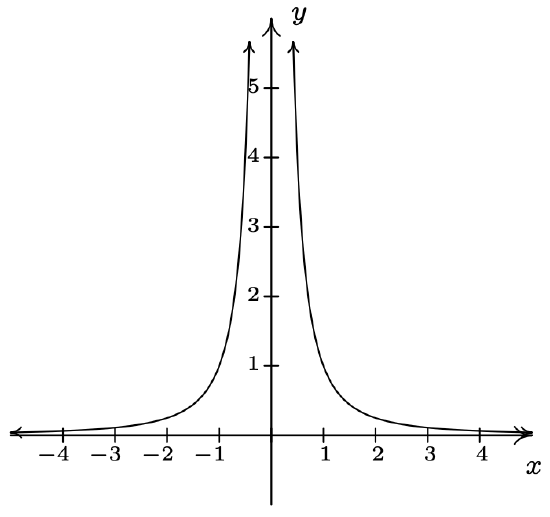
\(f(x) = \dfrac{1}{x^{2}}\) Domain: \((-\infty, 0) \cup (0, \infty)\) No \(x\)-intercepts No \(y\)-intercepts Vertical asymptote: \(x = 0\) As \(x \rightarrow 0^{-}, \; f(x) \rightarrow \infty\) As \(x \rightarrow 0^{+}, \; f(x) \rightarrow \infty\) Horizontal asymptote: \(y = 0\) As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\) As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)
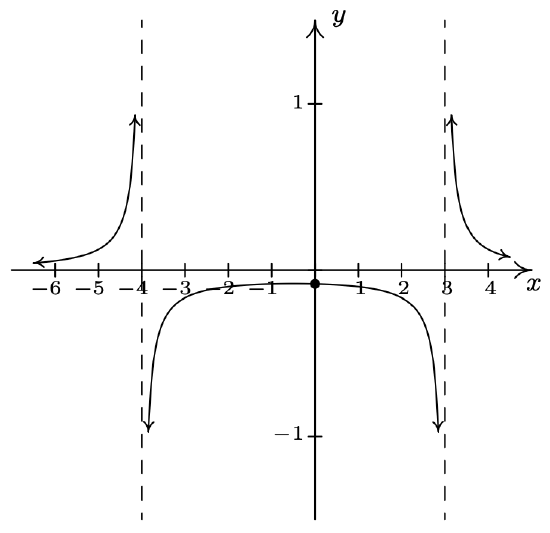
\(f(x) = \dfrac{1}{x^{2} + x - 12} = \dfrac{1}{(x - 3)(x + 4)}\) Domain: \((-\infty, -4) \cup (-4, 3) \cup (3, \infty)\) No \(x\)-intercepts \(y\)-intercept: \((0, -\frac{1}{12})\) Vertical asymptotes: \(x = -4\) and \(x = 3\) As \(x \rightarrow -4^{-}, \; f(x) \rightarrow \infty\) As \(x \rightarrow -4^{+}, \; f(x) \rightarrow -\infty\) As \(x \rightarrow 3^{-}, \; f(x) \rightarrow -\infty\) As \(x \rightarrow 3^{+}, \; f(x) \rightarrow \infty\) Horizontal asymptote: \(y = 0\) As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\) As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)
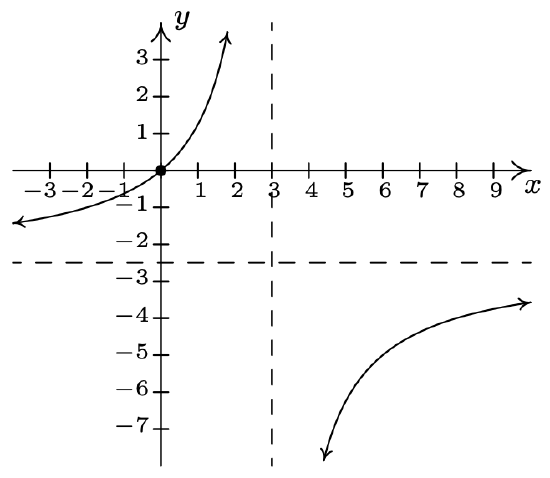
\(f(x) = \dfrac{2x - 1}{-2x^{2} - 5x + 3} = -\dfrac{2x - 1}{(2x - 1)(x + 3)}\) Domain: \((-\infty, -3) \cup (-3, \frac{1}{2}) \cup (\frac{1}{2}, \infty)\) No \(x\)-intercepts \(y\)-intercept: \((0, -\frac{1}{3})\) \(f(x) = \dfrac{-1}{x + 3}, \; x \neq \frac{1}{2}\) Hole in the graph at \((\frac{1}{2}, -\frac{2}{7})\) Vertical asymptote: \(x = -3\) As \(x \rightarrow -3^{-}, \; f(x) \rightarrow \infty\) As \(x \rightarrow -3^{+}, \; f(x) \rightarrow -\infty\) Horizontal asymptote: \(y = 0\) As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\) As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{-}\)
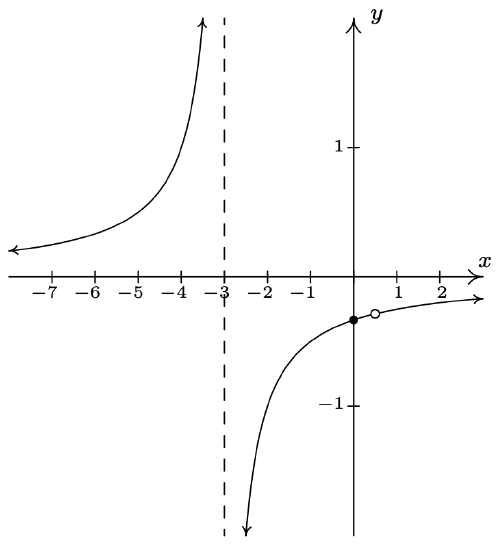
\(f(x) = \dfrac{x}{x^{2} + x - 12} = \dfrac{x}{(x - 3)(x + 4)}\) Domain: \((-\infty, -4) \cup (-4, 3) \cup (3, \infty)\) \(x\)-intercept: \((0, 0)\) \(y\)-intercept: \((0, 0)\) Vertical asymptotes: \(x = -4\) and \(x = 3\) As \(x \rightarrow -4^{-}, \; f(x) \rightarrow -\infty\) As \(x \rightarrow -4^{+}, \; f(x) \rightarrow \infty\) As \(x \rightarrow 3^{-}, \; f(x) \rightarrow -\infty\) As \(x \rightarrow 3^{+}, \; f(x) \rightarrow \infty\) Horizontal asymptote: \(y = 0\) As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\) As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)
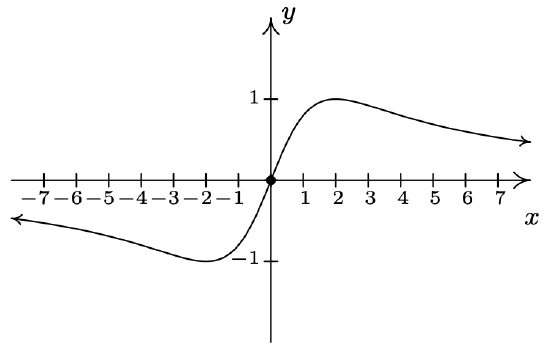
\(f(x) = \dfrac{4x}{x^{2} + 4}\) Domain: \((-\infty, \infty)\) \(x\)-intercept: \((0,0)\) \(y\)-intercept: \((0,0)\) No vertical asymptotes No holes in the graph Horizontal asymptote: \(y = 0\) As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\) As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)
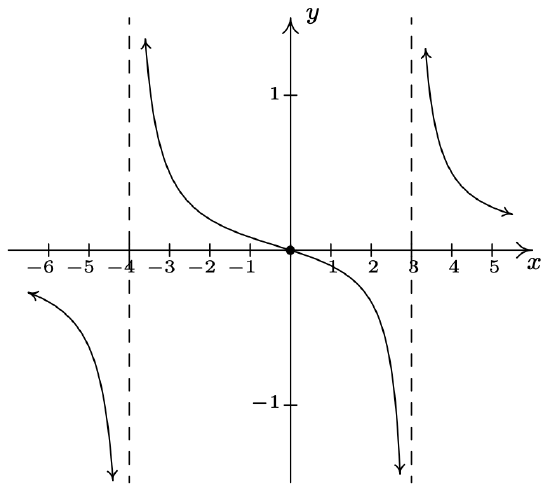
\(f(x) = \dfrac{4x}{x^{2} -4} = \dfrac{4x}{(x + 2)(x - 2)}\) Domain: \((-\infty, -2) \cup (-2, 2) \cup (2, \infty)\) \(x\)-intercept: \((0,0)\) \(y\)-intercept: \((0,0)\) Vertical asymptotes: \(x = -2, x = 2\) As \(x \rightarrow -2^{-}, f(x) \rightarrow -\infty\) As \(x \rightarrow -2^{+}, f(x) \rightarrow \infty\) As \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\) As \(x \rightarrow 2^{+}, f(x) \rightarrow \infty\) No holes in the graph Horizontal asymptote: \(y = 0\) As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\) As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)
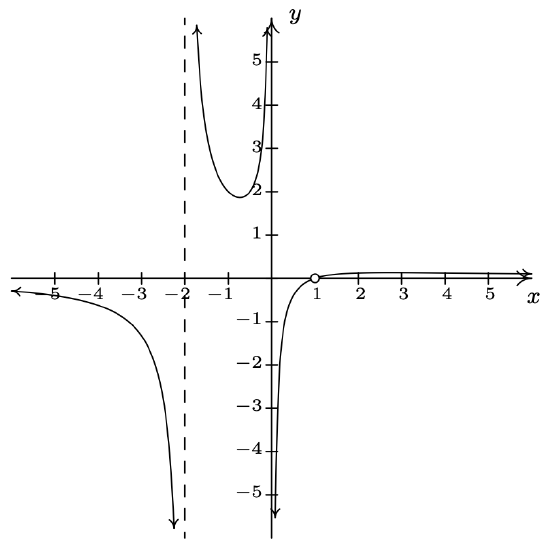
\(f(x) = \dfrac{x^2-x-12}{x^{2} +x - 6} = \dfrac{x-4}{x - 2} \, x \neq -3\) Domain: \((-\infty, -3) \cup (-3, 2) \cup (2, \infty)\) \(x\)-intercept: \((4,0)\) \(y\)-intercept: \((0,2)\) Vertical asymptote: \(x = 2\) As \(x \rightarrow 2^{-}, f(x) \rightarrow \infty\) As \(x \rightarrow 2^{+}, f(x) \rightarrow -\infty\) Hole at \(\left(-3, \frac{7}{5} \right)\) Horizontal asymptote: \(y = 1\) As \(x \rightarrow -\infty, f(x) \rightarrow 1^{+}\) As \(x \rightarrow \infty, f(x) \rightarrow 1^{-}\)
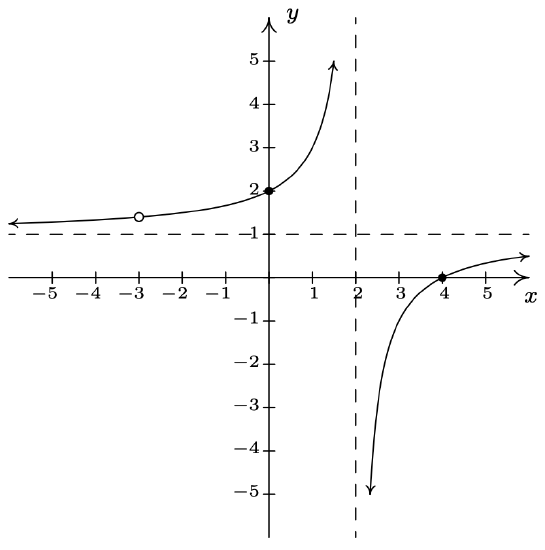
\(f(x) = \dfrac{3x^2-5x-2}{x^{2} -9} = \dfrac{(3x+1)(x-2)}{(x + 3)(x - 3)}\) Domain: \((-\infty, -3) \cup (-3, 3) \cup (3, \infty)\) \(x\)-intercepts: \(\left(-\frac{1}{3}, 0 \right)\), \((2,0)\) \(y\)-intercept: \(\left(0, \frac{2}{9} \right)\) Vertical asymptotes: \(x = -3, x = 3\) As \(x \rightarrow -3^{-}, f(x) \rightarrow \infty\) As \(x \rightarrow -3^{+}, f(x) \rightarrow -\infty\) As \(x \rightarrow 3^{-}, f(x) \rightarrow -\infty\) As \(x \rightarrow 3^{+}, f(x) \rightarrow \infty\) No holes in the graph Horizontal asymptote: \(y = 3\) As \(x \rightarrow -\infty, f(x) \rightarrow 3^{+}\) As \(x \rightarrow \infty, f(x) \rightarrow 3^{-}\)
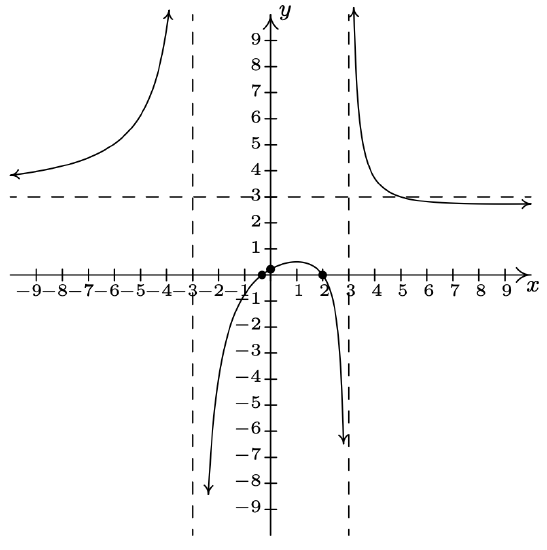
\(f(x) = \dfrac{x^2-x-6}{x+1} = \dfrac{(x-3)(x+2)}{x+1}\) Domain: \((-\infty, -1) \cup (-1, \infty)\) \(x\)-intercepts: \((-2,0)\), \((3,0)\) \(y\)-intercept: \((0,-6)\) Vertical asymptote: \(x = -1\) As \(x \rightarrow -1^{-}, f(x) \rightarrow \infty\) As \(x \rightarrow -1^{+}, f(x) \rightarrow -\infty\) Slant asymptote: \(y = x-2\) As \(x \rightarrow -\infty\), the graph is above \(y=x-2\) As \(x \rightarrow \infty\), the graph is below \(y=x-2\)
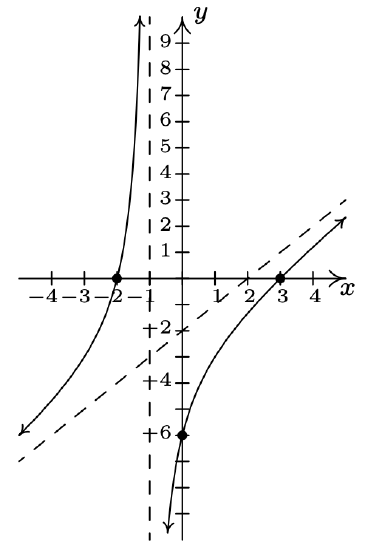
\(f(x) = \dfrac{x^2-x}{3-x} = \dfrac{x(x-1)}{3-x}\) Domain: \((-\infty, 3) \cup (3, \infty)\) \(x\)-intercepts: \((0,0)\), \((1,0)\) \(y\)-intercept: \((0,0)\) Vertical asymptote: \(x = 3\) As \(x \rightarrow 3^{-}, f(x) \rightarrow \infty\) As \(x \rightarrow 3^{+}, f(x) \rightarrow -\infty\) Slant asymptote: \(y = -x-2\) As \(x \rightarrow -\infty\), the graph is above \(y=-x-2\) As \(x \rightarrow \infty\), the graph is below \(y=-x-2\)
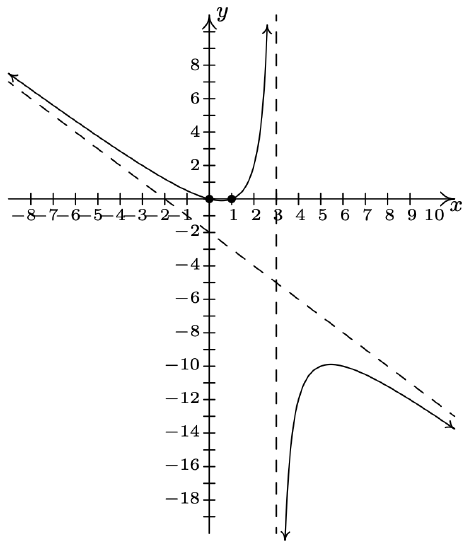
\(f(x) = \dfrac{x^3+2x^2+x}{x^{2} -x-2} = \dfrac{x(x+1)}{x - 2} \, x \neq -1\) Domain: \((-\infty, -1) \cup (-1, 2) \cup (2, \infty)\) \(x\)-intercept: \((0,0)\) \(y\)-intercept: \((0,0)\) Vertical asymptote: \(x = 2\) As \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\) As \(x \rightarrow 2^{+}, f(x) \rightarrow \infty\) Hole at \((-1,0)\) Slant asymptote: \(y = x+3\) As \(x \rightarrow -\infty\), the graph is below \(y=x+3\) As \(x \rightarrow \infty\), the graph is above \(y=x+3\)
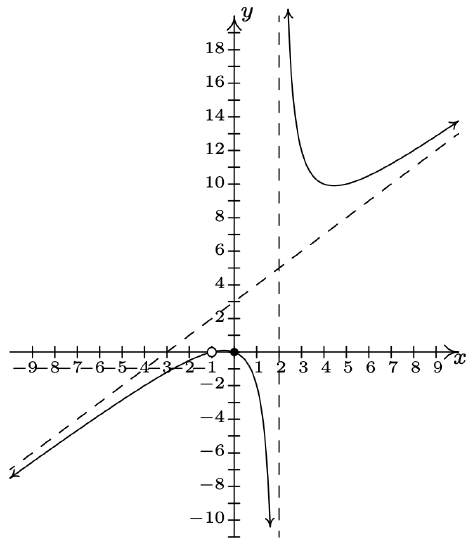
\(f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9}\) Domain: \((-\infty, -3) \cup (-3, 3) \cup (3, \infty)\) \(x\)-intercepts: \((-2, 0), (0, 0), (2, 0)\) \(y\)-intercept: \((0, 0)\) Vertical asymptotes: \(x = -3, x = 3\) As \(x \rightarrow -3^{-}, \; f(x) \rightarrow \infty\) As \(x \rightarrow -3^{+}, \; f(x) \rightarrow -\infty\) As \(x \rightarrow 3^{-}, \; f(x) \rightarrow \infty\) As \(x \rightarrow 3^{+}, \; f(x) \rightarrow -\infty\) Slant asymptote: \(y = -x\) As \(x \rightarrow -\infty\), the graph is above \(y=-x\) As \(x \rightarrow \infty\), the graph is below \(y=-x\)
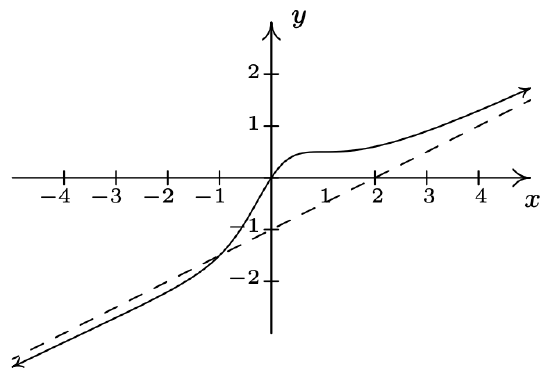
\(f(x) = \dfrac{x^3-2x^2+3x}{2x^2+2}\) Domain: \((-\infty,\infty)\) \(x\)-intercept: \((0,0)\) \(y\)-intercept: \((0,0)\) Slant asymptote: \(y = \frac{1}{2}x-1\) As \(x \rightarrow -\infty\), the graph is below \(y = \frac{1}{2}x-1\) As \(x \rightarrow \infty\), the graph is above \(y = \frac{1}{2}x-1\)
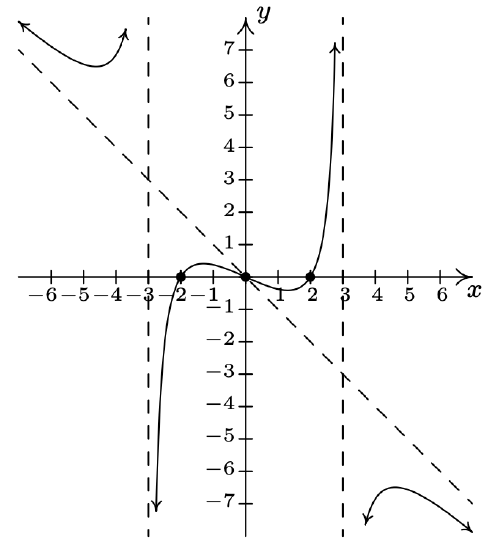
\(f(x) = \dfrac{x^{2} - 2x + 1}{x^{3} + x^{2} - 2x}\) Domain: \((-\infty, -2) \cup (-2, 0) \cup (0, 1) \cup (1, \infty)\) \(f(x) = \dfrac{x - 1}{x(x + 2)}, \; x \neq 1\) No \(x\)-intercepts No \(y\)-intercepts Vertical asymptotes: \(x = -2\) and \(x = 0\) As \(x \rightarrow -2^{-}, \; f(x) \rightarrow -\infty\) As \(x \rightarrow -2^{+}, \; f(x) \rightarrow \infty\) As \(x \rightarrow 0^{-}, \; f(x) \rightarrow \infty\) As \(x \rightarrow 0^{+}, \; f(x) \rightarrow -\infty\) Hole in the graph at \((1, 0)\) Horizontal asymptote: \(y = 0\) As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\) As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)
\(f(x) = \dfrac{1}{x - 2}\) Shift the graph of \(y = \dfrac{1}{x}\) to the right 2 units.
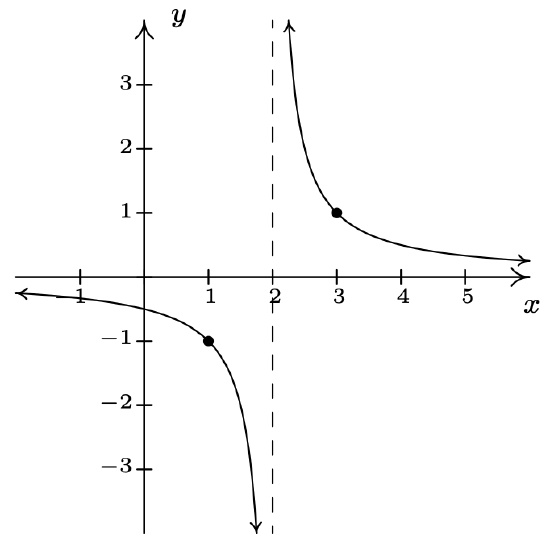
\(g(x) = 1 - \dfrac{3}{x}\) Vertically stretch the graph of \(y = \dfrac{1}{x}\) by a factor of 3. Reflect the graph of \(y = \dfrac{3}{x}\) about the \(x\)-axis. Shift the graph of \(y = -\dfrac{3}{x}\) up 1 unit.
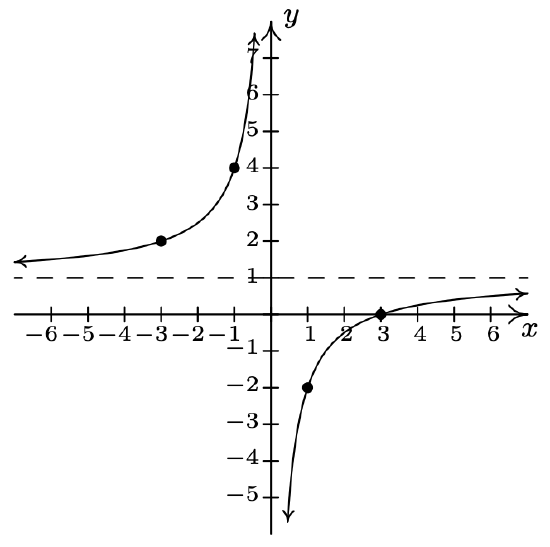
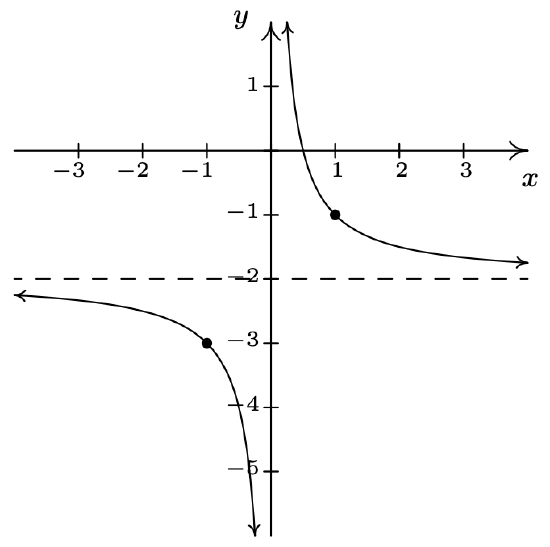
\(h(x) = \dfrac{-2x + 1}{x} = -2 + \dfrac{1}{x}\) Shift the graph of \(y = \dfrac{1}{x}\) down 2 units.
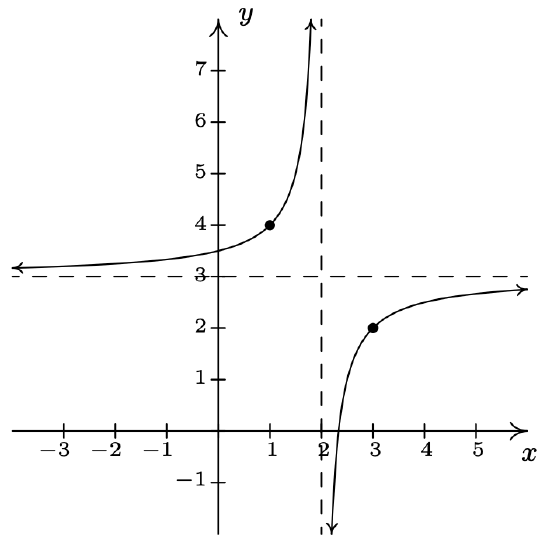
\(j(x) = \dfrac{3x - 7}{x - 2} = 3 - \dfrac{1}{x - 2}\) Shift the graph of \(y = \dfrac{1}{x}\) to the right 2 units. Reflect the graph of \(y = \dfrac{1}{x - 2}\) about the \(x\)-axis. Shift the graph of \(y = -\dfrac{1}{x - 2}\) up 3 units.
Holt Algebra 4.2 Relations and Functions Worksheet DOC & PDF


Description
Questions & answers, r squared creation.
- We're hiring
- Help & FAQ
- Privacy policy
- Student privacy
- Terms of service
- Tell us what you think
Have an account?

Functions Review
7th - 10th grade, mathematics.
26 questions

Introducing new Paper mode
No student devices needed. Know more
- 1. Multiple Choice Edit 1 minute 1 pt What is the definition of function? Has inputs and outputs Every input has only ONE output Inputs have different outputs every time x-values and y-values
- 2. Multiple Choice Edit 1 minute 1 pt Which set of values is a function? (9,5) (10,5) (9,-5) (10,-5) (3,4) (4,-3) (7,4) (3, 8) (6,-5) (7, -3) (8, -1) (9, 1) (2, -2) (5, 9) (5, -7) (1, 4)
- 21. Multiple Choice Edit 3 minutes 1 pt 1 Students were asked to state the different ways of determining if a relation is a function. Which student is not correct? - Jennifer said, “In a graph you can use the vertical line test and if the line intercepts only once, it is a function.” - Matthew said, “In a mapping diagram you could use the vertical line test and if the line intercepts only once, it is a function” - Maria said, “In a table, if the x values have more than one corresponding y value, it is not a function.” - Sam, “In an ordered pair, if the x values have more than one corresponding y value, it is not a function.”
- 25. Multiple Choice Edit 30 seconds 1 pt Which set of ordered pairs represents a function? {(2, 4), (2, 5), (2, 6), (2, 7) {(0, 0), (1, 1), (2, 2), (3, 3)} {(1.1, 2.2), (2.2, 1.1), (2.2, 3.4)} {(2,3), (3, 4), (4, 5), (4, 6)}
Explore all questions with a free account

Continue with email
Continue with phone
4.02 homework quiz relations and functions

- business plan
- course work
- research paper

IMAGES
VIDEO
COMMENTS
QUIZ 1: RELATIONS AND FUNCTIONS. x = { (2, 3), (2, 4), (2, 5), (2, 6)} Is x a function and why? Yes, there is more than one ordered pair in this list. No, each ordered pair in this list has the same first element. No, there is a limited number of ordered pairs in this list. Yes, no two ordered pairs in this list has the same second element.
From the list of sets A, B, and C, state the domain of set B. A function is always a relation. A relation is a function, if and only if, the x-values do not repeat in a given set. Which of the following statements best describes the relationship of a relation and a function? 2x^2 + 4x + 5. If f (x) = 2x^2 + 3, then which of the following ...
Example 4.2.21. For the function f(x) = 2x2 + 4x − 3, evaluate the function. In the last example, we found f(x) for a constant value of x. In the next example, we are asked to find g(x) with values of x that are variables. We still follow the same procedure and substitute the variables in for the x.
20. 30. 40. 50. Worksheet: 4.02 Functions and relations. Mathspace is an all-in-one learning resource, wherever you are. We bring all of your learning tools together in one place, from video lessons, textbooks, to adaptive practice. Encourage your students to become self-directed learners.
The answer is 3. Which graph represents f (x)=−2x^2. The graph should look like an upside down U. Which graph represents f (x)=−2x^4. The graph should look like an upside down U. Which functions have graphs that are less steep than the graph of f (x)=2x^2. h (x) = -2x^2. j (x) = -x^2. What is the end behavior of the graph?
the graph of a quadratic function. axis of symmetry. the line of symmetry that passes through the vertex. Vertex. the turning point of the curve. About us. About Quizlet; How Quizlet works; Careers; Advertise with us; Get the app; For students. Flashcards; Test; Learn; Solutions; Q-Chat: AI Tutor; Spaced Repetition; Modern Learning Lab; Quizlet ...
m (x)=4x2 and g (x)=−4x2. What is the end behavior of the graph? As x approaches infinity, f (x) approaches negative infinity. As x approaches negative infinity, f (x) approaches infinity. What is the degree of the power function represented in the table? 2. Honors Algebra 2 Learn with flashcards, games, and more — for free.
A relation is a relationship between sets of information. For example, think of the names of people in a class and their heights. If given a height (e.g. $162$162 cm), it would be possible to identify the names of all the people who are this tall in the class, and there may be more than one person. So, if someone came to the class looking for ...
4.07: Transform Linear Functions. 5 terms. alexander12322. Preview. Algebra 2 Honors 8.4-8.6. 6 terms. Shreck_2. Preview. the greatest degree & terms words (Algebra) 10 terms. Gisselle7135. ... Algebra Ch. 11 Quiz (Practice) Teacher 11 terms. MrVanWey. Preview. Terms in this set (11) what is the basic equation using rate, distance and time. s ...
Relations and Functions quiz for 7th grade students. Find other quizzes for Mathematics and more on Quizizz for free! ... Is the relation a function? Why. Yes, because the x-value 11 has two y-values pair with it. Yes, because each x-value has only one y-value paired with it.
Quiz 7A: Relations and Functions. 1. A) 0 B) 8 C) 3 D) 1. 2. A relation is a set of _____. A) frogs B) functions C) y-values D) ordered pairs. 3. Domain is a list of all of the ____ values of a relation or function. A) z B) x C) y. 4. Range is a list of all of the ____ values of a relation or function.
A relation is a set of inputs and outputs that are related in some way. In every relation, each input has exactly one output. All relations are functions. All of these are true statements ...
Application to evaluating functions. The polynomial function h(t) = −16t2 + 300 h ( t) = − 16 t 2 + 300 gives the height of a ball t seconds after it is dropped from a 100-foot tall bridge. Find the height after t = 3 t = 3 seconds. The polynomial function h(t) = −16t2 + 275 h ( t) = − 16 t 2 + 275 gives the height of a ball t seconds ...
Study with Quizlet and memorize flashcards containing terms like What are the domain and range of the function? f(x)=1/3^x7, Which graph represents the function? f(x)=1/x+1 +2, What are the equations of the asymptotes of the graph of f(x)=3/x−2 +9 ? and more.
Find the intervals on which the function is increasing, the intervals on which it is decreasing and the local extrema. Find all of the asymptotes of the graph of \(g\) and any holes in the graph, if they exist. Be sure to show all of your work including any polynomial or synthetic division. Sketch the graph of \(g\), using more than one picture ...
Each option violates the rule that a function only has one unique y-value for every x-value. <br />C) Each of x-values of 2, 1 and 9 are unique and correspond to one y-value.<br />D) Similar to C, each of x-values of 4, 8, and 0 are unique and correspond to one y-value.<br />So both option C and D strictly align with conditions for a function ...
Description. This r squared creation is the complementary worksheet for our 4.2 PowerPoint, which students will complete as homework. This worksheet is practice for the students on how to find the domain and range of a relation, decide if something is a function or not, and to express a relation using a table, graph, and mapping diagram.
Functions Review quiz for 7th grade students. Find other quizzes for Mathematics and more on Quizizz for free! ... 1 Students were asked to state the different ways of determining if a relation is a function. Which student is not correct? - Jennifer said, "In a graph you can use the vertical line test and if the line intercepts only once, it ...
Holt Algebra 4.2 Relations and Functions Worksheet DOC & PDF. Description. Questions & answers, r squared creation. We're hiring; Help & FAQ; Privacy policy; Student ...
View 4.02 math.pdf from MATH 238 at City College, Fort Lauderdale. ╰┈ 4.02 ; Pre-algebra ; Module 4 ; Assignment. 彡 ༺ ˎˊ- -ˋˏ ༻ ╔═════════════════╗ Work done by ; Giselle Medina. Teacher ; Deborah
Complete the project and notes and you can turn this in for credit for Project 4.02 Module 4 - Lesson 2: Comparing Functions Notes Space to Practice & Video Links Welcome to your Toolbox Watch this video first! Representing Data: Graphs, Tables, Equations, Verbal Descriptions & Ordered Pairs Vocabulary 1. Functions are displayed as: (pg. 2) a. Ordered Pairs (not listed)_____ b.
View Copy of 4.02 - Comparing Functions.docx from MNLKNKBJBHJH DJKJ at Florida Virtual School. Complete the project and notes and you can turn this in for credit for Project 4.02 Module 4 - Lesson 2:
View 4.02 Power Functions Classwork Document-B.pdf from MTH 306A at Ohio Virtual Academy. Unit 4 Lesson 2: Power Functions October 29, 2017 BEFORE CLASS: Get Ready: *Get this information from the Get ... week4 quiz.docx. Solutions Available. Southern New Hampshire University. CS 330. test prep. ... View Unit 1 Homework.pdf from MTH 306A at Ohio ...