what is the critical value in hypothesis testing

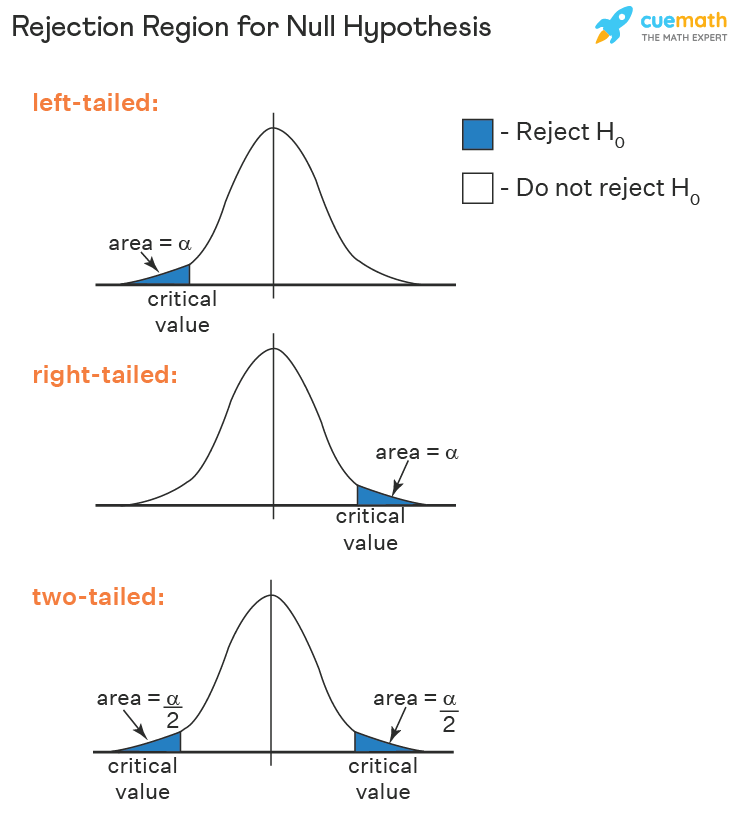
Critical Value

Critical value is a cut-off value that is used to mark the start of a region where the test statistic, obtained in hypothesis testing, is unlikely to fall in. In hypothesis testing, the critical value is compared with the obtained test statistic to determine whether the null hypothesis has to be rejected or not.

Graphically, the critical value splits the graph into the acceptance region and the rejection region for hypothesis testing. It helps to check the statistical significance of a test statistic. In this article, we will learn more about the critical value, its formula, types, and how to calculate its value.

What is Critical Value?

A critical value can be calculated for different types of hypothesis tests. The critical value of a particular test can be interpreted from the distribution of the test statistic and the significance level. A one-tailed hypothesis test will have one critical value while a two-tailed test will have two critical values.

Critical Value Definition

Critical value can be defined as a value that is compared to a test statistic in hypothesis testing to determine whether the null hypothesis is to be rejected or not. If the value of the test statistic is less extreme than the critical value, then the null hypothesis cannot be rejected. However, if the test statistic is more extreme than the critical value, the null hypothesis is rejected and the alternative hypothesis is accepted. In other words, the critical value divides the distribution graph into the acceptance and the rejection region. If the value of the test statistic falls in the rejection region, then the null hypothesis is rejected otherwise it cannot be rejected.

Critical Value Formula

Depending upon the type of distribution the test statistic belongs to, there are different formulas to compute the critical value. The confidence interval or the significance level can be used to determine a critical value. Given below are the different critical value formulas.

Critical Value Confidence Interval

The critical value for a one-tailed or two-tailed test can be computed using the confidence interval . Suppose a confidence interval of 95% has been specified for conducting a hypothesis test. The critical value can be determined as follows:

• Step 1: Subtract the confidence level from 100%. 100% - 95% = 5%.
• Step 2: Convert this value to decimals to get \(\alpha\). Thus, \(\alpha\) = 5%.
• Step 3: If it is a one-tailed test then the alpha level will be the same value in step 2. However, if it is a two-tailed test, the alpha level will be divided by 2.
• Step 4: Depending on the type of test conducted the critical value can be looked up from the corresponding distribution table using the alpha value.

The process used in step 4 will be elaborated in the upcoming sections.

T Critical Value

A t-test is used when the population standard deviation is not known and the sample size is lesser than 30. A t-test is conducted when the population data follows a Student t distribution . The t critical value can be calculated as follows:

• Determine the alpha level.
• Subtract 1 from the sample size. This gives the degrees of freedom (df).
• If the hypothesis test is one-tailed then use the one-tailed t distribution table. Otherwise, use the two-tailed t distribution table for a two-tailed test.
• Match the corresponding df value (left side) and the alpha value (top row) of the table. Find the intersection of this row and column to give the t critical value.

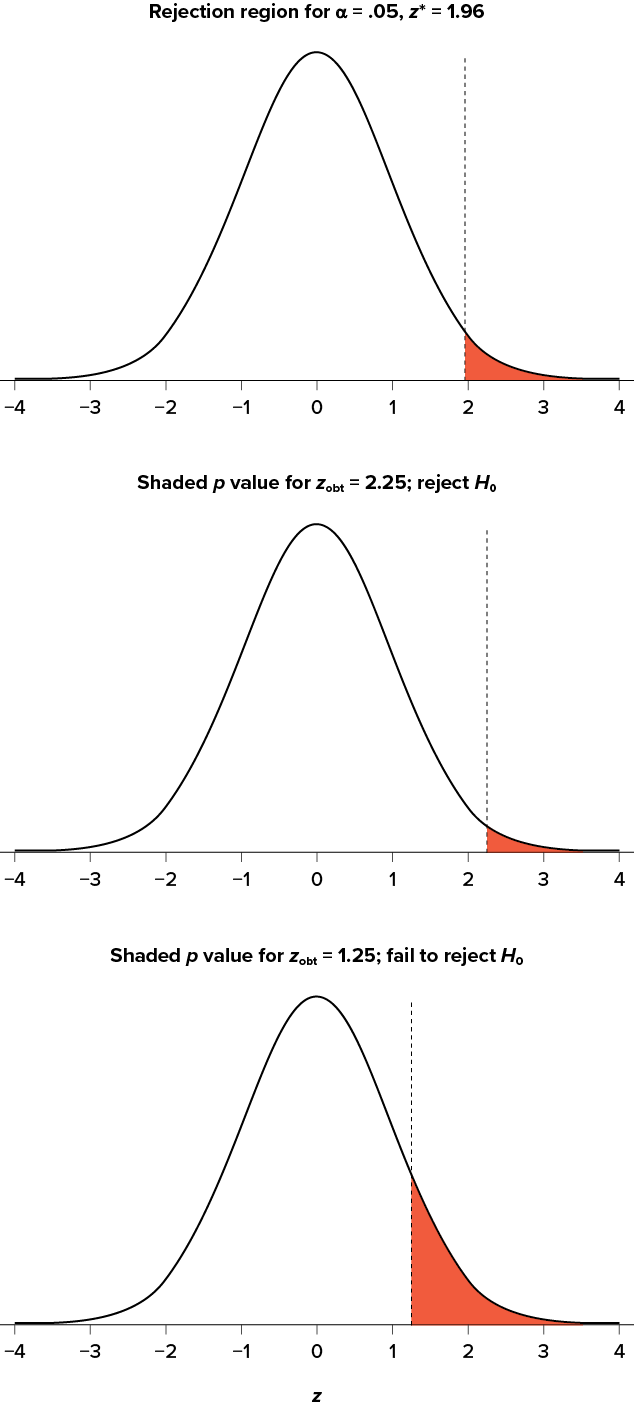
Test Statistic for one sample t test: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, s is the sample standard deviation and n is the size of the sample.

Test Statistic for two samples t test: \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Decision Criteria:

• Reject the null hypothesis if test statistic > t critical value (right-tailed hypothesis test).
• Reject the null hypothesis if test statistic < t critical value (left-tailed hypothesis test).
• Reject the null hypothesis if the test statistic does not lie in the acceptance region (two-tailed hypothesis test).

This decision criterion is used for all tests. Only the test statistic and critical value change.

Z Critical Value

A z test is conducted on a normal distribution when the population standard deviation is known and the sample size is greater than or equal to 30. The z critical value can be calculated as follows:

• Find the alpha level.
• Subtract the alpha level from 1 for a two-tailed test. For a one-tailed test subtract the alpha level from 0.5.
• Look up the area from the z distribution table to obtain the z critical value. For a left-tailed test, a negative sign needs to be added to the critical value at the end of the calculation.

Test statistic for one sample z test: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\sigma\) is the population standard deviation.

Test statistic for two samples z test: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

F Critical Value

The F test is largely used to compare the variances of two samples. The test statistic so obtained is also used for regression analysis. The f critical value is given as follows:

• Subtract 1 from the size of the first sample. This gives the first degree of freedom. Say, x
• Similarly, subtract 1 from the second sample size to get the second df. Say, y.
• Using the f distribution table, the intersection of the x column and y row will give the f critical value.

Test Statistic for large samples: f = \(\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}\). \(\sigma_{1}^{2}\) variance of the first sample and \(\sigma_{2}^{2}\) variance of the second sample.

Test Statistic for small samples: f = \(\frac{s_{1}^{2}}{s_{2}^{2}}\). \(s_{1}^{1}\) variance of the first sample and \(s_{2}^{2}\) variance of the second sample.

Chi-Square Critical Value

The chi-square test is used to check if the sample data matches the population data. It can also be used to compare two variables to see if they are related. The chi-square critical value is given as follows:

• Identify the alpha level.
• Subtract 1 from the sample size to determine the degrees of freedom (df).
• Using the chi-square distribution table, the intersection of the row of the df and the column of the alpha value yields the chi-square critical value.

Test statistic for chi-squared test statistic: \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\).

Critical Value Calculation

Suppose a right-tailed z test is being conducted. The critical value needs to be calculated for a 0.0079 alpha level. Then the steps are as follows:

• Subtract the alpha level from 0.5. Thus, 0.5 - 0.0079 = 0.4921
• Using the z distribution table find the area closest to 0.4921. The closest area is 0.4922. As this value is at the intersection of 2.4 and 0.02 thus, the z critical value = 2.42.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Critical Value

• Critical value can be defined as a value that is useful in checking whether the null hypothesis can be rejected or not by comparing it with the test statistic.
• It is the point that divides the distribution graph into the acceptance and the rejection region.
• There are 4 types of critical values - z, f, chi-square, and t.

Examples on Critical Value

Example 1: Find the critical value for a left tailed z test where \(\alpha\) = 0.012.

Solution: First subtract \(\alpha\) from 0.5. Thus, 0.5 - 0.012 = 0.488.

Using the z distribution table, z = 2.26.

However, as this is a left-tailed z test thus, z = -2.26

Answer: Critical value = -2.26

Example 2: Find the critical value for a two-tailed f test conducted on the following samples at a \(\alpha\) = 0.025

Variance = 110, Sample size = 41

Variance = 70, Sample size = 21

Solution: \(n_{1}\) = 41, \(n_{2}\) = 21,

\(n_{1}\) - 1= 40, \(n_{2}\) - 1 = 20,

Sample 1 df = 40, Sample 2 df = 20

Using the F distribution table for \(\alpha\) = 0.025, the value at the intersection of the 40 th column and 20 th row is

F(40, 20) = 2.287

Answer: Critical Value = 2.287

Example 3: Suppose a one-tailed t-test is being conducted on data with a sample size of 8 at \(\alpha\) = 0.05. Then find the critical value.

Solution: n = 8

df = 8 - 1 = 7

Using the one tailed t distribution table t(7, 0.05) = 1.895.

Answer: Crititcal Value = 1.895

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Critical Value

What is the critical value in statistics.

Critical value in statistics is a cut-off value that is compared with a test statistic in hypothesis testing to check whether the null hypothesis should be rejected or not.

What are the Different Types of Critical Value?

There are 4 types of critical values depending upon the type of distributions they are obtained from. These distributions are given as follows:

• Normal distribution (z critical value).
• Student t distribution (t).
• Chi-squared distribution (chi-squared).
• F distribution (f).

What is the Critical Value Formula for an F test?

To find the critical value for an f test the steps are as follows:

• Determine the degrees of freedom for both samples by subtracting 1 from each sample size.
• Find the corresponding value from a one-tailed or two-tailed f distribution at the given alpha level.
• This will give the critical value.

What is the T Critical Value?

The t critical value is obtained when the population follows a t distribution. The steps to find the t critical value are as follows:

• Subtract the sample size number by 1 to get the df.
• Use the t distribution table for the alpha value to get the required critical value.

How to Find the Critical Value Using a Confidence Interval for a Two-Tailed Z Test?

The steps to find the critical value using a confidence interval are as follows:

• Subtract the confident interval from 100% and convert the resultant into a decimal value to get the alpha level.
• Subtract this value from 1.
• Find the z value for the corresponding area using the normal distribution table to get the critical value.

Can a Critical Value be Negative?

If a left-tailed test is being conducted then the critical value will be negative. This is because the critical value will be to the left of the mean thus, making it negative.

How to Reject Null Hypothesis Based on Critical Value?

The rejection criteria for the null hypothesis is given as follows:

• Right-tailed test: Test statistic > critical value.
• Left-tailed test: Test statistic < critical value.
• Two-tailed test: Reject if the test statistic does not lie in the acceptance region.

Critical Value Calculator

How to use critical value calculator, what is a critical value, critical value definition, how to calculate critical values, z critical values, t critical values, chi-square critical values (χ²), f critical values, behind the scenes of the critical value calculator.

Welcome to the critical value calculator! Here you can quickly determine the critical value(s) for two-tailed tests, as well as for one-tailed tests. It works for most common distributions in statistical testing: the standard normal distribution N(0,1) (that is when you have a Z-score), t-Student, chi-square, and F-distribution .

What is a critical value? And what is the critical value formula? Scroll down – we provide you with the critical value definition and explain how to calculate critical values in order to use them to construct rejection regions (also known as critical regions).

The critical value calculator is your go-to tool for swiftly determining critical values in statistical tests, be it one-tailed or two-tailed. To effectively use the calculator, follow these steps:

In the first field, input the distribution of your test statistic under the null hypothesis: is it a standard normal N (0,1), t-Student, chi-squared, or Snedecor's F? If you are not sure, check the sections below devoted to those distributions, and try to localize the test you need to perform.

In the field What type of test? choose the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

If needed, specify the degrees of freedom of the test statistic's distribution. If you need more clarification, check the description of the test you are performing. You can learn more about the meaning of this quantity in statistics from the degrees of freedom calculator .

Set the significance level, α \alpha α . By default, we pre-set it to the most common value, 0.05, but you can adjust it to your needs.

The critical value calculator will display your critical value(s) and the rejection region(s).

Click the advanced mode if you need to increase the precision with which the critical values are computed.

For example, let's envision a scenario where you are conducting a one-tailed hypothesis test using a t-Student distribution with 15 degrees of freedom. You have opted for a right-tailed test and set a significance level (α) of 0.05. The results indicate that the critical value is 1.7531, and the critical region is (1.7531, ∞). This implies that if your test statistic exceeds 1.7531, you will reject the null hypothesis at the 0.05 significance level.

👩‍🏫 Want to learn more about critical values? Keep reading!

In hypothesis testing, critical values are one of the two approaches which allow you to decide whether to retain or reject the null hypothesis. The other approach is to calculate the p-value (for example, using the p-value calculator ).

The critical value approach consists of checking if the value of the test statistic generated by your sample belongs to the so-called rejection region , or critical region , which is the region where the test statistic is highly improbable to lie . A critical value is a cut-off value (or two cut-off values in the case of a two-tailed test) that constitutes the boundary of the rejection region(s). In other words, critical values divide the scale of your test statistic into the rejection region and the non-rejection region.

Once you have found the rejection region, check if the value of the test statistic generated by your sample belongs to it :

• If so, it means that you can reject the null hypothesis and accept the alternative hypothesis; and
• If not, then there is not enough evidence to reject H 0 .

But how to calculate critical values? First of all, you need to set a significance level , α \alpha α , which quantifies the probability of rejecting the null hypothesis when it is actually correct. The choice of α is arbitrary; in practice, we most often use a value of 0.05 or 0.01. Critical values also depend on the alternative hypothesis you choose for your test , elucidated in the next section .

To determine critical values, you need to know the distribution of your test statistic under the assumption that the null hypothesis holds. Critical values are then points with the property that the probability of your test statistic assuming values at least as extreme at those critical values is equal to the significance level α . Wow, quite a definition, isn't it? Don't worry, we'll explain what it all means.

First, let us point out it is the alternative hypothesis that determines what "extreme" means. In particular, if the test is one-sided, then there will be just one critical value; if it is two-sided, then there will be two of them: one to the left and the other to the right of the median value of the distribution.

Critical values can be conveniently depicted as the points with the property that the area under the density curve of the test statistic from those points to the tails is equal to α \alpha α :

Left-tailed test: the area under the density curve from the critical value to the left is equal to α \alpha α ;

Right-tailed test: the area under the density curve from the critical value to the right is equal to α \alpha α ; and

Two-tailed test: the area under the density curve from the left critical value to the left is equal to α / 2 \alpha/2 α /2 , and the area under the curve from the right critical value to the right is equal to α / 2 \alpha/2 α /2 as well; thus, total area equals α \alpha α .

As you can see, finding the critical values for a two-tailed test with significance α \alpha α boils down to finding both one-tailed critical values with a significance level of α / 2 \alpha/2 α /2 .

The formulae for the critical values involve the quantile function , Q Q Q , which is the inverse of the cumulative distribution function ( c d f \mathrm{cdf} cdf ) for the test statistic distribution (calculated under the assumption that H 0 holds!): Q = c d f − 1 Q = \mathrm{cdf}^{-1} Q = cdf − 1 .

Once we have agreed upon the value of α \alpha α , the critical value formulae are the following:

• Left-tailed test :
• Right-tailed test :
• Two-tailed test :

In the case of a distribution symmetric about 0 , the critical values for the two-tailed test are symmetric as well:

Unfortunately, the probability distributions that are the most widespread in hypothesis testing have somewhat complicated c d f \mathrm{cdf} cdf formulae. To find critical values by hand, you would need to use specialized software or statistical tables. In these cases, the best option is, of course, our critical value calculator! 😁

Use the Z (standard normal) option if your test statistic follows (at least approximately) the standard normal distribution N(0,1) .

In the formulae below, u u u denotes the quantile function of the standard normal distribution N(0,1):

Left-tailed Z critical value: u ( α ) u(\alpha) u ( α )

Right-tailed Z critical value: u ( 1 − α ) u(1-\alpha) u ( 1 − α )

Two-tailed Z critical value: ± u ( 1 − α / 2 ) \pm u(1- \alpha/2) ± u ( 1 − α /2 )

Check out Z-test calculator to learn more about the most common Z-test used on the population mean. There are also Z-tests for the difference between two population means, in particular, one between two proportions.

Use the t-Student option if your test statistic follows the t-Student distribution . This distribution is similar to N(0,1) , but its tails are fatter – the exact shape depends on the number of degrees of freedom . If this number is large (>30), which generically happens for large samples, then the t-Student distribution is practically indistinguishable from N(0,1). Check our t-statistic calculator to compute the related test statistic.

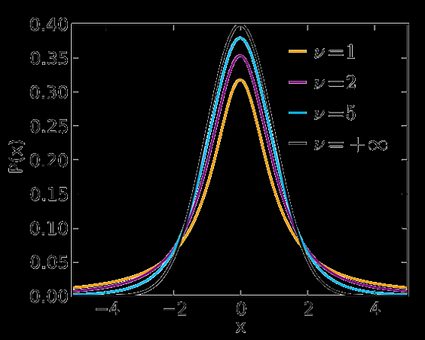
In the formulae below, Q t , d Q_{\text{t}, d} Q t , d ​ is the quantile function of the t-Student distribution with d d d degrees of freedom:

Left-tailed t critical value: Q t , d ( α ) Q_{\text{t}, d}(\alpha) Q t , d ​ ( α )

Right-tailed t critical value: Q t , d ( 1 − α ) Q_{\text{t}, d}(1 - \alpha) Q t , d ​ ( 1 − α )

Two-tailed t critical values: ± Q t , d ( 1 − α / 2 ) \pm Q_{\text{t}, d}(1 - \alpha/2) ± Q t , d ​ ( 1 − α /2 )

Visit the t-test calculator to learn more about various t-tests: the one for a population mean with an unknown population standard deviation , those for the difference between the means of two populations (with either equal or unequal population standard deviations), as well as about the t-test for paired samples .

Use the χ² (chi-square) option when performing a test in which the test statistic follows the χ²-distribution .

You need to determine the number of degrees of freedom of the χ²-distribution of your test statistic – below, we list them for the most commonly used χ²-tests.

Here we give the formulae for chi square critical values; Q χ 2 , d Q_{\chi^2, d} Q χ 2 , d ​ is the quantile function of the χ²-distribution with d d d degrees of freedom:

Left-tailed χ² critical value: Q χ 2 , d ( α ) Q_{\chi^2, d}(\alpha) Q χ 2 , d ​ ( α )

Right-tailed χ² critical value: Q χ 2 , d ( 1 − α ) Q_{\chi^2, d}(1 - \alpha) Q χ 2 , d ​ ( 1 − α )

Two-tailed χ² critical values: Q χ 2 , d ( α / 2 ) Q_{\chi^2, d}(\alpha/2) Q χ 2 , d ​ ( α /2 ) and Q χ 2 , d ( 1 − α / 2 ) Q_{\chi^2, d}(1 - \alpha/2) Q χ 2 , d ​ ( 1 − α /2 )

Several different tests lead to a χ²-score:

Goodness-of-fit test : does the empirical distribution agree with the expected distribution?

This test is right-tailed . Its test statistic follows the χ²-distribution with k − 1 k - 1 k − 1 degrees of freedom, where k k k is the number of classes into which the sample is divided.

Independence test : is there a statistically significant relationship between two variables?

This test is also right-tailed , and its test statistic is computed from the contingency table. There are ( r − 1 ) ( c − 1 ) (r - 1)(c - 1) ( r − 1 ) ( c − 1 ) degrees of freedom, where r r r is the number of rows, and c c c is the number of columns in the contingency table.

Test for the variance of normally distributed data : does this variance have some pre-determined value?

This test can be one- or two-tailed! Its test statistic has the χ²-distribution with n − 1 n - 1 n − 1 degrees of freedom, where n n n is the sample size.

Finally, choose F (Fisher-Snedecor) if your test statistic follows the F-distribution . This distribution has a pair of degrees of freedom .

Let us see how those degrees of freedom arise. Assume that you have two independent random variables, X X X and Y Y Y , that follow χ²-distributions with d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ degrees of freedom, respectively. If you now consider the ratio ( X d 1 ) : ( Y d 2 ) (\frac{X}{d_1}):(\frac{Y}{d_2}) ( d 1 ​ X ​ ) : ( d 2 ​ Y ​ ) , it turns out it follows the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom. That's the reason why we call d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ the numerator and denominator degrees of freedom , respectively.

In the formulae below, Q F , d 1 , d 2 Q_{\text{F}, d_1, d_2} Q F , d 1 ​ , d 2 ​ ​ stands for the quantile function of the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom:

Left-tailed F critical value: Q F , d 1 , d 2 ( α ) Q_{\text{F}, d_1, d_2}(\alpha) Q F , d 1 ​ , d 2 ​ ​ ( α )

Right-tailed F critical value: Q F , d 1 , d 2 ( 1 − α ) Q_{\text{F}, d_1, d_2}(1 - \alpha) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α )

Two-tailed F critical values: Q F , d 1 , d 2 ( α / 2 ) Q_{\text{F}, d_1, d_2}(\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( α /2 ) and Q F , d 1 , d 2 ( 1 − α / 2 ) Q_{\text{F}, d_1, d_2}(1 -\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α /2 )

Here we list the most important tests that produce F-scores: each of them is right-tailed .

ANOVA : tests the equality of means in three or more groups that come from normally distributed populations with equal variances. There are ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where k k k is the number of groups, and n n n is the total sample size (across every group).

Overall significance in regression analysis . The test statistic has ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where n n n is the sample size, and k k k is the number of variables (including the intercept).

Compare two nested regression models . The test statistic follows the F-distribution with ( k 2 − k 1 , n − k 2 ) (k_2 - k_1, n - k_2) ( k 2 ​ − k 1 ​ , n − k 2 ​ ) degrees of freedom, where k 1 k_1 k 1 ​ and k 2 k_2 k 2 ​ are the number of variables in the smaller and bigger models, respectively, and n n n is the sample size.

The equality of variances in two normally distributed populations . There are ( n − 1 , m − 1 ) (n - 1, m - 1) ( n − 1 , m − 1 ) degrees of freedom, where n n n and m m m are the respective sample sizes.

I'm Anna, the mastermind behind the critical value calculator and a PhD in mathematics from Jagiellonian University .

The idea for creating the tool originated from my experiences in teaching and research. Recognizing the need for a tool that simplifies the critical value determination process across various statistical distributions, I built a user-friendly calculator accessible to both students and professionals. After publishing the tool, I soon found myself using the calculator in my research and as a teaching aid.

Trust in this calculator is paramount to me. Each tool undergoes a rigorous review process , with peer-reviewed insights from experts and meticulous proofreading by native speakers. This commitment to accuracy and reliability ensures that users can be confident in the content. Please check the Editorial Policies page for more details on our standards.

What is a Z critical value?

A Z critical value is the value that defines the critical region in hypothesis testing when the test statistic follows the standard normal distribution . If the value of the test statistic falls into the critical region, you should reject the null hypothesis and accept the alternative hypothesis.

How do I calculate Z critical value?

To find a Z critical value for a given confidence level α :

Check if you perform a one- or two-tailed test .

For a one-tailed test:

Left -tailed: critical value is the α -th quantile of the standard normal distribution N(0,1).

Right -tailed: critical value is the (1-α) -th quantile.

Two-tailed test: critical value equals ±(1-α/2) -th quantile of N(0,1).

No quantile tables ? Use CDF tables! (The quantile function is the inverse of the CDF.)

Verify your answer with an online critical value calculator.

Is a t critical value the same as Z critical value?

In theory, no . In practice, very often, yes . The t-Student distribution is similar to the standard normal distribution, but it is not the same . However, if the number of degrees of freedom (which is, roughly speaking, the size of your sample) is large enough (>30), then the two distributions are practically indistinguishable , and so the t critical value has practically the same value as the Z critical value.

What is the Z critical value for 95% confidence?

The Z critical value for a 95% confidence interval is:

• 1.96 for a two-tailed test;
• 1.64 for a right-tailed test; and
• -1.64 for a left-tailed test.
• Sum of Squares Calculator
• Midrange Calculator
• Coefficient of Variation Calculator

Ascending order

Central limit theorem, plant spacing.

• Biology (101)
• Chemistry (100)
• Construction (145)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (571)
• Health (440)
• Physics (511)
• Sports (105)
• Statistics (184)
• Other (183)
• Discover Omni (40)

If you could change one thing about college, what would it be?

Graduate faster

Better quality online classes

Flexible schedule

Access to top-rated instructors

How To Find Critical Value In Statistics

10.28.2022 • 13 min read

Sarah Thomas

Subject Matter Expert

Learn how to find critical value, its importance, the different systems, and the steps to follow when calculating it.

In This Article

What Is a Critical Value?

The role of critical values in hypothesis tests, factors that influence critical values, critical values for one-tailed tests & two-tailed tests, commonly used critical values, how to find the critical value in statistics, how to find a critical value in r, don't overpay for college statistics.

Take Intro to Statistics Online with Outlier.org

From the co-founder of MasterClass, earn transferable college credits from the University of Pittsburgh (a top 50 global school). The world's best online college courses for 50% less than a traditional college.

In baseball, an ump cries “foul ball” any time a batter hits the ball into foul territory. In statistics, we have something similar to a foul zone. It’s called a rejection region. While foul lines, poles, and the stadium fence mark off the foul territory in baseball, in statistics numbers called critical values mark off rejection regions.

A critical value is a number that defines the rejection region of a hypothesis test. Critical values vary depending on the type of hypothesis test you run and the type of data you are working with.

In a hypothesis test called a two-tailed Z-test with a 95% confidence level, the critical values are 1.96 and -1.96. In this test, if the statistician’s results are greater than 1.96 or less than -1.96. We reject the null hypothesis in favor of the alternative hypothesis.

In Outlier's Intro to Statistics course, Dr. Gregory Matthews explains more about hypothesis testing and why to use it:

The figure below shows how the critical values mark the boundaries of two rejection regions (shaded in pink). Any test result greater than 1.96 falls into the rejection region in the distribution’s right tail, and any test result below -1.96 falls into the rejection region in the left tail of the distribution.

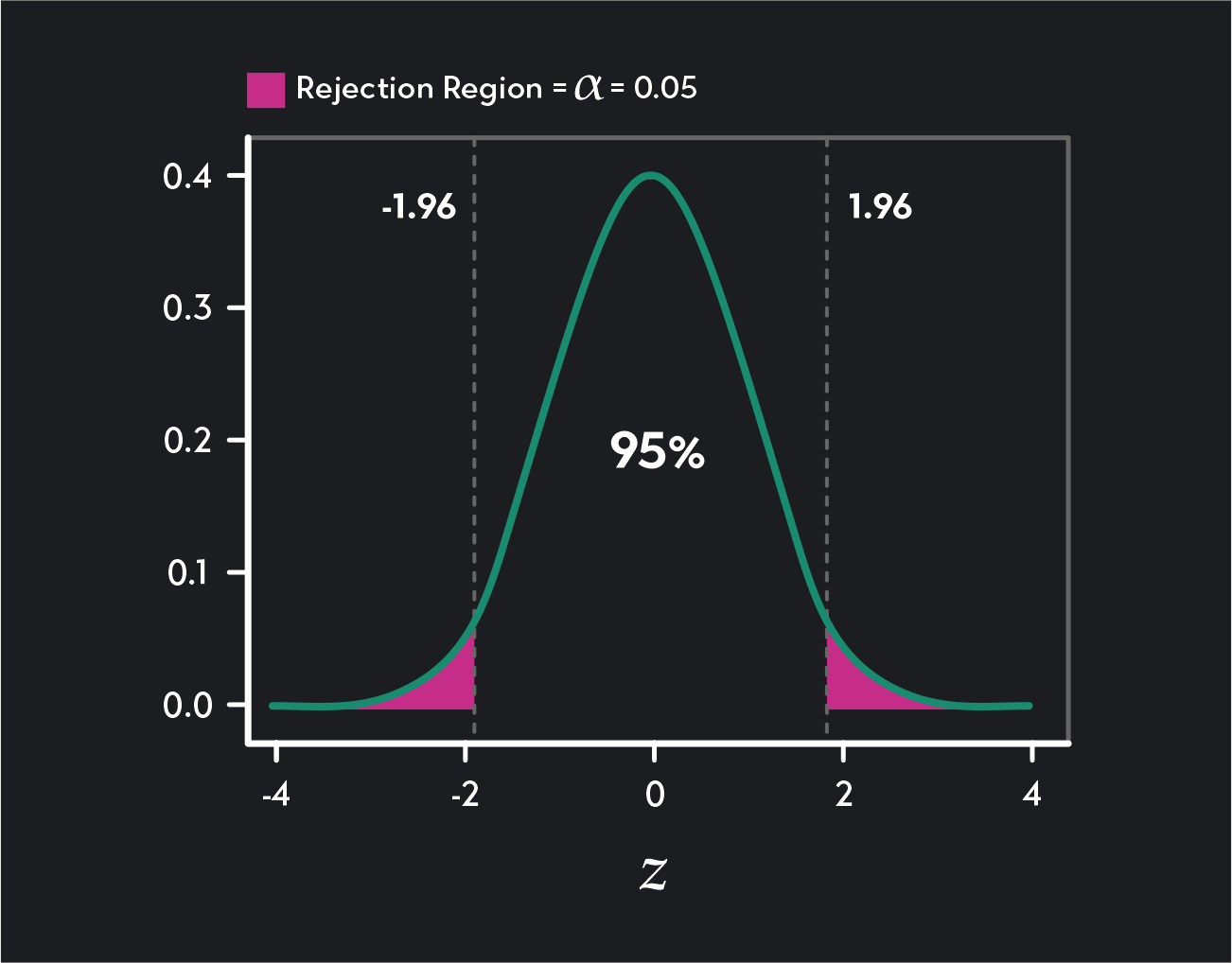
A two-tailed Z-test with a 95% confidence level (or a significance level of ɑ = 0.05) has two critical values 1.96 and -1.96.

Before we dive deeper, let’s do a quick refresher on hypothesis testing. In statistics, a hypothesis test is a statistical test where you test an “alternative” hypothesis against a “null” hypothesis. The null hypothesis represents the default hypothesis or the status quo. It typically represents what the academic community or the general public believes to be true. The alternative hypothesis represents what you suspect could be true in place of the null hypothesis.

For example, I may hypothesize that as times have changed, the average age of first-time mothers in the U.S. has increased and that first-time mothers, on average, are now older than 25. Meanwhile, conventional wisdom or existing research may say that the average age of first-time mothers in the U.S. is 25 years old.

In this example, my hypothesis is the alternative hypothesis, and the conventional wisdom is the null hypothesis.

Alternative Hypothesis H a H_a H a ​ = Average age of first-time mothers in the U.S. > 25

Null Hypothesis H 0 H_0 H 0 ​ = Average age of first-time mothers in the U.S. = 25

In a hypothesis test, the goal is to draw inferences about a population parameter (such as the population mean of first-time mothers in the U.S.) from sample data randomly drawn from the population.

The basic intuition behind hypothesis testing is this. If we assume that the null hypothesis is true, data collected from a random sample of first-time mothers should have a sample average that’s close to 25 years old. We don’t expect the sample to have the same average as the population, but we expect it to be pretty close. If we find this to be the case, we have evidence favoring the null hypothesis. If our sample average is far enough above 25, we have evidence that favors the alternative hypothesis.

A major conundrum in hypothesis testing is deciding what counts as “close to 25” and what counts as being “far enough above 25”? If you randomly sample a thousand first-time mothers and the sample mean is 26 or 27 years old, should you favor the null hypothesis or the alternative?

To make this determination, you need to do the following:

1. First, you convert your sample statistic into a test statistic.

In our first-time mother example, the sample statistic we have is the average age of the first-time mothers in our sample. Depending on the data we have, we might map this average to a Z-test statistic or a T-test statistic.

A test statistic is just a number that maps a sample statistic to a value on a standardized distribution such as a normal distribution or a T-distribution. By converting our sample statistic to a test statistic, we can easily see how likely or unlikely it is to get our sample statistic under the assumption that the null hypothesis is true.

2. Next, you select a significance level (also known as an alpha (ɑ) level) for your test.

The significance level is a measure of how confident you want to be in your decision to reject the null hypothesis in favor of the alternative. A commonly used significance level in hypothesis testing is 5% (or ɑ=0.05). An alpha-level of 0.05 means that you’ll only reject the null hypothesis if there is less than a 5% chance of wrongly favoring the alternative over the null.

3. Third, you find the critical values that correspond to your test statistic and significance level.

The critical value(s) tell you how small or large your test statistic has to be in order to reject the null hypothesis at your chosen significance level.

4. You check to see if your test statistic falls into the rejection region.

Check the value of the test statistic. Any test statistic that falls above a critical value in the right tail of the distribution is in the rejection region. Any test statistic located below a critical value in the left tail of the distribution is also in the rejection region. If your test statistic falls into the rejection region, you reject the null hypothesis in favor of the alternative hypothesis. If your test statistic does not fall into the rejection region, you fail to reject the null hypothesis.

Notice that critical values play a crucial role in hypothesis testing. Without knowing what your critical values are, you cannot make the final determination of whether or not to reject the null hypothesis.

Critical values vary with the following traits of a hypothesis test.

What test statistic are you using?

This will depend on the type of research question you have and the type of data you are working with. In a first-year statistics course, you will often conduct hypothesis tests using Z-statistics (these correspond to a standard normal distribution ), T-statistics (these correspond to a T-distribution), or chi-squared test statistics (these correspond to a chi-square distribution).

What significance level have you selected?

This is up to the person conducting the test. A significance level (or alpha level) is the probability of mistakenly rejecting the null hypothesis when it is actually true. By choosing a significance level, you are deciding how careful you want to be in avoiding such a mistake.

You might also hear a hypothesis test being described by a confidence level. Confidence levels are closely related to statistical significance. The confidence level of a test is equal to one minus the significance level or 1-ɑ.

Is it a one-tailed test or a two-tailed test?

Hypothesis tests can be one-tailed or two-tailed, depending on the alternative hypothesis. Null and alternative hypotheses are always mutually exclusive statements, but they can take different forms. If your alternative hypothesis is only concerned with positive effects or the right tail of the distribution, you will likely use a one-tailed upper-tail test.

If your alternative hypothesis is only concerned with negative effects or the left tail of the distribution, you will likely use a one-tailed lower-tail test. Finally, if your alternative hypothesis proposes a deviation in either direction from what the null hypothesis proposes, you’ll use a two-tailed test.

The number of critical values in a hypothesis test depends on whether the test is a one-tailed test or a two-tailed test.

Critical Values for Two-Tailed Tests

In a two-tailed test, we divide the rejection region into two equal parts: one in the right tail of the distribution and one in the left tail of the distribution. Each of these rejection regions will contain an area of the distribution equal to ɑ/2. For example, in a two-tailed test with a significance level of 0.05, each rejection region will contain 0.05/2 = 0.025 = 2.5% of the area under the distribution. Because we split the rejection region, a two-tailed test has two critical values.

Critical Values for One-Tailed Tests

A one-tailed test has one rejection region (either in the right tail or the left tail of the distribution) and one critical value. In a lower tail (or left-tailed) test, the critical value and rejection region will be in the left tail of the distribution. In an upper tail (or right-tailed) test, the critical value and rejection region will be in the right tail of the distribution.

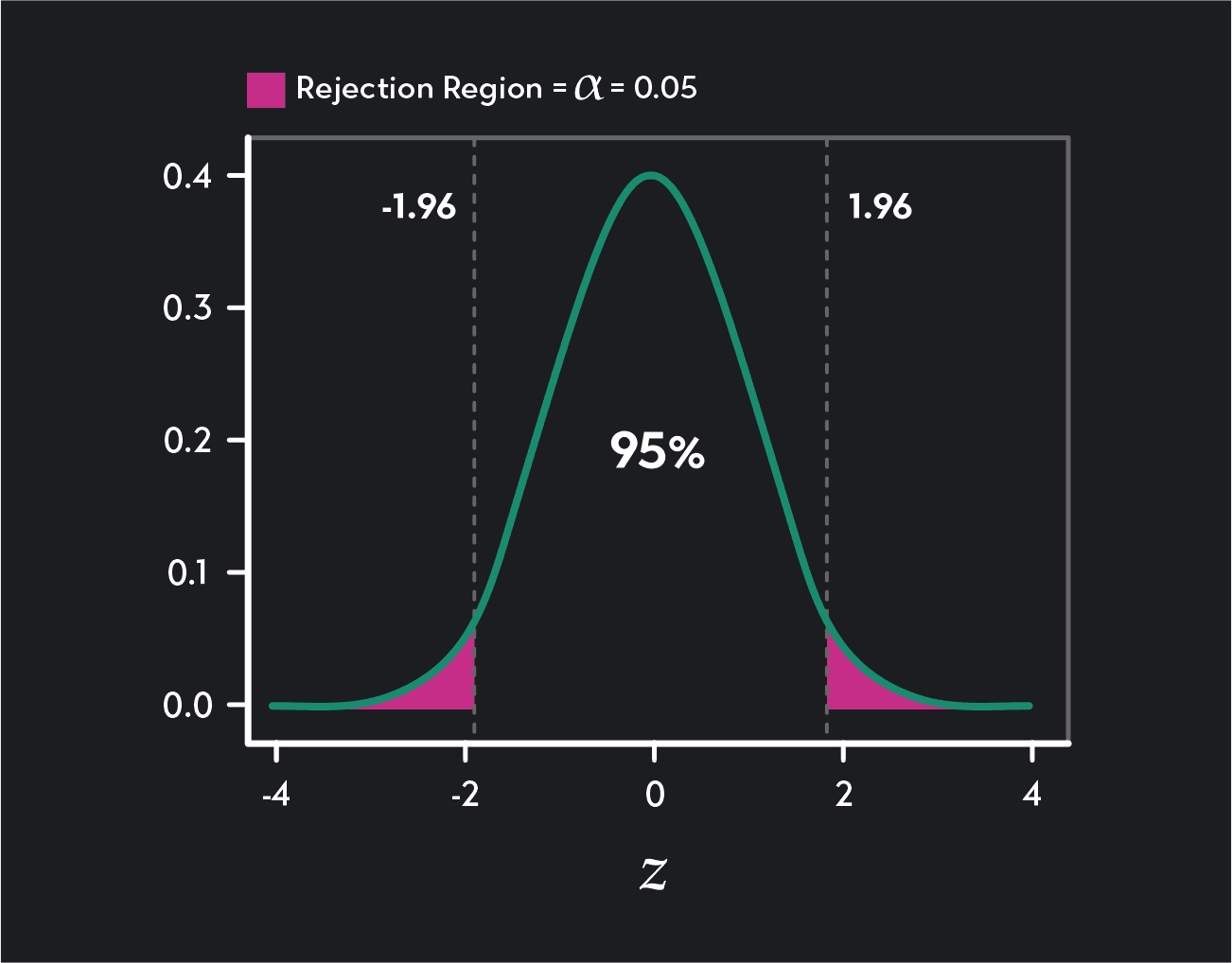
Two-tailed test

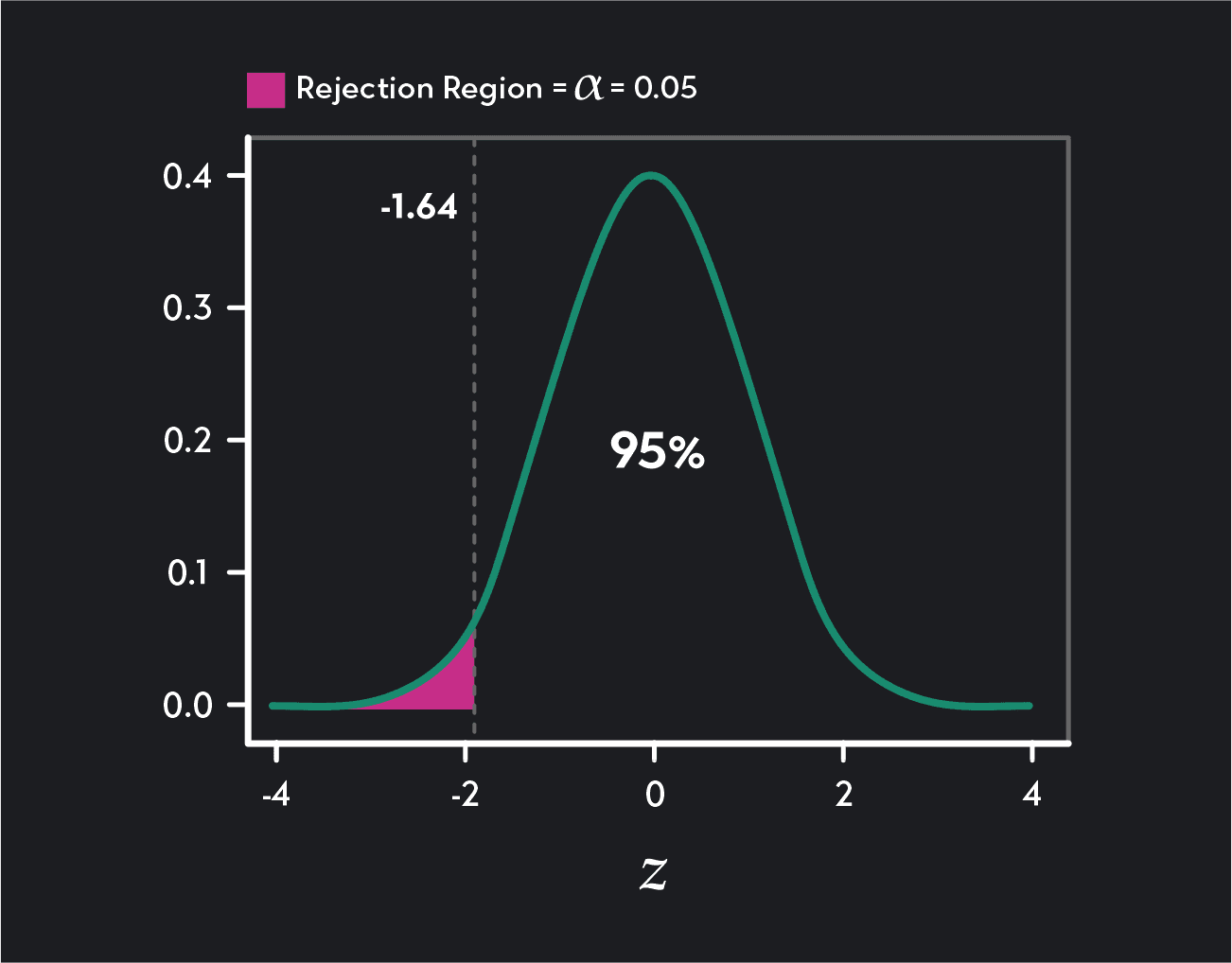
One-tailed lower tail test

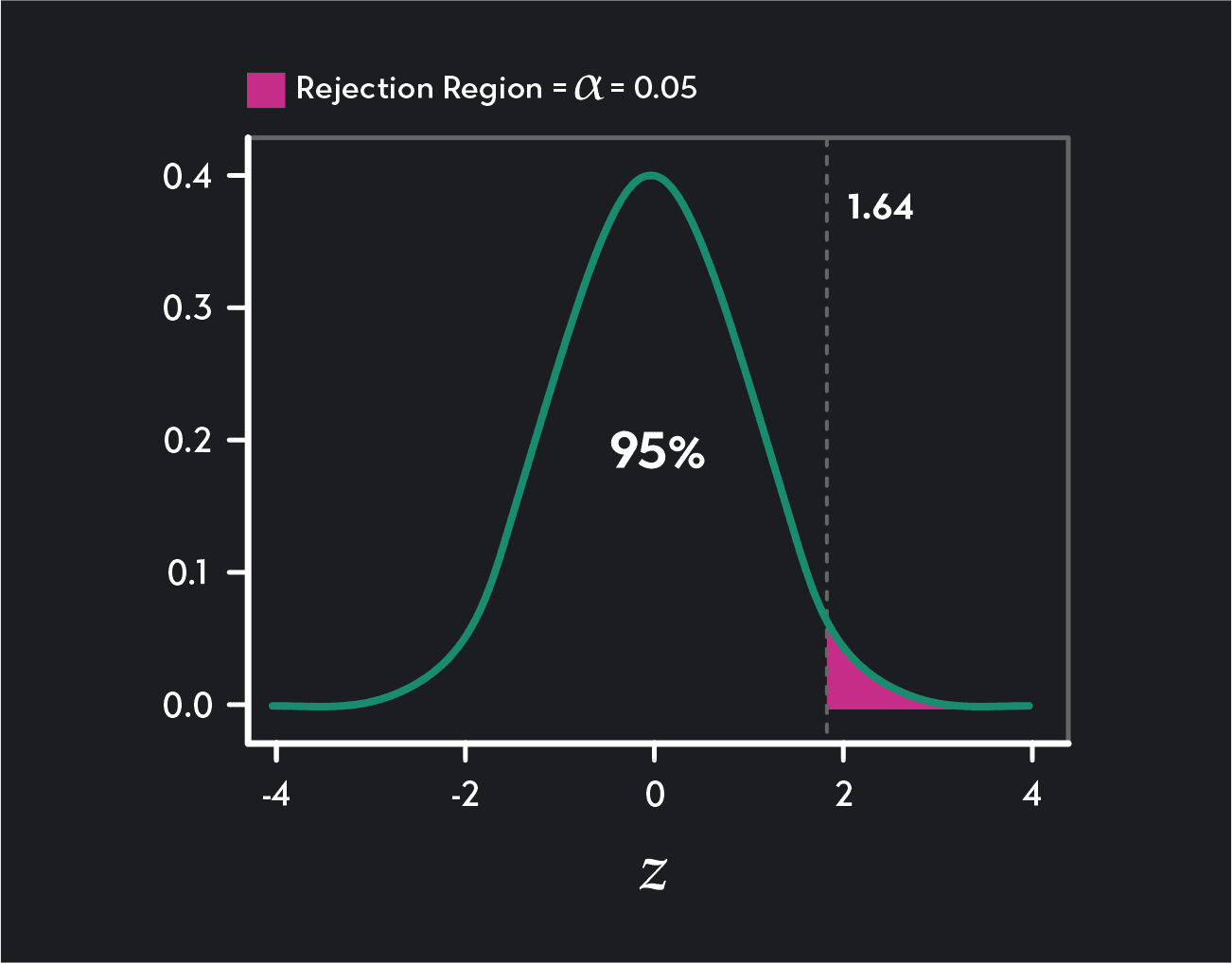
One-tailed upper tail test

The tables below provide a list of critical values that are commonly used in hypothesis testing.

Z-Test Statistics (Using a Normal Distribution)

T-test statistics (using a t distribution), degrees of freedom (df), finding a critical value for a two-tailed z-test.

Suppose you don’t remember what the critical values for a two-sided Z-test are. How would you go about finding them?

To find the critical value, you start with the significance level of your hypothesis test. Your significance level is equal to the total area of the rejection region. For example, with a 0.05 significance level, the entire rejection region will be equal to 5% of the area under the normal distribution.

In a two-tailed test Z-test, we split equally the rejection region into two parts. One rejection region is in the distribution’s right tail, and the other is in the left tail of the distribution. Each of these two parts will contain half of the total area of the rejection region. For a two-tailed Z-test with a significance level of ɑ=0.05, each rejection region will contain ɑ/2 = 0.025 or 2.5% of the distribution. This leaves a confidence interval of 0.95 (or 95%) between the two rejection regions.

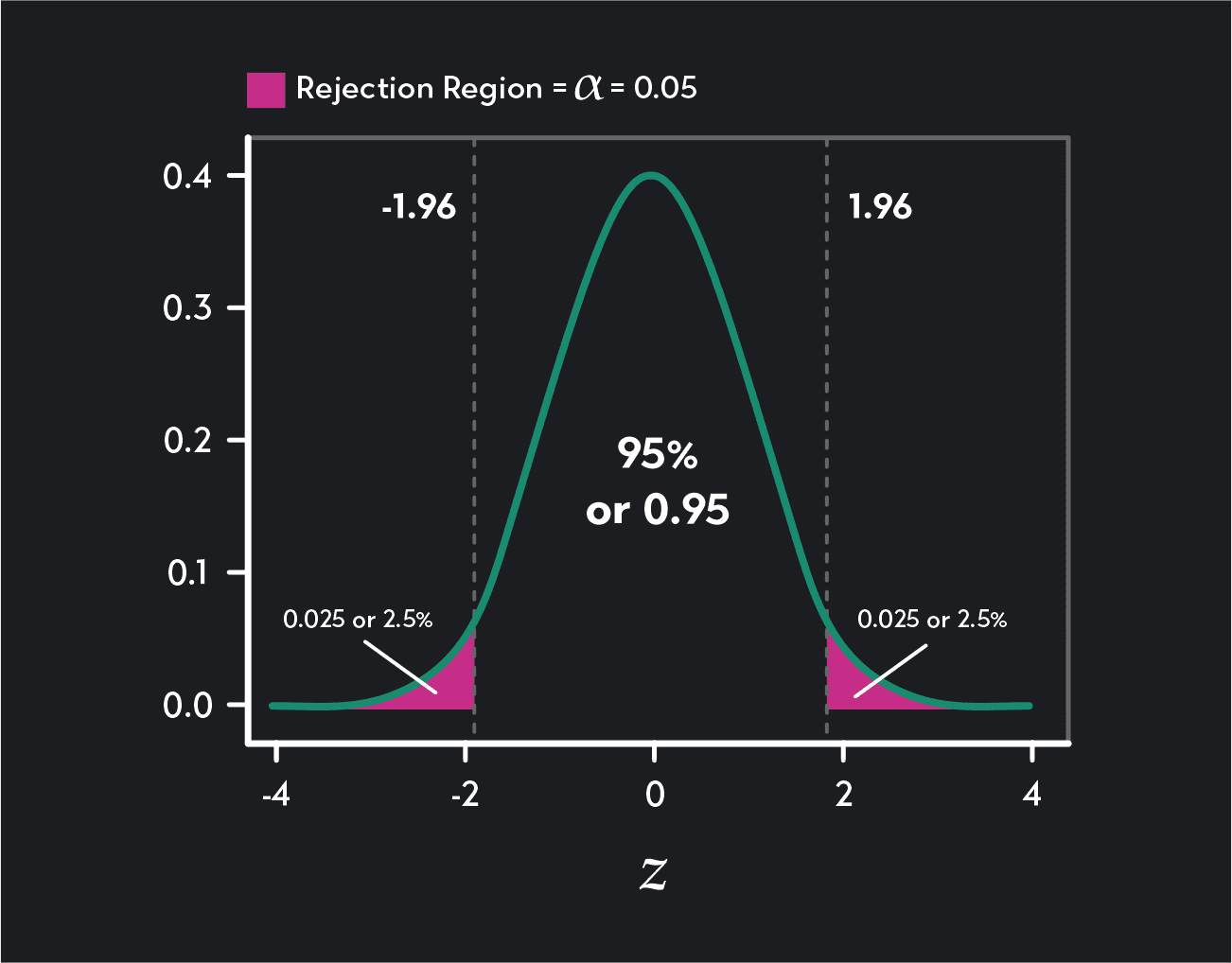
To find the critical values, you need to find the corresponding values (or Z-scores ) in the Z-distribution. Make sure the percentage lying to the left of the first critical value is equal to ɑ/2. Also, check that the percentage of the distribution lying to the right of the second critical value is equal to ɑ/2. You can use a Z-table to look up these figures.

Solved Example: Two-Tailed Z-Test

For a two-tailed Z-test with a significance level of ɑ=0.05, we are looking for two critical values such that ɑ/2 or 2.5% of the normal distribution lies to the left of the first critical value and ɑ/2 or 0.025 of the normal distribution lies to the right of the second critical value.

Z-tables will either show you probabilities to the LEFT or to the RIGHT of a particular value. We’ll stick to Z-tables showing probabilities to the LEFT.

For the first critical value, if the area to the left of the critical value is 0.025, we use the Z-table to find the number 0.025 in the table (we’ve shown this figure highlighted in an orange box). We then trace that value to the left to find the first two digits of the critical value (-1.9) and then up to the top to find the last digit (-0.06). If we put these together, we have the critical value -1.96. Z-tables provide Z-scores that are usually rounded to two decimal places.

For the second critical value, 2.5% of the distribution will lie to the right, meaning 97.5% of the distribution will lie to the left of the critical value (1-0.025=0.0975). To find this critical value, we look for the number 0.0975 in the Z-table (we’ve shown this figure highlighted in a green box). We trace that value to the left to find the first two digits of the critical value (1.9) and then up to the top to find the last digit (0.06). Our second critical value is 1.96.

Following similar steps, see if you can find the critical values for a Z-test with a significance level of ɑ=0.10. The critical values you find should be equal to -1.64 and 1.64.

Finding a Critical Value for a One-Tailed Z-Test

In a one-tailed test, there is just one rejection region, and the area of the rejection region is equal to the significance level.

For a one-tailed lower tail test, use the z-table to find a critical value where the total area to the left of the critical value is equal to alpha.

For a one-tailed upper tail test, use the z-table to find a critical value where the total area to the left of the critical value is equal to 1- alpha.

Solved Example: One-Tailed Z-Test

Let’s see if we can use the Z-table to find the critical value for a lower tail Z-test with a significance level of 0.01.

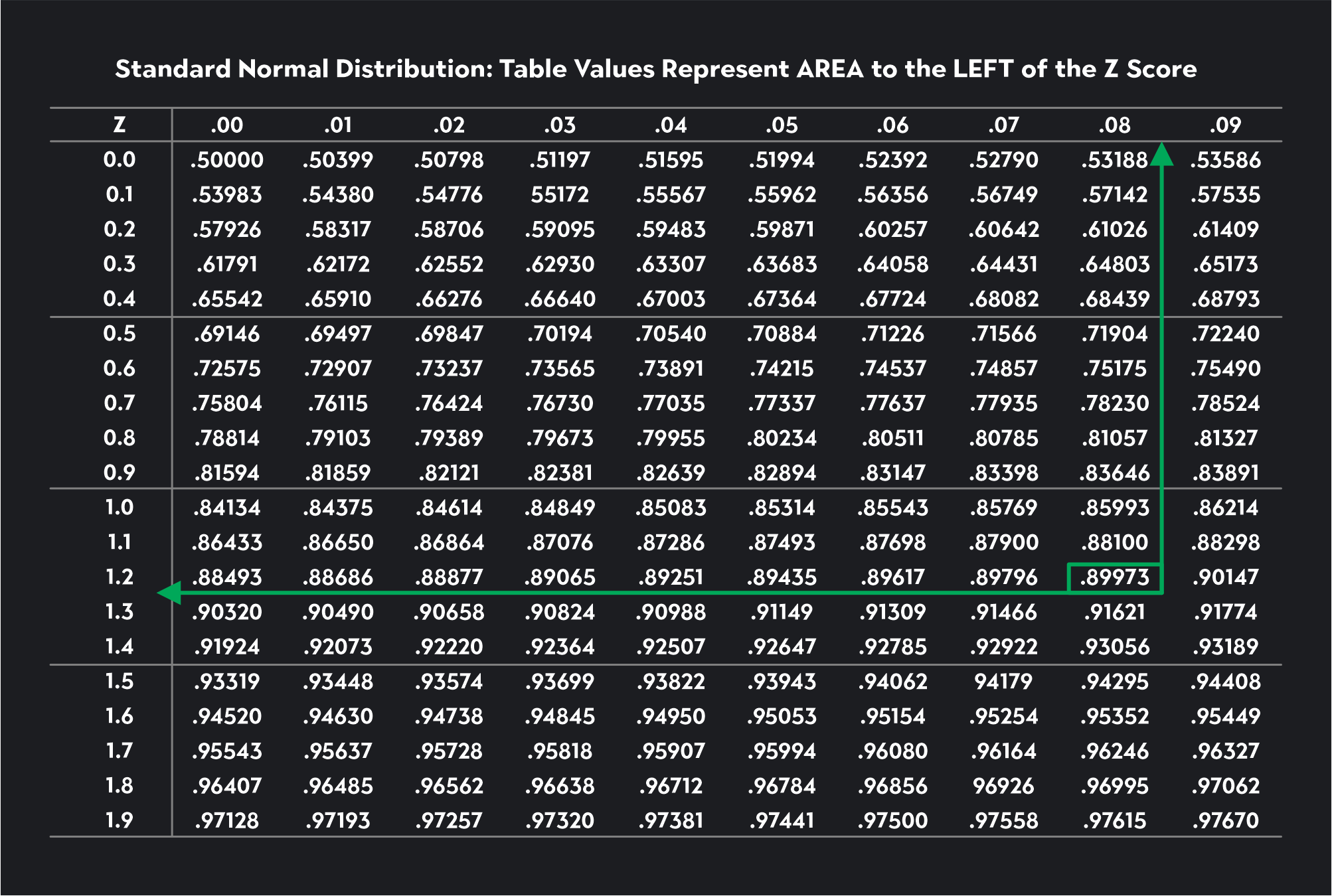
Since alpha equals 0.01, we are looking for this number in the Z-table. If you can’t find the exact number, you look for the closest number, which in this case is 0.0090. Once we’ve found this number, we trace the value to the first column to find the first two digits of the critical value and then up to the first row to find the last digit. The critical value is -2.33.

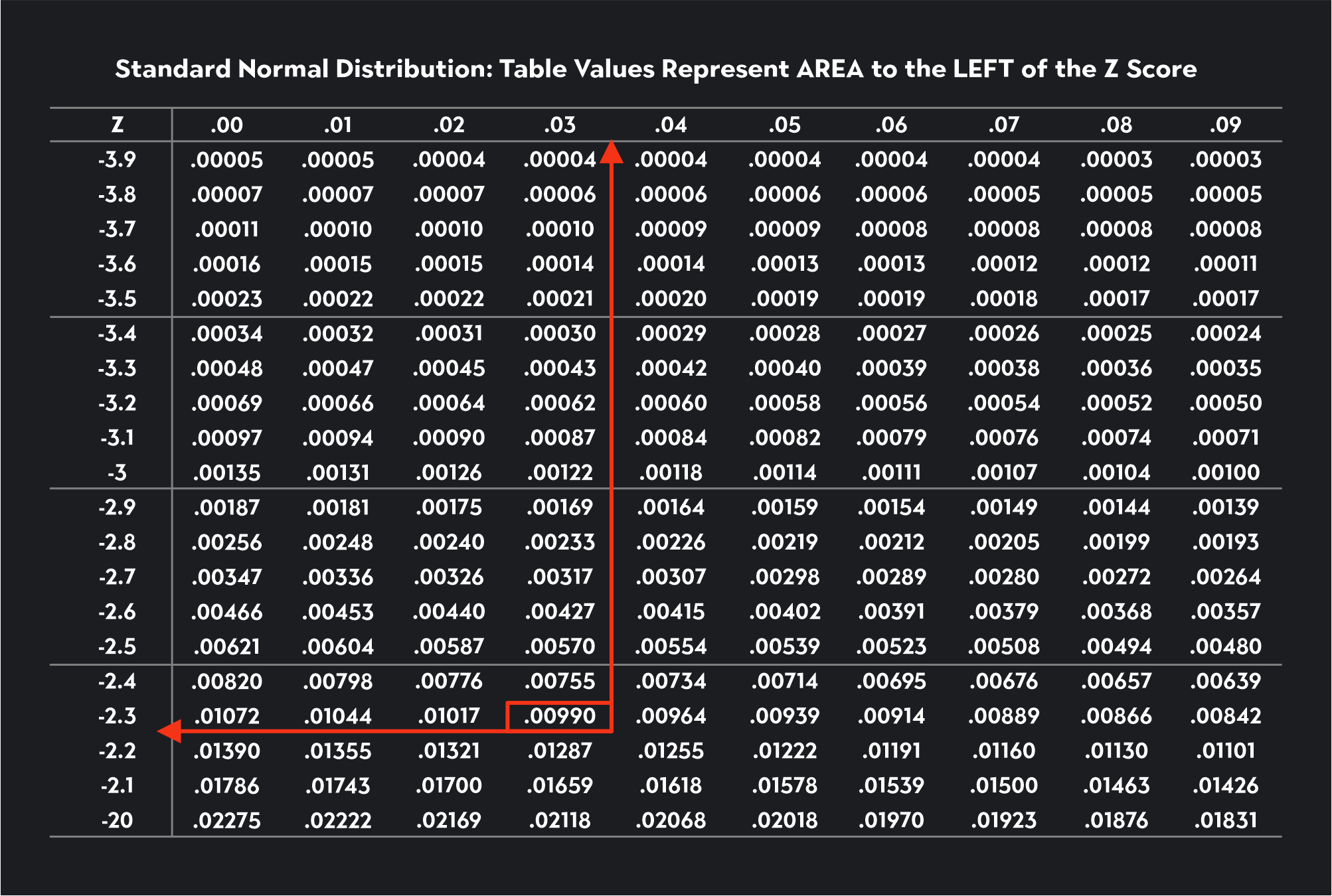
Now let’s see if we can use the Z-table to find the critical value for an upper tail Z-test with a significance level of 0.10.

Since this is an upper tail test, we need to use the Z-table to look for a critical value corresponding to 0.90 (1-ɑ = 1-0.10 = 0.90). The closest number to 0.90 we can find in the table is 0.89973. We trace this number to the left and then up to the top of the table to find a critical value of 1.28.

To find a critical value in R, you can use the qnorm() function for a Z-test or the qt() function for a T-test.

Here are some examples of how you could use these functions in your critical value approach.

Z-Critical Values Using R

For a two-tailed Z-test with a 0.05 significance level, you would type:

qnorm(p=0.05/2, lower.tail=FALSE)

This will give you one of your critical values. The second critical value is just the negative value of the first.

For a one-tailed lower tail Z-test with a 0.01 significance level, you would type:

qnorm(p=0.01, lower.tail=TRUE)

For a one-tailed upper tail Z-test with a 0.01 significance level, you would type:

qnorm(p=0.01, lower.tail=FALSE)

T-Critical Values Using R

For a two-tailed T-test with 15 degrees of freedom and a 0.1 significance level, you would type:

qt(p=0.1/2, df=15, lower.tail=FALSE)

For a one-tailed lower tail T-test with 10 degrees of freedom and a 0.05 significance level, you would type:

qt(p=0.05, df=10, lower.tail=TRUE)

For a one-tailed upper tail T-test with 20 degrees of freedom and a 0.01 significance level, you would type:

qt(p=0.01, df=20, lower.tail=FALSE)

Now that you know the ins and outs of critical values, you’re one step closer to conducting hypothesis tests with ease!

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Intro to Microeconomics

Why small choices have big impact.

Intro to Macroeconomics

How money moves our world.

Intro to Psychology

The science of the mind.

Related Articles

Binomial Distribution: Meaning & Formula

Learn what binomial distribution is in probability. Read a list of the criteria that must be present to apply the formula and learn how to calculate it.

Understanding Math Probability - Definition, Formula & How To Find It

This article is about what probability is, its definition, and the formula. You’ll also learn how to calculate it.

What Is a Residual in Stats?

This article gives a quick definition of what’s a residual equation, the best way to read it, and how to use it with proper statistical models.

Further Reading

Set operations: formulas, properties, examples & exercises, what is set notation [+ bonus practice], how to make a box plot, a guide to understand negative correlation, calculating p-value in hypothesis testing.

Critical Value Approach in Hypothesis Testing

by Nathan Sebhastian

Posted on Jun 05, 2023

Reading time: 5 minutes

The critical value is the cut-off point to determine whether to accept or reject the null hypothesis for your sample distribution.

The critical value approach provides a standardized method for hypothesis testing, enabling you to make informed decisions based on the evidence obtained from sample data.

After calculating the test statistic using the sample data, you compare it to the critical value(s) corresponding to the chosen significance level ( α ).

The critical value(s) represent the boundary beyond which you reject the null hypothesis. You will have rejection regions and non-rejection region as follows:

Two-sided test

A two-sided hypothesis test has 2 rejection regions, so you need 2 critical values on each side. Because there are 2 rejection regions, you must split the significance level in half.

Each rejection region has a probability of α / 2 , making the total likelihood for both areas equal the significance level.

In this test, the null hypothesis H0 gets rejected when the test statistic is too small or too large.

Left-tailed test

The left-tailed test has 1 rejection region, and the null hypothesis only gets rejected when the test statistic is too small.

Right-tailed test

The right-tailed test is similar to the left-tailed test, only the null hypothesis gets rejected when the test statistic is too large.

Now that you understand the definition of critical values, let’s look at how to use critical values to construct a confidence interval.

Using Critical Values to Construct Confidence Intervals

Confidence Intervals use the same Critical values as the test you’re running.

If you’re running a z-test with a 95% confidence interval, then:

• For a two-sided test, The CVs are -1.96 and 1.96
• For a one-tailed test, the critical value is -1.65 (left) or 1.65 (right)

To calculate the upper and lower bounds of the confidence interval, you need to calculate the sample mean and then add or subtract the margin of error from it.

To get the Margin of Error, multiply the critical value by the standard error:

Let’s see an example. Suppose you are estimating the population mean with a 95% confidence level.

You have a sample mean of 50, a sample size of 100, and a standard deviation of 10. Using a z-table, the critical value for a 95% confidence level is approximately 1.96.

Calculate the standard error:

Determine the margin of error:

Compute the lower bound and upper bound:

The 95% confidence interval is (48.04, 51.96). This means that we are 95% confident that the true population mean falls within this interval.

Finding the Critical Value

The formula to find critical values depends on the specific distribution associated with the hypothesis test or confidence interval you’re using.

Here are the formulas for some commonly used distributions.

Standard Normal Distribution (Z-distribution):

The critical value for a given significance level ( α ) in the standard normal distribution is found using the cumulative distribution function (CDF) or a standard normal table.

z(α) represents the z-score corresponding to the desired significance level α .

Student’s t-Distribution (t-distribution):

The critical value for a given significance level (α) and degrees of freedom (df) in the t-distribution is found using the inverse cumulative distribution function (CDF) or a t-distribution table.

t(α, df) represents the t-score corresponding to the desired significance level α and degrees of freedom df .

Chi-Square Distribution (χ²-distribution):

The critical value for a given significance level (α) and degrees of freedom (df) in the chi-square distribution is found using the inverse cumulative distribution function (CDF) or a chi-square distribution table.

where χ²(α, df) represents the chi-square value corresponding to the desired significance level α and degrees of freedom df .

F-Distribution:

The critical value for a given significance level (α), degrees of freedom for the numerator (df₁), and degrees of freedom for the denominator (df₂) in the F-distribution is found using the inverse cumulative distribution function (CDF) or an F-distribution table.

F(α, df₁, df₂) represents the F-value corresponding to the desired significance level α , df₁ , and df₂ .

As you can see, the specific formula to find critical values depends on the distribution and the parameters associated with the problem at hand.

Usually, you don’t calculate the critical values manually as you can use statistical tables or statistical software to determine the critical values.

I will update this tutorial with statistical tables that you can use later.

The critical value is as a threshold where you make a decision based on the observed test statistic and its relation to the significance level.

It provides a predetermined point of reference to objectively evaluate the strength of the evidence against the null hypothesis and guide the acceptance or rejection of the hypothesis.

If the test statistic falls in the critical region (beyond the critical value), it means the observed data provide strong evidence against the null hypothesis.

In this case, you reject the null hypothesis in favor of the alternative hypothesis, indicating that there is sufficient evidence to support the claim or relationship stated in the alternative hypothesis.

On the other hand, if the test statistic falls in the non-critical region (within the critical value), it means the observed data do not provide enough evidence to reject the null hypothesis.

In this case, you fail to reject the null hypothesis, indicating that there is insufficient evidence to support the alternative hypothesis.

Take your skills to the next level ⚡️

I'm sending out an occasional email with the latest tutorials on programming, web development, and statistics. Drop your email in the box below and I'll send new stuff straight into your inbox!

Hello! This website is dedicated to help you learn tech and data science skills with its step-by-step, beginner-friendly tutorials. Learn statistics, JavaScript and other programming languages using clear examples written for people.

Learn more about this website

Connect with me on Twitter

Or LinkedIn

Type the keyword below and hit enter

Click to see all tutorials tagged with:

What is a critical value?

A critical value is a point on the distribution of the test statistic under the null hypothesis that defines a set of values that call for rejecting the null hypothesis. This set is called critical or rejection region. Usually, one-sided tests have one critical value and two-sided test have two critical values. The critical values are determined so that the probability that the test statistic has a value in the rejection region of the test when the null hypothesis is true equals the significance level (denoted as α or alpha).

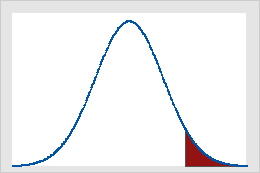
Critical values on the standard normal distribution for α = 0.05

Figure A shows that results of a one-tailed Z-test are significant if the value of the test statistic is equal to or greater than 1.64, the critical value in this case. The shaded area represents the probability of a type I error (α = 5% in this example) of the area under the curve. Figure B shows that results of a two-tailed Z-test are significant if the absolute value of the test statistic is equal to or greater than 1.96, the critical value in this case. The two shaded areas sum to 5% (α) of the area under the curve.

Examples of calculating critical values

In hypothesis testing, there are two ways to determine whether there is enough evidence from the sample to reject H 0 or to fail to reject H 0 . The most common way is to compare the p-value with a pre-specified value of α, where α is the probability of rejecting H 0 when H 0 is true. However, an equivalent approach is to compare the calculated value of the test statistic based on your data with the critical value. The following are examples of how to calculate the critical value for a 1-sample t-test and a One-Way ANOVA.

Calculating a critical value for a 1-sample t-test

• Select Calc > Probability Distributions > t .
• Select Inverse cumulative probability .
• In Degrees of freedom , enter 9 (the number of observations minus one).
• In Input constant , enter 0.95 (one minus one-half alpha).

This gives you an inverse cumulative probability, which equals the critical value, of 1.83311. If the absolute value of the t-statistic value is greater than this critical value, then you can reject the null hypothesis, H 0 , at the 0.10 level of significance.

Calculating a critical value for an analysis of variance (ANOVA)

• Choose Calc > Probability Distributions > F .
• In Numerator degrees of freedom , enter 2 (the number of factor levels minus one).
• In Denominator degrees of freedom , enter 9 (the degrees of freedom for error).
• In Input constant , enter 0.95 (one minus alpha).

This gives you an inverse cumulative probability (critical value) of 4.25649. If the F-statistic is greater than this critical value, then you can reject the null hypothesis, H 0 , at the 0.05 level of significance.

• Minitab.com
• License Portal
• Cookie Settings

You are now leaving support.minitab.com.

Click Continue to proceed to:

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7 Chapter 7: Introduction to Hypothesis Testing

alternative hypothesis

critical value

effect size

null hypothesis

probability value

rejection region

significance level

statistical power

statistical significance

test statistic

Type I error

Type II error

This chapter lays out the basic logic and process of hypothesis testing. We will perform z  tests, which use the z  score formula from Chapter 6 and data from a sample mean to make an inference about a population.

Logic and Purpose of Hypothesis Testing

A hypothesis is a prediction that is tested in a research study. The statistician R. A. Fisher explained the concept of hypothesis testing with a story of a lady tasting tea. Here we will present an example based on James Bond who insisted that martinis should be shaken rather than stirred. Let’s consider a hypothetical experiment to determine whether Mr. Bond can tell the difference between a shaken martini and a stirred martini. Suppose we gave Mr. Bond a series of 16 taste tests. In each test, we flipped a fair coin to determine whether to stir or shake the martini. Then we presented the martini to Mr. Bond and asked him to decide whether it was shaken or stirred. Let’s say Mr. Bond was correct on 13 of the 16 taste tests. Does this prove that Mr. Bond has at least some ability to tell whether the martini was shaken or stirred?

This result does not prove that he does; it could be he was just lucky and guessed right 13 out of 16 times. But how plausible is the explanation that he was just lucky? To assess its plausibility, we determine the probability that someone who was just guessing would be correct 13/16 times or more. This probability can be computed to be .0106. This is a pretty low probability, and therefore someone would have to be very lucky to be correct 13 or more times out of 16 if they were just guessing. So either Mr. Bond was very lucky, or he can tell whether the drink was shaken or stirred. The hypothesis that he was guessing is not proven false, but considerable doubt is cast on it. Therefore, there is strong evidence that Mr. Bond can tell whether a drink was shaken or stirred.

Let’s consider another example. The case study Physicians’ Reactions sought to determine whether physicians spend less time with obese patients. Physicians were sampled randomly and each was shown a chart of a patient complaining of a migraine headache. They were then asked to estimate how long they would spend with the patient. The charts were identical except that for half the charts, the patient was obese and for the other half, the patient was of average weight. The chart a particular physician viewed was determined randomly. Thirty-three physicians viewed charts of average-weight patients and 38 physicians viewed charts of obese patients.

The mean time physicians reported that they would spend with obese patients was 24.7 minutes as compared to a mean of 31.4 minutes for normal-weight patients. How might this difference between means have occurred? One possibility is that physicians were influenced by the weight of the patients. On the other hand, perhaps by chance, the physicians who viewed charts of the obese patients tend to see patients for less time than the other physicians. Random assignment of charts does not ensure that the groups will be equal in all respects other than the chart they viewed. In fact, it is certain the groups differed in many ways by chance. The two groups could not have exactly the same mean age (if measured precisely enough such as in days). Perhaps a physician’s age affects how long the physician sees patients. There are innumerable differences between the groups that could affect how long they view patients. With this in mind, is it plausible that these chance differences are responsible for the difference in times?

To assess the plausibility of the hypothesis that the difference in mean times is due to chance, we compute the probability of getting a difference as large or larger than the observed difference (31.4 − 24.7 = 6.7 minutes) if the difference were, in fact, due solely to chance. Using methods presented in later chapters, this probability can be computed to be .0057. Since this is such a low probability, we have confidence that the difference in times is due to the patient’s weight and is not due to chance.

The Probability Value

It is very important to understand precisely what the probability values mean. In the James Bond example, the computed probability of .0106 is the probability he would be correct on 13 or more taste tests (out of 16) if he were just guessing. It is easy to mistake this probability of .0106 as the probability he cannot tell the difference. This is not at all what it means.

The probability of .0106 is the probability of a certain outcome (13 or more out of 16) assuming a certain state of the world (James Bond was only guessing). It is not the probability that a state of the world is true. Although this might seem like a distinction without a difference, consider the following example. An animal trainer claims that a trained bird can determine whether or not numbers are evenly divisible by 7. In an experiment assessing this claim, the bird is given a series of 16 test trials. On each trial, a number is displayed on a screen and the bird pecks at one of two keys to indicate its choice. The numbers are chosen in such a way that the probability of any number being evenly divisible by 7 is .50. The bird is correct on 9/16 choices. We can compute that the probability of being correct nine or more times out of 16 if one is only guessing is .40. Since a bird who is only guessing would do this well 40% of the time, these data do not provide convincing evidence that the bird can tell the difference between the two types of numbers. As a scientist, you would be very skeptical that the bird had this ability. Would you conclude that there is a .40 probability that the bird can tell the difference? Certainly not! You would think the probability is much lower than .0001.

To reiterate, the probability value is the probability of an outcome (9/16 or better) and not the probability of a particular state of the world (the bird was only guessing). In statistics, it is conventional to refer to possible states of the world as hypotheses since they are hypothesized states of the world. Using this terminology, the probability value is the probability of an outcome given the hypothesis. It is not the probability of the hypothesis given the outcome.

This is not to say that we ignore the probability of the hypothesis. If the probability of the outcome given the hypothesis is sufficiently low, we have evidence that the hypothesis is false. However, we do not compute the probability that the hypothesis is false. In the James Bond example, the hypothesis is that he cannot tell the difference between shaken and stirred martinis. The probability value is low (.0106), thus providing evidence that he can tell the difference. However, we have not computed the probability that he can tell the difference.

The Null Hypothesis

The hypothesis that an apparent effect is due to chance is called the null hypothesis , written H 0 (“ H -naught”). In the Physicians’ Reactions example, the null hypothesis is that in the population of physicians, the mean time expected to be spent with obese patients is equal to the mean time expected to be spent with average-weight patients. This null hypothesis can be written as:

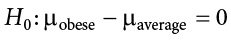
The null hypothesis in a correlational study of the relationship between high school grades and college grades would typically be that the population correlation is 0. This can be written as

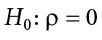
Although the null hypothesis is usually that the value of a parameter is 0, there are occasions in which the null hypothesis is a value other than 0. For example, if we are working with mothers in the U.S. whose children are at risk of low birth weight, we can use 7.47 pounds, the average birth weight in the U.S., as our null value and test for differences against that.

For now, we will focus on testing a value of a single mean against what we expect from the population. Using birth weight as an example, our null hypothesis takes the form:

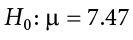
Keep in mind that the null hypothesis is typically the opposite of the researcher’s hypothesis. In the Physicians’ Reactions study, the researchers hypothesized that physicians would expect to spend less time with obese patients. The null hypothesis that the two types of patients are treated identically is put forward with the hope that it can be discredited and therefore rejected. If the null hypothesis were true, a difference as large as or larger than the sample difference of 6.7 minutes would be very unlikely to occur. Therefore, the researchers rejected the null hypothesis of no difference and concluded that in the population, physicians intend to spend less time with obese patients.

In general, the null hypothesis is the idea that nothing is going on: there is no effect of our treatment, no relationship between our variables, and no difference in our sample mean from what we expected about the population mean. This is always our baseline starting assumption, and it is what we seek to reject. If we are trying to treat depression, we want to find a difference in average symptoms between our treatment and control groups. If we are trying to predict job performance, we want to find a relationship between conscientiousness and evaluation scores. However, until we have evidence against it, we must use the null hypothesis as our starting point.

The Alternative Hypothesis

If the null hypothesis is rejected, then we will need some other explanation, which we call the alternative hypothesis, H A or H 1 . The alternative hypothesis is simply the reverse of the null hypothesis, and there are three options, depending on where we expect the difference to lie. Thus, our alternative hypothesis is the mathematical way of stating our research question. If we expect our obtained sample mean to be above or below the null hypothesis value, which we call a directional hypothesis, then our alternative hypothesis takes the form

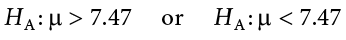
based on the research question itself. We should only use a directional hypothesis if we have good reason, based on prior observations or research, to suspect a particular direction. When we do not know the direction, such as when we are entering a new area of research, we use a non-directional alternative:

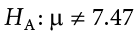
We will set different criteria for rejecting the null hypothesis based on the directionality (greater than, less than, or not equal to) of the alternative. To understand why, we need to see where our criteria come from and how they relate to z  scores and distributions.

Critical Values, p Values, and Significance Level

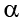
The significance level is a threshold we set before collecting data in order to determine whether or not we should reject the null hypothesis. We set this value beforehand to avoid biasing ourselves by viewing our results and then determining what criteria we should use. If our data produce values that meet or exceed this threshold, then we have sufficient evidence to reject the null hypothesis; if not, we fail to reject the null (we never “accept” the null).

Figure 7.1. The rejection region for a one-tailed test. (“ Rejection Region for One-Tailed Test ” by Judy Schmitt is licensed under CC BY-NC-SA 4.0 .)

The rejection region is bounded by a specific z  value, as is any area under the curve. In hypothesis testing, the value corresponding to a specific rejection region is called the critical value , z crit  (“ z  crit”), or z * (hence the other name “critical region”). Finding the critical value works exactly the same as finding the z  score corresponding to any area under the curve as we did in Unit 1 . If we go to the normal table, we will find that the z  score corresponding to 5% of the area under the curve is equal to 1.645 ( z = 1.64 corresponds to .0505 and z = 1.65 corresponds to .0495, so .05 is exactly in between them) if we go to the right and −1.645 if we go to the left. The direction must be determined by your alternative hypothesis, and drawing and shading the distribution is helpful for keeping directionality straight.

Suppose, however, that we want to do a non-directional test. We need to put the critical region in both tails, but we don’t want to increase the overall size of the rejection region (for reasons we will see later). To do this, we simply split it in half so that an equal proportion of the area under the curve falls in each tail’s rejection region. For a = .05, this means 2.5% of the area is in each tail, which, based on the z  table, corresponds to critical values of z * = ±1.96. This is shown in Figure 7.2 .

Figure 7.2. Two-tailed rejection region. (“ Rejection Region for Two-Tailed Test ” by Judy Schmitt is licensed under CC BY-NC-SA 4.0 .)

Thus, any z  score falling outside ±1.96 (greater than 1.96 in absolute value) falls in the rejection region. When we use z  scores in this way, the obtained value of z (sometimes called z  obtained and abbreviated z obt ) is something known as a test statistic , which is simply an inferential statistic used to test a null hypothesis. The formula for our z  statistic has not changed:

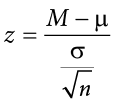
Figure 7.3. Relationship between a , z obt , and p . (“ Relationship between alpha, z-obt, and p ” by Judy Schmitt is licensed under CC BY-NC-SA 4.0 .)

When the null hypothesis is rejected, the effect is said to have statistical significance , or be statistically significant. For example, in the Physicians’ Reactions case study, the probability value is .0057. Therefore, the effect of obesity is statistically significant and the null hypothesis that obesity makes no difference is rejected. It is important to keep in mind that statistical significance means only that the null hypothesis of exactly no effect is rejected; it does not mean that the effect is important, which is what “significant” usually means. When an effect is significant, you can have confidence the effect is not exactly zero. Finding that an effect is significant does not tell you about how large or important the effect is.

Do not confuse statistical significance with practical significance. A small effect can be highly significant if the sample size is large enough.

Why does the word “significant” in the phrase “statistically significant” mean something so different from other uses of the word? Interestingly, this is because the meaning of “significant” in everyday language has changed. It turns out that when the procedures for hypothesis testing were developed, something was “significant” if it signified something. Thus, finding that an effect is statistically significant signifies that the effect is real and not due to chance. Over the years, the meaning of “significant” changed, leading to the potential misinterpretation.

The Hypothesis Testing Process

A four-step procedure.

The process of testing hypotheses follows a simple four-step procedure. This process will be what we use for the remainder of the textbook and course, and although the hypothesis and statistics we use will change, this process will not.

Step 1: State the Hypotheses

Your hypotheses are the first thing you need to lay out. Otherwise, there is nothing to test! You have to state the null hypothesis (which is what we test) and the alternative hypothesis (which is what we expect). These should be stated mathematically as they were presented above and in words, explaining in normal English what each one means in terms of the research question.

Step 2: Find the Critical Values

Step 3: calculate the test statistic and effect size.

Once we have our hypotheses and the standards we use to test them, we can collect data and calculate our test statistic—in this case z . This step is where the vast majority of differences in future chapters will arise: different tests used for different data are calculated in different ways, but the way we use and interpret them remains the same. As part of this step, we will also calculate effect size to better quantify the magnitude of the difference between our groups. Although effect size is not considered part of hypothesis testing, reporting it as part of the results is approved convention.

Step 4: Make the Decision

Finally, once we have our obtained test statistic, we can compare it to our critical value and decide whether we should reject or fail to reject the null hypothesis. When we do this, we must interpret the decision in relation to our research question, stating what we concluded, what we based our conclusion on, and the specific statistics we obtained.

Example A Movie Popcorn

Our manager is looking for a difference in the mean weight of popcorn bags compared to the population mean of 8. We will need both a null and an alternative hypothesis written both mathematically and in words. We’ll always start with the null hypothesis:

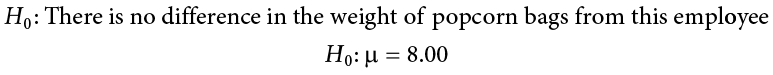
In this case, we don’t know if the bags will be too full or not full enough, so we do a two-tailed alternative hypothesis that there is a difference.

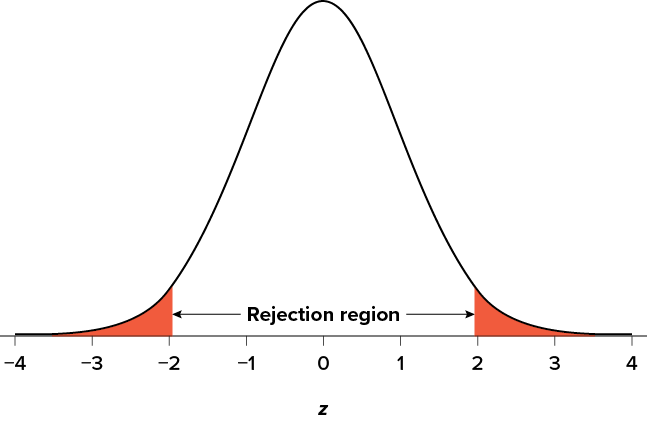
Our critical values are based on two things: the directionality of the test and the level of significance. We decided in Step 1 that a two-tailed test is the appropriate directionality. We were given no information about the level of significance, so we assume that a = .05 is what we will use. As stated earlier in the chapter, the critical values for a two-tailed z  test at a = .05 are z * = ±1.96. This will be the criteria we use to test our hypothesis. We can now draw out our distribution, as shown in Figure 7.4 , so we can visualize the rejection region and make sure it makes sense.

Figure 7.4. Rejection region for z * = ±1.96. (“ Rejection Region z+-1.96 ” by Judy Schmitt is licensed under CC BY-NC-SA 4.0 .)

Now we come to our formal calculations. Let’s say that the manager collects data and finds that the average weight of this employee’s popcorn bags is M = 7.75 cups. We can now plug this value, along with the values presented in the original problem, into our equation for z :

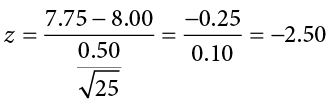
So our test statistic is z = −2.50, which we can draw onto our rejection region distribution as shown in Figure 7.5 .

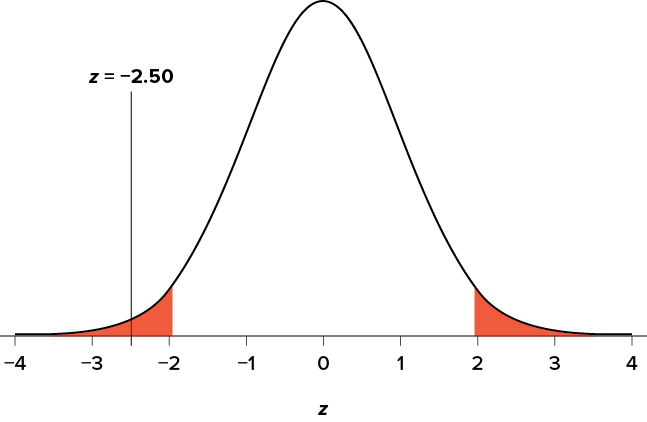
Figure 7.5. Test statistic location. (“ Test Statistic Location z-2.50 ” by Judy Schmitt is licensed under CC BY-NC-SA 4.0 .)

Effect Size

When we reject the null hypothesis, we are stating that the difference we found was statistically significant, but we have mentioned several times that this tells us nothing about practical significance. To get an idea of the actual size of what we found, we can compute a new statistic called an effect size. Effect size gives us an idea of how large, important, or meaningful a statistically significant effect is. For mean differences like we calculated here, our effect size is Cohen’s d :

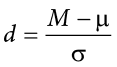
This is very similar to our formula for z , but we no longer take into account the sample size (since overly large samples can make it too easy to reject the null). Cohen’s d is interpreted in units of standard deviations, just like z . For our example:

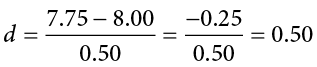
Cohen’s d is interpreted as small, moderate, or large. Specifically, d = 0.20 is small, d = 0.50 is moderate, and d = 0.80 is large. Obviously, values can fall in between these guidelines, so we should use our best judgment and the context of the problem to make our final interpretation of size. Our effect size happens to be exactly equal to one of these, so we say that there is a moderate effect.

Effect sizes are incredibly useful and provide important information and clarification that overcomes some of the weakness of hypothesis testing. Any time you perform a hypothesis test, whether statistically significant or not, you should always calculate and report effect size.

Looking at Figure 7.5 , we can see that our obtained z  statistic falls in the rejection region. We can also directly compare it to our critical value: in terms of absolute value, −2.50 > −1.96, so we reject the null hypothesis. We can now write our conclusion:

Reject H 0 . Based on the sample of 25 bags, we can conclude that the average popcorn bag from this employee is smaller ( M = 7.75 cups) than the average weight of popcorn bags at this movie theater, and the effect size was moderate, z = −2.50, p < .05, d = 0.50.

Example B Office Temperature

Let’s do another example to solidify our understanding. Let’s say that the office building you work in is supposed to be kept at 74 degrees Fahrenheit during the summer months but is allowed to vary by 1 degree in either direction. You suspect that, as a cost saving measure, the temperature was secretly set higher. You set up a formal way to test your hypothesis.

You start by laying out the null hypothesis:

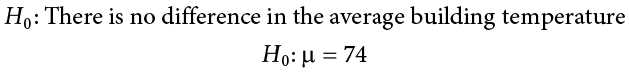
Next you state the alternative hypothesis. You have reason to suspect a specific direction of change, so you make a one-tailed test:

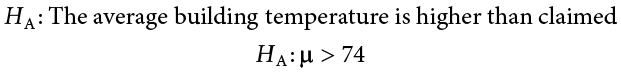
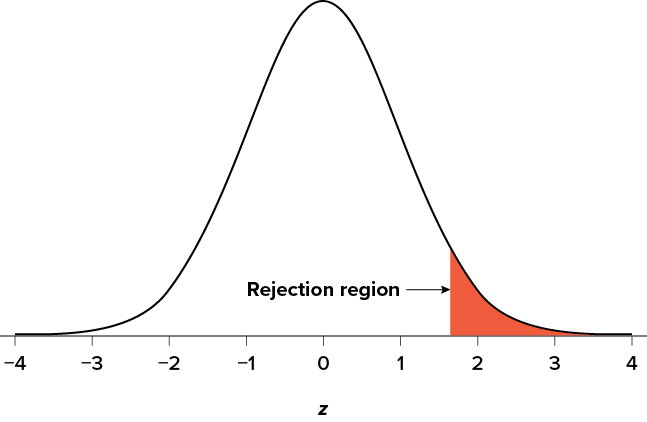
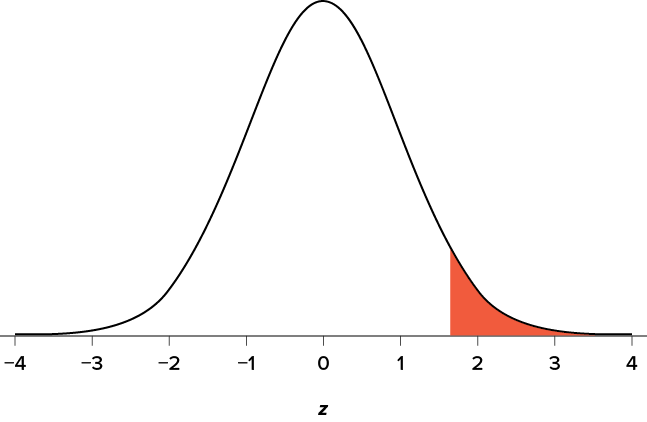
You know that the most common level of significance is a  = .05, so you keep that the same and know that the critical value for a one-tailed z  test is z * = 1.645. To keep track of the directionality of the test and rejection region, you draw out your distribution as shown in Figure 7.6 .

Figure 7.6. Rejection region. (“ Rejection Region z1.645 ” by Judy Schmitt is licensed under CC BY-NC-SA 4.0 .)

Now that you have everything set up, you spend one week collecting temperature data:

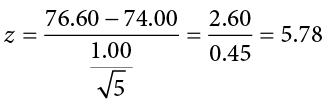
This value falls so far into the tail that it cannot even be plotted on the distribution ( Figure 7.7 )! Because the result is significant, you also calculate an effect size:

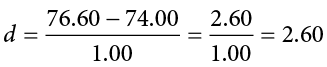
The effect size you calculate is definitely large, meaning someone has some explaining to do!

Figure 7.7. Obtained z statistic. (“ Obtained z5.77 ” by Judy Schmitt is licensed under CC BY-NC-SA 4.0 .)

You compare your obtained z  statistic, z = 5.77, to the critical value, z * = 1.645, and find that z > z *. Therefore you reject the null hypothesis, concluding:

Reject H 0 . Based on 5 observations, the average temperature ( M = 76.6 degrees) is statistically significantly higher than it is supposed to be, and the effect size was large, z = 5.77, p < .05, d = 2.60.

Example C Different Significance Level

Finally, let’s take a look at an example phrased in generic terms, rather than in the context of a specific research question, to see the individual pieces one more time. This time, however, we will use a stricter significance level, a = .01, to test the hypothesis.

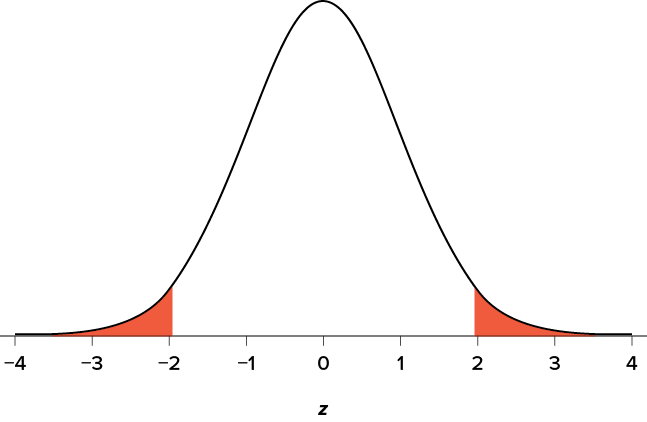
We will use 60 as an arbitrary null hypothesis value:

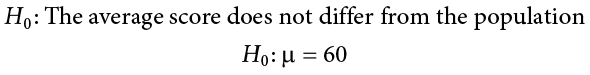
We will assume a two-tailed test:

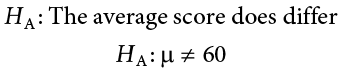
We have seen the critical values for z  tests at a = .05 levels of significance several times. To find the values for a = .01, we will go to the Standard Normal Distribution Table and find the z  score cutting off .005 (.01 divided by 2 for a two-tailed test) of the area in the tail, which is z * = ±2.575. Notice that this cutoff is much higher than it was for a = .05. This is because we need much less of the area in the tail, so we need to go very far out to find the cutoff. As a result, this will require a much larger effect or much larger sample size in order to reject the null hypothesis.

We can now calculate our test statistic. We will use s = 10 as our known population standard deviation and the following data to calculate our sample mean:

The average of these scores is M = 60.40. From this we calculate our z  statistic as:

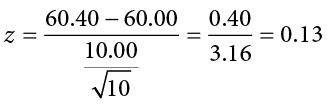
The Cohen’s d effect size calculation is:

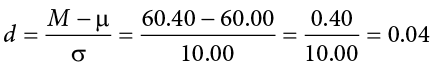
Our obtained z  statistic, z = 0.13, is very small. It is much less than our critical value of 2.575. Thus, this time, we fail to reject the null hypothesis. Our conclusion would look something like:

Fail to reject H 0 . Based on the sample of 10 scores, we cannot conclude that there is an effect causing the mean ( M  = 60.40) to be statistically significantly different from 60.00, z = 0.13, p > .01, d = 0.04, and the effect size supports this interpretation.

Other Considerations in Hypothesis Testing

There are several other considerations we need to keep in mind when performing hypothesis testing.

Errors in Hypothesis Testing

In the Physicians’ Reactions case study, the probability value associated with the significance test is .0057. Therefore, the null hypothesis was rejected, and it was concluded that physicians intend to spend less time with obese patients. Despite the low probability value, it is possible that the null hypothesis of no true difference between obese and average-weight patients is true and that the large difference between sample means occurred by chance. If this is the case, then the conclusion that physicians intend to spend less time with obese patients is in error. This type of error is called a Type I error. More generally, a Type I error occurs when a significance test results in the rejection of a true null hypothesis.

The second type of error that can be made in significance testing is failing to reject a false null hypothesis. This kind of error is called a Type II error . Unlike a Type I error, a Type II error is not really an error. When a statistical test is not significant, it means that the data do not provide strong evidence that the null hypothesis is false. Lack of significance does not support the conclusion that the null hypothesis is true. Therefore, a researcher should not make the mistake of incorrectly concluding that the null hypothesis is true when a statistical test was not significant. Instead, the researcher should consider the test inconclusive. Contrast this with a Type I error in which the researcher erroneously concludes that the null hypothesis is false when, in fact, it is true.

A Type II error can only occur if the null hypothesis is false. If the null hypothesis is false, then the probability of a Type II error is called b (“beta”). The probability of correctly rejecting a false null hypothesis equals 1 − b and is called statistical power . Power is simply our ability to correctly detect an effect that exists. It is influenced by the size of the effect (larger effects are easier to detect), the significance level we set (making it easier to reject the null makes it easier to detect an effect, but increases the likelihood of a Type I error), and the sample size used (larger samples make it easier to reject the null).

Misconceptions in Hypothesis Testing

Misconceptions about significance testing are common. This section lists three important ones.

• Misconception: The probability value ( p value) is the probability that the null hypothesis is false. Proper interpretation: The probability value ( p value) is the probability of a result as extreme or more extreme given that the null hypothesis is true. It is the probability of the data given the null hypothesis. It is not the probability that the null hypothesis is false.
• Misconception: A low probability value indicates a large effect. Proper interpretation: A low probability value indicates that the sample outcome (or an outcome more extreme) would be very unlikely if the null hypothesis were true. A low probability value can occur with small effect sizes, particularly if the sample size is large.
• Misconception: A non-significant outcome means that the null hypothesis is probably true. Proper interpretation: A non-significant outcome means that the data do not conclusively demonstrate that the null hypothesis is false.
• In your own words, explain what the null hypothesis is.
• What are Type I and Type II errors?
• Why do we phrase null and alternative hypotheses with population parameters and not sample means?
• Why do we state our hypotheses and decision criteria before we collect our data?
• Why do you calculate an effect size?
• z = 1.99, two-tailed test at a = .05
• z = 0.34, z * = 1.645
• p = .03, a = .05
• p = .015, a = .01

Answers to Odd-Numbered Exercises

Your answer should include mention of the baseline assumption of no difference between the sample and the population.

Alpha is the significance level. It is the criterion we use when deciding to reject or fail to reject the null hypothesis, corresponding to a given proportion of the area under the normal distribution and a probability of finding extreme scores assuming the null hypothesis is true.

We always calculate an effect size to see if our research is practically meaningful or important. NHST (null hypothesis significance testing) is influenced by sample size but effect size is not; therefore, they provide complimentary information.

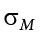
“ Null Hypothesis ” by Randall Munroe/xkcd.com is licensed under CC BY-NC 2.5 .)

Introduction to Statistics in the Psychological Sciences Copyright © 2021 by Linda R. Cote Ph.D.; Rupa G. Gordon Ph.D.; Chrislyn E. Randell Ph.D.; Judy Schmitt; and Helena Marvin is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Hypothesis Testing for Means & Proportions

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This is the first of three modules that will addresses the second area of statistical inference, which is hypothesis testing, in which a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The process of hypothesis testing involves setting up two competing hypotheses, the null hypothesis and the alternate hypothesis. One selects a random sample (or multiple samples when there are more comparison groups), computes summary statistics and then assesses the likelihood that the sample data support the research or alternative hypothesis. Similar to estimation, the process of hypothesis testing is based on probability theory and the Central Limit Theorem.  

This module will focus on hypothesis testing for means and proportions. The next two modules in this series will address analysis of variance and chi-squared tests. 

Learning Objectives

After completing this module, the student will be able to:

• Define null and research hypothesis, test statistic, level of significance and decision rule
• Distinguish between Type I and Type II errors and discuss the implications of each
• Explain the difference between one and two sided tests of hypothesis
• Estimate and interpret p-values
• Explain the relationship between confidence interval estimates and p-values in drawing inferences
• Differentiate hypothesis testing procedures based on type of outcome variable and number of sample

Introduction to Hypothesis Testing

Techniques for hypothesis testing  .

The techniques for hypothesis testing depend on

• the type of outcome variable being analyzed (continuous, dichotomous, discrete)
• the number of comparison groups in the investigation
• whether the comparison groups are independent (i.e., physically separate such as men versus women) or dependent (i.e., matched or paired such as pre- and post-assessments on the same participants).

In estimation we focused explicitly on techniques for one and two samples and discussed estimation for a specific parameter (e.g., the mean or proportion of a population), for differences (e.g., difference in means, the risk difference) and ratios (e.g., the relative risk and odds ratio). Here we will focus on procedures for one and two samples when the outcome is either continuous (and we focus on means) or dichotomous (and we focus on proportions).

General Approach: A Simple Example

The Centers for Disease Control (CDC) reported on trends in weight, height and body mass index from the 1960's through 2002. 1 The general trend was that Americans were much heavier and slightly taller in 2002 as compared to 1960; both men and women gained approximately 24 pounds, on average, between 1960 and 2002.   In 2002, the mean weight for men was reported at 191 pounds. Suppose that an investigator hypothesizes that weights are even higher in 2006 (i.e., that the trend continued over the subsequent 4 years). The research hypothesis is that the mean weight in men in 2006 is more than 191 pounds. The null hypothesis is that there is no change in weight, and therefore the mean weight is still 191 pounds in 2006.  

In order to test the hypotheses, we select a random sample of American males in 2006 and measure their weights. Suppose we have resources available to recruit n=100 men into our sample. We weigh each participant and compute summary statistics on the sample data. Suppose in the sample we determine the following:

Do the sample data support the null or research hypothesis? The sample mean of 197.1 is numerically higher than 191. However, is this difference more than would be expected by chance? In hypothesis testing, we assume that the null hypothesis holds until proven otherwise. We therefore need to determine the likelihood of observing a sample mean of 197.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true or under the null hypothesis). We can compute this probability using the Central Limit Theorem. Specifically,

(Notice that we use the sample standard deviation in computing the Z score. This is generally an appropriate substitution as long as the sample size is large, n > 30. Thus, there is less than a 1% probability of observing a sample mean as large as 197.1 when the true population mean is 191. Do you think that the null hypothesis is likely true? Based on how unlikely it is to observe a sample mean of 197.1 under the null hypothesis (i.e., <1% probability), we might infer, from our data, that the null hypothesis is probably not true.

Suppose that the sample data had turned out differently. Suppose that we instead observed the following in 2006:

How likely it is to observe a sample mean of 192.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true)? We can again compute this probability using the Central Limit Theorem. Specifically,

There is a 33.4% probability of observing a sample mean as large as 192.1 when the true population mean is 191. Do you think that the null hypothesis is likely true?  

Neither of the sample means that we obtained allows us to know with certainty whether the null hypothesis is true or not. However, our computations suggest that, if the null hypothesis were true, the probability of observing a sample mean >197.1 is less than 1%. In contrast, if the null hypothesis were true, the probability of observing a sample mean >192.1 is about 33%. We can't know whether the null hypothesis is true, but the sample that provided a mean value of 197.1 provides much stronger evidence in favor of rejecting the null hypothesis, than the sample that provided a mean value of 192.1. Note that this does not mean that a sample mean of 192.1 indicates that the null hypothesis is true; it just doesn't provide compelling evidence to reject it.

In essence, hypothesis testing is a procedure to compute a probability that reflects the strength of the evidence (based on a given sample) for rejecting the null hypothesis. In hypothesis testing, we determine a threshold or cut-off point (called the critical value) to decide when to believe the null hypothesis and when to believe the research hypothesis. It is important to note that it is possible to observe any sample mean when the true population mean is true (in this example equal to 191), but some sample means are very unlikely. Based on the two samples above it would seem reasonable to believe the research hypothesis when x̄ = 197.1, but to believe the null hypothesis when x̄ =192.1. What we need is a threshold value such that if x̄ is above that threshold then we believe that H 1 is true and if x̄ is below that threshold then we believe that H 0 is true. The difficulty in determining a threshold for x̄ is that it depends on the scale of measurement. In this example, the threshold, sometimes called the critical value, might be 195 (i.e., if the sample mean is 195 or more then we believe that H 1 is true and if the sample mean is less than 195 then we believe that H 0 is true). Suppose we are interested in assessing an increase in blood pressure over time, the critical value will be different because blood pressures are measured in millimeters of mercury (mmHg) as opposed to in pounds. In the following we will explain how the critical value is determined and how we handle the issue of scale.

First, to address the issue of scale in determining the critical value, we convert our sample data (in particular the sample mean) into a Z score. We know from the module on probability that the center of the Z distribution is zero and extreme values are those that exceed 2 or fall below -2. Z scores above 2 and below -2 represent approximately 5% of all Z values. If the observed sample mean is close to the mean specified in H 0 (here m =191), then Z will be close to zero. If the observed sample mean is much larger than the mean specified in H 0 , then Z will be large.  

In hypothesis testing, we select a critical value from the Z distribution. This is done by first determining what is called the level of significance, denoted α ("alpha"). What we are doing here is drawing a line at extreme values. The level of significance is the probability that we reject the null hypothesis (in favor of the alternative) when it is actually true and is also called the Type I error rate.

α = Level of significance = P(Type I error) = P(Reject H 0 | H 0 is true).

Because α is a probability, it ranges between 0 and 1. The most commonly used value in the medical literature for α is 0.05, or 5%. Thus, if an investigator selects α=0.05, then they are allowing a 5% probability of incorrectly rejecting the null hypothesis in favor of the alternative when the null is in fact true. Depending on the circumstances, one might choose to use a level of significance of 1% or 10%. For example, if an investigator wanted to reject the null only if there were even stronger evidence than that ensured with α=0.05, they could choose a =0.01as their level of significance. The typical values for α are 0.01, 0.05 and 0.10, with α=0.05 the most commonly used value.  

Suppose in our weight study we select α=0.05. We need to determine the value of Z that holds 5% of the values above it (see below).

The critical value of Z for α =0.05 is Z = 1.645 (i.e., 5% of the distribution is above Z=1.645). With this value we can set up what is called our decision rule for the test. The rule is to reject H 0 if the Z score is 1.645 or more.  

With the first sample we have

Because 2.38 > 1.645, we reject the null hypothesis. (The same conclusion can be drawn by comparing the 0.0087 probability of observing a sample mean as extreme as 197.1 to the level of significance of 0.05. If the observed probability is smaller than the level of significance we reject H 0 ). Because the Z score exceeds the critical value, we conclude that the mean weight for men in 2006 is more than 191 pounds, the value reported in 2002. If we observed the second sample (i.e., sample mean =192.1), we would not be able to reject the null hypothesis because the Z score is 0.43 which is not in the rejection region (i.e., the region in the tail end of the curve above 1.645). With the second sample we do not have sufficient evidence (because we set our level of significance at 5%) to conclude that weights have increased. Again, the same conclusion can be reached by comparing probabilities. The probability of observing a sample mean as extreme as 192.1 is 33.4% which is not below our 5% level of significance.

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.  

• Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);  

H 1 : Research hypothesis (investigator's belief); α =0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is a single number that summarizes the sample information.   An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

• Step 3.  Set up decision rule.  

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

• The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value.  In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
• The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.  
• The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value.   For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.  

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

• Step 4. Compute the test statistic.  

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

• Step 5. Conclusion.  

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).  

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .  

• Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191                 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

• Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

• Step 3. Set up decision rule.  

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05.   Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.  

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.                  

Type I and Type II Errors

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

 The most common reason for a Type II error is a small sample size.

Tests with One Sample, Continuous Outcome

Hypothesis testing applications with a continuous outcome variable in a single population are performed according to the five-step procedure outlined above. A key component is setting up the null and research hypotheses. The objective is to compare the mean in a single population to known mean (μ 0 ). The known value is generally derived from another study or report, for example a study in a similar, but not identical, population or a study performed some years ago. The latter is called a historical control. It is important in setting up the hypotheses in a one sample test that the mean specified in the null hypothesis is a fair and reasonable comparator. This will be discussed in the examples that follow.

Test Statistics for Testing H 0 : μ= μ 0

• if n > 30
• if n < 30

Note that statistical computing packages will use the t statistic exclusively and make the necessary adjustments for comparing the test statistic to appropriate values from probability tables to produce a p-value. 

The National Center for Health Statistics (NCHS) published a report in 2005 entitled Health, United States, containing extensive information on major trends in the health of Americans. Data are provided for the US population as a whole and for specific ages, sexes and races.  The NCHS report indicated that in 2002 Americans paid an average of $3,302 per year on health care and prescription drugs. An investigator hypothesizes that in 2005 expenditures have decreased primarily due to the availability of generic drugs. To test the hypothesis, a sample of 100 Americans are selected and their expenditures on health care and prescription drugs in 2005 are measured.   The sample data are summarized as follows: n=100, x̄

=$3,190 and s=$890. Is there statistical evidence of a reduction in expenditures on health care and prescription drugs in 2005? Is the sample mean of $3,190 evidence of a true reduction in the mean or is it within chance fluctuation? We will run the test using the five-step approach. 

• Step 1.  Set up hypotheses and determine level of significance

H 0 : μ = 3,302 H 1 : μ < 3,302           α =0.05

The research hypothesis is that expenditures have decreased, and therefore a lower-tailed test is used.

This is a lower tailed test, using a Z statistic and a 5% level of significance.   Reject H 0 if Z < -1.645.

•   Step 4. Compute the test statistic.  

We do not reject H 0 because -1.26 > -1.645. We do not have statistically significant evidence at α=0.05 to show that the mean expenditures on health care and prescription drugs are lower in 2005 than the mean of $3,302 reported in 2002.  

Recall that when we fail to reject H 0 in a test of hypothesis that either the null hypothesis is true (here the mean expenditures in 2005 are the same as those in 2002 and equal to $3,302) or we committed a Type II error (i.e., we failed to reject H 0 when in fact it is false). In summarizing this test, we conclude that we do not have sufficient evidence to reject H 0 . We do not conclude that H 0 is true, because there may be a moderate to high probability that we committed a Type II error. It is possible that the sample size is not large enough to detect a difference in mean expenditures.      

The NCHS reported that the mean total cholesterol level in 2002 for all adults was 203. Total cholesterol levels in participants who attended the seventh examination of the Offspring in the Framingham Heart Study are summarized as follows: n=3,310, x̄ =200.3, and s=36.8. Is there statistical evidence of a difference in mean cholesterol levels in the Framingham Offspring?

Here we want to assess whether the sample mean of 200.3 in the Framingham sample is statistically significantly different from 203 (i.e., beyond what we would expect by chance). We will run the test using the five-step approach.

H 0 : μ= 203 H 1 : μ≠ 203                       α=0.05

The research hypothesis is that cholesterol levels are different in the Framingham Offspring, and therefore a two-tailed test is used.

•   Step 3. Set up decision rule.  

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or is Z > 1.960.

We reject H 0 because -4.22 ≤ -1. .960. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level in the Framingham Offspring is different from the national average of 203 reported in 2002.   Because we reject H 0 , we also approximate a p-value. Using the two-sided significance levels, p < 0.0001.  

Statistical Significance versus Clinical (Practical) Significance

This example raises an important concept of statistical versus clinical or practical significance. From a statistical standpoint, the total cholesterol levels in the Framingham sample are highly statistically significantly different from the national average with p < 0.0001 (i.e., there is less than a 0.01% chance that we are incorrectly rejecting the null hypothesis). However, the sample mean in the Framingham Offspring study is 200.3, less than 3 units different from the national mean of 203. The reason that the data are so highly statistically significant is due to the very large sample size. It is always important to assess both statistical and clinical significance of data. This is particularly relevant when the sample size is large. Is a 3 unit difference in total cholesterol a meaningful difference?  

Consider again the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. Suppose a new drug is proposed to lower total cholesterol. A study is designed to evaluate the efficacy of the drug in lowering cholesterol.   Fifteen patients are enrolled in the study and asked to take the new drug for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows:   n=15, x̄ =195.9 and s=28.7. Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new drug for 6 weeks? We will run the test using the five-step approach. 

H 0 : μ= 203 H 1 : μ< 203                   α=0.05

•  Step 2. Select the appropriate test statistic.  

Because the sample size is small (n<30) the appropriate test statistic is

This is a lower tailed test, using a t statistic and a 5% level of significance. In order to determine the critical value of t, we need degrees of freedom, df, defined as df=n-1. In this example df=15-1=14. The critical value for a lower tailed test with df=14 and a =0.05 is -2.145 and the decision rule is as follows:   Reject H 0 if t < -2.145.

We do not reject H 0 because -0.96 > -2.145. We do not have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower than the national mean in patients taking the new drug for 6 weeks. Again, because we failed to reject the null hypothesis we make a weaker concluding statement allowing for the possibility that we may have committed a Type II error (i.e., failed to reject H 0 when in fact the drug is efficacious).

This example raises an important issue in terms of study design. In this example we assume in the null hypothesis that the mean cholesterol level is 203. This is taken to be the mean cholesterol level in patients without treatment. Is this an appropriate comparator? Alternative and potentially more efficient study designs to evaluate the effect of the new drug could involve two treatment groups, where one group receives the new drug and the other does not, or we could measure each patient's baseline or pre-treatment cholesterol level and then assess changes from baseline to 6 weeks post-treatment. These designs are also discussed here.

Video - Comparing a Sample Mean to Known Population Mean (8:20)

Link to transcript of the video

Tests with One Sample, Dichotomous Outcome

Hypothesis testing applications with a dichotomous outcome variable in a single population are also performed according to the five-step procedure. Similar to tests for means, a key component is setting up the null and research hypotheses. The objective is to compare the proportion of successes in a single population to a known proportion (p 0 ). That known proportion is generally derived from another study or report and is sometimes called a historical control. It is important in setting up the hypotheses in a one sample test that the proportion specified in the null hypothesis is a fair and reasonable comparator.    

In one sample tests for a dichotomous outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the sample proportion which is computed by taking the ratio of the number of successes to the sample size,

We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formula for the test statistic is given below.

Test Statistic for Testing H 0 : p = p 0

if min(np 0 , n(1-p 0 )) > 5

The formula above is appropriate for large samples, defined when the smaller of np 0 and n(1-p 0 ) is at least 5. This is similar, but not identical, to the condition required for appropriate use of the confidence interval formula for a population proportion, i.e.,

Here we use the proportion specified in the null hypothesis as the true proportion of successes rather than the sample proportion. If we fail to satisfy the condition, then alternative procedures, called exact methods must be used to test the hypothesis about the population proportion.

Example:  

The NCHS report indicated that in 2002 the prevalence of cigarette smoking among American adults was 21.1%.  Data on prevalent smoking in n=3,536 participants who attended the seventh examination of the Offspring in the Framingham Heart Study indicated that 482/3,536 = 13.6% of the respondents were currently smoking at the time of the exam. Suppose we want to assess whether the prevalence of smoking is lower in the Framingham Offspring sample given the focus on cardiovascular health in that community. Is there evidence of a statistically lower prevalence of smoking in the Framingham Offspring study as compared to the prevalence among all Americans?

H 0 : p = 0.211 H 1 : p < 0.211                     α=0.05

We must first check that the sample size is adequate.   Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 3,536(0.211), 3,536(1-0.211))=min(746, 2790)=746. The sample size is more than adequate so the following formula can be used:

This is a lower tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.645.

We reject H 0 because -10.93 < -1.645. We have statistically significant evidence at α=0.05 to show that the prevalence of smoking in the Framingham Offspring is lower than the prevalence nationally (21.1%). Here, p < 0.0001.  

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

Calculate this on your own before checking the answer.

Video - Hypothesis Test for One Sample and a Dichotomous Outcome (3:55)

Tests with Two Independent Samples, Continuous Outcome

There are many applications where it is of interest to compare two independent groups with respect to their mean scores on a continuous outcome. Here we compare means between groups, but rather than generating an estimate of the difference, we will test whether the observed difference (increase, decrease or difference) is statistically significant or not. Remember, that hypothesis testing gives an assessment of statistical significance, whereas estimation gives an estimate of effect and both are important.

Here we discuss the comparison of means when the two comparison groups are independent or physically separate. The two groups might be determined by a particular attribute (e.g., sex, diagnosis of cardiovascular disease) or might be set up by the investigator (e.g., participants assigned to receive an experimental treatment or placebo). The first step in the analysis involves computing descriptive statistics on each of the two samples. Specifically, we compute the sample size, mean and standard deviation in each sample and we denote these summary statistics as follows:

for sample 1:

for sample 2:

The designation of sample 1 and sample 2 is arbitrary. In a clinical trial setting the convention is to call the treatment group 1 and the control group 2. However, when comparing men and women, for example, either group can be 1 or 2.  

In the two independent samples application with a continuous outcome, the parameter of interest in the test of hypothesis is the difference in population means, μ 1 -μ 2 . The null hypothesis is always that there is no difference between groups with respect to means, i.e.,

The null hypothesis can also be written as follows: H 0 : μ 1 = μ 2 . In the research hypothesis, an investigator can hypothesize that the first mean is larger than the second (H 1 : μ 1 > μ 2 ), that the first mean is smaller than the second (H 1 : μ 1 < μ 2 ), or that the means are different (H 1 : μ 1 ≠ μ 2 ). The three different alternatives represent upper-, lower-, and two-tailed tests, respectively. The following test statistics are used to test these hypotheses.

Test Statistics for Testing H 0 : μ 1 = μ 2

• if n 1 > 30 and n 2 > 30
• if n 1 < 30 or n 2 < 30

NOTE: The formulas above assume equal variability in the two populations (i.e., the population variances are equal, or s 1 2 = s 2 2 ). This means that the outcome is equally variable in each of the comparison populations. For analysis, we have samples from each of the comparison populations. If the sample variances are similar, then the assumption about variability in the populations is probably reasonable. As a guideline, if the ratio of the sample variances, s 1 2 /s 2 2 is between 0.5 and 2 (i.e., if one variance is no more than double the other), then the formulas above are appropriate. If the ratio of the sample variances is greater than 2 or less than 0.5 then alternative formulas must be used to account for the heterogeneity in variances.    

The test statistics include Sp, which is the pooled estimate of the common standard deviation (again assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples as follows:

Because we are assuming equal variances between groups, we pool the information on variability (sample variances) to generate an estimate of the variability in the population. Note: Because Sp is a weighted average of the standard deviations in the sample, Sp will always be in between s 1 and s 2 .)

Data measured on n=3,539 participants who attended the seventh examination of the Offspring in the Framingham Heart Study are shown below.  

Suppose we now wish to assess whether there is a statistically significant difference in mean systolic blood pressures between men and women using a 5% level of significance.  

H 0 : μ 1 = μ 2

H 1 : μ 1 ≠ μ 2                       α=0.05

Because both samples are large ( > 30), we can use the Z test statistic as opposed to t. Note that statistical computing packages use t throughout. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The guideline suggests investigating the ratio of the sample variances, s 1 2 /s 2 2 . Suppose we call the men group 1 and the women group 2. Again, this is arbitrary; it only needs to be noted when interpreting the results. The ratio of the sample variances is 17.5 2 /20.1 2 = 0.76, which falls between 0.5 and 2 suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is

We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.

Notice that the pooled estimate of the common standard deviation, Sp, falls in between the standard deviations in the comparison groups (i.e., 17.5 and 20.1). Sp is slightly closer in value to the standard deviation in the women (20.1) as there were slightly more women in the sample.   Recall, Sp is a weight average of the standard deviations in the comparison groups, weighted by the respective sample sizes.  

Now the test statistic:

We reject H 0 because 2.66 > 1.960. We have statistically significant evidence at α=0.05 to show that there is a difference in mean systolic blood pressures between men and women. The p-value is p < 0.010.  

Here again we find that there is a statistically significant difference in mean systolic blood pressures between men and women at p < 0.010. Notice that there is a very small difference in the sample means (128.2-126.5 = 1.7 units), but this difference is beyond what would be expected by chance. Is this a clinically meaningful difference? The large sample size in this example is driving the statistical significance. A 95% confidence interval for the difference in mean systolic blood pressures is: 1.7 + 1.26 or (0.44, 2.96). The confidence interval provides an assessment of the magnitude of the difference between means whereas the test of hypothesis and p-value provide an assessment of the statistical significance of the difference.  

Above we performed a study to evaluate a new drug designed to lower total cholesterol. The study involved one sample of patients, each patient took the new drug for 6 weeks and had their cholesterol measured. As a means of evaluating the efficacy of the new drug, the mean total cholesterol following 6 weeks of treatment was compared to the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. At the end of the example, we discussed the appropriateness of the fixed comparator as well as an alternative study design to evaluate the effect of the new drug involving two treatment groups, where one group receives the new drug and the other does not. Here, we revisit the example with a concurrent or parallel control group, which is very typical in randomized controlled trials or clinical trials (refer to the EP713 module on Clinical Trials).  

A new drug is proposed to lower total cholesterol. A randomized controlled trial is designed to evaluate the efficacy of the medication in lowering cholesterol. Thirty participants are enrolled in the trial and are randomly assigned to receive either the new drug or a placebo. The participants do not know which treatment they are assigned. Each participant is asked to take the assigned treatment for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows.

Is there statistical evidence of a reduction in mean total cholesterol in patients taking the new drug for 6 weeks as compared to participants taking placebo? We will run the test using the five-step approach.

H 0 : μ 1 = μ 2 H 1 : μ 1 < μ 2                         α=0.05

Because both samples are small (< 30), we use the t test statistic. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The ratio of the sample variances, s 1 2 /s 2 2 =28.7 2 /30.3 2 = 0.90, which falls between 0.5 and 2, suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is:

This is a lower-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table (in More Resources to the right). In order to determine the critical value of t we need degrees of freedom, df, defined as df=n 1 +n 2 -2 = 15+15-2=28. The critical value for a lower tailed test with df=28 and α=0.05 is -1.701 and the decision rule is: Reject H 0 if t < -1.701.

Now the test statistic,

We reject H 0 because -2.92 < -1.701. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower in patients taking the new drug for 6 weeks as compared to patients taking placebo, p < 0.005.

The clinical trial in this example finds a statistically significant reduction in total cholesterol, whereas in the previous example where we had a historical control (as opposed to a parallel control group) we did not demonstrate efficacy of the new drug. Notice that the mean total cholesterol level in patients taking placebo is 217.4 which is very different from the mean cholesterol reported among all Americans in 2002 of 203 and used as the comparator in the prior example. The historical control value may not have been the most appropriate comparator as cholesterol levels have been increasing over time. In the next section, we present another design that can be used to assess the efficacy of the new drug.

Video - Comparison of Two Independent Samples With a Continuous Outcome (8:02)

Tests with Matched Samples, Continuous Outcome

In the previous section we compared two groups with respect to their mean scores on a continuous outcome. An alternative study design is to compare matched or paired samples. The two comparison groups are said to be dependent, and the data can arise from a single sample of participants where each participant is measured twice (possibly before and after an intervention) or from two samples that are matched on specific characteristics (e.g., siblings). When the samples are dependent, we focus on difference scores in each participant or between members of a pair and the test of hypothesis is based on the mean difference, μ d . The null hypothesis again reflects "no difference" and is stated as H 0 : μ d =0 . Note that there are some instances where it is of interest to test whether there is a difference of a particular magnitude (e.g., μ d =5) but in most instances the null hypothesis reflects no difference (i.e., μ d =0).  

The appropriate formula for the test of hypothesis depends on the sample size. The formulas are shown below and are identical to those we presented for estimating the mean of a single sample presented (e.g., when comparing against an external or historical control), except here we focus on difference scores.

Test Statistics for Testing H 0 : μ d =0

A new drug is proposed to lower total cholesterol and a study is designed to evaluate the efficacy of the drug in lowering cholesterol. Fifteen patients agree to participate in the study and each is asked to take the new drug for 6 weeks. However, before starting the treatment, each patient's total cholesterol level is measured. The initial measurement is a pre-treatment or baseline value. After taking the drug for 6 weeks, each patient's total cholesterol level is measured again and the data are shown below. The rightmost column contains difference scores for each patient, computed by subtracting the 6 week cholesterol level from the baseline level. The differences represent the reduction in total cholesterol over 4 weeks. (The differences could have been computed by subtracting the baseline total cholesterol level from the level measured at 6 weeks. The way in which the differences are computed does not affect the outcome of the analysis only the interpretation.)

Because the differences are computed by subtracting the cholesterols measured at 6 weeks from the baseline values, positive differences indicate reductions and negative differences indicate increases (e.g., participant 12 increases by 2 units over 6 weeks). The goal here is to test whether there is a statistically significant reduction in cholesterol. Because of the way in which we computed the differences, we want to look for an increase in the mean difference (i.e., a positive reduction). In order to conduct the test, we need to summarize the differences. In this sample, we have

The calculations are shown below.  

Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new medication for 6 weeks? We will run the test using the five-step approach.

H 0 : μ d = 0 H 1 : μ d > 0                 α=0.05

NOTE: If we had computed differences by subtracting the baseline level from the level measured at 6 weeks then negative differences would have reflected reductions and the research hypothesis would have been H 1 : μ d < 0. 

• Step 2 . Select the appropriate test statistic.

This is an upper-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table at the right, with df=15-1=14. The critical value for an upper-tailed test with df=14 and α=0.05 is 2.145 and the decision rule is Reject H 0 if t > 2.145.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

We reject H 0 because 4.61 > 2.145. We have statistically significant evidence at α=0.05 to show that there is a reduction in cholesterol levels over 6 weeks.  

Here we illustrate the use of a matched design to test the efficacy of a new drug to lower total cholesterol. We also considered a parallel design (randomized clinical trial) and a study using a historical comparator. It is extremely important to design studies that are best suited to detect a meaningful difference when one exists. There are often several alternatives and investigators work with biostatisticians to determine the best design for each application. It is worth noting that the matched design used here can be problematic in that observed differences may only reflect a "placebo" effect. All participants took the assigned medication, but is the observed reduction attributable to the medication or a result of these participation in a study.

Video - Hypothesis Testing With a Matched Sample and a Continuous Outcome (3:11)

Tests with Two Independent Samples, Dichotomous Outcome

There are several approaches that can be used to test hypotheses concerning two independent proportions. Here we present one approach - the chi-square test of independence is an alternative, equivalent, and perhaps more popular approach to the same analysis. Hypothesis testing with the chi-square test is addressed in the third module in this series: BS704_HypothesisTesting-ChiSquare.

In tests of hypothesis comparing proportions between two independent groups, one test is performed and results can be interpreted to apply to a risk difference, relative risk or odds ratio. As a reminder, the risk difference is computed by taking the difference in proportions between comparison groups, the risk ratio is computed by taking the ratio of proportions, and the odds ratio is computed by taking the ratio of the odds of success in the comparison groups. Because the null values for the risk difference, the risk ratio and the odds ratio are different, the hypotheses in tests of hypothesis look slightly different depending on which measure is used. When performing tests of hypothesis for the risk difference, relative risk or odds ratio, the convention is to label the exposed or treated group 1 and the unexposed or control group 2.      

For example, suppose a study is designed to assess whether there is a significant difference in proportions in two independent comparison groups. The test of interest is as follows:

H 0 : p 1 = p 2 versus H 1 : p 1 ≠ p 2 .  

The following are the hypothesis for testing for a difference in proportions using the risk difference, the risk ratio and the odds ratio. First, the hypotheses above are equivalent to the following:

• For the risk difference, H 0 : p 1 - p 2 = 0 versus H 1 : p 1 - p 2 ≠ 0 which are, by definition, equal to H 0 : RD = 0 versus H 1 : RD ≠ 0.
• If an investigator wants to focus on the risk ratio, the equivalent hypotheses are H 0 : RR = 1 versus H 1 : RR ≠ 1.
• If the investigator wants to focus on the odds ratio, the equivalent hypotheses are H 0 : OR = 1 versus H 1 : OR ≠ 1.  

Suppose a test is performed to test H 0 : RD = 0 versus H 1 : RD ≠ 0 and the test rejects H 0 at α=0.05. Based on this test we can conclude that there is significant evidence, α=0.05, of a difference in proportions, significant evidence that the risk difference is not zero, significant evidence that the risk ratio and odds ratio are not one. The risk difference is analogous to the difference in means when the outcome is continuous. Here the parameter of interest is the difference in proportions in the population, RD = p 1 -p 2 and the null value for the risk difference is zero. In a test of hypothesis for the risk difference, the null hypothesis is always H 0 : RD = 0. This is equivalent to H 0 : RR = 1 and H 0 : OR = 1. In the research hypothesis, an investigator can hypothesize that the first proportion is larger than the second (H 1 : p 1 > p 2 , which is equivalent to H 1 : RD > 0, H 1 : RR > 1 and H 1 : OR > 1), that the first proportion is smaller than the second (H 1 : p 1 < p 2 , which is equivalent to H 1 : RD < 0, H 1 : RR < 1 and H 1 : OR < 1), or that the proportions are different (H 1 : p 1 ≠ p 2 , which is equivalent to H 1 : RD ≠ 0, H 1 : RR ≠ 1 and H 1 : OR ≠

1). The three different alternatives represent upper-, lower- and two-tailed tests, respectively.  

The formula for the test of hypothesis for the difference in proportions is given below.

Test Statistics for Testing H 0 : p 1 = p

The formula above is appropriate for large samples, defined as at least 5 successes (np > 5) and at least 5 failures (n(1-p > 5)) in each of the two samples. If there are fewer than 5 successes or failures in either comparison group, then alternative procedures, called exact methods must be used to estimate the difference in population proportions.

The following table summarizes data from n=3,799 participants who attended the fifth examination of the Offspring in the Framingham Heart Study. The outcome of interest is prevalent CVD and we want to test whether the prevalence of CVD is significantly higher in smokers as compared to non-smokers.

The prevalence of CVD (or proportion of participants with prevalent CVD) among non-smokers is 298/3,055 = 0.0975 and the prevalence of CVD among current smokers is 81/744 = 0.1089. Here smoking status defines the comparison groups and we will call the current smokers group 1 (exposed) and the non-smokers (unexposed) group 2. The test of hypothesis is conducted below using the five step approach.

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2                 α=0.05

• Step 2.  Select the appropriate test statistic.  

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group. In this example, we have more than enough successes (cases of prevalent CVD) and failures (persons free of CVD) in each comparison group. The sample size is more than adequate so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5. Conclusion.

We do not reject H 0 because -1.960 < 0.927 < 1.960. We do not have statistically significant evidence at α=0.05 to show that there is a difference in prevalent CVD between smokers and non-smokers.  

A 95% confidence interval for the difference in prevalent CVD (or risk difference) between smokers and non-smokers as 0.0114 + 0.0247, or between -0.0133 and 0.0361. Because the 95% confidence interval for the risk difference includes zero we again conclude that there is no statistically significant difference in prevalent CVD between smokers and non-smokers.    

Smoking has been shown over and over to be a risk factor for cardiovascular disease. What might explain the fact that we did not observe a statistically significant difference using data from the Framingham Heart Study? HINT: Here we consider prevalent CVD, would the results have been different if we considered incident CVD?

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We now test whether there is a statistically significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using the five step approach.  

H 0 : p 1 = p 2     H 1 : p 1 ≠ p 2              α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group, i.e.,

In this example, we have min(50(0.46), 50(1-0.46), 50(0.22), 50(1-0.22)) = min(23, 27, 11, 39) = 11. The sample size is adequate so the following formula can be used

We reject H 0 because 2.526 > 1960. We have statistically significant evidence at a =0.05 to show that there is a difference in the proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever.

A 95% confidence interval for the difference in proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever is 0.24 + 0.18 or between 0.06 and 0.42. Because the 95% confidence interval does not include zero we concluded that there was a statistically significant difference in proportions which is consistent with the test of hypothesis result. 

Again, the procedures discussed here apply to applications where there are two independent comparison groups and a dichotomous outcome. There are other applications in which it is of interest to compare a dichotomous outcome in matched or paired samples. For example, in a clinical trial we might wish to test the effectiveness of a new antibiotic eye drop for the treatment of bacterial conjunctivitis. Participants use the new antibiotic eye drop in one eye and a comparator (placebo or active control treatment) in the other. The success of the treatment (yes/no) is recorded for each participant for each eye. Because the two assessments (success or failure) are paired, we cannot use the procedures discussed here. The appropriate test is called McNemar's test (sometimes called McNemar's test for dependent proportions).  

Vide0 - Hypothesis Testing With Two Independent Samples and a Dichotomous Outcome (2:55)

Here we presented hypothesis testing techniques for means and proportions in one and two sample situations. Tests of hypothesis involve several steps, including specifying the null and alternative or research hypothesis, selecting and computing an appropriate test statistic, setting up a decision rule and drawing a conclusion. There are many details to consider in hypothesis testing. The first is to determine the appropriate test. We discussed Z and t tests here for different applications. The appropriate test depends on the distribution of the outcome variable (continuous or dichotomous), the number of comparison groups (one, two) and whether the comparison groups are independent or dependent. The following table summarizes the different tests of hypothesis discussed here.

• Continuous Outcome, One Sample: H0: μ = μ0
• Continuous Outcome, Two Independent Samples: H0: μ1 = μ2
• Continuous Outcome, Two Matched Samples: H0: μd = 0
• Dichotomous Outcome, One Sample: H0: p = p 0
• Dichotomous Outcome, Two Independent Samples: H0: p1 = p2, RD=0, RR=1, OR=1

Once the type of test is determined, the details of the test must be specified. Specifically, the null and alternative hypotheses must be clearly stated. The null hypothesis always reflects the "no change" or "no difference" situation. The alternative or research hypothesis reflects the investigator's belief. The investigator might hypothesize that a parameter (e.g., a mean, proportion, difference in means or proportions) will increase, will decrease or will be different under specific conditions (sometimes the conditions are different experimental conditions and other times the conditions are simply different groups of participants). Once the hypotheses are specified, data are collected and summarized. The appropriate test is then conducted according to the five step approach. If the test leads to rejection of the null hypothesis, an approximate p-value is computed to summarize the significance of the findings. When tests of hypothesis are conducted using statistical computing packages, exact p-values are computed. Because the statistical tables in this textbook are limited, we can only approximate p-values. If the test fails to reject the null hypothesis, then a weaker concluding statement is made for the following reason.

In hypothesis testing, there are two types of errors that can be committed. A Type I error occurs when a test incorrectly rejects the null hypothesis. This is referred to as a false positive result, and the probability that this occurs is equal to the level of significance, α. The investigator chooses the level of significance in Step 1, and purposely chooses a small value such as α=0.05 to control the probability of committing a Type I error. A Type II error occurs when a test fails to reject the null hypothesis when in fact it is false. The probability that this occurs is equal to β. Unfortunately, the investigator cannot specify β at the outset because it depends on several factors including the sample size (smaller samples have higher b), the level of significance (β decreases as a increases), and the difference in the parameter under the null and alternative hypothesis.    

We noted in several examples in this chapter, the relationship between confidence intervals and tests of hypothesis. The approaches are different, yet related. It is possible to draw a conclusion about statistical significance by examining a confidence interval. For example, if a 95% confidence interval does not contain the null value (e.g., zero when analyzing a mean difference or risk difference, one when analyzing relative risks or odds ratios), then one can conclude that a two-sided test of hypothesis would reject the null at α=0.05. It is important to note that the correspondence between a confidence interval and test of hypothesis relates to a two-sided test and that the confidence level corresponds to a specific level of significance (e.g., 95% to α=0.05, 90% to α=0.10 and so on). The exact significance of the test, the p-value, can only be determined using the hypothesis testing approach and the p-value provides an assessment of the strength of the evidence and not an estimate of the effect.

Answers to Selected Problems

Dental services problem - bottom of page 5.

• Step 1: Set up hypotheses and determine the level of significance.

α=0.05

• Step 2: Select the appropriate test statistic.

First, determine whether the sample size is adequate.

Therefore the sample size is adequate, and we can use the following formula:

• Step 3: Set up the decision rule.

Reject H0 if Z is less than or equal to -1.96 or if Z is greater than or equal to 1.96.

• Step 4: Compute the test statistic
• Step 5: Conclusion.

We reject the null hypothesis because -6.15<-1.96. Therefore there is a statistically significant difference in the proportion of children in Boston using dental services compated to the national proportion.

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

• Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

• Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1]  When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3]  Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4]  When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5]  One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6]  Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7]  The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.  

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3]  In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12]  Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13]  A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14]  Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15]  confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14]  A larger width indicates a smaller sample size or a larger variability. [16]  A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15]  Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14]  In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13]  An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

• Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14]  Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4]  Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

• Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. 

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
• Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
• Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
• Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
• Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.

Recent Activity

• Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Introduction to Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 10211

• Kyle Siegrist
• University of Alabama in Huntsville via Random Services

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Basic Theory

Preliminaries.

As usual, our starting point is a random experiment with an underlying sample space and a probability measure \(\P\). In the basic statistical model, we have an observable random variable \(\bs{X}\) taking values in a set \(S\). In general, \(\bs{X}\) can have quite a complicated structure. For example, if the experiment is to sample \(n\) objects from a population and record various measurements of interest, then \[ \bs{X} = (X_1, X_2, \ldots, X_n) \] where \(X_i\) is the vector of measurements for the \(i\)th object. The most important special case occurs when \((X_1, X_2, \ldots, X_n)\) are independent and identically distributed. In this case, we have a random sample of size \(n\) from the common distribution.

The purpose of this section is to define and discuss the basic concepts of statistical hypothesis testing . Collectively, these concepts are sometimes referred to as the Neyman-Pearson framework, in honor of Jerzy Neyman and Egon Pearson, who first formalized them.

A statistical hypothesis is a statement about the distribution of \(\bs{X}\). Equivalently, a statistical hypothesis specifies a set of possible distributions of \(\bs{X}\): the set of distributions for which the statement is true. A hypothesis that specifies a single distribution for \(\bs{X}\) is called simple ; a hypothesis that specifies more than one distribution for \(\bs{X}\) is called composite .

In hypothesis testing , the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis . The null hypothesis is usually denoted \(H_0\) while the alternative hypothesis is usually denoted \(H_1\).

An hypothesis test is a statistical decision ; the conclusion will either be to reject the null hypothesis in favor of the alternative, or to fail to reject the null hypothesis. The decision that we make must, of course, be based on the observed value \(\bs{x}\) of the data vector \(\bs{X}\). Thus, we will find an appropriate subset \(R\) of the sample space \(S\) and reject \(H_0\) if and only if \(\bs{x} \in R\). The set \(R\) is known as the rejection region or the critical region . Note the asymmetry between the null and alternative hypotheses. This asymmetry is due to the fact that we assume the null hypothesis, in a sense, and then see if there is sufficient evidence in \(\bs{x}\) to overturn this assumption in favor of the alternative.

An hypothesis test is a statistical analogy to proof by contradiction, in a sense. Suppose for a moment that \(H_1\) is a statement in a mathematical theory and that \(H_0\) is its negation. One way that we can prove \(H_1\) is to assume \(H_0\) and work our way logically to a contradiction. In an hypothesis test, we don't prove anything of course, but there are similarities. We assume \(H_0\) and then see if the data \(\bs{x}\) are sufficiently at odds with that assumption that we feel justified in rejecting \(H_0\) in favor of \(H_1\).

Often, the critical region is defined in terms of a statistic \(w(\bs{X})\), known as a test statistic , where \(w\) is a function from \(S\) into another set \(T\). We find an appropriate rejection region \(R_T \subseteq T\) and reject \(H_0\) when the observed value \(w(\bs{x}) \in R_T\). Thus, the rejection region in \(S\) is then \(R = w^{-1}(R_T) = \left\{\bs{x} \in S: w(\bs{x}) \in R_T\right\}\). As usual, the use of a statistic often allows significant data reduction when the dimension of the test statistic is much smaller than the dimension of the data vector.

The ultimate decision may be correct or may be in error. There are two types of errors, depending on which of the hypotheses is actually true.

Types of errors:

• A type 1 error is rejecting the null hypothesis \(H_0\) when \(H_0\) is true.
• A type 2 error is failing to reject the null hypothesis \(H_0\) when the alternative hypothesis \(H_1\) is true.

Similarly, there are two ways to make a correct decision: we could reject \(H_0\) when \(H_1\) is true or we could fail to reject \(H_0\) when \(H_0\) is true. The possibilities are summarized in the following table:

Of course, when we observe \(\bs{X} = \bs{x}\) and make our decision, either we will have made the correct decision or we will have committed an error, and usually we will never know which of these events has occurred. Prior to gathering the data, however, we can consider the probabilities of the various errors.

If \(H_0\) is true (that is, the distribution of \(\bs{X}\) is specified by \(H_0\)), then \(\P(\bs{X} \in R)\) is the probability of a type 1 error for this distribution. If \(H_0\) is composite, then \(H_0\) specifies a variety of different distributions for \(\bs{X}\) and thus there is a set of type 1 error probabilities.

The maximum probability of a type 1 error, over the set of distributions specified by \( H_0 \), is the significance level of the test or the size of the critical region.

The significance level is often denoted by \(\alpha\). Usually, the rejection region is constructed so that the significance level is a prescribed, small value (typically 0.1, 0.05, 0.01).

If \(H_1\) is true (that is, the distribution of \(\bs{X}\) is specified by \(H_1\)), then \(\P(\bs{X} \notin R)\) is the probability of a type 2 error for this distribution. Again, if \(H_1\) is composite then \(H_1\) specifies a variety of different distributions for \(\bs{X}\), and thus there will be a set of type 2 error probabilities. Generally, there is a tradeoff between the type 1 and type 2 error probabilities. If we reduce the probability of a type 1 error, by making the rejection region \(R\) smaller, we necessarily increase the probability of a type 2 error because the complementary region \(S \setminus R\) is larger.

The extreme cases can give us some insight. First consider the decision rule in which we never reject \(H_0\), regardless of the evidence \(\bs{x}\). This corresponds to the rejection region \(R = \emptyset\). A type 1 error is impossible, so the significance level is 0. On the other hand, the probability of a type 2 error is 1 for any distribution defined by \(H_1\). At the other extreme, consider the decision rule in which we always rejects \(H_0\) regardless of the evidence \(\bs{x}\). This corresponds to the rejection region \(R = S\). A type 2 error is impossible, but now the probability of a type 1 error is 1 for any distribution defined by \(H_0\). In between these two worthless tests are meaningful tests that take the evidence \(\bs{x}\) into account.

If \(H_1\) is true, so that the distribution of \(\bs{X}\) is specified by \(H_1\), then \(\P(\bs{X} \in R)\), the probability of rejecting \(H_0\) is the power of the test for that distribution.

Thus the power of the test for a distribution specified by \( H_1 \) is the probability of making the correct decision.

Suppose that we have two tests, corresponding to rejection regions \(R_1\) and \(R_2\), respectively, each having significance level \(\alpha\). The test with region \(R_1\) is uniformly more powerful than the test with region \(R_2\) if \[ \P(\bs{X} \in R_1) \ge \P(\bs{X} \in R_2) \text{ for every distribution of } \bs{X} \text{ specified by } H_1 \]

Naturally, in this case, we would prefer the first test. Often, however, two tests will not be uniformly ordered; one test will be more powerful for some distributions specified by \(H_1\) while the other test will be more powerful for other distributions specified by \(H_1\).

If a test has significance level \(\alpha\) and is uniformly more powerful than any other test with significance level \(\alpha\), then the test is said to be a uniformly most powerful test at level \(\alpha\).

Clearly a uniformly most powerful test is the best we can do.

\(P\)-value

In most cases, we have a general procedure that allows us to construct a test (that is, a rejection region \(R_\alpha\)) for any given significance level \(\alpha \in (0, 1)\). Typically, \(R_\alpha\) decreases (in the subset sense) as \(\alpha\) decreases.

The \(P\)-value of the observed value \(\bs{x}\) of \(\bs{X}\), denoted \(P(\bs{x})\), is defined to be the smallest \(\alpha\) for which \(\bs{x} \in R_\alpha\); that is, the smallest significance level for which \(H_0\) is rejected, given \(\bs{X} = \bs{x}\).

Knowing \(P(\bs{x})\) allows us to test \(H_0\) at any significance level for the given data \(\bs{x}\): If \(P(\bs{x}) \le \alpha\) then we would reject \(H_0\) at significance level \(\alpha\); if \(P(\bs{x}) \gt \alpha\) then we fail to reject \(H_0\) at significance level \(\alpha\). Note that \(P(\bs{X})\) is a statistic . Informally, \(P(\bs{x})\) can often be thought of as the probability of an outcome as or more extreme than the observed value \(\bs{x}\), where extreme is interpreted relative to the null hypothesis \(H_0\).

Analogy with Justice Systems

There is a helpful analogy between statistical hypothesis testing and the criminal justice system in the US and various other countries. Consider a person charged with a crime. The presumed null hypothesis is that the person is innocent of the crime; the conjectured alternative hypothesis is that the person is guilty of the crime. The test of the hypotheses is a trial with evidence presented by both sides playing the role of the data. After considering the evidence, the jury delivers the decision as either not guilty or guilty . Note that innocent is not a possible verdict of the jury, because it is not the point of the trial to prove the person innocent. Rather, the point of the trial is to see whether there is sufficient evidence to overturn the null hypothesis that the person is innocent in favor of the alternative hypothesis of that the person is guilty. A type 1 error is convicting a person who is innocent; a type 2 error is acquitting a person who is guilty. Generally, a type 1 error is considered the more serious of the two possible errors, so in an attempt to hold the chance of a type 1 error to a very low level, the standard for conviction in serious criminal cases is beyond a reasonable doubt .

Tests of an Unknown Parameter

Hypothesis testing is a very general concept, but an important special class occurs when the distribution of the data variable \(\bs{X}\) depends on a parameter \(\theta\) taking values in a parameter space \(\Theta\). The parameter may be vector-valued, so that \(\bs{\theta} = (\theta_1, \theta_2, \ldots, \theta_n)\) and \(\Theta \subseteq \R^k\) for some \(k \in \N_+\). The hypotheses generally take the form \[ H_0: \theta \in \Theta_0 \text{ versus } H_1: \theta \notin \Theta_0 \] where \(\Theta_0\) is a prescribed subset of the parameter space \(\Theta\). In this setting, the probabilities of making an error or a correct decision depend on the true value of \(\theta\). If \(R\) is the rejection region, then the power function \( Q \) is given by \[ Q(\theta) = \P_\theta(\bs{X} \in R), \quad \theta \in \Theta \] The power function gives a lot of information about the test.

The power function satisfies the following properties:

• \(Q(\theta)\) is the probability of a type 1 error when \(\theta \in \Theta_0\).
• \(\max\left\{Q(\theta): \theta \in \Theta_0\right\}\) is the significance level of the test.
• \(1 - Q(\theta)\) is the probability of a type 2 error when \(\theta \notin \Theta_0\).
• \(Q(\theta)\) is the power of the test when \(\theta \notin \Theta_0\).

If we have two tests, we can compare them by means of their power functions.

Suppose that we have two tests, corresponding to rejection regions \(R_1\) and \(R_2\), respectively, each having significance level \(\alpha\). The test with rejection region \(R_1\) is uniformly more powerful than the test with rejection region \(R_2\) if \( Q_1(\theta) \ge Q_2(\theta)\) for all \( \theta \notin \Theta_0 \).

Most hypothesis tests of an unknown real parameter \(\theta\) fall into three special cases:

Suppose that \( \theta \) is a real parameter and \( \theta_0 \in \Theta \) a specified value. The tests below are respectively the two-sided test , the left-tailed test , and the right-tailed test .

• \(H_0: \theta = \theta_0\) versus \(H_1: \theta \ne \theta_0\)
• \(H_0: \theta \ge \theta_0\) versus \(H_1: \theta \lt \theta_0\)
• \(H_0: \theta \le \theta_0\) versus \(H_1: \theta \gt \theta_0\)

Thus the tests are named after the conjectured alternative. Of course, there may be other unknown parameters besides \(\theta\) (known as nuisance parameters ).

Equivalence Between Hypothesis Test and Confidence Sets

There is an equivalence between hypothesis tests and confidence sets for a parameter \(\theta\).

Suppose that \(C(\bs{x})\) is a \(1 - \alpha\) level confidence set for \(\theta\). The following test has significance level \(\alpha\) for the hypothesis \( H_0: \theta = \theta_0 \) versus \( H_1: \theta \ne \theta_0 \): Reject \(H_0\) if and only if \(\theta_0 \notin C(\bs{x})\)

By definition, \(\P[\theta \in C(\bs{X})] = 1 - \alpha\). Hence if \(H_0\) is true so that \(\theta = \theta_0\), then the probability of a type 1 error is \(P[\theta \notin C(\bs{X})] = \alpha\).

Equivalently, we fail to reject \(H_0\) at significance level \(\alpha\) if and only if \(\theta_0\) is in the corresponding \(1 - \alpha\) level confidence set. In particular, this equivalence applies to interval estimates of a real parameter \(\theta\) and the common tests for \(\theta\) given above .

In each case below, the confidence interval has confidence level \(1 - \alpha\) and the test has significance level \(\alpha\).

• Suppose that \(\left[L(\bs{X}, U(\bs{X})\right]\) is a two-sided confidence interval for \(\theta\). Reject \(H_0: \theta = \theta_0\) versus \(H_1: \theta \ne \theta_0\) if and only if \(\theta_0 \lt L(\bs{X})\) or \(\theta_0 \gt U(\bs{X})\).
• Suppose that \(L(\bs{X})\) is a confidence lower bound for \(\theta\). Reject \(H_0: \theta \le \theta_0\) versus \(H_1: \theta \gt \theta_0\) if and only if \(\theta_0 \lt L(\bs{X})\).
• Suppose that \(U(\bs{X})\) is a confidence upper bound for \(\theta\). Reject \(H_0: \theta \ge \theta_0\) versus \(H_1: \theta \lt \theta_0\) if and only if \(\theta_0 \gt U(\bs{X})\).

Pivot Variables and Test Statistics

Recall that confidence sets of an unknown parameter \(\theta\) are often constructed through a pivot variable , that is, a random variable \(W(\bs{X}, \theta)\) that depends on the data vector \(\bs{X}\) and the parameter \(\theta\), but whose distribution does not depend on \(\theta\) and is known. In this case, a natural test statistic for the basic tests given above is \(W(\bs{X}, \theta_0)\).

9.3: Critical Region, Critical Values and Significance Level

Chapter 1: understanding statistics, chapter 2: summarizing and visualizing data, chapter 3: measure of central tendency, chapter 4: measures of variation, chapter 5: measures of relative standing, chapter 6: probability distributions, chapter 7: estimates, chapter 8: distributions, chapter 9: hypothesis testing, chapter 10: analysis of variance, chapter 11: correlation and regression, chapter 12: statistics in practice.

The JoVE video player is compatible with HTML5 and Adobe Flash. Older browsers that do not support HTML5 and the H.264 video codec will still use a Flash-based video player. We recommend downloading the newest version of Flash here, but we support all versions 10 and above.

Hypothesis testing requires the sample statistics—such as proportion, mean, or standard deviation—to be converted into a value or score known as the test statistics.

Assuming that the null hypothesis is true, the test statistic for each sample statistic is calculated using the following equations.

As samples assume a particular distribution, a given test statistic value would fall into a specific area under the curve with some probability.

Such an area, which includes all the values of a test statistic that indicates that the null hypothesis must be rejected, is termed the rejection region or critical region.

The value that separates a critical region from the rest is termed the critical value. The critical values are the  z, t,  or chi-square values calculated at the desired confidence level.

The probability that the test statistic will fall in the critical region when the null hypothesis is actually true is called the significance level.

In the example of testing the proportion of healthy and scabbed apples, if the sample proportion is 0.9, the hypothesis can be tested as follows.

The critical region, critical value, and significance level are interdependent concepts crucial in hypothesis testing.

In hypothesis testing, a sample statistic is converted to a test statistic using z , t , or chi-square distribution. A critical region is an area under the curve in  probability distributions demarcated by the critical value. When the test statistic falls in this region, it suggests that the null hypothesis must be rejected. As this region contains all those values of the test statistic (calculated using the sample data) that suggest rejecting the null hypothesis, it is also known as the rejection region or region of rejection. The critical region may fall at the right, left, or both tails of the distribution based on the direction indicated in the alternative hypothesis and the calculated critical value.

A critical value is calculated using the z , t, or chi-square distribution table at a specific significance level. It is a fixed value for the given sample size and the significance level. The critical value creates a demarcation between all those values that suggest rejection of the null hypothesis and all those other values that indicate the opposite. A critical value is  based on a pre-decided significance level.

A significance level or level of significance or statistical significance is defined as the probability that the calculated test statistic will fall in the critical region. In other words, it is a statistical measure that indicates that the evidence for rejecting a true null hypothesis is strong enough. The significance level is indicated by α, and it is commonly 0.05 or 0.01.

Get cutting-edge science videos from J o VE sent straight to your inbox every month.

mktb-description

We use cookies to enhance your experience on our website.

By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

1.2 - the 7 step process of statistical hypothesis testing.

We will cover the seven steps one by one.

Step 1: State the Null Hypothesis

The null hypothesis can be thought of as the opposite of the "guess" the researchers made. In the example presented in the previous section, the biologist "guesses" plant height will be different for the various fertilizers. So the null hypothesis would be that there will be no difference among the groups of plants. Specifically, in more statistical language the null for an ANOVA is that the means are the same. We state the null hypothesis as:

\(H_0 \colon \mu_1 = \mu_2 = ⋯ = \mu_T\)

for  T levels of an experimental treatment.

Step 2: State the Alternative Hypothesis

\(H_A \colon \text{ treatment level means not all equal}\)

The alternative hypothesis is stated in this way so that if the null is rejected, there are many alternative possibilities.

For example, \(\mu_1\ne \mu_2 = ⋯ = \mu_T\) is one possibility, as is \(\mu_1=\mu_2\ne\mu_3= ⋯ =\mu_T\). Many people make the mistake of stating the alternative hypothesis as \(\mu_1\ne\mu_2\ne⋯\ne\mu_T\) which says that every mean differs from every other mean. This is a possibility, but only one of many possibilities. A simple way of thinking about this is that at least one mean is different from all others. To cover all alternative outcomes, we resort to a verbal statement of "not all equal" and then follow up with mean comparisons to find out where differences among means exist. In our example, a possible outcome would be that fertilizer 1 results in plants that are exceptionally tall, but fertilizers 2, 3, and the control group may not differ from one another.

Step 3: Set \(\alpha\)

If we look at what can happen in a hypothesis test, we can construct the following contingency table:

You should be familiar with Type I and Type II errors from your introductory courses. It is important to note that we want to set \(\alpha\) before the experiment ( a-priori ) because the Type I error is the more grievous error to make. The typical value of \(\alpha\) is 0.05, establishing a 95% confidence level. For this course, we will assume \(\alpha\) =0.05, unless stated otherwise.

Step 4: Collect Data

Remember the importance of recognizing whether data is collected through an experimental design or observational study.

Step 5: Calculate a test statistic

For categorical treatment level means, we use an F- statistic, named after R.A. Fisher. We will explore the mechanics of computing the F- statistic beginning in Lesson 2. The F- value we get from the data is labeled \(F_{\text{calculated}}\).

Step 6: Construct Acceptance / Rejection regions

As with all other test statistics, a threshold (critical) value of F is established. This F- value can be obtained from statistical tables or software and is referred to as \(F_{\text{critical}}\) or \(F_\alpha\). As a reminder, this critical value is the minimum value of the test statistic (in this case \(F_{\text{calculated}}\)) for us to reject the null.

The F- distribution, \(F_\alpha\), and the location of acceptance/rejection regions are shown in the graph below:

Step 7: Based on Steps 5 and 6, draw a conclusion about \(H_0\)

If \(F_{\text{calculated}}\) is larger than \(F_\alpha\), then you are in the rejection region and you can reject the null hypothesis with \(\left(1-\alpha \right)\) level of confidence.

Note that modern statistical software condenses Steps 6 and 7 by providing a p -value. The p -value here is the probability of getting an \(F_{\text{calculated}}\) even greater than what you observe assuming the null hypothesis is true. If by chance, the \(F_{\text{calculated}} = F_\alpha\), then the p -value would be exactly equal to \(\alpha\). With larger \(F_{\text{calculated}}\) values, we move further into the rejection region and the p- value becomes less than \(\alpha\). So, the decision rule is as follows:

If the p- value obtained from the ANOVA is less than \(\alpha\), then reject \(H_0\) in favor of \(H_A\).

Statistics Made Easy

5 Tips for Interpreting P-Values Correctly in Hypothesis Testing

Hypothesis testing is a critical part of statistical analysis and is often the endpoint where conclusions are drawn about larger populations based on a sample or experimental dataset. Central to this process is the p-value. Broadly, the p-value quantifies the strength of evidence against the null hypothesis. Given the importance of the p-value, it is essential to ensure its interpretation is correct. Here are five essential tips for ensuring the p-value from a hypothesis test is understood correctly. 

1. Know What the P-value Represents

First, it is essential to understand what a p-value is. In hypothesis testing, the p-value is defined as the probability of observing your data, or data more extreme, if the null hypothesis is true. As a reminder, the null hypothesis states no difference between your data and the expected population. 

For example, in a hypothesis test to see if changing a company’s logo drives more traffic to the website, a null hypothesis would state that the new traffic numbers are equal to the old traffic numbers. In this context, the p-value would be the probability that the data you observed, or data more extreme, would occur if this null hypothesis were true. 

Therefore, a smaller p-value indicates that what you observed is unlikely to have occurred if the null were true, offering evidence to reject the null hypothesis. Typically, a cut-off value of 0.05 is used where any p-value below this is considered significant evidence against the null. 

2. Understand the Directionality of Your Hypothesis

Based on the research question under exploration, there are two types of hypotheses: one-sided and two-sided. A one-sided test specifies a particular direction of effect, such as traffic to a website increasing after a design change. On the other hand, a two-sided test allows the change to be in either direction and is effective when the researcher wants to see any effect of the change. 

Either way, determining the statistical significance of a p-value is the same: if the p-value is below a threshold value, it is statistically significant. However, when calculating the p-value, it is important to ensure the correct sided calculations have been completed. 

Additionally, the interpretation of the meaning of a p-value will differ based on the directionality of the hypothesis. If a one-sided test is significant, the researchers can use the p-value to support a statistically significant increase or decrease based on the direction of the test. If a two-sided test is significant, the p-value can only be used to say that the two groups are different, but not that one is necessarily greater. 

3. Avoid Threshold Thinking

A common pitfall in interpreting p-values is falling into the threshold thinking trap. The most commonly used cut-off value for whether a calculated p-value is statistically significant is 0.05. Typically, a p-value of less than 0.05 is considered statistically significant evidence against the null hypothesis. 

However, this is just an arbitrary value. Rigid adherence to this or any other predefined cut-off value can obscure business-relevant effect sizes. For example, a hypothesis test looking at changes in traffic after a website design may find that an increase of 10,000 views is not statistically significant with a p-value of 0.055 since that value is above 0.05. However, the actual increase of 10,000 may be important to the growth of the business. 

Therefore, a p-value can be practically significant while not being statistically significant. Both types of significance and the broader context of the hypothesis test should be considered when making a final interpretation. 

4. Consider the Power of Your Study

Similarly, some study conditions can result in a non-significant p-value even if practical significance exists. Statistical power is the ability of a study to detect an effect when it truly exists. In other words, it is the probability that the null hypothesis will be rejected when it is false. 

Power is impacted by a lot of factors. These include sample size, the effect size you are looking for, and variability within the data. In the example of website traffic after a design change, if the number of visits overall is too small, there may not be enough views to have enough power to detect a difference. 

Simple ways to increase the power of a hypothesis test and increase the chances of detecting an effect are increasing the sample size, looking for a smaller effect size, changing the experiment design to control for variables that can increase variability, or adjusting the type of statistical test being run.

5. Be Aware of Multiple Comparisons

Whenever multiple p-values are calculated in a single study due to multiple comparisons, there is an increased risk of false positives. This is because each individual comparison introduces random fluctuations, and each additional comparison compounds these fluctuations. 

For example, in a hypothesis test looking at traffic before and after a website redesign, the team may be interested in making more than one comparison. This can include total visits, page views, and average time spent on the website. Since multiple comparisons are being made, there must be a correction made when interpreting the p-value. 

The Bonferroni correction is one of the most commonly used methods to account for this increased probability of false positives. In this method, the significance cut-off value, typically 0.05, is divided by the number of comparisons made. The result is used as the new significance cut-off value.  Applying this correction mitigates the risk of false positives and improves the reliability of findings from a hypothesis test. 

In conclusion, interpreting p-values requires a nuanced understanding of many statistical concepts and careful consideration of the hypothesis test’s context. By following these five tips, the interpretation of the p-value from a hypothesis test can be more accurate and reliable, leading to better data-driven decision-making.

Featured Posts

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Critical Points
• How to Find Z Critical Values in R
• Absolute Value
• Critical Velocity Formula
• P-Value Calculator
• How to Find the F Critical Value in R
• How to Calculate Critical t-Value in R ?
• How to Find the F Critical Value in Python?
• How to Find the Z Critical Value in Python?
• How to Find the Chi-Square Critical Value in R
• How to calculate P Value?
• Maximum value of int in C++
• C# | Byte.MinValue Field
• C# | Byte.MaxValue Field
• How to Find the T Critical Value in Python?
• P-value in Machine Learning
• JavaScript Number.MIN_VALUE Property
• JavaScript Number.MAX_VALUE Property
• Maximum value of short int in C++

Critical Value

Critical value is a cut-off value used to mark the beginning of a region where the test statistic obtained in the theoretical test is unlikely to fail. Compared to the obtained test statistic to determine the critical value at hypothesis testing, Null hypothesis is rejected or not. Graphically, the critical value divides the graph into an accepted and rejected region for hypothesis testing. It helps to check the statistical significance of the test statistics. So, critical values are simply the function’s output at these critical points.

In this article, we will learn more about the critical value, its formula, types, and how to calculate its value.

Table of Content

What is Critical Value?

Critical value formula, t-critical value, z-critical value, f-critical value, chi-square critical value.

Critical values are essential components in hypothesis testing. They are calculated to help determine the significance of test statistics in relation to a specific hypothesis. The distribution of these test statistics guides the identification of critical values. In a one-tailed hypothesis test, there is one critical value, while in a two-tailed test, there are two critical values, each corresponding to a specific level of significance.

Critical Value Definition

Critical values are often defined as specific points on a scale used in statistical tests. These points help determine whether the results of a test are statistically significant or not. They serve as thresholds for making decisions about hypotheses being tested.

There are different formulas for calculating the critical value, depending on the distributional nature of the test statistic. Confidence intervals or significance levels can be used to determine a critical value.

Critical Value Confidence Interval

Critical values play a crucial role in hypothesis testing, and they’re closely linked to confidence intervals. Let’s say we’ve set a 95% confidence interval for our test. To find the critical value:

• Step 1:  Subtract the confidence level from 100% (100% – 95% = 5%.
• Step 2:  Convert this to a decimal to get α (α = 5%).
• Step 3:  If it’s a one-tailed test, α remains the same as in step 2. For a two-tailed test, divide α by 2.
• Step 4:  Depending on the type of test, find the critical value in the distribution table using the α value.

T-test is used when the population trend is not observed and the sample size is less than 30. The t-test is conducted when the population data follow the Student t distribution. The t critical value can be calculated as follows.

Specify Alpha Level

• First, we set a level of confidence, which we call alpha (α). This is usually 0.05 or 0.01, but it can be different depending on the study.
• Next, we figure out the degrees of freedom (df). It’s just one less than the sample size. Degrees of freedom tell us how many values in the final calculation are free to vary.
• Now, we look at a table called the t-distribution table. If we’re doing a one-tailed test (meaning we’re only interested in one direction, like if something is greater or less than), we use a one-tailed t-distribution table. If it’s a two-tailed test (we’re interested in both directions), we use a two-tailed t-distribution table.
• In this table, we find the row that matches our degrees of freedom and the column that matches our alpha level. The number where they intersect is our t-critical value.

Decision criteria:

• Reject the null hypothesis if test statistic > critical t value (right-tailed hypothesis test).
• Reject the null hypothesis if test statistic < t critical value (left-tailed hypothesis test).
• Reject the null hypothesis if test statistic is not in the region of acceptance (two-tailed hypothesis test).

A ‘Z test’ is performed on a normal distribution when the population mean is known and the sample size is greater than or equal to 30. The critical value of Z can be calculated as follows.

To Find the alpha value

• Subtract the alpha level from 1 for a two-tailed test. For a one-tailed test, subtract the alpha level from 0.5
• The area from the Z distribution table to obtain the z critical value. For a left-tailed test, a negative sign needs to be added to the critical value at the end of the calculation.

The F test is commonly used to compare differences between two samples. The test statistic thus obtained is also used for regression analysis. The critical value of f is given as:

Find the alpha level

• Subtract 1 from the size of the original sample. This gives them the first freedom. Say, x.
• Similarly, subtract 1 from the second sample size to obtain the second df. Say, y.
• f Using the distribution x and row y, the distribution table will produce a critical value of f.

Test Statistic for small samples: f = s 1 2 / s 2 2 . S 1 1 variance of the first sample and S 2 2 variance of the second sample.

The chi-square test is used to check whether the sample data are consistent with the population data. It can also be used to compare two variables to see if they are correlated. The critical chi-square value is given as:

Select the alpha level

• Subtract 1 from the sample size to find the degree of freedom(df).
• Using the chi-square distribution table, the critical chi-square value is obtained by intersecting the df value in the row and column of the alpha value.

Also, Check:

Variance and Standard Deviation Difference Between Variance and Standard Deviation Mean, Variance and Standard Deviation

Solved Questions on Critical Value

Question 1: Find the critical value for a right-tailed t-test with a sample size of 15 and α = 0.025.

Given: n = 15, α = 0.025 Degrees of freedom (df) = n – 1 = 15 – 1 = 14 Using the t-distribution table for α = 0.025 and df = 14, the critical value is found to be t(14, 0.025) ≈ 2.145. Critical Value = 2.145

Question 2: Calculate the critical value for a left-tailed z-test with α = 0.05.

Given: α = 0.05 First, subtract α from 0.5: 0.5 – 0.05 = 0.45. Using the z-distribution table, the value corresponding to the cumulative probability of 0.45 is approximately -1.645. Critical Value = -1.645

Question 3: Determine the critical value for a two-tailed t-test with a sample size of 25 and α = 0.01.

Given: n = 25, α = 0.01 Degrees of freedom (df) = n – 1 = 25 – 1 = 24 Since this is a two-tailed test, we need to split α in half: 0.01/2 = 0.005. Using the t-distribution table for α = 0.005 and df = 24, the critical value is found to be t(24, 0.005) ≈ ±2.797. Critical Values = ±2.797

Practice Problems on Critical Value

The significance value is an important aspect of statistical hypothesis testing and is a requirement that the hypothesis based on sample data may not be rejected. When informed decisions are made, appropriate logic and the use of critical criteria are necessary to control Type I errors, ensure the validity of statistical inferences, facilitate comparison across studies, and increase both the rigor and reliability of statistical analysis in the evaluation and decision-making process.

Related Articles:

Probability and Statistics Data Handling Chi-Square Test Hypothesis Testing Formula

FAQs on Critical Value

What is the most important advantage of hypothesis testing.

A critical value is a threshold used in statistical hypothesis tests to determine whether the null hypothesis should be rejected on the sample data. to decide on the null hypothesis, it is compared with the test statistic.

How is the importance of the goal related to its importance?

The critical value is determined by the chosen level of significance ( ), which represents an acceptable probability of Type I error(false positive). Lower significance levels lead to more stringent critical values.

What are the differences between one-tailed and two-tailed critical values?

A single significant tree is used in trials in which the alternative hypothesis specifies a direction(greater than or less than), while a double significant tree is used when the alternative is scalar(not equal to).

How do degrees of freedom affect important values?

Significant differences in the t-distributions depend on the degree of freedom(sample size minus one).

What happens if the p-value is less than the mean?

A low p-value(less than alpha) indicates that the test statistic falls in the rejection region, resulting in the rejection hypothesis.

Why is it important to understand important values in hypothesis testing?

Important logic is important because it sets decision criteria for hypothesis testing, controls for type I errors, verifies statistical inferences, and guides decisions based on sample data.

Can important values be negative?

Depending on the classification and direction of the test(horizontal, vertical, two-tailed), the critical values can be negative or positive.

Please Login to comment...

Similar reads.

• Math-Statistics
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Open access
• Published: 26 May 2024

Are we romanticizing traditional knowledge? A plea for more experimental studies in ethnobiology

• Marco Leonti 1  

Journal of Ethnobiology and Ethnomedicine volume  20 , Article number:  56 ( 2024 ) Cite this article

248 Accesses

1 Altmetric

Metrics details

In answer to the debate question "Is ethnobiology romanticizing traditional practices, posing an urgent need for more experimental studies evaluating local knowledge systems?" I suggest to follow-up on field study results adopting an inclusive research agenda, and challenge descriptive data, theories, and hypotheses by means of experiments. Traditional and local knowledge are generally associated with positive societal values by ethnobiologists and, increasingly also by stakeholders. They are seen as a way for improving local livelihoods, biocultural diversity conservation and for promoting sustainable development. Therefore, it is argued that such knowledge needs to be documented, protected, conserved in situ, and investigated by hypothesis testing. Here I argue that a critical mindset is needed when assessing any kind of knowledge, whether it is modern, local, indigenous, or traditional.

Introduction

In this essay I take a broad view on ethnobiology highlighting the often-heterogenous origin and fuzzy character of local and traditional knowledge and the importance of being enriched with modern and outside knowledge. As a follow-up on a previous debate about the question of whether ethnobiology should “…abandon more classical folkloric studies” and instead “foster hypothesis-driven forefront research…” I asked for the approval of a call on “are we romanticizing traditional knowledge and is there a need for more experimental studies in ethnobiology” [full stop]. Here I acknowledge the need for descriptive and hypothesis-driven studies but also point out their limitations and the value of experimental studies as a means for overcoming the inherent subjectivity of human observation. Some of the experimental studies I refer to are not strictly ‘ethnobiological’, but they could have been so, if only experimental approaches were more frequently implemented.

Experimentations were instrumental for human cultural progress [ 1 ] and are also used for understanding cultural evolution [ 2 ]. Experiments are conducted to challenge hypotheses, assess the probabilities of efficacy, or have an exploratory character. It is distinguished between true experiments, where participants or treatments are assigned randomly or quasi-experiments where participants or treatments are selected for groups [ 3 ]. The scientific strength of experiments lies in their reproducibility and the consequent logical analysis of the results obtained. In laboratory experiments variables can be controlled for while field experiments are closer to reality [ 4 ]. Natural experiments are going on permanently around us and cannot be manipulated by researchers but only evaluated. Since the data is recorded in a natural setting it is crucial to capture the baseline data of the identified variables and to understand which hypothesis is actually being tested [ 1 , 4 ]. The experiment is an essential part of the scientific progress process [ 5 ]. Active involvement in descriptive studies, hypothesis testing and experimental research, grants a more nuanced sense of what evidence is, and insights into the difficulties of human observation.

What is traditional and local knowledge and what are the dynamics?

Traditional knowledge and customs (referred to also as indigenous and local knowledge) have been reported by natural philosophers and chroniclers since around 2000 years (e.g., [ 6 , 7 , 8 ]). With the help of written documents, cultural remains and archaeological artefacts, we understand persistence and dynamics of traditions and knowledge. Besides of being maintained or abandoned, traditional knowledge can synchronize with ‘outside’ knowledge and syncretize, blend with newly generated knowledge, evolve gradually, be reinvented, or invented intentionally [ 9 , 10 , 11 ]. For instance, the cheese ‘fondue’, a Swiss national dish, probably now considered traditional by many, was ad hoc invented to promote the consumption of Swiss cheese during the 1930ies and presented to an international audience at the New York World’s Fair 1939/40.

So, what is it that makes knowledge to become ‘traditional’? In the context of herbal medicine, traditional knowledge is defined and distinguished from a current fashion or a trend in that its transmission must involve at least three generations, including two steps of knowledge transmission or, alternatively, three ‘training generations’ where knowledge is being passed on to apprentices [ 12 ]. The definition of traditional knowledge in general is fuzzier and many of our daily activities, (e.g., preparing food) contain traditional elements. However, not all activities are traditional just because they have been practiced ever since or because they are sustainable. For instance, collecting rainwater for plant irrigation purposes, is not per se traditional ecological knowledge (TEK). People would collect rainwater for plant irrigation also if they had never observed this practice anywhere else. Moreover, having a theory of mind and observational skills individuals can understand the poor quality and unsustainability of (chlorinated) tap water for watering plants and thus try to avoid the associated economic costs. Collecting rainwater such as roof run-off is just intuitive and logic. On the other hand, complex and elaborate water collection and irrigation systems adapted to specific landscapes and climatic conditions are often grounded on traditional knowledge [ 13 ]. It is the culture-specific way of doing things that characterizes the local or the traditional and not necessarily actions per se.

From documents of culture-historical importance we learn that while many traditional practices and customs did not stand the test of time and were wisely abandoned, others persist to date. For instance, many medical treatments were not effective or even dangerous. Bloodletting or purging by means of poisonous botanical drugs with strong emetic and cathartic effects were eventually abandoned along with European humoral medicine [ 14 ]. Other botanical drugs have been used continuously throughout the centuries, many of them with acceptable safety profiles [ 15 , 16 , 17 , 18 , 19 ]. However, the European Medicines Agency (EMA) does not confuse generation-long use with efficacy or effectiveness. In absence of clinical data supporting traditional applications the EMA confers the status of ”traditional use” where “sufficient safety data and plausible efficacy are demonstrated” (e.g., any application of extracts derived from Panax ginseng C.A. Meyer, underground organs) which is different from products with “recognised efficacy” (e.g., application of 20 mg EtOH (60%) extract obtained from Vitex agnus-castus L. fruits with a DER of 6-12:1) for premenstrual syndrome.

The tradition of whaling (the hunting of whales, mainly for blubber) was not sustainable and brought several whale species to the brink of extinction which is the reason why whaling got banned in many countries by 1969. Some traditions were given up because of changing moral and ethical standards and by the introduction of new laws. Disputes about the expansion of slavery caused the American Civil War resulting in an official legal ban of slavery in 1865. Many other traditions ignoring individual’s freedom, right to integrity and equality such as female genital mutilation (in many African countries, the Near East and Indonesia), early child marriage (Africa, Near East, the Indian subcontinent, and South-East Asia) or the Indian caste system [ 20 ] continue to be practiced while the legacy of Roman law is still present in Western legal thought [ 21 ].

Example of Italy and the economization of TK

Let’s take for example modern Italian culture and economy which are rooted in the country’s rich history and local traditions. Italy shows a marked North–South economic disparity, associated with geography and culture. The varied history of the different Italian regions is reflected in the distinct traditions in food production, cuisine, and craftsmanship. Italy has currently the highest share of elderly people (> 65 years of age) and one of the lowest birth rates within all European countries. This is also conditioned by the late financial independence and economic insecurity of young Italians permitting them to start a family only relatively late in life. This situation poses serious challenges to health care, old age benefits and economy.

Small- and medium-sized enterprises constitute the backbone of the Italian economy with around 75% of all businesses in family hand [ 22 ]. The knowledge for securing the highest quality of raw products at the best conditions and the steps, processes, recipes, tools, and machines used during production are well-kept secrets and associated knowledge transmitted only within the family. Since it is easier to collect taxes from a few large businesses than from many small family businesses, Italian tax authorities face more difficulties than other European countries in this regard. Besides that, a low taxpayer commitment, organized crime, corruption, bureaucracy, low productivity due to lack of process innovation [ 22 , 23 ] are other traditional problems afflicting the Italian economy. Though Italy being a relatively wealthy country the traditional business structure and reliance on local knowledge is also a drawback for economic growth because innovation and modernization occur too often on a relatively low scale which reinforces Italy’s traditional set up.

Example of Switzerland and TEK

It was recently showcased how TEK is often maintained because of lack of economic resources that would permit the use of more technological equipment and not because of ecological concerns [ 24 ]. Also, others (e.g. [ 25 ]) concluded, that in the more economically developed regions TEK practices will have a chance to survive only in protected areas where they are used as a tool for biodiversity conservation and where they are fostered by consumers requesting organic and ecologically sustainable food. Topography also plays an important factor in the maintenance of TEK. In mountainous and alpine regions such as the European Alps, TEK and its application is more prominent than in the lowlands, conditioned by the fact that the inclination of the terrain and the marked seasonal changes do not allow for intensive land management and the use of heavy equipment and machinery. This applies also to natural estuaries, river, sea, and lake shores. Agriculture is subsidized all over Switzerland but more heavily in mountainous regions, where otherwise production would not be profitable at all. Switzerland is a wealthy and rich country, which can afford to subsidize agriculture and traditional ways of food production. Thereby, food sovereignty and indigenous food production systems including TEK are maintained at least partially. According to Article 104 of the Federal Constitution, agriculture has a mandate to provide public services. These are each subsidized with a specific type of direct payment. These services include, for example, near-natural, environmentally friendly, and animal-friendly production, the preservation of natural resources and the maintenance of the cultural landscape. In 2022, the federal government paid out a total of around CHF 2.8 billion in direct payments for agriculture [ 26 ].

Also, religious denomination can affect land management practices in Switzerland. The sociocultural differences between the protestant canton of Bern and the catholic canton of Lucerne are amongst others reflected in the fact that contrary to the practice followed in the canton of Lucerne, the grassland in the canton of Bern gets cleaned from bitter dock ( Rumex obtusifolius L.), a noxious weed [ 27 ]. In the past also a catholic and a protestant way of tilling the land existed in Switzerland [ 28 ]. Historically, the large number of non-working days in the canton of Lucerne and the heavy demands on the population were blamed by numerous travellers and writers for the region’s lagging behind in terms of industrialisation and agricultural development [ 29 ].

With the example of Italy, I tried to explain how traditional, and local knowledge can serve as a starting point for innovation, but that success depends on the effective adoption of global knowledge and economic structures. With the example of Switzerland, I tried to highlight that besides economic resources and consumers preferences also topographical particularities, and religion can have a direct influence on the maintenance and practice of TEK. With both, the example of Italy and Switzerland I also tried to highlight the difficulty of defining and identifying ‘systems’ of traditional knowledge. Thus, ‘traditional knowledge systems’ as such can be difficult to grasp because traditional and modern knowledge are often combined and blended in processes that may give way to new traditions. Therefore, here I rather focus on traditional and local knowledge as such and avoid talking about ‘systems’, which are nowadays to be found only in remote areas and isolated civilizations and communities [ 30 ].

In summary, history shows, that non-sustainable practices are often abandoned but, also that societal power structures can help to maintain archaic traditions and that traditional and local knowledge, in combinations with purposeful technological experimentation and invention led to innovation which was instrumental for shaping the world and the various human cultures we know today. However, in my view there is nothing wrong or dramatic about abandoning outdated traditions and practices. Here I argue that traditional knowledge should not only not be romanticized [ 24 ] but critically questioned, also with the help of experiments, like any other knowledge.

Are we howling at the moon?

The question as of whether there is an urgent need for more experimental studies evaluating local knowledge systems is related to a previous debate in this series focusing of whether ethnobiology and ethnomedicine should more decisively foster hypothesis-driven forefront research able to turn findings into policy and abandon more classical folkloric studies. I think that there is no need for dramatizing and that the ‘urgency’ is rather related to the question of whether or how proximate ethnobiology is thought to evolve into a branch of multidisciplinary science adopting an inclusive research protocol.

Clearly, for ethnobiology to prosper both, descriptive and hypothesis-driven approaches are needed. Primary data is the basis for all science and descriptive studies fuel hypothesis-driven studies [ 31 , 32 , 33 , 34 ]. Though I would agree with the statement that well conducted and solid descriptive studies contextualizing and highlighting new data and perspectives are worthier than hypotheses-driven studies pursuing hypotheses for the sake of confirming already known relationships and facts in an anachronistic or non-contextualized way [ 32 , 35 ].

However, analysing descriptive data for novelty is not simple and requires extensive background knowledge because the tradition of reporting the use of biodiversity by human societies is as old as written history and an immense quantity of recorded data exists. This complicates data accession, handling, and assessment. The inherent difficulty of assessing novelty of ethnomedical survey papers has been noted by Verpoorte in 2008 who proposed the use of a ‘repository’ (database) where the list of plant species and associated data can be integrated systematically, organized in a way that information for specific taxa or uses can be retrieved easily [ 31 ]. A brief paper mentioning methodological aspects and providing background data together with a short discussion was suggested to be published along with the database entry. However, this idea has not caught on. A Spanish initiative, however, has realized a reasonable way forward. Besides a national inventory database including traditional knowledge related to biodiversity that is based on descriptive reports, an online interactive platform was created that allows users to submit personal knowledge related to biodiversity and retrieve specific information [ 36 ].

While open databases allow for information exchange and their (changing) content for the formulation of hypotheses, Reyes-Garcia has correctly pointed out that results obtained from hypotheses-driven studies do not automatically translate to approved policies or scientific reorientations [ 33 ].  Here I must acknowledge that neither do experimental studies. The strengths of ethnobiology and ethnomedicine lie in the possibilities to “draw on theories and methods from the natural sciences, the social sciences, and the humanities” [ 33 ]. The flip side of this asset is that the vast breath of ethnobiology potentiates the complexity of seemingly simple research questions augmenting the possibility for overlooking or not being able to account for important confounders. Here lie the benefits of experiments. In experiments variables can be controlled, providing evidence of additional and specific support in favour or against theories and hypotheses. Ethnobiologists often blindly rely on their findings or on the motivation of researchers with different backgrounds and from different disciplines to pick up and draw on their data for experimental research, instead of taking on the challenge themselves and bring their research to the next level. I argue that by including experimental approaches and engaging in translational research next to describing reality and testing hypotheses the contribution of ethnobiology to the Sustainable Development Goals (SDGs) could be more relevant.

Clearly not all hypothesis testing, and experiments are automatically constructive. Lakatos proposed to focus on research programmes instead on isolated hypotheses as the descriptive unit of achievements [ 5 ] because research programmes have “auxiliary hypotheses” and a problem-solving machinery serving as a “protecting belt” in place. In the case of interdisciplinary research programmes such as ethnobiology, ethnobotany and ethnopharmacology the protecting disciplines are biology, history, phytochemistry, pharmacology, medicine, cultural anthropology, ecology, agronomy, and economy, including all their methodological and experimental approaches [ 35 ].

Experimental studies in the context of ethnobiology

Probably conditioned by Brent Berlin’s studies (e.g., [ 37 ]), for me ethnobiology is closely tied to human interpretation and classification of environmental sensory inputs and the perception of taste, smell, chemesthesis, vision, acoustics, and touch. Berlin and Kay’s research that led to the proposal of basic colour terms as a biological law was based on an experimental approach [ 38 ]. The proposed rule about the lexicalization of the colour space associated with stages of linguistic evolution got later relativized by Berlin and Kay themselves and by others [ 39 ] but breached a new dimension in ethnobiological research.

It was a natural experiment that lent support to the hypothesis that natural views as opposed to urban sceneries, may have a restorative effect. Patients assigned to a hospital room with a window view on trees were discharged earlier, required less analgesic medication, and suffered from fewer postoperative complications [ 40 ]. The positive effect on general health and well-being of practicing Shinrin-yoku (forest bathing) has been assessed by clinical trials [ 41 ]. This practice of mindful engagement with sensory stimuli emitted by forest environments originated in Japan. For instance, a comparative study of the physiological and psychological effects of Shinrin-yoku suggests a positive outcome on mental health and blood pressure [ 42 ]. A simultaneous contribution of different factors such as physical activity, overall relaxing effect of acoustic signals [ 43 ], green environment [ 44 ], the pharmacologic effect of plant volatiles and the volatilome [ 45 ] are plausible. Music is a universal cultural achievement used in healing rituals and ceremonies [ 46 ] and for directing emotions in general (e.g., film industry). Cumulative experimental evidence supports the idea that music has therapeutic potential [ 47 ] (especially for improving cognition and memory with patients suffering from dementia and Alzheimer’s disease [ 48 , 49 ].

In the specific case of forest bathing experiments could help to assess efficacy of individual factors, including their intensity or dose, and their potentiating and synergistic effects lending additional scientific credit to this practice. On the contrary, homeopathy, a more recent alternative and complementary form of medicine that was invented ad hoc has not shown any efficacy beyond the placebo effect, i.e., the meaning response [ 50 , 51 ]. Evidence-based data is important for informing practitioners, patients, and social security to allow for informed health care choices and health care provision. Clinical studies on the therapeutic efficacy of sensory inputs serves decision making so that, instead of getting prescribed homeopathic medicines or tranquillizers, patients eventually get prescribed a walk in the woods or a combination of different treatments. A meta-analysis including experimental studies found evidence for the efficacy of smell-training on the recovery of olfactory loss [ 52 ]. Olfactory loss (anosmia) and taste loss were also frequent symptoms of COVID-19 and found to be the only symptom associated with depressed mood and anxiety following infection [ 53 ]. A systematic review based on experimental studies highlighted that in general, depressed patients had increased olfactory dysfunction compared to healthy participants while patients with impaired olfactory performance showed depressive symptoms progressing in severity with increasing olfactory dysfunction [ 54 ]. On the other hand, aromatherapy was found to be effective in clinical trials with patients suffering from anxiety and stress [ 55 ]. There is thus substantial experimental evidence stemming from a variety of approaches, experiments and perspectives that spending time in nature and the frequent use of aromatic herbs in the treatment of psychological problems in traditional medicine [ 56 , 57 , 58 ] has an evidence base. I think this is very nice to know beyond any personal preferences or morbidities.

Also, taste and flavour properties of botanical drugs are often reported to be important selection cues in traditional medicine [ 14 , 59 , 60 , 61 , 62 ]. However, chemosensory qualities in ethnobiological studies are rarely experimentally assessed with the help of double-blind tasting panels and by challenging research participants with samples. Conducting a tasting panel can be fun and provides much more reliable data than simply asking for taste and flavour properties trying to retrieve participants’ memories. In fact, plant drugs can elicit a range of chemosensory perceptions and they do so to varying degrees. Recently we used chemosensory qualities of 700 botanical drugs assessed by 11 panel participants to predict therapeutic uses as described in an ancient medical text. The results, corrected for shared ancestry of botanical species, suggest that chemosensory perception and perceived physiologic effects guided ancient therapeutic knowledge linking it to modern pharmacology albeit aetiologies have completely changed [ 14 ]. Experimental evidence also suggests that it is not simply bitter which is the ‘better’ as suggested [ 62 ] but that those bitter tasting edible herbs are concomitantly salty or umami in taste which makes them more palatable and acceptable for food [ 63 ].

Especially in medicine many new discoveries were made through experimentations, evaluated by means of standardized experiments and due to serendipity in the context of experiments [ 64 , 65 ]. Without medical and pharmacological experiments most of us would not sit here and read these lines. If the claims made in traditional medicine were all correct there would be no need for ethnopharmacology or evidence-based medicine at all. The panacea would be within anyone’s reach, and we would probably live in a brave new world [ 66 ]. However, this is not the case and although indigenous people are generally not waiting for field researchers to poke their nose into community affairs, once accepted as a foreign investigator or collaborator of their medicinal customs, indigenous people are interested in knowing whether their medicines are effective (personal observation). Often, it is impossible to give an informed response because data are not available for all botanical drugs, or they are not meaningful for the traditional context (e.g., antioxidant in vitro effects). This anecdote highlights that also indigenous people may nurture doubts about the efficacy of their medicines and that there exists interest in knowing the other, Western perspective, as well. In this context it is important to distinguish between efficacy which describes the capacity of an agent to produce an effect under standardized conditions and effectiveness, describing the therapeutic success in real-life practice and within a cultural setting [ 67 , 68 ]. Traditional use can give some indications about safety profiles but adverse effects that manifest with delay such as hepatotoxicity or nephropathy (kidney disease) are not easily recognized. For many indications effectiveness is even more difficult to appreciate because of confounding factors such as severity of symptoms, self-limiting diseases (such as infections) and the restorative power of the human body. Therefore, ethnopharmacologists design laboratory experiments reflecting as accurately as possible the traditional application to provide information about the medicine’s efficacy and possible adverse effects [ 69 , 70 ].

Importantly, descriptive studies besides informing experimental studies also serve as a basis for meta-analyses and review papers that consider associated experimental studies. Lack of systematic reviews about experimental data providing evidence or its absence regarding traditional and complementary medicine in Mesoamerica and other regions of the world is linked with insufficient health care strategies and culturally pertinent health materials [ 58 ]. Integrative medicine is an important pillar for achieving universal health coverage (UHC) for underserved populations and access to appropriate medical care is central for achieving Sustainable Development Goal three (SDG 3 “Ensure healthy lives and promote well-being for all at all ages”; https://sdgs.un.org/goals/goal3 ) of the UN Agenda 2030 [ 71 , 72 ]. In order to fill this gap, we used a consensus approach based on the Mesoamerican Medicinal Plant Database to reflect acceptability and therapeutic importance for a critical assessment of the available pharmacological and toxicological data of botanical drugs [ 58 ].

The development of medicines for chronic illnesses and life-promoting medications that can be commercialized in the affluent Western world are appreciated more by stakeholders. In urban areas food supplements and remedies for life-style diseases are important product sectors sourced from herbal drugs and plant-based medicines. However, in a situation of health emergency termed double-burden of disease [ 73 ] marginalized populations, in addition to combatting insurging life-style diseases, continue to fight neglected infectious diseases with botanical drugs [ 58 , 74 ]. Investigations of traditional treatments of rare and neglected parasitic and infectious diseases [ 75 , 76 , 77 , 78 ] deserve more attention by ethnobiologists and ethnopharmacologists because major pharmaceutical companies show little interest in developing medications for a segment of the population with limited purchasing power [ 79 ]. Clinical studies involving humans are beyond what single academic groups can do. A possible way to assess the effectiveness of traditional medicines is by conducting retrospective treatment outcome (RTO) studies (open field experiments), where defined disease-related parameters are retrospectively assessed for clinical outcomes [ 80 ]. Food drugs qualify as good candidates for RTO studies because they generally show a high acceptance and are associated with low toxicity. Also, the field of veterinary research is accessible for ethnobiologists [ 81 ]. For instance, a placebo and antibiotic standard treatment-controlled study assessed the effect of garlic ( Allium sativum L.) on weight gain and postweaning diarrhoea in piglets. Garlic showed positive effects on weight gain but no prophylactic effect on postweaning diarrhoea leaving the search for anti-diarrhoeal herbal products able to reduce antibiotic treatment open [ 82 ].

The therapeutic value of crude animal drugs is often limited to culture-specific symbolism [ 83 ]. Belief in therapeutic effectiveness of animal products prompts illegal trade resulting in a negative impact on the probability of survival of wild animal populations as well as the welfare of individual animals [ 84 , 85 ]. Redirecting therapeutic demand towards products without conservation issues are more likely to be crowned by species conservation success than simply trying to reduce demand without offering alternatives. It was shown that Traditional Chinese Medicine (TCM) users remained unaffected by information appealing to reduced consumption but that especially the more regular TCM users had a positive attitude towards the idea of buying alternative botanical products [ 86 ]. In another study, using an online survey directed to 1000 medical practitioners in China, 86% of respondents reported the willingness to substitute animal-based materials with botanical drugs, provided, that safety and effectiveness was comparable [ 87 ]. Though it is challenging to find culturally acceptable plant-based substitutes this might be achieved in close collaboration with traditional healers, vendors, and an experimental assessment of consumers preferences. This proposal is not about trumping indigenous peoples’ rights to maintain their traditional health-care practises, but to actively involve them in generating information protecting their environment and traditions.

Conclusions

While we should avoid transfiguring modern knowledge and science as categorically superior over traditional knowledge there is also no need to romanticize traditional knowledge. Which approaches, strategies and knowledge can provide the best solutions depends always on the specific context. However, for achieving most of the SDGs there is no way around insights gained from experiments. There is much space for ethnobiologists for engaging in experimental research dedicated to sensory biology and health, traditional medicine, ethnopharmacology and ethnoveterinary research, traditional ecological knowledge, domestication of wild edible plant species, food preferences (landraces, wild vegetables and fruits versus commercial crops, evaluation of traditional recipes), pet-therapy (healing with animals), aromatherapy as well as the analysis of music, or incense and smoke constituents in the context or healing rituals. For an impactful ethnobiology, as with most scientific fields, broad interdisciplinary knowledge and a research agenda including next to descriptive, and hypothesis-driven studies also experimental work is essential. Though ethnobiology and TEK have a strong spiritual component, science as practiced today cannot capture it. It is important that ethnobiology avoids spiritual bypassing and that it builds its science on evidence and not on opinions.

Availability of data and materials

Not applicable.

Abbreviations

Drug extract ratio

European medicines agency

Ethyl alcohol

Sustainable development goal

Traditional Chinese medicine

Traditional ecological knowledge

Diamond J. Guns, Germs, and Steel. The Fates of Human Societies. New York/London: W.W. Norton and Company; 2005.

Mesoudi A, Whiten A. The multiple roles of cultural transmission experiments in understanding human cultural evolution. Philos Trans R Soc Lond B Biol Sci. 2008;363(1509):3489–501.

Article   PubMed   PubMed Central   Google Scholar  

Shadish WR, Cook TD, Campbell DT. Experimental and quasi-experimental designs for generalized causal inference. Boston: Houghton Mifflin; 2002.

Google Scholar  

Bernard HR. Research methods in anthropology—qualitative and quantitative approaches. Chapter 5: Research design: experiments and experimental thinking. New York: Altamira Press; 2006.

Lakatos I. The methodology of scientific research programmes. Philosophical papers, vol. 1. Cambridge: Cambridge University Press; 1989.

Pliny. Natural History, Volume I: Books 1–2. Translated by H. Rackham. Loeb Classical Library 330. Cambridge, MA: Harvard University Press; 1938.

Rousseau JJ. Abhandlung über den Ursprung und die Grundlagen der Ungleichheit unter den Menschen. Stuttgart: Reclam; 2012.

Schultes RE, Raffauf RF. The healing forest: medicinal and toxic plants of the northwest Amazonia. Portland: Dioscorides Press; 1990.

Bye R, Linares E, Estrada E. Biological diversity of medicinal plants in Mexico. In: Arnason, et al. (Eds.), Phytochemistry of medicinal plants pp. 65–82. New York: Plenium Press; 1995.

Hobsbawm E, Ranger T. The invention of tradition. Cambridge: Cambridge University Press; 2012.

Book   Google Scholar  

Richerson PJ, Christiansen MH. Cultural evolution: society, technology, language, and religion (Strüngmann forum reports). Cambridge: MIT Press Ltd; 2013.

Helmstädter A, Staiger C. Traditional use of medicinal agents: a valid source of evidence. Drug Discov Today. 2014;19(1):4–7.

Article   PubMed   Google Scholar  

Baba KM. Irrigation development strategies in sub-Saharan Africa: a comparative study of traditional and modern irrigation systems in Bauchi State of Nigeria. Agric Ecosyst Environ. 1993;45:47–58.

Article   Google Scholar  

Leonti M, Baker J, Staub P, Casu L, Hawkins J. Taste shaped the use of botanical drugs. Elife. 2024;12:RP90070.

Wichtl M. Teedrogen und Phytopharmaka: Ein Handbuch für die Praxis auf wissenschaftlicher Grundlage. 4th ed. Stuttgart: Wissenschaftliche Verlagsgesellschaft; 2002.

Lardos A, Heinrich M. Continuity and change in medicinal plant use: the example of monasteries on Cyprus and historical iatrosophia texts. J Ethnopharmacol. 2013;150(1):202–14.

Dal Cero M, Saller R, Leonti M, Weckerle CS. Trends of medicinal plant use over the last 2000 years in central Europe. Plants. 2022;12(1):135.

Sõukand R, Kalle R, Prakofjewa J, Sartori M, Pieroni A. The importance of the continuity of practice: ethnobotany of Kihnu island (Estonia) from 1937 to 2021. Plants People Planet. 2024;6:186–96.

EMA, (European Medicines Agency). https://www.ema.europa.eu/en/search?search_api_fulltext=Committee%20on%20Herbal%20Medicinal%20Products%20%28HMPC%29 ; 2024.

Desai S, Dubey A. Caste in 21st Century India: competing narratives. Econ Polit Wkly. 2012;46(11):40–9.

PubMed   PubMed Central   Google Scholar  

Wieacker F. The importance of roman law for western civilization and western legal thought. 4BC Int’l & Comp L Rev. 1981;4:257.

Glover S, Gibson K. “Made in Italy”; how culture and history has shaped modern Italian business environment, political landscape, and professional organizations. J Bus Divers. 2017;17(1):21–8.

Parisi ML, Schiantarelli F, Sembenelli A. Productivity, innovation and R&D: micro evidence for Italy. Eur Econ Rev. 2006;50(8):2037–61.

Hartel T, Fischer J, Shumi G, Apollinaire W. The traditional ecological knowledge conundrum. Trends Ecol Evol. 2023;38(3):211–4.

Gómez-Baggethun E, Mingorría S, Reyes-García V, Calvet L, Montes C. Traditional ecological knowledge trends in the transition to a market economy: empirical study in the Doñana natural areas. Conserv Biol. 2010;24(3):721–9.

Agrarbericht. https://agrarbericht.ch/de/politik/direktzahlungen/finanzielle-mittel-fuer-direktzahlungen ; 2023.

Poncet A, Schunko C, Vogl CR, Weckerle CS. Local plant knowledge and its variation among farmer’s families in the Napf region, Switzerland. J Ethnobiol Ethnomed. 2021;17(1):53.

Weiss R. Volkskunde der Schweiz. Grundriss, pp. 310. 2. Auflage, Erlenbach-Zürich: Rentsch-Verlag; 1978.

Bucher S. Bevölkerung und Wirtschaft des Amtes Entlebuch im 18. Jahrhundert. Eine Regional-studie zur Sozial- und Wirtschaftsgeschichte der Schweiz im Ancien Régime. Luzerner Historische Veröffentlichungen, Band 1. p 250. Luzern: Rex Verlag; 1974.

Fernández-Llamazares Á, Lepofsky D, Armstrong CG, Brondizio ES, Gavin MC, Lertzman K, Lyver POB, Nicholas GP, et al. Scientists’ warning to humanity on threats to indigenous and local knowledge systems. J Ethnobiol. 2021;41(2):144–69.

Verpoorte R. Primary data are the basis of all science! J Ethnopharmacol. 2012;139(3):683–4.

Łuczaj Ł. Descriptive ethnobotanical studies are needed for the rescue operation of documenting traditional knowledge. J Ethnobiol Ethnomed. 2023;19(1):37.

Reyes-García V. Beyond artificial academic debates: for a diverse, inclusive, and impactful ethnobiology and ethnomedicine. J Ethnobiol Ethnomed. 2023;19(1):36.

Albuquerque UP, Nóbrega Alves RRD. Integrating depth and rigor in ethnobiological and ethnomedical research. J Ethnobiol Ethnomed. 2024;20(1):6.

Leonti M, Casu L, de Oliveira Martins DT, Rodrigues E, Benítez G. Ecological theories and major hypotheses in ethnobotany: their relevance for ethnopharmacology and pharmacognosy in the context of historical data. Rev Bras Farmacogn. 2020;30:451–66.

Reyes-García V, Benyei P, Aceituno-Mata L, Gras A, Molina M, Tardío J, Pardo-de-Santayana M. Documenting and protecting traditional knowledge in the era of open science: Insights from two Spanish initiatives. J Ethnopharmacol. 2021;278:114295.

Berlin B, Breedlove DE, Raven PH. Folk taxonomies and biological classification. Science. 1966;154(3746):273–5.

Article   CAS   PubMed   Google Scholar  

Berlin B, Kay P. Basic color terms: their universality and evolution. Berkley: University of California Press; 1969.

Saunders B. Revisiting basic color terms. J R Anthropol Inst. 2000;6(1):81–99.

Ulrich RS. View through a window may influence recovery from surgery. Science. 1984;224(4647):420–1.

Doran-Sherlock R, Devitt S, Sood P. An integrative review of the evidence for Shinrin-Yoku (Forest Bathing) in the management of depression and its potential clinical application in evidence-based osteopathy. J Bodyw Mov Ther. 2023;35:244–55.

Furuyashiki A, Tabuchi K, Norikoshi K, Kobayashi T, Oriyama S. A comparative study of the physiological and psychological effects of forest bathing (Shinrin-yoku) on working age people with and without depressive tendencies. Environ Health Prev Med. 2019;24(1):46.

Song I, Baek K, Kim C, Song C. Effects of nature sounds on the attention and physiological and psychological relaxation. Urban For Urban Green. 2023;86:127987.

Briki W, Majed L. Adaptive effects of seeing green environment on psychophysiological parameters when walking or running. Front Psychol. 2019;10:252.

Maffei ME, Gertsch J, Appendino G. Plant volatiles: production, function and pharmacology. Nat Prod Rep. 2011;28(8):1359–80.

Gouk P. Musical healing in cultural contexts. London: Routledge; 2000.

Chanda ML, Levitin DJ. The neurochemistry of music. Trends Cogn Sci. 2013;17(4):179–93.

Moreira SV, Justi FRDR, Moreira M. Can musical intervention improve memory in Alzheimer’s patients? Evidence from a systematic review. Dement Neuropsychol. 2018;12(2):133–42.

Moreno-Morales C, Calero R, Moreno-Morales P, Pintado C. Music therapy in the treatment of dementia: a systematic review and meta-analysis. Front Med (Lausanne). 2020;7:160.

Shang A, Huwiler-Müntener K, Nartey L, Jüni P, Dörig S, Sterne JA, Pewsner D, Egger M. Are the clinical effects of homoeopathy placebo effects? Comparative study of placebo-controlled trials of homoeopathy and allopathy. Lancet. 2005;366(9487):726–32.

Singh S, Ernst E. Trick or treatment: the undeniable facts about alternative medicine. New York: WW Norton & Co Inc; 2009.

Sorokowska A, Drechsler E, Karwowski M, Hummel T. Effects of olfactory training: a meta-analysis. Rhinology. 2017;55(1):17–26.

Speth MM, Singer-Cornelius T, Oberle M, Gengler I, Brockmeier SJ, Sedaghat AR. Mood, anxiety and olfactory dysfunction in COVID-19: evidence of central nervous system involvement? Laryngoscope. 2020;130(11):2520–5.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Kohli P, Soler ZM, Nguyen SA, Muus JS, Schlosser RJ. The association between olfaction and depression: a systematic review. Chem Senses. 2016;41(6):479–86.

Perry N, Perry E. Aromatherapy in the management of psychiatric disorders: clinical and neuropharmacological perspectives. CNS Drugs. 2006;20:257–80.

Trotter RT. Susto: the context of community morbidity patterns. Ethnology. 1982;1982(21):215–26.

Hunn ES. A Zapotec natural history: trees, herbs, and flowers, birds, beasts, and bugs in the life of San Juan Gbëë. Tucson: University of Arizona Press; 2008. p. 2008.

Geck MS, Cristians S, Berger-González M, Casu L, Heinrich M, Leonti M. Traditional herbal medicine in mesoamerica: toward its evidence base for improving universal health coverage. Front Pharmacol. 2020;11:1160.

Casagrande DG. Human taste and cognition in tzeltal maya medicinal plant use. J Ecol Anthropol. 2000;4:57–69.

Molares S, Ladio A. Chemosensory perception and medicinal plants for digestive ailments in a Mapuche community in NW Patagonia, Argentina. J Ethnopharmacol. 2009;123(3):397–406.

Dragos D, Gilca M. Taste of phytocompounds: a better predictor for ethnopharmacological activities of medicinal plants than the phytochemical class? J Ethnopharmacol. 2018;220:129–46.

Pieroni A, Morini G, Piochi M, Sulaiman N, Kalle R, Haq SM, Devecchi A, Franceschini C, Zocchi DM, Migliavada R, Prakofjewa J, Sartori M, Krigas N, Ahmad M, Torri L, Sõukand R. Bitter is better: wild greens used in the blue Zone of Ikaria, Greece. Nutrients. 2023;15(14):3242.

Leonti M, Cabras S, Castellanos Nueda ME, Casu L. Food drugs as drivers of therapeutic knowledge and the role of chemosensory qualities. J Ethnopharmacol. 2024;28(328):118012.

Mann RD. Modern drug use: an enquiry on historical principles. Lancaster: MTP Press Limited; 1984.

Le Fanu J. The rise and fall of modern medicine. London: Hachette Digital; 2011.

Huxley A. Brave new world. London: Triad Grafton Books; 1932.

Last J, Spasoff RA, Harris S. A dictionary of epidemiology. 4th ed. Oxford: Oxford University Press; 2001.

Witt CM. Clinical research on traditional drugs and food items—the potential of comparative effectiveness research for interdisciplinary research. J Ethnopharmacol. 2013;147:254–8.

Gertsch J. How scientific is the science in ethnopharmacology? Historical perspectives and epistemological problems. J Ethnopharmacol. 2009;122(2):177–83.

Bruhn JG, Rivier L. Ethnopharmacology—a journal, a definition and a society. J Ethnopharmacol. 2019;242:112005.

UN General Assembly. Universal declaration of human rights.: New York City: UN General Assembly; 1948.

UN General Assembly. Transforming our world: the 2030 Agenda for sustainable development. New York City: UN General Assembly; 2015.

Marshall SJ. Developing countries face double burden of disease. Bull World Health Organ. 2004;82(7):556.

Engels D, Zhou XN. Neglected tropical diseases: an effective global response to local poverty-related disease priorities. Infect Dis Poverty. 2020;9(1):10.

Odonne G, Musset L, Cropet C, Philogene B, Gaillet M, Tareau MA, Douine M, Michaud C, Davy D, Epelboin L, Lazrek Y, Brousse P, Travers P, Djossou F, Mosnier E. When local phytotherapies meet biomedicine. Cross-sectional study of knowledge and intercultural practices against malaria in Eastern French Guiana. J Ethnopharmacol. 2021;279:114384.

Houël E, Ginouves M, Azas N, Bourreau E, Eparvier V, Hutter S, Knittel-Obrecht A, Jahn-Oyac A, Prévot G, Villa P, Vonthron-Sénécheau C, Odonne G. Treating leishmaniasis in Amazonia, part 2: multi-target evaluation of widely used plants to understand medicinal practices. J Ethnopharmacol. 2022;289:115054.

Salm A, Krishnan SR, Collu M, Danton O, Hamburger M, Leonti M, Almanza G, Gertsch J. Phylobioactive hotspots in plant resources used to treat Chagas disease. iScience. 2021;24(4):102310.

Elmi A, Said Mohamed A, Mérito A, Charneau S, Amina M, Grellier P, Bouachrine M, Lawson AM, Abdoul-Latif FM, Kordofani MAY. The ethnopharmacological study of plant drugs used traditionally in Djibouti for malaria treatment. J Ethnopharmacol. 2024;325:117839.

Feasey N, Wansbrough-Jones M, Mabey DC, Solomon AW. Neglected tropical diseases. Br Med Bull. 2010;93:179–200.

Willcox ML, Graz B, Falquet J, Diakite C, Giani S, Diallo D. A “reverse pharmacology” approach for developing an anti-malarial phytomedicine. Malar J. 2011;10(Suppl 1):8.

Mayer M, Vogl CR, Amorena M, Hamburger M, Walkenhorst M. Treatment of organic livestock with medicinal plants: a systematic review of European ethnoveterinary research. Forsch Komplementmed. 2014;21(6):375–86.

PubMed   Google Scholar  

Ayrle H, Nathues H, Bieber A, Durrer M, Quander N, Mevissen M, Walkenhorst M. Placebo-controlled study on the effects of oral administration of Allium sativum L. in postweaning piglets. Vet Rec. 2019;184(10):316.

Still J. Use of animal products in traditional Chinese medicine: environmental impact and health hazards. Complement Ther Med. 2003;11(2):118–22.

Starr C, Nekaris KAI, Streicher U, Leung L. Traditional use of slow lorises Nycticebus bengalensis and N. pygmaeus in Cambodia: an impediment to their conservation. Endange Spec Res. 2010;12:17–23.

Baker SE, Cain R, van Kesteren F, Zommers ZA, D’Cruze N, Macdonald DW. Rough trade: animal welfare in the global wildlife trade. Bioscience. 2013;63:928–38.

Moorhouse TP, Coals PGR, D’Cruze NC, Macdonald DW. Reduce or redirect? Which social marketing interventions could influence demand for traditional medicines. Biol Cons. 2020;242:108391.

Moorhouse TP, D’Cruze NC, Sun E, Elwin A, Macdonald DW. What are TCM doctors’ attitudes towards replacing animal-origin medicinal materials with plant-origin alternatives? Glob Ecol Conserv. 2020;34:e02045.

Download references

No funding received.

Author information

Authors and affiliations.

Department of Biomedical Sciences, University of Cagliari, Cittadella Universitaria, 09042, Monserrato, CA, Italy

Marco Leonti

You can also search for this author in PubMed   Google Scholar

Contributions

M.L. conceived and wrote the manuscript

Corresponding author

Correspondence to Marco Leonti .

Ethics declarations

Ethics approval, competing interests.

The author declares no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Leonti, M. Are we romanticizing traditional knowledge? A plea for more experimental studies in ethnobiology. J Ethnobiology Ethnomedicine 20 , 56 (2024). https://doi.org/10.1186/s13002-024-00697-6

Download citation

Received : 02 April 2024

Accepted : 22 May 2024

Published : 26 May 2024

DOI : https://doi.org/10.1186/s13002-024-00697-6

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Experimental studies ethnobiology
• Traditional knowledge
• Local knowledge
• Sustainability
• Knowledge dynamics

Journal of Ethnobiology and Ethnomedicine

ISSN: 1746-4269

• General enquiries: [email protected]