hypothesis graphs

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\(H_0\)) and an alternative hypothesis (\(H_a\)).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

• At this point we can write hypotheses for a single mean (\(\mu\)), paired means(\(\mu_d\)), a single proportion (\(p\)), the difference between two independent means (\(\mu_1-\mu_2\)), the difference between two proportions (\(p_1-p_2\)), a simple linear regression slope (\(\beta\)), and a correlation (\(\rho\)). 
• The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
• The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., \(\mu_0\) and \(p_0\)). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., \(p\) and \(\mu\)).  The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

• Quality Improvement
• Talk To Minitab

Understanding Hypothesis Tests: Why We Need to Use Hypothesis Tests in Statistics

Topics: Hypothesis Testing , Data Analysis , Statistics

Hypothesis testing is an essential procedure in statistics. A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. When we say that a finding is statistically significant, it’s thanks to a hypothesis test. How do these tests really work and what does statistical significance actually mean?

In this series of three posts, I’ll help you intuitively understand how hypothesis tests work by focusing on concepts and graphs rather than equations and numbers. After all, a key reason to use statistical software like Minitab is so you don’t get bogged down in the calculations and can instead focus on understanding your results.

To kick things off in this post, I highlight the rationale for using hypothesis tests with an example.

The Scenario

An economist wants to determine whether the monthly energy cost for families has changed from the previous year, when the mean cost per month was $260. The economist randomly samples 25 families and records their energy costs for the current year. (The data for this example is FamilyEnergyCost and it is just one of the many data set examples that can be found in Minitab’s Data Set Library.)

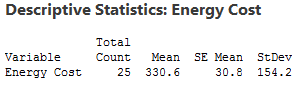
I’ll use these descriptive statistics to create a probability distribution plot that shows you the importance of hypothesis tests. Read on!

The Need for Hypothesis Tests

Why do we even need hypothesis tests? After all, we took a random sample and our sample mean of 330.6 is different from 260. That is different, right? Unfortunately, the picture is muddied because we’re looking at a sample rather than the entire population.

Sampling error is the difference between a sample and the entire population. Thanks to sampling error, it’s entirely possible that while our sample mean is 330.6, the population mean could still be 260. Or, to put it another way, if we repeated the experiment, it’s possible that the second sample mean could be close to 260. A hypothesis test helps assess the likelihood of this possibility!

Use the Sampling Distribution to See If Our Sample Mean is Unlikely

For any given random sample, the mean of the sample almost certainly doesn’t equal the true mean of the population due to sampling error. For our example, it’s unlikely that the mean cost for the entire population is exactly 330.6. In fact, if we took multiple random samples of the same size from the same population, we could plot a distribution of the sample means.

A sampling distribution is the distribution of a statistic, such as the mean, that is obtained by repeatedly drawing a large number of samples from a specific population. This distribution allows you to determine the probability of obtaining the sample statistic.

Fortunately, I can create a plot of sample means without collecting many different random samples! Instead, I’ll create a probability distribution plot using the t-distribution , the sample size, and the variability in our sample to graph the sampling distribution.

Our goal is to determine whether our sample mean is significantly different from the null hypothesis mean. Therefore, we’ll use the graph to see whether our sample mean of 330.6 is unlikely assuming that the population mean is 260. The graph below shows the expected distribution of sample means.

You can see that the most probable sample mean is 260, which makes sense because we’re assuming that the null hypothesis is true. However, there is a reasonable probability of obtaining a sample mean that ranges from 167 to 352, and even beyond! The takeaway from this graph is that while our sample mean of 330.6 is not the most probable, it’s also not outside the realm of possibility.

The Role of Hypothesis Tests

We’ve placed our sample mean in the context of all possible sample means while assuming that the null hypothesis is true. Are these results statistically significant?

As you can see, there is no magic place on the distribution curve to make this determination. Instead, we have a continual decrease in the probability of obtaining sample means that are further from the null hypothesis value. Where do we draw the line?

This is where hypothesis tests are useful. A hypothesis test allows us quantify the probability that our sample mean is unusual.

For this series of posts, I’ll continue to use this graphical framework and add in the significance level, P value, and confidence interval to show how hypothesis tests work and what statistical significance really means.

• Part Two: Significance Levels (alpha) and P values
• Part Three: Confidence Intervals and Confidence Levels

If you'd like to see how I made these graphs, please read: How to Create a Graphical Version of the 1-sample t-Test .

You Might Also Like

• Trust Center

© 2023 Minitab, LLC. All Rights Reserved.

• Terms of Use
• Privacy Policy
• Cookies Settings

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8: Hypothesis Testing with One Sample

• Last updated
• Save as PDF
• Page ID 10969

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

One job of a statistician is to make statistical inferences about populations based on samples taken from the population. Confidence intervals are one way to estimate a population parameter. Another way to make a statistical inference is to make a decision about a parameter. For instance, a car dealer advertises that its new small truck gets 35 miles per gallon, on average. A tutoring service claims that its method of tutoring helps 90% of its students get an A or a B. A company says that women managers in their company earn an average of $60,000 per year.

• 8.1.1: Null and Alternative Hypotheses
• 8.1.2: Outcomes and the Type I and Type II Errors
• 8.1.3: Distribution Needed for Hypothesis Testing
• 8.1.4: Rare Events, the Sample, Decision and Conclusion
• 8.1.5: Additional Information on Hypothesis Tests
• 8.2: Hypothesis Test Examples for Means The hypothesis test itself has an established process. This can be summarized as follows: Determine H0 and Ha. Remember, they are contradictory. Determine the random variable. Determine the distribution for the test. Draw a graph, calculate the test statistic, and use the test statistic to calculate the p-value. (A z-score and a t-score are examples of test statistics.) Compare the preconceived α with the p-value, make a decision (reject or do not reject H0), and write a clear conclusion.
• 8.3: Hypothesis Test Examples for Means with Unknown Standard Deviation The hypothesis test itself has an established process. This can be summarized as follows: Determine H0 and Ha. Remember, they are contradictory. Determine the random variable. Determine the distribution for the test. Draw a graph, calculate the test statistic, and use the test statistic to calculate the p-value. (A z-score and a t-score are examples of test statistics.) Compare the preconceived α with the p-value, make a decision (reject or do not reject H0), and write a clear conclusion.
• 8.4: Hypothesis Test Examples for Proportions The hypothesis test itself has an established process. This can be summarized as follows: Determine H0 and Ha. Remember, they are contradictory. Determine the random variable. Determine the distribution for the test. Draw a graph, calculate the test statistic, and use the test statistic to calculate the p-value. (A z-score and a t-score are examples of test statistics.) Compare the preconceived α with the p-value, make a decision (reject or do not reject H0), and write a clear conclusion.
• 8.E: Distribution Needed for Hypothesis Testing (Optional Exercises)
• 8.E: Hypothesis Testing with One Sample (Optional Exercises)
• 8.E: Null and Alternative Hypotheses (Optional Exercises)
• 8.E: Outcomes and the Type I and Type II Errors (Optional Exercises)
• 8.E: Rare Events, the Sample, Decision and Conclusion (Optional Exercises)

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

9.6 Hypothesis Testing of a Single Mean and Single Proportion

Hypothesis testing of a single mean and single proportion.

Class Time:

• The student will select the appropriate distributions to use in each case.
• The student will conduct hypothesis tests and interpret the results.

Television Survey In a recent survey, it was stated that Americans watch television on average four hours per day. Assume that σ = 2. Using your class as the sample, conduct a hypothesis test to determine if the average for students at your school is lower.

• H 0 : _____________
• H a : _____________
• In words, define the random variable. __________ = ______________________
• The distribution to use for the test is _______________________.
• Determine the test statistic using your data.
• Determine the p -value.
• Do you or do you not reject the null hypothesis? Why?
• Write a clear conclusion using a complete sentence.

Language Survey About 42.3% of Californians and 19.6% of all Americans over age five speak a language other than English at home. Using your class as the sample, conduct a hypothesis test to determine if the percent of the students at your school who speak a language other than English at home is different from 42.3%.

• H 0 : ___________
• H a : ___________
• In words, define the random variable. __________ = _______________
• The distribution to use for the test is ________________

Jeans Survey Suppose that young adults own an average of three pairs of jeans. Survey eight people from your class to determine if the average is higher than three. Assume the population is normal.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics
• Publication date: Sep 19, 2013
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics/pages/9-6-hypothesis-testing-of-a-single-mean-and-single-proportion

© Jun 23, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Null-Hypothesis Testing with Graphs

• First Online: 23 January 2016

Cite this chapter

• Ton J. Cleophas 3 &
• Aeilko H. Zwinderman 4  

99k Accesses

Because biological processes are full of variations, statistics will give no certainties only chances. What chances? Chances that hypotheses are true/untrue. What hypotheses? For example:

our mean effect is not different from a 0 effect,

it is really different from a 0 effect,

it is worse than a 0 effect,

where 0 effect means that your new treatment or any other intervention does not work. Statistics is about estimating such chances/testing such hypotheses. Please note that trials often calculate differences between a test treatment and a control treatment, and, subsequently, test whether this difference is larger than 0. A simple way to reduce a study of two groups of data, and, thus, two means to a single mean and single distribution of data, is to take the difference between the two means and compare it with 0. In Chap. 2 we explained that the data of a trial can be described in the form of a normal distribution graph with SEMs on the x-axis, and that this method is adequate for testing various statistical hypotheses. We will now focus on a very important hypothesis, the null-hypothesis. We will try and make a graph of this null-hypothesis, and then assess whether our result is significantly different from the null-hypothesis.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Author information

Authors and affiliations.

Department of Medicine, Albert Schweitzer Hospital, Dordrecht, The Netherlands

Ton J. Cleophas

Department Epidemiology and Biostatistics, Academic Medical Center, Amsterdam, The Netherlands

Aeilko H. Zwinderman

You can also search for this author in PubMed   Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 2016 Springer International Publishing Switzerland

About this chapter

Cleophas, T.J., Zwinderman, A.H. (2016). Null-Hypothesis Testing with Graphs. In: Clinical Data Analysis on a Pocket Calculator. Springer, Cham. https://doi.org/10.1007/978-3-319-27104-0_3

Download citation

DOI : https://doi.org/10.1007/978-3-319-27104-0_3

Published : 23 January 2016

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-27103-3

Online ISBN : 978-3-319-27104-0

eBook Packages : Biomedical and Life Sciences Biomedical and Life Sciences (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Stats Tools

Student's t-distribution calculator with graph generator

Critical value calculator - student's t-distribution.

This statistical calculator allows you to calculate the critical value corresponding to the Student's t-distribution, you can also see the result in a graph through our online graph generator and if you wish you can download the graph. Just enter the significance value (alpha), degrees of freedom, and left, right, or both tails.

Critical value result

P-value calculator - student's t distribution.

Use our online statistical calculator to calculate the p-value of the Student's t-distribution. You just need to enter the t-value and degrees of freedom and specify the tail. In addition to the p-value, you can get and download the graph created with our graph generator

p-value result

One sample t-test calculator.

The one sample t-test is a statistical hypothesis test calculator, use our calculator to check if you get a statistically significant result or not. To obtain it, fill in the corresponding fields and you will obtain the value of the t-score, p-value, critical value, and the degrees of freedom. You can also download a graph that will display your results in the form of the Student's t-distribution.

T-score result

Two sample t-test calculator.

To determine whether or not the means of two groups are equal, you can use our two-sample t-test calculator that applies the t-test. The results are displayed in a Student's t-distribution plot that you can download. To complete the form, you must include information for both groups, including the mean, standard deviation, sample size, significance level,and whether the test is left, right, or two-tailed.

Common questions related to the Student's t-distribution

In this section, we will try to address the most frequently asked questions about the Student's t-distribution. To give you a fundamental and complementary understanding, we will try to dive into the underlying ideas of the t-distribution. The approach we want to take is to answer the most common questions from students with relevant information. Let's tackle problems simply and offer short and understandable solutions.

Questions related to the student's t-distribution

The formula in relation to the probability density function (pdf) for Student's t-distribution, is given as follows:

Where: π is the pi (approximately 3.14), ν correspond to the degrees of freedom, and Γ is the Euler Gamma function.

A distribution of mean estimates derived from samples taken from a population is what is, by definition, the Student's t-distribution. The t-distribution, commonly known as the Student's t-distribution, is a type of symmetric bell-shaped distribution, it has a lower height but a wider spread than the normal distribution. It is symmetric around 0, but the t-distribution has a wider spread than the typical normal distribution curve, or put another way, the t-distribution has a high standard deviation. The variability of individual observations around their mean is measured by a standard deviation. The degrees of freedom (df) are n - 1. So, df is equal to n – 1, where n is the sample size. The degrees of freedom affect the shape of each t distribution curve.

When the sample size is less than 30 and the population standard deviation is unknown, the t-distribution is utilized in hypothesis testing. It is helpful when the sample size is relatively small or the population standard deviation is unknown. It resembles the normal distribution more closely as sample size grows.

A statistical metric known as the standard deviation is used to quantify the distances between each observation and the mean in a set of data. The standard deviation calculates the degree of dispersion or variability. In other words, it's used to calculate how much a random variable deviates from the mean.

The t-value and t-score have the same meanings. It is one of the relative position measurements. By definition, a value of t defines the location of a continuous random variable, X, in relation to the number of standard deviations from the mean.

The significance level is a point in the normal distribution that must be understood in order to either reject or fail to reject the null hypothesis and to assess whether or not the results are statistically significant. If you decide to make use of our t distribution calculator , you must enter the alpha value corresponding to the significance level. The most common alpha values are 0.1, 0.05 or 0.01. Generally, the most common confidence intervals are: 90%, 95% and 99% (1 − α is the confidence level).

The p-value is a probability with a value ranging from 0 to 1. It is used to test a hypothesis. As an example, in some experiment, we choose the significance level value as 0.05, in this case, the alternative hypothesis is more likely to be supported by stronger evidence when the p-value is less than 0.05 (p-value < 0.05), in case the p-value is high (p-value > 0.05), the probability of accepting the null hypothesis is also high.

The z and t distributions are symmetric and bell-shaped. However, what most characterizes the t distribution are its tails, since they are heavier than in the normal distribution. Furthermore, it can be seen that there are more values in the t-distribution located at the ends of the tail instead of the center of the distribution. You must have the population standard deviation to use the standard normal or z distribution. On the other hand, one of the important conditions for adopting the t distribution is that the population variance is unknown

The t-test , it is a parametric comparison test, is used if the means of two samples are compared using a hypothesis test, if they are independent, from two separate samples, or dependent, a sample evaluated at two different times. The procedure is carried out to evaluate if the differences between the means are significant, determining that they are not due to chance.

To interpret the results of a t-test, you can compare the t-score to the critical value and consider the p-value. A high t-score and low p-value indicate that there is a statistically significant difference between the two means, while a low t-score and high p-value indicate that the difference is not statistically significant. The degrees of freedom and the significance level (alpha) also play a role in determining the critical value and the p-value.

A one sample t-test is a statistical procedure used to test whether the mean of a single sample is significantly different from a hypothesized mean. It is used to determine whether the sample comes from a population with a mean that is different from the hypothesized mean. To perform a one sample t-test using a calculator, you need to input the following information: The sample data, including the mean and standard deviation. The hypothesized mean. The significance level (alpha). The type of tail (left, right, or two-tailed). The calculator will then calculate the t-score and p-value based on this information, and will also provide the critical value and degrees of freedom. To interpret the results, you can compare the t-score to the critical value and consider the p-value. If the t-score is greater than the critical value and the p-value is less than the significance level, you can reject the null hypothesis and conclude that the sample mean is significantly different from the hypothesized mean. If the t-score is less than the critical value or the p-value is greater than the significance level, you cannot reject the null hypothesis and must conclude that the sample mean is not significantly different from the hypothesized mean.

A two-sample t-test is a statistical procedure used to determine whether there is a significant difference between the means of two groups. It is often used to compare the means of two groups in order to determine whether a difference exists between them. For example, a researcher might use a two-sample t-test to determine whether there is a significant difference in the average scores on a test between males and females, or between two different treatment groups in a medical study. The t-test is based on the t-statistic , which is calculated from the sample data and represents the difference between the two groups in relation to the variation within the groups. The t-test is used to determine whether this difference is statistically significant, meaning that it is unlikely to have occurred by chance.