fraction decimal percent problem solving

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Fractions Decimals Percents Worksheets

Welcome to our Fractions Decimals Percents Worksheets page. Here you will find a wide range of printable Fraction Worksheets which will help your child understand and practice how to convert between fractions, decimals and percentages.

Looking to convert fractions to percentages or decimals; decimals to fractions or percentages; percentages to fractions or decimals?

Then look no further - we have what you need!

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Quicklinks to ...

• Fractions Decimals Percents Conversion Table

Fractions Decimals Percents Riddles

• More recommended resources

Fractions Decimals Percents Online Quiz

Fractions decimals percents.

Below are some common conversions for fractions into decimals and percents.

Where a digit is underlined, it means that the number has been rounded to 3 decimal places, or to the nearest 0.1%.

We have split up our fractions decimals percents worksheets into several different sections to make it easier for you to choose the skill you want to practice.

• The first section is just converting fractions into decimals and percents.
• The second sections is about converting decimals to percents and fractions.
• The third section covers convertig percents to fractions and decimals.
• The last section involves converting between all three.

The sheets are carefully graded so that the supported and easier sheets come first, and the most difficult sheet is the last one.

Using these sheets will help your child to:

• convert between fractions decimals and percents.

These sheets are aimed at 5th, 6th and 7th graders.

Converting Fractions to Decimals and Percents

• Fractions to Decimals and Percents Sheet 1
• PDF version
• Fractions to Decimals and Percents Sheet 2

Fractions to Decimals and Percents Walkthrough Video

This short video walkthrough shows several problems from our Fractions to Decimals and Percents Worksheet 1 being solved and has been produced by the West Explains Best math channel.

If you would like some support in solving the problems on these sheets, please check out the video below!

Converting Decimals to Percents and Fractions

• Decimals to Percents and Fractions Sheet 1
• Decimals to Percents and Fractions Sheet 2

Converting Percents to Decimals and Fraction s

• Percents to Decimals and Fractions Sheet 1
• Percents to Decimals and Fractions Sheet 2

Convert Between Fractions Decimals Percents Worksheets

• Fractions Decimals and Percents Sheet 1
• Fractions Decimals and Percents Sheet 2
• Fractions Decimals and Percents Sheet 3
• Fractions Decimals and Percents Sheet 4

Now is your chance to practice your fractions decimals and percents problem solving skills with some fun riddles!

• Fraction Decimal Percent Riddle 1
• Fraction Decimal Percent Riddle 2
• Fraction Decimal Percent Riddle 3

More Recommended Math Worksheets

Take a look at some more of our worksheets similar to these.

Equivalent Fractions

The printable fraction page below contains support, examples and practice using equivalent fractions.

• Finding Equivalent Fractions support page
• Equivalent Fractions Worksheets

Comparing Fractions

We have some carefully graded worksheets on comparing and ordering fractions.

You can choose from supported sheets with diagrams for students who need extra help to harder worksheets for those more confident.

• Comparing Fractions Worksheet page

Simplifying Fractions

Take a look at our Simplifying Fractions Practice Zone or try our worksheets for finding the simplest form for a range of fractions.

You can choose from proper fractions, improper fractions or both.

You can print out your results or benchmark your scores against future achievements.

Good for practising equivalent fractions as well as converting to simplest form.

Great for using with a group of children as well as individually.

• Simplify Fractions Practice Zone
• Simplifying Fractions Worksheet page

Fraction Riddles

Riddles are a great way to get children to apply their knowledge of fractions.

These riddles are a good way to start off a maths lesson, or also to use as a way of checking your child's understanding about fractions.

All the fraction riddles consist of 3 or 4 clues and a selection of 6 or 8 possible answers. Children have to read the clues and work out which is the correct answer.

The riddles can also be used as a template for the children to write their own clues for a partner to guess.

• Fraction Riddles for kids (easier)
• Free Printable Fraction Riddles (harder)

Are you looking for free fraction help or fraction support?

Here you will find a range of fraction help on a variety of fraction topics, from simplest form to converting fractions.

There are fraction videos, worked examples and practice fraction worksheets.

Our quizzes have been created using Google Forms.

At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.

This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.

For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.

We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.

We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.

For more information on the information we collect, please take a look at our Privacy Policy

We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.

This quick quiz tests your knowledge and skill at converting between fractions, decimals and percents.

Fun Quiz Facts

• This quiz was attempted 1,155 times in the last academic year.
• The average (mean) score was 13.4 out of 20 marks.
• Can you beat the mean score?

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to 5th Grade Math Worksheets

Return to Fraction Worksheets

Return from Fractions Decimals Percents Worksheets to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

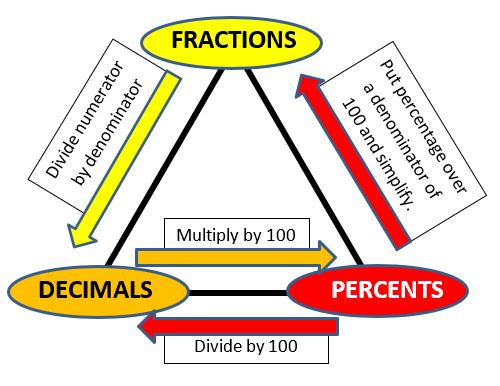
Decimals, Fractions and Percentages

Decimals, Fractions and Percentages are just different ways of showing the same value:

Here, have a play with it yourself:

Example Values

Here is a table of commonly used values shown in Percent, Decimal and Fraction form:

Conversions!

From percent to decimal.

To convert from percent to decimal divide by 100 and remove the % sign.

An easy way to divide by 100 is to move the decimal point 2 places to the left :

Don't forget to remove the % sign!

From Decimal to Percent

To convert from decimal to percent multiply by 100%

An easy way to multiply by 100 is to move the decimal point 2 places to the right :

 Don't forget to add the % sign!

From Fraction to Decimal

To convert a fraction to a decimal divide the top number by the bottom number:

Example: Convert 2 5 to a decimal

Divide 2 by 5: 2 ÷ 5 = 0.4

Answer: 2 5 = 0.4

From Decimal to Fraction

To convert a decimal to a fraction needs a little more work.

Example: To convert 0.75 to a fraction

From fraction to percentage.

To convert a fraction to a percentage divide the top number by the bottom number, then multiply the result by 100%

Example: Convert 3 8 to a percentage

First divide 3 by 8: 3 ÷ 8 = 0.375

Then multiply by 100%: 0.375 × 100% = 37.5%

Answer: 3 8 = 37.5%

From Percentage to Fraction

To convert a percentage to a fraction , first convert to a decimal (divide by 100), then use the steps for converting decimal to fractions (like above).

Example: To convert 80% to a fraction

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Fractions, Decimals & Percentages

Matching Fractions, Decimals and Percentages

Can you match pairs of fractions, decimals and percentages, and beat your previous scores?

Repetitiously

Can you express every recurring decimal as a fraction?

Ben, Jack and Emma passed counters to each other and ended with the same number of counters. How many did they start with?

A Chance to Win?

Imagine you were given the chance to win some money... and imagine you had nothing to lose...

Peaches Today, Peaches Tomorrow...

A monkey with peaches, keeps a fraction of them each day, gives the rest away, and then eats one. How long can his peaches last?

What do you notice about these families of recurring decimals?

Doughnut Percents

A task involving the equivalence between fractions, percentages and decimals which depends on members of the group noticing the needs of others and responding.

Fractions and Percentages Card Game

Can you find the pairs that represent the same amount of money?

Fractions, Decimals and Percentages - Short Problems

A collection of short problems on fractions, decimals and percentages.

Terminating or Not

Is there a quick way to work out whether a fraction terminates or recurs when you write it as a decimal?

Fractions, Decimals and Percentages Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Fractions, Decimals and Percentages

Fractions, Decimals and Percentages are three different ways of expressing a part of a whole.

We can convert between fractions, decimals and percentages.

Converting between Decimals and Percentages

To convert a decimal to a percentage we multiply by 100.

Example 1: Convert 0.7 to a percentage

0.7 × 100 = 70 0.7 = 70%

Example 2: Convert 0.19 to a percentage

0.19 × 100 = 19 0.19 = 19%

To convert a percentage to a decimal we divide by 100 Dividing by 100 is the opposite of multiplying by 100

Example 3: Convert 25% to a decimal

To convert a percentage to a decimal we divide by 100.

25 ÷ 100 = 0.25 25% = 0.25

Example 4: Convert 9% to a decimal

9 ÷ 100 = 0.09 9% = 0.09

Converting between Percentages and Fractions

A percentage is out of 100. We can re-write any percentage as a fraction by writing it over 100.

Example 5: Convert 11% to a fraction.

A percentage is the same as a fraction out of 100.

We can write 11% as 11 ⁄ 100

Example 6: Convert 36% to a fraction. Give your answer in it simplest form.

We can write 36% as 36 ⁄ 100

We have written 36% as a fraction, but it is not in its simplest form. To simplify we need to find a times table that 36 and 100 are both in. 36 and 100 are both in the 2 and the 4 times tables. 4 is the biggest so we will divide the denominator and the numerator by 4.

36 = 4 × 9 100 = 4 × 25

36% = 9 ⁄ 25

We could have also halved the top and bottom, and then halved again:

36 ⁄ 100 = 18 ⁄ 50 = 9 ⁄ 25

To convert a fraction to a percentage we can change the denominator to 100.

Example 7: Convert 7 ⁄ 20 to a percentage.

To convert the fraction to a percentage we need to make the denominator 100.

We can make the denominator 100 by multiplying by 5. 20 × 5 = 100

We have to multiply the numerator by 5 too keep the fraction equivalent. 7 × 5 = 35

7 ⁄ 20 = 35 ⁄ 100 = 35%

When the denominator is not a factor of 100 it may be easier to convert the fraction to a decimal first, and then from a decimal to a percentage.

Converting between Fractions and Decimals

To convert from a fraction to a decimal we can divide the numerator by the denominator.

Example 8: Convert 3 ⁄ 8 to a decimal.

We can convert 3 ⁄ 8 to a decimal by calculating 3 ÷ 8.

We can use a calculator or short division to do the calculation.

3 ÷ 8 = 0.375

3 ⁄ 8 = 0.375

If we are using a calculator we can also use the SD button.

Example 9 : Convert 7 ⁄ 12 to a decimal.

We need to calculate 7 ÷ 12

7 ÷ 12 = \(0.58\dot3\)

The dot above the 3 means that the 3 is recurring (it goes on forever), 0.5833333333333333333...

7 ⁄ 12 = \(0.58\dot3\)

To convert a decimal to a fraction we can convert it to a percentage (by multiplying by 100) and then write it is a fraction out of 100.

Example 10: Convert 0.88 to a fraction. Give your answer in its simplest form.

To convert 0.88 to a percentage we multiply by 100. 0.88 × 100 = 88

88% = 88 ⁄ 100

We can simplify our answer by dividing top and bottom by 4.

88 ⁄ 100 = 22 ⁄ 25

0.88 = 22 ⁄ 25

If the decimal involves a recurring numbers we can type it into the calculator instead and the calculator will do the conversion for us. The recurring button looks like this:

It may be found (depending on your calculator) by pressing SHIFT then the square button:

Example 11: Convert \(0.7\dot3\) to a fraction. Give your answer in its simplest form.

We can type \(0.7\dot3\) into a calculator by pressing:

The calculator should give an answer of 11 ⁄ 15

FRACTIONS DECIMALS AND PERCENTAGES WORD PROBLEMS

Problem 1 :

The numerator and denominator of a fraction add up to 10. Adding 3 to both numerator and denominator of the fraction results ⅗ . Find the fraction.

Let x be the numerator and y be the denominator of the fraction.

Given :  The numerator and denominator add up to 8.

x + y = 10 ----(1)

Given :  When 3 is added to both numerator and denominator, the fraction becomes ⅗ .

⁽ˣ ⁺ ³⁾⁄₍ y ₊ ₃₎  = ⅗

5(x + 3) = 3(y + 3)

5x + 15 = 3y + 9

5x - 3y = -6 ----(2)

3(1) + (2) :

Divide both sides by 8.

Substitute x = 3 in (1).

Subtract 3 from both sides.

ˣ⁄ y  =  ³⁄₇

The fraction is ³⁄₇ .

Problem 2 :

Three-fifth of the students in a school are girls. If there is a total of 750 students in the school, find the number of boys.

If three-fifth of the students are girls, then two-fifth of ths students are boys.

Because, in total 5 parts, 3 parts are girls and the remaning two parts are boys.

Number of boys in the school :

= 750  ⋅  ⅖

Problem 3 :

Sum of the length and width of a rectangle is 55 cm. If the length is 1.75 times of the width, find the area of the rectangle.

Let l be the length and w be the width of the rectangle.

Given :  The length and width add up to 55 cm.

l + w = 55 ----(1)

Given :  T he length is 1.75 times of the width.

l = 1.75w ----(2)

Substitute l = 1.75w in (1).

1.75w + w = 55

Divide both sides by 2.75.

Substitute w = 20 in (2).

l = 1.75(20)

Area of the rectangle :

= l  ⋅  w

= 35  ⋅ 20

= 700 square cm.

Problem 4 :

A chemist mixed 20 percent of 6.36 grams of one compound with 60 percent of 2.48 grams of another compound. How many grams were there in the mixture?

Quantity taken from the first compound is

= 20% of 6.36

= 0.2  ⋅ 6.36

= 60% of 2.48

= 0.6  ⋅ 2.48

Total quantity of mixture is

= Quantity from 1st comp + Quantity from 2nd comp

= 1.272 + 1.488

= 2.76 grams

Problem 5 :

David buys 3 pens where the price of each pen is $1.5 and the 4 pencils where the price of each pen is $0.75. If he gets a discount of 10% in the total bill, how much does he have to pay?

First, find the total bill.

Total bill = (3  ⋅  1.5) + (4  ⋅  0.75)

Given :  Discount is 10%.

The money that he has to pay is

= 90% of the total bill

= 0.9  ⋅  7.5

Problem 6 :

Joseph earned $24.60 for working 6 hours. How much will earn, if he works for 7.5 hours?

Given : Money earned in 6 hours is $24.60.

Then, m oney earned in 1 hour is

= 24.60 / 6

Therefore money earned in 7.5 hours is

= 7.5  ⋅  4.10

Problem 7 :

The length of a rope is 92.4 meters. If the rope is cut into pieces of length 7 meters each, find the maximum number of peices can be received.

The original length of the rope is 92.4 meters.

The length of each piece is 7 meters.

Number of pieces with length 7 meters each can be cut from the rope :

Number of pieces can not be decimal.

Therefore, maximum number of pieces of length 7 meters each can be cut from the rope is 13.

Problem 8 :

The original price of a suit is $1000. A salesman decides to discount it by 30%. Later on, the manager decides to give a 15% discount off the salesman's price. What is the final price of the suit? 

Price of the suit after 30% discount given by salesman :

= (100 - 30)% of 1000

= 70% of 1000

= 0.7  ⋅ 1000

Final price of the suit after 15% discount given by the manager :

= (100 - 15)% of 700

= 85% of 700

= 0.85  ⋅ 700

Problem 9 :

The cost of a toy is  $22.5. If the profit is 20%, what is the selling price of the toy?

The cost of a toy is $22.5.

If the profit is 20%, then the selling price is  120% of cost price.

Selling price = 120 % of cots price

= 1.2  ⋅ 22.5

Selling price of the toy is $27.

Problem 10 :

A sports equipment manufacturer produced 3,600 footballs and 2,200 basketballs during the fall. In the winter, it produced 3,060 footballs and a certain number of basketballs. If the manufacturer decreased the production of basketballs by the same percentage as it did foir footballs, how many basketballs did it produce in the winter?   

Percentage decrease in the production of footbals from the fall to the winter :

= [(3600 - 3060)/3600]  ⋅ 100%

= 540/3600 ⋅ 100%

Given :  From the fall to the winter, t he manufacturer decreased the production of basketballs by the same percentage as it did foir footballs.

Number of basketballs produced in the winter :

= (100 - 15)% of 2200

= 85% of 2200

= 0.85  ⋅ 2200

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Simplifying Algebraic Expressions with Fractional Coefficients

May 17, 24 08:12 AM

The Mean Value Theorem Worksheet

May 14, 24 08:53 AM

Mean Value Theorem

May 14, 24 02:48 AM

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.2.1: Solving Percent Problems

• Last updated
• Save as PDF
• Page ID 62169

• The NROC Project

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Identify the amount, the base, and the percent in a percent problem.
• Find the unknown in a percent problem.

Introduction

Percents are a ratio of a number and 100, so they are easier to compare than fractions, as they always have the same denominator, 100. A store may have a 10% off sale. The amount saved is always the same portion or fraction of the price, but a higher price means more money is taken off. Interest rates on a saving account work in the same way. The more money you put in your account, the more money you get in interest. It’s helpful to understand how these percents are calculated.

Parts of a Percent Problem

Jeff has a coupon at the Guitar Store for 15% off any purchase of $100 or more. He wants to buy a used guitar that has a price tag of $220 on it. Jeff wonders how much money the coupon will take off the original $220 price.

Problems involving percents have any three quantities to work with: the percent , the amount , and the base .

• The percent has the percent symbol (%) or the word “percent.” In the problem above, 15% is the percent off the purchase price.
• The base is the whole amount. In the problem above, the whole price of the guitar is $220, which is the base.
• The amount is the number that relates to the percent. It is always part of the whole. In the problem above, the amount is unknown. Since the percent is the percent off , the amount will be the amount off of the price.

You will return to this problem a bit later. The following examples show how to identify the three parts: the percent, the base, and the amount.

Identify the percent, amount, and base in this problem.

30 is 20% of what number?

Percent: The percent is the number with the % symbol: 20%.

Base : The base is the whole amount, which in this case is unknown.

Amount: The amount based on the percent is 30.

Percent=20%

Base=unknown

The previous problem states that 30 is a portion of another number. That means 30 is the amount. Note that this problem could be rewritten: 20% of what number is 30?

Identify the percent, base, and amount in this problem:

What percent of 30 is 3?

The percent is unknown, because the problem states " What percent?" The base is the whole in the situation, so the base is 30. The amount is the portion of the whole, which is 3 in this case.

Solving with Equations

Percent problems can be solved by writing equations. An equation uses an equal sign (=) to show that two mathematical expressions have the same value.

Percents are fractions, and just like fractions, when finding a percent (or fraction, or portion) of another amount, you multiply.

The percent of the base is the amount.

Percent of the Base is the Amount.

\[\ \text { Percent } {\color{red}\cdot}\text { Base }{\color{blue}=}\text { Amount } \nonumber \]

In the examples below, the unknown is represented by the letter \(\ n\). The unknown can be represented by any letter or a box \(\ \square\) or even a question mark.

Write an equation that represents the following problem.

\(\ 20 \% \cdot n=30\)

Once you have an equation, you can solve it and find the unknown value. To do this, think about the relationship between multiplication and division. Look at the pairs of multiplication and division facts below, and look for a pattern in each row.

Multiplication and division are inverse operations. What one does to a number, the other “undoes.”

When you have an equation such as \(\ 20 \% \cdot n=30\), you can divide 30 by 20% to find the unknown: \(\ n=30 \div 20 \%\).

You can solve this by writing the percent as a decimal or fraction and then dividing.

\(\ n=30 \div 20 \%=30 \div 0.20=150\)

What percent of 72 is 9?

\(\ 12.5 \% \text { of } 72 \text { is } 9\).

You can estimate to see if the answer is reasonable. Use 10% and 20%, numbers close to 12.5%, to see if they get you close to the answer.

\(\ 10 \% \text { of } 72=0.1 \cdot 72=7.2\)

\(\ 20 \% \text { of } 72=0.2 \cdot 72=14.4\)

Notice that 9 is between 7.2 and 14.4, so 12.5% is reasonable since it is between 10% and 20%.

What is 110% of 24?

\(\ 26.4 \text { is } 110 \% \text { of } 24\).

This problem is a little easier to estimate. 100% of 24 is 24. And 110% is a little bit more than 24. So, 26.4 is a reasonable answer.

18 is what percent of 48?

• \(\ 0.375 \%\)
• \(\ 8.64 \%\)
• \(\ 37.5 \%\)
• \(\ 864 \%\)

Incorrect. You may have calculated properly, but you forgot to move the decimal point when you rewrote your answer as a percent. The equation for this problem is \(\ n \cdot 48=18\). The corresponding division is \(\ 18 \div 48\), so \(\ n=0.375\). Rewriting this decimal as a percent gives the correct answer, \(\ 37.5 \%\).

Incorrect. You may have used \(\ 18\) or \(\ 48\) as the percent, rather than the amount or base. The equation for this problem is \(\ n \cdot 48=18\). The corresponding division is \(\ 18 \div 48\), so \(\ n=0.375\). Rewriting this decimal as a percent gives the correct answer, \(\ 37.5 \%\).

Correct. The equation for this problem is \(\ n \cdot 48=18\). The corresponding division is \(\ 18 \div 48\), so \(\ n=0.375\). Rewriting this decimal as a percent gives \(\ 37.5 \%\).

Incorrect. You probably used 18 or 48 as the percent, rather than the amount or base, and also forgot to rewrite the percent as a decimal before multiplying. The equation for this problem is \(\ n \cdot 48=18\). The corresponding division is \(\ 18 \div 48\), so \(\ n=0.375\). Rewriting this decimal as a percent gives the correct answer, \(\ 37.5 \%\).

Using Proportions to Solve Percent Problems

Percent problems can also be solved by writing a proportion. A proportion is an equation that sets two ratios or fractions equal to each other. With percent problems, one of the ratios is the percent, written as \(\ \frac{n}{100}\). The other ratio is the amount to the base.

\(\ \text { Percent }=\frac{\text { amount }}{\text { base }}\)

Write a proportion to find the answer to the following question.

30 is 20% of 150.

18 is 125% of what number?

• \(\ 0.144\)
• \(\ 694 \frac{4}{9}\) (or about \(\ 694.4\))

Incorrect. You probably didn’t write a proportion and just divided 18 by 125. Or, you incorrectly set up one fraction as \(\ \frac{18}{125}\) and set this equal to the base, \(\ n\). The percent in this case is 125%, so one fraction in the proportion should be \(\ \frac{125}{100}\). The base is unknown and the amount is 18, so the other fraction is \(\ \frac{18}{n}\). Solving the proportion \(\ \frac{125}{100}=\frac{18}{n}\) gives \(\ n=14.4\).

Correct. The percent in this case is 125%, so one fraction in the proportion should be \(\ \frac{125}{100}\). The base is unknown and the amount is 18, so the other fraction is \(\ \frac{18}{n}\). Solving the proportion \(\ \frac{125}{100}=\frac{18}{n}\) gives \(\ n=14.4\).

Incorrect. You probably put the amount (18) over 100 in the proportion, rather than the percent (125). Perhaps you thought 18 was the percent and 125 was the base. The correct percent fraction for the proportion is \(\ \frac{125}{100}\). The base is unknown and the amount is 18, so the other fraction is \(\ \frac{18}{n}\). Solving the proportion \(\ \frac{125}{100}=\frac{18}{n}\) gives \(\ n=14.4\).

Incorrect. You probably confused the amount (18) with the percent (125) when you set up the proportion. The correct percent fraction for the proportion is \(\ \frac{125}{100}\). The base is unknown and the amount is 18, so the other fraction is \(\ \frac{18}{n}\). Solving the proportion \(\ \frac{125}{100}=\frac{18}{n}\) gives \(\ n=14.4\).

Let’s go back to the problem that was posed at the beginning. You can now solve this problem as shown in the following example.

Jeff has a coupon at the Guitar Store for 15% off any purchase of $100 or more. He wants to buy a used guitar that has a price tag of $220 on it. Jeff wonders how much money the coupon will take off of the $220 original price .

The coupon will take $33 off the original price.

You can estimate to see if the answer is reasonable. Since 15% is half way between 10% and 20%, find these numbers.

\(\ \begin{array}{l} 10 \% \text { of } 220=0.1 \cdot 220=22 \\ 20 \% \text { of } 220=0.2 \cdot 220=44 \end{array}\)

The answer, 33, is between 22 and 44. So $33 seems reasonable.

There are many other situations that involve percents. Below are just a few.

Evelyn bought some books at the local bookstore. Her total bill was $31.50, which included 5% tax. How much did the books cost before tax?

The books cost $30 before tax.

Susana worked 20 hours at her job last week. This week, she worked 35 hours. In terms of a percent, how much more did she work this week than last week?

Since 35 is 175% of 20, Susana worked 75% more this week than she did last week. (You can think of this as, “Susana worked 100% of the hours she worked last week, as well as 75% more.”)

Percent problems have three parts: the percent, the base (or whole), and the amount. Any of those parts may be the unknown value to be found. To solve percent problems, you can use the equation, \(\ \text { Percent } \cdot \text { Base }=\text { Amount }\), and solve for the unknown numbers. Or, you can set up the proportion, \(\ \text { Percent }=\frac{\text { amount }}{\text { base }}\), where the percent is a ratio of a number to 100. You can then use cross multiplication to solve the proportion.

Decimals Worksheets

Thanks for visiting the Decimals Worksheets page at Math-Drills.Com where we make a POINT of helping students learn. On this page, you will find Decimals worksheets on a variety of topics including comparing and sorting decimals, adding, subtracting, multiplying and dividing decimals, and converting decimals to other number formats. To start, you will find the general use printables to be helpful in teaching the concepts of decimals and place value. More information on them is included just under the sub-title.

Further down the page, rounding, comparing and ordering decimals worksheets allow students to gain more comfort with decimals before they move on to performing operations with decimals. There are many operations with decimals worksheets throughout the page. It would be a really good idea for students to have a strong knowledge of addition, subtraction, multiplication and division before attempting these questions.

Most Popular Decimals Worksheets this Week

Grids and Charts Useful for Learning Decimals

General use decimal printables are used in a variety of contexts and assist students in completing math questions related to decimals.

The thousandths grid is a useful tool in representing decimals. Each small rectangle represents a thousandth. Each square represents a hundredth. Each row or column represents a tenth. The entire grid represents one whole. The hundredths grid can be used to model percents or decimals. The decimal place value chart is a tool used with students who are first learning place value related to decimals or for those students who have difficulty with place value when working with decimals.

• Thousandths and Hundredths Grids Thousandths Grid Hundredths Grids ( 4 on a page) Hundredths Grids ( 9 on a page) Hundredths Grids ( 20 on a page)
• Decimal Place Value Charts Decimal Place Value Chart ( Ones to Hundredths ) Decimal Place Value Chart ( Ones to Thousandths ) Decimal Place Value Chart ( Hundreds to Hundredths ) Decimal Place Value Chart ( Thousands to Thousandths ) Decimal Place Value Chart ( Hundred Thousands to Thousandths ) Decimal Place Value Chart ( Hundred Millions to Millionths )

Decimals in Expanded Form

For students who have difficulty with expanded form, try familiarizing them with the decimal place value chart, and allow them to use it when converting standard form numbers to expanded form. There are actually five ways (two more than with integers) to write expanded form for decimals, and which one you use depends on your application or preference. Here is a quick summary of the various ways using the decimal number 1.23. 1. Expanded Form using decimals: 1 + 0.2 + 0.03 2. Expanded Form using fractions: 1 + 2 ⁄ 10 + 3 ⁄ 100 3. Expanded Factors Form using decimals: (1 × 1) + (2 × 0.1) + (3 × 0.01) 4. Expanded Factors Form using fractions: (1 × 1) + (2 × 1 ⁄ 10 ) + (3 × 1 ⁄ 100 ) 5. Expanded Exponential Form: (1 × 10 0 ) + (2 × 10 -1 ) + (3 × 10 -2 )

• Converting Decimals from Standard Form to Expanded Form Using Decimals Converting Decimals from Standard to Expanded Form Using Decimals ( 3 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 4 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 5 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 6 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 7 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 8 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 9 Decimal Places)
• Converting Decimals from Standard Form to Expanded Form Using Fractions Converting Decimals from Standard to Expanded Form Using Fractions ( 3 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 4 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 5 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 6 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 7 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 8 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 9 Decimal Places)
• Converting Decimals from Standard Form to Expanded Factors Form Using Decimals Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 3 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 4 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 5 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 6 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 7 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 8 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 9 Decimal Places)
• Converting Decimals from Standard Form to Expanded Factors Form Using Fractions Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 3 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 4 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 5 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 6 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 7 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 8 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 9 Decimal Places)
• Converting Decimals from Standard Form to Expanded Exponential Form Converting Decimals from Standard to Expanded Exponential Form ( 3 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 4 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 5 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 6 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 7 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 8 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 9 Decimal Places)
• Retro Converting Decimals from Standard Form to Expanded Form Retro Standard to Expanded Form (3 digits before decimal; 2 after) Retro Standard to Expanded Form (4 digits before decimal; 3 after) Retro Standard to Expanded Form (6 digits before decimal; 4 after) Retro Standard to Expanded Form (12 digits before decimal; 3 after)
• Retro European Format Converting Decimals from Standard Form to Expanded Form Standard to Expanded Form (3 digits before decimal; 2 after) Standard to Expanded Form (4 digits before decimal; 3 after) Standard to Expanded Form (6 digits before decimal; 4 after)

Of course, being able to convert numbers already in expanded form to standard form is also important. All five versions of decimal expanded form are included in these worksheets.

• Converting Decimals to Standard Form from Expanded Form Using Decimals Converting Decimals from Expanded Form Using Decimals to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 9 Decimal Places)
• Converting Decimals to Standard Form from Expanded Form Using Fractions Converting Decimals from Expanded Form Using Fractions to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 9 Decimal Places)
• Converting Decimals to Standard Form from Expanded Factors Form Using Decimals Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 9 Decimal Places)
• Converting Decimals to Standard Form from Expanded Factors Form Using Fractions Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 9 Decimal Places)
• Converting Decimals to Standard Form from Expanded Exponential Form Converting Decimals from Expanded Exponential Form to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 9 Decimal Places)
• Retro Converting Decimals to Standard Form from Expanded Form Retro Expanded to Standard Form (3 digits before decimal; 2 after) Retro Expanded to Standard Form (4 digits before decimal; 3 after) Retro Expanded to Standard Form (6 digits before decimal; 4 after) Retro Expanded to Standard Form (12 digits before decimal; 3 after)
• Retro European Format Converting Decimals to Standard Form from Expanded Form Retro European Format Expanded to Standard Form (3 digits before decimal; 2 after) Retro European Format Expanded to Standard Form (4 digits before decimal; 3 after) Retro European Format Expanded to Standard Form (6 digits before decimal; 4 after)

Rounding Decimals Worksheets

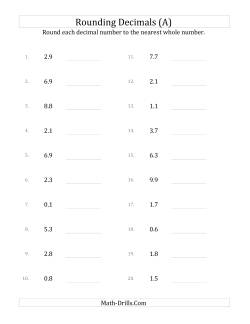
Rounding decimals is similar to rounding whole numbers; you have to know your place value! When learning about rounding, it is also useful to learn about truncating since it may help students to round properly. A simple strategy for rounding involves truncating, using the digits after the truncation to determine whether the new terminating digit remains the same or gets incremented, then taking action by incrementing if necessary and throwing away the rest. Here is a simple example: Round 4.567 to the nearest tenth. First, truncate the number after the tenths place 4.5|67. Next, look at the truncated part (67). Is it more than half way to 99 (i.e. 50 or more)? It is, so the decision will be to increment. Lastly, increment the tenths value by 1 to get 4.6. Of course, the situation gets a little more complicated if the terminating digit is a 9. In that case, some regrouping might be necessary. For example: Round 6.959 to the nearest tenth. Truncate: 6.9|59. Decide to increment since 59 is more than half way to 99. Incrementing results in the necessity to regroup the tenths into an extra one whole, so the result is 7.0. Watch that students do not write 6.10. You will want to correct them right away in that case. One last note: if there are three truncated digits then the question becomes is the number more than half way to 999. Likewise, for one digit; is the number more than half way to 9. And so on...

We should also mention that in some scientific and mathematical "circles," rounding is slightly different "on a 5". For example, most people would round up on a 5 such as: 6.5 --> 7; 3.555 --> 3.56; 0.60500 --> 0.61; etc. A different way to round on a 5, however, is to round to the nearest even number, so 5.5 would be rounded up to 6, but 8.5 would be rounded down to 8. The main reason for this is not to skew the results of a large number of rounding events. If you always round up on a 5, on average, you will have slightly higher results than you should. Because most pre-college students round up on a 5, that is what we have done in the worksheets that follow.

• Rounding Decimals to Whole Numbers Round Tenths to a Whole Number Round Hundredths to a Whole Number Round Thousandths to a Whole Number Round Ten Thousandths to a Whole Number Round Various Decimals to a Whole Number
• Rounding Decimals to Tenths Round Hundredths to Tenths Round Thousandths to Tenths Round Ten Thousandths to Tenths Round Various Decimals to Tenths
• Rounding Decimals to Hundredths Round Thousandths to Hundredths Round Ten Thousandths to Hundredths Round Various Decimals to Hundredths
• Rounding Decimals to Thousandths Round Ten Thousandths to Thousandths
• Rounding Decimals to Various Decimal Places Round Hundredths to Various Decimal Places Round Thousandths to Various Decimal Places Round Ten Thousandths to Various Decimal Places Round Various Decimals to Various Decimal Places
• European Format Rounding Decimals to Whole Numbers European Format Round Tenths to a Whole Number European Format Round Hundredths to a Whole Number European Format Round Thousandths to a Whole Number European Format Round Ten Thousandths to Whole Number
• European Format Rounding Decimals to Tenths European Format Round Hundredths to Tenths European Format Round Thousandths to Tenths European Format Round Ten Thousandths to Tenths
• European Format Rounding Decimals to Hundredths European Format Round Thousandths to Hundredths European Format Round Ten Thousandths to Hundredths
• European Format Rounding Decimals to Thousandths European Format Round Ten Thousandths to Thousandths

Comparing and Ordering/Sorting Decimals Worksheets.

The comparing decimals worksheets have students compare pairs of numbers and the ordering decimals worksheets have students compare a list of numbers by sorting them.

Students who have mastered comparing whole numbers should find comparing decimals to be fairly easy. The easiest strategy is to compare the numbers before the decimal (the whole number part) first and only compare the decimal parts if the whole number parts are equal. These sorts of questions allow teachers/parents to get a good idea of whether students have grasped the concept of decimals or not. For example, if a student thinks that 4.93 is greater than 8.7, then they might need a little more instruction in place value. Close numbers means that some care was taken to make the numbers look similar. For example, they could be close in value, e.g. 3.3. and 3.4 or one of the digits might be changed as in 5.86 and 6.86.

• Comparing Decimals up to Tenths Comparing Decimals up to Tenths ( Both Numbers Random ) Comparing Decimals up to Tenths ( One Digit Differs ) Comparing Decimals up to Tenths ( Both Numbers Close in Value ) Comparing Decimals up to Tenths ( Various Tricks )
• Comparing Decimals up to Hundredths Comparing Decimals up to Hundredths ( Both Numbers Random ) Comparing Decimals up to Hundredths ( One Digit Differs ) Comparing Decimals up to Hundredths ( Two Digits Swapped ) Comparing Decimals up to Hundredths ( Both Numbers Close in Value ) Comparing Decimals up to Hundredths ( One Number has an Extra Digit ) Comparing Decimals up to Hundredths ( Various Tricks )
• Comparing Decimals up to Thousandths Comparing Decimals up to Thousandths Comparing Decimals up to Thousandths ( One Digit Differs ) Comparing Decimals up to Thousandths ( Two Digits Swapped ) Comparing Decimals up to Thousandths ( Both Numbers Close in Value ) Comparing Decimals up to Thousandths ( One Number has an Extra Digit ) Comparing Decimals up to Thousandths ( Various Tricks )
• Comparing Decimals up to Ten Thousandths Comparing Decimals up to Ten Thousandths Comparing Decimals up to Ten Thousandths ( One Digit Differs ) Comparing Decimals up to Ten Thousandths ( Two Digits Swapped ) Comparing Decimals up to Ten Thousandths ( Both Numbers Close in Value ) Comparing Decimals up to Ten Thousandths ( One Number has an Extra Digit ) Comparing Decimals up to Ten Thousandths ( Various Tricks )
• Comparing Decimals up to Hundred Thousandths Comparing Decimals up to Hundred Thousandths Comparing Decimals up to Hundred Thousandths ( One Digit Differs ) Comparing Decimals up to Hundred Thousandths ( Two Digits Swapped ) Comparing Decimals up to Hundred Thousandths ( Both Numbers Close in Value ) Comparing Decimals up to Hundred Thousandths ( One Number has an Extra Digit ) Comparing Decimals up to Hundred Thousandths ( Various Tricks )
• European Format Comparing Decimals European Format Comparing Decimals up to Tenths European Format Comparing Decimals up to Tenths (tight) European Format Comparing Decimals up to Hundredths European Format Comparing Decimals up to Hundredths (tight) European Format Comparing Decimals up to Thousandths European Format Comparing Decimals up to Thousandths (tight)

Ordering decimals is very much like comparing decimals except there are more than two numbers. Generally, students determine the least (or greatest) decimal to start, cross it off the list then repeat the process to find the next lowest/greatest until they get to the last number. Checking the list at the end is always a good idea.

• Ordering/Sorting Decimals Ordering/Sorting Decimal Hundredths Ordering/Sorting Decimal Thousandths
• European Format Ordering/Sorting Decimals European Format Ordering/Sorting Decimal Tenths (8 per set) European Format Ordering/Sorting Decimal Hundredths (8 per set) European Format Ordering/Sorting Decimal Thousandths (8 per set) European Format Ordering/Sorting Decimal Ten Thousandths (8 per set) European Format Ordering/Sorting Decimals with Various Decimal Places(8 per set)

Converting Decimals to Fractions and Other Number Formats

There are many good reasons for converting decimals to other number formats. Dealing with a fraction in arithmetic is often easier than the equivalent decimal. Consider 0.333... which is equivalent to 1/3. Multiplying 300 by 0.333... is difficult, but multiplying 300 by 1/3 is super easy! Students should be familiar with some of the more common fraction/decimal conversions, so they can switch back and forth as needed.

• Converting Between Decimals and Fractions Converting Fractions to Terminating Decimals Converting Fractions to Terminating and Repeating Decimals Converting Terminating Decimals to Fractions Converting Terminating and Repeating Decimals to Fractions Converting Fractions to Hundredths
• Converting Between Decimals, Fraction, Percents and Ratios Converting Fractions to Decimals, Percents and Part-to-Part Ratios Converting Fractions to Decimals, Percents and Part-to-Whole Ratios Converting Decimals to Fractions, Percents and Part-to-Part Ratios Converting Decimals to Fractions, Percents and Part-to-Whole Ratios Converting Percents to Fractions, Decimals and Part-to-Part Ratios Converting Percents to Fractions, Decimals and Part-to-Whole Ratios Converting Part-to-Part Ratios to Fractions, Decimals and Percents Converting Part-to-Whole Ratios to Fractions, Decimals and Percents Converting Various Fractions, Decimals, Percents and Part-to-Part Ratios Converting Various Fractions, Decimals, Percents and Part-to-Whole Ratios Converting Various Fractions, Decimals, Percents and Part-to-Part Ratios with 7ths and 11ths Converting Various Fractions, Decimals, Percents and Part-to-Whole Ratios with 7ths and 11ths

Adding and Subtracting Decimals

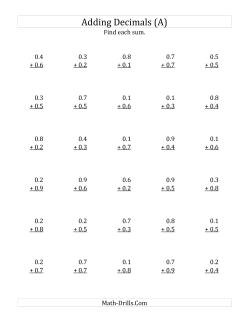
Try the following mental addition strategy for decimals. Begin by ignoring the decimals in the addition question. Add the numbers as if they were whole numbers. For example, 3.25 + 4.98 could be viewed as 325 + 498 = 823. Use an estimate to decide where to place the decimal. In the example, 3.25 + 4.98 is approximately 3 + 5 = 8, so the decimal in the sum must go between the 8 and the 2 (i.e. 8.23)

• Adding Tenths Adding Decimal Tenths with 0 Before the Decimal (range 0.1 to 0.9) Adding Decimal Tenths with 1 Digit Before the Decimal (range 1.1 to 9.9) Adding Decimal Tenths with 2 Digits Before the Decimal (range 10.1 to 99.9)
• Adding Hundredths Adding Decimal Hundredths with 0 Before the Decimal (range 0.01 to 0.99) Adding Decimal Hundredths with 1 Digit Before the Decimal (range 1.01 to 9.99) Adding Decimal Hundredths with 2 Digits Before the Decimal (range 10.01 to 99.99)
• Adding Thousandths Adding Decimal Thousandths with 0 Before the Decimal (range 0.001 to 0.999) Adding Decimal Thousandths with 1 Digit Before the Decimal (range 1.001 to 9.999) Adding Decimal Thousandths with 2 Digits Before the Decimal (range 10.001 to 99.999)
• Adding Ten Thousandths Adding Decimal Ten Thousandths with 0 Before the Decimal (range 0.0001 to 0.9999) Adding Decimal Ten Thousandths with 1 Digit Before the Decimal (range 1.0001 to 9.9999) Adding Decimal Ten Thousandths with 2 Digits Before the Decimal (range 10.0001 to 99.9999)
• Adding Various Decimal Places Adding Various Decimal Places with 0 Before the Decimal Adding Various Decimal Places with 1 Digit Before the Decimal Adding Various Decimal Places with 2 Digits Before the Decimal Adding Various Decimal Places with Various Numbers of Digits Before the Decimal
• European Format Adding Decimals European Format Adding decimal tenths with 0 before the decimal (range 0,1 to 0,9) European Format Adding decimal tenths with 1 digit before the decimal (range 1,1 to 9,9) European Format Adding decimal hundredths with 0 before the decimal (range 0,01 to 0,99) European Format Adding decimal hundredths with 1 digit before the decimal (range 1,01 to 9,99) European Format Adding decimal thousandths with 0 before the decimal (range 0,001 to 0,999) European Format Adding decimal thousandths with 1 digit before the decimal (range 1,001 to 9,999) European Format Adding decimal ten thousandths with 0 before the decimal (range 0,0001 to 0,9999) European Format Adding decimal ten thousandths with 1 digit before the decimal (range 1,0001 to 9,9999) European Format Adding mixed decimals with Various Decimal Places European Format Adding mixed decimals with Various Decimal Places (1 to 9 before decimal)

Base ten blocks can be used for decimal subtraction. Just redefine the blocks, so the big block is a one, the flat is a tenth, the rod is a hundredth and the little cube is a thousandth. Model and subtract decimals using base ten blocks, so students can "see" how decimals really work.

• Subtracting Tenths Subtracting Decimal Tenths with No Integer Part Subtracting Decimal Tenths with an Integer Part in the Minuend Subtracting Decimal Tenths with an Integer Part in the Minuend and Subtrahend
• Subtracting Hundredths Subtracting Decimal Hundredths with No Integer Part Subtracting Decimal Hundredths with an Integer Part in the Minuend and Subtrahend Subtracting Decimal Hundredths with a Larger Integer Part in the Minuend
• Subtracting Thousandths Subtracting Decimal Thousandths with No Integer Part Subtracting Decimal Thousandths with an Integer Part in the Minuend and Subtrahend
• Subtracting Ten Thousandths Subtracting Decimal Ten Thousandths with No Integer Part Subtracting Decimal Ten Thousandths with an Integer Part in the Minuend and Subtrahend
• Subtracting Various Decimal Places Subtracting Various Decimals to Hundredths Subtracting Various Decimals to Thousandths Subtracting Various Decimals to Ten Thousandths
• European Format Subtracting Decimals European Format Decimal subtraction (range 0,1 to 0,9) European Format Decimal subtraction (range 1,1 to 9,9) European Format Decimal subtraction (range 0,01 to 0,99) European Format Decimal subtraction (range 1,01 to 9,99) European Format Decimal subtraction (range 0,001 to 0,999) European Format Decimal subtraction (range 1,001 to 9,999) European Format Decimal subtraction (range 0,0001 to 0,9999) European Format Decimal subtraction (range 1,0001 to 9,9999) European Format Decimal subtraction with Various Decimal Places European Format Decimal subtraction with Various Decimal Places (1 to 9 before decimal)

Adding and subtracting decimals is fairly straightforward when all the decimals are lined up. With the questions arranged horizontally, students are challenged to understand place value as it relates to decimals. A wonderful strategy for placing the decimal is to use estimation. For example if the question is 49.2 + 20.1, the answer without the decimal is 693. Estimate by rounding 49.2 to 50 and 20.1 to 20. 50 + 20 = 70. The decimal in 693 must be placed between the 9 and the 3 as in 69.3 to make the number close to the estimate of 70.

The above strategy will go a long way in students understanding operations with decimals, but it is also important that they have a strong foundation in place value and a proficiency with efficient strategies to be completely successful with these questions. As with any math skill, it is not wise to present this to students until they have the necessary prerequisite skills and knowledge.

• Horizontally Arranged Adding Decimals Adding Decimals to Tenths Horizontally Adding Decimals to Hundredths Horizontally Adding Decimals to Thousandths Horizontally Adding Decimals to Ten Thousandths Horizontally Adding Decimals Horizontally With Up to Two Places Before and After the Decimal Adding Decimals Horizontally With Up to Three Places Before and After the Decimal Adding Decimals Horizontally With Up to Four Places Before and After the Decimal
• Horizontally Arranged Subtracting Decimals Subtracting Decimals to Tenths Horizontally Subtracting Decimals to Hundredths Horizontally Subtracting Decimals to Thousandths Horizontally Subtracting Decimals to Ten Thousandths Horizontally Subtracting Decimals Horizontally With Up to Two Places Before and After the Decimal Subtracting Decimals Horizontally With Up to Three Places Before and After the Decimal Subtracting Decimals Horizontally With Up to Four Places Before and After the Decimal
• Horizontally Arranged Mixed Adding and Subtracting Decimals Adding and Subtracting Decimals to Tenths Horizontally Adding and Subtracting Decimals to Hundredths Horizontally Adding and Subtracting Decimals to Thousandths Horizontally Adding and Subtracting Decimals to Ten Thousandths Horizontally Adding and Subtracting Decimals Horizontally With Up to Two Places Before and After the Decimal Adding and Subtracting Decimals Horizontally With Up to Three Places Before and After the Decimal Adding and Subtracting Decimals Horizontally With Up to Four Places Before and After the Decimal

Multiplying and Dividing Decimals

Multiplying decimals by whole numbers is very much like multiplying whole numbers except there is a decimal to deal with. Although students might initially have trouble with it, through the power of rounding and estimating, they can generally get it quite quickly. Many teachers will tell students to ignore the decimal and multiply the numbers just like they would whole numbers. This is a good strategy to use. Figuring out where the decimal goes at the end can be accomplished by counting how many decimal places were in the original question and giving the answer that many decimal places. To better understand this method, students can round the two factors and multiply in their head to get an estimate then place the decimal based on their estimate. For example, multiplying 9.84 × 91, students could first round the numbers to 10 and 91 (keep 91 since multiplying by 10 is easy) then get an estimate of 910. Actually multiplying (ignoring the decimal) gets you 89544. To get that number close to 910, the decimal needs to go between the 5 and the 4, thus 895.44. Note that there are two decimal places in the factors and two decimal places in the answer, but estimating made it more understandable rather than just a method.

• Multiplying Decimals by 1-Digit Whole Numbers Multiply 2-digit tenths by 1-digit whole numbers Multiply 2-digit hundredths by 1-digit whole numbers Multiply 2-digit thousandths by 1-digit whole numbers Multiply 3-digit tenths by 1-digit whole numbers Multiply 3-digit hundredths by 1-digit whole numbers Multiply 3-digit thousandths by 1-digit whole numbers Multiply various decimals by 1-digit whole numbers
• Multiplying Decimals by 2-Digit Whole Numbers Multiplying 2-digit tenths by 2-digit whole numbers Multiplying 2-digit hundredths by 2-digit whole numbers Multiplying 3-digit tenths by 2-digit whole numbers Multiplying 3-digit hundredths by 2-digit whole numbers Multiplying 3-digit thousandths by 2-digit whole numbers Multiplying various decimals by 2-digit whole numbers
• Multiplying Decimals by Tenths Multiplying 2-digit whole by 2-digit tenths Multiplying 2-digit tenths by 2-digit tenths Multiplying 2-digit hundredths by 2-digit tenths Multiplying 3-digit whole by 2-digit tenths Multiplying 3-digit tenths by 2-digit tenths Multiplying 3-digit hundredths by 2-digit tenths Multiplying 3-digit thousandths by 2-digit tenths Multiplying various decimals by 2-digit tenths
• Multiplying Decimals by Hundredths Multiplying 2-digit whole by 2-digit hundredths Multiplying 2-digit tenths by 2-digit hundredths Multiplying 2-digit hundredths by 2-digit hundredths Multiplying 3-digit whole by 2-digit hundredths Multiplying 3-digit tenths by 2-digit hundredths Multiplying 3-digit hundredths by 2-digit hundredths Multiplying 3-digit thousandths by 2-digit hundredths Multiplying various decimals by 2-digit hundredths
• Multiplying Decimals by Various Decimal Places Multiplying 2-digit by 2-digit numbers with various decimal places Multiplying 3-digit by 2-digit numbers with various decimal places
• Decimal Long Multiplication in Various Ranges Decimal Multiplication (range 0.1 to 0.9) Decimal Multiplication (range 1.1 to 9.9) Decimal Multiplication (range 10.1 to 99.9) Decimal Multiplication (range 0.01 to 0.99) Decimal Multiplication (range 1.01 to 9.99) Decimal Multiplication (range 10.01 to 99.99) Random # Digits Random # Places
• European Format Multiplying Decimals by 2-Digit Whole Numbers European Format 2-digit whole × 2-digit hundredths European Format 2-digit tenths × 2-digit whole European Format 2-digit hundredths × 2-digit whole European Format 3-digit tenths × 2-digit whole European Format 3-digit hundredths × 2-digit whole European Format 3-digit thousandths × 2-digit whole
• European Format Multiplying Decimals by 2-Digit Tenths European Format 2-digit whole × 2-digit tenths European Format 2-digit tenths × 2-digit tenths European Format 2-digit hundredths × 2-digit tenths European Format 3-digit whole × 2-digit tenths European Format 3-digit tenths × 2-digit tenths European Format 3-digit hundredths × 2-digit tenths European Format 3-digit thousandths × 2-digit tenths
• European Format Multiplying Decimals by 2-Digit Hundredths European Format 2-digit tenths × 2-digit hundredths European Format 2-digit hundredths × 2-digit hundredths European Format 3-digit whole × 2-digit hundredths European Format 3-digit tenths × 2-digit hundredths European Format 3-digit hundredths × 2-digit hundredths European Format 3-digit thousandths × 2-digit hundredths
• European Format Multiplying Decimals by Various Decimal Places European Format 2-digit × 2-digit with various decimal places European Format 3-digit × 2-digit with various decimal places
• Dividing Decimals by Whole Numbers Divide Tenths by a Whole Number Divide Hundredths by a Whole Number Divide Thousandths by a Whole Number Divide Ten Thousandths by a Whole Number Divide Various Decimals by a Whole Number

In case you aren't familiar with dividing with a decimal divisor, the general method for completing questions is by getting rid of the decimal in the divisor. This is done by multiplying the divisor and the dividend by the same amount, usually a power of ten such as 10, 100 or 1000. For example, if the division question is 5.32/5.6, you would multiply the divisor and dividend by 10 to get the equivalent division problem, 53.2/56. Completing this division will result in the exact same quotient as the original (try it on your calculator if you don't believe us). The main reason for completing decimal division in this way is to get the decimal in the correct location when using the U.S. long division algorithm.

A much simpler strategy, in our opinion, is to initially ignore the decimals all together and use estimation to place the decimal in the quotient. In the same example as above, you would complete 532/56 = 95. If you "flexibly" round the original, you will get about 5/5 which is about 1, so the decimal in 95 must be placed to make 95 close to 1. In this case, you would place it just before the 9 to get 0.95. Combining this strategy with the one above can also help a great deal with more difficult questions. For example, 4.584184 ÷ 0.461 can first be converted the to equivalent: 4584.184 ÷ 461 (you can estimate the quotient to be around 10). Complete the division question without decimals: 4584184 ÷ 461 = 9944 then place the decimal, so that 9944 is about 10. This results in 9.944.

Dividing decimal numbers doesn't have to be too difficult, especially with the worksheets below where the decimals work out nicely. To make these worksheets, we randomly generated a divisor and a quotient first, then multiplied them together to get the dividend. Of course, you will see the quotients only on the answer page, but generating questions in this way makes every decimal division problem work out nicely.

• Decimal Long Division with Quotients That Work Out Nicely Dividing Decimals by Various Decimals with Various Sizes of Quotients Dividing Decimals by 1-Digit Tenths (e.g. 0.72 ÷ 0.8 = 0.9) Dividing Decimals by 1-Digit Tenths with Larger Quotients (e.g. 3.2 ÷ 0.5 = 6.4) Dividing Decimals by 2-Digit Tenths (e.g. 10.75 ÷ 2.5 = 4.3) Dividing Decimals by 2-Digit Tenths with Larger Quotients (e.g. 387.75 ÷ 4.7 = 82.5) Dividing Decimals by 3-Digit Tenths (e.g. 1349.46 ÷ 23.8 = 56.7) Dividing Decimals by 2-Digit Hundredths (e.g. 0.4368 ÷ 0.56 = 0.78) Dividing Decimals by 2-Digit Hundredths with Larger Quotients (e.g. 1.7277 ÷ 0.39 = 4.43) Dividing Decimals by 3-Digit Hundredths (e.g. 31.4863 ÷ 4.61 = 6.83) Dividing Decimals by 4-Digit Hundredths (e.g. 7628.1285 ÷ 99.91 = 76.35) Dividing Decimals by 3-Digit Thousandths (e.g. 0.076504 ÷ 0.292 = 0.262) Dividing Decimals by 3-Digit Thousandths with Larger Quotients (e.g. 2.875669 ÷ 0.551 = 5.219)

These worksheets would probably be used for estimating and calculator work.

• Horizontally Arranged Decimal Division Random # Digits Random # Places
• European Format Dividing Decimals with Quotients That Work Out Nicely European Format Divide Tenths by a Whole Number European Format Divide Hundredths by a Whole Number European Format Divide Thousandths by a Whole Number European Format Divide Ten Thousandths by a Whole Number European Format Divide Various Decimals by a Whole Number

In the next set of questions, the quotient does not always work out well and may have repeating decimals. The answer key shows a rounded quotient in these cases.

• European Format Dividing Decimals by Whole Numbers European Format Divide Tenths by a Whole Number European Format Divide Hundredths by a Whole Number European Format Divide Thousandths by a Whole Number European Format Divide Ten Thousandths by a Whole Number European Format Divide Various Decimals by a Whole Number
• European Format Dividing Decimals by Decimals European Format Decimal Tenth (0,1 to 9,9) Divided by Decimal Tenth (1,1 to 9,9) European Format Decimal Hundredth (0,01 to 9,99) Divided by Decimal Tenth (1,1 to 9,9) European Format Decimal Thousandth (0,001 to 9,999) Divided by Decimal Tenth (1,1 to 9,9) European Format Decimal Ten Thousandth (0,0001 to 9,9999) Divided by Decimal Tenth (1,1 to 9,9) European Format Various Decimal Places (0,1 to 9,9999) Divided by Decimal Tenth (1,1 to 9,9) European Format Various Decimal Places (0,1 to 9,9999) Divided by Various Decimal Places (1,1 to 9,9999)

Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.

• International
• Schools directory
• Resources Jobs Schools directory News Search

Convert Fraction to Decimals Conversion Worksheets Math Problems

Subject: Mathematics

Age range: 7-11

Resource type: Worksheet/Activity

Last updated

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Convert Fraction to Decimals Conversion Worksheets Math Problems Make learning percentages and decimals engaging with our comprehensive set of worksheets designed to reinforce understanding and mastery of these essential mathematical concepts. Whether you’re a teacher looking for classroom resources or a parent seeking supplementary materials for at-home learning, our worksheets cater to various skill levels and learning styles. Variety of Problems: Each worksheet offers a diverse range of problems, including converting between percentages and decimals, calculating percentages of numbers, and solving word problems involving percentages and decimals. Progressive Difficulty: Worksheets are organized by difficulty level, allowing learners to gradually build their skills from basic to advanced concepts. Answer Keys: Each worksheet comes with an answer key for easy grading and self-assessment, facilitating independent learning. Enhanced Understanding: Through repeated practice, students develop a deeper comprehension of percentages and decimals, paving the way for proficiency in more advanced mathematical concepts. Improved Problem-Solving Skills: By tackling a variety of problems, learners sharpen their analytical and critical-thinking abilities, essential for solving mathematical problems and real-world challenges. Confidence Boost: Success in solving problems boosts students’ confidence and enthusiasm for learning mathematics, fostering a positive attitude towards the subject. Whether you’re introducing percentages and decimals for the first time or reinforcing existing knowledge, our worksheets provide valuable resources to support effective teaching and learning. Empower your students to excel in mathematics with our engaging and comprehensive materials. Worksheets are made in 8.5” x 11” Standard Letter Size. This resource is helpful in students’ assessment, Independent Studies, group activities, practice and homework. This product is available in PDF format and ready to print as well.

Tes paid licence How can I reuse this?

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

• May 21, 2024   •   24:14 The Crypto Comeback
• May 20, 2024   •   31:51 Was the 401(k) a Mistake?
• May 19, 2024   •   33:23 The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’
• May 17, 2024   •   51:10 The Campus Protesters Explain Themselves
• May 16, 2024   •   30:47 The Make-or-Break Testimony of Michael Cohen
• May 15, 2024   •   27:03 The Possible Collapse of the U.S. Home Insurance System
• May 14, 2024   •   35:20 Voters Want Change. In Our Poll, They See It in Trump.
• May 13, 2024   •   27:46 How Biden Adopted Trump’s Trade War With China
• May 10, 2024   •   27:42 Stormy Daniels Takes the Stand
• May 9, 2024   •   34:42 One Strongman, One Billion Voters, and the Future of India
• May 8, 2024   •   28:28 A Plan to Remake the Middle East
• May 7, 2024   •   27:43 How Changing Ocean Temperatures Could Upend Life on Earth

The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’

The answer involves a remarkable — and lucrative, and ridiculous — scheme to game the way we find music today..

By Brett Martin

Read by Eric Jason Martin

Produced by Adrienne Hurst and Aaron Esposito

Narration produced by Tanya Pérez and Krish Seenivasan

Edited by John Woo

Original music by Aaron Esposito

Engineered by Sophia Lanman and Devin Murphy

Listen and follow The Daily Apple Podcasts | Spotify

Have you heard the song “Brett Martin, You a Nice Man, Yes”?

Probably not. On Spotify, “Brett Martin, You a Nice Man, Yes” has not yet accumulated enough streams to even register a tally. Even Brett Martin, a contributing writer for The New York Times Magazine and the titular Nice Man, didn’t hear the 1 minute 14 second song until last summer, a full 11 years after it was uploaded by an artist credited as Papa Razzi and the Photogs.

When Martin stumbled on “Brett Martin, You a Nice Man, Yes,” he naturally assumed it was about a different, more famous Brett Martin: perhaps Brett Martin, the left-handed reliever who until recently played for the Texas Rangers; or Brett Martin, the legendary Australian squash player; or even Clara Brett Martin, the Canadian who in 1897 became the British Empire’s first female lawyer. Only when the singer began referencing details of stories that he made for public radio’s “This American Life” almost 20 years ago did he realize the song was actually about him. The song ended, “I really like you/Will you be my friend?/Will you call me on the phone?” Then it gave a phone number, with a New Hampshire area code.

So, he called.

There are a lot of ways to listen to ‘The Daily.’ Here’s how.

We want to hear from you. Tune in, and tell us what you think. Email us at [email protected] . Follow Michael Barbaro on X: @mikiebarb . And if you’re interested in advertising with The Daily, write to us at [email protected] .

Additional production for The Sunday Read was contributed by Isabella Anderson, Anna Diamond, Sarah Diamond, Elena Hecht, Emma Kehlbeck, Tanya Pérez, Frannie Carr Toth and Krish Seenivasan.

Advertisement

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.7: Solving Problems Using Ratios

• Last updated
• Save as PDF
• Page ID 45766
• Lumen Learning

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Outcome

• Use ratios to solve simple word problems

When you apply for a mortgage, the loan officer will compare your total debt to your total income to decide if you qualify for the loan. This comparison is called the debt-to-income ratio. The ratio must fall below a certain threshold for a lender to agree to loan you money. You can improve your debt to income ratio either by increasing your income, decreasing your debt, or both.

A ratio compares two numbers or two quantities and indicates their proportion to one another.

The ratio of \(a\) to \(b\) is written \(a\text{ to }b,{\Large\frac{a}{b}},\text{ or }\mathit{\text{a}}\text{ :}\mathit{\text{b}}\)

In this section, we will use the various notations interchangeably (i.e. \(\large\frac{5}{7}\) is the same as \(5\) : \(7\), is the same as \(5\) to \(7\)). When a ratio is written in fraction form, the fraction should be simplified. If it is an improper fraction, we do not change it to a mixed number. Because a ratio compares two quantities, we would leave a ratio as \({\large\frac{4}{1}}\) or \(4\) : \(1\) instead of simplifying it to \(4\) so that we can see the two parts of the ratio.

Write each ratio as a fraction:

• \(15\text{ to }27\)
• \(45\text{ to }18\)

Notice we leave the second ratio as an improper fraction.

[ohm_question]146453[/ohm_question]

In the following video you will see more examples of how to express a ratio as a fraction.

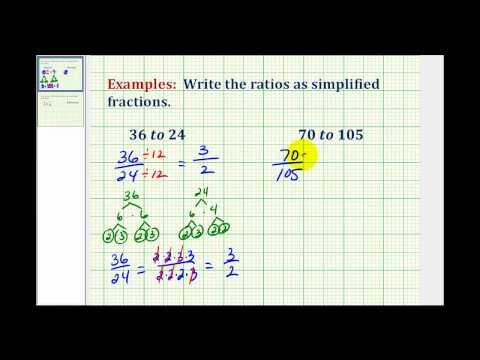
A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=74

Let’s consider some word problems with ratios. We will need to remember how to create equivalent ratios. As long as you are dividing or multiplying both parts of the ratio (or the numerator and denominator, if you are using a faction representation), then you are creating an equivalent ratio.

Take the ratio \(10\) : \(4\)

Let’s create an equivalent ratio by simplifying it. A common factor is \(2\), so let’s divide both values by \(2\). The result is a true statement of equivalent ratios.

\(10\) : \(4\) equals \(5\) : \(2\)

\(\frac{10}{4}\) = \(\frac{5}{2}\)

Let’s create another equivalent ratio by making it larger. Let’s multiply both values by \(3\). The result is a true statement of equivalent ratios.

\(10\) : \(4\) equals \(30\) : \(12\)

\(\frac{10}{4}\) = \(\frac{30}{12}\)

If Maria buys one dress for every three pairs of pants, and last year she bought nine pairs of pants, how many dresses did she buy last year?

We will set up two equivalent ratio sentences like this:

_____ dress : _____ pants (Maria’s purchase ratio)

_____ dress : _____ pants (last year’s actual purchases)

Then we will fill them out with the values we know:

__\(\color{red}{1}\)__ dress : __\(\color{red}{3}\)__ pants

__\(\color{red}{?}\)__ dress : __\(\color{red}{9}\)__ pants

To make an equivalent ratio and to get from \(3\) pants to \(9\) pants, we know that we must have multiplied the initial value by \(3\). Let’s do the same to the dresses to complete the equivalent ratio.

\(3\cdot1=3\)

Therefore, if Maria bought nine pairs of pants last year, based on her purchase ratio, she also bought three dresses.

The ratio of Sophomores to Seniors at Mauve Hills High School is seven to ten. If there are 154 Sophomores enrolled this year, how many Seniors are there?

[reveal-answer q=”368717″]Show Answer[/reveal-answer] [hidden-answer a=”368717″]

__\(\color{red}{7}\)__ Sophomores : __\(\color{red}{10}\)__ Seniors

__\(\color{red}{154}\)__ Sophomores : __\(\color{red}{?}\)__ Seniors

We know that to make equivalent fractions, the \(7\) must have been multiplied by something. So let’s divide \(154\) by \(7\) to find out what that multiplier was.

\(154\div{7}=22\)

Let’s take that multiplier of \(22\) and multiply it by the \(10\) Seniors in the original ratio to create an equivalent ratio.

\(10\cdot{22}=220\)

There are \(220\) Seniors at Mauve Hills High School.

[/hidden-answer]

The next examples go one step further and take a little more thought as to what value you are looking for and what to do with it after you calculate it.

The Pet Adoption Center in San Antonio houses a ratio of \(4\) cats to \(7\) dogs. If the shelter can house \(49\) dogs, how many total animals can they keep at the shelter?

[reveal-answer q=”587115″]Show Answer[/reveal-answer] [hidden-answer a=”587115″]

First, we need to figure out how many cats are at the shelter.

\(\large{\frac{4}{7}}=\large{\frac{?}{49}}\)

\(\large{\frac{4}{7}}\cdot\color{red}{\frac{7}{7}}=\large{\frac{28}{49}}\)

There are \(28\) cats at the shelter. So in total there are \(28+49=77\) animals housed at the Pet Adoption Center in San Antonio.

[ohm_question]156943[/ohm_question]