what is the difference between research hypothesis and null hypothesis

Null Hypothesis vs. Hypothesis

Published: November 3, 2022 by iSixSigma Staff

Null Hypothesis vs. Hypothesis: What’s the Difference?

What is null hypothesis.

A null hypothesis is a prediction that there is no statistical relationship between two variables or two sets of data. Essentially, a null hypothesis makes the assumption that any measured differences are the result of randomness and that the two possibilities are the same until proven otherwise.

The Benefits of a Null Hypothesis

A null hypothesis is commonly used in research to determine whether there is a real relationship between two measured phenomena. It offers the ability to distinguish between results that are the result of random chance or if there is a legitimate statistical relationship.

How to Create a Null Hypothesis

To create a null hypothesis, start by asking a few questions about the set of data or experiment. Then rephrase those questions into a statement that assumes no relationship. Null hypotheses usually include phrases such as “no relationship,” “no effect,” etc. For example, let’s say you are looking at some data about whether the number of people on a project affects the overall ability of the team to accomplish its goals.

A question might look like this:

“Does the number of people working on a team project impact the ability of the team to achieve the goals of the project?”

Rephrasing this into a null hypothesis that assumes no relationship would look like this:

“The number of people working on a team project does not impact the ability of the team to achieve the goals of the project.”

The null hypothesis is assumed true until proven otherwise.

What Is a Hypothesis?

A hypothesis, also known as an alternative hypothesis, is an educated theory or “guess” based on limited evidence that requires further testing to be proven true or false. It is used in an experiment to define a relationship between two variables.

The Benefits of a Hypothesis

A hypothesis helps a researcher prove or disprove their theories, or guesses, using limited data and knowledge. Researchers and scientists will create a formalized hypothesis based on past data or experiments. This hypothesis forces them to think about what they should be looking for in their experiments.

How to Create a Hypothesis

The best way to create a hypothesis is first to create a null hypothesis. Once you have your null hypothesis that states there is no relationship, you can then revise the statement that implies a relationship does exist. This is the reason it is referred to as an “alternative hypothesis.”

As an example:

Null hypothesis: There is no relationship between mediation and the reduction of depression. Alternative hypothesis: The practice of meditation reduces depression.

In this example, the research wants to disprove that there is no relationship between meditation and the reduction of depression and prove that meditation does, in fact, reduce depression. The researcher’s goal is to prove their hypothesis through statistical data.

In the simplest terms, a hypothesis is something that a researcher tries to prove, while a null hypothesis is something that a researcher tries to disprove. Both are used when performing research and evaluating data.

There are two variables in a hypothesis. The first is called the independent variable. This is the driving force of the experiment or research. The second is called the dependent variable, which is the measurable result.

The biggest difference between the two is that a null hypothesis cannot be proven; it can only be rejected.

Null Hypothesis vs. Hypothesis: Who Would Use Null Hypothesis and/or Hypothesis?

Having both a null hypothesis and hypothesis is beneficial and required in nearly all fields of research. Having both null and alternative hypothesis offer competing views into your research. Researchers weigh the evidence for and against the two hypotheses using a statistical test. The statistical data is used to prove or disprove the alternative hypothesis. If an alternative hypothesis is disproved, researchers can then modify their alternative hypothesis and look at their experimentation method(s) in order to achieve their goals and improve the accuracy of their experiments.

Choosing Between Null Hypothesis and Hypothesis: Real World Scenarios

Null and alternative hypotheses are used extensively in medical research. Let’s say a team of researchers is trying to determine if flossing decreases the number of cavities a person might experience.

Their null hypothesis might look like this:

“There is no relationship between tooth flossing and the number of cavities a person experiences.”

Their alternative hypothesis might be:

“Tooth flossing reduces the number of cavities a person experiences.”

In the world of investing, a null hypothesis is frequently used in the quantitative analysis of data to test theories about economies, investing strategies, and other financial markets.

An example of a null hypothesis: The mean annual return of a stock option is 3%.

An example of an alternative hypothesis: The mean annual return of a stock option is NOT 3%.

Essentially, the theories are the alternative hypothesis you are trying to prove, and the null hypothesis is the statement you are trying to disprove.

The bottom line is that both types of hypotheses are required for proper research and data evaluation. Create a null hypothesis to disprove and an alternative hypothesis to prove. Collect and evaluate the data to determine which hypothesis is favored.

About the Author

iSixSigma Staff

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 23459

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 66\)
• \(H_{a}: \mu \_ 66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 5\)
• \(H_{a}: \mu < 5\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 45\)
• \(H_{a}: \mu \_ 45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p \_ 0.40\)
• \(H_{a}: p \_ 0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Idea behind hypothesis testing

Examples of null and alternative hypotheses

• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations
• Using P-values to make conclusions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Indian J Crit Care Med
• v.23(Suppl 3); 2019 Sep

An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors

Priya ranganathan.

1 Department of Anesthesiology, Critical Care and Pain, Tata Memorial Hospital, Mumbai, Maharashtra, India

2 Department of Surgical Oncology, Tata Memorial Centre, Mumbai, Maharashtra, India

The second article in this series on biostatistics covers the concepts of sample, population, research hypotheses and statistical errors.

How to cite this article

Ranganathan P, Pramesh CS. An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors. Indian J Crit Care Med 2019;23(Suppl 3):S230–S231.

Two papers quoted in this issue of the Indian Journal of Critical Care Medicine report. The results of studies aim to prove that a new intervention is better than (superior to) an existing treatment. In the ABLE study, the investigators wanted to show that transfusion of fresh red blood cells would be superior to standard-issue red cells in reducing 90-day mortality in ICU patients. 1 The PROPPR study was designed to prove that transfusion of a lower ratio of plasma and platelets to red cells would be superior to a higher ratio in decreasing 24-hour and 30-day mortality in critically ill patients. 2 These studies are known as superiority studies (as opposed to noninferiority or equivalence studies which will be discussed in a subsequent article).

SAMPLE VERSUS POPULATION

A sample represents a group of participants selected from the entire population. Since studies cannot be carried out on entire populations, researchers choose samples, which are representative of the population. This is similar to walking into a grocery store and examining a few grains of rice or wheat before purchasing an entire bag; we assume that the few grains that we select (the sample) are representative of the entire sack of grains (the population).

The results of the study are then extrapolated to generate inferences about the population. We do this using a process known as hypothesis testing. This means that the results of the study may not always be identical to the results we would expect to find in the population; i.e., there is the possibility that the study results may be erroneous.

HYPOTHESIS TESTING

A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the “alternate” hypothesis, and the opposite is called the “null” hypothesis; every study has a null hypothesis and an alternate hypothesis. For superiority studies, the alternate hypothesis states that one treatment (usually the new or experimental treatment) is superior to the other; the null hypothesis states that there is no difference between the treatments (the treatments are equal). For example, in the ABLE study, we start by stating the null hypothesis—there is no difference in mortality between groups receiving fresh RBCs and standard-issue RBCs. We then state the alternate hypothesis—There is a difference between groups receiving fresh RBCs and standard-issue RBCs. It is important to note that we have stated that the groups are different, without specifying which group will be better than the other. This is known as a two-tailed hypothesis and it allows us to test for superiority on either side (using a two-sided test). This is because, when we start a study, we are not 100% certain that the new treatment can only be better than the standard treatment—it could be worse, and if it is so, the study should pick it up as well. One tailed hypothesis and one-sided statistical testing is done for non-inferiority studies, which will be discussed in a subsequent paper in this series.

STATISTICAL ERRORS

There are two possibilities to consider when interpreting the results of a superiority study. The first possibility is that there is truly no difference between the treatments but the study finds that they are different. This is called a Type-1 error or false-positive error or alpha error. This means falsely rejecting the null hypothesis.

The second possibility is that there is a difference between the treatments and the study does not pick up this difference. This is called a Type 2 error or false-negative error or beta error. This means falsely accepting the null hypothesis.

The power of the study is the ability to detect a difference between groups and is the converse of the beta error; i.e., power = 1-beta error. Alpha and beta errors are finalized when the protocol is written and form the basis for sample size calculation for the study. In an ideal world, we would not like any error in the results of our study; however, we would need to do the study in the entire population (infinite sample size) to be able to get a 0% alpha and beta error. These two errors enable us to do studies with realistic sample sizes, with the compromise that there is a small possibility that the results may not always reflect the truth. The basis for this will be discussed in a subsequent paper in this series dealing with sample size calculation.

Conventionally, type 1 or alpha error is set at 5%. This means, that at the end of the study, if there is a difference between groups, we want to be 95% certain that this is a true difference and allow only a 5% probability that this difference has occurred by chance (false positive). Type 2 or beta error is usually set between 10% and 20%; therefore, the power of the study is 90% or 80%. This means that if there is a difference between groups, we want to be 80% (or 90%) certain that the study will detect that difference. For example, in the ABLE study, sample size was calculated with a type 1 error of 5% (two-sided) and power of 90% (type 2 error of 10%) (1).

Table 1 gives a summary of the two types of statistical errors with an example

Statistical errors

In the next article in this series, we will look at the meaning and interpretation of ‘ p ’ value and confidence intervals for hypothesis testing.

Source of support: Nil

Conflict of interest: None

Statistics Resources

• Excel - Tutorials
• Basic Probability Rules
• Single Event Probability
• Complement Rule
• Intersections & Unions
• Compound Events
• Levels of Measurement
• Independent and Dependent Variables
• Entering Data
• Central Tendency
• Data and Tests
• Displaying Data
• Discussing Statistics In-text
• SEM and Confidence Intervals
• Two-Way Frequency Tables
• Empirical Rule
• Finding Probability
• Accessing SPSS
• Chart and Graphs
• Frequency Table and Distribution
• Descriptive Statistics
• Converting Raw Scores to Z-Scores
• Converting Z-scores to t-scores
• Split File/Split Output
• Partial Eta Squared
• Downloading and Installing G*Power: Windows/PC
• Correlation
• Testing Parametric Assumptions
• One-Way ANOVA
• Two-Way ANOVA
• Repeated Measures ANOVA
• Goodness-of-Fit
• Test of Association
• Pearson's r
• Point Biserial
• Mediation and Moderation
• Simple Linear Regression
• Multiple Linear Regression
• Binomial Logistic Regression
• Multinomial Logistic Regression
• Independent Samples T-test
• Dependent Samples T-test
• Testing Assumptions
• T-tests using SPSS
• T-Test Practice
• Predictive Analytics This link opens in a new window
• Quantitative Research Questions
• Null & Alternative Hypotheses
• One-Tail vs. Two-Tail
• Alpha & Beta
• Associated Probability
• Decision Rule
• Statement of Conclusion
• Statistics Group Sessions

ASC Chat Hours

ASC Chat is usually available at the following times ( Pacific Time):

If there is not a coach on duty, submit your question via one of the below methods:

  928-440-1325

  Ask a Coach

  [email protected]

Search our FAQs on the Academic Success Center's  Ask a Coach   page.

Once you have developed a clear and focused research question or set of research questions, you’ll be ready to conduct further research, a literature review, on the topic to help you make an educated guess about the answer to your question(s). This educated guess is called a hypothesis.

In research, there are two types of hypotheses: null and alternative. They work as a complementary pair, each stating that the other is wrong.

• Null Hypothesis (H 0 ) – This can be thought of as the implied hypothesis. “Null” meaning “nothing.”  This hypothesis states that there is no difference between groups or no relationship between variables. The null hypothesis is a presumption of status quo or no change.
• Alternative Hypothesis (H a ) – This is also known as the claim. This hypothesis should state what you expect the data to show, based on your research on the topic. This is your answer to your research question.

Null Hypothesis:   H 0 : There is no difference in the salary of factory workers based on gender. Alternative Hypothesis :  H a : Male factory workers have a higher salary than female factory workers.

Null Hypothesis :  H 0 : There is no relationship between height and shoe size. Alternative Hypothesis :  H a : There is a positive relationship between height and shoe size.

Null Hypothesis :  H 0 : Experience on the job has no impact on the quality of a brick mason’s work. Alternative Hypothesis :  H a : The quality of a brick mason’s work is influenced by on-the-job experience.

Was this resource helpful?

• << Previous: Hypothesis Testing
• Next: One-Tail vs. Two-Tail >>
• Last Updated: Apr 19, 2024 3:09 PM
• URL: https://resources.nu.edu/statsresources

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 13: Inferential Statistics

Understanding Null Hypothesis Testing

Learning Objectives

• Explain the purpose of null hypothesis testing, including the role of sampling error.
• Describe the basic logic of null hypothesis testing.
• Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called  parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s  r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called  sampling error . (Note that the term error  here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s  r  value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.

In fact, any statistical relationship in a sample can be interpreted in two ways:

• There is a relationship in the population, and the relationship in the sample reflects this.
• There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Null hypothesis testing  is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the   null hypothesis  (often symbolized  H 0  and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the  alternative hypothesis  (often symbolized as  H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:

• Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
• Determine how likely the sample relationship would be if the null hypothesis were true.
• If the sample relationship would be extremely unlikely, then reject the null hypothesis  in favour of the alternative hypothesis. If it would not be extremely unlikely, then  retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of  d  = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favour of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the  p value . A low  p  value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high  p  value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the  p  value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called  α (alpha)  and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be  statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood  p  Value

The  p  value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [1] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!

The most common misinterpretation is that the  p  value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the  p  value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The  p  value is really the probability of a result at least as extreme as the sample result  if  the null hypothesis  were  true. So a  p  value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.

You can avoid this misunderstanding by remembering that the  p  value is not the probability that any particular  hypothesis  is true or false. Instead, it is the probability of obtaining the  sample result  if the null hypothesis were true.

Role of Sample Size and Relationship Strength

Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the  p  value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the  p  value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s  d  is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s  d  is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word  Yes , then this combination would be statistically significant for both Cohen’s  d  and Pearson’s  r . If it contains the word  No , then it would not be statistically significant for either. There is one cell where the decision for  d  and  r  would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”

Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.

Statistical Significance Versus Practical Significance

Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word  significant  can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

This is why it is important to distinguish between the  statistical  significance of a result and the  practical  significance of that result.  Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.

Key Takeaways

• Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
• The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favour of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
• The probability of obtaining the sample result if the null hypothesis were true (the  p  value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
• Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
• Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
• The correlation between two variables is  r  = −.78 based on a sample size of 137.
• The mean score on a psychological characteristic for women is 25 ( SD  = 5) and the mean score for men is 24 ( SD  = 5). There were 12 women and 10 men in this study.
• In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
• In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
• A student finds a correlation of  r  = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.

Long Descriptions

“Null Hypothesis” long description: A comic depicting a man and a woman talking in the foreground. In the background is a child working at a desk. The man says to the woman, “I can’t believe schools are still teaching kids about the null hypothesis. I remember reading a big study that conclusively disproved it years ago.” [Return to “Null Hypothesis”]

“Conditional Risk” long description: A comic depicting two hikers beside a tree during a thunderstorm. A bolt of lightning goes “crack” in the dark sky as thunder booms. One of the hikers says, “Whoa! We should get inside!” The other hiker says, “It’s okay! Lightning only kills about 45 Americans a year, so the chances of dying are only one in 7,000,000. Let’s go on!” The comic’s caption says, “The annual death rate among people who know that statistic is one in six.” [Return to “Conditional Risk”]

Media Attributions

• Null Hypothesis by XKCD  CC BY-NC (Attribution NonCommercial)
• Conditional Risk by XKCD  CC BY-NC (Attribution NonCommercial)
• Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
• Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Values in a population that correspond to variables measured in a study.

The random variability in a statistic from sample to sample.

A formal approach to deciding between two interpretations of a statistical relationship in a sample.

The idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error.

The idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

When the relationship found in the sample would be extremely unlikely, the idea that the relationship occurred “by chance” is rejected.

When the relationship found in the sample is likely to have occurred by chance, the null hypothesis is not rejected.

The probability that, if the null hypothesis were true, the result found in the sample would occur.

How low the p value must be before the sample result is considered unlikely in null hypothesis testing.

When there is less than a 5% chance of a result as extreme as the sample result occurring and the null hypothesis is rejected.

Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

What Is A Research (Scientific) Hypothesis? A plain-language explainer + examples

By:  Derek Jansen (MBA)  | Reviewed By: Dr Eunice Rautenbach | June 2020

If you’re new to the world of research, or it’s your first time writing a dissertation or thesis, you’re probably noticing that the words “research hypothesis” and “scientific hypothesis” are used quite a bit, and you’re wondering what they mean in a research context .

“Hypothesis” is one of those words that people use loosely, thinking they understand what it means. However, it has a very specific meaning within academic research. So, it’s important to understand the exact meaning before you start hypothesizing. 

Research Hypothesis 101

• What is a hypothesis ?
• What is a research hypothesis (scientific hypothesis)?
• Requirements for a research hypothesis
• Definition of a research hypothesis
• The null hypothesis

What is a hypothesis?

Let’s start with the general definition of a hypothesis (not a research hypothesis or scientific hypothesis), according to the Cambridge Dictionary:

Hypothesis: an idea or explanation for something that is based on known facts but has not yet been proved.

In other words, it’s a statement that provides an explanation for why or how something works, based on facts (or some reasonable assumptions), but that has not yet been specifically tested . For example, a hypothesis might look something like this:

Hypothesis: sleep impacts academic performance.

This statement predicts that academic performance will be influenced by the amount and/or quality of sleep a student engages in – sounds reasonable, right? It’s based on reasonable assumptions , underpinned by what we currently know about sleep and health (from the existing literature). So, loosely speaking, we could call it a hypothesis, at least by the dictionary definition.

But that’s not good enough…

Unfortunately, that’s not quite sophisticated enough to describe a research hypothesis (also sometimes called a scientific hypothesis), and it wouldn’t be acceptable in a dissertation, thesis or research paper . In the world of academic research, a statement needs a few more criteria to constitute a true research hypothesis .

What is a research hypothesis?

A research hypothesis (also called a scientific hypothesis) is a statement about the expected outcome of a study (for example, a dissertation or thesis). To constitute a quality hypothesis, the statement needs to have three attributes – specificity , clarity and testability .

Let’s take a look at these more closely.

Need a helping hand?

Hypothesis Essential #1: Specificity & Clarity

A good research hypothesis needs to be extremely clear and articulate about both what’ s being assessed (who or what variables are involved ) and the expected outcome (for example, a difference between groups, a relationship between variables, etc.).

Let’s stick with our sleepy students example and look at how this statement could be more specific and clear.

Hypothesis: Students who sleep at least 8 hours per night will, on average, achieve higher grades in standardised tests than students who sleep less than 8 hours a night.

As you can see, the statement is very specific as it identifies the variables involved (sleep hours and test grades), the parties involved (two groups of students), as well as the predicted relationship type (a positive relationship). There’s no ambiguity or uncertainty about who or what is involved in the statement, and the expected outcome is clear.

Contrast that to the original hypothesis we looked at – “Sleep impacts academic performance” – and you can see the difference. “Sleep” and “academic performance” are both comparatively vague , and there’s no indication of what the expected relationship direction is (more sleep or less sleep). As you can see, specificity and clarity are key.

Hypothesis Essential #2: Testability (Provability)

A statement must be testable to qualify as a research hypothesis. In other words, there needs to be a way to prove (or disprove) the statement. If it’s not testable, it’s not a hypothesis – simple as that.

For example, consider the hypothesis we mentioned earlier:

Hypothesis: Students who sleep at least 8 hours per night will, on average, achieve higher grades in standardised tests than students who sleep less than 8 hours a night.  

We could test this statement by undertaking a quantitative study involving two groups of students, one that gets 8 or more hours of sleep per night for a fixed period, and one that gets less. We could then compare the standardised test results for both groups to see if there’s a statistically significant difference. 

Again, if you compare this to the original hypothesis we looked at – “Sleep impacts academic performance” – you can see that it would be quite difficult to test that statement, primarily because it isn’t specific enough. How much sleep? By who? What type of academic performance?

So, remember the mantra – if you can’t test it, it’s not a hypothesis 🙂

Defining A Research Hypothesis

You’re still with us? Great! Let’s recap and pin down a clear definition of a hypothesis.

A research hypothesis (or scientific hypothesis) is a statement about an expected relationship between variables, or explanation of an occurrence, that is clear, specific and testable.

So, when you write up hypotheses for your dissertation or thesis, make sure that they meet all these criteria. If you do, you’ll not only have rock-solid hypotheses but you’ll also ensure a clear focus for your entire research project.

What about the null hypothesis?

You may have also heard the terms null hypothesis , alternative hypothesis, or H-zero thrown around. At a simple level, the null hypothesis is the counter-proposal to the original hypothesis.

For example, if the hypothesis predicts that there is a relationship between two variables (for example, sleep and academic performance), the null hypothesis would predict that there is no relationship between those variables.

At a more technical level, the null hypothesis proposes that no statistical significance exists in a set of given observations and that any differences are due to chance alone.

And there you have it – hypotheses in a nutshell. 

If you have any questions, be sure to leave a comment below and we’ll do our best to help you. If you need hands-on help developing and testing your hypotheses, consider our private coaching service , where we hold your hand through the research journey.

Psst... there’s more!

This post was based on one of our popular Research Bootcamps . If you're working on a research project, you'll definitely want to check this out ...

You Might Also Like:

16 Comments

Very useful information. I benefit more from getting more information in this regard.

Very great insight,educative and informative. Please give meet deep critics on many research data of public international Law like human rights, environment, natural resources, law of the sea etc

In a book I read a distinction is made between null, research, and alternative hypothesis. As far as I understand, alternative and research hypotheses are the same. Can you please elaborate? Best Afshin

This is a self explanatory, easy going site. I will recommend this to my friends and colleagues.

Very good definition. How can I cite your definition in my thesis? Thank you. Is nul hypothesis compulsory in a research?

It’s a counter-proposal to be proven as a rejection

Please what is the difference between alternate hypothesis and research hypothesis?

It is a very good explanation. However, it limits hypotheses to statistically tasteable ideas. What about for qualitative researches or other researches that involve quantitative data that don’t need statistical tests?

In qualitative research, one typically uses propositions, not hypotheses.

could you please elaborate it more

I’ve benefited greatly from these notes, thank you.

This is very helpful

well articulated ideas are presented here, thank you for being reliable sources of information

Excellent. Thanks for being clear and sound about the research methodology and hypothesis (quantitative research)

I have only a simple question regarding the null hypothesis. – Is the null hypothesis (Ho) known as the reversible hypothesis of the alternative hypothesis (H1? – How to test it in academic research?

this is very important note help me much more

Trackbacks/Pingbacks

• What Is Research Methodology? Simple Definition (With Examples) - Grad Coach - […] Contrasted to this, a quantitative methodology is typically used when the research aims and objectives are confirmatory in nature. For example,…

Submit a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Print Friendly

• Privacy Policy

Home » What is a Hypothesis – Types, Examples and Writing Guide

What is a Hypothesis – Types, Examples and Writing Guide

Table of Contents

Definition:

Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation.

Hypothesis is often used in scientific research to guide the design of experiments and the collection and analysis of data. It is an essential element of the scientific method, as it allows researchers to make predictions about the outcome of their experiments and to test those predictions to determine their accuracy.

Types of Hypothesis

Types of Hypothesis are as follows:

Research Hypothesis

A research hypothesis is a statement that predicts a relationship between variables. It is usually formulated as a specific statement that can be tested through research, and it is often used in scientific research to guide the design of experiments.

Null Hypothesis

The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. It is often used as a starting point for testing the research hypothesis, and if the results of the study reject the null hypothesis, it suggests that there is a significant difference or relationship between variables.

Alternative Hypothesis

An alternative hypothesis is a statement that assumes there is a significant difference or relationship between variables. It is often used as an alternative to the null hypothesis and is tested against the null hypothesis to determine which statement is more accurate.

Directional Hypothesis

A directional hypothesis is a statement that predicts the direction of the relationship between variables. For example, a researcher might predict that increasing the amount of exercise will result in a decrease in body weight.

Non-directional Hypothesis

A non-directional hypothesis is a statement that predicts the relationship between variables but does not specify the direction. For example, a researcher might predict that there is a relationship between the amount of exercise and body weight, but they do not specify whether increasing or decreasing exercise will affect body weight.

Statistical Hypothesis

A statistical hypothesis is a statement that assumes a particular statistical model or distribution for the data. It is often used in statistical analysis to test the significance of a particular result.

Composite Hypothesis

A composite hypothesis is a statement that assumes more than one condition or outcome. It can be divided into several sub-hypotheses, each of which represents a different possible outcome.

Empirical Hypothesis

An empirical hypothesis is a statement that is based on observed phenomena or data. It is often used in scientific research to develop theories or models that explain the observed phenomena.

Simple Hypothesis

A simple hypothesis is a statement that assumes only one outcome or condition. It is often used in scientific research to test a single variable or factor.

Complex Hypothesis

A complex hypothesis is a statement that assumes multiple outcomes or conditions. It is often used in scientific research to test the effects of multiple variables or factors on a particular outcome.

Applications of Hypothesis

Hypotheses are used in various fields to guide research and make predictions about the outcomes of experiments or observations. Here are some examples of how hypotheses are applied in different fields:

• Science : In scientific research, hypotheses are used to test the validity of theories and models that explain natural phenomena. For example, a hypothesis might be formulated to test the effects of a particular variable on a natural system, such as the effects of climate change on an ecosystem.
• Medicine : In medical research, hypotheses are used to test the effectiveness of treatments and therapies for specific conditions. For example, a hypothesis might be formulated to test the effects of a new drug on a particular disease.
• Psychology : In psychology, hypotheses are used to test theories and models of human behavior and cognition. For example, a hypothesis might be formulated to test the effects of a particular stimulus on the brain or behavior.
• Sociology : In sociology, hypotheses are used to test theories and models of social phenomena, such as the effects of social structures or institutions on human behavior. For example, a hypothesis might be formulated to test the effects of income inequality on crime rates.
• Business : In business research, hypotheses are used to test the validity of theories and models that explain business phenomena, such as consumer behavior or market trends. For example, a hypothesis might be formulated to test the effects of a new marketing campaign on consumer buying behavior.
• Engineering : In engineering, hypotheses are used to test the effectiveness of new technologies or designs. For example, a hypothesis might be formulated to test the efficiency of a new solar panel design.

How to write a Hypothesis

Here are the steps to follow when writing a hypothesis:

Identify the Research Question

The first step is to identify the research question that you want to answer through your study. This question should be clear, specific, and focused. It should be something that can be investigated empirically and that has some relevance or significance in the field.

Conduct a Literature Review

Before writing your hypothesis, it’s essential to conduct a thorough literature review to understand what is already known about the topic. This will help you to identify the research gap and formulate a hypothesis that builds on existing knowledge.

Determine the Variables

The next step is to identify the variables involved in the research question. A variable is any characteristic or factor that can vary or change. There are two types of variables: independent and dependent. The independent variable is the one that is manipulated or changed by the researcher, while the dependent variable is the one that is measured or observed as a result of the independent variable.

Formulate the Hypothesis

Based on the research question and the variables involved, you can now formulate your hypothesis. A hypothesis should be a clear and concise statement that predicts the relationship between the variables. It should be testable through empirical research and based on existing theory or evidence.

Write the Null Hypothesis

The null hypothesis is the opposite of the alternative hypothesis, which is the hypothesis that you are testing. The null hypothesis states that there is no significant difference or relationship between the variables. It is important to write the null hypothesis because it allows you to compare your results with what would be expected by chance.

Refine the Hypothesis

After formulating the hypothesis, it’s important to refine it and make it more precise. This may involve clarifying the variables, specifying the direction of the relationship, or making the hypothesis more testable.

Examples of Hypothesis

Here are a few examples of hypotheses in different fields:

• Psychology : “Increased exposure to violent video games leads to increased aggressive behavior in adolescents.”
• Biology : “Higher levels of carbon dioxide in the atmosphere will lead to increased plant growth.”
• Sociology : “Individuals who grow up in households with higher socioeconomic status will have higher levels of education and income as adults.”
• Education : “Implementing a new teaching method will result in higher student achievement scores.”
• Marketing : “Customers who receive a personalized email will be more likely to make a purchase than those who receive a generic email.”
• Physics : “An increase in temperature will cause an increase in the volume of a gas, assuming all other variables remain constant.”
• Medicine : “Consuming a diet high in saturated fats will increase the risk of developing heart disease.”

Purpose of Hypothesis

The purpose of a hypothesis is to provide a testable explanation for an observed phenomenon or a prediction of a future outcome based on existing knowledge or theories. A hypothesis is an essential part of the scientific method and helps to guide the research process by providing a clear focus for investigation. It enables scientists to design experiments or studies to gather evidence and data that can support or refute the proposed explanation or prediction.

The formulation of a hypothesis is based on existing knowledge, observations, and theories, and it should be specific, testable, and falsifiable. A specific hypothesis helps to define the research question, which is important in the research process as it guides the selection of an appropriate research design and methodology. Testability of the hypothesis means that it can be proven or disproven through empirical data collection and analysis. Falsifiability means that the hypothesis should be formulated in such a way that it can be proven wrong if it is incorrect.

In addition to guiding the research process, the testing of hypotheses can lead to new discoveries and advancements in scientific knowledge. When a hypothesis is supported by the data, it can be used to develop new theories or models to explain the observed phenomenon. When a hypothesis is not supported by the data, it can help to refine existing theories or prompt the development of new hypotheses to explain the phenomenon.

When to use Hypothesis

Here are some common situations in which hypotheses are used:

• In scientific research , hypotheses are used to guide the design of experiments and to help researchers make predictions about the outcomes of those experiments.
• In social science research , hypotheses are used to test theories about human behavior, social relationships, and other phenomena.
• I n business , hypotheses can be used to guide decisions about marketing, product development, and other areas. For example, a hypothesis might be that a new product will sell well in a particular market, and this hypothesis can be tested through market research.

Characteristics of Hypothesis

Here are some common characteristics of a hypothesis:

• Testable : A hypothesis must be able to be tested through observation or experimentation. This means that it must be possible to collect data that will either support or refute the hypothesis.
• Falsifiable : A hypothesis must be able to be proven false if it is not supported by the data. If a hypothesis cannot be falsified, then it is not a scientific hypothesis.
• Clear and concise : A hypothesis should be stated in a clear and concise manner so that it can be easily understood and tested.
• Based on existing knowledge : A hypothesis should be based on existing knowledge and research in the field. It should not be based on personal beliefs or opinions.
• Specific : A hypothesis should be specific in terms of the variables being tested and the predicted outcome. This will help to ensure that the research is focused and well-designed.
• Tentative: A hypothesis is a tentative statement or assumption that requires further testing and evidence to be confirmed or refuted. It is not a final conclusion or assertion.
• Relevant : A hypothesis should be relevant to the research question or problem being studied. It should address a gap in knowledge or provide a new perspective on the issue.

Advantages of Hypothesis

Hypotheses have several advantages in scientific research and experimentation:

• Guides research: A hypothesis provides a clear and specific direction for research. It helps to focus the research question, select appropriate methods and variables, and interpret the results.
• Predictive powe r: A hypothesis makes predictions about the outcome of research, which can be tested through experimentation. This allows researchers to evaluate the validity of the hypothesis and make new discoveries.
• Facilitates communication: A hypothesis provides a common language and framework for scientists to communicate with one another about their research. This helps to facilitate the exchange of ideas and promotes collaboration.
• Efficient use of resources: A hypothesis helps researchers to use their time, resources, and funding efficiently by directing them towards specific research questions and methods that are most likely to yield results.
• Provides a basis for further research: A hypothesis that is supported by data provides a basis for further research and exploration. It can lead to new hypotheses, theories, and discoveries.
• Increases objectivity: A hypothesis can help to increase objectivity in research by providing a clear and specific framework for testing and interpreting results. This can reduce bias and increase the reliability of research findings.

Limitations of Hypothesis

Some Limitations of the Hypothesis are as follows:

• Limited to observable phenomena: Hypotheses are limited to observable phenomena and cannot account for unobservable or intangible factors. This means that some research questions may not be amenable to hypothesis testing.
• May be inaccurate or incomplete: Hypotheses are based on existing knowledge and research, which may be incomplete or inaccurate. This can lead to flawed hypotheses and erroneous conclusions.
• May be biased: Hypotheses may be biased by the researcher’s own beliefs, values, or assumptions. This can lead to selective interpretation of data and a lack of objectivity in research.
• Cannot prove causation: A hypothesis can only show a correlation between variables, but it cannot prove causation. This requires further experimentation and analysis.
• Limited to specific contexts: Hypotheses are limited to specific contexts and may not be generalizable to other situations or populations. This means that results may not be applicable in other contexts or may require further testing.
• May be affected by chance : Hypotheses may be affected by chance or random variation, which can obscure or distort the true relationship between variables.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

Institutional Review Board – Application Sample...

Evaluating Research – Process, Examples and...

Hypothesis Testing (cont...)

Hypothesis testing, the null and alternative hypothesis.

In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.

The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:

Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:

Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.

Significance levels

The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?

So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.

Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions

When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:

The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.

Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.

Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:

In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.

Rejecting or failing to reject the null hypothesis

Let's return finally to the question of whether we reject or fail to reject the null hypothesis.

If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.

Null Hypothesis and Alternative Hypothesis

• Inferential Statistics
• Statistics Tutorials
• Probability & Games
• Descriptive Statistics
• Applications Of Statistics
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade
• Ph.D., Mathematics, Purdue University
• M.S., Mathematics, Purdue University
• B.A., Mathematics, Physics, and Chemistry, Anderson University

Hypothesis testing involves the careful construction of two statements: the null hypothesis and the alternative hypothesis. These hypotheses can look very similar but are actually different.

How do we know which hypothesis is the null and which one is the alternative? We will see that there are a few ways to tell the difference.

The Null Hypothesis

The null hypothesis reflects that there will be no observed effect in our experiment. In a mathematical formulation of the null hypothesis, there will typically be an equal sign. This hypothesis is denoted by H 0 .

The null hypothesis is what we attempt to find evidence against in our hypothesis test. We hope to obtain a small enough p-value that it is lower than our level of significance alpha and we are justified in rejecting the null hypothesis. If our p-value is greater than alpha, then we fail to reject the null hypothesis.

If the null hypothesis is not rejected, then we must be careful to say what this means. The thinking on this is similar to a legal verdict. Just because a person has been declared "not guilty", it does not mean that he is innocent. In the same way, just because we failed to reject a null hypothesis it does not mean that the statement is true.

For example, we may want to investigate the claim that despite what convention has told us, the mean adult body temperature is not the accepted value of 98.6 degrees Fahrenheit . The null hypothesis for an experiment to investigate this is “The mean adult body temperature for healthy individuals is 98.6 degrees Fahrenheit.” If we fail to reject the null hypothesis, then our working hypothesis remains that the average adult who is healthy has a temperature of 98.6 degrees. We do not prove that this is true.

If we are studying a new treatment, the null hypothesis is that our treatment will not change our subjects in any meaningful way. In other words, the treatment will not produce any effect in our subjects.

The Alternative Hypothesis

The alternative or experimental hypothesis reflects that there will be an observed effect for our experiment. In a mathematical formulation of the alternative hypothesis, there will typically be an inequality, or not equal to symbol. This hypothesis is denoted by either H a or by H 1 .

The alternative hypothesis is what we are attempting to demonstrate in an indirect way by the use of our hypothesis test. If the null hypothesis is rejected, then we accept the alternative hypothesis. If the null hypothesis is not rejected, then we do not accept the alternative hypothesis. Going back to the above example of mean human body temperature, the alternative hypothesis is “The average adult human body temperature is not 98.6 degrees Fahrenheit.”

If we are studying a new treatment, then the alternative hypothesis is that our treatment does, in fact, change our subjects in a meaningful and measurable way.

The following set of negations may help when you are forming your null and alternative hypotheses. Most technical papers rely on just the first formulation, even though you may see some of the others in a statistics textbook.

• Null hypothesis: “ x is equal to y .” Alternative hypothesis “ x is not equal to y .”
• Null hypothesis: “ x is at least y .” Alternative hypothesis “ x is less than y .”
• Null hypothesis: “ x is at most y .” Alternative hypothesis “ x is greater than y .”
• Null Hypothesis Examples
• An Example of a Hypothesis Test
• Hypothesis Test for the Difference of Two Population Proportions
• What Is a P-Value?
• How to Conduct a Hypothesis Test
• Hypothesis Test Example
• What Level of Alpha Determines Statistical Significance?
• Chi-Square Goodness of Fit Test
• Maslow's Hierarchy of Needs Explained
• Popular Math Terms and Definitions
• The Difference Between Type I and Type II Errors in Hypothesis Testing
• How to Do Hypothesis Tests With the Z.TEST Function in Excel
• The Runs Test for Random Sequences
• Type I and Type II Errors in Statistics
• What 'Fail to Reject' Means in a Hypothesis Test
• What Is the Difference Between Alpha and P-Values?

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating ​ the dependent variable or due to random chance. 

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

When do we reject the null hypothesis .

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected. 

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables. 

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a  p  -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. 

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null. 

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists. 

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter. 

Purpose of a Null Hypothesis 

• The primary purpose of the null hypothesis is to disprove an assumption. 
• Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
• A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true. 

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables. 

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study. 

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”).  However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing.  Political research quarterly ,  52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method.  American Psychologist ,  56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing.  Behavior research methods ,  43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy.  Psychological methods ,  5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test.  Psychological bulletin ,  57 (5), 416.

Related Articles

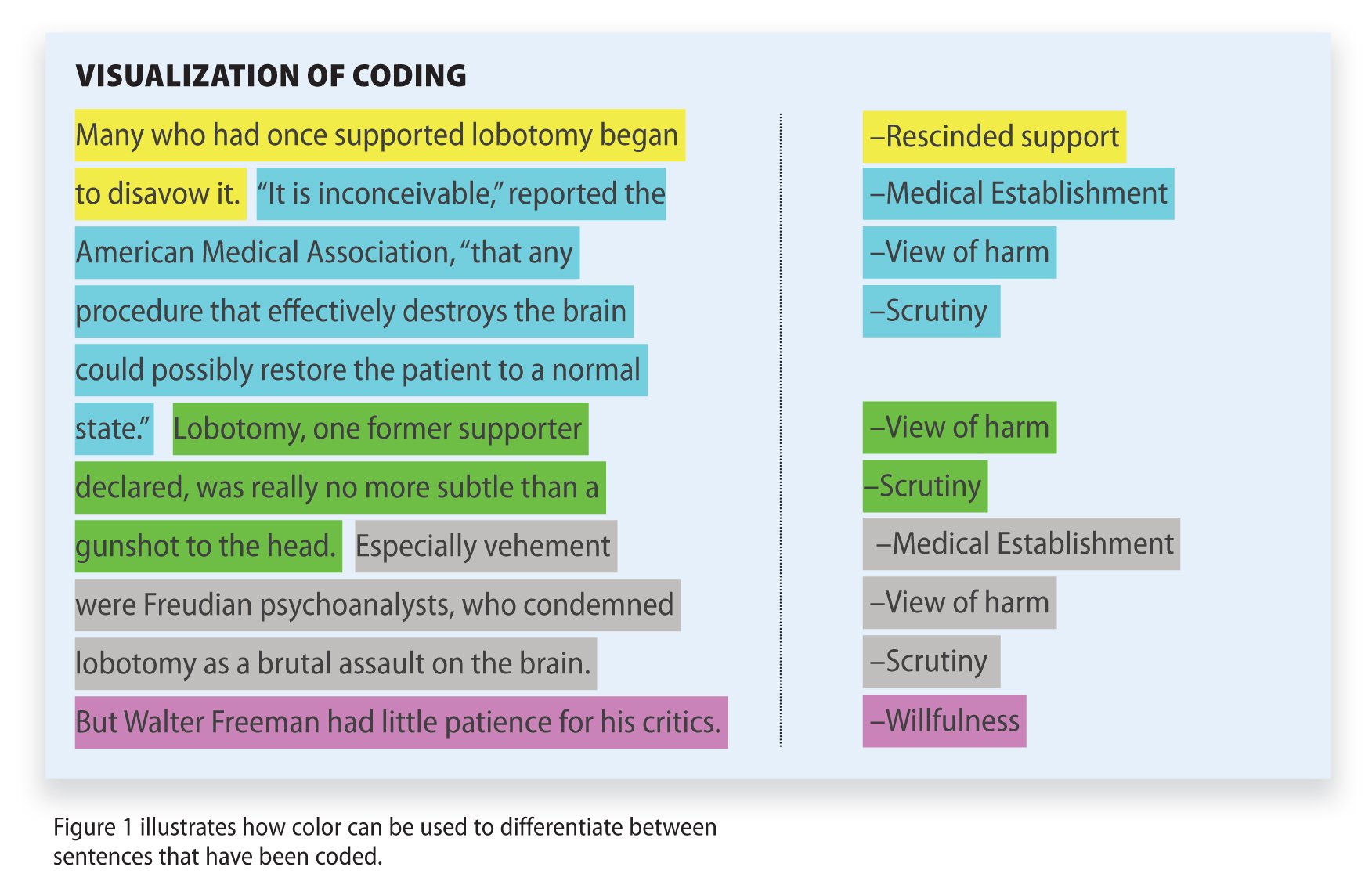
Research Methodology

Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

Frequently asked questions

What’s the difference between a research hypothesis and a statistical hypothesis.

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Frequently asked questions: Methodology

Quantitative observations involve measuring or counting something and expressing the result in numerical form, while qualitative observations involve describing something in non-numerical terms, such as its appearance, texture, or color.

To make quantitative observations , you need to use instruments that are capable of measuring the quantity you want to observe. For example, you might use a ruler to measure the length of an object or a thermometer to measure its temperature.

Scope of research is determined at the beginning of your research process , prior to the data collection stage. Sometimes called “scope of study,” your scope delineates what will and will not be covered in your project. It helps you focus your work and your time, ensuring that you’ll be able to achieve your goals and outcomes.

Defining a scope can be very useful in any research project, from a research proposal to a thesis or dissertation . A scope is needed for all types of research: quantitative , qualitative , and mixed methods .

To define your scope of research, consider the following:

• Budget constraints or any specifics of grant funding
• Your proposed timeline and duration
• Specifics about your population of study, your proposed sample size , and the research methodology you’ll pursue
• Any inclusion and exclusion criteria
• Any anticipated control , extraneous , or confounding variables that could bias your research if not accounted for properly.

Inclusion and exclusion criteria are predominantly used in non-probability sampling . In purposive sampling and snowball sampling , restrictions apply as to who can be included in the sample .

Inclusion and exclusion criteria are typically presented and discussed in the methodology section of your thesis or dissertation .

The purpose of theory-testing mode is to find evidence in order to disprove, refine, or support a theory. As such, generalisability is not the aim of theory-testing mode.

Due to this, the priority of researchers in theory-testing mode is to eliminate alternative causes for relationships between variables . In other words, they prioritise internal validity over external validity , including ecological validity .

Convergent validity shows how much a measure of one construct aligns with other measures of the same or related constructs .

On the other hand, concurrent validity is about how a measure matches up to some known criterion or gold standard, which can be another measure.

Although both types of validity are established by calculating the association or correlation between a test score and another variable , they represent distinct validation methods.

Validity tells you how accurately a method measures what it was designed to measure. There are 4 main types of validity :

• Construct validity : Does the test measure the construct it was designed to measure?
• Face validity : Does the test appear to be suitable for its objectives ?
• Content validity : Does the test cover all relevant parts of the construct it aims to measure.
• Criterion validity : Do the results accurately measure the concrete outcome they are designed to measure?

Criterion validity evaluates how well a test measures the outcome it was designed to measure. An outcome can be, for example, the onset of a disease.

Criterion validity consists of two subtypes depending on the time at which the two measures (the criterion and your test) are obtained:

• Concurrent validity is a validation strategy where the the scores of a test and the criterion are obtained at the same time
• Predictive validity is a validation strategy where the criterion variables are measured after the scores of the test

Attrition refers to participants leaving a study. It always happens to some extent – for example, in randomised control trials for medical research.

Differential attrition occurs when attrition or dropout rates differ systematically between the intervention and the control group . As a result, the characteristics of the participants who drop out differ from the characteristics of those who stay in the study. Because of this, study results may be biased .

Criterion validity and construct validity are both types of measurement validity . In other words, they both show you how accurately a method measures something.

While construct validity is the degree to which a test or other measurement method measures what it claims to measure, criterion validity is the degree to which a test can predictively (in the future) or concurrently (in the present) measure something.

Construct validity is often considered the overarching type of measurement validity . You need to have face validity , content validity , and criterion validity in order to achieve construct validity.

Convergent validity and discriminant validity are both subtypes of construct validity . Together, they help you evaluate whether a test measures the concept it was designed to measure.

• Convergent validity indicates whether a test that is designed to measure a particular construct correlates with other tests that assess the same or similar construct.
• Discriminant validity indicates whether two tests that should not be highly related to each other are indeed not related. This type of validity is also called divergent validity .

You need to assess both in order to demonstrate construct validity. Neither one alone is sufficient for establishing construct validity.

Face validity and content validity are similar in that they both evaluate how suitable the content of a test is. The difference is that face validity is subjective, and assesses content at surface level.

When a test has strong face validity, anyone would agree that the test’s questions appear to measure what they are intended to measure.

For example, looking at a 4th grade math test consisting of problems in which students have to add and multiply, most people would agree that it has strong face validity (i.e., it looks like a math test).

On the other hand, content validity evaluates how well a test represents all the aspects of a topic. Assessing content validity is more systematic and relies on expert evaluation. of each question, analysing whether each one covers the aspects that the test was designed to cover.

A 4th grade math test would have high content validity if it covered all the skills taught in that grade. Experts(in this case, math teachers), would have to evaluate the content validity by comparing the test to the learning objectives.

Content validity shows you how accurately a test or other measurement method taps  into the various aspects of the specific construct you are researching.

In other words, it helps you answer the question: “does the test measure all aspects of the construct I want to measure?” If it does, then the test has high content validity.

The higher the content validity, the more accurate the measurement of the construct.

If the test fails to include parts of the construct, or irrelevant parts are included, the validity of the instrument is threatened, which brings your results into question.

Construct validity refers to how well a test measures the concept (or construct) it was designed to measure. Assessing construct validity is especially important when you’re researching concepts that can’t be quantified and/or are intangible, like introversion. To ensure construct validity your test should be based on known indicators of introversion ( operationalisation ).

On the other hand, content validity assesses how well the test represents all aspects of the construct. If some aspects are missing or irrelevant parts are included, the test has low content validity.

• Discriminant validity indicates whether two tests that should not be highly related to each other are indeed not related

Construct validity has convergent and discriminant subtypes. They assist determine if a test measures the intended notion.

The reproducibility and replicability of a study can be ensured by writing a transparent, detailed method section and using clear, unambiguous language.

Reproducibility and replicability are related terms.

• A successful reproduction shows that the data analyses were conducted in a fair and honest manner.
• A successful replication shows that the reliability of the results is high.
• Reproducing research entails reanalysing the existing data in the same manner.
• Replicating (or repeating ) the research entails reconducting the entire analysis, including the collection of new data . 

Snowball sampling is a non-probability sampling method . Unlike probability sampling (which involves some form of random selection ), the initial individuals selected to be studied are the ones who recruit new participants.

Because not every member of the target population has an equal chance of being recruited into the sample, selection in snowball sampling is non-random.

Snowball sampling is a non-probability sampling method , where there is not an equal chance for every member of the population to be included in the sample .

This means that you cannot use inferential statistics and make generalisations – often the goal of quantitative research . As such, a snowball sample is not representative of the target population, and is usually a better fit for qualitative research .

Snowball sampling relies on the use of referrals. Here, the researcher recruits one or more initial participants, who then recruit the next ones. 

Participants share similar characteristics and/or know each other. Because of this, not every member of the population has an equal chance of being included in the sample, giving rise to sampling bias .

Snowball sampling is best used in the following cases:

• If there is no sampling frame available (e.g., people with a rare disease)
• If the population of interest is hard to access or locate (e.g., people experiencing homelessness)
• If the research focuses on a sensitive topic (e.g., extra-marital affairs)

Stratified sampling and quota sampling both involve dividing the population into subgroups and selecting units from each subgroup. The purpose in both cases is to select a representative sample and/or to allow comparisons between subgroups.

The main difference is that in stratified sampling, you draw a random sample from each subgroup ( probability sampling ). In quota sampling you select a predetermined number or proportion of units, in a non-random manner ( non-probability sampling ).

Random sampling or probability sampling is based on random selection. This means that each unit has an equal chance (i.e., equal probability) of being included in the sample.

On the other hand, convenience sampling involves stopping people at random, which means that not everyone has an equal chance of being selected depending on the place, time, or day you are collecting your data.

Convenience sampling and quota sampling are both non-probability sampling methods. They both use non-random criteria like availability, geographical proximity, or expert knowledge to recruit study participants.

However, in convenience sampling, you continue to sample units or cases until you reach the required sample size.

In quota sampling, you first need to divide your population of interest into subgroups (strata) and estimate their proportions (quota) in the population. Then you can start your data collection , using convenience sampling to recruit participants, until the proportions in each subgroup coincide with the estimated proportions in the population.

A sampling frame is a list of every member in the entire population . It is important that the sampling frame is as complete as possible, so that your sample accurately reflects your population.

Stratified and cluster sampling may look similar, but bear in mind that groups created in cluster sampling are heterogeneous , so the individual characteristics in the cluster vary. In contrast, groups created in stratified sampling are homogeneous , as units share characteristics.

Relatedly, in cluster sampling you randomly select entire groups and include all units of each group in your sample. However, in stratified sampling, you select some units of all groups and include them in your sample. In this way, both methods can ensure that your sample is representative of the target population .

When your population is large in size, geographically dispersed, or difficult to contact, it’s necessary to use a sampling method .

This allows you to gather information from a smaller part of the population, i.e. the sample, and make accurate statements by using statistical analysis. A few sampling methods include simple random sampling , convenience sampling , and snowball sampling .

The two main types of social desirability bias are:

• Self-deceptive enhancement (self-deception): The tendency to see oneself in a favorable light without realizing it.
• Impression managemen t (other-deception): The tendency to inflate one’s abilities or achievement in order to make a good impression on other people.

Response bias refers to conditions or factors that take place during the process of responding to surveys, affecting the responses. One type of response bias is social desirability bias .

Demand characteristics are aspects of experiments that may give away the research objective to participants. Social desirability bias occurs when participants automatically try to respond in ways that make them seem likeable in a study, even if it means misrepresenting how they truly feel.

Participants may use demand characteristics to infer social norms or experimenter expectancies and act in socially desirable ways, so you should try to control for demand characteristics wherever possible.

A systematic review is secondary research because it uses existing research. You don’t collect new data yourself.

Ethical considerations in research are a set of principles that guide your research designs and practices. These principles include voluntary participation, informed consent, anonymity, confidentiality, potential for harm, and results communication.

Scientists and researchers must always adhere to a certain code of conduct when collecting data from others .

These considerations protect the rights of research participants, enhance research validity , and maintain scientific integrity.

Research ethics matter for scientific integrity, human rights and dignity, and collaboration between science and society. These principles make sure that participation in studies is voluntary, informed, and safe.

Research misconduct means making up or falsifying data, manipulating data analyses, or misrepresenting results in research reports. It’s a form of academic fraud.

These actions are committed intentionally and can have serious consequences; research misconduct is not a simple mistake or a point of disagreement but a serious ethical failure.

Anonymity means you don’t know who the participants are, while confidentiality means you know who they are but remove identifying information from your research report. Both are important ethical considerations .

You can only guarantee anonymity by not collecting any personally identifying information – for example, names, phone numbers, email addresses, IP addresses, physical characteristics, photos, or videos.

You can keep data confidential by using aggregate information in your research report, so that you only refer to groups of participants rather than individuals.

Peer review is a process of evaluating submissions to an academic journal. Utilising rigorous criteria, a panel of reviewers in the same subject area decide whether to accept each submission for publication.

For this reason, academic journals are often considered among the most credible sources you can use in a research project – provided that the journal itself is trustworthy and well regarded.

In general, the peer review process follows the following steps:

• First, the author submits the manuscript to the editor.
• Reject the manuscript and send it back to author, or
• Send it onward to the selected peer reviewer(s)
• Next, the peer review process occurs. The reviewer provides feedback, addressing any major or minor issues with the manuscript, and gives their advice regarding what edits should be made.
• Lastly, the edited manuscript is sent back to the author. They input the edits, and resubmit it to the editor for publication.

Peer review can stop obviously problematic, falsified, or otherwise untrustworthy research from being published. It also represents an excellent opportunity to get feedback from renowned experts in your field.

It acts as a first defence, helping you ensure your argument is clear and that there are no gaps, vague terms, or unanswered questions for readers who weren’t involved in the research process.

Peer-reviewed articles are considered a highly credible source due to this stringent process they go through before publication.

Many academic fields use peer review , largely to determine whether a manuscript is suitable for publication. Peer review enhances the credibility of the published manuscript.

However, peer review is also common in non-academic settings. The United Nations, the European Union, and many individual nations use peer review to evaluate grant applications. It is also widely used in medical and health-related fields as a teaching or quality-of-care measure.

Peer assessment is often used in the classroom as a pedagogical tool. Both receiving feedback and providing it are thought to enhance the learning process, helping students think critically and collaboratively.

• In a single-blind study , only the participants are blinded.
• In a double-blind study , both participants and experimenters are blinded.
• In a triple-blind study , the assignment is hidden not only from participants and experimenters, but also from the researchers analysing the data.

Blinding is important to reduce bias (e.g., observer bias , demand characteristics ) and ensure a study’s internal validity .

If participants know whether they are in a control or treatment group , they may adjust their behaviour in ways that affect the outcome that researchers are trying to measure. If the people administering the treatment are aware of group assignment, they may treat participants differently and thus directly or indirectly influence the final results.

Blinding means hiding who is assigned to the treatment group and who is assigned to the control group in an experiment .

Explanatory research is a research method used to investigate how or why something occurs when only a small amount of information is available pertaining to that topic. It can help you increase your understanding of a given topic.

Explanatory research is used to investigate how or why a phenomenon occurs. Therefore, this type of research is often one of the first stages in the research process , serving as a jumping-off point for future research.

Exploratory research is a methodology approach that explores research questions that have not previously been studied in depth. It is often used when the issue you’re studying is new, or the data collection process is challenging in some way.

Exploratory research is often used when the issue you’re studying is new or when the data collection process is challenging for some reason.

You can use exploratory research if you have a general idea or a specific question that you want to study but there is no preexisting knowledge or paradigm with which to study it.

To implement random assignment , assign a unique number to every member of your study’s sample .

Then, you can use a random number generator or a lottery method to randomly assign each number to a control or experimental group. You can also do so manually, by flipping a coin or rolling a die to randomly assign participants to groups.

Random selection, or random sampling , is a way of selecting members of a population for your study’s sample.

In contrast, random assignment is a way of sorting the sample into control and experimental groups.

Random sampling enhances the external validity or generalisability of your results, while random assignment improves the internal validity of your study.

Random assignment is used in experiments with a between-groups or independent measures design. In this research design, there’s usually a control group and one or more experimental groups. Random assignment helps ensure that the groups are comparable.

In general, you should always use random assignment in this type of experimental design when it is ethically possible and makes sense for your study topic.

Clean data are valid, accurate, complete, consistent, unique, and uniform. Dirty data include inconsistencies and errors.

Dirty data can come from any part of the research process, including poor research design , inappropriate measurement materials, or flawed data entry.

Data cleaning takes place between data collection and data analyses. But you can use some methods even before collecting data.

For clean data, you should start by designing measures that collect valid data. Data validation at the time of data entry or collection helps you minimize the amount of data cleaning you’ll need to do.

After data collection, you can use data standardisation and data transformation to clean your data. You’ll also deal with any missing values, outliers, and duplicate values.

Data cleaning involves spotting and resolving potential data inconsistencies or errors to improve your data quality. An error is any value (e.g., recorded weight) that doesn’t reflect the true value (e.g., actual weight) of something that’s being measured.

In this process, you review, analyse, detect, modify, or remove ‘dirty’ data to make your dataset ‘clean’. Data cleaning is also called data cleansing or data scrubbing.

Data cleaning is necessary for valid and appropriate analyses. Dirty data contain inconsistencies or errors , but cleaning your data helps you minimise or resolve these.

Without data cleaning, you could end up with a Type I or II error in your conclusion. These types of erroneous conclusions can be practically significant with important consequences, because they lead to misplaced investments or missed opportunities.

Observer bias occurs when a researcher’s expectations, opinions, or prejudices influence what they perceive or record in a study. It usually affects studies when observers are aware of the research aims or hypotheses. This type of research bias is also called detection bias or ascertainment bias .

The observer-expectancy effect occurs when researchers influence the results of their own study through interactions with participants.

Researchers’ own beliefs and expectations about the study results may unintentionally influence participants through demand characteristics .

You can use several tactics to minimise observer bias .

• Use masking (blinding) to hide the purpose of your study from all observers.
• Triangulate your data with different data collection methods or sources.
• Use multiple observers and ensure inter-rater reliability.
• Train your observers to make sure data is consistently recorded between them.
• Standardise your observation procedures to make sure they are structured and clear.

Naturalistic observation is a valuable tool because of its flexibility, external validity , and suitability for topics that can’t be studied in a lab setting.

The downsides of naturalistic observation include its lack of scientific control , ethical considerations , and potential for bias from observers and subjects.

Naturalistic observation is a qualitative research method where you record the behaviours of your research subjects in real-world settings. You avoid interfering or influencing anything in a naturalistic observation.

You can think of naturalistic observation as ‘people watching’ with a purpose.

Closed-ended, or restricted-choice, questions offer respondents a fixed set of choices to select from. These questions are easier to answer quickly.

Open-ended or long-form questions allow respondents to answer in their own words. Because there are no restrictions on their choices, respondents can answer in ways that researchers may not have otherwise considered.

You can organise the questions logically, with a clear progression from simple to complex, or randomly between respondents. A logical flow helps respondents process the questionnaire easier and quicker, but it may lead to bias. Randomisation can minimise the bias from order effects.

Questionnaires can be self-administered or researcher-administered.

Self-administered questionnaires can be delivered online or in paper-and-pen formats, in person or by post. All questions are standardised so that all respondents receive the same questions with identical wording.

Researcher-administered questionnaires are interviews that take place by phone, in person, or online between researchers and respondents. You can gain deeper insights by clarifying questions for respondents or asking follow-up questions.

In a controlled experiment , all extraneous variables are held constant so that they can’t influence the results. Controlled experiments require:

• A control group that receives a standard treatment, a fake treatment, or no treatment
• Random assignment of participants to ensure the groups are equivalent

Depending on your study topic, there are various other methods of controlling variables .

An experimental group, also known as a treatment group, receives the treatment whose effect researchers wish to study, whereas a control group does not. They should be identical in all other ways.

A true experiment (aka a controlled experiment) always includes at least one control group that doesn’t receive the experimental treatment.

However, some experiments use a within-subjects design to test treatments without a control group. In these designs, you usually compare one group’s outcomes before and after a treatment (instead of comparing outcomes between different groups).

For strong internal validity , it’s usually best to include a control group if possible. Without a control group, it’s harder to be certain that the outcome was caused by the experimental treatment and not by other variables.

A questionnaire is a data collection tool or instrument, while a survey is an overarching research method that involves collecting and analysing data from people using questionnaires.

A Likert scale is a rating scale that quantitatively assesses opinions, attitudes, or behaviours. It is made up of four or more questions that measure a single attitude or trait when response scores are combined.

To use a Likert scale in a survey , you present participants with Likert-type questions or statements, and a continuum of items, usually with five or seven possible responses, to capture their degree of agreement.

Individual Likert-type questions are generally considered ordinal data , because the items have clear rank order, but don’t have an even distribution.

Overall Likert scale scores are sometimes treated as interval data. These scores are considered to have directionality and even spacing between them.

The type of data determines what statistical tests you should use to analyse your data.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess. It should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).

Cross-sectional studies are less expensive and time-consuming than many other types of study. They can provide useful insights into a population’s characteristics and identify correlations for further research.

Sometimes only cross-sectional data are available for analysis; other times your research question may only require a cross-sectional study to answer it.

Cross-sectional studies cannot establish a cause-and-effect relationship or analyse behaviour over a period of time. To investigate cause and effect, you need to do a longitudinal study or an experimental study .

Longitudinal studies and cross-sectional studies are two different types of research design . In a cross-sectional study you collect data from a population at a specific point in time; in a longitudinal study you repeatedly collect data from the same sample over an extended period of time.

Longitudinal studies are better to establish the correct sequence of events, identify changes over time, and provide insight into cause-and-effect relationships, but they also tend to be more expensive and time-consuming than other types of studies.

The 1970 British Cohort Study , which has collected data on the lives of 17,000 Brits since their births in 1970, is one well-known example of a longitudinal study .

Longitudinal studies can last anywhere from weeks to decades, although they tend to be at least a year long.

A correlation reflects the strength and/or direction of the association between two or more variables.

• A positive correlation means that both variables change in the same direction.
• A negative correlation means that the variables change in opposite directions.
• A zero correlation means there’s no relationship between the variables.

A correlational research design investigates relationships between two variables (or more) without the researcher controlling or manipulating any of them. It’s a non-experimental type of quantitative research .

A correlation coefficient is a single number that describes the strength and direction of the relationship between your variables.

Different types of correlation coefficients might be appropriate for your data based on their levels of measurement and distributions . The Pearson product-moment correlation coefficient (Pearson’s r ) is commonly used to assess a linear relationship between two quantitative variables.

Controlled experiments establish causality, whereas correlational studies only show associations between variables.

• In an experimental design , you manipulate an independent variable and measure its effect on a dependent variable. Other variables are controlled so they can’t impact the results.
• In a correlational design , you measure variables without manipulating any of them. You can test whether your variables change together, but you can’t be sure that one variable caused a change in another.

In general, correlational research is high in external validity while experimental research is high in internal validity .

The third variable and directionality problems are two main reasons why correlation isn’t causation .

The third variable problem means that a confounding variable affects both variables to make them seem causally related when they are not.

The directionality problem is when two variables correlate and might actually have a causal relationship, but it’s impossible to conclude which variable causes changes in the other.

As a rule of thumb, questions related to thoughts, beliefs, and feelings work well in focus groups . Take your time formulating strong questions, paying special attention to phrasing. Be careful to avoid leading questions , which can bias your responses.

Overall, your focus group questions should be:

• Open-ended and flexible
• Impossible to answer with ‘yes’ or ‘no’ (questions that start with ‘why’ or ‘how’ are often best)
• Unambiguous, getting straight to the point while still stimulating discussion
• Unbiased and neutral

Social desirability bias is the tendency for interview participants to give responses that will be viewed favourably by the interviewer or other participants. It occurs in all types of interviews and surveys , but is most common in semi-structured interviews , unstructured interviews , and focus groups .

Social desirability bias can be mitigated by ensuring participants feel at ease and comfortable sharing their views. Make sure to pay attention to your own body language and any physical or verbal cues, such as nodding or widening your eyes.

This type of bias in research can also occur in observations if the participants know they’re being observed. They might alter their behaviour accordingly.

A focus group is a research method that brings together a small group of people to answer questions in a moderated setting. The group is chosen due to predefined demographic traits, and the questions are designed to shed light on a topic of interest. It is one of four types of interviews .

The four most common types of interviews are:

• Structured interviews : The questions are predetermined in both topic and order.
• Semi-structured interviews : A few questions are predetermined, but other questions aren’t planned.
• Unstructured interviews : None of the questions are predetermined.
• Focus group interviews : The questions are presented to a group instead of one individual.

An unstructured interview is the most flexible type of interview, but it is not always the best fit for your research topic.

Unstructured interviews are best used when:

• You are an experienced interviewer and have a very strong background in your research topic, since it is challenging to ask spontaneous, colloquial questions
• Your research question is exploratory in nature. While you may have developed hypotheses, you are open to discovering new or shifting viewpoints through the interview process.
• You are seeking descriptive data, and are ready to ask questions that will deepen and contextualise your initial thoughts and hypotheses
• Your research depends on forming connections with your participants and making them feel comfortable revealing deeper emotions, lived experiences, or thoughts

A semi-structured interview is a blend of structured and unstructured types of interviews. Semi-structured interviews are best used when:

• You have prior interview experience. Spontaneous questions are deceptively challenging, and it’s easy to accidentally ask a leading question or make a participant uncomfortable.
• Your research question is exploratory in nature. Participant answers can guide future research questions and help you develop a more robust knowledge base for future research.

The interviewer effect is a type of bias that emerges when a characteristic of an interviewer (race, age, gender identity, etc.) influences the responses given by the interviewee.

There is a risk of an interviewer effect in all types of interviews , but it can be mitigated by writing really high-quality interview questions.

A structured interview is a data collection method that relies on asking questions in a set order to collect data on a topic. They are often quantitative in nature. Structured interviews are best used when:

• You already have a very clear understanding of your topic. Perhaps significant research has already been conducted, or you have done some prior research yourself, but you already possess a baseline for designing strong structured questions.
• You are constrained in terms of time or resources and need to analyse your data quickly and efficiently
• Your research question depends on strong parity between participants, with environmental conditions held constant

More flexible interview options include semi-structured interviews , unstructured interviews , and focus groups .

When conducting research, collecting original data has significant advantages:

• You can tailor data collection to your specific research aims (e.g., understanding the needs of your consumers or user testing your website).
• You can control and standardise the process for high reliability and validity (e.g., choosing appropriate measurements and sampling methods ).

However, there are also some drawbacks: data collection can be time-consuming, labour-intensive, and expensive. In some cases, it’s more efficient to use secondary data that has already been collected by someone else, but the data might be less reliable.

Data collection is the systematic process by which observations or measurements are gathered in research. It is used in many different contexts by academics, governments, businesses, and other organisations.

A mediator variable explains the process through which two variables are related, while a moderator variable affects the strength and direction of that relationship.

A confounder is a third variable that affects variables of interest and makes them seem related when they are not. In contrast, a mediator is the mechanism of a relationship between two variables: it explains the process by which they are related.

If something is a mediating variable :

• It’s caused by the independent variable
• It influences the dependent variable
• When it’s taken into account, the statistical correlation between the independent and dependent variables is higher than when it isn’t considered

Including mediators and moderators in your research helps you go beyond studying a simple relationship between two variables for a fuller picture of the real world. They are important to consider when studying complex correlational or causal relationships.

Mediators are part of the causal pathway of an effect, and they tell you how or why an effect takes place. Moderators usually help you judge the external validity of your study by identifying the limitations of when the relationship between variables holds.

You can think of independent and dependent variables in terms of cause and effect: an independent variable is the variable you think is the cause , while a dependent variable is the effect .

In an experiment, you manipulate the independent variable and measure the outcome in the dependent variable. For example, in an experiment about the effect of nutrients on crop growth:

• The  independent variable  is the amount of nutrients added to the crop field.
• The  dependent variable is the biomass of the crops at harvest time.

Defining your variables, and deciding how you will manipulate and measure them, is an important part of experimental design .

Discrete and continuous variables are two types of quantitative variables :

• Discrete variables represent counts (e.g., the number of objects in a collection).
• Continuous variables represent measurable amounts (e.g., water volume or weight).

Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).

Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).

You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .

Determining cause and effect is one of the most important parts of scientific research. It’s essential to know which is the cause – the independent variable – and which is the effect – the dependent variable.

You want to find out how blood sugar levels are affected by drinking diet cola and regular cola, so you conduct an experiment .

• The type of cola – diet or regular – is the independent variable .
• The level of blood sugar that you measure is the dependent variable – it changes depending on the type of cola.

No. The value of a dependent variable depends on an independent variable, so a variable cannot be both independent and dependent at the same time. It must be either the cause or the effect, not both.

Yes, but including more than one of either type requires multiple research questions .

For example, if you are interested in the effect of a diet on health, you can use multiple measures of health: blood sugar, blood pressure, weight, pulse, and many more. Each of these is its own dependent variable with its own research question.

You could also choose to look at the effect of exercise levels as well as diet, or even the additional effect of the two combined. Each of these is a separate independent variable .

To ensure the internal validity of an experiment , you should only change one independent variable at a time.

To ensure the internal validity of your research, you must consider the impact of confounding variables. If you fail to account for them, you might over- or underestimate the causal relationship between your independent and dependent variables , or even find a causal relationship where none exists.

A confounding variable is closely related to both the independent and dependent variables in a study. An independent variable represents the supposed cause , while the dependent variable is the supposed effect . A confounding variable is a third variable that influences both the independent and dependent variables.

Failing to account for confounding variables can cause you to wrongly estimate the relationship between your independent and dependent variables.

There are several methods you can use to decrease the impact of confounding variables on your research: restriction, matching, statistical control, and randomisation.

In restriction , you restrict your sample by only including certain subjects that have the same values of potential confounding variables.

In matching , you match each of the subjects in your treatment group with a counterpart in the comparison group. The matched subjects have the same values on any potential confounding variables, and only differ in the independent variable .

In statistical control , you include potential confounders as variables in your regression .

In randomisation , you randomly assign the treatment (or independent variable) in your study to a sufficiently large number of subjects, which allows you to control for all potential confounding variables.

In scientific research, concepts are the abstract ideas or phenomena that are being studied (e.g., educational achievement). Variables are properties or characteristics of the concept (e.g., performance at school), while indicators are ways of measuring or quantifying variables (e.g., yearly grade reports).

The process of turning abstract concepts into measurable variables and indicators is called operationalisation .

In statistics, ordinal and nominal variables are both considered categorical variables .

Even though ordinal data can sometimes be numerical, not all mathematical operations can be performed on them.

A control variable is any variable that’s held constant in a research study. It’s not a variable of interest in the study, but it’s controlled because it could influence the outcomes.

Control variables help you establish a correlational or causal relationship between variables by enhancing internal validity .

If you don’t control relevant extraneous variables , they may influence the outcomes of your study, and you may not be able to demonstrate that your results are really an effect of your independent variable .

‘Controlling for a variable’ means measuring extraneous variables and accounting for them statistically to remove their effects on other variables.

Researchers often model control variable data along with independent and dependent variable data in regression analyses and ANCOVAs . That way, you can isolate the control variable’s effects from the relationship between the variables of interest.

An extraneous variable is any variable that you’re not investigating that can potentially affect the dependent variable of your research study.

A confounding variable is a type of extraneous variable that not only affects the dependent variable, but is also related to the independent variable.

There are 4 main types of extraneous variables :

• Demand characteristics : Environmental cues that encourage participants to conform to researchers’ expectations
• Experimenter effects : Unintentional actions by researchers that influence study outcomes
• Situational variables : Eenvironmental variables that alter participants’ behaviours
• Participant variables : Any characteristic or aspect of a participant’s background that could affect study results

The difference between explanatory and response variables is simple:

• An explanatory variable is the expected cause, and it explains the results.
• A response variable is the expected effect, and it responds to other variables.

The term ‘ explanatory variable ‘ is sometimes preferred over ‘ independent variable ‘ because, in real-world contexts, independent variables are often influenced by other variables. This means they aren’t totally independent.

Multiple independent variables may also be correlated with each other, so ‘explanatory variables’ is a more appropriate term.

On graphs, the explanatory variable is conventionally placed on the x -axis, while the response variable is placed on the y -axis.

• If you have quantitative variables , use a scatterplot or a line graph.
• If your response variable is categorical, use a scatterplot or a line graph.
• If your explanatory variable is categorical, use a bar graph.

A correlation is usually tested for two variables at a time, but you can test correlations between three or more variables.

An independent variable is the variable you manipulate, control, or vary in an experimental study to explore its effects. It’s called ‘independent’ because it’s not influenced by any other variables in the study.

Independent variables are also called:

• Explanatory variables (they explain an event or outcome)
• Predictor variables (they can be used to predict the value of a dependent variable)
• Right-hand-side variables (they appear on the right-hand side of a regression equation)

A dependent variable is what changes as a result of the independent variable manipulation in experiments . It’s what you’re interested in measuring, and it ‘depends’ on your independent variable.

In statistics, dependent variables are also called:

• Response variables (they respond to a change in another variable)
• Outcome variables (they represent the outcome you want to measure)
• Left-hand-side variables (they appear on the left-hand side of a regression equation)

Deductive reasoning is commonly used in scientific research, and it’s especially associated with quantitative research .

In research, you might have come across something called the hypothetico-deductive method . It’s the scientific method of testing hypotheses to check whether your predictions are substantiated by real-world data.

Deductive reasoning is a logical approach where you progress from general ideas to specific conclusions. It’s often contrasted with inductive reasoning , where you start with specific observations and form general conclusions.

Deductive reasoning is also called deductive logic.

Inductive reasoning is a method of drawing conclusions by going from the specific to the general. It’s usually contrasted with deductive reasoning, where you proceed from general information to specific conclusions.

Inductive reasoning is also called inductive logic or bottom-up reasoning.

In inductive research , you start by making observations or gathering data. Then, you take a broad scan of your data and search for patterns. Finally, you make general conclusions that you might incorporate into theories.

Inductive reasoning is a bottom-up approach, while deductive reasoning is top-down.

Inductive reasoning takes you from the specific to the general, while in deductive reasoning, you make inferences by going from general premises to specific conclusions.

There are many different types of inductive reasoning that people use formally or informally.

Here are a few common types:

• Inductive generalisation : You use observations about a sample to come to a conclusion about the population it came from.
• Statistical generalisation: You use specific numbers about samples to make statements about populations.
• Causal reasoning: You make cause-and-effect links between different things.
• Sign reasoning: You make a conclusion about a correlational relationship between different things.
• Analogical reasoning: You make a conclusion about something based on its similarities to something else.

It’s often best to ask a variety of people to review your measurements. You can ask experts, such as other researchers, or laypeople, such as potential participants, to judge the face validity of tests.

While experts have a deep understanding of research methods , the people you’re studying can provide you with valuable insights you may have missed otherwise.

Face validity is important because it’s a simple first step to measuring the overall validity of a test or technique. It’s a relatively intuitive, quick, and easy way to start checking whether a new measure seems useful at first glance.

Good face validity means that anyone who reviews your measure says that it seems to be measuring what it’s supposed to. With poor face validity, someone reviewing your measure may be left confused about what you’re measuring and why you’re using this method.

Face validity is about whether a test appears to measure what it’s supposed to measure. This type of validity is concerned with whether a measure seems relevant and appropriate for what it’s assessing only on the surface.

Statistical analyses are often applied to test validity with data from your measures. You test convergent validity and discriminant validity with correlations to see if results from your test are positively or negatively related to those of other established tests.

You can also use regression analyses to assess whether your measure is actually predictive of outcomes that you expect it to predict theoretically. A regression analysis that supports your expectations strengthens your claim of construct validity .

When designing or evaluating a measure, construct validity helps you ensure you’re actually measuring the construct you’re interested in. If you don’t have construct validity, you may inadvertently measure unrelated or distinct constructs and lose precision in your research.

Construct validity is often considered the overarching type of measurement validity ,  because it covers all of the other types. You need to have face validity , content validity, and criterion validity to achieve construct validity.

Construct validity is about how well a test measures the concept it was designed to evaluate. It’s one of four types of measurement validity , which includes construct validity, face validity , and criterion validity.

There are two subtypes of construct validity.

• Convergent validity : The extent to which your measure corresponds to measures of related constructs
• Discriminant validity: The extent to which your measure is unrelated or negatively related to measures of distinct constructs

Attrition bias can skew your sample so that your final sample differs significantly from your original sample. Your sample is biased because some groups from your population are underrepresented.

With a biased final sample, you may not be able to generalise your findings to the original population that you sampled from, so your external validity is compromised.

There are seven threats to external validity : selection bias , history, experimenter effect, Hawthorne effect , testing effect, aptitude-treatment, and situation effect.

The two types of external validity are population validity (whether you can generalise to other groups of people) and ecological validity (whether you can generalise to other situations and settings).

The external validity of a study is the extent to which you can generalise your findings to different groups of people, situations, and measures.

Attrition bias is a threat to internal validity . In experiments, differential rates of attrition between treatment and control groups can skew results.

This bias can affect the relationship between your independent and dependent variables . It can make variables appear to be correlated when they are not, or vice versa.

Internal validity is the extent to which you can be confident that a cause-and-effect relationship established in a study cannot be explained by other factors.

There are eight threats to internal validity : history, maturation, instrumentation, testing, selection bias , regression to the mean, social interaction, and attrition .

A sampling error is the difference between a population parameter and a sample statistic .

A statistic refers to measures about the sample , while a parameter refers to measures about the population .

Populations are used when a research question requires data from every member of the population. This is usually only feasible when the population is small and easily accessible.

Systematic sampling is a probability sampling method where researchers select members of the population at a regular interval – for example, by selecting every 15th person on a list of the population. If the population is in a random order, this can imitate the benefits of simple random sampling .

There are three key steps in systematic sampling :

• Define and list your population , ensuring that it is not ordered in a cyclical or periodic order.
• Decide on your sample size and calculate your interval, k , by dividing your population by your target sample size.
• Choose every k th member of the population as your sample.

Yes, you can create a stratified sample using multiple characteristics, but you must ensure that every participant in your study belongs to one and only one subgroup. In this case, you multiply the numbers of subgroups for each characteristic to get the total number of groups.

For example, if you were stratifying by location with three subgroups (urban, rural, or suburban) and marital status with five subgroups (single, divorced, widowed, married, or partnered), you would have 3 × 5 = 15 subgroups.

You should use stratified sampling when your sample can be divided into mutually exclusive and exhaustive subgroups that you believe will take on different mean values for the variable that you’re studying.

Using stratified sampling will allow you to obtain more precise (with lower variance ) statistical estimates of whatever you are trying to measure.

For example, say you want to investigate how income differs based on educational attainment, but you know that this relationship can vary based on race. Using stratified sampling, you can ensure you obtain a large enough sample from each racial group, allowing you to draw more precise conclusions.

In stratified sampling , researchers divide subjects into subgroups called strata based on characteristics that they share (e.g., race, gender, educational attainment).

Once divided, each subgroup is randomly sampled using another probability sampling method .

Multistage sampling can simplify data collection when you have large, geographically spread samples, and you can obtain a probability sample without a complete sampling frame.

But multistage sampling may not lead to a representative sample, and larger samples are needed for multistage samples to achieve the statistical properties of simple random samples .

In multistage sampling , you can use probability or non-probability sampling methods.

For a probability sample, you have to probability sampling at every stage. You can mix it up by using simple random sampling , systematic sampling , or stratified sampling to select units at different stages, depending on what is applicable and relevant to your study.

Cluster sampling is a probability sampling method in which you divide a population into clusters, such as districts or schools, and then randomly select some of these clusters as your sample.

The clusters should ideally each be mini-representations of the population as a whole.

There are three types of cluster sampling : single-stage, double-stage and multi-stage clustering. In all three types, you first divide the population into clusters, then randomly select clusters for use in your sample.

• In single-stage sampling , you collect data from every unit within the selected clusters.
• In double-stage sampling , you select a random sample of units from within the clusters.
• In multi-stage sampling , you repeat the procedure of randomly sampling elements from within the clusters until you have reached a manageable sample.

Cluster sampling is more time- and cost-efficient than other probability sampling methods , particularly when it comes to large samples spread across a wide geographical area.

However, it provides less statistical certainty than other methods, such as simple random sampling , because it is difficult to ensure that your clusters properly represent the population as a whole.

If properly implemented, simple random sampling is usually the best sampling method for ensuring both internal and external validity . However, it can sometimes be impractical and expensive to implement, depending on the size of the population to be studied,

If you have a list of every member of the population and the ability to reach whichever members are selected, you can use simple random sampling.

The American Community Survey  is an example of simple random sampling . In order to collect detailed data on the population of the US, the Census Bureau officials randomly select 3.5 million households per year and use a variety of methods to convince them to fill out the survey.

Simple random sampling is a type of probability sampling in which the researcher randomly selects a subset of participants from a population . Each member of the population has an equal chance of being selected. Data are then collected from as large a percentage as possible of this random subset.

Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others.

In multistage sampling , or multistage cluster sampling, you draw a sample from a population using smaller and smaller groups at each stage.

This method is often used to collect data from a large, geographically spread group of people in national surveys, for example. You take advantage of hierarchical groupings (e.g., from county to city to neighbourhood) to create a sample that’s less expensive and time-consuming to collect data from.

In non-probability sampling , the sample is selected based on non-random criteria, and not every member of the population has a chance of being included.

Common non-probability sampling methods include convenience sampling , voluntary response sampling, purposive sampling , snowball sampling , and quota sampling .

Probability sampling means that every member of the target population has a known chance of being included in the sample.

Probability sampling methods include simple random sampling , systematic sampling , stratified sampling , and cluster sampling .

Samples are used to make inferences about populations . Samples are easier to collect data from because they are practical, cost-effective, convenient, and manageable.

While a between-subjects design has fewer threats to internal validity , it also requires more participants for high statistical power than a within-subjects design .

Advantages:

• Prevents carryover effects of learning and fatigue.
• Shorter study duration.

Disadvantages:

• Needs larger samples for high power.
• Uses more resources to recruit participants, administer sessions, cover costs, etc.
• Individual differences may be an alternative explanation for results.

In a factorial design, multiple independent variables are tested.

If you test two variables, each level of one independent variable is combined with each level of the other independent variable to create different conditions.

Yes. Between-subjects and within-subjects designs can be combined in a single study when you have two or more independent variables (a factorial design). In a mixed factorial design, one variable is altered between subjects and another is altered within subjects.

Within-subjects designs have many potential threats to internal validity , but they are also very statistically powerful .

• Only requires small samples
• Statistically powerful
• Removes the effects of individual differences on the outcomes
• Internal validity threats reduce the likelihood of establishing a direct relationship between variables
• Time-related effects, such as growth, can influence the outcomes
• Carryover effects mean that the specific order of different treatments affect the outcomes

Quasi-experimental design is most useful in situations where it would be unethical or impractical to run a true experiment .

Quasi-experiments have lower internal validity than true experiments, but they often have higher external validity  as they can use real-world interventions instead of artificial laboratory settings.

In experimental research, random assignment is a way of placing participants from your sample into different groups using randomisation. With this method, every member of the sample has a known or equal chance of being placed in a control group or an experimental group.

A quasi-experiment is a type of research design that attempts to establish a cause-and-effect relationship. The main difference between this and a true experiment is that the groups are not randomly assigned.

In a between-subjects design , every participant experiences only one condition, and researchers assess group differences between participants in various conditions.

In a within-subjects design , each participant experiences all conditions, and researchers test the same participants repeatedly for differences between conditions.

The word ‘between’ means that you’re comparing different conditions between groups, while the word ‘within’ means you’re comparing different conditions within the same group.

A confounding variable , also called a confounder or confounding factor, is a third variable in a study examining a potential cause-and-effect relationship.

A confounding variable is related to both the supposed cause and the supposed effect of the study. It can be difficult to separate the true effect of the independent variable from the effect of the confounding variable.

In your research design , it’s important to identify potential confounding variables and plan how you will reduce their impact.

Triangulation can help:

• Reduce bias that comes from using a single method, theory, or investigator
• Enhance validity by approaching the same topic with different tools
• Establish credibility by giving you a complete picture of the research problem

But triangulation can also pose problems:

• It’s time-consuming and labour-intensive, often involving an interdisciplinary team.
• Your results may be inconsistent or even contradictory.

There are four main types of triangulation :

• Data triangulation : Using data from different times, spaces, and people
• Investigator triangulation : Involving multiple researchers in collecting or analysing data
• Theory triangulation : Using varying theoretical perspectives in your research
• Methodological triangulation : Using different methodologies to approach the same topic

Experimental designs are a set of procedures that you plan in order to examine the relationship between variables that interest you.

To design a successful experiment, first identify:

• A testable hypothesis
• One or more independent variables that you will manipulate
• One or more dependent variables that you will measure

When designing the experiment, first decide:

• How your variable(s) will be manipulated
• How you will control for any potential confounding or lurking variables
• How many subjects you will include
• How you will assign treatments to your subjects

Exploratory research explores the main aspects of a new or barely researched question.

Explanatory research explains the causes and effects of an already widely researched question.

The key difference between observational studies and experiments is that, done correctly, an observational study will never influence the responses or behaviours of participants. Experimental designs will have a treatment condition applied to at least a portion of participants.

An observational study could be a good fit for your research if your research question is based on things you observe. If you have ethical, logistical, or practical concerns that make an experimental design challenging, consider an observational study. Remember that in an observational study, it is critical that there be no interference or manipulation of the research subjects. Since it’s not an experiment, there are no control or treatment groups either.

These are four of the most common mixed methods designs :

• Convergent parallel: Quantitative and qualitative data are collected at the same time and analysed separately. After both analyses are complete, compare your results to draw overall conclusions. 
• Embedded: Quantitative and qualitative data are collected at the same time, but within a larger quantitative or qualitative design. One type of data is secondary to the other.
• Explanatory sequential: Quantitative data is collected and analysed first, followed by qualitative data. You can use this design if you think your qualitative data will explain and contextualise your quantitative findings.
• Exploratory sequential: Qualitative data is collected and analysed first, followed by quantitative data. You can use this design if you think the quantitative data will confirm or validate your qualitative findings.

Triangulation in research means using multiple datasets, methods, theories and/or investigators to address a research question. It’s a research strategy that can help you enhance the validity and credibility of your findings.

Triangulation is mainly used in qualitative research , but it’s also commonly applied in quantitative research . Mixed methods research always uses triangulation.

Operationalisation means turning abstract conceptual ideas into measurable observations.

For example, the concept of social anxiety isn’t directly observable, but it can be operationally defined in terms of self-rating scores, behavioural avoidance of crowded places, or physical anxiety symptoms in social situations.

Before collecting data , it’s important to consider how you will operationalise the variables that you want to measure.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

There are five common approaches to qualitative research :

• Grounded theory involves collecting data in order to develop new theories.
• Ethnography involves immersing yourself in a group or organisation to understand its culture.
• Narrative research involves interpreting stories to understand how people make sense of their experiences and perceptions.
• Phenomenological research involves investigating phenomena through people’s lived experiences.
• Action research links theory and practice in several cycles to drive innovative changes.

There are various approaches to qualitative data analysis , but they all share five steps in common:

• Prepare and organise your data.
• Review and explore your data.
• Develop a data coding system.
• Assign codes to the data.
• Identify recurring themes.

The specifics of each step depend on the focus of the analysis. Some common approaches include textual analysis , thematic analysis , and discourse analysis .

In mixed methods research , you use both qualitative and quantitative data collection and analysis methods to answer your research question .

Methodology refers to the overarching strategy and rationale of your research project . It involves studying the methods used in your field and the theories or principles behind them, in order to develop an approach that matches your objectives.

Methods are the specific tools and procedures you use to collect and analyse data (e.g. experiments, surveys , and statistical tests ).

In shorter scientific papers, where the aim is to report the findings of a specific study, you might simply describe what you did in a methods section .

In a longer or more complex research project, such as a thesis or dissertation , you will probably include a methodology section , where you explain your approach to answering the research questions and cite relevant sources to support your choice of methods.

The research methods you use depend on the type of data you need to answer your research question .

• If you want to measure something or test a hypothesis , use quantitative methods . If you want to explore ideas, thoughts, and meanings, use qualitative methods .
• If you want to analyse a large amount of readily available data, use secondary data. If you want data specific to your purposes with control over how they are generated, collect primary data.
• If you want to establish cause-and-effect relationships between variables , use experimental methods. If you want to understand the characteristics of a research subject, use descriptive methods.

Ask our team

Want to contact us directly? No problem. We are always here for you.

• Chat with us
• Email [email protected]
• Call +44 (0)20 3917 4242
• WhatsApp +31 20 261 6040

Our support team is here to help you daily via chat, WhatsApp, email, or phone between 9:00 a.m. to 11:00 p.m. CET.

Our APA experts default to APA 7 for editing and formatting. For the Citation Editing Service you are able to choose between APA 6 and 7.

Yes, if your document is longer than 20,000 words, you will get a sample of approximately 2,000 words. This sample edit gives you a first impression of the editor’s editing style and a chance to ask questions and give feedback.

How does the sample edit work?

You will receive the sample edit within 24 hours after placing your order. You then have 24 hours to let us know if you’re happy with the sample or if there’s something you would like the editor to do differently.

Read more about how the sample edit works

Yes, you can upload your document in sections.

We try our best to ensure that the same editor checks all the different sections of your document. When you upload a new file, our system recognizes you as a returning customer, and we immediately contact the editor who helped you before.

However, we cannot guarantee that the same editor will be available. Your chances are higher if

• You send us your text as soon as possible and
• You can be flexible about the deadline.

Please note that the shorter your deadline is, the lower the chance that your previous editor is not available.

If your previous editor isn’t available, then we will inform you immediately and look for another qualified editor. Fear not! Every Scribbr editor follows the  Scribbr Improvement Model  and will deliver high-quality work.

Yes, our editors also work during the weekends and holidays.

Because we have many editors available, we can check your document 24 hours per day and 7 days per week, all year round.

If you choose a 72 hour deadline and upload your document on a Thursday evening, you’ll have your thesis back by Sunday evening!

Yes! Our editors are all native speakers, and they have lots of experience editing texts written by ESL students. They will make sure your grammar is perfect and point out any sentences that are difficult to understand. They’ll also notice your most common mistakes, and give you personal feedback to improve your writing in English.

Every Scribbr order comes with our award-winning Proofreading & Editing service , which combines two important stages of the revision process.

For a more comprehensive edit, you can add a Structure Check or Clarity Check to your order. With these building blocks, you can customize the kind of feedback you receive.

You might be familiar with a different set of editing terms. To help you understand what you can expect at Scribbr, we created this table:

View an example

When you place an order, you can specify your field of study and we’ll match you with an editor who has familiarity with this area.

However, our editors are language specialists, not academic experts in your field. Your editor’s job is not to comment on the content of your dissertation, but to improve your language and help you express your ideas as clearly and fluently as possible.

This means that your editor will understand your text well enough to give feedback on its clarity, logic and structure, but not on the accuracy or originality of its content.

Good academic writing should be understandable to a non-expert reader, and we believe that academic editing is a discipline in itself. The research, ideas and arguments are all yours – we’re here to make sure they shine!

After your document has been edited, you will receive an email with a link to download the document.

The editor has made changes to your document using ‘Track Changes’ in Word. This means that you only have to accept or ignore the changes that are made in the text one by one.

It is also possible to accept all changes at once. However, we strongly advise you not to do so for the following reasons:

• You can learn a lot by looking at the mistakes you made.
• The editors don’t only change the text – they also place comments when sentences or sometimes even entire paragraphs are unclear. You should read through these comments and take into account your editor’s tips and suggestions.
• With a final read-through, you can make sure you’re 100% happy with your text before you submit!

You choose the turnaround time when ordering. We can return your dissertation within 24 hours , 3 days or 1 week . These timescales include weekends and holidays. As soon as you’ve paid, the deadline is set, and we guarantee to meet it! We’ll notify you by text and email when your editor has completed the job.

Very large orders might not be possible to complete in 24 hours. On average, our editors can complete around 13,000 words in a day while maintaining our high quality standards. If your order is longer than this and urgent, contact us to discuss possibilities.

Always leave yourself enough time to check through the document and accept the changes before your submission deadline.

Scribbr is specialised in editing study related documents. We check:

• Graduation projects
• Dissertations
• Admissions essays
• College essays
• Application essays
• Personal statements
• Process reports
• Reflections
• Internship reports
• Academic papers
• Research proposals
• Prospectuses

Calculate the costs

The fastest turnaround time is 24 hours.

You can upload your document at any time and choose between four deadlines:

At Scribbr, we promise to make every customer 100% happy with the service we offer. Our philosophy: Your complaint is always justified – no denial, no doubts.

Our customer support team is here to find the solution that helps you the most, whether that’s a free new edit or a refund for the service.

Yes, in the order process you can indicate your preference for American, British, or Australian English .

If you don’t choose one, your editor will follow the style of English you currently use. If your editor has any questions about this, we will contact you.

• Key Differences

Know the Differences & Comparisons

Difference Between Null and Alternative Hypothesis

Null hypothesis implies a statement that expects no difference or effect. On the contrary, an alternative hypothesis is one that expects some difference or effect. Null hypothesis This article excerpt shed light on the fundamental differences between null and alternative hypothesis.

Content: Null Hypothesis Vs Alternative Hypothesis

Comparison chart, definition of null hypothesis.

A null hypothesis is a statistical hypothesis in which there is no significant difference exist between the set of variables. It is the original or default statement, with no effect, often represented by H 0 (H-zero). It is always the hypothesis that is tested. It denotes the certain value of population parameter such as µ, s, p. A null hypothesis can be rejected, but it cannot be accepted just on the basis of a single test.

Definition of Alternative Hypothesis

A statistical hypothesis used in hypothesis testing, which states that there is a significant difference between the set of variables. It is often referred to as the hypothesis other than the null hypothesis, often denoted by H 1 (H-one). It is what the researcher seeks to prove in an indirect way, by using the test. It refers to a certain value of sample statistic, e.g., x¯, s, p

The acceptance of alternative hypothesis depends on the rejection of the null hypothesis i.e. until and unless null hypothesis is rejected, an alternative hypothesis cannot be accepted.

Key Differences Between Null and Alternative Hypothesis

The important points of differences between null and alternative hypothesis are explained as under:

• A null hypothesis is a statement, in which there is no relationship between two variables. An alternative hypothesis is a statement; that is simply the inverse of the null hypothesis, i.e. there is some statistical significance between two measured phenomenon.
• A null hypothesis is what, the researcher tries to disprove whereas an alternative hypothesis is what the researcher wants to prove.
• A null hypothesis represents, no observed effect whereas an alternative hypothesis reflects, some observed effect.
• If the null hypothesis is accepted, no changes will be made in the opinions or actions. Conversely, if the alternative hypothesis is accepted, it will result in the changes in the opinions or actions.
• As null hypothesis refers to population parameter, the testing is indirect and implicit. On the other hand, the alternative hypothesis indicates sample statistic, wherein, the testing is direct and explicit.
• A null hypothesis is labelled as H 0 (H-zero) while an alternative hypothesis is represented by H 1 (H-one).
• The mathematical formulation of a null hypothesis is an equal sign but for an alternative hypothesis is not equal to sign.
• In null hypothesis, the observations are the outcome of chance whereas, in the case of the alternative hypothesis, the observations are an outcome of real effect.

There are two outcomes of a statistical test, i.e. first, a null hypothesis is rejected and alternative hypothesis is accepted, second, null hypothesis is accepted, on the basis of the evidence. In simple terms, a null hypothesis is just opposite of alternative hypothesis.

You Might Also Like:

Zipporah Thuo says

February 22, 2018 at 6:06 pm

The comparisons between the two hypothesis i.e Null hypothesis and the Alternative hypothesis are the best.Thank you.

Getu Gamo says

March 4, 2019 at 3:42 am

Thank you so much for the detail explanation on two hypotheses. Now I understood both very well, including their differences.

Jyoti Bhardwaj says

May 28, 2019 at 6:26 am

Thanks, Surbhi! Appreciate the clarity and precision of this content.

January 9, 2020 at 6:16 am

John Jenstad says

July 20, 2020 at 2:52 am

Thanks very much, Surbhi, for your clear explanation!!

Navita says

July 2, 2021 at 11:48 am

Thanks for the Comparison chart! it clears much of my doubt.

GURU UPPALA says

July 21, 2022 at 8:36 pm

Thanks for the Comparison chart!

Enock kipkoech says

September 22, 2022 at 1:57 pm

What are the examples of null hypothesis and substantive hypothesis

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.