research analysis gas

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

27.4: Applications of Gas Chromatography

• Last updated
• Save as PDF
• Page ID 350901

• David Harvey
• DePauw University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Quantitative Applications

Gas chromatography is widely used for the analysis of a diverse array of samples in environmental, clinical, pharmaceutical, biochemical, forensic, food science and petrochemical laboratories. Table 27.4.1 provides some representative examples of applications.

Quantitative Calculations

In a GC analysis the area under the peak is proportional to the amount of analyte injected onto the column. A peak’s area is determined by integration, which usually is handled by the instrument’s computer or by an electronic integrating recorder. If two peak are resolved fully, the determination of their respective areas is straightforward.

Before electronic integrating recorders and computers, two methods were used to find the area under a curve. One method used a manual planimeter; as you use the planimeter to trace an object’s perimeter, it records the area. A second approach for finding a peak’s area is the cut-and-weigh method. The chromatogram is recorded on a piece of paper and each peak of interest is cut out and weighed. Assuming the paper is uniform in thickness and density of fibers, the ratio of weights for two peaks is the same as the ratio of areas. Of course, this approach destroys your chromatogram.

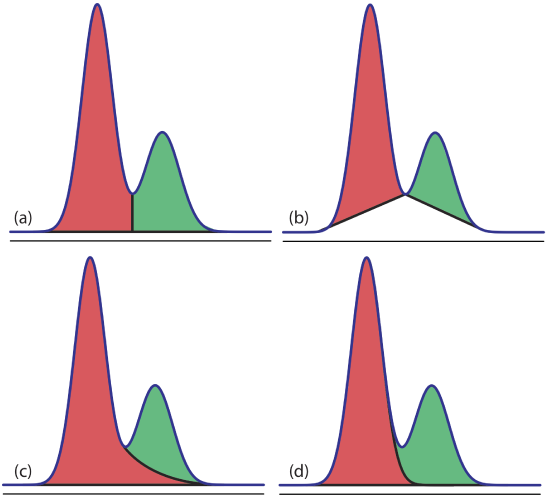
Overlapping peaks, however, require a choice between one of several options for dividing up the area shared by the two peaks (Figure 27.4.1 ). Which method we use depends on the relative size of the two peaks and their resolution. In some cases, the use of peak heights provides more accurate results [(a) Bicking, M. K. L. Chromatography Online, April 2006; (b) Bicking, M. K. L. Chromatography Online, June 2006].

For quantitative work we need to establish a calibration curve that relates the detector’s response to the analyte’s concentration. If the injection volume is identical for every standard and sample, then an external standardization provides both accurate and precise results. Unfortunately,even under the best conditions the relative precision for replicate injections may differ by 5%; often it is substantially worse. For quantitative work that requires high accuracy and precision, the use of internal standards is recommended.

Example 27.4.1

Marriott and Carpenter report the following data for five replicate injections of a mixture that contains 1% v/v methyl isobutyl ketone and 1% v/v p -xylene in dichloromethane [Marriott, P. J.; Carpenter, P. D. J. Chem. Educ. 1996 , 73 , 96–99].

Assume that p -xylene (peak 2) is the analyte, and that methyl isobutyl ketone (peak 1) is the internal standard. Determine the 95% confidence interval for a single-point standardization with and without using the internal standard.

For a single-point external standardization we ignore the internal standard and determine the relationship between the peak area for p -xylene, A 2 , and the concentration, C 2 , of p -xylene.

\[A_{2}=k C_{2} \nonumber \]

Substituting the known concentration for p -xylene (1% v/v) and the appropriate peak areas, gives the following values for the constant k .

\[78112 \quad 135404 \quad 132332 \quad 112889 \quad 91287 \nonumber \]

The average value for k is 110 000 with a standard deviation of 25 100 (a relative standard deviation of 22.8%). The 95% confidence interval is

\[\mu=\overline{X} \pm \frac{t s}{\sqrt{n}}=111000 \pm \frac{(2.78)(25100)}{\sqrt{5}}=111000 \pm 31200 \nonumber \]

For an internal standardization, the relationship between the analyte’s peak area, A 2 , the internal standard’s peak area, A 1 , and their respective concentrations, C 2 and C 1 , is

\[\frac{A_{2}}{A_{1}}=k \frac{C_{2}}{C_{1}} \nonumber \]

Substituting in the known concentrations and the appropriate peak areas gives the following values for the constant k .

\[1.5917 \quad 1.5776 \quad 1.5728 \quad 1.5749 \quad 1.5724 \nonumber \]

The average value for k is 1.5779 with a standard deviation of 0.0080 (a relative standard deviation of 0.507%). The 95% confidence interval is

\[\mu=\overline{X} \pm \frac{t s}{\sqrt{n}}=1.5779 \pm \frac{(2.78)(0.0080)}{\sqrt{5}}=1.5779 \pm 0.0099 \nonumber \]

Although there is a substantial variation in the individual peak areas for this set of replicate injections, the internal standard compensates for these variations, providing a more accurate and precise calibration.

Exercise 27.4.1

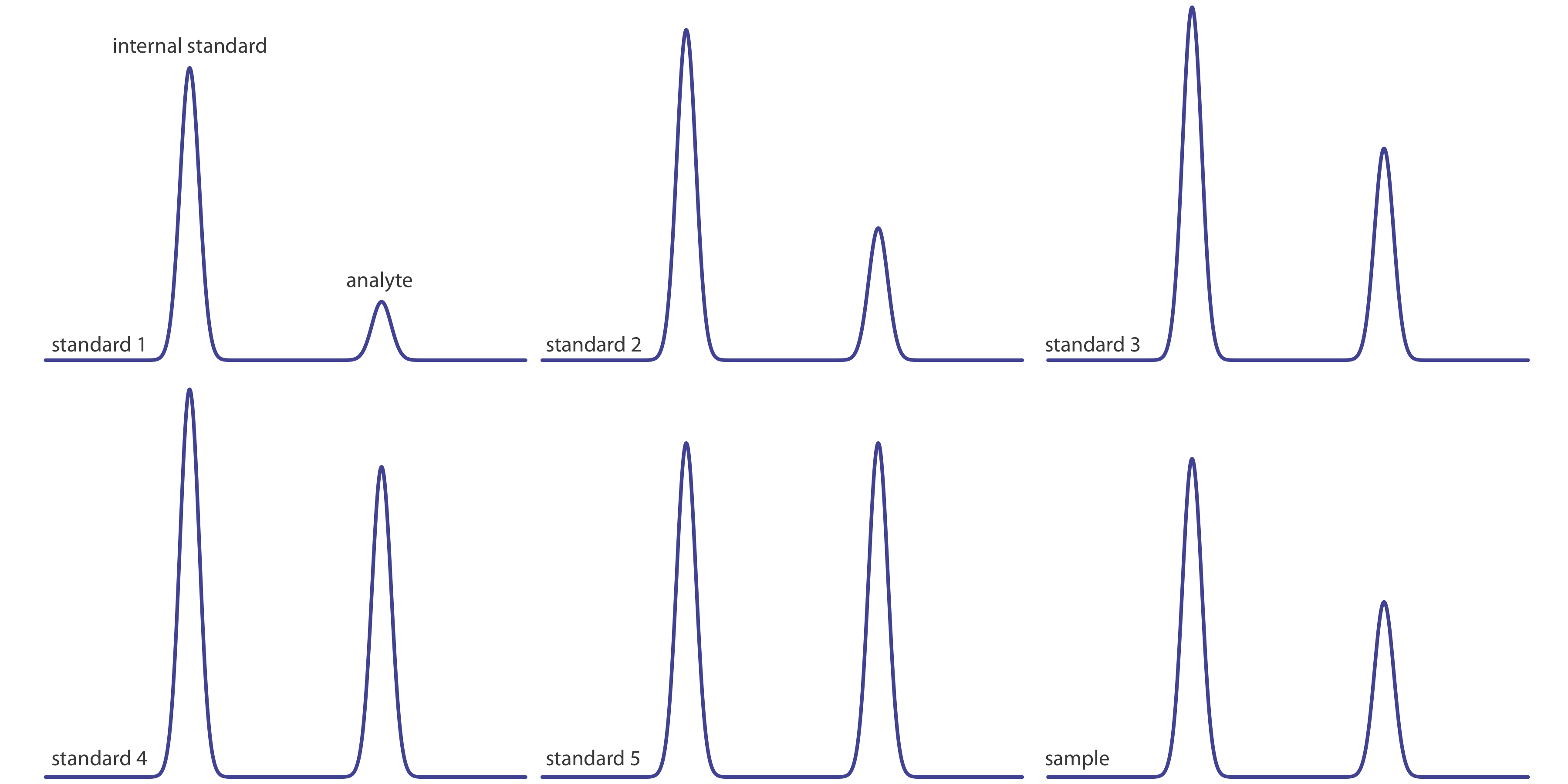
Figure 27.4.2 shows chromatograms for five standards and for one sample. Each standard and sample contains the same concentration of an internal standard, which is 2.50 mg/mL. For the five standards, the concentrations of analyte are 0.20 mg/mL, 0.40 mg/mL, 0.60 mg/mL, 0.80 mg/mL, and 1.00 mg/mL, respectively. Determine the concentration of analyte in the sample by (a) ignoring the internal standards and creating an external standards calibration curve, and by (b) creating an internal standard calibration curve. For each approach, report the analyte’s concentration and the 95% confidence interval. Use peak heights instead of peak areas.

The following table summarizes my measurements of the peak heights for each standard and the sample, and their ratio (although your absolute values for peak heights will differ from mine, depending on the size of your monitor or printout, your relative peak height ratios should be similar to mine).

Figure (a) shows the calibration curve and the calibration equation when we ignore the internal standard. Substituting the sample’s peak height into the calibration equation gives the analyte’s concentration in the sample as 0.49 mg/mL. The 95% confidence interval is ±0.24 mg/mL. The calibration curve shows quite a bit of scatter in the data because of uncertainty in the injection volumes.

Figure (b) shows the calibration curve and the calibration equation when we include the internal standard. Substituting the sample’s peak height ratio into the calibration equation gives the analyte’s concentration in the sample as 0.54 mg/mL. The 95% confidence interval is ±0.04 mg/mL.

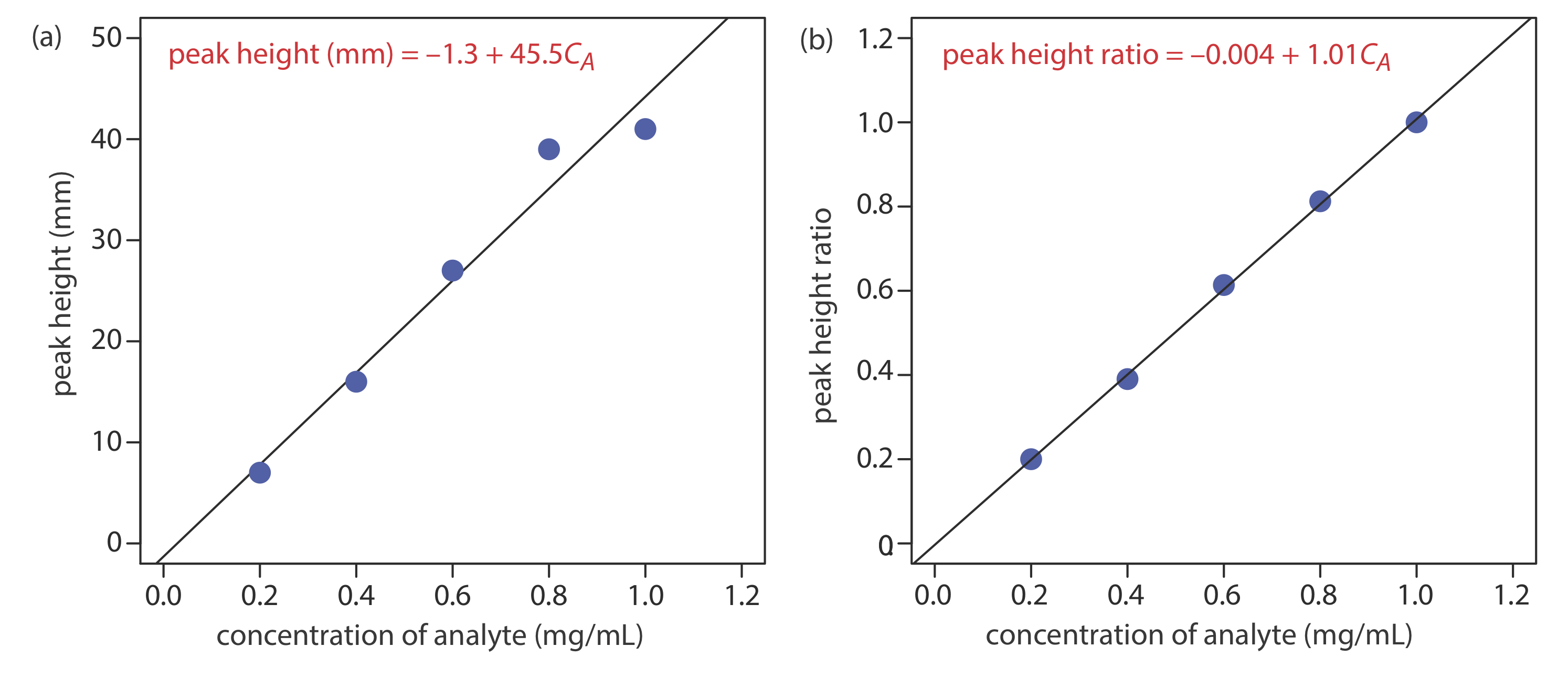
The data for this exercise were created so that the analyte’s actual concentration is 0.55 mg/mL. Given the resolution of my ruler’s scale, my answer is pretty reasonable. Your measurements may be slightly different, but your answers should be close to the actual values.

Qualitative Applications

In addition to a quantitative analysis, we also can use chromatography to identify the components of a mixture. As noted earlier, when we use an FT–IR or a mass spectrometer as the detector we have access to the eluent’s full spectrum for any retention time. By interpreting the spectrum or by searching against a library of spectra, we can identify the analyte responsible for each chromatographic peak.

In addition to identifying the component responsible for a particular chromatographic peak, we also can use the saved spectra to evaluate peak purity. If only one component is responsible for a chromatographic peak, then the spectra should be identical throughout the peak’s elution. If a spectrum at the beginning of the peak’s elution is different from a spectrum taken near the end of the peak’s elution, then at least two components are co-eluting.

When using a nonspectroscopic detector, such as a flame ionization detector, we must find another approach if we wish to identify the components of a mixture. One approach is to spike a sample with the suspected compound and look for an increase in peak height. We also can compare a peak’s retention time to the retention time for a known compound if we use identical operating conditions.

Because a compound’s retention times on two identical columns are not likely to be the same—differences in packing efficiency, for example, will affect a solute’s retention time on a packed column—creating a table of standard retention times is not possible. Kovat’s retention index provides one solution to the problem of matching retention times. Under isothermal conditions, the adjusted retention times for normal alkanes increase logarithmically. Kovat defined the retention index, I , for a normal alkane as 100 times the number of carbon atoms. For example, the retention index is 400 for butane, C 4 H 10 , and 500 for pentane, C 5 H 12 . To determine the a compound’s retention index, I cpd , we use the following formula

\[I_{cpd} = 100 \times \frac {\log t_{r,cpd}^{\prime} - \log t_{r,x}^{\prime}} {\log t_{r, x+1}^{\prime} - \log t_{r,x}^{\prime}} + I_x \label{12.1} \]

where \(t_{r,cpd}^{\prime}\) is the compound’s adjusted retention time, \(t_{r,x}^{\prime}\) and \(t_{r,x+1}^{\prime}\) are the adjusted retention times for the normal alkanes that elute immediately before the compound and immediately after the compound, respectively, and I x is the retention index for the normal alkane that elutes immediately before the compound. A compound’s retention index for a particular set of chromatographic conditions—such as the choice of stationary phase, mobile phase, column type, column length, and temperature—is reasonably consistent from day-to-day and between different columns and instruments.

Tables of Kovat’s retention indices are available; see, for example, the NIST Chemistry Webbook . A search for toluene returns 341 values of I for over 20 different stationary phases, and for both packed columns and capillary columns.

Example 27.4.2

In a separation of a mixture of hydrocarbons the following adjusted retention times are measured: 2.23 min for propane, 5.71 min for isobutane, and 6.67 min for butane. What is the Kovat’s retention index for each of these hydrocarbons?

Kovat’s retention index for a normal alkane is 100 times the number of carbons; thus, for propane, I = 300 and for butane, I = 400. To find Kovat’s retention index for isobutane we use Equation \ref{12.1}.

\[I_\text{isobutane} =100 \times \frac{\log (5.71)-\log (2.23)}{\log (6.67)-\log (2.23)}+300=386 \nonumber \]

Exercise 27.4.2

When using a column with the same stationary phase as in Example 27.4.2 , you find that the retention times for propane and butane are 4.78 min and 6.86 min, respectively. What is the expected retention time for isobutane?

Because we are using the same column we can assume that isobutane’s retention index of 386 remains unchanged. Using Equation \ref{12.1}, we have

\[386=100 \times \frac{\log x-\log (4.78)}{\log (6.86)-\log (4.78)}+300 \nonumber \]

where x is the retention time for isobutane. Solving for x , we find that

\[0.86=\frac{\log x-\log (4.78)}{\log (6.86)-\log (4.78)} \nonumber \]

\[0.135=\log x-0.679 \nonumber \]

\[0.814=\log x \nonumber \]

\[x=6.52 \nonumber \]

the retention time for isobutane is 6.5 min.

Making sense of gas measurements: quantification of multicomponent gas mixtures in biological and chemical laboratory experiments

• Lecture Text
• Open access
• Published: 28 September 2021
• Volume 7 , article number  27 , ( 2021 )

Cite this article

You have full access to this open access article

• Katharina Neubert   ORCID: orcid.org/0000-0003-1489-9806 1 ,
• Jörg Kretzschmar   ORCID: orcid.org/0000-0001-5970-6399 2 ,
• Tatiane Regina dos Santos 3 ,
• Claus Härtig 1 &
• Falk Harnisch   ORCID: orcid.org/0000-0002-0014-4640 1  

5714 Accesses

3 Citations

5 Altmetric

Explore all metrics

Textbooks in physical chemistry start from the treatise of the ideal gas. Gaseous compounds are important reactants and products of (bio)chemical reactions, and thus their absolute amounts are needed to establish mass balances. However, in contrast to solid, for dissolved and liquid compounds, their qualitative and especially quantitative analysis is less widely established in biological and chemical laboratories. This can be mainly ascribed to the seemingly simple chemical nature of gaseous compounds that is in contrast to the effort needed for their precise quantification. In this article, we will guide the reader through the considerations and steps needed to perform a meaningful analysis of multicomponent gas mixtures, which are reactants for or products of (bio)chemical reactions in aqueous solutions in the laboratory environment and scale. After a brief introduction, special focus is set on the methods for quantification and calculations needed to derive absolute amounts of gases in a mixture. The overall concept will be exemplified by biogas production as well as by an electroorganic reaction (Kolbe electrolysis of n -hexanoic acid), and general pitfalls will be highlighted.

Similar content being viewed by others

Determining modified reaction parameters for the real-time measurement of BTEX in biogas and nitrogen using Selected Ion Flow Tube Mass Spectrometry (SIFT-MS)

Gas Sensors

Introduction in Gas Sensing

Avoid common mistakes on your manuscript.

Introduction

Gas analysis can be defined as the qualitative and quantitative determination of the composition of a gas phase. This gas phase can either be pure, that is, containing one type of gas molecules, or it can be a multicomponent system, meaning that it comprises several gaseous compounds in different proportions (see Fig.  1 ). Footnote 1 Often we know the (bio)chemistry that leads to the consumption or production of gaseous reactants. Thus, the identity of the components in a multicomponent mixture is known or we are interested only in one or a few specific gaseous compounds. If the chemical identity of a compound needs to be determined, this information can be gained by different methods including chromatography, mass spectrometry or spectroscopy [ 1 , 2 , 3 ]. This identification of gases is not discussed in this article, and we refer the reader to the literature, for instance [ 4 , 5 ]. In the following we assume that all gaseous components are known.

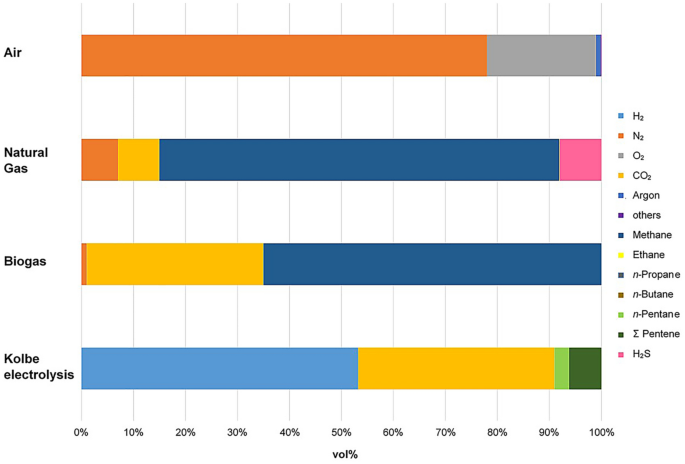
Chemical composition of different dry multicomponent gas mixtures: air, natural gas, biogas (see Sect.  4.1 ) and products of the Kolbe electrolysis of n -hexanoic acid (see Sect.  4.3 ) [ 6 ]

Quantitative measurements of gases are often an analytical challenge, especially when multicomponent systems are investigated and data of absolute gas quantities are required [ 7 ]. The acquisition of absolute gas quantities is indispensable to establish mass balances of (bio)chemical conversions involving gaseous reactants or products. To obtain absolute quantities of a gas mixture requires both information about the quantitative gas composition (absolute or relative values, see Table 1 ) and the total amount of gas (which usually means volume, \(v\) , or rarely mass, \(m\) ).

When looking at the quantitative chemical analysis of condensed phases, scales are extremely important. They permit the measurement of the mass of a sample as an absolute value at the given conditions. Normally, this gravimetric measurement is not possible for the analysis of gases. This is due to their low densities and hence masses as well as the lack of a defined volume and shape of the system to be analyzed. This means that there are only limited possibilities to weigh a gas phase. Gas mixtures can often be complex, but per se reach a chemical equilibrium quickly and then represent a homogeneous phase. This opens up the possibility of using volume instead of mass for quantitative gas analysis. Like masses, volumes can be measured precisely, provided that the compressibility of gases is considered. In addition to the number of moles of a gaseous component, the volume of a gas depends strongly on temperature and pressure. In many cases, especially under ambient conditions, we can describe the relation between these state variables by the ideal gas law (Eq.  1 ) [ 8 ].

According to the model of an ideal gas, gas molecules are not affected by intermolecular attractions. This is somewhat true for most gaseous compounds being analyzed in biological and chemical laboratories. Like all equations shown in this article, Eq.  1 is only valid when thermodynamic equilibrium is in place, including for instance the equilibration between the gas and liquid phases. Notably, it is not identical to steady state, and, strictly speaking, thermodynamic equilibrium is often not the case when gas analysis is performed. However, assumption of thermodynamic equilibrium is needed when performing gas analysis for practicability as well as to facilitate calculations. Therefore, time invariances are often leveled off by sequential analysis (see Sects.  4.2 and 4.3 ). In all cases, some particularities have to be considered in any analytical workflow for gas quantification. Gases spontaneously fill any free space and are often invisible and odorless. Therefore, the safe and defined containment of the measuring volume and the prevention of gas leaks for all experiments are of utmost importance, but often a challenge. Likewise, dead volumes, meaning the extra volumes of the experimental setup that do not contribute to the functionality of the system or that are not recorded by the used gas sensor, are always a source of uncertainty and error for gas quantification. Dead volumes must be recognized and avoided whenever possible when setting up the system. If this is not feasible, dead volumes need to be included in corrective calculations as we will illustrate below. As already mentioned above, the high compressibility of gases is an important property with effects that we cannot overestimate for precise gas measurement. Compressibility means that the volume of a gas changes as a function of the pressure it is exposed to [ 8 ]. Hence, any change in pressure has an immediate impact on the volume. As a consequence, temperature and pressure must be (1) known, (2) well defined and (3) constant during the entire gas analysis. Moreover, it must be ensured that temperature and pressure during the measurement are kept in a range in which the homogeneity of the gas phase is maintained. This means that condensation of components has to be avoided, which can be assured beforehand by estimating the dew point of the gas mixture to be analyzed (see Sect.  2.3 ) [ 9 ].

An arsenal of methods for the analysis of gases exists. Many of these are selective, meaning they are suitable to detect only one or a few gaseous compounds. This is particularly typical for industrial applications where only a few mostly known gases are of interest. These compounds are often determined in the process volume or volume stream without any separation from the gas mixture. This implies that the component to be determined exhibits a specific property that makes it suitable for selective detection in the industrial environment. Typical fields of application are heat gas industry for domestic use or natural gas industry [ 10 ] and chemical processes that involve the consumption or evolution of gaseous reactants, e.g., [ 11 ]. Since the handling of gases can generally be associated with considerable dangers, monitoring of diverse risk potentials (pressure, explosion limits, toxicity, etc.) is also important to provide workplace safety. Whereas specialized and routine methods dominate in industry, laboratories in academia require rather versatile but still very precise methods and workflows for gas analysis. Often mass balances have to be established to obtain information about reactions with gaseous reactants and unclear or unknown stoichiometry. In this case, we must reliably quantify all gaseous components.

In this article, we consider the quantification of multicomponent gaseous systems that are gas mixtures in biological and chemical laboratory experiments at ambient conditions and aqueous environment. The examples are selected to illustrate a typical workflow for converting gas mixtures to reference conditions and 0% humidity (see Sect.  4.1 ) as well as multicomponent gas analysis in a laboratory (see Sect.  4.3 ). The workflow starts from sampling and concludes with the calculations needed for setting up a mass balance (Figs. 2 and 10 ).

Typical workflow for a multicomponent gas analysis that is discussed in this article and exemplified for biogas production (Sect.  4.1 ) and Kolbe electrolysis of n -hexanoic acid (Sect.  4.3 )

Quantification of gas mixtures—basic principles

The focus of this contribution is on the quantification of gas mixtures. Therefore, we will first give a short overview of basic principles to be considered when gas volumes and the quantities of gaseous components are determined.

Pure substances

In thermodynamic equilibrium, the thermal state of any pure matter can be described unambiguously by its associated state variables volume ( \(v\) ), temperature ( \(T\) ), pressure ( \(p\) ) and mass ( \(m\) ) or amount of substance ( \(n\) ).

Changing the state variables independently from each other is impossible. The number of independent intensive variables needed to determine the system’s state, i.e., the number of degrees of freedom \((F)\) , depends on the number of components \((C)\) and the number of phases in equilibrium \((P)\) according to Gibbs' phase rule F  =  C  + 2 –  P [ 8 , 12 ]. For a pure phase and given amount of substance, two intensive state variables are sufficient for the unambiguous description of such a system (note that extensive variables are not degrees of freedom in the sense of the phase law). For instance, when considering the simple case of the ideal gas (Eq. 1 ), if temperature and pressure are given, the volume is automatically set and cannot be varied.

The mathematical expression for the relations between the thermal state variables for pure homogeneous systems are thermal state functions in the form \(f(p,T,v,n) = 0\) . This means that we cannot change a state variable without effecting at least one of the other three variables. For a general description of state changes, the total differential of the state function can be applied. For volume changes, this results in Eq.  2 :

For a given amount of substance \(n\) of a gas, the change in volume due to changes in \(p\) at constant \(T\) (which is isothermal) and due to change in \(T\) , at constant \(p\) (which is isobaric) can be calculated stepwise. Therefore, the partial differentials need to be known, which can be complex for real gases.

For the ideal gas, the partial differentials can be easily derived, and hence the state function can be represented explicitly and in a particularly simple way as an equation of state, also known as the combined gas law (Eqs. 1 and 3 ). It allows calculating all states of an ideal gas as the empirically found laws of Gay-Lussac/Charles, Amontons, Boyle/Mariotte and Avogadro are unified therein (see also Table 2 ) [ 8 ].

\(R\) is the universal gas constant. It is the product of the fundamental constants of nature, Avogadro's constant and Boltzmann's constant, and thus, since the redefinition of the SI base units in 2019, also exactly defined, precisely to R  = 8.31446261815324 J K −1  mol −1  = 8.31446261815324 Pa m 3  K −1  mol −1 [ 13 ].

We have to note that for the ideal gas the molar volume \(V = v/n\) is independent of the gas type. Thus, one mole of gas at the same temperature and pressure has the same volume (Avogadro's law) and there is proportionality between amount of substance and volume. For the reference point of IUPAC standard conditions (STP), which are \(T = 273.15 \text{ }\mathrm{K}\) and \(p = \mathrm{100,000} \text{ }\mathrm{Pa}\) , the molar volume of any ideal gas is \({V}^{\mathrm{STP}} = 22.711\text{ }\mathrm{ L }{\mathrm{mol}}^{-1}\) [ 14 ], see also Box 1 .

Box 1: The correct standard pressure is p  = 1 bar!

Standard conditions for temperature and pressure are important reference points for describing a gas state (see Eq.  1 ). Consequently, referring to standard conditions is also indispensable for any gas quantification that can only be carried out properly with appropriately calibrated devices and methods. Therefore, we strongly appreciate the efforts to define suitable and worldwide binding values for defining standard conditions, including a uniform terminology for their scientific use. In this publication, we consistently refer to the current IUPAC standard conditions for temperature and pressure (STP) [ 14 ]. They are well justified, internationally accepted, widely used and future-oriented.

While the IUPAC standard condition for temperature has remained unchanged at \(T=273.15\text{ }\mathrm{ K}\) , the IUPAC standard pressure was redefined in 1982. Until 1982, the standard pressure was \(p=1\mathrm{ atm}=\mathrm{ 101,325}\text{ }\mathrm{Pa}\) . According to the old definition, 1 atm refers to the mean air pressure at sea level. This reference state is poorly defined, the unit is not compliant with the system of SI units, and in calculations the converted value of 101,325 Pa always had to be used. Therefore, starting in 1982, the standard pressure condition was redefined by IUPAC to \(p=\mathrm{100,000} \text{ }\mathrm{Pa}=1\text{ }\mathrm{bar}\) . This is a freely defined fixed value, which, because of the unit 1 bar, has the advantage of being numerically well suited (as it was 1 atm previously) for describing the standard state of gases as simply as possible. Moreover, the newly defined standard pressure has the metrological advantage that it corresponds to the mean atmospheric pressure at an altitude of 105 m above sea level and is thus closer to the global mean altitude of human habitation (194 m) [ 15 ].

Actually, there is no scientific reason to continue using the old definition of standard pressure. However, many gas meter manufacturers still calibrate their devices to 1 atm. Thus, it is no wonder that people often want to continue using the old IUPAC definition for metrological reasons and ease of operation and calculation. We have decided to use the old IUPAC definition in the exceptional case of raw data acquisition with mass flow meters. For clarity, we mark the data obtained with the index "norm" instead of "STP" to indicate the changed reference conditions. Ultimately, for scientific clarity, we relate and report all results strictly to the STP conditions with \(p = 1 \text{ }\mathrm{bar}\) . We strongly advocate the reader to do so as well to assure clarity and allow easy comparison of gas quantities.

Homogeneous mixtures

Gas phases with more than one component are homogeneously mixed phases. In addition to \(p,\text{ } T,\text{ } v,\text{ } n\) composition variables for each component \(i\) are required for their description. Absolute values or relative values can be used to characterize the chemical composition of mixtures (Table 1 ).

Absolute composition values are extensive, i.e., they change with the size of system and hence the amount of substance changes. The absolute values are partial values of the component (in the system), such as partial pressure or partial volume. In a narrower sense, masses and amounts of substances can also be referred to as partial. The general advantage of all partial values is their additivity. This means that the total sum for all components of a partial value describes the corresponding overall property of a system (for volumes, however, this is only valid under ideal conditions). Of special importance in gas analysis is the use of partial pressures. Again, the sum of all partial pressures is equal to the whole pressure in the system (Dalton's law, Eq.  4 ) [ 8 ].

In contrast to the absolute values, the relative composition values are intensive values. This means that they are not proportional to the size of the system (see also Box 2 ). Intensive values describe the content of a defined compound in a mixture irrespective of the system size using the concepts of fraction values or concentrations.

Fraction values are dimensionless and defined as the proportion of a certain component in relation to the entire mixture. Thus, values between 0 and 1—or 0% and 100%—are possible. A fraction of 0 means absence of the respective component, whereas 1 means that a pure substance is present. Logically, the sum of fractions of all components in a mixture must be 1. Therefore, for C components, only ( C  − 1) fraction values are sufficient to fully describe a composition. Fraction values are mostly used for \(m,\text{ } n\) and \(v\) , but the concept is also useful for \(p\) . This allows us to provide “pressure fractions” or synonymously “relative partial pressures” of a component (see above). For an ideal gas, these are equal to the mole fractions, but not for a real gas, where mixture-dependent apparent or excess properties such as apparent molar volumes must be taken into account (see also Sect.  4.1 ). Here, the expression of pressure fractions does not make sense and is often inappropriate or even misleading.

Concentration values are mostly given as the ratio of an extensive variable such as \(m,\text{ } n,\text{ } v\) to the total volume. This has the consequence that, because the volume of gases is strongly dependent on environmental variables, these quantities are strongly dependent on temperature and pressure as well. The general advantage, however, is that intensive variables are created, i.e., the homogeneous mixture can be described independently of the size of the system. It should be noted that the volume concentration, \({\varphi }_{i}\) , only coincides with the partial volume fraction, \({\sigma }_{i}\) , for an ideal gas. In all real gas phases and even more in condensed phases, these two values are not identical. This is because by definition the total volume in volume concentrations always refers to values after mixing, while the total volume in volume fractions refers to values before mixing. Again, this illustrates the difference between intensive and extensive properties [ 8 ].

Box 2: Example calculations on intensive and extensive values

We assume now a gas volume of 500 mL that is filled with a mixture of N 2 and H 2 with each \({y}_{i}=50\%\) at \(p=198,000 \mathrm{Pa}\) . This means:

Now let us consider that the volume of the system increases by factor 20 to 10 L. According to the volume change, the pressure changes as follows:

We see that \({y}_{i}\) remains constant, while \({p}_{i}\) and \({v}_{i}\) scale with the size of the system.

The composition of gas mixtures in a system can be described in different ways. For each component, a partial pressure, a partial volume or a partial amount of substance (mass) can be stated. The total sum (over all components) of amount of substance and molar volume of the pure components leads to the total volume in ideal systems:

For mixtures of real gases, the partial volume of a compound is not identical to the molar volume of this compound in pure state. Thus, Eq.  5 cannot be used. The deviation of the volume from the ideal behavior can either be taken into account by including a so-called excess volume or the system has to be described by means of partial molar volumes, \({V}_{i}\) . The latter are the partial molar coefficients of the components in the total differential of the state function \(v\) :

The partial molar volume is not a fixed characteristic property of a component. The partial molar volume is a change function of the volume when the amount of substance of a component changes under the conditions of a quasi-constant composition of the mixed phase under isothermal and isobaric conditions. This means we have different \({V}_{i}\) for the same component in different mixtures. Using \({V}_{i}\) , the volume of a mixed phase can then be calculated additively again (Eq.  7 ):

It is often advantageous not to describe the composition of mixed phases with extensive values. Instead intensive values such as mass fraction, mole fraction or volume fraction could be used for this purpose. For a component of an ideal gas, according to the proportionality of \(n, v\) and \(p\) , the ratios of the different partial values to the respective total quantity are always the same for a given state, i.e., all fractional values are equal in the system:

As with all fractional values, the same applies here:

With Eq.  10 , it is possible to calculate partial pressures by mole fractions and vice versa:

Mean molar quantities such as average molar mass (Eq.  11 ), average molar volume (Eq.  12 ) and average molar density (Eq.  13 ) can be used to characterize a whole homogeneous mixture with a substance-related intensive average. These values can be calculated using the mole fraction, whereas volume-dependent quantities ( \(\overline{V }, \overline{\varrho })\) are only easily available when assuming an ideal gas.

The gas density of ideal gases is proportional to the molar mass; it holds:

Heterogeneous mixtures

Heterogeneous mixed phases often play a major role in the analysis and description of gas phase compositions, as exemplified in Sect.  4.3 . This applies in particular to the coexistence of mixed phases of liquids and gases. Due to the vapor pressures of all components in the liquid phase, corresponding partial pressures of these components are to be expected in the gas phase. The vapor pressure is an intrinsic property for a substance and depends strongly on the temperature, but not on the gas volume. For an ideal liquid mixture and an ideal behavior of the gas phase, the partial pressure of each component is equal to the product of the saturated vapor pressure of the pure component and its mole fraction in the liquid phase. This relationship is Raoult’s law (Eq.  15 ) [ 8 ].

Raoult’s law applies if the liquid phase is nearly pure or if very similar compounds (size, shape, polarity) are mixed. In contrast, especially for mixtures including water and organic solvents, it cannot be used. Generally, for real conditions, two correction factors for molecular interactions need to be applied: (1) For real gas behavior, the partial pressure is corrected by a fugacity coefficient to obtain the effective partial pressure (fugacity \(f\) of the component replaces partial pressure). (2) The non-ideal behavior of the liquid mixture is corrected by using an activity coefficient to describe the effective composition in a liquid phase (activity \(a\) of the component replaces its molar fraction). The interested reader can find more detailed information about this in literature, e.g., Wedler (1997) [ 16 ].

If ideal gases and liquids are in equilibrium with each other, the laws of Dalton and Raoult can be combined (with \({x}_{i}\) and \({y}_{i}\) as mole fraction in the liquid phase and gas phase, respectively) and lead to:

Equation  16 also allows the determination of the dew point of a gas mixture. The dew point is the temperature and pressure at which a first liquid droplet from a homogeneous gas mixture may condense. Knowing the dew point is of great importance, as gas analyses should generally be performed well above the dew point temperature (at a given pressure) or below the dew point pressure (at a given temperature) to avoid phase separation during analysis. Dew points can be determined using a system of two linear equations deduced from Eq.  16 and the boundary condition for mole fractions [ 8 ]:

For dew pressure, the system of equations mentioned above can be solved for a given complete set of \({y}_{i}\) and \({p}_{i}^{\mathrm{sat},*}\) at a specified temperature (Eq.  18 ).

In contrast, the dew temperature can only be calculated iteratively. Using a given complete set of \({y}_{i}\) and \({p}_{i}^{\mathrm{sat},*}\) at several temperatures around the assumed dew temperature, \({p}_{i}^{\mathrm{sat},*,f\left(\mathrm{temp}\right)}\) has to be approximated until Eq.  19 is valid [ 8 ].

Methods for gas measurements in chemical and biological laboratories

In general, gases can be analyzed regarding their quantity (usually volume) and their quality (composition). There is a whole arsenal of methods to determine gas volumes in the laboratory experiments available; most of these rely on displacement and are discussed in Sect.  3.1 .

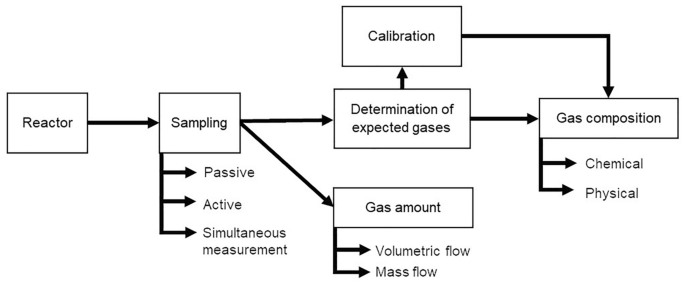
The sampling methods for the qualitative determination of different components can be divided into active sampling with or without enrichment, passive sampling or sampling with simultaneous measurement (Fig.  3 , Sect.  3.2 ). Which sampling technique is the most suitable depends on various factors such as the concentration and reactivity of the components, accompanying gases to be analyzed or the environmental conditions such as temperature and humidity as well as the availability of equipment. When taking samples with simultaneous measurement, a distinction can be made among the use of test tubes, sensors and spectroscopic or chromatographic methods [ 1 ]. The active sampling in laboratories is most often carried out using gasometers, gas collection tubes or similar gas collection containers such as gas bags. Another method of active sampling is the collection of the compound of interest using adsorption materials [ 1 , 17 ].

Examples for sampling methods: active sampling without enrichment using a a syringe and b gas bags and c sampling with online measurement using a sensor

How to measure the gas volume

Measurement of gas volume is commonly used. Reporting the gas volume is easy to understand and for process engineering has many practical advantages as it facilitates data exchange from laboratory to technical scale, for instance for the biogas process (see Sect.  4.1 ). Walker et al. evaluated the potential errors associated with the measurement of volume and calculation for the quantitative analysis of biogas. These include the measurement inaccuracy due to gas diffusion and the potential errors of volume calculation when converting the obtained values to STP conditions [ 18 ].

As the following paragraphs show, a variety of methods exist for the measurement of gas volumes. Given that the gas volume is pressure- and temperature-dependent, as discussed above, it is indispensable that both values be reported for each data point.

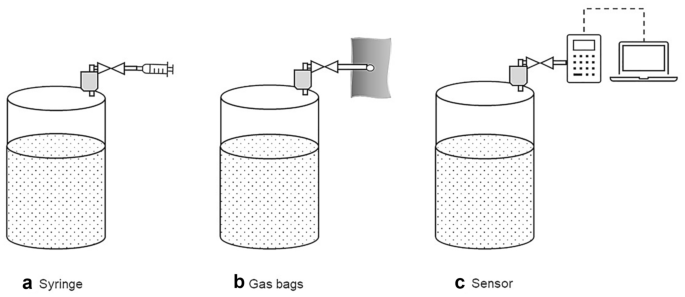
For measuring the volume of a gas in laboratories in academia, liquid displacement devices are commonly used, since they are inexpensive and easy to set up. However, the operation of simple liquid displacement devices is labor intensive and the accuracy is highly operator-dependent [ 18 , 19 ].

The liquid displacement method is used to determine the volume of gases independent of its composition. The basic principle is shown in the example devices presented in Fig.  4 . Commonly, the gas produced in a reactor is passed at the same pressure and temperature into a displacement tank that is filled with liquid, the so-called barrier solution. This leads to displacement of the barrier solution, which is quantified. The difference between the initial and final volume of the barrier solution corresponds to the volume of the produced gas. Different complexities of measurement setups for the displacement method are feasible and also include gravimetric measurements, as Fig.  4 B shows.

Examples of displacement methods used to determine the volume of gases [ 18 , 20 ]: a volume gasometer, b weight gasometer, c gas flow meter (Milligascounter)

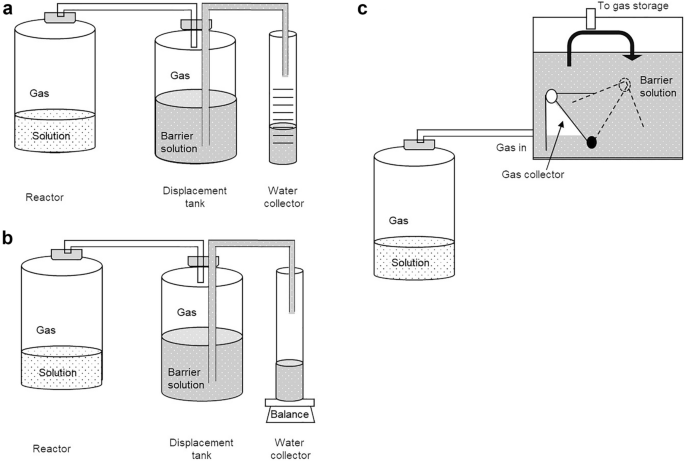
The accuracy of the measurement depends on the specific measuring device. Regardless of the complexity of the setup, the displacement method also permits the recording of the gas volume over time. Furthermore, the entire gas produced is collected in the displacement tank allowing determination of its composition (see Sect.  3.2 ). This allows the calculation of the absolute amount for each gaseous component. However, it is not possible to track the quantities of gaseous substances over time. Thus, whether the emission of certain components changes or remains constant over the duration of the measurement cannot be resolved. Furthermore, also intermittent gaseous reactants that are formed and subsequently consumed are not detected. An alternative to overcome this drawback is using more sophisticated and thus costly equipment. This comprises for instance Milligascounters (Fig.  4 C) fitted with a tipping bucket that is also based on the displacement principle. In summary, displacement methods are robust and yield the total amount for each gaseous component at the end of the experiment.

Another important point that should be noted using the displacement method for the quantification of the gas volume is the reactivity as well as the solubility of some compounds in the barrier solution, which depends, for example, on its pH value. The solubility can be predicted with knowledge of Henry's constants in different solutions. Henry’s law states that at a constant temperature, the amount of dissolved gas in a volume of a specified liquid is directly proportional to the partial pressure of the gas in equilibrium with the liquid. Looking at Henry's law constants of some species in water at ambient temperature (CO 2 : 3.6 × 10 –4  mol m −3  Pa −1 ; n -hexanoic acid: 7.5 mol m −3  Pa −1 ; n -butyric acid: 9.7 mol m −3  Pa −1 ), the effect of gas solubility can be estimated. This effect can cause major errors, since the absolute amount of dissolved gas can be considerable [ 21 , 22 ]. This needs to be considered when setting up the experiment and, according to the requirements, an acidified, alkaline or supersaturated saline barrier solution should be used. With an alkaline barrier solution, it is possible, for example, to dissolve the CO 2 from the gas stream as bicarbonate and thus exclude it from the volume measurement. Furthermore, a correction to the ambient temperature and the ambient pressure is necessary for all gas volumes being determined by displacement methods. It must further be noted that when using aqueous barrier solutions, water vapor (humidity of the gas) also plays a role and has to be included in the calculations (see Sect.  4.1 ).

Still, the Eudiometer unit (Fig.  5 ) is an important example for the widely applied displacement method that is even described in international standards and thus is of regulatory relevance [ 23 , 24 ]. The apparatus consists of a reactor that is connected to a sealed graduated gas collecting tube and a reservoir tank that is open to the atmosphere. Biogas produced in the reactor (see Box 4 ) passes from the headspace of the bioreactor to the headspace of the graduated gas collecting tube displacing the barrier solution in the reservoir tank. After pressure equalization, i.e., the same liquid level of the barrier solution, the volume of the displaced barrier solution is equivalent to the corresponding biogas volume. This method requires a specific adjustment of the barrier solution and allows achieving highly accurate results. Thus, it is a well established but labor-intensive method [ 21 , 22 ].

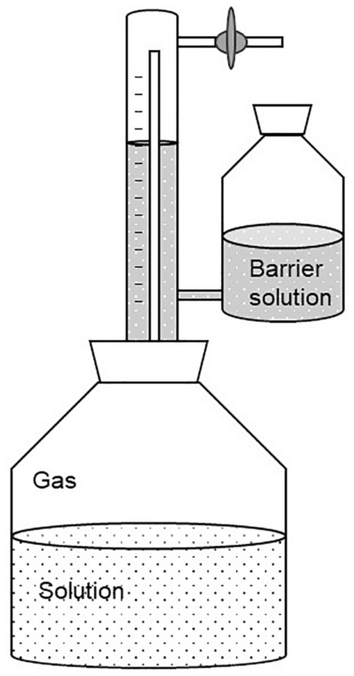
Eudiometer unit [ 25 ]

Among the more advanced techniques, one alternative method that we want to highlight here to determine the gas volume is using thermal mass flow meters (MFM). These allow the measurement of the mass flow directly and in real time. This has the advantage that the measurement is independent of temperature and pressure [ 26 ]. Yet, in contrast to the displacement method presented above, for the measurement with MFM, information on the gas composition is required.

There are two main measuring principles of thermal MFM; one is the bypass principle and the other is constant temperature anemometry (CTA) [ 26 ]. Both principles are based on two temperature measurements located in the direction of flow inside the gas stream. By convection, the gas flow creates a difference in temperature between the two measuring points. Using the bypass principle this temperature difference is directly correlated to the mass flow of the gas. For the CTA principle, the measurement sensors are kept at a constant temperature by heating. The power needed for keeping the temperature of the sensors constant is directly correlated to the mass flow. Depending on the gas composition and hence its heat capacity, the same mass flow influences the sensor temperature to a larger or smaller extent. Therefore, thermal MFMs are calibrated for a specific gas or gas mixture. If another gas or unknown gas mixture than the one used for calibration is analyzed with the MFM, a conversion factor is needed [ 27 ]. This can be easily done for pure gases. For gas mixtures, it is more tedious because each component needs its own conversion factor and the proportion of the components may change over time (see Sects.  4.2 and 4.3 ).

The output signal of mass flow meters is normally a volume flow and not mass flow because it is more common to use gas volume than gas mass. The volume flow refers to standard conditions, which means the mass flow is converted into a volume flow by using the specific density of the gas or gas mixture that the MFM is calibrated for at standard temperature and pressure (as requested by the manufacturer, see Box 1). In addition to mass flow meters, there are also mass flow controllers. These devices offer the possibility to fix the flow to a desired set point. The measured inflow mass flow is compared with the set point and is iteratively adjusted so that the outflow matches the set point.

How to measure the gas composition

Various methods are available for the qualitative and quantitative determination of individual components of a gas mixture. These methods can be grouped according to the principle of determination into chemical and physical methods. Chemical methods include volumetric and manometric gas analysis after the removal of specific gas components by specific reactions (e.g., precipitation, combustion) or specific absorption. The physical methods can be divided into condensation and distillation, fractional absorption and desorption and special methods exploiting specific physical properties of the gaseous components [ 17 ]. The latter include thermal conductivity, heat toning, magnetic properties and light absorption. Furthermore, gas chromatrography (GC) coupled to different kinds of detectors can be used (see below). In general, chemical methods for gas analysis offer the possibility to carry out a qualitative and quantitative determination in a short time with little equipment and operational expenditure. At the same time, these are limited to only one or a very few compounds and can often not be automatized. The physical methods, however, are more complex but are often considered to possess higher accuracy [ 17 ].

Chemical gas analysis

For chemical gas analysis that is based on precipitation, the gas mixture is passed through different barrier solutions one after the other. In each solution, a chemical reaction specific for a single component can take place and thus individual components can be determined [ 17 ]. Prominent examples are the determination of carbon dioxide using potassium hydroxide solution or oxygen using pyrogallol solution. The reactions lead to the formation of, for example, potassium carbonate when KOH reacts with CO 2 , precipitates of BaCO 3 if BaOH is used or a color change due to absorption of oxygen by alkaline pyrogallol. The formation of insoluble compounds or the change in color primarily provides a qualitative indication of the presence of a certain component. Since the gases are also bound (“trapped”) by the chemical reactions, they are removed from the gas mixture. For quantitative analysis, the chemical reactions have to be combined with volumetric or manometric analysis. Volumetric gas analysis means that the overall gas volume has been measured beforehand. When the overall gas volume changes because of the chemical reaction of one individual component, the volume of the individual component results from the difference in the overall gas volume before and after the reaction. A similar system is used for manometric gas analysis, except that it is not the volume difference after each chemical analysis that is determined but the pressure difference while the volume is kept constant. Since certain gases such as hydrogen cannot be determined by chemical gas analysis based on precipitation, a different approach is needed—e.g., chemical analysis based on the combustion of gases. The volumes of the burned gases can be calculated from the gas volume after combustion and the amount of oxygen required. The Orsat apparatus combines both approaches in one device. However, the Orsat apparatus, which was registered for a patent in 1874 [ 28 ], is no longer used as gas chromatography offers more efficient and precise quantification. Another method for the analysis of different gaseous components is using test tubes [ 1 ]. Their working principle is also based on a chemical reaction of a specific component in the test tube. These test tubes are commercially available and allow a simple and cheap qualitative analysis. The disadvantage of these test tubes is that no precise quantitative analysis is possible. They often only allow analysis with a large error range. For this reason, the test tubes are often only used to estimate the approximate concentration range in which a certain gaseous component is present.

Physical gas analysis

Gas analysis using physical methods offers many different options. In the context of this article, gas chromatography (GC) will be briefly introduced, since data from GC set the foundation for the example calculation shown in 4.3. GC is widely used because it can be automated, and the use of various separation columns and detectors enables the analysis of many different chemical compounds [ 1 ]. As with all chromatographic methods, the gas mixture is separated by the interaction of the gaseous analytes (that is the gas mixture) in the mobile gaseous phase with the stationary phase. The most commonly used columns today are capillary columns with a liquid or solid stationary phase [ 4 ]. The analytes are passed through the column using an inert carrier gas as mobile phase. Their separation occurs depending on the different interactions of the components in the gas mixture with the stationary phase and results in different retention times depending on the intensity of the interactions. The individual components can finally be analyzed using a detector. The thermal conductivity detector (TCD) is commonly used to analyze gases. By comparing the heat loss of two heating elements, each in a separate measuring chamber, due to the gas flow (sample or reference gas) around them, gas components can be quantified using a TCD. The amount of heat lost depends on the thermal conductivity of the gases. Hydrogen or helium is often used as reference gases because of their high thermal conductivity. Further detectors are: (1) infrared, (2) flame ionization, (3) mass selective and (4) flame photometric detectors, with the latter only being suitable for compounds that are combustible [ 4 ]. An important point to mention is that GC is a relative method for quantification meaning it requires calibration with external standards of different known concentrations (Box 3 ).

Box 3: Calibration of gas chromatographs for gas analysis—you have to accept the challenge

During calibration, the analyte signal, which means the peak area or peak height, is correlated with the analyte amount [ 1 ]. Thus, it is possible to create a calibration curve for each single gaseous component reflecting the correlation between signal intensity (seen in the chromatogram) and the amount of substance. Ultimately, the accuracy of this calibration determines the accuracy of the measurement of the analyte.

How to calculate the gas volume under STP conditions and the absolute amount of substance of gas components

A quantification of the absolute amount of gaseous component is only possible if the measurements of the gas volume and composition are combined. This combination enables the derivation of the absolute composition of a gas on a molar basis.

To calculate volumes of gas mixtures, first it is necessary to convert the measured volumes to the respective reference conditions. If humidity plays a role, the volume of the gas mixture has to be converted to dry conditions, i.e., 0% humidity. Here, we convert all volumes to STP conditions \({T}^{\mathrm{STP}}=273.15 \text{ }\mathrm{K}, {p}^{\mathrm{STP}}=1 \text{ }\mathrm{bar}\) and 0% humidity. Depending on the laboratory setup and the corresponding environmental conditions, the following scenarios with respect to the water vapor are possible: (1) assuming dry gases (described in Sect.  4.3 ), (2) water vapor saturated gases (Sect.  4.1 .) or (3) gases with a specific water vapor pressure. In the first case, the gas is dried, e.g., by cooling and condensation or water adsorption. Water-saturated gases can be assumed in reactors with high retention times of the gas phase over the aqueous phase, e.g., batch experiments. A specific water vapor can occur in continuous experiments, e.g., in a continuous stirred tank reactor (CSTR), with short retention times of the gas phase. In the latter case, the correct water vapor is accessible by careful measurement, e.g., using humidity sensors.

Several empirical equations exist to calculate water vapor pressure in gases, e.g., Antoine’s equation (Eq.  24 [ 29 ]) and the Magnus equation (Eq.  25 [ 30 ]) or the less known but more accurate Wagner equation [ 31 ] or Goff-Gratch equation [ 32 ] (both will not be discussed here). It should be noted that these equations represent approximations that are valid for certain environmental conditions. Several forms of the Magnus equation exist depending on the aggregate state of water (solid or liquid) and for different temperature ranges. Coefficients in Antoine’s equation to calculate \({p}_{{\mathrm{H}}_{2}\mathrm{o},\mathrm{sat}}\) depend on the temperature and pressure units that are used (e.g., [Pa], [mmHg], [°C], [K]) as well as on the basis of the logarithm. Therefore, it is vitally important to select the appropriate equation and correct coefficients that are valid for the conditions of the experiment and measurement.

If we want to analyze the quantity of single components from a gas mixture that includes water vapor (which is the case in almost all experiments under ambient conditions where the gas mixture has not been dried), it is very important to consider the method of quantification itself. If the gas mixture is directly injected in a GC with TCD, the water vapor is part of the injection volume and therefore needs to be considered during data processing. In this case, the molar or volume fractions of all components can only reach 100% if water vapor is included therein. Sometimes measured values of individual components of specific gas mixtures are related only to the calibrated components, i.e., all calibrated compounds sum up to 100%. Since the calibration is usually carried out with dry gases, water vapor leads to an overestimation of the individual components in gas mixtures.

Basic Example: Calculating the normal gas volume of biogas at 0% humidity

Box 4—the biogas process.

The biogas process, i.e., anaerobic digestion of organic material, called substrate, is a four-stage process performed by a wide range of anaerobic bacteria and archaea. In the first stage (hydrolysis), organic macromolecules such as fats, proteins and polysaccharides are broken down by different microbial hydrolases, e.g., lipases, proteases and hemicellulases, into soluble components such as volatile fatty acids (VFAs) and glycerin, amino acids and monosaccharides. In the second stage (acidogenesis), fermentation of monosaccharides, VFA and amino acids leads to the formation of different organic acids, hydrogen, carbon dioxide and alcohols. During the third stage (acetogenesis), the different fermentation products, e.g., longer chain fatty acids and alcohols, are converted to acetate, carbon dioxide and hydrogen. Finally, in the fourth stage (methanogenesis), archaea produce methane mainly from acetate (acetoclastic methanogenesis) or carbon dioxide and hydrogen (hydogenotrophic methanogenesis). Further pathways exist using methanoate (formate) instead of carbon dioxide or methylated compounds for methane production [ 33 ].

The produced biogas is a mixture of mainly methane and carbon dioxide, e.g., \({\varphi }_{{\mathrm{CH}}_{4}}\sim 0.5 , {\varphi }_{{\mathrm{CO}}_{2}}\sim 0.5)\) . The exact proportion of methane and carbon dioxide depends on the composition of the substrate used and the process temperature. A higher proportion of protein or fat in the substrate results in a higher proportion of methane in the biogas. Further trace gases in biogas are hydrogen sulfide ( \({\varphi }_{{\mathrm{H}}_{2}\mathrm{S}}<0.02\) ), hydrogen ( \({\varphi }_{{\mathrm{H}}_{2}}<0.02\) ), nitrogen ( \({\varphi }_{{\mathrm{N}}_{2}}<0.02\) ), oxygen ( \({\varphi }_{{\mathrm{O}}_{2}}<0.02\) ) and water (0.02–0.07 at 40–60 °C) [ 34 ].

To give an overview on the principal workflow for volume calculation of multicomponent gas mixtures at ambient conditions, we will first use the example of biogas production (Box 4 , Fig.  7 ). To quantify the biogas production from, e.g., liquid manure, one first has to choose a measurement method to determine the produced gas volume (for details, see Sect.  3.1 ). Let us assume a volume measurement with a displacement method such as the eudiometer unit (Figs. 5 and 6 C) that gives the volume of the produced biogas in milliliters or liters at ambient conditions. Let us further assume ideal environmental conditions, that is, no change of temperature and air pressure over the time of the experiment. To compare the measured gas volume with standard values in the literature, the measured volume must be normalized to STP conditions and 0% humidity using the ideal gas law (Eq.  1 ). Several gas laws exist that derive from the ideal gas law and allow the conversion or calculation of volume, pressure, and temperature from each other. Table 2 summarizes these gas laws.

Different devices for gas volume measurement commonly used in laboratories. a BlueVCount gas counter, b mass flow meter, c eudiometer, d drum-type gas meter, e MilliGascounter

As biogas originates from microbial processes in aqueous solutions, it contains a significant amount of water that needs to be considered. In this specific example, we use Antoine’s law (Eq.  24 ) and the Magnus equation (Eq.  25 ) to account for water vapor in the biogas (Fig.  7 ).

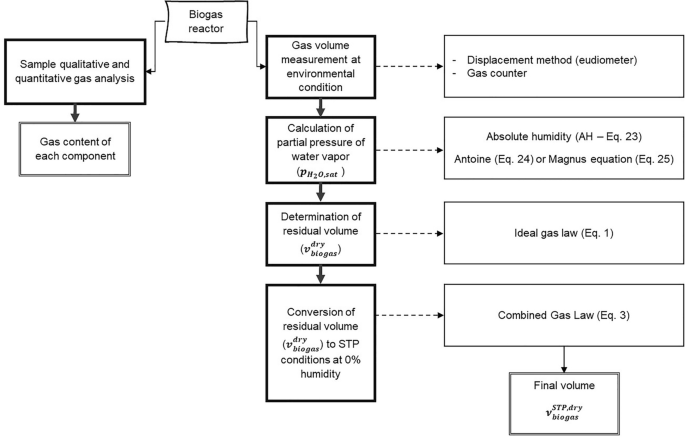
Principal workflow for volume measurement of multicomponent gas mixtures at ambient conditions on the example of biogas production as presented in the basic example

To illustrate the theory introduced above, in the following, some example calculations on biogas are performed. Therefore, we use real experimental data (given values).

Given values

\({v}_{\mathrm{biogas}}=1000 \text{ }\mathrm{mL} ({\varphi }_{{\mathrm{CH}}_{4}}\sim 50 \% , {\varphi }_{{\mathrm{CO}}_{2}}\sim 45 \%)\)

\({v}_{\mathrm{biogas}} \text{is saturated with water vapor}\left(100\mathrm{ \%} \text{ absolute humidity}\right)\)

\({\theta }_{\mathrm{biogas}} = 38\,^\circ\mathrm{C} \text{ or } {T}_{\mathrm{biogas}}=311.15 \text{}\,\mathrm{K}\)

\(p_{{{\text{biogas}}}} = {\text{99}},{\text{000 Pa }}(990{\text{ mbar}},{\text{ i}}.{\text{e}}.{\text{ atmospheric pressure}})\)

Biogas volume under STP conditions ( \({T}^{\mathrm{STP}}=273.15 \text{ }\mathrm{K}, {p}^{\mathrm{STP}}=1 \text{ }\mathrm{bar})\) and 0% humidity (dry gas), i.e., \({v}_{\mathrm{biogas}}^{\mathrm{STP},\mathrm{ dry}}\)

To convert the biogas volume to STP conditions and 0% humidity, one has to consider two issues. The first is the choice of an empirical equation to calculate water vapor pressure in gases, e.g., the Magnus equation or Antoine equation (for details, see Sect.  4 ). In our case, both equations are well suited and differ only slightly (see example below). The second issue is the order of mathematical removal of water vapor and the conversion to STP conditions in a way that avoids mistakes introduced by condensation of water vapor. For details, see Fig.  8 as well as the discussion. In our example, we will focus on two possible pathways to calculate the water vapor of biogas followed by converting the dry gas to STP conditions and afterwards shortly discuss possible sources of error.

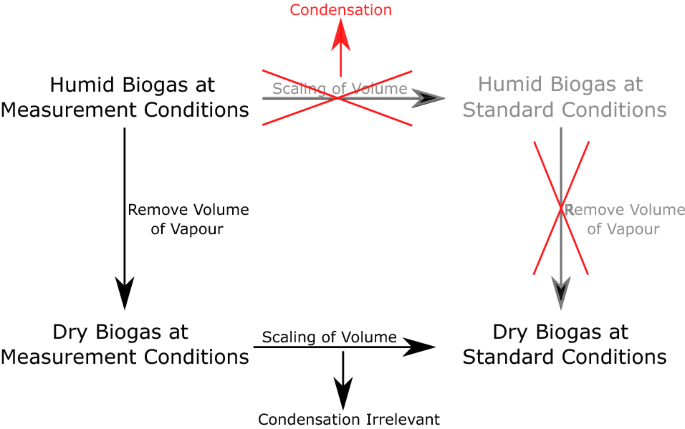
Effect of condensation on conversion of humid gas mixtures to reference conditions and 0% humidity

First case: Calculation of the volume of water vapor \({v}_{{\mathrm{H}}_{2}\mathrm{O},}\) in \({v}_{\mathrm{biogas}}\) using the Antoine equation (Eq.  24 ) or Magnus equation (Eq.  25 ) in combination with the equation for absolute humidity (AH, Eq.  23 ) followed by subtraction of \({v}_{{\mathrm{H}}_{2}\mathrm{O}}\) from \({v}_{\mathrm{biogas}}\) and converting the residual volume \({v}_{\mathrm{biogas}}^{\mathrm{dry}}\) to STP conditions at 0% humidity \({v}_{\mathrm{biogas} }^{\mathrm{STP},\mathrm{ dry}}\) using the combined gas law (Eq.  3 ).

Second case: Using a direct combination of the combined gas law (Eq.  3 ) and Antoine equation (Eq.  24 ) to directly convert \({v}_{\mathrm{biogas}}\) into \({v}_{\mathrm{biogas} }^{\mathrm{STP},\mathrm{ dry}}\) .

First case: Subtracting the volume of water vapor \({{\varvec{v}}}_{{\mathbf{H}}_{2}\mathbf{O}}\) from \({{\varvec{v}}}_{\mathbf{b}\mathbf{i}\mathbf{o}\mathbf{g}\mathbf{a}\mathbf{s}}\) followed by converting the residual gas volume to STP conditions at 0% absolute humidity \({{\varvec{v}}}_{\mathbf{b}\mathbf{i}\mathbf{o}\mathbf{g}\mathbf{a}\mathbf{s} }^{\mathbf{S}\mathbf{T}\mathbf{P}, \mathbf{d}\mathbf{r}\mathbf{y} }\)

Step 1: calculating the concentration of water vapor in biogas using the equation for absolute humidity (eq.  23 ).

Absolute humidity (AH) is defined as:

with \({R}_{{\mathrm{H}}_{2}\mathrm{O}}=461.52\mathrm{ J }{\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}\) being the individual gas constant of water.

The partial pressure of water vapor in water-saturated biogas \({p}_{{\mathrm{H}}_{2}\mathrm{O},\mathrm{sat}}\) is calculated here via (1) the Antoine equation (Eq.  24 ) or (2) the Magnus equation (Eq.  25 ).

Option 1 : Using the Antoine equation (Eq. 24 ) with A, B and C being substance as well as pressure and temperature unit specific parameters [ 29 , 35 ]:

For water at the given experimental conditions kPa and °C, the parameters A, B and C are tabulated, for instance, in Bierwerth 2011 [ 29 ] or Roizard 2014 [ 35 ], and Eq. 24 is solved as follows:

Note that multiplication with 1000 in the upper equation is due to the conversion of kPa to Pa.

Option 2: Using the Magnus equation (assuming saturation vapor pressure over flat water surfaces at \(\theta \ge - 45{\text{ }}^\circ {\text{C}} \le 60{\text{ }}^\circ {\text{C}}\) , Eq. 22) [ 36 ]:

For the given example, it follows:

Again, multiplication with 1000 in the upper equation is due to the conversion of kPa to Pa.

As we clearly see, calculation of \({p}_{{\mathrm{H}}_{2}\mathrm{O},\mathrm{ sat}}\) using the Antoine equation (Eq. 24 ) or the Magnus equation (Eq. 25 ) results in only slightly different values because of the empirical nature of both equations and their parameters. Both equations can be used without any limitation.

By inserting \({p}_{{\mathrm{H}}_{2}\mathrm{O},\mathrm{sat}}\) (here we use the result of the Antoine equation) into the equation for absolute humidity (Eq. 23 ), we get:

If we now consider \({v}_{\mathrm{biogas}}=1 \text{ }\mathrm{L}\) , it results in \({m}_{{\mathrm{H}}_{2}\mathrm{O}}=0.046 \text{ }\mathrm{g}\) .

Step 2: Calculation of \({v}_{\mathrm{biogas}}^{\mathrm{dry}}\) by calculation of \({v}_{{\mathrm{H}}_{2}\mathrm{O}}\) using the ideal gas law (Eq. 1 ) followed by subtraction from \({v}_{\mathrm{biogas}}\)

our example becomes:

Note that multiplication with 1000 in the calculation above is due to the conversion of m 3 to L.

The water vapor in our specific example is \({v}_{{\mathrm{H}}_{2}\mathrm{O}}=66.7 \mathrm{mL}\) and the volume of dry biogas under atmospheric conditions \({v}_{\mathrm{biogas}}^{\mathrm{dry}}\) calculates as follows:

Note: One may wonder why we did not use the density of water to calculate \({v}_{{\mathrm{H}}_{2}\mathrm{O}}\) out of \({m}_{{\mathrm{H}}_{2}\mathrm{O}}\) . This should generally not be done as \({v}_{{\mathrm{H}}_{2}\mathrm{O}}\) is part of a real mixture (biogas) and real gas mixtures have a non-ideal behavior. It has to be noted that for our specific biogas example (light gases, water, no carboxylic acids with vapor phase association), these effects are negligible. However, for other real gas mixtures, expansion or contraction effects may occur [ 8 , 37 ] (see also the discussion of excess volume below as well as Sects.  2.2 and 2.3 ).

Step 3: Converting \({v}_{\mathrm{biogas}}^{\mathrm{dry}}\) to \({\nu }_{\mathrm{biogas}}^{\mathrm{STP},\mathrm{ dry}}\) using the combined gas law Eq. 3 that derives from the ideal gas law (Eq. 1 )

For our specific example, it has to be noted that \({p}_{\mathrm{biogas}}\) equals atmospheric (isobaric) conditions, meaning \({p}_{\mathrm{biogas} }= {p}_{\mathrm{biogas}}^{ \mathrm{dry}}\) . Conversion of Eq.  3 to \({\nu }_{\mathrm{biogas}}^{\mathrm{STP},\mathrm{ dry}}\) results in Eq.  29 :

Thus, the combination of the equation of absolute humidity (Eq.  23 ) and the ideal gas law (Eq.  1 ) yields \({\nu }_{\mathrm{biogas}}^{\mathrm{STP},\mathrm{ dry}}= 811.13\mathrm{ mL}\) .

Second case: Converting \({{\varvec{v}}}_{\mathbf{b}\mathbf{i}\mathbf{o}\mathbf{g}\mathbf{a}\mathbf{s}}\) directly to \({{\varvec{v}}}_{\mathbf{b}\mathbf{i}\mathbf{o}\mathbf{g}\mathbf{a}\mathbf{s}}^{\mathbf{S}\mathbf{T}\mathbf{P},\mathbf{d}\mathbf{r}\mathbf{y}}\) by direct combination of the combined gas law (Eq.  3 ) and the Antoine equation (Eq.  24 )

In this example, the combined gas law (Eq.  3 ) and the Antoine equation (Eq.  24 ) are directly combined without intermediate conversion of \({p}_{{\mathrm{H}}_{2}\mathrm{O},\mathrm{ sat}}\) via \({m}_{{\mathrm{H}}_{2}\mathrm{O}}\) to \({v}_{{\mathrm{H}}_{2}\mathrm{O}}\) . This results in Eq.  30 [ 23 , 38 ]:

Inserting the values of our example yields:

In this case, the volume of dry biogas under STP conditions \({\nu }_{\mathrm{biogas}}^{\mathrm{STP},\mathrm{ dry}}=811.07 \mathrm{mL}\) . The results of both calculations are summarized in Table 3 .

The observed deviation shown in Table 3 of the first and second case is very little, only ~ 0.06 mL (or 0.07 ‰). This may seem negligible, but is a result of intermediate conversion of \({p}_{{\mathrm{H}}_{2}\mathrm{O},\mathrm{sat}}\) via \({m}_{{\mathrm{H}}_{2}\mathrm{O}}\) to \({v}_{{\mathrm{H}}_{2}\mathrm{O}}\) (rounding errors) in combination with the empirical nature of the equation for absolute humidity (Eq.  23 ) and the Antoine (Eq.  24 ) or Magnus equation (Eq.  25 ). From a practical point of view, the second case is easier to use as many fewer calculation steps are necessary, whereas the 1first case permits the calculation of parameters step by step, which may be necessary for further calculations.

Independent from the biogas example, several pitfalls exist when converting humid gas mixtures to the respective reference conditions. Here, we draw the attention again to the excess volume of real mixtures as already introduced in Sect.  2.2 and 2.3 as well the order of the conversion of humid gas mixtures to the respective reference conditions and 0% humidity.

Excess volume means the volume reduction or expansion when combining pure substances in a real mixture. Due to intermolecular forces, e.g., van der Waals forces, the distances between single molecules does vary resulting, for example, in changes of the partial density of the single components compared to the pure substances. Therefore, the volume of a component in a real mixture, e.g., water vapor, is not accessible via its density as a pure substance. Hence, the calculation of partial volumes of single gas components via the partial mass of the gaseous component is only possible regarding the molar amount of the respective component [ 8 , 37 ]. In such cases, the ideal gas model is not appropriate. For the given biogas example, these effects are negligible.

Furthermore, when converting humid gas mixtures at ambient conditions to the respective reference conditions and 0% humidity, the order of calculation can be important. One should always first mathematically remove the water volume from humid gas mixtures before converting the gas to reference conditions; otherwise, the effect of water condensation may falsify the calculation result (see Fig.  8 ).

General procedure for the quantification of multicomponent gas mixtures

Since the measurement with MFMs is independent of temperature and pressure, all that we need to do is convert the measured gas volume based on the gas composition into the real gas volume. This is presented below in general and illustrated in more detail using one case study in Sect.  4.3 .

For quantification of individual components in gas mixtures using a MFM and gas chromatography, it is necessary to combine the data from both devices. The MFM gives \({v}_{\mathrm{output}}^{\mathrm{norm}}\) as measured output volume of the gas mixture at norm conditions (see Box 1 ). The composition of the gas can be determined using GC in bypass, allowing to obtain the mole fraction \({y}_{i}\) of each individual gaseous component \(i\) . Since the MFM is calibrated for a specific gas, the nominally measured volume has to be corrected with a factor depending on the gas composition. Therefore, the first step is to convert the molar fraction of each gaseous component into a volume fraction \({\varphi }_{i}^{\mathrm{norm}}\) . For this conversion, it is necessary to calculate the average molar volume \({\overline{V} }_{\mathrm{mix}}^{\mathrm{norm}}\) of the real gas mixture (at the calibration conditions of the MFM: \(T = 273.15{\text{ K\, and\, }}p = 1.0132{\text{ bar}})\) for each sampling point. Then, the molar volume \({V}_{i}^{*,\mathrm{norm}}\) of each gaseous component at norm conditions is calculated by dividing the molecular weight \({M}_{i}^{*}\) by the gas density \({\varrho }_{i}^{*,\mathrm{norm}}\) of the component \(i\) (Eq.  31 ). Additionally, the molar volume \({V}_{i}^{*, \mathrm{STP}}\) of each component at STP conditions is also calculated (Eq.  32 ).

By multiplying the molar volume \({V}_{i}^{*,\mathrm{norm}}\) of each component with its molar fraction \({y}_{i}\) measured via GC the partial molar volume \({V}_{i}^{\mathrm{norm}}\) of each component in the mixture at norm conditions is gained (Eq.  33 ). To derive the average molar volume \({\overline{V} }_{\mathrm{mix}}^{\mathrm{norm}}\) of our specific gas mixture at norm conditions, we need to sum up all partial molar volume values of the different gaseous components (Eq.  34 ). It should be noted that, as the composition of the gas stream changes with time, this and all following calculations must be performed for each sampling point individually.

The partial molar volume of a component in relation to the average molar volume of the gas mixture gives the volume fraction \({\varphi }_{i}^{\mathrm{norm}}\) of each component (Eq.  35 ).

As mentioned above, MFMs can be used for gas flow measurements and are calibrated for a specific gas (or gas mixture). For MFM based on bypass measurements, the relationship between the signal output and mass flow or volume flow is:

with \(K\) as a device constant, \({c}_{p}\) specific heat capacity, \(\dot{m}\) mass flow and \(\dot{v}\) volume flow. To use the MFM for other gases than the calibration gas, a conversion factor \(C\) has to be defined.

in which the index cal stands for the calibration gas (indicated by MFM) and the index meas for any gas to be measured (real gas flow). Thus, equal signal outputs of the MFM are related to different volume flows.

Using a N 2 calibrated MFM (mL min −1 ) with an indicated output signal of 100, this means for a N 2 measurement a volume flow \({\dot{v}}_{\mathrm{meas}}\) of 100 mL min −1 N 2 ( \({c}_{p}^{*,\mathrm{norm}}=1045 \quad{\mathrm{J }}\quad{\mathrm{kg}}^{-1}{\mathrm{K}}^{-1},C=1\) ) or, if you measure CO 2 , a real flow of 80 mL min −1 CO 2 ( \({c}_{p}^{*,\mathrm{norm}}=\mathrm{828.2}\; \mathrm{J }{\mathrm{kg}}^{-1}{\mathrm{K}}^{-1}, C=0.80\) ).

Equation  38 shows that the conversion factor \({C}_{i}^{*,\mathrm{norm}}\) of a measured gas \(i\) in relation to the calibrated gas can be calculated as follows using the gas density and specific heat capacity at norm conditions. Sometimes also the manufacturers of MFMs provide the conversion factors for the most used gases.

For correcting the measured volume of the gas mixture, an average conversion factor \({\overline{C} }_{\mathrm{mix}}^{\mathrm{norm}}\) of the gas mixture has to be calculated.

If we assume an ideal gas mixture, the gas flows of the components are additive and \({\dot{v}}_{\mathrm{cal},\mathrm{mix}}\) (indicated gas flow at MFM) can be calculated as follows:

Finally, for gas mixtures a good approach is the following simplified Eq.  41 . The volume fraction \({\varphi }_{i}^{\mathrm{norm}}\) can be used to calculate the partial reciprocal conversion factor for each component \(\frac{1}{{C}_{i}^{\mathrm{norm}}}\) ; these are in the end summed up to the reciprocal conversion factor of the gas mixture \(\frac{1}{{\overline{C} }_{\mathrm{mix}}^{\mathrm{norm}}}\) .

At this point, we need to consider whether the gas composition remains constant or changes over the course of the experiment. Depending on the answer, the next calculation steps differ. If the gas composition does not change, we can use a constant conversion factor for the gas mixture (Eq.  42 ). Since the MFM is calibrated for norm conditions and all calculations so far are done for these conditions, a conversion to STP conditions is necessary to determine the amount of substance of each gaseous component (Eq.  43 ). Footnote 2

However, if the gas composition does change over the duration of the experiment, samples at different points of time need to be measured. The time intervals between samples need to be adjusted to the speed of the change in composition and generally should be kept as small as possible. We determine the real partial gas volume \(\Delta {v}_{\mathrm{real}}^{\mathrm{norm}}\) via the average of the conversion factors of the gas measurements at the two consecutive time points \({t}_{n}\) and \({t}_{n+1}\) and the measured partial gas volume \({\Delta v}_{\mathrm{output}}^{\mathrm{norm}}\) (Eq.  44 ) in between these two points. In addition, in this case also a conversion of the volume from norm to STP is necessary.

The next step is to calculate the real partial gas volumes of the individual components \({v}_{i}^{\mathrm{STP}}\) in the gas mixture. For this purpose, we multiply the average of the volume fractions of the two consecutive time points \({t}_{n}\) and \({t}_{n+1}\) with the previously calculated real partial gas volume at STP conditions between these time points (Eq.  46 ).

The last step is the calculation of the partial amount of substance of each component \({n}_{i}\) using the calculated partial gas volume at STP conditions and the calculated molar volume of the individual component at STP conditions (Eq.  47 ). The partial amounts of substance from each sampling point can then be summed up and the absolute amount of substance of each component \({n}_{\mathrm{total},i}\) of the gas mixture is obtained (Eq.  48 ).

Additionally, an important point to consider is the experimental setup. If there is a headspace of gas above the aqueous reaction solution that can be regarded as dead volume, we need to determine the corresponding amount of substance therein. It is calculated and added to the already calculated amount of substance of the individual components. The gas composition in the dead volume can be considered to correspond to the composition of the terminal measurement. The conversion of the determined dead volume \({v}_{\mathrm{dead}}^{x}\) into the dead volume \({v}_{\mathrm{dead}}^{\mathrm{STP}}\) at STP conditions considers the ambient temperature \({T}^{x}\) and the standard temperature \({T}^{\mathrm{STP}}\) (Eq.  49 ).

From the ratio of the dead volume at STP conditions and the partial gas volume between the last two measurements, including the partial amount of substance between these two measurements, the amount of substance in the dead volume \({n}_{dead,i}\) can be derived (Eq.  50 ).

Further to \({n}_{\mathrm{dead},i}\) substances could still be dissolved or precipitated. To account for these amounts of the component \(i\) , it may be necessary to subject the liquid or solid phase to post-treatment and analysis.

Case study for the quantification of gas mixtures

Reaction scheme 1 shows the electrochemical decarboxylation of medium chain carboxylic acids (MCCA) for the example of n -hexanoic acid [ 39 , 40 ]. The anions of the MCCA are oxidized by a one electron transfer at the anode of the electrolysis cell followed by a decarboxylation leading to radical formation. Subsequently, the radical can take different reaction pathways. Two of the formed radicals can combine spontaneously leading to dimers and hence the formation of an alkane—this is called the Kolbe reaction—or they can disproportionate, leading a short alkane and alkene. Alternatively, the radical can undergo a second electron transfer to the anode leading to the formation of a carbocation. This carbocation can react further to form an alkene, different alcohols or shorter chain carboxylic acid or lead to the formation of esters. All these side products are called non-Kolbe products. The overall reactions yield a complex mixture of products being soluble in an aqueous solution, but especially gaseous compounds, when starting from shorter chain acids such as n -hexanoic acid (see Reaction scheme 1 ). Beside CO 2 from decarboxylation at the anode, hydrogen is evolved from water electrolysis at the cathode. Further gaseous components can be formed during the reaction in the anode compartment such as 1-pentene, 2-methyl-2-butene, 2-cis-pentene, 2-trans-pentene and n -pentane. All gases have to be identified and quantified to establish a mass balance.

(Adapted from Stang et al. [ 39 ])

Kolbe electrolysis of n -hexanoic acid. Components marked with a green box are measured via microGC-TCD and those marked with an orange box via GC-MS

To illustrate the quantification of individual components in a gas mixture in the following, a case study on the Kolbe electrolysis of n -hexanoic acid to produce n -decane is discussed. Electrolysis was performed similarly to Stang et al. [ 39 ]. We further performed analysis of the quantitative gas composition at different time points during the experiment by gas chromatography (microGC-TCD) in bypass. The total gas volume evolved from the reactor was measured continuously with a MFM calibrated for N 2 . Since the setup was purged with nitrogen before the start of the electrolysis, N 2 is the most abundant gaseous component at the start of the experiment. The liquid products of such an electrolysis are of main interest as they can serve as fuel additives [ 41 ]. However, they are not of interest for the following consideration. Here, we will focus on gaseous products that are produced during electrolysis, which are listed in Table 4 together with the corresponding molar fractions measured with microGC-TCD and the gas volumes measured with a MFM at different time points. Many different gaseous products are formed in minor proportions during electrolysis that can hardly be distinguished using microGC-TCD, such as 1-pentene, 2-methyl-2-butene, 2-cis-pentene and 2-trans-pentene. Thus, they have been summed as Σ pentene for the sake of simplicity and also practical convenience.

Importantly and in contrast to case study 1 (see Sect.  4.1 ), in this example we did not consider the volume of water vapor in the total gas volume. Thus, we assume that the experimental setup is designed to allow drying the gas before the measurement. However, this is not always possible, since the distance between the reactor and microGC-TCD needs to be increased, which leads to a time delay in the measurement. Consequently, if the gas composition changes rapidly (which is not the case for the case study here), the real state inside the reactor is only reflected with delay.

As shown in Table 4 , the produced gas consists of H 2 , N 2 , CO 2 , Σ pentene and n -pentane. The distribution of the individual components changes over the course of the electrochemical conversion. In the beginning, there is nearly only N 2 , and in the last measurement after 240 min the main components are H 2 and CO 2 .

Step 1: Calculation of the conversion factors

First, the parameters \({V}_{i}^{*,\mathrm{norm}}\) , \({V}_{i}^{*,\mathrm{STP}}\) and \({C}_{i}^{*,\mathrm{norm}}\) (see Eqs. 31 , 32 and 38 ) of the individual gaseous components are calculated (Table 5 ). For \({V}_{i}^{*,\mathrm{norm}}\) , \({V}_{i}^{*,\mathrm{STP}}\) and \({C}_{i}^{*,\mathrm{norm}}\) of Σ pentene, the average was calculated from the individual molar volumes and conversion factors of the combined components.

To illustrate the importance of the conversion factor, n -pentane is used as example. The conversion factor of 0.249 means that the real flow in mL min −1 for n -pentane is only 24.9% of the nominal flow readout at a device calibrated for N 2 . Thus, if the MFM calibrated for N 2 provides a readout of 100 mL min −1 for a pure n -pentane stream, it means that only a flow of 24.9 mL min −1 is in place. The consequence of this is that the produced gas volume does not correspond to the nominal measured value when no correction for the different gases (actually their different thermal conductivity) takes place. This stresses clearly that it is important to correct the measured gas volume to quantify the individual gaseous components correctly.

Step 2: Calculating the partial molar volumes of components and the molar volume of the mixture

To calculate the partial molar volume \({V}_{i}^{\mathrm{norm}}\) (Eq.  33 ) of each component for each time point, we used the mole fractions \({y}_{i}\) measured with microGC-TCD (Table 4 ) and the molar volume \({V}_{i}^{*,\mathrm{norm}}\) of the individual products at norm conditions calculated in Table 5 . Thus, we ultimately obtain the average molar volume of the gas mixture for each time point according to Eq.  34 ; these are shown in Table 6 . This is shown using the example of H 2 after 20 min of electrolysis.

With the partial molar volume \({V}_{i}^{\mathrm{norm}}\) of each component and the average molar volume \({\overline{V} }_{\mathrm{mix}}^{\mathrm{norm}}\) of the gas mixture both at norm conditions listed in Table 6 , it is possible to calculate the volume fraction \({\varphi }_{i}^{\mathrm{norm}}\) of the individual gaseous products (Eq.  35 ) for each time point. Again shown for the example of H 2 after 20 min of electrolysis:

This means that 33 vol% of the gas mixture consists of H 2 after 20 min of electrolysis. After calculating \({\varphi }_{i}^{\mathrm{norm}}\) for all components at all sampling points (Table 7 ), it is possible to convert the measured gas volume with the conversion factor into the actually produced gas volume (Eqs. 36 – 45 ).

Step 3: Calculating the real volume of the gas mixture

To convert the volume fractions into an absolute volume of each gaseous component at the different time points, we need to know the real gas volume produced during the experiment. Therefore, we calculate the average conversion factor of the gas mixture \({\overline{C} }_{\mathrm{mix}}^{\mathrm{norm}}\) . Considering the volume fractions and conversion factor of each gaseous component (in relation to N 2 , which was used for calibration), the partial reciprocal conversion factor \(\frac{1}{{C}_{i}^{\mathrm{norm}}}\) of each gaseous component can be obtained and summed up to the reciprocal conversion factor of the gas mixture (Table 8 ).

This is shown with the example of H 2 after 20 min of electrolysis. First, we obtain the partial reciprocal conversion factor using Eq.  41 .

For converting the measured gas volume with the conversion factor of the gas mixture into the real produced gas volume, it is important to consider that the distribution of components may also change between two successive measurements. Therefore, in reality we may have a continuously changing conversion factor of the gas mixture that needs to be calculated by Eq.  41 . To include this dynamics, we consider the arithmetic mean of the conversion factors of two consecutive measurements to be representative of the corresponding interval. For the example of the measurement after 20 min, the real partial gas volume \({\Delta v}_{\mathrm{real}}^{\mathrm{norm}}\) is calculated by using the average \({\overline{C} }_{\mathrm{mix}}^{\mathrm{norm}}\) of the measurements after 10 and 20 min and multiplied with the measured partial gas volume \({\Delta v}_{\mathrm{output}}^{\mathrm{norm}}\) as shown using Eq.  44 . Since the MFM is calibrated for a temperature of 273.15 K and a pressure of 1.0132 bar \({\Delta v}_{\mathrm{real}}^{\mathrm{norm}}\) has to be converted to \({\Delta v}_{\mathrm{real}}^{\mathrm{STP}}\) according to the STP conditions of 273.15 K and 1 bar.

To illustrate the importance of this correction, Fig.  9 shows that the real gas volume deviates from the measured gas volume already after < 1 h of electrolysis, although there is still a large proportion of N 2 in the gas mixture. The lower the proportion of N 2 (the gas the MFM was calibrated for), the greater the deviation becomes. For the last measurement after 240 min, the difference between the measured and the real gas volume is 294.02 mL, which corresponds to a relative error of around 22.8%!

Readout of uncorrected volume of the gas mixture measured using a MFM calibrated for N 2 (black squares) and real gas volume at norm conditions calculated after applying the needed corrections (red dots) over the duration of the experiment

Step 4: Calculating the partial volumes and absolute amount of substance of each component

Having the real produced gas volume of the gas mixture at STP conditions, we can now calculate the real partial gas volume of each component. Subsequently, we gain the partial amounts of substance of each gaseous compound. These can be summed up to the absolute amount of substance of each component (Eqs. 46 – 48 ). Here, it is important to average the volume fractions of two successive measurements as described above, since within these two sampling points the volume fraction of each gaseous component in the total gas volume may change. For clarification, the calculation is shown using the example of H 2 after 20 min of electrolysis. We first use Eq.  46 to calculate the amount of H 2 after 20 min of electrolysis within the measured partial gas volume. Comparing both results for STP and norm, we see that the difference for the partial gas volume of H 2 is 0.10 mL, which corresponds to an error of 1.3% already for this single compound at one time point.

Now, we have absolute values for each gaseous component and do not rely on relative information anymore (Table 9 ). Summing up the real partial gas volumes of each component gives the total volume for the individual gaseous component that was produced during the experiment.

However, in (bio-)chemical and microbial experiments, the focus is usually on the quantification of the amount of components that are consumed or produced in the liquid phase. Thus, the entire process can only be balanced or evaluated if the values of the liquid and gas phase are combined. Therefore, it is necessary to convert the gas volume into the molar amount of substance. This is shown for the example of the conversion of the partial gas volume of H 2 produced between 10 and 20 min of electrolysis into the corresponding amount of substance using Eq.  47 :

The absolute amount of substance of each component is obtained by summing the partial values (Table 10 ).

Another important point during quantification of gaseous components is the calculation of the amount of substance in the dead volume of the experimental setup. Depending on the extent of the dead volume, this can have a major impact on the quantification. In the example presented, the dead volume of the system was \({v}_{\mathrm{dead}}^{x}=126 \text{ }\mathrm{mL}\) . If this is converted to STP conditions, it equals \({v}_{\mathrm{dead}}^{\mathrm{STP}}=117 \mathrm{mL}\) . Knowing the dead volume of the setup, we can calculate the amount of substance of each gas component in this dead volume at the end of the experiment (Eqs. 49 and 50 ).

Summing this up, with the amount of substance measured during the experiment, we obtained the final quantitative value for all individual gaseous components (Table 11 ).

In this article, we have shown that the correct and precise quantification of gases in biological and chemical laboratories can be a real challenge. This holds true for both measurement and data treatment. Several pitfalls exist that lead to incorrect results and in most cases to an overestimation of the amount of gaseous compounds. This is of special notice as especially gaseous products from biological and chemical conversions are intensively researched in light of a biobased economy.

In addition to the design and operation of the experimental setup that should avoid or at least minimize dead volumes, the instrumentation and methods have to be carefully chosen for the respective analytical task. Here, for pure gases and gas mixtures of well-known or even constant composition, (simple) chemical or physical methods can be an excellent choice, for instance, for quantification of biogas the use of eudiometers. The same device and method are rather unsuitable for the quantification of gases from other processes with an unknown composition. When it comes to less known mixtures of gases or those with fluctuating composition, more sophisticated instrumentation is required, for instance, the combined qualitative analysis using gas chromatography with quantitative measurements by thermal mass flow meters (see case study 2, Sect.  4.3 ).

In all circumstances, the quantification has to be performed with extreme care, and the data obtained, e.g., measured volumes, need further treatment. Here, only re-calculating of the volume to a state of reference is unequivocal, and only reporting values converted to reference conditions allows comparison across studies. However, by developing and rigorously following a fixed workflow and evaluation process, this challenge can be tackled. Figure  10 shows a workflow that can be used as blueprint and thereby summarizes the step-by-step procedures presented in this article.

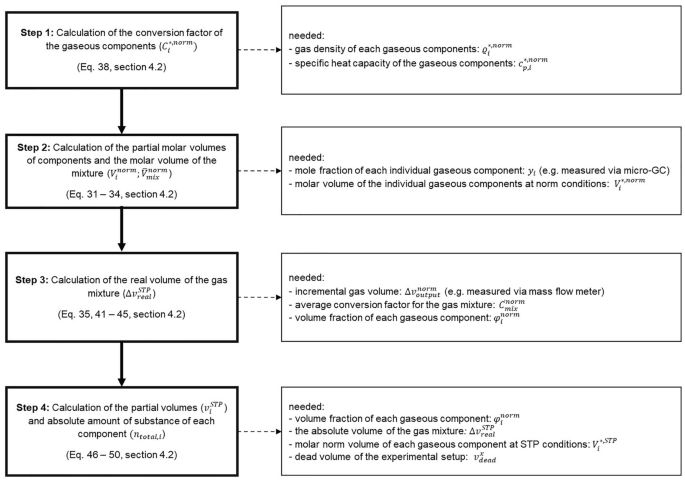
Workflow for calculations from raw data to final result

Availability of data and material

Not applicable.

Code availability

Within this article, we define a system in accordance with physical chemistry as a body of matter confined in space by walls that separate it from its surroundings, which is the environment.

Note that Eqs.  43 and 45 are special cases of Boyle’s law (Eq.  20 ). This illustrates both the interrelation of fundamental considerations with practical measurements and that here again an ideal gas is assumed for each step.

Abbreviations

Conversion factor of a pure substance i in a mixture

Partial conversion factor of component i in a mixture

Average conversion factor of gas mixture

Mole concentration of component i

Specific heat capacity of a pure substance i

Molecular weight \(M=\frac{m}{n}\)

Molecular weight of a pure substance i in a mixture

Average molecular weight of a mixture

Partial mass of component i \(\sum {m}_{i}=m\)

Amount of substance

Partial amount of substance of component i \(\sum {n}_{i}=n\)

Amount of substance of component i in the dead volume

Total amount of substance of component i

Partial pressure of component i  \(\sum {p}_{i}=p\)

Saturated vapor pressure of the pure component i

Temperature (Kelvin)

Molar volume \(V=\frac{v}{n}\)

Molar volume of a pure substance i in a mixture

Partial molar volume of component i in a mixture

Average molar volume of a mixture

Volume flow

Partial volume of component i \(\sum {v}_{i}=v\)

Dead volume

Temperature (°Celsius)

Mass fraction of component i \(\sum {\omega }_{i}=1\)

Mole fraction of component i in condensed phases \(\sum {x}_{i}=1\)

Mole fraction of component i in gas phases \(\sum {y}_{i}=1\)

Mass concentration (density) of a pure substance i in a mixture

Partial mass concentration (density) of component i in a mixture

Average density of a mixture

Volume concentration of component i

Volume fraction of component i \(\sum {\varphi }_{i}=1\)

Pure substance

Gas mixture

Outdated standard temperature and pressure conditions (273.15 K; 1.0132 bar)

Via mass flow meter measured volume of gas mixture

Real volume of the gas mixture

Ambient conditions

IUPAC standard temperature and pressure conditions (273.15 K; 1.0 bar)

Cammann K (2001) Instrumentelle Analytische Chemie. Spektrum Akademischer Verlag

Schwedt G, Schmidt TC, Schmitz OJ (2016) Analytische Chemie: Grundlagen, Methoden und Praxis, 3rd edn. WILEY-VCH Verlag

Flickinger MC, Pollard D, Christensen J (2010) Vent gas analysis. In: Flickinger MC (ed) Encyclopedia of Industrial Biotechnology. John Wiley & Sons

Dettmer-Wilde K, Engewald W, Adahchour M, et al (2014) Practical gas chromatography: a comprehensive reference. Springer-Verlag

Rood D (2007) The troubleshooting and maintenance guide for gas chromatographers. Wiley-VCH Verlag

Dörr H, Koturbash T, Kutcherov V (2019) Review of impacts of gas qualities with regard to quality determination and energy metering of natural gas. Meas Sci Technol 30:22001

Jones D, et al. (2013) Final Publishable JRP Report for ENG01 Gas Characterisation of Energy Gases. Project Number: ENG01. Euramet

Atkins P, Depaula J, Keeler J (2017) Physical Chemistry, 11th edn. Oxford University Press

NGC+ Liquid Hydrocarbon Drop Out Task Goup (2005) White paper on liquid hydrocarbon drop out in natural gas infrastructure. https://www.beg.utexas.edu/files/cee/legacy/NGC_HDP_Paper.pdf

Speight JG (2018) Handbook of natural gas analysis. John Wiley & Sons

McNeil B, Harvey LM (2008) Practical fermentation technology. John Wiley & Sons

Hillert M (2007) Phase equilibria, phase diagrams and phase transformations. Cambridge University Press

NIST SI Redefinition (2019) The NIST Reference on Constants, Units, and Uncertainty. In: NIST. https://physics.nist.gov/cgi-bin/cuu/Value?r

McNaught AD, Wilkinson A (2019) IUPAC Compendium of Chemical Terminology. The Gold Book. Blackwell Sci Publ Oxford

Cohen JE, Small C (1998) Hypsographic demography: the distribution of human population by altitude. Proc Natl Acad Sci USA. https://doi.org/10.1073/pnas.95.24.14009

Article   PubMed   PubMed Central   Google Scholar  

Wedler G (1997) Lehrbuch der physikalischen Chemie, 4, völlig. Wiley-VCH, Weinheim

Google Scholar  

Müller E (1953) A. Probenahme, Geräte und Verfahren. In: Bähr, Arndt, Bathe et al (eds) Analytische methoden. Georg Thieme Verlag, Stuttgart. https://doi.org/10.1055/b-003-117799

Walker M, Zhang Y, Heaven S, Banks C (2009) Potential errors in the quantitative evaluation of biogas production in anaerobic digestion processes. Bioresour Technol 100:6339–6346. https://doi.org/10.1016/j.biortech.2009.07.018

Article   CAS   PubMed   Google Scholar  

Strömberg S, Nistor M, Liu J (2014) Towards eliminating systematic errors caused by the experimental conditions in Biochemical Methane Potential (BMP) tests. Waste Manag 34:1939–1948. https://doi.org/10.1016/j.wasman.2014.07.018

Article   PubMed   Google Scholar  

Weinrich S, Schäfer F, Bochmann G, Liebetrau J (2018) Value of batch tests for biogas potential analysis-method comparison and challenges of substrate and efficiency evaluation of biogas plants. Murphy JD (Ed) IEA Bioenergy Task 37:10

Khan I, Brimblecombe P, Clegg SL (1995) Solubilities of pyruvic acid and the lower (C1–C6) carboxylic acids. Experimental determination of equilibrium vapour pressures above pure aqueous and salt solutions. J Atmos Chem 22:285–302. https://doi.org/10.1007/BF00696639

Article   CAS   Google Scholar  

Harvey A, Smith F (2007) Avoid Common Pitfalls when using Henry’s Law. Chem Eng Prog 103:33–39. https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=50449

VDI 4630:2014-04 E (2014) Fermentation of organic materials - Characterization of the substrate, sampling, collection of material data, fermentation tests, Beuth Verlag

DIN 38414-8:1985-06 (1985) German standard methods for the examination of water, waste water and sludge; sludge and sediments (group S); determination of the amenability to anaerobic digestion (S 8)

Guwy AJ (2004) Equipment used for testing anaerobic biodegradability and activity. Rev Environ Sci BioTechnol 3:131–139. https://doi.org/10.1007/s11157-004-1290-0

Wedler G Good to know - Thermal Mass Flow Sensor: Bypass versus CTA. https://www.bronkhorst.com/int/blog-1/good-to-know-thermal-mass-flow-sensor-bypass-versus-cta/ . Accessed 31 May 2021

Do you know why Mass Flow reference conditions matter? https://www.bronkhorst.com/int/blog-1/do-you-know-why-mass-flow-reference-conditions-matter/ . Accessed 31 May 2021

Rodhe O (1931) Orsat—Gasanalysen. tm Tech Mess 1–12:207. https://doi.org/10.1524/teme.1931.112.jg.207

Article   Google Scholar  

Bierwerth W (2011) Tabellenbuch Chemietechnik: Daten, Formeln, Normen, vergleichende Betrachtungen [Table book chemistry technology: Data, formulars, standards], 8th edn. Haan-Gruiten Verlag

Sonntag D (1990) Important new values of the physical constants of 1986, vapour pressure formulations based on the ITS-90, and psychrometer formulae. Z Meteorol 40:340–344

Wagner W (1973) New vapour pressure measurements for argon and nitrogen and a new method for establishing rational vapour pressure equations. Cryogenics (Guildf) 13:470–482. https://doi.org/10.1016/0011-2275(73)90003-9

Goff JA (1957) Saturation pressure of water on the new Kelvin temperature scale. Trans. Am. Soc. Heat. Vent. Eng. 347–354. presented at the semi-annual meeting of the American society of heating and ventilatingengineers, Canada.

Madigan MT, Martinko JM, Stahl DA, Clark DP (2012) Brock Biology of Microorganisms, 13th ed. Pearson

Kaltschmitt M, Scholwin F, Friehe J, et al. (2012) Guide to Biogas: From production to use. Fachagentur Nachwachsende Rohstoffe e. V. (FNR).

Roizard D (2014) Antoine equation. In: Drioli E, Giorno L (eds) Encyclopedia of membranes. Springer Berlin Heidelberg, Berlin Heidelberg

Alduchov OA, Eskridge RE (1996) Improved magnus form approximation of saturation vapor pressure. J Appl Meteorol Climatol 35:601–609. https://doi.org/10.1175/1520-0450(1996)035%3c0601:IMFAOS%3e2.0.CO;2

Elliott RJ, Lira CT (1999) Introductory chemical engineering thermodynamics. Prentice Hall PTR, Upper Saddle River, NJ

Liebetrau J, Pfeiffer D (2020) Collection of Methods for Biogas. Methods to determine parameters for analysis purposes and parameters that describe processes in the biogas sector, 2nd ed DBFZ

Stang C, Harnisch F (2016) The dilemma of supporting electrolytes for electroorganic synthesis: a case study on Kolbe electrolysis. Chemsuschem 9:50–60. https://doi.org/10.1002/cssc.201501407

Schäfer HJ (1990) Recent contributions of kolbe electrolysis to organic synthesis. In: Steckhan E (ed) Topics in current Chemistry, vol 152. Electrochemistry IV. Springer, Berlin, Heidelberg, pp 91–151

Urban C, Xu J, Sträuber H et al (2017) Production of drop-in fuels from biomass at high selectivity by combined microbial and electrochemical conversion. Energy Environ Sci 10:2231–2244. https://doi.org/10.1039/C7EE01303E

Download references

Acknowledgements

We acknowledge the numerous colleagues in our research groups in the last years who contributed to the setup and on-going optimization of gas measurements and data evaluation, especially Richard Hegner, Carolin Urban (neé Stang), Richard Hönig and Félix Delory.

Open Access funding enabled and organized by Projekt DEAL. This work was supported by the Helmholtz Association in the frame of the Integration Platform “Tapping nature’s potential for sustainable production and a healthy environment” at the UFZ.

Author information

Authors and affiliations.

Department of Environmental Microbiology, Helmholtz Center for Environmental Research GmbH—UFZ, Permoserstraße 15, 04318, Leipzig, Germany

Katharina Neubert, Claus Härtig & Falk Harnisch

Biochemical Conversion Department, DBFZ Deutsches Biomasseforschungszentrum gemeinnützige GmbH , Torgauer Straße 116, 04347, Leipzig, Germany

Jörg Kretzschmar

Faculdade de Engenharia Química, Universidade Estadual de Campinas—UNICAMP, Av. Albert Einstein, 500, 13083-852, Campinas, SP, Brasil

Tatiane Regina dos Santos

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Falk Harnisch .

Ethics declarations

Conflict of interest.

The authors have no conflicts of interest to declare that are relevant to the content of this article.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Neubert, K., Kretzschmar, J., dos Santos, T.R. et al. Making sense of gas measurements: quantification of multicomponent gas mixtures in biological and chemical laboratory experiments. ChemTexts 7 , 27 (2021). https://doi.org/10.1007/s40828-021-00151-0

Download citation

Received : 01 June 2021

Accepted : 19 August 2021

Published : 28 September 2021

DOI : https://doi.org/10.1007/s40828-021-00151-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Analytical chemistry
• Electrochemistry
• Quantitative analysis
• Mass balances
• Gas analysis
• Find a journal
• Publish with us
• Track your research

We've updated our Privacy Policy to make it clearer how we use your personal data. We use cookies to provide you with a better experience. You can read our Cookie Policy here.

Analysis & Separations

Stay up to date on the topics that matter to you

Gas Chromatography – How a Gas Chromatography Machine Works, How To Read a Chromatograph and GCxGC

Complete the form below to unlock access to ALL audio articles.

What is gas chromatography?

How does gas chromatography work, adding mass spectrometry to gas chromatography (gc-ms), how do you read a chromatogram and what does it tell you, taking gas chromatography into multiple dimensions.

• Quality control in the manufacture of many products from cars, 1 to chemicals and petrochemicals , to pharmaceuticals 2
• Research purposes from the analysis of meteorites 3 to natural products 4
• Safety and monitoring from environmental  samples, microplastics  and food 5 - 8 and wine , to forensics. 9

Gas chromatographs are frequently hyphenated to mass spectrometers (GC-MS) to enable the identification of the chemical components.

As the name implies, GC uses a carrier gas in the separation, this plays the part of the mobile phase (Figure 1 (1)). The carrier gas transports the sample molecules through the GC system, ideally without reacting with the sample or damaging the instrument components.

• The sample is first introduced into the gas chromatograph (GC), either with a syringe or transferred from an autosampler (Figure 1 (2)) that may also extract the chemical components from solid or liquid sample matrices. The sample is injected into the GC inlet (Figure 1 (3)) through a septum which enables the injection of the sample mixture without losing the mobile phase.
• Connected to the inlet is the analytical column (Figure 1 (4)), a long (10 – 150 m), narrow (0.1 – 0.53 mm internal diameter) fused silica or metal tube which contains the stationary phase coated on the inside walls.
• The analytical column is held in the column oven which is heated during the analysis to elute the less volatile components.
• The outlet of the column is inserted into the detector (Figure 1 (5)) which responds to the chemical components eluting from the column to produce a signal.
• The signal is recorded by the acquisition software on a computer to produce a chromatogram (Figure 1 (6)).

Once in the analytical column, the sample components are separated by their different interactions with the stationary phase. Therefore, when selecting the type of column to use, the volatility and functional groups of the analytes should be considered to match them to the stationary phase. Liquid stationary phases mainly fall into two types: polyethylene glycol (PEG) or polydimethylsiloxane (PDMS) based, the latter with varying percentages of dimethyl, diphenyl or mid-polar functional groups, for example cyanopropylphenyl. Like separates like, therefore non-polar columns with dimethyl or a low percentage of diphenyl are good for separating non-polar analytes. Those molecules capable of π-π interactions can be separated on stationary phases containing phenyl groups. Those capable of hydrogen bonding, for example acids and alcohols, are best separated with PEG columns, unless they have undergone derivatization to make them less polar.

Detectors for Gas Chromatography

The final step is the detection of the analyte molecules when they elute from the column. There are many types of GC detectors, for example: those that respond to C-H bonds like the flame ionization detector (FID); those that respond to specific elements for example sulfur, nitrogen or phosphorus; and those that respond to specific properties of the molecule, like the ability to capture an electron, as is used with the electron capture detector (ECD).

Mass spectrometry (MS) is an analytical technique that can be hyphenated to a GC and used instead of the GC detector. The neutral molecules elute from the analytical column and are ionized in the ion source to produce molecular ions which can degrade into fragment ions. The fragment and molecular ions are then separated in the mass analyzer by their mass:charge (m/z) ratio and are detected. Data from a GC-MS is three dimensional, providing mass spectra that can be used for identity confirmation, to identify unknown analytes and to determine structural and chemical properties of molecules, as well as the chromatogram that can be used for qualitative and quantitative analysis.

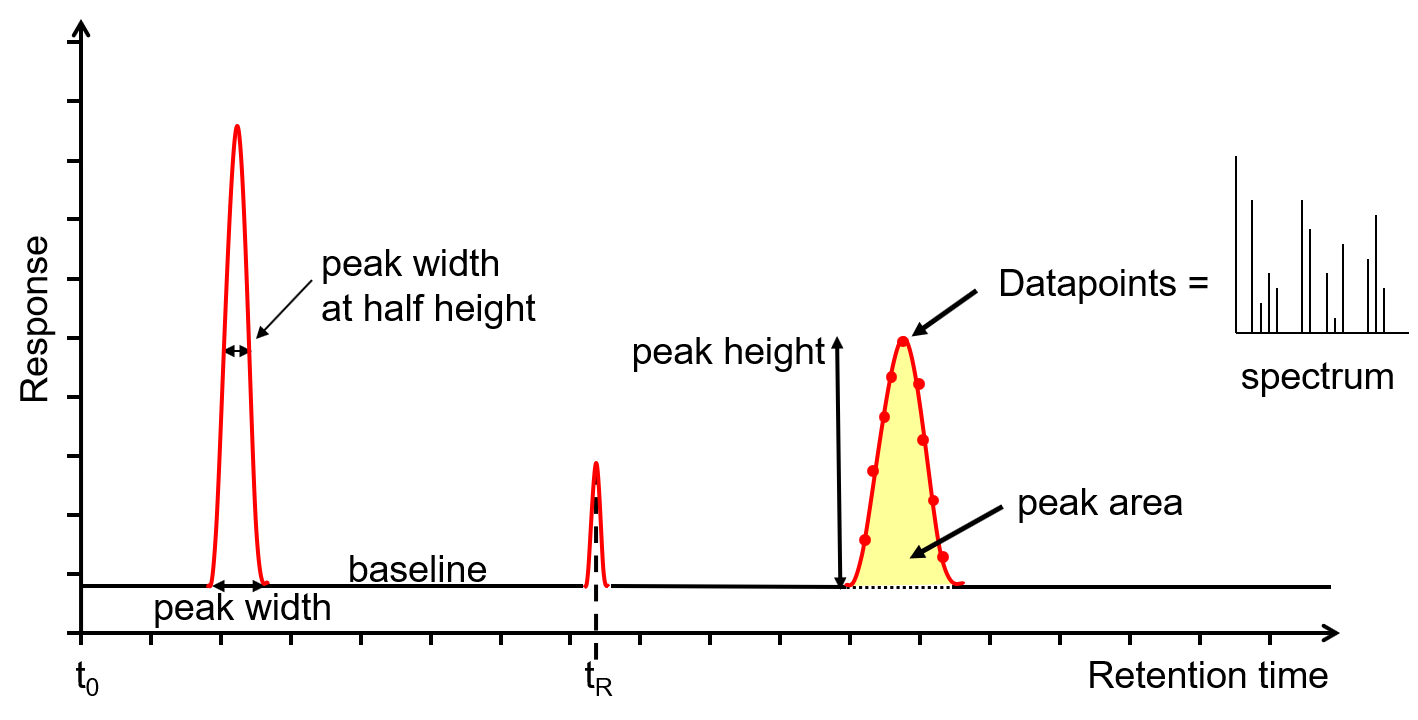
Much information can be gained from the chromatogram (Figure 2) on the health of the GC or GC-MS system as well as the data required to perform qualitative or quantitative analysis.

The x-axis is the retention time, taken from the time the sample was injected into the GC (t 0 ) to the end of the GC run. Each analyte peak has a retention time measured from the apex of the peak, for example t R . The y-axis is the measured response of the analyte peak in the detector. The baseline shows the signal from the detector when no analyte is eluting from the column, or it is below the detection limit. The baseline response is a mix of electrical noise (usually low) and chemical noise, such as impurities in the carrier gas, column stationary phase bleed and system contamination. Hence, if the baseline is higher than it should be, it is an indication of a problem or that maintenance is required. Various measurements can be taken from the peak, such as width at the baseline, width at half height, total height and area. The latter two are proportional to the concentration, however it is the area that is used for quantitation as it is less affected by band broadening. The measurements can be used to calculate the extent of band broadening, the spread of the analyte molecules on the column. Narrower, sharper peaks give better sensitivity (signal to noise ratio) and better resolution (peak separation). The peaks shown are Gaussian, however peak tailing (the right side of the peak is wider) indicates activity or a dead volume in the system, whereas a peak fronting (the left side of the peak is wider) indicates the column is overloaded. Accurate measurements are affected by the number of data points across a peak, with an ideal number being 15-25. Too few, makes the peak look like a child’s join-the-dots drawing, affecting peak area, resolution and, with GC-MS, deconvolution. Too many reduces the signal to noise, reducing sensitivity. For GC-MS data, each data point is a mass spectrum, the third dimension of data.

Compared to some other separation techniques, GC has a high peak capacity with the ability to separate hundreds of compounds. However, for some applications where thousands of peaks need to be separated, there aren’t enough theoretical plates to chromatographically separate them all. Examples may include the analysis of diesel, 10 or where trace analytes need to be detected in complex matrices like environmental, biological or food 11 samples. Spectral resolution, where an MS is hyphenated to a GC, enables analysis to be performed without full chromatographic resolution, however the coeluting peaks must have different spectra for this to be fully successful.

Figure 3:  Simplified diagram of GC x GC analysis.  Credit: Anthias Consulting.

Heart-cutting is useful where a column is selected to separate the majority of the peaks, then a few groups of coeluting peaks are “cut” and transferred onto a second column containing a different stationary phase and selectivity (Figure 3). Only a few cuts can be transferred through the run, therefore it can only be used where there are a few problem separations.

For complex samples where there are frequent coelutions, comprehensive two-dimensional chromatography (GC x GC) is used. Two columns, containing different stationary phases and therefore different separation mechanisms, are set-up in series. The “normal” set-up is a 1 st dimension non-polar column followed by a 2 nd dimension more polar column, as shown in Figure 4, for the analysis of diesel. A modulator is used between the two columns to take a cut from the first column and reinject in a narrow sample band onto the second column. Thermal modulators achieve this using temperature to trap and then release the molecules, flow modulators collect the effluent, compress and flush the molecules onto the second column. Cuts are taken throughout the run, usually every 1 to 10 seconds. Separation on the second column should be achieved before the next cut is introduced. This fast separation is achieved by using a short, narrow second column, usually 1-2 m of 0.1 mm internal diameter used with thermal modulators; or a short, wider second column, usually 5 m of 0.25 mm internal diameter used with flow modulators. GC x GC peaks are very narrow, down to 35 ms, therefore fast GC detectors or high acquisition rate mass spectrometers >100 Hz must be used to acquire enough data points.

Strengths and limitations of gas chromatography

GC is a widely used technique across most industries. It is used for routine analysis through to research, analysing a few to many hundreds (or thousands with GC x GC) of compounds in many different matrices, from solids to gases. It is a robust technique and is easily hyphenated to other techniques including mass spectrometry.

GC is limited to analysing volatile compounds from helium/hydrogen up to molecular weights of around 1250 u. Thermally labile compounds can degrade in a hot GC, therefore cold injection techniques and low temperatures should be used to minimize this. More polar analytes can become stuck or lost in the GC, therefore the system should be deactivated and well-maintained or these analytes derivatized.

Common problems with gas chromatography

The most common problem in GC is leaks. The mobile phase is a gas and flows throughout the system, therefore the correct installation of parts and consumables is important along with regular leak checking.

Perfecting Gas Chromatography Sample Preparation

Activity is another issue for more polar analytes, especially those at trace levels. Silanol groups on the glass liners and column, and also a build-up of dirt in the system can cause tailing peaks, irreversible adsorption or catalytic breakdown. The inlet is the area that causes most problems as it is here the sample is injected, vaporized and transferred into the GC column. Therefore, regular inlet maintenance along with using the correct consumables, for example a deactivated inlet liner, is important to keep the instrument trouble-free.

1. Kusch P. Application of gas chromatography/mass spectrometry (GC/MS) and pyrolysis-gas chromatography/mass spectrometry (Py-GC/MS) in failure analysis in the automotive industry.  Eng. Fail. Anal.  2017;82:726-732. doi: 10.1016/j.engfailanal.2017.06.033

2. Jwaili M. Pharmaceutical applications of gas chromatography.  Open J. Appl. Sci . 2019;9(9):683-690. doi: 10.4236/ojapps.2019.99055

3. Sephton MA, Gilmour I. Pyrolysis–gas chromatography–isotope ratio mass spectrometry of macromolecular material in meteorites.  Planet. Space Sci . 2001;49(5):465-471. doi: 10.1016/S0032-0633(00)00163-X

4. Ozek T, Demirci F. Isolation of natural products by preparative gas chromatography.  Methods Mol Biol . 2012;864:275-300. doi: 10.1007/978-1-61779-624-1_11 5. Lorenzo M, Pico Y. Chapter 2 - Gas chromatography and mass spectroscopy techniques for the detection of chemical contaminants and residues in foods. In: Schrenk D, Cartus A, eds.  Chemical Contaminants and Residues in Food (Second Edition) . Woodhead Publishing Series in Food Science, Technology and Nutrition. Woodhead Publishing; 2017:15-50. doi: 10.1016/B978-0-08-100674-0.00002-3 6. Ötleş S. 3 - Analysing the composition of fortified foods and supplements: the case of vitamins. In: Berginc K, Kreft S, eds.  Dietary Supplements . Woodhead Publishing Series in Food Science, Technology and Nutrition. Woodhead Publishing; 2015:37-44. doi: 10.1533/9781782420811.1.37

7. Hajšlová J, Čajka T. Chapter 12 - Gas chromatography–mass spectrometry (GC–MS). In: Picó Y, ed.  Food Toxicants Analysis . Elsevier; 2007:419-473. doi: 10.1016/B978-044452843-8/50013-4

8. Hopfer H. Gas chromatography. In: McSweeney PLH, McNamara JP, eds.  Encyclopedia of Dairy Sciences (Third Edition) . Academic Press; 2022:382-390. doi: 10.1016/B978-0-12-818766-1.00024-6 9. Shellie RA. Gas chromatography. In: Siegel JA, Saukko PJ, Houck MM, eds.  Encyclopedia of Forensic Sciences (Second Edition) . Academic Press; 2013:579-585. doi: 10.1016/B978-0-12-382165-2.00245-2

10. Wang FCY. Comprehensive three-dimensional gas chromatography mass spectrometry separation of diesel.  J Chromatogr. A . 2017;1489:126-133. doi: 10.1016/j.chroma.2017.01.091

11. Biedermann M, Grob K. Advantages of comprehensive two-dimensional gas chromatography for comprehensive analysis of potential migrants from food contact materials.  Anal. Chim. Acta . 2019;1057:11-17. doi: 10.1016/j.aca.2018.10.046

What is gas chromatography? Gas chromatography (GC) is an analytical technique used to separate the chemical components of a sample mixture and then detect them to determine their presence or absence and/or how much is present. These chemical components are usually organic molecules or gases.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List

Automatic real-time analysis and interpretation of arterial blood gas sample for Point-of-care testing: Clinical validation

Sancho rodríguez-villar.

1 Critical Care Department, King´s College Hospital, London, United Kingdom

Paloma Poza-Hernández

2 Hospital Virgen de la Salud, Servicio de Anestesia y Reanimación, Surgical Intensive Care Unit, Complejo Hospitalario de Toledo, Toledo, Spain

Sascha Freigang

3 Department of Neurosurgery, Neurosurgical Intensive Care Unit, Medical University of Graz, Graz, Austria

Idoia Zubizarreta-Ormazabal

4 Marqués de Valdecilla University Hospital (HUMV), Servicio de Anestesia y Reanimación, Santander, Cantabria, Spain

Daniel Paz-Martín

Etienne holl, osvaldo ceferino pérez-pardo, maría sherezade tovar-doncel, sonja maria wissa, bonifacio cimadevilla-calvo, guillermo tejón-pérez, ismael moreno-fernández.

5 Medical Software Specialist at Madrija Company, Toledo, Spain

Alejandro Escario-Méndez

Juan arévalo-serrano.

6 Internal Medicine Department, Príncipe de Asturias Hospital, Alcalá de Henares, Madrid, Spain

Antonio Valentín

7 Department of Basic and Clinical Neuroscience, Institute of Psychiatry, Psychology & Neuroscience (IoPPN) Academic Neuroscience Centre, London, United Kingdom

Bruno Manuel Do-Vale

8 Critical Care Department, Centro Hospitalar Universitário do Porto (CHUP), Porto, Portugal

Helen Marie Fletcher

9 Executive Nursing Department, King´s College Hospital, London, United Kingdom

Jesús Medardo Lorenzo- Fernández

10 External Consultant, Ingeniero de Caminos, Canales y Puertos e Ingeniero Técnico de Obras Públicas

Associated Data

In accordance with the Declaration of Helsinki regarding the confidentiality of the patient’s information, The General Data Protection Regulation (25 May 2018), local applicable regulatory requirements and the ethical approvals for the study, the deidentified study data can be made available to researchers upon request and after approval by the local Ethics Committee (Comité de Ética de la Investigación con Medicamentos (CEIm) de Toledo, Spain; Comité de Ética de la Investigación con Medicamentos (CEIm) de Cantabria, Spain and Vice-Rector for Research and International Affairs, Mag. a Caroline Schober-Trummler on behalf of the Med Uni Graz.) for researchers who meet the criteria for access to confidential data by contacting Comité de Ética de la Investigación con Medicamentos (CEIm) de Toledo, Spain (ref: 05/12/19. Number 461): se.mccj.macses@rimaicnecod .

Point-of-care arterial blood gas (ABG) is a blood measurement test and a useful diagnostic tool that assists with treatment and therefore improves clinical outcomes. However, numerically reported test results make rapid interpretation difficult or open to interpretation. The arterial blood gas algorithm (ABG-a) is a new digital diagnostics solution that can provide clinicians with real-time interpretation of preliminary data on safety features, oxygenation, acid-base disturbances and renal profile. The main aim of this study was to clinically validate the algorithm against senior experienced clinicians, for acid-base interpretation, in a clinical context.

We conducted a prospective international multicentre observational cross-sectional study. 346 sample sets and 64 inpatients eligible for ABG met strict sampling criteria. Agreement was evaluated using Cohen’s kappa index, diagnostic accuracy was evaluated with sensitivity, specificity, efficiency or global accuracy and positive predictive values (PPV) and negative predictive values (NPV) for the prevalence in the study population.

The concordance rates between the interpretations of the clinicians and the ABG-a for acid-base disorders were an observed global agreement of 84,3% with a Cohen’s kappa coefficient 0.81; 95% CI 0.77 to 0.86; p < 0.001. For detecting accuracy normal acid-base status the algorithm has a sensitivity of 90.0% (95% CI 79.9 to 95.3), a specificity 97.2% (95% CI 94.5 to 98.6) and a global accuracy of 95.9% (95% CI 93.3 to 97.6). For the four simple acid-base disorders, respiratory alkalosis: sensitivity of 91.2 (77.0 to 97.0), a specificity 100.0 (98.8 to 100.0) and global accuracy of 99.1 (97.5 to 99.7); respiratory acidosis: sensitivity of 61.1 (38.6 to 79.7), a specificity of 100.0 (98.8 to 100.0) and global accuracy of 98.0 (95.9 to 99.0); metabolic acidosis: sensitivity of 75.8 (59.0 to 87.2), a specificity of 99.7 (98.2 to 99.9) and a global accuracy of 97.4 (95.1 to 98.6); metabolic alkalosis sensitivity of 72.2 (56.0 to 84.2), a specificity of 95.5 (92.5 to 97.3) and a global accuracy of 93.0 (88.8 to 95.3); the four complex acid-base disorders, respiratory and metabolic alkalosis, respiratory and metabolic acidosis, respiratory alkalosis and metabolic acidosis, respiratory acidosis and metabolic alkalosis, the sensitivity, specificity and global accuracy was also high. For normal acid-base status the algorithm has PPV 87.1 (95% CI 76.6 to 93.3) %, and NPV 97.9 (95% CI 95.4 to 99.0) for a prevalence of 17.4 (95% CI 13.8 to 21.8). For the four-simple acid-base disorders and the four complex acid-base disorders the PPV and NPV were also statistically significant.

Conclusions

The ABG-a showed very high agreement and diagnostic accuracy with experienced senior clinicians in the acid-base disorders in a clinical context. The method also provides refinement and deep complex analysis at the point-of-care that a clinician could have at the bedside on a day-to-day basis. The ABG-a method could also have the potential to reduce human errors by checking for imminent life-threatening situations, analysing the internal consistency of the results, the oxygenation and renal status of the patient.

Introduction

The most imperative aspect of patients in emergency and critical care settings is their dynamic physiological status and potential for rapid deterioration that may require early diagnosis and clinical decisions for better patient outcome including pre-hospital medicine, using portable systems for the correct diagnosis of the patient’s condition. Along with various “vital signs” such as, blood pressure, heart rate and rhythm, temperature, and respiratory rate, some biochemical markers reflect these rapid changes resulting in patient’s unstable physiology [ 1 ]. Rapid provision of blood measurements, particularly blood gases and electrolytes, may translate into improved clinical outcomes. These situations require prompt lab results, most of which are done serially, ideally a point-of-care test (POCT), to meet the urgency of clinical decision and avoid subsequent damage to vital organs and systems [ 2 ]. Studies show that POCT carries advantages of providing reduced therapeutic turnaround time (TTAT), shorter door-to-clinical-decision time, rapid data availability, reduced pre-analytic and post-analytic testing errors, self-contained user-friendly instruments, small sample volume requirements, and frequent serial whole-blood testing [ 3 , 4 ]. This information provides vital in acute settings and patients on any type of extracorporeal support including extracorporeal membrane oxygenation (ECMO) especially on the initial set up until the patient is physiologically stable. This POCT is relevant also in chronic patients who attend on a regular basis to dialysis units or to respiratory outpatient clinics. In addition, the implementation and increased use of telemedicine in most countries is significant and thus the need for strong reliable software to support this new technology (e.g. supporting patients on home dialysis, clinics, small district/satellite hospitals, out-of-hours consultations, remote medicine, and district nurses) is essential.

A number of arterial blood gas (ABG) analysers from different manufactures exist which are commercially available. All such analysers, with more or less the same parameters, provide an output in the form of an on-screen or printed analysis which contains raw data, possibly with some standard reference values and indications as to whether the measured values fall inside or outside those reference values ( Fig 1 ).

All current analysers, with more or less the same parameters, provide an output in the form of an on-screen or printed analysis which contains raw data, possibly with some standard reference values and indications as to whether the measured values fall inside or outside those reference values.

However, there is significant potential for human error when interpreting the blood measurements, which can be very complex on occasions. This, together with other stressors facing healthcare professionals today may affect the best possible clinical treatment of patients in a critical condition. Such stressors include: inexperienced non-laboratorians, reduced in hospital presence particularly out of hours of senior clinicians, ever increasing workloads of clinical staff, extreme working conditions as a result of the Covid-19 pandemic, financial burdens of tests, operator-dependent processes, reduced medical workforce, pre-hospital medicine and difficulty in integrating test results with hospital information systems (HIS) [ 3 ].

In order to reduce the impact of these stressors and improve patient safety the ABG-a is a recent technique designed for the automatic real-time analysis and interpretation of the arterial blood gases in a form of a written report, using only data from the arterial blood gases or when available results from the laboratory biochemistry department. ABG-a can also be connected to an interface to help with the communication and integration of the results with HIS and other devices (Figs ​ (Figs2 2 and ​ and3 3 ).

Data can be fed into the ABG-a manually for example, into small devices or used in countries where the digital hospital data has not yet been fully developed. It can also be embedded directly into medical devices, such as an arterial blood gas machine (including portable blood gas analysers), extracorporeal support machines, a monitor, database or any other biochemistry/haematology programs available through an interface for the communication and integration of the results with HIS and other devices.

The communication and integration of the results with the hospital information system and other devices, can also be through the cloud and interface.

The method was evaluated initially by the developers in Emergency Departments, Theatres and Critical Care settings in different hospitals with subpopulations of patients across all ages. The main aim of the present study is to evaluate the agreement and clinical usefulness of the ABG-a comparing the final software conclusion with the independent and unbiased diagnostic decision of senior clinicians among hospitalized patients, eligible for arterial blood assessment with acid-base disturbances interpretation. The second aim is to explore if the ABG-a could be considered a safety tool integrated into regular clinical practice by providing default calculations with the results.

Materials and methods

Study design and eligibility.

This is a prospective multicentre, international, observational, cross sectional validation study: Complejo Hospitalario de Toledo (Spain), Marqués de Valdecilla University Hospital in Santander (Spain) and Medical University of Graz (Austria). The study conformed to the Declaration of Helsinki (a set of ethical principles regarding human experimentation developed for the medical community by the World Medical Association) and to local applicable regulatory requirements. The study was approved by each of the local Regional Research Ethics Committees [Comité de Ética de la Investigación con Medicamentos (CEIm) de Toledo, Spain; Comité de Ética de la Investigación con Medicamentos (CEIm) de Cantabria, Spain and Vice-Rector for Research and International Affairs, Mag. a Caroline Schober-Trummler on behalf of the Med Uni Graz. (References 461, 2020.008 and 32-104ex19/20 respectively)]. All participants (or the next of kin/legally authorized representative in minors) in accordance with applicable law.

The article is reported in accordance with recommendations for non-randomized trials [ 5 ] and comparing diagnostic tests [ 6 ].

For accuracy, reproducibility and consistency, we standardized the inclusion and exclusion criteria used for patient recruitment. Subjects aged over two days old (full-term pregnancy) that for clinical reasons required invasive arterial monitoring during their stay in the Emergency Department, Theatres, Recovery or Critical Care Units between January 2020 and September 2020 were included in the study. The exclusion criteria included patients without inserted arterial lines or lines that were not functioning properly, samples with time between taking and analysing of more than 5 minutes; and evidence of errors in sampling, processing and analysis such as visible gas bubbles and/or blood clots. All participants (or the next of kin) provided written informed consent.

Procedures and assessments

For the main study, patients admitted through the Emergency Department, Theatres, Recovery, interhospital transfers or any of the Critical Care Units were screened for eligibility by the responsible physician.

ABG samples were taken by qualified nurses directly from the arterial catheter (ensuring the monitor displayed arterial waveforms properly) according to standard criteria. They were analysed straight away using the closest certified routine diagnostic methods on the instruments ABL800 FLEX (Radiometer Medical ApS, Brønshøj, Denmark) in Marqués de Valdecilla University Hospital; ABL-90 FLEX analyzer (Radiometer Medical ApS, Brønshøj, Denmark) in Medical University of Graz, and the GEM Premier 3000 system and GEM Premier 5000 system (Instrumentation Laboratory) in Hospital Virgen de la Salud.

Data including IDs of the patient and temperature corrected arterial blood gas samples and the date and times of each sample was recorded on a standardized study sheet. Acid-base disorders have been grouped into a total of nine categories ( Table 1 ) from a total of 36 subcategories that the ABG-a can reproduce (Table in S1 Table ).

Normal arterial blood gas values: pH 7,35–7,45; pCO2 4,7–6,0 KPa or pCO2 35-45mmHg; HCO3 22–30 (mean 26) mmol/L (= 26 mEq/L); SBE-2 to +2 mmol/L (-2 to +2 mEq/L); lactate 0,5–2,0 mmol/L (0,5–2,0 mEq/L). To convert from KPa to mmHg multiply by 7,5 (mmHg = KPa x 7,5).

In order to reduce internal variability three senior Consultant level clinicians, with more than ten years of postgraduate experience, were assigned in each centre for the assessment. Initially, each ABG was individually interpreted, initially by two different senior clinicians (A and B). A research ABG-a demo was downloaded as an application on the principal investigator device from each centre, for the software to interpret the results. The clinicians in charge of the patient did not have access to the software results and they were not able to use it in their clinical practice or decisions. Concordance was reached if the interpretations by the ABG-a coincided with the two clinicians (A and B); partial concordance was reached if the interpretations by the ABG-a coincided with one of the two clinicians’ interpretations (A or B), in this case the two clinicians’ interpretations and the interpretation by the ABG-a were compared separately against a third independent as external opinion (C). Final discordance was reached if the interpretations of the ABG-a did not agree with at least two of the three clinicians (A, B, C) ( Table 2 ).

Then a third and independent clinician (C I ) answered the questionnaire. Questionnaire A R and B R = When software disagrees with any of the two clinicians or with both. The outcome of the software will not be used to suggest any treatment or any diagnosis in this study because it will not be available for the clinician. It is a blind study to the clinicians. The main objective is to compare the clinician’s interpretation with the software interpretation.

The ABG-a software by principle is an integrated mathematical algorithm, with foundations based on the current medical evidence for the analysis of oxygenation, acid-base and renal profiles. Some of the basis of this medical evidence have been previously published extensively elsewhere [ 7 – 11 ]. ABG-a has exclusive safety features such as an analysis of the internal consistency of the results with an identification of imminent life-threatening situations. Its preliminary diagnosis includes analysis of oxygenation, acid-base disturbances, blood urea nitrogen BUN (blood urea nitrogen)/creatinine ratio, and the URR (urea reduction ratio) as optional. The URR has been considered as useful in patients with presence of renal injury or renal replacement therapy [ 12 ]. Finally, ABG-a provides the clinician a differential physiological diagnosis and a potential list of causes of the identified disorder/s.

Data can be fed into the ABG-a manually for example, into small devices or used in countries where the digital hospital data has not yet been fully developed. It can also be embedded directly into medical devices, such as an arterial blood gas machine (including portable blood gas analysers), extracorporeal support machines, a monitor, database or any other biochemistry/haematology programs available through an interface for communication (Figs ​ (Figs2 2 and ​ and3). 3 ). The ABG-a software has been developed on a three-layer architecture to ensure that it can run under as many platforms as possible. The bottom layer of the software is the core algorithm, which is implemented in C++ and exchanges information in XML-format (Extensible Markup Language) with any other layer or piece of software.

The core algorithm can run on almost any device on the market, no matter whether it is Desktop, Mobile, Unix, Windows, cloud-based, on -premise or, even an embedded device. Furthermore, two different bridges, one for iOS devices to provide a software for testing, and a JNI (Java Native Interface) bridge has been developed, so it can interact with any piece of software written in Java. The described algorithm can also interact in seven different scenarios, with and without direct EHR/PDMS (Electronic Health Record)/(Patient Data Management System) integrations (Figs ​ (Figs2 2 and ​ and3 3 ).

Statistical analysis

Characteristics of patients and samples were tabulated as medians with range or interquartile range (IQR) for continuous variables. Categorical variables were expressed as frequencies and percentages.

The reliability also called agreement, reproducibility or consistency is the degree of coincidence of two or more measurements made on the same sample by one or more observers. The statistical tests used is the unweighted Cohen Kappa index with 95% asymptotic confidence interval for nominal measurements (also used was the observed agreement).

The diagnostic accuracy was evaluated with the index of sensitivity, specificity and efficiency of global accuracy. The clinical performance of the ABG-a was evaluated with the positive and negative predictive values for the prevalence of study population. The 95% confidence intervals of this diagnostic accuracy index were computed by de Wilson method. The analyses were performed using IBM SPSS Statistics 25.00 (IBM Corp., Armonk, NY, USA) and the Macro ’kappa for SPSS Statistics [ 13 ].

A preliminary version of ABG-a was tested initially with a total of 2348 calculations. A final ABG-a version of ABG-a was used for this validation study.

Between January and September 2020, 346 complete sample sets of consecutive ABG and biochemistry data (when available) was collected. The final analysis included 346 sample sets from 64 patients. Median age was 63, IQR (interquartile range) 54 to 73 years; 38 (59.4%) were men, and the primary source of admission was Theatre or Recovery by any speciality. Total number of patients with one or more organs support (intubated, dialysis, etc.) were 30 (46.9%).

Clinical characteristics were retrieved by the principal investigator in each centre and they are shown in Table 3 (source admission), Table 4 (admitting diagnosis group) and Table 5 (chronic diseases and comorbidities), organ support and circumstances at the time the arterial sample was taken on the day of each test ( Table 6 ).

& IQR (Interquartil range).

* No COPD /asthma exacerbation.

Clinical characteristics of patients

Arterial blood gas and biochemistry profile values.

The temperature corrected arterial blood gas (or staple ticket) and the most recent biochemistry values (or staple results) of the 346 samples is shown in Tables ​ Tables7 7 and ​ and8 8 respectively.

*Coversion to kPa (mmHg/7.5).

*Pre if dialysis or hemofiltration.

Reliability

The observed agreement and Cohen’s kappa index between the interpretations of the experienced clinicians A, B and clinician results (A, B and C) with the ABG-a for acid-base disorders is shown in Table 9 . For clinician results (A, B and C), observed agreement was 83.4% and Cohen’s kappa index 0.81; 95% CI (0.77 to 0.86); p < 0.001 ( Table 9 ).

Diagnostic accuracy

For detecting with accuracy normal acid-base status the ABG-a has a sensitivity of 90.0% (95% CI 79.9 to 95.3), a specificity of 97.2% (95% CI 94.5 to 98.6) and a global accuracy of 95.9% (95% CI 93.3 to 97.6). For the four simple acid-base disorders (Respiratory alkalosis, Respiratory acidosis, Metabolic acidosis and Metabolic alkalosis) and the four complex acid- base disorders (Respiratory and metabolic alkalosis, Respiratory and metabolic acidosis, Respiratory alkalosis and metabolic acidosis, Respiratory acidosis and metabolic alkalosis) the sensitivity, specificity and global accuracy were also high ( Table 10 ). The table also includes a column with the number of cases for each acid-base disorder in order to help with the interpretation. Since there are less positive cases than negative the sensitivity values are less than the specificity and the 95% CI are wider in the sensitivity and narrower in the specificity.

Likelihood ratios

Likelihood ratios of the ABG-a analysis and interpretation of the ABG was shown in Table 12 . For normal acid-base status the Positive Likelihood Ratio is 32.0, the Inverse Negative Likelihood Ratio is 9.7 (Negative Likelihood Ratio 0.1). Al the Positive and Inverse Negative Likelihood Ratios for the 4 simple and the 4 complex acid-base disorders are high and very high ( Table 11 ).

*No calculable, false positive is 0.0%.

Clinical performance

For normal acid-base status the algorithm has Positive Predictive Value 87.1 (95% CI 76.6 to 93.3) %, and Negative Predictive Value 97.9 (95% CI 95.4 to 99.0) % for a prevalence of 17.4 (95% CI 13.8 to 21.8) %. For the four simple acid-base disorders (Respiratory alkalosis, Respiratory acidosis, Metabolic acidosis and Metabolic alkalosis) and the four complex acid- base disorders (Respiratory and metabolic alkalosis, Respiratory and metabolic acidosis, respiratory alkalosis and metabolic acidosis, Respiratory acidosis and metabolic alkalosis the Positive and Negative Predictive Values were also high ( Table 12 ).

As reported by the National Committee for Clinical Laboratory Standards, ABG analysis has a prospective influence on patient care over any other laboratory determinants [ 14 ]. The sudden changes in these parameters may result in life-threatening situations hence; rapid results are frequently required for effective management. POCT is of enormous help in pre-hospital emergency settings and have been employed for many years with immense success [ 15 ]. The management strategies in these life-threatening conditions immensely rely on rapid blood gas analysis [ 16 ]. Early detection of rapid clinical deterioration and associated changes in treatment is recommended by the World Health Organisation (WHO) and Surviving Sepsis Campaign guidelines [ 17 , 18 ]. POCT devices with rapid blood gas analysis are essentially required in these situations. Accurate and timely interpretation of an ABG can be lifesaving but establishing a correct interpretation and therefore to conclude with a diagnosis may be challenging as well as time consuming, with a risk of error in the calculations without an automated process.

Currently, most clinical laboratories and ABG machine manufacturers report only numeric values for the ABG results ( Fig 1 ), and clinicians who are not specialists have difficulty interpreting the results and appropriately assessing a patient’s status for pertinent therapeutic action.

Thus, interpretation of the ABG results depends on the judgement of experienced clinicians for a precise interpretation. However, whilst clinicians who request and receive raw data from patients’ blood samples have considerable experience in this interpretation, they will not always be checking every aspect of the results and/or may overlook a particular aspect of the results if it was not part of the original reason for requesting ABG analysis. A thorough analysis can also be time consuming with a risk of error in the calculations without an automated process.

The ABG-a was designed to allow a detailed interpretation by the introduction of categories that reflect the extent of complexity for the four existing categories up to 36 categories. Given this, an algorithm for the automatic interpretation of ABG results would be useful for managing patients because it allows for the prompt and accurate interpretation of test results. We have assessed the validity of the algorithm by applying it to the interpretation of test results from clinical specimens. The main findings of our study are that ABG-a has very high agreement with the judgment of the senior clinician in all patients for the interpretation of acid-base status. This is the first published evaluation of ABG-a performed in independent centres from the developers. Strengths of the present study are that it includes a good sample size and a relevant target population on inpatients (emergency and elective) with a range of cardiopulmonary conditions and other pathologies eligible for blood gas measurement. Sampling was standardized and conducted by a dedicated specially trained nurse. The main analysis included only samples that met strict quality criteria. There were no signs of selection bias due to eligibility criteria as findings were robust when analysing all available samples. The analysis aligned to recent recommendations on the comparison of diagnostic tests [ 5 , 6 ].

At their broadest, aspects of the present method provide means of analysing an arterial blood sample, potentially at the point-of-care, which includes the following stages: safety analysis, oxygenation analysis, renal analysis and acid-base analysis. If any of the above sections are interpreted as abnormal or potential conditions identified, the software can then provide, for example, on screen or in printed form, a list of potential or likely causes and/or processes that explain the analytical findings.

As an initial step, the ABG-a carries out a number of safety checks by default to alert the clinician to potential problems with the analysis. Included within these checks is an analysis of the internal consistency of the results. Errors in the measurement of plasma pH, pCO 2 or serum (total CO 2 /HCO 3 - ) are not uncommon [ 7 ]. If the values do not fit, this could suggest an error in one or more of the parameters and the measurements should be taken with caution. The alert includes advice to check on one or more of the following (non-exhaustive) sources of inconsistency such as: machine calibration; sample taken with a tourniquet; sample taken from a patient on dialysis with an A-V fistula with a tourniquet in place. The data collected from the study also showed clinicians do not routinely complete checks on numeric results for internal consistency. The alert may advise repeating the sample as a first check. A second safety check is for imminent life-threatening situations. This may include the checking of one or more of the K + , Na + , Ca 2+ , lactate and/or glucose concentrations and/or the pH against thresholds [ 7 ].

Oxygenation

If the patient is on mechanical ventilation, the ABG-a checks for hypoxemia by calculating the PaO 2 /FiO 2 ratio on (PEEP 5cmH2O+) and if abnormal it will suggest or advise the clinician to rule out acute respiratory distress syndrome (ARDS) based on the Berlin definition [ 10 ]. If the patient is not on mechanical ventilation, the pO 2 is checked against normal values for group age and if abnormal, the A-a gradient is calculated and appropriate steps taken. From the questionnaire completed during the study, the Clinicians would welcome the routine automatic mathematical calculations of PaO 2 /FiO 2 ratio and A-a gradient.

The main limitation in order to be completely precise with the interpretation of the results from the ABG-a is the need of a clinical framework. The clinician should be aware that the assessment of an acid–base disorder is based on an accurate clinical evaluation and history. First, various signs and symptoms often provide clues regarding the underlying acid–base disorder; these include the patient’s vital signs (which may indicate shock or sepsis), neurologic state (consciousness vs. unconsciousness), signs of infection (e.g., fever), pulmonary status (respiratory rate and presence or absence of Kussmaul respiration, cyanosis, and clubbing of the fingers), and gastrointestinal symptoms (vomiting and diarrhoea). Secondly, it is the time and conditions at which the sample was taken and thus subsequent pathological processed. E.g. the result at the onset of septic shock will differ from that at the end when the patient may be hyperventilating or receiving mechanical ventilator/dialysis support respectively. Thirdly, certain underlying medical conditions such as liver, pregnancy, diabetes, and heart, lung, and kidney diseases may also affect the result. Finally, the clinician should determine whether the patient has taken any regular or new medications that affect acid–base balance (e.g. laxatives) and should consider signs of intoxication that may be associated with acid–base disturbances (e.g. acetone fetor as a sign of diabetic ketoacidosis).

In the physiological approach used by the ABG-a, a patient’s acid–base status (meaning the physiologic derangement occurring at “a point in time”) is classified according to one of the following four major acid-base disturbances defined as primary acid-base disorders: metabolic acidosis, metabolic alkalosis, respiratory acidosis and respiratory alkalosis. In many cases, however, a patient’s acid–base status cannot be precisely classified into only one of the aforementioned four categories. Instead, test results may fall into a combination of two or more types of acid–base conditions and even one acid–base disturbance can present a broad range of test results, depending on the extent of the secondary response, compensatory respiratory or metabolic [ 7 , 19 ]. In many patients, we are unable to identify the order of presentation of clinical events or physiological derangement thus making it problematic to assign a label to the primary disorder and subsequent secondary response. These explanations may partially explain the relatively low sensitivities in respiratory acidosis (61.1%), metabolic acidosis (75.8%), and metabolic alkalosis (72.2%) results in our study ( Table 10 ), all of which were identified by the clinician as a “simple” acid-base disorder. Furthermore, in our opinion, the software begins to calculate as soon as values are identified outside the normal range, and therefore, obtaining more refined conclusions than that of the clinicians. The clinicians however only considered the presence of “complex” acid-base disturbances when the results were obviously clearly deranged. This is likely due to multiple reasons including time pressures meaning not all ABG results can be rigorously examined with this approach.

Deviations from the prevailing normal value of the serum anion gap can reflect either errors in the measurements of its constituents or changes in the concentrations of unmeasured cations and/or anions. Given this wide inter-individual variability, it is important, where possible, to know the prevailing baseline value of the serum anion gap for a particular individual [ 20 ]. If the baseline serum anion gap of an individual is not known and the range of normal values of a particular laboratory is used to assess the anion gap, then it is possible that disorders that cause deviations in the serum anion gap might not be recognized since they are insufficient to shift the serum anion gap outside the normal range [ 20 ].

The advantage of the ABG-a is that it can successfully provide the identification and description of the acid-base disturbances and secondary responses associated from each sample and has the additional benefit of taking into account the basal anion gap and bicarbonate values to overcome the problems explained. Nevertheless, the clinician must review all results taking into account the clinical context of the situation they are presented with.

The concept of the automatic interpretation of acid-base using a computer program is not new. Since the first publications in the 1980’s [ 21 – 23 ], several web-based programs have been developed and are available online. However, the lack of a description of material and methods in most cases and a standard validation methodology make the comparison among studies and web-based programs impossible.

Renal analysis

The ABG-a analyses the BCR (BUN Creatinine ratio) automatically when the electrolytes, from either from ABG or/and HIS, are available. If it is not within the normal range, depending on what side of the range it lies, a selection of possible causes are identified. If the patient is on dialysis or CRRT (continuous renal replacement therapy), the algorithm can calculate the urea reduction ratio (URR) and determine if the dialysis is grossly performing adequately. The Kt/V is mathematically related to the URR (on average, a Kt/V of 1.2 is roughly equivalent to a URR of about 63 percent). The ABG-a can provide an initial estimation of the renal support treatment at POC. It was not the aim of this study to validate these features since they are mathematical calculations. The Clinicians reported via the study’s questionnaire that routine automatic calculation of BCR would be welcomed in order to obtain more initial information at Point-of-Care (POC).

The further benefit is the possibility of the ABG-a to be used outside of acute settings particularly for patients with chronic conditions such as long term respiratory pathologies e.g. chronic obstructed pulmonary disease (COPD) or renal patients on dialysis. This may provide reliable clinical interpretation with the option of taking into account known basal values of the anion gap and bicarbonate at the time of the analysis. Many of these patients are well known to the respiratory outpatients clinics or satellite dialysis units. The ABG-a could be a potential tool in the screening for an acute on chronic decompensation secondary to any other pathological process, to follow up clinical progression, monitoring during dialysis sessions or even telemedicine through application of the software to portable devices [ 21 , 24 ].

The ABG-a showed very high agreement and diagnostic accuracy with experienced senior clinicians in the acid-base disorders in a clinical context. The method also provides refinement and deep complex analysis for the point-of-care that a clinician could have at the bedside on a day-to-day basis. The ABG-a method could also have the potential to reduce human errors by checking for imminent life-threatening situations, analysing the internal consistency of the results and the oxygenation and renal statuses of the patient.

Supporting information

S1 raw data. raw blood gas data 06_02_21, acknowledgments.

The authors thank the patients and, in some cases, the next of kin who made this research possible.

Funding Statement

Financial support, including any institutional departmental funds, was not sought for the study. The authors received no specific funding for this work Medical Software Madrija Company provided financial support in the form of a salary to Moreno-Fernández I and Escario-Méndez A, but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The specific roles of these authors are articulated in the ‘author contributions’ section.

Data Availability

• PLoS One. 2021; 16(3): e0248264.

Decision Letter 0

PONE-D-20-32648

Automatic real-time analysis and interpretation of arterial blood gas for Point-of-Care testing: clinical validation

Dear Dr. Rodriguez-Villar,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Please submit your revised manuscript by Jan 18 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at gro.solp@enosolp . When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

• A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
• A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
• An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see:  http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

We look forward to receiving your revised manuscript.

Kind regards,

Tai-Heng Chen, M.D.

Academic Editor

Journal requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Thank you for including your ethics statement:  "This is a prospective multicentre, international, observational, cross sectional validation study: Complejo Hospitalario de Toledo (Spain), Marqués de Valdecilla University Hospital in Santander (Spain) and Medical University of Graz (Austria). The study conformed to the Declaration of Helsinki (a set of ethical principles regarding human experimentation developed for the medical community by the World Medical Association) and to local applicable regulatory requirements. The study was approved by each of the local Regional Research Ethics Committees (references 461, 2020.008 and 32-104ex19/20 respectively). All participants (or the next of kin/ legally authorized representative in minors) in accordance with applicable law.".   

Please amend your current ethics statement to include the full name of the ethics committee/institutional review board(s) that approved your specific study.

Once you have amended this/these statement(s) in the Methods section of the manuscript, please add the same text to the “Ethics Statement” field of the submission form (via “Edit Submission”).

For additional information about PLOS ONE ethical requirements for human subjects research, please refer to http://journals.plos.org/plosone/s/submission-guidelines#loc-human-subjects-research .

2. Please ensure you have thoroughly discussed any potential limitations of this study within the Discussion section, including the potential impact of confounding factors.

3. Thank you for stating the following in the Competing Interests section:

"All faculty and staff in a position to control or affect the content of this paper have declared that they have no competing financial interests or institutional conflicts. The authors have declared that no competing interests exist."

We note that one or more of the authors are employed by a commercial company: Madrija Company, External Consultant. Ingeniero de Caminos.

3.1. Please provide an amended Funding Statement declaring this commercial affiliation, as well as a statement regarding the Role of Funders in your study. If the funding organization did not play a role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript and only provided financial support in the form of authors' salaries and/or research materials, please review your statements relating to the author contributions, and ensure you have specifically and accurately indicated the role(s) that these authors had in your study. You can update author roles in the Author Contributions section of the online submission form.

Please also include the following statement within your amended Funding Statement.

“The funder provided support in the form of salaries for authors [insert relevant initials], but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The specific roles of these authors are articulated in the ‘author contributions’ section.”

If your commercial affiliation did play a role in your study, please state and explain this role within your updated Funding Statement.

3.2. Please also provide an updated Competing Interests Statement declaring this commercial affiliation along with any other relevant declarations relating to employment, consultancy, patents, products in development, or marketed products, etc.  

Within your Competing Interests Statement, please confirm that this commercial affiliation does not alter your adherence to all PLOS ONE policies on sharing data and materials by including the following statement: "This does not alter our adherence to  PLOS ONE policies on sharing data and materials.” (as detailed online in our guide for authors http://journals.plos.org/plosone/s/competing-interests ) . If this adherence statement is not accurate and  there are restrictions on sharing of data and/or materials, please state these. Please note that we cannot proceed with consideration of your article until this information has been declared.

Please include both an updated Funding Statement and Competing Interests Statement in your cover letter. We will change the online submission form on your behalf.

Please know it is PLOS ONE policy for corresponding authors to declare, on behalf of all authors, all potential competing interests for the purposes of transparency. PLOS defines a competing interest as anything that interferes with, or could reasonably be perceived as interfering with, the full and objective presentation, peer review, editorial decision-making, or publication of research or non-research articles submitted to one of the journals. Competing interests can be financial or non-financial, professional, or personal. Competing interests can arise in relationship to an organization or another person. Please follow this link to our website for more details on competing interests: http://journals.plos.org/plosone/s/competing-interests

4. We note that you have indicated that data from this study are available upon request. PLOS only allows data to be available upon request if there are legal or ethical restrictions on sharing data publicly. For more information on unacceptable data access restrictions, please see http://journals.plos.org/plosone/s/data-availability#loc-unacceptable-data-access-restrictions .

In your revised cover letter, please address the following prompts:

a) If there are ethical or legal restrictions on sharing a de-identified data set, please explain them in detail (e.g., data contain potentially sensitive information, data are owned by a third-party organization, etc.) and who has imposed them (e.g., an ethics committee). Please also provide contact information for a data access committee, ethics committee, or other institutional body to which data requests may be sent.

b) If there are no restrictions, please upload the minimal anonymized data set necessary to replicate your study findings as either Supporting Information files or to a stable, public repository and provide us with the relevant URLs, DOIs, or accession numbers. For a list of acceptable repositories, please see http://journals.plos.org/plosone/s/data-availability#loc-recommended-repositories .

We will update your Data Availability statement on your behalf to reflect the information you provide.

5. Your ethics statement should only appear in the Methods section of your manuscript. If your ethics statement is written in any section besides the Methods, please delete it from any other section.

6. Please include a separate caption for each figure in your manuscript.

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Partly

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #2: Yes

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #2: No

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: Based on the results, the arterial blood gas algorithm (ABG-a) is practical for acute and critical care. Only one questions are needed for explanation and one suggestion are recommended.

Question: Please explain the relatively low sensitivity in respiratory acidosis (61.1%), metabolic acidosis (75.8%), and metabolic alkalosis (72.2%).

Suggestion: The data (median & IQR) from enrolled samples in Table 7 & 8 seem so normal. The reports of minimum and maximum levels of tests may be demonstrated, as a kind of description of the severity and variability of tested samples.

Some errors need to correct.

Table 4: Acute renal failure or acute on chronic renal failure � acute kidney injury or acute on chronic kidney disease

Table 8: 4,1 --> 4.1

Line 352: 83,4%--> 83.4%

Reviewer #2: In this manuscript, authors compare the results of an automated acid-base disturbance algorithm to the opinions of experienced physicians. Acid base disorders are complicated, integrating many clinical observations, diagnosis, and recent treatment history into a mechanism underlying physiological perturbations. Thus the clinical relevance of an algorithmic solution is established.

As this manuscript is not describing the algorithm, but only its agreement with clinicians, there are some points that I think would add tremendous value to the work. Chief among them is a calculation of the interpretability of the algorithm. In machine learning, there are several tools that allow a user to test how a classification changes, among them ICE (individual continuous expectation) and partial dependence plots. These tools let you assess how a small change in one measurement would affect the algorithmic diagnosis. Other uncertainty quantification methods may be used instead, but some measure of interpretability may be useful.

Additionally, reporting the global accuracy in this type of work is misleading. The dataset is unbalanced (many more negative cases that positive cases, for at least some of the choices of acid base disorder. Without knowledge of the actual numbers of diagnoses (how many negative, how many metabolic acidosis, etc) it is impossible to interpret global accuracy, and its difficult to assess the importance of poor performance on some disease states. I would request that the authors include the number of patients with each disorder; this would be part of the PLOS requirement that "all data be made available". Additionally, reporting a beta-weighted F-score may give a more interpretable level of global accuracy, with beta chosen to reflect the relative cost between a false negative and a false positive.

There are some parts of the manuscript where English usage and idiom take away from the results being presented. Manuscript would be improved with editing.

6. PLOS authors have the option to publish the peer review history of their article ( what does this mean? ). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy .

Reviewer #1: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool,  https://pacev2.apexcovantage.com/ . PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at  gro.solp@serugif . Please note that Supporting Information files do not need this step.

Author response to Decision Letter 0

18 Dec 2020

REBUTTAL LETTER

Dear Academic Editor and Reviewers,

RE: PONE-D-20-32648

Thank you for reviewing and providing feedback to the paper. We will try to answer all your comments in a rigorous fashion by order.

Reviewer #1: Based on the results, the arterial blood gas algorithm (ABG-a) is practical for acute and critical care. Only one question are needed for explanation and one suggestion are recommended.

From the eight acid-base disorders, only three of them have a sensitivity of less than 80%. In the diagnosis of acid-base disorders, there is really no diagnostic test considered as reference “Gold standard” except for an expert opinion.

Firstly, it is very remarkable that only this relatively low sensitivity occurs with those acid-base disorders classified as “single” and not “complex” acid-base disorders. In our opinion based on the observations during the study, we can appreciate that the software is able to run calculations on extremely mild deranged values from the arterial blood gases, and therefore can obtain more refined conclusions than that of the clinicians. Also, the ABG-a follows the rules of certain values cutting points. The clinicians however only consider the presence of “complex” acid-base disturbances when the results are very obviously deranged. This approach from the clinicians maybe explained by many reasons, not least of all limited time for analysing every single ABG result in such a rigorous and complex manner. The diagnostic judgment of experienced clinicians has been taken as a reference test, which without denying its validity, can change from one clinician to another. Further studies in this regard would be necessary, after which it would be possible to consider our algorithm as a reference test.

Secondly, those diagnosis made by the ABG-a as “complex” still include the primary diagnosis of “respiratory acidosis”, “metabolic acidosis” and “metabolic alkalosis”. Not only keeping the safety standards but also improving the diagnosis. We know that in the human physiology, the presence of disturbances are complex and frequently not simple, making the ABG-a of great value in order to help with a more refined diagnosis.

We could understand that the suggestion relates to utilising means and standard deviations as opposed to medians and interquartile ranges because this form still present in some publications, but asking for the maximum and minimum values to describe and represent a quantitative variable is in our opinion inappropriate. The current trend is to describe quantitative values with median and interquartile range because they do not require compliance with normality; they are very robust, represent the data well and are not affected by the presence of extreme values. On the contrary, if they were described with the range and the minimum and maximum values, the representativeness of the data would be violated since those minimum and maximum values are usually atypical and remote values.

Some errors need to correct:

We agree and these errors have been corrected on the manuscript.

Reviewer #2:

Additionally, reporting the global accuracy in this type of work is misleading. The dataset is unbalanced (many more negative cases than positive cases, for at least some of the choices of acid base disorder. Without knowledge of the actual numbers of diagnoses (how many negative, how many metabolic acidosis, etc) it is impossible to interpret global accuracy, and it is difficult to assess the importance of poor performance on some disease states. I would request that the authors include the number of patients with each disorder; this would be part of the PLOS requirement that "all data be made available". Additionally, reporting a beta-weighted F-score may give a more interpretable level of global accuracy, with beta chosen to reflect the relative cost between a false negative and a false positive.

We agree that reporting global accuracy can be misleading and that reporting the frequency of each of the acid-base disorders helps with interpretation of the data. Table 10 has been modified to include a column with the number of cases of each of the acid-base disorders. It is observed that since there are fewer positive than negative cases, the sensitivity values are lower than those of specificity and the 95% CIs are wider in sensitivity and narrower in specificity. By reporting the global accuracy together with the sensitivity and specificity as well as the frequency of each disorder, as reflected in the modified table 10, there is less misunderstanding. The beta-weighted F-score could have been used as suggested, although it has the drawbacks that it ignores true negatives in its calculation and assigns equal importance to precision and recall. In our work we have chosen the analysis of reliability with the kappa index and accuracy with sensitivity, specificity and, together with them, and not in isolation, the global accuracy.

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

We are agreed as authors to be published our article peer review history

Best regards

Dr Sancho Rodriguez-Villar

Submitted filename: Response to Reviewers.docx

Decision Letter 1

PONE-D-20-32648R1

Please submit your revised manuscript by Mar 22 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at gro.solp@enosolp . When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #3: All comments have been addressed

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Partly

Reviewer #3: Yes

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #3: I Don't Know

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #3: No

5. Is the manuscript presented in an intelligible fashion and written in standard English?

6. Review Comments to the Author

Reviewer #1: (No Response)

Reviewer #3: I think this paper is very interesting and well written. But, I have only one serious concern.

According to Tables 7 and 8, both median and IQR are in the normal range. What are the values of the raw data that is the basis of this analysis? The author should show raw blood gas data as shown in PLOS Data policy.

7. PLOS authors have the option to publish the peer review history of their article ( what does this mean? ). If published, this will include your full peer review and any attached files.

Author response to Decision Letter 1

Reviewer #1: (No Response)

Reviewer #3: I think this paper is very interesting and well written. But, I have only one serious concern.

Anonymous raw blood gas data showed as per PLOS Data policy. Please, see attached .

Submitted filename: Response to Reviewers 09_02_21.docx

Decision Letter 2

17 Feb 2021

PONE-D-20-32648R2

Please submit your revised manuscript by Apr 03 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at gro.solp@enosolp . When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Reviewer #3: My concerns have been resolved. But, I don't know if the raw blood gas data does not have to be attached to the Manuscript. Leave it to the editor's judgment.

Author response to Decision Letter 2

21 Feb 2021

Dear Editor,

We are delighted that the Reviewer found our work to be of interest and value. We are grateful to him/her for taking time to comment on our manuscript and address each of the queries on a point-by-point basis. We think that the amended manuscript is improved and do very much hope that it is now considered acceptable for publication.

Our answers to the comment from Reviewer #3: follow below.

Reviewer #3: My concerns have been resolved. But I don't know if the raw blood gas data does not have to be attached to the Manuscript. Leave it to the editor's judgment.

Answer: From us there is no problem to add the raw arterial blood gas data. As authors we give consent and we leave that decision to the Editor-in -Chief.

Many thanks for your time.

Dr. Sancho Rodríguez-Villar

Honorary Senior Clinical Lecturer

Department of Basic and Clinical Neuroscience.

Institute of Psychiatry, Psychology & Neuroscience (IoPPN)

Academic Neuroscience Centre,

London SE5 8AF, UK

T: 0207 848 0293

Decision Letter 3

24 Feb 2021

PONE-D-20-32648R3

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/ , click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at gro.solp@gnillibrohtua .

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact gro.solp@sserpeno .

Reviewer #3: My concerns have been resolved. But I don't know if the raw blood gas data does not have to be attached to the Manuscript. Leave it to the editor's judgment.

Acceptance letter

25 Feb 2021

Automatic real-time analysis and interpretation of arterial blood gas sample for Point-of-Care testing: clinical validation

Dear Dr. Rodriguez-Villar:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact gro.solp@sserpeno .

If we can help with anything else, please email us at gro.solp@enosolp .

Thank you for submitting your work to PLOS ONE and supporting open access.

PLOS ONE Editorial Office Staff

on behalf of

Dr. Tai-Heng Chen

Research and Analysis of Insulating Gas in Unified Test Conditions

Affiliations.

• 1 School of Electrical and Automation, Wuhan University, 430072 Wuhan, China.
• 2 College of Chemistry and Molecular Sciences, Wuhan University, 430072 Wuhan, China.
• PMID: 35350321
• PMCID: PMC8945137
• DOI: 10.1021/acsomega.1c05760

In order to study the insulation mechanism of SF 6 substitute gas, it is suggested to calculate the dielectric strength of insulating gas from the molecular structure. The dielectric strength of a typical gas is modeled by a power frequency breakdown test under a uniform electric field. The molecular parameters of insulating gases are calculated by the density functional theory method, and the effect of molecular structure parameters on the breakdown voltage of power frequency is studied. Based on the molecular structure parameters, which are closely related to the breakdown voltage of power frequency, a model of pressure and distance variation of AC breakdown voltage of insulating gas is established. The breakdown voltages of insulating gases (CF 3 SO 2 F) are also derived from the proposed model. The calculated breakdown voltage of power frequency of two gases is compared with the experimental value. The average error is just 2.6%. This model provides a basis for the future search for potential alternative insulating gases.

© 2022 The Authors. Published by American Chemical Society.

Publication types

• Retracted Publication

Articles on Gas prices

Displaying 1 - 20 of 84 articles.

Why Jersey girls − and guys − still don’t pump their own gas

Robert H. Scott III , Monmouth University

5 tips for getting off gas at home – for a cleaner, cheaper, healthier all-electric  future

Trivess Moore , RMIT University ; Alan Pears , RMIT University , and Nicola Willand , RMIT University

Gas prices are falling but your energy bills still won’t be affordable any time soon

Karen Turner , University of Strathclyde

Inflation report is a mixed bag – an economist explains why some items are rising faster than others

Edouard Wemy , Clark University

Global economy 2023: how governments could make the energy crisis worse this year

Adi Imsirovic , University of Surrey

Power package: $3 billion for ‘targeted and temporary’ relief on bills

Michelle Grattan , University of Canberra

Despite soaring profits, oil companies are not paying enough for their environmental damage

Robert L. Ascah , University of Alberta

Still recovering from COVID-19 , US public transit tries to get back on track

Kari Edison Watkins , University of California, Davis

Politics with Michelle Grattan: Energy expert Bruce Mountain on what to do about the gas crisis

Why inflation will likely stay sky-high regardless of which party wins the midterms

William Chittenden , Texas State University

American voters are angry – that is a good thing for voter turnout, bad thing for democracy

Steven Webster , Indiana University

Sanctions on Russia are increasing, not decreasing, its revenue

Noha Razek , University of Regina and Brian McQuinn , University of Regina

Grattan on Friday: We must find a way to get gas prices down, but how?

Politics with Michelle Grattan: Rod Sims on the gas price crisis

Inflation: why France is holding up better than its neighbours (for now)

Mohamad Hassan Shahrour , IAE Nice - Université Côte d'Azur and Aymen Smondel , Université Côte d’Azur

Chalmers flags gas action, with escalating power prices a cost-of -living nightmare for government

How the UK energy crisis plan will affect bills and price inflation — an economist explains

Nasir Aminu , Cardiff Metropolitan University

Fed likely to stay the course on interest rate hike as inflation ticks up but gas prices ease

UK energy crisis: why rationing is likely to happen this winter, whether Liz Truss likes it or not

Renaud Foucart , Lancaster University

Energy price freezes and business support are sticking plasters – here’s how to protect UK families and companies from future crises

Phil Tomlinson , University of Bath and David Bailey , University of Birmingham

Related Topics

• Electricity
• Energy crisis
• Energy efficiency
• Energy prices
• Liquefied natural gas (LNG)
• Natural gas
• Renewable energy

Top contributors

Professorial Fellow, University of Canberra

Energy Advisor, formerly, The University of Melbourne

Senior Industry Fellow, RMIT University

Program Director, Energy, Grattan Institute

Professor, Deakin Law School, Deakin University

Professor of Global Energy, Warwick Business School, University of Warwick

Assistant Professor of Economics, Clark University

Professor and Director of the Centre for Energy Policy, University of Strathclyde

Lecturer, Jackson School of International Studies, University of Washington

Fellow, University of Surrey

Emeritus Professor of Sociology, Australian National University

Energy Fellow, Grattan Institute

Professor of Sustainable Energy Business and Policy, University of Strathclyde

Professor of Industrial Strategy, Co-Director Centre for Governance, Regulation and Industrial Strategy (CGR&IS), University of Bath

Adjunct Senior Research Fellow, Business Law and Taxation Dept, Monash Business School, Monash University

• X (Twitter)
• Unfollow topic Follow topic

New method could significantly reduce agricultural greenhouse gas emissions

N ew research by the Norwegian University of Life Sciences (NMBU) and International Institute for Applied Systems Analysis (IIASA) proposes using soil bacteria to cut greenhouse gas emissions from food production. The research is published in the journal Nature .

Nitrogen fertilization leads to emissions of the greenhouse gas nitrous oxide (N 2 O) from agricultural soils, accounting for a significant portion of total greenhouse gas emissions from agriculture. It has long been assumed that these N 2 O emissions are unavoidable.

However, an international team of researchers led by NMBU has discovered a method to reduce these emissions. They have identified bacteria that can "consume" nitrous oxide as it forms in the soil, preventing the gas from escaping into the atmosphere. The researchers believe that this method alone has the potential to reduce agricultural nitrous oxide emissions in Europe by one-third.

The N 2 O problem

Plants need a lot of nitrogen to grow. A productive agriculture, therefore, requires an abundant supply of nitrogenous fertilizer. This was a bottleneck in agriculture until Fritz Haber pioneered technology for the industrial production of nitrogen fertilizer from atmospheric nitrogen. This technology has contributed to the world's food production keeping pace with population growth for 120 years.

However, there are microorganisms in the soil that produce the greenhouse gas N 2 O, and fertilization stimulates this production.

"This greenhouse gas has an effect that is about 300 times stronger than CO 2 , and agriculture accounts for about three quarters of Europe's N 2 O emissions," explains Wilfried Winiwarter, one of the co-authors of the study and a senior researcher in the Pollution Management Research Group of the IIASA Energy, Climate, and Environment Program.

"Also, globally, agriculture is the primary source of nitrous oxide in the atmosphere. Nitrous oxide emissions are primarily regulated by soil bacteria, making reduction efforts challenging due to their elusive nature," he adds.

Bacteria can do the job

Researchers at NMBU have been conducting basic research for over 20 years on how microorganisms in the soil convert nitrogen. They have, among other things, thoroughly studied what happens when the microbes do not have access to enough oxygen, a condition called hypoxia.

When fertilization occurs (and during rainfall), some parts of the soil become hypoxic. Since the microbes then do not have access to oxygen, they are forced to find other ways to get energy. Many microbes can use nitrate instead of oxygen, and through a process called denitrification, they convert the nitrate into other gases. One of these is nitrous oxide, and in this way, the microorganisms contribute to greenhouse gas emissions.

The researchers have made significant discoveries regarding the regulation of this process, and they have developed a unique way to study denitrification. They use, among other things, robotic solutions both in the laboratory and in the field, and have developed a special robot that can make real-time measurements of nitrous oxide emissions from the soil.

The solution to reduce N 2 O emissions is to use a special type of bacteria that lacks the ability to produce nitrous oxide but can reduce nitrous oxide to harmless nitrogen gas (N 2 ).

"If we grow these microbes in organic waste used as fertilizer, we can reduce N 2 O emissions. This could mean a solution to the problem of N 2 O emissions from agriculture," says Lars Bakken, lead author of the study and a professor at NMBU.

"But it was not easy to find the right bacterium. It must be able to grow quickly in organic waste, function well in soil, and live long enough to reduce N 2 O emissions through an entire growing season. It was also a challenge to go from testing this in the laboratory to trying it out in nature, and to ensure that it actually reduced N 2 O emissions in the field," Bakken adds.

The research team is now working to find more bacteria that consume nitrous oxide and to test these in different types of organic waste used as fertilizers worldwide. The goal is to find a wide range of bacteria that can function in different types of soil and with various fertilizer mixtures.

More information: Elisabeth G. Hiis et al, Unlocking bacterial potential to reduce farmland N 2 O emissions, Nature (2024). DOI: 10.1038/s41586-024-07464-3

Provided by International Institute for Applied Systems Analysis

New research shows soil microorganisms could produce additional greenhouse gas emissions from thawing permafrost

As the planet has warmed, scientists have long been concerned about the potential for harmful greenhouse gasses to seep out of thawing Arctic permafrost. Recent estimates suggest that by 2100 the amount of carbon dioxide and methane released from these perpetually frozen lands could be on par with emissions from large industrial countries. However, new research led by a team of Colorado State University microbiome scientists suggests those estimates might be too low.

Microorganisms are responsible for the process that will generate greenhouse gasses from thawing northern peatlands, which contain about 50% of the world's soil carbon. For now, many of the microbes in this environment are frozen and inactive. But as the land thaws the microbes will "wake up" and begin to churn through carbon in the ground. This natural process, known as microbial respiration, is what produces the carbon dioxide and methane emissions forecasted by climate modelers.

Currently, these models assume that this community of microorganisms -- known as a microbiome -- will break down some types of carbon but not others. But the CSU-led work published this week in the journal Nature Microbiology provides new insight into how these microbes will behave once activated. The research demonstrates that the soil microbes embedded in the permafrost will go after a class of compounds previously thought to be untouchable under certain conditions: polyphenols.

"There were these pools of carbon -- say, donuts, pizza and chips -- and we were comfortable with the idea that microbes were going to use this stuff," said Bridget McGivern, a CSU postdoctoral researcher and the paper's first author. "But then there was this other stuff, spicy food; we didn't think the organisms liked spicy food. But what our work is showing is that actually there are organisms that are eating it, and so it's not going to just stay as carbon, it's going to be broken down."

More carbon being broken down by microbial respiration will produce additional greenhouse gas emissions. But this new finding has other implications, too. Some scientists had previously theorized that adding polyphenols to the thawing Arctic permafrost could potentially "turn off" these microorganisms altogether, effectively trapping a massive cache of potentially problematic carbon in the ground. The concept is known as the enzyme latch theory.

That no longer appears to be a viable option, said Kelly Wrighton, associate professor in the College of Agricultural Sciences' Department of Soil and Crop Sciences, whose lab led the work. "Not only did we think these microbes didn't eat polyphenols," Wrighton said, "we thought that if the polyphenols were there it was like they were toxic and would lock the microbes into inactivity."

The soil microbiome has often been considered something of a black box due of its complexity. Wrighton hopes this new information about the role of polyphenols in permafrost helps shift that perception. "I'd like to move past these black box assumptions," she said. "We can't engineer solutions if we don't understand the underlying wiring and plumbing of a system."

Probing the permafrost in Sweden

Unlocking the relationship between soil microbes and polyphenols has been years in the making for McGivern, who began examining this topic while working on her doctoral degree in Wrighton's lab in 2017.

McGivern started with a simple question. Scientists presumed that without oxygen, soil microbes could not break down polyphenols. Gut microbes, however, don't need oxygen to churn up the compound -- that's how humans extract healthy antioxidant benefits from polyphenol-rich substances such as chocolate and red wine. McGivern wondered why the process would be different in soils, a question that is particularly relevant to permafrost or waterlogged lands that contain little or no oxygen.

"The motivation for a lot of my Ph.D. was how could these two things exist?" McGivern said. "Organisms in our gut can breakdown polyphenols but organisms in the soil can't? The reality was that nobody in soils had really ever looked at it."

McGivern and Wrighton successfully tested the theory in a lab experiment and published a proof of concept study in 2021. The next step was testing it in the field. The team gained access to core samples from a research site in northern Sweden, a place that scientists have used for years to examine questions related to permafrost and the soil microbiome.

But before McGivern could look for evidence of polyphenol degradation in the core samples, she first had to create a database of gene sequences that corresponded to polyphenol metabolism. McGivern mined thousands of pages of existing scientific literature, cataloging the enzymes in cattle, the human gut, and some soils that were known to be responsible for the process. Once she built the database, McGivern compared the results to the gene sequences expressed by the microbes in the core samples. Sure enough, she said, polyphenol metabolism was happening.

"What we found was that genes across 58 different polyphenol pathways were expressed," McGivern said. "So, we're saying not only can the microorganisms potentially do it, but they actually are, in the field, expressing the genes for this metabolism."

Still, more work is needed, McGivern said. They don't know what might constrain the process or the rates at which the metabolism is happening -- both important factors for eventually quantifying the amount of additional greenhouse gas emissions that could be released from permafrost.

"The whole point of this is to build a better predictive understanding so that we have a framework we can actually manipulate," Wrighton said. "The climate crisis we're facing is so fast. But can we model it? Can we predict it? The only way we're going to get there is to actually understand how something works."

• Global Warming
• Air Quality
• Environmental Issues
• Geochemistry
• Climate change mitigation
• Greenhouse gas
• Climate engineering
• Fossil fuel
• Sulfur hexafluoride
• Carbon dioxide

Story Source:

Materials provided by Colorado State University . Original written by Christopher Outcalt. Note: Content may be edited for style and length.

Journal Reference :

• Bridget B. McGivern, Dylan R. Cronin, Jared B. Ellenbogen, Mikayla A. Borton, Eleanor L. Knutson, Viviana Freire-Zapata, John A. Bouranis, Lukas Bernhardt, Alma I. Hernandez, Rory M. Flynn, Reed Woyda, Alexandra B. Cory, Rachel M. Wilson, Jeffrey P. Chanton, Ben J. Woodcroft, Jessica G. Ernakovich, Malak M. Tfaily, Matthew B. Sullivan, Gene W. Tyson, Virginia I. Rich, Ann E. Hagerman, Kelly C. Wrighton. Microbial polyphenol metabolism is part of the thawing permafrost carbon cycle . Nature Microbiology , 2024; DOI: 10.1038/s41564-024-01691-0

Cite This Page :

Explore More

• Extinct Saber-Toothed Cat On Texas Coast
• Some Black Holes Survive in Globular Clusters
• People Altering Decomposition in Waterways
• Historic Iceberg Surges
• Food Groups Based On Level of Processing
• Computer Vision, Machine Learning Aid Driving
• Most Distant Known Galaxy
• A New Dinosaur from Zimbabwe
• The Case of the Missing Black Holes
• Menstrual Periods Arriving Earlier

Trending Topics

Strange & offbeat.

We use cookies to ensure best experience for you

We use cookies and other tracking technologies to improve your browsing experience on our site, show personalize content and targeted ads, analyze site traffic, and understand where our audience is coming from. You can also read our privacy policy , We use cookies to ensure the best experience for you on our website.

• The Middle East and Africa
• Leaders Speak
• Brand Solutions
• World's biggest companies snap up 'likely junk' carbon offsets: analysis

• Updated On May 31, 2024 at 11:59 AM IST

• Published On May 31, 2024 at 11:56 AM IST

All Comments

By commenting, you agree to the Prohibited Content Policy

Find this Comment Offensive?

• Foul Language
• Inciting hatred against a certain community
• Out of Context / Spam

Join the community of 2M+ industry professionals

Subscribe to our newsletter to get latest insights & analysis., download etenergyworld app.

• Get Realtime updates
• Save your favourite articles

• carbon offsets
• emissions reductions
• voluntary carbon markets
• greenwashing
• corporate accountability
• reduced emissions
• carbon credits
• environmentally friendly policies
• climate research
• rachel rose jackson

Today in Energy

• Recent articles
• liquid fuels
• natural gas
• electricity
• oil/petroleum
• production/supply
• consumption/demand
• exports/imports
• international
• forecasts/projections
• steo (short-term energy outlook)

Congo Brazzaville becomes a liquefied natural gas-exporting country

After years of either declining or stable domestic natural gas production, the Republic of the Congo, also known as Congo Brazzaville, began exporting liquefied natural gas (LNG) for the first time when the first phase of a two-phase floating LNG (FLNG) project began operating in February 2024. The development of LNG export capacity will allow the country to monetize natural gas production that was previously either flared or reinjected into oil wells.

Congo Brazzaville held an estimated 10 trillion cubic feet (Tcf) of proved natural gas reserves at the beginning of 2024, according to data from the Oil & Gas Journal . Before the FLNG facility began operating, any natural gas production that was not consumed domestically was either flared or reinjected into crude oil wells to enhance crude oil recovery. According to the World Bank Group , Congo Brazzaville flared about 64 billion cubic feet (Bcf) of natural gas in 2022, more than four times its domestic natural gas production in 2022.

In 2024, the Italian energy company Eni, the project operator, completed the first phase of Congo Brazzaville’s first LNG export project. The Tango FLNG facility exported its first LNG cargo at the end of February 2024, which Eni announced on February 27 . The Tango FLNG facility has a production capacity of 29 Bcf per year. The second, larger facility will have a production capacity of about 115 Bcf per year and is near the Marine XII block, the source of its natural gas supply. The second facility is under construction and is scheduled to begin operating in 2025.

More information about Congo Brazzaville’s energy sector is available in our recently updated Country Analysis Brief: Congo Brazzaville .

Principal contributors: Kimberly Peterson, Eric Han

Tags: natural gas , LNG (liquefied natural gas) , map , Africa , production/supply