problem solving skills in mathematics research

• Open supplemental data
• Reference Manager
• Simple TEXT file

People also looked at

Original research article, mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

• 1 Department of Education, Uppsala University, Uppsala, Sweden
• 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
• 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
• 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden

Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction

The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.

Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.

Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).

Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).

Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.

Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).

However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).

Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.

The Present Study

In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:

a) What is the effect of CL approach on students’ problem-solving in mathematics?

b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?

Participants

The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.

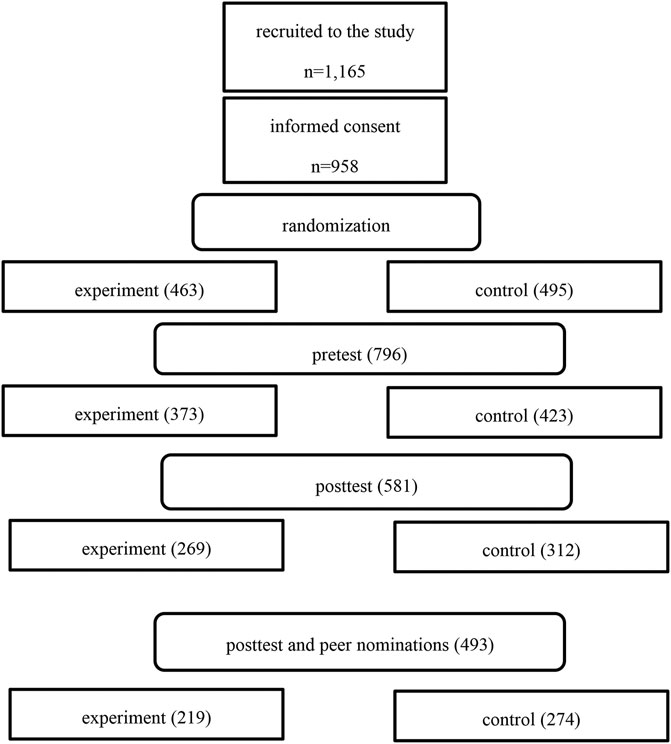
FIGURE 1 . Flow chart for participants included in data collection and data analysis.

As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.

Intervention

The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.

Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).

In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.

Implementation of the Intervention

To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.

Control Group

The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.

Tests of Mathematical Problem-Solving

Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).

The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.

Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.

The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.

The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.

Measures of Peer Acceptance and Friendships

To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).

Statistical Analyses

Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).

The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.

What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?

As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.

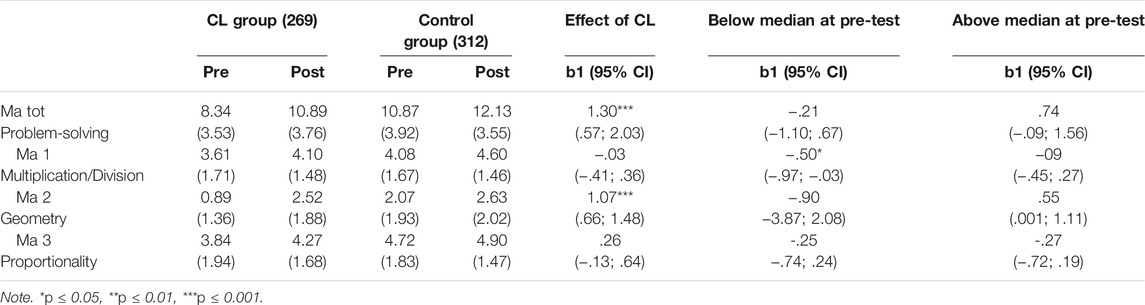
TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.

The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.

Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?

As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.

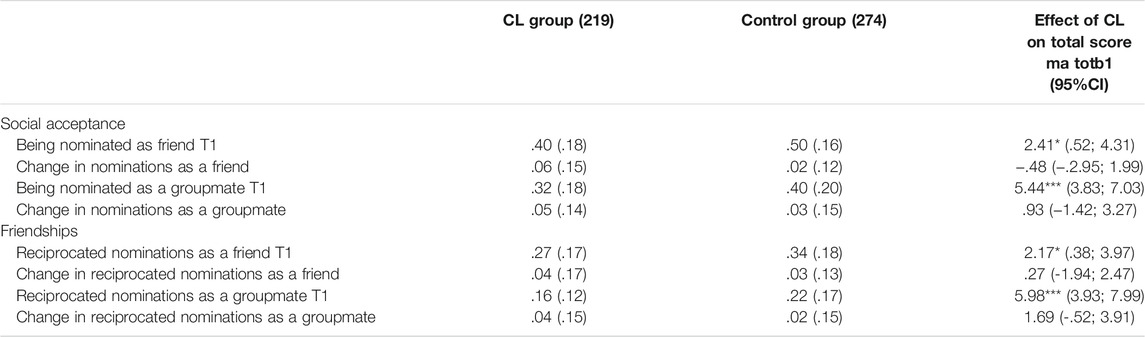
TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.

In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.

The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).

In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).

Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.

Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.

The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.

Limitations

The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.

Implications

The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.

The project was funded by the Swedish Research Council under Grant 2016-04,679.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to teachers who participated in the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material

Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430

Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001

Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.

Google Scholar

Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .

Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.

Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.

Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6

Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.

Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16

Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.

Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.

Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489

Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .

Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529

Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453

Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .

Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.

Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .

Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.

McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0

Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176

Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10

Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en

CrossRef Full Text

Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .

Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.

Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202

SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .

Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .

Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009

Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683

Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .

Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).

van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .

Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029

Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.

Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9

Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187

Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20

Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis

Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296

Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.

Reviewed by:

Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Nina Klang, [email protected]

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• v.9(5); 2023 May
• PMC10208825

Development and differences in mathematical problem-solving skills: A cross-sectional study of differences in demographic backgrounds

Ijtihadi kamilia amalina.

a Doctoral School of Education, University of Szeged, Hungary

Tibor Vidákovich

b Institute of Education, University of Szeged, Hungary

Associated Data

Data will be made available on request.

Problem-solving skills are the most applicable cognitive tool in mathematics, and improving the problem-solving skills of students is a primary aim of education. However, teachers need to know the best period of development and the differences among students to determine the best teaching and learning methods. This study aims to investigate the development and differences in mathematical problem-solving skills of students based on their grades, gender, and school locations. A scenario-based mathematical essay test was administered to 1067 students in grades 7–9 from schools in east Java, Indonesia, and their scores were converted into a logit scale for statistical analysis. The results of a one-way analysis of variance and an independent sample t -test showed that the students had an average level of mathematical problem-solving skills. The number of students who failed increased with the problem-solving phase. The students showed development of problem-solving skills from grade 7 to grade 8 but not in grade 9. A similar pattern of development was observed in the subsample of urban students, both male and female. The demographic background had a significant effect, as students from urban schools outperformed students from rural schools, and female students outperformed male students. The development of problem-solving skills in each phase as well as the effects of the demographic background of the participants were thoroughly examined. Further studies are needed with participants of more varied backgrounds.

1. Introduction

Problem-solving skills are a complex set of cognitive, behavioral, and attitudinal components that are situational and dependent on thorough knowledge and experience [ 1 , 2 ]. Problem-solving skills are acquired over time and are the most widely applicable cognitive tool [ 3 ]. Problem-solving skills are particularly important in mathematics education [ 3 , 4 ]. The development of mathematical problem-solving skills can differ based on age, gender stereotypes, and school locations [ [5] , [6] , [7] , [8] , [9] , [10] ]. Fostering the development of mathematical problem-solving skills is a major goal of educational systems because they provide a tool for success [ 3 , 11 ]. Mathematical problem-solving skills are developed through explicit training and enriching materials [ 12 ]. Teachers must understand how student profiles influence the development of mathematical problem-solving skills to optimize their teaching methods.

Various studies on the development of mathematical problem-solving skills have yielded mixed results. Grissom [ 13 ] concluded that problem-solving skills were fixed and immutable. Meanwhile, other researchers argued that problem-solving skills developed over time and were modifiable, providing an opportunity for their enhancement through targeted educational intervention when problem-solving skills developed quickly [ 3 , 4 , 12 ]. Tracing the development of mathematical problem-solving skills is crucial. Further, the results of previous studies are debatable, necessitating a comprehensive study in the development of students’ mathematical problem-solving skills.

Differences in mathematical problem-solving skills have been identified based on gender and school location [ [6] , [7] , [8] , [9] , [10] ]. School location affects school segregation and school quality [ 9 , 14 ]. The socioeconomic and sociocultural characteristics of a residential area where a school is located are the factors affecting academic achievement [ 14 ]. Studies in several countries have shown that students in urban schools demonstrated better performance and problem-solving skills in mathematics [ 9 , 10 , 15 ]. However, contradictory results have been obtained for other countries [ 6 , 10 ].

Studies on gender differences have shown that male students outperform female students in mathematics, which has piqued the interest of psychologists, sociologists, and educators [ 7 , 16 , 17 ]. The differences appear to be because of brain structure; however, sociologists argue that gender equality can be achieved by providing equal educational opportunities [ 8 , 16 , 18 , 19 ]. Because the results are debatable and no studies on gender differences across grades in schools have been conducted, it would be interesting to investigate gender differences in mathematical problem-solving skills.

Based on the previous explanations, teachers need to understand the best time for students to develop mathematical problem-solving skills because problem-solving is an obligatory mathematics skill to be mastered. However, no relevant studies focused on Indonesia have been conducted regarding the mathematical problem-solving skill development of students in middle school that can provide the necessary information for teachers. Further, middle school is the important first phase of developing critical thinking skills; thus relevant studies are required in this case [ 3 , 4 ]. In addition, a municipal policy-making system can raise differences in problem-solving skills based on different demographic backgrounds [ 10 ]. Moreover, the results of previous studies regarding the development and differences in mathematical problem-solving skills are debatable. Thus, the present study has been conducted to meet these gaps. This study investigated the development of mathematical problem-solving skills in students and the differences owing demographic backgrounds. Three aspects were considered: (1) student profiles of mathematical problem-solving skills, (2) development of their mathematical problem-solving skills across grades, and (3) significant differences in mathematical problem-solving skills based on gender and school location. The results of the present study will provide detailed information regarding the subsample that contributes to the development of mathematical problem-solving skills in students based on their demographic backgrounds. In addition, the description of the score is in the form of a logit scale from large-scale data providing consistent meaning and confident generalization. This study can be used to determine appropriate teaching and learning in the best period of students’ development in mathematical problem-solving skills as well as policies to achieve educational equality.

2. Theoretical background

2.1. mathematical problem-solving skills and their development.

Solving mathematical problems is a complex cognitive ability that requires students to understand the problem as well as apply mathematical concepts to them [ 20 ]. Researchers have described the phases of solving a mathematical problem as understanding the problem, devising a plan, conducting out the plan, and looking back [ [20] , [24] , [21] , [22] , [23] ]. Because mathematical problems are complex, students may struggle with several phases, including applying mathematical knowledge, determining the concepts to use, and stating mathematical sentences (e.g., arithmetic) [ 20 ]. Studies have concluded that more students fail at later stages of the solution process [ 25 , 26 ]. In other words, fewer students fail in the phase of understanding a problem than during the plan implementation phase. Different studies have stated that students face difficulties in understanding the problem, determining what to assume, and investigating relevant information [ 27 ]. This makes them unable to translate the problem into a mathematical form.

Age or grade is viewed as one factor that influences mathematical problem-solving skills because the skills of the students improve over time as a result of the teaching and learning processes [ 28 ]. Neuroscience research has shown that older students have fewer problems with arithmetic than younger students; however, the hemispheric asymmetry is reduced [ 29 ]. In other words, older students are more proficient, but their flexibility to switch among different strategies is less. Ameer & Sigh [ 28 ] obtained similar results and found a considerable difference in mathematical achievement; specifically, older students performed better than younger students in number sense and computation using one-way analysis of variance (ANOVA) ( F ) of F (2,411) = 4.82, p  < 0.01. Molnár et al. [ 3 ] found that the student grade affects domain-specific and complex problem-solving skills. They observed that the development of problem-solving skills was noticeable across grades in elementary school but stopped in secondary school. The fastest development of domain-specific problem-solving occurred in grades 7 and 8 [ 3 ], but the fastest development of complex problem-solving occurred in grades 5–7 [ 3 ]. No development was detected between grades 4 and 5 as well as grades 6 and 7 for domain-specific and complex problem-solving skills, respectively. Similarly, Greiff et al. [ 4 ] concluded that students developed problem-solving skills across grades 5–11 with older students being more skilled. However, the grade 9 students deviated from the development pattern, and their problem-solving skills dropped. The theories from Molnár et al. [ 3 ] and Greiff et al. [ 4 ] are the benchmark cases herein.

The above studies showed that problem-solving skills mostly developed during compulsory schooling and developed most quickly in specific grades. This indicates that specific development times can be targeted to enhance the problem-solving skills [ 3 ]. However, Jabor et al. [ 30 ] observed contradictory results showing statistically significant differences with small effects in mathematical performance between age groups: those under the age of 19 outperformed those over the age of 19 years old. Grissom [ 13 ] observed a negative correlation between age and school achievement that remained constant over time.

2.2. Effects of school location and gender on mathematical problem-solving skills

School location has been shown to affect mathematical achievement [ 9 , 14 ]. In 15 countries, students in rural schools performed considerably worse than students in urban schools in mathematics [ 9 , 10 ], science and reading [ 9 ]. In addition, Nepal [ 15 ] discovered that urban students significantly outperformed rural students in mathematical problem-solving skills ( t  = −5.11, p  < 0.001) and achievement ( t  = −4.45, p  < 0.001) using the results of an independent sample t -test (t). However, other countries have found that rural students outperformed urban students in mathematics [ 6 , 10 ]. These variations may be attributed to a lack of instructional resources (e.g., facilities, materials, and programs), professional training (e.g., poorly trained teachers), and progressive instruction [ 6 ]. The results of Williams's study [ 10 ] serve as the basis for the current study.

Gender differences in mathematics have received attention because studies show that male students outperform female students on higher-level cognitive tasks [ 31 ]. This is a shift from a meta-analysis study that found gender differences in mathematics to be insignificant and favored female students [ 32 ]. At the college level, female students slightly outperform male students in computation while male students outperform female students in problem solving. However, no gender differences have been observed among elementary and middle school students. This result was strengthened by other meta-analysis studies [ 7 , 8 ], which concluded that there was no gender difference in mathematical performance and problem-solving skills [ 15 , [33] , [35] , [34] ]. Gender similarity in mathematics is achieved when equal learning opportunities and educational choices are provided and the curriculum is expanded to include the needs and interests of the students [ 16 , 18 , 31 ].

From a sociological perspective, gender similarity in mathematics makes sense. If there is a gender difference in mathematics, this has been attributed to science, technology, engineering, and mathematics (STEM) being stereotyped as a male domain [ 8 ]. Stereotypes influence beliefs and self-efficacy of students and perceptions of their own abilities [ 8 , 19 ]. This is the reason for the low interest of female students in advanced mathematics courses [ 18 , 19 ]. However, Halpern et al. [ 16 ] found that more female students are entering many occupations that require a high level of mathematical knowledge. Moreover, Anjum [ 36 ] found that female students outperformed male students in mathematics. This may be because female students prepared better than the male students before the test and were more thorough [ 36 , 37 ]. The study of Anjum [ 36 ] is one of the basis cases of the current study.

Differences in brain structure support the argument that there are gender differences in mathematical performance [ 16 , 17 ]. Females have less brain lateralization (i.e., symmetric left and right hemispheres), which helps them perform better verbally. Meanwhile, males have more brain lateralization, which is important for spatial tasks [ 17 ]. In addition, the male hormone testosterone slows the development of the left hemisphere [ 16 ], which improves the performance of right brain-dominant mathematical reasoning and spatial tasks.

3.1. Instrumentation

In this study, a science-related mathematical problem-solving test was used. This is a mathematics essay test where the problems are in the form of scenarios related to environmental management. Problems are solved by using technology as a tool (e.g., calculator, grid paper). The test was developed in an interdisciplinary STEM framework, and it is targeted toward grades 7–9. There were six scenarios in total: some were given to multiple grades, and others were specific to a grade. They included ecofriendly packaging (grade 7), school park (grade 7), calorie vs. greenhouse gas emissions (grades 7–9), floodwater reservoir (grade 8), city park (grades 8–9), and infiltration well (grade 9). These scenarios cover topics such as number and measurement, ratio and proportion, geometry, and statistics. Every scenario had a challenge, and students were provided with eight metacognitive prompt items to help them explore their problem-solving skills.

The test was administered by using paper and pencils for a 3-h period with a break every hour. At the end of the test, students were asked to fill in their demographic information. Each prompt item had a maximum score of 5 points: a complete and correct answer (5 points), a complete answer with a minor error (4 points), an incomplete answer with a minor error (3 points), an incomplete answer with a major error (2 points), and a completely wrong and irrelevant answer (1 point). Each scenario had a maximum total score of 40 points.

The test was validated to determine whether it contained good and acceptable psychometric evidence. It had an acceptable content validity index (CVI >0.67), moderate intraclass correlation coefficient (ICC) (rxx = 0.63), and acceptable Cronbach's alpha (α = 0.84). The construct validity indicated all scenarios and prompt items were fit (0.77 ≤ weighted mean square ≤1.59) with an acceptable discrimination value (0.48 ≤ discrimination value ≤ 0.93), acceptable behavior of the rating score, and good reliability (scenario reliability = 0.86; prompt item reliability = 0.94).

3.2. Participants

The test was administered to grades 7–9 students in east Java, Indonesia (n = 1067). The students were selected from A-accreditation schools in urban and rural areas; random classes were selected for each grade. The majority of the students were Javanese (95.01%), with the remainder being Madurese (3.3%) and other ethnicities. Table 1 describes the demographics of the participants.

Demographic characteristics of participants.

3.3. Data analysis

Data were collected between July and September 2022. Prior to data collection, ethical approval was sought from the institutional review board (IRB) of the Doctoral School of Education, University of Szeged and was granted with the ethical approval number of 7/2022. In addition, permission letters were sent to several schools to request permission and confirm their participation. The test answers of the students were scored by two raters – the first author of this study and a rater with master's degree in mathematics education – to ensure that the rating scale was consistently implemented. The results showed good consistency with an ICC of 0.992 and Cronbach's alpha of 0.996.

The scores from one of the raters were converted to a logit scale by weighted likelihood estimation (WLE) using the ConQuest software. A logit scale provides a consistent value or meaning in the form of intervals. The logit scale represents the unit interval between locations on the person–item map. WLE was chosen rather than maximum likelihood estimation (MLE) because WLE is more central than MLE, which helps to correct for bias [ 38 ]. The WLE scale was represented by using descriptive statistics to profile the students' mathematical problem-solving skills in terms of the percentage, mean score ( M ) and standard deviation ( SD ) for each phase. The WLE scale was also used to describe common difficulties for each phase. The development of students’ mathematical problem-solving skills across grades was presented by a pirate plot, which is used in R to visualize the relationship between 1 and 3 categorical independent variables and 1 continuous dependent variable. It was chosen because it displays raw data, descriptive statistics, and inferential statistics at the same time. The data analysis was performed using R studio version 4.1.3 software with the YaRrr package. A one-way ANOVA was performed to find significant differences across grades. An independent sample t -test was used to analyze significant differences based on gender and school location. The descriptive statistics, one-way ANOVA test, and independent sample t -test were performed using the IBM SPSS Statistics 25 software.

4.1. Student profiles

The scores of students were converted to the WLE scale, where a score of zero represented a student with average ability, a positive score indicated above-average ability, and a negative score indicated below-average ability. A higher score indicated higher ability. The mean score represented a student with average mathematical problem-solving skills ( M  = 0.001, SD  = 0.39). Overall, 52.1% of students had a score below zero. The distribution of scores among students was predominantly in the interval between −1 and 0. When the problem-solving process was analyzed by phase, the results showed that exploring and understanding were the most mastered problem-solving skills ( M  = 0.24, SD  = 0.51). Only 27.9% of students had below-average scores for the exploring and understanding phases, which indicates that they mostly understood the given problem and recognized the important information. However, the problem-solving skills decreased with higher phases. The students had below-average abilities in the phases of representing and formulating ( M  = −0.01, SD  = 0.36), planning and executing ( M  = −0.15, SD  = 0.41), and monitoring and reflecting ( M  = −0.16, SD  = 0.36). About 57.9% of the students had below-average scores for the representing and formulating phase, which indicates that they had problems making hypotheses regarding science phenomena, representing problems in mathematical form, and designing a prototype. The obvious reason for their difficulty with making hypotheses was that they did not understand simple concepts of science (e.g., CO 2 vs. O 2 ). In the planning and executing phase, 66.8% of the students failed to achieve a score greater than zero. This happened because they failed to apply mathematical concepts and procedures. Because they were unable to plan and execute a strategy, this affected the next phase of the problem-solving process. In the monitoring and reflecting phase, 68.0% of the students had a below-average score.

4.2. Development of mathematical problem-solving skills across grades

The development of the mathematical problem-solving skills of the students across grades was observed based on the increase in the mean score. The problem-solving skills developed from grade 7 to grade 8. The students of grade 7 had a mean score of −0.04 while grade 8 students had the highest mean score of 0.03. The students in grades 7 and 8 also showed more varied problem-solving skills than the grade 9 students did. In contrast, the grade 9 students showed a different pattern of development, and their mean score dropped to 0.01. Although the difference was not large, further analysis was needed to determine its significance.

Fig. 1 displays the development of the mathematical problem-solving skills of the students. The dots represent raw data or WLE scores. The middle line shows the mean score. The beans represent a smoothed density curve showing the full data distribution. The scores of the students in grades 7 and 9 were concentrated in the interval between −0.5 and 0. However, the scores of the grade 8 students were concentrated in the interval between 0 and 0.5. The scores of the students in grades 7 and 8 showed a wider distribution than those of the grade 9 students. The bands which overlap with the line representing the mean score, define the inference around the mean (i.e., 95% of the data are in this interval). The inference of the WLE score was close to the mean.

Differences in students' mathematical problem-solving skills across grades.

Note : PS: Problem-Solving Skills of Students.

The one-way ANOVA results indicated a significant difference among the problem-solving skills of the students of grades 7–9 ( F (1,066) = 3.01, p  = 0.046). The students of grade 8 showed a significant difference in problem-solving skills and outperformed the other students. The students of grades 7 and 9 showed no significant difference in their mathematical problem-solving skills. Table 2 presents the one-way ANOVA results of the mathematical problem-solving skills across grades.

One-way ANOVA results of the mathematical problem-solving across grades.

Note. Post hoc test: Dunnett's T3. 7, 8, and 9: subsample grade. <: direction of significant difference ( p  < 0.05).

Fig. 2 shows the development of the mathematical problem-solving skills of the students across grades based on school location and gender. The problem-solving skills of the urban students increased from a mean score of 0.07 in grade 7 to 0.14 in grade 8. However, the mean score of urban students in grade 9 dropped. In contrast, the mean scores of the rural students increased continuously with grade. The improvements were significant for both the rural ( F (426) = 10.10, p  < 0.001) and urban ( F (639) = 6.10, p  < 0.01) students. For the rural students, grade 9 students showed a significant difference in problem-solving skills. In contrast, urban students in grades 8 and 9 showed significant differences in problem-solving skills but not in grade 7.

Differences in students' mathematical problem-solving skills across grades and different demographic backgrounds.

(a) Differences in students grade 7 of mathematical problem-solving skills across grades and different demographic backgrounds

(b) Differences in students grade 8 of mathematical problem-solving skills across grades and different demographic backgrounds

(c) Differences in students grade 9 of mathematical problem-solving skills across grades and different demographic backgrounds

Note: WLE_PS: The students' problem-solving skills in WLE scale; F: Female; M: Male; ScLoc: School location; R: Rural; U: Urban.

When divided by gender, both female and male students showed improvements in their problem-solving skills from grades 7 and 8. However, female students in grade 9 showed a stable score while the scores of male students in grade 9 declined. Only male students in grade 7 showed a significant difference in the mean score. In urban schools, the scores of male and female students increased and decreased, respectively, from grade 7 to grade 8. Male students in rural schools showed an increase in score from grade 7 to grade 9. However, the scores of female students in rural schools decreased from grade 7 to grade 8. Table 3 presents the one-way ANOVA results for the mathematical problem-solving skills of the students considering gender and school location.

One-way ANOVA results for mathematical problem-solving skills across grades and different demographic backgrounds.

Fig. 2 shows that the distributions of the male and female scores of students were similar for every grade except rural grade 9 students. The scores of the rural female students were concentrated in the interval between 0 and 0.5 while the scores of the rural male students were mostly below 0. The scores of rural students in grade 7 and urban students in grade 9 (both male and female) were concentrated in the interval between −0.5 and 0. The scores of urban students in grades 7 and 8 were concentrated in the interval between −0.5 and 0.5.

Fig. 3 shows a detailed analysis of the development of mathematical problem-solving skills across grades for each phase of the problem-solving process. Similar patterns were observed in the exploring and understanding and the representing and formulating phases: the mean score increased from grade 7 to grade 8 but decreased from grade 8 to grade 9. Grade 8 students had the highest mean score and differed significantly from the scores of students in other grades.

Differences in students' mathematical problem-solving skills in every phase across grades: (1) Exploring & understanding, (2) Representing & formulating, (3) Planning & executing, (4) Monitoring & reflecting.

(a) Differences in students' mathematical problem-solving skills in exploring and understanding phase

(b) Differences in students' mathematical problem-solving skills in representing and formulating phase

(c) Differences in students' mathematical problem-solving skills in planning and executing phase

(d) Differences in students' mathematical problem-solving skills in monitoring and reflecting phase

Note: WLE_Exp_Un: The WLE score in exploring and understanding; WLE_Rep_For: The WLE score in representing and formulating; WLE_Plan_Ex: The WLE score in planning and executing; WLE_Mon_Ref: The WLE score in monitoring and reflecting.

The scores of the students for the planning and executing phase increased with grade. However, the difference was only significant at grade 9. Grades 7 and 8 students showed an increase in score, but the improvement was not significant. There was no pattern detected in the monitoring and reflecting phase. The score was stable for grades 7 and 8 students but improved for grade 9 students. The mean score for each phase and the one-way ANOVA results are presented in Table 4 .

One-way ANOVA results for every phase of problem-solving across grades.

Fig. 3 shows that the distributions of the problem-solving skills of the students were similar across grades and phases. However, the distributions were different for grade 9 students in the representing and formulating, planning and executing, and monitoring and reflecting phases, where 95% of the data were in the interval between −0.5 and 0.5.

4.3. Effects of demographic background

4.3.1. school location.

The mathematical problem-solving skills of the students differed significantly based on school location. Urban students scored higher than rural students. The results of the t -test for mathematical problem-solving skills based on school location are presented in Table 5 .

T-test results for mathematical problem-solving skills based on school location.

The effects of the school's location on the performances of male and female students were analyzed. The results showed that the scores of the female students differed significantly based on school location ( t (613) = −6.09, p  < 0.001). Female students in urban schools ( M  = 0.18, SD  = 0.39) outperformed female students in rural schools ( M  = −0.08, SD  = 0.37). Similar results were observed for male students with urban students ( M  = −0.01, SD  = 0.35) outperforming rural students ( M  = −0.12, SD  = 0.39) by a significant margin ( t (382.764) = −3.25, p  < 0.01).

When analyzed by grade, grades 7 and 8 students contributed to the difference based on school location with t (377.952) = −6.34, p  < 0.001 and t (300.070) = −5.04, p  < 0.001, respectively. Urban students in grades 7 and 8 performed significantly better than their rural counterparts did. However, there was no significant difference between rural and urban students in grade 9 ( t (354) = 0.71, p  = 0.447).

4.3.2. Gender

Male and female students showed a significant difference in their mathematical problem-solving skills. Overall, female students outperformed male students. The detailed results of the independent sample t -test for mathematical problem-solving skills based on gender are presented in Table 6 .

T-test results for mathematical problem-solving skills based on gender.

The results were analyzed to determine whether the school location contributed to the gender difference. The gender difference was most significant among urban students ( t (596.796) = −4.36, p  < 0.001). Female students from urban schools ( M  = 0.12, SD  = 0.39) outperformed male students from urban schools ( M  = −0.01, SD  = 0.35). There was no significant difference between female and male students from rural schools ( t (425) = −1.31, p  = 0.191).

Grades 7 and 9 students contributed to the gender difference with t (372.996) = −3.90, p  < 0.001 and t (354) = −2.73, p  < 0.01, respectively. Female students in grades 7 and 9 outperformed their male counterparts. However, there was no significant gender difference among grade 8 students ( t (329) = −0.10, p  = 0.323).

5. Discussion

The mathematical problem-solving skills of the students were categorized as average. In addition, the difficulties of students increased in line with the problem-solving phase. Fewer students failed the exploring and understanding phase than the subsequent phases. This confirms the results of previous studies indicating that more students failed further along the problem-solving process [ 25 , 26 ]. Because the problem-solving process is sequential, students who have difficulty understanding a problem will fail the subsequent phases [ 27 ].

The development of mathematical problem-solving skills was evaluated according to the mean WLE score. The mathematical problem-solving skills of the students developed from grade 7 to grade 8 based on the increase in their mean scores. However, the development dropped in grade 9. This agrees with previous results that concluded that higher grades had the highest problem-solving skills, but the fastest skill development took place in grades 7–8 after which it dropped [ 3 , 4 ]. These results indicate that the mathematical problem-solving skills of the students should improve and be strengthened in grades 7–8, which will help them perform better in grade 9.

In this study, the effects of the demographic background of the students were analyzed in detail, which is an aspect missing from previous studies. The results showed that the mathematical problem-solving skills of urban students increased from grade 7 to grade 8 but decreased in grade 9. The same pattern was found among male and female students. However, a different pattern was observed for rural students, where the skills of grade 9 students continued to increase. The different patterns may be attributed to a structural reorganization of cognitive processes at a particular age [ 3 ]. However, more research is needed on the effects of the demographic backgrounds of students on mathematical problem-solving skills. These results were different from previous results because the previous studies only analyzed the development in general, without focusing on their demographic background. Hence, different patterns of development were observed when it was thoroughly examined.

Because solving problems is a cognitive process, the development of problem-solving skills for particular phases and processes needed to be analyzed. The students showed the same pattern for knowledge acquisition (i.e., exploring and understanding, and representing and formulating phases), with an increase in skill from grade 7 to grade 8 but a decrease in grade 9. However, the students showed increasing skill in knowledge application (i.e., planning and executing, as well as monitoring and reflecting phases) across grades. This means that the difference between the mean scores in grade 9 was not significant across phases. Grade 9 students had lower scores than grade 8 students for the knowledge acquisition phase but higher scores for the knowledge application phase. In contrast, the gap between the mean scores of grades 7 and 8 was large across phases.

These results proved that there is a significant difference in the mathematical problem-solving skills of students based on their demographic backgrounds. The urban students outperformed rural students, which confirms the results of previous studies [ 9 , 10 , 15 ]. The difference can be attributed to the availability of facilities, teacher quality, and interactive teaching and learning instruction [ 6 ]. In Indonesia, the policies for the public educational system for middle schools are set at the municipal level. This means that each city has its own policies for teacher training, teacher recruitment, teaching and learning processes, facilities, etc. Urban schools mostly have stricter policies as well as various programs to help students improve their knowledge and skills. In addition, they have supportive facilities for teaching and learning. This unequal environment is the strongest reason for the difference in mathematical problem-solving skills.

The results were analyzed in detail to observe which groups in the rural and urban schools contributed to the difference. Both male and female students in urban schools performed better than their counterparts in rural schools did. In addition, urban students in grades 7 and 8 outperformed their rural counterparts. There was no significant difference between urban and rural students in grade 9. This may be because grade 9 is the last grade in middle school, so students have to prepare for high school entrance requirements, including exam and/or grade point average scores. Hence, both rural and urban schools focus much effort on the teaching and learning process in this grade.

In this study, the female students surprisingly had better mathematical problem-solving skills than the male students did. This confirmed the results of the meta-analysis by Hyde et al. [ 32 ] and study by Anjum [ 36 ], which found that female students slightly outperformed male students in mathematics. This difference may be because of motivation and attitude [ 39 , 40 ]. Female Indonesian students are typically more diligent, thorough, responsible, persistent, and serious with their tasks.

A detailed analysis was performed to evaluate which group of students contributed to the gender differences. The results showed that female students outperformed male students in urban schools. This may be because male students at urban schools typically display an unserious attitude toward low-stake tests. In addition, female students outperformed their male counterparts in grades 7 and 9. The reason for this difference requires further analysis.

6. Conclusion

Studying the problem-solving skills of students is crucial to facilitating their development. In this study, the conclusions are presented as follows:

• • The mathematical problem-solving skills of the students were categorized as average. More students failed at higher phases of the problem-solving process.
• • Students showed development of their mathematical problem-solving skills from grade 7 to grade 8 but a decline in grade 9. The same pattern was detected across grades for urban students, both female and male. However, the problem-solving skills of rural students increased with the grade.
• • A similar development was observed for the individual problem-solving phases. In the knowledge acquisition phase, the problem-solving skills of the students developed from grade 7 to grade 8 but decreased in grade 9. However, problem-solving skills increased across grades in the knowledge application phase.
• • The school location was shown to have a significant effect on the mathematical problem-solving skills of the students. Urban students generally outperform students in rural schools. However, gender and grade contributed to differences in mathematical problem-solving skills based on school location. Female and male urban students in grades 7 and 8 outperformed their rural counterparts.
• • In general, female students outperformed male students in mathematical problem-solving skills, particularly those from urban schools and in grades 7 and 9.

The sampling method and the number of demographic backgrounds limited the scope of this study. Only students from A-accreditation schools were selected because higher-order problem-solving skills were considered assets. Moreover, the study only included three demographic factors: grade, gender, and school location. More demographic information, such as school type, can be added (public or private schools). Hence, future studies will need to broaden the sample size and consider more demographic factors. Despite these limitations, this study can help teachers determine the best period for enhancing the development of mathematical problem-solving skills. Moreover, the differences in mathematical problem-solving skills due to demographic background can be used as a basis for educational policymakers and teachers to provide equal opportunity and equitable education to students.

Author contribution statement

Ijtihadi Kamilia Amalina: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Tibor Vidákovich: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.

Funding statement

This work was supported by University of Szeged Open Access Fund with the grant number of 6020.

Data availability statement

Additional information.

No additional information is available for this paper.

Declaration of competing interest

No potential conflict of interest was reported by the authors.

• Future Students
• Current Students
• Faculty/Staff

News and Media

• News & Media Home
• Research Stories
• School's In
• In the Media

You are here

Softening the sharp edges in mathematics.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start — to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics — a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

“Mathematics should be flexible, conceptual, a place where we play with ideas and make connections," says Professor Jo Boaler. (Photo: Robert Houser Photography)

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced “How to Learn Math,” the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users. 

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer. 

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 — but the most common answer 13-year-olds gave was 19. The second most common was 21. 

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important? 

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mind-set. I think we all need a little more ish in our lives. 

You also argue that mathematics should be taught in more visual ways. What do you mean by that? 

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things — all of that contributes to our understanding of how it works. 

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking. 

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, ‘I’m in geometry class now, and I still remember that  sugar cube, what it looked like and felt like.’ His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing — elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

Click to enlarge: A depiction of various ways to calculate 38 x 5, numerically and visually. (Image: Courtesy of Jo Boaler)

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them. 

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

More Stories

⟵ Go to all Research Stories

Get the Educator

Subscribe to our monthly newsletter.

Stanford Graduate School of Education

482 Galvez Mall Stanford, CA 94305-3096 Tel: (650) 723-2109

• Contact Admissions
• GSE Leadership
• Site Feedback
• Web Accessibility
• Career Resources
• Faculty Open Positions
• Explore Courses
• Academic Calendar
• Office of the Registrar
• Cubberley Library
• StanfordWho
• StanfordYou

Improving lives through learning

• Stanford Home
• Maps & Directions
• Search Stanford
• Emergency Info
• Terms of Use
• Non-Discrimination
• Accessibility

© Stanford University , Stanford , California 94305 .

Mathematical Problem-Posing Research: Thirty Years of Advances Building on the Publication of “On Mathematical Problem Posing”

• First Online: 03 August 2023

Cite this chapter

• Jinfa Cai 6 ,
• Stephen Hwang 6 &
• Matthew Melville 7  

Part of the book series: Research in Mathematics Education ((RME))

381 Accesses

1 Citations

4 Altmetric

In 1994, Ed Silver published a seminal paper entitled “On Mathematical Problem Posing.” Silver both helped to lay a foundation for problem-posing research and pointed out key directions that problem-posing research could explore. This chapter provides a brief review of the problem-posing literature in the past three decades, showing that there have been marked advances in problem-posing research. We not only provide a review of the advances in problem-posing research, but also of the impact of Silver’s seminal paper on problem-posing research. The chapter ends with a discussion of three specific areas of research on mathematical problem posing (one of these areas is Problem-Posing-Based Learning [P-PBL]) that are ripe for progress and could significantly move the entire field forward.

During the preparation of this chapter, the authors were supported by a grant from the National Science Foundation (DRL 2101552). Any opinions expressed herein are those of the authors and do not necessarily represent the views of the National Science Foundation.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Data retrieved from Google Scholar on March 17, 2023.

Akay, H., & Boz, N. (2010). The effect of problem posing oriented analyses-II course on the attitudes toward mathematics and mathematics self-efficacy of elementary prospective mathematics teachers. Australian Journal of Teacher Education, 35 (1), 6.

Article   Google Scholar  

Baumanns, L., & Rott, B. (2021). Rethinking problem-posing situations: A review. Investigations in Mathematics Learning, 13 (2), 59–76.

Brown, S. I., & Walter, M. I. (1983). The art of problem posing . The Franklin Institute Press.

Google Scholar  

Butts, T. (1980). Posing problems properly. In S. Krulik & R. Reys (Eds.), Problem solving in school mathematics (pp. 23–33). National Council of Teachers of Mathematics.

Cai, J. (1998). An investigation of U.S. and Chinese students’ mathematical problem posing and problem solving. Mathematics Education Research Journal, 10 , 37–50.

Cai, J. (2003). Singaporean students’ mathematical thinking in problem solving and problem posing: An exploratory study. International Journal of Mathematical Education in Science and Technology, 34 (5), 719–737.

Cai, J. (2022). What research says about teaching mathematics through problem posing. Education & Didactique, 16 , 31–50.

Cai, J., & Cifarelli, V. V. (2005). Exploring mathematical exploration: How two college students formulated and solved their own mathematical problems. Focus on Learning Problems in Mathematics, 27 (3), 43–72.

Cai, J., & Hwang, S. (2002). Generalized and generative thinking in U.S. and Chinese students’ mathematical problem solving and problem posing. Journal of Mathematical Behavior, 21 , 401–421.

Cai, J., & Hwang, S. (2020). Learning to teach through mathematical problem posing: Theoretical considerations, methodology, and directions for future research. International Journal of Educational Research, 102 , 101391.

Cai, J., & Hwang, S. (2021). Teachers as redesigners of curriculum to teach mathematics through problem posing: Conceptualization and initial findings of a problem-posing project. ZDM–Mathematics Education, 53 , 1–14.

Cai, J., & Hwang, S. (2022). Making mathematics challenging through problem posing in the classroom. In R. Leikin, C. Christou, A. Karp, D. Pitta-Pantazi, & R. Zazkis (Eds.), Mathematical challenges for all . Springer.

Cai, J., & Jiang, C. (2017). An analysis of problem-posing tasks in Chinese and US elementary mathematics textbooks. International Journal of Science and Mathematics Education, 15 (8), 1521–1540.

Cai, J., & Leikin, R. (2020). Affect in mathematical problem posing: Conceptualization, advances, and future directions for research. Educational Studies in Mathematics, 105 (3), 287–301.

Cai, J., Moyer, J. C., Wang, N., Hwang, S., Nie, B., & Garber, T. (2013). Mathematical problem posing as a measure of curricular effect on students’ learning. Educational Studies in Mathematics, 83 , 57–69.

Cai, J., Hwang, S., Jiang, C., & Silber, S. (2015). Problem posing research in mathematics: Some answered and unanswered questions. In F. M. Singer, N. Ellerton, & J. Cai (Eds.), Mathematical problem posing: From research to effective practice (pp. 3–34). Springer.

Chapter   Google Scholar  

Cai, J., Chen, T., Li, X., Xu, R., Zhang, S., Hu, Y., Zhang, L., & Song, N. (2020). Exploring the impact of a problem-posing workshop on elementary school mathematics teachers’ conceptions on problem posing and lesson design. International Journal of Educational Research, 102 , 101404.

Cai, J., Muirhead, F., Cirillo, M., & Hwang, S. (2021). Supporting teachers to teach mathematics through problem posing: An early-stage longitudinal study [NSF Grant Proposal] . University of Delaware.

Cai, J., Koichu, B., Rott, B., Zazkis, R., & Jiang, C. (2022). Mathematical problem posing: Task variables, processes and products. In C. Fernández, S. Llinares, A. Gutiérrez, & N. Planas (Eds.), Proceedings of the 45th conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 119–145). PME.

Cai, J., Hwang, S., Melville, M., & Robison, V. (2023). Theories for teaching and teaching for theories: Artifacts as tangible entities for storing and improving professional knowledge for teaching. In A. Praetorius & C. Y. Charalambous (Eds.), Theorizing teaching . Springer.

Chen, T., & Cai, J. (2020). An elementary mathematics teacher learning to teach using problem posing: A case of the distributive property of multiplication over addition. International Journal of Educational Research, 102 , 101420.

Christou, C., Mousoulides, N., Pittalis, M., Pitta-Pantazi, D., & Sriraman, B. (2005). An empirical taxonomy of problem posing processes. ZDM, 37 (3), 149–158.

Cifarelli, V. V., & Cai, J. (2005). The evolution of mathematical explorations in open-ended problem-solving situations. The Journal of Mathematical Behavior, 24 (3–4), 302–324.

Crespo, S. (2003). Learning to pose mathematical problems: Exploring changes in preservice teachers’ practices. Educational Studies in Mathematics, 52 (3), 243–270.

Crespo, S., & Harper, F. (2020). Learning to pose collaborative mathematics problems with secondary prospective teachers. International Journal of Educational Research, 102 , 101430.

Crespo, S., & Sinclair, N. (2008). What makes a problem mathematically interesting? Inviting prospective teachers to pose better problems. Journal of Mathematics Teacher Education, 11 (5), 395–415.

Doig, B., & Groves, S. (2011). Japanese lesson study: Teacher professional development through communities of inquiry. Mathematics Teacher Education and Development, 13 (1), 77–93.

Ellerton, N. F. (1986). Children’s made-up mathematics problems – A new perspective on talented mathematicians. Educational Studies in Mathematics, 17 , 261–271.

English, L. D. (1998). Children’s problem posing within formal and informal contexts. Journal for Research in Mathematics Education, 29 (1), 83–106.

Fan, L., Chen, J., Zhu, Y., Qiu, X., & Hu, Q. (2004). Textbook use within and beyond Chinese mathematics classrooms: A study of 12 secondary schools in Kunming and Fuzhou of China. In L. Fan, N. Y. Wong, J. Cai, & S. Li (Eds.), How Chinese learn mathematics: Perspectives from insiders (pp. 228–261). World Scientific.

Garofalo, J., & Lester, F. K. (1985). Metacognition, cognitive monitoring, and mathematical performance. Journal for Research in Mathematics Education, 16 (3), 163–176.

Guo, Y., Yan, J., & Men, T. (2021). Chinese junior high school students’ mathematical problem-posing performance. ZDM–Mathematics Education, 53 , 1–13.

Guskey, T. R., & Yoon, K. S. (2009). What works in professional development? Phi Delta Kappan, 90 (7), 495–500.

Hart, K. M. (Ed.). (1981). Children’s understanding of mathematics (pp. 11–16). John Murray.

Healy, C. C. (1993). Creating miracles: A story of student discovery . Key Curriculum Press.

Hwang, S., & Cai, J. (2003). A perspective for examining the link between problem solving and problem posing. In N. A. Pateman, B. J. Dougherty, & J. Zilliox (Eds.), Proceedings of the 27th conference of the International Group for the Psychology of Mathematics Education held jointly with the 25th conference of PME-NA (Vol. 3, pp. 103–110). Center for Research and Development Group, University of Hawai’i.

Illustrative Mathematics. (n.d.). Supporting English-language learners. https://curriculum.illustrativemathematics.org/HS/teachers/supporting_ell.html

Jiang, C., & Cai, J. (2014). An analysis of mathematical problem-posing tasks in Chinese and US reform textbooks. In S. Oesterle, P. Liljedahl, C. Nicol, & D. Allan (Eds.), Proceedings of the Joint Meeting of PME 38 and PME-NA 36 (Vol. 3, pp. 393–400). PME.

Jiang, C., & Cai, J. (2015). An investigation of questions on the sixth grade students’ mathematical problem posing. In K. Beswick, T. Muir, & J. Fielding-Wells (Eds.), Proceedings of the 39th conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 113–120). PME.

Kar, T., Özdemir, E., İpek, A. S., & Albayrak, M. (2010). The relation between the problem posing and problem solving skills of prospective elementary mathematics teachers. Procedia-Social and Behavioral Sciences, 2 (2), 1577–1583.

Kilpatrick, J. (1987). Problem formulating: Where do good problems come from? In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 123–147). Erlbaum.

Koichu, B. (2020). Problem posing in the context of teaching for advanced problem solving. International Journal of Educational Research, 102 , 101428.

Koichu, B., & Kontorovich, I. (2013). Dissecting success stories on mathematical problem posing: A case of the Billiard Task. Educational Studies in Mathematics, 83 (1), 71–86.

Kotsopoulos, D., & Cordy, M. (2009). Investigating imagination as a cognitive space for learning mathematics. Educational Studies in Mathematics, 70 , 259–274.

Leikin, R. (2009). Exploring mathematical creativity using multiple solution tasks. In R. Leikin, A. Berman, & B. Koichu (Eds.), Creativity in mathematics and the education of gifted students (pp. 129–145). Sense.

Leikin, R., & Sriraman, B. (2017). Creativity and giftedness: Interdisciplinary perspectives from mathematics and beyond . Springer.

Book   Google Scholar  

Lesh, R. (1981). Applied mathematical problem solving. Educational Studies in Mathematics, 12 (2), 235–264.

Lesh, R., Landau, M., & Hamilton, E. (1983). Conceptual models and applied mathematical problem-solving research. In R. Lesh & M. Landau (Eds.), Acquisition of mathematics concepts and processes (pp. 264–343). Academic Press.

Leung, S. S., & Silver, E. A. (1997). The role of task format, mathematics knowledge, and creative thinking on the arithmetic problem posing of prospective elementary school teachers. Mathematics Education Research Journal, 9 (1), 5–24.

Lewis, W. M., & Colonnese, M. W. (2021). Fostering mathematical creativity through problem posing and three-act tasks. Gifted Child Today, 44 (3), 141–150.

Li, X., Song, N., Hwang, S., & Cai, J. (2020). Learning to teach mathematics through problem posing: Teachers’ beliefs and performance on problem posing. Educational Studies in Mathematics, 105 (3), 325–347.

Lubinski, D., & Benbow, C. P. (2006). Study of mathematically precocious youth after 35 years: Uncovering antecedents for the development of math-science expertise. Perspectives on Psychological Science, 1 (4), 316–345.

Ma, X. (1999). A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. Journal for Research in Mathematics Education, 30 , 520–540.

McLeod, D. B., & Adams, V. M. (1989). Affect and mathematical problem solving: A new perspective . Lawrence Erlbaum Associates.

Melville, M., & Corey, D. L. (2021). Kyouzaikenkyuu: An exploration of Japanese mathematics teachers’ daily planning practices. Journal of Mathematics Teacher Education. https://doi.org/10.1007/s10857-021-09493-5

Moses, B., Bjork, E., & Goldenberg, E. P. (1990). Beyond problem solving: Problem posing. In T. J. Cooney & C. R. Hirsch (Eds.), Teaching and learning mathematics in the 1990s (pp. 82–91). National Council of Teachers of Mathematics.

National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Journal for Research in Mathematics Education . https://doi.org/10.2307/749544

Philipp, R. A. (2007). Mathematics teachers’ beliefs and affect. In F. K. Lester Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 257–315). Information Age.

Polya, G. (1957). How to solve it: A new aspect of mathematical method . Princeton University Press.

Richardson, V. (1996). The role of attitudes and beliefs in learning to teach. In J. Sikula (Ed.), Handbook of research on teacher education (2nd ed., pp. 102–119). Macmillan.

Rott, B., Specht, B., & Knipping, C. (2021). A descriptive phase model of problem-solving processes. ZDM . https://doi.org/10.1007/s11858-021-01244-3

Schindler, M., & Bakker, A. (2020). Affective field during collaborative problem posing and problem solving: A case study. Educational Studies in Mathematics, 105 , 303–324. https://doi.org/10.1007/s10649-020-09973-0

Schoenfeld, A. H. (1985). Making sense of “out loud” problem-solving protocols. The Journal of Mathematical Behavior, 4 (2), 171–191.

Schroeder, T. L., & Lester, F. K. (1989). Developing understanding in mathematics via problem solving. New Directions for Elementary School Mathematics, 31 , 42.

Silber, S., & Cai, J. (2017). Pre-service teachers’ free and structured mathematical problem posing. International Journal of Mathematical Education in Science and Technology, 48 (2), 163–184.

Silber, S., & Cai, J. (2021). Exploring underprepared undergraduate students’ mathematical problem posing. ZDM–Mathematics Education, 53 , 1–13.

Silver, E. A. (1985). Research on teaching mathematical problem solving: Some underrepresented themes and needed directions. In Teaching and learning mathematical problem solving: Multiple research perspectives . Lawrence Erlbaum Associates.

Silver, E. A. (1994). On mathematical problem posing. For the Learning of Mathematics, 14 (1), 19–28.

Silver, E. A. (1997). Fostering creativity through instruction rich in mathematical problem solving and problem posing. ZDM–Mathematics Education, 97 (3), 75–80.

Silver, E. A. (Ed.). (2013). Teaching and learning mathematical problem solving: Multiple research perspectives . Routledge.

Silver, E. A., & Cai, J. (1996). An analysis of arithmetic problem posing by middle school students. Journal for Research in Mathematics Education, 27 (5), 521–539.

Silver, E. A., Mamona-Downs, J., Leung, S. S., & Kenney, P. A. (1996). Posing mathematical problems: An exploratory study. Journal for Research in Mathematics Education, 27 , 293–309.

Singer, F. M., Ellerton, N., & Cai, J. (2013). Problem-posing research in mathematics education: New questions and directions. Educational Studies in Mathematics, 83 (1), 1–7.

Singer, F. M., Sheffield, L. J., & Leikin, R. (2017). Advancements in research on creativity and giftedness in mathematics education: Introduction to the special issue. ZDM, 49 (1), 5–12.

Smith, M. S., & Friel, S. N. (Eds.). (2015). Cases in mathematics teacher education: Tools for developing knowledge needed for teaching . Information Age.

Stanic, G. M. A., & Kilpatrick, J. (1988). Historical perspectives on problem solving in mathematics curriculum. In R. I. Charles & E. A. Silver (Eds.), Research agenda for mathematics education: The teaching and assessing of mathematical problem solving (pp. 1–22). National Council of Teachers of Mathematics.

Stein, M. K., Smith, M. S., Henningsen, M. A., & Silver, E. A. (2000). Implementing standards-based mathematics instruction: A casebook for professional development . Teachers College Press.

Stoyanova, E., & Ellerton, N. F. (1996). A framework for research into students’ problem posing in school mathematics. In P. C. Clarkson (Ed.), Technology in mathematics education (pp. 518–525). Mathematics Education Research Group of Australasia.

Thompson, A. G. (1992). Teachers’ beliefs and conceptions: A synthesis of the research. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 127–146). Macmillan.

Tichá, M., & Hošpesová, A. (2013). Developing teachers’ subject didactic competence through problem posing. Educational Studies in Mathematics, 83 (1), 133–143.

Toluk-Uçar, Z. (2009). Developing pre-service teachers understanding of fractions through problem posing. Teaching and Teacher Education, 25 (1), 166–175.

Van Harpen, X. Y., & Sriraman, B. (2013). Creativity and mathematical problem posing: An analysis of high school students’ mathematical problem posing in China and the USA. Educational Studies in Mathematics, 82 (2), 201–221.

Voica, C., & Singer, F. M. (2012). Creative contexts as ways to strengthen mathematics learning. Procedia-Social and Behavioral Sciences, 33 , 538–542.

Williams, S. R., & Leatham, K. R. (2017). Journal quality in mathematics education. Journal for Research in Mathematics Education, 48 (4), 369–396.

Xie, J., & Masingila, J. O. (2017). Examining interactions between problem posing and problem solving with prospective primary teachers: A case of using fractions. Educational Studies in Mathematics, 96 (1), 101–118.

Xu, H., & Cai, J. (2020). Fostering the development of students’ thinking in teaching “Using letters to represent quantitative relationship” through collaborative learning and problem posing. Elementary Mathematics Teachers, 2020 (2), 14–16. [in Chinese].

Yao, Y., Hwang, S., & Cai, J. (2021). Preservice teachers’ mathematical understanding exhibited in problem posing and problem solving. ZDM–Mathematics Education, 53 , 1–13.

Yoon, K. S., Duncan, T., Lee, S. W.-Y., Scarloss, B., & Shapley, K. (2007). Reviewing the evidence on how teacher professional development affects student achievement (Issues & Answers Report, REL 2007–No. 033). U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance, Regional Educational Laboratory Southwest.

Zhang, H., & Cai, J. (2021). Teaching mathematics through problem posing: Insights from an analysis of teaching cases. ZDM–Mathematics Education, 53 , 1–13.

Zhang, L., Cai, J., Song, N., Zhang, H., Chen, T., Zhang, Z., & Guo, F. (2022). Mathematical problem posing of elementary school students: The impact of task format and its relationship to problem solving. ZDM–Mathematics Education, 54 , 497–512.

Download references

Author information

Authors and affiliations.

University of Delaware, Newark, DE, USA

Jinfa Cai & Stephen Hwang

Purdue University Fort Wayne, Fort Wayne, IN, USA

Matthew Melville

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Jinfa Cai .

Editor information

Editors and affiliations.

Department of Mathematical Sciences, University of Delaware, Newark, DE, USA

University of Oxford, Oxford, UK

Gabriel J. Stylianides

University of Michigan–Ann Arbor, Ann Arbor, MI, USA

Patricia Ann Kenney

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Cai, J., Hwang, S., Melville, M. (2023). Mathematical Problem-Posing Research: Thirty Years of Advances Building on the Publication of “On Mathematical Problem Posing”. In: Cai, J., Stylianides, G.J., Kenney, P.A. (eds) Research Studies on Learning and Teaching of Mathematics. Research in Mathematics Education. Springer, Cham. https://doi.org/10.1007/978-3-031-35459-5_1

Download citation

DOI : https://doi.org/10.1007/978-3-031-35459-5_1

Published : 03 August 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-35458-8

Online ISBN : 978-3-031-35459-5

eBook Packages : Education Education (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

News, Views & Insights

• Best of Blog (70)
• Astronomy (28)
• Computational Thinking (64)
• Current Events (36)
• Data Analysis and Visualization (138)
• Data Repository (11)
• Design (24)
• Developer Insights (76)
• Digital Humanities (7)
• Education (194)
• Events (44)
• Finance (24)
• Function Repository (12)
• Geosciences (12)
• High-Performance Computing (12)
• History (18)
• Image Processing (48)
• Machine Learning (16)
• Mathematica News (112)
• Mathematica Q&A (13)
• Mathematics (129)
• New Technology (41)
• Other Application Areas (136)
• Raspberry Pi (18)
• Recreational Computation (163)
• Software Development (35)
• System Modeler (49)
• Uncategorized (1)
• Wolfram Cloud (24)
• Wolfram Community (19)
• Wolfram Demonstrations Project (31)
• Wolfram Language (297)
• Wolfram News (278)
• Wolfram Notebooks (37)
• Wolfram U (29)
• Wolfram|Alpha (48)
• Wolfram|One (7)

Marking a Milestone: Four Years of Daily Study Groups

From data to discovery: studying computational biology with wolfram, navigating quantum computing: accelerating next-generation innovation, unlock innovative problem-solving skills with creative computation.

As computers continue to perform an increasing number of tasks for us, it’s never been more important to learn how to use computers in creative ways. Creative computing, an interdisciplinary subject combining coding with artistic expression, allows us to blend technology with human experiences. Learning to create in this way can help you unlock your innovative problem-solving skills. By mastering creative computation, you can create interactive artwork, design immersive experiences and develop creative solutions to real-world challenges.

Wolfram U ’s new Creative Computation course combines an introduction to Wolfram Language coding with a project-based exploration of various art forms, like visual art, poetry, audio and video game design. If you’ve never coded in Wolfram Language before, this course is a fantastic introduction to applied computing and will help you learn the language for any project. If you’ve already mastered the basics of coding, this course will help you apply your skills to fascinating new problems and projects.

We would love for you to join us in this interactive course as we explore what it means to work creatively with coding.

Motivation from History

Creative computing is a relatively new subject, but people have been using technology to make art for centuries. From the loom to the printing press or Walkman to Atari, technology has been part of art for as long as both have existed.

We now have a variety of exciting and creative ways to engage with computers, from AI-generated images to immersive virtual realities.

In this course, you will learn how to use Wolfram Language to create various forms of art. There are four main sections to the course: Computational Art, Computational Strings, Sound and Game Development. In each section, there are lessons teaching Wolfram Language skills, with associated exercises, and at the end of each section, there is a larger project. The projects are designed for you to stretch your creative muscles and use your new coding skills to create art. You’ll learn how to create visual art using images, how to write poetry using string manipulation, how to visualize audio and how to make text-based and graphics-based video games, all while learning how to code in Wolfram Language.

Here is a sneak peek at some of the topics in the course (shown in the left-hand column):

With 16 lessons, five quizzes and four projects, this course should take around five hours to complete. We recommend doing all the activities and projects to maximize your understanding and explore your new skills.

There is no background required to participate in this course. We will teach you all the coding skills you need to make the projects, so all that is required is your excitement and creativity.

Let’s explore what’s in the course.

There are 16 lessons in this course spread out over the five total sections (Computational Thinking and Coding, Computational Art, Computational Strings, Sound and Game Development). In each lesson, you will explore a different aspect of coding through a short video. You’ll start off by exploring the concept of computational thinking: how to translate your thoughts and your creativity into something the computer can understand and how to work with a computer to build creative artifacts. Here is a short excerpt from the video for this lesson:

Each lesson teaches a specific coding skill, with lots of examples and exploration of key concepts. In the Computational Art section, the goal is to use images and graphics to create a piece of art. In order to do that, we need to learn skills like variables, functions, lists, the Table and Map functions, colors, graphics and randomness, and image manipulation. Each skill is taught with an interactive video lesson in conjunction with exercises, before you use the project to test your knowledge.

The video lessons range from 5–13 minutes in length, and each video is accompanied by a transcript notebook displayed on the right-hand side of the screen. You can copy and paste Wolfram Language input directly from the transcript notebook to the embedded scratch notebook to try the examples for yourself.

Each lesson has a set of exercises to review the concepts covered during the lesson. Since this course is designed for independent study, a detailed solution is given for all exercises. Each exercise will help you practice a specific skill you’ve learned so that you are ready to use that skill in the project. Here is an example of an exercise from lesson 6 on image manipulation:

The exercise notebooks are interactive, so you can try variations of each problem in the Wolfram Cloud . You’re encouraged to blend skills together as you learn them. For example, for the aforementioned exercise, you could use the skills you just learned about randomness to replace the dominant colors in the image of the wolf with random colors, or you could import images to do the same exercise with a different image. When you’ve gotten further in the course, you could come back and build your own function that can do this to any two images.

Each section of the course includes a short project, and the Game Development section has two longer projects. In each case, you’ll use the skills you learned in that section to build something creative. In the first three sections, we provide detailed solutions and walk you though our processes, but in the Game Development section, we encourage you to build something unique.

In the Computational Art section, you’ll make art using images and shapes. In Computational Strings, you’ll write a Mad Libs haiku. In Sound, you’ll make an audio visualizer. In Game Development, you’ll make a text adventure game and a graphics-based Pac-Man –style game.

These projects will allow you to celebrate your successes and practice your new coding skills while cementing your understanding of creative computation.

Each section of the course ends with a short quiz, which allows you to demonstrate your understanding:

You will get instant feedback on your solutions, and you’re encouraged to try out the code.

Course Certificate

You are encouraged to watch all the lessons and attempt the projects and quizzes in the recommended sequence, since each topic in the course relies on earlier concepts and techniques. When you watch all 16 lesson videos and pass the five course quizzes, you will earn a certificate of course completion. The Track My Progress status bar in the course helps you to chart your progress, showing you where you left off from your previous course session. While you don’t have to submit projects to earn a certificate, they are a fundamental part of gaining computational skills, and we look forward to connecting with course users about their projects on Wolfram Community . Your course certificate represents completion of the basic course requirements, demonstrates your interest in exploring the latest technology and in building new computational skills, and it will add value to your resume or social media profile.

You are also encouraged to use the skills you learn in this course to go on to earn Level 1 certification for Wolfram Language proficiency . While the course does not require the same level of mathematics as the Level 1 certification exam, it will prepare you well for accomplishing the range of computational tasks that are required for Level 1 certification.

A Building Block for Success

A mastery of the fundamental concepts of creative computing will prepare you for working with computers to innovatively solve problems. Whether you’re interested in creating art or you’re interested in developing your coding skills, this course will provide a detailed foundation in both. Learning Wolfram Language is a valuable pursuit regardless of your career aspirations, as you can use the skills you learn in this course in any field.

Acknowledgements

I would like to thank my coauthor Eryn Gillam for their major contributions to the development of this course, as well as others who helped this course come together, including (but not limited to) Anisha Basil, Abrita Chakravarty, Cassidy Hinkle, Joyce Tracewell, Arben Kalziqi, Isabel Skidmore, Zach Shelton, Simeon Buttery, Ryan Domier and Eder Ordonez.

! Please enter your comment (at least 5 characters).

! Please enter your name.

! Please enter a valid email address.

Related Posts

The risk-taking activity that ‘helicopter parents’ should allow their kids to experience

Editor’s note: The views expressed in this commentary are solely those of the writers. CNN is showcasing the work of The Conversation , a collaboration between journalists and academics to provide news analysis and commentary. The content is produced solely by The Conversation.

There is ongoing concern about the impact of “ helicopter parenting ” on children’s growth and development.

Keen to ensure the best outcomes for their children, helicopter parents tend to hover over their kids, constantly trying to prevent misadventure or harm.

But child experts say this can lead to a  lack of resilience and tenacity  in children. Children can also struggle with problem-solving and initiative.

How can we overcome this?

We are educators who study risky environments. Our  new research  looks at parents’ perceptions of an outdoor play park. It shows how outdoor parks provide opportunities for children to engage in risky play and develop independence and problem-solving skills.

The importance of risk

Risk-taking means engaging in any behavior or activity with an uncertain physical, social, emotional or financial outcome.

Risk is an everyday part of life, from driving a car to buying a house at auction or climbing a ladder.

We cannot eliminate risk, so we need to learn how to navigate it. It means taking responsibility for assessing potential consequences and taking necessary precautions. For example, crossing the road carries risk, but we learn how to look for cars or cross at traffic lights if the road is busy.

Recognizing and appropriately responding to risk-taking is an integral aspect of children’s growth and development. In 1998, US educator and wilderness guide Jeff Liddle  observed risk was instrumental  to lifelong learning.

Outdoor experiences are particularly good places to  develop skills around risk  because they are not a controlled environment. For example, no two trees are the same to climb, and conditions can vary depending on the weather.

READ MORE: ‘It’s not fair!’ Kids grumble and complain for a reason. Here’s how to handle it

In a  new study , we surveyed parents and caregivers about children’s risk-taking in the Boongaree nature play park in Berry, New South Wales.

The park includes fixed equipment such as slides and climbing ropes as well as natural elements such as water, stone, timber, sand and greenery.

We chose Boongaree after it became the focus of media and social media debate due to a  spate of injuries , including broken bones. The Daily Mail  suggested  it was Australia’s “most dangerous playground.” Following community concerns, the park’s tunnel slide was  replaced  in May with another slide with less “momentum.”

Over multiple visits to the park in June, we recruited 302 adults to complete a survey about their children’s park use. We then followed up with a closed Facebook group of 56 parents from the same group.

READ MORE: From pests to pollutants, keeping schools healthy and clean is no simple task

The benefits of risk

We asked parents to share their views about the park, and they told us risky park play had many benefits. These included allowing children to:

• be challenged and solve problems

• connect to the outdoors

• direct their own play

• be physically active

• be creative and curious

• demonstrate confidence and independence and

• build social capacity, by sharing equipment and taking turns.

As one parent told us: “The look on children’s faces as they reach the top of climbing ropes and start walking across the bridges is fabulous — grit and determination, followed by a big deep breath. …”

Another parent spoke of the importance of giving kids the opportunity to “make their own decisions about the risk they want to take, how high or how fast they will go.”

Yet another parent described how the park gave children the “freedom to play in any way they feel comfortable.”

READ MORE: Bluey teaches children and parents alike about how play supports creativity — and other life lessons

How to support your child in outdoor, risky play

So next time you go to the park, how can you support your child to take appropriate risks? Here are some tips, based on  our work  on children, risk and outdoor play:

Start with a positive mindset:  Playgrounds are designed to develop physical and social skills. So be prepared for your child to try new things at the park (rather than just play it safe with the same old equipment).

Be ready to support — and to stand back:  There are times when it is best to stand back and let children experience the equipment or the area for themselves. There are others where parents are needed. So keep a monitoring eye on things. But don’t assume you will be helping all the time.

Language matters:  Try to steer away from language such as “be careful.” This can set children up to be afraid of a situation. Reframe your language to something more supportive such as “Is there a stronger piece of wood to put your foot on?” or “Have you seen the hole over there?”

You could also say something like, “Look around, do you want to explore left or right?” This prompts your child to think about the best approach for them and builds self-confidence and problem-solving skills.

Give useful advice:  Help children with specific guidance on how to use equipment safely. For example, when climbing you could say, “Use three points of contact, two hands and one foot on that ladder.”

Let the child decide:  Allow your child to decide what pieces of equipment they use and how far they climb. Do not push them to complete activities they are not comfortable with. And by the same token, intervene only when the equipment is clearly above their skill development level.

Have fun:  Show excitement, join in the imaginative games and reinforce the message that it is acceptable to say no or yes to challenge — both choices are OK!

READ MORE: Can parents give their children too much attention?

Tonia Gray is a professor in the Centre for Educational Research at Western Sydney University in Australia. Jaydene Barnes is an associate lecturer at Western Sydney University. Marion Sturges is an academic professional adviser and lecturer in education at Western Sydney University. The authors wish to acknowledge Amanda Lloyd, who contributed to the research on which this article is based. The authors do not work for, consult, own shares in or receive funding from any company or organization that would benefit from this article and have disclosed no relevant affiliations beyond their academic appointment.

For more CNN news and newsletters create an account at CNN.com