presentation on 18 electron rule

18 Electron Rule – Definition, Examples, and Applications

May 6, 2022
Coordination Compound

Table of Contents

18 electron rule , a chemical thumb rule is used to predict the stability of a metal atom in an organometallic compound by evaluating whether it has 18 valence electrons. According to this rule, “In order for a transition element to be stable, it must have 18 electrons in its valence shell in the configuration of inert gas, and these electrons must form chemical bonds”. It is considered a simplified version of the EAN rule. EAN rule considers the total number of electrons of the atom, while the 18 electron rule only considers the number of valence electrons. The advantage of this rule is that applies to all rows of the periodic table .

18 electron rule is one of the valuable tools for predicting the formula of stable compounds as organometallic compounds, particularly those containing carbonyl and nitrosyl ligands, follow the rule with a high frequency.

18 Electron Rule:

18 electron rule was proposed by Irving Langmuir, an American scientist in order to explain the stability of transition metals and the organometallic compounds they form. The law is based on the fact that there are 2 s electrons, 6 p electrons, and 10 d electrons in the valence shell of transition elements, for a total of 18 electrons that can be either bonding or non-bonding. This corresponds to nine molecular orbitals that are either metal-ligand bonding or non-bonding when these nine atomic orbitals are combined with ligand orbitals.

There are two popular procedures for electron counting: neutral atom and oxidation state method. It is necessary to know how many electrons each ligand in a complex provides to the metal in order to apply either electron counting approach. The neutral atom method is generally considered to be of high preference as it doesn’t require the correct assignment of oxidation state.

According to this rule in metal carbonyls, the sum of the metal atom’s valence electrons and the electrons provided by the CO ligand is equal to 18. Carbonyl compounds that follow the 18 electron rule are stable, while those that do not follow it are unstable and hence do not exist. The number of outer electrons of the central atoms of the polynuclear metal carbonyls can be calculated by the following rules:

For each metal atom, the number of valence electrons is added.
In a metal-metal bond, the electron should be assigned homolytically between the two metals. As a result, each M-M bond serves as an electron donor.
The terminal carbonyl group is a two-electron donor to a metal atom, while doubly bridging carbonyl or ketonic carbonyl groups give one electron.
Because the number of outside electrons is unaffected by tautomerism, if two isomers (bridge and non-bridge) occur as a result of terminal bridging tautomerism of the carbonyl group, the total number of outer electrons in both cases should be 18.

Examples of 18 electron rule

EAN rule vs 18 electron rule

Applications of 18 electron rule.

In the determination of the total number of metal-metal bonds
Used to Predict the stability of various organometallic compounds.
To know the reactivity of transition elements.
In the determination of the formula of organometallic compounds.

Limitations of 18 Electron Rule

Some of the major limitations of the 18 electron rules are:

16 electron compounds (both high spin octahedral and low spin square planar) fail to obey this rule.
High spin compounds usually do not follow this rule as it lacks vacant orbitals in order to gain electrons in their valence shell.
The metal complexes containing bulky ligands violate the 18 electron rule by interfering with the ligands for bonding.
𝛑-donating ligands do not follow the 18 electron rule.
When an organometallic compound consists of more than 6 metal atoms, the 18 electron rule does not apply.

18 Electron Rule Video

F.A. Cotton, G. Wilkinson, C.A. Murillo, and Manfred Bochmann Advanced Inorganic Chemistry , (6th Edition), John Wiley and Sons, 1999.
Huheey, James E, Ellen A. Keiter, and Richard L. Keiter. Inorganic Chemistry: Principles of Structure and Reactivity . New York, NY: HarperCollins College Publishers, 1993. Print.

Share this to:

Tags: 18 electron rule , 18 electron rule calculation , 18 electron rule definition , 18 electron rule examples , 18 electron rule table , 18 electron rule video , 18 electrons rule , applications of 18 electron rule , EAN rule vs 18 electron rule , examples of 18 electron rule , how to calculate 18 electron rule , limitations of 18 electron rule , the 18 electron rule , what is 18 electron rule

Balancing Redox Equations by Oxidation Number method

Lead: Properties, 7 Important Uses, Health Effects and Symptoms

Zinc – Chemistry, Deficiency, Side Effects, and its 4 important Health Benefits

Group 13 Elements: Boron Family- Easy Explanation

What is Activated complex? Easy Explanation

Ortho hydrogen and Para Hydrogen: Difference, interconversion

One Response

Excellent Explanation, easy to understand, and easy notes. Thanks

18 Electron Rule

The 18 Electron Rule is similar to the octet and duplet rules , as it is used to predict stability.

There are two 18 electron rules to be precise; one is applicable to the transition elements and another is for organometallic compounds . Though these 18 electron rules are different in their areas of application, their underlying theory and purpose are almost the same.

This rule was first proposed by the American chemist, Irving Langmuir . He proposed this rule in order to extend the Lewis static-atom model further than Argon in the periodic table.

Irving Langmuir(1881 - 1957) proposed 18 electron rule.

Later a new method to predict the stabilities of organometallic compounds was proposed by Nevil Sidgwick , called the Effective Atomic Number rule (EAN).

Due to this new EAN rule Irving’s 18 electron rule was less used by other scientists for a while. But later many reverted to the 18 electron rule as the EAN rule had different effective atomic numbers for every period of the transition group for a compound to be stable. Whereas the 18 electron rule is more like octet rule which can be applied to the whole group with the same numerical value.

18 Electron Rule Explained

The 18 electron rule states that,

For a transition element to be stable it needs to have 18 electrons in its valence shell so that they have the configuration of an inert gas, and that they form chemical bonds in order to attain this state.

This rule was proposed in order to explain the stability of transition metals and the organometallic compounds which they form.

The law is based on the fact that, in the valence shell of transition elements the total number of electrons is 2 s electrons, 6 p electrons and 10 d electrons making a total of 18 electrons.

Though this rule is often called a Chemical Rule of Thumb , transition elements often do not follow this rule .

Due to this fact, a condition called duodectet rule arises. Where the stability is determined by 12 electrons in the valence shell rather than 18 electrons. This condition arises due to the high energy and more diffuse p-orbitals which take part in a reaction only under specific conditions.

Effectively, the 12 and 18 electron rules describe the lower and upper bounds of valence electrons for a stable organometallic compound.

Though this rule just gives a bound on the maximum valence electrons of a transition element, it is also used to predict the stability of an organometallic compound and reactivity of a transition element.

Elements with valence electrons close to 18 are more reactive, so that they can achieve 18 electrons. The compounds with 18 electrons around their central metal atom are often relatively more stable than the others.

Limitations of 18 Electron Rule

There are many elements and compounds which do not follow the 18 electron rule as mentioned above.

16 Electron Compounds: The main group which do not follow this rule are those compounds which are called 16 electron compounds. There are two types of 16 electron compounds, high spin which are octahedral and low spin which are square planar. The low spin 16 electron compounds are relatively more stable due to their low energy bonding orbitals, due to which they do not follow this rule.

Bulky Ligands: The other group of compounds which commonly violate the rule are those with bulky ligands. The bulky ligands present in the compound block the participation of all the orbitals in bonding by hindering the approach of other ligands for bonding.
High Spin Compounds: High spin compounds often do not have enough vacant orbitals for accepting enough electron pairs from ligands to gain 18 electrons in their valence shells.
Higher Electron Compounds: There are compounds with electrons more than 18 in their valence shell after bonding. This usually happens when an element tries to balance its positive charge by gaining electrons from ligands, and sometimes it ends up with more than 18 electrons. This also happens when chelating(forming of rings) stabilises the molecule more than the rule .
?-donating Ligands: The ligands with lone-pairs on the coordinating atom stabilise unsaturated compounds. These ligands are called ?-donating ligands and hence the compound does not follow the 18 electron rule.
Other Block Elements: This rule is only applicable to transition elements and cannot be applied to find the stability and reactivity of elements of s- and p-blocks , as they do not have d-orbital in their valence shell to gain 18 electrons. It is not applicable even to f-block elements.
Multiple Metal Atoms: When there are more than 6 metal atoms in an organometallic compound the 18 electron rule is not obeyed by it.

Applications of 18 Electron Rule

Predicts the stability of various organometallic compounds.
Predicts the reactivity of transition elements.
Used to predict and refine the formulas of various complex compounds, especially organometallic compounds.
Used to predict the existence of metal-metal bonds in complexes.
Total number of metal-metal bonds in an element(N), \(N = \frac{(n*18)-A}{2}\) Here, \(n\) is the number of metal atoms in the complex. \(A\) is the total valence electrons (TVE) of the complex. (which is sum of valence electrons of the metal and the electrons gained from each ligand)

Question 1. Give examples of compounds that follow the 18 electron rule.

Answer. [Co(NH 3 ) 6 ]Cl 3 , Mo(CO) 6 and [Fe(CN) 6 ] 4- .

Question 2. Find the number of metal-metal bonds in the compounds:

Fe 3 (CO) 12
Co 4 (CO) 12

Answer. 1. Fe 3 (CO) 12 Here, the number of metal atoms(\(n\)) = 3 Total valence electrons(\(A\)) = 48

Then, \(N = \frac{(n*18)-A}{2} = \frac{(3*18)-48}{2} = 3\)

2. Co 4 (CO) 12 Here, the number of metal atoms(\(n\)) = 4 Total valence electrons(\(A\)) = 60

Then, \(N = \frac{(n*18)-A}{2} = \frac{(4*18)-60}{2} = 6\)

The 18 electron rule is a rule which the transition elements follow when forming bonds and also when forming complex compounds. They try to attain the inert gas configuration in their valence shell by forming bonds and complexes, hence following the 18 electron rule.

No, this rule can only be applied to transition elements and their complexes because they have s-, p- and d-orbitals, whereas p-block elements only have s- and p-orbitals in their valence shells.

The rule fails due to various reasons: a) bulky ligands b) high spin compounds c) multiple metal atoms d) other block elements e) compounds with more than 18 electrons due to stability reasons

The 18 electron rule and EAN rule are very similar but they are not the same as the EAN value of stable complexes changes with period(i.e. different for each period of the periodic table), whereas that value for the 18 electron rule is the same for the whole block of transition elements.

About The Author

The 18-electron rule and electron counting in transition metal compounds: theory and application

Lecture Text
Published: 05 March 2015
Volume 1 , article number 10 , ( 2015 )

Cite this article

Seth C. Rasmussen 1

59k Accesses

27 Citations

3 Altmetric

Explore all metrics

The 18-electron rule and the corresponding methods for counting the total valence electrons of transition metal complexes are among the most useful basic tools in modern inorganic chemistry, particularly in its application to organometallic species. While in its simplest representation, the 18-electron rule is explained in that a closed, stable noble gas configuration of ns 2 ( n -1) d 10 np 6 is achieved with 18 valence electrons, this does not adequately explain the trends and exceptions seen in practice. As such, this report presents a deeper discussion of the 18-electron rule via molecular orbital models, stressing the roles of both σ- and π-bonding effects. This discussion thus aims to provide a better understanding of the relationship between electron count and stability, while also illustrating which factors can determine adherence (or not) to this commonly utilized rule. Lastly, the two common methods for electron counting (ionic and covalent models) are also presented with practical examples to provide the complete ability to apply the 18-electron rule.

Computational Versus Experimental Spectroscopy for Transition Metals

Periodic Trends Revealed by Photoelectron Studies of Transition Metal and Lanthanide Compounds

Non-covalent interactions in selected transition metal complexes.

Avoid common mistakes on your manuscript.

Introduction

The 18-electron rule and the corresponding methods for determining the total number of valence electrons in metal compounds, commonly referred to as ‘electron counting’, are among the most useful basic tools in modern inorganic chemistry, particularly in its application to organometallic species. Not only can it be a predictive tool for evaluating the stability of some inorganic complexes, but can also be used to predict potential formulas of stable compounds. In addition, changes in the electron count of metal complexes during chemical processes can be a critical factor in determining mechanistic details of reaction pathways.

Historian William B. Jensen has traced the origins of the modern 18-electron rule to 1921 [ 1 ], when Irving Langmuir (1881–1957) [ 2 ] of the General Electric Company (Fig. 1 ) presented new models of valence, in an attempt to extend the Lewis static-atom model to cases not adequately explained by “octet theory” (i.e., the modern “octet rule”) [ 3 ]. In this early work, Langmuir derived an equation which related the number of shared (i.e., bonding) electrons or the covalence ( v c ) of a given atom in a compound to the difference between the number of valence electrons ( e ) in the isolated neutral atom and the number of valence electrons ( s ) after formation of the compound:

Irving Langmuir (1881–1957) [Edgar Fahs Smith Collection, Kislak Center for Special Collections, Rare Books and Manuscripts, University of Pennsylvania]

For any complete compound, s = 2, 8, 18, or 32. As such, the value of s corresponds to complete closed shell electron configurations and would correspond to the normal 8 for compounds of p -block elements as illustrated by the octet rule. Extending this model beyond the octet, however, leads to s = 18 for compounds of d -block elements and s = 32 for compounds f -block elements. Thus, for the d -block elements, a simple algebraic rearrangement leads to the relationship

which states that the sum of the metal valence electrons and the bonding electrons contributed by the ligands equals a total of 18 valence electrons. Langmuir then illustrated how the metal carbonyl compounds Ni(CO) 4 , Fe(CO) 5 , and Mo(CO) 6 all exhibited structures consistent with those predicted by this relationship [ 3 , 4 ].

An alternative electron count model, known as the effective atomic number (EAN) rule, was introduced in 1927 by Nevil Sidgwick (1873–1952) [ 5 ] of Oxford University [ 1 , 4 , 6 , 7 ]. Like the Langmuir model, stability was assumed to be dependent on obtaining a noble gas configuration for the central atom. In contrast, however, the EAN of a compound was analogous to the atomic number of an atom and thus focused not just on the number of valence-shell electrons, but the total electron count of the compound’s central atom. Thus, for transition metals, the EAN rule was said to be obeyed when d -block compounds obtained EAN values equal to the total electron configurations of noble gases Kr, Xe, and Rn (i.e. 36, 54, or 86) [ 7 ]. For the transition metals, attainment of an 18-electron valence configuration would therefore be equivalent to attaining the total electron count or EAN of the nearest noble gas [ 1 ].

As detailed by Jensen [ 1 ], there was a reversion to the earlier approach of Langmuir by the late 1960s. This was most likely due to the fact that Sidgwick’s model includes both the valence and core electrons, thus resulting in a different electron count in relation to stability for each row of the d -block. In contrast, Langmuir’s procedure, like the octet rule, has the advantage of using a single valence electron count for the three rows of the transition metals, thus eliminating the need to remember a different EAN value for each of the corresponding noble gases [ 1 , 6 ]. Another factor contributing to this shift in approach could also have been a paper by Craig and Doggett published in 1963 that tried to present a theoretical basis for Sidgwick’s model, which they referred to as the “rare-gas rule” [ 8 ]. In this treatment, they began with the full electron count model, but quickly refocused the discussion to present the work relative to the 18 valence electrons of the d -block elements.

Overall, the common aspects of the Langmuir and Sidgwick models relating to the d -block can be combined to make the general statement that when the metal of a complex obtains an outershell configuration of ns 2 ( n -1) d 10 np 6 , the valence orbitals contain 18 electrons and a closed, stable configuration is achieved. This basic relationship is commonly referred to as the “18-electron rule”, which has become a guiding principle of inorganic chemistry, particularly in organometallic chemistry [ 8 – 10 ]. It should be pointed out that some use the terms “18-electron rule” and “effective atomic number (or EAN) rule” interchangeably [ 9 , 11 – 13 ]. However, as the discussion above correctly demonstrates, the 18-electron rule is consistent with the EAN rule and may thus be considered a component or outcome of Sidgwick’s model, but these terms are not synonymous. In addition to the different emphasis on valence versus total electrons, the 18-electron rule is strictly limited to the d -block elements, while the EAN rule can be applied to all elements of the periodic table.

Much like the more common octet rule, the 18-electron rule is not always strictly obeyed and is subject to a number of apparent exceptions [ 10 ]. Thus, while this tool is extremely useful in predicting stability, examples of stable metal complexes with more or less than 18 valence electrons are also fairly common [ 1 , 6 , 9 ]. As such, the goal of this report is to present a deeper discussion of the 18-electron rule to better understand the relationship between electron count and stability, while also illustrating which factors can determine adherence (or not) to this commonly utilized rule.

18-Electron rule in terms of molecular orbital models, part I: simple view

Further insight into the connection between the stability of metal compounds and the 18-electron rule can be gained by addressing this relationship in terms of the molecular orbital (MO) description of bonding in metal complexes. As a starting point, let us consider just the simple σ bonding between a metal and six identical σ-donor ligands to generate an octahedral metal complex. Linear combination of the ligand orbitals with the s , p , and d atomic orbitals of the metal results in the formation of six bonding MOs ( a 1g , t 1u , and e g ) and six corresponding antibonding MOs, as illustrated in Fig. 2 . As there are a total of nine metal-based atomic orbitals and only six ligand-based donor orbitals, this results in three d orbitals remaining as non-bonding t 2 g MOs.

Nevil Sidgwick (1873–1952) [Reproduced from [ 5 ]; Courtesy of JSTOR]

For such an octahedral complex, the most stable arrangement will be that in which all of the bonding MOs ( a 1g , t 1u , and e g ) are fully occupied and the anti-bonding MOs are empty. Occupation of the six bonding MOs, as well as the three nonbonding MOs, would thus require 18 electrons, as predicted by the 18-electron rule [ 4 , 11 ]. As such, complexes will therefore tend to adhere to the rule if the energetic separation between the non-bonding t 2 g and anti-bonding e g MOs (commonly referred to as Δ O , Fig. 3 ) is large [ 6 , 12 ]. Here, as Δ O increases, the e g MOs are destabilized and ultimately reside at higher energies, thus making occupation of these anti-bonding orbitals unfavorable.

MO diagram for an octahedral metal complex (σ bonding only; for simplicity, degenerate orbitals are displayed as stacked sets)

The value of Δ O depends on both the central metal and the specific ligands involved. In terms of the metal, Δ O tends to increase down any particular periodic group (i.e. 3 d < 4 d < 5 d ) and for the same metal, it tends to increase with the metal charge (i.e. M 2+ < M 3+ < M 4+ ) [ 9 , 14 , 15 ]. As such, complexes of second and third row transition metals are typically not found to have more than 18 electrons [ 4 ].

The effect of the associated ligands is represented by the spectrochemical series (Fig. 4 ) [ 14 – 17 ], which orders the ligands from the smallest value of Δ O to the largest. In the most general sense, the order within the spectrochemical series is indicative of the ligand σ-donor strength. However, ligands low on the spectrochemical series also tend to exhibit π-donor characteristics, while those high on the series are typically strong π-accepting ligands. While these σ and π effects are typically additive, the π effects can sometimes play a more critical role than the simple σ-donor strength. The ligands within the series are generally ordered according to the periodic group of the ligand donor atom. As such, group 17 (i.e., the halogens) are low on the series, while group 14 are high on the spectrochemical series. Groups 15 and 16 then fall between these two extremes, as can be seen in Fig. 4 [ 14 ].

Spectrochemical series of ligands

Although the factors discussed above are a good start to understanding the working parameters of the 18-electron rule, it does not adequately explain the various limitations of this common rule. While not a complete list, the most common limitations can be given as:

This rule works best for low-valent (oxidation state ≤ 2) metal complexes, but many high valent metal complexes also work.

This rule works best for complexes containing π-acceptor ligands.

Square planar complexes are generally stable as 16-electron species.

There are always exceptions to the rule.

To understand the basis of these common limitations, it will be necessary to consider a number of additional factors.

18-Electron rule in terms of molecular orbital models, part II: more detailed view

In the initial treatment above, only σ donor interactions were considered and any potential π interactions were not taken into account. To deepen our insight into the factors that contribute to the 18-electron rule, it is now required to complicate our bonding picture by including any potential π-donor or π-acceptor contributions from the organic ligands. As outlined in Fig. 5 , the initial splitting of the d orbitals from the σ donors (i.e., the boxed orbitals in Figs. 3 , 5 ) is further modified via interactions between π ligands and the metal t 2 g orbitals, which are formally nonbonding in terms of the previous σ interactions. In the case of π-donor contributions, the ligand π-orbitals are filled and lower in energy than the metal t 2 g . Mixing of these orbitals with the metal t 2 g orbitals thus results in production of π-bonding metal–ligand MOs, while the t 2 g orbitals take on π* anti-bonding character, resulting in their destabilization and a decrease in Δ O (Fig. 5 ) [ 12 , 16 , 18 ].

Effect of π ligands on the MO diagram for octahedral metal complexes

Things are a bit different in the case of π-acceptor contributions. In this case, the ligand orbitals interacting with the metal are empty π*-orbitals which are high in energy (Fig. 5 ). As such, mixing of these high-lying orbitals with the metal t 2 g orbitals results in stabilization of the metal orbitals, that leads to an increase in the value of Δ O . Here, the stabilized t 2 g orbitals are now formally π-bonding in nature, while the e g orbitals retain their σ* anti-bonding character [ 12 , 16 , 18 , 19 ].

Transition metal complexes can be divided into three groups [ 9 , 18 ], which will be referred to here as Class I, Class II, and Class III. The first of these groups, Class I, are complexes with a relatively small Δ O and generally consist of first row transition metals with ligands low on the spectrochemical series (i.e., weak σ donors or π donors). If the bonding in these complexes is only weak σ bonding, then the metal t 2 g orbitals are formally nonbonding and can thus be either empty or filled without negatively affecting the extent of metal–ligand bonding. Here, the relatively weak σ bonding also results in the e g orbitals being low in energy and only weakly anti-bonding. As a result, the occupation of these MOs can also occur with little negative effect. Ligands with π-donor character, however, contribute to π bonding which results in the t 2 g orbitals taking on anti-bonding character as shown in Fig. 5 , and the occupation of these MOs is then not favored. It should be pointed out that strong π-donor ligands not only result in the t 2 g becoming anti-bonding, but also generate complementary filled π-donor bonding orbitals localized largely on the ligands. In this case, occupation of these π-bonding orbitals while keeping the t 2 g orbitals unoccupied maintains an 18 electron count [ 4 ]. For the most part, however, these complexes typically do not exhibit π-bonding of this magnitude and σ-bonding dominates the characteristics of these metal compounds. As such, the 18-electron rule has no special significance for the bulk of this class of complexes [ 12 ] and stable Class I species are possible with electron counts of 12–22 electrons depending on the extent that the t 2 g and e g orbitals are occupied [ 6 , 9 , 18 ].

Class II complexes have a larger Δ O and generally contain second and third row transition metals (especially in higher oxidation states) with σ ligands intermediate to high on the spectrochemical series. For this class, there is intermediate to strong σ bonding, but no π bonding. As such, the t 2 g orbitals are still nonbonding and can thus be either empty or filled. The relatively strong σ bonding, however, raises the energy of the e g orbitals and strengthens their anti-bonding nature, therefore making the occupation of these MOs disfavored. As a result, stable Class II complexes are possible with electron counts of 12–18 electrons, depending on the occupation of the t 2 g orbitals [ 6 , 9 , 18 ]. Class II complexes can follow the 18-electron rule, but a fair number do not.

The final group, Class III, is made up of complexes exhibiting the largest Δ O . These complexes generally consist of low oxidation state metals with ligands high on the spectrochemical series, particularly π-acceptor ligands. The metal–ligand interactions here constitute intermediate to strong σ bonding, as well as significant π back-bonding into the empty π* orbitals of any π-acceptor ligands. As such, the t 2 g orbitals now have π-bonding character and need to be filled for complex stability. In addition, the e g orbitals are still strongly anti-bonding and thus, the occupation of these MOs is again not favored. As a result, stable Class III complexes will always have the t 2 g orbitals occupied and the e g orbitals empty, resulting in 18 valence electrons and strict adherence to the 18-electron rule [ 9 , 18 ]. As almost all organometallic compounds of the d -block elements belong to Class III, the 18-electron rule becomes a very powerful and reliable predictive tool for organometallic chemistry.

Other compound geometries

Although the argument used above was developed using the example of an octahedral complex, precisely similar results are obtained for other coordination numbers. Generally it can be said that if the coordination number (CN) is greater than four, then [CN-4] d orbitals are required in addition to the metal s and p orbitals to form MOs with the corresponding ligand σ orbitals. As a result, this will result in [CN-4] low-lying anti-bonding orbitals and [9-CN] nonbonding orbitals. The energetic separation between these two general sets of orbitals will largely depend on the strength of the σ donors as discussed above [ 9 ].

This general relationship is illustrated for CN = 6 for the octahedral geometry given in Fig. 3 , but can also be shown for CN = 5 as given for the trigonal bipyramidal geometry shown in Fig. 6 . As with the octahedral example, filling the bonding and nonbonding MOs here would correspond to 18 electrons and be consistent with the 18-electron rule. Effects on adherence to this rule based on σ-donor strength and any contribution of π-bonding would again mirror those previously discussed for the octahedral case [ 4 , 19 ].

MO diagram for a trigonal bipyrimidal metal complex (σ bonding only)

The situation is more complicated for tetrahedral complexes (CN = 4) [ 6 , 9 , 19 ]. In this case, bonding with the four σ-donors can be proposed using either d 3 s or sp 3 sets of metal orbitals, although in practice a combination of both sets are used and the t 2 orbitals of the complex will involve both d and p orbitals from the metal (Fig. 7 ) [ 9 ]. As the resulting four bonding MOs can only accommodate a total of eight electrons, the remaining ten electrons must occupy the e and t 2 sets of d orbitals, which are formally nonbonding and at least partially antibonding [ 6 ]. The reduced number of ligands in comparison to the previous octahedral case results in a smaller energetic separation between these two sets of orbitals (Δ T ) and thus, there is little barrier to population of the t 2 orbitals [ 9 ].

MO diagram for a tetrahedral metal complex (σ bonding only)

Because of these factors, the 18-electron rule is only obeyed in tetrahedral complexes of π-acceptor ligands. In these cases, both the e and t 2 sets of d orbitals donate electrons to the empty π* orbitals of the ligands, resulting in both sets of orbitals becoming bonding in nature. In addition, MO calculations have shown that these π-bonding interactions contribute more to the metal–ligand bonding than the corresponding σ-donation from the ligand [ 19 , 20 ].

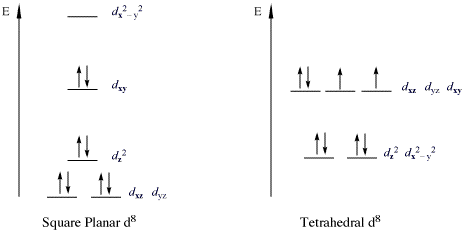
As stated in the general limitations above, the one major geometry that does not obey the 18-electron rule is that of four-coordinate, square planar complexes [ 4 , 6 , 9 , 19 ]. As shown in Fig. 8 , the metal-based orbitals are split into four sets, with the majority being nonbonding or having some partial bonding character. The remaining orbital (corresponding to the \(d_{{x^{ 2} - y^{ 2} }}\) ) is anti-bonding and is fairly high in energy [ 19 ]. For these complexes, filling the four low-lying σ bonding MOs requires 8 electrons and population of the metal-based bonding and nonbonding orbitals requires another 8 electrons. Any additional electrons would then populate the \(d_{{x^{ 2} - y^{ 2} }}\) ( b 1 g ) σ* orbital, resulting in a decrease in stability. As such, a total of 16 electrons represent the maximum population for a stable square planar complex [ 9 , 19 ]. This is sometimes referred to as the “16-electron rule” [ 6 ] or added to the 18-electron rule to become the “16 and 18 electron rule” [ 10 ], but most often is just recognized as the most consistent exception to the 18-electron rule.

MO diagram for a square planar metal complex (σ bonding only)

Electron counting methods

By counting the number of valence electrons surrounding a metal in a particular complex formula, it is possible not only to predict whether the complex should be stable, but in some cases give details concerning structural aspects of the complex (i.e., ligand binding modes, the presence of metal–metal bonds, etc.) [ 6 ]. Of course, as previously noted, while the electron count can be extremely useful in predicting stability, examples of stable metal complexes with more or less than 18 valence electrons are also fairly common [ 1 , 6 , 9 ]. Nevertheless, the ability to correctly determine the number of valence electrons from the complex formula is a critical step in the application of the 18-electron rule.

There are two methods for electron counting, the ionic model and the covalent model, each with its own advantages and limitations. Both models include the total valence electrons of the metal and those donated by the ligands, but differ in the way the division of electrons between the metal and the ligands are viewed. Either method can be used successfully and should provide the same answer, providing that care is taken not to mix aspects of the two models.

In the ionic model, the metal is treated as a cationic center and the ligands carry the charge associated with their non-coordinated state. As a consequence, this model requires that we correctly assign the metal a formal oxidation state. This in turn requires that we also know the formal charge on all the corresponding ligands. However, this model has the advantage that it treats most metal–ligand bonds as coordinate covalent (or dative) bonds which means each bond donates two electrons to the total electron count. The formal charge and corresponding electrons donating by a significant number of common ligands under the ionic model are given in Table 1 .

In contrast to the ionic model, the covalent model treats the metal as a neutral center and all ligands are likewise treated as neutral species. While this does not affect the way that neutral ligands are counted, ligands that would be typically viewed as charged are now treated as radical species for the electron count. This model removes the need to determine the formal oxidation state of the metal, but is somewhat awkward for anionic ligands such as the halides. However, this model is much more realistic for many organometallic ligands, such as the simple alkyls. The corresponding electrons donated under the covalent model are given for all common ligands in Table 1 .

The application of both models is illustrated via two examples given in Fig. 9 . The first example, [RhCl 2 (bpy) 2 ] + , represents a typical coordination complex including 2,2′-bipyridine (bpy) and chloride ligands. Under the ionic model, the combination of the overall 1+ charge and the two anionic ligands allows us to assign for formal 3+ oxidation state to the rhodium center. As such, this d 6 metal contributes six electrons, while each bpy and chloride ligand contributes four and two electrons, respectively, the sum of which gives the expected 18 electrons of a stable species.

Examples of electron counting via the ionic and covalent models

Under the covalent model, the rhodium of the same complex is treated as Rh(0) and is thus a d 9 metal, contributing nine electrons to the electron count. As bpy is a neutral ligand, it is treated the same under both models and is thus a four-electron donor as before. Under the covalent model, however, the anionic chloride ligand is treated as a neutral radical and is thus a one-electron donor. The sum thus comes to 19 electrons, but as all components have been treated as neutral species, it is necessary to subtract one electron to account for the overall positive charge of the cationic complex. Thus, the total electron count comes to 18 electrons and this is in complete agreement with the count from the ionic model.

In the second example, [Ni(Et) 2 (CO) 2 ], represents a typical organometallic complex including both alkyl (ethyl) and carbonyl ligands. Under the ionic model, the alkyl ligands are treated as anionic ligands and thus the nickel center is assigned a formal 2+ oxidation state to give an overall neutral complex. As such, this d 8 metal contributes eight electrons, while both the alkyl and carbonyl ligands contribute two electrons each, the sum of which gives the expected 16 electrons for a square planar species.

Under the covalent model, the nickel center is given a formal charge of zero and is thus a d 10 metal, contributing ten electrons to the electron count. The neutral carbonyl ligand is treated as before and is therefore still a two-electron donor. Under the covalent model, however, the ethyl ligands are now neutral radicals and are thus one-electron donors. As a result, the total electron count again comes to 16 electrons and is in complete agreement with the count from the ionic model. While the first example is more simply treated using the ionic model, this second example is more straight-forward under the covalent model. As such, both models have their benefits providing each are used independently.

Some additional structural factors that need to be considered are cases of bridging ligands and metal–metal bonding, both of which are somewhat common in organometallic species. A common class of bridging ligands are anionic species containing multiple lone pairs on the donor atom (halogens, RS − , RO − , R 2 P − , etc.). In this case, the ligand is able to utilize two different lone pairs to simultaneously donate to two separate metal centers. For such ligands, the first bond is treated exactly the same as a terminal anionic ligand and is thus a two-electron donor under the ionic model and a one-electron donor for the covalent model. As the second metal–ligand bond is via a full lone-pair under either model, this is treated the same as a neutral ligand and is thus a consistent two-electron donor to the second metal.

Two additional types of bridging ligands are bridging hydrides and bridging carbonyls, both of which only have a single lone-pair to donate. In the more simplistic case of the carbonyl, the donated electrons are split evenly between the two metal centers and this ligand is thus a one-electron donor to each metal under both models. The treatment of bridging hydrides, however, is a bit more complicated. Here the first bond is treated in the same way as a terminal hydride and is thus either a one- or two-electron donor. The second bond, however, is typically described as a donation of the first σ metal–ligand bond to the second metal. As such, it is treated as a two-electron donor to the second metal. Of course, this means that we are including the same two hydride-electrons in the electron count of both metals. Illustrations of electron counting examples that include all three types of bridging ligands are given in Fig. 10 .

Examples of bridging ligands in electron counting

Finally, metal–metal bonds are treated as classically covalent interactions under both models and thus always contribute one electron to the total electron count. In this case, the donated electron comes from the valence electrons of the second metal center, which means that the electron is technically included in the electron count for both metals. Examples of electron counting that include metal–metal bonds are given in Fig. 10 .

Adherence to the 18-electron count is strongest for metal complexes that include strong π-bonding. As such examples most commonly occur with π-acceptor ligands, strong π-bonding interactions require low-valent metals to provide sufficient electron density on the metal for back-donation to the empty ligand π* orbitals. Metal complexes with strong σ-donors, but no π-bonding can follow the 18-electron rule, but such complexes can exhibit stability with fewer than 18 valence electrons. While these relationships are not limited to octahedral geometries and hold true for many other common metal geometries, four-coordinate square planar complexes do not follow the 18-electron rule and are found to be stable with only 16 electrons. Lastly, proficient application of the 18-electron rule requires the ability to correctly count the total valence electrons for a given metal complex. This can be accomplished using one of two electron counting models (ionic or covalent), providing the chosen model is utilized exclusively.

Jensen WB (2005) The origin of the 18-electron rule. J Chem Educ 82:28

Article CAS Google Scholar

Rideal E (1959) Langmuir memorial lecture. Proc Chem Soc 1959:80

Google Scholar

Langmuir I (1921) Types of Valence. Science 54:59–67

Mingos DMP (2004) Complementary spherical electron density model and its implications for the 18 electron rule. J Organomet Chem 689:4420–4436

Tizard HT (1954) Nevil Vincent Sidgwick 1873–1952. Obit Not Fellows R Soc 9:236

Huheey JE, Keiter EA, Keiter RL (1993) Inorganic chemistry, principles of structure and reactivity, 4th edn. HarperCollins, New York, pp 624–630

Sidgwick NV (1927) The electronic theory of valency. Clarendon Press, Oxford, pp 163–184

Craig DP, Doggett G (1963) Theoretical basis of the “rare-gas rule”. J Chem Soc 1963:4189–4198

Mitchell PR, Parish RV (1969) The eighteen-electron rule. J Chem Educ 46:811–814

Tolman CA (1972) The 16 and 18 electron rule in organometallic chemistry and homogeneous catalysis. Chem Soc Rev 1:337–353

Collman JP, Hegedus LS, Norton JR, Finke RG (1987) Principles and applications of organotransition metal chemistry. University Science Books, Mill Valley, pp 22–34

Powell P (1988) Principles of organometallic chemistry, 2nd edn. Chapman and Hall, New York, pp 148–152

Book Google Scholar

Mingos DMP (1998) Essential trends in inorganic chemistry. Oxford University Press, Oxford, pp 297–309

Wulfsberg G (2000) Inorganic Chemistry. University Science Books, Sausalito, pp 367–374

Huheey JE, Keiter EA, Keiter RL (1993) Inorganic chemistry, principles of structure and reactivity, 4th edn. HarperCollins, New York, pp 404–405

Lever ABP (1968) Inorganic electronic spectroscopy. Elsevier Publishing Co., Amsterdam, pp 194–204

Osborn JA, Gillard RD, Wilkinson G (1964) J Chem Soc 1964:3168–3173

Porterfield WW (1993) Inorganic chemistry, a unified approach, 2nd edn. Academic Press Inc, San Diego, pp 604–609

Wulfsberg G (2000) Inorganic chemistry. University Science Books, Sausalito, pp 532–534

Bauschlicher CW, Bagus PS (1984) The metal-carbonyl bond in Ni(CO) 4 and Fe(CO) 5 : a clear-cut analysis. J Chem Phys 81:5889–5898

Article Google Scholar

Download references

Author information

Authors and affiliations.

Department of Chemistry and Biochemistry, North Dakota State University, NDSU Dept. 2735, P.O. Box 6050, Fargo, ND, 58108-6050, USA

Seth C. Rasmussen

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seth C. Rasmussen .

Rights and permissions

Reprints and permissions

About this article

Rasmussen, S.C. The 18-electron rule and electron counting in transition metal compounds: theory and application. ChemTexts 1 , 10 (2015). https://doi.org/10.1007/s40828-015-0010-4

Download citation

Received : 29 January 2015

Accepted : 18 February 2015

Published : 05 March 2015

DOI : https://doi.org/10.1007/s40828-015-0010-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Transition metal complexes
18-Electron rule
Electron counting
Effective atomic number (EAN) rule
Find a journal
Publish with us
Track your research

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

Chapter 6.1: The 18 Electron Rule

Last updated
Save as PDF
Page ID 290600

Kai Landskron
Lehigh University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Electron Counting In Transition Metal Complexes

In this chapter we will learn how to count valence electrons in coordination compounds. Electron counting is important because the number of electrons in a complex can tell us a lot about the stability and reactivity in a coordination compound. In addition, it allows us to predict and understand structures to a certain extent. Electron counting sounds trivial, but it is not as trivial as it seems, actually there are even two different methods for electron counting. Each method leads to the same result. Which method you prefer is “personal taste”, but each method is about equally common in the literature, so you need to know both of them.

The Neutral Atom Method

The first method is called the “neutral atom method”. As the name suggests, we will break up the complex into neutral fragments, and count the electrons that contribute to the bonding in each of the fragments. The neutral atom method is carried out according to the following three steps. First, we count the number of the valence electrons of the metal. We consider the metal as neutral atom. The number valence electrons is the same as the group number of the transition metal in the periodic table. For transition metals the group number varies from 3 to 12. In the second step, we account for the ionic charge of the complex, if the complex is not neutral. This will reduce the number of electrons for a complex cation, and increase the number of valence electrons for a complex anion. In the third step, we need to determine how many electrons are contributed by each ligand. This is the most complicated step. To determine the number of electrons must cleave each metal-ligand bond so that a ligand fragment results that is neutral. We then count the number of electrons at the ligand that contributed to the bond. The number of electrons contributed by each ligand is then summed up. This is sum is then added to the number of electrons determined by the previous steps. This is gives the overall number of valence electrons.

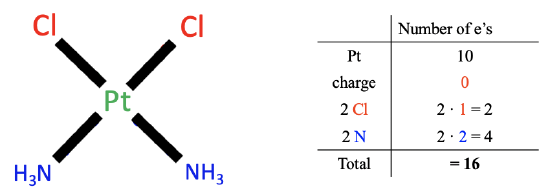
Figure \(\PageIndex{ 1}\): Example of neutral atom method

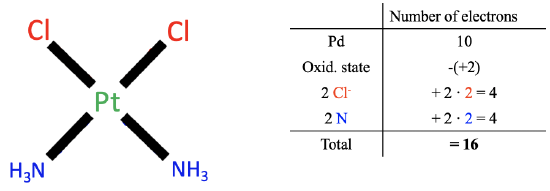
Let us apply these rules by an example, the cis-platinum complex (Figure \(\PageIndex{ 1}\) ). We first need to count the number of electrons of the metal. The metal is platinum which is located in group 10 of the periodic table. Therefore, a neutral platinum atom has ten valence electrons.

Next, we look at the charge of the complex. In this case, there is no charge, and therefore no electrons are added or subtracted.

Lastly, we count the electrons of the ligands. There are two types of ligands, the chloro-ligands and the ammine ligands. Now, our task is to cleave the Pt-ligand bond so that neutral ligand fragments result. We can see that for the chloro-ligands we must cleave the Pt-Cl bond, homoleptically, meaning in the middle, assigning one electron to the Pt and one electron to Cl, because doing so creates a neutral chlorine atom. The fact that we cleaved the bond homoleptically, means that the chloro ligand contributed one electron. Because we have two chloro ligands, there are overall two electrons.

Now, let us think about how many electrons the ammine ligands contribute. In this case we need to cleave the metal-ligand bond heteroleptically to produce a neutral ligand fragment. Both bonding electrons are assigned to the ligand. This produces a neutral NH 3 molecule. This means that each ammine ligand contributes two electrons. Overall, that makes four electrons, because we have two ammine ligands.

Finally, we need to sum up the electrons from all three steps. That is ten electrons from Pt, zero electrons due to charge, two electrons from the chloro ligands, and four electrons from the ammine ligands equaling 16 valence electrons total. This is the final result.

"Oxidation State" Method

The oxidation state method is also comprised of three steps. The first step is the same as in the neutral atom method. We determine the number of electrons of the neutral metal which the same as its group number in the periodic table. The next step is different though. It requires the determination of the oxidation state of the metal. How can we determine it? First, we cleave the metal-ligand bonds heteroleptically so that all bonding electrons are assigned to the ligands. Then we determine the charge of the ligands. Ligands can either be neutral or negatively charged. We determine the overall number of charges at the ligands. The difference between that number and the charge of the complex is the oxidation state of the metal. We either add or subtract electrons depending on the oxidation state of the metal. If the oxidation state is positive we subtract electrons, if it is negative, which is rare, then we add electrons. The third step counts the number of the electrons contributed by the ligands. Because we cleaved all bonds heteroleptically, all bonding electrons are considered to be contributed by the ligands, and we count them accordingly. Finally, we sum up the electrons of all three steps which gives the total number of electrons.

Let us apply the method to the previous example cis-platinum. Applying the first step gives us 10 valence electrons for the platinum.

Next, we need to determine the oxidation state of Pt. To do so, we must now cleave all metal-ligand bonds heteroleptically, so that all bonding electrons are assigned to the ligand. By the way, this is equivalent to saying that we treat all the bonds as dative bonds with all electrons coming from the ligands as the donors. When we do this for the chloro ligands we see that this created chloride anions with a 1- charge. Cleaving the Pt-N bonds heteroleptically leads to neutral NH 3 molecules. Therefore the overall number of charges at the ligands is 2x(-1)+2x0=-2. The charge at the complex is zero, therefore the oxidation state of Pt is 0-(-2)=+2. We must therefore subtract two electrons from the 10 electrons of the platinum.

Now we must determine the number electrons coming from the ligands. Because all bonds are considered as dative bonds, the chloro ligands contribute two electrons each, and the ammine ligands contribute two electrons each. That makes overall eight electrons.

In sum, 10 electrons from the neutral Pt atom minus two electrons due to the +2 oxidation state of Pt plus 2x2=4 electrons from Cl plus 2x2=4 electrons from NH 3 gives 16 electrons total. We can see that we have arrived at the same results as in the case of the oxidation state method.

We can discuss the advantages and disadvantages of both methods, also. The neutral atom method has the advantage that we do not have to think about charges at ligands and oxidation states. However, we have to think about how to cleave bonds to create neutral fragments. We may need to cleave bonds in an way that is not reflecting the donor-acceptor nature of a coordination compound. The oxidation method does account for the donor-acceptor nature of a coordination compound because the bonds are considered dative bonds, and the electrons are assigned to the ligands and metals accordingly. We do not need to think how to cleave bonds, because we cleave the bonds always heteroleptically. However, it requires us to think about charges at the ligands to determine oxidation states which is an additional, non-trivial step.

Counting Electrons: Ligand Contributions

The most difficult step in electron counting is usually the determination of the number of electrons a ligand provides. Therefore, let us practice this by a few examples.

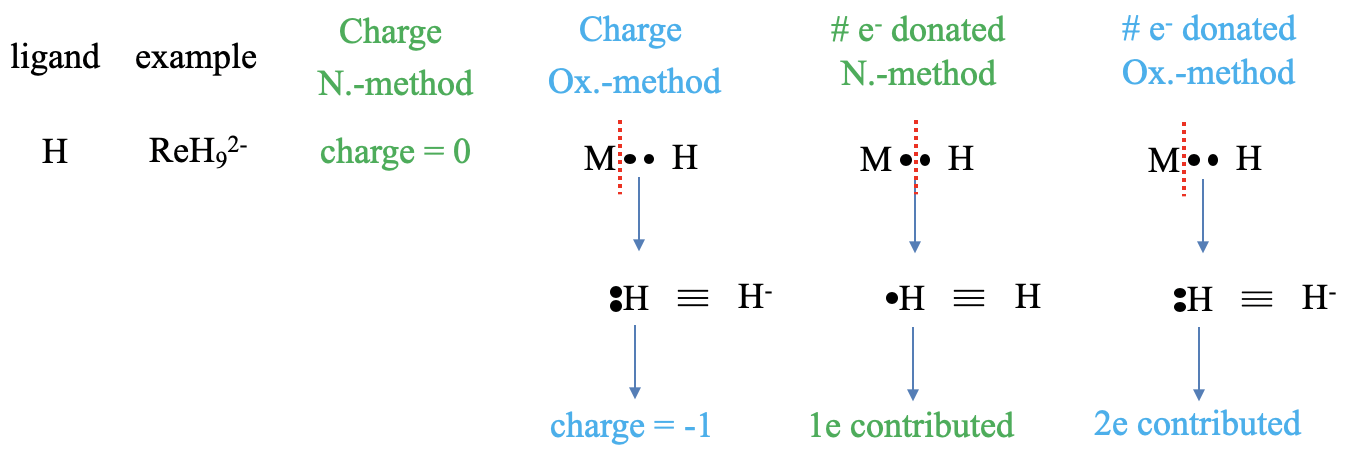
Let us first look at an hydrido ligand which is for example present in the nonahydridorhenate(2-) complex anion (Figure \(\PageIndex{ 3}\) ). What is the charge at the ligand in the two methods? In the neutral atom method, the charge is always zero, this is a no-brainer. In the case of the oxidation statement method, we need to treat the bond as a dative bond, and that means that we must cleave the bond heteroleptically, so that both bonding electrons can be assigned to the ligand. An H atom with two electrons is a hydride anion with a -1 charge. Next, let us think about the number of electrons donated. In the neutral atom method we need to produce neutral ligand fragments. To do so we must cleave the M-H bond homoleptically, because this will create a neutral hydrogen atom. How many electron will it contribute? It will contribute one electron, because we cleaved the bond homoleptically assigning only one of the two bonding electrons to H. In the oxidation state method, the hydrido ligand contributes two electrons because the bond was considered dative and therefore cleaved heteroleptically. Both bonding electrons were assigned to the ligand, therefore the ligand contributes two electrons.

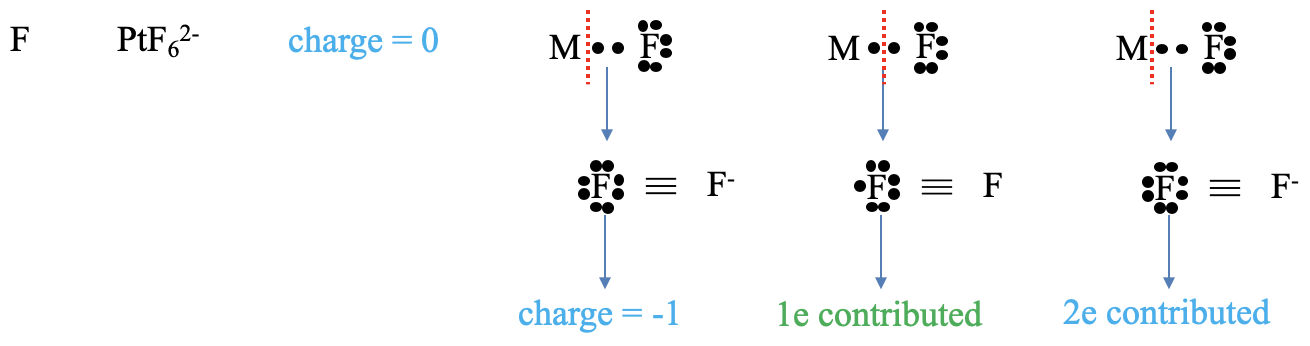
Next, let us consider a halogenide ligand (Figure \(\PageIndex{ 4}\) ). What is the charge at the ligand? For the neutral atom method, the answer is trivial, the charge is always zero. In the oxidation state method both bonding electrons in the metal-ligand bond get assigned to the ligand. This gives the ligand a -1 charge. What is the number of electrons contributed? In the neutral atom method we need to think again how to cleave the metal-ligand bond to create a neutral ligand fragment. We need to recognize that we must cleave the bond homoleptically to produce that fragment. Cleaving the bond homolopetically means that the ligand has contributed one electron. In the oxidation state method, we cleave the bond always heteroleptically so that all bonding electrons are assigned to the ligand. Thus, the ligand contributes two electrons.

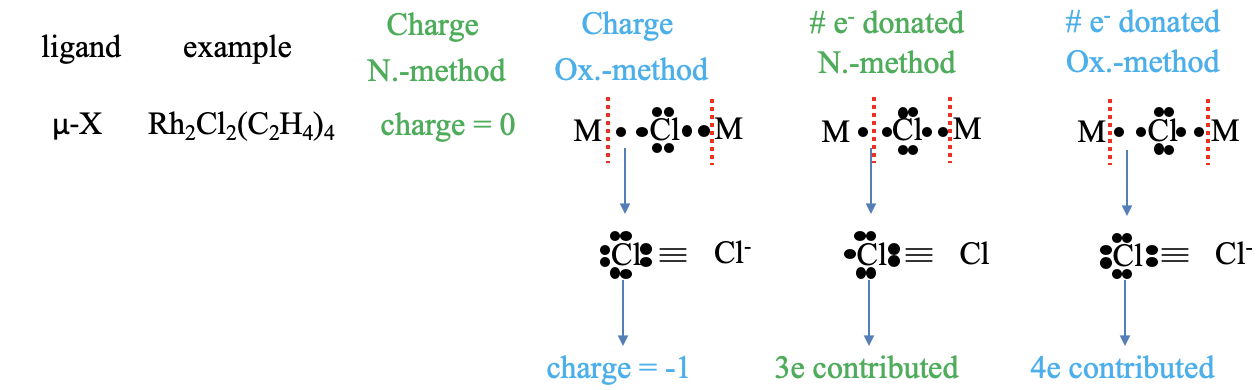
A halogenide anion as a ligand cannot only be terminal, but also bridging. An example is the μ-dichloro bis(tetraethylene rhodium(I)) complex in which two chloro-ligands bridge two rhodium atoms. What is the charge in the neutral atom method? Of course, it is zero. What is the charge in the oxidation state method? We can see that if we consider both metal-ligand bonds dative bonds, and cleave the bonds heteroleptically, that the Cl atom is surrounded by eight unshared electrons, which gives it a -1 charge. How, many electrons are contributed in the neutral atom method? To answer this question, we need to decide if we have to cleave the bonds homo- or heteroleptically to produce a neutral Cl atom. Can you see it? The answer is: We must cleave one bond homoleptically, and the other one heteroleptically. How many electrons are then contributed by the chloro ligand? It is the two electrons from the heteroleptically cleaved bond, and one electron from the homoleptically cleaved bond. So overall it is three electrons. What about the oxidation state method? In this case both bonds are cleaved heteroleptically, and this means that overall four electrons are contributed.

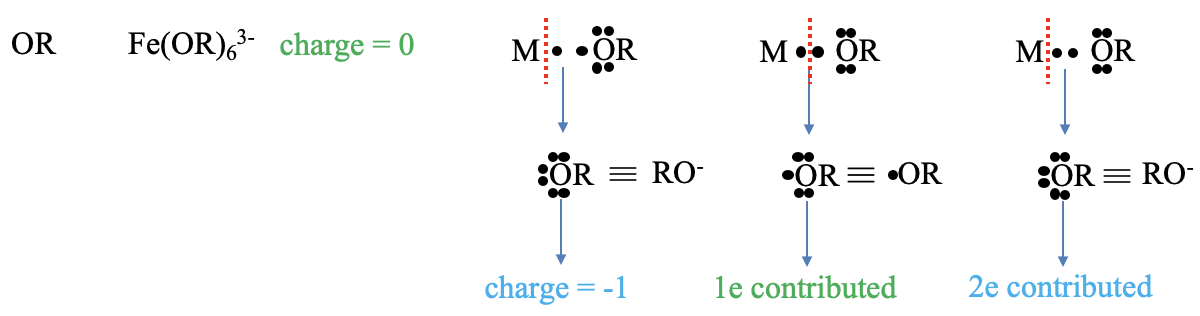
What are the charges and electrons contributed by an alkoxy ligand (OR), Figure \(\PageIndex{ 6}\) ? An example for a complex with such as ligand is hexaaphenoxy ferrate (3-). The charge according to the neutral atom method is zero. In the oxidation state method we cleave the bonds heteroleptically, and our ligand becomes an alkoxide anion. This anion has a 1- charge. How many electrons does the ligand contribute? To get a neutral fragment we must cleave the bond homoleptically. This actually produces an alkoxy radical. This radical contributes its radical electron, thus there is one contributed electron. In the oxidation state method we treat the bond as a dative bond and cleave the bond heteroleptically. Therefore two electrons are contributed according to the oxidation state method.

Next, let us apply electron counting to the carbonyl ligand. For example, five carbon monoxide molecules form an iron pentacarbonyl complex with iron. The charge at the ligand in the neutral atom method is zero. In the oxidation state method, we assign both bonding electrons to the ligand, and that produces a neutral carbon monoxide molecule. Note that the carbon atom is formally negatively charged, because it is surrounded by 5 electrons, but the oxygen atom is positively charged because it is surrounded by five electrons. So overall, the molecule is neutral. What is the number of electrons contributed in the neutral atom method? To produce a neutral ligand we must cleave the bond heteroleptically. This produces a neutral carbon monoxide molecule. Because we cleaved the bond heteroleptically, the ligand contributes two electrons. In the oxidation state method we always cleave the bonds heteroleptically, and thus two electrons come from the ligand, too.

The last ligand we discuss here is the isonitrile ligand. An example is the pentakis-(tert-butyl isonitrile) iron molecule. The charge of the ligand is zero in the neutral atom method, but what is it in the oxidation state method? Let us see what happens as we assign both bonding electrons to the ligand. We we see that the carbon is now surrounded by five electrons. Three are in the carbon-nitrogen triple bond and the other two come from the electron lone pair at the carbon atom. This means that the carbon atom has a -1 formal charge. Now, let us look at the N atom. We see that it is surrounded by four electrons, three coming from the C-N triple bond, and one from the C-R bond. That means that the N atom has a +1 charge. Overall, the molecule is neutral and does not carry a charge. What about the number of electrons contributed? We can see that we must cleave the bond heteroleptically to produce a neutral isonitrile, there are two electrons are contributed in the neutral atom method. The oxidation state method must cleave the bond heteroleptically, therefore, the number of electrons contributed is also two.

The 18 Electron Rule

Electron counting is important in the context of an important rule in coordination chemistry: The 18 electron rule. The 18 electron rule states that for d-block elements normally complexes with 18 electrons in the shell (ns 2 (n-1)d 10 np 6 configuration) are most stable. If this number is not reached, the species is coordinatively unsaturated and tends to add more ligands. It also tends to be reduced because adding electrons brings the complex to, or at least closer to 18 electrons. Coordinatively unsaturated complexes therefore tend to have a higher reactivity.

Definition: Coordinatively Unsaturated Complexes

A complex is coordinatively unsaturated when the 18 electrons are not reached in the (ns 2 (n-1)d 10 np 6 configuration) shell. It tends to add more ligands, and tends to be reduced. It is associated with higher reactivity.

If a species has more than 18 electrons it is coordinatively oversaturated and tends to lose ligands. It is usually easily oxidized. Both loss of ligands and oxidation reduces to the number of electrons to or at least closer to 18.

Definition: Coordinatively Oversaturated Complexes

A complex is coordinatively oversaturated when it has more than 18 electrons in the shell (ns 2 (n-1)d 10 np 6 configuration). It tends to lose ligands and tends to get oxidized.

The 18 electron rule has many exceptions, and therefore needs to be applied with caution. In particular, group 3, 4, and 10 complexes deviate often from the 18 electron rule.

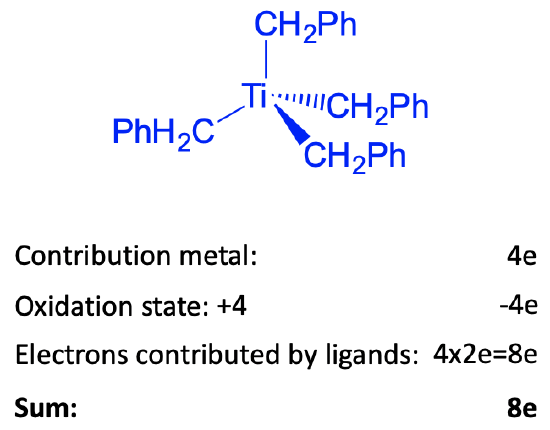
For illustration purposes, let us count the number of electrons of the tetrahedral tetrabenzyltitanium(0) complex by the oxidation state method. We could also use the neutral atom method, which would give the same results. This complex is a group 4 complex because titanium is in group 4. How many electrons will the titanium contribute? Because the number of electrons is always the same as the group number, it will contribute four electrons. Next, what is oxidation state of Ti? To determine it we must determine the charge at the ligands. To do that we cleave the bonds heteroleptically. This will give benzylate anions with -1 charge. There are four of these ions, and therefore there will be four negative charges overall. The complex is charge-neutral, and thus the oxidation state is +4 because -4+4=0. Therefore, we need to subtract four electrons. Because we cleaved the bond heteroleptically, each ligand contributes two electrons, giving overall eight electrons coming from the four ligands. This means that we have overall eight electrons, or an 8-electron complex. This is far, far away from 18 electrons. Nonetheless, the complex is stable. How can we explain this? The answer is that in order to achieve 18 electrons it would need to add five additional ligands if each ligand is considered a 2-electron donor. This would increase the coordination number to 9 which is too high to produce a stable complex. In order to reduce the complex to an 18 electron complex, 10 electrons would need to be added. This would produce a complex with a -10 charge which is way to high to be stable. The arguments are generalizable for group 3 and group 4 complexes. Because these elements only have a few d electrons, the ligands would need to contribute a lot of electrons to produce an 18 electron complex. This would require just too many ligands to add. The coordination numbers would get too high. If electrons are added instead of ligands, the negative charge at the complex would be to high to be stable based on electron-electron repulsion arguments.

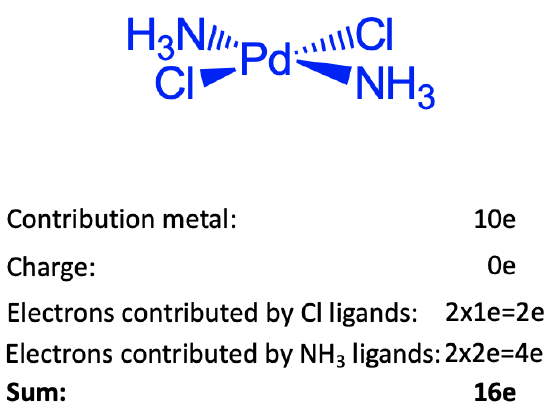
These arguments cannot be applied for group 10 elements, because these elements have many d electrons. The explanation in this case is that these elements like to make square planar complexes when in the oxidation number is +2. Square planar complexes prefer 16 instead of 18 electrons. We will learn later, when we discuss bonding in coordination compounds, why this is. You can see that the square planar diamminedichloro palladium complex shown is square planar and has sixteen electrons. There are 10 electrons coming from Pd. If we use the neutral atom method, no electrons need to be added or subtracted due to the charge at the complex. The complex is charge-neutral. To assess how many electrons come from the ligands we need to cleave the bonds so that neutral ligands are produced. The Pd-Cl bonds need to be cleave homoleptically, the Pd-N bonds need to be cleave heteroleptically. Therefore, the two chloro ligands are 1e donors, and the two ammine ligands are 2e donors. This gives 10+4+2=16 electrons.

Dr. Kai Landskron ( Lehigh University ). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate .

Preferences

18 electron rule: EAN rule (Effective Atomic Number) - PowerPoint PPT Presentation

Something went wrong! Please try again and reload the page.

18 electron rule: EAN rule (Effective Atomic Number)

18 electron rule: ean rule (effective atomic number) in 1927, developed by sidgwick d electrons of metal + electrons of ligand = 18 electrons – powerpoint ppt presentation.

4 5 6 7 8 9 10 11 12
d3 d4 d5 d6 d7 d8 d9 d10
Sc Ti V Cr Mn Fe Co Ni Cu Zn
Y Zr Nb Mo Tc Ru Rh Pd Ag Cd
Ta W Re Os Ir Pt Au Hg
oxidative addition (???????) and
reductive elimination (??? ???? )
2. insertion (????) and deinsertion
3. Oxidative coupling (???????)and
Reductive Cleavage (???????)

PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.

You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.

About the Developers

PowerShow.com is brought to you by CrystalGraphics , the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.

18 electron rule: EAN rule (Effective Atomic Number)

Aug 17, 2014

930 likes | 3.8k Views

18 electron rule: EAN rule (Effective Atomic Number). In 1927, developed by Sidgwick. d electrons of metal + electrons of ligand = 18 electrons. 4 5 6 7 8 9 10 11 12 d 3 d 4 d 5 d 6 d 7 d 8 d 9 d 10 Sc Ti V Cr Mn Fe Co Ni Cu Zn

Share Presentation

late transition metal
high valent metal species
zr nb mo tc

Presentation Transcript

18 electron rule: EAN rule (Effective Atomic Number) In 1927, developed by Sidgwick d electrons of metal + electrons of ligand = 18 electrons • 4 5 6 7 8 9 10 11 12 • d3 d4 d5 d6 d7 d8 d9 d10 • Sc Ti V Cr Mn Fe Co Ni Cu Zn • Y Zr Nb Mo Tc Ru RhPd Ag Cd • Ta W Re Os Ir Pt Au Hg

Ni: 1s22s22p63d84s2 : it is better to promote 4s electron to 3d, therefore Ni(0) is d10. Cu(I), Ag(I), and Au(I) is d10, Zn2+, Cd2+, andHg2+ is d10 Ti(IV) serves as a good index for memorizing the d electrons Because it is a d0 metal ion. TiCl4 is colorless, diamagnetic liquid TiCl3 is violet color

tetrahedral octahedral Square planar Trigonal bipyramid

Ni(CO)4, Fe(CO)5, Cr(CO)6, Ni(CO)4, For Mn, Mn(CO)5: 17 electrons Mn(CO)6: 19 electrons Mn(CO)5 (CO)5Mn-Mn(CO)5 HMn(CO)5, CH3Mn(CO)5, ClMn(CO)5 CH3Mn(CO)5 CH3- + Mn(CO)5+

18 Electron Rule: strong field ligand such as CO, Hydride, Cycanide anion. Not good for Aqua complex: Weak Field Ligand such as H2O is not matched with 18 electron rule. Late transition metal is better than early transition metals.

Exceptions Early trantion metals (η5-C5H5)2ZrCl2: 5ex2+4e+2e=16e, (CH3)3TaCl2는 1ex3+5e+2e=10e (CH3)6W는 1ex6+6e=12e For early transition metals, there is not enough room to attach many ligands to satisfy 18 electron rule. Coordination number: number of ligand to bind to metal. Coordination number cannot be larger than the maximun oxidation number or the group number of element. For Late transition Metals (PPh3)3Pt: 2ex3+10e=16e (η5-C5H5)2Ni:5ex2+10e=20e

d8complex: 16 electrons Pt(II), Pd(II), Cu(III), Ir(I), Rh(I): square planar For example, Cl(PPh3)3Rh(I) (Wilkinson’s complex), Cl(PPh3)2(CO)Ir(I) (Vaska’ complex), (PPh3)2(CCPh)2Pt(II) even though they contains strong field ligand

1.3 Mechanism in Organometallic Chemistry • oxidative addition (산화성부가반응) and • reductive elimination (환원성 제거반응 ) • 2. insertion (삽입반응) and deinsertion • (이탈반응) • 3. Oxidative coupling (산화성결합반응)and • Reductive Cleavage (환원성결합분열)

1. oxidative addition (산화성부가반응) and reductive elimination (환원성 제거반응 ) two electron oxidative addtion (이전자 산화성부가반응) and one electron oxidative addition (일전자 산화성부가반응) A; 16 electron complexes B: 18 electron complexes

H2Fe(CO)2-4 20 electron complex Na2Fe(CO)4 18 electron complex [RFe(CO)4]+X- 18 electron complex

Rh(II), Co(II) d7 complex

1965, Chatt and Davidson Kinetic Factor Thermodynamic Factor

In 1982, Bergman, Graham, Jones

Endo methyl migration: aromatic stablization energy

Reductive Elimination: spontaneous To do reductive elimination, two ligands should be placed at cis-position Concerted Mechanism

Transphos Ligand: Pd(II) is dsp2 (square planar): no reductive elimination Addition of CH3I allows to make cis-dimethyl to undergo reductive elimination.

2. Elimination of one of ligand to make T-shape to Y shape. 3. Reduce the electron density of central metal Ligand off from metal by heat or light, oxidize the metal, addition of strong pi-acceptor ligand such as CO, maleic anhydride, quinone, tetracyanoethylene

1. Insertion (삽입반응) and Deinsertion (이탈반응)

Migratory Insertion: cis position and concerted mechanism Order: h3-allyl ≥ Et 〉Me 〉PhCH2 〉vinyl ≥aryl, ROCH2 〉HOCH2 Hard to migrate to CO: Hydride(H-), acyl (CH3CO), CF3 ,Heteroatome: RO-, R2N

Decarbonylation

Hydride Insertion: cis-addition, 4-centered transition state For example: hydroboration, hydrosilylation, hydroformylation Reverse Reaction: b-Hydride Elimination The reason why it is hard to make a long chain alkylmetal complex

Alkyl Migration into olefin: olefin polymerization

Order of Migration of sigma liand-metal complex to Olefin: H >> R, vinyl, aryl> RCO>>RO, R2N Heteroatom is hard to migrate because of strong bond of heteroatom bearing lone pair to metal

Alkyne undergoes migratory insertion, but further successive reaction make polymer compounds, which make complication. Other Insertion, deinsertion substrate; isocyanide (:C≡NR), carbene(:CR2), SO2 , etc

Nucleophilic Addition Reaction (친핵부가반응) reverse sterechemistry to migratory insertion High valent metal species: electron deficient metal

Trans-Addition Product

Order of Reactivity 1.4.3 Oxidative coupling (산화성결합반응) Reductive Cleavage (환원성결합분열) M: +2 Increase

Electron withdrawing or strained molecules For alkyne, electron-withdrawing is no necessary

More by User

Chapter 4 Probability: Probabilities of Compound Events

Chapter 4 Probability: Probabilities of Compound Events 4.1THE ADDITION RULE 4.1.1 The General Addition Rule 4.1.2The Special Addition Rule for Mutually Exclusive Events 4.2 Conditional Probabilities 4.3 The Multiplication Rule 4.4 Independent Events and the Special Multiplication Rule

1.88k views • 21 slides

Significant Final Rule Makings of 2004

Biotech Partnership Meeting December 8, 2004. Significant Final Rule Makings of 2004. Bob Spar, Director Office of Patent Legal Administration (OPLA) (571) 272-7700 Deputy Commissioner for Patent Examination Policy (DCPEP) [email protected]. Final Rule Makings.

1.36k views • 104 slides

Chapter 5: Probability

Chapter 5: Probability. 5.1 Probability Rules 5.2 The Addition Rule and Complements 5.3 Independence and the Multiplication Rule 5.4 Conditional Probability and the General Multiplication Rule 5.5 Counting Techniques. November 4, 2008. 1. Example.

2.13k views • 99 slides

Recent Significant Rule Makings and Changes in USPTO Practice February 3, 2004

Recent Significant Rule Makings and Changes in USPTO Practice February 3, 2004. Robert Clarke Senior Legal Advisor Office of Patent Legal Administration (703) 305-9177, [email protected]. TOPICS . Final Rule Implementing Public Law 107-273 (2002) and Ancillary Matters – Rule Making

1.01k views • 73 slides

MO’s for Cyclobutadiene

MO’s for Cyclobutadiene. =>. Energy Diagram for Cyclobutadiene. Following Hund’s rule, two electrons are in separate orbitals. This diradical would be very reactive. =>. =>. Polygon Rule.

1.7k views • 10 slides

NEW RULE 25-30.029

NEW RULE 25-30.029. Legal Description of Service Area. Rule 25-30.029. The utility shall provide a complete legal description of the service area, as defined in Section 367.021(10), F.S., to be served, extended, deleted, or transferred in the following applications:

919 views • 69 slides

Rank Size Rule

Rank Size Rule. Settlement. Learning outcomes. To understand what the rank Size rule is and the pattern that it tries to outline. Rank Size Rule. This is an attempt to find a numerical relationship between population size of settlements within an area such as a country or county

1.76k views • 12 slides

Public Notification Rule State-EPA Training

Public Notification Rule State-EPA Training. Agenda. Welcome and Introductions Training Objectives PN Slide Presentation Background on development of the PN Rule Overview of the Rule Key areas that changed Summary of areas EPA believes are critical for state adoption

1.59k views • 124 slides

Revised Total Coliform Rule: Big Changes for the Little Coliform

Revised Total Coliform Rule: Big Changes for the Little Coliform. Maine Rural Water Association’s 13 th Annual Conference, Freeport, ME December 12, 2013 Kevin Reilly. Overview. Current Total Coliform Rule (TCR) – Major Provisions Revised Total Coliform Rule (RTCR) – History

1.25k views • 85 slides

Proper Plaintiff rule and Majority Rule Foss v Harbottle

Proper Plaintiff rule and Majority Rule Foss v Harbottle Two minority shareholders initiated legal proceedings against, among others, the directors of the company. They claimed that the directors had misapplied the company's assets.

3.92k views • 44 slides

Final Exam F 12/11 9 am We have the room until 12 pm.

Final Exam F 12/11 9 am We have the room until 12 pm. Review Session???. Some molecules have electron-dot structures that do not satisfy the octet rule. Some have an odd number of electrons, such as NO. Other molecules either have too few or too many electrons around the central atom.

1.18k views • 103 slides

Left Hand Rules

Left Hand Rules. by Richard J. Terwilliger. Left Hand Rule. st. Left Hand Rule. 1. Left Hand Rule. B. Click on a. i. N. LEFT HAND RULE. S. rd. 3. nd. 2. F. Left Hand Rules. Created by Richard J. Terwilliger July 2001. Left Hand Rule. st. Left Hand Rule. 1. Left Hand Rule.

1.51k views • 129 slides

Recent Patent-Related Rule Making and Changes in USPTO Practice Philadelphia IPLA 9/25/03

Recent Patent-Related Rule Making and Changes in USPTO Practice Philadelphia IPLA 9/25/03. Bob Spar Director Office of Patent Legal Administration (OPLA) (703) 308-5107, [email protected]. TOPICS. Recent Rule Making/ Notices: Image File Wrapper (IFW) – Final Rule

1.16k views • 98 slides

Chapter 4 Numerical Differentiation and Integration

Chapter 4 Numerical Differentiation and Integration. Numerical Analysis. Overview of Numerical Integration. Midpoint Rule. Midpoint Rule. Midpoint Rule. Midpoint Rule. Midpoint Rule. Trapezoidal Rule. Trapezoidal Rule. Trapezoidal Rule. Simpson Rule. Simpson Rule. Simpson Rule.

1.6k views • 82 slides

第七章網路資料庫之關連法則探勘

第七章網路資料庫之關連法則探勘. 內容概要. 簡介關連法則探勘 (Association Rule Mining) 多層次關連法則探勘 (Multilevel Association Rule Mining) 數量化關連法則探勘 (Quantitative Association Rule Mining) 關連分析 (Correlation Analysis) 總結. 簡介 (1). 單一購物車告訴我們個別顧客的消費行為，但是累積大量的購物車資料之後，可以分析整體顧客的消費習慣。

1.25k views • 98 slides

Asperger Syndrome Rethinking the Glass House Rule

Asperger Syndrome Rethinking the Glass House Rule. Dimitri Martin: Glass House Rule. Video clip. Complexity. Perhaps student profiles and behaviors are becoming more complex… The Real Question… What is your professional and ethical responsibility?.

1.39k views • 118 slides

Upendra shukla ECFY Consulting Pvt. Ltd. Upen@webxpress w w w. W e b X p r e s s. i n

Webxpress Visibility for Supply Chains. Control panel SOP. Contents General Setting Document Control Setting Operation rule Finance Rule Account Rule Fleet Rule Setting. Upendra shukla ECFY Consulting Pvt. Ltd. [email protected] w w w. W e b X p r e s s. i n. Login Page.

1.01k views • 84 slides

1.2k views • 98 slides

1.28k views • 104 slides

Chapter 4 Probability

Chapter 4 Probability. 4-1 Review and Preview 4-2 Basic Concepts of Probability 4-3 Addition Rule 4-4 Multiplication Rule: Basics 4-5 Multiplication Rule: Complements and Conditional Probability 4-6 Counting. Section 4-1 Review and Preview. Review.

2.68k views • 173 slides

Feeling the Stone When Crossing the River: China ’ s Efforts and Achievements in Promoting the Rule of Law. Zhang Fan. Contents. Part 1. Preliminary Definitions and Distinctions A The Rule of Law —— A Survey of Meanings B Fazhi, Renzhi, and Instrumentalism C A Rough-and-Ready Definition

1.65k views • 150 slides

Fact Check Team: Courts rule non-violent felons, some illegal migrants can own guns

by JANAE BOWENS | The National Desk

Gun safety firearm training holding gun (Photo: WZTV)

WASHINGTON (TND) — A pair of controversial court rulings permit some non-violent felons and illegal migrants to own a firearm.

The Ninth Circuit Court of Appeals ruled people convicted of non-violent crimes who have finished their prison sentence are allowed to own guns.

Steven Duarte is at the center of this ruling out of California. He has five prior non-violent state criminal convictions and then was convicted for tossing a handgun out of a moving car. The court ruled he was protected under the Second Amendment since he is a non-violent offender who has served his time in prison and reentered society. His last conviction was tossed out, and the court overturned a lower court ruling that made it legal for people like Duarte to have a gun.

The court cited the 2022 Supreme Court ruling, New York State Rifle & Pistol Association, Inc. v. Bruen as a reason for their ruling. It argued the Second Amendment applied to convicts who have reentered society.

However, the dissenting judge said the Supreme Court reiterated that the Second Amendment protects law-abiding citizens, not nonviolent offenders.

Illegal Migrants

Sharon Johnson Coleman, a judge on the U.S. District Court for the Northern District of Illinois, recently ruled some illegal migrants can own a gun.

In her opinion , Johnson had a slew of reasons why she ruled Heriberto Carbajal-Flores, an undocumented immigrant, should be able to own a gun. She wrote that Carbajal-Flores has a job, no felonies, no violent crimes, no crimes using a weapon, and no risk to public safety even though Title 18 of the U.S. Criminal Code prevents illegal migrants from possessing firearms.

Johnson also cited the 2022 Supreme Court ruling, New York State Rifle & Pistol Association, Inc. v. Bruen. The Bruen decision said law-abiding citizens with ordinary self-defense have the right to keep and bear arms in public for self-defense. Coleman said Carbajal-Flores had the gun for self-defense reasons and had committed no other crimes besides being in the country illegally. She said the Buren decision applies to him and he is allowed to have a firearm.

IMAGES

PPT
18 Electron Rule
The 18 Electron Rule for Transition Metal Complexes
PPT
PPT
More Practice With the 18 Electron Rule

VIDEO

18 Electron rule/Stability of the complexes/Coordination chemistry/PG TRB/POLYTRB/tamil
18 Electrons Rule + Examples
18 Electron Rule || Organometallic Chemistry
Chapter 18, example #5 (Accelerating an electron)
18 Electron Rule Chemistry Class 12th By Ubais sir #education#study
18 Electron rule and M-M bond

COMMENTS

24.3: The 18-electron Rule
The 18 electron rule allows one to predict the reactivity of a certain compound. The associative mechanism means that there is an addition of a ligand while a dissociative mechanism means that there is a loss of a ligand. When the electron count is less than 18, a molecule will most likely undergo an associative reaction. For example: (C 2 H 4 ...
18 Electron Rule
18 electron rule, a chemical thumb rule is used to predict the stability of a metal atom in an organometallic compound by evaluating whether it has 18 valence electrons.According to this rule, "In order for a transition element to be stable, it must have 18 electrons in its valence shell in the configuration of inert gas, and these electrons must form chemical bonds".
PPT
The 18-electron Rule is based on a similar concept. The central TM can accommodate electrons in the s, p, and d orbitals. s (2) , p (6) , and d (10) = maximum of 18 This means that a TM can add electrons from Lewis Bases (or ligands) in addition to its valence electrons to a total of 18.
PDF Understanding the eighteen-electron rule
Keywords: The 18-electron rule; Coordination chemistry; Tungsten hexacarbonyl; Ferrocene 1. Introduction The 18-electron principle for the stability of certain tran-sition-metal compounds was suggested in 1921 by Lang-muir [1], who quoted Mo(CO) 6, Fe(CO) 5 and Ni(CO) 4 as examples. Bose [2] included cyanides, chlorides and ammo-
PPT Chemistry 332 Basic Inorganic Chemistry II
This rule is only valid for Period 2 nonmetallic elements. The 18-electron Rule is based on a similar concept. The central TM can accommodate electrons in the s, p, and d orbitals. s (2) , p (6) , and d (10) = maximum of 18 This means that a TM can add electrons from Lewis Bases (or ligands) in addition to its valence electrons to a total of 18.
18-electron rule
The 18-electron rule is a chemical rule of thumb used primarily for predicting and rationalizing formulas for stable transition metal complexes, especially organometallic compounds. The rule is based on the fact that the valence orbitals in the electron configuration of transition metals consist of five (n−1)d orbitals, one ns orbital, and three np orbitals, where n is the principal quantum ...
PDF The 18-Electron Rule and Its Exceptions
The 18-Electron Rule and Its Exceptions (4) Linear complexes (d10, 14 electrons): More common for group 11 (Cu, Ag, Au) than group 12 (Zn, Cd, Hg) because the energy difference between the d, s and p-orbitals is smaller for group 11. More common for the heavier elements (AgI, AuI, HgII).
The 18 Electron Rule for Transition Metal Complexes
Ok, so we understand how ligands bond to metals to form transition metal complexes, but how many ligands will fit? Well, remember the octet rule from general...
The 18 and 16 Electron Rule
Problem. Using the 18-electron rule, explain why V (CO) 6 can be easily reduced to [V (CO) 6] -. Was this helpful? Learn The 18 and 16 Electron Rule with free step-by-step video explanations and practice problems by experienced tutors.
PDF 18- Electron Rule.
This rule assumes that the central atom in a compound will make bonds such that the total number of electrons around the central atom is 8. THIS IS THE MAXIMUM CAPACITY OF THE s and p orbitals. The 18-electron Rule is based on a similar concept. The central TM can accommodate electrons in the s, p, and d orbitals. This means that a TM can add ...
18 Electron Rule, Sigma and Pi Bonding
18 Electron Rule, Sigma and Pi Bonding Ppt - Free download as Powerpoint Presentation (.ppt / .pptx), PDF File (.pdf), Text File (.txt) or view presentation slides online. The document provides an overview of the 18 electron rule, sigma bonding, and pi bonding. It begins with the history and definition of the 18 electron rule, then discusses how to count valence electrons, examples of ...
18 Electron Rule
The 18 electron rule states that, For a transition element to be stable it needs to have 18 electrons in its valence shell so that they have the configuration of an inert gas, and that they form chemical bonds in order to attain this state. This rule was proposed in order to explain the stability of transition metals and the organometallic ...
Understanding the eighteen-electron rule
The 18-electron principle for the stability of certain transition-metal compounds was suggested in 1921 by Langmuir [1], who quoted Mo(CO) 6, Fe(CO) 5 and Ni(CO) 4 as examples. Bose [2] included cyanides, chlorides and ammonia as ligands, and Reiff [3] added nitrosyl. A comprehensive summary was given in 1934 by Sidgwick and Bailey [4], who included polynuclear complexes.
18-Electron rule
The 18-electron rule is a rule of thumb used primarily in transition metal chemistry for characterizing and predicting the stability of metal complexes. Valence shells of a transition metal can accommodate 18 electrons: 2 in each of the five d orbitals (10 in total); 2 in each of the three p orbitals (6 in total); and 2 in the s orbital (see Electron counting).
Organometallic compounds
6. The 18-Electron RuleThe 18-Electron Rule 18 electrons represent a filled valence shell for a transition metal. Why do many complexes (if not most) violate the 18- electron rule? The 18-electron rule does not consider the type of bonding and interactions. The interactions between the ligands and the metal need to be identified to determine if the complex will obey or violate the 18-electron ...
The 18-electron rule and electron counting in transition metal
The 18-electron rule and the corresponding methods for counting the total valence electrons of transition metal complexes are among the most useful basic tools in modern inorganic chemistry, particularly in its application to organometallic species. While in its simplest representation, the 18-electron rule is explained in that a closed, stable noble gas configuration of ns 2(n-1)d 10 np 6 is ...
Chapter 6.1: The 18 Electron Rule
The 18 electron rule states that for d-block elements normally complexes with 18 electrons in the shell (ns 2 (n-1)d 10 np 6 configuration) are most stable. If this number is not reached, the species is coordinatively unsaturated and tends to add more ligands. It also tends to be reduced because adding electrons brings the complex to, or at ...
Nomenclature and 18 Electron Rule
Nomenclature and 18 Electron rule - Free download as Powerpoint Presentation (.ppt), PDF File (.pdf), Text File (.txt) or view presentation slides online. Naming of organometallic compounds and predicting the stability of the compounds using 18 electron rule are discussed.
PPT
18 electron rule: EAN rule (Effective Atomic Number) In 1927, developed by Sidgwick d electrons of metal + electrons of ligand = 18 electrons - A free PowerPoint PPT presentation (displayed as an HTML5 slide show) on PowerShow.com - id: 50ff56-ZWU3N ... The PowerPoint PPT presentation: "18 electron rule: EAN rule (Effective Atomic Number)" is ...
18 electron rule: EAN rule (Effective Atomic Number)
An Image/Link below is provided (as is) to download presentation Download Policy: ... Weak Field Ligand such as H2O is not matched with 18 electron rule. Late transition metal is better than early transition metals. Exceptions Early trantion metals (η5-C5H5)2ZrCl2: 5ex2+4e+2e=16e, (CH3)3TaCl2는 1ex3+5e+2e=10e (CH3)6W는 1ex6+6e=12e For early ...
Courts rule non-violent felons, some illegal migrants can own guns
WASHINGTON (TND) — A pair of controversial court rulings permit some non-violent felons and illegal migrants to own a firearm. The Ninth Circuit Court of Appeals ruled people convicted of non-violent crimes who have finished their prison sentence are allowed to own guns.. Steven Duarte is at the center of this ruling out of California. He has five prior non-violent state criminal convictions ...

18 Electron Rule – Definition, Examples, and Applications

18 Electron Rule:

Examples of 18 electron rule

EAN rule vs 18 electron rule

Limitations of 18 Electron Rule

18 Electron Rule Video

You may also like to read:

Balancing Redox Equations by Oxidation Number method

Lead: Properties, 7 Important Uses, Health Effects and Symptoms

Zinc – Chemistry, Deficiency, Side Effects, and its 4 important Health Benefits

Group 13 Elements: Boron Family- Easy Explanation

What is Activated complex? Easy Explanation

Ortho hydrogen and Para Hydrogen: Difference, interconversion

One Response

Leave a Reply Cancel reply

18 Electron Rule

18 Electron Rule Explained

Limitations of 18 Electron Rule

Applications of 18 Electron Rule

About The Author

Leave a Comment Cancel Reply

The 18-electron rule and electron counting in transition metal compounds: theory and application

Cite this article

Similar content being viewed by others

Computational Versus Experimental Spectroscopy for Transition Metals

Periodic Trends Revealed by Photoelectron Studies of Transition Metal and Lanthanide Compounds

Introduction

18-Electron rule in terms of molecular orbital models, part I: simple view

18-Electron rule in terms of molecular orbital models, part II: more detailed view

Other compound geometries

Electron counting methods

Author information

Corresponding author

Rights and permissions

About this article

Share this article

Margin Size

Chapter 6.1: The 18 Electron Rule

Electron Counting In Transition Metal Complexes

The Neutral Atom Method

"Oxidation State" Method

Counting Electrons: Ligand Contributions

The 18 Electron Rule

18 electron rule: EAN rule (Effective Atomic Number) - PowerPoint PPT Presentation

18 electron rule: EAN rule (Effective Atomic Number)

18 electron rule: EAN rule (Effective Atomic Number)

Share Presentation

Presentation Transcript

Chapter 4 Probability: Probabilities of Compound Events

Significant Final Rule Makings of 2004

Chapter 5: Probability

Recent Significant Rule Makings and Changes in USPTO Practice February 3, 2004

MO’s for Cyclobutadiene

NEW RULE 25-30.029

Rank Size Rule

Public Notification Rule State-EPA Training

Revised Total Coliform Rule: Big Changes for the Little Coliform

Proper Plaintiff rule and Majority Rule Foss v Harbottle

Final Exam F 12/11 9 am We have the room until 12 pm.

Left Hand Rules

Recent Patent-Related Rule Making and Changes in USPTO Practice Philadelphia IPLA 9/25/03

Chapter 4 Numerical Differentiation and Integration

第七章 網路資料庫之關連法則探勘

Asperger Syndrome Rethinking the Glass House Rule

Upendra shukla ECFY Consulting Pvt. Ltd. Upen@webxpress w w w. W e b X p r e s s. i n

Chapter 4 Probability

Fact Check Team: Courts rule non-violent felons, some illegal migrants can own guns

IMAGES

VIDEO

COMMENTS

第七章網路資料庫之關連法則探勘