population in a research example

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Ind Psychiatry J
• v.19(1); Jan-Jun 2010

Statistics without tears: Populations and samples

Amitav banerjee.

Department of Community Medicine, D Y Patil Medical College, Pune, India

Suprakash Chaudhury

1 Department of Psychiatry, RINPAS, Kanke, Ranchi, India

Research studies are usually carried out on sample of subjects rather than whole populations. The most challenging aspect of fieldwork is drawing a random sample from the target population to which the results of the study would be generalized. In actual practice, the task is so difficult that some sampling bias occurs in almost all studies to a lesser or greater degree. In order to assess the degree of this bias, the informed reader of medical literature should have some understanding of the population from which the sample was drawn. The ultimate decision on whether the results of a particular study can be generalized to a larger population depends on this understanding. The subsequent deliberations dwell on sampling strategies for different types of research and also a brief description of different sampling methods.

Research workers in the early 19th century endeavored to survey entire populations. This feat was tedious, and the research work suffered accordingly. Current researchers work only with a small portion of the whole population (a sample) from which they draw inferences about the population from which the sample was drawn.

This inferential leap or generalization from samples to population, a feature of inductive or empirical research, can be full of pitfalls. In clinical medicine, it is not sufficient merely to describe a patient without assessing the underlying condition by a detailed history and clinical examination. The signs and symptoms are then interpreted against the total background of the patient's history and clinical examination including mental state examination. Similarly, in inferential statistics, it is not enough to just describe the results in the sample. One has to critically appraise the real worth or representativeness of that particular sample. The following discussion endeavors to explain the inputs required for making a correct inference from a sample to the target population.

TARGET POPULATION

Any inferences from a sample refer only to the defined population from which the sample has been properly selected. We may call this the target population. For example, if in a sample of lawyers from Delhi High Court it is found that 5% are having alcohol dependence syndrome, can we say that 5% of all lawyers all over the world are alcoholics? Obviously not, as the lawyers of Delhi High Court may be an institution by themselves and may not represent the global lawyers′ community. The findings of this study, therefore, apply only to Delhi High Court lawyers from which a representative sample was taken. Of course, this finding may nevertheless be interesting, but only as a pointer to further research. The data on lawyers in a particular city tell us nothing about lawyers in other cities or countries.

POPULATIONS IN INFERENTIAL STATISTICS

In statistics, a population is an entire group about which some information is required to be ascertained. A statistical population need not consist only of people. We can have population of heights, weights, BMIs, hemoglobin levels, events, outcomes, so long as the population is well defined with explicit inclusion and exclusion criteria. In selecting a population for study, the research question or purpose of the study will suggest a suitable definition of the population to be studied, in terms of location and restriction to a particular age group, sex or occupation. The population must be fully defined so that those to be included and excluded are clearly spelt out (inclusion and exclusion criteria). For example, if we say that our study populations are all lawyers in Delhi, we should state whether those lawyers are included who have retired, are working part-time, or non-practicing, or those who have left the city but still registered at Delhi.

Use of the word population in epidemiological research does not correspond always with its demographic meaning of an entire group of people living within certain geographic or political boundaries. A population for a research study may comprise groups of people defined in many different ways, for example, coal mine workers in Dhanbad, children exposed to German measles during intrauterine life, or pilgrims traveling to Kumbh Mela at Allahabad.

GENERALIZATION (INFERENCES) FROM A POPULATION

When generalizing from observations made on a sample to a larger population, certain issues will dictate judgment. For example, generalizing from observations made on the mental health status of a sample of lawyers in Delhi to the mental health status of all lawyers in Delhi is a formalized procedure, in so far as the errors (sampling or random) which this may hazard can, to some extent, be calculated in advance. However, if we attempt to generalize further, for instance, about the mental statuses of all lawyers in the country as a whole, we hazard further pitfalls which cannot be specified in advance. We do not know to what extent the study sample and population of Delhi is typical of the larger population – that of the whole country – to which it belongs.

The dilemmas in defining populations differ for descriptive and analytic studies.

POPULATION IN DESCRIPTIVE STUDIES

In descriptive studies, it is customary to define a study population and then make observations on a sample taken from it. Study populations may be defined by geographic location, age, sex, with additional definitions of attributes and variables such as occupation, religion and ethnic group.[ 1 ]

Geographic location

In field studies, it may be desirable to use a population defined by an administrative boundary such as a district or a state. This may facilitate the co-operation of the local administrative authorities and the study participants. Moreover, basic demographic data on the population such as population size, age, gender distribution (needed for calculating age- and sex-specific rates) available from census data or voters’ list are easier to obtain from administrative headquarters. However, administrative boundaries do not always consist of homogenous group of people. Since it is desirable that a modest descriptive study does not cover a number of different groups of people, with widely differing ways of life or customs, it may be necessary to restrict the study to a particular ethnic group, and thus ensure better genetic or cultural homogeneity. Alternatively, a population may be defined in relation to a prominent geographic feature, such as a river, or mountain, which imposes a certain uniformity of ways of life, attitudes, and behavior upon the people who live in the vicinity.

If cases of a disease are being ascertained through their attendance at a hospital outpatient department (OPD), rather than by field surveys in the community, it will be necessary to define the population according to the so-called catchment area of the hospital OPD. For administrative purposes, a dispensary, health center or hospital is usually considered to serve a population within a defined geographic area. But these catchment areas may only represent in a crude manner with the actual use of medical facilities by the local people. For example, in OPD study of psychiatric illnesses in a particular hospital with a defined catchment area, many people with psychiatric illnesses may not visit the particular OPD and may seek treatment from traditional healers or religious leaders.

Catchment areas depend on the demography of the area and the accessibility of the health center or hospital. Accessibility has three dimensions – physical, economic and social.[ 2 ] Physical accessibility is the time required to travel to the health center or medical facility. It depends on the topography of the area (e.g. hill and tribal areas with poor roads have problems of physical accessibility). Economic accessibility is the paying capacity of the people for services. Poverty may limit health seeking behavior if the person cannot afford the bus fare to the health center even if the health services may be free of charge. It may also involve absence from work which, for daily wage earners, is a major economic disincentive. Social factors such as caste, culture, language, etc. may adversely affect accessibility to health facility if the treating physician is not conversant with the local language and customs. In such situations, the patient may feel more comfortable with traditional healers.

Ascertainment of a particular disease within a particular area may be incomplete either because some patient may seek treatment elsewhere or some patients do not seek treatment at all. Focus group discussions (qualitative study) with local people, especially those residing away from the health center, may give an indication whether serious underreporting is occurring.

When it is impossible to relate cases of a disease to a population, perhaps because the cases were ascertained through a hospital with an undefined catchment area, proportional morbidity rates may be used. These rates have been widely used in cancer epidemiology where the number of cases of one form of cancer is expressed as a proportion of the number of cases of all forms of cancer among patients attending the same hospital during the same period.

POPULATIONS IN ANALYTIC STUDIES

Case control studies.

As opposed to descriptive studies where a study population is defined and then observations are made on a representative sample from it, in case control studies observations are made on a group of patients. This is known as the study group , which usually is not selected by sampling of a defined larger group. For instance, a study on patients of bipolar disorder may include every patient with this disorder attending the psychiatry OPD during the study period. One should not forget, however, that in this situation also, there is a hypothetical population consisting of all patients with bipolar disorder in the universe (which may be a certain region, a country or globally depending on the extent of the generalization intended from the findings of the study). Case control studies are often carried out in hospital settings because this is more convenient and accessible group than cases in the community at large. However, the two groups of cases may differ in many respects. At the outset of the study, it should be deliberated whether these differences would affect the external validity (generalization) of the study. Usually, analytic studies are not carried out in groups containing atypical cases of the disorder, unless there is a special indication to do so.

Populations in cohort studies

Basically, cohort studies compare two groups of people (cohorts) and demonstrate whether or not there are more cases of the disease among the cohort exposed to the suspected cause than among the cohort not exposed. To determine whether an association exists between positive family history of schizophrenia and subsequent schizophrenia in persons having such a history, two cohorts would be required: first, the exposed group, that is, people with a family history of mental disorders (the suspected cause) and second, the unexposed group, that is, people without a family history of mental disorders. These two cohorts would need to be followed up for a number of years and cases of schizophrenia in either group would be recorded. If a positive family history is associated with development of schizophrenia, then more cases would occur in the first group than in the second group.

The crucial challenges in a cohort study are that it should include participants exposed to a particular cause being investigated and that it should consist of persons who can be followed up for the period of time between exposure (cause) and development of the disorder. It is vital that the follow-up of a cohort should be complete as far as possible. If more than a small proportion of persons in the cohort cannot be traced (loss to follow-up or attrition), the findings will be biased , in case these persons differ significantly from those remaining in the study.

Depending on the type of exposure being studied, there may or may not be a range of choice of cohort populations exposed to it who may form a larger population from which one has to select a study sample. For instance, if one is exploring association between occupational hazard such as job stress in health care workers in intensive care units (ICUs) and subsequent development of drug addiction, one has to, by the very nature of the research question, select health care workers working in ICUs. On the other hand, cause effect study for association between head injury and epilepsy offers a much wider range of possible cohorts.

Difficulties in making repeated observations on cohorts depend on the length of time of the study. In correlating maternal factors (pregnancy cohort) with birth weight, the period of observation is limited to 9 months. However, if in a study it is tried to find the association between maternal nutrition during pregnancy and subsequent school performance of the child, the study will extend to years. For such long duration investigations, it is wise to select study cohorts that are firstly, not likely to migrate, cooperative and likely to be so throughout the duration of the study, and most importantly, easily accessible to the investigator so that the expense and efforts are kept within reasonable limits. Occupational groups such as the armed forces, railways, police, and industrial workers are ideal for cohort studies. Future developments facilitating record linkage such as the Unique Identification Number Scheme may give a boost to cohort studies in the wider community.

A sample is any part of the fully defined population. A syringe full of blood drawn from the vein of a patient is a sample of all the blood in the patient's circulation at the moment. Similarly, 100 patients of schizophrenia in a clinical study is a sample of the population of schizophrenics, provided the sample is properly chosen and the inclusion and exclusion criteria are well defined.

To make accurate inferences, the sample has to be representative. A representative sample is one in which each and every member of the population has an equal and mutually exclusive chance of being selected.

Sample size

Inputs required for sample size calculation have been dealt from a clinical researcher's perspective avoiding the use of intimidating formulae and statistical jargon in an earlier issue of the journal.[ 1 ]

Target population, study population and study sample

A population is a complete set of people with a specialized set of characteristics, and a sample is a subset of the population. The usual criteria we use in defining population are geographic, for example, “the population of Uttar Pradesh”. In medical research, the criteria for population may be clinical, demographic and time related.

• Clinical and demographic characteristics define the target population, the large set of people in the world to which the results of the study will be generalized (e.g. all schizophrenics).
• The study population is the subset of the target population available for study (e.g. schizophrenics in the researcher's town).
• The study sample is the sample chosen from the study population.

METHODS OF SAMPLING

Purposive (non-random samples).

• Volunteers who agree to participate
• Snowball sample, where one case identifies others of his kind (e.g. intravenous drug users)
• Convenient sample such as captive medical students or other readily available groups
• Quota sampling, at will selection of a fixed number from each group
• Referred cases who may be under pressure to participate
• Haphazard with combination of the above methods

Non-random samples have certain limitations. The larger group (target population) is difficult to identify. This may not be a limitation when generalization of results is not intended. The results would be valid for the sample itself (internal validity). They can, nevertheless, provide important clues for further studies based on random samples. Another limitation of non-random samples is that statistical inferences such as confidence intervals and tests of significance cannot be estimated from non-random samples. However, in some situations, the investigator has to make crucial judgments. One should remember that random samples are the means but representativeness is the goal. When non-random samples are representative (compare the socio-demographic characteristics of the sample subjects with the target population), generalization may be possible.

Random sampling methods

Simple random sampling.

A sample may be defined as random if every individual in the population being sampled has an equal likelihood of being included. Random sampling is the basis of all good sampling techniques and disallows any method of selection based on volunteering or the choice of groups of people known to be cooperative.[ 3 ]

In order to select a simple random sample from a population, it is first necessary to identify all individuals from whom the selection will be made. This is the sampling frame. In developing countries, listings of all persons living in an area are not usually available. Census may not catch nomadic population groups. Voters’ and taxpayers’ lists may be incomplete. Whether or not such deficiencies are major barriers in random sampling depends on the particular research question being investigated. To undertake a separate exercise of listing the population for the study may be time consuming and tedious. Two-stage sampling may make the task feasible.

The usual method of selecting a simple random sample from a listing of individuals is to assign a number to each individual and then select certain numbers by reference to random number tables which are published in standard statistical textbooks. Random number can also be generated by statistical software such as EPI INFO developed by WHO and CDC Atlanta.

Systematic sampling

A simple method of random sampling is to select a systematic sample in which every n th person is selected from a list or from other ordering. A systematic sample can be drawn from a queue of people or from patients ordered according to the time of their attendance at a clinic. Thus, a sample can be drawn without an initial listing of all the subjects. Because of this feasibility, a systematic sample may have some advantage over a simple random sample.

To fulfill the statistical criteria for a random sample, a systematic sample should be drawn from subjects who are randomly ordered. The starting point for selection should be randomly chosen. If every fifth person from a register is being chosen, then a random procedure must be used to determine whether the first, second, third, fourth, or fifth person should be chosen as the first member of the sample.

Multistage sampling

Sometimes, a strictly random sample may be difficult to obtain and it may be more feasible to draw the required number of subjects in a series of stages. For example, suppose we wish to estimate the number of CATSCAN examinations made of all patients entering a hospital in a given month in the state of Maharashtra. It would be quite tedious to devise a scheme which would allow the total population of patients to be directly sampled. However, it would be easier to list the districts of the state of Maharashtra and randomly draw a sample of these districts. Within this sample of districts, all the hospitals would then be listed by name, and a random sample of these can be drawn. Within each of these hospitals, a sample of the patients entering in the given month could be chosen randomly for observation and recording. Thus, by stages, we draw the required sample. If indicated, we can introduce some element of stratification at some stage (urban/rural, gender, age).

It should be cautioned that multistage sampling should only be resorted to when difficulties in simple random sampling are insurmountable. Those who take a simple random sample of 12 hospitals, and within each of these hospitals select a random sample of 10 patients, may believe they have selected 120 patients randomly from all the 12 hospitals. In statistical sense, they have in fact selected a sample of 12 rather than 120.[ 4 ]

Stratified sampling

If a condition is unevenly distributed in a population with respect to age, gender, or some other variable, it may be prudent to choose a stratified random sampling method. For example, to obtain a stratified random sample according to age, the study population can be divided into age groups such as 0–5, 6–10, 11–14, 15–20, 21–25, and so on, depending on the requirement. A different proportion of each group can then be selected as a subsample either by simple random sampling or systematic sampling. If the condition decreases with advancing age, then to include adequate number in the older age groups, one may select more numbers in older subsamples.

Cluster sampling

In many surveys, studies may be carried out on large populations which may be geographically quite dispersed. To obtain the required number of subjects for the study by a simple random sample method will require large costs and will be cumbersome. In such cases, clusters may be identified (e.g. households) and random samples of clusters will be included in the study; then, every member of the cluster will also be part of the study. This introduces two types of variations in the data – between clusters and within clusters – and this will have to be taken into account when analyzing data.

Cluster sampling may produce misleading results when the disease under study itself is distributed in a clustered fashion in an area. For example, suppose we are studying malaria in a population. Malaria incidence may be clustered in villages having stagnant water collections which may serve as a source of mosquito breeding. In villages without such water stagnation, there will be lesser malaria cases. The choice of few villages in cluster sampling may give erroneous results. The selection of villages as a cluster may be quite unrepresentative of the whole population by chance.[ 5 ]

Lot quality assurance sampling

Lot quality assurance sampling (LQAS), which originated in the manufacturing industry for quality control purposes, was used in the nineties to assess immunization coverage, estimate disease prevalence, and evaluate control measures and service coverage in different health programs.[ 6 ] Using only a small sample size, LQAS can effectively differentiate between areas that have or have not met the performance targets. Thus, this method is used not only to estimate the coverage of quality care but also to identify the exact subdivisions where it is deficient so that appropriate remedial measures can be implemented.

The choice of sampling methods is usually dictated by feasibility in terms of time and resources. Field research is quite messy and difficult like actual battle. It may be sometimes difficult to get a sample which is truly random. Most samples therefore tend to get biased. To estimate the magnitude of this bias, the researcher should have some idea about the population from which the sample is drawn. In conclusion, the following quote cited by Bradford Hill[ 4 ] elegantly sums up the benefit of random sampling:

…The actual practice of medicine is virtually confined to those members of the population who either are ill, or think they are ill, or are thought by somebody to be ill, and these so amply fill up the working day that in the course of time one comes unconsciously to believe that they are typical of the whole. This is not the case. The use of a random sample brings to light the individuals who are ill and know they are ill but have no intention of doing anything about it, as well as those who have never been ill, and probably never will be until their final illness. These would have been inaccessible to any other method of approach but that of the random sample… . J. H. Sheldon

Source of Support: Nil.

Conflict of Interest: None declared.

Introduction to Research Methods

7 samples and populations.

So you’ve developed your research question, figured out how you’re going to measure whatever you want to study, and have your survey or interviews ready to go. Now all your need is other people to become your data.

You might say ‘easy!’, there’s people all around you. You have a big family tree and surely them and their friends would have happy to take your survey. And then there’s your friends and people you’re in class with. Finding people is way easier than writing the interview questions or developing the survey. That reaction might be a strawman, maybe you’ve come to the conclusion none of this is easy. For your data to be valuable, you not only have to ask the right questions, you have to ask the right people. The “right people” aren’t the best or the smartest people, the right people are driven by what your study is trying to answer and the method you’re using to answer it.

Remember way back in chapter 2 when we looked at this chart and discussed the differences between qualitative and quantitative data.

One of the biggest differences between quantitative and qualitative data was whether we wanted to be able to explain something for a lot of people (what percentage of residents in Oklahoma support legalizing marijuana?) versus explaining the reasons for those opinions (why do some people support legalizing marijuana and others not?). The underlying differences there is whether our goal is explain something about everyone, or whether we’re content to explain it about just our respondents.

‘Everyone’ is called the population . The population in research is whatever group the research is trying to answer questions about. The population could be everyone on planet Earth, everyone in the United States, everyone in rural counties of Iowa, everyone at your university, and on and on. It is simply everyone within the unit you are intending to study.

In order to study the population, we typically take a sample or a subset. A sample is simply a smaller number of people from the population that are studied, which we can use to then understand the characteristics of the population based on that subset. That’s why a poll of 1300 likely voters can be used to guess at who will win your states Governor race. It isn’t perfect, and we’ll talk about the math behind all of it in a later chapter, but for now we’ll just focus on the different types of samples you might use to study a population with a survey.

If correctly sampled, we can use the sample to generalize information we get to the population. Generalizability , which we defined earlier, means we can assume the responses of people to our study match the responses everyone would have given us. We can only do that if the sample is representative of the population, meaning that they are alike on important characteristics such as race, gender, age, education. If something makes a large difference in people’s views on a topic in your research and your sample is not balanced, you’ll get inaccurate results.

Generalizability is more of a concern with surveys than with interviews. The goal of a survey is to explain something about people beyond the sample you get responses from. You’ll never see a news headline saying that “53% of 1250 Americans that responded to a poll approve of the President”. It’s only worth asking those 1250 people if we can assume the rest of the United States feels the same way overall. With interviews though we’re looking for depth from their responses, and so we are less hopefully that the 15 people we talk to will exactly match the American population. That doesn’t mean the data we collect from interviews doesn’t have value, it just has different uses.

There are two broad types of samples, with several different techniques clustered below those. Probability sampling is associated with surveys, and non-probability sampling is often used when conducting interviews. We’ll first describe probability samples, before discussing the non-probability options.

The type of sampling you’ll use will be based on the type of research you’re intending to do. There’s no sample that’s right or wrong, they can just be more or less appropriate for the question you’re trying to answer. And if you use a less appropriate sampling strategy, the answer you get through your research is less likely to be accurate.

7.1 Types of Probability Samples

So we just hinted at the idea that depending on the sample you use, you can generalize the data you collect from the sample to the population. That will depend though on whether your sample represents the population. To ensure that your sample is representative of the population, you will want to use a probability sample. A representative sample refers to whether the characteristics (race, age, income, education, etc) of the sample are the same as the population. Probability sampling is a sampling technique in which every individual in the population has an equal chance of being selected as a subject for the research.

There are several different types of probability samples you can use, depending on the resources you have available.

Let’s start with a simple random sample . In order to use a simple random sample all you have to do is take everyone in your population, throw them in a hat (not literally, you can just throw their names in a hat), and choose the number of names you want to use for your sample. By drawing blindly, you can eliminate human bias in constructing the sample and your sample should represent the population from which it is being taken.

However, a simple random sample isn’t quite that easy to build. The biggest issue is that you have to know who everyone is in order to randomly select them. What that requires is a sampling frame , a list of all residents in the population. But we don’t always have that. There is no list of residents of New York City (or any other city). Organizations that do have such a list wont just give it away. Try to ask your university for a list and contact information of everyone at your school so you can do a survey? They wont give it to you, for privacy reasons. It’s actually harder to think of popultions you could easily develop a sample frame for than those you can’t. If you can get or build a sampling frame, the work of a simple random sample is fairly simple, but that’s the biggest challenge.

Most of the time a true sampling frame is impossible to acquire, so researcher have to settle for something approximating a complete list. Earlier generations of researchers could use the random dial method to contact a random sample of Americans, because every household had a single phone. To use it you just pick up the phone and dial random numbers. Assuming the numbers are actually random, anyone might be called. That method actually worked somewhat well, until people stopped having home phone numbers and eventually stopped answering the phone. It’s a fun mental exercise to think about how you would go about creating a sampling frame for different groups though; think through where you would look to find a list of everyone in these groups:

Plumbers Recent first-time fathers Members of gyms

The best way to get an actual sampling frame is likely to purchase one from a private company that buys data on people from all the different websites we use.

Let’s say you do have a sampling frame though. For instance, you might be hired to do a survey of members of the Republican Party in the state of Utah to understand their political priorities this year, and the organization could give you a list of their members because they’ve hired you to do the reserach. One method of constructing a simple random sample would be to assign each name on the list a number, and then produce a list of random numbers. Once you’ve matched the random numbers to the list, you’ve got your sample. See the example using the list of 20 names below

and the list of 5 random numbers.

Systematic sampling is similar to simple random sampling in that it begins with a list of the population, but instead of choosing random numbers one would select every kth name on the list. What the heck is a kth? K just refers to how far apart the names are on the list you’re selecting. So if you want to sample one-tenth of the population, you’d select every tenth name. In order to know the k for your study you need to know your sample size (say 1000) and the size of the population (75000). You can divide the size of the population by the sample (75000/1000), which will produce your k (750). As long as the list does not contain any hidden order, this sampling method is as good as the random sampling method, but its only advantage over the random sampling technique is simplicity. If we used the same list as above and wanted to survey 1/5th of the population, we’d include 4 of the names on the list. It’s important with systematic samples to randomize the starting point in the list, otherwise people with A names will be oversampled. If we started with the 3rd name, we’d select Annabelle Frye, Cristobal Padilla, Jennie Vang, and Virginia Guzman, as shown below. So in order to use a systematic sample, we need three things, the population size (denoted as N ), the sample size we want ( n ) and k , which we calculate by dividing the population by the sample).

N= 20 (Population Size) n= 4 (Sample Size) k= 5 {20/4 (kth element) selection interval}

We can also use a stratified sample , but that requires knowing more about the population than just their names. A stratified sample divides the study population into relevant subgroups, and then draws a sample from each subgroup. Stratified sampling can be used if you’re very concerned about ensuring balance in the sample or there may be a problem of underrepresentation among certain groups when responses are received. Not everyone in your sample is equally likely to answer a survey. Say for instance we’re trying to predict who will win an election in a county with three cities. In city A there are 1 million college students, in city B there are 2 million families, and in City C there are 3 million retirees. You know that retirees are more likely than busy college students or parents to respond to a poll. So you break the sample into three parts, ensuring that you get 100 responses from City A, 200 from City B, and 300 from City C, so the three cities would match the population. A stratified sample provides the researcher control over the subgroups that are included in the sample, whereas simple random sampling does not guarantee that any one type of person will be included in the final sample. A disadvantage is that it is more complex to organize and analyze the results compared to simple random sampling.

Cluster sampling is an approach that begins by sampling groups (or clusters) of population elements and then selects elements from within those groups. A researcher would use cluster sampling if getting access to elements in an entrie population is too challenging. For instance, a study on students in schools would probably benefit from randomly selecting from all students at the 36 elementary schools in a fictional city. But getting contact information for all students would be very difficult. So the researcher might work with principals at several schools and survey those students. The researcher would need to ensure that the students surveyed at the schools are similar to students throughout the entire city, and greater access and participation within each cluster may make that possible.

The image below shows how this can work, although the example is oversimplified. Say we have 12 students that are in 6 classrooms. The school is in total 1/4th green (3/12), 1/4th yellow (3/12), and half blue (6/12). By selecting the right clusters from within the school our sample can be representative of the entire school, assuming these colors are the only significant difference between the students. In the real world, you’d want to match the clusters and population based on race, gender, age, income, etc. And I should point out that this is an overly simplified example. What if 5/12s of the school was yellow and 1/12th was green, how would I get the right proportions? I couldn’t, but you’d do the best you could. You still wouldn’t want 4 yellows in the sample, you’d just try to approximiate the population characteristics as best you can.

7.2 Actually Doing a Survey

All of that probably sounds pretty complicated. Identifying your population shouldn’t be too difficult, but how would you ever get a sampling frame? And then actually identifying who to include… It’s probably a bit overwhelming and makes doing a good survey sound impossible.

Researchers using surveys aren’t superhuman though. Often times, they use a little help. Because surveys are really valuable, and because researchers rely on them pretty often, there has been substantial growth in companies that can help to get one’s survey to its intended audience.

One popular resource is Amazon’s Mechanical Turk (more commonly known as MTurk). MTurk is at its most basic a website where workers look for jobs (called hits) to be listed by employers, and choose whether to do the task or not for a set reward. MTurk has grown over the last decade to be a common source of survey participants in the social sciences, in part because hiring workers costs very little (you can get some surveys completed for penny’s). That means you can get your survey completed with a small grant ($1-2k at the low end) and get the data back in a few hours. Really, it’s a quick and easy way to run a survey.

However, the workers aren’t perfectly representative of the average American. For instance, researchers have found that MTurk respondents are younger, better educated, and earn less than the average American.

One way to get around that issue, which can be used with MTurk or any survey, is to weight the responses. Because with MTurk you’ll get fewer responses from older, less educated, and richer Americans, those responses you do give you want to count for more to make your sample more representative of the population. Oversimplified example incoming!

Imagine you’re setting up a pizza party for your class. There are 9 people in your class, 4 men and 5 women. You only got 4 responses from the men, and 3 from the women. All 4 men wanted peperoni pizza, while the 3 women want a combination. Pepperoni wins right, 4 to 3? Not if you assume that the people that didn’t respond are the same as the ones that did. If you weight the responses to match the population (the full class of 9), a combination pizza is the winner.

Because you know the population of women is 5, you can weight the 3 responses from women by 5/3 = 1.6667. If we weight (or multiply) each vote we did receive from a woman by 1.6667, each vote for a combination now equals 1.6667, meaning that the 3 votes for combination total 5. Because we received a vote from every man in the class, we just weight their votes by 1. The big assumption we have to make is that the people we didn’t hear from (the 2 women that didn’t vote) are similar to the ones we did hear from. And if we don’t get any responses from a group we don’t have anything to infer their preferences or views from.

Let’s go through a slightly more complex example, still just considering one quality about people in the class. Let’s say your class actually has 100 students, but you only received votes from 50. And, what type of pizza people voted for is mixed, but men still prefer peperoni overall, and women still prefer combination. The class is 60% female and 40% male.

We received 21 votes from women out of the 60, so we can weight their responses by 60/21 to represent the population. We got 29 votes out of the 40 for men, so their responses can be weighted by 40/29. See the math below.

53.8 votes for combination? That might seem a little odd, but weighting isn’t a perfect science. We can’t identify what a non-respondent would have said exactly, all we can do is use the responses of other similar people to make a good guess. That issue often comes up in polling, where pollsters have to guess who is going to vote in a given election in order to project who will win. And we can weight on any characteristic of a person we think will be important, alone or in combination. Modern polls weight on age, gender, voting habits, education, and more to make the results as generalizable as possible.

There’s an appendix later in this book where I walk through the actual steps of creating weights for a sample in R, if anyone actually does a survey. I intended this section to show that doing a good survey might be simpler than it seemed, but now it might sound even more difficult. A good lesson to take though is that there’s always another door to go through, another hurdle to improve your methods. Being good at research just means being constantly prepared to be given a new challenge, and being able to find another solution.

7.3 Non-Probability Sampling

Qualitative researchers’ main objective is to gain an in-depth understanding on the subject matter they are studying, rather than attempting to generalize results to the population. As such, non-probability sampling is more common because of the researchers desire to gain information not from random elements of the population, but rather from specific individuals.

Random selection is not used in nonprobability sampling. Instead, the personal judgment of the researcher determines who will be included in the sample. Typically, researchers may base their selection on availability, quotas, or other criteria. However, not all members of the population are given an equal chance to be included in the sample. This nonrandom approach results in not knowing whether the sample represents the entire population. Consequently, researchers are not able to make valid generalizations about the population.

As with probability sampling, there are several types of non-probability samples. Convenience sampling , also known as accidental or opportunity sampling, is a process of choosing a sample that is easily accessible and readily available to the researcher. Researchers tend to collect samples from convenient locations such as their place of employment, a location, school, or other close affiliation. Although this technique allows for quick and easy access to available participants, a large part of the population is excluded from the sample.

For example, researchers (particularly in psychology) often rely on research subjects that are at their universities. That is highly convenient, students are cheap to hire and readily available on campuses. However, it means the results of the study may have limited ability to predict motivations or behaviors of people that aren’t included in the sample, i.e., people outside the age of 18-22 that are going to college.

If I ask you to get find out whether people approve of the mayor or not, and tell you I want 500 people’s opinions, should you go stand in front of the local grocery store? That would be convinient, and the people coming will be random, right? Not really. If you stand outside a rural Piggly Wiggly or an urban Whole Foods, do you think you’ll see the same people? Probably not, people’s chracteristics make the more or less likely to be in those locations. This technique runs the high risk of over- or under-representation, biased results, as well as an inability to make generalizations about the larger population. As the name implies though, it is convenient.

Purposive sampling , also known as judgmental or selective sampling, refers to a method in which the researcher decides who will be selected for the sample based on who or what is relevant to the study’s purpose. The researcher must first identify a specific characteristic of the population that can best help answer the research question. Then, they can deliberately select a sample that meets that particular criterion. Typically, the sample is small with very specific experiences and perspectives. For instance, if I wanted to understand the experiences of prominent foreign-born politicians in the United States, I would purposefully build a sample of… prominent foreign-born politicians in the United States. That would exclude anyone that was born in the United States or and that wasn’t a politician, and I’d have to define what I meant by prominent. Purposive sampling is susceptible to errors in judgment by the researcher and selection bias due to a lack of random sampling, but when attempting to research small communities it can be effective.

When dealing with small and difficult to reach communities researchers sometimes use snowball samples , also known as chain referral sampling. Snowball sampling is a process in which the researcher selects an initial participant for the sample, then asks that participant to recruit or refer additional participants who have similar traits as them. The cycle continues until the needed sample size is obtained.

This technique is used when the study calls for participants who are hard to find because of a unique or rare quality or when a participant does not want to be found because they are part of a stigmatized group or behavior. Examples may include people with rare diseases, sex workers, or a child sex offenders. It would be impossible to find an accurate list of sex workers anywhere, and surveying the general population about whether that is their job will produce false responses as people will be unwilling to identify themselves. As such, a common method is to gain the trust of one individual within the community, who can then introduce you to others. It is important that the researcher builds rapport and gains trust so that participants can be comfortable contributing to the study, but that must also be balanced by mainting objectivity in the research.

Snowball sampling is a useful method for locating hard to reach populations but cannot guarantee a representative sample because each contact will be based upon your last. For instance, let’s say you’re studying illegal fight clubs in your state. Some fight clubs allow weapons in the fights, while others completely ban them; those two types of clubs never interreact because of their disagreement about whether weapons should be allowed, and there’s no overlap between them (no members in both type of club). If your initial contact is with a club that uses weapons, all of your subsequent contacts will be within that community and so you’ll never understand the differences. If you didn’t know there were two types of clubs when you started, you’ll never even know you’re only researching half of the community. As such, snowball sampling can be a necessary technique when there are no other options, but it does have limitations.

Quota Sampling is a process in which the researcher must first divide a population into mutually exclusive subgroups, similar to stratified sampling. Depending on what is relevant to the study, subgroups can be based on a known characteristic such as age, race, gender, etc. Secondly, the researcher must select a sample from each subgroup to fit their predefined quotas. Quota sampling is used for the same reason as stratified sampling, to ensure that your sample has representation of certain groups. For instance, let’s say that you’re studying sexual harassment in the workplace, and men are much more willing to discuss their experiences than women. You might choose to decide that half of your final sample will be women, and stop requesting interviews with men once you fill your quota. The core difference is that while stratified sampling chooses randomly from within the different groups, quota sampling does not. A quota sample can either be proportional or non-proportional . Proportional quota sampling refers to ensuring that the quotas in the sample match the population (if 35% of the company is female, 35% of the sample should be female). Non-proportional sampling allows you to select your own quota sizes. If you think the experiences of females with sexual harassment are more important to your research, you can include whatever percentage of females you desire.

7.4 Dangers in sampling

Now that we’ve described all the different ways that one could create a sample, we can talk more about the pitfalls of sampling. Ensuring a quality sample means asking yourself some basic questions:

• Who is in the sample?
• How were they sampled?
• Why were they sampled?

A meal is often only as good as the ingredients you use, and your data will only be as good as the sample. If you collect data from the wrong people, you’ll get the wrong answer. You’ll still get an answer, it’ll just be inaccurate. And I want to reemphasize here wrong people just refers to inappropriate for your study. If I want to study bullying in middle schools, but I only talk to people that live in a retirement home, how accurate or relevant will the information I gather be? Sure, they might have grandchildren in middle school, and they may remember their experiences. But wouldn’t my information be more relevant if I talked to students in middle school, or perhaps a mix of teachers, parents, and students? I’ll get an answer from retirees, but it wont be the one I need. The sample has to be appropriate to the research question.

Is a bigger sample always better? Not necessarily. A larger sample can be useful, but a more representative one of the population is better. That was made painfully clear when the magazine Literary Digest ran a poll to predict who would win the 1936 presidential election between Alf Landon and incumbent Franklin Roosevelt. Literary Digest had run the poll since 1916, and had been correct in predicting the outcome every time. It was the largest poll ever, and they received responses for 2.27 million people. They essentially received responses from 1 percent of the American population, while many modern polls use only 1000 responses for a much more populous country. What did they predict? They showed that Alf Landon would be the overwhelming winner, yet when the election was held Roosevelt won every state except Maine and Vermont. It was one of the most decisive victories in Presidential history.

So what went wrong for the Literary Digest? Their poll was large (gigantic!), but it wasn’t representative of likely voters. They polled their own readership, which tended to be more educated and wealthy on average, along with people on a list of those with registered automobiles and telephone users (both of which tended to be owned by the wealthy at that time). Thus, the poll largely ignored the majority of Americans, who ended up voting for Roosevelt. The Literary Digest poll is famous for being wrong, but led to significant improvements in the science of polling to avoid similar mistakes in the future. Researchers have learned a lot in the century since that mistake, even if polling and surveys still aren’t (and can’t be) perfect.

What kind of sampling strategy did Literary Digest use? Convenience, they relied on lists they had available, rather than try to ensure every American was included on their list. A representative poll of 2 million people will give you more accurate results than a representative poll of 2 thousand, but I’ll take the smaller more representative poll than a larger one that uses convenience sampling any day.

7.5 Summary

Picking the right type of sample is critical to getting an accurate answer to your reserach question. There are a lot of differnet options in how you can select the people to participate in your research, but typically only one that is both correct and possible depending on the research you’re doing. In the next chapter we’ll talk about a few other methods for conducting reseach, some that don’t include any sampling by you.

Root out friction in every digital experience, super-charge conversion rates, and optimize digital self-service

Uncover insights from any interaction, deliver AI-powered agent coaching, and reduce cost to serve

Increase revenue and loyalty with real-time insights and recommendations delivered to teams on the ground

Know how your people feel and empower managers to improve employee engagement, productivity, and retention

Take action in the moments that matter most along the employee journey and drive bottom line growth

Whatever they’re are saying, wherever they’re saying it, know exactly what’s going on with your people

Get faster, richer insights with qual and quant tools that make powerful market research available to everyone

Run concept tests, pricing studies, prototyping + more with fast, powerful studies designed by UX research experts

Track your brand performance 24/7 and act quickly to respond to opportunities and challenges in your market

Explore the platform powering Experience Management

• Free Account
• For Digital
• For Customer Care
• For Human Resources
• For Researchers
• Financial Services
• All Industries

Popular Use Cases

• Customer Experience
• Employee Experience
• Net Promoter Score
• Voice of Customer
• Customer Success Hub
• Product Documentation
• Training & Certification
• XM Institute
• Popular Resources
• Customer Stories
• Artificial Intelligence
• Market Research
• Partnerships
• Marketplace

The annual gathering of the experience leaders at the world’s iconic brands building breakthrough business results, live in Salt Lake City.

• English/AU & NZ
• Español/Europa
• Español/América Latina
• Português Brasileiro
• REQUEST DEMO
• Experience Management
• What Is A Research Panel?
• Population and Samples

Try Qualtrics for free

Population and samples: the complete guide.

9 min read What are the differences between populations and samples? In this guide, we’ll discuss the two, as well as how to use them effectively in your research.

When we hear the term population, the first thing that comes to mind is a large group of people.

In market research, however, a population is an entire group that you want to draw conclusions about and possesses a standard parameter that is consistent throughout the group.

It’s important to note that a population doesn’t always refer to people, it can mean anything you want to study: objects, organizations, animals, chemicals and so on.

For example, all the countries in the world are an example of a population — or even the number of males in the UK. The size of the population can vary according to the target entities in question and the scope of the research.

When do you need to collect data from a population?

You use populations when your research calls for or requires you to collect data from every member of the population. Note: it’s normally far easier to collect data from whole populations when they’re small and accessible.

For larger and more diverse populations, on the other hand — e.g. a regional study on people living in Europe — while you would get findings representative of the entire population (as they’re all included in the study), it would take a considerable amount of time.

It’s in these instances that you use sampling. It allows you to make more precise inferences about the population as a whole, and streamline your research project. They’re typically used when population sizes are too large to include all possible members or inferences.

Let’s talk about samples.

What is a sample?

In statistical methods, a sample consists of a smaller group of entities, which are taken from the entire population. This creates a subset group that is easier to manage and has the characteristics of the larger population.

This smaller subset is then surveyed to gain information and data. The sample should reflect the population as a whole, without any bias towards a specific attribute or characteristic. In this way, researchers can ensure their results are representative and statistically significant.

To remove unconscious selection bias, a researcher may choose to randomize the selection of the sample.

Types of samples

There are two categories of sampling generally used – probability sampling and non-probability sampling :

• Probability sampling , also known as random sampling, is a kind of sample selection where randomization is used instead of deliberate choice.
• Non-probability sampling techniques involve the researcher deliberately picking items or individuals for the sample based on their research goals or knowledge

These two sampling techniques have several methods:

Probability sampling types include:

• Simple random sampling Every element in the population has an equal chance of being selected as part of the sample. Find out more about simple random sampling.
• Systematic sampling Also known as systematic clustering, in this method, random selection only applies to the first item chosen. A rule then applies so that every nth item or person after that is picked. Find out more about systematic sampling .
• Stratified random sampling Sampling uses random selection within predefined groups. Find out more about stratified random sampling .
• Cluster sampling Groups rather than individual units of the target population are selected at random.

Non-probability sampling types include:

• Convenience sampling People or elements in a sample are selected based on their availability.
• Quota sampling The sample is formed according to certain groups or criteria.
• Purposive sampling Also known as judgmental sampling. The sample is formed by the researcher consciously choosing entities, based on the survey goals.
• Snowball sampling Also known as referral sampling. The sample is formed by sample participants recruiting connections.

Find out more about sampling methods with our ultimate guide to sampling methods and best practices

Calculating sample size

Worried about sample sizes? You can also use our sample size calculator to determine how many responses you need to be confident in your data.

Go to sample size calculator

When to use sampling

As mentioned, sampling is useful for dealing with population data that is too large to process as a whole or is inaccessible. Sampling also helps to keep costs down and reduce time to insight.

Advantages of using sampling to collect data

• Provide researchers with a representative view of the population through the sample subset.
• The researcher has flexibility and control over what kind of sample they want to make, depending on their needs and the goals of the research.
• Reduces the volume of data, helping to save time.
• With proper methods, researchers can achieve a higher level of accuracy
• Researchers can get detailed information on a population with a smaller amount of resource
• Significantly cheaper than other methods
• Allows for deeper study of some aspects of data — rather than asking 15 questions to every individual, it’s better to use 50 questions on a representative sample

Disadvantages of using sampling to collect data

• Researcher bias can affect the quality and accuracy of results
• Sampling studies require well-trained experts
• Even with good survey design, there’s no way to eliminate sampling errors entirely
• People in the sample may refuse to respond
• Probability sampling methods can be less representative in favor of random allocation.
• Improper selection of sampling techniques can affect the entire process negatively

How can you use sampling in business?

Depending on the nature of your study and the conclusions you wish to draw, you’ll have to select an appropriate sampling method as mentioned above. That said, here are a few examples of how you can use sampling techniques in business.

Creating a new product

If you’re looking to create a new product line, you may want to do panel interviews or surveys with a representative sample for the new market. By showing your product or concept to a sample that represents your target audience (population), you ensure that the feedback you receive is more reflective of how that customer segment will feel.

Average employee performance

If you wanted to understand the average employee performance for a specific group, you could use a random sample from a team or department (population). As every person in the department has a chance of being selected, you’ll have a truly random — yet representative sample. From the data collected, you can make inferences about the team/department’s average performance.

Store feedback

Let’s say you want to collect feedback from customers who are shopping or have just finished shopping at your store. To do this, you could use convenience sampling. It’s fast, affordable and done at a point of convenience. You can use this to get a quick gauge of how people feel about your store’s shopping experience — but it won’t represent the true views of all your customers.

Manage your population and sample data easily

Whatever the sample size of your target audience, there are several things to consider:

• How can you save time in conducting the research?
• How do you analyze and compare all the responses?
• How can you track and chase non-respondents easily?
• How can you translate the data into a usable presentation format?
• How can you share this easily?

These questions can make the task of supporting internal teams and management difficult.

This is where the Qualtrics CoreXM technology solution can help you progress through research with ease.

It includes:

• Advanced AI and machine learning tools to easily analyze data from open-text responses and data, giving you actionable insights at scale.
• Intuitive drag-and-drop survey building with powerful logic, 100+ question types, and pre-built survey templates . For more information on how to get started on your survey creation, visit our complete guide on creating a survey.
• Stylish, accessible and easy-to-understand reporting that automatically updates in real time, so everyone in your organization has the latest insights at their fingertips.
• Powerful automation to get up and running quickly with out-of-the-box workflows, including guided setup and proactive recommendations to help you connect with other teams and react fast to changes.

Also, the Qualtrics online research panels and samples help you to:

• Choose a target audience and get access to a representative sample
• Boost the accuracy of your research with a sample methodology that’s 47% more consistent than standard sampling methods
• Get dedicated support at every stage, from launching your survey to reporting on the results.

Want to learn more?

Related resources

Panels & Samples

Representative Samples 13 min read

Reward survey participants 15 min read, panel management 14 min read, what is a research panel 10 min read.

Analysis & Reporting

Data Saturation In Qualitative Research 8 min read

How to determine sample size 12 min read.

Market Segmentation

User Personas 14 min read

Request demo.

Ready to learn more about Qualtrics?

3. Populations and samples

Populations, unbiasedness and precision, randomisation, variation between samples, standard error of the mean.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.1: Samples, Populations and Sampling

• Last updated
• Save as PDF
• Page ID 36115

• Danielle Navarro
• University of New South Wales

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In the prelude to Part I discussed the riddle of induction, and highlighted the fact that all learning requires you to make assumptions. Accepting that this is true, our first task to come up with some fairly general assumptions about data that make sense. This is where sampling theory comes in. If probability theory is the foundations upon which all statistical theory builds, sampling theory is the frame around which you can build the rest of the house. Sampling theory plays a huge role in specifying the assumptions upon which your statistical inferences rely. And in order to talk about “making inferences” the way statisticians think about it, we need to be a bit more explicit about what it is that we’re drawing inferences from (the sample) and what it is that we’re drawing inferences about (the population).

In almost every situation of interest, what we have available to us as researchers is a sample of data. We might have run experiment with some number of participants; a polling company might have phoned some number of people to ask questions about voting intentions; etc. Regardless: the data set available to us is finite, and incomplete. We can’t possibly get every person in the world to do our experiment; a polling company doesn’t have the time or the money to ring up every voter in the country etc. In our earlier discussion of descriptive statistics (Chapter 5, this sample was the only thing we were interested in. Our only goal was to find ways of describing, summarising and graphing that sample. This is about to change.

Defining a population

A sample is a concrete thing. You can open up a data file, and there’s the data from your sample. A population , on the other hand, is a more abstract idea. It refers to the set of all possible people, or all possible observations, that you want to draw conclusions about, and is generally much bigger than the sample. In an ideal world, the researcher would begin the study with a clear idea of what the population of interest is, since the process of designing a study and testing hypotheses about the data that it produces does depend on the population about which you want to make statements. However, that doesn’t always happen in practice: usually the researcher has a fairly vague idea of what the population is and designs the study as best he/she can on that basis.

Sometimes it’s easy to state the population of interest. For instance, in the “polling company” example that opened the chapter, the population consisted of all voters enrolled at the a time of the study – millions of people. The sample was a set of 1000 people who all belong to that population. In most situations the situation is much less simple. In a typical a psychological experiment, determining the population of interest is a bit more complicated. Suppose I run an experiment using 100 undergraduate students as my participants. My goal, as a cognitive scientist, is to try to learn something about how the mind works. So, which of the following would count as “the population”:

• All of the undergraduate psychology students at the University of Adelaide?
• Undergraduate psychology students in general, anywhere in the world?
• Australians currently living?
• Australians of similar ages to my sample?
• Anyone currently alive?
• Any human being, past, present or future?
• Any biological organism with a sufficient degree of intelligence operating in a terrestrial environment?
• Any intelligent being?

Each of these defines a real group of mind-possessing entities, all of which might be of interest to me as a cognitive scientist, and it’s not at all clear which one ought to be the true population of interest. As another example, consider the Wellesley-Croker game that we discussed in the prelude. The sample here is a specific sequence of 12 wins and 0 losses for Wellesley. What is the population?

• All outcomes until Wellesley and Croker arrived at their destination?
• All outcomes if Wellesley and Croker had played the game for the rest of their lives?
• All outcomes if Wellseley and Croker lived forever and played the game until the world ran out of hills?
• All outcomes if we created an infinite set of parallel universes and the Wellesely/Croker pair made guesses about the same 12 hills in each universe?

Again, it’s not obvious what the population is.

Irrespective of how I define the population, the critical point is that the sample is a subset of the population, and our goal is to use our knowledge of the sample to draw inferences about the properties of the population. The relationship between the two depends on the procedure by which the sample was selected. This procedure is referred to as a sampling method , and it is important to understand why it matters.

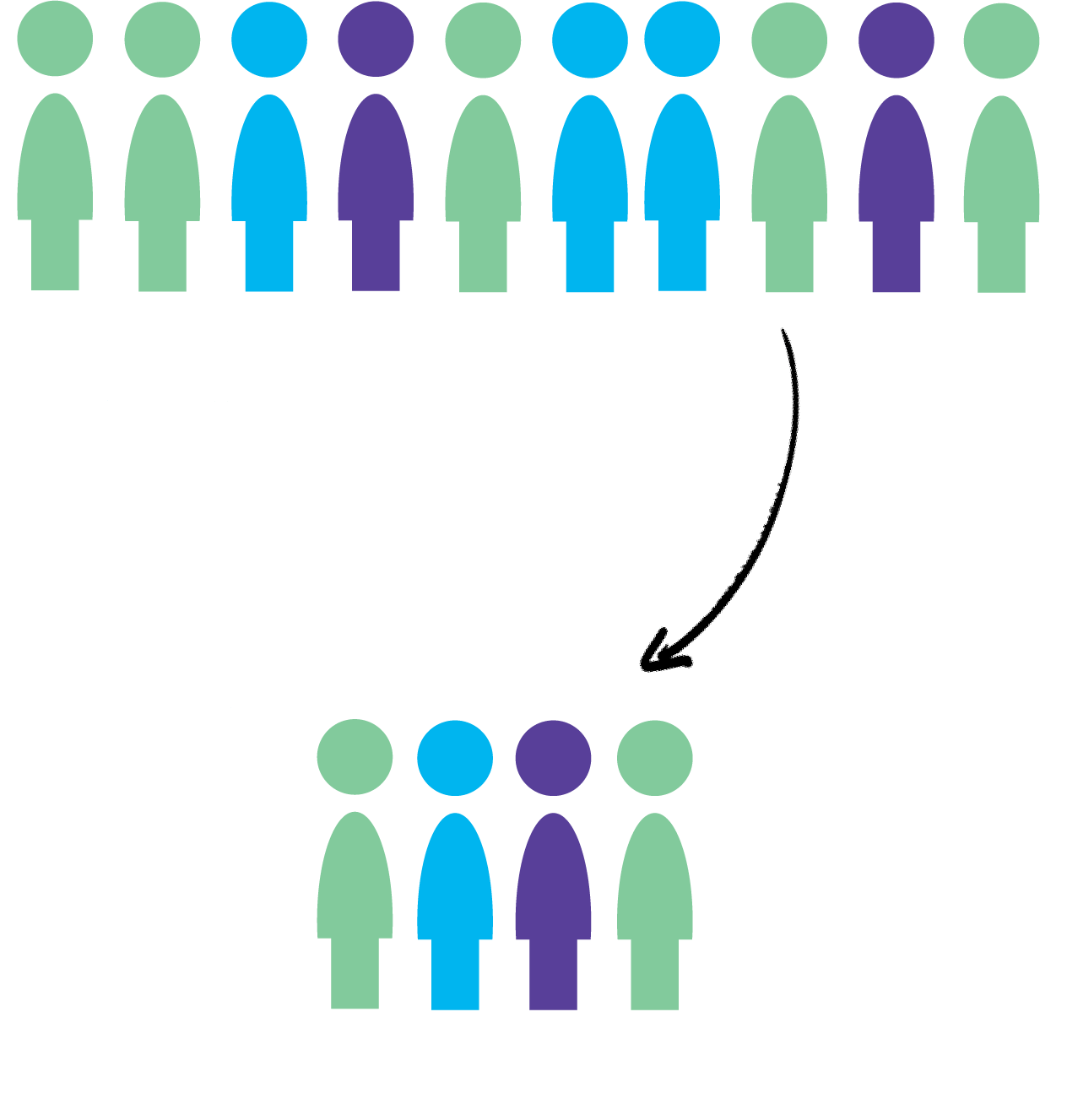
To keep things simple, let’s imagine that we have a bag containing 10 chips. Each chip has a unique letter printed on it, so we can distinguish between the 10 chips. The chips come in two colours, black and white. This set of chips is the population of interest, and it is depicted graphically on the left of Figure 10.1. As you can see from looking at the picture, there are 4 black chips and 6 white chips, but of course in real life we wouldn’t know that unless we looked in the bag. Now imagine you run the following “experiment”: you shake up the bag, close your eyes, and pull out 4 chips without putting any of them back into the bag. First out comes the a chip (black), then the c chip (white), then j (white) and then finally b (black). If you wanted, you could then put all the chips back in the bag and repeat the experiment, as depicted on the right hand side of Figure 10.1. Each time you get different results, but the procedure is identical in each case. The fact that the same procedure can lead to different results each time, we refer to it as a random process. 147 However, because we shook the bag before pulling any chips out, it seems reasonable to think that every chip has the same chance of being selected. A procedure in which every member of the population has the same chance of being selected is called a simple random sample . The fact that we did not put the chips back in the bag after pulling them out means that you can’t observe the same thing twice, and in such cases the observations are said to have been sampled without replacement .

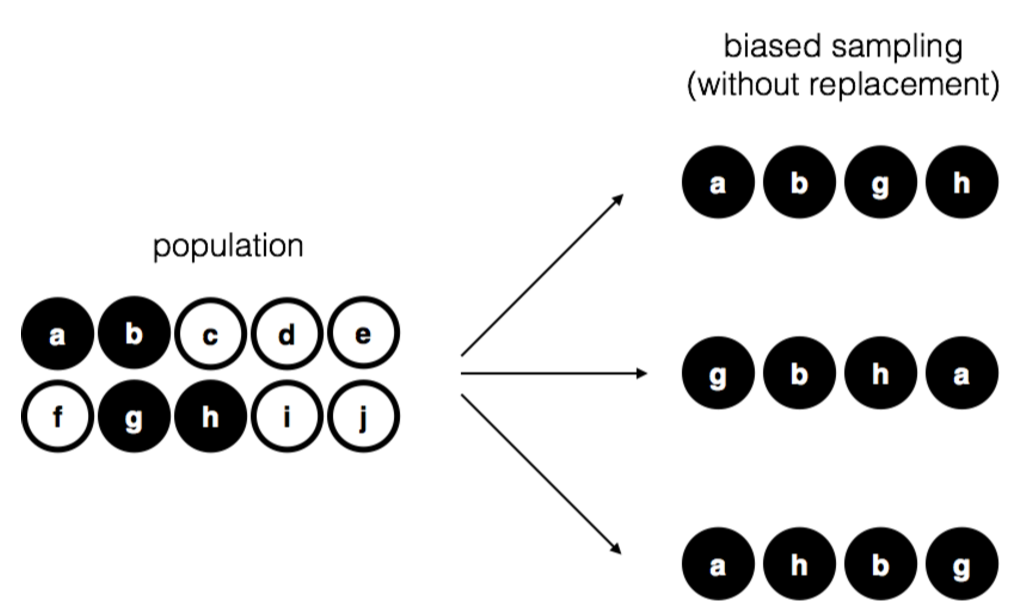
To help make sure you understand the importance of the sampling procedure, consider an alternative way in which the experiment could have been run. Suppose that my 5-year old son had opened the bag, and decided to pull out four black chips without putting any of them back in the bag. This biased sampling scheme is depicted in Figure 10.2. Now consider the evidentiary value of seeing 4 black chips and 0 white chips. Clearly, it depends on the sampling scheme, does it not? If you know that the sampling scheme is biased to select only black chips, then a sample that consists of only black chips doesn’t tell you very much about the population! For this reason, statisticians really like it when a data set can be considered a simple random sample, because it makes the data analysis much easier.

A third procedure is worth mentioning. This time around we close our eyes, shake the bag, and pull out a chip. This time, however, we record the observation and then put the chip back in the bag. Again we close our eyes, shake the bag, and pull out a chip. We then repeat this procedure until we have 4 chips. Data sets generated in this way are still simple random samples, but because we put the chips back in the bag immediately after drawing them it is referred to as a sample with replacement . The difference between this situation and the first one is that it is possible to observe the same population member multiple times, as illustrated in Figure 10.3.

In my experience, most psychology experiments tend to be sampling without replacement, because the same person is not allowed to participate in the experiment twice. However, most statistical theory is based on the assumption that the data arise from a simple random sample with replacement. In real life, this very rarely matters. If the population of interest is large (e.g., has more than 10 entities!) the difference between sampling with- and without- replacement is too small to be concerned with. The difference between simple random samples and biased samples, on the other hand, is not such an easy thing to dismiss.

Most samples are not simple random samples

As you can see from looking at the list of possible populations that I showed above, it is almost impossible to obtain a simple random sample from most populations of interest. When I run experiments, I’d consider it a minor miracle if my participants turned out to be a random sampling of the undergraduate psychology students at Adelaide university, even though this is by far the narrowest population that I might want to generalise to. A thorough discussion of other types of sampling schemes is beyond the scope of this book, but to give you a sense of what’s out there I’ll list a few of the more important ones:

• Stratified sampling . Suppose your population is (or can be) divided into several different subpopulations, or strata . Perhaps you’re running a study at several different sites, for example. Instead of trying to sample randomly from the population as a whole, you instead try to collect a separate random sample from each of the strata. Stratified sampling is sometimes easier to do than simple random sampling, especially when the population is already divided into the distinct strata. It can also be more efficient that simple random sampling, especially when some of the subpopulations are rare. For instance, when studying schizophrenia it would be much better to divide the population into two 148 strata (schizophrenic and not-schizophrenic), and then sample an equal number of people from each group. If you selected people randomly, you would get so few schizophrenic people in the sample that your study would be useless. This specific kind of of stratified sampling is referred to as oversampling because it makes a deliberate attempt to over-represent rare groups.
• Snowball sampling is a technique that is especially useful when sampling from a “hidden” or hard to access population, and is especially common in social sciences. For instance, suppose the researchers want to conduct an opinion poll among transgender people. The research team might only have contact details for a few trans folks, so the survey starts by asking them to participate (stage 1). At the end of the survey, the participants are asked to provide contact details for other people who might want to participate. In stage 2, those new contacts are surveyed. The process continues until the researchers have sufficient data. The big advantage to snowball sampling is that it gets you data in situations that might otherwise be impossible to get any. On the statistical side, the main disadvantage is that the sample is highly non-random, and non-random in ways that are difficult to address. On the real life side, the disadvantage is that the procedure can be unethical if not handled well, because hidden populations are often hidden for a reason. I chose transgender people as an example here to highlight this: if you weren’t careful you might end up outing people who don’t want to be outed (very, very bad form), and even if you don’t make that mistake it can still be intrusive to use people’s social networks to study them. It’s certainly very hard to get people’s informed consent before contacting them, yet in many cases the simple act of contacting them and saying “hey we want to study you” can be hurtful. Social networks are complex things, and just because you can use them to get data doesn’t always mean you should.
• Convenience sampling is more or less what it sounds like. The samples are chosen in a way that is convenient to the researcher, and not selected at random from the population of interest. Snowball sampling is one type of convenience sampling, but there are many others. A common example in psychology are studies that rely on undergraduate psychology students. These samples are generally non-random in two respects: firstly, reliance on undergraduate psychology students automatically means that your data are restricted to a single subpopulation. Secondly, the students usually get to pick which studies they participate in, so the sample is a self selected subset of psychology students not a randomly selected subset. In real life, most studies are convenience samples of one form or another. This is sometimes a severe limitation, but not always.

much does it matter if you don’t have a simple random sample?

Okay, so real world data collection tends not to involve nice simple random samples. Does that matter? A little thought should make it clear to you that it can matter if your data are not a simple random sample: just think about the difference between Figures 10.1 and 10.2. However, it’s not quite as bad as it sounds. Some types of biased samples are entirely unproblematic. For instance, when using a stratified sampling technique you actually know what the bias is because you created it deliberately, often to increase the effectiveness of your study, and there are statistical techniques that you can use to adjust for the biases you’ve introduced (not covered in this book!). So in those situations it’s not a problem.

More generally though, it’s important to remember that random sampling is a means to an end, not the end in itself. Let’s assume you’ve relied on a convenience sample, and as such you can assume it’s biased. A bias in your sampling method is only a problem if it causes you to draw the wrong conclusions. When viewed from that perspective, I’d argue that we don’t need the sample to be randomly generated in every respect: we only need it to be random with respect to the psychologically-relevant phenomenon of interest. Suppose I’m doing a study looking at working memory capacity. In study 1, I actually have the ability to sample randomly from all human beings currently alive, with one exception: I can only sample people born on a Monday. In study 2, I am able to sample randomly from the Australian population. I want to generalise my results to the population of all living humans. Which study is better? The answer, obviously, is study 1. Why? Because we have no reason to think that being “born on a Monday” has any interesting relationship to working memory capacity. In contrast, I can think of several reasons why “being Australian” might matter. Australia is a wealthy, industrialised country with a very well-developed education system. People growing up in that system will have had life experiences much more similar to the experiences of the people who designed the tests for working memory capacity. This shared experience might easily translate into similar beliefs about how to “take a test”, a shared assumption about how psychological experimentation works, and so on. These things might actually matter. For instance, “test taking” style might have taught the Australian participants how to direct their attention exclusively on fairly abstract test materials relative to people that haven’t grown up in a similar environment; leading to a misleading picture of what working memory capacity is.

There are two points hidden in this discussion. Firstly, when designing your own studies, it’s important to think about what population you care about, and try hard to sample in a way that is appropriate to that population. In practice, you’re usually forced to put up with a “sample of convenience” (e.g., psychology lecturers sample psychology students because that’s the least expensive way to collect data, and our coffers aren’t exactly overflowing with gold), but if so you should at least spend some time thinking about what the dangers of this practice might be.

Secondly, if you’re going to criticise someone else’s study because they’ve used a sample of convenience rather than laboriously sampling randomly from the entire human population, at least have the courtesy to offer a specific theory as to how this might have distorted the results. Remember, everyone in science is aware of this issue, and does what they can to alleviate it. Merely pointing out that “the study only included people from group BLAH” is entirely unhelpful, and borders on being insulting to the researchers, who are of course aware of the issue. They just don’t happen to be in possession of the infinite supply of time and money required to construct the perfect sample. In short, if you want to offer a responsible critique of the sampling process, then be helpful . Rehashing the blindingly obvious truisms that I’ve been rambling on about in this section isn’t helpful.

Population parameters and sample statistics

Okay. Setting aside the thorny methodological issues associated with obtaining a random sample and my rather unfortunate tendency to rant about lazy methodological criticism, let’s consider a slightly different issue. Up to this point we have been talking about populations the way a scientist might. To a psychologist, a population might be a group of people. To an ecologist, a population might be a group of bears. In most cases the populations that scientists care about are concrete things that actually exist in the real world. Statisticians, however, are a funny lot. On the one hand, they are interested in real world data and real science in the same way that scientists are. On the other hand, they also operate in the realm of pure abstraction in the way that mathematicians do. As a consequence, statistical theory tends to be a bit abstract in how a population is defined. In much the same way that psychological researchers operationalise our abstract theoretical ideas in terms of concrete measurements (Section 2.1, statisticians operationalise the concept of a “population” in terms of mathematical objects that they know how to work with. You’ve already come across these objects in Chapter 9: they’re called probability distributions.

The idea is quite simple. Let’s say we’re talking about IQ scores. To a psychologist, the population of interest is a group of actual humans who have IQ scores. A statistician “simplifies” this by operationally defining the population as the probability distribution depicted in Figure ?? . IQ tests are designed so that the average IQ is 100, the standard deviation of IQ scores is 15, and the distribution of IQ scores is normal. These values are referred to as the population parameters because they are characteristics of the entire population. That is, we say that the population mean μ is 100, and the population standard deviation σ is 15.

Now suppose I run an experiment. I select 100 people at random and administer an IQ test, giving me a simple random sample from the population. My sample would consist of a collection of numbers like this:

Each of these IQ scores is sampled from a normal distribution with mean 100 and standard deviation 15. So if I plot a histogram of the sample, I get something like the one shown in Figure 10.4b. As you can see, the histogram is roughly the right shape, but it’s a very crude approximation to the true population distribution shown in Figure 10.4a. When I calculate the mean of my sample, I get a number that is fairly close to the population mean 100 but not identical. In this case, it turns out that the people in my sample have a mean IQ of 98.5, and the standard deviation of their IQ scores is 15.9. These sample statistics are properties of my data set, and although they are fairly similar to the true population values, they are not the same. In general, sample statistics are the things you can calculate from your data set, and the population parameters are the things you want to learn about. Later on in this chapter I’ll talk about how you can estimate population parameters using your sample statistics (Section 10.4 and how to work out how confident you are in your estimates (Section 10.5 but before we get to that there’s a few more ideas in sampling theory that you need to know about.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, automatically generate references for free.

• Knowledge Base
• Methodology
• Population vs Sample | Definitions, Differences & Examples

Population vs Sample | Definitions, Differences & Examples

Published on 3 May 2022 by Pritha Bhandari . Revised on 5 December 2022.

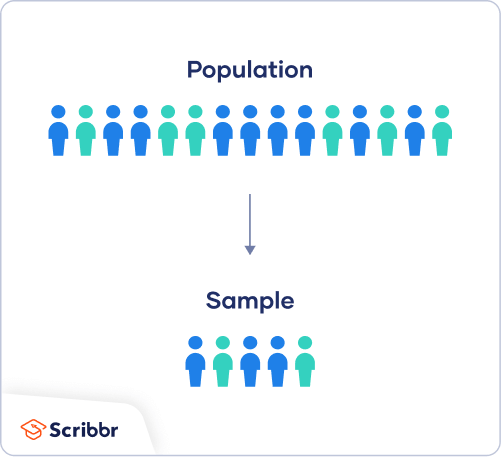
A population is the entire group that you want to draw conclusions about.

A sample is the specific group that you will collect data from. The size of the sample is always less than the total size of the population.

In research, a population doesn’t always refer to people. It can mean a group containing elements of anything you want to study, such as objects, events, organisations, countries, species, or organisms.

Table of contents

Collecting data from a population, collecting data from a sample, population parameter vs sample statistic, practice questions: populations vs samples, frequently asked questions about samples and populations.

Populations are used when your research question requires, or when you have access to, data from every member of the population.

Usually, it is only straightforward to collect data from a whole population when it is small, accessible and cooperative.

For larger and more dispersed populations, it is often difficult or impossible to collect data from every individual. For example, every 10 years, the federal US government aims to count every person living in the country using the US Census. This data is used to distribute funding across the nation.

However, historically, marginalised and low-income groups have been difficult to contact, locate, and encourage participation from. Because of non-responses, the population count is incomplete and biased towards some groups, which results in disproportionate funding across the country.

In cases like this, sampling can be used to make more precise inferences about the population.

Prevent plagiarism, run a free check.

When your population is large in size, geographically dispersed, or difficult to contact, it’s necessary to use a sample. With statistical analysis , you can use sample data to make estimates or test hypotheses about population data.

Ideally, a sample should be randomly selected and representative of the population. Using probability sampling methods (such as simple random sampling or stratified sampling ) reduces the risk of sampling bias and enhances both internal and external validity .

For practical reasons, researchers often use non-probability sampling methods . Non-probability samples are chosen for specific criteria; they may be more convenient or cheaper to access. Because of non-random selection methods, any statistical inferences about the broader population will be weaker than with a probability sample.

Reasons for sampling

• Necessity : Sometimes it’s simply not possible to study the whole population due to its size or inaccessibility.
• Practicality : It’s easier and more efficient to collect data from a sample.
• Cost-effectiveness : There are fewer participant, laboratory, equipment, and researcher costs involved.
• Manageability : Storing and running statistical analyses on smaller datasets is easier and reliable.

When you collect data from a population or a sample, there are various measurements and numbers you can calculate from the data. A parameter is a measure that describes the whole population. A statistic is a measure that describes the sample.

You can use estimation or hypothesis testing to estimate how likely it is that a sample statistic differs from the population parameter.

Sampling error

A sampling error is the difference between a population parameter and a sample statistic. In your study, the sampling error is the difference between the mean political attitude rating of your sample and the true mean political attitude rating of all undergraduate students in the Netherlands.

Sampling errors happen even when you use a randomly selected sample. This is because random samples are not identical to the population in terms of numerical measures like means and standard deviations .

Because the aim of scientific research is to generalise findings from the sample to the population, you want the sampling error to be low. You can reduce sampling error by increasing the sample size.

Samples are used to make inferences about populations . Samples are easier to collect data from because they are practical, cost-effective, convenient, and manageable.

Populations are used when a research question requires data from every member of the population. This is usually only feasible when the population is small and easily accessible.

A statistic refers to measures about the sample , while a parameter refers to measures about the population .

A sampling error is the difference between a population parameter and a sample statistic .

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Bhandari, P. (2022, December 05). Population vs Sample | Definitions, Differences & Examples. Scribbr. Retrieved 7 June 2024, from https://www.scribbr.co.uk/research-methods/population-versus-sample/

Is this article helpful?

Pritha Bhandari

Other students also liked, sampling methods | types, techniques, & examples, a quick guide to experimental design | 5 steps & examples, what is quantitative research | definition & methods.

Study Population

• Reference work entry
• pp 6412–6414
• Cite this reference work entry

3335 Accesses

Study population is a subset of the target population from which the sample is actually selected. It is broader than the concept sample frame . It may be appropriate to say that sample frame is an operationalized form of study population. For example, suppose that a study is going to conduct a survey of high school students on their social well-being . High school students all over the world might be considered as the target population. Because of practicalities, researchers decide to only recruit high school students studying in China who are the study population in this example. Suppose there is a list of high school students of China, this list is used as the sample frame .

Description

Study population is the operational definition of target population (Henry, 1990 ; Bickman & Rog, 1998 ). Researchers are seldom in a position to study the entire target population, which is not always readily accessible. Instead, only part of it—respondents who are both eligible for the study...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Babbie, E. R. (2010). The practice of social research . Belmont, CA: Wadsworth Publishing Company.

Google Scholar  

Bickman, L., & Rog, D. J. (1998). Handbook of applied social research methods . Thousand Oaks, CA: Sage Publications.

Friedman, L. M., Furberg, C. D., & DeMets, D. L. (2010). Fundamentals of clinical trials . New York: Springer.

Gerrish, K., & Lacey, A. (2010). The research process in nursing . West Sussex: Wiley-Blackwell.

Henry, G. T. (1990). Practical sampling . Newbury Park, CA: Sage Publications.

Kumar, R. (2011). Research methodology: A step-by-step guide for beginners . London: Sage Publications Limited.

Riegelman, R. K. (2005). Studying a study and testing a test: How to read the medical evidence . Philadelphia: Lippincott Williams & Wilkins.

Download references

Author information

Authors and affiliations.

Sociology Department, National University of Singapore, 11 Arts Link, 117570, Singapore, Singapore

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Shu Hu .

Editor information

Editors and affiliations.

University of Northern British Columbia, Prince George, BC, Canada

Alex C. Michalos

(residence), Brandon, MB, Canada

Rights and permissions

Reprints and permissions

Copyright information

© 2014 Springer Science+Business Media Dordrecht

About this entry

Cite this entry.

Hu, S. (2014). Study Population. In: Michalos, A.C. (eds) Encyclopedia of Quality of Life and Well-Being Research. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-0753-5_2893

Download citation

DOI : https://doi.org/10.1007/978-94-007-0753-5_2893

Publisher Name : Springer, Dordrecht

Print ISBN : 978-94-007-0752-8

Online ISBN : 978-94-007-0753-5

eBook Packages : Humanities, Social Sciences and Law

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• Foundations
• Write Paper

Search form

• Experiments
• Anthropology
• Self-Esteem
• Social Anxiety

Research Population

All research questions address issues that are of great relevance to important groups of individuals known as a research population.

This article is a part of the guide:

• Non-Probability Sampling
• Convenience Sampling
• Random Sampling
• Stratified Sampling
• Systematic Sampling

Browse Full Outline

• 1 What is Sampling?
• 2.1 Sample Group
• 2.2 Research Population
• 2.3 Sample Size
• 2.4 Randomization
• 3.1 Statistical Sampling
• 3.2 Sampling Distribution
• 3.3.1 Random Sampling Error
• 4.1 Random Sampling
• 4.2 Stratified Sampling
• 4.3 Systematic Sampling
• 4.4 Cluster Sampling
• 4.5 Disproportional Sampling
• 5.1 Convenience Sampling
• 5.2 Sequential Sampling
• 5.3 Quota Sampling
• 5.4 Judgmental Sampling
• 5.5 Snowball Sampling

A research population is generally a large collection of individuals or objects that is the main focus of a scientific query. It is for the benefit of the population that researches are done. However, due to the large sizes of populations, researchers often cannot test every individual in the population because it is too expensive and time-consuming. This is the reason why researchers rely on sampling techniques .

A research population is also known as a well-defined collection of individuals or objects known to have similar characteristics. All individuals or objects within a certain population usually have a common, binding characteristic or trait.

Usually, the description of the population and the common binding characteristic of its members are the same. "Government officials" is a well-defined group of individuals which can be considered as a population and all the members of this population are indeed officials of the government.

Relationship of Sample and Population in Research

A sample is simply a subset of the population. The concept of sample arises from the inability of the researchers to test all the individuals in a given population. The sample must be representative of the population from which it was drawn and it must have good size to warrant statistical analysis.

The main function of the sample is to allow the researchers to conduct the study to individuals from the population so that the results of their study can be used to derive conclusions that will apply to the entire population. It is much like a give-and-take process. The population “gives” the sample, and then it “takes” conclusions from the results obtained from the sample.

Two Types of Population in Research

Target population.

Target population refers to the ENTIRE group of individuals or objects to which researchers are interested in generalizing the conclusions. The target population usually has varying characteristics and it is also known as the theoretical population.

Accessible Population

The accessible population is the population in research to which the researchers can apply their conclusions. This population is a subset of the target population and is also known as the study population. It is from the accessible population that researchers draw their samples.

• Psychology 101
• Flags and Countries
• Capitals and Countries

Explorable.com (Nov 15, 2009). Research Population. Retrieved Jun 05, 2024 from Explorable.com: https://explorable.com/research-population

You Are Allowed To Copy The Text

The text in this article is licensed under the Creative Commons-License Attribution 4.0 International (CC BY 4.0) .

This means you're free to copy, share and adapt any parts (or all) of the text in the article, as long as you give appropriate credit and provide a link/reference to this page.

That is it. You don't need our permission to copy the article; just include a link/reference back to this page. You can use it freely (with some kind of link), and we're also okay with people reprinting in publications like books, blogs, newsletters, course-material, papers, wikipedia and presentations (with clear attribution).

Want to stay up to date? Follow us!

Save this course for later.

Don't have time for it all now? No problem, save it as a course and come back to it later.

Footer bottom

• Privacy Policy

• Subscribe to our RSS Feed
• Like us on Facebook
• Follow us on Twitter

• Search Search Please fill out this field.

What Is Population?

Understanding populations, how to measure a population, population and investing, the bottom line.

• Fundamental Analysis

Population Definition in Statistics and How to Measure It

Pete Rathburn is a copy editor and fact-checker with expertise in economics and personal finance and over twenty years of experience in the classroom.

Investopedia / Matthew Collins

In statistics, a population is the pool from which a sample is drawn for a study. Thus, any selection grouped by a common feature can be considered a population. A sample is a statistically significant portion of a population.

Key Takeaways

• In statistics, a population is the entire group on which data is being gathered and analyzed.
• It is generally difficult in terms of cost and time to gather the data needed on an entire population, so samples are often used to make inferences about a population.
• A sample of a population must be randomly selected for the results of the study to accurately reflect the whole.

Statisticians , scientists, and analysts prefer to know the characteristics of every entity in a population to draw the most precise conclusions possible. However, this is impossible or impractical most of the time since population sets tend to be quite large. A sample of a population must usually be taken since the characteristics of every individual in a population cannot be measured due to constraints of time, resources, and accessibility.

It's important to note that when referring to an individual in statistics, the term does not always mean a person. Statistically, an individual is a single entity in the group being studied.

For example, there is no real way to gather data on all of the great white sharks in the ocean (a population) because finding and tagging each one isn't feasible. So, marine biologists tag the great whites they can (a sample) and begin collecting information on them to make inferences about the entire population of great whites. This is a random sampling approach because the initial encounters with tagged great whites are entirely random.

A valid statistic may be drawn from either a sample or a study of an entire population. The objective of a random sample is to avoid bias in the results. A sample is random if every member of the whole population has an equal chance to be selected to participate.

The difficulty of measuring a population lies in whatever you're attempting to analyze and what you're trying to accomplish. Data must be collected through surveys, measurements, observation, or other methods.

Therefore, gathering the data on a large population is generally not done because of the costs, time, and resources necessary to obtain it. For instance, when you see advertisements claiming, "62% of doctors recommend XYZ for their patients,"—all of the doctors with patients who could use XYZ in the U.S. were likely not contacted. Of the doctors who responded to the several hundred or thousand surveys that were requested, 62% responded that they would recommend XYZ—this is a population sample.

While a parameter is a characteristic of a population, a statistic is a characteristic of a sample, and samples can only result in inferences about a population characteristic. Inferential statistics enables you to make an educated guess about a population parameter based on a statistic computed from a sample randomly drawn from that population.

Statistics such as  averages  (means) and  standard deviations , when taken from populations, are referred to as population parameters. Many, such as a population's mean and standard deviation, are represented by Greek letters like µ (mu) and σ (sigma). Much of the time, these statistics are inferential in nature because samples are used rather than populations.

If you have all the data for the population being studied, you do not need to use statistical inference because you won't need to use a sample of the population.

Market and investment analysts use statistics to analyze investment data and make inferences about the market, a specific investment, or an index. In some cases, financial analysts can evaluate an entire population because price data has been recorded for decades. For example, the price of every publicly traded stock could be analyzed for a total market evaluation because the prices are recorded—this is a population, in terms of investment analysis. Another population might be the stock prices of all tech companies since 2010.

An analyst can calculate parameters with all of this data; however, the parameters used by analysts are only occasionally used in the same way statisticians and scientists use them.

Some of the parameters you might see used by investment analysts, statisticians, and scientists and their differences are:

Alpha : The excess returns of an asset compared to a benchmark

Standard Deviation : Average amount of variability in prices, used to measure volatility and risk

Moving Average : Used to smooth out short-term price fluctuations to indicate trends

Beta : Measures the performance of an investment/portfolio against the market as a whole

Alpha : The probability of making a Type I error, or rejecting the null hypothesis when it is true

Standard Deviation : Average amount of variability in data

Moving Average : Smooths out short-term fluctuations in data values

Beta : The probability of making a Type II error, or incorrectly failing to reject the null hypothesis

What Is the Population Mean?

A population mean is the average of whatever value you're measuring in a given population.

What Are 2 Examples of Population?

One example of a population might be all green-eyed children in the U.S. under age 12. Another could be all the great white sharks in the ocean.

What Is the Best Example of a Population?

Imagine you're a teacher trying to see how well your fifth-grade math class did on a standardized test compared to all fifth-graders in the U.S. The population would be all fifth-grade math scores in the country.

In statistics, a population is the pool being studied from which data is extracted. Populations can be difficult to gather data on, especially if the studied topic is expansive and widely dispersed. Studying humans is an excellent example—there is no way to gather data on every brown-eyed person in the world (a statistical population), so random sampling is the only way to infer anything about that population.

In investment analysis, populations are generally specific types of assets being analyzed. These data sets are generally small (in statistical terms) and easy to acquire because they have been recorded, unlike data on living organisms, which is much more difficult to obtain.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• Open access
• Published: 26 May 2024

The sense of coherence scale: psychometric properties in a representative sample of the Czech adult population

• Martin Tušl 1 ,
• Ivana Šípová 2 ,
• Martin Máčel 2 ,
• Kristýna Cetkovská 2 &
• Georg F. Bauer 1  

BMC Psychology volume  12 , Article number:  293 ( 2024 ) Cite this article

851 Accesses

Metrics details

Sense of coherence (SOC) is a personal resource that reflects the extent to which one perceives the world as comprehensible, manageable, and meaningful. Decades of empirical research consistently show that SOC is an important protective resource for health and well-being. Despite the extensive use of the 13-item measure of SOC, there remains uncertainty regarding its factorial structure. Additionally, a valid and reliable Czech version of the scale is lacking. Therefore, the present study aims to examine the psychometric properties of the SOC-13 scale in a representative sample of Czech adults.

An online survey was completed by 498 Czech adults (18–86 years old) between November 2021 and December 2021. We used confirmatory factor analysis to examine the factorial structure of the scale. Further, we examined the variations in SOC based on age and gender, and we tested the criterion validity of the scale using the short form of the Mental Health Continuum (MHC) scale and the Generalized Anxiety Disorder (GAD) scale as mental health outcomes.

SOC-13 showed an acceptable one- and three-factor fit only with specified residual covariance between items 2 and 3. We tested alternative short versions by systematically removing poorly performing items. The fit significantly improved for all shorter versions with SOC-9 having the best psychometric properties with a clear one-factorialstructure. We found that SOC increases with age and males score higher than females. SOC showed a moderately strong positive correlation with MHC, and a moderately strong negative correlation with GAD. These findings were similar for all tested versions supporting the criterion validity of the SOC scale.

Our findings suggest that shortened versions of the SOC-13 scale have better psychometric properties than the original 13-item version in the Czech adult population. Particularly, SOC-9 emerges as a viable alternative, showing comparable reliability and validity as the 13-item version and a clear one-factorial structure in our sample.

Peer Review reports

Sense of coherence (SOC) was introduced by the sociologist Aaron Antonovsky as the main pillar of his salutogenic theory, which explains how individuals cope with stressors and stay healthy even in case of adverse life situations [ 1 ]. SOC is a personal resource defined as a global orientation to life determining the degree to which one perceives life as comprehensible, manageable, and meaningful [ 2 ]. A strong SOC enables individuals to cope with stressors and manage tension, thus moving to the ease-end of the ease/disease continuum [ 2 , 3 ]. A person’s strength of SOC can be measured with the Orientation to Life Questionnaire commonly referred to as the SOC scale [ 4 ]. The original version is composed of 29 items (SOC-29) and Antonovsky recommended 13 items for the short version of the scale (SOC-13). To date, both versions of the scale have been used across diverse populations in at least 51 languages and 51 countries [ 5 ]. Studies have consistently shown that SOC correlates strongly with different health and well-being outcomes [ 6 , 7 ] and quality of life measures [ 8 ]. In the context of the recent COVID-19 pandemic, SOC has been identified as the most important protective resource in relation to mental health [ 9 ]. Regarding individual differences, SOC has been shown to strengthen over the life course [ 10 ], males usually score higher than females [ 11 ], and some studies indicate that SOC increases with the level of education [ 12 ]. However, despite the extensive evidence on the criterion validity of the scale, there is still a lack of clarity about its underlying factor structure and dimensionality.

The SOC scale was conceptualized as unidimensional suggesting that SOC in its totality, as a global orientation, influences the movement along the ease/dis-ease continuum [ 2 ]. However, the structure of the scale is rather multidimensional as each item is composed of multiple elements. Antonovsky developed the scale according to the facet theory [ 13 , 14 ] which assumes that social phenomena are best understood when they are seen as multidimensional. Facet theory involves the construction of a mapping sentence which consists of the facets and the sentence linking the facets together [ 15 ]. The SOC scale is composed of five facets: (i) the response mode (comprehensibility, manageability, meaningfulness); (ii) the modality of stimulus (instrumental, cognitive, affective), (iii) its source (internal, external, both), (iv) the nature of the demand it poses (concrete, diffuse, affective), (v) and its time reference (past, present, future). For example, item 3 “Has it happened that people whom you counted on disappointed you?” is a manageability item that can be described with the mapping sentence as follows: "Respondent X responds to an instrumental stimulus (“counted on”), which originated from the external environment (“people”), and which poses a diffuse demand (“disappointed”) being in the past (“has it happened”)." Although each item can be categorized along the SOC component comprehensibility, manageability, or meaningfulness, the items also share elements from the other four facets with items within the same, but also within the other SOC components (see 2, Chap. 4 for details). As Antonovsky states [ 2 , p. 87]: “The SOC facet pulls the items apart; the other facets push them together.”

Thus, the multi-facet nature of the scale can create difficulties in identifying the three theorized SOC components using statistical methods such as factor analysis. In fact, both the unidimensional and the three-dimensional SOC-13 rarely yield an acceptable fit without specifying residual covariance between single items (see 5 for an overview). This has been further exemplified in a recent study which examined the dimensionality of SOC-13 using a network perspective. The authors were unable to identify a clear structure and concluded that SOC is composed of multiple elements that are deeply linked and not necessarily distinct [ 16 ]. As a result, several researchers have suggested modified [ 17 ] or abbreviated versions of the scale, such as SOC-12 [ 18 , 19 ], SOC-11 [ 20 , 21 , 22 ], or SOC-9 [ 23 ], which have empirically shown a better factorial structure. This prompts the general question, whether an alternative short version should be preferred over the 13-item version. In fact, looking into the original literature [ 2 ], it is not clear why Antonovsky chose specifically these 13 items from the 29-item scale. We will address this question with the Czech version of the SOC-13 scale.

Salutogenesis in the Czech Republic

Salutogenesis and the SOC scale were introduced to the Czech audience in the early 90s by a Czech psychologist Jaro Křivohlavý. His work included the Czech translation of the SOC-29 scale [ 24 ] and the application of the concept in research on resilience [ 25 ] and behavioral medicine [ 26 ]. Unfortunately, the early Czech translation of the scale by Křivohlavý is not available electronically, nor could we locate it in library repositories. Later studies examined SOC-29 in relation to resilience [ 27 , 28 ] and self-reported health [ 29 , 30 ], however, it is not clear which translation of SOC-29 the authors used in the studies. A new Czech translation of the SOC-13 scale has recently been developed by the authors of this paper to examine the protective role of SOC for mental health during the COVID-19 crisis [ 31 ]. In line with earlier studies [ 9 ], SOC was identified as an important protective resource for individual mental health. This recent Czech translation of the SOC-13 scale [ 31 ] is the subject of the present study.

Present study

Our study aims to investigate the psychometric properties of the SOC-13 scale within a representative sample of the Czech adult population. Specifically, we will examine the factorial structure of the SOC-13 scale to understand its underlying dimensions and evaluate its internal consistency to ensure its reliability as a measure of SOC. Additionally, we aim to assess criterion validity by examining the scale’s association with established measures of positive and negative mental health outcomes - the Mental Health Continuum [ 32 ] and Generalized Anxiety Disorder [ 33 ]. We anticipate a strong correlation between these measures and the SOC construct [ 6 ]. Furthermore, we will investigate demographic variations in SOC, considering factors such as age, gender, and education. Understanding these variations will provide valuable insights into the applicability of the SOC-13 scale across different population subgroups. Finally, we will explore whether alternative short versions of the SOC scale should be preferred over the 13-item version. This analysis will help determine the most efficient version of the SOC scale for future research.

Study design and data collection

Our study design is a cross-sectional online survey of the Czech adult population. We contracted a professional agency DataCollect ( www.datacollect.cz ) to collect data from a representative sample for our study. Participants were recruited using quota sampling. The inclusion criteria were: being of adult age (18+), speaking the Czech language, and having permanent residence in the Czech Republic. Exclusion criteria related to study participation were predetermined to minimize the risk of biases in the collected data. The order of items in all measures was randomized and we implemented two attention checks in the questionnaire (e.g. “Please, choose option number 2”). Participants were excluded if they did not finish the survey, completed the survey in less than five minutes, did not pass the attention checks, or gave the same answer to more than 10 consecutive items. Data collection was conducted via the online platform Survey Monkey between November 2021 and December 2021.

Translation into the Czech language

Translation of the SOC scale was carried out by the authors of the paper with the help of a qualified translator. We followed the translation guidelines provided on the website of the Society for Research and Theory on Salutogenesis ( www.stars-society.org ), where the original English version of the SOC scale is available for download. Two translations were conducted independently, then compared and checked for differences. Based on this comparison, the agreed version of the scale was back translated into English by a Czech-English translator. The final version was checked for resemblance to the original version in content and in form. Although we used only the short version of the scale in our study (i.e., SOC-13), the translation included the full SOC-29 scale. The Czech translation of the full SOC scale is available as supplementary material.

Sense of coherence. We used the short version of the Orientation to Life Questionnaire [ 3 ] to assess SOC. The measure consists of 13 items evaluated on a 7-point Likert-type scale with different response options. Five items measure comprehensibility (e.g., “Does it happen that you experience feelings that you would rather not have to endure?”), four items measure manageability (e.g., “Has it happened that people whom you counted on disappointed you?”), and four items measure meaningfulness (e.g., “Do you have the feeling that you really don’t care about what is going on around you?”). In our sample, Cronbach’s alpha for the full scale was α = 0.88, for comprehensibility α = 0.76, manageability α = 0.72, and meaningfulness α = 0.70.

Mental health continuum - short form (MHC-SF; 32). This scale consists of 14 items that capture three dimensions of well-being: (i) emotional (e.g. “During the past month, how often did you feel interested in life?”); (ii) social (e.g. “During the past month, how often did you feel that the way our society works makes sense to you?”); (iii) psychological (e.g. “During the past month, how often did you feel confident to think or express your own ideas and opinions?”). The items assess the experiences the participants had over the past two weeks, the response options ranged from 1 (never) to 6 (every day). Internal consistency of the scale was α = 0.90.

Generalized anxiety disorder (GAD; 33). The scale consists of seven items that measure symptoms of anxiety over the past two weeks. Sample items include, e.g. “Over the past two weeks, how often have you been bothered by the following problems?” (i) “feeling nervous, anxious, or on edge”, (ii) “worrying too much about different things”, (iii) “becoming easily annoyed or irritable”. The response options ranged from 0 (not at all) to 3 (almost every day). Internal consistency of the scale was α = 0.92.

Sociodemographic characteristics included age, gender, and level of education (i.e., primary/vocational, secondary, tertiary).

Analytical procedure

Data analysis was conducted in R [ 34 ]. For confirmatory factor analysis, we used the cfa function of the lavaan package 0.6–16 [ 35 ]. We compared a one-factor model of SOC-13 to a correlated three-factor model (correlated latent factors comprehensibility, manageability, and meaningfulness) and a bi-factor model (general SOC dimension and specific dimensions comprehensibility, manageability, meaningfulness). Based on the empirical findings we further assessed the fit of alternative shorter versions of the SOC scale. We assessed the model fit using the comparative-fit index (CFI), Tucker-Lewis index (TLI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR) with the conventional cut-off values. The goodness-of-fit values for CFI and TLI surpassing 0.90 indicate an acceptable fit and exceeding 0.95 a good fit [ 36 ]. A value under 0.08 for RMSEA and SRMR indicates a good fit [ 37 ]. Nested models were compared using chi-square difference tests and the Bayesian Information Criterion (BIC). Models with lower BIC values should be preferred over models with higher BIC values [ 38 ]. All models were fitted using maximum likelihood estimation.

Further, we used the cor function of the stats package 4.3.2 [ 34 ] for Pearson correlation analysis to explore the association between SOC-13 and age, the t.test function of the same package for between groups t-test for differences based on gender, and the aov function with posthoc tests of the same package for one-way between-subjects ANOVA to test for differences based on level of education. To examine the criterion validity of the scale, we used the cor function for Pearson correlation analysis to examine the associations between SOC-13, MHC-SF, and GAD. We conducted the same analyses for the alternative short versions of the scale.

Participants

The median survey completion time was 11 min. In total, 676 participants started the survey and 557 completed it. Of those, 56 were excluded due to exclusion criteria. One additional respondent was excluded because of dubious responses on demographic items (e.g., 100 years old and a student), and two respondents were excluded for not meeting the inclusion criteria (under 18 years old). The final sample included N  = 498 participants. Of those, 53.4% were female, the average age was 49 years ( SD  = 16.6; range = 18–86), 43% had completed primary, 35% secondary, and 22% tertiary education. The sample is a good representation of the Czech adult population Footnote 1 with regard to gender (51% females), age ( M  = 50 years), and education level (44% primary, 33% secondary, 18% tertiary). Representativeness was tested using chi-squared test which yielded non-significant results for all domains.

Descriptive statistics

In Table  1 , we present an inter-item correlation matrix along with skewness, kurtosis, means and standard deviations of single items for SOC-13. Item correlations ranged from r  = 0.07 (items 2 and 4) to r  = 0.67 (items 8 and 9). Strong and moderately strong correlations were found also across the three SOC dimensions (e.g., r  = 0.77 comprehensibility and manageability).

• Confirmatory factor analysis

A one-factor model showed inadequate fit to the data [χ2(65) = 338.2, CFI = 0.889, TLI = 0.867, RMSEA = 0.092, SRMR = 0.062]. Based on existing evidence [ 6 ], we specified residual covariance between items 2 and 3 and tested a modified one-factor model. The model showed an acceptable fit to the data [χ2(64) = 242.6, CFI = 0.927, TLI = 0.911, RMSEA = 0.075, SRMR = 0.050], and it was superior to the one-factor model (Δχ2 = 95.5, Δ df  = 1, p  < 0.001).

A correlated three-factor model showed an acceptable fit considering CFI and SRMR [χ2(63) = 286.6, CFI = 0.909, TLI = 0.885, RMSEA = 0.085, SRMR = 0.058]. The model was superior to the one-factor model (Δχ2 = 51.5, Δ df  = 2, p  < 0.001), however, it was inferior to the modified one-factor model (ΔBIC = -56). We further tested a modified three-factor model with residual covariance between items 2 and 3 which showed an acceptable fit to the data based on CFI and TLI and a good fit based on RMSEA and SRMR [χ2(62) = 191.7, CFI = 0.947, TLI = 0.932, RMSEA = 0.066, SRMR = 0.046]. The model was superior to the three-factor model (Δχ2 = 97.1, Δ df  = 1, p  < 0.001) as well as to the modified one-factor model (Δχ2 = 50.9, Δ df  = 3, p  < 0.001). See Fig.  1 for a detailed illustration of the model.

Finally, we tested a bi-factor model with one general SOC factor and three specific factors (comprehensibility, manageability, meaningfulness), however, the model was not identified.

Correlated three-factor model of SOC-13 with residual covariance between item 2 and item 3

Alternative short versions of the SOC scale

We further tested the fit of alternative shorter versions of the SOC scale by systematically removing poorly performing items. In SOC-12, item 2 was excluded (“Has it happened in the past that you were surprised by the behavior of people whom you thought you knew well?”). This item measures comprehensibility, hence SOC-12 has even distribution of items for each dimension (i.e., comprehensibility, manageability, meaningfulness). Item 2 has previously been identified as problematic [ 6 ] and also in our sample it did not perform well in any of the fitted SOC-13 models (i.e., low factor loading and explained variance). A one-factor SOC-12 model showed an acceptable fit to the data based on CFI and TLI and a good fit based on RMSEA and SRMR [χ2(54) = 221.1, CFI = 0.927, RMSEA = 0.079, SRMR = 0.048]. A correlated three-factor model showed an acceptable fit based on CFI and TLI and a good fit based on RMSEA and SRMR [χ2(52) = 171.1, CFI = 0.948, TLI = 0.932, RMSEA = 0.069 SRMR = 0.043]. The model was superior to the one-factor model (Δχ2 = 50, Δ df  = 3, p  < 0.001). Bi-factor model was not identified.

In SOC-11, we removed item 3 (“Has it happened that people whom you counted on disappointed you?”), which measures manageability. The item had the lowest factor loading and the lowest explained variance in the one-factor SOC-12. A one-factor SOC-11 model showed a good fit to the data [χ2 (44) = 138.5, CFI = 0.955, TLI = 0.944, RMSEA = 0.066, SRMR = 0.038]. A correlated three-factor model was identified but not acceptable due to covariance between comprehensibility and manageability higher than 1 (i.e., Heywood case; 39).

In SOC-10, we removed item 1 (“Do you have the feeling that you don’t really care about what goes on around you?”), which measures meaningfulness. The item had the lowest factor loading and the lowest explained variance in one-factor SOC-11. A one-factor SOC-10 model showed a good fit to the data [χ2 (35) = 126.6, CFI = 0.956, TLI = 0.943, RMSEA = 0.072, SRMR = 0.039]. As in the case of SOC-11, a correlated three-factor model was identified but not acceptable due to covariance between comprehensibility and manageability higher than 1.

Finally, in SOC-9, we removed item 11 (“When something happened, have you generally found that… you overestimated or underestimated its importance / you saw the things in the right proportion”), which measures comprehensibility. The item had the lowest factor loading and the lowest explained variance in one-factor SOC-10. SOC-9 has an even distribution of three items for each dimension. A one-factor model showed a good fit to the data [χ2 (27) = 105.6, CFI = 0.959, TLI = 0.946, RMSEA = 0.076, SRMR = 0.038]. As in the previous models, a correlated three-factor model was identified but not acceptable due to covariance between comprehensibility and manageability higher than 1. See Fig.  2 for an illustration of one-factor SOC-9 model. Detailed results of the confirmatory factor analysis are shown in Table  2 . In Table 3 , we present the items of the SOC-13 (and SOC-9) scale with details about their facet structure.

One-factor model of SOC-9

Differences by gender, age, and education

Correlation analysis indicated that SOC-13 increases with age ( r  = 0.32, p  < 0.001), this finding was identical for all alternative short versions of the SOC scale (see Table  2 ). Further, the results of the two-tailed t-test showed that males ( M  = 4.8, SD  = 1.08) had a significantly higher SOC-13 score [ t (497) = 3.06, p  = 0.002, d  = 0.27] than females ( M  = 4.5, SD  = 1.07). A one-way between-subjects ANOVA did not show any significant effect of level of education on SOC-13 score [F(2, 497) = 1.78, p  = 0.169, η p 2  = 0.022]. These results were similar for all alternative short versions of the SOC scale.

Criterion validity

We found a moderately strong positive correlation ( r  = 0.61, p  < 0.001) between SOC-13 and the positive mental health measure MHC, and a moderately strong negative correlation between SOC-13 and the negative mental health measure GAD ( r = -0.68, p  < 0.001). These findings were similar for all alternative short versions of the SOC scale (see Table  4 ).

Our study examined the psychometric properties of the SOC-13 scale and its alternative short versions SOC-12, SOC-11, SOC-10, and SOC-9 in a representative sample of the Czech adult population. In line with existing studies [ 40 ], we found that SOC increases with age and that males score higher than females. In contrast to some prior findings [ 12 ], we did not find any significant differences in SOC based on the level of education. Further, we tested criterion validity using both positive and negative mental health outcomes (i.e., MHC and GAD). SOC had a strong positive correlation with MHC and a strong negative correlation with GAD, thus adding to the evidence about the criterion validity of the scale [ 6 , 40 ].

Analysis of the factor structure showed that a one-factor SOC-13 had an inadequate fit to our data, however, an acceptable fit was achieved for a modified one-factor model with specified residual covariance between item 2 (“Has it happened in the past that you were surprised by the behavior of people whom you thought you knew well?”) and item 3 (“Has it happened that people whom you counted on disappointed you?”). A correlated three factor model with latent factors comprehensibility, manageability, and meaningfulness showed a better fit than the one factor-model. However, it was also necessary to specify residual covariance between item 2 and item 3 to reach an acceptable fit for all fit indices. A recent Slovenian study [ 41 ] found a similar result and several prior studies (see 6 for an overview) have noted that items 2 and 3 of the SOC-13 scale are problematic. Although the items pertain to different SOC dimensions (item 2 to comprehensibility, item 3 to manageability), multiple studies [e.g., 20 , 42 , 43 ] have reported moderately strong correlation between them and this is also the case in our study ( r  = 0.5, p  < 0.001). The two items aptly illustrate the facet theory behind the scale construction as the SOC component represents only one building block of each item. Although items 2 and 3 theoretically pertain to different SOC components, they share the same elements from the other four facets (i.e., modality, source, demand, and time) which is reflected in the similarity of their wording. Therefore, they will necessarily share residual variance and this needs to be specified to achieve a good model fit. Drageset and Haugan [ 18 ] explain this similarity in that the people whom we know well are usually the ones that we count on, and feeling disappointed and surprised by the behavior of people we know well is closely related. Therefore, it should be theoretically justifiable to specify residual covariance between item 2 and item 3 as a possible solution to improve the fit. As we could show in our sample, the model fit significantly improved for both one-factor and three-factor solutions.

In addition, we examined the fit of alternative short versions of the SOC scale by systematically removing single items that performed poorly. First, in line with previous studies [ 6 ], we addressed the issue of residual covariance in SOC-13 by removing item 2, examining the factor structure of SOC-12. The remaining 12 items were equally distributed within the three SOC components with four items per each component. Interestingly, a one-factor model reached an acceptable fit and the fit further improved for a correlated three-factor model with latent factors of comprehensibility, manageability, and meaningfulness. Although correlated three-factor models were superior to one-factor models, we observed extreme covariances between latent variables, especially in case of comprehensibility and manageability (cov = 0.98). This suggests that the SOC components are not empirically separable and that, indeed, SOC is rather a one-dimensional global orientation with multiple components that are dynamically interrelated as Antonovsky proposed [ 2 ]. This notion was supported in a recent study that explored the dimensionality of the scale using a network perspective [ 16 ]. Our examination of SOC-11, SOC-10 and SOC-9 provided further support for a one-factor structure of the scale. All shorter versions yielded a good one-dimensional fit, however, we could not identify a correlated three-factor model fit due to the Heywood case. This refers to the situation when a solution that otherwise is satisfactory produces communality greater than one explained by the latent factor, which implies that the residual variance of the variable is negative [ 39 ]. In our case, this was true for the latent factors comprehensibility and manageability. However, we demonstrated that we could attain a good one-dimensional fit for all alternative short versions of SOC, and, importantly, they all showed comparable reliability and validity metrics to their longer counterpart SOC-13. In particular, SOC-9 shows very good fit indices and it performs equally well in validity analyses as SOC-13. Given these findings and existing evidence [ 5 ], we propose that future investigations may consider utilizing the SOC-9 scale instead of the SOC-13. It is interesting to point out that the majority of items that were removed for the shorter versions of the scale are negatively worded or reverse-scored (expect for item 11). This is in line with the latest research suggesting that such items can cause problems in model identification as they create additional method factors [ 44 , 45 , 46 ].

Finally, it is important to highlight that Antonovsky did not provide any information about the selection of the 13 items for the short version of the SOC scale [ 2 ]. For example, a detailed examination of the facet structure reveals that none of the items included in SOC-13 refers to future which is part of facet referring to time (i.e., past, present, future). Hence, considering the absence of explicit criteria for item selection in the SOC-13 scale, it would be interesting to gather data from diverse populations utilizing the full SOC-29 scale. Subsequently, through exploratory factor analysis, researchers could derive a new, theory- and empirical-driven, short version of the SOC scale.

Strengths and limitations

A clear strength of our study is that our findings are based on a representative sample that accurately reflects the Czech adult population. Moreover, we implemented rigorous data cleaning procedures, meticulously excluding participants who provided potentially careless or low-quality responses. By doing so, we ensured that our conclusions are based on high-quality data and that they are generalizable to our target population of Czech adults. Finally, we conducted a thorough back-translation procedure to achieve an accurate Czech version of the SOC scale and we carried out systematic testing of different short versions of the SOC scale.

However, our study also has some limitations. First, our conclusions are based on data from a culturally specific country and they may not be generalizable to other populations. It is important to note, however, that most of our findings are in line with multiple existing studies which supports the validity of our conclusions. Second, the data were collected during a later stage of the COVID-19 pandemic, which may have impacted particularly the mental health outcomes we used for criterion validity. It would be worthwhile to investigate whether the data replicate in our population outside of this exceptional situation. Third, it should be noted that we did not examine test-retest reliability of the scale due to the cross-sectional design of our study. Finally, self-reported data are subject to common method biases such as social desirability, recall bias, or consistency motive [ 47 ]. We aimed to minimize this risk by implementing various strategies in the questionnaire, such as randomization of items and the use of disqualifying items (e.g. “Please, choose option number 2”) to disqualify careless answers.

Our study contributes to decades of ongoing research on SOC, the main pillar of the theory of salutogenesis. In line with existing research, we found evidence for the validity of the SOC as a construct, but we could not identify a clear factorial structure of the SOC-13 scale. However, following Antonovsky’s conception of the scale, we believe it is theoretically sound to aim for a one-factor solution of the scale and we could show that this is possible with shorter versions of the SOC scale. We particularly recommend using the SOC-9 scale in future research which shows an excellent one-factor fit and validity indices comparable to SOC-13. Finally, since Antonovsky does not explain how he selected the items of the SOC-13 scale, it would be interesting to examine the possibility of developing a new one-dimensional short version based on exploratory factor analysis of the original SOC-29 scale.

Data availability

The datasets used and analyzed during the current study and the R code used for the statistical analysis are available as supplementary material.

www.czso.cz .

Antonovsky A. The salutogenic model as a theory to guide health promotion. Health Promot Int. 1996;11(1).

Antonovsky A. Unraveling the mystery of Health how people manage stress and stay well. Jossey-Bass; 1987.

Antonovsky A. Health stress and coping. Jossey-Bass; 1979.

Antonovsky A. The structure and Properties of the sense of coherence scale. Soc Sci Med. 1993;36(6):125–733.

Article   Google Scholar  

Eriksson M, Contu P. The sense of coherence: Measurement issues. The Handbook of Salutogenesis. Springer International Publishing; 2022. pp. 79–91.

Eriksson M. The sense of coherence: the Concept and its relationship to Health. The Handbook of Salutogenesis. Springer International Publishing; 2022. pp. 61–8.

Eriksson M, Lindström B. Antonovsky’s sense of coherence scale and the relation with health: a systematic review. J Epidemiol Community Health (1978). 2006;60(5):376–81.

Eriksson M, Lindström B. Antonovsky’s sense of coherence scale and its relation with quality of life: a systematic review. J Epidemiol Community Health. 2007;61(11):938–44.

Article   PubMed   PubMed Central   Google Scholar  

Mana A, Super S, Sardu C, Juvinya Canal D, Moran N, Sagy S. Individual, social and national coping resources and their relationships with mental health and anxiety: A comparative study in Israel, Italy, Spain, and the Netherlands during the Coronavirus pandemic. Glob Health Promot [Internet]. 2021;28(2):17–26.

Silverstein M, Heap J. Sense of coherence changes with aging over the second half of life. Adv Life Course Res. 2015;23:98–107.

Article   PubMed   Google Scholar  

Rivera F, García-Moya I, Moreno C, Ramos P. Developmental contexts and sense of coherence in adolescence: a systematic review. J Health Psychol. 2013;18(6):800–12.

Volanen SM, Lahelma E, Silventoinen K, Suominen S. Factors contributing to sense of coherence among men and women. Eur J Public Health [Internet]. 2004;14(3):322–30.

Guttman L. Measurement as structural theory. Psychometrika. 1971;3(4):329–47.

Guttman R, Greenbaum CW. Facet theory: its development and current status. Eur Psychol. 1998;3(1):13–36.

Shye S. Theory Construction and Data Analysis in the behavioral sciences. San Francisco: Jossey-Bass; 1978.

Google Scholar  

Portoghese I, Sardu C, Bauer G, Galletta M, Castaldi S, Nichetti E, Petrocelli L, Tassini M, Tidone E, Mereu A, Contu P. A network perspective to the measurement of sense of coherence (SOC): an exploratory graph analysis approach. Current Psychology. 2024;12:1-3.

Bachem R, Maercker A. Development and psychometric evaluation of a revised sense of coherence scale. Eur J Psychol Assess. 2016;34(3):206–15.

Drageset J, Haugan G. Psychometric properties of the orientation to Life Questionnaire in nursing home residents. Scand J Caring Sci. 2016;30(3):623–30.

Kanhai J, Harrison VE, Suominen AL, Knuuttila M, Uutela A, Bernabé E. Sense of coherence and incidence of periodontal disease in adults. J Clin Periodontol. 2014;41(8):760–5.

Naaldenberg J, Tobi H, van den Esker F, Vaandrager L. Psychometric properties of the OLQ-13 scale to measure sense of coherence in a community-dwelling older population. Health Qual Life Outcomes. 2011;9.

Luyckx K, Goossens E, Apers S, Rassart J, Klimstra T, Dezutter J et al. The 13-item sense of coherence scale in Dutch-speaking adolescents and young adults: structural validity, age trends, and chronic disease. Psychol Belg. 2012;52(4):351–68.

Lerdal A, Opheim R, Gay CL, Moum B, Fagermoen MS, Kottorp A. Psychometric limitations of the 13-item sense of coherence scale assessed by Rasch analysis. BMC Psychol. 2017;5(1).

Klepp OM, Mastekaasa A, Sørensen T, Sandanger I, Kleiner R. Structure analysis of Antonovsky’s sense of coherence from an epidemiological mental health survey with a brief nine-item sense of coherence scale. Int J Methods Psychiatr Res. 2007;16(1):11–22.

Křivohlavý J. Sense of coherence: methods and first results. II. Sense of coherence and cancer. Czechoslovak Psychol. 1990;34:511–7.

Křivohlavý J. Nezdolnost v pojetí SOC. Czechoslovak Psychol. 1990;34(6).

Křivohlavý J. Salutogenesis and behavioral medicine. Cas Lek Cesk. 1990;126(36):1121–4.

Kebza V, Šolcová I. Hlavní Koncepce psychické odolnosti. Czechoslovak Psychol. 2008;52(1):1–19.

Šolcová I, Blatný M, Kebza V, Jelínek M. Relation of toddler temperament and perceived parenting styles to adult resilience. Czechoslovak Psychol. 2016;60(1):61–70.

Šolcová I, Kebza V, Kodl M, Kernová V. Self-reported health status predicting resilience and burnout in longitudinal study. Cent Eur J Public Health. 2017;25(3):222–7.

Šolcová I, Kebza V. Subjective health: current state of knowledge and results of two Czech studies. Czechoslovak Psychol. 2006;501:1–15.

Šípová I, Máčel M, Zubková A, Tušl M. Association between coping resources and mental health during the COVID-19 pandemic: a cross-sectional study in the Czech Republic. Int J Environ Health Res. 2022;1–9.

Keyes CLM. The Mental Health Continuum: from languishing to flourishing in life. J Health Soc Behav. 2002;43(2):207–22.

Löwe B, Decker O, Müller S, Brähler E, Schellberg D, Herzog W, et al. Validation and standardization of the generalized anxiety disorder screener (GAD-7) in the General Population. Med Care. 2008;46(3):266–74.

R Core Team. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2022.

Rosseel Y. Lavaan: an R Package for Structural equation modeling. J Stat Softw. 2012;48(2):1–36.

Bentler PM, Bonett DG. Significance tests and goodness of fit in the analysis of covariance structures. Psychol Bull. 1980;88(3):588–606.

Beauducel A, Wittmann WW. Simulation study on fit indexes in CFA based on data with slightly distorted simple structure. Struct Equ Model. 2005;12(1):41–75.

Raftery AE. Bayesian model selection in Social Research. Sociol Methodol. 1995;25:111–63.

Farooq R. Heywood cases: possible causes and solutions. Int J Data Anal Techniques Strategies. 2022;14(1):79.

Eriksson M, Lindström B. Validity of Antonovsky’s sense of coherence scale: a systematic review. J Epidemiol Community Health (1978). 2005;59(6):460–6.

Stern B, Socan G, Rener-Sitar K, Kukec A, Zaletel-Kragelj L. Validation of the Slovenian version of short sense of coherence questionnaire (SOC-13) in multiple sclerosis patients. Zdr Varst. 2019;58(1):31–9.

PubMed   PubMed Central   Google Scholar  

Bernabé E, Tsakos G, Watt RG, Suominen-Taipale AL, Uutela A, Vahtera J, et al. Structure of the sense of coherence scale in a nationally representative sample: the Finnish Health 2000 survey. Qual Life Res. 2009;18(5):629–36.

Sardu C, Mereu A, Sotgiu A, Andrissi L, Jacobson MK, Contu P. Antonovsky’s sense of coherence scale: cultural validation of soc questionnaire and socio-demographic patterns in an Italian Population. Clin Pract Epidemiol Mental Health. 2012;8:1–6.

Chyung SY, Barkin JR, Shamsy JA. Evidence-based Survey Design: the Use of negatively worded items in surveys. Perform Improv. 2018;57(3):16–25.

Suárez-Alvarez J, Pedrosa I, Lozano LM, García-Cueto E, Cuesta M, Muñiz J. Using reversed items in likert scales: a questionable practice. Psicothema. 2018;30(2):149–58.

PubMed   Google Scholar  

van Sonderen E, Sanderman R, Coyne JC. Ineffectiveness of reverse wording of questionnaire items: let’s learn from cows in the rain. PLoS ONE. 2013;8(7).

Podsakoff PM, MacKenzie SB, Lee JY, Podsakoff NP. Common method biases in behavioral research: a critical review of the literature and recommended remedies. J Appl Psychol. 2003;88(5):879–903.

Download references

Acknowledgements

The authors would like to thank to the team of Center of Salutogenesis at the University of Zurich for their helpful comments on the adapted version of the SOC scale.

MT received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 801076, through the SSPH + Global PhD Fellowship Program in Public Health Sciences (GlobalP3HS) of the Swiss School of Public Health. Data collection was supported by the Charles University Strategic Partnerships Fund 2021. The University of Zurich Foundation supported the contribution of GB.

Author information

Authors and affiliations.

Division of Public and Organizational Health, Center of Salutogenesis, Epidemiology, Biostatistics and Prevention Institute, University of Zurich, Hirschengraben 84, Zurich, 8001, Switzerland

Martin Tušl & Georg F. Bauer

Department of Psychology, Faculty of Arts, Charles University, Prague, Czech Republic

Ivana Šípová, Martin Máčel & Kristýna Cetkovská

You can also search for this author in PubMed   Google Scholar

Contributions

All authors contributed to the conception and design of the study. MT wrote the manuscript, conducted data analysis, and contributed to data collection. MM and IS conducted data collection, contributed to data analysis, interpretation of results, edited and commented on the manuscript. KC and GB contributed to interpretation of results, edited and commented on the manuscript. All authors have read and approved the final manuscript.

Corresponding author

Correspondence to Martin Tušl .

Ethics declarations

Ethics approval and consent to participate.

The study was conducted in accordance with the general principles of the Declaration of Helsinki and with the ethical principles defined by the university and by the national law ( https://cuni.cz/UK-5317.html ). Informed consent was obtained from all participants prior to the completion of the survey. Participation was voluntary and participants could withdraw from the study at any time without any consequences. For anonymous online surveys in adult population no ethical review by an ethics committee was necessary under national law and university rules. See: https://www.muni.cz/en/about-us/organizational-structure/boards-and-committees/research-ethics-committee/evaluation-request .

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary Material 1

Supplementary material 2, supplementary material 3, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Tušl, M., Šípová, I., Máčel, M. et al. The sense of coherence scale: psychometric properties in a representative sample of the Czech adult population. BMC Psychol 12 , 293 (2024). https://doi.org/10.1186/s40359-024-01805-7

Download citation

Received : 22 March 2023

Accepted : 21 May 2024

Published : 26 May 2024

DOI : https://doi.org/10.1186/s40359-024-01805-7

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Salutogenesis
• Sense of coherence
• Psychometrics
• Czech adult population
• Mental health

BMC Psychology

ISSN: 2050-7283

• General enquiries: [email protected]

• Election 2024
• Entertainment
• Newsletters
• Photography
• Personal Finance
• AP Investigations
• AP Buyline Personal Finance
• AP Buyline Shopping
• Press Releases
• Israel-Hamas War
• Russia-Ukraine War
• Global elections
• Asia Pacific
• Latin America
• Middle East
• Election Results
• Delegate Tracker
• AP & Elections
• Auto Racing
• 2024 Paris Olympic Games
• Movie reviews
• Book reviews
• Personal finance
• Financial Markets
• Business Highlights
• Financial wellness
• Artificial Intelligence
• Social Media

They’re big. They’re colorful. But Joro spiders aren’t nightmare fodder

FILE - The Joro spider, a large spider native to East Asia, is seen in Johns Creek, Ga., Oct. 24, 2021. Populations of the species have been growing in parts of the South and East Coast for years now, and many researchers think it’s only a matter of time before they spread to much of the continental U.S. (AP Photo/Alex Sanz, File)

FILE - A Joro spider makes a web, Sept. 27, 2022, in Atlanta. Populations of the species have been growing in parts of the South and East Coast for years now, and many researchers think it’s only a matter of time before they spread to much of the continental U.S. (AP Photo/Brynn Anderson, File)

• Copy Link copied

A large, brightly colored invasive species called the Joro spider is on the move in the United States. Populations have been growing in parts of the South and East Coast for years, and many researchers think it’s only a matter of time before they spread to much of the continental U.S.

But spider experts say we shouldn’t be too worried about them.

“My sense is people like the weird and fantastic and potentially dangerous,” said David Nelsen, a professor of biology at Southern Adventist University who has studied the growing range of Joro spiders. “This is one of those things that sort of checks all the boxes for public hysteria.”

Scientists instead worry about the growing prevalence of invasive species that can do damage to our crops and trees — a problem made worse by global trade and climate change , which is making local environmental conditions more comfortable for pests that previously couldn’t survive frigid winters.

“I think this is one of those ‘canary in the coal mine’ type species where it’s showy, it’s getting a lot of attention,” said Hannah Burrack, professor and chair of the entomology department at Michigan State University. But the shy critter poses little risk to humans. Instead, Burrack said, introduced pests like fruit flies and tree borers can do more damage.

“This is a global concern, because it makes all the things that we do in terms of conservation, in terms of agricultural production, in terms of human health, harder to manage,” she said.

WHAT IS THE JORO SPIDER?

The Joro spider is one of a group of spiders called orb-weavers, named for their wheel-shaped webs. They’re native to East Asia, have bright yellow and black coloring and can grow as long as three inches (8 cm) when their legs are fully extended.

However, they’re pretty hard to spot at this time of year because they’re still early in their life cycle, only about the size of a grain of rice. A trained eye can spot their softball-sized webs on a front porch, or their gossamer threads of golden silk blanketing the grass. Adults are most commonly seen in August and September.

WHERE ARE THEY HEADED?

Scientists are still trying to figure that out, said David Coyle, an assistant professor at Clemson University who worked with Nelsen on a study on the Joro’s range, published last November . Their central population is primarily in Atlanta but expanding to the Carolinas and southeastern Tennessee. A satellite population has taken hold in Baltimore over the last two years, Coyle said.

As for when the species will become more prevalent in the Northeast, an eventual outcome suggested by their research? “Maybe this year, maybe a decade, we really don’t know,” he said. “They’re probably not going to get that far in a single year. It’s going to take a bunch of incremental steps.”

CAN THEY FLY?

The babies can: using a tactic called “ballooning,” young Joro spiders can use their webs to harness the winds and electromagnetic currents of the Earth to travel relatively long distances. But you won’t see fully-grown Joro spiders taking flight.

WHAT DO THEY EAT?

Joro spiders will eat whatever lands in their web, which mainly ends up being insects. That could mean they’ll compete with native spiders for food, but it might not all be bad — a Joro’s daily catch could also feed native bird species, something Andy Davis, a research scientist at the University of Georgia, has personally documented.

As for some observers’ hope that Joro spiders could gobble up the invasive spotted lanternflies destroying trees on the East Coast? They might eat a few, but there’s “zero chance” they’ll make a dent in the population, Coyle said.

ARE THEY DANGEROUS TO HUMANS?

Joro spiders have venom like all spiders, but they aren’t deadly or even medically relevant to humans, Nelsen said. At worst, a Joro bite might itch or cause an allergic reaction. But the shy creatures tend to stay out of humans’ way.

What could one day truly cause damage to humans is the widespread introduction of other creatures like the emerald ash borer or a fruit fly called the spotted wing drosophila that threaten the natural resources we rely upon.

“I try to stay scientifically objective about it. And that’s a way to protect myself from maybe the sadness of it. But there’s so much ecological damage being done all over the world for, for so many reasons, mostly because of humans,” Davis said. “This to me is just one more example of mankind’s influence on the environment.”

The Associated Press’ climate and environmental coverage receives financial support from multiple private foundations. AP is solely responsible for all content. Find AP’s standards for working with philanthropies, a list of supporters and funded coverage areas at AP.org .

Numbers, Facts and Trends Shaping Your World

Read our research on:

Full Topic List

Regions & Countries

• Publications
• Our Methods
• Short Reads
• Tools & Resources

Read Our Research On:

Table of Contents

Which social media platforms are most common, who uses each social media platform, find out more, social media fact sheet.

Many Americans use social media to connect with one another, engage with news content, share information and entertain themselves. Explore the patterns and trends shaping the social media landscape.

To better understand Americans’ social media use, Pew Research Center surveyed 5,733 U.S. adults from May 19 to Sept. 5, 2023. Ipsos conducted this National Public Opinion Reference Survey (NPORS) for the Center using address-based sampling and a multimode protocol that included both web and mail. This way nearly all U.S. adults have a chance of selection. The survey is weighted to be representative of the U.S. adult population by gender, race and ethnicity, education and other categories.

Polls from 2000 to 2021 were conducted via phone. For more on this mode shift, read our Q&A.

Here are the questions used for this analysis , along with responses, and  its methodology ­­­.

A note on terminology: Our May-September 2023 survey was already in the field when Twitter changed its name to “X.” The terms  Twitter  and  X  are both used in this report to refer to the same platform.

YouTube and Facebook are the most-widely used online platforms. About half of U.S. adults say they use Instagram, and smaller shares use sites or apps such as TikTok, LinkedIn, Twitter (X) and BeReal.

Note: The vertical line indicates a change in mode. Polls from 2012-2021 were conducted via phone. In 2023, the poll was conducted via web and mail. For more details on this shift, please read our Q&A . Refer to the topline for more information on how question wording varied over the years. Pre-2018 data is not available for YouTube, Snapchat or WhatsApp; pre-2019 data is not available for Reddit; pre-2021 data is not available for TikTok; pre-2023 data is not available for BeReal. Respondents who did not give an answer are not shown.

Source: Surveys of U.S. adults conducted 2012-2023.

Usage of the major online platforms varies by factors such as age, gender and level of formal education.

% of U.S. adults who say they ever use __ by …

• RACE & ETHNICITY
• POLITICAL AFFILIATION

This fact sheet was compiled by Research Assistant  Olivia Sidoti , with help from Research Analyst  Risa Gelles-Watnick , Research Analyst  Michelle Faverio , Digital Producer  Sara Atske , Associate Information Graphics Designer Kaitlyn Radde and Temporary Researcher  Eugenie Park .

Follow these links for more in-depth analysis of the impact of social media on American life.

• Americans’ Social Media Use  Jan. 31, 2024
• Americans’ Use of Mobile Technology and Home Broadband  Jan. 31 2024
• Q&A: How and why we’re changing the way we study tech adoption  Jan. 31, 2024

Find more reports and blog posts related to  internet and technology .

1615 L St. NW, Suite 800 Washington, DC 20036 USA (+1) 202-419-4300 | Main (+1) 202-857-8562 | Fax (+1) 202-419-4372 |  Media Inquiries

Research Topics

• Email Newsletters

ABOUT PEW RESEARCH CENTER  Pew Research Center is a nonpartisan fact tank that informs the public about the issues, attitudes and trends shaping the world. It conducts public opinion polling, demographic research, media content analysis and other empirical social science research. Pew Research Center does not take policy positions. It is a subsidiary of  The Pew Charitable Trusts .

© 2024 Pew Research Center