example of problem solving fraction

Fractions Questions and Problems with Solutions

Questions and problems with solutions on fractions are presented. Detailed solutions to the examples are also included. In order to master the concepts and skills of fractions, you need a thorough understanding (NOT memorizing) of the rules and properties and lot of practice and patience. I hope the examples, questions, problems in the links below will help you.

• Fractions and Mixed Numbers , define fractions and mixed numbers, and introduce important vocabulary.
• Evaluate Fractions of Quantities .
• Fractions Rules including questions with Solutions
• Properties of Fractions
• Complex Fractions with Variables
• Equivalent Fractions examples and questions with solutions.
• Reduce Fractions examples and questions with solutions.
• Reduce Fractions Calculator
• Simplify Fractions , examples and questions including solutions.
• Factor Fractions , examples with questions including solutions.
• Adding Fractions. Add fractions with same denominator or different denominator. Several examples with detailed solutions and exercises.
• Multiply Fractions. Multiply a fraction by another fraction or a number by a fraction. Examples with solutions and exercises.
• Divide Fractions. Divide a fraction by a fraction, a fraction by a number of a number by a fraction. Several examples with solutions and exercises with answers.

Fractions Per Grade

• Fractions and Mixed Numbers , questions and problems with solutions for grade 7
• Fractions and Mixed Numbers , questions and problems with solutions for grade 6
• Fractions , questions for grade 5 and their solutions
• Fractions , questions for grade 4 their answers.

Fractions Calculators

• Fractions Calculator including reducing, adding and multiplying fractions.
• Add Mixed Numbers Calculator

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Fraction Questions in Math

Last Updated: April 14, 2024 Fact Checked

This article was co-authored by Mario Banuelos, PhD and by wikiHow staff writer, Sophia Latorre . Mario Banuelos is an Associate Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,201,367 times.

Fraction questions can look tricky at first, but they become easier with practice and know-how. Start by learning the terminology and fundamentals, then pratice adding, subtracting, multiplying, and dividing fractions. [1] X Research source Once you understand what fractions are and how to manipulate them, you'll be breezing through fraction problems in no time.

Doing Calculations with Fractions

• For instance, to solve 5/9 + 1/9, just add 5 + 1, which equals 6. The answer, then, is 6/9 which can be reduced to 2/3.

• For instance, to solve 6/8 - 2/8, all you do is take away 2 from 6. The answer is 4/8, which can be reduced to 1/2.

• For example, if you need to add 1/2 and 2/3, start by determining a common multiple. In this case, the common multiple is 6 since both 2 and 3 can be converted to 6. To turn 1/2 into a fraction with a denominator of 6, multiply both the numerator and denominator by 3: 1 x 3 = 3 and 2 x 3 = 6, so the new fraction is 3/6. To turn 2/3 into a fraction with a denominator of 6, multiply both the numerator and denominator by 2: 2 x 2 = 4 and 3 x 2 = 6, so the new fraction is 4/6. Now, you can add the numerators: 3/6 + 4/6 = 7/6. Since this is an improper fraction, you can convert it to the mixed number 1 1/6.
• On the other hand, say you're working on the problem 7/10 - 1/5. The common multiple in this case is 10, since 1/5 can be converted into a fraction with a denominator of 10 by multiplying it by 2: 1 x 2 = 2 and 5 x 2 = 10, so the new fraction is 2/10. You don't need to convert the other fraction at all. Just subtract 2 from 7, which is 5. The answer is 5/10, which can also be reduced to 1/2.

• For instance, to multiply 2/3 and 7/8, find the new numerator by multiplying 2 by 7, which is 14. Then, multiply 3 by 8, which is 24. Therefore, the answer is 14/24, which can be reduced to 7/12 by dividing both the numerator and denominator by 2.

• For example, to solve 1/2 ÷ 1/6, flip 1/6 upside down so it becomes 6/1. Then just multiply 1 x 6 to find the numerator (which is 6) and 2 x 1 to find the denominator (which is 2). So, the answer is 6/2 which is equal to 3.

Joseph Meyer

Think about fractions as portions of a whole. Imagine dividing objects like pizzas or cakes into equal parts. Visualizing fractions this way improves comprehension, compared to relying solely on memorization. This approach can be helpful when adding, subtracting, and comparing fractions.

Practicing the Basics

• For instance, in 3/5, 3 is the numerator so there are 3 parts and 5 is the denominator so there are 5 total parts. In 7/8, 7 is the numerator and 8 is the denominator.

• If you need to turn 7 into a fraction, for instance, write it as 7/1.

• For example, if you have the fraction 15/45, the greatest common factor is 15, since both 15 and 45 can be divided by 15. Divide 15 by 15, which is 1, so that's your new numerator. Divide 45 by 15, which is 3, so that's your new denominator. This means that 15/45 can be reduced to 1/3.

• Say you have the mixed number 1 2/3. Stary by multiplying 3 by 1, which is 3. Add 3 to 2, the existing numerator. The new numerator is 5, so the mixed fraction is 5/3.

Tip: Typically, you'll need to convert mixed numbers to improper fractions if you're multiplying or dividing them.

• Say that you have the improper fraction 17/4. Set up the problem as 17 ÷ 4. The number 4 goes into 17 a total of 4 times, so the whole number is 4. Then, multiply 4 by 4, which is equal to 16. Subtract 16 from 17, which is equal to 1, so that's the remainder. This means that 17/4 is the same as 4 1/4.

Fraction Calculator, Practice Problems, and Answers

Community Q&A

• Check with your teacher to find out if you need to convert improper fractions into mixed numbers and/or reduce fractions to their lowest terms to get full marks. Thanks Helpful 2 Not Helpful 1
• Take the time to carefully read through the problem at least twice so you can be sure you know what it's asking you to do. Thanks Helpful 2 Not Helpful 2
• To take the reciprocal of a whole number, just put a 1 over it. For example, 5 becomes 1/5. Thanks Helpful 1 Not Helpful 1

You Might Also Like

• ↑ https://www.sparknotes.com/math/prealgebra/fractions/terms/
• ↑ https://www.bbc.co.uk/bitesize/articles/z9n4k7h
• ↑ https://www.mathsisfun.com/fractions_multiplication.html
• ↑ https://www.mathsisfun.com/fractions_division.html
• ↑ https://medium.com/i-math/the-no-nonsense-straightforward-da76a4849ec
• ↑ https://www.youtube.com/watch?v=PcEwj5_v75g
• ↑ https://sciencing.com/solve-math-problems-fractions-7964895.html

About This Article

To solve a fraction multiplication question in math, line up the 2 fractions next to each other. Multiply the top of the left fraction by the top of the right fraction and write that answer on top, then multiply the bottom of each fraction and write that answer on the bottom. Simplify the new fraction as much as possible. To divide fractions, flip one of the fractions upside-down and multiply them the same way. If you need to add or subtract fractions, keep reading! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Sebastian Maxwell

Jun 1, 2017

Did this article help you?

Jul 19, 2017

Sep 16, 2017

Kamaria Albert

Feb 28, 2017

Oct 17, 2016

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Inverse operations

Solve equations with fractions

Here you will learn about how to solve equations with fractions, including solving equations with one or more operations. You will also learn about solving equations with fractions where the unknown is the denominator of a fraction.

Students will first learn how to solve equations with fractions in 7th grade as part of their work with expressions and equations and expand that knowledge in 8th grade.

What are equations with fractions?

Equations with fractions involve solving equations where the unknown variable is part of the numerator and/or denominator of a fraction.

The numerator (top number) in a fraction is divided by the denominator (bottom number).

To solve equations with fractions, you will use the “balancing method” to apply the inverse operation to both sides of the equation in order to work out the value of the unknown variable.

The inverse operation of addition is subtraction.

The inverse operation of subtraction is addition.

The inverse operation of multiplication is division.

The inverse operation of division is multiplication.

For example,

\begin{aligned} \cfrac{2x+3}{5} \, &= 7\\ \colorbox{#cec8ef}{$\times \, 5$} \; & \;\; \colorbox{#cec8ef}{$\times \, 5$} \\\\ 2x+3&=35 \\ \colorbox{#cec8ef}{$-\,3$} \; & \;\; \colorbox{#cec8ef}{$- \, 3$} \\\\ 2x & = 32 \\ \colorbox{#cec8ef}{$\div \, 2$} & \; \; \; \colorbox{#cec8ef}{$\div \, 2$}\\\\ x & = 16 \end{aligned}

Common Core State Standards

How does this relate to 7th grade and 8th grade math?

• Grade 7: Expressions and Equations (7.EE.A.1) Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
• Grade 8: Expressions and Equations (8.EE.C.7) Solve linear equations in one variable.
• Grade 8: Expressions and Equations (8.EE.C.7b) Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.

How to solve equations with fractions

In order to solve equations with fractions:

Identify the operations that are being applied to the unknown variable.

• Apply the inverse operations, one at a time, to both sides of the equation .
• When you have the variable on one side, you have the final answer.
• Check the answer by substituting the answer back into the original equation .

[FREE] Solve Equations with Fractions Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of solving equations with fractions. 15 questions with answers to identify areas of strength and support!

Solve equations with fractions examples

Example 1: equations with one operation.

Solve for x \text{: } \cfrac{x}{5}=4 .

The unknown is x.

Looking at the left hand side of the equation, the x is divided by 5.

\cfrac{x}{5}

2 Apply the inverse operations, one at a time, to both sides of the equation.

The inverse of “dividing by 5 ” is “multiplying by 5 ”.

You will multiply both sides of the equation by 5.

3 When you have the variable on one side, you have the final answer.

The final answer is x=20.

4 Check the answer by substituting the answer back into the original equation.

You can check the answer by substituting the answer back into the original equation.

\cfrac{20}{5}=20\div5=4

Example 2: equations with one operation

Solve for x \text{: } \cfrac{x}{3}=8 .

Looking at the left hand side of the equation, the x is divided by 3.

\cfrac{x}{3}

Apply the inverse operations, one at a time, to both sides of the equation.

The inverse of “dividing by 3 ” is “multiplying by 3 ”.

You will multiply both sides of the equation by 3.

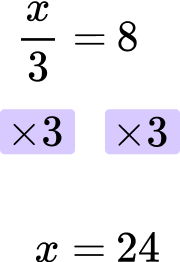
Write the final answer, checking that it is correct.

The final answer is x=24.

\cfrac{24}{3}=24\div3=8

Example 3: equations with two operations

Solve for x \text{: } \cfrac{x \, + \, 1}{2}=7 .

Looking at the left hand side of the equation, 1 is added to x and then divided by 2 (the denominator of the fraction).

\cfrac{x \, + \, 1}{2}

First, clear the fraction by multiplying both sides of the equation by 2.

Then, subtract 1 from both sides.

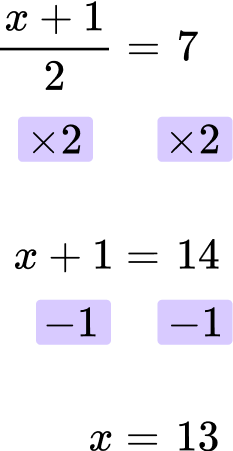
The final answer is x=13.

\cfrac{13 \, +1 \, }{2}=\cfrac{14}{2}=14\div2=7

Example 4: equations with two operations

Solve for x \text{: } \cfrac{x}{4}-2=3 .

Looking at the left hand side of the equation, x is divided by 4 and then 2 is subtracted.

\cfrac{x}{4}-2

First, add 2 to both sides of the equation.

Then, multiply both sides of the equation by 4.

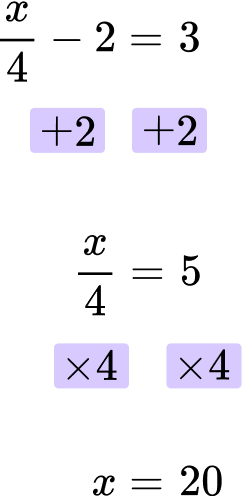
\cfrac{20}{4}-2=20\div4-2=5-2=3

Example 5: equations with three operations

Solve for x \text{: } \cfrac{3x}{5}+1=7 .

Looking at the left hand side of the equation, x is multiplied by 3, then divided by 5 , and then 1 is added.

\cfrac{3x}{5}+1

First, subtract 1 from both sides of the equation.

Then, multiply both sides of the equation by 5.

Finally, divide both sides by 3.

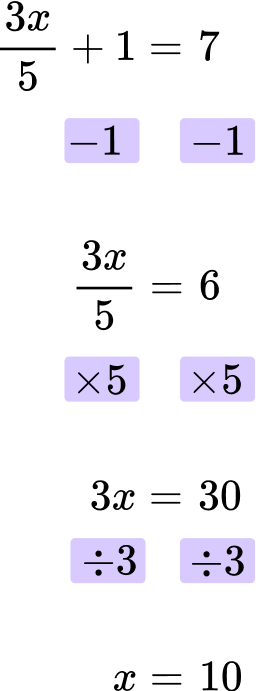
The final answer is x=10.

\cfrac{3 \, \times \, 10}{5}+1=\cfrac{30}{5}+1=6+1=7

Example 6: equations with three operations

Solve for x \text{: } \cfrac{2x-1}{7}=3 .

Looking at the left hand side of the equation, x is multiplied by 2, then 1 is subtracted, and the last operation is divided by 7 (the denominator).

\cfrac{2x-1}{7}

First, multiply both sides of the equation by 7.

Next, add 1 to both sides.

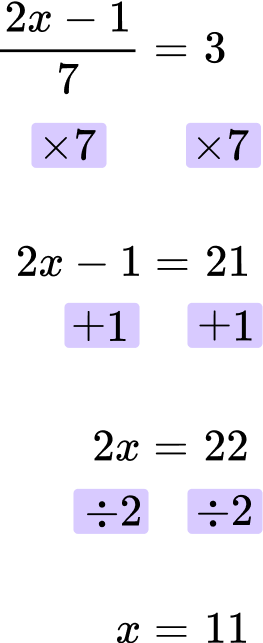
The final answer is x=11.

\cfrac{2 \, \times \, 11-1}{7}=\cfrac{22-1}{7}=\cfrac{21}{7}=3

Example 7: equations with the unknown as the denominator

Solve for x \text{: } \cfrac{24}{x}=6 .

Looking at the left hand side of the equation, x is the denominator. 24 is divided by x.

\cfrac{24}{x}

You need to multiply both sides of the equation by x.

Then, you can divide both sides by 6.

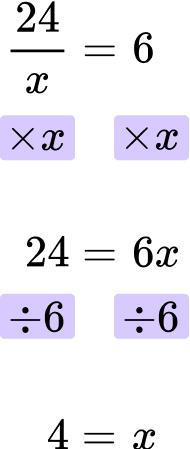
The final answer is x=4.

\cfrac{24}{4}=24\div4=6

Example 8: equations with the unknown as the denominator

Solve for x \text{: } \cfrac{18}{x}-6=3 .

Looking at the left hand side of the equation, x is the denominator. 18 is divided by x , and then 6 is subtracted.

\cfrac{18}{x}-6

First, add 6 to both sides of the equation.

Then, multiply both sides of the equation by x.

Finally, divide both sides by 9.

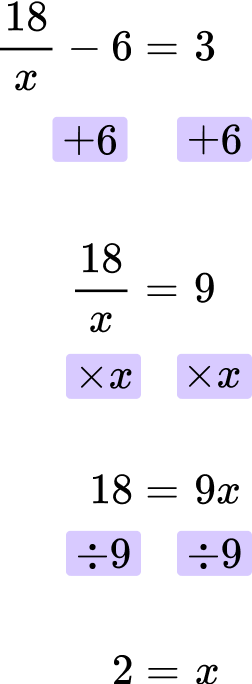
The final answer is x=2.

\cfrac{18}{2}-6=9-6=3

Teaching tips for solving equations with fractions

• When students first start working through practice problems and word problems, provide step-by-step instructions to assist them with solving linear equations.
• Introduce solving equations with fractions with one-step problems, then two-step problems, before introducing multi-step problems.
• Students will need lots of practice with solving linear equations. These standards provide the foundation for work with future linear equations in Algebra I and II.
• Provide opportunities for students to explain their thinking through writing. Ensure that they are using key vocabulary, such as, absolute value, coefficient, equation, common factors, inequalities, simplify, etc.

Easy mistakes to make

• The solution to an equation can be any type of number The unknowns do not have to be integers (whole numbers and their negative opposites). The solutions can be fractions or decimals. They can also be positive or negative numbers.
• The unknown of an equation can be on either side of the equation The unknown, represented by a letter, is often on the left hand side of the equations; however, it doesn’t have to be. It could also be on the right hand side of an equation.

• Lowest common denominator (LCD) It is common to get confused between solving equations involving fractions and adding and subtracting fractions. When adding and subtracting, you need to work out the lowest/least common denominator (sometimes called the least common multiple or LCM). When you solve equations involving fractions, multiply both sides of the equation by the denominator of the fraction.

Related math equations lessons

• Math equations
• Rearranging equations
• How to find the equation of a line
• Substitution
• Linear equations
• Writing linear equations
• Solving equations
• Identity math
• One step equations

Practice solve equations with fractions questions

1. Solve: \cfrac{x}{6}=3

You will multiply both sides of the equation by 6, because the inverse of “dividing by 6 ” is “multiplying by 6 ”.

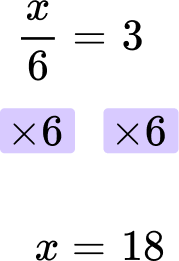
The final answer is x = 18.

\cfrac{18}{6}=18 \div 6=3

2. Solve: \cfrac{x \, + \, 4}{2}=7

Then subtract 4 from both sides.

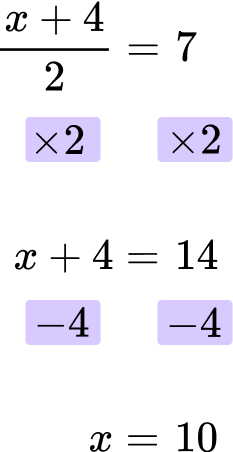
The final answer is x = 10.

\cfrac{10 \, + \, 4}{2}=\cfrac{14}{2}=14 \div 2=7

3. Solve: \cfrac{x}{8}-5=1

First, add 5 to both sides of the equation.

Then multiply both sides of the equation by 8.

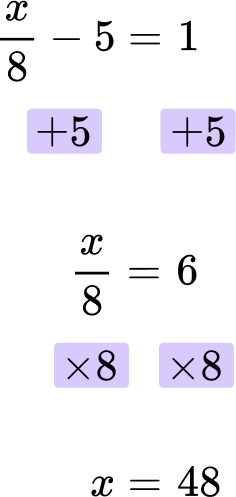
The final answer is x = 48.

\cfrac{48}{8}-5=48 \div 8-5=1

4. Solve: \cfrac{3x \, + \, 2}{4}=2

First, multiply both sides of the equation by 4.

Next, subtract 2 from both sides.

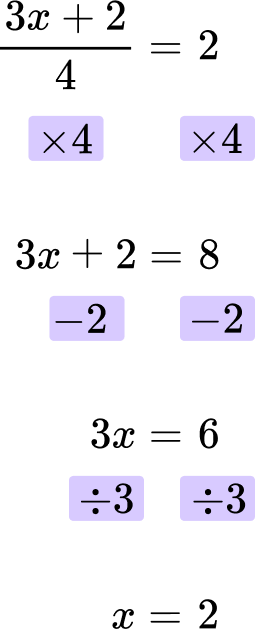
The final answer is x = 2.

\cfrac{3 \, \times \, 2+2}{4}=\cfrac{6 \, + \, 2}{4}=\cfrac{8}{4}=8 \div 4=2

5. Solve: \cfrac{4x}{7}-2=6

Then multiply both sides of the equation by 7.

Finally, divide both sides by 4.

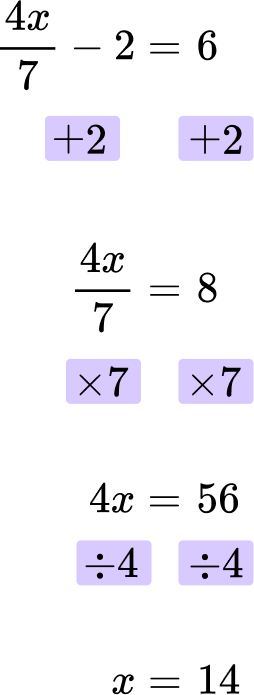
The final answer is x = 14.

\cfrac{4 \, \times \, 14}{7}-2=\cfrac{56}{7}-2=56 \div 7-2=6

6. Solve: \cfrac{42}{x}=7

Then you divide both sides by 7.

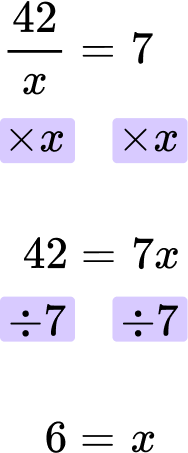
The final answer is x = 6.

\cfrac{42}{6}=42 \div 6=7

Solve equations with fractions FAQs

Yes, you still follow the order of operations when solving equations with fractions. You will start with any operations in the numerator and follow PEMDAS (parenthesis, exponents, multiply/divide, add/subtract), followed by any operations in the denominator. Then you will solve the rest of the equation as usual.

The next lessons are

• Inequalities
• Types of graphs
• Math formulas
• Coordinate plane
• Number patterns
• Algebraic expressions

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2013 Revised 2019

Exploring Fractions

• The first group  gives you some starting points to explore with your class, which are applicable to a wide range of ages.  The tasks in this first group will build on children's current understanding of fractions and will help them get to grips with the concept of the part-whole relationship. 
• The second group of tasks  focuses on the progression of ideas associated with fractions, through a problem-solving lens.  So, the tasks in this second group are curriculum-linked but crucially also offer opportunities for learners to develop their problem-solving and reasoning skills.   

• are applicable to a range of ages;
• provide contexts in which to explore the part-whole relationship in depth;
• offer opportunities to develop conceptual understanding through talk.

Fraction Word Problems (Difficult)

Here are some examples of more difficult fraction word problems. We will illustrate how block models (tape diagrams) can be used to help you to visualize the fraction word problems in terms of the information given and the data that needs to be found.

Related Pages Fraction Word Problems Singapore Math Lessons Fraction Problems Using Algebra Algebra Word Problems

Block modeling (also known as tape diagrams or bar models) are widely used in Singapore Math and the Common Core to help students visualize and understand math word problems.

Example: 2/9 of the people on a restaurant are adults. If there are 95 more children than adults, how many children are there in the restaurant?

Solution: Draw a diagram with 9 equal parts: 2 parts to represent the adults and 7 parts to represent the children.

5 units = 95 1 unit = 95 ÷ 5 = 19 7 units = 7 × 19 = 133

Answer: There are 133 children in the restaurant.

Example: Gary and Henry brought an equal amount of money for shopping. Gary spent $95 and Henry spent $350. After that Henry had 4/7 of what Gary had left. How much money did Gary have left after shopping?

350 – 95 = 255 3 units = 255 1 unit = 255 ÷ 3 = 85 7 units = 85 × 7 = 595

Answer: Gary has $595 after shopping.

Example: 1/9 of the shirts sold at Peter’s shop are striped. 5/8 of the remainder are printed. The rest of the shirts are plain colored shirts. If Peter’s shop has 81 plain colored shirts, how many more printed shirts than plain colored shirts does the shop have?

Solution: Draw a diagram with 9 parts. One part represents striped shirts. Out of the remaining 8 parts: 5 parts represent the printed shirts and 3 parts represent plain colored shirts.

3 units = 81 1 unit = 81 ÷ 3 = 27 Printed shirts have 2 parts more than plain shirts. 2 units = 27 × 2 = 54

Answer: Peter’s shop has 54 more printed colored shirts than plain shirts.

Solve a problem involving fractions of fractions and fractions of remaining parts

Example: 1/4 of my trail mix recipe is raisins and the rest is nuts. 3/5 of the nuts are peanuts and the rest are almonds. What fraction of my trail mix is almonds?

How to solve fraction word problem that involves addition, subtraction and multiplication using a tape diagram or block model

Example: Jenny’s mom says she has an hour before it’s bedtime. Jenny spends 3/5 of the hour texting a friend and 3/8 of the remaining time brushing her teeth and putting on her pajamas. She spends the rest of the time reading her book. How long did Jenny read?

How to solve a four step fraction word problem using tape diagrams?

Example: In an auditorium, 1/6 of the students are fifth graders, 1/3 are fourth graders, and 1/4 of the remaining students are second graders. If there are 96 students in the auditorium, how many second graders are there?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Module 1: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 10352

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1

1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.

After understanding, then make a plan.

Carry out the plan.

Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Notice we are going in the wrong direction! The total number of feet is decreasing!

Better! The total number of feet are increasing!

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Videos to watch:

1. Click on this link to see an example of “Guess and Test”

http://www.mathstories.com/strategies.htm

2. Click on this link to see another example of Guess and Test.

http://www.mathinaction.org/problem-solving-strategies.html

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)

Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!

Videos to watch demonstrating how to use "Draw a Picture".

1. Click on this link to see an example of “Draw a Picture”

2. Click on this link to see another example of Draw a Picture.

Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences.

last term = fixed number ( n -1) + first term

The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Ex: 2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2

Sum = (2 + 599) (200) then divide by 2

Sum = 60,100

Check in question 3: (10 points)

Find the 320 th term of 7, 10, 13, 16 …

Then find the sum of the first 320 terms.

Problem Solving Strategy 4 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Videos to watch demonstrating of “Working Backwards”

https://www.youtube.com/watch?v=5FFWTsMEeJw

Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 5 (Looking for a Pattern)

Definition: A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example 1: 1, 4, 7, 10, 13…

Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.

So the next number would be

25 + 11 = 36

Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5

-5 – 3 = -8

Example 4: 1, 2, 4, 8 … find the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

1. Click on this link to see an example of “Looking for a Pattern”

2. Click on this link to see another example of Looking for a Pattern.

Problem Solving Strategy 6 (Make a List)

Example 1 : Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Videos demonstrating "Make a List"

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 7 (Solve a Simpler Problem)

Geometric Sequences:

How would we find the nth term?

Solve a simpler problem:

1, 3, 9, 27.

1. To get from 1 to 3 what did we do?

2. To get from 3 to 9 what did we do?

Let’s set up a table:

Term Number what did we do

Looking back: How would you find the nth term?

Find the 10 th term of the above sequence.

Let L = the tenth term

Problem Solving Strategy 8 (Process of Elimination)

This strategy can be used when there is only one possible solution.

I’m thinking of a number.

The number is odd.

It is more than 1 but less than 100.

It is greater than 20.

It is less than 5 times 7.

The sum of the digits is 7.

It is evenly divisible by 5.

a. We know it is an odd number between 1 and 100.

b. It is greater than 20 but less than 35

21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.

c. The sum of the digits is 7

21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

Check in question 6: (8 points)

Jose is thinking of a number.

The number is not odd.

The sum of the digits is divisible by 2.

The number is a multiple of 11.

It is greater than 5 times 4.

It is a multiple of 6

It is less than 7 times 8 +23

What is the number?

Click on this link for a quick review of the problem solving strategies.

https://garyhall.org.uk/maths-problem-solving-strategies.html

• Trending Now
• Foundational Courses
• Data Science
• Practice Problem
• Machine Learning
• System Design
• DevOps Tutorial

Fractions Practice Questions

Master fractions with our comprehensive practice questions.

Welcome to our in-depth video on Fractions Practice Questions ! This video is crafted to help you understand and excel in fractions through a variety of engaging and challenging practice problems. Perfect for students looking to boost their math skills or teachers in search of high-quality educational materials.

What You Will Learn

In this video, you will explore:

• Detailed explanations of fraction concepts.
• Step-by-step solutions to a wide range of practice questions.
• Effective strategies for solving fraction problems.
• Real-world examples to illustrate the use of fractions.

Why Practice Fractions?

Fractions are a fundamental part of mathematics, essential for understanding more complex topics. Practicing fractions helps:

• Strengthen your mathematical foundation.
• Enhance your problem-solving abilities.
• Prepare you for exams and daily mathematical applications.

Keywords for Better Learning

We focus on several key areas to maximize your learning experience:

• Fraction Practice Questions
• Math Skills Improvement
• Solving Fraction Problems
• Fraction Concepts and Applications

Additional Resources

Be sure to explore our other math practice videos and resources to further enhance your skills. Subscribe to our channel and hit the notification bell to stay updated with the latest content.

Search Functionality Update!

To optimize your search experience, please refresh the page.

Windows: Press Ctrl + F5

Mac: Use Command + Option + R

Mobile: Tap and hold the refresh icon, then select "Hard Refresh" or "Reload Without Cache" for an instant upgrade!

• Child Login
• Number Sense
• Measurement
• Pre Algebra
• Figurative Language
• Reading Comprehension
• Reading and Writing
• Science Worksheets
• Social Studies Worksheets
• Math Worksheets
• ELA Worksheets
• Online Worksheets

Browse By Grade

• Become a Member

• Kindergarten

• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even Numbers
• Prime and Composite Numbers
• Roman Numerals
• Ordinal Numbers

• Big vs Small
• Long vs Short
• Tall vs Short
• Heavy vs Light
• Full and Empty
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature

• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem and Leaf Plot
• Box and Whisker Plot
• Permutations
• Combinations

• Lines, Rays, and Line Segments
• Points, Lines, and Planes
• Transformation
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel and Perpendicular Lines
• Surface Area
• Pythagorean Theorem

• Significant Figures
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Scientific Notation
• Absolute Value

• Translating Algebraic Phrases
• Simplifying Algebraic Expressions
• Evaluating Algebraic Expressions
• Systems of Equations
• Slope of a Line
• Equation of a Line
• Quadratic Equations
• Polynomials
• Inequalities
• Determinants
• Arithmetic Sequence
• Arithmetic Series
• Geometric Sequence
• Complex Numbers
• Trigonometry

Fraction Division Word Problems Worksheets

• Pre-Algebra >
• Fractions >
• Division >

Trawl through a host of free printable dividing fractions word problems worksheets and add life to division of fractions with fascinating everyday scenarios. Equal parts exciting and challenging, our practice word problems pdfs with included answer keys ensure children's computation skills will substantially improve. With diverse exercises like solving division word problems involving fractions, mixed numbers, and whole numbers, students will be spoiled for choice!

Our pdf fraction division word problem worksheets are suitable for grade 5, grade 6, and grade 7.

Dividing Fractions and Whole Numbers Word Problems - Customary

Let the young prodigies stir up enthusiasm as they grasp the concept of dividing fractions and whole numbers by solving word problems. The trick is for them to multiply with the reciprocal of the fractions and get the solutions.

Dividing Fractions and Whole Numbers Word Problems - Metric

Master dividing fractions and whole numbers by getting your hands on these pdf worksheets. Take the reciprocal of the divisor and multiply it with the dividend, and you're all set. Remember, this set involves metric units.

Dividing Fractions Word Problems - Customary

Watch how this printable set impels 6th grade and 7th grade students to solve real-world problems involving division of fractions. Deceptively simple, these pdfs get children to perform fraction division with wit and skill.

Dividing Fractions Word Problems - Metric

Looking for ways to make dividing fractions a fun-filled affair? Grade 6 and grade 7 students will work their way through interactive word problems on dividing fractions, featuring metric units of measurement.

Dividing Mixed Numbers Word Problems - Customary

Excitement never ends in our dividing mixed numbers word problems worksheets pdf. Each situation involves a pair of mixed numbers with customary units of measurement. Convert them to fractions and obtain the answers.

Dividing Mixed Numbers Word Problems - Metric

Introduce 5th grade kids to these word problems worksheet pdfs on dividing mixed fractions to hone their skills in fraction division. Convert mixed numbers into improper fractions, and proceed to divide.

Dividing Mixed Numbers and Fractions Word Problems - Customary

Run out of resources to divide fractions and mixed numbers on and on? Grab our pdf toolkit on dividing mixed numbers and fractions, brimming with exciting word problems involving customary units of measurement.

Dividing Mixed Numbers and Fractions Word Problems - Metric

Assess the division chops of learners in grade 5 by putting into use this set of pdf worksheets on dividing fractions and mixed numbers involving metric units of measurements.

Related Printable Worksheets

▶ Dividing Fractions Using Visual Models

▶ Dividing Fractions and Whole Numbers

Tutoringhour

What we offer, information.

• Membership Benefits
• How to Use Online Worksheets
• How to Use Printable Worksheets
• Printing Help
• Testimonial
• Privacy Policy
• Refund Policy

Copyright © 2024 - Tutoringhour

You must be a member to unlock this feature!

Sign up now for only $29.95/year — that's just 8 cents a day!

Printable Worksheets

• 20,000+ Worksheets Across All Subjects
• Access to Answer Key
• Add Worksheets to "My Collections"
• Create Custom Workbooks

Digitally Fillable Worksheets

• 1100+ Math and ELA Worksheets
• Preview and Assign Worksheets
• Create Groups and Add Children
• Track Progress

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

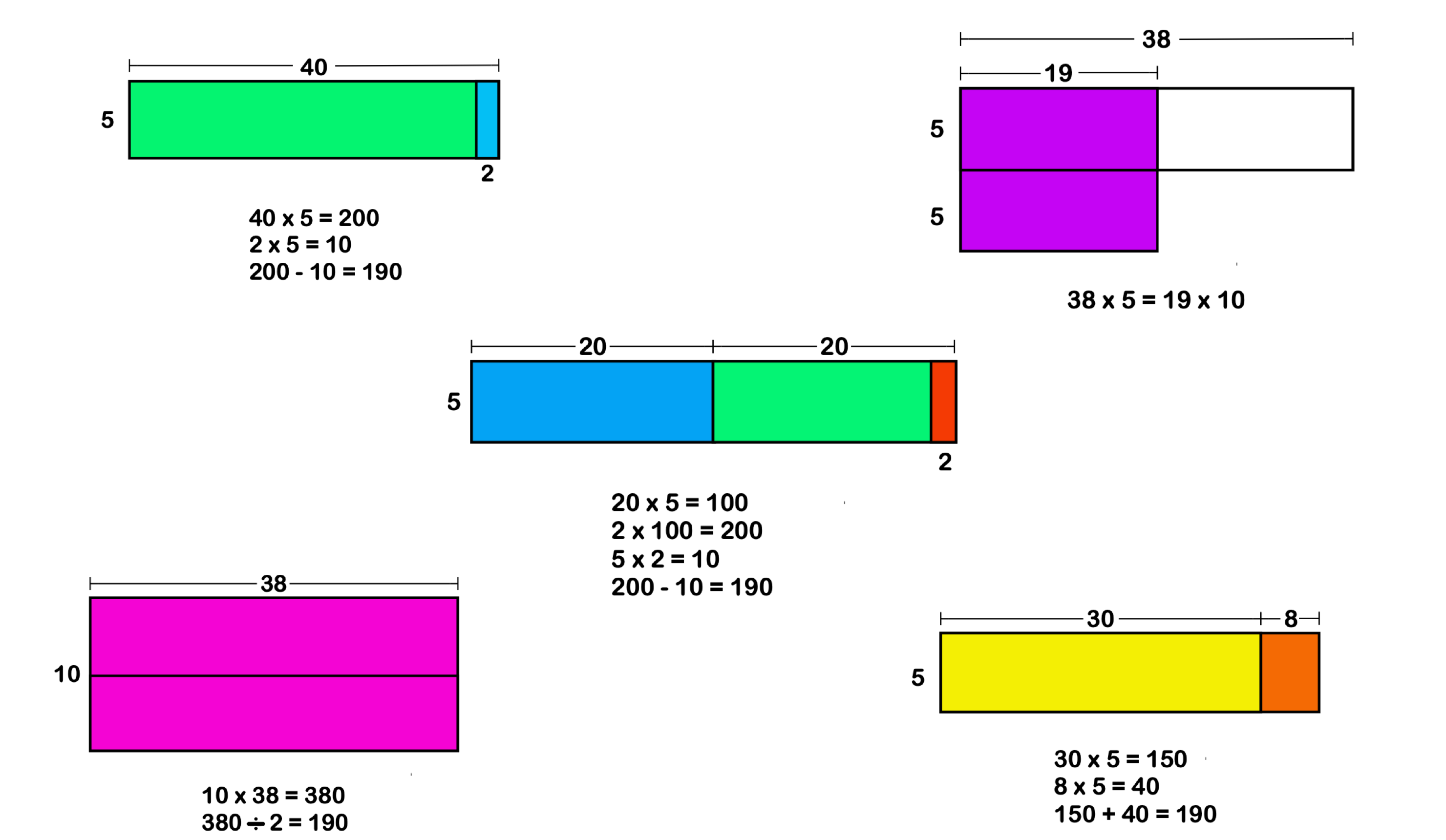
A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

• Spencer Greenberg
• 14 min read

Problem-Solving Techniques That Work For All Types of Challenges

Essay by Spencer Greenberg, Clearer Thinking founder

A lot of people don’t realize that there are general purpose problem solving techniques that cut across domains. They can help you deal with thorny challenges in work, your personal life, startups, or even if you’re trying to prove a new theorem in math.

Below are the 26 general purpose problem solving techniques that I like best, along with a one-word name I picked for each, and hypothetical examples to illustrate what sort of strategy I’m referring to.

Consider opening up this list whenever you’re stuck solving a challenging problem. It’s likely that one or more of these techniques can help!

1. Clarifying

Try to define the problem you are facing as precisely as you can, maybe by writing down a detailed description of exactly what the problem is and what constraints exist for a solution, or by describing it in detail to another person. This may lead to you realizing the problem is not quite what you had thought, or that it has a more obvious solution than you thought.

Life Example

“I thought that I needed to find a new job, but when I thought really carefully about what I don’t like about my current job, I realized that I could likely fix those things by talking to my boss or even, potentially, just by thinking about them differently.”

Startup Example

“we thought we had a problem with users not wanting to sign up for the product, but when we carefully investigated what the problem really was, we discovered it was actually more of a problem of users wanting the product but then growing frustrated because of bad interface design.”

2. Subdividing

Break the problem down into smaller problems in such a way that if you solve each of the small problems, you will have solved the entire problem. Once a problem is subdivided it can also sometimes be parallelized (e.g., by involving different people to work on the different components).

“My goal is to get company Z to become a partner with my company, and that seems hard, so let me break that goal into the steps of (a) listing the ways that company Z would benefit from becoming a partner with us, (b) finding an employee at company Z who would be responsive to hearing about these benefits, and (c) tracking down someone who can introduce me to that employee.”

Math Example

“I want to prove that a certain property applies to all functions of a specific type, so I start by (a) showing that every function of that type can be written as a sum of a more specific type of function, then I show that (b) the property applies to each function of the more specific type, and finally I show that (c) if the property applies to each function in a set of functions then it applies to arbitrary sums of those functions as well.”

3. Simplifying

Think of the simplest variation of the problem that you expect you can solve that shares important features in common with your problem, and see if solving this simpler problem gives you ideas for how to solve the more difficult version.

“I don’t know how to hire a CTO, but I do know how to hire a software engineer because I’ve done it many times, and good CTOs will often themselves be good software engineers, so how can I tweak my software engineer hiring to make it appropriate for hiring a CTO?”

“I don’t know how to calculate this integral as it is, but if I remove one of the free parameters, I actually do know how to calculate it, and maybe doing that calculation will give me insight into the solution of the more complex integral.”

4. Crowd-sourcing 

Use suggestions from multiple people to gain insight into how to solve the problem, for instance by posting on Facebook or Twitter requesting people’s help, or by posting to a Q&A site like Quora, or by sending emails to 10 people you know explaining the problem and requesting assistance.

Business Example

“Do you have experience outsourcing manufacturing to China? If so, I’d appreciate hearing your thoughts about how to approach choosing a vendor.”

Health Example

“I have trouble getting myself to stick to doing exercise daily. If you also used to have trouble getting yourself to exercise but don’t anymore, I’d love to know what worked to make it easier for you.”

5. Splintering

If the problem you are trying to solve has special cases that a solution to the general problem would also apply to, consider just one or two of these special cases as examples and solve the problem just for those cases first. Then see if a solution to one of those special cases helps you solve the problem in general.

“I want to figure out how to improve employee retention in general, let me examine how I could have improved retention in the case of the last three people that quit.”

“I want to figure out how to convince a large number of people to become customers, let me first figure out how to convince just Bill and John to become customers since they seem like the sort of customer I want to attract, and see what general lessons I learn from doing that.”

Read the books or textbooks that seem most related to the topic, and see whether they provide a solution to the problem, or teach you enough related information that you can now solve it yourself.

Economics Example

“Economists probably have already figured out reasonable ways to estimate demand elasticity, let’s see what an econometrics textbook says rather than trying to invent a technique from scratch.”

Mental Health Example

“I’ve been feeling depressed for a long time, maybe I should read some well-liked books about depression.”

7. Searching

Think of a similar problem that you think practitioners, bloggers or academics might have already solved and search online (e.g., via google, Q&A sites, or google scholar academic paper search) to see if anyone has done a write-up about how they solved it.

Advertising Example

“I’m having trouble figuring out the right advertising keywords to bid on for my specific product, I bet someone has a blog post describing how to approach choosing keywords for other related products.”

Machine Learning Example

“I can’t get this neural network to train properly in my specific case, I wonder if someone has written a tutorial about how to apply neural networks to related problems.”

8. Unconstraining

List all the constraints of the problem, then temporarily ignore one or more of the constraints that make the problem especially hard, and try to solve it without those constraints. If you can, then see if you can modify that unconstrained solution until it becomes a solution for the fully constrained problem.

“I need to hire someone who can do work at the intersection of machine learning and cryptography, let me drop the constraint of having cryptography experience and recruit machine learning people, then pick from among them a person that seems both generally capable and well positioned to learn the necessary cryptography.”

Computer Science Example

“I need to implement a certain algorithm, and it needs to be efficient, but that seems very difficult, so let me first figure out how to implement an inefficient version of the algorithm (i.e., drop the efficiency constraint), then at the end I will try to figure out how to optimize that algorithm for efficiency.”

9. Distracting

Fill your mind with everything you know about the problem, including facts, constraints, challenges, considerations, etc. and then stop thinking about the problem, and go and do a relaxing activity that requires little focus, such as walking, swimming, cooking, napping or taking a bath to see if new ideas or potential solutions pop into your mind unexpectedly as your subconscious continues to work on the problem without your attention.

“For three days, I’ve been trying to solve this problem at work, but the solution only came to me when I was strolling in the woods and not even thinking about it.”

Example from mathematician Henri Poincaré

“The incidents of the travel made me forget my mathematical work. Having reached Coutances, we entered an omnibus to go someplace or other. At the moment when I put my foot on the step, the idea came to me, without anything in my former thoughts seeming to have paved the way for it, that the transformations I had used to define the Fuchsian functions were identical with those of non-Euclidean geometry.”

10. Reexamining

Write down all the assumptions you’ve been making about the problem or about what a solution should I look like (yes – make an actual list). Then start challenging them one by one to see if they are actually needed or whether some may be unnecessary or mistaken.

Psychology Example

“We were assuming in our lab experiments that when people get angry they have some underlying reason behind it, but there may be some anger that is better modeled as a chemical fluctuation that is only loosely related to what happens in the lab, such as when people are quick to anger because they are hungry.”

“I need to construct a function that has this strange property, and so far I’ve assumed that the function must be smooth, but if it doesn’t actually need to be then perhaps I can construct just such a function out of simple linear pieces that are glued together.”

11. Reframing

Try to see the problem differently. For instance, by flipping the default, analyzing the inverse of the problem instead, thinking about how you would achieve the opposite of what you want, or shifting to an opposing perspective.

If we were building this company over again completely from scratch, what would we do differently in the design of our product, and can we pivot the product in that direction right now?”

“Should move to New York to take a job that pays $20,000 more per year? Well, if I already lived in New York, the decision to stay there rather than taking a $20,000 pay cut to move here would be an easy one. So maybe I’m overly focused on the current default of not being in New York and the short term unpleasantness of relocating.”

Marketing Example

“If I were one of our typical potential customers, what would I do to try to find a product like ours?”

12. Brainstorming

Set a timer for at least 5 minutes, and generate as many plausible solutions or ideas that you can without worrying about quality at all. Evaluate the ideas only at the end after the timer goes off.

“I’m going to set a timer for 5 minutes and come up with at least three new ways I could go about looking for a co-founder.”

“I’m going to set a timer for 20 minutes and come up with at least five possible explanations for why I’ve been feeling so anxious lately.”

13. Experting

Find an expert (or someone highly knowledgeable) in the topic area and ask their opinion about the best way to solve the problem.

“Why do you think most attempts at creating digital medical records failed, and what would someone have to do differently to have a reasonable chance at success?”

“What sort of optimization algorithm would be most efficient for minimizing the objective functions of this type?”

14. Eggheading

Ask the smartest person you know how they would solve the problem. Be sure to send an email in advance, describing the details so that this person has time to deeply consider the problem before you discuss it.

“Given the information I sent you about our competitors and the interviews we’ve done with potential customers, in which direction would you pivot our product if you were me (and why)?”

Research Example

“Given the information I sent you about our goals and the fact that our previous research attempts have gotten nowhere, how would you approach researching this topic to find the answer we need?”

15. Guessing

Start with a guess for what the solution could be, now check if it actually works and if not, start tweaking that guess to see if you can morph it into something that could work.

“I don’t know what price to use for the product we’re selling, so let me start with an initial guess and then begin trying to sell the thing, and tweak the price down if it seems to be a sticking point for customers, and tweak the price up if the customers don’t seem to pay much attention to the price.”

“My off the cuff intuition says that this differential equation might have a solution of the form x^a * e^(b x)for some a or b, let me plug it into the equation to see if indeed it satisfies the equation for any choice of a and b, and if not, let me see if I can tweak it to make something similar work.”

“I don’t know what the most effective diet for me would be, so I’ll just use my intuition to ban from my diet some foods that seem both unhealthy and addictive, and see if that helps.”

16. Comparing

Think of similar domains you already understand or similar problems you have already solved in the past, and see whether your knowledge of those domains or solutions to those similar problems may work as a complete or partial solution here.

“I don’t know how to find someone to fix things in my apartment, but I have found a good house cleaner before by asking a few friends who they use, so maybe I can simply use the same approach for finding a person to fix things.”

“This equation I’m trying to simplify reminds me of work I’m familiar with related to Kullback-Leibler divergence, I wonder if results from information theory could be applied in this case.”

17. Outsourcing

Consider whether you can hire someone to solve this problem, instead of figuring out how to solve it yourself.

“I don’t really understand how to get media attention for my company, so let me hire a public relations firm and let them handle the process.”

“I have no fashion sense, but I’d like to look better. Maybe I should hire someone fashionable who works in apparel to go shopping with me and help me choose what I should wear.”

18. Experimenting

Rapidly develop possible solutions and test them out (in sequence, or in parallel) by applying cheap and fast experiments. Discard those that don’t work, or iterate on them to improve them based on what you learn from the experiments.

“We don’t know if people will like a product like the one we have in mind, but we can put together a functioning prototype quickly, show five people that seem like they could be potential users, and iterate or create an entirely new design based on how they respond.”

“I don’t know if cutting out sugar will help improve my energy levels, but I can try it for two weeks and see if I notice any differences.”

19. Generalizing

Consider the more general case of the specific problem you are trying to solve, and then work on solving the general version instead. Paradoxically, it is sometimes easier to make progress on the general case rather than a specific one because it increases your focus on the structure of the problem rather than unimportant details.

“I want to figure out how to get this particular key employee more motivated to do good work, let me construct a model of what makes employees motivated to do good work in general, then I’ll apply it to this case.”

“I want to solve this specific differential equation, but it’s clearly a special case of a more general class of differential equations, let me study the general class and see what I can learn about them first and then apply what I learn to the specific case.”

20. Approximating

Consider whether a partial or approximate solution would be acceptable and, if so, aim for that instead of a full or exact solution.

“Our goal is to figure out which truck to send out for which delivery, which theoretically depends on many factors such as current location, traffic conditions, truck capacity, fuel efficiency, how many hours the driver has been on duty, the number of people manning each truck, the hourly rate we pay each driver, etc. etc. Maybe if we focus on just the three variables that we think are most important, we can find a good enough solution.”

“Finding a solution to this equation seems difficult, but if I approximate one of the terms linearly it becomes much easier, and maybe for the range of values we’re interested in, that’s close enough to an exact solution!”

21. Annihilating

Try to prove that the problem you are attempting to solve is actually impossible. If you succeed, you may save yourself a lot of time working on something impossible. Furthermore, in attempting to prove that the problem is impossible, you may gain insight into what makes it actually possible to solve, or if it turns out to truly be impossible, figure out how you could tweak the problem to make it solvable.

“I’m struggling to find a design for a theoretical voting system that has properties X, Y, and Z, let me see if I can instead prove that no such voting system with these three properties could possibly exist.”

“My goal has been to prove that this property always applies to this class of functions, let me see if I can generate a counterexample to prove that this goal is actually impossible.”

Physics Example

“I was trying to design a physical system with certain properties, but I now realize that if such a system could be realized, then it would allow for perpetual motion, and therefore it is impossible to build the sort of system I had in mind.”

22. Modeling

Try to build an explicit model of the situation, including what elements there are and how they related to each other. For instance, try drawing a diagram or flow chart that encapsulates your understanding of all the important information that relates to the problem.

“I’ve noticed that there are certain situations that cause me to freak out that would not bother other people. So what are the common elements when this happens, and how do they seem to relate to each other and to the way I end up feeling? Let me see if I can draw a diagram of this on paper.”

“What are all the different groups (e.g., providers, payers, patients) involved in the healthcare system, and if we diagram how they interact with each other, will that give us ideas for how we can sell our healthcare product?”

23. Brute forcing

One-by-one, consider every possible solution to the problem until you’ve found a good one or exhausted them all.

Startup example

“We’re not sure the order that these four parts of the user registration process should go in, so let’s make a list of all 24 possible orderings, and examine them one by one to see which makes the most sense.”

“It’s not clear how to pick which of these machine learning methods to use on this problem, but since we have lots of data, we can just try each of the algorithms and see which makes the most accurate predictions on data we’ve held to the side for testing.”

24. Refocusing

Forget about trying to solve the problem, and instead consider why you are trying to solve it. Then consider if there is a different problem you can work on that is aimed at producing the same sort of value in a different way.

Startup Example 1

“Maybe instead of trying increasingly hard to figure out how to get this type of consumer to buy, we need to switch our focus to the problem of how to sell to businesses, since what we actually care about is selling it, not selling it to one particular group.”

Startup Example 2

“I’ve been banging my head against the wall trying to implement this extremely complex feature, but there are lots of features that users would find just as valuable that are much easier to implement, maybe I should focus on those instead.”

25. Sidestepping

Consider whether you really want to spend more time trying to solve this problem and whether you can avoid the problem by instead working on totally different problems that you also care about.

“We’ve tried selling our solution to replace Excel for 12 months without much success, maybe we should go back to the drawing board and consider designing a totally new product. Our assumptions about customer needs seem to simply have been wrong.”

“I’ve spent six months on this math problem with little progress, but there are two other math problems I’m equally excited about, so maybe I should spend some time investigating whether one of those may be more tractable.”

26. Aggregating

Consider whether multiple problems you’re now experiencing might, in fact, be caused by the same source of difficulty, rather than being independent problems.

“I seem to be having conflict with a few different friends right now – could it be that I’m doing something without realizing it that is increasing my chance of conflict with all of them?”

“Three employees have quit in the last month. Perhaps the primary problem isn’t really about convincing this one important employee to stay, which is how I was framing it, but rather, about identifying why people keep leaving more generally.”

Recent Posts

We're launching a scientific test of astrology, and anyone can participate!

Remembering Daniel Kahneman: 7 theories that can help you understand how you think

Test how well you understand human psychology with our new quiz

Basic Math Definitions

We have collected some basic definitions on this page. For more definitions, explanations, etc, use search above. Or look up your word in the Illustrated Mathematics Dictionary :

The Basic Operations

In basic mathematics there are many ways of saying the same thing:

Addition is ...

... bringing two or more numbers (or things) together to make a new total.

The numbers to be added together are called the " Addends ":

Subtraction is ...

... taking one number away from another.

Minuend :The number that is to be subtracted from. Subtrahend :The number that is to be subtracted. Difference : The result of subtracting one number from another.

Multiplication is ...

... (in its simplest form) repeated addition .

Here we see that 6+6+6 (three 6s) make 18:

It can also be said that 3+3+3+3+3+3 (six 3s) make 18

But we can also multiply by fractions or decimals, which goes beyond the simple idea of repeated addition:

Example: 3.5 × 5 = 17.5

which is 3.5 lots of 5, or 5 lots of 3.5

Division is ...

... splitting into equal parts or groups. It is the result of "fair sharing".

Division has its own special words to remember.

Let's take the simple question of 22 divided by 5 . The answer is 4 , with 2 left over.

Here we see the important words:

Which can also be in this form:

A Fraction is ...

... part of a whole.

The top part (the numerator) says how many parts we have .

The bottom part (the denominator) says how many parts the whole is divided into .

See Fractions for more details.

A Decimal Number is ...

... a number that contains a Decimal Point.

See Decimals for more details.

A Percentage is ...

... parts per 100. The symbol is %

Example: 25% means 25 per 100 (25% of this box is green)

See Percentages for more details.

Average (Mean) is ...

... the sum divided by the count .

We calculate the average by adding up all the values , then divide by how many values .

Example: What is the average of 9, 2, 12 and 5?

Add up all the values: 9 + 2 + 12 + 5 = 28

Divide by how many values (there are four of them): 28 ÷ 4 = 7

So the average is 7

See Mean for more details.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 5th grade   >   Unit 6

• Multiplying 2 fractions: fraction model
• Multiplying 2 fractions: number line
• Represent fraction multiplication with visuals
• Multiplying fractions with visuals
• Multiplying 2 fractions: 5/6 x 2/3

Multiplying fractions

• (Choice A)   11 8 ‍   A 11 8 ‍  
• (Choice B)   16 56 ‍   B 16 56 ‍  
• (Choice C)   18 15 ‍   C 18 15 ‍  
• (Choice D)   9 28 ‍   D 9 28 ‍