ratio and rate problem solving

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Section 12: Solving Ratio and Rate Problems

• Last updated
• Save as PDF
• Page ID 35051

• Illustrative Mathematics
• OpenUp Resources

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Ratio Problem Solving

Here we will learn about ratio problem solving, including how to set up and solve problems. We will also look at real life ratio problems.

There are also ratio problem solving worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is ratio problem solving?

Ratio problem solving is a collection of word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities . They are usually written in the form a:b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are,

• What is the ratio involved?
• What order are the quantities in the ratio?
• What is the total amount / what is the part of the total amount known?
• What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that we can use to help us find an answer. 

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods we can use when given certain pieces of information.

When solving ratio problems it is very important that you are able to use ratios. This includes being able to use ratio notation. 

For example, Charlie and David share some sweets in the ratio of 3:5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

We use the ratio to divide 40 sweets into 8 equal parts. 

Then we multiply each part of the ratio by 5.

3 x 5:5 x 5 = 15:25

This means that Charlie will get 15 sweets and David will get 25 sweets.

• Dividing ratios

Step-by-step guide: Dividing ratios (coming soon)

Ratios and fractions (proportion problems)

We also need to consider problems involving fractions. These are usually proportion questions where we are stating the proportion of the total amount as a fraction.

Simplifying and equivalent ratios

• Simplifying ratios

Equivalent ratios

Units and conversions ratio questions

Units and conversions are usually equivalent ratio problems (see above).

• If £1:\$1.37 and we wanted to convert £10 into dollars, we would multiply both sides of the ratio by 10 to get £10 is equivalent to \$13.70.
• The scale on a map is 1:25,000. I measure 12cm on the map. How far is this in real life, in kilometres? After multiplying both parts of the ratio by 12 you must then convert 12 \times 25000=300000 \ cm to km by dividing the solution by 100 \ 000 to get 3km.

Notice that for all three of these examples, the units are important. For example if we write the mapping example as the ratio 4cm:1km, this means that 4cm on the map is 1km in real life.

Top tip: if you are converting units, always write the units in your ratio.

Usually with ratio problem solving questions, the problems are quite wordy . They can involve missing values , calculating ratios , graphs , equivalent fractions , negative numbers , decimals and percentages .

Highlight the important pieces of information from the question, know what you are trying to find or calculate , and use the steps above to help you start practising how to solve problems involving ratios.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

Explain how to do ratio problem solving

Ratio problem solving worksheet

Get your free ratio problem solving worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on ratio

Ratio problem solving is part of our series of lessons to support revision on ratio . You may find it helpful to start with the main ratio lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• How to work out ratio  
• Ratio to fraction
• Ratio scale
• Ratio to percentage

Ratio problem solving examples

Example 1: part:part ratio.

Within a school, the number of students who have school dinners to packed lunches is 5:7. If 465 students have a school dinner, how many students have a packed lunch?

Within a school, the number of students who have school dinners to packed lunches is \bf{5:7.} If \bf{465} students have a school dinner , how many students have a packed lunch ?

Here we can see that the ratio is 5:7 where the first part of the ratio represents school dinners (S) and the second part of the ratio represents packed lunches (P).

We could write this as

Where the letter above each part of the ratio links to the question.

We know that 465 students have school dinner.

2 Know what you are trying to calculate.

From the question, we need to calculate the number of students that have a packed lunch, so we can now write a ratio below the ratio 5:7 that shows that we have 465 students who have school dinners, and p students who have a packed lunch.

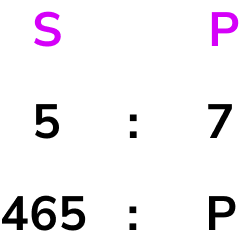
We need to find the value of p.

3 Use prior knowledge to structure a solution.

We are looking for an equivalent ratio to 5:7. So we need to calculate the multiplier. We do this by dividing the known values on the same side of the ratio by each other.

So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

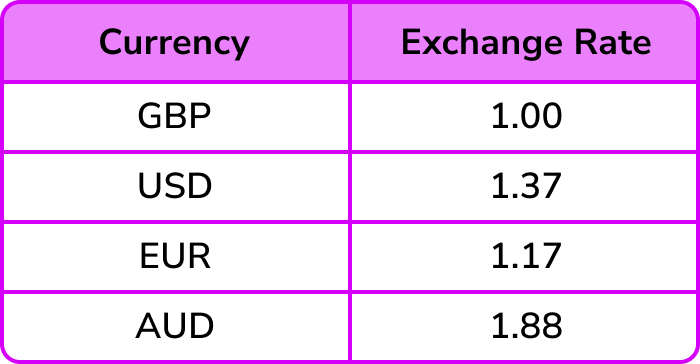
Use the table above to convert £520 (GBP) to Euros € (EUR).

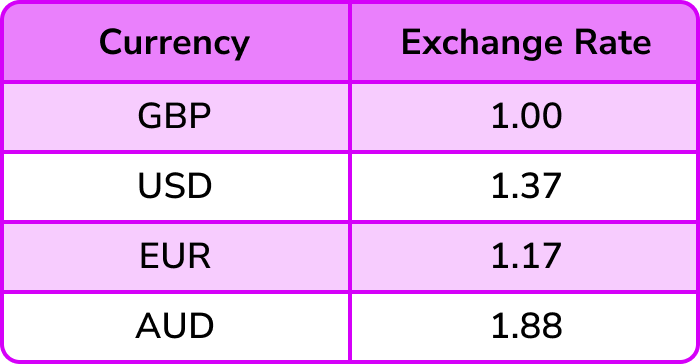
Use the table above to convert \bf{£520} (GBP) to Euros \bf{€} (EUR).

The two values in the table that are important are GBP and EUR. Writing this as a ratio, we can state

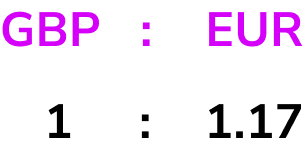
We know that we have £520.

We need to convert GBP to EUR and so we are looking for an equivalent ratio with GBP = £520 and EUR = E.

To get from 1 to 520, we multiply by 520 and so to calculate the number of Euros for £520, we need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520 = €608.40.

Example 3: writing a ratio 1:n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500ml of concentrated plant food must be diluted into 2l of water. Express the ratio of plant food to water respectively in the ratio 1:n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500ml} of concentrated plant food must be diluted into \bf{2l} of water . Express the ratio of plant food to water respectively as a ratio in the form 1:n.

Using the information in the question, we can now state the ratio of plant food to water as 500ml:2l. As we can convert litres into millilitres, we could convert 2l into millilitres by multiplying it by 1000.

2l = 2000ml

So we can also express the ratio as 500:2000 which will help us in later steps.

We want to simplify the ratio 500:2000 into the form 1:n.

We need to find an equivalent ratio where the first part of the ratio is equal to 1. We can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

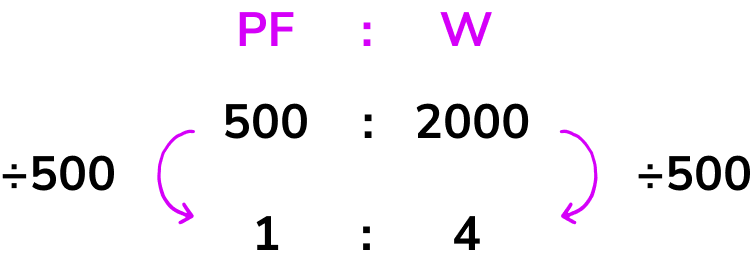
So the ratio of plant food to water in the form 1:n is 1:4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives £8 pocket money, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their ages. Kieran is \bf{3} years older than Josh . Luke is twice Josh’s age. If Luke receives \bf{£8} pocket money, how much money do the three siblings receive in total ?

We can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, we have

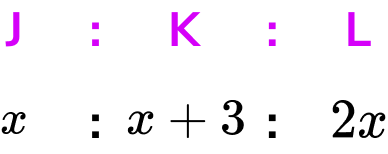
We also know that Luke receives £8.

We want to calculate the total amount of pocket money for the three siblings.

We need to find the value of x first. As Luke receives £8, we can state the equation 2x=8 and so x=4.

Now we know the value of x, we can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

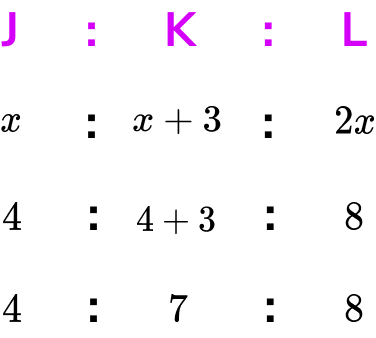
The total amount of pocket money is therefore 4+7+8=£19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colours of counters in a bag.

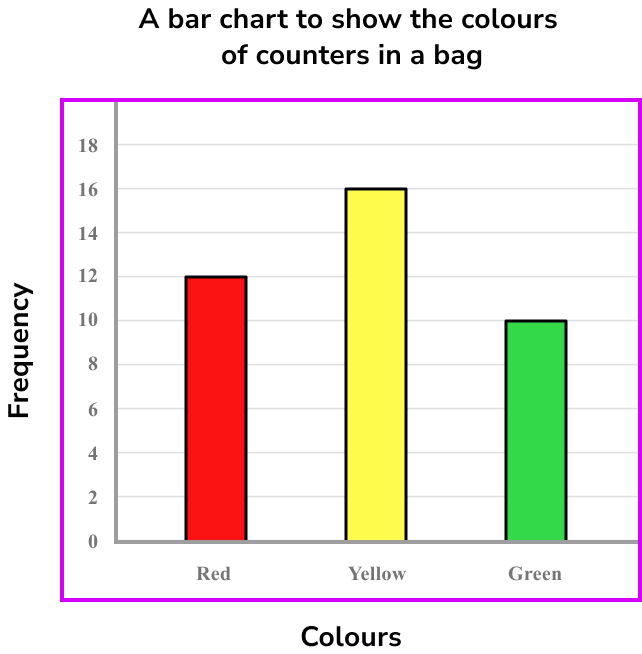
Express this data as a ratio in its simplest form.

From the bar chart, we can read the frequencies to create the ratio.

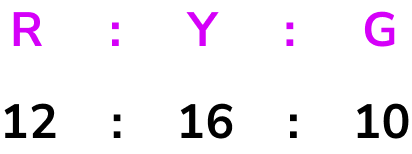
We need to simplify this ratio.

To simplify a ratio, we need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} &12 = 1, {\color{red} 2}, 3, 4, 6, 12 \\\\ &16 = 1, {\color{red} 2}, 4, 8, 16 \\\\ &10 = 1, {\color{red} 2}, 5, 10 \end{aligned}

HCF (12,16,10) = 2

Dividing all the parts of the ratio by 2 , we get

Our solution is 6:8:5 .

Example 6: combining two ratios

Glass is made from silica, lime and soda. The ratio of silica to lime is 15:2. The ratio of silica to soda is 5:1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15:2.} The ratio of silica to soda is \bf{5:1.} State the ratio of silica:lime:soda .

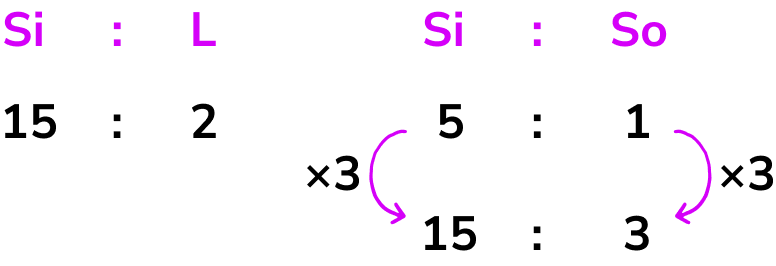
We know the two ratios

We are trying to find the ratio of all 3 components: silica, lime and soda.

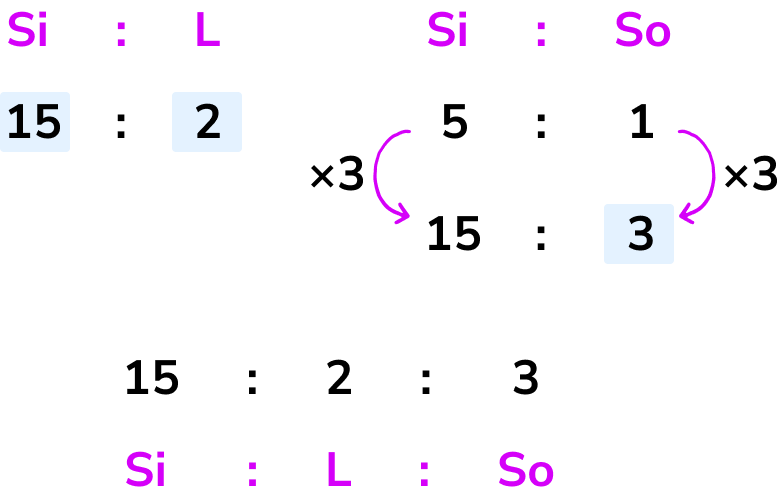
Using equivalent ratios we can say that the ratio of silica:soda is equivalent to 15:3 by multiplying the ratio by 3.

We now have the same amount of silica in both ratios and so we can now combine them to get the ratio 15:2:3.

Example 7: using bar modelling

India and Beau share some popcorn in the ratio of 5:2. If India has 75g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5:2.} If India has \bf{75g} more popcorn than Beau , what was the original quantity?

We know that the initial ratio is 5:2 and that India has three more parts than Beau.

We want to find the original quantity.

Drawing a bar model of this problem, we have

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if we can find out this value, we can then find the total quantity.

From the question, India’s share is 75g more than Beau’s share so we can write this on the bar model.

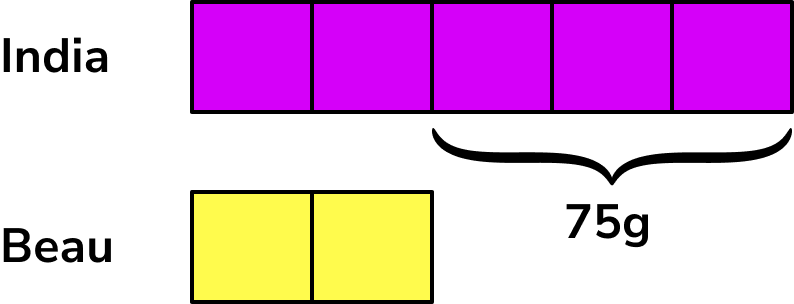
We can find the value of one share by working out 75 \div 3=25g.

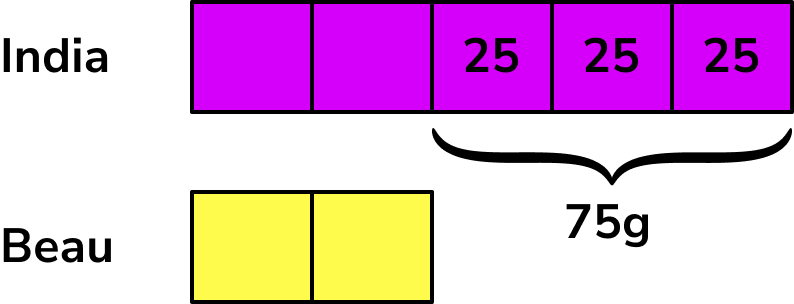
We can fill in each share to be 25g.

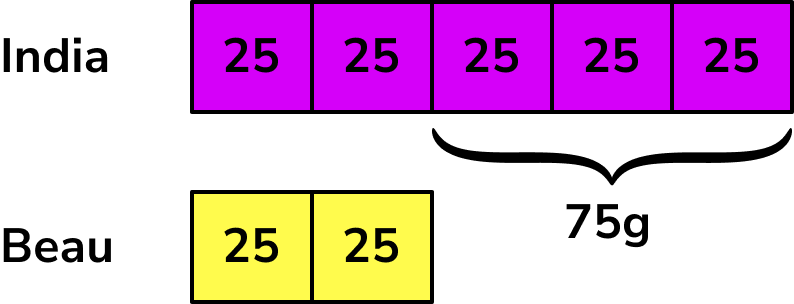
Adding up each share, we get

India = 5 \times 25=125g

Beau = 2 \times 25=50g

The total amount of popcorn was 125+50=175g.

Common misconceptions

• Mixing units

Make sure that all the units in the ratio are the same. For example, in example 6 , all the units in the ratio were in millilitres. We did not mix ml and l in the ratio.

• Ratio written in the wrong order

For example the number of dogs to cats is given as the ratio 12:13 but the solution is written as 13:12.

• Ratios and fractions confusion

Take care when writing ratios as fractions and vice-versa. Most ratios we come across are part:part. The ratio here of red:yellow is 1:2. So the fraction which is red is \frac{1}{3} (not \frac{1}{2} ).

• Counting the number of parts in the ratio, not the total number of shares

For example, the ratio 5:4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.

• Ratios of the form \bf{1:n}

The assumption can be incorrectly made that n must be greater than 1 , but n can be any number, including a decimal.

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3:8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

3. The ratio of prime numbers to non-prime numbers from 1-200 is 45:155. Express this as a ratio in the form 1:n.

4. The angles in a triangle are written as the ratio x:2x:3x. Calculate the size of each angle.

5. A clothing company has a sale on tops, dresses and shoes. \frac{1}{3} of sales were for tops, \frac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

6. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2:3 and the ratio of cloud to rain was 9:11. State the ratio that compares sunshine:cloud:rain for the month.

Ratio problem solving GCSE questions

1. One mole of water weighs 18 grams and contains 6.02 \times 10^{23} water molecules.

Write this in the form 1gram:n where n represents the number of water molecules in standard form.

2. A plank of wood is sawn into three pieces in the ratio 3:2:5. The first piece is 36cm shorter than the third piece.

Calculate the length of the plank of wood.

5-3=2 \ parts = 36cm so 1 \ part = 18cm

3. (a) Jenny is x years old. Sally is 4 years older than Jenny. Kim is twice Jenny’s age. Write their ages in a ratio J:S:K.

(b) Sally is 16 years younger than Kim. Calculate the sum of their ages.

Learning checklist

You have now learned how to:

• Relate the language of ratios and the associated calculations to the arithmetic of fractions and to linear functions
• Develop their mathematical knowledge, in part through solving problems and evaluating the outcomes, including multi-step problems
• Make and use connections between different parts of mathematics to solve problems

The next lessons are

• Compound measures
• Best buy maths

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

A free service from Mattecentrum

Rates and ratios

• Class ratio I
• Class ratio II
• Class ratio III

The ratio is the relationship of two numbers. For example you have 2 flashlights and 5 batteries. To compare the ratio between the flashlights and the batteries we divide the set of flashlights with the set of batteries.

The ratio is 2 to 5 or 2:5 or 2/5. All these describe the ratio in different forms of fractions. The ratio can consequently be expressed as fractions or as a decimal. 2:5 in decimals is 0.4.

A rate is a little bit different than the ratio, it is a special ratio. It is a comparison of measurements that have different units, like cents and grams. A unit rate is a rate with a denominator of 1.

Sarah is buying jellybeans for her best friend's birthday party. She buys a bag of 10 lb of jellybeans that costs $45. Sarah is wondering how much 1 lb of jellybeans cost.

$$\$ 45=4500 \, cents$$

$$\frac{4500 \: cents}{10\: lb}=\frac{4500 \: cents{\color{green} {\, \div\, 10}}}{10\: lb{\color{green} {\, \div\, 10}}}=\frac{450 \: cents}{1\: lb}$$

$$1\: lb=450\: cents=\$ 4.50$$

Video lesson

Express the ratio as a fraction in simplest form and as a decimal

• Pre-Algebra
• The mean, the median and the mode
• Stem-and-Leaf Plots and Box-and-Whiskers Plot
• Calculating the outcome
• Combinations and permutations
• Finding the odds
• Probability of events
• Geometry – fundamental statements
• Circle graphs
• Angles and parallel lines
• Quadrilaterals, polygons and transformations
• Measure areas
• Pyramids, prisms, cylinders and cones
• Square roots and real numbers
• The Pythagorean Theorem
• Trigonometry
• Algebra 1 Overview
• Algebra 2 Overview
• Geometry Overview
• SAT Overview
• ACT Overview

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Ratio, Proportion and Rates of Change - Short Problems

Eating Beans

The Bean family are very particular about beans. At every meal all Beans eat some beans... At their last meal they ate 23 beans altogether. How many beans did Pa Bean eat?

24 Hour Conundrum

It is 225 minutes until midnight. What time is it on a 24-hour digital clock?

Roman Distances

Marcus' atrium was a square with each side 50 pedes long. How many times did Marcus have to walk round his atrium to complete his daily exercise of 8 stadia?

Thunder and Lightning

How far away was the lightning if the flash and the thunderclap were 6 seconds apart?

Three of a Kind

How long is it between 5:55 and the next time all three digits on a digital clock are the same?

Printer Ink

A small ink cartridge has enough ink to print 600 pages. How many pages can be printed using a large ink cartridge?

Flying Down Under

Fred flew to Melbourne, Australia. What time was it in Melbourne when Fred's flight arrived?

A Classy Ratio

There are six more girls than boys in Miss Spelling's class of 24 pupils. What is the ratio of girls to boys in the class?

Turbo Tortoise

Harriet Hare and Turbo Tortoise want to cross the finish line together on their 12 mile race.... What time should Harriet set off?

Brothers and Sisters

Can you work out how many brothers and sisters are in the family?

Dean's Mountain

Dean runs down the mountain at 12 km per hour. How long does it take him to run down the mountain?

Draining a Pool

The water is being drained from a pool. After how long will the depth of the pool be 144 cm?

Frank and Gabriel competed in a 200m race. Interpret the different units used for their times to work out who won.

Athletics Club

An athletics club has girl, boy and adult members. How many members does the club have?

Minutes in Between

How many minutes are there between 11:41 and 14:02?

Speed over a Bridge

How fast is the train travelling as it goes over the bridge?

Family Fortune

If three brothers will get £20 more if they do not share their money with their sister, how much money is there?

A recipe for flapjacks calls for a certain quantity of butter, sugar and oats. Given the amount of these ingredients I have, how many flapjacks can I make?

Don't Be Late

Mary is driving to Birmingham Airport. Using her average speed for the entire journey, find how long her journey took.

How many adults would need to join this group of people to reverse this ratio?

Sharing Sweets

Maria and Lucy spun a coin 30 times, and gave each other sweets depending on the outcome of the spin. How many times was tails spun?

A car with 5 tyres (four road tyres and a spare) travelled 30,000 km. All 5 tyres were used equally. How many kilometres' wear did each tyre receive?

A Leg to Stand On

Can you work out the number of chairs at a cafe from the number of legs?

Fruit Basket Ratio

From two ratios of apples and oranges in a fruit bowl, can you work out how many fruits there are?

How Many Swimmers?

Given the ratios of junior to senior and senior to veteran members, can you work out what the smallest possible number of members in a swimming club is?

How far from the finishing line should these runners start to make the race 'fair'?

Out of Sync

Albert Einstein could see two clocks which were out of sync. For what fraction of the day did they show the same time?

Stair Climb

Three people run up stairs at different rates. If they each start from a different point - who will win, come second and come last?

Decimal Clock

A decimal clock is started at midnight. What time would it show at 6 o'clock in the morning?

Off the Cuff

Can you work out the ratio of shirt types made by a factory, if you know the ratio of button types used?

Musical Maths

Approximately how long is five hundred and twenty five thousand six hundred minutes?

The Elephant Diet

Use the relationship between the elephant and the rabbit to find out how many carrots the rabbit eats in a day

Revolutions

Jack and Jill run at different speeds in opposite directions around the maypole. How many times do they pass in the first minute?

Washing Elephants

How long will it take Mary and Nigel to wash an elephant if they work together?

How many bees could fly 1000 miles if they had 10 gallons of honey?

Timmy, Tammy and Tommy all go to the doctors. In what order do they arrive at the surgery?

Hiking the Hill

Sarah's average speed for a journey was 2 mph, and her return average speed was 4 mph. What is her average speed for the whole journey?

The London Eye

The 80 spokes of The London Eye are made from 4 miles of cable. What is the approximate circumference of the wheel?

Caught in the Web

Can you estimate the mass of insects caught by spiders in the UK each year?

Ratio Riddle

Can you work out the ratio b:c given the ratios a:b and a:c?

Very Long Line

If the line on the right were 0.2mm thick, how long would it need to be to cover an area of one square metre?

Tom and Tim are travelling towards Glasgow, but leave at different times. If Tim overtakes Tom, how fast is he travelling?

Tyneside Average Speed

Can you work out the average speed of the van?

Platinum Puzzle

What is the approximate total volume of platinum that has ever been produced?

Pond Runners

Can you work out how much time it will be before Katherine laps James around the pond?

Dolly Dolphin

Can you find Dolly Dolphin's average speed as she swims with and against the current?

If I walk to the bike shop, but then cycle back, what is my average speed?

Crude Calculation

Louise has noticed that the price of petrol has changed. Can you work out the percentage that it has increased by?

Walking in the Mountains

Heidi and Peter pass two signs which say how far their destination is. How long will it take them to get there?

How much more antifreeze is needed to make the proportion 30%?

Inches and Barleycorns

How many barleycorns are there in one inch?

Travelling by Train

Stephen stops at Darlington on his way to Durham. At what time does he arrive at Durham?

Shepherd's Flock

Does Joseph have too many sheep in his flock...

When Andrew arrives at the end of the walkway, how far is he ahead of Bill?

Hillwalking

Andrew walks along a flat path, then up and down a hill, then back along the path. Is it possible to work out how far he has walked?

On which of the hare's laps will she first pass the tortoise?

Two trains started simultaneously, each travelling towards the other. How long did each train need to complete the journey?

Fraction of Percentages

What is $W$ as a fraction of $Z?$

Traffic Jam

Emily's journey home took 25% longer than usual. By what percentage was her average speed reduced?

Late for Work

What average speed should Ms Fanthorpe drive at to arrive at work on time?

Backwards Laps

If two friends run in opposite directions around a track, and they pass each other every 24 seconds, how long do they take to complete a lap?

Chris cycled faster than expected. Can you work out his average speed?

What is the ratio of the lengths of the candles?

Petrol Stop

From the information given, can you work out how long Roberto drove for after putting petrol in his car?

Marathon Mission

Minnie trained more for the London Marathon this year, so her speed increased. By what percentage did her time decrease?

Walk up the Escalator

Can you work out how long Aimee would take to get up the escalator if she walked?

100m Sprint

Anna, Bridget and Carol run a race. Can you work out where Carol was when Anna finished?

Flower Show

How long will it take six gardeners to dig six circular flower beds?

Boys and Girls

Can you find the total number of students in the school, given some information about ratios?

Televisual Technology

If a new and an old television have screens of the same area, what is the ratio of their widths?

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation

Table of Contents

Last modified on April 25th, 2024

#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline

Ratios and rates.

Ratio and rates are frequently used together in everyday life to compare two quantities. While calculating the amount to be paid to shopkeepers to the changes, we will get back; all involve calculating rates of quantities in the form of a ratio.

They also calculate a population’s birth, mortality, or death rate. The incidence of COVID-19 over a region, district, or state and its death rate in a country are all calculated based on ratios and rates.

A ratio compares two quantities having the same units. It is written using a colon ‘:’, for example, 2:3, and is also written in fraction form as ${\dfrac{2}{3}}$.

For example, the expression between 20kg of sugar and 14 kg of wheat represents a ratio.

A rate is a unique ratio that compares 2 quantities with different units.

For example, if a man covers 3 km in 30 minutes, it is written as 3 km/30 minutes.

A unit rate is a rate with a denominator of 1.

Let us use the concept of ratios and rates to solve some problems.

Solved Examples

A frog limps 180 times in 10 seconds. Write the rate as a fraction in the lowest terms.

${\dfrac{180 \ times}{10 \ seconds}}$ = ${\dfrac{180}{10}=\dfrac{18}{1}}$ So, the rate is 18 limps per second.

A swimmer swims 30 laps in 60 minutes. Find the time it takes the swimmer to cover one lap.

${\dfrac{60 \ laps}{30 \ minutes}}$ = ${\dfrac{60}{30}=\dfrac{2}{1}}$ = 2 minutes Thus, the time taken by the swimmer to cover one lap is 2 minutes

If a truck travels 24 miles in 2 hours, calculate the average speed of the truck.

= ${\dfrac{24 \ miles}{2 \ hours}}$ = ${\dfrac{24}{2}=\dfrac{12}{1}}$ = 12 miles/hour Thus, the average speed of the truck is 12 miles/hour.

Ratio and rates are frequently used together in our everyday life for comparing two quantities. Calculating the amount to be paid to a shopkeeper and the amount of return we will get back involves finding rates of quantities in the form of ratios.

They are also used to calculate a population’s birth, mortality, or death rate.

A ratio is a comparison of two quantities having the same units. It is written using a colon ‘:’, for example, 2:3, and is also written in fraction form as ${\dfrac{2}{3}}$.

For example, the expression between 20kg of sugar and 14 kg of wheat is an example of a ratio.

A rate is a special kind of ratio that compares between 2 quantities having different units.

For example, if a man covers 3 km in 30 minutes, it is written as 3 km/30 minutes as an example of the rate.

If a car travels 24 miles in 2 hours, calculate the average speed of the car.

= ${\dfrac{24 \ miles}{2 \ hours}}$ = ${\dfrac{24}{2}=\dfrac{12}{1}}$ = 12 miles/hour Thus, the average speed of the car is 12 miles/hour

One thought on “ Ratios and Rates ”

This helped me alot

Leave a comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Privacy Policy
• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

How to Solve Rate Problems - Grade 7 Math Questions With Detailed Solutions

How to solve questions on rates in math? Grade 7 math questions are presented along with detailed Solutions and explanations included.

What are rates in math and where are they needed? The rate is a ratio of two quantities having different units. Where are they needed? Example 1: Car A travels 150 kilometers in 3 hours. Car B travels 220 kilometers in 4 hours. We assume that both car travels at constant speeds. Which of the two cars travels faster? Solution Car A travels 150 kilometers in 3 hours. In one hour it travels \( \dfrac{150 \,\, \text{kilometers}}{3 \,\, \text{hours}} = \dfrac{50 \,\, \text{km}}{1 \,\, \text{hour}} \) = 50 km / hour Car B travels 220 kilometers in 4 hours. In one hour it travels \( \dfrac{220 \,\, \text{kilometers}}{4 \,\, \text{hours}} = \dfrac{55 \,\, \text{km}}{1 \,\, \text{hour}} \) = 55 km / hour The quantities 50 km / hour and 55 km / hour are called unit rates because the denominator is one unit of time: 1 hour. In this case the unit rates can be used to find out which car travels faster because we now know how many kilometers are traveled by each car in one hour and we can therefore compare the speed (or rates) and say that car B travels faster.

Example 2: A car travels 150 kilometers in 3 hours. We assume that the car travels at a constant speed. How many hours are needed for this car to travel 250 kilometers at the same speed? Let t be the number of hours needed to travel 250 kilometers. Since the car travels at a constant rate (speed), we can write that the unit rate is the same whatever values for distance and time we use. Hence we write \( \dfrac{150 \,\, \text{km}}{3\,\,\text{hour}} = \dfrac{250 \,\, \text{km}}{\text{t}} \) , t in hours The above equation in t has the form. \( \dfrac{a}{b} = \dfrac{c}{d} \) Multiply both terms of the above by the product of the denominators \(b \times d\). \( b \times d \times \dfrac{a}{b} = b \times d \times \dfrac{c}{d} \) Simplify \( \cancel{b}\times d \times\dfrac{a}{\cancel{b}} = b \times \cancel{d} \times \dfrac{c}{\cancel{d}} \) to obtain \( a \times d = b \times c \) Hence the equations \( \dfrac{a}{b} = \dfrac{c}{d} \) and \( a \times d = b \times c \) are equivalent and have the same solution. This method of changing an equation from fractions on each side to products on each side is called "cross muliply" method which we will use to solve our problems. We now go back to our equation \( \dfrac{150 \,\, \text{km}}{3\,\,\text{hour}} = \dfrac{250 \,\, \text{km}}{\text{t}} \) and use the "cross multiply" method to write it as follows. \( 150 \,\, \text{km} \times t = 250 \text{km}\times 3 \text{hours} \) Since we need to find t, we then isolate it by dividing both sides of the above equation by \( 150 \,\, \text{km} \). \( \dfrac{150 \,\, \text{km} \times t}{150 \,\, \text{km}} = \dfrac{250 \text{km}\times 3 \text{hours}}{150 \,\, \text{km}} \) Simplify. \( \dfrac{\cancel{150 \,\, \text{km}} \times t}{\cancel{150 \,\, \text{km}}} = \dfrac{250 \cancel{\text{km}}\times 3 \text{hours}}{150 \,\, \cancel{\text{km}}} \) \( t = \dfrac{250 \times 3}{150} \, \, \text{hours} = 5 \,\, \text{hours}\)

The exercises below with solutions and explanations are all about solving rate problems.

Solve the following rate problems.

• The distance between two cities on the map is 15 centimeters. The scales on the map is 5 centimeters to 15 kilometers. What is the real distance, in kilometers, between the two cities?
• A car consumes 10 gallons of fuel to travel a distance of 220 miles. Assuming a constant rate of consumption, how many gallons are needed to travel 330 miles?
• Ten tickets to a cinema theater costs $66. Wha is the cost of 22 tickets to the same cinema theater?
• Cans of soda are packaged in boxes containing the same number of cans. There are 36 cans in 4 boxes. a) How many cans are there in 7 boxes? b) How many boxes are needed to package 99 cans of soda?
• Joe bought 4 kilograms of apples at the cost of $15. How much would he pay for 11 kilograms of the same apples in the same shop?
• It takes a pump 10 minutes to move 55 gallons of water up a hill. Using the same pump under the same condition; a) how much water is moved in 22 minutes? b) how long does it take to move 165 gallons of water?
• A container with 324 liters of water, leaks 3 liters every 5 hours. How long does it take for the container to become empty?
• Twenty one cans of tomato paste of the same size have a weight of 7300 grams. What is the weight of 5 cans?
• An empty container is being filled with water at the rate of 5 liters every 45 seconds and leaks water at the rate of one liter every 180 seconds. What is the quantity of water in the container after one hour?

Middle School Maths (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers High School Maths (Grades 10, 11 and 12) - Free Questions and Problems With Answers Primary Maths (Grades 4 and 5) with Free Questions and Problems With Answers Home Page

Ratio Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

Word Problems Involving Rates and Ratios

The ratio is to compare two numbers. Rate is one type of ratio and is used to measure the variety of one thing or quantity in comparison to other. Word problems involving comparing rates deal with distances, time, rates, wind or water current, money, and age.

A step-by-step guide to solving rates and ratios word problems

To solve the word problems involving rates and ratios, follow these steps: Step 1: Find the known ratio and the unknown ratio. Step 2: Write the proportion. Step 3: Use cross-multiply and solve. Step 4: Plug the result into the unknown ratio to check the answers.

Word Problems Involving Rates and Ratios – Examples 1

If 11 apple pies cost $88, what will 8 apple pies cost? Solution: Write as a rate. \(\frac{88÷11}{11÷11}=\frac{8}{1}\) Write a proportion to know the cost of 8 apple pies. \(\frac{8}{1}=\frac{x}{6}→8×6=1×x→x=48\)

Word Problems Involving Rates and Ratios – Examples 2

If 6 cookbooks cost $120, how much would a dozen cookbooks cost? Solution: Write as a rate. \(\frac{120÷6}{6÷6}=\frac{20}{1}\) Write a proportion to know the cost of 12 cookbooks. \(\frac{20}{1}=\frac{x}{12}→20×12=1×x→x=240\)

by: Effortless Math Team about 1 year ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• 3rd Grade LEAP Math Worksheets: FREE & Printable
• Let’s Do the Math on Tesla’s Electric Cars
• How is the ASTB Test Scored?
• How to Use Basic Techniques for Solving Trigonometric Equations
• Full-Length 7th Grade Common Core Math Practice Test
• How to Balance the Scales: Inequalities in Decimal Addition and Subtraction
• Algebra Puzzle – Challenge 32
• 4th Grade PSSA Math Worksheets: FREE & Printable
• Geometry Puzzle – Challenge 76
• Number Properties Puzzle -Critical Thinking 1

What people say about "Word Problems Involving Rates and Ratios - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems

Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Use the generator to make customized ratio worksheets. Experiment with the options to see what their effect is.

Primary Grade Challenge Math by Edward Zaccaro

A good book on problem solving with very varied word problems and strategies on how to solve problems. Includes chapters on: Sequences, Problem-solving, Money, Percents, Algebraic Thinking, Negative Numbers, Logic, Ratios, Probability, Measurements, Fractions, Division. Each chapter’s questions are broken down into four levels: easy, somewhat challenging, challenging, and very challenging.

Can Economic Growth Help Solve Our Debt Problem?

The U.S. is among the most indebted countries in the world—and the problem is only getting worse.

The federal government’s debt is currently $33 trillion and annual deficits just reached the highest in U.S. history outside of the pandemic years (at nearly $2 trillion ). Not only are we spending more than we’re taking in, but the long-run growth in our spending is outpacing the growth in our revenue.

If the lessons from other countries dealing with similar problems are any indication, fixing this problem is going to require a combination of spending cuts and tax hikes. But there’s a third factor that could help alleviate some of the pain involved: economic growth .

Economic Growth, Deficits, and Debt

The faster the economy grows, the less pressure there is to raise taxes and cut spending.

With more businesses and workers, the tax base The tax base is the total amount of income, property, assets, consumption, transactions, or other economic activity subject to taxation by a tax authority. A narrow tax base is non-neutral and inefficient. A broad tax base reduces tax administration costs and allows more revenue to be raised at lower rates. expands, meaning the government can collect more tax revenue without raising rates.

To illustrate, suppose we have an economy with a GDP of $1 trillion and an average tax rate The average tax rate is the total tax paid divided by taxable income . While marginal tax rates show the amount of tax paid on the next dollar earned, average tax rates show the overall share of income paid in taxes. of 20 percent. Total tax revenue would be $200 billion. Let’s say the economy grows by 5 percent, bringing the new GDP to $1.05 trillion. With the tax rate unchanged at 20 percent, the new tax revenue would be $210 billion—a $10 billion increase without touching the tax rate.

A growing economy brings in more tax revenue, which reduces the relative debt burden. This gives lawmakers some breathing room to address fiscal imbalances (think gradual tweaks, not drastic measures).

What Is the Debt-to-GDP Ratio and Why Does It Matter?

The debt-to-GDP ratio is a measure of how much debt the federal government holds compared to how much it produces (i.e., the size of its economy) in a year. For example, say you borrowed $10,000 to start a business and you sold $50,000 worth of products. Your personal “debt-to-GDP” ratio would be 20 percent.

But what would happen if your debt-to-GDP ratio was 115 percent (like the U.S. in 2021)? You’d owe more than you produced in a year.

This ratio gives valuable insight into the sustainability of a country’s economy. If it gets too high, a country might struggle to pay back its debts, leading to a host of undesirable consequences. For example, interest costs to service the debt would become a bigger part of the budget, taking resources away from other priorities. And sometimes governments are tempted to print money to deal with the problem, which causes inflation Inflation is when the general price of goods and services increases across the economy, reducing the purchasing power of a currency and the value of certain assets. The same paycheck covers less goods, services, and bills. It is sometimes referred to as a “ hidden tax ,” as it leaves taxpayers less well-off due to higher costs and “bracket creep,” while increasing the government’s spending power. . While there’s disagreement about how high is too high, a debt-to-GDP ratio of 100 percent is a common milestone economists look out for.

How Taxes Affect Economic Growth

One way policymakers can promote economic growth is through tax policies that encourage people to work, save , and invest .

For example, allowing businesses to write off investments in the year they occur rather than over time (which decreases their value) makes investments more profitable. This, in turn, encourages more investments, which boosts productivity and can lead to more jobs and higher wages.

To be sure, some of these tax policies would decrease revenue, but the growing economy could help partially offset the reduction.

The Way Forward

With much of the 2017 tax reform law expiring in less than two years, Congress will get the chance to rewrite the tax code. And while a sustainable approach will require addressing the underlying drivers of the debt—i.e., mandatory spending programs like Social Security and Medicare—lawmakers should prioritize policies that lower the country’s debt-to-GDP ratio the most.

The bottom line: improving the country’s fiscal situation won’t be comfortable, but economic growth can help cushion the blow.

Level-up your tax knowledge with free educational resources—primers, glossary terms, videos, and more—delivered monthly.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 6th grade   >   Unit 3

• Intro to rates
• Solving unit rate problem
• Solving unit price problem

Rate problems

• Comparing rates example
• Comparing rates
• Rate review

• Your answer should be
• an integer, like 6 ‍  
• an exact decimal, like 0.75 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  

We've detected unusual activity from your computer network

To continue, please click the box below to let us know you're not a robot.

Why did this happen?

Please make sure your browser supports JavaScript and cookies and that you are not blocking them from loading. For more information you can review our Terms of Service and Cookie Policy .

For inquiries related to this message please contact our support team and provide the reference ID below.