prime number problem solving year 5

Prime numbers: Reasoning and Problem Solving

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Factors, Multiple and Primes - Short Problems

Prime Order

Weekly Problem 24 - 2006 How many of the rearrangements of the digits 1, 3 and 5 give prime numbers?

Almost a Million

Weekly Problem 26 - 2014 Which of the given numbers is divisible by 6?

Divisible Digits

Can you find the missing digits, given that the number is divisible by 3, 4, 5 and 6?

Little Goldbach

How many of the numbers 1 to 20 are not the sum of two primes?

What's on the Back?

Four cards have a number on one side and a phrase on the back. On each card, the number does not have the property described on the back. What do the four cards have on them?

Multiplication Table Puzzle

In the multiplication table on the right, only some of the numbers have been given. What is the value of A+B+C+D+E?

Producing Zeros

Weekly Problem 10 - 2008 If the numbers 1 to 10 are all multiplied together, how many zeros are at the end of the answer?

Factor Trio

Which of the numbers shown is the product of exactly 3 distinct prime factors?

Reversible Primes

How many two-digit primes are there between 10 and 99 which are also prime when reversed?

Multiple Years

Weekly Problem 18 - 2016 The year 2010 is one in which the sum of the digits is a factor of the year itself. What is the next year that has the same property?

Product 100

The product of four different positive integers is 100. What is the sum of these four integers?

The numbers 72, 8, 24, 10, 5, 45, 36, 15 are grouped in pairs so that each pair has the same product. Which number is paired with 10?

Tricky Customer

Charlie doesn't want his new house number to be divisible by 3 or 5. How many choices of house does he have?

Calculation 2000

Weekly Problem 49 - 2013 What is the value of 2000 + 1999 × 2000?

Stamp Collecting

Last week, Tom and Sophie bought some stamps and they spent exactly £10. Can you work out how many stamps they bought?

Halloween Day

One year there were exactly four Tuesdays and four Fridays in October. On what day of the week was Halloween.

Red Card Blue Card

Can you arrange the red and blue cards so that the rules are all followed?

A whole number less than 100 gives remainders of 2, 3 and 4 when divided by 3, 4 and 5. What is the remainder when it is divided by 7?

Grandma's Cake

What is the smallest number of pieces grandma should cut her cake into to guarantee each grandchild gets the same amount of cake and none is left over?

Cakes and Buns

Helen buys some cakes and some buns for her party. Can you work out how many of each she buys?

Find from Factors

Weekly Problem 35 - 2006 A number has exactly eight factors, two of which are 21 and 35. What is the number?

Jenny's Logic

Weekly Problem 52 - 2009 How did Jenny figure out that Tom's cards added to an even number?

Back of the Queue

Weekly Problem 48 - 2013 What is the remainder when the number 743589×301647 is divided by 5?

Digital Division

How many three digit numbers formed with three different digits from 0, 1, 2, 3 and 5 are divisible by 6?

Smallest Abundant Number

Weekly Problem 34 - 2017 An abundant number is a positive integer N such that the sum of the factors of N is larger than 2N. What is the smallest abundant number?

The five digit number A679B, in base ten, is divisible by 72. What are the values of A and B?

Adjacent Factors

Two numbers can be placed adjacent if one of them divides the other. Using only $1,...,10$, can you write the longest such list?

Ones, Twos and Threes

Each digit of a positive integer is 1, 2 or 3, and each of these occurs at least twice. What is the smallest such integer that is not divisible by 2 or 3?

Trailing Zeros

How many zeros does 50! have at the end?

Four or Five

The diagram shows a large rectangle composed of 9 smaller rectangles. If each of these rectangles has integer sides, what could the area of the large rectangle be?

Big Blackboard

Can you work out which numbers between 1 and 2016 have exactly two of 2, 3, 4 as factors?

17s and 23s

Can you form this 2010-digit number...

Common Remainder

144 divided by n leaves a remainder of 11. 220 divided by n also leaves a remainder of 11. What is n?

Cinema Costs

Weekly Problem 41 - 2009 At a cinema a child's ticket costs £4.20 and an adult's ticket costs £7.70. How much did is cost this group of adults and children to see a film?

Seven from Nine

In how many ways can seven of the numbers 1-9 be chosen such that they add up to a multiple of 3?

Colossal Sum

What is the units digit in this sum of powers of 9?

HCF Expression

Find out which two distinct primes less than $7$ will give the largest highest common factor of these two expressions.

Powerful Finale

Weekly Problem 24 - 2017 What is the last digit of $3^{2011}$?

Given any positive integer n, Paul adds together the factors of n, apart from n itself. Which of the numbers 1, 3, 5, 7 and 9 can never be Paul's answer?

Leap Monday

Can you find the next time that the 29th of February will fall on a Monday?

Missing Digit

What digit must replace the star to make the number a multiple of 11?

Threes and Fours

What is the smallest integer where every digit is a 3 or a 4 and it is divisible by both 3 and 4?

Essential Supplies

Chocolate bars come in boxes of 5 or boxes of 12. How many boxes do you need to have exactly 2005 chocolate bars?

Peter's Primes

Peter wrote a list of all the numbers that can be formed by changing one digit of the number 200. How many of Peter's numbers are prime?

Indivisible

Each time a class lines up in different sized groups, a different number of people are left over. How large can the class be?

Flora the Florist

Flora has roses in three colours. What is the greatest number of identical bunches she can make, using all the flowers?

A male punky fish has 9 stripes and a female punky fish has 8 stripes. I count 86 stripes on the fish in my tank. What is the ratio of male fish to female fish?

End of a Prime

I made a list of every number that is the units digit of at least one prime number. How many digits appear in the list?

Sticky Fingers

Ruth wants to puts stickers on the cuboid she has made from little cubes. Will she have any stickers left over?

Eight Factors Only

We are given two factors of a number with eight factors. Can you work out the other factors of the number?

One of these numbers is the largest of nine consecutive positive integers whose sum is a perfect square. Which one is it?

Last-but-one

What is the last-but-one digit of 99! ?

Powerful Zeros

How many zeros are there at the end of $3^4 \times 4^5 \times 5^6$?

Weekly Problem 47 - 2017 How many numbers do I need in a list to have two squares, two primes and two cubes?

Divisible Palindrome

What is the sum of the digits of the largest 4-digit palindromic number which is divisible by 15?

Triangular Algebra

Weekly Problem 26 - 2017 The angles in the triangle are shown in the diagram in terms of x and y. If x and y are positive integers, what is the value of x+y?

Relative Time

Albert Einstein is experimenting with two unusual clocks. At what time do they next agree?

Times and Square

Roger multiplies two consecutive integers and squares the result. Can you find the last two digits of his new number?

Coin Collection

When coins are put into piles of six 3 remain and in piles of eight 7 remain. How many remain when they are put into piles of 24?

Added Power

How many integers $n$ are there for which $n$ and $n^3+3$ are both prime?

Rational Integer

Weekly Problem 39 - 2012 For how many values of $n$ are both $n$ and $\frac{n+3}{n−1}$ integers?

Factorised Factorial

Weekly Problem 17 - 2010 The value of the factorial $n!$ is written in a different way. Can you work what $n$ must be?

Super Computer

What is the units digit of the given expression?

Square Product

Weekly Problem 10 - 2011 Will this product give a perfect square?

Integer Indices

From this sum of powers, can you find the sum of the indices?

Primes and Six

Weekly Problem 1 - 2015 If $p$ and $q$ are prime numbers greater than $3$ and $q=p+2$, prove that $pq+1$ is divisible by $36$.

Adding a Square to a Cube

If you take a number and add its square to its cube, how often will you get a perfect square?

Cancelling Fractions

Can you find a fraction with the following properties?

Factor List

Tina has chosen a number and has noticed something about its factors. What number could she have chosen? Are there multiple possibilities?

Three Primes

Weekly Problem 6 - 2010 Can you find three primes such that their product is exactly five times their sum? Do you think you have found all possibilities?

Fortunate Inflation

The price of an item in pounds and pence is increased by 4%. The new price is an integer number of pounds. Can you find it?

Weekly Problem 26 - 2008 If $n$ is a positive integer, how many different values for the remainder are obtained when $n^2$ is divided by $n+4$?

Using the hcf and lcf of the numerators, can you deduce which of these fractions are square numbers?

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Year 5 Maths Worksheets UK Hub Page

Welcome to our Year 5 Maths Worksheets area.

Here you will find a wide range of free printable Maths Worksheets for pupils in Year 5, and Math activities for your child to enjoy.

Take a look at our decimal place value sheets, our mental math sheets, or maybe some of our equivalent fraction worksheets. Perhaps you would prefer our statistics worksheets, or how to measure angles?

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

• This page contains links to other Math webpages where you will find a range of activities and resources.
• If you can't find what you are looking for, try searching the site using the Google search box at the top of each page.

Year 5 Maths Learning

Here are some of the key learning objectives for the end of Year 5:

• know and use Place value up to 1 million
• Compare and order numbers up to 1 million
• Counting on and back in steps of powers of 10 from any number up to 1 million
• Round numbers to the nearest 10, 100, 1000, 10000 or 100000.
• Count forwards and backwards through zero with positive and negative numbers.
• Read Roman numerals to 1000
• add and subtract with more than 4 digits in columns
• add or subtract larger numbers mentally
• solve multi-step problems using addition and subtraction
• Multiply and divide whole numbers and decimals up to 2dp by 10, 100 or 1000
• identify multiples and factors including common factors
• multiply up to 4-digit numbers by a 1-digit number
• multiply up to 3-digits numbers by 2-digits
• divide numbers up to 4-digits by a 1-digit number
• recognise and use squared and cubed numbers
• solve problems using multiplication and division
• know what a prime number is and recall prime numbers up to 20
• compare and order fractions whose denominators are multiples of the same number
• identify, name and write equivalent fractions
• convert between mixed numbers and improper fractions
• add and subtract fractions with the same denominator or whose denominators are multiples of the same number
• multiply proper fractions and mixed numbers by whole numbers
• read and write decimal numbers as fractions.
• Multiply and divide whole numbers and decimals by 10, 100 or 1000
• read, write, order and compare numbers up to 2dp
• round decimals with up to 2dp to the nearest whole
• solve problems with numbers up to 2dp
• understand and use the percent symbol
• convert percentages to fractions with a denominator of 100
• know fraction-percentage equivalence for halves, quarters, fifths and tenths
• solve problems using simple percentages
• measure, compare and calculate using different measures
• find the area and perimeter of a range of rectilinear shapes
• convert between different units of time
• convert between different units of metric measure
• convert between simple imperial and metric units
• solve more complex money and measure problems
• draw and measure angles in degrees
• know the sum of angles at a point (360°rees;) and angles at a point along a line (180°rees;)
• identify 3D shapes from 2D representations
• Identify, describe and represent the position of a shape following a reflection or translation
• find the area and perimeter of composite rectilinear shapes
• know properties of regular and irregular shapes

Please note:

Our site is mainly based around the US Elementary school math standards.

Though the links on this page are all designed primarily for students in the US, but they are also at the correct level and standard for UK students.

The main issue is that some of the spelling is different and this site uses US spelling.

Year 5 is generally equivalent to 4th Grade in the US.

On this page you will find link to our range of math worksheets for Year 5.

Quicklinks to Year 5 ...

• Place Value Zone
• Mental Math Zone

Word Problems Zone

• Fractions & Percentages Zone
• Measurement Zone

Geometry Zone

Data analysis zone.

• Fun Zone: games and puzzles

Coronavirus Stay At Home Support

For those parents who have found themselves unexpectedly at home with the kids and need some emergency activities for them to do, we have started to develop some Maths Grab Packs for kids in the UK.

Each pack consists of at least 10 mixed math worksheets on a variety of topics to help you keep you child occupied and learning.

The idea behind them is that they can be used out-of-the-box for some quick maths activities for your child.

They are completely FREE - take a look!

• Free Maths Grabs Packs

Place Value & Number Sense Zone

Year 5 place value worksheets.

Using these Year 5 maths worksheets will help your child to:

• Understand decimals;
• Use place value notation with tenths and hundredths;
• Know how to read and write numbers to 10 million;
• Understand place value to 10 million.
• Decimal Place Value Worksheets
• Year 5 Place Value up to 6 digits
• Comparing and Ordering Whole Numbers up to 6 Digits
• Ordering Decimals Worksheets
• Roman Numerals worksheets

Year 5 Number Worksheets

Using these Year 5 Maths worksheets will help your child to:

• learn to estimate and approximate;
• order numbers, including negative numbers and decimals;
• learn how to place decimal numbers on a number line;
• understand and use multiples and factors, and know what a prime number is;
• complete the missing number to balance a math equation.
• Factors and Multiples Worksheet
• Rounding Decimals to the nearest whole
• Rounding to the nearest tenth
• Balancing Math Equations

Year 5 Counting Worksheets

Using these sheets will support you child to:

• count on and back by multiples of 10;
• fill in the missing numbers in sequences;
• count on and back into negative numbers.
• Counting on and back by tens

Year 5 Mental Maths Zone

Here you will find a range of printable Year 5 mental maths sheets for your child to enjoy.

Each quiz tests the children on a range of maths topics from number facts and mental arithmetic to geometry, fraction and measures questions.

A great way to revise topics, or use as a weekly math test or math quiz!

• Year 5 Mental Maths Worksheet

Top of Page

Year 5 Addition Worksheets

• add multiple numbers in columns up to 5 digits;
• add numbers in columns, including money amounts with up to two decimal places.
• Decimal Addition Worksheets (mental)
• Free Addition Worksheets (randomly generated)
• Addition Worksheets with Multi-Addends
• Money Addition Worksheets (£ )
• Money Worksheets (randomly generated)

Year 5 Subtraction Worksheets

• learn to subtract numbers with up to 5 digits;
• learn to subtract numbers involving money with decimals with up to two decimal places.
• Free Subtraction Worksheets (randomly generated)
• 5 Digit Subtraction Worksheets
• Money Subtraction Worksheets UK (£ )
• Subtracting Decimals Worksheets (mental)

Year 5 Multiplication Worksheets

Using these 4th grade math worksheets will help your child to:

• use their multiplication table knowledge to multiply by 10s and 100s mentally
• multiply any whole number by a single digit;
• multiply a two or three digit number by a two digit number.
• Times Table Worksheets Circles 1 to 12 tables
• Times Tables Worksheets (randomly generated)
• Multiplying Decimals by 10 and 100
• Multiply and Divide by 10 100 (decimals)
• Multiplying by Multiples of 10 and 100
• Single Digit Multiplication Graded Sheets
• Double Digit Multiplication Worksheets (Graded)
• Single Digit Multiplication Worksheets Generator
• Multi-Digit Multiplication Generator
• Multiplication Word Problems

Year 5 Division Worksheets

Using these Year 5 maths worksheets will help your child learn to:

• apply their division facts up to 10x10 to answer related questions involving 10s and 100s.
• divide any whole number by a single digit.
• Divding by Multiples of 10 and 100 Worksheets
• Year 5 (4th Grade) Long Division Worksheets

These sheets involve solving a range of division problems.

• Division Worksheets (Grade 4) Word Problems
• Division Facts Worksheets (randomly generated)

Year 5 Math Problems

• apply their addition, subtraction and problem solving skills;
• apply their knowledge of rounding and place value;
• solve a range of 'real life' problems;
• attempt more challenging longer problems.

Using the problems in this section will help your child develop their problem solving and reasoning skills.

These sheets involve solving one or two more challenging longer problems.

• 4th Grade Math Problems

These sheets involve solving many 'real-life' problems involving data.

• 4th Grade Math Word Problems

These sheets involve solving a range of multiplciation problems.

• Division Worksheets Grade 4 Word Problems

Fractions & Percentage Zone

Quicklinks to ...

• Year 5 Fractions Worksheets

Year 5 Percentage Worksheets

Year 5 fraction worksheets.

• position different fractions on a number line;
• understand equivalent fractions;
• understand what a mixed number is;
• compare two or more fractions;
• begin to convert fractions to decimals and decimals to fractions.
• Equivalent Fractions Worksheets
• Comparing Fractions Worksheet page
• Improper Fraction Worksheets
• Fractions of Numbers
• Convert Fractions to Decimal Sheets
• Convert Decimal to Fraction Sheets
• Free Printable Fraction Riddles (harder)

Take a look at our percentage worksheets for finding the percentage of a number or money amount.

We have a range of percentage sheets from quite a basic level to much harder.

• Fractions Decimals Percents Worksheets
• Percentage Word Problems

Year 5 Geometry Worksheets

Using these sheets will help you to:

• classify angles - acute, obtuse, right, reflex, straight;
• classify triangles - acute, obtuse, right;
• measure angles using a protractor;
• know that angles in a triangle add up to 180°
• know the properties of regular and irregular shapes
• plot and write coordinates in the first quadrant.
• 4th Grade Geometry Worksheets
• Symmetry Activities
• Coordinate Worksheets (1st Quadrant)

Measurement Zone, including Time & Money

Year 5 measurement worksheets.

Using these sheets will help your child understand how to:

• read scales in both the standard and metric systems;
• read a scale going up in a range of fractions: halves, quarters and eighths;
• read a scale going up in tenths, fives, tens, fifties, and hundreds.
• 4th Grade Measurement Worksheets
• Converting Customary Units Worksheets
• Metric Conversion Worksheets

Area and Perimeter Worksheets

• understand area and perimeter;
• learn how to find the area and perimeter of rectangles and rectilinear shapes.
• Area Worksheets
• Perimeter Worksheets

Year 5 Time Worksheets (4th Grade)

Using the sheets in this section will help your child to:

• tell the time to the nearest minute;
• become familiar with both digital and analogue times;
• add and subtract time intervals.
• Telling Time Worksheets Grade 4 (1 minute intervals)
• 24 Hour Clock Conversion Worksheets

On this webpage there is a selection of printable 24 hour (military time) conversion worksheets which will help you learn to convert from 24 hour clock to standard 12 hour time, and from standard time to 24 hour time.

Time Interval Worksheets

These sheets will help you learn to add and subtract hours and minutes from times as well as working out a range of time intervals.

• Add and Subtract Time Worksheets
• Elapsed Time Worksheets

Time Puzzles - harder

Here you will find our selection of harder time puzzles.

• Time Word Problems Worksheets - Riddles (harder)

Using these 4th grade math worksheets will help you to:

• draw and read bar graphs with increasingly complex numbers;
• read, interpret and draw line graphs;
• Year 5 Bar Graph Worksheets (4th grade)
• Year 5 Line Graph Worksheets

Fun Zone: Puzzles, Games and Riddles

Year 5 maths games.

• Year 5 Math Games (4th Grade)

Year 5 Maths Puzzles

The puzzles will help your child practice and apply their addition, subtraction, multiplication and division facts as well as developing their thinking and reasoning skills in a fun and engaging way.

• Year 5 Maths Puzzles (4th Grade)

Math Salamanders Year 5 Maths Games Ebook

Our Year 5 Maths Games Ebook contains all of our fun maths games, complete with instructions and resources.

This ebooklet is available in our store - use the link below to find out more!

• Year 5 Maths Games Ebook

Other UK Maths Worksheet pages

See below for our other maths worksheets hub pages designed for children in the UK.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to Math Salamanders UK Home Page

Return from Year 5 Maths Worksheets to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Prime Numbers

Here we will learn about prime numbers, including what they are, how we can determine whether a number is prime, and how to solve problems that involve prime numbers.

There are also prime number worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are prime numbers?

Prime numbers are positive integers (whole numbers) that have only two factors , themselves and 1.

This means that you cannot divide a prime number by any number apart from 1 or itself, and get an integer answer.

A number that is not prime is called a composite number .

There are 25 prime numbers between 1 and 100. These are:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29,  31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.

Notice that,

1 is not a prime number as it has only 1 factor.

2 is the only even prime number.

You should be able to recall the first 8 prime numbers (up to 20 ) and be able to determine whether a number is prime by looking at the factors of the number.

To determine whether the number is prime, check whether it has any factors other than itself and 1, either manually or by using a number trick. If the number has a factor that is not itself or 1, it is not prime.

There are a few useful number tricks that can help us determine whether a number is divisible by an integer and therefore has that integer as a factor:

Once we have considered these number tricks, we need to look for divisibility by other numbers. We don’t, however, need to consider every number.

The reason for this is that for a number to be divisible by 4 or 6 or any multiple of 2, it must also be divisible by 2, which is something we have already checked. 

For a number to be divisible by 6 or 9 or any multiple of 3, it must also be divisible by 3, which is something that we have already checked.

This pattern continues and means that we only need to check for divisibility by other prime numbers, starting with the number 7.

How to find prime numbers

In order to determine whether a number is a prime number:

Use the number tricks to see whether \bf{2, 3} or \bf{5} is a factor.

If they are not factors, test for divisibility by other prime numbers, starting with \bf{7} .

State your conclusion with a reason.

Explain how to find prime numbers

Prime numbers worksheet

Get your free prime numbers worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on   factors, multiples and primes

Prime numbers  is part of our series of lessons to support revision on  factors, multiples and primes . You may find it helpful to start with the main  factors, multiples and primes  lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Factors, multiples and primes
• Factors and multiples
• HCF and LCM
• Highest common factor
• Lowest common multiple
• Prime factors
• Factor trees

Prime numbers examples

Example 1: two digit number.

Is 53 a prime number?

The last digit is not a 2, 4, 6, 8, or 0 so it is not a multiple of 2.

Adding the digits together we have 5+3=8 and so it is not a multiple of 3.

The last digit is not a 5 or a 0 and so it is not a multiple of 5.

2 If they are not factors, test for divisibility by other prime numbers, starting with \bf{7} .

We need to continue dividing 53 by successive prime numbers until we reach the first prime number that is greater than \sqrt{53}.

\sqrt{53} \approx 7.3 so we only need to try prime numbers less than this.

Start by dividing by 7:

As 53\div{7}=7.57142857 \ 7 is not a factor of 53.

The next prime number is 11, which is greater than 7.3 so there are no more integers that we need to try.

3 State your conclusion with a reason.

53 is a prime number as it only has two factors, 1 and 53.

Example 2: three digit number

Is 223 a prime number?

Adding the digits together we have 2+2+3=7 and so it is not a multiple of 3.

As 223 is not divisible by 2, 3, or 5, we need to divide 223 by prime numbers until we reach the prime number that is greater than \sqrt{223}.

223 \approx 14.9

The prime numbers up to 14.9 (excluding 2, 3, and 5 ) are: 7, 11 and 13.

Completing these calculations, and rounding when necessary, we have:

\begin{aligned} 223\div{7}&=31.9 \text{ (1dp)}\\\\ 223\div{11}&=20.3 \text{ (1dp)}\\\\ 223\div{13}&=17.2 \text{ (1dp)} \end{aligned}

There are no other numbers that we can divide 223 by and get an integer answer except for 1 and 223.

223 is a prime number as it has only two factors, 1 and 223.

Example 3: four digit number

Is 2073 a prime number?

Adding the digits together we have 2+0+7+3=12 which is a multiple of 3.

Dividing 2073 by 3 we have:

2073\div{3}=691

As we know that 2073 is divisible by 3, we do not need to carry out any further divisions.

2073 is not a prime number because 3\times{691}=2073.

Example 4: determine the prime number from a list of numbers

One of the following numbers is prime. Identify the prime number.

The last digit of 14 is a 4 and so 14 is a multiple of 2.

The last digit of 25 is a 5 and so 25 is a multiple of 5.

9 is a multiple of 3.

The final two numbers are 61 and 259. As 61 is a smaller number, it is easiest to determine whether 61 is prime.

61 does not end in a 2, 4, 6, 8, or 0 and so 61 is not a multiple of 2.

6+1=7 and so 61 is not a multiple of 3.

61 does not end in a 5 or 0 and so it is not a multiple of 5.

We need to see whether 61 is divisible by any other prime number up to \sqrt{61} which is approximately 7.8. Therefore we only need to check to see whether 61 is divisible by 7.

61\div{7}=8.71\text{ (2dp)}

61 is not divisible by 7 and is therefore prime.

61 is the prime number as it only has 2 factors, 1 and 61.

Note: 259=7\times{37}

Problem solving with prime numbers

In order to place numbers into a diagram / table:

Determine what each box / section of the diagram represents.

Place each number one-by-one into the diagram.

Determine the frequency of values in each box / section if required.

Problem solving with prime numbers examples

Example 5: complete the diagram (two way table).

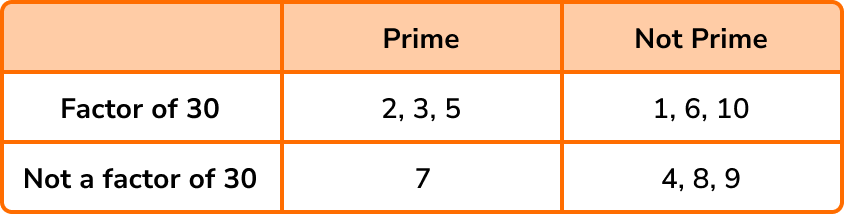
Place the set of numbers N=\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} into the two-way table below.

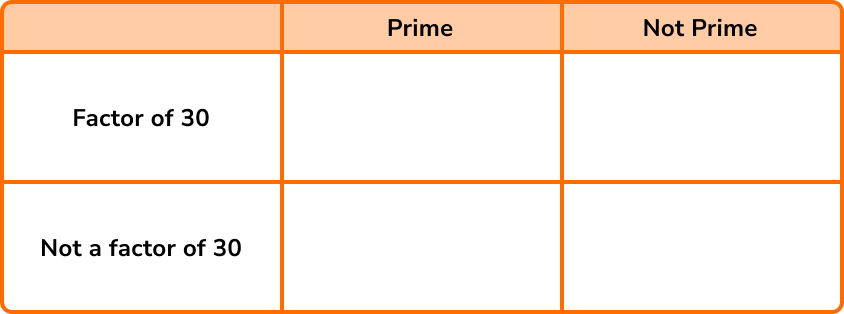
Make a mental note of what each box represents:

The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, and 30.

Given that the values we need to place in the two way table are 1-10, we do not need to include 15 and 30 in the table.

1 is not a prime number but it is a factor of 30.

2 is a prime number and it is a factor of 30.

3 is a prime number and it is a factor of 30…

and so on until we get:

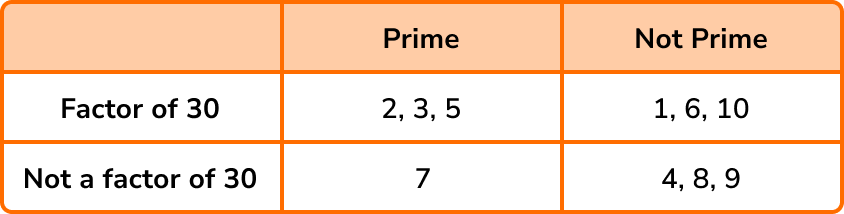
This question does not require us to show the frequency of values in each box and so the final solution is:

Example 6: complete the diagram (Venn diagram)

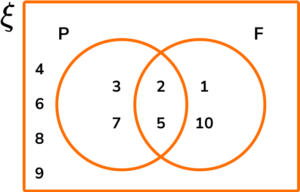
The Venn diagram below represents the two sets P=\{ Prime \} and F=\{ Factor of 24 \}.

Given that ξ=\{x is an integer such that 0 < x \leq 24 \}, complete the Venn diagram.

Use your Venn diagram to write down the frequency of values in the sets.

ii) P \cap F

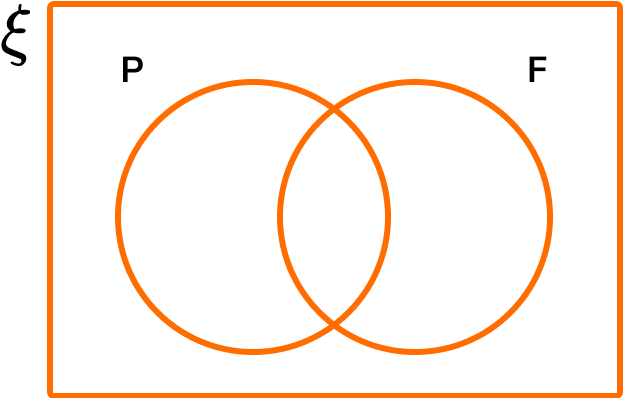
Making a mental note of what each section of the venn diagram represents, we have:

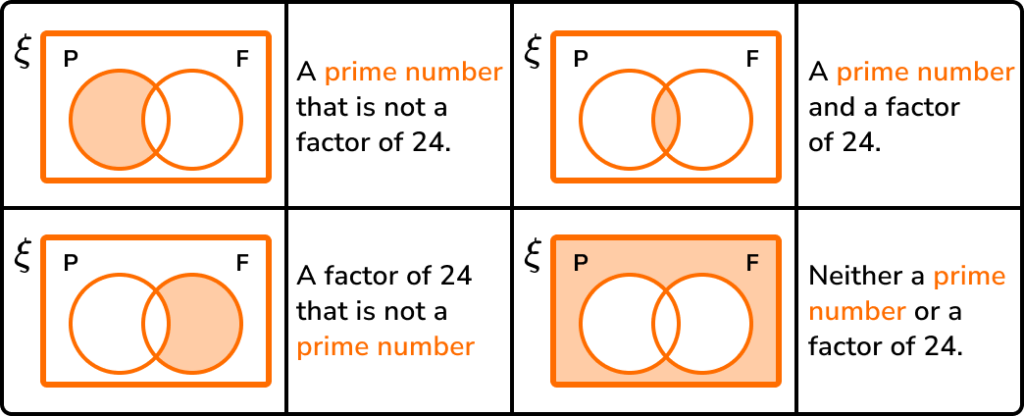
The question asks us for the frequency of values in set P, which is 9.

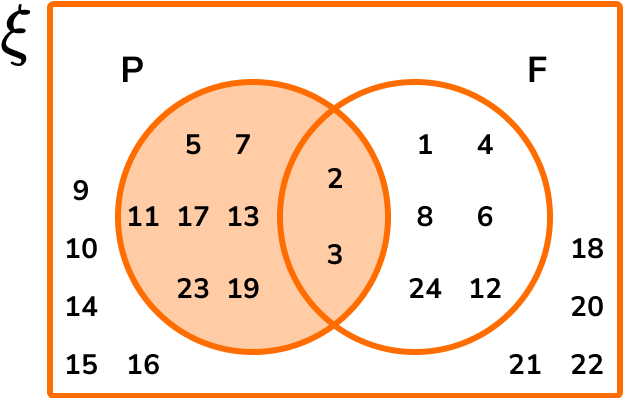
We are also asked to find the frequency of values in P \cap F which is the section ‘P and F’. There are 2 values in P \cap F.

Common misconceptions

• \bf{1} is not a prime number

1 is not a prime number. This is because it only has one factor, rather than the 2 factors needed to be a prime number.

• \bf{2} is a prime number

2 is the only even prime number. This is because it only has two factors, 1 and itself, and therefore by definition, it is a prime number. Every other even number is divisible by 2. \ 2 is therefore known as a special case when discussing prime numbers.

• Prime numbers and the odd numbers

As all but one of the prime numbers are odd (remember that 2 is the only even prime number), it is sometimes assumed that all odd numbers are prime. Take the number 9. It is an odd number, however 9 is a multiple of 3 and so we can divide 9 by 3 (and get 3 ). Not all odd numbers are prime, and not all prime numbers are odd.

• Decimals cannot be prime numbers

All prime numbers are positive integers but a common misconception is that decimals can be prime. For example, the decimal 2.3 is considered to be a prime number as 23 is a prime number.

Practice prime numbers questions

1. Determine what type of number 71 is from the list below.

Multiple of 3

Multiple of 4

Multiple of 5

Prime number

71 does not end in 0, 2, 4, 6 or 8 and so is not a multiple of 2. It cannot therefore be a multiple of 4.

7+1=4 so 71 is not a multiple of 3 .

71 does not end in 0 or 5 therefore it is not a multiple of 5.

71 \div 7=10.14 therefore it is not a multiple of 7.

This tells us that 71 is a prime number.

2. Determine what type of number 513 is from the list below.

Multiple of 2

513 is a multiple of 3 as 5+1+3=9 which is a multiple of 3.

3. Determine what type of number 143 is from the list below.

Multiple of 7

Multiple of 11

1+4+3=8 so 143 is not a multiple of 3 .

143\div 7=20.42857… so 143 is not a multiple of 7 .

143\div{11}=13 so 143 is a multiple of 11 .

4. Which number from the list is prime?

2 is the only even prime number. It has two factors, 1 and itself.

81 has factors of 1, 3, 9, 27 and 81.

343 has factors of 1, 7, 49 and 343.

3\times{10}^{2} written as an ordinary number is 300 which has many factors.

5. Let N=\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}. Which two way table correctly sorts the set N?

Factors of 12: 1, 2, 3, 4, 6, 12

Prime Numbers: 2, 3, 5, 7, 11

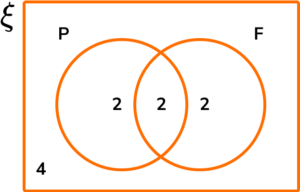
6. The Venn diagram below represents the two sets P=\{ Prime \} and F=\{ Factor of 10\}. Given that ξ= \{x is an integer such that 0 < x \leq 12 \}, work out the frequency of values that would appear in P \cap F.

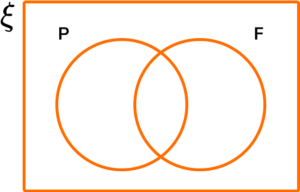
Factors of 10: 1, 2, 5, and 10.

Prime Numbers: 2, 3, 5, and 7.

Each value placed correctly in the Venn diagram gives the result:

The frequency that corresponds to each set is therefore:

Prime numbers GCSE questions

1. (a) Write the first 8 prime numbers.

(b) Peter says “every prime number is odd”. Is Peter correct? Explain your answer.

2. (a) The perimeter of a rectangle can be written as P=2(l+w) where l and w are integer side lengths.

Given that the area of the rectangle is 23cm^{2}, calculate the perimeter of the rectangle.

(b) A square has an area of A=x^{2}, where x is an integer. Is the area always, sometimes or never a prime number? Explain your answer.

l=1 and w=23 or l=23 and w=1

All square numbers have an odd number of factors, whereas all prime numbers have 2 factors.

1 is not prime and any other square number has a factor of its square root meaning it is not prime.

3.  Below is a list of numbers:

(a) Which of the values is a prime number ?

(b) Which of the values is 2 more than a prime number, and 2 less than another prime number?

(c) Which of the values gives a prime number when it is squared?

(c) \sqrt{5}

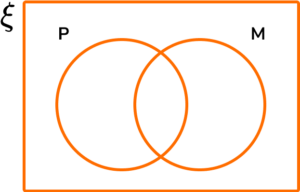
4. (a) On the Venn diagram below, P=\{ Prime numbers \} and M=\{ Multiples of 4\}.

For the set of numbers ξ=\{x such that 20 < x \leq 40 \}, complete the Venn diagram.

(b) Write down the numbers that are in the set P .

(c) How many numbers are in the set P \cap M?

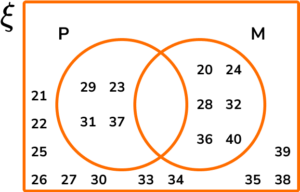
Prime Numbers: 23, 29, 31, 37.

Multiples of 4: 20, 24, 28, 32, 36, 40.

No values in the intersection (P \cap M).

(b) 23, 29, 31, 37

Learning checklist

You have now learned how to:

• Identify prime numbers
• Know and use the vocabulary of prime numbers, prime factors and composite (non-prime) numbers
• Establish whether a number up to 100 is prime and recall prime numbers up to 19

The next lessons are

• Rounding numbers
• Negative numbers

The sieve of Eratosthenes

The ancient greek mathematician Eratosthenes of Cyrene lived nearly 2300 years ago. He devised a way of determining the prime numbers using the method that we know of today called the Sieve of Eratosthenes (or Eratosthenes Sieve).

Below is a number square from 1 to 100.

Our aim is to cross out every number that is not prime.

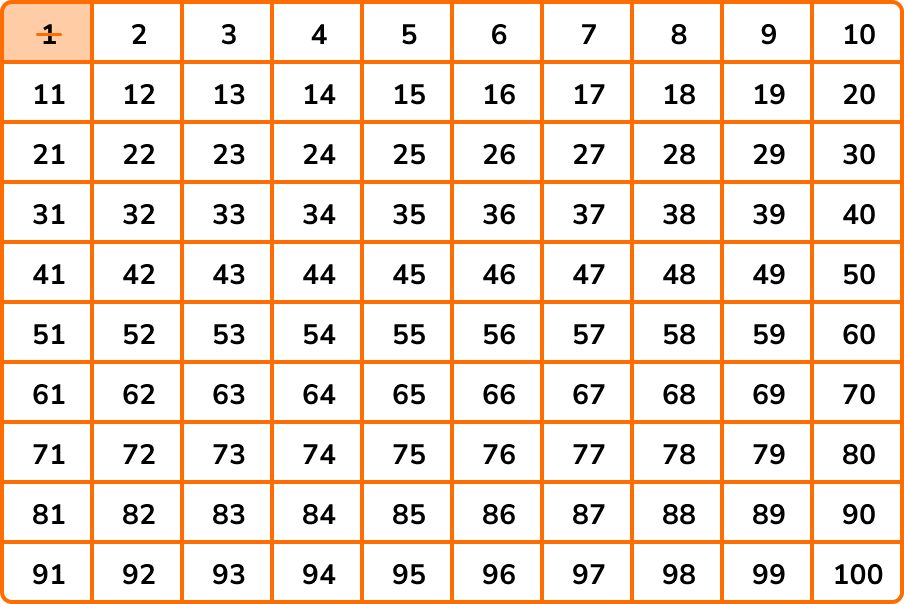
We start by crossing out the number 1 because a prime number has two factors, itself and 1, however the number 1 is itself and so by definition, 1 has only 1 factor and is therefore not prime.

Any number that is a multiple of 2 can divide by 2. The number 2 is prime because we can only divide 2 by 1 and 2 (itself).

All the other multiples of 2 have a factor of 2 and so we highlight 2, and then cross out all of the other multiples of 2 .

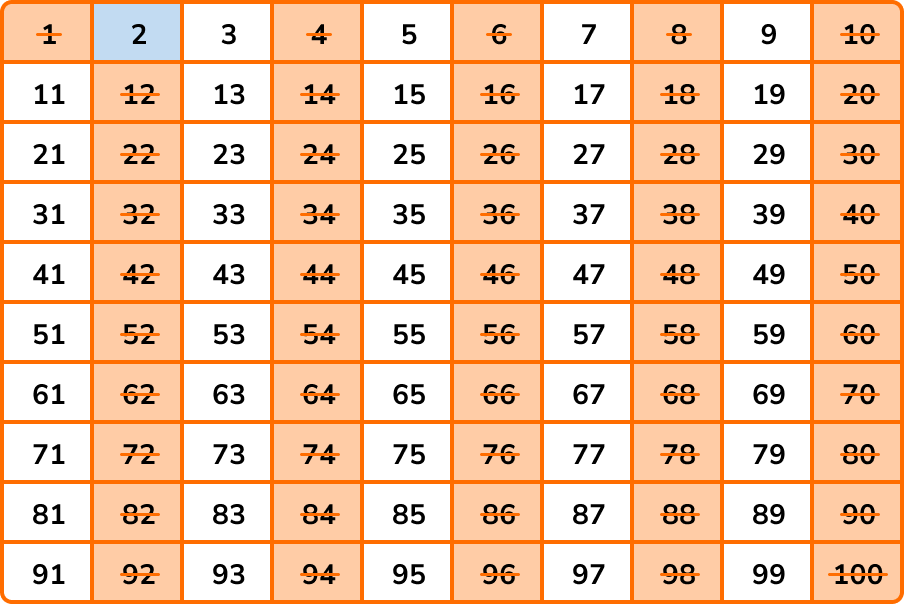
The next number that is not crossed out is 3. \ 3 is prime as we can only divide it by 1 and 3. All of the multiples of 3 have a factor of 3, and so we highlight 3, and cross out all of the other multiples of 3 .

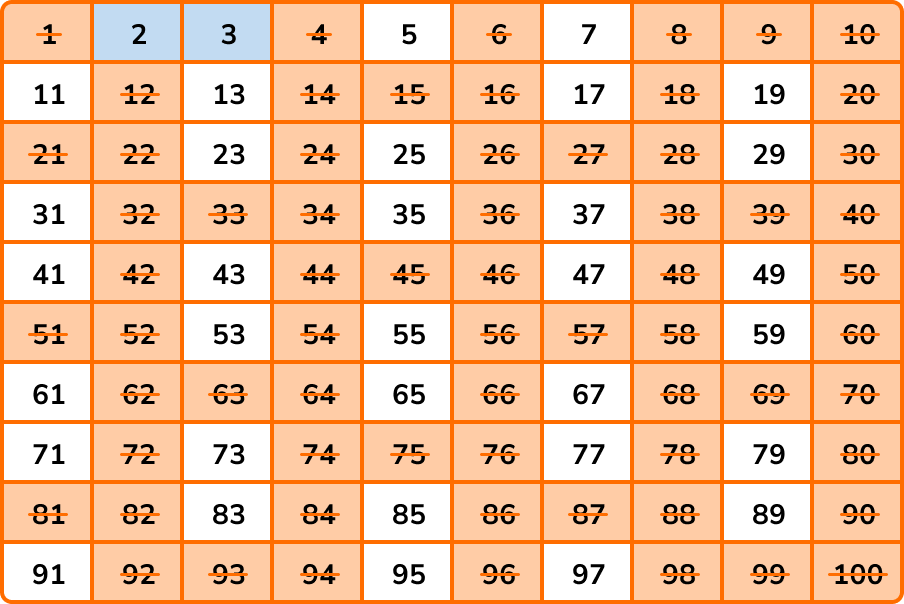
Continuing with the sieve of Eratosthenes, every multiple of 4 can be divided by 2, and so all of the multiples of 4 are already crossed out.

The next number that is not crossed out is 5. \ 5 is prime so we highlight 5 and cross out all of the other multiples of 5 .

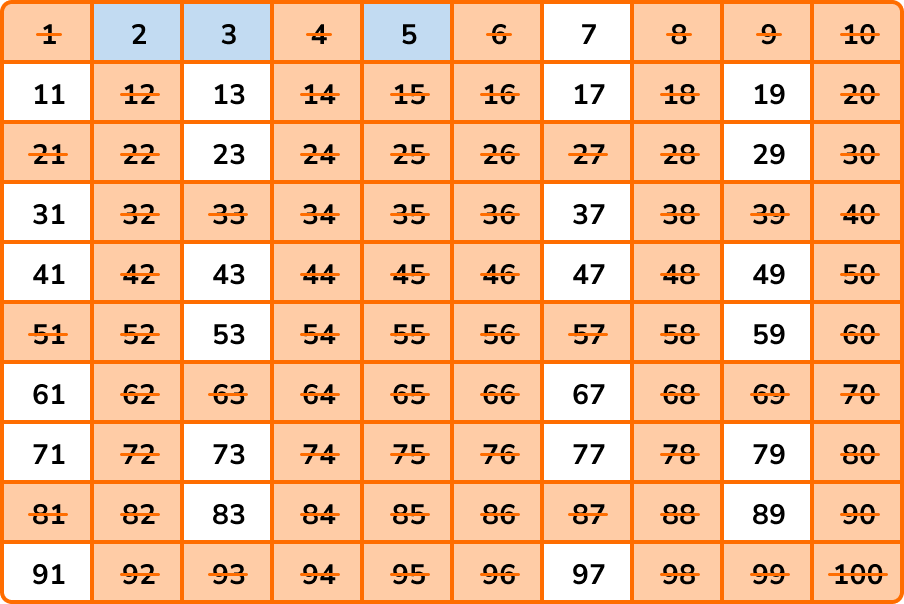
As we continue, the next number that is not crossed out will always be prime.

The next number in the list is a 7, so we highlight 7 and cross out the multiples of 7 .

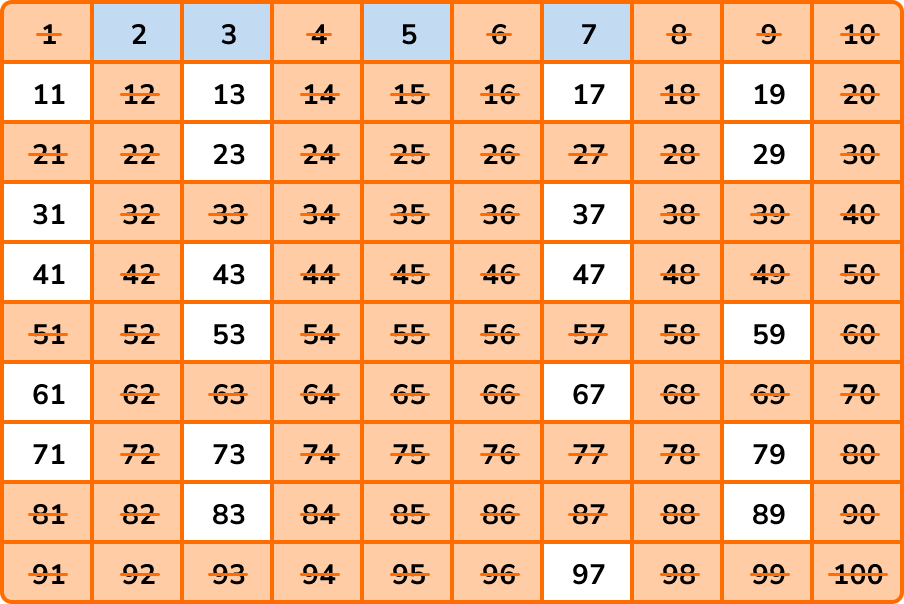
Amazingly, once you have crossed out the multiples of 7, all of the remaining numbers between 1 and 100 have no multiples that are not already crossed out between 1 and 100, and so we can highlight the rest of the numbers like this:

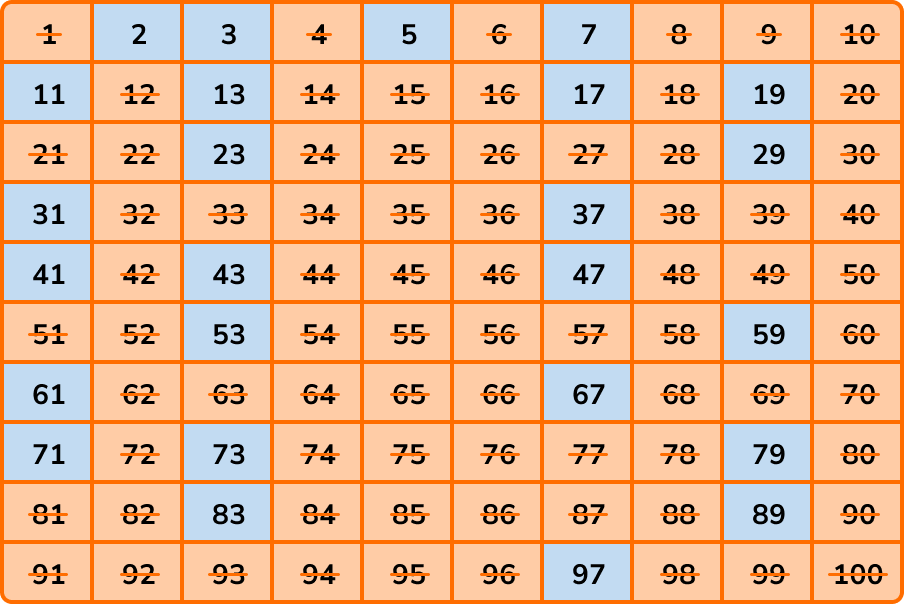
This leaves us with the list of prime numbers between 1 and 100 which are,

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.

The downside to this method is that it is very time consuming, especially if you want to determine whether certain large numbers are prime numbers.

Other facts about prime numbers

The square root of any prime number is a surd.

Step-by-step guide: Surds

The ancient Egyptians are believed to be the first civilisation to recognise prime numbers. Today, prime numbers are considered to be the building blocks of mathematics as every number is itself prime, or can be built by multiplying two or more prime numbers together.

In number theory, the fundamental theorem of arithmetic states that any given number can be represented by a unique product of prime numbers. This is useful when we calculate prime factors of a number.

Step-by-step guide: Prime factors

The greek mathematician Euclid derived the Prime Number Theorem, which states that there are infinitely many prime numbers. Computers are used today to calculate large primes. In March 2022, the largest known prime number was 2^{82,589,933}-1 which has 24,862,048 digits! This number was found in 2018 by the great internet mersenne prime search. If there are an infinite number of prime numbers, the challenge is always to find the next largest prime number.

Prime numbers are used a lot in cryptology and cryptography. Cryptology is the process used to convert plaintext into ciphertext, and vice versa, whereas cryptography is just the conversion of plaintext to ciphertext. Public key cryptography utilises very large prime numbers within message encryption; you can only decode the message if you know the prime numbers and it is very difficult to calculate them.

A primality test is an algorithm that determines whether a number is prime. We used a form of primality test when using positive divisors to determine whether a number is prime.

A mathematical conjecture is an incomplete mathematical proof. Once a conjecture is fully proven, it is a theorem.

The twin prime conjecture, also known as Polignac’s conjecture asserts that there are infinitely many twin primes (pairs of primes that differ by 2 ) such as 3 and 5, 11 and 13, and 17 and 19.

Christian Goldbach in 1742 derived Goldbach’s conjecture. Goldbach’s conjecture states that any even whole number greater than 2 is the sum of two prime numbers.

A Fermat number or Fermat prime is a type of prime number. If 2^{k}+1 is a prime number and k > 0, then k is a power of 2. In March 2022, there are only 6 known Fermat primes: 3, 5, 17, 257, and 65537.

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Prime Numbers Textbook Exercise

Click here for questions, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Prime Numbers Questions

The prime numbers questions and answers are provided here for students to understand the concept quickly. Prime Numbers is one of the most basic concepts taught in primary classes. The questions framed are based on the NCERT curriculum. Students can use these questions to take a quick review of the concepts, and become familiar with the topics by practising them. Check your answers against the detailed explanations provided for each question. To learn more about prime numbers, click here .

Go through the below prime numbers questions and answers, and practise them as well.

Prime Numbers Questions with Solutions

1. The smallest prime number is _____.

The smallest prime number is 2 . The number “2” is the only even prime number, which has only two factors, such as 1 and 2.

2. What are the first 10 prime numbers?

The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

3. Is 9 a prime number?

No, the number 9 is not a prime number.

This is because the number 9 has more than 2 factors. The factors of 9 are 1, 3 and 9. Hence, we can consider 9 as a composite number.

Also, read : Composite Numbers .

4. What is the sum of the first 10 prime numbers?

As we know, the first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

Therefore, sum = 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29.

Hence, the sum of the first ten prime numbers is 129.

5. What is the mean of the first ten prime numbers?

First 10 prime numbers = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

As we know, Mean = Sum of all values / Total number of values

Mean = 129 / 10

Mean = 12.9

Hence, the mean of the first ten prime numbers is 12.9.

6. What is the median of the first ten prime numbers?

As we know,

The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

The prime number sequence is already in ascending order.

So, we have 10 terms here.

Therefore, Median = Mean of 5th and 6th term

Here, 5th term = 11 and 6th term = 13.

Median = (11+13)/2 = 24/2 = 12

Hence, the median of the first ten prime numbers is 12.

7. What is the sum of the first seven prime numbers divided by 2?

We know that the first seven prime numbers are 2, 3, 5, 7, 11, 13, 17.

Therefore, sum = 2+3+5+7+11+13+17 = 58

When the sum is divided by 2, we get

Hence, the sum of the first seven prime numbers divided by 2 is 29.

8. If “p” is the prime number, find the number of factors p 2 has.

As we know, p 2 can be written as the product of p and P. (i.e., p×p). Hence, the factors of p 2 are 1, p and p 2 .

For example, let us take p = 2, the factors of 2 are 1, 2 and 4.

Therefore, p 2 has exactly three factors.

9. Identify the twin primes among the given pair of numbers:

(1, 3), (3, 5), (13, 19), (1, 2)

As know that the number 1 is neither prime nor composite. Hence, we can ignore the pairs (1, 3) and (1, 2).

As we know, twin prime numbers are the pair of prime numbers with a difference of 2.

Here, (3, 5) is a pair of prime numbers with a difference of 2 (i.e) 5 – 3 = 2.

Whereas (13, 19) is also a pair of prime numbers, in which the difference between them is not equal to 2.

Hence, (3, 5) is a twin prime.

Also, read : What are Twin Primes?

10. How many prime numbers are there between 1 and 50?

The list of prime numbers between 1 and 50 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47.

Hence, the number of prime numbers between 1 and 50 is 15.

Video Lesson on Prime Numbers

Practice Questions

• What is the sum of the first 20 prime numbers?
• What is the mean of the first 50 prime numbers?
• If “p” is the prime number, find the number of factors p 3 has.
• Is 15 a prime number?
• Which is the smallest odd prime number?

Stay tuned to BYJU’S – The Learning App, and learn all Maths-related topics easily by exploring more videos.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• £ 0.00 0 items

Year 5 Prime Numbers Maths Challenge

This Year 5 Prime Numbers Maths Challenge checks your child’s understanding of prime numbers while developing their problem solving ability. Children will have to apply their knowledge of prime numbers to work out where children are on a board game.

If you would like to access additional resources which link to this maths challenge, you can purchase a subscription for only £5.31 per month on our sister site, Classroom Secrets .

Teacher Specific Information

This Year 5 Prime Numbers Maths Challenge checks pupils’ understanding of prime numbers while developing their problem solving ability. Pupils will have to apply their knowledge of prime numbers to work out where children are on a board game.

National Curriculum Objectives

Calculation – multiplication and division (5C5b) Know and use the vocabulary of prime numbers, prime factors and composite (non-prime) numbers

Have you visited our sister site yet?

Primary resources for teachers

Classroom Secrets provides high-quality, affordable teaching resources that children love, and teachers trust.

Stay in touch

01422 419608

[email protected]

Interested in getting weekly updates from us? Then sign up to our newsletter here!

Information

• Cookie Policy
• Privacy Settings
• Terms and Conditions
• End User License Agreement

Copyright: Classroom Secrets 2024

Company number: 8401067

VAT number: 248824574

Designed by Classroom Secrets

Bootstrap Modal Title

Bootstrap modal body text should be here.

• International
• Schools directory
• Resources Jobs Schools directory News Search

Prime numbers - Year 5 Multiplication and Division

Subject: Mathematics

Age range: 7-11

Resource type: Lesson (complete)

Last updated

5 November 2019

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

This is a whole lesson based on the Year 5 Multiplication and Division objective of Prime numbers”. This resource includes the teacher input ( learning journey), independent worksheet and a depth activity to deepen the children’s understanding of the concept being learned.

The questions have been inspired and adapted from the White Rose Small Steps Guidance and Teaching for Mastery documents. This document is useful for teachers who have adapted Maths Mastery and need guidance in the approach or those who are looking for variation in fluency, reasoning and problem solving or simply those who don’t want to plan it themselves but want high quality resources and quality first teaching. =)

All of the documents that are uploaded as an Activinspire file are interactive and all of the concrete/pictorial manipulative can be used, moved and manipulated.

This document can be downloaded on Activinspire and it is also available as a PDF for those who do not have Activinspire.

Please note - these resources are not compatible with Smart Notebook and the PDF file is not interactive.

Thank you for taking the time to review my resources. =) I hope this helps you with your teaching and if it does please could you be kind enough to leave some positive feedback. =)

Kind regards,

@MasteryMaths01

Tes paid licence How can I reuse this?

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource: