operations with fractions problem solving

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

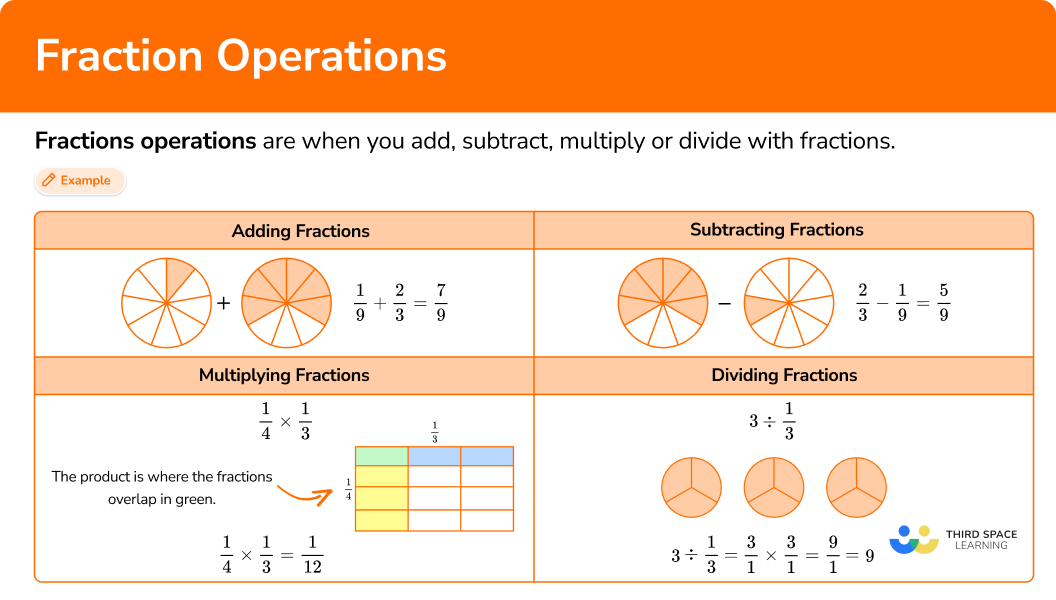
Fractions operations

Here you will learn about fractions operations, including how to add, subtract, multiply and divide with fractions.

Students will first learn about fractions operations as part of number and operations in fractions in elementary school. They will continue to build on this knowledge in the number system in 6th grade and 7th grade.

What are fractions operations?

Fractions operations are when you add, subtract, multiply or divide with fractions.

For example,

[FREE] Fraction Operations Worksheet (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!

Adding and subtracting fractions

Adding and subtracting fractions means finding the sum or the difference of two or more fractions. To do this, find a common denominator (bottom number), add the two numerators (top numbers), and keep the denominators the same.

The numerator shows the number of parts out of the whole and the denominator shows how many equal parts the whole is divided into.

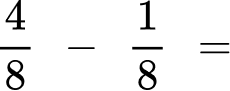
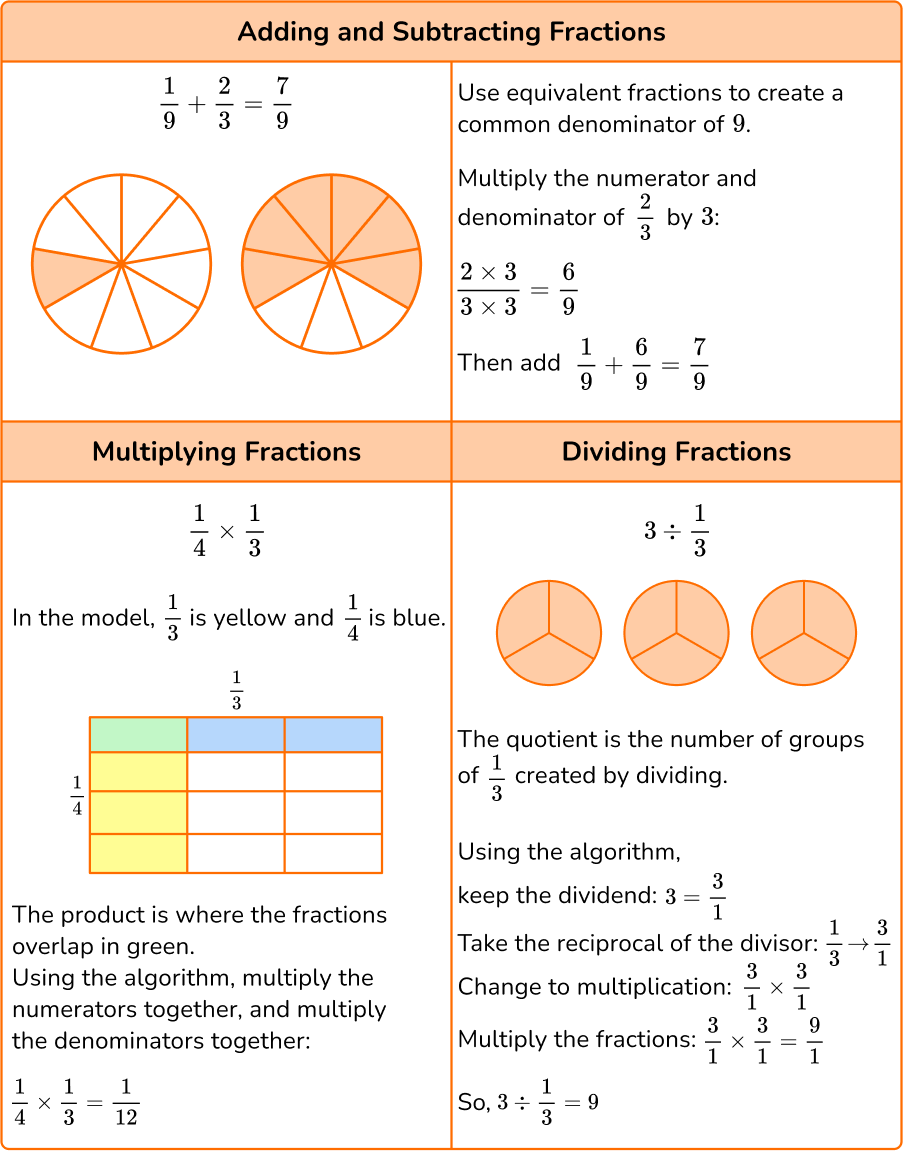
The equation is taking \, \cfrac{1}{8} \, away from \, \cfrac{4}{8} \, .

Since the denominators are the same, the parts are the same size.

You subtract to see how many parts are left: 4-1 = 3.

There are 3 parts and the size is still eighths, so the denominator stays the same.

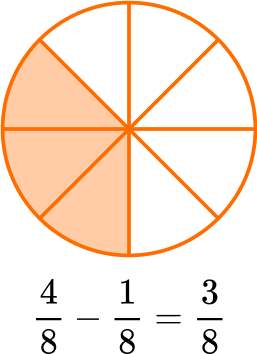
When fractions have unlike denominators, create equivalent fractions with common denominators to solve.

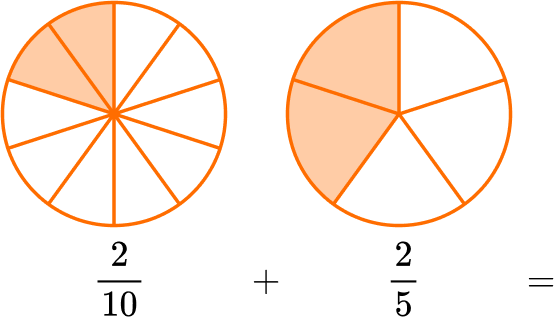
The parts are NOT the same size, since the denominators are different.

Use equivalent fractions to create a common denominator of 10.

Multiply the numerator and denominator of \, \cfrac{2}{5} \, by 2.

\cfrac{2 \, \times \, 2}{5 \, \times \, 2}=\cfrac{4}{10}

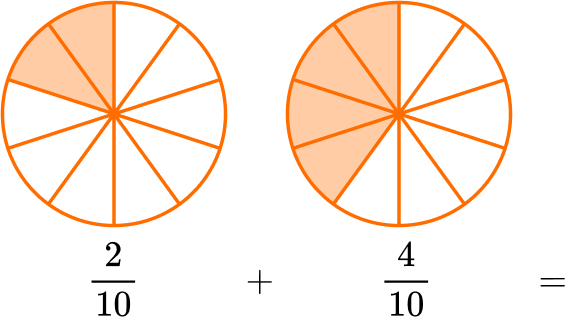
Add to find how many parts there are in all: 2 + 4 = 6.

There are 6 parts and the size is still tenths, so the denominator stays the same.

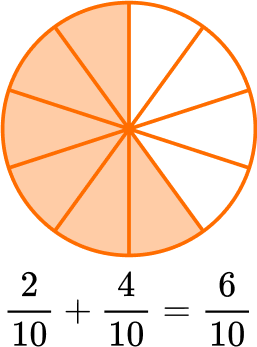
The sum could also be written as the equivalent fraction \, \cfrac{3}{5} \, .

Step-by-step guide: Adding fractions

Step-by-step guide: Subtracting fractions

Step-by-step guide: Adding and subtracting fractions

Multiplying and dividing fractions

Multiplying and dividing fractions means using multiplication and division to calculate with fractions. Fraction multiplication and division can be solved using models or an algorithm.

Using models:

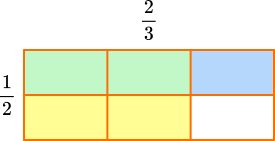
In the model, \, \cfrac{2}{3} \, is yellow and \, \cfrac{1}{2} \, is blue.

The product is where the fractions overlap in green.

The model shows \, \cfrac{2}{3} \, of \, \cfrac{1}{2}, \, so \, \cfrac{1}{2} \times \cfrac{2}{3} = \cfrac{2}{6} \, .

Using the algorithm:

To multiply fractions , you multiply the numerators together, and multiply the denominators together:

\cfrac{1}{2} \, \times \, \cfrac{2}{3}=\cfrac{2}{6} \, .

You can also divide fractions with a model or an algorithm.

Think of this equation as how many \, \cfrac{1}{4} \, fit into \, \cfrac{1}{2} \, .

In the model, \, \cfrac{1}{2} \, is orange and \, \cfrac{1}{4} \, is yellow.

To divide into equal groups, use the equivalent fraction \, \cfrac{2}{4} \, .

The quotient is the final fraction formed when \, \cfrac{2}{4} \, is put into a group of \, \cfrac{1}{4} \, .

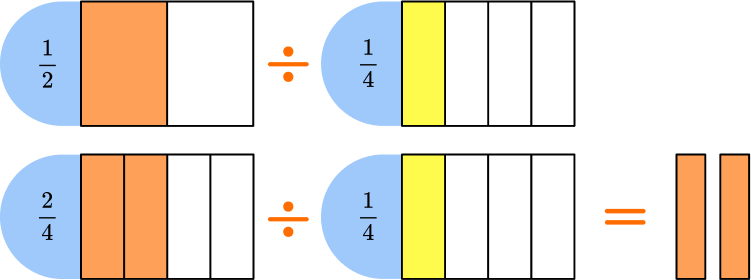
Two groups of \cfrac{1}{4} can be made, so \cfrac{1}{2} \div \cfrac{1}{4}=2.

KEEP the first fraction, FLIP the second fraction, CHANGE to multiplication.

\cfrac{1}{2} \div \cfrac{1}{4}

Keep the dividend (first fraction): \, \cfrac{1}{2}

Take the reciprocal of the divisor (flip the second fraction): \, \cfrac{1}{4} \rightarrow \cfrac{4}{1}

Change to multiplication: \, \cfrac{1}{2} \times \cfrac{4}{1}

Multiply the fractions: \, \cfrac{1}{2} \times \cfrac{4}{1}=\cfrac{4}{2} \, which simplifies to 2.

\cfrac{1}{2} \div \cfrac{1}{4}=2

Since \, \cfrac{1}{2} \, is larger than \, \cfrac{1}{4} \, , the answer makes sense.

A larger number divided by a smaller number, will have a quotient of greater than 1.

Notice that it is not necessary to create a common denominator to multiply and divide fractions when using the algorithm, like it is to add and subtract fractions.

Step-by-step guide: Multiplying fractions

Step-by-step guide: Dividing fractions

Step-by-step guide: Multiplying and dividing fractions

The algorithm for dividing fractions involves using the reciprocal .

When two numbers are multiplied by something other than 1, and have a product of 1, they are reciprocals.

This is also known as the multiplicative inverse.

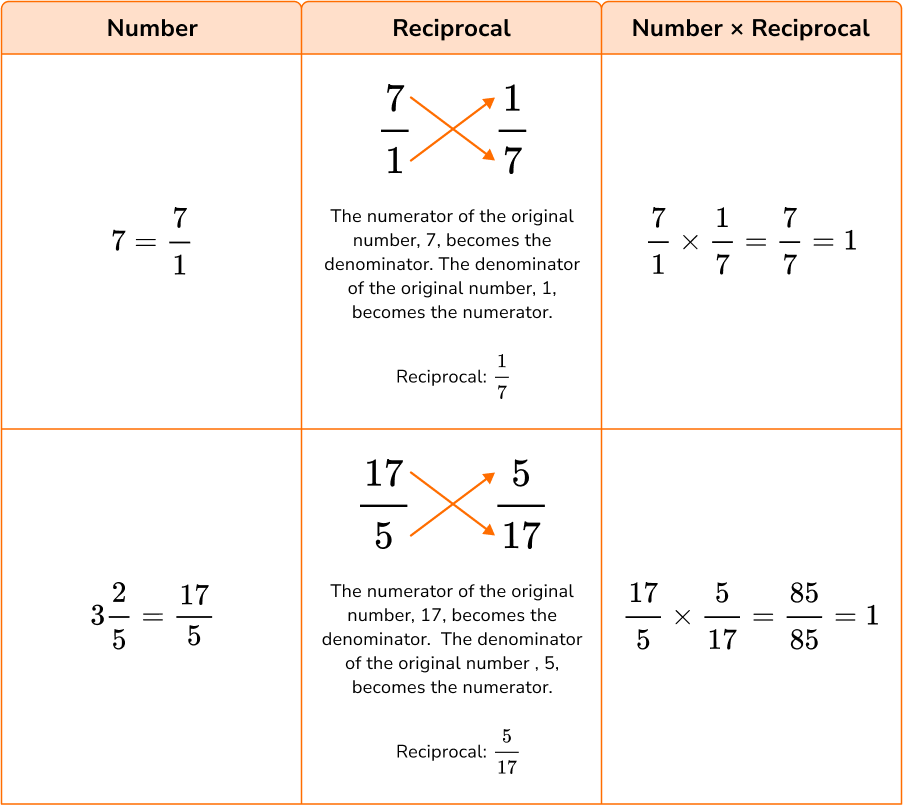
The reciprocal of all numbers can be found by writing the number as a fraction and then flipping it so that the numerator becomes the denominator and the denominator becomes the numerator.

Step-by-step guide: Reciprocal

Step-by-step guide: Multiplicative inverse

Common Core State Standards

How does this relate to 4th grade math, 5th grade math, and 6th grade math?

• Grade 4 – Number and Operations – Fractions (4.NF.B.3a) Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
• Grade 4 – Number and Operations – Fractions (4.NF.B.3c) Add and subtract mixed numbers with like denominators, for example, by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
• Grade 4 – Number and Operations – Fractions (4.NF.B.4b) ​​Understand a multiple of \, \cfrac{a}{b} \, as a multiple of \, \cfrac{1}{b} \, , and use this understanding to multiply a fraction by a whole number.
• Grade 5 – Number and Operations – Fractions (5.NF.A.1) Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. For example, \, \cfrac{2}{3} + \cfrac{5}{4} = \cfrac{8}{12} + \cfrac{15}{12} = \cfrac{23}{12} \, . \; ( In general, \, \cfrac{a}{b} + \cfrac{c}{d} = \cfrac{(ad \, + \, bc)}{bd} \, . )
• Grade 5 – Number and Operations – Fractions (5.NF.B.4b) Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
• Grade 6 – Number System (6.NS.A.1) Apply and extend previous understandings of multiplication and division to divide fractions by fractions.

How to use fractions operations

There are a lot of ways to use fractions operations. For more specific step-by-step guides, check out the fraction pages linked in the “What are fractions operations?” section above or read through the examples below.

Fractions operations examples

Example 1: adding fractions with like denominators.

Solve \, \cfrac{5}{8}+\cfrac{7}{8} \, .

Add or subtract the numerators (top numbers).

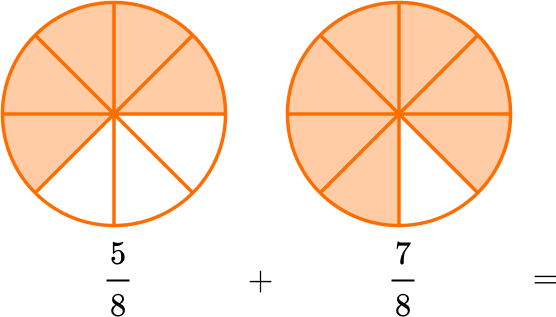
Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 5 + 7 = 12.

2 Write your answer as a fraction.

There are 12 parts, and the size is still eighths, so the denominator stays the same.

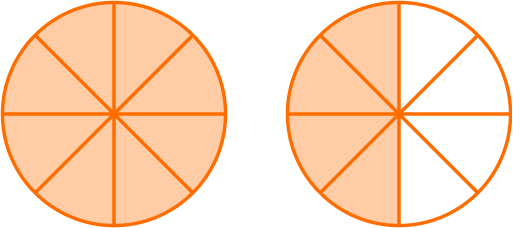
\cfrac{12}{8} \, is an improper fraction and converts to the mixed number 1 \, \cfrac{4}{8} \, .

\cfrac{5}{8}+\cfrac{7}{8}=1 \cfrac{4}{8}

You can also write this answer as the equivalent mixed number \, 1 \cfrac{1}{2} \, .

Example 2: subtracting fractions with unlike denominators

Solve \cfrac{6}{10}-\cfrac{1}{3} \, .

Create common denominators (bottom numbers).

Since \, \cfrac{6}{10} \, and \, \cfrac{1}{3} \, do not have like denominators, the parts are NOT the same size.

Multiply the numerator and denominator by the opposite denominator to create equivalent fractions with common denominators.

\cfrac{6 \, \times \, 3}{10 \, \times \, 3}=\cfrac{18}{30} \quad and \quad \cfrac{1 \, \times \, 10}{3 \, \times \, 10}=\cfrac{10}{30}

Now use the equivalent fractions to solve: \, \cfrac{18}{30}-\cfrac{10}{30} \, .

Since the denominators are the same, the parts are the same size. You subtract to see how many parts are left: 18-10 = 8.

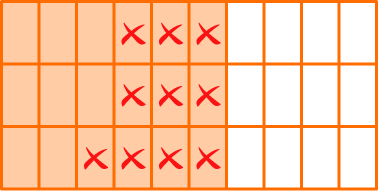
Write your answer as a fraction.

There are 8 parts and the size is still thirtieths, so the denominator stays the same.

\cfrac{18}{30}-\cfrac{10}{30}=\cfrac{8}{30}

You can also write this answer as the equivalent fraction \, \cfrac{4}{15} \, .

Example 3: multiplying a mixed number by a fraction with the algorithm

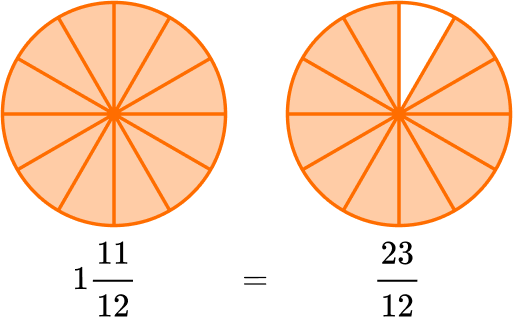
Solve 1 \, \cfrac{11}{12} \times \cfrac{3}{4} \, .

Convert whole numbers and mixed numbers to improper fractions.

Convert the mixed number to an improper fraction.

Multiply the numerators together.

\cfrac{23}{12} \times \cfrac{3}{4}=\cfrac{69}{}

Multiply the denominators together.

\cfrac{23}{12} \times \cfrac{3}{4}=\cfrac{69}{48}

If possible, simplify or convert to a mixed number.

The numerator is greater than the denominator, so the improper fraction can be converted to a mixed number.

\cfrac{69}{48}=1 \, \cfrac{21}{48}

The product can be simplified. 21 and 48 have a common factor of 3.

\cfrac{21 \, \div \, 3}{48 \, \div \, 3}=\cfrac{7}{16}

So, \, \cfrac{23}{12} \times \cfrac{3}{4}=\cfrac{69}{48} \, or 1 \, \cfrac{7}{16} \, .

Example 4: dividing a fraction by a fraction

Divide the numbers \, \cfrac{1}{12} \div \cfrac{1}{4} \, .

Take the reciprocal (flip) of the divisor (second fraction).

\cfrac{1}{4} \, → \, \cfrac{4}{1}

Change the division sign to a multiplication sign.

\cfrac{1}{12} \, \times \, \cfrac{4}{1}

Multiply the fractions together.

\cfrac{1}{12} \, \times \, \cfrac{4}{1}=\cfrac{4}{12}

\cfrac{4}{12}=\cfrac{1}{3}

This can also be solved with a model.

You can think of this equation as how many \, \cfrac{1}{4} \, fit into \, \cfrac{1}{12} \, .

In the model, \, \cfrac{1}{12} \, is yellow and \, \cfrac{1}{4} \, is orange.

To divide into equal groups, the fractional pieces need to be the same size.

Use \, \cfrac{1}{12} \, and \, \cfrac{3}{12} \, to solve.

The quotient is the final fraction formed when \, \cfrac{1}{12} \, is put into groups of \, \cfrac{3}{12} \, .

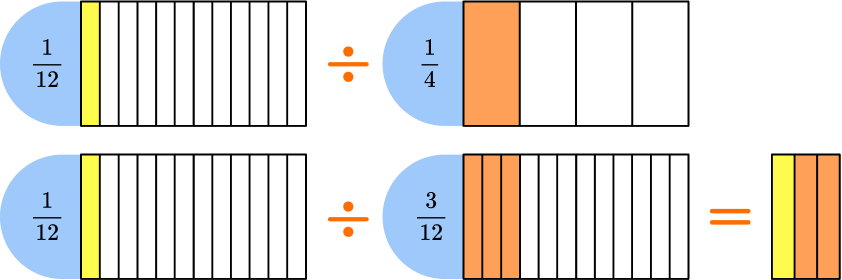
One out of the three parts are filled, so \, \cfrac{1}{12} \div \cfrac{3}{12}=\cfrac{1}{3} \, .

Example 5: adding mixed numbers with unlike denominators

There are 2 \, \cfrac{1}{3} \, pounds of red apples and 4 \, \cfrac{1}{6} \, pounds of green apples.

How many pounds of apples are there in all?

Create an equation to model the problem.

2 \cfrac{1}{3}+4 \cfrac{1}{6}= \, ?

Add or subtract the whole numbers.

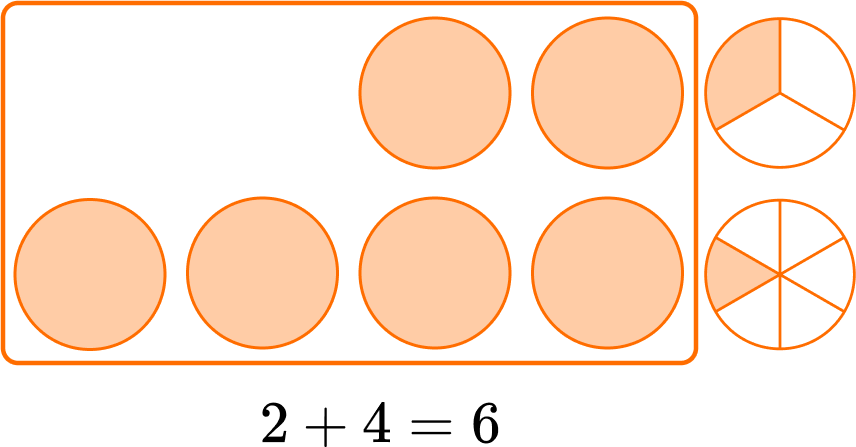
Since \, \cfrac{1}{3} \, and \, \cfrac{1}{6} \, do not have like denominators, the parts are NOT the same size.

Use equivalent fractions to create a common denominator.

A common denominator of 6 can be used.

Multiply the numerator and denominator of \, \cfrac{1}{3} \, by 2 to create an equivalent fraction.

\cfrac{1}{3}=\cfrac{1 \, \times \, 2}{3 \, \times \, 2}=\cfrac{2}{6} \quad and \quad \cfrac{1}{6}

Add or subtract the fractions.

Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 2 + 1 = 3.

There are 3 parts, and the size is still sixths, so the denominator stays the same.

Write your answer as a mixed number.

Add the whole number and fraction together.

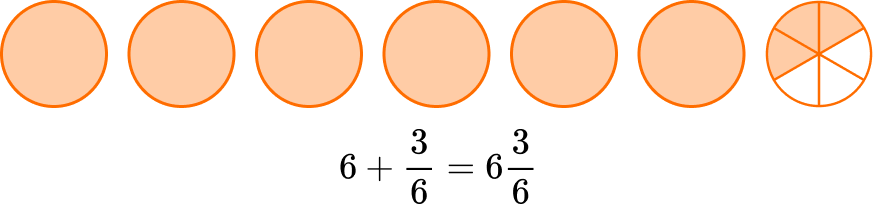
You can also write this answer as the equivalent mixed number 6 \, \cfrac{1}{2} \, .

There are 6 \, \cfrac{1}{2} \, pounds of apples in all.

Example 6: word problem dividing with fractions

Each seed needs \, \cfrac{1}{5} \, cup of soil. How many seeds can be planted with 11 cups of soil?

11 \div \cfrac{1}{5}= \, ?

Change any mixed numbers to an improper fraction.

Change 11 to an improper fraction.

11=\cfrac{11}{1}

Take the reciprocal (flip) of the divisor (second fractions).

\cfrac{1}{5} \, → \, \cfrac{5}{1}

\cfrac{11}{1} \times \cfrac{5}{1}

\cfrac{11}{1} \times \cfrac{5}{1}=\cfrac{55}{1}

If possible, simplify or convert to a mixed number (mixed fraction).

\cfrac{55}{1}=55

55 seeds can be planted with 11 cups of soil.

Teaching tips for fractions operations

• Fraction work in lower grades emphasizes understanding through models, including area models and number lines. To support students in upper grades, always have digital or physical models available for students to use as they work with fractions operations.
• Fraction worksheets can be useful when students are developing understanding around basic operations with fractions. However, when students have successful strategies and can flexibly operate, make the practice more engaging by using math games or real world projects that allow students to use fractions in a variety of situations.
• Highlight patterns within and between the operations as students are learning and encourage them to look for patterns on their own. This will help students make sense of the algorithms used to operate with fractions and minimize conceptual errors.
• Let students find reciprocal numbers on their own by consistently asking questions such as, “What number multiplied by 7 will have a product of 1 ?” Each time this is discussed, write these equations on an anchor chart and students will begin to see a pattern over time. Although worksheets can serve a purpose and help with skill and test prep practice, having students discover and make sense of mathematical concepts is more meaningful for building long lasting understanding.

Easy mistakes to make

• Forgetting how to find the reciprocal of a whole number Whole numbers can be written as an improper fraction and then the numerator and denominator of the improper fraction can be flipped to find the reciprocal of the whole number. For example, 16 can be written as \, \cfrac{16}{1} \, and the reciprocal is \, \cfrac{1}{16} \, .

Practice fractions operations questions

1. Solve \, \cfrac{5}{9}+\cfrac{2}{9} \, .

Since the denominators are the same, the parts are the same size. You add to see how many parts there are in total: 5 + 2 = 7.

There are 7 parts and the size is still ninths, so the denominator stays the same.

\cfrac{5}{9}+\cfrac{2}{9}=\cfrac{7}{9}

2. Solve \, 2 \, \cfrac{3}{10}-1 \, \cfrac{4}{5} \, .

The equation is taking \, 1 \cfrac{4}{5} \, away from \, 2 \cfrac{3}{10} \, .

Start with the fractions. Since \, \cfrac{3}{10} \, and \, \cfrac{4}{5} \, do not have like denominators, the parts are NOT the same size.

Use equivalent fractions to create a common denominator. Both denominators are multiples of 10.

\cfrac{3}{10} \quad and \quad \cfrac{4 \, \times \, 2}{5 \, \times \, 2}=\cfrac{8}{10}

Now use the equivalent fraction to solve: 2 \, \cfrac{3}{10}-1 \, \cfrac{8}{10}

However, there are not enough parts to take 8 away from 3.

You can break one of the wholes into \cfrac{10}{10} \, …

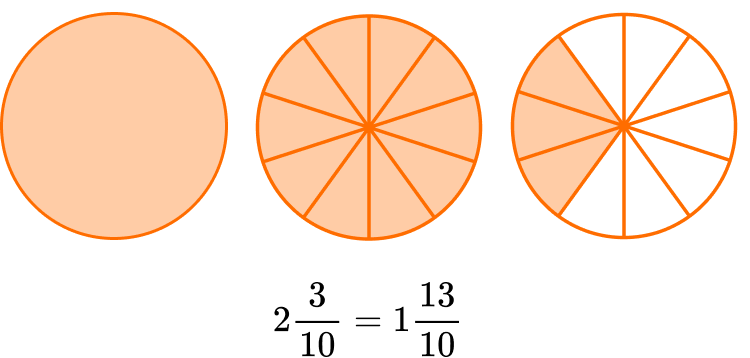
Now you can solve 1 \, \cfrac{13}{10}-1 \, \cfrac{8}{10}.

You subtract to see how many parts are left: 13-8 = 5.

There are 5 parts and the size is still tenths, so the denominator stays the same.

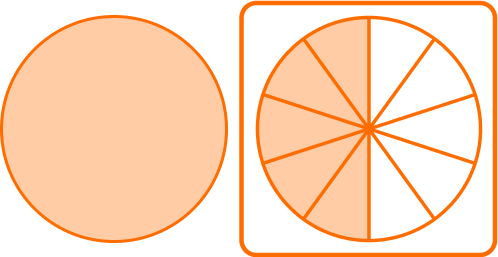
\cfrac{13}{10}-\cfrac{8}{10}=\cfrac{5}{10}

Subtract the whole numbers.

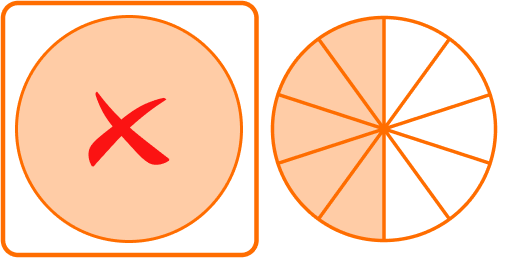
1 \, \cfrac{13}{10}-1 \, \cfrac{8}{10}=\cfrac{5}{10}

You can also write this answer as the equivalent fraction \, \cfrac{1}{2} \, .

3. Solve \, \cfrac{1}{4} \times \cfrac{2}{5} \, .

To solve using a model, draw a rectangle. Divide one side into fourths.

Divide the other side into fifths.

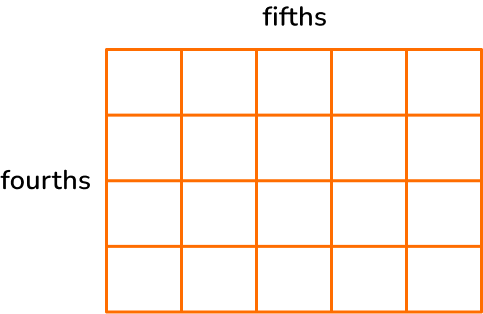
Shade in \, \cfrac{1}{4} \, with yellow and \, \cfrac{2}{5} with blue.

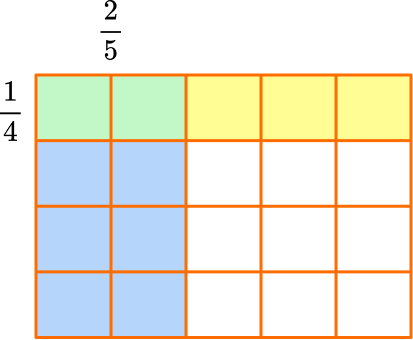
The model shows \, \cfrac{2}{5} \, of \, \cfrac{1}{4} \, , so \, \cfrac{1}{4} \times \cfrac{2}{5}=\cfrac{2}{20} \, , because there are 2 green squares and the whole has 20 squares in total.

The product can be simplified. Both 2 and 20 have a factor of 2, so they can be divided by 2 :

\, \cfrac{2 \, \div \, 2}{20 \, \div \, 2}=\cfrac{1}{10} \, .

So, \, \cfrac{1}{4} \times \cfrac{2}{5}=\cfrac{2}{20} \; or \; \cfrac{1}{10}

4. Solve \, 2 \, \cfrac{1}{6} \div 1 \, \cfrac{2}{3} \, . Write the quotient in lowest terms.

Change the mixed numbers to improper fractions:

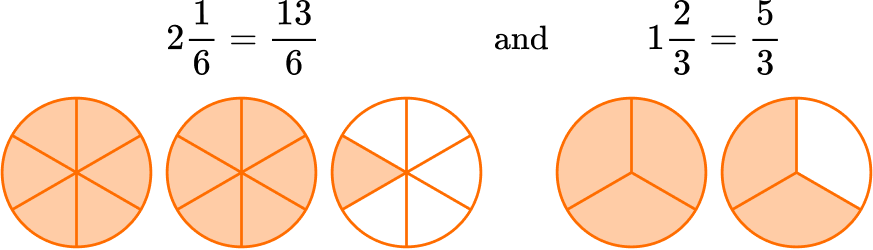
Keep the dividend (first fraction): \, \cfrac{13}{6}

Take the reciprocal of the divisor (flip the second fraction): \, \cfrac{5}{3} → \cfrac{3}{5}

Change to multiplication: \, \cfrac{13}{6} \times \cfrac{3}{5}

Multiply the fractions: \, \cfrac{13}{6} \times \cfrac{3}{5}=\cfrac{39}{30}

Change back into a mixed number: \, \cfrac{39}{30}=1 \, \cfrac{9}{30}

Simplify: \, \cfrac{9 \, \div \, 3}{30 \, \div \, 3}=\cfrac{3}{10} \, , so the answer in lowest terms is \, 1 \, \cfrac{3}{10} \, .

5. Rashad is cutting a 12 \, ft rope into smaller \, \cfrac{2}{3} \, ft pieces. How many smaller pieces of rope will he have?

8 smaller pieces of rope

12 smaller pieces of rope

18 smaller pieces of rope

\cfrac{24}{3} smaller pieces of rope

Use the equation \, 12 \div \cfrac{2}{3}= \, ?

Draw 12 wholes and break them up into thirds.

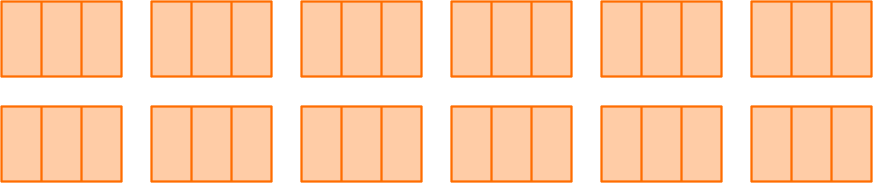
Create groups of \, \cfrac{2}{3} \, .

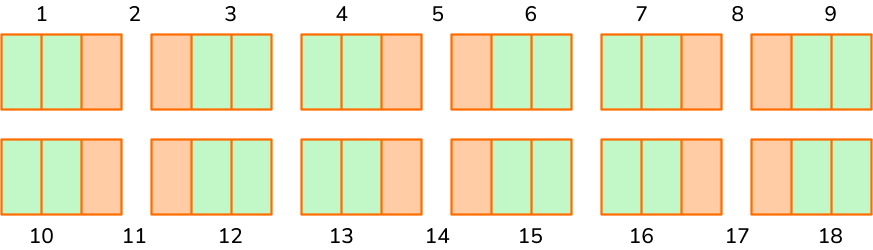
There are 18 groups of \, \cfrac{2}{3} \, .

Rashad will have 18 pieces of smaller rope.

6. A recipe calls for 3 \, \cfrac{1}{4} \, cups of strawberries. If Tyler has 5 \, \cfrac{5}{8} \, cups of strawberries, how many will he have left after he makes 1 recipe?

2 \, \cfrac{3}{8} cups

2 \, \cfrac{4}{4} cups

8 \, \cfrac{7}{8} cups

8 \, \cfrac{6}{12} cups

Use the equation 5 \cfrac{5}{8}-3 \cfrac{1}{4}= \, ?

Start with the fraction.

Since \, \cfrac{5}{8} \, and \, \cfrac{1}{4} \, do not have like denominators, the parts are NOT the same size.

A common denominator of 8 can be used.

Multiply the numerator and denominator of \, \cfrac{1}{4} \, by 2 to create an equivalent fraction.

\cfrac{5}{8} \quad and \quad \cfrac{1}{4}=\cfrac{1 \, \times \, 2}{4 \, \times \, 2}=\cfrac{2}{8}

You subtract to see how many parts there are in total: 5-2 = 3.

There are 2 parts and the size is still eighths, so the denominator stays the same.

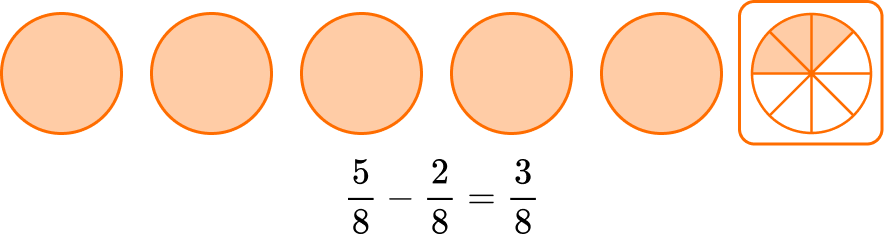
There will be \, 2 \cfrac{3}{8} \, cups of strawberries left.

Fractions operations FAQs

No, although using these operations will create different denominators and numerators, as long as they are multiplied or divided by the same thing, the value of the fraction will remain the same.

No, unless the question specifies the lowest terms, it is valid to answer without using the least common denominator (LCD). However, as students progress in their understanding of fractions, it is a good idea to encourage them to practice this skill. Also be mindful of standard expectations, as they may vary from state to state.

Yes, just like any other type of number, to solve multistep problems correctly, the order of operations must be followed.

The multiplicative inverse of a number is the reciprocal. For any integer, that is the number written as the numerator over a denominator of 1. For any rational number, that is switching the numerator and denominator.

The next lessons are

• Algebraic expression
• Converting fractions decimals and percents
• Interpret fractions as division
• Fraction word problems

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Fractions Worksheets

Welcome to the fractions worksheets page at Math-Drills.com where the cup is half full! This is one of our more popular pages most likely because learning fractions is incredibly important in a person's life and it is a math topic that many approach with trepidation due to its bad rap over the years. Fractions really aren't that difficult to master especially with the support of our wide selection of worksheets.

This page includes Fractions worksheets for understanding fractions including modeling, comparing, ordering, simplifying and converting fractions and operations with fractions. We start you off with the obvious: modeling fractions. It is a great idea if students can actually understand what a fraction is, so please do spend some time with the modeling aspect. Relating modeling to real life helps a great deal too as it is much easier to relate to half a cookie than to half a square. Ask most students what you get if you add half a cookie and another half a cookie, and they'll probably let you know that it makes one delicious snack.

The other fractions worksheets on this page are devoted to helping students understand the concept of fractions. From comparing and ordering to simplifying and converting... by the time students master the material on this page, operations of fractions will be a walk in the park.

Most Popular Fractions Worksheets this Week

Fraction Circles

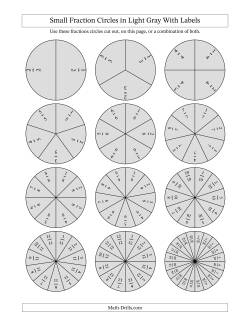
Fraction circle manipulatives are mainly used for comparing fractions, but they can be used for a variety of other purposes such as representing and identifying fractions, adding and subtracting fractions, and as probability spinners. There are a variety of options depending on your purpose. Fraction circles come in small and large versions, labeled and unlabeled versions and in three different color schemes: black and white, color, and light gray. The color scheme matches the fraction strips and use colors that are meant to show good contrast among themselves. Do note that there is a significant prevalence of color-blindness in the population, so don't rely on all students being able to differentiate the colors.

Suggested activity for comparing fractions: Photocopy the black and white version onto an overhead projection slide and another copy onto a piece of paper. Alternatively, you can use two pieces of paper and hold them up to the light for this activity. Use a pencil to represent the first fraction on the paper copy. Use a non-permanent overhead pen to represent the second fraction. Lay the slide over the paper and compare the two circles. You should easily be able to tell which is greater or lesser or if the two fractions are equal. Re-use both sheets by erasing the pencil and washing off the marker.

Adding fractions with fraction circles will involve two copies on paper. Cut out the fraction circles and segments of one copy and leave the other copy intact. To add 1/3 + 1/2, for example, place a 1/3 segment and a 1/2 segment into a circle and hold it over various fractions on the intact copy to see what 1/2 + 1/3 is equivalent to. 5/6 or 10/12 should work.

• Small Fraction Circles Small Fraction Circles in Black and White with Labels Small Fraction Circles in Color with Labels Small Fraction Circles in Light Gray with Labels Small Fraction Circles in Black and White Unlabeled Small Fraction Circles in Color Unlabeled Small Fraction Circles in Light Gray Unlabeled
• Large Fraction Circles Large Fraction Circles in Black and White with Labels Large Fraction Circles in Color with Labels Large Fraction Circles in Light Gray with Labels Large Fraction Circles in Black and White Unlabeled Large Fraction Circles in Color Unlabeled Large Fraction Circles in Light Gray Unlabeled

Fraction Strips

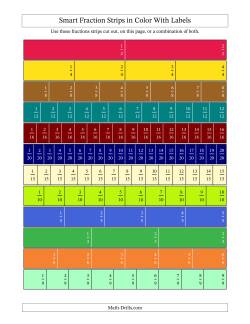
Fractions strips are often used for comparing fractions. Students are able to see quite easily the relationships and equivalence between fractions with different denominators. It can be quite useful for students to have two copies: one copy cut into strips and the other copy kept intact. They can then use the cut-out strips on the intact page to individually compare fractions. For example, they can use the halves strip to see what other fractions are equivalent to one-half. This can also be accomplished with a straight edge such as a ruler without cutting out any strips. Pairs or groups of strips can also be compared side-by-side if they are cut out. Addition and subtraction (etc.) are also possibilities; for example, adding a one-quarter and one-third can be accomplished by shifting the thirds strip so that it starts at the end of one-quarter then finding a strip that matches the end of the one-third mark (7/12 should do it).

Teachers might consider copying the fraction strips onto overhead projection acetates for whole class or group activities. Acetate versions are also useful as a hands-on manipulative for students in conjunction with an uncut page.

The "Smart" Fraction Strips include strips in a more useful order, eliminate the 7ths and 11ths strips as they don't have any equivalents and include 15ths and 16ths. The colors are consistent with the classic versions, so the two sets can be combined.

• Classic Fraction Strips with Labels Classic Fraction Strips in Black and White With Labels Classic Fraction Strips in Color With Labels Classic Fraction Strips in Gray With Labels
• Unlabeled Classic Fraction Strips Classic Fraction Strips in Black and White Unlabeled Classic Fraction Strips in Color Unlabeled Classic Fraction Strips in Gray Unlabeled
• Smart Fraction Strips with Labels Smart Fraction Strips in Black and White With Labels Smart Fraction Strips in Color With Labels Smart Fraction Strips in Gray With Labels

Modeling fractions

Fractions can represent parts of a group or parts of a whole. In these worksheets, fractions are modeled as parts of a group. Besides using the worksheets in this section, you can also try some more interesting ways of modeling fractions. Healthy snacks can make great models for fractions. Can you cut a cucumber into thirds? A tomato into quarters? Can you make two-thirds of the grapes red and one-third green?

• Modeling Fractions with Groups of Shapes Coloring Groups of Shapes to Represent Fractions Identifying Fractions from Colored Groups of Shapes (Only Simplified Fractions up to Eighths) Identifying Fractions from Colored Groups of Shapes (Halves Only) Identifying Fractions from Colored Groups of Shapes (Halves and Thirds) Identifying Fractions from Colored Groups of Shapes (Halves, Thirds and Fourths) Identifying Fractions from Colored Groups of Shapes (Up to Fifths) Identifying Fractions from Colored Groups of Shapes (Up to Sixths) Identifying Fractions from Colored Groups of Shapes (Up to Eighths) Identifying Fractions from Colored Groups of Shapes (OLD Version; Print Too Light)
• Modeling Fractions with Rectangles Modeling Halves Modeling Thirds Modeling Halves and Thirds Modeling Fourths (Color Version) Modeling Fourths (Grey Version) Coloring Fourths Models Modeling Fifths Coloring Fifths Models Modeling Sixths Coloring Sixths Models
• Modeling Fractions with Circles Modeling Halves, Thirds and Fourths Coloring Halves, Thirds and Fourths Modeling Halves, Thirds, Fourths, and Fifths Coloring Halves, Thirds, Fourths, and Fifths Modeling Halves to Sixths Coloring Halves to Sixths Modeling Halves to Eighths Coloring Halves to Eighths Modeling Halves to Twelfths Coloring Halves to Twelfths

Ratio and Proportion Worksheets

The equivalent fractions models worksheets include only the "baking fractions" in the A versions. To see more difficult and varied fractions, please choose the B to J versions after loading the A version. More picture ratios can be found on holiday and seasonal pages. Try searching for picture ratios to find more.

• Picture Ratios Autumn Trees Part-to-Part Picture Ratios ( Grouped ) Autumn Trees Part-to-Part and Part-to-Whole Picture Ratios ( Grouped )
• Equivalent Fractions Equivalent Fractions With Blanks ( Multiply Right ) ✎ Equivalent Fractions With Blanks ( Divide Left ) ✎ Equivalent Fractions With Blanks ( Multiply Right or Divide Left ) ✎ Equivalent Fractions With Blanks ( Divide Right ) ✎ Equivalent Fractions With Blanks ( Multiply Left ) ✎ Equivalent Fractions With Blanks ( Multiply Left or Divide Right ) ✎ Equivalent Fractions With Blanks ( Multiply or Divide Right ) ✎ Equivalent Fractions With Blanks ( Multiply or Divide Left ) ✎ Equivalent Fractions With Blanks ( Multiply or Divide in Either Direction ) ✎ Are These Fractions Equivalent? (Multiplier 2 to 5) Are These Fractions Equivalent? (Multiplier 5 to 15) Equivalent Fractions Models Equivalent Fractions Models with the Simplified Fraction First Equivalent Fractions Models with the Simplified Fraction Second
• Equivalent Ratios Equivalent Ratios with Blanks Only on Right Equivalent Ratios with Blanks Anywhere Equivalent Ratios with x 's

Comparing and Ordering Fractions

Comparing fractions involves deciding which of two fractions is greater in value or if the two fractions are equal in value. There are generally four methods that can be used for comparing fractions. First is to use common denominators . If both fractions have the same denominator, comparing the fractions simply involves comparing the numerators. Equivalent fractions can be used to convert one or both fractions, so they have common denominators. A second method is to convert both fractions to a decimal and compare the decimal numbers. Visualization is the third method. Using something like fraction strips , two fractions can be compared with a visual tool. The fourth method is to use a cross-multiplication strategy where the numerator of the first fraction is multiplied by the denominator of the second fraction; then the numerator of the second fraction is multiplied by the denominator of the first fraction. The resulting products can be compared to decide which fraction is greater (or if they are equal).

• Comparing Proper Fractions Comparing Proper Fractions to Sixths ✎ Comparing Proper Fractions to Ninths (No Sevenths) ✎ Comparing Proper Fractions to Ninths ✎ Comparing Proper Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Proper Fractions to Twelfths ✎

The worksheets in this section also include improper fractions. This might make the task of comparing even easier for some questions that involve both a proper and an improper fraction. If students recognize one fraction is greater than one and the other fraction is less than one, the greater fraction will be obvious.

• Comparing Proper and Improper Fractions Comparing Proper and Improper Fractions to Sixths ✎ Comparing Proper and Improper Fractions to Ninths (No Sevenths) ✎ Comparing Proper and Improper Fractions to Ninths ✎ Comparing Proper and Improper Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Proper and Improper Fractions to Twelfths ✎ Comparing Improper Fractions to Sixths ✎ Comparing Improper Fractions to Ninths (No Sevenths) ✎ Comparing Improper Fractions to Ninths ✎ Comparing Improper Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Improper Fractions to Twelfths ✎

This section additionally includes mixed fractions. When comparing mixed and improper fractions, it is useful to convert one of the fractions to the other's form either in writing or mentally. Converting to a mixed fraction is probably the better route since the first step is to compare the whole number portions, and if one is greater than the other, the proper fraction portion can be ignored. If the whole number portions are equal, the proper fractions must be compared to see which number is greater.

• Comparing Proper, Improper and Mixed Fractions Comparing Proper, Improper and Mixed Fractions to Sixths ✎ Comparing Proper, Improper and Mixed Fractions to Ninths (No Sevenths) ✎ Comparing Proper, Improper and Mixed Fractions to Ninths ✎ Comparing Proper, Improper and Mixed Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Proper, Improper and Mixed Fractions to Twelfths ✎
• Comparing Improper and Mixed Fractions Comparing Improper and Mixed Fractions to Sixths ✎ Comparing Improper and Mixed Fractions to Ninths (No Sevenths) ✎ Comparing Improper and Mixed Fractions to Ninths ✎ Comparing Improper and Mixed Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Improper and Mixed Fractions to Twelfths ✎
• Comparing Mixed Fractions Comparing Mixed Fractions to Sixths ✎ Comparing Mixed Fractions to Ninths (No Sevenths) ✎ Comparing Mixed Fractions to Ninths ✎ Comparing Mixed Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Mixed Fractions to Twelfths ✎

Many of the same strategies that work for comparing fractions also work for ordering fractions. Using manipulatives such as fraction strips, using number lines, or finding decimal equivalents will all have your student(s) putting fractions in the correct order in no time. We've probably said this before, but make sure that you emphasize that when comparing or ordering fractions, students understand that the whole needs to be the same. Comparing half the population of Canada with a third of the population of the United States won't cut it. Try using some visuals to reinforce this important concept. Even though we've included number lines below, feel free to use your own strategies.

• Ordering Fractions with Easy Denominators on a Number Line Ordering Fractions with Easy Denominators to 10 on a Number Line Ordering Fractions with Easy Denominators to 24 on a Number Line Ordering Fractions with Easy Denominators to 60 on a Number Line Ordering Fractions with Easy Denominators to 100 on a Number Line
• Ordering Fractions with Easy Denominators on a Number Line (Including Negative Fractions) Ordering Fractions with Easy Denominators to 10 + Negatives on a Number Line Ordering Fractions with Easy Denominators to 24 + Negatives on a Number Line Ordering Fractions with Easy Denominators to 60 + Negatives on a Number Line Ordering Fractions with Easy Denominators to 100 + Negatives on a Number Line
• Ordering Fractions with All Denominators on a Number Line Ordering Fractions with All Denominators to 10 on a Number Line Ordering Fractions with All Denominators to 24 on a Number Line Ordering Fractions with All Denominators to 60 on a Number Line Ordering Fractions with All Denominators to 100 on a Number Line
• Ordering Fractions with All Denominators on a Number Line (Including Negative Fractions) Ordering Fractions with All Denominators to 10 + Negatives on a Number Line Ordering Fractions with All Denominators to 24 + Negatives on a Number Line Ordering Fractions with All Denominators to 60 + Negatives on a Number Line Ordering Fractions with All Denominators to 100 + Negatives on a Number Line

The ordering fractions worksheets in this section do not include a number line, to allow for students to use various sorting strategies.

• Ordering Positive Fractions Ordering Positive Fractions with Like Denominators Ordering Positive Fractions with Like Numerators Ordering Positive Fractions with Like Numerators or Denominators Ordering Positive Fractions with Proper Fractions Only Ordering Positive Fractions with Improper Fractions Ordering Positive Fractions with Mixed Fractions Ordering Positive Fractions with Improper and Mixed Fractions
• Ordering Positive and Negative Fractions Ordering Positive and Negative Fractions with Like Denominators Ordering Positive and Negative Fractions with Like Numerators Ordering Positive and Negative Fractions with Like Numerators or Denominators Ordering Positive and Negative Fractions with Proper Fractions Only Ordering Positive and Negative Fractions with Improper Fractions Ordering Positive and Negative Fractions with Mixed Fractions Ordering Positive and Negative Fractions with Improper and Mixed Fractions

Simplifying & Converting Fractions Worksheets

Rounding fractions helps students to understand fractions a little better and can be applied to estimating answers to fractions questions. For example, if one had to estimate 1 4/7 × 6, they could probably say the answer was about 9 since 1 4/7 is about 1 1/2 and 1 1/2 × 6 is 9.

• Rounding Fractions with Helper Lines Rounding Fractions to the Nearest Whole with Helper Lines Rounding Mixed Numbers to the Nearest Whole with Helper Lines Rounding Fractions to the Nearest Half with Helper Lines Rounding Mixed Numbers to the Nearest Half with Helper Lines
• Rounding Fractions Rounding Fractions to the Nearest Whole Rounding Mixed Numbers to the Nearest Whole Rounding Fractions to the Nearest Half Rounding Mixed Numbers to the Nearest Half

Learning how to simplify fractions makes a student's life much easier later on when learning operations with fractions. It also helps them to learn that different-looking fractions can be equivalent. One way of demonstrating this is to divide out two equivalent fractions. For example 3/2 and 6/4 both result in a quotient of 1.5 when divided. By practicing simplifying fractions, students will hopefully recognize unsimplified fractions when they start adding, subtracting, multiplying and dividing with fractions.

• Simplifying Fractions Simplify Fractions (easier) Simplify Fractions (harder) Simplify Improper Fractions (easier) Simplify Improper Fractions (harder)
• Converting Between Improper and Mixed Fractions Converting Mixed Fractions to Improper Fractions Converting Improper Fractions to Mixed Fractions Converting Between (both ways) Mixed and Improper Fractions
• Converting Between Fractions and Decimals Converting Fractions to Terminating Decimals Converting Fractions to Terminating and Repeating Decimals Converting Terminating Decimals to Fractions Converting Terminating and Repeating Decimals to Fractions Converting Fractions to Hundredths
• Converting Between Fractions, Decimals, Percents and Ratios with Terminating Decimals Only Converting Fractions to Decimals, Percents and Part-to- Part Ratios ( Terminating Decimals Only) Converting Fractions to Decimals, Percents and Part-to- Whole Ratios ( Terminating Decimals Only) Converting Decimals to Fractions, Percents and Part-to- Part Ratios ( Terminating Decimals Only) Converting Decimals to Fractions, Percents and Part-to- Whole Ratios ( Terminating Decimals Only) Converting Percents to Fractions, Decimals and Part-to- Part Ratios ( Terminating Decimals Only) Converting Percents to Fractions, Decimals and Part-to- Whole Ratios ( Terminating Decimals Only) Converting Part-to-Part Ratios to Fractions, Decimals and Percents ( Terminating Decimals Only) Converting Part-to-Whole Ratios to Fractions, Decimals and Percents ( Terminating Decimals Only) Converting Various Fractions, Decimals, Percents and Part-to- Part Ratios ( Terminating Decimals Only) Converting Various Fractions, Decimals, Percents and Part-to- Whole Ratios ( Terminating Decimals Only)
• Converting Between Fractions, Decimals, Percents and Ratios with Terminating and Repeating Decimals Converting Fractions to Decimals, Percents and Part-to- Part Ratios Converting Fractions to Decimals, Percents and Part-to- Whole Ratios Converting Decimals to Fractions, Percents and Part-to- Part Ratios Converting Decimals to Fractions, Percents and Part-to- Whole Ratios Converting Percents to Fractions, Decimals and Part-to- Part Ratios Converting Percents to Fractions, Decimals and Part-to- Whole Ratios Converting Part-to-Part Ratios to Fractions, Decimals and Percents Converting Part-to-Whole Ratios to Fractions, Decimals and Percents Converting Various Fractions, Decimals, Percents and Part-to- Part Ratios Converting Various Fractions, Decimals, Percents and Part-to- Whole Ratios Converting Various Fractions, Decimals, Percents and Part-to- Part Ratios with 7ths and 11ths Converting Various Fractions, Decimals, Percents and Part-to- Whole Ratios with 7ths and 11ths

Multiplying Fractions

Multiplying fractions is usually less confusing operationally than any other operation and can be less confusing conceptually if approached in the right way. The algorithm for multiplying is simply multiply the numerators then multiply the denominators. The magic word in understanding the multiplication of fractions is, "of." For example what is two-thirds OF six? What is a third OF a half? When you use the word, "of," it gets much easier to visualize fractions multiplication. Example: cut a loaf of bread in half, then cut the half into thirds. One third OF a half loaf of bread is the same as 1/3 x 1/2 and tastes delicious with butter.

• Multiplying Two Proper Fraction Multiplying Two Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ ✎ Multiplying Two Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Proper Fractions with No Simplifying (Printable Only) Multiplying Two Proper Fractions with All Simplifying (Printable Only) Multiplying Two Proper Fractions with Some Simplifying (Printable Only)
• Multiplying Proper and Improper Fractions Multiplying Proper and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Improper Fractions with No Simplifying (Printable Only) Multiplying Proper and Improper Fractions with All Simplifying (Printable Only) Multiplying Proper and Improper Fractions with Some Simplifying (Printable Only)
• Multiplying Two Improper Fractions Multiplying Two Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Improper Fractions with No Simplifying (Printable Only) Multiplying Two Improper Fractions with All Simplifying (Printable Only) Multiplying Two Improper Fractions with Some Simplifying (Printable Only)
• Multiplying Proper and Mixed Fractions Multiplying Proper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Mixed Fractions with No Simplifying (Printable Only) Multiplying Proper and Mixed Fractions with All Simplifying (Printable Only) Multiplying Proper and Mixed Fractions with Some Simplifying (Printable Only)
• Multiplying Two Mixed Fractions Multiplying Two Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Mixed Fractions with No Simplifying (Printable Only) Multiplying Two Mixed Fractions with All Simplifying (Printable Only) Multiplying Two Mixed Fractions with Some Simplifying (Printable Only)
• Multiplying Whole Numbers and Proper Fractions Multiplying Whole Numbers and Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Proper Fractions with No Simplifying (Printable Only) Multiplying Whole Numbers and Proper Fractions with All Simplifying (Printable Only) Multiplying Whole Numbers and Proper Fractions with Some Simplifying (Printable Only)
• Multiplying Whole Numbers and Improper Fractions Multiplying Whole Numbers and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Improper Fractions with No Simplifying (Printable Only) Multiplying Whole Numbers and Improper Fractions with All Simplifying (Printable Only) Multiplying Whole Numbers and Improper Fractions with Some Simplifying (Printable Only)
• Multiplying Whole Numbers and Mixed Fractions Multiplying Whole Numbers and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Mixed Fractions with No Simplifying (Printable Only) Multiplying Whole Numbers and Mixed Fractions with All Simplifying (Printable Only) Multiplying Whole Numbers and Mixed Fractions with Some Simplifying (Printable Only)
• Multiplying Proper, Improper and Mixed Fractions Multiplying Proper, Improper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper, Improper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper, Improper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper, Improper and Mixed Fractions with No Simplifying (Printable Only) Multiplying Proper, Improper and Mixed Fractions with All Simplifying (Printable Only) Multiplying Proper, Improper and Mixed Fractions with Some Simplifying (Printable Only)
• Multiplying 3 Fractions Multiplying 3 Proper Fractions (Fillable, Savable, Printable) ✎ Multiplying 3 Proper and Improper Fractions (Fillable, Savable, Printable) ✎ Multiplying Proper and Improper Fractions and Whole Numbers (3 factors) (Fillable, Savable, Printable) ✎ Multiplying Fractions and Mixed Fractions (3 factors) (Fillable, Savable, Printable) ✎ Multiplying 3 Mixed Fractions (Fillable, Savable, Printable) ✎

Dividing Fractions

Conceptually, dividing fractions is probably the most difficult of all the operations, but we're going to help you out. The algorithm for dividing fractions is just like multiplying fractions, but you find the inverse of the second fraction or you cross-multiply. This gets you the right answer which is extremely important especially if you're building a bridge. We told you how to conceptualize fraction multiplication, but how does it work with division? Easy! You just need to learn the magic phrase: "How many ____'s are there in ______? For example, in the question 6 ÷ 1/2, you would ask, "How many halves are there in 6?" It becomes a little more difficult when both numbers are fractions, but it isn't a giant leap to figure it out. 1/2 ÷ 1/4 is a fairly easy example, especially if you think in terms of U.S. or Canadian coins. How many quarters are there in a half dollar?

• Dividing Two Proper Fractions Dividing Two Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Proper Fractions with No Simplifying (Printable Only) Dividing Two Proper Fractions with All Simplifying (Printable Only) Dividing Two Proper Fractions with Some Simplifying (Printable Only)
• Dividing Proper and Improper Fractions Dividing Proper and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Improper Fractions with No Simplifying (Printable Only) Dividing Proper and Improper Fractions with All Simplifying (Printable Only) Dividing Proper and Improper Fractions with Some Simplifying (Printable Only)
• Dividing Two Improper Fractions Dividing Two Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Improper Fractions with No Simplifying (Printable Only) Dividing Two Improper Fractions with All Simplifying (Printable Only) Dividing Two Improper Fractions with Some Simplifying (Printable Only)
• Dividing Proper and Mixed Fractions Dividing Proper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Mixed Fractions with No Simplifying (Printable Only) Dividing Proper and Mixed Fractions with All Simplifying (Printable Only) Dividing Proper and Mixed Fractions with Some Simplifying (Printable Only)
• Dividing Two Mixed Fractions Dividing Two Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Mixed Fractions with No Simplifying (Printable Only) Dividing Two Mixed Fractions with All Simplifying (Printable Only) Dividing Two Mixed Fractions with Some Simplifying (Printable Only)
• Dividing Whole Numbers and Proper Fractions Dividing Whole Numbers and Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Proper Fractions with No Simplifying (Printable Only) Dividing Whole Numbers and Proper Fractions with All Simplifying (Printable Only) Dividing Whole Numbers and Proper Fractions with Some Simplifying (Printable Only)
• Dividing Whole Numbers and Improper Fractions Dividing Whole Numbers and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Improper Fractions with No Simplifying (Printable Only) Dividing Whole Numbers and Improper Fractions with All Simplifying (Printable Only) Dividing Whole Numbers and Improper Fractions with Some Simplifying (Printable Only)
• Dividing Whole Numbers and Mixed Fractions Dividing Whole Numbers and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Mixed Fractions with No Simplifying (Printable Only) Dividing Whole Numbers and Mixed Fractions with All Simplifying (Printable Only) Dividing Whole Numbers and Mixed Fractions with Some Simplifying (Printable Only)
• Dividing Proper, Improper and Mixed Fractions Dividing Proper, Improper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper, Improper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper, Improper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper, Improper and Mixed Fractions with No Simplifying (Printable Only) Dividing Proper, Improper and Mixed Fractions with All Simplifying (Printable Only) Dividing Proper, Improper and Mixed Fractions with Some Simplifying (Printable Only)
• Dividing 3 Fractions Dividing 3 Fractions Dividing 3 Fractions (Some Whole Numbers) Dividing 3 Fractions (Some Mixed) Dividing 3 Mixed Fractions

Multiplying and Dividing Fractions

This section includes worksheets with both multiplication and division mixed on each worksheet. Students will have to pay attention to the signs.

• Multiplying and Dividing Two Proper Fractions Multiplying and Dividing Two Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Proper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Two Proper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Two Proper Fractions with Some Simplifying (Printable Only)
• Multiplying and Dividing Proper and Improper Fractions Multiplying and Dividing Proper and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Improper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Proper and Improper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Proper and Improper Fractions with Some Simplifying (Printable Only)
• Multiplying and Dividing Two Improper Fractions Multiplying and Dividing Two Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Improper Fractions (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Improper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Two Improper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Two Improper Fractions (Printable Only)
• Multiplying and Dividing Proper and Mixed Fractions Multiplying and Dividing Proper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Mixed Fractions with No Simplifying (Printable Only) Multiplying and Dividing Proper and Mixed Fractions with All Simplifying (Printable Only) Multiplying and Dividing Proper and Mixed Fractions with Some Simplifying (Printable Only)
• Multiplying and Dividing Two Mixed Fractions Multiplying and Dividing Two Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Mixed Fractions with No Simplifying (Printable Only) Multiplying and Dividing Two Mixed Fractions with All Simplifying (Printable Only) Multiplying and Dividing Two Mixed Fractions with Some Simplifying (Printable Only)
• Multiplying and Dividing Whole Numbers and Proper Fractions Fractions Multiplying and Dividing Whole Numbers and Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Proper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Proper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Proper Fractions with Some Simplifying (Printable Only)
• Multiplying and Dividing Whole Numbers and Improper Fractions Multiplying and Dividing Whole Numbers and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Improper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Improper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Improper Fractions with Some Simplifying (Printable Only)
• Multiplying and Dividing Whole Numbers and Mixed Fractions Multiplying and Dividing Whole Numbers and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Mixed Fractions with No Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Mixed Fractions with All Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Mixed Fractions with Some Simplifying (Printable Only)
• Multiplying and Dividing Proper, Improper and Mixed Fractions Multiplying and Dividing Proper, Improper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper, Improper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper, Improper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper, Improper and Mixed Fractions with No Simplifying (Printable Only) Multiplying and Dividing Proper, Improper and Mixed Fractions with All Simplifying (Printable Only) Multiplying and Dividing Proper, Improper and Mixed Fractions with Some Simplifying (Printable Only)
• Multiplying and Dividing 3 Fractions Multiplying/Dividing Fractions (three factors) Multiplying/Dividing Mixed Fractions (3 factors)

Adding Fractions

Adding fractions requires the annoying common denominator. Make it easy on your students by first teaching the concepts of equivalent fractions and least common multiples. Once students are familiar with those two concepts, the idea of finding fractions with common denominators for adding becomes that much easier. Spending time on modeling fractions will also help students to understand fractions addition. Relating fractions to familiar examples will certainly help. For example, if you add a 1/2 banana and a 1/2 banana, you get a whole banana. What happens if you add a 1/2 banana and 3/4 of another banana?

• Adding Two Proper Fractions with Equal Denominators and Proper Fraction Results Adding Two Proper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Proper Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Equal Denominators, Proper Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Equal Denominators, Proper Fractions Result, and Some Simplifying (Printable Only)
• Adding Two Proper Fractions with Equal Denominators and Mixed Fraction Results Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Result, and Some Simplifying (Printable Only)
• Adding Two Proper Fractions with Similar Denominators and Proper Fraction Results Adding Two Proper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Proper Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Similar Denominators, Proper Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Similar Denominators, Proper Fractions Result, and Some Simplifying (Printable Only)
• Adding Two Proper Fractions with Similar Denominators and Mixed Fraction Results Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Result, and Some Simplifying (Printable Only)
• Adding Two Proper Fractions with Unlike Denominators and Proper Fraction Results Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Result, and Some Simplifying (Printable Only)
• Adding Two Proper Fractions with Unlike Denominators and Mixed Fraction Results Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Result, and Some Simplifying (Printable Only)
• Adding Proper and Improper Fractions with Equal Denominators Adding Proper and Improper Fractions with Equal Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Equal Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Equal Denominators and No Simplifying (Printable Only) Adding Proper and Improper Fractions with Equal Denominators and All Simplifying (Printable Only) Adding Proper and Improper Fractions with Equal Denominators and Some Simplifying (Printable Only)
• Adding Proper and Improper Fractions with Similar Denominators Adding Proper and Improper Fractions with Similar Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Similar Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Similar Denominators and No Simplifying (Printable Only) Adding Proper and Improper Fractions with Similar Denominators and All Simplifying (Printable Only) Adding Proper and Improper Fractions with Similar Denominators and Some Simplifying (Printable Only)
• Adding Proper and Improper Fractions with Unlike Denominators Adding Proper and Improper Fractions with Unlike Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Unlike Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Unlike Denominators and No Simplifying (Printable Only) Adding Proper and Improper Fractions with Unlike Denominators and All Simplifying (Printable Only) Adding Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Printable Only)

A common strategy to use when adding mixed fractions is to convert the mixed fractions to improper fractions, complete the addition, then switch back. Another strategy which requires a little less brainpower is to look at the whole numbers and fractions separately. Add the whole numbers first. Add the fractions second. If the resulting fraction is improper, then it needs to be converted to a mixed number. The whole number portion can be added to the original whole number portion.

• Adding Two Mixed Fractions with Equal Denominators Adding Two Mixed Fractions with Equal Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Equal Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Equal Denominators and No Simplifying (Printable Only) Adding Two Mixed Fractions with Equal Denominators and All Simplifying (Printable Only) Adding Two Mixed Fractions with Equal Denominators and Some Simplifying (Printable Only)
• Adding Two Mixed Fractions with Similar Denominators Adding Two Mixed Fractions with Similar Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Similar Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Similar Denominators and Some Simplifying Adding Two Mixed Fractions with Similar Denominators and No Simplifying (Printable Only) Adding Two Mixed Fractions with Similar Denominators and All Simplifying (Printable Only) Adding Two Mixed Fractions with Similar Denominators and Some Simplifying (Printable Only)
• Adding Two Mixed Fractions with Unlike Denominators Adding Two Mixed Fractions with Unlike Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Unlike Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Unlike Denominators and No Simplifying (Printable Only) Adding Two Mixed Fractions with Unlike Denominators and All Simplifying (Printable Only) Adding Two Mixed Fractions with Unlike Denominators and Some Simplifying (Printable Only)

Subtracting Fractions

There isn't a lot of difference between adding and subtracting fractions. Both require a common denominator which requires some prerequisite knowledge. The only difference is the second and subsequent numerators are subtracted from the first one. There is a danger that you might end up with a negative number when subtracting fractions, so students might need to learn what it means in that case. When it comes to any concept in fractions, it is always a good idea to relate it to a familiar or easy-to-understand situation. For example, 7/8 - 3/4 = 1/8 could be given meaning in the context of a race. The first runner was 7/8 around the track when the second runner was 3/4 around the track. How far ahead was the first runner? (1/8 of the track).

• Subtracting Two Proper Fractions with Equal Denominators and Proper Fraction Results Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Two Proper Fractions with Similar Denominators and Proper Fraction Results Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Two Proper Fractions with Unlike Denominators and Proper Fraction Results Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Proper and Improper Fractions with Equal Denominators and Proper Fraction Results Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Proper and Improper Fractions with Similar Denominators and Proper Fraction Results Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Proper and Improper Fractions with Unlike Denominators and Proper Fraction Results Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Proper and Improper Fractions with Equal Denominators and Mixed Fraction Results Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Proper and Improper Fractions with Similar Denominators and Mixed Fraction Results Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Proper and Improper Fractions with Unlike Denominators and Mixed Fraction Results Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and Some Simplifying (Printable Only)
• Subtracting Mixed Fractions with Equal Denominators Subtracting Mixed Fractions with Equal Denominators, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Equal Denominators, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Equal Denominators, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Equal Denominators, and No Simplifying (Printable Only) Subtracting Mixed Fractions with Equal Denominators, and All Simplifying (Printable Only) Subtracting Mixed Fractions with Equal Denominators, and Some Simplifying (Printable Only)
• Subtracting Mixed Fractions with Similar Denominators Subtracting Mixed Fractions with Similar Denominators, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Similar Denominators, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Similar Denominators, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Similar Denominators, and No Simplifying (Printable Only) Subtracting Mixed Fractions with Similar Denominators, and All Simplifying (Printable Only) Subtracting Mixed Fractions with Similar Denominators, and Some Simplifying (Printable Only)
• Subtracting Mixed Fractions with Unlike Denominators Subtracting Mixed Fractions with Unlike Denominators, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Unlike Denominators, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Unlike Denominators, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Unlike Denominators, and No Simplifying (Printable Only) Subtracting Mixed Fractions with Unlike Denominators, and All Simplifying (Printable Only) Subtracting Mixed Fractions with Unlike Denominators, and Some Simplifying (Printable Only)

Adding and Subtracting Fractions

Mixing up the signs on operations with fractions worksheets makes students pay more attention to what they are doing and allows for a good test of their skills in more than one operation.

• Adding and Subtracting Proper and Improper Fractions Adding and Subtracting Proper and Improper Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Proper and Improper Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Proper and Improper Fractions with Equal Denominators and Some Simplifying (Printable Only) Adding and Subtracting Proper and Improper Fractions with Similar Denominators and Some Simplifying (Printable Only) Adding and Subtracting Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Printable Only)
• Adding and Subtracting Mixed Fractions Adding and Subtracting Mixed Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Mixed Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Mixed Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Mixed Fractions with Equal Denominators and Some Simplifying (Printable Only) Adding and Subtracting Mixed Fractions with Similar Denominators and Some Simplifying (Printable Only) Adding and Subtracting Mixed Fractions with Unlike Denominators and Some Simplifying (Printable Only) Adding/Subtracting Three Fractions/Mixed Fractions

All Operations Fractions Worksheets

• All Operations with Two Proper Fractions with Equal Denominators and Proper Fraction Results All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and No Simplifying (Printable Only) All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and All Simplifying (Printable Only) All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and Some Simplifying (Printable Only)
• All Operations with Two Proper Fractions with Similar Denominators and Proper Fraction Results All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and No Simplifying (Printable Only) All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and All Simplifying (Printable Only) All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and Some Simplifying (Printable Only)
• All Operations with Two Proper Fractions with Unlike Denominators and Proper Fraction Results All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and No Simplifying (Printable Only) All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and All Simplifying (Printable Only) All Operations with Two Proper Fractions with Unlike Denominators, Mixed Fractions Results and Some Simplifying (Printable Only)
• All Operations with Proper and Improper Fractions with Equal Denominators All Operations with Proper and Improper Fractions with Equal Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Equal Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Equal Denominators and No Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Equal Denominators and All Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Equal Denominators and Some Simplifying (Printable Only)
• All Operations with Proper and Improper Fractions with Similar Denominators All Operations with Proper and Improper Fractions with Similar Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Similar Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Similar Denominators and No Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Similar Denominators and All Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Similar Denominators and Some Simplifying (Printable Only)
• All Operations with Proper and Improper Fractions with Unlike Denominators All Operations with Proper and Improper Fractions with Unlike Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Unlike Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Unlike Denominators and No Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Unlike Denominators and All Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Printable Only)
• All Operations with Two Mixed Fractions with Equal Denominators All Operations with Two Mixed Fractions with Equal Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Equal Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Equal Denominators and No Simplifying (Printable Only) All Operations with Two Mixed Fractions with Equal Denominators and All Simplifying (Printable Only) All Operations with Two Mixed Fractions with Equal Denominators and Some Simplifying (Printable Only)
• All Operations with Two Mixed Fractions with Similar Denominators All Operations with Two Mixed Fractions with Similar Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Similar Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Similar Denominators and No Simplifying (Printable Only) All Operations with Two Mixed Fractions with Similar Denominators and All Simplifying (Printable Only) All Operations with Two Mixed Fractions with Similar Denominators and Some Simplifying (Printable Only)
• All Operations with Two Mixed Fractions with Unlike Denominators All Operations with Two Mixed Fractions with Unlike Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Unlike Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Unlike Denominators and No Simplifying (Printable Only) All Operations with Two Mixed Fractions with Unlike Denominators and All Simplifying (Printable Only) All Operations with Two Mixed Fractions with Unlike Denominators and Some Simplifying (Printable Only)
• All Operations with 3 Fractions All Operations with Three Fractions Including Some Improper Fractions All Operations with Three Fractions Including Some Negative and Some Improper Fractions

Operations with Negative Fractions Worksheets

Although some of these worksheets are single operations, it should be helpful to have all of these in the same location. There are some special considerations when completing operations with negative fractions. It is usually very helpful to change any mixed numbers to an improper fraction before proceeding. It is important to pay attention to the signs and know the rules for multiplying positives and negatives (++ = +, +- = -, -+ = - and -- = +).

• Adding with Negative Fractions Adding Negative Proper Fractions with Unlike Denominators Up to Sixths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Negative Proper Fractions with Unlike Denominators Up to Twelfths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Negative Mixed Fractions with Unlike Denominators Up to Sixths, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Adding Negative Mixed Fractions with Unlike Denominators Up to Twelfths, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Adding Negative Proper Fractions with Denominators Up to Sixths, Proper Fraction Results and Some Simplifying (Printable Only) Adding Negative Proper Fractions with Denominators Up to Twelfths, Proper Fraction Results and Some Simplifying (Printable Only) Adding Negative Mixed Fractions with Denominators Up to Sixths and Some Simplifying (Printable Only) Adding Negative Mixed Fractions with Denominators Up to Twelfths and Some Simplifying (Printable Only)
• Subtracting with Negative Fractions Subtracting Negative Proper Fractions with Unlike Denominators Up to Sixths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Negative Proper Fractions with Unlike Denominators Up to Twelfths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Negative Mixed Fractions with Unlike Denominators Up to Sixths, Mixed Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Negative Mixed Fractions with Unlike Denominators Up to Twelfths, Mixed Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Negative Proper Fractions with Denominators Up to Sixths, Proper Fraction Results and Some Simplifying (Printable Only) Subtracting Negative Proper Fractions with Denominators Up to Twelfths, Proper Fraction Results and Some Simplifying (Printable Only) Subtracting Negative Mixed Fractions with Denominators Up to Sixths and Some Simplifying (Printable Only) Subtracting Negative Mixed Fractions with Denominators Up to Twelfths and Some Simplifying (Printable Only)
• Multiplying with Negative Fractions Multiplying Negative Proper Fractions with Denominators Up to Sixths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Negative Proper Fractions with Denominators Up to Twelfths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Negative Mixed Fractions with Denominators Up to Sixths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Negative Mixed Fractions with Denominators Up to Twelfths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Negative Proper Fractions with Denominators Up to Sixths, Proper Fraction Results and Some Simplifying (Printable Only) Multiplying Negative Proper Fractions with Denominators Up to Twelfths, Proper Fraction Results and Some Simplifying (Printable Only) Multiplying Negative Mixed Fractions with Denominators Up to Sixths and Some Simplifying (Printable Only) Multiplying Negative Mixed Fractions with Denominators Up to Twelfths and Some Simplifying (Printable Only)
• Dividing with Negative Fractions Dividing Negative Proper Fractions with Denominators Up to Sixths, Mixed Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Negative Proper Fractions with Denominators Up to Twelfths, Mixed Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Negative Mixed Fractions with Denominators Up to Twelfths, Mixed Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Dividing Negative Mixed Fractions with Denominators Up to Twelfths, Mixed Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Dividing Negative Proper Fractions with Denominators Up to Sixths, Proper Fraction Results and Some Simplifying (Printable Only) Dividing Negative Proper Fractions with Denominators Up to Twelfths, Proper Fraction Results and Some Simplifying (Printable Only) Dividing Negative Mixed Fractions with Denominators Up to Sixths and Some Simplifying (Printable Only) Dividing Negative Mixed Fractions with Denominators Up to Twelfths and Some Simplifying (Printable Only)

Order of Operations with Fractions Worksheets

The order of operations worksheets in this section actually reside on the Order of Operations page, but they are included here for your convenience.

• Order of Operations with Fractions 2-Step Order of Operations with Fractions 3-Step Order of Operations with Fractions 4-Step Order of Operations with Fractions 5-Step Order of Operations with Fractions 6-Step Order of Operations with Fractions
• Order of Operations with Fractions (No Exponents) 2-Step Order of Operations with Fractions (No Exponents) 3-Step Order of Operations with Fractions (No Exponents) 4-Step Order of Operations with Fractions (No Exponents) 5-Step Order of Operations with Fractions (No Exponents) 6-Step Order of Operations with Fractions (No Exponents)
• Order of Operations with Positive and Negative Fractions 2-Step Order of Operations with Positive & Negative Fractions 3-Step Order of Operations with Positive & Negative Fractions 4-Step Order of Operations with Positive & Negative Fractions 5-Step Order of Operations with Positive & Negative Fractions 6-Step Order of Operations with Positive & Negative Fractions

Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.

Lectures, Courses, Problem Examples

Operations with Fractions

Doing operations with fractions means applying the four basic mathematical operations:  addition , subtraction , multiplication and division .

Adding and subtracting fractions with the same denominator

Adding and subtracting fraction with the same denominator is easy. All you have to do is add or subtract the numerator while the denominator remains as it is. If the fraction that we get can be reduced to lowest terms then it’s better to do so.

Exam ple 1:  Add the fractions $ \displaystyle \frac{1}{9}+\frac{2}{9}$

Since the denominator is the same we add the numerators and keep the same denominator

$\displaystyle \frac{1}{9}+\frac{2}{9}=\frac{{1+2}}{9}=\frac{3}{9}$

The we reduce the sum to the lowest term

$\displaystyle \frac{3}{9}=\frac{3}{{3\times 3}}=\frac{1}{3}$

So $\displaystyle \frac{1}{9}+\frac{2}{9}=\frac{3}{9}=\frac{1}{3}$

Example 2 : Subtract the fractions $ \displaystyle \frac{5}{7}-\frac{3}{7}$

Solution : Since the denominator is the same we substract the numerators and keep the same denominator

$ \displaystyle \frac{5}{7}-\frac{3}{7}=\frac{{5-3}}{7}=\frac{2}{7}$

So, $\displaystyle \frac{5}{7}-\frac{3}{7}=\frac{2}{7}$

Adding and subtracting fractions with different denominator

When adding and subtracting fraction with different denominators you have to turn the fractions into equivalent fractions by finding the least common denominator.Then reduce the sum into the lowest term if possible.

Example 3: Add the fractions $ \displaystyle \frac{2}{5}+\frac{3}{{15}}$

Since the fractions have diffrent denominator we find the LCD

LCD(5, 15) = 3 x 5 = 15

Converting the fractions into  equivalent fractions    with 15 as a denominator.

$\displaystyle \frac{2}{5}\times \frac{3}{3}=\frac{6}{{15}}$

$\displaystyle \frac{3}{{15}}$ is a fraction with the denominator 15 so no need to be converted.

Now since our fractions have similar denominators we add the numerators, the denominator stays the same and then we reduce the sum.

$\displaystyle \frac{6}{{15}}+\frac{3}{{15}}=\frac{9}{{15}}=\frac{3}{5}$

So, $ \displaystyle \frac{2}{5}+\frac{3}{{15}}=\frac{3}{5}$

Example 4 : Subtract the fraction $ \displaystyle \frac{1}{{12}}-\frac{2}{9}$

We find the LCD since we have different denominators

12 = 2 x 2 x 3

LCD(9, 12) = 2 x 2 x 3 x 3 = 36

Converting the fractions into equivalent fractions with 36 as a denominator.

$ \displaystyle \frac{1}{{12}}\times \frac{3}{3}=\frac{3}{{36}}$

$\displaystyle \frac{2}{9}\times \frac{4}{4}=\frac{8}{{36}}$

Now since the fractions have similar denominators we substract the numerators, the denominator stays the same.

$ \displaystyle \frac{3}{{36}}-\frac{8}{{36}}=-\frac{5}{{36}}$.

So,$ \displaystyle \frac{1}{{12}}-\frac{2}{9}=-\frac{5}{{36}}$

Adding and subtracting a fraction with a mixed one or two mixed fractions

• Convert the mixed fraction into a improper fraction.
• If the proper fractions have unlike denominators then find the LCD and change the fractions into equivalent one.
• Subtract or add the numerators and leave the dominator as it is.
• Reduce to lowest term if possible.

Example 5: Add the fractions $\displaystyle \frac{6}{7}+2\frac{3}{5}$

Firstly we convert the mixed fraction $\displaystyle 2\frac{3}{5}$ into a improper one .

The whole number is 2 and the denominator is 5, so 5 x 2 = 10

We add the product 10 to the numerator of our fraction: 3+10=13

Since the denominator stays the same our improper fraction is: $\displaystyle \frac{{13}}{5}$

The fractions $\displaystyle\frac{6}{7}$ and $\displaystyle \frac{{13}}{5}$ have diffrent denominators, so we find the LCD to turn them into equivalent one´s.

LCD(7, 5) = 35

$ \displaystyle \frac{6}{7}\times \frac{5}{5}=\frac{{30}}{{35}}$

$\displaystyle \frac{{13}}{5}\times \frac{7}{7}=\frac{{91}}{{35}}$

Add the numerators and leave the denominator as it is :$\displaystyle \frac{{30}}{{35}}+\frac{{91}}{{35}}=\frac{{121}}{{35}}$

So, $\displaystyle \frac{6}{7}+2\frac{3}{5}=\frac{{121}}{{35}}$

Example 6: Subtract the mixed fractions $ \displaystyle 3\frac{2}{7}-2\frac{3}{4}$

Firstly convert the mixed fractions into improper one.

$\displaystyle 2\frac{3}{4}=\frac{{11}}{4}$ and $\displaystyle 3\frac{2}{7}=\frac{{23}}{7}$

Since they have different denominator we change them into equaivalent fractions by finding the LCD.

LCD(4,7)=28

$ \displaystyle \frac{{11}}{4}\times \frac{7}{7}=\frac{{77}}{{28}}$

$\displaystyle \frac{{23}}{7}\times \frac{4}{4}=\frac{{92}}{{28}}$

Subtract the numerators and leave the denominator as it is:

$\displaystyle \frac{{92}}{{28}}-\frac{{77}}{{28}}=\frac{{15}}{{28}}$

So,  $ \displaystyle 3\frac{2}{7}-2\frac{3}{4}=$

$ \displaystyle \frac{{92}}{{28}}-\frac{{77}}{{28}}=\frac{{15}}{{28}}$

Adding and Subtracting Fractions by Using Formulas

There is an easy way to add and subtract fractions without having to find the LCD. This method consist in using formulas that involves cross multiplication of the fractions.

Adding  Fraction

The formula for adding fractions is:

$\displaystyle \frac{a}{b}+\frac{c}{d}=\frac{{ad+bc}}{{bd}}$

Subtracting Fraction

The formula for subtracting fractions is:

$\displaystyle \frac{a}{b}-\frac{c}{d}=\frac{{ad-cd}}{{bd}}$

Example 7:  Add $ \displaystyle \frac{5}{9}+\frac{2}{5}$by using the formula above.

Solution : $\displaystyle \frac{5}{9}+\frac{2}{5}=\frac{{(5\times 5)+(9\times 2)}}{{9\times 5}}=\frac{{25+18}}{{45}}=\frac{{43}}{{45}}$

Example 8:  Subtract$\displaystyle \frac{2}{3}-\frac{3}{9}$ by using the formula above.

Solution : $\displaystyle \frac{2}{3}-\frac{3}{9}=\frac{{(2\times 9)-(3\times 3)}}{{3\times 9}}=\frac{{18-9}}{{27}}=\frac{9}{{27}}=\frac{1}{3}$

Multiplying and Dividing Fractions

$ \displaystyle n(A\cup B)=n(A)+n(B)-n(A\cap B)$

$ \displaystyle n(A\cap B)=n(A)+n(B)-n(A\cup B)$

$ \displaystyle n(A\cap B)=12+10-18=4$

$ \displaystyle n(A/B)=n(A)-n(A\cap B)$

$ \displaystyle n(A/B)=12-4=8$

Multiplying Fractions Multiplying fractions is even easier than adding and substracting them.All you have to do is multiply the numerators  and the denominators of the fraction then reduce the fraction if possible.If mixed fractions are involved don`t forget to turn them to improper fractions.

The formula for multiplying fractions is:  $\displaystyle \frac{a}{b}\times \frac{c}{d}=\frac{{ac}}{{bd}}$

Example 9:  Multiply $\displaystyle \frac{2}{9}\times \frac{3}{5}$.

Solution:   $\displaystyle \frac{2}{9}\times \frac{3}{5}=\frac{{(2\times 3)}}{{(9\times 5)}}=\frac{6}{{45}}=\frac{2}{{15}}$

Example 10:  Multiply $\displaystyle 2\frac{1}{7}\times \frac{3}{8}$.

Solution:  Firstly we have to turn the mixed fraction into a improper one.

$\displaystyle 2\frac{1}{7}=\frac{{15}}{7}$

Then we multiply by using the formula above.

$\displaystyle 2\frac{1}{7}\times \frac{3}{8}=\frac{{15}}{7}\times \frac{3}{8}=\frac{{45}}{{56}}$

Dividing Fractions

Dividing two fractions is the same as multiplying the first fraction with the reciprocal of the second fraction. So all you have to do is keep the first fraction, change the division sign to multiplication and then flip the second fraction. Then we use the multiplication formula. Don´t forget to reduce the fraction if possible. If it´s easier for you, you can apply directly the formula for dividing fractions.

The formula for dividing fractions is:  $ \displaystyle \frac{a}{b}\div \frac{c}{d}=\frac{{ad}}{{bc}}$

Example 11:  Divide $\displaystyle \frac{2}{4}\div \frac{5}{9}$.

Three simply steps:

Keep the first fraction, flip the second one and then multiply them.

$\displaystyle \frac{2}{4}\div \frac{5}{9}=\frac{2}{4}\times \frac{9}{5}=\frac{{18}}{{20}}=\frac{9}{{10}}$

Using the formula

$ \displaystyle \frac{2}{4}\div \frac{5}{9}=\frac{{(2\times 9)}}{{(4\times 5)}}=\frac{{18}}{{20}}=\frac{9}{{10}}$

Share this:

Related posts:.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 3: Operations on fractions

Mixed fractions.

• Writing mixed numbers as improper fractions (Opens a modal)
• Writing improper fractions as mixed numbers (Opens a modal)
• Write mixed numbers and improper fractions Get 5 of 7 questions to level up!

Fractions on the number line

• Fractions on a number line (Opens a modal)
• Fractions greater than 1 on the number line (Opens a modal)
• Fractions on the number line Get 5 of 7 questions to level up!
• Fractions greater than 1 on the number line Get 3 of 4 questions to level up!

Multiplication of fractions

• Intro to multiplying 2 fractions (Opens a modal)
• Multiplying 2 fractions: number line (Opens a modal)
• Multiply fractions and whole numbers Get 5 of 7 questions to level up!
• Multiplying fractions Get 5 of 7 questions to level up!

Division of fractions

• Understanding division of fractions (Opens a modal)
• Dividing unit fractions by whole numbers Get 3 of 4 questions to level up!
• Dividing whole numbers by unit fractions Get 3 of 4 questions to level up!
• Dividing fractions Get 3 of 4 questions to level up!

Word problems on fractions

• Multiplying fractions word problem: laundry (Opens a modal)
• Dividing fractions by whole numbers: studying (Opens a modal)
• Multiply fractions word problems Get 3 of 4 questions to level up!
• Divide fractions and whole numbers word problems Get 3 of 4 questions to level up!

Number Sense

Understanding numbers, their relationships and numerical reasoning

Using symbols to solve equations and express patterns

Studying shapes, sizes and spatial relationships in mathematics

Measurement

Quantifying and comparing attributes like length, weight and volume

Performing mathematical operations like addition, subtraction, division

Probability and Statistics

Analyzing uncertainty and likelihood of events and outcomes

Calculator Suite

Exploring functions, solving equations, constructing geometric shapes

Graphing Calculator

Visualizing equations and functions with interactive graphs and plots

Exploring geometric concepts and constructions in a dynamic environment

3D Calculator

Graphing functions and performing calculations in 3D

Scientific Calculator

Performing calculations with fractions, statistics and exponential functions

Exploring apps bundle including free tools for geometry, spreadsheet and CAS

Operations with Fractions

Learn and practice operating with fractions with interactive resources from GeoGebra.

Upper Elementary

Adding and subtracting fractions and mixed numbers.

Add and subtract fractions and mixed numbers using models and pictures to explain the process and record the results in number and word problems.

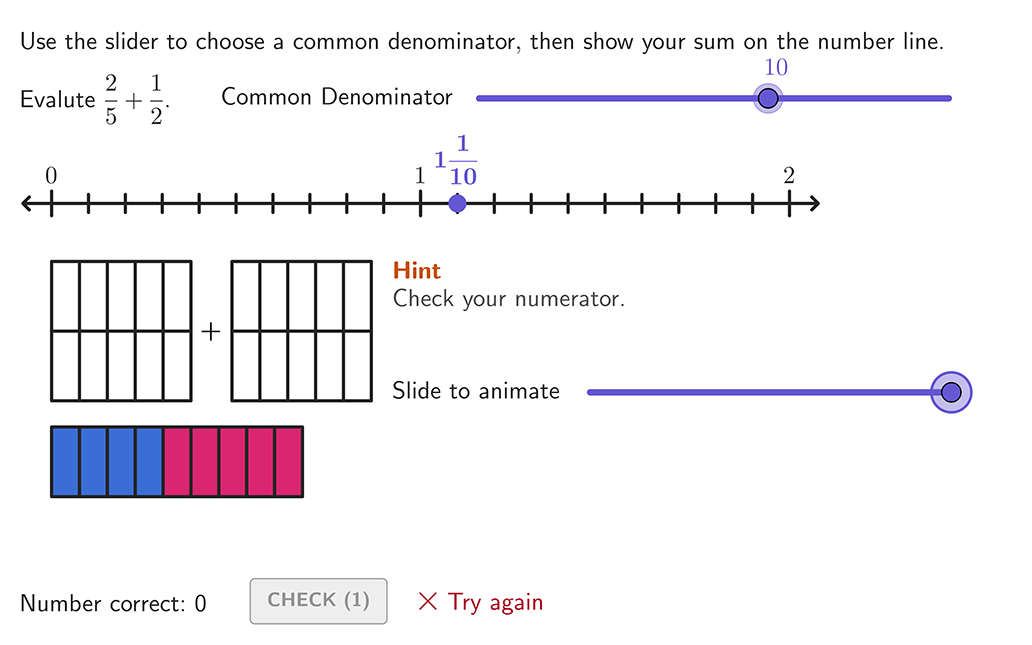
Adding Fractions with Like and Unlike Denominators

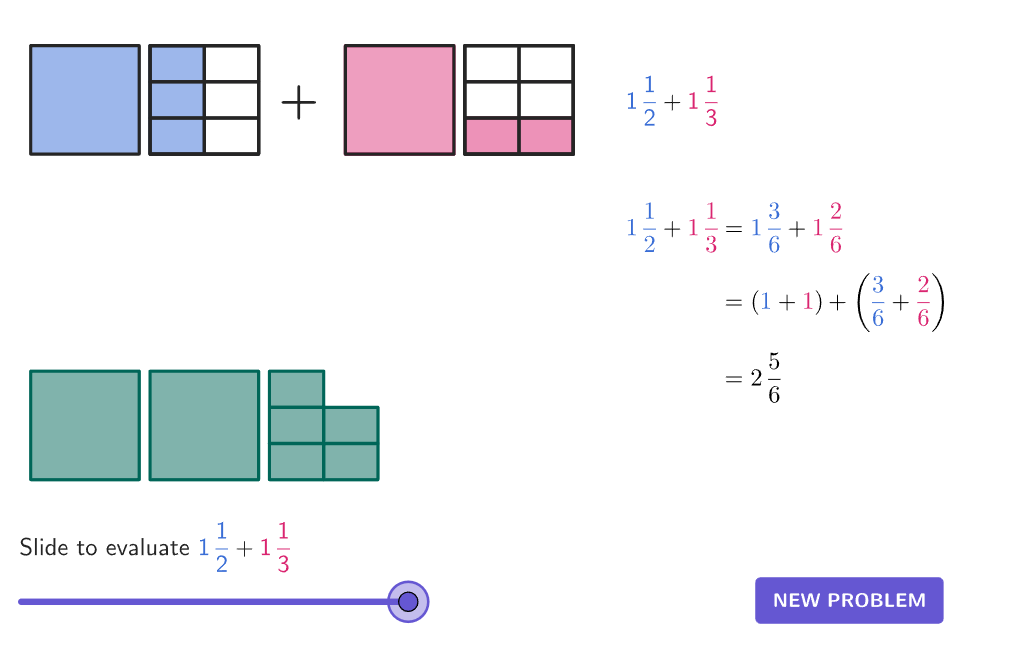
Adding and Subtracting Mixed Numbers Using Visual Models

Adding and subtracting fractions or mixed numbers with like denominators.

Add and subtract fractions and mixed numbers with like denominators (without regrouping) in number and word problems.

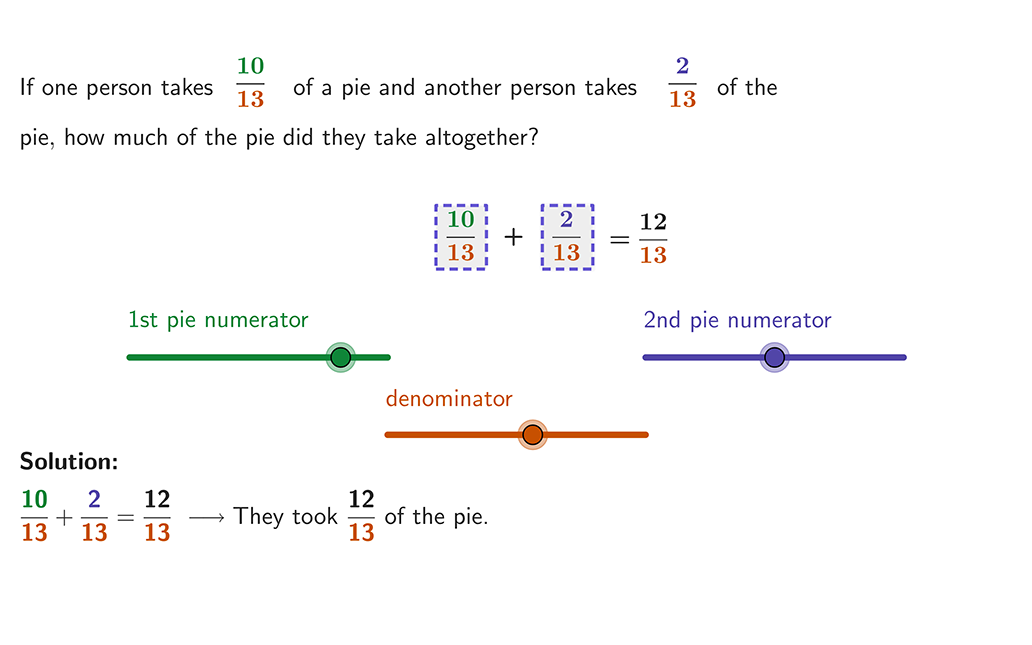
Adding Fractions with Like Denominators in Word Problems

Adding Fractions with Like Denominators

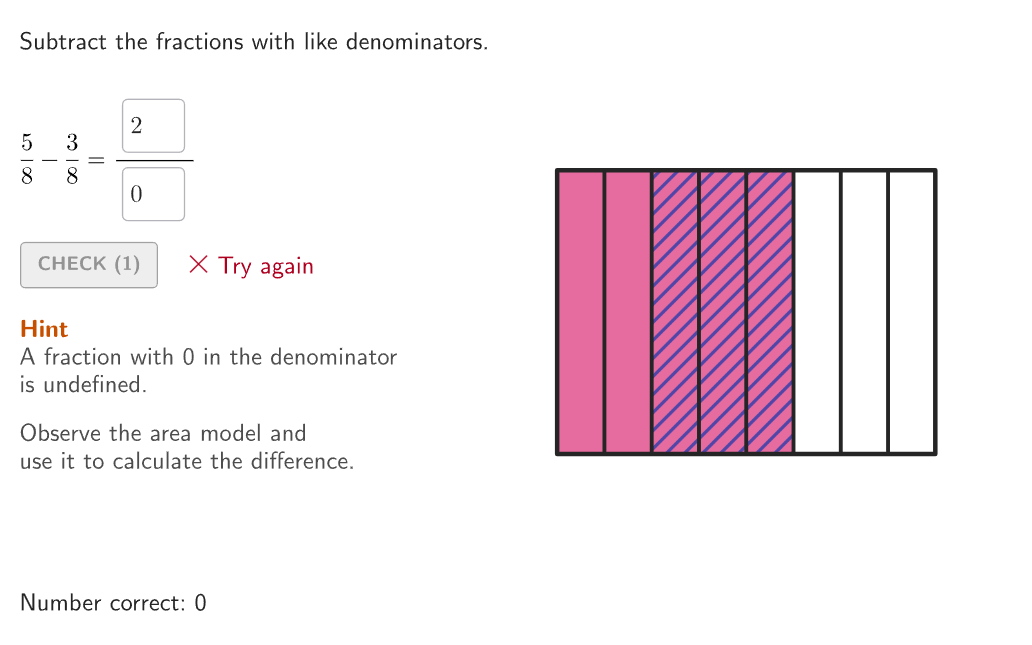
Subtracting Fractions with Like Denominators

Adding and subtracting fractions and mixed numbers with unlike denominators.

Add and subtract fractions and mixed numbers with unlike denominators in number and word problems.

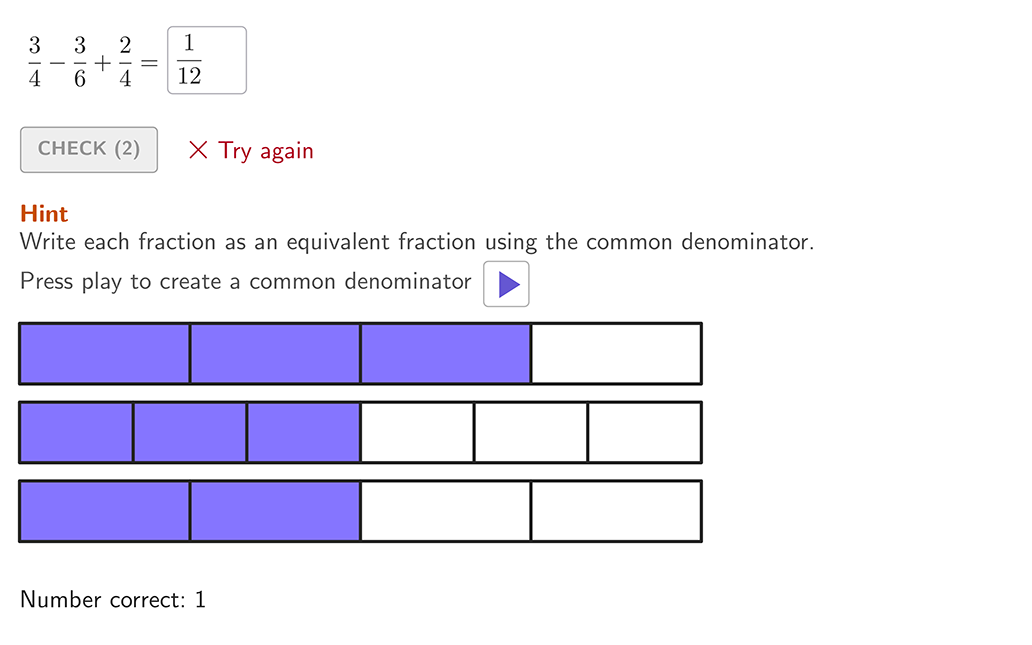
Adding and Subtracting Multiple Fractions With Unlike Denominators

Combinations of fractions.

Identify combinations of fractions that make one whole.

Making One Whole Using Fraction Tiles

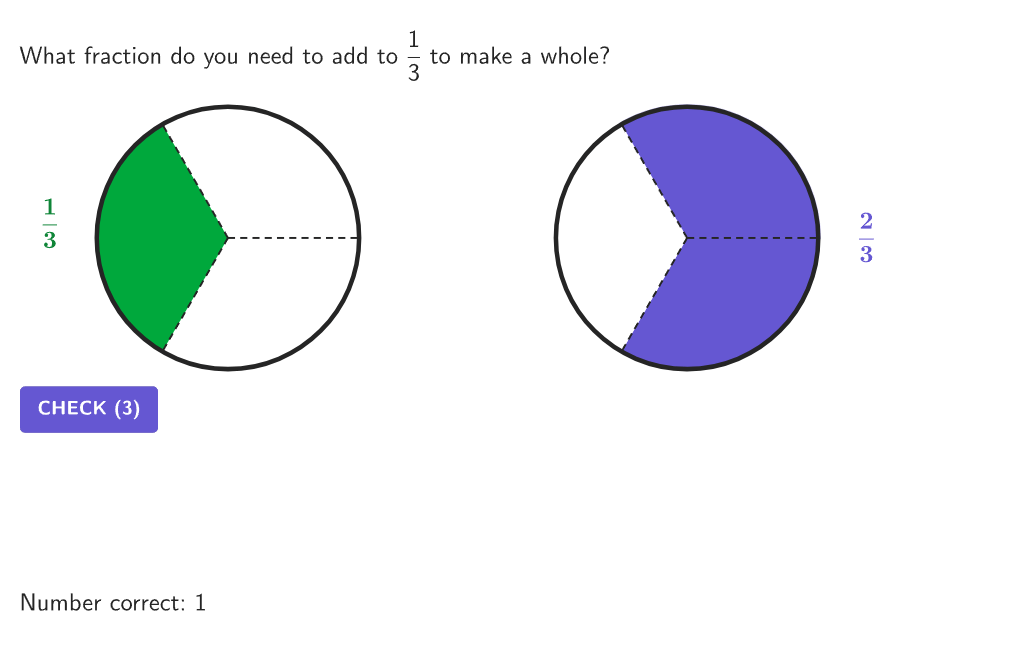
Finding the Missing Fraction to Make a Whole

Dividing fractions.

Divide two fractions or a fraction and a whole number in number or word problems.

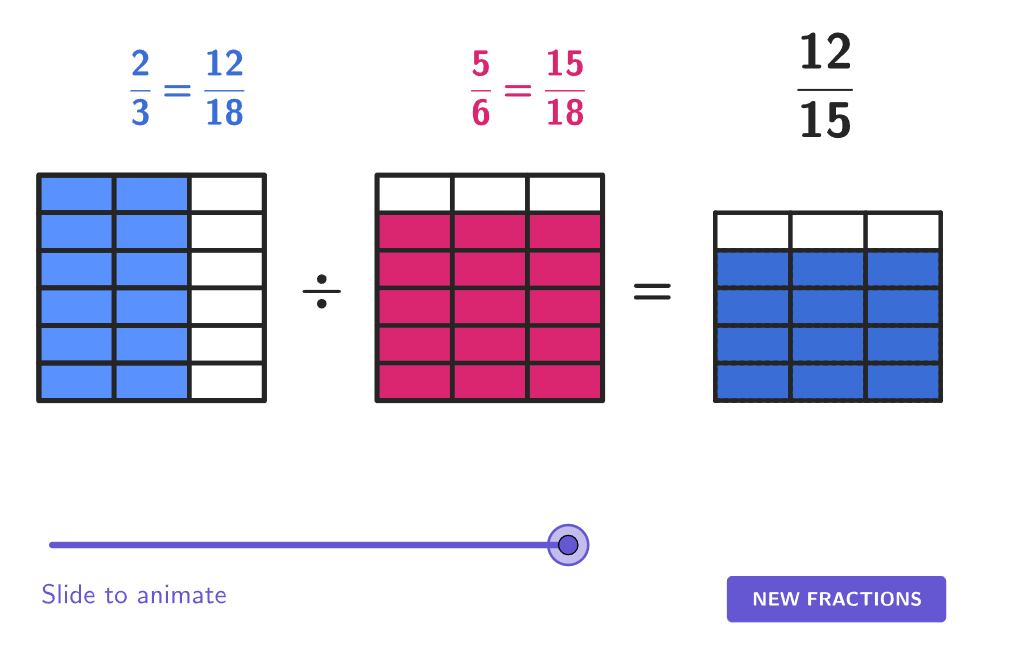
Dividing Fractions Using Visual Models

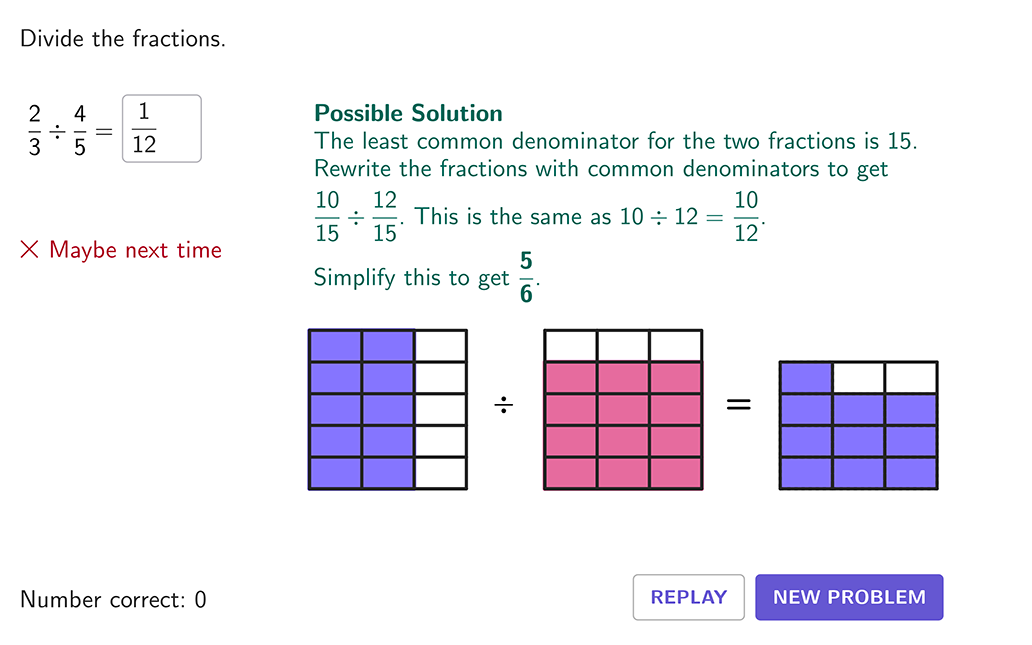
Dividing Unit Fractions

Represent division of a unit fraction by a whole number or a whole number by a unit fraction using models to explain the process in number and word problems.

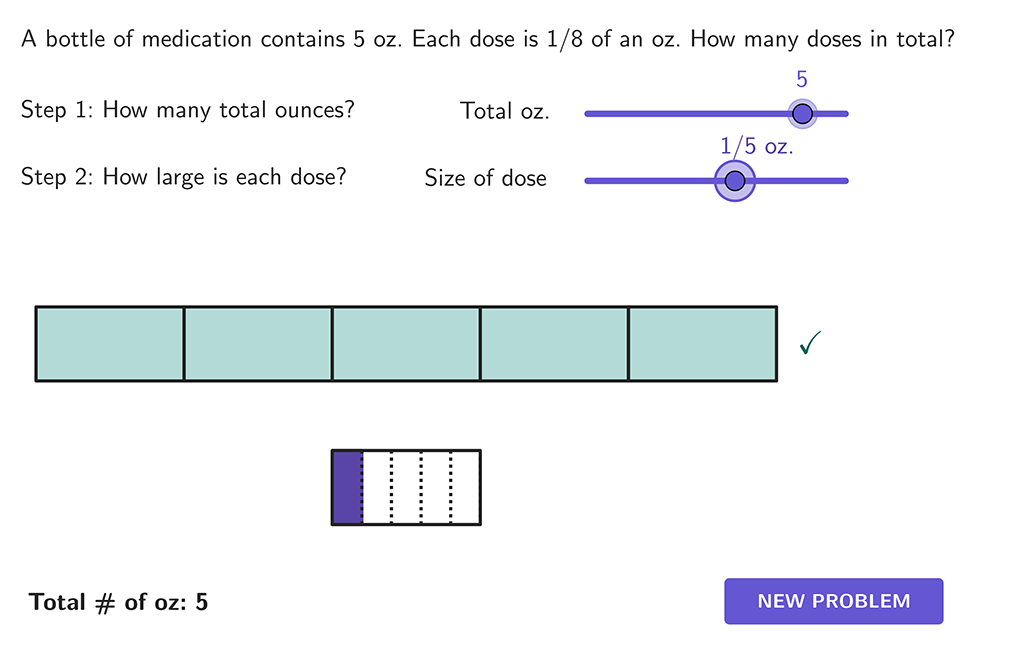
Dividing Whole Numbers by Unit Fractions

Estimating sums and differences of fractions and mixed numbers.

Estimate sums and differences with fractions and mixed numbers.

Estimating Sums of Fractions and Mixed Numbers Using a Number Line

Finding the fractional part.

Find the fractional part of a whole number or fraction with and without models and pictures.

Modeling the Fractional Part of a Set

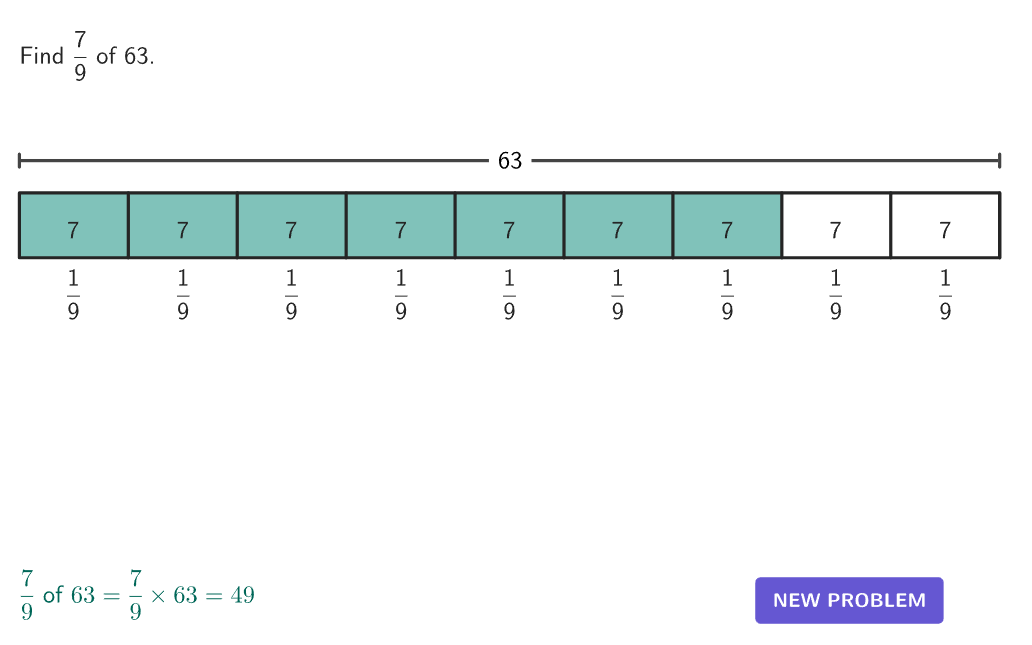
Modeling the Fractional Part of a Whole Number

Finding the Fractional Part of a Whole Number

Fraction as division.

Represent division of whole numbers as a fraction in number and word problems.

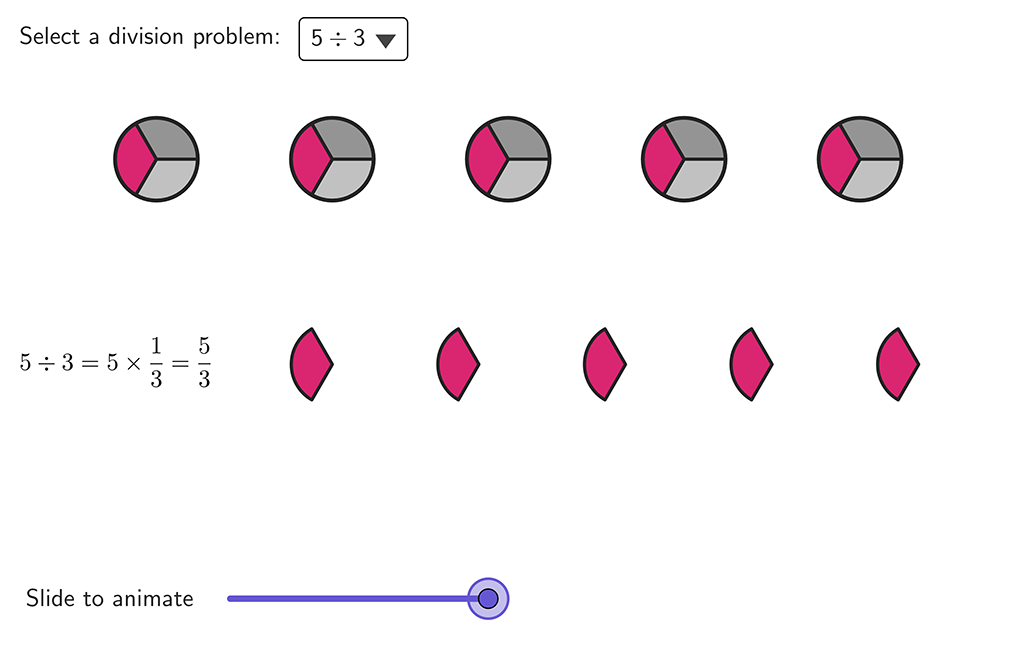
Modeling Division as a Fraction

Multiplying fractions.

Multiply two fractions or a fraction and a whole number in number and word problems.

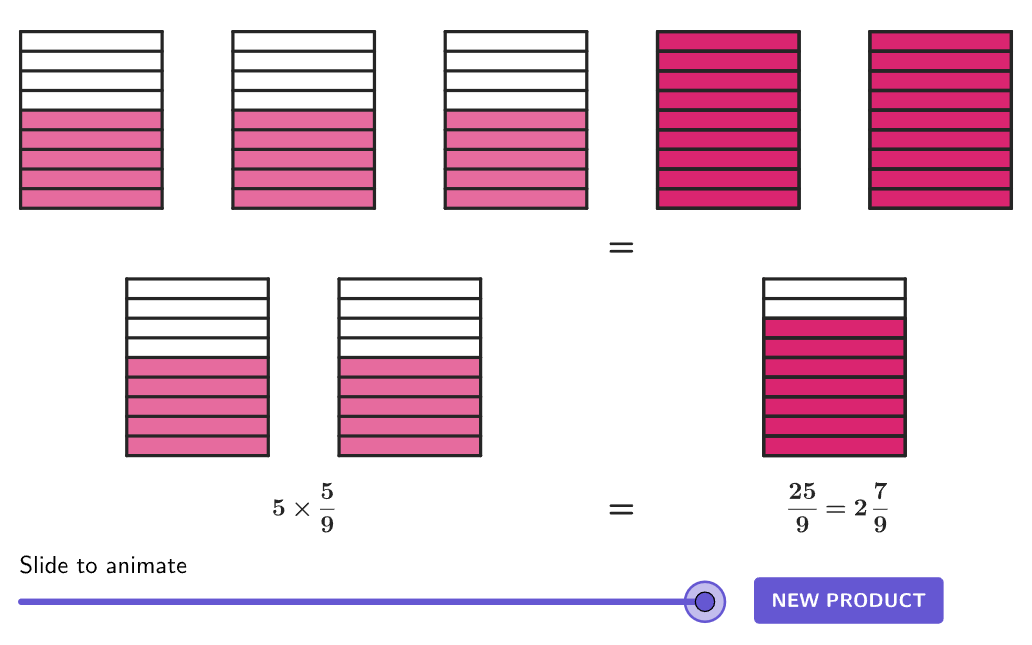
Whole Number of Fractions

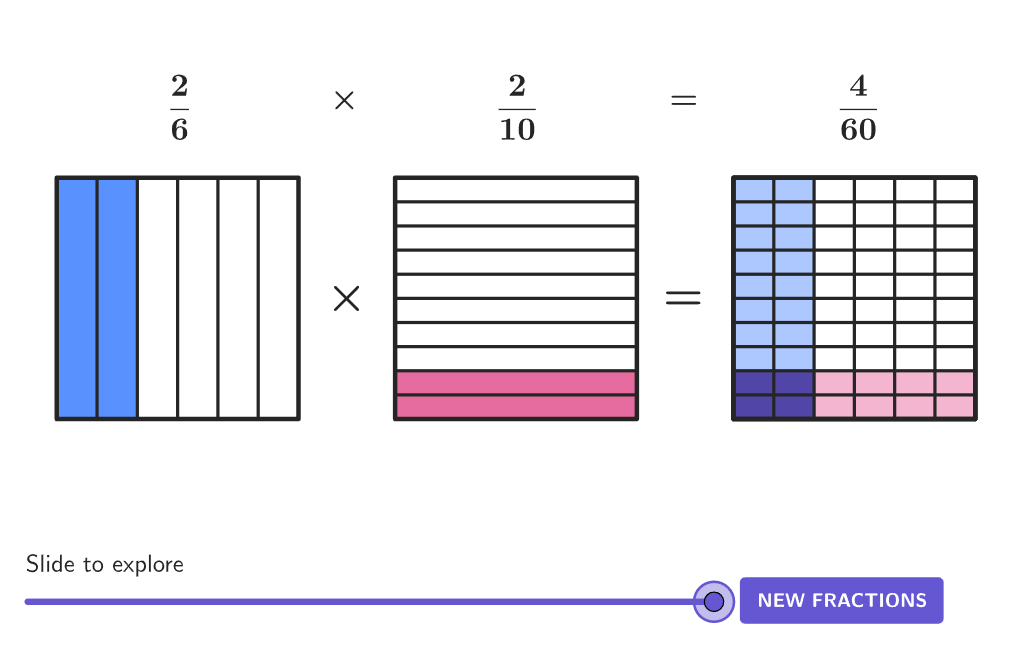
Multiplying Fractions Using Visual Models

Unit fractions.

Use models to represent a fraction as a product of a whole number and a unit fraction in number and word problems.

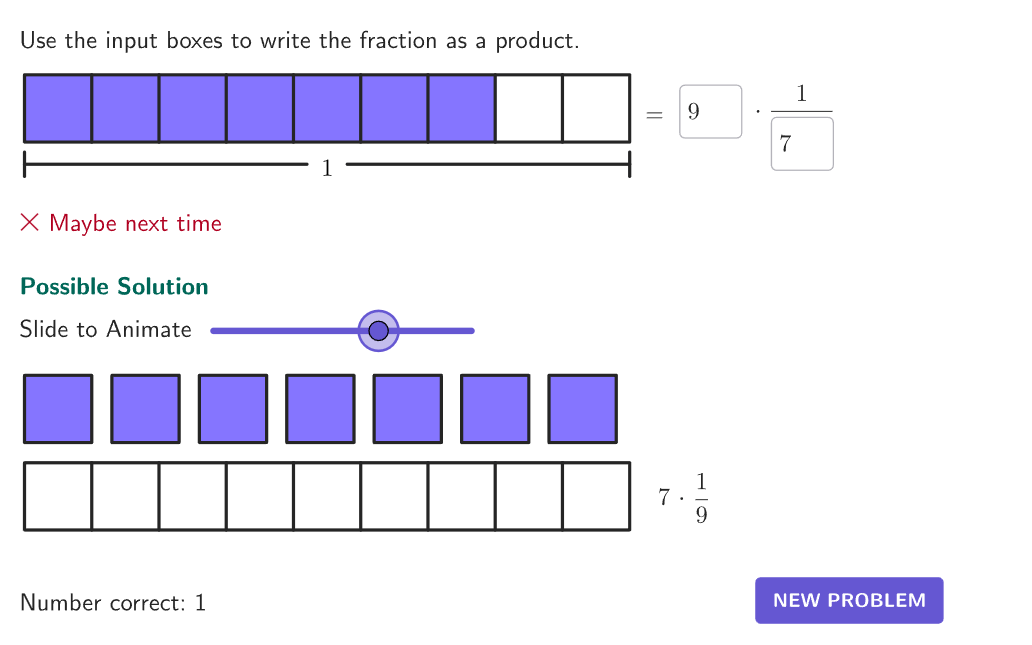
Writing Fractions as a Product of Unit Fractions Using a Tape Diagram

Middle school, dividing fractions and mixed numbers.

Represent division of fractions and mixed numbers with and without models and pictures in number and word problems; describe the inverse relationship between multiplication and division.

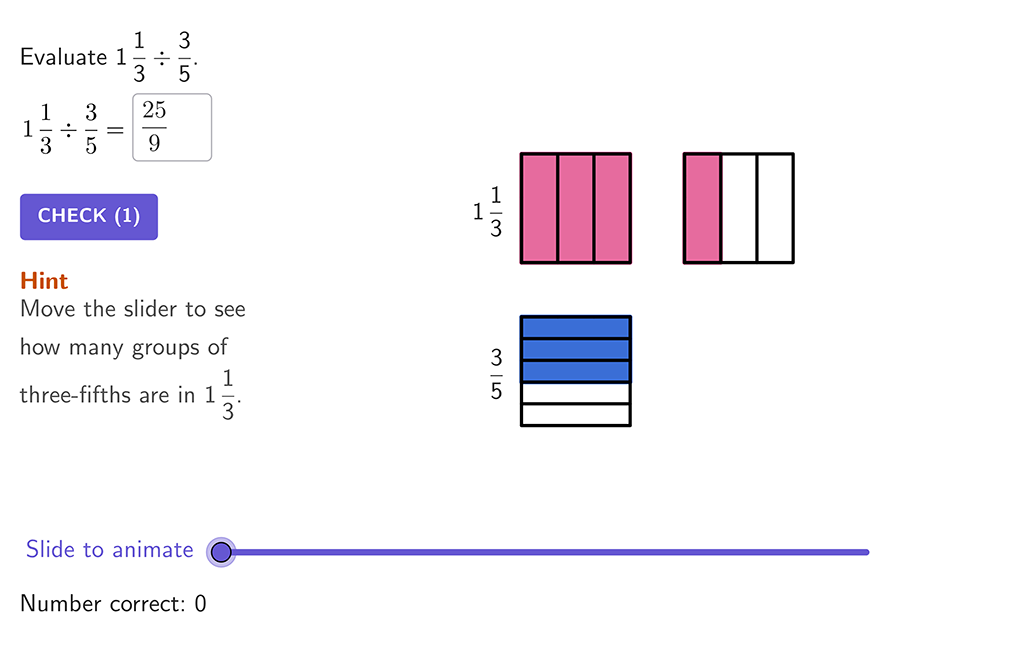
Mixed Number and Fraction Division

Estimating products and quotients of fractions and mixed numbers.

Estimate products and quotients of decimals or of mixed numbers.

Estimating Products of Decimals Using Area Models

Related topics.

Absolute Value

Decimal Numbers

Mathematical Expressions

Mixed Numbers

Multiplication

Community Resources

Explore an extensive collection of over one million math and science activities, exercises and lessons meticulously crafted by our global GeoGebra community. Immerse yourself in the boundless possibilities that await you.

Get started using GeoGebra today

Create a free account so you can save your progress any time and access thousands of math resources for you to customize and share with others

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.8: Order of Operations with Fractions

• Last updated
• Save as PDF
• Page ID 24081

• David Arnold
• College of the Redwoods

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Let’s begin by taking powers of fractions. Recall that

\[ a^m = \underbrace{a \cdot a \cdot ... \cdot a}_{m \text{ times}}\nonumber \]

Simplify: (−3/4) 2 .

By definition,

\[ \begin{aligned} \left( - \frac{3}{4} \right)^2 = \left( - \frac{3}{4} \right) \left( - \frac{3}{4} \right) ~& \textcolor{red}{ \text{ Fact: } a^2 = a \cdot a.} \\ = \frac{3 \cdot 3}{4 \cdot 4} ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply numerators and denominators.} \\ \text{ Product of even number of negative factors is positive.} \end{array}} \\ = \frac{9}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

\[ \left( - \frac{2}{5} \right)^2\nonumber \]

Simplify: (−2/3) 3 .

\[ \begin{aligned} \left( - \frac{2}{3}\right)^3 = \left( - \frac{2}{3} \right) \left( - \frac{2}{3} \right) \left( - \frac{2}{3} \right) ~ & \textcolor{red}{ \text{ Fact: } a^3 = a \cdot a \cdot a.} \\ = - \frac{2 \cdot 2 \cdot 2}{3 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array} ~ \text{ Multiply numerators and denominators.} \\ \text{ Product of odd number of negative factors is negative.} \end{array}} \\ = - \frac{8}{27} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

\[ \left( - \frac{1}{6} \right)^3\nonumber \]

−1/216

The last two examples reiterate a principle learned earlier.

Odd and Even

• The product of an even number of negative factors is positive.
• The product of an odd number of negative factors is negative.

Order of Operations

For convenience, we repeat here the rules guiding order of operations.

Rules Guiding Order of Operations

When evaluating expressions, proceed in the following order.

• Evaluate expressions contained in grouping symbols first. If grouping symbols are nested, evaluate the expression in the innermost pair of grouping symbols first.
• Evaluate all exponents that appear in the expression.
• Perform all multiplications and divisions in the order that they appear in the expression, moving left to right.
• Perform all additions and subtractions in the order that they appear in the expression, moving left to right.

Simplify: \(- \frac{1}{2} + \frac{1}{4} \left( - \frac{1}{3} \right)\).

Multiply first, then add.

\[ \begin{aligned} - \frac{1}{2} + \frac{1}{4} \left( - \frac{1}{3} \right) = - \frac{1}{2} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{4} \left( - \frac{1}{3} \right) = - \frac{1}{12}.} \\ = - \frac{1 \cdot \textcolor{red}{6}}{2 \cdot \textcolor{red}{6}} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 12.}} \\ = - \frac{6}{12} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = - \frac{7}{12} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

Simplify: \( - \frac{2}{3} + \frac{3}{4} \left( - \frac{1}{2} \right)\)

−25/24

Simplify: \(2 \left( - \frac{1}{2} \right)^2 +4 \left( - \frac{1}{2} \right)\).

Exponents first, then multiply, then add.

\[ \begin{aligned} 2 \left( - \frac{1}{2} \right)^2 + 4 \left( - \frac{1}{2} \right) = 2 \left( \frac{1}{4} \right) + 4 \left( - \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Exponent first: } \left( - \frac{1}{2} \right)^2 = \frac{1}{4}.} \\ = \frac{1}{2} + \left( - \frac{2}{1} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply: } 2 \left( \frac{1}{4} \right) = \frac{1}{2} \\ \text{ and } 4 \left( - \frac{1}{2} \right) = - \frac{2}{1}. \end{array}} \\ = \frac{1}{2} + \left( - \frac{2 \cdot \textcolor{red}{2}}{1 \cdot \textcolor{red}{2}} \right) ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 2.}} \\ = \frac{1}{2} + \left( - \frac{4}{2} \right) ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = - \frac{3}{2} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

Simplify: \(3 \left( - \frac{1}{3} \right)^2 - 2 \left( - \frac{1}{3} \right)\)

Given a = −3/4, b = 1/2, c = 1/3, and d = −1/4, evaluate the expression ab − cd .

Recall that it is good practice to prepare parentheses before substituting.

\[ ad - bc = ( ~ ) (~) - (~)(~)\nonumber \]

Substitute the given values into the algebraic expression, then simplify using order of operations.

\[ \begin{aligned} ab - cd = \left( - \frac{3}{4} \right) \left( \frac{1}{2} \right) - \left( \frac{1}{3} \right) \left( - \frac{1}{4} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Substitute: } -3/4 \text{ for } a, ~ 1/2 \text{ for } b, \\ 1/3 \text{ for } c, ~ \text{ and } -1/4 \text{ for } d. \end{array}} \\ = - \frac{3}{8} - \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply first: } \left( - \frac{3}{4} \right) \left( \frac{1}{2} \right) = - \frac{3}{8} \\ \text{ and } \left( \frac{1}{3} \right) \left( - \frac{1}{4} \right) = - \frac{1}{12}. \end{array}} \\ = - \frac{3}{8} + \frac{1}{12} ~ & \textcolor{red}{ \text{ Subtract by adding opposite.}} \\ = - \frac{3 \cdot \textcolor{red}{3}}{8 \cdot \textcolor{red}{3}} + \frac{1 \cdot \textcolor{red}{2}}{12 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions; LCD = 24.}} \\ = - \frac{9}{24} + \frac{2}{24} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = - \frac{7}{24} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

Given a = −1/2, b = 1/3, and c = −1/5, evaluate a + bc .

−17/30

Given a = −1/4 and b = 1/2, evaluate ( a 2 − b 2 ) ÷ ( a + b ).

\[ (a^2 - b^2 ) \div (a+b) - \left( (~)^2 - (~)^2 \right) \div \left( (~) + (~) \right)\nonumber \]

Substitute the given values into the algebraic expression, then evaluate exponents first.

\[ \begin{array}{l} (a^2 -b^2) \div (a+b) & = \left( \left( - \frac{1}{4} \right)^2 - \left( \frac{1}{2} \right)^2 \right) \div \left( \left( - \frac{1}{4} \right) + \left( \frac{1}{2} \right) \right) \\ ~ & = \left( \frac{1}{16} - \frac{1}{4} \right) \div \left( - \frac{1}{4} + \frac{1}{2} \right) \end{array}\nonumber \]

We must evaluate parentheses first. Inside each set of parentheses, create equivalent fractions and perform subtractions and additions next.

\[ \begin{array}{l} = \left( \frac{1}{16} - \frac{1 \cdot 4}{4 \cdot 4} \right) \div \left( - \frac{1}{4} + \frac{1 \cdot 2}{2 \cdot 2} \right) \\ = \left( \frac{1}{16} - \frac{4}{16} \right) \div \left( - \frac{1}{4} + \frac{2}{4} \right) \\ = - \frac{3}{16} \div \frac{1}{4} \end{array}\nonumber \]

Invert and multiply.

\[ \begin{aligned} = - \frac{3}{16} \cdot \frac{4}{1} \\ = - \frac{12}{16} \end{aligned}\nonumber \]

\[ \begin{aligned} = - \frac{12 \div 4}{16 \div 4} \\ - \frac{3}{4} \end{aligned}\nonumber \]

Note: In the last step, you could also reduce by prime factoring numerator and denominator and canceling common factors.

Give a = −1/2 and b = −1/3, evaluate ab ÷ ( a + b ).

Complex Fractions

When the numerator and denominator of a fraction contain fractions themselves, such an expression is called a complex fraction .

You can use the standard order of operations to simplify a complex fraction. Recall the advice when a fraction is present.

Fractional Expressions

If a fractional expression is present, simplify the numerator and denominator separately, then divide.

\[ \frac{ - \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}}\nonumber \]

We have addition in the numerator, subtraction in the denominator. In each case, we need equivalent fractions with a common denominator.

\[ \begin{aligned} \frac{- \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}} = \frac{- \frac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \frac{1 \cdot \textcolor{red}{2}}{3 \cdot \textcolor{red}{2}}} ~ & \textcolor{red}{ \text{ Create equivalent fractions.}} \\ = \frac{- \frac{3}{6} + \frac{2}{6}}{ \frac{3}{4} - \frac{6}{4}} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = \frac{- \frac{1}{6}}{- \frac{3}{4}} ~ & \textcolor{red}{ \begin{array}{l} ~ \text{ Numerator: } - \frac{3}{6} + \frac{2}{6} = - \frac{1}{6}. \\ \text{ Denominator: } \frac{3}{4} - \frac{6}{4} = - \frac{3}{4}. \end{array}} \end{aligned}\nonumber \]

The last expression asks us to divide. Invert and multiply.

\[ \begin{aligned} = - \frac{1}{6} \div \left( - \frac{3}{4} \right) ~ & \textcolor{red}{ \text{ A complex fraction means divide.}} \\ = - \frac{1}{6} \cdot \left( - \frac{4}{3} \right) ~ & \textcolor{red}{ \text{ Invert and multiply.}} \end{aligned}\nonumber \]

Like signs (two negatives) give a positive product. Multiply numerators and denominators, then reduce.

\[ \begin{aligned} = \frac{4}{18} ~ & \textcolor{red}{ \begin{array}{l} \text{ Like signs yields positive answer.} \\ \text{ Multiply numerators and denominators.} \end{array}} \\ = \frac{4 \div 2}{18 \div 2} ~ & \textcolor{red}{ \text{ Divide both numerator and denominator by 2.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Alternatively, one could prime factor and cancel to reduce to lowest terms; that is,

\[ \begin{aligned} \frac{4}{18} = \frac{2 \cdot 2}{2\cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = \frac{ \cancel{2} \cdot 2}{ \cancel{2} \cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

\[ \frac{ \frac{1}{4} - \frac{1}{3}}{ \frac{1}{4} + \frac{1}{3}}\nonumber \]

Clearing Fractions

An alternate technique for simplifying complex fractions is available.

Clearing Fractions from Complex Fractions

You can clear fractions from a complex fraction using the following algorithm:

• Determine an LCD1 for the numerator.
• Determine an LCD2 for the denominator.
• Determine an LCD for both LCD1 and LCD2.
• Multiply both numerator and denominator by this “combined” LCD.

Let’s apply this technique to the complex fraction of Example 7.

\[ \frac{- \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}}\nonumber \]

As we saw in the solution in Example 7, common denominators of 6 and 4 were used for the numerator and denominator, respectively. Thus, a common denominator for both numerator and denominator would be 12. We begin the alternate solution technique by multiplying both numerator and denominator by 12.

\[ \begin{aligned} \frac{ - \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}} = \frac{ \textcolor{red}{12} \left( - \frac{1}{2} + \frac{1}{3} \right)}{ \textcolor{red}{12} \left( \frac{3}{4} - \frac{3}{2} \right)} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 12.}} \\ = \frac{ \textcolor{red}{12} \left( - \frac{1}{2} \right) + \textcolor{red}{12} \left( \frac{1}{3} \right)}{ \textcolor{red}{12} \left( \frac{3}{4} \right) - \textcolor{red}{12} \left( \frac{3}{2} \right)} ~ & \textcolor{red}{ \text{ Distribute the 12.}} \\ = \frac{-6+4}{9-18} ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply: } 12(-1/2)=-6,~ 12(1/2) = 4. \\ 12(3/4)=9, \text{ and } 12(3/2)=18. \end{array}} \\ = \frac{-2}{-9} ~ & \textcolor{red}{ \text{ Simplify.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Like signs yield positive.}} \end{aligned}\nonumber \]

Simplify: \( \frac{- \frac{2}{3} + \frac{1}{5}}{ \frac{4}{5} - \frac{1}{2}}\)

−14/9

Application — Trapezoid

A trapezoid is a special type of quadrilateral (four-sided polygon).

A quadrilateral with one pair of parallel opposite sides is called a trapezoid .

The pair of parallel sides are called the bases of the trapezoid. Their lengths are marked by the variables b 1 and b 2 in the figure above. The distance between the parallel bases is called the height or altitude of the trapezoid. The height is marked by the variable h in the figure above.

Mathematicians use subscripts to create new variables. Thus, b 1 (“ b sub 1”) and b 2 (“ b sub 2”) are two distinct variables, used in this case to represent the length of the bases of the trapezoid.

By drawing in a diagonal, we can divide the trapezoid into two triangles (see Figure 4.14).

We can find the area of the trapezoid by summing the areas of the two triangles.

• The shaded triangle in Figure 4.14 has base b 1 and height h . Hence, the area of the shaded triangle is (1/2) b 1 h .
• The unshaded triangle in Figure 4.14 has base b 2 and height h . Hence, the area of the unshaded triangle is (1/2) b 2 h .

Summing the areas, the area of the trapezoid is

\[ \text{Area of Trapezoid} = \frac{1}{2} b_1h + \frac{1}{2} b_2h.\nonumber \]

We can use the distributive property to factor out a (1/2) h .

Area of a Trapezoid

A trapezoid with bases b 1 and b 2 and height h has area

\[A = \frac{1}{2} h (b_1 + b_2).\nonumber \]

That is, to find the area, sum the bases, multiply by the height, and take one-half of the result.

Find the area of the trapezoid pictured below.

The formula for the area of a trapezoid is

\[A = \frac{1}{2} h (b_1 + b_2)\nonumber \]

Substituting the given bases and height, we get

\[A = \frac{1}{2} (3) \left( 4 \frac{1}{4} + 2 \frac{1}{2} \right).\nonumber \]

Simplify the expression inside the parentheses first. Change mixed fractions to improper fractions, make equivalent fractions with a common denominator, then add.

\[\begin{array}{c} A = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{5}{2} \right) \\ = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{5 \cdot 2}{2 \cdot 2} \right) \\ = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{10}{4} \right) \\ = \frac{1}{2} \left( \frac{3}{1} \right) \left( \frac{27}{4} \right) \end{array}\nonumber \]

Multiply numerators and denominators.

\[ = \frac{81}{8}\nonumber \]

This improper fraction is a perfectly good answer, but let’s change this result to a mixed fraction (81 divided by 8 is 10 with a remainder of 1). Thus, the area of the trapezoid is

\[A = 10 \frac{1}{8} \text{ square inches.}\nonumber \]

A trapezoid has bases measuring 6 and 15 feet, respectively. The height of the trapezoid is 5 feet. Find the area of the trapezoid.

\(52 \frac{1}{2} \text{ square feet}\)

In Exercises 1-8, simplify the expression.

1. \( \left( − \frac{7}{3} \right)^3\)

2. \( \left( \frac{1}{2} \right)^3\)

3. \( \left( \frac{5}{3} \right)^4\)

4. \( \left( − \frac{3}{5} \right)^4\)

5. \( \left( \frac{1}{2} \right)^5\)

6. \( \left( \frac{3}{4} \right)^5\)

7. \( \left( \frac{4}{3} \right)^2\)

8. \( \left( − \frac{8}{5} \right)^2\)

9. If a = 7/6, evaluate a 3 .

10. If e = 1/6, evaluate e 3 .

11. If e = −2/3, evaluate − e 2 .

12. If c = −1/5, evaluate − c 2 .

13. If b = −5/9, evaluate b 2 .

14. If c = 5/7, evaluate c 2 .

15. If b = −1/2, evaluate − b 3 .

16. If a = −2/9, evaluate − a 3 .

In Exercises 17-36, simplify the expression.

17. \( \left( − \frac{1}{2} \right) \left( \frac{1}{6} \right) − \left( \frac{7}{8} \right) \left( − \frac{7}{9} \right)\)

18. \( \left( − \frac{3}{4} \right) \left( \frac{1}{2} \right) − \left( \frac{3}{5} \right) \left( \frac{1}{4} \right)\)

19. \( \left( − \frac{9}{8} \right)^2 − \left( − \frac{3}{2} \right) \left( \frac{7}{3} \right)\)

20. \( \left( \frac{3}{2} \right)^2 − \left( \frac{7}{8} \right) \left( − \frac{1}{2} \right)\)

21. \( \left( − \frac{1}{2} \right) \left( − \frac{7}{4} \right) − \left( − \frac{1}{2} \right)^2\)

22. \( \left( \frac{1}{5} \right) \left( − \frac{9}{4} \right) − \left( \frac{7}{4} \right)^2\)

23. \(− \frac{7}{6} − \frac{1}{7} \cdot \frac{7}{9}\)

24. \( − \frac{4}{9} − \frac{8}{5} \cdot \frac{8}{9}\)

25. \( \frac{3}{4} + \frac{9}{7} \left( − \frac{7}{6} \right)\)

26. \( \frac{3}{2} + \frac{1}{4} \left( − \frac{9}{8} \right)\)

27. \( \left( − \frac{1}{3} \right)^2 + \left( \frac{7}{8} \right) \left( − \frac{1}{3} \right)\)

28. \( \left( − \frac{2}{9} \right)^2 + \left( \frac{2}{3} \right) \left( \frac{1}{2} \right)\)

29. \(\frac{5}{9} + \frac{5}{9} \cdot \frac{7}{9}\)

30. \( − \frac{1}{2} + \frac{9}{8} \cdot \frac{1}{3}\)

31. \( \left( − \frac{5}{6} \right) \left( \frac{3}{8} \right) + \left( − \frac{7}{9} \right) \left( − \frac{3}{4} \right)\)

32. \( \left( \frac{7}{4} \right) \left( \frac{6}{5} \right) + \left( − \frac{2}{5} \right) \left( \frac{8}{3} \right)\)

33. \( \frac{4}{3} − \frac{2}{9} \left( − \frac{3}{4} \right)\)

34. \(− \frac{1}{3} − \frac{1}{5} \left( − \frac{4}{3} \right)\)

35. \( \left( − \frac{5}{9} \right) \left( \frac{1}{2} \right) + \left( − \frac{1}{6} \right)^2\)

36. \( \left( \frac{1}{4} \right) \left( \frac{1}{6} \right) + \left( − \frac{5}{6} \right)^2\)

37. Given a = −5/4, b = 1/2, and c = 3/8, evaluate a + bc .

38. Given a = −3/5, b = 1/5, and c = 1/3, evaluate a + bc .

39. Given x = −1/8, y = 5/2, and z = −1/2, evaluate the expression x + yz .

40. Given x = −5/9, y = 1/4, and z = −2/3, evaluate the expression x + yz .

41. Given a = 3/4, b = 5/7, and c = 1/2, evaluate the expression a − bc .

42. Given a = 5/9, b = 2/3, and c = 2/9, evaluate the expression a − bc .

43. Given x = −3/2, y = 1/4, and z = −5/7, evaluate x 2 − yz .

44. Given x = −3/2, y = −1/2, and z = 5/3, evaluate x 2 − yz .

45. Given a = 6/7, b = 2/3, c = −8/9, and d = −6/7, evaluate ab + cd .

46. Given a = 4/9, b = −3/2, c = 7/3, and d = −8/9, evaluate ab + cd .

47. Given w = −1/8, x = −2/7, y = −1/2, and z = 8/7, evaluate wx − yz .

48. Given w = 2/7, x = −9/4, y = −3/4, and z = −9/2, evaluate wx − yz .

49. Given x = 3/8, y = 3/5, and z = −3/2, evaluate xy + z 2 .

50. Given x = −1/2, y = 7/5, and z = −3/2, evaluate xy + z 2 .

51. Given u = 9/7, v = 2/3, and w = −3/7, evaluate uv − w 2 .

52. Given u = 8/7, v = −4/3, and w = 2/3, evaluate uv − w 2 .

53. Given a = 7/8, b = −1/4, and c = −3/2, evaluate a 2 + bc .

54. Given a = −5/8, b = 3/2, and c = −3/2, evaluate a 2 + bc .

55. Given u = 1/3, v = 5/2, and w = −2/9, evaluate the expression u − vw .

56. Given u = −1/2, v = 1/4, and w = −1/4, evaluate the expression u − vw .

In Exercises 57-68, simplify the complex rational expression.

57. \(\frac{ \frac{8}{3} + \frac{7}{6}}{− \frac{9}{2} − \frac{1}{4}}\)

58. \( \frac{ \frac{7}{8} + \frac{1}{9}}{ \frac{8}{9} − \frac{1}{6}}\)

59. \( \frac{ \frac{3}{4} + \frac{4}{3}}{ \frac{1}{9} + \frac{5}{3}}\)

60. \( \frac{− \frac{9}{8} − \frac{6}{5}}{ \frac{7}{4} + \frac{1}{2}}\)

61. \( \frac{ \frac{7}{5} + \frac{5}{2}}{− \frac{1}{4} + \frac{1}{2}}\)

62. \( \frac{ \frac{5}{6} + \frac{2}{3}}{ \frac{3}{5} + \frac{2}{3}}\)

63. \( \frac{− \frac{3}{2} − \frac{2}{3}}{− \frac{7}{4} − \frac{2}{3}}\)

64. \( \frac{ \frac{8}{9} + \frac{3}{4}}{− \frac{2}{3} − \frac{1}{6}}\)

65. \( \frac{− \frac{1}{2} − \frac{4}{7}}{− \frac{5}{7} + \frac{1}{6}}\)

66. \( \frac{− \frac{3}{2} − \frac{5}{8}}{ \frac{3}{4} − \frac{1}{2}}\)

67. \(\frac{− \frac{3}{7} − \frac{1}{3}}{ \frac{1}{3} − \frac{6}{7}}\)

68. \( \frac{− \frac{5}{8} − \frac{6}{5}}{− \frac{5}{4} − \frac{3}{8}}\)

69. A trapezoid has bases measuring \(3 \frac{3}{8}\) and \(5 \frac{1}{2}\) feet, respectively. The height of the trapezoid is 7 feet. Find the area of the trapezoid.

70. A trapezoid has bases measuring \(2 \frac{1}{2}\) and \(6 \frac{7}{8}\) feet, respectively. The height of the trapezoid is 3 feet. Find the area of the trapezoid.

71. A trapezoid has bases measuring \(2 \frac{1}{4}\) and \(7 \frac{3}{8}\) feet, respectively. The height of the trapezoid is 7 feet. Find the area of the trapezoid.

72. A trapezoid has bases measuring \(3 \frac{1}{8}\) and \(6 \frac{1}{2}\) feet, respectively. The height of the trapezoid is 3 feet. Find the area of the trapezoid.

73. A trapezoid has bases measuring \(2 \frac{3}{4}\) and \(6 \frac{5}{8}\) feet, respectively. The height of the trapezoid is 3 feet. Find the area of the trapezoid.

74. A trapezoid has bases measuring \(2 \frac{1}{4}\) and \(7 \frac{1}{8}\) feet, respectively. The height of the trapezoid is 5 feet. Find the area of the trapezoid.

1. \(\frac{−343}{27}\)

3. \(\frac{625}{81}\)

5. \(\frac{1}{32}\)

7. \(\frac{16}{9}\)

9. \(\frac{343}{216}\)

11. \(\frac{−4}{9}\)

13. \(\frac{25}{81}\)

15. \(\frac{1}{8}\)

17. \(\frac{43}{72}\)

19. \(\frac{305}{64}\)

21. \(\frac{5}{8}\)

23. \(\frac{−23}{18}\)

25. \(\frac{−3}{4}\)

27. \(\frac{−13}{72}\)

29. \(\frac{80}{81}\)

31. \(\frac{13}{48}\)

33. \(\frac{3}{2}\)

35. \(\frac{−1}{4}\)

37. \(\frac{−17}{16}\)

39. \(\frac{−11}{8}\)

41. \(\frac{11}{28}\)

43. \(\frac{17}{7}\)

45. \(\frac{4}{3}\)

47. \(\frac{17}{28}\)

49. \(\frac{99}{40}\)

51. \(\frac{33}{49}\)

53. \(\frac{73}{64}\)

55. \(\frac{8}{9}\)

57. \(\frac{−46}{57}\)

59. \(\frac{75}{64}\)

61. \(\frac{78}{5}\)

63. \(\frac{26}{29}\)

65. \(\frac{45}{23}\)

67. \(\frac{16}{11}\)

69. \(31 \frac{1}{16}\)

71. \(33 \frac{11}{16}\)

73. \(14 \frac{1}{16}\)

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• About Varsity Tutors

Basic Arithmetic : Operations with Fractions

Study concepts, example questions & explanations for basic arithmetic, all basic arithmetic resources, example questions, example question #1 : operations with fractions.

Multiply the numerators together, then multiply the denominators together.

First, find out how many girls and boys are in the class.

Then, subtract the number of girls from the total number of students in the class to find the number of boys.

Now, we can figure out how many girls enjoy eating strawberries. Multiply the total number of girls by the fraction of girls who enjoy eating strawberries.

Now, do the same with the boys.

Add these two numbers together to get the total number of students who enjoy eating strawberries.

Example Question #191 : Basic Arithmetic

Solve and simplify. 

When multiplying fractions, you simply multiply the numerators and then multiply the denominators. Then simplify the fraction.

Evaluate the following:

This problem involves order of operations.  

The correct order is:  Parenthesis, Exponents, Multiplication, Division, Addition, and Subtraction.  

Rewrite the exponent and cancel out the 4 on the numerator and denominator.

Example Question #1 : Multiplication With Fractions

Please choose the best answer for the question below. 

To do this problem, simply multiply through (i.e. numerator by numerator and denominator by denominator):

Example Question #6 : Multiplication With Fractions

Multiply these fractions:

When multiplying fractions, all we have to do is multiply the numerators together and multiply the denominators together:

Simply the fraction to get the final answer:

Example Question #4521 : Algebra Ii

Example Question #4522 : Algebra Ii

Example Question #10 : Multiplication With Fractions

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

Fraction Worksheets

Conversion :: Addition :: Subtraction :: Multiplication :: Division

Conversions

Fractions - addition, fractions - subtraction, fractions - multiplication, fractions - division.

Visual Fractions Blog

Operations with Fractions

Introduction.

Fractions are an essential part of mathematics that represent a part of a whole. They are used in many real-life situations, such as cooking, sharing resources, and measurements. Understanding how to perform operations with fractions is crucial in solving math problems and working with fractions in everyday life.

In this blog post, we will cover the basics of operations with fractions, including addition, subtraction, multiplication, and division. We will also provide examples and tips to help you master these operations and simplify fractions.

Check Out Our Online Calculators and Tools

Adding and Subtracting Fractions

For adding or subtracting fractions, a common denominator is necessary. The common denominator is the same number that both fractions can be written with. Here’s how you can add or subtract fractions:

• Determine the smallest common multiple (LCM) of the denominators.
• Convert each fraction to an equivalent fraction with the LCM as the denominator.
• Combine or deduct the numerators and express the result with the common denominator.

Let’s work through an example problem:

Suppose we need to subtract 3/7 from 4/9.

Step 1: Determine the least common multiple (LCM) of 7 and 9.

The numbers that are divisible by 7 are: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70…

The numbers that are divisible by 9 are: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90…

63 is the least common multiple (LCM) of 7 and 9.

Step 2: Convert each fraction to an equivalent fraction with a denominator of 63.

4/9 x 7/7 = 28/63

3/7 x 9/9 = 27/63

Step 3: Subtract the numerators and write the result over the common denominator.

28/63 – 27/63 = 1/63

Therefore, 4/9 – 3/7 = 1/63.

By following these steps, we can successfully subtract fractions with different denominators.

Reduce a fraction to its lowest terms with Fraction Simplifier

Multiplying and Dividing Fractions

Multiplying fractions is straightforward. You simply multiply the numerators and denominators separately and write the result as a fraction. Here’s how:

• Multiply the numerators of the fractions.
• Multiply the denominators of the fractions.
• Write the result as a fraction.

Let’s take a different example:

Suppose we need to multiply 3/4 by 2/5.

3/4 x 2/5=(3×2)÷(4×5)= 6/20.

To simplify the result, we need to find the greatest common factor (GCF) of 6 and 20, which is 2. Then, we divide both the numerator and denominator by 2 to get the simplified fraction:

6/20 = 3/10.

Therefore, 3/4 multiplied by 2/5 is equal to 3/10.

By following these steps, we can successfully multiply fractions and simplify the result to its lowest terms.

Dividing fractions is a little more complicated than multiplying fractions. Here’s how:

• Invert the second fraction (the one you’re dividing by).
• Multiply the first fraction by the inverted second fraction.
• Simplify the result if possible.

Let’s consider an example:

Divide 2/3 by 4/5.

2/3 ÷ 4/5 = 2/3 x 5/4 = (2 x 5) / (3 x 4) = 10/12.

To simplify the result, we need to find the GCF of 10 and 12, which is 2. Then, we divide both the numerator and denominator by 2 to get the simplified fraction:

10/12 = 5/6.

Tips for Simplifying Fractions

Simplifying fractions is important because it makes them easier to work with and understand. Here are some tips to help you simplify fractions:

• Find the Greatest Common Factor (GCF) of the numerator and denominator and divide both by it.
• Look for common factors in the numerator and denominator and cancel them out.
• If the numerator and denominator have no common factors, the fraction is already in its simplest form.
• If the numerator is larger than the denominator, the fraction can be written as a mixed number. For example, 7/4 can be written as 1 3/4.
• If the denominator is a multiple of 10, the fraction can be converted to a decimal by dividing the numerator by the denominator.

Simplify the fraction 12/24.

Step 1: Find the GCF of 12 and 24, which is 12.

Step 2: Divide the numerator and denominator by a common factor of 12.

12/24 = 1/2.

Therefore, 12/24 simplifies to 1/2.

Solve multiple types of fraction math problems with the Fractions Calculator

Operations with fractions are an essential part of mathematics that are used in many real-life situations. Understanding how to perform these operations is crucial in solving math problems and working with fractions in everyday life. Adding, subtracting, multiplying, and dividing fractions can be easily mastered with practice and the use of common techniques like finding the common denominator, inverting the second fraction, and simplifying fractions. Simplifying fractions is important because it makes them easier to work with and understand. With these tips and techniques, you can easily perform operations with fractions and simplify them to their simplest form.

Special May offer - 7 days free unlimited access to all premium content Try Premium

• Interactive

Fractions Problems

Fractions problems interactive.

Filter by Grade:

Filter by subject:.

Fraction Operations Activities

Teach your child all about fractions operations with amazing educational resources for children. These online fractions operations learning resources break down the topic into smaller parts for better conceptual understanding and grasp. Get started now to make fractions operations practice a smooth, easy and fun process for your child!

CONTENT TYPE

• Lesson Plans
• Math (8,010)
• Number Sense (1,465)
• Number Recognition (515)
• Number Recognition Within 3 (82)
• Number Recognition Within 5 (75)
• Number Recognition Within 10 (146)
• Number Recognition Within 20 (216)
• Number Sequence (86)
• Number Sequence Within 3 (6)
• Number Sequence Within 5 (15)
• Number Sequence Within 10 (28)
• Number Sequence Within 20 (15)
• Number Sequence Within 50 (5)
• Number Sequence Within 100 (5)
• Number Sequence Within 120 (4)
• Backward Sequence from 20 (10)
• Counting (330)
• Counting Objects Within 3 (13)
• Counting Objects Within 5 (54)
• Counting Objects Within 10 (86)
• Counting Objects Within 20 (13)
• Writing Numbers (470)
• Writing Numbers Within 3 (70)
• Writing Numbers Within 5 (65)
• Writing Numbers Within 10 (125)
• Writing Numbers Within 20 (210)
• Number Representation (82)
• Represent Numbers Using Place Value Blocks (10)
• Compare and Order Numbers (205)
• Compare Numbers (163)
• Compare Numbers within 10 (45)
• Compare Objects within 10 (16)
• Compare Without Visual Support (10)
• Compare Numbers within 20 (31)
• Compare Numbers Using Place Value Blocks (10)
• Compare Numbers Without Visual Support (10)
• Compare Numbers within 100 (46)
• Use Place Value Blocks to Compare Numbers (10)
• Compare Two 2-Digit Numbers (10)
• Compare 3-Digit Numbers (10)
• Compare Multi-Digit Numbers (10)
• Order Numbers (44)
• Order Numbers within 10 (3)
• Order Numbers within 20 (3)
• Order 3-Digit Numbers (10)
• Order Multi-Digit Numbers (11)
• Skip Counting (37)
• Skip Count by 2 (6)
• Skip Count by 5 (7)
• Skip Count by 10 (18)
• Skip Count by 100 (3)
• Even and Odd Numbers (28)
• Place Value (335)
• Read and Write Numbers (177)
• Numbers up to 10 (55)
• Numbers up to 20 (6)
• Numbers up to 50 (7)
• Numbers up to 100 (17)
• Identify Teen Numbers (12)
• Expanded Form (8)
• 3-Digit Numbers in Expanded Form (6)
• 4-Digit Numbers in Expanded Form (1)
• 5-Digit Numbers in Expanded Form (1)
• Standard Form (11)
• 3-Digit Numbers in Standard Form (6)
• 4-Digit Numbers in Standard Form (4)
• 5-Digit Numbers in Standard Form (1)
• Word Form (3)
• 3-Digit Numbers in Word Form (1)
• 4-Digit Numbers in Word Form (1)
• 5-Digit Numbers in Word Form (1)
• Unit Form (17)
• 3-Digit Numbers in Unit Form (5)
• 4-Digit Numbers in Unit Form (4)
• 5-Digit Numbers in Unit Form (3)
• Place Value Chart (17)
• 3-Digit Numbers on Place Value Chart (14)
• 4-Digit Numbers on Place Value Chart (1)
• 5-Digit Numbers on Place Value Chart (1)
• Round Numbers (47)
• Round Numbers to the Nearest 10 (18)
• Round Numbers to the Nearest 100 (14)
• Addition (1,331)
• Embedded Numbers (13)
• Addition Sentences (64)
• Addition Sentence within 5 (20)
• Addition Sentence within 10 (44)
• Add with Pictures (33)
• Add with Pictures within 5 (22)
• Add with Pictures within 10 (11)
• Model Addition (235)
• Addition Properties (16)
• Commutative Property of Addition (10)
• Add Using Models (18)
• Addition Strategies (500)
• Addition Strategies within 10 (287)
• Count All to Add (21)
• Count All to add within 5 (5)
• Count All to add within 10 (16)
• Count On to Add Strategy (40)
• Add using number line (10)
• Compose and Decompose Numbers (226)
• Number Bonds (197)
• Addition Strategies within 20 (130)
• Anchor 5 and 10 (21)
• Count On Strategy (24)
• Add with 10 (13)
• Make 10 Strategy (20)
• Doubles and Near Doubles Strategy to Add (38)
• Doubles Facts (13)
• Add Three Whole Numbers (18)
• Addition Strategies within 100 (54)
• Add using multiples of 10 (19)
• Addition Strategies within 1000 (36)
• Add using multiples of 100 (25)
• Addition Facts (208)
• Fluently Add within 5 (16)
• Fluently Add within 10 (83)
• Fluently Add within 20 (116)
• Equal Expressions (33)
• Addition Without Regrouping (238)
• Add within 100 without Regrouping (72)
• Add 2-digit number to 1-digit (17)
• Add 2-digit number to 2-digit (54)
• Add within 1000 without Regrouping (124)
• Add 10 to 3-digit numbers (15)
• Add 100 to 3-digit numbers (16)
• Add 3-digit number to 1-digit (16)
• Add 3-digit number to 2-digit (24)
• Add two 3-digit numbers (44)
• Add within 10000 without Regrouping (42)
• Addition With Regrouping (152)
• Add within 100 with Regrouping (51)
• Regroup and add 2-digit number to 1-digit (17)
• Regroup and add 2-digit numbers (17)
• Add within 1000 with Regrouping (57)
• Regroup ones and add (13)
• Regroup ones and tens and add (13)
• Regroup tens and add (3)
• Add within 10000 with Regrouping (44)
• Multi-digit Addition (108)
• Addition within 100000 (53)
• Addition within 1000000 (53)
• Subtraction (943)
• Subtraction Sentences (52)
• Subtraction Sentences within 5 (19)
• Subtraction Sentences within 10 (32)
• Subtract with Pictures (52)
• Subtract with Pictures within 5 (33)
• Subtract with Pictures within 10 (19)
• Model Subtraction (49)
• Subtract using Models (14)
• Subtraction Strategies (172)
• Subtraction Strategies within 10 (32)
• Count Back Strategy within 10 (25)
• Relate Addition and Subtraction within 10 (6)
• Subtraction Strategies within 20 (84)
• Count Back Strategy within 20 (44)
• Subtract using number line (10)
• Relate Addition and Subtraction within 20 (13)
• Doubles and Near Doubles Strategy to Subtract (4)
• Subtract from 10 Strategy (12)
• Subtraction Strategies within 100 (36)
• Subtract using multiples of 10 (20)
• Subtraction Strategies within 1000 (22)
• Subtract using multiples of 100 (11)
• Subtraction Facts (198)
• Fluently Subtract within 5 (17)
• Fluently Subtract within 10 (82)
• Fluently Subtract within 20 (110)
• Equal Expressions in Subtraction (28)
• Subtraction Without Regrouping (227)
• Subtract within 100 without Regrouping (83)
• Subtract Multiples of 10 (19)
• Subtract within 1000 without Regrouping (104)
• Subtract within 10000 without Regrouping (40)
• Subtraction With Regrouping (137)
• Subtract within 100 with Regrouping (49)
• Subtract within 1000 with Regrouping (52)
• Subtract across Zeros (5)
• Subtract within 10000 with Regrouping (36)
• Multi-digit Subtraction (110)
• Subtraction within 100000 (56)
• Subtraction within 1000000 (52)
• Multiplication (670)
• Arrays (23)
• Equal Groups (26)
• Multiplication Sentences (53)
• Repeated Addition to Multiply (18)
• Multiplication on Number Line (6)
• Multi-digit Multiplication (162)
• Multiply 2-digit by 1-digit Numbers (35)
• Multiply 2-digit by 2-digit numbers (55)
• Multiply 3-digit by 1-digit Numbers (18)
• Multiply 3-digit by 2-digit numbers (25)
• Multiply 4-digit by 1-digit Numbers (17)
• Multiplication Properties (105)
• Associative Property (12)
• Commutative Property (14)
• Distributive Property (61)
• Multiply by 0 and 1 (13)
• Estimate Products (12)
• Multiply by multiples of 10 (27)
• Times Tables (206)
• Multiplication Facts (193)
• Multiplication Facts of 2 (19)
• Multiplication Facts of 3 (19)
• Multiplication Facts of 4 (19)
• Multiplication Facts of 5 (19)
• Multiplication Facts of 6 (19)
• Multiplication Facts of 7 (18)
• Multiplication Facts of 8 (18)
• Multiplication Facts of 9 (19)
• Multiplication Facts of 10 (17)
• Multiply by 11 (15)
• Multiply by 12 (15)
• Division (383)
• Division Facts (138)
• Division Facts of 2 (15)
• Division Facts of 3 (17)
• Division Facts of 4 (17)
• Division Facts of 5 (15)
• Division Facts of 6 (18)
• Division Facts of 7 (15)
• Division Facts of 8 (16)
• Division Facts of 9 (15)
• Division Facts of 10 (14)
• Divide on a Number Line (13)
• Long Division (116)
• Divide 2-digit by 1-digit Numbers (21)
• Divide 3-digit by 1-digit Numbers (19)
• Divide 4-digit by 1-digit Numbers (15)
• Divide Multiples of 10 or 100 (20)
• Estimate Quotients (29)
• Fractions (609)
• Identify Fractions (54)
• Identify fractions using models (18)
• Identify fractions on the number line (17)
• Represent Fractions (44)
• Represent fractions on the number line (10)
• Mark fractions on the number line (10)
• Represent fractions using models (10)
• Represent fractions using real-word objects (10)
• Represent Mixed Numbers (10)
• Represent mixed numbers using models (10)
• Compare Fractions (65)
• Compare fractions using visual models (13)
• Compare fractions using number lines (14)
• Compare fractions without visual models (11)
• Benchmark Fractions (16)
• Order Fractions (20)
• Order fractions using visual models (10)
• Order fractions without visual models (10)
• Equivalent Fractions (52)
• Equivalent fractions using models (10)
• Equivalent fractions using number lines (10)
• Equivalent fractions without visual models (15)
• Identify equivalent fractions (10)
• Convert Fractions (35)
• Fractions as Mixed Numbers (10)
• Mixed Numbers as Fractions (25)
• Fractions Operations (324)
• Add and Subtract Fractions (110)
• Add Fractions (57)
• Represent Fraction Addition (9)
• Add fractions using models (12)
• Add like fractions (12)
• Add unlike fractions (10)
• Estimate fraction sums (13)
• Subtract Fractions (39)
• Represent Fraction Subtraction (9)
• Subtract fractions using models (9)
• Subtract like fractions (12)
• Subtract unlike fractions (10)
• Add and Subtract mixed numbers (81)
• Add mixed numbers (40)
• Add mixed numbers using models (10)
• Add a mixed number to a fraction (12)
• Add two mixed numbers (11)
• Subtract mixed numbers (41)
• Subtract mixed numbers using models (10)
• Subtract a fraction from a mixed number (14)
• Subtract two mixed numbers (10)
• Multiply Fractions (122)
• Multiply fractions by whole numbers (14)
• Multiply fractions by whole numbers without models (10)
• Multiply two fractions (20)
• Multiply fractions using models (10)
• Multiply fractions without models (10)
• Multiply mixed numbers (32)
• Multiply mixed numbers by whole numbers (10)
• Multiply mixed numbers by fractions (10)
• Multiply two mixed numbers (10)
• Fraction multiplication as scaling (10)
• Divide fractions (8)
• Decimals (1,729)
• Identify tenths (7)
• Identify hundredths (8)
• Represent Decimals (32)
• Represent Decimals Using Models (18)
• Represent Decimals on Number Lines (14)
• Read and Write Decimals (42)
• Decimals Expanded Form (20)
• Compose Decimals (10)
• Decompose Decimals (10)
• Decimals Standard Form (11)
• Decimals Word Form (10)
• Decimal Place Value (34)
• Digits at the given decimal place (10)
• Place values of digits in decimals (10)
• Compare and Order Decimals (76)
• Compare decimals (45)
• Compare decimals using models (20)
• Compare using decimal grids (10)
• Compare using decimal number lines (10)
• Compare decimals using place value (10)
• Order decimals (31)
• Order decimals using place value (10)
• Round Decimals (42)
• Round decimals to the nearest whole (12)
• Round decimals to the nearest tenths (10)
• Round decimals to the nearest hundredths (10)
• Convert Between Decimals and Fractions (7)
• Convert Decimals to Fractions (7)
• Equivalent Decimals (27)
• Tenths to hundredths (9)
• Hundredths to tenths (8)
• Decimal Operations (1,459)
• Add Decimals (699)
• Add tenths and hundredths (360)
• Add decimals without regrouping (194)
• Add decimals with regrouping (188)
• Subtract Decimals (705)
• Subtract decimals without regrouping (194)
• Subtract decimals with regrouping (184)
• Multiply Decimals (237)
• Multiply decimals by powers of 10 (83)
• Multiply decimals by whole numbers (128)
• Multiply decimals by decimals (72)
• Divide Decimals (161)
• Divide decimals by powers of 10 (20)
• Divide decimals by whole numbers (41)
• Divide whole numbers by decimals (45)
• Divide decimals by decimals (41)
• Types of Decimals (12)
• Geometry (292)
• Parallel lines (5)
• Angles (15)
• Positional Words (15)
• Sides and Corners (12)
• Corners (11)
• Shapes (200)
• 2d Shapes (162)
• Identify Quadrilaterals (24)
• Trapezoids (10)
• Identify triangles (14)
• Identify polygons (10)
• Attributes of 2D shapes (20)
• Sort 2D shapes (14)
• Partition 2D Shapes (28)
• Partition into equal parts (24)
• Halves, Thirds, and Fourths (18)
• 3d Shapes (20)
• Flat and Solid Shapes (23)
• Match 2D Shapes (9)
• Match 3D Shapes (10)
• 3D Shapes in real life (10)
• Coordinate Planes (28)
• Identify Points on the Coordinate Plane (10)
• Plot on the Coordinate Plane (11)
• Measurement (282)
• Capacity (22)
• Comparing Measurements (53)
• Compare Weights (13)
• Group of Objects (4)
• Compare Lengths (24)
• Compare Heights (14)
• Conversion of Measurement Units (16)
• Data Handling (73)
• Organize and Interpret Data (57)
• Organize data in bar graphs (7)
• Organize data in line plots (6)
• Organize data in picture graphs (4)
• Interpret data in bar graphs (5)
• Interpret data in line plots (7)
• Interpret data in picture graphs (6)
• Sort Objects (11)
• Length (39)
• Measure Lengths (19)
• Measure Lengths using the ruler (17)
• Estimate Lengths (4)
• Area of Shapes (18)
• Area of 2D Shapes (5)
• Area as Additive (5)
• Perimeter (19)
• Perimeter of Shapes (19)
• AM and PM (12)
• Analog Clock (32)
• Hour hand (12)
• Set time (10)
• Digital Clock (9)
• Elapsed Time (3)
• Time in Half Hours (19)
• Time in Hours (17)
• Time in Quarter Hours (19)
• Time to the Nearest 5 Minutes (21)
• Time to the Nearest Minute (2)
• Money (128)
• Identify Coins (20)
• Value of the Coins (10)
• Make Amounts (10)
• Counting Money (103)
• Compare Money (15)
• Count Money with Coins (37)
• Penny, Nickel, and Dime (20)
• Quarters and Half Dollar (9)
• Operations With Money (24)
• Add and Subtract Money (12)
• Multiply and Divide Money (7)
• Algebra (146)
• Patterns (35)
• Number Patterns (35)
• Extend Number Patterns (10)
• Generate Number Patterns (10)
• Relationship Between Patterns (10)
• Numerical Expressions (41)
• Interpret Numerical Expressions (10)
• Evaluate Numerical Expressions (21)
• Evaluate Exponents (10)
• Order of Operations (10)
• Factors and Multiples (51)
• Factors (30)
• Multiples (14)
• Prime and Composite Numbers (15)
• Word Problems (705)
• Addition and Subtraction Word Problems (396)
• Addition Word Problems (174)
• Addition Word Problems within 10 (29)
• Addition Word Problems within 20 (28)
• Addition Word Problems within 100 (44)
• Add to Compare Word Problems (21)
• Subtraction Word Problems (112)
• Subtraction Word Problems within 10 (17)
• Subtraction Word Problems within 20 (14)
• Subtraction Word Problems within 100 (28)
• Subtract to Compare Word Problems (16)
• Decimal Subtraction Word Problems (25)
• Multiplication and Division Word Problems (180)
• Multiplication Word Problems (104)
• Division Word Problems (73)
• Fraction Word Problems (34)
• Multi-step Word Problems (81)
• Money Word Problems (10)
• ELA (7,781)
• Reading (5,206)
• Phonics (4,916)
• Bossy R (27)
• Words with AR (10)
• Words with ER (8)
• Words With IR (8)
• Words with OR (7)
• Words with UR (8)
• Diphthongs (28)
• Words with OI (11)
• Words with OU (11)
• Words with OW (11)
• Words with OY (11)
• Ending Consonant Blends (91)
• CK Blend (7)
• LF Blend (13)
• LK Blend (14)
• LT Blend (13)
• MP Blend (12)
• ND Blend (13)
• NK Blend (14)
• SK Blend (12)
• ST Blend (12)
• NG Blend (7)
• Beginning Consonant Blends (101)
• L Blend Words (40)
• BL Blend (14)
• CL Blend (13)
• FL Blend (13)
• GL Blend (10)
• PL Blend (11)
• SL Blend (10)
• R Blend Words (36)
• CR Blend (12)
• FR Blend (12)
• GR Blend (11)
• PR Blend (13)
• TR Blend (12)
• SPL Blend (9)
• SQU Blend (8)
• STR Blend (8)
• Alphabet (581)
• Letter A (23)
• Letter B (27)
• Letter C (22)
• Letter D (28)
• Letter E (22)
• Letter F (23)
• Letter G (28)
• Letter H (24)
• Letter I (26)
• Letter J (26)
• Letter K (22)
• Letter L (22)
• Letter M (23)
• Letter N (25)
• Letter O (22)
• Letter P (29)
• Letter Q (27)
• Letter R (22)
• Letter S (22)
• Letter T (23)
• Letter U (22)
• Letter V (22)
• Letter W (22)
• Letter X (22)
• Letter Y (22)
• Letter Z (22)
• Letter Sequence (64)
• ABC Song (20)
• Alphabetical Order (34)
• Letter Sounds (468)
• Letter Sound A (21)
• Letter Sound B (21)
• Letter Sound C (21)
• Letter Sound D (22)
• Letter Sound E (20)
• Letter Sound F (21)
• Letter Sound G (22)
• Letter Sound H (22)
• Letter Sound I (19)
• Letter Sound J (19)
• Letter Sound K (21)
• Letter Sound L (20)
• Letter Sound M (21)
• Letter Sound N (17)
• Letter Sound O (20)
• Letter Sound P (21)
• Letter Sound Q (17)
• Letter Sound R (21)
• Letter Sound S (21)
• Letter Sound T (21)
• Letter Sound U (17)
• Letter Sound V (18)
• Letter Sound W (20)
• Letter Sound X (16)
• Letter Sound Y (19)
• Letter Sound Z (17)
• Beginning and Ending Sounds (25)
• Letter Recognition (365)
• Lowercase Letters (78)
• Uppercase Letters (78)
• Matching Lowercase and Uppercase Letters (209)
• Match Aa - Dd (9)
• Match Ee - Gg (7)
• Match Hh - Kk (9)
• Match Ll - Pp (11)
• Match Qq - Ss (7)
• Match Tt - Vv (7)
• Match Ww - Zz (9)
• Vowels (321)
• Long Vowel Sounds (128)
• Long A Vowel Sound (28)
• Long E Vowel Sound (27)
• Long I Vowel Sound (26)
• Long O Vowel Sound (24)
• Long U Vowel Sound (25)
• Magic - E (37)
• Magic E Words with Long Vowel A (12)
• Magic E Words with Long Vowel E (6)
• Magic E Words with Long Vowel I (12)
• Magic E Words with Long Vowel O (11)
• Magic E Words with Long Vowel U (11)
• Short Vowel Sounds (151)
• Short A Vowel Sound (77)
• Short E Vowel Sound (38)
• Short I Vowel Sound (77)
• Short O Vowel Sound (55)
• Short U Vowel Sound (35)
• Vowel Teams (49)
• Words with AI and AY (13)
• Words with EA and EE (14)
• Words with IE and Y (11)
• Words with OA and OW (13)
• Words with OO (11)
• Words with UE and UI (9)
• Blending (955)
• CCVC Words (64)
• CCVCC Words (36)
• CVC Words (453)
• CVCC Words (156)
• Beginning Blending (34)
• CCVC and CCVCC Words (28)
• CVCC and CCVCC Words (46)
• Words With Bossy R (45)
• Words With Diphthongs (18)
• Words With Three Letter Blends (14)
• Words With Trigraphs (28)
• Words With Vowel Teams (50)
• Consonant Digraphs (39)
• Digraph CH (17)
• Digraph CK (5)
• Digraph NG (5)
• Digraph PH (11)
• Digraph SH (18)
• Digraph TH (17)
• Digraph WH (17)
• Double Consonants (43)
• FF Words (13)
• LL Words (17)
• SS Words (15)
• ZZ Words (12)
• Rhyming Words (174)
• Trigraphs (29)
• Trigraph DGE (9)
• Trigraph IGH (7)
• Trigraph SHR (8)
• Trigraph TCH (7)
• Trigraph THR (7)
• Soft Sounds (2)
• Words with Soft C (1)
• Words with Soft G (1)
• Three Letter Blends (5)
• Sight Words (1,943)
• Dolch Sight Words (567)
• Fry Sight Words (444)
• Syllables (8)
• Hard and Soft Sounds of C and G (2)
• Segmenting Phonemes (1)
• Adding Deleting and Substituting Phonemes (6)
• Silent Letter Words (11)
• Reading Skills (276)
• Cause and Effect (21)
• Inference (19)
• Identify the Main Idea (40)
• Categorize Pictures into Groups (4)
• Choose a Suitable Heading (5)
• Prediction (14)
• Sequencing (28)
• Arrange Pictures in Order (3)
• Arrange Sentences in Order (4)
• Story Elements (20)
• Authors Purpose (9)
• Compare and Contrast (14)
• Ask and Answer Questions (6)
• Central Message (4)
• Point of View (12)
• Sensory Words (3)
• Comprehension (21)
• Character Analysis (16)
• Text Structure (9)
• Fact or Opinion (2)
• Reality and Fantasy (6)
• Using Illustrations (15)
• Using Text Features (8)
• Context Clues (13)
• Evaluating Authors Argument and Evidence (6)
• Communication Skills (14)
• Listening Skills (3)
• Speaking Skills (11)
• Writing (1,836)
• Handwriting (1,652)
• Letter Tracing (356)
• Letter Tracing A (33)
• Letter Tracing B (34)
• Letter Tracing C (33)
• Letter Tracing D (33)
• Letter Tracing E (33)
• Letter Tracing F (34)
• Letter Tracing G (33)
• Letter Tracing H (34)
• Letter Tracing I (33)
• Letter Tracing J (33)
• Letter Tracing K (33)
• Letter Tracing L (33)
• Letter Tracing M (34)
• Letter Tracing N (33)
• Letter Tracing O (33)
• Letter Tracing P (33)
• Letter Tracing Q (33)
• Letter Tracing R (33)
• Letter Tracing S (33)
• Letter Tracing T (33)
• Letter Tracing U (33)
• Letter Tracing V (33)
• Letter Tracing W (33)
• Letter Tracing X (33)
• Letter Tracing Y (33)
• Letter Tracing Z (33)
• Word Tracing (300)
• Cursive Writing (742)
• Writing Sight Words (60)
• Creative Writing (124)
• Grammar (392)
• Adverbs and Adjectives (71)
• Nouns and Pronouns (135)
• Pronouns (25)
• Parts of Speech (12)
• Prepositions and Conjunctions (36)
• Conjunctions (6)
• Prepositions (13)
• Punctuation (23)
• Sentences (27)
• Verbs and Tenses (100)
• Determiners (2)
• Article A An The (2)
• Spelling (29)
• Common Misspellings (10)
• Unscramble (16)
• Vocabulary (307)
• Abbreviations and Contractions (11)
• Affixes (17)
• Inflectional Endings (2)
• Commonly Confused Words (28)
• Compound Words (10)
• Figures of Speech (14)
• Similes and Metaphors (6)
• Alliteration (2)
• Synonyms and Antonyms (23)
• Word Puzzles (81)
• Shades of Meaning (4)
• Sorting Words into Categories (21)
• Making Connections in Reading (6)
• Flashcards (45)
• Vocabulary Flashcards (1)
• Phonics Flashcards (42)
• Grammar Flashcards (2)
• General Knowledge (295)
• Vegetables (19)
• Fruits (24)
• Dessert (9)
• Animals (58)
• Underwater (9)
• Dinosaurs (8)
• Reptiles (9)
• Seasonal (28)
• Christmas (12)
• Halloween (8)
• Kitchen (11)
• Utensils (6)
• Musical Instruments (30)
• Transport (9)
• Vehicles (9)
• Insects (9)
• Professions (8)
• Monuments (8)
• Household Items (8)
• Flowers (8)
• Buildings (8)
• Art & Creativity (236)
• Coloring (181)
• Animals (32)
• Underwater (8)
• Reptiles (8)
• Vegetables (8)
• Transport (8)
• Vehicles (8)
• Musical Instruments (8)
• Kitchen (8)
• Utensils (5)
• Insects (8)
• Rhymes (25)
• Cooking (7)
• Stories (10)
• Logic & Thinking (16)
• Puzzles (11)
• Matching (3)
• Multiplayer (12)
• Time Based (12)
• Player vs Player (12)
• Motor Skills (16)
• Fine Finger Movement (9)
• Aiming and Precision (6)

Add and Subtract Fractions

Estimate the Sum using Number Line Game

Enjoy the marvel of mathematics by exploring how to estimate the sum using a number line.

Estimate the Sum of Two Fractions Game

Have your own math-themed party by learning how to estimate the sum of two fractions.

Estimate and Sort Fraction Sums Worksheet

Boost your fraction skills with this worksheet on estimating and sorting fraction sums.

Estimate Fraction Sum and Verify Worksheet

A worksheet designed to practice and confirm your skills in estimating the sums of fractions.

Add and Subtract mixed numbers

FIll in the Blank to add the Fraction and the Mixed Number Game

FIll in the blanks to add the fraction and the mixed number.

Find the Sum of Mixed Numbers Game

Apply your knowledge of fractions to find the sum of mixed numbers.

Add Mixed Numbers Without Models Worksheet

Put your skills to the test by practicing to add mixed numbers without models.

Adding Fractions & Mixed Numbers Word Problems Worksheet

Help your child solve word problems on adding fractions & mixed numbers.

Multiply Fractions

Choose the Multiplication Expression Representing Fraction Models Game

Kids must choose the multiplication expression representing fraction models.

Complete the Multiplication Expression Using the Fraction Models Game

Use fraction models to complete the multiplication expression.

Express a Fraction as Product in Different Ways Worksheet

Learn to express a fraction as a product in different ways in this fun worksheet.

Express a Fraction as Product in Multiple Ways Worksheet

Pack your math practice time with fun by expressing a fraction as a product in multiple ways.

All Fractions Operations Resources

Represent Unit Fraction Multiplication on a Number Line Game

Dive deep into the world of math by representing unit fraction multiplication on a number line.

Multiply Unit Fraction by a Whole Number on a Number Line Game

Kids must multiply unit fractions by a whole number on a number line.

Represent a Fraction as Product in Different Ways Worksheet

Learners must represent a fraction as a product in different ways to enhance their math skills.

Multiplying Unit Fractions Worksheet

Make math practice a joyride by multiplying unit fractions.

Select the Multiplication Expression Represented by Fraction Models Game

Select the multiplication expression represented by fraction models correctly.

Fill in the Correct Number Using Fraction Models Game

Utilise your fraction knowledge to fill in the correct number using fraction models.

Multiplying Non Unit Fractions Worksheet

Make math practice a joyride by multiplying non unit fractions.

Word Problems on Multiplying Fractions Worksheet

Make math practice a joyride by solving word problems on multiplying fractions.

Represent Fraction Multiplication on a Number Line Game

Use your fraction skills to represent fraction multiplication on a number line.

Multiply Fraction by a Whole Number on a Number Line Game

Use your fraction skills to multiply fractions by a whole number on a number line.

Real Life Problems on Multiplying Fractions Worksheet

Be on your way to become a mathematician by solving real life problems on multiplying fractions.

Estimate the Fraction Products Worksheet

In this worksheet, learners will get to estimate fraction products.

Choose the Correct Addition Sentence Related to the Fraction Game

Kids must choose the correct addition sentence related to the fraction.

Multiply Unit Fraction by Whole Number Game

Enjoy the marvel of math-multiverse by exploring how to multiply unit fractions by whole numbers.

Estimate Fractions Products by Rounding Worksheet

Reinforce math concepts by practicing to estimate fraction products by rounding.

Multiply Fractions and Compare the Products Worksheet

Enhance your skills with this worksheet on multiplying fractions and comparing outcomes!

Fill in and Find the Product of Unit Fraction and the Whole Number Game

Kids must fill in and find the product of unit fractions and whole numbers.

Complete the Multiplication Between Fractions and Whole Numbers Game

Use your fraction skills to complete the multiplication between fractions and whole numbers.

Multiply Improper Fractions Worksheet

This worksheet focuses on multiplying improper fractions without the use of models.

Multiply Unit Fractions Worksheet

This worksheet provides exercises for students to practice multiplying unit fractions without the use of visual models.

Find the Product of Fractions and the Whole Numbers Game

Dive deep into the world of fractions by finding the product of fractions and whole numbers.

Solve Word Problems on Fraction-Whole Number Multiplication Game

Apply your knowledge to solve word problems on fraction-whole number multiplication.

Write Missing Fractions in Fraction Multiplication Worksheet

Enhance your fraction multiplication skills with this worksheet on writing missing fractions!

Write Product of Fractions as Mixed Number Worksheet

A worksheet on converting the product of fraction multiplication into mixed numbers.

Find Fraction of a Whole Number Game

Shine bright in the math world by learning how to solve a fraction to make a whole number.

Multiply a Fraction and a Whole Number Game

Ask your little one to multiply a fraction and a whole number to play this game.

Create Area Models to Multiply Unit Fractions Worksheet

Help your child revise fractions by creating area models to multiply unit fractions.

Draw Area Models to Multiply Unit Fractions Worksheet

Assess your math skills by drawing area models to multiply unit fractions in this worksheet.

Simplify the Product of Whole Number and Fraction Game

Use your fraction skills to simplify the product of whole numbers and fractions.

Find the Product of Fractions Game

Take a deep dive into the world of math by finding the product of fractions.

Represent Fractions on Area Models and Multiply Worksheet

Engage with this worksheet to learn multiplying fractions using area models effectively.

Represent Unit Fractions on Area Models and Multiply Worksheet

An engaging worksheet for learning to multiply unit fractions using area models.

Multiply Fractions using Models Game

Shine bright in the math world by learning how to multiply fractions using models.

Determine the Correct Fraction Game

Practice how to determine the correct fraction with this game.

Shade the Models and Multiply Fractions Worksheet

An interactive worksheet to learn multiplying fractions by shading models and solving problems.

Shade the Models and Multiply Unit Fractions Worksheet

This worksheet focuses on multiplying unit fractions using visual models for better understanding.

Identify the Expression for the Model Game

Add more arrows to your child’s math quiver by helping them identify the expression for the model.

Simplify the Product of Fractions Game

Enjoy the marvel of math-multiverse by exploring how to simplify the product of fractions.

Use the Models and Multiply Fractions Worksheet

This worksheet provides exercises on multiplying fractions using visual models to enhance understanding and proficiency.

Use the Models and Multiply Unit Fractions Worksheet

This worksheet provides exercises on using visual models to solve multiplication problems involving unit fractions.

Multiply a Fraction by Whole Worksheet

Help your child revise fractions by solving to multiply fraction by a whole.

Problems on Multiplying Unit Fraction by Whole Worksheet

Learners must solve problems on multiplying a unit fraction by a whole to enhance their math skills.

Word Problems on Product of Unit Fraction & Whole Worksheet

Use this worksheet to solve word problems to find the product of a unit fraction & a whole.

Problems on Multiplying Non-Unit Fraction & Whole Worksheet

Focus on core math skills by solving problems on multiplying a non-unit fraction & a whole.

Your one stop solution for all grade learning needs.

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation

Table of Contents

Last modified on August 3rd, 2023

#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline

Order of operations with fractions.

Just like solving equations with whole numbers, solving equations with fractions follows the same PEMDAS rule.

Let us recap the PEMDAS rule before we solve some expressions involving fractions.

• Step 1: P for Parentheses
• Step 2: E for Exponent
• Step 3: MD for Multiplication and Division
• Step 4: AS for Addition and Subtraction

We can simplify expressions having both like and unlike fractions involving PEMDAS.

With Like Fractions

Let us consider a simple example with like fractions (having the same denominators)

Simplify: ${\begin{aligned}\left( \dfrac{2}{3}\times \dfrac{4}{3}\right) +\dfrac{6}{3}\\ .\end{aligned}}$

Solving this expression using PEMDAS rule, we will first perform the operation within the parenthesis involving multiplication and then we will add the result with 6/3

= ${\dfrac{8}{3}+\dfrac{6}{3}}$ (∵ Multiplication of ${\begin{aligned}\dfrac{2}{3}\times \dfrac{4}{3}=\dfrac{8}{3}\\ .\end{aligned}}$)

= ${\dfrac{14}{3}}$ (∵ Addition of ${\dfrac{8}{3}+\dfrac{6}{3}=\dfrac{14}{3}}$)

Let us solve some more expressions using PEMDAS having like fraction

Simplify: ${\dfrac{1}{3}\times \left( \dfrac{2}{3}\right) ^{2}-\dfrac{1}{3}}$

Using PEMDAS, = ${\dfrac{1}{3}\times \dfrac{4}{9}-\dfrac{1}{3}}$ (Evaluating the exponents) = ${\dfrac{4}{27}-\dfrac{1}{3}}$ (Multiplying) = ${\dfrac{4}{27}-\dfrac{9}{27}}$ (Making the fractions equivalent) = ${-\dfrac{5}{27}}$ (Subtracting) Answer: ${-\dfrac{5}{27}}$

Solve: ${\dfrac{1}{14}\div \dfrac{2}{14}-\dfrac{1}{2}}$

Using PEMDAS, = ${\dfrac{1}{14}\times \dfrac{14}{2}-\dfrac{1}{2}}$ (Dividing: Inverting the 2nd fraction)  = ${\dfrac{1}{2}-\dfrac{1}{2}}$ (Multiplying) = 0 (Subtracting)

With Unlike Fractions

When, we consider an expression involving improper fractions, we follow the same rule but an extra step is involved, making the fractions equivalent

Simplify: ${-\dfrac{1}{3}+\dfrac{1}{3}\left( -\dfrac{1}{5}\right)}$

Here, we will use the rule of PEMDAS

${-\dfrac{1}{3}-\dfrac{1}{15}}$ (∵ Multiplication of ${\dfrac{1}{3}\left( -\dfrac{1}{5}\right) =-\dfrac{1}{15}}$)

= ${-1\times \dfrac{5}{3}\times 5-\dfrac{1}{15}}$ (Making the fractions equivalent, Lowest Common Denominator (LCD) = 15)

= ${-\dfrac{5}{15}-\dfrac{1}{15}}$ (Subtracting the like fractions)

= ${-\dfrac{6}{15}}$

Let us solve another expression using PEMDAS having unlike fraction

Simplify: ${\dfrac{1}{3}\div \dfrac{4}{5}-\dfrac{1}{7}}$

Using PEMDAS, = ${\dfrac{1}{3}\times \dfrac{5}{4}-\dfrac{1}{6}}$ (Dividing: Inverting the 2nd fraction) = ${\dfrac{5}{12}-\dfrac{1}{6}}$ (Multiplying) = ${\dfrac{5}{12}-1\times \dfrac{2}{6}\times 2}$ (Making the fractions equivalent) = ${\dfrac{5}{12}-\dfrac{2}{12}}$ (Subtracting = ${\dfrac{3}{12}}$

Leave a comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Privacy Policy
• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice

Measurement

• Factoring & prime factors

Proportions

• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

Download & Print From only $2.60

Sixth Grade Math Worksheets

Free grade 6 worksheets from k5 learning.

Our printable grade 6 math worksheets delve deeper into earlier grade math topics (4 operations, fractions, decimals, measurement, geometry) as well as introduce exponents, proportions, percents and integers .

Choose your grade 6 topic:

4 operations.

Place Value & Scientific Notation

Add & Subtract

Multiply & Divide

Decimals & Percents

Fractions to / from Decimals

Decimals - Add and Subtract

Decimals  - Multiply

Decimals - Divide

Add & Subtract Fractions

Multiply & Divide Fractions

Converting Fractions

Sample Grade 6 Math Worksheet

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

Join K5 to save time, skip ads and access more content. Learn More

• Forgot Password?