balancing equations and types of reactions assignment

• Sign in / Register
• Administration
• Edit profile

The PhET website does not support your browser. We recommend using the latest version of Chrome, Firefox, Safari, or Edge.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.3: Balancing Equations

• Last updated
• Save as PDF
• Page ID 53781

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Any leftovers?

When you cook a meal, quite often there are leftovers because you prepared more than people would eat at one sitting. Sometimes when you repair a piece of equipment, you end up with what are called "pocket parts"—small pieces you put in your pocket because you're not sure where they belong. Chemistry tries to avoid leftovers and pocket parts. In normal chemical processes, we cannot create or destroy matter (law of conservation of mass). If we start out with ten carbon atoms, we need to end up with ten carbon atoms. John Dalton's atomic theory said that chemical reactions basically involve the rearrangement of atoms. Chemical equations need to follow these principles in order to be correct.

Balancing Chemical Equations

A balanced equation is a chemical equation in which mass is conserved and there are equal numbers of atoms of each element on both sides of the equation. We can write a chemical equation for the reaction of carbon with hydrogen gas to form methane \(\left( \ce{CH_4} \right)\):

\[\begin{array}{ccccc} \ce{C} \left( s \right) & + & \ce{H_2} \left( g \right) & \rightarrow & \ce{CH_4} \left( g \right) \\ 2 \: \ce{C} \: \text{atoms} & & 2 \: \ce{H} \: \text{atoms} & & 1 \: \ce{C} \: \text{atom,} \: 4 \: \ce{H} \: \text{atoms} \end{array}\nonumber \]

In order to write a correct equation, you must first write the correct skeleton equation with the correct chemical formulas. Recall that hydrogen is a diatomic molecule and so is written as \(\ce{H_2}\).

When we count the number of atoms of both elements, shown under the equation, we see that the equation is not balanced. There are only 2 atoms of hydrogen on the reactant side of the equation, while there are 4 atoms of hydrogen on the product side. We can balance the above equation by adding a coefficient of 2 in front of the formula for hydrogen.

\[\ce{C} \left( s \right) + 2 \ce{H_2} \left( g \right) \rightarrow \ce{CH_4} \left( g \right)\nonumber \]

A coefficient is a small whole number placed in front of a formula in an equation in order to balance it. The 2 in front of the \(\ce{H_2}\) means that there are a total of \(2 \times 2 = 4\) atoms of hydrogen as reactants. Visually, the reaction looks like the figure below.

In the balanced equation, there is one atom of carbon and four atoms of hydrogen on both sides of the arrow. Below are guidelines for writing and balancing chemical equations.

• Determine the correct chemical formulas for each reactant and product.
• Write the skeleton equation.
• Count the number of atoms of each element that appears as a reactant and as a product. If a polyatomic ion is unchanged on both sides of the equation, count it as a unit.
• It is best to begin by balancing elements that only appear in one chemical formula on each side of the equation.
• No coefficient is written for a 1.
• NEVER change the subscripts in a chemical formula—you can only balance equations by using coefficients.
• Check each atom or polyatomic ion to be sure that they are equal on both sides of the equation.
• Make sure that all coefficients are in the lowest possible ratio. If necessary, reduce to the lowest ratio.

Example \(\PageIndex{1}\): Balancing Chemical Equations

Aqueous solutions of lead (II) nitrate and sodium chloride are mixed. The products of the reaction are an aqueous solution of sodium nitrate and a solid precipitate of lead (II) chloride. Write the balanced chemical equation for this reaction.

Step 1: Plan the problem.

Follow the steps for writing and balancing a chemical equation listed in the text.

Step 2: Solve.

Write the skeleton equation with the correct formulas.

\[\ce{Pb(NO_3)_2} \left( aq \right) + \ce{NaCl} \left( aq \right) \rightarrow \ce{NaNO_3} \left( aq \right) + \ce{PbCl_2} \left( s \right)\nonumber \]

Count the number of each atom or polyatomic ion on both sides of the equation.

\[\begin{array}{ll} \textbf{Reactants} & \textbf{Products} \\ 1 \: \ce{Pb} \: \text{atom} & 1 \: \ce{Pb} \: \text{atom} \\ 2 \: \ce{NO_3^-} \: \text{ions} & 1 \: \ce{NO_3^-} \: \text{ions} \\ 1 \: \ce{Na} \: \text{atom} & 1 \: \ce{Na} \: \text{atom} \\ 1 \: \ce{Cl} \: \text{atom} & 2 \: \ce{Cl} \: \text{atoms} \end{array}\nonumber \]

The nitrate ions and the chlorine atoms are unbalanced. Start by placing a 2 in front of the \(\ce{NaCl}\). This increases the reactant counts to 2 \(\ce{Na}\) atoms and 2 \(\ce{Cl}\) atoms. Then place a 2 in front of the \(\ce{NaNO_3}\). The result is:

\[\ce{Pb(NO_3)_2} \left( aq \right) + 2 \ce{NaCl} \left( aq \right) \rightarrow 2 \ce{NaNO_3} \left( aq \right) + \ce{PbCl_2} \left( s \right)\nonumber \]

The new count for each atom and polyatomic ion becomes:

\[\begin{array}{ll} \textbf{Reactants} & \textbf{Products} \\ 1 \: \ce{Pb} \: \text{atom} & 1 \: \ce{Pb} \: \text{atom} \\ 2 \: \ce{NO_3^-} \: \text{ions} & 2 \: \ce{NO_3^-} \: \text{ions} \\ 2 \: \ce{Na} \: \text{atom} & 2 \: \ce{Na} \: \text{atom} \\ 2 \: \ce{Cl} \: \text{atom} & 2 \: \ce{Cl} \: \text{atoms} \end{array}\nonumber \]

Step 3: Think about your result.

The equation is now balanced since there are equal numbers of atoms of each element on both sides of the equation.

Practice balancing chemical equations with this simulation:

Can you balance a chemical equation?

• The process of balancing chemical equations is described.
• What is the law of conservation of mass?
• How did Dalton describe the process of a chemical reaction?
• Why don’t we change the subscripts in order to balance an equation?

4.1 Writing and Balancing Chemical Equations

Learning objectives.

By the end of this section, you will be able to:

• Derive chemical equations from narrative descriptions of chemical reactions.
• Write and balance chemical equations in molecular, total ionic, and net ionic formats.

An earlier chapter of this text introduced the use of element symbols to represent individual atoms. When atoms gain or lose electrons to yield ions, or combine with other atoms to form molecules, their symbols are modified or combined to generate chemical formulas that appropriately represent these species. Extending this symbolism to represent both the identities and the relative quantities of substances undergoing a chemical (or physical) change involves writing and balancing a chemical equation . Consider as an example the reaction between one methane molecule (CH 4 ) and two diatomic oxygen molecules (O 2 ) to produce one carbon dioxide molecule (CO 2 ) and two water molecules (H 2 O). The chemical equation representing this process is provided in the upper half of Figure 4.2 , with space-filling molecular models shown in the lower half of the figure.

This example illustrates the fundamental aspects of any chemical equation:

• The substances undergoing reaction are called reactants , and their formulas are placed on the left side of the equation.
• The substances generated by the reaction are called products , and their formulas are placed on the right side of the equation.
• Plus signs (+) separate individual reactant and product formulas, and an arrow (⟶) (⟶) separates the reactant and product (left and right) sides of the equation.
• The relative numbers of reactant and product species are represented by coefficients (numbers placed immediately to the left of each formula). A coefficient of 1 is typically omitted.

It is common practice to use the smallest possible whole-number coefficients in a chemical equation, as is done in this example. Realize, however, that these coefficients represent the relative numbers of reactants and products, and, therefore, they may be correctly interpreted as ratios. Methane and oxygen react to yield carbon dioxide and water in a 1:2:1:2 ratio. This ratio is satisfied if the numbers of these molecules are, respectively, 1-2-1-2, or 2-4-2-4, or 3-6-3-6, and so on ( Figure 4.3 ). Likewise, these coefficients may be interpreted with regard to any amount (number) unit, and so this equation may be correctly read in many ways, including:

• One methane molecule and two oxygen molecules react to yield one carbon dioxide molecule and two water molecules.
• One dozen methane molecules and two dozen oxygen molecules react to yield one dozen carbon dioxide molecules and two dozen water molecules.
• One mole of methane molecules and 2 moles of oxygen molecules react to yield 1 mole of carbon dioxide molecules and 2 moles of water molecules.

Balancing Equations

The chemical equation described in section 4.1 is balanced , meaning that equal numbers of atoms for each element involved in the reaction are represented on the reactant and product sides. This is a requirement the equation must satisfy to be consistent with the law of conservation of matter. It may be confirmed by simply summing the numbers of atoms on either side of the arrow and comparing these sums to ensure they are equal. Note that the number of atoms for a given element is calculated by multiplying the coefficient of any formula containing that element by the element’s subscript in the formula. If an element appears in more than one formula on a given side of the equation, the number of atoms represented in each must be computed and then added together. For example, both product species in the example reaction, CO 2 and H 2 O, contain the element oxygen, and so the number of oxygen atoms on the product side of the equation is

The equation for the reaction between methane and oxygen to yield carbon dioxide and water is confirmed to be balanced per this approach, as shown here:

A balanced chemical equation often may be derived from a qualitative description of some chemical reaction by a fairly simple approach known as balancing by inspection. Consider as an example the decomposition of water to yield molecular hydrogen and oxygen. This process is represented qualitatively by an unbalanced chemical equation:

Comparing the number of H and O atoms on either side of this equation confirms its imbalance:

The numbers of H atoms on the reactant and product sides of the equation are equal, but the numbers of O atoms are not. To achieve balance, the coefficients of the equation may be changed as needed. Keep in mind, of course, that the formula subscripts define, in part, the identity of the substance, and so these cannot be changed without altering the qualitative meaning of the equation. For example, changing the reactant formula from H 2 O to H 2 O 2 would yield balance in the number of atoms, but doing so also changes the reactant’s identity (it’s now hydrogen peroxide and not water). The O atom balance may be achieved by changing the coefficient for H 2 O to 2.

The H atom balance was upset by this change, but it is easily reestablished by changing the coefficient for the H 2 product to 2.

These coefficients yield equal numbers of both H and O atoms on the reactant and product sides, and the balanced equation is, therefore:

Example 4.1

Balancing chemical equations.

Next, count the number of each type of atom present in the unbalanced equation.

Though nitrogen is balanced, changes in coefficients are needed to balance the number of oxygen atoms. To balance the number of oxygen atoms, a reasonable first attempt would be to change the coefficients for the O 2 and N 2 O 5 to integers that will yield 10 O atoms (the least common multiple for the O atom subscripts in these two formulas).

The N atom balance has been upset by this change; it is restored by changing the coefficient for the reactant N 2 to 2.

The numbers of N and O atoms on either side of the equation are now equal, and so the equation is balanced.

Check Your Learning

It is sometimes convenient to use fractions instead of integers as intermediate coefficients in the process of balancing a chemical equation. When balance is achieved, all the equation’s coefficients may then be multiplied by a whole number to convert the fractional coefficients to integers without upsetting the atom balance. For example, consider the reaction of ethane (C 2 H 6 ) with oxygen to yield H 2 O and CO 2 , represented by the unbalanced equation:

Following the usual inspection approach, one might first balance C and H atoms by changing the coefficients for the two product species, as shown:

This results in seven O atoms on the product side of the equation, an odd number—no integer coefficient can be used with the O 2 reactant to yield an odd number, so a fractional coefficient, 7 2 , 7 2 , is used instead to yield a provisional balanced equation:

A conventional balanced equation with integer-only coefficients is derived by multiplying each coefficient by 2:

Finally with regard to balanced equations, recall that convention dictates use of the smallest whole-number coefficients . Although the equation for the reaction between molecular nitrogen and molecular hydrogen to produce ammonia is, indeed, balanced,

the coefficients are not the smallest possible integers representing the relative numbers of reactant and product molecules. Dividing each coefficient by the greatest common factor, 3, gives the preferred equation:

Link to Learning

Use this interactive tutorial for additional practice balancing equations.

Additional Information in Chemical Equations

The physical states of reactants and products in chemical equations very often are indicated with a parenthetical abbreviation following the formulas. Common abbreviations include s for solids, l for liquids, g for gases, and aq for substances dissolved in water ( aqueous solutions , as introduced in the preceding chapter). These notations are illustrated in the example equation here:

This equation represents the reaction that takes place when sodium metal is placed in water. The solid sodium reacts with liquid water to produce molecular hydrogen gas and the ionic compound sodium hydroxide (a solid in pure form, but readily dissolved in water).

Special conditions necessary for a reaction are sometimes designated by writing a word or symbol above or below the equation’s arrow. For example, a reaction carried out by heating may be indicated by the uppercase Greek letter delta (Δ) over the arrow.

Other examples of these special conditions will be encountered in more depth in later chapters.

Equations for Ionic Reactions

Given the abundance of water on earth, it stands to reason that a great many chemical reactions take place in aqueous media. When ions are involved in these reactions, the chemical equations may be written with various levels of detail appropriate to their intended use. To illustrate this, consider a reaction between ionic compounds taking place in an aqueous solution. When aqueous solutions of CaCl 2 and AgNO 3 are mixed, a reaction takes place producing aqueous Ca(NO 3 ) 2 and solid AgCl:

This balanced equation, derived in the usual fashion, is called a molecular equation because it doesn’t explicitly represent the ionic species that are present in solution. When ionic compounds dissolve in water, they may dissociate into their constituent ions, which are subsequently dispersed homogenously throughout the resulting solution (a thorough discussion of this important process is provided in the chapter on solutions). Ionic compounds dissolved in water are, therefore, more realistically represented as dissociated ions, in this case:

Unlike these three ionic compounds, AgCl does not dissolve in water to a significant extent, as signified by its physical state notation, s .

Explicitly representing all dissolved ions results in a complete ionic equation . In this particular case, the formulas for the dissolved ionic compounds are replaced by formulas for their dissociated ions:

Examining this equation shows that two chemical species are present in identical form on both sides of the arrow, Ca 2+ ( aq ) and NO 3 − ( a q ) . NO 3 − ( a q ) . These spectator ions —ions whose presence is required to maintain charge neutrality—are neither chemically nor physically changed by the process, and so they may be eliminated from the equation to yield a more succinct representation called a net ionic equation :

Following the convention of using the smallest possible integers as coefficients, this equation is then written:

This net ionic equation indicates that solid silver chloride may be produced from dissolved chloride and silver(I) ions, regardless of the source of these ions. These molecular and complete ionic equations provide additional information, namely, the ionic compounds used as sources of Cl − and Ag + .

Example 4.2

Ionic and molecular equations.

Balance is achieved easily in this case by changing the coefficient for NaOH to 2, resulting in the molecular equation for this reaction:

The two dissolved ionic compounds, NaOH and Na 2 CO 3 , can be represented as dissociated ions to yield the complete ionic equation:

Finally, identify the spectator ion(s), in this case Na + ( aq ), and remove it from each side of the equation to generate the net ionic equation:

Write balanced molecular, complete ionic, and net ionic equations for this process.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/chemistry-2e/pages/1-introduction

• Authors: Paul Flowers, Klaus Theopold, Richard Langley, William R. Robinson, PhD
• Publisher/website: OpenStax
• Book title: Chemistry 2e
• Publication date: Feb 14, 2019
• Location: Houston, Texas
• Book URL: https://openstax.org/books/chemistry-2e/pages/1-introduction
• Section URL: https://openstax.org/books/chemistry-2e/pages/4-1-writing-and-balancing-chemical-equations

© Jan 8, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Please log in to save materials. Log in

• Resource Library

Education Standards

Wyoming science content and performance standards.

Learning Domain: Matter and Its Interactions

Standard: Use mathematical representations to support the claim that atoms, and therefore mass, are conserved during a chemical reaction.

Next Generation Science Standards

Science Domain: Physical Sciences

Topic: Chemical Reactions

Standard: Use mathematical representations to support the claim that atoms, and therefore mass, are conserved during a chemical reaction. [Clarification Statement: Emphasis is on using mathematical ideas to communicate the proportional relationships between masses of atoms in the reactants and the products, and the translation of these relationships to the macroscopic scale using the mole as the conversion from the atomic to the macroscopic scale. Emphasis is on assessing students’ use of mathematical thinking and not on memorization and rote application of problem-solving techniques.] [Assessment Boundary: Assessment does not include complex chemical reactions.]

Example Packets

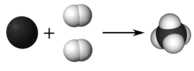
Particle Diagrams

Hands-on balancing equations and reaction types.

Objectives:

To use models and particle diagrams to represent the law of conservation of matter and energy in a chemical reaction.

To write and determine the ratio of reactants to products, through the use of adding coefficients.

To classify various types of chemical reactions.

Hands-on Balancing

Connection to Prior Knowledge:

What is the Law of Conservation of Matter? How does this apply to chemical reactions?

Materials: Balancing Packets, Molecular Model kits or the PhET Balancing Activity and possibly a whiteboard.

https://phet.colorado.edu/en/simulation/balancing-chemical-equations

Procedure: (Students choose if they will be using the pre-made packets or the PhET simulation prior to beginning.)

From the packets or PhET simulation, write down the first equation. Draw a particle diagram representing the unbalanced equation. Using the substances in the packet or simply adding more compounds or atoms on the simulation, continue to add until both sides of the equation have equal amounts of each element.

Draw the particle diagram for the balanced equation and write in the proper coefficients.

Using the chemical reaction particle diagram document provided on Schoology, determine which type of reaction the equation is demonstrating. Have the teacher initial to check for accuracy after completing each equation. The PhET simulation will tell if you are correct with balancing and you will only need the teacher signature at the end of each game level. There are a total of 15 equations.

*The pre-made packets can be 15 of any equations that you would like the students to practice balancing. Make sure to have a variety of reaction types for the second type. To create the packets, cut out a variety of possible elements and compounds that could be used in balancing the equations. I place some extra elements that are not correct, to really check their understanding of equations. 

First determine if you will be using the packets available in class or the online simulation. From the packets or PhET simulation, write down the first equation. Draw a particle diagram representing the unbalanced equation. Using the substances in the packet or simply adding more compounds or atoms on the simulation, continue to add until both sides of the equation have equal amounts of each element.

Analysis: Students could answer these questions on a discussion board or whiteboard, whatever the teacher's preference. 

Determine and explain how the law of conservation of mass has been represented throughout this activity.

What do the subscripts tell you in an equation?

What do the coefficients tell you about an equation?

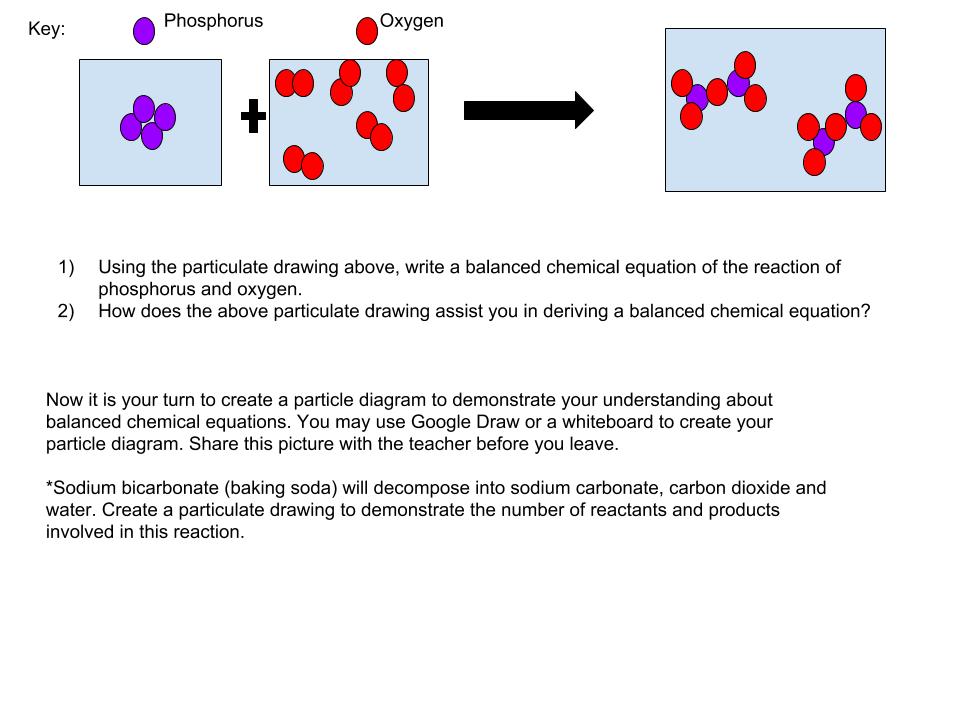
Once the students have finished the activity and the analysis portion, they must individually answer the questions on the particulate drawings document. Students may use Google Draw, paper and colored pencils, or even everyday items to demonstrate their understanding of particulate drawings and balanced chemical equations. This assessment leads you into be able to use this skill when introducing stoichiometry. 

Once you have finished the activity and analysis, open the following link and individually answer the questions presented. When asked to create your own particulate drawing, you may use a variety of resources; Google Draw, paper and colored pencils, M & M candies, etc.. Whatever allows you to represent the balanced chemical equation. You may take a picture of your drawing and submit it to your teacher before you leave, along with the answers to the beginning questions. 

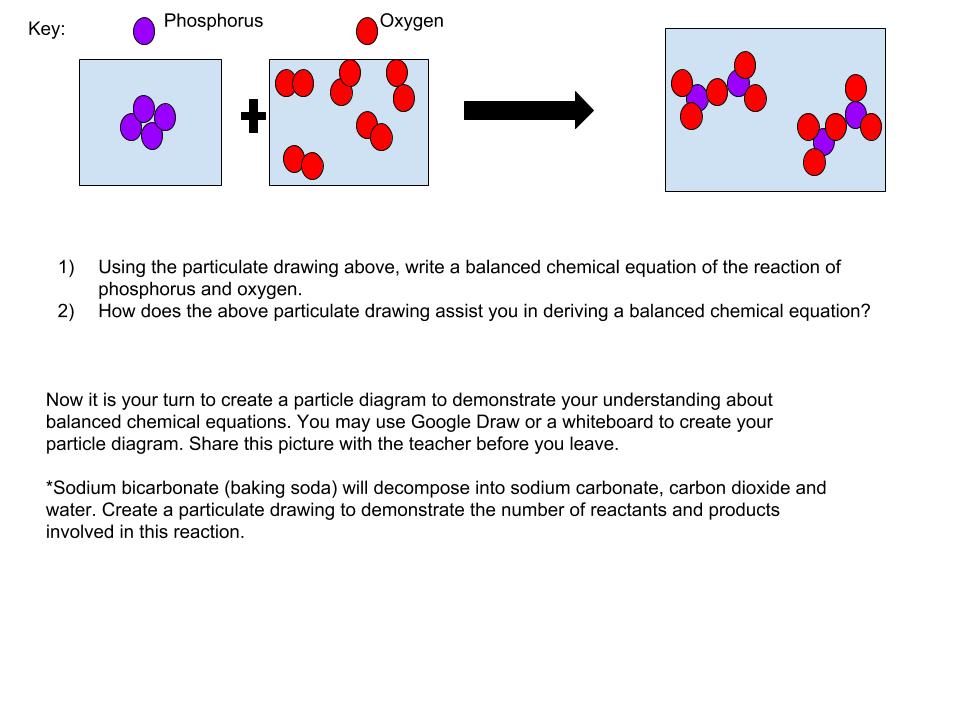
Version History

Unit 3: The Mole – Chemical Formulas, Stoichiometry, Limiting Reactant, Percent Yield

Writing and balancing chemical equations, learning objectives.

By the end of this section, you will be able to:

• Derive chemical equations from narrative descriptions of chemical reactions.
• Write and balance chemical equations in molecular formats.

The preceding chapter introduced the use of element symbols to represent individual atoms. When atoms gain or lose electrons to yield ions, or combine with other atoms to form molecules, their symbols are modified or combined to generate chemical formulas that appropriately represent these species. Extending this symbolism to represent both the identities and the relative quantities of substances undergoing a chemical (or physical) change involves writing and balancing a chemical equation . Consider as an example the reaction between one methane molecule (CH 4 ) and two diatomic oxygen molecules (O 2 ) to produce one carbon dioxide molecule (CO 2 ) and two water molecules (H 2 O). The chemical equation representing this process is provided in the upper half of Figure 1, with space-filling molecular models shown in the lower half of the figure.

Figure 1. The reaction between methane and oxygen to yield carbon dioxide in water (shown at bottom) may be represented by a chemical equation using formulas (top).

This example illustrates the fundamental aspects of any chemical equation:

• The substances undergoing reaction are called reactants , and their formulas are placed on the left side of the equation.
• The substances generated by the reaction are called products , and their formulas are placed on the right sight of the equation.
• Plus signs (+) separate individual reactant and product formulas, and an arrow ([latex]\rightarrow[/latex]) separates the reactant and product (left and right) sides of the equation.
• The relative numbers of reactant and product species are represented by coefficients (numbers placed immediately to the left of each formula). A coefficient of 1 is typically omitted.

It is common practice to use the smallest possible whole-number coefficients in a chemical equation, as is done in this example. Realize, however, that these coefficients represent the relative numbers of reactants and products, and, therefore, they may be correctly interpreted as ratios. Methane and oxygen react to yield carbon dioxide and water in a 1:2:1:2 ratio. This ratio is satisfied if the numbers of these molecules are, respectively, 1-2-1-2, or 2-4-2-4, or 3-6-3-6, and so on (Figure 2). Likewise, these coefficients may be interpreted with regard to any amount (number) unit, and so this equation may be correctly read in many ways, including:

• One methane molecule and two oxygen molecules react to yield one carbon dioxide molecule and two water molecules.
• One dozen methane molecules and two dozen oxygen molecules react to yield one dozen carbon dioxide molecules and two dozen water molecules.
• One mole of methane molecules and 2 moles of oxygen molecules react to yield 1 mole of carbon dioxide molecules and 2 moles of water molecules.

Figure 2. Regardless of the absolute number of molecules involved, the ratios between numbers of molecules are the same as that given in the chemical equation.

Balancing Equations

A  balanced chemical is equation  has equal numbers of atoms for each element involved in the reaction are represented on the reactant and product sides. This is a requirement the equation must satisfy to be consistent with the law of conservation of matter. It may be confirmed by simply summing the numbers of atoms on either side of the arrow and comparing these sums to ensure they are equal. Note that the number of atoms for a given element is calculated by multiplying the coefficient of any formula containing that element by the element’s subscript in the formula. If an element appears in more than one formula on a given side of the equation, the number of atoms represented in each must be computed and then added together. For example, both product species in the example reaction, CO 2 and H 2 O, contain the element oxygen, and so the number of oxygen atoms on the product side of the equation is

[latex]\left(1{\text{CO}}_{2}\text{ molecule }\times \frac{\text{2 O atoms}}{{\text{CO}}_{2}\text{ molecule }}\right)+\left(2{\text{H}}_{2}\text{O molecule }\times \frac{\text{1 O atom}}{{\text{H}}_{2}\text{O molecule }}\right)=\text{4 O atoms}[/latex]

The equation for the reaction between methane and oxygen to yield carbon dioxide and water is confirmed to be balanced per this approach, as shown here:

[latex]{\text{CH}}_{4}+2{\text{O}}_{2}\rightarrow{\text{CO}}_{2}+2{\text{H}}_{2}\text{O}[/latex]

A balanced chemical equation often may be derived from a qualitative description of some chemical reaction by a fairly simple approach known as balancing by inspection. Consider as an example the decomposition of water to yield molecular hydrogen and oxygen. This process is represented qualitatively by an unbalanced chemical equation:

[latex]{\text{H}}_{2}\text{O}\rightarrow{\text{H}}_{2}+{\text{O}}_{2}\text{(unbalanced)}[/latex]

Comparing the number of H and O atoms on either side of this equation confirms its imbalance:

The numbers of H atoms on the reactant and product sides of the equation are equal, but the numbers of O atoms are not. To achieve balance, the coefficients of the equation may be changed as needed. Keep in mind, of course, that the formula subscripts define, in part, the identity of the substance, and so these cannot be changed without altering the qualitative meaning of the equation. For example, changing the reactant formula from H 2 O to H 2 O 2 would yield balance in the number of atoms, but doing so also changes the reactant’s identity (it’s now hydrogen peroxide and not water). The O atom balance may be achieved by changing the coefficient for H 2 O to 2.

[latex]\mathbf{2}\text{H}_{2}\text{O}\rightarrow{\text{H}}_{2}+{\text{O}}_{2}\text{(unbalanced)}[/latex]

The H atom balance was upset by this change, but it is easily reestablished by changing the coefficient for the H 2 product to 2.

[latex]2{\text{H}}_{2}\text{O}\rightarrow\mathbf{2}{\text{H}}_{2}+{\text{O}}_{2}\text{(balanced)}[/latex]

These coefficients yield equal numbers of both H and O atoms on the reactant and product sides, and the balanced equation is, therefore:

[latex]2{\text{H}}_{2}\text{O}\rightarrow 2{\text{H}}_{2}+{\text{O}}_{2}[/latex]

Example 1:  Balancing Chemical Equations

Write a balanced equation for the reaction of molecular nitrogen (N 2 ) and oxygen (O 2 ) to form dinitrogen pentoxide.

First, write the unbalanced equation:

[latex]{\text{N}}_{2}+{\text{O}}_{2}\rightarrow{\text{N}}_{2}{\text{O}}_{5}\text{(unbalanced)}[/latex]

Next, count the number of each type of atom present in the unbalanced equation.

Though nitrogen is balanced, changes in coefficients are needed to balance the number of oxygen atoms. To balance the number of oxygen atoms, a reasonable first attempt would be to change the coefficients for the O 2 and N 2 O 5 to integers that will yield 10 O atoms (the least common multiple for the O atom subscripts in these two formulas).

[latex]{\text{N}}_{2}+\mathbf{5}{\text{O}}_{2}\rightarrow\mathbf{2}{\text{N}}_{2}{\text{O}}_{5}\text{(unbalanced)}[/latex]

The N atom balance has been upset by this change; it is restored by changing the coefficient for the reactant N 2 to 2.

[latex]2{\text{N}}_{2}+5{\text{O}}_{2}\rightarrow 2{\text{N}}_{2}{\text{O}}_{5}[/latex]

The numbers of N and O atoms on either side of the equation are now equal, and so the equation is balanced.

Check Your Learning

Write a balanced equation for the decomposition of ammonium nitrate to form molecular nitrogen, molecular oxygen, and water. (Hint: Balance oxygen last, since it is present in more than one molecule on the right side of the equation.)

It is sometimes convenient to use fractions instead of integers as intermediate coefficients in the process of balancing a chemical equation. When balance is achieved, all the equation’s coefficients may then be multiplied by a whole number to convert the fractional coefficients to integers without upsetting the atom balance. For example, consider the reaction of ethane (C 2 H 6 ) with oxygen to yield H 2 O and CO 2 , represented by the unbalanced equation:

[latex]{\text{C}}_{2}{\text{H}}_{6}+{\text{O}}_{2}\rightarrow{\text{H}}_{2}\text{O}+{\text{CO}}_{2}\text{(unbalanced)}[/latex]

Following the usual inspection approach, one might first balance C and H atoms by changing the coefficients for the two product species, as shown:

[latex]{\text{C}}_{2}{\text{H}}_{6}+{\text{O}}_{2}\rightarrow 3{\text{H}}_{2}\text{O}+2{\text{CO}}_{2}\text{(unbalanced)}[/latex]

This results in seven O atoms on the product side of the equation, an odd number—no integer coefficient can be used with the O 2 reactant to yield an odd number, so a fractional coefficient, [latex]\displaystyle\frac{7}{2}[/latex] , is used instead to yield a provisional balanced equation:

[latex]{\text{C}}_{2}{\text{H}}_{6}+\frac{7}{2}{\text{O}}_{2}\rightarrow 3{\text{H}}_{2}\text{O}+2{\text{CO}}_{2}[/latex]

A conventional balanced equation with integer-only coefficients is derived by multiplying each coefficient by 2:

[latex]2{\text{C}}_{2}{\text{H}}_{6}+7{\text{O}}_{2}\rightarrow 6{\text{H}}_{2}\text{O}+4{\text{CO}}_{2}[/latex]

Finally with regard to balanced equations, recall that convention dictates use of the smallest whole-number coefficients . Although the equation for the reaction between molecular nitrogen and molecular hydrogen to produce ammonia is, indeed, balanced,

[latex]3{\text{N}}_{2}+9{\text{H}}_{2}\rightarrow 6{\text{NH}}_{3}[/latex]

the coefficients are not the smallest possible integers representing the relative numbers of reactant and product molecules. Dividing each coefficient by the greatest common factor, 3, gives the preferred equation:

[latex]{\text{N}}_{2}+3{\text{H}}_{2}\rightarrow 2{\text{NH}}_{3}[/latex]

Balance the following equations:

• [latex]{\text{PCl}}_{5}\text{(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}\rightarrow{\text{POCl}}_{3}\text{(}l\text{)}+\text{HCl(}aq\text{)}[/latex]
• [latex]\text{Ag}\text{(}s\text{)}+{\text{H}}_{2}\text{S}\text{(}g\text{)}+{\text{O}}_{2}\text{(}g\text{)}\rightarrow{\text{Ag}}_{2}\text{S}\text{(}s\text{)}+{\text{H}}_{2}\text{O}\text{(}l\text{)}[/latex]
• [latex]\text{Cu(}s\text{)}+{\text{HNO}}_{3}\text{(}aq\text{)}\rightarrow\text{Cu}{\text{(}{\text{NO}}_{3}\text{)}}_{2}\text{(}aq\text{)}+{\text{H}}_{2}\text{O(}l\text{)}+\text{NO(}g\text{)}[/latex]
• [latex]{\text{P}}_{4}\text{(}s\text{)}+{\text{O}}_{2}\text{(}g\text{)}\rightarrow{\text{P}}_{4}{\text{O}}_{10}\text{(}s\text{)}[/latex]
• [latex]{\text{H}}_{2}\text{(}g\text{)}+{\text{I}}_{2}\text{(}s\text{)}\rightarrow\text{HI(}s\text{)}[/latex]
• [latex]\text{Pb(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}+{\text{O}}_{2}\text{(}g\text{)}\rightarrow{\text{Pb(OH)}}_{2}\text{(}s\text{)}[/latex]
• [latex]\text{Fe(}s\text{)}+{\text{O}}_{2}\text{(}g\text{)}\rightarrow{\text{Fe}}_{2}{\text{O}}_{3}\text{(}s\text{)}[/latex]
• [latex]\text{Fe(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}\rightarrow{\text{Fe}}_{3}{\text{O}}_{4}\text{(}s\text{)}+{\text{H}}_{2}\text{(}g\text{)}[/latex]
• [latex]\text{Na(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}\rightarrow\text{NaOH}\text{(}aq\text{)}+{\text{H}}_{2}\text{(}g\text{)}[/latex]
• [latex]{\text{Sc}}_{2}{\text{O}}_{3}\text{(}s\text{)}+{\text{SO}}_{3}\text{(}l\text{)}\rightarrow{\text{Sc}}_{2}{\text{(}{\text{SO}}_{4}\text{)}}_{3}\text{(}s\text{)}[/latex]
• [latex]{\text{(}{\text{NH}}_{4}\text{)}}_{2}{\text{Cr}}_{2}{\text{O}}_{7}\text{(}s\text{)}\rightarrow{\text{Cr}}_{2}{\text{O}}_{3}\text{(}s\text{)}+{\text{N}}_{2}\text{(}g\text{)}+{\text{H}}_{2}\text{O(}g\text{)}[/latex]
• [latex]{\text{Ca}}_{3}{\text{(}{\text{PO}}_{4}\text{)}}_{2}\text{(}aq\text{)}+{\text{H}}_{3}{\text{PO}}_{4}\text{(}aq\text{)}\rightarrow\text{Ca}{\text{(}{\text{H}}_{2}{\text{PO}}_{4}\text{)}}_{2}\text{(}aq\text{)}[/latex]
• [latex]{\text{P}}_{4}\text{(}s\text{)}+{\text{Cl}}_{2}\text{(}g\text{)}\rightarrow{\text{PCl}}_{3}\text{(}l\text{)}[/latex]
• [latex]\text{Al(}s\text{)}+{\text{H}}_{2}{\text{SO}}_{4}\text{(}aq\text{)}\rightarrow{\text{Al}}_{2}{\text{(}{\text{SO}}_{4}\text{)}}_{3}\text{(}aq\text{)}+{\text{H}}_{2}\text{(}g\text{)}[/latex]
• [latex]{\text{PtCl}}_{4}\text{(}s\text{)}\rightarrow\text{Pt}\text{(}s\text{)}+{\text{Cl}}_{2}\text{(}g\text{)}[/latex]
• [latex]{\text{TiCl}}_{4}\text{(}s\text{)}+{\text{H}}_{2}\text{O(}g\text{)}\rightarrow{\text{TiO}}_{2}\text{(}s\text{)}+\text{HCl(}g\text{)}[/latex]

The balanced equations are as follows:

1. [latex]{\text{PCl}}_{5}\text{(}s\text{)}+{\text{H}}_{2}\text{O(}l\text{)}\rightarrow{\text{POCl}}_{3}\text{(}l\text{)}+2\text{HCl(}aq\text{);}[/latex]

3. [latex]3\text{Cu}\text{(}s\text{)}+8{\text{HNO}}_{3}\text{(}aq\text{)}\rightarrow 3\text{Cu}{\text{(}{\text{NO}}_{3}\text{)}}_{2}\text{(}aq\text{)}+4{\text{H}}_{2}\text{O(}l\text{)}+2\text{NO(}g\text{);}[/latex]

5. [latex]{\text{H}}_{2}\text{(}g\text{)}+{\text{I}}_{2}\text{(}s\text{)}\rightarrow 2\text{HI(}s\text{);}[/latex]

7. [latex]4\text{Fe(}s\text{)}+3{\text{O}}_{2}\text{(}g\text{)}\rightarrow 2{\text{Fe}}_{2}{\text{O}}_{3}\text{(}s\text{);}[/latex]

9. [latex]2\text{Na(}s\text{)}+2{\text{H}}_{2}\text{O(}l\text{)}\rightarrow 2\text{NaOH(}aq\text{)}+{\text{H}}_{2}\text{(}g\text{);}[/latex]

11. [latex]{\text{(}{\text{NH}}_{4}\text{)}}_{2}+{\text{Cr}}_{5}{\text{O}}_{7}\text{(}s\text{)}\rightarrow{\text{Cr}}_{2}{\text{O}}_{3}\text{(}s\text{)}+{\text{N}}_{2}\text{(}g\text{)}+4{\text{H}}_{2}\text{O(}g\text{);}[/latex]

13. [latex]{\text{P}}_{4}\text{(}s\text{)}+6{\text{Cl}}_{2}\text{(}g\text{)}\rightarrow 4{\text{PCl}}_{3}\text{(}l\text{);}[/latex]

15. [latex]{\text{PtCl}}_{4}\text{(}s\text{)}\rightarrow\text{Pt(}s\text{)}+2{\text{Cl}}_{2}\text{(}g\text{)}[/latex]

balanced equation:  chemical equation with equal numbers of atoms for each element in the reactant and product

chemical equation:  symbolic representation of a chemical reaction

coefficient:  number placed in front of symbols or formulas in a chemical equation to indicate their relative amount

product:  substance formed by a chemical or physical change; shown on the right side of the arrow in a chemical equation

reactant:  substance undergoing a chemical or physical change; shown on the left side of the arrow in a chemical equation

• Chemistry. Provided by : OpenStax College. Located at : http://openstaxcollege.org . License : CC BY: Attribution . License Terms : Download for free at https://openstaxcollege.org/textbooks/chemistry/get

• Chemical Reactions and Equations

Balancing Chemical Equations

Balancing chemical equations involves the addition of stoichiometric coefficients to the reactants and products. This is important because a chemical equation must obey the law of conservation of mass and the law of constant proportions , i.e. the same number of atoms of each element must exist on the reactant side and the product side of the equation.

Two quick and easy methods of balancing a chemical equation are discussed in this article. The first method is the traditional balancing method and the second one is the algebraic balancing method.

Table of Content

Related terminology, chemical equation, stoichiometric coefficient, the traditional balancing method, the algebraic balancing method, solved examples.

• A chemical equation is a symbolic representation of a chemical reaction in which the reactants and products are denoted by their respective chemical formulae.
• An example of a chemical equation is 2H 2 + O 2 → 2H 2 O which describes the reaction between hydrogen and oxygen to form water
• The reactant side is the part of the chemical equation to the left of the ‘→’ symbol whereas the product side is the part to the right of the arrow symbol.
• A stoichiometric coefficient describes the total number of molecules of a chemical species that participate in a chemical reaction.
• It provides a ratio between the reacting species and the products formed in the reaction.
• In the reaction described by the equation CH 4 + 2O 2 → CO 2 + 2H 2 O , the stoichiometric coefficient of O 2 and H 2 O is 2 whereas that of CH 4 and CO 2 is 1.
• The total number of atoms of an element present in a species (in a balanced chemical equation) is equal to the product of the stoichiometric coefficient and the number of atoms of the element in one molecule of the species.
• For example, the total number of oxygen atoms in the reacting species ‘2O 2 ’ is 4.
• While balancing chemical equations, stoichiometric coefficients are assigned in a manner that balances the total number of atoms of an element on the reactant and product side.

The first step that must be followed while balancing chemical equations is to obtain the complete unbalanced equation. In order to illustrate this method, the combustion reaction between propane and oxygen is taken as an example.

• The unbalanced equation must be obtained from the chemical formulae of the reactants and the products (if it is not already provided).
• The chemical formula of propane is C 3 H 8 . It burns with oxygen (O 2 ) to form carbon dioxide (CO 2 ) and water (H 2 O)
• The unbalanced chemical equation can be written as C 3 H 8 + O 2 → CO 2 + H 2 O

The total number of atoms of each element on the reactant side and the product side must be compared. For this example, the number of atoms on each side can be tabulated as follows.

• Now, stoichiometric coefficients are added to molecules containing an element which has a different number of atoms in the reactant side and the product side.
• The coefficient must balance the number of atoms on each side.
• Generally, the stoichiometric coefficients are assigned to hydrogen and oxygen atoms last.
• Now, the number of atoms of the elements on the reactant and product side must be updated.
• It is important to note that the number of atoms of an element in one species must be obtained by multiplying the stoichiometric coefficient with the total number of atoms of that element present in 1 molecule of the species.
• For example, when the coefficient 3 is assigned to the CO 2 molecule, the total number of oxygen atoms in CO 2 becomes 6. In this example, the coefficient is first assigned to carbon, as tabulated below.

Step 3 is repeated until all the number of atoms of the reacting elements are equal on the reactant and product side. In this example, hydrogen is balanced next. The chemical equation is transformed as follows.

Now that the hydrogen atoms are balanced, the next element to be balanced is oxygen. There are 10 oxygen atoms on the product side, implying that the reactant side must also contain 10 oxygen atoms.

Each O 2 molecule contains 2 oxygen atoms. Therefore, the stoichiometric coefficient that must be assigned to the O 2 molecule is 5. The updated chemical equation is tabulated below.

• Once all the individual elements are balanced, the total number of atoms of each element on the reactant and product side are compared once again.
• If there are no inequalities, the chemical equation is said to be balanced.
• In this example, every element now has an equal number of atoms in the reactant and product side.
• Therefore, the balanced chemical equation is C 3 H 8 + 5O 2 → 3CO 2 + 4H 2 O .

This method of balancing chemical equations involves assigning algebraic variables as stoichiometric coefficients to each species in the unbalanced chemical equation. These variables are used in mathematical equations and are solved to obtain the values of each stoichiometric coefficient. In order to better explain this method, the reaction between glucose and oxygen that yields carbon dioxide and water has been considered as an example.

• The unbalanced chemical equation must be obtained by writing the chemical formulae of the reactants and the products.
• In this example, the reactants are glucose (C 6 H 12 O 6 ) and oxygen (O 2 ) and the products are carbon dioxide (CO 2 ) and water (H 2 O)
• The unbalanced chemical equation is C 6 H 12 O 6 + O 2 → CO 2 + H 2 O

Now, algebraic variables are assigned to each species (as stoichiometric coefficients) in the unbalanced chemical equation. In this example, the equation can be written as follows.

a C 6 H 12 O 6 + b O 2 → c CO 2 + d H 2 O

Now, a set of equations must be formulated (between the reactant and product side) in order to balance each element in the reaction. In this example, the following equations can be formed.

The equation for Carbon

• On the reactant side, ‘a’ molecules of C 6 H 12 O 6 will contain ‘6a’ carbon atoms.
• On the product side, ‘c’ molecules of CO 2 will contain ‘c’ carbon atoms.
• In this equation, the only species containing carbon are C 6 H 12 O 6 and CO 2 .

Therefore, the following equation can be formulated for carbon: 6a = c

  The equation for Hydrogen

• The species that contain hydrogen in this equation are C 6 H 12 O 6 and H 2
• ‘a’ molecules of C 6 H 12 O 6 contains ‘12a’ hydrogen atoms whereas ‘d’ H 2 O molecules will contain ‘2d’ hydrogen atoms.
• Therefore, the equation for hydrogen becomes 12a = 2d .

Simplifying this equation (by dividing both sides by 2), the equation becomes:

The equation for Oxygen

Every species in this chemical equation contains oxygen. Therefore, the following relations can be made to obtain the equation for oxygen:

• For ‘a’ molecules of C 6 H 12 O 6 , there exist ‘6a’ oxygen atoms.
• ‘b’ molecules of O 2 contain a total of ‘2b’ oxygens.
• ‘c’ molecules of CO 2 contain ‘2c’ number of oxygen atoms.
• ‘d’ molecules of H 2 O hold ‘d’ oxygen atoms.

Therefore, the equation for oxygen can be written as:

6a + 2b = 2c+ d

The equations for each element are listed together to form a system of equations. In this example, the system of equations is as follows:

6a = c (for carbon); 6a = d (for hydrogen); 6a + 2b = 2c + d (for oxygen)

This system of equations can have multiple solutions, but the solution with minimal values of the variables is required. To obtain this solution, a value is assigned to one of the coefficients. In this case, the value of a is assumed to be 1. Therefore, the system of equations is transformed as follows:

c = 6a = 6*1 = 6

Substituting the values of a,c, and d in the equation 6a + 2b = 2c + d , the value of ‘b’ can be obtained as follows:

6*1 + 2b = 2*6 + 6

2b = 12; b = 6

It is important to note that these equations must be solved in a manner that each variable is a positive integer. If fractional values are obtained, the lowest common denominator between all the variables must be multiplied with each variable. This is necessary because the variables hold the values of the stoichiometric coefficients, which must be a positive integer.

• Now that the smallest value of each variable is obtained, their values can be substituted into the chemical equation obtained in step 2.
• Therefore, aC 6 H 12 O 6 + bO 2 → cCO 2 + dH 2 O becomes: C 6 H 12 O 6 + 6O 2 → 6CO 2 + 6H 2 O
• Thus, the balanced chemical equation is obtained.

The algebraic method of balancing chemical equations is considered to be more efficient than the traditional method. However, it can yield fractional values for the stoichiometric coefficients, which must then be converted into integers.

Recommended Videos

Session 1 – balancing of chemical equations.

How to Balance Any Chemical Equation in 30 Secs

Some examples describing the balancing of chemical equations are provided in this subsection. These equations have been balanced using both the methods described above.

Unbalanced chemical equation: Al + O 2 → Al 2 O 3

Traditional Method

Following the traditional method, the reaction can be balanced as follows:

First, the aluminium atoms are balanced. The equation becomes 2Al + O 2 → Al 2 O 3

Now, the oxygen atoms must be balanced, there are two oxygen atoms on the reactant side and 3 on the product side. Therefore, there must be 3 O 2 molecules that yield 2 Al 2 O 3 atoms. The chemical equation is transformed into 2Al + 3O 2 → 2Al 2 O 3

Since the number of aluminium atoms on the product side has doubled, so must the number on the reactant side.

Since each element is balanced, the balanced chemical equation is found to be 4Al + 3O 2 → 2Al 2 O 3

Algebraic Method

Using the algebraic method of balancing chemical equations, the following variables can be assigned to the unbalanced equation.

a Al + b O 2 → c Al 2 O 3

The equation for Aluminum: a = 2c

The equation for Oxygen: 2b = 3c

Assuming a = 1, we get:

c = a/2 ; c = 1/2

2b = 3*(½) = 3/2 ; b = ¾

Since fractional values of b and c are obtained, the lowest common denominator between the variables a, b, and c must be found and multiplied with each variable. Since the lowest common denominator is 4, each of the variables must be multiplied by 4.

Therefore, a = 4*1 = 4 ;  b = (¾)*4 = 3 ; c = (½)*4 = 2

Substituting the values of a, b, and c in the unbalanced equation, the following balanced chemical equation is obtained.

4Al + 3O 2 → 2Al 2 O 3

Unbalanced chemical equation: N 2 + H 2 → NH 3

In this reaction, the nitrogen atoms are balanced first. The reactant side has two nitrogen atoms, implying that 2 molecules of NH 3 must be formed for each N 2 molecule.

Each H 2 molecule contains 2 hydrogen atoms. In order to balance the number of hydrogen atoms in the equation, the total number of hydrogen atoms must be equal to 6. Therefore, the stoichiometric coefficient that must be assigned to hydrogen is 3.

Thus, the balanced chemical equation is N 2 + 3H 2 → 2NH 3

The variables a, b, and c must be assigned to N 2 , H 2 , and NH 3 respectively. The chemical equation can be written as:

a N 2 + b H 2 → c NH 3

The equation for nitrogen: 2a = c

The equation for hydrogen: 2b = 3c

Assuming a = 1 , the values of b and c can be obtained as follows.

2b = 3c = 3*2 = 6; b = 6/2 = 3

Since a, b, and c have no common multiples, they can be substituted into the equation as follows.

N 2 + 3H 2 → 2NH 3

This is the balanced form of the given chemical equation.

In order to practice different methods of balancing chemical equations, the following unbalanced equations can be worked on.

• FeCl 3 + NaOH → NaCl + Fe(OH) 3
• Zn + HCl → ZnCl 2 + H 2
• P 2 O 5 + H 2 O → H 3 PO 4
• FeSO 4 + NaOH → Na 2 SO 4 + Fe(OH) 2
• Mg + HCl →  MgCl 2 + H 2

To learn more about balancing chemical equations and other related concepts, register with BYJU’S and download the mobile application on your smartphone.

Access NCERT Solutions for Class 10 Chapter 1 Chemical Reactions and Equations here . 

Related Videos

How to balance chemical equations.

5 Easy Steps on How to Balance Chemical Equation

Frequently Asked Questions – FAQs

What is the balanced form of the reaction between calcium hydroxide and nitric acid [ca(oh) 2 + hno 3  → ca(no 3 ) 2 + h 2 o], if water is reacted with oxygen to form hydrogen peroxide, what would be the balanced chemical equation for the reaction, what is the balanced chemical equation for the reaction between ferric chloride and sodium hydroxide.

The chemical formula of ferric chloride is FeCl 3 and that of sodium hydroxide is NaOH. The unbalanced chemical equation is:

FeCl 3 + NaOH → Fe(OH) 3 + NaCl

balancing the number of oxygen and hydrogen atoms first and then balancing the number of sodium atoms, the balanced chemical equation is found to be:

FeCl 3 + 3NaOH → Fe(OH) 3 + 3NaCl

What is the most crucial thing about balancing chemical equations?

What is a chemical equation, what is a stoichiometric coefficient, do charges matter when balancing a chemical equation, what happens if a chemical equation is not balanced, write a balanced equation for photosynthesis., write a balanced equation for molecular dinitrogen and dioxygen reaction to form dinitrogen pentoxide..

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Chemistry related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Interesting, knowledgeable 🤓

Helpful,nice

It is really helpful for the beginners

OK it was nice thank you for the hlep

Very helpful

Its helpful and very easy to understand

Helpful and good to understand 🌝🌝🙂🙂

VERY HELPFUL .THANK YOU

This is very helpful and interesting thanks

Byjuis is the best app

Very nicely explained. However, a few complex examples with hydroxyl ions should have been explained

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Class 10 Chemistry (India)

Course: class 10 chemistry (india)   >   unit 1, balancing chemical equations.

• Balancing more complex chemical equations
• Visually understanding balancing chemical equations
• Balancing another combustion reaction
• Balancing chemical equation with substitution

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍