what is hypothesis testing ap stats

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6a.2 - steps for hypothesis tests, the logic of hypothesis testing section  .

A hypothesis, in statistics, is a statement about a population parameter, where this statement typically is represented by some specific numerical value. In testing a hypothesis, we use a method where we gather data in an effort to gather evidence about the hypothesis.

How do we decide whether to reject the null hypothesis?

• If the sample data are consistent with the null hypothesis, then we do not reject it.
• If the sample data are inconsistent with the null hypothesis, but consistent with the alternative, then we reject the null hypothesis and conclude that the alternative hypothesis is true.

Six Steps for Hypothesis Tests Section  

In hypothesis testing, there are certain steps one must follow. Below these are summarized into six such steps to conducting a test of a hypothesis.

• Set up the hypotheses and check conditions : Each hypothesis test includes two hypotheses about the population. One is the null hypothesis, notated as \(H_0 \), which is a statement of a particular parameter value. This hypothesis is assumed to be true until there is evidence to suggest otherwise. The second hypothesis is called the alternative, or research hypothesis, notated as \(H_a \). The alternative hypothesis is a statement of a range of alternative values in which the parameter may fall. One must also check that any conditions (assumptions) needed to run the test have been satisfied e.g. normality of data, independence, and number of success and failure outcomes.
• Decide on the significance level, \(\alpha \): This value is used as a probability cutoff for making decisions about the null hypothesis. This alpha value represents the probability we are willing to place on our test for making an incorrect decision in regards to rejecting the null hypothesis. The most common \(\alpha \) value is 0.05 or 5%. Other popular choices are 0.01 (1%) and 0.1 (10%).
• Calculate the test statistic: Gather sample data and calculate a test statistic where the sample statistic is compared to the parameter value. The test statistic is calculated under the assumption the null hypothesis is true and incorporates a measure of standard error and assumptions (conditions) related to the sampling distribution.
• Calculate probability value (p-value), or find the rejection region: A p-value is found by using the test statistic to calculate the probability of the sample data producing such a test statistic or one more extreme. The rejection region is found by using alpha to find a critical value; the rejection region is the area that is more extreme than the critical value. We discuss the p-value and rejection region in more detail in the next section.
• Make a decision about the null hypothesis: In this step, we decide to either reject the null hypothesis or decide to fail to reject the null hypothesis. Notice we do not make a decision where we will accept the null hypothesis.
• State an overall conclusion : Once we have found the p-value or rejection region, and made a statistical decision about the null hypothesis (i.e. we will reject the null or fail to reject the null), we then want to summarize our results into an overall conclusion for our test.

We will follow these six steps for the remainder of this Lesson. In the future Lessons, the steps will be followed but may not be explained explicitly.

Step 1 is a very important step to set up correctly. If your hypotheses are incorrect, your conclusion will be incorrect. In this next section, we practice with Step 1 for the one sample situations.

Teach yourself statistics

What is Hypothesis Testing?

A statistical hypothesis is an assumption about a population parameter . This assumption may or may not be true. Hypothesis testing refers to the formal procedures used by statisticians to accept or reject statistical hypotheses.

Statistical Hypotheses

The best way to determine whether a statistical hypothesis is true would be to examine the entire population. Since that is often impractical, researchers typically examine a random sample from the population. If sample data are not consistent with the statistical hypothesis, the hypothesis is rejected.

There are two types of statistical hypotheses.

• Null hypothesis . The null hypothesis, denoted by H o , is usually the hypothesis that sample observations result purely from chance.
• Alternative hypothesis . The alternative hypothesis, denoted by H 1 or H a , is the hypothesis that sample observations are influenced by some non-random cause.

For example, suppose we wanted to determine whether a coin was fair and balanced. A null hypothesis might be that half the flips would result in Heads and half, in Tails. The alternative hypothesis might be that the number of Heads and Tails would be very different. Symbolically, these hypotheses would be expressed as

H o : P = 0.5 H a : P ≠ 0.5

Suppose we flipped the coin 50 times, resulting in 40 Heads and 10 Tails. Given this result, we would be inclined to reject the null hypothesis. We would conclude, based on the evidence, that the coin was probably not fair and balanced.

Can We Accept the Null Hypothesis?

Some researchers say that a hypothesis test can have one of two outcomes: you accept the null hypothesis or you reject the null hypothesis. Many statisticians, however, take issue with the notion of "accepting the null hypothesis." Instead, they say: you reject the null hypothesis or you fail to reject the null hypothesis.

Why the distinction between "acceptance" and "failure to reject?" Acceptance implies that the null hypothesis is true. Failure to reject implies that the data are not sufficiently persuasive for us to prefer the alternative hypothesis over the null hypothesis.

Hypothesis Tests

Statisticians follow a formal process to determine whether to reject a null hypothesis, based on sample data. This process, called hypothesis testing , consists of four steps.

• State the hypotheses. This involves stating the null and alternative hypotheses. The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false.
• Formulate an analysis plan. The analysis plan describes how to use sample data to evaluate the null hypothesis. The evaluation often focuses around a single test statistic.
• Analyze sample data. Find the value of the test statistic (mean score, proportion, t statistic, z-score, etc.) described in the analysis plan.
• Interpret results. Apply the decision rule described in the analysis plan. If the value of the test statistic is unlikely, based on the null hypothesis, reject the null hypothesis.

Decision Errors

Two types of errors can result from a hypothesis test.

• Type I error . A Type I error occurs when the researcher rejects a null hypothesis when it is true. The probability of committing a Type I error is called the significance level . This probability is also called alpha , and is often denoted by α.
• Type II error . A Type II error occurs when the researcher fails to reject a null hypothesis that is false. The probability of committing a Type II error is called Beta , and is often denoted by β. The probability of not committing a Type II error is called the Power of the test.

Decision Rules

The analysis plan for a hypothesis test must include decision rules for rejecting the null hypothesis. In practice, statisticians describe these decision rules in two ways - with reference to a P-value or with reference to a region of acceptance.

• P-value. The strength of evidence in support of a null hypothesis is measured by the P-value . Suppose the test statistic is equal to S . The P-value is the probability of observing a test statistic as extreme as S , assuming the null hypothesis is true. If the P-value is less than the significance level, we reject the null hypothesis.

The set of values outside the region of acceptance is called the region of rejection . If the test statistic falls within the region of rejection, the null hypothesis is rejected. In such cases, we say that the hypothesis has been rejected at the α level of significance.

These approaches are equivalent. Some statistics texts use the P-value approach; others use the region of acceptance approach.

One-Tailed and Two-Tailed Tests

A test of a statistical hypothesis, where the region of rejection is on only one side of the sampling distribution , is called a one-tailed test . For example, suppose the null hypothesis states that the mean is less than or equal to 10. The alternative hypothesis would be that the mean is greater than 10. The region of rejection would consist of a range of numbers located on the right side of sampling distribution; that is, a set of numbers greater than 10.

A test of a statistical hypothesis, where the region of rejection is on both sides of the sampling distribution, is called a two-tailed test . For example, suppose the null hypothesis states that the mean is equal to 10. The alternative hypothesis would be that the mean is less than 10 or greater than 10. The region of rejection would consist of a range of numbers located on both sides of sampling distribution; that is, the region of rejection would consist partly of numbers that were less than 10 and partly of numbers that were greater than 10.

Find what you need to study

9.6 Skills Focus: Selecting an Appropriate Inference Procedure

5 min read • january 8, 2023

Jed Quiaoit

One of the most important skills in AP Statistics is being able to identify the best inference procedure to use in order to complete a hypothesis test or confidence interval. We have covered all of the following types of procedures: 📄

One Proportion Z Test

One Proportion Z Interval

One Sample T Test

One Sample T Interval

Matched Pairs T Test

Two Proportion Z Test

Two Proportion Z Interval

Two Sample T Test

Two Sample T Interval

Chi Squared Goodness of Fit Test

Chi Squared Test for Independence

Chi Squared Test for Homogeneity

Linear Regression T Interval

Linear Regression T Test

For example, If given a problem involving one of the linear regression t procedures, it is most common that you will be given a computer output and be asked to make a conclusion or construct an interval.

Here are a couple illustrative flowchart "cheat sheets" on picking the right inferential procedure. Good luck! ⭐

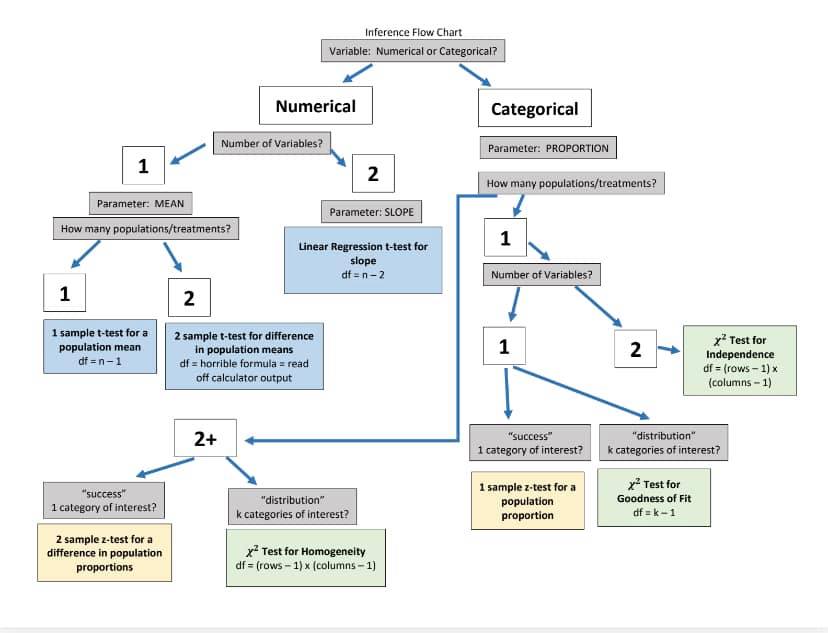
Source: Mr. Sardinha

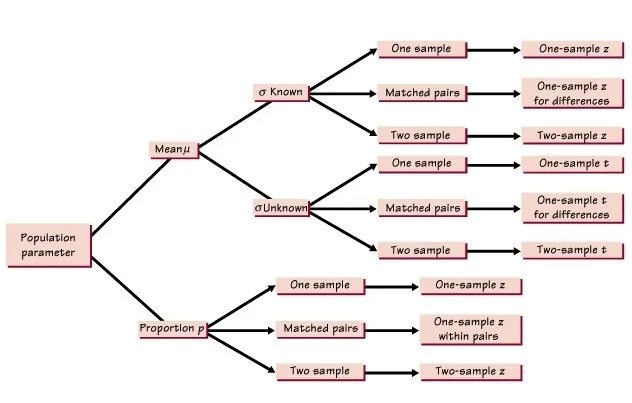
Source: Reddit

Here is a computer output similar to what you would see on the AP test. This is based on a study with a sample size of 30.

Remember from Unit 2, that we are only focusing on the inference values associated with the slope, which is the row entitled “Sick Days.”

Confidence Interval

In order to construct a confidence interval like we discussed in Section 9.2, we will need the point estimate (sample slope), t-score and standard error.

Everything except our t-score is given in the computer output, so we have to calculate our t-score based on our confidence level and sample size. We will first calculate our degrees of freedom of 28 and then use that with the invT function to calculate our t-score . We get a t-score of 2.05 for a 95% confidence level.

For the computer output above, our confidence interval would be:

0.962.05(0.12)

Which comes out to be (0.714, 1.206).

In this case, we can be sure that the two variables of interest (sick days and wellness visits) because 0 is not contained in our interval and therefore there is evidence that the two have some correlation. This is also supported by our high r value that could be easily computed by the R2 value.

Hypothesis Test

The other option for inference would be to use the p-value to make a judgment on the hypothesis test. In this example, our p-value for the slope is 0.02, which is usually considered significant enough to reject our null hypothesis.

In this instance, our conclusion would be:

Since our p value 0.02<0.05, we reject the null hypothesis. We have significant evidence that the true slope of the regression model between the number of sick days taken and the number of wellness visits is not 0.

Again, since we have some evidence that the slope is not 0, this shows that these two things are correlated, which is also evidenced by the R2 and resulting correlation coefficient .

Example 2: Pick a Test!

(1) A marketing research firm is interested in determining whether the proportion of adults in the United States who use a certain brand of toothpaste is significantly different from 50%. They survey a random sample of 500 adults and find that 270 of them use the toothpaste. Which of the following tests is/are appropriate to use?

(2) A high school statistics teacher wants to determine whether the mean score on a certain statistics exam is significantly different from 80. They administer the exam to a random sample of 25 students and find that the mean score is 78. Which of the following tests is/are appropriate to use?

(3) A psychology researcher is interested in determining whether there is a significant difference in anxiety levels between a treatment group and a control group. They measure anxiety levels in both groups before and after an intervention and find that the mean difference in anxiety levels between the two groups is -5. Which of the following tests is/are appropriate to use?

(4) A political pollster is interested in determining whether the proportion of registered voters who support a certain candidate is significantly different from 40%. They survey a random sample of 1000 registered voters and find that 400 of them support the candidate. They also survey a random sample of 1000 registered voters from a different region and find that 300 of them support the candidate. Which of the following tests is/are appropriate to use?

(5) A nutritionist is interested in determining whether the mean daily caloric intake of a certain population is significantly different from 2000 calories. They collect data from a random sample of 50 individuals from the population and find that the mean caloric intake is 1950 calories. Which of the following tests is/are appropriate to use?

(6) A historian is interested in determining whether the distribution of birth months among a group of people is significantly different from a uniform distribution. They collect data on the birth months of a random sample of 100 people and find that there are more births in the summer months than in the winter months. Which of the following tests is/are appropriate to use?

(7) A sociologist is interested in determining whether there is a significant association between the type of car a person drives and their political party affiliation. They collect data on the car types and political party affiliations of a random sample of 100 people and find that there are more Democrats who drive sedans than Republicans. Which of the following tests is/are appropriate to use?

(8) A medical researcher is interested in determining whether there is a significant difference in the effectiveness of two different treatments for a certain medical condition. They randomly assign patients to receive either treatment A or treatment B and measure the percentage of patients who show improvement after receiving each treatment. They find that the percentage of patients who show improvement is significantly higher for treatment A than for treatment B. Which of the following tests is/are appropriate to use?

(9) A real estate agent is interested in determining whether there is a significant relationship between the size of a house (in square feet) and its sale price. They collect data on the sizes and sale prices of a random sample of houses and find that there is a positive relationship between the two variables. Which of the following tests is/are appropriate to use?

(1) One Proportion Z-Test, One Proportion Z-Interval

(2) One Sample T-Test, One Sample T-Interval

(3) Matched Pairs T-Test

(4) Two Proportion Z-Test, Two Proportion Z-Interval

(5) Two Sample T-Test, Two Sample T-Interval

(6) Chi Squared Goodness of Fit Test

(7) Chi-Squared Test for Independence

(8) Chi-Squared Test for Homogeneity

(9) Linear Regression T-Test, Linear Regression T-Interval

🎥  Watch: AP Stats Unit 9 - Inference for Slopes

Key Terms to Review ( 13 )

Chi-Squared Test for Homogeneity

Chi-Squared Test for Independence

Correlation Coefficient

invT function

Stay Connected

© 2024 Fiveable Inc. All rights reserved.

AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Introduction to Type I and Type II errors
• Examples identifying Type I and Type II errors
• Type I vs Type II error

Introduction to power in significance tests

• Examples thinking about power in significance tests
• Error probabilities and power
• Consequences of errors and significance

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• Quality Improvement
• Talk To Minitab

Understanding Hypothesis Tests: Significance Levels (Alpha) and P values in Statistics

Topics: Hypothesis Testing , Statistics

What do significance levels and P values mean in hypothesis tests? What is statistical significance anyway? In this post, I’ll continue to focus on concepts and graphs to help you gain a more intuitive understanding of how hypothesis tests work in statistics.

To bring it to life, I’ll add the significance level and P value to the graph in my previous post in order to perform a graphical version of the 1 sample t-test. It’s easier to understand when you can see what statistical significance truly means!

Here’s where we left off in my last post . We want to determine whether our sample mean (330.6) indicates that this year's average energy cost is significantly different from last year’s average energy cost of $260.

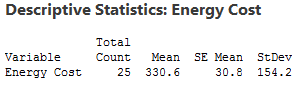
The probability distribution plot above shows the distribution of sample means we’d obtain under the assumption that the null hypothesis is true (population mean = 260) and we repeatedly drew a large number of random samples.

I left you with a question: where do we draw the line for statistical significance on the graph? Now we'll add in the significance level and the P value, which are the decision-making tools we'll need.

We'll use these tools to test the following hypotheses:

• Null hypothesis: The population mean equals the hypothesized mean (260).
• Alternative hypothesis: The population mean differs from the hypothesized mean (260).

What Is the Significance Level (Alpha)?

The significance level, also denoted as alpha or α, is the probability of rejecting the null hypothesis when it is true. For example, a significance level of 0.05 indicates a 5% risk of concluding that a difference exists when there is no actual difference.

These types of definitions can be hard to understand because of their technical nature. A picture makes the concepts much easier to comprehend!

The significance level determines how far out from the null hypothesis value we'll draw that line on the graph. To graph a significance level of 0.05, we need to shade the 5% of the distribution that is furthest away from the null hypothesis.

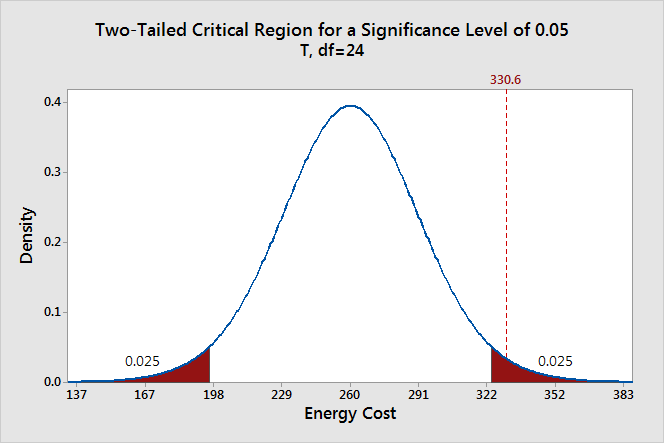
In the graph above, the two shaded areas are equidistant from the null hypothesis value and each area has a probability of 0.025, for a total of 0.05. In statistics, we call these shaded areas the critical region for a two-tailed test. If the population mean is 260, we’d expect to obtain a sample mean that falls in the critical region 5% of the time. The critical region defines how far away our sample statistic must be from the null hypothesis value before we can say it is unusual enough to reject the null hypothesis.

Our sample mean (330.6) falls within the critical region, which indicates it is statistically significant at the 0.05 level.

We can also see if it is statistically significant using the other common significance level of 0.01.

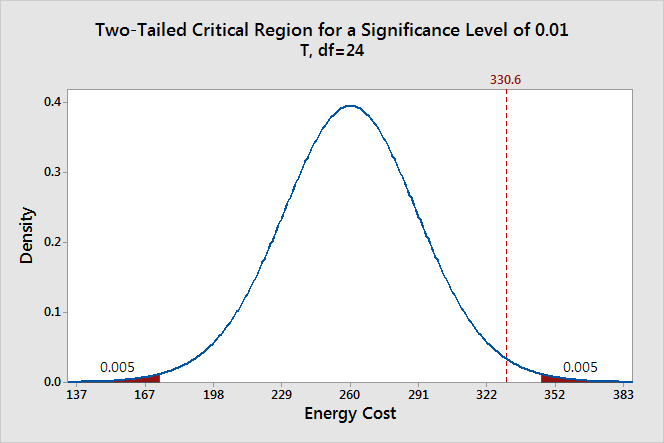
The two shaded areas each have a probability of 0.005, which adds up to a total probability of 0.01. This time our sample mean does not fall within the critical region and we fail to reject the null hypothesis. This comparison shows why you need to choose your significance level before you begin your study. It protects you from choosing a significance level because it conveniently gives you significant results!

Thanks to the graph, we were able to determine that our results are statistically significant at the 0.05 level without using a P value. However, when you use the numeric output produced by statistical software , you’ll need to compare the P value to your significance level to make this determination.

Ready for a demo of Minitab Statistical Software? Just ask! 

What Are P values?

P-values are the probability of obtaining an effect at least as extreme as the one in your sample data, assuming the truth of the null hypothesis.

This definition of P values, while technically correct, is a bit convoluted. It’s easier to understand with a graph!

To graph the P value for our example data set, we need to determine the distance between the sample mean and the null hypothesis value (330.6 - 260 = 70.6). Next, we can graph the probability of obtaining a sample mean that is at least as extreme in both tails of the distribution (260 +/- 70.6).

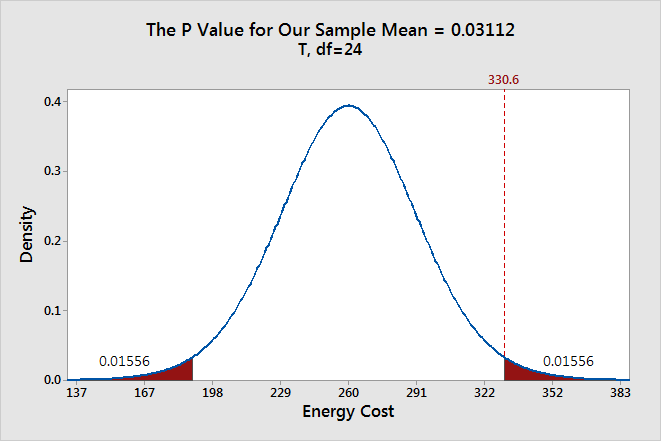
In the graph above, the two shaded areas each have a probability of 0.01556, for a total probability 0.03112. This probability represents the likelihood of obtaining a sample mean that is at least as extreme as our sample mean in both tails of the distribution if the population mean is 260. That’s our P value!

When a P value is less than or equal to the significance level, you reject the null hypothesis. If we take the P value for our example and compare it to the common significance levels, it matches the previous graphical results. The P value of 0.03112 is statistically significant at an alpha level of 0.05, but not at the 0.01 level.

If we stick to a significance level of 0.05, we can conclude that the average energy cost for the population is greater than 260.

A common mistake is to interpret the P-value as the probability that the null hypothesis is true. To understand why this interpretation is incorrect, please read my blog post  How to Correctly Interpret P Values .

Discussion about Statistically Significant Results

A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. A test result is statistically significant when the sample statistic is unusual enough relative to the null hypothesis that we can reject the null hypothesis for the entire population. “Unusual enough” in a hypothesis test is defined by:

• The assumption that the null hypothesis is true—the graphs are centered on the null hypothesis value.
• The significance level—how far out do we draw the line for the critical region?
• Our sample statistic—does it fall in the critical region?

Keep in mind that there is no magic significance level that distinguishes between the studies that have a true effect and those that don’t with 100% accuracy. The common alpha values of 0.05 and 0.01 are simply based on tradition. For a significance level of 0.05, expect to obtain sample means in the critical region 5% of the time when the null hypothesis is true . In these cases, you won’t know that the null hypothesis is true but you’ll reject it because the sample mean falls in the critical region. That’s why the significance level is also referred to as an error rate!

This type of error doesn’t imply that the experimenter did anything wrong or require any other unusual explanation. The graphs show that when the null hypothesis is true, it is possible to obtain these unusual sample means for no reason other than random sampling error. It’s just luck of the draw.

Significance levels and P values are important tools that help you quantify and control this type of error in a hypothesis test. Using these tools to decide when to reject the null hypothesis increases your chance of making the correct decision.

If you like this post, you might want to read the other posts in this series that use the same graphical framework:

• Previous: Why We Need to Use Hypothesis Tests
• Next: Confidence Intervals and Confidence Levels

If you'd like to see how I made these graphs, please read: How to Create a Graphical Version of the 1-sample t-Test .

You Might Also Like

• Trust Center

© 2023 Minitab, LLC. All Rights Reserved.

• Terms of Use
• Privacy Policy
• Cookies Settings

Statistics Made Easy

5 Tips for Interpreting P-Values Correctly in Hypothesis Testing

Hypothesis testing is a critical part of statistical analysis and is often the endpoint where conclusions are drawn about larger populations based on a sample or experimental dataset. Central to this process is the p-value. Broadly, the p-value quantifies the strength of evidence against the null hypothesis. Given the importance of the p-value, it is essential to ensure its interpretation is correct. Here are five essential tips for ensuring the p-value from a hypothesis test is understood correctly. 

1. Know What the P-value Represents

First, it is essential to understand what a p-value is. In hypothesis testing, the p-value is defined as the probability of observing your data, or data more extreme, if the null hypothesis is true. As a reminder, the null hypothesis states no difference between your data and the expected population. 

For example, in a hypothesis test to see if changing a company’s logo drives more traffic to the website, a null hypothesis would state that the new traffic numbers are equal to the old traffic numbers. In this context, the p-value would be the probability that the data you observed, or data more extreme, would occur if this null hypothesis were true. 

Therefore, a smaller p-value indicates that what you observed is unlikely to have occurred if the null were true, offering evidence to reject the null hypothesis. Typically, a cut-off value of 0.05 is used where any p-value below this is considered significant evidence against the null. 

2. Understand the Directionality of Your Hypothesis

Based on the research question under exploration, there are two types of hypotheses: one-sided and two-sided. A one-sided test specifies a particular direction of effect, such as traffic to a website increasing after a design change. On the other hand, a two-sided test allows the change to be in either direction and is effective when the researcher wants to see any effect of the change. 

Either way, determining the statistical significance of a p-value is the same: if the p-value is below a threshold value, it is statistically significant. However, when calculating the p-value, it is important to ensure the correct sided calculations have been completed. 

Additionally, the interpretation of the meaning of a p-value will differ based on the directionality of the hypothesis. If a one-sided test is significant, the researchers can use the p-value to support a statistically significant increase or decrease based on the direction of the test. If a two-sided test is significant, the p-value can only be used to say that the two groups are different, but not that one is necessarily greater. 

3. Avoid Threshold Thinking

A common pitfall in interpreting p-values is falling into the threshold thinking trap. The most commonly used cut-off value for whether a calculated p-value is statistically significant is 0.05. Typically, a p-value of less than 0.05 is considered statistically significant evidence against the null hypothesis. 

However, this is just an arbitrary value. Rigid adherence to this or any other predefined cut-off value can obscure business-relevant effect sizes. For example, a hypothesis test looking at changes in traffic after a website design may find that an increase of 10,000 views is not statistically significant with a p-value of 0.055 since that value is above 0.05. However, the actual increase of 10,000 may be important to the growth of the business. 

Therefore, a p-value can be practically significant while not being statistically significant. Both types of significance and the broader context of the hypothesis test should be considered when making a final interpretation. 

4. Consider the Power of Your Study

Similarly, some study conditions can result in a non-significant p-value even if practical significance exists. Statistical power is the ability of a study to detect an effect when it truly exists. In other words, it is the probability that the null hypothesis will be rejected when it is false. 

Power is impacted by a lot of factors. These include sample size, the effect size you are looking for, and variability within the data. In the example of website traffic after a design change, if the number of visits overall is too small, there may not be enough views to have enough power to detect a difference. 

Simple ways to increase the power of a hypothesis test and increase the chances of detecting an effect are increasing the sample size, looking for a smaller effect size, changing the experiment design to control for variables that can increase variability, or adjusting the type of statistical test being run.

5. Be Aware of Multiple Comparisons

Whenever multiple p-values are calculated in a single study due to multiple comparisons, there is an increased risk of false positives. This is because each individual comparison introduces random fluctuations, and each additional comparison compounds these fluctuations. 

For example, in a hypothesis test looking at traffic before and after a website redesign, the team may be interested in making more than one comparison. This can include total visits, page views, and average time spent on the website. Since multiple comparisons are being made, there must be a correction made when interpreting the p-value. 

The Bonferroni correction is one of the most commonly used methods to account for this increased probability of false positives. In this method, the significance cut-off value, typically 0.05, is divided by the number of comparisons made. The result is used as the new significance cut-off value.  Applying this correction mitigates the risk of false positives and improves the reliability of findings from a hypothesis test. 

In conclusion, interpreting p-values requires a nuanced understanding of many statistical concepts and careful consideration of the hypothesis test’s context. By following these five tips, the interpretation of the p-value from a hypothesis test can be more accurate and reliable, leading to better data-driven decision-making.

Featured Posts

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.