sample size for hypothesis test

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

25.3 - calculating sample size.

Before we learn how to calculate the sample size that is necessary to achieve a hypothesis test with a certain power, it might behoove us to understand the effect that sample size has on power. Let's investigate by returning to our IQ example.

Example 25-3 Section

Let $X$ denote the IQ of a randomly selected adult American. Assume, a bit unrealistically again, that $X$ is normally distributed with unknown mean $\mu$ and (a strangely known) standard deviation of 16. This time, instead of taking a random sample of $n=16$ students, let's increase the sample size to $n=64$. And, while setting the probability of committing a Type I error to $\alpha=0.05$, test the null hypothesis $H_0:\mu=100$ against the alternative hypothesis that $H_A:\mu>100$.

What is the power of the hypothesis test when $\mu=108$, $\mu=112$, and $\mu=116$?

Setting $\alpha$, the probability of committing a Type I error, to 0.05, implies that we should reject the null hypothesis when the test statistic $Z\ge 1.645$, or equivalently, when the observed sample mean is 103.29 or greater:

$ \bar{x} = \mu + z \left(\dfrac{\sigma}{\sqrt{n}} \right) = 100 +1.645\left(\dfrac{16}{\sqrt{64}} \right) = 103.29$

Therefore, the power function \K(\mu)\), when $\mu>100$ is the true value, is:

$ K(\mu) = P(\bar{X} \ge 103.29 | \mu) = P \left(Z \ge \dfrac{103.29 - \mu}{16 / \sqrt{64}} \right) = 1 - \Phi \left(\dfrac{103.29 - \mu}{2} \right)$

Therefore, the probability of rejecting the null hypothesis at the $\alpha=0.05$ level when $\mu=108$ is 0.9907, as calculated here:

$K(108) = 1 - \Phi \left( \dfrac{103.29-108}{2} \right) = 1- \Phi(-2.355) = 0.9907 $

And, the probability of rejecting the null hypothesis at the $\alpha=0.05$ level when $\mu=112$ is greater than 0.9999, as calculated here:

$ K(112) = 1 - \Phi \left( \dfrac{103.29-112}{2} \right) = 1- \Phi(-4.355) = 0.9999\ldots $

And, the probability of rejecting the null hypothesis at the $\alpha=0.05$ level when $\mu=116$ is greater than 0.999999, as calculated here:

$ K(116) = 1 - \Phi \left( \dfrac{103.29-116}{2} \right) = 1- \Phi(-6.355) = 0.999999... $

In summary, in the various examples throughout this lesson, we have calculated the power of testing $H_0:\mu=100$ against $H_A:\mu>100$ for two sample sizes ( $n=16$ and $n=64$) and for three possible values of the mean ( $\mu=108$, $\mu=112$, and $\mu=116$). Here's a summary of our power calculations:

As you can see, our work suggests that for a given value of the mean $\mu$ under the alternative hypothesis, the larger the sample size $n$, the greater the power $K(\mu)$ . Perhaps there is no better way to see this than graphically by plotting the two power functions simultaneously, one when $n=16$ and the other when $n=64$:

As this plot suggests, if we are interested in increasing our chance of rejecting the null hypothesis when the alternative hypothesis is true, we can do so by increasing our sample size $n$. This benefit is perhaps even greatest for values of the mean that are close to the value of the mean assumed under the null hypothesis. Let's take a look at two examples that illustrate the kind of sample size calculation we can make to ensure our hypothesis test has sufficient power.

Example 25-4 Section

Let $X$ denote the crop yield of corn measured in the number of bushels per acre. Assume (unrealistically) that $X$ is normally distributed with unknown mean $\mu$ and standard deviation $\sigma=6$. An agricultural researcher is working to increase the current average yield from 40 bushels per acre. Therefore, he is interested in testing, at the $\alpha=0.05$ level, the null hypothesis $H_0:\mu=40$ against the alternative hypothesis that $H_A:\mu>40$. Find the sample size $n$ that is necessary to achieve 0.90 power at the alternative $\mu=45$.

As is always the case, we need to start by finding a threshold value $c$, such that if the sample mean is larger than $c$, we'll reject the null hypothesis:

That is, in order for our hypothesis test to be conducted at the $\alpha=0.05$ level, the following statement must hold (using our typical $Z$ transformation):

$c = 40 + 1.645 \left( \dfrac{6}{\sqrt{n}} \right) $ (**)

But, that's not the only condition that $c$ must meet, because $c$ also needs to be defined to ensure that our power is 0.90 or, alternatively, that the probability of a Type II error is 0.10. That would happen if there was a 10% chance that our test statistic fell short of $c$ when $\mu=45$, as the following drawing illustrates in blue:

This illustration suggests that in order for our hypothesis test to have 0.90 power, the following statement must hold (using our usual $Z$ transformation):

$c = 45 - 1.28 \left( \dfrac{6}{\sqrt{n}} \right) $ (**)

Aha! We have two (asterisked (**)) equations and two unknowns! All we need to do is equate the equations, and solve for $n$. Doing so, we get:

$40+1.645\left(\frac{6}{\sqrt{n}}\right)=45-1.28\left(\frac{6}{\sqrt{n}}\right)$ $\Rightarrow 5=(1.645+1.28)\left(\frac{6}{\sqrt{n}}\right), \qquad \Rightarrow 5=\frac{17.55}{\sqrt{n}}, \qquad n=(3.51)^2=12.3201\approx 13$

Now that we know we will set $n=13$, we can solve for our threshold value c :

$ c = 40 + 1.645 \left( \dfrac{6}{\sqrt{13}} \right)=42.737 $

So, in summary, if the agricultural researcher collects data on $n=13$ corn plots, and rejects his null hypothesis $H_0:\mu=40$ if the average crop yield of the 13 plots is greater than 42.737 bushels per acre, he will have a 5% chance of committing a Type I error and a 10% chance of committing a Type II error if the population mean $\mu$ were actually 45 bushels per acre.

Example 25-5 Section

Consider $p$, the true proportion of voters who favor a particular political candidate. A pollster is interested in testing at the $\alpha=0.01$ level, the null hypothesis $H_0:9=0.5$ against the alternative hypothesis that $H_A:p>0.5$. Find the sample size $n$ that is necessary to achieve 0.80 power at the alternative $p=0.55$.

In this case, because we are interested in performing a hypothesis test about a population proportion $p$, we use the $Z$-statistic:

$Z = \dfrac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} $

Again, we start by finding a threshold value $c$, such that if the observed sample proportion is larger than $c$, we'll reject the null hypothesis:

That is, in order for our hypothesis test to be conducted at the $\alpha=0.01$ level, the following statement must hold:

$c = 0.5 + 2.326 \sqrt{ \dfrac{(0.5)(0.5)}{n}} $ (**)

But, again, that's not the only condition that c must meet, because $c$ also needs to be defined to ensure that our power is 0.80 or, alternatively, that the probability of a Type II error is 0.20. That would happen if there was a 20% chance that our test statistic fell short of $c$ when $p=0.55$, as the following drawing illustrates in blue:

This illustration suggests that in order for our hypothesis test to have 0.80 power, the following statement must hold:

$c = 0.55 - 0.842 \sqrt{ \dfrac{(0.55)(0.45)}{n}} $ (**)

Again, we have two (asterisked (**)) equations and two unknowns! All we need to do is equate the equations, and solve for $n$. Doing so, we get:

$0.5+2.326\sqrt{\dfrac{0.5(0.5)}{n}}=0.55-0.842\sqrt{\dfrac{0.55(0.45)}{n}} \\ 2.326\dfrac{\sqrt{0.25}}{\sqrt{n}}+0.842\dfrac{\sqrt{0.2475}}{\sqrt{n}}=0.55-0.5 \\ \dfrac{1}{\sqrt{n}}(1.5818897)=0.05 \qquad \Rightarrow n\approx \left(\dfrac{1.5818897}{0.05}\right)^2 = 1000.95 \approx 1001 $

Now that we know we will set $n=1001$, we can solve for our threshold value $c$:

$c = 0.5 + 2.326 \sqrt{\dfrac{(0.5)(0.5)}{1001}}= 0.5367 $

So, in summary, if the pollster collects data on $n=1001$ voters, and rejects his null hypothesis $H_0:p=0.5$ if the proportion of sampled voters who favor the political candidate is greater than 0.5367, he will have a 1% chance of committing a Type I error and a 20% chance of committing a Type II error if the population proportion $p$ were actually 0.55.

Incidentally, we can always check our work! Conducting the survey and subsequent hypothesis test as described above, the probability of committing a Type I error is:

$\alpha= P(\hat{p} >0.5367 \text { if } p = 0.50) = P(Z > 2.3257) = 0.01 $

and the probability of committing a Type II error is:

$\beta = P(\hat{p} <0.5367 \text { if } p = 0.55) = P(Z < -0.846) = 0.199 $

just as the pollster had desired.

We've illustrated several sample size calculations. Now, let's summarize the information that goes into a sample size calculation. In order to determine a sample size for a given hypothesis test, you need to specify:

The desired $\alpha$ level, that is, your willingness to commit a Type I error.

The desired power or, equivalently, the desired $\beta$ level, that is, your willingness to commit a Type II error.

A meaningful difference from the value of the parameter that is specified in the null hypothesis.

The standard deviation of the sample statistic or, at least, an estimate of the standard deviation (the "standard error") of the sample statistic.

Power and Sample Size Determination

Lisa Sullivan, PhD

Professor of Biosatistics

Boston Univeristy School of Public Health

Introduction

A critically important aspect of any study is determining the appropriate sample size to answer the research question. This module will focus on formulas that can be used to estimate the sample size needed to produce a confidence interval estimate with a specified margin of error (precision) or to ensure that a test of hypothesis has a high probability of detecting a meaningful difference in the parameter.

Studies should be designed to include a sufficient number of participants to adequately address the research question. Studies that have either an inadequate number of participants or an excessively large number of participants are both wasteful in terms of participant and investigator time, resources to conduct the assessments, analytic efforts and so on. These situations can also be viewed as unethical as participants may have been put at risk as part of a study that was unable to answer an important question. Studies that are much larger than they need to be to answer the research questions are also wasteful.

The formulas presented here generate estimates of the necessary sample size(s) required based on statistical criteria. However, in many studies, the sample size is determined by financial or logistical constraints. For example, suppose a study is proposed to evaluate a new screening test for Down Syndrome. Suppose that the screening test is based on analysis of a blood sample taken from women early in pregnancy. In order to evaluate the properties of the screening test (e.g., the sensitivity and specificity), each pregnant woman will be asked to provide a blood sample and in addition to undergo an amniocentesis. The amniocentesis is included as the gold standard and the plan is to compare the results of the screening test to the results of the amniocentesis. Suppose that the collection and processing of the blood sample costs $250 per participant and that the amniocentesis costs $900 per participant. These financial constraints alone might substantially limit the number of women that can be enrolled. Just as it is important to consider both statistical and clinical significance when interpreting results of a statistical analysis, it is also important to weigh both statistical and logistical issues in determining the sample size for a study.

Learning Objectives

After completing this module, the student will be able to:

Provide examples demonstrating how the margin of error, effect size and variability of the outcome affect sample size computations.
Compute the sample size required to estimate population parameters with precision.
Interpret statistical power in tests of hypothesis.
Compute the sample size required to ensure high power when hypothesis testing.

Issues in Estimating Sample Size for Confidence Intervals Estimates

The module on confidence intervals provided methods for estimating confidence intervals for various parameters (e.g., μ , p, ( μ 1 - μ 2 ), μ d , (p 1 -p 2 )). Confidence intervals for every parameter take the following general form:

Point Estimate + Margin of Error

In the module on confidence intervals we derived the formula for the confidence interval for μ as

In practice we use the sample standard deviation to estimate the population standard deviation. Note that there is an alternative formula for estimating the mean of a continuous outcome in a single population, and it is used when the sample size is small (n<30). It involves a value from the t distribution, as opposed to one from the standard normal distribution, to reflect the desired level of confidence. When performing sample size computations, we use the large sample formula shown here. [Note: The resultant sample size might be small, and in the analysis stage, the appropriate confidence interval formula must be used.]

The point estimate for the population mean is the sample mean and the margin of error is

In planning studies, we want to determine the sample size needed to ensure that the margin of error is sufficiently small to be informative. For example, suppose we want to estimate the mean weight of female college students. We conduct a study and generate a 95% confidence interval as follows 125 + 40 pounds, or 85 to 165 pounds. The margin of error is so wide that the confidence interval is uninformative. To be informative, an investigator might want the margin of error to be no more than 5 or 10 pounds (meaning that the 95% confidence interval would have a width (lower limit to upper limit) of 10 or 20 pounds). In order to determine the sample size needed, the investigator must specify the desired margin of error . It is important to note that this is not a statistical issue, but a clinical or a practical one. For example, suppose we want to estimate the mean birth weight of infants born to mothers who smoke cigarettes during pregnancy. Birth weights in infants clearly have a much more restricted range than weights of female college students. Therefore, we would probably want to generate a confidence interval for the mean birth weight that has a margin of error not exceeding 1 or 2 pounds.

The margin of error in the one sample confidence interval for μ can be written as follows:

Our goal is to determine the sample size, n, that ensures that the margin of error, " E ," does not exceed a specified value. We can take the formula above and, with some algebra, solve for n :

First, multipy both sides of the equation by the square root of n . Then cancel out the square root of n from the numerator and denominator on the right side of the equation (since any number divided by itself is equal to 1). This leaves:

Now divide both sides by "E" and cancel out "E" from the numerator and denominator on the left side. This leaves:

Finally, square both sides of the equation to get:

This formula generates the sample size, n , required to ensure that the margin of error, E , does not exceed a specified value. To solve for n , we must input " Z ," " σ ," and " E ."

Z is the value from the table of probabilities of the standard normal distribution for the desired confidence level (e.g., Z = 1.96 for 95% confidence)
E is the margin of error that the investigator specifies as important from a clinical or practical standpoint.
σ is the standard deviation of the outcome of interest.

Sometimes it is difficult to estimate σ . When we use the sample size formula above (or one of the other formulas that we will present in the sections that follow), we are planning a study to estimate the unknown mean of a particular outcome variable in a population. It is unlikely that we would know the standard deviation of that variable. In sample size computations, investigators often use a value for the standard deviation from a previous study or a study done in a different, but comparable, population. The sample size computation is not an application of statistical inference and therefore it is reasonable to use an appropriate estimate for the standard deviation. The estimate can be derived from a different study that was reported in the literature; some investigators perform a small pilot study to estimate the standard deviation. A pilot study usually involves a small number of participants (e.g., n=10) who are selected by convenience, as opposed to by random sampling. Data from the participants in the pilot study can be used to compute a sample standard deviation, which serves as a good estimate for σ in the sample size formula. Regardless of how the estimate of the variability of the outcome is derived, it should always be conservative (i.e., as large as is reasonable), so that the resultant sample size is not too small.

Sample Size for One Sample, Continuous Outcome

In studies where the plan is to estimate the mean of a continuous outcome variable in a single population, the formula for determining sample size is given below:

where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), σ is the standard deviation of the outcome variable and E is the desired margin of error. The formula above generates the minimum number of subjects required to ensure that the margin of error in the confidence interval for μ does not exceed E .

An investigator wants to estimate the mean systolic blood pressure in children with congenital heart disease who are between the ages of 3 and 5. How many children should be enrolled in the study? The investigator plans on using a 95% confidence interval (so Z=1.96) and wants a margin of error of 5 units. The standard deviation of systolic blood pressure is unknown, but the investigators conduct a literature search and find that the standard deviation of systolic blood pressures in children with other cardiac defects is between 15 and 20. To estimate the sample size, we consider the larger standard deviation in order to obtain the most conservative (largest) sample size.

In order to ensure that the 95% confidence interval estimate of the mean systolic blood pressure in children between the ages of 3 and 5 with congenital heart disease is within 5 units of the true mean, a sample of size 62 is needed. [ Note : We always round up; the sample size formulas always generate the minimum number of subjects needed to ensure the specified precision.] Had we assumed a standard deviation of 15, the sample size would have been n=35. Because the estimates of the standard deviation were derived from studies of children with other cardiac defects, it would be advisable to use the larger standard deviation and plan for a study with 62 children. Selecting the smaller sample size could potentially produce a confidence interval estimate with a larger margin of error.

An investigator wants to estimate the mean birth weight of infants born full term (approximately 40 weeks gestation) to mothers who are 19 years of age and under. The mean birth weight of infants born full-term to mothers 20 years of age and older is 3,510 grams with a standard deviation of 385 grams. How many women 19 years of age and under must be enrolled in the study to ensure that a 95% confidence interval estimate of the mean birth weight of their infants has a margin of error not exceeding 100 grams? Try to work through the calculation before you look at the answer.

Sample Size for One Sample, Dichotomous Outcome

In studies where the plan is to estimate the proportion of successes in a dichotomous outcome variable (yes/no) in a single population, the formula for determining sample size is:

where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%) and E is the desired margin of error. p is the proportion of successes in the population. Here we are planning a study to generate a 95% confidence interval for the unknown population proportion, p . The equation to determine the sample size for determining p seems to require knowledge of p, but this is obviously this is a circular argument, because if we knew the proportion of successes in the population, then a study would not be necessary! What we really need is an approximate value of p or an anticipated value. The range of p is 0 to 1, and therefore the range of p(1-p) is 0 to 1. The value of p that maximizes p(1-p) is p=0.5. Consequently, if there is no information available to approximate p, then p=0.5 can be used to generate the most conservative, or largest, sample size.

Example 2:

An investigator wants to estimate the proportion of freshmen at his University who currently smoke cigarettes (i.e., the prevalence of smoking). How many freshmen should be involved in the study to ensure that a 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion?

Because we have no information on the proportion of freshmen who smoke, we use 0.5 to estimate the sample size as follows:

In order to ensure that the 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion, a sample of size 385 is needed.

Suppose that a similar study was conducted 2 years ago and found that the prevalence of smoking was 27% among freshmen. If the investigator believes that this is a reasonable estimate of prevalence 2 years later, it can be used to plan the next study. Using this estimate of p, what sample size is needed (assuming that again a 95% confidence interval will be used and we want the same level of precision)?

An investigator wants to estimate the prevalence of breast cancer among women who are between 40 and 45 years of age living in Boston. How many women must be involved in the study to ensure that the estimate is precise? National data suggest that 1 in 235 women are diagnosed with breast cancer by age 40. This translates to a proportion of 0.0043 (0.43%) or a prevalence of 43 per 10,000 women. Suppose the investigator wants the estimate to be within 10 per 10,000 women with 95% confidence. The sample size is computed as follows:

A sample of size n=16,448 will ensure that a 95% confidence interval estimate of the prevalence of breast cancer is within 0.10 (or to within 10 women per 10,000) of its true value. This is a situation where investigators might decide that a sample of this size is not feasible. Suppose that the investigators thought a sample of size 5,000 would be reasonable from a practical point of view. How precisely can we estimate the prevalence with a sample of size n=5,000? Recall that the confidence interval formula to estimate prevalence is:

Assuming that the prevalence of breast cancer in the sample will be close to that based on national data, we would expect the margin of error to be approximately equal to the following:

Thus, with n=5,000 women, a 95% confidence interval would be expected to have a margin of error of 0.0018 (or 18 per 10,000). The investigators must decide if this would be sufficiently precise to answer the research question. Note that the above is based on the assumption that the prevalence of breast cancer in Boston is similar to that reported nationally. This may or may not be a reasonable assumption. In fact, it is the objective of the current study to estimate the prevalence in Boston. The research team, with input from clinical investigators and biostatisticians, must carefully evaluate the implications of selecting a sample of size n = 5,000, n = 16,448 or any size in between.

Sample Sizes for Two Independent Samples, Continuous Outcome

In studies where the plan is to estimate the difference in means between two independent populations, the formula for determining the sample sizes required in each comparison group is given below:

where n i is the sample size required in each group (i=1,2), Z is the value from the standard normal distribution reflecting the confidence level that will be used and E is the desired margin of error. σ again reflects the standard deviation of the outcome variable. Recall from the module on confidence intervals that, when we generated a confidence interval estimate for the difference in means, we used Sp, the pooled estimate of the common standard deviation, as a measure of variability in the outcome (based on pooling the data), where Sp is computed as follows:

If data are available on variability of the outcome in each comparison group, then Sp can be computed and used in the sample size formula. However, it is more often the case that data on the variability of the outcome are available from only one group, often the untreated (e.g., placebo control) or unexposed group. When planning a clinical trial to investigate a new drug or procedure, data are often available from other trials that involved a placebo or an active control group (i.e., a standard medication or treatment given for the condition under study). The standard deviation of the outcome variable measured in patients assigned to the placebo, control or unexposed group can be used to plan a future trial, as illustrated below.

Note that the formula for the sample size generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used.

An investigator wants to plan a clinical trial to evaluate the efficacy of a new drug designed to increase HDL cholesterol (the "good" cholesterol). The plan is to enroll participants and to randomly assign them to receive either the new drug or a placebo. HDL cholesterol will be measured in each participant after 12 weeks on the assigned treatment. Based on prior experience with similar trials, the investigator expects that 10% of all participants will be lost to follow up or will drop out of the study over 12 weeks. A 95% confidence interval will be estimated to quantify the difference in mean HDL levels between patients taking the new drug as compared to placebo. The investigator would like the margin of error to be no more than 3 units. How many patients should be recruited into the study?

The sample sizes are computed as follows:

A major issue is determining the variability in the outcome of interest (σ), here the standard deviation of HDL cholesterol. To plan this study, we can use data from the Framingham Heart Study. In participants who attended the seventh examination of the Offspring Study and were not on treatment for high cholesterol, the standard deviation of HDL cholesterol is 17.1. We will use this value and the other inputs to compute the sample sizes as follows:

Samples of size n 1 =250 and n 2 =250 will ensure that the 95% confidence interval for the difference in mean HDL levels will have a margin of error of no more than 3 units. Again, these sample sizes refer to the numbers of participants with complete data. The investigators hypothesized a 10% attrition (or drop-out) rate (in both groups). In order to ensure that the total sample size of 500 is available at 12 weeks, the investigator needs to recruit more participants to allow for attrition.

N (number to enroll) * (% retained) = desired sample size

Therefore N (number to enroll) = desired sample size/(% retained)

N = 500/0.90 = 556

If they anticipate a 10% attrition rate, the investigators should enroll 556 participants. This will ensure N=500 with complete data at the end of the trial.

An investigator wants to compare two diet programs in children who are obese. One diet is a low fat diet, and the other is a low carbohydrate diet. The plan is to enroll children and weigh them at the start of the study. Each child will then be randomly assigned to either the low fat or the low carbohydrate diet. Each child will follow the assigned diet for 8 weeks, at which time they will again be weighed. The number of pounds lost will be computed for each child. Based on data reported from diet trials in adults, the investigator expects that 20% of all children will not complete the study. A 95% confidence interval will be estimated to quantify the difference in weight lost between the two diets and the investigator would like the margin of error to be no more than 3 pounds. How many children should be recruited into the study?

Again the issue is determining the variability in the outcome of interest (σ), here the standard deviation in pounds lost over 8 weeks. To plan this study, investigators use data from a published study in adults. Suppose one such study compared the same diets in adults and involved 100 participants in each diet group. The study reported a standard deviation in weight lost over 8 weeks on a low fat diet of 8.4 pounds and a standard deviation in weight lost over 8 weeks on a low carbohydrate diet of 7.7 pounds. These data can be used to estimate the common standard deviation in weight lost as follows:

We now use this value and the other inputs to compute the sample sizes:

Samples of size n 1 =56 and n 2 =56 will ensure that the 95% confidence interval for the difference in weight lost between diets will have a margin of error of no more than 3 pounds. Again, these sample sizes refer to the numbers of children with complete data. The investigators anticipate a 20% attrition rate. In order to ensure that the total sample size of 112 is available at 8 weeks, the investigator needs to recruit more participants to allow for attrition.

N = 112/0.80 = 140

Sample Size for Matched Samples, Continuous Outcome

In studies where the plan is to estimate the mean difference of a continuous outcome based on matched data, the formula for determining sample size is given below:

where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), E is the desired margin of error, and σ d is the standard deviation of the difference scores. It is extremely important that the standard deviation of the difference scores (e.g., the difference based on measurements over time or the difference between matched pairs) is used here to appropriately estimate the sample size.

Sample Sizes for Two Independent Samples, Dichotomous Outcome

In studies where the plan is to estimate the difference in proportions between two independent populations (i.e., to estimate the risk difference), the formula for determining the sample sizes required in each comparison group is:

where n i is the sample size required in each group (i=1,2), Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), and E is the desired margin of error. p 1 and p 2 are the proportions of successes in each comparison group. Again, here we are planning a study to generate a 95% confidence interval for the difference in unknown proportions, and the formula to estimate the sample sizes needed requires p 1 and p 2 . In order to estimate the sample size, we need approximate values of p 1 and p 2 . The values of p 1 and p 2 that maximize the sample size are p 1 =p 2 =0.5. Thus, if there is no information available to approximate p 1 and p 2 , then 0.5 can be used to generate the most conservative, or largest, sample sizes.

Similar to the situation for two independent samples and a continuous outcome at the top of this page, it may be the case that data are available on the proportion of successes in one group, usually the untreated (e.g., placebo control) or unexposed group. If so, the known proportion can be used for both p 1 and p 2 in the formula shown above. The formula shown above generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used. Interested readers can see Fleiss for more details. 4

An investigator wants to estimate the impact of smoking during pregnancy on premature delivery. Normal pregnancies last approximately 40 weeks and premature deliveries are those that occur before 37 weeks. The 2005 National Vital Statistics report indicates that approximately 12% of infants are born prematurely in the United States. 5 The investigator plans to collect data through medical record review and to generate a 95% confidence interval for the difference in proportions of infants born prematurely to women who smoked during pregnancy as compared to those who did not. How many women should be enrolled in the study to ensure that the 95% confidence interval for the difference in proportions has a margin of error of no more than 4%?

The sample sizes (i.e., numbers of women who smoked and did not smoke during pregnancy) can be computed using the formula shown above. National data suggest that 12% of infants are born prematurely. We will use that estimate for both groups in the sample size computation.

Samples of size n 1 =508 women who smoked during pregnancy and n 2 =508 women who did not smoke during pregnancy will ensure that the 95% confidence interval for the difference in proportions who deliver prematurely will have a margin of error of no more than 4%.

Is attrition an issue here?

Issues in Estimating Sample Size for Hypothesis Testing

In the module on hypothesis testing for means and proportions, we introduced techniques for means, proportions, differences in means, and differences in proportions. While each test involved details that were specific to the outcome of interest (e.g., continuous or dichotomous) and to the number of comparison groups (one, two, more than two), there were common elements to each test. For example, in each test of hypothesis, there are two errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. In the first step of any test of hypothesis, we select a level of significance, α , and α = P(Type I error) = P(Reject H 0 | H 0 is true). Because we purposely select a small value for α , we control the probability of committing a Type I error. The second type of error is called a Type II error and it is defined as the probability we do not reject H 0 when it is false. The probability of a Type II error is denoted β , and β =P(Type II error) = P(Do not Reject H 0 | H 0 is false). In hypothesis testing, we usually focus on power, which is defined as the probability that we reject H 0 when it is false, i.e., power = 1- β = P(Reject H 0 | H 0 is false). Power is the probability that a test correctly rejects a false null hypothesis. A good test is one with low probability of committing a Type I error (i.e., small α ) and high power (i.e., small β, high power).

Here we present formulas to determine the sample size required to ensure that a test has high power. The sample size computations depend on the level of significance, aα, the desired power of the test (equivalent to 1-β), the variability of the outcome, and the effect size. The effect size is the difference in the parameter of interest that represents a clinically meaningful difference. Similar to the margin of error in confidence interval applications, the effect size is determined based on clinical or practical criteria and not statistical criteria.

The concept of statistical power can be difficult to grasp. Before presenting the formulas to determine the sample sizes required to ensure high power in a test, we will first discuss power from a conceptual point of view.

Suppose we want to test the following hypotheses at aα=0.05: H 0 : μ = 90 versus H 1 : μ ≠ 90. To test the hypotheses, suppose we select a sample of size n=100. For this example, assume that the standard deviation of the outcome is σ=20. We compute the sample mean and then must decide whether the sample mean provides evidence to support the alternative hypothesis or not. This is done by computing a test statistic and comparing the test statistic to an appropriate critical value. If the null hypothesis is true (μ=90), then we are likely to select a sample whose mean is close in value to 90. However, it is also possible to select a sample whose mean is much larger or much smaller than 90. Recall from the Central Limit Theorem (see page 11 in the module on Probability), that for large n (here n=100 is sufficiently large), the distribution of the sample means is approximately normal with a mean of

If the null hypothesis is true, it is possible to observe any sample mean shown in the figure below; all are possible under H 0 : μ = 90.

Normal distribution of X when the mean of X is 90. A bell-shaped curve with a value of X-90 at the center.

Rejection Region for Test H 0 : μ = 90 versus H 1 : μ ≠ 90 at α =0.05

Standard normal distribution showing a mean of 90. The rejection areas are in the two tails at the extremes above and below the mean. If the alpha level is 0.05, then each tail accounts for an arean of 0.025.

The areas in the two tails of the curve represent the probability of a Type I Error, α= 0.05. This concept was discussed in the module on Hypothesis Testing.

Now, suppose that the alternative hypothesis, H 1 , is true (i.e., μ ≠ 90) and that the true mean is actually 94. The figure below shows the distributions of the sample mean under the null and alternative hypotheses.The values of the sample mean are shown along the horizontal axis.

Two overlapping normal distributions, one depicting the null hypothesis with a mean of 90 and the other showing the alternative hypothesis with a mean of 94. A more complete explanation of the figure is provided in the text below the figure.

If the true mean is 94, then the alternative hypothesis is true. In our test, we selected α = 0.05 and reject H 0 if the observed sample mean exceeds 93.92 (focusing on the upper tail of the rejection region for now). The critical value (93.92) is indicated by the vertical line. The probability of a Type II error is denoted β, and β = P(Do not Reject H 0 | H 0 is false), i.e., the probability of not rejecting the null hypothesis if the null hypothesis were true. β is shown in the figure above as the area under the rightmost curve (H 1 ) to the left of the vertical line (where we do not reject H 0 ). Power is defined as 1- β = P(Reject H 0 | H 0 is false) and is shown in the figure as the area under the rightmost curve (H 1 ) to the right of the vertical line (where we reject H 0 ).

Note that β and power are related to α, the variability of the outcome and the effect size. From the figure above we can see what happens to β and power if we increase α. Suppose, for example, we increase α to α=0.10.The upper critical value would be 92.56 instead of 93.92. The vertical line would shift to the left, increasing α, decreasing β and increasing power. While a better test is one with higher power, it is not advisable to increase α as a means to increase power. Nonetheless, there is a direct relationship between α and power (as α increases, so does power).

β and power are also related to the variability of the outcome and to the effect size. The effect size is the difference in the parameter of interest (e.g., μ) that represents a clinically meaningful difference. The figure above graphically displays α, β, and power when the difference in the mean under the null as compared to the alternative hypothesis is 4 units (i.e., 90 versus 94). The figure below shows the same components for the situation where the mean under the alternative hypothesis is 98.

Overlapping bell-shaped distributions - one with a mean of 90 and the other with a mean of 98

Notice that there is much higher power when there is a larger difference between the mean under H 0 as compared to H 1 (i.e., 90 versus 98). A statistical test is much more likely to reject the null hypothesis in favor of the alternative if the true mean is 98 than if the true mean is 94. Notice also in this case that there is little overlap in the distributions under the null and alternative hypotheses. If a sample mean of 97 or higher is observed it is very unlikely that it came from a distribution whose mean is 90. In the previous figure for H 0 : μ = 90 and H 1 : μ = 94, if we observed a sample mean of 93, for example, it would not be as clear as to whether it came from a distribution whose mean is 90 or one whose mean is 94.

Ensuring That a Test Has High Power

In designing studies most people consider power of 80% or 90% (just as we generally use 95% as the confidence level for confidence interval estimates). The inputs for the sample size formulas include the desired power, the level of significance and the effect size. The effect size is selected to represent a clinically meaningful or practically important difference in the parameter of interest, as we will illustrate.

The formulas we present below produce the minimum sample size to ensure that the test of hypothesis will have a specified probability of rejecting the null hypothesis when it is false (i.e., a specified power). In planning studies, investigators again must account for attrition or loss to follow-up. The formulas shown below produce the number of participants needed with complete data, and we will illustrate how attrition is addressed in planning studies.

In studies where the plan is to perform a test of hypothesis comparing the mean of a continuous outcome variable in a single population to a known mean, the hypotheses of interest are:

H 0 : μ = μ 0 and H 1 : μ ≠ μ 0 where μ 0 is the known mean (e.g., a historical control). The formula for determining sample size to ensure that the test has a specified power is given below:

where α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α/2 below it. For example, if α=0.05, then 1- α/2 = 0.975 and Z=1.960. 1- β is the selected power, and Z 1-β is the value from the standard normal distribution holding 1- β below it. Sample size estimates for hypothesis testing are often based on achieving 80% or 90% power. The Z 1-β values for these popular scenarios are given below:

For 80% power Z 0.80 = 0.84
For 90% power Z 0.90 =1.282

ES is the effect size , defined as follows:

where μ 0 is the mean under H 0 , μ 1 is the mean under H 1 and σ is the standard deviation of the outcome of interest. The numerator of the effect size, the absolute value of the difference in means | μ 1 - μ 0 |, represents what is considered a clinically meaningful or practically important difference in means. Similar to the issue we faced when planning studies to estimate confidence intervals, it can sometimes be difficult to estimate the standard deviation. In sample size computations, investigators often use a value for the standard deviation from a previous study or a study performed in a different but comparable population. Regardless of how the estimate of the variability of the outcome is derived, it should always be conservative (i.e., as large as is reasonable), so that the resultant sample size will not be too small.

Example 7:

An investigator hypothesizes that in people free of diabetes, fasting blood glucose, a risk factor for coronary heart disease, is higher in those who drink at least 2 cups of coffee per day. A cross-sectional study is planned to assess the mean fasting blood glucose levels in people who drink at least two cups of coffee per day. The mean fasting blood glucose level in people free of diabetes is reported as 95.0 mg/dL with a standard deviation of 9.8 mg/dL. 7 If the mean blood glucose level in people who drink at least 2 cups of coffee per day is 100 mg/dL, this would be important clinically. How many patients should be enrolled in the study to ensure that the power of the test is 80% to detect this difference? A two sided test will be used with a 5% level of significance.

The effect size is computed as:

The effect size represents the meaningful difference in the population mean - here 95 versus 100, or 0.51 standard deviation units different. We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

Therefore, a sample of size n=31 will ensure that a two-sided test with α =0.05 has 80% power to detect a 5 mg/dL difference in mean fasting blood glucose levels.

In the planned study, participants will be asked to fast overnight and to provide a blood sample for analysis of glucose levels. Based on prior experience, the investigators hypothesize that 10% of the participants will fail to fast or will refuse to follow the study protocol. Therefore, a total of 35 participants will be enrolled in the study to ensure that 31 are available for analysis (see below).

N (number to enroll) * (% following protocol) = desired sample size

N = 31/0.90 = 35.

Sample Size for One Sample, Dichotomous Outcome

In studies where the plan is to perform a test of hypothesis comparing the proportion of successes in a dichotomous outcome variable in a single population to a known proportion, the hypotheses of interest are:

where p 0 is the known proportion (e.g., a historical control). The formula for determining the sample size to ensure that the test has a specified power is given below:

where α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α/2 below it. 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it , and ES is the effect size, defined as follows:

where p 0 is the proportion under H 0 and p 1 is the proportion under H 1 . The numerator of the effect size, the absolute value of the difference in proportions |p 1 -p 0 |, again represents what is considered a clinically meaningful or practically important difference in proportions.

Example 8:

A recent report from the Framingham Heart Study indicated that 26% of people free of cardiovascular disease had elevated LDL cholesterol levels, defined as LDL > 159 mg/dL. 9 An investigator hypothesizes that a higher proportion of patients with a history of cardiovascular disease will have elevated LDL cholesterol. How many patients should be studied to ensure that the power of the test is 90% to detect a 5% difference in the proportion with elevated LDL cholesterol? A two sided test will be used with a 5% level of significance.

We first compute the effect size:

We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

A sample of size n=869 will ensure that a two-sided test with α =0.05 has 90% power to detect a 5% difference in the proportion of patients with a history of cardiovascular disease who have an elevated LDL cholesterol level.

A medical device manufacturer produces implantable stents. During the manufacturing process, approximately 10% of the stents are deemed to be defective. The manufacturer wants to test whether the proportion of defective stents is more than 10%. If the process produces more than 15% defective stents, then corrective action must be taken. Therefore, the manufacturer wants the test to have 90% power to detect a difference in proportions of this magnitude. How many stents must be evaluated? For you computations, use a two-sided test with a 5% level of significance. (Do the computation yourself, before looking at the answer.)

In studies where the plan is to perform a test of hypothesis comparing the means of a continuous outcome variable in two independent populations, the hypotheses of interest are:

where μ 1 and μ 2 are the means in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is:

where n i is the sample size required in each group (i=1,2), α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α /2 below it, and 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as:

where | μ 1 - μ 2 | is the absolute value of the difference in means between the two groups expected under the alternative hypothesis, H 1 . σ is the standard deviation of the outcome of interest. Recall from the module on Hypothesis Testing that, when we performed tests of hypothesis comparing the means of two independent groups, we used Sp, the pooled estimate of the common standard deviation, as a measure of variability in the outcome.

Sp is computed as follows:

If data are available on variability of the outcome in each comparison group, then Sp can be computed and used to generate the sample sizes. However, it is more often the case that data on the variability of the outcome are available from only one group, usually the untreated (e.g., placebo control) or unexposed group. When planning a clinical trial to investigate a new drug or procedure, data are often available from other trials that may have involved a placebo or an active control group (i.e., a standard medication or treatment given for the condition under study). The standard deviation of the outcome variable measured in patients assigned to the placebo, control or unexposed group can be used to plan a future trial, as illustrated.

Note also that the formula shown above generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used (see Howell 3 for more details).

An investigator is planning a clinical trial to evaluate the efficacy of a new drug designed to reduce systolic blood pressure. The plan is to enroll participants and to randomly assign them to receive either the new drug or a placebo. Systolic blood pressures will be measured in each participant after 12 weeks on the assigned treatment. Based on prior experience with similar trials, the investigator expects that 10% of all participants will be lost to follow up or will drop out of the study. If the new drug shows a 5 unit reduction in mean systolic blood pressure, this would represent a clinically meaningful reduction. How many patients should be enrolled in the trial to ensure that the power of the test is 80% to detect this difference? A two sided test will be used with a 5% level of significance.

In order to compute the effect size, an estimate of the variability in systolic blood pressures is needed. Analysis of data from the Framingham Heart Study showed that the standard deviation of systolic blood pressure was 19.0. This value can be used to plan the trial.

The effect size is:

Samples of size n 1 =232 and n 2 = 232 will ensure that the test of hypothesis will have 80% power to detect a 5 unit difference in mean systolic blood pressures in patients receiving the new drug as compared to patients receiving the placebo. However, the investigators hypothesized a 10% attrition rate (in both groups), and to ensure a total sample size of 232 they need to allow for attrition.

N = 232/0.90 = 258.

The investigator must enroll 258 participants to be randomly assigned to receive either the new drug or placebo.

An investigator is planning a study to assess the association between alcohol consumption and grade point average among college seniors. The plan is to categorize students as heavy drinkers or not using 5 or more drinks on a typical drinking day as the criterion for heavy drinking. Mean grade point averages will be compared between students classified as heavy drinkers versus not using a two independent samples test of means. The standard deviation in grade point averages is assumed to be 0.42 and a meaningful difference in grade point averages (relative to drinking status) is 0.25 units. How many college seniors should be enrolled in the study to ensure that the power of the test is 80% to detect a 0.25 unit difference in mean grade point averages? Use a two-sided test with a 5% level of significance.

Answer

In studies where the plan is to perform a test of hypothesis on the mean difference in a continuous outcome variable based on matched data, the hypotheses of interest are:

where μ d is the mean difference in the population. The formula for determining the sample size to ensure that the test has a specified power is given below:

where α is the selected level of significance and Z 1-α/2 is the value from the standard normal distribution holding 1- α/2 below it, 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it and ES is the effect size, defined as follows:

where μ d is the mean difference expected under the alternative hypothesis, H 1 , and σ d is the standard deviation of the difference in the outcome (e.g., the difference based on measurements over time or the difference between matched pairs).

Example 10:

An investigator wants to evaluate the efficacy of an acupuncture treatment for reducing pain in patients with chronic migraine headaches. The plan is to enroll patients who suffer from migraine headaches. Each will be asked to rate the severity of the pain they experience with their next migraine before any treatment is administered. Pain will be recorded on a scale of 1-100 with higher scores indicative of more severe pain. Each patient will then undergo the acupuncture treatment. On their next migraine (post-treatment), each patient will again be asked to rate the severity of the pain. The difference in pain will be computed for each patient. A two sided test of hypothesis will be conducted, at α =0.05, to assess whether there is a statistically significant difference in pain scores before and after treatment. How many patients should be involved in the study to ensure that the test has 80% power to detect a difference of 10 units on the pain scale? Assume that the standard deviation in the difference scores is approximately 20 units.

First compute the effect size:

Then substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

A sample of size n=32 patients with migraine will ensure that a two-sided test with α =0.05 has 80% power to detect a mean difference of 10 points in pain before and after treatment, assuming that all 32 patients complete the treatment.

Sample Sizes for Two Independent Samples, Dichotomous Outcomes

In studies where the plan is to perform a test of hypothesis comparing the proportions of successes in two independent populations, the hypotheses of interest are:

H 0 : p 1 = p 2 versus H 1 : p 1 ≠ p 2

where p 1 and p 2 are the proportions in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is given below:

where n i is the sample size required in each group (i=1,2), α is the selected level of significance and Z 1-α/2 is the value from the standard normal distribution holding 1- α/2 below it, and 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as follows:

where |p 1 - p 2 | is the absolute value of the difference in proportions between the two groups expected under the alternative hypothesis, H 1 , and p is the overall proportion, based on pooling the data from the two comparison groups (p can be computed by taking the mean of the proportions in the two comparison groups, assuming that the groups will be of approximately equal size).

Example 11:

An investigator hypothesizes that there is a higher incidence of flu among students who use their athletic facility regularly than their counterparts who do not. The study will be conducted in the spring. Each student will be asked if they used the athletic facility regularly over the past 6 months and whether or not they had the flu. A test of hypothesis will be conducted to compare the proportion of students who used the athletic facility regularly and got flu with the proportion of students who did not and got flu. During a typical year, approximately 35% of the students experience flu. The investigators feel that a 30% increase in flu among those who used the athletic facility regularly would be clinically meaningful. How many students should be enrolled in the study to ensure that the power of the test is 80% to detect this difference in the proportions? A two sided test will be used with a 5% level of significance.

We first compute the effect size by substituting the proportions of students in each group who are expected to develop flu, p 1 =0.46 (i.e., 0.35*1.30=0.46) and p 2 =0.35 and the overall proportion, p=0.41 (i.e., (0.46+0.35)/2):

We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

Samples of size n 1 =324 and n 2 =324 will ensure that the test of hypothesis will have 80% power to detect a 30% difference in the proportions of students who develop flu between those who do and do not use the athletic facilities regularly.

Donor Feces? Really? Clostridium difficile (also referred to as "C. difficile" or "C. diff.") is a bacterial species that can be found in the colon of humans, although its numbers are kept in check by other normal flora in the colon. Antibiotic therapy sometimes diminishes the normal flora in the colon to the point that C. difficile flourishes and causes infection with symptoms ranging from diarrhea to life-threatening inflammation of the colon. Illness from C. difficile most commonly affects older adults in hospitals or in long term care facilities and typically occurs after use of antibiotic medications. In recent years, C. difficile infections have become more frequent, more severe and more difficult to treat. Ironically, C. difficile is first treated by discontinuing antibiotics, if they are still being prescribed. If that is unsuccessful, the infection has been treated by switching to another antibiotic. However, treatment with another antibiotic frequently does not cure the C. difficile infection. There have been sporadic reports of successful treatment by infusing feces from healthy donors into the duodenum of patients suffering from C. difficile. (Yuk!) This re-establishes the normal microbiota in the colon, and counteracts the overgrowth of C. diff. The efficacy of this approach was tested in a randomized clinical trial reported in the New England Journal of Medicine (Jan. 2013). The investigators planned to randomly assign patients with recurrent C. difficile infection to either antibiotic therapy or to duodenal infusion of donor feces. In order to estimate the sample size that would be needed, the investigators assumed that the feces infusion would be successful 90% of the time, and antibiotic therapy would be successful in 60% of cases. How many subjects will be needed in each group to ensure that the power of the study is 80% with a level of significance α = 0.05?

Determining the appropriate design of a study is more important than the statistical analysis; a poorly designed study can never be salvaged, whereas a poorly analyzed study can be re-analyzed. A critical component in study design is the determination of the appropriate sample size. The sample size must be large enough to adequately answer the research question, yet not too large so as to involve too many patients when fewer would have sufficed. The determination of the appropriate sample size involves statistical criteria as well as clinical or practical considerations. Sample size determination involves teamwork; biostatisticians must work closely with clinical investigators to determine the sample size that will address the research question of interest with adequate precision or power to produce results that are clinically meaningful.

The following table summarizes the sample size formulas for each scenario described here. The formulas are organized by the proposed analysis, a confidence interval estimate or a test of hypothesis.

Buschman NA, Foster G, Vickers P. Adolescent girls and their babies: achieving optimal birth weight. Gestational weight gain and pregnancy outcome in terms of gestation at delivery and infant birth weight: a comparison between adolescents under 16 and adult women. Child: Care, Health and Development. 2001; 27(2):163-171.
Feuer EJ, Wun LM. DEVCAN: Probability of Developing or Dying of Cancer. Version 4.0 .Bethesda, MD: National Cancer Institute, 1999.
Howell DC. Statistical Methods for Psychology. Boston, MA: Duxbury Press, 1982.
Fleiss JL. Statistical Methods for Rates and Proportions. New York, NY: John Wiley and Sons, Inc.,1981.
National Center for Health Statistics. Health, United States, 2005 with Chartbook on Trends in the Health of Americans. Hyattsville, MD : US Government Printing Office; 2005.
Plaskon LA, Penson DF, Vaughan TL, Stanford JL. Cigarette smoking and risk of prostate cancer in middle-aged men. Cancer Epidemiology Biomarkers & Prevention. 2003; 12: 604-609.
Rutter MK, Meigs JB, Sullivan LM, D'Agostino RB, Wilson PW. C-reactive protein, the metabolic syndrome and prediction of cardiovascular events in the Framingham Offspring Study. Circulation. 2004;110: 380-385.
Ramachandran V, Sullivan LM, Wilson PW, Sempos CT, Sundstrom J, Kannel WB, Levy D, D'Agostino RB. Relative importance of borderline and elevated levels of coronary heart disease risk factors. Annals of Internal Medicine. 2005; 142: 393-402.
Wechsler H, Lee JE, Kuo M, Lee H. College Binge Drinking in the 1990s:A Continuing Problem Results of the Harvard School of Public Health 1999 College Health, 2000; 48: 199-210.

Answers to Selected Problems

Answer to birth weight question - page 3.

In order to ensure that the 95% confidence interval estimate of the mean birthweight is within 100 grams of the true mean, a sample of size 57 is needed. In planning the study, the investigator must consider the fact that some women may deliver prematurely. If women are enrolled into the study during pregnancy, then more than 57 women will need to be enrolled so that after excluding those who deliver prematurely, 57 with outcome information will be available for analysis. For example, if 5% of the women are expected to delivery prematurely (i.e., 95% will deliver full term), then 60 women must be enrolled to ensure that 57 deliver full term. The number of women that must be enrolled, N, is computed as follows:

N (number to enroll) * (% retained) = desired sample size

N (0.95) = 57

N = 57/0.95 = 60.

Answer Freshmen Smoking - Page 4

In order to ensure that the 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion, a sample of size 303 is needed. Notice that this sample size is substantially smaller than the one estimated above. Having some information on the magnitude of the proportion in the population will always produce a sample size that is less than or equal to the one based on a population proportion of 0.5. However, the estimate must be realistic.

Answer to Medical Device Problem - Page 7

Then substitute the effect size and the appropriate z values for the selected alpha and power to comute the sample size.

A sample size of 364 stents will ensure that a two-sided test with α=0.05 has 90% power to detect a 0.05, or 5%, difference in jthe proportion of defective stents produced.

Answer to Alcohol and GPA - Page 8

First compute the effect size.

Now substitute the effect size and the appropriate z values for alpha and power to compute the sample size.

Sample sizes of n i =44 heavy drinkers and 44 who drink few fewer than five drinks per typical drinking day will ensure that the test of hypothesis has 80% power to detect a 0.25 unit difference in mean grade point averages.

Answer to Donor Feces - Page 8

We first compute the effect size by substituting the proportions of patients expected to be cured with each treatment, p 1 =0.6 and p 2 =0.9, and the overall proportion, p=0.75:

We now substitute the effect size and the appropriate Z values for the selected a and power to compute the sample size.

Samples of size n 1 =33 and n 2 =33 will ensure that the test of hypothesis will have 80% power to detect this difference in the proportions of patients who are cured of C. diff. by feces infusion versus antibiotic therapy.

In fact, the investigators enrolled 38 into each group to allow for attrition. Nevertheless, the study was stopped after an interim analysis. Of 16 patients in the infusion group, 13 (81%) had resolution of C. difficile–associated diarrhea after the first infusion. The 3 remaining patients received a second infusion with feces from a different donor, with resolution in 2 patients. Resolution of C. difficile infection occurred in only 4 of 13 patients (31%) receiving the antibiotic vancomycin.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

Advanced Search
Journal List
Indian J Psychol Med
v.42(1); Jan-Feb 2020

Sample Size and its Importance in Research

Chittaranjan andrade.

Clinical Psychopharmacology Unit, Department of Clinical Psychopharmacology and Neurotoxicology, National Institute of Mental Health and Neurosciences, Bengaluru, Karnataka, India

The sample size for a study needs to be estimated at the time the study is proposed; too large a sample is unnecessary and unethical, and too small a sample is unscientific and also unethical. The necessary sample size can be calculated, using statistical software, based on certain assumptions. If no assumptions can be made, then an arbitrary sample size is set for a pilot study. This article discusses sample size and how it relates to matters such as ethics, statistical power, the primary and secondary hypotheses in a study, and findings from larger vs. smaller samples.

Studies are conducted on samples because it is usually impossible to study the entire population. Conclusions drawn from samples are intended to be generalized to the population, and sometimes to the future as well. The sample must therefore be representative of the population. This is best ensured by the use of proper methods of sampling. The sample must also be adequate in size – in fact, no more and no less.

SAMPLE SIZE AND ETHICS

A sample that is larger than necessary will be better representative of the population and will hence provide more accurate results. However, beyond a certain point, the increase in accuracy will be small and hence not worth the effort and expense involved in recruiting the extra patients. Furthermore, an overly large sample would inconvenience more patients than might be necessary for the study objectives; this is unethical. In contrast, a sample that is smaller than necessary would have insufficient statistical power to answer the primary research question, and a statistically nonsignificant result could merely be because of inadequate sample size (Type 2 or false negative error). Thus, a small sample could result in the patients in the study being inconvenienced with no benefit to future patients or to science. This is also unethical.

In this regard, inconvenience to patients refers to the time that they spend in clinical assessments and to the psychological and physical discomfort that they experience in assessments such as interviews, blood sampling, and other procedures.

ESTIMATING SAMPLE SIZE

So how large should a sample be? In hypothesis testing studies, this is mathematically calculated, conventionally, as the sample size necessary to be 80% certain of identifying a statistically significant outcome should the hypothesis be true for the population, with P for statistical significance set at 0.05. Some investigators power their studies for 90% instead of 80%, and some set the threshold for significance at 0.01 rather than 0.05. Both choices are uncommon because the necessary sample size becomes large, and the study becomes more expensive and more difficult to conduct. Many investigators increase the sample size by 10%, or by whatever proportion they can justify, to compensate for expected dropout, incomplete records, biological specimens that do not meet laboratory requirements for testing, and other study-related problems.

Sample size calculations require assumptions about expected means and standard deviations, or event risks, in different groups; or, upon expected effect sizes. For example, a study may be powered to detect an effect size of 0.5; or a response rate of 60% with drug vs. 40% with placebo.[ 1 ] When no guesstimates or expectations are possible, pilot studies are conducted on a sample that is arbitrary in size but what might be considered reasonable for the field.

The sample size may need to be larger in multicenter studies because of statistical noise (due to variations in patient characteristics, nonspecific treatment characteristics, rating practices, environments, etc. between study centers).[ 2 ] Sample size calculations can be performed manually or using statistical software; online calculators that provide free service can easily be identified by search engines. G*Power is an example of a free, downloadable program for sample size estimation. The manual and tutorial for G*Power can also be downloaded.

PRIMARY AND SECONDARY ANALYSES

The sample size is calculated for the primary hypothesis of the study. What is the difference between the primary hypothesis, primary outcome and primary outcome measure? As an example, the primary outcome may be a reduction in the severity of depression, the primary outcome measure may be the Montgomery-Asberg Depression Rating Scale (MADRS) and the primary hypothesis may be that reduction in MADRS scores is greater with the drug than with placebo. The primary hypothesis is tested in the primary analysis.

Studies almost always have many hypotheses; for example, that the study drug will outperform placebo on measures of depression, suicidality, anxiety, disability and quality of life. The sample size necessary for adequate statistical power to test each of these hypotheses will be different. Because a study can have only one sample size, it can be powered for only one outcome, the primary outcome. Therefore, the study would be either overpowered or underpowered for the other outcomes. These outcomes are therefore called secondary outcomes, and are associated with secondary hypotheses, and are tested in secondary analyses. Secondary analyses are generally considered exploratory because when many hypotheses in a study are each tested at a P < 0.05 level for significance, some may emerge statistically significant by chance (Type 1 or false positive errors).[ 3 ]

INTERPRETING RESULTS

Here is an interesting question. A test of the primary hypothesis yielded a P value of 0.07. Might we conclude that our sample was underpowered for the study and that, had our sample been larger, we would have identified a significant result? No! The reason is that larger samples will more accurately represent the population value, whereas smaller samples could be off the mark in either direction – towards or away from the population value. In this context, readers should also note that no matter how small the P value for an estimate is, the population value of that estimate remains the same.[ 4 ]

On a parting note, it is unlikely that population values will be null. That is, for example, that the response rate to the drug will be exactly the same as that to placebo, or that the correlation between height and age at onset of schizophrenia will be zero. If the sample size is large enough, even such small differences between groups, or trivial correlations, would be detected as being statistically significant. This does not mean that the findings are clinically significant.

Financial support and sponsorship

Conflicts of interest.

There are no conflicts of interest.

Power & Sample Size Calculator

Use this advanced sample size calculator to calculate the sample size required for a one-sample statistic, or for differences between two proportions or means (two independent samples). More than two groups supported for binomial data. Calculate power given sample size, alpha, and the minimum detectable effect (MDE, minimum effect of interest).

Experimental design

Data parameters

Related calculators

Using the power & sample size calculator

Parameters for sample size and power calculations

Calculator output.

Why is sample size determination important?
What is statistical power?

Post-hoc power (Observed power)

Sample size formula
Types of null and alternative hypotheses in significance tests
Absolute versus relative difference and why it matters for sample size determination

Using the power & sample size calculator

This calculator allows the evaluation of different statistical designs when planning an experiment (trial, test) which utilizes a Null-Hypothesis Statistical Test to make inferences. It can be used both as a sample size calculator and as a statistical power calculator . Usually one would determine the sample size required given a particular power requirement, but in cases where there is a predetermined sample size one can instead calculate the power for a given effect size of interest.

1. Number of test groups. The sample size calculator supports experiments in which one is gathering data on a single sample in order to compare it to a general population or known reference value (one-sample), as well as ones where a control group is compared to one or more treatment groups ( two-sample, k-sample ) in order to detect differences between them. For comparing more than one treatment group to a control group the sample size adjustments based on the Dunnett's correction are applied. These are only approximately accurate and subject to the assumption of about equal effect size in all k groups, and can only support equal sample sizes in all groups and the control. Power calculations are not currently supported for more than one treatment group due to their complexity.

2. Type of outcome . The outcome of interest can be the absolute difference of two proportions (binomial data, e.g. conversion rate or event rate), the absolute difference of two means (continuous data, e.g. height, weight, speed, time, revenue, etc.), or the relative difference between two proportions or two means (percent difference, percent change, etc.). See Absolute versus relative difference for additional information. One can also calculate power and sample size for the mean of just a single group. The sample size and power calculator uses the Z-distribution (normal distribution) .

3. Baseline The baseline mean (mean under H 0 ) is the number one would expect to see if all experiment participants were assigned to the control group. It is the mean one expects to observe if the treatment has no effect whatsoever.

4. Minimum Detectable Effect . The minimum effect of interest, which is often called the minimum detectable effect ( MDE , but more accurately: MRDE, minimum reliably detectable effect) should be a difference one would not like to miss , if it existed. It can be entered as a proportion (e.g. 0.10) or as percentage (e.g. 10%). It is always relative to the mean/proportion under H 0 ± the superiority/non-inferiority or equivalence margin. For example, if the baseline mean is 10 and there is a superiority alternative hypothesis with a superiority margin of 1 and the minimum effect of interest relative to the baseline is 3, then enter an MDE of 2 , since the MDE plus the superiority margin will equal exactly 3. In this case the MDE (MRDE) is calculated relative to the baseline plus the superiority margin, as it is usually more intuitive to be interested in that value.

If entering means data, one needs to specify the mean under the null hypothesis (worst-case scenario for a composite null) and the standard deviation of the data (for a known population or estimated from a sample).

5. Type of alternative hypothesis . The calculator supports superiority , non-inferiority and equivalence alternative hypotheses. When the superiority or non-inferiority margin is zero, it becomes a classical left or right sided hypothesis, if it is larger than zero then it becomes a true superiority / non-inferiority design. The equivalence margin cannot be zero. See Types of null and alternative hypothesis below for an in-depth explanation.

6. Acceptable error rates . The type I error rate, α , should always be provided. Power, calculated as 1 - β , where β is the type II error rate, is only required when determining sample size. For an in-depth explanation of power see What is statistical power below. The type I error rate is equivalent to the significance threshold if one is doing p-value calculations and to the confidence level if using confidence intervals.

The sample size calculator will output the sample size of the single group or of all groups, as well as the total sample size required. If used to solve for power it will output the power as a proportion and as a percentage.

Why is sample size determination important?

While this online software provides the means to determine the sample size of a test, it is of great importance to understand the context of the question, the "why" of it all.

Estimating the required sample size before running an experiment that will be judged by a statistical test (a test of significance, confidence interval, etc.) allows one to:

determine the sample size needed to detect an effect of a given size with a given probability
be aware of the magnitude of the effect that can be detected with a certain sample size and power
calculate the power for a given sample size and effect size of interest

This is crucial information with regards to making the test cost-efficient. Having a proper sample size can even mean the difference between conducting the experiment or postponing it for when one can afford a sample of size that is large enough to ensure a high probability to detect an effect of practical significance.

For example, if a medical trial has low power, say less than 80% (β = 0.2) for a given minimum effect of interest, then it might be unethical to conduct it due to its low probability of rejecting the null hypothesis and establishing the effectiveness of the treatment. Similarly, for experiments in physics, psychology, economics, marketing, conversion rate optimization, etc. Balancing the risks and rewards and assuring the cost-effectiveness of an experiment is a task that requires juggling with the interests of many stakeholders which is well beyond the scope of this text.

What is statistical power?

Statistical power is the probability of rejecting a false null hypothesis with a given level of statistical significance , against a particular alternative hypothesis. Alternatively, it can be said to be the probability to detect with a given level of significance a true effect of a certain magnitude. This is what one gets when using the tool in "power calculator" mode. Power is closely related with the type II error rate: β, and it is always equal to (1 - β). In a probability notation the type two error for a given point alternative can be expressed as [1] :

β(T α ; μ 1 ) = P(d(X) ≤ c α ; μ = μ 1 )

It should be understood that the type II error rate is calculated at a given point, signified by the presence of a parameter for the function of beta. Similarly, such a parameter is present in the expression for power since POW = 1 - β [1] :

POW(T α ; μ 1 ) = P(d(X) > c α ; μ = μ 1 )

In the equations above c α represents the critical value for rejecting the null (significance threshold), d(X) is a statistical function of the parameter of interest - usually a transformation to a standardized score, and μ 1 is a specific value from the space of the alternative hypothesis.

One can also calculate and plot the whole power function, getting an estimate of the power for many different alternative hypotheses. Due to the S-shape of the function, power quickly rises to nearly 100% for larger effect sizes, while it decreases more gradually to zero for smaller effect sizes. Such a power function plot is not yet supported by our statistical software, but one can calculate the power at a few key points (e.g. 10%, 20% ... 90%, 100%) and connect them for a rough approximation.

Statistical power is directly and inversely related to the significance threshold. At the zero effect point for a simple superiority alternative hypothesis power is exactly 1 - α as can be easily demonstrated with our power calculator. At the same time power is positively related to the number of observations, so increasing the sample size will increase the power for a given effect size, assuming all other parameters remain the same.

Power calculations can be useful even after a test has been completed since failing to reject the null can be used as an argument for the null and against particular alternative hypotheses to the extent to which the test had power to reject them. This is more explicitly defined in the severe testing concept proposed by Mayo & Spanos (2006).

Computing observed power is only useful if there was no rejection of the null hypothesis and one is interested in estimating how probative the test was towards the null . It is absolutely useless to compute post-hoc power for a test which resulted in a statistically significant effect being found [5] . If the effect is significant, then the test had enough power to detect it. In fact, there is a 1 to 1 inverse relationship between observed power and statistical significance, so one gains nothing from calculating post-hoc power, e.g. a test planned for α = 0.05 that passed with a p-value of just 0.0499 will have exactly 50% observed power (observed β = 0.5).

I strongly encourage using this power and sample size calculator to compute observed power in the former case, and strongly discourage it in the latter.

Sample size formula

The formula for calculating the sample size of a test group in a one-sided test of absolute difference is:

where Z 1-α is the Z-score corresponding to the selected statistical significance threshold α , Z 1-β is the Z-score corresponding to the selected statistical power 1-β , σ is the known or estimated standard deviation, and δ is the minimum effect size of interest. The standard deviation is estimated analytically in calculations for proportions, and empirically from the raw data for other types of means.

The formula applies to single sample tests as well as to tests of absolute difference between two samples. A proprietary modification is employed when calculating the required sample size in a test of relative difference . This modification has been extensively tested under a variety of scenarios through simulations.

Types of null and alternative hypotheses in significance tests

When doing sample size calculations, it is important that the null hypothesis (H 0 , the hypothesis being tested) and the alternative hypothesis is (H 1 ) are well thought out. The test can reject the null or it can fail to reject it. Strictly logically speaking it cannot lead to acceptance of the null or to acceptance of the alternative hypothesis. A null hypothesis can be a point one - hypothesizing that the true value is an exact point from the possible values, or a composite one: covering many possible values, usually from -∞ to some value or from some value to +∞. The alternative hypothesis can also be a point one or a composite one.

In a Neyman-Pearson framework of NHST (Null-Hypothesis Statistical Test) the alternative should exhaust all values that do not belong to the null, so it is usually composite. Below is an illustration of some possible combinations of null and alternative statistical hypotheses: superiority, non-inferiority, strong superiority (margin > 0), equivalence.

All of these are supported in our power and sample size calculator.

Careful consideration has to be made when deciding on a non-inferiority margin, superiority margin or an equivalence margin . Equivalence trials are sometimes used in clinical trials where a drug can be performing equally (within some bounds) to an existing drug but can still be preferred due to less or less severe side effects, cheaper manufacturing, or other benefits, however, non-inferiority designs are more common. Similar cases exist in disciplines such as conversion rate optimization [2] and other business applications where benefits not measured by the primary outcome of interest can influence the adoption of a given solution. For equivalence tests it is assumed that they will be evaluated using a two one-sided t-tests (TOST) or z-tests, or confidence intervals.

Note that our calculator does not support the schoolbook case of a point null and a point alternative, nor a point null and an alternative that covers all the remaining values. This is since such cases are non-existent in experimental practice [3][4] . The only two-sided calculation is for the equivalence alternative hypothesis, all other calculations are one-sided (one-tailed) .

Absolute versus relative difference and why it matters for sample size determination

When using a sample size calculator it is important to know what kind of inference one is looking to make: about the absolute or about the relative difference, often called percent effect, percentage effect, relative change, percent lift, etc. Where the fist is μ 1 - μ the second is μ 1 -μ / μ or μ 1 -μ / μ x 100 (%). The division by μ is what adds more variance to such an estimate, since μ is just another variable with random error, therefore a test for relative difference will require larger sample size than a test for absolute difference. Consequently, if sample size is fixed, there will be less power for the relative change equivalent to any given absolute change.

For the above reason it is important to know and state beforehand if one is going to be interested in percentage change or if absolute change is of primary interest. Then it is just a matter of fliping a radio button.

References

1 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.

2 Georgiev G.Z. (2017) "The Case for Non-Inferiority A/B Tests", [online] https://blog.analytics-toolkit.com/2017/case-non-inferiority-designs-ab-testing/ (accessed May 7, 2018)

3 Georgiev G.Z. (2017) "One-tailed vs Two-tailed Tests of Significance in A/B Testing", [online] https://blog.analytics-toolkit.com/2017/one-tailed-two-tailed-tests-significance-ab-testing/ (accessed May 7, 2018)

4 Hyun-Chul Cho Shuzo Abe (2013) "Is two-tailed testing for directional research hypotheses tests legitimate?", Journal of Business Research 66:1261-1266

5 Lakens D. (2014) "Observed power, and what to do if your editor asks for post-hoc power analyses" [online] http://daniellakens.blogspot.bg/2014/12/observed-power-and-what-to-do-if-your.html (accessed May 7, 2018)

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Sample Size Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/power-sample-size-calculator.php URL [Accessed Date: 24 May, 2024].

Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

Statistical calculators

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 9: Data Analysis – Hypothesis Testing, Estimating Sample Size, and Modeling

This chapter provides the foundational concepts and tools for analyzing data commonly seen in the transportation profession. The concepts include hypothesis testing, assessing the adequacy of the sample sizes, and estimating the least square model fit for the data. These applications are useful in collecting and analyzing travel speed data, conducting before-after comparisons, and studying the association between variables, e.g., travel speed and congestion as measured by traffic density on the road.

Learning Objectives

At the end of the chapter, the reader should be able to do the following:

Estimate the required sample size for testing.
Use specific significance tests including, z-test, t-test (one and two samples), chi-squared test.
Compute corresponding p-value for the tests.
Compute and interpret simple linear regression between two variables.
Estimate a least-squares fit of data.
Find confidence intervals for parameter estimates.
Use of spreadsheet tools (e.g., MS Excel) and basic programming (e.g., R or SPSS) to calculate complex and repetitive mathematical problems similar to earthwork estimates (cut, fill, area, etc.), trip generation and distribution, and linear optimization.
Use of spreadsheet tools (e.g., MS Excel) and basic programming (e.g., R or SPSS) to create relevant graphs and charts from data points.
Identify topics in the introductory transportation engineering courses that build on the concepts discussed in this chapter.

Central Limit Theorem

In this section, you will learn about the the central limit theorem by reading each description along with watching the videos. Also, short problems to check your understanding are included.

The Central Limit theorem for Sample Means

The sampling distribution is a theoretical distribution. It is created by taking many samples of size n from a population. Each sample mean is then treated like a single observation of this new distribution, the sampling distribution. The genius of thinking this way is that it recognizes that when we sample, we are creating an observation and that observation must come from some particular distribution. The Central Limit Theorem answers the question: from what distribution dis a sample mean come? If this is discovered, then we can treat a sample mean just like any other observation and calculate probabilities about what values it might take on. We have effectively moved from the world of statistics where we know only what we have from the sample to the world of probability where we know the distribution from which the same mean came and the parameters of that distribution.

The reasons that one samples a population are obvious. The time and expense of checking every invoice to determine its validity or every shipment to see if it contains all the items may well exceed the cost of errors in billing or shipping. For some products, sampling would require destroying them, called destructive sampling. One such example is measuring the ability of a metal to withstand saltwater corrosion for parts on ocean going vessels.

Sampling thus raises an important question; just which sample was drawn. Even if the sample were randomly drawn, there are theoretically an almost infinite number of samples. With just 100 items, there are more than 75 million unique samples of size five that can be drawn. If six are in the sample, the number of possible samples increases to just more than one billion. Of the 75 million possible samples, then, which one did you get? If there is variation in the items to be sampled, there will be variation in the samples. One could draw an “unlucky” sample and make very wrong conclusions concerning the population. This recognition that any sample we draw is really only one from a distribution of samples provides us with what is probably the single most important theorem is statistics: the Central Limit Theorem. Without the Central Limit Theorem, it would be impossible to proceed to inferential statistics from simple probability theory. In its most basic form, the Central Limit Theorem states that regardless of the underlying probability density function of the population data, the theoretical distribution of the means of samples from the population will be normally distributed. In essence, this says that the mean of a sample should be treated like an observation drawn from a normal distribution. The Central Limit Theorem only holds if the sample size is “large enough” which has been shown to be only 30 observations or more.

Figure 1 graphically displays this very important proposition.

Graph of the population and normal sampling distribution

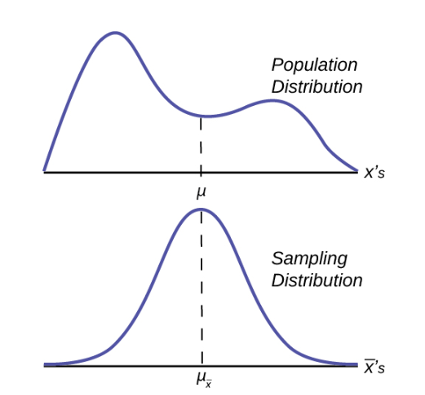
Notice that the horizontal axis in the top panel is labeled X. These are the individual observations of the population. This is the unknown distribution of the population values. The graph is purposefully drawn all squiggly to show that it does not matter just how odd ball it really is. Remember, we will never know what this distribution looks like, or its mean or standard deviation for that matter.

$\overline{X^{\prime} s}$

The Central Limit Theorem goes even further and tells us the mean and standard deviation of this theoretical distribution.

$\overline{X^{\prime}}$

Sampling Distribution of the Sample Mean

Sampling Distribution of the Sample Mean (Part 2)

Sampling Distributions: Sampling Distribution of the Mean

Using the Central Limit Theorem

Law of Large Numbers

$\bar{X} \text { is } \frac{\sigma}{\sqrt{n}}$

Indeed, there are two critical issues that flow from the Central Limit Theorem and the application of the Law of Large numbers to it. These are listed below.

The probability density function of the sampling distribution of means is normally distributed regardless of the underlying distribution of the population observations and
Standard deviation of the sampling distribution decreases as the size of the samples that were used to calculate the means for the sampling distribution increases.

Taking these in order. It would seem counterintuitive that the population may have any distribution and the distribution of means coming from it would be normally distributed. With the use of computers, experiments can be simulated that show the process by which the sampling distribution changes as the sample size is increased. These simulations show visually the results of the mathematical proof of the Central Limit Theorem.

$\bar{x}^{\prime} s$

At non-extreme values of n, this relationship between the standard deviation of the sampling distribution and the sample size plays a very important part in our ability to estimate the parameters in which we are interested.

Figure 3 shows three sampling distributions. The only change that was made is the sample size that was used to get the sample means for each distribution. As the sample size increases, n goes from 10 to 30 to 50, the standard deviations of the respective sampling distributions decrease because the sample size is in the denominator of the standard deviations of the sampling distributions.

Normal distribution with variety of sample sizes.

The Central Limit Theorem for Proportions

$\overline{x^{\prime}} s$

In order to find the distribution from which sample proportions come we need to develop the sampling distribution of sample proportions just as we did for sample means. So again, imagine that we randomly sample say 50 people and ask them if they support the new school bond issue. From this we find a sample proportion, p’, and graph it on the axis of p’s. We do this again and again etc., etc. until we have the theoretical distribution of p’s. Some sample proportions will show high favorability toward the bond issue and others will show low favorability because random sampling will reflect the variation of views within the population. What we have done can be seen in Figure 5. The top panel is the population distributions of probabilities for each possible value of the random variable X. While we do not know what the specific distribution looks like because we do not know p, the population parameter, we do know that it must look something like this. In reality, we do not know either the mean or the standard deviation of this population distribution, the same difficulty we faced when analyzing the X’s previously.

Bar group of population and the corresponding normal sampling distribution

Importantly, in the case of the analysis of the distribution of sample means, the Central Limit Theorem told us the expected value of the mean of the sample means in the sampling distribution, and the standard deviation of the sampling distribution. Again, the Central Limit Theorem provides this information for the sampling distribution for proportions. The answers are:

$\mu_{p^{\prime}}$

Both these conclusions are the same as we found for the sampling distribution for sample means. However, in this case, because mean and standard deviation of the binomial distribution both rely upon p , the formula for the standard deviation of the sampling distribution requires algebraic manipulation to be useful. The standard deviation of the sampling distribution for proportions is thus:

$\sigma_{p^{\prime}}=\sqrt{\frac{p(1-P)}{n}}$

Table 2 summarizes these results and shows the relationship between the population, sample, and sampling distribution.

$\mu \text { or } p$

Find Confidence Intervals for Parameter Estimates

In this section, you will learn how to find and estimate confidence intervals by reading each description along with watching the videos included. Also, short problems to check your understanding are included.

Confidence Intervals & Estimation: Point Estimates Explained

Introduction to Confidence Intervals

Suppose you were trying to determine the mean rent of a two-bedroom apartment in your town. You might look in the classified section of the newspaper, write down several rents listed, and average them together. You would have obtained a point estimate of the true mean. If you are trying to determine the percentage of times you make a basket when shooting a basketball, you might count the number of shots you make and divide that by the number of shots you attempted. In this case, you would have obtained a point estimate for the true proportion the parameter p in the binomial probability density function.

We use sample data to make generalizations about an unknown population. This part of statistics is called inferential statistics . The sample data help us to make an estimate of a population parameter. We realize that the point estimate is most likely not the exact value of the population parameter, but close to it. After calculating point estimates, we construct interval estimates, called confidence intervals. What statistics provides us beyond a simple average , or point estimate, is an estimate to which we can attach a probability of accuracy, what we will call a confidence level. We make inferences with a known level of probability.

$\sigma$

A confidence interval is another type of estimate but, instead of being just one number, it is an interval of numbers. The interval of numbers is a range of values calculated from a given set of sample data. The confidence interval is likely to include the unknown population parameter.

$\sigma=1$

We say that we are 95% confident that the unknown population mean number of songs downloaded from iTunes per month is between 1.8 and 2.2. The 95% confidence interval is (1.8, 2.2). Please note that we talked in terms of 95% confidence using the empirical rule. The empirical rule for two standard deviations is only approximately 95% of the probability under the normal distribution. To be precise, two standard deviations under a normal distribution is actually 95.44% of the probability. To calculate the exact 95% confidence level, we would use 1.96 standard deviations.

Remember that a confidence interval is created for an unknown population parameter like the population mean, 𝜇 "> 𝜇 .

For the confidence interval for a mean the formula would be:

$\mu=\bar{X} \pm Z_\alpha \sigma / \sqrt{n}$

Or written another way as:

$\bar{X}-Z_\alpha \sigma / \sqrt{n} \leq \mu \leq \bar{X}+Z_\alpha \sigma / \sqrt{n}$

A Confidence Interval for a Population Standard Deviation, Known or Large Sample Size

A confidence interval for a population mean, when the population standard deviation is known based on the conclusion of the Central Limit Theorem that the sampling distribution of the sample means follow an approximately normal distribution.

Calculating the Confidence Interval

Consider the standardizing formula for the sampling distribution developed in the discussion of the Central Limit Theorem:

$Z_1=\frac{\bar{X}-\mu_{-}}{\sigma_{-}}=\frac{\bar{X}-\mu}{\sigma / \sqrt{n}}$

This is the formula for a confidence interval for the mean of a population.

$Z_\alpha$

Let us say we know that the actual population mean number of iTunes downloads is 2.1. The true population mean falls within the range of the 95% confidence interval. There is absolutely nothing to guarantee that this will happen . Further, if the true mean falls outside of the interval, we will never know it. We must always remember that we will never ever know the true mean. Statistics simply allows us, with a given level of probability (confidence), to say that the true mean is within the range calculated.

Changing the Confidence Level or Sample Size

Here again is the formula for a confidence interval for an unknown population mean assuming we know the population standard deviation:

$\bar{X}-Z_\alpha(\alpha / \sqrt{n}) \leq \mu \leq \bar{X}+Z_\alpha(\alpha / \sqrt{n})$

For a moment we should ask just what we desire in a confidence interval. Our goal was to estimate the population mean from a sample. We have forsaken the hope that we will ever find the true population mean, and population standard deviation for that matter, for any case except where we have an extremely small population and the cost of gathering the data of interest is very small. In all other cases we must rely on samples. With the Central Limit Theorem, we have the tools to provide a meaningful confidence interval with a given level of confidence, meaning a known probability of being wrong. By meaningful confidence interval we mean one that is useful. Imagine that you are asked for a confidence interval for the ages of your classmates. You have taken a sample and find a mean of 19.8 years. You wish to be very confident, so you report an interval between 9.8 years and 29.8 years. This interval would certainly contain the true population mean and have a very high confidence level. However, it hardly qualifies as meaningful. The very best confidence interval is narrow while having high confidence. There is a natural tension between these two goals. The higher the level of confidence the wider the confidence interval as the case of the students’ ages above. We can see this tension in the equation for the confidence interval.

$\mu=\bar{x} \pm Z_\alpha\left(\frac{\sigma}{\sqrt{n}}\right)$

Calculating the Confidence Interval: An Alternative Approach

The confidence interval estimate will have the form:

(Point estimate – error bound, point estimate + error bound) or, in symbols,

$(\bar{x}-E B M, \bar{x}+E B M) .$

The mathematical formula for this confidence interval is:

The margin of error (EBM) depends on the confidence level (abbreviated CL ). The confidence level is often considered the probability that the calculated confidence interval estimate will contain the true population parameter. However, it is more accurate to state that the confidence level is the percent of confidence intervals that contain the true population parameter when repeated samples are taken. Most often, it is the choice of the person constructing the confidence interval to choose a confidence level of 90% or higher because that person wants to be reasonably certain of his or her conclusions.

$(\alpha) . \alpha$

To capture the central 90%, we must go out 1.645 standard deviations on either side of the calculated sample mean. The value 1.645 is the z-score from a standard normal probability distribution that puts an area of 0.90 in the center, an area of 0.05 in the far-left tail, and an area of 0.05 in the far-right tail.

$\frac{\sigma}{\sqrt{n}}$

Calculating the Confidence Interval Using EBM

To construct a confidence interval, estimate for an unknown population mean, we need data from a random sample. The steps to construct and interpret the confidence interval are listed below.

Find the z-score from the standard normal table that corresponds to the confidence level desired.
Calculate the error bound EBM.
Construct the confidence interval.
Write a sentence that interprets the estimate in the context of the situation in the problem.

Finding the z-score for the Stated Confidence Level

$Z \sim N(0,1)$

Calculating the Error Bound (EBM)

$E B M=\left(Z_{\frac{\alpha}{2}}\right)\left(\frac{\sigma}{\sqrt{n}}\right)$

Constructing the Confidence Interval

$(\bar{x}-E M B, \bar{x}+E B M)$

The graph gives a picture of the entire situation.

$C L+\frac{\alpha}{2}+\frac{\alpha}{2}=C L+\alpha=1$

Confidence Interval for Mean: 1 Sample Z Test (Using Formula)

Check Your Understanding: Confidence Interval for Mean

A Confidence Interval for a Population Standard Deviation Unknown, Small Sample Case

Up until the mid-1970s, some statisticians used the normal distribution approximation for large sample sizes and used the Student’s t-distribution only for sample sizes of at most 30 observations.

$t=\frac{\bar{x}-\mu}{\left(\frac{s}{\sqrt{n}}\right)}$

Properties of the Student’s t-distribution

The graph for the Student’s t-distribution is similar to the standard normal curve and at infinite degrees of freedom it is the normal distribution. You can confirm this by reading the bottom line at infinite degrees of freedom for a familiar level of confidence, e.g., at column 0.05, 95% level of confidence, we find the t-value of 1.96 at infinite degrees of freedom.
The mean for the Student’s t-distribution is zero and the distribution is symmetric about zero, again like the standard normal distribution.
The Student’s t-distribution has more probability in its tails than the standard normal distribution because the spread of the t-distribution is greater than the spread of the standard normal. So, the graph of the Student’s t-distribution will be thicker in the tails and shorter in the center than the graph of the standard normal distribution.
The exact shape of the Student’s t-distribution depends on the degrees of freedom. As the degrees of freedom increases, the graph of Student’s t-distribution becomes more like the graph of the standard normal distribution.

A probability table for the Student’s t-distribution is used to calculate t-values at various commonly used levels of confidence. The table gives t-scores that correspond to the confidence level (column) and degrees of freedom (row). When using a t-table, note that some tables are formatted to show the confidence level in the column headings, while the column headings in some tables may show only corresponding area in one or both tails. Notice that at the bottom the table will show the t-value for infinite degrees of freedom. Mathematically, as the degrees of freedom increase, the t-distribution approaches the standard normal distribution. You can find familiar Z-values by looking in the relevant alpha column and reading value in the last row.

A Student’s t-table gives t-scores given the degrees of freedom and the right-tailed probability.

The Student’s t-distribution has one of the most desirable properties of the normal: it is symmetrical. What the Student’s t-distribution does is spread out the horizontal axis, so it takes a larger number of standard deviations to capture the same amount of probability. In reality there are an infinite number of Student’s t-distributions, one for each adjustment to the sample size. As the sample size increases, the Student’s t-distribution become more and more like the normal distribution. When the sample size reaches 30 the normal distribution is usually substituted for the Student’s t because they are so much alike. This relationship between the Student’s t-distribution and the normal distribution is shown in Figure 8.

Graph of the relationship between the normal and t distribution

Confidence Intervals: Using the t Distribution

Check Your Understanding: Confidence Intervals

A Confidence Interval for a Population Proportion

During an election year, we see articles in the newspaper that state confidence intervals in terms of proportions or percentages. For example, a poll for a particular candidate running for president might show that the candidate has 40% of the vote within three percentage points (if the sample is large enough). Often, election polls are calculated with 95% confidence, so, the pollsters would be 95% confident that the true proportion of voters who favored the candidate would be between 0.37 and 0.43.

The procedure to find the confidence interval for a population proportion is similar to that for the population mean, but the formulas are a bit different although conceptually identical. While the formulas are different, they are based upon the same mathematical foundation given to us by the Central Limit Theorem. Because of this we will see the same basic format using the same three pieces of information: the sample value of the parameter in question, the standard deviation of the relevant sampling distribution, and the number of standard deviations we need to have the confidence in our estimate that we desire.

$X \sim B(n, p)$

x = the number of successes in the sample

n = the size of the sample

The formula for the confidence interval for a population proportion follows the same format as that for an estimate of a population mean. Remembering the sampling distribution for the proportion, the standard deviation was found to be:

$\sigma_{p^{\prime}}=\sqrt{\frac{p(1-p)}{n}}$

The confidence interval for a population proportion, therefore, becomes:

$p=p^{\prime} \pm\left[Z_{\left(\frac{\alpha}{2}\right)} \sqrt{\frac{p^{\prime}\left(1-p^{\prime}\right)}{n}}\right]$

The sample proportions p’ and q’ are estimates of the unknown population proportions p and q . The estimated proportions p’ and q’ are used because p and q are not known.

Remember that as p moves further from 0.5 the binomial distribution becomes less symmetrical. Because we are estimating the binomial with the symmetrical normal distribution the further away from symmetrical the binomial becomes the less confidence we have in the estimate.

This conclusion can be demonstrated through the following analysis. Proportions are based upon the binomial probability distribution. The possible outcomes are binary, either “success” or “failure.” This gives rise to a proportion, meaning the percentage of the outcomes that are “successes.” It was shown that the binomial distribution could be fully understood if we knew only the probability of a success in any one trial, called p. The mean and the standard deviation of the binomial were found to be:

$\sigma=\sqrt{n p q}$

It was also shown that the binomial could be estimated by the normal distribution if BOTH np AND nq were greater than 5. From the discussion above, it was found that the standardizing formula for the binomial distribution is:

$Z=\frac{p^{\prime}-p}{\sqrt{\left(\frac{p q}{n}\right)}}$

We can now manipulate this formula in just the same way we did for finding the confidence intervals for a mean, but to find the confidence interval for the binomial population parameter, p .

$p^{\prime}-Z_\alpha \sqrt{\frac{p^{\prime} q^{\prime}}{n}} \leq p \leq p^{\prime}+Z_\alpha \sqrt{\frac{p^{\prime} q^{\prime}}{n}}$

x = number of successes.

n = the number in the sample.

$q^{\prime}=\left(1-p^{\prime}\right)$

Unfortunately, there is no correction factor for cases where the sample size is small so np’ and nq’ must always be greater than 5 to develop an interval estimate for p .

Also written as:

$p^{\prime}-Z_\alpha \sqrt{\frac{p^{\prime}\left(1-p^{\prime}\right)}{n}} \leq p \leq p^{\prime}+Z_\alpha \sqrt{\frac{p^{\prime}\left(1-p^{\prime}\right)}{n}}$

How to Construct a Confidence Interval for Population Proportion

Check Your Understanding: How to Construct a Confidence Interval for Population Proportion

Estimate the Required Sample Size for Testing

In this section, you will learn how to calculate sample size with continuous and binary random samples. by reading each description along with watching the videos included. Also, short problems to check your understanding are included.

Calculating the Sample Size n: Continuous and Binary Random Variables

Continuous Random Variables

Usually, we have no control over the sample size of a data set. However, if we are able to set the sample size, as in cases where we are taking a survey, it is very helpful to know just how large it should be to provide the most information. Sampling can be very costly in both time and product. Simple telephone surveys will cost approximately $30.00 each, for example, and some sampling requires the destruction of the product.

$(\bar{X}-\mu)$

Binary Random Variables

What was done in cases when looking for the mean of a distribution can also be done when sampling to determine the population parameter p for proportions. Manipulation of the standardizing formula for proportions gives:

$n=\frac{Z_\alpha^2 p q}{e^2}$

There is an interesting trade-off between the level of confidence and the sample size that shows up here when considering the cost of sampling. Table 4 shows the appropriate sample size at different levels of confidence and different level of the acceptable error, or tolerance.

$p=0.5 \text { and } q=0.5$

The acceptable error, called tolerance in the table, is measured in plus or minus values from the actual proportion. For example, an acceptable error of 5% means that if the sample proportion was found to be 26 percent, the conclusion would be that the actual population proportion is between 21 and 31 percent with a 90 percent level of confidence if a sample of 271 had been taken. Likewise, if the acceptable error was set at 2%, then the population proportion would be between 24 and 28 percent with a 90 percent level of confidence but would require that the sample size be increased from 271 to 1,691. If we wished a higher level of confidence, we would require a larger sample size. Moving from a 90 percent level of confidence to a 95 percent level at a plus or minus 5% tolerance requires changing the sample size from 271 to 384. A very common sample size often seen reported in political surveys is 384. With the survey results it is frequently stated that the results are good to a plus or minus 5% level of “accuracy”.

Example: Suppose a mobile phone company wants to determine the current percentage of customers aged 50+ who use text messaging on their cell phones. How many customers aged 50+ should the company survey in order to be 90% confident that the estimated (sample) proportion is within three percentage points of the true population proportion of customers aged 50+ who use text messaging on their cell phones.

$z_{\frac{\alpha}{2}}, z_{0.05}=1.645$

Round the answer to the next higher value. The sample size should be 752 cell phone customers aged 50+ in order to be 90% confident that the estimated (sample) proportion is within three percentage points of the true population proportion of all customers aged 50+ who use text messaging on their cell phones.

Estimation and Confidence Intervals: Calculate Sample Size

Calculating Sample size to Predict a Population Proportion

Use Specific Significance Tests Including, Z-Test, T-Test (one and two samples), Chi-Squared Test

In this section, you will learn the fundamentals of hypothesis testing along with hypothesis testing with errors by reading each description along with watching the videos. Also, short problems to check your understanding are included.

Hypothesis Testing with One Sample

Statistical testing is part of a much larger process known as the scientific method. The scientific method, briefly, states that only by following a careful and specific process can some assertion be included in the accepted body of knowledge. This process begins with a set of assumptions upon which a theory, sometimes called a model, is built. This theory, if it has any validity, will lead to predictions; what we call hypotheses.

Statistics and statisticians are not necessarily in the business of developing theories, but in the business of testing others’ theories. Hypotheses come from these theories based upon an explicit set of assumptions and sound logic. The hypothesis comes first, before any data are gathered. Data do not create hypotheses; they are used to test them. If we bear this in mind as we study this section, the process of forming and testing hypotheses will make more sense.

One job of a statistician is to make statistical inferences about populations based on samples taken from the population. Confidence intervals are one way to estimate a population parameter. Another way to make a statistical inference is to make a decision about the value of a specific parameter. For instance, a car dealer advertises that its new small truck gets 35 miles per gallon, on average. A tutoring service claims that its method of tutoring helps 90% of its students get an A or a B. A company says that women managers in their company earn an average of $60,000 per year.

A statistician will make a decision about these claims. This process is called "hypothesis testing." A hypothesis test involves collecting data from a sample and evaluating the data. Then, the statistician makes a decision as to whether or not there is sufficient evidence, based upon analyses of the data, to reject the null hypothesis.

Hypothesis Testing: The Fundamentals

Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

Table 5 presents the various hypotheses in the relevant pairs. For example, if the null hypothesis is equal to some value, the alternative has to be not equal to that value.

$\boldsymbol{H}_0$

Example 2: We wants to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

$H_0: \mu=2.0$

Example 3: We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

$H_0: \mu \geq 5$

Hypothesis Testing: Setting up the Null and Alternative Hypothesis Statements

Outcomes and the Type I and Type II Errors

The four possible outcomes in the table are:

$\beta$

The easiest way to see the relationship between the alpha error and the level of confidence is in Figure 9.

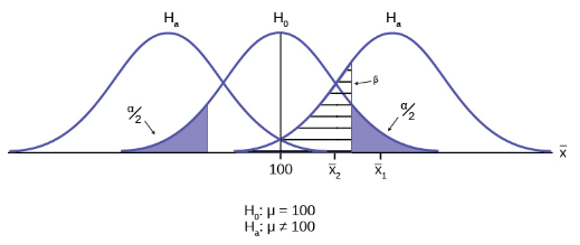
By way of example, the American judicial system begins with the concept that a defendant is “presumed innocent”. This is the status quo and is the null hypothesis. The judge will tell the jury that they cannot find the defendant guilty unless the evidence indicates guilt beyond a “reasonable doubt” which is usually defined in criminal cases as 95% certainty of guilt. If the jury cannot accept the null, innocent, then action will be taken, jail time. The burden of proof always lies with the alternative hypothesis. (In civil cases, the jury needs only to be more than 50% certain of wrongdoing to find culpability, called “a preponderance of the evidence”).

The example above was for a test of a mean, but the same logic applies to tests of hypotheses for all statistical parameters one may wish to test.

Type I error: Frank thinks that his rock-climbing equipment may not be safe when, in fact, it really is safe.

Type II error: Frank thinks that his rock-climbing equipment may be safe when, in fact, it is not safe.

$\boldsymbol{\beta}=$

Notice that, in this case, the error with the greater consequence is the Type II error. (If Frank thinks his rock-climbing equipment is safe, he will go ahead and use it.)

This is a situation described as “accepting a false null”.

Hypothesis Testing: Type I and Type II Errors

Check Your Understanding: H ypothesis Testing: Type I and Type II Errors

Distribution Needed for Hypothesis Testing

$1-p^{\prime}$

Hypothesis Test for the Mean

Going back to the standardizing formula we can derive the test statistic for testing hypotheses concerning means.

$Z_c=\frac{\bar{x}-\mu_0}{\sigma / \sqrt{n}}$

This gives us the decision rule for testing a hypothesis for a two-tailed test:

Hypothesis testing: Finding Critical Values

Normal Distribution: Finding Critical Values of Z

P-Value Approach

$\alpha,$

Both decision rules will result in the same decision, and it is a matter of preference which one is used.

What is a “P-Value?”

One and Two-Tailed Tests

$\mu \neq 100$

The claim would be in the alternative hypothesis. The burden of proof in hypothesis testing is carried in the alternative. This is because failing to reject the null, the status quo, must be accomplished with 90 or 95 percent confidence that it cannot be maintained. Said another way, we want to have only a 5 or 10 percent probability of making a Type I error, rejecting a good null; overthrowing the status quo.

Figure 13 shows two possible cases and the form of the null and alternative hypothesis that give rise to them.

Two normal distributions one with the higher tail shaded and the other the lower tail.

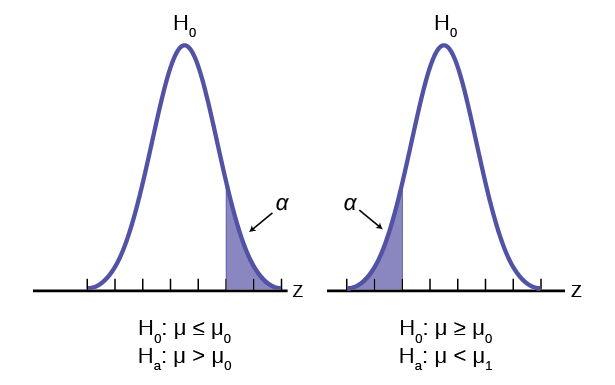
Effects of Sample Size on Test Statistic

Table 8 summarizes these rules.

A Systematic Approach for Testing a Hypothesis

A systematic approach to hypothesis testing follows the following steps and in this order. This template will work for all hypotheses that you will ever test.

Set up the null and alternative hypothesis. This is typically the hardest part of the process. Here the question being asked is reviewed. What parameter is being tested, a mean, a proportion, differences in means, etc. Is this a one-tailed test or two-tailed test?

$Z_\alpha, t_\alpha$

Take a sample(s) and calculate the relevant parameters: sample mean, standard deviation, or proportion. Using the formula for the test statistic from above in step 2, now calculate the test statistic for this particular case using the parameters you have just calculated.
The test statistic is in the tail: Cannot Accept the null, the probability that this sample mean (proportion) came from the hypothesized distribution is too small to believe that it is the real home of these sample data.
The test statistic is not in the tail: Cannot Reject the null, the sample data are compatible with the hypothesized population parameter.
Reach a conclusion. It is best to articulate the conclusion two different ways. First a formal statistical conclusion such as “With a 5 % level of significance we cannot accept the null hypotheses that the population mean is equal to XX (units of measurement)”. The second statement of the conclusion is less formal and states the action, or lack of action, required. If the formal conclusion was that above, then the informal one might be, “The machine is broken, and we need to shut it down and call for repairs.”

All hypotheses tested will go through this same process. The only changes are the relevant formulas and those are determined by the hypothesis required to answer the original question.

Hypothesis Testing: One Sample Z Test of the Mean (Critical Value Approach)

Hypothesis Testing: t Test for the Mean (Critical Value Approach)

Hypothesis Testing: 1 Sample Z Test of the Mean (Confidence Interval Approach)

Hypothesis Testing: 1 Sample Z Test for Mean (P-Value Approach)

Hypothesis Test for Proportions

Just as there were confidence intervals for proportions, or more formally, the population parameter p of the binomial distribution, there is the ability to test hypotheses concerning p .

$p^{\prime}=x / n, x$

Again, we begin with the standardizing formula modified because this is the distribution of a binomial.

$Z=\frac{p^{\prime}-p}{\sqrt{\frac{p q}{n}}}$

This is the test statistic for testing hypothesized values of p , where the null and alternative hypotheses take one of the following forms:

Hypothesis Testing: 1 Proportion using the Critical Value Approach

Hypothesis Testing with Two Samples

Studies often compare two groups. For example, researchers are interested in the effect aspirin has in preventing heart attacks. Over the last few years, newspapers and magazines have reported various aspirin studies involving two groups. Typically, one group is given aspirin and the other group is given a placebo. Then, the heart attack rate is studied over several years.

There are other situations that deal with the comparison of two groups. For example, studies compare various diet and exercise programs. Politicians compare the proportion of individuals from different income brackets who might vote for them. Students are interested in whether SAT or GRE preparatory courses really help raise their scores. Many business applications require comparing two groups. It may be the investment returns of two different investment strategies, or the differences in production efficiency of different management styles.

To compare two means or two proportions, you work with two groups. The groups are classified either as independent or matched pairs . Independent groups consist of two samples that are independent, that is, sample values selected from one population are not related in any way to sample values selected from the other population. Matched pairs consist of two samples that are dependent. The parameter tested using matched pairs is the population mean. The parameters tested using independent groups are either population means or population proportions of each group.

Comparing Two Independent Population Means

The comparison of two independent population means is very common and provides a way to test the hypothesis that the two groups differ from each other. Is the night shift less productive than the day shift, are the rates of return from fixed asset investments different from those from common stock investments, and so on? An observed difference between two sample means depends on both the means and the sample standard deviations. Very different means can occur by chance if there is great variation among the individual samples. The test statistic will have to account for this fact. The test comparing two independent population means with unknown and possibly unequal population standard deviations is called the Aspin-Welch t-test. The degrees of freedom formula we will see later was developed by Aspin-Welch.

When we developed the hypothesis test for the mean and proportions, we began with the Central Limit Theorem. We recognized that a sample mean came from a distribution of sample means, and sample proportions came from the sampling distribution of sample proportions. This made our sample parameters, the sample means and sample proportions, into random variables. It was important for us to know the distribution that these random variables came from. The Central Limit Theorem gave us the answer: the normal distribution. Our Z and t statistics came from this theorem. This provided us with the solution to our question of how to measure the probability that a sample mean came from a distribution with a particular hypothesized value of the mean or proportion. In both cases that was the question: what is the probability that the mean (or proportion) from our sample data came from a population distribution with the hypothesized value we are interested in?

Now we are interested in whether or not two samples have the same mean. Our question has not changed: Do these two samples come from the same population distribution? We recognize that we have two sample means, one from each set of data, and thus we have two random variables coming from two unknown distributions. To solve the problem, we create a new random variable, the difference between the sample means. This new random variable also has a distribution and, again, the Central Limit Theorem tells us that this new distribution is normally distributed, regardless of the underlying distributions of the original data. A graph may help to understand this concept.

Two population graphs forming into one sampling distribution.

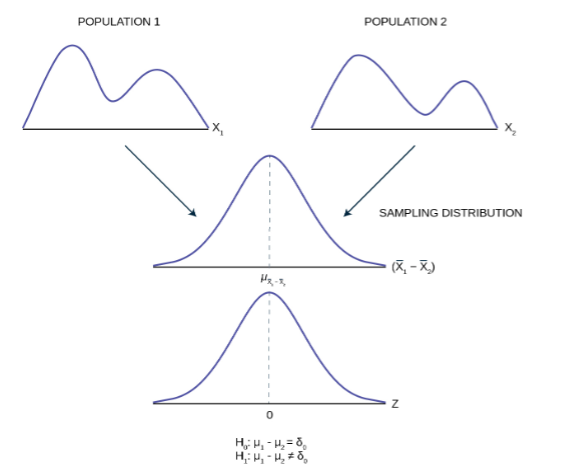
The Central Limit Theorem, as before, provides us with the standard deviation of the sampling distribution, and further, that the expected value of the mean of the distribution of differences in sample means is equal to the differences in the population means. Mathematically this can be stated:

$E\left(\mu_{x_1}-\mu_{x_2}\right)=\mu_1-\mu_2$

The standard error is:

$\sqrt{\frac{\left(s_1\right)^2}{n_1}+\frac{\left(s_2\right)^2}{n_2}}$

We remember that substituting the sample variance for the population variance when we did not have the population variance was the technique we used when building the confidence interval and the test statistic for the test of hypothesis for a single mean back in Confidence Intervals and Hypothesis Testing with One Sample. The test statistic (t-score) is calculated as follows:

$t_c=\frac{\left(\bar{x}-\bar{x}_2\right)-\delta_0}{\sqrt{\frac{\left(s_1\right)^2}{n_1}+\frac{\left(s_2\right)^2}{n_2}}}$

The number of degrees of freedom (df) requires a somewhat complicated calculation. The df are not always a whole number. The test statistic above is approximated by the Student’s t-distribution with df as follows:

$d f=\frac{\left(\frac{\left(s_1\right)^2}{n_1}+\frac{\left(s_2\right)^2}{n_2}\right)^2}{\left(\frac{1}{n_1-1}\right)\left(\frac{\left(s_1\right)^2}{n_1}\right)^2+\left(\frac{1}{n_2-1}\right)\left(\frac{\left(s_2\right)^2}{n_2}\right)^2}$

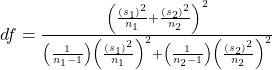
The format of the sampling distribution, differences in sample means, specifies that the format of the null and alternative hypothesis is:

$H_0: \mu_1-\mu_2=\delta_0$

Hypothesis Testing – Two Population Means

Two Population Means, One Tail Test

Two Population Means, Two Tail Test

Check Your Understanding: Hypothesis Testing (Two Population Means)

Cohen’s Standards for Small, Medium, and Large Effect Sizes

Cohen's d is a measure of “effect size” based on the differences between two means. Cohen’s d, named for United States statistician Jacob Cohen, measures the relative strength of the differences between the means of two populations based on sample data. The calculated value of effect size is then compared to Cohen’s standards of small, medium, and large effect sizes.

Cohen’s d is the measure of the difference between two means divided by the pooled standard deviation:

$d=\frac{\bar{x}_1-\bar{x}_2}{s_{\text {pooled }}} \text { where } s_{\text {pooled }}=\sqrt{\frac{\left(n_1-1\right) s_1^2+\left(n_2-1\right) s_2^2}{n_1+n_2-2}}$

It is important to note that Cohen’s d does not provide a level of confidence as to the magnitude of the size of the effect comparable to the other tests of hypothesis we have studied. The sizes of the effects are simply indicative.

Effect Size for a Significant Difference of Two Sample Means

Test for Differences in Means: Assuming Equal Population Variances

Typically, we can never expect to know any of the population parameters, mean, proportion, or standard deviation. When testing hypotheses concerning differences in means we are faced with the difficulty of two unknown variances that play a critical role in the test statistic. We have been substituting the sample variances just as we did when testing hypotheses for a single mean. And as we did before, we used a Student’s t to compensate for this lack of information on the population variance. There may be situations, however, when we do not know the population variances, but we can assume that the two populations have the same variance. If this is true, then the pooled sample variance will be smaller than the individual sample variances. This will give more precise estimates and reduce the probability of discarding a good null. The null and alternative hypotheses remain the same, but the test statistic changes to:

$t_c=\frac{\left(\overline{x_1}-\bar{x}_2\right)-\delta_0}{\sqrt{S_p^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$

Example: A drug trial is attempted using a real drug and a pill made of just sugar. 18 people are given the real drug in hopes of increasing the production of endorphins. The increase in endorphins is found to be on average 8 micrograms per person, and the sample standard deviation is 5.4 micrograms. 11 people are given the sugar pill, and their average endorphin increase is 4 micrograms with a standard deviation of 2.4. From previous research on endorphins, it is determined that it can be assumed that the variances within the two samples can be assumed to be the same. Test at 5% to see if the population mean for the real drug had a significantly greater impact on the endorphins than the population mean with the sugar pill.

First, we begin by designating one of the two groups Group 1 and the other Group 2. This will be needed to keep track of the null and alternative hypotheses. Let us set Group 1 as those who received the actual new medicine being tested and therefore Group 2 is those who received the sugar pill. We can now set up the null and alternative hypothesis as:

$H_0: \mu_1 \leq \mu_2$

The test statistic is clearly in the tail, 2.31 is larger than the critical value of 1.703, and therefore we cannot maintain the null hypothesis. Thus, we conclude that there is significant evidence at the 95% level of confidence that the new medicine produces the effect desired.

Two Population Means with Known Standard Deviations

The standard deviation is:

$\sqrt{\frac{\left(\sigma_1\right)^2}{n_1}+\frac{\left(\sigma_2\right)^2}{n_2}}$

The test statistic (z-score) is:

$Z_c=\frac{\left(\bar{x}_1-\bar{x}_2\right)-\delta_0}{\sqrt{\frac{\left(\sigma_1\right)^2}{n_1}+\frac{\left(\sigma_2\right)^2}{n_2}}}$

Check Your Understanding: Two Population Means

Matched or Paired Samples

$\bar{X}_d$

When using a hypothesis test for matched or paired samples, the following characteristics may be present:

Simple random sampling is used.
Sample sizes are often small.
Two measurements (samples) are drawn from the same pair of individuals or objects.
Differences are calculated from the matched or paired samples.
The differences form the sample that is used for the hypothesis test.
Either the matched pairs have differences that come from a population that is normal or the number of differences is sufficiently large so that distribution of the sample mean of differences is approximately normal.

$\mu_d$

The null and alternative hypotheses for this test are:

$H_0: \mu_d=0$

The test statistic is:

$t_c=\frac{\bar{x}_d-\mu_d}{\left(\frac{s_d}{\sqrt{n}}\right)}$

Two Population Means, One Tail Test, Matched Sample

Two Population Means, One Tail test, Matched Sample (Hypothesized Test Different from Zero)

Matched Sample, Two Tail Test

Check Your Understanding: Matched Sample, Two Tail Test

Comparing Two Independent Population Proportions

When conducting a hypothesis test that compares two independent population proportions, the following characteristics should be present:

The two independent samples are random samples are independent.
The number of successes is at least five, and the number of failures is at least five, for each of the samples.
Growing literature states that the population must be at least ten or even perhaps 20 times the size of the sample. This keeps each population from being over-sampled and causing biased results.

Comparing two proportions, like comparing two means, is common. If two estimated proportions are different, it may be due to a difference in the populations or it may be due to chance in the sampling. A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the two population proportions.

$\left(p_A^{\prime}-p_B^{\prime}\right)$

Most common, however, is the test that the two proportions are the same. That is,

The pooled proportion is calculated as follows:

$p_c=\frac{x_A+x_B}{n_A+n_B}$

Two Population Proportions, One Tail Test

Two Population Proportion, Two Tail Test

Check Your Understanding: Comparing Two Independent Population Proportions

The Chi-Square Distribution

Have you ever wondered if lottery winning numbers were evenly distributed or if some numbers occurred with a greater frequency? How about if the types of movies people preferred were different across different age groups? What about if a coffee machine was dispensing approximately the same amount of coffee each time? You could answer these questions by conducting a hypothesis test.

You will now study a new distribution, one that is used to determine the answers to such questions. This distribution is called the chi-square distribution.

In this section, you will learn the three major applications of the chi-square distribution:

The test of a single variance, which tests variability, such as in the coffee example
The goodness-of-fit test, which determines if data fit a particular distribution, such as in the lottery example
the test of independence, which determines if events are independent, such as in the movie example

Facts About the Chi-Square Distribution

The notation for the chi-square distribution is:

$\chi \sim X_{d f}^2$

The random variable for a chi-square distribution with k degrees of freedom is the sum of k independent, squared standard normal variables.

$\chi^2=\left(Z_1\right)^2+\left(Z_2\right)^2+\ldots+\left(Z_k\right)^2$

The curve is nonsymmetrical and skewed to the right.
There is a different chi-square curve for each df.

The difference of distributions according to sample size

3. The test statistic for any test is always greater than or equal to zero.

Test of a Single Variance

A test of a single variance assumes that the underlying distribution is normal. The null and alternative hypotheses are stated in terms of the population variance . The test statistic is:

$\chi_c^2=\frac{(n-1) s^2}{\sigma_0^2}$

Example: Math instructors are not only interested in how their students do on exams, on average, but how the exam scores vary. To many instructors, the variance (or standard deviation) may be more important than the average.

Suppose a math instructor believes that the standard deviation for his final exam is five points. One of his best students thinks otherwise. The student claims that the standard deviation is more than five points. If the student were to conduct a hypothesis test, what would the null and alternative hypotheses be?

Solution: Even though we are given the population standard deviation, we can set up the test using the population variance as follows:

$H_0: \sigma^2 \leq 5^2$

Single Population Variances, One-Tail Test

Check Your Understanding: Test of a Single Variance

Goodness-Of-Fit Test

In this type of hypothesis test, you determine whether the data “fit” a particular distribution or not. For example, you may suspect your unknown data fit a binomial distribution. You use a chi-square test (meaning the distribution for the hypothesis test is chi-square) to determine if there is a fit or not. The null and the alternative hypotheses for this test may be written in sentences or may be stated as equations or inequalities.

The test statistic for a goodness-of -fit test is:

$\sum_k \frac{(O-E)^2}{E}$

O = observed values (data)
E = expected values (from theory)
k = the number of different data cells or categories

$\frac{(O-E)^2}{E}$

The goodness-of-fit test is almost always right-tailed. If the observed values and the corresponding expected values are not close to each other, then the test statistic can get very large and will be way out in the right tail of the chi-square curve.

Note: The number of expected values inside each cell needs to be at least five in order to use this test.

Chi-Square Statistic for Hypothesis Testing

Chi-Square Goodness-of-Fit Example

Check Your Understanding: Goodness-of-Fit Test

Test of Independence

Tests of independence involve using a contingency table of observed (data) values.

The test statistic of a test of independence is similar to that of a goodness-of-fit test:

$\sum_{i \bullet j} \frac{(O-E)^2}{E}$

O = observed values
E = expected values
i = the number of rows in the table
j = the number of columns in the table

$i \cdot j \text { terms of the form } \frac{(O-E)^2}{E}$

A test of independence determines whether two factors are independent or not.

Note: The expected value inside each cell needs to be at least five in order for you to use this test.

The test of independence is always right tailed because of the calculation of the test statistic. If the expected and observed values are not close together, then the test statistic is very large and way out in the right tail of the chi-square curve, as it is in a goodness-of-fit.

The number of degrees of freedom for the test of independence is:

$d f=(\text { Number of columns }-1 \text { ) (number of rows }-1 \text { ) }$

The following formula calculates the expected number (E):

$E=\frac{(\text { row total })(\text { column total })}{\text { total number surveyed }}$

Simple Explanation of Chi-Squared

Chi-Square Test for Association (independence)

Check Your Understanding: Test of Independence

Test for Homogeneity

The goodness-of-fit test can be used to decide whether a population fits a given distribution, but it will not suffice to decide whether two populations follow the same unknown distribution. A different test, called the test of homogeneity , can be used to draw a conclusion about whether two populations have the same distribution. To calculate the test statistic for a test for homogeneity, follow the same procedure as with the test of independence.

Test Statistic

Degrees of Freedom (df)

$d f=\text { number of columns }-1$

Requirements

All values in the table must be greater than or equal to five

Common uses

Comparing two populations. For example: men vs. women, before vs. after, east vs. west. The variable is categorical with more than two possible response values.

Introduction to the Chi-Square Test for Homogeneity

Check Your Understanding: Test for Homogeneity

Comparison of the Chi-Square Tests

Goodness-of-fit: Use the goodness-of-fit test to decide whether a population with an unknown distribution “fits” a known distribution. In this case there will be a single qualitative survey question or a single outcome of an experiment from a single population. Goodness-of-Fit is typically used to see if the population is uniform (all outcomes occur with equal frequency), the population is normal, or the population is the same as another population with a known distribution. The null and alternative hypotheses are:

Independence: Use the test for independence to decide whether two variables (factors) are independent or dependent. In this case there will be two qualitative survey questions or experiments and a contingency table will be constructed. The goal is to see if the two variables are unrelated (independent) or related (dependent). The null and alternative hypotheses are:

Homogeneity: Use the test for homogeneity to decide if two populations with unknown distributions have the same distribution as each other. In this case there will be a single qualitative survey question or experiment given to two different populations. The null and alternative hypotheses are:

F Distribution and One-Way ANOVA

Many statistical applications in psychology, social science, business administration, and the natural sciences involve several groups. For example, an environmentalist is interested in knowing if the average amount of pollution varies in several bodies of water. A sociologist is interested in knowing if the amount of income a person earns varies according to his or her upbringing. A consumer looking for a new car might compared the average gas mileage of several models.

For hypothesis tests comparing averages among more than two groups, statisticians have developed a method called “Analysis of Variance” (abbreviated ANOVA). In this chapter, you will study the simplest form of ANOVA called single factor or one-way ANOVA . You will also study the F distribution, used for one-way ANOVA, and the test for differences between two variances. This is just a very brief overview of one-way ANOVA. One-Way ANOVA, as it is presented here, relies heavily on a calculator or computer.

Test of Two Variances

This chapter introduces a new probability density function, the F distribution. This distribution is used for many applications including ANOVA and for testing equality across multiple means. We begin with the F distribution and the test of hypothesis of differences in variances. It is often desirable to compare two variances rather than two averages. For instance, college administrators would like two college professors grading exams to have the same variation in their grading. In order for a lid to fit a container, the variation in the lid and the container should be approximately the same. A supermarket might be interested in the variability of check-out times for two checkers. In finance, the variance is a measure of risk and thus an interesting question would be to test the hypothesis that two different investment portfolios have the same variance, the volatility.

In order to perform a F test of two variances, it is important that the following are true:

The populations from which the two samples are drawn are approximately normally distributed.
The two populations are independent of each other.

Unlike most other hypothesis tests in this Module, the F test for equality of two variances is very sensitive to deviations from normality. If the two distributions are not normal, or close, the test can give a biased result for the test statistic.

$\sigma_1^2 \text { and } \sigma_2^2$

The various forms of the hypotheses tested are:

A more general form of the null and alternative hypothesis for a two tailed test would be:

$H_0: \frac{\sigma_1^2}{\sigma_2^2}=\delta_0$

Therefore, if F is close to one, the evidence favors the null hypothesis (the two population variances are equal). But if F is much larger than one, then the evidence is against the null hypothesis. In essence, we are asking if the calculated F statistic, test statistic, is significantly different from one.

$F_{\alpha, d f 1, d f 2}$

To find the critical value for the lower end of the distribution, reverse the degrees of freedom and divide the F-value from the table into one.

$1 / F_{\alpha, d f 2, d f 1}$

When the calculated value of F is between the critical values, not in the tail, we cannot reject the null hypothesis that the two variances came from a population with the same variance. If the calculated F-value is in either tail we cannot accept the null hypothesis just as we have been doing for all of the previous tests of hypothesis.

An alternative way of finding the critical values of the F distribution makes the use of the F-table easier. We note in the F-table that all the values of F are greater than one therefore the critical F value for the left-hand tail will always be less than one because to find the critical value on the left tail we divide an F value into the number one as shown above. We also note that if the sample variance in the numerator of the test statistic is larger than the sample variance in the denominator, the resulting F value will be greater than one. The shorthand method for this test is thus to be sure that the larger of the two sample variances is placed in the numerator to calculate the test statistic. This will mean that only the right-hand tail critical value will have to be found in the F-table.

Hypothesis Test Two Population Variances

Check Your Understanding: F Distribution

One-Way ANOVA

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test actually uses variances to help determine if the means are equal or not. In order to perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:

Each population from which a sample is taken is assumed to be normal.
All samples are randomly selected and independent.
The populations are assumed to have equal standard deviations (or variances).
The factor is a categorical variable.
The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is simply that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are k groups:

$H_0: \mu_1=\mu_2=\mu_3=\ldots \mu_k$

If the null hypothesis is false, then the variance of the combined data is larger which is caused by the different means as shown in the second graph (green box plots).

The F Distribution and the F-Ratio

The distribution used for the hypothesis test is a new one. It is called the F distribution, invented by George Snedecor but named in honor of Sir Ronald Fisher, an English statistician. The F statistic is a ratio (a fraction). There are two sets of degrees of freedom: one for the numerator and one for the denominator.

$F \sim F_{4,10}$

To calculate the F ratio , two estimates of the variance are made.

$\sigma^2$

To find a “sum of squares” means to add together squared quantities that, in some cases, may be weighted.

$M S_{\text {between }}$

Calculation of Sum of Squares and Mean Square

k = the number of different groups

$n_j=\text { the size of the } j_{t h}$

Note: The null hypothesis says that all the group population means are equal. The hypothesis of equal means implies that the populations have the same normal distribution, because it is assumed that the populations are normal and that they have equal variances.

F-Ration or F Statistic

$F=\frac{M S_{\text {between }}}{M S_{\text {within }}}$

The foregoing calculations were done with groups of different sizes. If the groups are the same size, the calculations simplify somewhat, and the F-ratio can be written as:

F-Ratio Formula when the groups are the same size

$F=\frac{n \cdot s_{-}^2}{s_{\text {pooled }}^2}$

n = the sample size

$d f_{\text {numerator }}=k-1$

Data are typically put into a table for easy viewing. One-Way ANOVA results are often displayed is this manner by computer software.

Example: Three different diet plans are to be tested for mean weight loss. The entries in the table are the weight losses for the different plans. The one-way ANOVA results are shown in Table 13.

Following are the calculations needed to fill in the one-way ANOVA table. The table is used to conduct a hypothesis test.

$S S_{\text {between }}=\sum\left[\frac{\left(s_j\right)^2}{n_j}\right]-\frac{\left(\sum s_j\right)^2}{n}$

Calculating SST (total sum of squares)

Calculating

Hypothesis Test with F-Statistic

Check Your Understanding: The F Distribution and the F-Ratio

Facts About the F Distribution

The curve is not symmetrical but skewed to the right.
There is a different curve for each set of degrees of freedom.
The F statistic is greater than or equal to zero.
As the degrees of freedom for the numerator and for the denominator get larger, the curve approximates the normal as can be seen in Figure 18. Remember that the F cannot ever be less than zero, so the distribution does not have a tail that goes to infinity on the left as the normal distribution does.
Other uses for the F distribution include comparing two variances and two-way Analysis of Variances. Two-Way Analysis is beyond the scope of this section.

F Distribution graph with various sample sizes

Compute and Interpret Simple Linear Regression Between Two Variables

Linear regression and correlation.

Professionals often want to know how two or more numeric variables are related. For example, is there a relationship between the grade on the second math exam a student takes and the grade on the final exam? If there is a relationship, what is the relationship and how strong is it?

This example may or may not be tied to a model, meaning that some theory suggested that a relationship exists. This link between a cause and an effect is the foundation of the scientific method and is the core of how we determine what we believe about how the world works. Beginning with a theory and developing a model of the theoretical relationship should result in a prediction, what we have called a hypothesis earlier. Now the hypothesis concerns a full set of relationships.

In this section we will begin with correlation, the investigation of relationships among variables that may or may not be founded on a cause-and-effect model. The variables simply move in the same, or opposite, direction. That is to say, they do not move randomly. Correlation provides a measure of the degree to which this is true. From there we develop a tool to measure cause and effect relationships, regression analysis. We will be able to formulate models and tests to determine if they are statistically sound. If they are found to be so, then we can use them to make predictions: if as a matter of policy, we changed the value of this variable what would happen to this other variable? If we imposed a gasoline tax of 50 cents per gallon how would that effect the carbon emissions, sales of Hummers/Hybrids, use of mass transit, etc.? The ability to provide answers to these types of questions is the value of regression as both a tool to help us understand our world and to make thoughtful policy decisions.

The Correlation Coefficient r

As we begin this section, we note that the type of data we will be working with has changed. Perhaps unnoticed, all the data we have been using is for a single variable. It may be from two samples, but it is still a univariate variable. The type of data described for any model of cause and effect is bivariate data — “bi” for two variables. In reality, statisticians use multivariate data, meaning many variables.

Data can be classified into three broad categories: time series data, cross-section data, and panel data. Time series data measures a single unit of observation; say a person, or a company or a country, as time passes. What are measures will be at least two characteristics, say the person’s income, the quantity of a particular good they buy and the price they paid. This would be three pieces of information in one time period, say 1985. If we followed that person across time we would have those same pieces of information for 1985, 1986, 1987, etc. This would constitute a time series data set.

A second type of data set is for cross-section data. Here the variation is not across time for a single unit of observation, but across units of observation during one point in time. For a particular period of time, we would gather the price paid, amount purchased, and income of many individual people.

A third type of data set is panel data. Here a panel of units of observation is followed across time. If we take our example from above, we might follow 500 people, the unit of observation, through time, ten years, and observe their income, price paid and quantity of the good purchased. If we had 500 people and data for ten years for price, income and quantity purchased we would have 15,000 pieces of information. These types of data sets are very expensive to construct and maintain. They do, however, provide a tremendous amount of information that can be used to answer very important questions. As an example, what is the effect on the labor force participation rate of women as their family of origin, mother and father, age? Or are there differential effects on health outcomes depending upon the age at which a person started smoking? Only panel data can give answers to these and related questions because we must follow multiple people across time.

Beginning with a set of data with two independent variables we ask the question: are these related? One way to visually answer this question is to create a scatter plot of the data. We could not do that before when we were doing descriptive statistics because those data were univariate. Now we have bivariate data so we can plot in two dimensions. Three dimensions are possible on a flat piece of paper but become very hard to fully conceptualize. Of course, more than three dimensions cannot be graphed although the relationships can be measured mathematically.

To provide mathematical precision to the measurement of what we see we use the correlation coefficient. The correlation tells us something about the co-movement of two variables, but nothing about why this movement occurred. Formally, correlation analysis assumes that both variables being analyzed are independent variables. This means that neither one causes the movement in the other. Further, it means that neither variable is dependent on the other, or for that matter, on any other variable. Even with these limitations, correlation analysis can yield some interesting results.

$\rho$

In practice all correlation and regression analysis will be provided through computer software designed for these purposes. Anything more than perhaps one-half a dozen observations creates immense computational problems. It was because of this fact that correlation, and even more so, regression, were not widely used research tools until after the advent of “computing machines.” Now the computing power required to analyze data using regression packages is deemed almost trivial by comparison to just a decade ago.

$1 \text { or }-1$

Remember, all the correlation coefficient tells us is whether or not the data are linearly related. In panel (d) the variables obviously have some type of very specific relationship to each other, but the correlation coefficient is zero, indicating no linear relationship exists.

$X_1 \text { and } X_2 \text { then } r$

What the VALUE of r tells us:

$-1 \text { and }+1:-1 \leq r \leq 1$

What the SIGN of r tells us

$X_1 \text { increases, } X_2$

Bivariate Relationship Linearity, Strength, and Direction

Check Your Understanding: The Correlation Coefficient r

Calculating Correlation Coefficient r

Example: Correlation Coefficient Intuition

Linear Equations

Linear regression to two variables is based on a linear equation with one independent variable. The equation has the form:

Where a and b are constant numbers.

The variable x is the independent variable, and y is the dependent variable . Another way to think about this equation is a statement of cause and effect. The X variable is the cause, and the Y variable is the hypothesized effect. Typically, you choose a value to substitute for the independent variable and then solve for the dependent variable.

Slope and Y-Intercept of a Linear Equation

The Regression Equation

Regression analysis is a statistical technique that can test the hypothesis that a variable is dependent upon one or more other variables. Further, regression analysis can provide an estimate of the magnitude of the impact of a change in one variable on another. This last feature, of course, is all important in predicting future values.

Regression analysis is based upon a functional relationship among variables and further, assumes that the relationship is linear. This linearity assumption is required because, for the most part, the theoretical statistical properties of non-linear estimation are not well worked out yet by the mathematicians and econometricians. This presents us with some difficulties in economic analysis because many of our theoretical models are nonlinear. The marginal cost curve, for example, is decidedly nonlinear as is the total cost function, if we are to believe in the effect of specialization of labor and the Law of Diminishing Marginal Product. There are techniques for overcoming some of these difficulties, exponential and logarithmic transformation of the data for example, but at the outset we must recognize that standard ordinary least squares (OLS) regression analysis will always use a linear function to estimate what might be a nonlinear relationship.

The general linear regression model can be stated by the equation:

$y_i=\beta_0+\beta_1 X_{1 i}+\beta_2 X_{2 i}+\ldots+\beta_k X_{k i}+\varepsilon_i$

As with our earlier work with probability distributions, this model works only if certain assumptions hold. These are that the Y is normally distributed, the errors are also normally distributed with a mean of zero and a constant standard deviation, and that the error terms are independent of the size of X and independent of each other.

Assumptions of the Ordinary Least Squares Regression Model

Each of these assumptions needs a bit more explanation. If one of these assumptions fails to be true, then it will have an effect on the quality of the estimates. Some of the failures of these assumptions can be fixed while others result in estimates that quite simply provide no insight into the questions the model is trying to answer or worse, give biased estimates.

The error term is a random variable with a mean of zero and a constant variance. The meaning of this is that the variances of the independent variables are independent of the value of the variable. Consider the relationship between personal income and the quantity of a good purchased as an example of a case where the variance is dependent upon the value of the independent variable, income. It is plausible that as income increases the variation around the amount purchased will also increase simply because of the flexibility provided with higher levels of income. The assumption is for constant variance with respect to the magnitude of the independent variable called homoscedasticity. If the assumption fails, then it is called heteroscedasticity. Figure 21 shows the case of homoscedasticity where all three distributions have the same variance around the predicted value of Y regardless of the magnitude of X.
Error terms should be normally distributed. This can be seen in Figure 21 by the shape of the distributions placed on the predicted line at the expected value of the relevant value of Y.
The independent variables are independent of Y but are also assumed to be independent of the other X variables. The model is designed to estimate the effects of independent variables on some dependent variable in accordance with a proposed theory. The case where some or more of the independent variables are correlated is not unusual. There may be no cause and effect relationship among the independent variables, but nevertheless they move together. Take the case of a simple supply curve where quantity supplied is theoretically related to the price of the product and the prices of inputs. There may be multiple inputs that may over time move together from general inflationary pressure. The input prices will therefore violate this assumption of regression analysis. This condition is called multicollinearity.
The error terms are uncorrelated with each other. This situation arises from an effect on one error term from another error term. While not exclusively a time series problem, it is here that we most often see this case. An X variable in time period one has an effect on the Y variable, but this effect then has an effect in the next time period. This effect gives rise to a relationship among the error terms. This case is called autocorrelation, “self-correlated.” The error terms are now not independent of each other, but rather have their own effect on subsequent error terms.

$\widehat{y}=a+b x$

This is the general form that is most often called the multiple regression model. So-called “simple” regression analysis has only one independent (right-hand) variable rather than many independent variables. Simple regression is just a special case of multiple regression. There is some value in beginning with simple regression: it is easy to graph in two dimensions, difficult to graph in three dimensions, and impossible to graph in more than three dimensions. Consequently, our graphs will be for the simple regression case. Figure 22 presents the regression problem in the form of a scatter plot graph of the data set where it is hypothesized that Y is dependent upon the single independent variable X.

The regression problem comes down to determining which straight line would best represent the data in Figure 23. Regression analysis is sometimes called “least squares” analysis because the method of determining which line best “fits” the data is to minimize the sum of the squared residuals of a line put through the data.

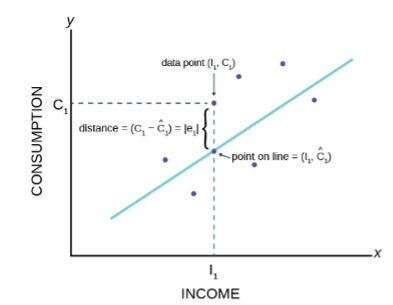
Consider the graph in Figure 24. The notation has returned to that for the more general model rather than the specific case of the Macroeconomic consumption function in our example.

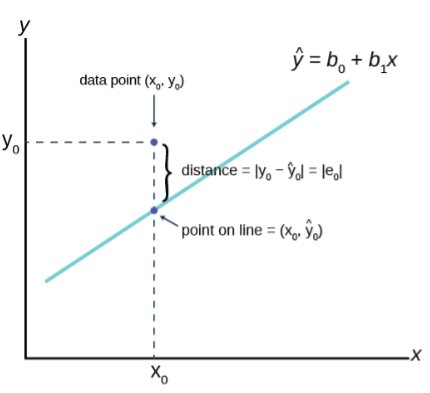
If the observed data point lies above the line, the residual is positive, and the line underestimates the actual data value for y.

If the observed data point lies below the line, the residual is negative, and the line overestimates that actual data value for y.

$y_0-\hat{y}_0=e_0$

The sum of the errors squared is the term obviously called Sum of Squared Errors (SSE).

$b_0 \text { and } b_1$

The slope b can also be written as:

$b_1=r_{y, x}\left(\frac{s_y}{s_x}\right)$

The variance of the errors is fundamental in testing hypotheses for a regression. It tells us just how “tight” the dispersion is about the line. As we will see shortly, the greater the dispersion about the line, meaning the larger the variance of the errors, the less probable that the hypothesized independent variable will be found to have a significant effect on the dependent variable. In short, the theory being tested will more likely fail if the variance of the error term is high. Upon reflection this should not be a surprise. As we tested hypotheses about a mean we observed that large variances reduced the calculated test statistic and thus it failed to reach the tail of the distribution. In those cases, the null hypotheses could not be rejected. If we cannot reject the null hypothesis in a regression problem, we must conclude that the hypothesized independent variable has no effect on the dependent variable.

A way to visualize this concept is to draw two scatter plots of x and y data along a predetermined line. The first will have little variance of the errors, meaning that all the data points will move close to the line. Now do the same except the data points will have a large estimate of the error variance, meaning that the data points are scattered widely along the line. Clearly the confidence about a relationship between x and y is affected by this difference between the estimate of the error variance.

Introduction to Residuals and Least-Squares Regression

Calculating Residual Example

Check Your Understanding: Linear Equations

Residual Plots

Check Your Understanding: Residual Plots

Calculating the Equation of a Regression Line

Check Your Understanding: Calculating the Equation of a Regression Line

Interpreting Slope of Regression Line

Interpreting y-intercept in Regression Model

Check Your Understanding: Interpreting Slope of Regression Line and Interpreting y-intercept in Regression Model

Using Least Squares Regression Output

Check Your Understanding: Using Least Squares Regression Output

How Good is the Equation?

The multiple correlation coefficient, also called the coefficient of multiple determination or the coefficient of determination , is given by the formula:

$R^2=\frac{S S R}{S S T}$

R-Squared or Coefficient of Determination

Data Analysis Tools (Spreadsheets and Basic Programming)

Descriptive statistics, using microsoft excel’s “descriptive statistics” tool.

How to Run Descriptive Statistics in R

Descriptive Statistics in R Part 2

Regression Analysis

How to use microsoft excel for regression analysis.

Please read this text on how to use Microsoft Excel for regression analysis.

Simple Linear Regression in Excel

Simple Linear Regression, fit and interpretations in R

Relevance to Transportation Engineering Coursework

This section explains the relevance of the regression models for trip generation, mode choice, traffic flow-speed-density relationship, traffic safety, and appropriate sample size for spot speed study to transportation engineering coursework.

Regression Models for Trip Generation

The trip generation step is the first of the four-step process for estimating travel demand for infrastructure planning. It involves estimating the number of trips made to and from each traffic analysis zone (TAZ). Trip generation models are estimated based on land use and trip-making data. They use either linear regression or cross-tabulation of household characteristics. Simple linear regression is described in the section above titled “ Compute and Interpret Simple Linear Regression Between Two Variables” , and the tools to conduct the linear regression are discussed in “ Data Analysis Tools (Spreadsheets and Basic Programming)”.

Mode Choice

Estimation of Mode Choice is also part of the four-step process for estimating travel demand. It entails estimating the trip makers’ transportation mode (drive alone, walk, take public transit, etc.) choices. The results of this step are the counts of trips categorized by mode. The most popular mode choice model is the discrete choice, multinomial logit model. Hypothesis tests are conducted for the estimated model parameters to assess whether they are “statistically significant.” The section titled “ Use Specific Significance Tests Including, Z-Test, T-Test (one and two samples), Chi-Squared Test” of this chapter provides extensive information on hypothesis testing.

Traffic Flow-Speed-Density Relationship

Greenshield’s model is used to represent the traffic flow-speed-density relationship. Traffic speed and traffic density (number of vehicles per unit mile) are collected to estimate a linear regression model for speed as a function of density. “ Compute and Interpret Simple Linear Regression Between Two Variables” above provides information on simple linear regression. “ Data Analysis Tools (Spreadsheets and Basic Programming)” provides guidance for implementing the linear regression technique using tools available in Microsoft Excel and the programing language R.

Traffic Safety

Statistical analyses of traffic collisions are used to estimate traffic safety in roadway locations. A variety of regression models, most of which are beyond the scope of this book, are implemented to investigate the association between crashes and characteristics of the roadway locations. Hypothesis tests are conducted for the estimated model parameters to assess whether they are “statistically significant.” “ Find Confidence Intervals for Parameter Estimates” above describes the confidence intervals of the parameters, and “ Use Specific Significance Tests Including, Z-Test, T-Test (one and two samples), Chi-Squared Test” discusses the different types of hypothesis tests. Programing language R includes statistical analysis toolkits or packages that may be used to estimate the regression models for crash data.

Appropriate Sample Size for Spot Speed Study

Spot speed studies during relatively congestion-free durations are conducted to estimate mean speed, modal speed, pace, standard deviation, and different percentile of speeds at a roadway location. An adequate number of data points (i.e., the number of vehicle speeds recorded) are required to ensure reliable results within an acceptable margin of error. “ Estimate the Required Sample Size for Testing” in this chapter discusses the approach to assessing the adequacy of sample size.

Key Takeaways

Estimating the total number of trips made to and from each traffic analysis zone (TAZ)is typically the first step in the four-step travel demand modeling process. Simple linear regression models and the tools (such as MS Excel and R) to estimate these models are used this step of the travel demand modeling process. The independent variables for these models are the total number of trips with demographic and employment data for the zones as independent variables.
Hypothesis testing is used to determine the statistical significance of coefficients estimated for the discrete choice multinomial models. Such models are used for the mode choice step of the travel demand modeling process.
Linear regression models are also used to estimate the relationship between speed and density on uninterrupted flow facilities such as freeway segments.
Regression models are also implemented to investigate the association between crashes and characteristics of the roadway locations. Tools described in the chapter for linear regression may also be used for estimating these models, including negative binomial regression models.
Statistical analysis is also used to ensure that an adequate number of data points (i.e., the number of vehicle speeds recorded) are used to obtain estimates of the mean, median, and 85th percentile of speed within an acceptable margin of error in a spot speed study.

Glossary – Key Terms

Analysis of Variance [1] – also referred to as ANOVA, is a method of testing whether or not the means of three or more populations are equal. The method is applicable if: (1) all populations of interest are normally distributed (2) the populations have equal standard deviations (3) samples (not necessarily of the same size) are randomly and independently selected from each population (4) there is one independent variable and one dependent variable. The test statistic for analysis of variance is the F-ratio

Average [1] – a number that describes the central tendency of the data; there are a number of specialized averages, including the arithmetic mean, weighted mean, median, mode, and geometric mean.

B is the Symbol for Slope [1] – the word coefficient will be used regularly for the slope, because it is a number that will always be next to the letter “x.” It will be written a 𝑏 1 when a sample is used, and 𝛽 1 will be used with a population or when writing the theoretical linear model.

$P(X=x)=\left(\begin{array}{l} n \\ x \end{array}\right) p^x q^{n-x}$

Bivariate [1] – two variables are present in the model where one is the “cause” or independent variable and the other is the “effect” of dependent variable.

$\bar{X} \sim N\left(\mu, \frac{\sigma}{\sqrt{n}}\right)$

Cohen’s d [1] – a measure of effect size based on the differences between two means. If d is between 0 and 0.2 then the effect is small. If d approaches is 0.5, then the effect is medium, and if d approaches 0.8, then it is a large effect.

Confidence Interval (CI) [1] – an interval estimate for an unknown population parameter. This depends on: (1) the desired confidence level (2) information that is known about the distribution (for example, known standard deviation) (3) the sample and its size

Confidence Level (CL) [1] – the percent expression for the probability that the confidence interval contains the true population parameter; for example, if the CL = 90%, then in 90 out of 100 samples the interval estimate will enclose the true population parameter.

Contingency Table [1] – a table that displays sample values for two different factors that may be dependent or contingent on one another; it facilitates determining conditional probabilities.

Critical Value [1] – The t or Z value set by the researcher that measures the probability of a Type I error, 𝛼

Degrees of Freedom (df) [1] – the number of objects in a sample that are free to vary

Error Bound for a Population Mean (EBM) [1] – the margin of error; depends on the confidence level, sample size, and known or estimated population standard deviation.

Error Bound for a Population Proportion (EBP) [1] – the margin of error; depends on the confidence level, the sample size, and the estimated (from the sample) proportion of successes.

Goodness-of-Fit [1] – a hypothesis test that compares expected and observed values in order to look for significant differences within one non-parametric variable. The degrees of freedom used equals the (number of categories – 1).

Hypothesis [1] – a statement about the value of a population parameter, in case of two hypotheses, the statement assumed to be true is called the null hypothesis (notation 𝐻 0 ) and the contradictory statement is called the alternative hypothesis (notation 𝐻 𝑎 )

Hypothesis Testing [1] – Based on sample evidence, a procedure for determining whether the hypothesis stated is a reasonable statement and should not be rejected, or is unreasonable and should be rejected.

Independent Groups [1] – two samples that are selected from two populations, and the values from one population are not related in any way to the values from the other population.

Inferential Statistics [1] – also called statistical inference or inductive statistics; this facet of statistics deals with estimating a population parameter based on a sample statistic. For example, if four out of the 100 calculators sampled are defective we might infer that four percent of the production is defective.

Linear [1] – a model that takes data and regresses it into a straight line equation.

Matched Pairs [1] – two samples that are dependent. Differences between a before and after scenario are tested by testing one population mean of differences.

$\bar{x}) \text { is } \bar{x}=\frac{\text { sum of all values in the sample }}{\text { number of values in the sample }}$

Multivariate [1] – a system or model where more than one independent variable is being used to predict an outcome. There can only ever be one dependent variable, but there is no limit to the number of independent variables.

$f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{\frac{-(x-\mu)^2}{2 \sigma^2}}$

One-Way ANOVA [1] – a method of testing whether or not the means of three or more populations are equal; the method is applicable if: (1) all populations of interest are normally distributed (2) the populations have equal standard deviations (3) samples (not necessarily of the same size) are randomly and independently selected from each population. The test statistic for analysis of variance is the F-ratio

Parameter [1] – a numerical characteristic of a population

Point Estimate [1] – a single number computed from a sample and used to estimate a population parameter

Pooled Variance [1] – a weighted average of two variances that can then be used when calculating standard error.

R – Correlation Coefficient [1] – A number between −1 and 1 that represents the strength and direction of the relationship between “X” and “Y.” The value for “r” will equal 1 or −1 only if all the plotted points form a perfectly straight line.

Sampling Distribution [1] – Given simple random samples of size n from a given population with a measured characteristic such as mean, proportion, or standard deviation for each sample, the probability distribution of all the measured characteristics is called a sampling distribution.

Standard Deviation [1] – a number that is equal to the square root of the variance and measures how far data values are from their mean; notation: s for sample standard deviation and 𝜎 for population standard deviation

Standard Error of the Proportion [1] – the standard deviation of the sampling distribution of proportions

Student’s t-Distribution [1] – investigated and reported by William S. Gossett in 1908 and published under the pseudonym Student; the major characteristics of this random variable are: (1) it is continuous and assumes any real values (2) the pdf is symmetrical about its mean of zero (3) it approaches the standard normal distribution as n gets larger (4) there is a “family” of t-distributions: each representative of the family is completely defined by the number of degrees of freedom, which depends upon the application for which the t is being used.

Sum of Squared Errors (SSE) [1] – the calculated value from adding up all the squared residual terms. The hope is that this value is very small when creating a model.

Test for Homogeneity [1] – a test used to draw a conclusion about whether two populations have the same distribution. The degrees of freedom used equals the (number of columns – 1).

Test of Independence [1] – a hypothesis test that compares expected and observed values for contingency tables in order to test for independence between two variables. The degrees of freedom used equals the (number of columns – 1) multiplied by the (number of rows – 1).

Test Statistic [1] – the formula that counts the number of standard deviations on the relevant distribution that estimated parameter is away from the hypothesized value.

Type I Error [1] – the decision is to reject the null hypothesis when, in fact, the null hypothesis is true.

Type II Error [1] – the decision is not to reject the null hypothesis when, in fact, the null hypothesis is false.

$x-\bar{x}$

X – the Independent Variable [1] – This will sometimes be referred to as the “predictor” variable, because these values were measured in order to determine what possible outcomes could be predicted.

[1] “Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean on OpenStax. Access for free at https://openstax.org/books/introductory-business-statistics/pages/1-introduction

Media Attributions

Video 1: Central Limit Theorem by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 2: Sampling Distribution of the Sample Mean by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 3: Sampling Distribution of the Sample Mean (Part 2) by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 4: Sampling Distributions: Sampling Distribution of the Mean by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 5: Confidence Intervals & Estimation: Point Estimates Explained by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 6: Confidence Interval for Mean: 1 Sample Z Test (Using Formula) by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 7: Confidence Intervals: Using the t Distribution by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 8: How to Construct a Confidence Interval for Population Proportion by Simple Science and Maths is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 9: Estimation and Confidence Intervals: Calculate Sample Size by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 10: Calculating Sample size to Predict a Population Proportion by Matthew Simmons is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 11: Hypothesis Testing: The Fundamentals by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 12: Hypothesis Testing: Setting up the Null and Alternative Hypothesis Statements by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 13: Hypothesis Testing: Type I and Type II Errors by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 14: Hypothesis testing: Finding Critical Values by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 15: Normal Distribution: Finding Critical Values of Z by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 16: What is a “P-Value?” by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 17: Hypothesis Testing: One Sample Z Test of the Mean (Critical Value Approach) by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 18: Hypothesis Testing: t Test for the Mean (Critical Value Approach) by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 19: Hypothesis Testing: 1 Sample Z Test of the Mean (Confidence Interval Approach) by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 20: Hypothesis Testing: 1 Sample Z Test for Mean (P-Value Approach ) by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 21: Hypothesis Testing: 1 Proportion using the Critical Value Approach by Linda Williams is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 22: Hypothesis Testing – Two Population Means by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 23: Two Population Means, One Tail Test, unknown by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 24: Two Population Means, Two Tail Test, unknown by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 25: Effect Size for a Significant Difference of Two Sample Means by Dana Lee Ling is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 26: Two Population Means, One Tail Test, Known by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 27: Two Population Means, Two Tail Test, Known by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 28: Two Population Means, One Tail Test, Matched Sample by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 29: Two Population Means, One Tail test, Matched Sample by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 30: Matched Sample, Two Tail Test by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 31: Two Population Proportions, One Tail Test by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 32: Two Population Proportion, Two Tail Test by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 33: Single Population Variances, One-Tail Test by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 34: Chi-Square Statistic for Hypothesis Testing by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 35: Chi-Square Goodness-of-Fit Example by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 36: Simple Explanation of Chi-Squared by J David Eisenberg is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 37: Chi-Square Tet for Association (independence) by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 38: Introduction to the Chi-Square Test for Homogeneity by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 39: Hypothesis Test Two Population Variances by Peter Dalley is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 40: ANOVA by J David Eisenberg is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 41: Calculating SST (total sum of squares) by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 42: Calculating by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 43: Hypothesis Test with F-Statistic by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 44: Bivariate Relationship Linearity, Strength, and Direction by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 45: Calculating Correlation Coefficient r by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 46: Example: Correlation Coefficient Intuition by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 47: Introduction to Residuals and Least-Squares Regression by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 48: Calculating Residual Example by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 49: Residual Plots by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 50: Calculating the Equation of a Regression Line by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 51: Interpreting Slope of Regression Line by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 52: Interpreting y-intercept in Regression Model by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 53: Using Least Squares Regression Output by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 54: R-Squared or Coefficient of Determination by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
Video 55: Using Microsoft Excel’s “Descriptive Statistics” Tool by Linda Weiser Friedman is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 56: How to Run Descriptive Statistics in R by Learning Puree is licensed by Creative Commons 4.0 International (CC BY 4.0)
Video 57: Descriptive Statistics in R Part 2 by Learning Puree is licensed by Creative Commons 4.0 International (CC BY 4.0)
Video 58: Simple Linear Regression in Excel by Ramya Rachel is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Video 59: Simple Linear Regression, fit and interpretations in R is licensed by Creative Commons 3.0 Unported (CC BY 3.0)
Figure 1: “Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 2: “Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 3: “Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 4: “Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 5: “Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 6: “ Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 7: “ Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 8 : “ Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 9: “ Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 10 : “ Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 11: “ Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 12: “ Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 13: “ Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 14: by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 15 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 16 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 17 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 18 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 19 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 20 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 21 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 22 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 23 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 24 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
Figure 25 by Alexander Holmes, Barbara Illowsky , and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)

Note: All Khan Academy content is available for free at ( www.khanacademy.org ).

“Unit: Sampling Distributions” by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
“Unit: Inference for Categorical Data: Chi-Square” by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
“Unit: Analysis of Variance (ANOVA)” by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
“Unit: Exploring Two-Variable Quantitative Data” by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
“Statistics” by Barbara Illosky and Susan Dean is licensed by Creative Commons 4.0 International (CC BY 4.0)
“Introduction to Probability and Statistics” by Jeremy Orloff and Jonathan Bloom is licensed by Creative Commons NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0)
Farid, A. (2022). Transportation Planning 1 . Personal Collection of Ahmed Farid, California Polytechnic State University, San Luis Obispo, CA.
Farid, A. (2022). Transportation Planning 2 . Personal Collection of Ahmed Farid, California Polytechnic State University, San Luis Obispo, CA.
Farid, A. (2022). Fundamentals of Traffic Flow Theory . Personal Collection of Ahmed Farid, California Polytechnic State University, San Luis Obispo, CA.
Washington, S., Karlaftis, M., Mannering, F., and Anastasopoulos, P. (2020). Statistical and Econometric Methods for Transportation Data Analysis 3rd Edition . Chemical Rubber Company (CRC) Press, Taylor and Francis Group, Boca Raton, FL.
Farid, A. (2022). Spot Speed Study. Personal Collection of Ahmed Farid, California Polytechnic State University, San Luis Obispo, CA.

Given simple random samples of size n from a given population with a measured characteristic such as mean, proportion, or standard deviation for each sample, the probability distribution of all the measured characteristics is called a sampling distribution.

a mean score is an average score. It is the sum of individual scores divided by the number of individuals.

a numerical characteristic of a population

The standard deviation is a numerical value used to indicate how widely individuals in a group vary. If individual observations vary greatly from the group mean, the standard deviation is big; and vice versa. It is important to distinguish between the standard deviation of a population and the standard deviation of a sample. They have different notation, and they are computed differently. The standard deviation of a population is denoted by 𝜎 and the standard deviation of a sample, by 𝑠

a single number computed from a sample and used to estimate a population parameter

also called statistical inference or inductive statistics; this facet of statistics deals with estimating a population parameter based on a sample statistic. For example, if four out of the 100 calculators sampled are defective we might infer that four percent of the production is defective.

a number that describes the central tendency of the data; there are a number of specialized averages, including the arithmetic mean, weighted mean, median, mode, and geometric mean.

an interval estimate for an unknown population parameter. This depends on: (1) the desired confidence level (2) information that is known about the distribution (for example, known standard deviation) (3) the sample and its size

the margin of error; depends on the confidence level, sample size, and known or estimated population standard deviation.

the percent expression for the probability that the confidence interval contains the true population parameter; for example, if the CL = 90%, then in 90 out of 100 samples the interval estimate will enclose the true population parameter.

investigated and reported by William S. Gossett in 1908 and published under the pseudonym Student; the major characteristics of this random variable are: (1) it is continuous and assumes any real values (2) the pdf is symmetrical about its mean of zero (3) it approaches the standard normal distribution as n gets larger (4) there is a “family” of t-distributions: each representative of the family is completely defined by the number of degrees of freedom, which depends upon the application for which the t is being used.

the number of objects in a sample that are free to vary

a statement about the value of a population parameter, in case of two hypotheses, the statement assumed to be true is called the null hypothesis (notation and the contradictory statement is called the alternative hypothesis

Based on sample evidence, a procedure for determining whether the hypothesis stated is a reasonable statement and should not be rejected, or is unreasonable and should be rejected.

The decision is to reject the null hypothesis when, in fact, the null hypothesis is true.

The decision is not to reject the null hypothesis when, in fact, the null hypothesis is false.

The formula that counts the number of standard deviations on the relevant distribution that estimated parameter is away from the hypothesized value.

The t or Z value set by the researcher that measures the probability of a Type I error, 𝛼

a discrete random variable which arises from Bernoulli trials; there are a fixed number, n, of independent trials. “Independent” means that the result of any trial (for example, trial 1) does not affect the results of the following trials, and all trials are conducted under the same conditions.

two samples that are dependent. Differences between a before and after scenario are tested by testing one population mean of differences.

two samples that are selected from two populations, and the values from one population are not related in any way to the values from the other population.

a measure of effect size based on the differences between two means. If d is between 0 and 0.2 then the effect is small. If d approaches is 0.5, then the effect is medium, and if d approaches 0.8, then it is a large effect.

the variance is a numerical value used to indicate how widely individuals in a group vary. If individual observations vary greatly from the group mean, the variance is big; and vice versa. It is important to distinguish between the variance of a population and the variance of a sample. They have different notation, and they are computed differently.

a hypothesis test that compares expected and observed values in order to look for significant differences within one non-parametric variable. The degrees of freedom used equals the (number of categories – 1).

a table that displays sample values for two different factors that may be dependent or contingent on one another; it facilitates determining conditional probabilities.

a hypothesis test that compares expected and observed values for contingency tables in order to test for independence between two variables. The degrees of freedom used equals the (number of columns – 1) multiplied by the (number of rows – 1).

a test used to draw a conclusion about whether two populations have the same distribution. The degrees of freedom used equals the (number of columns – 1).

also referred to as ANOVA, is a method of testing whether or not the means of three or more populations are equal. The method is applicable if: (1) all populations of interest are normally distributed (2) the populations have equal standard deviations (3) samples (not necessarily of the same size) are randomly and independently selected from each population (4) there is one independent variable and one dependent variable. The test statistic for analysis of variance is the F-ratio

a method of testing whether or not the means of three or more populations are equal; the method is applicable if: (1) all populations of interest are normally distributed (2) the populations have equal standard deviations (3) samples (not necessarily of the same size) are randomly and independently selected from each population. The test statistic for analysis of variance is the F-ratio

a weighted average of two variances that can then be used when calculating standard error.

two variables are present in the model where one is the “cause” or independent variable and the other is the “effect” of dependent variable.

a system or model where more than one independent variable is being used to predict an outcome. There can only ever be one dependent variable, but there is no limit to the number of independent variables.

A number between −1 and 1 that represents the strength and direction of the relationship between “X” and “Y.” The value for “r” will equal 1 or −1 only if all the plotted points form a perfectly straight line.

a model that takes data and regresses it into a straight line equation.

This will sometimes be referred to as the “predictor” variable, because these values were measured in order to determine what possible outcomes could be predicted.

also, using the letter “y” represents actual values while 𝑦ˆ represents predicted or estimated values. Predicted values will come from plugging in observed “x” values into a linear model

The absolute value of a residual measures the vertical distance between the actual value of y and the estimated value of y that appears on the best-fit line.

the calculated value from adding up all the squared residual terms. The hope is that this value is very small when creating a model.

this is a number between 0 and 1 that represents the percentage variation of the dependent variable that can be explained by the variation in the independent variable.

the standard deviation of the distribution of the sample means

OERTransport: Fundamentals of Math, Physics, and Statistics for Future Transportation Professionals Copyright © by Anurag Pande, Ph.D. in Civil Engineering (Transportation); Peyton Ratto, Civil Engineering MS/MCRP; and Ahmed Farid, Ph.D. in Civil Engineering is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

8.4: Small Sample Tests for a Population Mean

Last updated
Save as PDF
Page ID 522

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Learning Objectives

To learn how to apply the five-step test procedure for test of hypotheses concerning a population mean when the sample size is small.

In the previous section hypotheses testing for population means was described in the case of large samples. The statistical validity of the tests was insured by the Central Limit Theorem, with essentially no assumptions on the distribution of the population. When sample sizes are small, as is often the case in practice, the Central Limit Theorem does not apply. One must then impose stricter assumptions on the population to give statistical validity to the test procedure. One common assumption is that the population from which the sample is taken has a normal probability distribution to begin with. Under such circumstances, if the population standard deviation is known, then the test statistic

\[\frac{(\bar{x}-\mu _0)}{\sigma /\sqrt{n}} \nonumber \]

still has the standard normal distribution, as in the previous two sections. If $\sigma$ is unknown and is approximated by the sample standard deviation $s$, then the resulting test statistic

\[\dfrac{(\bar{x}-\mu _0)}{s/\sqrt{n}} \nonumber \]

follows Student’s $t$-distribution with $n-1$ degrees of freedom.

Standardized Test Statistics for Small Sample Hypothesis Tests Concerning a Single Population Mean

If $\sigma$ is known: \[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}} \nonumber \]

If $\sigma$ is unknown: \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}} \nonumber \]

The first test statistic ($\sigma$ known) has the standard normal distribution.
The second test statistic ($\sigma$ unknown) has Student’s $t$-distribution with $n-1$ degrees of freedom.
The population must be normally distributed.

The distribution of the second standardized test statistic (the one containing $s$) and the corresponding rejection region for each form of the alternative hypothesis (left-tailed, right-tailed, or two-tailed), is shown in Figure $\PageIndex{1}$. This is just like Figure 8.2.1 except that now the critical values are from the $t$-distribution. Figure 8.2.1 still applies to the first standardized test statistic (the one containing ($\sigma$) since it follows the standard normal distribution.

The $p$-value of a test of hypotheses for which the test statistic has Student’s $t$-distribution can be computed using statistical software, but it is impractical to do so using tables, since that would require $30$ tables analogous to Figure 7.1.5, one for each degree of freedom from $1$ to $30$. Figure 7.1.6 can be used to approximate the $p$-value of such a test, and this is typically adequate for making a decision using the $p$-value approach to hypothesis testing, although not always. For this reason the tests in the two examples in this section will be made following the critical value approach to hypothesis testing summarized at the end of Section 8.1, but after each one we will show how the $p$-value approach could have been used.

Example $\PageIndex{1}$

The price of a popular tennis racket at a national chain store is $\$179$. Portia bought five of the same racket at an online auction site for the following prices:

\[155\; 179\; 175\; 175\; 161 \nonumber \]

Assuming that the auction prices of rackets are normally distributed, determine whether there is sufficient evidence in the sample, at the $5\%$ level of significance, to conclude that the average price of the racket is less than $\$179$ if purchased at an online auction.

Step 1 . The assertion for which evidence must be provided is that the average online price $\mu$ is less than the average price in retail stores, so the hypothesis test is \[H_0: \mu =179\\ \text{vs}\\ H_a: \mu <179\; @\; \alpha =0.05 \nonumber \]
Step 2 . The sample is small and the population standard deviation is unknown. Thus the test statistic is \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}} \nonumber \] and has the Student $t$-distribution with $n-1=5-1=4$ degrees of freedom.
Step 3 . From the data we compute $\bar{x}=169$ and $s=10.39$. Inserting these values into the formula for the test statistic gives \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{169-179}{10.39/\sqrt{5}}=-2.152 \nonumber \]
Step 4 . Since the symbol in $H_a$ is “$<$” this is a left-tailed test, so there is a single critical value, $-t_\alpha =-t_{0.05}[df=4]$. Reading from the row labeled $df=4$ in Figure 7.1.6 its value is $-2.132$. The rejection region is $(-\infty ,-2.132]$.
Step 5 . As shown in Figure $\PageIndex{2}$ the test statistic falls in the rejection region. The decision is to reject $H_0$. In the context of the problem our conclusion is:

The data provide sufficient evidence, at the $5\%$ level of significance, to conclude that the average price of such rackets purchased at online auctions is less than $\$179$.

To perform the test in Example $\PageIndex{1}$ using the $p$-value approach, look in the row in Figure 7.1.6 with the heading $df=4$ and search for the two $t$-values that bracket the unsigned value $2.152$ of the test statistic. They are $2.132$ and $2.776$, in the columns with headings $t_{0.050}$ and $t_{0.025}$. They cut off right tails of area $0.050$ and $0.025$, so because $2.152$ is between them it must cut off a tail of area between $0.050$ and $0.025$. By symmetry $-2.152$ cuts off a left tail of area between $0.050$ and $0.025$, hence the $p$-value corresponding to $t=-2.152$ is between $0.025$ and $0.05$. Although its precise value is unknown, it must be less than $\alpha =0.05$, so the decision is to reject $H_0$.

Example $\PageIndex{2}$

A small component in an electronic device has two small holes where another tiny part is fitted. In the manufacturing process the average distance between the two holes must be tightly controlled at $0.02$ mm, else many units would be defective and wasted. Many times throughout the day quality control engineers take a small sample of the components from the production line, measure the distance between the two holes, and make adjustments if needed. Suppose at one time four units are taken and the distances are measured as

Determine, at the $1\%$ level of significance, if there is sufficient evidence in the sample to conclude that an adjustment is needed. Assume the distances of interest are normally distributed.

Step 1 . The assumption is that the process is under control unless there is strong evidence to the contrary. Since a deviation of the average distance to either side is undesirable, the relevant test is \[H_0: \mu =0.02\\ \text{vs}\\ H_a: \mu \neq 0.02\; @\; \alpha =0.01 \nonumber \] where $\mu$ denotes the mean distance between the holes.
Step 2 . The sample is small and the population standard deviation is unknown. Thus the test statistic is \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}} \nonumber \] and has the Student $t$-distribution with $n-1=4-1=3$ degrees of freedom.
Step 3 . From the data we compute $\bar{x}=0.02075$ and $s=0.00171$. Inserting these values into the formula for the test statistic gives \[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{0.02075-0.02}{0.00171\sqrt{4}}=0.877 \nonumber \]
Step 4 . Since the symbol in $H_a$ is “$\neq$” this is a two-tailed test, so there are two critical values, $\pm t_{\alpha/2} =-t_{0.005}[df=3]$. Reading from the row in Figure 7.1.6 labeled $df=3$ their values are $\pm 5.841$. The rejection region is $(-\infty ,-5.841]\cup [5.841,\infty )$.
Step 5 . As shown in Figure $\PageIndex{3}$ the test statistic does not fall in the rejection region. The decision is not to reject $H_0$. In the context of the problem our conclusion is:

The data do not provide sufficient evidence, at the $1\%$ level of significance, to conclude that the mean distance between the holes in the component differs from $0.02$ mm.

To perform the test in "Example $\PageIndex{2}$" using the $p$-value approach, look in the row in Figure 7.1.6 with the heading $df=3$ and search for the two $t$-values that bracket the value $0.877$ of the test statistic. Actually $0.877$ is smaller than the smallest number in the row, which is $0.978$, in the column with heading $t_{0.200}$. The value $0.978$ cuts off a right tail of area $0.200$, so because $0.877$ is to its left it must cut off a tail of area greater than $0.200$. Thus the $p$-value, which is the double of the area cut off (since the test is two-tailed), is greater than $0.400$. Although its precise value is unknown, it must be greater than $\alpha =0.01$, so the decision is not to reject $H_0$.

Key Takeaway

There are two formulas for the test statistic in testing hypotheses about a population mean with small samples. One test statistic follows the standard normal distribution, the other Student’s $t$-distribution.
The population standard deviation is used if it is known, otherwise the sample standard deviation is used.
Either five-step procedure, critical value or $p$-value approach, is used with either test statistic.

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as $H_{0}$. Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as $H_{1}$ or $H_{a}$. For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, $\alpha$ or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$. $\overline{x}$ is the sample mean, $\mu$ is the population mean, $\sigma$ is the population standard deviation and n is the size of the sample.
t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$. s is the sample standard deviation.
$\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}$. $O_{i}$ is the observed value and $E_{i}$ is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

One sample: z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$.
Two samples: z = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}$.

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

One sample: t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$.
Two samples: t = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}$.

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

$H_{0}$: The population parameter is ≤ some value

$H_{1}$: The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

$H_{0}$: The population parameter is ≥ some value

$H_{1}$: The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

$H_{0}$: the population parameter = some value

$H_{1}$: the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
Step 2: Set up the alternative hypothesis.
Step 3: Choose the correct significance level, $\alpha$, and find the critical value.
Step 4: Calculate the correct test statistic (z, t or $\chi$) and p-value.
Step 5: Compare the test statistic with the critical value or compare the p-value with $\alpha$ to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as $H_{0}$: $\mu$ = 100.

Step 2: The alternative hypothesis is given by $H_{1}$: $\mu$ > 100.

Step 3: As this is a one-tailed test, $\alpha$ = 100% - 95% = 5%. This can be used to determine the critical value.

1 - $\alpha$ = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$.

$\mu$ = 100, $\overline{x}$ = 112.5, n = 30, $\sigma$ = 15

z = $\frac{112.5-100}{\frac{15}{\sqrt{30}}}$ = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Probability and Statistics
Data Handling

Important Notes on Hypothesis Testing

Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
It involves the setting up of a null hypothesis and an alternate hypothesis.
There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. $H_{0}$: $\mu$ = 90, $H_{1}$: $\mu$ > 90 $\overline{x}$ = 110, $\mu$ = 90, n = 5, s = 18. $\alpha$ = 0.05 Using the t-distribution table, the critical value is 2.132 t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$ t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. $H_{0}$: $\mu$ = 80, $H_{1}$: $\mu$ ≠ 80 $\overline{x}$ = 88, $\mu$ = 80, n = 36, $\sigma$ = 10. $\alpha$ = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$ z = $\frac{88-80}{\frac{10}{\sqrt{36}}}$ = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. $H_{0}$: $\mu$ = 90, $H_{1}$: $\mu$ < 90 $\overline{x}$ = 110, $\mu$ = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$ t = $\frac{82-90}{\frac{18}{\sqrt{6}}}$ t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$ and for two samples is z = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}$.

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide $\alpha$ by 2. This is done as there are two rejection regions in the curve.

Download PDF
Share X Facebook Email LinkedIn
Permissions

Sample Size Calculation for a Hypothesis Test

1 Department of Statistical Science, Southern Methodist University, Dallas, Texas
Original Investigation Varenicline and Nicotine Replacement Therapy for Smoking Cessation Coenraad F. N. Koegelenberg, MD, PhD; Firdows Noor, MD; Eric D. Bateman, MD, PhD; Richard N. van Zyl-Smit, MD, PhD; Axel Bruning, MD; John A. O’Brien, MD; Clifford Smith, MD; Mohamed S. Abdool-Gaffar, MD; Shaunagh Emanuel, MD; Tonya M. Esterhuizen, MSc; Elvis M. Irusen, MD, PhD JAMA

In this issue of JAMA , Koegelenberg et al 1 report the results of a randomized clinical trial (RCT) that investigated whether treatment with a nicotine patch in addition to varenicline produced higher rates of smoking abstinence than varenicline alone. The primary results were positive; that is, patients receiving the combination therapy were more likely to achieve continuous abstinence at 12 weeks than patients receiving varenicline alone. The absolute difference in the abstinence rate was estimated to be approximately 14%, which was statistically significant at level α = .05.

Manage citations:

Artificial Intelligence Resource Center

Cardiology in JAMA : Read the Latest

Browse and subscribe to JAMA Network podcasts!

Others Also Liked

Select your interests.

Customize your JAMA Network experience by selecting one or more topics from the list below.

Academic Medicine
Acid Base, Electrolytes, Fluids
Allergy and Clinical Immunology
American Indian or Alaska Natives
Anesthesiology
Anticoagulation
Art and Images in Psychiatry
Artificial Intelligence
Assisted Reproduction
Bleeding and Transfusion
Caring for the Critically Ill Patient
Challenges in Clinical Electrocardiography
Climate and Health
Climate Change
Clinical Challenge
Clinical Decision Support
Clinical Implications of Basic Neuroscience
Clinical Pharmacy and Pharmacology
Complementary and Alternative Medicine
Consensus Statements
Coronavirus (COVID-19)
Critical Care Medicine
Cultural Competency
Dental Medicine
Dermatology
Diabetes and Endocrinology
Diagnostic Test Interpretation
Drug Development
Electronic Health Records
Emergency Medicine
End of Life, Hospice, Palliative Care
Environmental Health
Equity, Diversity, and Inclusion
Facial Plastic Surgery
Gastroenterology and Hepatology
Genetics and Genomics
Genomics and Precision Health
Global Health
Guide to Statistics and Methods
Hair Disorders
Health Care Delivery Models
Health Care Economics, Insurance, Payment
Health Care Quality
Health Care Reform
Health Care Safety
Health Care Workforce
Health Disparities
Health Inequities
Health Policy
Health Systems Science
History of Medicine
Hypertension
Images in Neurology
Implementation Science
Infectious Diseases
Innovations in Health Care Delivery
JAMA Infographic
Law and Medicine
Leading Change
Less is More
LGBTQIA Medicine
Lifestyle Behaviors
Medical Coding
Medical Devices and Equipment
Medical Education
Medical Education and Training
Medical Journals and Publishing
Mobile Health and Telemedicine
Narrative Medicine
Neuroscience and Psychiatry
Notable Notes
Nutrition, Obesity, Exercise
Obstetrics and Gynecology
Occupational Health
Ophthalmology
Orthopedics
Otolaryngology
Pain Medicine
Palliative Care
Pathology and Laboratory Medicine
Patient Care
Patient Information
Performance Improvement
Performance Measures
Perioperative Care and Consultation
Pharmacoeconomics
Pharmacoepidemiology
Pharmacogenetics
Pharmacy and Clinical Pharmacology
Physical Medicine and Rehabilitation
Physical Therapy
Physician Leadership
Population Health
Primary Care
Professional Well-being
Professionalism
Psychiatry and Behavioral Health
Public Health
Pulmonary Medicine
Regulatory Agencies
Reproductive Health
Research, Methods, Statistics
Resuscitation
Rheumatology
Risk Management
Scientific Discovery and the Future of Medicine
Shared Decision Making and Communication
Sleep Medicine
Sports Medicine
Stem Cell Transplantation
Substance Use and Addiction Medicine
Surgical Innovation
Surgical Pearls
Teachable Moment
Technology and Finance
The Art of JAMA
The Arts and Medicine
The Rational Clinical Examination
Tobacco and e-Cigarettes
Translational Medicine
Trauma and Injury
Treatment Adherence
Ultrasonography
Users' Guide to the Medical Literature
Vaccination
Venous Thromboembolism
Veterans Health
Women's Health
Workflow and Process
Wound Care, Infection, Healing
Register for email alerts with links to free full-text articles
Access PDFs of free articles
Manage your interests
Save searches and receive search alerts

IMAGES

Sample Size Calculation: Hypothesis Testing || Randomized control trial (RCT)
Hypothesis Testing
PPT
hypothesis test formula statistics
Hypothesis testing tutorial using p value method
Hypothesis testing tutorial using p value method

VIDEO

Small Sample Hypothesis Testing, Example 1
Hypothesis Testing for Mean: p-value is more than the level of significance (Hat Size Example)
Hypothesis Testing 3
Calculate Sample Size for Hypothesis Tests
Large Sample Hypothesis Tests Sample Size
Hypothesis testing

COMMENTS

25.3
Let's take a look at two examples that illustrate the kind of sample size calculation we can make to ensure our hypothesis test has sufficient power. Example 25-4 Section Let $X$ denote the crop yield of corn measured in the number of bushels per acre.
How to Calculate Sample Size Needed for Power
Statistical power and sample size analysis provides both numeric and graphical results, as shown below. The text output indicates that we need 15 samples per group (total of 30) to have a 90% chance of detecting a difference of 5 units. The dot on the Power Curve corresponds to the information in the text output.
Sample size, power and effect size revisited: simplified and practical
The sample size critically affects the hypothesis and the study design, and there is no straightforward way of calculating the effective sample size for reaching an accurate conclusion. ... Study design (Statistical test) Minimum sample size / group Maximum sample size / group; Group comparison (ANOVA) = (10 / k) + 1 = (20 / k) + 1: One group ...
Issues in Estimating Sample Size for Hypothesis Testing
Suppose we want to test the following hypotheses at aα=0.05: H 0: μ = 90 versus H 1: μ ≠ 90. To test the hypotheses, suppose we select a sample of size n=100. For this example, assume that the standard deviation of the outcome is σ=20. We compute the sample mean and then must decide whether the sample mean provides evidence to support the ...
Power and Sample Size Determination
Sample size estimates for hypothesis testing are often based on achieving 80% or 90% power. The Z 1-β values for these popular scenarios are given below: For 80% power Z 0.80 = 0.84; For 90% power Z 0.90 =1.282; ES is the effect size, defined as follows:
Sample size calculation: Basic principles
Sample size can be calculated either using confidence interval method or hypothesis testing method. In the former, the main objective is to obtain narrow intervals with high reliability. In the latter, the hypothesis is concerned with testing whether the sample estimate is equal to some specific value.
7.1: Basics of Hypothesis Testing
State and check the assumptions for a hypothesis test. A random sample of size n is taken. The population standard derivation is known. The sample size is at least 30 or the population of the random variable is normally distributed. Find the sample statistic, test statistic, and p-value. Conclusion; Interpretation; Solution. 1. x = life of battery
Sample Size Essentials: The Foundation of Reliable Statistics
Sample size is the number of observations or data points collected in a study. It is a crucial element in any statistical analysis because it is the foundation for drawing inferences and conclusions about a larger population. When delving into the world of statistics, the phrase "sample size" often pops up, carrying with it the weight of ...
9.8: Effect Size, Sample Size and Power
In other words, power increases with the sample size. This is illustrated in Figure 11.7, which shows the power of the test for a true parameter of θ=0.7, for all sample sizes N from 1 to 100, where I'm assuming that the null hypothesis predicts that θ 0 =0.5.
Sample Size and its Importance in Research
ESTIMATING SAMPLE SIZE. So how large should a sample be? In hypothesis testing studies, this is mathematically calculated, conventionally, as the sample size necessary to be 80% certain of identifying a statistically significant outcome should the hypothesis be true for the population, with P for statistical significance set at 0.05. Some investigators power their studies for 90% instead of 80 ...
Sample size determination
Toggle Required sample sizes for hypothesis tests subsection. 3.1 Tables. 3.2 Mead's resource equation. 3.3 Cumulative distribution function. 4 Stratified sample size. 5 Qualitative research. ... The table shown on the right can be used in a two-sample t-test to estimate the sample sizes of an experimental group and a control group that are of ...
Test Statistic: Definition, Types & Formulas
Performing a hypothesis test on a sample produces a single test statistic. Now, imagine you carry out the following process: ... The sampling distribution below shows a t-distribution with 20 degrees of freedom, equating to a 1-sample t-test with a sample size of 21. The distribution centers on zero because it assumes the null hypothesis is ...
Type I & II Errors and Sample Size Calculation in Hypothesis Testing
Photo by Scott Graham on Unsplash. In the world of statistics and data analysis, hypothesis testing is a fundamental concept that plays a vital role in making informed decisions. In this blog, we will delve deeper into hypothesis testing, specifically focusing on how to reduce type I and type II errors.We will discuss the factors that influence these errors, such as significance level, sample ...
Hypothesis Testing
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
8.2: Large Sample Tests for a Population Mean
The sample is large and the population standard deviation is known. Thus the test statistic is Z = ˉx − μ0 σ / √n and has the standard normal distribution. Step 3. Inserting the data into the formula for the test statistic gives Z = ˉx − μ0 σ / √n = 8.2 − 8.1 0.22 / √30 = 2.490. Step 4.
BI Guide: Determining Hypothesis Test Sample Size
For your hypothesis test, you aim for high power, typically 80% or above, which means there's an 80% chance of correctly rejecting a false null hypothesis. By calculating the effect size, desired ...
Hypothesis Testing Explained (How I Wish It Was Explained to Me)
In this article, I won't delve into how sample size is computed (I will probably do it in a follow-up). For now, let's simply use the Statmodel's function for testing the difference between sample means as a black box: ### input (hypothesis + confusion matrix) control_mean = 10 control_std = 8 treatment_mean = 10.5 treatment_std = 9 confidence = .975 power = .80 ### compute sample size ...
Probing into Minimum Sample Size Formula: Derivation and Usage
The key idea to calculating the minimum required sample size is just the reverse of hypothesis testing, or put it differently, asking the sample size "as if the p-value is known to be the significance level 𝛼". Given two samples, we could compute the p-value based on the sample mean, standard deviation, and N.
Sample Size Calculator & Statistical Power Calculator
The formula for calculating the sample size of a test group in a one-sided test of absolute difference is: ... In a Neyman-Pearson framework of NHST (Null-Hypothesis Statistical Test) the alternative should exhaust all values that do not belong to the null, so it is usually composite. Below is an illustration of some possible combinations of ...
Chapter 9: Data Analysis
The concepts include hypothesis testing, assessing the adequacy of the sample sizes, and estimating the least square model fit for the data. These applications are useful in collecting and analyzing travel speed data, conducting before-after comparisons, and studying the association between variables, e.g., travel speed and congestion as ...
8.4: Small Sample Tests for a Population Mean
Solution. Step 1. The assertion for which evidence must be provided is that the average online price μ is less than the average price in retail stores, so the hypothesis test is H0: μ = 179vsHa: μ < 179 @ α = 0.05. Step 2. The sample is small and the population standard deviation is unknown.
PDF Hypothesis Testing
Why do hypothesis testing? Sample mean may be di↵erent from the population mean. Type of Test to Apply: Rightailed T. µ>kuYo believe that µ is more than value stated in H 0. ... use a sample size n 30. csusm.edu/stemsc XXXX @csusm_stemcenter Tel: STEM SC (N): (760) 750-4101 STEM SC (S): (760) 750-7324; Title: Hypothesis Testing.pdf Created ...
Hypothesis Testing
However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is ...
Sample Size Calculation for a Hypothesis Test
For this scenario, the authors' target sample size of 398 (199 in each group) will produce a power of 80%. All these values (45%, 14%, .05, 80%) must be selected at the planning stage of the study to carry out this calculation. The significance level and power are "rule-of-thumb" choices and are typically not based on the specifics of the ...
Reply to Comment on 'Self-thinning forest understoreys reduce wildfire
We tested their hypothesis by repeating the analysis of Zylstra et al (2022 Environ. Res. Lett. 17 044022) with a better suited statistical method on an improved and expanded dataset after removing the small patches that Miller et al (2024 Environ.