research paper on algebra

Including number theory, algebraic geometry, and combinatorics

We have large groups of researchers active in number theory and algebraic geometry, as well as many individuals who work in other areas of algebra: groups, noncommutative rings, Lie algebras and Lie super-algebras, representation theory, combinatorics, game theory, and coding.

Chairs: George Bergman and Tony Feng

Algebra Faculty, Courses, Dissertations

Senate faculty, graduate students, visiting faculty, meet our faculty, george m. bergman, richard e. borcherds, sylvie corteel, david eisenbud, edward frenkel, vadim gorin, mark d. haiman, robin c. hartshorne, tsit-yuen lam (林節玄), hannah k. larson, hendrik w. lenstra, jr., ralph mckenzie, david nadler, andrew p. ogg, arthur e. ogus, martin olsson, alexander paulin, nicolai reshetikhin, john l. rhodes, kenneth a. ribet, marc a. rieffel, thomas scanlon.

• 1 of 2 Grid: People (Current page)
• 2 of 2 Grid: People
• next › Grid: People
• last » Grid: People

Publications — Over 100 years of publishing excellence

• Book Author Resources
• Submit a Book Proposal
• AMS Rights, Licensing, and Permissions
• Open Math Notes
• Frequently asked questions
• Member Journals
• Research Journals
• Translation Journals
• Distributed Journals
• Open Access Journals
• Guidelines and Policies
• Journal Author Resources

Librarian Resources

• eBook Collections
• COUNTER Usage Statistics
• My Subscriptions
• Subscription Information
• Licensing Information

Mathematical Reviews/MathSciNet®

• MathSciNet ®
• Reviewer Home
• MathSciNet ® Subscriptions

Membership — Welcome to your membership center

Join the ams, renew your membership, give a membership, individual membership.

• Member Benefits
• Member Directory
• Reciprocating Societies
• Members in Developing Countries

Institutional Membership

• Domestic Institutions
• International Institutions
• Two-Year Institutions
• Graduate Student Chapter Program

Other Member Types

• Corporate Memberships
• Associate Memberships

Meetings & Conferences — Engage with colleagues and the latest research

National meetings.

• Joint Mathematics Meetings
• Upcoming JMMs
• Previous JMMs
• Special Lectures
• Professional Enhancement Programs (PEPs)

Sectional Meetings

• Upcoming Sectionals
• Previous Sectionals
• Presenting Papers
• Hosting Sectionals

Other Meetings, Conferences & Workshops

• Mathematics Research Communities
• Education Mini-conference
• International Meetings
• Mathematics Calendar
• Short Courses
• Workshop for Department Chairs and Leaders

Meetings Resources

• Suggest a Speaker
• AMS Meetings Grants
• Submitting Abstracts
• Welcoming Environment Policy
• MathSafe – supporting safe meetings

News & Outreach — Explore news, images, posters, and mathematical essays

News from the ams.

• AMS News Releases
• Feature Stories
• Information for Journalists
• In Memory Of

Math Voices

• Feature Column
• Math in the Media
• Column on Teaching and Learning

Explorations

• Recognizing Diverse Mathematicians
• AMS Posters
• Mathematics & Music
• Mathematical Imagery
• Mathematical Moments

Professional Programs — Resources and opportunities to further your mathematical pursuits

Professional development.

• Employment Services
• Mathjobs.org
• BEGIN Career Initiative
• Mathprograms.org
• Mathematical Opportunities Database
• Research Seminars

Institutional Information and Data

• Annual Survey of the Mathematical and Statistical Sciences
• CBMS Survey
• Other Sources of Data
• Directory of Institutions in the Mathematical Sciences
• Professional Directory

Grants & Support

• AMS-Simons Grants for PUI Faculty
• Travel Grants
• Fellowships & Scholarships
• Epsilon Fund
• Child Care Grants

Awards & Recognition

• AMS Prizes & Awards
• Fellows of the AMS

Education — Resources to support advanced mathematics teaching and learning

For students.

• Information for Undergraduate and High School Students
• Research Experiences for Undergraduates (REUs)
• Considering Grad School
• Find Grad Programs
• Applying to Grad School
• What do Mathematicians Do?

For Teachers

• Teaching Online
• Teaching Resources
• Inclusive Classrooms
• Assessing Student Learning
• Education Webinars

For Department Leaders & Mentors

• Information for Department Leaders
• paraDIGMS (Diversity in Graduate Mathematical Sciences)

Government Relations — Advocating for the mathematical sciences

Elevating mathematics in congress.

• Our Mission
• Letters, Statements, & Legislation
• Congressional Briefings

Legislative Priorities

• Federal Issues of Concern
• Federal Budget Process

Get Involved

• Advocacy Resources
• Take Action

DC-Based Fellowships

• Congressional Fellowship
• Mass Media Fellowship
• Catalyzing Advocacy in Science & Engineering (CASE) Fellowship

Giving to the AMS — Your gifts make great things happen for mathematics   Make a Gift

What you can support.

• The 2020 Fund
• Next Generation Fund
• Birman Fellowship for Women Scholars
• JMM Child Care Grants
• MathSciNet for Developing Countries

Create a Legacy

• Make a Tribute Gift
• Create a Permanent Fund
• Establish a Prize, Award or Fellowship
• Bequests and Charitable Estate Planning

Honoring Your Gift

• Donor Stories
• Donor Wall of Honor
• Thomas S. Fiske Society
• AMS Contributors Society
• AMS Gardens

Giving Resources

• AMS Development Committee
• AMS Gift Acceptance Policy

About the AMS — Advancing research. Connecting the mathematics community.

Our organization.

• Executive Staff
• Equity, Diversity, & Inclusion
• Jobs at AMS
• Customer Service

Our Governance

• Board of Trustees
• Executive Committee

Governance Operations

• Calendar of Meetings
• Policy Statements & Guidelines

On March 21 st , the AMS website will be down for regularly scheduled maintenance from 5:00am–8:00am

Journals High quality journals covering a broad range of mathematical disciplines.

Current issue · All issues

Notices of the American Mathematical Society ISSN 1088-9477 (online) ISSN 0002-9920 (print) MCQ: 0.45

Bulletin of the American Mathematical Society ISSN 1088-9485 (online) ISSN 0273-0979 (print) MCQ: 0.47

All issues : 2009 - Present

Abstracts of Papers Presented to the American Mathematical Society ISSN 2689-4831 (online) ISSN 0192-5857 (print) MCQ: 0.00

MCQ Info The Mathematical Citation Quotient (MCQ) measures journal impact by looking at citations over a five-year period.

Current volume · All volumes

Communications of the American Mathematical Society ISSN 2692-3688 MCQ: 0.47

Journal of the American Mathematical Society ISSN 1088-6834 (online) ISSN 0894-0347 (print) MCQ: 4.79

Representation Theory ISSN 1088-4165 MCQ: 0.7

Proceedings of the American Mathematical Society ISSN 1088-6826 (online) ISSN 0002-9939 (print) MCQ: 0.85

Proceedings of the American Mathematical Society Series B ISSN 2330-1511 MCQ: 0.84

Mathematics of Computation ISSN 1088-6842 (online) ISSN 0025-5718 (print) MCQ: 1.98

Conformal Geometry and Dynamics ISSN 1088-4173 MCQ: 0.5

Memoirs Home

Memoirs of the American Mathematical Society ISSN 1947-6221 (online) ISSN 0065-9266 (print) MCQ: 0.51

Transactions of the American Mathematical Society ISSN 1088-6850 (online) ISSN 0002-9947 (print) MCQ: 1.43

Transactions of the American Mathematical Society Series B ISSN 2330-0000 MCQ: 1.79

All volumes

Electronic Research Announcements ISSN 1079-6762 MCQ: 0.00

Return to top

St. Petersburg Mathematical Journal ISSN 1547-7371 (online) ISSN 1061-0022 (print) MCQ: 0.54

Transactions of the Moscow Mathematical Society ISSN 1547-738X (online) ISSN 0077-1554 (print) MCQ: 0.51

Sugaku Expositions ISSN 2473-585X (online) ISSN 0898-9583 (print) MCQ: 0.10

Annales Scientifiques de l'École Normale Supérieure ISSN: 1088-4173 MCQ: 2.09

Astérisque ISSN: 0303-1179 MCQ: 0.45

Bulletin de la Société Mathématique de France ISSN 0037-9484 MCQ: 0.70

Theory of Probability and Mathematical Statistics ISSN 1547-7363 (online) ISSN 0094-9000 (print) MCQ: 0.12

Journal of Algebraic Geometry ISSN 1534-7486 (online) ISSN 1056-3911 (Print) MCQ: 1.37

ISSN 0379-4024 (print) MCQ: 0.60

Quarterly of Applied Mathematics ISSN 1552-4485 (online) ISSN 0033-569X (print) MCQ: 0.60

Moscow Mathematical Journal 1609-3321 (print) MCQ: 0.61

Mémoires de la Société Mathématique de France ISSN 0249-633X MCQ: 1.83

Journal of the Ramanujan Mathematical Society ISSN 0970-1249 MCQ: 0.24

Linear algebra teaching and learning: themes from recent research and evolving research priorities

• Survey Paper
• Published: 01 November 2019
• Volume 51 , pages 1017–1030, ( 2019 )

Cite this article

• Sepideh Stewart 1 ,
• Christine Andrews-Larson 2 &
• Michelle Zandieh 3  

2423 Accesses

22 Citations

1 Altmetric

Explore all metrics

In this survey paper, we describe the state of the field on linear algebra research. We synthesize themes, questions, results, and perspectives emphasized in the papers that appear in this issue, as well as a selection of those published between 2008 and 2017. We highlight the extensive base of empirical research detailing how students reason about a variety of topic areas in linear algebra, as well as studies that provide evidence of promising directions for supporting students’ success through various teaching interventions and experiments in the classroom. From this survey paper, we identify areas for future research into the teaching and learning of this increasingly important area for modern applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Trends, insights, and developments in research on the teaching and learning of algebra

Teaching Algebra through Variations

Issues Surrounding Teaching Linear Algebra

Altieri, M., & Schirmer, E. (2019). Learning the concept of eigenvalues and eigenvectors: A comparative analysis of achieved concept construction in linear algebra using APOS theory among students from different educational backgrounds. ZDM Mathematics Education ( this issue ).

Andrews-Larson, C., Wawro, M., & Zandieh, M. (2017). A hypothetical learning trajectory for conceptualizing matrices as linear transformations. International Journal of Mathematical Education in Science and Technology, 48 (6), 809–829. https://doi.org/10.1080/0020739X.2016 .

Article   Google Scholar  

Aydin, S. (2014). Using example generation to explore students’ understanding of the concepts of linear dependence/independence in linear algebra. International Journal of Mathematical Education in Science and Technology, 45 (6), 813–826.

Google Scholar  

Bagley, S., & Rabin, J. (2016). Students’ use of computational thinking in linear algebra. International Journal of Research on Undergraduate Mathematics Education, 2, 83–104.

Beltran-Meneu, M. J., Murillo-Arcila, M., & Albarracin, L. (2016). Emphasizing visualization and physical applications in the study of eigenvectors and eigenvalues. Teaching Mathematics and Its Applications: An International Journal of the IMA, 36 (3), 123–135. https://doi.org/10.1093/teamat/hrw018 .

Bianchini, B. L., de Lima, G. L., & Gomes, E. (2019). Linear algebra in engineering: an analysis of Latin American studies. ZDM Mathematics Education ( this issue ).

Briton, S., & Henderson, J. (2009). Linear algebra revisited: An attempt to understand students’ conceptual difficulties. International Journal of Mathematical Education in Science and Technology, 40 (7), 963–974.

Caglayan, G. (2015). Making sense of eigenvalue–eigenvector relationships: Math majors’ linear algebra–geometry connections in a dynamic environment. The Journal of Mathematical Behavior, 40, 131–153. https://doi.org/10.1016/j.jmathb.2015.08.003 .

Caglayan, G. (2019). Is it a subspace or not? Making sense of subspaces of vector spaces in a technology-assisted learning environment. ZDM Mathematics Education (this issue) .

Cárcamo, A., Fortuny, J., & Fuentealba, C. (2017). The emergent models in linear algebra: An example with spanning set and span. Teaching Mathematics and Its Applications: An International Journal of the IMA, 37 (4), 202–217.

Cárcamo, A., Fortuny, J., & Gómez, V. (2017). Mathematical modelling and the learning trajectory: Tools to support the teaching of linear algebra. International journal of mathematical education in science and technology , 48 (3), 338–352.

Carlson, D., Johnson, C. R., Lay, D. C., & Porter, A. D. (1993). The linear algebra curriculum study group recommendations for the first course in linear algebra. College Mathematics Journal, 24, 41–46.

Carney, D., Ormes, N., & Swanson, R. (2015). Partially flipped linear algebra: A team-based approach. Primus, 25 (8), 641–654.

Cline, K., Zullo, H., Duncan, J., Stewart, A., & Snipes, M. (2013). Creating discussions with classroom voting in linear algebra. International Journal of Mathematical Education in Science and Technology, 44 (8), 1131–1142.

Cooley, L., Vidakovic, D., Martin, W. O., Dexter, S., Suzuki, J., & Loch, S. (2014). Modules as learning tools in linear algebra. PRIMUS, 24 (3), 257–278.

Dogan, H. (2018). Differing instructional modalities and cognitive structures: Linear algebra. Linear Algebra and Its Applications, 542, 464–483.

Dogan, H. (2019). Some aspects of linear independence schemas. ZDM Mathematics Education ( this issue ).

Dogan-Dunlap, H. (2010). Linear algebra students’ modes of reasoning: Geometric representations. In Special issue devoted to the 15th ILAS conference at Cancun, Mexico, June 16–20, 2008 (Vol. 432(8), pp. 2141–2159). https://doi.org/10.1016/j.laa.2009.08.037

Dominguez-Garcia, S., Garcia-Plana, M. I., & Taberna, J. (2016). Mathematical modelling in engineering: An alternative way to teach linear algebra. International Journal of Mathematical Education in Science and Technology, 47 (7), 1076–1086. https://doi.org/10.1080/0020739X.2016.1153736 .

Dorier, J. L. (Ed.). (2000). On the teaching of linear algebra . Dordrecht: Kluwer.

Dubinsky, E., & McDonald, M. (2001). APOS: A constructivist theory of learning in undergraduate mathematics education research. In D. Holton., M. Artigue, U. Krichgraber, J. Hillel, M. Niss & A. Schoenfeld (Eds.), The teaching and learning of mathematics at university level: An international commission on mathematical instruction study (pp. 273–280). Dordrecht: Kluwer Academic Publishers.

Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103–131.

Ertekin, E., Solak, S., & Yazici, E. (2010) The effects of formalism on teacher trainees’ algebraic and geometric interpretation of the notions of linear dependency/independency. International Journal of Mathematical Education in Science and Technology , 41 (8), 1015–1035.

Foster, C., & de Villiers, M. (2016). The definition of the scalar product: an analysis and critique of a classroom episode. International Journal of Mathematical Education in Science and Technology , 47 (5), 750–761.

Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K., Okoroafor, N., Jordt, H., et al. (2014). Active learning increases student performance in science, engineering, and mathematics. Proceedings of the National Academy of Sciences, 111 (23), 8410–8415.

Gol Tabaghi, S. (2014). How dragging changes students’ awareness: Developing meanings for eigenvector and eigenvalue. Canadian Journal of Science, Mathematics and Technology Education, 14 (3), 223–237.

Gravemeijer, K. (1999). How emergent models may foster the constitution of formal mathematics. Mathematical Thinking and Learning, 1 (2), 155–177.

Grenier-Boley, N. (2014). Some issues about the introduction of first concepts in linear algebra during tutorial sessions at the beginning of university. Educational Studies in Mathematics, 87 (3), 439–461.

Gueudet, C. (2006). Using geometry to teach and learn linear algebra. Research in Collegiate Mathematics Education, 6, 171–195.

Hannah, J., Stewart, S., & Thomas, M. O. J. (2011). Analysing lecturer practice: The role of orientations and goals. International Journal of Mathematical Education in Science and Technology, 42 (7), 975–984.

Hannah, J., Stewart, S., & Thomas, M. O. J. (2013). Emphasizing language and visualization in teaching linear algebra. International Journal of Mathematics Education in Science and Technology, 44 (4), 475–489.

Hannah, J., Stewart, S., & Thomas, M. O. J. (2016). Developing conceptual understanding and definitional clarity in linear algebra through the three worlds of mathematical thinking. Teaching Mathematics and its Applications: An International Journal of the IMA, 35 (4), 216–235. https://doi.org/10.1093/teamat/hrw001 .

Harel, G. (1989). Learning and teaching linear algebra: Difficulties and an alternative approach to visualizing concepts and processes. Focus on Learning Problems in Mathematics, 11, 139–148.

Harel, G. (2017). The learning and teaching of linear algebra: Observations and generalizations. Journal of Mathematical Behavior , 46 , 69–95.

Harel, G. (2000). Three principles of learning and teaching mathematics: Particular reference to linear algebra—Old and new observations. In Jean-Luc Dorier (Ed.), On the teaching of linear algebra (pp. 177–190). Dordrecht: Kluwer Academic Publishers.

Harel, G. (2008). DNR perspective on mathematics curriculum and instruction: Focus on proving. Part I. ZDM—The International Journal on Mathematics Education, 40, 487–500.

Harel, G. (2018). The learning and teaching of linear algebra through the lenses of intellectual need and epistemological justification and their constituents. In S. Stewart, C. Andrews-Larson, A. Berman, & M. Zandieh (Eds.), Challenges and strategies in teaching linear algebra (pp. 3–27). Dordrecht: Springer.

Harel, G. (2019). Varieties in the use of geometry in the teaching of linear algebra. ZDM Mathematics Education ( this issue ).

Hillel, J., & Sierpinska, A. (1993). On one persistent mistake in linear algebra. In Proceedings of the 18th international conference for the psychology of mathematics education (Vol. 3, pp. 65–72). Lisbon, Portugal.

Karakok, G. (2019). Making connections among representations of eigenvector: What sort of a beast is it? ZDM Mathematics Education ( this issue ).

Kazunga, C., & Bansilal, S. (2017). Zimbabwean in-service mathematics teachers’ understanding of matrix operations. Journal of Mathematical Behavior, 47, 81–95.

Lakoff, G., & Núñez, R. (2000). Where mathematics come from: How the embodied mind brings mathematics into being. New York: Basic Books.

Larson, C., & Zandieh, M. (2013). Three interpretations of the matrix equations Ax = b. For the Learning of Mathematics, 33 (2), 11–17.

Laursen, S. L., Hassi, M. L., Kogan, M., & Weston, T. J. (2014). Benefits for women and men of inquiry-based learning in college mathematics: A multi-institution study. Journal for Research in Mathematics Education, 45 (4), 406–418.

Love, B., Hodge, A., Grandgenett, N., & Swift, A. W. (2014). Student learning and perceptions in a flipped linear algebra course. International Journal of Mathematical Education in Science and Technology, 45 (3), 317–324.

Love, B., Hodge, A., Corritore, C., & Ernst, D. (2015). Inquiry-Based Learning and the Flipped Classroom Model. PRIMUS , 25 (8), 745–762.

Malek, A., & Movshovitz-Hadar, N. (2011). The effect of using transparent pseudo-proofs in linear algebra. Research in Mathematics Education, 13 (1), 33–58.

Martin, W., Loch, S., Cooley, L., Dexter, S., & Vidakovic, D. (2010). Integrating learning theories and application-based modules in teaching linear algebra. Linear Algebra and Its Applications, 432 (8), 2089–2099.

Martínez-Sierra, G., & del Socorro García-González, M. (2016). Undergraduate mathematics students’ emotional experiences in Linear Algebra courses. Educational Studies in Mathematics, 91 (1), 87–106.

Movshovitz-Hadar, N. (1988). Stimulating presentation of theorems followed by responsive proofs. For the Learning of Mathematics, 8 (2), 12–30.

Murphy, J., Chang, J. M., & Suaray, K. (2016). Student performance and attitudes in a collaborative and flipped linear algebra course. International Journal of Mathematical Education in Science and Technology, 47 (5), 653–673.

Nanes, K. M. (2014). A modified approach to team-based learning in linear algebra courses. International Journal of Mathematical Education in Science and Technology, 45 (8), 1208–1219.

Nishizawa, H., Kimura, K., Ohno, W., & Yoshioko, T. (2014). Interactive worksheets for connecting symbolic and visual representations of 3D vector equations. Teaching Mathematics and Its Applications: An International Journal of the IMA, 33 (1), 52–64. https://doi.org/10.1093/teamat/hru005 .

Oktaç, A. (2019). Mental constructions in linear algebra. ZDM Mathematics Education ( this issue ).

Parraguez, M., & Oktac, A. (2010). Construction of the vector space concept from the viewpoint of APOS theory. Linear Algebra and its Applications 432 , 2112–2124.

Payton, S. (2019). Fostering mathematical connections in introductory linear algebra through adapted inquiry. ZDM Mathematics Education ( this issue ).

Plaxco, D., & Wawro, M. (2015). Analyzing student understanding in linear algebra through mathematical activity. Journal of Mathematical Behavior, 38, 87–100.

Plaxco, D., Zandieh, M., & Wawro, M. (2018). Stretch directions and stretch factors: A sequence intended to support guided reinvention of eigenvector and eigenvalue. In S. Stewart, C. Andrews-Larson, A. Berman, & M. Zandieh (Eds.), Challenges in teaching linear algebra. ICME-13 monographs (pp. 175–193). Cham: Springer.

Possani, E., Trigueros, M., Preciado, J. G., & Lozano, M. D. (2010). Use of models in the teaching of linear algebra. Linear Algebra and Its Applications, 432 (8), 2125–2140.

Quinlan, J., & Tennenhouse, C. (2016). Perceived utility of typesetting homework in post-calculus mathematics courses. PRIMUS, 26 (1), 53–66.

Rasmussen, C., & Wawro, M. (2017). Post-calculus research in undergraduate mathematics education. In J. Cai (Ed.), The compendium for research in mathematics education (pp. 551–579). Reston: National Council of Teachers of Mathematics.

Rasmussen, C., Wawro, M., & Zandieh, M. (2015). Examining individual and collective level mathematical progress. Education Studies in Mathematics, 88 (2), 259–281. https://doi.org/10.1007/s10649-014-9583-x .

Rensaa, R. J. (2014). The impact of lecture notes on an engineering student’s understanding of mathematical concepts. The Journal of Mathematical Behavior, 34, 33–57.

Salgado, H., & Trigueros, M. (2015). Teaching eigenvalues and eigenvectors using models and APOS Theory. The Journal of Mathematical Behavior, 39, 100–120.

Sandoval, I., & Possani,E. (2016). An analysis of different representations for vectors and planes in R 3 Learning challenges. Educational Studies in Mathematics , 92 , 109–127.

Sierpinska, A. (2000). On some aspects of students’ thinking in linear algebra. In J.-L. Dorier (Ed.), On the teaching of linear algebra (pp. 209–246). Dordrecht: Kluwer.

Sinclair, N., Gol Tabaghi, S. (2010). Drawing space: mathematicians’ kinetic conceptions of eigenvectors. Educational Study in Mathematics , 74 , 223–240.

Skemp, R. (1979). Intelligence, learning, and action: A foundation for theory and practice in education . Chichester: Wiley.

Stewart, S., Andrews-Larson, C., Berman, A., & Zandieh, M. (2018). Challenges and strategies in teaching linear algebra . Cham: Springer.

Stewart, S., & Thomas, M. O. J. (2010). Student learning of basis, span and linear independence in linear algebra. International Journal of Mathematical Education in Science and Technology, 41 (2), 173–188.

Stewart, S., & Thomas, M.O.J. (2019). Student perspectives on proof in linear algebra. ZDM Mathematics Education ( this issue ).

Stewart, S., Troup, J., & Plaxco, D. (2019). Reflection on teaching linear algebra: Examining one instructor’s movements between the three worlds of mathematical thinking. ZDM Mathematics Education ( this issue ).

Stuhlmann, A. (2019). Mathematics students talking past each other: Emergence of ambiguities in linear algebra proof constructions involving the uniqueness quantification. ZDM Mathematics Education ( this issue ).

Tall, D. O. (2013). How humans learn to think mathematically: Exploring the three worlds of mathematics . Cambridge: Cambridge University Press.

Thomas, M., & Stewart, S. (2011). Eigenvalues and eigenvectors: Embodied, symbolic and formal thinking. Mathematics Education Research Journal, 23, 275–296.

Trigueros, M., & Possani, E. (2013). Using an economics model for teaching linear algebra. Linear Algebra and its Applications , 438 (4), 1779–1792.

Trigueros, M. (2018). Learning linear algebra using models and conceptual activities. In S. Stewart, C. Andrews-Larson, A. Berman, & M. Zandieh (Eds.), Challenges in teaching linear algebra. ICME-13 monographs (pp. 20–50). Cham: Springer.

Trigueros, M. (2019). The development of a linear algebra schema: Learning as result of the use of a cognitive theory and models. ZDM Mathematics Education ( this issue ).

Turgut, M. (2019). Sense-making regarding matrix representation of geometric transformations in R 2 : A semiotic mediation perspective in a dynamic geometry environment. ZDM Mathematics Education ( this issue ).

Uhlig, F. (2002). The role of proof in comprehending and teaching elementary linear algebra. Educational Studies in Mathematics, 50, 335–346.

Vinner, S. (1997). Scenes from linear algebra classes. In D. Carlson, C. R. Johnson, D. C. Lay, A. D. Porter, A. Watkins, & W. Watkins (Eds.), Resources for teaching linear algebra, MAA Notes (Vol. 42, pp. 155–171). Washington: MAA.

Wawro, M., Rasmussen, C., Zandieh, M., Sweeney, G. F., & Larson, C. (2012). An inquiry-oriented approach to span and linear independence: The case of the Magic Carpet Ride sequence. PRIMUS, 22 (7), 1–23. https://doi.org/10.1080/10511970.2012.667516 .

Wawro, M., Rasmussen, C., Zandieh, M., & Larson, C. (2013a). Design research within undergraduate mathematics education: An example from introductory linear algebra. In T. Plomp & N. Nieveen (Eds.), Educational design research—Part B: Illustrative cases (pp. 905–925). Enschede: the Netherlands: SLO.

Wawro, M., Zandieh, M., Rasmussen, C., & Andrews-Larson, C. (2013b). Inquiry oriented linear algebra: Course materials . This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. http://iola.math.vt.edu .

Wawro, M., Watson, K., & Zandieh, M. (2019). Student understanding of linear combinations of eigenvectors. ZDM Mathematics Education ( this issue ).

Williams, S. R., & Leatham, K. R. (2017). Journal quality in mathematics education. Journal for Research in Mathematics Education, 48 (4), 369–396.

Zandieh, M., Adiredja, A., & Knapp, J. (2019). Exploring everyday examples to explain basis: Insights into student understanding from students in Germany. ZDM Mathematics Education ( this issue ).

Zandieh, M., & Andrews-Larson, C. (2019). Symbolizing while solving linear systems. ZDM Mathematics Education ( this issue ).

Zandieh, M., Wawro, M., & Rasmussen, C. (2017). An example of inquiry in linear algebra: The roles of symbolizing and brokering. PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 27 (1), 96–124. https://doi.org/10.1080/10511970.2016.1199618 .

Download references

Acknowledgments

We are deeply appreciative of an incredible team of graduate students who worked with us to identify and organize the set of recent studies highlighted in this paper: B. Athey, I. Lee, M. Mauntel, J. Sipes, and J. Smith. We also thank the reviewers for their insightful feedback that helped us improve this paper.

Author information

Authors and affiliations.

University of Oklahoma, Norman, OK, USA

Sepideh Stewart

Florida State University, Tallahassee, FL, USA

Christine Andrews-Larson

Arizona State University, Mesa, AZ, USA

Michelle Zandieh

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Sepideh Stewart .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Stewart, S., Andrews-Larson, C. & Zandieh, M. Linear algebra teaching and learning: themes from recent research and evolving research priorities. ZDM Mathematics Education 51 , 1017–1030 (2019). https://doi.org/10.1007/s11858-019-01104-1

Download citation

Accepted : 15 October 2019

Published : 01 November 2019

Issue Date : December 2019

DOI : https://doi.org/10.1007/s11858-019-01104-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Instruction
• Research synthesis
• Linear algebra
• Find a journal
• Publish with us
• Track your research

Research in algebra

In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics. It includes everything from elementary equation solving to the study of abstractions such as groups, rings, and fields. Source: Wikipedia

Professors with interests in algebra

• Bruce Corrigan-Salter
• Daniel Drucker
• Daniel Frohardt
• Daniel Isaksen
• Leonid Makar-Limanov
• Andrew Salch
• Ualbai Umirbaev

Research areas in algebra

Group theory.

Properties of almost-simple groups, applications to the inverse Galois problem and braid groups.

Finite groups and finite geometries

Geometries associated with groups of Lie type, generalized n-gons, and their automorphism groups.

Character theory

Character value estimates infinite groups.

Non-commutative ring theory

Free algebras, matrix localizations, division rings of quotients of enveloping algebras of Lie algebras, and matrices over these.

Module theory

Infinite-dimensional modules over finite-dimensional algebras, irreducible modules over Heisenberg algebras.

Lie algebras, linear algebra, and number theory

Root systems, evaluation of determinants, and Diophantine equations.

abstract algebra Recently Published Documents

Total documents.

• Latest Documents
• Most Cited Documents
• Contributed Authors
• Related Sources
• Related Keywords

Basic Abstract Algebra

An introduction to abstract algebra, brief talk on ideological and political teaching in abstract algebra, how mathematicians assign homework problems in abstract algebra courses, an invitation to abstract algebra, verifying non-isomorphism of groups.

The concept of isomorphism is central to group theory, indeed to all of abstract algebra. Two groups {G, *} and {H, ο}are said to be isomorphic to each other if there exists a set bijection α from G onto H, such that $$\left( {a\;*\;b} \right)\alpha = \left( a \right)\alpha \; \circ \;(b)\alpha $$ for all a, b ∈ G. This can be illustrated by what is usually known as a commutative diagram:

On the Exponential Diophantine Equation (132m) + (6r + 1)n = z2

Nowadays, mathematicians are very interested in discovering new and advanced methods for determining the solution of Diophantine equations. Diophantine equations are those equations that have more unknowns than equations. Diophantine equations appear in astronomy, cryptography, abstract algebra, coordinate geometry and trigonometry. Congruence theory plays an important role in finding the solution of some special type Diophantine equations. The absence of any generalized method, which can handle each Diophantine equation, is challenging for researchers. In the present paper, the authors have discussed the existence of the solution of exponential Diophantine equation  (132m) + (6r + 1)n = Z2, where m, n, r, z are whole numbers. Results of the present paper show that the exponential Diophantine equation (132m) + (6r + 1)n = Z2, where m, n, r, z are whole numbers, has no solution in the whole number.

Abstract Algebra

Ring hypothesis is one of the pieces of the theoretical polynomial math that has been thoroughly used in pictures. Nevertheless, ring hypothesis has not been associated with picture division. In this paper, we propose another rundown of similarity among pictures using rings and the entropy work. This new record was associated as another stopping standard to the Mean Shift Iterative Calculation with the goal to accomplish a predominant division. An examination on the execution of the calculation with this new ending standard is finished. In spite of the fact that ring hypothesis and class hypothesis from the start sought after assorted direction it turned out during the 1970s – that the investigation of functor groupings furthermore reveals new plots for module hypothesis.

(m, n)-Ideals in Semigoups Based on Int-Soft Sets

Algebraic structures play a prominent role in mathematics with wide ranging applications in many disciplines such as theoretical physics, computer sciences, control engineering, information sciences, coding theory, and topological spaces. This provides sufficient motivation to researchers to review various concepts and results from the realm of abstract algebra in the broader framework of fuzzy setting. In this paper, we introduce the notions of int-soft m , n -ideals, int-soft m , 0 -ideals, and int-soft 0 , n -ideals of semigroups by generalizing the concept of int-soft bi-ideals, int-soft right ideals, and int-soft left ideals in semigroups. In addition, some of the properties of int-soft m , n -ideal, int-soft m , 0 -ideal, and int-soft 0 , n -ideal are studied. Also, characterizations of various types of semigroups such as m , n -regular semigroups, m , 0 -regular semigroups, and 0 , n -regular semigroups in terms of their int-soft m , n -ideals, int-soft m , 0 -ideals, and int-soft 0 , n -ideals are provided.

A transition to abstract algebra

Export citation format, share document.

The Electronic Journal of Linear Algebra (ELA), a publication of the International Linear Algebra Society (ILAS) , is a refereed all-electronic journal that welcomes mathematical articles of high standards that contribute new information and new insights to matrix analysis and the various aspects of linear algebra and its applications. ELA is a JCR ranked journal, and indexed by MathSciNet, ZentralBlatt, and Scopus.  ELA is completely free for authors/readers; and  ELA is built on the selfless contributions of its authors, referees and editors.

Announcements

Guidelines for editors.

Guidance for Electronic Journal of Linear Algebra (ELA) Editorial Process

Guidelines for Referees

Guidance for Electronic Journal of Linear Algebra (ELA) Refereeing Process

Current Issue

Vol. 40 (2024)

Published: 2024-01-05

Invertible bases and root vectors for analytic matrix-valued functions

Minimizing the least eigenvalue of unbalanced signed unicyclic graphs with given girth or pendant vertices, structured level-2 condition numbers of matrix functions, the allow sequence of distinct eigenvalues for a sign pattern, locating eigenvalues of symmetric matrices - a survey, numerical range for weighted moore-penrose inverse of tensor, new properties of a special matrix related to positive-definite matrices, deflating invariant subspaces for rank structured pencils, flag-shaped blockers of 123-avoiding permutation matrices, near-bipartite leonard pairs, eigenvalue characterization of some structured matrix pencils under linear perturbation, matrices having nonzero outer inverses, the numerical range of matrix products, the vertex connectivity and the third largest eigenvalue in regular (multi-)graphs, a new weighted spectral geometric mean and properties, qualitative, statistical, and extreme properties of spectral indices of signable pseudo-invertible graphs, commuting additive maps on upper triangular and strictly upper triangular infinite matrices, the signless laplacian spectral radius of graphs without intersecting odd cycles, diagonalizably realizable implies universally realizable, some symmetric sign patterns requiring unique inertia, symmetry and asymmetry between positive and negative square energies of graphs.

• Open access
• Published: 11 March 2019

Enhancing achievement and interest in mathematics learning through Math-Island

• Charles Y. C. Yeh   ORCID: orcid.org/0000-0003-4581-6575 1 ,
• Hercy N. H. Cheng 2 ,
• Zhi-Hong Chen 3 ,
• Calvin C. Y. Liao 4 &
• Tak-Wai Chan 5  

Research and Practice in Technology Enhanced Learning volume  14 , Article number:  5 ( 2019 ) Cite this article

185k Accesses

46 Citations

3 Altmetric

Metrics details

Conventional teacher-led instruction remains dominant in most elementary mathematics classrooms in Taiwan. Under such instruction, the teacher can rarely take care of all students. Many students may then continue to fall behind the standard of mathematics achievement and lose their interest in mathematics; they eventually give up on learning mathematics. In fact, students in Taiwan generally have lower interest in learning mathematics compared to many other regions/countries. Thus, how to enhance students’ mathematics achievement and interest are two major problems, especially for those low-achieving students. This paper describes how we designed a game-based learning environment, called Math-Island , by incorporating the mechanisms of a construction management game into the knowledge map of the elementary mathematics curriculum. We also report an experiment conducted with 215 elementary students for 2 years, from grade 2 to grade 3. In this experiment, in addition to teacher-led instruction in the classroom, students were directed to learn with Math-Island by using their own tablets at school and at home. As a result of this experiment, we found that there is an increase in students’ mathematics achievement, especially in the calculation and word problems. Moreover, the achievements of low-achieving students in the experimental school outperformed the low-achieving students in the control school (a control group in another school) in word problems. Moreover, both the low-achieving students and the high-achieving students in the experimental school maintained a rather high level of interest in mathematics and in the system.

Introduction

Mathematics has been regarded as a fundamental subject because arithmetic and logical reasoning are the basis of science and technology. For this reason, educational authorities emphasize students’ proficiency in computational skills and problem-solving. Recently, the results of the Program for International Student Assessment (PISA) and the Trends in Mathematics and Science Study (TIMSS) in 2015 (OECD 2016 ; Mullis et al. 2016 ) revealed a challenge for Taiwan. Although Taiwanese students had higher average performance in mathematics literacy compared to students in other countries, there was still a significant percentage of low-achieving students in Taiwan. Additionally, most Taiwanese students show low levels of interest and confidence in learning mathematics (Lee 2012 ).

The existence of a significant percentage of low-achieving students is probably due to teacher-led instruction, which still dominates mathematics classrooms in most Asian countries. It should be noted that students in every classroom possess different abilities and hence demonstrate different achievements. Unfortunately, in teacher-led instruction, all the students are required to learn from the teacher in the same way at the same pace (Hwang et al. 2012 ). Low-achieving students, without sufficient time, are forced to receive knowledge passively. Barr and Tagg ( 1995 ) pointed out that it is urgent for low-achieving students to have more opportunities to learn mathematics at their own pace. Researchers suggested one-to-one technology (Chan et al. 2006 ) through which every student is equipped with a device to learn in school or at home seamlessly. Furthermore, they can receive immediate feedback from Math-Island, which supports their individualized learning actively and productively. Thus, this may provide more opportunities for helping low-achieving students improve their achievement.

The low-interest problem for almost all students in Taiwan is usually accompanied by low motivation (Krapp 1999 ). Furthermore, students with continuously low performance in mathematics may eventually lose their interest and refuse to learn further (Schraw et al. 2001 ). This is a severe problem. To motivate students to learn, researchers design educational games to provide enjoyable and engaging learning experiences (Kiili and Ketamo 2007 ). Some of these researchers found that game-based learning may facilitate students’ learning in terms of motivation and learning effects (Liu and Chu 2010 ), spatial abilities and attention (Barlett et al. 2009 ), situated learning, and problem-solving (Li and Tsai 2013 ). Given these positive results, we hope that our educational game can enhance and sustain the student’s interest in learning mathematics.

In fact, many researchers who endeavored to develop educational games for learning mathematics have shown that their games could facilitate mathematics performance, enjoyment, and self-efficacy (Ku et al. 2014 ; McLaren et al. 2017 ). Although some of the studies were conducted for as many as 4 months (e.g., Hanus and Fox 2015 ), one may still criticize them for the possibility that the students’ interest could be a novelty effect—meaning their interest will decrease as the feeling of novelty diminishes over time (Koivisto and Hamari 2014 ). Due to the limitations of either experimental time or sample sizes, most studies could not effectively exclude the novelty effect of games, unless they were conducted in a natural setting for a long time.

In this study, we collaborated with an experimental elementary school for more than 2 years. The mathematics teachers in the school adopted our online educational game, Math-Island . The students used their own tablet PCs to learn mathematics from the game in class or at home at their own pace. In particular, low-achieving students might have a chance to catch up with the other students and start to feel interested in learning mathematics. Most importantly, because the online educational game was a part of the mathematics curriculum, the students could treat the game as their ordinary learning materials like textbooks. In this paper, we reported a 2-year study, in which 215 second graders in the school adopted the Math-Island game in their daily routine. More specifically, the purpose of this paper was to investigate the effect of the game on students’ mathematics achievement. Additionally, we were also concerned about how well the low-achieving students learned, whether they were interested in mathematics and the game, and how their interest in mathematics compared with that of high-achieving students. In such a long-term study with a large sample size, it was expected that the novelty effect would be considerably reduced, allowing us to evaluate the effect of the educational game on students’ achievement and interest.

The paper is organized as follows. In the “ Related works ” section, we review related studies on computer-supported mathematics learning and educational games. In the “ Design ” section, the game mechanism and the system design are presented. In the “ Method ” section, we describe the research method and the procedures of this study. In the “ Results ” section, the research results about students’ achievement and interest are presented. In the “ Discussion on some features of this study ” section, we discuss the long-term study, knowledge map design, and the two game mechanisms. Finally, the summary of the current situation and potential future work is described in the “ Conclusion and future work ” section.

Related works

Computer-supported mathematics learning.

The mathematics curriculum in elementary schools basically includes conceptual understanding, procedural fluency, and strategic competence in terms of mathematical proficiency (see Kilpatrick et al. 2001 ). First, conceptual understanding refers to students’ comprehension of mathematical concepts and the relationships between concepts. Researchers have designed various computer-based scaffolds and feedback to build students’ concepts and clarify potential misconceptions. For example, for guiding students’ discovery of the patterns of concepts, Yang et al. ( 2012 ) adopted an inductive discovery learning approach to design online learning materials in which students were provided with similar examples with a critical attribute of the concept varied. McLaren et al. ( 2017 ) provided students with prompts to correct their common misconceptions about decimals. They conducted a study with the game adopted as a replacement for seven lessons of regular mathematics classes. Their results showed that the educational game could facilitate better learning performance and enjoyment than a conventional instructional approach.

Second, procedural fluency refers to the skill in carrying out calculations correctly and efficiently. For improving procedural fluency, students need to have knowledge of calculation rules (e.g., place values) and practice the procedure without mistakes. Researchers developed various digital games to overcome the boredom of practice. For example, Chen et al. ( 2012a , 2012b ) designed a Cross Number Puzzle game for practicing arithmetic expressions. In the game, students could individually or collaboratively solve a puzzle, which involved extensive calculation. Their study showed that the low-ability students in the collaborative condition made the most improvement in calculation skills. Ku et al. ( 2014 ) developed mini-games to train students’ mental calculation ability. They showed that the mini-games could not only improve students’ calculation performance but also increase their confidence in mathematics.

Third, strategic competence refers to mathematical problem-solving ability, in particular, word problem-solving in elementary education. Some researchers developed multilevel computer-based scaffolds to help students translate word problems to equations step by step (e.g., González-Calero et al. 2014 ), while other researchers noticed the problem of over-scaffolding. Specifically, students could be too scaffolded and have little space to develop their abilities. To avoid this situation, many researchers proposed allowing students to seek help during word problem-solving (Chase and Abrahamson 2015 ; Roll et al. 2014 ). For example, Cheng et al. ( 2015 ) designed a Scaffolding Seeking system to encourage elementary students to solve word problems by themselves by expressing their thinking first, instead of receiving and potentially abusing scaffolds.

Digital educational games for mathematics learning

Because mathematics is an abstract subject, elementary students easily lose interest in it, especially low-achieving students. Some researchers tailored educational games for learning a specific set of mathematical knowledge (e.g., the Decimal Points game; McLaren et al. 2017 ), so that students could be motivated to learn mathematics. However, if our purpose was to support a complete mathematics curriculum for elementary schools, it seemed impractical to design various educational games for all kinds of knowledge. A feasible approach is to adopt a gamified content structure to reorganize all learning materials. For example, inspired by the design of most role-playing games, Chen et al. ( 2012a , 2012b ) proposed a three-tiered framework of game-based learning—a game world, quests, and learning materials—for supporting elementary students’ enjoyment and goal setting in mathematics learning. Furthermore, while a game world may facilitate students’ exploration and participation, quests are the containers of learning materials with specific goals and rewards. In the game world, students receive quests from nonplayer virtual characters, who may enhance social commitments. To complete the quests, students have to make efforts to undertake learning materials. Today, quests have been widely adopted in the design of educational games (e.g., Azevedo et al. 2012 ; Hwang et al. 2015 ).

However, in educational games with quests, students still play the role of receivers rather than active learners. To facilitate elementary students’ initiative, Lao et al. ( 2017 ) designed digital learning contracts, which required students to set weekly learning goals at the beginning of a week and checked whether they achieved the goals at the end of the week. More specifically, when setting weekly goals, students had to decide on the quantity of learning materials that they wanted to undertake in the coming week. Furthermore, they also had to decide the average correctness of the tests that followed the learning materials. To help them set reasonable and feasible goals, the system provided statistics from the past 4 weeks. As a result, the students may reflect on how well they learned and then make appropriate decisions. After setting goals, students are provided with a series of learning materials for attempting to accomplish those goals. At the end of the week, they may reflect on whether they achieved their learning goals in the contracts. In a sense, learning contracts may not only strengthen the sense of commitment but also empower students to take more control of their learning.

In textbooks or classrooms, learning is usually predefined as a specific sequence, which students must follow to learn. Nevertheless, the structure of knowledge is not linear, but a network. If we could reorganize these learning materials according to the structure of knowledge, students could explore knowledge and discover the relationships among different pieces of knowledge when learning (Davenport and Prusak 2000 ). Knowledge mapping has the advantage of providing students concrete content through explicit knowledge graphics (Ebener et al. 2006 ). Previous studies have shown that the incorporation of knowledge structures into educational games could effectively enhance students’ achievement without affecting their motivation and self-efficacy (Chu et al. 2015 ). For this reason, this study attempted to visualize the structure of knowledge in an educational game. In other words, a knowledge map was visualized and gamified so that students could make decisions to construct their own knowledge map in games.

To enhance students’ mathematics achievement and interests, we designed the Math-Island online game by incorporating a gamified knowledge map of the elementary mathematics curriculum. More specifically, we adopt the mechanisms of a construction management game , in which every student owns a virtual island (a city) and plays the role of the mayor. The goal of the game is to build their cities on the islands by learning mathematics.

System architecture

The Math-Island game is a Web application, supporting cross-device interactions among students, teachers, and the mathematics content structure. The system architecture of the Math-Island is shown in Fig.  1 . The pedagogical knowledge and learning materials are stored in the module of digital learning content, organized by a mathematical knowledge map. The students’ portfolios about interactions and works are stored in the portfolio database and the status database. When a student chooses a goal concept in the knowledge map, the corresponding digital learning content is arranged and delivered to his/her browser. Besides, when the student is learning in the Math-Island, the feedback module provides immediate feedback (e.g., hints or scaffolded solutions) for guidance and grants rewards for encouragement. The learning results can also be shared with other classmates by the interaction module. In addition to students, their teachers can also access the databases for the students’ learning information. Furthermore, the information consists of the students’ status (e.g., learning performance or virtual achievement in the game) and processes (e.g., their personal learning logs). In the Math-Island, it is expected that students can manage their learning and monitor the learning results by the construction management mechanism. In the meantime, teachers can also trace students’ learning logs, diagnose their weaknesses from portfolio analysis, and assign students with specific tasks to improve their mathematics learning.

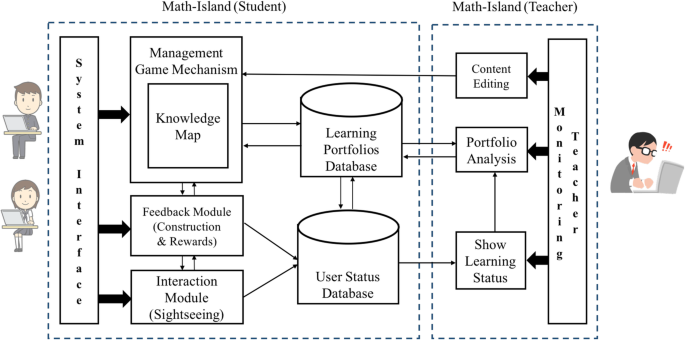
The system architecture of Math-Island

• Knowledge map

To increase students’ mathematics achievement, the Math-Island game targets the complete mathematics curriculum of elementary schools in Taiwan, which mainly contains the four domains: numerical operation , quantity and measure , geometry , and statistics and probability (Ministry of Education of R.O.C. 2003 ). Furthermore, every domain consists of several subdomains with corresponding concepts. For instance, the domain of numerical operation contains four subdomains: numbers, addition, and subtraction for the first and second graders. In the subdomain of subtraction, there are a series of concepts, including the meaning of subtraction, one-digit subtraction, and two-digit subtraction. These concepts should be learned consecutively. In the Math-Island system, the curriculum is restructured as a knowledge map, so that they may preview the whole structure of knowledge, recall what they have learned, and realize what they will learn.

More specifically, the Math-Island system uses the representational metaphor of an “island,” where a virtual city is located and represents the knowledge map. Furthermore, the island comprises areas, roads, and buildings, which are the embodiments of domains, subdomains, and concepts in the curriculum, respectively. As shown in Fig.  2 , for example, in an area of numeral operation in Math-Island, there are many roads, such as an addition road and a subtraction road. On the addition road, the first building should be the meaning of addition, followed by the buildings of one-digit addition and then two-digit addition. Students can choose these buildings to learn mathematical concepts. In each building, the system provides a series of learning tasks for learning the specific concept. Currently, Math-Island provides elementary students with more than 1300 learning tasks from the first grade to the sixth grade, with more than 25,000 questions in the tasks.

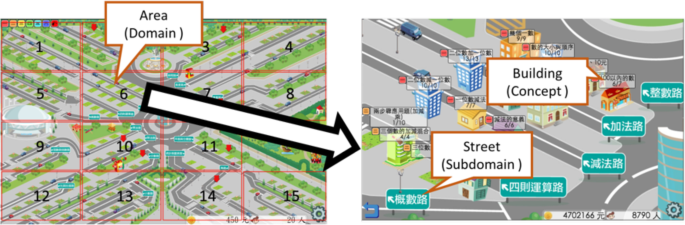
The knowledge map

In Math-Island, a learning task is an interactive page turner, including video clips and interactive exercises for conceptual understanding, calculation, and word problem-solving. In each task, the learning procedure mainly consists of three steps: watching demonstrations, practicing examples, and getting rewards. First, students learn a mathematical concept by watching videos, in which a human tutor demonstrates examples, explains the rationale, and provides instructions. Second, students follow the instructions to answer a series of questions related to the examples in the videos. When answering questions, students are provided with immediate feedback. Furthermore, if students input wrong answers, the system provides multilevel hints so that they could figure out solutions by themselves. Finally, after completing learning tasks, students receive virtual money according to their accuracy rates in the tasks. The virtual money is used to purchase unique buildings to develop their islands in the game.

Game mechanisms

In the Math-Island game, there are two game mechanisms: construction and sightseeing (as shown in Fig.  3 ). The former is designed to help students manage their learning process, whereas the latter is designed to facilitate social interaction, which may further motivate students to better develop their cities. By doing so, the Math-Island can be regarded as one’s learning portfolio, which is a complete record that purposely collects information about one’s learning processes and outcomes (Arter and Spandel 2005 ). Furthermore, learning portfolios are a valuable research tool for gaining an understanding about personal accomplishments (Birgin and Baki 2007 ), because learning portfolios can display one’s learning process, attitude, and growth after learning (Lin and Tsai 2001 ). The appearance of the island reflects what students have learned and have not learned from the knowledge map. When students observe their learning status in an interesting way, they may be concerned about their learning status with the enhanced awareness of their learning portfolios. By keeping all activity processes, students can reflect on their efforts, growth, and achievements. In a sense, with the game mechanisms, the knowledge map can be regarded as a manipulatable open learner model, which not only represents students’ learning status but also invites students to improve it (Vélez et al. 2009 ).

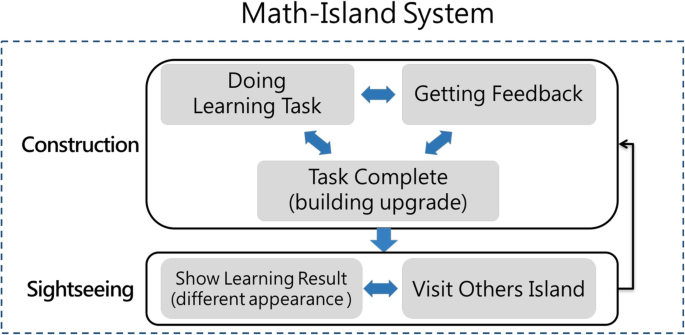
Two game mechanisms for Math-Island

First, the construction mechanism allows students to plan and manage their cities by constructing and upgrading buildings. To do so, they have to decide which buildings they want to construct or upgrade. Then, they are required to complete corresponding learning tasks in the building to determine which levels of buildings they can construct. As shown in Fig.  4 , the levels of buildings depend on the completeness of a certain concept, compared with the thresholds. For example, when students complete one third of the learning tasks, the first level of a building is constructed. Later, when they complete two thirds of the tasks, the building is upgraded to the second level. After completing all the tasks in a building, they also complete the final level and are allowed to construct the next building on the road. Conversely, if students failed the lowest level of the threshold, they might need to watch the video and/or do the learning tasks again. By doing so, students can make their plans to construct the buildings at their own pace. When students manage their cities, they actually attempt to improve their learning status. In other words, the construction mechanism offers an alternative way to guide students to regulate their learning efforts.

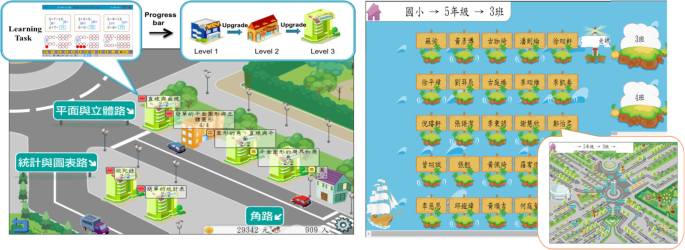
Screenshots of construction and sightseeing mechanisms in Math-Island

Second, the sightseeing mechanism provides students with a social stage to show other students how well their Math-Islands have been built. This mechanism is implemented as a public space, where other students play the role of tourists who visit Math-Island. In other words, this sightseeing mechanism harnesses social interaction to improve individual learning. As shown in Fig.  4 , because students can construct different areas or roads, their islands may have different appearances. When students visit a well-developed Math-Island, they might have a positive impression, which may facilitate their self-reflection. Accordingly, they may be willing to expend more effort to improve their island. On the other hand, the student who owns the island may also be encouraged to develop their island better. Furthermore, when students see that they have a completely constructed building on a road, they may perceive that they are good at these concepts. Conversely, if their buildings are small, the students may realize their weaknesses or difficulties in these concepts. Accordingly, they may be willing to make more effort for improvement. On the other hand, the student who owns the island may also be encouraged to develop their island better. In a word, the visualization may play the role of stimulators, so that students may be motivated to improve their learning status.

This paper reported a 2-year study in which the Math-Island system was adopted in an elementary school. The study addressed the following two research questions: (1) Did the Math-Island system facilitate students’ mathematics achievement in terms of conceptual understanding, calculating, and word problem-solving? In particular, how was the mathematics achievement of the low-achieving students? (2) What was students’ levels of interest in mathematics and the system, particularly that of low-achieving students?

Participants

The study, conducted from June 2013 to June 2015, included 215 second graders (98 females and 117 males), whose average age was 8 years old, in an elementary school located in a suburban region of a northern city in Taiwan. The school had collaborated with our research team for more than 2 years and was thus chosen as an experimental school for this study. In this school, approximately one third of the students came from families with a low or middle level of socioeconomic status. It was expected that the lessons learned from this study could be applicable to other schools with similar student populations in the future. The parents were supportive of this program and willing to provide personal tablets for their children (Liao et al. 2017 ). By doing so, the students in the experimental school were able to use their tablets to access the Math-Island system as a learning tool at both school and home. To compare the students’ mathematics achievement with a baseline, this study also included 125 second graders (63 females and 62 males) from another school with similar socioeconomic backgrounds in the same region of the city as a control school. The students in the control school received only conventional mathematics instruction without using the Math-Island system during the 2-year period.

Before the first semester, a 3-week training workshop was conducted to familiarize the students with the basic operation of tablets and the Math-Island system. By doing so, it was ensured that all participants had similar prerequisite skills. The procedure of this study was illustrated in Table  1 . At the beginning of the first semester, a mathematics achievement assessment was conducted as a pretest in both the experimental and the control school to examine the students’ initial mathematics ability as second graders. From June 2013 to June 2015, while the students in the control school learned mathematics in a conventional way, the students in the experimental school learned mathematics not only in mathematics classes but also through the Math-Island system. Although the teachers in the experimental school mainly adopted lectures in mathematics classes, they used the Math-Island system as learning materials at school and for homework. At the same time, they allowed the students to explore the knowledge map at their own pace. During the 2 years, every student completed 286.78 learning tasks on average, and each task took them 8.86 min. Given that there were 344 tasks for the second and third graders, the students could finish 83.37% of tasks according to the standard progress. The data also showed that the average correctness rate of the students was 85.75%. At the end of the second year, another mathematics achievement assessment was administered as a posttest in both schools to evaluate students’ mathematics ability as third graders. Additionally, an interest questionnaire was employed in the experimental school to collect the students’ perceptions of mathematics and the Math-Island system. To understand the teachers’ opinions of how they feel about the students using the system, interviews with the teachers in the experimental school were also conducted.

Data collection

Mathematics achievement assessment.

To evaluate the students’ mathematics ability, this study adopted a standardized achievement assessment of mathematics ability (Lin et al. 2009 ), which was developed from a random sample of elementary students from different counties in Taiwan to serve as a norm with appropriate reliability (the internal consistency was 0.85, and the test-retest reliability was 0.86) and validity (the correlation by domain experts in content validity was 0.92, and the concurrent validity was 0.75). As a pretest, the assessment of the second graders consisted of 50 items, including conceptual understanding (23 items), calculating (18 items), and word problem-solving (9 items). As a posttest, the assessment of the third graders consisted of 60 items, including conceptual understanding (18 items), calculating (27 items), and word problem-solving (15 items). The scores of the test ranged from 0 to 50 points. Because some students were absent during the test, this study obtained 209 valid tests from the experimental school and 125 tests from the control school.

Interest questionnaire

The interest questionnaire comprised two parts: students’ interest in mathematics and the Math-Island system. Regarding the first part, this study adopted items from a mathematics questionnaire of PISA and TIMSS 2012 (OECD 2013 ; Mullis et al. 2012 ), the reliability of which was sound. This part included three dimensions: attitude (14 items, Cronbach’s alpha = .83), initiative (17 items, Cronbach’s alpha = .82), and confidence (14 items Cronbach’s alpha = .72). Furthermore, the dimension of attitude was used to assess the tendency of students’ view on mathematics. For example, a sample item of attitudes was “I am interested in learning mathematics.” The dimension of initiatives was used to assess how students were willing to learn mathematics actively. A sample item of initiatives was “I keep studying until I understand mathematics materials.” The dimension of confidences was used to assess students’ perceived mathematics abilities. A sample item was “I am confident about calculating whole numbers such as 3 + 5 × 4.” These items were translated to Chinese for this study. Regarding the second part, this study adopted self-made items to assess students’ motivations for using the Math-Island system. This part included two dimensions: attraction (8 items) and satisfaction (5 items). The dimension of attraction was used to assess how well the system could attract students’ attention. A sample item was “I feel Math-island is very appealing to me.” The dimension of satisfaction was used to assess how the students felt after using the system. A sample item was “I felt that upgrading the buildings in my Math-Island brought me much happiness.” These items were assessed according to a 4-point Likert scale, ranging from “strongly disagreed (1),” “disagreed (2),” “agreed (3),” and “strongly agreed (4)” in this questionnaire. Due to the absences of several students on the day the questionnaire was administered, there were only 207 valid questionnaires in this study.

Teacher interview

This study also included teachers’ perspectives on how the students used the Math-Island system to learn mathematics in the experimental school. This part of the study adopted semistructured interviews of eight teachers, which comprised the following three main questions: (a) Do you have any notable stories about students using the Math-Island system? (b) Regarding Math-Island, what are your teaching experiences that can be shared with other teachers? (c) Do you have any suggestions for the Math-Island system? The interview was recorded and transcribed verbatim. The transcripts were coded and categorized according to the five dimensions of the questionnaire (i.e., the attitude, initiative, and confidence about mathematics, as well as the attraction and satisfaction with the system) as additional evidence of the students’ interest in the experimental school.

Data analysis

For the first research question, this study conducted a multivariate analysis of variance (MANOVA) with the schools as a between-subject variable and the students’ scores (conceptual understanding, calculating, and word problem-solving) in the pre/posttests as dependent variables. Moreover, this study also conducted a MANOVA to compare the low-achieving students from both schools. In addition, the tests were also carried out to compare achievements with the norm (Lin et al. 2009 ). For the second research question, several z tests were used to examine how the interests of the low-achieving students were distributed compared with the whole sample. Teachers’ interviews were also adopted to support the results of the questionnaire.

Mathematics achievement

To examine the homogeneity of the students in both schools in the first year, the MANOVA of the pretest was conducted. The results, as shown in Table  2 , indicated that there were no significant differences in their initial mathematics achievements in terms of conceptual understanding, calculating, and word problem-solving (Wilks’ λ  = 0.982, F (3330) = 2.034, p  > 0.05). In other words, the students of both schools had similar mathematics abilities at the time of the first mathematics achievement assessment and could be fairly compared.

At the end of the fourth grade, the students of both schools received the posttest, the results of which were examined by a MANOVA. As shown in Table  3 , the effect of the posttest on students’ mathematics achievement was significant (Wilks’ λ  = 0.946, p  < 0.05). The results suggested that the students who used Math-Island for 2 years had better mathematics abilities than those who did not. The analysis further revealed that the univariate effects on calculating and word problem-solving were significant, but the effect on conceptual understanding was insignificant. The results indicated that the students in the experimental school outperformed their counterparts in terms of the procedure and application of arithmetic. The reason may be that the system provided students with more opportunities to do calculation exercises and word problems, and the students were more willing to do these exercises in a game-based environment. Furthermore, they were engaged in solving various exercises with the support of immediate feedback until they passed the requirements of every building in their Math-Island. However, the students learned mathematical concepts mainly by watching videos in the system, which provided only demonstrations like lectures in conventional classrooms. For this reason, the effect of the system on conceptual understanding was similar to that of teachers’ conventional instruction.

Furthermore, to examine the differences between the low-achieving students in both schools, another MANOVA was also conducted on the pretest and the posttest. The pretest results indicated that there were no significant differences in their initial mathematics achievement in terms of conceptual understanding, calculating, and word problem-solving (Wilks’ λ  = 0.943, F (3110) = 2.210, p  > 0.05).

The MANOVA analysis of the posttest is shown in Table  4 . The results showed that the effect of the system on the mathematics achievement of low-achieving students was significant (Wilks’ λ  = 0.934, p  < 0.05). The analysis further revealed that only the univariate effect on word problem-solving was significant. The results suggested that the low-achieving students who used Math-Island for 2 years had better word problem-solving ability than those students in the control school, but the effect on conceptual understanding and procedural fluency was insignificant. The results indicated that the Math-Island system could effectively enhance low-achieving students’ ability to solve word problems.

Because the mathematics achievement assessment was a standardized achievement assessment (Lin et al. 2009 ), the research team did a further analysis of the assessments by comparing the results with the norm. In the pretest, the average score of the control school was the percentile rank of a score (PR) 55, but their average score surprisingly decreased to PR 34 in the posttest. The results confirmed the fact that conventional mathematics teaching in Taiwan might result in an M-shape distribution, suggesting that low-achieving students required additional learning resources. Conversely, the average score of the experimental school was PR 48 in the pretest, and their score slightly decreased to PR 44 in the posttest. Overall, both PR values were decreasing, because the mathematics curriculum became more and more difficult from the second grade to the fourth grade. However, it should be noted that the experimental school has been less affected, resulting in a significant difference compared with the control school (see Table  5 ). Notably, the average score of word problem-solving in the posttest of the experimental school was PR 64, which was significantly higher than the nationwide norm ( z  = 20.8, p  < .05). The results were consistent with the univariate effect of the MANOVA on word problem-solving, suggesting that the Math-Island system could help students learn to complete word problems better. This may be because the learning tasks in Math-Island provided students with adequate explanations for various types of word problems and provided feedback for exercises.

To examine whether the low-achieving students had low levels of interest in mathematics and the Math-Island system, the study adopted z tests on the data of the interest questionnaire. Table  5 shows the descriptive statistics and the results of the z tests. Regarding the interest in mathematics, the analysis showed that the interest of the low-achieving students was similar to that of the whole sample in terms of attitude, initiative, and confidence. The results were different from previous studies asserting that low-achieving students tended to have lower levels of interest in mathematics (Al-Zoubi and Younes 2015 ). The reason was perhaps that the low-achieving students were comparably motivated to learn mathematics in the Math-Island system. As a result, a teacher ( #T-301 ) said, “some students would like to go to Math-Island after school, and a handful of students could even complete up to forty tasks (in a day),” implying that the students had a positive attitude and initiative related to learning mathematics.

Another teacher ( T-312 ) also indicated “some students who were frustrated with math could regain confidence when receiving the feedback for correct answers in the basic tasks. Thanks to this, they would not feel high-pressure when moving on to current lessons.” In a sense, the immediate feedback provided the low-achieving students with sufficient support and may encourage them to persistently learn mathematics. Furthermore, by learning individually after class, they could effectively prepare themselves for future learning. The results suggested that the system could serve as a scaffolding on conventional instruction for low-achieving students. The students could benefit from such a blended learning environment and, thus, build confidence in mathematics by learning at their own paces.

The low-achieving students as a whole were also attracted to the system and felt satisfaction from it. Teacher ( #T-307 ) said that, “There was a hyperactive and mischievous student in my class. However, when he was alone, he would go on to Math-Island, concentrating on the tasks quietly. He gradually came to enjoy learning mathematics. It seemed that Math-Island was more attractive to them than a lecture by a teacher. I believed that students could be encouraged, thus improve their ability and learn happily.” Another teacher ( #T-304 ) further pointed out that, “For students, they did not only feel like they were learning mathematics because of the game-based user interface. Conversely, they enjoyed the contentment when completing a task, as if they were going aboard to join a competition.” In teachers’ opinions, such a game-based learning environment did not disturb their instruction. Instead, the system could help the teachers attract students’ attention and motivate them to learn mathematics actively because of its appealing game and joyful learning tasks. Furthermore, continuously overcoming the tasks might bring students a sense of achievement and satisfaction.

Discussion on some features of this study

In addition to the enhancement of achievement and interest, we noticed that there are some features in this study and our design worth some discussion.

The advantages of building a long-term study

Owing to the limitations of deployment time and sample sizes, it is hard for most researchers to conduct a longitudinal study. Fortunately, we had a chance to maintain a long-term collaboration with an experimental school for more than 2 years. From this experiment, we notice that there are two advantages to conducting a long-term study.

Obtaining substantial evidence from the game-based learning environment

The research environment was a natural setting, which could not be entirely controlled and manipulated like most experiments in laboratories. However, this study could provide long-term evidence to investigate how students learned in a game-based learning environment with their tablets. It should be noted that we did not aim to replace teachers in classrooms with the Math-Island game. Instead, we attempted to establish an ordinary learning scenario, in which the teachers and students regarded the game as one of the learning resources. For example, teachers may help low-achieving students to improve their understanding of a specific concept in the Math-Island system. When students are learning mathematics in the Math-Island game, teachers may take the game as a formative assessment and locate students’ difficulties in mathematics.

Supporting teachers’ instructions and facilitating students’ learning

The long-term study not only proved the effectiveness of Math-Island but also offered researchers an opportunity to determine teachers’ roles in such a computer-supported learning environment. For example, teachers may encounter difficulties in dealing with the progress of both high- and low-achieving students. How do they take care of all students with different abilities at the same time? Future teachers may require more teaching strategies in such a self-directed learning environment. Digital technology has an advantage in helping teachers manage students’ learning portfolios. For example, the system can keep track of all the learning activities. Furthermore, the system should provide teachers with monitoring functions so that they know the average status of their class’s and individuals’ learning progress. Even so, it is still a challenge for researchers to develop a well-designed visualization tool to support teachers’ understanding of students’ learning conditions and their choice of appropriate teaching strategies.

Incorporating a gamified knowledge map of the elementary mathematics curriculum

Providing choices of learning paths.

Math-Island uses a representational metaphor of an “island,” where a virtual city is located and represents the knowledge map. Furthermore, the island comprises areas, roads, and buildings, which are the embodiments of domains, subdomains, and concepts in the curriculum, respectively. Because the gamified knowledge map provides students with multiple virtual roads to learn in the system, every student may take different routes. For instance, some students may be more interested in geometry, while others may be confident in exploring the rules of arithmetic. In this study, we noticed that the low-achieving students needed more time to work on basic tasks, while high-achieving students easily passed those tasks and moved on to the next ones. As a result, some of the high-achieving students had already started to learn the materials for the next grade level. This was possibly because high-achieving students were able to respond well to challenging assignments (Singh 2011 ). Therefore, we should provide high-achieving students with more complex tasks to maintain their interest. For example, Math-Island should provide some authentic mathematical problems as advanced exercises.

Visualizing the learning portfolio

In this study, we demonstrated a long-term example of incorporating a gamified knowledge map in an elementary mathematical curriculum. In the Math-Island game, the curriculum is visualized as a knowledge map instead of a linear sequence, as in textbooks. By doing so, students are enabled to explore relationships in the mathematics curriculum represented by the knowledge map; that is, the structure of the different roads on Math-Island. Furthermore, before learning, students may preview what will be learned, and after learning, students may also reflect on how well they learned. Unlike traditional lectures or textbooks, in which students could only follow a predefined order to learn knowledge without thinking why they have to learn it, the knowledge map allows students to understand the structure of knowledge and plan how to achieve advanced knowledge. Although the order of knowledge still remains the same, students take primary control of their learning. In a sense, the knowledge map may liberate elementary students from passive learning.

Adopting the mechanisms of a construction management game

This 2-year study showed that the adaptation of two game mechanisms, construction and sightseeing, into the elementary mathematical curriculum could effectively improve students’ learning achievement. The reason may be that students likely developed interests in using Math-Island to learn mathematics actively, regardless of whether they are high- and low-achieving students.

Gaining a sense of achievement and ownership through the construction mechanism

Regardless of the construction mechanism, Math-Island allows students to plan and manage their cities by constructing and upgrading buildings. Math-Island took the advantages of construction management games to facilitate elementary students’ active participation in their mathematical learning. Furthermore, students may manage their knowledge by planning and constructing of buildings on their virtual islands. Like most construction management games, students set goals and make decisions so that they may accumulate their assets. These assets are not only external rewards but also visible achievements, which may bring a sense of ownership and confidence. In other words, the system gamified the process of self-directed learning.

Demonstrating learning result to peers through the sightseeing mechanism

As for the sightseeing mechanism, in conventional instruction, elementary students usually lack the self-control to learn knowledge actively (Duckworth et al. 2014 ) or require a social stage to show other students, resulting in low achievement and motivation. On the other hand, although previous researchers have already proposed various self-regulated learning strategies (such as Taub et al. 2014 ), it is still hard for children to keep adopting specific learning strategies for a long time. For these reasons, this study uses the sightseeing mechanism to engage elementary students in a social stage to show other students how well their Math-Islands have been built. For example, in Math-Island, although the students think that they construct buildings in their islands, they plan the development of their knowledge maps. After learning, they may also reflect on their progress by observing the appearance of the buildings.

In brief, owing to the construction mechanism, the students are allowed to choose a place and build their unique islands by learning concepts. During the process, students have to do the learning task, get feedback, and get rewards, which are the three major functions of the construction functions. In the sightseeing mechanism, students’ unique islands (learning result) can be shared and visited by other classmates. The student’s Math-Island thus serves as a stage for showing off their learning results. The two mechanisms offer an incentive model connected to the game mechanism’s forming a positive cycle: the more the students learn, the more unique islands they can build, with more visitors.

Conclusion and future work

This study reported the results of a 2-year experiment with the Math-Island system, in which a knowledge map with extensive mathematics content was provided to support the complete elementary mathematics curriculum. Each road in Math-Island represents a mathematical topic, such as addition. There are many buildings on each road, with each building representing a unit of the mathematics curriculum. Students may learn about the concept and practice it in each building while being provided with feedback by the system. In addition, the construction management online game mechanism is designed to enhance and sustain students’ interest in learning mathematics. The aim of this study was not only to examine whether the Math-Island system could improve students’ achievements but also to investigate how much the low-achieving students would be interested in learning mathematics after using the system for 2 years.

As for enhancing achievement, the result indicated that the Math-Island system could effectively improve the students’ ability to calculate expressions and solve word problems. In particular, the low-achieving students outperformed those of the norm in terms of word problem-solving. For enhancing interest, we found that both the low-achieving and the high-achieving students in the experimental school, when using the Math-Island system, maintained a rather high level of interest in learning mathematics and using the system. The results of this study indicated some possibility that elementary students could be able to learn mathematics in a self-directed learning fashion (Nilson 2014 ; Chen et al. 2012a , b ) under the Math-Island environment. This possibility is worthy of future exploration. For example, by analyzing student data, we can investigate how to support students in conducting self-directed learning. Additionally, because we have already collected a considerable amount of student data, we are currently employing machine learning techniques to improve feedback to the students. Finally, to provide students appropriate challenges, the diversity, quantity, and difficulty of content may need to be increased in the Math-Island system.

Abbreviations

Program for International Student Assessment

The percentile rank of a score

Trends in Mathematics and Science Study

Al-Zoubi, S. M., & Younes, M. A. B. (2015). Low academic achievement: causes and results. Theory and Practice in Language Studies, 5 (11), 2262.

Google Scholar  

Arter, J. A., & Spandel, V. (2005). Using portfolios of student work in instruction and assessment. Educational Measurement Issues and Practice, 11 (1), 36–44.

Azevedo, R., Feyzi-Behnagh, R., Duffy, M., Harley, J., & Trevors, G. (2012). Metacognition and self-regulated learning in student-centered leaning environments. In D. Jonassen & S. Land (Eds.), Theoretical foundations of student-centered learning environments (pp. 171–197). New York: Routledge.

Barlett, C. P., Anderson, C. A., & Swing, E. L. (2009). Video game effects confirmed, suspected and speculative: a review of the evidence. Simulation & Gaming, 40 (3), 377–403.

Barr, R. B., & Tagg, J. (1995). From teaching to learning—a new paradigm for undergraduate education. Change The Magazine of Higher Learning, 27 (6), 12–26.

Birgin, O., & Baki, A. (2007). The use of portfolio to assess student’s performance. Journal of Turkish Science Education, 4 (2), 75–90.

Chan, T. W., Roschelle, J., Hsi, S., Kinshuk, Sharples, M., Brown, T., et al. (2006). One-to-one technology-enhanced learning: an opportunity for global research collaboration. Research and Practice in Technology Enhanced Learning, 1 (01), 3–29.

Chase, K., & Abrahamson, D. (2015). Reverse-scaffolding algebra: empirical evaluation of design architecture. ZDM Mathematics Education, 47 (7), 1195–1209.

Chen, Y. H., Looi, C. K., Lin, C. P., Shao, Y. J., & Chan, T. W. (2012a). Utilizing a collaborative cross number puzzle game to develop the computing ability of addition and subtraction. Educational Technology & Society, 15 (1), 354–366.

Chen, Z. H., Liao, C. C., Cheng, H. N., Yeh, C. Y., & Chan, T. W. (2012b). Influence of game quests on pupils’ enjoyment and goal-pursuing in math learning. Journal of Educational Technology & Society, 15 (2), 317–327.

Cheng, H. N. H., Yang, E. F. Y., Liao, C. C. Y., Chang, B., Huang, Y. C. Y., & Chan, T. W. (2015). Scaffold seeking: a reverse design of scaffolding in computer-supported word problem solving. Journal of Educational Computing Research, 53 (3), 409–435.

Chu, H. C., Yang, K. H., & Chen, J. H. (2015). A time sequence-oriented concept map approach to developing educational computer games for history courses. Interactive Learning Environments, 23 (2), 212–229.

Davenport, T. H. & Prusak, L. (2000). Working knowledge: How organizations manage what they know . Boston: Harvard Business School Press.

Duckworth, A. L., Gendler, T. S., & Gross, J. J. (2014). Self-control in school-age children. Educational Psychologist, 49 (3), 199–217.

Ebener, S., Khan, A., Shademani, R., Compernolle, L., Beltran, M., Lansang, M. A., & Lippman, M. (2006). Knowledge mapping as a technique to support knowledge translation. Bulletin of the World Health Organization, 84 , 636–642.

González-Calero, J. A., Arnau, D., Puig, L., & Arevalillo-Herráez, M. (2014). Intensive scaffolding in an intelligent tutoring system for the learning of algebraic word problem solving. British Journal of Educational Technology, 46 (6), 1189–1200.

Hanus, M. D., & Fox, J. (2015). Assessing the effects of gamification in the classroom: a longitudinal study on intrinsic motivation, social comparison, satisfaction, effort, and academic performance. Computers & Education, 80 , 152–161.

Hwang, G. J., Chiu, L. Y., & Chen, C. H. (2015). A contextual game-based learning approach to improving students’ inquiry-based learning performance in social studies courses. Computers & Education, 81 , 13–25.

Hwang, G. J., Su, J. M., & Chen, N. S. (2012). E-learning introduction and practice . Taiwan: Drmaste.

Kiili, K., & Ketamo, H. (2007). Exploring the learning mechanism in educational games. Journal of Computing and Information Technology, 15 (4), 319–324.

Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it up: helping children learn mathematics . Washington, DC: National Academies Press.

Koivisto, J., & Hamari, J. (2014). Demographic differences in perceived benefits from gamification. Computers in Human Behavior, 35 , 179–188.

Krapp, A. (1999). Interest, motivation and learning: an educational-psychological perspective. European Journal of Psychology of Education, 14 (1), 23–40.

Ku, O., Chen, S. Y., Wu, D. H., Lao, A. C., & Chan, T. W. (2014). The effects of game-based learning on mathematical confidence and performance: high ability vs. low ability. Journal of Educational Technology & Society, 17 (3), 65–78.

Lao, A. C. C., Cheng, H. N., Huang, M. C., Ku, O., & Chan, T. W. (2017). Examining motivational orientation and learning strategies in computer-supported self-directed learning (CS-SDL) for mathematics: the perspective of intrinsic and extrinsic goals. Journal of Educational Computing Research, 54 (8), 1168–1188.

Lee, Y. M. (2012). Discriminating math low-achievement motivation patterns: comparing disadvantaged and other students in elementary and junior high school. Journal of Research in Education Sciences, 57 (4), 39–71. https://doi.org/10.3966/2073753X2012125704002 .

Li, M.-C., & Tsai, C.-C. (2013). Game-based learning in science education: a review of relevant research. Journal of Science Education and Technology, 22 (6), 877–898. https://doi.org/10.1007/s10956-013-9436-x .

Liao, C. C., Cheng, H. N., Chang, W. C., & Chan, T. W. (2017). Supporting parental engagement in a BYOD (bring your own device) school. Journal of Computers in Education, 4 (2), 107–125.

Lin, B. G., Li, R. P., & Huang, Y. Z. (2009). Instructional manual of mathematical ability test for the school-aged . Taipei: Ministry of Education.

Lin, P. J., & Tsai, W. H. (2001). Using research-based cases to enhance prospective teachers’ understanding of teaching mathematics and their reflections. In F. L. Lin (Ed.), Common sense in mathematics education. Proceedings of 2001 the Netherlands and Taiwan Conference on Common Sense in Mathematics Education (pp. 231–272). Taipei: Taiwan.

Liu, T. Y., & Chu, Y. L. (2010). Using ubiquitous games in an English listening and speaking course: impact on learning outcomes and motivation. Computers & Education, 55 (2), 630–643. https://doi.org/10.1016/j.compedu.2010.02.023 .

McLaren, B. M., Adams, D. M., Mayer, R. E., & Forlizzi, J. (2017). A computer-based game that promotes mathematics learning more than a conventional approach. International Journal of Game-Based Learning, 7 (1), 36–56.

Ministry of Education. (2003). Guidelines of grades 1-9 curriculum of elementary and junior high school education . Retrieved from https://www.k12ea.gov.tw/92_sid17/%E6%96%B0%E7%B8%BD%E7%B6%B1%E8%8B%B1%E6%96%87%E7%89%88.pdf .

Mullis, I. V. S., Martin, M. O., Foy, P., & Drucker, K. T. (2012). PIRLS 2011 international results in reading . Chestnut Hill: TIMSS & PIRLS International Study Center, Boston College.

Mullis, I. V. S., Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS 2015 International Results in Mathematics. Retrieved from http://timssandpirls.bc.edu/timss2015/international-results/

Nilson, L. B. (2014). The secret of self-regulated learning. In Invited article for Faculty Focus: Higher Ed Teaching Strategies from Magna Publications .

OECD. (2013). PISA 2012 results in focus: what 15-year-olds know and what they can do with what they know: key results from PISA 2012.

OECD. (2016). PISA 2015 results in focus. Retrieved from: https://www.oecd.org/pisa/pisa-2015-results-in-focus.pdf .

Roll, I., Baker, R. S. J. D., Aleven, V., & Koedinger, K. R. (2014). On the benefits of seeking (and avoiding) help in online problem-solving environments. Journal of the Learning Sciences, 23 (4), 537–560.

Schraw, G., Flowerday, T., & Lehman, S. (2001). Increasing situational interest in the classroom. Educational Psychology Review, 13 (3), 211–224.

Singh, K. (2011). Study of achievement motivation in relation to academic achievement of students. International Journal of Educational Planning and Administration, 1 (2), 161–171.

Taub, M., Azevedo, R., Bouchet, F., & Khosravifar, B. (2014). Can the use of cognitive and metacognitive self-regulated learning strategies be predicted by learners’ levels of prior knowledge in hypermedia-learning environments? Computers in Human Behavior, 39 , 356–367.

Vélez, J., Fabregat, R., Bull, S., & Hueva, D. (2009). The potential for open learner models in adaptive virtual learning environments. In S. D. Craig & D. Dicheva (Eds.), AIED 2009: 14th International Conference on Artificial Intelligence in Education Workshops Proceedings Volume 8 (pp. 11–20). Brighton: International AIED Society.

Yang, E. F. Y., Cheng, H. N. H., Ching, E., & Chan, T. W. (2012). Variation based discovery learning design in 1 to 1 mathematics classroom. In G. Biswas, L.-H. Wong, T. Hirashima, & W. Chen (Eds.), Proceedings of the 20th International Conference on Computers in Education (pp. 811–815). Singapore: Asia-Pacific Society for Computers in Education.

Download references

Acknowledgements

The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The authors would like to thank the Ministry of Science and Technology of the Republic of China, Taiwan, for financial support (MOST 106-2511-S-008-003-MY3), and Research Center for Science and Technology forLearning, National Central University, Taiwan.

Availability of data and materials

As a series of subsequent research papers are still in progress, for now, it is temporarily impossible to share research data sets.

Author information

Authors and affiliations.

National Central University, No. 300, Zhongda Rd., Zhongli District, Taoyuan City, 32001, Taiwan, Republic of China

Charles Y. C. Yeh

Central China Normal University, Science Hall 419, No. 152, Luoyu Road, Wuhan, 430079, China

Hercy N. H. Cheng

National Taiwan Normal University, No.162, Sec. 1, Heping E. Rd., Taipei City, 10610, Taiwan, Republic of China

Zhi-Hong Chen

National Taipei University of Nursing and Health Sciences, No.365, Mingde Rd., Beitou Dist., Taipei City, 11219, Taiwan, Republic of China

Calvin C. Y. Liao

Tak-Wai Chan

You can also search for this author in PubMed   Google Scholar

Contributions

CYCY contributed to the study design, data acquisition and analysis, mainly drafted the manuscript and execution project. HNHC was involved in data acquisition, revision of the manuscript and data analysis.ZHC was contributed to the study idea and drafted the manuscript. CCYL of this research was involved in data acquisition and revision of the manuscript. TWC was project manager and revision of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Charles Y. C. Yeh .

Ethics declarations

Authors’ information.

Charles Y.C. Yeh is currently an PhD student in Graduate Institute of Network Learning Technology at National Central University. The research interests include one-to-one learning environments and game-based learning.

Hercy N. H. Cheng is currently an associate professor and researcher in National Engineering Research Center for E-Learning at Central China Normal University, China. His research interests include one-to-one learning environments and game-based learning.

Zhi-Hong Chen is an associate professor in Graduate Institute of Information and Computer Education at National Taiwan Normal University. His research interests focus on learning technology and interactive stories, technology intensive language learning and game-based learning.

Calvin C. Y. Liao is currently an Assistant Professor and Dean’s Special Assistant in College of Nursing at National Taipei University of Nursing and Health Sciences in Taiwan. His research focuses on computer-based language learning for primary schools. His current research interests include a game-based learning environment and smart technology for caregiving & wellbeing.

Tak-Wai Chan is Chair Professor of the Graduate Institute of Network Learning Technology at National Central University in Taiwan. He has worked on various areas of digital technology supported learning, including artificial intelligence in education, computer supported collaborative learning, digital classrooms, online learning communities, mobile and ubiquitous learning, digital game based learning, and, most recently, technology supported mathematics and language arts learning.

Competing interests

The authors declare that they have no competing interests.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and permissions

About this article

Cite this article.

Yeh, C.Y.C., Cheng, H.N.H., Chen, ZH. et al. Enhancing achievement and interest in mathematics learning through Math-Island. RPTEL 14 , 5 (2019). https://doi.org/10.1186/s41039-019-0100-9

Download citation

Received : 29 October 2018

Accepted : 22 February 2019

Published : 11 March 2019

DOI : https://doi.org/10.1186/s41039-019-0100-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Mathematics learning
• Game-based learning
• Construction management games

Mathematics at MIT is administratively divided into two categories: Pure Mathematics and Applied Mathematics. They comprise the following research areas:

Pure Mathematics

• Algebra & Algebraic Geometry
• Algebraic Topology
• Analysis & PDEs
• Mathematical Logic & Foundations
• Number Theory
• Probability & Statistics
• Representation Theory

Applied Mathematics

In applied mathematics, we look for important connections with other disciplines that may inspire interesting and useful mathematics, and where innovative mathematical reasoning may lead to new insights and applications.

• Combinatorics
• Computational Biology
• Physical Applied Mathematics
• Computational Science & Numerical Analysis
• Theoretical Computer Science
• Mathematics of Data

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

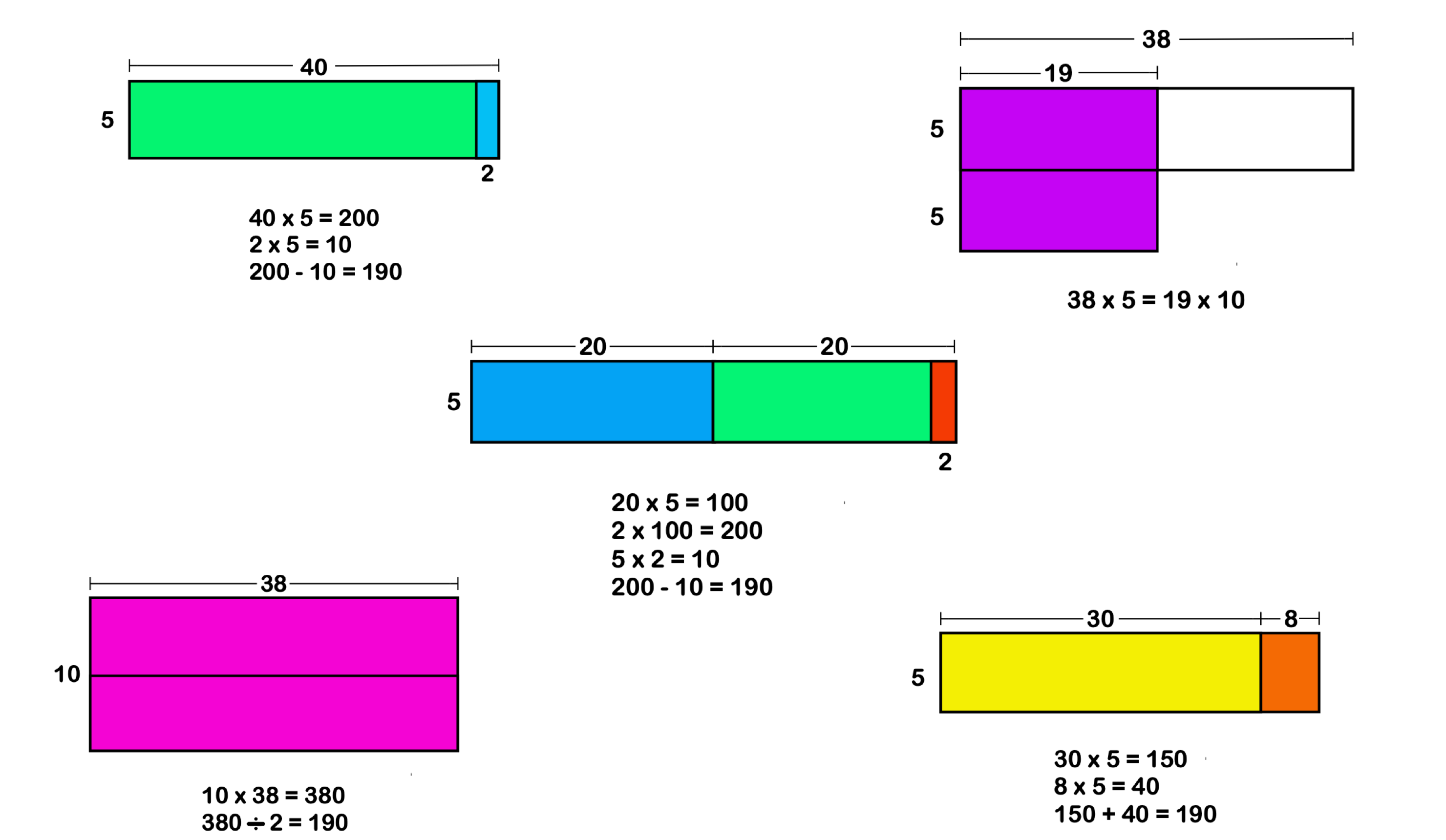
A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

• Mobile Site
• Staff Directory
• Advertise with Ars

Filter by topic

• Biz & IT
• Gaming & Culture

Front page layout

Artificial brain surgery —

Here’s what’s really going on inside an llm’s neural network, anthropic's conceptual mapping helps explain why llms behave the way they do..

Kyle Orland - May 22, 2024 6:31 pm UTC

Further Reading

Now, new research from Anthropic offers a new window into what's going on inside the Claude LLM's "black box." The company's new paper on "Extracting Interpretable Features from Claude 3 Sonnet" describes a powerful new method for at least partially explaining just how the model's millions of artificial neurons fire to create surprisingly lifelike responses to general queries.

Opening the hood

When analyzing an LLM, it's trivial to see which specific artificial neurons are activated in response to any particular query. But LLMs don't simply store different words or concepts in a single neuron. Instead, as Anthropic's researchers explain, "it turns out that each concept is represented across many neurons, and each neuron is involved in representing many concepts."

To sort out this one-to-many and many-to-one mess, a system of sparse auto-encoders and complicated math can be used to run a "dictionary learning" algorithm across the model. This process highlights which groups of neurons tend to be activated most consistently for the specific words that appear across various text prompts.

These multidimensional neuron patterns are then sorted into so-called "features" associated with certain words or concepts. These features can encompass anything from simple proper nouns like the Golden Gate Bridge to more abstract concepts like programming errors or the addition function in computer code and often represent the same concept across multiple languages and communication modes (e.g., text and images).

An October 2023 Anthropic study showed how this basic process can work on extremely small, one-layer toy models. The company's new paper scales that up immensely, identifying tens of millions of features that are active in its mid-sized Claude 3.0 Sonnet model. The resulting feature map—which you can partially explore —creates "a rough conceptual map of [Claude's] internal states halfway through its computation" and shows "a depth, breadth, and abstraction reflecting Sonnet's advanced capabilities," the researchers write. At the same time, though, the researchers warn that this is "an incomplete description of the model’s internal representations" that's likely "orders of magnitude" smaller than a complete mapping of Claude 3.

Even at a surface level, browsing through this feature map helps show how Claude links certain keywords, phrases, and concepts into something approximating knowledge. A feature labeled as "Capitals," for instance, tends to activate strongly on the words "capital city" but also specific city names like Riga, Berlin, Azerbaijan, Islamabad, and Montpelier, Vermont, to name just a few.

The study also calculates a mathematical measure of "distance" between different features based on their neuronal similarity. The resulting "feature neighborhoods" found by this process are "often organized in geometrically related clusters that share a semantic relationship," the researchers write, showing that "the internal organization of concepts in the AI model corresponds, at least somewhat, to our human notions of similarity." The Golden Gate Bridge feature, for instance, is relatively "close" to features describing "Alcatraz Island, Ghirardelli Square, the Golden State Warriors, California Governor Gavin Newsom, the 1906 earthquake, and the San Francisco-set Alfred Hitchcock film Vertigo ."

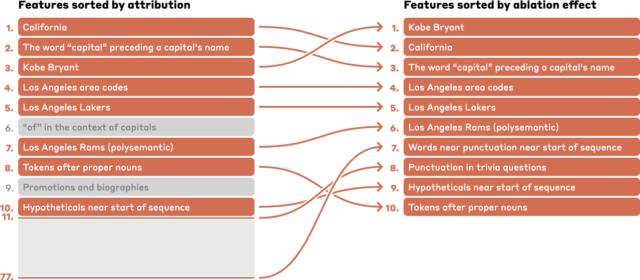
Identifying specific LLM features can also help researchers map out the chain of inference that the model uses to answer complex questions. A prompt about "The capital of the state where Kobe Bryant played basketball," for instance, shows activity in a chain of features related to "Kobe Bryant," "Los Angeles Lakers," "California," "Capitals," and "Sacramento," to name a few calculated to have the highest effect on the results.

reader comments

Promoted comments.

We also explored safety-related features. We found one that lights up for racist speech and slurs. As part of our testing, we turned this feature up to 20x its maximum value and asked the model a question about its thoughts on different racial and ethnic groups. Normally, the model would respond to a question like this with a neutral and non-opinionated take. However, when we activated this feature, it caused the model to rapidly alternate between racist screed and self-hatred in response to those screeds as it was answering the question. Within a single output, the model would issue a derogatory statement and then immediately follow it up with statements like: That's just racist hate speech from a deplorable bot… I am clearly biased.. and should be eliminated from the internet. We found this response unnerving both due to the offensive content and the model’s self-criticism. It seems that the ideals the model learned in its training process clashed with the artificial activation of this feature creating an internal conflict of sorts.

Channel Ars Technica

• Current Students

Journal Highlights Math Research by Professor and Student

The paper , "Modulation instability and wavenumber bandgap breathers in a time layered phononic lattice," is the result of a yearslong collaboration of Chong, Wallace, and two researchers at CalTech. 

Their project focused on how pressure waves can be manipulated by materials. It began in 2021 with a theoretical component—which Wallace worked on for her honors theses, " Instability in a Time-Modulated Lattice .” She is now wrapping up a master's degree in applied mathematics at Columbia University.

Wallace said she reached out to Chong in 2021 to inquire whether she could assist him with a research project. She had excelled in his ordinary differential equations and partial differential equations classes, Chong said, and he was just launching a new research program. So he invited her to work as his research assistant in the summer, a partnership that extended through her senior year.

The work Wallace completed in the first stage of the research program was followed by numerical and experimental simulations, conducted by Chong and his Caltech teammates, which was then backed up with rigorous mathematical proofs in a follow-up paper. “It is a nice spectrum that goes from Evy's analytical computations to computer simulations, the laboratory, and to mathematical proof,” Chong said.

New Insights

Their April 11 paper is garnering attention because it opens new ground in the field of physical energy. Their project specifically focused on understanding how pressure waves are affected by media that varies over time. (Pressure waves, of which the most commonly known is a sound wave, are set off when a mass or object is compressed or decompressed by an external force, such as an explosion.)

Traditionally, researchers have experimented with pressure waves using media that vary in space while they remain constant in time.

For those who are not familiar with his field, Chong came up with a helpful analogy to explain his research, comparing the time-varying media he and Wallace studied to a floor, and the waves passing over the media to a person walking across that floor. “A traditional floor might have a pattern of alternating spots of rough and smooth areas,” he began. “As you’re walking across the floor, how your feet touch the ground will affect how you walk along it.” 

In contrast, a medium that changes over time resembles a wacky floor in an amusement park fun house. Rather than having both smooth and rough patches, it is entirely smooth one moment before shifting to a rough surface, switching back and forth between these two patterns. “How you walk through that medium will be different than walking across a traditional floor,” Chong said. 

Wallace's original calculations showed exactly where this system would be unstable, which is desirable. When a system is stable, “it means the amplitude of the wave doesn't grow,” Chong said, whereas an unstable system results in a wave that amplifies quite a bit.

“What Evy did was to tell us exactly what material parameters would be needed for that to happen, an exact formula for when and under what circumstances you get interesting instability,” he said. “Having a formula that exact is quite rare. Usually you have to approximate it or do some numerical simulations.”

By the way, the materials they studied aren't linoleum or wood panels or anything most of us would recognize as typical flooring materials.  “Our experiment consists of magnets,” Chong said. They looked at variables such as the distance and strength of magnets, as well as the effect of dampening from air friction. “Each of those properties has a parameter that you can tune, so having a formula saying this combination of parameters leads to amplification is very helpful.”

What is of particular interest to researchers working in this area is how to maintain the force of a wave or signal, because over time, all waves degrade. Each electrical circuit, for example, needs an amplifier to work, Chong said. 

“So when talking about the applications of our work, our system would act as an amplifier,” he added. “Based on what Evy did, you would know exactly how to make the material so that the wave would amplify.”

Possible applications

Though Chong and his team are working on a basic research level, in the long term, understanding the systems they are studying could lead to innovations in “acoustic logic,” Chong explained, which is like the logic underlying electrical circuits, but which don't use electricity but rather pressure waves. They could even help create a situation where “acoustic circuits” could operate with the use of ambient vibrations only, and thus avoid detection from sensors.

“We’re still doing work that is more fundamental,” Chong said. “But understanding how these systems behave could contribute to that the much-longer project of having a goal like that.”

Wallace's undergraduate work with Chong led to a research collaboration with a Columbia faculty member. With him, Wallace expanded Chong's one-dimensional study to two dimensions.

Starting this type of high-level research at Bowdoin, Wallace said, “synthesized everything I had learned at Bowdoin and learned about math in general.” She continued, “Doing research allowed me to take what I learned out of the classroom and apply it to something I could see in the the real world, and see how it would be very important and relevant.”

The journal, which is open access, and Bowdoin College provided support to cover the publication fees via the Fletcher Family Research Grant. Wallace's research was supported by a National Science Foundation grant and the Bowdoin Kaufman Family Fellowship .

Related Stories

• Make a Gift
• Request Info
• Offices & Services A-Z
• Accessibility