neural networks and deep learning research papers

• Survey Paper
• Open access
• Published: 31 March 2021

Review of deep learning: concepts, CNN architectures, challenges, applications, future directions

• Laith Alzubaidi   ORCID: orcid.org/0000-0002-7296-5413 1 , 5 ,
• Jinglan Zhang 1 ,
• Amjad J. Humaidi 2 ,
• Ayad Al-Dujaili 3 ,
• Ye Duan 4 ,
• Omran Al-Shamma 5 ,
• J. Santamaría 6 ,
• Mohammed A. Fadhel 7 ,
• Muthana Al-Amidie 4 &
• Laith Farhan 8  

Journal of Big Data volume  8 , Article number:  53 ( 2021 ) Cite this article

413k Accesses

2358 Citations

37 Altmetric

Metrics details

In the last few years, the deep learning (DL) computing paradigm has been deemed the Gold Standard in the machine learning (ML) community. Moreover, it has gradually become the most widely used computational approach in the field of ML, thus achieving outstanding results on several complex cognitive tasks, matching or even beating those provided by human performance. One of the benefits of DL is the ability to learn massive amounts of data. The DL field has grown fast in the last few years and it has been extensively used to successfully address a wide range of traditional applications. More importantly, DL has outperformed well-known ML techniques in many domains, e.g., cybersecurity, natural language processing, bioinformatics, robotics and control, and medical information processing, among many others. Despite it has been contributed several works reviewing the State-of-the-Art on DL, all of them only tackled one aspect of the DL, which leads to an overall lack of knowledge about it. Therefore, in this contribution, we propose using a more holistic approach in order to provide a more suitable starting point from which to develop a full understanding of DL. Specifically, this review attempts to provide a more comprehensive survey of the most important aspects of DL and including those enhancements recently added to the field. In particular, this paper outlines the importance of DL, presents the types of DL techniques and networks. It then presents convolutional neural networks (CNNs) which the most utilized DL network type and describes the development of CNNs architectures together with their main features, e.g., starting with the AlexNet network and closing with the High-Resolution network (HR.Net). Finally, we further present the challenges and suggested solutions to help researchers understand the existing research gaps. It is followed by a list of the major DL applications. Computational tools including FPGA, GPU, and CPU are summarized along with a description of their influence on DL. The paper ends with the evolution matrix, benchmark datasets, and summary and conclusion.

Introduction

Recently, machine learning (ML) has become very widespread in research and has been incorporated in a variety of applications, including text mining, spam detection, video recommendation, image classification, and multimedia concept retrieval [ 1 , 2 , 3 , 4 , 5 , 6 ]. Among the different ML algorithms, deep learning (DL) is very commonly employed in these applications [ 7 , 8 , 9 ]. Another name for DL is representation learning (RL). The continuing appearance of novel studies in the fields of deep and distributed learning is due to both the unpredictable growth in the ability to obtain data and the amazing progress made in the hardware technologies, e.g. High Performance Computing (HPC) [ 10 ].

DL is derived from the conventional neural network but considerably outperforms its predecessors. Moreover, DL employs transformations and graph technologies simultaneously in order to build up multi-layer learning models. The most recently developed DL techniques have obtained good outstanding performance across a variety of applications, including audio and speech processing, visual data processing, natural language processing (NLP), among others [ 11 , 12 , 13 , 14 ].

Usually, the effectiveness of an ML algorithm is highly dependent on the integrity of the input-data representation. It has been shown that a suitable data representation provides an improved performance when compared to a poor data representation. Thus, a significant research trend in ML for many years has been feature engineering, which has informed numerous research studies. This approach aims at constructing features from raw data. In addition, it is extremely field-specific and frequently requires sizable human effort. For instance, several types of features were introduced and compared in the computer vision context, such as, histogram of oriented gradients (HOG) [ 15 ], scale-invariant feature transform (SIFT) [ 16 ], and bag of words (BoW) [ 17 ]. As soon as a novel feature is introduced and is found to perform well, it becomes a new research direction that is pursued over multiple decades.

Relatively speaking, feature extraction is achieved in an automatic way throughout the DL algorithms. This encourages researchers to extract discriminative features using the smallest possible amount of human effort and field knowledge [ 18 ]. These algorithms have a multi-layer data representation architecture, in which the first layers extract the low-level features while the last layers extract the high-level features. Note that artificial intelligence (AI) originally inspired this type of architecture, which simulates the process that occurs in core sensorial regions within the human brain. Using different scenes, the human brain can automatically extract data representation. More specifically, the output of this process is the classified objects, while the received scene information represents the input. This process simulates the working methodology of the human brain. Thus, it emphasizes the main benefit of DL.

In the field of ML, DL, due to its considerable success, is currently one of the most prominent research trends. In this paper, an overview of DL is presented that adopts various perspectives such as the main concepts, architectures, challenges, applications, computational tools and evolution matrix. Convolutional neural network (CNN) is one of the most popular and used of DL networks [ 19 , 20 ]. Because of CNN, DL is very popular nowadays. The main advantage of CNN compared to its predecessors is that it automatically detects the significant features without any human supervision which made it the most used. Therefore, we have dug in deep with CNN by presenting the main components of it. Furthermore, we have elaborated in detail the most common CNN architectures, starting with the AlexNet network and ending with the High-Resolution network (HR.Net).

Several published DL review papers have been presented in the last few years. However, all of them have only been addressed one side focusing on one application or topic such as the review of CNN architectures [ 21 ], DL for classification of plant diseases [ 22 ], DL for object detection [ 23 ], DL applications in medical image analysis [ 24 ], and etc. Although these reviews present good topics, they do not provide a full understanding of DL topics such as concepts, detailed research gaps, computational tools, and DL applications. First, It is required to understand DL aspects including concepts, challenges, and applications then going deep in the applications. To achieve that, it requires extensive time and a large number of research papers to learn about DL including research gaps and applications. Therefore, we propose a deep review of DL to provide a more suitable starting point from which to develop a full understanding of DL from one review paper. The motivation behinds our review was to cover the most important aspect of DL including open challenges, applications, and computational tools perspective. Furthermore, our review can be the first step towards other DL topics.

The main aim of this review is to present the most important aspects of DL to make it easy for researchers and students to have a clear image of DL from single review paper. This review will further advance DL research by helping people discover more about recent developments in the field. Researchers would be allowed to decide the more suitable direction of work to be taken in order to provide more accurate alternatives to the field. Our contributions are outlined as follows:

This is the first review that almost provides a deep survey of the most important aspects of deep learning. This review helps researchers and students to have a good understanding from one paper.

We explain CNN in deep which the most popular deep learning algorithm by describing the concepts, theory, and state-of-the-art architectures.

We review current challenges (limitations) of Deep Learning including lack of training data, Imbalanced Data, Interpretability of data, Uncertainty scaling, Catastrophic forgetting, Model compression, Overfitting, Vanishing gradient problem, Exploding Gradient Problem, and Underspecification. We additionally discuss the proposed solutions tackling these issues.

We provide an exhaustive list of medical imaging applications with deep learning by categorizing them based on the tasks by starting with classification and ending with registration.

We discuss the computational approaches (CPU, GPU, FPGA) by comparing the influence of each tool on deep learning algorithms.

The rest of the paper is organized as follows: “ Survey methodology ” section describes The survey methodology. “ Background ” section presents the background. “ Classification of DL approaches ” section defines the classification of DL approaches. “ Types of DL networks ” section displays types of DL networks. “ CNN architectures ” section shows CNN Architectures. “ Challenges (limitations) of deep learning and alternate solutions ” section details the challenges of DL and alternate solutions. “ Applications of deep learning ” section outlines the applications of DL. “ Computational approaches ” section explains the influence of computational approaches (CPU, GPU, FPGA) on DL. “ Evaluation metrics ” section presents the evaluation metrics. “ Frameworks and datasets ” section lists frameworks and datasets. “ Summary and conclusion ” section presents the summary and conclusion.

Survey methodology

We have reviewed the significant research papers in the field published during 2010–2020, mainly from the years of 2020 and 2019 with some papers from 2021. The main focus was papers from the most reputed publishers such as IEEE, Elsevier, MDPI, Nature, ACM, and Springer. Some papers have been selected from ArXiv. We have reviewed more than 300 papers on various DL topics. There are 108 papers from the year 2020, 76 papers from the year 2019, and 48 papers from the year 2018. This indicates that this review focused on the latest publications in the field of DL. The selected papers were analyzed and reviewed to (1) list and define the DL approaches and network types, (2) list and explain CNN architectures, (3) present the challenges of DL and suggest the alternate solutions, (4) assess the applications of DL, (5) assess computational approaches. The most keywords used for search criteria for this review paper are (“Deep Learning”), (“Machine Learning”), (“Convolution Neural Network”), (“Deep Learning” AND “Architectures”), ((“Deep Learning”) AND (“Image”) AND (“detection” OR “classification” OR “segmentation” OR “Localization”)), (“Deep Learning” AND “detection” OR “classification” OR “segmentation” OR “Localization”), (“Deep Learning” AND “CPU” OR “GPU” OR “FPGA”), (“Deep Learning” AND “Transfer Learning”), (“Deep Learning” AND “Imbalanced Data”), (“Deep Learning” AND “Interpretability of data”), (“Deep Learning” AND “Overfitting”), (“Deep Learning” AND “Underspecification”). Figure  1 shows our search structure of the survey paper. Table  1 presents the details of some of the journals that have been cited in this review paper.

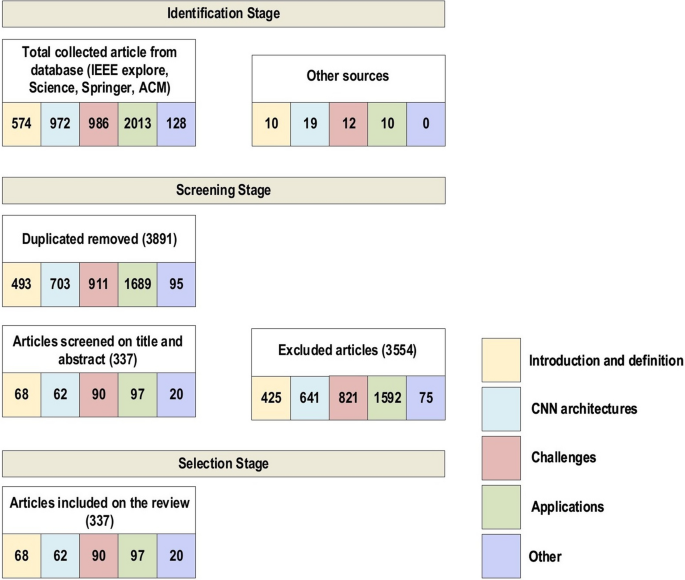
Search framework

This section will present a background of DL. We begin with a quick introduction to DL, followed by the difference between DL and ML. We then show the situations that require DL. Finally, we present the reasons for applying DL.

DL, a subset of ML (Fig.  2 ), is inspired by the information processing patterns found in the human brain. DL does not require any human-designed rules to operate; rather, it uses a large amount of data to map the given input to specific labels. DL is designed using numerous layers of algorithms (artificial neural networks, or ANNs), each of which provides a different interpretation of the data that has been fed to them [ 18 , 25 ].

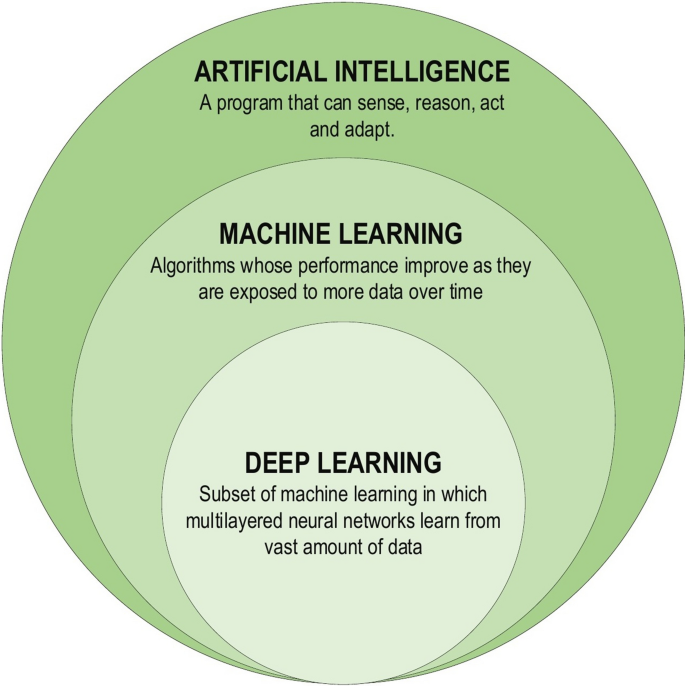
Deep learning family

Achieving the classification task using conventional ML techniques requires several sequential steps, specifically pre-processing, feature extraction, wise feature selection, learning, and classification. Furthermore, feature selection has a great impact on the performance of ML techniques. Biased feature selection may lead to incorrect discrimination between classes. Conversely, DL has the ability to automate the learning of feature sets for several tasks, unlike conventional ML methods [ 18 , 26 ]. DL enables learning and classification to be achieved in a single shot (Fig.  3 ). DL has become an incredibly popular type of ML algorithm in recent years due to the huge growth and evolution of the field of big data [ 27 , 28 ]. It is still in continuous development regarding novel performance for several ML tasks [ 22 , 29 , 30 , 31 ] and has simplified the improvement of many learning fields [ 32 , 33 ], such as image super-resolution [ 34 ], object detection [ 35 , 36 ], and image recognition [ 30 , 37 ]. Recently, DL performance has come to exceed human performance on tasks such as image classification (Fig.  4 ).

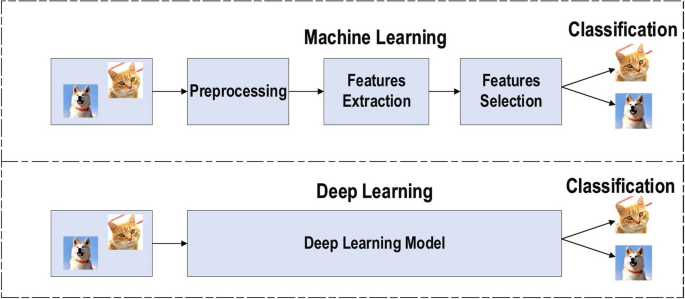
The difference between deep learning and traditional machine learning

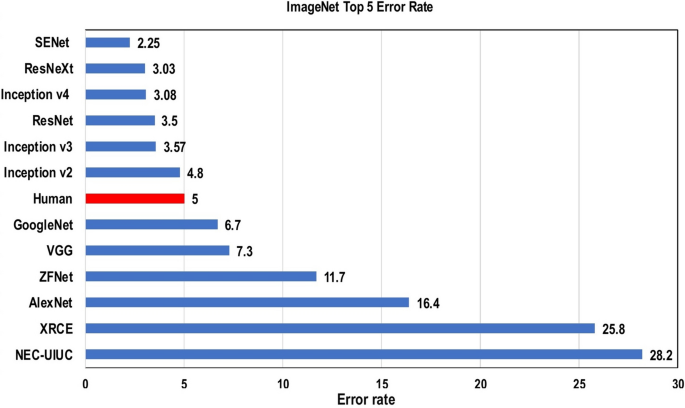
Deep learning performance compared to human

Nearly all scientific fields have felt the impact of this technology. Most industries and businesses have already been disrupted and transformed through the use of DL. The leading technology and economy-focused companies around the world are in a race to improve DL. Even now, human-level performance and capability cannot exceed that the performance of DL in many areas, such as predicting the time taken to make car deliveries, decisions to certify loan requests, and predicting movie ratings [ 38 ]. The winners of the 2019 “Nobel Prize” in computing, also known as the Turing Award, were three pioneers in the field of DL (Yann LeCun, Geoffrey Hinton, and Yoshua Bengio) [ 39 ]. Although a large number of goals have been achieved, there is further progress to be made in the DL context. In fact, DL has the ability to enhance human lives by providing additional accuracy in diagnosis, including estimating natural disasters [ 40 ], the discovery of new drugs [ 41 ], and cancer diagnosis [ 42 , 43 , 44 ]. Esteva et al. [ 45 ] found that a DL network has the same ability to diagnose the disease as twenty-one board-certified dermatologists using 129,450 images of 2032 diseases. Furthermore, in grading prostate cancer, US board-certified general pathologists achieved an average accuracy of 61%, while the Google AI [ 44 ] outperformed these specialists by achieving an average accuracy of 70%. In 2020, DL is playing an increasingly vital role in early diagnosis of the novel coronavirus (COVID-19) [ 29 , 46 , 47 , 48 ]. DL has become the main tool in many hospitals around the world for automatic COVID-19 classification and detection using chest X-ray images or other types of images. We end this section by the saying of AI pioneer Geoffrey Hinton “Deep learning is going to be able to do everything”.

When to apply deep learning

Machine intelligence is useful in many situations which is equal or better than human experts in some cases [ 49 , 50 , 51 , 52 ], meaning that DL can be a solution to the following problems:

Cases where human experts are not available.

Cases where humans are unable to explain decisions made using their expertise (language understanding, medical decisions, and speech recognition).

Cases where the problem solution updates over time (price prediction, stock preference, weather prediction, and tracking).

Cases where solutions require adaptation based on specific cases (personalization, biometrics).

Cases where size of the problem is extremely large and exceeds our inadequate reasoning abilities (sentiment analysis, matching ads to Facebook, calculation webpage ranks).

Why deep learning?

Several performance features may answer this question, e.g

Universal Learning Approach: Because DL has the ability to perform in approximately all application domains, it is sometimes referred to as universal learning.

Robustness: In general, precisely designed features are not required in DL techniques. Instead, the optimized features are learned in an automated fashion related to the task under consideration. Thus, robustness to the usual changes of the input data is attained.

Generalization: Different data types or different applications can use the same DL technique, an approach frequently referred to as transfer learning (TL) which explained in the latter section. Furthermore, it is a useful approach in problems where data is insufficient.

Scalability: DL is highly scalable. ResNet [ 37 ], which was invented by Microsoft, comprises 1202 layers and is frequently applied at a supercomputing scale. Lawrence Livermore National Laboratory (LLNL), a large enterprise working on evolving frameworks for networks, adopted a similar approach, where thousands of nodes can be implemented [ 53 ].

Classification of DL approaches

DL techniques are classified into three major categories: unsupervised, partially supervised (semi-supervised) and supervised. Furthermore, deep reinforcement learning (DRL), also known as RL, is another type of learning technique, which is mostly considered to fall into the category of partially supervised (and occasionally unsupervised) learning techniques.

Deep supervised learning

Deep semi-supervised learning.

In this technique, the learning process is based on semi-labeled datasets. Occasionally, generative adversarial networks (GANs) and DRL are employed in the same way as this technique. In addition, RNNs, which include GRUs and LSTMs, are also employed for partially supervised learning. One of the advantages of this technique is to minimize the amount of labeled data needed. On other the hand, One of the disadvantages of this technique is irrelevant input feature present training data could furnish incorrect decisions. Text document classifier is one of the most popular example of an application of semi-supervised learning. Due to difficulty of obtaining a large amount of labeled text documents, semi-supervised learning is ideal for text document classification task.

Deep unsupervised learning

This technique makes it possible to implement the learning process in the absence of available labeled data (i.e. no labels are required). Here, the agent learns the significant features or interior representation required to discover the unidentified structure or relationships in the input data. Techniques of generative networks, dimensionality reduction and clustering are frequently counted within the category of unsupervised learning. Several members of the DL family have performed well on non-linear dimensionality reduction and clustering tasks; these include restricted Boltzmann machines, auto-encoders and GANs as the most recently developed techniques. Moreover, RNNs, which include GRUs and LSTM approaches, have also been employed for unsupervised learning in a wide range of applications. The main disadvantages of unsupervised learning are unable to provide accurate information concerning data sorting and computationally complex. One of the most popular unsupervised learning approaches is clustering [ 54 ].

Deep reinforcement learning

For solving a task, the selection of the type of reinforcement learning that needs to be performed is based on the space or the scope of the problem. For example, DRL is the best way for problems involving many parameters to be optimized. By contrast, derivative-free reinforcement learning is a technique that performs well for problems with limited parameters. Some of the applications of reinforcement learning are business strategy planning and robotics for industrial automation. The main drawback of Reinforcement Learning is that parameters may influence the speed of learning. Here are the main motivations for utilizing Reinforcement Learning:

It assists you to identify which action produces the highest reward over a longer period.

It assists you to discover which situation requires action.

It also enables it to figure out the best approach for reaching large rewards.

Reinforcement Learning also gives the learning agent a reward function.

Reinforcement Learning can’t utilize in all the situation such as:

In case there is sufficient data to resolve the issue with supervised learning techniques.

Reinforcement Learning is computing-heavy and time-consuming. Specially when the workspace is large.

Types of DL networks

The most famous types of deep learning networks are discussed in this section: these include recursive neural networks (RvNNs), RNNs, and CNNs. RvNNs and RNNs were briefly explained in this section while CNNs were explained in deep due to the importance of this type. Furthermore, it is the most used in several applications among other networks.

Recursive neural networks

RvNN can achieve predictions in a hierarchical structure also classify the outputs utilizing compositional vectors [ 57 ]. Recursive auto-associative memory (RAAM) [ 58 ] is the primary inspiration for the RvNN development. The RvNN architecture is generated for processing objects, which have randomly shaped structures like graphs or trees. This approach generates a fixed-width distributed representation from a variable-size recursive-data structure. The network is trained using an introduced back-propagation through structure (BTS) learning system [ 58 ]. The BTS system tracks the same technique as the general-back propagation algorithm and has the ability to support a treelike structure. Auto-association trains the network to regenerate the input-layer pattern at the output layer. RvNN is highly effective in the NLP context. Socher et al. [ 59 ] introduced RvNN architecture designed to process inputs from a variety of modalities. These authors demonstrate two applications for classifying natural language sentences: cases where each sentence is split into words and nature images, and cases where each image is separated into various segments of interest. RvNN computes a likely pair of scores for merging and constructs a syntactic tree. Furthermore, RvNN calculates a score related to the merge plausibility for every pair of units. Next, the pair with the largest score is merged within a composition vector. Following every merge, RvNN generates (a) a larger area of numerous units, (b) a compositional vector of the area, and (c) a label for the class (for instance, a noun phrase will become the class label for the new area if two units are noun words). The compositional vector for the entire area is the root of the RvNN tree structure. An example RvNN tree is shown in Fig.  5 . RvNN has been employed in several applications [ 60 , 61 , 62 ].

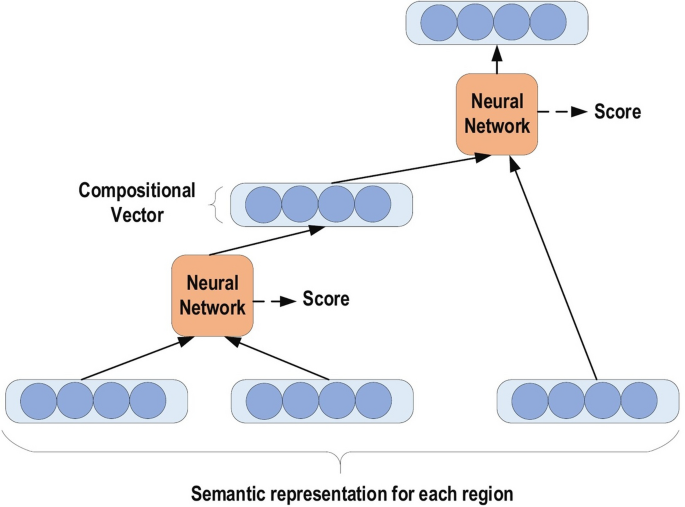
An example of RvNN tree

Recurrent neural networks

RNNs are a commonly employed and familiar algorithm in the discipline of DL [ 63 , 64 , 65 ]. RNN is mainly applied in the area of speech processing and NLP contexts [ 66 , 67 ]. Unlike conventional networks, RNN uses sequential data in the network. Since the embedded structure in the sequence of the data delivers valuable information, this feature is fundamental to a range of different applications. For instance, it is important to understand the context of the sentence in order to determine the meaning of a specific word in it. Thus, it is possible to consider the RNN as a unit of short-term memory, where x represents the input layer, y is the output layer, and s represents the state (hidden) layer. For a given input sequence, a typical unfolded RNN diagram is illustrated in Fig.  6 . Pascanu et al. [ 68 ] introduced three different types of deep RNN techniques, namely “Hidden-to-Hidden”, “Hidden-to-Output”, and “Input-to-Hidden”. A deep RNN is introduced that lessens the learning difficulty in the deep network and brings the benefits of a deeper RNN based on these three techniques.

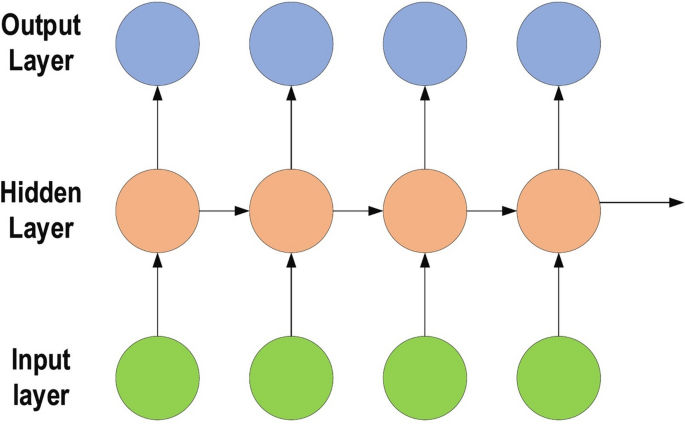
Typical unfolded RNN diagram

However, RNN’s sensitivity to the exploding gradient and vanishing problems represent one of the main issues with this approach [ 69 ]. More specifically, during the training process, the reduplications of several large or small derivatives may cause the gradients to exponentially explode or decay. With the entrance of new inputs, the network stops thinking about the initial ones; therefore, this sensitivity decays over time. Furthermore, this issue can be handled using LSTM [ 70 ]. This approach offers recurrent connections to memory blocks in the network. Every memory block contains a number of memory cells, which have the ability to store the temporal states of the network. In addition, it contains gated units for controlling the flow of information. In very deep networks [ 37 ], residual connections also have the ability to considerably reduce the impact of the vanishing gradient issue which explained in later sections. CNN is considered to be more powerful than RNN. RNN includes less feature compatibility when compared to CNN.

Convolutional neural networks

In the field of DL, the CNN is the most famous and commonly employed algorithm [ 30 , 71 , 72 , 73 , 74 , 75 ]. The main benefit of CNN compared to its predecessors is that it automatically identifies the relevant features without any human supervision [ 76 ]. CNNs have been extensively applied in a range of different fields, including computer vision [ 77 ], speech processing [ 78 ], Face Recognition [ 79 ], etc. The structure of CNNs was inspired by neurons in human and animal brains, similar to a conventional neural network. More specifically, in a cat’s brain, a complex sequence of cells forms the visual cortex; this sequence is simulated by the CNN [ 80 ]. Goodfellow et al. [ 28 ] identified three key benefits of the CNN: equivalent representations, sparse interactions, and parameter sharing. Unlike conventional fully connected (FC) networks, shared weights and local connections in the CNN are employed to make full use of 2D input-data structures like image signals. This operation utilizes an extremely small number of parameters, which both simplifies the training process and speeds up the network. This is the same as in the visual cortex cells. Notably, only small regions of a scene are sensed by these cells rather than the whole scene (i.e., these cells spatially extract the local correlation available in the input, like local filters over the input).

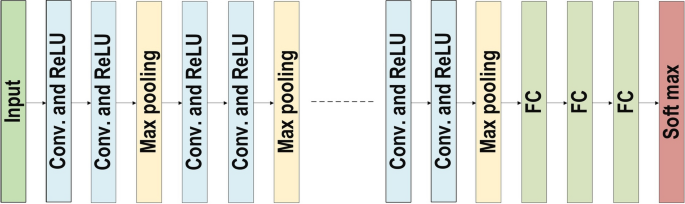
A commonly used type of CNN, which is similar to the multi-layer perceptron (MLP), consists of numerous convolution layers preceding sub-sampling (pooling) layers, while the ending layers are FC layers. An example of CNN architecture for image classification is illustrated in Fig.  7 .

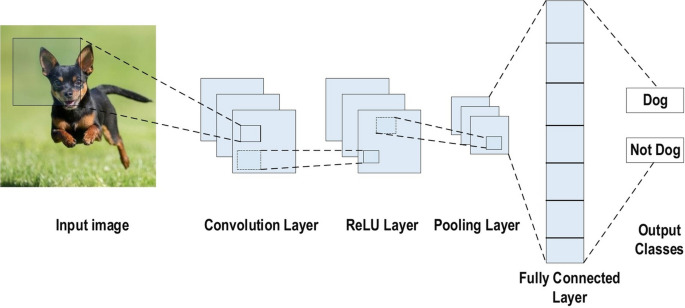
An example of CNN architecture for image classification

The input x of each layer in a CNN model is organized in three dimensions: height, width, and depth, or \(m \times m \times r\) , where the height (m) is equal to the width. The depth is also referred to as the channel number. For example, in an RGB image, the depth (r) is equal to three. Several kernels (filters) available in each convolutional layer are denoted by k and also have three dimensions ( \(n \times n \times q\) ), similar to the input image; here, however, n must be smaller than m , while q is either equal to or smaller than r . In addition, the kernels are the basis of the local connections, which share similar parameters (bias \(b^{k}\) and weight \(W^{k}\) ) for generating k feature maps \(h^{k}\) with a size of ( \(m-n-1\) ) each and are convolved with input, as mentioned above. The convolution layer calculates a dot product between its input and the weights as in Eq. 1 , similar to NLP, but the inputs are undersized areas of the initial image size. Next, by applying the nonlinearity or an activation function to the convolution-layer output, we obtain the following:

The next step is down-sampling every feature map in the sub-sampling layers. This leads to a reduction in the network parameters, which accelerates the training process and in turn enables handling of the overfitting issue. For all feature maps, the pooling function (e.g. max or average) is applied to an adjacent area of size \(p \times p\) , where p is the kernel size. Finally, the FC layers receive the mid- and low-level features and create the high-level abstraction, which represents the last-stage layers as in a typical neural network. The classification scores are generated using the ending layer [e.g. support vector machines (SVMs) or softmax]. For a given instance, every score represents the probability of a specific class.

Benefits of employing CNNs

The benefits of using CNNs over other traditional neural networks in the computer vision environment are listed as follows:

The main reason to consider CNN is the weight sharing feature, which reduces the number of trainable network parameters and in turn helps the network to enhance generalization and to avoid overfitting.

Concurrently learning the feature extraction layers and the classification layer causes the model output to be both highly organized and highly reliant on the extracted features.

Large-scale network implementation is much easier with CNN than with other neural networks.

The CNN architecture consists of a number of layers (or so-called multi-building blocks). Each layer in the CNN architecture, including its function, is described in detail below.

Convolutional Layer: In CNN architecture, the most significant component is the convolutional layer. It consists of a collection of convolutional filters (so-called kernels). The input image, expressed as N-dimensional metrics, is convolved with these filters to generate the output feature map.

Kernel definition: A grid of discrete numbers or values describes the kernel. Each value is called the kernel weight. Random numbers are assigned to act as the weights of the kernel at the beginning of the CNN training process. In addition, there are several different methods used to initialize the weights. Next, these weights are adjusted at each training era; thus, the kernel learns to extract significant features.

Convolutional Operation: Initially, the CNN input format is described. The vector format is the input of the traditional neural network, while the multi-channeled image is the input of the CNN. For instance, single-channel is the format of the gray-scale image, while the RGB image format is three-channeled. To understand the convolutional operation, let us take an example of a \(4 \times 4\) gray-scale image with a \(2 \times 2\) random weight-initialized kernel. First, the kernel slides over the whole image horizontally and vertically. In addition, the dot product between the input image and the kernel is determined, where their corresponding values are multiplied and then summed up to create a single scalar value, calculated concurrently. The whole process is then repeated until no further sliding is possible. Note that the calculated dot product values represent the feature map of the output. Figure  8 graphically illustrates the primary calculations executed at each step. In this figure, the light green color represents the \(2 \times 2\) kernel, while the light blue color represents the similar size area of the input image. Both are multiplied; the end result after summing up the resulting product values (marked in a light orange color) represents an entry value to the output feature map.

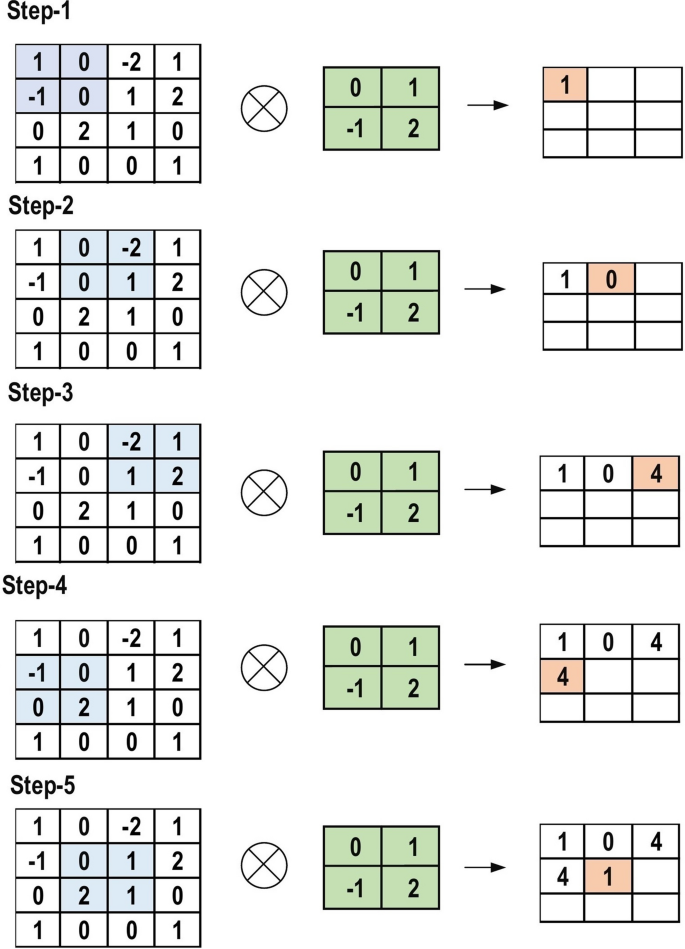
The primary calculations executed at each step of convolutional layer

However, padding to the input image is not applied in the previous example, while a stride of one (denoted for the selected step-size over all vertical or horizontal locations) is applied to the kernel. Note that it is also possible to use another stride value. In addition, a feature map of lower dimensions is obtained as a result of increasing the stride value.

On the other hand, padding is highly significant to determining border size information related to the input image. By contrast, the border side-features moves carried away very fast. By applying padding, the size of the input image will increase, and in turn, the size of the output feature map will also increase. Core Benefits of Convolutional Layers.

Sparse Connectivity: Each neuron of a layer in FC neural networks links with all neurons in the following layer. By contrast, in CNNs, only a few weights are available between two adjacent layers. Thus, the number of required weights or connections is small, while the memory required to store these weights is also small; hence, this approach is memory-effective. In addition, matrix operation is computationally much more costly than the dot (.) operation in CNN.

Weight Sharing: There are no allocated weights between any two neurons of neighboring layers in CNN, as the whole weights operate with one and all pixels of the input matrix. Learning a single group of weights for the whole input will significantly decrease the required training time and various costs, as it is not necessary to learn additional weights for each neuron.

Pooling Layer: The main task of the pooling layer is the sub-sampling of the feature maps. These maps are generated by following the convolutional operations. In other words, this approach shrinks large-size feature maps to create smaller feature maps. Concurrently, it maintains the majority of the dominant information (or features) in every step of the pooling stage. In a similar manner to the convolutional operation, both the stride and the kernel are initially size-assigned before the pooling operation is executed. Several types of pooling methods are available for utilization in various pooling layers. These methods include tree pooling, gated pooling, average pooling, min pooling, max pooling, global average pooling (GAP), and global max pooling. The most familiar and frequently utilized pooling methods are the max, min, and GAP pooling. Figure  9 illustrates these three pooling operations.

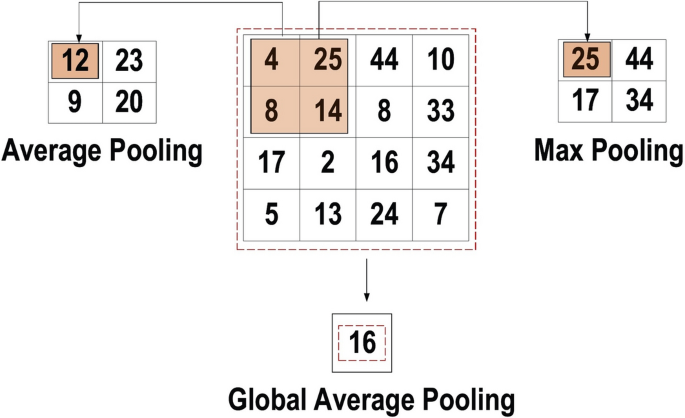
Three types of pooling operations

Sometimes, the overall CNN performance is decreased as a result; this represents the main shortfall of the pooling layer, as this layer helps the CNN to determine whether or not a certain feature is available in the particular input image, but focuses exclusively on ascertaining the correct location of that feature. Thus, the CNN model misses the relevant information.

Activation Function (non-linearity) Mapping the input to the output is the core function of all types of activation function in all types of neural network. The input value is determined by computing the weighted summation of the neuron input along with its bias (if present). This means that the activation function makes the decision as to whether or not to fire a neuron with reference to a particular input by creating the corresponding output.

Non-linear activation layers are employed after all layers with weights (so-called learnable layers, such as FC layers and convolutional layers) in CNN architecture. This non-linear performance of the activation layers means that the mapping of input to output will be non-linear; moreover, these layers give the CNN the ability to learn extra-complicated things. The activation function must also have the ability to differentiate, which is an extremely significant feature, as it allows error back-propagation to be used to train the network. The following types of activation functions are most commonly used in CNN and other deep neural networks.

Sigmoid: The input of this activation function is real numbers, while the output is restricted to between zero and one. The sigmoid function curve is S-shaped and can be represented mathematically by Eq. 2 .

Tanh: It is similar to the sigmoid function, as its input is real numbers, but the output is restricted to between − 1 and 1. Its mathematical representation is in Eq. 3 .

ReLU: The mostly commonly used function in the CNN context. It converts the whole values of the input to positive numbers. Lower computational load is the main benefit of ReLU over the others. Its mathematical representation is in Eq. 4 .

Occasionally, a few significant issues may occur during the use of ReLU. For instance, consider an error back-propagation algorithm with a larger gradient flowing through it. Passing this gradient within the ReLU function will update the weights in a way that makes the neuron certainly not activated once more. This issue is referred to as “Dying ReLU”. Some ReLU alternatives exist to solve such issues. The following discusses some of them.

Leaky ReLU: Instead of ReLU down-scaling the negative inputs, this activation function ensures these inputs are never ignored. It is employed to solve the Dying ReLU problem. Leaky ReLU can be represented mathematically as in Eq. 5 .

Note that the leak factor is denoted by m. It is commonly set to a very small value, such as 0.001.

Noisy ReLU: This function employs a Gaussian distribution to make ReLU noisy. It can be represented mathematically as in Eq. 6 .

Parametric Linear Units: This is mostly the same as Leaky ReLU. The main difference is that the leak factor in this function is updated through the model training process. The parametric linear unit can be represented mathematically as in Eq. 7 .

Note that the learnable weight is denoted as a.

Fully Connected Layer: Commonly, this layer is located at the end of each CNN architecture. Inside this layer, each neuron is connected to all neurons of the previous layer, the so-called Fully Connected (FC) approach. It is utilized as the CNN classifier. It follows the basic method of the conventional multiple-layer perceptron neural network, as it is a type of feed-forward ANN. The input of the FC layer comes from the last pooling or convolutional layer. This input is in the form of a vector, which is created from the feature maps after flattening. The output of the FC layer represents the final CNN output, as illustrated in Fig.  10 .

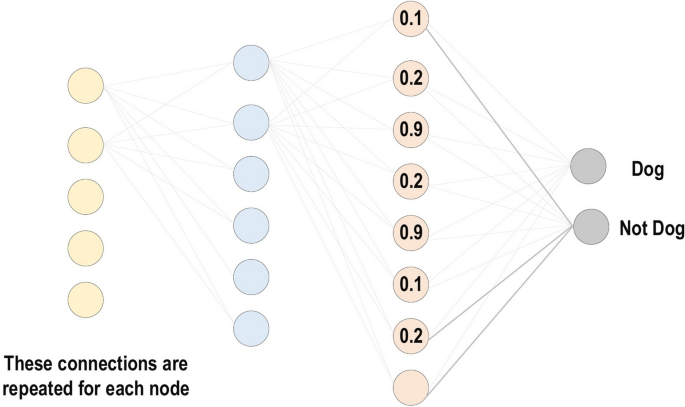
Fully connected layer

Loss Functions: The previous section has presented various layer-types of CNN architecture. In addition, the final classification is achieved from the output layer, which represents the last layer of the CNN architecture. Some loss functions are utilized in the output layer to calculate the predicted error created across the training samples in the CNN model. This error reveals the difference between the actual output and the predicted one. Next, it will be optimized through the CNN learning process.

However, two parameters are used by the loss function to calculate the error. The CNN estimated output (referred to as the prediction) is the first parameter. The actual output (referred to as the label) is the second parameter. Several types of loss function are employed in various problem types. The following concisely explains some of the loss function types.

Cross-Entropy or Softmax Loss Function: This function is commonly employed for measuring the CNN model performance. It is also referred to as the log loss function. Its output is the probability \(p \in \left\{ 0\left. , 1 \right\} \right. \) . In addition, it is usually employed as a substitution of the square error loss function in multi-class classification problems. In the output layer, it employs the softmax activations to generate the output within a probability distribution. The mathematical representation of the output class probability is Eq. 8 .

Here, \(e^{a_{i}}\) represents the non-normalized output from the preceding layer, while N represents the number of neurons in the output layer. Finally, the mathematical representation of cross-entropy loss function is Eq. 9 .

Euclidean Loss Function: This function is widely used in regression problems. In addition, it is also the so-called mean square error. The mathematical expression of the estimated Euclidean loss is Eq. 10 .

Hinge Loss Function: This function is commonly employed in problems related to binary classification. This problem relates to maximum-margin-based classification; this is mostly important for SVMs, which use the hinge loss function, wherein the optimizer attempts to maximize the margin around dual objective classes. Its mathematical formula is Eq. 11 .

The margin m is commonly set to 1. Moreover, the predicted output is denoted as \(p_{_{i}}\) , while the desired output is denoted as \(y_{_{i}}\) .

Regularization to CNN

For CNN models, over-fitting represents the central issue associated with obtaining well-behaved generalization. The model is entitled over-fitted in cases where the model executes especially well on training data and does not succeed on test data (unseen data) which is more explained in the latter section. An under-fitted model is the opposite; this case occurs when the model does not learn a sufficient amount from the training data. The model is referred to as “just-fitted” if it executes well on both training and testing data. These three types are illustrated in Fig.  11 . Various intuitive concepts are used to help the regularization to avoid over-fitting; more details about over-fitting and under-fitting are discussed in latter sections.

Dropout: This is a widely utilized technique for generalization. During each training epoch, neurons are randomly dropped. In doing this, the feature selection power is distributed equally across the whole group of neurons, as well as forcing the model to learn different independent features. During the training process, the dropped neuron will not be a part of back-propagation or forward-propagation. By contrast, the full-scale network is utilized to perform prediction during the testing process.

Drop-Weights: This method is highly similar to dropout. In each training epoch, the connections between neurons (weights) are dropped rather than dropping the neurons; this represents the only difference between drop-weights and dropout.

Data Augmentation: Training the model on a sizeable amount of data is the easiest way to avoid over-fitting. To achieve this, data augmentation is used. Several techniques are utilized to artificially expand the size of the training dataset. More details can be found in the latter section, which describes the data augmentation techniques.

Batch Normalization: This method ensures the performance of the output activations [ 81 ]. This performance follows a unit Gaussian distribution. Subtracting the mean and dividing by the standard deviation will normalize the output at each layer. While it is possible to consider this as a pre-processing task at each layer in the network, it is also possible to differentiate and to integrate it with other networks. In addition, it is employed to reduce the “internal covariance shift” of the activation layers. In each layer, the variation in the activation distribution defines the internal covariance shift. This shift becomes very high due to the continuous weight updating through training, which may occur if the samples of the training data are gathered from numerous dissimilar sources (for example, day and night images). Thus, the model will consume extra time for convergence, and in turn, the time required for training will also increase. To resolve this issue, a layer representing the operation of batch normalization is applied in the CNN architecture.

The advantages of utilizing batch normalization are as follows:

It prevents the problem of vanishing gradient from arising.

It can effectively control the poor weight initialization.

It significantly reduces the time required for network convergence (for large-scale datasets, this will be extremely useful).

It struggles to decrease training dependency across hyper-parameters.

Chances of over-fitting are reduced, since it has a minor influence on regularization.

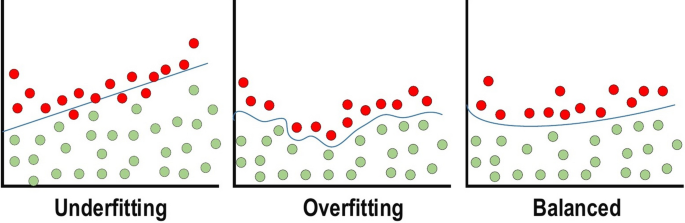
Over-fitting and under-fitting issues

Optimizer selection

This section discusses the CNN learning process. Two major issues are included in the learning process: the first issue is the learning algorithm selection (optimizer), while the second issue is the use of many enhancements (such as AdaDelta, Adagrad, and momentum) along with the learning algorithm to enhance the output.

Loss functions, which are founded on numerous learnable parameters (e.g. biases, weights, etc.) or minimizing the error (variation between actual and predicted output), are the core purpose of all supervised learning algorithms. The techniques of gradient-based learning for a CNN network appear as the usual selection. The network parameters should always update though all training epochs, while the network should also look for the locally optimized answer in all training epochs in order to minimize the error.

The learning rate is defined as the step size of the parameter updating. The training epoch represents a complete repetition of the parameter update that involves the complete training dataset at one time. Note that it needs to select the learning rate wisely so that it does not influence the learning process imperfectly, although it is a hyper-parameter.

Gradient Descent or Gradient-based learning algorithm: To minimize the training error, this algorithm repetitively updates the network parameters through every training epoch. More specifically, to update the parameters correctly, it needs to compute the objective function gradient (slope) by applying a first-order derivative with respect to the network parameters. Next, the parameter is updated in the reverse direction of the gradient to reduce the error. The parameter updating process is performed though network back-propagation, in which the gradient at every neuron is back-propagated to all neurons in the preceding layer. The mathematical representation of this operation is as Eq. 12 .

The final weight in the current training epoch is denoted by \(w_{i j^{t}}\) , while the weight in the preceding \((t-1)\) training epoch is denoted \(w_{i j^{t-1}}\) . The learning rate is \(\eta \) and the prediction error is E . Different alternatives of the gradient-based learning algorithm are available and commonly employed; these include the following:

Batch Gradient Descent: During the execution of this technique [ 82 ], the network parameters are updated merely one time behind considering all training datasets via the network. In more depth, it calculates the gradient of the whole training set and subsequently uses this gradient to update the parameters. For a small-sized dataset, the CNN model converges faster and creates an extra-stable gradient using BGD. Since the parameters are changed only once for every training epoch, it requires a substantial amount of resources. By contrast, for a large training dataset, additional time is required for converging, and it could converge to a local optimum (for non-convex instances).

Stochastic Gradient Descent: The parameters are updated at each training sample in this technique [ 83 ]. It is preferred to arbitrarily sample the training samples in every epoch in advance of training. For a large-sized training dataset, this technique is both more memory-effective and much faster than BGD. However, because it is frequently updated, it takes extremely noisy steps in the direction of the answer, which in turn causes the convergence behavior to become highly unstable.

Mini-batch Gradient Descent: In this approach, the training samples are partitioned into several mini-batches, in which every mini-batch can be considered an under-sized collection of samples with no overlap between them [ 84 ]. Next, parameter updating is performed following gradient computation on every mini-batch. The advantage of this method comes from combining the advantages of both BGD and SGD techniques. Thus, it has a steady convergence, more computational efficiency and extra memory effectiveness. The following describes several enhancement techniques in gradient-based learning algorithms (usually in SGD), which further powerfully enhance the CNN training process.

Momentum: For neural networks, this technique is employed in the objective function. It enhances both the accuracy and the training speed by summing the computed gradient at the preceding training step, which is weighted via a factor \(\lambda \) (known as the momentum factor). However, it therefore simply becomes stuck in a local minimum rather than a global minimum. This represents the main disadvantage of gradient-based learning algorithms. Issues of this kind frequently occur if the issue has no convex surface (or solution space).

Together with the learning algorithm, momentum is used to solve this issue, which can be expressed mathematically as in Eq. 13 .

The weight increment in the current \(t^{\prime} \text{th}\) training epoch is denoted as \( \Delta w_{i j^{t}}\) , while \(\eta \) is the learning rate, and the weight increment in the preceding \((t-1)^{\prime} \text{th}\) training epoch. The momentum factor value is maintained within the range 0 to 1; in turn, the step size of the weight updating increases in the direction of the bare minimum to minimize the error. As the value of the momentum factor becomes very low, the model loses its ability to avoid the local bare minimum. By contrast, as the momentum factor value becomes high, the model develops the ability to converge much more rapidly. If a high value of momentum factor is used together with LR, then the model could miss the global bare minimum by crossing over it.

However, when the gradient varies its direction continually throughout the training process, then the suitable value of the momentum factor (which is a hyper-parameter) causes a smoothening of the weight updating variations.

Adaptive Moment Estimation (Adam): It is another optimization technique or learning algorithm that is widely used. Adam [ 85 ] represents the latest trends in deep learning optimization. This is represented by the Hessian matrix, which employs a second-order derivative. Adam is a learning strategy that has been designed specifically for training deep neural networks. More memory efficient and less computational power are two advantages of Adam. The mechanism of Adam is to calculate adaptive LR for each parameter in the model. It integrates the pros of both Momentum and RMSprop. It utilizes the squared gradients to scale the learning rate as RMSprop and it is similar to the momentum by using the moving average of the gradient. The equation of Adam is represented in Eq. 14 .

Design of algorithms (backpropagation)

Let’s start with a notation that refers to weights in the network unambiguously. We denote \({\varvec{w}}_{i j}^{h}\) to be the weight for the connection from \(\text {ith}\) input or (neuron at \(\left. (\text {h}-1){\text{th}}\right) \) to the \(j{\text{t }}\) neuron in the \(\text {hth}\) layer. So, Fig. 12 shows the weight on a connection from the neuron in the first layer to another neuron in the next layer in the network.

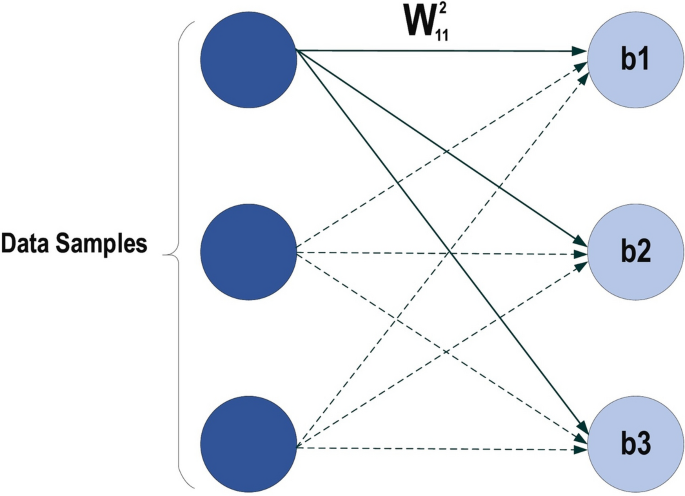
MLP structure

Where \(w_{11}^{2}\) has represented the weight from the first neuron in the first layer to the first neuron in the second layer, based on that the second weight for the same neuron will be \(w_{21}^{2}\) which means is the weight comes from the second neuron in the previous layer to the first layer in the next layer which is the second in this net. Regarding the bias, since the bias is not the connection between the neurons for the layers, so it is easily handled each neuron must have its own bias, some network each layer has a certain bias. It can be seen from the above net that each layer has its own bias. Each network has the parameters such as the no of the layer in the net, the number of the neurons in each layer, no of the weight (connection) between the layers, the no of connection can be easily determined based on the no of neurons in each layer, for example, if there are ten input fully connect with two neurons in the next layer then the number of connection between them is \((10 * 2=20\) connection, weights), how the error is defined, and the weight is updated, we will imagine there is there are two layers in our neural network,

where \(\text {d}\) is the label of induvial input \(\text {ith}\) and \(\text {y}\) is the output of the same individual input. Backpropagation is about understanding how to change the weights and biases in a network based on the changes of the cost function (Error). Ultimately, this means computing the partial derivatives \(\partial \text {E} / \partial \text {w}_{\text {ij}}^{h}\) and \(\partial \text {E} / \partial \text {b}_{\text {j}}^{h}.\) But to compute those, a local variable is introduced, \(\delta _{j}^{1}\) which is called the local error in the \(j{\text{th} }\) neuron in the \(h{\text{th} }\) layer. Based on that local error Backpropagation will give the procedure to compute \(\partial \text {E} / \partial \text {w}_{\text {ij}}^{h}\) and \(\partial \text {E} / \partial \text {b}_{\text {j}}^{h}\) how the error is defined, and the weight is updated, we will imagine there is there are two layers in our neural network that is shown in Fig. 13 .

Neuron activation functions

Output error for \(\delta _{\text {j}}^{1}\) each \(1=1: \text {L}\) where \(\text {L}\) is no. of neuron in output

where \(\text {e}(\text {k})\) is the error of the epoch \(\text {k}\) as shown in Eq. ( 2 ) and \(\varvec{\vartheta }^{\prime }\left( {\varvec{v}}_{j}({\varvec{k}})\right) \) is the derivate of the activation function for \(v_{j}\) at the output.

Backpropagate the error at all the rest layer except the output

where \(\delta _{j}^{1}({\mathbf {k}})\) is the output error and \(w_{j l}^{h+1}(k)\) is represented the weight after the layer where the error need to obtain.

After finding the error at each neuron in each layer, now we can update the weight in each layer based on Eqs. ( 16 ) and ( 17 ).

Improving performance of CNN

Based on our experiments in different DL applications [ 86 , 87 , 88 ]. We can conclude the most active solutions that may improve the performance of CNN are:

Expand the dataset with data augmentation or use transfer learning (explained in latter sections).

Increase the training time.

Increase the depth (or width) of the model.

Add regularization.

Increase hyperparameters tuning.

CNN architectures

Over the last 10 years, several CNN architectures have been presented [ 21 , 26 ]. Model architecture is a critical factor in improving the performance of different applications. Various modifications have been achieved in CNN architecture from 1989 until today. Such modifications include structural reformulation, regularization, parameter optimizations, etc. Conversely, it should be noted that the key upgrade in CNN performance occurred largely due to the processing-unit reorganization, as well as the development of novel blocks. In particular, the most novel developments in CNN architectures were performed on the use of network depth. In this section, we review the most popular CNN architectures, beginning from the AlexNet model in 2012 and ending at the High-Resolution (HR) model in 2020. Studying these architectures features (such as input size, depth, and robustness) is the key to help researchers to choose the suitable architecture for the their target task. Table  2 presents the brief overview of CNN architectures.

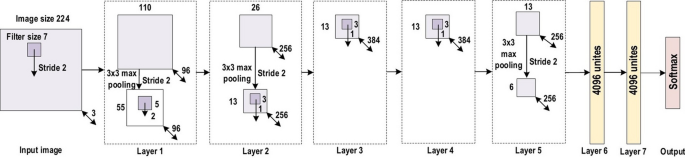
The history of deep CNNs began with the appearance of LeNet [ 89 ] (Fig.  14 ). At that time, the CNNs were restricted to handwritten digit recognition tasks, which cannot be scaled to all image classes. In deep CNN architecture, AlexNet is highly respected [ 30 ], as it achieved innovative results in the fields of image recognition and classification. Krizhevesky et al. [ 30 ] first proposed AlexNet and consequently improved the CNN learning ability by increasing its depth and implementing several parameter optimization strategies. Figure  15 illustrates the basic design of the AlexNet architecture.

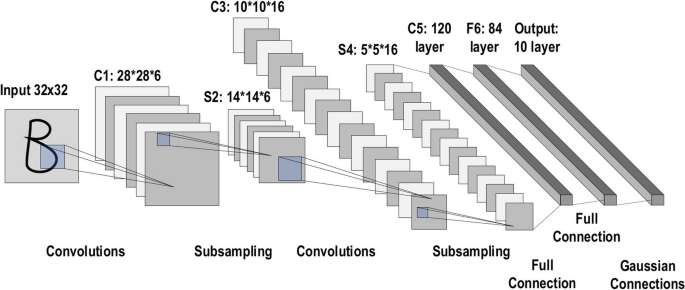
The architecture of LeNet

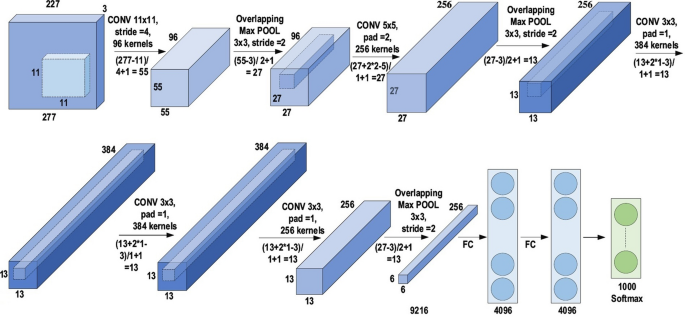
The architecture of AlexNet

The learning ability of the deep CNN was limited at this time due to hardware restrictions. To overcome these hardware limitations, two GPUs (NVIDIA GTX 580) were used in parallel to train AlexNet. Moreover, in order to enhance the applicability of the CNN to different image categories, the number of feature extraction stages was increased from five in LeNet to seven in AlexNet. Regardless of the fact that depth enhances generalization for several image resolutions, it was in fact overfitting that represented the main drawback related to the depth. Krizhevesky et al. used Hinton’s idea to address this problem [ 90 , 91 ]. To ensure that the features learned by the algorithm were extra robust, Krizhevesky et al.’s algorithm randomly passes over several transformational units throughout the training stage. Moreover, by reducing the vanishing gradient problem, ReLU [ 92 ] could be utilized as a non-saturating activation function to enhance the rate of convergence [ 93 ]. Local response normalization and overlapping subsampling were also performed to enhance the generalization by decreasing the overfitting. To improve on the performance of previous networks, other modifications were made by using large-size filters \((5\times 5 \; \text{and}\; 11 \times 11)\) in the earlier layers. AlexNet has considerable significance in the recent CNN generations, as well as beginning an innovative research era in CNN applications.

Network-in-network

This network model, which has some slight differences from the preceding models, introduced two innovative concepts [ 94 ]. The first was employing multiple layers of perception convolution. These convolutions are executed using a 1×1 filter, which supports the addition of extra nonlinearity in the networks. Moreover, this supports enlarging the network depth, which may later be regularized using dropout. For DL models, this idea is frequently employed in the bottleneck layer. As a substitution for a FC layer, the GAP is also employed, which represents the second novel concept and enables a significant reduction in the number of model parameters. In addition, GAP considerably updates the network architecture. Generating a final low-dimensional feature vector with no reduction in the feature maps dimension is possible when GAP is used on a large feature map [ 95 , 96 ]. Figure  16 shows the structure of the network.

The architecture of network-in-network

Before 2013, the CNN learning mechanism was basically constructed on a trial-and-error basis, which precluded an understanding of the precise purpose following the enhancement. This issue restricted the deep CNN performance on convoluted images. In response, Zeiler and Fergus introduced DeconvNet (a multilayer de-convolutional neural network) in 2013 [ 97 ]. This method later became known as ZefNet, which was developed in order to quantitively visualize the network. Monitoring the CNN performance via understanding the neuron activation was the purpose of the network activity visualization. However, Erhan et al. utilized this exact concept to optimize deep belief network (DBN) performance by visualizing the features of the hidden layers [ 98 ]. Moreover, in addition to this issue, Le et al. assessed the deep unsupervised auto-encoder (AE) performance by visualizing the created classes of the image using the output neurons [ 99 ]. By reversing the operation order of the convolutional and pooling layers, DenconvNet operates like a forward-pass CNN. Reverse mapping of this kind launches the convolutional layer output backward to create visually observable image shapes that accordingly give the neural interpretation of the internal feature representation learned at each layer [ 100 ]. Monitoring the learning schematic through the training stage was the key concept underlying ZefNet. In addition, it utilized the outcomes to recognize an ability issue coupled with the model. This concept was experimentally proven on AlexNet by applying DeconvNet. This indicated that only certain neurons were working, while the others were out of action in the first two layers of the network. Furthermore, it indicated that the features extracted via the second layer contained aliasing objects. Thus, Zeiler and Fergus changed the CNN topology due to the existence of these outcomes. In addition, they executed parameter optimization, and also exploited the CNN learning by decreasing the stride and the filter sizes in order to retain all features of the initial two convolutional layers. An improvement in performance was accordingly achieved due to this rearrangement in CNN topology. This rearrangement proposed that the visualization of the features could be employed to identify design weaknesses and conduct appropriate parameter alteration. Figure  17 shows the structure of the network.

The architecture of ZefNet

Visual geometry group (VGG)

After CNN was determined to be effective in the field of image recognition, an easy and efficient design principle for CNN was proposed by Simonyan and Zisserman. This innovative design was called Visual Geometry Group (VGG). A multilayer model [ 101 ], it featured nineteen more layers than ZefNet [ 97 ] and AlexNet [ 30 ] to simulate the relations of the network representational capacity in depth. Conversely, in the 2013-ILSVRC competition, ZefNet was the frontier network, which proposed that filters with small sizes could enhance the CNN performance. With reference to these results, VGG inserted a layer of the heap of \(3\times 3\) filters rather than the \(5\times 5\) and 11 × 11 filters in ZefNet. This showed experimentally that the parallel assignment of these small-size filters could produce the same influence as the large-size filters. In other words, these small-size filters made the receptive field similarly efficient to the large-size filters \((7 \times 7 \; \text{and}\; 5 \times 5)\) . By decreasing the number of parameters, an extra advantage of reducing computational complication was achieved by using small-size filters. These outcomes established a novel research trend for working with small-size filters in CNN. In addition, by inserting \(1\times 1\) convolutions in the middle of the convolutional layers, VGG regulates the network complexity. It learns a linear grouping of the subsequent feature maps. With respect to network tuning, a max pooling layer [ 102 ] is inserted following the convolutional layer, while padding is implemented to maintain the spatial resolution. In general, VGG obtained significant results for localization problems and image classification. While it did not achieve first place in the 2014-ILSVRC competition, it acquired a reputation due to its enlarged depth, homogenous topology, and simplicity. However, VGG’s computational cost was excessive due to its utilization of around 140 million parameters, which represented its main shortcoming. Figure  18 shows the structure of the network.

The architecture of VGG

In the 2014-ILSVRC competition, GoogleNet (also called Inception-V1) emerged as the winner [ 103 ]. Achieving high-level accuracy with decreased computational cost is the core aim of the GoogleNet architecture. It proposed a novel inception block (module) concept in the CNN context, since it combines multiple-scale convolutional transformations by employing merge, transform, and split functions for feature extraction. Figure  19 illustrates the inception block architecture. This architecture incorporates filters of different sizes ( \(5\times 5, 3\times 3, \; \text{and} \; 1\times 1\) ) to capture channel information together with spatial information at diverse ranges of spatial resolution. The common convolutional layer of GoogLeNet is substituted by small blocks using the same concept of network-in-network (NIN) architecture [ 94 ], which replaced each layer with a micro-neural network. The GoogLeNet concepts of merge, transform, and split were utilized, supported by attending to an issue correlated with different learning types of variants existing in a similar class of several images. The motivation of GoogLeNet was to improve the efficiency of CNN parameters, as well as to enhance the learning capacity. In addition, it regulates the computation by inserting a \(1\times 1\) convolutional filter, as a bottleneck layer, ahead of using large-size kernels. GoogleNet employed sparse connections to overcome the redundant information problem. It decreased cost by neglecting the irrelevant channels. It should be noted here that only some of the input channels are connected to some of the output channels. By employing a GAP layer as the end layer, rather than utilizing a FC layer, the density of connections was decreased. The number of parameters was also significantly decreased from 40 to 5 million parameters due to these parameter tunings. The additional regularity factors used included the employment of RmsProp as optimizer and batch normalization [ 104 ]. Furthermore, GoogleNet proposed the idea of auxiliary learners to speed up the rate of convergence. Conversely, the main shortcoming of GoogleNet was its heterogeneous topology; this shortcoming requires adaptation from one module to another. Other shortcomings of GoogleNet include the representation jam, which substantially decreased the feature space in the following layer, and in turn occasionally leads to valuable information loss.

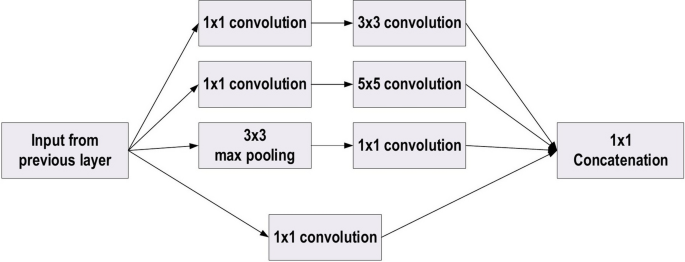
The basic structure of Google Block

Highway network

Increasing the network depth enhances its performance, mainly for complicated tasks. By contrast, the network training becomes difficult. The presence of several layers in deeper networks may result in small gradient values of the back-propagation of error at lower layers. In 2015, Srivastava et al. [ 105 ] suggested a novel CNN architecture, called Highway Network, to overcome this issue. This approach is based on the cross-connectivity concept. The unhindered information flow in Highway Network is empowered by instructing two gating units inside the layer. The gate mechanism concept was motivated by LSTM-based RNN [ 106 , 107 ]. The information aggregation was conducted by merging the information of the \(\i{\text{th}}-k\) layers with the next \(\i{\text{th}}\) layer to generate a regularization impact, which makes the gradient-based training of the deeper network very simple. This empowers the training of networks with more than 100 layers, such as a deeper network of 900 layers with the SGD algorithm. A Highway Network with a depth of fifty layers presented an improved rate of convergence, which is better than thin and deep architectures at the same time [ 108 ]. By contrast, [ 69 ] empirically demonstrated that plain Net performance declines when more than ten hidden layers are inserted. It should be noted that even a Highway Network 900 layers in depth converges much more rapidly than the plain network.

He et al. [ 37 ] developed ResNet (Residual Network), which was the winner of ILSVRC 2015. Their objective was to design an ultra-deep network free of the vanishing gradient issue, as compared to the previous networks. Several types of ResNet were developed based on the number of layers (starting with 34 layers and going up to 1202 layers). The most common type was ResNet50, which comprised 49 convolutional layers plus a single FC layer. The overall number of network weights was 25.5 M, while the overall number of MACs was 3.9 M. The novel idea of ResNet is its use of the bypass pathway concept, as shown in Fig.  20 , which was employed in Highway Nets to address the problem of training a deeper network in 2015. This is illustrated in Fig.  20 , which contains the fundamental ResNet block diagram. This is a conventional feedforward network plus a residual connection. The residual layer output can be identified as the \((l - 1){\text{th}}\) outputs, which are delivered from the preceding layer \((x_{l} - 1)\) . After executing different operations [such as convolution using variable-size filters, or batch normalization, before applying an activation function like ReLU on \((x_{l} - 1)\) ], the output is \(F(x_{l} - 1)\) . The ending residual output is \(x_{l}\) , which can be mathematically represented as in Eq. 18 .

There are numerous basic residual blocks included in the residual network. Based on the type of the residual network architecture, operations in the residual block are also changed [ 37 ].

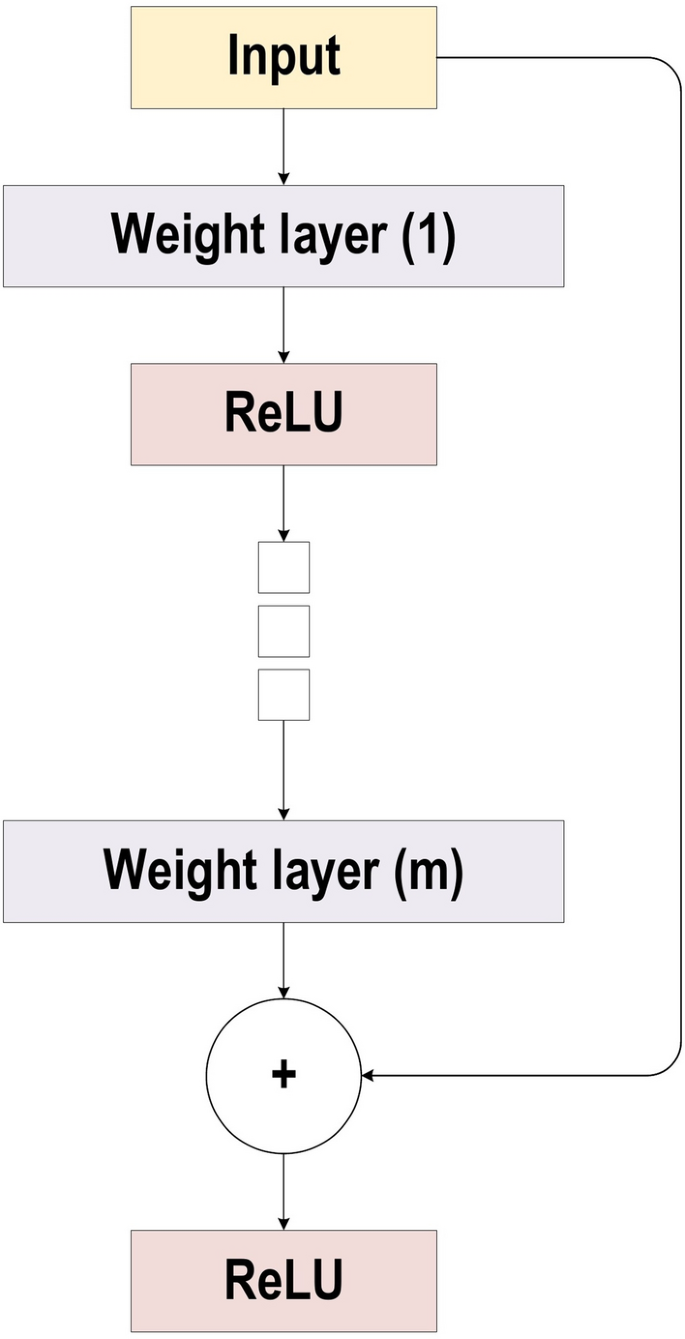
The block diagram for ResNet

In comparison to the highway network, ResNet presented shortcut connections inside layers to enable cross-layer connectivity, which are parameter-free and data-independent. Note that the layers characterize non-residual functions when a gated shortcut is closed in the highway network. By contrast, the individuality shortcuts are never closed, while the residual information is permanently passed in ResNet. Furthermore, ResNet has the potential to prevent the problems of gradient diminishing, as the shortcut connections (residual links) accelerate the deep network convergence. ResNet was the winner of the 2015-ILSVRC championship with 152 layers of depth; this represents 8 times the depth of VGG and 20 times the depth of AlexNet. In comparison with VGG, it has lower computational complexity, even with enlarged depth.

Inception: ResNet and Inception-V3/4

Szegedy et al. [ 103 , 109 , 110 ] proposed Inception-ResNet and Inception-V3/4 as upgraded types of Inception-V1/2. The concept behind Inception-V3 was to minimize the computational cost with no effect on the deeper network generalization. Thus, Szegedy et al. used asymmetric small-size filters ( \(1\times 5\) and \(1\times 7\) ) rather than large-size filters ( \( 7\times 7\) and \(5\times 5\) ); moreover, they utilized a bottleneck of \(1\times 1\) convolution prior to the large-size filters [ 110 ]. These changes make the operation of the traditional convolution very similar to cross-channel correlation. Previously, Lin et al. utilized the 1 × 1 filter potential in NIN architecture [ 94 ]. Subsequently, [ 110 ] utilized the same idea in an intelligent manner. By using \(1\times 1\) convolutional operation in Inception-V3, the input data are mapped into three or four isolated spaces, which are smaller than the initial input spaces. Next, all of these correlations are mapped in these smaller spaces through common \(5\times 5\) or \(3\times 3\) convolutions. By contrast, in Inception-ResNet, Szegedy et al. bring together the inception block and the residual learning power by replacing the filter concatenation with the residual connection [ 111 ]. Szegedy et al. empirically demonstrated that Inception-ResNet (Inception-4 with residual connections) can achieve a similar generalization power to Inception-V4 with enlarged width and depth and without residual connections. Thus, it is clearly illustrated that using residual connections in training will significantly accelerate the Inception network training. Figure  21 shows The basic block diagram for Inception Residual unit.

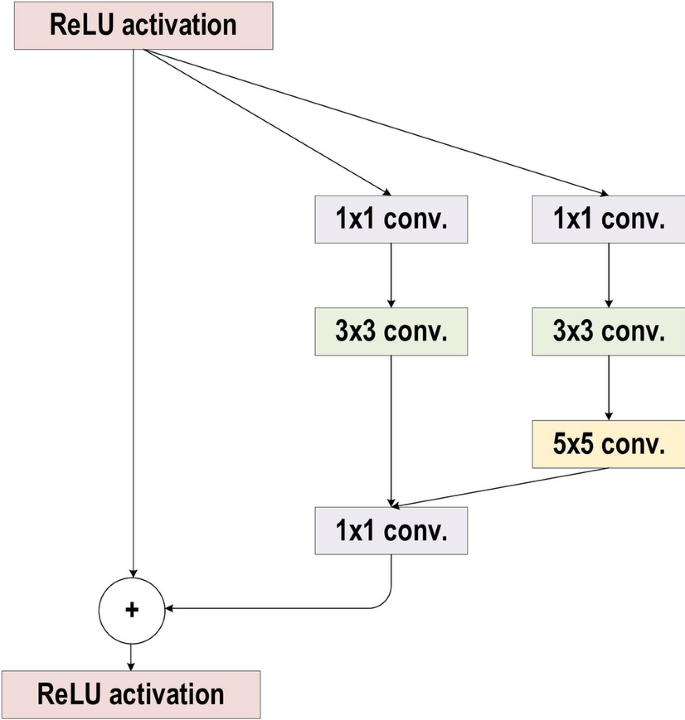
The basic block diagram for Inception Residual unit

To solve the problem of the vanishing gradient, DenseNet was presented, following the same direction as ResNet and the Highway network [ 105 , 111 , 112 ]. One of the drawbacks of ResNet is that it clearly conserves information by means of preservative individuality transformations, as several layers contribute extremely little or no information. In addition, ResNet has a large number of weights, since each layer has an isolated group of weights. DenseNet employed cross-layer connectivity in an improved approach to address this problem [ 112 , 113 , 114 ]. It connected each layer to all layers in the network using a feed-forward approach. Therefore, the feature maps of each previous layer were employed to input into all of the following layers. In traditional CNNs, there are l connections between the previous layer and the current layer, while in DenseNet, there are \(\frac{l(l+1)}{2}\) direct connections. DenseNet demonstrates the influence of cross-layer depth wise-convolutions. Thus, the network gains the ability to discriminate clearly between the added and the preserved information, since DenseNet concatenates the features of the preceding layers rather than adding them. However, due to its narrow layer structure, DenseNet becomes parametrically high-priced in addition to the increased number of feature maps. The direct admission of all layers to the gradients via the loss function enhances the information flow all across the network. In addition, this includes a regularizing impact, which minimizes overfitting on tasks alongside minor training sets. Figure  22 shows the architecture of DenseNet Network.

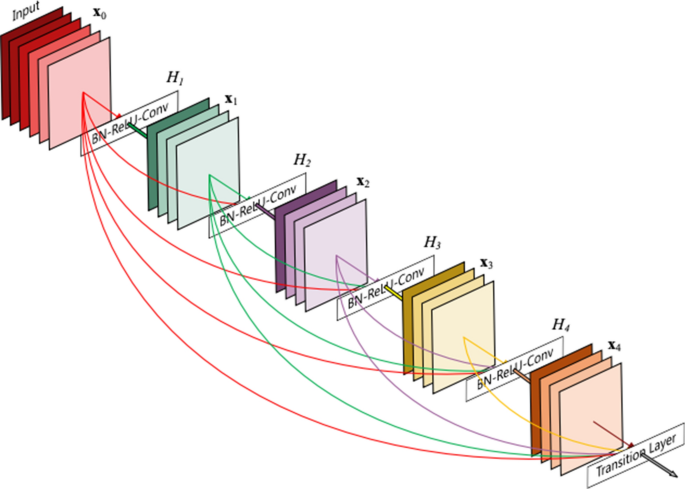
(adopted from [ 112 ])

The architecture of DenseNet Network

ResNext is an enhanced version of the Inception Network [ 115 ]. It is also known as the Aggregated Residual Transform Network. Cardinality, which is a new term presented by [ 115 ], utilized the split, transform, and merge topology in an easy and effective way. It denotes the size of the transformation set as an extra dimension [ 116 , 117 , 118 ]. However, the Inception network manages network resources more efficiently, as well as enhancing the learning ability of the conventional CNN. In the transformation branch, different spatial embeddings (employing e.g. \(5\times 5\) , \(3\times 3\) , and \(1\times 1\) ) are used. Thus, customizing each layer is required separately. By contrast, ResNext derives its characteristic features from ResNet, VGG, and Inception. It employed the VGG deep homogenous topology with the basic architecture of GoogleNet by setting \(3\times 3\) filters as spatial resolution inside the blocks of split, transform, and merge. Figure  23 shows the ResNext building blocks. ResNext utilized multi-transformations inside the blocks of split, transform, and merge, as well as outlining such transformations in cardinality terms. The performance is significantly improved by increasing the cardinality, as Xie et al. showed. The complexity of ResNext was regulated by employing \(1\times 1\) filters (low embeddings) ahead of a \(3\times 3\) convolution. By contrast, skipping connections are used for optimized training [ 115 ].

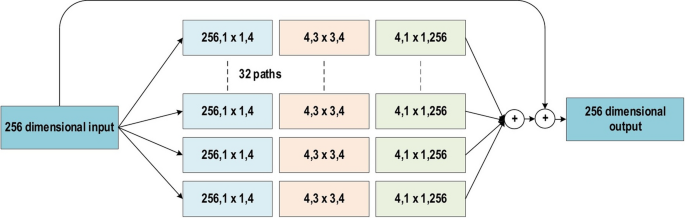
The basic block diagram for the ResNext building blocks

The feature reuse problem is the core shortcoming related to deep residual networks, since certain feature blocks or transformations contribute a very small amount to learning. Zagoruyko and Komodakis [ 119 ] accordingly proposed WideResNet to address this problem. These authors advised that the depth has a supplemental influence, while the residual units convey the core learning ability of deep residual networks. WideResNet utilized the residual block power via making the ResNet wider instead of deeper [ 37 ]. It enlarged the width by presenting an extra factor, k, which handles the network width. In other words, it indicated that layer widening is a highly successful method of performance enhancement compared to deepening the residual network. While enhanced representational capacity is achieved by deep residual networks, these networks also have certain drawbacks, such as the exploding and vanishing gradient problems, feature reuse problem (inactivation of several feature maps), and the time-intensive nature of the training. He et al. [ 37 ] tackled the feature reuse problem by including a dropout in each residual block to regularize the network in an efficient manner. In a similar manner, utilizing dropouts, Huang et al. [ 120 ] presented the stochastic depth concept to solve the slow learning and gradient vanishing problems. Earlier research was focused on increasing the depth; thus, any small enhancement in performance required the addition of several new layers. When comparing the number of parameters, WideResNet has twice that of ResNet, as an experimental study showed. By contrast, WideResNet presents an improved method for training relative to deep networks [ 119 ]. Note that most architectures prior to residual networks (including the highly effective VGG and Inception) were wider than ResNet. Thus, wider residual networks were established once this was determined. However, inserting a dropout between the convolutional layers (as opposed to within the residual block) made the learning more effective in WideResNet [ 121 , 122 ].

Pyramidal Net

The depth of the feature map increases in the succeeding layer due to the deep stacking of multi-convolutional layers, as shown in previous deep CNN architectures such as ResNet, VGG, and AlexNet. By contrast, the spatial dimension reduces, since a sub-sampling follows each convolutional layer. Thus, augmented feature representation is recompensed by decreasing the size of the feature map. The extreme expansion in the depth of the feature map, alongside the spatial information loss, interferes with the learning ability in the deep CNNs. ResNet obtained notable outcomes for the issue of image classification. Conversely, deleting a convolutional block—in which both the number of channel and spatial dimensions vary (channel depth enlarges, while spatial dimension reduces)—commonly results in decreased classifier performance. Accordingly, the stochastic ResNet enhanced the performance by decreasing the information loss accompanying the residual unit drop. Han et al. [ 123 ] proposed Pyramidal Net to address the ResNet learning interference problem. To address the depth enlargement and extreme reduction in spatial width via ResNet, Pyramidal Net slowly enlarges the residual unit width to cover the most feasible places rather than saving the same spatial dimension inside all residual blocks up to the appearance of the down-sampling. It was referred to as Pyramidal Net due to the slow enlargement in the feature map depth based on the up-down method. Factor l, which was determined by Eq. 19 , regulates the depth of the feature map.

Here, the dimension of the l th residual unit is indicated by \(d_{l}\) ; moreover, n indicates the overall number of residual units, the step factor is indicated by \(\lambda \) , and the depth increase is regulated by the factor \(\frac{\lambda }{n}\) , which uniformly distributes the weight increase across the dimension of the feature map. Zero-padded identity mapping is used to insert the residual connections among the layers. In comparison to the projection-based shortcut connections, zero-padded identity mapping requires fewer parameters, which in turn leads to enhanced generalization [ 124 ]. Multiplication- and addition-based widening are two different approaches used in Pyramidal Nets for network widening. More specifically, the first approach (multiplication) enlarges geometrically, while the second one (addition) enlarges linearly [ 92 ]. The main problem associated with the width enlargement is the growth in time and space required related to the quadratic time.

Extreme inception architecture is the main characteristic of Xception. The main idea behind Xception is its depthwise separable convolution [ 125 ]. The Xception model adjusted the original inception block by making it wider and exchanging a single dimension ( \(3 \times 3\) ) followed by a \(1 \times 1\) convolution to reduce computational complexity. Figure  24 shows the Xception block architecture. The Xception network becomes extra computationally effective through the use of the decoupling channel and spatial correspondence. Moreover, it first performs mapping of the convolved output to the embedding short dimension by applying \(1 \times 1\) convolutions. It then performs k spatial transformations. Note that k here represents the width-defining cardinality, which is obtained via the transformations number in Xception. However, the computations were made simpler in Xception by distinctly convolving each channel around the spatial axes. These axes are subsequently used as the \(1 \times 1\) convolutions (pointwise convolution) for performing cross-channel correspondence. The \(1 \times 1\) convolution is utilized in Xception to regularize the depth of the channel. The traditional convolutional operation in Xception utilizes a number of transformation segments equivalent to the number of channels; Inception, moreover, utilizes three transformation segments, while traditional CNN architecture utilizes only a single transformation segment. Conversely, the suggested Xception transformation approach achieves extra learning efficiency and better performance but does not minimize the number of parameters [ 126 , 127 ].

The basic block diagram for the Xception block architecture

Residual attention neural network

To improve the network feature representation, Wang et al. [ 128 ] proposed the Residual Attention Network (RAN). Enabling the network to learn aware features of the object is the main purpose of incorporating attention into the CNN. The RAN consists of stacked residual blocks in addition to the attention module; hence, it is a feed-forward CNN. However, the attention module is divided into two branches, namely the mask branch and trunk branch. These branches adopt a top-down and bottom-up learning strategy respectively. Encapsulating two different strategies in the attention model supports top-down attention feedback and fast feed-forward processing in only one particular feed-forward process. More specifically, the top-down architecture generates dense features to make inferences about every aspect. Moreover, the bottom-up feedforward architecture generates low-resolution feature maps in addition to robust semantic information. Restricted Boltzmann machines employed a top-down bottom-up strategy as in previously proposed studies [ 129 ]. During the training reconstruction phase, Goh et al. [ 130 ] used the mechanism of top-down attention in deep Boltzmann machines (DBMs) as a regularizing factor. Note that the network can be globally optimized using a top-down learning strategy in a similar manner, where the maps progressively output to the input throughout the learning process [ 129 , 130 , 131 , 132 ].

Incorporating the attention concept with convolutional blocks in an easy way was used by the transformation network, as obtained in a previous study [ 133 ]. Unfortunately, these are inflexible, which represents the main problem, along with their inability to be used for varying surroundings. By contrast, stacking multi-attention modules has made RAN very effective at recognizing noisy, complex, and cluttered images. RAN’s hierarchical organization gives it the capability to adaptively allocate a weight for every feature map depending on its importance within the layers. Furthermore, incorporating three distinct levels of attention (spatial, channel, and mixed) enables the model to use this ability to capture the object-aware features at these distinct levels.

Convolutional block attention module

The importance of the feature map utilization and the attention mechanism is certified via SE-Network and RAN [ 128 , 134 , 135 ]. The convolutional block attention (CBAM) module, which is a novel attention-based CNN, was first developed by Woo et al. [ 136 ]. This module is similar to SE-Network and simple in design. SE-Network disregards the object’s spatial locality in the image and considers only the channels’ contribution during the image classification. Regarding object detection, object spatial location plays a significant role. The convolutional block attention module sequentially infers the attention maps. More specifically, it applies channel attention preceding the spatial attention to obtain the refined feature maps. Spatial attention is performed using 1 × 1 convolution and pooling functions, as in the literature. Generating an effective feature descriptor can be achieved by using a spatial axis along with the pooling of features. In addition, generating a robust spatial attention map is possible, as CBAM concatenates the max pooling and average pooling operations. In a similar manner, a collection of GAP and max pooling operations is used to model the feature map statistics. Woo et al. [ 136 ] demonstrated that utilizing GAP will return a sub-optimized inference of channel attention, whereas max pooling provides an indication of the distinguishing object features. Thus, the utilization of max pooling and average pooling enhances the network’s representational power. The feature maps improve the representational power, as well as facilitating a focus on the significant portion of the chosen features. The expression of 3D attention maps through a serial learning procedure assists in decreasing the computational cost and the number of parameters, as Woo et al. [ 136 ] experimentally proved. Note that any CNN architecture can be simply integrated with CBAM.

Concurrent spatial and channel excitation mechanism

To make the work valid for segmentation tasks, Roy et al. [ 137 , 138 ] expanded Hu et al. [ 134 ] effort by adding the influence of spatial information to the channel information. Roy et al. [ 137 , 138 ] presented three types of modules: (1) channel squeeze and excitation with concurrent channels (scSE); (2) exciting spatially and squeezing channel-wise (sSE); (3) exciting channel-wise and squeezing spatially (cSE). For segmentation purposes, they employed auto-encoder-based CNNs. In addition, they suggested inserting modules following the encoder and decoder layers. To specifically highlight the object-specific feature maps, they further allocated attention to every channel by expressing a scaling factor from the channel and spatial information in the first module (scSE). In the second module (sSE), the feature map information has lower importance than the spatial locality, as the spatial information plays a significant role during the segmentation process. Therefore, several channel collections are spatially divided and developed so that they can be employed in segmentation. In the final module (cSE), a similar SE-block concept is used. Furthermore, the scaling factor is derived founded on the contribution of the feature maps within the object detection [ 137 , 138 ].

CNN is an efficient technique for detecting object features and achieving well-behaved recognition performance in comparison with innovative handcrafted feature detectors. A number of restrictions related to CNN are present, meaning that the CNN does not consider certain relations, orientation, size, and perspectives of features. For instance, when considering a face image, the CNN does not count the various face components (such as mouth, eyes, nose, etc.) positions, and will incorrectly activate the CNN neurons and recognize the face without taking specific relations (such as size, orientation etc.) into account. At this point, consider a neuron that has probability in addition to feature properties such as size, orientation, perspective, etc. A specific neuron/capsule of this type has the ability to effectively detect the face along with different types of information. Thus, many layers of capsule nodes are used to construct the capsule network. An encoding unit, which contains three layers of capsule nodes, forms the CapsuleNet or CapsNet (the initial version of the capsule networks).

For example, the MNIST architecture comprises \(28\times 28\) images, applying 256 filters of size \(9\times 9\) and with stride 1. The \(28-9+1=20\) is the output plus 256 feature maps. Next, these outputs are input to the first capsule layer, while producing an 8D vector rather than a scalar; in fact, this is a modified convolution layer. Note that a stride 2 with \(9\times 9\) filters is employed in the first convolution layer. Thus, the dimension of the output is \((20-9)/2+1=6\) . The initial capsules employ \(8\times 32\) filters, which generate 32 × 8 × 6 × 6 (32 for groups, 8 for neurons, while 6 × 6 is the neuron size).

Figure  25 represents the complete CapsNet encoding and decoding processes. In the CNN context, a max-pooling layer is frequently employed to handle the translation change. It can detect the feature moves in the event that the feature is still within the max-pooling window. This approach has the ability to detect the overlapped features; this is highly significant in detection and segmentation operations, since the capsule involves the weighted features sum from the preceding layer.

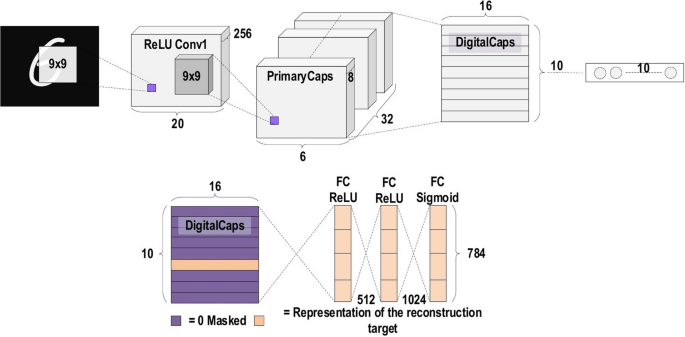
The complete CapsNet encoding and decoding processes

In conventional CNNs, a particular cost function is employed to evaluate the global error that grows toward the back throughout the training process. Conversely, in such cases, the activation of a neuron will not grow further once the weight between two neurons turns out to be zero. Instead of a single size being provided with the complete cost function in repetitive dynamic routing alongside the agreement, the signal is directed based on the feature parameters. Sabour et al. [ 139 ] provides more details about this architecture. When using MNIST to recognize handwritten digits, this innovative CNN architecture gives superior accuracy. From the application perspective, this architecture has extra suitability for segmentation and detection approaches when compared with classification approaches [ 140 , 141 , 142 ].

High-resolution network (HRNet)

High-resolution representations are necessary for position-sensitive vision tasks, such as semantic segmentation, object detection, and human pose estimation. In the present up-to-date frameworks, the input image is encoded as a low-resolution representation using a subnetwork that is constructed as a connected series of high-to-low resolution convolutions such as VGGNet and ResNet. The low-resolution representation is then recovered to become a high-resolution one. Alternatively, high-resolution representations are maintained during the entire process using a novel network, referred to as a High-Resolution Network (HRNet) [ 143 , 144 ]. This network has two principal features. First, the convolution series of high-to-low resolutions are connected in parallel. Second, the information across the resolutions are repeatedly exchanged. The advantage achieved includes getting a representation that is more accurate in the spatial domain and extra-rich in the semantic domain. Moreover, HRNet has several applications in the fields of object detection, semantic segmentation, and human pose prediction. For computer vision problems, the HRNet represents a more robust backbone. Figure  26 illustrates the general architecture of HRNet.

The general architecture of HRNet

Challenges (limitations) of deep learning and alternate solutions

When employing DL, several difficulties are often taken into consideration. Those more challenging are listed next and several possible alternatives are accordingly provided.

Training data

DL is extremely data-hungry considering it also involves representation learning [ 145 , 146 ]. DL demands an extensively large amount of data to achieve a well-behaved performance model, i.e. as the data increases, an extra well-behaved performance model can be achieved (Fig.  27 ). In most cases, the available data are sufficient to obtain a good performance model. However, sometimes there is a shortage of data for using DL directly [ 87 ]. To properly address this issue, three suggested methods are available. The first involves the employment of the transfer-learning concept after data is collected from similar tasks. Note that while the transferred data will not directly augment the actual data, it will help in terms of both enhancing the original input representation of data and its mapping function [ 147 ]. In this way, the model performance is boosted. Another technique involves employing a well-trained model from a similar task and fine-tuning the ending of two layers or even one layer based on the limited original data. Refer to [ 148 , 149 ] for a review of different transfer-learning techniques applied in the DL approach. In the second method, data augmentation is performed [ 150 ]. This task is very helpful for use in augmenting the image data, since the image translation, mirroring, and rotation commonly do not change the image label. Conversely, it is important to take care when applying this technique in some cases such as with bioinformatics data. For instance, when mirroring an enzyme sequence, the output data may not represent the actual enzyme sequence. In the third method, the simulated data can be considered for increasing the volume of the training set. It is occasionally possible to create simulators based on the physical process if the issue is well understood. Therefore, the result will involve the simulation of as much data as needed. Processing the data requirement for DL-based simulation is obtained as an example in Ref. [ 151 ].

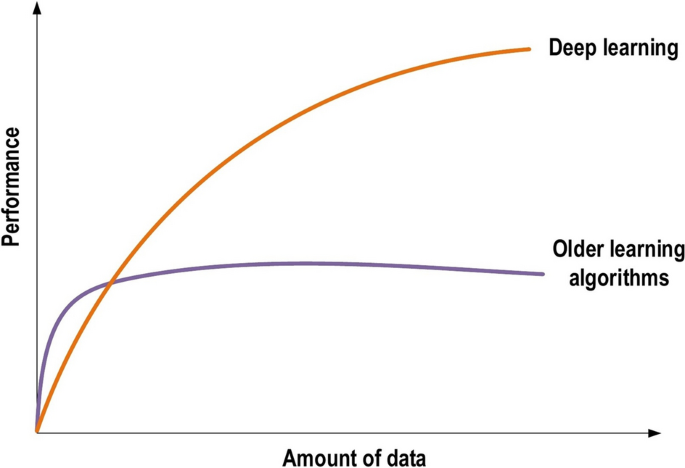
The performance of DL regarding the amount of data

• Transfer learning

Recent research has revealed a widespread use of deep CNNs, which offer ground-breaking support for answering many classification problems. Generally speaking, deep CNN models require a sizable volume of data to obtain good performance. The common challenge associated with using such models concerns the lack of training data. Indeed, gathering a large volume of data is an exhausting job, and no successful solution is available at this time. The undersized dataset problem is therefore currently solved using the TL technique [ 148 , 149 ], which is highly efficient in addressing the lack of training data issue. The mechanism of TL involves training the CNN model with large volumes of data. In the next step, the model is fine-tuned for training on a small request dataset.

The student-teacher relationship is a suitable approach to clarifying TL. Gathering detailed knowledge of the subject is the first step [ 152 ]. Next, the teacher provides a “course” by conveying the information within a “lecture series” over time. Put simply, the teacher transfers the information to the student. In more detail, the expert (teacher) transfers the knowledge (information) to the learner (student). Similarly, the DL network is trained using a vast volume of data, and also learns the bias and the weights during the training process. These weights are then transferred to different networks for retraining or testing a similar novel model. Thus, the novel model is enabled to pre-train weights rather than requiring training from scratch. Figure  28 illustrates the conceptual diagram of the TL technique.

Pre-trained models: Many CNN models, e.g. AlexNet [ 30 ], GoogleNet [ 103 ], and ResNet [ 37 ], have been trained on large datasets such as ImageNet for image recognition purposes. These models can then be employed to recognize a different task without the need to train from scratch. Furthermore, the weights remain the same apart from a few learned features. In cases where data samples are lacking, these models are very useful. There are many reasons for employing a pre-trained model. First, training large models on sizeable datasets requires high-priced computational power. Second, training large models can be time-consuming, taking up to multiple weeks. Finally, a pre-trained model can assist with network generalization and speed up the convergence.

A research problem using pre-trained models: Training a DL approach requires a massive number of images. Thus, obtaining good performance is a challenge under these circumstances. Achieving excellent outcomes in image classification or recognition applications, with performance occasionally superior to that of a human, becomes possible through the use of deep convolutional neural networks (DCNNs) including several layers if a huge amount of data is available [ 37 , 148 , 153 ]. However, avoiding overfitting problems in such applications requires sizable datasets and properly generalizing DCNN models. When training a DCNN model, the dataset size has no lower limit. However, the accuracy of the model becomes insufficient in the case of the utilized model has fewer layers, or if a small dataset is used for training due to over- or under-fitting problems. Due to they have no ability to utilize the hierarchical features of sizable datasets, models with fewer layers have poor accuracy. It is difficult to acquire sufficient training data for DL models. For example, in medical imaging and environmental science, gathering labelled datasets is very costly [ 148 ]. Moreover, the majority of the crowdsourcing workers are unable to make accurate notes on medical or biological images due to their lack of medical or biological knowledge. Thus, ML researchers often rely on field experts to label such images; however, this process is costly and time consuming. Therefore, producing the large volume of labels required to develop flourishing deep networks turns out to be unfeasible. Recently, TL has been widely employed to address the later issue. Nevertheless, although TL enhances the accuracy of several tasks in the fields of pattern recognition and computer vision [ 154 , 155 ], there is an essential issue related to the source data type used by the TL as compared to the target dataset. For instance, enhancing the medical image classification performance of CNN models is achieved by training the models using the ImageNet dataset, which contains natural images [ 153 ]. However, such natural images are completely dissimilar from the raw medical images, meaning that the model performance is not enhanced. It has further been proven that TL from different domains does not significantly affect performance on medical imaging tasks, as lightweight models trained from scratch perform nearly as well as standard ImageNet-transferred models [ 156 ]. Therefore, there exists scenarios in which using pre-trained models do not become an affordable solution. In 2020, some researchers have utilized same-domain TL and achieved excellent results [ 86 , 87 , 88 , 157 ]. Same-domain TL is an approach of using images that look similar to the target dataset for training. For example, using X-ray images of different chest diseases to train the model, then fine-tuning and training it on chest X-ray images for COVID-19 diagnosis. More details about same-domain TL and how to implement the fine-tuning process can be found in [ 87 ].

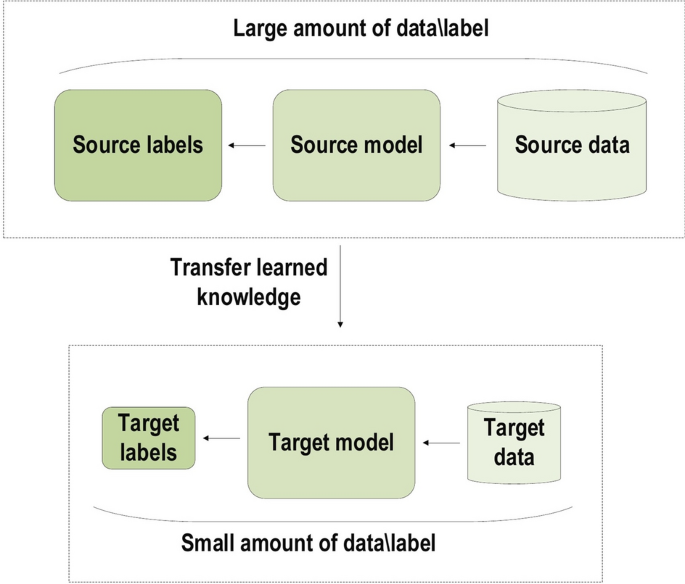
The conceptual diagram of the TL technique

Data augmentation techniques

If the goal is to increase the amount of available data and avoid the overfitting issue, data augmentation techniques are one possible solution [ 150 , 158 , 159 ]. These techniques are data-space solutions for any limited-data problem. Data augmentation incorporates a collection of methods that improve the attributes and size of training datasets. Thus, DL networks can perform better when these techniques are employed. Next, we list some data augmentation alternate solutions.

Flipping: Flipping the vertical axis is a less common practice than flipping the horizontal one. Flipping has been verified as valuable on datasets like ImageNet and CIFAR-10. Moreover, it is highly simple to implement. In addition, it is not a label-conserving transformation on datasets that involve text recognition (such as SVHN and MNIST).

Color space: Encoding digital image data is commonly used as a dimension tensor ( \(height \times width \times color channels\) ). Accomplishing augmentations in the color space of the channels is an alternative technique, which is extremely workable for implementation. A very easy color augmentation involves separating a channel of a particular color, such as Red, Green, or Blue. A simple way to rapidly convert an image using a single-color channel is achieved by separating that matrix and inserting additional double zeros from the remaining two color channels. Furthermore, increasing or decreasing the image brightness is achieved by using straightforward matrix operations to easily manipulate the RGB values. By deriving a color histogram that describes the image, additional improved color augmentations can be obtained. Lighting alterations are also made possible by adjusting the intensity values in histograms similar to those employed in photo-editing applications.

Cropping: Cropping a dominant patch of every single image is a technique employed with combined dimensions of height and width as a specific processing step for image data. Furthermore, random cropping may be employed to produce an impact similar to translations. The difference between translations and random cropping is that translations conserve the spatial dimensions of this image, while random cropping reduces the input size [for example from (256, 256) to (224, 224)]. According to the selected reduction threshold for cropping, the label-preserving transformation may not be addressed.

Rotation: When rotating an image left or right from within 0 to 360 degrees around the axis, rotation augmentations are obtained. The rotation degree parameter greatly determines the suitability of the rotation augmentations. In digit recognition tasks, small rotations (from 0 to 20 degrees) are very helpful. By contrast, the data label cannot be preserved post-transformation when the rotation degree increases.

Translation: To avoid positional bias within the image data, a very useful transformation is to shift the image up, down, left, or right. For instance, it is common that the whole dataset images are centered; moreover, the tested dataset should be entirely made up of centered images to test the model. Note that when translating the initial images in a particular direction, the residual space should be filled with Gaussian or random noise, or a constant value such as 255 s or 0 s. The spatial dimensions of the image post-augmentation are preserved using this padding.

Noise injection This approach involves injecting a matrix of arbitrary values. Such a matrix is commonly obtained from a Gaussian distribution. Moreno-Barea et al. [ 160 ] employed nine datasets to test the noise injection. These datasets were taken from the UCI repository [ 161 ]. Injecting noise within images enables the CNN to learn additional robust features.

However, highly well-behaved solutions for positional biases available within the training data are achieved by means of geometric transformations. To separate the distribution of the testing data from the training data, several prospective sources of bias exist. For instance, when all faces should be completely centered within the frames (as in facial recognition datasets), the problem of positional biases emerges. Thus, geometric translations are the best solution. Geometric translations are helpful due to their simplicity of implementation, as well as their effective capability to disable the positional biases. Several libraries of image processing are available, which enables beginning with simple operations such as rotation or horizontal flipping. Additional training time, higher computational costs, and additional memory are some shortcomings of geometric transformations. Furthermore, a number of geometric transformations (such as arbitrary cropping or translation) should be manually observed to ensure that they do not change the image label. Finally, the biases that separate the test data from the training data are more complicated than transitional and positional changes. Hence, it is not trivial answering to when and where geometric transformations are suitable to be applied.

Imbalanced data

Commonly, biological data tend to be imbalanced, as negative samples are much more numerous than positive ones [ 162 , 163 , 164 ]. For example, compared to COVID-19-positive X-ray images, the volume of normal X-ray images is very large. It should be noted that undesirable results may be produced when training a DL model using imbalanced data. The following techniques are used to solve this issue. First, it is necessary to employ the correct criteria for evaluating the loss, as well as the prediction result. In considering the imbalanced data, the model should perform well on small classes as well as larger ones. Thus, the model should employ area under curve (AUC) as the resultant loss as well as the criteria [ 165 ]. Second, it should employ the weighted cross-entropy loss, which ensures the model will perform well with small classes if it still prefers to employ the cross-entropy loss. Simultaneously, during model training, it is possible either to down-sample the large classes or up-sample the small classes. Finally, to make the data balanced as in Ref. [ 166 ], it is possible to construct models for every hierarchical level, as a biological system frequently has hierarchical label space. However, the effect of the imbalanced data on the performance of the DL model has been comprehensively investigated. In addition, to lessen the problem, the most frequently used techniques were also compared. Nevertheless, note that these techniques are not specified for biological problems.

Interpretability of data

Occasionally, DL techniques are analyzed to act as a black box. In fact, they are interpretable. The need for a method of interpreting DL, which is used to obtain the valuable motifs and patterns recognized by the network, is common in many fields, such as bioinformatics [ 167 ]. In the task of disease diagnosis, it is not only required to know the disease diagnosis or prediction results of a trained DL model, but also how to enhance the surety of the prediction outcomes, as the model makes its decisions based on these verifications [ 168 ]. To achieve this, it is possible to give a score of importance for every portion of the particular example. Within this solution, back-propagation-based techniques or perturbation-based approaches are used [ 169 ]. In the perturbation-based approaches, a portion of the input is changed and the effect of this change on the model output is observed [ 170 , 171 , 172 , 173 ]. This concept has high computational complexity, but it is simple to understand. On the other hand, to check the score of the importance of various input portions, the signal from the output propagates back to the input layer in the back-propagation-based techniques. These techniques have been proven valuable in [ 174 ]. In different scenarios, various meanings can represent the model interpretability.

Uncertainty scaling

Commonly, the final prediction label is not the only label required when employing DL techniques to achieve the prediction; the score of confidence for every inquiry from the model is also desired. The score of confidence is defined as how confident the model is in its prediction [ 175 ]. Since the score of confidence prevents belief in unreliable and misleading predictions, it is a significant attribute, regardless of the application scenario. In biology, the confidence score reduces the resources and time expended in proving the outcomes of the misleading prediction. Generally speaking, in healthcare or similar applications, the uncertainty scaling is frequently very significant; it helps in evaluating automated clinical decisions and the reliability of machine learning-based disease-diagnosis [ 176 , 177 ]. Because overconfident prediction can be the output of different DL models, the score of probability (achieved from the softmax output of the direct-DL) is often not in the correct scale [ 178 ]. Note that the softmax output requires post-scaling to achieve a reliable probability score. For outputting the probability score in the correct scale, several techniques have been introduced, including Bayesian Binning into Quantiles (BBQ) [ 179 ], isotonic regression [ 180 ], histogram binning [ 181 ], and the legendary Platt scaling [ 182 ]. More specifically, for DL techniques, temperature scaling was recently introduced, which achieves superior performance compared to the other techniques.

Catastrophic forgetting

This is defined as incorporating new information into a plain DL model, made possible by interfering with the learned information. For instance, consider a case where there are 1000 types of flowers and a model is trained to classify these flowers, after which a new type of flower is introduced; if the model is fine-tuned only with this new class, its performance will become unsuccessful with the older classes [ 183 , 184 ]. The logical data are continually collected and renewed, which is in fact a highly typical scenario in many fields, e.g. Biology. To address this issue, there is a direct solution that involves employing old and new data to train an entirely new model from scratch. This solution is time-consuming and computationally intensive; furthermore, it leads to an unstable state for the learned representation of the initial data. At this time, three different types of ML techniques, which have not catastrophic forgetting, are made available to solve the human brain problem founded on the neurophysiological theories [ 185 , 186 ]. Techniques of the first type are founded on regularizations such as EWC [ 183 ] Techniques of the second type employ rehearsal training techniques and dynamic neural network architecture like iCaRL [ 187 , 188 ]. Finally, techniques of the third type are founded on dual-memory learning systems [ 189 ]. Refer to [ 190 , 191 , 192 ] in order to gain more details.

Model compression

To obtain well-trained models that can still be employed productively, DL models have intensive memory and computational requirements due to their huge complexity and large numbers of parameters [ 193 , 194 ]. One of the fields that is characterized as data-intensive is the field of healthcare and environmental science. These needs reduce the deployment of DL in limited computational-power machines, mainly in the healthcare field. The numerous methods of assessing human health and the data heterogeneity have become far more complicated and vastly larger in size [ 195 ]; thus, the issue requires additional computation [ 196 ]. Furthermore, novel hardware-based parallel processing solutions such as FPGAs and GPUs [ 197 , 198 , 199 ] have been developed to solve the computation issues associated with DL. Recently, numerous techniques for compressing the DL models, designed to decrease the computational issues of the models from the starting point, have also been introduced. These techniques can be classified into four classes. In the first class, the redundant parameters (which have no significant impact on model performance) are reduced. This class, which includes the famous deep compression method, is called parameter pruning [ 200 ]. In the second class, the larger model uses its distilled knowledge to train a more compact model; thus, it is called knowledge distillation [ 201 , 202 ]. In the third class, compact convolution filters are used to reduce the number of parameters [ 203 ]. In the final class, the information parameters are estimated for preservation using low-rank factorization [ 204 ]. For model compression, these classes represent the most representative techniques. In [ 193 ], it has been provided a more comprehensive discussion about the topic.

Overfitting

DL models have excessively high possibilities of resulting in data overfitting at the training stage due to the vast number of parameters involved, which are correlated in a complex manner. Such situations reduce the model’s ability to achieve good performance on the tested data [ 90 , 205 ]. This problem is not only limited to a specific field, but involves different tasks. Therefore, when proposing DL techniques, this problem should be fully considered and accurately handled. In DL, the implied bias of the training process enables the model to overcome crucial overfitting problems, as recent studies suggest [ 205 , 206 , 207 , 208 ]. Even so, it is still necessary to develop techniques that handle the overfitting problem. An investigation of the available DL algorithms that ease the overfitting problem can categorize them into three classes. The first class acts on both the model architecture and model parameters and includes the most familiar approaches, such as weight decay [ 209 ], batch normalization [ 210 ], and dropout [ 90 ]. In DL, the default technique is weight decay [ 209 ], which is used extensively in almost all ML algorithms as a universal regularizer. The second class works on model inputs such as data corruption and data augmentation [ 150 , 211 ]. One reason for the overfitting problem is the lack of training data, which makes the learned distribution not mirror the real distribution. Data augmentation enlarges the training data. By contrast, marginalized data corruption improves the solution exclusive to augmenting the data. The final class works on the model output. A recently proposed technique penalizes the over-confident outputs for regularizing the model [ 178 ]. This technique has demonstrated the ability to regularize RNNs and CNNs.

Vanishing gradient problem

In general, when using backpropagation and gradient-based learning techniques along with ANNs, largely in the training stage, a problem called the vanishing gradient problem arises [ 212 , 213 , 214 ]. More specifically, in each training iteration, every weight of the neural network is updated based on the current weight and is proportionally relative to the partial derivative of the error function. However, this weight updating may not occur in some cases due to a vanishingly small gradient, which in the worst case means that no extra training is possible and the neural network will stop completely. Conversely, similarly to other activation functions, the sigmoid function shrinks a large input space to a tiny input space. Thus, the derivative of the sigmoid function will be small due to large variation at the input that produces a small variation at the output. In a shallow network, only some layers use these activations, which is not a significant issue. While using more layers will lead the gradient to become very small in the training stage, in this case, the network works efficiently. The back-propagation technique is used to determine the gradients of the neural networks. Initially, this technique determines the network derivatives of each layer in the reverse direction, starting from the last layer and progressing back to the first layer. The next step involves multiplying the derivatives of each layer down the network in a similar manner to the first step. For instance, multiplying N small derivatives together when there are N hidden layers employs an activation function such as the sigmoid function. Hence, the gradient declines exponentially while propagating back to the first layer. More specifically, the biases and weights of the first layers cannot be updated efficiently during the training stage because the gradient is small. Moreover, this condition decreases the overall network accuracy, as these first layers are frequently critical to recognizing the essential elements of the input data. However, such a problem can be avoided through employing activation functions. These functions lack the squishing property, i.e., the ability to squish the input space to within a small space. By mapping X to max, the ReLU [ 91 ] is the most popular selection, as it does not yield a small derivative that is employed in the field. Another solution involves employing the batch normalization layer [ 81 ]. As mentioned earlier, the problem occurs once a large input space is squashed into a small space, leading to vanishing the derivative. Employing batch normalization degrades this issue by simply normalizing the input, i.e., the expression | x | does not accomplish the exterior boundaries of the sigmoid function. The normalization process makes the largest part of it come down in the green area, which ensures that the derivative is large enough for further actions. Furthermore, faster hardware can tackle the previous issue, e.g. that provided by GPUs. This makes standard back-propagation possible for many deeper layers of the network compared to the time required to recognize the vanishing gradient problem [ 215 ].

Exploding gradient problem

Opposite to the vanishing problem is the one related to gradient. Specifically, large error gradients are accumulated during back-propagation [ 216 , 217 , 218 ]. The latter will lead to extremely significant updates to the weights of the network, meaning that the system becomes unsteady. Thus, the model will lose its ability to learn effectively. Grosso modo, moving backward in the network during back-propagation, the gradient grows exponentially by repetitively multiplying gradients. The weight values could thus become incredibly large and may overflow to become a not-a-number (NaN) value. Some potential solutions include:

Using different weight regularization techniques.

Redesigning the architecture of the network model.

Underspecification

In 2020, a team of computer scientists at Google has identified a new challenge called underspecification [ 219 ]. ML models including DL models often show surprisingly poor behavior when they are tested in real-world applications such as computer vision, medical imaging, natural language processing, and medical genomics. The reason behind the weak performance is due to underspecification. It has been shown that small modifications can force a model towards a completely different solution as well as lead to different predictions in deployment domains. There are different techniques of addressing underspecification issue. One of them is to design “stress tests” to examine how good a model works on real-world data and to find out the possible issues. Nevertheless, this demands a reliable understanding of the process the model can work inaccurately. The team stated that “Designing stress tests that are well-matched to applied requirements, and that provide good “coverage” of potential failure modes is a major challenge”. Underspecification puts major constraints on the credibility of ML predictions and may require some reconsidering over certain applications. Since ML is linked to human by serving several applications such as medical imaging and self-driving cars, it will require proper attention to this issue.

Applications of deep learning

Presently, various DL applications are widespread around the world. These applications include healthcare, social network analysis, audio and speech processing (like recognition and enhancement), visual data processing methods (such as multimedia data analysis and computer vision), and NLP (translation and sentence classification), among others (Fig.  29 ) [ 220 , 221 , 222 , 223 , 224 ]. These applications have been classified into five categories: classification, localization, detection, segmentation, and registration. Although each of these tasks has its own target, there is fundamental overlap in the pipeline implementation of these applications as shown in Fig.  30 . Classification is a concept that categorizes a set of data into classes. Detection is used to locate interesting objects in an image with consideration given to the background. In detection, multiple objects, which could be from dissimilar classes, are surrounded by bounding boxes. Localization is the concept used to locate the object, which is surrounded by a single bounding box. In segmentation (semantic segmentation), the target object edges are surrounded by outlines, which also label them; moreover, fitting a single image (which could be 2D or 3D) onto another refers to registration. One of the most important and wide-ranging DL applications are in healthcare [ 225 , 226 , 227 , 228 , 229 , 230 ]. This area of research is critical due to its relation to human lives. Moreover, DL has shown tremendous performance in healthcare. Therefore, we take DL applications in the medical image analysis field as an example to describe the DL applications.

Examples of DL applications

Workflow of deep learning tasks

Classification

Computer-Aided Diagnosis (CADx) is another title sometimes used for classification. Bharati et al. [ 231 ] used a chest X-ray dataset for detecting lung diseases based on a CNN. Another study attempted to read X-ray images by employing CNN [ 232 ]. In this modality, the comparative accessibility of these images has likely enhanced the progress of DL. [ 233 ] used an improved pre-trained GoogLeNet CNN containing more than 150,000 images for training and testing processes. This dataset was augmented from 1850 chest X-rays. The creators reorganized the image orientation into lateral and frontal views and achieved approximately 100% accuracy. This work of orientation classification has clinically limited use. As a part of an ultimately fully automated diagnosis workflow, it obtained the data augmentation and pre-trained efficiency in learning the metadata of relevant images. Chest infection, commonly referred to as pneumonia, is extremely treatable, as it is a commonly occurring health problem worldwide. Conversely, Rajpurkar et al. [ 234 ] utilized CheXNet, which is an improved version of DenseNet [ 112 ] with 121 convolution layers, for classifying fourteen types of disease. These authors used the CheXNet14 dataset [ 235 ], which comprises 112,000 images. This network achieved an excellent performance in recognizing fourteen different diseases. In particular, pneumonia classification accomplished a 0.7632 AUC score using receiver operating characteristics (ROC) analysis. In addition, the network obtained better than or equal to the performance of both a three-radiologist panel and four individual radiologists. Zuo et al. [ 236 ] have adopted CNN for candidate classification in lung nodule. Shen et al. [ 237 ] employed both Random Forest (RF) and SVM classifiers with CNNs to classify lung nodules. They employed two convolutional layers with each of the three parallel CNNs. The LIDC-IDRI (Lung Image Database Consortium) dataset, which contained 1010-labeled CT lung scans, was used to classify the two types of lung nodules (malignant and benign). Different scales of the image patches were used by every CNN to extract features, while the output feature vector was constructed using the learned features. Next, these vectors were classified into malignant or benign using either the RF classifier or SVM with radial basis function (RBF) filter. The model was robust to various noisy input levels and achieved an accuracy of 86% in nodule classification. Conversely, the model of [ 238 ] interpolates the image data missing between PET and MRI images using 3D CNNs. The Alzheimer Disease Neuroimaging Initiative (ADNI) database, containing 830 PET and MRI patient scans, was utilized in their work. The PET and MRI images are used to train the 3D CNNs, first as input and then as output. Furthermore, for patients who have no PET images, the 3D CNNs utilized the trained images to rebuild the PET images. These rebuilt images approximately fitted the actual disease recognition outcomes. However, this approach did not address the overfitting issues, which in turn restricted their technique in terms of its possible capacity for generalization. Diagnosing normal versus Alzheimer’s disease patients has been achieved by several CNN models [ 239 , 240 ]. Hosseini-Asl et al. [ 241 ] attained 99% accuracy for up-to-date outcomes in diagnosing normal versus Alzheimer’s disease patients. These authors applied an auto-encoder architecture using 3D CNNs. The generic brain features were pre-trained on the CADDementia dataset. Subsequently, the outcomes of these learned features became inputs to higher layers to differentiate between patient scans of Alzheimer’s disease, mild cognitive impairment, or normal brains based on the ADNI dataset and using fine-tuned deep supervision techniques. The architectures of VGGNet and RNNs, in that order, were the basis of both VOXCNN and ResNet models developed by Korolev et al. [ 242 ]. They also discriminated between Alzheimer’s disease and normal patients using the ADNI database. Accuracy was 79% for Voxnet and 80% for ResNet. Compared to Hosseini-Asl’s work, both models achieved lower accuracies. Conversely, the implementation of the algorithms was simpler and did not require feature hand-crafting, as Korolev declared. In 2020, Mehmood et al. [ 240 ] trained a developed CNN-based network called “SCNN” with MRI images for the tasks of classification of Alzheimer’s disease. They achieved state-of-the-art results by obtaining an accuracy of 99.05%.

Recently, CNN has taken some medical imaging classification tasks to different level from traditional diagnosis to automated diagnosis with tremendous performance. Examples of these tasks are diabetic foot ulcer (DFU) (as normal and abnormal (DFU) classes) [ 87 , 243 , 244 , 245 , 246 ], sickle cells anemia (SCA) (as normal, abnormal (SCA), and other blood components) [ 86 , 247 ], breast cancer by classify hematoxylin–eosin-stained breast biopsy images into four classes: invasive carcinoma, in-situ carcinoma, benign tumor and normal tissue [ 42 , 88 , 248 , 249 , 250 , 251 , 252 ], and multi-class skin cancer classification [ 253 , 254 , 255 ].

In 2020, CNNs are playing a vital role in early diagnosis of the novel coronavirus (COVID-2019). CNN has become the primary tool for automatic COVID-19 diagnosis in many hospitals around the world using chest X-ray images [ 256 , 257 , 258 , 259 , 260 ]. More details about the classification of medical imaging applications can be found in [ 226 , 261 , 262 , 263 , 264 , 265 ].

Localization

Although applications in anatomy education could increase, the practicing clinician is more likely to be interested in the localization of normal anatomy. Radiological images are independently examined and described outside of human intervention, while localization could be applied in completely automatic end-to-end applications [ 266 , 267 , 268 ]. Zhao et al. [ 269 ] introduced a new deep learning-based approach to localize pancreatic tumor in projection X-ray images for image-guided radiation therapy without the need for fiducials. Roth et al. [ 270 ] constructed and trained a CNN using five convolutional layers to classify around 4000 transverse-axial CT images. These authors used five categories for classification: legs, pelvis, liver, lung, and neck. After data augmentation techniques were applied, they achieved an AUC score of 0.998 and the classification error rate of the model was 5.9%. For detecting the positions of the spleen, kidney, heart, and liver, Shin et al. [ 271 ] employed stacked auto-encoders on 78 contrast-improved MRI scans of the stomach area containing the kidneys or liver. Temporal and spatial domains were used to learn the hierarchal features. Based on the organs, these approaches achieved detection accuracies of 62–79%. Sirazitdinov et al. [ 268 ] presented an aggregate of two convolutional neural networks, namely RetinaNet and Mask R-CNN for pneumonia detection and localization.

Computer-Aided Detection (CADe) is another method used for detection. For both the clinician and the patient, overlooking a lesion on a scan may have dire consequences. Thus, detection is a field of study requiring both accuracy and sensitivity [ 272 , 273 , 274 ]. Chouhan et al. [ 275 ] introduced an innovative deep learning framework for the detection of pneumonia by adopting the idea of transfer learning. Their approach obtained an accuracy of 96.4% with a recall of 99.62% on unseen data. In the area of COVID-19 and pulmonary disease, several convolutional neural network approaches have been proposed for automatic detection from X-ray images which showed an excellent performance [ 46 , 276 , 277 , 278 , 279 ].

In the area of skin cancer, there several applications were introduced for the detection task [ 280 , 281 , 282 ]. Thurnhofer-Hemsi et al. [ 283 ] introduced a deep learning approach for skin cancer detection by fine-tuning five state-of-art convolutional neural network models. They addressed the issue of a lack of training data by adopting the ideas of transfer learning and data augmentation techniques. DenseNet201 network has shown superior results compared to other models.

Another interesting area is that of histopathological images, which are progressively digitized. Several papers have been published in this field [ 284 , 285 , 286 , 287 , 288 , 289 , 290 ]. Human pathologists read these images laboriously; they search for malignancy markers, such as a high index of cell proliferation, using molecular markers (e.g. Ki-67), cellular necrosis signs, abnormal cellular architecture, enlarged numbers of mitotic figures denoting augmented cell replication, and enlarged nucleus-to-cytoplasm ratios. Note that the histopathological slide may contain a huge number of cells (up to the thousands). Thus, the risk of disregarding abnormal neoplastic regions is high when wading through these cells at excessive levels of magnification. Ciresan et al. [ 291 ] employed CNNs of 11–13 layers for identifying mitotic figures. Fifty breast histology images from the MITOS dataset were used. Their technique attained recall and precision scores of 0.7 and 0.88 respectively. Sirinukunwattana et al. [ 292 ] utilized 100 histology images of colorectal adenocarcinoma to detect cell nuclei using CNNs. Roughly 30,000 nuclei were hand-labeled for training purposes. The novelty of this approach was in the use of Spatially Constrained CNN. This CNN detects the center of nuclei using the surrounding spatial context and spatial regression. Instead of this CNN, Xu et al. [ 293 ] employed a stacked sparse auto-encoder (SSAE) to identify nuclei in histological slides of breast cancer, achieving 0.83 and 0.89 recall and precision scores respectively. In this field, they showed that unsupervised learning techniques are also effectively utilized. In medical images, Albarquoni et al. [ 294 ] investigated the problem of insufficient labeling. They crowd-sourced the actual mitoses labeling in the histology images of breast cancer (from amateurs online). Solving the recurrent issue of inadequate labeling during the analysis of medical images can be achieved by feeding the crowd-sourced input labels into the CNN. This method signifies a remarkable proof-of-concept effort. In 2020, Lei et al. [ 285 ] introduced the employment of deep convolutional neural networks for automatic identification of mitotic candidates from histological sections for mitosis screening. They obtained the state-of-the-art detection results on the dataset of the International Pattern Recognition Conference (ICPR) 2012 Mitosis Detection Competition.

Segmentation

Although MRI and CT image segmentation research includes different organs such as knee cartilage, prostate, and liver, most research work has concentrated on brain segmentation, particularly tumors [ 295 , 296 , 297 , 298 , 299 , 300 ]. This issue is highly significant in surgical preparation to obtain the precise tumor limits for the shortest surgical resection. During surgery, excessive sacrificing of key brain regions may lead to neurological shortfalls including cognitive damage, emotionlessness, and limb difficulty. Conventionally, medical anatomical segmentation was done by hand; more specifically, the clinician draws out lines within the complete stack of the CT or MRI volume slice by slice. Thus, it is perfect for implementing a solution that computerizes this painstaking work. Wadhwa et al. [ 301 ] presented a brief overview on brain tumor segmentation of MRI images. Akkus et al. [ 302 ] wrote a brilliant review of brain MRI segmentation that addressed the different metrics and CNN architectures employed. Moreover, they explain several competitions in detail, as well as their datasets, which included Ischemic Stroke Lesion Segmentation (ISLES), Mild Traumatic brain injury Outcome Prediction (MTOP), and Brain Tumor Segmentation (BRATS).

Chen et al. [ 299 ] proposed convolutional neural networks for precise brain tumor segmentation. The approach that they employed involves several approaches for better features learning including the DeepMedic model, a novel dual-force training scheme, a label distribution-based loss function, and Multi-Layer Perceptron-based post-processing. They conducted their method on the two most modern brain tumor segmentation datasets, i.e., BRATS 2017 and BRATS 2015 datasets. Hu et al. [ 300 ] introduced the brain tumor segmentation method by adopting a multi-cascaded convolutional neural network (MCCNN) and fully connected conditional random fields (CRFs). The achieved results were excellent compared with the state-of-the-art methods.

Moeskops et al. [ 303 ] employed three parallel-running CNNs, each of which had a 2D input patch of dissimilar size, for segmenting and classifying MRI brain images. These images, which include 35 adults and 22 pre-term infants, were classified into various tissue categories such as cerebrospinal fluid, grey matter, and white matter. Every patch concentrates on capturing various image aspects with the benefit of employing three dissimilar sizes of input patch; here, the bigger sizes incorporated the spatial features, while the lowest patch sizes concentrated on the local textures. In general, the algorithm has Dice coefficients in the range of 0.82–0.87 and achieved a satisfactory accuracy. Although 2D image slices are employed in the majority of segmentation research, Milletrate et al. [ 304 ] implemented 3D CNN for segmenting MRI prostate images. Furthermore, they used the PROMISE2012 challenge dataset, from which fifty MRI scans were used for training and thirty for testing. The U-Net architecture of Ronnerberger et al. [ 305 ] inspired their V-net. This model attained a 0.869 Dice coefficient score, the same as the winning teams in the competition. To reduce overfitting and create the model of a deeper 11-convolutional layer CNN, Pereira et al. [ 306 ] applied intentionally small-sized filters of 3x3. Their model used MRI scans of 274 gliomas (a type of brain tumor) for training. They achieved first place in the 2013 BRATS challenge, as well as second place in the BRATS challenge 2015. Havaei et al. [ 307 ] also considered gliomas using the 2013 BRATS dataset. They investigated different 2D CNN architectures. Compared to the winner of BRATS 2013, their algorithm worked better, as it required only 3 min to execute rather than 100 min. The concept of cascaded architecture formed the basis of their model. Thus, it is referred to as an InputCascadeCNN. Employing FC Conditional Random Fields (CRFs), atrous spatial pyramid pooling, and up-sampled filters were techniques introduced by Chen et al. [ 308 ]. These authors aimed to enhance the accuracy of localization and enlarge the field of view of every filter at a multi-scale. Their model, DeepLab, attained 79.7% mIOU (mean Intersection Over Union). In the PASCAL VOC-2012 image segmentation, their model obtained an excellent performance.

Recently, the Automatic segmentation of COVID-19 Lung Infection from CT Images helps to detect the development of COVID-19 infection by employing several deep learning techniques [ 309 , 310 , 311 , 312 ].

Registration

Usually, given two input images, the four main stages of the canonical procedure of the image registration task are [ 313 , 314 ]:

Target Selection: it illustrates the determined input image that the second counterpart input image needs to remain accurately superimposed to.

Feature Extraction: it computes the set of features extracted from each input image.

Feature Matching: it allows finding similarities between the previously obtained features.

Pose Optimization: it is aimed to minimize the distance between both input images.

Then, the result of the registration procedure is the suitable geometric transformation (e.g. translation, rotation, scaling, etc.) that provides both input images within the same coordinate system in a way the distance between them is minimal, i.e. their level of superimposition/overlapping is optimal. It is out of the scope of this work to provide an extensive review of this topic. Nevertheless, a short summary is accordingly introduced next.

Commonly, the input images for the DL-based registration approach could be in various forms, e.g. point clouds, voxel grids, and meshes. Additionally, some techniques allow as inputs the result of the Feature Extraction or Matching steps in the canonical scheme. Specifically, the outcome could be some data in a particular form as well as the result of the steps from the classical pipeline (feature vector, matching vector, and transformation). Nevertheless, with the newest DL-based methods, a novel conceptual type of ecosystem issues. It contains acquired characteristics about the target, materials, and their behavior that can be registered with the input data. Such a conceptual ecosystem is formed by a neural network and its training manner, and it could be counted as an input to the registration approach. Nevertheless, it is not an input that one might adopt in every registration situation since it corresponds to an interior data representation.

From a DL view-point, the interpretation of the conceptual design enables differentiating the input data of a registration approach into defined or non-defined models. In particular, the illustrated phases are models that depict particular spatial data (e.g. 2D or 3D) while a non-defined one is a generalization of a data set created by a learning system. Yumer et al. [ 315 ] developed a framework in which the model acquires characteristics of objects, meaning ready to identify what a more sporty car seems like or a more comfy chair is, also adjusting a 3D model to fit those characteristics while maintaining the main characteristics of the primary data. Likewise, a fundamental perspective of the unsupervised learning method introduced by Ding et al. [ 316 ] is that there is no target for the registration approach. In this instance, the network is able of placing each input point cloud in a global space, solving SLAM issues in which many point clouds have to be registered rigidly. On the other hand, Mahadevan [ 317 ] proposed the combination of two conceptual models utilizing the growth of Imagination Machines to give flexible artificial intelligence systems and relationships between the learned phases through training schemes that are not inspired on labels and classifications. Another practical application of DL, especially CNNs, to image registration is the 3D reconstruction of objects. Wang et al. [ 318 ] applied an adversarial way using CNNs to rebuild a 3D model of an object from its 2D image. The network learns many objects and orally accomplishes the registration between the image and the conceptual model. Similarly, Hermoza et al. [ 319 ] also utilize the GAN network for prognosticating the absent geometry of damaged archaeological objects, providing the reconstructed object based on a voxel grid format and a label selecting its class.

DL for medical image registration has numerous applications, which were listed by some review papers [ 320 , 321 , 322 ]. Yang et al. [ 323 ] implemented stacked convolutional layers as an encoder-decoder approach to predict the morphing of the input pixel into its last formation using MRI brain scans from the OASIS dataset. They employed a registration model known as Large Deformation Diffeomorphic Metric Mapping (LDDMM) and attained remarkable enhancements in computation time. Miao et al. [ 324 ] used synthetic X-ray images to train a five-layer CNN to register 3D models of a trans-esophageal probe, a hand implant, and a knee implant onto 2D X-ray images for pose estimation. They determined that their model achieved an execution time of 0.1 s, representing an important enhancement against the conventional registration techniques based on intensity; moreover, it achieved effective registrations 79–99% of the time. Li et al. [ 325 ] introduced a neural network-based approach for the non-rigid 2D–3D registration of the lateral cephalogram and the volumetric cone-beam CT (CBCT) images.

Computational approaches

For computationally exhaustive applications, complex ML and DL approaches have rapidly been identified as the most significant techniques and are widely used in different fields. The development and enhancement of algorithms aggregated with capabilities of well-behaved computational performance and large datasets make it possible to effectively execute several applications, as earlier applications were either not possible or difficult to take into consideration.

Currently, several standard DNN configurations are available. The interconnection patterns between layers and the total number of layers represent the main differences between these configurations. The Table  2 illustrates the growth rate of the overall number of layers over time, which seems to be far faster than the “Moore’s Law growth rate”. In normal DNN, the number of layers grew by around 2.3× each year in the period from 2012 to 2016. Recent investigations of future ResNet versions reveal that the number of layers can be extended up to 1000. However, an SGD technique is employed to fit the weights (or parameters), while different optimization techniques are employed to obtain parameter updating during the DNN training process. Repetitive updates are required to enhance network accuracy in addition to a minorly augmented rate of enhancement. For example, the training process using ImageNet as a large dataset, which contains more than 14 million images, along with ResNet as a network model, take around 30K to 40K repetitions to converge to a steady solution. In addition, the overall computational load, as an upper-level prediction, may exceed 1020 FLOPS when both the training set size and the DNN complexity increase.

Prior to 2008, boosting the training to a satisfactory extent was achieved by using GPUs. Usually, days or weeks are needed for a training session, even with GPU support. By contrast, several optimization strategies were developed to reduce the extensive learning time. The computational requirements are believed to increase as the DNNs continuously enlarge in both complexity and size.

In addition to the computational load cost, the memory bandwidth and capacity have a significant effect on the entire training performance, and to a lesser extent, deduction. More specifically, the parameters are distributed through every layer of the input data, there is a sizeable amount of reused data, and the computation of several network layers exhibits an excessive computation-to-bandwidth ratio. By contrast, there are no distributed parameters, the amount of reused data is extremely small, and the additional FC layers have an extremely small computation-to-bandwidth ratio. Table  3 presents a comparison between different aspects related to the devices. In addition, the table is established to facilitate familiarity with the tradeoffs by obtaining the optimal approach for configuring a system based on either FPGA, GPU, or CPU devices. It should be noted that each has corresponding weaknesses and strengths; accordingly, there are no clear one-size-fits-all solutions.

Although GPU processing has enhanced the ability to address the computational challenges related to such networks, the maximum GPU (or CPU) performance is not achieved, and several techniques or models have turned out to be strongly linked to bandwidth. In the worst cases, the GPU efficiency is between 15 and 20% of the maximum theoretical performance. This issue is required to enlarge the memory bandwidth using high-bandwidth stacked memory. Next, different approaches based on FPGA, GPU, and CPU are accordingly detailed.

CPU-based approach

The well-behaved performance of the CPU nodes usually assists robust network connectivity, storage abilities, and large memory. Although CPU nodes are more common-purpose than those of FPGA or GPU, they lack the ability to match them in unprocessed computation facilities, since this requires increased network ability and a larger memory capacity.

GPU-based approach

GPUs are extremely effective for several basic DL primitives, which include greatly parallel-computing operations such as activation functions, matrix multiplication, and convolutions [ 326 , 327 , 328 , 329 , 330 ]. Incorporating HBM-stacked memory into the up-to-date GPU models significantly enhances the bandwidth. This enhancement allows numerous primitives to efficiently utilize all computational resources of the available GPUs. The improvement in GPU performance over CPU performance is usually 10-20:1 related to dense linear algebra operations.

Maximizing parallel processing is the base of the initial GPU programming model. For example, a GPU model may involve up to sixty-four computational units. There are four SIMD engines per each computational layer, and each SIMD has sixteen floating-point computation lanes. The peak performance is 25 TFLOPS (fp16) and 10 TFLOPS (fp32) as the percentage of the employment approaches 100%. Additional GPU performance may be achieved if the addition and multiply functions for vectors combine the inner production instructions for matching primitives related to matrix operations.

For DNN training, the GPU is usually considered to be an optimized design, while for inference operations, it may also offer considerable performance improvements.

FPGA-based approach

FPGA is wildly utilized in various tasks including deep learning [ 199 , 247 , 331 , 332 , 333 , 334 ]. Inference accelerators are commonly implemented utilizing FPGA. The FPGA can be effectively configured to reduce the unnecessary or overhead functions involved in GPU systems. Compared to GPU, the FPGA is restricted to both weak-behaved floating-point performance and integer inference. The main FPGA aspect is the capability to dynamically reconfigure the array characteristics (at run-time), as well as the capability to configure the array by means of effective design with little or no overhead.

As mentioned earlier, the FPGA offers both performance and latency for every watt it gains over GPU and CPU in DL inference operations. Implementation of custom high-performance hardware, pruned networks, and reduced arithmetic precision are three factors that enable the FPGA to implement DL algorithms and to achieve FPGA with this level of efficiency. In addition, FPGA may be employed to implement CNN overlay engines with over 80% efficiency, eight-bit accuracy, and over 15 TOPs peak performance; this is used for a few conventional CNNs, as Xillinx and partners demonstrated recently. By contrast, pruning techniques are mostly employed in the LSTM context. The sizes of the models can be efficiently minimized by up to 20×, which provides an important benefit during the implementation of the optimal solution, as MLP neural processing demonstrated. A recent study in the field of implementing fixed-point precision and custom floating-point has revealed that lowering the 8-bit is extremely promising; moreover, it aids in supplying additional advancements to implementing peak performance FPGA related to the DNN models.

Evaluation metrics

Evaluation metrics adopted within DL tasks play a crucial role in achieving the optimized classifier [ 335 ]. They are utilized within a usual data classification procedure through two main stages: training and testing. It is utilized to optimize the classification algorithm during the training stage. This means that the evaluation metric is utilized to discriminate and select the optimized solution, e.g., as a discriminator, which can generate an extra-accurate forecast of upcoming evaluations related to a specific classifier. For the time being, the evaluation metric is utilized to measure the efficiency of the created classifier, e.g. as an evaluator, within the model testing stage using hidden data. As given in Eq. 20 , TN and TP are defined as the number of negative and positive instances, respectively, which are successfully classified. In addition, FN and FP are defined as the number of misclassified positive and negative instances respectively. Next, some of the most well-known evaluation metrics are listed below.

Accuracy: Calculates the ratio of correct predicted classes to the total number of samples evaluated (Eq. 20 ).

Sensitivity or Recall: Utilized to calculate the fraction of positive patterns that are correctly classified (Eq. 21 ).

Specificity: Utilized to calculate the fraction of negative patterns that are correctly classified (Eq. 22 ).

Precision: Utilized to calculate the positive patterns that are correctly predicted by all predicted patterns in a positive class (Eq. 23 ).

F1-Score: Calculates the harmonic average between recall and precision rates (Eq. 24 ).

J Score: This metric is also called Youdens J statistic. Eq. 25 represents the metric.

False Positive Rate (FPR): This metric refers to the possibility of a false alarm ratio as calculated in Eq. 26

Area Under the ROC Curve: AUC is a common ranking type metric. It is utilized to conduct comparisons between learning algorithms [ 336 , 337 , 338 ], as well as to construct an optimal learning model [ 339 , 340 ]. In contrast to probability and threshold metrics, the AUC value exposes the entire classifier ranking performance. The following formula is used to calculate the AUC value for two-class problem [ 341 ] (Eq. 27 )

Here, \(S_{p}\) represents the sum of all positive ranked samples. The number of negative and positive samples is denoted as \(n_{n}\) and \(n_{p}\) , respectively. Compared to the accuracy metrics, the AUC value was verified empirically and theoretically, making it very helpful for identifying an optimized solution and evaluating the classifier performance through classification training.

When considering the discrimination and evaluation processes, the AUC performance was brilliant. However, for multiclass issues, the AUC computation is primarily cost-effective when discriminating a large number of created solutions. In addition, the time complexity for computing the AUC is \(O \left( |C|^{2} \; n\log n\right) \) with respect to the Hand and Till AUC model [ 341 ] and \(O \left( |C| \; n\log n\right) \) according to Provost and Domingo’s AUC model [ 336 ].

Frameworks and datasets

Several DL frameworks and datasets have been developed in the last few years. various frameworks and libraries have also been used in order to expedite the work with good results. Through their use, the training process has become easier. Table  4 lists the most utilized frameworks and libraries.

Based on the star ratings on Github, as well as our own background in the field, TensorFlow is deemed the most effective and easy to use. It has the ability to work on several platforms. (Github is one of the biggest software hosting sites, while Github stars refer to how well-regarded a project is on the site). Moreover, there are several other benchmark datasets employed for different DL tasks. Some of these are listed in Table  5 .

Summary and conclusion

Finally, it is mandatory the inclusion of a brief discussion by gathering all the relevant data provided along this extensive research. Next, an itemized analysis is presented in order to conclude our review and exhibit the future directions.

DL already experiences difficulties in simultaneously modeling multi-complex modalities of data. In recent DL developments, another common approach is that of multimodal DL.

DL requires sizeable datasets (labeled data preferred) to predict unseen data and to train the models. This challenge turns out to be particularly difficult when real-time data processing is required or when the provided datasets are limited (such as in the case of healthcare data). To alleviate this issue, TL and data augmentation have been researched over the last few years.

Although ML slowly transitions to semi-supervised and unsupervised learning to manage practical data without the need for manual human labeling, many of the current deep-learning models utilize supervised learning.

The CNN performance is greatly influenced by hyper-parameter selection. Any small change in the hyper-parameter values will affect the general CNN performance. Therefore, careful parameter selection is an extremely significant issue that should be considered during optimization scheme development.

Impressive and robust hardware resources like GPUs are required for effective CNN training. Moreover, they are also required for exploring the efficiency of using CNN in smart and embedded systems.

In the CNN context, ensemble learning [ 342 , 343 ] represents a prospective research area. The collection of different and multiple architectures will support the model in improving its generalizability across different image categories through extracting several levels of semantic image representation. Similarly, ideas such as new activation functions, dropout, and batch normalization also merit further investigation.

The exploitation of depth and different structural adaptations is significantly improved in the CNN learning capacity. Substituting the traditional layer configuration with blocks results in significant advances in CNN performance, as has been shown in the recent literature. Currently, developing novel and efficient block architectures is the main trend in new research models of CNN architectures. HRNet is only one example that shows there are always ways to improve the architecture.

It is expected that cloud-based platforms will play an essential role in the future development of computational DL applications. Utilizing cloud computing offers a solution to handling the enormous amount of data. It also helps to increase efficiency and reduce costs. Furthermore, it offers the flexibility to train DL architectures.

With the recent development in computational tools including a chip for neural networks and a mobile GPU, we will see more DL applications on mobile devices. It will be easier for users to use DL.

Regarding the issue of lack of training data, It is expected that various techniques of transfer learning will be considered such as training the DL model on large unlabeled image datasets and next transferring the knowledge to train the DL model on a small number of labeled images for the same task.

Last, this overview provides a starting point for the community of DL being interested in the field of DL. Furthermore, researchers would be allowed to decide the more suitable direction of work to be taken in order to provide more accurate alternatives to the field.

Availability of data and materials

Not applicable.

Rozenwald MB, Galitsyna AA, Sapunov GV, Khrameeva EE, Gelfand MS. A machine learning framework for the prediction of chromatin folding in Drosophila using epigenetic features. PeerJ Comput Sci. 2020;6:307.

Article   Google Scholar  

Amrit C, Paauw T, Aly R, Lavric M. Identifying child abuse through text mining and machine learning. Expert Syst Appl. 2017;88:402–18.

Hossain E, Khan I, Un-Noor F, Sikander SS, Sunny MSH. Application of big data and machine learning in smart grid, and associated security concerns: a review. IEEE Access. 2019;7:13960–88.

Crawford M, Khoshgoftaar TM, Prusa JD, Richter AN, Al Najada H. Survey of review spam detection using machine learning techniques. J Big Data. 2015;2(1):23.

Deldjoo Y, Elahi M, Cremonesi P, Garzotto F, Piazzolla P, Quadrana M. Content-based video recommendation system based on stylistic visual features. J Data Semant. 2016;5(2):99–113.

Al-Dulaimi K, Chandran V, Nguyen K, Banks J, Tomeo-Reyes I. Benchmarking hep-2 specimen cells classification using linear discriminant analysis on higher order spectra features of cell shape. Pattern Recogn Lett. 2019;125:534–41.

Liu W, Wang Z, Liu X, Zeng N, Liu Y, Alsaadi FE. A survey of deep neural network architectures and their applications. Neurocomputing. 2017;234:11–26.

Pouyanfar S, Sadiq S, Yan Y, Tian H, Tao Y, Reyes MP, Shyu ML, Chen SC, Iyengar S. A survey on deep learning: algorithms, techniques, and applications. ACM Comput Surv (CSUR). 2018;51(5):1–36.

Alom MZ, Taha TM, Yakopcic C, Westberg S, Sidike P, Nasrin MS, Hasan M, Van Essen BC, Awwal AA, Asari VK. A state-of-the-art survey on deep learning theory and architectures. Electronics. 2019;8(3):292.

Potok TE, Schuman C, Young S, Patton R, Spedalieri F, Liu J, Yao KT, Rose G, Chakma G. A study of complex deep learning networks on high-performance, neuromorphic, and quantum computers. ACM J Emerg Technol Comput Syst (JETC). 2018;14(2):1–21.

Adeel A, Gogate M, Hussain A. Contextual deep learning-based audio-visual switching for speech enhancement in real-world environments. Inf Fusion. 2020;59:163–70.

Tian H, Chen SC, Shyu ML. Evolutionary programming based deep learning feature selection and network construction for visual data classification. Inf Syst Front. 2020;22(5):1053–66.

Young T, Hazarika D, Poria S, Cambria E. Recent trends in deep learning based natural language processing. IEEE Comput Intell Mag. 2018;13(3):55–75.

Koppe G, Meyer-Lindenberg A, Durstewitz D. Deep learning for small and big data in psychiatry. Neuropsychopharmacology. 2021;46(1):176–90.

Dalal N, Triggs B. Histograms of oriented gradients for human detection. In: 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR’05), vol. 1. IEEE; 2005. p. 886–93.

Lowe DG. Object recognition from local scale-invariant features. In: Proceedings of the seventh IEEE international conference on computer vision, vol. 2. IEEE; 1999. p. 1150–7.

Wu L, Hoi SC, Yu N. Semantics-preserving bag-of-words models and applications. IEEE Trans Image Process. 2010;19(7):1908–20.

Article   MathSciNet   MATH   Google Scholar  

LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–44.

Yao G, Lei T, Zhong J. A review of convolutional-neural-network-based action recognition. Pattern Recogn Lett. 2019;118:14–22.

Dhillon A, Verma GK. Convolutional neural network: a review of models, methodologies and applications to object detection. Prog Artif Intell. 2020;9(2):85–112.

Khan A, Sohail A, Zahoora U, Qureshi AS. A survey of the recent architectures of deep convolutional neural networks. Artif Intell Rev. 2020;53(8):5455–516.

Hasan RI, Yusuf SM, Alzubaidi L. Review of the state of the art of deep learning for plant diseases: a broad analysis and discussion. Plants. 2020;9(10):1302.

Xiao Y, Tian Z, Yu J, Zhang Y, Liu S, Du S, Lan X. A review of object detection based on deep learning. Multimed Tools Appl. 2020;79(33):23729–91.

Ker J, Wang L, Rao J, Lim T. Deep learning applications in medical image analysis. IEEE Access. 2017;6:9375–89.

Zhang Z, Cui P, Zhu W. Deep learning on graphs: a survey. IEEE Trans Knowl Data Eng. 2020. https://doi.org/10.1109/TKDE.2020.2981333 .

Shrestha A, Mahmood A. Review of deep learning algorithms and architectures. IEEE Access. 2019;7:53040–65.

Najafabadi MM, Villanustre F, Khoshgoftaar TM, Seliya N, Wald R, Muharemagic E. Deep learning applications and challenges in big data analytics. J Big Data. 2015;2(1):1.

Goodfellow I, Bengio Y, Courville A, Bengio Y. Deep learning, vol. 1. Cambridge: MIT press; 2016.

MATH   Google Scholar  

Shorten C, Khoshgoftaar TM, Furht B. Deep learning applications for COVID-19. J Big Data. 2021;8(1):1–54.

Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Commun ACM. 2017;60(6):84–90.

Bhowmick S, Nagarajaiah S, Veeraraghavan A. Vision and deep learning-based algorithms to detect and quantify cracks on concrete surfaces from uav videos. Sensors. 2020;20(21):6299.

Goh GB, Hodas NO, Vishnu A. Deep learning for computational chemistry. J Comput Chem. 2017;38(16):1291–307.

Li Y, Zhang T, Sun S, Gao X. Accelerating flash calculation through deep learning methods. J Comput Phys. 2019;394:153–65.

Yang W, Zhang X, Tian Y, Wang W, Xue JH, Liao Q. Deep learning for single image super-resolution: a brief review. IEEE Trans Multimed. 2019;21(12):3106–21.

Tang J, Li S, Liu P. A review of lane detection methods based on deep learning. Pattern Recogn. 2020;111:107623.

Zhao ZQ, Zheng P, Xu ST, Wu X. Object detection with deep learning: a review. IEEE Trans Neural Netw Learn Syst. 2019;30(11):3212–32.

He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2016. p. 770–8.

Ng A. Machine learning yearning: technical strategy for AI engineers in the era of deep learning. 2019. https://www.mlyearning.org .

Metz C. Turing award won by 3 pioneers in artificial intelligence. The New York Times. 2019;27.

Nevo S, Anisimov V, Elidan G, El-Yaniv R, Giencke P, Gigi Y, Hassidim A, Moshe Z, Schlesinger M, Shalev G, et al. Ml for flood forecasting at scale; 2019. arXiv preprint arXiv:1901.09583 .

Chen H, Engkvist O, Wang Y, Olivecrona M, Blaschke T. The rise of deep learning in drug discovery. Drug Discov Today. 2018;23(6):1241–50.

Benhammou Y, Achchab B, Herrera F, Tabik S. Breakhis based breast cancer automatic diagnosis using deep learning: taxonomy, survey and insights. Neurocomputing. 2020;375:9–24.

Wulczyn E, Steiner DF, Xu Z, Sadhwani A, Wang H, Flament-Auvigne I, Mermel CH, Chen PHC, Liu Y, Stumpe MC. Deep learning-based survival prediction for multiple cancer types using histopathology images. PLoS ONE. 2020;15(6):e0233678.

Nagpal K, Foote D, Liu Y, Chen PHC, Wulczyn E, Tan F, Olson N, Smith JL, Mohtashamian A, Wren JH, et al. Development and validation of a deep learning algorithm for improving Gleason scoring of prostate cancer. NPJ Digit Med. 2019;2(1):1–10.

Google Scholar  

Esteva A, Kuprel B, Novoa RA, Ko J, Swetter SM, Blau HM, Thrun S. Dermatologist-level classification of skin cancer with deep neural networks. Nature. 2017;542(7639):115–8.

Brunese L, Mercaldo F, Reginelli A, Santone A. Explainable deep learning for pulmonary disease and coronavirus COVID-19 detection from X-rays. Comput Methods Programs Biomed. 2020;196(105):608.

Jamshidi M, Lalbakhsh A, Talla J, Peroutka Z, Hadjilooei F, Lalbakhsh P, Jamshidi M, La Spada L, Mirmozafari M, Dehghani M, et al. Artificial intelligence and COVID-19: deep learning approaches for diagnosis and treatment. IEEE Access. 2020;8:109581–95.

Shorfuzzaman M, Hossain MS. Metacovid: a siamese neural network framework with contrastive loss for n-shot diagnosis of COVID-19 patients. Pattern Recogn. 2020;113:107700.

Carvelli L, Olesen AN, Brink-Kjær A, Leary EB, Peppard PE, Mignot E, Sørensen HB, Jennum P. Design of a deep learning model for automatic scoring of periodic and non-periodic leg movements during sleep validated against multiple human experts. Sleep Med. 2020;69:109–19.

De Fauw J, Ledsam JR, Romera-Paredes B, Nikolov S, Tomasev N, Blackwell S, Askham H, Glorot X, O’Donoghue B, Visentin D, et al. Clinically applicable deep learning for diagnosis and referral in retinal disease. Nat Med. 2018;24(9):1342–50.

Topol EJ. High-performance medicine: the convergence of human and artificial intelligence. Nat Med. 2019;25(1):44–56.

Kermany DS, Goldbaum M, Cai W, Valentim CC, Liang H, Baxter SL, McKeown A, Yang G, Wu X, Yan F, et al. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell. 2018;172(5):1122–31.

Van Essen B, Kim H, Pearce R, Boakye K, Chen B. Lbann: livermore big artificial neural network HPC toolkit. In: Proceedings of the workshop on machine learning in high-performance computing environments; 2015. p. 1–6.

Saeed MM, Al Aghbari Z, Alsharidah M. Big data clustering techniques based on spark: a literature review. PeerJ Comput Sci. 2020;6:321.

Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, Graves A, Riedmiller M, Fidjeland AK, Ostrovski G, et al. Human-level control through deep reinforcement learning. Nature. 2015;518(7540):529–33.

Arulkumaran K, Deisenroth MP, Brundage M, Bharath AA. Deep reinforcement learning: a brief survey. IEEE Signal Process Mag. 2017;34(6):26–38.

Socher R, Perelygin A, Wu J, Chuang J, Manning CD, Ng AY, Potts C. Recursive deep models for semantic compositionality over a sentiment treebank. In: Proceedings of the 2013 conference on empirical methods in natural language processing; 2013. p. 1631–42.

Goller C, Kuchler A. Learning task-dependent distributed representations by backpropagation through structure. In: Proceedings of international conference on neural networks (ICNN’96), vol 1. IEEE; 1996. p. 347–52.

Socher R, Lin CCY, Ng AY, Manning CD. Parsing natural scenes and natural language with recursive neural networks. In: ICML; 2011.

Louppe G, Cho K, Becot C, Cranmer K. QCD-aware recursive neural networks for jet physics. J High Energy Phys. 2019;2019(1):57.

Sadr H, Pedram MM, Teshnehlab M. A robust sentiment analysis method based on sequential combination of convolutional and recursive neural networks. Neural Process Lett. 2019;50(3):2745–61.

Urban G, Subrahmanya N, Baldi P. Inner and outer recursive neural networks for chemoinformatics applications. J Chem Inf Model. 2018;58(2):207–11.

Hewamalage H, Bergmeir C, Bandara K. Recurrent neural networks for time series forecasting: current status and future directions. Int J Forecast. 2020;37(1):388–427.

Jiang Y, Kim H, Asnani H, Kannan S, Oh S, Viswanath P. Learn codes: inventing low-latency codes via recurrent neural networks. IEEE J Sel Areas Inf Theory. 2020;1(1):207–16.

John RA, Acharya J, Zhu C, Surendran A, Bose SK, Chaturvedi A, Tiwari N, Gao Y, He Y, Zhang KK, et al. Optogenetics inspired transition metal dichalcogenide neuristors for in-memory deep recurrent neural networks. Nat Commun. 2020;11(1):1–9.

Batur Dinler Ö, Aydin N. An optimal feature parameter set based on gated recurrent unit recurrent neural networks for speech segment detection. Appl Sci. 2020;10(4):1273.

Jagannatha AN, Yu H. Structured prediction models for RNN based sequence labeling in clinical text. In: Proceedings of the conference on empirical methods in natural language processing. conference on empirical methods in natural language processing, vol. 2016, NIH Public Access; 2016. p. 856.

Pascanu R, Gulcehre C, Cho K, Bengio Y. How to construct deep recurrent neural networks. In: Proceedings of the second international conference on learning representations (ICLR 2014); 2014.

Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. In: Proceedings of the thirteenth international conference on artificial intelligence and statistics; 2010. p. 249–56.

Gao C, Yan J, Zhou S, Varshney PK, Liu H. Long short-term memory-based deep recurrent neural networks for target tracking. Inf Sci. 2019;502:279–96.

Zhou DX. Theory of deep convolutional neural networks: downsampling. Neural Netw. 2020;124:319–27.

Article   MATH   Google Scholar  

Jhong SY, Tseng PY, Siriphockpirom N, Hsia CH, Huang MS, Hua KL, Chen YY. An automated biometric identification system using CNN-based palm vein recognition. In: 2020 international conference on advanced robotics and intelligent systems (ARIS). IEEE; 2020. p. 1–6.

Al-Azzawi A, Ouadou A, Max H, Duan Y, Tanner JJ, Cheng J. Deepcryopicker: fully automated deep neural network for single protein particle picking in cryo-EM. BMC Bioinform. 2020;21(1):1–38.

Wang T, Lu C, Yang M, Hong F, Liu C. A hybrid method for heartbeat classification via convolutional neural networks, multilayer perceptrons and focal loss. PeerJ Comput Sci. 2020;6:324.

Li G, Zhang M, Li J, Lv F, Tong G. Efficient densely connected convolutional neural networks. Pattern Recogn. 2021;109:107610.

Gu J, Wang Z, Kuen J, Ma L, Shahroudy A, Shuai B, Liu T, Wang X, Wang G, Cai J, et al. Recent advances in convolutional neural networks. Pattern Recogn. 2018;77:354–77.

Fang W, Love PE, Luo H, Ding L. Computer vision for behaviour-based safety in construction: a review and future directions. Adv Eng Inform. 2020;43:100980.

Palaz D, Magimai-Doss M, Collobert R. End-to-end acoustic modeling using convolutional neural networks for hmm-based automatic speech recognition. Speech Commun. 2019;108:15–32.

Li HC, Deng ZY, Chiang HH. Lightweight and resource-constrained learning network for face recognition with performance optimization. Sensors. 2020;20(21):6114.

Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 1962;160(1):106.

Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift; 2015. arXiv preprint arXiv:1502.03167 .

Ruder S. An overview of gradient descent optimization algorithms; 2016. arXiv preprint arXiv:1609.04747 .

Bottou L. Large-scale machine learning with stochastic gradient descent. In: Proceedings of COMPSTAT’2010. Springer; 2010. p. 177–86.

Hinton G, Srivastava N, Swersky K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited on. 2012;14(8).

Zhang Z. Improved Adam optimizer for deep neural networks. In: 2018 IEEE/ACM 26th international symposium on quality of service (IWQoS). IEEE; 2018. p. 1–2.

Alzubaidi L, Fadhel MA, Al-Shamma O, Zhang J, Duan Y. Deep learning models for classification of red blood cells in microscopy images to aid in sickle cell anemia diagnosis. Electronics. 2020;9(3):427.

Alzubaidi L, Fadhel MA, Al-Shamma O, Zhang J, Santamaría J, Duan Y, Oleiwi SR. Towards a better understanding of transfer learning for medical imaging: a case study. Appl Sci. 2020;10(13):4523.

Alzubaidi L, Al-Shamma O, Fadhel MA, Farhan L, Zhang J, Duan Y. Optimizing the performance of breast cancer classification by employing the same domain transfer learning from hybrid deep convolutional neural network model. Electronics. 2020;9(3):445.

LeCun Y, Jackel LD, Bottou L, Cortes C, Denker JS, Drucker H, Guyon I, Muller UA, Sackinger E, Simard P, et al. Learning algorithms for classification: a comparison on handwritten digit recognition. Neural Netw Stat Mech Perspect. 1995;261:276.

Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res. 2014;15(1):1929–58.

MathSciNet   MATH   Google Scholar  

Dahl GE, Sainath TN, Hinton GE. Improving deep neural networks for LVCSR using rectified linear units and dropout. In: 2013 IEEE international conference on acoustics, speech and signal processing. IEEE; 2013. p. 8609–13.

Xu B, Wang N, Chen T, Li M. Empirical evaluation of rectified activations in convolutional network; 2015. arXiv preprint arXiv:1505.00853 .

Hochreiter S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int J Uncertain Fuzziness Knowl Based Syst. 1998;6(02):107–16.

Lin M, Chen Q, Yan S. Network in network; 2013. arXiv preprint arXiv:1312.4400 .

Hsiao TY, Chang YC, Chou HH, Chiu CT. Filter-based deep-compression with global average pooling for convolutional networks. J Syst Arch. 2019;95:9–18.

Li Z, Wang SH, Fan RR, Cao G, Zhang YD, Guo T. Teeth category classification via seven-layer deep convolutional neural network with max pooling and global average pooling. Int J Imaging Syst Technol. 2019;29(4):577–83.

Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. In: European conference on computer vision. Springer; 2014. p. 818–33.

Erhan D, Bengio Y, Courville A, Vincent P. Visualizing higher-layer features of a deep network. Univ Montreal. 2009;1341(3):1.

Le QV. Building high-level features using large scale unsupervised learning. In: 2013 IEEE international conference on acoustics, speech and signal processing. IEEE; 2013. p. 8595–8.

Grün F, Rupprecht C, Navab N, Tombari F. A taxonomy and library for visualizing learned features in convolutional neural networks; 2016. arXiv preprint arXiv:1606.07757 .

Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition; 2014. arXiv preprint arXiv:1409.1556 .

Ranzato M, Huang FJ, Boureau YL, LeCun Y. Unsupervised learning of invariant feature hierarchies with applications to object recognition. In: 2007 IEEE conference on computer vision and pattern recognition. IEEE; 2007. p. 1–8.

Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going deeper with convolutions. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2015. p. 1–9.

Bengio Y, et al. Rmsprop and equilibrated adaptive learning rates for nonconvex optimization; 2015. arXiv:1502.04390 corr abs/1502.04390

Srivastava RK, Greff K, Schmidhuber J. Highway networks; 2015. arXiv preprint arXiv:1505.00387 .

Kong W, Dong ZY, Jia Y, Hill DJ, Xu Y, Zhang Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans Smart Grid. 2017;10(1):841–51.

Ordóñez FJ, Roggen D. Deep convolutional and LSTM recurrent neural networks for multimodal wearable activity recognition. Sensors. 2016;16(1):115.

CireşAn D, Meier U, Masci J, Schmidhuber J. Multi-column deep neural network for traffic sign classification. Neural Netw. 2012;32:333–8.

Szegedy C, Ioffe S, Vanhoucke V, Alemi A. Inception-v4, inception-resnet and the impact of residual connections on learning; 2016. arXiv preprint arXiv:1602.07261 .

Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z. Rethinking the inception architecture for computer vision. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2016. p. 2818–26.

Wu S, Zhong S, Liu Y. Deep residual learning for image steganalysis. Multimed Tools Appl. 2018;77(9):10437–53.

Huang G, Liu Z, Van Der Maaten L, Weinberger KQ. Densely connected convolutional networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2017. p. 4700–08.

Rubin J, Parvaneh S, Rahman A, Conroy B, Babaeizadeh S. Densely connected convolutional networks for detection of atrial fibrillation from short single-lead ECG recordings. J Electrocardiol. 2018;51(6):S18-21.

Kuang P, Ma T, Chen Z, Li F. Image super-resolution with densely connected convolutional networks. Appl Intell. 2019;49(1):125–36.

Xie S, Girshick R, Dollár P, Tu Z, He K. Aggregated residual transformations for deep neural networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2017. p. 1492–500.

Su A, He X, Zhao X. Jpeg steganalysis based on ResNeXt with gauss partial derivative filters. Multimed Tools Appl. 2020;80(3):3349–66.

Yadav D, Jalal A, Garlapati D, Hossain K, Goyal A, Pant G. Deep learning-based ResNeXt model in phycological studies for future. Algal Res. 2020;50:102018.

Han W, Feng R, Wang L, Gao L. Adaptive spatial-scale-aware deep convolutional neural network for high-resolution remote sensing imagery scene classification. In: IGARSS 2018-2018 IEEE international geoscience and remote sensing symposium. IEEE; 2018. p. 4736–9.

Zagoruyko S, Komodakis N. Wide residual networks; 2016. arXiv preprint arXiv:1605.07146 .

Huang G, Sun Y, Liu Z, Sedra D, Weinberger KQ. Deep networks with stochastic depth. In: European conference on computer vision. Springer; 2016. p. 646–61.

Huynh HT, Nguyen H. Joint age estimation and gender classification of Asian faces using wide ResNet. SN Comput Sci. 2020;1(5):1–9.

Takahashi R, Matsubara T, Uehara K. Data augmentation using random image cropping and patching for deep cnns. IEEE Trans Circuits Syst Video Technol. 2019;30(9):2917–31.

Han D, Kim J, Kim J. Deep pyramidal residual networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2017. p. 5927–35.

Wang Y, Wang L, Wang H, Li P. End-to-end image super-resolution via deep and shallow convolutional networks. IEEE Access. 2019;7:31959–70.

Chollet F. Xception: Deep learning with depthwise separable convolutions. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2017. p. 1251–8.

Lo WW, Yang X, Wang Y. An xception convolutional neural network for malware classification with transfer learning. In: 2019 10th IFIP international conference on new technologies, mobility and security (NTMS). IEEE; 2019. p. 1–5.

Rahimzadeh M, Attar A. A modified deep convolutional neural network for detecting COVID-19 and pneumonia from chest X-ray images based on the concatenation of xception and resnet50v2. Inform Med Unlocked. 2020;19:100360.

Wang F, Jiang M, Qian C, Yang S, Li C, Zhang H, Wang X, Tang X. Residual attention network for image classification. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2017. p. 3156–64.

Salakhutdinov R, Larochelle H. Efficient learning of deep boltzmann machines. In: Proceedings of the thirteenth international conference on artificial intelligence and statistics; 2010. p. 693–700.

Goh H, Thome N, Cord M, Lim JH. Top-down regularization of deep belief networks. Adv Neural Inf Process Syst. 2013;26:1878–86.

Guan J, Lai R, Xiong A, Liu Z, Gu L. Fixed pattern noise reduction for infrared images based on cascade residual attention CNN. Neurocomputing. 2020;377:301–13.

Bi Q, Qin K, Zhang H, Li Z, Xu K. RADC-Net: a residual attention based convolution network for aerial scene classification. Neurocomputing. 2020;377:345–59.

Jaderberg M, Simonyan K, Zisserman A, et al. Spatial transformer networks. In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2015. p. 2017–25.

Hu J, Shen L, Sun G. Squeeze-and-excitation networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2018. p. 7132–41.

Mou L, Zhu XX. Learning to pay attention on spectral domain: a spectral attention module-based convolutional network for hyperspectral image classification. IEEE Trans Geosci Remote Sens. 2019;58(1):110–22.

Woo S, Park J, Lee JY, So Kweon I. CBAM: Convolutional block attention module. In: Proceedings of the European conference on computer vision (ECCV); 2018. p. 3–19.

Roy AG, Navab N, Wachinger C. Concurrent spatial and channel ‘squeeze & excitation’ in fully convolutional networks. In: International conference on medical image computing and computer-assisted intervention. Springer; 2018. p. 421–9.

Roy AG, Navab N, Wachinger C. Recalibrating fully convolutional networks with spatial and channel “squeeze and excitation’’ blocks. IEEE Trans Med Imaging. 2018;38(2):540–9.

Sabour S, Frosst N, Hinton GE. Dynamic routing between capsules. In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2017. p. 3856–66.

Arun P, Buddhiraju KM, Porwal A. Capsulenet-based spatial-spectral classifier for hyperspectral images. IEEE J Sel Topics Appl Earth Obs Remote Sens. 2019;12(6):1849–65.

Xinwei L, Lianghao X, Yi Y. Compact video fingerprinting via an improved capsule net. Syst Sci Control Eng. 2020;9:1–9.

Ma B, Li X, Xia Y, Zhang Y. Autonomous deep learning: a genetic DCNN designer for image classification. Neurocomputing. 2020;379:152–61.

Wang J, Sun K, Cheng T, Jiang B, Deng C, Zhao Y, Liu D, Mu Y, Tan M, Wang X, et al. Deep high-resolution representation learning for visual recognition. IEEE Trans Pattern Anal Mach Intell. 2020. https://doi.org/10.1109/TPAMI.2020.2983686 .

Cheng B, Xiao B, Wang J, Shi H, Huang TS, Zhang L. Higherhrnet: scale-aware representation learning for bottom-up human pose estimation. In: CVPR 2020; 2020. https://www.microsoft.com/en-us/research/publication/higherhrnet-scale-aware-representation-learning-for-bottom-up-human-pose-estimation/ .

Karimi H, Derr T, Tang J. Characterizing the decision boundary of deep neural networks; 2019. arXiv preprint arXiv:1912.11460 .

Li Y, Ding L, Gao X. On the decision boundary of deep neural networks; 2018. arXiv preprint arXiv:1808.05385 .

Yosinski J, Clune J, Bengio Y, Lipson H. How transferable are features in deep neural networks? In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2014. p. 3320–8.

Tan C, Sun F, Kong T, Zhang W, Yang C, Liu C. A survey on deep transfer learning. In: International conference on artificial neural networks. Springer; 2018. p. 270–9.

Weiss K, Khoshgoftaar TM, Wang D. A survey of transfer learning. J Big Data. 2016;3(1):9.

Shorten C, Khoshgoftaar TM. A survey on image data augmentation for deep learning. J Big Data. 2019;6(1):60.

Wang F, Wang H, Wang H, Li G, Situ G. Learning from simulation: an end-to-end deep-learning approach for computational ghost imaging. Opt Express. 2019;27(18):25560–72.

Pan W. A survey of transfer learning for collaborative recommendation with auxiliary data. Neurocomputing. 2016;177:447–53.

Deng J, Dong W, Socher R, Li LJ, Li K, Fei-Fei L. Imagenet: a large-scale hierarchical image database. In: 2009 IEEE conference on computer vision and pattern recognition. IEEE; 2009. p. 248–55.

Cook D, Feuz KD, Krishnan NC. Transfer learning for activity recognition: a survey. Knowl Inf Syst. 2013;36(3):537–56.

Cao X, Wang Z, Yan P, Li X. Transfer learning for pedestrian detection. Neurocomputing. 2013;100:51–7.

Raghu M, Zhang C, Kleinberg J, Bengio S. Transfusion: understanding transfer learning for medical imaging. In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2019. p. 3347–57.

Pham TN, Van Tran L, Dao SVT. Early disease classification of mango leaves using feed-forward neural network and hybrid metaheuristic feature selection. IEEE Access. 2020;8:189960–73.

Saleh AM, Hamoud T. Analysis and best parameters selection for person recognition based on gait model using CNN algorithm and image augmentation. J Big Data. 2021;8(1):1–20.

Hirahara D, Takaya E, Takahara T, Ueda T. Effects of data count and image scaling on deep learning training. PeerJ Comput Sci. 2020;6:312.

Moreno-Barea FJ, Strazzera F, Jerez JM, Urda D, Franco L. Forward noise adjustment scheme for data augmentation. In: 2018 IEEE symposium series on computational intelligence (SSCI). IEEE; 2018. p. 728–34.

Dua D, Karra Taniskidou E. Uci machine learning repository. Irvine: University of california. School of Information and Computer Science; 2017. http://archive.ics.uci.edu/ml

Johnson JM, Khoshgoftaar TM. Survey on deep learning with class imbalance. J Big Data. 2019;6(1):27.

Yang P, Zhang Z, Zhou BB, Zomaya AY. Sample subset optimization for classifying imbalanced biological data. In: Pacific-Asia conference on knowledge discovery and data mining. Springer; 2011. p. 333–44.

Yang P, Yoo PD, Fernando J, Zhou BB, Zhang Z, Zomaya AY. Sample subset optimization techniques for imbalanced and ensemble learning problems in bioinformatics applications. IEEE Trans Cybern. 2013;44(3):445–55.

Wang S, Sun S, Xu J. Auc-maximized deep convolutional neural fields for sequence labeling 2015. arXiv preprint arXiv:1511.05265 .

Li Y, Wang S, Umarov R, Xie B, Fan M, Li L, Gao X. Deepre: sequence-based enzyme EC number prediction by deep learning. Bioinformatics. 2018;34(5):760–9.

Li Y, Huang C, Ding L, Li Z, Pan Y, Gao X. Deep learning in bioinformatics: introduction, application, and perspective in the big data era. Methods. 2019;166:4–21.

Choi E, Bahadori MT, Sun J, Kulas J, Schuetz A, Stewart W. Retain: An interpretable predictive model for healthcare using reverse time attention mechanism. In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2016. p. 3504–12.

Ching T, Himmelstein DS, Beaulieu-Jones BK, Kalinin AA, Do BT, Way GP, Ferrero E, Agapow PM, Zietz M, Hoffman MM, et al. Opportunities and obstacles for deep learning in biology and medicine. J R Soc Interface. 2018;15(141):20170,387.

Zhou J, Troyanskaya OG. Predicting effects of noncoding variants with deep learning-based sequence model. Nat Methods. 2015;12(10):931–4.

Pokuri BSS, Ghosal S, Kokate A, Sarkar S, Ganapathysubramanian B. Interpretable deep learning for guided microstructure-property explorations in photovoltaics. NPJ Comput Mater. 2019;5(1):1–11.

Ribeiro MT, Singh S, Guestrin C. “Why should I trust you?” explaining the predictions of any classifier. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining; 2016. p. 1135–44.

Wang L, Nie R, Yu Z, Xin R, Zheng C, Zhang Z, Zhang J, Cai J. An interpretable deep-learning architecture of capsule networks for identifying cell-type gene expression programs from single-cell RNA-sequencing data. Nat Mach Intell. 2020;2(11):1–11.

Sundararajan M, Taly A, Yan Q. Axiomatic attribution for deep networks; 2017. arXiv preprint arXiv:1703.01365 .

Platt J, et al. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv Large Margin Classif. 1999;10(3):61–74.

Nair T, Precup D, Arnold DL, Arbel T. Exploring uncertainty measures in deep networks for multiple sclerosis lesion detection and segmentation. Med Image Anal. 2020;59:101557.

Herzog L, Murina E, Dürr O, Wegener S, Sick B. Integrating uncertainty in deep neural networks for MRI based stroke analysis. Med Image Anal. 2020;65:101790.

Pereyra G, Tucker G, Chorowski J, Kaiser Ł, Hinton G. Regularizing neural networks by penalizing confident output distributions; 2017. arXiv preprint arXiv:1701.06548 .

Naeini MP, Cooper GF, Hauskrecht M. Obtaining well calibrated probabilities using bayesian binning. In: Proceedings of the... AAAI conference on artificial intelligence. AAAI conference on artificial intelligence, vol. 2015. NIH Public Access; 2015. p. 2901.

Li M, Sethi IK. Confidence-based classifier design. Pattern Recogn. 2006;39(7):1230–40.

Zadrozny B, Elkan C. Obtaining calibrated probability estimates from decision trees and Naive Bayesian classifiers. In: ICML, vol. 1, Citeseer; 2001. p. 609–16.

Steinwart I. Consistency of support vector machines and other regularized kernel classifiers. IEEE Trans Inf Theory. 2005;51(1):128–42.

Lee K, Lee K, Shin J, Lee H. Overcoming catastrophic forgetting with unlabeled data in the wild. In: Proceedings of the IEEE international conference on computer vision; 2019. p. 312–21.

Shmelkov K, Schmid C, Alahari K. Incremental learning of object detectors without catastrophic forgetting. In: Proceedings of the IEEE international conference on computer vision; 2017. p. 3400–09.

Zenke F, Gerstner W, Ganguli S. The temporal paradox of Hebbian learning and homeostatic plasticity. Curr Opin Neurobiol. 2017;43:166–76.

Andersen N, Krauth N, Nabavi S. Hebbian plasticity in vivo: relevance and induction. Curr Opin Neurobiol. 2017;45:188–92.

Zheng R, Chakraborti S. A phase ii nonparametric adaptive exponentially weighted moving average control chart. Qual Eng. 2016;28(4):476–90.

Rebuffi SA, Kolesnikov A, Sperl G, Lampert CH. ICARL: Incremental classifier and representation learning. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2017. p. 2001–10.

Hinton GE, Plaut DC. Using fast weights to deblur old memories. In: Proceedings of the ninth annual conference of the cognitive science society; 1987. p. 177–86.

Parisi GI, Kemker R, Part JL, Kanan C, Wermter S. Continual lifelong learning with neural networks: a review. Neural Netw. 2019;113:54–71.

Soltoggio A, Stanley KO, Risi S. Born to learn: the inspiration, progress, and future of evolved plastic artificial neural networks. Neural Netw. 2018;108:48–67.

Parisi GI, Tani J, Weber C, Wermter S. Lifelong learning of human actions with deep neural network self-organization. Neural Netw. 2017;96:137–49.

Cheng Y, Wang D, Zhou P, Zhang T. Model compression and acceleration for deep neural networks: the principles, progress, and challenges. IEEE Signal Process Mag. 2018;35(1):126–36.

Wiedemann S, Kirchhoffer H, Matlage S, Haase P, Marban A, Marinč T, Neumann D, Nguyen T, Schwarz H, Wiegand T, et al. Deepcabac: a universal compression algorithm for deep neural networks. IEEE J Sel Topics Signal Process. 2020;14(4):700–14.

Mehta N, Pandit A. Concurrence of big data analytics and healthcare: a systematic review. Int J Med Inform. 2018;114:57–65.

Esteva A, Robicquet A, Ramsundar B, Kuleshov V, DePristo M, Chou K, Cui C, Corrado G, Thrun S, Dean J. A guide to deep learning in healthcare. Nat Med. 2019;25(1):24–9.

Shawahna A, Sait SM, El-Maleh A. Fpga-based accelerators of deep learning networks for learning and classification: a review. IEEE Access. 2018;7:7823–59.

Min Z. Public welfare organization management system based on FPGA and deep learning. Microprocess Microsyst. 2020;80:103333.

Al-Shamma O, Fadhel MA, Hameed RA, Alzubaidi L, Zhang J. Boosting convolutional neural networks performance based on fpga accelerator. In: International conference on intelligent systems design and applications. Springer; 2018. p. 509–17.

Han S, Mao H, Dally WJ. Deep compression: compressing deep neural networks with pruning, trained quantization and huffman coding; 2015. arXiv preprint arXiv:1510.00149 .

Chen Z, Zhang L, Cao Z, Guo J. Distilling the knowledge from handcrafted features for human activity recognition. IEEE Trans Ind Inform. 2018;14(10):4334–42.

Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network; 2015. arXiv preprint arXiv:1503.02531 .

Lenssen JE, Fey M, Libuschewski P. Group equivariant capsule networks. In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2018. p. 8844–53.

Denton EL, Zaremba W, Bruna J, LeCun Y, Fergus R. Exploiting linear structure within convolutional networks for efficient evaluation. In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2014. p. 1269–77.

Xu Q, Zhang M, Gu Z, Pan G. Overfitting remedy by sparsifying regularization on fully-connected layers of CNNs. Neurocomputing. 2019;328:69–74.

Zhang C, Bengio S, Hardt M, Recht B, Vinyals O. Understanding deep learning requires rethinking generalization. Commun ACM. 2018;64(3):107–15.

Xu X, Jiang X, Ma C, Du P, Li X, Lv S, Yu L, Ni Q, Chen Y, Su J, et al. A deep learning system to screen novel coronavirus disease 2019 pneumonia. Engineering. 2020;6(10):1122–9.

Sharma K, Alsadoon A, Prasad P, Al-Dala’in T, Nguyen TQV, Pham DTH. A novel solution of using deep learning for left ventricle detection: enhanced feature extraction. Comput Methods Programs Biomed. 2020;197:105751.

Zhang G, Wang C, Xu B, Grosse R. Three mechanisms of weight decay regularization; 2018. arXiv preprint arXiv:1810.12281 .

Laurent C, Pereyra G, Brakel P, Zhang Y, Bengio Y. Batch normalized recurrent neural networks. In: 2016 IEEE international conference on acoustics, speech and signal processing (ICASSP), IEEE; 2016. p. 2657–61.

Salamon J, Bello JP. Deep convolutional neural networks and data augmentation for environmental sound classification. IEEE Signal Process Lett. 2017;24(3):279–83.

Wang X, Qin Y, Wang Y, Xiang S, Chen H. ReLTanh: an activation function with vanishing gradient resistance for SAE-based DNNs and its application to rotating machinery fault diagnosis. Neurocomputing. 2019;363:88–98.

Tan HH, Lim KH. Vanishing gradient mitigation with deep learning neural network optimization. In: 2019 7th international conference on smart computing & communications (ICSCC). IEEE; 2019. p. 1–4.

MacDonald G, Godbout A, Gillcash B, Cairns S. Volume-preserving neural networks: a solution to the vanishing gradient problem; 2019. arXiv preprint arXiv:1911.09576 .

Mittal S, Vaishay S. A survey of techniques for optimizing deep learning on GPUs. J Syst Arch. 2019;99:101635.

Kanai S, Fujiwara Y, Iwamura S. Preventing gradient explosions in gated recurrent units. In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2017. p. 435–44.

Hanin B. Which neural net architectures give rise to exploding and vanishing gradients? In: Advances in neural information processing systems. San Mateo: Morgan Kaufmann Publishers; 2018. p. 582–91.

Ribeiro AH, Tiels K, Aguirre LA, Schön T. Beyond exploding and vanishing gradients: analysing RNN training using attractors and smoothness. In: International conference on artificial intelligence and statistics, PMLR; 2020. p. 2370–80.

D’Amour A, Heller K, Moldovan D, Adlam B, Alipanahi B, Beutel A, Chen C, Deaton J, Eisenstein J, Hoffman MD, et al. Underspecification presents challenges for credibility in modern machine learning; 2020. arXiv preprint arXiv:2011.03395 .

Chea P, Mandell JC. Current applications and future directions of deep learning in musculoskeletal radiology. Skelet Radiol. 2020;49(2):1–15.

Wu X, Sahoo D, Hoi SC. Recent advances in deep learning for object detection. Neurocomputing. 2020;396:39–64.

Kuutti S, Bowden R, Jin Y, Barber P, Fallah S. A survey of deep learning applications to autonomous vehicle control. IEEE Trans Intell Transp Syst. 2020;22:712–33.

Yolcu G, Oztel I, Kazan S, Oz C, Bunyak F. Deep learning-based face analysis system for monitoring customer interest. J Ambient Intell Humaniz Comput. 2020;11(1):237–48.

Jiao L, Zhang F, Liu F, Yang S, Li L, Feng Z, Qu R. A survey of deep learning-based object detection. IEEE Access. 2019;7:128837–68.

Muhammad K, Khan S, Del Ser J, de Albuquerque VHC. Deep learning for multigrade brain tumor classification in smart healthcare systems: a prospective survey. IEEE Trans Neural Netw Learn Syst. 2020;32:507–22.

Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, Van Der Laak JA, Van Ginneken B, Sánchez CI. A survey on deep learning in medical image analysis. Med Image Anal. 2017;42:60–88.

Mukherjee D, Mondal R, Singh PK, Sarkar R, Bhattacharjee D. Ensemconvnet: a deep learning approach for human activity recognition using smartphone sensors for healthcare applications. Multimed Tools Appl. 2020;79(41):31663–90.

Zeleznik R, Foldyna B, Eslami P, Weiss J, Alexander I, Taron J, Parmar C, Alvi RM, Banerji D, Uno M, et al. Deep convolutional neural networks to predict cardiovascular risk from computed tomography. Nature Commun. 2021;12(1):1–9.

Wang J, Liu Q, Xie H, Yang Z, Zhou H. Boosted efficientnet: detection of lymph node metastases in breast cancer using convolutional neural networks. Cancers. 2021;13(4):661.

Yu H, Yang LT, Zhang Q, Armstrong D, Deen MJ. Convolutional neural networks for medical image analysis: state-of-the-art, comparisons, improvement and perspectives. Neurocomputing. 2021. https://doi.org/10.1016/j.neucom.2020.04.157 .

Bharati S, Podder P, Mondal MRH. Hybrid deep learning for detecting lung diseases from X-ray images. Inform Med Unlocked. 2020;20:100391.

Dong Y, Pan Y, Zhang J, Xu W. Learning to read chest X-ray images from 16000+ examples using CNN. In: 2017 IEEE/ACM international conference on connected health: applications, systems and engineering technologies (CHASE). IEEE; 2017. p. 51–7.

Rajkomar A, Lingam S, Taylor AG, Blum M, Mongan J. High-throughput classification of radiographs using deep convolutional neural networks. J Digit Imaging. 2017;30(1):95–101.

Rajpurkar P, Irvin J, Zhu K, Yang B, Mehta H, Duan T, Ding D, Bagul A, Langlotz C, Shpanskaya K, et al. Chexnet: radiologist-level pneumonia detection on chest X-rays with deep learning; 2017. arXiv preprint arXiv:1711.05225 .

Wang X, Peng Y, Lu L, Lu Z, Bagheri M, Summers RM. ChestX-ray8: Hospital-scale chest X-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2017. p. 2097–106.

Zuo W, Zhou F, Li Z, Wang L. Multi-resolution CNN and knowledge transfer for candidate classification in lung nodule detection. IEEE Access. 2019;7:32510–21.

Shen W, Zhou M, Yang F, Yang C, Tian J. Multi-scale convolutional neural networks for lung nodule classification. In: International conference on information processing in medical imaging. Springer; 2015. p. 588–99.

Li R, Zhang W, Suk HI, Wang L, Li J, Shen D, Ji S. Deep learning based imaging data completion for improved brain disease diagnosis. In: International conference on medical image computing and computer-assisted intervention. Springer; 2014. p. 305–12.

Wen J, Thibeau-Sutre E, Diaz-Melo M, Samper-González J, Routier A, Bottani S, Dormont D, Durrleman S, Burgos N, Colliot O, et al. Convolutional neural networks for classification of Alzheimer’s disease: overview and reproducible evaluation. Med Image Anal. 2020;63:101694.

Mehmood A, Maqsood M, Bashir M, Shuyuan Y. A deep siamese convolution neural network for multi-class classification of Alzheimer disease. Brain Sci. 2020;10(2):84.

Hosseini-Asl E, Ghazal M, Mahmoud A, Aslantas A, Shalaby A, Casanova M, Barnes G, Gimel’farb G, Keynton R, El-Baz A. Alzheimer’s disease diagnostics by a 3d deeply supervised adaptable convolutional network. Front Biosci. 2018;23:584–96.

Korolev S, Safiullin A, Belyaev M, Dodonova Y. Residual and plain convolutional neural networks for 3D brain MRI classification. In: 2017 IEEE 14th international symposium on biomedical imaging (ISBI 2017). IEEE; 2017. p. 835–8.

Alzubaidi L, Fadhel MA, Oleiwi SR, Al-Shamma O, Zhang J. DFU_QUTNet: diabetic foot ulcer classification using novel deep convolutional neural network. Multimed Tools Appl. 2020;79(21):15655–77.

Goyal M, Reeves ND, Davison AK, Rajbhandari S, Spragg J, Yap MH. Dfunet: convolutional neural networks for diabetic foot ulcer classification. IEEE Trans Emerg Topics Comput Intell. 2018;4(5):728–39.

Yap MH., Hachiuma R, Alavi A, Brungel R, Goyal M, Zhu H, Cassidy B, Ruckert J, Olshansky M, Huang X, et al. Deep learning in diabetic foot ulcers detection: a comprehensive evaluation; 2020. arXiv preprint arXiv:2010.03341 .

Tulloch J, Zamani R, Akrami M. Machine learning in the prevention, diagnosis and management of diabetic foot ulcers: a systematic review. IEEE Access. 2020;8:198977–9000.

Fadhel MA, Al-Shamma O, Alzubaidi L, Oleiwi SR. Real-time sickle cell anemia diagnosis based hardware accelerator. In: International conference on new trends in information and communications technology applications, Springer; 2020. p. 189–99.

Debelee TG, Kebede SR, Schwenker F, Shewarega ZM. Deep learning in selected cancers’ image analysis—a survey. J Imaging. 2020;6(11):121.

Khan S, Islam N, Jan Z, Din IU, Rodrigues JJC. A novel deep learning based framework for the detection and classification of breast cancer using transfer learning. Pattern Recogn Lett. 2019;125:1–6.

Alzubaidi L, Hasan RI, Awad FH, Fadhel MA, Alshamma O, Zhang J. Multi-class breast cancer classification by a novel two-branch deep convolutional neural network architecture. In: 2019 12th international conference on developments in eSystems engineering (DeSE). IEEE; 2019. p. 268–73.

Roy K, Banik D, Bhattacharjee D, Nasipuri M. Patch-based system for classification of breast histology images using deep learning. Comput Med Imaging Gr. 2019;71:90–103.

Hameed Z, Zahia S, Garcia-Zapirain B, Javier Aguirre J, María Vanegas A. Breast cancer histopathology image classification using an ensemble of deep learning models. Sensors. 2020;20(16):4373.

Hosny KM, Kassem MA, Foaud MM. Skin cancer classification using deep learning and transfer learning. In: 2018 9th Cairo international biomedical engineering conference (CIBEC). IEEE; 2018. p. 90–3.

Dorj UO, Lee KK, Choi JY, Lee M. The skin cancer classification using deep convolutional neural network. Multimed Tools Appl. 2018;77(8):9909–24.

Kassem MA, Hosny KM, Fouad MM. Skin lesions classification into eight classes for ISIC 2019 using deep convolutional neural network and transfer learning. IEEE Access. 2020;8:114822–32.

Heidari M, Mirniaharikandehei S, Khuzani AZ, Danala G, Qiu Y, Zheng B. Improving the performance of CNN to predict the likelihood of COVID-19 using chest X-ray images with preprocessing algorithms. Int J Med Inform. 2020;144:104284.

Al-Timemy AH, Khushaba RN, Mosa ZM, Escudero J. An efficient mixture of deep and machine learning models for COVID-19 and tuberculosis detection using X-ray images in resource limited settings 2020. arXiv preprint arXiv:2007.08223 .

Abraham B, Nair MS. Computer-aided detection of COVID-19 from X-ray images using multi-CNN and Bayesnet classifier. Biocybern Biomed Eng. 2020;40(4):1436–45.

Nour M, Cömert Z, Polat K. A novel medical diagnosis model for COVID-19 infection detection based on deep features and Bayesian optimization. Appl Soft Comput. 2020;97:106580.

Mallio CA, Napolitano A, Castiello G, Giordano FM, D’Alessio P, Iozzino M, Sun Y, Angeletti S, Russano M, Santini D, et al. Deep learning algorithm trained with COVID-19 pneumonia also identifies immune checkpoint inhibitor therapy-related pneumonitis. Cancers. 2021;13(4):652.

Fourcade A, Khonsari R. Deep learning in medical image analysis: a third eye for doctors. J Stomatol Oral Maxillofac Surg. 2019;120(4):279–88.

Guo Z, Li X, Huang H, Guo N, Li Q. Deep learning-based image segmentation on multimodal medical imaging. IEEE Trans Radiat Plasma Med Sci. 2019;3(2):162–9.

Thakur N, Yoon H, Chong Y. Current trends of artificial intelligence for colorectal cancer pathology image analysis: a systematic review. Cancers. 2020;12(7):1884.

Lundervold AS, Lundervold A. An overview of deep learning in medical imaging focusing on MRI. Zeitschrift für Medizinische Physik. 2019;29(2):102–27.

Yadav SS, Jadhav SM. Deep convolutional neural network based medical image classification for disease diagnosis. J Big Data. 2019;6(1):113.

Nehme E, Freedman D, Gordon R, Ferdman B, Weiss LE, Alalouf O, Naor T, Orange R, Michaeli T, Shechtman Y. DeepSTORM3D: dense 3D localization microscopy and PSF design by deep learning. Nat Methods. 2020;17(7):734–40.

Zulkifley MA, Abdani SR, Zulkifley NH. Pterygium-Net: a deep learning approach to pterygium detection and localization. Multimed Tools Appl. 2019;78(24):34563–84.

Sirazitdinov I, Kholiavchenko M, Mustafaev T, Yixuan Y, Kuleev R, Ibragimov B. Deep neural network ensemble for pneumonia localization from a large-scale chest X-ray database. Comput Electr Eng. 2019;78:388–99.

Zhao W, Shen L, Han B, Yang Y, Cheng K, Toesca DA, Koong AC, Chang DT, Xing L. Markerless pancreatic tumor target localization enabled by deep learning. Int J Radiat Oncol Biol Phys. 2019;105(2):432–9.

Roth HR, Lee CT, Shin HC, Seff A, Kim L, Yao J, Lu L, Summers RM. Anatomy-specific classification of medical images using deep convolutional nets. In: 2015 IEEE 12th international symposium on biomedical imaging (ISBI). IEEE; 2015. p. 101–4.

Shin HC, Orton MR, Collins DJ, Doran SJ, Leach MO. Stacked autoencoders for unsupervised feature learning and multiple organ detection in a pilot study using 4D patient data. IEEE Trans Pattern Anal Mach Intell. 2012;35(8):1930–43.

Li Z, Dong M, Wen S, Hu X, Zhou P, Zeng Z. CLU-CNNs: object detection for medical images. Neurocomputing. 2019;350:53–9.

Gao J, Jiang Q, Zhou B, Chen D. Convolutional neural networks for computer-aided detection or diagnosis in medical image analysis: an overview. Math Biosci Eng. 2019;16(6):6536.

Article   MathSciNet   Google Scholar  

Lumini A, Nanni L. Review fair comparison of skin detection approaches on publicly available datasets. Expert Syst Appl. 2020. https://doi.org/10.1016/j.eswa.2020.113677 .

Chouhan V, Singh SK, Khamparia A, Gupta D, Tiwari P, Moreira C, Damaševičius R, De Albuquerque VHC. A novel transfer learning based approach for pneumonia detection in chest X-ray images. Appl Sci. 2020;10(2):559.

Apostolopoulos ID, Mpesiana TA. COVID-19: automatic detection from X-ray images utilizing transfer learning with convolutional neural networks. Phys Eng Sci Med. 2020;43(2):635–40.

Mahmud T, Rahman MA, Fattah SA. CovXNet: a multi-dilation convolutional neural network for automatic COVID-19 and other pneumonia detection from chest X-ray images with transferable multi-receptive feature optimization. Comput Biol Med. 2020;122:103869.

Tayarani-N MH. Applications of artificial intelligence in battling against COVID-19: a literature review. Chaos Solitons Fractals. 2020;142:110338.

Toraman S, Alakus TB, Turkoglu I. Convolutional capsnet: a novel artificial neural network approach to detect COVID-19 disease from X-ray images using capsule networks. Chaos Solitons Fractals. 2020;140:110122.

Dascalu A, David E. Skin cancer detection by deep learning and sound analysis algorithms: a prospective clinical study of an elementary dermoscope. EBioMedicine. 2019;43:107–13.

Adegun A, Viriri S. Deep learning techniques for skin lesion analysis and melanoma cancer detection: a survey of state-of-the-art. Artif Intell Rev. 2020;54:1–31.

Zhang N, Cai YX, Wang YY, Tian YT, Wang XL, Badami B. Skin cancer diagnosis based on optimized convolutional neural network. Artif Intell Med. 2020;102:101756.

Thurnhofer-Hemsi K, Domínguez E. A convolutional neural network framework for accurate skin cancer detection. Neural Process Lett. 2020. https://doi.org/10.1007/s11063-020-10364-y .

Jain MS, Massoud TF. Predicting tumour mutational burden from histopathological images using multiscale deep learning. Nat Mach Intell. 2020;2(6):356–62.

Lei H, Liu S, Elazab A, Lei B. Attention-guided multi-branch convolutional neural network for mitosis detection from histopathological images. IEEE J Biomed Health Inform. 2020;25(2):358–70.

Celik Y, Talo M, Yildirim O, Karabatak M, Acharya UR. Automated invasive ductal carcinoma detection based using deep transfer learning with whole-slide images. Pattern Recogn Lett. 2020;133:232–9.

Sebai M, Wang X, Wang T. Maskmitosis: a deep learning framework for fully supervised, weakly supervised, and unsupervised mitosis detection in histopathology images. Med Biol Eng Comput. 2020;58:1603–23.

Sebai M, Wang T, Al-Fadhli SA. Partmitosis: a partially supervised deep learning framework for mitosis detection in breast cancer histopathology images. IEEE Access. 2020;8:45133–47.

Mahmood T, Arsalan M, Owais M, Lee MB, Park KR. Artificial intelligence-based mitosis detection in breast cancer histopathology images using faster R-CNN and deep CNNs. J Clin Med. 2020;9(3):749.

Srinidhi CL, Ciga O, Martel AL. Deep neural network models for computational histopathology: a survey. Med Image Anal. 2020;67:101813.

Cireşan DC, Giusti A, Gambardella LM, Schmidhuber J. Mitosis detection in breast cancer histology images with deep neural networks. In: International conference on medical image computing and computer-assisted intervention. Springer; 2013. p. 411–8.

Sirinukunwattana K, Raza SEA, Tsang YW, Snead DR, Cree IA, Rajpoot NM. Locality sensitive deep learning for detection and classification of nuclei in routine colon cancer histology images. IEEE Trans Med Imaging. 2016;35(5):1196–206.

Xu J, Xiang L, Liu Q, Gilmore H, Wu J, Tang J, Madabhushi A. Stacked sparse autoencoder (SSAE) for nuclei detection on breast cancer histopathology images. IEEE Trans Med Imaging. 2015;35(1):119–30.

Albarqouni S, Baur C, Achilles F, Belagiannis V, Demirci S, Navab N. Aggnet: deep learning from crowds for mitosis detection in breast cancer histology images. IEEE Trans Med Imaging. 2016;35(5):1313–21.

Abd-Ellah MK, Awad AI, Khalaf AA, Hamed HF. Two-phase multi-model automatic brain tumour diagnosis system from magnetic resonance images using convolutional neural networks. EURASIP J Image Video Process. 2018;2018(1):97.

Thaha MM, Kumar KPM, Murugan B, Dhanasekeran S, Vijayakarthick P, Selvi AS. Brain tumor segmentation using convolutional neural networks in MRI images. J Med Syst. 2019;43(9):294.

Talo M, Yildirim O, Baloglu UB, Aydin G, Acharya UR. Convolutional neural networks for multi-class brain disease detection using MRI images. Comput Med Imaging Gr. 2019;78:101673.

Gabr RE, Coronado I, Robinson M, Sujit SJ, Datta S, Sun X, Allen WJ, Lublin FD, Wolinsky JS, Narayana PA. Brain and lesion segmentation in multiple sclerosis using fully convolutional neural networks: a large-scale study. Mult Scler J. 2020;26(10):1217–26.

Chen S, Ding C, Liu M. Dual-force convolutional neural networks for accurate brain tumor segmentation. Pattern Recogn. 2019;88:90–100.

Hu K, Gan Q, Zhang Y, Deng S, Xiao F, Huang W, Cao C, Gao X. Brain tumor segmentation using multi-cascaded convolutional neural networks and conditional random field. IEEE Access. 2019;7:92615–29.

Wadhwa A, Bhardwaj A, Verma VS. A review on brain tumor segmentation of MRI images. Magn Reson Imaging. 2019;61:247–59.

Akkus Z, Galimzianova A, Hoogi A, Rubin DL, Erickson BJ. Deep learning for brain MRI segmentation: state of the art and future directions. J Digit Imaging. 2017;30(4):449–59.

Moeskops P, Viergever MA, Mendrik AM, De Vries LS, Benders MJ, Išgum I. Automatic segmentation of MR brain images with a convolutional neural network. IEEE Trans Med Imaging. 2016;35(5):1252–61.

Milletari F, Navab N, Ahmadi SA. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In: 2016 fourth international conference on 3D vision (3DV). IEEE; 2016. p. 565–71.

Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In: International conference on medical image computing and computer-assisted intervention. Springer; 2015. p. 234–41.

Pereira S, Pinto A, Alves V, Silva CA. Brain tumor segmentation using convolutional neural networks in MRI images. IEEE Trans Med Imaging. 2016;35(5):1240–51.

Havaei M, Davy A, Warde-Farley D, Biard A, Courville A, Bengio Y, Pal C, Jodoin PM, Larochelle H. Brain tumor segmentation with deep neural networks. Med Image Anal. 2017;35:18–31.

Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL. DeepLab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans Pattern Anal Mach Intell. 2017;40(4):834–48.

Yan Q, Wang B, Gong D, Luo C, Zhao W, Shen J, Shi Q, Jin S, Zhang L, You Z. COVID-19 chest CT image segmentation—a deep convolutional neural network solution; 2020. arXiv preprint arXiv:2004.10987 .

Wang G, Liu X, Li C, Xu Z, Ruan J, Zhu H, Meng T, Li K, Huang N, Zhang S. A noise-robust framework for automatic segmentation of COVID-19 pneumonia lesions from CT images. IEEE Trans Med Imaging. 2020;39(8):2653–63.

Khan SH, Sohail A, Khan A, Lee YS. Classification and region analysis of COVID-19 infection using lung CT images and deep convolutional neural networks; 2020. arXiv preprint arXiv:2009.08864 .

Shi F, Wang J, Shi J, Wu Z, Wang Q, Tang Z, He K, Shi Y, Shen D. Review of artificial intelligence techniques in imaging data acquisition, segmentation and diagnosis for COVID-19. IEEE Rev Biomed Eng. 2020;14:4–5.

Santamaría J, Rivero-Cejudo M, Martos-Fernández M, Roca F. An overview on the latest nature-inspired and metaheuristics-based image registration algorithms. Appl Sci. 2020;10(6):1928.

Santamaría J, Cordón O, Damas S. A comparative study of state-of-the-art evolutionary image registration methods for 3D modeling. Comput Vision Image Underst. 2011;115(9):1340–54.

Yumer ME, Mitra NJ. Learning semantic deformation flows with 3D convolutional networks. In: European conference on computer vision. Springer; 2016. p. 294–311.

Ding L, Feng C. Deepmapping: unsupervised map estimation from multiple point clouds. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2019. p. 8650–9.

Mahadevan S. Imagination machines: a new challenge for artificial intelligence. AAAI. 2018;2018:7988–93.

Wang L, Fang Y. Unsupervised 3D reconstruction from a single image via adversarial learning; 2017. arXiv preprint arXiv:1711.09312 .

Hermoza R, Sipiran I. 3D reconstruction of incomplete archaeological objects using a generative adversarial network. In: Proceedings of computer graphics international 2018. Association for Computing Machinery; 2018. p. 5–11.

Fu Y, Lei Y, Wang T, Curran WJ, Liu T, Yang X. Deep learning in medical image registration: a review. Phys Med Biol. 2020;65(20):20TR01.

Haskins G, Kruger U, Yan P. Deep learning in medical image registration: a survey. Mach Vision Appl. 2020;31(1):8.

de Vos BD, Berendsen FF, Viergever MA, Sokooti H, Staring M, Išgum I. A deep learning framework for unsupervised affine and deformable image registration. Med Image Anal. 2019;52:128–43.

Yang X, Kwitt R, Styner M, Niethammer M. Quicksilver: fast predictive image registration—a deep learning approach. NeuroImage. 2017;158:378–96.

Miao S, Wang ZJ, Liao R. A CNN regression approach for real-time 2D/3D registration. IEEE Trans Med Imaging. 2016;35(5):1352–63.

Li P, Pei Y, Guo Y, Ma G, Xu T, Zha H. Non-rigid 2D–3D registration using convolutional autoencoders. In: 2020 IEEE 17th international symposium on biomedical imaging (ISBI). IEEE; 2020. p. 700–4.

Zhang J, Yeung SH, Shu Y, He B, Wang W. Efficient memory management for GPU-based deep learning systems; 2019. arXiv preprint arXiv:1903.06631 .

Zhao H, Han Z, Yang Z, Zhang Q, Yang F, Zhou L, Yang M, Lau FC, Wang Y, Xiong Y, et al. Hived: sharing a {GPU} cluster for deep learning with guarantees. In: 14th {USENIX} symposium on operating systems design and implementation ({OSDI} 20); 2020. p. 515–32.

Lin Y, Jiang Z, Gu J, Li W, Dhar S, Ren H, Khailany B, Pan DZ. DREAMPlace: deep learning toolkit-enabled GPU acceleration for modern VLSI placement. IEEE Trans Comput Aided Des Integr Circuits Syst. 2020;40:748–61.

Hossain S, Lee DJ. Deep learning-based real-time multiple-object detection and tracking from aerial imagery via a flying robot with GPU-based embedded devices. Sensors. 2019;19(15):3371.

Castro FM, Guil N, Marín-Jiménez MJ, Pérez-Serrano J, Ujaldón M. Energy-based tuning of convolutional neural networks on multi-GPUs. Concurr Comput Pract Exp. 2019;31(21):4786.

Gschwend D. Zynqnet: an fpga-accelerated embedded convolutional neural network; 2020. arXiv preprint arXiv:2005.06892 .

Zhang N, Wei X, Chen H, Liu W. FPGA implementation for CNN-based optical remote sensing object detection. Electronics. 2021;10(3):282.

Zhao M, Hu C, Wei F, Wang K, Wang C, Jiang Y. Real-time underwater image recognition with FPGA embedded system for convolutional neural network. Sensors. 2019;19(2):350.

Liu X, Yang J, Zou C, Chen Q, Yan X, Chen Y, Cai C. Collaborative edge computing with FPGA-based CNN accelerators for energy-efficient and time-aware face tracking system. IEEE Trans Comput Soc Syst. 2021. https://doi.org/10.1109/TCSS.2021.3059318 .

Hossin M, Sulaiman M. A review on evaluation metrics for data classification evaluations. Int J Data Min Knowl Manag Process. 2015;5(2):1.

Provost F, Domingos P. Tree induction for probability-based ranking. Mach Learn. 2003;52(3):199–215.

Rakotomamonyj A. Optimizing area under roc with SVMS. In: Proceedings of the European conference on artificial intelligence workshop on ROC curve and artificial intelligence (ROCAI 2004), 2004. p. 71–80.

Mingote V, Miguel A, Ortega A, Lleida E. Optimization of the area under the roc curve using neural network supervectors for text-dependent speaker verification. Comput Speech Lang. 2020;63:101078.

Fawcett T. An introduction to roc analysis. Pattern Recogn Lett. 2006;27(8):861–74.

Huang J, Ling CX. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans Knowl Data Eng. 2005;17(3):299–310.

Hand DJ, Till RJ. A simple generalisation of the area under the ROC curve for multiple class classification problems. Mach Learn. 2001;45(2):171–86.

Masoudnia S, Mersa O, Araabi BN, Vahabie AH, Sadeghi MA, Ahmadabadi MN. Multi-representational learning for offline signature verification using multi-loss snapshot ensemble of CNNs. Expert Syst Appl. 2019;133:317–30.

Coupé P, Mansencal B, Clément M, Giraud R, de Senneville BD, Ta VT, Lepetit V, Manjon JV. Assemblynet: a large ensemble of CNNs for 3D whole brain MRI segmentation. NeuroImage. 2020;219:117026.

Download references

Acknowledgements

We would like to thank the professors from the Queensland University of Technology and the University of Information Technology and Communications who gave their feedback on the paper.

This research received no external funding.

Author information

Authors and affiliations.

School of Computer Science, Queensland University of Technology, Brisbane, QLD, 4000, Australia

Laith Alzubaidi & Jinglan Zhang

Control and Systems Engineering Department, University of Technology, Baghdad, 10001, Iraq

Amjad J. Humaidi

Electrical Engineering Technical College, Middle Technical University, Baghdad, 10001, Iraq

Ayad Al-Dujaili

Faculty of Electrical Engineering & Computer Science, University of Missouri, Columbia, MO, 65211, USA

Ye Duan & Muthana Al-Amidie

AlNidhal Campus, University of Information Technology & Communications, Baghdad, 10001, Iraq

Laith Alzubaidi & Omran Al-Shamma

Department of Computer Science, University of Jaén, 23071, Jaén, Spain

J. Santamaría

College of Computer Science and Information Technology, University of Sumer, Thi Qar, 64005, Iraq

Mohammed A. Fadhel

School of Engineering, Manchester Metropolitan University, Manchester, M1 5GD, UK

Laith Farhan

You can also search for this author in PubMed   Google Scholar

Contributions

Conceptualization: LA, and JZ; methodology: LA, JZ, and JS; software: LA, and MAF; validation: LA, JZ, MA, and LF; formal analysis: LA, JZ, YD, and JS; investigation: LA, and JZ; resources: LA, JZ, and MAF; data curation: LA, and OA.; writing–original draft preparation: LA, and OA; writing—review and editing: LA, JZ, AJH, AA, YD, OA, JS, MAF, MA, and LF; visualization: LA, and MAF; supervision: JZ, and YD; project administration: JZ, YD, and JS; funding acquisition: LA, AJH, AA, and YD. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Laith Alzubaidi .

Ethics declarations

Ethics approval and consent to participate, consent for publication, competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Alzubaidi, L., Zhang, J., Humaidi, A.J. et al. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. J Big Data 8 , 53 (2021). https://doi.org/10.1186/s40537-021-00444-8

Download citation

Received : 21 January 2021

Accepted : 22 March 2021

Published : 31 March 2021

DOI : https://doi.org/10.1186/s40537-021-00444-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Deep learning
• Machine learning
• Convolution neural network (CNN)
• Deep neural network architectures
• Deep learning applications
• Image classification
• Medical image analysis
• Supervised learning

• Reference Manager
• Simple TEXT file

People also looked at

Review article, an introductory review of deep learning for prediction models with big data.

• 1 Predictive Society and Data Analytics Lab, Faculty of Information Technology and Communication Sciences, Tampere University, Tampere, Finland
• 2 Institute of Biosciences and Medical Technology, Tampere, Finland
• 3 School of Management, University of Applied Sciences Upper Austria, Steyr, Austria
• 4 Department of Biomedical Computer Science and Mechatronics, University for Health Sciences, Medical Informatics and Technology (UMIT), Hall in Tyrol, Austria
• 5 College of Artificial Intelligence, Nankai University, Tianjin, China

Deep learning models stand for a new learning paradigm in artificial intelligence (AI) and machine learning. Recent breakthrough results in image analysis and speech recognition have generated a massive interest in this field because also applications in many other domains providing big data seem possible. On a downside, the mathematical and computational methodology underlying deep learning models is very challenging, especially for interdisciplinary scientists. For this reason, we present in this paper an introductory review of deep learning approaches including Deep Feedforward Neural Networks (D-FFNN), Convolutional Neural Networks (CNNs), Deep Belief Networks (DBNs), Autoencoders (AEs), and Long Short-Term Memory (LSTM) networks. These models form the major core architectures of deep learning models currently used and should belong in any data scientist's toolbox. Importantly, those core architectural building blocks can be composed flexibly—in an almost Lego-like manner—to build new application-specific network architectures. Hence, a basic understanding of these network architectures is important to be prepared for future developments in AI.

1. Introduction

We are living in the big data era where all areas of science and industry generate massive amounts of data. This confronts us with unprecedented challenges regarding their analysis and interpretation. For this reason, there is an urgent need for novel machine learning and artificial intelligence methods that can help in utilizing these data. Deep learning (DL) is such a novel methodology currently receiving much attention ( Hinton et al., 2006 ). DL describes a family of learning algorithms rather than a single method that can be used to learn complex prediction models, e.g., multi-layer neural networks with many hidden units ( LeCun et al., 2015 ). Importantly, deep learning has been successfully applied to several application problems. For instance, a deep learning method set the record for the classification of handwritten digits of the MNIST data set with an error rate of 0.21% ( Wan et al., 2013 ). Further application areas include image recognition ( Krizhevsky et al., 2012a ; LeCun et al., 2015 ), speech recognition ( Graves et al., 2013 ), natural language understanding ( Sarikaya et al., 2014 ), acoustic modeling ( Mohamed et al., 2011 ) and computational biology ( Leung et al., 2014 ; Alipanahi et al., 2015 ; Zhang S. et al., 2015 ; Smolander et al., 2019a , b ).

Models of artificial neural networks have been used since about the 1950s ( Rosenblatt, 1957 ); however, the current wave of deep learning neural networks started around 2006 ( Hinton et al., 2006 ). A common characteristic of the many variations of supervised and unsupervised deep learning models is that these models have many layers of hidden neurons learned, e.g., by a Restricted Boltzmann Machine (RBM) in combination with Backpropagation and error gradients of the Stochastic Gradient Descent ( Riedmiller and Braun, 1993 ). Due to the heterogeneity of deep learning approaches a comprehensive discussion is very challenging, and for this reason, previous reviews aimed at dedicated sub-topics. For instance, a bird's eye view without detailed explanations can be found in LeCun et al. (2015) , a historic summary with many detailed references in Schmidhuber (2015) and reviews about application domains, e.g., image analysis ( Rawat and Wang, 2017 ; Shen et al., 2017 ), speech recognition ( Yu and Li, 2017 ), natural language processing ( Young et al., 2018 ), and biomedicine ( Cao et al., 2018 ).

In contrast, our review aims at an intermediate level, providing also technical details usually omitted. Given the interdisciplinary interest in deep learning, which is part of data science ( Emmert-Streib and Dehmer, 2019a ), this makes it easier for people new to the field to get started. The topics we selected are focused on the core methodology of deep learning approaches including Deep Feedforward Neural Networks (D-FFNN), Convolutional Neural Networks (CNNs), Deep Belief Networks (DBNs), Autoencoders (AEs), and Long Short-Term Memory (LSTM) networks. Further network architectures which we discuss help in understanding these core approaches.

This paper is organized as follows. In the section 2, we provide a historical overview of general developments of neural networks. Then in section 3, we discuss major architectures distinguishing neural networks. Thereafter, we discuss Deep Feedforward Neural Networks (section 4), Convolutional Neural Networks (section 5), Deep Belief Networks (section 6), Autoencoders (section 7) and Long Short-Term Memory networks (section 8) in detail. In section 9, we provide a discussion of important issues when learning neural network models. Finally, this paper finishes in section 10 with conclusions.

2. Key Developments of Neural Networks: A Time Line

The history of neural networks is long, and many people have contributed toward their development over the decades. Given the recent explosion of interest in deep learning, it is not surprising that the assignment of credit for key developments is not uncontroversial. In the following, we were aiming at an unbiased presentation highlighting only the most distinguished contributions.

In   1943 , the first mathematical model of a neuron was created by McCulloch and Pitts (1943) . This model aimed at providing an abstract formulation for the functioning of a neuron without mimicking the biophysical mechanism of a real biological neuron. It is interesting to note that this model did not consider learning.

In   1949 , the first idea about biologically motivated learning in neural networks was introduced by Hebb (1949) . Hebbian learning is a form of unsupervised learning of neural networks.

In   1957 , the Perceptron was introduced by Rosenblatt (1957) . The Perceptron is a single-layer neural network serving as a linear binary classifier. In the modern language of ANNs, a Perceptron uses the Heaviside function as an activation function (see Table 1 ).

Table 1 . An overview of frequently used activation functions for neuron models.

In   1960 , the Delta Learning rule for learning a Perceptron was introduced by Widrow and Hoff (1960) . The Delta Learning rule, also known as Widrow & Hoff Learning rule or the Least Mean Square rule, is a gradient descent learning rule for updating the weights of the neurons. It is a special case of the backpropagation algorithm.

In   1968 , a method called Group Method of Data Handling (GMDH) for training neural networks was introduced by Ivakhnenko (1968) . These networks are widely considered the first deep learning networks of the Feedforward Multilayer Perceptron type. For instance, the paper ( Ivakhnenko, 1971 ) used a deep GMDH network with 8 layers. Interestingly, the numbers of layers and units per layer could be learned and were not fixed from the beginning.

In   1969 , an important paper by Minsky and Papert (1969) was published which showed that the XOR problem cannot be learned by a Perceptron because it is not linearly separable. This triggered a pause phase for neural networks called the “AI winter.”

In   1974 , error backpropagation (BP) has been suggested to use in neural networks ( Werbos, 1974 ) for learning the weighted in a supervised manner and applied in Werbos (1981) . However, the method itself is older (see e.g., Linnainmaa, 1976 ).

In   1980 , a hierarchical multilayered neural network for visual pattern recognition called Neocognitron was introduced by Fukushima (1980) . After the deep GMDH networks (see above), the Neocognitron is considered the second artificial NN that deserved the attribute deep . It introduced convolutional NNs (today called CNNs). The Neocognitron is very similar to the architecture of modern, supervised , deep Feedforward Neural Networks (D-FFNN) ( Fukushima, 2013 ).

In   1982 , Hopfield introduced a content-addressable memory neural network, nowadays called Hopfield Network ( Hopfield, 1982 ). Hopfield Networks are an example for recurrent neural networks.

In   1986 , backpropagation reappeared in a paper by Rumelhart et al. (1986) . They showed experimentally that this learning algorithm can generate useful internal representations and, hence, be of use for general neural network learning tasks.

In   1987 , Terry Sejnowski introduced the NETtalk algorithm ( Sejnowski and Rosenberg, 1987 ). The program learned how to pronounce English words and was able to improve over time.

In   1989 , a Convolutional Neural Network was trained with the backpropagation algorithm to learn handwritten digits ( LeCun et al., 1989 ). A similar system was later used to read handwritten checks and zip codes, processing cashed checks in the United States in the late 90s and early 2000s.

Note: In the 1980s, the second wave of neural network research emerged in great part via a movement called connectionism ( Fodor and Pylyshyn, 1988 ). This wave lasted until the mid 1990s.

In   1991 , Hochreiter studied a fundamental problem of any deep learning network, which relates to the problem of not being trainable with the backpropagation algorithm ( Hochreiter, 1991 ). His study revealed that the signal propagated by backpropagation either decreases or increases without bounds. In case of a decay, this is proportional to the depth of the network. This is now known as the vanishing or exploding gradient problem.

In   1992 , a first partial remedy to this problem has been suggested by Schmidhuber (1992) . The idea was to pre-train a RNN in an unsupervised way to accelerate subsequent supervised learning. The studied network had more than 1,000 layers in the recurrent neural network.

In   1995 , oscillatory neural networks have been introduced in Wang and Terman (1995) . They have been used in various applications like image and speech segmentation and generating complex time series ( Wang and Terman, 1997 ; Hoppensteadt and Izhikevich, 1999 ; Wang and Brown, 1999 ; Soman et al., 2018 ).

In   1997 , the first supervised model for learning RNN was introduced by Hochreiter and Schmidhuber (1997) , which was called Long Short-Term Memory (LSTM). A LSTM prevents the decaying error signal problem between layers by making the LSTM networks “remember” information for a longer period of time.

In   1998 , the Stochastic Gradient Descent algorithm (gradient-based learning) was combined with the backpropagation algorithm for improving learning in CNN ( LeCun et al., 1989 ). As a result, LeNet-5, a 7-level convolutional network, was introduced for classifying hand-written numbers on checks.

In   2006 , is widely considered a breakthrough year because in Hinton et al. (2006) it was shown that neural networks called Deep Belief Networks can be efficiently trained by using a strategy called greedy layer-wise pre-training. This initiated the third wave of neural networks that made also the use of the term deep learning popular.

In   2012 , Alex Krizhevsky won the ImageNet Large Scale Visual Recognition Challenge by using AlexNet, a Convolutional Neural Network utilizing a GPU and improved upon LeNet5 (see above) ( LeCun et al., 1989 ). This success started a convolutional neural network renaissance in the deep learning community (see Neocognitron).

In   2014 , generative adversarial networks were introduced in Goodfellow et al. (2014) . The idea is that two neural networks compete with each other in a game-like manner. Overall, this establishes a generative model that can produce new data. This has been called “the coolest idea in machine learning in the last 20 years” by Yann LeCun.

In   2019 , Yoshua Bengio, Geoffrey Hinton, and Yann LeCun were awarded the Turing Award for conceptual and engineering breakthroughs that have made deep neural networks a critical component of computing.

The reader interested in a more detailed early history of neural networks is referred to Schmidhuber (2015) .

In Figure 1 , we show the evolution of publications related to deep learning from the Web of Science publication database. Specifically, the figure shows the number of publications in dependence on the publication year for DL, deep learning; CNN, convolutional neural network; DBN, deep belief network; LSTM, long short-term memory; AEN, autoencoder; and MLP, multilayer perceptron. The two dashed lines are scaled by a factor of 5 (deep learning) and 3 (convolutional neural network), i.e., overall, for deep learning we found the majority of publications (in total 30, 230). Interestingly, most of these are in computer science (52.1%) and engineering (41.5%). In application areas, medical imaging (6.2%), robotics (2.6%), and computational biology (2.5%) received most attention. These observations are a reflection of the brief history of deep learning indicating that the methods are still under development.

Figure 1 . Number of publications in dependence on the publication year for DL, deep learning; CNN, convolutional neural network; DBN, deep belief network; LSTM, long short-term memory; AEN, autoencoder; and MLP, multilayer perceptron. The legend shows the search terms used to query the Web of Science publication database. The two dashed lines are scaled by a factor of 5 (deep learning) and 3 (convolutional neural network).

In the following sections, we will discuss all of these methods in more detail because they represent the core methodology of deep learning. In addition, we present background information about general artificial neural networks as far as this is needed for a better understanding of the DL methods.

3. Architectures of Neural Networks

Artificial Neural Networks (ANNs) are mathematical models that have been motivated by the functioning of the brain. However, the models we discuss in the following do not aim at providing biologically realistic models. Instead, the purpose of these models is to analyze data.

3.1. Model of an Artificial Neuron

The basic entity of any neural network is a model of a neuron. In Figure 2A , we show such a model of an artificial neuron.

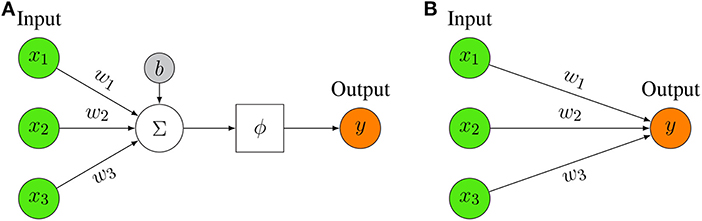
Figure 2. (A) Representation of a mathematical artificial neuron model. The input to the neuron is summed up and filtered by activation function ϕ (for examples see Table 1 ). (B) Simplified Representation of an artificial neuron model. Only the key elements are depicted, i.e., the input, the output, and the weights.

The basic idea of a neuron model is that an input, x , together with a bias, b is weighted by, w , and then summarized together. The bias, b , is a scalar value whereas the input x and the weights w are vector valued, i.e., x ∈ ℝ n and w ∈ ℝ n with n ∈ ℕ corresponding to the dimension of the input. Note that the bias term is not always present but is sometimes omitted. The sum of these terms, i.e., z = w T x + b forms then the argument of an activation function, ϕ, resulting in the output of the neuron model,

Considering only the argument of ϕ one obtains a linear discriminant function ( Webb and Copsey, 2011 ).

The activation function, ϕ, (also known as unit function or transfer function) performs a non-linear transformation of z . In Table 1 , we give an overview of frequently used activation functions.

The ReLU activation function is called Rectified Linear Unit or rectifier ( Nair and Hinton, 2010 ). The ReLU activation function is the most popular activation function for deep neural networks. Another useful activation function is the softmax function ( Lawrence et al., 1997 ):

The softmax maps a n -dimensional vector x into a n -dimensional vector y having the property ∑ i y i = 1 . Hence, the components of y represent probabilities for each of the n elements. The softmax is often used in the final layer of a network. If the Heaviside step function is used as activation function, the neuron model is known as perceptron ( Rosenblatt, 1957 ).

Usually, the model neuron shown in Figure 2A is represented in a more ergonomic way by limiting the focus on its key elements. In Figure 2B , we show such a representation that highlights merely the input part.

3.2. Feedforward Neural Networks

In order to build neural networks (NNs), the neurons need to be connected with each other. The simplest architecture of a NN is a feedforward structure. In Figures 3A,B , we show examples for a shallow and a deep architecture.

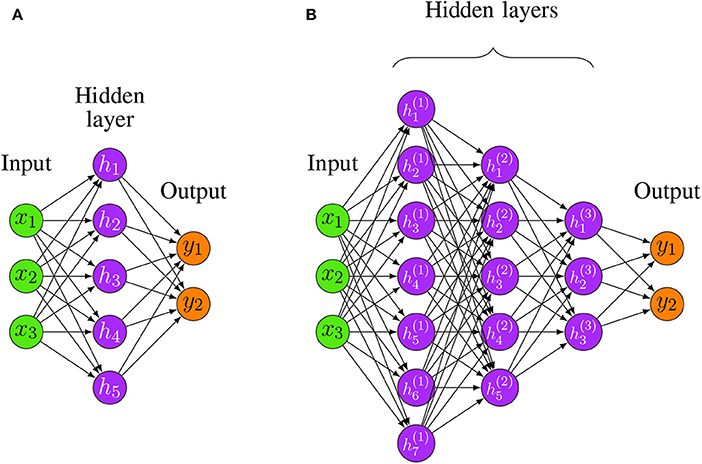
Figure 3 . Two examples for Feedforward Neural Networks. (A) A shallow FFNN. (B) A Deep Feedforward Neural Network (D-FFNN) with 3 hidden layers.

In general, the depth of a network denotes the number of non-linear transformations between the separating layers whereas the dimensionality of a hidden layer, i.e., the number of hidden neurons, is called its width. For instance, the shallow architecture in Figure 3A has a depth of 2 whereas Figure 3B has a depth of 4 [total number of layers minus one (input layer)]. The required number to call a Feedforward Neural Network (FFNN) architecture deep is debatable, but architectures with more than two hidden layers are commonly considered as deep ( Yoshua, 2009 ).

A Feedforward Neural Network, also called a Multilayer Perceptron (MLP), can use linear or non-linear activation functions ( Goodfellow et al., 2016 ). Importantly, there are no cycles in the NN that would allow a direct feedback. Equation (3) defines how the output of a MLP is obtained from the input ( Webb and Copsey, 2011 ).

Equation (3) is the discriminant function of the neural network ( Webb and Copsey, 2011 ). For finding the optimal parameters one needs a learning rule. A common approach is to define an error function (or cost function) together with an optimization algorithm to find the optimal parameters by minimizing the error for training data.

3.3. Recurrent Neural Networks

The family of Recurrent Neural Network (RNN) models has two subclasses that can be distinguished based on their signal processing behavior. The first contains finite impulse recurrent networks (FRNs) and the second infinite impulse recurrent networks (IIRNs). That difference is that a FRN is given by a directed acyclic graph (DAG) that can be unrolled in time and replaced with a Feedforward Neural Network, whereas an IIRN is a directed cyclic graph (DCG) for which such an unrolling is not possible.

3.3.1. Hopfield Networks

A Hopfield Network (HN) ( Hopfield, 1982 ) is an example for a FRN. A HN is defined as a fully connected network consisting of McCulloch-Pitts neurons. A McCulloch-Pitts neuron is a binary model with an activation function given by

The activity of the neurons x i , i.e.,

is either updated synchronously or asynchronously. To be precise, x j refers to x j t and x i to x i t + 1 (time progression).

Hopfield Networks have been introduced to serve as a model of a content-addressable (“associative”) memory, i.e., for storing patterns. In this case, it has been shown that the weights are obtained by

whereas P is the number of patterns, t ( k ) is the k-th pattern and t i ( k ) its i-th component. From Equation (6), one can see that the weights are symmetrical. An interesting question in this context is what is the maximal value of P or P / N , called the network capacity (here N is the total number of patterns). In Hertz et al. (1991) it was shown that the network capacity is ≈0.138. It is interesting to note that the neurons in a Hopfield Network cannot be distinguished as input neurons, hidden neurons and output neurons because at the beginning every neuron is an input neuron, during the processing every neuron is a hidden neuron and at the end every neuron is an output neuron.

3.3.2. Boltzmann Machine

A Boltzmann Machine ( Hinton and Sejnowski, 1983 ) can be described as a noisy Hopfield network because it uses a probabilistic activation function

whereas x i is obtained as in Equation (5). This model is important because it is one of the first neural networks that uses hidden units (latent variables). For learning the weights, the Contrastive Divergence algorithm (see Algorithm 9) can be used to train Boltzmann Machines. Put simply, Boltzmann Machines are neural networks consisting of two layers—a visible layer and a hidden layer. Each edge between the two layers is undirected, implying that information can flow in a bi-directional way. The whole network is fully connected, which means that each neuron in the network is connected to all other neurons via undirected edges (see Figures 8A,B ).

3.4. An Overview of Network Architectures

There is a large variety of different network architectures used as deep learning models. The following Table 2 does not aim to provide a comprehensive list, but it includes the most popular models currently used ( Yoshua, 2009 ; LeCun et al., 2015 ).

Table 2 . List of popular deep learning models, available learning algorithms (unsupervised, supervised) and software implementations in R or python.

It is interesting to note that some of the models in Table 2 are composed by other networks. For instance, CDBNs are based on RBMs and CNNs ( Lee et al., 2009 ); DBMs are based on RBMs ( Salakhutdinov and Hinton, 2009 ); DBNs are based on RBMs and MLPs; dAEs are stochastic Autoencoders that can be stacked on top of each other to build stacked denoising Autoencoders (SdAEs).

In the following sections, we discuss the major core architectures Deep Feedforward Neural Networks (D-FFNN), Convolutional Neural Networks (CNNs), Deep Belief Networks (DBNs), Autoencoders (AEs), and Long Short-Term Memory networks (LSTMs) in more detail.

4. Deep Feedforward Neural Networks

It can be proven that a Feedforward Neural Network with one hidden layer and a finite number of neurons can approximate any continuous function on a compact subset of ℝ n ( Hornik, 1991 ). This is called the universal approximation theorem . The reason for using a FFNN with more than one hidden layer is that the universal approximation theorem does not provide information on how to learn such a network, which turned out to be very difficult. A related issue that contributes to the difficulty of learning such networks is that their width can become exponentially large. Interestingly, the universal approximation theorem can also be proven for FFNN with many hidden layers and a bounded number of hidden neurons ( Lu et al., 2017 ) for which learning algorithms have been found. Hence, D-FFNNs are used instead of (shallow) FFNNs for practical reasons of learnability.

Formally, the idea of approximating an unknown function f * can be written as

Here f is a function from a specific family that depends on the parameters θ, and ϕ is a non-linear activation function with one layer. For many hidden layers ϕ has the form

Instead of guessing the correct family of functions from which f should be chosen, D-FFNNs learn this function by approximating it via ϕ , which itself is approximated by the n hidden layers.

The practical learning of the parameters of a D-FFNN (see Figure 3B ) can be accomplished with the backpropagation algorithm, although for computational efficiency nowadays the Stochastic Gradient Descent is used ( Bottou, 2010 ). The Stochastic Gradient Descent calculates a gradient for a set of randomly chosen training samples (batch) and updates the parameters for this batch sequentially. This results in a faster learning. A drawback is an increase in imprecision. However, for data sets with a large number of samples (big data), the speed advantage outweighs this drawback.

5. Convolutional Neural Networks

A Convolutional Neural Network (CNN) is a special Feedforward Neural Network utilizing convolution, ReLU and pooling layers. Standard CNNs are normally composed of several Feedforward Neural Network layers including convolution, pooling, and fully-connected layers.

Typically, in traditional ANNs, each neuron in a layer is connected to all neurons in the next layer, whereas each connection is a parameter in the network. This can result in a very large number of parameters. Instead of using fully connected layers, a CNN uses a local connectivity between neurons, i.e., a neuron is only connected to nearby neurons in the next layer. This can significantly reduce the total number of parameters in the network.

Furthermore, all the connections between local receptive fields and neurons use a set of weights, and we denote this set of weights as a kernel. A kernel will be shared with all the other neurons that connect to their local receptive fields, and the results of these calculations between the local receptive fields and neurons using the same kernel will be stored in a matrix denoted as activation map . The sharing property is referred to as weight sharing of CNNs ( Le Cun, 1989 ). Consequently, different kernels will result in different activation maps, and the number of kernels can be adjusted with hyper-parameters. Thus, regardless of the total number of connections between the neurons in a network, the total number of weights corresponds only to the size of the local receptive field, i.e., the size of the kernel. This is visualized in Figure 4B , where the total number of connections between the two layers is 9 but the size of the kernel is only 3.

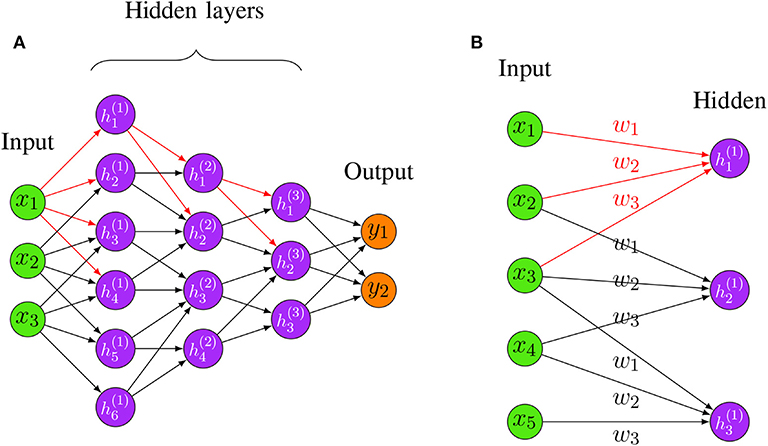
Figure 4. (A) An example for a Convolutional Neural Network. The red edges highlight the fact that hidden layers are connected in a “local” way, i.e., only very few neurons connect the succeeding layers. (B) An example for shared weights and local connectivity in CNN. The red edges highlight the fact that hidden layers are connected in a “local” way, i.e., only very few neurons connect the succeeding layers. The labels w 1 , w 2 , w 3 indicate the assigned weight for each connection, three hidden nodes share the same set of weights w 1 , w 2 , w 3 when connecting to three local patches.

By combining weight sharing and the local connectivity property, a CNN is able to handle data with high dimensions. See Figure 4A for a visualization of a CNN with three hidden layers. In Figure 4A , the red edges highlight the locality property of hidden neurons, i.e., only very few neurons connect to the succeeding layers. This locality property of CNN makes the network sparse compared to a FFNN which is fully connected.

5.1. Basic Components of CNN

5.1.1. convolutional layer.

A convolutional layer is an essential part in building a convolutional neural network. Similar to a hidden layer of an ordinary neural network, a convolutional layer has the same goal, which is to convert the input into a representation of a more abstract level. However, instead of using a full connectivity, the convolutional layer uses a local connectivity to perform the calculations between input and the hidden neurons. A convolutional layer uses at least one kernel to slide across the input, performing a convolution operation between each input region and the kernel. The results are stored in the activation maps, which can be seen as the output of the convolutional layer. Importantly, the activation maps can contain features extracted by different kernels. Each kernel can act as a feature extractor and will share its weights with all neurons.

For the convolution process, some spatial arguments need to be defined in order to produce the activation maps of a certain size. Essential attributes include:

1. Size of kernels (N). Each kernel has a window size, which is also referred to as receptive field. The kernel will perform a convolution operation with a region matching its window size from the input, and produce results in its activation map.

2. Stride (S). This parameter defines the number of pixels the kernel will move for the next position. If it is set to 1, each kernel will make convolution operations around the input volume and then shift 1 pixel at a time until it reaches the specified border of the input. Hence, the stride can be used to downsize the dimension of the activation maps as the larger the stride the smaller the activation maps.

3. Zero-padding (P). This parameter is used to specify how many zeros one wants to pad around the border of the input. This is very useful for preserving the dimension of the input.

These three parameters are the most common hyper-parameters used for controlling the output volume of a convolutional layer. Specifically, for an input of dimension W input × H input × Z , for the hyper-parameters size of the kernel (N), Stride (S), and Zero-padding (P) the dimension of the activation map, i.e., W out × H out × D can be calculated by:

An example of how to calculate the result between an input matrix and a kernel can be seen in Figure 5 .

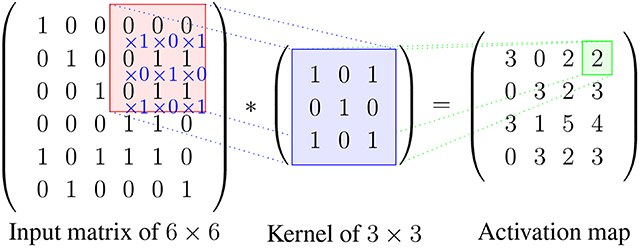
Figure 5 . An example for calculating the values in the activation map. Here, the stride is 1 and the zero-padding is 0. The kernel slides by 1 pixel at a time from left to right starting from the left top position, after reaching the boarder the kernel will start from the second row and repeat the process until the whole input is covered. The red area indicates the local patch to be convoluted with the kernel, and the result is stored in the green field in the activation map.

The shared weights and the local connectivity help significantly in reducing the total number of parameters of the network. For example, assuming that an input has dimension 100 × 100 × 3, and that the convolutional layer and the number of kernels is 2 and each kernel has a local receptive field of size 4, then the dimension of each kernel is 4 × 4 × 3 (3 is the depth of the kernel which will be the same as the depth of the input volume). For 100 neurons in the layer there will be in total only 4 × 4 × 3 × 2 = 96 parameters in this layer because all the 100 neurons will share the same weights for each kernel. This considers only the number of kernels and the size of the local connectivity but does not depend on the number neurons in the layer.

In addition to reducing the number of parameters, shared weights and a local connectivity are important in processing images efficiently. The reason therefore is that local convolutional operations in an image result in values that contain certain characteristics of the image, because in images local values are generally highly correlated and the statistics formed by the local values are often invariant in the location ( LeCun et al., 2015 ). Hence, using a kernel that shares the same weights can detect patterns from all the local regions in the image, and different kernels can extract different types of patterns from the image.

A non-linear activation function (for instance ReLu, tanh, sigmoid, etc.) is often applied to the values from the convolutional operations between the kernel and the input. These values are stored in the activation maps, which will be later passed to the next layer of the network.

5.1.2. Pooling Layer

A pooling layer is usually inserted between a convolutional layer and the following layer. Pooling layers aim at reducing the dimension of the input with some pre-specified pooling method, resulting in a smaller input by conserving as much information as possible. Also, a pooling layer is able to introduce spatial invariance into the network ( Scherer et al., 2010 ), which can help to improve the generalization of the model. In order to perform pooling, a pooling layer uses stride, zero-padding, and a pooling window size as hyper-parameters. The pooling layer will scan the entire input with the specified pooling window size in the same manner as the kernel in a convolutional layer. For instance, using a stride of 2, window size of 2 and 0 zeros-padding for pooling will half the size of the input dimension.

There are many types of pooling methods, e.g., averaging-pooling, min-pooling and some advanced pooling methods, such as fractional max-pooling and stochastic pooling. The most common used pooling method is max-pooling, as it has been shown to be superior in dealing with images by capturing invariances efficiently ( Scherer et al., 2010 ). Max-pooling extracts the maximum value within each specified sub-window across the activation map. The max-pooling can be formulated as A i, j, k = max ( R i − n : i + n, j − n : j + n, k ), where A i, j, k is the maximum activation value from the matrix R of size n × n centered at index i, j in the kth activation map with n is the window size.

5.1.3. Fully-Connected Layer

A fully-connected layer is the basic hidden layer unit in FFNN (see section 3.2). Interestingly, also for traditional CNN architectures, a fully connected layer is often added between the penultimate layer and the output layer to further model non-linear relationships of the input features ( Krizhevsky et al., 2012b ; Simonyan and Zisserman, 2014 ; Szegedy et al., 2015 ). However, recently the benefit of this has been questioned because of the many parameters introduced by this, leading potentially to overfitting ( Simonyan and Zisserman, 2014 ). As a result, more and more researchers started to construct CNN architecture without such a fully connected layer using other techniques like max-over-time pooling ( Lin et al., 2013 ; Kim, 2014 ) to replace the role of linear layers.

5.2. Important Variants of CNN

5.2.1. vggnet.

VGGNet ( Simonyan and Zisserman, 2014 ) was a pioneer in exploring how the depth of the network influences the performance of a CNN. VGGNet was proposed by the Visual Geometry Group and Google DeepMind, and they studied architectures with a depth of 19 (e.g., compared to 11 for AlexNet Krizhevsky et al., 2012b ).

VGG19 extended the network from eight weight layers (a structure proposed by AlexNet) to 19 weights layers by adding 11 more convolutional layers. In total, the parameters increased from 61 million to 144 million, however, the fully connected layer takes up most of the parameters. According to their reported results, the error rate dropped from 29.6 to 25.5 regrading top-1 val.error (percentage of times the classifier did not give the correct class with the highest score) on the ILSVRC dataset, and from 10.4 to 8.0 regarding top-5 val.error (percentage of times the classifier did not include the correct class among its top 5) on the ILSVRC dataset in ILSVRC2014. This indicates that a deeper CNN structure is able to achieve better results than shallower networks. In addition, they stacked multiple 3 × 3 convolutional layers without a pooling layer placed in between to replace the convolutional layer with a large filter sizes, e.g., 7 × 7 or 11 × 11. They suggested such an architecture is capable of receiving the same receptive fields as those composed of larger filter sizes. Consequently, two stacked 3 × 3 layers can learn features from a 5 × 5 receptive field, but with less parameters and more non-linearity.

5.2.2. GoogLeNet With Inception

The most intuitive way for improving the performance of a Convolutional Neural Network is to stack more layers and add more parameters to the layers ( Simonyan and Zisserman, 2014 ). However, this will impose two major problems. One is that too many parameters will lead to overfitting, and the other is that the model becomes hard to train.

GoogLeNet ( Szegedy et al., 2015 ) was introduced by Google. Until the introduction of inception, traditional state-of-the-art CNN architectures mainly focused on increasing the size and depth of the neural network, which also increased the computation cost of the network. In contrast, GoogLeNet introduced an architecture to achieve state-of-the-art performance with a light-weight network structure.

The idea underlying an inception network architecture is to keep the network as sparse as possible while utilizing the fast matrix computation feature provided by a computer. This idea facilitates the first inception structure (see Figure 6 ).

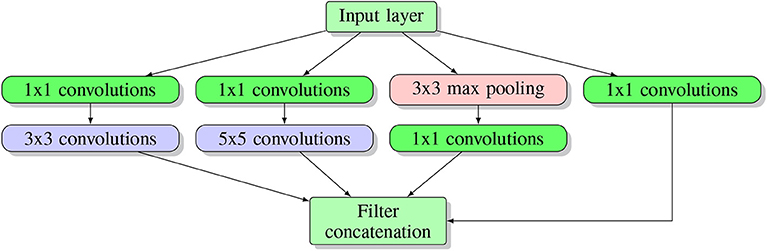
Figure 6 . Inception block structure. Here multiple blocks are stacked on top of each other, forming the input layer for the next block.

As one can see in the Figure 6 , several parallel layers including 1 × 1 convolution and 3 × 3 max pooling operate at the same level on the input. Each tunnel (namely one separated sequential operation) has a different child layer, including 3 × 3 convolutions, 5 × 5 convolutions and 1 × 1 convolution layer. All the results from each tunnel are concatenated together at the output layer. In this architecture, a 1x1 convolution is used to downscale the input image while reserving input information ( Lin et al., 2013 ). They argued that concatenating all the features extracted by different filters corresponds to the idea that image information should be processed at different scales and only the aggregated features should be sent to the next level. Hence, the next level can extract features from different scales. Moreover, this sparse structure introduced by an inception block requires much fewer parameters and, hence, is much more efficient.

By stacking the inception structure throughout the network, GoogLeNet won first place in the classification task of ILSVRC2014, demonstrating the quality of the inception structure. Followed by the inception v1, inception v2, v3, and the latest version v4 were introduced. Each generation introduced some new features, making the network faster, more light-weight and more powerful.

5.2.3. ResNet

In principle, CNNs with a deeper structure perform better than shallow ones ( Simonyan and Zisserman, 2014 ). In theory, deeper networks have a better ability to represent high level features from the input, therefore improving the accuracy of predictions ( Donahue et al., 2014 ). However, one cannot simply stack more and more layers. In the paper ( He et al., 2016 ), the authors observed the phenomena that more layers can actually hurt the performance. Specifically, in their experiment, network A had N layers, and network B had N + M layers, while the initial N layers had the same structure. Interestingly, when training on the CIFAR-10 and ImageNet dataset, network B showed a higher training error than network B. In theory, the extra M layers should result in a better performance, but instead they obtained higher errors which cannot be explained by overfitting. The reason for this is that the loss is getting optimized to local minima, which is different to the vanishing gradient phenomena. This is referred to as the degradation problem ( He et al., 2016 ).

ResNet ( He et al., 2016 ) was introduced to overcome the degradation problem of CNNs to push the depth of a CNN to its limit. In ( He et al., 2016 ), the authors proposed a novel structure of a CNN, which is in theory capable of being extended to an infinite depth without losing accuracy. In their paper, they proposed a deep residual learning framework, which consists of multiple residual blocks to address the degradation problem. The structure of a residual block is shown in the Figure 7 .

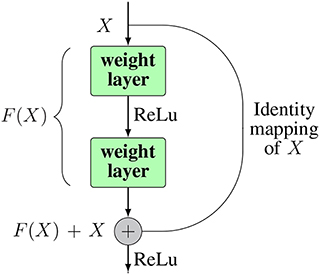
Figure 7 . The structure of a residual block. Inside a block there can be as many weight layers as desired.

Instead of trying to learn the desired underlying mapping H ( x ) from each few stacked layers, they used an identity mapping for input x from input to the output of the layer, and then let the network learn the residual mapping F ( x ) = H ( x ) − x . After adding the identity mapping, the original mapping can be reformulated as H ( x ) = F ( x ) + x . The identity mapping is realized by making shortcut connections from the input node directly to the output node. This can help to address the degradation problem as well as the vanishing (exploding) gradient issue of deep networks. In extreme cases, deeper layers can just learn the identity map of the input to the output layer, by simply calculating the residuals as 0. This enables the ability for a deep network to perform at least not worse than shallow ones. Also, in practice, the residuals are never 0, which makes it possible for very deeper layers to always learn something new from the residuals therefore producing better results. The implementation of ResNet helped to push the layers of CNNs to 152 by stacking so-called residual blocks through out the network. ResNet achieved the best result in the ILSVRC2016 competition, with an error rate of 3.57.

6. Deep Belief Networks

A Deep Belief Network (DBN) is a model that combines different types of neural networks with each other to form a new neural network model. Specifically, DBNs integrate Restricted Boltzmann Machines (RBMs) with Deep Feedforward Neural Networks (D-FFNN). The RBMs form the input unit whereas the D-FFNNs form the output unit. Frequently, RBMs are stacked on top of each other, which means more than one RBM is used sequentially. This adds to the depth of the DBN.

Due to the different nature of the networks RBM and D-FFNN, two different types of learning algorithms are used. Practically, the Restricted Boltzmann Machines are used for initializing a model in an unsupervised way. Thereafter, a supervised method is applied for the fine tuning of the parameters ( Yoshua, 2009 ). In the following, we describe these two phases of the training of a DBN in more detail.

6.1. Pre-training Phase: Unsupervised

Theoretically, neural networks can be learned by using supervised methods only. However, in practice it was found that such a learning process can be very slow. For this reason, unsupervised learning is used to initialize the model parameters. The standard neural network learning algorithm (backpropagation) was initially only able to learn shallow architectures. However, by using a Restricted Boltzmann Machine for the unsupervised initialization of the parameters one obtains a more efficient training of the neural network ( Hinton et al., 2006 ).

A Restricted Boltzmann Machine is a special type of a Boltzmann Machine (BM), see section 3.3.2. The difference between a Restricted Boltzmann Machine and a Boltzmann Machine is that Restricted Boltzmann Machines (RBMs) have constraints in the connectivity of their structure ( Fischer and Igel, 2012 ). Specifically, there can be no connections between nodes in the same layer. For an example, see Figure 8C .

Figure 8 . Examples for Boltzmann Machines. (A) The neurons are arranged on a circle. (B) The neurons are separated according to their type. Both Boltzmann Machines are identical and differ only in their visualization. (C) Transition from a Boltzmann Machine (left) to a Restricted Boltzmann Machine (right).

The values of neurons, v , in the visible layer are known, but the neuron values, h , in the hidden layer are unknown. The parameters of the network are learned by defining an energy function, E , of the model which is then minimized.

Frequently, a RBM is used with binary values, i.e., v i ∈ {0, 1} and h i ∈ {0, 1}. The energy function for such a network is given by ( Hinton, 2012 ):

whereas Θ = { a, b , W } is the set of model parameters.

Each configuration of the system corresponds to a probability defined via the Boltzmann distribution in Equation (11):

In Equation (12), Z is the partition function given by:

The probability for the network assigning to a visible vector v is given by summing over all possible hidden vectors:

Maximum-likelihood estimation (MLE) is used for estimating the optimal parameters of the probabilistic model ( Hayter, 2012 ). For a training data set D = D t r a i n = { v 1 , … , v l } consisting of l patterns, assuming that the patterns are iid (independent and identical) distributed, the log-likelihood function is given by:

For simple cases, one may be able to find an analytical solution for Equation (15) by solving ∂ ∂ θ ln  L ( θ | D ) = 0 . However, usually the parameters need to be found numerically. For this, the gradient of the log-likelihood is a typical approach for estimating the optimal parameters:

In Equation (16), the constant, η, in front of the gradient is the learning rate and the first regularization term, −λθ ( t ) , is the weight-decay. The weight-decay is used to constrain the optimization problem by penalizing large values of θ ( Hinton, 2012 ). The parameter λ is also called the weight-cost . The second regularization term in Equation (16) is called momentum. The purpose of the momentum is to make learning faster and to reduce possible oscillations. Overall, this should stabilize the learning process.

For the optimization, the Stochastic Gradient Ascent (SGA) is utilized using mini-batches . That means one selects randomly a number of samples from the training set, k , which are much smaller than the total sample size, and then estimates the gradient. The parameters, θ, are then updated for the mini-batch. This process is repeated iteratively until an epoch is completed. An epoch is characterized by using the whole training set once. A common problem is encountered when using mini-batches that are too large, because this can slow down the learning process considerably. Frequently, k is chosen between 10 and 100 ( Hinton, 2012 ).

Before the gradient can be used, one needs to approximate the gradient of Equation (16). Specifically, the derivatives with respect to the parameters can be written in the following form:

In Equation (17), H i denotes the value of hidden unit i and p ( v ) is the probability defined in Equation (14). For the conditional probability, one finds

and correspondingly

Using the above equations in the presented form would be inefficient because these equations require a summation over all visible vectors. For this reason, the Contrastive Divergence (CD) method is used for increasing the speed for the estimation of the gradient. In Figure 9A , we show pseudocode of the CD algorithm.

Figure 9. (A) Contrastive Divergence k-step algorithm using Gibbs sampling. (B) Backpropagation algorithm. (C) iRprop + algorithm.

The CD uses Gibbs sampling for drawing samples from conditional distributions, so that the next value depends only on the previous one. This generates a Markov chain ( Hastie et al., 2009 ). Asymptotically, for k → ∞ the distribution becomes the true stationary distribution. In this case, the CD → ML . Interestingly, already k = 1 can lead to satisfactory approximations for the pre-training ( Carreira-Perpinan and Hinton, 2005 ).

In general, pre-training of DBNs consists of stacking RBMs. That means the next RBM is trained using the hidden layer of the previous RBM as visible layer. This initializes the parameters for each layer ( Hinton and Salakhutdinov, 2006 ). Interestingly, the order of this training is not fixed but can vary. For instance, first, the last layer can be trained and then the remaining layers can be trained ( Hinton et al., 2006 ). In Figure 10 , we show an example for the stacking of RBMs.

Figure 10 . Visualizing the stacking of RBMs in order to learn the parameters Θ of a model in an unsupervised way.

6.2. Fine-Tuning Phase: Supervised

After the initialization of the parameters of the neural network, as described in the previous step, these can now be fine-tuned. For this step, a supervised learning approach is used, i.e., the labels of the samples, omitted in the pre-training phase, are now utilized.

For learning the model, one minimizes an error function (also called loss function or sometimes objective function). An example for such an error function is the mean squared error (MSE).

In Equation (20), o i = ϕ ( x i ) is the i th output from the network function ϕ :ℝ m → ℝ n given the i th input x i from the training set D = D t r a i n = { ( x 1 , t 1 ) , … ( x l , t l ) } and t i is the target output.

Similarly, for maximizing the log-likelihood function of a RBM (see Equation 16), one uses gradient descent to find the parameters that minimize the error function.

Here, the parameters (η, λ and ν) have the same meaning as explained above. Again, the gradient is typically not used for the entire training data D , but instead smaller batches are used via the Stochastic Gradient Descent (SGD).

The gradient of the RBM log-likelihood can be approximated using the CD algorithm (see Figure 9A ). For this, the backpropagation algorithm is used ( LeCun et al., 2015 ).

Let us denote by a i l the activation of the ith unit in the lth layer ( l ∈ {2, …, L }), b i t the corresponding bias and w i j l the weight for the edge between the jth unit of the ( l − 1)th layer and the ith unit of the lth layer. For activation function, φ, the activation of the lth layer with the (l - 1)th layer as input is a l = φ( z ( l ) ) = φ( w ( l ) a ( l −1) + b ( l ) ).

Application of the chain rule leads to ( Nielsen, 2015 ):

In Equation (22), the vector δ L contains the errors of the output layer ( L ), whereas the vector δ l contains the errors of the lth layer. Here, · indicates the element-wise product of vectors. From this the gradient of the error of the output layer is given by

In general, the result of this depends on E . For instance, for the MSE we obtain ∂ E ∂ a j ( L ) = ( a j - t j ) . As a result, the pseudocode for the backpropagation algorithm can be formulated as shown in Figure 9B ( Nielsen, 2015 ). The estimated gradients from Figure 9B are then used to update the parameters (weights and biases) via SGD (see Equation 21). More updates are performed using mini-batches until all training data have been used ( Smolander, 2016 ).

The resilient backpropagation algorithm (Rprop) is a modification of the backpropagation algorithm that was originally introduced to speed up the basic backpropagation (Bprop) algorithm ( Riedmiller and Braun, 1993 ). There exist at least four different versions of Rprop ( Igel and Hüsken, 2000 ) and in Algorithm 9 pseudocode for the iRprop + algorithm (which improves Rprop with weight-backtracking) is shown ( Smolander, 2016 ).

As one can see in Algorithm 9, iRprop + uses information about the sign of the partial derivative from time step ( t − 1) to make a decision for the update of the parameter. Importantly, the results of comparisons have shown that the iRprop + algorithm is faster than Bprop ( Igel and Hüsken, 2000 ).

It has been shown that the backpropagation algorithm with SGD can learn good neural network models even without a pre-training stage when the training data are sufficiently large ( LeCun et al., 2015 ).

In Figure 11 , we show an example of the overall DBN learning procedure. The left-hand side shows the pre-training phase and the right-hand side the fine-tuning.

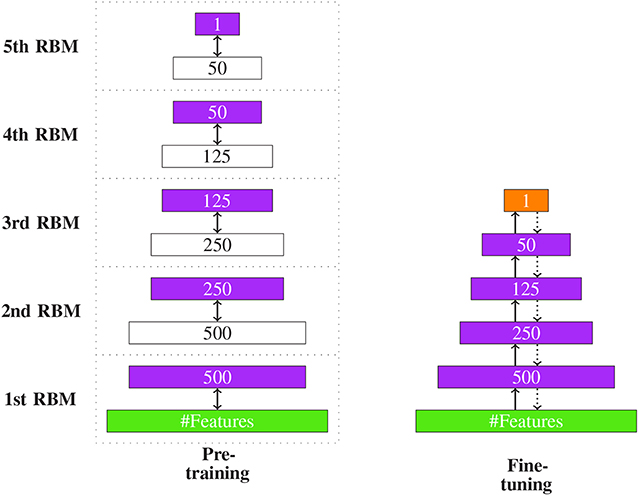
Figure 11 . The two stages of DBN learning. (Left) The hidden layer (purple) of one RBM is the input of the next RBM. For this reason their dimensions are equal. (Right) The two edges in fine-tuning denote the two stages of the backpropagation algorithm: the input feedforwarding and the error backpropagation. The orange layer indicated the output.

DBNs have been used successfully for many application tasks, e.g., natural language processing ( Sarikaya et al., 2014 ), acoustic modeling ( Mohamed et al., 2011 ), image recognition ( Hinton et al., 2006 ) and computational biology ( Zhang S. et al., 2015 ).

7. Autoencoder

An Autoencoder is an unsupervised neural network model used for representation learning, e.g., feature selection or dimension reduction. A common property of autoencoders is that the size of the input and output layer is the same with a symmetric architecture ( Hinton and Salakhutdinov, 2006 ). The underlying idea is to learn a mapping from an input pattern x to a new encoding c = h ( x ), which ideally gives as output pattern the same as the input pattern, i.e., x ≈ y = g ( c ). Hence, the encoding c , which has usually lower dimension than x , allows to reproduce (or code for) x .

The construction of Autoencoders is similar to DBNs. Interestingly, the original implementation of an autoencoder ( Hinton and Salakhutdinov, 2006 ) pre-trained only the first half of the network with RBMs and then unrolled the network, creating in this way the second part of the network. Similar to DBNs, a pre-training phase is followed by a fine-tuning phase. In Figure 12 , an illustration of the learning process is shown. Here, the coding layer corresponds to the new encoding c providing, e.g., a reduced dimension of x .

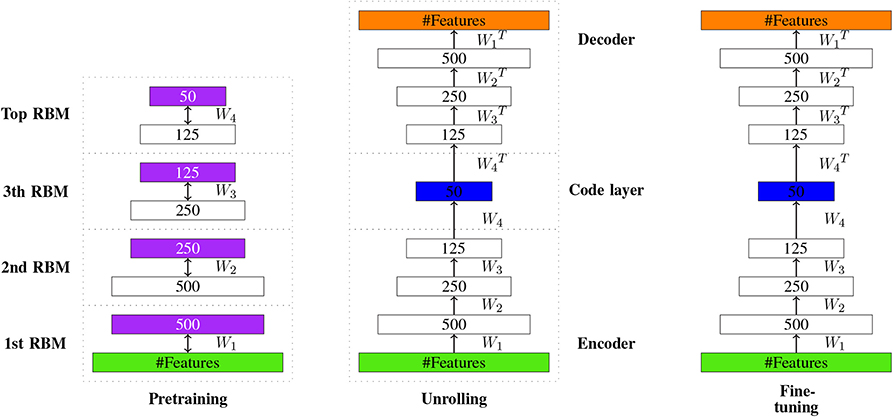
Figure 12 . Visualizing the idea of autoencoder learning. The learned new encoding of the input is represented in the code layer (shown in blue).

An Autoencoder does not utilize labels and, hence, it is an unsupervised learning model. In applications, the model has been successfully used for dimensionality reduction. Autoencoders can achieve a much better two-dimensional representation of array data, when an adequate amount of data is available ( Hinton and Salakhutdinov, 2006 ). Importantly, PCAs implement a linear transformation, whereas Autoencoders are non-linear. Usually, this results in a better performance. We would like to highlight that there are many extensions of these models, e.g., sparse autoencoder, denoising autoencoder or variational autoencoder ( Vincent et al., 2010 ; Deng et al., 2013 ; Pu et al., 2016 ).

8. Long Short-Term Memory Networks

Long short-term memory (LSTM) networks were introduced by Hochreiter and Schmidhuber in 1997 ( Hochreiter and Schmidhuber, 1997 ). LSTM is a variant of a RNN that has the ability to address the shortcomings of RNNs which do not perform well, e.g., when handling long-term dependencies ( Graves, 2013 ). Furthermore, LSTMs avoid the gradient vanishing or exploding problem ( Hochreiter, 1998 ; Gers et al., 1999 ). In 1999, a LSTM with a forget gate was introduced which could reset the cell memory. This improved the initial LSTM and became the standard structure of LSTM networks ( Gers et al., 1999 ). In contrast to Deep Feedforward Neural Networks, LSTMs contain feedback connections. Furthermore, they can not only process single data points, such as vectors or arrays, but sequences of data. For this reason, LSTMs are particularly useful for analyzing speech or video data.

8.1. LSTM Network Structure With Forget Gate

Figure 13 shows an unrolled structure of a LSTM network model ( Wang et al., 2016 ). In this model, the input and output are organized vertically, while information is delivered horizontally over the time series.

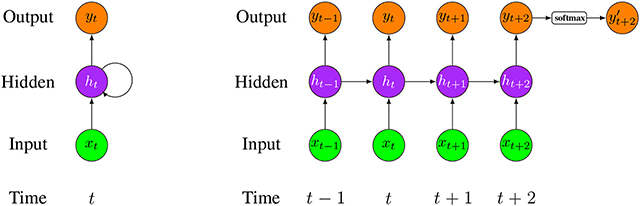
Figure 13. (Left) A folded structure of a LSTM network model. (Right) An unfolded structure of a LSTM network model. x i is the input data at time i and y i is the corresponding output ( i is the time step starting from ( t − 1)). In this network, only y t + 2 ′ activated by softmax function is the final network output.

In a standard LSTM network, the basic entity is called LSTM unit or a memory block ( Gers et al., 1999 ). Each unit is composed of a cell, the memory part of the unit, and three gates: an input gate, an output gate and a forget gate (also called keep gate) ( Gers et al., 2002 ). A LSTM unit can remember values over arbitrary time intervals and the three gates control the flow of information through the cell. The central feature of a LSTM cell is a part called “constant error carousel” (CEC) ( Lipton et al., 2015 ). In general, a LSTM network is formed exactly like a RNN, except that the neurons in the hidden layers are replaced by memory blocks.

In the following, we discuss some core concepts and the corresponding technicalities ( W and U stand for the weights and b for the bias). In Figure 14 , we show a schematic description of a LSTM block with one cell.

• Input gate: A unit with sigmoidal function that controls the flow of information into the cell. It receives its activation from both output of the previous time h ( t −1) and current input x ( t ) . Under the effect of the sigmoid function, an input gate i t generates values between zero and one. Zero indicates it blocks the information entirely, whereas values of one allow all the information to pass.

• Cell input layer: The cell input has a similar flow as the input gate, receiving h ( t −1) and x ( t ) as input. However, a tanh activation is used to squish input values to a range between -1 and 1 (denoted by l t in Equation 25).

• Forget gate: A unit with a sigmoidal function determines which information from previous steps of the cell should be memorized or forgotten. The forget gate f t assumes values between zero and one based on the input, h ( t −1) and x ( t ) . In the next step, f t is given by a Hadamard product with an old cell state c t −1 to update to a new cell state c t (Equation 26). In this case, a value of zero means the gate is closed, so it will completely forget the information of the old cell state c t −1 , whereas values of one will make all information memorable. Therefore, a forget gate has the right to reset the cell state if the old information is considered meaningless.

• Cell state: A cell state stores the memory of a cell over a longer time period ( Ming et al., 2017 ). Each cell has a recurrently self-connected linear unit which is called Constant Error Carousel (CEC) ( Hochreiter and Schmidhuber, 1997 ). The CEC mechanism ensures that a LSTM network does not suffer from the vanishing or exploding gradient problem ( Elsayed et al., 2018 ). The CEC is regulated by a forget gate and it can also be reset by the forget gate. At time t , the current cell state c t is updated by the previous cell state c t −1 controlled by the forget gate and the product of the current input and the cell input, i.e., ( i t ∘ l t ). Overall, Equation (27) describes the combined update of a cell state,

• Output gate: A unit with a sigmoidal function can control the flow of information out of the cell. A LSTM uses the values of the output gate at time t (denoted by o t ) to control the current cell state c t activated by a tanh function, to obtain the final output vector h ( t ) ,

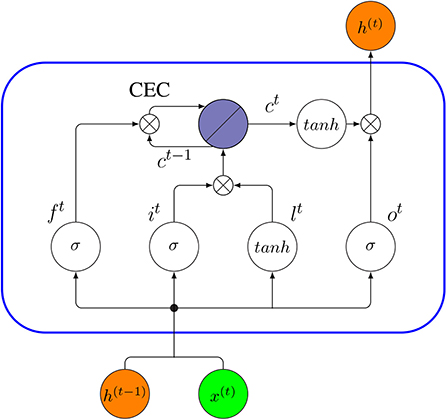
Figure 14 . Internal connectivity pattern of a standard LSTM unit (blue rectangle). The output from the previous time step, h ( t −1) , and x ( t ) , are the input to the block at time t , then the output h ( t ) at time t will be an input to the same block in the next time step ( t + 1).

8.2. Peephole LSTM

A Peephole LSTM is a variant of a LSTM proposed by Gers and Schmidhuber (2000) . In contrast to a standard LSTM discussed above, a Peephole LSTM uses the cell state c , instead of h for regulating the forget gate, input gate and output gate. In Figure 15 , we show the internal connectivity of a Peephole LSTM unit whereas the red arrows represent the new peephole connections.

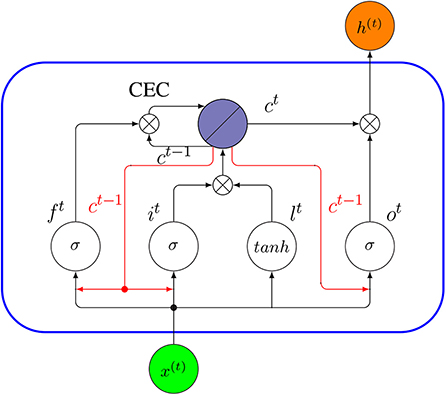
Figure 15 . Internal connectivity of a Peephole LSTM unit (blue rectangle). Here x ( t ) is the input to the cell at time t , and h ( t ) is its output. The red arrows are the new peephole connections added, compared to the standard LSTM in Figure 14 .

The key difference between a Peephole LSTM and a standard LSTM is that the forget gate f t , input gate i t and output gate o t do not use h ( t −1) as input. Instead, these gates use the cell state c t −1 . In order to understand the base idea behind a Peephole LSTM, let us assume the output gate o t −1 in a traditional LSTM network is closed. Then the output of the network h ( t −1) at time ( t − 1) will be 0, according to Equation (29), and in the next time step t , the regulating mechanism of all three gates will only depend on the network input x ( t −1) . Therefore, the historical information will be lost completely. A Peephole LSTM avoids this problem by using a cell state instead of output h to control the gates. The following equations describe a Peephole LSTM formally.

Aside from these main forms of LSTMs described above, there are further variants. For instance, a Bidirectional LSTM Network (BLSTM) has been introduced by ( Graves and Schmidhuber, 2005 ), which can access long-range context in both input directions. Furthermore, in 2014, the concept of “Gated Recurrent Unit” was proposed, which is viewed as a simplified version of LSTM ( Cho et al., 2014 ) and in 2015, Wai-kin Wong and Wang-chun Woo introduced a Convolutional LSTM Network (ConvLSTM) for precipitation nowcasting ( Xingjian et al., 2015 ). There are further variants of LSTM networks; however, most of them are designed for specific application domains without clear performance advantage.

8.3. Applications

LSTMs have a wide range of applications in text generation, text classification, language translation or image captioning ( Hwang and Sung, 2015 ; Vinyals et al., 2015 ). In Figure 16 , an LSTM classifier model for text classification is shown. In this figure, the input of the LSTM structure at each time step is a word embedding vector V i , which is a common choice for text classification problems. A word embedding technique maps the words or phrases in the vocabulary to vectors consisting of real numbers. Some common word embedding techniques include word2vec, GloVe, FastText, etc. Zhou (2019) . The output y N is the corresponding output at the Nth time step and y N ′ is the final output after softmax activation of y N , which will determine the classification of the input text.

Figure 16 . An LSTM classifier model for text classification. N is the sequence length of the input text (the number of words). Input from V 1 to V N is a sequence of word embedding vectors used as input to the model at different time steps. y N ′ is the final prediction result.

9. Discussion

9.1. general characteristics of deep learning.

A property common to all deep learning models is that they perform so-called representation learning. Sometimes this is also called feature learning. This denotes a model that learns new and better representations compared to the raw data. Importantly, deep learning models do not learn the final representation within one step but multiple ones corresponding to multi-level representation transformations between the hidden layers ( LeCun et al., 2015 ).

Another common property of deep learning models is that the subsequent transformations between layers are non-linear (see Figure 3 ). This increases the expressive power of the model ( Duda et al., 2000 ). Furthermore, individual representations are not designed manually, but learned via training data ( LeCun et al., 2015 ). This makes deep learning models very flexible.

9.2. Differences Between Models

Currently, CNNs are the dominating deep learning models for computer vision tasks ( LeCun et al., 2015 ). They are effective when the data consist of arrays where nearby values in an array are correlated with each other, e.g., as is the case for images, videos, and sound data. A convolutional layer can easily process high-dimensional input by using the local connectivity and shared weights, while a pooling layer can down-sample the input without losing essential information. Each convolutional layer is capable of converting the input image into groups of more abstract features using different kernels; therefore, by stacking multiple convolution layers, the network is able to transform the input image to a representation that captures essential patterns from the input, thus making precise predictions.

However, also in other areas, CNNs have shown very competitive results compared to other deep learning architectures, e.g., in natural language processing ( Kim, 2014 ; Yang et al., 2020 ). Specifically, CNNs can be good at extracting local information from text and exploring meaningful semantic and syntactic meanings between phrases and words. Also, the natural composition of text data can be easily handled by a CNN architecture. Hence, CNNs show very strong potential in performing classification tasks where successful predictions heavily rely on extracting key information from input text ( Yin et al., 2017 ).

The classical network architecture is fully connected and feedforward corresponding to a D-FFNN. Interestingly, in ( Mayr et al., 2016 ), it has been shown that a D-FFNN outperformed other methods for predicting the toxicity of drugs. Also for drug target predictions, a D-FFNN has been shown to be superior compared to other methods ( Mayr et al., 2018 ). This shows that even such an architecture can be successfully used in modern applications.

Commonly, RNNs are used for problems with sequential data, such as speech and language processing or modeling ( Sundermeyer et al., 2012 ; Graves et al., 2013 ; Luong and Manning, 2015 ). While DBNs and CNNs are feedforward networks, connections in RNNs can form cycles. This allows the modeling of dynamical changes over time ( LeCun et al., 2015 ).

A problem with finding the right application for a deep learning model is that their application domains are not mutually exclusive from each other. Instead, as the discussion above shows, there is a considerable overlap and the best model can in many cases only be found by conducting a comparative study. In Table 3 , we show several examples of different applications involving images, audio, text, and genomics data.

Table 3 . Overview of applications of deep learning methods.

9.3. Interpretable Models vs. Black-Box Models

Any model in data science can be categorized either as an inferential model or a prediction model ( Breiman, 2001 ; Shmueli, 2010 ). An inferential model does not only make predictions but provides also an interpretable structure. Hence, it is a model of the prediction process itself, e.g., a causal model. In contrast, a prediction model is merely a black-box model for making predictions.

The models discussed in this review neither aim at providing physiological models of biological neurons nor offer an interpretable structure. Instead, they are prediction models. An example for a biologically motivated learning rule for neural networks is the Hebbian learning rule ( Hebb, 1949 ). Hebbian learning is a form of unsupervised learning of neural networks that does not use global information about the error as backpropagation. Instead, only local information is used from adjacent neurons. There are many extensions of Hebb's basic learning rule that have been introduced based on new biological insights (see e.g., Emmert-Streib, 2006 ).

Recently, there is great interest in interpretable or explainable AI (XAI) ( Biran and Cotton, 2017 ; Doshi-Velez and Kim, 2017 ). Especially in the clinical and medical area, one would like to have understandable decisions of statistical prediction models because patients are affected ( Holzinger et al., 2017 ). The field is still in its infancy, but if meaningful interpretations of general deep learning models could be found this would certainly revolutionize the field.

As a note, we would like to add that the distinction between an explainable AI model and a non-explainable model is not well-defined. For instance, the sparse coding model by Olshausen and Field (1997) was shown to be similar to the coding of images in the human visual cortex ( Tosic and Frossard, 2011 ) and an application of this model can be found in Charles et al. (2011) , where an unsupervised learning approach was used to learn an optimal sparse coding dictionary for the classification of high spectral imagery (HIS) data. Some may consider this model as an XAI model because of the similarity to the working mechanism of the human cortex, whereas others may question this explanation.

9.4. Big Data vs. Small Data

In statistics, the field of experimental design is concerned with assessing if the available sample sizes are sufficient to conduct a particular analysis (for a practical example see Stupnikov et al., 2016 ). In contrast, for all methods discussed in this paper, we assumed that we are in the big data domain implying sufficient samples. This corresponds to the ideal case. However, we would like to point out that for practical applications, one needs to assess this situation case-by-case to ensure the available data (respectively the sample sizes) are sufficient to use deep learning models. Unfortunately, this issue is not well-represented in the current literature. As a rule-of-thumb , deep learning models usually perform well for tens of thousands of samples but it is largely unclear how they perform in a small data setting. This leaves it to the user to estimate learning curves of the generalization error for a given model to avoid spurious results ( Emmert-Streib and Dehmer, 2019b ).

As an example to demonstrate this problem, we conducted an analysis to explore the influence of the sample size on the accuracy of the classification of the EMNIST data. EMNIST (Extended MNIST) ( Cohen et al., 2017 ) consists of 280, 000 handwritten characters (240, 000 training samples and 40, 000 test samples) for 10 balanced classes (0–9). We used a multilayered Long Short-Term Memory (LSTM) model for the 10-class handwritten digit classification task. The model we used is a four-layer network (three hidden layers and one fully connected layer), and each hidden layer contains 200 neurons. For this analysis, we set the batch size to 100 and the training samples were randomly drawn if the number of training samples was < 240, 000 (subsampling).

From the results in Figure 17 , one can see that thousands of training samples are needed to achieve a classification error below 5% (blue dashed line). Specifically, more than 25, 000 training samples are needed. Given the relative simplicity of the problem—classification of ten digits, compared to classification or diagnosis of cancer patients—the severity of this issue should become clear. Also, these results show that a deep learning model cannot do miracles. If the number of samples is too small, the method breaks down. Hence, the combination of a model and data is crucial for solving a task.

Figure 17 . Classification error of the EMNIST data in dependence on the number of training samples. The standard errors are shown in red and the horizontal dashed line corresponds to an error of 5% (reference). The results are averaged over 10 independent runs.

9.5. Data Types

A related problem to the sample size issue discussed above is the type of data. Examples for different data types are text data, image data, audio data, network data or measurement/sensor data (for instance from genomics) to name just a few. One can further subdivide these data according to the application domain from which these originate, e.g., text data from medical publications, text data from social media or text data from novels. Considering such categorizations, it becomes clear that the information content of 'one sample' does not have the same meaning for each data type and for each application domain. Hence, the assessment of deep learning models needs to be always conducted in a domain specific manner because the transfer of knowledge between such models is not straight forward.

9.6. Further Advanced Models

Finally, we would like to emphasize that there are additional but more advanced models of deep learning networks, which are outside the core architectures. For instance, deep learning and reinforcement learning have been combined with each other to form deep reinforcement learning ( Mnih et al., 2015 ; Arulkumaran et al., 2017 ; Henderson et al., 2018 ). Such models have found application in problems from robotics, games and healthcare.

Another example for an advanced model is a graph CNN, which is particularly suitable when data have the form of graphs ( Henaff et al., 2015 ; Wu et al., 2019 ). Such models have been used in natural language processing, recommender systems, genomics and chemistry ( Li et al., 2018 ; Yao et al., 2019 ).

Lastly, a further advanced model is a Variational Autoencoder (VAE) ( An and Cho, 2015 ; Doersch, 2016 ). Put simply, a VAR is a regularized Autoencoder that uses a distribution over the latent spaces as encoding for the input, instead of a single point. The major application of VAE is as a generative model for generating similar data in an unsupervised manner, e.g., for image or text generation.

10. Conclusion

In this paper, we provided an introductory review for deep learning models including Deep Feedforward Neural Networks, (D-FFNN), Convolutional Neural Networks (CNNs), Deep Belief Networks (DBNs), Autoencoders (AE) and Long Short-Term Memory networks (LSTMs). These models can be considered the core architectures that currently dominate deep learning. In addition, we discussed related concepts needed for a technical understanding of these models, e.g., Restricted Boltzmann Machines and resilient backpropagation. Given the flexibility of network architectures allowing a “ Lego-like ” construction of new models, an unlimited number of neural network models can be constructed by utilizing elements of the core architectural building blocks discussed in this review. Hence, a basic understanding of these elements is key to be equipped for future developments in AI.

Author Contributions

FE-S conceived the study. All authors contributed to all aspects of the preparation and the writing of the manuscript.

MD thanks the Austrian Science Funds for supporting this work (project P 30031).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Johannes Smolander for discussions about Deep Belief Networks.

Alipanahi, B., Delong, A., Weirauch, M. T., and Frey, B. J. (2015). Predicting the sequence specificities of DNA-and RNA-binding proteins by deep learning. Nat. Biotechnol. 33, 831–838. doi: 10.1038/nbt.3300

PubMed Abstract | CrossRef Full Text | Google Scholar

An, J., and Cho, S. (2015). Variational Autoencoder Based Anomaly Detection Using Reconstruction Probability . Special Lecture on IE 2.

Google Scholar

Arulkumaran, K., Deisenroth, M. P., Brundage, M., and Bharath, A. A. (2017). Deep reinforcement learning: a brief survey. IEEE Signal Process. Mag. 34, 26–38. doi: 10.1109/MSP.2017.2743240

CrossRef Full Text | Google Scholar

Bergmeir, C., and Benítez, J. M. (2012). Neural networks in R using the stuttgart neural network simulator: RSNNS. J. Stat. Softw. 46, 1–26. doi: 10.18637/jss.v046.i07

Biran, O., and Cotton, C. (2017). “Explanation and justification in machine learning: a survey,” in IJCAI-17 Workshop on Explainable AI (XAI) . Vol. 8, 1.

Bottou, L. (2010). “Large-scale machine learning with stochastic gradient descent,” in Proceedings of COMPSTAT'2010 (Springer), 177–186.

Breiman, L. (2001). Statistical modeling: the two cultures (with comments and a rejoinder by the author). Stat. Sci. 16, 199–231. doi: 10.1214/ss/1009213726

Cao, C., Liu, F., Tan, H., Song, D., Shu, W., Li, W., et al. (2018). Deep learning and its applications in biomedicine. Genomics Proteomics Bioinform. 16, 17–32. doi: 10.1016/j.gpb.2017.07.003

Cao, S., Lu, W., and Xu, Q. (2016). “Deep neural networks for learning graph representations,” in Thirtieth AAAI Conference on Artificial Intelligence .

Carreira-Perpinan, M. A., and Hinton, G. E. (2005). “On contrastive divergence learning,” in Proceedings of the Tenth International Workshop on Artificial Intelligence and Statistics (Citeseer), 33–40.

Charles, A. S., Olshausen, B. A., and Rozell, C. J. (2011). Learning sparse codes for hyperspectral imagery. IEEE J. Select. Top. Signal Process. 5, 963–978. doi: 10.1109/JSTSP.2011.2149497

Chen, T., Li, M., Li, Y., Lin, M., Wang, N., Wang, M., et al. (2015). Mxnet: a flexible and efficient machine learning library for heterogeneous distributed systems.

Chimera (2019). Pydbm . arXiv:1512.01274.

Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., et al. (2014). Learning phrase representations using rnn encoder-decoder for statistical machine translation. arXiv [Preprint] . arXiv:1406.1078. doi: 10.3115/v1/D14-1179

Chollet, F. (2015). Keras . Available online at: https://github.com/fchollet/keras

Cohen, G., Afshar, S., Tapson, J., and van Schaik, A. (2017). Emnist: an extension of mnist to handwritten letters. arXiv[Preprint]. arXiv:1702.05373. doi: 10.1109/IJCNN.2017.7966217

Dai, J., Wang, Y., Qiu, X., Ding, D., Zhang, Y., Wang, Y., et al. (2018). BigDL: a distributed deep learning framework for big data. arXiv:1804.05839.

[Dataset] Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2016). Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv:1603.04467.

[Dataset] Bondarenko, Y. (2017). Boltzman-Machines .

[Dataset] Candel, A., Pramar, V., LeDell, E., and Arora, A. (2015). Deep Learning With H2O .

[Dataset] Dieleman, S., Schlüter, J., Raffel, C., Olson, E., Sonderby, S. K., Nouri, D., et al. (2015). Lasagne: First Release .

[Dataset] Howard J., and Gugger S. (2018). fastai: A Layered API for Deep Learning . arXiv:2002.04688.

Deng, J., Zhang, Z., Marchi, E., and Schuller, B. (2013). “Sparse autoencoder-based feature transfer learning for speech emotion recognition,” in 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction (IEEE), 511–516.

Dixon, M., Klabjan, D., and Wei, L. (2017). Ostsc: over sampling for time series classification in R.

Doersch, C. (2016). Tutorial on variational autoencoders. arXiv [Preprint] . arXiv:1606.05908.

Donahue, J., Jia, Y., Vinyals, O., Hoffman, J., Zhang, N., Tzeng, E., et al. (2014). “Decaf: a deep convolutional activation feature for generic visual recognition,” in International Conference on Machine Learning , 647–655.

Doshi-Velez, F., and Kim, B. (2017). Towards a rigorous science of interpretable machine learning. arXiv [Preprint] . arXiv:1702.08608.

Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pattern Classification. 2nd Edn. Wiley.

Elsayed, N., Maida, A. S., and Bayoumi, M. (2018). Reduced-gate convolutional LSTM using predictive coding for spatiotemporal prediction. arXiv [Preprint] . arXiv:1810.07251.

Emmert-Streib, F. (2006). A heterosynaptic learning rule for neural networks. Int. J. Mod. Phys. C 17, 1501–1520. doi: 10.1142/S0129183106009916

Emmert-Streib, F., and Dehmer, M. (2019a). Defining data science by a data-driven quantification of the community. Mach. Learn. Knowl. Extract. 1, 235–251. doi: 10.3390/make1010015

Emmert-Streib, F., and Dehmer, M. (2019b). Evaluation of regression models: model assessment, model selection and generalization error. Mach. Learn. Knowl. Extract. 1, 521–551. doi: 10.3390/make1010032

Enarvi, S., and Kurimo, M. (2016). TheanoLM–an extensible toolkit for neural network language modeling. Proc. Interspeech 3052–3056 doi: 10.21437/Interspeech.2016-618

Esteva, A., Kuprel, B., Novoa, R. A., Ko, J., Swetter, S. M., Blau, H. M., et al. (2017). Dermatologist-level classification of skin cancer with deep neural networks. Nature 542:115. doi: 10.1038/nature21056

Fischer, A., and Igel, C. (2012). “An introduction to restricted boltzmann machines,” in Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications (Springer), 14–36.

Fodor, J. A., and Pylyshyn, Z. W. (1988). Connectionism and cognitive architecture: a critical analysis. Cognition 28, 3–71.

PubMed Abstract | Google Scholar

Fukushima, K. (1980). Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybernet. 36, 193–202.

Fukushima, K. (2013). Training multi-layered neural network neocognitron. Neural Netw. 40, 18–31. doi: 10.1016/j.neunet.2013.01.001

Gers, F. A., and Schmidhuber, J. (2000). “Recurrent nets that time and count,” in Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium (IEEE), Vol. 3, 189–194.

Gers, F. A., Schmidhuber, J., and Cummins, F. (1999). Learning to forget: continual prediction with LSTM. Neural Comput . 12, 2451–2471. doi: 10.1162/089976600300015015

PubMed Abstract | CrossRef Full Text

Gers, F. A., Schraudolph, N. N., and Schmidhuber, J. (2002). Learning precise timing with lstm recurrent networks. J. Mach. Learn. Res. 3, 115–143. Available online at: http://www.jmlr.org/papers/v3/gers02a.html

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning . MIT Press.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative adversarial nets,” in Advances in Neural Information Processing Systems , 2672–2680.

Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin, V., Mirza, M., Pascanu, R., et al. (2013). Pylearn2: a machine learning research library. arXiv:1308.4214.

Graves, A. (2013). Generating sequences with recurrent neural networks. arXiv [Preprint]. arXiv:1308.0850.

Graves, A., Mohamed, A., and Hinton, G. E. (2013). “Speech recognition with deep recurrent neural networks,” in 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) .

Graves, A., and Schmidhuber, J. (2005). Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 18, 602–610. doi: 10.1016/j.neunet.2005.06.042

Hastie, T. J., Tibshirani, R. J., and Friedman, J. H. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction . Springer Series in Statistics. Springer.

Hayter, H. O. (2012). Probability and Statistics for Engineers and Scientists. 4th Edn. Duxbury Press).

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition , 770–778.

Hebb, D. (1949). The Organization of Behavior . New York, NY: Wiley.

Henaff, M., Bruna, J., and LeCun, Y. (2015). Deep convolutional networks on graph-structured data. arXiv [Preprint] . arXiv:1506.05163.

Henderson, P., Islam, R., Bachman, P., Pineau, J., Precup, D., and Meger, D. (2018). “Deep reinforcement learning that matters,” in Thirty-Second AAAI Conference on Artificial Intelligence .

Hertz, J., Krogh, A., and Palmer, R. (1991). Introduction to the Theory of Neural Compuation . Addison-Wesley.

Hinton, G. E. (2012). Neural Networks: Tricks of the Trade. 2nd Edn. Chapter. A Practical Guide to Training Restricted Boltzmann Machines. Berlin; Heidelberg: Springer Berlin Heidelberg, 599–619.

Hinton, G. E., Osindero, S., and Teh, Y.-W. (2006). A fast learning algorithm for deep belief nets. Neural Comput. 18, 1527–1554. doi: 10.1162/neco.2006.18.7.1527

Hinton, G. E., and Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Science 313, 504–507. doi: 10.1126/science.1127647

Hinton, G. E., and Sejnowski, T. J. (1983). “Optimal perceptual inference,” in Proceedings of the IEEE conference on Computer Vision and Pattern Recognition (Citeseer), 448–453.

Hochreiter, S. (1991). Untersuchungen zu Dynamischen Neuronalen Netzen . Diploma, Technische Universität München 91.

Hochreiter, S. (1998). The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertainty Fuzziness Knowl. Based Syst. 6, 107–116.

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780.

Holzinger, A., Biemann, C., Pattichis, C. S., and Kell, D. B. (2017). What do we need to build explainable AI systems for the medical domain? arXiv [Preprint] . arXiv:1712.09923.

Hopfield, J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558.

Hoppensteadt, F. C., and Izhikevich, E. M. (1999). Oscillatory neurocomputers with dynamic connectivity. Phys. Rev. Lett. 82:2983.

Hornik, K. (1991). Approximation capabilities of multilayer feedforward networks. Neural Netw. 4, 251–257.

Hosny, A., Parmar, C., Coroller, T. P., Grossmann, P., Zeleznik, R., Kumar, A., et al. (2018). Deep learning for lung cancer prognostication: a retrospective multi-cohort radiomics study. PLoS Med. 15:e1002711. doi: 10.1371/journal.pmed.1002711

Hwang, K., and Sung, W. (2015). “Single stream parallelization of generalized LSTM-like rnns on a GPU,” in 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (IEEE), 1047–1051.

Igel, C., and Hüsken, M. (2000). “Improving the RPROP learning algorithm,” in Proceedings of the Second International ICSC Symposium on Neural Computation (NC 2000) , Vol. 2000 (Citeseer), 115–121.

Ivakhnenko, A. G. (1968). The group method of data of handling; a rival of the method of stochastic approximation. Soviet Autom. Control 13, 43–55.

Ivakhnenko, A. G. (1971). Polynomial theory of complex systems. IEEE Trans. Syst. Man Cybernet. SMC-1, 364–378.

Jia, Y., Shelhamer, E., Donahue, J., Karayev, S., Long, J., Girshick, R., et al. (2014). “Caffe: convolutional architecture for fast feature embedding,” in Proceedings of the 22Nd ACM International Conference on Multimedia , MM '14 (New York, NY: ACM), 675–678.

Jiang, M., Liang, Y., Feng, X., Fan, X., Pei, Z., Xue, Y., et al. (2018). Text classification based on deep belief network and softmax regression. Neural Comput. Appl. 29, 61–70. doi: 10.1007/s00521-016-2401-x

Kim, Y. (2014). Convolutional neural networks for sentence classification. arXiv [Preprint]. arXiv:1408.5882. doi: 10.3115/v1/D14-1181

Kou, Q., and Sugomori, Y. (2014). Rcppdl .

Kraemer, G., and Reichstein, M., and D., M. M. (2018). dimRed and coRanking—unifying dimensionality reduction in R. R J. 10, 342–358. doi: 10.32614/RJ-2018-039

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012a). ImageNet Classification with Deep Convolutional Neural Networks . Curran Associates, Inc.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012b). “Imagenet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems , 1097–1105.

Lai, S., Xu, L., Liu, K., and Zhao, J. (2015). “Recurrent convolutional neural networks for text classification,” in Twenty-Ninth AAAI Conference on Artificial Intelligence .

Lawrence, S., Giles, C. L., Tsoi, A. C., and Back, A. D. (1997). Face recognition: a convolutional neural-network approach. IEEE Trans. Neural Netw. 8, 98–113.

Le Cun, Y. (1989). Generalization and Network Design Strategies . Technical Report CRG-TR-89-4, Connectionism in Perspective. University of Toronto Connectionist Research Group, Toronto, ON.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521:436.

LeCun, Y., Boser, B., Denker, J. S., Henderson, D., Howard, R. E., Hubbard, W., et al. (1989). Backpropagation applied to handwritten zip code recognition. Neural Comput. 1, 541–551.

Lee, H., Pham, P., Largman, Y., and Ng, A. Y. (2009). “Unsupervised feature learning for audio classification using convolutional deep belief networks,” in Advances in Neural Information Processing Systems , 1096–1104.

Leung, M. K. K., Xiong, H. Y., Lee, L. J., and Frey, B. J. (2014). Deep learning of the tissue-regulated splicing code. Bioinformatics 30, 121–129. doi: 10.1093/bioinformatics/btu277

Li, R., Wang, S., Zhu, F., and Huang, J. (2018). “Adaptive graph convolutional neural networks,” in Thirty-Second AAAI Conference on Artificial Intelligence .

Lin, M., Chen, Q., and Yan, S. (2013). Network in network. arXiv [Preprint] . arXiv:1312.4400.

Linnainmaa, S. (1976). Taylor expansion of the accumulated rounding error. BIT Numer. Math. 16, 146–160.

Liou, C.-Y., Cheng, W.-C., Liou, J.-W., and Liou, D.-R. (2014). Autoencoder for words. Neurocomputing 139, 84–96. doi: 10.1016/j.neucom.2013.09.055

Lipton, Z. C., Berkowitz, J., and Elkan, C. (2015). A critical review of recurrent neural networks for sequence learning. arXiv [Preprint] . arXiv:1506.00019.

Lu, Z., Pu, H., Wang, F., Hu, Z., and Wang, L. (2017). “The expressive power of neural networks: a view from the width,” in Advances in Neural Information Processing Systems , 6231–6239.

Luong, M.-T., and Manning, C. D. (2015). “Stanford neural machine translation systems for spoken language domains,” in Proceedings of the International Workshop on Spoken Language Translation , 76–79.

Mayr, A., Klambauer, G., Unterthiner, T., and Hochreiter, S. (2016). Deeptox: toxicity prediction using deep learning. Front. Environ. Sci. 3:80. doi: 10.3389/fenvs.2015.00080

Mayr, A., Klambauer, G., Unterthiner, T., Steijaert, M., Wegner, J. K., Ceulemans, H., et al. (2018). Large-scale comparison of machine learning methods for drug target prediction on chembl. Chem. Sci. 9, 5441–5451. doi: 10.1039/C8SC00148K

McCulloch, W., and Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5, 115–133.

Ming, Y., Cao, S., Zhang, R., Li, Z., Chen, Y., Song, Y., et al. (2017). “Understanding hidden memories of recurrent neural networks,” in 2017 IEEE Conference on Visual Analytics Science and Technology (VAST) (IEEE), 13–24.

Minsky, M., and Papert, S. (1969). Perceptrons . MIT Press.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature 518:529. doi: 10.1038/nature14236

Mohamed, A.-R., Dahl, G. E., and Hinton, G. (2011). Acoustic modeling using deep belief networks. IEEE Trans. Audio Speech Lang. Process. 20, 14–22. doi: 10.1109/TASL.2011.2109382

Nair, V., and Hinton, G. E. (2010). “Rectified linear units improve restricted boltzmann machines,” in Proceedings of the 27th International Conference on Machine Learning (ICML-10) , 807–814.

Nielsen, M. A. (2015). Neural Networks and Deep Learning . Determination Press.

Olshausen, B. A., and Field, D. J. (1997). Sparse coding with an overcomplete basis set: a strategy employed by v1? Vision Res. 37, 3311–3325.

Palangi, H., Deng, L., Shen, Y., Gao, J., He, X., Chen, J., et al. (2016). Deep sentence embedding using long short-term memory networks: Analysis and application to information retrieval. IEEE/ACM Trans. Audio Speech Lang. Process. 24, 694–707. doi: 10.1109/TASLP.2016.2520371

Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E., DeVito, Z., et al. (2017). Automatic differentiation in pytorch . Available online at: https://www.semanticscholar.org/paper/Automatic-differentiation-in-PyTorch-Paszke-Gross/b36a5bb1707bb9c70025294b3a310138aae8327a

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830. Available online at: http://www.jmlr.org/papers/v12/pedregosa11a

Pham, T., Tran, T., Phung, D., and Venkatesh, S. (2016). “Deepcare: a deep dynamic memory model for predictive medicine,” in Pacific-Asia Conference on Knowledge Discovery and Data Mining (Springer), 30–41.

Pu, Y., Gan, Z., Henao, R., Yuan, X., Li, C., Stevens, A., et al. (2016). “Variational autoencoder for deep learning of images, labels and captions,” in Advances in Neural Information Processing Systems , 2352–2360.

Quast, B. (2016). RNN: A Recurrent Neural Network in R . Working Papers.

Rawat, W., and Wang, Z. (2017). Deep convolutional neural networks for image classification: a comprehensive review. Neural Comput. 29, 2352–2449. doi: 10.1162/neco_a_00990

Riedmiller, M., and Braun, H. (1993). “A direct adaptive method for faster backpropagation learning: the rprop algorithm,” in IEEE International Conference on Neural Networks (IEEE), 586–591.

Rong, X. (2014). Deep Learning Toolkit in R .

Rosenblatt, F. (1957). The Perceptron, A Perceiving and Recognizing Automaton Project Para . Cornell Aeronautical Laboratory.

Rumelhart, D., Hinton, G., and Williams, R. (1986). Learning representations by back-propagating errors. Nature 323, 533–536.

Sahu, S. K., and Anand, A. (2018). Drug-drug interaction extraction from biomedical texts using long short-term memory network. J. Biomed. Inform. 86, 15–24. doi: 10.1016/j.jbi.2018.08.005

Salakhutdinov, R., and Hinton, G. E. (2009). “Deep boltzmann machines,” in International conference on artificial intelligence and statistics , 448–455.

Sarikaya, R., Hinton, G. E., and Deoras, A. (2014). Application of deep belief networks for natural language understanding. IEEE/ACM Trans. Audio Speech Lang. Process. 22, 778–784. doi: 10.1109/TASLP.2014.2303296

Scherer, D., Müller, A., and Behnke, S. (2010). “Evaluation of pooling operations in convolutional architectures for object recognition,” in International Conference on Artificial Neural Networks (Springer), 92–101.

Schmidhuber, J. (1992). Learning complex, extended sequences using the principle of history compression. Neural Comput. 4, 234–242.

Schmidhuber, J. (2015). Deep learning in neural networks: an overview. Neural Netw. 61, 85–117. doi: 10.1016/j.neunet.2014.09.003

Sejnowski, T. J., and Rosenberg, C. R. (1987). Parallel networks that learn to pronounce english text. Complex Syst. 1, 145–168.

Shen, D., Wu, G., and Suk, H.-I. (2017). Deep learning in medical image analysis. Annu. Rev. Biomed. Eng. 19, 221–248. doi: 10.1146/annurev-bioeng-071516-044442

Shmueli, G. (2010). To explain or to predict? Stat. Sci. 25, 289–310. doi: 10.1214/10-STS330

Simonyan, K., and Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. arXiv [Preprint] . arXiv:1409.1556.

Smolander, J. (2016). Deep learning classification methods for complex disorders (Master's thesis), The School of the thesis, Tampere University of Technology, Tampere, Finland . Available online at: https://dspace.cc.tut.fi/dpub/handle/123456789/23845

Smolander, J., Dehmer, M., and Emmert-Streib, F. (2019a). Comparing deep belief networks with support vector machines for classifying gene expression data from complex disorders. FEBS Open Bio 9, 1232–1248. doi: 10.1002/2211-5463.12652

Smolander, J., Stupnikov, A., Glazko, G., Dehmer, M., and Emmert-Streib, F. (2019b). Comparing biological information contained in mRNA and non-coding RNAs for classification of lung cancer patients. BMC Cancer 19:1176. doi: 10.1186/s12885-019-6338-1

Soman, K., Muralidharan, V., and Chakravarthy, V. S. (2018). An oscillatory neural autoencoder based on frequency modulation and multiplexing. Front. Comput. Neurosci. 12:52. doi: 10.3389/fncom.2018.00052

Stupnikov, A., Tripathi, S., de Matos Simoes, R., McArt, D., Salto-Tellez, M., Glazko, G., et al. (2016). samExploreR: exploring reproducibility and robustness of RNA-seq results based on SAM files. Bioinformatics 32, 3345–3347. doi: 10.1093/bioinformatics/btw475

Sundermeyer, M., Schlüter, R., and Ney, H. (2012). “LSTM neural networks for language modeling,” in Thirteenth Annual Conference of the International Speech Communication Association .

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., et al. (2015). “Going deeper with convolutions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition , 1–9.

Theano Development Team (2016). Theano: a Python framework for fast computation of mathematical expressions. arXiv [Preprint] . arXiv:abs/1605.02688.

Tosic, I., and Frossard, P. (2011). Dictionary learning. IEEE Signal Process. Mag. 28, 27–38.

Venkataraman, S., Yang, Z., Liu, D., Liang, E., Falaki, H., Meng, X., et al. (2016). “Sparkr: Scaling R programs with spark,” in Proceedings of the 2016 International Conference on Management of Data , SIGMOD '16 (New York, NY: ACM), 1099–1104. doi: 10.1145/2882903.2903740

Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y., and Manzagol, P. -A. (2010). Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 11, 3371–3408. Available online at: http://www.jmlr.org/papers/v11/vincent10a.html

Vinyals, O., Toshev, A., Bengio, S., and Erhan, D. (2015). “Show and tell: a neural image caption generator,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition , 3156–3164.

Wan, L., Zeiler, M., Zhang, S., Cun, Y. L., and Fergus, R. (2013). “Regularization of neural networks using dropconnect,” in Proceedings of the 30th International Conference on Machine Learning (ICML-13) , 1058–1066.

Wang, D., and Terman, D. (1995). Locally excitatory globally inhibitory oscillator networks. IEEE Trans. Neural Netw. 6, 283–286.

Wang, D., and Terman, D. (1997). Image segmentation based on oscillatory correlation. Neural Comput. 9, 805–836.

Wang, D. L., and Brown, G. J. (1999). Separation of speech from interfering sounds based on oscillatory correlation. IEEE Trans. Neural Netw. 10, 684–697.

Wang, Y., Huang, M., Zhao, L., et al. (2016). “Attention-based lstm for aspect-level sentiment classification,” in Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing , 606–615.

Webb, A. R., and Copsey, K. D. (2011). Statistical Pattern Recognition. 3rd Edn. Wiley.

Werbos, P. (1974). Beyond regression: new tools for prediction and analysis in the behavioral sciences (Ph.D. thesis), Harvard University, Harvard, MA, United States.

Werbos, P. J. (1981). “Applications of advances in nonlinear sensitivity analysis,” in Proceedings of the 10th IFIP Conference, 31.8–4.9 , New York, 762–770.

Widrow, B., and Hoff, M. E. (1960). Adaptive Switching Circuits . Technical Report, Stanford University, California; Stanford Electronics Labs.

Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Yu, P. S. (2019). A comprehensive survey on graph neural networks. arXiv [Preprint] . arXiv:1901.00596.

Xingjian, S., Chen, Z., Wang, H., Yeung, D.-Y., Wong, W.-K., and Woo, W.-C. (2015). “Convolutional lstm network: a machine learning approach for precipitation nowcasting,” in Advances in Neural Information Processing Systems , 802–810.

Yang, Z., Dehmer, M., Yli-Harja, O., and Emmert-Streib, F. (2020). Combining deep learning with token selection for patient phenotyping from electronic health records. Sci. Rep. 10:1432. doi: 10.1038/s41598-020-58178-1

Yao, L., Mao, C., and Luo, Y. (2019). “Graph convolutional networks for text classification,” in Proceedings of the AAAI Conference on Artificial Intelligence , Vol. 33, 7370–7377.

Yin, W., Kann, K., Yu, M., and Schütze, H. (2017). Comparative study of cnn and rnn for natural language processing. arXiv [Preprint] . arXiv:1702.01923.

Yoshua, B. (2009). Learning deep architectures for AI. Foundat. Trends Mach. Learn. 2, 1–127. doi: 10.1561/2200000006

Young, T., Hazarika, D., Poria, S., and Cambria, E. (2018). Recent trends in deep learning based natural language processing. IEEE Comput. Intell. Mag. 13, 55–75. doi: 10.1109/MCI.2018.2840738

Yu, D., and Li, J. (2017). Recent progresses in deep learning based acoustic models. IEEE/CAA J. Autom. Sinica 4, 396–409. doi: 10.1109/JAS.2017.7510508

Zhang, S., Zhou, J., Hu, H., Gong, H., Chen, L., Cheng, C., et al. (2015). A deep learning framework for modeling structural features of rna-binding protein targets. Nucleic Acids Res. 43:e32. doi: 10.1093/nar/gkv1025

Zhang, X., Zhao, J., and LeCun, Y. (2015). “Character-level convolutional networks for text classification,” in Advances in Neural Information Processing Systems , 649–657.

Zhou, Y. (2019). Sentiment classification with deep neural networks (Master's thesis). Tampere University, Tampere, Finland.

Keywords: deep learning, artificial intelligence, machine learning, neural networks, prediction models, data science

Citation: Emmert-Streib F, Yang Z, Feng H, Tripathi S and Dehmer M (2020) An Introductory Review of Deep Learning for Prediction Models With Big Data. Front. Artif. Intell. 3:4. doi: 10.3389/frai.2020.00004

Received: 24 October 2019; Accepted: 31 January 2020; Published: 28 February 2020.

Reviewed by:

Copyright © 2020 Emmert-Streib, Yang, Feng, Tripathi and Dehmer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Frank Emmert-Streib, v@bio-complexity.com

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Review Article
• Open access
• Published: 22 April 2020

Deep learning in mental health outcome research: a scoping review

• Chang Su 1 ,
• Zhenxing Xu 1 ,
• Jyotishman Pathak 1 &
• Fei Wang 1  

Translational Psychiatry volume  10 , Article number:  116 ( 2020 ) Cite this article

49k Accesses

138 Citations

20 Altmetric

Metrics details

• Psychiatric disorders

Mental illnesses, such as depression, are highly prevalent and have been shown to impact an individual’s physical health. Recently, artificial intelligence (AI) methods have been introduced to assist mental health providers, including psychiatrists and psychologists, for decision-making based on patients’ historical data (e.g., medical records, behavioral data, social media usage, etc.). Deep learning (DL), as one of the most recent generation of AI technologies, has demonstrated superior performance in many real-world applications ranging from computer vision to healthcare. The goal of this study is to review existing research on applications of DL algorithms in mental health outcome research. Specifically, we first briefly overview the state-of-the-art DL techniques. Then we review the literature relevant to DL applications in mental health outcomes. According to the application scenarios, we categorize these relevant articles into four groups: diagnosis and prognosis based on clinical data, analysis of genetics and genomics data for understanding mental health conditions, vocal and visual expression data analysis for disease detection, and estimation of risk of mental illness using social media data. Finally, we discuss challenges in using DL algorithms to improve our understanding of mental health conditions and suggest several promising directions for their applications in improving mental health diagnosis and treatment.

Similar content being viewed by others

Major depressive disorder: hypothesis, mechanism, prevention and treatment

Adults who microdose psychedelics report health related motivations and lower levels of anxiety and depression compared to non-microdosers

The serotonin theory of depression: a systematic umbrella review of the evidence

Introduction.

Mental illness is a type of health condition that changes a person’s mind, emotions, or behavior (or all three), and has been shown to impact an individual’s physical health 1 , 2 . Mental health issues including depression, schizophrenia, attention-deficit hyperactivity disorder (ADHD), and autism spectrum disorder (ASD), etc., are highly prevalent today and it is estimated that around 450 million people worldwide suffer from such problems 1 . In addition to adults, children and adolescents under the age of 18 years also face the risk of mental health disorders. Moreover, mental health illnesses have also been one of the most serious and prevalent public health problems. For example, depression is a leading cause of disability and can lead to an increased risk for suicidal ideation and suicide attempts 2 .

To better understand the mental health conditions and provide better patient care, early detection of mental health problems is an essential step. Different from the diagnosis of other chronic conditions that rely on laboratory tests and measurements, mental illnesses are typically diagnosed based on an individual’s self-report to specific questionnaires designed for the detection of specific patterns of feelings or social interactions 3 . Due to the increasing availability of data pertaining to an individual’s mental health status, artificial intelligence (AI) and machine learning (ML) technologies are being applied to improve our understanding of mental health conditions and have been engaged to assist mental health providers for improved clinical decision-making 4 , 5 , 6 . As one of the latest advances in AI and ML, deep learning (DL), which transforms the data through layers of nonlinear computational processing units, provides a new paradigm to effectively gain knowledge from complex data 7 . In recent years, DL algorithms have demonstrated superior performance in many data-rich application scenarios, including healthcare 8 , 9 , 10 .

In a previous study, Shatte et al. 11 explored the application of ML techniques in mental health. They reviewed literature by grouping them into four main application domains: diagnosis, prognosis, and treatment, public health, as well as research and clinical administration. In another study, Durstewitz et al. 9 explored the emerging area of application of DL techniques in psychiatry. They focused on DL in the studies of brain dynamics and subjects’ behaviors, and presented the insights of embedding the interpretable computational models into statistical context. In contrast, this study aims to provide a scoping review of the existing research applying DL methodologies on the analysis of different types of data related to mental health conditions. The reviewed articles are organized into four main groups according to the type of the data analyzed, including the following: (1) clinical data, (2) genetic and genomics data, (3) vocal and visual expression data, and (4) social media data. Finally, the challenges the current studies faced with, as well as future research directions towards bridging the gap between the application of DL algorithms and patient care, are discussed.

Deep learning overview

ML aims at developing computational algorithms or statistical models that can automatically infer hidden patterns from data 12 , 13 . Recent years have witnessed an increasing number of ML models being developed to analyze healthcare data 4 . However, conventional ML approaches require a significant amount of feature engineering for optimal performance—a step that is necessary for most application scenarios to obtain good performance, which is usually resource- and time-consuming.

As the newest wave of ML and AI technologies, DL approaches aim at the development of an end-to-end mechanism that maps the input raw features directly into the outputs through a multi-layer network structure that is able to capture the hidden patterns within the data. In this section, we will review several popular DL model architectures, including deep feedforward neural network (DFNN), recurrent neural network (RNN) 14 , convolutional neural network (CNN) 15 , and autoencoder 16 . Figure 1 provides an overview of these architectures.

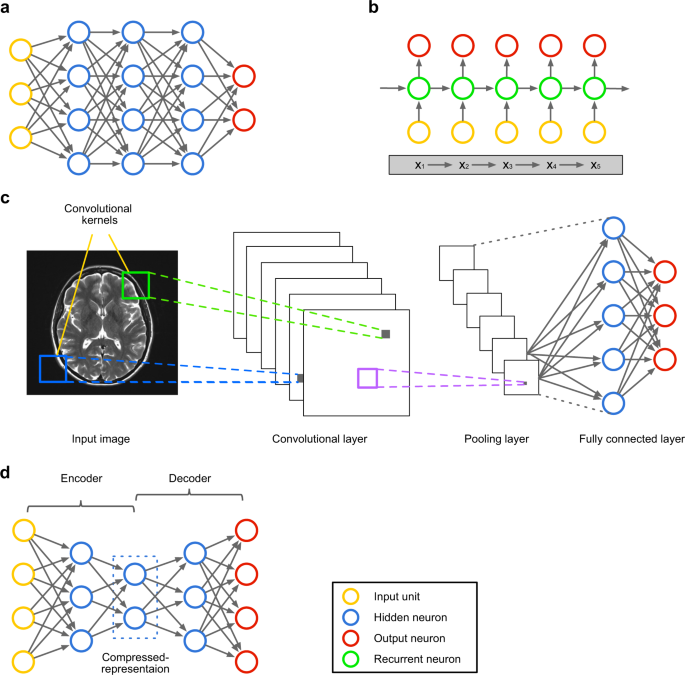
a Deep feedforward neural network (DFNN). It is the basic design of DL models. Commonly, a DFNN contains multiple hidden layers. b A recurrent neural network (RNN) is presented to process sequence data. To encode history information, each recurrent neuron receives the input element and the state vector of the predecessor neuron, and yields a hidden state fed to the successor neuron. For example, not only the individual information but also the dependence of the elements of the sequence x 1  → x 2  → x 3  → x 4  → x 5 is encoded by the RNN architecture. c Convolutional neural network (CNN). Between input layer (e.g., input neuroimage) and output layer, a CNN commonly contains three types of layers: the convolutional layer that is to generate feature maps by sliding convolutional kernels in the previous layer; the pooling layer is used to reduce dimensionality of previous convolutional layer; and the fully connected layer is to make prediction. For the illustrative purpose, this example only has one layer of each type; yet, a real-world CNN would have multiple convolutional and pooling layers (usually in an interpolated manner) and one fully connected layer. d Autoencoder consists of two components: the encoder, which learns to compress the input data into a latent representation layer by layer, whereas the decoder, inverse to the encoder, learns to reconstruct the data at the output layer. The learned compressed representations can be fed to the downstream predictive model.

Deep feedforward neural network

Artificial neural network (ANN) is proposed with the intention of mimicking how human brain works, where the basic element is an artificial neuron depicted in Fig. 2a . Mathematically, an artificial neuron is a nonlinear transformation unit, which takes the weighted summation of all inputs and feeds the result to an activation function, such as sigmoid, rectifier (i.e., rectified linear unit [ReLU]), or hyperbolic tangent (Fig. 2b ). An ANN is composed of multiple artificial neurons with different connection architectures. The simplest ANN architecture is the feedforward neural network (FNN), which stacks the neurons layer by layer in a feedforward manner (Fig. 1a ), where the neurons across adjacent layers are fully connected to each other. The first layer of the FNN is the input layer that each unit receives one dimension of the data vector. The last layer is the output layer that outputs the probabilities that a subject belonging to different classes (in classification). The layers between the input and output layers are the hidden layers. A DFNN usually contains multiple hidden layers. As shown in Fig. 2a , there is a weight parameter associated with each edge in the DFNN, which needs to be optimized by minimizing some training loss measured on a specific training dataset (usually through backpropagation 17 ). After the optimal set of parameters are learned, the DFNN can be used to predict the target value (e.g., class) of any testing data vectors. Therefore, a DFNN can be viewed as an end-to-end process that transforms a specific raw data vector to its target layer by layer. Compared with the traditional ML models, DFNN has shown superior performance in many data mining tasks and have been introduced to the analysis of clinical data and genetic data to predict mental health conditions. We will discuss the applications of these methods further in the Results section.

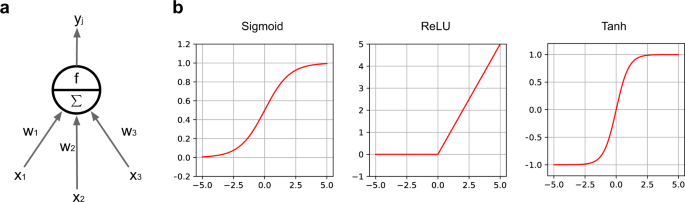
a An illustration of basic unit of neural networks, i.e., artificial neuron. Each input x i is associated with a weight w i . The weighted sum of all inputs Σ w i x i is fed to a nonlinear activation function f to generate the output y j of the j -th neuron, i.e., y j  =  f (Σ w i x i ). b Illustrations of the widely used nonlinear activation function.

Recurrent neural network

RNNs were designed to analyze sequential data such as natural language, speech, and video. Given an input sequence, the RNN processes one element of the sequence at a time by feeding to a recurrent neuron. To encode the historical information along the sequence, each recurrent neuron receives the input element at the corresponding time point and the output of the neuron at previous time stamp, and the output will also be provided to the neuron at next time stamp (this is also where the term “recurrent” comes from). An example RNN architecture is shown in Fig. 1b where the input is a sequence of words (a sentence). The recurrence link (i.e., the edge linking different neurons) enables RNN to capture the latent semantic dependencies among words and the syntax of the sentence. In recent years, different variants of RNN, such as long short-term memory (LSTM) 18 and gated recurrent unit 19 have been proposed, and the main difference among these models is how the input is mapped to the output for the recurrent neuron. RNN models have demonstrated state-of-the-art performance in various applications, especially natural language processing (NLP; e.g., machine translation and text-based classification); hence, they hold great premise in processing clinical notes and social media posts to detect mental health conditions as discussed below.

Convolutional neural network

CNN is a specific type of deep neural network originally designed for image analysis 15 , where each pixel corresponds to a specific input dimension describing the image. Similar to a DFNN, CNN also maps these input image pixels to the corresponding target (e.g., image class) through layers of nonlinear transformations. Different from DFNN, where only fully connected layers are considered, there are typically three types of layers in a CNN: a convolution–activation layer, a pooling layer, and a fully connected layer (Fig. 1c ). The convolution–activation layer first convolves the entire feature map obtained from previous layer with small two-dimensional convolution filters. The results from each convolution filter are activated through a nonlinear activation function in the same way as a DFNN. A pooling layer reduces the size of the feature map through sub-sampling. The fully connected layer is analogous to the hidden layer in a DFNN, where each neuron is connected to all neurons of the previous layer. The convolution–activation layer extracts locally invariant patterns from the feature maps. The pooling layer effectively reduces the feature dimensionality to avoid model overfitting. The fully connected layer explores the global feature interactions as in DFNNs. Different combinations of these three types of layers constitute different CNN architectures. Because of the various characteristics of images such as local self-similarity, compositionality, and translational and deformation invariance, CNN has demonstrated state-of-the-art performance in many computer vision tasks 7 . Hence, the CNN models are promising in processing clinical images and expression data (e.g., facial expression images) to detect mental health conditions. We will discuss the application of these methods in the Results section.

Autoencoder

Autoencoder is a special variant of the DFNN aimed at learning new (usually more compact) data representations that can optimally reconstruct the original data vectors 16 , 20 . An autoencoder typically consists of two components (Fig. 1d ) as follows: (1) the encoder, which learns new representations (usually with reduced dimensionality) from the input data through a multi-layer FNN; and (2) the decoder, which is exactly the reverse of the encoder, reconstructs the data in their original space from the representations derived from the encoder. The parameters in the autoencoder are learned through minimizing the reconstruction loss. Autoencoder has demonstrated the capacity of extracting meaningful features from raw data without any supervision information. In the studies of mental health outcomes, the use of autoencoder has resulted in desirable improvement in analyzing clinical and expression image data, which will be detailed in the Results section.

The processing and reporting of the results of this review were guided by the Preferred Reporting Items for Systematic Reviews and Meta-Analyses guidelines 21 . To thoroughly review the literature, a two-step method was used to retrieve all the studies on relevant topics. First, we conducted a search of the computerized bibliographic databases including PubMed and Web of Science. The search strategy is detailed in Supplementary Appendix 1 . The literature search comprised articles published until April 2019. Next, a snowball technique was applied to identify additional studies. Furthermore, we manually searched other resources, including Google Scholar, and Institute of Electrical and Electronics Engineers (IEEE Xplore), to find additional relevant articles.

Figure 3 presents the study selection process. All articles were evaluated carefully and studies were excluded if: (1) the main outcome is not a mental health condition; (2) the model involved is not a DL algorithm; (3) full-text of the article is not accessible; and (4) the article is written not in English.

In total, 57 studies, in terms of clinical data analysis, genetic data analysis, vocal and visual expression data analysis, and social media data analysis, which met our eligibility criteria, were included in this review.

A total of 57 articles met our eligibility criteria. Most of the reviewed articles were published between 2014 and 2019. To clearly summarize these articles, we grouped them into four categories according to the types of data analyzed, including (1) clinical data, (2) genetic and genomics data, (3) vocal and visual expression data, and (4) social media data. Table 1 summarizes the characteristics of these selected studies.

Clinical data

Neuroimages.

Previous studies have shown that neuroimages can record evidence of neuropsychiatric disorders 22 , 23 . Two common types of neuroimage data analyzed in mental health studies are functional magnetic resonance imaging (fMRI) and structural MRI (sMRI) data. In fMRI data, the brain activity is measured by identification of the changes associated with blood flow, based on the fact that cerebral blood flow and neuronal activation are coupled 24 . In sMRI data, the neurological aspect of a brain is described based on the structural textures, which show some information in terms of the spatial arrangements of voxel intensities in 3D. Recently, DL technologies have been demonstrated in analyzing both fMRI and sMRI data.

One application of DL in fMRI and sMRI data is the identification of ADHD 25 , 26 , 27 , 28 , 29 , 30 , 31 . To learn meaningful information from the neuroimages, CNN and deep belief network (DBN) models were used. In particular, the CNN models were mainly used to identify local spatial patterns and DBN models were to obtain a deep hierarchical representation of the neuroimages. Different patterns were discovered between ADHDs and controls in the prefrontal cortex and cingulated cortex. Also, several studies analyzed sMRIs to investigate schizophrenia 32 , 33 , 34 , 35 , 36 , where DFNN, DBN, and autoencoder were utilized. These studies reported abnormal patterns of cortical regions and cortical–striatal–cerebellar circuit in the brain of schizophrenia patients, especially in the frontal, temporal, parietal, and insular cortices, and in some subcortical regions, including the corpus callosum, putamen, and cerebellum. Moreover, the use of DL in neuroimages also targeted at addressing other mental health disorders. Geng et al. 37 proposed to use CNN and autoencoder to acquire meaningful features from the original time series of fMRI data for predicting depression. Two studies 31 , 38 integrated the fMRI and sMRI data modalities to develop predictive models for ASDs. Significant relationships between fMRI and sMRI data were observed with regard to ASD prediction.

Challenges and opportunities

The aforementioned studies have demonstrated that the use of DL techniques in analyzing neuroimages can provide evidence in terms of mental health problems, which can be translated into clinical practice and facilitate the diagnosis of mental health illness. However, multiple challenges need to be addressed to achieve this objective. First, DL architectures generally require large data samples to train the models, which may pose a difficulty in neuroimaging analysis because of the lack of such data 39 . Second, typically the imaging data lie in a high-dimensional space, e.g., even a 64 × 64 2D neuroimage can result in 4096 features. This leads to the risk of overfitting by the DL models. To address this, most existing studies reported to utilize MRI data preprocessing tools such as Statistical Parametric Mapping ( https://www.fil.ion.ucl.ac.uk/spm/ ), Data Processing Assistant for Resting-State fMRI 40 , and fMRI Preprocessing Pipeline 41 to extract useful features before feeding to the DL models. Even though an intuitive attribute of DL is the capacity to learn meaningful features from raw data, feature engineering tools are needed especially in the case of small sample size and high-dimensionality, e.g., the neuroimage analysis. The use of such tools mitigates the overfitting risk of DL models. As reported in some selected studies 28 , 31 , 35 , 37 , the DL models can benefit from feature engineering techniques and have been shown to outperform the traditional ML models in the prediction of multiple conditions such as depression, schizophrenia, and ADHD. However, such tools extract features relying on prior knowledge; hence may omit some information that is meaningful for mental outcome research but unknown yet. An alternative way is to use CNN to automatically extract information from the raw data. As reported in the previous study 10 , CNNs perform well in processing raw neuroimage data. Among the studies reviewed in this study, three 29 , 30 , 37 reported to involve CNN layers and achieved desirable performances.

Electroencephalogram data

As a low-cost, small-size, and high temporal resolution signal containing up to several hundred channels, analysis of electroencephalogram (EEG) data has gained significant attention to study brain disorders 42 . As the EEG signal is one kind of streaming data that presents a high density and continuous characteristics, it challenges traditional feature engineering-based methods to obtain sufficient information from the raw EEG data to make accurate predictions. To address this, recently the DL models have been employed to analyze raw EEG signal data.

Four articles reviewed proposed to use DL in understanding mental health conditions based on the analysis of EEG signals. Acharya et al. 43 used CNN to extract features from the input EEG signals. They found that the EEG signals from the right hemisphere of the human brain are more distinctive in terms of the detection of depression than those from the left hemisphere. The findings provided shreds of evidence that depression is associated with a hyperactive right hemisphere. Mohan et al. 44 modeled the raw EEG signals by DFNN to obtain information about the human brain waves. They found that the signals collected from the central (C3 and C4) regions are marginally higher compared with other brain regions, which can be used to distinguish the depressed and normal subjects from the brain wave signals. Zhang et al. 45 proposed a concatenated structure of deep recurrent and 3D CNN to obtain EEG features across different tasks. They reported that the DL model can capture the spectral changes of EEG hemispheric asymmetry to distinguish different mental workload effectively. Li et al. 46 presented a computer-aided detection system by extracting multiple types of information (e.g., spectral, spatial, and temporal information) to recognize mild depression based on CNN architecture. The authors found that both spectral and temporal information of EEG are crucial for prediction of depression.

EEG data are usually classified as streaming data that are continuous and are of high density. Despite the initial success in applying DL algorithms to analyze EEG data for studying multiple mental health conditions, there exist several challenges. One major challenge is that raw EEG data gathered from sensors have a certain degree of erroneous, noisy, and redundant information caused by discharged batteries, failures in sensor readings, and intermittent communication loss in wireless sensor networks 47 . This may challenge the model in extracting meaningful information from noise. Multiple preprocessing steps (e.g., data denoising, data interpolation, data transformation, and data segmentation) are necessary for dealing with the raw EEG signal before feeding to the DL models. Besides, due to the dense characteristics in the raw EEG data, analysis of the streaming data is computationally more expensive, which poses a challenge for the model architecture selection. A proper model should be designed relatively with less training parameters. This is one reason why the reviewed studies are mainly based on the CNN architecture.

Electronic health records

Electronic health records (EHRs) are systematic collections of longitudinal, patient-centered records. Patients’ EHRs consist of both structured and unstructured data: the structured data include information about a patient’s diagnosis, medications, and laboratory test results, and the unstructured data include information in clinical notes. Recently, DL models have been applied to analyze EHR data to study mental health disorders 48 .

The first and foremost issue for analyzing the structured EHR data is how to appropriately handle the longitudinal records. Traditional ML models address this by collapsing patients’ records within a certain time window into vectors, which comprised the summary of statistics of the features in different dimensions 49 . For instance, to estimate the probability of suicide deaths, Choi et al. 50 leveraged a DFNN to model the baseline characteristics. One major limitation of these studies is the omittance of temporality among the clinical events within EHRs. To overcome this issue, RNNs are more commonly used for EHR data analysis as an RNN intuitively handles time-series data. DeepCare 51 , a long short-term memory network (LSTM)-based DL model, encodes patient’s long-term health state trajectories to predict the future outcomes of depressive episodes. As the LSTM architecture appropriately captures disease progression by modeling the illness history and the medical interventions, DeepCare achieved over 15% improvement in prediction, compared with the conventional ML methods. In addition, Lin et al. 52 designed two DFNN models for the prediction of antidepressant treatment response and remission. The authors reported that the proposed DFNN can achieve an area under the receiver operating characteristic curve (AUC) of 0.823 in predicting antidepressant response.

Analyzing the unstructured clinical notes in EHRs refers to the long-standing topic of NLP. To extract meaningful knowledge from the text, conventional NLP approaches mostly define rules or regular expressions before the analysis. However, it is challenging to enumerate all possible rules or regular expressions. Due to the recent advance of DL in NLP tasks, DL models have been developed to mine clinical text data from EHRs to study mental health conditions. Geraci et al. 53 utilized term frequency-inverse document frequency to represent the clinical documents by words and developed a DFNN model to identify individuals with depression. One major limitation of such an approach is that the semantics and syntax of sentences are lost. In this context, CNN 54 and RNN 55 have shown superiority in modeling syntax for text-based prediction. In particular, CNN has been used to mine the neuropsychiatric notes for predicting psychiatric symptom severity 56 , 57 . Tran and Kavuluru 58 used an RNN to analyze the history of present illness in neuropsychiatric notes for predicting mental health conditions. The model engaged an attention mechanism 55 , which can specify the importance of the words in prediction, making the model more interpretable than their previous CNN model 56 .

Although DL has achieved promising results in EHR analysis, several challenges remain unsolved. On one hand, different from diagnosing physical health condition such as diabetes, the diagnosis of mental health conditions lacks direct quantitative tests, such as a blood chemistry test, a buccal swab, or urinalysis. Instead, the clinicians evaluate signs and symptoms through patient interviews and questionnaires during which they gather information based on patient’s self-report. Collection and deriving inferences from such data deeply relies on the experience and subjectivity of the clinician. This may account for signals buried in noise and affect the robustness of the DL model. To address this challenge, a potential way is to comprehensively integrate multimodal clinical information, including structured and unstructured EHR information, as well as neuroimaging and EEG data. Another way is to incorporate existing medical knowledge, which can guide model being trained in the right direction. For instance, the biomedical knowledge bases contain massive verified interactions between biomedical entities, e.g., diseases, genes, and drugs 59 . Incorporating such information brings in meaningful medical constraints and may help to reduce the effects of noise on model training process. On the other hand, implementing a DL model trained from one EHR system into another system is challenging, because EHR data collection and representation is rarely standardized across hospitals and clinics. To address this issue, national/international collaborative efforts such as Observational Health Data Sciences and Informatics ( https://ohdsi.org ) have developed common data models, such as OMOP, to standardize EHR data representation for conducting observational data analysis 60 .

Genetic data

Multiple studies have found that mental disorders, e.g., depression, can be associated with genetic factors 61 , 62 . Conventional statistical studies in genetics and genomics, such as genome-wide association studies, have identified many common and rare genetic variants, such as single-nucleotide polymorphisms (SNPs), associated with mental health disorders 63 , 64 . Yet, the effect of the genetic factors is small and many more have not been discovered. With the recent developments in next-generation sequencing techniques, a massive volume of high-throughput genome or exome sequencing data are being generated, enabling researchers to study patients with mental health disorders by examining all types of genetic variations across an individual’s genome. In recent years, DL 65 , 66 has been applied to identify genetic risk factors associated with mental illness, by borrowing the capacity of DL in identifying highly complex patterns in large datasets. Khan and Wang 67 integrated genetic annotations, known brain expression quantitative trait locus, and enhancer/promoter peaks to generate feature vectors of variants, and developed a DFNN, named ncDeepBrain, to prioritized non-coding variants associated with mental disorders. To further prioritize susceptibility genes, they designed another deep model, iMEGES 68 , which integrates the ncDeepBrain score, general gene scores, and disease-specific scores for estimating gene risk. Wang et al. 69 developed a novel deep architecture that combines deep Boltzmann machine architecture 70 with conditional and lateral connections derived from the gene regulatory network. The model provided insights about intermediate phenotypes and their connections to high-level phenotypes (disease traits). Laksshman et al. 71 used exome sequencing data to predict bipolar disorder outcomes of patients. They developed a CNN and used the convolution mechanism to capture correlations of the neighboring loci within the chromosome.

Although the use of genetic data in DL in studying mental health conditions shows promise, multiple challenges need to be addressed. For DL-based risk c/gene prioritization efforts, one major challenge is the limitation of labeled data. On one hand, the positive samples are limited, as known risk SNPs or genes associated with mental health conditions are limited. For example, there are about 108 risk loci that were genome-wide significant in ASD. On the other hand, the negative samples (i.e., SNPs, variants, or genes) may not be the “true” negative, as it is unclear whether they are associated with the mental illness yet. Moreover, it is also challenging to develop DL models for analyzing patient’s sequencing data for mental illness prediction, as the sequencing data are extremely high-dimensional (over five million SNPs in the human genome). More prior domain knowledge is needed to guide the DL model extracting patterns from the high-dimensional genomic space.

Vocal and visual expression data

The use of vocal (voice or speech) and visual (video or image of facial or body behaviors) expression data has gained the attention of many studies in mental health disorders. Modeling the evolution of people’s emotional states from these modalities has been used to identify mental health status. In essence, the voice data are continuous and dense signals, whereas the video data are sequences of frames, i.e., images. Conventional ML models for analyzing such types of data suffer from the sophisticated feature extraction process. Due to the recent success of applying DL in computer vision and sequence data modeling, such models have been introduced to analyze the vocal and/or visual expression data. In this work, most articles reviewed are to predict mental health disorders based on two public datasets: (i) the Chi-Mei corpus, collected by using six emotional videos to elicit facial expressions and speech responses of the subjects of bipolar disorder, unipolar depression, and healthy controls; 72 and (ii) the International Audio/Visual Emotion Recognition Challenges (AVEC) depression dataset 73 , 74 , 75 , collected within human–computer interaction scenario. The proposed models include CNNs, RNNs, autoencoders, as well as hybrid models based on the above ones. In particular, CNNs were leveraged to encode the temporal and spectral features from the voice signals 76 , 77 , 78 , 79 , 80 and static facial or physical expression features from the video frames 79 , 81 , 82 , 83 , 84 . Autoencoders were used to learn low-dimensional representations for people’s vocal 85 , 86 and visual expression 87 , 88 , and RNNs were engaged to characterize the temporal evolution of emotion based on the CNN-learned features and/or other handcraft features 76 , 81 , 84 , 85 , 86 , 87 , 88 , 89 , 90 . Few studies focused on analyzing static images using a CNN architecture to predict mental health status. Prasetio et al. 91 identified the stress types (e.g., neutral, low stress, and high stress) from facial frontal images. Their proposed CNN model outperforms the conventional ML models by 7% in terms of prediction accuracy. Jaiswal et al. 92 investigated the relationship between facial expression/gestures and neurodevelopmental conditions. They reported accuracy over 0.93 in the diagnostic prediction of ADHD and ASD by using the CNN architecture. In addition, thermal images that track persons’ breathing patterns were also fed to a deep model to estimate psychological stress level (mental overload) 93 .

From the above summary, we can observe that analyzing vocal and visual expression data can capture the pattern of subjects’ emotion evolution to predict mental health conditions. Despite the promising initial results, there remain challenges for developing DL models in this field. One major challenge is to link vocal and visual expression data with the clinical data of patients, given the difficulties involved in collecting such expression data during clinical practice. Current studies analyzed vocal and visual expression over individual datasets. Without clinical guidance, the developed prediction models have limited clinical meanings. Linking patients’ expression information with clinical variables may help to improve both the interpretability and robustness of the model. For example, Gupta et al. 94 designed a DFNN for affective prediction from audio and video modalities. The model incorporated depression severity as the parameter, linking the effects of depression on subjects’ affective expressions. Another challenge is the limitation of the samples. For example, the Chi-Mei dataset contains vocal–visual data from only 45 individuals (15 with bipolar disorder, 15 with unipolar disorder, and 15 healthy controls). Also, there is a lack of “emotion labels” for people’s vocal and visual expression. Apart from improving the datasets, an alternative way to solve this challenge is to use transfer learning, which transfers knowledge gained with one dataset (usually more general) to the target dataset. For example, some studies trained autoencoder in public emotion database such as eNTERFACE 95 to generate emotion profiles (EPs). Other studies 83 , 84 pre-trained CNN over general facial expression datasets 96 , 97 for extracting face appearance features.

Social media data

With the widespread proliferation of social media platforms, such as Twitter and Reddit, individuals are increasingly and publicly sharing information about their mood, behavior, and any ailments one might be suffering. Such social media data have been used to identify users’ mental health state (e.g., psychological stress and suicidal ideation) 6 .

In this study, the articles that used DL to analyze social media data mainly focused on stress detection 98 , 99 , 100 , 101 , depression identification 102 , 103 , 104 , 105 , 106 , and estimation of suicide risk 103 , 105 , 107 , 108 , 109 . In general, the core concept across these work is to mine the textual, and where applicable graphical, content of users’ social media posts to discover cues for mental health disorders. In this context, the RNN and CNN were largely used by the researchers. Especially, RNN usually introduces an attention mechanism to specify the importance of the input elements in the classification process 55 . This provides some interpretability for the predictive results. For example, Ive et al. 103 proposed a hierarchical RNN architecture with an attention mechanism to predict the classes of the posts (including depression, autism, suicidewatch, anxiety, etc.). The authors observed that, benefitting from the attention mechanism, the model can predict risk text efficiently and extract text elements crucial for making decisions. Coppersmith et al. 107 used LSTM to discover quantifiable signals about suicide attempts based on social media posts. The proposed model can capture contextual information between words and obtain nuances of language related to suicide.

Apart from text, users also post images on social media. The properties of the images (e.g., color theme, saturation, and brightness) provide some cues reflecting users’ mental health status. In addition, millions of interactions and relationships among users can reflect the social environment of individuals that is also a kind of risk factors for mental illness. An increasing number of studies attempted to combine these two types of information with text content for predictive modeling. For example, Lin et al. 99 leveraged the autoencoder to extract low-level and middle-level representations from texts, images, and comments based on psychological and art theories. They further extended their work with a hybrid model based on CNN by integrating post content and social interactions 101 . The results provided an implication that the social structure of the stressed users’ friends tended to be less connected than that of the users without stress.

The aforementioned studies have demonstrated that using social media data has the potential to detect users with mental health problems. However, there are multiple challenges towards the analysis of social media data. First, given that social media data are typically de-identified, there is no straightforward way to confirm the “true positives” and “true negatives” for a given mental health condition. Enabling the linkage of user’s social media data with their EHR data—with appropriate consent and privacy protection—is challenging to scale, but has been done in a few settings 110 . In addition, most of the previous studies mainly analyzed textual and image data from social media platforms, and did not consider analyzing the social network of users. In one study, Rosenquist et al. 111 reported that the symptoms of depression are highly correlated inside the circle of friends, indicating that social network analysis is likely to be a potential way to study the prevalence of mental health problems. However, comprehensively modeling text information and network structure remains challenging. In this context, graph convolutional networks 112 have been developed to address networked data mining. Moreover, although it is possible to discover online users with mental illness by social media analysis, translation of this innovation into practical applications and offer aid to users, such as providing real-time interventions, are largely needed 113 .

Discussion: findings, open issues, and future directions

Principle findings.

The purpose of this study is to investigate the current state of applications of DL techniques in studying mental health outcomes. Out of 2261 articles identified based on our search terms, 57 studies met our inclusion criteria and were reviewed. Some studies that involved DL models but did not highlight the DL algorithms’ features on analysis were excluded. From the above results, we observed that there are a growing number of studies using DL models for studying mental health outcomes. Particularly, multiple studies have developed disease risk prediction models using both clinical and non-clinical data, and have achieved promising initial results.

DL models “think to learn” like a human brain relying on their multiple layers of interconnected computing neurons. Therefore, to train a deep neural network, there are multiple parameters (i.e., weights associated links between neurons within the network) being required to learn. This is one reason why DL has achieved great success in the fields where a massive volume of data can be easily collected, such as computer vision and text mining. Yet, in the health domain, the availability of large-scale data is very limited. For most selected studies in this review, the sample sizes are under a scale of 10 4 . Data availability is even more scarce in the fields of neuroimaging, EEG, and gene expression data, as such data reside in a very high-dimensional space. This then leads to the problem of “curse of dimensionality” 114 , which challenges the optimization of the model parameters.

One potential way to address this challenge is to reduce the dimensionality of the data by feature engineering before feeding information to the DL models. On one hand, feature extraction approaches can be used to obtain different types of features from the raw data. For example, several studies reported in this review have attempted to use preprocessing tools to extract features from neuroimaging data. On the other hand, feature selection that is commonly used in conventional ML models is also an option to reduce data dimensionality. However, the feature selection approaches are not often used in the DL application scenario, as one of the intuitive attributes of DL is the capacity to learn meaningful features from “all” available data. The alternative way to address the issue of data bias is to use transfer learning where the objective is to improve learning a new task through the transfer of knowledge from a related task that has already been learned 115 . The basic idea is that data representations learned in the earlier layers are more general, whereas those learned in the latter layers are more specific to the prediction task 116 . In particular, one can first pre-train a deep neural network in a large-scale “source” dataset, then stack fully connected layers on the top of the network and fine-tune it in the small “target” dataset in a standard backpropagation manner. Usually, samples in the “source” dataset are more general (e.g., general image data), whereas those in the “target” dataset are specific to the task (e.g., medical image data). A popular example of the success of transfer learning in the health domain is the dermatologist-level classification of skin cancer 117 . The authors introduced Google’s Inception v3 CNN architecture pre-trained over 1.28 million general images and fine-tuned in the clinical image dataset. The model achieved very high-performance results of skin cancer classification in epidermal (AUC = 0.96), melanocytic (AUC = 0.96), and melanocytic–dermoscopic images (AUC = 0.94). In facial expression-based depression prediction, Zhu et al. 83 pre-trained CNN on the public face recognition dataset to model the static facial appearance, which overcomes the issue that there is no facial expression label information. Chao et al. 84 also pre-trained CNN to encode facial expression information. The transfer scheme of both of the two studies has been demonstrated to be able to improve the prediction performance.

Diagnosis and prediction issues

Unlike the diagnosis of physical conditions that can be based on lab tests, diagnoses of the mental illness typically rely on mental health professionals’ judgment and patient self-report data. As a result, such a diagnostic system may not accurately capture the psychological deficits and symptom progression to provide appropriate therapeutic interventions 118 , 119 . This issue accordingly accounts for the limitation of the prediction models to assist clinicians to make decisions. Except for several studies using the unsupervised autoencoder for learning low-dimensional representations, most studies reviewed in this study reported using supervised DL models, which need the training set containing “true” (i.e., expert provided) labels to optimize the model parameters before the model being used to predict labels of new subjects. Inevitably, the quality of the expert-provided diagnostic labels used for training sets the upper-bound for the prediction performance of the model.

One intuitive route to address this issue is to use an unsupervised learning scheme that, instead of learning to predict clinical outcomes, aims at learning compacted yet informative representations of the raw data. A typical example is the autoencoder (as shown in Fig. 1d ), which encodes the raw data into a low-dimensional space, from which the raw data can be reconstructed. Some studies reviewed have proposed to leverage autoencoder to improve our understanding of mental health outcomes. A constraint of the autoencoder is that the input data should be preprocessed to vectors, which may lead to information loss for image and sequence data. To address this, recently convolutional-autoencoder 120 and LSTM-autoencoder 121 have been developed, which integrate the convolution layers and recurrent layers with the autoencoder architecture and enable us to learn informative low-dimensional representations from the raw image data and sequence data, respectively. For instance, Baytas et al. 122 developed a variation of LSTM-autoencoder on patient EHRs and grouped Parkinson’s disease patients into meaningful subtypes. Another potential way is to predict other clinical outcomes instead of the diagnostic labels. For example, several selected studies proposed to predict symptom severity scores 56 , 57 , 77 , 82 , 84 , 87 , 89 . In addition, Du et al. 108 attempted to identify suicide-related psychiatric stressors from users’ posts on Twitter, which plays an important role in the early prevention of suicidal behaviors. Furthermore, training model to predict future outcomes such as treatment response, emotion assessments, and relapse time is also a promising future direction.

Multimodal modeling

The field of mental health is heterogeneous. On one hand, mental illness refers to a variety of disorders that affect people’s emotions and behaviors. On the other hand, though the exact causes of most mental illnesses are unknown to date, it is becoming increasingly clear that the risk factors for these diseases are multifactorial as multiple genetic, environmental, and social factors interact to influence an individual’s mental health 123 , 124 . As a result of domain heterogeneity, researchers have the chance to study the mental health problems from different perspectives, from molecular, genomic, clinical, medical imaging, physiological signal to facial, and body expressive and online behavioral. Integrative modeling of such multimodal data means comprehensively considering different aspects of the disease, thus likely obtaining deep insight into mental health. In this context, DL models have been developed for multimodal modeling. As shown in Fig. 4 , the hierarchical structure of DL makes it easily compatible with multimodal integration. In particular, one can model each modality with a specific network and combine them by the final fully connected layers, such that parameters can be jointly learned by a typical backpropagation manner. In this review, we found an increasing number of studies have attempted to use multimodal modeling. For example, Zou et al. 28 developed a multimodal model composed of two CNNs for modeling fMRI and sMRI modalities, respectively. The model achieved 69.15% accuracy in predicting ADHD, which outperformed the unimodal models (66.04% for fMRI modal-based and 65.86% for sMRI modal-based). Yang et al. 79 proposed a multimodal model to combine vocal and visual expression for depression cognition. The model results in 39% lower prediction error than the unimodal models.

One can model each modality with a specific network and combine them using the final fully-connected layers. In this way, parameters of the entire neural network can be jointly learned in a typical backpropagation manner.

Model interpretability

Due to the end-to-end design, the DL models usually appear to be “black boxes”: they take raw data (e.g., MRI images, free-text of clinical notes, and EEG signals) as input, and yield output to reach a conclusion (e.g., the risk of a mental health disorder) without clear explanations of their inner working. Although this might not be an issue in other application domains such as identifying animals from images, in health not only the model’s prediction performance but also the clues for making the decision are important. For example in the neuroimage-based depression identification, despite estimation of the probability that a patient suffers from mental health deficits, the clinicians would focus more on recognizing abnormal regions or patterns of the brain associated with the disease. This is really important for convincing the clinical experts about the actions recommended from the predictive model, as well as for guiding appropriate interventions. In addition, as discussed above, the introduction of multimodal modeling leads to an increased challenge in making the models more interpretable. Attempts have been made to open the “black box” of DL 59 , 125 , 126 , 127 . Currently, there are two general directions for interpretable modeling: one is to involve the systematic modification of the input and the measure of any resulting changes in the output, as well as in the activation of the artificial neurons in the hidden layers. Such a strategy is usually used in CNN in identifying specific regions of an image being captured by a convolutional layer 128 . Another way is to derive tools to determine the contribution of one or more features of the input data to the output. In this case, the widely used tools include Shapley Additive Explanation 129 , LIME 127 , DeepLIFT 130 , etc., which are able to assign each feature an importance score for the specific prediction task.

Connection to therapeutic interventions

According to the studies reviewed, it is now possible to detect patients with mental illness based on different types of data. Compared with the traditional ML techniques, most of the reviewed DL models reported higher prediction accuracy. The findings suggested that the DL models are likely to assist clinicians in improved diagnosis of mental health conditions. However, to associate diagnosis of a condition with evidence-based interventions and treatment, including identification of appropriate medication 131 , prediction of treatment response 52 , and estimation of relapse risk 132 still remains a challenge. Among the reviewed studies, only one 52 proposed to target at addressing these issues. Thus, further efforts are needed to link the DL techniques with the therapeutic intervention of mental illness.

Domain knowledge

Another important direction is to incorporate domain knowledge. The existing biomedical knowledge bases are invaluable sources for solving healthcare problems 133 , 134 . Incorporating domain knowledge could address the limitation of data volume, problems of data quality, as well as model generalizability. For example, the unified medical language system 135 can help to identify medical entities from the text and gene–gene interaction databases 136 could help to identify meaningful patterns from genomic profiles.

Recent years have witnessed the increasing use of DL algorithms in healthcare and medicine. In this study, we reviewed existing studies on DL applications to study mental health outcomes. All the results available in the literature reviewed in this work illustrate the applicability and promise of DL in improving the diagnosis and treatment of patients with mental health conditions. Also, this review highlights multiple existing challenges in making DL algorithms clinically actionable for routine care, as well as promising future directions in this field.

World Health Organization. The World Health Report 2001: Mental Health: New Understanding, New Hope (World Health Organization, Switzerland, 2001).

Google Scholar  

Marcus, M., Yasamy, M. T., van Ommeren, M., Chisholm, D. & Saxena, S. Depression: A Global Public Health Concern (World Federation of Mental Health, World Health Organisation, Perth, 2012).

Hamilton, M. Development of a rating scale for primary depressive illness. Br. J. Soc. Clin. Psychol. 6 , 278–296 (1967).

CAS   PubMed   Google Scholar  

Dwyer, D. B., Falkai, P. & Koutsouleris, N. Machine learning approaches for clinical psychology and psychiatry. Annu. Rev. Clin. Psychol. 14 , 91–118 (2018).

PubMed   Google Scholar  

Lovejoy, C. A., Buch, V. & Maruthappu, M. Technology and mental health: the role of artificial intelligence. Eur. Psychiatry 55 , 1–3 (2019).

Wongkoblap, A., Vadillo, M. A. & Curcin, V. Researching mental health disorders in the era of social media: systematic review. J. Med. Internet Res. 19 , e228 (2017).

PubMed   PubMed Central   Google Scholar  

LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521 , 436 (2015).

Miotto, R., Wang, F., Wang, S., Jiang, X. & Dudley, J. T. Deep learning for healthcare: review, opportunities and challenges. Brief. Bioinformatics 19 , 1236–1246 (2017).

Durstewitz, D., Koppe, G. & Meyer-Lindenberg, A. Deep neural networks in psychiatry. Mol. Psychiatry 24 , 1583–1598 (2019).

Vieira, S., Pinaya, W. H. & Mechelli, A. Using deep learning to investigate the neuroimaging correlates of psychiatric and neurological disorders: methods and applications. Neurosci. Biobehav. Rev. 74 , 58–75 (2017).

Shatte, A. B., Hutchinson, D. M. & Teague, S. J. Machine learning in mental health: a scoping review of methods and applications. Psychol. Med. 49 , 1426–1448 (2019).

Murphy, K. P. Machine Learning: A Probabilistic Perspective (MIT Press, Cambridge, 2012).

Biship, C. M. Pattern Recognition and Machine Learning (Information Science and Statistics) (Springer-Verlag, Berlin, 2007).

Bengio, Y., Simard, P. & Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. Learn. Syst. 5 , 157–166 (1994).

CAS   Google Scholar  

LeCun, Y., Bottou, L., Bengio, Y. & Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 86 , 2278–2324 (1998).

Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y. & Manzagol, P. A. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 11 , 3371–3408 (2010).

Rumelhart, D. E., Hinton, G. E. & Williams, R. J. Learning representations by back-propagating errors. Cogn. modeling. 5 , 1 (1988).

Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9 , 1735–1780 (1997).

Cho, K., Van Merriënboer, B., Bahdanau, D. & Bengio, Y. On the properties of neural machine translation: encoder-decoder approaches. In Proc . SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation 103–111 (Doha, Qatar, 2014).

Liou, C., Cheng, W., Liou, J. & Liou, D. Autoencoder for words. Neurocomputing 139 , 84–96 (2014).

Moher, D., Liberati, A., Tetzlaff, J. & Altman, D. G. Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. Ann. Intern. Med. 151 , 264–269 (2009).

Schnack, H. G. et al. Can structural MRI aid in clinical classification? A machine learning study in two independent samples of patients with schizophrenia, bipolar disorder and healthy subjects. Neuroimage 84 , 299–306 (2014).

O’Toole, A. J. et al. Theoretical, statistical, and practical perspectives on pattern-based classification approaches to the analysis of functional neuroimaging data. J. Cogn. Neurosci. 19 , 1735–1752 (2007).

Logothetis, N. K., Pauls, J., Augath, M., Trinath, T. & Oeltermann, A. Neurophysiological investigation of the basis of the fMRI signal. Nature 412 , 150 (2001).

Kuang, D. & He, L. Classification on ADHD with deep learning. In Proc . Int. Conference on Cloud Computing and Big Data 27–32 (Wuhan, China, 2014).

Kuang, D., Guo, X., An, X., Zhao, Y. & He, L. Discrimination of ADHD based on fMRI data with deep belief network. In Proc . Int. Conference on Intelligent Computing 225–232 (Taiyuan, China, 2014).

Farzi, S., Kianian, S. & Rastkhadive, I. Diagnosis of attention deficit hyperactivity disorder using deep belief network based on greedy approach. In Proc . 5th Int. Symposium on Computational and Business Intelligence 96–99 (Dubai, United Arab Emirates, 2017).

Zou, L., Zheng, J. & McKeown, M. J. Deep learning based automatic diagnoses of attention deficit hyperactive disorder. In Proc . 2017 IEEE Global Conference on Signal and Information Processing (GlobalSIP) 962–966 (Montreal, Canada, 2017).

Riaz A. et al. Deep fMRI: an end-to-end deep network for classification of fMRI data. In Proc . 2018 IEEE 15th Int. Symposium on Biomedical Imaging . 1419–1422 (Washington, DC, USA, 2018).

Zou, L., Zheng, J., Miao, C., Mckeown, M. J. & Wang, Z. J. 3D CNN based automatic diagnosis of attention deficit hyperactivity disorder using functional and structural MRI. IEEE Access. 5 , 23626–23636 (2017).

Sen, B., Borle, N. C., Greiner, R. & Brown, M. R. A general prediction model for the detection of ADHD and Autism using structural and functional MRI. PLoS ONE 13 , e0194856 (2018).

Zeng, L. et al. Multi-site diagnostic classification of schizophrenia using discriminant deep learning with functional connectivity MRI. EBioMedicine 30 , 74–85 (2018).

Pinaya, W. H. et al. Using deep belief network modelling to characterize differences in brain morphometry in schizophrenia. Sci. Rep. 6 , 38897 (2016).

CAS   PubMed   PubMed Central   Google Scholar  

Pinaya, W. H., Mechelli, A. & Sato, J. R. Using deep autoencoders to identify abnormal brain structural patterns in neuropsychiatric disorders: a large-scale multi-sample study. Hum. Brain Mapp. 40 , 944–954 (2019).

Ulloa, A., Plis, S., Erhardt, E. & Calhoun, V. Synthetic structural magnetic resonance image generator improves deep learning prediction of schizophrenia. In Proc . 25th IEEE Int. Workshop on Machine Learning for Signal Processing (MLSP) 1–6 (Boston, MA, USA, 2015).

Matsubara, T., Tashiro, T. & Uehara, K. Deep neural generative model of functional MRI images for psychiatric disorder diagnosis. IEEE Trans. Biomed. Eng . 99 (2019).

Geng, X. & Xu, J. Application of autoencoder in depression diagnosis. In 2017 3rd Int. Conference on Computer Science and Mechanical Automation (Wuhan, China, 2017).

Aghdam, M. A., Sharifi, A. & Pedram, M. M. Combination of rs-fMRI and sMRI data to discriminate autism spectrum disorders in young children using deep belief network. J. Digit. Imaging 31 , 895–903 (2018).

Shen, D., Wu, G. & Suk, H. -I. Deep learning in medical image analysis. Annu. Rev. Biomed. Eng. 19 , 221–248 (2017).

Yan, C. & Zang, Y. DPARSF: a MATLAB toolbox for “pipeline” data analysis of resting-state fMRI. Front. Syst. Neurosci. 4 , 13 (2010).

Esteban, O. et al. fMRIPrep: a robust preprocessing pipeline for functional MRI. Nat. Methods 16 , 111–116 (2019).

Herrmann, C. & Demiralp, T. Human EEG gamma oscillations in neuropsychiatric disorders. Clin. Neurophysiol. 116 , 2719–2733 (2005).

Acharya, U. R. et al. Automated EEG-based screening of depression using deep convolutional neural network. Comput. Meth. Prog. Biol. 161 , 103–113 (2018).

Mohan, Y., Chee, S. S., Xin, D. K. P. & Foong, L. P. Artificial neural network for classification of depressive and normal. In EEG Proc . 2016 IEEE EMBS Conference on Biomedical Engineering and Sciences 286–290 (Kuala Lumpur, Malaysia, 2016).

Zhang, P., Wang, X., Zhang, W. & Chen, J. Learning spatial–spectral–temporal EEG features with recurrent 3D convolutional neural networks for cross-task mental workload assessment. IEEE Trans. Neural Syst. Rehabil. Eng. 27 , 31–42 (2018).

Li, X. et al. EEG-based mild depression recognition using convolutional neural network. Med. Biol. Eng. Comput . 47 , 1341–1352 (2019).

Patel, S., Park, H., Bonato, P., Chan, L. & Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 9 , 21 (2012).

Smoller, J. W. The use of electronic health records for psychiatric phenotyping and genomics. Am. J. Med. Genet. B Neuropsychiatr. Genet. 177 , 601–612 (2018).

Wu, J., Roy, J. & Stewart, W. F. Prediction modeling using EHR data: challenges, strategies, and a comparison of machine learning approaches. Med. Care. 48 , S106–S113 (2010).

Choi, S. B., Lee, W., Yoon, J. H., Won, J. U. & Kim, D. W. Ten-year prediction of suicide death using Cox regression and machine learning in a nationwide retrospective cohort study in South Korea. J. Affect. Disord. 231 , 8–14 (2018).

Pham, T., Tran, T., Phung, D. & Venkatesh, S. Predicting healthcare trajectories from medical records: a deep learning approach. J. Biomed. Inform. 69 , 218–229 (2017).

Lin, E. et al. A deep learning approach for predicting antidepressant response in major depression using clinical and genetic biomarkers. Front. Psychiatry 9 , 290 (2018).

Geraci, J. et al. Applying deep neural networks to unstructured text notes in electronic medical records for phenotyping youth depression. Evid. Based Ment. Health 20 , 83–87 (2017).

Kim, Y. Convolutional neural networks for sentence classification. arXiv Prepr. arXiv 1408 , 5882 (2014).

Yang, Z. et al. Hierarchical attention networks for document classification. In Proc . 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies 1480–1489 (San Diego, California, USA, 2016).

Rios, A. & Kavuluru, R. Ordinal convolutional neural networks for predicting RDoC positive valence psychiatric symptom severity scores. J. Biomed. Inform. 75 , S85–S93 (2017).

Dai, H. & Jonnagaddala, J. Assessing the severity of positive valence symptoms in initial psychiatric evaluation records: Should we use convolutional neural networks? PLoS ONE 13 , e0204493 (2018).

Tran, T. & Kavuluru, R. Predicting mental conditions based on “history of present illness” in psychiatric notes with deep neural networks. J. Biomed. Inform. 75 , S138–S148 (2017).

Samek, W., Binder, A., Montavon, G., Lapuschkin, S. & Müller, K.-R. Evaluating the visualization of what a deep neural network has learned. IEEE Trans. Neural Netw. Learn. Syst. 28 , 2660–2673 (2016).

Hripcsak, G. et al. Characterizing treatment pathways at scale using the OHDSI network. Proc. Natl. Acad. Sci . USA 113 , 7329–7336 (2016).

McGuffin, P., Owen, M. J. & Gottesman, I. I. Psychiatric Genetics and Genomics (Oxford Univ. Press, New York, 2004).

Levinson, D. F. The genetics of depression: a review. Biol. Psychiatry 60 , 84–92 (2006).

Wray, N. R. et al. Genome-wide association analyses identify 44 risk variants and refine the genetic architecture of major depression. Nat. Genet. 50 , 668 (2018).

Mullins, N. & Lewis, C. M. Genetics of depression: progress at last. Curr. Psychiatry Rep. 19 , 43 (2017).

Zou, J. et al. A primer on deep learning in genomics. Nat. Genet. 51 , 12–18 (2019).

Yue, T. & Wang, H. Deep learning for genomics: a concise overview. Preprint at arXiv:1802.00810 (2018).

Khan, A. & Wang, K. A deep learning based scoring system for prioritizing susceptibility variants for mental disorders. In Proc . 2017 IEEE Int. Conference on Bioinformatics and Biomedicine (BIBM) 1698–1705 (Kansas City, USA, 2017).

Khan, A., Liu, Q. & Wang, K. iMEGES: integrated mental-disorder genome score by deep neural network for prioritizing the susceptibility genes for mental disorders in personal genomes. BMC Bioinformatics 19 , 501 (2018).

Wang, D. et al. Comprehensive functional genomic resource and integrative model for the human brain. Science 362 , eaat8464 (2018).

Salakhutdinov, R. & Hinton, G. Deep Boltzmann machines. In Proc . 12th Int. Conference on Artificial Intelligence and Statistics 448–455 (Clearwater, Florida, USA, 2009).

Laksshman, S., Bhat, R. R., Viswanath, V. & Li, X. DeepBipolar: Identifying genomic mutations for bipolar disorder via deep learning. Hum. Mutat. 38 , 1217–1224 (2017).

CAS   PubMed Central   Google Scholar  

Huang, K.-Y. et al. Data collection of elicited facial expressions and speech responses for mood disorder detection. In Proc . 2015 Int. Conference on Orange Technologies (ICOT) 42–45 (Hong Kong, China, 2015).

Valstar, M. et al. AVEC 2013: the continuous audio/visual emotion and depression recognition challenge. In Proc . 3rd ACM Int. Workshop on Audio/Visual Emotion Challenge 3–10 (Barcelona, Spain, 2013).

Valstar, M. et al. Avec 2014: 3d dimensional affect and depression recognition challenge. In Proc . 4th Int. Workshop on Audio/Visual Emotion Challenge 3–10 (Orlando, Florida, USA, 2014).

Valstar, M. et al. Avec 2016: depression, mood, and emotion recognition workshop and challenge. In Proc . 6th Int. Workshop on Audio/Visual Emotion Challenge 3–10 (Amsterdam, The Netherlands, 2016).

Ma, X., Yang, H., Chen, Q., Huang, D. & Wang, Y. Depaudionet: an efficient deep model for audio based depression classification. In Proc . 6th Int. Workshop on Audio/Visual Emotion Challenge 35–42 (Amsterdam, The Netherlands, 2016).

He, L. & Cao, C. Automated depression analysis using convolutional neural networks from speech. J. Biomed. Inform. 83 , 103–111 (2018).

Li, J., Fu, X., Shao, Z. & Shang, Y. Improvement on speech depression recognition based on deep networks. In Proc . 2018 Chinese Automation Congress (CAC) 2705–2709 (Xi’an, China, 2018).

Yang, L., Jiang, D., Han, W. & Sahli, H. DCNN and DNN based multi-modal depression recognition. In Proc . 2017 7th Int. Conference on Affective Computing and Intelligent Interaction 484–489 (San Antonio, Texas, USA, 2017).

Huang, K. Y., Wu, C. H. & Su, M. H. Attention-based convolutional neural network and long short-term memory for short-term detection of mood disorders based on elicited speech responses. Pattern Recogn. 88 , 668–678 (2019).

Dawood, A., Turner, S. & Perepa, P. Affective computational model to extract natural affective states of students with Asperger syndrome (AS) in computer-based learning environment. IEEE Access. 6 , 67026–67034 (2018).

Song, S., Shen, L. & Valstar, M. Human behaviour-based automatic depression analysis using hand-crafted statistics and deep learned spectral features. In Proc . 13th IEEE Int. Conference on Automatic Face & Gesture Recognition 158–165 (Xi’an, China, 2018).

Zhu, Y., Shang, Y., Shao, Z. & Guo, G. Automated depression diagnosis based on deep networks to encode facial appearance and dynamics. IEEE Trans. Affect. Comput. 9 , 578–584 (2018).

Chao, L., Tao, J., Yang, M. & Li, Y. Multi task sequence learning for depression scale prediction from video. In Proc . 2015 Int. Conference on Affective Computing and Intelligent Interaction (ACII) 526–531 (Xi’an, China, 2015).

Yang, T. H., Wu, C. H., Huang, K. Y. & Su, M. H. Detection of mood disorder using speech emotion profiles and LSTM. In Proc . 10th Int. Symposium on Chinese Spoken Language Processing (ISCSLP) 1–5 (Tianjin, China, 2016).

Huang, K. Y., Wu, C. H., Su, M. H. & Chou, C. H. Mood disorder identification using deep bottleneck features of elicited speech. In Proc . 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC) 1648–1652 (Kuala Lumpur, Malaysia, 2017).

Jan, A., Meng, H., Gaus, Y. F. B. A. & Zhang, F. Artificial intelligent system for automatic depression level analysis through visual and vocal expressions. IEEE Trans. Cogn. Dev. Syst. 10 , 668–680 (2017).

Su, M. H., Wu, C. H., Huang, K. Y. & Yang, T. H. Cell-coupled long short-term memory with l-skip fusion mechanism for mood disorder detection through elicited audiovisual features. IEEE Trans. Neural Netw. Learn. Syst . 31 (2019).

Harati, S., Crowell, A., Mayberg, H. & Nemati, S. Depression severity classification from speech emotion. In Proc . 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) 5763–5766 (Honolulu, HI, USA, 2018).

Su, M. H., Wu, C. H., Huang, K. Y., Hong, Q. B. & Wang, H. M. Exploring microscopic fluctuation of facial expression for mood disorder classification. In Proc . 2017 Int. Conference on Orange Technologies (ICOT) 65–69 (Singapore, 2017).

Prasetio, B. H., Tamura, H. & Tanno, K. The facial stress recognition based on multi-histogram features and convolutional neural network. In Proc . 2018 IEEE Int. Conference on Systems, Man, and Cybernetics (SMC) 881–887 (Miyazaki, Japan, 2018).

Jaiswal, S., Valstar, M. F., Gillott, A. & Daley, D. Automatic detection of ADHD and ASD from expressive behaviour in RGBD data. In Proc . 12th IEEE Int. Conference on Automatic Face & Gesture Recognition 762–769 (Washington, DC, USA, 2017).

Cho, Y., Bianchi-Berthouze, N. & Julier, S. J. DeepBreath: deep learning of breathing patterns for automatic stress recognition using low-cost thermal imaging in unconstrained settings. In Proc . 2017 7th Int. Conference on Affective Computing and Intelligent Interaction (ACII) 456–463 (San Antonio, Texas, USA, 2017).

Gupta, R., Sahu, S., Espy-Wilson, C. Y. & Narayanan, S. S. An affect prediction approach through depression severity parameter incorporation in neural networks. In Proc . 2017 Int. Conference on INTERSPEECH 3122–3126 (Stockholm, Sweden, 2017).

Martin, O., Kotsia, I., Macq, B. & Pitas, I. The eNTERFACE'05 audio-visual emotion database. In Proc . 22nd Int. Conference on Data Engineering Workshops 8–8 (Atlanta, GA, USA, 2006).

Goodfellow, I. J. et al. Challenges in representation learning: A report on three machine learning contests. In Proc . Int. Conference on Neural Information Processing 117–124 (Daegu, Korea, 2013).

Yi, D., Lei, Z., Liao, S. & Li, S. Z.. Learning face representation from scratch. Preprint at arXiv 1411.7923 (2014).

Lin, H. et al. User-level psychological stress detection from social media using deep neural network. In Proc . 22nd ACM Int. Conference on Multimedia 507–516 (Orlando, Florida, USA, 2014).

Lin, H. et al. Psychological stress detection from cross-media microblog data using deep sparse neural network. In Proc . 2014 IEEE Int. Conference on Multimedia and Expo 1–6 (Chengdu, China, 2014).

Li, Q. et al. Correlating stressor events for social network based adolescent stress prediction. In Proc . Int. Conference on Database Systems for Advanced Applications 642–658 (Suzhou, China, 2017).

Lin, H. et al. Detecting stress based on social interactions in social networks. IEEE Trans. Knowl. Data En. 29 , 1820–1833 (2017).

Cong, Q. et al. X-A-BiLSTM: a deep learning approach for depression detection in imbalanced data. In Proc . 2018 IEEE Int. Conference on Bioinformatics and Biomedicine (BIBM) 1624–1627 (Madrid, Spain, 2018).

Ive, J., Gkotsis, G., Dutta, R., Stewart, R. & Velupillai, S. Hierarchical neural model with attention mechanisms for the classification of social media text related to mental health. In Proc . Fifth Workshop on Computational Linguistics and Clinical Psychology: From Keyboard to Clinic 69–77 (New Orleans, Los Angeles, USA, 2018).

Sadeque, F., Xu, D. & Bethard, S. UArizona at the CLEF eRisk 2017 pilot task: linear and recurrent models for early depression detection. CEUR Workshop Proc . 1866 (2017).

Fraga, B. S., da Silva, A. P. C. & Murai, F. Online social networks in health care: a study of mental disorders on Reddit. In Proc . 2018 IEEE/WIC/ACM Int. Conference on Web Intelligence (WI) 568–573 (Santiago, Chile, 2018).

Gkotsis, G. et al. Characterisation of mental health conditions in social media using Informed Deep Learning. Sci. Rep. 7 , 45141 (2017).

Coppersmith, G., Leary, R., Crutchley, P. & Fine, A. Natural language processing of social media as screening for suicide risk. Biomed. Inform. Insights 10 , 1178222618792860 (2018).

Du, J. et al. Extracting psychiatric stressors for suicide from social media using deep learning. BMC Med. Inform. Decis. Mak. 18 , 43 (2018).

Alambo, A. et al. Question answering for suicide risk assessment using Reddit. In Proc . IEEE 13th Int. Conference on Semantic Computing 468–473 (Newport Beach, California, USA, 2019).

Eichstaedt, J. C. et al. Facebook language predicts depression in medical records. Proc. Natl Acad. Sci. USA 115 , 11203–11208 (2018).

Rosenquist, J. N., Fowler, J. H. & Christakis, N. A. Social network determinants of depression. Mol. Psychiatry 16 , 273 (2011).

Kipf, T. N. & Welling, M. Semi-supervised classification with graph convolutional networks. In Proc. 2017 Int. Conference on Learning Representations (Toulon, France, 2017).

Rice, S. M. et al. Online and social networking interventions for the treatment of depression in young people: a systematic review. J. Med. Internet Res. 16 , e206 (2014).

Hastie, T., Tibshirani, R. & Friedman, J. The elements of statistical learning: data mining, inference, and prediction. Springer Series in Statistics. Math. Intell. 27 , 83–85 (2009).

Torrey, L. & Shavlik, J. in Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods, and Techniques 242–264 (IGI Global, 2010).

Yosinski, J., Clune, J., Bengio, Y. & Lipson, H. How transferable are features in deep neural networks? In Proc . Advances in Neural Information Processing Systems 3320–3328 (Montreal, Canada, 2014).

Esteva, A. et al. Dermatologist-level classification of skin cancer with deep neural networks. Nature 542 , 115 (2017).

Insel, T. et al. Research domain criteria (RDoC): toward a new classification framework for research on mental disorders. Am. Psychiatr. Assoc. 167 , 748–751 (2010).

Nelson, B., McGorry, P. D., Wichers, M., Wigman, J. T. & Hartmann, J. A. Moving from static to dynamic models of the onset of mental disorder: a review. JAMA Psychiatry 74 , 528–534 (2017).

Guo, X., Liu, X., Zhu, E. & Yin, J. Deep clustering with convolutional autoencoders. In Proc . Int. Conference on Neural Information Processing 373–382 (Guangzhou, China, 2017).

Srivastava, N., Mansimov, E. & Salakhudinov, R. Unsupervised learning of video representations using LSTMs. In Proc . Int. Conference on Machine Learning 843–852 (Lille, France, 2015).

Baytas, I. M. et al. Patient subtyping via time-aware LSTM networks. In Proc . 23rd ACM SIGKDD Int. Conference on Knowledge Discovery and Data Mining 65–74 (Halifax, Canada, 2017).

American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders (DSM-5®) (American Psychiatric Pub, Washington, DC, 2013).

Biological Sciences Curriculum Study. In: NIH Curriculum Supplement Series (Internet) (National Institutes of Health, USA, 2007).

Noh, H., Hong, S. & Han, B. Learning deconvolution network for semantic segmentation. In Proc . IEEE Int. Conference on Computer Vision 1520–1528 (Santiago, Chile, 2015).

Grün, F., Rupprecht, C., Navab, N. & Tombari, F. A taxonomy and library for visualizing learned features in convolutional neural networks. In Proc. 33rd Int. Conference on Machine Learning (ICML) Workshop on Visualization for Deep Learning (New York, USA, 2016).

Ribeiro, M. T., Singh, S. & Guestrin, C. Why should I trust you?: Explaining the predictions of any classifier. In Proc . 22nd ACM SIGKDD Int. Conference on Knowledge Discovery and Data Mining 1135–1144 (San Francisco, CA, 2016).

Zhang, Q. S. & Zhu, S. C. Visual interpretability for deep learning: a survey. Front. Inf. Technol. Electron. Eng. 19 , 27–39 (2018).

Lundberg, S. M. & Lee, S. I. A unified approach to interpreting model predictions. In Proc . 31st Conference on Neural Information Processing Systems 4765–4774 (Long Beach, CA, 2017).

Shrikumar, A., Greenside, P., Shcherbina, A. & Kundaje, A. Not just a black box: learning important features through propagating activation differences. In Proc . 33rd Int. Conference on Machine Learning (New York, NY, 2016).

Gawehn, E., Hiss, J. A. & Schneider, G. Deep learning in drug discovery. Mol. Inform. 35 , 3–14 (2016).

Jerez-Aragonés, J. M., Gómez-Ruiz, J. A., Ramos-Jiménez, G., Muñoz-Pérez, J. & Alba-Conejo, E. A combined neural network and decision trees model for prognosis of breast cancer relapse. Artif. Intell. Med. 27 , 45–63 (2003).

Zhu, Y., Elemento, O., Pathak, J. & Wang, F. Drug knowledge bases and their applications in biomedical informatics research. Brief. Bioinformatics 20 , 1308–1321 (2018).

Su, C., Tong, J., Zhu, Y., Cui, P. & Wang, F. Network embedding in biomedical data science. Brief. Bioinform . https://doi.org/10.1093/bib/bby117 (2018).

Bodenreider, O. The unified medical language system (UMLS): integrating biomedical terminology. Nucleic Acids Res. 32 (suppl_1), D267–D270 (2004).

Szklarczyk, D. et al. STRING v10: protein–protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 43 , D447–D452 (2014).

Download references

Acknowledgements

The work is supported by NSF 1750326, R01 MH112148, R01 MH105384, R01 MH119177, R01 MH121922, and P50 MH113838.

Author information

Authors and affiliations.

Department of Healthcare Policy and Research, Weill Cornell Medicine, New York, NY, USA

Chang Su, Zhenxing Xu, Jyotishman Pathak & Fei Wang

You can also search for this author in PubMed   Google Scholar

Contributions

C.S., Z.X. and F.W. planned and structured the whole paper. C.S. and Z.X. conducted the literature review and drafted the manuscript. J.P. and F.W. reviewed and edited the manuscript.

Corresponding author

Correspondence to Fei Wang .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplemental material, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Su, C., Xu, Z., Pathak, J. et al. Deep learning in mental health outcome research: a scoping review. Transl Psychiatry 10 , 116 (2020). https://doi.org/10.1038/s41398-020-0780-3

Download citation

Received : 31 August 2019

Revised : 17 February 2020

Accepted : 26 February 2020

Published : 22 April 2020

DOI : https://doi.org/10.1038/s41398-020-0780-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Automated mood disorder symptoms monitoring from multivariate time-series sensory data: getting the full picture beyond a single number.

• Filippo Corponi
• Bryan M. Li
• Antonio Vergari

Translational Psychiatry (2024)

Detecting your depression with your smartphone? – An ethical analysis of epistemic injustice in passive self-tracking apps

• Mirjam Faissner
• Sebastian Laacke

Ethics and Information Technology (2024)

Development of intelligent system based on synthesis of affective signals and deep neural networks to foster mental health of the Indian virtual community

• Mandeep Kaur Arora
• Jaspreet Singh

Social Network Analysis and Mining (2024)

Prevalence and predictors of self-rated mental health among farm and non-farm adult rural residents of Saskatchewan

• Md Saiful Alam
• Bonnie Janzen
• Punam Pahwa

Current Psychology (2024)

Unraveling minds in the digital era: a review on mapping mental health disorders through machine learning techniques using online social media

Quick links.

• Explore articles by subject
• Guide to authors
• Editorial policies

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Transl Vis Sci Technol
• v.9(2); 2020 Feb

Introduction to Machine Learning, Neural Networks, and Deep Learning

Rene y. choi.

1 Department of Ophthalmology, Casey Eye Institute, Oregon Health & Science University (OHSU), Portland, Oregon, United States

Aaron S. Coyner

2 Department of Medical Informatics and Clinical Epidemiology, Oregon Health & Science University, Portland, Oregon, United States

Jayashree Kalpathy-Cramer

3 Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Charlestown, Massachusetts, United States

Michael F. Chiang

J. peter campbell.

To present an overview of current machine learning methods and their use in medical research, focusing on select machine learning techniques, best practices, and deep learning.

A systematic literature search in PubMed was performed for articles pertinent to the topic of artificial intelligence methods used in medicine with an emphasis on ophthalmology.

A review of machine learning and deep learning methodology for the audience without an extensive technical computer programming background.

Conclusions

Artificial intelligence has a promising future in medicine; however, many challenges remain.

Translational Relevance

The aim of this review article is to provide the nontechnical readers a layman's explanation of the machine learning methods being used in medicine today. The goal is to provide the reader a better understanding of the potential and challenges of artificial intelligence within the field of medicine.

Introduction

Over the past decade, artificial intelligence (AI) has become a popular subject both within and outside of the scientific community; an abundance of articles in technology and non-technology-based journals have covered the topics of machine learning (ML), deep learning (DL), and AI. 1 – 6 Yet there still remains confusion around AI, ML, and DL. The terms are highly associated, but are not interchangeable. In this review, we (attempt to) forgo technical jargon to better explain these concepts to a clinical audience.

In 1956, a group of computer scientists proposed that computers could be programmed to think and reason, “that every aspect of learning or any other feature of intelligence [could], in principle, be so precisely described that a machine [could] be made to simulate it.” 7 They described this principle as “artificial intelligence.” 7 Simply put, AI is a field focused on automating intellectual tasks normally performed by humans, and ML and DL are specific methods of achieving this goal. That is, they are within the realm of AI ( Fig. 1 ). However, AI includes approaches that do not involve any form of “learning.” For instance, the subfield known as symbolic AI focuses on hardcoding (i.e., explicitly writing) rules for every possible scenario in a particular domain of interest. These rules, written by humans, come from a priori knowledge of the particular subject and task to be completed. For example, if one were to program an algorithm to modulate room temperature of an office, he or she likely already know what temperatures are comfortable for humans to work in and would program the room to cool if temperatures rise above a specific threshold and heat if they drop below a lower threshold. Although symbolic AI is proficient at solving clearly defined logical problems, it often fails for tasks that require higher-level pattern recognition, such as speech recognition or image classification. These more complicated tasks are where ML and DL methods perform well. This review summarizes machine learning and deep learning methodology for the audience without an extensive technical computer programming background.

Umbrella of select data science techniques. Artificial intelligence (AI) falls within the realm of data science, and includes classical programming and machine learning (ML). ML contains many models and methods, including deep learning (DL) and artificial neural networks (ANN).

We conducted a literature search in PubMed for articles that were pertinent to leading artificial intelligence methods being utilized in medical research. Selection of articles was at the sole discretion of the authors. The goal of our literature search was to provide the nontechnical readers a layman's explanation of the machine learning methods being used in medicine today.

We found 33 articles that were pertinent to the main AI methods being used in medicine today.

Introduction to Machine Learning

ML is a field that focuses on the learning aspect of AI by developing algorithms that best represent a set of data. In contrast to classical programming ( Fig. 2 A), in which an algorithm can be explicitly coded using known features, ML uses subsets of data to generate an algorithm that may use novel or different combinations of features and weights than can be derived from first principles ( Fig. 2 B). 8 , 9 In ML, there are four commonly used learning methods, each useful for solving different tasks: supervised, unsupervised, semisupervised, and reinforcement learning. 8 – 10 To better understand these methods, they will be defined via an example of a hypothetical real estate company that specializes in predicting housing prices and features associated with those houses.

Classical programming versus machine learning paradigm. (A) In classical programming, a computer is supplied with a dataset and an algorithm. The algorithm informs the computer how to operate upon the dataset to create outputs. (B) In machine learning, a computer is supplied with a dataset and associated outputs. The computer learns and generates an algorithm that describes the relationship between the two. This algorithm can be used for inference on future datasets.

Supervised Learning

Suppose the real estate company would like to predict the price of a house based on specific features of the house. To begin, the company would first gather a dataset that contains many instances. 8 , 9 , 11 Each instance represents a singular observation of a house and associated features. Features are the recorded properties of a house that might be useful for predicting prices (e.g., total square-footage, number of floors, the presence of a yard). 8 , 9 , 11 The target is the feature to be predicted, in this case the housing price. 8 , 9 , 11 Datasets are generally split into training, validation, and testing datasets (models will always perform optimally on the data they are trained on). 8 , 9 Supervised learning uses patterns in the training dataset to map features to the target so that an algorithm can make housing price predictions on future datasets. This approach is supervised because the model infers an algorithm from feature-target pairs and is informed, by the target, whether it has predicted correctly. 8 – 10 That is, features, x , are mapped to the target, Y , by learning the mapping function, f , so that future housing prices may be approximated using the algorithm Y   =   f ( x ). The performance of the algorithm is evaluated on the test dataset, data that the algorithm has never seen before. 8 , 9 The basic steps of supervised machine learning are (1) acquire a dataset and split it into separate training, validation, and test datasets; (2) use the training and validation datasets to inform a model of the relationship between features and target; and (3) evaluate the model via the test dataset to determine how well it predicts housing prices for unseen instances. In each iteration, the performance of the algorithm on the training data is compared with the performance on the validation dataset. In this way, the algorithm is tuned by the validation set. Insofar as the validation set may differ from the test set, the performance of the algorithm may or may not generalize. This concept will be discussed further in the section on performance evaluation.

The most common supervised learning tasks are regression and classification. 8 – 10 Regression involves predicting numeric data, such as test scores, laboratory values, or prices of an item, much like the housing price example. 8 – 10 Classification, on the other hand, entails predicting to which category an example belongs. 8 – 10 Sticking with the previous example, imagine that rather than predicting exact housing prices in a fluctuating market, the real estate company would now like to predict a range of prices for which a house will likely sell, such as (0, 125K), (125K, 250K), (250K, 375K), and (375K, ∞). To accomplish this, data scientists would transform the numeric target variable into a categorical variable by binning housing prices into separate classes. These classes would be ordinal, meaning that there is a natural order associated with the categories. 9 However, if their task was to determine whether houses had wood, plastic, or metal siding, classes would be nominal; they are independent of one another and have no natural order. 9

Unsupervised Learning

In contrast to supervised learning, unsupervised learning aims to detect patterns in a dataset and categorize individual instances in the dataset to said categories. 8 – 10 These algorithms are unsupervised because the patterns that may or may not exist in a dataset are not informed by a target and are left to be determined by the algorithm. Some of the most common unsupervised learning tasks are clustering, association, and anomaly detection. 8 – 10 Clustering, as the name suggests, groups instances in a dataset into separate clusters based upon specific combinations of their features . 8 – 10 Say the real estate company now uses a clustering algorithm on its dataset and it finds three distinct clusters. Upon further investigation, it might find that the clusters represent the three separate architects responsible for designing the homes in their dataset, which is a feature that was not present in the training dataset.

Semisupervised Learning

Semisupervised learning can be thought of as the “happy medium” between supervised and unsupervised learning and is particularly useful for datasets that contain both labeled and unlabeled data (i.e., all features are present, but not all features have associated targets). 10 This situation typically arises when labeling images become time-intensive or cost-prohibitive. Semisupervised learning is often used for medical images, where a physician might label a small subset of images and use them to train a model. This model is then used to classify the rest of the unlabeled images in the dataset. The resultant labeled dataset is then used to train a working model that should, in theory, outperform unsupervised models. 10

Reinforcement Learning

Finally, reinforcement learning is the technique of training an algorithm for a specific task where no single answer is correct, but an overall outcome is desired. 9 , 10 It is arguably the closest attempt at modeling the human learning experience because it also learns from trial and error rather than data alone. 9 , 10 Although reinforcement learning is a powerful technique, its applications in medicine are currently limited and thus will be presented with a new example. Imagine one would like to train an algorithm to play the video game Super Mario Bros, where the purpose of the game is to move the character Mario from the left side of the screen to the right side in order to reach the flag pole at the end of each level while avoiding hazards such as enemies and pits. There is no correct sequence of controller inputs; there are sequences that lead to a win and those that do not. In reinforcement learning, an algorithm would be allowed to “play” on its own. It would attempt many different controller inputs and when it finally moves Mario forward (without receiving damage), the algorithm is “rewarded” (i.e., the behavior is reinforced). Through this process, the algorithm begins to learn what behavior is desired (e.g., moving forward is better than moving backward, jumping over enemies is better than running into them). Eventually, the algorithm learns how to move from start to finish. Although reinforcement has its place in the field of computer science and machine learning, it has yet to make a substantial impact in clinical medicine.

Performance Evaluation

To maximize the chance of generalizability to the performance of the algorithm on unseen data, the training dataset is usually split into a slightly smaller training dataset and a separate validation dataset. 8 , 9 Metrics used for evaluation of a model depend upon the model itself and whether it is in the training or testing phase. The validation dataset is meant to mimic the test dataset and helps data scientists tune an algorithm by identifying when a model may generalize well and work in a new population. Because the validation dataset is a small sample of the true (larger) population, it may not accurately represent the population itself due to an unknown sampling bias. Therefore, model performance and generalizability should not be assessed via validation set performance. It is conceivable that a data scientist could create a validation dataset with an unknown bias and use it to tune a model. Although the model might perform well on the validation dataset, it would likely not perform well on the much larger test dataset (i.e., it would not be a generalizable model)

Typically, model performance is monitored via some form of accuracy on the training and validation datasets during this phase. So long as the accuracy of the model on the training set ( X %) and validation set ( Y %) are increasing and converging after each training iteration, the model is considered to be learning. If both converge, but do not increase (e.g., X converges on Y at 50%), the model is not learning and may be underfit to the data, that is, it may not have learned enough of the relationship between features and targets in a way that it would be expected to work in another population. Finally, if training performance increases far more than validation set performance (e.g., the model has an accuracy of 99% on the data it was trained on, but only 80% on the validation data), the model is overfit. That is, it has learned features specific to the training dataset population at the expense of generalizability to another population. Although the validation dataset is not specifically used to train the algorithm, it is used to iteratively tune the algorithm. Therefore, the validation dataset is not necessarily a reliable indicator of model performance on unseen data. 8 , 9

Upon completion of the training phase, a data scientist has, ideally, trained a highly generalizable model; however, this must be confirmed via a separate test dataset. In the case of supervised learning, which will be the focus of this review from here on, the performance of a learned model can be evaluated in a number of ways, but is most commonly evaluated based on prediction accuracy (classification) or error and residuals (regression). 8 , 9 As previously mentioned, the test dataset contains instances of the original dataset that have not been seen by the algorithm during the training phase. If the predictive power of a model is strong on the training dataset, but poor on the test dataset, then the model is too specific to the patterns from the training data and is considered to be overfit to the training dataset. 8 , 9 That is, it has memorized patterns rather than learned a generalizable model. An underfit model, on the other hand, is one that performs poorly on both training and test datasets and has neither learned nor memorized the training dataset and still is not generalizable. 8 , 9 An ideally fitted model is one that performs strongly on both datasets, suggesting it is generalizable (i.e., it will perform well on other similar datasets). 8 , 9

With regression models, the average mean squared error (MSE) can be an indicator of model performance. 8 , 9 MSE measures how close a predicted value is to the intended target value. MSE is calculated by summing the differences between predicted values and target values, squaring the results, and dividing by the total number of instances ( MSE = 1 n ∑ i = 1 n ( y i - y ^ i ) 2 ) . 8 , 9 There are many other measures of performance for regression models that are out of the scope of this review.

For binary classification, the output of the model is a class. However, before the class designation, the probability of an instance belonging to class A or class B is determined. 8 , 9 Normally, this probability threshold is set at 0.5. A receiver operating characteristic curve evaluates a model's true positive rate (TPR; i.e., sensitivity, recall), the number of samples correctly identified as positive divided by the total number of positive samples, versus its false-positive rate (FPR; i.e., 1 - specificity), the number of samples incorrectly identified as positive divided by the total number of negative samples ( Fig. 3 ,  Fig. 4 A). 8 , 9 Similarly, the precision-recall curve evaluates a model's positive predictive value (PPV; i.e., precision), the number of samples correctly identified as positive divided by the total number of samples identified as positive, versus its recall ( Fig. 3 ,  Fig. 4 B). 8 , 9 Each curve is evaluated across the range of model probability thresholds from 1 to 0, left to right. A receiver operating characteristic curve starts at the point (FPR = 0, TPR = 0), which corresponds to a decision threshold of 1 (every sample is classified as negative, and thus there are no false or true positives). It ends at the point (FPR = 1, TPR = 1), which corresponds to a decision threshold of 0 (where every sample is classified as positive, and thus all points are either truly or falsely labeled positive). The points in between, which create the curve, are obtained by calculating the TPR and FPR for different decision thresholds between 1 and 0, trading off sensitivity (minimizing false negatives) with specificity (minimizing false positives). The area under the curve (AUC) of the receiver operating characteristics curve (AUROC) can be calculated and used as a metric for evaluating the overall performance of a classifier, assuming the classes of the dataset are balanced. If classes are not balanced, the area under the precision-recall curve (AUPR) may be a better metric of model performance because the threshold (set at 0.5 in  Fig. 4 B) may be adjusted. For example, if a dataset comprised 75% of class A and 25% of class B, the ratio between the two would be computed as the threshold (0.75). In practice, an AUROC value of 0.50 indicates a model that performs no better than chance, and an AUC of 1.00 indicates that the model performs perfectly; the higher the value of the AUC, the stronger the performance of the ML model. 8 , 9 Similarly, an AUPR value at the preset threshold indicates a model that performs no better than chance, and an AUPR value of 1.00 indicates a perfect model. 8 , 9

Sensitivity, specificity, positive predictive value, and negative predictive value. A population (dataset) is represented as circles colored blue if positive or orange if negative. The dataset is input to an algorithm that predicts each instance's class association. If an instance is correctly predicted as positive or negative, it is a true positive (TP) or true negative (TN), respectively. If an instance is incorrectly labeled positive or negative, it is a false positive (FP) or false negative (FN), respectively. (A) A model with perfect sensitivity ( ∑ T P T P + F N ) and specificity ( ∑ T N T N + F P ). (B) A model with perfect sensitivity (ability to correctly classify all positive cases), but poor specificity (ability to correctly classify all negative cases) and (C) a model with perfect specificity, but poor sensitivity. Although a model might have perfect sensitivity (B), it can have many false positives. Similarly, a model with perfect specificity (C) might have many false negatives. Therefore, it is also useful to evaluate the positive predictive value (PPV; ∑ T P T P + F P ) and the negative predictive value (NPV; ∑ T N T N + F N ). PPV and NPV are also thus dependent on the prevalence of disease in a population.

Example receiver operating characteristics and precision-recall curves. Red line : a model that performs no better than chance has an area under the curve (AUC) of the receiver operating characteristics curve (AUROC) of 0.50 or area under the precision-recall curve (AUPR) at the class ratio ( red shaded area ). Blue line : a model that performs better than chance, but not perfectly, will have an AUC between 0.50 and 1.00 ( blue + red shaded areas ). Green line : a model that performs perfectly has an AUC of 1.00 ( red + blue + green shaded areas ).

Classic Machine Learning Methods

There are many machine learning algorithms used in medicine. Described next are some of the most popular to date.

Linear Regression

Linear regression is arguably the simplest ML algorithm. The main idea behind regression analysis is to specify a relationship between one or more numeric features and a single numeric target. 8 , 9 Linear regression is an analysis technique used to solve a regression problem by using a straight line to describe a dataset. Univariate linear regression, a regression problem where only a single feature is used for predicting a target value, can be represented in a slope-intercept form: y   =   ax   +   b . 8 , 9 Here, a is a weight describing the slope, which describes how much a line increases on the y-axis for each increase in x . The intercept, b , describes the point where the line intercepts the y-axis. Linear regression models a dataset using this slope-intercept form, where the machine's task is to identify values of a and b such that the determined line is best able to relate the supplied values of x values to the values of y . Multivariate linear regression is similar; however, there are multiple weights in the algorithm, each describing to what degree each feature influences the target. 8 , 9

In practice, there is rarely a single function that fits a dataset perfectly. To measure the error associated with a fit, the residuals are measured. Conceptually, residuals are the vertical distances between predicted values, y ^ , and actual values, y . In machine learning, the cost function is a calculus derived term that aims to minimize errors associated with a model. 8 , 9 The process of minimizing the cost function involves an iterative optimization algorithm known as gradient descent, of which the mathematical calculations involved are outside the scope of this article. 8 , 9 , 12 In linear regression, the cost function is the previously described MSE. Minimizing this function often obtains estimates of a and b that best model a dataset. All model-based learning algorithms have a cost function, and the goal is to minimize this function to find the best-fit model. 8 , 9

Logistic Regression

Logistic regression is a classification algorithm where the goal is to find a relationship between features and the probability of a particular outcome. Rather than using the straight line produced by linear regression to estimate class probability, logistic regression uses a sigmoidal curve to estimate class probability ( Fig. 5 ). This curve is determined by the sigmoid function, y = 1 1 + e - x , which produces an S-shaped curve that converts discrete or continuous numeric features ( x ) into a single numerical value ( y ) between 0 and 1. 8 , 9 The major advantage of this method is that probabilities are bounded between 0 and 1 (i.e., probabilities cannot be negative or greater than 1). It can be either binomial, where there are only two possible outcomes, or multinomial, where there can be three or more possible outcomes. 8 , 9

Example class probability prediction using linear and logistic regression. Presented are linear ( blue line ) and logistic ( red line ) regression models for predicting the probability of various samples ( gray circles ) as belonging to a particular class using a single variable, variable X , which ranges from -10 to 10. With logistic regression, variable X is transformed into class probabilities that are bounded between 0 and 1 using the sigmoid function. Simple linear regression attempts to estimate class probabilities, but is not bounded between 0 and 1; thus, it breaks a fundamental law of probability that does not allow for negative probabilities or those greater than 1.

Decision Trees and Random Forests

A decision tree is a supervised learning technique, primarily used for classification tasks, but can also be used for regression. 8 , 9 A decision tree begins with a root node, the first decision point for splitting the dataset, and contains a single feature that best splits the data into their respective classes ( Fig. 6 ). 8 , 9 Each split has an edge that connects either to a new decision node that contains another feature to further split the data into homogenous groups or to a terminal node that predicts the class. This process of separating data into two binary partitions is known as recursive partitioning . 8 , 9 A random forest is an extension of this method, known as an ensemble method, that produces multiple decision trees. 8 , 9 Rather than using every feature to create every decision tree in a random forest, a subsample of features are used to create each decision tree. Trees then predict a class outcome, and the majority vote among trees is used as the model's final class prediction. 8 , 9

Structure of a decision tree. Splitting of the dataset begins at the root node. Each split connects to either another decision node, which results in further splitting of the data, or a terminal node that predicts the class of the data.

Classic Machine Learning in Ophthalmology

Although DL has become a highly popular technique in ophthalmology, there are a multitude of examples of classic ML algorithms being used in the field. Simple linear models have been used to predict patients who would develop advanced age-related macular degeneration and to discern which factors separate patients into who will respond to anti-vascular endothelial growth factor treatment versus those who will not. 13 – 16 Random forest algorithms have been used to discover features that are most predictive of progression to geographic atrophy in age-related macular degeneration and find prognostic features for visual acuity outcomes of intravitreal anti-vascular endothelial growth factor treatment. 17 , 18 Random forest classifiers have also been applied to diagnose and grade cataracts from ultrasound images, as well as identify patients with glaucoma based on retinal nerve fiber layer and visual field data. 19 , 20

Neural Networks and Deep Learning

An artificial neural network (ANN) is a machine learning algorithm inspired by biological neural networks. 8 , 9 , 21 Each ANN contains nodes (analogous to cell bodies) that communicate with other nodes via connections (analogous to axons and dendrites). Much in the way synapses between neurons are strengthened when their neurons have correlated outputs in a biological neural network (the Hebbian theory postulates that “nerves that fire together, wire together”), connections between nodes in an ANN are weighted based upon their ability to provide a desired outcome. 8 , 9 , 21

Feedforward Neural Networks

A perceptron is a machine learning algorithm that takes in a series of features and their targets as input and attempts to find a line, plane, or hyperplane that separates the classes in a two-, three-, or hyper-dimensional space, respectively. 9 , 22 , 23 These features are transformed using the sigmoid function ( Fig. 7 A). Thus, this method is similar to logistic regression; however, it only provides class associations, and not the probability of an instance belonging to a class.

Components of a neural network. (A) The basis of an artificial neural network, the perceptron. This algorithm uses the sigmoid function to scale and transform multiple inputs into a single output ranging from 0 to 1. (B) An artificial neural network connects multiple perceptron units, so that the output of one unit is used as input to another. Additionally, these units are not limited to using the sigmoid activation function. (C) Examples of four different activation functions: sigmoid, hyperbolic tangent, identity, and rectified linear unit. The sigmoid scales inputs between 0 and 1 using an S-shaped curved. Similarly, the hyperbolic tangent function uses an S-shaped curve, but scales inputs between -1 and 1. The identity function can multiply its input by any number to produce a linear output. The rectified linear unit is similar to the identity function, however all inputs < 0 are given an output value of 0. There are other activation functions outside of these, but these are arguably.

When multiple perceptrons are connected, the model is referred to as a multilayer perceptron algorithm or an ANN. Commonly, ANNs contain a layer of input nodes, a layer of output nodes, and a number of “hidden layers” between the two. 9 In simple ANNs, there exists an input layer between zero and three hidden layers and an output layer, whereas deep neural networks contain tens or even hundreds of hidden layers. 9 , 24 For most tasks, ANNs feed information forward. This is known as a feedforward neural network, meaning information from each node in the previous layer is passed to each node in the next layer, transformed, and passed forward to each node in the next layer ( Fig. 7 B). 9 In recurrent neural networks, which are out of the scope of this paper, information can be passed between nodes within a layer or to previous layers, where their output is operated on and fed forward once again. 22

Each layer in an ANN can contain any number of nodes; however, the number of nodes in the output layer typically corresponds to the number of classes being predicted if the goal is multiclass classification, a single node with a sigmoidal activation for binary classification, or a linear activation function if the goal is regression. 9 , 24 These activation functions simply transform a node's input into a desired output ( Fig. 7 C). Each node in an ANN contains an activation function (not just the output layer;  Fig. 7 B). These activation functions, although not always linear, do not have to be complex. For instance, the rectified linear unit applies a linear transformation to inputs ≥ 0, and sets inputs < 0 to 0. 25 It follows that as inputs proceed through an ANN, they are progressively modified at each layer so that at the final layer they no longer resemble their original state. However, this final representation of the input is, in theory, more predictive of the specified outcome.

Convolutional Neural Networks

For image recognition tasks, each input into a feedforward ANN corresponds to a pixel in the image. However, this is not ideal because there are no connections between nodes in a layer. In practice, this means that the spatial context of features in the image are lost. 24 , 26 , 27 In other words, pixels that are close to one another in an image are likely more correlated than pixels on opposite sides of the image, but a feedforward ANN does not take this into account.

A convolutional neural network (CNN) is a special case of the ANN that overcomes this issue by preserving the spatial relationship between pixels in an image. 24 , 26 , 27 Rather than using single pixels as input, a CNN feeds patches of an image to specific nodes in the next layer of nodes (rather than all nodes), thereby preserving the spatial context from which a feature was extracted. 9 , 24 , 26 , 27 These patches of nodes learn to extract specific features and are known as convolutional filters.

Convolutions are widely used in the realm of image processing, and are often used to blur or sharpen images, or for other tasks such as edge detection. 28 A visible-light digital image is simply a single matrix if the image is grayscale or three stacked matrices if the image is color (red, green, and blue color channels). 28 These matrices contain values, typically between 0 and 255, that represent pixels in the image and the intensity of each color channel at each pixel. 28 A convolutional filter is a much smaller matrix that is typically square and range in size from 2 × 2 to 9 × 9. 28 This filter is passed over the original image and, at each position, element-wise matrix multiplication is performed ( Fig. 8 ). 28 The output of this convolution is mapped to a new matrix (a feature map) that contains values corresponding to whether or not the convolutional filter detected a feature of interest. 24 , 26 – 29

Example of a digital image convolved with a filter. The image ( left ) is transformed into the feature map ( right ) via a convolutional filter ( center ). The convolutional filter is designed to locate diagonal lines running from top left to bottom right of the image. The filter passes over the image in a specified manner and each element in the image ( red ) is multiplied by the corresponding element in the convolutional filter ( blue ). The summation of these elements ( orange ) is output into a new matrix that reports the presence of a diagonal line. The feature map indicates 2 when the specified diagonal line is found, 1 if a portion of it is found, and 0 if none of it is found.

In CNNs, filters are trained to extract specific features from images (e.g., vertical lines, U-shaped objects,) and mark their location on the feature map. 26 , 27 A deep CNN then uses the feature map as input for the next layer, which uses new filters to create another new feature map. 24 , 26 , 27 This can continue for many layers and, as it continues, the extracted features become abstract, but highly useful for prediction. The final features maps are then compressed from their square representations and input to a feedforward ANN, where classification of the image based on the extracted features and textures can occur. 24 , 26 , 27 This process is referred to as DL. 24

Aside from image classification tasks, DL has shown promise for image segmentation tasks. 1 , 30 , 31 Rather than classifying images as a whole, this method aims to identify objects within an image. To accomplish this task, DL classifies individual pixels given surrounding pixel information. For example, in diabetic retinopathy, a segmentation algorithm might segment (outline) the retinal vasculature by assigning probabilities to individual pixels as belonging to a retinal blood vessel or not belonging to a retinal blood vessel. A similar method for breast cancer detection could mark pixels as belonging to a mass or not belonging to a mass, and the output image could be provided to a radiologist for further review.

Deep Learning in Ophthalmology

The popularity for DL has especially risen in the field of ophthalmology for image-based diagnostic systems. On the simpler end of visual interpretation tasks, Coyner et al. devised a DL system for automated assessment of retinal fundus image quality with an output of “acceptable” or “not acceptable” based on multiple graded expert labels. 3 Presumably, the network learned that the retinal vasculature must be easily distinguishable for an image to be deemed acceptable. In a more complex task, Gulshan et al. demonstrated that DL could classify diabetic retinopathy, in agreement with the Early Treatment for Diabetic Retinopathy Study scale, using only retinal fundus images as input and the consensus diagnoses of multiple clinicians as the “class labels.” 2 The presence of features such as microaneurysms, intraretinal hemorrhages, or neovascularization were not supplied to the DL method as signs of diabetic retinopathy. Rather, the DL model either learned these features or learned novel features that aid in the diagnosis of diabetic retinopathy. Further, Brown et al. trained a similar DL network for the diagnosis of plus disease in retinopathy of prematurity. First, an algorithm was trained to segment retinal vasculature into binary vessel maps. Then another DL algorithm was trained to examine the vessel maps and conclude whether the vasculature appeared normal or abnormal. 1 This network, too, performs on par or better than most experts in the field. One of the most impressive examples of DL in ophthalmology was conducted by De Fauw et al. Using three-dimensional optical coherence tomography images, a DL framework was trained to not only detect a single disease, but more than 50 common retinal diseases. 6

Challenges with DL Models

In recent years, DL has become a hot topic within the field of medicine given the digital availability of information; however, many challenges still exist. DL is limited by the quantity and quality of data used to train the model. It is difficult to estimate how much data are necessary to sufficiently and reliably train DL systems because it depends both on the quality of the input training data as well as the complexity of the task. Typically, thousands of training examples are required to create a model that is both accurate and generalizable. Thus, developing models for identification of rare diseases, where large datasets may not be readily available, is especially challenging. On the other hand, although one might assume that more data will always lead to better models, if the quality of the training data is imprecise, mislabeled, or somehow systematically different than the test population, training on very large datasets may result in models that do not perform well in real-world scenarios. Furthermore, there is an implicit assumption that datasets are accurately labeled by human graders. Unfortunately, this is often not the case, and noisy and/or missing labels are often a bane for data scientists.

DL methods also suffer from the “black box” problem: input is supplied to the algorithm and an output emerges, but it is not exactly clear what features were identified or how they informed the model output. 29 , 32 , 33 In contrast, simple linear algorithms, although not always as powerful as DL, are easily interpretable. The computed weights for each feature are supplied upon completion of the training process, which allow for one to interrogate exactly how the model works and possibly discover important predictors that may be useful for prevention of a disease. With deep learning, a complex series of matrix multiplication and abstract filters makes interpretability significantly more challenging. 29 , 32 , 33 Activation maps, or heatmaps, are methods that attempt to address the “black box” issue by highlighting areas of images that highlight regions of an image that “fire together” with the output classification label. 29 , 32 , 33 Unfortunately, these methods still require human interpretation, as they are often not examined critically (examples are cherry picked for publication, highly subject to confirmation bias, etc.), and thus this remains an active area of research. For instance, if a DL model classifies a fundus image as having proliferative diabetic retinopathy, a heatmap will highlight feature areas on that fundus image that contributed to the decision of being classified as having proliferative diabetic retinopathy. It is up to the physician to interpret whether these DL model identified features are the same features the physician would use to diagnose the disease, and the implications of such findings.

AI methods have shown to be a promising tool in the field of medicine. Recent work has demonstrated that these methods can develop effective diagnostic and predictive tools to identify various diseases. In the future, AI-based programs may become an integral part of patients’ clinic visits with their ability to assist in diagnosis and management of various diseases. Physicians should take an active approach to understand the theories behind AI and its utility in medicine with the goal of providing optimal patient care.

Acknowledgments

This project was supported by grants R01EY19474, K12 EY027720, and P30EY10572 from the National Institutes of Health; SCH-1622679, SCH-1622542, and SCH-1622536 from the National Science Foundation; and by unrestricted departmental funding and a Career Development Award (JPC) from Research to Prevent Blindness.

Disclosure: R.Y. Choi, None; A.S. Coyner, None; J. Kalpathy-Cramer, None; M.F. Chiang, None; J.P. Campbell, None

Object Detection Using Deep Learning, CNNs and Vision Transformers: A Review

Ieee account.

• Change Username/Password
• Update Address

Purchase Details

• Payment Options
• Order History
• View Purchased Documents

Profile Information

• Communications Preferences
• Profession and Education
• Technical Interests
• US & Canada: +1 800 678 4333
• Worldwide: +1 732 981 0060
• Contact & Support
• About IEEE Xplore
• Accessibility
• Terms of Use
• Nondiscrimination Policy
• Privacy & Opting Out of Cookies

A not-for-profit organization, IEEE is the world's largest technical professional organization dedicated to advancing technology for the benefit of humanity. © Copyright 2024 IEEE - All rights reserved. Use of this web site signifies your agreement to the terms and conditions.

• Open access
• Published: 08 June 2020

Deep learning in finance and banking: A literature review and classification

• Jian Huang 1 ,
• Junyi Chai   ORCID: orcid.org/0000-0003-1560-845X 2 &
• Stella Cho 2  

Frontiers of Business Research in China volume  14 , Article number:  13 ( 2020 ) Cite this article

65k Accesses

91 Citations

68 Altmetric

Metrics details

Deep learning has been widely applied in computer vision, natural language processing, and audio-visual recognition. The overwhelming success of deep learning as a data processing technique has sparked the interest of the research community. Given the proliferation of Fintech in recent years, the use of deep learning in finance and banking services has become prevalent. However, a detailed survey of the applications of deep learning in finance and banking is lacking in the existing literature. This study surveys and analyzes the literature on the application of deep learning models in the key finance and banking domains to provide a systematic evaluation of the model preprocessing, input data, and model evaluation. Finally, we discuss three aspects that could affect the outcomes of financial deep learning models. This study provides academics and practitioners with insight and direction on the state-of-the-art of the application of deep learning models in finance and banking.

Introduction

Deep learning (DL) is an advanced technique of machine learning (ML) based on artificial neural network (NN) algorithms. As a promising branch of artificial intelligence, DL has attracted great attention in recent years. Compared with conventional ML techniques such as support vector machine (SVM) and k-nearest neighbors (kNN), DL possesses advantages of the unsupervised feature learning, a strong capability of generalization, and a robust training power for big data. Currently, DL has been applied comprehensively in classification and prediction tasks, computer visions, image processing, and audio-visual recognition (Chai and Li 2019 ). Although DL was developed in the field of computer science, its applications have penetrated diversified fields such as medicine, neuroscience, physics and astronomy, finance and banking (F&B), and operations management (Chai et al. 2013 ; Chai and Ngai 2020 ). The existing literature lacks a good overview of DL applications in F&B fields. This study attempts to bridge this gap.

While DL is the focus of computer vision (e.g., Elad and Aharon 2006 ; Guo et al. 2016 ) and natural language processing (e.g., Collobert et al. 2011 ) in the mainstream, DL applications in F&B are developing rapidly. Shravan and Vadlamani (2016) investigated the tools of text mining for F&B domains. They examined the representative ML algorithms, including SVM, kNN, genetic algorithm (GA), and AdaBoost. Butaru et al. ( 2016 ) compared performances of DL algorithms, including random forests, decision trees, and regularized logistic regression. They found that random forests gained the highest classification accuracy in the delinquency status.

Cavalcante et al. ( 2016 ) summarized the literature published from 2009 to 2015. They analyzed DL models, including multi-layer perceptron (MLP) (a fast library for approximate nearest neighbors), Chebyshev functional link artificial NN, and adaptive weighting NN. Although the study constructed a prediction framework in financial trading, some notable DL techniques such as long short-term memory (LSTM) and reinforcement learning (RL) models are neglect. Thus, the framework cannot ascertain the optimal model in a specific condition.

The reviews of the existing literature are either incomplete or outdated. However, our study provides a comprehensive and state-of-the-art review that could capture the relationships between typical DL models and various F&B domains. We identified critical conditions to limit our collection of articles. We employed academic databases in Science Direct, Springer-Link Journal, IEEE Xplore, Emerald, JSTOR, ProQuest Database, EBSCOhost Research Databases, Academic Search Premier, World Scientific Net, and Google Scholar to search for articles. We used two groups of keywords for our search. One group is related to the DL, including “deep learning,” “neural network,” “convolutional neural networks” (CNN), “recurrent neural network” (RNN), “LSTM,” and “RL.” The other group is related to finance, including “finance,” “market risk,” “stock risk,” “credit risk,” “stock market,” and “banking.” It is important to conduct cross searches between computer-science-related and finance-related literature. Our survey exclusively focuses on the financial application of DL models rather than other DL models like SVM, kNN, or random forest. The time range of our review was set between 2014 and 2018. In this stage, we collected more than 150 articles after cross-searching. We carefully reviewd each article and considered whether it is worthy of entering our pool of articles for review. We removed the articles if they are not from reputable journals or top professional conferences. Moreover, articles were discarded if the details of financial DL models presented were not clarified. Thus, 40 articles were selected for this review eventually.

This study contributes to the literature in the following ways. First, we systematically review the state-of-the-art applications of DL in F&B fields. Second, we summarize multiple DL models regarding specified F&B domains and identify the optimal DL model of various application scenarios. Our analyses rely on the data processing methods of DL models, including preprocessing, input data, and evaluation rules. Third, our review attempts to bridge the technological and application levels of DL and F&B, respectively. We recognize the features of various DL models and highlight their feasibility toward different F&B domains. The penetration of DL into F&B is an emerging trend. Researchers and financial analysts should know the feasibilities of particular DL models toward a specified financial domain. They usually face difficulties due to the lack of connections between core financial domains and numerous DL models. This study will fill this literature gap and guide financial analysts.

The rest of this paper is organized as follows. Section 2 provides a background of DL techniques. Section 3 introduces our research framework and methodology. Section 4 analyzes the established DL models. Section 5 analyzes key methods of data processing, including data preprocessing and data inputs. Section 6 captures appeared criteria for evaluating the performance of DL models. Section 7 provides a general comparison of DL models against identified F&B domains. Section 8 discusses the influencing factors in the performance of financial DL models. Section 9 concludes and outlines the scope for promising future studies.

Background of deep learning

Regarding DL, the term “deep” presents the multiple layers that exist in the network. The history of DL can be traced back to stochastic gradient descent in 1952, which is employed for an optimization problem. The bottleneck of DL at that time was the limit of computer hardware, as it was very time-consuming for computers to process the data. Today, DL is booming with the developments of graphics processing units (GPUs), dataset storage and processing, distributed systems, and software such as Tensor Flow. This section briefly reviews the basic concept of DL, including NN and deep neural network (DNN). All of these models have greatly contributed to the applications in F&B.

The basic structure of NN can be illustrated as Y  =  F ( X T w  +  c ) regarding the independent (input) variables X , the weight terms w , and the constant terms c . Y is the dependent variable and X is formed as an n  ×  m matrix for the number of training sample n and the number of input variables m . To apply this structure in finance, Y can be considered as the price of next term, the credit risk level of clients, or the return rate of a portfolio. F is an activation function that is unique and different from regression models. F is usually formulated as sigmoid functions and tanh functions. Other functions can also be used, including ReLU functions, identity functions, binary step functions, ArcTan functions, ArcSinh functions, ISRU functions, ISRLU functions, and SQNL functions. If we combine several perceptrons in each layer and add a hidden layer from Z 1 to Z 4 in the middle, we term a single layer as a neural network, where the input layers are the X s , and the output layers are the Y s . In finance, Y can be considered as the stock price. Moreover, multiple Y s are also applicable; for instance, fund managers often care about future prices and fluctuations. Figure  1 illustrates the basic structure.

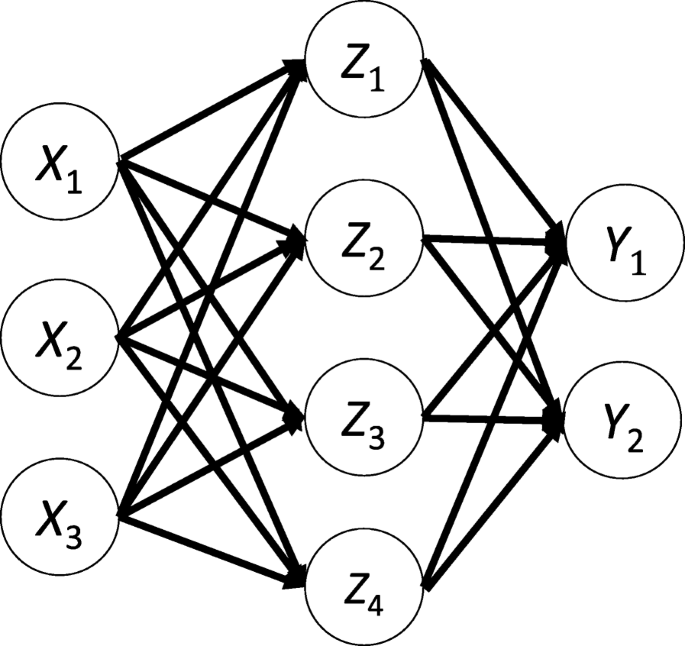
The structure of NN

Based on the basic structure of NN shown in Fig.  1 , traditional networks include DNN, backpropagation (BP), MLP, and feedforward neural network (FNN). Using these models can ignore the order of data and the significance of time. As shown in Fig.  2 , RNN has a new NN structure that can address the issues of long-term dependence and the order between input variables. As financial data in time series are very common, uncovering hidden correlations is critical in the real world. RNN can be better at solving this problem, as compared to other moving average (MA) methods that have been frequently adopted before. A detailed structure of RNN for a sequence over time is shown in Part B of the Appendix (see Fig. 7 in Appendix ).

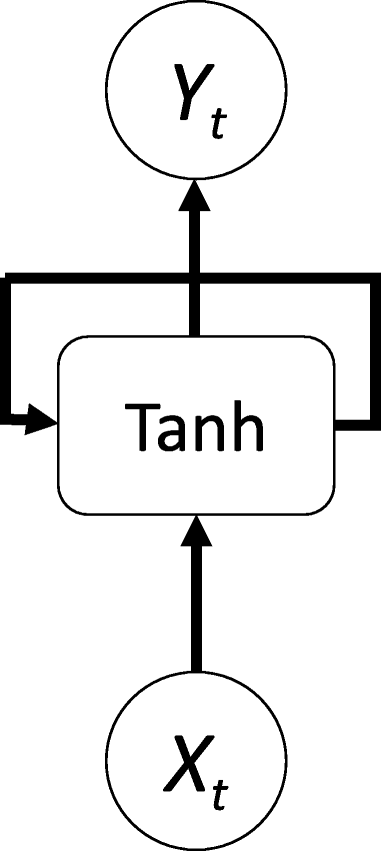
The abstract structure of RNN

Although RNN can resolve the issue of time-series order, the issue of long-term dependencies remains. It is difficult to find the optimal weight for long-term data. LSTM, as a type of RNN, added a gated cell to overcome long-term dependencies by combining different activation functions (e.g., sigmoid or tanh). Given that LSTM is frequently used for forecasting in the finance literature, we extract LSTM from RNN models and name other structures of standard RNN as RNN(O).

As we focus on the application rather than theoretical DL aspect, this study will not consider other popular DL algorithms, including CNN and RL, as well as Latent variable models such as variational autoencoders and generative adversarial network. Table 6 in Appendix shows a legend note to explain the abbreviations used in this paper. We summarize the relationship between commonly used DL models in Fig.  3 .

Relationships of reviewed DL models for F&B domains

Research framework and methodology

Our research framework is illustrated in Fig.  4 . We combine qualitative and quantitative analyses of the articles in this study. Based on our review, we recognize and identify seven core F&B domains, as shown in Fig.  5 . To connect the DL side and the F&B side, we present our review on the application of the DL model in seven F&B domains in Section 4. It is crucial to analyze the feasibility of a DL model toward particular domains. To do so, we provide summarizations in three key aspects, including data preprocessing, data inputs, and evaluation rules, according to our collection of articles. Finally, we determine optimal DL models regarding the identified domains. We further discuss two common issues in using DL models for F&B: overfitting and sustainability.

The research framework of this study

The identified domains of F&B for DL applications

Figure  5 shows that the application domains can be divided into two major areas: (1) banking and credit risk and (2) financial market investment. The former contains two domains: credit risk prediction and macroeconomic prediction. The latter contains financial prediction, trading, and portfolio management. Prediction tasks are crucial, as emphasized by Cavalcante et al. ( 2016 ). We study this domain from three aspects of prediction, including exchange rate, stock market, and oil price. We illustrate this structure of application domains in F&B.

Figure  6 shows a statistic in the listed F&B domains. We illustrate the domains of financial applications on the X-axis and count the number of articles on the Y-axis. Note that a reviewed article could cover more than one domain in this figure; thus, the sum of the counts (45) is larger than the size of our review pool (40 articles). As shown in Fig.  6 , stock marketing prediction and trading dominate the listed domains, followed by exchange rate prediction. Moreover, we found two articles on banking credit risk and two articles on portfolio management. Price prediction and macroeconomic prediction are two potential topics that deserve more studies.

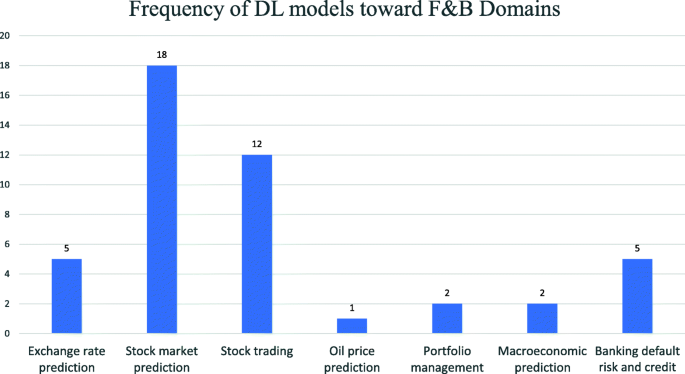
A count of articles over seven identified F&B domains

Application of DL models in F&B domains

Based on our review, six types of DL models are reported. They are FNN, CNN, RNN, RL, deep belief networks (DBN), and restricted Boltzmann machine (RBM). Regarding FNN, several papers use the alternative terms of backpropagation artificial neural network (ANN), FNN, MLP, and DNN. They have an identical structure. Regarding RNN, one of its well-known models in the time-series analysis is called LSTM. Nearly half of the reviewed articles apply FNN as the primary DL technique. Nine articles apply LSTM, followed by eight articles for RL, and six articles for RNN. Minor ones that are applied in F&B include CNN, DBM, and RBM. We count the number of articles that use various DL models in seven F&B domains, as shown in Table  1 . FNN is the principal model used in exchange rate, price, and macroeconomic predictions, as well as banking default risk and credit. LSTM and FNN are two kinds of popular models for stock market prediction. Differently, RL and FNN are frequently used regarding stock trading. FNN, RL, and simple RNN can be conducted in portfolio management. FNN is the primary model in macroeconomic and banking risk prediction. CNN, LSTM, and RL are emerging research approaches in banking risk prediction. The detailed statistics that contain specific articles can be found in Table 5 in Appendix .

Exchange rate prediction

Shen et al. ( 2015 ) construct an improved DBN model by including RBM and find that their model outperforms the random walk algorithm, auto-regressive-moving-average (ARMA), and FNN with fewer errors. Zheng et al. ( 2017 ) examine the performance of DBN and find that the DBN model estimates the exchange rate better than FNN model does. They find that a small number of layer nodes engender a more significant effect on DBN.

Several scholars believe that a hybrid model should have better performance. Ravi et al. ( 2017 ) contribute a hybrid model by using MLP (FNN), chaos theory, and multi-objective evolutionary algorithms. Their Chaos+MLP + NSGA-II model Footnote 1 has a mean squared error (MSE) with 2.16E-08 that is very low. Several articles point out that only a complicated neural network like CNN can gain higher accuracy. For example, Galeshchuk and Mukherjee ( 2017 ) conduct experiments and claim that a single hidden layer NN or SVM performs worse than a simple model like moving average (MA). However, they find that CNN could achieve higher classification accuracy in predicting the direction of the change of exchange rate because of successive layers of DNN.

Stock market prediction

In stock market prediction, some studies suggest that market news may influence the stock price and DL model, such as using a magic filter to extract useful information for price prediction. Matsubara et al. ( 2018 ) extract information from the news and propose a deep neural generative model to predict the movement of the stock price. This model combines DNN and a generative model. It suggests that this hybrid approach outperforms SVM and MLP.

Minh et al. ( 2017 ) develop a novel framework with two streams combining the gated recurrent unit network and the Stock2vec. It employs a word embedding and sentiment training system on financial news and the Harvard IV-4 dataset. They use the historical price and news-based signals from the model to predict the S&P500 and VN-index price directions. Their model shows that the two-stream gated recurrent unit is better than the gated recurrent unit or the LSTM. Jiang et al. ( 2018 ) establish a recurrent NN that extracts the interaction between the inner-domain and cross-domain of financial information. They prove that their model outperforms the simple RNN and MLP in the currency and stock market. Krausa and Feuerriegel ( 2017 ) propose that they can transform financial disclosure into a decision through the DL model. After training and testing, they point out that LSTM works better than the RNN and conventional ML methods such as ridge regression, Lasso, elastic net, random forest, SVR, AdaBoost, and gradient boosting. They further pre-train words embeddings with transfer learning (Krausa and Feuerriegel 2017 ). They conclude that better performance comes from LSTM with word embeddings. In the sentiment analysis, Sohangir et al. ( 2018 ) compares LSTM, doc2vec, and CNN to evaluate the stock opinions on the StockTwits. They conclude that CNN is the optimal model to predict the sentiment of authors. This result may be further applied to predict the stock market trend.

Data preprocessing is conducted to input data into the NN. Researchers may apply numeric unsupervised methods of feature extraction, including principal component analysis, autoencoder, RBM, and kNN. These methods can reduce the computational complexity and prevent overfitting. After the input of high-frequency transaction data, Chen et al. ( 2018b ) establish a DL model with an autoencoder and an RBM. They compare their model with backpropagation FNN, extreme learning machine, and radial basis FNN. They claim that their model can better predict the Chinese stock market. Chong et al. ( 2017 ) apply the principal component analysis (PCA) and RBM with high-frequency data of the South Korean market. They find that their model can explain the residual of the autoregressive model. The DL model can thus extract additional information and improve prediction performance. More so, Singh and Srivastava ( 2017 ) describe a model involving 2-directional and 2-dimensional (2D 2 ) PCA and DNN. Their model outperforms 2D 2 with radial basis FNN and RNN.

For time-series data, sometimes it is difficult to judge the weight of long-term and short-term data. The LSTM model is just for resolving this problem in financial prediction. The literature has attempted to prove that LSTM models are applicable and outperform conventional FNN models. Yan and Ouyang ( 2017 ) apply LSTM to challenge the MLP, SVM, and kNN in predicting a static and dynamic trend. After a wavelet decomposition and a reconstruction of the financial time series, their model can be used to predict a long-term dynamic trend. Baek and Kim ( 2018 ) apply LSTM not only in predicting the price of S&P500 and KOSPI200 but also in preventing overfitting. Kim and Won ( 2018 ) apply LSTM in the prediction of stock price volatility. They propose a hybrid model that combines LSTM with three generalized autoregressive conditional heteroscedasticity (GARCH)-type models. Hernandez and Abad ( 2018 ) argue that RBM is inappropriate for dynamic data modeling in the time-series analysis because it cannot retain memory. They apply a modified RBM model called p -RBM that can retain the memory of p past states. This model is used in predicting market directions of the NASDAQ-100 index. Compared with vector autoregression (VAR) and LSTM, notwithstanding, they find that LSTM is better because it can uncover the hidden structure within the non-linear data while VAR and p -RBM cannot capture the non-linearity in data.

CNN was established to predict the price with a complicated structure. Making the best use of historical price, Dingli and Fournier ( 2017 ) develop a new CNN model. This model can predict next month’s price. Their results cannot surpass other comparable models, such as logistic regression (LR) and SVM. Tadaaki ( 2018 ) applies the financial ratio and converts them into a “grayscale image” in the CNN model. The results reveal that CNN is more efficient than decision trees (DT), SVM, linear discriminant analysis, MLP, and AdaBoost. To predict the stock direction, Gunduz et al. ( 2017 ) establish a CNN model with a so-called specially ordered feature set whose classifier outperforms either CNN or LR.

Stock trading

Many studies adopt the conventional FNN model and try to set up a profitable trading system. Sezer et al. ( 2017 ) combine GA with MLP. Chen et al. ( 2017 ) adopt a double-layer NN and discover that its accuracy is better than ARMA-GARCH and single-layer NN. Hsu et al. ( 2018 ) equip the Black-Scholes model and a three-layer fully-connected feedforward network to estimate the bid-ask spread of option price. They argue that this novel model is better than the conventional Black-Scholes model with lower RMSE. Krauss et al. ( 2017 ) apply DNN, gradient-boosted-trees, and random forests in statistical arbitrage. They argue that their returns outperform the market index S&P500.

Several studies report that RNN and its derivate models are potential. Deng et al. ( 2017 ) extend the fuzzy learning into the RNN model. After comparing their model to different DL models like CNN, RNN, and LSTM, they claim that their model is the optimal one. Fischer and Krauss ( 2017 ) and Bao et al. ( 2017 ) argue that LSTM can create an optimal trading system. Fischer and Krauss ( 2017 ) claim that their model has a daily return of 0.46 and a sharp ratio of 5.8 prior to the transaction cost. Given the transaction cost, however, LSTM’s profitability fluctuated around zero after 2010. Bao et al. ( 2017 ) advance Fischer and Krauss’s ( 2017 ) work and propose a novel DL model (i.e., WSAEs-LSTM model). It uses wavelet transforms to eliminate noise, stacked autoencoders (SAEs) to predict stock price, and LSTM to predict the close price. The result shows that their model outperforms other models such as WLSTM, Footnote 2 LSTM, and RNN in predictive accuracy and profitability.

RL is popular recently despite its complexity. We find that five studies apply this model. Chen et al. ( 2018a ) propose an agent-based RL system to mimic 80% professional trading strategies. Feuerriegel and Prendinger ( 2016 ) convert the news sentiment into the signal in the trading system, although their daily returns and abnormal returns are nearly zero. Chakraborty ( 2019 ) cast the general financial market fluctuation into a stochastic control problem and explore the power of two RL models, including Q-learning Footnote 3 and state-action-reward-state-action (SARSA) algorithm. Both models can enhance profitability (e.g., 9.76% for Q-learning and 8.52% for SARSA). They outperform the buy-and-hold strategy. Footnote 4 Zhang and Maringer ( 2015 ) conduct a hybrid model called GA, with recurrent RL. GA is used to select an optimal combination of technical indicators, fundamental indicators, and volatility indicators. The out-of-sample trading performance is improved due to a significantly positive Sharpe ratio. Martinez-Miranda et al. ( 2016 ) create a new topic of trading. It uses a market manipulation scanner model rather than a trading system. They use RL to model spoofing-and-pinging trading. This study reveals that their model just works on the bull market. Jeong and Kim ( 2018 ) propose a model called deep Q-network that is constructed by RL, DNN, and transfer learning. They use transfer learning to solve the overfitting issue incurred as a result of insufficient data. They argue that the profit yields in this system increase by four times the amount in S&P500, five times in KOSPI, six times in EuroStoxx50, and 12 times in HIS.

Banking default risk and credit

Most articles in this domain focus on FNN applications. Rönnqvist and Sarlin ( 2017 ) propose a model for detecting relevant discussions in texting and extracting natural language descriptions of events. They convert the news into a signal of the bank-distress report. In their back-test, their model reflects the distressing financial event of the 2007–2008 period.

Zhu et al. ( 2018 ) propose a hybrid CNN model with a feature selection algorithm. Their model outperforms LR and random forest in consumer credit scoring. Wang et al. ( 2019 ) consider that online operation data can be used to predict consumer credit scores. They thus convert each kind of event into a word and apply the Event2vec model to transform the word into a vector in the LSTM network. The probability of default yields higher accuracy than other models. Jurgovsky et al. ( 2018 ) employs the LSTM to detect credit card fraud and find that LSTM can enhance detection accuracy.

Han et al. ( 2018 ) report a method that adopts RL to assess the credit risk. They claim that high-dimensional partial differential equations (PDEs) can be reformulated by using backward stochastic differential equations. NN approximates the gradient of the unknown solution. This model can be applied to F&B risk evaluation after considering all elements such as participating agents, assets, and resources, simultaneously.

Portfolio management

Song et al. ( 2017 ) establish a model after combining ListNet and RankNet to make a portfolio. They take a long position for the top 25% stocks and hold the short position for the bottom 25% stocks weekly. The ListNetlong-short model is the optimal one, which can achieve a return of 9.56%. Almahdi and Yang ( 2017 ) establish a better portfolio with a combination of RNN and RL. The result shows that the proposed trading system respond to transaction cost effects efficiently and outperform hedge fund benchmarks consistently.

Macroeconomic prediction

Sevim et al. ( 2014 ) develops a model with a back-propagation learning algorithm to predict the financial crises up to a year before it happened. This model contains three-layer perceptrons (i.e., MLP) and can achieve an accuracy rate of approximately 95%, which is superior to DT and LR. Chatzis et al. ( 2018 ) examine multiple models such as classification tree, SVM, random forests, DNN, and extreme gradient boosting to predict the market crisis. The results show that crises encourage persistence. Furthermore, using DNN increases the classification accuracy that makes global warning systems more efficient.

Price prediction

For price prediction, Sehgal and Pandey ( 2015 ) review ANN, SVM, wavelet, GA, and hybrid systems. They separate the time-series models into stochastic models, AI-based models, and regression models to predict oil prices. They reveal that researchers prevalently use MLP for price prediction.

Data preprocessing and data input

Data preprocessing.

Data preprocessing is conducted to denoise before data training of DL. This section summarizes the methods of data preprocessing. Multiple preprocessing techniques discussed in Part 4 include the principal component analysis (Chong et al. 2017 ), SVM (Gunduz et al. 2017 ), autoencoder, and RBM (Chen et al. 2018b ). There are several additional techniques of feature selection as follows.

Relief: The relief algorithm (Zhu et al. 2018 ) is a simple approach to weigh the importance of the feature. Based on NN algorithms, relief repeats the process for n times and divides each final weight vector by n . Thus, the weight vectors are the relevance vectors, and features are selected if their relevance is larger than the threshold τ .

Wavelet transforms: Wavelet transforms are used to fix the noise feature of the financial time series before feeding into a DL network. It is a widely used technique for filtering and mining single-dimensional signals (Bao et al. 2017 ).

Chi-square: Chi-square selection is commonly used in ML to measure the dependence between a feature and a class label. The representative usage is by Gunduz et al. ( 2017 ).

Random forest: Random forest algorithm is a two-stage process that contains random feature selection and bagging. The representative usage is by Fischer and Krauss ( 2017 ).

Data inputs

Data inputs are an important criterion for judging whether a DL model is feasible for particular F&B domains. This section summarizes the method of data inputs that have been adopted in the literature. Based on our review, five types of input data in the F&B domain can be presented. Table  2 provides a detailed summary of the input variable in F&B domains.

History price: The daily exchange rate can be considered as history price. The price can be the high, low, open, and close price of the stock. Related articles include Bao et al. ( 2017 ), Chen et al. ( 2017 ), Singh and Srivastava ( 2017 ), and Yan and Ouyang ( 2017 ).

Technical index: Technical indexes include MA, exponential MA, MA convergence divergence, and relative strength index. Related articles include Bao et al. ( 2017 ), Chen et al. ( 2017 ), Gunduz et al. ( 2017 ), Sezer et al. ( 2017 ), Singh and Srivastava ( 2017 ), and Yan and Ouyang ( 2017 ).

Financial news: Financial news covers financial message, sentiment shock score, and sentiment trend score. Related articles include Feuerriegel and Prendinger ( 2016 ), Krausa and Feuerriegel ( 2017 ), Minh et al. ( 2017 ), and Song et al. ( 2017 ).

Financial report data: Financial report data can account for items in the financial balance sheet or the financial report data (e.g., return on equity, return on assets, price to earnings ratio, and debt to equity ratio). Zhang and Maringer ( 2015 ) is a representative study on the subject.

Macroeconomic data: This kind of data includes macroeconomic variables. It may affect elements of the financial market, such as exchange rate, interest rate, overnight interest rate, and gross foreign exchange reserves of the central bank. Representative articles include Bao et al. ( 2017 ), Kim and Won ( 2018 ), and Sevim et al. ( 2014 ).

Stochastic data: Chakraborty ( 2019 ) provides a representative implementation.

Evaluation rules

It is critical to judge whether an adopted DL model works well in a particular financial domain. We, thus, need to consider evaluation systems of criteria for gauging the performance of a DL model. This section summarizes the evaluation rules of F&B-oriented DL models. Based on our review, three evaluation rules dominate: the error term, the accuracy index, and the financial index. Table  3 provides a detailed summary. The evaluation rules can be boiled down to the following categories.

Error term: Suppose Y t  +  i and F t  +  i are the real data and the prediction data, respectively, where m is the total number. The following is a summary of the functional formula commonly employed for evaluating DL models.

Mean Absolute Error (MAE): \( {\sum}_{i=1}^m\frac{\left|{Y}_{t+i}-{F}_{t+i}\right|}{m} \) ;

Mean Absolute Percent Error (MAPE): \( \frac{100}{m}{\sum}_{i=1}^m\frac{\left|{Y}_{t+i}-{F}_{t+i}\right|}{Y_{t+i}} \) ;

Mean Squared Error (MSE): \( {\sum}_{i=1}^m\frac{{\left({Y}_{t+i}-{F}_{t+i}\right)}^2}{m} \) ;

Root Mean Squared Error (RMSE): \( \sqrt{\sum_{i=1}^m\frac{{\left({Y}_{t+i}-{F}_{t+i}\right)}^2}{m}} \) ;

Normalized Mean Square Error (NMSE): \( \frac{1}{m}\frac{\sum {\left({Y}_{t+i}-{F}_{t+i}\right)}^2}{\mathit{\operatorname{var}}\left({Y}_{t+i}\right)} \) .

Accuracy index: According to Matsubara et al. ( 2018 ), we use TP, TN, FP, and FN to represent the number of true positives, true negatives, false positives, and false negatives, respectively, in a confusion matrix for classification evaluation. Based on our review, we summarize the accuracy indexes as follows.

Directional Predictive Accuracy (DPA): \( \frac{1}{N}{\sum}_{t=1}^N{D}_t \) , if ( Y t  + 1  −  Y t ) × ( F t  + 1  −  Y t ) ≥ 0, D t  = 1, otherwise, D t  = 0;

Actual Correlation Coefficient (ACC): \( \frac{TP+ TN}{TP+ FP+ FN+ TN} \) ;

Matthews Correlation Coefficient (MCC): \( \frac{TP\times TN- FP\times FN}{\sqrt{\left( TP+ FP\right)\left( TP+ FN\right)\left( TN+ FP\right)\left( TN+ FN\right)}} \) .

Financial index: Financial indexes involve total return, Sharp ratio, abnormal return, annualized return, annualized number of transaction, percentage of success, average profit percent per transaction, average transaction length, maximum profit percentage in the transaction, maximum loss percentage in the transaction, maximum capital, and minimum capital.

For the prediction by regressing the numeric dependent variables (e.g., exchange rate prediction or stock market prediction), evaluation rules are mostly error terms. For the prediction by classification in the category data (e.g., direction prediction on oil price), the accuracy indexes are widely conducted. For stock trading and portfolio management, financial indexes are the final evaluation rules.

General comparisons of DL models

This study identifies the most efficient DL model in each identified F&B domain. Table  4 illustrates our comparisons of the error terms in the pool of reviewed articles. Note that “A > B” means that the performance of model A is better than that of model B. “A + B” indicates the hybridization of multiple DL models.

At this point, we have summarized three methods of data processing in DL models against seven specified F&B domains, including data preprocessing, data inputs, and evaluation rules. Apart from the technical level of DL, we find the following:

NN has advantages in handling cross-sectional data;

RNN and LSTM are more feasible in handling time series data;

CNN has advantages in handling the data with multicollinearity.

Apart from application domains, we can induce the following viewpoints. Cross-sectional data usually appear in exchange rate prediction, price prediction, and macroeconomic prediction, for which NN could be the most feasible model. Time series data usually appear in stock market prediction, for which LSTM and RNN are the best options. Regarding stock trading, a feasible DL model requires the capabilities of decision and self-learning, for which RL can be the best. Moreover, CNN is more suitable for the multivariable environment of any F&B domains. As shown in the statistics of the Appendix , the frequency of using corresponding DL models corresponds to our analysis above. Selecting proper DL models according to the particular needs of financial analysis is usually challenging and crucial. This study provides several recommendations.

We summarize emerging DL models in F&B domains. Nevertheless, can these models refuse the efficient market hypothesis (EMH)? Footnote 5 According to the EMH, the financial market has its own discipline. There is no long-term technical tool that could outperform an efficient market. If so, using DL models may not be practical in long-term trading as it requires further experimental tests. However, why do most of the reviewed articles argue that their DL models of trading outperform the market returns? This argument has challenged the EMH. A possible explanation is that many DL algorithms are still challenging to apply in the real-world market. The DL models may raise trading opportunities to gain abnormal returns in the short-term. In the long run, however, many algorithms may lose their superiority, whereas EMH still works as more traders recognize the arbitrage gap offered by these DL models.

This section discusses three aspects that could affect the outcomes of DL models in finance.

Training and validation of data processing

The size of the training set.

The optimal way to improve the performance of models is by enhancing the size of the training data. Bootstrap can be used for data resampling, and generative adversarial network (GAN) can extend the data features. However, both can recognize numerical parts of features. Sometimes, the sample set is not diverse enough; thus, it loses its representativeness. Expanding the data size could make the model more unstable. The current literature reported diversified sizes of training sets. The requirements of data size in the training stage could vary by different F&B tasks.

The number of input factors

Input variables are independent variables. Based on our review, multi-factor models normally perform better than single-factor models in the case that the additional input factors are effective. In the time-series data model, long-term data have less prediction errors than that for a short period. The number of input factors depends on the employment of the DL structure and the specific environment of F&B tasks.

The quality of data

Several methods can be used to improve the data quality, including data cleaning (e.g., dealing with missing data), data normalization (e.g., taking the logarithm, calculating the changes of variables, and calculating the t -value of variables), feature selection (e.g., Chi-square test), and dimensionality reduction (e.g., PCA). Financial DL models require that the input variables should be interpretable in economics. When inputting the data, researchers should clarify the effective variables and noise. Several financial features, such as technical indexes, are likely to be created and added into the model.

Selection on structures of DL models

DL model selection should depend on problem domains and cases in finance. NN is suitable for processing cross-sectional data. LSTM and other RNNs are optimal choices for time-series data in prediction tasks. CNN can settle the multicollinearity issue through data compression. Latent variable models like GAN can be better for dimension reduction and clustering. RL is applicable in the cases with judgments like portfolio management and trading. The return levels and outcomes on RL can be affected significantly by environment (observation) definitions, situation probability transfer matrix, and actions.

The setting of objective functions and the convexity of evaluation rules

Objective function selection affects training processes and expected outcomes. For predictions on stock price, low MAE merely reflects the effectiveness of applied models in training; however, it may fail in predicting future directions. Therefore, it is vital for additional evaluation rules for F&B. Moreover, it can be more convenient to resolve the objective functions if they are convex.

The influence of overfitting (underfitting)

Overfitting (underfitting) commonly happens in using DL models, which is clearly unfavorable. A generated model performs perfectly in one case but usually cannot replicate good performance with the same model and identical coefficients. To solve this problem, we have to trade off the bias against variances. Bias posits that researchers prefer to keep it small to illustrate the superiority of their models. Generally, a deeper (i.e., more layered) NN model or neurons can reduce errors. However, it is more time-consuming and could reduce the feasibility of applied DL models.

One solution is to establish validation sets and testing sets for deciding the numbers of layers and neurons. After setting optimal coefficients in the validation set (Chong et al. 2017 ; Sevim et al. 2014 ), the result in the testing sets reveals the level of errors that could mitigate the effect of overfitting. One can input more samples of financial data to check the stability of the model’s performance. This method is known as the early stopping. It stops training more layers in the network once the testing result has achieved an optimal level.

Moreover, regularization is another approach to conquer the overfitting. Chong et al. ( 2017 ) introduces a constant term for the objective function and eventually reduces the variates of the result. Dropout is also a simple method to address overfitting. It reduces the dimensions and layers of the network (Minh et al. 2017 ; Wang et al. 2019 ). Finally, the data cleaning process (Baek and Kim 2018 ; Bao et al. 2017 ), to an extent, could mitigate the impact of overfitting.

Financial models

The sustainability of the model.

According to our reviews, the literature focus on evaluating the performance of historical data. However, crucial problems remain. Given that prediction is always complicated, the problem of how to justify the robustness of the used DL models in the future remains. More so, whether a DL model could survive in dynamic environments must be considered.

The following solutions could be considered. First, one can divide the data into two groups according to the time range; performance can subsequently be checked (e.g., using the data for the first 3 years to predict the performance of the fourth year). Second, the feature selection can be used in the data preprocessing, which could improve the sustainability of models in the long run. Third, stochastic data can be generated for each input variable by fixing them with a confidence interval, after which a simulation to examine the robustness of all possible future situations is conducted.

The popularity of the model

Whether a DL model is effective for trading is subject to the popularity of the model in the financial market. If traders in the same market conduct an identical model with limited information, they may run identical results and adopt the same trading strategy accordingly. Thus, they may lose money because their strategy could sell at a lower price after buying at a higher.

Conclusion and future works

Concluding remarks.

This paper provides a comprehensive survey of the literature on the application of DL in F&B. We carefully review 40 articles refined from a collection of 150 articles published between 2014 and 2018. The review and refinement are based on a scientific selection of academic databases. This paper first recognizes seven core F&B domains and establish the relationships between the domains and their frequently-used DL models. We review the details of each article under our framework. Importantly, we analyze the optimal models toward particular domains and make recommendations according to the feasibility of various DL models. Thus, we summarize three important aspects, including data preprocessing, data inputs, and evaluation rules. We further analyze the unfavorable impacts of overfitting and sustainability when applying DL models and provide several possible solutions. This study contributes to the literature by presenting a valuable accumulation of knowledge on related studies and providing useful recommendations for financial analysts and researchers.

Future works

Future studies can be conducted from the DL technical and F&B application perspectives. Regarding the perspective of DL techniques, training DL model for F&B is usually time-consuming. However, effective training could greatly enhance accuracy by reducing errors. Most of the functions can be simulated with considerable weights in complicated networks. First, one of the future works should focus on data preprocessing, such as data cleaning, to reduce the negative effect of data noise in the subsequent stage of data training. Second, further studies on how to construct layers of networks in the DL model are required, particularly when considering a reduction of the unfavorable effects of overfitting and underfitting. According to our review, the comparisons between the discussed DL models do not hinge on an identical source of input data, which renders these comparisons useless. Third, more testing regarding F&B-oriented DL models would be beneficial.

In addition to the penetration of DL techniques in F&B fields, more structures of DL models should be explored. From the perspective of F&B applications, the following problems need further research to investigate desirable solutions. In the case of financial planning, can a DL algorithm transfer asset recommendations to clients according to risk preferences? In the case of corporate finance, how can a DL algorithm benefit capital structure management and, thus, maximize the values of corporations? How can managers utilize DL technical tools to gauge the investment environment and financial data? How can they use such tools to optimize cash balances and cash inflow and outflow? Until recently, DL models like RL and generative adversarial networks are rarely used. More investigations on constructing DL structures for F&B regarding preferences would be beneficial. Finally, the developments of professional F&B software and system platforms that implement DL techniques are highly desirable.

Availability of data and materials

Not applicable.

In the model, NSGA stands for non-dominated sorting genetic algorithm.

A combination of Wavelet transforms (WT) and long-short term memory (LSTM) is called WLSTM in Bao et al. ( 2017 ).

Q-learning is a model-free reinforcement learning algorithm.

Buy-and-hold is a passive investment strategy in which an investor buys stocks (or ETFs) and holds them for a long period regardless of fluctuations in the market.

EMH was developed from a Ph.D. dissertation by economist Eugene Fama in the 1960s. It says that at any given time, stock prices reflect all available information and trade at exactly their fair value at all times. It is impossible to consistently choose stocks that will beat the returns of the overall stock market. Therefore, this hypothesis implies that the pursuit of market-beating performance is more about chance than it is about researching and selecting the right stocks.

Almahdi, S., & Yang, S. Y. (2017). An adaptive portfolio trading system: A risk-return portfolio optimization using recurrent reinforcement learning with expected maximum drawdown. Expert Systems with Applications, 87 , 267–279.

Article   Google Scholar  

Baek, Y., & Kim, H. Y. (2018). ModAugNet: A new forecasting framework for stock market index value with an overfitting prevention LSTM module and a prediction LSTM module. Expert Systems with Applications, 113 , 457–480.

Bao, W., Yue, J., & Rao, Y. (2017). A deep learning framework for financial time series using stacked autoencoders and long-short-term memory. PLoS One, 12 (7), e0180944.

Butaru, F., Chen, Q., Clark, B., Das, S., Lo, A. W., & Siddique, A. (2016). Risk and risk management in the credit card industry. Journal of Banking & Finance, 72 , 218–239.

Cavalcante, R. C., Brasileiro, R. C., Souza, V. L. F., Nobrega, J. P., & Oliveira, A. L. I. (2016). Computational intelligence and financial markets: A survey and future directions. Expert System with Application, 55 , 194–211.

Chai, J. Y., & Li, A. M. (2019). Deep learning in natural language processing: A state-of-the-art survey. In The proceeding of the 2019 international conference on machine learning and cybernetics (pp. 535–540). Japan: Kobe.

Google Scholar  

Chai, J. Y., Liu, J. N. K., & Ngai, E. W. T. (2013). Application of decision-making techniques in supplier selection: A systematic review of literature. Expert Systems with Applications, 40 (10), 3872–3885.

Chai, J. Y., & Ngai, E. W. T. (2020). Decision-making techniques in supplier selection: Recent accomplishments and what lies ahead. Expert Systems with Applications, 140 , 112903. https://doi.org/10.1016/j.eswa.2019.112903 .

Chakraborty, S. (2019). Deep reinforcement learning in financial markets Retrieved from https://arxiv.org/pdf/1907.04373.pdf . Accessed 04 Apr 2020.

Chatzis, S. P., Siakoulis, V., Petropoulos, A., Stavroulakis, E., & Vlachogiannakis, E. (2018). Forecasting stock market crisis events using deep and statistical machine learning techniques. Expert Systems with Applications, 112 , 353–371.

Chen, C. T., Chen, A. P., & Huang, S. H. (2018a). Cloning strategies from trading records using agent-based reinforcement learning algorithm. In The proceeding of IEEE international conference on agents (pp. 34–37).

Chen, H., Xiao, K., Sun, J., & Wu, S. (2017). A double-layer neural network framework for high-frequency forecasting. ACM Transactions on Management Information Systems, 7 (4), 11.

Chen, L., Qiao, Z., Wang, M., Wang, C., Du, R., & Stanley, H. E. (2018b). Which artificial intelligence algorithm better predicts the Chinese stock market? IEEE Access, 6 , 48625–48633.

Chong, E., Han, C., & Park, F. C. (2017). Deep learning networks for stock market analysis and prediction: Methodology, data representations, and case studies. Expert Systems with Applications, 83 , 187–205.

Collobert, R., Weston, J., Bottou, L., Karlen, M., Kavukcuoglu, K., & Kuksa, P. (2011). Natural language processing (almost) from scratch. Journal of Machine Learning Research, 12 , 2493–2537.

Deng, Y., Bao, F., Kong, Y., Ren, Z., & Dai, Q. (2017). Deep direct reinforcement learning for financial signal representation and trading. IEEE Transactions on Neural Networks and Learning Systems, 28 (3), 653–664.

Dingli, A., & Fournier, K. S. (2017). Financial time series forecasting—A machine learning approach. International Journal of Machine Learning and Computing, 4 , 11–27.

Elad, M., & Aharon, M. (2006). Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing, 15 (12), 3736–3745.

Feuerriegel, S., & Prendinger, H. (2016). News-based trading strategies. Decision Support Systems, 90 , 65–74.

Fischer, T., & Krauss, C. (2017). Deep learning with long short-term memory networks for financial market predictions. European Journal of Operational Research, 270 (2), 654–669.

Galeshchuk, S., & Mukherjee, S. (2017). Deep networks for predicting the direction of change in foreign exchange rates. Intelligent Systems in Accounting, Finance and Maangement, 24 (4), 100–110.

Gunduz, H., Yaslan, Y., & Cataltepe, Z. (2017). Intraday prediction of Borsa Istanbul using convolutional neural networks and feature correlations. Knowledge-Based Systems, 137 , 138–148.

Guo, Y., Liu, Y., Oerlemans, A., Lao, S., Wu, S., & Lew, M. S. (2016). Deep learning for visual understanding: A review. Neurocomputing, 187 , 27–48.

Han, J., Jentzen, A., & Weinan, E. (2018). Solving high-dimensional partial differential equations using deep learning. The proceedings of the National Academy of Sciences of the United States of America (PNAS) ; 8505–10).

Hernandez, J., & Abad, A. G. (2018). Learning from multivariate discrete sequential data using a restricted Boltzmann machine model. In The proceeding of IEEE 1st Colombian conference on applications in computational intelligence (ColCACI) (pp. 1–6).

Hsu, P. Y., Chou, C., Huang, S. H., & Chen, A. P. (2018). A market making quotation strategy based on dual deep learning agents for option pricing and bid-ask spread estimation.   The proceeding of IEEE international conference on agents (pp. 99–104).

Jeong, G., & Kim, H. Y. (2018). Improving financial trading decisions using deep Q-learning: Predicting the number of shares, action strategies and transfer learning. Expert Systems with Applications, 117 , 125–138.

Jiang, X., Pan, S., Jiang, J., & Long, G. (2018). Cross-domain deep learning approach for multiple financial market predictions. The proceeding of international joint conference on neural networks (pp. 1–8).

Jurgovsky, J., Granitzer, M., Ziegler, K., Calabretto, S., Portier, P. E., Guelton, L. H., & Caelen, O. (2018). Sequence classification for credit-card fraud detection. Expert Systems with Applications, 100 , 234–245.

Kim, H. Y., & Won, C. H. (2018). Forecasting the volatility of stock price index: A hybrid model integrating LSTM with multiple GARCH-type models. Expert Systems with Applications, 103 , 25–37.

Krausa, M., & Feuerriegel, S. (2017). Decision support from financial disclosures with deep neural networks and transfer learning Retrieved from https://arxiv.org/pdf/1710.03954.pdf Accessed 04 Apr 2020.

Book   Google Scholar  

Krauss, C., Do, X. A., & Huck, N. (2017). Deep neural networks, gradient-boosted trees, random forests: Statistical arbitrage on the S&P500. European Journal of Operational Research, 259 (2), 689–702.

Martinez-Miranda, E., McBurney, P., & Howard, M. J. W. (2016). Learning unfair trading: A market manipulation analysis from the reinforcement learning perspective. In The proceeding of 2016 IEEE conference on evolving and adaptive intelligent systems (EAIS) (pp. 103–109).

Chapter   Google Scholar  

Matsubara, T., Akita, R., & Uehara, K. (2018). Stock price prediction by deep neural generative model of news articles. IEICE Transactions on Information and Systems, 4 , 901–908.

Minh, D. L., Sadeghi-Niaraki, A., Huy, H. D., Min, K., & Moon, H. (2017). Deep learning approach for short-term stock trends prediction based on two-stream gated recurrent unit network. IEEE Access, 6 , 55392–55404.

Ravi, V., Pradeepkumar, D., & Deb, K. (2017). Financial time series prediction using hybrids of chaos theory, multi-layer perceptron and multi-objective evolutionary algorithms. Swarm and Evolutionary Computation, 36 , 136–149.

Rönnqvist, S., & Sarlin, P. (2017). Bank distress in the news describing events through deep learning. Neurocomputing, 264 (15), 57–70.

Sehgal, N., & Pandey, K. K. (2015). Artificial intelligence methods for oil price forecasting: A review and evaluation. Energy System, 6 , 479–506.

Sevim, C., Oztekin, A., Bali, O., Gumus, S., & Guresen, E. (2014). Developing an early warning system to predict currency crises. European Journal of Operational Research, 237 (3), 1095–1104.

Sezer, O. B., Ozbayoglu, M., & Gogdu, E. (2017). A deep neural-network-based stock trading system based on evolutionary optimized technical analysis parameters. Procedia Computer Science, 114 , 473–480.

Shen, F., Chao, J., & Zhao, J. (2015). Forecasting exchange rate using deep belief networks and conjugate gradient method. Neurocomputing, 167 , 243–253.

Singh, R., & Srivastava, S. (2017). Stock prediction using deep learning. Multimedia Tools Application, 76 , 18569–18584.

Sohangir, S., Wang, D., Pomeranets, A., & Khoshgoftaar, T. M. (2018). Big data: Deep learning for financial sentiment analysis. Journal of Big Data, 5 (3), 1–25.

Song, Q., Liu, A., & Yang, S. Y. (2017). Stock portfolio selection using learning-to-rank algorithms with news sentiment. Neurocomputing, 264 , 20–28.

Tadaaki, H. (2018). Bankruptcy prediction using imaged financial ratios and convolutional neural networks. Expert Systems with Applications, 117 , 287–299.

Wang, C., Han, D., Liu, Q., & Luo, S. (2019). A deep learning approach for credit scoring of peer-to-peer lending using attention mechanism LSTM. IEEE Access, 7 , 2161–2167.

Yan, H., & Ouyang, H. (2017). Financial time series prediction based on deep learning. Wireless Personal Communications, 102 , 683–700.

Zhang, J., & Maringer, D. (2015). Using a genetic algorithm to improve recurrent reinforcement learning for equity trading. Computational Economics, 47 , 551–567.

Zheng, J., Fu, X., & Zhang, G. (2017). Research on exchange rate forecasting based on a deep belief network. Neural Computing and Application, 31 , 573–582.

Zhu, B., Yang, W., Wang, H., & Yuan, Y. (2018). A hybrid deep learning model for consumer credit scoring. In The proceeding of international conference on artificial intelligence and big data (pp. 205–208).

Download references

Acknowledgments

The constructive comments of the editor and three anonymous reviewers on an earlier version of this paper are greatly appreciated. The authors are indebted to seminar participants at 2019 China Accounting and Financial Innovation Form at Zhuhai for insightful discussions. The corresponding author thanks the financial supports from BNU-HKBU United International College Research Grant under Grant R202026.

BNU-HKBU United International College Research Grant under Grant R202026.

Author information

Authors and affiliations.

Department of Mathematics, The Hong Kong University of Science and Technology, Hong Kong, China

Division of Business and Management, BNU-HKBU United International College, Zhuhai, China

Junyi Chai & Stella Cho

You can also search for this author in PubMed   Google Scholar

Contributions

JH carried out the collections and analyses of the literature, participated in the design of this study and preliminarily drafted the manuscript. JC initiated the idea and research project, identified the research gap and motivations, carried out the collections and analyses of the literature, participated in the design of this study, helped to draft the manuscript and proofread the manuscript. SC participated in the design of the study and the analysis of the literature, helped to draft the manuscript and proofread the manuscript. The authors read and approved the final manuscript.

Corresponding author

Correspondence to Junyi Chai .

Ethics declarations

Competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Part A. Summary of publications in DL and F&B domains

Part b. detailed structure of standard rnn.

The abstract structure of RNN for a sequence cross over time can be extended, as shown in Fig. 7 in Appendix , which presents the inputs as X , the outputs as Y , the weights as w , and the Tanh functions.

The detailed structure of RNN

Part C. List of abbreviations

Rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Huang, J., Chai, J. & Cho, S. Deep learning in finance and banking: A literature review and classification. Front. Bus. Res. China 14 , 13 (2020). https://doi.org/10.1186/s11782-020-00082-6

Download citation

Received : 02 September 2019

Accepted : 30 April 2020

Published : 08 June 2020

DOI : https://doi.org/10.1186/s11782-020-00082-6

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Literature review
• Deep learning

These computer science terms are often used interchangeably, but what differences make each a unique technology?

Technology is becoming more embedded in our daily lives by the minute. To keep up with the pace of consumer expectations, companies are relying more heavily on machine learning algorithms to make things easier. You can see its application in social media (through object recognition in photos) or in talking directly to devices (like Alexa or Siri).

While  artificial intelligence  (AI),  machine learning  (ML),  deep learning  and  neural networks  are related technologies, the terms are often used interchangeably, which frequently leads to confusion about their differences. This blog post clarifies some of the ambiguity.

The easiest way to think about AI, machine learning, deep learning and neural networks is to think of them as a series of AI systems from largest to smallest, each encompassing the next.

AI is the overarching system. Machine learning is a subset of AI. Deep learning is a subfield of machine learning, and neural networks make up the backbone of deep learning algorithms. It’s the number of node layers, or depth, of neural networks that distinguishes a single neural network from a deep learning algorithm, which must have more than three.

Artificial intelligence or AI, the broadest term of the three, is used to classify machines that mimic human intelligence and human cognitive functions like problem-solving and learning. AI uses predictions and automation to optimize and solve complex tasks that humans have historically done, such as facial and speech recognition, decision-making and translation.

Categories of AI

The three main categories of AI are:

• Artificial Narrow Intelligence (ANI)
• Artificial General Intelligence (AGI)
• Artificial Super Intelligence (ASI)

ANI is considered “weak” AI, whereas the other two types are classified as “strong” AI. We define weak AI by its ability to complete a specific task, like winning a chess game or identifying a particular individual in a series of photos. Natural language processing and computer vision, which let companies automate tasks and underpin  chatbots  and virtual assistants such as Siri and Alexa, are examples of ANI. Computer vision is a factor in the development of self-driving cars.

Stronger forms of AI, like AGI and ASI, incorporate human behaviors more prominently, such as the ability to interpret tone and emotion. Strong AI is defined by its ability compared to humans. AGI would perform on par with another human, while ASI—also known as superintelligence—would surpass a human’s intelligence and ability. Neither form of Strong AI exists yet, but research in this field is ongoing.

Using AI for business

An increasing number of businesses, about  35%  globally, are using AI, and another 42% are exploring the technology. The development of  generative AI , which uses powerful foundation models that train on large amounts of unlabeled data, can be adapted to new use cases and bring flexibility and scalability that is likely to accelerate the adoption of AI significantly. In early tests, IBM has seen generative AI bring time to value up to 70% faster than traditional AI.

Whether you use AI applications based on ML or foundation models, AI can give your business a competitive advantage. Integrating customized AI models into your workflows and systems, and automating functions such as customer service, supply chain management and cybersecurity, can help a business meet customers’ expectations, both today and as they increase in the future.

The key is identifying the right data sets from the start to help ensure that you use quality data to achieve the most substantial competitive advantage. You’ll also need to create a hybrid, AI-ready architecture that can successfully use data wherever it lives—on mainframes, data centers, in private and public clouds and at the edge.

Your AI must be trustworthy because anything less means risking damage to a company’s reputation and bringing regulatory fines. Misleading models and those containing bias or that  hallucinate  (link resides outside ibm.com) can come at a high cost to customers’ privacy, data rights and trust. Your AI must be explainable, fair and transparent.

Machine learning is a subset of AI that allows for optimization. When set up correctly, it helps you make predictions that minimize the errors that arise from merely guessing. For example, companies like Amazon use machine learning to recommend products to a specific customer based on what they’ve looked at and bought before.

Classic or “nondeep” machine learning depends on human intervention to allow a computer system to identify patterns, learn, perform specific tasks and provide accurate results. Human experts determine the hierarchy of features to understand the differences between data inputs, usually requiring more structured data to learn.

For example, let’s say I showed you a series of images of different types of fast food—“pizza,” “burger” and “taco.” A human expert working on those images would determine the characteristics distinguishing each picture as a specific fast food type. The bread in each food type might be a distinguishing feature. Alternatively, they might use labels, such as “pizza,” “burger” or “taco” to streamline the learning process through supervised learning.

While the subset of AI called deep machine learning can leverage labeled data sets to inform its algorithm in supervised learning, it doesn’t necessarily require a labeled data set. It can ingest unstructured data in its raw form (for example, text, images), and it can automatically determine the set of features that distinguish “pizza,” “burger” and “taco” from one another. As we generate more big data, data scientists use more machine learning. For a deeper dive into the differences between these approaches, check out  Supervised versus Unsupervised Learning: What’s the Difference?

A third category of machine learning is reinforcement learning, where a computer learns by interacting with its surroundings and getting feedback (rewards or penalties) for its actions. And online learning is a type of ML where a data scientist updates the ML model as new data becomes available.

To learn more about machine learning, check out the following video:

As our article on  deep learning  explains, deep learning is a subset of machine learning. The primary difference between machine learning and deep learning is how each algorithm learns and how much data each type of algorithm uses.

Deep learning automates much of the feature extraction piece of the process, eliminating some of the manual human intervention required. It also enables the use of large data sets, earning the title of  scalable machine learning . That capability is exciting as we explore the use of unstructured data further, particularly since  over 80% of an organization’s data is estimated to be unstructured  (link resides outside ibm.com). 

Observing patterns in the data allows a deep-learning model to cluster inputs appropriately. Taking the same example from earlier, we might group pictures of pizzas, burgers and tacos into their respective categories based on the similarities or differences identified in the images. A deep-learning model requires more data points to improve accuracy, whereas a machine-learning model relies on less data given its underlying data structure. Enterprises generally use deep learning for more complex tasks, like virtual assistants or fraud detection.

Neural networks, also called artificial neural networks or simulated neural networks, are a subset of machine learning and are the backbone of deep learning algorithms. They are called “neural” because they mimic how neurons in the brain signal one another.

Neural networks are made up of node layers—an input layer, one or more hidden layers and an output layer. Each node is an artificial neuron that connects to the next, and each has a weight and threshold value. When one node’s output is above the threshold value, that node is activated and sends its data to the network’s next layer. If it’s below the threshold, no data passes along.

Training data teach neural networks and help improve their accuracy over time. Once the learning algorithms are fined-tuned, they become powerful computer science and AI tools because they allow us to quickly classify and cluster data. Using neural networks, speech and image recognition tasks can happen in minutes instead of the hours they take when done manually. Google’s search algorithm is a well-known example of a neural network.

As mentioned in the explanation of neural networks above, but worth noting more explicitly, the “deep” in deep learning refers to the depth of layers in a neural network. A neural network of more than three layers, including the inputs and the output, can be considered a deep-learning algorithm. That can be represented by the following diagram:

Most deep neural networks are feed-forward, meaning they only flow in one direction from input to output. However, you can also train your model through back-propagation, meaning moving in the opposite direction, from output to input. Back-propagation allows us to calculate and attribute the error that is associated with each neuron, allowing us to adjust and fit the algorithm appropriately.

While all these areas of AI can help streamline areas of your business and improve your customer experience, achieving AI goals can be challenging because you’ll first need to ensure that you have the right systems to construct learning algorithms to manage your data. Data management is more than merely building the models that you use for your business. You need a place to store your data and mechanisms for cleaning it and controlling for bias before you can start building anything.

At IBM we are combining the power of machine learning and artificial intelligence in our new studio for foundation models, generative AI and machine learning, watsonx.ai™.

Get the latest tech insights and expert thought leadership in your inbox.

Learn more about watsonx.ai

Get our newsletters and topic updates that deliver the latest thought leadership and insights on emerging trends.

Deep Cybersecurity: A Comprehensive Overview from Neural Network and Deep Learning Perspective

• Survey Article
• Published: 20 March 2021
• Volume 2 , article number  154 , ( 2021 )

Cite this article

• Iqbal H. Sarker   ORCID: orcid.org/0000-0003-1740-5517 1 , 2  

8302 Accesses

84 Citations

1 Altmetric

Explore all metrics

Deep learning, which is originated from an artificial neural network (ANN), is one of the major technologies of today’s smart cybersecurity systems or policies to function in an intelligent manner. Popular deep learning techniques, such as multi-layer perceptron, convolutional neural network, recurrent neural network or long short-term memory, self-organizing map, auto-encoder, restricted Boltzmann machine, deep belief networks, generative adversarial network, deep transfer learning, as well as deep reinforcement learning, or their ensembles and hybrid approaches can be used to intelligently tackle the diverse cybersecurity issues. In this paper, we aim to present a comprehensive overview from the perspective of these neural networks and deep learning techniques according to today’s diverse needs. We also discuss the applicability of these techniques in various cybersecurity tasks such as intrusion detection, identification of malware or botnets, phishing, predicting cyberattacks, e.g. denial of service, fraud detection or cyberanomalies, etc. Finally, we highlight several research issues and future directions within the scope of our study in the field. Overall, the ultimate goal of this paper is to serve as a reference point and guidelines for the academia and professionals in the cyber industries, especially from the deep learning point of view.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

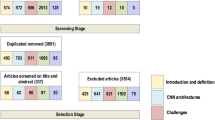
Review of deep learning: concepts, CNN architectures, challenges, applications, future directions

Development and application of artificial neural network.

AI-Driven Cybersecurity: An Overview, Security Intelligence Modeling and Research Directions

Li S, Da LX, Zhao S. The internet of things: a survey. Inf Syst Front. 2015;17(2):243–59.

Article   Google Scholar  

McIntosh T, Jang-Jaccard J, Watters P, Susnjak T. The inadequacy of entropy-based ransomware detection. In: International conference on neural information processing. Springer; 2019. pp. 181–189.

Alazab M, Venkatraman S, Watters P, Alazab M et al. Zero-day malware detection based on supervised learning algorithms of API call signatures. 2010.

Sun N, Zhang J, Rimba P, Gao S, Zhang LY, Xiang Y. Data-driven cybersecurity incident prediction: a survey. IEEE Commun Surv Tutor. 2018;21(2):1744–72.

Google Scholar  

Abraham S. Data breach: from notification to prevention using PCI DSS. Colum JL Soc Probs. 2009;43:517.

Brij BG, Aakanksha T, Ankit KJ, Dharma PA. Fighting against phishing attacks: state of the art and future challenges. Neural Comput Appl. 2017;28(12):3629–54.

Ibm security report. https://www.ibm.com/security/data-breach . Accessed 20 Oct 2019.

Fischer EA. Cybersecurity issues and challenges: In brief. 2014.

Sarker IH, Kayes ASM, Badsha S, Alqahtani H, Watters P, Ng A. Cybersecurity data science: an overview from machine learning perspective. J Big Data. 2020;7(1):1–29.

Steven A. Cybersecurity: the cold war online. Nature. 2017;547(7661):30.

Anwar S, Mohamad Zain J, Zolkipli MF, Inayat Z, Khan S, Anthony B, Chang V. From intrusion detection to an intrusion response system: fundamentals, requirements, and future directions. Algorithms. 2017;10(2):39.

MATH   Google Scholar  

Sara M, Hamid M, Mostafa G-A, Hadis K. Cyber intrusion detection by combined feature selection algorithm. J Inf Secur Appl. 2019;44:80–8.

Tapiador JE, Orfila A, Ribagorda A, Ramos B. Key-recovery attacks on kids, a keyed anomaly detection system. IEEE Trans Depend Secure Comput. 2013;12(3):312–25.

Tavallaee M, Stakhanova N, Ghorbani AA. Toward credible evaluation of anomaly-based intrusion-detection methods. IEEE Trans Syst Man Cybern Part C (Appl Rev). 2010;40(5):516–24.

Farhad F, Peter L. Data science methodology for cybersecurity projects. arXiv preprint arXiv:1803.04219 . 2018.

Saxe J, Sanders H. Malware data science: attack detection and attribution. 2018.

Ślusarczyk B. Industry 4.0: Are we ready? Pol J Manag Stud. 2018; 17.

Google trends. In https://trends.google.com/trends/ , 2021.

Yang X, Lingshuang K, Zhi L, Yuling C, Yanmiao L, Hongliang Z, Mingcheng G, Haixia H, Chunhua W. Machine learning and deep learning methods for cybersecurity. IEEE Access. 2018;6:35365–81.

Aya R, Ahmed E. Data science: developing theoretical contributions in information systems via text analytics. J Big Data. 2020;7(1):1–26.

Lippmann RP, Fried DJ, Graf I, Haines JW, Kendall KR, McClung D, Weber D, Webster SE, Wyschogrod D, Cunningham RK, et al. Evaluating intrusion detection systems: the 1998 Darpa off-line intrusion detection evaluation. In: Proceedings DARPA information survivability conference and exposition. DISCEX’00, vol 2. IEEE; 2000. pp. 12–26.

Kdd cup 99. available online: http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html Accessed 20 Oct 2019.

Tavallaee M, Bagheri E, Lu W , Ghorbani AA. A detailed analysis of the KDD cup 99 data set. In: 2009 IEEE symposium on computational intelligence for security and defense applications. IEEE; 2009, pp. 1–6.

Sarker IH, Abushark YB, Alsolami F, Khan AI. Intrudtree: a machine learning based cyber security intrusion detection model. Symmetry. 2020;12(5):754.

Canadian institute of cybersecurity, university of new brunswick, ISCX dataset. http://www.unb.ca/cic/datasets/index.html/ . Accessed 20 Oct 2019.

CSE-CIC-IDS 2018 [online]. https://www.unb.ca/cic/ datasets/ids-2018.html/ . Accessed 20 Oct 2019.

Xuyang J, Zheng Y, Xueqin J, Witold P. Network traffic fusion and analysis against DDOS flooding attacks with a novel reversible sketch. Inf Fusion. 2019;51:100–13.

Xie M, Hu J, Yu CE. Evaluating host-based anomaly detection systems: application of the frequency-based algorithms to adfa-ld. In: International conference on network and system security. Springer (2015).

Caida ddos attack 2007 dataset. http://www.caida.org/data/ passive/ddos-20070804-dataset.xml/ . Accessed 20 October 2019.

Caida anonymized internet traces 2008 dataset. http://www.caida.org/data/passive/passive-2008-dataset.xml/ . Accessed 20 Oct 2019.

Isot botnet dataset. https://www.uvic.ca/engineering/ece/isot/ datasets/index.php/ . Accessed 20 Oct 2019.

The honeynet project. http://www.honeynet.org/chapters/france/ . Accessed 20 Oct 2019.

The ctu-13 dataset. https://stratosphereips.org/category/datasets-ctu13 . Accessed 20 Oct 2019.

Alexa top sites. https://aws.amazon.com/alexa-top-sites/ . Accessed 20 Oct 2019.

Bambenek consulting–master feeds. http://osint.bambenekconsulting.com/feeds/ . Accessed 20 October 2019.

Dgarchive. https://dgarchive.caad.fkie.fraunhofer.de/site/ . Accessed 20 Oct 2019.

Moustafa N, Slay J. UNSW-NB15: a comprehensive data set for network intrusion detection systems (UNSW-NB15 network data set). In: 2015 military communications and information systems conference (MilCIS). IEEE; 2015, pp. 1–6.

Shiravi A, Shiravi H, Tavallaee M, Ghorbani AA. Toward developing a systematic approach to generate benchmark datasets for intrusion detection. Comput Secur. 2012;31(3):357–74.

Google play store. available online: https://play.google.com/store/ . Accessed 20 Oct 2019.

Virustotal. https://virustotal.com/ . Accessed 20 Oct 2019.

Zhou Y, Jiang X. Dissecting android malware: characterization and evolution. In: 2012 IEEE symposium on security and privacy. IEEE; 2012. pp. 95–109.

Virusshare. http://virusshare.com/ . Accessed 20 Oct 2019.

Comodo. https://www.comodo.com/home/internet-security/updates/vdp/database.php . Accessed 20 Oct 2019.

Contagio. http://contagiodump.blogspot.com/ . Accessed 20 Oct 2019.

Kumar R, Zhang X, Ullah Khan R, Kumar J, Ahad I. Effective and explainable detection of android malware based on machine learning algorithms. In: Proceedings of the 2018 international conference on computing and artificial intelligence. ACM; 2018. pp. 35–40.

Microsoft malware classification (big 2015). http://arxiv.org/abs/1802.10135/ . Accessed 20 Oct 2019.

Berman DS, Buczak AL, Chavis JS, Corbett CL. A survey of deep learning methods for cyber security. Information. 2019;10(4):122.

Lindauer B, Glasser J, Rosen M, Wallnau KC, Exactdata L. Generating test data for insider threat detectors. JoWUA. 2014;5(2):80–94.

Joshua G, Brian L. Bridging the gap: a pragmatic approach to generating insider threat data. In: 2013 IEEE security and privacy workshops, pp. 98–104. IEEE. 2013.

Enronspam. https://labs-repos.iit.demokritos.gr/skel/i-config/downloads/enron-spam/ . Accessed 20 Oct 2019.

Spamassassin. available online: http://www.spamassassin.org/publiccorpus/ . Accessed 20 Oct 2019.

Lingspam. https://labs-repos.iit.demokritos.gr/skel/i-config/downloads/lingspampublic.tar.gz/ . Accessed 20 Oct 2019.

Nickolaos K, Nour M, Elena S, Benjamin T. Towards the development of realistic botnet dataset in the internet of things for network forensic analytics: Bot-iot dataset. Future Gener Comput Syst. 2019;100:779–96.

Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al . Scikit-learn: machine learning in python. J Mach Learn Res. 2011;12:2825–30.

MathSciNet   MATH   Google Scholar  

Sarker IH. Ai-driven cybersecurity: an overview, security intelligence modeling and research directions. 2021.

Jiawei H, Jian P, Micheline K. Data mining: concepts and techniques. Amsterdam: Elsevier; 2011.

Felipe De AF, Edward DMO, Hendrik TM, Ricardo JPDBS, Filipe Barreto Do N, Flavio AOS. Intrusion detection via MLP neural network using an arduino embedded system. In: 2018 VIII Brazilian symposium on computing systems engineering (SBESC), pp 190–195. IEEE. 2018.

ElMouatez BK, Mourad D, Abdelouahid D, Djedjiga M. Maldozer: Automatic framework for android malware detection using deep learning. Digit Investig. 2018;24:S48–59.

Hodo E, Bellekens X, Hamilton A, Dubouilh P-L, Iorkyase E, Christos T, Robert A. Threat analysis of IoT networks using artificial neural network intrusion detection system. In: 2016 international symposium on networks, computers and communications (ISNCC). IEEE; 2016, pp. 1–6

Yousra J, Navid R. Multi-layer perceptron artificial neural network based IoT botnet traffic classification. In: Proceedings of the future technologies conference. Springer; 2019, pp. 973–84.

Iván G-M, Rajarajan M, Jaime L. Human-centric AI for trustworthy IoT systems with explainable multilayer perceptrons. IEEE Access. 2019;7:125562–74.

Yann LC, Léon B, Yoshua B, Patrick H. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86(11):2278–324.

Aurélien G. Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow: concepts, tools, and techniques to build intelligent systems. O’Reilly Media, 2019.

Susilo B, Sari RF. Intrusion detection in IoT networks using deep learning algorithm. Information. 2020;11(5):279.

Yan J, Qi Y, Rao Q. Detecting malware with an ensemble method based on deep neural network. Secur Commun Netw. 2018; 2018.

McLaughlin N, Martinez del RJ, Kang BJ, Yerima S, Miller P, Sezer S, Safaei Y, Trickel E, Zhao Z, Doupé A et al. Deep android malware detection. In: Proceedings of the seventh ACM on conference on data and application security and privacy; 2017. pp. 301–308.

Xiao X, Zhang D , Hu G Jiang Y, Xia S. CNN-MHSA: a convolutional neural network and multi-head self-attention combined approach for detecting phishing websites. Neural Netw (2020).

Yanmiao L, Yingying X, Zhi L, Haixia H, Yushuo Z, Yang X, Yuefeng Z, Lizhen C. Robust detection for network intrusion of industrial IoT based on multi-CNN fusion. Measurement. 2020;154:107450.

Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. In: Advances in neural information processing systems; 2012, pp. 1097–1105.

Chollet F. Xception: Deep learning with depthwise separable convolutions. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 1251–1258. 2017.

Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going deeper with convolutions. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2015, pp. 1–9.

Kaiming H, Xiangyu Z, Shaoqing R, Jian S. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans Pattern Anal Mach Intell. 2015;37(9):1904–16.

Kaiming H, Xiangyu Z, Shaoqing R, Jian S. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778. 2016.

Ian G, Yoshua B, Aaron C, Yoshua B. Deep learning, vol. 1. Cambridge: MIT press Cambridge; 2016.

Changhui J, Yuwei C, Shuai C, Yuming B, Wei L, Wenxin T, Jun G. A mixed deep recurrent neural network for mems gyroscope noise suppressing. Electronics. 2019;8(2):181.

Jihyun K, Jaehyun K, Huong LTT, Howon K. Long short term memory recurrent neural network classifier for intrusion detection. In: 2016 international conference on platform technology and service (PlatCon). IEEE; 2016. pp. 1–5.

Vinayakumar R, Soman KP, Poornachandran P. Deep android malware detection and classification. In: 2017 International conference on advances in computing, communications and informatics (ICACCI). IEEE; 2017, pp. 1677–1683.

Adebowale MA, Lwin KT, Hossain MA. Intelligent phishing detection scheme using deep learning algorithms. J Enterp Inf Manag. 2020.

Tran D, Mac H, Tong V, Tran HA, Nguyen LG. A LSTM based framework for handling multiclass imbalance in DGA botnet detection. Neurocomputing. 2018;275:2401–13.

Teuvo K. The self-organizing map. Proc IEEE. 1990;78(9):1464–80.

Juha V, Esa A. Clustering of the self-organizing map. IEEE Trans Neural Netw. 2000;11(3):586–600.

Teuvo K. Essentials of the self-organizing map. Neural Netw. 2013;37:52–65.

Qu X, Yang L, Guo K, Ma L, Sun M, Ke M, Li M. A survey on the development of self-organizing maps for unsupervised intrusion detection. Mob Netw Appl. 2019; 1–22.

Langin C, Zhou H, Rahimi S, Gupta B, Zargham M, Sayeh MR. A self-organizing map and its modeling for discovering malignant network traffic. In: 2009 IEEE symposium on computational intelligence in cyber security. IEEE, 2009; pp. 122–129.

Ameya M, Roberto C, Iluju K, Michelangelo C, Nathalie J. Spark-GHSOM: growing hierarchical self-organizing map for large scale mixed attribute datasets. Inf Sci. 2019;496:572–91.

Le Duc C, Zincir-Heywood AN, Heywood MI. Data analytics on network traffic flows for botnet behaviour detection. In: 2016 IEEE symposium series on computational intelligence (SSCI), pp. 1–7. IEEE, 2016.

López AU, Mateo F, Navío-Marco J, Martínez-Martínez JM, Gómez-Sanchís J, Vila-Francés J, José Serrano-López A. Analysis of computer user behavior, security incidents and fraud using self-organizing maps. Comput Secur. 2019;83:38–51.

Liu W, Wang Z, Liu X, Zeng N, Liu Y, Alsaadi FE. A survey of deep neural network architectures and their applications. Neurocomputing. 2017;234:11–26.

Sarker IH, Abushark YB, Khan AI. Contextpca: Predicting context-aware smartphone apps usage based on machine learning techniques. Symmetry. 2020;12(4):499.

Guijuan Z, Yang L, Xiaoning J. A survey of autoencoder-based recommender systems. Front Comput Sci. 2020;14(2):430–50.

Sarker IH, Hoque MM, Uddin MK, Alsanoosy T. Mobile data science and intelligent apps: Concepts, AI-based modeling and research directions. Mob Netw Appl 1–19; 2020.

Yousefi-Azar M, Varadharajan V, Hamey L, Tupakula U. Autoencoder-based feature learning for cyber security applications. In: 2017 International joint conference on neural networks (IJCNN). IEEE; 2017. pp. 3854–3861.

Liu L, De Vel O, Chen C, Zhang J, Xiang Y. Anomaly-based insider threat detection using deep autoencoders. In: 2018 IEEE international conference on data mining workshops (ICDMW). IEEE, 2018, pp. 39–48.

Wei W, Mengxue Z, Jigang W. Effective android malware detection with a hybrid model based on deep autoencoder and convolutional neural network. J Ambient Intel Humaniz Comput. 2019;10(8):3035–43.

Binghao Y, Guodong H. Effective feature extraction via stacked sparse autoencoder to improve intrusion detection system. IEEE Access. 2018;6:41238–48.

Memisevic R, Hinton GE. Learning to represent spatial transformations with factored higher-order Boltzmann machines. Neural Comput. 2010;22(6):1473–92.

Benjamin M, Kevin S, Bo C, Nando F. Inductive principles for restricted Boltzmann machine learning. In: Proceedings of the thirteenth international conference on artificial intelligence and statistics. JMLR workshop and conference proceedings; 2010, pp. 509–516.

Hinton GE, Osindero S, Yee-Whye T. A fast learning algorithm for deep belief nets. Neural Comput. 2006;18(7):1527–54.

Fiore U, Palmieri F, Castiglione A, De Santis A. Network anomaly detection with the restricted Boltzmann machine. Neurocomputing. 2013;122:13–23.

Yadigar I, Fargana A. Deep learning method for denial of service attack detection based on restricted Boltzmann machine. Big Data. 2018;6(2):159–69.

Seo S, Park S, Kim J. Improvement of network intrusion detection accuracy by using restricted boltzmann machine. In: 2016 8th international conference on computational intelligence and communication networks (CICN). IEEE; 2016. pp. 413–417.

Hinton GE. Deep belief networks. Scholarpedia. 2009;4(5):5947.

Peng W, Yufeng L, Zhen Z, Tao H, Ziyong L, Diyang L. An optimization method for intrusion detection classification model based on deep belief network. IEEE Access. 2019;7:87593–605.

Salama MA, Eid HF , Ramadan RA , Darwish A, Hassanien AE. Hybrid intelligent intrusion detection scheme. In: Soft computing in industrial applications. Springer; 2011, pp. 293–303.

Qu F, Zhang J Shao Z, Qi S. An intrusion detection model based on deep belief network. In: Proceedings of the 2017 VI international conference on network, communication and computing; 2017. pp. 97–101.

Ian G, Jean P-A, Mehdi M, Bing X, David W-F, Sherjil O, Aaron C, Yoshua B. Generative adversarial nets. In: Advances in neural information processing systems, pp. 2672–2680. 2014.

Jin-Young K, Seok-Jun B, Sung-Bae C. Malware detection using deep transferred generative adversarial networks. In: International conference on neural information processing. Springer; 2017. pp. 556–564.

Jin-Young K, Seok-Jun B, Sung-Bae C. Zero-day malware detection using transferred generative adversarial networks based on deep autoencoders. Inf Sci. 2018;460:83–102.

Yin C, Zhu Y, Liu S , Fei J, Zhang H. An enhancing framework for botnet detection using generative adversarial networks. In: 2018 international conference on artificial intelligence and big data (ICAIBD). IEEE; 2018. pp. 228–234.

Heng L, ShiYao Z, Wei Y, Jiahuan L, Henry L. Adversarial-example attacks toward android malware detection system. IEEE Syst J. 2019;14(1):653–6.

Merino T, Stillwell M, Steele M, Coplan M, Patton J, Stoyanov A, Deng L. Expansion of cyber attack data from unbalanced datasets using generative adversarial networks. In: International conference on software engineering research, management and applications. Springer; 2019, pp. 131–145.

Weiss K, Khoshgoftaar TM, Wang DD. A survey of transfer learning. J Big Data. 2016;3(1):9.

Pan SJ, Qiang Y. A survey on transfer learning. IEEE Trans Knowl Data Eng. 2009;22(10):1345–59.

Wu P, Guo H, Buckland R. A transfer learning approach for network intrusion detection. In 2019 IEEE 4th international conference on big data analytics (ICBDA), pp. 281–285. IEEE (2019).

Daniel N, Aviad C, Nir N, Yuval E. Deep feature transfer learning for trusted and automated malware signature generation in private cloud environments. Neural Networks. 2020;124:243–57.

Nahmias D, Cohen A, Nissim N, Elovici Y. Trustsign: trusted malware signature generation in private clouds using deep feature transfer learning. In: 2019 international joint conference on neural networks (IJCNN). IEEE; 2019, pp. 1–8.

Zhao J, Shetty S, Pan JW, Kamhoua C, Kwiat K. Transfer learning for detecting unknown network attacks. EURASIP J Inf Secur. 2019;2019(1):1.

Xianwei G, Changzhen H, Chun S, Baoxu L, Zequn N, Hui X. Malware classification for the cloud via semi-supervised transfer learning. J Inf Secur Appl. 2020;55:102661.

Rezende E , Ruppert G, Carvalho T, Ramos F, De Geus P. Malicious software classification using transfer learning of resnet-50 deep neural network. In: 2017 16th IEEE international conference on machine learning and applications (ICMLA). IEEE; 2017. pp. 1011–1014.

Vu L, Nguyen QU, Nguyen DN, Hoang DT, Dutkiewicz E. Deep transfer learning for IoT attack detection. IEEE Access. 2020;8:107335–44.

Taekeun H, Chang C, Juhyun S. CNN-based malicious user detection in social networks. Concurr Comput Pract Exp. 2018;30(2):e4163.

Li Q, Cheng M, Wang J, Sun B. LSTM based phishing detection for big email data. IEEE Trans Big Data. 2020.

Shi W-C, Sun H-M. Deepbot: a time-based botnet detection with deep learning. Soft Comput. 2020.

Abuhamad M, Abuhmed T, Mohaisen D, Nyang D. AUToSen: Deep-learning-based implicit continuous authentication using smartphone sensors. IEEE Internet Things J. 2020;7(6):5008–20.

Mayuranathan M, Murugan M,Dhanakoti V. Best features based intrusion detection system by RBM model for detecting DDOS in cloud environment. J Ambient Intel Humaniz Comput 2019;1–11.

Alom MZ, Taha TM. Network intrusion detection for cyber security using unsupervised deep learning approaches. In: 2017 IEEE national aerospace and electronics conference (NAECON), pp 63–69. IEEE. 2017.

Yi P, Guan Y, Zou F, Yao Y , Wang W , Zhu T. Web phishing detection using a deep learning framework. Wirel Commun Mob Comput. 2018; 2018.

Arshey M, Angel VKS. An optimization-based deep belief network for the detection of phishing. Data Technol. Appl. 2020.

Saif D, El-Gokhy SM, Sallam E. Deep belief networks-based framework for malware detection in android systems. Alex Eng J. 2018;57(4):4049–57.

Shifu H, Aaron S, Yanfang Y, Lifei C. Droiddelver: an android malware detection system using deep belief network based on API call blocks. In: International conference on web-age information management. Springer; 2016. pp. 54–66.

Manuel L-M, Belen C, Antonio S-E. Application of deep reinforcement learning to intrusion detection for supervised problems. Expert Syst Appl. 2020;141:112963.

Sethi K, Kumar R, Prajapati N, Bera P. Deep reinforcement learning based intrusion detection system for cloud infrastructure. In: 2020 international conference on communication systems & networks (COMSNETS). IEEE. 2020; pp. 1–6.

Zhiyang F, Junfeng W, Jiaxuan G, Xuan K. Feature selection for malware detection based on reinforcement learning. IEEE Access. 2019;7:176177–87.

Shakeel PM, Baskar S, Dhulipala VRS, Mishra S, Jaber MM. Maintaining security and privacy in health care system using learning based deep-q-networks. J Med Syst. 2018;42(10):186.

Arulkumaran K, Deisenroth MP, Brundage M, Bharath AA. Deep reinforcement learning: a brief survey. IEEE Signal Process Mag. 2017;34(6):26–38.

Parra GDLT, Rad P, Kim-Kwang RC, Nicole B. Detecting internet of things attacks using distributed deep learning. J Netw Comput Appl.; 2020. 102662.

Sarker IH, Kayes ASM, Watters P. Effectiveness analysis of machine learning classification models for predicting personalized context-aware smartphone usage. J Big Data. 2019;6(1):57.

Sarker IH. A machine learning based robust prediction model for real-life mobile phone data. Internet Things. 2019;5:180–93.

Sarker IH. Context-aware rule learning from smartphone data: survey, challenges and future directions. J Big Data. 2019;6(1):95.

Sarker IH, Colman A, Kabir MA, Han J. Individualized time-series segmentation for mining mobile phone user behavior. Comput J. 2018;61(3):349–68.

Sarker IH, Kayes ASM. ABC-ruleminer: user behavioral rule-based machine learning method for context-aware intelligent services. J Netw Comput Appl. 2020;168:102762.

Sarker IH, Colman A, Han J. Recencyminer: mining recency-based personalized behavior from contextual smartphone data. J Big Data. 2019;6(1):1–21.

Download references

Author information

Authors and affiliations.

Swinburne University of Technology, Melbourne, VIC, 3122, Australia

Iqbal H. Sarker

Department of Computer Science and Engineering, Chittagong University of Engineering & Technology, Chittagong, 4349, Bangladesh

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Iqbal H. Sarker .

Ethics declarations

Conflict of interest.

The author declares no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This article is part of the topical collection “Deep learning approaches for data analysis: A practical perspective” guest edited by D. Jude Hemanth, Lipo Wang and Anastasia Angelopoulou.

Rights and permissions

Reprints and permissions

About this article

Sarker, I.H. Deep Cybersecurity: A Comprehensive Overview from Neural Network and Deep Learning Perspective. SN COMPUT. SCI. 2 , 154 (2021). https://doi.org/10.1007/s42979-021-00535-6

Download citation

Received : 19 November 2020

Accepted : 19 February 2021

Published : 20 March 2021

DOI : https://doi.org/10.1007/s42979-021-00535-6

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Cybersecurity
• Deep learning
• Artificial neural network
• Artificial intelligence
• Cyberattacks
• Cybersecurity analytics
• Cyber threat intelligence

Advertisement

• Find a journal
• Publish with us
• Track your research

An Improved Face Recognition Method Based on Convolutional Neural Network

• Syed Muhammad Daniyal Faculty of Engineering, Science and Technology Iqra University Karachi, Pakistan
• Atiya Masood Faculty of Engineering, Science and Technology Iqra University Karachi, Pakistan
• Mansoor Ebrahim Faculty of Engineering, Science and Technology Iqra University Karachi, Pakistan
• Syed Hasan Adil Faculty of Engineering, Science and Technology Iqra University Karachi, Pakistan
• Kamran Raza Faculty of Engineering, Science and Technology Iqra University Karachi, Pakistan

Face recognition using an image-processing technique is a valuable and effective approach to verifying the identity of a human being. Authorizing users based on human face identification remains one of the biggest challenges. However, with the improvement of deep learning and the creation of deep convolutional neural networks, the performance of face recognition has significantly improved. However, the outcomes from different models and networks are quite different in terms of accuracy. This paper proposes a face recognition model based on a Convolutional neural network (CNN). The recognition rate of the AT&T and AR data set on the proposed model is 99.17% and 99.12%.

K. Hamann and R. Smith, “Facial recognition technology,” Criminal Justice, vol. 34, no. 1, pp. 9–13, 2019.

Y. Kortli, M. Jridi, A. Al Falou, and M. Atri, “Face recognition systems: A survey,” Sensors, vol. 20, no. 2, p. 342, 2020.

A. Hazra, P. Choudhary, S. Inunganbi, and M. Adhikari, “Bangla-meitei mayek scripts handwritten character recognition using convolutional neural network,” Applied Intelligence, vol. 51, no. 4, pp. 2291–2311, 2021.

W. McNally, K. Vats, A. Wong, and J. McPhee, “Evopose2d: Pushing the boundaries of 2d human pose estimation using accelerated neuroevolution with weight transfer,” IEEE Access, vol. 9, pp. 139 403–139 414, 2021.

S. A. Sovitkar and S. S. Kawathekar, “Comparative study of feature- based algorithms and classifiers in face recognition for automated attendance system,” in 2020 2nd international conference on innovative mechanisms for industry applications (ICIMIA). IEEE, 2020, pp. 195– 200.

K. Pranav and J. Manikandan, “Design and evaluation of a real-time face recognition system using convolutional neural networks,” Procedia Computer Science, vol. 171, pp. 1651–1659, 2020.

N. Sabri, J. Henry, Z. Ibrahim, N. Ghazali, N. N. A. Mangshor, N. F. M. Johari, and S. Ibrahim, “A comparison of face detection classifier using facial geometry distance measure,” in 2018 9th IEEE Control and System Graduate Research Colloquium (ICSGRC). IEEE, 2018, pp. 116–120.

M. Arsenovic, S. Sladojevic, A. Anderla, and D. Stefanovic, “Face- time—deep learning based face recognition attendance system,” in 2017 IEEE 15th International symposium on intelligent systems and informatics (SISY). IEEE, 2017, pp. 000 053–000 058.

S. Saleem, J. Shiney, B. P. Shan, and V. K. Mishra, “Face recognition using facial features,” Materials Today: Proceedings, vol. 80, pp. 3857– 3862, 2023.

K. Sarvakar, R. Senkamalavalli, S. Raghavendra, J. S. Kumar, R. Man- junath, and S. Jaiswal, “Facial emotion recognition using convolutional neural networks,” Materials Today: Proceedings, vol. 80, pp. 3560– 3564, 2023.

B. Sowmya, S. A. Alex, A. Kanavalli, S. Supreeth, G. Shruthi, S. Rohith et al., “Machine learning model for emotion detection and recognition using an enhanced convolutional neural network,” Journal of Integrated Science and Technology, vol. 12, no. 4, pp. 786–786, 2024.

K. Yan, S. Huang, Y. Song, W. Liu, and N. Fan, “Face recognition based on convolution neural network,” in 2017 36th Chinese Control Conference (CCC). IEEE, 2017, pp. 4077–4081.

A. F. Agarap, “Deep learning using rectified linear units (relu),” arXiv preprint arXiv:1803.08375, 2018.

M. Wang, P. Tan, X. Zhang, Y. Kang, C. Jin, and J. Cao, “Facial expression recognition based on cnn,” in Journal of Physics: Conference Series, vol. 1601, no. 5. IOP Publishing, 2020, p. 052027.

L. Alzubaidi, J. Zhang, A. J. Humaidi, A. Al-Dujaili, Y. Duan, O. Al- Shamma, J. Santamar´ıa, M. A. Fadhel, M. Al-Amidie, and L. Farhan, “Review of deep learning: Concepts, cnn architectures, challenges, applications, future directions,” Journal of big Data, vol. 8, no. 1, pp. 1–74, 2021.

T. Jin, Z. Liu, Z. Yu, X. Min, and L. Li, “Locality preserving collab- orative representation for face recognition,” Neural Processing Letters, vol. 45, pp. 967–979, 2017.

M. Wang, Z. Wang, and J. Li, “Deep convolutional neural network applies to face recognition in small and medium databases,” in 2017 4th International Conference on Systems and Informatics (ICSAI). IEEE, 2017, pp. 1368–1372.

H. ben Fredj, S. Sghaier, and C. Souani, “An efficient face recognition method using cnn,” in 2021 International Conference of Women in Data Science at Taif University (WiDSTaif). IEEE, 2021, pp. 1–5.

S. Jain, V. Chaudhari, R. Chuadhari, T. Chavan, and P. Shahane, “A sur- vey on face recognition techniques in machine learning,” International Journal of Scientific Research in Computer Science, Engineering and Information Technology (IJSRCSEIT), vol. 8, no. 6, pp. 50–66, 2022.

M. Norouzi et al., “A survey on face recognition based on deep neural networks,” 2022.

M. Tamilselvi and S. Karthikeyan, “An ingenious face recognition system based on hrpsm cnn under unrestrained environmental condition,” Alexandria Engineering Journal, vol. 61, no. 6, pp. 4307–4321, 2022.

Information

• For Readers
• For Authors
• For Librarians