importance of mathematics research paper

Importance and Application of Mathematics in Everyday Life

Abstract: Mathematics is a field of science that studies numbers and how they are used. It includes calculations, computations, and problem solving, among other things. It is a subject that is accurate, precise, methodical, and logical. Mathematics has been defined in a variety of ways throughout history; it is an indispensible component of science and is utilized in virtually every discipline, including natural science, engineering, art, and economics. Mathematics is a vital instrument in our lives and in every scientific field that promotes personal growth and development on a broad scale. To avoid chaos and confusion, mathematics makes life smoother and more organized. Problem solving, creativity, critical thinking, and reasoning capacity are some of the traits and talents fostered by mathematics. Other unique skills include analyzing and communicating effectively. Everyone requires mathematics in their daily lives, whether they are a cook or a farmer, a carpenter or a mechanic, a shopkeeper or a doctor, an engineer or a scientist, a musician or a magician. Therefore, it would be impossible to summarize mathematics applications in each field. Through this research document, it is intended to talk about the importance and applications of mathematics in our daily lives. Keywords: Mathematics, Importance of Mathematics, Application of Mathematics, Analysis, Problem Solving and Critical Thinking Abilities.

• Related Documents

Leading Learning Communities with Creative Practice

Reflective leadership stories from various fields including, instructional technology, education and humanities guide the reader to reflect upon practice. Leadership theories that support personal growth, caring, interpersonal communication, problem solving, and creativity are discussed (Bass, 2008). Furthermore, the authors describe how creative leaders can use Communities of Practice (CoPs) as a mechanism to share and build knowledge, solve problems, and foster professional growth and development.

Engaging Students in Critical Thinking and Problem Solving: A Brief Review of the Literature

<p>Problem solving and critical thinking skills are beneficial across all fields of collegiate studies and provide lasting value in the workplace and everyday life.  In problem solving, students employ critical thinking skills in the analyses of problems and the synthesis and applications of previously learned concepts.  For decades, researchers and academics have deliberated on ways to engage students in the classroom to train them in these skills.  The collective research on teaching critical thinking and problem solving reveal overarching themes, which include student involvement, learning styles, student motivation, and instructor perceptions and behaviors.</p>

Basic Approaches to Adjustment Services in Rehabilitation

Work acclimation, problem solving, personal growth and development, and education are described as four basic approaches to the treatment/training process known as Adjustment Services in Rehabilitation. Techniques common to each approach are discussed for rehabilitation counselors and facility professionals. Although not mutually exclusive, the separate treatment of each approach illustrates the current state of the art of adjustment services.

Aspects of Free Market Economy & Autonomy in Applied Philosophy

The aim of the course is to engage students in a wide variety of activities and experiences that will assist in the development of critical thinking, analysis and problem solving skills. Through exposure to a wide range of historical perspectives across different domains of knowledge (including History, Science, Art, Ethics, Psychology and Literature) and the opportunity to discuss problems and scenarios from everyday life, students will develop a deeper understanding of their personal values and the perspectives of others. This course aims to develop students into inquirers with a critical disposition and a thirst for knowledge.

INQUIRY AS A KEY TO DEEPER LEARNING

In spite of the fact that critical thinking is a vital skill not only during studying at university but in everyday life either, students are often unprepared for critically thinking when they start their studies. That is why it is so necessary to explain how to use practical strategies for developing these skills for a successful academic life. First of all, teachers should always bear in mind Bloom’s Taxonomy as it helps them to find the correct way for teaching showing the nearest and the furthest goals in their work. The levels start from the simplest and go to the most complicated ones showing that no one can acquire a higher level without mastering the lower ones and that their acquiring is necessary for bringing up critically thinking students. Creating a culture of inquiry is constant work which grows problem-solving learners with deeper understanding of important knowledge. Being convinced that a significant tool for creating a culture of inquiry is essential questions that drive and motivate learning, the authors have designed some recommendations that can encourage inquiry-based learning process and involve students in it. As inquiry-based learning elevates students’ autonomy and collaboration, and helps to create a culture focused on researching rather than reproducing information, the authors consider that teachers should focus on question formulation technique. Besides, four phases of inquiry-based learning have been distinguished and described in details.  

Problem-based Learning: Nursing students’ attitude, self-reported competence, tutorial performance and self-directed learning readiness

Background and objectives: Problem-based learning (PBL) is widely recognized as progressive pedagogy for the preparation of a range of health professionals. Despite the prominence of PBL in contemporary discussions about the education of future health professionals, its value is increasingly being contested in light of shrinking resources and increasing student enrolments in universities.  The objectives were to ascertain Bachelor of Nursing (BN) students’ attitude towards the value of PBL as a learning strategy; to determine BN students’ degree of certainty about their competence in PBL processes; to determine whether student performance in PBL tutorials improve over four years of study; and to compare the self-directed learning readiness of PBL students to those who are not exposed to PBL.Methods: The study followed a descriptive and comparative survey design to collect the data. Participants were BN students who were invited to participate in the descriptive survey (n = 92), and purposively selected (n = 159) for comparison between PBL (n = 54) and non-PBL (n = 105) groups.Results: The majority of students found PBL a stimulating (59.8%; n = 55), useful (65.2%; n = 60), empowering (70.6%; n = 65) and enlightening (60.8%; n = 56) learning strategy; most students (53.2%; n = 49) expressed certainty about their competence in “accessing relevant literature/evidence” but more (56.3%; n = 52) were less certain about their ability to “integrate information into nursing care”. First year students performed poorly in PBL tutorials but showed a significant improvement in the final year of study in problem-solving (p = .0001), contribution to the group (p = .000), communication (p = .000), critical thinking (p = .001), learning skills (p = .001), personal growth (p = .000) and leadership skills (p = .041). There was no significant difference between PBL and non-PBL students’ overall readiness for self-directed learning (p = .69).Conclusions: The findings suggest that BN students generally have a positive attitude towards PBL, finding it stimulating, useful, empowering and enlightening in a transformative learning environment. However, fewer students feel that they are competent in the majority of the PBL processes. The biggest learning gains for students during PBL tutorials are in problem-solving, contributions to the group, communication, learning skills, critical thinking, personal growth and leadership. PBL and non-PBL students are similar in their self-directed learning readiness regardless of the learning strategy used.

Problem based learning (PBL) in Organic Chemistry

Background: PBL appears to answer many concerns regarding educational methods, encourages students to look for new solutions to relevant problems using available knowledge and resources. The process expands students' critical thinking and problem solving skills while enhancing their creative capabilities Objective: To develop a PBL modules for teaching of organic chemistry. Methods: This module was developed for implementation in the curriculum of Chemistry Departments in Colleges of Sciences and Education. This is an innovations to be developed for increasing the wide-ranging abilities of students. A series of strategies which are involved in PBL, concept mapping and online communications, are suggested and discussed in terms of encouraging student-centered learning.  

PERBEDAAN PENINGKATAN KETERAMPILAN BERPIKIR KRITIS SISWA PADA MATERI TERMOKIMIA MELALUI PEMBELAJARAN GROUP DAN INDIVIDUAL PROBLEM SOLVING

ABSTRACTThis research is aimed to know the differences increase critical thinking skills through learning group and individual problem solving in thermochemical material. This research uses a quasi-experimental design with nonequivalent control group design and study sample consisted of 103 students, divided into the first experimental (group problem solving) (35 students), the two group experimental (individual problem solving) (34 students). The collected through pretest-posttest. The analyzed with the Kruskal Wallis test, the results showed that the learning problem solving as a group or individually can improve students’ critical thinking skills. Statistical test there are significant differences in the students critical thinking skills thermochemical material between students who received group and individual problem solving. Critical thinking skills improvement with problem solving individual learning higher compared with group learning problem solving.Keywords: problem solving learning, critical thinking skillsABSTRAKPenelitian ini bertujuan untuk mengetahui perbedaan peningkatan keterampilan berpikir kritis siswa melalui pembelajaran group dan individual problem solving pada materi termokimia. Penelitian ini menggunakan metode quasi experimen dengan desain Nonequivalent Control Group Design dan sampel penelitian ini terdiri dari 103 siswa yang terbagi ke dalam kelompok eksperimen pertama (pembelajaran group problem solving) (35 siswa), kelompok eksperimen kedua (pembelajaran individual problem solving) (34 siswa).Pengumpulan data dilakukan melalui pretest-posttest. Data dianalisis dengan uji Kruskal Wallis Test, hasil penelitian menunjukkan bahwa pembelajaran problem solving secara group maupun secara individual dapat meningkatkan keterampilan berpikir kritis siswa. Data uji statistik, terdapat perbedaan yang signifikan keterampilan berpikir kritis siswa pada materi termokimia antara siswa yang mendapat pembelajaran group problem solving dan individual problem solving. Peningkatan keterampilan berpikir kritis dengan pembelajaran individual problem solving lebih tinggi dibandingkan dengan pembelajaran group problem solving.Kata Kunci: Pembelajaran Problem Solving, Keterampilan Berpikir Kritis

The effect of Havruta discussion activities on critical thinking dispositions and problem solving abilities of child care teacher

Export citation format, share document.

• Open access
• Published: 11 March 2019

Enhancing achievement and interest in mathematics learning through Math-Island

• Charles Y. C. Yeh   ORCID: orcid.org/0000-0003-4581-6575 1 ,
• Hercy N. H. Cheng 2 ,
• Zhi-Hong Chen 3 ,
• Calvin C. Y. Liao 4 &
• Tak-Wai Chan 5  

Research and Practice in Technology Enhanced Learning volume  14 , Article number:  5 ( 2019 ) Cite this article

45 Citations

3 Altmetric

Metrics details

Conventional teacher-led instruction remains dominant in most elementary mathematics classrooms in Taiwan. Under such instruction, the teacher can rarely take care of all students. Many students may then continue to fall behind the standard of mathematics achievement and lose their interest in mathematics; they eventually give up on learning mathematics. In fact, students in Taiwan generally have lower interest in learning mathematics compared to many other regions/countries. Thus, how to enhance students’ mathematics achievement and interest are two major problems, especially for those low-achieving students. This paper describes how we designed a game-based learning environment, called Math-Island , by incorporating the mechanisms of a construction management game into the knowledge map of the elementary mathematics curriculum. We also report an experiment conducted with 215 elementary students for 2 years, from grade 2 to grade 3. In this experiment, in addition to teacher-led instruction in the classroom, students were directed to learn with Math-Island by using their own tablets at school and at home. As a result of this experiment, we found that there is an increase in students’ mathematics achievement, especially in the calculation and word problems. Moreover, the achievements of low-achieving students in the experimental school outperformed the low-achieving students in the control school (a control group in another school) in word problems. Moreover, both the low-achieving students and the high-achieving students in the experimental school maintained a rather high level of interest in mathematics and in the system.

Introduction

Mathematics has been regarded as a fundamental subject because arithmetic and logical reasoning are the basis of science and technology. For this reason, educational authorities emphasize students’ proficiency in computational skills and problem-solving. Recently, the results of the Program for International Student Assessment (PISA) and the Trends in Mathematics and Science Study (TIMSS) in 2015 (OECD 2016 ; Mullis et al. 2016 ) revealed a challenge for Taiwan. Although Taiwanese students had higher average performance in mathematics literacy compared to students in other countries, there was still a significant percentage of low-achieving students in Taiwan. Additionally, most Taiwanese students show low levels of interest and confidence in learning mathematics (Lee 2012 ).

The existence of a significant percentage of low-achieving students is probably due to teacher-led instruction, which still dominates mathematics classrooms in most Asian countries. It should be noted that students in every classroom possess different abilities and hence demonstrate different achievements. Unfortunately, in teacher-led instruction, all the students are required to learn from the teacher in the same way at the same pace (Hwang et al. 2012 ). Low-achieving students, without sufficient time, are forced to receive knowledge passively. Barr and Tagg ( 1995 ) pointed out that it is urgent for low-achieving students to have more opportunities to learn mathematics at their own pace. Researchers suggested one-to-one technology (Chan et al. 2006 ) through which every student is equipped with a device to learn in school or at home seamlessly. Furthermore, they can receive immediate feedback from Math-Island, which supports their individualized learning actively and productively. Thus, this may provide more opportunities for helping low-achieving students improve their achievement.

The low-interest problem for almost all students in Taiwan is usually accompanied by low motivation (Krapp 1999 ). Furthermore, students with continuously low performance in mathematics may eventually lose their interest and refuse to learn further (Schraw et al. 2001 ). This is a severe problem. To motivate students to learn, researchers design educational games to provide enjoyable and engaging learning experiences (Kiili and Ketamo 2007 ). Some of these researchers found that game-based learning may facilitate students’ learning in terms of motivation and learning effects (Liu and Chu 2010 ), spatial abilities and attention (Barlett et al. 2009 ), situated learning, and problem-solving (Li and Tsai 2013 ). Given these positive results, we hope that our educational game can enhance and sustain the student’s interest in learning mathematics.

In fact, many researchers who endeavored to develop educational games for learning mathematics have shown that their games could facilitate mathematics performance, enjoyment, and self-efficacy (Ku et al. 2014 ; McLaren et al. 2017 ). Although some of the studies were conducted for as many as 4 months (e.g., Hanus and Fox 2015 ), one may still criticize them for the possibility that the students’ interest could be a novelty effect—meaning their interest will decrease as the feeling of novelty diminishes over time (Koivisto and Hamari 2014 ). Due to the limitations of either experimental time or sample sizes, most studies could not effectively exclude the novelty effect of games, unless they were conducted in a natural setting for a long time.

In this study, we collaborated with an experimental elementary school for more than 2 years. The mathematics teachers in the school adopted our online educational game, Math-Island . The students used their own tablet PCs to learn mathematics from the game in class or at home at their own pace. In particular, low-achieving students might have a chance to catch up with the other students and start to feel interested in learning mathematics. Most importantly, because the online educational game was a part of the mathematics curriculum, the students could treat the game as their ordinary learning materials like textbooks. In this paper, we reported a 2-year study, in which 215 second graders in the school adopted the Math-Island game in their daily routine. More specifically, the purpose of this paper was to investigate the effect of the game on students’ mathematics achievement. Additionally, we were also concerned about how well the low-achieving students learned, whether they were interested in mathematics and the game, and how their interest in mathematics compared with that of high-achieving students. In such a long-term study with a large sample size, it was expected that the novelty effect would be considerably reduced, allowing us to evaluate the effect of the educational game on students’ achievement and interest.

The paper is organized as follows. In the “ Related works ” section, we review related studies on computer-supported mathematics learning and educational games. In the “ Design ” section, the game mechanism and the system design are presented. In the “ Method ” section, we describe the research method and the procedures of this study. In the “ Results ” section, the research results about students’ achievement and interest are presented. In the “ Discussion on some features of this study ” section, we discuss the long-term study, knowledge map design, and the two game mechanisms. Finally, the summary of the current situation and potential future work is described in the “ Conclusion and future work ” section.

Related works

Computer-supported mathematics learning.

The mathematics curriculum in elementary schools basically includes conceptual understanding, procedural fluency, and strategic competence in terms of mathematical proficiency (see Kilpatrick et al. 2001 ). First, conceptual understanding refers to students’ comprehension of mathematical concepts and the relationships between concepts. Researchers have designed various computer-based scaffolds and feedback to build students’ concepts and clarify potential misconceptions. For example, for guiding students’ discovery of the patterns of concepts, Yang et al. ( 2012 ) adopted an inductive discovery learning approach to design online learning materials in which students were provided with similar examples with a critical attribute of the concept varied. McLaren et al. ( 2017 ) provided students with prompts to correct their common misconceptions about decimals. They conducted a study with the game adopted as a replacement for seven lessons of regular mathematics classes. Their results showed that the educational game could facilitate better learning performance and enjoyment than a conventional instructional approach.

Second, procedural fluency refers to the skill in carrying out calculations correctly and efficiently. For improving procedural fluency, students need to have knowledge of calculation rules (e.g., place values) and practice the procedure without mistakes. Researchers developed various digital games to overcome the boredom of practice. For example, Chen et al. ( 2012a , 2012b ) designed a Cross Number Puzzle game for practicing arithmetic expressions. In the game, students could individually or collaboratively solve a puzzle, which involved extensive calculation. Their study showed that the low-ability students in the collaborative condition made the most improvement in calculation skills. Ku et al. ( 2014 ) developed mini-games to train students’ mental calculation ability. They showed that the mini-games could not only improve students’ calculation performance but also increase their confidence in mathematics.

Third, strategic competence refers to mathematical problem-solving ability, in particular, word problem-solving in elementary education. Some researchers developed multilevel computer-based scaffolds to help students translate word problems to equations step by step (e.g., González-Calero et al. 2014 ), while other researchers noticed the problem of over-scaffolding. Specifically, students could be too scaffolded and have little space to develop their abilities. To avoid this situation, many researchers proposed allowing students to seek help during word problem-solving (Chase and Abrahamson 2015 ; Roll et al. 2014 ). For example, Cheng et al. ( 2015 ) designed a Scaffolding Seeking system to encourage elementary students to solve word problems by themselves by expressing their thinking first, instead of receiving and potentially abusing scaffolds.

Digital educational games for mathematics learning

Because mathematics is an abstract subject, elementary students easily lose interest in it, especially low-achieving students. Some researchers tailored educational games for learning a specific set of mathematical knowledge (e.g., the Decimal Points game; McLaren et al. 2017 ), so that students could be motivated to learn mathematics. However, if our purpose was to support a complete mathematics curriculum for elementary schools, it seemed impractical to design various educational games for all kinds of knowledge. A feasible approach is to adopt a gamified content structure to reorganize all learning materials. For example, inspired by the design of most role-playing games, Chen et al. ( 2012a , 2012b ) proposed a three-tiered framework of game-based learning—a game world, quests, and learning materials—for supporting elementary students’ enjoyment and goal setting in mathematics learning. Furthermore, while a game world may facilitate students’ exploration and participation, quests are the containers of learning materials with specific goals and rewards. In the game world, students receive quests from nonplayer virtual characters, who may enhance social commitments. To complete the quests, students have to make efforts to undertake learning materials. Today, quests have been widely adopted in the design of educational games (e.g., Azevedo et al. 2012 ; Hwang et al. 2015 ).

However, in educational games with quests, students still play the role of receivers rather than active learners. To facilitate elementary students’ initiative, Lao et al. ( 2017 ) designed digital learning contracts, which required students to set weekly learning goals at the beginning of a week and checked whether they achieved the goals at the end of the week. More specifically, when setting weekly goals, students had to decide on the quantity of learning materials that they wanted to undertake in the coming week. Furthermore, they also had to decide the average correctness of the tests that followed the learning materials. To help them set reasonable and feasible goals, the system provided statistics from the past 4 weeks. As a result, the students may reflect on how well they learned and then make appropriate decisions. After setting goals, students are provided with a series of learning materials for attempting to accomplish those goals. At the end of the week, they may reflect on whether they achieved their learning goals in the contracts. In a sense, learning contracts may not only strengthen the sense of commitment but also empower students to take more control of their learning.

In textbooks or classrooms, learning is usually predefined as a specific sequence, which students must follow to learn. Nevertheless, the structure of knowledge is not linear, but a network. If we could reorganize these learning materials according to the structure of knowledge, students could explore knowledge and discover the relationships among different pieces of knowledge when learning (Davenport and Prusak 2000 ). Knowledge mapping has the advantage of providing students concrete content through explicit knowledge graphics (Ebener et al. 2006 ). Previous studies have shown that the incorporation of knowledge structures into educational games could effectively enhance students’ achievement without affecting their motivation and self-efficacy (Chu et al. 2015 ). For this reason, this study attempted to visualize the structure of knowledge in an educational game. In other words, a knowledge map was visualized and gamified so that students could make decisions to construct their own knowledge map in games.

To enhance students’ mathematics achievement and interests, we designed the Math-Island online game by incorporating a gamified knowledge map of the elementary mathematics curriculum. More specifically, we adopt the mechanisms of a construction management game , in which every student owns a virtual island (a city) and plays the role of the mayor. The goal of the game is to build their cities on the islands by learning mathematics.

System architecture

The Math-Island game is a Web application, supporting cross-device interactions among students, teachers, and the mathematics content structure. The system architecture of the Math-Island is shown in Fig.  1 . The pedagogical knowledge and learning materials are stored in the module of digital learning content, organized by a mathematical knowledge map. The students’ portfolios about interactions and works are stored in the portfolio database and the status database. When a student chooses a goal concept in the knowledge map, the corresponding digital learning content is arranged and delivered to his/her browser. Besides, when the student is learning in the Math-Island, the feedback module provides immediate feedback (e.g., hints or scaffolded solutions) for guidance and grants rewards for encouragement. The learning results can also be shared with other classmates by the interaction module. In addition to students, their teachers can also access the databases for the students’ learning information. Furthermore, the information consists of the students’ status (e.g., learning performance or virtual achievement in the game) and processes (e.g., their personal learning logs). In the Math-Island, it is expected that students can manage their learning and monitor the learning results by the construction management mechanism. In the meantime, teachers can also trace students’ learning logs, diagnose their weaknesses from portfolio analysis, and assign students with specific tasks to improve their mathematics learning.

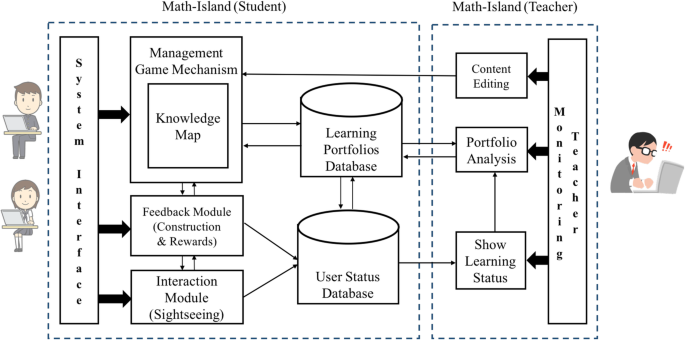
The system architecture of Math-Island

• Knowledge map

To increase students’ mathematics achievement, the Math-Island game targets the complete mathematics curriculum of elementary schools in Taiwan, which mainly contains the four domains: numerical operation , quantity and measure , geometry , and statistics and probability (Ministry of Education of R.O.C. 2003 ). Furthermore, every domain consists of several subdomains with corresponding concepts. For instance, the domain of numerical operation contains four subdomains: numbers, addition, and subtraction for the first and second graders. In the subdomain of subtraction, there are a series of concepts, including the meaning of subtraction, one-digit subtraction, and two-digit subtraction. These concepts should be learned consecutively. In the Math-Island system, the curriculum is restructured as a knowledge map, so that they may preview the whole structure of knowledge, recall what they have learned, and realize what they will learn.

More specifically, the Math-Island system uses the representational metaphor of an “island,” where a virtual city is located and represents the knowledge map. Furthermore, the island comprises areas, roads, and buildings, which are the embodiments of domains, subdomains, and concepts in the curriculum, respectively. As shown in Fig.  2 , for example, in an area of numeral operation in Math-Island, there are many roads, such as an addition road and a subtraction road. On the addition road, the first building should be the meaning of addition, followed by the buildings of one-digit addition and then two-digit addition. Students can choose these buildings to learn mathematical concepts. In each building, the system provides a series of learning tasks for learning the specific concept. Currently, Math-Island provides elementary students with more than 1300 learning tasks from the first grade to the sixth grade, with more than 25,000 questions in the tasks.

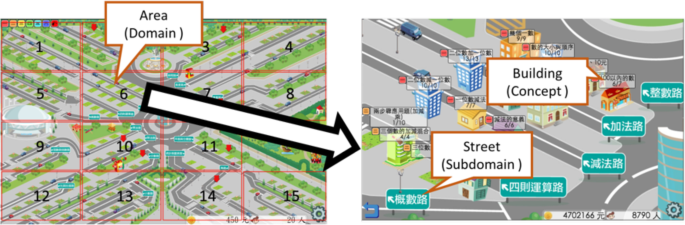
The knowledge map

In Math-Island, a learning task is an interactive page turner, including video clips and interactive exercises for conceptual understanding, calculation, and word problem-solving. In each task, the learning procedure mainly consists of three steps: watching demonstrations, practicing examples, and getting rewards. First, students learn a mathematical concept by watching videos, in which a human tutor demonstrates examples, explains the rationale, and provides instructions. Second, students follow the instructions to answer a series of questions related to the examples in the videos. When answering questions, students are provided with immediate feedback. Furthermore, if students input wrong answers, the system provides multilevel hints so that they could figure out solutions by themselves. Finally, after completing learning tasks, students receive virtual money according to their accuracy rates in the tasks. The virtual money is used to purchase unique buildings to develop their islands in the game.

Game mechanisms

In the Math-Island game, there are two game mechanisms: construction and sightseeing (as shown in Fig.  3 ). The former is designed to help students manage their learning process, whereas the latter is designed to facilitate social interaction, which may further motivate students to better develop their cities. By doing so, the Math-Island can be regarded as one’s learning portfolio, which is a complete record that purposely collects information about one’s learning processes and outcomes (Arter and Spandel 2005 ). Furthermore, learning portfolios are a valuable research tool for gaining an understanding about personal accomplishments (Birgin and Baki 2007 ), because learning portfolios can display one’s learning process, attitude, and growth after learning (Lin and Tsai 2001 ). The appearance of the island reflects what students have learned and have not learned from the knowledge map. When students observe their learning status in an interesting way, they may be concerned about their learning status with the enhanced awareness of their learning portfolios. By keeping all activity processes, students can reflect on their efforts, growth, and achievements. In a sense, with the game mechanisms, the knowledge map can be regarded as a manipulatable open learner model, which not only represents students’ learning status but also invites students to improve it (Vélez et al. 2009 ).

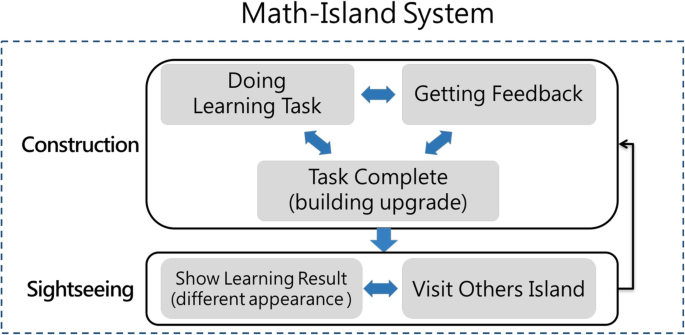
Two game mechanisms for Math-Island

First, the construction mechanism allows students to plan and manage their cities by constructing and upgrading buildings. To do so, they have to decide which buildings they want to construct or upgrade. Then, they are required to complete corresponding learning tasks in the building to determine which levels of buildings they can construct. As shown in Fig.  4 , the levels of buildings depend on the completeness of a certain concept, compared with the thresholds. For example, when students complete one third of the learning tasks, the first level of a building is constructed. Later, when they complete two thirds of the tasks, the building is upgraded to the second level. After completing all the tasks in a building, they also complete the final level and are allowed to construct the next building on the road. Conversely, if students failed the lowest level of the threshold, they might need to watch the video and/or do the learning tasks again. By doing so, students can make their plans to construct the buildings at their own pace. When students manage their cities, they actually attempt to improve their learning status. In other words, the construction mechanism offers an alternative way to guide students to regulate their learning efforts.

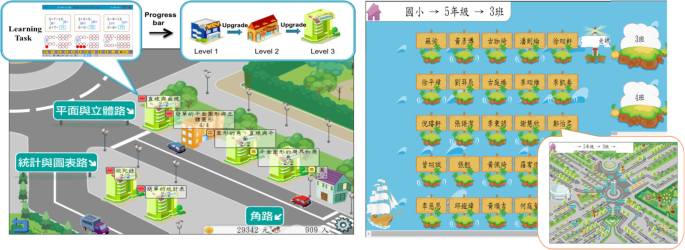
Screenshots of construction and sightseeing mechanisms in Math-Island

Second, the sightseeing mechanism provides students with a social stage to show other students how well their Math-Islands have been built. This mechanism is implemented as a public space, where other students play the role of tourists who visit Math-Island. In other words, this sightseeing mechanism harnesses social interaction to improve individual learning. As shown in Fig.  4 , because students can construct different areas or roads, their islands may have different appearances. When students visit a well-developed Math-Island, they might have a positive impression, which may facilitate their self-reflection. Accordingly, they may be willing to expend more effort to improve their island. On the other hand, the student who owns the island may also be encouraged to develop their island better. Furthermore, when students see that they have a completely constructed building on a road, they may perceive that they are good at these concepts. Conversely, if their buildings are small, the students may realize their weaknesses or difficulties in these concepts. Accordingly, they may be willing to make more effort for improvement. On the other hand, the student who owns the island may also be encouraged to develop their island better. In a word, the visualization may play the role of stimulators, so that students may be motivated to improve their learning status.

This paper reported a 2-year study in which the Math-Island system was adopted in an elementary school. The study addressed the following two research questions: (1) Did the Math-Island system facilitate students’ mathematics achievement in terms of conceptual understanding, calculating, and word problem-solving? In particular, how was the mathematics achievement of the low-achieving students? (2) What was students’ levels of interest in mathematics and the system, particularly that of low-achieving students?

Participants

The study, conducted from June 2013 to June 2015, included 215 second graders (98 females and 117 males), whose average age was 8 years old, in an elementary school located in a suburban region of a northern city in Taiwan. The school had collaborated with our research team for more than 2 years and was thus chosen as an experimental school for this study. In this school, approximately one third of the students came from families with a low or middle level of socioeconomic status. It was expected that the lessons learned from this study could be applicable to other schools with similar student populations in the future. The parents were supportive of this program and willing to provide personal tablets for their children (Liao et al. 2017 ). By doing so, the students in the experimental school were able to use their tablets to access the Math-Island system as a learning tool at both school and home. To compare the students’ mathematics achievement with a baseline, this study also included 125 second graders (63 females and 62 males) from another school with similar socioeconomic backgrounds in the same region of the city as a control school. The students in the control school received only conventional mathematics instruction without using the Math-Island system during the 2-year period.

Before the first semester, a 3-week training workshop was conducted to familiarize the students with the basic operation of tablets and the Math-Island system. By doing so, it was ensured that all participants had similar prerequisite skills. The procedure of this study was illustrated in Table  1 . At the beginning of the first semester, a mathematics achievement assessment was conducted as a pretest in both the experimental and the control school to examine the students’ initial mathematics ability as second graders. From June 2013 to June 2015, while the students in the control school learned mathematics in a conventional way, the students in the experimental school learned mathematics not only in mathematics classes but also through the Math-Island system. Although the teachers in the experimental school mainly adopted lectures in mathematics classes, they used the Math-Island system as learning materials at school and for homework. At the same time, they allowed the students to explore the knowledge map at their own pace. During the 2 years, every student completed 286.78 learning tasks on average, and each task took them 8.86 min. Given that there were 344 tasks for the second and third graders, the students could finish 83.37% of tasks according to the standard progress. The data also showed that the average correctness rate of the students was 85.75%. At the end of the second year, another mathematics achievement assessment was administered as a posttest in both schools to evaluate students’ mathematics ability as third graders. Additionally, an interest questionnaire was employed in the experimental school to collect the students’ perceptions of mathematics and the Math-Island system. To understand the teachers’ opinions of how they feel about the students using the system, interviews with the teachers in the experimental school were also conducted.

Data collection

Mathematics achievement assessment.

To evaluate the students’ mathematics ability, this study adopted a standardized achievement assessment of mathematics ability (Lin et al. 2009 ), which was developed from a random sample of elementary students from different counties in Taiwan to serve as a norm with appropriate reliability (the internal consistency was 0.85, and the test-retest reliability was 0.86) and validity (the correlation by domain experts in content validity was 0.92, and the concurrent validity was 0.75). As a pretest, the assessment of the second graders consisted of 50 items, including conceptual understanding (23 items), calculating (18 items), and word problem-solving (9 items). As a posttest, the assessment of the third graders consisted of 60 items, including conceptual understanding (18 items), calculating (27 items), and word problem-solving (15 items). The scores of the test ranged from 0 to 50 points. Because some students were absent during the test, this study obtained 209 valid tests from the experimental school and 125 tests from the control school.

Interest questionnaire

The interest questionnaire comprised two parts: students’ interest in mathematics and the Math-Island system. Regarding the first part, this study adopted items from a mathematics questionnaire of PISA and TIMSS 2012 (OECD 2013 ; Mullis et al. 2012 ), the reliability of which was sound. This part included three dimensions: attitude (14 items, Cronbach’s alpha = .83), initiative (17 items, Cronbach’s alpha = .82), and confidence (14 items Cronbach’s alpha = .72). Furthermore, the dimension of attitude was used to assess the tendency of students’ view on mathematics. For example, a sample item of attitudes was “I am interested in learning mathematics.” The dimension of initiatives was used to assess how students were willing to learn mathematics actively. A sample item of initiatives was “I keep studying until I understand mathematics materials.” The dimension of confidences was used to assess students’ perceived mathematics abilities. A sample item was “I am confident about calculating whole numbers such as 3 + 5 × 4.” These items were translated to Chinese for this study. Regarding the second part, this study adopted self-made items to assess students’ motivations for using the Math-Island system. This part included two dimensions: attraction (8 items) and satisfaction (5 items). The dimension of attraction was used to assess how well the system could attract students’ attention. A sample item was “I feel Math-island is very appealing to me.” The dimension of satisfaction was used to assess how the students felt after using the system. A sample item was “I felt that upgrading the buildings in my Math-Island brought me much happiness.” These items were assessed according to a 4-point Likert scale, ranging from “strongly disagreed (1),” “disagreed (2),” “agreed (3),” and “strongly agreed (4)” in this questionnaire. Due to the absences of several students on the day the questionnaire was administered, there were only 207 valid questionnaires in this study.

Teacher interview

This study also included teachers’ perspectives on how the students used the Math-Island system to learn mathematics in the experimental school. This part of the study adopted semistructured interviews of eight teachers, which comprised the following three main questions: (a) Do you have any notable stories about students using the Math-Island system? (b) Regarding Math-Island, what are your teaching experiences that can be shared with other teachers? (c) Do you have any suggestions for the Math-Island system? The interview was recorded and transcribed verbatim. The transcripts were coded and categorized according to the five dimensions of the questionnaire (i.e., the attitude, initiative, and confidence about mathematics, as well as the attraction and satisfaction with the system) as additional evidence of the students’ interest in the experimental school.

Data analysis

For the first research question, this study conducted a multivariate analysis of variance (MANOVA) with the schools as a between-subject variable and the students’ scores (conceptual understanding, calculating, and word problem-solving) in the pre/posttests as dependent variables. Moreover, this study also conducted a MANOVA to compare the low-achieving students from both schools. In addition, the tests were also carried out to compare achievements with the norm (Lin et al. 2009 ). For the second research question, several z tests were used to examine how the interests of the low-achieving students were distributed compared with the whole sample. Teachers’ interviews were also adopted to support the results of the questionnaire.

Mathematics achievement

To examine the homogeneity of the students in both schools in the first year, the MANOVA of the pretest was conducted. The results, as shown in Table  2 , indicated that there were no significant differences in their initial mathematics achievements in terms of conceptual understanding, calculating, and word problem-solving (Wilks’ λ  = 0.982, F (3330) = 2.034, p  > 0.05). In other words, the students of both schools had similar mathematics abilities at the time of the first mathematics achievement assessment and could be fairly compared.

At the end of the fourth grade, the students of both schools received the posttest, the results of which were examined by a MANOVA. As shown in Table  3 , the effect of the posttest on students’ mathematics achievement was significant (Wilks’ λ  = 0.946, p  < 0.05). The results suggested that the students who used Math-Island for 2 years had better mathematics abilities than those who did not. The analysis further revealed that the univariate effects on calculating and word problem-solving were significant, but the effect on conceptual understanding was insignificant. The results indicated that the students in the experimental school outperformed their counterparts in terms of the procedure and application of arithmetic. The reason may be that the system provided students with more opportunities to do calculation exercises and word problems, and the students were more willing to do these exercises in a game-based environment. Furthermore, they were engaged in solving various exercises with the support of immediate feedback until they passed the requirements of every building in their Math-Island. However, the students learned mathematical concepts mainly by watching videos in the system, which provided only demonstrations like lectures in conventional classrooms. For this reason, the effect of the system on conceptual understanding was similar to that of teachers’ conventional instruction.

Furthermore, to examine the differences between the low-achieving students in both schools, another MANOVA was also conducted on the pretest and the posttest. The pretest results indicated that there were no significant differences in their initial mathematics achievement in terms of conceptual understanding, calculating, and word problem-solving (Wilks’ λ  = 0.943, F (3110) = 2.210, p  > 0.05).

The MANOVA analysis of the posttest is shown in Table  4 . The results showed that the effect of the system on the mathematics achievement of low-achieving students was significant (Wilks’ λ  = 0.934, p  < 0.05). The analysis further revealed that only the univariate effect on word problem-solving was significant. The results suggested that the low-achieving students who used Math-Island for 2 years had better word problem-solving ability than those students in the control school, but the effect on conceptual understanding and procedural fluency was insignificant. The results indicated that the Math-Island system could effectively enhance low-achieving students’ ability to solve word problems.

Because the mathematics achievement assessment was a standardized achievement assessment (Lin et al. 2009 ), the research team did a further analysis of the assessments by comparing the results with the norm. In the pretest, the average score of the control school was the percentile rank of a score (PR) 55, but their average score surprisingly decreased to PR 34 in the posttest. The results confirmed the fact that conventional mathematics teaching in Taiwan might result in an M-shape distribution, suggesting that low-achieving students required additional learning resources. Conversely, the average score of the experimental school was PR 48 in the pretest, and their score slightly decreased to PR 44 in the posttest. Overall, both PR values were decreasing, because the mathematics curriculum became more and more difficult from the second grade to the fourth grade. However, it should be noted that the experimental school has been less affected, resulting in a significant difference compared with the control school (see Table  5 ). Notably, the average score of word problem-solving in the posttest of the experimental school was PR 64, which was significantly higher than the nationwide norm ( z  = 20.8, p  < .05). The results were consistent with the univariate effect of the MANOVA on word problem-solving, suggesting that the Math-Island system could help students learn to complete word problems better. This may be because the learning tasks in Math-Island provided students with adequate explanations for various types of word problems and provided feedback for exercises.

To examine whether the low-achieving students had low levels of interest in mathematics and the Math-Island system, the study adopted z tests on the data of the interest questionnaire. Table  5 shows the descriptive statistics and the results of the z tests. Regarding the interest in mathematics, the analysis showed that the interest of the low-achieving students was similar to that of the whole sample in terms of attitude, initiative, and confidence. The results were different from previous studies asserting that low-achieving students tended to have lower levels of interest in mathematics (Al-Zoubi and Younes 2015 ). The reason was perhaps that the low-achieving students were comparably motivated to learn mathematics in the Math-Island system. As a result, a teacher ( #T-301 ) said, “some students would like to go to Math-Island after school, and a handful of students could even complete up to forty tasks (in a day),” implying that the students had a positive attitude and initiative related to learning mathematics.

Another teacher ( T-312 ) also indicated “some students who were frustrated with math could regain confidence when receiving the feedback for correct answers in the basic tasks. Thanks to this, they would not feel high-pressure when moving on to current lessons.” In a sense, the immediate feedback provided the low-achieving students with sufficient support and may encourage them to persistently learn mathematics. Furthermore, by learning individually after class, they could effectively prepare themselves for future learning. The results suggested that the system could serve as a scaffolding on conventional instruction for low-achieving students. The students could benefit from such a blended learning environment and, thus, build confidence in mathematics by learning at their own paces.

The low-achieving students as a whole were also attracted to the system and felt satisfaction from it. Teacher ( #T-307 ) said that, “There was a hyperactive and mischievous student in my class. However, when he was alone, he would go on to Math-Island, concentrating on the tasks quietly. He gradually came to enjoy learning mathematics. It seemed that Math-Island was more attractive to them than a lecture by a teacher. I believed that students could be encouraged, thus improve their ability and learn happily.” Another teacher ( #T-304 ) further pointed out that, “For students, they did not only feel like they were learning mathematics because of the game-based user interface. Conversely, they enjoyed the contentment when completing a task, as if they were going aboard to join a competition.” In teachers’ opinions, such a game-based learning environment did not disturb their instruction. Instead, the system could help the teachers attract students’ attention and motivate them to learn mathematics actively because of its appealing game and joyful learning tasks. Furthermore, continuously overcoming the tasks might bring students a sense of achievement and satisfaction.

Discussion on some features of this study

In addition to the enhancement of achievement and interest, we noticed that there are some features in this study and our design worth some discussion.

The advantages of building a long-term study

Owing to the limitations of deployment time and sample sizes, it is hard for most researchers to conduct a longitudinal study. Fortunately, we had a chance to maintain a long-term collaboration with an experimental school for more than 2 years. From this experiment, we notice that there are two advantages to conducting a long-term study.

Obtaining substantial evidence from the game-based learning environment

The research environment was a natural setting, which could not be entirely controlled and manipulated like most experiments in laboratories. However, this study could provide long-term evidence to investigate how students learned in a game-based learning environment with their tablets. It should be noted that we did not aim to replace teachers in classrooms with the Math-Island game. Instead, we attempted to establish an ordinary learning scenario, in which the teachers and students regarded the game as one of the learning resources. For example, teachers may help low-achieving students to improve their understanding of a specific concept in the Math-Island system. When students are learning mathematics in the Math-Island game, teachers may take the game as a formative assessment and locate students’ difficulties in mathematics.

Supporting teachers’ instructions and facilitating students’ learning

The long-term study not only proved the effectiveness of Math-Island but also offered researchers an opportunity to determine teachers’ roles in such a computer-supported learning environment. For example, teachers may encounter difficulties in dealing with the progress of both high- and low-achieving students. How do they take care of all students with different abilities at the same time? Future teachers may require more teaching strategies in such a self-directed learning environment. Digital technology has an advantage in helping teachers manage students’ learning portfolios. For example, the system can keep track of all the learning activities. Furthermore, the system should provide teachers with monitoring functions so that they know the average status of their class’s and individuals’ learning progress. Even so, it is still a challenge for researchers to develop a well-designed visualization tool to support teachers’ understanding of students’ learning conditions and their choice of appropriate teaching strategies.

Incorporating a gamified knowledge map of the elementary mathematics curriculum

Providing choices of learning paths.

Math-Island uses a representational metaphor of an “island,” where a virtual city is located and represents the knowledge map. Furthermore, the island comprises areas, roads, and buildings, which are the embodiments of domains, subdomains, and concepts in the curriculum, respectively. Because the gamified knowledge map provides students with multiple virtual roads to learn in the system, every student may take different routes. For instance, some students may be more interested in geometry, while others may be confident in exploring the rules of arithmetic. In this study, we noticed that the low-achieving students needed more time to work on basic tasks, while high-achieving students easily passed those tasks and moved on to the next ones. As a result, some of the high-achieving students had already started to learn the materials for the next grade level. This was possibly because high-achieving students were able to respond well to challenging assignments (Singh 2011 ). Therefore, we should provide high-achieving students with more complex tasks to maintain their interest. For example, Math-Island should provide some authentic mathematical problems as advanced exercises.

Visualizing the learning portfolio

In this study, we demonstrated a long-term example of incorporating a gamified knowledge map in an elementary mathematical curriculum. In the Math-Island game, the curriculum is visualized as a knowledge map instead of a linear sequence, as in textbooks. By doing so, students are enabled to explore relationships in the mathematics curriculum represented by the knowledge map; that is, the structure of the different roads on Math-Island. Furthermore, before learning, students may preview what will be learned, and after learning, students may also reflect on how well they learned. Unlike traditional lectures or textbooks, in which students could only follow a predefined order to learn knowledge without thinking why they have to learn it, the knowledge map allows students to understand the structure of knowledge and plan how to achieve advanced knowledge. Although the order of knowledge still remains the same, students take primary control of their learning. In a sense, the knowledge map may liberate elementary students from passive learning.

Adopting the mechanisms of a construction management game

This 2-year study showed that the adaptation of two game mechanisms, construction and sightseeing, into the elementary mathematical curriculum could effectively improve students’ learning achievement. The reason may be that students likely developed interests in using Math-Island to learn mathematics actively, regardless of whether they are high- and low-achieving students.

Gaining a sense of achievement and ownership through the construction mechanism

Regardless of the construction mechanism, Math-Island allows students to plan and manage their cities by constructing and upgrading buildings. Math-Island took the advantages of construction management games to facilitate elementary students’ active participation in their mathematical learning. Furthermore, students may manage their knowledge by planning and constructing of buildings on their virtual islands. Like most construction management games, students set goals and make decisions so that they may accumulate their assets. These assets are not only external rewards but also visible achievements, which may bring a sense of ownership and confidence. In other words, the system gamified the process of self-directed learning.

Demonstrating learning result to peers through the sightseeing mechanism

As for the sightseeing mechanism, in conventional instruction, elementary students usually lack the self-control to learn knowledge actively (Duckworth et al. 2014 ) or require a social stage to show other students, resulting in low achievement and motivation. On the other hand, although previous researchers have already proposed various self-regulated learning strategies (such as Taub et al. 2014 ), it is still hard for children to keep adopting specific learning strategies for a long time. For these reasons, this study uses the sightseeing mechanism to engage elementary students in a social stage to show other students how well their Math-Islands have been built. For example, in Math-Island, although the students think that they construct buildings in their islands, they plan the development of their knowledge maps. After learning, they may also reflect on their progress by observing the appearance of the buildings.

In brief, owing to the construction mechanism, the students are allowed to choose a place and build their unique islands by learning concepts. During the process, students have to do the learning task, get feedback, and get rewards, which are the three major functions of the construction functions. In the sightseeing mechanism, students’ unique islands (learning result) can be shared and visited by other classmates. The student’s Math-Island thus serves as a stage for showing off their learning results. The two mechanisms offer an incentive model connected to the game mechanism’s forming a positive cycle: the more the students learn, the more unique islands they can build, with more visitors.

Conclusion and future work

This study reported the results of a 2-year experiment with the Math-Island system, in which a knowledge map with extensive mathematics content was provided to support the complete elementary mathematics curriculum. Each road in Math-Island represents a mathematical topic, such as addition. There are many buildings on each road, with each building representing a unit of the mathematics curriculum. Students may learn about the concept and practice it in each building while being provided with feedback by the system. In addition, the construction management online game mechanism is designed to enhance and sustain students’ interest in learning mathematics. The aim of this study was not only to examine whether the Math-Island system could improve students’ achievements but also to investigate how much the low-achieving students would be interested in learning mathematics after using the system for 2 years.

As for enhancing achievement, the result indicated that the Math-Island system could effectively improve the students’ ability to calculate expressions and solve word problems. In particular, the low-achieving students outperformed those of the norm in terms of word problem-solving. For enhancing interest, we found that both the low-achieving and the high-achieving students in the experimental school, when using the Math-Island system, maintained a rather high level of interest in learning mathematics and using the system. The results of this study indicated some possibility that elementary students could be able to learn mathematics in a self-directed learning fashion (Nilson 2014 ; Chen et al. 2012a , b ) under the Math-Island environment. This possibility is worthy of future exploration. For example, by analyzing student data, we can investigate how to support students in conducting self-directed learning. Additionally, because we have already collected a considerable amount of student data, we are currently employing machine learning techniques to improve feedback to the students. Finally, to provide students appropriate challenges, the diversity, quantity, and difficulty of content may need to be increased in the Math-Island system.

Abbreviations

Program for International Student Assessment

The percentile rank of a score

Trends in Mathematics and Science Study

Al-Zoubi, S. M., & Younes, M. A. B. (2015). Low academic achievement: causes and results. Theory and Practice in Language Studies, 5 (11), 2262.

Google Scholar  

Arter, J. A., & Spandel, V. (2005). Using portfolios of student work in instruction and assessment. Educational Measurement Issues and Practice, 11 (1), 36–44.

Azevedo, R., Feyzi-Behnagh, R., Duffy, M., Harley, J., & Trevors, G. (2012). Metacognition and self-regulated learning in student-centered leaning environments. In D. Jonassen & S. Land (Eds.), Theoretical foundations of student-centered learning environments (pp. 171–197). New York: Routledge.

Barlett, C. P., Anderson, C. A., & Swing, E. L. (2009). Video game effects confirmed, suspected and speculative: a review of the evidence. Simulation & Gaming, 40 (3), 377–403.

Barr, R. B., & Tagg, J. (1995). From teaching to learning—a new paradigm for undergraduate education. Change The Magazine of Higher Learning, 27 (6), 12–26.

Birgin, O., & Baki, A. (2007). The use of portfolio to assess student’s performance. Journal of Turkish Science Education, 4 (2), 75–90.

Chan, T. W., Roschelle, J., Hsi, S., Kinshuk, Sharples, M., Brown, T., et al. (2006). One-to-one technology-enhanced learning: an opportunity for global research collaboration. Research and Practice in Technology Enhanced Learning, 1 (01), 3–29.

Chase, K., & Abrahamson, D. (2015). Reverse-scaffolding algebra: empirical evaluation of design architecture. ZDM Mathematics Education, 47 (7), 1195–1209.

Chen, Y. H., Looi, C. K., Lin, C. P., Shao, Y. J., & Chan, T. W. (2012a). Utilizing a collaborative cross number puzzle game to develop the computing ability of addition and subtraction. Educational Technology & Society, 15 (1), 354–366.

Chen, Z. H., Liao, C. C., Cheng, H. N., Yeh, C. Y., & Chan, T. W. (2012b). Influence of game quests on pupils’ enjoyment and goal-pursuing in math learning. Journal of Educational Technology & Society, 15 (2), 317–327.

Cheng, H. N. H., Yang, E. F. Y., Liao, C. C. Y., Chang, B., Huang, Y. C. Y., & Chan, T. W. (2015). Scaffold seeking: a reverse design of scaffolding in computer-supported word problem solving. Journal of Educational Computing Research, 53 (3), 409–435.

Chu, H. C., Yang, K. H., & Chen, J. H. (2015). A time sequence-oriented concept map approach to developing educational computer games for history courses. Interactive Learning Environments, 23 (2), 212–229.

Davenport, T. H. & Prusak, L. (2000). Working knowledge: How organizations manage what they know . Boston: Harvard Business School Press.

Duckworth, A. L., Gendler, T. S., & Gross, J. J. (2014). Self-control in school-age children. Educational Psychologist, 49 (3), 199–217.

Ebener, S., Khan, A., Shademani, R., Compernolle, L., Beltran, M., Lansang, M. A., & Lippman, M. (2006). Knowledge mapping as a technique to support knowledge translation. Bulletin of the World Health Organization, 84 , 636–642.

González-Calero, J. A., Arnau, D., Puig, L., & Arevalillo-Herráez, M. (2014). Intensive scaffolding in an intelligent tutoring system for the learning of algebraic word problem solving. British Journal of Educational Technology, 46 (6), 1189–1200.

Hanus, M. D., & Fox, J. (2015). Assessing the effects of gamification in the classroom: a longitudinal study on intrinsic motivation, social comparison, satisfaction, effort, and academic performance. Computers & Education, 80 , 152–161.

Hwang, G. J., Chiu, L. Y., & Chen, C. H. (2015). A contextual game-based learning approach to improving students’ inquiry-based learning performance in social studies courses. Computers & Education, 81 , 13–25.

Hwang, G. J., Su, J. M., & Chen, N. S. (2012). E-learning introduction and practice . Taiwan: Drmaste.

Kiili, K., & Ketamo, H. (2007). Exploring the learning mechanism in educational games. Journal of Computing and Information Technology, 15 (4), 319–324.

Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it up: helping children learn mathematics . Washington, DC: National Academies Press.

Koivisto, J., & Hamari, J. (2014). Demographic differences in perceived benefits from gamification. Computers in Human Behavior, 35 , 179–188.

Krapp, A. (1999). Interest, motivation and learning: an educational-psychological perspective. European Journal of Psychology of Education, 14 (1), 23–40.

Ku, O., Chen, S. Y., Wu, D. H., Lao, A. C., & Chan, T. W. (2014). The effects of game-based learning on mathematical confidence and performance: high ability vs. low ability. Journal of Educational Technology & Society, 17 (3), 65–78.

Lao, A. C. C., Cheng, H. N., Huang, M. C., Ku, O., & Chan, T. W. (2017). Examining motivational orientation and learning strategies in computer-supported self-directed learning (CS-SDL) for mathematics: the perspective of intrinsic and extrinsic goals. Journal of Educational Computing Research, 54 (8), 1168–1188.

Lee, Y. M. (2012). Discriminating math low-achievement motivation patterns: comparing disadvantaged and other students in elementary and junior high school. Journal of Research in Education Sciences, 57 (4), 39–71. https://doi.org/10.3966/2073753X2012125704002 .

Li, M.-C., & Tsai, C.-C. (2013). Game-based learning in science education: a review of relevant research. Journal of Science Education and Technology, 22 (6), 877–898. https://doi.org/10.1007/s10956-013-9436-x .

Liao, C. C., Cheng, H. N., Chang, W. C., & Chan, T. W. (2017). Supporting parental engagement in a BYOD (bring your own device) school. Journal of Computers in Education, 4 (2), 107–125.

Lin, B. G., Li, R. P., & Huang, Y. Z. (2009). Instructional manual of mathematical ability test for the school-aged . Taipei: Ministry of Education.

Lin, P. J., & Tsai, W. H. (2001). Using research-based cases to enhance prospective teachers’ understanding of teaching mathematics and their reflections. In F. L. Lin (Ed.), Common sense in mathematics education. Proceedings of 2001 the Netherlands and Taiwan Conference on Common Sense in Mathematics Education (pp. 231–272). Taipei: Taiwan.

Liu, T. Y., & Chu, Y. L. (2010). Using ubiquitous games in an English listening and speaking course: impact on learning outcomes and motivation. Computers & Education, 55 (2), 630–643. https://doi.org/10.1016/j.compedu.2010.02.023 .

McLaren, B. M., Adams, D. M., Mayer, R. E., & Forlizzi, J. (2017). A computer-based game that promotes mathematics learning more than a conventional approach. International Journal of Game-Based Learning, 7 (1), 36–56.

Ministry of Education. (2003). Guidelines of grades 1-9 curriculum of elementary and junior high school education . Retrieved from https://www.k12ea.gov.tw/92_sid17/%E6%96%B0%E7%B8%BD%E7%B6%B1%E8%8B%B1%E6%96%87%E7%89%88.pdf .

Mullis, I. V. S., Martin, M. O., Foy, P., & Drucker, K. T. (2012). PIRLS 2011 international results in reading . Chestnut Hill: TIMSS & PIRLS International Study Center, Boston College.

Mullis, I. V. S., Martin, M. O., Foy, P., & Hooper, M. (2016). TIMSS 2015 International Results in Mathematics. Retrieved from http://timssandpirls.bc.edu/timss2015/international-results/

Nilson, L. B. (2014). The secret of self-regulated learning. In Invited article for Faculty Focus: Higher Ed Teaching Strategies from Magna Publications .

OECD. (2013). PISA 2012 results in focus: what 15-year-olds know and what they can do with what they know: key results from PISA 2012.

OECD. (2016). PISA 2015 results in focus. Retrieved from: https://www.oecd.org/pisa/pisa-2015-results-in-focus.pdf .

Roll, I., Baker, R. S. J. D., Aleven, V., & Koedinger, K. R. (2014). On the benefits of seeking (and avoiding) help in online problem-solving environments. Journal of the Learning Sciences, 23 (4), 537–560.

Schraw, G., Flowerday, T., & Lehman, S. (2001). Increasing situational interest in the classroom. Educational Psychology Review, 13 (3), 211–224.

Singh, K. (2011). Study of achievement motivation in relation to academic achievement of students. International Journal of Educational Planning and Administration, 1 (2), 161–171.

Taub, M., Azevedo, R., Bouchet, F., & Khosravifar, B. (2014). Can the use of cognitive and metacognitive self-regulated learning strategies be predicted by learners’ levels of prior knowledge in hypermedia-learning environments? Computers in Human Behavior, 39 , 356–367.

Vélez, J., Fabregat, R., Bull, S., & Hueva, D. (2009). The potential for open learner models in adaptive virtual learning environments. In S. D. Craig & D. Dicheva (Eds.), AIED 2009: 14th International Conference on Artificial Intelligence in Education Workshops Proceedings Volume 8 (pp. 11–20). Brighton: International AIED Society.

Yang, E. F. Y., Cheng, H. N. H., Ching, E., & Chan, T. W. (2012). Variation based discovery learning design in 1 to 1 mathematics classroom. In G. Biswas, L.-H. Wong, T. Hirashima, & W. Chen (Eds.), Proceedings of the 20th International Conference on Computers in Education (pp. 811–815). Singapore: Asia-Pacific Society for Computers in Education.

Download references

Acknowledgements

The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The authors would like to thank the Ministry of Science and Technology of the Republic of China, Taiwan, for financial support (MOST 106-2511-S-008-003-MY3), and Research Center for Science and Technology forLearning, National Central University, Taiwan.

Availability of data and materials

As a series of subsequent research papers are still in progress, for now, it is temporarily impossible to share research data sets.

Author information

Authors and affiliations.

National Central University, No. 300, Zhongda Rd., Zhongli District, Taoyuan City, 32001, Taiwan, Republic of China

Charles Y. C. Yeh

Central China Normal University, Science Hall 419, No. 152, Luoyu Road, Wuhan, 430079, China

Hercy N. H. Cheng

National Taiwan Normal University, No.162, Sec. 1, Heping E. Rd., Taipei City, 10610, Taiwan, Republic of China

Zhi-Hong Chen

National Taipei University of Nursing and Health Sciences, No.365, Mingde Rd., Beitou Dist., Taipei City, 11219, Taiwan, Republic of China

Calvin C. Y. Liao

Tak-Wai Chan

You can also search for this author in PubMed   Google Scholar

Contributions

CYCY contributed to the study design, data acquisition and analysis, mainly drafted the manuscript and execution project. HNHC was involved in data acquisition, revision of the manuscript and data analysis.ZHC was contributed to the study idea and drafted the manuscript. CCYL of this research was involved in data acquisition and revision of the manuscript. TWC was project manager and revision of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Charles Y. C. Yeh .

Ethics declarations

Authors’ information.

Charles Y.C. Yeh is currently an PhD student in Graduate Institute of Network Learning Technology at National Central University. The research interests include one-to-one learning environments and game-based learning.

Hercy N. H. Cheng is currently an associate professor and researcher in National Engineering Research Center for E-Learning at Central China Normal University, China. His research interests include one-to-one learning environments and game-based learning.

Zhi-Hong Chen is an associate professor in Graduate Institute of Information and Computer Education at National Taiwan Normal University. His research interests focus on learning technology and interactive stories, technology intensive language learning and game-based learning.

Calvin C. Y. Liao is currently an Assistant Professor and Dean’s Special Assistant in College of Nursing at National Taipei University of Nursing and Health Sciences in Taiwan. His research focuses on computer-based language learning for primary schools. His current research interests include a game-based learning environment and smart technology for caregiving & wellbeing.

Tak-Wai Chan is Chair Professor of the Graduate Institute of Network Learning Technology at National Central University in Taiwan. He has worked on various areas of digital technology supported learning, including artificial intelligence in education, computer supported collaborative learning, digital classrooms, online learning communities, mobile and ubiquitous learning, digital game based learning, and, most recently, technology supported mathematics and language arts learning.

Competing interests

The authors declare that they have no competing interests.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and permissions

About this article

Cite this article.

Yeh, C.Y.C., Cheng, H.N.H., Chen, ZH. et al. Enhancing achievement and interest in mathematics learning through Math-Island. RPTEL 14 , 5 (2019). https://doi.org/10.1186/s41039-019-0100-9

Download citation

Received : 29 October 2018

Accepted : 22 February 2019

Published : 11 March 2019

DOI : https://doi.org/10.1186/s41039-019-0100-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Mathematics learning
• Game-based learning
• Construction management games

• Open supplemental data
• Reference Manager
• Simple TEXT file

People also looked at

Original research article, mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

• 1 Department of Education, Uppsala University, Uppsala, Sweden
• 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
• 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
• 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden

Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction

The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.

Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.

Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).

Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).

Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.

Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).

However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).

Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.

The Present Study

In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:

a) What is the effect of CL approach on students’ problem-solving in mathematics?

b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?

Participants

The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.

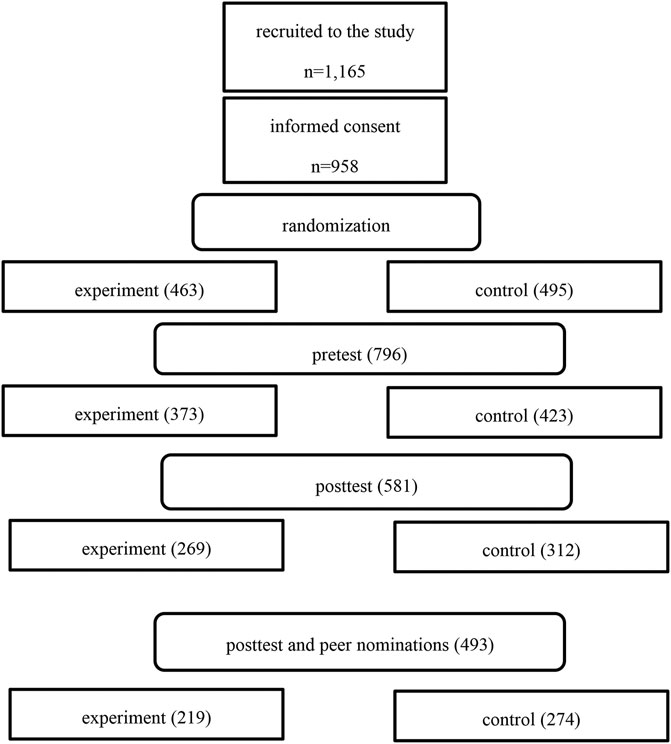
FIGURE 1 . Flow chart for participants included in data collection and data analysis.

As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.

Intervention

The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.

Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).

In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.

Implementation of the Intervention

To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.

Control Group

The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.

Tests of Mathematical Problem-Solving

Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).

The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.

Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.

The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.

The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.

Measures of Peer Acceptance and Friendships

To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).

Statistical Analyses

Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).

The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.

What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?

As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.

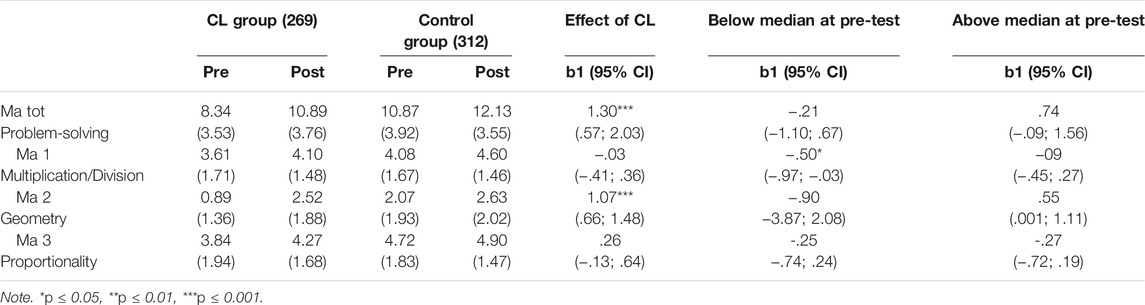
TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.

The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.

Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?

As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.

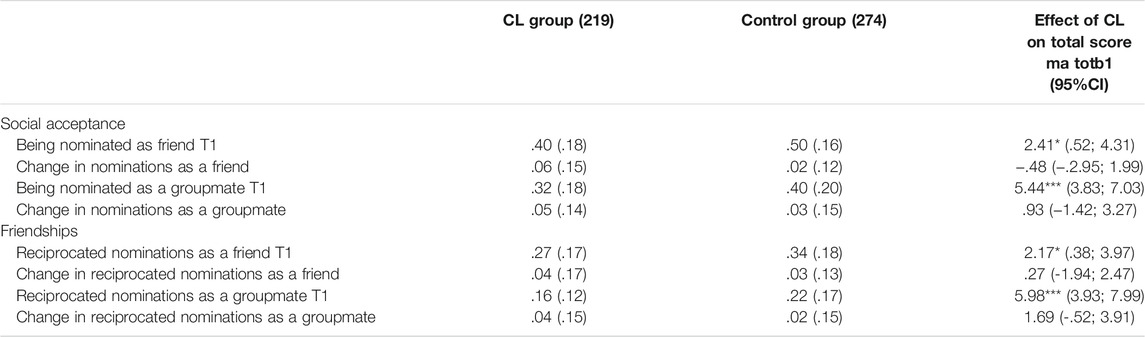
TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.

In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.

The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).

In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).

Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.

Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.

The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.

Limitations

The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.

Implications

The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.

The project was funded by the Swedish Research Council under Grant 2016-04,679.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to teachers who participated in the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material

Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430

Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001

Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.

Google Scholar

Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .

Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.

Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.

Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6

Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.

Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16

Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.

Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.

Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489

Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .

Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529

Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453

Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .

Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.

Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .

Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.

McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0

Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176

Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10

Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en

CrossRef Full Text

Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .

Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.

Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202

SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .

Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .

Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009

Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683

Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .

Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).

van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .

Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029

Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.

Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9

Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187

Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20

Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis

Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296

Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.

Reviewed by:

Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Nina Klang, [email protected]

all the numbers are changing, but what doesn't change is the relationship between x and y: y is always one more than twice x. That is, y=2x+1. Finding what doesn't change "tames" the situation. So, you have tamed this problem! Yay. And if you want a fancy mathematical name for things that don’t vary, we call these things "invariants." The number of messed-up recruits is invariant, even though they are all wiggling back and forth, trying to figure out which way is right!

3) Encourage generalizations

So, of course, the next question that comes to my mind is how to generalize what you’ve already discovered: there are 15 ways that 2 mistakes can be arranged in a line of 6 recruits. What about a different number of mistakes? Or a different number of recruits? Is there some way to predict? Or, alternatively, is there some way to predict how these 15 ways of making mistakes will play out as the recruits try to settle themselves down? Which direction interests you?

4) Inquire about reasoning and rigor

The students were looking at the number of ways the recruits could line up with 2 out of n faced the wrong way: Anyway, I had a question of my own. It looks like the number of possibilities increases pretty fast, as the number of recruits increases. For example, I counted 15 possibilities in your last set (the line of six). What I wonder is this: when the numbers get that large, how you can possibly know that you've found all the possibilities? (For example, I noticed that >>>><< is missing.) The question "How do I know I've counted 'em all?" is actually quite a big deal in mathematics, as mathematicians are often called upon to find ways of counting things that nobody has ever listed (exactly like the example you are working on).

The students responded by finding a pattern for generating the lineups in a meaningful order: The way that we can prove that we have all the possibilities is that we can just add the number of places that the second wrong person could be in. For example, if 2 are wrong in a line of 6, then the first one doesn’t move and you count the space in which the second one can move in. So for the line of six, it would be 5+4+3+2+1=15. That is the way to make sure that we have all the ways. Thanks so much for giving challenges. We enjoyed thinking!

5) Work towards proof

a) The group wrote the following: When we found out that 6 recruits had 15 different starting arrangements, we needed more information. We needed to figure out how many starting positions are there for a different number of recruits.

By drawing out the arrangements for 5 recruits and 7 recruits we found out that the number of starting arrangements for the recruit number before plus that recruit number before it would equal the number of starting arrangements for that number of recruits.

We also found out that if you divide the starting arrangements by the number of recruits there is a pattern.

To which the mentor replied: Wow! I don't think (in all the years I've been hanging around mathematics) I've ever seen anyone describe this particular pattern before! Really nice! If you already knew me, you'd be able to predict what I'm about to ask, but you don't, so I have to ask it: "But why?" That is, why is this pattern (the 6, 10, 15, 21, 28…) the pattern that you find for this circumstance (two recruits wrong in lines of lengths, 4, 5, 6, 7, 8…)? Answering that—explaining why you should get those numbers and why the pattern must continue for longer lines—is doing the kind of thing that mathematics is really about.

b) Responding to students studying a circular variation of raw recruits that never settled down: This is a really interesting conclusion! How can you show that it will always continue forever and that it doesn’t matter what the original arrangement was? Have you got a reason or did you try all the cases or…? I look forward to hearing more from you.

6) Distinguish between examples and reasons

a) You have very thoroughly dealt with finding the answer to the problem you posed—it really does seem, as you put it, "safe to say" how many there will be. Is there a way that you can show that that pattern must continue? I guess I’d look for some reason why adding the new recruit adds exactly the number of additional cases that you predict. If you could say how the addition of one new recruit depends on how long the line already is, you’d have a complete proof. Want to give that a try?

b) A student, working on Amida Kuji and having provided an example, wrote the following as part of a proof: In like manner, to be given each relationship of objects in an arrangement, you can generate the arrangement itself, for no two different arrangements can have the same object relationships. The mentor response points out the gap and offers ways to structure the process of extrapolating from the specific to the general: This statement is the same as your conjecture, but this is not a proof. You repeat your claim and suggest that the example serves as a model for a proof. If that is so, it is up to you to make the connections explicit. How might you prove that a set of ordered pairs, one per pair of objects forces a unique arrangement for the entire list? Try thinking about a given object (e.g., C) and what each of its ordered pairs tells us? Try to generalize from your example. What must be true for the set of ordered pairs? Are all sets of n C2 ordered pairs legal? How many sets of n C2 ordered pairs are there? Do they all lead to a particular arrangement? Your answers to these questions should help you work toward a proof of your conjecture.

9) Encourage extensions

What you’ve done—finding the pattern, but far more important, finding the explanation (and stating it so clearly)—is really great! (Perhaps I should say "finding and stating explanations like this is real mathematics"!) Yet it almost sounded as if you put it down at the very end, when you concluded "making our project mostly an interesting coincidence." This is a truly nice piece of work!

The question, now, is "What next?" You really have completely solved the problem you set out to solve: found the answer, and proved that you’re right!

I began looking back at the examples you gave, and noticed patterns in them that I had never seen before. At first, I started coloring parts red, because they just "stuck out" as noticeable and I wanted to see them better. Then, it occurred to me that I was coloring the recruits that were back-to-back, and that maybe I should be paying attention to the ones who were facing each other, as they were "where the action was," so I started coloring them pink. (In one case, I recopied your example to do the pinks.) To be honest, I’m not sure what I’m looking for, but there was such a clear pattern of the "action spot" moving around that I thought it might tell me something new. Anything come to your minds?

10) Build a Mathematical Community

I just went back to another paper and then came back to yours to look again. There's another pattern in the table. Add the recruits and the corresponding starting arrangements (for example, add 6 and 15) and you get the next number of starting arrangements. I don't know whether this, or your 1.5, 2, 2.5, 3, 3.5… pattern will help you find out why 6, 10, 15… make sense as answers, but they might. Maybe you can work with [your classmates] who made the other observation to try to develop a complete understanding of the problem.

11) Highlight Connections

Your rule—the (n-1)+(n-2)+(n-3)+… +3+2+1 part—is interesting all by itself, as it counts the number of dots in a triangle of dots. See how?

12) Wrap Up

This is really a very nice and complete piece of work: you've stated a problem, found a solution, and given a proof (complete explanation of why that solution must be correct). To wrap it up and give it the polish of a good piece of mathematical research, I'd suggest two things.

The first thing is to extend the idea to account for all but two mistakes and the (slightly trivial) one mistake and all but one mistake. (If you felt like looking at 3 and all but 3, that'd be nice, too, but it's more work—though not a ton—and the ones that I suggested are really not more work.)

The second thing I'd suggest is to write it all up in a way that would be understandable by someone who did not know the problem or your class: clear statement of the problem, the solution, what you did to get the solution, and the proof.

I look forward to seeing your masterpiece!

Advice for Keeping a Formal Mathematics Research Logbook

As part of your mathematics research experience, you will keep a mathematics research logbook. In this logbook, keep a record of everything you do and everything you read that relates to this work. Write down questions that you have as you are reading or working on the project. Experiment. Make conjectures. Try to prove your conjectures. Your journal will become a record of your entire mathematics research experience. Don’t worry if your writing is not always perfect. Often journal pages look rough, with notes to yourself, false starts, and partial solutions. However, be sure that you can read your own notes later and try to organize your writing in ways that will facilitate your thinking. Your logbook will serve as a record of where you are in your work at any moment and will be an invaluable tool when you write reports about your research.

Ideally, your mathematics research logbook should have pre-numbered pages. You can often find numbered graph paper science logs at office supply stores. If you can not find a notebook that has the pages already numbered, then the first thing you should do is go through the entire book putting numbers on each page using pen.

• Date each entry.

• Work in pen.

• Don’t erase or white out mistakes. Instead, draw a single line through what you would like ignored. There are many reasons for using this approach:

– Your notebook will look a lot nicer if it doesn’t have scribbled messes in it.

– You can still see what you wrote at a later date if you decide that it wasn’t a mistake after all.

– It is sometimes useful to be able to go back and see where you ran into difficulties.

– You’ll be able to go back and see if you already tried something so you won’t spend time trying that same approach again if it didn’t work.

• When you do research using existing sources, be sure to list the bibliographic information at the start of each section of notes you take. It is a lot easier to write down the citation while it is in front of you than it is to try to find it at a later date.

• Never tear a page out of your notebook. The idea is to keep a record of everything you have done. One reason for pre-numbering the pages is to show that nothing has been removed.

• If you find an interesting article or picture that you would like to include in your notebook, you can staple or tape it onto a page.

Advice for Keeping a Loose-Leaf Mathematics Research Logbook

Get yourself a good loose-leaf binder, some lined paper for notes, some graph paper for graphs and some blank paper for pictures and diagrams. Be sure to keep everything that is related to your project in your binder.

– Your notebook will look a lot nicer if it does not have scribbled messes in it.

• Be sure to keep everything related to your project. The idea is to keep a record of everything you have done.

• If you find an interesting article or picture that you would like to include in your notebook, punch holes in it and insert it in an appropriate section in your binder.

Making Mathematics Home | Mathematics Projects | Students | Teachers | Mentors | Parents | Hard Math Café |

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

Explaining research performance: investigating the importance of motivation

• Original Paper
• Open access
• Published: 23 May 2024
• Volume 4 , article number  105 , ( 2024 )

Cite this article

You have full access to this open access article

• Silje Marie Svartefoss   ORCID: orcid.org/0000-0001-5072-1293 1   nAff4 ,
• Jens Jungblut 2 ,
• Dag W. Aksnes 1 ,
• Kristoffer Kolltveit 2 &
• Thed van Leeuwen 3  

5 Altmetric

In this article, we study the motivation and performance of researchers. More specifically, we investigate what motivates researchers across different research fields and countries and how this motivation influences their research performance. The basis for our study is a large-N survey of economists, cardiologists, and physicists in Denmark, Norway, Sweden, the Netherlands, and the UK. The analysis shows that researchers are primarily motivated by scientific curiosity and practical application and less so by career considerations. There are limited differences across fields and countries, suggesting that the mix of motivational aspects has a common academic core less influenced by disciplinary standards or different national environments. Linking motivational factors to research performance, through bibliometric data on publication productivity and citation impact, our data show that those driven by practical application aspects of motivation have a higher probability for high productivity. Being driven by career considerations also increases productivity but only to a certain extent before it starts having a detrimental effect.

Similar content being viewed by others

How to design bibliometric research: an overview and a framework proposal

Literature reviews as independent studies: guidelines for academic practice

Research Methodology: An Introduction

Avoid common mistakes on your manuscript.

Introduction

Motivation and abilities are known to be as important factors in explaining employees’ job performance of employees (Van Iddekinge et al. 2018 ), and in the vast scientific literature on motivation, it is common to differentiate between intrinsic and extrinsic motivation factors (Ryan and Deci 2000 ). In this context, path-breaking individuals are said to often be intrinsically motivated (Jindal-Snape and Snape 2006 ; Thomas and Nedeva 2012 ; Vallerand et al. 1992 ), and it has been found that the importance of these of types of motivations differs across occupations and career stages (Duarte and Lopes 2018 ).

In this article, we address the issue of motivation for one specific occupation, namely: researchers working at universities. Specifically, we investigate what motivates researchers across fields and countries (RQ1) and how this motivation is linked to their research performance (RQ2). The question of why people are motivated to do their jobs is interesting to address in an academic context, where work is usually harder to control, and individuals tend to have a lot of much freedom in structuring their work. Moreover, there have been indications that academics possess an especially high level of motivation for their tasks that is not driven by a search for external rewards but by an intrinsic satisfaction from academic work (Evans and Meyer 2003 ; Leslie 2002 ). At the same time, elements of researchers’ performance are measurable through indicators of their publication activity: their productivity through the number of outputs they produce and the impact of their research through the number of citations their publications receive (Aksnes and Sivertsen 2019 ; Wilsdon et al. 2015 ).

Elevating research performance is high on the agenda of many research organisations (Hazelkorn 2015 ). How such performance may be linked to individuals’ motivational aspects has received little attention. Thus, a better understanding of this interrelation may be relevant for developing institutional strategies to foster environments that promote high-quality research and research productivity.

Previous qualitative research has shown that scientists are mainly intrinsically motivated (Jindal-Snape and Snape 2006 ). Other survey-based contributions suggest that there can be differences in motivations across disciplines (Atta-Owusu and Fitjar 2021 ; Lam 2011 ). Furthermore, the performance of individual scientists has been shown to be highly skewed in terms of publication productivity and citation rates (Larivière et al. 2010 ; Ruiz-Castillo and Costas 2014 ). There is a large body of literature explaining these differences. Some focus on national and institutional funding schemes (Hammarfelt and de Rijcke 2015 ; Melguizo and Strober 2007 ) and others on the research environment, such as the presence of research groups and international collaboration (Jeong et al. 2014 ), while many studies address the role of academic rank, age, and gender (see e.g. Baccini et al. 2014 ; Rørstad and Aksnes 2015 ). Until recently, less emphasis has been placed on the impact of researchers’ motivation. Some studies have found that different types of motivations drive high levels of research performance (see e.g. Horodnic and Zaiţ 2015 ; Ryan and Berbegal-Mirabent 2016 ). However, researchers are only starting to understand how this internal drive relates to research performance.

While some of the prior research on the impact of motivation depends on self-reported research performance evaluations (Ryan 2014 ), the present article combines survey responses with actual bibliometric data. To investigate variation in research motivation across scientific fields and countries, we draw on a large-N survey of economists, cardiologists, and physicists in Denmark, Norway, Sweden, the Netherlands, and the UK. To investigate how this motivation is linked to their research performance, we map the survey respondents’ publication and citation data from the Web of Science (WoS).

This article is organised as follows. First, we present relevant literature on research performance and motivation. Next, the scientific fields and countries are then presented before elaborating on our methodology. In the empirical analysis, we investigate variations in motivation across fields, gender, age, and academic position and then relate motivation to publications and citations as our two measures of research performance. In the concluding section, we discuss our findings and implications for national decision-makers and individual researchers.

Motivation and research performance

As noted above, the concepts of intrinsic and extrinsic motivation play an important role in the literature on motivation and performance. Here, intrinsic motivation refers to doing something for its inherent satisfaction rather than for some separable consequence. Extrinsic motivation refers to doing something because it leads to a separable outcome (Ryan and Deci 2000 ).

Some studies have found that scientists are mainly intrinsically motivated (Jindal-Snape and Snape 2006 ; Lounsbury et al. 2012 ). Research interests, curiosity, and a desire to contribute to new knowledge are examples of such motivational factors. Intrinsic motives have also been shown to be crucial when people select research as a career choice (Roach and Sauermann 2010 ). Nevertheless, scientists are also motivated by extrinsic factors. Several European countries have adopted performance-based research funding systems (Zacharewicz et al. 2019 ). In these systems, researchers do not receive direct financial bonuses when they publish, although such practices may occur at local levels (Stephan et al. 2017 ). Therefore, extrinsic motivation for such researchers may include salary increases, peer recognitions, promotion, or expanded access to research resources (Lam 2011 ). According to Tien and Blackburn ( 1996 ), both types of motivations operate simultaneously, and their importance vary and may depend on the individual’s circumstances, personal situation, and values.

The extent to which different kinds of motivations play a role in scientists’ performance has been investigated in several studies. In these studies, bibliometric indicators based on the number of publications are typically used as outcome measures. Such indicators play a critical role in various contexts in the research system (Wilsdon et al. 2015 ), although it has also been pointed out that individuals can have different motivations to publish (Hangel and Schmidt-Pfister 2017 ).

Based on a survey of Romanian economics and business administration academics combined with bibliometric data, Horodnic and Zait ( 2015 ) found that intrinsic motivation was positively correlated with research productivity, while extrinsic motivation was negatively correlated. Their interpretations of the results are that researchers motivated by scientific interest are more productive, while researchers motivated by extrinsic forces will shift their focus to more financially profitable activities. Similarly, based on the observation that professors continue to publish even after they have been promoted to full professor, Finkelstein ( 1984 ) concluded that intrinsic rather than extrinsic motivational factors have a decisive role regarding the productivity of academics.

Drawing on a survey of 405 research scientists working in biological, chemical, and biomedical research departments in UK universities, Ryan ( 2014 ) found that (self-reported) variations in research performance can be explained by instrumental motivation based on financial incentives and internal motivation based on the individual’s view of themselves (traits, competencies, and values). In the study, instrumental motivation was found to have a negative impact on research performance: As the desire for financial rewards increase, the level of research performance decreases. In other words, researchers mainly motivated by money will be less productive and effective in their research. Contrarily, internal motivation was found to have a positive impact on research performance. This was explained by highlighting that researchers motivated by their self-concept set internal standards that become a reference point that reinforces perceptions of competency in their environments.

Nevertheless, it has also been argued that intrinsic and extrinsic motivations for publishing are intertwined (Ma 2019 ). According to Tien and Blackburn ( 1996 ), research productivity is neither purely intrinsically nor purely extrinsically motivated. Publication activity is often a result of research, which may be intrinsically motivated or motivated by extrinsic factors such as a wish for promotion, where the number of publications is often a part of the assessment (Cruz-Castro and Sanz-Menendez 2021 ; Tien 2000 , 2008 ).

The negative relationship between external/instrumental motivation and performance and the positive relationship between internal/self-concept motivation and performance are underlined by Ryan and Berbegal-Mirabent ( 2016 ). Drawing on a fuzzy set qualitative comparative analysis of a random sampling of 300 of the original respondents from Ryan ( 2014 ), they find that scientists working towards the standards and values they identify with, combined with a lack of concern for instrumental rewards, contribute to higher levels of research performance.

Based on the above, this article will address two research questions concerning different forms of motivation and the relationship between motivation and research performance.

How does the motivation of researchers vary across fields and countries?

How do different types of motivations affect research performance?

In this study, the roles of three different motivational factors are analysed. These are scientific curiosity, practical and societal applications, and career progress. The study aims to assess the role of these specific motivational factors and not the intrinsic-extrinsic distinction more generally. Of the three factors, scientific curiosity most strongly relates to intrinsic motivation; practical and societal applications also entail strong intrinsic aspects. On the other hand, career progress is linked to extrinsic motivation.

In addition to variation in researchers’ motivations by field and country, we consider differences in relation to age, position and gender. Additionally, when investigating how motivation relates to scientific performance we control for the influence of age, gender, country and funding. These are dimensions where differences might be found in motivational factors given that scientific performance, particularly publication productivity, has been shown to differ along these dimensions (Rørstad and Aksnes 2015 ).

Research context: three fields, five countries

To address the research question about potential differences across fields and countries, the study is based on a sample consisting of researchers in three different fields (cardiology, economics, and physics) and five countries (Denmark, Norway, Sweden, the Netherlands, and the UK). Below, we describe this research context in greater detail.

The fields represent three different domains of science: medicine, social sciences, and the natural sciences, where different motivational factors may be at play. This means that the fields cover three main areas of scientific investigations: the understanding of the world, the functioning of the human body, and societies and their functions. The societal role and mission of the fields also differ. While a primary aim of cardiology research and practice is to reduce the burden of cardiovascular disease, physics research may drive technology advancements, which impacts society. Economics research may contribute to more effective use of limited resources and the management of people, businesses, markets, and governments. In addition, the fields also differ in publication patterns (Piro et al. 2013 ). The average number of publications per researcher is generally higher in cardiology and physics than in economics (Piro et al. 2013 ). Moreover, cardiologists and physicists mainly publish in international scientific journals (Moed 2005 ; Van Leeuwen 2013 ). In economics, researchers also tend to publish books, chapters, and articles in national languages, in addition to international journal articles (Aksnes and Sivertsen 2019 ; van Leeuwen et al. 2016 ).

We sampled the countries with a twofold aim. On the one hand, we wanted to have countries that are comparable so that differences in the development of the science systems, working conditions, or funding availability would not be too large. On the other hand, we also wanted to assure variation among the countries regarding these relevant framework conditions to ensure that our findings are not driven by a specific contextual condition.

The five countries in the study are all located in the northwestern part of Europe, with science systems that are foremost funded by block grant funding from the national governments (unlike, for example, the US, where research grants by national funding agencies are the most important funding mechanism) (Lepori et al. 2023 ).

In all five countries, the missions of the universities are composed of a blend of education, research, and outreach. Furthermore, the science systems in Norway, Denmark, Sweden, and the Netherlands have a relatively strong orientation towards the Anglo-Saxon world in the sense that publishing in the national language still exists, but publishing in English in internationally oriented journals in which English is the language of publications is the norm (Kulczycki et al. 2018 ). These framework conditions ensure that those working in the five countries have somewhat similar missions to fulfil in their professions while also belonging to a common mainly Anglophone science system.

However, in Norway, Denmark, Sweden, and the Netherlands, research findings in some social sciences, law, and the humanities are still oriented on publishing in various languages. Hence, we avoided selecting the humanities field for this study due to a potential issue with cross-country comparability (Sivertsen 2019 ; Sivertsen and Van Leeuwen 2014 ; Van Leeuwen 2013 ).

Finally, the chosen countries vary regarding their level of university autonomy. When combining the scores for organisational, financial, staffing, and academic autonomy presented in the latest University Autonomy in Europe Scorecard presented by the European University Association (EUA), the UK, the Netherlands, and Denmark have higher levels of autonomy compared to Norway and Sweden, with Swedish universities having less autonomy than their Norwegian counterparts (Pruvot et al. 2023 ). This variation is relevant for our study, as it ensures that our findings are not driven by response from a higher education system with especially high or low autonomy, which can influence the motivation and satisfaction of academics working in it (Daumiller et al. 2020 ).

Data and methods

The data used in this article are a combination of survey data and bibliometric data retrieved from the WoS. The WoS database was chosen for this study due to its comprehensive coverage of research literature across all disciplines, encompassing the three specific research areas under analysis. Additionally, the WoS database is well-suited for bibliometric analyses, offering citation counts essential for this study.

Two approaches were used to identify the sample for the survey. Initially, a bibliometric analysis of the WoS using journal categories (‘Cardiac & cardiovascular systems’, ‘Economics’, and ‘Physics’) enabled the identification of key institutions with a minimum number of publications within these journal categories. Following this, relevant organisational units and researchers within these units were identified through available information on the units’ webpages. Included were employees in relevant academic positions (tenured academic personnel, post-docs, and researchers, but not PhD students, adjunct positions, guest researchers, or administrative and technical personnel).

Second, based on the WoS data, people were added to this initial sample if they had a minimum number of publications within the field and belonged to any of the selected institutions, regardless of unit affiliation. For economics, the minimum was five publications within the selected period (2011–2016). For cardiology and physics, where the individual publication productivity is higher, the minimum was 10 publications within the same period. The selection of the minimum publication criteria was based on an analysis of publication outputs in these fields between 2011 and 2016. The thresholds were applied to include individuals who are more actively engaged in research while excluding those with more peripheral involvement. The higher thresholds for cardiology and physics reflect the greater frequency of publications (and co-authorship) observed in these fields.

The benefit of this dual-approach strategy to sampling is that we obtain a more comprehensive sample: the full scope of researchers within a unit and the full scope of researchers that publish within the relevant fields. Overall, 59% of the sample were identified through staff lists and 41% through the second step involving WoS data.

The survey data were collected through an online questionnaire first sent out in October 2017 and closed in December 2018. In this period, several reminders were sent to increase the response rate. Overall, the survey had a response rate of 26.1% ( N  = 2,587 replies). There were only minor variations in response rates between scientific fields; the variations were larger between countries. Tables  1 and 2 provide an overview of the response rate by country and field.

Operationalisation of motivation

Motivation was measured by a question in the survey asking respondents what motivates or inspires them to conduct research, of which three dimensions are analysed in the present paper. The two first answer categories were related to intrinsic motivation (‘Curiosity/scientific discovery/understanding the world’ and ‘Application/practical aims/creating a better society’). The third answer category was more related to extrinsic motivation (‘Progress in my career [e.g. tenure/permanent position, higher salary, more interesting/independent work]’). Appendix Table A1 displays the distribution of respondents and the mean value and standard deviation for each item.

These three different aspects of motivation do not measure the same phenomenon but seem to capture different aspects of motivation (see Pearson’s correlation coefficients in Appendix Table A2 ). There is no correlation between curiosity/scientific discovery, career progress, and practical application. However, there is a weak but significant positive correlation between career progress and practical application. These findings indicate that those motivated by career considerations to some degrees also are motivated by practical application.

In addition to investigating how researchers’ motivation varies by field and country, we consider the differences in relation to age, position and gender as well. Field of science differentiates between economics, cardiology, physics, and other fields. The country variables differentiate between the five countries. Age is a nine-category variable. The position variable differentiates between full professors, associate professors, and assistant professors. The gender variable has two categories (male or female). For descriptive statistics on these additional variables, see Appendix Table A3 .

Publication productivity and citation impact

To analyse the respondents’ bibliometric performance, the Centre for Science and Technology Studies (CWTS) in-house WoS database was used. We identified the publication output of each respondent during 2011–2017 (limited to regular articles, reviews, and letters). For 16% of the respondents, no publications were identified in the database. These individuals had apparently not published in international journals covered by the database. However, in some cases, the lack of publications may be due to identification problems (e.g. change of names). Therefore, we decided not to include the latter respondents in the analysis.

Two main performance measures were calculated: publication productivity and citation impact. As an indicator of productivity, we counted the number of publications for each individual (as author or co-author) during the period. To analyse the citation impact, a composite measure using three different indicators was used: total number of citations (total citations counts for all articles they have contributed to during the period, counting citations up to and including 2017), normalised citation score (MNCS), and proportion of publications among the 10% most cited articles in their fields (Waltman and Schreiber 2013 ). Here, the MNCS is an indicator for which the citation count of each article is normalised by subject, article type, and year, where 1.00 corresponds to the world average (Waltman et al. 2011 ). Based on these data, averages for the total publication output of each respondent were calculated. By using three different indicators, we can avoid biases or limitations attached to each of them. For example, using the MNCS, a respondent with only one publication would appear as a high impact researcher if this article was highly cited. However, when considering the additional indicator, total citation counts, this individual would usually perform less well.

The bibliometric scores were skewedly distributed among the respondents. Rather than using the absolute numbers, in this paper, we have classified the respondents into three groups according to their scores on the indicators. Here, we have used percentile rank classes (tertiles). Percentile statistics are increasingly applied in bibliometrics (Bornmann et al. 2013 ; Waltman and Schreiber 2013 ) due to the presence of outliers and long tails, which characterise both productivity and citation distributions.

As the fields analysed have different publication patterns, the respondents within each field were ranked according to their scores on the indicators, and their percentile rank was determined. For the productivity measure, this means that there are three groups that are equal in terms of number of individuals included: 1: Low productivity (the group with the lowest publication numbers, 0–33 percentile), 2: Medium productivity (33–67 percentile), and 3: High productivity (67–100 percentile). For the citation impact measure, we conducted a similar percentile analysis for each of the three composite indicators. Then everyone was assigned to one of the three percentile groups based on their average score: 1: Low citation impact (the group with lowest citation impact, 0–33 percentile), 2: Medium citation impact (33–67 percentile), and 3: High citation impact (67–100 percentile), cf. Table  3 . Although it might be argued that the application of tertile groups rather than absolute numbers leads to a loss of information, the advantage is that the results are not influenced by extreme values and may be easier to interpret.

Via this approach, we can analyse the two important dimensions of the respondents’ performance. However, it should be noted that the WoS database does not cover the publication output of the fields equally. Generally, physics and cardiology are very well covered, while the coverage of economics is somewhat lower due to different publication practices (Aksnes and Sivertsen 2019 ). This problem is accounted for in our study by ranking the respondents in each field separately, as described above. In addition, not all respondents may have been active researchers during the entire 2011–2017 period, which we have not adjusted for. Despite these limitations, the analysis provides interesting information on the bibliometric performance of the respondents at an aggregated level.

Regression analysis

To analyse the relationship between motivation and performance, we apply multinomial logistic regression rather then ordered logistic regression because we assume that the odds for respondents belonging in each category of the dependent variables are not equal (Hilbe 2017 ). The implication of this choice of model is that the model tests the probability of respondents being in one category compared to another (Hilbe 2017 ). This means that a reference or baseline category must be selected for each of the dependent variables (productivity and citation impact). Furthermore, the coefficient estimates show how the probability of being in one of the other categories decreases or increases compared to being in the reference category.

For this analysis, we selected the medium performers as the reference or baseline category for both our dependent variables. This enables us to evaluate how the independent variables affect the probability of being in the low performers group compared to the medium performers and the high performers compared to the medium performers.

To evaluate model fit, we started with a baseline model where only types of motivations were included as independent variables. Subsequently, the additional variables were introduced into the model, and based on measures for model fit (Pseudo R 2 , -2LL, and Akaike Information Criterion (AIC)), we concluded that the model with all additional variables included provides the best fit to the data for both the dependent variables (see Appendix Tables A5 and A6 ). Additional control variables include age, gender, country, and funding. We include these variables as controls to obtain robust effects of motivation and not effects driven by other underlying factors. The type of funding was measured by variables where the respondent answered the following question: ‘How has your research been funded the last five years?’ The funding variable initially consisted of four categories: ‘No source’, ‘Minor source’, ‘Moderate source’, and ‘Major source’. In this analysis, we have combined ‘No source’ and ‘Minor source’ into one category (0) and ‘Moderate source’ and ‘Major source’ into another category (1). Descriptive statistics for the funding variables are available in Appendix Table A4 . We do not control for the influence of field due to how the scientific performance variables are operationalised, the field normalisation implies that there are no variations across fields. We also do not control for position, as this variable is highly correlated with age, and we are therefore unable to include these two variables in the same model.

The motivation of researchers

In the empirical analysis, we first investigate variation in motivation and then relate it to publications and citations as our two measures of research performance.

As Fig.  1 shows, the respondents are mainly driven by curiosity and the wish to make scientific discoveries. This is by far the most important motivation. Practical application is also an important source of motivation, while making career progress is not identified as being very important.

Motivation of researchers– percentage

As Table  4 shows, at the level of fields, there are no large differences, and the motivational profiles are relatively similar. However, physicists tend to view practical application as somewhat less important than cardiologists and economists. Moreover, career progress is emphasised most by economists. Furthermore, as table 5 shows, there are some differences in motivation between countries. For curiosity/scientific discovery and practical application, the variations across countries are minor, but researchers in Denmark tend to view career progress as somewhat more important than researchers in the other countries.

Furthermore, as table 6 shows, women seem to view practical application and career progress as a more important motivation than men; these differences are also significant. Similar gender disparities have also been reported in a previous study (Zhang et al. 2021 ).

There are also some differences in motivation across the additional variables worth mentioning, as Table  7 shows. Unsurprisingly, perhaps, there is a significant moderate negative correlation between age, position, and career progress. This means that the importance of career progress as a motivation seems to decrease with increased age or a move up the position hierarchy.

In the second part of the analysis, we relate motivation to research performance. We first investigate publications and productivity using the percentile groups. Here, we present the results we use using predicted probabilities because they are more easily interpretable than coefficient estimates. For the model with productivity percentile groups as the dependent variable, the estimates for career progress were negative when comparing the medium productivity group to the high productivity group and the medium productivity group to the low productivity group. This result indicates that the probability of being in the high and low productivity groups decreases compared to the medium productivity group as the value of career progress increases, which may point towards a curvilinear relationship between the variables. A similar pattern was also found in the model with the citation impact group as the dependent variable, although it was not as apparent.

As a result of this apparent curvilinear relationship, we included quadric terms for career progress in both models, and these were significant. Likelihood ratio tests also show that the models with quadric terms included have a significant better fit to the data. Furthermore, the AIC was also lower for these models compared to the initial models where quadric terms were not included (see Appendix Tables A5 – A7 ). Consequently, we base our results on these models, which can be found in Appendix Table A7 . Due to a low number of respondents in the low categories of the scientific curiosity/discovery variable, we also combined the first three values into one to include it as a variable in the regression analysis, which results in a reduced three-value variable for scientific curiosity/discovery.

Results– productivity percentile group

Using the productivity percentile group as the dependent variable, we find that the motivational aspects of practical application and career progress have a significant effect on the probability of being in the low, medium, or high productivity group but not curiosity/scientific discovery. In Figs.  2 and 3 , each line represents the probability of being in each group across the scale of each motivational aspect.

Predicted probability for being in each of the productivity groups according to the value on the ‘practical application’ variable

Predicted probability of being in the low and high productivity groups according to the value on the ‘progress in my career’ variable

Figure  2 shows that at low values of application, there are no significant differences between the probability of being in either of the groups. However, from around value 3 of application, the differences between the probability of being in each group increases, and these are also significant. As a result, we concluded that high scores on practical application is related to increased probability of being in the high productivity group.

In Fig.  3 , we excluded the medium productivity group from the figure because there are no significant differences between this group and the high and low productivity group. Nevertheless, we found significant differences between the low productivity and the high productivity group. Since we added a quadric term for career progress, the two lines in Fig.  3 have a curvilinear shape. Figure  3 shows that there are only significant differences between the probability of being in the low or high productivity group at mid and high values of career progress. In addition, the probability of being in the high productivity group is at its highest value at mid values of career progress. This indicates that being motivated by career progress increases the probability of being in the high productivity group but only up to a certain point before it begins to have a negative effect on the probability of being in this group.

We also included age and gender as variables in the model, and Figs.  4 and 5 show the results. Figure  4 shows that age especially impacts the probability of being in the high productivity and low productivity groups. The lowest age category (< 30–34 years) has the highest probability for being in the low productivity group, while from the mid age category (50 years and above), the probability is highest for being in the high productivity group. This means that increased age is related to an increased probability of high productivity. The variable controlling for the effect of funding also showed some significant results (see Appendix Table A7 ). The most relevant finding is that receiving competitive grants from external public sources had a very strong and significant positive effect on being in the high productivity group and a medium-sized significant negative effect on being in the low productivity group. This shows that receiving external funding in the form of competitive grants has a strong effect on productivity.

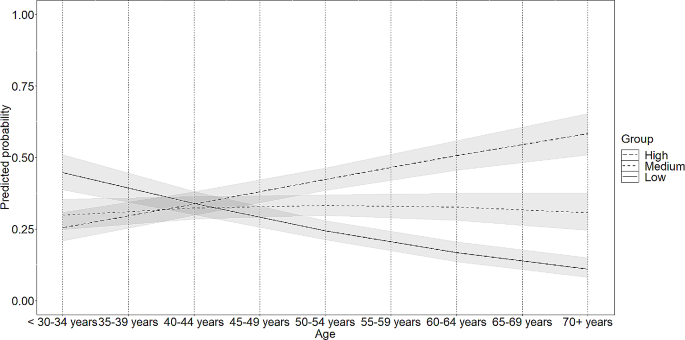
Predicted probability of being in each of the productivity groups according to age

Figure  5 shows that there is a difference between male and female respondents. For females, there are no differences in the probability of being in either of the groups, while males have a higher probability of being in the high productivity group compared to the medium and low productivity groups.

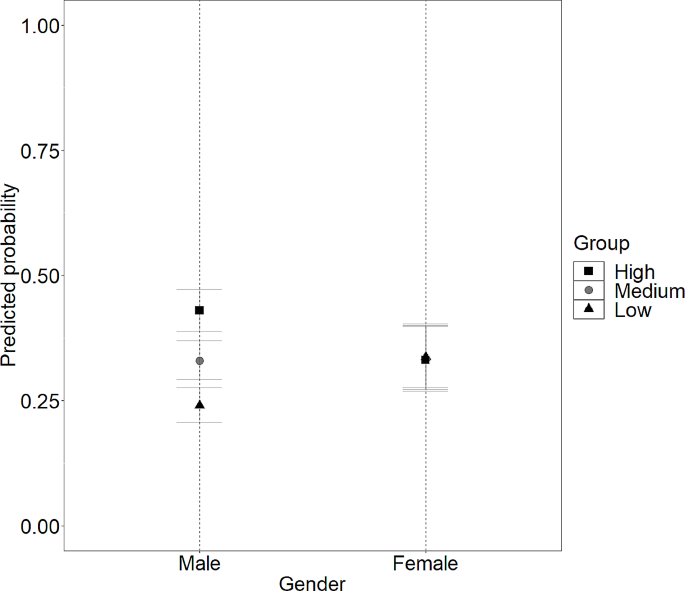
Results– citation impact group

For the citation impact group as the dependent variable, we found that career progress has a significant effect on the probability of being in the low citation impact group or the high citation group but not curiosity/scientific discovery or practical application. Figure  6 shows how the probability of being in the high citation impact group increases as the value on career progress increases and is higher than that of being in the low citation impact group, but only up to a certain point. This indicates that career progress increases the probability of being in the high citation impact group to some degree but that too high values are not beneficial for high citation impact. However, it should also be noted that the effect of career progress is weak and that it is difficult to conclude on how very low or very high values of career progress affect the probability of being in the two groups.

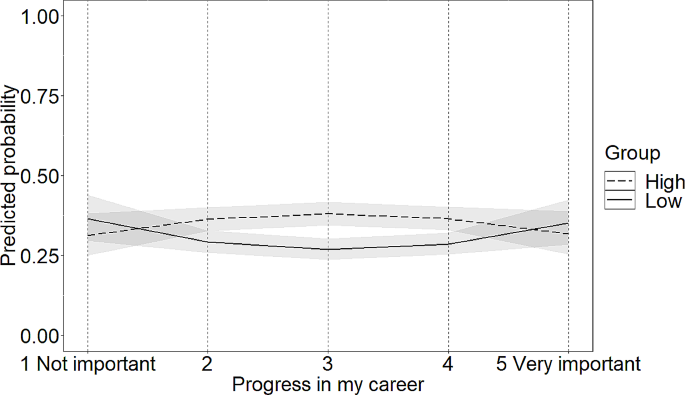
Predicted probability for being in each of the citation impact groups according to the value on the ‘progress in my career’ variable

We also included age and gender as variables in the model, and we found a similar pattern as in the model with productivity percentile group as the dependent variable. However, the relationship between the variables is weaker in this model with the citation impact group as the dependent variable. Figure  7 shows that the probability of being in the high citation impact group increases with age, but there is no significant difference between the probability of being in the high citation impact group and the medium citation impact group. We only see significant differences when each of these groups is compared to the low citation impact group. In addition, the increase in probability is more moderate in this model.

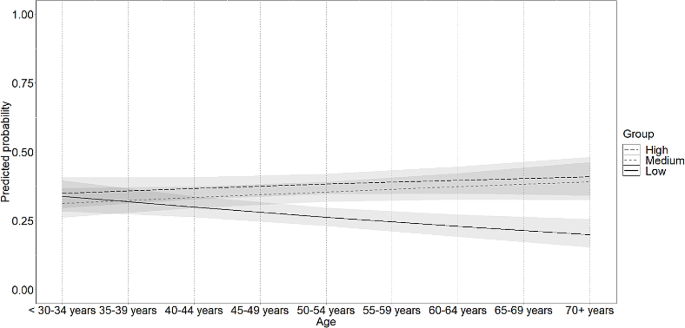
Predicted probability of being in each of the citation impact groups according to age

Figure  8 shows that there are differences between male and female respondents. Male respondents have a significant higher probability of being in the medium or high citation impact group compared to the low citation impact group, but there is no significant difference in the probability between the high and medium citation impact groups. For female respondents, there are no significant differences. Similarly, for age, the effect also seems to be more moderate in this model compared to the model with productivity percentile groups as the dependent variable. In addition, the effect of funding sources is more moderate on citation impact compared to productivity (see Appendix Table A7 ). Competitive grants from external public sources still have the most relevant effect, but the effect size and level of significance is lower than for the model where productivity groups are the dependent variable. Respondents who received a large amount of external funding through competitive grants are more likely to be highly cited, but the effect size is much smaller, and the result is only significant at p  < 0.1. Those who do not receive much funding from this source are more likely to be in the low impact group. Here, the effect size is large, and the coefficient is highly significant.

Predicted probability for being in each of the citation impact groups according to gender

Concluding discussion

This article aimed to explore researchers’ motivations and investigate the impact of motivation on research performance. By addressing these issues across several fields and countries, we provided new evidence on the motivation and performance of researchers.

Most researchers in our large-N survey found curiosity/scientific discovery to be a crucial motivational factor, with practical application being the second most supported aspect. Only a smaller number of respondents saw career progress as an important inspiration to conduct their research. This supports the notion that researchers are mainly motivated by core aspects of academic work such as curiosity, discoveries, and practical application of their knowledge and less so by personal gains (see Evans and Meyer 2003 ). Therefore, our results align with earlier research on motivation. In their interview study of scientists working at a government research institute in the UK, Jindal-Snape and Snape ( 2006 ) found that the scientists were typically motivated by the ability to conduct high quality, curiosity-driven research and de-motivated by the lack of feedback from management, difficulty in collaborating with colleagues, and constant review and change. Salaries, incentive schemes, and prospects for promotion were not considered a motivator for most scientists. Kivistö and colleagues ( 2017 ) also observed similar patterns in more recent survey data from Finnish academics.

As noted in the introduction, the issue of motivation has often been analysed in the literature using the intrinsic-extrinsic distinction. In our study, we have not applied these concepts directly. However, it is clear that the curiosity/scientific discovery item should be considered a type of intrinsic motivation, as it involves performing the activity for its inherent satisfaction. Moreover, the practical application item should probably be considered mainly intrinsic, as it involves creating a better society (for others) without primarily focusing on gains for oneself. The career progress item explicitly mentions personal gains such as position and higher salary and is, therefore, a type of extrinsic motivation. This means that our results support the notion that there are very strong elements of intrinsic motivation among researchers (Jindal-Snape and Snape 2006 ).

When analysing the three aspects of motivation, we found some differences. Physicists tend to view practical application as less important than researchers in the two other fields, while career progress was most emphasised by economists. Regarding country differences, our data suggest that career progress is most important for researchers in Denmark. Nevertheless, given the limited effect sizes, the overall picture is that motivational factors seem to be relatively similar regarding disciplinary and country dimensions.

Regarding gender aspects of motivation, our data show that women seem to view practical application and career progress as more important than men. One explanation for this could be the continued gender differences in academic careers, which tend to disadvantage women, thus creating a greater incentive for female scholars to focus on and be motivated by career progress aspects (Huang et al. 2020 ; Lerchenmueller and Sorenson 2018 ). Unsurprisingly, respondents’ age and academic position influenced the importance of different aspects of motivation, especially regarding career progress. Here, increased age and moving up the positional hierarchy are linked to a decrease in importance. This highlights that older academics and those in more senior positions drew more motivation from other sources that are not directly linked to their personal career gains. This can probably be explained by the academic career ladder plateauing at a certain point in time, as there are often no additional titles and very limited recognition beyond becoming a full professor. Finally, the type of funding that scholars received also had an influence on their productivity and, to a certain extent, citation impact.

Overall, there is little support that researchers across various fields and countries are very different when it comes to their motivation for conducting research. Rather, there seems to be a strong common core of academic motivation that varies mainly by gender and age/position. Rather than talking about researchers’ motivation per se, our study, therefore, suggests that one should talk about motivation across gender, at different stages of the career, and, to a certain degree, in different fields. Thus, motivation seems to be a multi-faceted construct, and the importance of different aspects of motivation vary between different groups.

In the second step of our analysis, we linked motivation to performance. Here, we focused on both scientific productivity and citation impact. Regarding the former, our data show that both practical application and career progress have a significant effect on productivity. The relationship between practical application aspects and productivity is linear, meaning that those who indicate that this aspect of motivation is very important to them have a higher probability of being in the high productivity group. The relationship between career aspects of motivation and productivity is curve linear, and we found only significant differences between the high and low productivity groups at mid and high values of the motivation scale. This indicates that being more motivated by career progress increases productivity but only to a certain extent before it starts having a detrimental effect. A common assumption has been that intrinsic motivation has a positive and instrumental effect and extrinsic motivation has a negative effect on the performance of scientists (Peng and Gao 2019 ; Ryan and Berbegal-Mirabent 2016 ). Our results do not generally support this, as motives related to career progress are positively linked with productivity only to a certain point. Possibly, this can be explained by the fact that the number of publications is often especially important in the context of recruitment and promotion (Langfeldt et al. 2021 ; Reymert et al. 2021 ). Thus, it will be beneficial from a scientific career perspective to have many publications when trying to get hired or promoted.

Regarding citation impact, our analysis highlights that only the career aspects of motivation have a significant effect. Similar to the results regarding productivity, being more motivated by career progress increases the probability of being in the high citation impact group, but only to a certain value when the difference stops being significant. It needs to be pointed out that the effect strength is weaker than in the analysis that focused on productivity. Thus, these results should be treated with greater caution.

Overall, our results shed light on some important aspects regarding the motivation of academics and how this translates into research performance. Regarding our first research question, it seems to be the case that there is not one type of motivation but rather different contextual mixes of motivational aspects that are strongly driven by gender and the academic position/age. We found only limited effects of research fields and even less pronounced country effects, suggesting that while situational, the mix of motivational aspects also has a common academic core that is less influenced by different national environments or disciplinary standards. Regarding our second research question, our results challenge the common assumption that intrinsic motivation has a positive effect and extrinsic motivation has a negative effect on the performance of scientists. Instead, we show that motives related to career are positively linked to productivity at least to a certain point. Our analysis regarding citation patterns achieved similar results. Combined with the finding regarding the importance of current academic position and age for specific patterns of motivation, it could be argued that the fact that the number of publications is often used as a measurement in recruitment and promotion makes academics that are more driven by career aspects publish more, as this is perceived as a necessary condition for success.

Our study has a clear focus on the research side of academic work. However, most academics do both teaching and research, which raises the question of how far our results can also inform our knowledge regarding the motivation for teaching. On the one hand, previous studies have highlighted that intrinsic motivation is also of high importance for the quality of teaching (see e.g. Wilkesmann and Lauer 2020 ), which fits well with our findings. At the same time, the literature also highlights persistent goal conflicts of academics (see e.g. Daumiller et al. 2020 ), given that extra time devoted to teaching often comes at the costs of publications and research. Given that other findings in the literature show that research performance continues to be of higher importance than teaching in academic hiring processes (Reymert et al. 2021 ), the interplay between research performance, teaching performance, and different types of motivation is most likely more complicated and demands further investigation.

While offering several relevant insights, our study still comes with certain limitations that must be considered. First, motivation is a complex construct. Thus, there are many ways one could operationalise it, and not one specific understanding so far seems to have emerged as best practice. Therefore, our approach to operationalisation and measurement should be seen as an addition to this broader field of measurement approaches, and we do not claim that this is the only sensible way of doing it. Second, we rely on self-reported survey data to measure the different aspects of motivation in our study. This means that aspects such as social desirability could influence how far academics claim to be motivated by certain aspects. For example, claiming to be mainly motivated by personal career gains may be considered a dubious motive among academics.

With respect to the bibliometric analyses, it is important to realise that we have lumped researchers into categories, thereby ‘smoothening’ the individual performances into group performances under the various variables. This has an effect that some extraordinary scores might have become invisible in our study, which might have been interesting to analyse separately, throwing light on the relationships we studied. However, breaking the material down to the lower level of analysis of individual researchers also comes with a limitation, namely that at the level of the individual academic, bibliometrics tend to become quite sensitive for the underlying numbers, which in itself is then hampered by the coverage of the database used, the publishing cultures in various countries and fields, and the age and position of the individuals. Therefore, the level of the individual academic has not been analysed in our study, how interesting and promising outcomes might have been. even though we acknowledge that such a study could yield interesting results.

Finally, our sample is drawn from northwestern European countries and a limited set of disciplines. We would argue that we have sufficient variation in countries and disciplines to make the results relevant for a broader audience context. While our results show rather small country or discipline differences, we are aware that there might be country- or discipline-specific effects that we cannot capture due to the sampling approach we used. Moreover, as we had to balance sufficient variation in framework conditions with the comparability of cases, the geographical generalisation of our results has limitations.

This article investigated what motivates researchers across different research fields and countries and how this motivation influences their research performance. The analysis showed that the researchers are mainly motivated by scientific curiosity and practical application and less so by career considerations. Furthermore, the analysis shows that researchers driven by practical application aspects of motivation have a higher probability of high productivity. Being driven by career considerations also increases productivity but only to a certain extent before it starts having a detrimental effect.

The article is based on a large-N survey of economists, cardiologists, and physicists in Denmark, Norway, Sweden, the Netherlands, and the UK. Building on this study, future research should expand the scope and study the relationship between motivation and productivity as well as citation impact in a broader disciplinary and geographical context. In addition, we encourage studies that develop and validate our measurement and operationalisation of aspects of researchers’ motivation.

Finally, a long-term panel study design that follows respondents throughout their academic careers and investigates how far their motivational patterns shift over time would allow for more fine-grained analysis and thereby a richer understanding of the important relationship between motivation and performance in academia.

Data availability

The data set for this study is available from the corresponding author upon reasonable request.

Aksnes DW, Sivertsen G (2019) A criteria-based assessment of the coverage of Scopus and web of Science. J Data Inform Sci 4(1):1–21. https://doi.org/10.2478/jdis-2019-0001

Article   Google Scholar  

Atta-Owusu K, Fitjar RD (2021) What motivates academics for external engagement? Exploring the effects of motivational drivers and organizational fairness. Sci Public Policy. https://doi.org/10.1093/scipol/scab075 . November, scab075

Baccini A, Barabesi L, Cioni M, Pisani C (2014) Crossing the hurdle: the determinants of individual. Sci Perform Scientometrics 101(3):2035–2062. https://doi.org/10.1007/s11192-014-1395-3

Bornmann L, Leydesdorff L, Mutz R (2013) The use of percentiles and percentile rank classes in the analysis of bibliometric data: opportunities and limits. J Informetrics 7(1):158–165. https://doi.org/10.1016/j.joi.2012.10.001

Cruz-Castro L, Sanz-Menendez L (2021) What should be rewarded? Gender and evaluation criteria for tenure and promotion. J Informetrics 15(3):1–22. https://doi.org/10.1016/j.joi.2021.101196

Daumiller M, Stupnisky R, Janke S (2020) Motivation of higher education faculty: theoretical approaches, empirical evidence, and future directions. Int J Educational Res 99:101502. https://doi.org/10.1016/j.ijer.2019.101502

Duarte H, Lopes D (2018) Career stages and occupations impacts on workers motivations. Int J Manpow 39(5):746–763. https://doi.org/10.1108/IJM-02-2017-0026

Evans IM, Meyer LH (2003) Motivating the professoriate: why sticks and carrots are only for donkeys. High Educ Manage Policy 15(3):151–167. https://doi.org/10.1787/hemp-v15-art29-en

Finkelstein MJ (1984) The American academic profession: a synthesis of social scientific inquiry since World War II. Ohio State University, Columbus

Google Scholar  

Hammarfelt B, de Rijcke S (2015) Accountability in context: effects of research evaluation systems on publication practices, disciplinary norms, and individual working routines in the Faculty of arts at Uppsala University. Res Evaluation 24(1):63–77. https://doi.org/10.1093/reseval/rvu029

Hangel N, Schmidt-Pfister D (2017) Why do you publish? On the tensions between generating scientific knowledge and publication pressure. Aslib J Inform Manage 69(5):529–544. https://doi.org/10.1108/AJIM-01-2017-0019

Hazelkorn E (2015) Rankings and the reshaping of higher education: the battle for world-class excellence. Palgrave McMillan, Basingstoke

Book   Google Scholar  

Hilbe JM (2017) Logistic regression models. Taylor & Francis Ltd, London

Horodnic IA, Zaiţ A (2015) Motivation and research productivity in a university system undergoing transition. Res Evaluation 24(3):282–292

Huang J, Gates AJ, Sinatra R, Barabási A-L (2020) Historical comparison of gender inequality in scientific careers across countries and disciplines. Proceedings of the National Academy of Sciences 117(9):4609–4616. https://doi.org/10.1073/pnas.1914221117

Jeong S, Choi JY, Kim J-Y (2014) On the drivers of international collaboration: the impact of informal communication, motivation, and research resources. Sci Public Policy 41(4):520–531. https://doi.org/10.1093/scipol/sct079

Jindal-Snape D, Snape JB (2006) Motivation of scientists in a government research institute: scientists’ perceptions and the role of management. Manag Decis 44(10):1325–1343. https://doi.org/10.1108/00251740610715678

Kivistö J, Pekkola E, Lyytinen A (2017) The influence of performance-based management on teaching and research performance of Finnish senior academics. Tert Educ Manag 23(3):260–275. https://doi.org/10.1080/13583883.2017.1328529

Kulczycki E, Engels TCE, Pölönen J, Bruun K, Dušková M, Guns R et al (2018) Publication patterns in the social sciences and humanities: evidence from eight European countries. Scientometrics 116(1):463–486. https://doi.org/10.1007/s11192-018-2711-0

Lam A (2011) What motivates academic scientists to engage in research commercialization: gold, ribbon or puzzle? Res Policy 40(10):1354–1368. https://doi.org/10.1016/j.respol.2011.09.002

Langfeldt L, Reymert I, Aksnes DW (2021) The role of metrics in peer assessments. Res Evaluation 30(1):112–126. https://doi.org/10.1093/reseval/rvaa032

Larivière V, Macaluso B, Archambault É, Gingras Y (2010) Which scientific elites? On the concentration of research funds, publications and citations. Res Evaluation 19(1):45–53. https://doi.org/10.3152/095820210X492495

Lepori B, Jongbloed B, Hicks D (2023) Introduction to the handbook of public funding of research: understanding vertical and horizontal complexities. In: Lepori B, Hicks BJ D (eds) Handbook of public funding of research. Edward Elgar Publishing, Cheltenham, pp 1–19

Chapter   Google Scholar  

Lerchenmueller MJ, Sorenson O (2018) The gender gap in early career transitions in the life sciences. Res Policy 47(6):1007–1017. https://doi.org/10.1016/j.respol.2018.02.009

Leslie DW (2002) Resolving the dispute: teaching is academe’s core value. J High Educ 73(1):49–73

Lounsbury JW, Foster N, Patel H, Carmody P, Gibson LW, Stairs DR (2012) An investigation of the personality traits of scientists versus nonscientists and their relationship with career satisfaction: relationship of personality traits and career satisfaction of scientists and nonscientists. R&D Manage 42(1):47–59. https://doi.org/10.1111/j.1467-9310.2011.00665.x

Ma L (2019) Money, morale, and motivation: a study of the output-based research support scheme. Univ Coll Dublin Res Evaluation 28(4):304–312. https://doi.org/10.1093/reseval/rvz017

Melguizo T, Strober MH (2007) Faculty salaries and the maximization of prestige. Res High Educt 48(6):633–668

Moed HF (2005) Citation analysis in research evaluation. Springer, Dordrecht

Netherlands Observatory of Science (NOWT) (2012) Report to the Dutch Ministry of Science, Education and Culture (OC&W). Den Haag 1998

Peng J-E, Gao XA (2019) Understanding TEFL academics’ research motivation and its relations with research productivity. SAGE Open 9(3):215824401986629. https://doi.org/10.1177/2158244019866295

Piro FN, Aksnes DW, Rørstad K (2013) A macro analysis of productivity differences across fields: challenges in the measurement of scientific publishing. J Am Soc Inform Sci Technol 64(2):307–320. https://doi.org/10.1002/asi.22746

Pruvot EB, Estermann T, Popkhadze N (2023) University autonomy in Europe IV. The scorecard 2023. Retrieved from Brussels. https://eua.eu/downloads/publications/eua autonomy scorecard.pdf

Reymert I, Jungblut J, Borlaug SB (2021) Are evaluative cultures national or global? A cross-national study on evaluative cultures in academic recruitment processes in Europe. High Educ 82(5):823–843. https://doi.org/10.1007/s10734-020-00659-3

Roach M, Sauermann H (2010) A taste for science? PhD scientists’ academic orientation and self-selection into research careers in industry. Res Policy 39(3):422–434. https://doi.org/10.1016/j.respol.2010.01.004

Rørstad K, Aksnes DW (2015) Publication rate expressed by age, gender and academic position– A large-scale analysis of Norwegian academic staff. J Informetrics 9(2):317–333. https://doi.org/10.1016/j.joi.2015.02.003

Ruiz-Castillo J, Costas R (2014) The skewness of scientific productivity. J Informetrics 8(4):917–934. https://doi.org/10.1016/j.joi.2014.09.006

Ryan JC (2014) The work motivation of research scientists and its effect on research performance: work motivation of research scientists. R&D Manage 44(4):355–369. https://doi.org/10.1111/radm.12063

Ryan JC, Berbegal-Mirabent J (2016) Motivational recipes and research performance: a fuzzy set analysis of the motivational profile of high-performing research scientists. J Bus Res 69(11):5299–5304. https://doi.org/10.1016/j.jbusres.2016.04.128

Ryan RM, Deci EL (2000) Intrinsic and extrinsic motivations: classic definitions and new directions. Contemp Educ Psychol 25(1):54–67. https://doi.org/10.1006/ceps.1999.1020

Sivertsen G (2019) Understanding and evaluating research and scholarly publishing in the social sciences and humanities (SSH). Data Inform Manage 3(2):61–71. https://doi.org/10.2478/dim-2019-0008

Sivertsen G, Van Leeuwen T (2014) Scholarly publication patterns in the social sciences and humanities and their relationship with research assessment

Stephan P, Veugelers R, Wang J (2017) Reviewers are blinkered by bibliometrics. Nature 544(7651):411–412. https://doi.org/10.1038/544411a

Thomas D, Nedeva M (2012) Characterizing researchers to study research funding agency impacts: the case of the European Research Council’s starting grants. Res Evaluation 21(4):257–269. https://doi.org/10.1093/reseval/rvs020

Tien FF (2000) To what degree does the desire for promotion motivate faculty to perform research? Testing the expectancy theory. Res High Educt 41(6):723–752. https://doi.org/10.1023/A:1007020721531

Tien FF (2008) What kind of faculty are motivated to perform research by the desire for promotion? High Educ 55(1):17–32. https://doi.org/10.1007/s10734-006-9033-5

Tien FF, Blackburn RT (1996) Faculty rank system, research motivation, and faculty research productivity: measure refinement and theory testing. J High Educ 67(1):2. https://doi.org/10.2307/2943901

Vallerand RJ, Pelletier LG, Blais MR, Briere NM, Senecal C, Vallieres EF (1992) The academic motivation scale: a measure of intrinsic, extrinsic, and amotivation in education. Educ Psychol Meas 52(4):1003–1017. https://doi.org/10.1177/0013164492052004025

Van Iddekinge CH, Aguinis H, Mackey JD, DeOrtentiis PS (2018) A meta-analysis of the interactive, additive, and relative effects of cognitive ability and motivation on performance. J Manag 44(1):249–279. https://doi.org/10.1177/0149206317702220

Van Leeuwen T (2013) Bibliometric research evaluations, Web of Science and the social sciences and humanities: A problematic relationship? Bibliometrie - Praxis Und Forschung, September, Bd. 2(2013). https://doi.org/10.5283/BPF.173

Van Leeuwen T, van Wijk E, Wouters PF (2016) Bibliometric analysis of output and impact based on CRIS data: a case study on the registered output of a Dutch university. Scientometrics 106(1):1–16. https://doi.org/10.1007/s11192-015-1788-y

Waltman L, Schreiber M (2013) On the calculation of percentile-based bibliometric indicators. J Am Soc Inform Sci Technol 64(2):372–379. https://doi.org/10.1002/asi.22775

Waltman L, van Eck NJ, van Leeuwen TN, Visser MS, van Raan AFJ (2011) Towards a new crown indicator: an empirical analysis. Scientometrics 87(3):467–481. https://doi.org/10.1007/s11192-011-0354-5

Wilkesmann U, Lauer S (2020) The influence of teaching motivation and new public management on academic teaching. Stud High Educ 45(2):434–451. https://doi.org/10.1080/03075079.2018.1539960

Wilsdon J, Allen L, Belfiore E, Campbell P, Curry S, Hill S, Jones R et al (2015) The metric tide: report of the independent review of the role of metrics in research assessment and management. https://doi.org/10.13140/RG.2.1.4929.1363

Zacharewicz T, Lepori B, Reale E, Jonkers K (2019) Performance-based research funding in EU member states—A comparative assessment. Sci Public Policy 46(1):105–115. https://doi.org/10.1093/scipol/scy041

Zhang L, Sivertsen G, Du H, Huang Y, Glänzel W (2021) Gender differences in the aims and impacts of research. Scientometrics 126(11):8861–8886. https://doi.org/10.1007/s11192-021-04171-y

Download references

Acknowledgements

We are thankful to the R-QUEST team for input and comments to the paper.

The authors disclosed the receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the Research Council Norway (RCN) [grant number 256223] (R-QUEST).

Open access funding provided by University of Oslo (incl Oslo University Hospital)

Author information

Silje Marie Svartefoss

Present address: TIK Centre for Technology, Innovation and Culture, University of Oslo, 0317, Oslo, Norway

Authors and Affiliations

Nordic Institute for Studies in Innovation, Research and Education (NIFU), Økernveien 9, 0608, Oslo, Norway

Silje Marie Svartefoss & Dag W. Aksnes

Department of Political Science, University of Oslo, 0315, Oslo, Norway

Jens Jungblut & Kristoffer Kolltveit

Centre for Science and Technology Studies (CWTS), Leiden University, 2311, Leiden, The Netherlands

Thed van Leeuwen

You can also search for this author in PubMed   Google Scholar

Contributions

All authors contributed to the study conception and design. Material preparation, data collection, and analysis were performed by Silje Marie Svartefoss, Jens Jungblut, Dag W. Aksnes, Kristoffer Kolltveit, and Thed van Leeuwen. The first draft of the manuscript was written by all authors in collaboration, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Silje Marie Svartefoss .

Ethics declarations

Competing interests.

The authors have no competing interests to declare that are relevant to the content of this article.

Informed consent

was retrieved from the participants in this study.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.

Supplementary Material 1

Rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Svartefoss, S.M., Jungblut, J., Aksnes, D.W. et al. Explaining research performance: investigating the importance of motivation. SN Soc Sci 4 , 105 (2024). https://doi.org/10.1007/s43545-024-00895-9

Download citation

Received : 14 December 2023

Accepted : 15 April 2024

Published : 23 May 2024

DOI : https://doi.org/10.1007/s43545-024-00895-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Performance
• Productivity
• Find a journal
• Publish with us
• Track your research