hypothesis test t value calculator

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

T test calculator

A t test compares the means of two groups. There are several types of two sample t tests and this calculator focuses on the three most common: unpaired, welch's, and paired t tests. Directions for using the calculator are listed below, along with more information about two sample t tests and help on which is appropriate for your analysis. NOTE: This is not the same as a one sample t test; for that, you need this One sample t test calculator .

1. Choose data entry format

Caution: Changing format will erase your data.

2. Choose a test

Help me choose

3. Enter data

Help me arrange the data

4. View the results

What is a t test.

A t test is used to measure the difference between exactly two means. Its focus is on the same numeric data variable rather than counts or correlations between multiple variables. If you are taking the average of a sample of measurements, t tests are the most commonly used method to evaluate that data. It is particularly useful for small samples of less than 30 observations. For example, you might compare whether systolic blood pressure differs between a control and treated group, between men and women, or any other two groups.

This calculator uses a two-sample t test, which compares two datasets to see if their means are statistically different. That is different from a one sample t test , which compares the mean of your sample to some proposed theoretical value.

The most general formula for a t test is composed of two means (M1 and M2) and the overall standard error (SE) of the two samples:

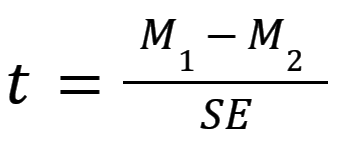
See our video on How to Perform a Two-sample t test for an intuitive explanation of t tests and an example.

How to use the t test calculator

• Choose your data entry format . This will change how section 3 on the page looks. The first two options are for entering your data points themselves, either manually or by copy & paste. The last two are for entering the means for each group, along with the number of observations (N) and either the standard error of that mean (SEM) or standard deviation of the dataset (SD) standard error. If you have already calculated these summary statistics, the latter options will save you time.
• Choose a test from the three options: Unpaired t test, Welch's unpaired t test, or Paired t test. Use our Ultimate Guide to t tests if you are unsure which is appropriate, as it includes a section on "How do I know which t test to use?". Notice not all options are available if you enter means only.
• Enter data for the test, based on the format you chose in Step 1.
• Click Calculate Now and View the results. All options will perform a two-tailed test .

Performing t tests? We can help.

Sign up for more information on how to perform t tests and other common statistical analyses.

Common t test confusion

In addition to the number of t test options, t tests are often confused with completely different techniques as well. Here's how to keep them all straight.

Correlation and regression are used to measure how much two factors move together. While t tests are part of regression analysis, they are focused on only one factor by comparing means in different samples.

ANOVA is used for comparing means across three or more total groups. In contrast, t tests compare means between exactly two groups.

Finally, contingency tables compare counts of observations within groups rather than a calculated average. Since t tests compare means of continuous variable between groups, contingency tables use methods such as chi square instead of t tests.

Assumptions of t tests

Because there are several versions of t tests, it's important to check the assumptions to figure out which is best suited for your project. Here are our analysis checklists for unpaired t tests and paired t tests , which are the two most common. These (and the ultimate guide to t tests ) go into detail on the basic assumptions underlying any t test:

• Exactly two groups
• Sample is normally distributed
• Independent observations
• Unequal or equal variance?
• Paired or unpaired data?

Interpreting results

The three different options for t tests have slightly different interpretations, but they all hinge on hypothesis testing and P values. You need to select a significance threshold for your P value (often 0.05) before doing the test.

While P values can be easy to misinterpret , they are the most commonly used method to evaluate whether there is evidence of a difference between the sample of data collected and the null hypothesis. Once you have run the correct t test, look at the resulting P value. If the test result is less than your threshold, you have enough evidence to conclude that the data are significantly different.

If the test result is larger or equal to your threshold, you cannot conclude that there is a difference. However, you cannot conclude that there was definitively no difference either. It's possible that a dataset with more observations would have resulted in a different conclusion.

Depending on the test you run, you may see other statistics that were used to calculate the P value, including the mean difference, t statistic, degrees of freedom, and standard error. The confidence interval and a review of your dataset is given as well on the results page.

Graphing t tests

This calculator does not provide a chart or graph of t tests, however, graphing is an important part of analysis because it can help explain the results of the t test and highlight any potential outliers. See our Prism guide for some graphing tips for both unpaired and paired t tests.

Prism is built for customized, publication quality graphics and charts. For t tests we recommend simply plotting the datapoints themselves and the mean, or an estimation plot . Another popular approach is to use a violin plot, like those available in Prism.

For more information

Our ultimate guide to t tests includes examples, links, and intuitive explanations on the subject. It is quite simply the best place to start if you're looking for more about t tests!

If you enjoyed this calculator, you will love using Prism for analysis. Take a free 30-day trial to do more with your data, such as:

• Clear guidance to pick the right t test and detailed results summaries
• Custom, publication quality t test graphics, violin plots, and more
• More t test options, including normality testing as well as nested and multiple t tests
• Non-parametric test alternatives such as Wilcoxon, Mann-Whitney, and Kolmogorov-Smirnov

Check out our video on how to perform a t test in Prism , for an example from start to finish!

Remember, this page is just for two sample t tests. If you only have one sample, you need to use this calculator instead.

We Recommend:

Analyze, graph and present your scientific work easily with GraphPad Prism. No coding required.

• PRE-ALGEBRA
• MORE MATH FINANCE BUSINESS ENGINEERING FINANCE CHARTS MATH WORKSHEETS CURRENCY CONVERTER MULTIPLICATION TABLES DEPRECIATION SPORTS CALCULATORS HEALTH equations tricks history notes register login

• Engineering

t-Test Calculator

T-test - work with steps.

Input Data : Data set x = 3, 11, 17, 28, 34 Data set y = 5, 8, 13, 19, 28 Total number of elements = 5 Objective : Find the t-score by using mean and standard deviation. Solution : Mean 1 = (3 + 11 + 17 + 28 + 34)/5 = 93/5 Mean 1 = 18.6 Mean 2 = (5 + 8 + 13 + 19 + 28)/5 = 73/5 Mean 2 = 14.6 SD1 = √(1/5 - 1) x ((3 - 18.6) 2 + ( 11 - 18.6) 2 + ( 17 - 18.6) 2 + ( 28 - 18.6) 2 + ( 34 - 18.6) 2 ) = √(1/4) x ((-15.6) 2 + (-7.6) 2 + (-1.6) 2 + (9.4) 2 + (15.4) 2 ) = √(0.25) x ((243.36) + (57.76) + (2.56) + (88.36) + (237.16)) = √(0.25) x 629.2 = √157.3 SD1 = 12.5419 SD2 = √(1/5 - 1) x ((5 - 14.6) 2 + ( 8 - 14.6) 2 + ( 13 - 14.6) 2 + ( 19 - 14.6) 2 + ( 28 - 14.6) 2 ) = √(1/4) x ((-9.6) 2 + (-6.6) 2 + (-1.6) 2 + (4.4) 2 + (13.4) 2 ) = √(0.25) x ((92.16) + (43.56) + (2.56) + (19.36) + (179.56)) = √(0.25) x 337.2 = √84.3 SD2 = 9.1815 t-score = x 1 - x 2 √(SD1 2 /n1 + SD2 2 /n2) = 18.6 - 14.6 √((12.5419) 2 /5 + (9.1815) 2 /5) = 4 √((157.3)/5 + (84.3)/5) = 4 √(31.46 + 16.86) = 4 √(48.32) = 4 6.9513 t-score = 0.5754

t-test calculator is an online statistics tool to estimate the significance of observed differences between the means of two samples when there is a null hypothesis that is no significant difference between the means by using standard deviation. It is necessary to follow the next steps:

• Enter two samples (observed values) in the box. These values must be real numbers or variables and may be separated by commas. The values can be copied from a text document or a spreadsheet.
• Press the "GENERATE WORK" button to make the computation.
• t-Test calculator will give a test whether samples from two independent populations provide that the populations have different means.

What is t-Test?

A hypothesis test consists of two hypotheses, the null hypothesis and the alternative hypothesis or research hypothesis. The symbol $H_0$ represents the null hypothesis. The null hypothesis reflects that there will be no observed effect on the experiment. The null hypothesis consists of an equal sign. The alternative hypothesis reflects that there is an observed effect on the experiment. The symbol $H_a$ represents the alternative hypothesis. The first step in testing is to determine the null hypothesis and the alternative hypothesis. Regarding the testing hypothesis, there are some important terms. Rejection region is the set of values leads to rejection of the null hypothesis. Non-rejection region is the set of values that leads to nonrejection of the null hypothesis. Critical values are the value that separates the rejection and non-rejection regions. The t-Test is used in comparing the means of two populations. There are two approaches:

• When the samples from the two populations are independent;
• When the samples from the two populations are depended, i.e. when they are paired.
• If populations standard deviations are equal, $\sigma_1-\sigma_2$
• If populations standard deviations are different

How to Find t-Critical Value

To perform a hypothesis test to compare two population means, $\mu_1$ and $\mu_2$, we have some assumptions:

• Simple and independent random samples;
• Normal populations or large samples.

t-Test with Mean and Standard Deviation

A t-Test is one of the most frequently used tests in statistics. A t-Test is useful to conclude if the results are correct and applicable to the entire population. If we want to analyze simple experiments or when making simple comparisons between levels of independent variable we use the t-Test. It's used in comparison between two separate groups of individuals, for example: male vs female, experimental vs control group, etc. Practice Problem 1: There are two company A and B. We want to test average age of employees at these companies so we use a random sample of employee ages from each company.

• Hypergeometric distribution Calculator
• Error Function Calculator
• Beta Function Calculator
• Gamma Function Calculator
• Digamma Function Calculator
• F-Test Calculator
• Statistical Data Set Range Calculator
• Effect of Size Calculator
• Sampling Error Calculator
• Percent Error Calculator
• Percentile Calculator
• Signal to Noise Ratio Calculator

• Salary & Income Tax Calculators
• Mortgage Calculators
• Retirement Calculators
• Depreciation Calculators
• Statistics and Analysis Calculators
• Date and Time Calculators
• Contractor Calculators
• Budget & Savings Calculators
• Loan Calculators
• Forex Calculators
• Real Function Calculators
• Engineering Calculators
• Tax Calculators
• Volume Calculators
• 2D Shape Calculators
• 3D Shape Calculators
• Logistics Calculators
• HRM Calculators
• Sales & Investments Calculators
• Grade & GPA Calculators
• Conversion Calculators
• Ratio Calculators
• Sports & Health Calculators
• Other Calculators

Student T-Value Calculator

You can use this T-Value Calculator to calculate the Student's t-value based on the significance level and the degrees of freedom in the standard deviation.

How to use the calculator

• Enter the degrees of freedom (df)
• Enter the significance level alpha (α is a number between 0 and 1)
• Click the "Calculate" button to calculate the Student's t-critical value.

Degrees of Freedom (df) :

Significance Level (α) :

• Currently 4.76/5

Rating: 4.8 /5 (823 votes)

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Statistics and probability
• T-test calculator

T-Test calculator

The Student's t-test is used to determine if means of two data sets differ significantly. This calculator will generate a step by step explanation on how to apply t - test.

• Factoring Polynomials
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Rationalize Denominator
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance calculator
• Midpoint Calculator
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Twelve younger adults and twelve older adults conducted a life satisfaction test. The data are presented in the table below. Compute the appropriate t-test.

Are the means between two data sets are significantly different at level $\alpha < 0.05$.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

T-Value Calculator / Critical Value Calculator

A T value is the “cut-off point” on a T distribution. The T value is almost the same with the Z value which is the “cut-off point” on a normal distribution. The only variation between these two is that they have different shapes. Therefore, the values for their cut-off points vary slightly too. When conducting a hypothesis test, you can use the T value to compare against a T score that you’ve calculated. The easiest way to get the T value is by using this T value calculator.

Table of Contents

How to use the T value calculator?

Calculations can be quite intimidating for a lot of people, especially if the formulas have a very complex nature. Fortunately, there are online tools such as this critical value calculator which can do the computations for you. Here are the steps to use this calculator:

• First, enter the value for the Degrees of Freedom.
• Then, enter the value for the Significance level. This value should be between 0 and 1 only.
• After entering these values, the T score calculator will generate the T value (right-tailed) and the T value (two-tailed).

How do you calculate the T value?

  There are two main ways you can calculate the T value without using the T value calculator:

Perform the calculation using Excel

You can calculate the T value using Microsoft Excel by combining custom formulas with its built-in functions. Aside from the T value, you can also get other values such as the degrees of freedom, standard deviation, and the means.

Perform the calculation by hand

Start with the value of the sample size then subtract one to get the degrees of freedom.

Select an alpha level. Usually, you would get this value in the problem, but the most common value is 0.05 or 5%.

Determine which distribution table you will use. This will depend on whether you will run a one or two-tailed test. Use the distribution table to find the intersection of the column and the row. Then you can check the correctness of your answer using the T distribution calculator.

What is T in confidence interval?  

There are other concepts to learn about when using a T distribution calculator one of which is the T value in confidence interval. This is a type of function that falls under the statistical functions category.

Use this function to calculate the confidence value which you can use to build the confidence interval. This is very useful for population means for sample size and supplied probability. It’s also very useful when you’re trying to determine the T value for a confidence interval of 95. The T in confidence interval has the following formula:

  T Confidence Interval Formula = CONFIDENCE.T(alpha,standard_dev,size)

alpha refers to the significance level you use when computing the confidence level

standard_dev refers to the data range’s population standard deviation

size refers to the standard size

What does T score mean in statistics?  

In statistics, the T score is inextricably linked to the P score. When performing a T-test, it means that you’re attempting to obtain evidence of a significant variation between a hypothesized value and a population means or between two population means.

In statistics, you use the T value or T score to measure how big the difference is in relation to the variation in your data sample. In other words, the T score is the difference which you’ve calculated, and you represent this in units of standard error.

You can calculate the T score in the output from a single sample taken from the whole population. If you take recurring samples of random data from a single population, you will obtain T scores which are slightly different every time. This is because of a random sampling error. This isn’t really a mistake, it’s simply a random variation that you would expect in the data.

But when you think about it, how different should the T scores be from the random samples you take from just one population? Also, how does the T score from the sample data compare to the T scores you’re expecting? To answer these questions, you can use a T-distribution .

T scores with higher magnitudes whether positive or negative, aren’t very likely. This is because the far right and left tails of the distribution curves correspond to situations where you obtain extreme T scores which are very far from zero. On the other hand, if you have a P score that’s very low, you can reject the null hypothesis. Also, you can conclude that, in fact, there’s a difference that’s statistically significant.

Going back to the link between the T score and P score , we’ve mentioned that both of these are inextricably linked. You can consider them as various ways you can use to quantify your results’ extremeness under a null hypothesis. Because of their link, it’s not possible to change one of the values without also altering the other. If you have a large absolute T score value, you would have a smaller P score value. Also, you would have greater evidence against the nullity of your hypothesis.

What is the critical value for the test statistic?  

We define a critical value for the test statistic using the context of probability and population distribution. It can be mathematically expressed using the following formula:  

Pr[X <= critical value] = probability

Pr refers to the probability calculation

X refers to the population observations

critical value refers to the calculated critical value

probability refers to the selected probability

You can calculate critical values using a critical value calculator. You can also perform the calculation using the mathematical formula above. For the distributions which are very common, you can’t calculate the value analytically. Instead, you can estimate the value through numerical methods.

You can also use critical values in statistical significance testing. We often express the probability as the “significance” with the Greek letter alpha as the symbol. Use the standard alpha values which you’re computing critical values. These values provide an equivalent and alternative way for you to interpret the hypothesis of your statistical tests.

T-Test Calculator

Compare the means of two samples using a single-sample or two-sample t-test below.

• Single Sample
• Two Sample (Unpaired)

Have a Question or Feedback?

Chevron Down Icon scroll down

On this page:

How to do a t-test, types of t-tests, how to calculate t using a one-sample t-test, how to calculate t using a student’s t-test, how to calculate t using welch’s t-test, find the p-value.

Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.

Full bio Chevron Right Icon

Brian specializes in political science and statistics with several advanced degrees from Harvard.

A t-test calculates how significant the difference between the means of two groups are. The results let you know if those differences could have occurred by chance, or rather, whether the difference is statistically significant.

A t-test uses the test statistic, sometimes called a t-value or t-score, the t-distribution values, and the degrees of freedom to calculate the statistical significance of the difference.

Since a t-test is a parametric test, it relies on assumptions about the process that generated the underlying data. In particular, the likelihood or unlikelihood that the t-test provides for a difference being due to chance depends on the assumption that the data are normally distributed and each data point’s values are independent of one another.

Depending on how plausible those assumptions are, the analysis that follows will be more or less useful. If your data is continuous and comes from a relatively large random sample from some population, the central limit theorem implies that these assumptions will likely be approximately satisfied.

The first part of doing a t-test is determining which type of t-test you need to do.

There are three different types of t-tests:

• one-sample t-test: used to compare the mean of a sample to the known mean of a population
• two-sample t-test: used to compare the mean of two different independent samples
• paired t-test: used to compare the mean of two different samples after an intervention or change

A one-sample t-test, or single-sample test, is used to compare a sample mean to a population mean when the null hypothesis is that the sample mean is equal to the population mean.

Those who first encounter this test often wonder why they would use it, since the population mean is often not known (and the data is often collected to determine the population mean in the first place).

It often does make sense to use a one-sample t-test if you have a particular interest in whether a sample’s mean is different from some reference value that is determined to be substantively important for other reasons.

For example, let’s suppose that 5 micrograms of lead per liter of blood is the maximum safe amount, according to most medical references. Then, you may well consider doing a one-sample t-test to examine whether the average blood lead level of a sample of individuals was above that medically acceptable limit.

One-Sample T-Test Formula

To calculate the t value using a one-sample t-test, use the following formula:

Where: x̄ = sample mean μ = population mean s = sample standard deviation n = sample size

Thus, the test statistic t is equal to the difference between the sample mean x̄ and the population mean μ , divided by the standard error s / √n .

A Student’s t-test is used for test statistics that follow a Student’s t-distribution under the null hypothesis that two populations have equal means.

The name “Student” refers to the pseudonym of the author who first proposed the test in an academic journal, and does not refer to the fact it is one of the most commonly taught tests in statistics courses (although the latter is also true).

The Student’s t-test assumes that the variances of two populations are equal and asks whether their means differ significantly.

This is a type of two-sample test used to compare two sample means, where a large t-value suggests that the samples are very different, and a small t-value suggests that they are similar.

Similar to the one-sample t-test, individuals who first encounter this test may wonder about the plausibility of its assumptions. In particular, you might question how the variances in two samples could possibly be equal if the means are different.

In some contexts (for example, the industrial experiments that motivated Student’s efforts), there might be substantive reasons to assume equal variances. More informally, if you calculate the standard deviations in each sample and sees that they are close, you might proceed to calculate Student’s t-test.

More formally, some analysts would recommend that you initially conduct an F-test to determine whether variances are different, and then proceed to consider the means. But many analysts would also simply not make the equal variances assumption and proceed directly to Welch’s t-test.

Student’s T-Test Formula

The formula for a Student’s t-test is:

Given the formula to calculate the pooled standard deviation s p :

Where: x̄ 1 = first sample mean x̄ 2 = second sample mean n 1 = first sample size n 2 = second sample size s 1 = first sample standard deviation s 2 = second sample standard deviation n 1 + n 2 – 2 = degrees of freedom ν

In a Student’s t-test, the test statistic t is equal to the difference between sample means x̄ 1 and x̄ 2 , divided by the pooled standard deviation s p times the square root of 1 divided by the first sample size n 1 plus 1 divided by the second sample size n 2 .

The pooled standard deviation s p is equal to the first sample size n 1 minus 1 times the first sample standard deviation s 1 plus the second sample size n 2 minus 1 times the second sample standard deviation s 2 , divided by the degrees of freedom, in this case the sum of the sample sizes minus two.

It is called the “pooled” standard deviation because it combines or “pools” the data between both samples to determine the overall variability of the data.

This formula can be broken down into a few simple steps.

Step One: Calculate the Degrees of Freedom

Step two: calculate the pooled standard deviation, step three: calculate the test statistic.

Recall that the Student’s t-test assumes that the variances of two populations are equal. As was mentioned above, this is often a questionable assumption, and ultimately unverifiable.

In this case, you can use Welch’s t-test, which is sometimes also called an unequal variances t-test or an “unpooled” t-test. Like before, the null hypothesis with this test is that two populations have equal means.

Welch’s T-Test Formula

The formula for Welch’s t-test is:

Degrees of Freedom Formula

To find the degrees of freedom when using Welch’s t-test, use the Satterthwaite formula:

The next step is to find the p-value for the test statistic. The p-value is a measure of how “surprising” or “unlikely” some statistic would be given the particular assumptions that the analyst makes.

In the case of these t-tests for differences in means, the p-value is the probability of calculating a t-statistic that is as large or larger than what was actually calculated from the observed data if, in fact, the population means were identical.

More generally, a p-value is used to determine whether to reject the null hypothesis. In formal hypothesis testing, you would specify beforehand the p-value that would lead you to conclude that the two samples came from different populations.

What is the Right P-Value?

These standards differ by field and disciplines a lot, for example, in social and biological sciences, a p-value of 0.05 or smaller (implying 5% or lower chance of observing the data under the null hypothesis) is common, although in some cases 0.1 or 0.01 might be the standard.

In the physical sciences, it is not uncommon to pre-specify a “6 sigma” standard for certain kinds of evidence, which requires an astronomically small p-value.

How to Calculate the P-Value

To calculate the p-value from a t-statistic, use a t-table and locate the degrees of freedom in the leftmost column. Then, locate the desired p-value in the heading row, 0.05 is most commonly used for a 95% confidence level.

Then, find the intersection of the row and column to find the critical value.

Drawing Conclusions Using the P-Value

If the calculated t-value is larger than the critical value, then you can reject the null hypothesis. If it is less than the critical value, then you fail to reject the null hypothesis.

The t-distribution is related to the normal distribution; indeed, it can be thought of as the normal distribution’s “heavy-tailed” cousin. The degrees of freedom in the t-distribution determines how heavy the tails are, with fewer degrees of freedom resulting in greater departures from normality.

As the degrees of freedom increase, it becomes harder and harder to tell the differences between the associated t-distribution and the normal distribution.

Because of this fact, experienced statistical analysts are often able to approximately estimate the p-value of a particular t-statistic through their familiarity with the normal distribution.

A t-statistic of 2 or greater is typically enough to confirm statistical significance in the social and biological contexts.

Recommended Statistics Resources

• Winning Percentage Calculator Right Arrow Icon
• Standard Error Calculator Right Arrow Icon
• Average Calculator Right Arrow Icon
• Central Limit Theorem Calculator Right Arrow Icon
• T Table Right Arrow Icon

P-value Calculator

Statistical significance calculator to easily calculate the p-value and determine whether the difference between two proportions or means (independent groups) is statistically significant. T-test calculator & z-test calculator to compute the Z-score or T-score for inference about absolute or relative difference (percentage change, percent effect). Suitable for analysis of simple A/B tests.

Related calculators

• Using the p-value calculator
• What is "p-value" and "significance level"
• P-value formula
• Why do we need a p-value?
• How to interpret a statistically significant result / low p-value
• P-value and significance for relative difference in means or proportions

    Using the p-value calculator

This statistical significance calculator allows you to perform a post-hoc statistical evaluation of a set of data when the outcome of interest is difference of two proportions (binomial data, e.g. conversion rate or event rate) or difference of two means (continuous data, e.g. height, weight, speed, time, revenue, etc.). You can use a Z-test (recommended) or a T-test to find the observed significance level (p-value statistic). The Student's T-test is recommended mostly for very small sample sizes, e.g. n < 30. In order to avoid type I error inflation which might occur with unequal variances the calculator automatically applies the Welch's T-test instead of Student's T-test if the sample sizes differ significantly or if one of them is less than 30 and the sampling ratio is different than one.

If entering proportions data, you need to know the sample sizes of the two groups as well as the number or rate of events. These can be entered as proportions (e.g. 0.10), percentages (e.g. 10%) or just raw numbers of events (e.g. 50).

If entering means data, simply copy/paste or type in the raw data, each observation separated by comma, space, new line or tab. Copy-pasting from a Google or Excel spreadsheet works fine.

The p-value calculator will output : p-value, significance level, T-score or Z-score (depending on the choice of statistical hypothesis test), degrees of freedom, and the observed difference. For means data it will also output the sample sizes, means, and pooled standard error of the mean. The p-value is for a one-sided hypothesis (one-tailed test), allowing you to infer the direction of the effect (more on one vs. two-tailed tests ). However, the probability value for the two-sided hypothesis (two-tailed p-value) is also calculated and displayed, although it should see little to no practical applications.

Warning: You must have fixed the sample size / stopping time of your experiment in advance, otherwise you will be guilty of optional stopping (fishing for significance) which will inflate the type I error of the test rendering the statistical significance level unusable. Also, you should not use this significance calculator for comparisons of more than two means or proportions, or for comparisons of two groups based on more than one metric. If a test involves more than one treatment group or more than one outcome variable you need a more advanced tool which corrects for multiple comparisons and multiple testing. This statistical calculator might help.

    What is "p-value" and "significance level"

The p-value is a heavily used test statistic that quantifies the uncertainty of a given measurement, usually as a part of an experiment, medical trial, as well as in observational studies. By definition, it is inseparable from inference through a Null-Hypothesis Statistical Test (NHST) . In it we pose a null hypothesis reflecting the currently established theory or a model of the world we don't want to dismiss without solid evidence (the tested hypothesis), and an alternative hypothesis: an alternative model of the world. For example, the statistical null hypothesis could be that exposure to ultraviolet light for prolonged periods of time has positive or neutral effects regarding developing skin cancer, while the alternative hypothesis can be that it has a negative effect on development of skin cancer.

In this framework a p-value is defined as the probability of observing the result which was observed, or a more extreme one, assuming the null hypothesis is true . In notation this is expressed as:

p(x 0 ) = Pr(d(X) > d(x 0 ); H 0 )

where x 0 is the observed data (x 1 ,x 2 ...x n ), d is a special function (statistic, e.g. calculating a Z-score), X is a random sample (X 1 ,X 2 ...X n ) from the sampling distribution of the null hypothesis. This equation is used in this p-value calculator and can be visualized as such:

Therefore the p-value expresses the probability of committing a type I error : rejecting the null hypothesis if it is in fact true. See below for a full proper interpretation of the p-value statistic .

Another way to think of the p-value is as a more user-friendly expression of how many standard deviations away from the normal a given observation is. For example, in a one-tailed test of significance for a normally-distributed variable like the difference of two means, a result which is 1.6448 standard deviations away (1.6448σ) results in a p-value of 0.05.

The term "statistical significance" or "significance level" is often used in conjunction to the p-value, either to say that a result is "statistically significant", which has a specific meaning in statistical inference ( see interpretation below ), or to refer to the percentage representation the level of significance: (1 - p value), e.g. a p-value of 0.05 is equivalent to significance level of 95% (1 - 0.05 * 100). A significance level can also be expressed as a T-score or Z-score, e.g. a result would be considered significant only if the Z-score is in the critical region above 1.96 (equivalent to a p-value of 0.025).

    P-value formula

There are different ways to arrive at a p-value depending on the assumption about the underlying distribution. This tool supports two such distributions: the Student's T-distribution and the normal Z-distribution (Gaussian) resulting in a T test and a Z test, respectively.

In both cases, to find the p-value start by estimating the variance and standard deviation, then derive the standard error of the mean, after which a standard score is found using the formula [2] :

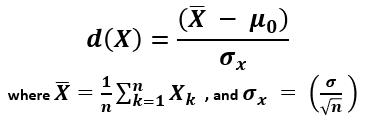
X (read "X bar") is the arithmetic mean of the population baseline or the control, μ 0 is the observed mean / treatment group mean, while σ x is the standard error of the mean (SEM, or standard deviation of the error of the mean).

When calculating a p-value using the Z-distribution the formula is Φ(Z) or Φ(-Z) for lower and upper-tailed tests, respectively. Φ is the standard normal cumulative distribution function and a Z-score is computed. In this mode the tool functions as a Z score calculator.

When using the T-distribution the formula is T n (Z) or T n (-Z) for lower and upper-tailed tests, respectively. T n is the cumulative distribution function for a T-distribution with n degrees of freedom and so a T-score is computed. Selecting this mode makes the tool behave as a T test calculator.

The population standard deviation is often unknown and is thus estimated from the samples, usually from the pooled samples variance. Knowing or estimating the standard deviation is a prerequisite for using a significance calculator. Note that differences in means or proportions are normally distributed according to the Central Limit Theorem (CLT) hence a Z-score is the relevant statistic for such a test.

    Why do we need a p-value?

If you are in the sciences, it is often a requirement by scientific journals. If you apply in business experiments (e.g. A/B testing) it is reported alongside confidence intervals and other estimates. However, what is the utility of p-values and by extension that of significance levels?

First, let us define the problem the p-value is intended to solve. People need to share information about the evidential strength of data that can be easily understood and easily compared between experiments. The picture below represents, albeit imperfectly, the results of two simple experiments, each ending up with the control with 10% event rate treatment group at 12% event rate.

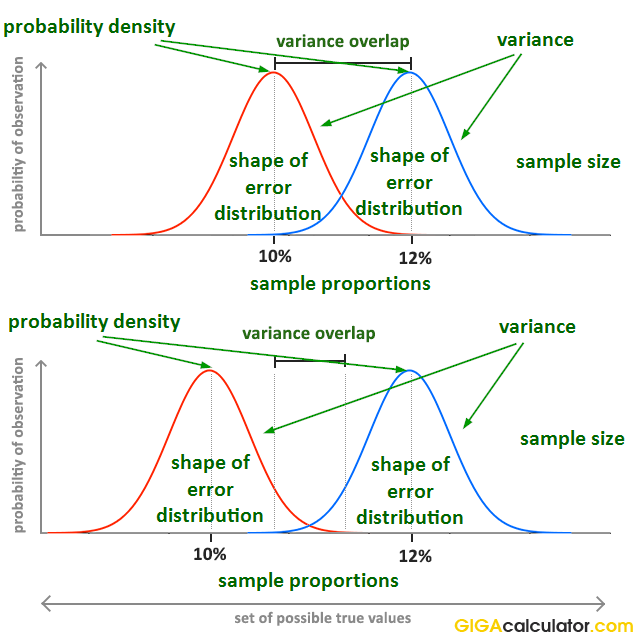
However, it is obvious that the evidential input of the data is not the same, demonstrating that communicating just the observed proportions or their difference (effect size) is not enough to estimate and communicate the evidential strength of the experiment. In order to fully describe the evidence and associated uncertainty , several statistics need to be communicated, for example, the sample size, sample proportions and the shape of the error distribution. Their interaction is not trivial to understand, so communicating them separately makes it very difficult for one to grasp what information is present in the data. What would you infer if told that the observed proportions are 0.1 and 0.12 (e.g. conversion rate of 10% and 12%), the sample sizes are 10,000 users each, and the error distribution is binomial?

Instead of communicating several statistics, a single statistic was developed that communicates all the necessary information in one piece: the p-value . A p-value was first derived in the late 18-th century by Pierre-Simon Laplace, when he observed data about a million births that showed an excess of boys, compared to girls. Using the calculation of significance he argued that the effect was real but unexplained at the time. We know this now to be true and there are several explanations for the phenomena coming from evolutionary biology. Statistical significance calculations were formally introduced in the early 20-th century by Pearson and popularized by Sir Ronald Fisher in his work, most notably "The Design of Experiments" (1935) [1] in which p-values were featured extensively. In business settings significance levels and p-values see widespread use in process control and various business experiments (such as online A/B tests, i.e. as part of conversion rate optimization, marketing optimization, etc.).

    How to interpret a statistically significant result / low p-value

Saying that a result is statistically significant means that the p-value is below the evidential threshold (significance level) decided for the statistical test before it was conducted. For example, if observing something which would only happen 1 out of 20 times if the null hypothesis is true is considered sufficient evidence to reject the null hypothesis, the threshold will be 0.05. In such case, observing a p-value of 0.025 would mean that the result is interpreted as statistically significant.

But what does that really mean? What inference can we make from seeing a result which was quite improbable if the null was true?

Observing any given low p-value can mean one of three things [3] :

• There is a true effect from the tested treatment or intervention.
• There is no true effect, but we happened to observe a rare outcome. The lower the p-value, the rarer (less likely, less probable) the outcome.
• The statistical model is invalid (does not reflect reality).

Obviously, one can't simply jump to conclusion 1.) and claim it with one hundred percent certainty, as this would go against the whole idea of the p-value and statistical significance. In order to use p-values as a part of a decision process external factors part of the experimental design process need to be considered which includes deciding on the significance level (threshold), sample size and power (power analysis), and the expected effect size, among other things. If you are happy going forward with this much (or this little) uncertainty as is indicated by the p-value calculation suggests, then you have some quantifiable guarantees related to the effect and future performance of whatever you are testing, e.g. the efficacy of a vaccine or the conversion rate of an online shopping cart.

Note that it is incorrect to state that a Z-score or a p-value obtained from any statistical significance calculator tells how likely it is that the observation is "due to chance" or conversely - how unlikely it is to observe such an outcome due to "chance alone". P-values are calculated under specified statistical models hence 'chance' can be used only in reference to that specific data generating mechanism and has a technical meaning quite different from the colloquial one. For a deeper take on the p-value meaning and interpretation, including common misinterpretations, see: definition and interpretation of the p-value in statistics .

    P-value and significance for relative difference in means or proportions

When comparing two independent groups and the variable of interest is the relative (a.k.a. relative change, relative difference, percent change, percentage difference), as opposed to the absolute difference between the two means or proportions, the standard deviation of the variable is different which compels a different way of calculating p-values [5] . The need for a different statistical test is due to the fact that in calculating relative difference involves performing an additional division by a random variable: the event rate of the control during the experiment which adds more variance to the estimation and the resulting statistical significance is usually higher (the result will be less statistically significant). What this means is that p-values from a statistical hypothesis test for absolute difference in means would nominally meet the significance level, but they will be inadequate given the statistical inference for the hypothesis at hand.

In simulations I performed the difference in p-values was about 50% of nominal: a 0.05 p-value for absolute difference corresponded to probability of about 0.075 of observing the relative difference corresponding to the observed absolute difference. Therefore, if you are using p-values calculated for absolute difference when making an inference about percentage difference, you are likely reporting error rates which are about 50% of the actual, thus significantly overstating the statistical significance of your results and underestimating the uncertainty attached to them.

In short - switching from absolute to relative difference requires a different statistical hypothesis test. With this calculator you can avoid the mistake of using the wrong test simply by indicating the inference you want to make.

    References

1 Fisher R.A. (1935) – "The Design of Experiments", Edinburgh: Oliver & Boyd

2 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.

3 Georgiev G.Z. (2017) "Statistical Significance in A/B Testing – a Complete Guide", [online] https://blog.analytics-toolkit.com/2017/statistical-significance-ab-testing-complete-guide/ (accessed Apr 27, 2018)

4 Mayo D.G., Spanos A. (2006) – "Severe Testing as a Basic Concept in a Neyman–Pearson Philosophy of Induction", British Society for the Philosophy of Science , 57:323-357

5 Georgiev G.Z. (2018) "Confidence Intervals & P-values for Percent Change / Relative Difference", [online] https://blog.analytics-toolkit.com/2018/confidence-intervals-p-values-percent-change-relative-difference/ (accessed May 20, 2018)

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "P-value Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/p-value-significance-calculator.php URL [Accessed Date: 29 May, 2024].

Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

     Statistical calculators

“extremely user friendly”

“truly amazing!”

“so easy to use!”

Statistics Calculator

You want to analyze your data effortlessly? DATAtab makes it easy and online.

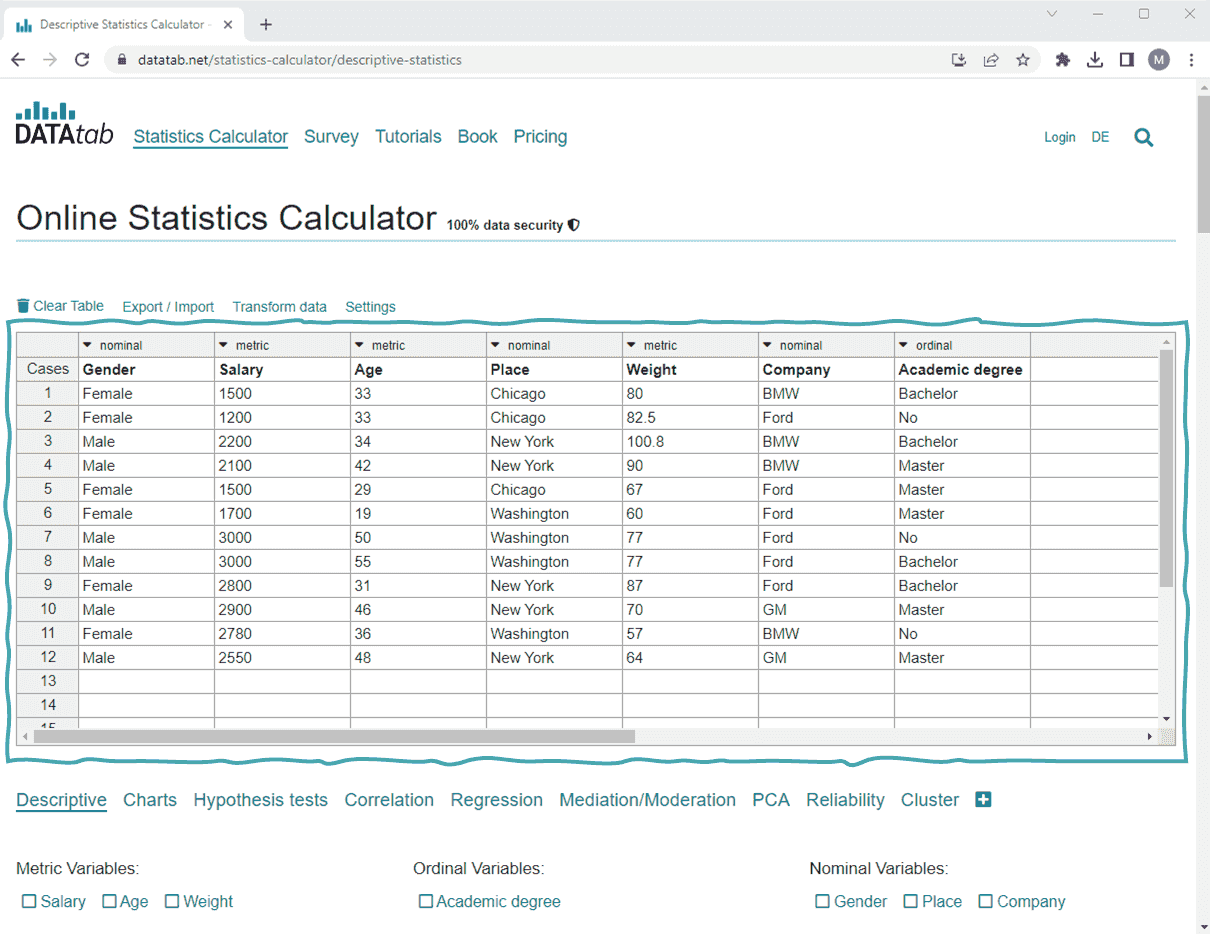
Online Statistics Calculator

What do you want to calculate online? The online statistics calculator is simple and uncomplicated! Here you can find a list of all implemented methods!

Create charts online with DATAtab

Create your charts for your data directly online and uncomplicated. To do this, insert your data into the table under Charts and select which chart you want.

The advantages of DATAtab

Statistics, as simple as never before..

DATAtab is a modern statistics software, with unique user-friendliness. Statistical analyses are done with just a few clicks, so DATAtab is perfect for statistics beginners and for professionals who want more flow in the user experience.

Directly in the browser, fully flexible.

Directly in the browser, fully flexible. DATAtab works directly in your web browser. You have no installation and maintenance effort whatsoever. Wherever and whenever you want to use DATAtab, just go to the website and get started.

All the statistical methods you need.

DATAtab offers you a wide range of statistical methods. We have selected the most central and best known statistical methods for you and do not overwhelm you with special cases.

Data security is a top priority.

All data that you insert and evaluate on DATAtab always remain on your end device. The data is not sent to any server or stored by us (not even temporarily). Furthermore, we do not pass on your data to third parties in order to analyze your user behavior.

Many tutorials with simple examples.

In order to facilitate the introduction, DATAtab offers a large number of free tutorials with focused explanations in simple language. We explain the statistical background of the methods and give step-by-step explanations for performing the analyses in the statistics calculator.

Practical Auto-Assistant.

DATAtab takes you by the hand in the world of statistics. When making statistical decisions, such as the choice of scale or measurement level or the selection of suitable methods, Auto-Assistants ensure that you get correct results quickly.

Charts, simple and clear.

With DATAtab data visualization is fun! Here you can easily create meaningful charts that optimally illustrate your results.

New in the world of statistics?

DATAtab was primarily designed for people for whom statistics is new territory. Beginners are not overwhelmed with a lot of complicated options and checkboxes, but are encouraged to perform their analyses step by step.

Online survey very simple.

DATAtab offers you the possibility to easily create an online survey, which you can then evaluate immediately with DATAtab.

Our references

Alternative to statistical software like SPSS and STATA

DATAtab was designed for ease of use and is a compelling alternative to statistical programs such as SPSS and STATA. On datatab.net, data can be statistically evaluated directly online and very easily (e.g. t-test, regression, correlation etc.). DATAtab's goal is to make the world of statistical data analysis as simple as possible, no installation and easy to use. Of course, we would also be pleased if you take a look at our second project Statisty .

Extensive tutorials

Descriptive statistics.

Here you can find out everything about location parameters and dispersion parameters and how you can describe and clearly present your data using characteristic values.

Hypothesis Test

Here you will find everything about hypothesis testing: One sample t-test , Unpaired t-test , Paired t-test and Chi-square test . You will also find tutorials for non-parametric statistical procedures such as the Mann-Whitney u-Test and Wilcoxon-Test . mann-whitney-u-test and the Wilcoxon test

The regression provides information about the influence of one or more independent variables on the dependent variable. Here are simple explanations of linear regression and logistic regression .

Correlation

Correlation analyses allow you to analyze the linear association between variables. Learn when to use Pearson correlation or Spearman rank correlation . With partial correlation , you can calculate the correlation between two variables to the exclusion of a third variable.

Partial Correlation

The partial correlation shows you the correlation between two variables to the exclusion of a third variable.

Levene Test

The Levene Test checks your data for variance equality. Thus, the levene test is used as a prerequisite test for many hypothesis tests .

The p-value is needed for every hypothesis test to be able to make a statement whether the null hypothesis is accepted or rejected.

Distributions

DATAtab provides you with tables with distributions and helpful explanations of the distribution functions. These include the Table of t-distribution and the Table of chi-squared distribution

Contingency table

With a contingency table you can get an overview of two categorical variables in the statistics.

Equivalence and non-inferiority

In an equivalence trial, the statistical test aims at showing that two treatments are not too different in characteristics and a non-inferiority trial wants to show that an experimental treatment is not worse than an established treatment.

If there is a clear cause-effect relationship between two variables, then we can speak of causality. Learn more about causality in our tutorial.

Multicollinearity

Multicollinearity is when two or more independent variables have a high correlation.

Effect size for independent t-test

Learn how to calculate the effect size for the t-test for independent samples.

Reliability analysis calculator

On DATAtab, Cohen's Kappa can be easily calculated online in the Cohen’s Kappa Calculator . there is also the Fleiss Kappa Calculator . Of course, the Cronbach's alpha can also be calculated in the Cronbach's Alpha Calculator .

Analysis of variance with repeated measurement

Repeated measures ANOVA tests whether there are statistically significant differences in three or more dependent samples.

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

Critical Value Calculator

How to use critical value calculator, what is a critical value, critical value definition, how to calculate critical values, z critical values, t critical values, chi-square critical values (χ²), f critical values, behind the scenes of the critical value calculator.

Welcome to the critical value calculator! Here you can quickly determine the critical value(s) for two-tailed tests, as well as for one-tailed tests. It works for most common distributions in statistical testing: the standard normal distribution N(0,1) (that is when you have a Z-score), t-Student, chi-square, and F-distribution .

What is a critical value? And what is the critical value formula? Scroll down – we provide you with the critical value definition and explain how to calculate critical values in order to use them to construct rejection regions (also known as critical regions).

The critical value calculator is your go-to tool for swiftly determining critical values in statistical tests, be it one-tailed or two-tailed. To effectively use the calculator, follow these steps:

In the first field, input the distribution of your test statistic under the null hypothesis: is it a standard normal N (0,1), t-Student, chi-squared, or Snedecor's F? If you are not sure, check the sections below devoted to those distributions, and try to localize the test you need to perform.

In the field What type of test? choose the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

If needed, specify the degrees of freedom of the test statistic's distribution. If you need more clarification, check the description of the test you are performing. You can learn more about the meaning of this quantity in statistics from the degrees of freedom calculator .

Set the significance level, α \alpha α . By default, we pre-set it to the most common value, 0.05, but you can adjust it to your needs.

The critical value calculator will display your critical value(s) and the rejection region(s).

Click the advanced mode if you need to increase the precision with which the critical values are computed.

For example, let's envision a scenario where you are conducting a one-tailed hypothesis test using a t-Student distribution with 15 degrees of freedom. You have opted for a right-tailed test and set a significance level (α) of 0.05. The results indicate that the critical value is 1.7531, and the critical region is (1.7531, ∞). This implies that if your test statistic exceeds 1.7531, you will reject the null hypothesis at the 0.05 significance level.

👩‍🏫 Want to learn more about critical values? Keep reading!

In hypothesis testing, critical values are one of the two approaches which allow you to decide whether to retain or reject the null hypothesis. The other approach is to calculate the p-value (for example, using the p-value calculator ).

The critical value approach consists of checking if the value of the test statistic generated by your sample belongs to the so-called rejection region , or critical region , which is the region where the test statistic is highly improbable to lie . A critical value is a cut-off value (or two cut-off values in the case of a two-tailed test) that constitutes the boundary of the rejection region(s). In other words, critical values divide the scale of your test statistic into the rejection region and the non-rejection region.

Once you have found the rejection region, check if the value of the test statistic generated by your sample belongs to it :

• If so, it means that you can reject the null hypothesis and accept the alternative hypothesis; and
• If not, then there is not enough evidence to reject H 0 .

But how to calculate critical values? First of all, you need to set a significance level , α \alpha α , which quantifies the probability of rejecting the null hypothesis when it is actually correct. The choice of α is arbitrary; in practice, we most often use a value of 0.05 or 0.01. Critical values also depend on the alternative hypothesis you choose for your test , elucidated in the next section .

To determine critical values, you need to know the distribution of your test statistic under the assumption that the null hypothesis holds. Critical values are then points with the property that the probability of your test statistic assuming values at least as extreme at those critical values is equal to the significance level α . Wow, quite a definition, isn't it? Don't worry, we'll explain what it all means.

First, let us point out it is the alternative hypothesis that determines what "extreme" means. In particular, if the test is one-sided, then there will be just one critical value; if it is two-sided, then there will be two of them: one to the left and the other to the right of the median value of the distribution.

Critical values can be conveniently depicted as the points with the property that the area under the density curve of the test statistic from those points to the tails is equal to α \alpha α :

Left-tailed test: the area under the density curve from the critical value to the left is equal to α \alpha α ;

Right-tailed test: the area under the density curve from the critical value to the right is equal to α \alpha α ; and

Two-tailed test: the area under the density curve from the left critical value to the left is equal to α / 2 \alpha/2 α /2 , and the area under the curve from the right critical value to the right is equal to α / 2 \alpha/2 α /2 as well; thus, total area equals α \alpha α .

As you can see, finding the critical values for a two-tailed test with significance α \alpha α boils down to finding both one-tailed critical values with a significance level of α / 2 \alpha/2 α /2 .

The formulae for the critical values involve the quantile function , Q Q Q , which is the inverse of the cumulative distribution function ( c d f \mathrm{cdf} cdf ) for the test statistic distribution (calculated under the assumption that H 0 holds!): Q = c d f − 1 Q = \mathrm{cdf}^{-1} Q = cdf − 1 .

Once we have agreed upon the value of α \alpha α , the critical value formulae are the following:

• Left-tailed test :
• Right-tailed test :
• Two-tailed test :

In the case of a distribution symmetric about 0 , the critical values for the two-tailed test are symmetric as well:

Unfortunately, the probability distributions that are the most widespread in hypothesis testing have somewhat complicated c d f \mathrm{cdf} cdf formulae. To find critical values by hand, you would need to use specialized software or statistical tables. In these cases, the best option is, of course, our critical value calculator! 😁

Use the Z (standard normal) option if your test statistic follows (at least approximately) the standard normal distribution N(0,1) .

In the formulae below, u u u denotes the quantile function of the standard normal distribution N(0,1):

Left-tailed Z critical value: u ( α ) u(\alpha) u ( α )

Right-tailed Z critical value: u ( 1 − α ) u(1-\alpha) u ( 1 − α )

Two-tailed Z critical value: ± u ( 1 − α / 2 ) \pm u(1- \alpha/2) ± u ( 1 − α /2 )

Check out Z-test calculator to learn more about the most common Z-test used on the population mean. There are also Z-tests for the difference between two population means, in particular, one between two proportions.

Use the t-Student option if your test statistic follows the t-Student distribution . This distribution is similar to N(0,1) , but its tails are fatter – the exact shape depends on the number of degrees of freedom . If this number is large (>30), which generically happens for large samples, then the t-Student distribution is practically indistinguishable from N(0,1). Check our t-statistic calculator to compute the related test statistic.

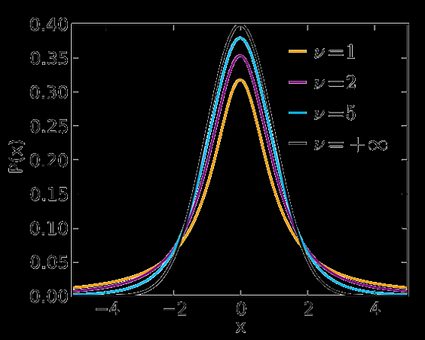
In the formulae below, Q t , d Q_{\text{t}, d} Q t , d ​ is the quantile function of the t-Student distribution with d d d degrees of freedom:

Left-tailed t critical value: Q t , d ( α ) Q_{\text{t}, d}(\alpha) Q t , d ​ ( α )

Right-tailed t critical value: Q t , d ( 1 − α ) Q_{\text{t}, d}(1 - \alpha) Q t , d ​ ( 1 − α )

Two-tailed t critical values: ± Q t , d ( 1 − α / 2 ) \pm Q_{\text{t}, d}(1 - \alpha/2) ± Q t , d ​ ( 1 − α /2 )

Visit the t-test calculator to learn more about various t-tests: the one for a population mean with an unknown population standard deviation , those for the difference between the means of two populations (with either equal or unequal population standard deviations), as well as about the t-test for paired samples .

Use the χ² (chi-square) option when performing a test in which the test statistic follows the χ²-distribution .

You need to determine the number of degrees of freedom of the χ²-distribution of your test statistic – below, we list them for the most commonly used χ²-tests.

Here we give the formulae for chi square critical values; Q χ 2 , d Q_{\chi^2, d} Q χ 2 , d ​ is the quantile function of the χ²-distribution with d d d degrees of freedom:

Left-tailed χ² critical value: Q χ 2 , d ( α ) Q_{\chi^2, d}(\alpha) Q χ 2 , d ​ ( α )

Right-tailed χ² critical value: Q χ 2 , d ( 1 − α ) Q_{\chi^2, d}(1 - \alpha) Q χ 2 , d ​ ( 1 − α )

Two-tailed χ² critical values: Q χ 2 , d ( α / 2 ) Q_{\chi^2, d}(\alpha/2) Q χ 2 , d ​ ( α /2 ) and Q χ 2 , d ( 1 − α / 2 ) Q_{\chi^2, d}(1 - \alpha/2) Q χ 2 , d ​ ( 1 − α /2 )

Several different tests lead to a χ²-score:

Goodness-of-fit test : does the empirical distribution agree with the expected distribution?

This test is right-tailed . Its test statistic follows the χ²-distribution with k − 1 k - 1 k − 1 degrees of freedom, where k k k is the number of classes into which the sample is divided.

Independence test : is there a statistically significant relationship between two variables?

This test is also right-tailed , and its test statistic is computed from the contingency table. There are ( r − 1 ) ( c − 1 ) (r - 1)(c - 1) ( r − 1 ) ( c − 1 ) degrees of freedom, where r r r is the number of rows, and c c c is the number of columns in the contingency table.

Test for the variance of normally distributed data : does this variance have some pre-determined value?

This test can be one- or two-tailed! Its test statistic has the χ²-distribution with n − 1 n - 1 n − 1 degrees of freedom, where n n n is the sample size.

Finally, choose F (Fisher-Snedecor) if your test statistic follows the F-distribution . This distribution has a pair of degrees of freedom .

Let us see how those degrees of freedom arise. Assume that you have two independent random variables, X X X and Y Y Y , that follow χ²-distributions with d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ degrees of freedom, respectively. If you now consider the ratio ( X d 1 ) : ( Y d 2 ) (\frac{X}{d_1}):(\frac{Y}{d_2}) ( d 1 ​ X ​ ) : ( d 2 ​ Y ​ ) , it turns out it follows the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom. That's the reason why we call d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ the numerator and denominator degrees of freedom , respectively.

In the formulae below, Q F , d 1 , d 2 Q_{\text{F}, d_1, d_2} Q F , d 1 ​ , d 2 ​ ​ stands for the quantile function of the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom:

Left-tailed F critical value: Q F , d 1 , d 2 ( α ) Q_{\text{F}, d_1, d_2}(\alpha) Q F , d 1 ​ , d 2 ​ ​ ( α )

Right-tailed F critical value: Q F , d 1 , d 2 ( 1 − α ) Q_{\text{F}, d_1, d_2}(1 - \alpha) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α )

Two-tailed F critical values: Q F , d 1 , d 2 ( α / 2 ) Q_{\text{F}, d_1, d_2}(\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( α /2 ) and Q F , d 1 , d 2 ( 1 − α / 2 ) Q_{\text{F}, d_1, d_2}(1 -\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α /2 )

Here we list the most important tests that produce F-scores: each of them is right-tailed .

ANOVA : tests the equality of means in three or more groups that come from normally distributed populations with equal variances. There are ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where k k k is the number of groups, and n n n is the total sample size (across every group).

Overall significance in regression analysis . The test statistic has ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where n n n is the sample size, and k k k is the number of variables (including the intercept).

Compare two nested regression models . The test statistic follows the F-distribution with ( k 2 − k 1 , n − k 2 ) (k_2 - k_1, n - k_2) ( k 2 ​ − k 1 ​ , n − k 2 ​ ) degrees of freedom, where k 1 k_1 k 1 ​ and k 2 k_2 k 2 ​ are the number of variables in the smaller and bigger models, respectively, and n n n is the sample size.

The equality of variances in two normally distributed populations . There are ( n − 1 , m − 1 ) (n - 1, m - 1) ( n − 1 , m − 1 ) degrees of freedom, where n n n and m m m are the respective sample sizes.

I'm Anna, the mastermind behind the critical value calculator and a PhD in mathematics from Jagiellonian University .

The idea for creating the tool originated from my experiences in teaching and research. Recognizing the need for a tool that simplifies the critical value determination process across various statistical distributions, I built a user-friendly calculator accessible to both students and professionals. After publishing the tool, I soon found myself using the calculator in my research and as a teaching aid.

Trust in this calculator is paramount to me. Each tool undergoes a rigorous review process , with peer-reviewed insights from experts and meticulous proofreading by native speakers. This commitment to accuracy and reliability ensures that users can be confident in the content. Please check the Editorial Policies page for more details on our standards.

What is a Z critical value?

A Z critical value is the value that defines the critical region in hypothesis testing when the test statistic follows the standard normal distribution . If the value of the test statistic falls into the critical region, you should reject the null hypothesis and accept the alternative hypothesis.

How do I calculate Z critical value?

To find a Z critical value for a given confidence level α :

Check if you perform a one- or two-tailed test .

For a one-tailed test:

Left -tailed: critical value is the α -th quantile of the standard normal distribution N(0,1).

Right -tailed: critical value is the (1-α) -th quantile.

Two-tailed test: critical value equals ±(1-α/2) -th quantile of N(0,1).

No quantile tables ? Use CDF tables! (The quantile function is the inverse of the CDF.)

Verify your answer with an online critical value calculator.

Is a t critical value the same as Z critical value?

In theory, no . In practice, very often, yes . The t-Student distribution is similar to the standard normal distribution, but it is not the same . However, if the number of degrees of freedom (which is, roughly speaking, the size of your sample) is large enough (>30), then the two distributions are practically indistinguishable , and so the t critical value has practically the same value as the Z critical value.

What is the Z critical value for 95% confidence?

The Z critical value for a 95% confidence interval is:

• 1.96 for a two-tailed test;
• 1.64 for a right-tailed test; and
• -1.64 for a left-tailed test.
• Sum of Squares Calculator
• Midrange Calculator
• Coefficient of Variation Calculator

Pie chart percentage

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (571)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (184)
• Other (183)
• Discover Omni (40)

Statistics Made Easy

Two Sample t-test Calculator

t = -1.608761

p-value (one-tailed) = 0.060963

p-value (two-tailed) = 0.121926

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

5 Replies to “Two Sample t-test Calculator”

Hi! Thanks for efforts.

-1.838687427 I get this for t value.

Could you please check? Classical two independant samples formula: t = (ma- mb)/ sqrt( s*s/12 – s*s/12)

Thank you learnt something. For df = 12, I had to subtract one from each of the samples

good work zach

Hi, I noticed that in using the calculators for hypothesis testing, the default level of significance is 0.05 and you cannot change it. Is there a way I can change the level of significance to 0.1 or say 0.01?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Paired T Test Calculator (Dependent T test)

Enter sample data, reporting results in apa style, paired t-test online, what is a paired t-test, how to use the paired t-test calculator, calculators.

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

T Test Calculator for 2 Dependent Means

The t -test for dependent means (also called a repeated-measures t -test, paired samples t -test, matched pairs t -test and matched samples t -test) is used to compare the means of two sets of scores that are directly related to each other. So, for example, it could be used to test whether subjects' galvanic skin responses are different under two conditions - first, on exposure to a photograph of a beach scene; second, on exposure to a photograph of a spider.

Requirements

• The data is normally distributed
• Scale of measurement should be interval or ratio
• The two sets of scores are paired or matched in some way

Null Hypothesis

H 0 : U D = U 1 - U 2 = 0, where U D equals the mean of the population of difference scores across the two measurements.

• Typing Test
• Image Converters
• Code Formatters
• File Converters
• Image Editor
• Image Cropper
• Image Resizer
• Mortgage Calculator
• Age Calculator
• Qr-Code Generator
• HTML Formatter
• CSS Formatter
• JS Formatter
• PHP Formatter
• XML Formatter
• Slope Calculator - Free Online Calculator
• Rounding Numbers Calculator - Free Online Calculator
• Percentage Decrease Calculator - Free Online Calculator
• Percentage Difference Calculator - Free Online Calculator
• Decimal to Fraction Calculator - Free Online Calculator
• Percent Off Calculator (Free Online Tool to Calculate Percent Off)
• Hourly to Salary Calculator (Free Calculator for Employees)
• Create a Scientific Calculator using React-Native
• Ratio Calculator GUI using Tkinter
• Build a Calculator using React Native
• Love Calculator GUI Application in Python
• Scientific Calculator using React
• Creating a Calculator using Calculator Widget in Flutter
• Use Pandas to Calculate Statistics in Python
• How to Make a Calculator in C# ?
• Calculator using Classes in C++
• Create a GPA Calculator using React Native
• How to install Gnome-Calculator in Ubuntu
• Calculator in PHP using If-Else Statement

t-statistic Calculator – Free Online Calculator

t-statistic Calculator: A t-statistic is a value used in statistics to determine if there is a significant difference between the means of two groups. The t-statistic calculator helps you quickly calculate this value. The GeeksforGeeks free online calculator makes it easy to find the t-statistic. This is especially important in fields like research and data analysis , where accuracy is key. Whether you’re new to statistics or an experienced analyst, this simple tool will help you be more precise in your calculations and ensure your results are reliable.

How to use the t-statistic Calculator

Calculating the t-statistic manually involves a series of steps to ensure accuracy. Here’s a simplified guide:

• Compute the Difference in Sample Means: Calculate the difference between the means of the two groups being compared.
• Determine the Standard Error of the Difference: Calculate the standard error of the difference using the standard deviations and sample sizes of the two groups.
• Calculate the t-statistic: Divide the difference in sample means by the standard error of the difference to obtain the t-statistic.

What is a t-statistic Calculator?

A t-statistic Calculator is a powerful guide designed to streamline the computation of t-statistics for statistical analysis. By inputting the relevant data, such as sample means, standard deviations, and sample sizes, users can quickly obtain the t-statistic value, facilitating hypothesis testing and statistical decision-making.

t-statistic Calculator 

Suppose we have two groups, Group A and Group B, with sample means of 15 and 18, respectively. The standard deviations for Group A and Group B are 3 and 4, and the sample sizes are 25 and 30, respectively. Let’s calculate the t-statistic:

• Difference in Means = 18 – 15 = 3
• Standard Error of the Difference = sqrt((3^2/25) + (4^2/30)) ≈ sqrt((9/25) + (16/30)) ≈ sqrt(0.36 + 0.5333) ≈ sqrt(0.8933) ≈ 0.9451
• t-statistic = 3 / Standard Error of the Difference ≈ 3 / 0.9451 ≈ 3.1766

t-statistic Calculator Examples 

• Group 1: Mean (?¯₁) = 10, Standard Deviation (?₁) = 2, Sample Size (?₁) = 20
• Group 2: Mean (?¯₂) = 12, Standard Deviation (?₂) = 3, Sample Size (?₂) = 25

Difference in Means (?¯₁ – ?¯₂) = 10 – 12 = -2 Pooled Standard Deviation (?ₚ) ≈ 2.608 (Calculated similarly as in Example 1) t-statistic (?) ≈ -2.5561

• Group 1: Mean (?¯₁) = 25, Standard Deviation (?₁) = 5, Sample Size (?₁) = 30
• Group 2: Mean (?¯₂) = 28, Standard Deviation (?₂) = 6, Sample Size (?₂) = 35

Difference in Means (?¯₁ – ?¯₂) = 25 – 28 = -3 Pooled Standard Deviation (?ₚ) ≈ 2.991 (Calculated similarly as in Example 1) t-statistic (?) ≈ -2.009

• Group 1: Mean (?¯₁) = 18, Standard Deviation (?₁) = 4, Sample Size (?₁) = 15
• Group 2: Mean (?¯₂) = 20, Standard Deviation (?₂) = 5, Sample Size (?₂) = 20

Difference in Means (?¯₁ – ?¯₂) = 18 – 20 = -2 Pooled Standard Deviation (?ₚ) ≈ 4.457 (Calculated similarly as in Example 1) t-statistic (?) ≈ -1.341

3 Practice Questions on t-statistic Calculator

1. Compute the t-statistic for two groups with sample means 15 and 17, standard deviations 3 and 4, and sample sizes 25 and 30, respectively.

2. Calculate the t-statistic for groups with means 20 and 22, standard deviations 4 and 5, and sample sizes 35 and 40, respectively.

3. Determine the t-statistic for groups with means 22 and 25, standard deviations 6 and 7, and sample sizes 20 and 25, respectively.

In conclusion, the t-statistic Calculator serves as an indispensable guide for statisticians, researchers, and analysts alike, offering a convenient solution for computing t-statistics and facilitating statistical analyses. By simplifying complex calculations and providing accurate results, this calculator empowers users to make informed decisions and draw meaningful insights from their data.

t-statistic Calculator – Free Online Calculator – FAQs 

What is t-statistics.

t-statistics, also known as Student’s t-statistics, is a measure used in hypothesis testing to determine if there is a significant difference between the means of two groups.

When should I use t-statistics?

t-statistics are typically used when comparing the means of two groups (e.g., experimental vs. control group) and the sample size is small (usually less than 30) or the population standard deviation is unknown.

What does the t-statistic value indicate?

The t-statistic value indicates the number of standard errors the sample mean is from the population mean. A larger absolute t-value suggests a greater difference between the sample means.

How do I interpret the t-statistic?

If the absolute value of the t-statistic is greater than the critical value (obtained from a t-distribution table or calculated using statistical software) at a given significance level (e.g., 0.05), then the difference between the means is considered statistically significant.

What is the difference between t-statistics and z-statistics?

t-statistics are used when the sample size is small or the population standard deviation is unknown, whereas z-statistics are used when the sample size is large (typically greater than 30) and the population standard deviation is known.

What are the assumptions of t-statistics?

The main assumptions of t-statistics include: the data are normally distributed, the samples are independent, and the populations have equal variances (for a two-sample t-test). Violations of these assumptions can affect the accuracy of the results.

Please Login to comment...

Similar reads.

• tools-converters

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• All Products

Hypothesis Testing - One Way Analysis of Variance (ANOVA) with F-Test

This article describes how to perform a one-way ANOVA with F-test.

To learn about statistical functions in MAQL, see our Documentation .

In Hypothesis Testing - One Sample T-Tests and Z-Tests , we examined comparisons of a single sample mean with the population mean. For situations in which three or more sample means are compared with each other, the ANOVA test can be used to measure statistically significant differences among those means and, in turn, among the means for their populations.

ANOVA should be viewed as an extension of the t-test when there are more than two comparison groups.

The size of a difference that is statistically significant depends on the sample sizes and the amount of certainty desired in the testing. In our significance tests, we use p-values (levels of statistical significance).

For example, a company’s marketing team may want to answer, “Does the day of the week have an impact on the number of clicks?” To frame the question in other terms, we wish to measure whether there is any difference between the number of clicks on different days of the week.

The first step of any hypothesis testing is to convert the question into null and alternative hypotheses:

• null hypothesis (H0): x? Mon = x? Tue = x? Wed = x? Thu = x? Fri = x? Sat = x? Sun (where x? is the average number of clicks in a given day of the week). If the average number of clicks on each day of the week is consistent, the day of the week does not have an impact.
• alternative hypothesis (H1): At least one of the mean values does not equal the others.

To perform this test, we must calculate the F-test statistical value and compare it with the critical value from the F-distribution table, based on the chosen significance level or p-value (usually 0.05) and the degrees of freedom.

Computing ANOVA Table

An ANOVA table comprises the following components:

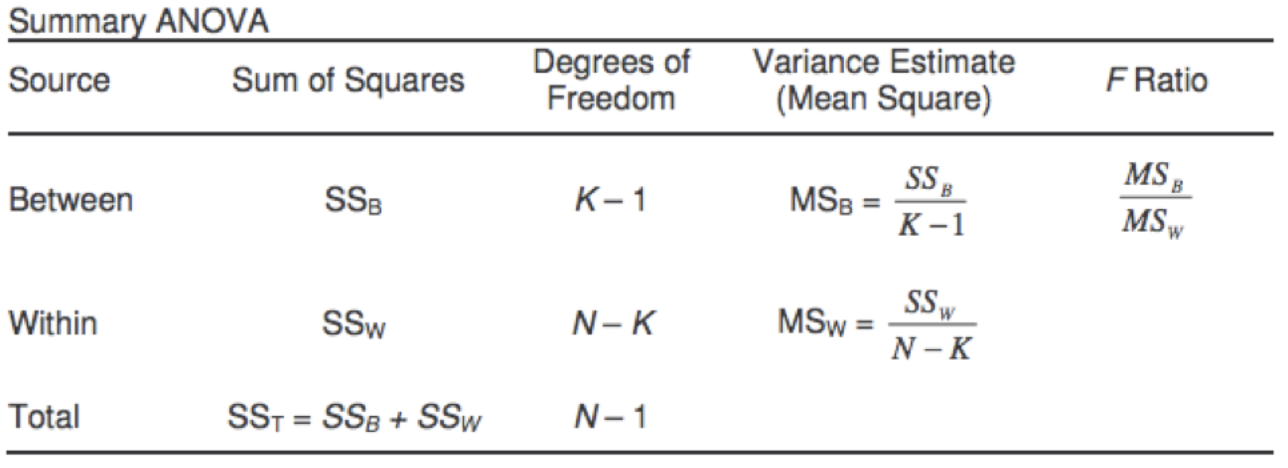
Our goal is to calculate the value of F Ratio in the last column as the final result of computing the values in all of the other columns. Let’s review what these table values mean and how we can calculate them in MAQL.

Column 1 - Sum of Squares

SS B = ∑n( x? i -μ)², is the Sum of Squares (deviations) between the group means and the grand mean, where *x?*i is the group mean and μ represents the grand mean.

Avg Clicks(Mon) The following MAQL metric computes the average number of clicks for the specified day of the week: SELECT AVG( Clicks ) WHERE Day of Week (Mon-Sun) (Date) =Mon We calculate this metric for each day of the week. These are our group means (*x?*i).

Avg Clicks(ALL) The following MAQL calculates the average clicks across all days of the week. This value is our grand mean (μ). SELECT AVG( Clicks ) BY ALL OTHER

Count(Mon) The following metric calculates the count of clicks for Monday: SELECT COUNT( Date(Date) , Records of Website ) WHERE Day of Week (Mon-Sun) (Date) =Mon We calculate this metric for each day of the week to get the number of records in each group. In our example, the unique identifier for clicks is the Date attribute.

Dev(B,Mon) (The B above stands for “Between”) SELECT ( Avg Clicks(Mon) - Avg Clicks(ALL) ) BY ALL OTHER This metric gives us the deviation between the groups and the grand mean (*x?*i-μ). We calculate this for each day of the week.

SSB Finally, we add n (x?i-μ) for all the groups to get the value for SSB. SELECT ((POWER( Dev(B,Mon) ,2)* Count(Mon) ) + ((POWER( Dev(B,Tue) ,2)* Count(Tue) ) + ((POWER(Dev(B,Wed) ,2)* Count(Wed) ) ...

SST SS T = ∑(xi -μ)² is the Sum of Squares of all the observations from the grand mean (μ), regardless of which group produced them. SELECT SUM(POWER((SELECT (SUM( Clicks )- Avg Clicks(ALL) ) BY Date (Date) ),2)) Note how we used the BY Date(Date) clause to compute the difference between each observation and the grand mean. In our example, Date is the unique identifier for Clicks.

SSW SS W = SS T - SS B , is the Sum of Squares within the groups. It is also called Error Sum of Squares and can be calculated by subtracting Sum of Squares between the groups from total Sum of Squares. SELECT SST - SSB

Column 2 - Degrees of Freedom

K-1 measures the degrees of freedom between groups, where K is number of groups. In this example, the value is 7 because we are analyzing days of the week.

N-K measures within degrees of freedom, where N is total number of records.

Count(N) SELECT COUNT( Date(Date) , Records of Website )

Column 3 - Mean Square

MS B = SS B / K-1 is the Mean Sum of Squares between the groups. It is calculated by dividing the Sum of Squares between the groups by the between-group degrees of freedom.

MSB SELECT SSB / ( K -1)

MS W = SS W / N-K is the Mean Sum of Squares within the group. It is calculated by dividing the Sum of Squares within the groups by the within-group degrees of freedom.

MSW SELECT SSW / ( Count(N) - K )

Column 4 - F Ratio

F Ratio = MS B / MS W SELECT MSB / MSW

After we have calculated the F-value, we can compare it to the critical value using an F-distribution table and then evaluate the significance of the analysis.

Evaluating Significance

F-Distribution Table

The first step is to upload a table of F-distribution critical values, which you can find in any statistical textbook. Download an example table of F-statistic values in the attached file. The example table has 4 columns:

df1 - Between-group degrees of freedom

df2 - Within-group degrees of freedom

alpha - Significance level that we desire in our analysis (usually 0.05, 0.01, 0.005)

X - This column contains the critical value of F-statistic. We compare the F Ratio metric calculated above with this value using the other three columns as lookup values

Fact Dataset in LDM

We create a fact dataset in our logical data model, as shown below, to store these values:

Note that all the four columns are stored as facts.

Upload F-Distribution Data

After you have created the dataset in your logical data model, build a simple ETL graph to upload the data in the file to your project.

Calculate Metrics

After the values have been uploaded to the project, we can use the following metrics to evaluate whether our analysis is significant.

df1(Clicks) SELECT CASE WHEN ( K -1) > 150 THEN 1000, WHEN ( K -1) > 90 THEN 120, WHEN ( K -1) > 50 THEN 60,WHEN ( K -1) > 35 THEN 40, WHEN ( K -1) > 29 THEN 30 ELSE ( K -1) END

df2(Clicks) SELECT CASE WHEN (COUNT(N)-K) > 150 THEN 1000, WHEN (COUNT(N)-K) > 90 THEN 120, WHEN(COUNT(N)-K) > 50 THEN 60,WHEN (COUNT(N)-K) > 35 THEN 40, WHEN (COUNT(N)-K) > 29 THEN 30 ELSE (COUNT(N)-K) END

X(Clicks) SELECT (SELECT SUM( X ) WHERE df1 = df1(Clicks) AND df2 = df2(Clicks) AND alpha = Sig Level ) BY ALL OTHER

The Sig Level variable is used to depict significance level, which is usually 0.05 or 0.01.

• If the F Ratio metric is larger than this X value, our analysis is significant.
• If the analysis is valid, we can reject the null hypothesis. In our example, day of the week does have an impact on the number of clicks.