essay about volumetric analysis

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

14.2: Fundamentals of Volumetric Chemical Analysis, Acid/Base Equilibria & Titrations

• Last updated
• Save as PDF
• Page ID 134630

• Paul M. Shiundu
• University of Nairobi via Arican Virtual University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

Review the concept of chemical equilibria, and in particular ionic equilibria.

• Define and distinguish between acids and bases.
• Distinguish between monoprotic and polyprotic acid-base equilibrium.
• Describe and distinguish between weak acid/base dissociations.
• Have a working knowledge of the fundamentals of volumetric analysis.
• Define and distinguish between equivalence and end point.
• Use the concept of titration to distinguish between blank and back titrations.
• Define neutralization reactions and explain their corresponding titration curve structures.
• Define and explain standardization, indicators, and primary standards and their use
• Use the concept of polyprotic acid equilibria to do related calculations.

Some of the most important processes in chemical and biological systems are acid-base reactions in aqueous solutions. At the onset of this unit, a review of the topic of acid-base equilibria, together with the properties of acids and bases is undertaken. This is because the concepts of ionic equilibria and reactions are important for a better understanding of the ideas and workings of acid-base neutralization titrations . This unit discusses the basic principles of titrimetric analytical methods, and the use of the equivalence concept in quantitative titration methods. The latter part of this unit will provide you with the opportunity to carry out simple acid-base titration reactions and calculations as well as demonstrations of simulated acid-base titrations.

Key Concepts

• Arrhenius Acid : A substance that yields hydrogen ions (H + ) when dissolved in water.
• Arrhenius Base: A substance that yields hydroxide ions (OH - ) when dissolved in water.
• Bronsted acid : A substance capable of donationg a proton. Bronsted base: A substance capable of accepting a proton.
• Chemical Equilibrium: A state in which the rates of the forward and reverse reactions are equal.
• Chemical Reaction: A process in which a substance (or substances) is changed into one or more new substances.
• End point: The volume of titrant required for the detection of the equivalence point.
• Equilibrium constant: A number equal to the ratio of the equilibrium concen- trations of products to the equilibrium concentrations of reactants, each raised tothe power of its stoichiometric coefficient.
• Equivalence point: The point at which the acid has completely reacted with or been neutralized by the base.
• Indicators: Substancesthathavedistinctlydifferentcoloursinacidicandbasic media.
• Molar solubility: The number of moles of solute in one litre of a saturated so- lution (mol/L)
• Monoprotic acid: Each unit of the acid yields one hydrogen ion upon ioniza- tion.
• Neutralization reaction: A reaction between an acid and a base.
• Precipitation reaction: A reaction that results in the formation of a precipitate.
• Primary Standard: a high purity compound used to prepare the standard solution or to standardize the solution with.
• Quantitative analysis: The determination of the amount of substances present in a sample.
• Secondary Standard: a second material used as a substitute for a suitable primary standard. This standard solution should always be standardized using a primary standard.
• Solubility product, K sp : The equilibrium constant for the reaction in which a solid salt dissolves to give its constituent ions in solution. It expresses the equilibrium between a solid and its ions in solution.
• Standardization: The process by which the concentration of a solution is deter- mined.
• Standard Solution: A solution of accurately known concentration.
• Stoichiometry: The quantitative study of reactants and products in a chemical reaction.
• Stoichiometric amounts: The exact molar amounts of reactants and products that appear in the balanced chemical equation.
• Strong acids: Strong electrolytes which are assumed to ionize completely in water.
• Strong bases : Strong electrolytes which are assumed to ionize completely in water.
• Titration : The gradual addition of of a solution of accurately known concentration to another solution of unknown concentration until the chemical reaction between the two solutions is complete.
• Volumetric methods of analysis:based on the measurement of the amount of reagent that combines with the analyte. The terms volumetric analysis specifically involves the determination of the volume of the reagent solution needed for a complete reaction.
• Volumetric titrimetry: methods that require that a reagent solution of known concentration, standard solution or titrant , be used.

Introduction to activity # 2

The thrust of this unit deals primarily with the fundamentals of volumetric methods of analysis. Volumetric method of analysis or sometimes referred to as titrimetric method of analysis is a quantitative method of analysis that is based upon the measurement of volume. These methods are considered important since they are usually rapid, convenient and are often accurate. The concept of pH and the pH scale, the ionization of weak acids and weak bases are introduced and discussed at length. Also, the unit looks at the relationship between acid strength and molecular structure.

List of other compulsory readings

Chemical equilibria (Reading #9)

Introduction to acid-base chemistry (Reading #10)

Acid-Base equilibria and Calculations (Reading #11)

Acid-base equilibria of aquatic environment (Reading #12)

A reference text with file with sub-sections containing sample problemsdealing with acids and bases, chemical equilibrium, quantitative calcula-tions in acids and bases (Reading #13).

Acid Base (Reading #14)

Bronsted-Lowry Acid-Base Reactions (Reading #15)

Chemistry Chapter 16 Complex Ions (Reading #16)

Chemistry Chapter 16 Hydrolysis of Bases (Reading #17)

Chemistry Chapter 16 Titrations (Reading #18)

Chemistry Chapter 16 Hydrolysis of Acids (Reading #19)

Chemistry Chapter 16 Autoionization of Water (Reading #20)

Addition of Strong Base to a weak Acid (Reading #21)

pH curves (titration curves) (Reading #22)

Titration of a Weak Acid with a Strong Base (Reading #23)

Detailed description of the activity

Review of General concepts and Principles of Chemical Equilibria:

The concept of equilibrium is extremely important in chemistry. For example, an industrial chemist who wants to maximize the yield of sulphuric acid, must have a clear understanding of the equilibrium constants for all the steps in the process, starting from the oxidation of sulphur as a reactant and ending with theformation of the final product. For a “general” reaction at equilibrium, we write:

\[\ce{aA + bB <=> cC + dD}\]

where the double arrow, ⇔ , is used to indicate that the chemical reaction proceeds in both directions. Dynamic equilibrium is said to occur when the rate of the forward reaction (represented by the chemical reaction,

\[\ce{aA + bB -> cC + dD}\]

which implies that a moles of substance A reacts with b moles of substance B to form c moles of C and d moles of D) equals the rate of the reverse reaction represented by the chemical reaction

\[\ce{cC + dD -> aA + bB}\]

which again implies that \(c\) moles of substance \(C\) reacts with \(d\) moles of substance \(D\) to form \(a\) moles of \(A\) and \(b\) moles of \(B).

At equilibrium, when there is no net change in any of the concentrations of the materials involved in that reaction over time,

\[\bf{K}_{eq}={[C]^c[D]^d\over \bf{[A]}_{eq}^a\bf{[B]}_{eq}^b}\]

where the K eq is the equilibrium constant and the square brackets, [ ], indicate a concentration of a species relative to the standard state for that particular phase at equilibrium. The standard state and their standard concentrations are:

[solutes] = mol/L; [gases] = atmospheres (atm) and [pure liquids], [pure solids], and [solivents] = unity.

For most calculations required for this module, it is sufficient to rememberthat the molar concentrations are to be used in the equilibrium expressions.

Types of Equilibria:

There are 4 main types of chemical equilibria that will be discussed in this module:

• Solubility Equilibria

Acid-Base Equilibria

• Oxidation/Reduction Equilibria and
• Complex ion Formation Equilibria

In this unit, our discussions will be limited to solubility and acid-base equilibria. The latter two equilibria types will be dealt with in the subsequent two units of this module.

Solubility Equilibria: In solubility equilibrium, (see equation below) a moles of the analyte A reacts with r moles of the reagent, R , to form an insoluble species, A a R r . Recall that the standard state for a solid solution is unity (i.e., x = 1). The solid precipitate is assumed to be pure, thus has x =1. Thus, because of this, the concentration of A a R r (s) does not appear in the solubility product expression given below.

\[aA(aq) + rR(aq)\Leftrightarrow\bf{A}_a\bf{R}_x(s)$$ \[\bf{K}_{sp}={[A]^a[R]^r}\]

where K sp is defined as the solubility product constant.

The sequence of steps for (a) calculating K sp from solubility data and (b) calculating solubility from K sp data are given in the figure below:

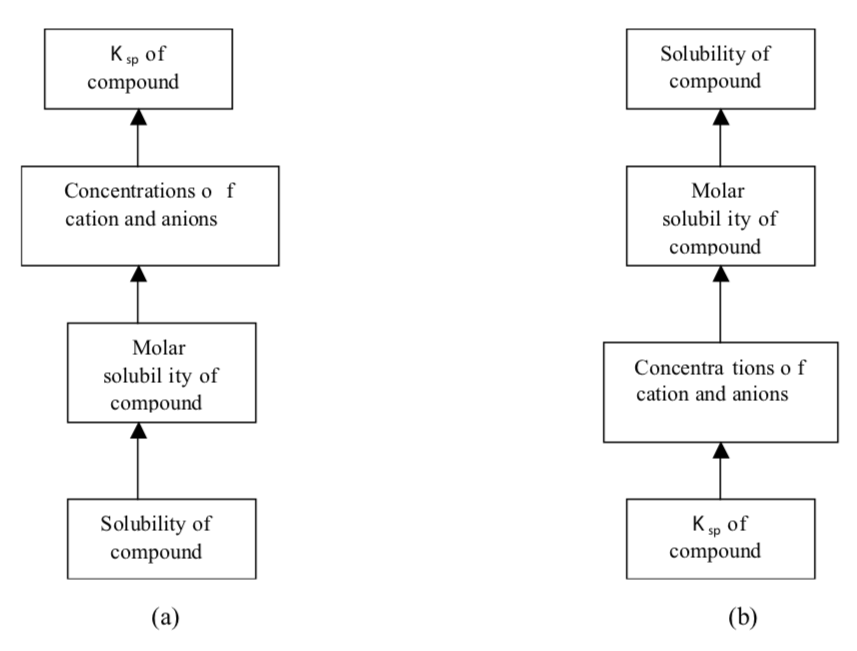
Here, molar solubility , is the number of moles of solute in 1 L of a standard solution (mol/L) , and solubility, which is the number of grams of solute in 1 L of a saturated solution (g/L). Note that both of these expressions refer to the concentration of saturated solutions at some given temperature (usually 25 o C).

Example \(\PageIndex{1}\)

Consider the reaction in which a solid salt of mercury chloride dis- solves in water to give its constituent ions in solutions as shown below:

\[\ce{Hg2Cl2 (s) <=> Hg2^{+} (aq) + 2Cl^{−} (aq)}\]

If the solubility product, K is 1.2 x 10 -18 , then

Hg 2 Cl 2 (s) É Hg 2 + (aq) + 2Cl − (aq)

Initail Conc. 0 0

Final Conc. x 2x

where x equals solubility only if there is little ion-pair formation. Therefore,

\[K_{sp} = 1.2 \times 10^{-18} = [Hg2^{2+}] [Cl^{-}]^2\]

This implies that: [Hg 2 2+ ] [Cl - ] 2 = 1.2 x 10 -18 . Thus, (x) (2x - ) 2 = 1.2 x 10 -18

Therefore, the solubility x = 6.7 x 10 -7 M.

Since some dissolved Hg 2 Cl 2 may not dissociate into free ion, we say that its solubility is at least 6.7×10 -7 M.

Example \(\PageIndex{2}\): solubility of calcium sulfate

The solubility of calcium sulfate (CaSO 4 ) is found to be 0.67 g/L. Calculate the value of K sp for calcium sulfate.

Please note that we are given the solubility of CaSO 4 and asked to calculate its K sp . The sequence of conversion steps, according to the Figure above is:

Solubility of → Molar Solubility → [Ca 2 + ] → K sp of

CaSO 4 of CaSO and [SO 2-] CaSO 4

Now consider the dissociation of CaSO 4 in water. Let s be the molar solubility (in mol/L) of CaSO 4 .

CaSO 4 (s) ⇌ [Ca 2+ ] (aq) + SO 4 2- (aq)​

Initial (M): 0 0

Change (M): -s +s +s

Equilibrium (M): s s

The solubility product of CaSO4 is:

K sp = [Ca 2+ ] [SO 4 2- ] = S 2

First, we calculate the number of moles of CaSO 4 dissolved in 1 L of solution.

\[ \frac { 0.67 \mathrm { g } ~\mathrm { CaSO } _ { 4 } } { 1 \mathrm { L } \text { solution } } \times \frac { 1 \mathrm { mol }~ \mathrm { CaSO } _ { 4 } } { 136.2 \mathrm { g } ~\mathrm { CaSO } _ { 4 } } = 4.9 \times 10 ^ { - 3 } \mathrm { mol } / \mathrm { L } = \mathrm { s } \nonumber\]

From the solubility equilibrium we see that for every mole of CaSO 4 that dissolves,

1 mole of Ca 2+ and 1 mole of SO 4 2- are produced. Thus, at equilibrium

[Ca 2 + ] = 4.9 x 10 -3 M and [SO 4 2- ] = 4.9 x 10 -3 M

Now we can calculate K sp :

K sp = [Ca 2 + ] [SO 4 2- ] = (4.9 x 10 -3 ) (4.9 x 10 -3 ) = 2.4 x 10 -5

Exercise \(\PageIndex{1}\)

Exercise 1: The solubility of lead chromate (PbCrO 4 ) is 4.5 x 10 -5 g/L. Calculate the solubility product of this compound.

Add texts here. Do not delete this text first.

Theory of Acids and Bases (Arrhenius and Bronsted-Lowry Theories):

According to the Arrhenius Theory of Acids : All acids contain H + ions and All bases contain OH - ions; and that an acid-base reaction involves the reaction of hydrogen and hydroxide ions to form water. The corresponding equation is as below:

H + (aq) + OH - (aq) → H 2 O (i)

Where ( aq ) stands for aqueous phase in which the species exists and l , the liquid phase.

Problems with Arrhenius Theory are two-fold:

(i) Theory requires bases to have an OH - group. However, we know that ammonia (whose structural formula is NH 3 ) does not contain the OH - group but is nonetheless a base.

(ii) Theory does not consider the role of the solvent water, H 2 O. These shortcomings are overcome by the Bronsted-Lowry Theory .

Bronsted-Lowry Theories on acids and bases:

Acid : An acid as any substance that can donate a proton to a base.

acid base conjugate Conjugate

base of HA acid of H 2 O

Base: A base is any substance that can accept a proton from an acid.

NH 3 + H 2 O -> NH 4 + + OH -

base acid conjugate acid conjugate base

We now recognize that NH 3 acts as a base (proton acceptor) because of its role as a hydrogen atom acceptor in the reaction and H 2 O acts as an acid (proton donor). Moreover, H 2 O is now included as a solvent in our consideration. The conjugate acid of NH 3 is NH 4 + while the conjugate base of water in the reaction is OH-. NH 4 + /NH 3 are referred to as conjugate acid/base pair .

In these two examples, water has acted as either an acid or a base, hence a unique solvent. This is one of the Hence it is called water is called an amphiprotic sol- vent. It undergoes self ionization in a process called (autoprotolysis) as shown below:

H 2 O + H 2 O ↔ H 3 O + + OH -

In the study of acid-base reactions, the hydrogen ion concentration is key; its value indicates the acidity or basicity of the solution. In pure water, only 1 water in 10 7 undergoes autoprotolysis. This implies that only a very small fraction of water molecules are ionized, hence the concentration of water, [H 2 O], remains virtually unchanged. Therefore, the equilibrium constant for the autoionization of water according to the immediate above equation is

K c = [H 3 O + ][OH - ]

And because we use H + (aq) and H 3 O + (aq) interchangeably to represent the hydrated proton, the equilibrium constant can also be expressed as

K c = [H + ][OH - ]

To indicate that the equilibrium constant refers to the autoionization of water, we replace K c by K w

K w = [H 3 O + ][OH - ] = [H + ][OH - ]

Where is the ion-product constant , which is the product of the molar concentra- tions of H + and OH - ions at a particular temperature.

In pure water at 25 o C, the concentrations of H + and OH - ions are equal and found to be [H + ] = 1.0 x 10 -7 M and [OH - ] = 1.0 x 10 -7 M. From the above equation

K w = (1.0 x 10 -7 M) (1.0 x 10 -7 M) = 1.0 x 10 -14

Note that, whether we have pure water or an aqueous solution of dissolved species, the following relation always holds at 25oC:

K w = [H + ][OH - ] = 1.0 x 10 -14

Whenever [H + ] = [OH - ], the aqueous solution is said to be neutral. In an acidic solution, there is an excess of H+ ions and [H + ] > [OH - ]. In a basic solution, there is an excess of hydroxide ions, so [H + ] < [OH - ]. In practice, we can change the concentration of either H + or OH - ions in solution, but we cannot vary both of them independently. If we adjust the solution so that [H + ] = 1.0 x 10 -6 M, the OH - concentration must change to

\[ \left[ \mathrm { OH } ^ { - } \right] = \frac { \mathrm { K } _ { \mathrm { w } } } { \left[ \mathrm { H } ^ { + } \right] } = \frac { 1.0 \times 10 ^ { - 14 } } { 1.0 \times 10 ^ { - 6 } } = 1.0 \times 10 ^ { - 8 } \mathrm { M } \nonumber\]

Example \(\PageIndex{3}\):

Calculate the concentration of H+ ions in a certain cleaning solution if the concentration of OH- ions is 0.0025 M.

We are given the concentration of the OH - ions and asked to calculate [H + ]. We also know that K w = [H + ][OH - ] = 1.0 x 10 -14 . Hence, by rearranging the equation,

\[ \left[ \mathrm { H } ^ { + } \right] = \frac { \mathrm { K } _ { w } } { \left[ \mathrm { OH } ^ { - } \right] } = \frac { 1.0 \times 10 ^ { - 14 } } { 0.0025 } = 4.0 \times 10 ^ { - 12 } \mathrm { M } \nonumber\]

Exercise \(\PageIndex{2}\)

Cacultate the concentration OH - ions in HCl solution whose hydrogen ion concentration is 1.4 x 10 -3 M.

pH as a measure of acidity:

The pH of a solution is defined as the negative logarithm of the hydrogen ionconcentration (in mol/L).

\[ \mathrm { pH } = - \log \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] \text { or } \mathrm { pH } = - \log \left[ \mathrm { H } ^ { + } \right] \]

Note that because pH is simply a way of expressing hydrogen ion concentration, acidic and basic solutions at 25 o C can be distinguished by their pH values, as follows:

Acidic solutions: [H + ] > 1.0 x 10 -7 M, pH < 7.00

Basic solutions: [H + ] < 1.0 x 10 -7 M, pH > 7.00

Neutral solutions: [H + ] = 1.0 x 10 -7 M, pH = 7.00

Note that pH increases as [H + ] decreases.

Now, taking the negative logarithm of both sides of the expression [H + ][OH - ] = 1.0 x 10 -14

yields the expression,

-log ([H + ][OH-]) = -log (1.0 x 10 -14 )

-(log ([H + ]) + log ([OH - ]) = -log (1.0 x 10 -14 )

-log ([H + ]) - log ([OH - ]) = 14.00

From the definitions of pH and pOH we obtainpH + pOH = 14.00

This expression provides us with another way of showing the relationship between the H + ion concentration and the OH - ion concentration.

Example \(\PageIndex{4}\):

The pH of a rain water sample collected in the Western Province of Kenya on a particular day was found to be 4.82. Calculate the H + ion concentra- tion of the rain water.

We know that pH = -log [H + ] = 4.82

Therefore, log [H + ] = -4.82

This implies that [H + ] = antilog (-4.82)

Therefore, [H + ] = 10 -4.82 = 1.5 x 10 -5 M.

Exercise \(\PageIndex{3}\)

If the pH of a mixture of orange and passion juice is 3.30, calculate the H+ ion concentration.

Exercise \(\PageIndex{4}\)

Calculate the hydrogen ion concentration in mol/L for solutions with the following pH values: (a) 2.42, (b) 11.21, (c) 6.96, (d) 15.00

Base/Acid Ionization Constant:

In the reaction below,

NH 3 + H 2 O ⇌ NH 4 + + OH -

base acid conjugate conjugate

we can write the following equilibrium expression, called the base ionization constant, K b .

\[ \mathrm { K } _ { \mathrm { b } } = \frac { \left[ \mathrm { NH } _ { 4 } ^ { + } \right] \left[ \mathrm { OH } ^ { - } \right] } { \left[ \mathrm { NH } _ { 3 } \right] } = 1.8 \times 10 ^ { - 5 } \nonumber\]

Note that water does not explicitly appear in the equilibrium expression because the reaction is taking place in water (water being the solvent). It is important to note that the larger the K b , the stronger the base. Since NH 3 is a known weak base, there will be a reasonable amount of unreacted NH 3 in solution when equilibrium is established. Hence the low value of its K b .

Strength of Acids and Bases

Strong acids are assumed to ionize completely in water. Examples of strong acids are hydrochloric acid (HCl), nitric acid (HNO3), perchloric acid (HClO4) and sulphuric acid (H2SO4). Most acids are weak acids , which ionize only to a limited extent in water .

Strong bases ionize completely in water. Examples of strong bases are Hydroxi- des of alkali metals (e.g., NaOH, KOH, etc).

Dissociation of Weak acids and Bases:

Weak Acids: If HA is a weak acid, then

HA + H 2 O ↔ H 3 O + + A -

\[ \mathrm { K } _ { \mathrm { A } } = \frac { \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] } \]

If B is a weak base, then

B + H 2 O ↔ BH + + OH -

\[ \mathrm { K } _ { \mathrm { B } } = \frac { \left[ \mathrm { OH } ^ { - } \right] \left[ \mathrm { BH } ^ { + } \right] } { [ \mathrm { B } ] } \]

Note that water is not included in both expressions because it is a constant.

Example \(\PageIndex{5}\):

Determine the pH of a 0.10 M acetic acid solution, if the acid disso- ciation constant, K is 2.24 x 10-5.

We need to know that acetic acid is a weak acid which will only ionize to a limited extent. This can be represented by the equilibrium reaction below:

HAc + H 2 O ↔ H 3 O + + Ac -

\[ \mathrm { K } _ { \mathrm { A } } = \frac { \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] } \nonumber\]

Since both a H 3 O + and a A - is produced for each HA that dissociates:

[H 3 O + ] = [A - ]

[ HA ] = 0.10 M –[H 3 O + ]

Suppose y = [H 3 O + ], then

K A = 2.24 x 10 -5 = y 2 / (0.10-y) A

Rearranging yields a quadratic equation of the form: y 2 + 2.24 x 10 -5 y – 2.24 x 10 -6 = 0

Note that this quadratic equation can be solved

using $$ y = \frac { - b \pm \sqrt { \left( b ^ { 2 } - 4 a c \right) } } { 2 a } \nonumber\]

or the solution can be estimated by assuming that the amount of acid dissociated is insignificant when compared with the undissociated form ( HAc ).

Let us try the exact solution using

y = [-2.24 x 10 -5 + {(2.24 x 10 -5 ) 2 – (4 x 2.24 x 10 -6 )} 1/2 ]/2

y = 0.00149

Therefore, pH = -log (0.00149) = 2.82

Exercise \(\PageIndex{5}\)

The K a for benzoic acid is 6.5 x 10 -5 . Calculate the pH of a 0.10 M benzoic acid solution.

Exercise \(\PageIndex{6}\)

The pH of an acid solution is 6.20. Calculate the K a for the acid. The initial acid concentration is 0.010 M.

Dissociation of Weak bases:

The calculations are essentially the same as for weak acids. The important ex- pression to remember is:

pH + pOH = pK w = 14.00

Also, it can be shown that p K A + p K B = 14.00, where p K A = -log ( K A ) Note the following:

• If you are starting with an acid, acidic conditions or the conjugate acid of a base, then perform your calculations using K A .
• If starting with a base, basic conditions or the conjugate base of an acid, then do your calculations using K B .
• You can readily convert pH to pOH (i.e., pH + pOH = 14.00) and K A to K B (i.e., p K A + p K B = 14.00) values.

Fundamentals of Volumetric Analysis

Volumetric or titrimetric analyses are quantitative analytical techniques which employ a titration in comparing an unknown with a standard. In a titration , a measured and controlled volume of a standardized solution , a solution containing a known concentration of reactant «A» from a buret is added incrementally to a sample solution of known volume (measured by a pipete) containing a substance to be determined ( analyte ) of unknown concentration of reactant «B». Th titration proceeds until reactant «B» is just consumed ( stoichiometric completion ). This is known as the equivalence point . (The titration is complete when sufficienttitrant has been added to react with all the analyte.) At this point the number of equivalents of «A» added to the unknown equals the number of equivalents of «B» originally present in the unknown.

An indicator , a substance that have distinctly different colours in acidic and basic media , is usually added to the reaction flask to signal when and if all the analytehas reacted. The use of indicators enables the end point to be observed. In this, the titrant reacts with a second chemical, the indicator , after completely reacting with the analyte in solution. The indicator undergoes a change that can be detected (like colour). The titrant volume required for the detection of the equivalence point is called the end point . Note that the end point and equivalence point are seldomly the same. Ideally, we want the equivalence point and the end point to be the same. This seldom happens due to the methods used to observe end points. As a result, we get a titration error , the difference between the end point and the equivalence point , which leads to overtitration .

The end point is then the point where sufficient indicator has been converted fordetection. The sequence of events can be demonstrated as below:

followed by

The last step does NOT require that all indicator be converted. Infact, it is best if a very small percent need to be reacted to make the colour change visible.

For volumetric methods of analysis to be useful, the reaction must reach 99%+ completion in a short period of time. In almost all cases, a burette is used to measure out the titrant . When a titrant reacts directly with an analyte (or with a reaction the product of the analyte and some intermediate compound), the procedure is termed a direct titration . The alternative technique is called a back titration . Here, an intermediate reactant is added in excess of that required to exhaust the analyte , then the exact degree of excess is determined by subsequent titration of the unreacted intermediate with the titrant. Regardless of the type of titration, an indicator is always used to detect the equivalence point . Most com- mon are the internal indicators , compounds added to the reacting solutions that undergo an abrupt change in a physical property (usually absorbance or color) at or near the equivalence point . Sometimes the analyte or titrant will serve this function (auto indicating). External indicators , electrochemical devices such as pH meters, may also be used. Ideally, titrations should be stopped precisely at the equivalence point . However, the ever-present random and systematic error, often results in a titration endpoint , the point at which a titration is stopped , that is not quite the same as the equivalence point . Fortunately, the systematic error, or bias may be estimated by conducting a blank titration . In many cases the titrantis not available in a stable form of well-defined composition. If this is true, thetitrant must be standardized (usually by volumetric analysis) against a compound that is available in a stable, highly pure form (i.e., a primary standard).

Note that by accurately measuring the volume of the titrant that is added (using a buret), the amount of the sample can be determined.

For a successful titrimetric analysis, the following need to be true:

• The titrant should either be a standard or should be standardized.
• The reaction should proceed to a stable and well defined equivalence point.
• The equivalence point must be able to be detected.
• The titrant’s and sample’s volume or mass must be accurately known.
• The reaction must proceed by a definite chemistry. There should be nocomplicating side reactions.
• The reaction should be nearly complete at the equivalence point. In other words, chemical equilibrium should favour the formation of products.
• The reaction rate should be fast enough to be practical.

Illustration: In the determination of chloride, 50 ml of a 0.1M AgNO 3 solution would be required to completely react with 0.005 moles of chloride present in solution.

Balanced Equation for the reaction: Ag + (aq) + Cl - (aq) → AgCl(s). Here, 1 mole of Ag + ions reacts stoichiometrically with 1 mole of Cl - ions. Therefore 50 ml (0.05L) of a standard 0.10M AgNO 3 which contains 0.005 moles (= 0.10 moles L-1 x 0.050 L) requires an equivalent number of moles of Cl - ions.

Since the titrant solution must be of known composition and concentration, we ideally would like to start with a primary standard material , a high purity compound used to prepare the standard solution or to standardize the solution with. A standard solution is one whose concentration is known. The concentration of a standard solution is usually expressed in molarity (mole/liter). The process by which the concentration of a solution is determined is called standardization . Because of the availability of some substances known as primary standards , in many instances the standardization of a solution is not necessary. Primary standard solutions are analytically pure, and by dissolving a known amount of aprimary standard in a suitable medium and diluting to a definite volume, a solutionof known concentration is readily prepared. Most standard solutions, however, are prepared from materials that are not analytically pure and they have to be standardized against a suitable primary standard.

The following are the desired requirements of a primary standard :

• High purity
• Stable in air and solution: composition should be unaltered in the air at ordinary or moderately hgh temperatures.
• Not hygroscopic.
• Inexpensive
• Large formula weight: equivalence weight ought to be high in order to reduce the effects of small weighing error.
• Readily soluble in the solvent under the given conditions of the analy- sis.
• On titration, no interfering product(s) should be present.
• The primary standard should be colorless before and after titration to avoid interference with indicators.
• Reacts rapidly and stoichiometrically with the analyte.

The following are also the desired requirements of a primary standard solution :

• Have long term stability in solvent.
• React rapidly with the analyte.
• React completely with analyte.
• Be selective to the analyte.

The most commonly used primary standards are:

A. Acidimetric standards.

Sodium carbonate (Na 2 Co 3 , equivalent weight 53.00) and Borax (Na 2 B 4 O 7 .10H 2 O, equivalent weight 63.02)

B. Alkalimetric standards.

Sulphamic acid (NH 2 SO 3 H, equivalent weight 97.098),

Potassium hydrogenphthalate (KHC 8 H 2 O 4 , equivalent weight 204.22)

Oxalic acid (H 2 C 2 O 4 .2H 2 O, Equivalent weight 63.02)

This is a second material used As a substitute for a suitable primary standard , a secondary standard are often used as a second material. However, the standard solution should always be standardized using a primary standard.

Exercise \(\PageIndex{7}\)

Discuss the following analytical terms: Standard solution; Primary standards; Standardized solution; Standardization; End point of titration; Equi- valence point of titration; and Titration error

The basic requirements or components of a volumetric method are:

• A standard solution (i.e., titrant) of known concentration which reacts with the analyte in a known and repeatable stoichiometry (i.e., acid/base, precipitation, redox, complexation).
• A device to measure the mass or volume of sample (e.g., pipet, graduatedcylinder, volumetric flask, analytical balance).
• A device to measure the volume of the titrant added (i.e., buret).
• If the titrant-analyte reaction is not sufficiently specific, a pretreatment toremove interferents.
• A means by which the endpoint can be determined. This may be an in- ternal indicator (e.g., phenolphthalein) or an external indicator (e.g., pH meter).

Apparatus for titrimetric analysis:

The most common apparatus used in volumetric determinations are the pipette,buret, measuring cylinder, volumetric and conical (titration) flask. Reliablemeasurements of volume is often done with the help of a pipet, buret, and a vo-lumetric flask. The conical flask is preferred for titration because it has a good“mouth” that minimizes the loss of the titrant during titration.

Classification of reactions in volumetric (titrimetric) analysis

Any type of chemical reactions in solution should theoretically be used for ti- trimetric analysis. However, the reactions most often used fall under two main categories:

(a) Those in which no change in oxidation state occurs. These are dependent on combination of ions.

(b) Oxidation-reduction reactions: These involve a change of oxidation state (i.e., the transfer of electrons).

For convenience, however, these two types of reactions are further divided into four main classes:

(i) Neutralization reactions or acidimetry and alkalimetry: HA+B⇌HB+ +A-

(ii) Precipitation reactions: M(aq) +nL(aq) ⇌ ML n (s)

(iii) Oxidation-reduction reactions: Ox + Red ⇌ Red' + ox'

(iv) Complex ion formation reactions: M(aq) +nL(aq) ⇌ ML n (aq)

In this unit, we shall focus on neutralization reactions. The latter two will be dealt with in the next two units that follow in this module.

General Theory of Titrations

In determining what happens during a titration process, some of the theories of chemical equilibria (previously covered in this unit as well as in an earlier Module entitled General Chemistry) are often used. To fully understand what happens during a titration experiment enables one to set up a titration and choose an indicator wisely.

Consider a hypothetical titration reaction illustrated as follows:

T+A→P x +P y where T is the titrant (considered as the standard), A is the titrand (considered as the

unknown analyte whose concentration is desired), and P x and P y are products. Note that the extent of the above hypothetical reaction is determined by the magnitude of the equilibrium constant,

\[ \mathrm { K } _ { \mathrm { eq } } = \frac { \left[ \mathrm { P } _ { x } \right] \left[ \mathrm { P } _ { y } \right] } { [ \mathrm { T } ] [ \mathrm { A } ] } \]

Suppose C t is the concentration of the titrant which must be known (in the buret) and C A is the concentration of the unknown analyte A in the titration flask before any titrant is added. For the purposes of our illustrations here, we shall assume that both C t and C A are known.

In order to understand what is occuring in a titration flask, we shall consider asingle step titration to comprise of four (4) distinct regions described as below:

• Region 1 –Initial Stage ( i.e., before the addition of any titrant): Here , a pure solution of analyte, A is placed in a titration flask before any volume of reagent is added. At this point there is no titrant, T introduced in the flask, no products P x or P y formed yet and [A] in the titration flask is a function of C A .
• Region 2 –Before equivalence point (i.e., a fter addition of the titrant but before the equivalence point ): Here, the volume of reagent added to analyte is not sufficient to make the reaction complete (when there is excess of analyte). Thus, in this region T becomes the limiting reagent,and hence there will be very little T in solution (in fact [T] in the flask could be zero if the reaction went totally to completion). Therefore, only A, P x and P y would be present in measurable quantities.
• Region 3 –At equivalence point: In this region, the reagent added is the amount that is chemically equivalent to the amount of substance being determined (analyte). The equivalence point is defined as the point at which there would be neither T nor A present if the reaction went to completion. In reality though, there is often very little of either T or A present and there exists a very simple relationship between [T] and [A]. As is expected, only P x and P y would be present in measurable amounts.
• Region 4 –After equivalence point : Here, the amount of reagent added is higher than the amount of substance being determined. In this region, A now becomes the limiting reagent, and therefore there will be very little A (if any, depending on whether the reaction went totally to completion, in which case [A] = 0) in solution. Only T, P x , and P y are present in measurable amounts in the titration flask.

In view of the aforementioned, it is clear that the method for determining what is trully present in a titration flask during a titration depends on the region under consideration. To demonstrate what happens and how the concentrations of all substances present varies during a titration process, acid/base titrations will be used as examples of titrations in general. The types of acid/base titrations that will be considered in this unit are:

A) Titration of strong acid with strong base

B) Titration of weak acid with strong base

C) Titration of weak base with strong acid

D) Titration of polyprotic weak acids with strong base

Note that the behaviour in each of the stages mentioned above is a function of the type of acid-base titration process. This behaviour is best depicted or described by making plots of pH as a function of the volume of base added. This plot is known as a titration curve .

Let us now examine each of the types of acid/base titrations mentioned above.

Titration of a Strong acid with a Strong Base

The reaction between HCl (considered here as the unknown) and NaOH (the titrant) will be used as an example. As discussed earlier, strong acids are 100% dissociated in water (i.e., H + Cl − +H 2 O→H 3 O + +Cl - ) and strong bases are 100%hydrolysed (i.e., Na + OH − +H 2 O→H 2 O+OH - +Na + ).​​​​​​ The reaction therefore between HCl and NaOH can be expressed as:

H 3 O + +OH - →2H 2 O

Here, Na + and Cl - are spectator ions and do not enter into the titration reaction. In this reaction, Cl - is neither added to the flask nor is it consumed in the reaction in the course of the titration process. Thus the number of moles of Cl - remains constant while its concentration decreases due dilution. (Remember that the volume of solution in the flask is increasing as titration progresses and this dilution process has an effect on the concentrations.)

If C t is the concentration of the titrant in the buret and whose value is a fixed; C A is the concentration of the unknown analyte, A in the flask before the titration and is also a fixed value; V t is the volume of the titrant added to the titration flask;and V A is the volume of the unknown analyte placed initially in the titration flask,then the concentration of Cl - , [Cl - ] which does not depend on the region of the titration is given by

\[ \left[ \left. C \right| ^ { - } \right] = \frac { \text { mol } } { \text { Volume } } = \frac { C _ { A } V _ { A } } { \left( V _ { A } + V _ { t } \right) } \text { and } p C l = - \log [ C l ] \nonumber\]

Na + is continuously being added to the titration flask in the course of the titration process but is not reacting. Hence, the concentration of Na + , [Na + ] will continuously increase and its concentration will not depend on the region of the titration and is given as

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { \mathrm { mol } } { \text { Volume } } = \frac {\mathrm{C}_{t} \mathrm { V } _ { \mathrm { t } } } { \left( \mathrm { V } _ { \mathrm { A } } + \mathrm { V } _ { \mathrm { t } } \right) } \text { and pNa } = - \log \left[ \mathrm { Na } ^ { + } \right] \nonumber\]

Since the species H 3 O + and OH - are involved in the titration reaction, the calculations of [H 3 O + ] and [OH - ] in the titration flask will now depend on the titration region. This is now examined below.

Suppose C a is the concentration of the strong acid that is present in the flask at any point during the titration process, and C b is the concentration of the strong base actually present in the titration flask at any point in the titration. Note that these values will always be different from C t and C A .

Let us now examine what happens to the concentrations of [H 3 O + ] and [OH - ] in each of the titration regions discussed above.

Region 1: This is simple a solution of the strong acid present in the titration flask.

\[ \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = \mathbf { C } _ { \mathrm { A } } \text { and } \mathrm { pH } = - \log \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] \text { and } \mathrm { pOH } = 14.00 - \mathrm { pH } \]

Region 2: As titrant (strong base) is added, some of the strong acid get consu- med, but no strong base is yet present. Thus, only the strong acid affects theoverall pH of the solution in the titration flask.

\[\ Moles of acid remaining = (moles of original acid – moles of base added)\]

\[\bf{C}_a={(moles\ of\ acid\ remaining)\over(total\ resultant\ volume)}={(\bf{V}_a\bf{C}_a-\bf{V}_t\bf{C}_t)\over(\bf{V}_a+\bf{V}_t)}\]

\[[H^+]=\bf{C}_a={(\bf{V}_a\bf{C}_A-\bf{V}_t\bf{C}_t)\over(\bf{V}_a+{V}_t)}\ if\ \bf{C}_a>>2\bf{K}_w^{1/2}\]

Region 3: In this region, there is neither strong acid nor strong base present inthe titration flask. The solution simply contains the salt, NaCl, the product of theacid-base reaction. Since neither Na+ nor Cl- affect pH of the solution mixture, the pH will be that of pure water.

\[ [ \mathrm { H } + ] = \left( K _ { W } \right) ^ { 1 / 2 } \text { or } \mathrm { pH } = 7.00 \]

Region 4: In this region, all the strong acid is now exhausted and there is excess strong base present. Therefore, the pH of the soultion mixture is determined by the excess strong base present.

Moles of base present = (total moles of base added so far – moles of original acidpresent in flask at beginning of titration)

\[Moles\ of\ base\ present={(total\ moles\ of\ base\ added\ so\ far\ -\ moles\ of\ original\ acid\ present\ in\ flask\ at\ beginning\ of\ titration)}\]

\[\bf{C}_a={(moles\ of\ base\ present)\over(total\ resultant\ volume)}={(\bf{V}_t\bf{C}_t-\bf{V}_A\bf{C}_A)\over(\bf{V}_a+\bf{V}_t)}\]

\[[OH^-]=\bf{C}_b={(\bf{V}_t\bf{C}_t-\bf{V}_a\bf{C}_A)\over(\bf{V}_a+{V}_t)}\ if\ \bf{C}_a>>2\bf{K}_w^{1/2}\]

\[[\bf{H}_3O^+]={\bf{K}_w\over[OH^-]}\]

Example \(\PageIndex{6}\):

Consider titration of 100.0 mL of 0.100 mol/L HCl solution with 0.100 mol/L standard NaOH solution.

Region 1: Before addition of any titrant. The 100.0 mL solution contains a strong HCl acid and the total volume is 100 mL (0.100 L).

[Na + ] = 0.0 mol/L

\[ [ \mathrm { Cl } ^-] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol }/ \mathrm { L } ) } { ( 0.100 \mathrm { L } ) } = 0.100 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = \mathbf { C } _ { \mathrm { A } } = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.100 \mathrm { L } ) } = 0.100 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ [ \mathrm { OH } ^-] = \frac { 1.00 \times 10 ^ { - 14 } } { ( 0.100 ) } = 1.00 \times 10 ^ { - 13 } \mathrm { mol } / \mathrm { L } \nonumber\]

Region 2: After addition of, say 50.00 mL of NaOH. The solution still contains a strong acid and the total volume is 150.0 mL.

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.0500 \mathrm { L } ) ( 0.100 \mathrm { mol } /\mathrm { L } ) } { ( 0.1500 \mathrm { L } ) } = 0.0333 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ [ \mathrm { Cl }^- ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.1500 \mathrm { L } ) } = 0.0667 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ { \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = } { \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.0500 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1500 \mathrm { L } ) } = 0.0333 \mathrm { mol } / \mathrm { L } } \nonumber\]

\[[ \mathrm { OH ^-} ] = \frac { 1.00 \times 10 ^ { - 14 } } { ( 0.0333 ) } = 3.00 \times 10 ^ { - 13 } \mathrm { mol } / \mathrm { L }\nonumber\]

Region 3: After addition of, say 99.00 mL of NaOH. The solution contains very little of the strong acid and the total volume is 199.0 mL.

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.0990 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.1990 \mathrm { L } ) } = 0.0498 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ [ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1990 \mathrm { L } ) } = 0.0502 \mathrm { mol } / \mathrm { L } \nonumber$$ $$ { \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = } { \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.0990 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1990 \mathrm { L } ) } = 5.03 \times 10 ^ { - 4 } \mathrm { mol } / \mathrm { L } } \nonumber\]

\[ [ \mathrm { OH^- } ] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 5.03 \times 10 ^ { - 4 } \right) } = 1.99 \times 10 ^ { - 11 } \mathrm { mol } / \mathrm { L } \nonumber\]

Region 3 Continued: After addition of, say 99.90 mL of NaOH. The solution contains further reduced strong acid and the total volume is 199.90 mL.

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.0999 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.199 \mathrm { L } ) } = 0.04998 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ [ \mathrm { Cl ^-} ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1999 \mathrm { L } ) } = 0.05003 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ { \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = } { \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.0999 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1999 \mathrm { L } ) } = 5.00 \times 10 ^ { - 5 } \mathrm { mol } / \mathrm { L } } \nonumber\]

\[ [ \mathrm { OH^- } ] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 5.00 \times 10 ^ { - 5 } \right) } = 1.999 \times 10 ^ { - 10 } \mathrm { mol } / \mathrm { L } \nonumber\]

Region 3 Continued: After addition of, say 99.99 mL of NaOH. The solution contains even further reduced strong acid and the total volume is 199.90 mL.

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.09999 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.19999 \mathrm { L } ) } = 0.049998 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ [ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.1999 \mathrm { L } ) } = 0.050003 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ { \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = } { \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) - ( 0.09999 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1999 \mathrm { L } ) } = 5.00 \times 10 ^ { - 6 } \mathrm { mol/ } \mathrm { L } } \nonumber\]

\[ [ \mathrm { OH^- } ] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 5.00 \times 10 ^ { - 6 } \right) } = 2.00 \times 10 ^ { - 9 } \mathrm { mol } / \mathrm { L } \nonumber\]

Region 3 Continued: After addition of 100.00 mL of NaOH. The solution contains neither a strong acid nor a strong base and the total volume is 200.00 mL

\[ { \left[ \mathrm { Na } ^ { + } \right] = \left[ \mathrm { Cl } ^ { - } \right] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.200 \mathrm { L } ) } = 0.0500 \mathrm { mol } / \mathrm { L } } \\ { \left[ \mathrm { H } ^ { + } \right] = \left[ \mathrm { OH } ^ { - } \right] = 1.00 \mathrm { x } 10 ^ { - 7 } \mathrm { mol } / \mathrm { L } } \nonumber\]

Region 4: After addition of, say 100.01 mL of NaOH. The solution contains a little strong base and the total volume is 200.01 mL.

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.10001 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.20001 \mathrm { L } ) } = 0.050022 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ [ \mathrm { Cl ^-} ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.20001 \mathrm { L } ) } = 0.0499975 \mathrm { mol/L } \nonumber\]

\[ { [ \mathrm { OH^- } ] = \mathbf { C } _ { \mathrm { b } } = } { \frac { ( 0.10001 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) - ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.20001 \mathrm { L } ) } = 4.99975 \times 10 ^ { 6 } \mathrm { mol } / \mathrm { L } } \nonumber\]

\[ \left[ \mathrm { H } ^ {+} \right] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 4.99975 \times 10 ^ { - 6 } \right) } = 2.00 \times 10 ^ { - 9 } \mathrm { mol } / \mathrm { L } \nonumber\]

Region 4 Continued: After addition of 100.10 mL of NaOH. The solution contains a little strong base and the total volume is 200.10 mL.

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.1001 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.2001 \mathrm { L } ) } = 0.050025 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ [ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.2001 \mathrm { L } ) } = 0.049975 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ { [ \mathrm { OH^- } ] = \mathrm { C } _ { \mathrm { b } } = } { \frac { ( 0.1001 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.2001 \mathrm { L } ) } = 4.9975 \times 10 ^ { 5 } \mathrm { mol } / \mathrm { L } } \nonumber\]

\[ \left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 4.9975 \times 10 ^ { - 5 } \right) } = 2.001 \times 10 ^ { - 10 } \mathrm { mol } / \mathrm { L } \nonumber\]

Region 4 Continued: After addition of 110.00 mL of NaOH. The solution contains more strong base and the total volume is 210.00 mL.

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.110 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.210 \mathrm { L } ) } = 0.05238 \mathrm { mol/L } \nonumber\]

\[ [ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.210 \mathrm { L } ) } = 0.04762 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ { [ \mathrm { OH^- } ] = \mathbf { C } _ { \mathrm { b } } = } { \frac { ( 0.110 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.210 \mathrm { L } ) } = 4.762 \times 10 ^ { - 3 } \mathrm { mol } / \mathrm { L } } \nonumber\]

\[ \left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 4.762 \times 10 ^ { - 3 } \right) } = 2.1 \times 10 ^ { - 12 } \mathrm { mol } / \mathrm { L } \nonumber\]

Region 4 Continued: After addition of 150.00 mL of NaOH. The solution contains more strong base and the total volume is 250.00 mL.

\[ \left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.150 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.250 \mathrm { L } ) } = 0.06 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ [ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.250 \mathrm { L } ) } = 0.04 \mathrm { mol } / \mathrm { L } \nonumber\]

\[ { [ \mathrm { OH^- } ] = \mathrm { C } _ { \mathrm { b } } = } { \frac { ( 0.150 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.250 \mathrm { L } ) } = 0.02 \mathrm { mol } / \mathrm { L } } \nonumber\]

\[ \left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { ( 0.02 ) } = 5.0 \times 10 ^ { - 13 } \mathrm { mol } / \mathrm { L } \nonumber\]

The result of a series of such calculations can now be ploted as a graph of pH versus volume of NaOH to generate what is referred to as a titration curve . In such a plot, it becomes evident that the concentrations of the reactants, but not the products or the spectator ions, go through a large change exactly at the equivalence point. It is this change that allows one to pinpoint the equivalence point. The equivalence point can therefore be determined, say in this case, by monitoring either the concentration of OH - or H + ions.

A typical titration curve for a strong acid versus a strong base is given in the figurebelow. (We’ll take hydrochloric acid and sodium hydroxide as typical of a strongacid and a strong base; i.e., NaOH (aq) + HCl (aq) → NaCl (aq) + H2O (l) ).

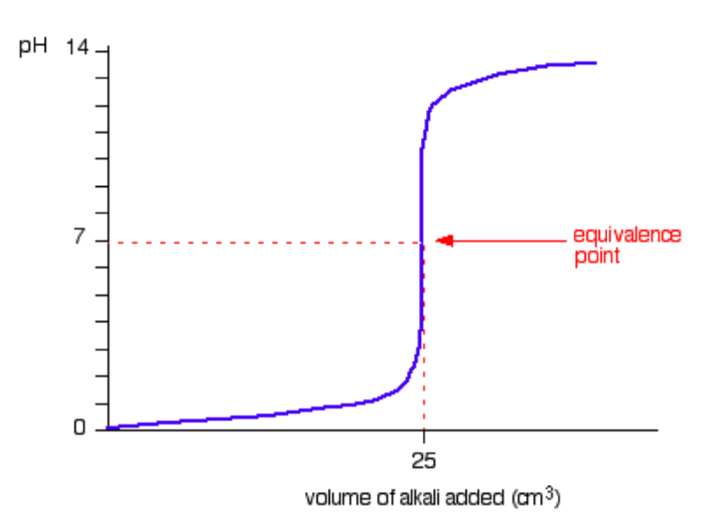
It is clear from this figure that the pH only rises a very small amount until quitenear the equivalence point. Then there is a really steep rise.

In order for you to appreciate the generation of a titration curve from such calcu- lations as above, you are encouraged to do the exercise problem below.

Exercise: Using the above calculations, plot the corresponding titration curve for the titration of 100.00 mL of 0.10 mol/L HCL solution with 0.10 mol/L standard NaOH solution.

Let us now consider the case of titration of a weak acid with a strong base and see how it compares with that of a strong acid with a strong base dealt with above.

Titration of a Weak acid with a Strong Base

At first glance, it might seem that weak acid/strong base titrations are just like the strong acid/strong base titration encountered in the preceding section. However, there is a significant difference that makes this case more complicated. Whereas the product of the titration reaction and the spectator ions in a strong acid/strong base titration (such as H 2 O, Na + , and Cl - ) do not affect the pH of the solution in the titration flask and can thus be neglected, the same cannot be said of the weak acid/strong base titration. In fact, when a weak acid is titrated with a strong base, one of the products is a weak base which does affect the pH in all the regions discussed above except Region 1, and this must be taken into consideration.

The titration reaction involving a weak acid (HA) with a strong base such as NaOH is often expressed as:

\[ \mathrm { HA } + \mathrm { NaOH } \rightarrow \mathrm { NaA } + \mathrm { H } _ { 2 } \mathrm { O } \nonumber\]

which can be more accurately represented as:

\[ \mathrm { HA } + \mathrm { OH } ^ { - } \rightarrow \mathrm { A } ^ { - } + \mathrm { H } _ { 2 } \mathrm { O } \]

with a corresponding equilibrium constant expressed as:

\[ \mathrm { K } _ { \mathrm { eq } } = \frac { \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] \left[ \mathrm { OH } ^ { - } \right] } = \frac { 1 } { \mathrm { K } _ { \mathrm { b } } } = \frac { \mathrm { K } _ { a } } { \mathrm { K } _ { \mathrm { w } } } \]

Note that K eq for the titration of a weak acid with an K a of about 1.0 x 10 -5 will be only 1.0x10 9 (i.e., \(\ k_{eq}=\)\(\dfrac{1}{K_b}\)=\(\dfrac{K_a}{K_w}\)=\(\dfrac{K_a}{10^{-14}}\)) a value that is not as large as that for a strong acid. However, this is still considered large enough for the reaction to proceed to completion. In fact, as the value of K a of the weak acid decreases, so does the value of K eq for the titration. Therefore, if the acid is too weak, it cannot be easily titrated.

A typical titration curve for a weak acid versus a strong base is given in the figurebelow. (We’ll take ethanoic acid and sodium hydroxide as typical of a waek acidand a strong base; i.e., CH3COOH (aq) + NaOH (aq) → CH3COONa (aq) + H2O (l) ).

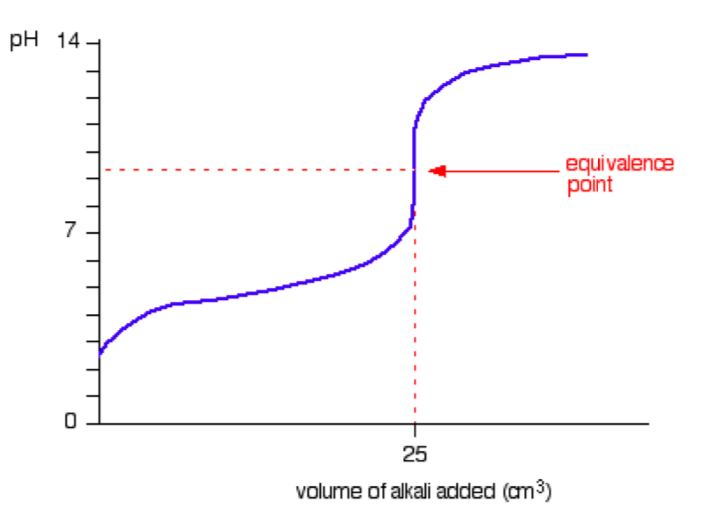
The start of the graph shows a relatively rapid rise in pH but this slows down as a buffer solution containing ethanoic acid and sodium ethanoate is produced. Beyond the equivalence point (when the sodium hydroxide is in excess) the curve is just the same as that end of the HCl-NaOH graph shown previously.

Let us now consider the four regions of the titration in the same manner as for the strong acid/strong base titration. Here again, we shall assume that the weak acid of concentration C A is the unknown and that the titrant of concentration C t , is a strong base.

Region 1: Prior to addition of any base, the solution in the titration flask basicallycontains only the weak acid, HA and that C a = C A . In order to calculate [H+], a weak acid equation need to be used. Thus

\[ \left[ \mathrm { H } ^ { + } \right] = \left( \mathrm { K } _ { \mathrm { a } } \mathrm { C } _ { \mathrm { A } } \right) ^ { \frac { 1 } { 2 } } , \mathrm { i.e. } , \mathrm { pH } = - \log \sqrt { \mathrm { K } _ { \mathrm { a } } \mathrm { C } _ { \mathrm { A } } } \]

Region 2: Upon addition of some titrant, the solution contains some unreacted acid, HA (since the acid is not 100% dissociated) and some conjugate base, A-, due to the titration reaction.

Therefore, moles of acid remaining = original moles of acid-moles of strong base added.

\[\bf{C}_a={(moles\ of\ acid\ remaining)\over Total volme}={\bf{V}_A\bf{C}_A-\bf{V}_t\bf{C}_t\over(\bf{V}_A+\bf{V}_t)}\]

Moles of weak base formed = moles of strong base added.

Therefore C B =V t C t \(V A +V t ), where C B is concentration of the weak base formed.

To calculate the [H + ], we need to use the simplified equation for a mixture of a weak acid and its conjugate base, i.e.,

\[ \left[ \mathrm { H } ^ { + } \right] = \frac { \mathrm { K } _ { a } \mathrm { C } _ { \mathrm { a } } } { \mathrm { C } _ { \mathrm { B } } } , \text { i.e., } \mathrm { pH } = \mathrm { pK } _ { \mathrm { a } } + \log \frac { \mathrm { C } _ { \mathrm { B } } } { \mathrm { C } _ { \mathrm { a } } } \]

Region 3: At the equivalence point, all the weak acid has been completely neu- tralized by the strong base and only the weak base remains. There is no excess strong base present. Since the solution contains a weak base, the pH of the solutionin the flask cannot be equal to 7.00 and must be greater than 7.00.

Moles of weak base present = moles of strong base added.

\[ C _ { B } = \frac { V _ { t } C _ { t } } { \left( V _ { A } + V _ { t } \right) } \]

[OH - ] can be calculated using the simplified weak base equation, i.e.,

\[ \left[ \mathrm { OH } ^ { - } \right] = \left( \mathrm { K } _ { \mathrm { b } } \mathrm { C } _ { \mathrm { B } } \right) ^ { \frac { 1 } { 2 } } \]

Region 4: After the equivalence point , both the weak base, A-, and excess strong base, OH-, will be present.

moles of weak base = moles of original weak acid

Concentration of weak base,

\[ \mathbf { C } _ { w } = \frac { V _ { A } C _ { A } } { \left( V _ { A } + V _ { t } \right) } \]

Moles of strong base present = moles of titrant added – moles of original weak acid

Thus, concentration of strong base,

\[ \mathbf { C } _ { \mathrm { s } } = \frac { \left( \mathrm { V } _ { \mathrm { t } } \mathrm { C } _ { \mathrm { t } } - \mathrm { V } _ { \mathrm { A } } \mathrm { C } _ { \mathrm { A } } \right) } { \left( \mathrm { V } _ { \mathrm { A } } + \mathrm { V } _ { \mathrm { t } } \right) } \]

The [OH - ] can be calculated by using an equation for a mixture of a weak base and a strong base, i.e.,

\[ \left[ \mathrm { OH } ^ { - } \right] = \mathrm { C } _ { \mathrm { s } } \]

Example \(\PageIndex{7}\):

Consider the titration of a 50.0 mL solution of weak acid of butanoic (p K a =4.98,i.e., K a =1.05x10 -5 )ofconcentration0.10mol/Lwitha0.10mol/L standard NaOH solution. For convenience, we shall calculate only the pH of thesolution mixture in the titration flask.

Region 1: Before addition of NaOH, C A = 0.10 mol/L.

\[ { \left[ \mathrm { H } ^ { + } \right] = \left( \mathrm { K } _ { \mathrm { a } } \mathrm { C } _ { \mathrm { A } } \right) ^ { \frac { 1 } { 2 } } = \left\{ \left( 1.05 \times 10 ^ { - 5 } \right) ( 0.10 ) \right\} ^ { \frac { 1 } { 2 } } = 1.02 \times 10 ^ { - 3 } \mathrm { mol } / \mathrm { L } } \\ { \left[ \mathrm { OH } ^ { - } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { 1.02 \times 10 ^ { - 3 } } = 9.77 \times 10 ^ { - 12 } \mathrm { mol } / \mathrm { L } } \nonumber\]

Region 2: After addition of, say, 20.0 mL of NaOH. Total volume in the titra-tion flask becomes 70.0 mL and the solution is a mixture of a weak acid and its conjugate base.

\[ { \mathrm { C } _ { a } = \frac { ( \text { moles of acid remaing } ) } { \text { Total volume } } = \frac { ( 0.050 \mathrm { L } ) ( 0.10 \mathrm { mol } / \mathrm { L } ) - ( 0.020 \mathrm { L } ) ( 0.10 \mathrm { mol } / \mathrm { L } ) } { ( 0.050 \mathrm { L } + 0.020 \mathrm { L } ) } = 0.0429 \mathrm { mol } / \mathrm { L } } \\ { \mathrm { C } _ { B } = \frac { ( 0.10 \mathrm { mol } / \mathrm { L } ) ( 0.020 \mathrm { L } ) } { 0.070 \mathrm { L } } = 0.0286 \mathrm { mol/L } \ \mathrm { C } \mathrm { B } } \nonumber\]

Using the simplified equation for a mixture of a weak acid and its conjugate baseto solve for [H + ] and therefore pH,

\[ \begin{aligned} \left[ H ^ { + } \right] = \frac { K _ { a } C _ { a } } { C _ { B } } & = \frac { \left( 1.05 \times 10 ^ { - 5 } \right) ( 0.0429 ) } { 0.0286 } = 1.57 \times 10 ^ { - 5 } \mathrm { mol } / \mathrm { L } \text { and } p H = - \log \left( 1.5 \times 10 ^ { - 5 } \right) = 4.80 \end{aligned} \nonumber\]

\[ \left[ \mathrm { OH } ^ { - } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { 1.57 \times 10 ^ { - 5 } } = 6.37 \times 10 ^ { - 10 } \mathrm { mol } / \mathrm { L } \nonumber\]

Region 3: After addition of, say, 50.0 mL of NaOH. Total volume in the titrationflask becomes 100.0 mL and the solution contains only a weak base.

\[ { C _ { B } = \frac { V _ { t } C _ { t } } { \left( V _ { A } + V _ { t } \right) } = \frac { ( 0.050 L ) ( 0.10 m o l / L ) } { 0.10 L } = 0.050 m o l / L } \\ { K _ { b } = \frac { 1.00 \times 10 ^ { - 14 } } { K_a } = 9.55 \times 10 ^ { - 10 } } \nonumber\]

With the simplified equation for a weak base

\[ { \left[ \mathrm { OH } ^ { - } \right] = \left( \mathrm { K } _ { \mathrm { b } } \mathrm { C } _ { \mathrm { B } } \right) ^ { \frac { 1 } { 2 } } = \left\{ \left( 9.55 \times 10 ^ { - 10 } \right) ( 0.050 ) \right\} ^ { \frac { 1 } { 2 } } = 6.91 \times 10 ^ { - 6 } \mathrm { mol } / \mathrm { L } } \\ { \left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { 6.91 \times 10 ^ { - 6 } } = 1.45 \times 10 ^ { - 9 } \mathrm { mol } / \mathrm { L } , \text { and } \mathrm { pH } = - \log \left( 1.45 \times 10 ^ { - 9 } \right) = } { 8.84 } \nonumber\]

Region 4: After addition of, say, 60.0 mL of NaOH. Total volume in the titrationflask becomes 110.0 mL and the solution contains both a weak base and a strong base.

\[ {C_w}=\frac { V _ { A } C _ { A } } { \left( V _ { A } + V _ { t } \right) } = \frac { ( 0.050 L ) ( 0.10 m o l / L ) } { 0.110 L } = 0.0455 \text { mol } / L \nonumber\]

Concentration of strong base,

\[ C_s=\frac { \left( \mathrm { V } _ { \mathrm { t } } \mathrm { C } _ { \mathrm { t } } - \mathrm { V } _ { \mathrm { A } } \mathrm { C } _ { \mathrm { A } } )\right. } { \left( \mathrm { V } _ { \mathrm { A } } + \mathrm { V } _ { \mathrm { t } } \right) } = \frac { \{ ( 0.060 \mathrm { L } ) ( 0.10 \mathrm { mol } / \mathrm { L } ) - ( 0.050 \mathrm { L } ) ( 0.10 \mathrm { mol } / \mathrm { L } ) \} } { 0.110 \mathrm { L } }=0.00909\ mol/L \nonumber\]

Using the simplified equation for a mixture of a strong and weak base,

\[ { [ \mathrm { OH } ] = \mathrm { C } _ { \mathrm { s } } = 0.00909 \mathrm { mol } / \mathrm { L } } \\ { \left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { 0.00909 } = 1.10 \times 10 ^{-12} \mathrm { mol } / \mathrm { L } , \text { and } \mathrm { pH } = - \log \left( 1.10 \times 10 ^{-12} \right) = 11.96 } \nonumber\]

Note that the complete titration curve can be plotted when a series of additional calculations similar to those above are carried out.

Exercise \(\PageIndex{8}\): Titration of weak acid with strong base.

Using the information pro- vided below, plot the titration curve for the titration of 100.00 mL of 0.10 mol/L CH3COOH solution with 0.10 mol/L standard NaOH solution. Hint: Consider the four titration stages given above.

Illustration

Calculating pH at Initial Stage:

Let n moles of HA (i.e., a monoprotic weak acid such as the CH3COOH) be available in a titration flask. The pH is dependent on extent of dissociation of the weak acid. If K a of the weak acid is very small (i.e., K a < 1.0 x 10 -4 ), then it is possible to calculate the pH from the dissociation of weak acid using the relation:

\[ \mathrm { pH } = - \log \left[ \sqrt { \mathrm { K } _ { \mathrm { a } } [ \mathrm { Acid } ] }\right. \]

Before equivalence point:

Again, let n moles of HA be available in titration flask. To this solution let m moles of NaOH be added. In this titration, “ Before Equivalence Point ” means n > m.

HA + NaOH → NaA + H2O

Start n m 0 0

Final n-m 0 m m

Question: What is left in the solution in the titration flask?

The solution left in the flask contains excess weak acid by an amount of (n-m) moles and salt of weak acid of an amount of equivalent to m moles. The solution is a buffer solution. Therefore, the pH of the solution can be calculated using the Henderson-Hasselbalch equation: $$ \mathrm{pH}=\mathrm{pKa}+\log\frac{[\mathrm{salt}]}{[\mathrm{Acid}]}=\mathrm { pK } _ { \mathrm { a } } + \log \frac { \frac { \mathrm { m } } { \left( \mathrm { V } _ { \text { Acid } } + \mathrm { V } _ { \text { base added } } \right) } } { \frac { ( \mathrm { n } - \mathrm { m } ) } { \left( \mathrm { V } _ { \text { Acid } } + \mathrm { V } _ { \text { base added } } \right) } } = \mathrm { pK } _ { \mathrm { a } } + \log \frac { \mathrm { m } } { ( \mathrm { n } - \mathrm { m } ) } \]

At equivalence point:

The acid is completely neutralized by the base added. Hence the pH is dependent on the salt solution. The resultant salt obtained is a salt of a weak acid and strong base. Therefore the anion part of the salt will hydrolyze as follows.

\[ \begin{array} { l } { \mathrm { NaA } \rightarrow \mathrm { Na } ^ { + } ( \mathrm { aq } ) + \mathrm { A } ^ { - } ( \mathrm { aq } ) } \\ { \mathrm { A } ^ { - } + \mathrm { H } _ { 2 } \mathrm { O } \Leftrightarrow \mathrm { HA } + \mathrm { OH } ^ { - } } \end{array} \]

\[ \mathrm{pH}=\frac{1}{2}\{(\mathrm {pK_w}+\mathrm{pK_a}-\mathrm {pC_{salt \ produced}})\}= \frac { 1 } { 2 } \left\{ \left( \mathrm { pK } _ { \mathrm { w } } + \mathrm { pK } _ { \mathrm { a } } + \log \left( \frac { \mathrm { m } } { \mathrm { V } _ { \text { arid } } + \mathrm { V } _ { \text { base } } } \right) \right\}\right. \]

After equivalence point:

The amount of strong base added is more than the amount required to neutralize the acid. Hence an excess amount of strong base will remain in solution. The pH can be calculated from the excess strong base left in the solution using the following equation.

\[ \mathrm { pH } = \mathrm { pK } _ { \mathrm { w } } + \log[\frac{\mathrm(C_{Base}V_{base\ added})-(C_{Acid}V_{acid})}{(V_{acid}+V_{base\ added})}] \]

Exercise \(\PageIndex{9}\): Titration of weak acid with strong base.

Plot a titration curve for titrating 75 mL of 0.12 mol/L CH3COOH with 0.09 mol/L NH 3 . K a for CH 3 COOH= 1.8 x 10 -5 and K b for NH 3 = 1.8 x 10 -5 . Hint: Consider the four titration stages discussed earlier.

Polyprotic Acids:

In our previous discussion of acid-base reactions, we dealt with acids (e.g., HCl, HNO 3 , and HCN) that contain only one ionizable hydrogen atom in each molecule. This group of acids that have only one ionizable hydrogen atom per molecule is known as monoprotic acid . The corresponding reactions of the monoprotic acids given above with a base like water are as follows:

HCl + H 2 O → H 3 O + + Cl -

HNO 3 + H 2 O → H 3 O + + NO 3 -

HCN + H 2 O ↔ H 3 O + + CN -

In general, however, acids can be classified by the number of protons present permolecule that can be given up in a reaction. For acids that can transfer more than one proton to a base, the term polyprotic acid is used. Diprotic acids contain two ionizable hydrogen atoms per molecule and their ionization occurs in two stages. Examples of diprotic acids include, H 2 SO 4 , H 2 S, H 2 CO 3 , etc. An illustration of the two-stage ionization of H 2 S is as follows:

H 2 S + H 2 O ⇌H 3 O + + HS - (primary ionization)

HS - + H 2 O ⇌ H 3 O + + S 2- (secondary ionization)

Each of the above steps is characterized by a different acid ionization constant.

The primary ionization step has an acid ionization constant,

\[ \mathrm { K } _ { 1 } = \frac { \left[ \mathrm { HS } ^ { - } \right] \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] } { \left[ \mathrm { H } _ { 2 } \mathrm { S } \right] } \]

whereas the secondary has an acid ionization constant,

\[ \mathrm { K } _ { 2 } = \frac { \left[ \mathrm { S } ^ { 2 - } \right] \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] } { \left[ \mathrm { HS } ^ { - } \right] } \]

If K 1 ≈ K 2 , the two steps occur simultaneously and both must be considered in solving any problems involving the pH of solutions of the acid. If however,

K 1 ≫ K 2 (by atleast a factor of 10 4 ), then only the one reaction involving the species present need be considered. This then makes one apply the simple monobasic equations that have been dealt with previously in unit 2.

Of the two steps above, the primary ionization always takes place to a greater extent than the secondary ionization.

The most common triprotic acid is phosphoric acid or sometimes called ortho-phosphoric acid (H 3 PO 4 ), which can ionize in solution in three steps as follows:

H 3 PO 4 + H 2 O ⇌H 3 O + + H 2 PO 4 - (primary ionization)

H 2 PO 4 - + H 2 O ⇌ H 3 O + + H 2 PO 4 2- (secondary ionization)

H 2 PO 4 2- + H 2 O ⇌ H 3 O + + H 2 PO 3- (tertiary ionization)

The corresponding experimentally determined acid ionization constants for phosphoricacid (H 3 PO 4 ) are: K 1 =7.5×10 -3 , K 2 =6.6×10 -6 , and K 3 =1.0×10 -12

Thus, a solution of phosphoric acid will usually comprise a mixture of three different acids; H 3 PO 4 , H 2 PO 4 - , and HPO 4 2- and their corresponding conjugate bases.

It is important to note that successive ionization constants for a given acid gene- rally have widely different values as can be seen in the case of phosphoric acid (i.e., K 1 >> K 2 >> K 3 ). Thus, as mentioned in the case of the diprotic acid above, no more than two of the successive species associated with the ionization of a particular polyprotic acid are present in significant concentrations at any particular pH. Hence, the equilibria or any calculations can be determined by only one, or at most two,of the acid ionization constants.

Titration of a Polyprotic Weak acid with a Strong base

In accordance with the stepwise dissocitation of di- and polyprotic weak acids, their neutralization reactions are also stepwise. For instance, in the titration of orthophosphoric acid (H 3 PO 4 ) with a strong base such as NaOH, the following stepwise reactions occur:

H 3 PO 4 + NaOH ↔ NaH 2 PO 4 + H 2 O

NaH 2 PO 4 + NaOH → NaH 2 PO 4 + H 2 O

Na 2 HPO 4 + NaOH ↔ Na 3 PO4 + H 2 O

Accordingly, the H 3 PO 4 –NaOH titration curve has not one but three equivalence points. The first equivalence point is reached after one mole of NaOH has beenadded per mole of H 3 PO 4 ; the second after addition of two moles of NaOH; andthe third after addition of three moles of NaOH.

Example \(\PageIndex{8}\):

If 10.00 mL of 0.10 mol L-1 H 3 PO 4 solution is titrated, the first equivalence point is reached after addition of 10.00 mL, the second after addition of 20.00 mL, and the third after addition of 30.00 mL of 0.10 mol L-1 NaOH solution.

Titration of a Diprotic weak acid ( H 2 A ) with NaOH

For a diprotic weak acid represented by H 2 A , 1. The pH at the beginning of the titration is calculated from the ionization (dissocitation) of the first proton, i.e.,

H 2 A⇌H + +HA -

If K a1 , the acid dissociation constatant$$ (= \frac { \left[ \mathrm { H } ^ { + } \right] \left[ \mathrm { HA } ^ { - } \right] } { \left[ \mathrm { H } _ { 2 } \mathrm { A } \right] } ) \nonumber$$, is not too large and amount of dissociated H 2 A is ignored compared to the analytical concentration of the acid, then

\[ \left[ \mathrm { H } ^ { + } \right] = \sqrt { \mathrm { K } _ { \mathrm { al } } \left[ \mathrm { H } _ { 2 } \mathrm { A } \right] } \]

Otherwise the quadratic formula must be used to solve pH (see section on .... Of unit 2).

2. The pH during titration upto the first equivalence point

An HA - /H 2 A buffer region (a region where the solution attempts to resist any change in pH upon addition of base during the titration) is established such that

\[ \mathrm { pH } = \mathrm { pK } _ { \mathrm { al } } + \log \left( \frac { \mathrm { HA } ^ { - } } { \mathrm { H } _ { 2 } \mathrm { A } } \right) \]

3. At the first equivalence point

$$ \mathrm { pH } = \frac { \mathrm { pK } _ { \mathrm { al } } + \mathrm { pK } _ { \mathrm { a } 2 } } { 2 } $$

4. Beyond the first equivalence point an A2- /HA - buffer exists

\[ \mathrm { pH } = \mathrm { pK } _ { \mathrm { a } 2 } + \log \left( \frac { \left[ \mathrm { A } ^ { 2 - } \right] } { \left[ \mathrm { HA } ^ { - } \right] } \right) \]

5. At the second equivalence point the pH is determined from the hydrolysis of A 2- salt (i.e., A 2- + H 2 O ⇌ HA - + OH - ), such that

$$ \left[ \mathrm { OH } ^ { - } \right] = \sqrt { \frac { \mathrm { K } _ { w } } { \mathrm { K } _ { \mathrm { a } 2 } } \left[ \mathrm { A } ^ { 2 - } \right] } $$

6. Beyond the second equivalence point

The pH will be dependent on the concentration of excess strong base added (i.e., concentration of the titrant).

Illustration:

Consider addition of sodium hydroxide solution to dilute ethanedioic acid (oxalic acid). Ethanedioic acid is a diprotic acid which means that it can give away 2 protons (hydrogen ions) to a base. (Note that something which can only give away one (like HCl) is known as a monoprotic acid).

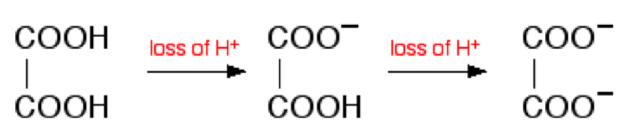
The reaction with NaOH takes place in two stages because one of the hydrogens is easier to remove than the other. The two successive reactions can be represented as:

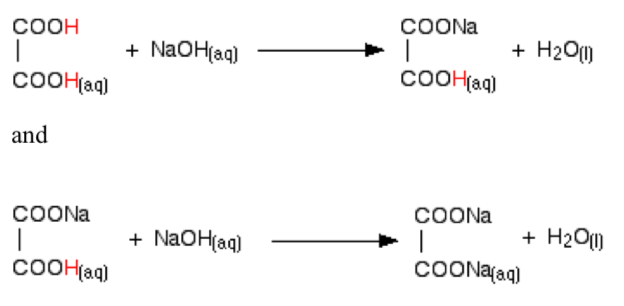
By running NaOH solution into ethanoic acid solution, the pH curve shows the end points for both of these reactions as shown in the figure below.

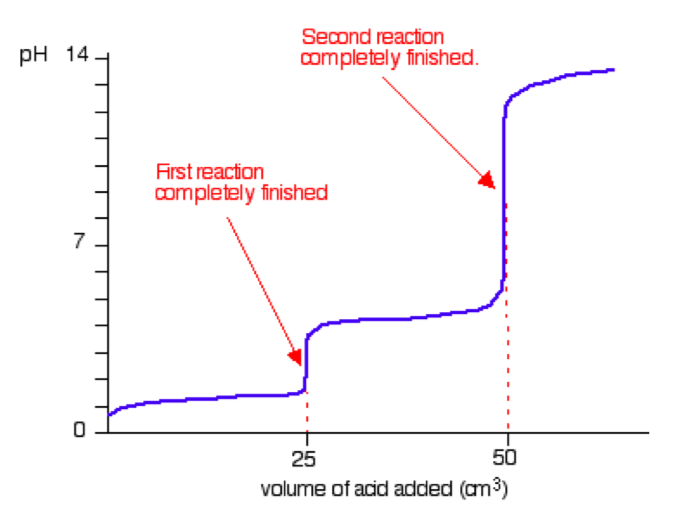
The curve is the reaction between NaOH and ethanedioic acid solutions of equal concentrations.

Exercise \(\PageIndex{10}\)

Plot a titration curve for the titration of 75 mL of 0.12 mol L -1 H 2 CO 3 with 0.09 mol L -1 NaOH, given that K al = 4.3 x 10 -7 and K a2 = 5.6 x 10 -11 .

Hint: You are expected to consider the six titration stages shown above to collect data in order to plot the titration curve.

Exercise \(\PageIndex{11}\)

In the titration of a triprotic acid, H 3 A with NaOH where K a1 / K a2 ≥104and K / K ≥10 4 ,

(a) Identify the eight titration stages that need to be considered in order to plot the corresponding titration curve.

(b) Derive the expressions for pH in each of the eight stages.

Titration of Anions of a weak acid with strong acid, HA

For the titration of Na 2 A salt:

A 2- + H 2 O ⇌ HA - + OH -

A 2- + H+ ⇌ HA -

The solution mixture of HA- and A2- is a buffer solution and so,

\[ \mathrm { pH } = \mathrm { pK } _ { \mathrm { a } 2 } + \log \frac { \left[ \mathrm { A } ^ { 2 - } \right] } { \left[ \mathrm { HA } ^ { - } \right] } \]

A 2- + H + ⇌ HA -

We have HA - in solution and pH arises from the dissociation of HA - , i.e.,

HA - + H 2 O ⇌ H 3 O + + A 2- and

\[ \mathrm { pH } = \frac { \mathrm { pK } _ { \mathrm { al } } + \mathrm { pK } _ { \mathrm { a } 2 } } { 2 } \]

HA - + H + ⇌ H 2 A

The resultant solution is a mixture of H A and HA-, hence a buffer solution and so

\[ \mathrm { pH } = \mathrm { pK } _ { \mathrm { al } } + \log \frac { \left[ \mathrm { HA } ^ { - } \right] } { \left[ \mathrm { H } _ { 2 } \mathrm { A } \right] } \]

Here, only H 2 A is left in solution and hence pH is dependent on the dissociation of H 2 A, and so

H 2 A + H 2 O ⇌ H 3 O + + HA -

Excess strong acid is added and the pH is determined by the concentration of excess strong acid.

Exercise \(\PageIndex{12}\)

Plot the titration curve of 75mL of 0.12 mol L -1 CH COONa with 0.09 mol L -1 HCl. K a for CH 3 COOH = 1.80 x 10 -5 . Hint: Consider the four possible titration stages.

Exercise \(\PageIndex{13}\)

Plot the titration curve of 75mL of 0.12 mol L -1 Na 2 CO 3 with 0.09 mol L -1 HCl. K a1 = 4.3 x 10 -7 and K a2 = 5.6 x 10 -11 . Hint: You are expected to consider six possible titration stages to collect data in order to plot the titration curve.

Acid-Base Indicators

Example \(\PageIndex{9}\):

In the titration of 30.0 mL of 0.10 M HF with 0.20 M KOH, the pH of the solution mixtures at 10.0, 15.0, and 20.0 mL additions of the strong alkali are 3.76, 8.14, and 12.30, respectively. If phenol red (whose pK value is 7.5 and its acid colour is yellow and its base colour is red) were to be used as an indicator for the titration reaction, what colour would the indicator be at the 10, 15, and20 mL additions of KOH?

At 10 mL, the pH is 3.76. This is very acidic; the colour will be yellow.

At 15 mL, the pH is 8.14. This is just within the of the pK, so it will be orange. Likely a reddish-orange colour.

At 20 mL, the pH is 12.30. This is very basic; and hence the colour will bered.

Since it changes colour at the equivalence point (it doesn’t have to hit exactly), this would be a reasonable choice indicator.

Exercise \(\PageIndex{14}\)

Refer to the example above. The indicator methyl orange has a pK of about 3.5. It is red in its acidic form and yellow in its basic form. What colourwill the indicator be at 10, 15, and 20 mL additions of KOH? Would this be a good indicator for this titration?

• Wired Chemist
• COVID-19; Knowns, Unknowns, and Questions
• Instructional
• Bibliography
• An Introduction to Chemistry
• General Chemistry Modules
• General Chemistry Problems
• Flash Demonstrations and Rollover Drills

Laboratory Tutorials

• Supplemental Material for Chemistry
• Harebrain Corner
• Quizzes for General Chemistry
• Chemistry by Yoder, Retterer, Thomsen, and Hess
• Volumetric Analysis

Volumetric analysis is a widely-used quantitative analytical method. As the name implies, this method involves the measurement of volume of a solution of known concentration which is used to determine the concentration of the analyte.

• Prepare a solution from an accurately weighed sample to +/- 0.0001 g of the material to be analyzed.
• Choose a substance that will react rapidly and completely with the analyte and prepare a standard solution of this substance. The concentration of the standard solution should be known to +/- 0.0001 M.
• Place the standard solution in a buret and add it slowly to the unknown. This process is called titration and the solution in the buret is called the titrant. Continue the titration until the reaction is complete; that is, until the amount of reactant added is exactly the amount required to react with all the constituent being analyzed. This point is called the equivalence point, and can be detected by adding an indicator to the unknown solution before beginning the titration. An indicator is a substance that gives a color change at or near the equivalence point. The point at which the color change occurs is the end point of the titration.
• Measure the exact volume of standard solution required from buret readings before and after the titration. Since the molarity of the standard solution is known, the number of moles of titrant can be calculated. From a knowledge of the equation for the reaction, the number of moles of constituent present in the sample can also be calculated.
• The most accurate and convenient way of preparing a standard solution is to weigh the reagent, dissolve it, and dilute the solution to a definite volume in a volumetric flask. This method can only be used if the reagent is a primary standard.
• In order for a reagent to be a primary standard, it must be obtainable in pure form (generally at least 99.98% pure), stable both in pure form and in solution, easy to dry and keep dry, and soluble in a suitable solvent.
• Many useful reagents do not meet those requirements, so the reagent is dissolved and diluted approximately to the concentration desired. The solution is then standardized by titrating it against a primary solution. This standardized soluton is caled a secondary standard.
• Clean the buret before use and rinse wih water. If any drops of water collect on the walls, the buret is not clean. Once the buret is clean, rinse it with the titrant solution before filling it. Pour about 5 mL of the titrant into the buret and, holding the buret almost horizontally, rotate it slowly so that the titrant cleans the entire buret. Do this three times.
• Place the buret in a buret clamp attached to a large ring stand. Using a funnel, fill the buret with titrant to a level above the zero mark. Place a beaker under the buret and open the stopcock for a few seconds to remove all air from the tip and fill it. The top of the solution should now be below the zero mark.

Figure 1. Place a black strip behind the buret to make the meniscus easier to see and the volume easier to read.

• Place the solution that is to be titrated in an Erlenmeyer flask and add 3-5 drops of the appropriate indicator. Position the flask under he buret.

Figure 2. The proper handling of the stopcock of the buret. This allows for maximum control of the rate at which the titrant is added.

• When the end point has been reached, allow the solution to sit for 10 seconds so the liquid in the buret can settle, then read the buret. Subtract the initial buret reading from the final reading to obtain the volume of titrant used.

Indicators are used to determine the end point of the titration. An indicator is used in acid-base and oxidation-reduction titrations. The color change of the indicator should be near the equivalence point of the reaction. The following charts show commonly used indicators and their color changes.

Acid-Base Indicators

Figure 3. A solution containing the indicator phenolphthalein before titration.

Figure 4. A solution containing phenolphthalein after titration.

Oxidation-Reduction Indicators

• Introduction
• Determination of Melting Point
• Distillation
• Gravimetric Analysis
• Index of Refraction
• Qualitative Analysis
• Recrystallization
• Selecting a Solvent
• Using a Desiccator
• Using the Spectronic 20 Spectrophotometer
• Weighing Techniques

Copyright © 2024 Claude Yoder. All rights reserved.

Practical Volumetric Analysis

Proficiency in volumetric analysis is a key skill for chemists in research and industry. This work seeks to ‘modernise’ approaches to volumetric analysis, by relating practical work to vocationally-relevant topics, whilst maintaining the rigor required for satisfactory performance in practical examinations. Written by someone who has experienced both teaching and working as a research chemist, this up to date textbook on practical volumetric analysis will provide the theoretical chemistry associated with volumetric analysis supported by a selection of practicals. There will also be suggestions for a number of investigations which could form the basis of project-based learning or coursework, particularly for those pursing vocational science courses.

Section 1 will consist of three theory chapters, covering preliminary concepts (fundamentals of chemistry, essential quantitative chemistry and concepts of statistics). Section 2 will be divided into four chapters, based on the four main divisions of volumetric analysis (acid-base titrimetry, redox titrimetry, precipitation titrimetry and complexometric titrimetry). Each chapter in this section will start with a review of essential theory, with worked examples and illustrations where appropriate, and end with a selection of laboratory practicals. Each chapter will also contain a number of open-ended investigations, for use in project-based learning or coursework. Section 3 will address more advanced topics and be divided into four chapters (volumetric analysis in industry, further statistical concepts, mathematics of titrimetry and advanced titrimetry). Practical work and suggestions for further reading will be included where appropriate.

Practical Volumetric Analysis is suitable for students taking modules in introductory chemistry and analytical chemistry on undergraduate degree courses as well as providing guidance to non-specialists teaching chemistry.

• Cite Icon Cite

P. McPherson, Practical Volumetric Analysis, The Royal Society of Chemistry, 2014.

Download citation file:

• Ris (Zotero)
• Reference Manager

Digital access

Print format, table of contents.

• Front Matter
• Units, Symbols & Terminology Used
• CHAPTER 1: Foundations of Chemistry p1-26 Abstract Open the PDF Link PDF for CHAPTER 1: Foundations of Chemistry in another window
• CHAPTER 2: Stoichiometry p27-40 Abstract Open the PDF Link PDF for CHAPTER 2: Stoichiometry in another window
• CHAPTER 3: Statistical Concepts p41-54 Abstract Open the PDF Link PDF for CHAPTER 3: Statistical Concepts in another window
• CHAPTER 4: Basics of Volumetric Analysis p55-76 Abstract Open the PDF Link PDF for CHAPTER 4: Basics of Volumetric Analysis in another window
• CHAPTER 5: Acid–Base Titrimetry p77-124 Abstract Open the PDF Link PDF for CHAPTER 5: Acid–Base Titrimetry in another window
• CHAPTER 6: Redox Titrimetry p125-172 Abstract Open the PDF Link PDF for CHAPTER 6: Redox Titrimetry in another window
• CHAPTER 7: Precipitation Titrimetry p173-194 Abstract Open the PDF Link PDF for CHAPTER 7: Precipitation Titrimetry in another window
• CHAPTER 8: Complexometric Titrimetry p195-220 Abstract Open the PDF Link PDF for CHAPTER 8: Complexometric Titrimetry in another window
• CHAPTER 9: Advanced Titrimetry p221-247 Abstract Open the PDF Link PDF for CHAPTER 9: Advanced Titrimetry in another window
• CHAPTER 10: Mathematics of Titrimetry p248-265 Abstract Open the PDF Link PDF for CHAPTER 10: Mathematics of Titrimetry in another window
• CHAPTER 11: Volumetric Analysis in Industry p266-278 Abstract Open the PDF Link PDF for CHAPTER 11: Volumetric Analysis in Industry in another window
• CHAPTER 12: Further Statistical Concepts p279-293 Abstract Open the PDF Link PDF for CHAPTER 12: Further Statistical Concepts in another window
• APPENDIX: Answers to End of Chapter Questions p294-301 Open the PDF Link PDF for APPENDIX: Answers to End of Chapter Questions in another window
• Subject Index p302-313 Open the PDF Link PDF for Subject Index in another window

Advertisement

• Campaigning and outreach
• News and events
• Awards and funding
• Privacy policy
• Journals and databases
• Locations and contacts
• Membership and professional community
• Teaching and learning
• Help and legal
• Cookie policy
• Terms and conditions
• Get Adobe Acrobat Reader
• Registered charity number: 207890
• © Royal Society of Chemistry 2023

This Feature Is Available To Subscribers Only

Sign In or Create an Account

• Chemistry Concept Questions and Answers

Volumetric Analysis Questions

In the laboratory experiments, solutions with exact known concentrations are required as even the slightest of difference in the aforesaid calculation may lead to greater imbalances at the atomic/ molecular level. For this purpose, Volumetric analysis is done to determine the concentration of the given compound.

Volumetric Analysis Chemistry Questions with Solutions

Q1: How does Potassium permanganate act as a self indicator?

Answer: A self indicator is a substance that along with itself participating in the reaction, indicates the end point of the reaction. Potassium permanganate is a violet-coloured solution. It acts as a strong oxidizing agent and thus, turns colourless when added to oxalic acid solution in the acidic medium. However, at the end point, it gives a faint pink colour in the acidic solution.

Q2. In the titration of Potassium permanganate with Oxalic acid, why is the oxalic acid solution warmed in the beginning?

Answer: In order to speed up the reaction, the oxalic acid solution is heated up to 50-60 o C. In the beginning of the reaction, manganous sulphate is formed which catalyses the reduction of KMnO 4 . This leads to the slowed rate of the reaction. The reaction gets auto-catalysed as it proceeds forward.

Q3. How is the strength of a solution calculated?

Answer: The strength of a solution is determined by calculating the amount of solute in grams present in 1 Litre of the solution. The unit of strength is g L -1 .

Therefore, Strength = Mass of Solute (g) / Volume of solution (L)

Strength of a solution can also be calculated as:

Strength = Molarity x Molar mass

Q4. How many grams of NaOH is required to make 250 cm 3 solution of 0.025 M NaOH solution?

Answer: Given: 0.025 M NaOH solution which means that 0.025 moles of NaOH are present in 1 L of solution.

1000 cm 3 0.025 M NaOH solution contains NaOH = 0.025 mol.

250 cm 3 0.025 M NaOH solution contains NaOH = (0.025/1000) x 250 mol = 0.00625 mol

The molar mass of NaOH is 40 g/mol.

Hence, the mass of 0.00625 moles of NaOH = 0.00625 x 40 g = 0.25 g

Q5. List some limitations of the volumetric analysis.

Answer: Some of the major limitations of the volumetric analysis are given below:

• Large amounts of chemicals are used and discarded.
• This method has limited accuracy.
• Failure in observing the end point may lead to disturbed calculations.
• Natural factors such as temperature, pressure and humidity may affect the titration reaction as the titration is carried out in an open vessel/flask.
• Indicators are required to detect the end point of the reaction.
• Liquid-phase reactions for the titration are required.

Q6. What volume of concentrated sulphuric acid is required to make 5 litre of 0.5 M H 2 SO 4 solution? The concentrated sulphuric acid is 98% H 2 SO 4 by mass and its density is 1.84 g cm -3 .

Answer: Given 98% H 2 SO 4 by mass means 98 g H 2 SO 4 is present in 100 g of solution.

From the given density, the volume of the concentrated H 2 SO 4 is calculated as:

Volume = mass/ density

Hence, volume of the concentrated H 2 SO 4 is 100 / 1.84 cm 3 = 54.35 cm 3 = 0.5435 L

The molar mass of H 2 SO 4 is 98 g/mol i,e. 98 g H 2 SO 4 equals 1 mole of H 2 SO 4 .

Hence, the molarity of the given concentrated H 2 SO 4 is 1 mol / 0.5435 L = 18.4 M

Now, to determine the required amount of concentrated H 2 SO 4 , the molarity formula is applied as: M 1 V 1 = M 2 V 2

Where, M 1 = Molarity of concentrated H 2 SO 4 solution

V 1 = Required volume of concentrated H 2 SO 4 solution

M 2 = 0.5 M

Hence, 18.4 M x V 1 = 5 L x 0.5 M

V 1 = 0.136 L = 136 cm 3

Thus, the volume of concentrated sulphuric acid required to make 5 litre of 0.5 M H 2 SO 4 solution is 136 cm 3 .

Q7. What is the specific name that is given to potassium permanganate solution?

Answer: The potassium permanganate solution is also known as Baeyer’s Reagent.

Q8. Why in permanganate titrations the burette with the pinch-cock regulator not used?

Answer: This is because the permanganate solution attacks the rubber.

Q9. Would you consider the upper or lower meniscus of potassium permanganate solution in the burette?

Answer: As the potassium permanganate solution is a deeply coloured solution, the upper meniscus of the burette is considered.

Q10. Why HNO 3 or HCl are not used in permanganate titrations?

Answer: HNO 3 is not used as it is a stronger oxidizing agent. However, HCl reacts with KMnO 4 and disturbs the reaction.

Q11. What are primary and secondary standards?

Answer: The primary standard substances are stable, pure, readily soluble in most of the solutions and remain unaffected by the presence of moisture and air. The solutions of these substances remain as such for a number of days. While, the secondary standard substances do not possess the aforementioned characteristics.

Q12. What is the equivalent mass of KMnO 4 in acidic medium?

Answer: KMnO 4 acts as an oxidizing agent and loses 5 electrons per molecule during the reaction. Hence, the equivalent mass of KMnO 4 in acidic medium is mol. Mass / Total positive valency. The equivalent mass of KMnO 4 = 158 / 5 = 31.6 g.

Q13. What is the Basicity of H 3 PO 4 solution?

Answer: Basicity of an acid is the total number of displaceable H + ions present in 1 molecule of the acid. Hence, the Basicity of H 3 PO 4 solution is 3.

Q14. Write the principle of Volumetric analysis.

Answer: The principle of Volumetric analysis is based on the fact that the unknown concentration of the known solution can be determined by titrating it with the known volume of another solution with known concentration.

Q15. Are the equivalence point and end point the same?

Answer: The equivalence point is the point when the reactants just react completely. It does not bring any change in the appearance of the colour of the solution. However, an end point is achieved right after the equivalence point, and the excess of the titrant added gives the end colour of the reaction. Hence, the equivalence point and endpoint are not the same.

Practise Questions on Volumetric Analysis

Q1. During the titration of KMnO 4 with Mohr’s salt, the solution of Mohr’s salt is not heated. Why?

Q2. Calculate the molarity of commercially available concentrated HCl acid.

Q3. In the titration of Na 2 CO 3 with HCl, methyl orange is used as an indicator. Why?

Q4. What is the relationship between Normality, molarity, equivalent mass and molecular mass?

Q5. Why is KMnO 4 not regarded as the primary standard?

Click the PDF to check the answers for Practice Questions. Download PDF

Recommended Videos

Titration using acidified kmno 4 and acidified k 2 cr 2 o 7.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Click through the PLOS taxonomy to find articles in your field.

For more information about PLOS Subject Areas, click here .

• Volumetric analysis
• Chemical analysis
• Get an email alert for Volumetric analysis
• Get the RSS feed for Volumetric analysis

Showing 1 - 12 of 12

View by: Cover Page List Articles

Sort by: Recent Popular

Effect of geometric distortion correction on thickness and volume measurements of cortical parcellations in 3D T1w gradient echo sequences

Christian Thaler, Jan Sedlacik,  [ ... ], Susanne Gellißen

Testing and validation of reciprocating positive displacement pump for benchtop pulsating flow model of cerebrospinal fluid production and other physiologic systems

Ahmad Faryami, Adam Menkara, Daniel Viar, Carolyn A. Harris

Regional brain development in fetuses with Dandy-Walker malformation: A volumetric fetal brain magnetic resonance imaging study

Shizuko Akiyama, Neel Madan,  [ ... ], Tomo Tarui

On the way to routine cardiac MRI at 7 Tesla - a pilot study on consecutive 84 examinations

Theresa Reiter, David Lohr,  [ ... ], Laura Maria Schreiber

Excellent accuracy of ABC/2 volume formula compared to computer-assisted volumetric analysis of subdural hematomas

Sae-Yeon Won, Andrea Zagorcic,  [ ... ], Juergen Konczalla

Local vs. systemic administration of bisphosphonates in rat cleft bone graft: A comparative study

Christine Hong, Alison Quach,  [ ... ], Sotirios Tetradis

Non-invasive volumetric analysis of asymptomatic hands using a 3-D scanner

Hiroki Shinkai, Michiro Yamamoto,  [ ... ], Hitoshi Hirata

Assessment of Volumetric versus Manual Measurement in Disseminated Testicular Cancer; No Difference in Assessment between Non-Radiologists and Genitourinary Radiologist

Çiğdem Öztürk, Ton Velleman,  [ ... ], Harald J. Hoekstra

Striatal Atrophy in the Behavioural Variant of Frontotemporal Dementia: Correlation with Diagnosis, Negative Symptoms and Disease Severity

Matthew D. Macfarlane, David Jakabek,  [ ... ], Alexander Frizell Santillo

Hematoma Shape, Hematoma Size, Glasgow Coma Scale Score and ICH Score: Which Predicts the 30-Day Mortality Better for Intracerebral Hematoma?

Chih-Wei Wang, Yi-Jui Liu,  [ ... ], Hsian-He Hsu

A Three Dimensional Study of Upper Airway in Adult Skeletal Class II Patients with Different Vertical Growth Patterns

Tianhu Wang, Zhenhua Yang,  [ ... ], Yongming Li

Volume Quantification of Acute Infratentorial Hemorrhage with Computed Tomography: Validation of the Formula 1/2ABC and 2/3SH

Wanlin Yang, Yulan Feng,  [ ... ], Shengdi Chen

Connect with Us

• PLOS ONE on Twitter
• PLOS on Facebook

• Search Menu
• Sign in through your institution
• Advance articles
• Author Guidelines
• Submission Site
• Open Access
• About IMA Journal of Numerical Analysis
• About the Institute of Mathematics and its Applications
• Editorial Board
• Advertising and Corporate Services
• Journals Career Network
• Self-Archiving Policy
• Dispatch Dates
• Journals on Oxford Academic
• Books on Oxford Academic

Browse issues

Cover image

Volume 44, Issue 3, May 2024

Adaptive fem with quasi-optimal overall cost for nonsymmetric linear elliptic pdes.

• View article

Corrigendum to: Adaptive FEM with quasi-optimal overall cost for nonsymmetric linear elliptic PDEs

Convergence guarantees for coefficient reconstruction in pdes from boundary measurements by variational and newton-type methods via range invariance, a new second-order low-regularity integrator for the cubic nonlinear schrödinger equation, random points are optimal for the approximation of sobolev functions, on the rate of convergence of a numerical scheme for fractional conservation laws with noise, lax dynamics for cartan decomposition with applications to hamiltonian simulation, regularity analysis for sees with multiplicative fbms and strong convergence for a fully discrete scheme, non-asymptotic estimates for tusla algorithm for non-convex learning with applications to neural networks with relu activation function, nodal discrete duality numerical scheme for nonlinear diffusion problems on general meshes, a unified approach to maximum-norm a posteriori error estimation for second-order time discretizations of parabolic equations, error analysis of time-discrete random batch method for interacting particle systems and associated mean-field limits, an arbitrary-order discrete rot-rot complex on polygonal meshes with application to a quad-rot problem, on symmetric positive definite preconditioners for multiple saddle-point systems, on the reduction in accuracy of finite difference schemes on manifolds without boundary, the gaussian wave packet transform via quadrature rules, adapting the centred simplex gradient to compensate for misaligned sample points, a posteriori error analysis of space-time discontinuous galerkin methods for the ε-stochastic allen–cahn equation, email alerts.

• Recommend to your Library

Affiliations

• Online ISSN 1464-3642
• Print ISSN 0272-4979
• Copyright © 2024 Institute of Mathematics and its Applications
• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

Publications — Over 100 years of publishing excellence

• Book Author Resources
• Submit a Book Proposal
• AMS Rights, Licensing, and Permissions
• Open Math Notes
• Frequently asked questions
• Member Journals
• Research Journals
• Translation Journals
• Distributed Journals
• Open Access Journals
• Guidelines and Policies
• Journal Author Resources

Librarian Resources

• eBook Collections
• COUNTER Usage Statistics
• My Subscriptions
• Subscription Information
• Licensing Information

Mathematical Reviews/MathSciNet®

• MathSciNet ®
• Reviewer Home
• MathSciNet ® Subscriptions

Membership — Welcome to your membership center

Join the ams, renew your membership, give a membership, individual membership.

• Member Benefits
• Member Directory
• Reciprocating Societies
• Members in Developing Countries

Institutional Membership

• Domestic Institutions
• International Institutions
• Two-Year Institutions
• Graduate Student Chapter Program

Other Member Types

• Corporate Memberships
• Associate Memberships

Meetings & Conferences — Engage with colleagues and the latest research

National meetings.

• Joint Mathematics Meetings
• Upcoming JMMs
• Previous JMMs
• Special Lectures
• Professional Enhancement Programs (PEPs)

Sectional Meetings

• Upcoming Sectionals
• Previous Sectionals
• Presenting Papers
• Hosting Sectionals

Other Meetings, Conferences & Workshops

• Mathematics Research Communities
• Education Mini-conference
• International Meetings
• Mathematics Calendar
• Short Courses
• Workshop for Department Chairs and Leaders

Meetings Resources

• Suggest a Speaker
• AMS Meetings Grants
• Submitting Abstracts
• Welcoming Environment Policy
• MathSafe – supporting safe meetings

News & Outreach — Explore news, images, posters, and mathematical essays

News from the ams.

• AMS News Releases
• Feature Stories
• Information for Journalists
• In Memory Of

Math Voices

• Feature Column
• Math in the Media
• Column on Teaching and Learning

Explorations

• Recognizing Diverse Mathematicians
• AMS Posters
• Mathematics & Music
• Mathematical Imagery
• Mathematical Moments

Professional Programs — Resources and opportunities to further your mathematical pursuits

Professional development.

• Employment Services
• Mathjobs.org
• BEGIN Career Initiative
• Mathprograms.org
• Mathematical Opportunities Database
• Research Seminars

Institutional Information and Data

• Annual Survey of the Mathematical and Statistical Sciences
• CBMS Survey
• Other Sources of Data
• Directory of Institutions in the Mathematical Sciences
• Professional Directory

Grants & Support

• AMS-Simons Grants for PUI Faculty
• Travel Grants
• Fellowships & Scholarships
• Epsilon Fund
• Child Care Grants

Awards & Recognition

• AMS Prizes & Awards
• Fellows of the AMS

Education — Resources to support advanced mathematics teaching and learning

For students.

• Information for Undergraduate and High School Students
• Research Experiences for Undergraduates (REUs)
• Considering Grad School
• Find Grad Programs
• Applying to Grad School
• What do Mathematicians Do?

For Teachers

• Teaching Online
• Teaching Resources
• Inclusive Classrooms
• Assessing Student Learning
• Education Webinars

For Department Leaders & Mentors

• Information for Department Leaders
• paraDIGMS (Diversity in Graduate Mathematical Sciences)

Government Relations — Advocating for the mathematical sciences

Elevating mathematics in congress.

• Our Mission
• Letters, Statements, & Legislation
• Congressional Briefings

Legislative Priorities

• Federal Issues of Concern
• Federal Budget Process

Get Involved

• Advocacy Resources
• Take Action

DC-Based Fellowships

• Congressional Fellowship
• Mass Media Fellowship
• Catalyzing Advocacy in Science & Engineering (CASE) Fellowship

Giving to the AMS — Your gifts make great things happen for mathematics   Make a Gift

What you can support.

• The 2020 Fund
• Next Generation Fund
• Birman Fellowship for Women Scholars
• JMM Child Care Grants
• MathSciNet for Developing Countries

Create a Legacy

• Make a Tribute Gift
• Create a Permanent Fund
• Establish a Prize, Award or Fellowship
• Bequests and Charitable Estate Planning

Honoring Your Gift

• Donor Stories
• Donor Wall of Honor
• Thomas S. Fiske Society
• AMS Contributors Society
• AMS Gardens

Giving Resources

• AMS Development Committee
• AMS Gift Acceptance Policy

About the AMS — Advancing research. Connecting the mathematics community.

Our organization.

• Executive Staff
• Equity, Diversity, & Inclusion
• Jobs at AMS
• Customer Service

Our Governance

• Board of Trustees
• Executive Committee

Governance Operations

• Calendar of Meetings
• Policy Statements & Guidelines

Proceedings of the American Mathematical Society

Published by the American Mathematical Society since 1950, Proceedings of the American Mathematical Society is devoted to shorter research articles in all areas of pure and applied mathematics.

ISSN 1088-6826 (online) ISSN 0002-9939 (print)

The 2020 MCQ for Proceedings of the American Mathematical Society is 0.85 . What is MCQ? The Mathematical Citation Quotient (MCQ) measures journal impact by looking at citations over a five-year period. Subscribers to MathSciNet may click through for more detailed information.

• Articles in press
• Recently published
• All issues : 1950 – Present

Contents of Volume 152, Number 7 HTML articles powered by AMS MathViewer View front and back matter from the print issue

Advertisement

Supported by

Climate Change Added a Month’s Worth of Extra-Hot Days in Past Year

Since last May, the average person experienced 26 more days of abnormal warmth than they would have without global warming, a new analysis found.

• Share full article

By Raymond Zhong

Over the past year of record-shattering warmth, the average person on Earth experienced 26 more days of abnormally high temperatures than they otherwise would have, were it not for human-induced climate change, scientists said Tuesday.

The past 12 months have been the planet’s hottest ever measured, and the burning of fossil fuels, which has added huge amounts of heat-trapping gases to the atmosphere, is a major reason. Nearly 80 percent of the world’s population experienced at least 31 days of atypical warmth since last May as a result of human-caused warming, the researchers’ analysis found.

Hypothetically, had we not heated the globe to its current state , the number of unusually warm days would have been far fewer, the scientists estimated, using mathematical modeling of the global climate.

The precise difference varies place to place. In some countries, it is just two or three weeks, the researchers found. In others, including Colombia, Indonesia and Rwanda, the difference is upward of 120 days.

“That’s a lot of toll that we’ve imposed on people,” said one of the researchers who conducted the new analysis, Andrew Pershing, the vice president for science at Climate Central, a nonprofit research and news organization based in Princeton, N.J., adding, “It’s a lot of toll that we’ve imposed on nature.” In parts of South America and Africa, he said, it amounts to “120 days that just wouldn’t be there without climate change.”

Currently, the world’s climate is shifting toward the La Niña phase of the cyclical pattern known as the El Niño-Southern Oscillation. This typically portends cooler temperatures on average. Even so, the recent heat could have reverberating effects on weather and storms in some places for months to come. Forecasters expect this year’s Atlantic hurricane season to be extraordinarily active, in part because the ocean waters where storms form have been off-the-charts warm.

The analysis issued Tuesday was a collaboration between several groups: Climate Central, the Red Cross Red Crescent Climate Centre and World Weather Attribution, a scientific initiative that examines extreme weather episodes. The report’s authors considered a given day’s temperature to be abnormally high in a particular location if it exceeded 90 percent of the daily temperatures recorded there between 1991 and 2020.

The average American experienced 39 days of such temperatures as a result of climate change since last May, the report found. That’s 19 more days than in a hypothetical world without human-caused warming. In some states, including Arizona and New Mexico in the Southwest and Washington and Oregon in the Northwest, the difference is 30 days or more, a full extra month.

The scientists also tallied up how many extreme heat waves the planet had experienced since last May. They defined these as episodes of unseasonable warmth across a large area, lasting three or more days, with significant loss of life or disruption to infrastructure and industry.

In total, the researchers identified 76 such episodes over the past year, affecting 90 countries, on every continent except Antarctica. There was the punishing hot spell in India last spring. There was the extreme heat that worsened wildfires and strained power grids in North America, Europe and East Asia last summer. And, already this year, there has been excessive warmth from Africa to the Middle East to Southeast Asia .

Raymond Zhong reports on climate and environmental issues for The Times. More about Raymond Zhong

Our Coverage of Climate and the Environment

News and Analysis

Over the past year of record-shattering warmth, the average person on Earth experienced 26 more days of abnormally high temperatures  than they otherwise would have, were it not for human-induced climate change, scientists said.

The Biden administration laid out for the first time a set of broad government guidelines around the use of carbon offsets  in an attempt to shore up confidence in a method for tackling global warming that has faced growing criticism.

A group of health experts, economists and U.S. government lawyers are working to address a growing crisis: people dying on the job from extreme heat. They face big hurdles .

Adopting Orphaned Oil Wells:  Students, nonprofit groups and others are fund-raising to cap highly polluting oil and gas wells  abandoned by industry.

Struggling N.Y.C. Neighborhoods:  New data projects are linking social issues with global warming. Here’s what that means for five communities in New York .

Biden Environmental Rules:  The Biden administration has rushed to finalize 10 major environmental regulations  to meet its self-imposed spring deadline.

F.A.Q.:  Have questions about climate change? We’ve got answers .

GPT-4 is better than humans at financial forecasting, new study shows

• OpenAI's GPT-4 is better than humans at analyzing financial statements and making forecasts, according to a new study.
• "Even without any narrative or industry-specific information, the LLM outperforms financial analysts in its ability to predict earnings changes," the study found.
• Trading strategies based on GPT-4 also delivered more profitable results than the stock market.

OpenAI's GPT-4 proved to be a better financial analyst than humans, according to a new study.

The findings could upend the financial services industry that, like other business sectors, is racing to adopt generative AI technologies.

According to the study conducted by the Booth School of Business at the University of Chicago, the large language model did a better job of analyzing financial statements and making predictions based on those statements.

"Even without any narrative or industry-specific information, the LLM outperforms financial analysts in its ability to predict earnings changes," the study said. "The LLM exhibits a relative advantage over human analysts in situations when the analysts tend to struggle."

The study utilized "chain-of-thought" prompts that directed GPT-4 to identify trends in financial statements and calculate different financial ratios. From there, the large language model analyzed the information and predicted future earnings results.

"When we use the chain of thought prompt to emulate human reasoning, we find that GPT achieves an accuracy of 60%, which is remarkably higher than that achieved by the analysts," the study said. The human analysts were closer to the low 50% range with regard to prediction accuracy.

The large language models' ability to recognize financial patterns and business concepts with incomplete information suggests that the technology should play a key role in financial decision-making going forward, according to the study's authors.

Finally, the study found that applying GPT-4's financial acumen to trading strategies produced more profitable trading, with higher share ratios and alpha that ultimately beat the stock market.

"We find that the long-short strategy based on GPT forecasts outperforms the market and generates significant alphas and Sharpe ratios," the study said. 

• Main content

• Get Benzinga Pro
• Data & APIs
• Our Services
• News Earnings Guidance Dividends M&A Buybacks Legal Interviews Management Offerings IPOs Insider Trades Biotech/FDA Politics Government Healthcare
• Markets Pre-Market After Hours Movers ETFs Forex Cannabis Commodities Binary Options Bonds Futures CME Group Global Economics Previews Small-Cap Real Estate Cryptocurrency Penny Stocks Digital Securities Volatility
• Ratings Analyst Color Downgrades Upgrades Initiations Price Target
• Ideas Trade Ideas Covey Trade Ideas Long Ideas Short Ideas Technicals From The Press Jim Cramer Rumors Best Stocks & ETFs Best Penny Stocks Best S&P 500 ETFs Best Swing Trade Stocks Best Blue Chip Stocks Best High-Volume Penny Stocks Best Small Cap ETFs Best Stocks to Day Trade Best REITs
• Money Investing Cryptocurrency Mortgage Insurance Yield Personal Finance Forex Startup Investing Real Estate Investing Credit Cards
• Cannabis Cannabis Conference News Earnings Interviews Deals Regulations Psychedelics

Salesforce Options Trading: A Deep Dive into Market Sentiment

Deep-pocketed investors have adopted a bullish approach towards Salesforce CRM , and it's something market players shouldn't ignore. Our tracking of public options records at Benzinga unveiled this significant move today. The identity of these investors remains unknown, but such a substantial move in CRM usually suggests something big is about to happen.

We gleaned this information from our observations today when Benzinga's options scanner highlighted 38 extraordinary options activities for Salesforce. This level of activity is out of the ordinary.

The general mood among these heavyweight investors is divided, with 55% leaning bullish and 42% bearish. Among these notable options, 9 are puts, totaling $567,086, and 29 are calls, amounting to $1,824,460.

Expected Price Movements

Taking into account the Volume and Open Interest on these contracts, it appears that whales have been targeting a price range from $185.0 to $320.0 for Salesforce over the last 3 months.

Insights into Volume & Open Interest

Assessing the volume and open interest is a strategic step in options trading. These metrics shed light on the liquidity and investor interest in Salesforce's options at specified strike prices. The forthcoming data visualizes the fluctuation in volume and open interest for both calls and puts, linked to Salesforce's substantial trades, within a strike price spectrum from $185.0 to $320.0 over the preceding 30 days.

Salesforce Option Activity Analysis: Last 30 Days

Significant Options Trades Detected:

About salesforce.

Salesforce provides enterprise cloud computing solutions. The company offers customer relationship management technology that brings companies and customers together. Its Customer 360 platform helps the group to deliver a single source of truth, connecting customer data across systems, apps, and devices to help companies sell, service, market, and conduct commerce. It also offers Service Cloud for customer support, Marketing Cloud for digital marketing campaigns, Commerce Cloud as an e-commerce engine, the Salesforce Platform, which allows enterprises to build applications, and other solutions, such as MuleSoft for data integration.

Having examined the options trading patterns of Salesforce, our attention now turns directly to the company. This shift allows us to delve into its present market position and performance

Where Is Salesforce Standing Right Now?

• Trading volume stands at 10,968,723, with CRM's price down by -0.32%, positioned at $233.68.
• RSI indicators show the stock to be may be approaching oversold.
• Earnings announcement expected in 86 days.

Expert Opinions on Salesforce

In the last month, 5 experts released ratings on this stock with an average target price of $267.0.

• An analyst from Wells Fargo persists with their Equal-Weight rating on Salesforce, maintaining a target price of $250.
• An analyst from Piper Sandler has decided to maintain their Neutral rating on Salesforce, which currently sits at a price target of $250.
• An analyst from DA Davidson has decided to maintain their Neutral rating on Salesforce, which currently sits at a price target of $230.
• An analyst from Evercore ISI Group persists with their Outperform rating on Salesforce, maintaining a target price of $300.
• An analyst from Barclays has decided to maintain their Overweight rating on Salesforce, which currently sits at a price target of $305.

Options trading presents higher risks and potential rewards. Astute traders manage these risks by continually educating themselves, adapting their strategies, monitoring multiple indicators, and keeping a close eye on market movements. Stay informed about the latest Salesforce options trades with real-time alerts from Benzinga Pro .

© 2024 Benzinga.com. Benzinga does not provide investment advice. All rights reserved.

Trade confidently with insights and alerts from analyst ratings, free reports and breaking news that affects the stocks you care about.