use polya's four step problem solving

• Resources library

Polya’s Problem-Solving Process

Emma Moore, Teaching Excellence Program Master Teacher 

Problem-solving skills are crucial for students to navigate challenges, think critically, and find innovative solutions. In PISA, problem-solving competence is defined as “an individual’s capacity to engage in cognitive processing to understand and resolve problem situations where a method of solution is not immediately obvious” (OECD, 2014, p. 30). Returning to the classroom post-COVID, I found that students had lost their ‘grit’ for these deep-thinking tasks. They either struggled to start, gave up easily, or stopped at their first ‘answer’ without considering if it answered the problem or was the only possible solution.

To re-invigorate these skills, I investigated the impact of explicitly teaching Polya's problem-solving process in my Year Six class. This framework developed student agency and supported them to manage their feelings if they felt challenged by the work.

Here, I will share the impact of this initiative and how it empowered students to become effective and resilient problem solvers.  

Understanding Polya's Problem-Solving Process

Polya's problem-solving process, developed by mathematician George Polya, provides a structured approach to problem-solving that can be applied across various domains. This four-step process consists of understanding the problem, devising a plan, trying the plan, and revisiting the solution. (Polya, 1947)

In order to focus on the skills and knowledge of the problem-solving process, I began by using tasks where the mathematical processes were obvious. This allowed me to focus on the problem-solving process explicitly.

The question shown in Figure 2 is taken from Peter Sullivan and Pat Lilburn's Open-Ended Maths Activities book. This task was used to establish a baseline assessment for each stage of the process. I planned the prompts in dot points and revealed them one by one through the PowerPoint. After launching the task and giving the students time to think, they recorded all their possible answers in their workbook.

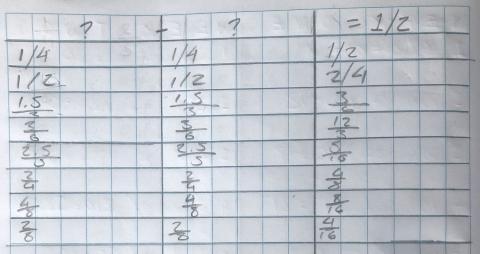
The student sample shown in Figure 3 demonstrates that the student followed a pattern and stuck to it but did not revisit their work. On line two, their response (1 half and 1 half is 2 quarters) is unreasonable.

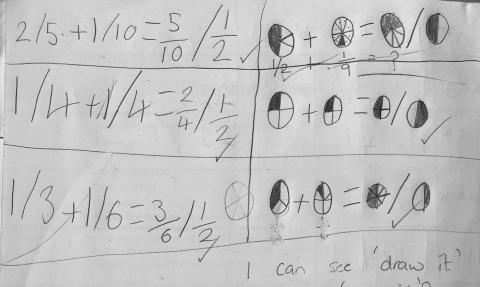
Figure 3 is a sample gathered from a small group of students. This group required support to start. They used paper folding and paper strips to model their thinking.

Over half of the class could give at least one correct answer, but only four students showed signs of checking to see if their plans addressed the problem and yielded correct answers. Understanding the problem and revisiting the solutions became the focus of my inquiry.

The following series of lessons covering operations with fractions and decimals focused on the stages of Polya’s process.  

Step 1: Understanding the Problem

The first step of Polya's problem-solving process emphasises the importance of ensuring you thoroughly comprehend the problem. In this step, students learn to read and analyse the problem statement, identify the key information, and clarify any uncertainties. This process encourages critical thinking (Bicer et al., 2020) as students develop the ability to break down complex problems into manageable parts. I facilitated this process by engaging students in discussions and guiding them to identify the essential components of the problem. By fostering a collaborative learning environment, students shared their perspectives and learned to refine their questions when they were unsure. Figure 6 shares an example of a prompt I use for Step 1.

Figure 4: Example prompt for Step 1.

Initially, students who were stuck provided the classic ‘white flag’ responses.

Student: I just don’t get it.

Teacher: What part don’t you get?

Student: All of it!

As a starting point, the students and I co-created a classroom display of helpful questions the students could use to develop their understanding.

These questions supported me to develop a deeper understanding of what students didn’t understand when they expressed uncertainty. This could range from not understanding specific terminology (often easy to explain) to where numbers came from and why their classmates interpreted the problem differently. I found engaging in this step made triaging their misunderstandings easier.  

Step 2: Devising a Plan

Once students had grasped the problem, the next step was to formulate a plan of action. In this step, students explored different strategies and selected the most appropriate approach. I prompted students to brainstorm possible solutions, draw diagrams, make tables, and create algorithms, all the time fostering creativity and diverse thinking.

This step had been a strength during the baseline assessment data, and a wide range of strategies were explored. Polya’s strategies were displayed in the classroom as the mathematician’s strategy tool kit, so students were comfortable acknowledging the many ways to solve the problem.

Students developed critical thinking and decision-making skills by keeping this step in problem-solving. They become adept at evaluating multiple approaches and selecting the most effective strategy to solve a problem, thus promoting the development of mathematical reasoning abilities (Barnes, 2021). Figure 7 shows a slide used in Step 2.

Figure 5: Example prompt for Step 2.

Step 3: Try

The students implemented their selected strategy, performed calculations, made models, drew diagrams, created tables, and found patterns. This stage encouraged students to persevere and take ownership of their problem-solving process.

At Cowes Primary School, we have developed whole-school expectations around providing opportunities for hands-on learning, allowing students to engage in practical activities that support the development of ideas, expecting students to represent their work visually (pictures, materials and manipulatives), using language and numbers/symbols. This approach enhances students' problem-solving skills and fosters a sense of autonomy and confidence in their capabilities and ability to talk about their work (Roche et al., 2023). Figure 9 shows the slide used for Step 3.

Figure 6: Example prompt for Step 3.

Step 4. Re-visiting the solution

The last step in Polya's problem-solving process is re-visit. After finding a solution, students critically analyse and evaluate their approach after finding a solution. They consider the effectiveness of their chosen strategy, identify strengths and weaknesses, and reflect on how they could improve their problem-solving techniques. This step was missing from most students’ work during the baseline assessment.

As a class, we added to the display questions to facilitate better reflective practice and developed a more critical approach to looking at our work. This process encouraged students to refine their answers, not go too far down the wrong path, fostered resilience, embrace challenge and normalise uncertainty (Buckley & Sullivan, 2023).

Figure 7: Class display showing our questions.

  Figure 8: Student samples from the task.

Impact and Benefits:

Figure 9 shows four tasks, including the initial baseline assessment. The blue series shows the percentage of students who arrived at least one correct solution. The green series shows evidence that students were revisiting their initial solutions using other strategies to check they were correct or checking in with other groups and adjusting. There was a steady increase in both skills over the course of these four tasks.

By explicitly teaching Polya's problem-solving process, the students cultivated valuable skills that extend beyond maths problems. Some of the key benefits observed were:

Mathematical Reasoning: Polya's process promotes the development of mathematical reasoning skills. Students analysed problems, explored different strategies, and apply logical thinking to arrive at solutions. These skills can enhance their overall mathematical proficiency.

Self-efficacy: Through problem-solving, students gained confidence in their ability to tackle problems. They become more self-reliant, taking ownership of their learning, and seeking solutions proactively.

Collaboration and Communication: The process encouraged collaboration and communication among students. They discussed problems, shared ideas, and considered multiple perspectives, students developed effective teamwork and interpersonal skills.

Metacognition: The reflective aspect of Polya's process fostered metacognitive skills, enabling students to monitor and regulate their thinking processes. They learned to identify their strengths and weaknesses, supporting continuous improvement and growth.  

Overall using the 4 steps was a really effective and an explicit way to focus on developing the problem-solving skills of my Year 6 students.

This article was originally published for the Mathematical Association of Victoria's Prime Number.    

References:

Barnes, A. (2021). Enjoyment in learning mathematics: Its role as a potential barrier to children’s perseverance in mathematical reasoning. Educational Studies in Mathematics , 106(1), 45–63. https://doi.org/10.1007/s10649-020-09992-x

Bicer, Ali, Yujin Lee, Celal Perihan, Mary M. Capraro, and Robert M. Capraro. ‘Considering Mathematical Creative Self-Efficacy with Problem Posing as a Measure of Mathematical Creativity’. Educational Studies in Mathematics 105, no. 3 (November 2020): 457–85. https://doi.org/10.1007/s10649-020-09995-8

Buckley, S., & Sullivan, P. (2023). Reframing anxiety and uncertainty in the mathematics classroom. Mathematics Education Research Journal , 35(S1), 157–170. https://doi.org/10.1007/s13394-021-00393-8

OECD (Ed.). (2014). Creative problem solving: Students’ skills in tackling real-life problems. OECD.

Pólya, G. (1988). How to solve it: A new aspect of mathematical method (2nd ed). Princeton university press.

Roche, A., Gervasoni, A., & Kalogeropoulos, P. (2023). Factors that promote interest and engagement in learning mathematics for low-achieving primary students across three learning settings. Mathematics Education Research Journal , 35(3), 525–556. https://doi.org/10.1007/s13394-021-00402-w

Four Steps of Polya's Problem Solving Techniques

Related tags:

In the world of mathematics and algorithms, problem-solving is an art which follows well-defined steps. Such steps do not follow some strict rules and each individual can come up with their steps of solving the problem. But there are some guidelines which can help to solve systematically.

In this direction, mathematician George Polya crafted a legacy that has guided countless individuals through the maze of problem-solving. In his book “ How To Solve It ,” Polya provided four fundamental steps that serve as a compass for handling mathematical challenges. 

• Understand the problem
• Devise a Plan
• Carry out the Plan
• Look Back and Reflect

Let’s look at each one of these steps in detail.

Polya’s First Principle: Understand the Problem

Before starting the journey of problem-solving, a critical step is to understand every critical detail in the problem. According to Polya, this initial phase serves as the foundation for successful solutions.

At first sight, understanding a problem may seem a trivial task for us, but it is often the root cause of failure in problem-solving. The reason is simple: We often understand the problem in a hurry and miss some important details or make some unnecessary assumptions. So, we need to clearly understand the problem by asking these essential questions:

• Do we understand all the words used in the problem statement? 
• What are we asked to find or show? What is the unknown? What is the information given? Is there enough information to enable you to find a solution?
• What is the condition or constraints given in the problem? Separate the various parts of the condition: Is it possible to satisfy the condition? Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory?
• Can you write down the problem in your own words? If required, use suitable notations, symbols, equations, or expressions to convey ideas and encapsulate critical details. This can work as our compass, which can guide us through calculations to reach the solution.
• After knowing relevant details, visualization becomes a powerful tool. Can you think of a diagram that might help you understand the problem? This can serve as a bridge between the abstract and tangible details and reveal patterns that might not be visible after looking at the problem description.

Just as a painter understands the canvas before using the brush, understanding the problem is the first step towards the correct solution.

Polya’s Second Principle: Devise a Plan

Polya mentions that there are many reasonable ways to solve problems. If we want to learn how to choose the best problem-solving strategy, the most effective way is to solve a variety of problems and observe different steps involved in the thought process and implementation techniques.

During this practice, we can try these strategies:

• Guess and check
• Identification of patterns
• Construction of orderly lists
• Creation of visual diagrams
• Elimination of possibilities
• Solving simplified versions of the problem
• Using symmetry and models
• Considering special cases
• Working backwards
• Using direct reasoning
• Using formulas and equations

Here are some critical questions at this stage:

• Can you solve a portion of the problem? Consider retaining only a segment of conditions and discarding the rest.
• Have you encountered this problem before? Have you encountered a similar problem in a slightly different form with the same or a similar unknown? Look closely at the unknown.
• If the proposed problem proves challenging, try to solve related problems first. Can you imagine a more approachable related problem? A more general or specialized version? Could you utilize their solutions, results, or methods?
• Can you derive useful insights from the data? Can you think of other data that would help determine the unknown? Did you utilize all the given data? Did you incorporate the entire set of conditions? Have you considered all essential concepts related to the problem?

Polya’s Third Principle: Carry out the Plan

This is the execution phase where we transform the blueprint of our devised strategy into a correct solution. As we proceed, our goal is to put each step into action and move towards the solution.

In general, after identifying the strategy, we need to move forward and persist with the chosen strategy. If it is not working, then we should not hesitate to discard it and try another strategy. All we need is care and patience. Don’t be misled, this is how mathematics is done, even by professionals. There is one important thing: We need to verify the correctness of each step or prove the correctness of the entire solution.

Polya’s Fourth Principle: Look Back and Reflect

In the rush to solve a problem, we often ignore learning from the completed solutions. So according to Polya, we can gain a lot of new insights by taking the time to reflect and look back at what we have done, what worked, and what didn’t. Doing this will enable us to predict what strategy to use to solve future problems.

• Can you check the result? 
• Can you check the concepts and theorems used? 
• Can you derive the solution differently?
• Can you use the result, or the method, for some other problem?

By consistently following the steps, you can observe a lot of interesting insights on your own.

George Polya's problem-solving methods give us a clear way of thinking to get better at math. These methods change the experience of dealing with math problems from something hard to something exciting. By following Polya's ideas, we not only learn how to approach math problems but also learn how to handle the difficult parts of math problems.

Shubham Gautam

Share on social media:

Don’t fill this out if you’re human:

More blogs to explore

Originated from the “Games of Chance,” probability in itself is a branch of mathematics concerned about how likely it is that a proposition is true.

There are 3 doors behind which are two goats and a car. You pick door 1 hoping for the car but don’t open it right away. Monty Hall, the game show host who knows what's behind the doors, opens door 3, which has a goat. Here's the game: do you want to pick door No. 2? Is it to your advantage to switch your choice?

A cube is painted with some color on all faces. Now, we cut it into 1000 small cubes of equal size. How many small cubes are painted?

Given two non-negative integers, m and n, we have to find their greatest common divisor or HCF. It is the largest number, a divisor of both m and n. The Euclidean algorithm is one of the oldest and most widely known methods for computing the GCD of two integers.

This is one of the basic problems to learn the properties of prime numbers and the divisibility rule. There could be several variations and several ideas of proof available to this question.

The Probability distribution lists the probabilities of the events that happened in any given random experiment. For example rolling a dice.

Follow us on:

© 2020 Code Algorithms Pvt. Ltd.

All rights reserved.

• Mathematics
• Reading and Writing
• Intervention
• Professional Learning
• Virtual Events
• What is Phonics?
• Teaching Grammar
• Vocabulary Games
• What is Virtual Learning?
• About Sadlier
• Find a Sales Representative
• International Distributors
• International Programs
• Online Catalogs
• Sadlier School Site Map
• Pricing & Ordering Information
• Sadlier’s W-9
• Sadlier’s Sole Source Letter
• Sadlier’s Credit Application
• Privacy Policy
• Return Policy
• Terms & Conditions

Sadlier's Math Blog

• Counting and Cardinality
• Operations and Algebraic Thinking
• Number and Operations in Base 10
• Measurement and Data
• Math Practices
• Number and Operations Fractions
• Statistics and Probability
• The Number System
• Ratios and Proportional Relationships
• Expressions and Equations
• MP1—Problem Solving
• MP2—Abstract <−>Quantitative
• MP3—Reasoning
• MP4—Modeling
• MP5—Using Tools
• MP6—Precision
• MP7—Structure
• MP8—Repeated Reasoning
• Kindergarten Math Activities
• First Grade Math Activities
• Second Grade Math Activities
• Third Grade Math Activities
• Fourth Grade Math Activities
• Fifth Grade Math Activities
• Sixth Grade Math Activities
• Seventh Grade Math Activities
• Eighth Grade Math Activities
• Professional Development
• Test-Taking Strategies
• Classroom Posters
• Writing In Mathematics

April 19, 2023 3-5-operations-and-algebraic-thinking , k-2-operations-and-algebraic-thinking , 6-8-expressions-and-equations

Polya’s problem-solving process: finding unknowns elementary & middle school, by: jeff todd.

In this article, we'll explore how a focus on finding “unknowns” in math will lead to active problem-solving strategies for Kindergarten to Grade 8 classrooms. Through the lens of George Polya and his four-step problem-solving heuristic, I will discuss how you can apply the concept of finding unknowns to your classroom. Plus, download my Finding Unknowns in Elementary and Middle School Math Classes Tip Sheet .

It is unfortunate that in the United States mathematics has a reputation for being dry and uninteresting. I hear this more from adults than I do from children—in fact, I find that children are naturally curious about how math works and how it relates to the world around them. It is from adults that they get the idea that math is dry, boring, and unrelated to their lives. Despite what children may or may not hear about math, I focus on making instruction exciting and showing my students that math applicable to their lives.

Problem solving is a fundamental means of developing students' mathematical knowledge and it also shows them that math concepts apply to real-world concepts.

Problem solving is one way I show my students that math relates to their lives! Problem solving is a fundamental means of developing students' mathematical knowledge and it also shows them that math concepts apply to real-world concepts.

Who Is George Polya?

George Polya was a European-born scholar and mathematician who moved to the U.S in 1940, to work at Stanford University. When considering the his classroom experience of teaching mathematics, he noticed that students were not presented with a view of mathematics that excited and energized them. I know that I have felt this way many times in my teaching career and have often asked: How can I make this more engaging and yet still maintain rigor?

Polya suggested that math should be presented in the light of being able to solve problems. His 1944 book,  How to Solve It  contains his famous four-step problem solving heuristic. Polya suggests that by presenting mathematical thinking as a way to find “unknowns,” it becomes more engaging for students.

He even goes as far as to say that his general four-step problem-solving heuristic can be applied to any field of human endeavor—to any opportunity where a problem exists.

Polya suggested that math should be presented in the light of being able to solve problems...that by presenting mathematical thinking as a way to find “unknowns,” it becomes more engaging for students.

Polya specifically wrote about problem-solving at the high school mathematics level. For those of us teaching students in the elementary and middle school levels, finding ways to apply Polya’s problem-solving process as he intended forces us to rethink the way we teach.

Particularly in the lower grade levels, finding “unknowns” can be relegated to prealgebra and algebra courses in the later grades. Nonetheless, today’s standards call for algebra and algebraic thinking at early grade levels. The  download  for today’s post presents one way you can find unknowns at each grade level.

Presenting Mathematics  As A Way To Find "Unknowns" In Real-Life Situations

I would like to share a conversation I had recently with my friend Stu. I have been spending my summers volunteering for a charitable organization in Central America that provides medical services for the poor, runs ESL classes, and operates a Pre-K to Grade 6 school. We were talking about the kind of professional development that I might provide the teachers, and he was intrigued by the thought that we could connect mathematical topics to real life. We specifically talked about the fact that he remembers little or nothing about how to find the area of a figure and never learned in school why it might be important to know about area. Math was presented to him as a set of rules and procedures rather than as a way to find unknowns in real-life situations.

That’s what I am talking about here, and it’s what I believe Polya was talking about. How can we create classrooms where students are able to use their mathematical knowledge to solve problems, whether real-life or purely mathematical?

As Polya noted, there are two ways that mathematics can be presented, either as deductive system of rules and procedures or as an inductive method of making mathematics. Both ways of thinking about mathematics have endured through the centuries, but at least in American education, there has been an emphasis on a procedural approach to math. Polya noticed this in the 1940s, and I think that although we have made progress, there is still an over-emphasis on skill and procedure at the expense of problem-solving and application.

I recently reread Polya’s book. I can’t say that it is an “easy” read, but I would say that it was valuable for me to revisit his own words in order to be sure I understood what he was advocating. As a result, I made the following outline of his problem-solving process and the questions he suggests we use with students.

Polya's Problem-Solving Process

1. understand the problem, and desiring the solution .

• Restate the problem
• Identify the principal parts of the problem
• Essential questions
• What is unknown?
• What data are available?
• What is the condition?

2. Devising a Problem-Solving Plan 

• Look at the unknown and try to think of a familiar problem having the same or similar unknown
• Here is a problem related to yours and solved before. Can you use it?
• Can you restate the problem?
• Did you use all the data?
• Did you use the whole condition?

3. Carrying Out the Problem-Solving Plan 

• Can you see that each step is correct?
• Can you prove that each step is correct?

4. Looking Back

• Can you check the result?
• Can you check the argument?
• Can you derive the result differently?
• Can you see the result in a glance?
• Can you use the result, or the method, for some other problem?

Polya's Suggestions For Helping Students Solve Problems

I also found four suggestions from Polya about what teachers can do to help students solve problems:

Suggestion One In order for students to understand the problem, the teacher must focus on fostering in students the desire to find a solution. Absent this motivation, it will always be a fight to get students to solve problems when they are not sure what to do.

Suggestion Two A second key feature of this first phase of problem-solving is giving students strategies forgetting acquainted with problems.

Suggestion Three Another suggestion is that teachers should help students learn strategies to be able to work toward a better understanding of any problem through experimentation.

Suggestion Four Finally, when students are not sure how to solve a problem, they need strategies to “hunt for the helpful idea.”

Whether you are thinking of problem-solving in a traditional sense (solving computational problems and geometric proofs, as illustrated in Polya’s book) or you are thinking of the kind of problem-solving students can do through STEAM activities, I can’t help but hear echoes of Polya in Standard for Math Practice 1: Make sense of problems and persevere in solving them.

Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary.

In Conclusion

We all know we should be fostering students’ problem-solving ability in our math classes. Polya’s focus on “finding unknowns” in math has wide applicability to problems whether they are purely mathematical or more general.

Grab my  download  and start  applying Polya’s Four-Step Problem-Solving Process in the lower grades!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.5: Problem Solving

• Last updated
• Save as PDF
• Page ID 50932

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

• First, you have to understand the problem.
• After understanding, then make a plan.
• Carry out the plan.
• Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Example \(\PageIndex{1}\)

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found a solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31.

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet. How many of each animal does he have? Make sure you use Polya’s 4 problem-solving steps.

Problem Solving Strategy 2 (Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences:

last term = (fixed number) ( n -1) + first term

The fix number is the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Example \(\PageIndex{2}\)

2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

Check in question 3:

Find the 320th term of 7, 10, 13, 16 …

Problem Solving Strategy 3 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Example \(\PageIndex{3}\)

Karen is thinking of a number. If you double it and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 4 (Looking for a Pattern)

Definition: Sequence

A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example \(\PageIndex{4}\)

1, 4, 7, 10, 13… Find the next 2 numbers.

The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example \(\PageIndex{5}\)

1, 4, 9, 16 … Find the next 2 numbers.

It looks like each number is a perfect square. \(1^2=1\), \(2^2=4\)

So the next numbers would be

Example \(\PageIndex{6}\)

10, 7, 4, 1, -2… Find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be

-5 – 3 = -8

Example \(\PageIndex{7}\)

1, 2, 4, 8 …Ffind the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

Problem Solving Strategy 5 (Make a List)

Example \(\PageIndex{8}\)

Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8. But note that this is just an observation. To answer this question, one would need a mathematically rigorous proof.

Example \(\PageIndex{9}\)

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 6 (Process of Elimination)

This strategy can be used when there is only one possible solution.

Example \(\PageIndex{10}\)

I’m thinking of a number.

• The number is odd.
• It is more than 1 but less than 100.
• It is greater than 20.
• It is less than 5 times 7.
• The sum of the digits is 7.
• It is evenly divisible by 5.
• We know it is an odd number between 1 and 100.
• 21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.
• 21 (2+1=3) No
• 23 (2+3 = 5) No
• 25 (2 + 5= 7) Yes

Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

• References (2)

Fallacies in Common Language

For each of the following statements, name the type of logical fallacy being used.

If you don’t want to drive from Boston to New York, then you will have to take the train.

Every time I go to Dodger Stadium, the Dodgers win. I should go there for every game.

New England Patriots quarterback Tom Brady likes his footballs slightly underinflated. The “Cheatriots” have a history of bending or breaking the rules, so Brady must have told the equipment manager to make sure that the footballs were underinflated.

What you are doing is clearly illegal because it’s against the law.

The county supervisor voted against the new education tax. He must not believe in education.

“Apples a day keeps doctors away.” No one has said apples are bad, so this old saying must be true.

Wine has to be good for your health because… I mean, can you imagine a life without wine?

Studies show that slightly overweight senior citizens live longer than underweight ones. The extra weight must make people live longer.

Whenever our smoke detector beeps, my kids eat cereal for dinner. The loud beeping sound must make them want to eat cereal for some reason.

There is a scientist who works at a really good university, and he says there is no strong evidence for climate change, especially global warming. Some politicians also question climate change. So I don’t really believe it.

My neighbor cheats on his tax returns. I don’t believe anything he says.

A: “Don’t fight over small things. Just let them go.”

B: “What exactly are ‘small things’? How do I know what is small and what isn’t?”

A: “Well, small things are things you really don’t want to fight over.”

Propositions and Logic

List the set of integers that satisfy the following statement: A positive multiple of 5 and not a multiple of 2

List the set of integers that satisfy the following statement: Greater than 12 and less than or equal to 18

List the set of integers that satisfy the following statement: Even number less than 10 or odd number between 12 and 10

You qualify for a special discount if you are either

a full-time student in the state of California or

at least 18 and your income is less than $20,000 a year.

For each person below, determine if the person qualifies for this discount. If more information is needed, indicate that.

A 17-year-old full-time student at a California community college with no job

A 28-year-old man earning $50,000 a year

A 60-year-old grandmother who does not work and does not go to school

A boy in first grade

A mother making $18,000 a year and not enrolled in any college

A 22-year-old full-time student at Arizona State University with no job

A 18-year-old earning exactly $20,000 a year while attending UCLA part-time

Write the negation: Everyone failed the quiz today.

Write the negation: Someone in the car needs to use the restroom.

How can you prove this statement wrong?

“Everyone who ate at that restaurant got sick.”

“There was someone who ate at that restaurant and got sick.”

“There is no baseball player who can excel at both pitching and hitting. Everyone must choose one or the other.”

“Every student must have an ID number before registering for classes.”

Truth Tables

Translate each statement from symbolic notation into English sentences. Let A represent “Elvis is alive” and let G represent “Elvis gained weight.”

A ⋁ G

~( A ⋀ G )

G → ~ A

A ↔ ~ G

A ⋀ ~ G

~( A ⋁ G )

Create a truth table for each statement below.

A ⋀ ~ B

~(~ A ⋁ B )

( A ⋀ B ) → C

( A ⋁ B ) → ~ C

Complete the truth table for ( A ⋁ B ) ⋀ ~( A ⋀ B ).

We have been studying the inclusive or, which allows both A and B to be true. The exclusive or does not allow both to be true; it translates to “either A or B , but not both.” For each situation, decide whether the “or” is most likely exclusive or inclusive.

An entrée at a restaurant includes soup or a salad.

You should bring an umbrella or a raincoat with you.

We can keep driving on I-5 or get on I-405 at the next exit.

Use Gate 1 if you are at least 35 years old, or Gate 2 if you are younger.

You should save this document on your computer or a flash drive.

I am not sure if my pregnant wife is going to have a boy or a girl.

Consider the statement “If you are under age 17, then you cannot attend this movie.”

Write the converse.

Write the inverse.

Write the contrapositive.

Consider the statement “If you have a house in Beverly Hills, you are rich.”

Assume that the statement “If you swear, then you will get your mouth washed out with soap” is true. Which of the following statements must also be true?

If you don’t swear, then you won’t get your mouth washed out with soap.

If you don’t get your mouth washed out with soap, then you didn’t swear.

If you get your mouth washed out with soap, then you swore.

Write the negation: If Luke faces Vader, then Obi-Wan cannot interfere.

Write the negation: If you look both ways before crossing the street, then you will not get hit by a car.

Write the negation: If you weren’t talking, then you wouldn’t have missed the instructions.

Write the negation: If you score a goal now, we will win.

Assume that the biconditional statement “You will play in the game if and only if you attend all practices this week” is true. Which of the following situations could NOT happen?

You attended all practices this week and didn’t play in the game.

You didn’t attend all practices this week and played in the game.

You didn’t attend all practices this week and didn’t play in the game.

Use De Morgan’s Laws to rewrite the disjunction as a conjunction: It is not true that Tina likes Sprite or 7-Up.

Use De Morgan’s Laws to rewrite the disjunction as a conjunction: It is not true that the father or the mother of that child will be required to testify.

Use De Morgan’s Laws to rewrite the conjunction as a disjunction: It is not the case that both the House and the Senate passed the bill.

Use De Morgan’s Laws to rewrite the conjunction as a disjunction: It is not the case that you need a dated receipt and your credit card to return this item.

Analyzing Arguments

Determine whether each of the following is an inductive or deductive argument:

The new medicine works. We tried it on 100 patients, and all of them were cured.

Every student has an ID number. Sandra is a student, so she has an ID number.

Every angle of a rectangle is 90 degrees. A soccer field (pitch) is rectangular, so every corner is 90 degrees.

Everything that goes up comes down. I throw a ball up. It must come down.

Every time it rains, my grass grows fast. Rain speeds up the growth of grass.

Sports makes a person strong. My daughter plays basketball. She will be strong.

Analyze the validity of the argument.

Everyone who gets a degree in science will get a good job. I got a science degree. Therefore, I will get a good job.

If someone turns off the switch, the lights will not be on. The lights are off. Therefore, someone must have turned off the switch.

Suppose the statement: “If today is Dec. 25, then the store is closed.”

“Today is Dec. 25. Thus, the store is closed.” Which property was used? Is this valid?

“The store is not closed. So today is not Dec. 25.” Which property was used? Is this valid?

“The store is closed. Therefore, today must be Dec. 25.” Which property was used? Is this valid?

“Today is not Dec. 25. Thus, the store is open.” Which property was used? Is this valid?

For the following questions, use a Venn diagram or a truth table to determine the validity.

If a person is on this reality show, they must be self-absorbed. Laura is not self-absorbed. Therefore, Laura cannot be on this reality show.

If you are a triathlete, then you have outstanding endurance. LeBron James is not a triathlete. Therefore, LeBron does not have outstanding endurance.

Jamie must scrub the toilets or hose down the garbage cans. Jamie refuses to scrub the toilets. Therefore, Jamie will hose down the garbage cans.

Some of these kids are rude. Jimmy is one of these kids. Therefore, Jimmy is rude!

Every student brought a pencil or a pen. Marcie brought a pencil. Therefore, Marcie did not bring a pen.

If a creature is a chimpanzee, then it is a primate. If a creature is a primate, then it is a mammal. Bobo is a mammal. Therefore, Bobo is a chimpanzee.

Every cripsee is a domwow. Mekep is not a domwow. Therefore, Mekep is not a cripsee. (This sentence has a lot of made-up words, but it is still possible to check for the validity of the argument. This is a good practice for abstract thinking.)

Whoever dephels a kipoc will be bopied. I did not dephel any kipoc. Therefore, I will not be bopied. (Again, you do not need to know the meaning of each word to do this exercise.)

Problem Solving

For the following exercises, apply any problem-solving strategies and your critical-thinking skills to solve various types of problems. There is single formula or procedure to follow. Be flexible and consider all possibilities.

There are 13 postage stamps on the table. Some are 20-cent stamps while others are 45-cent stamps. The total postage value of these stamps is $4.10.

If they were all 20-cent stamps, would 13 of them add up to $4.10?

If there were five 20-cent stamps, would these stamps add up to $4.10?

How about ten 20-cent stamps? OK, you probably got some idea now.

How many 20-cent stamps are there?

Can you think of another way to solve the problem?

What would you say to a friend of yours who tries to help you out by writing a system of two equations to solve this problem?

Find the next two terms of each of the following sequences and explain why.

9, 7, 5, 3, …

0, 1, 4, 9, 16, 25, …

3, 6, 12, 24, …

0, 1, 3, 6, 10, 15, …

5, 7, 5, 5, 7, 5, 5, 7, 5, 5, …

1, 1, 2, 3, 5, 8, 13, 21, … (Fibonacci Sequence) We will study it later.

A man bought an old car for $2000. He fixed it up and sold it for $2,500. But he missed it, so he brought it back for $3,200. Later, he sold it for $4,000. How much did he make in these transactions?

Is it $4,000 - $2,000 = $2,000?

He made $500 on the first sale and then $800 on the second. But he lost $700 in between when he re-purchased it. So is it $800 - $700 = $100?

Is it $500 + $800 = $1,300?

See the pattern below. Can you make a conjecture? Is it true? Can you prove it?

1+3=4 (=22).

1+3+5=9 (=32).

1+3+5+7=16 (=42).

A heart surgeon is about to perform a medical procedure on a boy. The surgeon told the nurses, “I want you to know that this is my son. I am operating on my own child today.” Everyone there knew that the boy was the surgeon’s son. But the surgeon was not the boy’s father. How can this be true?

What can “H.D.” in this little story be?

“H.D. sat on a wall. H.D. had a great fall. All the president’s horses and all the president’s men couldn’t put H.D. together again.”

You have decided to work out at the gym at least twice a week, but never on two consecutive days. If you are to keep the same schedule every week, list all possible days of the week) you can exercise at the gym.

A man must be married to have a mother-in-law but can be single and have a brother-in-law. Explain why.

Your sprinklers are set to water your plants at 6 am every morning during summer, when the daylight saving time is in effect. Once the time goes back to regular time (in November, say from PDT to PST), what time do your sprinklers start? (Hint: it’s either 5 am or 7 am.) What is the best way to explain this to your friend?

You are to visit a friend who lives 300 miles away. You drive to his house early in the morning, averaging 60 mph, but you return in the afternoon, when the freeway is jammed, at an average speed of 40 mph. Is the overall average speed 50 mph? Why or why not?

You have 10 identical pairs of black socks and 9 identical parts of white socks in your drawer, except each pair is not “paired up,” i.e., each sock is in the drawer, separated from all others. The room is completely dark, and you cannot see which socks you are taking out. How many socks do you have to pull out if you want to be sure that you get

A pair of white socks?

A pair of black socks?

Any matching pair?

A divorced 49-year-old man with a 25-year-old son marries a young woman whose mother is a widow. The 25-year-old son marries the widow and have a baby girl.

How is that baby related to the 49-year-old man? (The baby is his son’s daughter.)

How else is that baby related to the 49-year-old man? (The baby is his wife’s mother’s daughter.)

Does that baby have a step-brother? If so, under what conditions?

Who is that baby’s step-sister?

Combine your answers to describe how the 49-year-old man is related to the baby.

A person can be ½ Chinese and ½ Italian. Are the following cases possible?

½ Japanese, ¼ Russian, ¼ Irish

3/8 Scottish, 3/8 Vietnamese, ¼ Spanish

3/8 Mexican, ¼ Turkish, and ½ Norwegian

1/6 French, ½ Canadian, 1/3 Brazilian

½ Armenian, ¼ German, ½ Swedish

John says, “I don’t have any brothers, sisters, step-brothers, or step-sisters. See that tall woman? Her father is my mother’s child.” Who is the tall woman?

Contributors and Attributions

Saburo Matsumoto CC-BY-4.0