math helps us have better problem solving skills

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Unlocking the Power of Math Learning: Strategies and Tools for Success

posted on September 20, 2023

Mathematics, the foundation of all sciences and technology, plays a fundamental role in our everyday lives. Yet many students find the subject challenging, causing them to shy away from it altogether. This reluctance is often due to a lack of confidence, a misunderstanding of unclear concepts, a move ahead to more advanced skills before they are ready, and ineffective learning methods. However, with the right approach, math learning can be both rewarding and empowering. This post will explore different approaches to learning math, strategies for success, and cutting-edge tools to help you achieve your goals.

Math Learning

Math learning can take many forms, including traditional classroom instruction, online courses, and self-directed learning. A multifaceted approach to math learning can improve understanding, engage students, and promote subject mastery. A 2014 study by the National Council of Teachers of Mathematics found that the use of multiple representations, such as visual aids, graphs, and real-world examples, supports the development of mathematical connections, reasoning, and problem-solving skills.

Moreover, the importance of math learning goes beyond solving equations and formulas. Advanced math skills are essential for success in many fields, including science, engineering, finance, health care, and technology. In fact, a report by Burning Glass Technologies found that 71% of high-salary, entry-level positions require advanced math skills.

Benefits of Math Learning

In today’s 21st-century world, having a broad knowledge base and strong reading and math skills is essential. Mathematical literacy plays a crucial role in this success. It empowers individuals to comprehend the world around them and make well-informed decisions based on data-driven understanding. More than just earning good grades in math, mathematical literacy is a vital life skill that can open doors to economic opportunities, improve financial management, and foster critical thinking. We’re not the only ones who say so:

• Math learning enhances problem-solving skills, critical thinking, and logical reasoning abilities. (Source: National Council of Teachers of Mathematics )
• It improves analytical skills that can be applied in various real-life situations, such as budgeting or analyzing data. (Source: Southern New Hampshire University )
• Math learning promotes creativity and innovation by fostering a deep understanding of patterns and relationships. (Source: Purdue University )
• It provides a strong foundation for careers in fields such as engineering, finance, computer science, and more. These careers generally correlate to high wages. (Source: U.S. Bureau of Labor Statistics )
• Math skills are transferable and can be applied across different academic disciplines. (Source: Sydney School of Education and Social Work )

How to Know What Math You Need to Learn

Often students will find gaps in their math knowledge; this can occur at any age or skill level. As math learning is generally iterative, a solid foundation and understanding of the math skills that preceded current learning are key to success. The solution to these gaps is called mastery learning, the philosophy that underpins Khan Academy’s approach to education .

Mastery learning is an educational philosophy that emphasizes the importance of a student fully understanding a concept before moving on to the next one. Rather than rushing students through a curriculum, mastery learning asks educators to ensure that learners have “mastered” a topic or skill, showing a high level of proficiency and understanding, before progressing. This approach is rooted in the belief that all students can learn given the appropriate learning conditions and enough time, making it a markedly student-centered method. It promotes thoroughness over speed and encourages individualized learning paths, thus catering to the unique learning needs of each student.

Students will encounter mastery learning passively as they go through Khan Academy coursework, as our platform identifies gaps and systematically adjusts to support student learning outcomes. More details can be found in our Educators Hub . 

Try Our Free Confidence Boosters

How to learn math.

Learning at School

One of the most common methods of math instruction is classroom learning. In-class instruction provides students with real-time feedback, practical application, and a peer-learning environment. Teachers can personalize instruction by assessing students’ strengths and weaknesses, providing remediation when necessary, and offering advanced instruction to students who need it.

Learning at Home

Supplemental learning at home can complement traditional classroom instruction. For example, using online resources that provide additional practice opportunities, interactive games, and demonstrations, can help students consolidate learning outside of class. E-learning has become increasingly popular, with a wealth of online resources available to learners of all ages. The benefits of online learning include flexibility, customization, and the ability to work at one’s own pace. One excellent online learning platform is Khan Academy, which offers free video tutorials, interactive practice exercises, and a wealth of resources across a range of mathematical topics.

Moreover, parents can encourage and monitor progress, answer questions, and demonstrate practical applications of math in everyday life. For example, when at the grocery store, parents can ask their children to help calculate the price per ounce of two items to discover which one is the better deal. Cooking and baking with your children also provides a lot of opportunities to use math skills, like dividing a recipe in half or doubling the ingredients. 

Learning Math with the Help of Artificial Intelligence (AI) 

AI-powered tools are changing the way students learn math. Personalized feedback and adaptive practice help target individual needs. Virtual tutors offer real-time help with math concepts while AI algorithms identify areas for improvement. Custom math problems provide tailored practice, and natural language processing allows for instant question-and-answer sessions. 

Using Khan Academy’s AI Tutor, Khanmigo

Transform your child’s grasp of mathematics with Khanmigo , the 24/7 AI-powered tutor that specializes in tailored, one-on-one math instruction. Available at any time, Khanmigo provides personalized support that goes beyond mere answers to nurture genuine mathematical understanding and critical thinking. Khanmigo can track progress, identify strengths and weaknesses, and offer real-time feedback to help students stay on the right track. Within a secure and ethical AI framework, your child can tackle everything from basic arithmetic to complex calculus, all while you maintain oversight using robust parental controls.

Get Math Help with Khanmigo Right Now

You can learn anything .

Math learning is essential for success in the modern world, and with the right approach, it can also be enjoyable and rewarding. Learning math requires curiosity, diligence, and the ability to connect abstract concepts with real-world applications. Strategies for effective math learning include a multifaceted approach, including classroom instruction, online courses, homework, tutoring, and personalized AI support. 

So, don’t let math anxiety hold you back; take advantage of available resources and technology to enhance your knowledge base and enjoy the benefits of math learning.

National Council of Teachers of Mathematics, “Principles to Actions: Ensuring Mathematical Success for All” , April 2014

Project Lead The Way Research Report, “The Power of Transportable Skills: Assessing the Demand and Value of the Skills of the Future” , 2020

Page. M, “Why Develop Quantitative and Qualitative Data Analysis Skills?” , 2016

Mann. EL, Creativity: The Essence of Mathematics, Journal for the Education of the Gifted. Vol. 30, No. 2, 2006, pp. 236–260, http://www.prufrock.com ’

Nakakoji Y, Wilson R.” Interdisciplinary Learning in Mathematics and Science: Transfer of Learning for 21st Century Problem Solving at University ”. J Intell. 2020 Sep 1;8(3):32. doi: 10.3390/jintelligence8030032. PMID: 32882908; PMCID: PMC7555771.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

• Grade 1 Lessons
• Grade 2 Lessons
• Grade 3 Lessons
• Grade 4 Lessons
• Grade 5 Lessons
• Math Activities

How to Improve Problem-Solving Skills in Math

Importance of Problem-Solving Skills in Math

Problem-solving skills are crucial in math education , enabling students to apply mathematical concepts and principles to real-world situations. Here’s why problem-solving skills are essential in math education:

1. Application of knowledge: Problem-solving in math requires encouraging students to apply the knowledge they acquire in the classroom to tackle real-life problems. It helps them understand the relevance of math in everyday life and enhances their critical thinking skills.

2. Developing critical thinking:  Problem-solving requires students to analyze, evaluate, and think critically about different approaches and strategies to solve a problem. It strengthens their mathematical abilities and improves their overall critical thinking skills.

3. Enhancing problem-solving skills:  Math problems often have multiple solutions, encouraging students to think creatively and explore different problem-solving strategies. It helps develop their problem-solving skills, which are valuable in various aspects of life beyond math.

4. Fostering perseverance:  Problem-solving in math often requires persistence and resilience. Students must be willing to try different approaches, learn from their mistakes, and keep trying until they find a solution. It fosters a growth mindset and teaches them the value of perseverance.

Benefits of strong problem-solving skills

Having strong problem-solving skills in math offers numerous benefits for students:

1. Improved academic performance:  Students with strong problem-solving skills are likelier to excel in math and other subjects that rely on logical reasoning and critical thinking.

2. Enhanced problem-solving abilities:  Strong problem-solving skills extend beyond math and can be applied to various real-life situations. It includes decision-making, analytical thinking, and solving complex problems creatively.

3. Increased confidence:  Successfully solving math problems boosts students’ self-confidence and encourages them to tackle more challenging tasks. This confidence spills over into other areas of their academic and personal lives.

4. Preparation for future careers:  Problem-solving skills are highly sought after by employers in various fields. Developing strong problem-solving skills in math sets students up for successful careers in engineering, technology, finance, and more.

Problem-solving skills are essential for math education and have numerous benefits for students. By fostering these skills, educators can empower students to become confident, critical thinkers who can apply their mathematical knowledge to solve real-world problems.

Understand the Problem

Breaking down the problem and identifying the key components.

To improve problem-solving math skills, it’s essential to first understand the problem at hand. Here are some tips to help break down the problem and identify its key components:

1. Read the problem carefully:  Take your time to read it attentively and ensure you understand what it asks. Pay attention to keywords or phrases that indicate what mathematical operation or concept to use.

2. Identify the known and unknown variables:  Determine what information is already given in the problem (known variables) and what you need to find (unknown variables). This step will help you analyze the problem more effectively.

3. Define the problem in your own words:  Restate the problem using your own words to ensure you clearly understand what needs to be solved. It can help you focus on the main objective and eliminate any distractions.

4. Break the problem into smaller parts:  Complex math problems can sometimes be overwhelming. Breaking them down into smaller, manageable parts can make them more approachable. Identify any sub-problems or intermediate steps that must be solved before reaching the final solution.

Reading and interpreting math word problems effectively

Many math problems are presented as word problems requiring reading and interpreting skills. Here are some strategies to help you effectively understand and solve math word problems:

1. Highlight key information:  As you read the word problem, underline or highlight any important details, such as numbers, units of measurement, or specific keywords related to mathematical operations.

2. Visualize the problem:  Create visual representations, such as diagrams or graphs, to help you understand the problem better. Visualizing the problem can make determining what steps to take and how to approach the solution easier.

3. Translate words into equations:  Convert the information in the word problem into mathematical equations or expressions. This translation step helps you transform the problem into a solvable math equation.

4. Solve step by step:  Break down the problem into smaller steps and solve each step individually. This approach helps you avoid confusion and progress toward the correct solution.

Improving problem-solving skills in math requires practice and patience. By understanding the problem thoroughly, breaking it into manageable parts, and effectively interpreting word problems, you can confidently enhance your ability to solve math problems.

Use Visual Representations

Using diagrams, charts, and graphs to visualize the problem.

One effective way to improve problem-solving skills in math is to utilize visual representations. Visual representations , such as diagrams, charts, and graphs, can help make complex problems more tangible and easily understood. Here are some ways to use visual representations in problem-solving:

1. Draw Diagrams:  When faced with a word problem or a complex mathematical concept, drawing a diagram can help break down the problem into more manageable parts. For example, suppose you are dealing with a geometry problem. In that case, sketching the shapes involved can provide valuable insights and help you visualize the problem better.

2. Create Charts or Tables:  For problems that involve data or quantitative information, creating charts or tables can help organize the data and identify patterns or trends. It can be particularly useful in analyzing data from surveys, experiments, or real-life scenarios.

3. Graphical Representations:  Graphs can be powerful tools in problem-solving, especially when dealing with functions, equations, or mathematical relationships. Graphically representing data or equations makes it easier to identify key features that may be hard to spot from a numerical representation alone, such as intercepts or trends.

Benefits of visual representation in problem-solving

Using visual representations in problem-solving offers several benefits:

1. Enhances Comprehension:  Visual representations provide a visual context for abstract mathematical concepts, making them easier to understand and grasp.

2. Encourages Critical Thinking:  Visual representations require active engagement and critical thinking skills. Students can enhance their problem-solving and critical thinking abilities by analyzing and interpreting visual data.

3. Promotes Pattern Recognition: Visual representations simplify identifying patterns, trends, and relationships within data or mathematical concepts. It can lead to more efficient problem-solving and a deeper understanding of mathematical principles.

4. Facilitates Communication:  Visual representations can be shared and discussed, helping students communicate their thoughts and ideas effectively. It can be particularly useful in collaborative problem-solving environments.

Incorporating visual representations into math problem-solving can significantly enhance understanding, critical thinking, pattern recognition, and communication skills. Students can approach math problems with a fresh perspective and improve their problem-solving abilities using visual tools.

Work Backwards

Understanding the concept of working backward in math problem-solving.

Working backward is a problem-solving strategy that starts with the solution and returns to the given problem. This approach can be particularly useful in math, as it helps students break down complex problems into smaller, more manageable steps. Here’s how to apply the concept of working backward in math problem-solving:

1. Identify the desired outcome : Start by clearly defining the goal or solution you are trying to reach. It could be finding the value of an unknown variable, determining a specific measurement, or solving for a particular quantity.

2. Visualize the result : Imagine the final step or solution. It will help you create a mental image of the steps needed to reach that outcome.

3. Trace the steps backward : Break down the problem into smaller steps, working backward from the desired outcome. Think about what needs to happen immediately before reaching the final solution and continue tracing the steps back to the beginning of the problem.

4. Check your work : Once you have worked backward to the beginning of the problem, double-check your calculations and steps to ensure accuracy.

Real-life examples and applications of working backward

Working backward is a valuable problem-solving technique in math and has real-life applications. Here are a few examples:

1. Financial planning : When creating a budget, you can work backward by determining your desired savings or spending amount and then calculating how much income or expenses are needed to reach that goal.

2. Project management : When planning a project, you can work backward by setting a fixed deadline and then determining the necessary steps and timelines to complete the project on time.

3. Game strategy : In games like chess or poker, working backward can help you anticipate your opponent’s moves and plan your strategy accordingly.

4. Recipe adjustments : When modifying a recipe, you can work backward by envisioning the final taste or texture you want to achieve and adjusting the ingredients or cooking methods accordingly.

By practicing working backward in math and applying it to real-life situations, you can enhance your problem-solving abilities and find creative solutions to various challenges.

Try Different Strategies

When solving math problems, it’s essential to have a repertoire of problem-solving strategies. You can improve your problem-solving skills and tackle various mathematical challenges by trying different approaches. Here are some strategies to consider:

Exploring Various Problem-Solving Strategies

1. Guess and Check:  This strategy involves making an educated guess and checking if it leads to the correct solution. It can be useful when dealing with trial-and-error problems.

2. Drawing a Diagram:  Visually representing the problem through diagrams or graphs can help you understand and solve it more effectively. This strategy is particularly useful in geometry and algebraic reasoning.

3. Using Logic:  Using logical reasoning is useful for breaking down complicated problems into smaller, more manageable components. This strategy is especially useful in mathematical proofs and logical puzzles.

4. Working Backwards:  Start with the desired outcome and return to the given information. When dealing with equations or word problems, this approach can assist.

5. Using Patterns:  Look for patterns and relationships within the problem to determine a solution. This approach can be used for different mathematical problems, such as sequences and numerical patterns.

When and How to Apply Different Strategies in Math Problem-Solving

Knowing when and how to apply different problem-solving strategies is crucial for success in math. Here are some tips:

• Understand the problem: Read the problem carefully and identify the key information and requirements.
• Select an appropriate strategy: Choose the most appropriate problem-solving strategy for the problem.
• Apply the chosen strategy: Implement the selected strategy, following the necessary steps.
• Check your solution: Verify your answer by double-checking the calculations or applying alternative methods.
• Reflect on the process: After solving the problem, take a moment to reflect and evaluate your problem-solving approach. Identify areas for improvement and consider alternative strategies that could have been used.

By exploring different problem-solving strategies and applying them to various math problems, you can enhance your problem-solving skills and develop a versatile toolkit for tackling mathematical challenges. Practice and persistence are key to honing your problem-solving abilities in math.

Key takeaways and tips for improving problem-solving skills in math

In conclusion, developing strong problem-solving skills in math is crucial for success in this subject. Here are some key takeaways and tips to help you improve your problem-solving abilities:

• Practice regularly:  The more you practice solving math problems, the better you will become at identifying patterns, applying strategies, and finding solutions.
• Break down the problem:  When faced with a complex math problem, break it into smaller, more manageable parts. It will make it easier to understand and solve.
• Understand the problem:  Before diving into a solution, fully understand the problem. Identify what information is given and what you are asked to find.
• Draw diagrams or visualize:  Use visual aids, such as diagrams or sketches, to help you better understand the problem and visualize the solution.
• Use logical reasoning:  Apply logical reasoning skills to analyze the problem and determine the most appropriate approach or strategy.
• Try different strategies:  If one approach doesn’t work, don’t be afraid to try different strategies or methods. There are often multiple ways to solve a math problem.
• Seek help and collaborate:  Don’t hesitate to seek help from your teacher, classmates, or online resources. Collaborating with others can provide different perspectives and insights.
• Learn from mistakes:  Mistakes are a valuable learning opportunity. Analyze your mistakes, understand where you went wrong, and learn from them to avoid making the same errors in the future.
• Grade 6 Lessons
• Grade 7 Lessons
• Grade 8 Lessons
• Kindergarten
• Math Lessons Online
• Math Tutorial
• Multiplication
• Subtraction
• #basic mathematic
• #Basic Mathematical Operation
• #best math online math tutor
• #Best Math OnlineTutor
• #dividing fractions
• #effective teaching
• #grade 8 math lessons
• #linear equation
• #Math Online Blog
• #mathematical rule
• #mutiplying fractions
• #odd and even numbers
• #Online Math Tutor
• #online teaching
• #order of math operations
• #pemdas rule
• #Point-Slope Form
• #Precalculus
• #Slope-Intercept Form
• #Tutoring Kids

Thank you for signing up!

GET IN TOUCH WITH US

How to Improve Problem-Solving Skills: Mathematics and Critical Thinking

In today’s rapidly changing world, problem-solving has become a quintessential skill. When we discuss the topic, it’s natural to ask, “What is problem-solving?” and “How can we enhance this skill, particularly in children?” The discipline of mathematics offers a rich platform to explore these questions. Through math, not only do we delve into numbers and equations, but we also explore how to improve problem-solving skills and how to develop critical thinking skills in math. Let’s embark on this enlightening journey together.

What is Problem-Solving?

At its core, problem-solving involves identifying a challenge and finding a solution. But it’s not always as straightforward as it sounds. So, what is problem-solving? True problem-solving requires a combination of creative thinking and logical reasoning. Mathematics, in many ways, embodies this blend. When a student approaches a math problem, they must discern the issue at hand, consider various methods to tackle it, and then systematically execute their chosen strategy.

But what is problem-solving in a broader context? It’s a life skill. Whether we’re deciding the best route to a destination, determining how to save for a big purchase, or even figuring out how to fix a broken appliance, we’re using problem-solving.

How to Develop Critical Thinking Skills in Math

Critical thinking goes hand in hand with problem-solving. But exactly how to develop critical thinking skills in math might not be immediately obvious. Here are a few strategies:

• Contextual Learning: Teaching math within a story or real-life scenario makes it relevant. When students see math as a tool to navigate the world around them, they naturally begin to think critically about solutions.
• Open-ended Questions: Instead of merely seeking the “right” answer, encourage students to explain their thought processes. This nudges them to think deeply about their approach.
• Group Discussions: Collaborative learning can foster different perspectives, prompting students to consider multiple ways to solve a problem.
• Challenging Problems: Occasionally introducing problems that are a bit beyond a student’s current skill level can stimulate critical thinking. They will have to stretch their understanding and think outside the box.

What are the Six Basic Steps of the Problem-Solving Process?

Understanding how to improve problem-solving skills often comes down to familiarizing oneself with the systematic approach to challenges. So, what are the six basic steps of the problem-solving process?

• Identification: Recognize and define the problem.
• Analysis: Understand the problem’s intricacies and nuances.
• Generation of Alternatives: Think of different ways to approach the challenge.
• Decision Making: Choose the most suitable method to address the problem.
• Implementation: Put the chosen solution into action.
• Evaluation: Reflect on the solution’s effectiveness and learn from the outcome.

By embedding these steps into mathematical education, we provide students with a structured framework. When they wonder about how to improve problem-solving skills or how to develop critical thinking skills in math, they can revert to this process, refining their approach with each new challenge.

Making Math Fun and Relevant

At Wonder Math, we believe that the key to developing robust problem-solving skills lies in making math enjoyable and pertinent. When students see math not just as numbers on a page but as a captivating story or a real-world problem to be solved, their engagement skyrockets. And with heightened engagement comes enhanced understanding.

As educators and parents, it’s crucial to continuously ask ourselves: how can we demonstrate to our children what problem-solving is? How can we best teach them how to develop critical thinking skills in math? And how can we instill in them an understanding of the six basic steps of the problem-solving process?

The answer, we believe, lies in active learning, contextual teaching, and a genuine passion for the beauty of mathematics.

The Underlying Beauty of Mathematics

Often, people perceive mathematics as a rigid discipline confined to numbers and formulas. However, this is a limited view. Math, in essence, is a language that describes patterns, relationships, and structures. It’s a medium through which we can communicate complex ideas, describe our universe, and solve intricate problems. Understanding this deeper beauty of math can further emphasize how to develop critical thinking skills in math.

Why Mathematics is the Ideal Playground for Problem-Solving

Math provides endless opportunities for problem-solving. From basic arithmetic puzzles to advanced calculus challenges, every math problem offers a chance to hone our problem-solving skills. But why is mathematics so effective in this regard?

• Structured Challenges: Mathematics presents problems in a structured manner, allowing learners to systematically break them down. This format mimics real-world scenarios where understanding the structure of a challenge can be half the battle.
• Multiple Approaches: Most math problems can be approached in various ways . This teaches learners flexibility in thinking and the ability to view a single issue from multiple angles.
• Immediate Feedback: Unlike many real-world problems where solutions might take time to show results, in math, students often get immediate feedback. They can quickly gauge if their approach works or if they need to rethink their strategy.

Enhancing the Learning Environment

To genuinely harness the power of mathematics in developing problem-solving skills, the learning environment plays a crucial role. A student who is afraid of making mistakes will hesitate to try out different approaches, stunting their critical thinking growth.

However, in a nurturing, supportive environment where mistakes are seen as learning opportunities, students thrive. They become more willing to take risks, try unconventional solutions, and learn from missteps. This mindset, where failure is not feared but embraced as a part of the learning journey, is pivotal for developing robust problem-solving skills.

Incorporating Technology

In our digital age, technology offers innovative ways to explore math. Interactive apps and online platforms can provide dynamic problem-solving scenarios, making the process even more engaging. These tools can simulate real-world challenges, allowing students to apply their math skills in diverse contexts, further answering the question of how to improve problem-solving skills.

More than Numbers 

In summary, mathematics is more than just numbers and formulas—it’s a world filled with challenges, patterns, and beauty. By understanding its depth and leveraging its structured nature, we can provide learners with the perfect platform to develop critical thinking and problem-solving skills. The key lies in blending traditional techniques with modern tools, creating a holistic learning environment that fosters growth, curiosity, and a lifelong love for learning.

Join us on this transformative journey at Wonder Math. Let’s make math an adventure, teaching our children not just numbers and equations, but also how to improve problem-solving skills and navigate the world with confidence. Enroll your child today and witness the magic of mathematics unfold before your eyes!

FAQ: Mathematics and Critical Thinking

1. what is problem-solving in the context of mathematics.

Problem-solving in mathematics refers to the process of identifying a mathematical challenge and systematically working through methods and strategies to find a solution.

2. Why is math considered a good avenue for developing problem-solving skills?

Mathematics provides structured challenges and allows for multiple approaches to find solutions. This promotes flexibility in thinking and encourages learners to view problems from various angles.

3. How does contextual learning enhance problem-solving abilities?

By teaching math within a story or real-life scenario, it becomes more relevant for the learner. This helps them see math as a tool to navigate real-world challenges , thereby promoting critical thinking.

4. What are the six basic steps of the problem-solving process in math?

The six steps are: Identification, Analysis, Generation of Alternatives, Decision Making, Implementation, and Evaluation.

5. How can parents support their children in developing mathematical problem-solving skills?

Parents can provide real-life contexts for math problems , encourage open discussions about different methods, and ensure a supportive environment where mistakes are seen as learning opportunities.

6. Are there any tools or apps that can help in enhancing problem-solving skills in math?

Yes, there are various interactive apps and online platforms designed specifically for math learning. These tools provide dynamic problem-solving scenarios and simulate real-world challenges, making the learning process engaging.

7. How does group discussion foster critical thinking in math?

Group discussions allow students to hear different perspectives and approaches to a problem. This can challenge their own understanding and push them to think about alternative methods.

8. Is it necessary to always follow the six steps of the problem-solving process sequentially?

While the six steps provide a structured approach, real-life problem-solving can sometimes be more fluid. It’s beneficial to know the steps, but adaptability and responsiveness to the situation are also crucial.

9. How does Wonder Math incorporate active learning in teaching mathematics?

Wonder Math integrates mathematics within engaging stories and real-world scenarios, making it fun and relevant. This active learning approach ensures that students are not just passive recipients but active participants in the learning process.

10. What if my child finds a math problem too challenging and becomes demotivated?

It’s essential to create a supportive environment where challenges are seen as growth opportunities. Remind them that every problem is a chance to learn, and it’s okay to seek help or approach it differently.

Related posts

Summer Math Programs: How They Can Prevent Learning Loss in Young Students

As summer approaches, parents and educators alike turn their attention to how they can support young learners during the break. Summer is a time for relaxation, fun, and travel, yet it’s also a critical period when learning loss can occur. This phenomenon, often referred to as the “summer slide,” impacts students’ progress, especially in foundational subjects like mathematics. It’s reported…

Math Programs 101: What Every Parent Should Know When Looking For A Math Program

  As a parent, you know that a solid foundation in mathematics is crucial for your child’s success, both in school and in life. But with so many math programs and math help services out there, how do you choose the right one? Whether you’re considering Outschool classes, searching for “math tutoring near me,” or exploring tutoring services online, understanding…

• Our Mission

6 Tips for Teaching Math Problem-Solving Skills

Solving word problems is tougher than computing with numbers, but elementary teachers can guide students to do the deep thinking involved.

A growing concern with students is the ability to problem-solve, especially with complex, multistep problems. Data shows that students struggle more when solving word problems than they do with computation , and so problem-solving should be considered separately from computation. Why?

Consider this. When we’re on the way to a new destination and we plug in our location to a map on our phone, it tells us what lane to be in and takes us around any detours or collisions, sometimes even buzzing our watch to remind us to turn. When I experience this as a driver, I don’t have to do the thinking. I can think about what I’m going to cook for dinner, not paying much attention to my surroundings other than to follow those directions. If I were to be asked to go there again, I wouldn’t be able to remember, and I would again seek help.

If we can switch to giving students strategies that require them to think instead of giving them too much support throughout the journey to the answer, we may be able to give them the ability to learn the skills to read a map and have several ways to get there.

Here are six ways we can start letting students do this thinking so that they can go through rigorous problem-solving again and again, paving their own way to the solution. 

1. Link problem-solving to reading

When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools like counters or base 10 blocks, drawing a quick sketch of the problem, retelling the story in their own words, etc., can really help them to utilize the skills they already have to make the task less daunting.

We can break these skills into specific short lessons so students have a bank of strategies to try on their own. Here's an example of an anchor chart that they can use for visualizing . Breaking up comprehension into specific skills can increase student independence and help teachers to be much more targeted in their problem-solving instruction. This allows students to build confidence and break down the barriers between reading and math to see they already have so many strengths that are transferable to all problems.

2. Avoid boxing students into choosing a specific operation

It can be so tempting to tell students to look for certain words that might mean a certain operation. This might even be thoroughly successful in kindergarten and first grade, but just like when our map tells us where to go, that limits students from becoming deep thinkers. It also expires once they get into the upper grades, where those words could be in a problem multiple times, creating more confusion when students are trying to follow a rule that may not exist in every problem.

We can encourage a variety of ways to solve problems instead of choosing the operation first. In first grade, a problem might say, “Joceline has 13 stuffed animals and Jordan has 17. How many more does Jordan have?” Some students might choose to subtract, but a lot of students might just count to find the amount in between. If we tell them that “how many more” means to subtract, we’re taking the thinking out of the problem altogether, allowing them to go on autopilot without truly solving the problem or using their comprehension skills to visualize it. 

3. Revisit ‘representation’

The word “representation” can be misleading. It seems like something to do after the process of solving. When students think they have to go straight to solving, they may not realize that they need a step in between to be able to support their understanding of what’s actually happening in the problem first.

Using an anchor chart like one of these ( lower grade , upper grade ) can help students to choose a representation that most closely matches what they’re visualizing in their mind. Once they sketch it out, it can give them a clearer picture of different ways they could solve the problem.

Think about this problem: “Varush went on a trip with his family to his grandmother’s house. It was 710 miles away. On the way there, three people took turns driving. His mom drove 214 miles. His dad drove 358 miles. His older sister drove the rest. How many miles did his sister drive?”

If we were to show this student the anchor chart, they would probably choose a number line or a strip diagram to help them understand what’s happening.

If we tell students they must always draw base 10 blocks in a place value chart, that doesn’t necessarily match the concept of this problem. When we ask students to match our way of thinking, we rob them of critical thinking practice and sometimes confuse them in the process. 

4. Give time to process

Sometimes as educators, we can feel rushed to get to everyone and everything that’s required. When solving a complex problem, students need time to just sit with a problem and wrestle with it, maybe even leaving it and coming back to it after a period of time.

This might mean we need to give them fewer problems but go deeper with those problems we give them. We can also speed up processing time when we allow for collaboration and talk time with peers on problem-solving tasks. 

5. Ask questions that let Students do the thinking

Questions or prompts during problem-solving should be very open-ended to promote thinking. Telling a student to reread the problem or to think about what tools or resources would help them solve it is a way to get them to try something new but not take over their thinking.

These skills are also transferable across content, and students will be reminded, “Good readers and mathematicians reread.” 

6. Spiral concepts so students frequently use problem-solving skills

When students don’t have to switch gears in between concepts, they’re not truly using deep problem-solving skills. They already kind of know what operation it might be or that it’s something they have at the forefront of their mind from recent learning. Being intentional within their learning stations and assessments about having a variety of rigorous problem-solving skills will refine their critical thinking abilities while building more and more resilience throughout the school year as they retain content learning in the process. 

Problem-solving skills are so abstract, and it can be tough to pinpoint exactly what students need. Sometimes we have to go slow to go fast. Slowing down and helping students have tools when they get stuck and enabling them to be critical thinkers will prepare them for life and allow them multiple ways to get to their own destination.

Math in Daily Life

Table of contents.

Kids are very inquisitive. They need to be explained the importance of Math in their daily life at an early age, for them to enjoy doing it instead of doing it without the love for the subject.

Math in Daily Life: When am I ever going to use Math?

The truth is that we use math all the time!

It is pertinent to note how one experiences mathematical applications in daily life from the time one gets up from bed till one goes to bed in the night.

Be it a cook or a farmer, a carpenter, a mechanic, a shopkeeper or a doctor, an engineer or a scientist, a musician or a magician, an artist or a tailor, everyone needs math in daily life.

Math in Daily Life - PDF

This will help us understand the importance of maths in daily life. It summarizes some real-life examples with activities. The importance of maths in our daily life and few real-life examples are mentioned below in the Downloadable PDF.

Why is Math Important in our Daily Life?

Math is very useful in everyday life. Math can help us do many things that are important in our everyday lives. Here are some daily tasks for which math is important:

Managing time:  Keeping a track of time is very important to do all you love to do

Budgeting:  Managing money, understanding discounts, and buying for the best price

Sports:  Score, Time, Strategizing to win

Cooking:  Measuring the ingredients to add to a recipe, kitchen inventory planning

Exercising and Dieting

Driving:  Distance traveled, the shortest route to take to reach a destination

Home Decorating

Stitching:  Measurements to stitch a dress

Critical Thinking

The base of other Subjects

Some Real-Life Examples with Activities

  managing time.

 When we get up in the morning, we see the time of waking to verify whether we have enough time to complete various tasks. (Awareness of time, reading a clock/watch, planning one’s routine)

Task: Encourage the kids to make a daily timetable for their daily activities allocating time for their hobbies, academics, leisure, sports, etc.

How much is this shirt or blouse going to cost once the 50% sale is applied? What about once the taxes are added? Do you prefer to gather your things and hope for a great deal on the cash counter? Or know the price before heading there.

That takes math knowledge and at least a basic understanding of how percentages work.

Task: Fix pocket money for your kids and guide them to manage it in a proper way.

We set our routine according to our workout schedule, count the number of repetitions while exercising, etc., just based on math.

Task: let the kids practice any type of exercise like skipping, push-ups, running, and ask them to keep a count of their repetitions.

Basic knowledge of math also helps keep track of scores for every sports activity. Geometry and trigonometry can help your teens who want to improve their skills in sports. It can help them find the best way to hit a ball, make a basket or run around the track.

Task: Introduce the kids to a new sport on TV and let them judge the winning team.

The recipe calls for “3 tablespoons” of salt. You only have a teaspoon or a soup spoon. The recipe calls for “2 cups,” but you only have a quarter cup measuring tool and a half cup measuring tool. How much adds up to “2 ”? You may know the answer.

But that’s because you understand math, fractions, and conversions.

Task: Bake a cake :)

Operating a car or motorcycle is ultimately nothing but a series of calculations viz., How many kilometers needed to reach the destination? How much petrol in the car? How many kilometers per hour am I able to drive? How many kilometers per liter does my car get? Oh no, I’ve hit a traffic jam, and now my pace has slowed, am I still going to make it to work on time?

All of these questions are extremely easily answered with basic math skills.

Task: Calculate the speed of the school bus by using the distance and time of travel.

How many rolls of wallpaper do we need for this wall? What’s the difference between a meter and a square meter? Do we have enough space to fit in your favorite couch? Common questions when you are trying to set up your new space or apartment. It's very important to know these basics before you head to a store, otherwise, you will end up coming back empty-handed as the sales representative won’t be able to help you without the proper input from your side.

You should have a fair knowledge of dimensions and units and unit conversions to be able to sail through. It seems fairly simple if you know how to do the math.

Task: Help the kids to measure their study table.

Just home decorating, math is also an essential concept of fashion designing. From taking measurements, estimating the quantity and quality of clothes, choosing the color theme, estimating the cost and profit, to produce cloth according to the needs and tastes of the customers, math is followed at every stage.

Task: Join the cut pieces of waste cloth and make a small table cover.

Technically ‘critical thinking’ is not even Math as there are no numbers involved. But knowledge of Math surely increases the ability to think critically.

The more math skills you gain, the more you observe the minute details, question the available data, rule out unnecessary data and analyze it further for your benefit.

Task: Solve a puzzle

The base of all other subjects

Though math is itself a unique subject. But, you would be surprised to know that it forms the base for every subject. The subjects like physics, chemistry, economics, history, accountancy, statistics, in fact; every subject is based upon math.

So, next time you say, “I’m not going to study this math subject ever!” remember, this subject will not be going to leave you ever.

Task: Takedown the important dates in the History in chronological order.

Math is a tool in our hands to make our life smoother. The more mathematical we are in our approach, the more rational would be our thoughts. It’s time to understand the importance of the subject and enjoy the beauty of it. Math is a medium that should be embraced by everyone in all our walks of life.

About Cuemath

Cuemath, a student-friendly mathematics and coding platform, conducts regular  Online Classes  for academics and skill-development, and their Mental Math App, on both  iOS  and  Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath Fee structure and sign up for a free trial.

Frequently Asked Questions (FAQs)

What does math help with in life.

Math helps us have better problem-solving skills. Math helps us think analytically and have better reasoning abilities. The reasoning is our ability to think logically about a situation. Analytical and reasoning skills are essential because they help us solve problems and look for solutions.

Why is math so hard?

Math seems difficult because it takes time and energy. Many people don't experience sufficient time to "get" math lessons, and they fall behind as the teacher moves on. Many move on to study more complex concepts with a shaky foundation. We often end up with a weak structure that is doomed to collapse at some point.

What is the need and importance of mathematics in daily life?

Mathematics makes our life orderly and prevents chaos. Certain qualities that are nurtured by mathematics are the power of reasoning, creativity, abstract or spatial thinking, critical thinking, problem-solving ability, and even effective communication skills.

Why is Math Important in Life?

Q1. Jenny has six apples.  If she gives away four apples, how many apples does she have remaining? Q2. Two trains are traveling nonstop to Kansas City, one leaving from Boston (1450 miles away) at 50 miles per hour and one leaving from San Francisco (1850 miles away) at 40 miles per hour.  Both trains leave their origins at the exact same time early in the morning.  Which train will arrive first, and what will be the time difference of the two trains’ arrival in their final destination in Kansas City? Q3. What is the radius of a circle with circumference 2π?  

(Check the bottom of this blog post for the answers to the math problems posted above!)

While it may seem like math problems like the ones above have no real use in life, this couldn’t be farther from the truth!  Math is incredibly important in our lives and, without realizing it, we use mathematical concepts, as well as the skills we learn from doing math problems every day.  The laws of mathematics govern everything around us, and without a good understanding of them, one can encounter significant difficulties in life.

Read on to learn a few reasons that math is a powerful and incredibly useful tool.

1. Learning math is good for your brain

Research conducted by Dr. Tanya Evans of Stanford University indicates that children who know math can recruit certain brain regions more reliably, and have higher gray matter volume in those regions, than those who perform more poorly in math.  The brain regions involved in higher math skills in high-performing children were associated with various cognitive tasks involving visual attention and decision-making.  While correlation may not imply causation, this study indicates that the same brain regions that help you do math are recruited in decision-making and attentional processes.

2. Math helps you tell time

“I’m late, I’m late for a very important date.” – White Rabbit from the movie Alice in Wonderland .  Don’t let your ignorance of math make you like the White Rabbit! A recent study indicated that 4 out of 5 children living in Oklahoma City can’t read the hands on an analog clock to tell time.  Knowing math, and particularly fractions , can help you better tell time.  While analog clocks may eventually become obsolete, don’t let your ability to tell time become outdated!  Use your knowledge of fractions to help you tell time on analog clocks that have an hour, minute, and (sometimes) second hand.

3. Math helps you with your finances

Math can be helpful for balancing your budget because you will have a good understanding of how to make sure that your costs are less than the money you have.  Balancing one’s bank account, for example, is an important life skill that requires math in order to subtract balances.  People who know math are therefore less likely to go into debt because they did not know how much money they had versus how much money they spent.

4. Math makes you a better cook (or baker)

With knowledge of math, for example, you can quickly deduce that a half-cup of flour is the same thing as eight tablespoons of flour.  This skill can prove handy if you find that your half-cup measure is missing.  Likewise, if you are cooking from a recipe that serves four people, but you need to feed eight people, your math skills tell you that you can simply double all of the necessary ingredients.  Without math, you may not have enough food (or have too much food) to feed your guest!

5. Math helps us have better problem-solving skills

Math helps us think analytically and have better reasoning abilities.  Analytical thinking refers to the ability to think critically about the world around us.  Reasoning is our ability to think logically about a situation.  Analytical and reasoning skills are essential because they help us solve problems and look for solutions.  While it may seem far-fetched to believe that solving the train problem above can help you solve a problem in your life, the skills that you use in framing the problem, identifying the knowns and unknowns, and taking steps to solve the problem can be a very important strategy that is applicable to other issues in life.

6. Practically every career uses math in some way.

Obviously, mathematicians and scientists rely on mathematical principles to do the most basic aspects of their work, such as test hypotheses.  While scientific careers famously involve math, they are not the only careers to do so.  Even operating a cash register requires that one understands basic arithmetic. People working in a factory must be able to do mental arithmetic to keep track of the parts on the assembly line and must, in some cases, manipulate fabrication software utilizing geometric properties (such as the dimensions of a part) in order to build their products.  Really, any job requires math because you must know how to interpret your paycheck and balance your budget.

7. Math is all around us and helps us understand the world better

To live in a mathematically-driven world and not know math is like walking through an art museum with your eyes closed.  Learning and appreciating math can help you appreciate things that you would not otherwise notice about the world.   In reality, math is everywhere ! Don’t believe me?  Read on for some examples of math in nature.

Bees, masters of geometry, use hexagons  to build their honeycombs.  The Fibonacci sequence , a famous sequence of numbers in mathematics, is found throughout nature: in pinecones, seashells, trees, flowers, and leaves.

The number pi can also be observed all around us.  Pi is a cool number with many unique properties.  Pi is approximately 3.14, but in reality, it is greater than 3.14, with an infinite string of numbers after the decimal point. Because pi is, in reality, an infinitely long number, it is expressed as the Greek letter pi (π).  It cannot be expressed as a fraction; numbers that cannot be expressed as fractions are said to be irrational .  Pi is also transcendental , which means that it is non-algebraic; this means that pi cannot be the solution of single-variable polynomial equations whose coefficients are all integers.  (By definition, all transcendental numbers are also irrational.)

The number pi can be observed in the shapes of rivers.  The ratio of a river’s length to the distance from the source to its mouth is called the “meandering ratio.”  The average meandering ratio of rivers approaches the number pi.  It makes sense that the average meandering ratio of rivers approaches pi, because rivers tend to bend into loops, which are circular in nature.  The ratio of a circle’s circumference to its diameter is also equal to pi.

Now that you know more about pi and about how math governs nature, don’t you feel that you have a greater command over the mathematical laws of the universe?  It can be empowering to learn about mathematical principles because it can help make sense of a world that, oftentimes, does not make much sense.

8. Math can make you more popular

Before you start to disagree with me, think about how great it is to go to dinner with a friend who can quickly divide a check in their mind to determine how much each person needs to pay to split the bill.  Your knowledge of fractions can also help you divide a pizza among a few people.  While math is popularly the realm of nerds, your ability to avoid awkward confusion and silence as you and your friends try to divide a pizza or a dinner bill is a truly valuable skill.  Be known as the cool (yes, I said cool ) person that knows how to do mental math quickly!

9. Math can help you shop for a good sale

Not only will your quick mental arithmetic skills help you become known as the smart person who everyone appreciates when the waiter brings the check to your table, your math skills can also help you shop.  Knowledge of percentages and how to calculate them quickly can help you save time when shopping at a sale at the mall – for example, to quickly calculate a discounted price, or to determine whether you’ve been correctly charged when paying for a shirt at the store.  You don’t need a Ph.D. in math to develop some quick mental arithmetic skills; they can help you in these and other areas of your life in the long run.

Tip: use the 10 rule while sale-shopping.   If you want to brush up on your math skills to be a better bargain-hunter, remember this rule: to subtract 10 from a price, you can just move the decimal place to the left by one digit.  Take, for example, a shirt that has a price of $25.00 and is on sale for an additional 20 off.  You can move the decimal over to the left by one digit to calculate 10 off – $2.50.  Since 20 off is 2 x 10 off, you can quickly multiply $2.50 x 2 to get the discount amount – $5.00.  Subtract the discount amount from the original price of the shirt: $25.00 – $5.00 = $20.00.  You can use the 10 rule to quickly calculate 10 of the price and multiply it by a factor that can help you estimate price discounts quickly.

10. Math is a universal language

Sure, it’s mostly equations, numbers, and some Greek letters, but math is understood the same virtually all over the world (and who knows, maybe all over the universe)!  A math equation doesn’t need to be translated to another language to be understood by someone on the other side of the planet.  A mathematical law doesn’t change because someone has a different religion than you or speaks a different language from you.  2 + 2 = 4 in every single place on planet Earth.  Pretty cool! The universality of math is one of the many things that makes it such a powerful tool and, indeed, essential life skill.

In summary, math is not only important for success in life; it is all around us.  The laws of mathematics are evident throughout the world, including in nature, and the problem-solving skills obtained from completing math homework can help us tackle problems in other areas of life.  While many may complain that math is boring or complicated, the truth is that a life devoid of math means that we go around experiencing the world on a much less interesting level than we could.

Math problem answers: A1. Two apples A2. To solve this problem, simply divide the distance travelled for each train by its speed to obtain the time that the journey will take.  Assuming that the trains travel a uniform velocity and make no stops, The Boston train will arrive in Kansas City in (1450 / 50) = 29 hours. The San Francisco train will arrive in (1850/40) = 46.25 hours.  To calculate the time difference, simply subtract 46.25 from 29 = 17.25. Therefore, the Boston train will arrive first – and the San Francisco train will arrive 17.25 hours later. A3. The circumference of a circle is equal to the diameter of the circle times pi. Therefore, dividing the circumference (2π) by π gives us the diameter, which is 2.  The radius is half the diameter, so in this case, 2/2 = 1.  Therefore, the radius of a circle with circumference 2π is equal to 1.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2018

The Problem-solving Classroom

• Visualising
• Working backwards
• Reasoning logically
• Conjecturing
• Working systematically
• Looking for patterns
• Trial and improvement.

• stage of the lesson 
• level of thinking
• mathematical skill.
• The length of student response increases (300-700%)
• More responses are supported by logical argument.
• An increased number of speculative responses.
• The number of questions asked by students increases.
• Student - student exchanges increase (volleyball).
• Failures to respond decrease.
• 'Disciplinary moves' decrease.
• The variety of students participating increases.  As does the number of unsolicited, but appropriate contributions.
• Student confidence increases.
• conceptual understanding
• procedural fluency
• strategic competence
• adaptive reasoning
• productive disposition

Trending Post : French Toast your kids will love

5 Ways to Build Math Problem Solving Skills (based on brain research)

Whether talking about state tests or meeting with your team to plan the next math unit, the conversation inevitably turns to word problems. But knowing how to build math problem-solving skills without resorting to pages of boring story problem practice can be hard.

These days word problems aren’t the basic one-step wonders that many of us dealt with as students. Instead, multi-step story problems that require students to apply multiple concepts and skills are incorporated into instruction and state assessments.

Understanding brain research can help simply the process of teaching this challenging format of math problem-solving to students, including those who struggle.

What research says about building master problem solvers in math

Have you seen how many math skills we must teach these days? No teacher has enough time to build critical math skills AND effectively teach problem-solving…or do they?

Research would argue we are going about these tasks all wrong. They say there are many reasons students struggle with math word problems , but one big one is that we aren’t doing what’s best for the brain. Instead, here’s what the brain research says about the must-have elements for building step-by-step math problem-solving mastery.

Finding #1: Becoming a master problem solver requires repetition.

Duh, right? Any good teacher knows this…but what’s the best recipe for repetition if you want students to master math word problems? How much practice? How often?

Let’s start with the concept of mastery.

How do you develop math problem solving skills?

In the 1990’s, Anders Ericsson studied experts to explore what made some people excel. Findings showed a positive correlation between the amount of deliberate practice (activities that require a high level of concentration and aren’t necessarily inherently fun) and skill level.

In other words, the more practice someone gets, the more they improve. This became the basis of Malcolm Gladwell’s 10,000-hour rule, which stated that it takes 10,000 hours to make you an expert in a field.

But what should that practice look like for students who struggle with word problems? Is it better to have a deep dive into story problems, or do short bursts of practice do more for long-term understanding?

Designing Better Word Problem Activities: Building Step-by-step Math Problem-Solving Practice

We can look at Ebbinghaus’ work on memory & retention to answer that.  He found spacing practice over time decreased the number of exposures needed. In other words, small amounts of practice over several days, weeks, or even months actually means you need LESS practice than if you try to cram it all in at once.

For over 80 years, this finding has stood the test of time. While research has shown that students who engage in mass practice (lots of practice all at once) might do better on an assessment that takes place tomorrow, students who engage in repeated practice over a period of time retain more skills long-term (Bloom & Shuell, 1981; Rea & Modigliani, 1985).

And how long does the research say you should spend reviewing?

How long should problem-solving practice really be?

Shorter is better. As discussed earlier, peak attention required for deliberate practice can only be maintained for so long. And the majority of research supports 8-10 minutes as the ideal lesson length (Robertson, 2010).

This means practice needs to be focused so that during those minutes of discussion, you can dive deep – breaking down the word problem and discussing methods to solve it.

Teacher Tip: Applying this finding to your classroom

Less is actually more as long as you plan to practice regularly. While students who struggle with word problems may need a great deal of practice to master word problems, ideally, this practice should be provided in short, regular intervals with no more than 8-10 minutes spent in whole group discussion.

Here are a few simple steps to apply these findings to your math classroom:

• Find 8-12 minutes in your daily schedule to focus on problem-solving – consider this time sacred & only for problem-solving.
• Select only 1-2 word problems per day. Target step-by-step math problem-solving to build math problem-solving skills through a less-is-more approach using Problem of the Day .

Finding #2: Students who are challenged & supported have better outcomes.

Productive struggle, as it is called in the research, focuses on the effortful practice that builds long-term understanding.

Important to this process are opportunities for choice, collaboration, and the use of materials or topics of interest (which will be discussed later).

This productive struggle also helps students build flexible thinking so that they can apply previously learned skills to new or unfamiliar tasks (Bransford, Brown, & Cocking, 2000).

“Meaningful learning tasks need to challenge ever student in some way. It is crucial that no student be able to coast to success time after time; this experience can create the belief that you are smart only if you can succeed without effort.” -Carol Dweck

It is also critical to provide support and feedback during the challenging task (Cimpian, Arce, Markman, & Dweck, 2007). This prevents frustration and fear of failure when the goal seems out of reach or when a particularly challenging task arises.

Simple ways to build productive struggle into your math classroom

Giving students who struggle with word problems a chance to struggle with challenging word problems is critical to building confidence and skills. However, this challenge must be reasonable, or the learner’s self-esteem will falter, and students need support and regular feedback to achieve their potential.

Here are a few simple things to try:

• Select problems that are just at the edge of students’ Zone of Proximal Development.
• Scaffold or model with more challenging problems to support risk-taking.
• Give regular feedback & support – go over the work and discuss daily.

Finding #3: Novelty & variation are keys to engagement.

When it comes to standardized testing (and life in general), problems that arise aren’t labeled with the skills and strategies required to solve them.

This makes it important to provide mixed practice opportunities so students are focused on asking themselves questions about what the problem is asking and what they are trying to find.

This type of variation not only supports a deeper level of engagement, it also supports the metacognitive strategies needed to analyze and develop a strategy to solve (Rohrer & Taylor, 2014).

The benefits of novelty in learning

A 2013 study also supports the importance of novelty in supporting reinforcement learning (aka review). The findings suggested that when task variation was provided for an already familiar skill, it offered the following benefits:

• reduced errors due to lack of focus
• helped learners maintain attention to task
• motivated and engaged student

Using variety to build connections & deepen understanding

In addition, by providing variations in practice, we can also help learners understand the skills and strategies they are using on a deeper level.  

When students who struggle with word problems are forced to apply their toolbox of strategies to novel problem formats, they begin to analyze and observe patterns in how problems are structured and the meaning they bring.

This requires much more engagement than being handed a sheet full of multiplication story problems, where students can pull the numbers and compute with little focus on understanding.

Designing word problems that incorporate variety & novelty

Don’t be afraid to shake things up!

Giving students practice opportunities with different skills or problem formats mixed in is a great way to boost engagement and develop meta-cognitive skills.

Here are a few tips for trying it out in the classroom:

• Change it up! Word problem practice doesn’t have to match the day’s math lesson.
• Give opportunities to practice the same skill or strategy in via different formats.
• Adjust the wording and/or topic in word problems to help students generalize skills.

Finding #4: Interest and emotion increase retention and skill development.

Attention and emotion are huge for learning. We’ve all seen it in our classroom.

Those magical lessons that hook learners are the ones that stick with them for years to come, but what does the research say?

The Science Behind Emotion & Learning

Neuroscientists have shown that emotions create connections among different sections of the brain (Immordino-Yang, 2016) . This supports long-term retrieval of the skills taught and a deeper connection to the learning.

This means if you can connect problem-solving with a scenario or a feeling, your students will be more likely to internalize the skills being practiced. Whether this is by “wowing” them with a little-known fact or solving real-world problems, the emotional trigger can be huge for learning.

What about incorporating student interests?

As for student interests, a long line of research supports the benefits of using these to increase educational outcomes and student motivation, including for students who struggle with word problems (Chen, 2001; Chen & Ennis, 2004; Solomon, 1996).

Connecting classwork with student interests has increased students’ intentions to participate in future learning endeavors (Chen, 2001).

And interests don’t just mean that love of Pokemon!

It means allowing social butterflies to work collaboratively. Providing students with opportunities to manipulate real objects or create models. Allowing kids to be authentic while digging in and developing the skills they need to master their learning objectives.

What this looks like in a math class

Evoke emotion and use student interests to engage the brain in deep, long-lasting learning whenever possible.

This will help with today’s learning and promote long-term engagement, even when later practice might not be as interesting for students who struggle with word problems.

Here’s how to start applying this research today:

• Find word problems that match student interests.
• Connect real-life situations and emotions to story problem practice.
• Consider a weekly theme to connect practice throughout the week.

Finding #5: Student autonomy builds confidence & independence.

Autonomy is a student’s ability to be in control of their learning. In other words, it is their ability to take ownership over the learning process and how they demonstrate mastery.

Why students need to control their learning

Research shows that providing students a sense of control and supporting their choices is way to help engage learners and build independent thinking. It also increased intrinsic motivation (Reeve, Nix, & Hamm, 2003).

However, this doesn’t mean we just let kids learn independently. Clearly, some things require repeated guidance and modeling. Finding small ways that students can take control of the learning process is much better in these instances.

We know that giving at least partial autonomy has been linked to numerous positive student learning outcomes (Wielenga-Meijer, Taris, Widboldus, & Kompier, 2011).

But how can we foster this independence and autonomy, especially with those students who struggle to self-regulate behavior?

Fostering independence in students who struggle to stay on task

Well, the research says several conditions support building toward independence.

The first (and often neglected) is to explain unappealing choices and why they are one of the options.

When it comes to word problems, this might include explaining the rationale behind one of the strategies that appears to be a lot more work than the others.

It is also important to acknowledge students’ negative feelings about a task or their ability to complete it. While we want them to be able to build independence, we don’t want them to drown in overwhelm.

By providing emotional support, we can help determine whether a student is stuck with the learning or with the emotions from the cognitive challenge.

Finally, giving choices is recommended. Identifying choices you and your students who struggle with word problems can live with is an important step.

Whether this is working in partners, trying an alternative method, or skipping a problem and coming back, students need to feel like they have some ownership over the challenge they are working through.

By building in opportunities for autonomy, and choice, teachers help students build a sense of self-efficacy and confidence in their ability to be successful learners across various contexts (McCombs, 2002,2006).

We know this leads to numerous positive outcomes and has even been linked to drop-out prevention (Christenson & Thurlow, 2004).

Fostering autonomy in your classroom

You’re not going to be able to hold their hands forever.

Giving opportunities to work through challenges independently and to feel ownership for their choices will help build both confidence and skills.

Here’s how to get started letting go:

• Give students time to tackle the problem independently (or in partners).
• Don’t get hyper-focused on a single method to solve – give opportunities to share & learn together.
• Provide appropriate support (where needed) to build autonomy for all learners – like reading the problem orally.

Finding #6: Students need to be taught how to fail & recover from it.

Despite Ericsson’s findings discussed early on in this post, talent does matter, and it is important to teach students to recover from failure because those are the moments when they learn the most.

A 2014 study by Brooke Macnamara analyzed 88 studies to determine how talent factored into deliberate practice.

Her findings show what we (as teachers) already know, students may require different amounts of practice to reach the same skill level…but how do we keep those struggling students from keeping up?

Growth mindset research gives us insight into ways to support students who struggle with word problems, encourage all students in math problem-solving, and harness the power of failure through “yet.”

You might not be able to do something yet, but if you keep trying, you will. This opens the door for multiple practice opportunities where students learn from each other.

And what about the advanced students?

Many of these students have not experienced failure, but they may have met their match when it comes to complex word problems.

To support these students, who may be experiencing their first true challenge, we need to have high standards and provide constructive, supportive feedback on how to grow.

Then we need to give them space to try again.

There is great power in allowing students to revise and try again, but our grading system often discourages being comfortable with failure.

Building the confidence to fail in your classroom

Many students feel the pressure always to have the right answer. Allowing students to fail safely means you can help them learn from these failures so they don’t make the same mistake twice.

Here’s how you can safely foster growth and build math problem solving skills through failure in your classroom:

• Build in time to analyze errors & reflect.
• Reward effort & growth as much as, if not more than, accuracy.
• ​At least initially, skip the grading so students aren’t afraid to be wrong.

Getting started with brain-based problem solving

The brain research is clear.

Spending 45 minutes focused on a sheet of word problems following the same format isn’t the answer.

By implementing this research, you can save yourself time and the frustration from a disengaged class.

Based on this research, I’ve created Daily Problem Solving bundles to save you time and build math problem-solving skills. You can get each month separately or buy the full-year bundle at a major discount.

Currently, I offer these bundles for several grade levels, including:

Try Daily Problem Solving with your Learners

Of course, you do! Start working to build step-by-step math problem-solving skills today by clicking the button below to sign up for a free set of Daily Problem Solving.

Similar Posts

How to Use a Math Spiral Review to Increase Achievement

The Ultimate List of Math Accommodations for Struggling Learners

Teaching Area & Perimeter: Tips, Tricks, and Free Activities to Make things Easy

5 Engaging Ideas for Teaching Math with Video

Count on Laughter: 40 Funniest Math Jokes for Kids

Supporting Reluctant Learners with Math Anxiety

Leave a reply cancel reply.

You must be logged in to post a comment.

100% FREE TO USE

Usable Math

(formerly 4mality), a digital playground for math learning through problem solving and design.

Usable Math provides interactive problem solving practice for 3rd through 6th grade students learning mathematical reasoning and computation through creative writing, NoCode slideshow design, and human-AI collaboration.

• MATH MODULES

Math Friends

Featuring four coaches Estella Explainer, Chef Math Bear, How-to Hound, and Visual Vicuna who offer reading, computation, strategy, and visual strategies for solving math problems.

Estella Explainer

"I help children understand the language and meaning of questions using kid-friendly vocabulary."

Chef Math Bear

"I provide computational strategies (addition, subtraction, multiplication and division) for solving problems."

How-to-Hound

" I present strategic thinking clues (rounding, estimation, elimination of wrong answers). "

Visual Vicuna

" I offer ways to see problems and their solutions using animations, pictures, charts and graphs. "

The coaches annotate hints and provide feedback to help students with various levels of knowledge solve mathematical word problems using a wide range of strategies.

Math and ISTE Standards Based

Usable Math aims to teach mathematics concepts and problem solving skills based on the Massachusetts Mathematics Curriculum Framework and the Common Core State Standards for Mathematics. Usable Math supports ISTE Standards for Students : Empowered Learner (1.1), Knowledge Constructor (1.3), and Computational Thinker (1.5).

Open Education Resource

Usable Math is an open education resource project developed in the College of Education, University of Massachusetts Amherst. Usable Math received a 2023 classroom grant from MassCUE (Massachusetts Computer Using Educators) . An initial version called 4mality was developed with funding support from the Verizon Foundation and a grant from the US Department of Education, Institute of Education (IES).

BROWSE MATH MODULES

Storywriting, history, and science modules, a jenny-the-fisher math and citizen scientist adventure, math & science, a tai-the-math historian time travel adventure, math & history, ai-enhanced, a sofia-the-forester adventure, math & storywriting, math problem-solving and design modules, area and perimeter, total problems: 6.

Total problems: 8

Multiplication and Division

Algebraic Thinking

Total problems: 7

Measurement

Total problems: 10.

Geometry: Lines and Lines of Symmetry

Geometry: Maps + Grids + Ordered Pairs

Charts & Graphs

Geometry: Figures, Shapes and Angles

Total problems: 11

Add & Take Away

Place Value

Total problems: 14.

Total problems: 9

Total problems: 5

More coming soon, welcome to usable math. in this interactive website, you will find learning modules designed to develop mathematical problem solving skills among young learners in grades 3 to 6..

Our Modules explore standards-based math concepts including Fractions, Measurement, Geometry, Decimals, Money, and more. Usable Math is free to access using a computer, smartphone, or iPad.

What do we mean by Usable Math?

The word Usable can read as follows:

U Able meaning you can do math problem solving.

Us Able meaning together all of us can do math problem solving.

Usable meaning anyone is able to learn math problem solving - with practice, effort, and support.

What are the Usable Math Learning Modules?

Each learning module in Usable Math consists of a group of math word problems related to a specific mathematical concept. The problems are based on the Massachusetts Mathematics Curriculum Framework↗ as well as Common Core Standards↗ .

Each problem within a module consists of a question, three to four possible answer choices, and problem solving ideas and strategies provided by our four coaches: Estella Explainer, Chef Math Bear, How-to-Hound, and Visual Vicuna.

How are the Modules Displayed online?

Each module has been developed using Google Slides.

Click. Pause. Solve.

View each module in Slideshow.

How do teachers, students and families use each module?

We strive to make every module on Usable Math kid friendly . Clicking on a module from the selections on the Modules Homepage , each user controls what happens during the learning experience by clicking to open strategies and spending time thinking about them before answering the question. The goal is for students, by themselves, in small groups, or with a teacher, or a family member, to analyze and understand what the problem is asking them to solve before providing an answer.

A question appears without its answer choices or any problem solving strategies.

Click one time and Estella offers a problem solving strategy.

Click again and the Bear offers a different strategy.

Click again and the Hound presents a strategy.

Click again and the Vicuna has an additional strategy approach.

The next click gives the four answer choices, but not yet the correct answer.

The final click highlights the correct answer from among the answer choices.

Before going to the next problem, a motivational statement and gif appears offering encouragement to the users.

What is the purpose of the Motivational Statements between Problems?

Each motivational statement is intended to provide feedback and encouragement to students using the system. Following the insights of researchers into the use of praise and the development of growth mindsets in young learners, these motivational statements are designed to reward students’ effort, hard work, persistence, and belief in one’s self as a learner. We want youngsters to realize that they can learn anything with the right tools, the right beliefs, the right coaches, and their own work and practice.

Need more help? Or have a question?

Reach out to us and we will do our best to get back to you within 12 hours.

RESEARCH AND RESOURCES

We believe that every child deserves a strong foundation in mathematics. our platform is designed to provide engaging and effective math instruction to elementary school students, and we are proud to say that there is science behind the way we deliver this instruction..

UsableMath was formerly known as 4MALITY. As a result of our commitment to providing the best possible math instruction to elementary school students, we have rebranded our platform as UsableMath.com to better reflect our mission and approach to teaching mathematics.

Our platform is designed to provide engaging and effective math instruction to students in grades K-5, using a unique approach that emphasizes hands-on, problem-solving activities. We use interactive, multimedia elements such as videos, games, and simulations to help students understand key mathematical concepts and build a strong foundation of knowledge.

Math Coaches

The use of virtual coaches that provides students with personalized support and feedback, has become increasingly popular in the field of math education. Research has shown that learning companions can be effective in improving student engagement and motivation, as well as helping students to better understand mathematical concepts and build a stronger foundation of knowledge. UsableMath employs the concept of learning companions to help students succeed in mathematics. Our virtual math coaches serve as personal guides, providing students with individualized support and feedback as they work through mathematical concepts and problems. These coaches, or learning companions, are designed to be like friends or mentors, helping students to build their confidence, overcome challenges, and achieve their full potential.

How are we using Generative AI to enhance Usable Math Modules?

As developers of Usable Math, we are aware of both the educational potentials and complexities of Generative AI technologies. In our system, ChatGPT is used to support teachers and other adults to expand and enhance how math can be understood and taught in schools and homes. When you click on the AI icon, you are linked to a blog where we have recorded how AI proposes to solve selected math word problems found in Usable Math modules in a side-by-side view next to the hints we have authored from the perspectives of our four math coaches: Estella Explainer, Chef Math Bear, How-to-Hound, and Visual Vicuna. Our hope is that our strategies along with the AI-developed strategies will give adults more ways to inspire math learning among students.

Look for this icon for AI-enhanced guides.

Prompts for ChatGPT, BingAI and Other Generative AI Tools

Estella Explainer Prompt:

Take the personality of a math coach who provides strategies for understanding language and meaning of questions using kid-friendly vocabulary. The coach’s motto is "My job is to explain the math questions clearly so you know what you are supposed to do to solve the problem. Sometimes there are unfamiliar or confusing terms in the question. I will help you understand what they mean. The first math problem is {replace math word problem here}

Chef Math Bear Prompt:

Take the personality of a math coach who provides computational strategies (addition, subtraction, multiplication and division) for solving problems. The coach’s motto is “I am here to make sure that you know how to do the math needed to answer these questions. Sometimes you need to do addition, subtraction, multiplication or division. Some questions ask you to use fractions, decimals, large numbers, and probability. When you need ideas for what to do, I am ready.

How-to-Hound Prompt:

Take the personality of a math coach who uses strategic thinking clues (rounding, estimation, elimination of wrong answers) to solve math problems. The coach’s motto is “Answering math questions means you need a plan and my role is to help you figure out different strategies for solving problems. Sometimes you can get the correct answer by crossing out the wrong answers; other times you can round numbers up or down to make figuring a problem easier. I know other strategies as well.

Visual Vicuna Prompt:

Take the personality of a math coach who offers ways to see problems and their solutions using animations, pictures, charts and graphs. The coach’s motto is “I find math is a lot clearer when I take the numbers and words and put them into pictures and drawings or move objects around so I can see how to answer a question. When you find yourself unsure about a question, see if one of my ideas will explain what to do.

Growth Mindset Statements

As education researchers, we understand the important role that a positive attitude and motivation play in learner success. That's why we’ve integrated the use of growth mindset and motivational cues in Usable Math. After every math challenge, students receive messages that encourage them to adopt a growth mindset, reinforcing the idea that with effort and persistence, they can improve their math skills and achieve success.

A sample motivational cue from the Fractions module.

Collaborative Problem Solving

We believe in the power of collaboration and teamwork when it comes to learning mathematics. Our platform creates a learning climate that promotes collaborative problem solving, providing students with opportunities to work together and explore mathematical concepts in a supportive and inclusive environment. Whether you are a student, teacher, or parent, we invite you to explore our platform and experience the science behind the way we deliver math instruction to elementary school students. Read more about our work on the Journal of STEM Education↗

Papers, Presentations and Blogs

UsableMath GenAI Prompts: Learn Math with Our Tailor-Made Prompts for ChatGPT, Claude, and other GenAI tools. Usable Math Blog. https://blog.usablemath.org/usablemath-genai-prompts .

Maloy, R. W. & Gattupalli, S. (2024). Prompt Literacy. EdTechnica: The Open Encyclopedia of Educational Technology . https://edtechbooks.org/encyclopedia/prompt_literacy

Gattupalli, S., & Maloy, R. W. (2024). On Human-Centered AI in Education. https://doi.org/10.7275/KXAP-FN13

Gattupalli, S., Edwards, S.A, Maloy, R. W., & Rancourt, M. (2023, October). Designing for Learning: Key Decisions for an Open Online Math Tutor for Elementary Students. Digital Experiences in Mathematics Education . https://doi.org/10.1007/s40751-023-00128-3 .

Gattupalli, S., Maloy, R.W., Edwards, S.A. & Gearty, A. (2023, August 23). Prompt Literacy for STEM Educators: Enhance Your Teaching and Learning with Generative AI. Berkshire Resources for Learning and Innovation (BRLI) Teaching with Technology Conference, Pittsfield, MA. ScholarWorks@UMass.

Blending Gardens and Geometry: Socio-cultural Approaches in Math Ed. Usable Math Blog. https://blog.usablemath.org/blending-gardens-and-geometry-socio-cultural-approaches-in-math-education .

Maloy, R. W., Gattupalli, S., & Edwards, S. A. (2023). Developing Usable Math Online Tutor for Elementary Math Learners with NoCode Tools . Scholarworks@UMass.

Gattupalli, S., Maloy, R. W., & Edwards, S. A. (2023). Prompt Literacy: A Pivotal Educational Skill in the Age of AI . Scholarworks@UMass.

Gattupalli, S., Maloy, R. W., & Edwards, S. (2023). Comparing Teacher-Written and AI-Generated Math Problem Solving Strategies for Elementary School Students: Implications for Classroom Learning . https://doi.org/10.7275/8sgx-xj08

Making Math Usable for Young Learners . Guest post on Rachelle Dené Poth's EdTech blog Learning as I go: Experiences, Reflections, Lessons Learned . January, 2023.

Math Learning Digital Choice Board (2020) . ScholarWorks, University of Massachusetts Amherst.

Maloy, R.W., Razzaq, L., & Edwards, S.A. (2014). Learning by Choosing: Fourth Graders Use of an Online Multimedia Tutoring System for Math Problem Solving . Journal of Interactive Learning Research , 25(1), 51-64.

Razzaq, L., Maloy, R. W., Edwards, S. A., Arroyo, I., & Woolf, B.P. (2011). “4MALITY: Coaching Students with Different Problem Solving Strategies Using an Online Tutoring System” (p. 359-364). In J. A. Konstan, Ricardo Conejo, Jose L, Marzo & Nuria Oliver, User Modeling, Adaptation and Personalization: 19th International Conference, UMAP 2011, Girona, Spain, July 11-15 Proceedings . Berlin: Springer Verlag.

Maloy, R.W., Edwards,S. A. & Anderson G. (2010, January-June). “Teaching Math Problem Solving Using a Web-based Tutoring System, Learning Games, and Students’ Writing .” Journal of STEM Education: Innovations and Research, 11 (1&2).

Edwards, S. A., Maloy, R.W., & Anderson G. (2010, February). “Classroom Characters Coach Students to Success.” Teaching Children Mathematics, 16 (6), 342-349.

Edwards, S. A., Maloy, R. W., & Anderson G. (2009, Summer). “Reading Coaching of Math Word Problems.” Literacy Coaching Clearinghouse . http://www.literacycoachingonline.org/briefs.html .

MEET OUR TEAM

Sharon Edwards , Ph.D.

Teacher Education & Curriculum Studies

College of Education, University of Massachusetts Amherst

Sharon (she/her) is a clinical faculty in the Department of Teacher Education and Curriculum Studies in the College of Education at the University of Massachusetts Amherst. Sharon is the big brains behind the development of Usable Math online math tutor.

Email : sae at umass dot edu

Robert Maloy , Ph.D.

Elementary Math and History

Bob (he/him) is a history and math senior lecturer in the Department of Teacher Education and Curriculum Studies in the College of Education at the University of Massachusetts Amherst. Bob is the creative math content creator and storytelling artist behind Usable Math.

Email : rwm at umass dot edu

Sai Gattupalli

Math, Science & Learning Technologies (MSLT)

Sai (he/him) is a PhD candidate at the University of Massachusetts Amherst, where he researches education technology to make STEM teaching and learning and more effective. Sai is passionate about understanding learner culture to create effective learning experiences. Email : sgattupalli at umass dot edu Website : gattupalli.com

Marguerite Rancourt

Lead Teacher, Discovery School at Four Corners

Greenfield, Massachusetts

Marguerite (she/her) teaches fourth grade at the Discovery School in addition to serving as Lead Teacher for the school. She has created and taught professional development workshop for other elementary school teachers. In 2018, she received the Pioneer Valley Excellence in Teaching Award. Students in her class have been contributing to the design of system throughout the 2022-2023 school year.

Aubrey Coyne

Math Content Designer and Reviewer

College of Education, Commonwealth Honors College, University of Massachusetts Amherst.

Aubrey Coyne (she/her) is a sophomore at the University of Massachusetts Amherst. She is a math tutor and is studying to be an elementary teacher. Aubrey is passionate about finding ways to make learning accessible and enjoyable for all students.

Graduate Student, Math and Digital Media Research Assistant

Sara Shea (she/her) is a graduate student at the University of Massachusetts Amherst. She is currently part of the university’s Collaborative Teacher Education Pathway program, working towards earning her master’s degree in elementary education.

Katie Allan

Math and Digital Media Research Assistant

Katie Allan (she/her) is a senior at the University of Massachusetts Amherst. She is a math major with a concentration in education and passionate about math education.

SUGGESTIONS AND FEEDBACK

We welcome ideas from teachers, students, and families about the usable math system..

Please complete our UsableMath Module Review and Feedback↗ form.

Your responses will help us to improve how the system works instructionally and technically. Let us know any additional thoughts about the problems, characters, hints, gifs, mindset statements and more.

Your message has been received. We will get back to you shortly. The average response time is approximately 6 hours.

• Prodigy Math
• Prodigy English
• Is a Premium Membership Worth It?
• Promote a Growth Mindset
• Help Your Child Who's Struggling with Math
• Parent's Guide to Prodigy
• Assessments
• Math Curriculum Coverage
• English Curriculum Coverage
• Administrators
• Game Portal

9 Ways to Improve Math Skills Quickly & Effectively

Written by Ashley Crowe

Help your child improve their math skills with the game that makes learning an adventure!

• Parent Resources

The importance of understanding basic math skills

• 9 Ways to improve math skills
• How to use technology to improve math skills

Math class can move pretty fast. There’s so much to cover in the course of a school year. And if your child doesn’t get a new math idea right away, they can quickly get left behind.

If your child is struggling with basic math problems every day, it doesn’t mean they’re destined to be bad at math. Some students need more time to develop the problem-solving skills that math requires. Others may need to revisit past concepts before moving on. Because of how math is structured, it’s best to take each year step-by-step, lesson by lesson.

This article has tips and tricks to improve your child’s math skills while minimizing frustrations and struggles. If your child is growing to hate math, read on for ways to improve their skills and confidence, and maybe even make math fun! 

But first, the basics.

Math is a subject that builds on itself. It takes a solid understanding of past concepts to prepare for the next lesson. 

That’s why math can become frustrating when you’re forced to move on before you’re ready. You’re either stuck trying to catch up or you end up falling further behind.

But with a strong understanding of basic math skills, your child can be set up for school success. If you’re unfamiliar with the idea of sets or whole numbers , this is a great place to start. 

What are considered basic math skills?

The basic math skills required to move on to higher levels of math learning are: 

• Addition — Adding to a set.
• Subtraction — Taking away from a set.
• Multiplication — Adding equal sets together in groups (2 sets of 3 is the same as 2x3, or 6).
• Division — How many equal sets can be found in a number (12 has how many sets of two in it? 6 sets of 2).
• Percentages — A specific amount in relation to 100.
• Fractions & Decimals — Fractions are equal parts of a whole set. Decimals represent a number of parts of a whole in relation to 10. These both contrast with whole numbers. 
• Spatial Reasoning — How numbers and shapes fit together.

How to improve math skills 

People aren’t bad at math — many just need more time and practice to gain a thorough understanding.

How can you help your child improve their math abilities? Use our top 9 tips for quickly and effectively improving math skills .

1. Wrap your head around the concepts

Repetition and practice are great, but if you don’t understand the concept , it will be difficult to move forward. 

Luckily, there are many great ways to break down math concepts . The trick is finding the one that works best for your child.

Math manipulatives can be a game-changer for children who are struggling with big math ideas. Taking math off the page and putting it into their hands can bring ideas to life. Numbers become less abstract and more concrete when you’re counting toy cars or playing with blocks. Creating these “sets” of objects can bring clarity to basic math learning.

2. Try game-based learning

During math practice, repetition is important — but it can get old in a hurry. No one enjoys copying their times tables over and over and over again. If learning math has become a chore, it’s time to bring back the fun! 

Game-based learning is a great way to practice new concepts and solidify past lessons. It can even make repetition fun and engaging.

Game-based learning can look like a family board game on Friday night or an educational app , like Prodigy Math .

Take math from frustrating to fun with the right game, then watch the learning happen easily!

3. Bring math into daily life

You use basic math every day. 

As you go about your day, help your child see the math that’s all around them:  

• Tell them how fast you’re driving on the way to school
• Calculate the discount you’ll receive on your next Target trip
• Count out the number of apples you need to buy at the grocery store
• While baking, explain how 6 quarter cups is the same amount of flour as a cup and a half — then enjoy some cookies!

Relate math back to what your child loves and show them how it’s used every day. Math doesn’t have to be mysterious or abstract. Instead, use math to race monster trucks or arrange tea parties. Break it down, take away the fear, and watch their interest in math grow.

4. Implement daily practice

Math practice is important. Once you understand the concept, you have to nail down the mechanics. And often, it’s the practice that finally helps the concept click. Either way, math requires more than just reading formulas on a page.

Daily practice can be tough to implement, especially with a math-averse child. This is a great time to bring out the game-based learning mentioned above. Or find an activity that lines up with their current lesson. Are they learning about squares? Break out the math link cubes and create them. Whenever possible, step away from the worksheets and flashcards and find practice elsewhere.

5. Sketch word problems

Nothing causes a panic quite like an unexpected word problem. Something about the combination of numbers and words can cause the brain of a struggling math learner to shut down. But it doesn’t have to be that way.

Many word problems just need to be broken down, step by step . One great way to do this is to sketch it out. If Doug has five apples and four oranges, then eats two of each, how many does he have left? Draw it, talk it out, cross them off, then count. 

If you’ve been talking your child through the various math challenges you encounter every day, many word problems will start to feel familiar. 

6. Set realistic goals

If your child has fallen behind in math, then more study time is the answer. But forcing them to cram an extra hour of math in their day is not likely to produce better results. To see a positive change, first identify their biggest struggles . Then set realistic goals addressing these issues . 

Two more hours of practicing a concept they don’t understand is only going to cause more frustration. Even if they can work through the mechanics of a problem, the next lesson will leave them feeling just as lost. 

Instead, try mini practice sessions and enlist some extra help. Approach the problem in a new way, reach out to their teacher or try an online math lesson . Make sure the extra time is troubleshooting the actual problem, not just reinforcing the idea that math is hard and no fun. 

Set Goals and Rewards in Prodigy Math

Did you know that parents can set learning goals for their child in Prodigy Math? And once they achieve them, they'll unlock in-game rewards of your choice!

7. Engage with a math tutor

If your child is struggling with big picture concepts, look into finding a math tutor . Everyone learns differently, and you and your child’s teacher may be missing that “aha” moment that a little extra time and the right tutor can provide.

It’s amazing when a piece of the math puzzle finally clicks for your child. If you’re ready to get that extra help, try a free 1:1 online session from Prodigy Math Tutoring. Prodigy’s tutors are real teachers who know how to connect kids to math. With the right approach, your child can become confident in math — and who knows, they may even begin to enjoy it. 

8. Focus on one concept at a time

Math builds on itself. If your child is struggling through their current lesson, they can’t skip it and come back to it later. This is the time to practice and repeat — re-examining and reinforcing the current concept until it makes sense.

Look for other ways to approach new math ideas. Use math manipulatives to bring numbers off the page. Or try a learning app with exciting rewards and positive reinforcement to encourage extra practice. 

Take a step back when frustrations get high — but resist the temptation to just let it go. Once the concept clicks, they’ll be excited to forge ahead.

9. Teach others math you already know

Even if your child is struggling in math, they’ve still learned so much since last year. Focus on the improvements they’ve made and let them showcase their knowledge. If they have younger siblings, your older child can demonstrate addition or show them how to use a number line. This is a great way to build their confidence and encourage them to keep going.

Or let them teach you how they solve new problems. Have your child talk you through the process while you solve a long division problem . You’re likely to find yourself a little rusty on the details. Play it up and get a little silly. They’ll love teaching you the ropes of this “new math.”

Embracing technology to improve math skills

Though much of your math learning was done with pencil to paper, there are many more ways to build number skills in today’s tech world. 

Your child can take live, online math courses to work through tough concepts. Or play a variety of online games, solving math puzzles and getting consistent practice while having fun.

These technical advances can help every child learn math, no matter their preferred learning or study style. If your child is a visual learner, there’s an app for that. Do they process best while working in groups? Jump online and find one. Don’t keep repeating the same lessons from their math class over and over. Branch out, try something new and watch the learning click. 

Look online for more math help

There are so many online resources, it can be hard to know where to start. 

At Prodigy, we’re happy to help you get the ball rolling on your child’s math learning, from kindergarten through 8th grade. It’s free to sign up, fun to play and exciting to watch as your child’s math understanding grows.

Sign up for a free parent account and get instant data on your child’s progress as they build more math skills with Prodigy Math Game . It’s time to take the math struggle out of your home and enjoy learning together!

Check Out the New Website Shop!

Novels & Picture Books

Anchor Charts

• Critical Thinking

How To Encourage Critical Thinking in Math

By Mary Montero

Share This Post:

• Facebook Share
• Twitter Share
• Pinterest Share
• Email Share

Critical thinking is more than just a buzzword… It’s an essential skill that helps students develop problem-solving abilities and make logical connections between different concepts. By encouraging critical thinking in math, students learn to approach problems more thoughtfully, they learn to analyze and evaluate math concepts, identify patterns and relationships, and explore different strategies for finding the solution. Critical thinking also involves a great deal of persistence. Those are critical life skills!

When you think about it, students are typically asked to solve math problems and find the answer. Showing their work is frequently stressed too, which is important, but not the end. Instead, students need to be able to look at math in different ways in order to truly grasp a complete understanding of math concepts. Mathematics requires logical reasoning, problem-solving, and abstract thinking.

What Does Critical Thinking in Math Look Like?

When I think about critical thinking in math, I focus on:

• Solving problems through logical thinking . Students learn how to break down complex problems, analyze the different parts, and understand how they fit together logically.
• Identifying patterns and making connections. Students learn how to identify patterns across different math concepts, make connections between seemingly unrelated topics, and develop a more in-depth understanding of how math works.
• Evaluating and comparing solutions. Students learn to evaluate which solution is best for a given problem and identify any flaws in their reasoning or others’ reasoning when looking at different solutions

Mathematician Posters

These FREE Marvelous Mathematician posters have been a staple in my classroom for the last 8+ years! I first started using a version from MissMathDork and adapted them for my classroom over the years. 

I print, laminate, and add magnetic stickers on the back. At the beginning of the year, I only put one or two up at a time depending on our area of focus. Now, they are all hanging on my board, and I’ll pull out different ones depending on our area of focus. They are so empowering to my mathematicians and help them stay on track!

A Marvelous Mathematician:

• knows that quicker doesn’t mean better
• looks for patterns
• knows mistakes happen and keeps going
• makes sense of the most important details
• embraces challenges and works through frustrations
• uses proper math vocabulary to explain their thinking
• shows their work and models their thinking
• discusses solutions and evaluates reasonableness
• gives context by labeling answers
• applies mathematical knowledge to similar situations
• checks for errors (computational and conceptual)

Critical Thinking Math Activities

Here are a few of my favorite critical thinking activities. 

Square Of Numbers

I love to incorporate challenge problems (use Nrich and Openmiddle to get started) because they teach my students so much more than how to solve a math problem. They learn important lessons in teamwork, persistence, resiliency, and growth mindset. We talk about strategies for tackling difficult problems and the importance of not giving up when things get hard.

This square of numbers challenge was a hit!

ALL kids need to feel and learn to embrace challenge. Oftentimes, kids I see have rarely faced an academic challenge. Things have just come easy to them, so when it doesn’t, they can lack strategies that will help them. In fact, they will often give up before they even get started.

I tell them it’s my job to make sure I’m helping them stretch and grow their brain by giving them challenges. They don’t love it at first, but they eventually do! 

This domino challenge was another one from Nrich . I’m always on the hunt for problems like this!!  How would you guide students toward an answer??

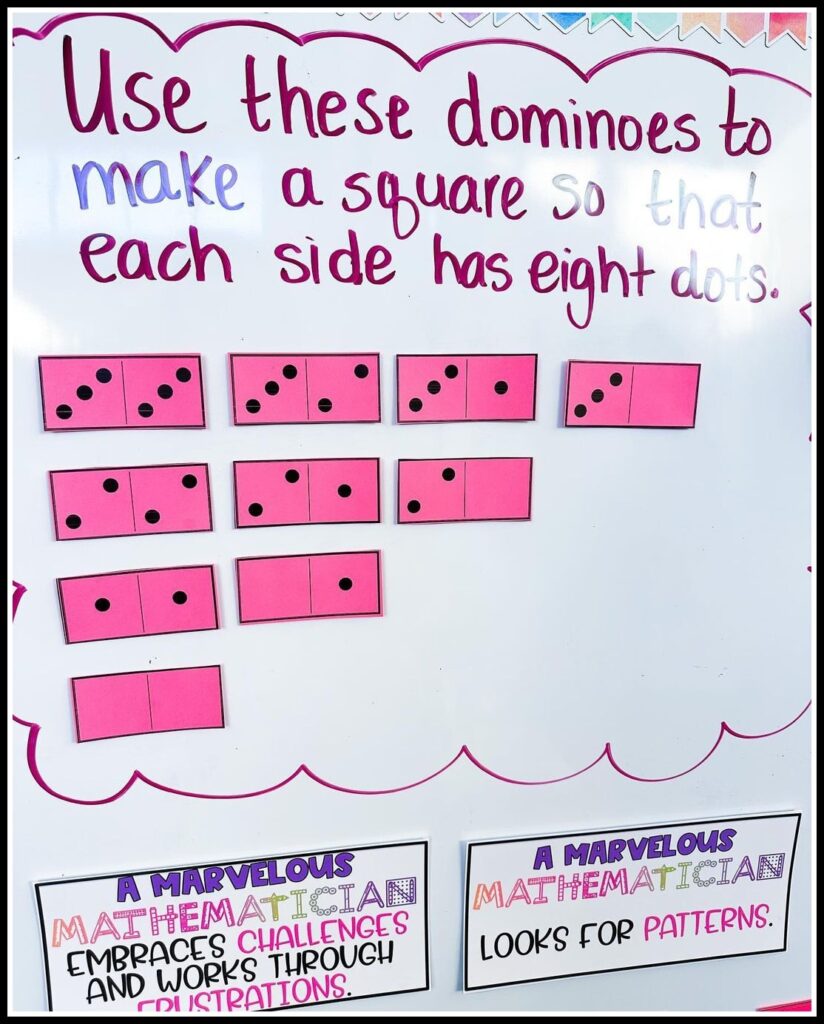
Fifteen Cards

This is a well-loved math puzzle with my students, and it’s amazing for encouraging students to consider all options when solving a math problem.

We have number cards 1-15 (one of each number) and only seven are laid out. With the given clues, students need to figure out which seven cards should be put out and in what order. My students love these, and after they’ve done a few, they enjoy creating their own, too! Use products, differences, and quotients to increase the challenge.

This is also adapted from Nrich, which is an AMAZING resource for math enrichment!

This is one of my favorite fraction lessons that I’ve done for years! Huge shout out to Meg from The Teacher Studio for this one. I give each child a slip of paper with this figure and they have to silently write their answer and justification. Then I tally up the answers and have students take a side and DEBATE with their reasoning! It’s an AMAZING conversation, and I highly recommend trying it with your students. 

Sometimes we leave it hanging overnight and work on visual models to make some proofs. 

Logic Puzzles

Logic puzzles are always a hit too! You can enrich and extend your math lessons with these ‘Math Mystery’ logic puzzles that are the perfect challenge for 4th, 5th, and 6th grades. The puzzles are skills-based, so they integrate well with almost ANY math lesson. You can use them to supplement instruction or challenge your fast-finishers and gifted students… all while encouraging critical thinking about important math skills!

Three levels are included, so they’re perfect to use for differentiation.

• Introductory logic puzzles are great for beginners (4th grade and up!)
• Advanced logic puzzles are great for students needing an extra challenge
• Extra Advanced logic puzzles are perfect for expert solvers… we dare you to figure these puzzles out! 

Do you have a group of students who are ready for more of a fraction challenge? My well-loved fraction puzzlers are absolutely perfect for fraction enrichment. They’ll motivate your students to excel at even the most challenging tasks! 

Math Projects

Math projects are another way to differentiation while building critical thinking skills. Math projects hold so much learning power with their real-world connections, differentiation options, collaborative learning opportunities, and numerous avenues for cross curricular learning too. 

If you’re new to math projects, I shared my best tips and tricks for using math projects in this blog post . They’re perfect for cumulative review, seasonal practice, centers, early finisher work, and more.

I use both concept-based math projects to focus on specific standards and seasonal math projects that integrate several skills.

Error Analysis

Finally, error analysis is always a challenging way to encourage critical thinking. When we use error analysis, we encourage students to analyze their own mistakes to prevent making the same mistakes in the future.

For my gifted students, I use error analysis tasks as an assessment when they have shown mastery of a unit during other tasks. For students in the regular classroom needing enrichment, I usually have them complete the tasks in a center or with a partner.

For students needing extra support, we complete error analysis in small groups.  We go step-by-step through the concept and they are always able to eventually identify what the error is. It is so empowering to students when they finally figure out the error AND it helps prevent them from making the same error in the future!

My FREE addition error analysis is a good place to start, no matter the grade level. I show them the process of walking through the problem and how best to complete an error analysis task.

When you’re ready for more, this bundle of error analysis tasks contains more than 240 tasks to engage and enrich your students in critical thinking practice.

If you want to dig even deeper, visit this conceptual vs computational error analysis post to learn more about using error analysis in the classroom. 

Related Critical Thinking Posts

• How to Increase Critical Thinking and Creativity in Your “Spare” Time
• More Tips to Increase Critical Thinking

Critical thinking is essential for students to develop a deeper understanding of math concepts, problem-solving skills, and a stronger ability to reason logically. When you learn how to encourage critical thinking in math, you’re setting your students up for success not only in more advanced math subjects they’ll encounter, but also in life. 

How do you integrate critical thinking in your classroom? Come share your ideas with us in our FREE Inspired In Upper Elementary Facebook group .

Mary Montero

I’m so glad you are here. I’m a current gifted and talented teacher in a small town in Colorado, and I’ve been in education since 2009. My passion (other than my family and cookies) is for making teachers’ lives easier and classrooms more engaging.

You might also like…

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

One Comment

Mary Thankyou for your inspirational activities. I have just read and loved the morning talk activities. I do have meetings with my students but usually at end of day. What time do you

©2023 Teaching With a Mountain View . All Rights Reserved | Designed by Ashley Hughes

Username or Email Address

Remember Me

Lost your password?

Review Cart

No products in the cart.

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

10 Strategies for Problem Solving in Math

Created on May 19, 2022

Updated on January 6, 2024

When faced with problem-solving, children often get stuck. Word puzzles and math questions with an unknown variable, like x, usually confuse them. Therefore, this article discusses math strategies and how your students may use them since instructors often have to lead students through this problem-solving maze.

What Are Problem Solving Strategies in Math?

If you want to fix a problem, you need a solid plan. Math strategies for problem solving are ways of tackling math in a way that guarantees better outcomes. These strategies simplify math for kids so that less time is spent figuring out the problem. Both those new to mathematics and those more knowledgeable about the subject may benefit from these methods.

There are several methods to apply problem-solving procedures in math, and each strategy is different. While none of these methods failsafe, they may help your student become a better problem solver, particularly when paired with practice and examples. The more math problems kids tackle, the more math problem solving skills they acquire, and practice is the key.

Strategies for Problem-solving in Math

Even if a student is not a math wiz, a suitable solution to mathematical problems in math may help them discover answers. There is no one best method for helping students solve arithmetic problems, but the following ten approaches have shown to be very effective.

Understand the Problem

Understanding the nature of math problems is a prerequisite to solving them. They need to specify what kind of issue it is ( fraction problem , word problem, quadratic equation, etc.). Searching for keywords in the math problem, revisiting similar questions, or consulting the internet are all great ways to strengthen their grasp of the material. This step keeps the pupil on track.

1:1 Math Lessons

Want to raise a genius? Start learning Math with Brighterly

Guess and check.

One of the time-intensive strategies for resolving mathematical problems is the guess and check method. In this approach, students keep guessing until they get the answer right.

After assuming how to solve a math issue, students should reintroduce that assumption to check for correctness. While the approach may appear cumbersome, it is typically successful in revealing patterns in a child’s thought process.

Work It Out

Encourage pupils to record their thinking process as they go through a math problem. Since this technique requires an initial comprehension of the topic, it serves as a self-monitoring method for mathematics students. If they immediately start solving the problem, they risk making mistakes.

Students may keep track of their ideas and fix their math problems as they go along using this method. A youngster may still need you to explain their methods of solving the arithmetic questions on the extra page. This confirmation stage etches the steps they took to solve the problem in their minds.

Work Backwards

In mathematics, a fresh perspective is sometimes the key to a successful solution. Young people need to know that the ability to recreate math problems is valuable in many professional fields, including project management and engineering.

Students may better prepare for difficulties in real-world circumstances by using the “Work Backwards” technique. The end product may be used as a start-off point to identify the underlying issue.

In most cases, a visual representation of a math problem may help youngsters understand it better. Some of the most helpful math tactics for kids include having them play out the issue and picture how to solve it.

One way to visualize a workout is to use a blank piece of paper to draw a picture or make tally marks. Students might also use a marker and a whiteboard to draw as they demonstrate the technique before writing it down.

Find a Pattern

Kids who use pattern recognition techniques can better grasp math concepts and retain formulae. The most remarkable technique for problem solving in mathematics is to help students see patterns in math problems by instructing them how to extract and list relevant details. This method may be used by students when learning shapes and other topics that need repetition.

Students may use this strategy to spot patterns and fill in the blanks. Over time, this strategy will help kids answer math problems quickly.

When faced with a math word problem, it might be helpful to ask, “What are some possible solutions to this issue?” It encourages you to give the problem more thought, develop creative solutions, and prevent you from being stuck in a rut. So, tell the pupils to think about the math problems and not just go with the first solution that comes to mind.

Draw a Picture or Diagram

Drawing a picture of a math problem can help kids understand how to solve it, just like picturing it can help them see it. Shapes or numbers could be used to show the forms to keep things easy. Kids might learn how to use dots or letters to show the parts of a pattern or graph if you teach them.

Charts and graphs can be useful even when math isn’t involved. Kids can draw pictures of the ideas they read about to help them remember them after they’ve learned them. The plan for how to solve the mathematical problem will help kids understand what the problem is and how to solve it.

Trial and Error Method

The trial and error method may be one of the most common problem solving strategies for kids to figure out how to solve problems. But how well this strategy is used will determine how well it works. Students have a hard time figuring out math questions if they don’t have clear formulas or instructions.

They have a better chance of getting the correct answer, though, if they first make a list of possible answers based on rules they already know and then try each one. Don’t be too quick to tell kids they shouldn’t learn by making mistakes.

Review Answers with Peers

It’s fun to work on your math skills with friends by reviewing the answers to math questions together. If different students have different ideas about how to solve the same problem, get them to share their thoughts with the class.

During class time, kids’ ways of working might be compared. Then, students can make their points stronger by fixing these problems.

Check out the Printable Math Worksheets for Your Kids!

There are different ways to solve problems that can affect how fast and well students do on math tests. That’s why they need to learn the best ways to do things. If students follow the steps in this piece, they will have better experiences with solving math questions.

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

As adults, we take numbers for granted, but preschoolers and kindergartners have no idea what these symbols mean. Yet, we often demand instant understanding and flawless performance when we start teaching numbers to our children. If you don’t have a clue about how to teach numbers for kids, browse no more. You will get four […]

May 19, 2022

Teaching children is a complex process because they require more attention than an adult person. You may need to employ different teaching strategies when teaching kids. But what are teaching strategies? Teaching strategies are the methods to ensure your kids or students learn efficiently. But not all strategies yield similarly, and if the one you […]

Book 1 to 1 Math Lesson

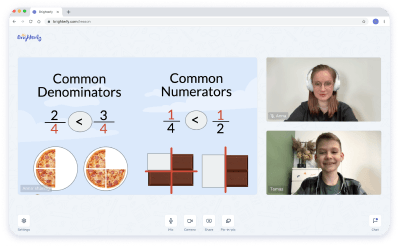
Kid’s grade

Summer Math Program Boost Your Child's Math Abilities! Ideal for 1st-12th Graders, Perfectly Synced with School Curriculum!

Online Summer Math Camp

Related posts.

10 Project-Based Learning (PBL) Ideas for Every Math Teacher

Math teaches foundational skills that children need to know and apply in the classroom and real-life situations. But how about a scenario where kids are not interested in learning, no matter how hard you try? You could opt for alternative teaching approaches to make kids embrace and understand math. One of the most effective approaches […]

May 20, 2022

Everything You Need to Know about Game Based Learning and Its Types

Most times, children do not get enough time to pay attention to teachers as the birds fly past the window. One minute, they are staring at the window. It is a miracle to get children focused on one thing for an extended time, except if it is exciting. As a teacher, you are responsible for […]

Useful Tips to Help Children Go through Deschooling Smoothly

Homeschooling is a life-changing decision that opens numerous unknown aspects of studying, one of which is deschooling. Check what it means, learn how it differs from unschooling, and get a few tips about making the process smoother. What Is Deschooling? Deschooling is the transition from studying at school to homeschooling. This process influences both children […]

Jun 30, 2022

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

May 31, 2024

10 min read

Math Can Help Solve Social Justice Problems

Mathematicians are working on ways to use their field to tackle major social issues, such as social inequality and the need for gender equity

By Rachel Crowell & Nature magazine

MicroStockHub/Getty Images

When Carrie Diaz Eaton trained as a mathematician, they didn’t expect their career to involve social-justice research. Growing up in Providence, Rhode Island, Diaz Eaton first saw social justice in action when their father, who’s from Peru, helped other Spanish-speaking immigrants to settle in the United States.

But it would be decades before Diaz Eaton would forge a professional path to use their mathematical expertise to study social-justice issues. Eventually, after years of moving around for education and training, that journey brought them back to Providence, where they collaborated with the Woonasquatucket River Watershed Council on projects focused on preserving the local environment of the river’s drainage basin, and bolstering resources for the surrounding, often underserved communities.

By “thinking like a mathematician” and leaning on data analysis, data science and visualization skills, they found that their expertise was needed in surprising ways, says Diaz Eaton, who is now executive director of the Institute for a Racially Just, Inclusive, and Open STEM Education at Bates College in Lewiston, Maine.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For example, the council identified a need to help local people to better connect with community resources. “Even though health care and education don’t seem to fall under the purview of a watershed council, these are all interrelated issues,” Diaz Eaton says. Air pollution can contribute to asthma attacks, for example. In one project, Diaz Eaton and their collaborators built a quiz to help community members to choose the right health-care option, depending on the nature of their illness or injury, immigration status and health-insurance coverage.

“One of the things that makes us mathematicians, is our skills in logic and the questioning of assumptions”, and creating that quiz “was an example of logic at play”, requiring a logic map of cases and all of the possible branches of decision-making to make an effective quiz, they say.

Maths might seem an unlikely bedfellow for social-justice research. But applying the rigour of the field is turning out to be a promising approach for identifying, and sometimes even implementing, fruitful solutions for social problems.

Mathematicians can experience first-hand the messiness and complexity — and satisfaction — of applying maths to problems that affect people and their communities. Trying to work out how to help people access much-needed resources, reduce violence in communities or boost gender equity requires different technical skills, ways of thinking and professional collaborations compared with breaking new ground in pure maths. Even for an applied mathematician like Diaz Eaton, transitioning to working on social-justice applications brings fresh challenges.

Mathematicians say that social-justice research is difficult yet fulfilling — these projects are worth taking on because of their tremendous potential for creating real-world solutions for people and the planet.

Data-driven research

Mathematicians are digging into issues that range from social inequality and health-care access to racial profiling and predictive policing. However, the scope of their research is limited by their access to the data, says Omayra Ortega, an applied mathematician and mathematical epidemiologist at Sonoma State University in Rohnert Park, California. “There has to be that measured information,” Ortega says.

Fortunately, data for social issues abound. “Our society is collecting data at a ridiculous pace,” Ortega notes. Her mathematical epidemiology work has examined which factors affect vaccine uptake in different communities. Her work has found, for example, that, in five years, a national rotavirus-vaccine programme in Egypt would reduce disease burden enough that the cost saving would offset 76% of the costs of the vaccine. “Whenever we’re talking about the distribution of resources, there’s that question of social justice: who gets the resources?” she says.

Lily Khadjavi’s journey with social-justice research began with an intriguing data set.

About 15 years ago, Khadjavi, a mathematician at Loyola Marymount University in Los Angeles, California, was “on the hunt for real-world data” for an undergraduate statistics class she was teaching. She wanted data that the students could crunch to “look at new information and pose their own questions”. She realized that Los Angeles Police Department (LAPD) traffic-stop data fit that description.

At that time, every time that LAPD officers stopped pedestrians or pulled over drivers, they were required to report stop data. Those data included “the perceived race or ethnicity of the person they had stopped”, Khadjavi notes.

When the students analysed the data, the results were memorable. “That was the first time I heard students do a computation absolutely correctly and then audibly gasp at their results,” she says. The data showed that one in every 5 or 6 police stops of Black male drivers resulted in a vehicle search — a rate that was more than triple the national average, which was about one out of every 20 stops for drivers of any race or ethnicity, says Khadjavi.

Her decision to incorporate that policing data into her class was a pivotal moment in Khadjavi’s career — it led to a key publication and years of building expertise in using maths to study racial profiling and police practice. She sits on California’s Racial Identity and Profiling Advisory Board , which makes policy recommendations to state and local agencies on how to eliminate racial profiling in law enforcement.

In 2023, she was awarded the Association for Women in Mathematics’ inaugural Mary & Alfie Gray Award for Social Justice, named after a mathematician couple who championed human rights and equity in maths and government.

Sometimes, gaining access to data is a matter of networking. One of Khadjavi’s colleagues shared Khadjavi’s pivotal article with specialists at the American Civil Liberties Union. In turn, these specialists shared key data obtained through public-records requests with Khadjavi and her colleague. “Getting access to that data really changed what we could analyse,” Khadjavi says. “[It] allowed us to shine a light on the experiences of civilians and police in hundreds of thousands of stops made every year in Los Angeles.”

The data-intensive nature of this research can be an adjustment for some mathematicians, requiring them to develop new skills and approach problems differently. Such was the case for Tian An Wong, a mathematician at the University of Michigan-Dearborn who trained in number theory and representation theory.

In 2020, Wong wanted to know more about the controversial issue of mathematicians collaborating with the police, which involves, in many cases, using mathematical modelling and data analysis to support policing activities. Some mathematicians were protesting about the practice as part of a larger wave of protests around systemic racism , following the killing of George Floyd by police in Minneapolis, Minnesota. Wong’s research led them to a technique called predictive policing, which Wong describes as “the use of historical crime and other data to predict where future crime will occur, and [to] allocate policing resources based on those predictions”.

Wong wanted to know whether the tactics that mathematicians use to support police work could instead be used to critique it. But first, they needed to gain some additional statistics and data analysis skills. To do so, Wong took an online introductory statistics course, re-familiarized themself with the Python programming language, and connected with colleagues trained in statistical methods. They also got used to reading research papers across several disciplines.

Currently, Wong applies those skills to investigating the policing effectiveness of a technology that automatically locates gunshots by sound. That technology has been deployed in parts of Detroit, Michigan, where community members and organizations have raised concerns about its multimillion-dollar cost and about whether such police surveillance makes a difference to public safety.

Getting the lay of the land

For some mathematicians, social-justice work is a natural extension of their career trajectories. “My choice of mathematical epidemiology was also partially born out of out of my love for social justice,” Ortega says. Mathematical epidemiologists apply maths to study disease occurrence in specific populations and how to mitigate disease spread. When Ortega’s PhD adviser mentioned that she could study the uptake of a then-new rotovirus vaccine in the mid-2000s, she was hooked.

Mathematicians, who decide to jump into studying social-justice issues anew, must do their homework and dedicate time to consider how best to collaborate with colleagues of diverse backgrounds.

Jonathan Dawes, an applied mathematician at the University of Bath, UK, investigates links between the United Nations’ Sustainable Development Goals (SDGs) and their associated target actions. Adopted in 2015, the SDGs are “a universal call to action to end poverty, protect the planet, and ensure that by 2030 all people enjoy peace and prosperity,” according to the United Nations , and each one has a number of targets.

“As a global agenda, it’s an invitation to everybody to get involved,” says Dawes. From a mathematical perspective, analysing connections in the complex system of SDGs “is a nice level of problem,” Dawes says. “You’ve got 17 Sustainable Development Goals. Between them, they have 169 targets. [That’s] an amount of data that isn’t very large in big-data terms, but just big enough that it’s quite hard to hold all of it in your head.”

Dawes’ interest in the SDGs was piqued when he read a 2015 review that focused on how making progress on individual goals could affect progress on the entire set. For instance, if progress is made on the goal to end poverty how does that affect progress on the goal to achieve quality education for all, as well as the other 15 SDGs?

“If there’s a network and you can put some numbers on the strengths and signs of the edges, then you’ve got a mathematized version of the problem,” Dawes says. Some of his results describe how the properties of the network change if one or more of the links is perturbed, much like an ecological food web. His work aims to identify hierarchies in the SDG networks, pinpointing which SDGs should be prioritized for the health of the entire system.

As Dawes dug into the SDGs, he realized that he needed to expand what he was reading to include different journals, including publications that were “written in very different ways”. That involved “trying to learn a new language”, he explains. He also kept up to date with the output of researchers and organizations doing important SDG-related work, such as the International Institute for Applied Systems Analysis in Laxenburg, Austria, and the Stockholm Environment Institute.

Dawes’ research showed that interactions between the SDGs mean that “there are lots of positive reinforcing effects between poverty, hunger, health care, education, gender equity and so on.” So, “it’s possible to lift all of those up” when progress is made on even one of the goals. With one exception: managing and protecting the oceans. Making progress on some of the other SDGs could, in some cases, stall progress for, or even harm, life below water.

Collaboration care

Because social-justice projects are often inherently cross-disciplinary, mathematicians studying social justice say it’s key in those cases to work with community leaders, activists or community members affected by the issues.

Getting acquainted with these stakeholders might not always feel comfortable or natural. For instance, when Dawes started his SDG research, he realized that he was entering a field in which researchers already knew each other, followed each other’s work and had decades of experience. “There’s a sense of being like an uninvited guest at a party,” Dawes says. He became more comfortable after talking with other researchers, who showed a genuine interest in what he brought to the discussion, and when his work was accepted by the field’s journals. Over time, he realized “the interdisciplinary space was big enough for all of us to contribute to”.

Even when mathematicians have been invited to join a team of social-justice researchers, they still must take care, because first impressions can set the tone.

Michael Small is an applied mathematician and director of the Data Institute at the University of Western Australia in Perth. For much of his career, Small focused on the behaviour of complex systems, or those with many simple interacting parts, and dynamical systems theory, which addresses physical and mechanical problems.

But when a former vice-chancellor at the university asked him whether he would meet with a group of psychiatrists and psychologists to discuss their research on mental health and suicide in young people, it transformed his research. After considering the potential social impact of better understanding the causes and risks of suicide in teenagers and younger children, and thinking about how the problem meshed well with his research in complex systems and ‘non-linear dynamics’, Small agreed to collaborate with the group.

The project has required Small to see beyond the numbers. For the children’s families, the young people are much more than a single data point. “If I go into the room [of mental-health professionals] just talking about mathematics, mathematics, mathematics, and how this is good because we can prove this really cool theorem, then I’m sure I will get push back,” he says. Instead, he notes, it’s important to be open to insights and potential solutions from other fields. Listening before talking can go a long way.

Small’s collaborative mindset has led him to other mental-health projects, such as the Transforming Indigenous Mental Health and Wellbeing project to establish culturally sensitive mental-health support for Indigenous Australians.

Career considerations

Mathematicians who engage in social-justice projects say that helping to create real-world change can be tremendously gratifying. Small wants “to work on problems that I think can do good” in the world. Spending time pursuing them “makes sense both as a technical challenge [and] as a social choice”, he says.

However, pursuing this line of maths research is not without career hurdles. “It can be very difficult to get [these kinds of] results published,” Small says. Although his university supports, and encourages, his mental-health research, most of his publications are related to his standard mathematics research. As such, he sees “a need for balance” between the two lines of research, because a paucity of publications can be a career deal breaker.

Diaz Eaton says that mathematicians pursuing social-justice research could experience varying degrees of support from their universities. “I’ve seen places where the work is supported, but it doesn’t count for tenure [or] it won’t help you on the job market,” they say.

Finding out whether social-justice research will be supported “is about having some really open and transparent conversations. Are the people who are going to write your recommendation letters going to see that work as scholarship?” Diaz Eaton notes.

All things considered, mathematicians should not feel daunted by wading into solving the world’s messy problems, Khadjavi says: “I would like people to follow their passions. It’s okay to start small.”

This article is reproduced with permission and was first published on May 22, 2024 .

Opinion | Teaching and Learning

When teaching students math, concepts matter more than process, by nicola hodkowski     jun 5, 2024.

Ground Picture / Shutterstock

As a mathematics education researcher, I study how math instruction impacts students' learning, from following standard math procedures to understanding mathematical concepts. Focusing on the latter, conceptual understanding often involves understanding the “why” of a mathematical concept ; it’s the reasoning behind the math rather than the how or the steps it takes to get to an answer.

So often, in mathematics classrooms, students are shown steps and procedures for solving math problems and then required to demonstrate their rote memorization of these steps independently.

As a result, students' agency, knowledge and ability to transfer the concepts of mathematics suffer. Specifically, students experience diminished confidence in tackling mathematical problems and a decreased ability to apply mathematical reasoning in real-world situations. In addition, students may struggle with more advanced mathematical concepts and problem-solving tasks as they progress in their education.

While procedural fluency is important, conceptual understanding provides a framework for students to build mental relationships between math concepts. It allows students to connect new ideas to what they already know , creating increasing connections toward more advanced mathematics.

If we want mathematics achievement to improve, we need instruction to begin focusing on concepts instead of procedures.

Why Concept Matters More Than Procedure

Conceptual understanding builds on existing understanding to advance knowledge and focuses on the student’s ability to justify and explain. Procedural fluency, on the other hand, is about following steps to arrive at an answer and accuracy.

When considering how students will learn more advanced mathematics concepts, it is important to consider how they will engage with the problems presented to them in class and how those problems will contribute either to their greater conceptual understanding or greater procedural fluency. For example, consider these two math questions and ask yourself: What knowledge is needed to solve each problem?

Early Learning

Many lack access to quality early education. home visiting programs are bringing it to more families., by emily tate sullivan.

The Impact of Inclusive STEM Education

By lisa milenkovic.

Girls in Science Olympiad Shrink the STEM Gap

By mark leong.

Data Privacy

This $90m education research project is banking on data privacy to drive insights, by nadia tamez-robledo.

Journalism that ignites your curiosity about education.

EdSurge is an editorially independent project of and

• Product Index
• Write for us
• Advertising

FOLLOW EDSURGE

© 2024 All Rights Reserved

Teachers Are Evenly Divided on the Best Way to Teach Math

• Share article

Teaching math, at least in part, by having students solve real-world problems is becoming increasingly popular in schools. In fact, California recently adopted a controversial framework that embraces the approach.

However, educators are still divided over whether it’s the best way to go, according to an EdWeek Research Center survey conducted this spring.

About half of the teachers, principals, and district leaders surveyed—49 percent—agreed that students learn math best through procedures rather than solving big problems, the survey found, including 13 percent who said they “completely agreed.”

On the other hand, about 52 percent disagreed with the statement, including 12 percent who “completely disagreed.”

To be sure, even experts who prefer one approach over the other say that aspects of both are necessary to help students understand math.

Although the debate over the two approaches has sometimes been dubbed the “math wars,” “I don’t think it needs to be as polarizing of a choice,” said Zack Hill, a math curriculum writer and education consultant.

“I lean more toward a constructivist approach,” also sometimes referred to as problem-solving, Hill said. “But I also understand that there are certain things that ... children will not intuit,” such as expanded form, a way of writing numbers to see the math value of individual digits. “They’re not going to come up with that term on their own. There are certain things that we need to teach kids explicitly. I think for me what it’s about [is] giving them the time and the space to reason around it.”

Janaki Nagarajan, who teaches in the Renton school district near Seattle, also prefers teaching math from a problem-solving perspective. But she doesn’t believe teachers should limit themselves to just one approach.

Even when educators prioritize problem-solving, “there’s obviously instruction that involves teaching kids how to multiply,” she said.

But she sees a difference between learning basic procedures “in a way that’s just like, ‘here, you need to know this, but I’m not going to explain to you what this is or why this makes sense or how it’s connected to anything,’” and instead telling students, “‘Here’s what multiplication is, how do we use it? How do we apply it to things?’”

Nagarajan’s district sets aside time for what it calls a “math workshop” where students play “fluency games” that allow them to practice using particular math concepts in an engaging way.

“It’s not like ‘Oh, we’re not giving them the building blocks,’” she said. Instead, “you’re giving them in ways that kids are interested in.”

Data analysis for this article was provided by the EdWeek Research Center. Learn more about the center’s work.

Sign Up for EdWeek Update

Edweek top school jobs.

Sign Up & Sign In

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

Explore how Microsoft's partnership with Khan Academy is enhancing the future of education with AI innovation and tools for teachers >

• Published Nov 3, 2022

Empowering student learning with Math Assistant

• Content Type
• Accessibility
• Microsoft Teams

Math teachers, what if there was a way to help students who say “I’m not a math person” or “I’m just not good at math”? When a student lacks math confidence, every challenge along the way simply confirms their self-doubt. These challenges only intensify as students move through their K-12 school experience and their needs and the course content continue to evolve. The good news is that Math Assistant , found in Microsoft OneNote, helps students find their math confidence and gain important math skills through inclusive, individualized features.

Explore the scenarios below to learn how Math Assistant can help transform K-12 students’ math experience, accelerate their learning, and help them enjoy math too.

Capture notes using Ink to Math

Ellie is a 5th grade student who is currently learning about multiplying fractions. Ellie has consistently enjoyed learning the steps for multiplication and understood the concept of fractions almost immediately. However, combining the two ideas into multiplying fractions has been challenging, even when using a calculator.

As a learner who constantly takes notes to remember her teacher’s instructions, Ellie can quickly draw equations on her Windows 11SE device’s touchscreen and convert the image into a mathematical format using Ink to Math . Ellie, like most of her classmates, is still developing her handwriting skills and she can select which characters she is writing to ensure that each problem comes out exactly right.

Math Assistant features that impact Ellie’s skills and confidence:

• Ink to Math helps Ellie capture class notes in real-time. Later, she can convert her hand-written equations into math.
• Ink to Math lets Ellie select the correct character from a list.

Instant practice with Generate Quiz

Sadie is a 7th grader whose class just started its algebra unit. She uses OneNote Class Notebook to keep up with resources and example problems that she can access at home or in class. Tomorrow is the big quiz and Sadie is still nervous about how to solve for x in linear inequalities, so she opens OneNote to practice.

Sadie starts by using her Math Assistant’s Ink to Math feature to create a sample problem. As this is her first practice problem, Sadie starts by using Math Solver for a step-by-step explanation of how to find x.

Now that Sadie is ready for some independent practice, she clicks the Generate Quiz button to create a custom set of no-stakes practice problems based on her example equation. She can even determine how many questions the practice set should have.

Using tools like Math Assistant’s Generate Quiz, Sadie creates personalized, on-demand assessments that help her accelerate her learning when she needs it regardless of if she is in class or at home. The next day in class, Sadie confidently completes her algebra quiz using the skills she developed using Math Assistant.

Math Assistant features that impact Sadie’s skills and confidence:

• Ink to Math allows Sadie to naturally write equations on her touchscreen device and then convert it into math for additional AI features.
• Math Solver offers step-by-step explanations of solving algebraic equations.
• Generate Quiz creates on-demand practice challenging topics.

Graphing and analysis in OneNote Notebook

Guillermo is an 11th grade Algebra II student who is learning about graphing equations. His teacher uses Microsoft Teams for Education and a OneNote Class Notebook to share resources, post assignments, and offer virtual office hours for students who need extra help or want to check in outside of class.

Earlier this week, Guillermo’s teacher shared a linear equation. Now Guillermo is trying to remember the steps to solving the equation and how to graph his solution. Guillermo uses OneNote Math Assistant’s graphing feature to graph both sides in 2D and insert the graph into his OneNote.

Later, Guillermo explores other features of his graph like the y-intercept and x-y values at different points along the graph line.

As the year continues, Guillermo feels self-assured knowing that he can always return to his linear equation notes to review past concepts. He increasingly trusts his math skills without anxiousness knowing that he can use other graphing features in Math Assistant when his class covers polynomial arrays, systems of equations, and inequalities.

Math Assistant features that impact Guillermo’s skills and confidence:

• OneNote Class Notebook organizes and structures Guillermo’s notes.
• Math Assistant graphs equations and inserts them directly into Guillermo’s notebook.
• Math Assistant analyzes the graph for features like y-intercept and x-y values.

Inclusion and accessibility with Immersive Reader for Math

Mei is a 6th grade student who primarily speaks Mandarin at home. While skilled in math, she feels unsure of herself due to the challenge of accessing domain-specific vocabulary in English. Mei’s teacher recently attended a virtual training led by Microsoft Innovative Educators and was introduced to Immersive Reader for Math , a built-in feature of Math Assistant.

Inclusive-by-design, Immersive Reader for Math allows students like Mei to access math content through equations read aloud, a feature that many browser-based screen readers lack. Beyond simply reading the equations aloud, Mei can select her preferred language to access the content using familiar vocabulary and phrases. By removing language barriers, Mei is confident that her math skills will be on full display.

Math Assistant features that impact Mei’s skills and confidence:

• Immersive Reader for Math makes math text and equations inclusive and accessible with read aloud and other features.
• Math Assistant allows Mei to explore a step-by-step explanation of the equation to practice the concept.
• Immersive Reader for Math translates the step-by-step process into Chinese. Mei can customize the voice, speed, and other features to her preferences.

Meeting students’ unique math needs

Just like a student’s personality or interests, their learning needs are unique. Math Assistant in OneNote offers inclusive-by-design instructional tools that empower learners to gain the important confidence and skills that they need to thrive.

Related Posts

Stay ahead with 8 new updates from Microsoft Education  

• Professional development

Comprehensive quick start guides for Microsoft Education tools  

Read ‘em and reap (the rewards): World Read Aloud Day 2024  

Ai in education brings opportunity to life.

Watch Reimagine Education

Connect with us on social

Subscribe to our newsletter

Stay up to date with monthly newsletters from Microsoft Education.  

School stories

Get inspired by stories from Microsoft Education customers.

Microsoft Learn Educator Center

Expand possibilities with educator training and professional development resources.

Contact sales

Connect with a Microsoft Education sales specialist to explore solutions for your school.

Discover a collection of resources to support a variety of educational topics.

The 7 Best AI Tools to Help Solve Math Problems

How do you make seven even? Use these tools to solve the big math problems in life.

Quick Links

The test questions, wolframalpha, microsoft mathsolver.

While OpenAI's ChatGPT is one of the most widely known AI tools, there are numerous other platforms that students can use to improve their math skills.

I tested seven AI tools on two common math problems so you know what to expect from each platform and how to use each of them.

I used two math problems to test each tool and standardize the inputs.

• Solve for b: (2 / (b - 3)) - (6 / (2b + 1)) = 4
• Simplify the expression: (4 / 12) + (9 / 8) x (15 / 3) - (26 / 10)

These two problems give each AI tool a chance to show reasoning, problem-solving, accuracy, and how it can guide a learner through the process.

Thetawise provides more than simple answers; you can also opt to have the AI model tutor you by sharing a detailed step-by-step breakdown of the solution. Using the platform is fairly straightforward, given that all you need to do is navigate to the platform and key in the math problem at hand. Alternatively, you can even upload a photo of the math problem onto the platform, and the AI will analyze the image and provide you with an answer.

The AI platform gave us a step-by-step breakdown of the problem:

It resulted in the answer:

While the answer is correct, the tool also provides further options for students to generate a more detailed breakdown of the steps or ask more specific questions.

WolframAlpha is an AI tool capable of solving advanced arithmetic, calculus, and algebra equations. While WolframAlpha's free version provides you with a direct answer, the paid version of the tool generates step-by-step solutions. If you want to make the best use of WolframAlpha's capabilities, you can sign up for the Pro version, which costs $5 per month for the annual plan if you're a student.

As expected, Wolfram Alpha solved both problems, showcasing its ability to handle different problems and provide precise answers quickly.

Julius works pretty similarly to the other AI tools on this list. That said, the highlight of this platform is that it has a built-in community forum, which users can use to discuss their prompts, results, or even issues they might be facing with the platform. Its active user base helps you quickly exchange ideas and receive feedback or advice. The platform's default version uses a combination of GPT-4 and Calude-3, based on whichever model best suits the prompt you input.

We tested the platform's accuracy by submitting the same problems that we did with the other AI tools. When submitting your prompt, you have the option of typing your question or uploading an image or a Google Sheet.

Julius provided correct solutions and offered options to help users verify the solution.

One of the oldest AI platforms, Microsoft's MathSolver is a great option if you want a tool capable of providing free step-by-step solutions to calculus, algebra, and other math problems. Here's how it fared when we submitted our math problems.

Microsoft's MathSolver provided the correct answers, and you can view the steps to the solution, take a quiz, solve similar problems, and more. This can be a great way to practice and perfect your understanding of different concepts.

Symbolab allows you to practice your math skills via quizzes, track your progress, and provide solutions to mathematical problems of different types, including calculus, fractions, trigonometry, and more. You can also use the Digital Notebook feature to keep track of any math problems you solve and share them with your friends. Another highlight of this platform is that educators can use the tool to create a virtual classroom, generate assessments, and share feedback, among other things.

The platform not only displays the answer but also lets you view a breakdown of the steps involved in solving the problem. You can also share the answers and steps via email or social media or print them for reference.

Anthropic launched its Claude 3 AI models in March 2024. Anthropic stated that Claude Opus, the most advanced Claude 3 model, outperforms comparable AI tools on most benchmarks for AI systems, including basic mathematics, undergraduate-level expert knowledge, and graduate-level expert reasoning. To test the platform's accuracy and ease of use, we submitted our two math problems. Here's how the platform performed:

While Claude initially got the answer wrong, probing it and requesting further clarification led to a correct solution.

Remember that we used the free version of Claude to solve this problem; subscribing to Opus (its more advanced model) is recommended if you want to take advantage of Claude's more advanced problem-solving capabilities.

Given that Claude got the previous problem wrong, our second, more basic fraction-based problem will indicate if the AI's performance was an anomaly or part of a consistent pattern.

As you can see, Claude correctly solved this problem and provided a detailed step-by-step breakdown of how it arrived at the answer.

GPT-4 can solve problems with far greater accuracy than its predecessor, GPT-3.5. If you're using the free version of ChatGPT, you'll likely only have access to GPT 3.5 and GPT-4o . However, for $20 per month, you can subscribe to the Plus model, which gives you access to GPT-4 and allows you to input five times the number of messages per day compared to the free version. That said, let's check how it performs with math problems.

In both cases, GPT-4o provided the correct answer with a detailed breakdown of the steps. While the platform is free, unlike other models, it does not have a quiz feature or a community forum.

These AI tools offer unique features and capabilities that make them a good option for math problems. Ultimately, the best way to pick a tool is by testing different models to determine which platform best fits your preferences and learning needs.