introduction to quadratic functions assignment quizlet

Quadratic Functions

Introduction to quadratic functions, learning objectives.

By the end of this lesson, you will be able to:

• Recognize characteristics of parabolas.
• Understand how the graph of a parabola is related to its quadratic function.
• Determine a quadratic function’s minimum or maximum value.
• Solve problems involving a quadratic function’s minimum or maximum value.

Figure 1. An array of satellite dishes. (credit: Matthew Colvin de Valle, Flickr)

Curved antennas, such as the ones shown in the photo, are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.

In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior.

• Precalculus. Authored by : Jay Abramson, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download For Free at : http://cnx.org/contents/[email protected].

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Study Guides > College Algebra

Graphs of quadratic functions.

Characteristics of Parabolas

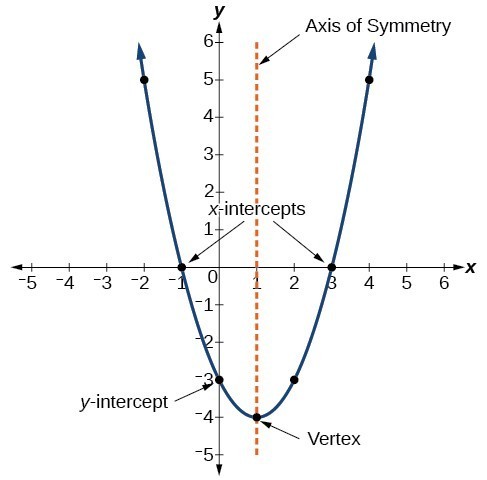
Example: Identifying the Characteristics of a Parabola

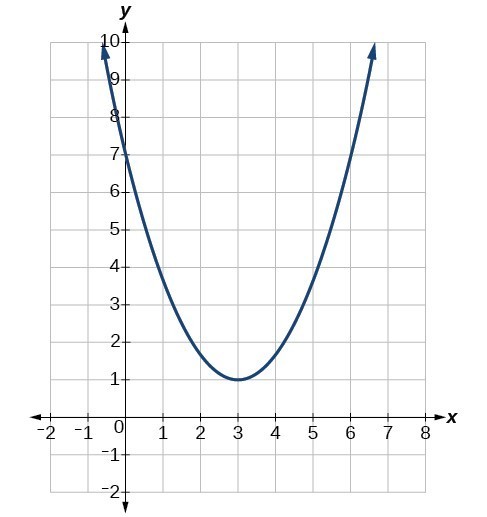
Answer: The vertex is the turning point of the graph. We can see that the vertex is at (3, 1). Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is x  = 3. This parabola does not cross the x -axis, so it has no zeros. It crosses the y -axis at (0, 7) so this is the y -intercept.

Equations of Quadratic Functions

[latex]f\left(x\right)=a{x}^{2}+bx+c[/latex]

[latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]

Given a quadratic function in general form, find the vertex of the parabola.

[latex]f(x)=ax^2+bx+c[/latex]

• Identify a ,  b , and  c .
• Find h , the x -coordinate of the vertex, by substituting a and b  into [latex]h=-\frac{b}{2a}[/latex].
• Find k , the y -coordinate of the vertex, by evaluating [latex]k=f\left(h\right)=f\left(-\frac{b}{2a}\right)[/latex]

Example: Finding the Vertex of a Quadratic Function

[latex]\begin{array}{c}h=-\frac{b}{2a}\hfill \\ \text{ }=-\frac{-6}{2\left(2\right)}\hfill \\ \text{ }=\frac{6}{4}\hfill \\ \text{ }=\frac{3}{2}\hfill \end{array}[/latex]

[latex]\begin{array}{c}k=f\left(h\right)\hfill \\ \text{ }=f\left(\frac{3}{2}\right)\hfill \\ \text{ }=2{\left(\frac{3}{2}\right)}^{2}-6\left(\frac{3}{2}\right)+7\hfill \\ \text{ }=\frac{5}{2}\hfill \end{array}[/latex]

[latex]\begin{array}{c}f\left(x\right)=a{x}^{2}+bx+c\hfill \\ f\left(x\right)=2{x}^{2}-6x+7\hfill \end{array}[/latex]

[latex]f\left(x\right)=2{\left(x-\frac{3}{2}\right)}^{2}+\frac{5}{2}[/latex]

Answer: [latex]g\left(x\right)={x}^{2}-6x+13[/latex] in general form; [latex]g\left(x\right)={\left(x - 3\right)}^{2}+4[/latex] in standard form

Finding the Domain and Range of a Quadratic Function

A general note: domain and range of a quadratic function, how to: given a quadratic function, find the domain and range..

• Identify the domain of any quadratic function as all real numbers.
• Determine whether a  is positive or negative. If a  is positive, the parabola has a minimum. If a  is negative, the parabola has a maximum.
• Determine the maximum or minimum value of the parabola, k .
• If the parabola has a minimum, the range is given by [latex]f\left(x\right)\ge k[/latex], or [latex]\left[k,\infty \right)[/latex]. If the parabola has a maximum, the range is given by [latex]f\left(x\right)\le k[/latex], or [latex]\left(-\infty ,k\right][/latex].

Example: Finding the Domain and Range of a Quadratic Function

[latex]\begin{array}{c}h=-\frac{b}{2a}\hfill \\ \text{ }=-\frac{9}{2\left(-5\right)}\hfill \\ \text{ }=\frac{9}{10}\hfill \end{array}[/latex]

[latex]\begin{array}{c}f\left(\frac{9}{10}\right)=5{\left(\frac{9}{10}\right)}^{2}+9\left(\frac{9}{10}\right)-1\hfill \\ \text{ }=\frac{61}{20}\hfill \end{array}[/latex]

Answer: The domain is all real numbers. The range is [latex]f\left(x\right)\ge \frac{8}{11}[/latex], or [latex]\left[\frac{8}{11},\infty \right)[/latex].

Transformations of Quadratic Functions

[latex]\begin{array}{c}a{\left(x-h\right)}^{2}+k=a{x}^{2}+bx+c\hfill \\ a{x}^{2}-2ahx+\left(a{h}^{2}+k\right)=a{x}^{2}+bx+c\hfill \end{array}[/latex]

[latex]-2ah=b,\text{ so }h=-\frac{b}{2a}[/latex].

[latex]\begin{array}{c}a{h}^{2}+k=c\hfill \\ \text{ }k=c-a{h}^{2}\hfill \\ \text{ }=c-a-{\left(\frac{b}{2a}\right)}^{2}\hfill \\ \text{ }=c-\frac{{b}^{2}}{4a}\hfill \end{array}[/latex]

A General Note: Forms of Quadratic Functions

[latex]h=-\frac{b}{2a},\text{ }k=f\left(h\right)=f\left(\frac{-b}{2a}\right)[/latex].

How To: Given a graph of a quadratic function, write the equation of the function in general form.

• Identify the horizontal shift of the parabola; this value is h . Identify the vertical shift of the parabola; this value is k .
• Substitute the values of the horizontal and vertical shift for h  and k . in the function [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex].
• Substitute the values of any point, other than the vertex, on the graph of the parabola for x  and [latex]f\left(x\right)[/latex].
• Solve for the stretch factor, | a |.
• If the parabola opens up, [latex]a>0[/latex]. If the parabola opens down, [latex]a<0[/latex] since this means the graph was reflected about the x -axis.
• Expand and simplify to write in general form.

Example: Writing the Equation of a Quadratic Function from the Graph

[latex]\begin{array}{c}-1=a{\left(0+2\right)}^{2}-3\hfill \\ \text{ }2=4a\hfill \\ \text{ }a=\frac{1}{2}\hfill \end{array}[/latex]

[latex]\begin{array}{c}g\left(x\right)=\frac{1}{2}{\left(x+2\right)}^{2}-3\hfill \\ \text{ }=\frac{1}{2}\left(x+2\right)\left(x+2\right)-3\hfill \\ \text{ }=\frac{1}{2}\left({x}^{2}+4x+4\right)-3\hfill \\ \text{ }=\frac{1}{2}{x}^{2}+2x+2 - 3\hfill \\ \text{ }=\frac{1}{2}{x}^{2}+2x - 1\hfill \end{array}[/latex]

Analysis of the Solution

Answer: The path passes through the origin and has vertex at [latex]\left(-4,\text{ }7\right)[/latex], so [latex]\left(h\right)x=-\frac{7}{16}{\left(x+4\right)}^{2}+7[/latex]. To make the shot, [latex]h\left(-7.5\right)[/latex] would need to be about 4 but [latex]h\left(-7.5\right)\approx 1.64[/latex]; he doesn’t make it.

Key Equations

Key concepts.

• A polynomial function of degree two is called a quadratic function.
• The graph of a quadratic function is a parabola. A parabola is a U-shaped curve that can open either up or down.
• The axis of symmetry is the vertical line passing through the vertex.
• Quadratic functions are often written in general form. Standard or vertex form is useful to easily identify the vertex of a parabola. Either form can be written from a graph.
• The vertex can be found from an equation representing a quadratic function.
• The domain of a quadratic function is all real numbers. The range varies with the function.

Licenses & Attributions

Cc licensed content, original.

• Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .

CC licensed content, Shared previously

• College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .
• Question ID 120303, 120300. Authored by: Lumen Learning. License: CC BY: Attribution . License terms: IMathAS Community License CC-BY + GPL.

Please add a message.

Message received. Thanks for the feedback.

Introduction to Functions

Chapter outline.

Toward the end of the twentieth century, the values of stocks of Internet and technology companies rose dramatically. As a result, the Standard and Poor’s stock market average rose as well. The graph above tracks the value of that initial investment of just under $100 over the 40 years. It shows that an investment that was worth less than $500 until about 1995 skyrocketed up to about $1100 by the beginning of 2000. That five-year period became known as the “dot-com bubble” because so many Internet startups were formed. As bubbles tend to do, though, the dot-com bubble eventually burst. Many companies grew too fast and then suddenly went out of business. The result caused the sharp decline represented on the graph beginning at the end of 2000.

Notice, as we consider this example, that there is a definite relationship between the year and stock market average. For any year we choose, we can determine the corresponding value of the stock market average. In this chapter, we will explore these kinds of relationships and their properties.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/3-introduction-to-functions

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.7: Modeling with Quadratic Functions

• Last updated
• Save as PDF
• Page ID 93930

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Recognize characteristics of parabolas
• Understand how the graph of a parabola is related to its quadratic function
• Solve problems involving a quadratic function’s minimum or maximum value

in order to apply mathematical modeling to solve real-world applications.

Curved antennas, such as the ones shown in Figure \(\PageIndex{1}\), are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.

In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior.

Recognizing Characteristics of Parabolas

The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex . If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value . In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry . These features are illustrated in Figure \(\PageIndex{2}\).

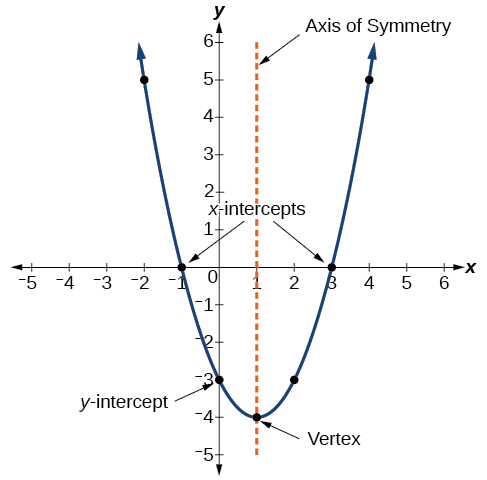
The y-intercept is the point at which the parabola crosses the \(y\)-axis. The x-intercepts are the points at which the parabola crosses the \(x\)-axis. If they exist, the x-intercepts represent the zeros , or roots , of the quadratic function, the values of \(x\) at which \(y=0\).

Example \(\PageIndex{1}\): Identifying the Characteristics of a Parabola

Determine the vertex, axis of symmetry, zeros, and y-intercept of the parabola shown in Figure \(\PageIndex{3}\).

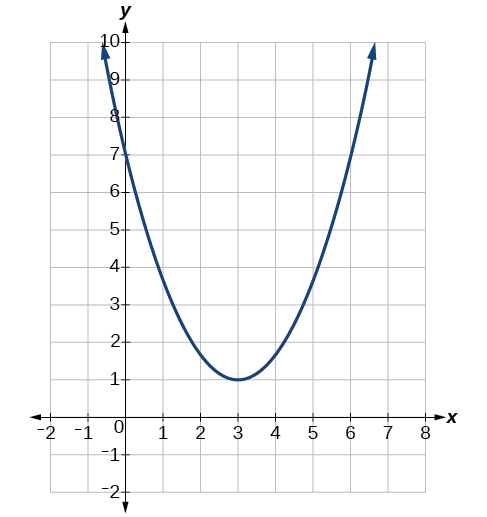
The vertex is the turning point of the graph. We can see that the vertex is at \((3,1)\). Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is \(x=3\). This parabola does not cross the x-axis, so it has no zeros. It crosses the \(y\)-axis at \((0,7)\) so this is the y-intercept.

Understanding How the Graphs of Parabolas are Related to Their Quadratic Functions

The general form of a quadratic function presents the function in the form

\[f(x)=ax^2+bx+c\]

where \(a\), \(b\), and \(c\) are real numbers and \(a{\neq}0\). If \(a>0\), the parabola opens upward. If \(a<0\), the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.

The axis of symmetry is defined by \(x=−\frac{b}{2a}\). If we use the quadratic formula, \(x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}\), to solve \(ax^2+bx+c=0\) for the x-intercepts, or zeros, we find the value of \(x\) halfway between them is always \(x=−\frac{b}{2a}\), the equation for the axis of symmetry.

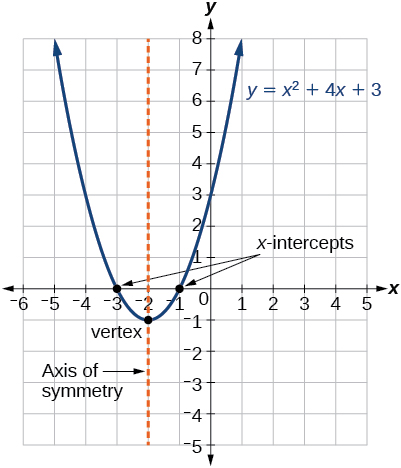
Figure \(\PageIndex{4}\) represents the graph of the quadratic function written in general form as \(y=x^2+4x+3\). In this form, \(a=1\), \(b=4\), and \(c=3\). Because \(a>0\), the parabola opens upward. The axis of symmetry is \(x=−\frac{4}{2(1)}=−2\). This also makes sense because we can see from the graph that the vertical line \(x=−2\) divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, \((−2,−1)\). The x-intercepts, those points where the parabola crosses the x-axis, occur at \((−3,0)\) and \((−1,0)\).

The standard form of a quadratic function presents the function in the form

\[f(x)=a(x−h)^2+k\]

where \((h, k)\) is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function .

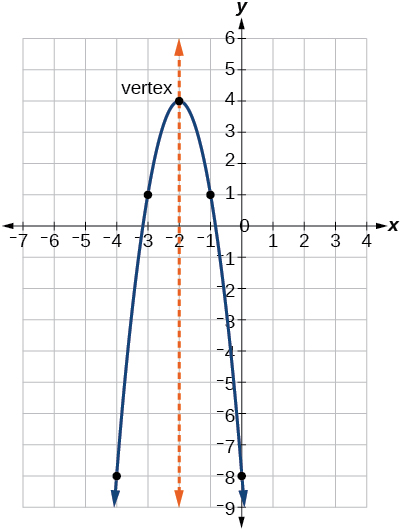
As with the general form, if \(a>0\), the parabola opens upward and the vertex is a minimum. If \(a<0\), the parabola opens downward, and the vertex is a maximum. Figure \(\PageIndex{5}\) represents the graph of the quadratic function written in standard form as \(y=−3(x+2)^2+4\). Since \(x–h=x+2\) in this example, \(h=–2\). In this form, \(a=−3\), \(h=−2\), and \(k=4\). Because \(a<0\), the parabola opens downward. The vertex is at \((−2, 4)\).

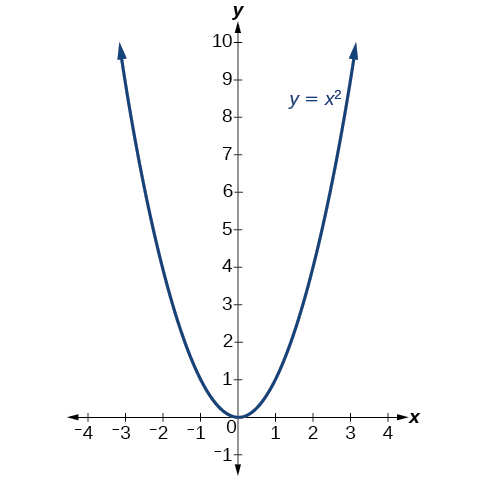
The standard form is useful for determining how the graph is transformed from the graph of \(y=x^2\). Figure \(\PageIndex{6}\) is the graph of this basic function.

If \(k>0\), the graph shifts upward, whereas if \(k<0\), the graph shifts downward. In Figure \(\PageIndex{5}\), \(k>0\), so the graph is shifted 4 units upward. If \(h>0\), the graph shifts toward the right and if \(h<0\), the graph shifts to the left. In Figure \(\PageIndex{5}\), \(h<0\), so the graph is shifted 2 units to the left. The magnitude of \(a\) indicates the stretch of the graph. If \(|a|>1\), the point associated with a particular x-value shifts farther from the x-axis, so the graph appears to become narrower, and there is a vertical stretch. But if \(|a|<1\), the point associated with a particular x-value shifts closer to the x-axis, so the graph appears to become wider, but in fact there is a vertical compression. In Figure \(\PageIndex{5}\), \(|a|>1\), so the graph becomes narrower.

The standard form and the general form are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the standard form.

\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]

For the linear terms to be equal, the coefficients must be equal.

\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]

This is the axis of symmetry we defined earlier. Setting the constant terms equal:

\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a−\Big(\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\]

In practice, though, it is usually easier to remember that \(k\) is the output value of the function when the input is \(h\), so \(f(h)=k\).

Definitions: Forms of Quadratic Functions

A quadratic function is a function of degree two. The graph of a quadratic function is a parabola.

• The general form of a quadratic function is \(f(x)=ax^2+bx+c\) where \(a\), \(b\), and \(c\) are real numbers and \(a{\neq}0\).
• The standard form of a quadratic function is \(f(x)=a(x−h)^2+k\).
• The vertex \((h,k)\) is located at \[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]

HOWTO: Write a quadratic function in a general form

Given a graph of a quadratic function, write the equation of the function in general form.

• Identify the horizontal shift of the parabola; this value is \(h\). Identify the vertical shift of the parabola; this value is \(k\).
• Substitute the values of the horizontal and vertical shift for \(h\) and \(k\). in the function \(f(x)=a(x–h)^2+k\).
• Substitute the values of any point, other than the vertex, on the graph of the parabola for \(x\) and \(f(x)\).
• Solve for the stretch factor, \(|a|\).
• If the parabola opens up, \(a>0\). If the parabola opens down, \(a<0\) since this means the graph was reflected about the x-axis.
• Expand and simplify to write in general form.

Example \(\PageIndex{2}\): Writing the Equation of a Quadratic Function from the Graph

Write an equation for the quadratic function \(g\) in Figure \(\PageIndex{7}\) as a transformation of \(f(x)=x^2\), and then expand the formula, and simplify terms to write the equation in general form.

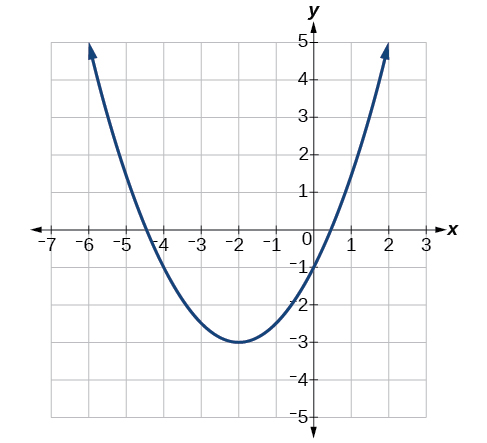
We can see the graph of \(g\) is the graph of \(f(x)=x^2\) shifted to the left 2 and down 3, giving a formula in the form \(g(x)=a(x+2)^2–3\).

Substituting the coordinates of a point on the curve, such as \((0,−1)\), we can solve for the stretch factor.

\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]

In standard form, the algebraic model for this graph is \(g(x)=\dfrac{1}{2}(x+2)^2–3\).

To write this in general polynomial form, we can expand the formula and simplify terms.

\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]

Notice that the horizontal and vertical shifts of the basic graph of the quadratic function determine the location of the vertex of the parabola; the vertex is unaffected by stretches and compressions.

We can check our work using the table feature on a graphing utility. First enter \(\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}\). Next, select \(\mathrm{TBLSET}\), then use \(\mathrm{TblStart=–6}\) and \(\mathrm{ΔTbl = 2}\), and select \(\mathrm{TABLE}\). See Table \(\PageIndex{1}\)

The ordered pairs in the table correspond to points on the graph.

Exercise \(\PageIndex{2}\)

A coordinate grid has been superimposed over the quadratic path of a basketball in Figure \(\PageIndex{8}\). Find an equation for the path of the ball. Does the shooter make the basket?

Figure \(\PageIndex{8}\): Stop motioned picture of a boy throwing a basketball into a hoop to show the parabolic curve it makes. (credit: modification of work by Dan Meyer)

The path passes through the origin and has vertex at \((−4, 7)\), so \(h(x)=–\frac{7}{16}(x+4)^2+7\). To make the shot, \(h(−7.5)\) would need to be about 4 but \(h(–7.5){\approx}1.64\); he doesn’t make it.

• Identify \(a\), \(b\), and \(c\).
• Find \(h\), the x-coordinate of the vertex, by substituting \(a\) and \(b\) into \(h=–\frac{b}{2a}\).
• Find \(k\), the y-coordinate of the vertex, by evaluating \(k=f(h)=f\Big(−\frac{b}{2a}\Big)\).

Example \(\PageIndex{3}\): Finding the Vertex of a Quadratic Function

Find the vertex of the quadratic function \(f(x)=2x^2–6x+7\). Rewrite the quadratic in standard form (vertex form).

The horizontal coordinate of the vertex will be at

\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]

The vertical coordinate of the vertex will be at

\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]

Rewriting into standard form, the stretch factor will be the same as the \(a\) in the original quadratic.

\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]

Using the vertex to determine the shifts,

\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]

One reason we may want to identify the vertex of the parabola is that this point will inform us what the maximum or minimum value of the function is, \((k)\),and where it occurs, \((h)\).

Exercise \(\PageIndex{3}\)

Given the equation \(g(x)=13+x^2−6x\), write the equation in general form and then in standard form.

\(g(x)=x^2−6x+13\) in general form; \(g(x)=(x−3)^2+4\) in standard form.

Determining the Maximum and Minimum Values of Quadratic Functions

The output of the quadratic function at the vertex is the maximum or minimum value of the function, depending on the orientation of the parabola . We can see the maximum and minimum values in Figure \(\PageIndex{9}\).

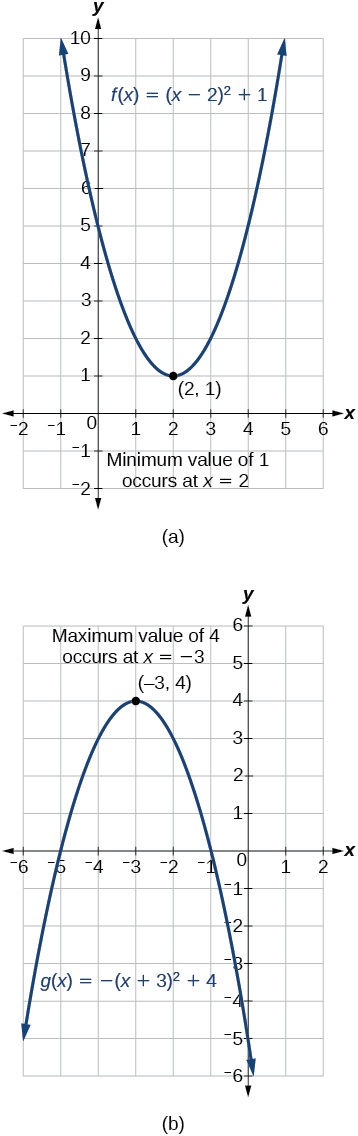
There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.

Example \(\PageIndex{5}\): Finding the Maximum Value of a Quadratic Function

A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.

• Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length \(L\).
• What dimensions should she make her garden to maximize the enclosed area?

Let’s use a diagram such as Figure \(\PageIndex{10}\) to record the given information. It is also helpful to introduce a temporary variable, \(W\), to represent the width of the garden and the length of the fence section parallel to the backyard fence.

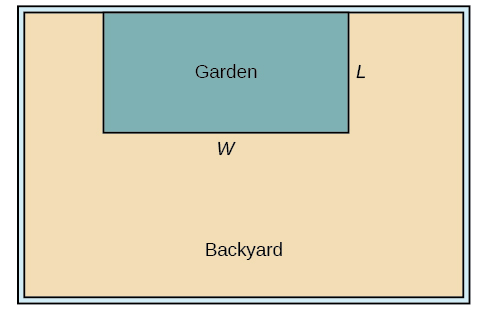
a. We know we have only 80 feet of fence available, and \(L+W+L=80\), or more simply, \(2L+W=80\). This allows us to represent the width, \(W\), in terms of \(L\).

\[W=80−2L\]

Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]

This formula represents the area of the fence in terms of the variable length \(L\). The function, written in general form, is

\[A(L)=−2L^2+80L\].

The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since \(a\) is the coefficient of the squared term, \(a=−2\), \(b=80\), and \(c=0\).

To find the vertex:

\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]

The maximum value of the function is an area of 800 square feet, which occurs when \(L=20\) feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.

This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function in Figure \(\PageIndex{11}\).

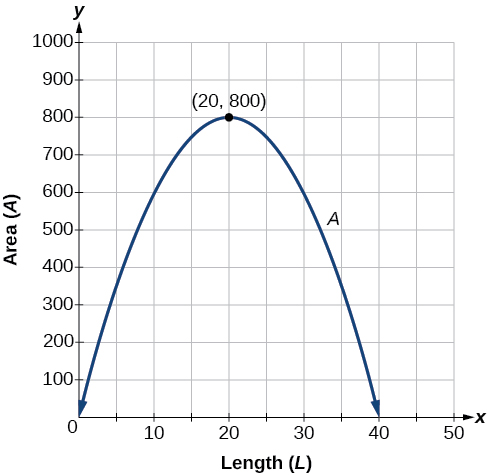
• Write a quadratic equation for revenue.
• Find the vertex of the quadratic equation.
• Determine the y-value of the vertex.

Example \(\PageIndex{6}\): Finding Maximum Revenue

The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?

Revenue is the amount of money a company brings in. In this case, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity. We can introduce variables, \(p\) for price per subscription and \(Q\) for quantity, giving us the equation \(\text{Revenue}=pQ\).

Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently \(p=30\) and \(Q=84,000\). We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, \(p=32\) and \(Q=79,000\). From this we can find a linear equation relating the two quantities. The slope will be

\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]

This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the y-intercept.

\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]

This gives us the linear equation \(Q=−2,500p+159,000\) relating cost and subscribers. We now return to our revenue equation.

\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]

We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.

\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]

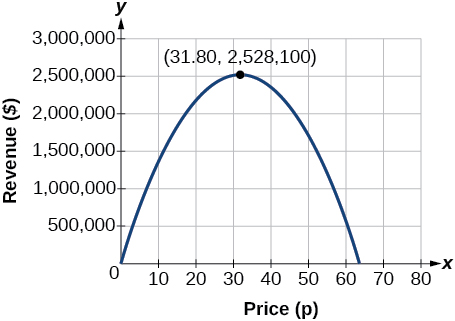
The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.

\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]

This could also be solved by graphing the quadratic as in Figure \(\PageIndex{12}\). We can see the maximum revenue on a graph of the quadratic function.

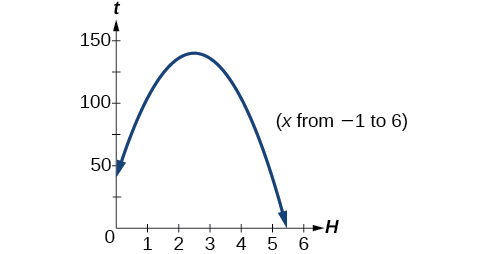
Example \(\PageIndex{10}\): Applying the Vertex and x-Intercepts of a Parabola

A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation \(H(t)=−16t^2+80t+40\).

When does the ball reach the maximum height? What is the maximum height of the ball? When does the ball hit the ground?

The ball reaches the maximum height at the vertex of the parabola. \[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]

The ball reaches a maximum height after 2.5 seconds.

To find the maximum height, find the y-coordinate of the vertex of the parabola. \[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]

The ball reaches a maximum height of 140 feet.

To find when the ball hits the ground, we need to determine when the height is zero, \(H(t)=0\).

We use the quadratic formula.

\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]

Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.

\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds. See Figure \(\PageIndex{16}\).

Example \(\PageIndex{11}\): Using Technology to Find the Best Fit Quadratic Model

A ball is thrown into the air, and the following data is collected where x represents the time in seconds after the ball is thrown up and y represents the height in meters of the ball. We can use desmos to create a quadratic model that fits the given data.

On desmos, type the data into a table with the x-values in the first column and the y-values in the second column. Then, to tell desmos to compute a quadratic model, type in y 1 ~ a x 1 2 + b x 1 + c. You will get a result that looks like this:

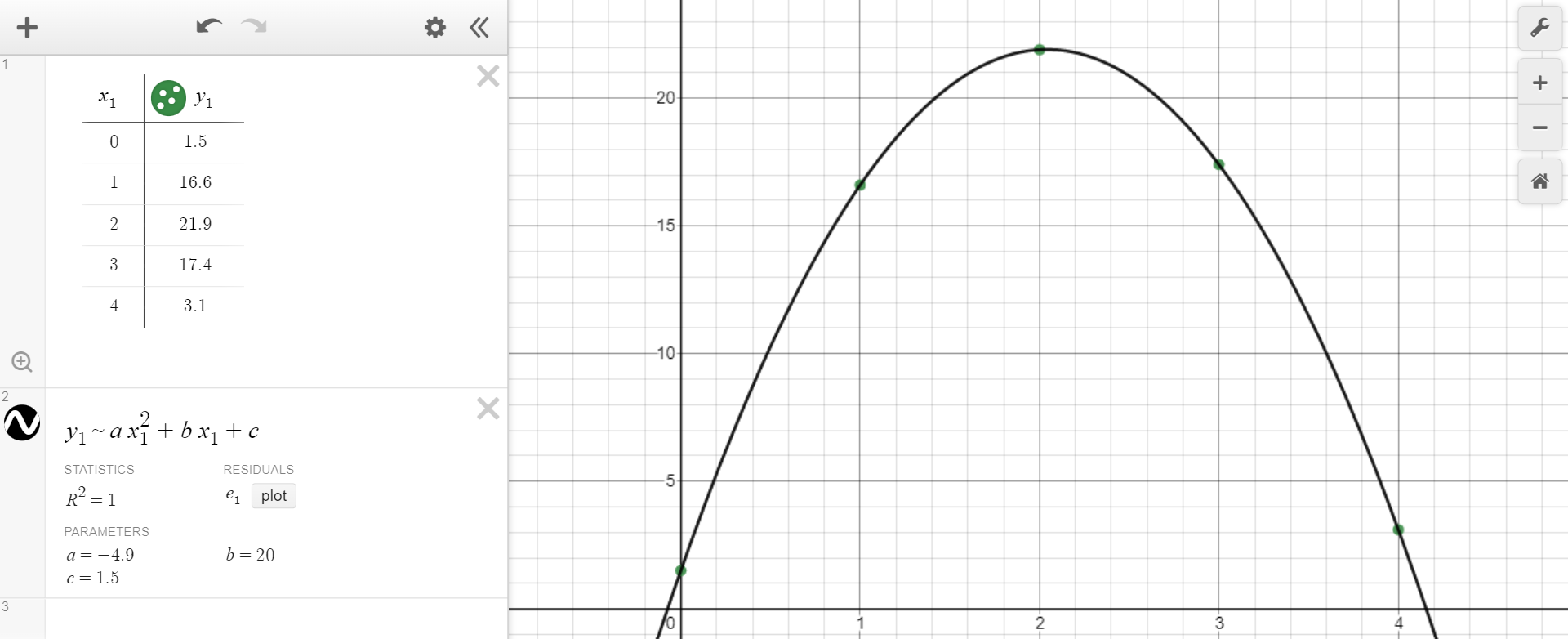
You can go to this problem in desmos by clicking https://www.desmos.com/calculator/u8ytorpnhk . Looking at the results, the quadratic model that fits the data is \[y = -4.9 x^2 + 20 x + 1.5\]