examples of a problem solving heuristic

Heuristic Problem Solving: A comprehensive guide with 5 Examples

What are heuristics, advantages of using heuristic problem solving, disadvantages of using heuristic problem solving, heuristic problem solving examples, frequently asked questions.

• Speed: Heuristics are designed to find solutions quickly, saving time in problem solving tasks. Rather than spending a lot of time analyzing every possible solution, heuristics help to narrow down the options and focus on the most promising ones.
• Flexibility: Heuristics are not rigid, step-by-step procedures. They allow for flexibility and creativity in problem solving, leading to innovative solutions. They encourage thinking outside the box and can generate unexpected and valuable ideas.
• Simplicity: Heuristics are often easy to understand and apply, making them accessible to anyone regardless of their expertise or background. They don’t require specialized knowledge or training, which means they can be used in various contexts and by different people.
• Cost-effective: Because heuristics are simple and efficient, they can save time, money, and effort in finding solutions. They also don’t require expensive software or equipment, making them a cost-effective approach to problem solving.
• Real-world applicability: Heuristics are often based on practical experience and knowledge, making them relevant to real-world situations. They can help solve complex, messy, or ill-defined problems where other problem solving methods may not be practical.
• Potential for errors: Heuristic problem solving relies on generalizations and assumptions, which may lead to errors or incorrect conclusions. This is especially true if the heuristic is not based on a solid understanding of the problem or the underlying principles.
• Limited scope: Heuristic problem solving may only consider a limited number of potential solutions and may not identify the most optimal or effective solution.
• Lack of creativity: Heuristic problem solving may rely on pre-existing solutions or approaches, limiting creativity and innovation in problem-solving.
• Over-reliance: Heuristic problem solving may lead to over-reliance on a specific approach or heuristic, which can be problematic if the heuristic is flawed or ineffective.
• Lack of transparency: Heuristic problem solving may not be transparent or explainable, as the decision-making process may not be explicitly articulated or understood.
• Trial and error: This heuristic involves trying different solutions to a problem and learning from mistakes until a successful solution is found. A software developer encountering a bug in their code may try other solutions and test each one until they find the one that solves the issue.
• Working backward: This heuristic involves starting at the goal and then figuring out what steps are needed to reach that goal. For example, a project manager may begin by setting a project deadline and then work backward to determine the necessary steps and deadlines for each team member to ensure the project is completed on time.
• Breaking a problem into smaller parts: This heuristic involves breaking down a complex problem into smaller, more manageable pieces that can be tackled individually. For example, an HR manager tasked with implementing a new employee benefits program may break the project into smaller parts, such as researching options, getting quotes from vendors, and communicating the unique benefits to employees.
• Using analogies: This heuristic involves finding similarities between a current problem and a similar problem that has been solved before and using the solution to the previous issue to help solve the current one. For example, a salesperson struggling to close a deal may use an analogy to a successful sales pitch they made to help guide their approach to the current pitch.
• Simplifying the problem: This heuristic involves simplifying a complex problem by ignoring details that are not necessary for solving it. This allows the problem solver to focus on the most critical aspects of the problem. For example, a customer service representative dealing with a complex issue may simplify it by breaking it down into smaller components and addressing them individually rather than simultaneously trying to solve the entire problem.

Test your problem-solving skills for free in just a few minutes.

The free problem-solving skills for managers and team leaders helps you understand mistakes that hold you back.

What are the three types of heuristics?

What are the four stages of heuristics in problem solving.

Other Related Blogs

Top 15 Tips for Effective Conflict Mediation at Work

Top 10 games for negotiation skills to make you a better leader, manager effectiveness: a complete guide for managers in 2024, 5 proven ways managers can build collaboration in a team.

Heuristics: Definition, Examples, And How They Work

Benjamin Frimodig

Science Expert

B.A., History and Science, Harvard University

Ben Frimodig is a 2021 graduate of Harvard College, where he studied the History of Science.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

On This Page:

Every day our brains must process and respond to thousands of problems, both large and small, at a moment’s notice. It might even be overwhelming to consider the sheer volume of complex problems we regularly face in need of a quick solution.

While one might wish there was time to methodically and thoughtfully evaluate the fine details of our everyday tasks, the cognitive demands of daily life often make such processing logistically impossible.

Therefore, the brain must develop reliable shortcuts to keep up with the stimulus-rich environments we inhabit. Psychologists refer to these efficient problem-solving techniques as heuristics.

Heuristics can be thought of as general cognitive frameworks humans rely on regularly to reach a solution quickly.

For example, if a student needs to decide what subject she will study at university, her intuition will likely be drawn toward the path that she envisions as most satisfying, practical, and interesting.

She may also think back on her strengths and weaknesses in secondary school or perhaps even write out a pros and cons list to facilitate her choice.

It’s important to note that these heuristics broadly apply to everyday problems, produce sound solutions, and helps simplify otherwise complicated mental tasks. These are the three defining features of a heuristic.

While the concept of heuristics dates back to Ancient Greece (the term is derived from the Greek word for “to discover”), most of the information known today on the subject comes from prominent twentieth-century social scientists.

Herbert Simon’s study of a notion he called “bounded rationality” focused on decision-making under restrictive cognitive conditions, such as limited time and information.

This concept of optimizing an inherently imperfect analysis frames the contemporary study of heuristics and leads many to credit Simon as a foundational figure in the field.

Kahneman’s Theory of Decision Making

The immense contributions of psychologist Daniel Kahneman to our understanding of cognitive problem-solving deserve special attention.

As context for his theory, Kahneman put forward the estimate that an individual makes around 35,000 decisions each day! To reach these resolutions, the mind relies on either “fast” or “slow” thinking.

The fast thinking pathway (system 1) operates mostly unconsciously and aims to reach reliable decisions with as minimal cognitive strain as possible.

While system 1 relies on broad observations and quick evaluative techniques (heuristics!), system 2 (slow thinking) requires conscious, continuous attention to carefully assess the details of a given problem and logically reach a solution.

Given the sheer volume of daily decisions, it’s no surprise that around 98% of problem-solving uses system 1.

Thus, it is crucial that the human mind develops a toolbox of effective, efficient heuristics to support this fast-thinking pathway.

Heuristics vs. Algorithms

Those who’ve studied the psychology of decision-making might notice similarities between heuristics and algorithms. However, remember that these are two distinct modes of cognition.

Heuristics are methods or strategies which often lead to problem solutions but are not guaranteed to succeed.

They can be distinguished from algorithms, which are methods or procedures that will always produce a solution sooner or later.

An algorithm is a step-by-step procedure that can be reliably used to solve a specific problem. While the concept of an algorithm is most commonly used in reference to technology and mathematics, our brains rely on algorithms every day to resolve issues (Kahneman, 2011).

The important thing to remember is that algorithms are a set of mental instructions unique to specific situations, while heuristics are general rules of thumb that can help the mind process and overcome various obstacles.

For example, if you are thoughtfully reading every line of this article, you are using an algorithm.

On the other hand, if you are quickly skimming each section for important information or perhaps focusing only on sections you don’t already understand, you are using a heuristic!

Why Heuristics Are Used

Heuristics usually occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind at the same moment

When studying heuristics, keep in mind both the benefits and unavoidable drawbacks of their application. The ubiquity of these techniques in human society makes such weaknesses especially worthy of evaluation.

More specifically, in expediting decision-making processes, heuristics also predispose us to a number of cognitive biases .

A cognitive bias is an incorrect but pervasive judgment derived from an illogical pattern of cognition. In simple terms, a cognitive bias occurs when one internalizes a subjective perception as a reliable and objective truth.

Heuristics are reliable but imperfect; In the application of broad decision-making “shortcuts” to guide one’s response to specific situations, occasional errors are both inevitable and have the potential to catalyze persistent mistakes.

For example, consider the risks of faulty applications of the representative heuristic discussed above. While the technique encourages one to assign situations into broad categories based on superficial characteristics and one’s past experiences for the sake of cognitive expediency, such thinking is also the basis of stereotypes and discrimination.

In practice, these errors result in the disproportionate favoring of one group and/or the oppression of other groups within a given society.

Indeed, the most impactful research relating to heuristics often centers on the connection between them and systematic discrimination.

The tradeoff between thoughtful rationality and cognitive efficiency encompasses both the benefits and pitfalls of heuristics and represents a foundational concept in psychological research.

When learning about heuristics, keep in mind their relevance to all areas of human interaction. After all, the study of social psychology is intrinsically interdisciplinary.

Many of the most important studies on heuristics relate to flawed decision-making processes in high-stakes fields like law, medicine, and politics.

Researchers often draw on a distinct set of already established heuristics in their analysis. While dozens of unique heuristics have been observed, brief descriptions of those most central to the field are included below:

Availability Heuristic

The availability heuristic describes the tendency to make choices based on information that comes to mind readily.

For example, children of divorced parents are more likely to have pessimistic views towards marriage as adults.

Of important note, this heuristic can also involve assigning more importance to more recently learned information, largely due to the easier recall of such information.

Representativeness Heuristic

This technique allows one to quickly assign probabilities to and predict the outcome of new scenarios using psychological prototypes derived from past experiences.

For example, juries are less likely to convict individuals who are well-groomed and wearing formal attire (under the assumption that stylish, well-kempt individuals typically do not commit crimes).

This is one of the most studied heuristics by social psychologists for its relevance to the development of stereotypes.

Scarcity Heuristic

This method of decision-making is predicated on the perception of less abundant, rarer items as inherently more valuable than more abundant items.

We rely on the scarcity heuristic when we must make a fast selection with incomplete information. For example, a student deciding between two universities may be drawn toward the option with the lower acceptance rate, assuming that this exclusivity indicates a more desirable experience.

The concept of scarcity is central to behavioral economists’ study of consumer behavior (a field that evaluates economics through the lens of human psychology).

Trial and Error

This is the most basic and perhaps frequently cited heuristic. Trial and error can be used to solve a problem that possesses a discrete number of possible solutions and involves simply attempting each possible option until the correct solution is identified.

For example, if an individual was putting together a jigsaw puzzle, he or she would try multiple pieces until locating a proper fit.

This technique is commonly taught in introductory psychology courses due to its simple representation of the central purpose of heuristics: the use of reliable problem-solving frameworks to reduce cognitive load.

Anchoring and Adjustment Heuristic

Anchoring refers to the tendency to formulate expectations relating to new scenarios relative to an already ingrained piece of information.

Put simply, this anchoring one to form reasonable estimations around uncertainties. For example, if asked to estimate the number of days in a year on Mars, many people would first call to mind the fact the Earth’s year is 365 days (the “anchor”) and adjust accordingly.

This tendency can also help explain the observation that ingrained information often hinders the learning of new information, a concept known as retroactive inhibition.

Familiarity Heuristic

This technique can be used to guide actions in cognitively demanding situations by simply reverting to previous behaviors successfully utilized under similar circumstances.

The familiarity heuristic is most useful in unfamiliar, stressful environments.

For example, a job seeker might recall behavioral standards in other high-stakes situations from her past (perhaps an important presentation at university) to guide her behavior in a job interview.

Many psychologists interpret this technique as a slightly more specific variation of the availability heuristic.

How to Make Better Decisions

Heuristics are ingrained cognitive processes utilized by all humans and can lead to various biases.

Both of these statements are established facts. However, this does not mean that the biases that heuristics produce are unavoidable. As the wide-ranging impacts of such biases on societal institutions have become a popular research topic, psychologists have emphasized techniques for reaching more sound, thoughtful and fair decisions in our daily lives.

Ironically, many of these techniques are themselves heuristics!

To focus on the key details of a given problem, one might create a mental list of explicit goals and values. To clearly identify the impacts of choice, one should imagine its impacts one year in the future and from the perspective of all parties involved.

Most importantly, one must gain a mindful understanding of the problem-solving techniques used by our minds and the common mistakes that result. Mindfulness of these flawed yet persistent pathways allows one to quickly identify and remedy the biases (or otherwise flawed thinking) they tend to create!

Further Information

• Shah, A. K., & Oppenheimer, D. M. (2008). Heuristics made easy: an effort-reduction framework. Psychological bulletin, 134(2), 207.
• Marewski, J. N., & Gigerenzer, G. (2012). Heuristic decision making in medicine. Dialogues in clinical neuroscience, 14(1), 77.
• Del Campo, C., Pauser, S., Steiner, E., & Vetschera, R. (2016). Decision making styles and the use of heuristics in decision making. Journal of Business Economics, 86(4), 389-412.

What is a heuristic in psychology?

A heuristic in psychology is a mental shortcut or rule of thumb that simplifies decision-making and problem-solving. Heuristics often speed up the process of finding a satisfactory solution, but they can also lead to cognitive biases.

Bobadilla-Suarez, S., & Love, B. C. (2017, May 29). Fast or Frugal, but Not Both: Decision Heuristics Under Time Pressure. Journal of Experimental Psychology: Learning, Memory, and Cognition .

Bowes, S. M., Ammirati, R. J., Costello, T. H., Basterfield, C., & Lilienfeld, S. O. (2020). Cognitive biases, heuristics, and logical fallacies in clinical practice: A brief field guide for practicing clinicians and supervisors. Professional Psychology: Research and Practice, 51 (5), 435–445.

Dietrich, C. (2010). “Decision Making: Factors that Influence Decision Making, Heuristics Used, and Decision Outcomes.” Inquiries Journal/Student Pulse, 2(02).

Groenewegen, A. (2021, September 1). Kahneman Fast and slow thinking: System 1 and 2 explained by Sue. SUE Behavioral Design. Retrieved March 26, 2022, from https://suebehaviouraldesign.com/kahneman-fast-slow-thinking/

Kahneman, D., Lovallo, D., & Sibony, O. (2011). Before you make that big decision .

Kahneman, D. (2011). Thinking, fast and slow . Macmillan.

Pratkanis, A. (1989). The cognitive representation of attitudes. In A. R. Pratkanis, S. J. Breckler, & A. G. Greenwald (Eds.), Attitude structure and function (pp. 71–98). Hillsdale, NJ: Erlbaum.

Simon, H.A., 1956. Rational choice and the structure of the environment. Psychological Review .

Tversky, A., & Kahneman, D. (1974). Judgment under Uncertainty: Heuristics and Biases. Science, 185 (4157), 1124–1131.

Related Articles

Cognitive Psychology

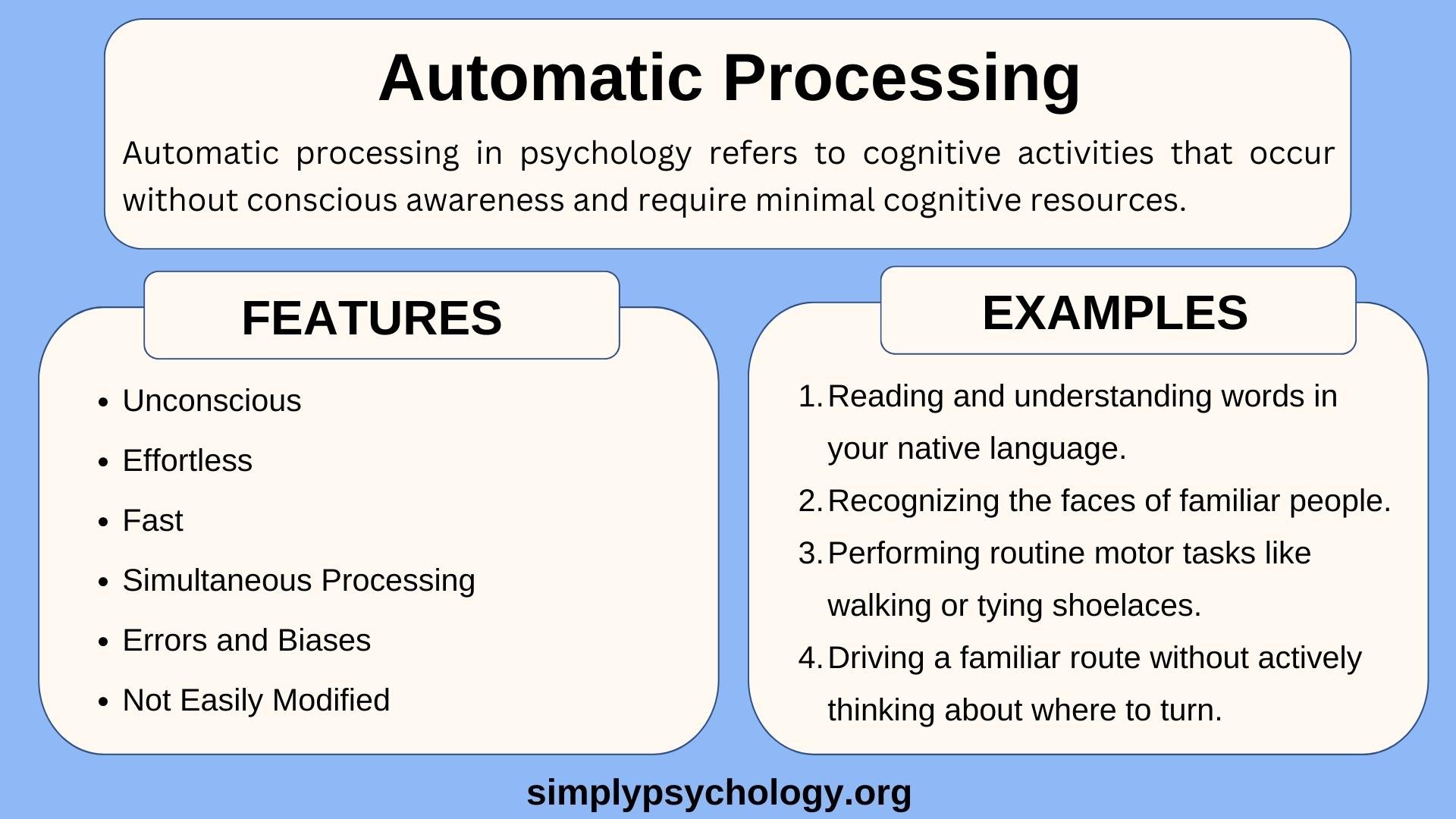
Automatic Processing in Psychology: Definition & Examples

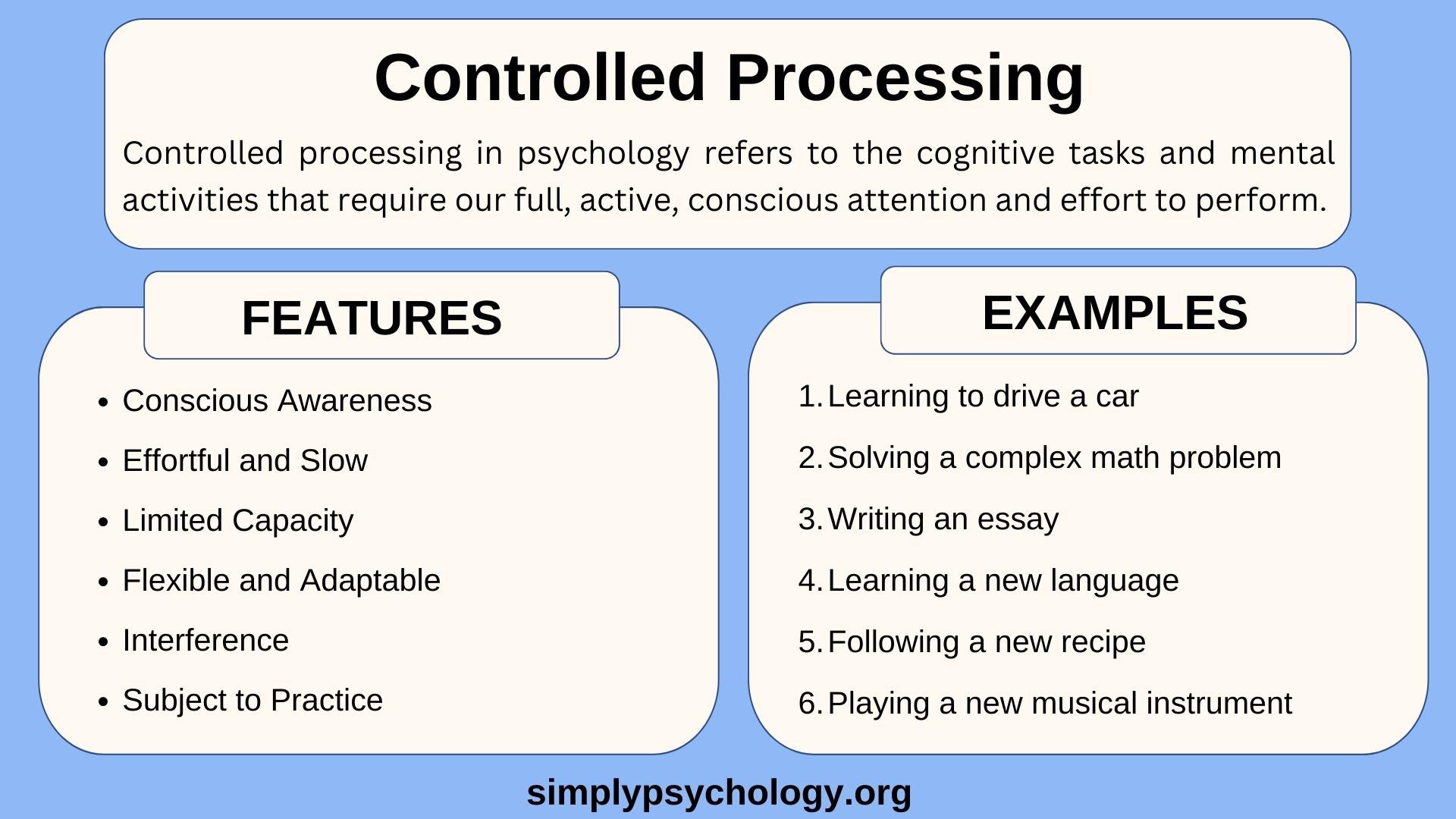
Controlled Processing in Psychology: Definition & Examples

How Ego Depletion Can Drain Your Willpower

What is the Default Mode Network?

Theories of Selective Attention in Psychology

Availability Heuristic and Decision Making

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

What Are Heuristics?

These mental shortcuts can help people make decisions more efficiently

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Steven Gans, MD is board-certified in psychiatry and is an active supervisor, teacher, and mentor at Massachusetts General Hospital.

Verywell / Cindy Chung 

• History and Origins
• Heuristics vs. Algorithms
• Heuristics and Bias

How to Make Better Decisions

Heuristics are mental shortcuts that allow people to solve problems and make judgments quickly and efficiently. These rule-of-thumb strategies shorten decision-making time and allow people to function without constantly stopping to think about their next course of action.

However, there are both benefits and drawbacks of heuristics. While heuristics are helpful in many situations, they can also lead to  cognitive biases . Becoming aware of this might help you make better and more accurate decisions.

Press Play for Advice On Making Decisions

Hosted by therapist Amy Morin, LCSW, this episode of The Verywell Mind Podcast shares a simple way to make a tough decision. Click below to listen now.

Follow Now : Apple Podcasts / Spotify / Google Podcasts

The History and Origins of Heuristics

Nobel-prize winning economist and cognitive psychologist Herbert Simon originally introduced the concept of heuristics in psychology in the 1950s. He suggested that while people strive to make rational choices, human judgment is subject to cognitive limitations. Purely rational decisions would involve weighing all the potential costs and possible benefits of every alternative.

But people are limited by the amount of time they have to make a choice as well as the amount of information they have at their disposal. Other factors such as overall intelligence and accuracy of perceptions also influence the decision-making process.

During the 1970s, psychologists Amos Tversky and Daniel Kahneman presented their research on cognitive biases. They proposed that these biases influence how people think and the judgments people make.

As a result of these limitations, we are forced to rely on mental shortcuts to help us make sense of the world. Simon's research demonstrated that humans were limited in their ability to make rational decisions, but it was Tversky and Kahneman's work that introduced the study of heuristics and the specific ways of thinking that people rely on to simplify the decision-making process.

How Heuristics Are Used

Heuristics play important roles in both  problem-solving  and  decision-making , as we often turn to these mental shortcuts when we need a quick solution.

Here are a few different theories from psychologists about why we rely on heuristics.

• Attribute substitution : People substitute simpler but related questions in place of more complex and difficult questions.
• Effort reduction : People use heuristics as a type of cognitive laziness to reduce the mental effort required to make choices and decisions.
• Fast and frugal : People use heuristics because they can be fast and correct in certain contexts. Some theories argue that heuristics are actually more accurate than they are biased.

In order to cope with the tremendous amount of information we encounter and to speed up the decision-making process, our brains rely on these mental strategies to simplify things so we don't have to spend endless amounts of time analyzing every detail.

You probably make hundreds or even thousands of decisions every day. What should you have for breakfast? What should you wear today? Should you drive or take the bus? Fortunately, heuristics allow you to make such decisions with relative ease and without a great deal of agonizing.

There are many heuristics examples in everyday life. When trying to decide if you should drive or ride the bus to work, for instance, you might remember that there is road construction along the bus route. You realize that this might slow the bus and cause you to be late for work. So you leave earlier and drive to work on an alternate route.

Heuristics allow you to think through the possible outcomes quickly and arrive at a solution.

Are Heuristics Good or Bad?

Heuristics aren't inherently good or bad, but there are pros and cons to using them to make decisions. While they can help us figure out a solution to a problem faster, they can also lead to inaccurate judgments about other people or situations.

Types of Heuristics

There are many different kinds of heuristics. While each type plays a role in decision-making, they occur during different contexts. Understanding the types can help you better understand which one you are using and when.

Availability

The availability heuristic  involves making decisions based upon how easy it is to bring something to mind. When you are trying to make a decision, you might quickly remember a number of relevant examples. Since these are more readily available in your memory, you will likely judge these outcomes as being more common or frequently occurring.

For example, if you are thinking of flying and suddenly think of a number of recent airline accidents, you might feel like air travel is too dangerous and decide to travel by car instead. Because those examples of air disasters came to mind so easily, the availability heuristic leads you to think that plane crashes are more common than they really are.

Familiarity

The familiarity heuristic refers to how people tend to have more favorable opinions of things, people, or places they've experienced before as opposed to new ones. In fact, given two options, people may choose something they're more familiar with even if the new option provides more benefits.

Representativeness

The representativeness heuristic  involves making a decision by comparing the present situation to the most representative mental prototype. When you are trying to decide if someone is trustworthy, you might compare aspects of the individual to other mental examples you hold.

A soft-spoken older woman might remind you of your grandmother, so you might immediately assume that she is kind, gentle, and trustworthy. However, this is an example of a heuristic bias, as you can't know someone trustworthy based on their age alone.

The affect heuristic involves making choices that are influenced by the emotions that an individual is experiencing at that moment. For example, research has shown that people are more likely to see decisions as having benefits and lower risks when they are in a positive mood. Negative emotions, on the other hand, lead people to focus on the potential downsides of a decision rather than the possible benefits.

The anchoring bias involves the tendency to be overly influenced by the first bit of information we hear or learn. This can make it more difficult to consider other factors and lead to poor choices. For example, anchoring bias can influence how much you are willing to pay for something, causing you to jump at the first offer without shopping around for a better deal.

Scarcity is a principle in heuristics in which we view things that are scarce or less available to us as inherently more valuable. The scarcity heuristic is one often used by marketers to influence people to buy certain products. This is why you'll often see signs that advertise "limited time only" or that tell you to "get yours while supplies last."

Trial and Error

Trial and error is another type of heuristic in which people use a number of different strategies to solve something until they find what works. Examples of this type of heuristic are evident in everyday life. People use trial and error when they're playing video games, finding the fastest driving route to work, and learning to ride a bike (or learning any new skill).

Difference Between Heuristics and Algorithms

Though the terms are often confused, heuristics and algorithms are two distinct terms in psychology.

Algorithms are step-by-step instructions that lead to predictable, reliable outcomes; whereas heuristics are mental shortcuts that are basically best guesses. Algorithms always lead to accurate outcomes, whereas, heuristics do not.

Examples of algorithms include instructions for how to put together a piece of furniture or a recipe for cooking a certain dish. Health professionals also create algorithms or processes to follow in order to determine what type of treatment to use on a patient.

How Heuristics Can Lead to Bias

While heuristics can help us solve problems and speed up our decision-making process, they can introduce errors. As in the examples above, heuristics can lead to inaccurate judgments about how commonly things occur and about how representative certain things may be.

Just because something has worked in the past does not mean that it will work again, and relying on a heuristic can make it difficult to see alternative solutions or come up with new ideas.

Heuristics can also contribute to stereotypes and  prejudice . Because people use mental shortcuts to classify and categorize people, they often overlook more relevant information and create stereotyped categorizations that are not in tune with reality.

While heuristics can be a useful tool, there are ways you can improve your decision-making and avoid cognitive bias at the same time.

We are more likely to make an error in judgment if we are trying to make a decision quickly or are under pressure to do so. Whenever possible, take a few deep breaths . Do something to distract yourself from the decision at hand. When you return to it, you may find you have a fresh perspective, or notice something you didn't before.

Identify the Goal

We tend to focus automatically on what works for us and make decisions that serve our best interest. But take a moment to know what you're trying to achieve. Are there other people who will be affected by this decision? What's best for them? Is there a common goal that can be achieved that will serve all parties?

Process Your Emotions

Fast decision-making is often influenced by emotions from past experiences that bubble to the surface. Is your decision based on facts or emotions? While emotions can be helpful, they may affect decisions in a negative way if they prevent us from seeing the full picture.

Recognize All-or-Nothing Thinking

When making a decision, it's a common tendency to believe you have to pick a single, well-defined path, and there's no going back. In reality, this often isn't the case.

Sometimes there are compromises involving two choices, or a third or fourth option that we didn't even think of at first. Try to recognize the nuances and possibilities of all choices involved, instead of using all-or-nothing thinking .

Rachlin H. Rational thought and rational behavior: A review of bounded rationality: The adaptive toolbox . J Exp Anal Behav . 2003;79(3):409–412. doi:10.1901/jeab.2003.79-409

Shah AK, Oppenheimer DM. Heuristics made easy: An effort-reduction framework . Psychol Bull. 2008;134(2):207-22. doi:10.1037/0033-2909.134.2.207

Marewski JN, Gigerenzer G. Heuristic decision making in medicine .  Dialogues Clin Neurosci . 2012;14(1):77–89. PMID: 22577307

Schwikert SR, Curran T. Familiarity and recollection in heuristic decision making .  J Exp Psychol Gen . 2014;143(6):2341-2365. doi:10.1037/xge0000024

Finucane M, Alhakami A, Slovic P, Johnson S. The affect heuristic in judgments of risks and benefits . J Behav Decis Mak . 2000; 13(1):1-17. doi:10.1002/(SICI)1099-0771(200001/03)13:1<1::AID-BDM333>3.0.CO;2-S

Cheung TT, Kroese FM, Fennis BM, De Ridder DT. Put a limit on it: The protective effects of scarcity heuristics when self-control is low . Health Psychol Open . 2015;2(2):2055102915615046. doi:10.1177/2055102915615046

Mohr H, Zwosta K, Markovic D, Bitzer S, Wolfensteller U, Ruge H. Deterministic response strategies in a trial-and-error learning task . Inman C, ed. PLoS Comput Biol. 2018;14(11):e1006621. doi:10.1371/journal.pcbi.1006621

Lang JM, Ford JD, Fitzgerald MM.  An algorithm for determining use of trauma-focused cognitive-behavioral therapy .  Psychotherapy   (Chic) . 2010;47(4):554-69. doi:10.1037/a0021184

Bigler RS, Clark C. The inherence heuristic: A key theoretical addition to understanding social stereotyping and prejudice. Behav Brain Sci . 2014;37(5):483-4. doi:10.1017/S0140525X1300366X

del Campo C, Pauser S, Steiner E, et al.  Decision making styles and the use of heuristics in decision making .  J Bus Econ.  2016;86:389–412. doi:10.1007/s11573-016-0811-y

Marewski JN, Gigerenzer G. Heuristic decision making in medicine .  Dialogues Clin Neurosci . 2012;14(1):77-89. doi:10.31887/DCNS.2012.14.1/jmarewski

Zheng Y, Yang Z, Jin C, Qi Y, Liu X. The influence of emotion on fairness-related decision making: A critical review of theories and evidence .  Front Psychol . 2017;8:1592. doi:10.3389/fpsyg.2017.01592

Bazerman MH. Judgment and decision making. In: Biswas-Diener R, Diener E, eds.,  Noba Textbook Series: Psychology.  DEF Publishers.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Computer Science Principles

Course: ap®︎/college computer science principles   >   unit 4, using heuristics.

• Undecidable problems
• Solving hard problems

Traveling Salesperson Problem

The brute force approach, developing a heuristic, the nearest-neighbor heuristic, heuristics everywhere, want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• Memberships

Heuristic Method

Heuristic Method: this article explains the concept of the Heuristic Method , developed by George Pólya in a practical way. After reading it, you will understand the basics of this powerful Problem Solving tool.

What is the Heuristic Method?

A heuristic method is an approach to finding a solution to a problem that originates from the ancient Greek word ‘eurisko’, meaning to ‘find’, ‘search’ or ‘discover’. It is about using a practical method that doesn’t necessarily need to be perfect. Heuristic methods speed up the process of reaching a satisfactory solution.

Previous experiences with comparable problems are used that can concern problem situations for people, machines or abstract issues. One of the founders of heuristics is the Hungarian mathematician György (George) Pólya , who published a book about the subject in 1945 called ‘How to Solve It’. He used four principles that form the basis for problem solving.

Heuristic method: Four principles

Pólya describes the following four principles in his book:

• try to understand the problem
• make a plan
• carry out this plan
• evaluate and adapt

If this sequence doesn’t lead to the right solution, Pólya advises to first look for a simpler problem.

A solution may potentially be found by first looking at a similar problem that was possible to solve. With this experience, it’s possible to look at the current problem in another way.

First principle of the heuristic method: understand the problem

It’s more difficult than it seems, because it seems obvious. In truth, people are hindered when it comes to finding an initially suitable approach to the problem.

It can help to draw the problem and to look at it from another angle. What is the problem, what is happening, can the problem be explained in other words, is there enough information available, etc. Such questions can help with the first evaluation of a problem issue.

Second principle of the heuristic method: make a plan

There are many ways to solve problems. This section is about choosing the right strategy that best fits the problem at hand. The reversed ‘working backwards’ can help with this; people assume to have a solution and use this as a starting point to work towards the problem.

It can also be useful to make an overview of the possibilities, delete some of them immediately, work with comparisons, or to apply symmetry. Creativity comes into play here and will improve the ability to judge.

Third principle of the heuristic method: carry out the plan

Once a strategy has been chosen, the plan can quickly be implemented. However, it is important to pay attention to time and be patient, because the solution will not simply appear.

If the plan doesn’t go anywhere, the advice is to throw it overboard and find a new way.

Fourth principle of the heuristic method: evaluate and adapt

Take the time to carefully consider and reflect upon the work that’s already been done. The things that are going well should be maintained, those leading to a lesser solution, should be adjusted. Some things simply work, while others simply don’t.

There are many different heuristic methods, which Pólya also used. The most well-known heuristics are found below:

1. Dividing technique

The original problem is divided into smaller sub-problems that can be solved more easily. These sub-problems can be linked to each other and combined, which will eventually lead to the solving of the original problem.

2. Inductive method

This involves a problem that has already been solved, but is smaller than the original problem. Generalisation can be derived from the previously solved problem, which can help in solving the bigger, original problem.

3. Reduction method

Because problems are often larger than assumed and deal with different causes and factors, this method sets limits for the problem in advance. This reduces the leeway of the original problem, making it easier to solve.

4. Constructive method

This is about working on the problem step by step. The smallest solution is seen as a victory and from that point consecutive steps are taken. This way, the best choices keep being made, which will eventually lead to a successful end result.

5. Local search method

This is about the search for the most attainable solution to the problem. This solution is improved along the way. This method ends when improvement is no longer possible.

Exact solutions versus the heuristic method

The heuristic approach is a mathmatical method with which proof of a good solution to a problem is delivered. There is a large number of different problems that could use good solutions. When the processing speed is equally as important as the obtained solution, we speak of a heuristic method.

The Heuristic Method only tries to find a good, but not necessarily optimal, solution. This is what differentiates heuristics from exact solution methods, which are about finding the optimal solution to a problem. However, that’s very time consuming, which is why a heuristic method may prove preferable. This is much quicker and more flexible than an exact method, but does have to satisfy a number of criteria.

It’s Your Turn

What do you think? Is the Heuristic Method applicable in your personal or professional environment? Do you recognize the practical explanation or do you have more suggestions? What are your success factors for solving problems

Share your experience and knowledge in the comments box below.

More information

• Groner, R., Groner, M., & Bischof, W. F. (2014). Methods of heuristics . Routledge .
• Newell, A. (1983). The heuristic of George Polya and its relation to artificial intelligence . Methods of heuristics, 195-243.
• Polya, G. (2014, 1945). How to solve it: A new aspect of mathematical method . Princeton university press .

How to cite this article: Mulder, P. (2018). Heuristic Method . Retrieved [insert date] from ToolsHero: https://www.toolshero.com/problem-solving/heuristic-method/

Add a link to this page on your website: <a href=”https://www.toolshero.com/problem-solving/heuristic-method/”>ToolsHero: Heuristic Method</a>

Published on: 29/05/2018 | Last update: 04/03/2022

Did you find this article interesting?

Your rating is more than welcome or share this article via Social media!

Average rating 4.6 / 5. Vote count: 13

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you!

Let us improve this post!

Tell us how we can improve this post?

Patty Mulder

Patty Mulder is an Dutch expert on Management Skills, Personal Effectiveness and Business Communication. She is also a Content writer, Business Coach and Company Trainer and lives in the Netherlands (Europe). Note: all her articles are written in Dutch and we translated her articles to English!

ALSO INTERESTING

Soft Systems Methodology (SSM) by Peter Checkland

Crowdsourcing: the meaning, definition and some examples

Systematic Inventive Thinking (SIT)

Leave a reply cancel reply.

You must be logged in to post a comment.

BOOST YOUR SKILLS

Toolshero supports people worldwide ( 10+ million visitors from 100+ countries ) to empower themselves through an easily accessible and high-quality learning platform for personal and professional development.

By making access to scientific knowledge simple and affordable, self-development becomes attainable for everyone, including you! Join our learning platform and boost your skills with Toolshero.

POPULAR TOPICS

• Change Management
• Marketing Theories
• Problem Solving Theories
• Psychology Theories

ABOUT TOOLSHERO

• Free Toolshero e-book
• Memberships & Pricing

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.2 Problem-Solving: Heuristics and Algorithms

Learning objectives.

• Describe the differences between heuristics and algorithms in information processing.

When faced with a problem to solve, should you go with intuition or with more measured, logical reasoning? Obviously, we use both of these approaches. Some of the decisions we make are rapid, emotional, and automatic. Daniel Kahneman (2011) calls this “fast” thinking. By definition, fast thinking saves time. For example, you may quickly decide to buy something because it is on sale; your fast brain has perceived a bargain, and you go for it quickly. On the other hand, “slow” thinking requires more effort; applying this in the same scenario might cause us not to buy the item because we have reasoned that we don’t really need it, that it is still too expensive, and so on. Using slow and fast thinking does not guarantee good decision-making if they are employed at the wrong time. Sometimes it is not clear which is called for, because many decisions have a level of uncertainty built into them. In this section, we will explore some of the applications of these tendencies to think fast or slow.

We will look further into our thought processes, more specifically, into some of the problem-solving strategies that we use. Heuristics are information-processing strategies that are useful in many cases but may lead to errors when misapplied. A heuristic is a principle with broad application, essentially an educated guess about something. We use heuristics all the time, for example, when deciding what groceries to buy from the supermarket, when looking for a library book, when choosing the best route to drive through town to avoid traffic congestion, and so on. Heuristics can be thought of as aids to decision making; they allow us to reach a solution without a lot of cognitive effort or time.

The benefit of heuristics in helping us reach decisions fairly easily is also the potential downfall: the solution provided by the use of heuristics is not necessarily the best one. Let’s consider some of the most frequently applied, and misapplied, heuristics in the table below.

In many cases, we base our judgments on information that seems to represent, or match, what we expect will happen, while ignoring other potentially more relevant statistical information. When we do so, we are using the representativeness heuristic . Consider, for instance, the data presented in the table below. Let’s say that you went to a hospital, and you checked the records of the babies that were born on that given day. Which pattern of births do you think you are most likely to find?

Most people think that list B is more likely, probably because list B looks more random, and matches — or is “representative of” — our ideas about randomness, but statisticians know that any pattern of four girls and four boys is mathematically equally likely. Whether a boy or girl is born first has no bearing on what sex will be born second; these are independent events, each with a 50:50 chance of being a boy or a girl. The problem is that we have a schema of what randomness should be like, which does not always match what is mathematically the case. Similarly, people who see a flipped coin come up “heads” five times in a row will frequently predict, and perhaps even wager money, that “tails” will be next. This behaviour is known as the gambler’s fallacy . Mathematically, the gambler’s fallacy is an error: the likelihood of any single coin flip being “tails” is always 50%, regardless of how many times it has come up “heads” in the past.

The representativeness heuristic may explain why we judge people on the basis of appearance. Suppose you meet your new next-door neighbour, who drives a loud motorcycle, has many tattoos, wears leather, and has long hair. Later, you try to guess their occupation. What comes to mind most readily? Are they a teacher? Insurance salesman? IT specialist? Librarian? Drug dealer? The representativeness heuristic will lead you to compare your neighbour to the prototypes you have for these occupations and choose the one that they seem to represent the best. Thus, your judgment is affected by how much your neibour seems to resemble each of these groups. Sometimes these judgments are accurate, but they often fail because they do not account for base rates , which is the actual frequency with which these groups exist. In this case, the group with the lowest base rate is probably drug dealer.

Our judgments can also be influenced by how easy it is to retrieve a memory. The tendency to make judgments of the frequency or likelihood that an event occurs on the basis of the ease with which it can be retrieved from memory is known as the availability heuristic (MacLeod & Campbell, 1992; Tversky & Kahneman, 1973). Imagine, for instance, that I asked you to indicate whether there are more words in the English language that begin with the letter “R” or that have the letter “R” as the third letter. You would probably answer this question by trying to think of words that have each of the characteristics, thinking of all the words you know that begin with “R” and all that have “R” in the third position. Because it is much easier to retrieve words by their first letter than by their third, we may incorrectly guess that there are more words that begin with “R,” even though there are in fact more words that have “R” as the third letter.

The availability heuristic may explain why we tend to overestimate the likelihood of crimes or disasters; those that are reported widely in the news are more readily imaginable, and therefore, we tend to overestimate how often they occur. Things that we find easy to imagine, or to remember from watching the news, are estimated to occur frequently. Anything that gets a lot of news coverage is easy to imagine. Availability bias does not just affect our thinking. It can change behaviour. For example, homicides are usually widely reported in the news, leading people to make inaccurate assumptions about the frequency of murder. In Canada, the murder rate has dropped steadily since the 1970s (Statistics Canada, 2018), but this information tends not to be reported, leading people to overestimate the probability of being affected by violent crime. In another example, doctors who recently treated patients suffering from a particular condition were more likely to diagnose the condition in subsequent patients because they overestimated the prevalence of the condition (Poses & Anthony, 1991).

The anchoring and adjustment heuristic is another example of how fast thinking can lead to a decision that might not be optimal. Anchoring and adjustment is easily seen when we are faced with buying something that does not have a fixed price. For example, if you are interested in a used car, and the asking price is $10,000, what price do you think you might offer? Using $10,000 as an anchor, you are likely to adjust your offer from there, and perhaps offer $9000 or $9500. Never mind that $10,000 may not be a reasonable anchoring price. Anchoring and adjustment does not just happen when we’re buying something. It can also be used in any situation that calls for judgment under uncertainty, such as sentencing decisions in criminal cases (Bennett, 2014), and it applies to groups as well as individuals (Rutledge, 1993).

In contrast to heuristics, which can be thought of as problem-solving strategies based on educated guesses, algorithms are problem-solving strategies that use rules. Algorithms are generally a logical set of steps that, if applied correctly, should be accurate. For example, you could make a cake using heuristics — relying on your previous baking experience and guessing at the number and amount of ingredients, baking time, and so on — or using an algorithm. The latter would require a recipe which would provide step-by-step instructions; the recipe is the algorithm. Unless you are an extremely accomplished baker, the algorithm should provide you with a better cake than using heuristics would. While heuristics offer a solution that might be correct, a correctly applied algorithm is guaranteed to provide a correct solution. Of course, not all problems can be solved by algorithms.

As with heuristics, the use of algorithmic processing interacts with behaviour and emotion. Understanding what strategy might provide the best solution requires knowledge and experience. As we will see in the next section, we are prone to a number of cognitive biases that persist despite knowledge and experience.

Key Takeaways

• We use a variety of shortcuts in our information processing, such as the representativeness, availability, and anchoring and adjustment heuristics. These help us to make fast judgments but may lead to errors.
• Algorithms are problem-solving strategies that are based on rules rather than guesses. Algorithms, if applied correctly, are far less likely to result in errors or incorrect solutions than heuristics. Algorithms are based on logic.

Bennett, M. W. (2014). Confronting cognitive ‘anchoring effect’ and ‘blind spot’ biases in federal sentencing: A modest solution for reforming and fundamental flaw. Journal of Criminal Law and Criminology , 104 (3), 489-534.

Kahneman, D. (2011). Thinking, fast and slow. New York, NY: Farrar, Straus and Giroux.

MacLeod, C., & Campbell, L. (1992). Memory accessibility and probability judgments: An experimental evaluation of the availability heuristic.  Journal of Personality and Social Psychology, 63 (6), 890–902.

Poses, R. M., & Anthony, M. (1991). Availability, wishful thinking, and physicians’ diagnostic judgments for patients with suspected bacteremia.  Medical Decision Making,  11 , 159-68.

Rutledge, R. W. (1993). The effects of group decisions and group-shifts on use of the anchoring and adjustment heuristic. Social Behavior and Personality, 21 (3), 215-226.

Statistics Canada. (2018). Ho micide in Canada, 2017 . Retrieved from https://www150.statcan.gc.ca/n1/en/daily-quotidien/181121/dq181121a-eng.pdf

Tversky, A., & Kahneman, D. (1973). Availability: A heuristic for judging frequency and probability.  Cognitive Psychology, 5 , 207–232.

Psychology - 1st Canadian Edition Copyright © 2020 by Sally Walters is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Home Blog Business Using Heuristic Problem-Solving Methods for Effective Decision-Making

Using Heuristic Problem-Solving Methods for Effective Decision-Making

Problem-solving capability and effective decision making are two of the most prized capabilities of any leader. However, one cannot expect these traits to be simply present by default in an individual, as both require extensive analysis of the root cause of issues and to know what to look for when anticipating a gain. In a previous article, we brought you  5 Problem-Solving Strategies to Become a Better Problem Solver . This time we have something that can help you dig deep to resolve problems, i.e. using heuristic problem-solving methods for effective decision-making.

What are Heuristics?

Heuristics are essentially problem-solving tools that can be used for solving non-routine and challenging problems. A heuristic method is a practical approach for a short-term goal, such as solving a problem. The approach might not be perfect but can help find a quick solution to help move towards a reasonable way to resolve a problem.

Example: A computer that is to be used for an event to allow presenters to play PowerPoint presentations via a projector malfunctions due to an operating system problem. In such a case a system administrator might quickly refresh the system using a backup to make it functional for the event. Once the event concludes the system administrator can run detailed diagnostic tests to see if there are any further underlying problems that need to be resolved.

In this example, restoring the system using a backup was a short-term solution to solve the immediate problem, i.e. to make the system functional for the event that was to start in a few hours. There are a number of heuristic methods that can lead to such a decision to resolve a problem. These are explained in more detail in the sections below.

Examples of Heuristic Methods Used for Challenging and Non-Routine Problems

Heuristic methods can help ease the cognitive load by making it easy to process decisions. These include various basic methods that aren’t rooted in any theory per se but rather rely on past experiences and common sense. Using heuristics one can, therefore, resolve challenging and non-routine problems. Let’s take a look at some examples.

A Rule of Thumb

This includes using a method based on practical experience. A rule of thumb can be applied to find a short-term solution to a problem to quickly resolve an issue during a situation where one might be pressed for time.

Example: In the case of the operating system failure mentioned earlier, we assume that the PC on which PowerPoint presentations are to be run by presenters during an event is getting stuck on the start screen. Considering that the event is about to start in 2 hours, it is not practical for the system administrator to reinstall the operating system and all associated applications, hotfixes and updates, as it might take several hours. Using a rule of thumb, he might try to use various tried and tested methods, such as trying to use a system restore point to restore the PC without deleting essential files or to use a backup to restore the PC to an earlier environment.

An Educated Guess

An educated guess or guess and check can help resolve a problem by using knowledge and experience. Based on your knowledge of a subject, you can make an educated guess to resolve a problem.

Example: In the example of the malfunctioning PC, the system administrator will have to make an educated guess regarding the best possible way to resolve the problem. The educated guess, in this case, can be to restore the system to a backup instead of using system restore, both of which might take a similar amount of time; however, the former is likely to work better as a quick fix based on past experience and knowledge of the system administrator.

Trial and Error

This is another heuristic method to problem-solving where one might try various things that are expected to work until a solution is achieved.

Example: The system administrator might try various techniques to fix the PC using trial and error. He might start with checking if the system is accessible in safe mode. And if so, does removing a newly installed software or update solve the problem? If he can’t access the system at all, he might proceed with restoring it from a backup. If that too fails, he might need to quickly opt for a wipe and load installation and only install PowerPoint to ensure that at least presenters can run presentations on the PC. In this case he can perform other required software installations after the event.

An Intuitive Judgment

Intuitive judgment does not result from a rational analysis of a situation or based on reasoning. It is more of a feeling one has which may or may not lead to the desired outcome. Sometimes, intuitive judgement can help resolve problems. Perhaps the most rational way to describe an intuition is that it is some type of calculation at the subconscious level, where you can’t put your finger on the reason why you think something might be the way it is.

Example: The system administrator might have a feeling that the PC is not working because the hard drive has failed. This might be an intuitive judgment without hard evidence. He might quickly replace the hard drive to resolve the problem. Later, after he runs diagnostics on the old hard drive, he might realize that it was indeed that hard drive that was faulty and trying to fix it would have been a waste of time. In this case, he might be able to solve a problem using intuitive judgment.

Stereotyping

A stereotype is an opinion which is judgmental rather than rational. Certain types of possessions for example create a stereotype of social status. A person who wears an expensive watch might be deemed rich, although he might simply have received it as a gift from someone, instead of being rich himself.

Example: A certain company might have developed a bad reputation of developing faulty hard drives. If the systems administrator sees the name of that company on the hard drive when opening the faulty PC, he might think that the hard drive is faulty based on stereotyping and decide to replace it.

Profiling is used to systematically analyze data to understand its dynamics. Profiling as a heuristic method for problem-solving might entail analyzing data to understand and resolve a problem or to look for patterns, just like a root cause analysis .

Example: To solve the issue of the faulty PC, a system administrator might look for similar patterns which might have led to the problem. He might search online for solutions via online forums to understand what might have caused the issue. He might also look at the information associated with recently installed software and updates to see if something conflicted with the operating system. During the profiling process, he might realize that software he installed yesterday before shutting down the PC is the cause of the problem, since similar issues have been reported by other users. He might try to remove the software using Safe Mode or by removing its files by running the computer from a bootable disc drive.

Common Sense

Common sense is the use of practical judgment to understand something. The use of common sense is also a heuristic method used for problem-solving.

Example: When dealing with a faulty PC the system administrator sees smoke coming out of the PC. In this case, it is common sense that a hardware component is faulty. He shuts down the PC, removes the power cord and investigates the issue further based on common sense. This is because keeping the system linked to a power socket amidst smoke emitting from the PC can only make things worse. It is common sense to turn off everything and take the necessary precautions to investigate the issue further.

How are Heuristic Methods Used in Decision-Making?

There are a number of formal and informal models of heuristics used for decision making. Let’s take a look at a few of the formal models of heuristics used for decision making.

Formal Models of Heuristics

Fast-and-frugal tree.

A fast-and-frugal tree is a classification or decision tree. It is a graphical form that helps make decisions. For example, a fast-and-frugal tree might help doctors determine if a patient should be sent to a regular ward or for an emergency procedure. fast-and-frugal trees are methods for making decisions based on hierarchical models, where one has to make a decision based on little information.

Fluency Heuristic

In psychology, fluency heuristic implies an object that can be easily processed and deemed to have a higher value, even if it is not logical to assume this. Understanding the application of fluency heuristic can help make better decisions in a variety of fields. Fluency heuristic is more like sunk cost fallacy .

For example, a designer might design a user interface that is easier for users to process, with fewer buttons and easily labeled options. This can help them think fast, work quicker and improve productivity. Similarly, the concept might be used in marketing to sell products using effective marketing techniques. Even if two products are identical, a consumer might pick one over the other based on fluency heuristic. The consumer might deem the product to be better for his needs, even if it is the same as the other one.

Gaze Heuristic

Assume that you aim to catch a ball. Based on your judgment you would leap to catch the ball. If you were to leave yourself to instinct, you will end up at the same spot to catch the ball at a spot you would predict it to fall. This is essentially gaze heuristic. The concept of gaze heuristic is thought to be applied for simple situations and its applications are somewhat limited.

Recognition Heuristic

If there are two objects, one recognizable and the one isn’t, the person is likely to deem the former to be of greater value. A simple example of recognition heuristic is branding. People get used to brand logos, assuming them to be of high quality. This helps brands to sell multiple products using recognition heuristic. So, if you are looking to buy an air conditioner and come across two products, A and B, where A is a brand you know and B is a new company you don’t recognize, you might opt for A. Even if B is of better quality, you might simply trust A because you have been buying electronics from the brand for many years and they have been of good quality.

Satisficing

Satisficing entails looking for alternatives until an acceptable threshold can be ensured. Satisficing in decision making implies selecting an option which meets most needs or the first option which can meet a need, even if it is not the optimal solution. For example, when choosing between early retirement or continuing service for 2 or 3 more years, one might opt for early retirement assuming that it would meet the individual’s needs.

Similarity Heuristic

Similarity heuristic is judgment based on which is deemed similar, if something reminds someone of good or bad days, something similar might be considered the same. Similarity heuristics is often used by brands to remind people of something that they might have sentimental value for.

Someone might buy a limited-edition bottle of perfume that is being sold in a packaging style that was replaced 20 years ago. Assuming that sales were great in those days, the company might sell such limited-edition perfume bottles in the hope of boosting sales. Consumers might buy them simply because they remind them of the ‘good old days’, even though the product inside might not even be of the same but rather similar to what it used to be. Many consumers claim to buy these types of products claiming that it reminds them of a fond memory, such as their youth, marriage or  first job, when they used the product back in the day.

Final Words

Heuristics play a key role in decision making and affect the way we make decisions. Understanding heuristics can not only help resolve problems but also understand biases that affect effective decision making. A business decision or one that affects one’s health, life, or well-being cannot rely merely on a hunch. Understanding heuristics and applying them effectively can therefore help make the best possible decisions. Heuristic methods are not only used in different professions and personal decision making but are also used in artificial intelligence and programming.

Modern anti-virus software for instance uses heuristic methods to dig out the most elusive malware. The same rule can be essentially applied to decision making, by effectively using heuristics to resolve problems and to make decisions based on better judgment.

Like this article? Please share

Common Sense, Decision Making, Educated Guess, Heuristics, Judgment, Problem Solving, Profiling, Rule of Thumb, Stereotyping, Trial and Error Filed under Business

Related Articles

Filed under Business • January 16th, 2024

The OODA Loop Decision-Making Model and How to Use it for Presentations

OODA Loop is a model that supports people and companies when defining important decisions in teams or individuals. See here how to apply it in presentation slide design.

Filed under Business • October 5th, 2023

SCAMPER Technique & Ideation Method (Quick Guide for Interactive Presentations)

SCAMPER is a technique that provides a structured approach towards thinking outside the box. In this article, we explore how this technique can be used.

Filed under Business • October 2nd, 2023

How to Write a Problem Statement: Hands-On Guide With Examples

A well-written problem statement defines the stage for successful solution development and garnering support from stakeholders. Helpful tips here.

Leave a Reply

How it works

For Business

Join Mind Tools

Article • 7 min read

Heuristic Methods

Going back to basics.

By the Mind Tools Content Team

You've likely had computer problems in the past. We all have. But did you call up the IT department in a panic? Or did you use the tried-and-tested method of "turning it off and on again"?

This simple step is often all it takes to solve the problem. And it's much quicker and cheaper than sending a technician out to look at your computer every time you encounter a problem.

This is a prime example of a heuristic method at work. It's a simple, standard rule that we refer to when we're problem solving .

What Are Heuristic Methods?

Heuristics are most commonly referred to as "rules of thumb," a term thought to have been coined by Scottish preacher James Durham in his book, "Heaven Upon Earth," published in 1685. In it, Durham refers to "foolish builders, who build by guess, and by rule of thumb." [1]

This method of measurement has its origins in carpenters' ages-old habit of using the tip of their thumb to estimate an inch. (In fact, in Dutch (along with several other European languages), the word for thumb – "duim" – also means inch.)

Heuristic methods are reliable and convenient mental shortcuts that you can use to narrow down your options when you're faced with several different choices, to ease your cognitive load , or to solve problems.

Perhaps you're a hiring manager, and you decide to dismiss any résumés that contain spelling mistakes. Or maybe you're an office manager and you have to make an educated guess about the amount of stationery you need to order every month. In both instances, you are using an heuristic method to meet your objective.

However, it's also important to realize the limitations of heuristic methods. They are best used when the consequences of getting what you're doing wrong is relatively low. Certainly, you might use a heuristic method to help you to sift through a big pile of résumés, but when you make your final decision about who to recruit , greater deliberation and judgment will be needed.

Formalizing a Heuristic Method

Heuristic methods need to be formalized to be most useful to your organization as a whole. This raises them above the level of "gut instinct," and means that you can share them with your colleagues.

Whenever you find yourself calling on your experience to make a judgment, try to work out the rule of thumb that you used to find the solution. Find out what heuristics methods your team members employ as part of your use of explorative techniques such as Management By Walking Around and DILO (Day In the Life Of) . Identify whether any of the methods that you discover could be applied elsewhere within your organization, and if they should even be incorporated into its formal procedures and guidelines.

Heuristic methods can also play an important role in your problem-solving processes. The straw man technique, for example, is similar in approach to heuristics, and it is designed to help you to build on or refine a basic idea. Another approach is to adapt the solution to a different problem to fix yours. TRIZ is a powerful methodology for adopting just such an approach, and is a great source of reliable, experience-based problem-solving approaches.

Heuristics Checklists

It can be helpful to incorporate the heuristic methods that you have discovered into a checklist for newer employees. This way, they can learn from the tried-and-tested knowledge that has been accumulated by their more experienced colleagues.

Such checklists can also be used to refine your decision-making process. For example, in the food industry, the following heuristic checklist might help the product development team to decide whether it's worth test marketing a new pie:

• Does the pie look appetizing in its packaging?
• Can it be packaged so that it won't be damaged in transit?
• Can it be cooked in under 20 minutes, so that busy people will buy it?
• Does it have a shelf life of at least five days from manufacture to expiration date?

This type of list is based on previous product development processes, and on market research. Of course, there's no guarantee that a pie that meets all of these criteria will be successful. But the checklist can help the development team to make a quick "go/no-go" decision , before moving on to the next stage of product development.

The Disadvantages of Using Heuristics

Heuristics are best used when the benefits of making a quick decision outweigh the potential risk of oversimplifying the problem. Remember that heuristics are not about precision, but about having a rough idea of the problem. When you need a more precise answer, you'll need to use a more comprehensive tool. See our problem solving and decision making sections for more than 80 of these, which all focus on different situations.

Heuristic methods are also a great starting point when you or your team are brainstorming but, again, you'll likely need to follow a more detailed and formal procedure when you come to refine your ideas.

The temptation to use mental shortcuts to solve problems and make decisions can be great, particularly if we are under a lot of pressure or have heavy workloads. But cutting corners consistently can lead us to miss important solutions, mishandle problem resolution, and can make us prone to cognitive bias . (The TDODAR decision-making process can help you make good decisions in these situations.)

Instead of rushing to a conclusion that is based on an easy mental shortcut, assess whether the problem is high or low risk. If it is high risk, a more rigorous, knowledge-based approach will likely be needed.

Heuristics, or "rules of thumb," are problem-solving methods that are based on practical experience and knowledge. They allow you to use a "quick fix" to solve a minor problem or to narrow down options. They're also a great starting point for brainstorming or exploring new ideas.

However, remember to be aware of the limitations of heuristic methods. They shouldn't be applied in situations where inaccuracy carries a high degree of risk, or where the consequences of getting things wrong are significant.

[1] Durham, J. (1685). 'Heaven Upon Earth,' Edinburgh: Thomas Lumisden & John Robertson. Sermon ii, p235.

You've accessed 1 of your 2 free resources.

Get unlimited access

Discover more content

Developing a communications charter.

Delivering Clear Messages

Expert Interviews

Extraordinary Groups

With Geoffrey Bellman

Add comment

Comments (0)

Be the first to comment!

Gain essential management and leadership skills

Busy schedule? No problem. Learn anytime, anywhere. 

Subscribe to unlimited access to meticulously researched, evidence-based resources.

Join today and take advantage of our 30% offer, available until May 31st .

Sign-up to our newsletter

Subscribing to the Mind Tools newsletter will keep you up-to-date with our latest updates and newest resources.

Subscribe now

Business Skills

Personal Development

Leadership and Management

Member Extras

Most Popular

Latest Updates

Winning Body Language

Business Stripped Bare

Mind Tools Store

About Mind Tools Content

Discover something new today

Nine ways to get the best from x (twitter).

Growing Your Business Quickly and Safely on Social Media

Managing Your Emotions at Work

Controlling Your Feelings... Before They Control You

How Emotionally Intelligent Are You?

Boosting Your People Skills

Self-Assessment

What's Your Leadership Style?

Learn About the Strengths and Weaknesses of the Way You Like to Lead

Recommended for you

Top tips for managing redundancy survivors.

Address the Effects of Survivor Syndrome in Your Team.

Business Operations and Process Management

Strategy Tools

Customer Service

Business Ethics and Values

Handling Information and Data

Project Management

Knowledge Management

Self-Development and Goal Setting

Time Management

Presentation Skills

Learning Skills

Career Skills

Communication Skills

Negotiation, Persuasion and Influence

Working With Others

Difficult Conversations

Creativity Tools

Self-Management

Work-Life Balance

Stress Management and Wellbeing

Coaching and Mentoring

Change Management

Team Management

Managing Conflict

Delegation and Empowerment

Performance Management

Leadership Skills

Developing Your Team

Talent Management

Problem Solving

Decision Making

Member Podcast

Heuristics and Problem Solving

• Reference work entry
• pp 1421–1424
• Cite this reference work entry

• Erik De Corte 2 ,
• Lieven Verschaffel 2 &
• Wim Van Dooren 2  

539 Accesses

3 Citations

Definitions

In a general sense heuristics are guidelines or methods for problem solving. Therefore, we will first define problem solving before presenting a specific definition of heuristics.

Problem Solving

In contrast to a routine task, a problem is a situation in which a person is trying to attain a goal but does not dispose of a ready-made solution or solution method. Problem solving involves then “cognitive processing directed at transforming the given situation into a goal situation when no obvious method of solution is available” (Mayer and Wittrock 2006 , p. 287). An implication is that a task can be a problem for one person, but not for someone else. For instance, the task “divide 120 marbles equally among 8 children” may be a problem for beginning elementary school children, but not for people who master the algorithm for long division, or know how to use a calculator.

The term “heuristic” originates from the Greek word heuriskein which means “to find.” Heuristics ...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

De Corte, E., Verschaffel, L., & Op’t Eynde, P. (2000). Self-regulation: a characteristic and a goal of mathematics education. In M. Boekaerts, P. R. Pintrich, & M. Zeidner (Eds.), Handbook of self-regulation (pp. 687–726). San Diego, CA: Academic.

Google Scholar  

De Corte, E., Verschaffel, L., & Masui, C. (2004). The CLIA-model: a framework for designing powerful learning environments for thinking and problem solving. European Journal of Psychology of Education, 19 , 365–384.

Article   Google Scholar  

Dignath, C., & Büttner, G. (2008). Components of fostering self-regulated learning among students. a meta-analysis on intervention studies at primary and secondary school level. Metacognition and Learning, 3 , 231–264.

Groner, R., Groner, M., & Bischof, W. F. (Eds.). (1983). Methods of heuristics . Hillsdale, NJ: Erlbaum.

Mayer, R. E., & Wittrock, M. C. (2006). Problem solving. In P. A. Alexander & P. H. Winne (Eds.), Handbook of educational psychology (pp. 287–303). New York: Macmillan.

Polya, G. (1945). How to solve it . Princeton, NJ: Princeton University Press.

Schoenfeld, A. H. (1985). Mathematical problem solving . New York: Academic.

Download references

Author information

Authors and affiliations.

Department of Education, Center for Instructional Psychology and Technology (CIP&T), Katholieke Universiteit Leuven, Dekenstraat 2, P.O. box 3773, B-3000, Leuven, Belgium

Dr. Erik De Corte, Prof. Dr. Lieven Verschaffel & Wim Van Dooren

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Erik De Corte .

Editor information

Editors and affiliations.

Faculty of Economics and Behavioral Sciences, Department of Education, University of Freiburg, 79085, Freiburg, Germany

Norbert M. Seel

Rights and permissions

Reprints and permissions

Copyright information

© 2012 Springer Science+Business Media, LLC

About this entry

Cite this entry.

De Corte, E., Verschaffel, L., Van Dooren, W. (2012). Heuristics and Problem Solving. In: Seel, N.M. (eds) Encyclopedia of the Sciences of Learning. Springer, Boston, MA. https://doi.org/10.1007/978-1-4419-1428-6_420

Download citation

DOI : https://doi.org/10.1007/978-1-4419-1428-6_420

Publisher Name : Springer, Boston, MA

Print ISBN : 978-1-4419-1427-9

Online ISBN : 978-1-4419-1428-6

eBook Packages : Humanities, Social Sciences and Law

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Ohio State nav bar

The Ohio State University

• BuckeyeLink
• Find People
• Search Ohio State

Some Helpful Problem-Solving Heuristics

A  heuristic  is a thinking strategy, something that can be used to tease out further information about a problem and thus help you figure out what to do when you don’t know what to do. Here are 25 heuristics that can be useful in solving problems. They help you monitor your thought processes, to step back and watch yourself at work, and thus keep your cool in a challenging situation.

• Ask somebody else  how to do the problem. This strategy is probably the most used world-wide, though it is not one we encourage our students to use, at least not initially.
• Guess and try  (guess, check, and revise). Your first guess might be right! But incorrect guesses can often suggest a direction toward a solution. (N.B. A spreadsheet is a powerful aid in guessing and trying. Set up the relationships and plug in a number to see if you get what you want. If you don’t, it is easy to try another number. And another.)
• Restate the problem  using words that make sense to you. One way to do this is to explain the problem to someone else. Often this is all it takes for the light to dawn.
• Organize information  into a table or chart. Having it laid out clearly in front of you frees up your mind for thinking. And perhaps you can use the organized data to generate more information.
• Draw a picture  of the problem. Translate problem information into pictures, diagrams, sketches, glyphs, arrows, or some other kind of representation.
• Make a model  of the problem. The model might be a physical or mental model, perhaps using a computer. You might vary the problem information to see whether and how the model may be affected.
• Look for patterns , any kind of patterns: number patterns, verbal patterns, spatial/visual patterns, patterns in time, patterns in sound. (Some people define mathematics as the science of patterns.)
• Act out the problem , if it is stated in a narrative form. Acting it out can have the same effect as drawing a picture. What’s more, acting out the problem might disclose incorrect assumptions you are making.
• Invent notation . Name things in the problem (known or unknown) using words or symbols, including relationships between problem components.
• Write equations . An equation is simply the same thing named two different ways.
• Check all possibilities  in a systematic way. A table or chart may help you to be systematic.
• Work backwards  from the end condition to the beginning condition. Working backwards is particularly helpful when letting a variable (letter) represent an unknown.
• Identify subgoals  in the problem. Break up the problem into a sequence of smaller problems (“If I knew this, then I could get that”).
• Simplify the problem . Use easier or smaller numbers, or look at extreme cases (e.g., use the minimum or maximum value of one of the varying quantities).
• Restate the problem again . After working on the problem for a time, back off a bit and put it into your own words in still a different way, since now you know more about it.
• Change your point of view . Use your imagination to change the way you are looking at the problem. Turn it upside down, or pull it inside out.
• Check for hidden assumptions  you may be making (you might be making the problem harder than it really is). These assumptions are often found by changing the given numbers or conditions and looking to see what happens.
• Identify needed and given information clearly . You may not need to find everything you think you need to find, for instance.
• Make up your own technique . It is your mind, after all; use mental actions that make sense to you. The key is to do something that engages you with the problem.
• Try combinations of the above heuristics .

These heuristics can be readily pointed out to students as they engage problems in the classroom. However, real-world problems are often confronted many times over or on increasingly complex levels. For those kinds of problems, George Polya, the father of modern problem-solving heuristics, identified a fifth class (E) of looking-back heuristics. We include these here for completeness, but also with the teaching caveat that solutions often improve and insights grow deeper after the initial pressure to produce a solution has been resolved. Subsequent considerations of a problem situation are invariably deeper than the first attempt.

• Check your solution . Substitute your answer or results back into the problem. Are all of the conditions satisfied?
• Find another solution . There may be more than one answer. Make sure you have them all.
• Solve the problem a different way . Your first solution will seldom be the best solution. Now that the pressure is off, you may readily find other ways to solve the problem.
• Solve a related problem . Steve Brown and Marion Walter in their book,  The Art of Problem Posing , suggest the “What if not?” technique. What if the train goes at a different speed? What if there are 8 children, instead of 9? What if . . .? Fascinating discoveries can be made in this way, leading to:
• Generalize the solution . Can you glean from your solution how it can be made to fit a whole class of related situations? Can you prove your result?

7.3 Problem Solving

Learning objectives.

By the end of this section, you will be able to:

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving and decision making

People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

Problem-Solving Strategies

When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them ( Table 7.2 ). For example, a well-known strategy is trial and error . The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Everyday Connection

Solving puzzles.

Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below ( Figure 7.7 ) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

Here is another popular type of puzzle ( Figure 7.8 ) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Take a look at the “Puzzling Scales” logic puzzle below ( Figure 7.9 ). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

Pitfalls to Problem Solving

Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but they just need to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. Duncker (1945) conducted foundational research on functional fixedness. He created an experiment in which participants were given a candle, a book of matches, and a box of thumbtacks. They were instructed to use those items to attach the candle to the wall so that it did not drip wax onto the table below. Participants had to use functional fixedness to overcome the problem ( Figure 7.10 ). During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

Link to Learning

Check out this Apollo 13 scene about NASA engineers overcoming functional fixedness to learn more.

Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in Table 7.3 .

Watch this teacher-made music video about cognitive biases to learn more.

Were you able to determine how many marbles are needed to balance the scales in Figure 7.9 ? You need nine. Were you able to solve the problems in Figure 7.7 and Figure 7.8 ? Here are the answers ( Figure 7.11 ).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/psychology-2e/pages/1-introduction

• Authors: Rose M. Spielman, William J. Jenkins, Marilyn D. Lovett
• Publisher/website: OpenStax
• Book title: Psychology 2e
• Publication date: Apr 22, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/psychology-2e/pages/1-introduction
• Section URL: https://openstax.org/books/psychology-2e/pages/7-3-problem-solving

© Jan 6, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Heuristic Approach to Problem-solving: Examples

Related Topics: More Lessons for Singapore Math Math Worksheets

Videos, worksheets, solutions, and activities to help students learn how to use the heuristic approach to solve word problems in Singapore Math.

Use A Picture / Diagram / Model Example: The total cost of 2 similar bags, 3 wallets and 4 belts is $1188. A bag cost thrice as much as a wallet and a wallet costs twice as much as a belt. How much will Ted have to pay for a bag, a wallet and a belt?

Heuristic Approach to problem-solving Example: 7/10 of the boys who participated in a marathon race were Chinese. The rest of the boys were made up of Eurasians and Malays in the ratio 5:7 respectively. There were 756 more Chinese than Malay boys. Find the total number of boys who participated in the marathon race.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Reviewed by Psychology Today Staff

A heuristic is a mental shortcut that allows an individual to make a decision, pass judgment, or solve a problem quickly and with minimal mental effort. While heuristics can reduce the burden of decision-making and free up limited cognitive resources, they can also be costly when they lead individuals to miss critical information or act on unjust biases.

• Understanding Heuristics
• Different Heuristics
• Problems with Heuristics

As humans move throughout the world, they must process large amounts of information and make many choices with limited amounts of time. When information is missing, or an immediate decision is necessary, heuristics act as “rules of thumb” that guide behavior down the most efficient pathway.

Heuristics are not unique to humans; animals use heuristics that, though less complex, also serve to simplify decision-making and reduce cognitive load.

Generally, yes. Navigating day-to-day life requires everyone to make countless small decisions within a limited timeframe. Heuristics can help individuals save time and mental energy, freeing up cognitive resources for more complex planning and problem-solving endeavors.

The human brain and all its processes—including heuristics— developed over millions of years of evolution . Since mental shortcuts save both cognitive energy and time, they likely provided an advantage to those who relied on them.

Heuristics that were helpful to early humans may not be universally beneficial today . The familiarity heuristic, for example—in which the familiar is preferred over the unknown—could steer early humans toward foods or people that were safe, but may trigger anxiety or unfair biases in modern times.

The study of heuristics was developed by renowned psychologists Daniel Kahneman and Amos Tversky. Starting in the 1970s, Kahneman and Tversky identified several different kinds of heuristics, most notably the availability heuristic and the anchoring heuristic.

Since then, researchers have continued their work and identified many different kinds of heuristics, including:

Familiarity heuristic

Fundamental attribution error

Representativeness heuristic

Satisficing

The anchoring heuristic, or anchoring bias , occurs when someone relies more heavily on the first piece of information learned when making a choice, even if it's not the most relevant. In such cases, anchoring is likely to steer individuals wrong .

The availability heuristic describes the mental shortcut in which someone estimates whether something is likely to occur based on how readily examples come to mind . People tend to overestimate the probability of plane crashes, homicides, and shark attacks, for instance, because examples of such events are easily remembered.

People who make use of the representativeness heuristic categorize objects (or other people) based on how similar they are to known entities —assuming someone described as "quiet" is more likely to be a librarian than a politician, for instance. 

Satisficing is a decision-making strategy in which the first option that satisfies certain criteria is selected , even if other, better options may exist.

Heuristics, while useful, are imperfect; if relied on too heavily, they can result in incorrect judgments or cognitive biases. Some are more likely to steer people wrong than others.

Assuming, for example, that child abductions are common because they’re frequently reported on the news—an example of the availability heuristic—may trigger unnecessary fear or overprotective parenting practices. Understanding commonly unhelpful heuristics, and identifying situations where they could affect behavior, may help individuals avoid such mental pitfalls.

Sometimes called the attribution effect or correspondence bias, the term describes a tendency to attribute others’ behavior primarily to internal factors—like personality or character— while attributing one’s own behavior more to external or situational factors .

If one person steps on the foot of another in a crowded elevator, the victim may attribute it to carelessness. If, on the other hand, they themselves step on another’s foot, they may be more likely to attribute the mistake to being jostled by someone else .

Listen to your gut, but don’t rely on it . Think through major problems methodically—by making a list of pros and cons, for instance, or consulting with people you trust. Make extra time to think through tasks where snap decisions could cause significant problems, such as catching an important flight.

Artificial intelligence already plays a role in deciding who’s getting hired. The way to improve AI is very similar to how we fight human biases.

Think you are avoiding the motherhood penalty by not having children? Think again. Simply being a woman of childbearing age can trigger discrimination.

Psychological experiments on human judgment under uncertainty showed that people often stray from presumptions about rational economic agents.

Psychology, like other disciplines, uses the scientific method to acquire knowledge and uncover truths—but we still ask experts for information and rely on intuition. Here's why.

We all experience these 3 cognitive blind spots at work, frequently unaware of their costs in terms of productivity and misunderstanding. Try these strategies to work around them.

Have you ever fallen for fake news? This toolkit can help you easily evaluate whether a claim is real or phony.

An insidious form of prejudice occurs when a more powerful group ignores groups with less power and keeps them out of the minds of society.

We can never know everything and yet unconscious biases often convince us that we do. Being alert to your own ignorance is crucial for more efficient thinking in daily life.

Chatbot designers engage in dishonest anthropomorphism by designing features to exploit our heuristic processing and dupe us into overtrusting and assigning moral responsibility.

How do social media influencers convert a scroll into a like, follow, and sale? Here are the psychological principles used by digital influencers.

• Find a Therapist
• Find a Treatment Center
• Find a Psychiatrist
• Find a Support Group
• Find Online Therapy
• United States
• Brooklyn, NY
• Chicago, IL
• Houston, TX
• Los Angeles, CA
• New York, NY
• Portland, OR
• San Diego, CA
• San Francisco, CA
• Seattle, WA
• Washington, DC
• Asperger's
• Bipolar Disorder
• Chronic Pain
• Eating Disorders
• Passive Aggression
• Personality
• Goal Setting
• Positive Psychology
• Stopping Smoking
• Low Sexual Desire
• Relationships
• Child Development
• Self Tests NEW
• Therapy Center
• Diagnosis Dictionary
• Types of Therapy

At any moment, someone’s aggravating behavior or our own bad luck can set us off on an emotional spiral that threatens to derail our entire day. Here’s how we can face our triggers with less reactivity so that we can get on with our lives.

• Emotional Intelligence
• Gaslighting
• Affective Forecasting
• Neuroscience

7.3 Problem-Solving

Learning objectives.

By the end of this section, you will be able to:

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving

   People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

The study of human and animal problem solving processes has provided much insight toward the understanding of our conscious experience and led to advancements in computer science and artificial intelligence. Essentially much of cognitive science today represents studies of how we consciously and unconsciously make decisions and solve problems. For instance, when encountered with a large amount of information, how do we go about making decisions about the most efficient way of sorting and analyzing all the information in order to find what you are looking for as in visual search paradigms in cognitive psychology. Or in a situation where a piece of machinery is not working properly, how do we go about organizing how to address the issue and understand what the cause of the problem might be. How do we sort the procedures that will be needed and focus attention on what is important in order to solve problems efficiently. Within this section we will discuss some of these issues and examine processes related to human, animal and computer problem solving.

PROBLEM-SOLVING STRATEGIES

   When people are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

Problems themselves can be classified into two different categories known as ill-defined and well-defined problems (Schacter, 2009). Ill-defined problems represent issues that do not have clear goals, solution paths, or expected solutions whereas well-defined problems have specific goals, clearly defined solutions, and clear expected solutions. Problem solving often incorporates pragmatics (logical reasoning) and semantics (interpretation of meanings behind the problem), and also in many cases require abstract thinking and creativity in order to find novel solutions. Within psychology, problem solving refers to a motivational drive for reading a definite “goal” from a present situation or condition that is either not moving toward that goal, is distant from it, or requires more complex logical analysis for finding a missing description of conditions or steps toward that goal. Processes relating to problem solving include problem finding also known as problem analysis, problem shaping where the organization of the problem occurs, generating alternative strategies, implementation of attempted solutions, and verification of the selected solution. Various methods of studying problem solving exist within the field of psychology including introspection, behavior analysis and behaviorism, simulation, computer modeling, and experimentation.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them (table below). For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

   Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Further problem solving strategies have been identified (listed below) that incorporate flexible and creative thinking in order to reach solutions efficiently.

Additional Problem Solving Strategies :

• Abstraction – refers to solving the problem within a model of the situation before applying it to reality.
• Analogy – is using a solution that solves a similar problem.
• Brainstorming – refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal solution is reached.
• Divide and conquer – breaking down large complex problems into smaller more manageable problems.
• Hypothesis testing – method used in experimentation where an assumption about what would happen in response to manipulating an independent variable is made, and analysis of the affects of the manipulation are made and compared to the original hypothesis.
• Lateral thinking – approaching problems indirectly and creatively by viewing the problem in a new and unusual light.
• Means-ends analysis – choosing and analyzing an action at a series of smaller steps to move closer to the goal.
• Method of focal objects – putting seemingly non-matching characteristics of different procedures together to make something new that will get you closer to the goal.
• Morphological analysis – analyzing the outputs of and interactions of many pieces that together make up a whole system.
• Proof – trying to prove that a problem cannot be solved. Where the proof fails becomes the starting point or solving the problem.
• Reduction – adapting the problem to be as similar problems where a solution exists.
• Research – using existing knowledge or solutions to similar problems to solve the problem.
• Root cause analysis – trying to identify the cause of the problem.

The strategies listed above outline a short summary of methods we use in working toward solutions and also demonstrate how the mind works when being faced with barriers preventing goals to be reached.

One example of means-end analysis can be found by using the Tower of Hanoi paradigm . This paradigm can be modeled as a word problems as demonstrated by the Missionary-Cannibal Problem :

Missionary-Cannibal Problem

Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.

Hint : At one point in your solution, you will have to send more people back to the original side than you just sent to the destination.

The actual Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape. The objective of the puzzle is to move the entire stack to another rod obeying the following rules:

• 1. Only one disk can be moved at a time.
• 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• 3. No disc may be placed on top of a smaller disk.

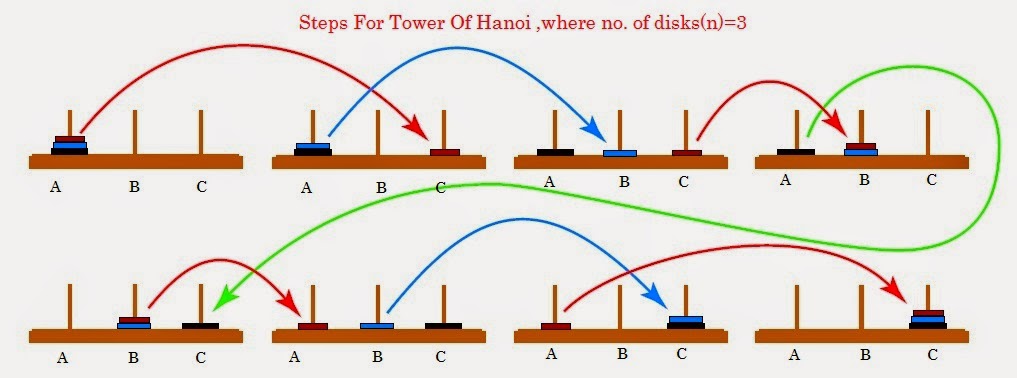
  Figure 7.02. Steps for solving the Tower of Hanoi in the minimum number of moves when there are 3 disks.

Figure 7.03. Graphical representation of nodes (circles) and moves (lines) of Tower of Hanoi.

The Tower of Hanoi is a frequently used psychological technique to study problem solving and procedure analysis. A variation of the Tower of Hanoi known as the Tower of London has been developed which has been an important tool in the neuropsychological diagnosis of executive function disorders and their treatment.

GESTALT PSYCHOLOGY AND PROBLEM SOLVING

As you may recall from the sensation and perception chapter, Gestalt psychology describes whole patterns, forms and configurations of perception and cognition such as closure, good continuation, and figure-ground. In addition to patterns of perception, Wolfgang Kohler, a German Gestalt psychologist traveled to the Spanish island of Tenerife in order to study animals behavior and problem solving in the anthropoid ape.

As an interesting side note to Kohler’s studies of chimp problem solving, Dr. Ronald Ley, professor of psychology at State University of New York provides evidence in his book A Whisper of Espionage  (1990) suggesting that while collecting data for what would later be his book  The Mentality of Apes (1925) on Tenerife in the Canary Islands between 1914 and 1920, Kohler was additionally an active spy for the German government alerting Germany to ships that were sailing around the Canary Islands. Ley suggests his investigations in England, Germany and elsewhere in Europe confirm that Kohler had served in the German military by building, maintaining and operating a concealed radio that contributed to Germany’s war effort acting as a strategic outpost in the Canary Islands that could monitor naval military activity approaching the north African coast.

While trapped on the island over the course of World War 1, Kohler applied Gestalt principles to animal perception in order to understand how they solve problems. He recognized that the apes on the islands also perceive relations between stimuli and the environment in Gestalt patterns and understand these patterns as wholes as opposed to pieces that make up a whole. Kohler based his theories of animal intelligence on the ability to understand relations between stimuli, and spent much of his time while trapped on the island investigation what he described as  insight , the sudden perception of useful or proper relations. In order to study insight in animals, Kohler would present problems to chimpanzee’s by hanging some banana’s or some kind of food so it was suspended higher than the apes could reach. Within the room, Kohler would arrange a variety of boxes, sticks or other tools the chimpanzees could use by combining in patterns or organizing in a way that would allow them to obtain the food (Kohler & Winter, 1925).

While viewing the chimpanzee’s, Kohler noticed one chimp that was more efficient at solving problems than some of the others. The chimp, named Sultan, was able to use long poles to reach through bars and organize objects in specific patterns to obtain food or other desirables that were originally out of reach. In order to study insight within these chimps, Kohler would remove objects from the room to systematically make the food more difficult to obtain. As the story goes, after removing many of the objects Sultan was used to using to obtain the food, he sat down ad sulked for a while, and then suddenly got up going over to two poles lying on the ground. Without hesitation Sultan put one pole inside the end of the other creating a longer pole that he could use to obtain the food demonstrating an ideal example of what Kohler described as insight. In another situation, Sultan discovered how to stand on a box to reach a banana that was suspended from the rafters illustrating Sultan’s perception of relations and the importance of insight in problem solving.

Grande (another chimp in the group studied by Kohler) builds a three-box structure to reach the bananas, while Sultan watches from the ground.  Insight , sometimes referred to as an “Ah-ha” experience, was the term Kohler used for the sudden perception of useful relations among objects during problem solving (Kohler, 1927; Radvansky & Ashcraft, 2013).

Solving puzzles.

   Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (see figure) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)

   Here is another popular type of puzzle (figure below) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.

   Take a look at the “Puzzling Scales” logic puzzle below (figure below). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

What steps did you take to solve this puzzle? You can read the solution at the end of this section.

Pitfalls to problem solving.

   Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

   Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the table below.

Were you able to determine how many marbles are needed to balance the scales in the figure below? You need nine. Were you able to solve the problems in the figures above? Here are the answers.

   Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

References:

Openstax Psychology text by Kathryn Dumper, William Jenkins, Arlene Lacombe, Marilyn Lovett and Marion Perlmutter licensed under CC BY v4.0. https://openstax.org/details/books/psychology

Review Questions:

1. A specific formula for solving a problem is called ________.

a. an algorithm

b. a heuristic

c. a mental set

d. trial and error

2. Solving the Tower of Hanoi problem tends to utilize a  ________ strategy of problem solving.

a. divide and conquer

b. means-end analysis

d. experiment

3. A mental shortcut in the form of a general problem-solving framework is called ________.

4. Which type of bias involves becoming fixated on a single trait of a problem?

a. anchoring bias

b. confirmation bias

c. representative bias

d. availability bias

5. Which type of bias involves relying on a false stereotype to make a decision?

6. Wolfgang Kohler analyzed behavior of chimpanzees by applying Gestalt principles to describe ________.

a. social adjustment

b. student load payment options

c. emotional learning

d. insight learning

7. ________ is a type of mental set where you cannot perceive an object being used for something other than what it was designed for.

a. functional fixedness

c. working memory

Critical Thinking Questions:

1. What is functional fixedness and how can overcoming it help you solve problems?

2. How does an algorithm save you time and energy when solving a problem?

Personal Application Question:

1. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?

anchoring bias

availability heuristic

confirmation bias

functional fixedness

hindsight bias

problem-solving strategy

representative bias

trial and error

working backwards

Answers to Exercises

algorithm:  problem-solving strategy characterized by a specific set of instructions

anchoring bias:  faulty heuristic in which you fixate on a single aspect of a problem to find a solution

availability heuristic:  faulty heuristic in which you make a decision based on information readily available to you

confirmation bias:  faulty heuristic in which you focus on information that confirms your beliefs

functional fixedness:  inability to see an object as useful for any other use other than the one for which it was intended

heuristic:  mental shortcut that saves time when solving a problem

hindsight bias:  belief that the event just experienced was predictable, even though it really wasn’t

mental set:  continually using an old solution to a problem without results

problem-solving strategy:  method for solving problems

representative bias:  faulty heuristic in which you stereotype someone or something without a valid basis for your judgment

trial and error:  problem-solving strategy in which multiple solutions are attempted until the correct one is found

working backwards:  heuristic in which you begin to solve a problem by focusing on the end result

Share This Book

• Increase Font Size

• Search Search Please fill out this field.

What Are Heuristics?

Understanding heuristics.

• Pros and Cons
• Examples in Behavioral Economics

Heuristics and Psychology

The bottom line.

• Investing Basics

Heuristics: Definition, Pros & Cons, and Examples

James Chen, CMT is an expert trader, investment adviser, and global market strategist.

Heuristics are mental shortcuts that help people make quick decisions. They are rules or methods that help people use reason and past experience to solve problems efficiently. Commonly used to simplify problems and avoid cognitive overload, heuristics are part of how the human brain evolved and is wired, allowing individuals to quickly reach reasonable conclusions or solutions to complex problems. These solutions may not be optimal ones but are often sufficient given limited timeframes and calculative capacity.

These cognitive shortcuts feature prominently in behavioral economics .

Key Takeaways

• Heuristics are mental shortcuts for solving problems in a quick way that delivers a result that is sufficient enough to be useful given time constraints.
• Investors and financial professionals use a heuristic approach to speed up analysis and investment decisions.
• Heuristics can lead to poor decision-making based on a limited data set, but the speed of decisions can sometimes make up for the disadvantages.
• Behavioral economics has focused on heuristics as one limitation of human beings behaving like rational actors.
• Availability, anchoring, confirmation bias, and the hot hand fallacy are some examples of heuristics people use in their economic lives.

Investopedia / Danie Drankwalter

People employ heuristics naturally due to the evolution of the human brain. The brain can only process so much information at once and therefore must employ various shortcuts or practical rules of thumb . We would not get very far if we had to stop to think about every little detail or collect every piece of available information and integrate it into an analysis.

Heuristics therefore facilitate timely decisions that may not be the absolute best ones but are appropriate enough. Individuals are constantly using this sort of intelligent guesswork, trial and error, process of elimination, and past experience to solve problems or chart a course of action. In a world that is increasingly complex and overloaded with big data, heuristic methods make decision-making simpler and faster through shortcuts and good-enough calculations.

First identified in economics by the political scientist and organizational scholar Herbert Simon in his work on bounded rationality, heuristics have now become a cornerstone of behavioral economics.

Rather than subscribing to the idea that economic behavior was rational and based upon all available information to secure the best possible outcome for an individual ("optimizing"), Simon believed decision-making was about achieving outcomes that were "good enough" for the individual based on their limited information and balancing the interests of others. Simon called this " satisficing ," a portmanteau of the words "satisfy" and "suffice."

Advantages and Disadvantages of Using Heuristics

The main advantage to using heuristics is that they allow people to make good enough decisions without having all of the information and without having to undertake complex calculations.

Because humans cannot possibly obtain or process all the information needed to make fully rational decisions, they instead seek to use the information they do have to produce a satisfactory result, or one that is good enough. Heuristics allow people to go beyond their cognitive limits.

Heuristics are also advantageous when speed or timeliness matters—for example, deciding to enter a trade or making a snap judgment about some important decision. Heuristics are thus handy when there is no time to carefully weigh all options and their merits.

Disadvantages

There are also drawbacks to using heuristics. While they may be quick and dirty, they will likely not produce the optimal decision and can also be wrong entirely. Quick decisions without all the information can lead to errors in judgment, and miscalculations can lead to mistakes.

Moreover, heuristics leave us prone to biases that tend to lead us toward irrational economic behavior and sway our understanding of the world. Such heuristics have been identified and cataloged by the field of behavioral economics.

Quick & easy

Allows decision-making that goes beyond our cognitive capacity

Allows for snap judgments when time is limited

Often inaccurate

Can lead to systemic biases or errors in judgment

Example of Heuristics in Behavioral Economics

Representativeness.

A popular shortcut method in problem-solving identified in behavioral economics is called representativeness heuristics. Representativeness uses mental shortcuts to make decisions based on past events or traits that are representative of or similar to the current situation.

Say, for example, Fast Food ABC expanded its operations to India and its stock price soared. An analyst noted that India is a profitable venture for all fast-food chains. Therefore, when Fast Food XYZ announced its plan to explore the Indian market the following year, the analyst wasted no time in giving XYZ a "buy" recommendation.

Although their shortcut approach saved reviewing data for both companies, it may not have been the best decision. Fast Food XYZ may have food that is not appealing to Indian consumers, which research would have revealed.

Anchoring and Adjustment

Anchoring and adjustment is another prevalent heuristic approach. With anchoring and adjustment, a person begins with a specific target number or value—called the anchor—and subsequently adjusts that number until an acceptable value is reached over time. The major problem with this method is that if the value of the initial anchor is not the true value, then all subsequent adjustments will be systematically biased toward the anchor and away from the true value.

An example of anchoring and adjustment is a car salesman beginning negotiations with a very high price (that is arguably well above the  fair value ). Because the high price is an anchor, the final price will tend to be higher than if the car salesman had offered a fair or low price to start.

Availability (Recency) Heuristic

The availability (or recency) heuristic is an issue where people give too much weight to the probability of an event happening again if it recently has occurred. For instance, if a shark attack is reported in the news, those headlines make the event salient and can lead people to stay away from the water, even though shark attacks remain very rare.

Another example is the case of the " hot hand ," or the sense that following a string of successes, an individual is likely to continue being successful. Whether at the casino, in the markets, or playing basketball, the hot hand has been debunked. A string of recent good luck does not alter the overall probability of events occurring.

Confirmation Bias

Confirmation bias is a well-documented heuristic whereby people give more weight to information that fits with their existing worldviews or beliefs. At the same time, information that contradicts these beliefs is discounted or rejected.

Investors should be aware of their own tendency toward confirmation bias so that they can overcome poor decision-making, missing chances, and avoid falling prey to bubbles . Seeking out contrarian views and avoiding affirmative questions are two ways to counteract confirmation bias.

Hindsight Bias

Hindsight is always 20/20. However, the hindsight bias leads us to forget that we made incorrect predictions or estimates prior to them occurring. Rather, we become convinced that we had accurately predicted an event before it occurred, even when we did not. This can lead to overconfidence for making future predictions, or regret for not taking past opportunities.

Stereotypes

Stereotypes are a kind of heuristic that allows us to form opinions or judgments about people whom we have never met. In particular, stereotyping takes group-level characteristics about certain social groups—often ones that are racist, sexist, or otherwise discriminatory—and casts those characteristics onto all of the members in that group, regardless of their individual personalities, beliefs, skills, or behaviors.

By imposing oversimplified beliefs onto people, we can quickly judge potential interactions with them or individual outcomes of those people. However, these judgments are often plain wrong, derogatory, and perpetuate social divisions and exclusions.

Heuristics were first identified and taken seriously by scholars in the middle of the 20th century with the work of Herbert Simon, who asked why individuals and firms don't act like rational actors in the real world, even with market pressures punishing irrational decisions. Simon found that corporate managers do not usually optimize but instead rely on a set of heuristics or shortcuts to get the job done in a way that is good enough (to "satisfice").

Later, in the 1970s and '80s, psychologists Amos Tversky and Daniel Kahneman working at the Hebrew University in Jerusalem, built off of Herbert Simon's work and developed what is known as Prospect Theory . A cornerstone of behavioral economics, Prospect Theory catalogs several heuristics used subconsciously by people as they make financial evaluations.

One major finding is that people are loss-averse —that losses loom larger than gains (i.e., the pain of losing $50 is far more than the pleasure of receiving $50). Here, people adopt a heuristic to avoid realizing losses, sometimes spurring them to take excessive risks in order to do so—but often leading to even larger losses.

More recently, behavioral economists have tried to develop policy measures or "nudges" to help correct people's irrational use of heuristics in order to help them achieve more optimal outcomes—for instance, by having people enroll in a retirement savings plan by default instead of having to opt in.

What Are the Types of Heuristics?

To date, several heuristics have been identified by behavioral economics—or else developed to aid people in making otherwise complex decisions. In behavioral economics, representativeness, anchoring and adjustment, and availability (recency) are among the most widely cited. Heuristics may be categorized in many ways, such as cognitive versus emotional biases or errors in judgment versus errors in calculation.

What Is Heuristic Thinking?

Heuristic thinking uses mental shortcuts—often unconsciously—to quickly and efficiently make otherwise complex decisions or judgments. These can be in the form of a "rule of thumb" (e.g., saving 5% of your income in order to have a comfortable retirement) or cognitive processes that we are largely unaware of like the availability bias.

What Is Another Word for Heuristic?

Heuristic may also go by the following terms: rule of thumb; mental shortcut; educated guess; or satisfice.

How Does a Heuristic Differ From an Algorithm?

An algorithm is a step-by-step set of instructions that are followed to achieve some goal or outcome, often optimizing that outcome. They are formalized and can be expressed as a formula or "recipe." As such, they are reproducible in the sense that an algorithm will always provide the same output, given the same input.

A heuristic amounts to an educated guess or gut feeling. Rather than following a set of rules or instructions, a heuristic is a mental shortcut. Moreover, it often produces sub-optimal and even irrational outcomes that may differ even when given the same input.

What Are Computer Heuristics?

In computer science, a heuristic refers to a method of solving a problem that proves to be quicker or more efficient than traditional methods. This may involve using approximations rather than precise calculations or techniques that circumvent otherwise computationally intensive routines.

Heuristics are practical rules of thumb that manifest as mental shortcuts in judgment and decision-making. Without heuristics, our brains would not be able to function given the complexity of the world, the amount of data to process, and the calculative abilities required to form an optimal decision. Instead, heuristics allow us to make quick, good-enough choices.

However, these choices may also be subject to inaccuracies and systemic biases, such as those identified by behavioral economics.

Simon, Herbert. " Herbert Simon, Innovation, and Heuristics ." Mind & Society, vol. 17, 2019, pp. 97-109.

Kahneman, Daniel, and Tversky, Amos. " Prospect Theory: An Analysis of Decision Under Risk ." The Econometric Society, vol. 47, no. 2, 1979, pp. 263-292.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Into all problem-solving, a little dissent must fall

Events of the past several years have reiterated for executives the importance of collaboration and of welcoming diverse perspectives when trying to solve complicated workplace problems. Companies weren’t fully prepared for the onset of a global pandemic, for instance, and all that it engendered—including supply chain snarls and the resulting Great Attrition  and shift to remote (and now hybrid) work, which required employers to fundamentally rethink their talent strategies . But in most cases leaders have been able to collaborate their way through the uncertainty, engage in rigorous debate and analyses about the best steps to take, and work with employees, suppliers, partners, and other critical stakeholders to react and, ultimately, recover.

And It’s not just COVID-19: many organisations have had to rethink their business strategies and practices in the wake of environmental concerns, the war in Ukraine, and social movements sparked by racial injustice, sexual misconduct, and widespread economic inequity . Ours are fast-moving, complex times, rich not just in worrisome challenges but also in exciting potential—organisations that enable innovation will find ample opportunities to thrive. So now more than ever, decision makers can’t act alone; they must bring diverse perspectives to the table and ensure that those voices are fully heard . 1 Sundiatu Dixon-Fyle, Kevin Dolan, Vivian Hunt, and Sara Prince, “ Diversity wins: How inclusion matters ,” McKinsey, May 19, 2020.

But while many leaders say they welcome dissent, their reactions often change when they actually get some. They may feel defensive. They may question their own judgment. They may resent having to take time to revisit the decision-making process. These are natural responses, of course; employees’ loyalty and affirmation are more reassuring to leaders than robust challenges from the group. There is discomfort, too, for potential dissenters; it is much safer to keep your thoughts to yourself and conform  than to risk expulsion from the group. 2 Derived from this work on the evolutionary origins of social and political behavior: Christopher Boehm, Hierarchy in the Forest: The Evolution of Egalitarian Behavior , Cambridge, Massachusetts: Harvard University Press, 2001.

What’s missing in many companies, in our experience, is the use of “contributory dissent” or the capabilities required to engage in healthy if divergent discussions about critical business problems. Contributory dissent allows individuals and groups to air their differences in a way that moves the discussion toward a positive outcome and doesn’t undermine leadership or group cohesion . 3 McKinsey itself has established obligation to dissent as one of its core values alongside those focused on client service and talent development. For more, see Bill Taylor, “True leaders believe dissent is an obligation,” Harvard Business Review , January 12, 2017.

McKinsey’s research and experience in the field point to several steps leaders can take to engage in healthy dissent and build a culture where constructive feedback is expected and where communication is forthright. These include modeling “open” behaviors, embedding psychological safety  and robust debate into decision-making processes, and equipping employees with the communication skills that will allow them to contribute dissenting opinions effectively.

In this article we outline the steps leaders can take to encourage healthy dissent, and the actions teams and individuals can take to share their voices and perspectives most effectively. It takes both sides, after all, to engage in robust debate, find the right solutions, and enable lasting, positive change.

How leaders can encourage contributory dissent

Senior leaders in an organisation play a central role in ensuring that individuals and teams see contributory dissent as a normal part of any discussion. They can signal the importance of dissent by taking a series of steps to institutionalise the practice within an organisation and empower employees to share their ideas freely and productively. Specifically, senior leaders should strive to inspire rather than direct employees to collaborate, explicitly demand dissent and, taking that one step further, actively engage with naysayers (see sidebar “How to encourage healthy dissent”). 4 Leaders can also draw on McKinsey’s “influence model” for changing mindsets and behaviors: role modeling, fostering understanding and conviction, reinforcing with formal mechanisms, and developing talent and skills. For more, see Tessa Basford and Bill Schaninger, “ The four building blocks of change ,” McKinsey Quarterly , April 11, 2016.

Inspire, don’t direct

How to encourage healthy dissent.

To encourage dissent through personal leadership:

Lead to inspire, not to direct:

• Empower the group to come up with ideas: “None of us knows the answer yet, but we can work it out together if we harness the best of everyone’s thinking.”

Foster dissent by actively seeking it:

• Explicitly seek dissent; give people permission and encouragement.
• Consider including dissent as a stated organisational value.
• Make provision for open discussion in the buildup to decisions.

Welcome open discussion when it comes:

• Listen to dissenters and naysayers, and thank them for their insights.
• Recognise this as a usefully unfiltered channel for understanding the organisation’s perceptions on issues.
• Seek to bring dissenters along the decision journey, so they become positive influencers later during implementation.
• Employ deliberate techniques such as red teaming and pre-mortems to widen the debate and mitigate groupthink.

As the inspirational speaker Simon Sinek put it, “The role of a leader is not to come up with all the great ideas. The role of a leader is to create an environment in which great ideas can happen.” 5 Simon Sinek, Start with Why: How Great Leaders Inspire Everyone to Take Action , New York, NY: Portfolio, 2009. That is especially important for fostering an atmosphere of collaboration and contributory dissent. Rather than immediately jump into a discussion about solutions, one senior leader in an international organisation addressed his team’s anxiety in the wake of a crisis. “Let me guess,” he said, “you’re all feeling confused and uncertain about the way ahead. Terrific. I’m so glad we are of one mind and that we all understand our situation correctly! I’m sure that we can work it out together, but it’s going to require the best of everyone’s thinking. Let’s get started.” His authenticity and understated humor allowed him to connect with the group and inspired them to keep calm, carry on, and generate solutions that the leader alone couldn’t have come up with. Harvard professor Ron Heifetz describes this as creating a holding environment, a key element of adaptive leadership. 6 Ronald A. Heifetz and Mary Linksy, Leadership on the Line: Staying Alive through the Dangers of Leading , Boston, MA: Harvard Business School Press, 2002; Ronald Heifetz, Alexander Grashow, and Marty Linksy, The Practice of Adaptive Leadership: Tools and Tactics for Changing Your Organization and the World , Boston, MA: Harvard Business Press, 2009.

Explicitly demand dissent

It’s not enough for leaders to give people permission to dissent; they must demand it of people. In many companies, individuals and teams may (understandably) default to collegiality, not realizing that there are ways to challenge ideas while still respecting colleagues’ roles and intellect. It’s on senior leaders, then, to help employees understand where the boundaries are. In World War 1, Australia’s General Sir John Monash was determined to develop better tactics to overcome the catastrophic impasse of trench warfare. He knew there were answers to be found from the experience of soldiers in the trenches, but he needed to loosen the military discipline of blind obedience: “I don’t care a damn for your loyal service when you think I am right; when I really want it most is when you think I am wrong.” Monash scheduled open battle planning sessions and pulled in advice from whoever offered it. In doing so, he built ownership of and confidence in his plans among all ranks. The resulting orchestration of tanks, artillery, aircraft, and troops led to rapid advances along the Somme Valley, and Monash garnered respect and appreciation from his troops, whose chances of survival and ultimate victory had increased markedly.

Actively engage with naysayers

Taking the demand imperative one step further, it’s beneficial for leaders to actively seek out the views of vocal naysayers , who can turn into influential champions just by being part of the conversation. They can immediately improve the nature of business debate and may boost the quality of the final decision, although engaging with naysayers can be tough. Some dissenting opinions can be ill-informed or uncomfortable to hear. The objective for senior leaders, then, is to put their discomfort aside and listen for signs of cognitive dissonance within an organisation. As an example, front-line employees may say things like “We’re not considered strategic thinkers,” or “The company doesn’t put people first,” while senior management may actually feel as though they have made strides in both of those areas. Still, leaders need to absorb such comments, treat them as useful data points, assess their validity, and engage in what may be a challenging discussion. They may want to use red teams  and premortems , in which teams at the outset anticipate all the ways a project could fail, to frame up dissenting opinions, mitigate groupthink, and find a positive resolution. These behaviours also serve to enhance organizational agility and resilience .

How leaders can establish psychological safety

Senior leaders need to establish a work environment in which it is safe to offer dissenting views. The McKinsey Health Institute’s work on employee well-being points to a strong correlation between leadership behaviors, collaborative culture, and resistance to mental health problems and burnout : only 15 percent of employees in environments with low inclusivity and low support for personal growth are highly engaged, compared with 38 percent in high-scoring environments. 7 “ Addressing employee burnout: Are you solving the right problem? ,” McKinsey, May 27, 2022. Leaders can build psychological safety (where team members feel they can take interpersonal risks and remain respected and accepted) and set the conditions for contributory dissent by rethinking how they engage in debate—both the dynamics and the choreography of it.

The dynamics of debate

The poet and playwright Oscar Wilde described a healthy debating culture as one in which people are “playing gracefully with ideas”— listening to, and even nourishing, opposing points of view in a measured and respectful way. 8 The Complete Works of Oscar Wilde, Volume 2: De Profundis, “Epistola: In Carcere et Vinculis,” Oxford, United Kingdom: Clarendon Press, 2005. Indeed, the best ideas can emerge at the intersection of cultures and opinions. In 15th century Florence, for instance, the Medici family attracted and funded creators from across the arts and sciences to establish an epicenter of innovative thinking that sparked the Renaissance. 9 Frans Johansson, The Medici Effect: Breakthrough Insights at the Intersection of Ideas, Concepts, and Culture , Boston, MA: Harvard Business School Press, 2004. Closer to this century, we have seen cross-discipline innovations like the application of biologists’ research on ant colonies to solve problems in telecommunications routing. And in the business world, extraordinary innovations have been achieved by open-minded leaders bringing together smart people and creating the conditions for playful exploration.

To achieve a state of “graceful play,” senior leaders must carefully manage group dynamics during debates. Rather than lead with their own opinions, for instance, which might immediately carry outsize weight in the group and stifle discussion, senior leaders can hold back and let others lead the discussion . They can lean in to show genuine curiosity or to explicitly recognise when a dissenting view has changed their thinking. But by letting other, more junior voices carry the agenda and work through ideas, however imperfect, senior leaders can establish a climate of psychological safety—and garner more respect from colleagues long term. 10 Amy C. Edmondson, The Fearless Organization: Creating Psychological Safety in the Workplace for Learning, Innovation, and Growth , Hoboken, NJ: John Wiley & Sons, 2019.

Leaders will also need to be aware of cultural differences that may crop up during debates. For example, many Australians speak candidly and are happy to address issues squarely. By contrast, the concept of “face” is so important in many Asian cultures that a more circumspect approach is taken. And the Pacific and Maori cultures emphasize displays of both strength and respect. 11 Erin Meyer, The Culture Map: Breaking through the Invisible Boundaries of Global Business , Philadelphia, PA: PublicAffairs, 2014. These differences in debate dynamics really matter. They can be a great source of hybrid vigour, 12 “Heterosis, also called hybrid vigour: the increase in such characteristics as size, growth rate, fertility, and yield of a hybrid organism over those of its parents. The first-generation offspring generally show, in greater measure, the desired characteristics of both parents.” Encyclopedia Britannica , accessed September 19, 2022. if sensitively managed, or a source of conflict and disenfranchisement if not. To approach these differences in a positive way, senior leaders could undertake a mapping exercise that identifies the different styles of the cultures present, thereby providing validation and enabling pragmatic measures to integrate them.

Choreographing debate

Beyond just managing debate dynamics, business leaders must take a hand in choreographing the debate and, specifically, in helping to design collective-thinking processes  so people know how best to play their part. Business leaders may adopt a structured approach  to brainstorming, for instance, or plan strategic off-site schedules that combine deliberate thinking with “distracted” thinking—taking time to engage in a social activity, for instance—to take advantage of employees’ deep-thinking processes.

How deliberate choices by the leader can optimise a decision-making process

A leader must consciously assess each new situation and design the collective-thinking process accordingly, then articulate this so that people know how best to play their part.

In doing so, the leader should consider an array of questions, the answers to which will determine the context, for example:

• What does success look like?
• Will the organisation underwrite initial failures in the interests of agility and innovation?
• How broad and freethinking an analysis is required?
• What are the explicit expectations for contributory dissent?
• Are any topics and behaviours out of bounds?
• Who will lead the discussion, and how will comments be captured?
• Does urgency mean that it’s better to be directive?
• Who will be consulted?
• Which decisions can be delegated, and to whom?
• Whose support needs to be built?
• What parameters and boundaries exist?
• Are there interim decisions and communications required?
• What form should the deliverable outcomes take?
• When are the deliverables required?
• Direction setting on these parameters by the leader focuses the team, while also creating space for creativity and iterative learning.

To create a sustainable structure for debate, business leaders will need to consider questions relating to team structure and rules of engagement: What does success look like when it comes to contributory dissent? What topics and behaviors are out of bounds? Who will lead the discussion, and how will comments be captured? Who has the final say on decisions, or which decisions can be delegated, and to whom? (For a more comprehensive explanation, see sidebar “How deliberate choices by the leader can optimise a decision-making process.”)

Having these parameters in place can free up the team to think more creatively about the issue at hand. Establishing such protocols can also make it easier to raise dissenting opinions. At one company, people are asked to call out their underlying values or potential biases when expressing a dissenting view. During meetings of the promotion committee, for instance, a statement like “I think we are making the wrong decision” would be rephrased as “I am someone who values experience over collaboration, and this decision would risk losing too much institutional knowledge.”

How individuals and teams can engage and dissent

As we’ve shared, senior leaders can take steps to set conditions for robust discussion and problem-solving, but individuals and teams themselves must also have the right mindsets and skills for contributory dissent to work well (see sidebar “How teams and individuals can dissent effectively”). In particular, they must embrace the obligation to dissent, actively make space to analyse ideas that are different from their own, and then find ways to either iterate on others’ ideas or respectfully agree to disagree.

Embrace the obligation to dissent

How teams and individuals can dissent effectively.

For dissent to be effective, its delivery requires courage and tactical skills underpinned by sincere respect and grace. Speaking up with respect is the right thing to do, and the responsibility to do so exists, even if there is uncertainty. The following guidelines are useful in enabling effective dissent:

Prepare a welcome for dissenting views:

• Understand the context and motivations of others, appreciate their views, and syndicate your own.
• Stop and strategise before wading into the conversations, establish a solid platform for agreement, and explicitly seek permission to dissent.

Play the long game:

• Be open minded and iterative. Don’t expect to succeed on the first try.
• Listen to others for what their views might add rather than to defend your own.

Withhold assent if you need to, but do it carefully:

• Withholding assent is a legitimate option if done judiciously.
• Minimise offense to and loss of face for the decision maker.
• If principles or legality is at stake, document your dissent.

Individuals and teams need to exhibit a certain amount of humility and confidence in order to speak truth to power with respect; they must be sure for themselves that doing so is the right thing to do. To build this confidence, individuals and teams should remember that the very act of dissent can be valuable, even if the contribution itself isn’t 100 percent baked. Others can react or build on the dissenting view—which, in itself, can be a satisfying process for a dissenter. If the ultimate decision isn’t what they proposed, they still helped shape it by offering and testing a worthy possibility.

Make space to analyse different views

Individuals and teams may need time to determine their positions on an issue. During this period, it’s important to be (and seen to be) open-minded and respectful of others’ views. That means asking lots of questions, gathering information, assessing others’ motivations, and acknowledging their views before syndicating alternatives of your own. Much of this fact gathering can be done one-on-one, in a nonconfrontational way, in offline conversations rather than in a tension-filled meeting room. In these conversations, individuals could start by reaffirming a shared commitment to finding a solution to the issue at hand, their respect for the decision-making process and the group, and areas of broad agreement. They could also signal their possible intention to dissent and seek permission to do so rather than confronting people head-on. People will find it harder to refuse that permission, and will be less likely to get defensive, when approached with statements like “This is a great discussion, and I love the vision of where we are headed, but would it be OK for us to explore some alternatives for how to get there?”

Agree to iterate …

Individuals and teams that decide to offer dissenting views should agree to iterate on other solutions, rather than digging in. Their dissenting opinions should be cogent, persuasive, and open-minded—but dissenters shouldn’t expect to change hearts and minds on the first try. They should plant seeds gently and bide their time; they might even see their idea come back as someone else’s. The critical skill required here is active, open listening: dissenters should listen carefully for others’ additive insights and find ways to build on them. In their contributory dissent, individuals and teams can take a moment to summarize what others have said and then use statements like “Can I offer another take?” and then allow the momentum of the conversation to take over.

… or agree to disagree

But what happens if, after all the considered and tactful input, the dissenter still believes a decision is heading in the wrong direction? In our experience, withholding assent then becomes a legitimate option: people shouldn’t agree if they don’t agree. This is where all the careful, respectful groundwork the dissenter has done can pay dividends. In fact, a dissenting view gains even more power when an individual can say something like, “I still believe in my alternate solution, but I’m grateful for the opportunity to contribute to this process, and I respect that you have the final say.” In this case, the dissenter is supporting the leader while flagging that the open debate hasn’t convinced them to change their initial view.

Of course, withholding assent should be a relatively rare action, taken only after an individual or team has shown that they can accommodate other views and have aligned with the consensus when they believe it’s right to do so. Think of US Supreme Court associate justice Ruth Bader Ginsburg, who joined the consensus view on many decisions but who is especially celebrated for the positive changes that arose from her highly influential dissenting opinions on issues such as gender equity, human rights, and religious freedom.

Contributory dissent can help strengthen employee engagement, unlock hidden insights, and help organisations solve tough challenges. But putting it into practice takes courage and humility, and it won’t just happen by accident. Leaders need to be intentional about welcoming challenges to their plans and opinions, even when it’s uncomfortable to do so. They need to establish cultures and structures where respectful debate can occur and where individuals and teams feel free to bring innovative—and often better—alternative solutions to the table.

Ben Fletcher is a senior partner in McKinsey’s Sydney office, Chris Hartley is a partner in the Melbourne office, Rupe Hoskin is a senior expert in the Canberra office, and Dana Maor is a senior partner in the Tel Aviv office.

The authors wish to thank Jacqueline Brassey, Nikki Dines, Richard Fitzgerald, Sam Hemphill, Ayush Jain, Jemma King, and Martin Nimmo for their contributions to this article.

Explore a career with us

Related articles.

Psychological safety and the critical role of leadership development

How to demonstrate calm and optimism in a crisis

The four building blocks of change

Cross-Problem Learning for Solving Vehicle Routing Problems

Existing neural heuristics often train a deep architecture from scratch for each specific vehicle routing problem (VRP), ignoring the transferable knowledge across different VRP variants. This paper proposes the cross-problem learning to assist heuristics training for different downstream VRP variants. Particularly, we modularize neural architectures for complex VRPs into 1) the backbone Transformer for tackling the travelling salesman problem (TSP), and 2) the additional lightweight modules for processing problem-specific features in complex VRPs. Accordingly, we propose to pre-train the backbone Transformer for TSP, and then apply it in the process of fine-tuning the Transformer models for each target VRP variant. On the one hand, we fully fine-tune the trained backbone Transformer and problem-specific modules simultaneously. On the other hand, we only fine-tune small adapter networks along with the modules, keeping the backbone Transformer still. Extensive experiments on typical VRPs substantiate that 1) the full fine-tuning achieves significantly better performance than the one trained from scratch, and 2) the adapter-based fine-tuning also delivers comparable performance while being notably parameter-efficient. Furthermore, we empirically demonstrate the favorable effect of our method in terms of cross-distribution application and versatility.

1 Introduction

Recently, there has been a growing trend toward applying neural methods based on deep learning to solve Combinatorial Optimization Problems (COPs), commonly known as Neural Combinatorial Optimization (NCO) Bengio et al. ( 2021 ) . Among the studied COPs, the Vehicle Routing Problems (VRPs) are often favoured and chosen to verify the effectiveness of the NCO methods, especially the Traveling Salesman Problem (TSP) and Capacitated Vehicle Routing Problem (CVRP). On the one hand, VRPs are widely applied in real-world scenarios such as logistics, and drone delivery  Wang and Sheu ( 2019 ); Konstantakopoulos et al. ( 2022 ) . On the other hand, VRPs are known to be NP-complete problems, and many of them are challenging to be solved efficiently. With the advances of deep learning and its power to automatically learn neural heuristics, NCO methods have demonstrated notable promise against traditional heuristics  Kool et al. ( 2018 ); Kwon et al. ( 2020 ); Li et al. ( 2021 ); Luo et al. ( 2023 ) . To further strengthen NCO methods, a number of recent endeavors have been paid to enhance generalization capabilities, which attempt to ameliorate the performance of the neural heuristics in solving the VRP instances with distributions or sizes unseen during training  Geisler et al. ( 2022 ); Bi et al. ( 2022 ); Qiu et al. ( 2022 ) .

While gaining promising outcomes, current NCO methods generally learn a neural heuristic solely for each specific VRP, which brings about several issues. Firstly, such a learning paradigm would not be practical, since considerable models need to be trained from scratch when a number of VRPs are supposed to be solved, such as TSP and its variants like Orienteering Problem (OP) and Prize Collecting TSP (PCTSP). Secondly, the mainstream neural heuristics for VRPs are mostly developed based on heavy deep architectures like the Transformer model, and thus training neural heuristic even for a middle-sized problem may incur massive computational overhead and memory cost  Kwon et al. ( 2020 ); Kim et al. ( 2022b ); Luo et al. ( 2023 ) . Lastly, the learned neural heuristic for a VRP tends to be ignored entirely when another VRP needs to be solved, with potentially transferable knowledge wasted. In practice, many VRP variants share the same or similar problem structure (e.g., VRPs are always featured by customer locations denoted by node coordinates), and only differ in a few constraints in their mathematical formulations. Accordingly, the corresponding neural heuristics are only distinct in a few layers of their respective neural architectures. Hence a more efficient training paradigm could leverage common parts of neural networks to transfer learned parameters, e.g., the part of neural network trained for TSP could be re-used to train the neural heuristic for OP.

This paper mainly answers the question “whether the trained neural heuristic for a VRP could benefit the training for other similar variants, and how could it be deployed?” To this end, we first pre-train a neural heuristic for TSP using the Transformer model, and then leverage the pre-trained model as the backbone to foster the learning of neural heuristics for other (relatively) complex VRP variants via fine-tuning. Specifically, we first modularize neural architectures for complex VRPs based on the backbone Transformer model for TSP, where additional lightweight modules beyond the backbone are applied to process problem-specific features in complex VRPs. Then, we directly apply the pre-trained backbone for TSP  Kool et al. ( 2018 ); Kwon et al. ( 2020 ) in the training process of neural heuristics for the complex VRPs, by fully fine-tuning the backbone along with problem-specific modules. Finally, we propose three adapter-based fine-tuning methods to further increase the efficiency of parameter usage. Extensive experiments substantiate that the fully fine-tuned Transformers on complex VRPs significantly outperform Transformers trained from scratch on each of the VRPs. Adapter-based fine-tuning methods are inferior to full fine-tuning, but comparable to the ones trained from scratch, with significantly fewer trained parameters. Moreover, we empirically verify the efficacy of key designs in the fine-tuning process and the favorable effect of our method in the cross-distribution application. Notably, the proposed method is versatile enough to be used for different models to learn effective neural heuristics for VRPs. In summary, this paper contributes in the following four aspects:

As an early attempt, we propose cross-problem learning for solving VRPs. The pre-trained backbone Transformer for a basic VRP (i.e., TSP) is used to foster the training of Transformers for downstream complex VRPs through fine-tuning.

We propose the modularization of Transformers for complex VRPs, which centers around the neural architecture of the backbone Transformer for TSP. The obtained problem-specific modules are used in the process of fine-tuning.

We develop different fine-tuning methods for cross-problem learning, i.e., the full and adapter-based fine-tuning, by which we fine-tune the entire Transformers or only the lightweight problem-specific modules along with small adapter networks.

We empirically testify that the knowledge learned in the Transformer for TSP is well transferred to aid in training neural heuristics for other VRPs. While full fine-tuning achieves better performance than Transformer trained from scratch, adapter-based fine-tuning methods attain comparable performance, with far fewer parameters to be trained and stored.

2 Related Work

In this section, we introduce the literature on neural heuristics for solving VRPs, and briefly discuss the pre-training-then-fine-tuning works in different fields.

2.1 Neural Heuristics for VRP

Current neural heuristics for VRPs mostly learn policies to construct a solution in an autoregressive way. Among diverse neural construction heuristics  Bello et al. ( 2017 ); Nazari et al. ( 2018 ); Dai et al. ( 2017 ); Ma et al. ( 2023 ) , the first breakthrough is made by the Transformer  Vaswani et al. ( 2017 ) , which is cast as Attention Model (AM) to solve VRP variants such as TSP, OP and PCTSP  Kool et al. ( 2018 ) . After that, numerous neural heuristics are proposed based on AM for solving VRPs  Xin et al. ( 2021a ); Kwon et al. ( 2020 ); Hottung et al. ( 2022 ) . Among them, Kwon et al. significantly ameliorate AM with policy optimization with multiple optima (POMO)  Kwon et al. ( 2020 ) , and enlighten considerable follow-up works with Transformers to solve VRPs  Kim et al. ( 2022b ); Kwon et al. ( 2021 ); Choo et al. ( 2022 ) . As alternatives, some works endeavor to predict probabilities of edges in optimal solutions to VRPs, which are then leveraged to efficiently construct high-quality solutions with search algorithms such as greedy search, sampling, and Monte Carlo tree search  Fu et al. ( 2021 ); Qiu et al. ( 2022 ); Hudson et al. ( 2022 ) . On the other hand, neural improvement heuristics aim to learn policies to iteratively improve an initial but complete solution. Inspired by traditional local search algorithms, a few works learn local operations such as 2-opt and swap to promote the solution   Wu et al. ( 2021 ); Ma et al. ( 2021 ); Wang et al. ( 2021 ); Kim et al. ( 2022a ) . Inspired by specialized algorithms or solvers for VRPs, some literature attempts to learn repair or destroy operations in Large Neighborhood Search (LNS)  Hottung and Tierney ( 2020 ); Gao et al. ( 2020 ) . Deep learning is also applied to enhance solvers like Lin-Kernighan-Helsgaun (LKH)  Xin et al. ( 2021b ); Kim et al. ( 2021 ) and Hybrid Genetic Search (HGS)  Santana et al. ( 2022 ) .

2.2 Pre-training, Fine-tuning

The pre-training-then-fine-tuning paradigm has been widely verified effective in domains of Natural Language Processing (NLP)  Dong et al. ( 2019 ); Devlin et al. ( 2018 ) , Graph Neural Network (GNN)  Qiu et al. ( 2020 ); Hu et al. ( 2020 ) , Computer Vision (CV)  Bao et al. ( 2022 ); Chen et al. ( 2020 ) , etc. In this line of work, large models such as Transformers are first trained on basic tasks  Dong et al. ( 2019 ); Ribeiro et al. ( 2020 ); Hu et al. ( 2020 ); You et al. ( 2020 ); Dosovitskiy et al. ( 2021 ); Touvron et al. ( 2021 ) . Then the pre-trained model is fine-tuned to solve downstream tasks, with the neural network adapted by introducing additional structures or layers (which possess far fewer parameters than the pre-trained model)  Houlsby et al. ( 2019 ); Pfeiffer et al. ( 2021 ); Zhao et al. ( 2020 ); Kitaev et al. ( 2020 ); Hu et al. ( 2021 ) . In this manner, the pre-training can be conducted on considerable unlabeled data to learn general patterns and features, which are re-used in downstream tasks. Also, the knowledge learned during pre-training is transferred to fine-tuning process to facilitate more efficient training.

In this paper, the cross-problem learning method brings a similar pre-training-then-fine-tuning paradigm to the field of learning to route . A Transformer is pre-trained for solving TSP by DRL with massive unlabeled data, which is then leveraged to fine-tune Transformers for downstream VRPs.

3 Preliminaries

In this section, we describe VRPs including TSP, OP, PCTSP and CVRP, which are used in experiments to evaluate our method. Afterwards, we introduce the general DRL method to learn construction heuristics with Transformers. Finally, we analyze the paucity of existing neural heuristics.

3.1 VRP Description

Feasibility. The solution to a VRP instance is feasible if it satisfies the problem-specific constraints. For example, a feasible solution to a TSP instance is a tour that goes through every node on the graph exactly once. A solution to OP is feasible if the length of a tour is not larger than a given value. Other VRPs like PCTSP and CVRP are defined on graphs in a similar fashion. Their details can be found in Appendix A. 1 1 1 https://arxiv.org/abs/2404.11677

3.2 Transformer based Construction Heuristics

where ℒ ⁢ ( θ | 𝒢 ) = 𝔼 p θ ⁢ ( π | 𝒢 ) ⁢ μ ⁢ ( π ) ℒ conditional 𝜃 𝒢 subscript 𝔼 subscript 𝑝 𝜃 conditional 𝜋 𝒢 𝜇 𝜋 \mathcal{L}(\theta|\mathcal{G})=\mathbb{E}_{p_{\theta}(\pi|\mathcal{G})}\mu(\pi) caligraphic_L ( italic_θ | caligraphic_G ) = blackboard_E start_POSTSUBSCRIPT italic_p start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT ( italic_π | caligraphic_G ) end_POSTSUBSCRIPT italic_μ ( italic_π ) is the expected cost and b ⁢ ( ⋅ ) 𝑏 ⋅ b(\cdot) italic_b ( ⋅ ) is a baseline function to reduce the variance of the estimation and raise the training efficiency  Sutton and Barto ( 2018 ) .

4 The Proposed Method

The cross-problem learning for solving VRPs falls within the pre-training-then-fine-tuning paradigm. Given the Transformer for a basic VRP (TSP in this paper), we train it to learn neural heuristics for solving the basic VRP with a DRL algorithm. Then, the pre-trained Transformer as the backbone is applied to train neural heuristics for downstream VRPs by fine-tuning. According to the modularization of Transformers, we propose different fine-tuning methods, which fully fine-tune the backbone with problem-specific modules, or only fine-tune lightweight problem-specific modules with small adapter networks. In the below, we elaborate on the modularization of Transformers for VRPs, the pre-training method for TSP by DRL, and different fine-tuning methods in detail.

4.1 Modularization of Transformers for VRPs

Most neural heuristics for VRPs are developed from Transformers  Kool et al. ( 2018 ); Kwon et al. ( 2020 , 2021 ) with similar neural architectures. To learn heuristics for TSP, the coordinates of customer nodes { x i } i = 1 n superscript subscript subscript 𝑥 𝑖 𝑖 1 𝑛 \{x_{i}\}_{i=1}^{n} { italic_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT } start_POSTSUBSCRIPT italic_i = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT are linearly projected to initial embeddings { h i 0 } i = 1 n superscript subscript superscript subscript ℎ 𝑖 0 𝑖 1 𝑛 \{h_{i}^{0}\}_{i=1}^{n} { italic_h start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 0 end_POSTSUPERSCRIPT } start_POSTSUBSCRIPT italic_i = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT . The encoder in a Transformer processes { h i 0 } i = 1 n superscript subscript superscript subscript ℎ 𝑖 0 𝑖 1 𝑛 \{h_{i}^{0}\}_{i=1}^{n} { italic_h start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 0 end_POSTSUPERSCRIPT } start_POSTSUBSCRIPT italic_i = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT to derive the advanced node embeddings { h i L } i = 1 n superscript subscript superscript subscript ℎ 𝑖 𝐿 𝑖 1 𝑛 \{h_{i}^{L}\}_{i=1}^{n} { italic_h start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_L end_POSTSUPERSCRIPT } start_POSTSUBSCRIPT italic_i = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT , which are then used in the decoder to output probabilities of nodes to be selected, as shown in Figure  1(a) . Based on the Transformer for TSP, we modularize neural architectures for complex VRPs into the backbone Transformer (for TSP) and problem-specific modules.

Taking OP as an example (shown in Figure  1(b) ), the Transformer resorts to additional modules (i.e., linear layers) to process the coordinate of depot x 0 subscript 𝑥 0 x_{0} italic_x start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT and prizes on customer nodes { p i } i = 1 n superscript subscript subscript 𝑝 𝑖 𝑖 1 𝑛 \{p_{i}\}_{i=1}^{n} { italic_p start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT } start_POSTSUBSCRIPT italic_i = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT , respectively. The linearly transformed prizes are added to the initial embeddings of coordinates to complement the information on customer nodes in OP. Then the resulting embeddings { h i 0 } i = 1 n superscript subscript superscript subscript ℎ 𝑖 0 𝑖 1 𝑛 \{h_{i}^{0}\}_{i=1}^{n} { italic_h start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 0 end_POSTSUPERSCRIPT } start_POSTSUBSCRIPT italic_i = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT are concatenated with the initial embedding of the depot node h 0 0 superscript subscript ℎ 0 0 h_{0}^{0} italic_h start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 0 end_POSTSUPERSCRIPT , which together are taken as input to the encoder. Similarly, the decoder uses one additional module (i.e., linear layer) to inject the dynamic feature, i.e., the remaining max length T t subscript 𝑇 𝑡 T_{t} italic_T start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT at the t 𝑡 t italic_t -th step, into the query vector for the subsequent computation. Note that we also dump the unnecessary information in TSP from the query embedding, e.g., the embedding of the firstly selected node, which is always the depot and thus senseless in OP.

Consequently, the Transformer for OP is modularized into the backbone Transformer (for TSP) plus the three additional linear layers to process additional features. Similarly, we can modularize Transformers for other VRPs such as PCTSP and CVRP. Taking PCTSP as an example, we only need modules to transform 1) the depot’s coordinate, prizes, and penalties before the encoder, and 2) the remaining prize in the decoder.

4.2 Pre-training on TSP

Given the above modularization, we propose to first train the backbone Transformer for TSP, and then fine-tune the problem-specific modules for downstream tasks. The rationale behind the use of TSP as the basic task for pre-training is that 1) as showed in the modularization, the Transformer for TSP is included in Transformers for other VRPs (e.g., OP, PCTSP); 2) as a basic VRP, TSP is merely featured by node coordinates, which are also included in other VRPs. Hence, we can leverage the backbone Transformer for TSP to learn useful node representations to reflect the common knowledge in VRPs (e.g., node locations and their distances), and then insert the backbone in Transformers for downstream VRPs.

In this paper, we take Transformer based AM as the backbone to pre-train the neural heuristic for TSP, since AM is able to solve a wide range of VRPs with strong performance. We illustrate the neural architecture of AM in Figure  1(a) , and refer interested readers to the original work in  Kool et al. ( 2018 ) for more details. We will focus more on the usage of the pre-trained AM in fine-tuning for downstream VRPs.

4.3 Full Fine-tuning for VRPs

4.4 adapter-based fine-tuning for vrps.

Despite the handy implementation of full fine-tuning, it still depends on massive parameters to be trained for every downstream VRP. Given a broad spectrum of VRP variants, it would not be realistic to train and store many heavy models with limited memory resources. An ideal alternative is that we only store problem-specific modules along with small networks for a VRP, which can be used with the backbone (for TSP) to assemble the Transformer for solving it. To this end, we provide three adapter-based fine-tuning methods, i.e., inside tuning, side tuning and LoRA. For each downstream VRP, we only train its problem-specific modules and small adapter networks, while freezing the parameters of the pre-trained backbone. Despite similar adaptation techniques in other domains  Zhang et al. ( 2020 ); Sung et al. ( 2022 ); Hu et al. ( 2021 ) , we take an early step to propose three fine-tuning methods with adapter networks for solving VRPs.

Inside Tuning. The adapter network in the inside tuning comprises two linear layers with a LeakyReLU (LR) activation function in between such that:

where i ∈ { 0 , … , n } 𝑖 0 … 𝑛 i\in\{0,\ldots,n\} italic_i ∈ { 0 , … , italic_n } is the node index. We set the trainable parameters 𝐖 0 in ∈ ℝ d × ( d / 2 ) superscript subscript 𝐖 0 in superscript ℝ 𝑑 𝑑 2 \mathbf{W}_{0}^{\text{in}}\in\mathbb{R}^{d\times(d/2)} bold_W start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT in end_POSTSUPERSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_d × ( italic_d / 2 ) end_POSTSUPERSCRIPT ; 𝐖 1 in ∈ ℝ ( d / 2 ) × d superscript subscript 𝐖 1 in superscript ℝ 𝑑 2 𝑑 \mathbf{W}_{1}^{\text{in}}\in\mathbb{R}^{(d/2)\times d} bold_W start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT in end_POSTSUPERSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT ( italic_d / 2 ) × italic_d end_POSTSUPERSCRIPT ; 𝐛 0 in ∈ ℝ d / 2 superscript subscript 𝐛 0 in superscript ℝ 𝑑 2 \mathbf{b}_{0}^{\text{in}}\in\mathbb{R}^{d/2} bold_b start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT in end_POSTSUPERSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_d / 2 end_POSTSUPERSCRIPT ; 𝐛 1 in ∈ ℝ d superscript subscript 𝐛 1 in superscript ℝ 𝑑 \mathbf{b}_{1}^{\text{in}}\in\mathbb{R}^{d} bold_b start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT in end_POSTSUPERSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_d end_POSTSUPERSCRIPT , which are uniformly initialized with the range ( − 1 / d , 1 / d ) 1 𝑑 1 𝑑 (-1/\sqrt{d},1/\sqrt{d}) ( - 1 / square-root start_ARG italic_d end_ARG , 1 / square-root start_ARG italic_d end_ARG ) . We put the above adapter network right after the self-attention layer and fully-connected layer in the backbone Transformer’s encoder, as shown in Figure  2(a) .

Side Tuning. Instead of adjusting intermediate embeddings in the encoder, the side tuning adjusts the output from the encoder, with the following neural architecture:

LoRA. Inspired by Low-Rank Adaptation (LoRA) in  Hu et al. ( 2021 ) , we design a low-rank decomposition to adjust the output from any matrix in the pre-trained Transformer,

where i ∈ { 0 , … , n } 𝑖 0 … 𝑛 i\in\{0,\ldots,n\} italic_i ∈ { 0 , … , italic_n } is the node index. 𝐖 p ∈ ℝ d × d subscript 𝐖 𝑝 superscript ℝ 𝑑 𝑑 \mathbf{W}_{p}\in\mathbb{R}^{d\times d} bold_W start_POSTSUBSCRIPT italic_p end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_d × italic_d end_POSTSUPERSCRIPT represents the pre-trained weight matrix in the backbone Transformer for TSP; 𝐁 p ∈ ℝ d × r subscript 𝐁 𝑝 superscript ℝ 𝑑 𝑟 \mathbf{B}_{p}\in\mathbb{R}^{d\times r} bold_B start_POSTSUBSCRIPT italic_p end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_d × italic_r end_POSTSUPERSCRIPT and 𝐀 p ∈ ℝ r × d subscript 𝐀 𝑝 superscript ℝ 𝑟 𝑑 \mathbf{A}_{p}\in\mathbb{R}^{r\times d} bold_A start_POSTSUBSCRIPT italic_p end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_r × italic_d end_POSTSUPERSCRIPT are two trainable matrices with r = 2 ≪ d 𝑟 2 much-less-than 𝑑 r=2\ll d italic_r = 2 ≪ italic_d , which we initialize by 0 0 and Gaussian(0,1). We apply Eq. ( 6 ) to adjust the output from query, key, and value matrices in the encoder of pre-trained Transformer, with one example shown in Figure  2(c) . Meanwhile, we exert LoRA on the weight matrix in the initial linear projection for better results we can find.

5 Experiments

We empirically evaluate cross-problem learning from different perspectives. Firstly, we compare it with other baselines to show its performance on OP and PCTSP. Then, we ablate on the key designs in the fine-tuning methods. Finally, we demonstrate the effectiveness of our method, in terms of cross-distribution application and versatility.

Settings. Following the existing works, we generate the coordinates of nodes by uniformly sampling from the unit square [ 0 , 1 ] × [ 0 , 1 ] 0 1 0 1 [0,1]\times[0,1] [ 0 , 1 ] × [ 0 , 1 ] . For OP, we set prizes all equal to 1. For PCTSP, we randomly sample prizes and penalties from Uniform distributions, following  Kool et al. ( 2018 ) . Meanwhile, we generate different-sized instances for OP and PCTSP, by setting the number of customer nodes to n = 𝑛 absent n= italic_n = 20, 50, and 100. We then use the Transformer based AM in  Kool et al. ( 2018 ) to implement the cross-problem learning, and maintain most of the original experimental settings for a fair comparison. Specifically, we train the model with 2500 batches in each epoch and use 512 instances in each batch (except for the problem with n = 𝑛 absent n= italic_n = 100, where we use 256 instances). For each epoch, the training instances are generated on the fly, and we use 10,000 instances for the validation. Then the paired t-test ( α = 5 % 𝛼 percent 5 \alpha=5\% italic_α = 5 % ) is conducted after each epoch to replace the baseline model, according to the improvement significance. For all problems and sizes, we train 100 epochs for the full convergence of the training curves. The learning rate is set as 10 − 4 superscript 10 4 10^{-4} 10 start_POSTSUPERSCRIPT - 4 end_POSTSUPERSCRIPT in all our methods, as the one for the original AM 2 2 2 We tried to assign different learning rates to adapter networks and problem-specific modules for fine-tuning, which did not result in better performance. . The server with Intel Core i9-10940X CPU and NVIDIA GeForce RTX 2080Ti is used in our experiments.

Baselines. We compare our method with AM  Kool et al. ( 2018 ) , the DRL based method with a strong performance on a variety of VRPs. We deploy the cross-problem learning based on its Transformer models. We also compare various baselines as follows. Regarding OP, we include 1) Gurobi, the state-of-the-art exact solver for various COPs  Gurobi Optimization, LLC ( 2022 ) ; 2) Compass, the specialized Genetic Algorithm (GA) for OP  Kobeaga et al. ( 2018 ) ; 3) Tsili, a classic randomized construction heuristic for OP with the manually crafted node probabilities   Tsiligirides ( 1984 ) . As for PCTSP, besides Gurobi, we run two additional baselines: 4) ILS, the iterated local search metaheuristic that is widely used for routing problems; and 5) OR-Tools, a mature metaheuristics based solver for routing problems.

Bold means the best results among learning based methods. ∗ * ∗ means the results of the method reported in  Kool et al. ( 2018 ) .

5.1 Comparison

We test all methods with 10,000 instances of OP and PCTSP, two typical VRPs that aim to maximize the total prize and minimize the distance plus the total penalty in the tour, respectively. We report the results of AM and Tsili by two decoding strategies, i.e., greedy search and sampling. For our method, we only report the better results derived by sampling. The sampling size is 1,280 for these methods, following  Kool et al. ( 2018 ) . For adapter-based fine-tuning, we only report results derived by inside tuning, since it significantly outstrips side tuning and LoRA (see Section  5.2 ). We compare the methods by different metrics, including the average objective value, average gap (to the best solutions), total runtime, and the number of trained parameters (for learning based methods). In Table  1 , we can observe that our method with either full fine-tuning or inside tuning consistently outperforms AM with either greedy search or sampling, with significantly smaller gaps and similar runtime. While Gurobi achieves the optimal solutions for small problems, it cannot derive solutions for middle-sized OP and PCTSP ( n 𝑛 n italic_n =50, 100). Instead, we run Gurobi as a heuristic with a 30s limit, but it is inferior to our methods on OP ( n 𝑛 n italic_n =50, 100) or fails to obtain any solutions on PCTSP ( n 𝑛 n italic_n =100). While Compass and ILS are specialized algorithms for OP and PCTSP respectively, our method achieves comparable results in all cases, with most gap differences smaller than 1 % percent 1 1\% 1 % . Moreover, our methods significantly surpass Tsili on OP ( n 𝑛 n italic_n =20, 50, 100), and outperform OR-Tools on PCTSP ( n 𝑛 n italic_n =100). Lastly, the inside tuning costs far fewer parameters for training, in contrast to AM and the full fine-tuning, which reduces considerable memory resources for solving each VRP (except the backbone Transformer for TSP). Besides transferring knowledge between problems with the same (Uniform) distribution, the cross-problem learning effectively can solve downstream VRPs with different distributions. Results on such cross-distribution applications are provided in Appendix B.

5.2 Ablation Study

In this part, we conduct an ablation study to demonstrate the impact of key designs for the proposed fine-tuning methods. Given the same pre-trained backbone, we first compare the inside tuning, the side tuning, and LoRA. Then, we show the sensitivity of the inside tuning approach by varying activation functions, including Sigmoid, Tanh, and LeakyReLU. With the changed components, we draw training curves on PCTSP ( n 𝑛 n italic_n =20, 50, 100) and display them in Figure  3 . To investigate the effects of different training methods, we also add the curves for the training from scratch and the full-tuning. As shown, although side tuning is equipped with a larger adapter network (i.e., 332K vs. 199K), it is significantly inferior to inside tuning on all sizes. On the other hand, despite the disconcerting performance of LoRA on PCTSP ( n 𝑛 n italic_n =20), it achieves similar results with side tuning for n 𝑛 n italic_n =50 and is significantly superior to side tuning for n 𝑛 n italic_n =100 with only 127K parameters. In addition, the activation function influences the performance, and the inside tuning with LeakyReLU outperforms the one with Sigmoid or Tanh. Notably, the curves of the inside tuning drop faster in the early epochs than the original AM trained from scratch on PCTSP ( n 𝑛 n italic_n =50, 100), and the inside tuning with LeakyReLU achieves similar convergences to AM on all sizes, with far fewer trained parameters.

5.3 Versatility

6 conclusion and future work.

This paper presents a cross-problem learning method for solving VRPs, which assists heuristics training for downstream VRPs by using the pre-trained Transformer for a basic VRP. We modularize Transformers for VRPs based on the backbone (Transformer) for TSP, and propose different fine-tuning methods to train the backbone or problem-specific modules in the target VRP. Results show that the full fine-tuning significantly outperforms Transformer trained from scratch, and the adapter-based fine-tuning delivers comparable performance, with far fewer parameters. We also verify the favorable cross-distribution application and versatility of our method, along with the efficacy of key components. In the future, we will improve our methods with more advanced techniques such as neural architecture search. We also plan to apply our method to solve other COPs, such as job shop scheduling problem or bin packing problem.

Acknowledgments

This research is supported by the National Research Foundation, Singapore under its AI Singapore Programme (AISG Award No: AISG3-RP-2022-031), and the Singapore Ministry of Education (MOE) Academic Research Fund (AcRF) Tier 1 grant.

• Bao et al. [2022] Hangbo Bao, Li Dong, Songhao Piao, and Furu Wei. Beit: Bert pre-training of image transformers. In ICLR , 2022.
• Bello et al. [2017] Irwan Bello, Hieu Pham, Quoc V. Le, Mohammad Norouzi, and Samy Bengio. Neural combinatorial optimization with reinforcement learning. In ICLR , 2017.
• Bengio et al. [2021] Yoshua Bengio, Andrea Lodi, and Antoine Prouvost. Machine learning for combinatorial optimization: a methodological tour d’horizon. European Journal of Operational Research , 290(2):405–421, 2021.
• Bi et al. [2022] Jieyi Bi, Yining Ma, Jiahai Wang, Zhiguang Cao, Jinbiao Chen, Yuan Sun, and Yeow Meng Chee. Learning generalizable models for vehicle routing problems via knowledge distillation. In NeurIPS , 2022.
• Chen et al. [2020] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for contrastive learning of visual representations. In ICML , pages 1597–1607, 2020.
• Choo et al. [2022] Jinho Choo, Yeong-Dae Kwon, Jihoon Kim, Jeongwoo Jae, André Hottung, Kevin Tierney, and Youngjune Gwon. Simulation-guided beam search for neural combinatorial optimization. In NeurIPS , 2022.
• Dai et al. [2017] Hanjun Dai, Elias B. Khalil, Yuyu Zhang, Bistra Dilkina, and Le Song. Learning combinatorial optimization algorithms over graphs. In NeurIPS , 2017.
• Devlin et al. [2018] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 , 2018.
• Dong et al. [2019] Li Dong, Nan Yang, Wenhui Wang, Furu Wei, Xiaodong Liu, Yu Wang, Jianfeng Gao, Ming Zhou, and Hsiao-Wuen Hon. Unified language model pre-training for natural language understanding and generation. In NeurIPS , pages 13063–13075, 2019.
• Dosovitskiy et al. [2021] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, et al. An image is worth 16x16 words: Transformers for image recognition at scale. In ICLR , 2021.
• Fu et al. [2021] Zhang-Hua Fu, Kai-Bin Qiu, and Hongyuan Zha. Generalize a small pre-trained model to arbitrarily large tsp instances. In AAAI , pages 7474–7482, 2021.
• Gao et al. [2020] Lei Gao, Mingxiang Chen, Qichang Chen, Ganzhong Luo, Nuoyi Zhu, and Zhixin Liu. Learn to design the heuristics for vehicle routing problem. arXiv preprint arXiv:2002.08539 , 2020.
• Geisler et al. [2022] Simon Geisler, Johanna Sommer, Jan Schuchardt, Aleksandar Bojchevski, and Stephan Günnemann. Generalization of neural combinatorial solvers through the lens of adversarial robustness. In ICLR , 2022.
• Gurobi Optimization, LLC [2022] Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual, 2022.
• Hottung and Tierney [2020] André Hottung and Kevin Tierney. Neural large neighborhood search for the capacitated vehicle routing problem. In ECAI , pages 443–450, 2020.
• Hottung et al. [2022] André Hottung, Yeong-Dae Kwon, and Kevin Tierney. Efficient active search for combinatorial optimization problems. In ICLR , 2022.
• Houlsby et al. [2019] Neil Houlsby, Andrei Giurgiu, Stanislaw Jastrzebski, Bruna Morrone, Quentin De Laroussilhe, Andrea Gesmundo, Mona Attariyan, and Sylvain Gelly. Parameter-efficient transfer learning for nlp. In ICML , pages 2790–2799, 2019.
• Hu et al. [2020] W Hu, B Liu, J Gomes, M Zitnik, P Liang, V Pande, and J Leskovec. Strategies for pre-training graph neural networks. In ICLR , 2020.
• Hu et al. [2021] Edward J Hu, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, Weizhu Chen, et al. Lora: Low-rank adaptation of large language models. In ICLR , 2021.
• Hudson et al. [2022] Benjamin Hudson, Qingbiao Li, Matthew Malencia, and Amanda Prorok. Graph neural network guided local search for the traveling salesperson problem. In ICLR , 2022.
• Kim et al. [2021] Minsu Kim, Jinkyoo Park, et al. Learning collaborative policies to solve np-hard routing problems. In NeurIPS , pages 10418–10430, 2021.
• Kim et al. [2022a] Minjun Kim, Junyoung Park, and Jinkyoo Park. Learning to cross exchange to solve min-max vehicle routing problems. In ICLR , 2022.
• Kim et al. [2022b] Minsu Kim, Junyoung Park, and Jinkyoo Park. Sym-NCO: Leveraging symmetricity for neural combinatorial optimization. In NeurIPS , 2022.
• Kitaev et al. [2020] Nikita Kitaev, Lukasz Kaiser, and Anselm Levskaya. Reformer: The efficient transformer. In ICLR , 2020.
• Kobeaga et al. [2018] Gorka Kobeaga, María Merino, and Jose A Lozano. An efficient evolutionary algorithm for the orienteering problem. Computers & Operations Research , 90:42–59, 2018.
• Konstantakopoulos et al. [2022] Grigorios D Konstantakopoulos, Sotiris P Gayialis, and Evripidis P Kechagias. Vehicle routing problem and related algorithms for logistics distribution: A literature review and classification. Operational research , pages 1–30, 2022.
• Kool et al. [2018] Wouter Kool, Herke van Hoof, and Max Welling. Attention, learn to solve routing problems! In ICLR , 2018.
• Kwon et al. [2020] Yeong-Dae Kwon, Jinho Choo, Byoungjip Kim, Iljoo Yoon, Youngjune Gwon, and Seungjai Min. Pomo: Policy optimization with multiple optima for reinforcement learning. In NeurIPS , pages 21188–21198, 2020.
• Kwon et al. [2021] Yeong-Dae Kwon, Jinho Choo, Iljoo Yoon, Minah Park, Duwon Park, and Youngjune Gwon. Matrix encoding networks for neural combinatorial optimization. In NeurIPS , pages 5138–5149, 2021.
• Li et al. [2021] Sirui Li, Zhongxia Yan, and Cathy Wu. Learning to delegate for large-scale vehicle routing. In NeurIPS , pages 26198–26211, 2021.
• Luo et al. [2023] Fu Luo, Xi Lin, Fei Liu, Qingfu Zhang, and Zhenkun Wang. Neural combinatorial optimization with heavy decoder: Toward large scale generalization. In NeurIPS , 2023.
• Ma et al. [2021] Yining Ma, Jingwen Li, Zhiguang Cao, Wen Song, Le Zhang, Zhenghua Chen, and Jing Tang. Learning to iteratively solve routing problems with dual-aspect collaborative transformer. In NeurIPS , pages 11096–11107, 2021.
• Ma et al. [2023] Zeyuan Ma, Hongshu Guo, Jiacheng Chen, Zhenrui Li, Guojun Peng, Yue-Jiao Gong, Yining Ma, and Zhiguang Cao. Metabox: A benchmark platform for meta-black-box optimization with reinforcement learning. In Advances in Neural Information Processing Systems , volume 36, 2023.
• Nazari et al. [2018] Mohammadreza Nazari, Afshin Oroojlooy, Lawrence Snyder, and Martin Takác. Reinforcement learning for solving the vehicle routing problem. In NeurIPS , page 9861–9871, 2018.
• Pfeiffer et al. [2021] Jonas Pfeiffer, Aishwarya Kamath, Andreas Rücklé, Kyunghyun Cho, and Iryna Gurevych. Adapterfusion: Non-destructive task composition for transfer learning. In EACL , pages 487–503, 2021.
• Qiu et al. [2020] Jiezhong Qiu, Qibin Chen, Yuxiao Dong, Jing Zhang, Hongxia Yang, Ming Ding, Kuansan Wang, and Jie Tang. Gcc: Graph contrastive coding for graph neural network pre-training. In KDD , pages 1150–1160, 2020.
• Qiu et al. [2022] Ruizhong Qiu, Zhiqing Sun, and Yiming Yang. DIMES: A differentiable meta solver for combinatorial optimization problems. In NeurIPS , 2022.
• Ribeiro et al. [2020] Marco Tulio Ribeiro, Tongshuang Wu, Carlos Guestrin, and Sameer Singh. Beyond accuracy: Behavioral testing of nlp models with checklist. In ACL , pages 4902–4912, 2020.
• Santana et al. [2022] Ítalo Santana, Andrea Lodi, and Thibaut Vidal. Neural networks for local search and crossover in vehicle routing: A possible overkill? arXiv preprint arXiv:2210.12075 , 2022.
• Sung et al. [2022] Yi-Lin Sung, Jaemin Cho, and Mohit Bansal. Lst: Ladder side-tuning for parameter and memory efficient transfer learning. In NeurIPS , pages 12991–13005, 2022.
• Sutton and Barto [2018] Richard S Sutton and Andrew G Barto. Reinforcement learning: An introduction . MIT press, 2018.
• Touvron et al. [2021] Hugo Touvron, Matthieu Cord, Matthijs Douze, Francisco Massa, Alexandre Sablayrolles, and Hervé Jégou. Training data-efficient image transformers & distillation through attention. In ICML , pages 10347–10357, 2021.
• Tsiligirides [1984] Theodore Tsiligirides. Heuristic methods applied to orienteering. Journal of the Operational Research Society , 35:797–809, 1984.
• Vaswani et al. [2017] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In NeurIPS , page 6000–6010, 2017.
• Wang and Sheu [2019] Zheng Wang and Jiuh-Biing Sheu. Vehicle routing problem with drones. Transportation research part B: methodological , 122:350–364, 2019.
• Wang et al. [2021] Runzhong Wang, Zhigang Hua, Gan Liu, Jiayi Zhang, Junchi Yan, Feng Qi, Shuang Yang, Jun Zhou, and Xiaokang Yang. A bi-level framework for learning to solve combinatorial optimization on graphs. In NeurIPS , pages 21453–21466, 2021.
• Williams [1992] Ronald J Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning , 8(3):229–256, 1992.
• Wu et al. [2021] Yaoxin Wu, Wen Song, Zhiguang Cao, Jie Zhang, and Andrew Lim. Learning improvement heuristics for solving routing problems. IEEE transactions on neural networks and learning systems , 2021.
• Xin et al. [2021a] Liang Xin, Wen Song, Zhiguang Cao, and Jie Zhang. Multi-decoder attention model with embedding glimpse for solving vehicle routing problems. In AAAI , pages 12042–12049, 2021.
• Xin et al. [2021b] Liang Xin, Wen Song, Zhiguang Cao, and Jie Zhang. Neurolkh: Combining deep learning model with lin-kernighan-helsgaun heuristic for solving the traveling salesman problem. In NeurIPS , pages 7472–7483, 2021.
• You et al. [2020] Yuning You, Tianlong Chen, Yongduo Sui, Ting Chen, Zhangyang Wang, and Yang Shen. Graph contrastive learning with augmentations. In NeurIPS , pages 5812–5823, 2020.
• Zhang et al. [2020] Jeffrey O Zhang, Alexander Sax, Amir Zamir, Leonidas Guibas, and Jitendra Malik. Side-tuning: a baseline for network adaptation via additive side networks. In ECCV , pages 698–714. Springer, 2020.
• Zhao et al. [2020] Mengjie Zhao, Tao Lin, Fei Mi, Martin Jaggi, and Hinrich Schütze. Masking as an efficient alternative to finetuning for pretrained language models. In EMNLP , pages 2226–2241, 2020.